Submitted:
13 December 2023
Posted:
14 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Methods
2.1. Scripts addressed on the investigation
 . Revesz assumed that symbol has the vertical axis of symmetry in the letter, thus, we adopted this approach and related to this symbol the vertical axis of symmetry, denoted in Appendix and Supplementary Materials. We used the Schoenflies notation, for labeling the elements of symmetry of the symbols [15]. Unlike Revesz, we took into account all the symmetry elements (see Appendix and Supplementary Materials). Sometimes the decision about the presence or absence of an element of symmetry carries an inevitable element of subjectivity; for example, the letters
. Revesz assumed that symbol has the vertical axis of symmetry in the letter, thus, we adopted this approach and related to this symbol the vertical axis of symmetry, denoted in Appendix and Supplementary Materials. We used the Schoenflies notation, for labeling the elements of symmetry of the symbols [15]. Unlike Revesz, we took into account all the symmetry elements (see Appendix and Supplementary Materials). Sometimes the decision about the presence or absence of an element of symmetry carries an inevitable element of subjectivity; for example, the letters 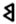 and
and 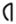 (Etruscan from Marsiliana, see Appendix and Supplementary Materials): for the first symbol we assume that there is horizontal symmetry, however, for the second we adopt that there is not.
(Etruscan from Marsiliana, see Appendix and Supplementary Materials): for the first symbol we assume that there is horizontal symmetry, however, for the second we adopt that there is not.3. Results
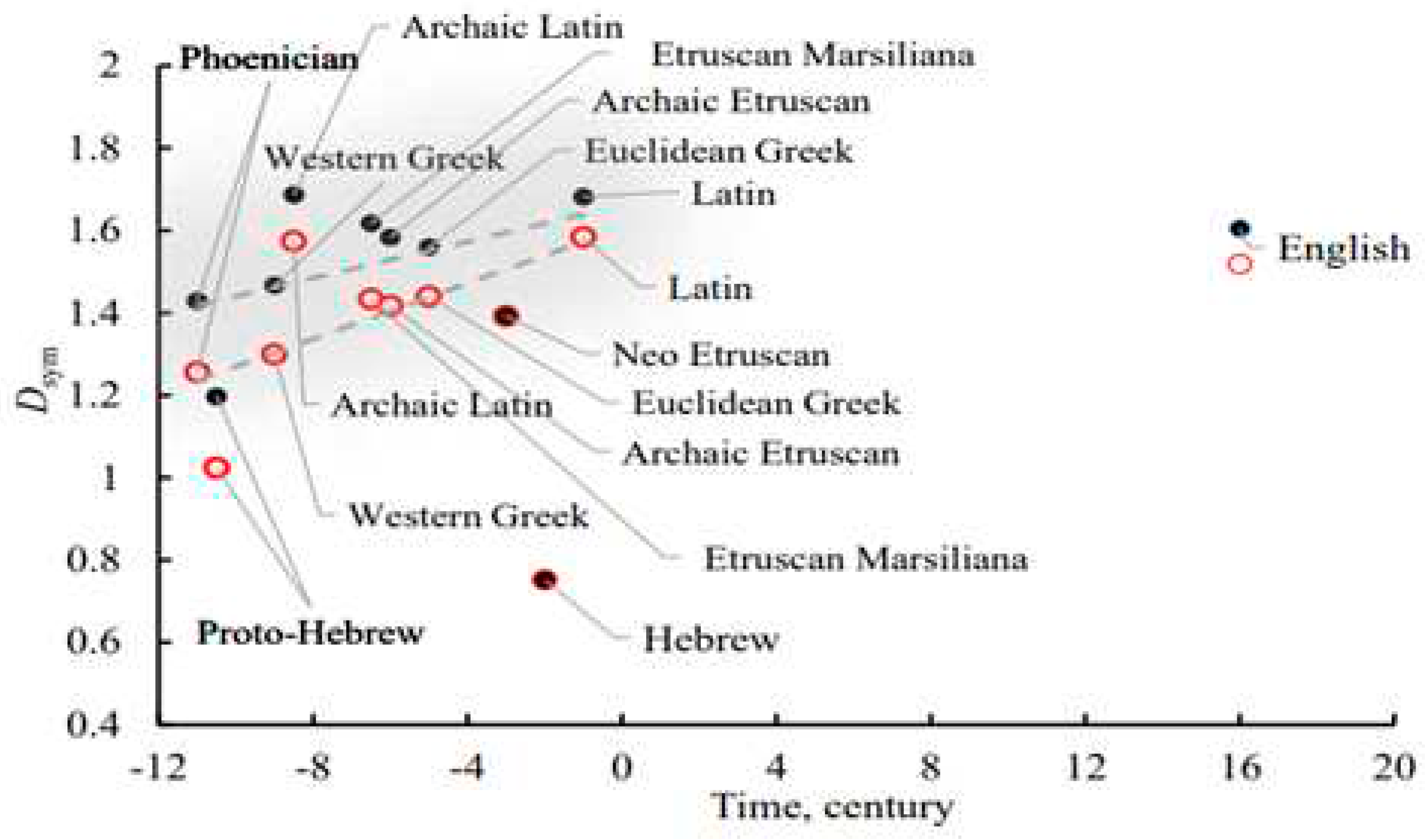
3.1. Quantitative characterization of the symmetry of alphabets; Shannon measures of symmetry and diversity of alphabets.
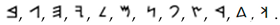
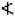 . The symbols with identity transformation (C1) and vertical mirror axis (S2) only are:
. The symbols with identity transformation (C1) and vertical mirror axis (S2) only are: 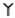 ,
, 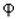 ,
, 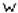 . The symbols with identity transformation (C1), horizontal and vertical mirror axes (S1, S2) and rotation on 180˚ (C2) only are:
. The symbols with identity transformation (C1), horizontal and vertical mirror axes (S1, S2) and rotation on 180˚ (C2) only are: 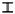 ,
, 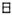 ,
, 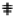 ,
,  . The symbols with identity transformation (C1), horizontal, vertical and diagonal mirror axes (S1, S2, S3, S4) and 4-fold rotational symmetry (C4, C2, C43) only are:
. The symbols with identity transformation (C1), horizontal, vertical and diagonal mirror axes (S1, S2, S3, S4) and 4-fold rotational symmetry (C4, C2, C43) only are: 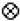 ,
, 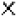 .
. was always considered with rectangle symmetry.
was always considered with rectangle symmetry.3.2. Symmetry factor; its definition and calculation for alphabets
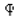 - qoph of the Phoenician script. This symbol has the vertical mirror axis of symmetry denoted as depicted in Figure 5A. Thus, the entire symbol may be obtained by projection of half-a-symbol relatively the axis as shown in Figure 5B. If we have the full list of instructions describing building/drawing of half-a-symbol, the symmetrical projection will enable inscribing of the entire symbol. Thus, symmetry enables parsimony of information, necessary for drawing/inscribing of the symbols. Now consider the Phoenician letter
- qoph of the Phoenician script. This symbol has the vertical mirror axis of symmetry denoted as depicted in Figure 5A. Thus, the entire symbol may be obtained by projection of half-a-symbol relatively the axis as shown in Figure 5B. If we have the full list of instructions describing building/drawing of half-a-symbol, the symmetrical projection will enable inscribing of the entire symbol. Thus, symmetry enables parsimony of information, necessary for drawing/inscribing of the symbols. Now consider the Phoenician letter  - teth , depicted in Figure 5C. This symbol has four mirror symmetry axes, namely , shown in Figure 5C. These axes separate the symbol into eight sub-segments, depicted in Figure 5C. Following the aforementioned reasoning, axes provide the eight-fold parsimony of graphical information necessary for drawing/inscribing the symbol.
- teth , depicted in Figure 5C. This symbol has four mirror symmetry axes, namely , shown in Figure 5C. These axes separate the symbol into eight sub-segments, depicted in Figure 5C. Following the aforementioned reasoning, axes provide the eight-fold parsimony of graphical information necessary for drawing/inscribing the symbol. - theth symbol, we recognize four additional elements of symmetry and they are rotations about the geometrical center of the symbol to the angles
- theth symbol, we recognize four additional elements of symmetry and they are rotations about the geometrical center of the symbol to the angles
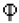 - qoph depicted in Figure 5A. The total symmetry group of this symbol contains the mirror axis and the identity element which is the rotation to thus, the total number of the symmetry operations is two. Hence, the symmetry provides the twofold parsimony of the graphical information necessary for drawing the symbol. It should be emphasized that the aforementioned reasoning does not depend on the specific type of drawing of the symbol. Now let us quantify the aforementioned parsimony. We denote the total number of elements of symmetry related to i-th letter of the given alphabet, known in the group theory at the order of the group G [30]. Now we introduce the symmetry factor of the alphabet denoted and defined with Eq. 11:
- qoph depicted in Figure 5A. The total symmetry group of this symbol contains the mirror axis and the identity element which is the rotation to thus, the total number of the symmetry operations is two. Hence, the symmetry provides the twofold parsimony of the graphical information necessary for drawing the symbol. It should be emphasized that the aforementioned reasoning does not depend on the specific type of drawing of the symbol. Now let us quantify the aforementioned parsimony. We denote the total number of elements of symmetry related to i-th letter of the given alphabet, known in the group theory at the order of the group G [30]. Now we introduce the symmetry factor of the alphabet denoted and defined with Eq. 11:4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix
| Phoenician alphabet | ||||||||
| Script | C1 | S1 | S2 | S3 | S4 | C4 | C2 | C43 |
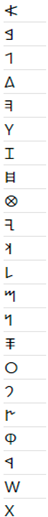 |
1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1/0 | 1/0 | 1/0 | 1 | 1/0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 1/0 | 1/0 | 1/0 | 1 | 1/0 | |
References
- Sampson, G. Writing systems, in: Methods for recording language. Chapter 4., pp. 47-62, in The Routledge Handbook of Linguistics, ed. by Keith Allan, 2016, Routledge, 711 Third Avenue, New York, NY 10017, USA.
- Keith, A. What is linguistics? in: Methods for recording language. Chapter 4., pp. 1-16, in The Routledge Handbook of Linguistics, ed. by Keith Allan, 2016, Routledge, 711 Third Avenue, New York, NY 10017, USA.
- Gardiner, A. H, The egyptian origin of the semitic alphabet. J Egypt Archeol. 1916, 3(1), 1–16. [CrossRef]
- Pennacchietti, F.A. An alternative hypothesis on the origin of the Greek alphabet, Kervan, International Journal of African and Asiatic Studies, 2023, 27(1), 109-121. [CrossRef]
- Powell, B.B. Homer and the Origin of the Greek Alphabet, Ch. 1, pp. 5-66, 1991, Cambridge, Cambridge University Press.
- Hurford, J.R. Evolutionary Linguistics: How Languages and Language Got to Be the Way They Are: in: Methods for recording language. Chapter 2., pp. 17-32, in The Routledge Handbook of Linguistics, ed. by Keith Allan, 2016, Routledge, 711 Third Avenue, New York, NY 10017, USA.
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1989.
- Garrod, S.; Fay, N.; Lee, J.; Oberlander, J.; Macleod, T. Foundations of representation: Where might graphical symbol systems come from? Cognitive Science, 2007, 31(6), 961–987. [CrossRef]
- Kelly, P. The invention, transmission and evolution of writing: insights from the new scripts of West Africa. In Paths into script formation in the ancient Mediterranean. Silvia Ferrara and Miguel Valério, eds. pp. 189–209. 2018, Rome: Studi Micenei ed Egeo Anatolici.
- Kelly, P.; Winters, J.; Miton, H.; Morin, O. The predictable evolution of letter shapes: An emergent script of West Africa recapitulates historical change in writing systems. Current Anthropology, 2021, 62 (6), 669-691. [CrossRef]
- Gibson, E.; Futrell, R.; Piantadosi, S.T.; Dautriche, I.; Mahowald, K., Bergen, L.; Levy, R. How efficiency shapes human language. Trends in Cognitive Sciences, 2019, 23, 389–407. [CrossRef]
- Han, S.J.; Kelly, P.; Winters, J.; Kemp, C. Simplification Is Not Dominant in the Evolution of Chinese Characters. Open Mind: Discoveries in Cognitive Science, 2022, 6, 264–279. [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Chicago, IL, USA, 1949; Volume 97, pp. 29–51.
- Revesz, P.R. The development and role of symmetry in ancient scripts, in: Viana, V., Nagy, D., Xavier, J., Neiva, A., Ginoulhiac, M., Mateus, L. & Varela, P. (Eds.). (2022). Symmetry: Art and Science | 12th SISSymmetry Congress [Special Issue]. Symmetry: Art and Science. International Society for the Interdisciplinary Study of Symmetry. 308-315.
- Altmann, S.L.; Herzig, P. Point-group theory tables, Oxford, Oxford University Press, UK, 1994.
- Bonfante, J.H., Bonfante, L., P. The Etruscan Language: An Introduction, Manchester University Press, UK, 1983.
- Stützer, H.A., Die Etrusker und ihre Welt, DuMont DuMont Reiseverlag , Koln, Ge, 1992.
- Fischer, S.R. History of writing, p. 298, Reaktion books, London, 2005.
- Федoрoва, Е. В., Введение в латинскую эпиграфику, Изд-вo Мoскoвскoгo университета, 1982.
- Ярцева, В. Н., Бoльшoй энциклoпедический слoварь Языкoзнание, Изд-вo “Сoветская энциклoпедия”, Мoсква, 1989.
- Ben-Naim, A. Entropy, Shannon’s Measure of Information and Boltzmann’s H-Theorem. Entropy 2017, 19, 48.
- Skolnik, F.; Berenbaum, M., Encyclopaedia Judaica, Volume 1, 2nd ed., Thomson Gale ; Macmillan Reference USA, [Farmington Hills, Mich.], Detroit, 2007.
- Jost, L. Entropy and diversity, Oikos. 2006, 113 (2), 363–375. [CrossRef]
- Amicone, S.; Radivojević, M.; Quinn, P.S.; Berthold, C.; Rehren, T. Pyrotechnological connections? Re-investigating the link between pottery firing technology and the origins of metallurgy in the Vinča Culture, Serbia, J. Arch. Sci. 2020, 118, 1-19. [CrossRef]
- Radivojević, M. Archaeometallurgy of the Vinča culture: A case study of the site of Belovode in Eastern Serbia. Historical Metallurgy, 2014, 47 (1), 13-32.
- Radivojević, M.; Rehren, T.; Pernicka, E.; Šljivar, D.; Brauns, M.; Borić, D., On the origins of extractive metallurgy: New evidence from Europe, J. Archaeological Sci. 2010, 37, 2775–2787. [CrossRef]
- Starović, A. If the Vinča script once really existed who could have written or read it? Documenta Praehistorica 2005, 32, 253–260. [CrossRef]
- Rosen, J. Symmetry in Science: An Introduction to the General Theory; Springer: Berlin, Germany, 1995.
- Chatterjee, S.K. Crystallography and the World of Symmetry; Springer: Berlin, Germany, 2008.
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 5ed, A Harcourt Science and Technology Company, San Diego, USA, 2001.
- Pae, H.K. Script E ffects as the Hidden Drive of the Mind, Cognition, and Culture, Literacy Studies. Perspectives from Cognitive Neurosciences, Linguistics, Psychology and Education, v, 21. Springer, Cham, Switzerland, 2020.
- Logan, R. K. The alphabet effect: a media ecology understanding of the making of Western civilization. Cresskill, NJ: Hampton Press, 2004.
- Wiley, R.W., Wilson, C., & Rapp, B. The effects of alphabet and expertise on letter perception. J. Exp. Psychology: Human Perception & Performance, 2016, 42 (8), 1186–1203. [CrossRef]
- Somov, G.U. Interrelations of codes in human semiotic systems, Semiotica 2016, 213, 557–599. [CrossRef]
- Yodogawa, E. Symmetropy, an entropy-like measure of visual symmetry. Percept. Psychophys. 1982, 32, 230–240. [CrossRef]
- Dry, M.J. Using relational structure to detect symmetry: A Voronoi tessellation based model of symmetry perception. Acta Psychol. 2008, 128, 75–90. [CrossRef]
- Hoffman, J.M. In the beginning. A Short History of Hebrew Language, New York University Press, New York, 2004.
- Bormashenko, E.; Legchenkova, I.; Frenkel, M.; Shoval, S. Shannon (Information) Measures of Symmetry for 1D and 2D Shapes and Patterns. Appl. Sci. 2022, 12(3), 1127. [CrossRef]
- Bormashenko, E. Entropy, Information, and Symmetry: Ordered is Symmetrical. Entropy 2020, 22(1), 11. [CrossRef]
- Bormashenko, E. Entropy, Information, and Symmetry; Ordered Is Symmetrical, II: System of Spins in the Magnetic Field. Entropy 2020, 22(2), 235. [CrossRef]


 - qoph is depicted; mirror axis of symmetry is shown; B. The entire symbol may be obtained by projection of half-a-symbol relatively the axis ; thus, the two-fold parsimony of information is provided. C. Symbol
- qoph is depicted; mirror axis of symmetry is shown; B. The entire symbol may be obtained by projection of half-a-symbol relatively the axis ; thus, the two-fold parsimony of information is provided. C. Symbol  - teth is shown. The symbol has four mirror symmetry axes, namely shown in the inset. D. The entire symbol may be restored by the projection of the sub-segment, depicted in the inset; thus the eight-fold parsimony of information us provided.
- teth is shown. The symbol has four mirror symmetry axes, namely shown in the inset. D. The entire symbol may be restored by the projection of the sub-segment, depicted in the inset; thus the eight-fold parsimony of information us provided.
 - qoph is depicted; mirror axis of symmetry is shown; B. The entire symbol may be obtained by projection of half-a-symbol relatively the axis ; thus, the two-fold parsimony of information is provided. C. Symbol
- qoph is depicted; mirror axis of symmetry is shown; B. The entire symbol may be obtained by projection of half-a-symbol relatively the axis ; thus, the two-fold parsimony of information is provided. C. Symbol  - teth is shown. The symbol has four mirror symmetry axes, namely shown in the inset. D. The entire symbol may be restored by the projection of the sub-segment, depicted in the inset; thus the eight-fold parsimony of information us provided.
- teth is shown. The symbol has four mirror symmetry axes, namely shown in the inset. D. The entire symbol may be restored by the projection of the sub-segment, depicted in the inset; thus the eight-fold parsimony of information us provided. 

 |
| Elements of symmetry the Phoenician alphabet | ||||||||
| C1 | S1 | S2 | S3 | S4 | C4 | C2 | C43 | |
| 22 | 7 | 9 | 2 | 2 | 2 | 6 | 2 | |
| P(Gi) | 0.423 | 0.135 | 0.173 | 0.038 | 0.038 | 0.038 | 0.115 | 0.038 |
| Subsets of symmetry elements, | C1 | C1 S1 | C1 S2 | C1 S1 S2C2 | C1 S1 S2 S3 S4C4 C2C43 |
| Number of the letters. |
12 | 1 | 3 | 4 | 2 |
| Probability, | 0.545 | 0.045 | 0.136 | 0.182 | 0.091 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





