1. Introduction
Evaporation involves the conversion of a solvent into vapor, which is then removed from a solution or slurry. In most cases, water is the solvent used in evaporation systems. This process entails vaporizing a portion of the solvent to create a concentrated solution, thick liquor, or slurry [
1].
Dairy manufacturers commonly employ concentration techniques to produce dairy products with higher levels of dry matter, increased value, reduced volume, and extended shelf-life [
2]. Lowering the water activity and reducing transportation and storage costs are key benefits of dehydrating dairy products. This process involves converting a liquid product into a dry powder by removing nearly all the available water. However, dairy products are sensitive to heat, and their functional properties and digestibility can be negatively affected by excessive heat during the dehydration process. Therefore, a single water removal method cannot consistently achieve optimal performance. It thus, becomes necessary to employ multiple processing steps tailored to the specific properties of the material being processed, while considering both product quality considerations and processing costs [
3].
Typically, the main steps involved in the production of milk powder include standardisation, homogenisation, pasteurisation, evaporation and drying [
4]. Evaporation is a significant step in milk-powder production plants, serving not only to concentrate milk to the desired viscosity for subsequent spray drying but also to reduce the energy requirements during the spray drying process. In the evaporation stage, sterilized milk is concentrated under vacuum conditions at temperatures ranging from 40 to 70°C. This process leads to a significant increase in the total solids content, which typically rises from around 13% to 50% [
5]. Vacuum conditions are used to mitigate the negative effects of heat on heat-sensitive milk components like fats and to prevent the degradation of essential nutrients, such as vitamins.
Milk powder production consists of many thermal processes, including evaporation and drying, and is responsible for 15% of the total energy use in the dairy industry [
4]. In France, approximately 25% of the total energy consumption in food industry is attributed to the dairy sector [
3]. Therefore, energy consumption attributed to the process of evaporation has a substantial impact on the cost of milk powder production.
To this end, there are several energy consumption optimization strategies in the evaporation of milk that have been discussed in the literature. The ones that are examined in this work involve the most commonly used in the industrial practice, such as the Mechanical Vapor Recompression (MVR) and the Thermal Vapor Recompression (TVR) technologies.
In the evaporator unit, the excess heat generated by the secondary steam from the evaporator is typically released as waste heat. However, this waste heat can be effectively utilized to preheat the feed. An important feature of MVR technology is the utilization of the secondary steam cycle. MVR employs a mechanical fan, typically powered by electricity, to recompress low-pressure vapor to a slightly higher pressure and temperature.
On the other hand, TVR utilizes a thermos-compressor, which employs high-pressure vapor to recompress low-pressure vapor to a slightly higher pressure and temperature. Numerous studies have demonstrated that multi-effect evaporation reduces energy consumption costs by enhancing steam economy. This is achieved by utilizing the secondary steam generated by the preceding effect as the heat source for the subsequent effect [
6].
Jebson and Chen [
7] assessed the effectiveness of falling film evaporators used in the New Zealand dairy sector for concentrating whole milk by calculating the kg steam utilized to kg water evaporated ratio and the heat transfer coefficient of each evaporator pass. The steam consumption of full and skim milk was comparable. Schuck et al. [
3] introduced a methodology for assessing and comparing the energy consumption involved in the production of dairy and feed powders at various stages of the dehydration process. The findings of the study revealed that the energy consumption for fat-filled and demineralized whey powders were 9.072 kJ/kg and 15.120 kJ/kg, respectively.
Walmsley et al. [
8] conducted a study on applying Pinch Analysis to an industrial milk evaporator case study to quantify the potential energy savings. By the appropriate placement of mechanical vapor recompression in a new improved two-effect milk evaporation system design, a 78% reduction to steam (6397 kW) at the expense of 16% (364 kW) more electricity use was achieved and the emissions reduction was 3416 t CO
2-e/y. Srinivasan et al. [
9] studied the energy efficiency at India’s largest milk processing plant and proposed retrofits for improving the plant’s sustainability. The results reveal that exergy efficiency of certain units is very low (<20%) while significant improvements in energy efficiencies can be achieved through simple, low-cost retrofits to these units. Moejes [
4] studied the possibilities of upcoming milk processing technologies such as membrane distillation, monodisperse-droplet drying, air dehumidification, radio frequency heating, and radio frequency heating paired with renewable energy sources such as solar thermal systems. It was illustrated that the combination of developing technologies has the potential to cut operational energy consumption for milk powder manufacturing by up to 60%.
Zhang et al. [
10] conducted a study by simulating a "pseudo" milk composition using hypothetical components in a commercial process simulator. The purpose of their work was to model a falling film evaporator commonly (FFE) employed in milk powder production plants. The study demonstrated that commercial process simulators have the ability to accurately simulate dairy processes. Building upon this research, Munir et al. [
11] further enhanced the capabilities of commercial process simulators, providing valuable insights for practicing engineers to identify potential process improvements in the dairy industry. Bojnourd et al. [
12] developed two types of dynamic models for an industrial four-effect falling-film evaporator used to condense whole milk: lumped and distributed. The findings indicate that while the distributed model demonstrates slightly better predictive capabilities compared to the lumped model, the latter outshines in terms of performance due to its simpler structure and significantly reduced simulation time. Zhang et al. [
5] developed models for two commonly used types of milk powder evaporators: a conventional five-effect FFE without MVR and a three-effect evaporator with MVR. Heat-recovery processes were incorporated into the models to enable a comparison of energy consumption between the two processes. The results revealed that a three-effect FFE with MVR could achieve a 60% reduction in energy consumption compared to a conventional five-effect evaporator.
Gourdon and Mura [
13] created a modeling tool based on experimental correlations built at industrial scale circumstances. The complicated interaction between the generated vapor and the liquid flow is included in their model. The results show that pressure drop is important in evaporator performance because of its influence on saturation temperature. Daz-Ovalle et al. [
14] provided a set of dynamic models to study fouling of falling-film evaporators by considering fouling thickness, film thickness, temperature, and solids mass percentage. Hu et al. [
15] developed a model for a water-to-water FFE simulation, which was employed in water vapor heat pump systems. That study focused on an existing FFE with four working tubes.
Bouman et al. [
16] conducted experiments with a one-tube evaporator using whole and skim milk to ascertain the heat transfer and pressure decrease in evaporator tubes. Based on the findings, a computer software was created to optimize the design of multistage falling-film evaporators for dairy products. Silveira et al. [
17] investigated the evaporation of water and skim milk using a pilot-scale, single-stage falling-film evaporator. In comparison to water, a thicker and slower film was formed at the end of the skim milk concentration procedure. They concluded that the behavior of a product during the evaporation process cannot be predicted solely by the overall heat transfer coefficient, and that a wide range of information, such as residence time distribution, product viscosity, and surface tension, is required to understand the evaporation process. Gourdon et al. [
18] examined the flow behavior of a dairy product under falling film evaporation. The effects of varying dry solids concentrations, flow rates, and driving temperature changes were investigated. All three factors were shown to have a significant impact on the flow characteristics. Mura et al. [
19] investigated the absolute vapor flow pressure losses during dairy product falling film evaporation using an experimental internal tube evaporator setup, adjusting the co-flow input velocity and product dry solid content. They concluded that pressure losses are strongly dependent on the co-flowing vapor rate for dry solid content between 13 and 40%.
Wijck et al. [
20] conducted an evaluation of tools used for dynamic modeling and supervisory multivariable control design of multiple-effect falling-film evaporators. They specifically focused on the NIZO four-effect evaporator as a case study. The research aimed to achieve improved process operation for industries, leading to economic benefits such as increased yield, enhanced product quality, reduced energy consumption, and minimized material waste. Sharma et al. [
21] created an Excel-based multi-objective optimization tool based on the elitist non-dominated sorting genetic algorithm (NSGA-II) and tested it on benchmark tasks. It is then used for multi-objective optimization (MOO) of the design of a falling-film evaporator system for milk concentration, which includes a pre-heater, evaporator, vapor condenser, and steam jet ejector. Haasbroek et al. [
22], conducted a study utilizing historical data from a FFE to develop models for control purposes, without requiring knowledge of the plant's physical dimensions. The results indicated that fuzzy predictive controllers and LQR control exhibited the highest performance, followed by cascade control, and finally, PI control. Galvản-Ángeles et al. [
23] analyzed a thermo-compression evaporation method for milk. The suggested tool considers the cost optimization of the evaporation system while incorporating thermo-physical parameters of the foodstuff as a function of composition and temperature. The results revealed that the evaporation economy is proportional to the percentage of recycled steam and the location of the effect that recycles the steam, and inverse to the thermodynamic efficiency of the thermo-compressor.
This work aims at optimizing the milk evaporation process by minimizing steam consumption under the operational and product quality constraints. To this end, 5 different Cases of evaporator layouts are examined using a global system analysis (GSA) and an advanced optimization approach. GSA is employed to revise decisions to improve system robustness, validate the process and reduce parameter uncertainty. An uncertainty analysis allowed the investigation of the impact of design and operational decisions and environmental inputs on Key Performance Indicators (KPIs). Afterwards, Cases 1-4 are optimized under 5 different scenarios, either minimizing the cost of steam while maximizing product yield or minimizing the total annualized cost which is applicable to a new plant design or a capacity expansion option. Steam economy, energy consumption profile and heat transfer areas are assessed and compared. Moreover, this study investigates to what extend switching from milk powders to new products known as milk concentrates effects the energy consumption in the evaporation process. Thus, Cases 1-4 are optimized under different end-product specifications (30, 35 or 50% solid content). Finally, it is evaluated whether the use of MVR or TVR is more economical for the evaporation process, based on current steam and electricity prices, economic trends, and costs of steam generated from renewable energy sources.
The remaining of the article is structured as follows:
Section 2 describes the material composition along with some of its properties.
Section 3 provides a detailed presentation of the mathematical model that describes the operation of a falling film evaporator. Sectio 4 presents the studied evaporator layouts. The attained global system analysis and optimization results of each studied Case/evaporator layout are presented and thoroughly discussed in
Section 5. Finally,
Section 6 summarizes the concluded remarks emerging from the study.
3. Process model
The concentration of milk in this study is focused on falling film evaporators. In this process, the milk, which is close to its boiling point, is introduced in a uniform manner at the upper section of the inner surface of a tube. These tubes are arranged side by side, fixed in place, and surrounded by a jacket. As the milk descends within each tube, it forms a thin film and undergoes boiling as a result of the heat exchanged with the steam. The concentrated liquid is collected at the lower part of the equipment, while the remaining portion is separated from the steam in a subsequent separator. In evaporators equipped with multiple effects, the concentrated liquid is pumped to the next stage, while the steam serves the purpose of heating the subsequent [
2].
A dynamic model of a simple falling-film evaporator is developed in this Section. The model examines the flash calculations of liquid entering the evaporator, its distribution through distributor plates, and its evaporation as it flows downwards through pipes. The model has been developed based on the following assumptions:
It is assumed that the product immediately reaches its boiling temperature once it passes above the distributor plate, with either steam flashing or condensing.
All the heating steam condenses at its saturation temperature. The heat released during condensation is utilized to preheat and evaporate the feed stream.
The pressure difference on the steam side is insignificant, thus resulting in a constant temperature on the steam side.
The unit is assumed to be perfectly mixed at all times, implying there are no spatial variations in intensive properties within it.
A steady state balance is applied to the tube flow, but the mass hold-up of liquid on the distributed plate is calculated.
3.1. Mass balance
The rate of change of the mass hold-up,
, of any given species in phase
in the unit is given by Equation (4):
Where
is the mass flowrate of the
jth feed stream in phase
p,
is the mass fraction of species
i in the
jth feed stream in phase
p,
is the mass flowrate of material phase
p in the outlet stream,
is the mass fraction of species
i in the outlet stream of phase
p and
is the rate of mass transfer between the phase
p and the phase
pn.
Assuming that the unit is perfectly mixed, the composition of any outlet stream is the same as the composition within the unit:
Where
is the mass fraction of species
i in phase
p in the unit.
The composition of material within the unit is given by Equations (6),(7):
Where
is the total holdup of material in phase
p within the unit.
3.2. Energy balance
The rate of accumulation of enthalpy,
, within the unit is given by Equations (8),(9):
Where
is the specific enthalpy of the material in the unit in phase
p,
is the specific enthalpy of the
jth feed stream in phase
p,
is the specific enthalpy of the outlet stream in phase
p,
is the enthalpy of phase change between phase
p and phase
pn and
is the enthalpy transferred into the unit through boundary due to heat loss, heating and so forth.
Due to the assumption that the unit is perfectly mixed, the specific enthalpy of each of the outlet streams is equal to the specific enthalpy of the material within the unit:
The specific enthalpy is assumed to be a function of the composition and temperature,
, of the material within the unit:
3.3. Heat transfer rates
The total heat transfer rate,
, is the sum of energy transfer by steam,
and energy loss,
, to the environment:
Where is the overall heat transfer coefficient, is the heat transfer area, is the number of tubes, is the length of the tubes and finally and are the linear and logarithmic temperature differences, respectively.
3.4. Flow through distribute plate
The distribute plate is an inserted plate that distributes product stream evenly around the inner periphery of the evaporator tubes. Aside from the liquid holes that allow liquid to pass through, there are also openings to let steam flow through the plate. Two designs for vapor transport through the distribute plate are considered:
The vapor flowing downwards or upwards through the distribute plate causes a vapor pressure drop, while the liquid flowing downwards through the distribute plate and liquid holdup above the plate cause a liquid pressure drop.
The vapor flow through plate,
, for plate design with upstanding vapor tubes is expressed by the following relation.
Where
is the number of vapour uprising tubes,
is the diameter of each uprising tube,
is the length of each tube,
is the vapor density above plate,
is the vapor friction factor and
is the vapor pressure drop.
The vapor flow through plate for plate design with upstanding rim at the edges is expressed by Equations (18)-(19):
Where
are the diameter of the evaporator body and the plate respectively and
is the height of the outer rim.
The liquid flow through plate,
, is expressed by Equations (20)-(21):
Where
is the number of liquid holes,
is the diameter of liquid holes,
is the thickness of the distribute plate,
is the liquid density above plate,
is the liquid flow velocity through plate,
is the liquid friction factor and
is the liquid pressure drop.
3.5. Liquid flow through pipes
The wetting rate,
, of a falling film evaporator tube is correlated to the liquid mass flow of the tube,
and the tube diameter
through:
The Reynolds number,
, in the falling film evaporation used in empirical relations is defined by Equation (23):
Where is the liquid dynamic viscosity.
The liquid characteristic length,
, is given as:
Where is the liquid density and is the gravity acceleration.
The film thickness,
, is calculated by Equation (25):
Assuming that the film thickness is small compared to the tube diameter, the liquid velocity downwards on the tube,
, and the residence time,
, for liquid flow to the bottom are calculated based on Equations (26)-(27):
3.6. Boiling point elevation
The boiling point elevation of a solution can be calculated by combining the laws of Raoult and Clausius Clapeyron:
Where is the gas constant, is the boiling temperature of water, is heat of evaporation, is molar weight and is the molar fraction of water in the solution.
It is assumed that fat does not dissolve in the solvent and therefore does not affect the boiling point. The molar fraction of water in the fat-free product can therefore be calculated:
Where denotes for the mass fraction and refers to all but fat components.
3.7. Liquid friction factor
The most widely used correlations for liquid friction factor is the Wallis correlation for annular falling film and it is incorporated to the model for better prediction of the liquid friction factor [
19].
3.8. Energy cost
In order to compare the energy consumption of TVR and MVR, the variable
Energy cost is used, defined by Equation (31). When employing TVR technology, the annual cost is given as:
For MVR technology, the annual energy cost is expressed as:
The current price of steam based on natural gas is 20.01
$/t [
25]. According to Eurostat [
26], the electricity unit cost for non-household users in 2023 is 0.21
$/kWh. The operating hours per year are considered as 7,920h/year, thus variable
Energy cost refers to annual energy cost.
6. Conclusion
In this work, five different and industrially relevant milk evaporator Cases have been studied using a model-based approach. For each Case study various conclusions were drawn regarding the simulation, model validation, global system analysis and process optimization. In this section, the results are discussed in terms of comparing TVR and MVR.
Comparing Cases 2, 3 and 4 for current steam and electricity prices, when processing 1,000 kg/h raw milk the most economical option includes 3 evaporator effects with TVR (Case 3) to meet the desired 50% product dry mass content. The same figure is reported for optimization Scenarios 2 and 3. However, Case 4 indicates the most significant reduction in the annual cost when reducing the product specification to 30 or 35% dry mass content.
It is worth mentioning that current high electricity prices (0.21$/kWh) lead to Case 4 being the most unprofitable choice. When producing product with 35% dry mass content, only a 11% reduction in the unit electricity price leads to Case 4 being more cost effective than Case 2 with only a single evaporator effect. Simultaneous reduction by 7% of electricity price along with a 5% increase of gas-based steam price would also lead to Case 4 being the most profitable option among these Cases.
Regarding the maximum values of product yield in Cases 2-4 (Scenario 4), Case 2 can achieve slightly higher values than Cases 3 and 4 (0.28 as opposed to 0.25 respectively). Moreover, for a new plant design, the minimum total annualized cost is achieved in Case 4 which includes a single evaporator effect with MVR, thus indicating that the capital fixed cost in such processes has the dominant contribution on the total annualized cost compared to the operating costs.
Cases 1 and 2 can be compared as they both include 2 evaporator effects with TVR, the former relevant to a plant scale and the latter to a pilot scale. The annual steam cost seems to have a relatively linear relationship with capacity while lower product yield values can be achieved in Case 1 when producing products with 50% dry mass content.
Overall, switching from milk powder production to milk concentrates results to a reduction in the annual cost from 10.75 to 44% depending on the Case under consideration. Furthermore, a forecasted reduction of biomass-based steam cost by only 20% (or more) leads to lower values of the annual expenditure in all Cases, than that of the currently used NG-based steam. As predictions indicate a rise in natural gas’ price, renewable-based steam would potentially become more and more competitive. Finally, assuming a simultaneous increase in the price of NG-based steam by 10% and a reduction of biomass-based steam by 10%, the former one is no longer the most economically attractive solution.
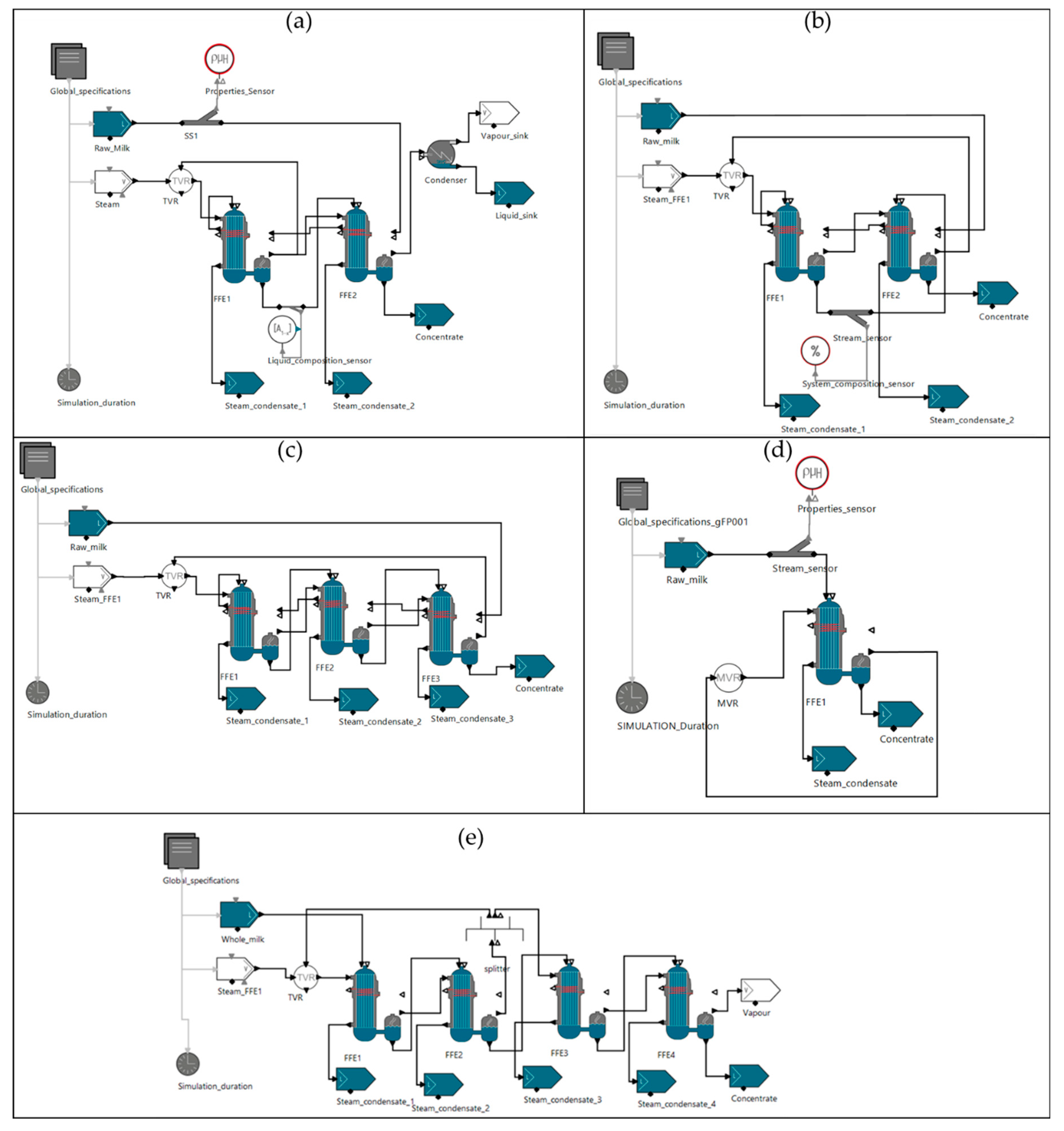
Figure 1.
(a) Case 1: 2 stage FFE layout with TVR technology with vapor recycling from 1st to 1st stage, (b) Case 2: 2 stage FFE layout with TVR technology with vapor recycling from 2nd to 1st stage, (c) Case 3: 3 stage FFE layout with TVR technology with vapor recycling from 3rd to 1st stage, (d) Case 4: 1 stage FFE layout with MVR technology, (e) Case 5: 4 stage FFE with TVR technology with vapor recycling from 2nd to 1st stage.
Figure 1.
(a) Case 1: 2 stage FFE layout with TVR technology with vapor recycling from 1st to 1st stage, (b) Case 2: 2 stage FFE layout with TVR technology with vapor recycling from 2nd to 1st stage, (c) Case 3: 3 stage FFE layout with TVR technology with vapor recycling from 3rd to 1st stage, (d) Case 4: 1 stage FFE layout with MVR technology, (e) Case 5: 4 stage FFE with TVR technology with vapor recycling from 2nd to 1st stage.
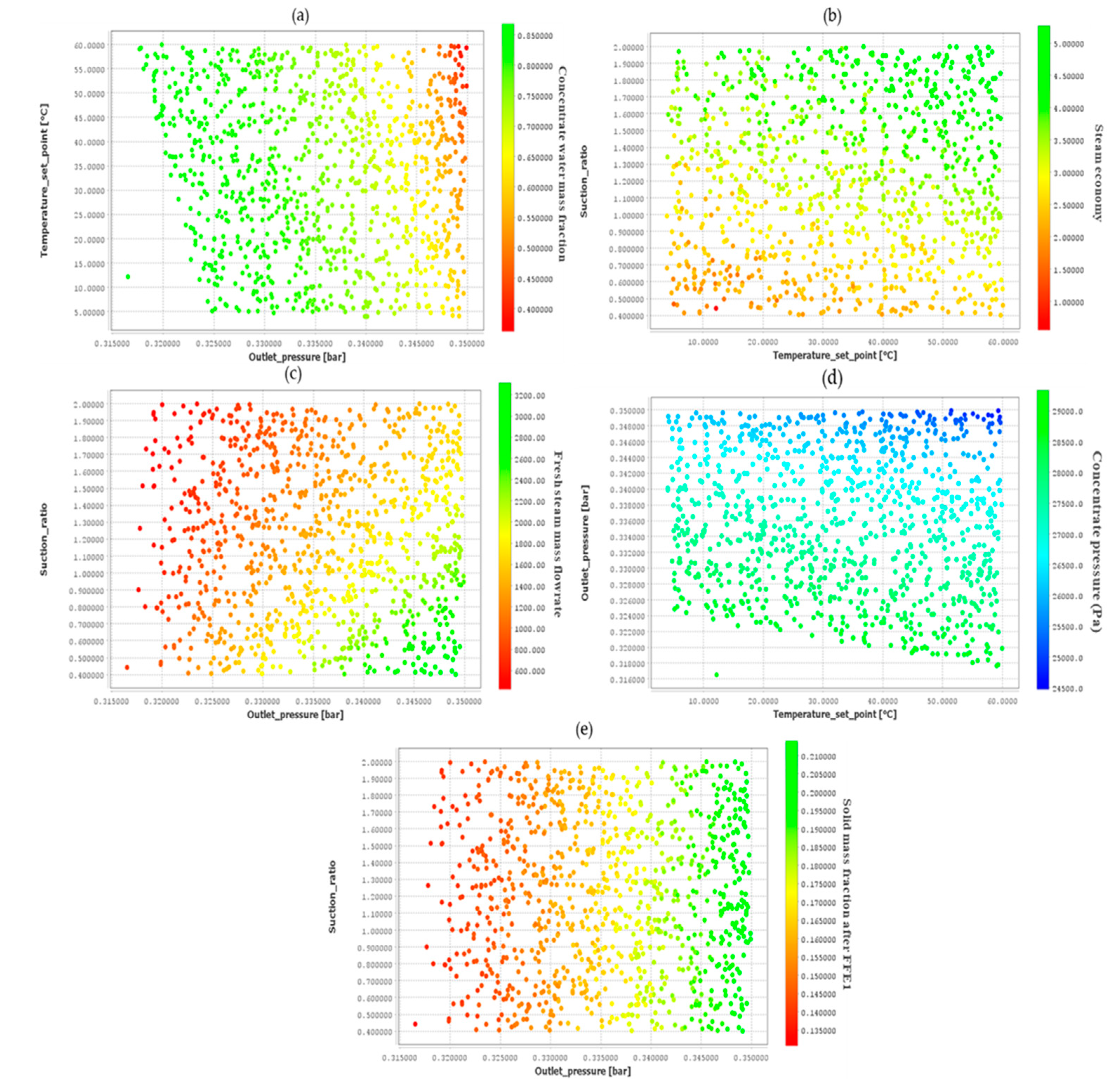
Figure 2.
Case 1 uncertainty analysis results: (a) Concentrate water mass fraction versus feed temperature and TVR discharge pressure, (b) Steam economy versus TVR suction ratio and feed temperature, (c) Steam mass flowrate versus suction ratio and TVR discharge pressure, (d) Concentrate pressure versus TVR discharge pressure and feed temperature, (e) FFE1 product dry mass fraction versus TVR suction ratio and discharge pressure.
Figure 2.
Case 1 uncertainty analysis results: (a) Concentrate water mass fraction versus feed temperature and TVR discharge pressure, (b) Steam economy versus TVR suction ratio and feed temperature, (c) Steam mass flowrate versus suction ratio and TVR discharge pressure, (d) Concentrate pressure versus TVR discharge pressure and feed temperature, (e) FFE1 product dry mass fraction versus TVR suction ratio and discharge pressure.
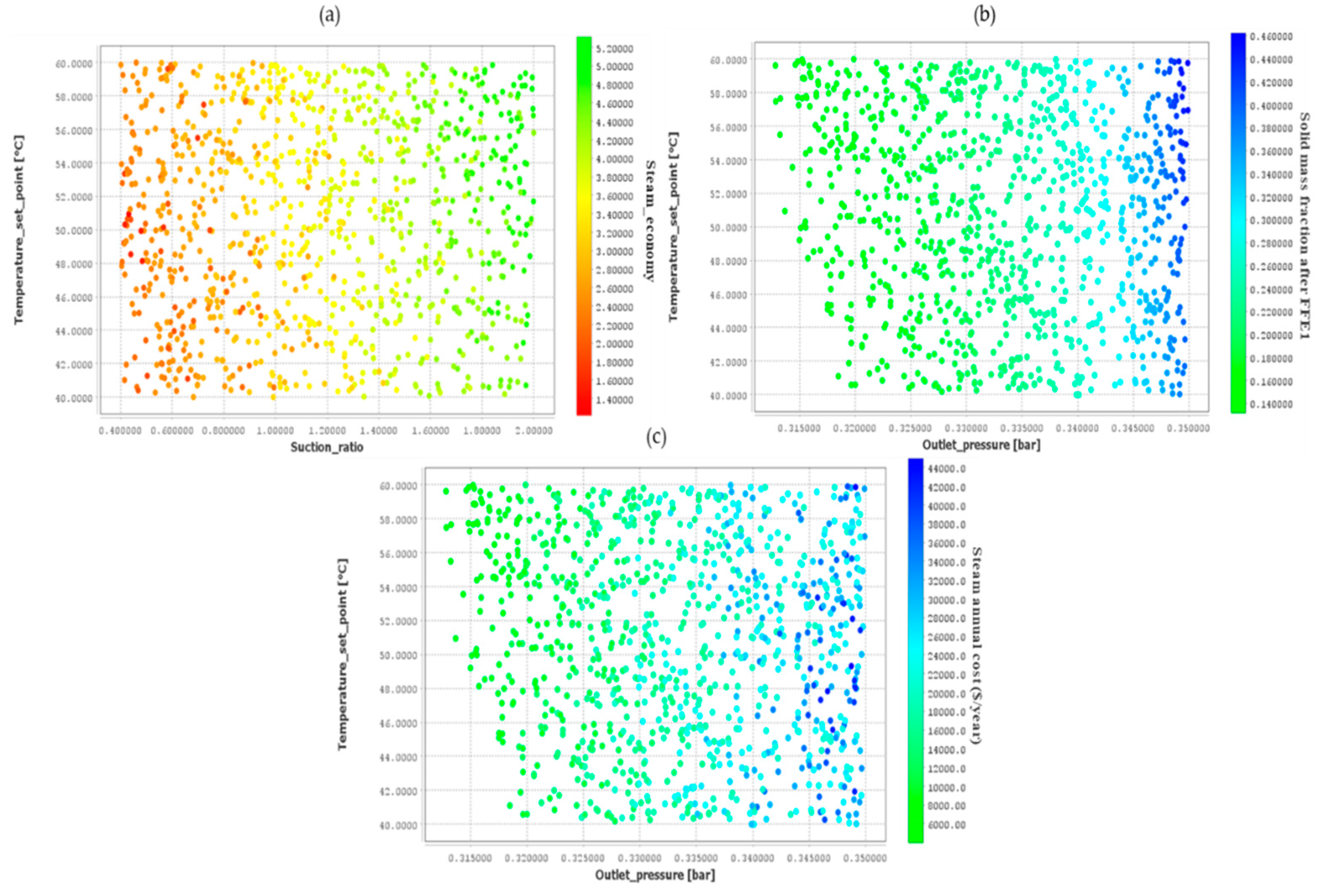
Figure 3.
Case 2 uncertainty analysis results: (a) Steam economy versus TVR suction ratio and feed temperature, (b) FFE1 product dry mass fraction versus feed temperature and discharge pressure, (c) Steam annual cost versus feed temperature and TVR discharge pressure.
Figure 3.
Case 2 uncertainty analysis results: (a) Steam economy versus TVR suction ratio and feed temperature, (b) FFE1 product dry mass fraction versus feed temperature and discharge pressure, (c) Steam annual cost versus feed temperature and TVR discharge pressure.
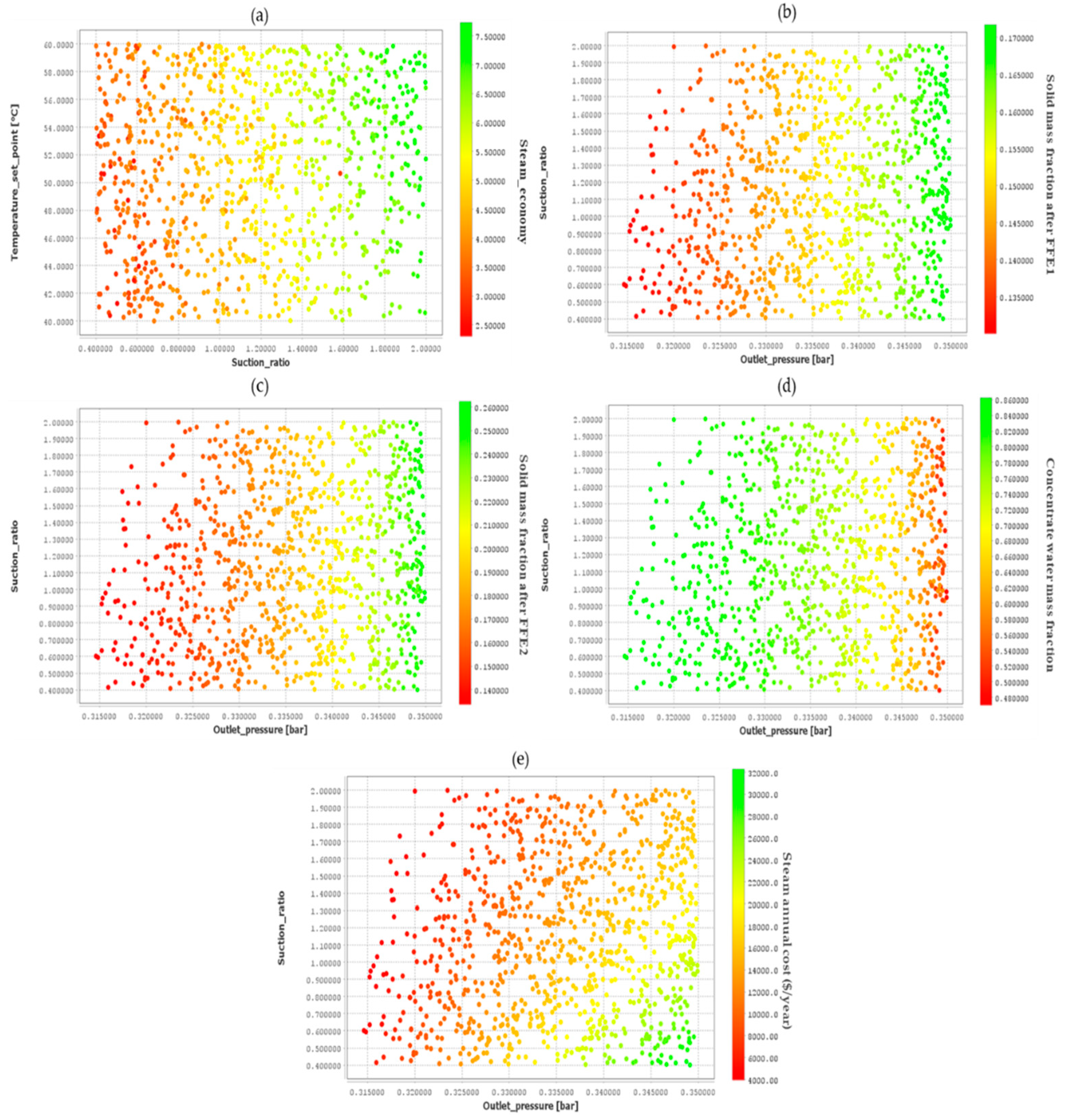
Figure 4.
Case 3 uncertainty analysis results: (a) Steam economy versus feed temperature and suction ratio, (b) Dry mass fraction of product after FFE1 versus suction ratio and TVR discharge pressure, (c) Dry mass fraction of product after FFE2 versus suction ratio and TVR discharge pressure, (d) Water mass fraction of concentrate versus TVR suction ratio and TVR discharge pressure, (e) Steam annual cost versus TVR suction ratio and TVR discharge pressure.
Figure 4.
Case 3 uncertainty analysis results: (a) Steam economy versus feed temperature and suction ratio, (b) Dry mass fraction of product after FFE1 versus suction ratio and TVR discharge pressure, (c) Dry mass fraction of product after FFE2 versus suction ratio and TVR discharge pressure, (d) Water mass fraction of concentrate versus TVR suction ratio and TVR discharge pressure, (e) Steam annual cost versus TVR suction ratio and TVR discharge pressure.
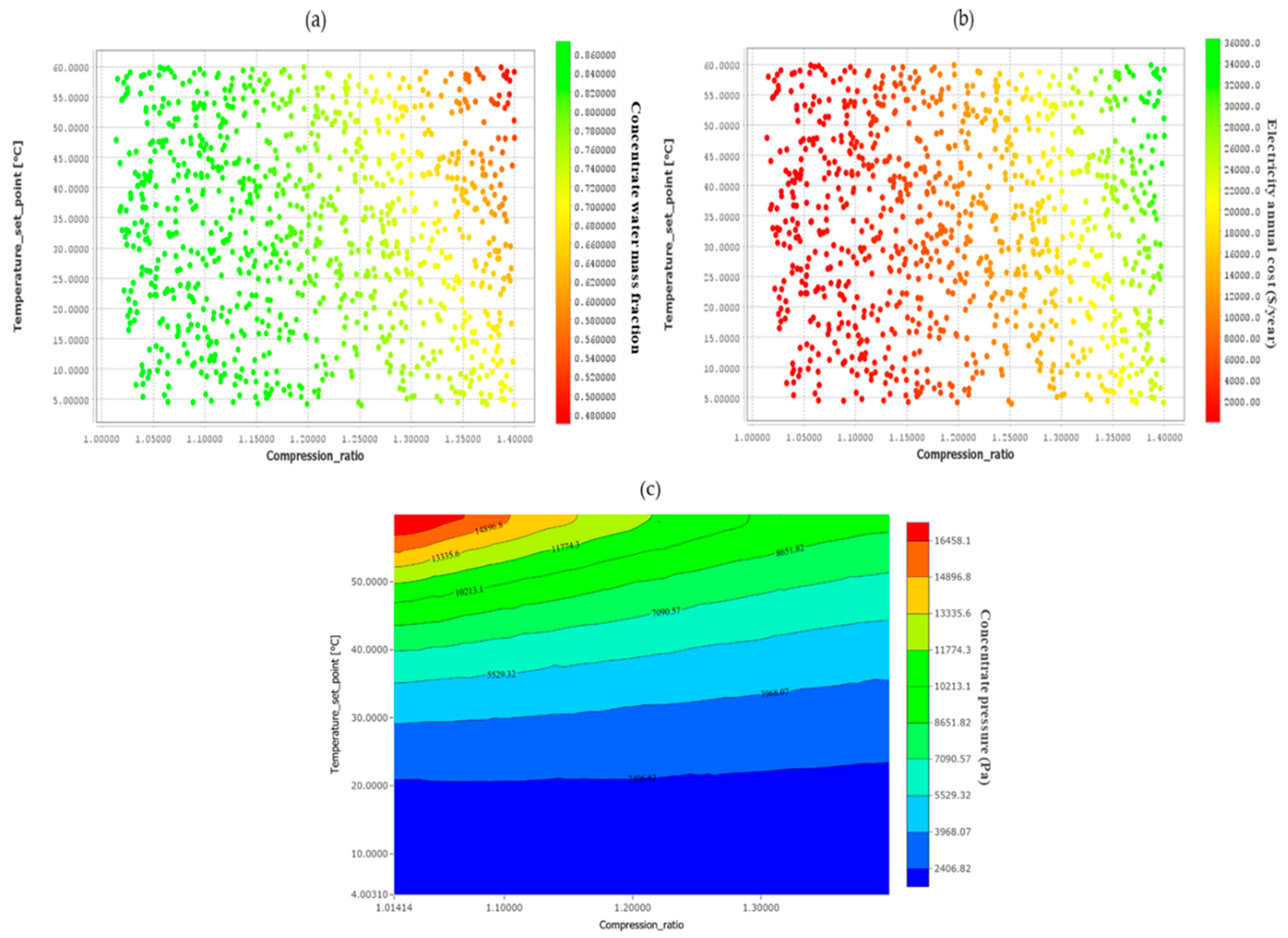
Figure 5.
Case 4 uncertainty analysis results: (a) Water mass fraction of concentrate versus feed temperature and MVR compression ratio, (b) Steam annual cost versus feed temperature and compression ratio, (c) Concentrate pressure versus MVR compression ratio and feed temperature.
Figure 5.
Case 4 uncertainty analysis results: (a) Water mass fraction of concentrate versus feed temperature and MVR compression ratio, (b) Steam annual cost versus feed temperature and compression ratio, (c) Concentrate pressure versus MVR compression ratio and feed temperature.
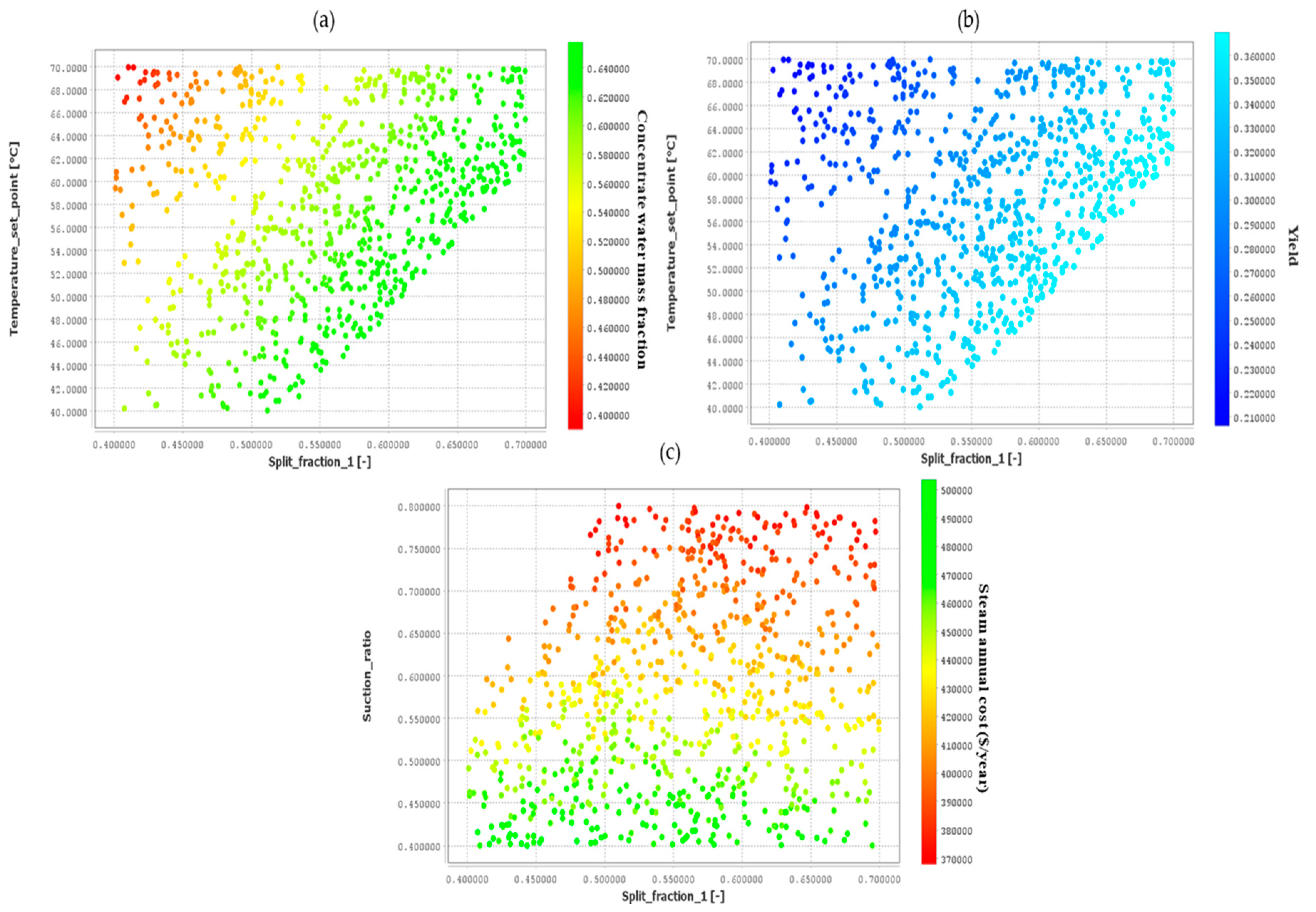
Figure 6.
Case 5 uncertainty analysis results: (a) Water mass fraction of concentrate versus feed temperature and split fraction, (b) Yield versus feed temperature and split fraction, (c) Steam annual cost versus TVR suction ratio and split fraction.
Figure 6.
Case 5 uncertainty analysis results: (a) Water mass fraction of concentrate versus feed temperature and split fraction, (b) Yield versus feed temperature and split fraction, (c) Steam annual cost versus TVR suction ratio and split fraction.
Table 1.
Whole milk composition.
Table 1.
Whole milk composition.
| Whole milk components [24] |
Weight (%)
[24] |
Whole milk components [5] |
Weight (%)
[5] |
| Water |
|
Water |
|
| Carbohydrates |
|
Fat |
|
| Proteins |
|
Protein |
|
| Fat |
|
Lactose |
|
| Ash |
|
NaCl |
|
| |
|
KCl |
|
Table 2.
Equations of properties calculation.
Table 2.
Equations of properties calculation.
| Property |
Equation [23] |
|
| Specific heat capacity |
|
|
| Thermal conductivity |
|
|
| Density |
|
|
Table 3.
Properties of whole milk before evaporation at 4°C, 101 kPa.
Table 3.
Properties of whole milk before evaporation at 4°C, 101 kPa.
| Property |
Value [23] |
Value [5] |
Simulated data |
| Density |
|
|
|
|
|
|
|
|
|
|
|
Table 4.
Steam prices examined in GSA.
Table 4.
Steam prices examined in GSA.
| Cost ($/tn) |
-40% |
-30% |
-20% |
-10% |
0% |
+10% |
+20% |
+30% |
| Biomass- based steam |
12.222 |
14.259 |
16.296 |
18.333 |
20.37 |
22.407 |
24.444 |
26.481 |
| Solar-based steam |
19.5 |
22.75 |
26 |
29.25 |
32.5 |
35.75 |
39 |
42.25 |
| Biogas-based steam |
16.452 |
19.194 |
21.936 |
24.678 |
27.42 |
30.162 |
32.904 |
35.646 |
| NG-based steam |
10.086 |
11.767 |
13.448 |
15.129 |
16.81 |
18.491 |
20.172 |
21.853 |
Table 5.
Minimum & maximum annual cost values of evaporation process depending on steam source.
Table 5.
Minimum & maximum annual cost values of evaporation process depending on steam source.
| |
-40% |
-30% |
-20% |
-10% |
0% |
+10% |
+20% |
+30% |
| Minimum Annual Cost ($) |
| Biomass- based steam |
82,477 |
96,221 |
109,969 |
123,715 |
137,461 |
151,207 |
164,953 |
178,699 |
| Solar-based steam |
131,590 |
153,522 |
175,453 |
197,385 |
219,317 |
241,248 |
263,180 |
285,112 |
| Biogas-based steam |
111,025 |
129,525 |
148,028 |
166,532 |
185,036 |
203,539 |
222,043 |
240,546 |
| NG-based steam |
68,062 |
79,406 |
90,750 |
102,094 |
113,438 |
124,781 |
136,125 |
147,469 |
| Maximum Annual Cost ($) |
| Biomass- based steam |
278,931 |
325,419 |
371,908 |
418,396 |
464,885 |
511,373 |
557,862 |
604,350 |
| Solar-based steam |
445,029 |
519,201 |
593,373 |
667,544 |
741,716 |
815,887 |
890,059 |
964,231 |
| Biogas-based steam |
375,468 |
438,046 |
500,624 |
563,202 |
625,780 |
688,358 |
750,936 |
813,514 |
| NG-based steam |
230,183 |
268,547 |
306,911 |
345,275 |
383,638 |
422,002 |
460,366 |
498,730 |
Table 6.
Minimum and maximum values of outlet dry mass fraction of each effect.
Table 6.
Minimum and maximum values of outlet dry mass fraction of each effect.
| Variable |
Minimum |
Maximum |
| FFE1 Outlet dry mass fraction (kg/kg) |
0.162 |
0.169 |
| FFE2 Outlet dry mass fraction (kg/kg) |
0.225 |
0.254 |
| FFE3 Outlet dry mass fraction (kg/kg) |
0.278 |
0.359 |
| FFE4 Outlet dry mass fraction (kg/kg) |
0.341 |
0.610 |
Table 7.
Optimization scenarios examined – Cases 1-4.
Table 7.
Optimization scenarios examined – Cases 1-4.
| Scenario |
Objective function |
Product quality specifications |
| 1 |
Minimization of annual steam cost ($/year) |
Product dry mass fraction = 0.5 |
| 2 |
Minimization of annual steam cost ($/year) |
Product dry mass fraction = 0.35 |
| 3 |
Minimization of annual steam cost ($/year) |
Product dry mass fraction = 0.30 |
| 4 |
Maximization of yield |
Product dry mass fraction = 0.5 |
| 5 |
Minimization of total cost |
Product dry mass fraction = 0.5 |
| 6 |
Maximization of yield |
0.3 <Product dry mass fraction < 0.5 |
Table 8.
Operating constraints for Case 1.
Table 8.
Operating constraints for Case 1.
| Constraints |
Explanation |
|
The final water content must be equal to 0.5 in Scenarios 1,4 and 5, 0.65 in Scenario 2 and 0.7 in Scenario 3. |
|
FFE1 temperature should be under 70°C to mitigate the negative effects of heat on heat-sensitive milk components and prevent the degradation of essential nutrients. |
|
The temperature of each evaporator effect must be at least 2°C lower than the previous one to ensure proper vacuum. |
|
Only for Scenario 6, the final water content varies between 0.5 and 0.7 |
Table 9.
Optimal values of performance indices, time-invariant optimization variables, and final process variables at each Scenario – Case 1.
Table 9.
Optimal values of performance indices, time-invariant optimization variables, and final process variables at each Scenario – Case 1.
| Scenario |
1 |
2 |
3 |
4 |
5 |
6 |
Base Case |
| Steam annual cost ($/year) |
232,118 |
199,609 |
181,563 |
319,363 |
228,307 |
261,481 |
368,653 |
| Total annualized cost ($/year) |
3.90·106
|
3.86·106
|
3.85·106
|
3.98·106
|
2.33·106
|
3.92·106
|
4.03·106
|
| Yield |
0.24 |
0.36 |
0.42 |
0.252 |
0.252 |
0.42 |
0.27 |
| TVR – Discharge Pressure (bar) |
0.347 |
0.341 |
0.338 |
0.35 |
0.35 |
0.342 |
0.35 |
| TVR – Suction ratio |
2 |
2 |
2 |
1.4 |
2 |
1.4 |
1.1 |
| Feed Temperature (°C) |
60 |
60 |
60 |
31.84 |
60 |
26.74 |
20 |
| FFE1/FFE2 tube inner diameter (m) |
0.0508 |
0.0508 |
0.0508 |
0.0508 |
0.0435/0.0254 |
0.0508 |
0.0508 |
| FFE1/FFE2 tube length (m) |
16 |
16 |
16 |
16 |
17/5 |
16 |
16 |
| FFE2 Temperature (K) |
339.81 |
340.2 |
340.4 |
339.85 |
326.54 |
340.5 |
340 |
| Concentrate water content |
0.5 |
0.65 |
0.7 |
0.5 |
0.5 |
0.7 |
0.543 |
Table 10.
Optimal values of performance indices, time-invariant optimization variables, and final process variables at each Scenario – Case 2.
Table 10.
Optimal values of performance indices, time-invariant optimization variables, and final process variables at each Scenario – Case 2.
| Scenario |
1 |
2 |
3 |
4 |
5 |
6 |
Base Case |
| Steam annual cost ($/year) |
21,159 |
18,887 |
17,184 |
30,719 |
20,663 |
25,326 |
30,740 |
| Total annualized cost ($/year) |
504,490 |
502,217 |
500,514 |
514,049 |
274,768 |
508,657 |
514,070 |
| Yield |
0.279 |
0.36 |
0.42 |
0.28 |
0.252 |
0.42 |
0.28 |
| TVR – Discharge Pressure (bar) |
0.349 |
0.345 |
0.341 |
0.35 |
0.35 |
0.342 |
0.35 |
| TVR – Suction ratio |
2 |
2 |
2 |
1.1 |
2 |
1.1 |
1.1 |
| Feed Temperature (°C) |
60 |
60 |
60 |
55.87 |
60 |
53.47 |
55 |
| FFE1/FFE2 tube inner diameter (m) |
0.0508 |
0.0508 |
0.0508 |
0.0508 |
0.0508/ |
|
|
| FFE1/FFE2 tube length (m) |
6 |
6 |
6 |
6 |
5.7/0.6 |
6 |
6 |
| FFE2 Temperature (K) |
340 |
340.3 |
340.5 |
340 |
293.15 |
340.5 |
340 |
| Concentrate water content |
0.5 |
0.65 |
0.7 |
0.5 |
0.5 |
0.7 |
0.55 |
Table 11.
Operating constraints for Case 3.
Table 11.
Operating constraints for Case 3.
| Constraints |
Explanation |
|
The final water content must be equal to 0.5 in Scenarios 1,4 and 5, 0.65 in Scenario 2 and 0.7 in Scenario 3. |
|
FFE1 temperature should be under 70°C to mitigate the negative effects of heat on heat-sensitive milk components and prevent the degradation of essential nutrients. |
|
|
The temperature of each evaporator effect must be at least 2°C lower than the previous one to ensure proper vacuum. |
|
Only for Scenario 6, final water content can vary between 0.5 and 0.7 |
Table 12.
Optimal values of performance indices, time-invariant optimization variables, and final process variables at each Scenario – Case 3.
Table 12.
Optimal values of performance indices, time-invariant optimization variables, and final process variables at each Scenario – Case 3.
| Scenario |
1 |
2 |
3 |
4 |
5 |
6 |
Base Case |
| Steam annual cost ($/year) |
15,078 |
12,989 |
11,300 |
22,069 |
18,900 |
19,200 |
22,088 |
| Total annualized cost ($/year) |
681,251 |
679,163 |
677,474 |
688,242 |
449,236 |
685,374 |
688,262 |
| Yield |
0.25 |
0.35 |
0.36 |
0.252 |
0.25 |
0.36 |
0.25 |
| TVR – Discharge Pressure (bar) |
0.35 |
0.342 |
0.34 |
0.35 |
0.349 |
0.344 |
0.35 |
| TVR – Suction ratio |
2 |
2 |
2 |
1.1 |
1.37 |
1.1 |
1.1 |
| Feed Temperature (°C) |
60 |
60 |
60 |
54.9 |
60 |
53.6 |
55 |
| FFE1/FFE2/FFE3 tube inner diameter (m) |
0.0508 |
0.0508 |
0.0508 |
0.0508 |
0.0508 / 0.0381/0.0381 |
0.0508 |
0.0508 |
| FFE1/FFE2/FFE3 tube length (m) |
6 |
6 |
6 |
6 |
4.25/4.12/4.13 |
6 |
6 |
| FFE2 Temperature (K) |
340.7 |
341 |
341 |
340.7 |
338.5 |
341 |
340.7 |
| FFE3 Temperature (K) |
338.3 |
338.9 |
339 |
338.4 |
334 |
339 |
338.4 |
| Concentrate water content |
0.5 |
0.65 |
0.7 |
0.5 |
0.5 |
0.7 |
0.5 |
Table 13.
Constraints and explanations - Case 4.
Table 13.
Constraints and explanations - Case 4.
| Constraints |
Explanation |
|
The final water content must be equal to 0.5 in Scenarios 1,4 and 5, 0.65 in Scenario 2 and 0.7 in Scenario 3. |
|
FFE1 temperature should be under 70°C to mitigate the negative effects of heat on heat-sensitive milk components and prevent the degradation of essential nutrients. |
|
Only for Scenario 6, final water content can vary between 0.5 and 0.7 |
Table 14.
Optimal values of performance indices, time-invariant optimization variables, and final process variables at each Scenario – Case 4.
Table 14.
Optimal values of performance indices, time-invariant optimization variables, and final process variables at each Scenario – Case 4.
| Scenario |
1 |
2 |
3 |
4 |
5 |
6 |
Base Case |
| Electricity annual cost ($/year) |
34,319 |
23,815 |
19,299 |
35,950 |
39,522 |
20,466 |
34,582 |
| Total annualized cost ($/year) |
275,985 |
265,480 |
260,964 |
277,616 |
251,240 |
262,131 |
276,248 |
| Yield |
0.252 |
0.36 |
0.42 |
0.252 |
0.252 |
0.42 |
0.26 |
| MVR – Adiabatic efficiency |
1 |
1 |
1 |
0.98 |
1 |
1 |
1 |
| MVR – Compression ratio |
1.38 |
1.3 |
1.26 |
1.4 |
1.45 |
1.29 |
1.4 |
| Feed Temperature (°C) |
60 |
60 |
60 |
50.35 |
60 |
44.17 |
50 |
| FFE1 tube inner diameter (m) |
0.0508 |
0.0508 |
0.0508 |
0.0508 |
0.0508 |
0.0508 |
0.0508 |
| FFE1 tube length (m) |
6 |
6 |
6 |
6 |
5.7 |
6 |
6 |
| FFE1 Temperature (K) |
319.2 |
321 |
322.1 |
312.5 |
318.6 |
310.3 |
312.3 |
| Concentrate water content |
0.5 |
0.65 |
0.7 |
0.5 |
0.5 |
0.7 |
0.514 |