Submitted:
05 December 2023
Posted:
07 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Experimentals
2.1. Specimen preparation
2.2. Quasi-Static State Compression Tests
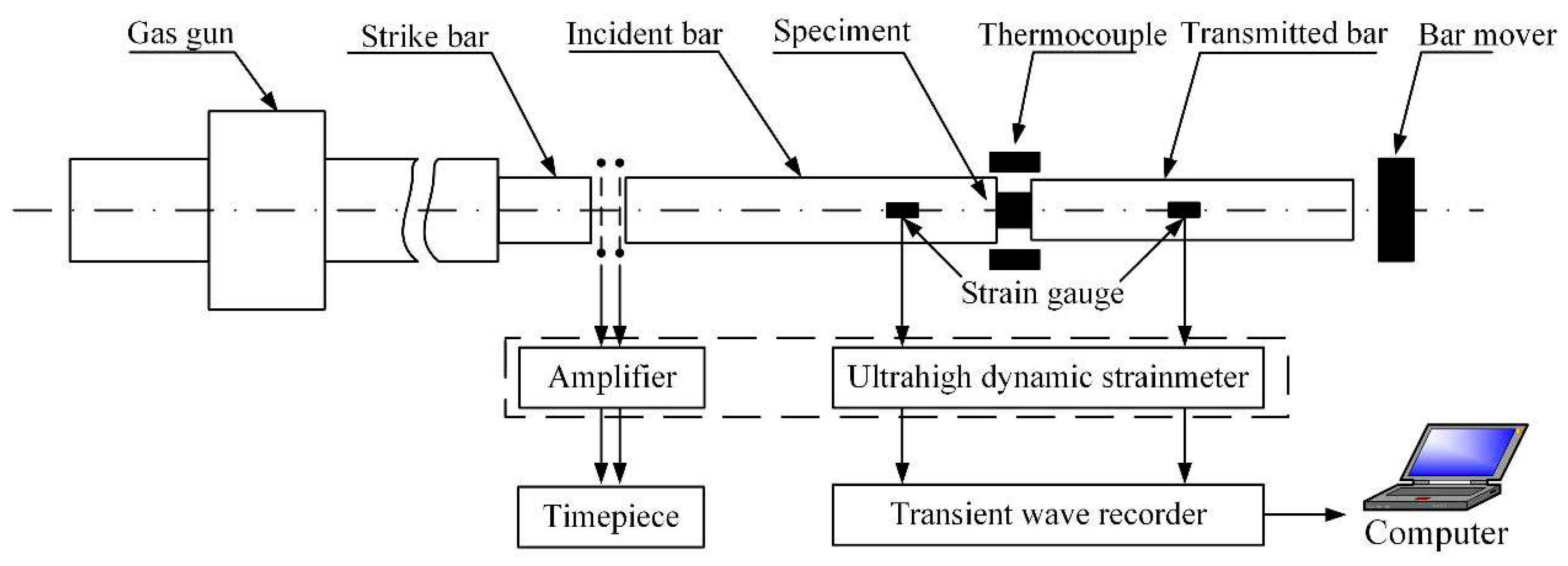
2.3. SHPB Tests
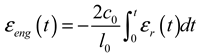
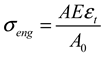
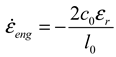
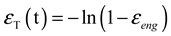
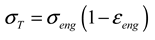
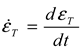
3. Modified Constitutive Model
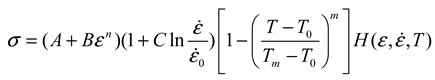
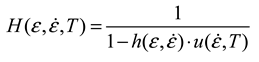
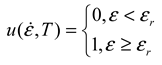
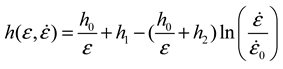
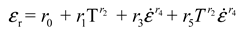
4. Results and Discussion
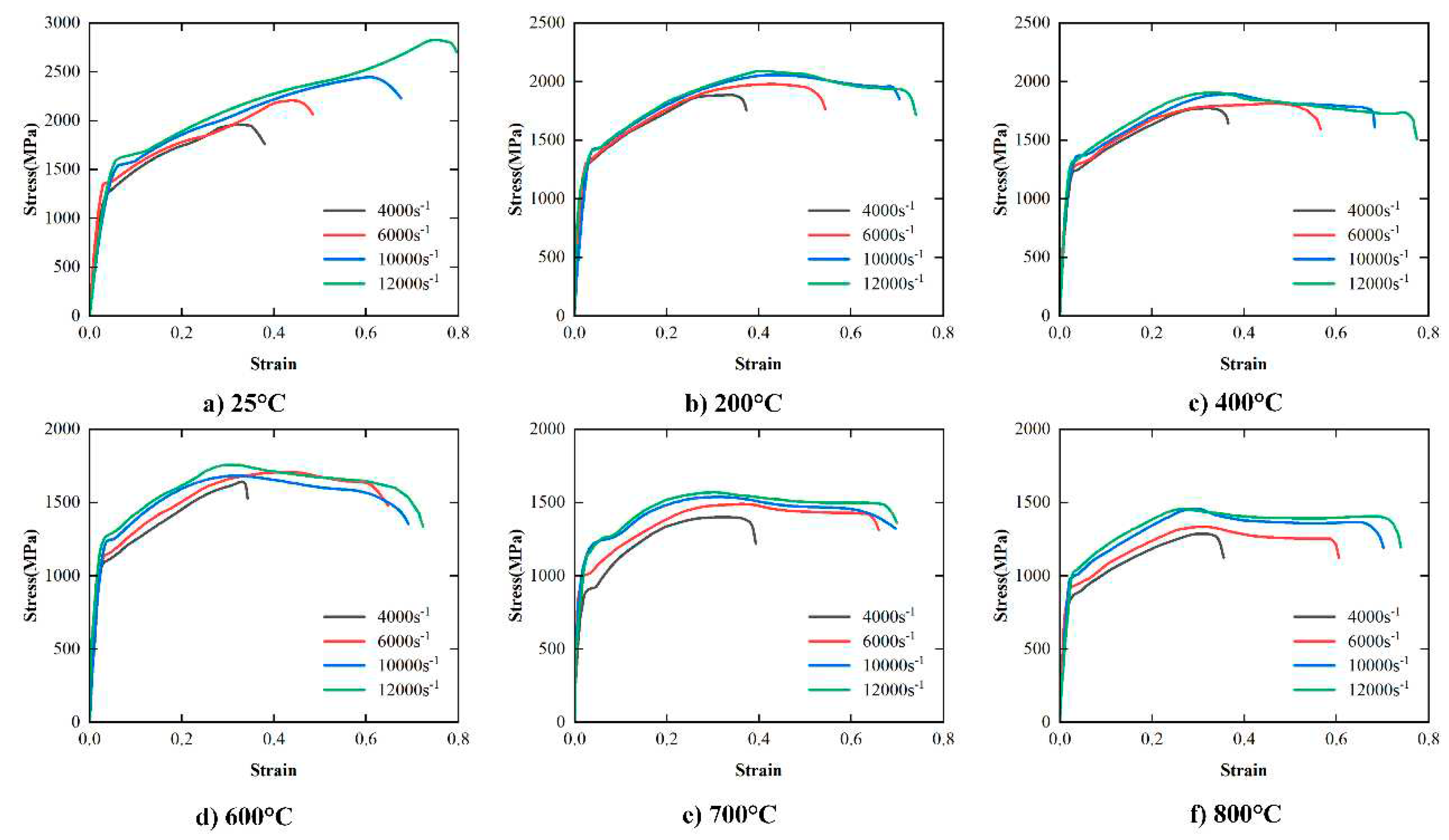
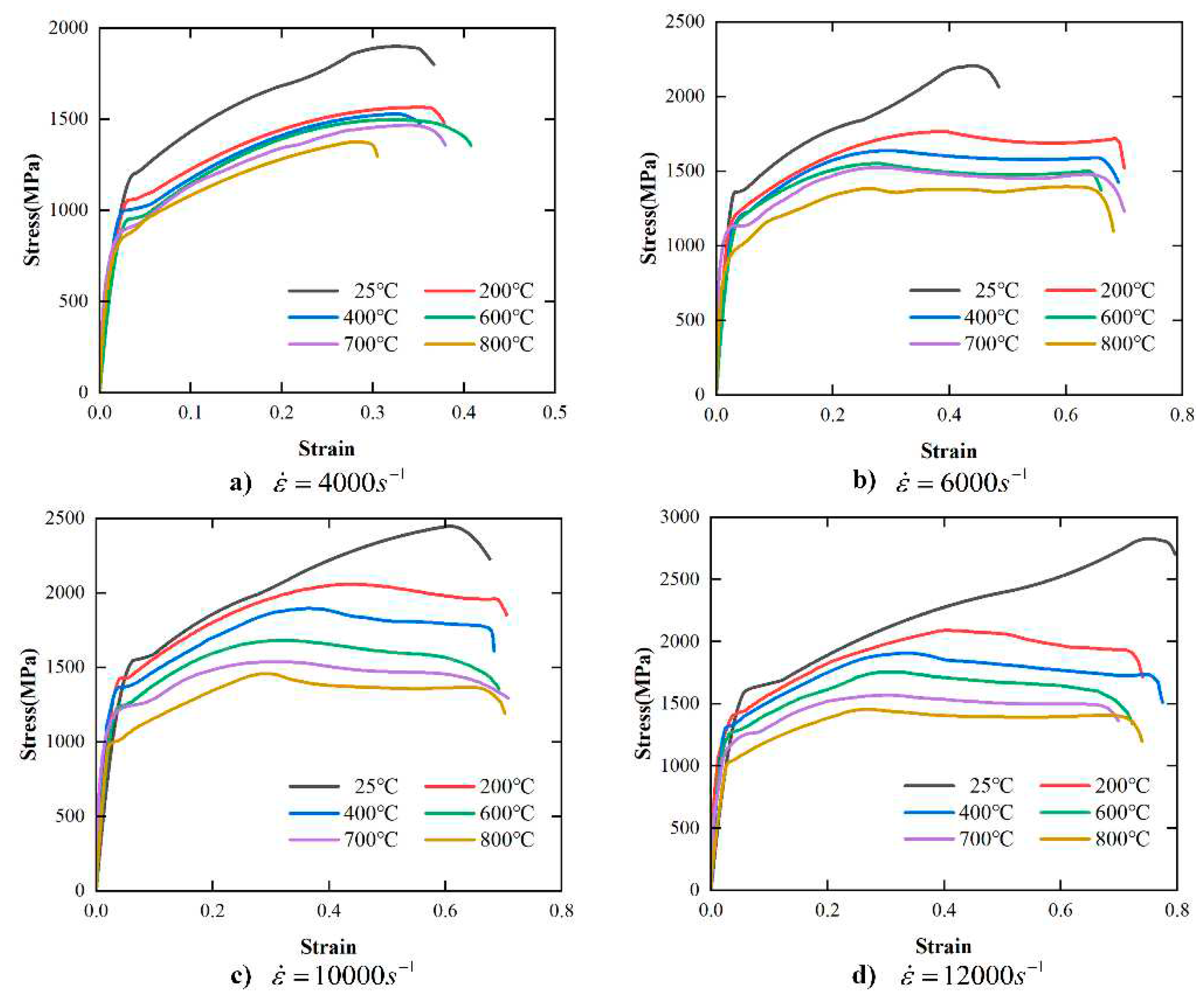
4.1. Dynamic Mechanical Properties
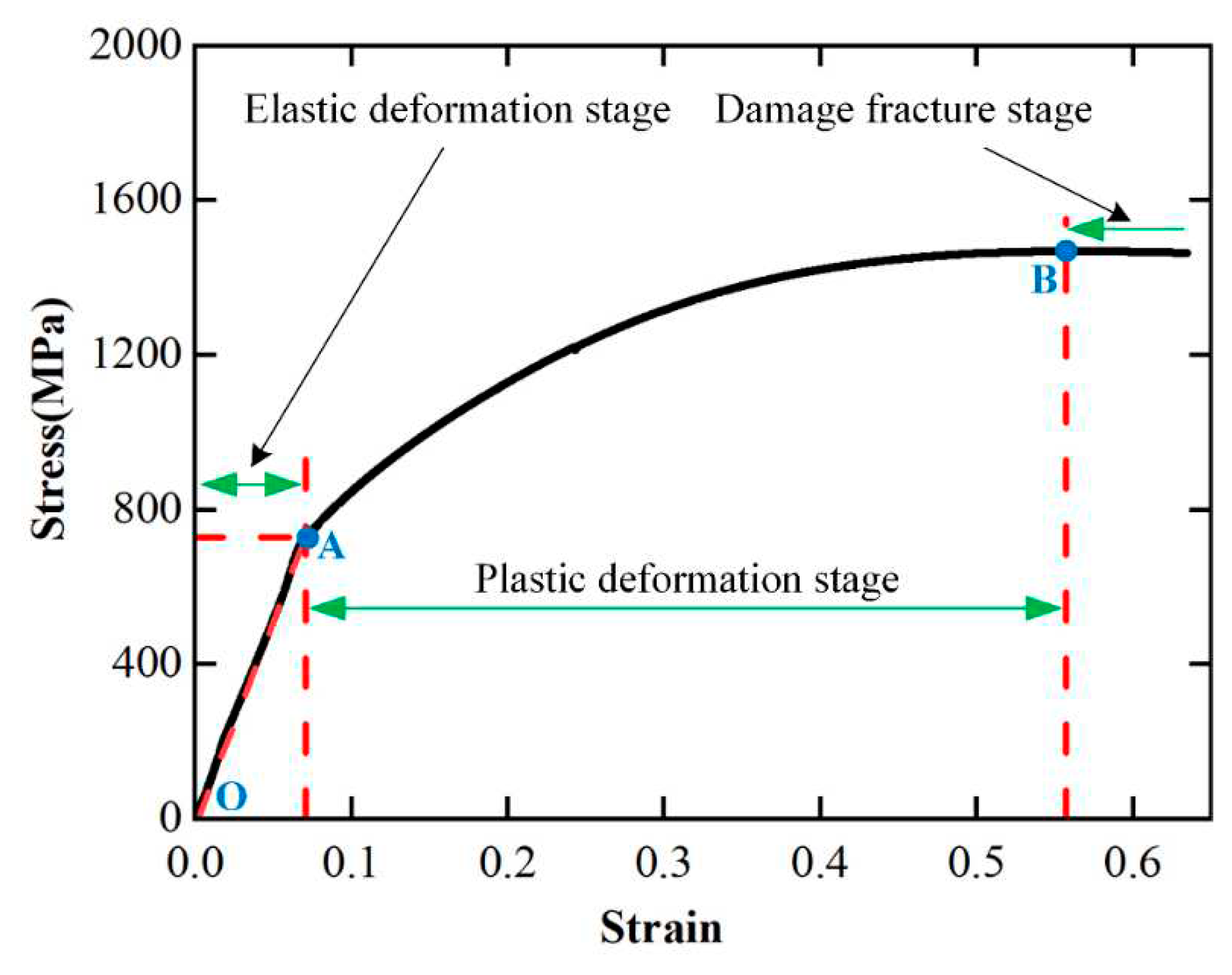
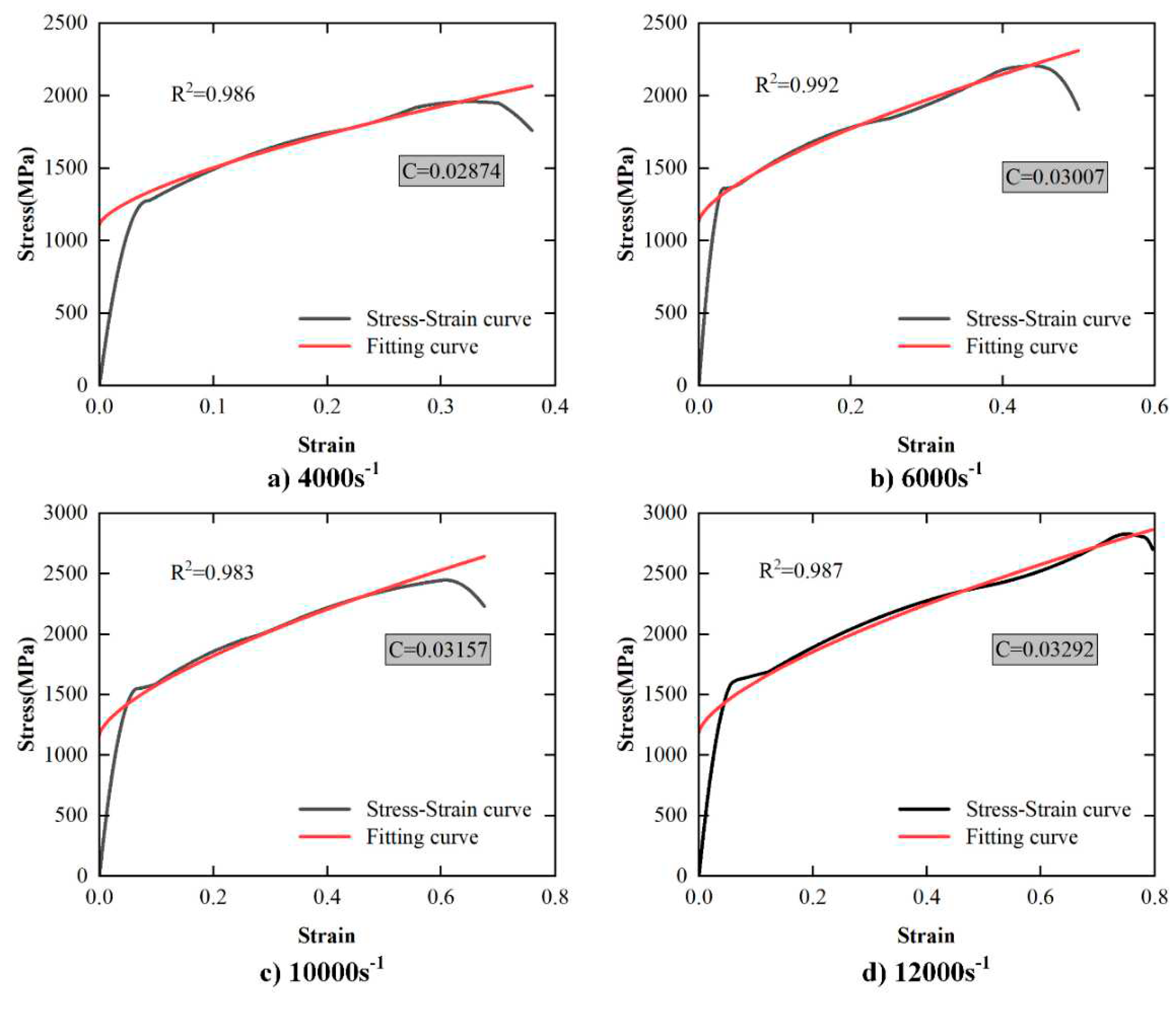
4.1.1. Characteristics of Stress-Strain Curve
| Strain rate (s-1) | Temperature, T (℃) | |||||
|---|---|---|---|---|---|---|
| 25 | 200 | 400 | 600 | 700 | 800 | |
| 4000 | 1315 | 1305 | 1234 | 1097 | 903 | 883 |
| 6000 | 1359 | 1318 | 1280 | 1142 | 1001 | 926 |
| 10000 | 1544 | 1544 | 1322 | 1227 | 1182 | 994 |
| 12000 | 1616 | 1616 | 1355 | 1271 | 1205 | 1043 |
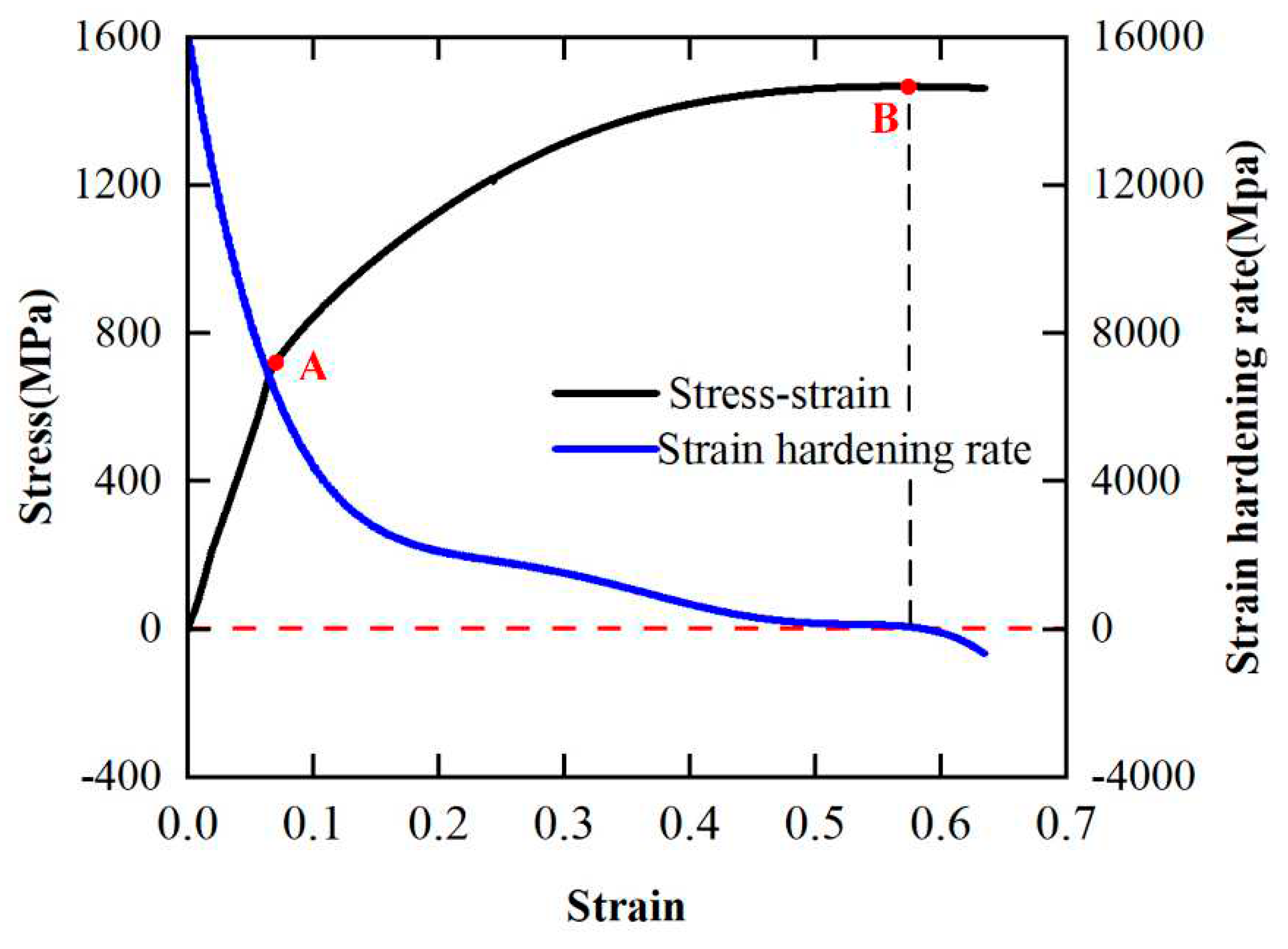
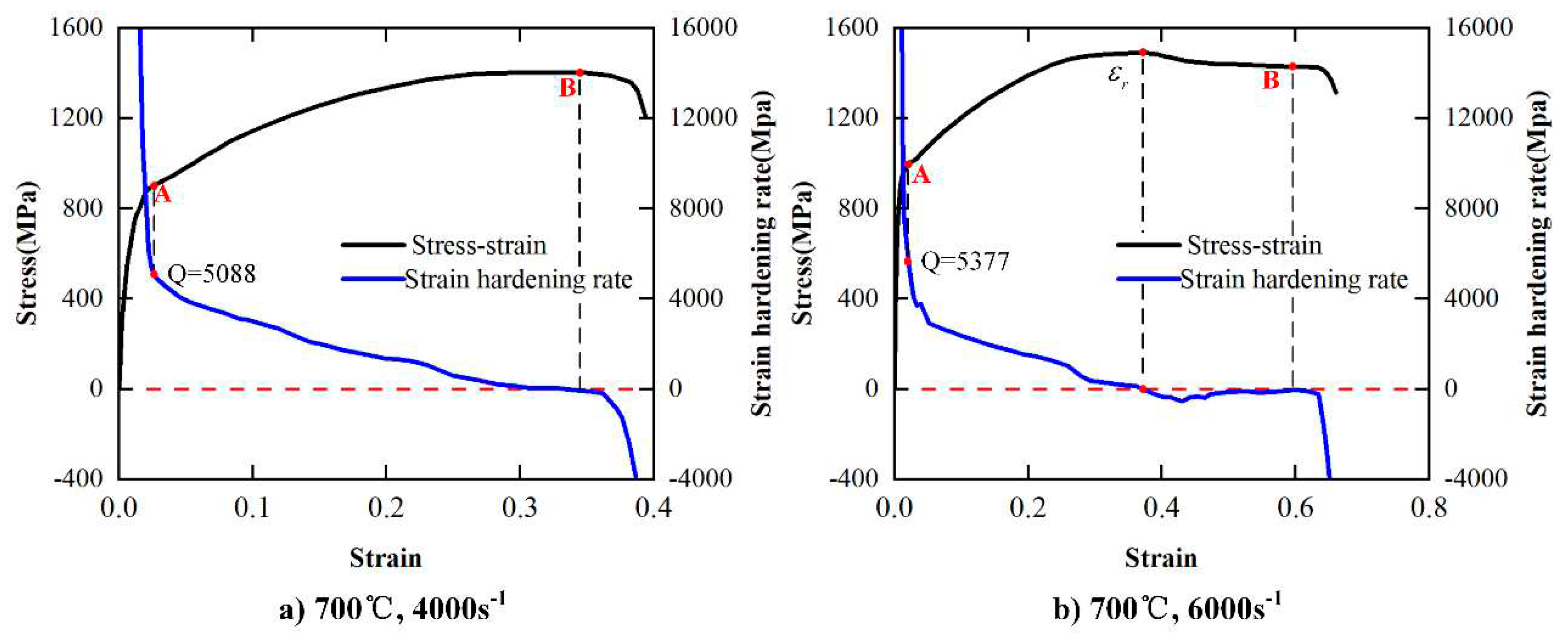
4.1.2. Strain-Hardening
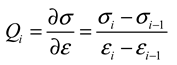
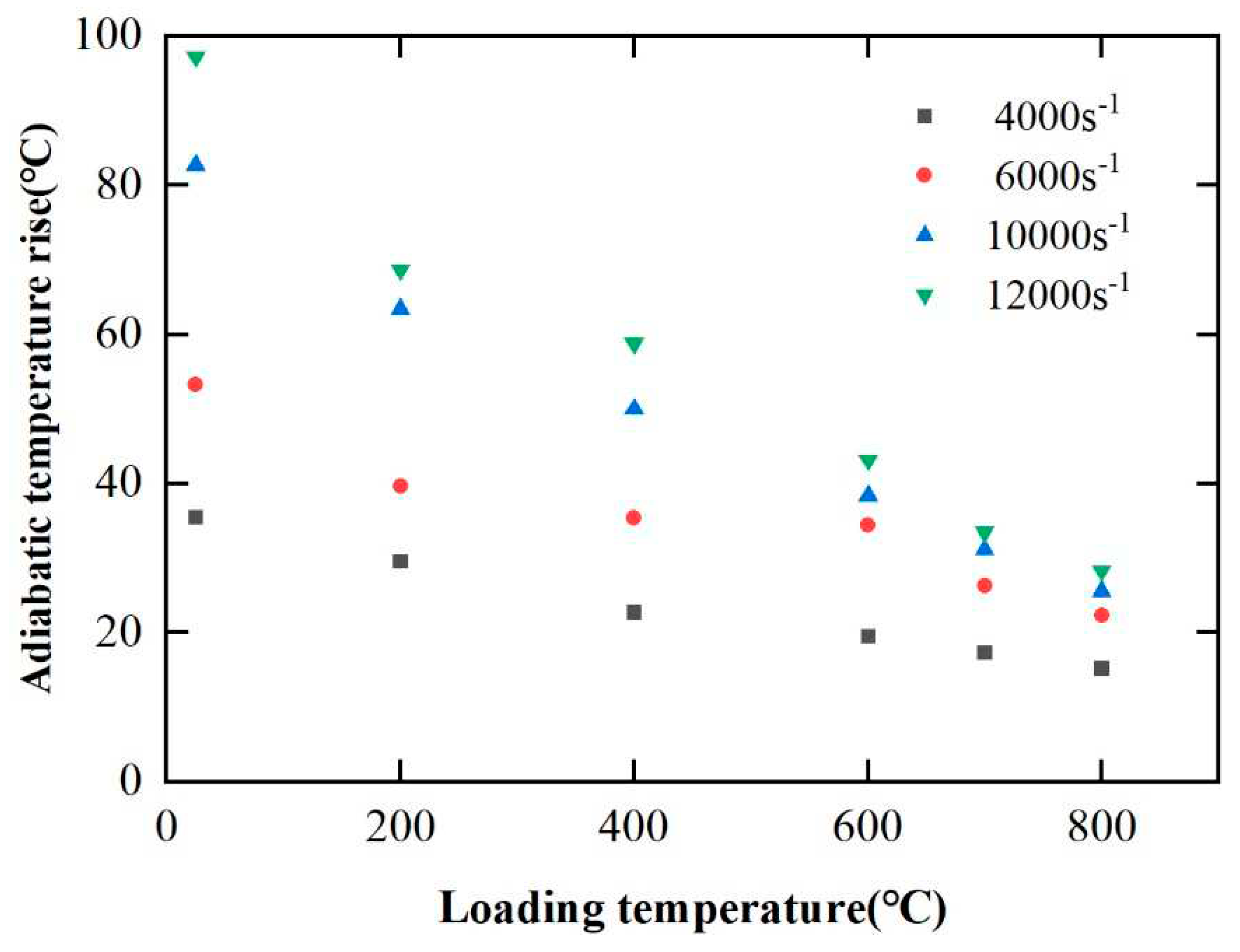
4.1.3. Adiabatic induced Increase of Temperature

| Temperature, T (℃) | 25 | 200 | 400 | 600 | 700 | 800 |
| Cp (kJ/ (kg‧K)) | 0.391 | 0.422 | 0.455 | 0.487 | 0.503 | 0.525 |
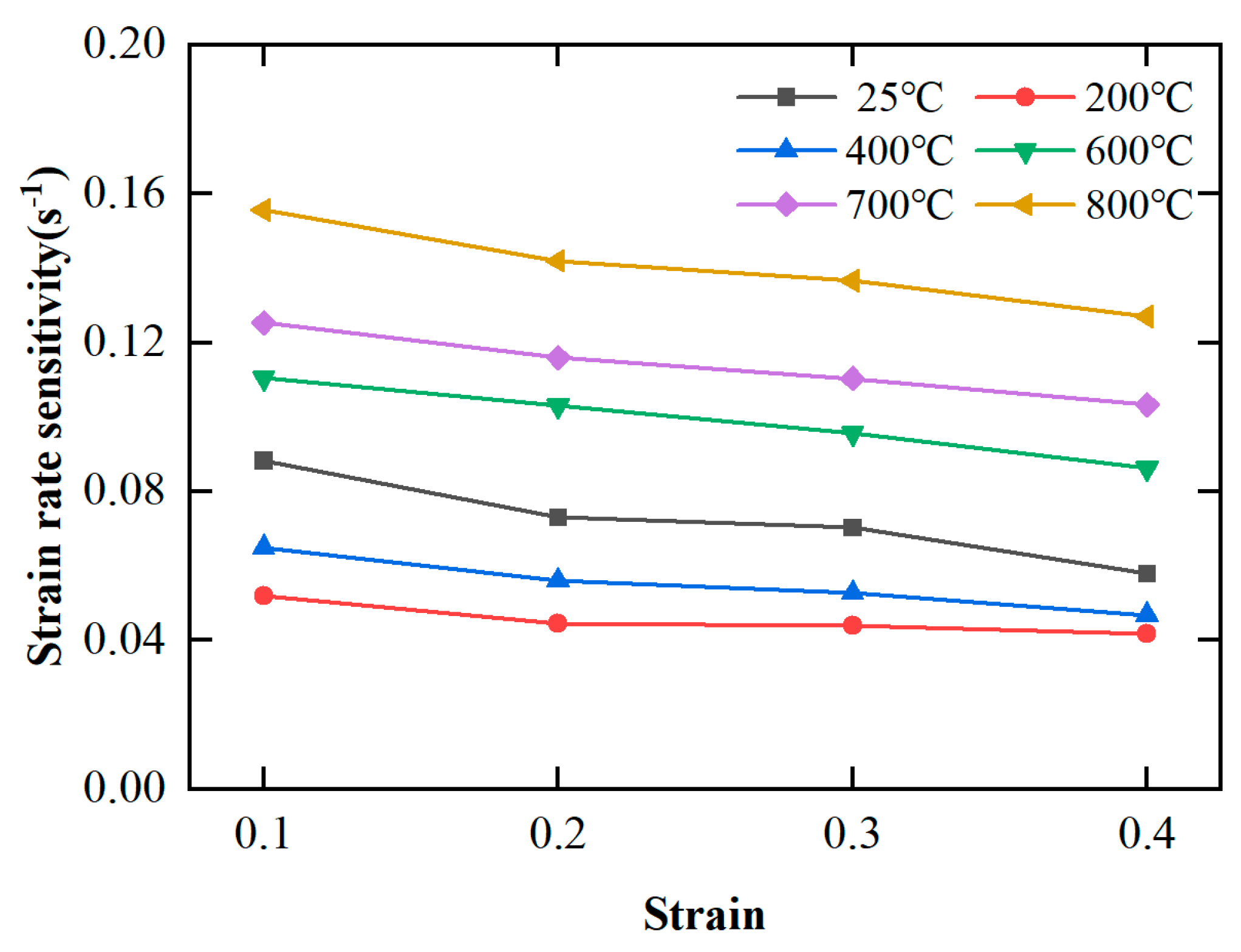
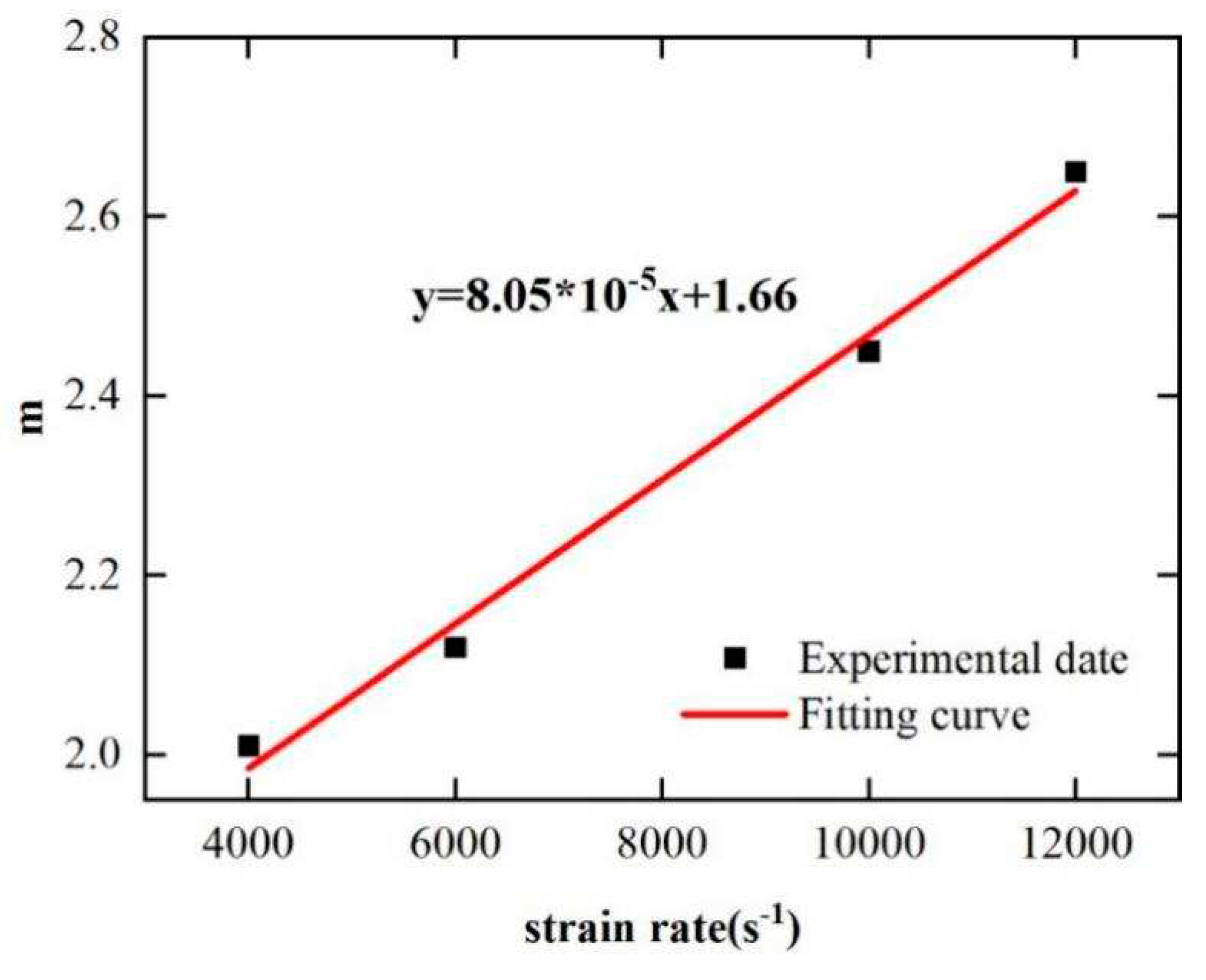
4.1.4. The Strain Rate Sensitivity
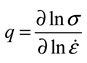
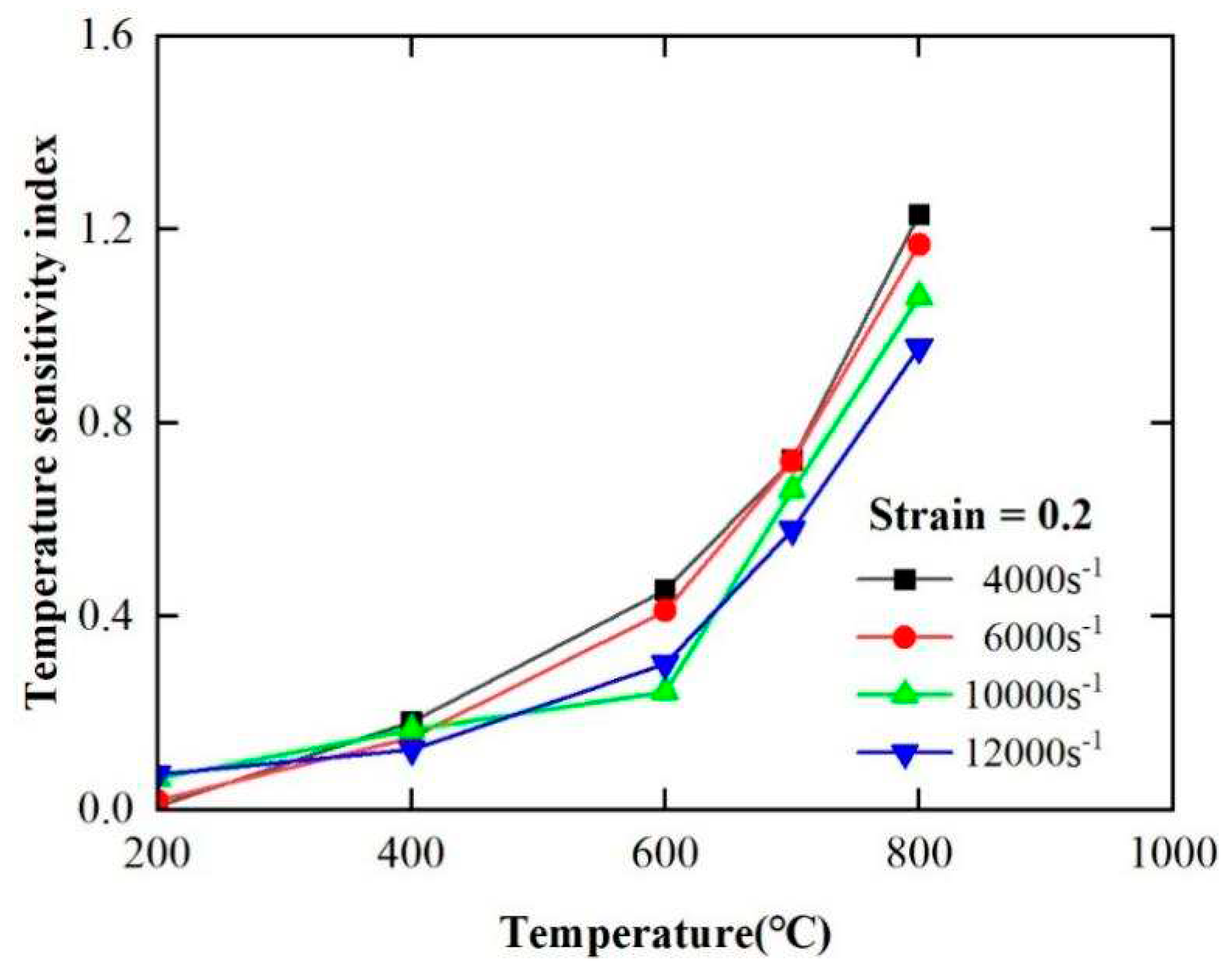
4.1.5. The Temperature Sensitivity
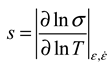
4.2. Construction of Constitutive Model
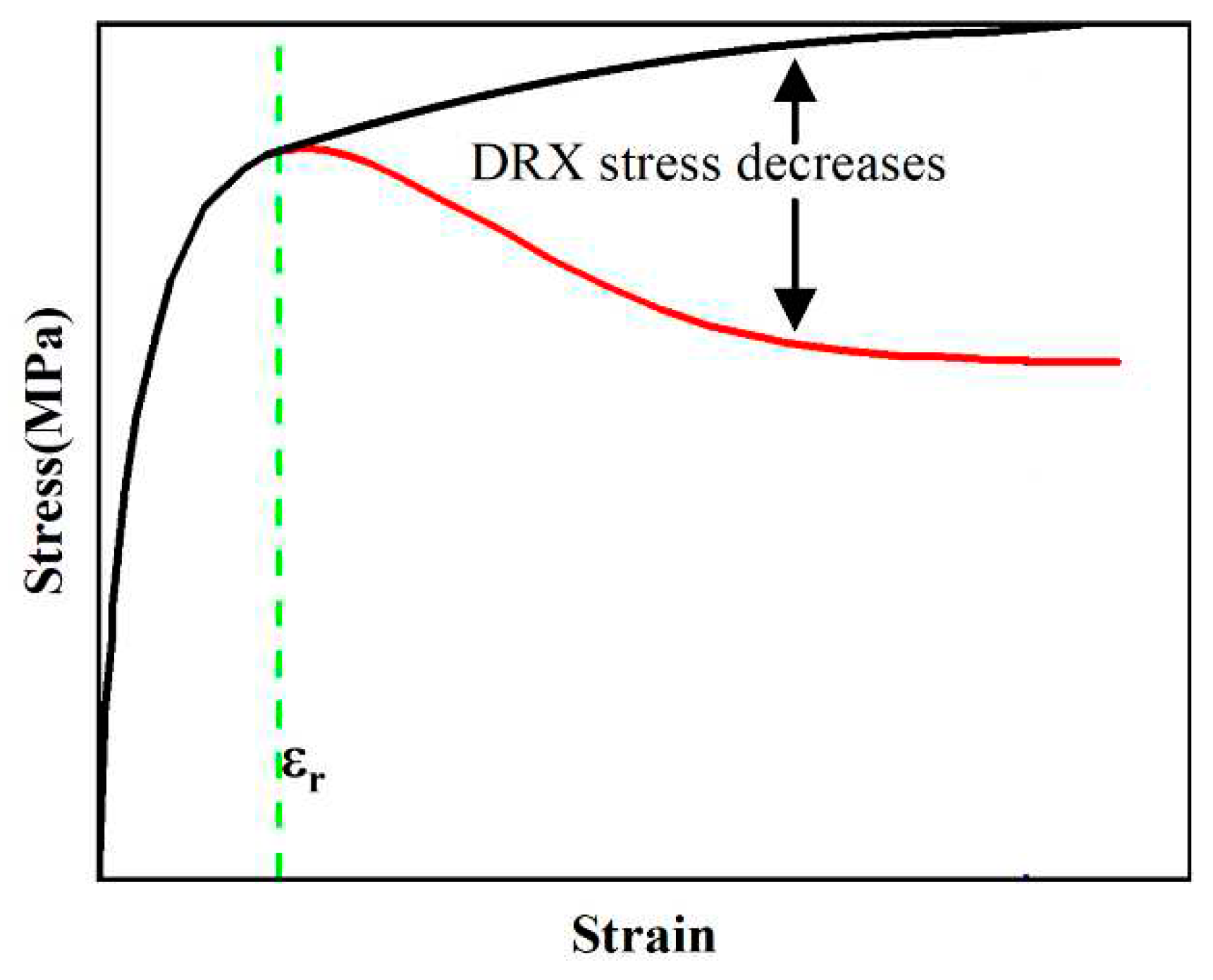
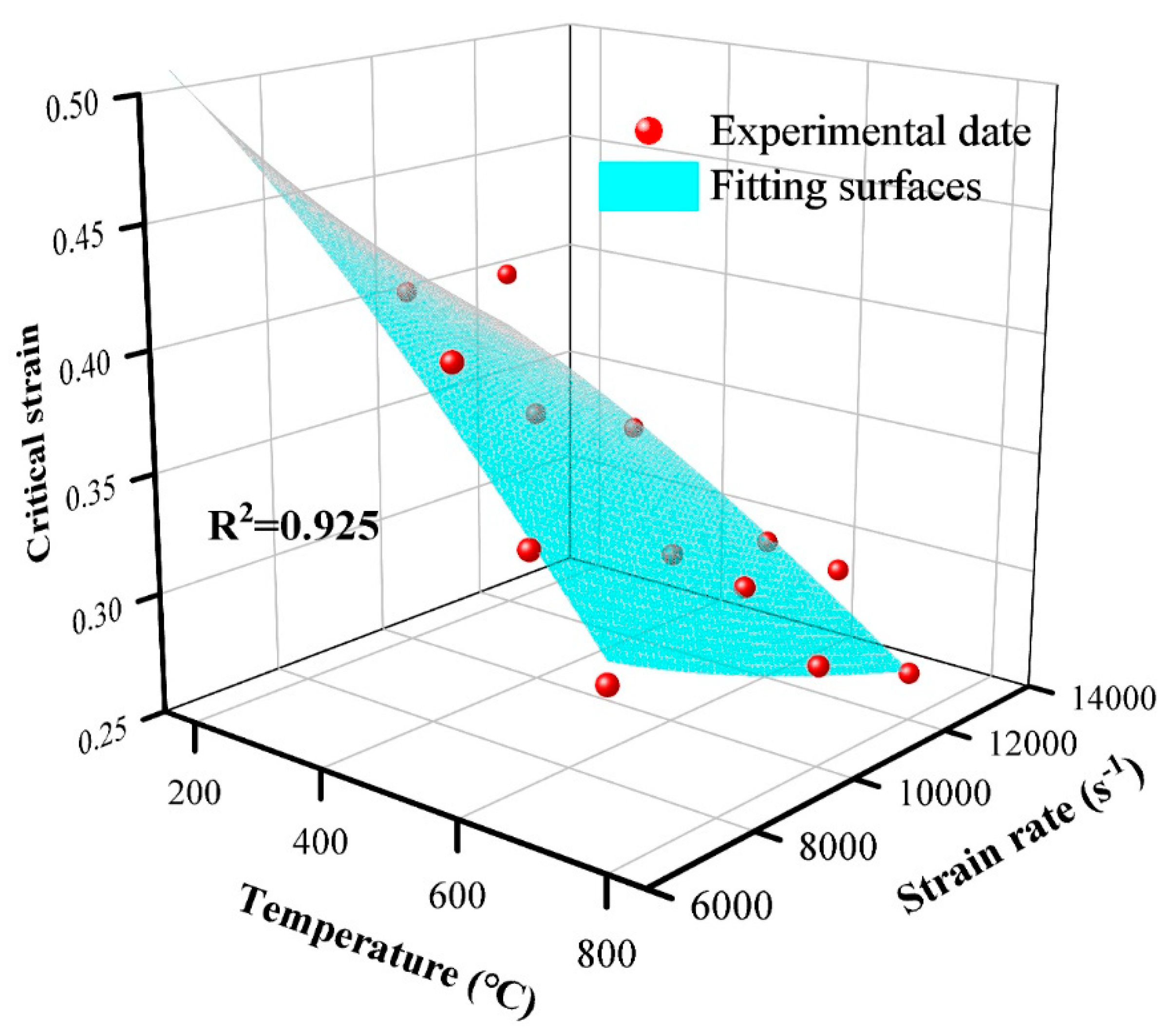
4.2.1. Recrystallization Critical Condition
| strain rate (s-1) | Temperature, T (℃) | ||||
|---|---|---|---|---|---|
| 200 | 400 | 600 | 700 | 800 | |
| 6000 10000 12000 |
0.4233 | 0.3621 | 0.3211 | ||
| 0.4033 | 0.3640 | 0.3199 | 0.3144 | 0.2911 | |
| 0.3999 | 0.3443 | 0.3091 | 0.3051 | 0.2698 | |
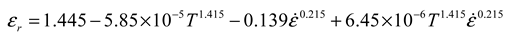
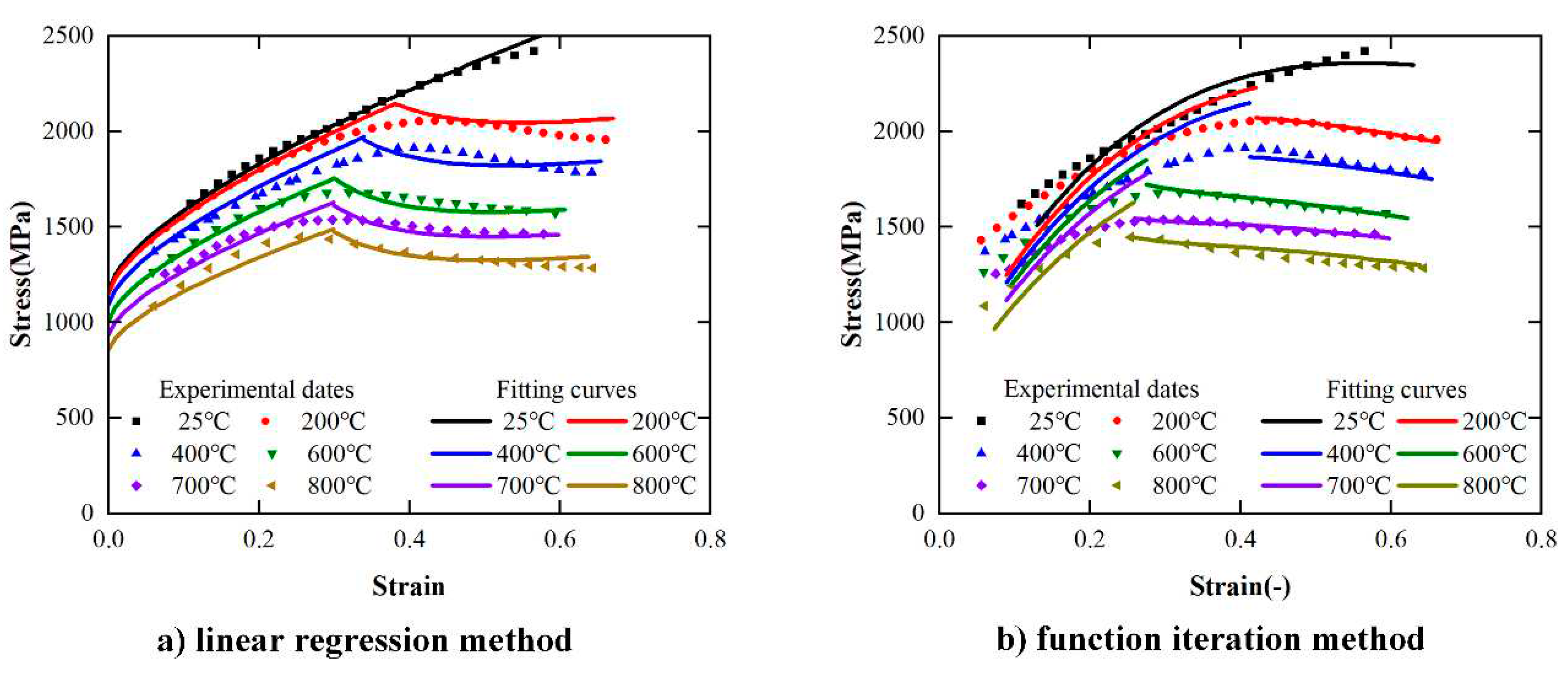
4.2.2. Identification of Constitutive Model’s Coefficients
- (1)
- Linear regression method
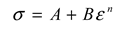
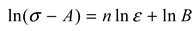

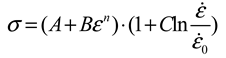
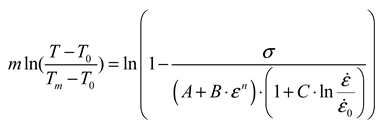
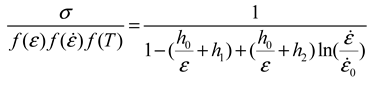
- (2)
- Function iteration method
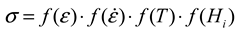
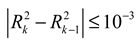
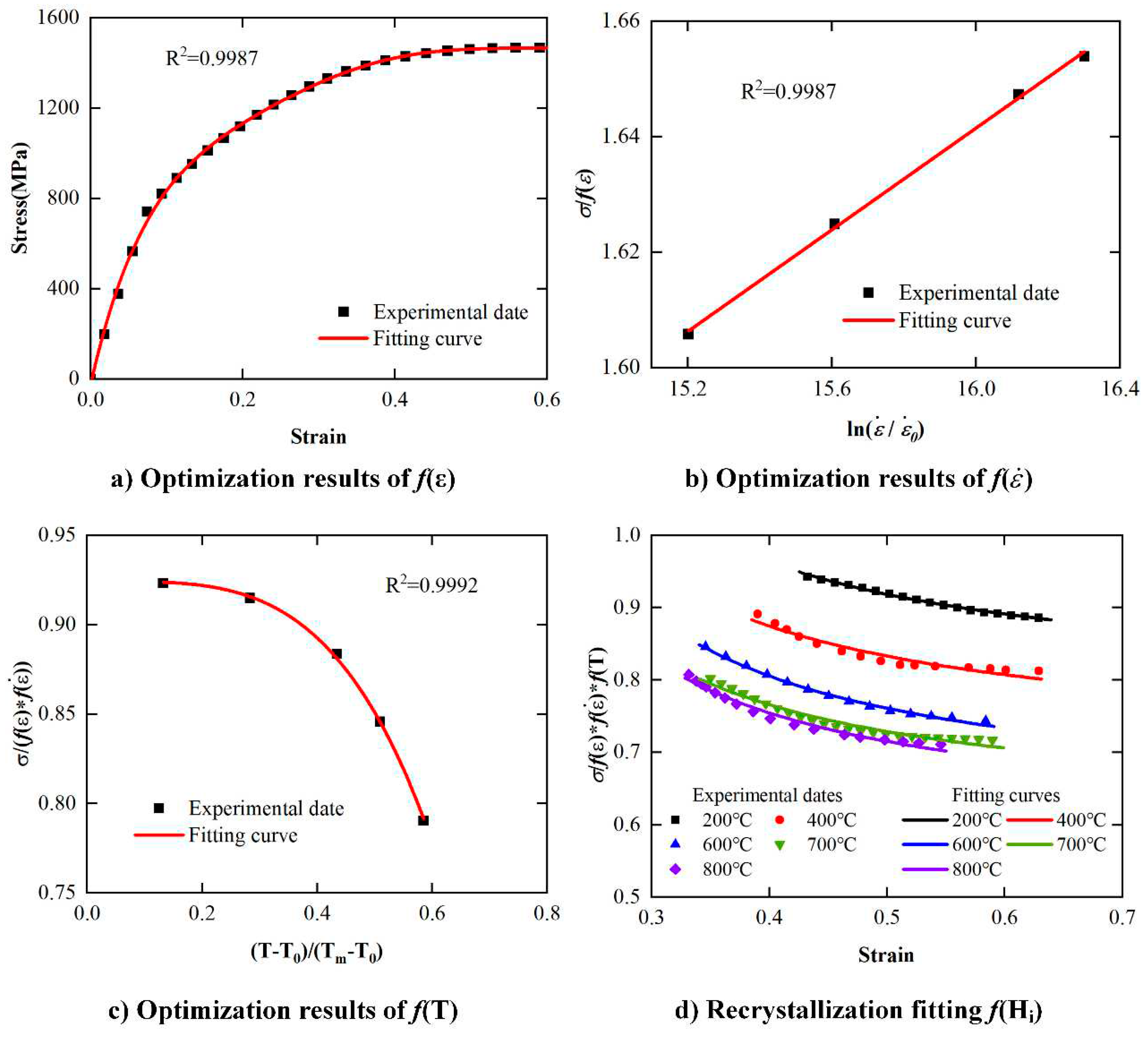
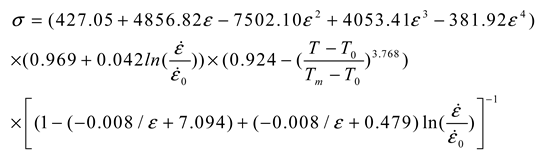
- (3)
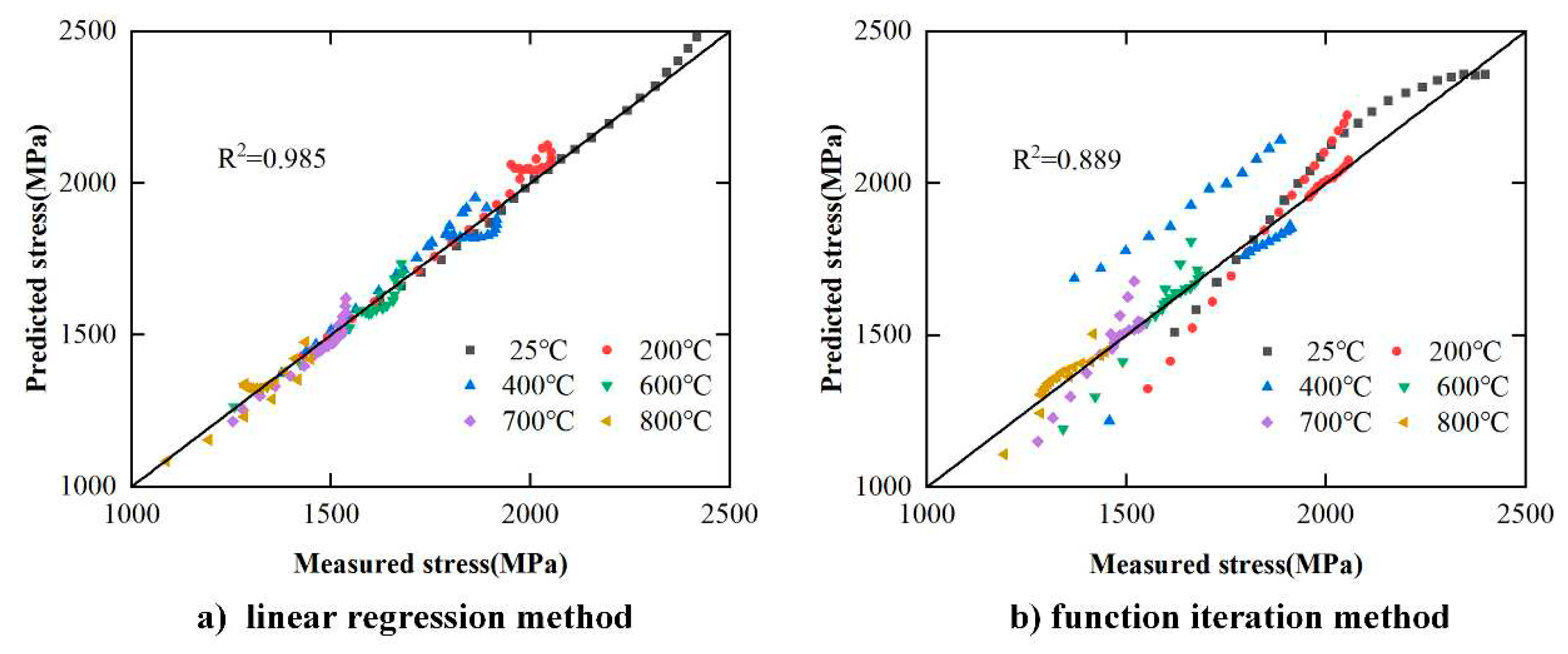
- Comparison of different methods
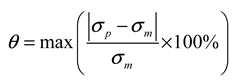
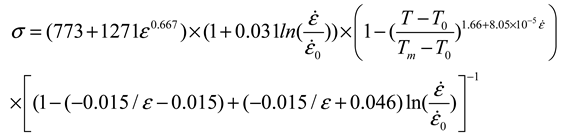
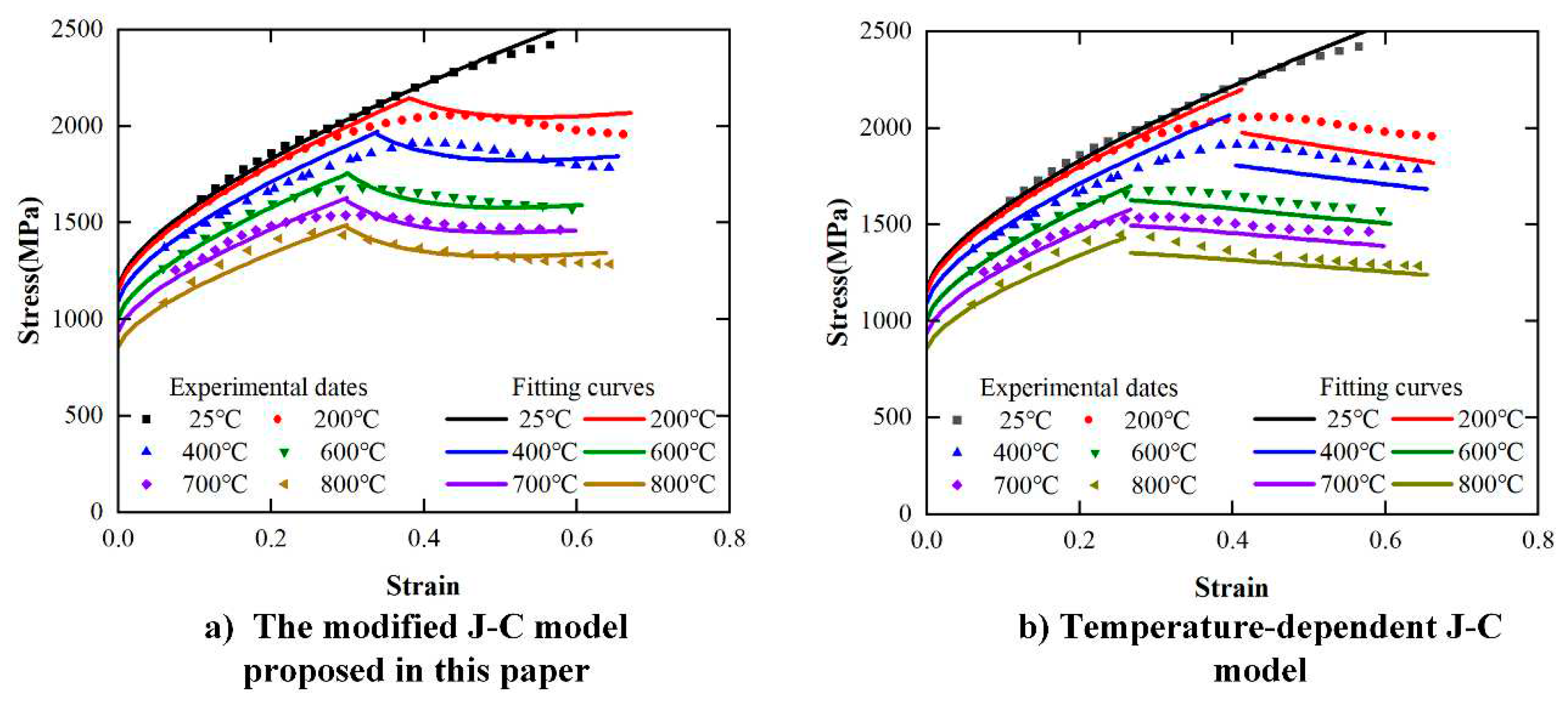
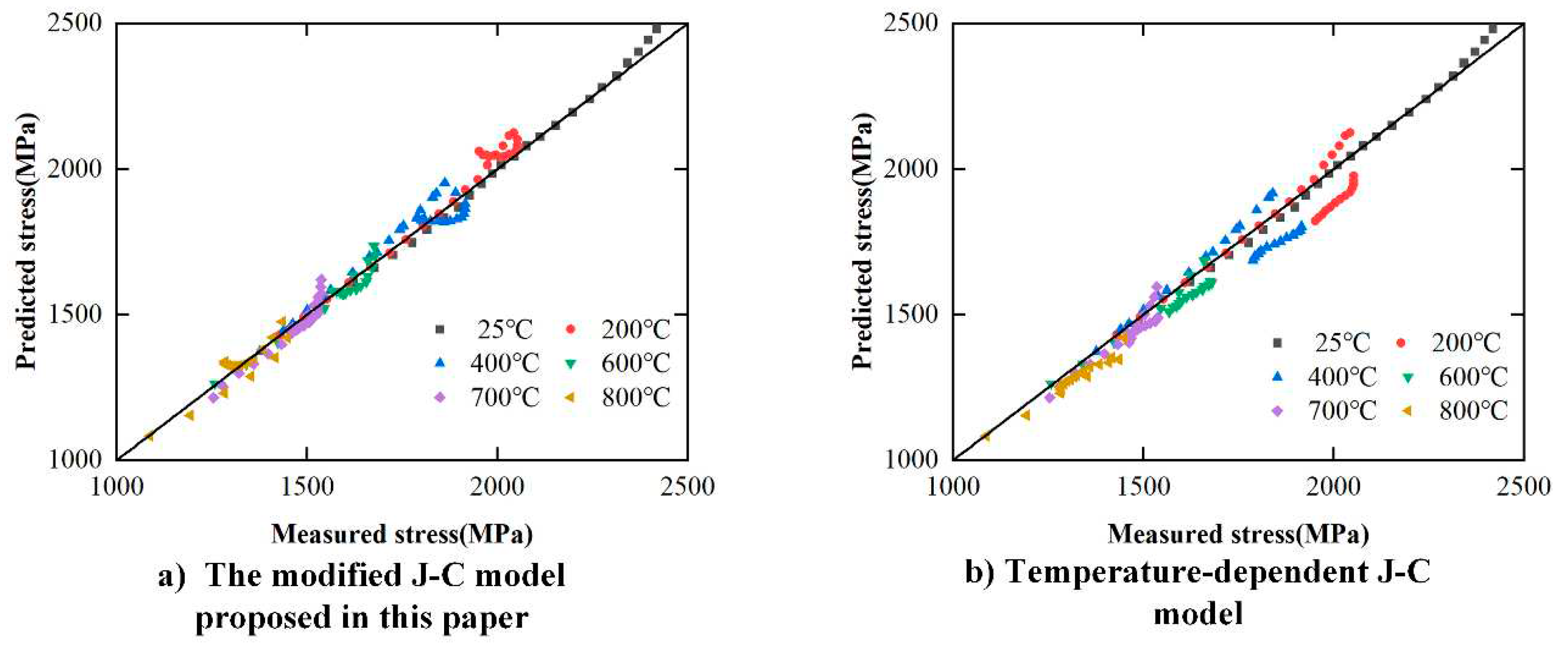
4.3. Validation of Modified J-C constitutive Model
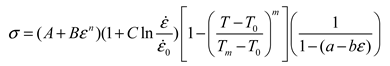
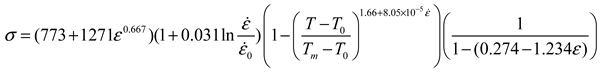
5. Conclusion
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boyer R, Cotton J, Mohaghegh M, Schafrik R J M B. Materials considerations for aerospace applications[J]. 2015, 40, 1055–1066. [CrossRef]
- Yang L, Ren X, Ge C, Yan Q J I J o M R. Status and development of powder metallurgy nickel-based disk superalloys[J]. 2019, 110, 901–910. [CrossRef]
- Yang L, Ren X, Ge C, Yan Q. Status and development of powder metallurgy nickel-based disk superalloys[J]. International Journal of Materials Research. 2019, 110, 901–910. [CrossRef]
- Selvaraj S K, Sundaramali G, Jithin Dev S, et al. Recent Advancements in the Field of Ni-Based Superalloys[J]. Advances in Materials Science and Engineering. 2021, 2021, 1–60. [CrossRef]
- Zhang X, Chen Y, Hu J. Recent advances in the development of aerospace materials[J]. Progress in Aerospace Sciences, 2018, 97: 22-34. [CrossRef]
- Guo N, Leu M C. Additive manufacturing: technology, applications and research needs[J]. Frontiers of mechanical engineering, 2013, 8: 215-243. [CrossRef]
- Zhang H, Zeng H, Yan R, Wang W, Peng F J T I J o A M T. Analytical modeling of cutting forces considering material softening effect in laser-assisted milling of AerMet100 steel[J]. 2021, 113: 247-260. [CrossRef]
- Melkote S N, Grzesik W, Outeiro J, et al. Advances in material and friction data for modelling of metal machining[J]. 2017, 66, 731–754. [CrossRef]
- Ucun İ, Aslantas K J T I J o A M T. Numerical simulation of orthogonal machining process using multilayer and single-layer coated tools[J]. 2011, 54: 899-910. [CrossRef]
- Hou X, Liu Z, Wang B, et al. Stress-strain curves and modified material constitutive model for Ti-6Al-4V over the wide ranges of strain rate and temperature[J]. Materials. 2018, 11, 938. [CrossRef]
- Liu H, Xu X, Zhang J, et al. The state-of-the-art on numerical simulation of the effect of microstructure and its evolution in metal cutting processes[J]. International Journal of Machine Tools and Manufacture, 2022: 103890. [CrossRef]
- Johnson G, R. A constitutive model and data for materials subjected to large strains, high strain rates, and high temperatures[J]. Proc 7th Inf Sympo Ballistics, 1983: 541-547.
- He A, Xie G, Zhang H, Wang X. A comparative study on Johnson–Cook, modified Johnson–Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel[J]. Materials & Design (1980-2015), 2013, 52: 677-685. [CrossRef]
- Shokry A, Gowid S, Mulki H, Kharmanda G. On the Prediction of the Flow Behavior of Metals and Alloys at a Wide Range of Temperatures and Strain Rates Using Johnson–Cook and Modified Johnson–Cook-Based Models: A Review[J]. Materials. 2023, 16, 1574. [CrossRef]
- Su X, Wang G, Li J, Rong Y J S. Dynamic mechanical response and a constitutive model of Fe-based high temperature alloy at high temperatures and strain rates[J]. 2016, 5, 1–14. [CrossRef]
- Sakai T, Belyakov A, Kaibyshev R, Miura H, Jonas J J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions[J]. Progress in materials science, 2014, 60: 130-207. [CrossRef]
- Shin H, Ju Y, Choi M K, Ha D H. Flow stress description characteristics of some constitutive models at wide strain rates and temperatures[J]. . Technologies 2022, 10, 52. [CrossRef]
- Calamaz M, Coupard D, Girot F J I J o M T, Manufacture. A new material model for 2D numerical simulation of serrated chip formation when machining titanium alloy Ti–6Al–4V[J]. 2008, 48(3-4): 275-288. [CrossRef]
- Ulutan D, Sima M, Özel T J A M R. Prediction of machining induced surface integrity using elastic-viscoplastic simulations and temperature-dependent flow softening material models in titanium and nickel-based alloys[J]. 2011, 223: 401-410. [CrossRef]
- Rotella G, Umbrello D. Finite element modeling of microstructural changes in dry and cryogenic cutting of Ti6Al4V alloy[J]. Cirp Annals 2014, 63, 69–72. [CrossRef]
- Liang X, Liu Z, Wang B, Hou X J I J o M S. Modeling of plastic deformation induced by thermo-mechanical stresses considering tool flank wear in high-speed machining Ti-6Al-4V[J]. 2018, 140: 1-12. [CrossRef]
- Denguir L, Outeiro J, Fromentin G, Vignal V, Besnard R J J o M P T. A physical-based constitutive model for surface integrity prediction in machining of OFHC copper[J]. 2017, 248: 143-160. [CrossRef]
- Pan Z, Wu Z, Xiong J J P T. High-speed infrared imaging and mesostructural analysis of localized temperature rise in damage and failure behavior of 3-D braided carbon/epoxy composite subjected to high strain-rate compression[J]. 2019, 80: 106151. [CrossRef]
- Liang H, Guo H, Nan Y, et al. The construction of constitutive model and identification of dynamic softening mechanism of high-temperature deformation of Ti–5Al–5Mo–5V–1Cr–1Fe alloy[J]. 2014, 615: 42-50. [CrossRef]
- Guo Y, Ruan Q, Zhu S, et al. Temperature rise associated with adiabatic shear band: causality clarified[J]. 2019, 122, 015503. [CrossRef]
- Su X, Wang G, Li J, Rong Y J S. Dynamic mechanical response and a constitutive model of Fe-based high temperature alloy at high temperatures and strain rates[J]. 2016, 5, 1–14. [CrossRef]
- Lin Y, Chen X-M, Liu G J M S, A E. A modified Johnson–Cook model for tensile behaviors of typical high-strength alloy steel[J]. 2010, 527, 6980–6986. [CrossRef]
- Murugesan M, Jung D W J M. Johnson Cook material and failure model parameters estimation of AISI-1045 medium carbon steel for metal forming applications[J]. 2019, 12, 609. [CrossRef]
- Andrade U, Meyers M, Vecchio K, Chokshi A H J A m e m. Dynamic recrystallization in high-strain, high-strain-rate plastic deformation of copper[J]. 1994, 42, 3183–3195. [CrossRef]
- Ashrafian M M, Hosseini Kordkheili S A J P o t I o M E, Part G: Journal of Aerospace Engineering. A novel phenomenological constitutive model for Ti-6Al-4V at high temperature conditions and quasi-static strain rates[J]. 2021, 235, 1831–1842. [CrossRef]
| Element | C | Al | Ti | Cr | Co | Nb | Mo | W | Ni |
| Wt. (%) | 0.03 | 2.2 | 3.7 | 16 | 13 | 0.8 | 4 | 4 | Bal |
| Variable | Values |
|---|---|
| Strain rate (s-1) | 4000, 6000, 10000, 12000 |
| Temperature T (°C) | 25, 200, 400, 600, 700, 800 |
| Coefficients | Value |
|---|---|
| A (MPa) | 773 |
| B (MPa) | 1271 |
| C | 0.031 |
| n | 0.667 |
| m | 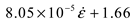 |
|
h0 h1 h2 |
-0.015 -0.015 0.046 |
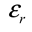 |
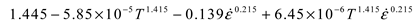 |
| Maximum relative errors | Linear regression method | Function iteration method |
|---|---|---|
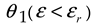 |
4.74% | 11.21% |
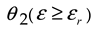 |
5.11% | 4.11% |
| 4.93% | 7.66% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





