Prerpints.org logo
Preprint
Review

A Review of Numerical and Physical Methods to Analyze the Coupled Hydro-Aero-Structural Dynamics of Floating Wind Turbine Systems

Altmetrics

Downloads

234

Views

105

Comments

0

Submitted:

28 November 2023

Posted:

30 November 2023

You are already at the latest version

Alerts
Abstract
Recently, more wind turbine systems are being installed in deep waters far from the coast. Several concepts of floating wind turbine systems (FWTSs) are developed, among which the semisubmersible platform, due to its applicability in different water depths, good hydrodynamic performance, and facility in the installation process, constitutes the most explored technology compared to the others. However, a significant obstacle to the industrialization of this technology is a design of a cost-effective FWTS, which can be achieved by optimizing the geometry, size and weight of the floating platform, along with the mooring system. This is only possible by selecting a method capable of accurately analyzing the FWTS coupled hydro-aero-structural dynamics at each design stage. Accordingly, this paper aims at providing a detailed overview of the most common coupled numerical and physical methods, including their basic assumptions, formulations, limitations, and costs, used for analyzing the dynamics of FWTSs, mainly those supported by a semisubmersible, to assist the choice of the most suitable method at each design phase of FWTSs. Finally, the article discusses possible future research to address challenges in modeling FWTSs dynamics that persist to date.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

The offshore wind industry is growing continuously over the last few years. Recently, more wind turbines are being installed in deeper waters and further away from shore, which comprise a considerable share of the offshore wind resources with less turbulence [1]. However, over deep-sea sites, the bottom-fixed concepts are no longer viable as these structures are not an economical solution for water depths more than 50 m [2]. Therefore, several floating wind turbine system (FWTS) concepts are developed for use in deeper waters [3,4]. Among these floating concepts, the semisubmersible platform, stabilized mainly by buoyancy, is a promising technology and constitutes the most explored technology compared to the others. This is due to the applicability of these platforms in different water depths, good hydrodynamic performance, and facility in the installation process [3,5,6].
Several examples of commissioned semisubmersible FWTSs are the 2 MW WindFloat Semisubmersible in Portugal [7], 3x8.4 MW WindFloat Atlantic Semisubmersibles in Portugal [8], 2 MW Fukushima Mirai 4-column Semisubmersible in Japan [9], 7 MW Fukushima Shimpuu V-shape 3-column Semisubmersible [9] and 5x9.5 MW plus 2 MW Kincardine Semisubmersibles in Scotland [10]. Several FWTSs are under construction, such as 5MW Eolink 4-column Semisubmersible in France and 10MW concrete OO-Star Norway Semisubmersible [8]. Some popular semisubmersible configurations are the WindFloat, Braceless platform, and VolturnUS-S, as shown in Figure 1 [11,12,13,14,15].
Figure 1 depicts the layout of two semisubmersible platforms. Figure 2 (a) presents DeepCwind semisubmersible platform [18] designed within the phase II of the Offshore Code Comparison Collaboration Continuation (OC4) project to support the National Renewable Energy Laboratory (NREL) offshore 5-MW wind turbine [19]; while Figure 1 (b) shows UMaine VolturnUS-S reference platform, which is developed to sustain the IEA 15-MW Offshore Reference Wind Turbine [13]. Semisubmersible platforms may possess different offset columns. As shown by [20], increasing these columns can reduce the platform motions. Although most of the semisubmersibles are made of steel, there is a tendency to use concrete for FWTS structures owing to lower construction cost, as well as superior durability and fatigue resistance of concrete compared to steel [21,22,23,24].
Nonetheless, FWTSs are less mature than their bottom-fixed counterparts owing to their more complicated operating conditions and higher prices. The FWTSs are subject to loads emanating from several sources, namely wave, current, wind, and, in certain locations, ice [25,26]. Although the similarities between FWTSs and floating platforms in the industry of oil and gas lead to a partial transfer of the technology [27], there are numerous differences between the two industries, such as the aerodynamic loads acting on the wind turbines, which affect significantly the dynamics of FWTSs and give rise to several new technical challenges [25,28]. For instance, the coupled current-wave-wind loads acting on the FWTSs, as shown schematically in Figure 3, may cause large platform motions along the degrees of freedom of motion of the structure, which combined with the blade aeroelastic deformations results in a highly dynamic inflow to the turbine rotor affecting the turbine structural integrity [29,30]. Additionally, to guarantee safe turbine operations, the platform motions induced by the offshore environmental loads need to be restrained to an acceptable limit [31].
Accordingly, floating wind turbines are complex systems subject to coupled hydro-aerodynamic loads, and a better understanding of the behavior of these machines, which is substantial for their efficient design, requires the accurate evaluation of the nature and order of these coupled loading on the structure. The design of a cost-effective FWTS is a major obstacle to the industrialization of this technology [21]. Cost reduction can be achieved by optimizing the floating platform’s size and weight, along with mooring, anchors, and installation and maintenance processes [5,21,32]. Further cost reduction, particularly the levelized energy cost, can be achieved by improving the power production by enhancing the platform’s motion, a function of platform geometry, control system, and mooring [33]. This is only possible by selecting a method able to analyze accurately the coupled hydro-aero-structural dynamics of FWTSs in each design stage while incorporating control algorithms, such as power and pitch control [34,35]. Thus, a rather detailed overview of the basic assumptions, formulations, accuracy, and computational demand of the most common methods capable of evaluating the coupled behavior of FWTSs in various design stages is required. This provides the necessary knowledge to identify the most suitable method at each design stage. For this purpose, based on the review carried out in this paper, a wide range of methods with different fidelities, as shown in Figure 4, can be used.
Generally, from right to left, the fidelity increases. The higher the method’s fidelity, the more closely it represents reality by producing more detailed information. However, this comes at the cost of more computational demand and less efficiency. Therefore, the choice of a method at each design stage is a compromise between the accuracy and computational cost.
The simplest methods, as shown on the extreme-right of Figure 4, are the linear frequency-domain models with the lowest level of fidelity, which, due to their ability to provide results in a short time period, are suitable in the early conceptual design phases for sizing and optimization purposes [36]. The hydrodynamics and aerodynamics of the rigid FWTS structure are evaluated by strip theory based on potential flow (PF) together with Morison’s Equation (ME) and a simplified blade element momentum (BEM) approach or tabular data, respectively. In this stage, in addition to structure sizing and static analysis, one must also optimize the response amplitude operators (RAOs) [37]. QuLAF [38] and SLOW [39] codes are examples of low-fidelity frequency-domain tools.
Fully coupled nonlinear time-domain models, used at the basic design stages, are categorized as mid-fidelity models (see Figure 4). These models are more accurate than the low-fidelity tools, which come at the cost of higher computational demand. The aerodynamic part is modeled using either a BEM, Generalized Dynamic Wake (GDW) model, or Free Vortex Wake (FVW) method. Note that, in the case of FWTSs, the large blade deformations combined with the platform motions may lead to an interaction of the blades with their own shed vortices, which is a violation of basic assumptions of BEM method [29,40]. In this regard, FVW is better capable of modeling these complex physics than the BEM method while maintaining the computational cost to an acceptable level. The hydrodynamic loads are modeled based on PF, ME, or a combination of them. Further, the structural dynamics is modeled using multi-body dynamics (MBD) formulations, where flexibility is considered in selected components, such as blades and towers. Due to the efficiency and accuracy offered by the MBD for slender bodies, it has turned into a common tool for wind turbine structural simulations [41].
The mid-fidelity simulation tools based on nonlinear time-domain methods are used for the analysis of dynamic responses of FWTSs under a variety of operating and extreme conditions. These tools, through a time-domain analysis, make it possible to assess properly the fatigue and extreme loads impact on FWTSs in various operating and extreme conditions [42]. These tools are also excellent for the control design of the floating offshore wind plant, which may be more complex for this technology as the objective function, in addition to power production optimization, can be extended to reduce the structural loads and platform motions [43,44,45,46,47,48,49,50,51]. The OpenFAST software from NREL is an example of these tools, which can perform the real-time coupled hydro-aero-servo-elastic simulations for FWTSs [52,53].
Next, as presented in Figure 4, are the high-fidelity methods on the basis of both finite element analysis (FEA) and computational fluid dynamics (CFD). These tools are employed at last design phases, where more in-depth investigations are required for extreme conditions, as well as intricate flow conditions, e.g., vortex detachment from heave plates [42]. These models involve less modeling than the other categories, which makes them computationally more expensive. These models are also suitable for fine tuning of the design, as well as the calibration of the low- and mid-fidelity models [42,54,55,56,57,58]. CFD uses either large eddy simulation (LES) or Reynolds-averaged Navier-Stokes (RANS) equations or hybrid LES-RANS, to predict the aero-hydrodynamic loads acting on FWTSs. Contrary to BEM and FVW methods, which rely on external input of aerodynamic loads and semi-empirical corrections for considering 3D effects, dynamic stall etc., CFD naturally accounts for all these effects. CFD can also better capture the turbulent wake behind a turbine, which leads to transient loads on the downstream machines in a wind farm.
Further, the FEA can better capture complex blade deformations at a higher computational cost than the MBD. Structural failure commonly emanates from local stress raisers, which the MBD cannot capture properly. Despite that, MBD can provide reasonable boundary conditions for the local finite element analyses.
The high-fidelity tools are an attractive option for evaluating FWTS dynamics; however, the results of these tools depend on several factors, such as temporal and spatial resolutions, turbulence modeling, free surface modeling, etc. Accordingly, reliable measurements from physical testing, including hybrid testing, full physical testing, and field testing, as shown in Figure 4, are required to gain more confidence in these numerical tools.
Therefore, the low-, mid-, and high-fidelity models, as shown in Figure 4, are obtained by combining numerical models able to evaluate the structural dynamics, hydrodynamics, and aerodynamics of FWTSs at different levels of accuracy. As one advance in the design stages, more accurate and detailed methods are required.
The present paper aims to provide a detailed overview of the most common coupled methods, as depicted in Figure 4, including their basic assumptions, formulations, limitations, and costs, used for FWTSs, mainly those supported by a semisubmersible, to assist the choice of the most suitable method at each design stage of FWTSs. Note that several review papers are available about the hydro-aero-structural dynamic evaluation of FWTSs [5,8,25,30,42,59,60,61,62].
In this regard, experimental testing and numerical models employed to assess FWTSs are reviewed by [8]. However, full physical testing, field testing, numerical methods such as FVW methods, structural dynamics, and nonlinear second-order wave loads are not covered. An overview of the numerical methods, as well as the physical and hybrid tests, are covered by [42]. However, the field tests, as well as the physical basis and formulations of the numerical models, are not presented. An overview of the coupled numerical models for optimizing an FWTS structure in conceptual, basic, and detailed design stages is given by [5]. An overview of the coupled numerical tools and full physical tests for FWTSs is presented by [25]. A review of the experimental and numerical methods is presented by [59], without giving any detail about numerical methods. A general view of the numerical and physical models is given by [30]. The physical and hybrid model tests is reviewed by [60,61,62].
The present review is built upon the previous review efforts by giving a more detailed and up-to-date overview of the physical and numerical coupled modeling techniques for FWTSs, as presented in Figure 4.
The paper is organized as follows: Section 2 presents the coupled CFD-FEA modeling of FWTSs. Afterward, the nonlinear coupled time-domain methods are described in Section 3. This is followed by the presentation of the linear frequency-domain models and mooring systems in Section 4 and Section 5, respectively. Moreover, some final notes about numerical models are given in Section 6, and after that Section 7 focuses on physical testing. Finally, a summary and conclusions are given in Section 8.

2. Coupled CFD-FEA models

2.1. CFD

2.1.1. Hydrodynamics

The hydrodynamic loads acting on FWTSs can be most accurately computed using CFD methods capable of accounting for viscosity and free surface effects [63]. Generally, the RANS equations with a turbulence model are solved numerically utilizing the finite volume method [8,64,65,66,67,68,69].
The RANS equations, which are the result of ensemble averaging of the Navier-Stokes equations (NSE), are written as [66,67,70]:
∂ u i ∂ x i = 0 ,
∂ u i ∂ t + ∂ u j u i ∂ x j = − 1 ρ ∂ p ∂ x i + ∂ 2 ν s i j + τ i j ∂ x j .
Here, the variables u i and p are the ensemble mean velocity components and pressure, which may vary over both time t, and space x i . Additionally, ρ , ν and s i j are the fluid density, fluid kinematic viscosity, and mean strain rate tensor, respectively.
The term τ i j is called the Reynolds stress tensor representing the turbulence effect. This term is most commonly modeled using eddy viscosity (EV) models based on the Boussinesq hypothesis [71]:
τ i j = 2 ρ ν t s i j − 2 3 ρ k δ i j ,
where k is the turbulence kinetic energy and δ i j is the kronecker delta function and ν t is the EV. In the simplest way, the EV can be determined without solving any further transport equations, e.g., the mixing-length model of Prandtl [72,73]. Later, more sophisticated one-equation and two-equation turbulence models are developed to compute directly or indirectly the EV [63,64,65,67,74,75]. The most popular models for the hydrodynamic evaluation of FWTSs are the two-equation models, such as k − ε , k − ω and k − ω Shear Stress Transport (SST) [57,65,68,74,76], in which by solving two transport equations the turbulence is modeled.
To model the free surface, CFD uses two main approaches: interface tracking and interface capturing [77,78] (see Figure 5).
The interface tracking method, as its name implies, tracks the free surface through implementing a Lagrangian grid fitted to the free surface interface (see Figure 5 (a)). Nevertheless, tracking the free surface where this interface experiences large motions imposes certain difficulties, which can only be remedied by remeshing techniques. Using this technique, in addition to increasing the computational demand, can introduce errors in the numerical solutions.
Nonetheless, the method of interface capturing, which is also called the Eulerian grid method, as its name implies, captures the free surface interface by computing a volume inside a computational domain encompassing the free surface. Contrary to the interface tracking method, the grid does not track the free surface evolution over time (see Figure 5 (b)).
The free surface modeling in case of FWTSs is most commonly performed using the volume of fluid (VOF) and level set both belonging to the interface capturing methods [35,57,63,64,65,66,74,76,79,80,81,82,83].
To capture the free surface profile using the interface capturing method an increased cell density is required close to the free surface. The common approach is to employ a certain number of cells perpendicular and normal to the free surface for spatial discretization [84]. The increased cell density on the free surface can also be achieved based on the kinetic wave energy [74,85].
Two methods exist to ensure that no wave-reflection will occur on the boundaries of the numerical domain. The first method is dampening the waves by coarsening the grid towards the boundaries [68,84]. Another method is using a damping (relaxation) function over a damping (relaxation) zone close to the boundaries to force the wave field towards the undisturbed either free surface or wave [64,66,74,82,86].

2.1.2. Aerodynamics

The aerodynamics of FWTSs can be most accurately captured by solving the NSE based on CFD [69]. The NSE, in the case of incompressible Newtonian fluids for Cartesian coordinates, is as follows:
∂ U i ∂ t + ∂ ( U j U i ) ∂ x j = − 1 ρ ∂ P ∂ x i + ∂ 2 ν S i j ∂ x j .
Here, the variables U i and P are the instantaneous velocity components and pressure, which vary over both time t, and space x i . S i j is the instantaneous strain rate tensor. Note that in the case of wind turbine simulations, several new terms may be added to the NSE to consider the effects of Coriolis and buoyancy forces [87,88].
To compute the pressure and velocity fields, the NSE is solved together with the continuity equation:
∂ U i ∂ x i = 0 .
A reliable aerodynamic evaluation of the FWTSs depends on the accurate turbulence modeling around these machines [89]. In this regard, in the case of turbulent flows, CFD solves the NSE using three different approaches: Direct numerical simulation (DNS), LES and (unsteady) RANS equations. An adequately formulated DNS captures all the relevant turbulence scales up till the Kolmogorov scale using an extremely refined grid [90], which is not viable due to being prohibitively expensive. Therefore, LES and RANS are used to model partially or entirely the turbulence effect on the flow [91].
The important energetic large eddies are captured by LES, while the influence of the smaller eddies, whose properties are more universal, is parametrized based on a subgrid-scale (SGS) model [91]. A spatial filtering operation is used by LES to divide the scales into large eddies constituting the resolved scales and small eddies representing the unresolved scales [69,92]. Applying this filtering operation transforms the NSE as follows:
∂ u ˜ i ∂ x i = 0 .
∂ u ˜ i ∂ t + ∂ u ˜ j u ˜ i ∂ x j = − 1 ρ ∂ p ˜ ∂ x i + 2 ν ∂ S ˜ i j ∂ x j − ∂ τ i j ∂ x j .
Here, the variables u ˜ i and p ˜ are the filtered velocity components and pressure. Additionally, S ˜ i j is the tensor of strain rate defined as a function of the resolved velocity components. The new term τ i j is the tensor of SGS Reynolds stress that emerges in the NSE due to spatial filtering. Through this term, the influence of the unresolved smaller eddies is parametrized. The most common approach to compute τ i j is the Smagorinsky model [93,94]:
τ i j − 1 3 τ k k δ i j = − 2 ν t S ˜ i j ,
where ν t is the EV, which is characterized in terms of the resolved velocity field [95]. However, this model is unable to account for the turbulence anisotropy and secondary flows due to the use of Boussinesq hypothesis [90,96,97]. To overcome these limitations, several other SGS turbulence models are proposed, such as Scale-Dependent Dynamic, anisotropic minimum dissipation, dynamic Smagorinsky, and mixed SGS [79,98,99,100].
However, the LES requirement of grid refinement in three directions close to a solid wall to compute the turbulent boundary layer makes applying LES to the turbine blades infeasible. Thus, LES is generally used for simulating turbine wakes where the turbine rotor is parametrized using actuator methods, including actuator disk, actuator line, and actuator surface, as shown schematically in Figure 6 [101,102,103,104]. Using actuator methods leads to a drastic drop in computational cost due to eliminating the need for resolving the boundary layer close to the blades. Another way to decrease the computational demand of LES is to utilize hybrid RANS-LES methods, in which RANS equations are used for modeling the boundary layer close to the body, while LES is employed over the separated unsteady region far from the body [105,106,107,108].
The simulations based on RANS equations constitute the most popular approach for the aerodynamic evaluation of turbines [109,110]. Here, it is also possible to use the zero-equation, one-equation, and two-equation models presented in the hydrodynamic section. However, again the most popular models are the two-equation models, especially k − ω and k − ω SST [111,112,113,114,115,116,117,118]. Nevertheless, due to the use of the Boussinesq hypothesis, these models are incapable of considering the turbulence anisotropy [96,97,119,120,121]. Thus, more sophisticated models such as realizable models [122,123] or even Reynolds stress turbulence (RST) models and nonlinear EV models are recommended [96,97,124,125,126,127]. The RST models, in which each Reynolds stress term is computed from a separate transport equation, provide the most accurate results at the cost of higher computational demand [96,97,126,128]. An alternative is the use of nonlinear quadratic and cubic EV models, which are able to account for the turbulence anisotropy at a much lower computational cost. It is worth mentioning that to diminish the computational demand, the use of actuator methods to represent the turbine rotor is also common in the RANS context [129].

2.2. Structural dynamics

The FEA method is usually applied to model the structural responses, but it is also used for fluid dynamics [130].
The FEA, similar to CFD uses the blade’s exact geometry and is based on a methodology similar to other numerical methods that approximate continuous governing partial differential equations with a set of algebraic equations [131].
The governing equation is obtained by assuming that the amount of virtual work performed by external loads equals the amount of virtual work absorbed by dissipation, inertia, and internal forces [30].
In the first step, the turbine geometry is discretized into a finite number of elements. These elements are typically triangles, quadrilaterals, tetrahedra, and hexahedra. The blades are typically discretized into 3D composite shell elements [25,132].
In each element, the displacement values at the element nodes are used to construct the distribution of this variable within the element [133]. Note that the stresses and strains, which are also of interest, are expressed in terms of nodal values of displacements based on Cauchy relations and Hook’s law [134]. Based on local distributions of the displacement, shape functions, usually based on polynomial forms, are used to interpolate the displacement values to any other point inside the element. The global system of algebraic equations is obtained by assembling all the element equations. This system of algebraic equations is solved using direct or iterative methods to obtain the nodal values of the displacements.

2.3. Recent research

The coupled CFD-FEA method provides an intriguing option for investigating hydro-aero-structural dynamics of an FWTS under coupled loading due to its high accuracy and minimum level of parametrization. However, this method is rarely used to evaluate the hydro-aero-structural dynamics of these structures due to its high computational demand. [83] carries out an example of these types of studies to evaluate the fluid-structure interaction for the NREL 5MW supported by the OC3-Hywind SPAR floater [135], where the free-surface is modeled using the NSE with the level set method. Additionally, the FEA is used for the fluid dynamic governing equations discretization and the FWTS structural dynamics is modeled based on an isogeometric analysis. However, the developed coupled model is only applied to the parked configuration of the wind turbine. Thus, considering the prohibitively high computational cost of a coupled CFD-FEA method, the researchers has reduced the coupled analyses of FWTSs to aerodynamic analysis under prescribed platform motions, aeroelastic and hydro-aerodynamic analyses.

2.3.1. Aerodynamic analysis under prescribed platform motions

In these analyses, to reduce the computational cost, the hydrodynamic part is simplified to focus on the aerodynamic part. Therefore, harmonic motion will be prescribed on the platform in predetermined degree-of-freedom (DOF) of motion to emulate the reaction of oscillating wave loads on FWTSs.
In this regard, the aerodynamics of the NREL 5-MW turbine [19] subject to prescribed harmonic motions in surge and pitch directions induced by a floating platform is evaluated by [136] using a CFD code based on URANS with k − ω Kok turbulence model. Due to ignoring the blade aeroelastic deformations, discrepancies are observed between the CFD predictions and the results given by OpenFAST.
The aerodynamics of the NREL 5MW FWTS under harmonic pitch and yaw motions is assessed by [40] based on URANS equations with k − ω SST model.
By modeling the NREL 5 MW turbine blades as actuator line (AL) based on RANS simulations without any turbulence model, the researchers in [137] investigate the aerodynamics of this turbine undergoing harmonic surge and pitch motions induced by platform motions. The results show that the pitching motion influences the aerodynamic loads and wake flow more than the surging motion.
The aerodynamics of the NREL 5MW turbine under harmonic surge and pitch motions of its supporting platform is investigated by [138,139] based URANS equations with k − ω SST model. The results show the significant impact of both pitch and surge motions of the platform on the turbine aerodynamics.
The aerodynamics of the NREL 5 MW turbine undergoing harmonic motions is investigated by [140] based on RANS equations with SST k − ω turbulence model. For large platform motions in which the grid is highly deformed, leading to a low-quality mesh, a remeshing method is used to regenerate the mesh in the locals with low quality based on criteria such as cell volume and skewness. The results show that the interaction between the rotor and its own shed vortices certainly affects the machine aerodynamics.
The aerodynamics of an FWTS subject to harmonic pitch motions is simulated by [141] using URANS-based CFD solver, where the turbulence modeling is carried out using the k − ω SST model.
[142] investigates the 5-MW NREL turbine wake pattern under prescribed platform motions using RANS with a Realizable k − ε model where the turbine rotor is represented by an AL method.
A few works are also performed to evaluate the platform motions under prescribed aerodynamic loads. For instance, the hydrodynamics of an FWTS is evaluated by [68] for various wind-wave conditions using RANS equations with k − ω SST model without the turbine presence. The corresponding aerodynamic loads for each wind speed are exerted at the center of rotation of the platform.

2.3.2. Aeroelastic simulations

Although both the aerodynamic and hydrodynamic loads impact the elastic deformations of FWTS structure, considering the high costs of coupled CFD-FEA studies, such studies are mainly restricted to aeroelastic investigations, where the interaction between aerodynamic loads and blade structural dynamics are assessed. This is because the larger and more flexible modern wind turbine blades typically have lower flexural rigidity provoking a more intensified coupled aero-structural dynamics, which accentuate the importance of aeroelastic evaluation of these large machines [109,143,144,145,146,147]. The blades are discretized in these simulations into 3D composite shell elements [25,148,149].
[146] investigates the wind gust effect on the structural responses of a large-scale turbine through coupling a CFD solver based on RANS equations with k − ε model and an FEA code based on shell elements.
The performance of geometrically adaptive blades implemented to the NREL 5MW turbine to mitigate the destructive effects of the typhoon is tested by [150] through a coupled FEA-CFD method. The blade discretization in the FEA is performed using 3D composite shell elements, and the flow field in the CFD code is modeled using unsteady RANS equations with k − ω SST model.

2.3.3. Hydro-aerodynamic simulations

A coupled hydro-aerodynamic CFD model is developed by [82] to evaluate the dynamics of the OC4 semisubmersible FWTS subject to different wind and wave conditions. The turbulence effect is captured using the k − ω SST model.
Similar CFD models are also developed by [76,151,152,153,154,155,156] based on URANS equations with k − ω SST model for the evaluation of hydro-aerodynamics of FWTSs.
In this regard, [151] simulate the hydro-aerodynamic behavior of the DeepCwind OC4 semisubmersible FWTS, where the effects of both waves and wind are considered. The researchers in [152,153], based on a hydro-aerodynamic model, evaluate the responses of the NREL-5MW mounted on a semisubmersible platform where the wind turbine blades are modeled using an AL technique. The researchers in [155] perform the coupled hydro-aerodynamic simulations of a 5-WM semisubmersible FWTS under combined wind–wave conditions. The platform motion is shown to be responsible for a 10% decrease in the mean turbine power production. The full-scale OC4 semisubmersible FWTS is simulated by [76] to evaluate the dynamic responses of this machine to focused waves. Comparing the results with those obtained from the OpenFAST indicates the importance of using nonlinear models with increased wave steepness. The dynamics of an FWTS under a blade pitch control action is simulated by [156] using a hydro-aerodynamic model under different operating conditions.

2.3.4. Final remarks on coupled CFD-FEA models

As inferred from the previous sections, most of the coupled analyses of FWTSs are performed within a CFD code to assess the hydro-aerodynamic behavior of the system, except for the aeroelastic simulations, which are carried out through coupled CFD-FEA simulations. This may be associated with most of these studies adopting a 5 MW wind turbine in which the structural deformations have little impact on the whole system dynamics.
In this regard, as shown in Figure 7, the most popular CFD software used in the coupled simulations of FWTSs is the open-source CFD code OpenFOAM, followed by the commercial CFD software STAR-CCM+.
By considering both viscous effects and detailed FWTS geometry, CFD can simulate the FWTS dynamic responses more realistically. To predict accurately both the loads and dynamic responses of an FWTS based on CFD, the correct reproduction of the environmental conditions, including the atmospheric boundary layer (ABL) is critical. In the case of LES, the most reliable approach for generating a realistic inflow condition is using a precursor method, where the ABL is simulated in a separate numerical domain without the turbine’s presence. The resultant wind flow field is then utilized as the inflow condition to a second domain, which encompasses the turbine geometry [157,158,159]. In the case of RANS simulations of turbines, the wind profile must remain homogeneous in the horizontal direction as it propagates toward the body. This is guaranteed typically through a proper combination of the boundary conditions and the addition of new source terms into the momentum equations [160,161,162,163,164].
Another critical issue regarding the CFD simulations is the choice of an adequate turbulence model. The coupled simulations of FWTSs are consistently performed using RANS equations. As shown in Figure 8, the most popular RANS-based turbulence model used in these simulations is the k − ω SST model, followed by the Spalart-Allmaras model, where both of them are based on Boussinesq approximation ignoring the turbulence anisotropy. However, one can use nonlinear eddy viscosity models, which offer better accuracy in capturing the turbulent flow characteristics while maintaining the computational cost to an acceptable level.
Another important issue that has not been evaluated sufficiently is the accurate representation of the turbulent boundary layer near the FWTS body in the coupled simulations of these structures. For this purpose, a highly refined grid with a y+ value smaller than 5 is usually required. However, this may lead to a large number of mesh cells, which significantly increases the computational cost. Therefore, an alternative is using wall functions together with a relatively coarse grid with a y+ value from 30 to 100 to model the turbulent flow behavior within the boundary layer. Based on the review carried out here, little attention has been paid to this topic in the studies on the FWTSs. In a majority of coupled CFD simulations of FWTS, such as [40,68,136,138,139,151], it is not clear how the turbulent boundary layer close to the FWTSs is treated. As shown in Figure 9, a considerable percentage of coupled CFD simulations of FWTSs avoid capturing the turbulent boundary layer close to the rotor blades by using an actuator method, such as the actuator line [152,153]. Additionally, several works have used Wall-functions (WF) [82,146], and a few works have resolved the boundary layer all the way down to the viscous sublayer by adopting a grid with a y+ less than 1 [143,155].
In this regard, one of the few studies that assess the impact of near-wall grid resolution on CFD simulations of FWTSs is carried out by [141] where the effect of different values of y+ ranging from 10 to 100 on the aerodynamic performance of the NREL 5 MW reference wind turbine is evaluated. In this work, the k − ω SST turbulence model with wall functions is used to represent the effect of turbulence. The results indicate that the best predictions are obtained with y+ around 30, which makes sense since the y+ values used here coincide with the buffer and log-law sublayers of the boundary layer, and as is well known, the wall functions work well when applied to the log-law region.
Moreover, the coupled analyses of FWTSs are restricted to regular wave conditions, where the system behavior is investigated under several monochromatic wave conditions. In other words, simulations of realistic irregular sea states are not common due mainly to a high computational cost emanating from the requirement of a relatively long simulation physical time, which is usually up to 3 hours to capture all the necessary nonlinear and low-frequency effects [165]. This kind of simulation has become more common very recently, especially for assessing floater behavior in real sea states, where the irregular sea is generated by a low-order model typically based on nonlinear PF theory and then imported to a CFD model using a one-way coupling scheme. This allows for the reduction of the CFD domains, which consequently reduces the computational demand [165,166].
Finally, it is worthwhile mentioning that to capture the transient motions of the moving part of an FWTS, several methods, such as moving reference frame, sliding mesh, and overset methods, are used [40,65,75,82,140,141,167].

3. Nonlinear coupled time-domain models

3.1. Hydrodynamics

Both PF and ME are employed for the assessment of the hydrodynamic behavior of FWTSs based on the characteristic length of the floating platform compared to the incident wavelength [65,168,169].
In this regard, when the characteristic length of the floating platform (D) is much larger than the incident wavelength ( λ ), the diffraction theory from linear PF is used for the assessment of the hydrodynamic loads.
The governing equation of PF theory is obtained by assuming the flow is incompressible, inviscid, and irrotational. Thus, there will be a velocity potential Φ , whose gradient describe the velocity field as:
∂ 2 Φ ∂ x 2 + ∂ 2 Φ ∂ y 2 + ∂ 2 Φ ∂ z 2 = 0 .
This Laplace equation is solved using proper linearized boundary conditions, as shown in Figure 10. In this Figure, n is the vector normal to the body surface. Thus, having calculated the velocity potential and, as a consequence, the velocity components, the pressure on the surface of the floating structure is computed using Bernoulli’s equation. Solving this equation with linearized boundary conditions leads to deriving the linear (Airy) wave theory for surface propagating waves. Although there are other wave theories like stream function and stokes to compute the wave kinematics based on wave steepness and water depth, the linear Airy wave theory is the most predominant wave theory employed in offshore industry [30,168,169,170].
To compute the hydrodynamic loads, the incident, diffraction, and radiation wave linear potentials are obtained [65,171,172,173]. Note that as the linear assumption is employed, it is possible to consider that the potential function is a summation of these three potential functions:
Φ = Φ i n c + Φ d i f + Φ r a d ,
where Φ i n c is the velocity potential related to the incident waves, Φ d i f is the velocity potential related to the diffraction of the incident waves, and Φ r a d is the velocity potential related to the radiation.
The radiation part is related to the case without the presence of any incident waves, and the floating platform is forced to oscillate along its DOFs of motion, as shown schematically in Figure 11, which leads to the calculation of added mass and damping loads [171].
The diffraction part is related to the case where a floating platform is fixed, causing the scattering of the incident waves, as shown schematically in Figure 12. The diffraction loads come from the undisturbed pressure field (Froude-Kriloff) and the disturbed pressure field due to wave scattering (diffraction) [65].
Note that numerical solutions are obtained using the panel methods where the floating platform is discretized into a limited number of panels [174,175,176,177,177]. A convergence study may be required to determine the minimum number of panels to obtain a precise solution [175,177].
On the other hand, for λ > 5 D [171], the diffraction effects are negligible, and the semi-empirical ME capable of accounting for viscous effects can be used for the calculation of the hydrodynamic loads [168,169,173]. The total hydrodynamic load acting on each structural element modeled as a line beam, considering the local velocity and acceleration of the floating system to account for the structure motion effects, is estimated as:
F T = π D 2 4 ρ C M u ˙ − X ¨ + π D 2 4 ρ u ˙ + 1 2 ρ C D D u − X ˙ u − X ˙ .
Here, C D is the drag coefficient, C M is the added-mass coefficient, u and u ˙ are the water particles velocity and acceleration, and X ˙ and X ¨ are the velocity and acceleration of the floating structure.
To ensure the accuracy of the ME, a proper estimation of the inertial and drag coefficients is crucial [63]. A wide range of methods, from high-fidelity experiments and CFD to semi-empirical equations, can be used to determine these coefficients [178]. To include the loads due to water current, one needs to modify the velocity of water particles to account for the presence of the current.
Note that the ME may be combined with strip theory to calculate both the linear wave loads and nonlinear viscous loads for slender structural elements [179]. The strip theory in hydrodynamics, as in BEM theory in aerodynamics, splits the slender structure into a finite number of strips, where two-dimensional hydrodynamic loads are utilized to calculate the overall hydrodynamic forces acting on the structure [171].
Most of the time, as the part of FWTSs in contact with water has members with characteristic lengths both much larger and smaller than the incident wavelength, a combination of ME and PF is employed to calculate the hydrodynamic loads due to viscous drag, as well as incident, radiation and diffraction wave potentials [18,173,180].
Note that the predictions provided by linear potential flow theory are inadequate for several cases, such as severe sea states with platforms experiencing large motions, accurate description of the horizontal motions of a moored platform, and reliable determination of the excitations related to a semisubmersible natural frequencies in the horizontal plane, which typically fall outside the wave-excitation frequency region [173,178,181,182,183]. To overcome these limitations, it is necessary to consider the nonlinear second-order or higher-order effects [173,180,181,184,185,186,186].
The second-order effects, which are functions of the square of wave height, are considered commonly by using quadratic transfer functions (QTFs) obtained from the second-order potential-flow problem, which requires detailed knowledge of the first-order potential quantities [171,181,182,187]. In this regard, second-order hydrodynamic loads are expressed in terms of the sum and difference of frequencies of sets of two incident waves with amplitudes A k and A l and frequencies ω k and ω l using typically the following double Fourier transform [181,188]:
F e x − i ( 2 ) = Re ∑ k = 1 N ∑ l = 1 N A k A l Q T F i + ω k , ω l e j ω k + ω l t + A k A l * Q T F i − ω k , ω l e j ω k − ω l t , i = 1 , 2 , … , 6 ,
where Q T F i + ω k , ω l and Q T F i − ω k , ω l , which are the QTFs to be determined, represent the ith component of sum- and difference-frequency second-order loads, and asterisk (*) is an indication of the complex conjugate. Note that, for k = l (diagonal terms), the difference-frequency term results in mean hydrodynamic loads, also known as mean-drift loads, which are responsible for an average displacement of floating platforms from their undisturbed initial positions [189,190].
The full sum- and difference-frequency QTF matrices can be computed using available hydrodynamic codes such as WAMIT, ANSYS-AQWA and WADAM module from the SESAM code [12,186,189,191,192,193,194]. Alternatively, as outlined by [181], one can make use of the symmetry properties of the QTFs by dividing the matrices into three different regions: l = k , l > k , and l < k to reduce the numerical difficulties and the computational cost.
Thus, the frequencies in the second-order effects contain the sum and difference of the frequencies of the waves that make up the irregular sea state [195,196]. The high-frequency hydrodynamic loads emanating from the sum of frequencies may lead to higher ultimate and fatigue loads due to the excitation of structural natural frequencies, especially in the case of fixed-bottom and tension-leg offshore wind turbines [144,188,189,193,196]. The low-frequency hydrodynamic loads originating from the difference of frequencies are extremely important for an optimum mooring system design for floating structures [173,180,181,183,184]. This is because a moored floating platform, unlike an unrestricted platform, has natural frequencies in the horizontal plane, generally smaller than the frequency range of the incident waves. The natural frequencies in the horizontal plane are, in fact, excited by the low second-order frequencies emanating from the second-order potential problem. Consequently, increasing attention has been given to the evaluation of the second-order low-frequency hydrodynamic loads in the case of FWTSs [186,197,198,199].
Due to its complexity, using the full QTF matrices is sometimes avoided in the offshore industry, and instead, Newman’s approximation has been the most common approach to account for second-order effects. This method estimates the slow-drift forces based on the symmetry of the matrix of the difference-frequency QTF and the mean drift forces [200]. However, the reliability of this method is questionable for intermediate and shallow waters [186,188,198,201].
Another option to compute the matrix of the difference-frequency QTF is the white-noise approach proposed by [201,202]. In this approach, by decoupling the degrees of freedom of motion, it is assumed that the slow-drift motion is excited mainly by a limited portion of frequencies around the platform’s natural frequency, and consequently, the spectrum of the second-order force can be considered constant within this band. The advantage of this method is that the QTF matrix is computed based only on the sets of two frequencies, whose difference gives the drift motion natural frequency.
To improve the predictions of second-order wave loads, one can use the results from wave basin tests or high-fidelity simulations to tune the QTFs obtained from PF solvers [57,203,204].
To consider second-order effects, alternatively, the full second-order velocity potential can be obtained through perturbation analysis, and then the loads can be calculated through direct integration of the pressure acting on the instantaneous wetted surface of FWTSs [182,183,187,205]. Second-order loads are computed more accurately using this approach, which is computationally more demanding.
Another important subject is the assessment of the dynamic responses of an FWTS subject to extreme sea states such as freak waves [206,207,208]. These extreme waves can be generated by dividing the wave spectrum into uniform N parts, which are then summed up after modifying the initial phases of some of these components.
Finally, to perform the time-domain simulations using the frequency-dependent loads presented so far, the Cummins equation, where a convolution integral formulation is used to capture the fluid memory effects, is employed [12,174,209,210]:
( M + A ∞ ) X ¨ ( t ) + ∫ − ∞ t K ( t − τ ) X ˙ ( τ ) d τ + C X ( t ) = F e x t ( t )
Here, M is the inertia matrix, A ∞ is the added-mass matrix at infinite frequency, C is the restoring (hydrostatic stiffness) matrix, X ( t ) is the displacement vector of the floating platform, K ( t ) is the retardation function (fluid memory) and F e x t ( t ) is the time-varying external forces.

3.2. Aerodynamics

3.2.1. BEM method

The BEM theory forms the most popular method to evaluate a wind turbine aerodynamics. This method is a combination of two theories: blade element and momentum. The blade element theory considers that the blades comprise a finite number of elements with negligible interaction with the nearby elements. It is further considered that these elements operate as two-dimensional airfoils. The momentum theory is also used to calculate the induced axial and tangential velocities. Thus, combining these two theories gives origin to the BEM theory, an iterative process to evaluate turbine aerodynamics.
In this regard, the elements along the blade span located at the radial position of r, which extend to r + δ r , as shown in Figure 13, affect the airflow momentum that travels across the circular ring area covered by these rotating elements due to their aerodynamic loads.
The element aerodynamic loads are calculated using the two-dimensional airfoil properties based on an angle of attack ( α ), which is defined in terms of the total incident wind speed W written as follows based on Figure 14:
W = 1 + a ′ 2 r 2 Ω 2 + ( 1 − a ) 2 U 2 ,
where a ′ and a are the tangential and axial induction factors, U the freestream wind speed and Ω the angular rotor speed.
To improve the predictions given by BEM method, several corrections are introduced to account for the effects such as blade-tip and -root losses, a finite number of blades, tower shadow, three-dimensional stall delay, dynamic stall, yawed condition, unsteady loading and dynamic inflow [29,211,212,213,214,215].
However, both the large platform motions and blade aeroelastic deformations result in the rotor interaction with its own shed vortices, a condition that BEM may give unrealistic results [140,180,216,217]. FWTSs are more frequently subject to yawed inflow conditions since they have little yaw stiffness. However, the BEM theory is originally developed for the inflow condition perpendicular to the rotor plane, and the commonly used corrections may give erroneous results [167,180,199,216].
To evaluate turbine aerodynamics, the GDW model can be used alternatively to consider intrinsically the three-dimensional effects and the dynamic wake effects [218,219]. The GDW method is normally employed to model the tip losses at the blades and the performance of a turbine under yawed conditions more accurately. Albeit, its limitations at small wind speeds lead to unstable computations [220]. Generally, the BEM method is more commonly used in the coupled analyses of FWTSs. This can be deduced from the availability of this method in most of the codes used for the investigation of the coupled dynamics of FWTSs such as Bladed, OpenFAST, OrcaFlex, SIMA, SESAM and HAWC2 [141,173,211,221,222,223,224].

3.2.2. FVW method

The FVW method is capable of characterizing the wake evolution of a wind turbine over time, which may give more reliable predictions in case of FWTSs due to the possibility of movement of the rotor into its own wake [29,225,226].
The FVW belongs to the vorticity-based methods, such as the vortex lattice method (VLM) [145,211,213] assuming that the flow is inviscid, incompressible and irrotational [227], and have long been used in the field of wind energy [228,229,230,231,232,233].
The FVW method is used to solve the turbine wake based on a time-accurate manner, in which, contrary to the prescribed vortex methods, the convection, stretching, and diffusion of vortices are captured [29]. This is performed using a Lagrangian approach able to discretize the turbine wake into Lagrangian markers defined as a function of wake age ζ and azimuthal blade location ψ , as shown in Figure 15[29,227]. A wide range of methods are available for the representation of the wake using Lagrangian markers [230], such as the hybrid lattice/filament, which is used within the OpenFAST code [226] (see Figure 15). Over the near-wake region, a lattice method is used, as shown schematically in Figure 15. A user-defined angle is used to specify the near-wake span [234], which is usually assumed to be Δ ψ = 30 degrees [234]. This angle may not be sufficient for challenging operating conditions, e.g., high thrust conditions [226]. The near-wake region is followed by instantaneous wake aggregation into tip vortices, which are considered the principal flow characteristics over the rest of the wake [235]. Straight-line vortex filaments with second-order accuracy are used to connect the Lagrangian markers together [235] (see Figure 15).
The vortex-filament motion is expressed as [233,236,237,238]:
d r → ( ψ , ζ ) d t = V → r → ( ψ , ζ ) , t .
Here, r → ( ψ , ζ ) is the position of the Lagrangian markers and V → r → ( ψ , ζ ) , t is the velocity vector [233,239]. This vector is the summation of three components: the freestream, induced velocity, and velocity emanated from the platform movements due to environmental loading [227,233,239,240]. Each straight-line vortex filament creates an induced velocity at point k, which is calculated based on the Biot-Savart law [235]:
d V → k = F ν Γ 4 π d l → × r → r → 3 ,
where Γ is the vortex filament circulation strength, l is the vector used to connect the endpoint locations of filaments, and r → is the normal distance from l to point k. The factor F ν is used to consider the effect of viscosity on the vortex core [241,242,243]. Γ is obtained regarding the lift force acting on the blade element airfoil using the Kutta-Joukowski theorem [30].
The blade can be represented using either a lifting line or lifting surface [237], or more attractive options such as the Weissinger-L blade model, which has been demonstrated to give more reliable results than the lifting line model with a computational cost lower than the lifting-surface model [226,237,238]. Based on a blade model, the circulation along the blade span is computed by discretizing the blade into a finite number of panels, and then connection to the wake is performed by dependence on the induced velocities.
The FVW is available only in a few simulation tools for coupled analysis of FWTSs, such as QBlade and OpenFAST [52,244]. This method, despite being able to consider the turbine-wake interaction, has not been commonly used in the coupled analyses of FWTSs [245].

3.3. Structural dynamics

Coupled analyses of floating wind turbine systems are performed using a wide range of structural models, from modal analysis methods to more sophisticated finite element methods such as Euler-Bernoulli and Timoshenko, all based on the following second-order differential equation:
M x ¨ + B x ˙ + C x = F ,
where M, B, and C are the structural inertia, damping, and stiffness matrices, respectively. Additionally, x is the vector of structural displacements (deformations), and F is the vector of external forces. The structural dynamics is typically considered through the use of an MBD formulation, where the flexibility is considered in selected components, such as blades and towers, as shown schematically in Figure 16. The MBD formulation, the most common approach for the structural dynamic assessment of FWTSs, is available in many low- and mid-fidelity simulation tools, such as HAWC2, OpenFAST, SIMA, Bladed, QBlade, and Virtual.Lab Motion and Multibody Bladed [52,135,246,247,248,249,250,251,252].
In this technique, the geometry of the wind turbine is split into a limited number of interconnected rigid or flexible bodies, which may undergo translational and rotational motions [8]. The connection between the bodies is via force and joint elements that express their dynamic and kinematic restrictions. The description of the motion of the bodies is performed through a group of differential-algebraic equations, including the differential equations describing the motion of the bodies and a set of algebraic equations expressing the motion restrictions [35,107]. Among the turbine structural elements, the blades normally have the largest number of bodies due to being the most flexible components [35,107].
The long flexible blades and towers are commonly modeled as beam members based on either a linear modal analysis (MA) or more sophisticated beam theories, such as Euler-Bernoulli and Timoshenko [35].
The simplest form of representing the flexible turbine structural components is using the linear MA [30], which is available in many coupled analysis tools for FWTSs, such as OpenFAST, Bladed and QBlade [52,135,247,248,249,253,254,255]. Briefly, in this method, a modal transformation is used to separate the structural responses into various eigenfrequencies resulting in distinct vibration modes, whose linear superposition gives the total structural response [25,256,257]. Thus, due to its linearity assumption, its use is restricted to small deflections [25]. To specify the flexibility properties of blades and towers, the spanwise mass and stiffness distributions and their mode shapes based on equivalent polynomial coefficients are defined [257,258]. These mode shapes, which typically the first few of them are considered in the modal representation, are commonly determined using a finite element method [258,259]. Therefore, the accuracy of a modal analysis depends highly on the correct determination of the mode shapes, which is a principal disadvantage of this method [30].
However, in the case of large blade deformations, using more advanced beam theories such as Euler-Bernoulli and Timoshenko is preferred over the modal approach [42,260]. For example, using nonlinear beam theories, the OpenFAST from NREL and HAWC2 from DTU can simulate flexible blades. More specifically, OpenFAST employs both theories of Euler-Bernoulli beam and geometrically exact beam with Legendre spectral finite elements. The latter can better model the geometric nonlinearities and large blade deformations compared to the former [261]. While HAWC2 uses the Timeshenko finite-element modeling approach [262]. The results obtained from these codes are expected to be similar, as shown by [263].
The floating structure is typically modeled as a rigid body, the same practice adopted in the oil and gas industry. However, accounting for floating platform flexibility can be crucial in the floating wind system design and optimization process, considering the increasing use of large platforms for offshore wind power and the growing tendency to reduce substructure costs.

3.4. Recent research

The aerodynamics of the NREL 5MW FWTS under prescribed motions over single and multiple DOFs is investigated by [29] using an FVW code. The platform motions are estimated using OpenFAST. The obtained results demonstrate the importance of using the FVW method to capture the complex physics due to the interaction between the rotor and its own shed vortices.
A coupled FVW-geometrically-exact beam theory model is developed by [261] to evaluate the aeroelastic behavior of the NREL 5 MW wind turbine.
An FVW-MBD coupled model is developed by [236,239] to assess the aeroelastic behavior of the NREL 5 MW wind turbine under harmonic platform motions.
[136] evaluates the aerodynamics of an FWTS subject to prescribed harmonic motions using a code based on FVW method. Due to ignoring the blade aeroelasticity, discrepancies exist between the predictions and the results given by OpenFAST.
An FVW solver is used [264,265] to evaluate the aerodynamic performance of a rigid FWTS under harmonic surge motions with various amplitudes and frequencies. It is shown that, for tip speed ratios close to the optimum value, the turbine power can surpass the Betz limit mainly because of the platform’s axial motion induced on the rotor.
The coupled analysis of a 15MW FWTS is performed by [266] using a coupled HAWC2-FVW code, and the results are compared against those obtained from a HAWC2-BEM code. The results highlight a large difference between these codes for high wind speeds.
The performance of different codes to simulate the dynamics of the semisubmersible floating NREL 5 MW wind turbine is assessed by [11,173] under different load cases. The structural part is modeled using a wide range of methods from MBD to FEM. The aerodynamics are represented based on mid-fidelity methods, such as BEM and FVW. The hydrodynamic modeling is mainly based on PF theory with or without the ME. It is shown that the codes based on the Morison approach need to consider the effect of the heave plates as an additional damping force [11,173].
2D harmonic polynomial cell wave tank [267] is used by [169] to calculate linear and nonlinear wave kinematics based on potential flow theory to be used in a coupled analysis for the 5MW OC4 semisubmersible FWTS [18] based on HAWC2 code [248,262,268]. The results show the importance of considering a fully nonlinear wave theory for FWTS in shallow and intermediate water depths.
The wave-body interaction for an FWTS is simulated by [174] through coupling a hydrodynamic model based on PF theory and BEM aerodynamic code.
The performance of two codes Simo-Riflex and HAWC2, in modeling the coupled dynamic behavior of an FWTS is evaluated by [269]. The structural dynamics and hydrodynamics are modeled in both codes using an MBD and PF plus ME, respectively.
A hydrodynamic model based on PF and ME able to account for second-order wave loading is coupled to an aero-servo-elastic model based on BEM and MBD by [270] to predict the responses of GustoMSC Tri-Floater FWTS.
The SIMPACK tool based on ME via strip theory, BEM method, and MBD is used by [271] to evaluate the dynamics of a 10 MW FWTS. The numerical results are compared against the measurements from a scaled OC4 semisubmersible platform supporting a 1:60 scaled DTU 10MW wind turbine. The comparison of the calculations and measurements highlights the significance of accounting for the second-order wave effects in coupled dynamic analysis of FWTSs.
[188] conducts the coupled analysis of a conceptual 10 MW FWTS using OpenFAST. The second-order effects are considered through a full QTFs and Newman approximation. The BEM method is used to model the wind turbine aerodynamics. The results show that using the full QTFs is necessary to model second-order responses accurately.
To evaluate the importance of the second-order effects, the coupled behavior of a 6-MW FWTS at a depth of 100 m is evaluated by [272] using both experimental and numerical methods. The numerical model is developed using the OpenFAST. The results show the importance of using the full QTFs compared to Newman’s approximation to consider the second-order effects.
The responses of two FWTSs, 15-MW spar WindCrete [273], and 15-MW Activefloat semisubmersible [274], both made of concrete, under static and dynamic conditions are evaluated by [12] using OpenFAST. The results show that the second-order wave loads dominate the platforms’ responses more than the first-order wave forces.
[275] assesses the coupled behavior of a novel catamaran FWTS, where OpenFAST is used for the aero-elastic part while ANSYS AQWA is utilized to predict the hydrodynamic loads.
[276] performs the numerical investigation of the behavior of a 5MW FWTS through a combination of the PF ANSYS-AQWA capable of accounting for second-order loads based on the full QTFs and a BEM code. The flexible blades are modeled using a nonlinear deflection model.
The dynamic behavior of four different platforms supporting the NREL 5-MW turbine are compared by [277] against the onshore turbine performance using the OpenFAST code.
The dynamics of the 5-MW WindFloat FWTS is investigated by [278] using a coupled PF-ME-BEM-MBD code under coupled wave-wind conditions.
Coupled simulations of a V-shaped semisubmersible FWTS is carried out by [279,280,281] using the coupled PF-BEM-MBD Simo-Riflex-Aerodyn code [282].
[283] extends the OpenFAST code to analyze three wind turbines’ coupled hydro-aero-structural dynamic behavior mounted on the same semisubmersible platform.
The dynamics of the OC4 semisubmersible supporting the NREL 5-MW turbine with a broken mooring line is simulated by [284] using the OpenFAST code.
The dynamics of a 5-MW braceless steel semisubmersible FWTS is carried out by [285] by coupling a structural model based on beam elements, a first-order PF model and a BEM method available in the coupled Simo/Riflex/Aerodyn code [286].
[173,287] use the OpenFAST software to model the hydro-aero-servo-elastic behavior of the OC5 DeepCwind semisubmersible FWTS, where the full QTFs are used to account for the second-order effects. The same code is also used by [288] to evaluate the coupled behavior of OC4 DeepCwind semisubmersible FWTS.
The coupled analysis of a 5-MW and a 13.2-MW FWTSs is performed by [289,290] using a coupled BEM-PF-ME model. The second-order hydrodynamic loads are considered through the full QTFs. The structural responses are modeled using an MBD with Euler-Bernoulli beams for flexible blades and towers.
[291] tests different mooring configurations for a 5-MW FWTS using the OpenFAST code.
[222] analyzes the low-frequency second-order wave effects on the 5-MW OC4 FWTS using both SIMA (SIMO/RIFLEX/AERODYN) and OpenFAST codes.
The second-order wave effects based on the full QTFs on 10 MW and 5 MW FWTSs is evaluated by [188,196] using the OpenFAST code.
The OpenFAST code is also used by [292] to assess the behavior of a 5-MW V-shaped FWTS in moderate water depths.
Motions and loads predicted by the open-source OpenFAST and commercial OrcaFlex codes for an FWTS are compared together by [293] and it is shown that the predictions provided by these codes are generally in good agreement.
A coupled numerical model, based on BEM-PF-ME is developed by [294] to investigate the dynamic responses of FWTSs.
The impact of substructure hydroelastic deformations on the dynamic responses of a 20MW FWTS is assessed by [295], using the nonlinear aero-hydro-servo-elastic code SIMA, which is a combination of RIFLEX and SIMO software. RIFLEX is responsible for structural analysis based on a nonlinear beam theory approach, which here models platform, tower and turbine blades. The hydro-aerodynamic loads are computed from a coupled BEM-PF-ME with the difference-frequency second-order loads.
[296] uses the OpenFAST code to evaluate the impact of the motions of two types of floating platforms, including OC3-UMaine spar and OC4-DeepCWind semisubmersible, on the power generation of the NREL 5MW turbine subjected to irregular waves and various wind conditions imported from the LES code SOWFA from NREL [297].
[298] uses the OpenFAST code to evaluate the impact of second-order wave hydrodynamic forces based on the full QTFs method as well as Newman’s approximation on the time-domain analyses of three FWTSs supporting the NREL 5 MW turbine.
The behavior of the OC4 DeepCwind semisubmersible FWTS with a mooring line failure is assessed by [299] by coupling the BEM aerodynamic model available in OpenFAST to ANSYS-AQWA, which is responsible for the computation of the hydrodynamic loads. The responses of the drivetrain is also considered through a multibody drivetrain model using SIMPACK [300].
The dynamics of the OC4 FWTS after one of its mooring lines is broken is assessed by [301] using both ANSYS-AQWA and OrcaFlex software.
[302] analyzes the coupled behavior of a 5-MW FWTS, where the aero-servo-elastic part of the OpenFAST code is coupled to ANSYS-AQWA capable of modeling nonlinear hydrodynamics and mooring line behavior.

4. Linear frequency-domain models

These models are based on a linear frequency-domain mathematical model able to provide the FWTS steady-state responses [36,303,304]. The FWTS responses are computed using the following six DOF equations [304,305]:
− ω 2 M + A ( ω ) + i ω B ( ω ) + C ξ ^ ( ω ) = F ^ ( ω ) .
Here, ω is the frequency of the incident wave, ξ ^ the DOF dynamic response of a FWTS, F ^ the excitation forces and moments vector due to wind and waves, M the FWTS mass and inertia matrices, A added mass and inertia matrix, B damping matrix and C restoring matrix. Note that the matrices A and B contain the contributions from aerodynamics and hydrodynamics, while the C matrix, in addition to the hydrostatic forces, includes the mooring loads. The mooring loads are computed using either analytical equations based on a simple linear spring model or a quasi-static approach [30,38,303,304,306]. The hydrodynamic loads are estimated using a linearized PF theory or strip theory combined with a linearized ME [304,305,307]. The ME may be modified to account for the effect of heave plates [308]. Additionally, aerodynamic loads are considered as a point force at the hub, which is computed using either a steady-state BEM method or tabular pre-computed data [38,303,305,307]. Note that these models can typically capture only the rigid-body dynamics [30,39,140].
Examples of these models are the open-source frequency-domain code developed by [303], as well as the in-house codes developed by [305,307,309].

5. Mooring system

A mooring system serves as a station-keeping system for a floating platform. Proper implementation of the mooring system is crucial for maintaining the wind turbine nearly fixed in its position in such a manner to guarantee the safe operation of the machine.
Generally, there are two types of mooring line systems: catenary and taut, as shown in Figure 17.
In the case of the catenary system, the station keeping is performed through the weight of the portion of the mooring lines in contact with the seafloor [21,310]. In the case of the taut system, this is performed by the high tension in the cables. In other words, while the mooring line weight provides the restoring force in the catenary mooring system, the elasticity of the mooring line provides this force in the taut mooring system.
The catenary mooring lines are typically made of steel chains and/or wires [311,312], while the taut mooring lines are made of synthetic fibers, such as polyester, nylon or wires [312,313,314,315,316,317]. Recent studies have shown that a taut system composed of nylon may significantly reduce the cost of the floating wind turbine system, especially for shallow water applications, compared to the same system with polyester [313,315].
It is also possible to use a combination of materials for catenary applications (the semi-taut mooring system) to reduce the weight and cost of the mooring system [318]. The chain is typically used to adjust the length and tension of the upper portion, where the mooring line is connected to the floater at the fairlead. Again, the chain is preferred due to its stiffness at the seabed, where the mooring line rests on the sea floor. Synthetic fibers, nylon, or wire can be used for cost and weight reduction. The Hywind project, for instance, uses a combination of steel chain and wire [318].
The catenary configuration is usually applied to the floating platforms at water depths between 100 m to 250 m, where it can be considered an optimum solution for station keeping of the system [319]. Based on Figure 18, which shows the cost evolution of a traditional steel chain catenary system regarding water depth, in the case of shallow waters with a depth smaller than 100, the highly dynamic condition in which the floater operates calls for a more expensive station-keeping system [320]. Additionally, the additional mooring line length increases the cost as the water depth exceeds the values larger than 250 m.
On the other hand, the taut configuration can be used in water depths smaller than 100 m or larger than 250 m [320]. An example of a taut system used at a water depth shallower than 100 m is the Ideol platform installed close to the French coastline at a water depth of nearly 30 m [321].
A floating platform equipped with a catenary system can have some horizontal movement. However, a floating platform with a taut system, typically has limited horizontal movement. The disadvantages of the catenary system are its more seabed disruption and larger footprint. On the other hand, as the anchor experiences relatively less loads, the catenary system has more economical anchors. Considering a taut system, the disadvantage is the higher cost of installation and anchoring due to the large horizontal and vertical loads acting on the anchor [27,322]. However, its lower seafloor disruption, smaller footprint, and suitability for shallow and deep waters are the main advantages of a taut system.
In the case of catenary systems, to increase the mooring line tension and, consequently, the restoring force acting on the floating platform, especially in the case of shallow waters, the clump weights can be used, as shown schematically in Figure 19. It is also possible to reduce the mooring line dynamics and weight effects on the platform in the case of deep waters using buoyancy modules, as shown in Figure 19.
One main challenge related to floating wind turbines is the high cost of anchoring for a single floating platform. An alternative to reduce these costs is using shared mooring or shared anchoring systems [324,325,326].
However, the use of shared mooring lines is accompanied by a number of challenges as follows [327,328]:
  • The installation process is more complex.
  • Difficulty in towing a single floating wind turbine to a nearby port when it is necessary for operation and maintenance.
  • complexity in a mooring line may increase to a point where it is exposed to failure risk.
  • The Natural period of several mooring lines may have coupled effects with their surrounding floating wind turbines.
  • In the event of a mooring line or anchor failure, this scenario may affect several turbines.
The use of shared anchors is only beneficial under certain situations, which calls for a site-specific investigation [328]. Saving due to shared anchors can be lost due to an increase in the length of mooring lines to respect the minimum spacing between turbines, which depends highly on the energy yield calculations of the specific site. Shared anchors are more feasible for sites where it is possible to have smaller turbines’ spacing [327].
The coupled analysis of a floating wind turbine system is generally accompanied by a mooring line modeling, which is performed using either a quasi-static or dynamic method.

5.1. Quasi-static method

The quasi-static models can be as a simple linear stiffness matrix to more complex catenary equations, where Newton’s force equation is solved for each node of connection [329]. These models consider that the mooring is in the balance between the anchor and the FWTS attachment point [30]. Additionally, the dynamic effects, such as inertia, hydrodynamic drag force, and vortex shedding, are not considered [65,66,67,75,82,182].
Figure 20 illustrates schematically how the responses of a mooring line can be affected when dynamic effects are ignored. As can be seen, although the mooring line close to the fairlead tends to follow the floating platform motions, the lower portion of the mooring line may respond with a delay to this displacement. This can be regarded as a violation of the quasi-static assumption, which considers that the line is in static equilibrium at each time step [330].
The quasi-static models tend to underestimate the restoring load, particularly for extreme sea states [42,331,332], and as shown by [333] they are unable to estimate reliably the fairlead load amplitudes.

5.2. Dynamic method

Considering or neglecting the dynamic effects of mooring lines for FWTSs is a hot topic in the hydrodynamics of these structures. Due to the smallness of mass and motions, the dynamics may be neglected in the case of mooring systems used in shallow waters. However, it is crucial to consider the dynamic effects of deep water conditions. The oil and gas platform and vessel demonstrate the importance of considering line dynamics for water depth larger than 150 m [180]. Further, using dynamic models is essential for reliable estimation of the ultimate and fatigue loads in a mooring line and correct modeling of the peak tension in extreme events [30,173].
The dynamic models are based on either lumped-mass approach (similar to MBD) [186,195,334,335,336], FEA [182,183,299,330,299] or finite difference (FD) method [337]. The hydrodynamic drag and added mass are considered for all the elements resulting from the line discretization.
The simplest model is the lumped mass, where the mooring line model is a set of compact masses connected through massless spring-damper elements [195]. A sensitivity study may be required to determine the number of multibodies beyond which the results remain unchanged. The drawback of this method is that it neglects the mooring line torsional stiffness [333,338]. Due to its simplistic nature, the lumped-mass method is available in many simulation tools of FWTSs, such as OpenFAST and OrcaFlex [180]
A higher fidelity solution can be achieved using either the FD or FE methods. However, the results obtained from lumped mass, FD, and FE methods are expected to be very similar under sufficient resolution [30,333,339].

6. Final notes on numerical models

Table 1 summarizes the tools used to perform the coupled hydro-aero-structural analysis of floating wind turbines based on low- and mid-fidelity codes.
As can be inferred, most of these tools use BEM with various corrections to compute the aerodynamic loads. The main difference between the BEM, GDW, and FVW methods is their consideration of the dynamic inflow condition. A correction referred to as a dynamic inflow model is typically used within the BEM method for the better representation of the aerodynamic responses under unsteady conditions emanating from changes in incoming wind speed, rotor speed, and blade pitch angle, as well as platform motions. However, the dynamic inflow is directly considered by the GDW method. A limitation of the GDW method is the assumption of the smallness of the induced velocities compared to the free flow, which creates instability at low wind speeds. Finally, the FVW method is able to account for the dynamic inflow due to its basic formulation.
In this regard, the Offshore Code Comparison Collaboration (OC6) evaluates the validation of 54 aerodynamic numerical models for a floating wind turbine subject to large harmonic support platform motions in both surge and pitch directions [340]. The validation uses wind tunnel measurements from a 1:75 scaled DTU 10 MW wind turbine. A wide range of modeling approaches, such as BEM, dynamic BEM (DBEM) (which considers the effects of dynamic inflow), GDW, FVW, and blade-resolved/actuator-based CFD methods, are evaluated. The tests are performed at a wind speed of 4.19 m/s and an angular velocity of the rotor of 240 rpm, equivalent to the scaled model’s rated condition. The measured and calculated torque moment and thrust force of the turbine during one harmonic surge motion of the platform with a frequency of 1 Hz and an amplitude of 0.035 of rotor diameter are presented in Figure 21. Note that the numerical results are median values for each modeling technique. As can be inferred, the predictions provided by the FVW are comparable to those provided by CFD and even better in the case of thrust force. The poorest predictions are produced consistently by the BEM and DBEM methods.
Regarding the hydrodynamics, as shown in Table 1, either the Morison equation or potential flow theory or a combination of both is employed. Second-order potential flow theory based on QTFs is employed to account for the fundamental second-order effects. Considering these effects is crucial because a moored floating platform, unlike an unrestricted platform, has natural frequencies in the horizontal plane, generally outside the frequency range of the incident waves. The natural frequencies in the horizontal plane are excited by the low second-order frequencies emanating from the second-order potential problem. As shown in the OC5 Phase II validation project [173], underestimation of low-frequency loads can lead to a 20% underestimation of the loads and motions of a floating structure. This underestimation remarkably affects the correct estimation of the fatigue and ultimate loads acting on the floating structure. As suggested in the project of OC6 Phase I, improvement in the low-frequency predictions can be achieved by tuning the QTFs using data from physical tests or high-fidelity CFD simulations [203].
Accordingly, a RANS-based CFD model, together with the VOF method, is used by [57] to fine-tune the QTFs of an FWTS obtained from potential flow theory for a group of bichromatic regular waves, with a frequency difference correspondent to the natural frequency of the FWTS in surge or pitch direction. In this regard, Figure 22 shows the phases and magnitudes of the QTFs related to the force in surge direction and the moment in pitch direction obtained from both CFD (new QTF) using the commercial finite volume code OpenFOAM and potential flow theory (old QTF) using the commercial code WAMIT. As can be seen, a considerable difference exists between the predictions; regarding the QTFs related to the force and moment magnitudes, this difference increases even more at higher frequencies, while regarding the phase, there is consistently a substantial difference between the predictions with CFD showing nearly an opposite trends for phase angle when compared with potential flow theory.
The frequency-dependent characteristics of a floating platform are obtained most commonly using either AQWA [177,186,195,196,199] or WAMIT [198]. As shown by [195]. Generally, a good agreement exists between the two codes. AQWA can perform the time-domain simulations [177,186]. However, one needs to specify how the aerodynamic loads are computed. These loads can be either calculated using simple expressions within the software or through coupling with other codes such as OpenFAST.
As seen in Table 1, the structural flexibility is accounted for through an MBD formulation, where flexibility is considered by either a modal method or finite element representation. The flexibility is generally applied to the wind turbines, and substructures are typically assumed to be rigid.
Note that in addition to the coupled numerical models presented so far, the coupled dynamic analysis of FWTSs may be carried out through other coupling schemes as follows:
-
- coupled CFD-MBD models [35,75,107,143,341,342,343]:
An aeroelastic model is developed by [341] by combining the CFD-based AL method with a beam solver to evaluate the couple aero-structural responses of the NREL 5MW wind turbine in both isolation and wakefield of an upstream wind turbine. It is shown that considering the aeroelastic deformations leads to an aggravation of the tower shadow effect.
A CFD solver based on URANS equations with a k − ω model coupled with an FEA code based on non-linear Timoshenko beam elements is used by [143] to investigate the aeroelastic behavior of the reference 10MW DTU wind turbine at various uniform wind speeds [342]. [343] evaluates the NREL 5 MW wind turbine’s aeroelastic behavior by coupling a URANS-based CFD model with a geometrically exact beam formulation FEA code under harmonic platform surge motions. The turbulence model in CFD is the k − ω SST model.
[107] proposes an aero-elastic model that considers the drivetrain dynamics through coupling the Hybrid RANS-LES CFD model responsible for the flow field prediction with an MBF. The model is applied to the NREL 5 MW wind turbine to investigate the interaction between turbine aerodynamics, flexible blades, and drivetrain dynamics. A coupled hydro-aero-elastic model is developed by [75] to simulate the OC4 semisubmersible FOWT under a combined wind/wave operating condition. The hydrodynamic model is based on RANS with k − ω SST model and VOF method, and the structural model is based on an MBF. An overset grid CFD solver based on the DDES model derived from the k − ω SST coupled with an MBD solver is used by [35] to predict the aeroelastic behavior of the floating NREL 5 MW wind turbine subject to an ABL. Blades and tower are considered as flexible one-dimensional structures.
-
- coupled CFD-BEM-MBD models [344]:
A CFD model, which is responsible for the platform hydrodynamics, is coupled to the aero-servo-elastic OpenFAST code by [344] to simulate the OC4 DeepCWind FOWT dynamic responses under various operating conditions. More accurate results are obtained using this coupled tool compared to the OpenFAST alone simulations.
-
- coupled CFD-PF models [79]:
[79] proposes a coupled fluid-structure interaction model based on LES to study FWTS motions in waves. The domain is divided into two parts: near-field, where a two-phase LES solver based on the level set method is used, and a far-field model, where an aerodynamic model based on LES without viscosity is combined with a hydrodynamic model based on a fully nonlinear-potential-flow-theory. The modeling of the subgrid-scale turbulence over the near-field region is performed using the dynamic Smagorinsky model, while the scale-dependent Lagrangian dynamic model is used over the far-field region.
-
- coupled CFD-PF-MBD models [345,346]:
The wakefield of the OC4 semisubmersible FWTS is compared against its fixed-bottom counterpart under ABL condition by [345]. The wind turbine rotors are represented using an AL method based on OpenFAST code, where the wind flow is simulated using the SOWFA LES solver from NREL with standard Smagorinsky model responsible for subgrid-scale turbulence modeling [346]. The results indicate a small deviation between the wake patterns of the FWTS and its fixed-bottom counterpart.
-
- coupled PF-FEA models [347,348]:
[347] analyzes the ship-FWTS collision using a coupled linear PF-FEA model. The aerodynamic thrust force is considered to be a point load acting at the hub based on the thrust curve of the 5MW NREL wind turbine. The linear diffraction theory and an FEA model are combined by [348] to evaluate the hydro-elastic behavior of a novel triangular floating platform capable of accommodating three wind turbines on its vertices.

7. Physical testing

7.1. Lab testing

7.1.1. Full physical testing

The importance of physical tests is twofold. First, they are crucial for the validation of the numerical model. Additionally, they sometimes enhance our understanding of the physical aspect of the problem by revealing the complex phenomena that may only be recognized using physical modeling techniques. This enhanced understanding eventually leads to an improvement in the low- and mid-fidelity numerical models.
The main challenge of performing the full physical experiments is the need to address the Reynolds scaling problem of the Froude-scaled FWTS model in such a manner to decrease the scale effects during the tests [8,42,59,118,349,350]. This is because satisfying at the same time both platform Froude-number scaling and turbine Reynolds-number scaling is impossible [42,350,351]. The lower Reynolds number of the Froude-scaled FWTS model leads to a misrepresentation of the aerodynamic loads in a Froude-scaled environment, which consequently leads to the dissimilar dynamic response of the model and the prototype [118,350,351,352]. To solve this issue, several solutions are proposed to diminish mainly the difference between the model’s and prototype’s thrust coefficients, which is shown to impact an FWTS response significantly [353]. The most popular solutions are as follows:
  • Using a mechanical pulley system [354].
  • Applying an increased wind speed to the Froude-scaled FWTS model [42,355,356].
  • Redesigning the blades’ geometry [173,353,357,358,359,360,361]
  • Implementing an active control for blade pitch on the Froude-scaled model [270,362,363,364,365,365].
In this regard, a 1:47 Froude-scaled FWTS model is tested by [366,367] to validate the results of dynamic responses of its equivalent prototype obtained from a coupled SIMO/RIFLEX/HAWC2 code. A rotor pitch control system is implemented to ensure the FWTS model has a dynamic behavior similar to the prototype.
[353] designs a scaled-down NREL 5MW wind turbine model to have a similar thrust coefficient as the full-scale prototype wind turbine, which guarantees the similarity of the dynamic behavior of the model to the prototype when it is subject to Froude-scaled wind-wave operating conditions.
[270] implements an active blade pitch control in a 1:50 Froude-scaled model of the GustoMSC Tri-Floater FWTS, where the NREL 5MW wind turbine is used. The results show the potential of the active blade pitch control to reproduce an improved level of thrust force.
Through tests on the DeepCwind-OC5 floating platform supporting a 1:50 scaled NREL 5MW turbine, it is shown by [362] that implementing an active blade pitch control in a wind field scaled properly based on Froude number together with a turbine model with a thrust coefficient similar to the full-scale prototype can result in a model capable of reproducing the motions of the full-scaled FWTS.
[368] carries out tests on a 1:50 Froude-scaled OC4 semisubmersible FWTS model with two different blade designs, including geometrically matched and performance-matched blade models. In the former the wind speed is adjusted to ensure that the scaled model and prototype have similar thrust coefficients. It is shown that the performance-matched blade model can better capture the dynamics of the FWTS model.
The scaled OC4 semisubmersible platform supporting a 1:60 scaled DTU 10MW wind turbine along with active control of blade pitch is tested by [271], where the rotor blades are redesigned to reduce model and prototype thrust coefficients.
[272] tests a 1:65.3 Froude-based scaled FWTS model, where structural stiffness similarity is also satisfied by manufacturing the model with lightweight materials. Additionally, the blades are redesigned to guarantee the same thrust force coefficient between the model and the prototype.
[369] performs tests on a 1:50 Froude-scaled OC4 DeepCwind semisubmersible FWTS in a wave basin, where the wind speed in the wave basin is increased to guarantee the similarity of the thrust coefficients between the model and real-scale FWTS. Later, the same model is used by [356] to propose an improvement in generating a thrust force on the model equivalent to that of the prototype by permitting the rotor to be driven purely by the inflow wind.
[370,371] test a 1:40 Froude-scaled model of a 750-kW FWTS, where the rotor blades are redesigned to guarantee that the model has a thrust force coefficient similar to the full-scale machine.
[372] designs an FWTS model, where to guarantee that both model and prototype have similar aerodynamic performance, the blades’ pitch angle and rotor rotational speed are adjusted in the model.
The responses of a novel FWTS model with a steel fish farming cage as a support structure are investigated by [373] through tests in a wave basin on a 1:30 Froude-scaled of the FWTS. The inflow wind speed in the wave basin is adjusted to ensure that the thrust coefficient remains the same between the model and prototype.
The tests on a 1:64 Froude-scaled 10 MW FWTS are performed by [374,375,376], where the blades are redesigned to ensure the similarity of the thrust coefficient between the model and prototype.

7.1.2. Hybrid testing

Another option to solve the Reynolds scaling issue of FWTS models is using hybrid testing (real-time hybrid simulation or hardware-in-the-loop testing), in which efficient numerical models are combined with realistic physical experiments.
During hybrid testing, the interaction between the physical testing part and the numerical model occurs in real time through one or more actuators at the transition interface between the physical and numerical models. Hybrid testing faces certain challenges, such as the accuracy of the numerical model needs to be improved and the time delays in the actuators and movement measurements must be optimized [61,62]. Hybrid testing can be performed in various configurations, which can be categorized into numerically modeled aerodynamics and numerically modeled hydrodynamics.
  • Numerically modeled aerodynamics
In the numerically modeled aerodynamics, also referred to as aerodynamics in the virtual subsystem, the aerodynamics is treated within a numerical model, while the hydrodynamics is modeled physically through a model test within a wave tank. The full-scale aerodynamics are calculated in a computer model and then dictated to the Froude-scaled FWTS model through actuators. Therefore, using this method eliminates the need to physically generate the wind flow, which can reduce the costs related to testing, even though the question arises of properly controlling mechanical actuators, which certainly is easier than controlling the physically generated wind flow [377]. The aerodynamic loads are typically calculated using a BEM method.
The coupling between the physical and numerical models can be either tower-base or aero-rotor, as shown schematically in Figure 23.
In the tower-base coupling scheme, the physical and numerical models are separated from each other by means of a clear boundary, plus the rotor elasticity can be more realistically represented for the scaled model through the numerical model [378,379]. However, the coupling strategy must respond with a relatively high frequency to properly mimic the dynamic behavior at the tower-platform connection. Consequently, it is relatively sensitive to the bandwidth and time delay of the platform motion measurements and actuators[378]. The actuation mechanism requirements to guarantee the hybrid model testing accuracy using the tower-base coupling method is presented by [380]. Additionally, the effects of ignoring some aerodynamic load components on the same testing method are evaluated by [381].
In the aero-rotor coupling, the blades are modeled physically as non-rotating mass and inertia. The numerical model computes the aerodynamic loads acting on rotor blades, which are assumed to be rigid and massless, neglecting the tower loads [15,378].
[15] designs hybrid testing based on aero-rotor coupling to assess the behavior of a 1:30 scaled of a 5MW braceless semisubmersible FWTS in a wave basin. The hybrid testing procedure is later verified by [382], where it is shown that the test results are highly repeatable, allowing the assessment of the responses of the FWTS. The hybrid testing model presented by [15,382] is used by [383] to calibrate the viscous drag coefficients of ME of a coupled PF-ME-BEM numerical model developed for the braceless FWTS.
The aerodynamic loads can be applied to the physical model within a wave basin using a duct fan, which replaces the rotor, as shown by [384,385]. By controlling the fan rpm based on the simulation results, it is able to generate a thrust force equivalent to the full-scale prototype.
A 1:80 scaled model of a 5 MW FWTS is modeled physically by [386] in a wave basin, where the thrust force is accounted for by a fan mounted on top of the tower.
[387] tests a 1:36 Froude-scaled FWTS with two rotors, where the steady wind loads are simulated by two ducted fans and gyroscopic loads by weighted rotating beams. It is shown that the uncertainty is highly affected by the simulated thrust loads, while the gyroscopic loads have negligible effects.
The single-fan method, which is only able to generate the thrust force, is later extended by [388,389,390], where a multi-fan system is used to consider the effects from other aerodynamic loads besides the thrust force.
[377,391] develops a new hybrid testing approach where a cable-based actuator prescribes the correct thrust force value to a FWTS model in a wave basin. [15,382,383] also use a similar approach to test the 1:30 scale braceless FWTS mentioned earlier, where the nacelle is substituted with a square frame connected to several pulleys through thin cables, which are used as actuators.
  • Numerically modeled hydrodynamics
In the numerically modeled hydrodynamics hybrid tests, which is also referred to as hydrodynamics in the virtual subsystem, the hydrodynamics is treated within a numerical model, while the aerodynamics is represented physically through a model test within a wind tunnel, as shown schematically in Figure 24. This type of test gains importance, especially in the case of wake evaluation of FWTSs. The main focus of this type of test is the development of a reliable actuation system to prescribe the platform movements in the wind turbine.
In the simplest case of this kind of test, the scaled wind turbine model undergoes a forced harmonic motion due to the platform motions in a certain degree of freedom [392,393,394,395,396,397,398].
The complexity increases when the platform motions are estimated from a numerical model and then prescribed to the wind turbine through an actuation mechanism.
In this regard, a two-degree freedom mechanism that can reproduce the pitch/roll rotations and the surge/sway movements for an FWTS is developed by [399]. The movements are calculated using the results from a real-time simulation of a hydrodynamic numerical model based on ME implemented in MATLAB/Simulink. The arrangement is later used by [392] to evaluate the OC5 FWTS motions by accounting for the first-order and second-order low-frequency hydrodynamic loads using the WAMIT software. Additionally, the same system is tested by [400] to assess an FWTS behavior under the actions of active blade and pitch control, as proposed by [401]. The system is later extended by [402] into a six-degree of freedom mechanism called HexaFloat, which is able to simulate the FWTS dynamics subject to normal operational conditions. [403,404,405] use the HexaFloat to evaluate the dynamic responses of an FWTS under unsteady aerodynamics and turbine controller action.

7.2. Field testing

Despite the existence of several real-scale FWTSs, such as Hywind in Norway and WindFloat in Portugal [406,407], there is a shortage of full-scale field measurements of the responses of these structures in the public domain, which leads to a limited number of validation studies of simulation tools against field data. This is crucial for better understanding the coupled dynamic behavior of these machines and gaining confidence in the predictions provided by simulation tools. Over the recent years, a few works have reported data from field measurements and used these data to validate numerical simulation tools for a range of FWTS concepts [22,408,409,410,411,412].
In this regard, the field measurements from a 2MW hybrid concrete-steel HAENKAZE FWTS commissioned in 2013 in Japan are used by [410,411] to validate a coupled hydro-aeroelastic simulation tool for FWTSs. It is argued that the spatial coherence of the wind field plays a significant role in the accurate prediction of the FWTS responses.
The measured and calculated data for a 7MW V-shaped semisubmersible FWTS in Japan are reported by [413], where the calculations are performed using the commercial code Bladed.
The measurement data during a six-month operation for a concrete barge-type FWTS installed 2018 in France are presented by [414]. [415] calculates the motion RAOs and turbine loads using OpenFAST-OrcaFlex code.
The validation of the OpenFAST code using the measurements from the Statoil Hywind Demo by [408,409]. Except for the roll and yaw responses at low frequencies, the OpenFAST reasonably reproduces the measured platform motions.
A 20kW VorturnUS, a 1:8 Froude-scaled model of the concrete 6 MW VolturnUS semisubmersible floating wind turbine, tested in the US for 18 months [22]. The test site environmental conditions are chosen so that the turbine model produces a thrust force equivalent to the prototype.
The influence of wave/wind-induced oscillations on the energy production of the WindFloat is assessed by [416]. The nacelle movements are recorded using accelerometer sensors. The wind data are measured using a nacelle-mounted LiDAR system, and the wave data are recorded using a buoy equipped with a LiDAR system.

8. Summary and Conclusions

Various methods with various fidelity levels are available to analyze the FWTS coupled hydro-aero-structural dynamics at each design stage.
The linear models in the frequency domain with the lowest level of fidelity are suitable in the early conceptual design phases for dimensioning and optimizing the FWTSs.
At the preliminary design stages, the mid-fidelity fully coupled nonlinear time-domain models are used to analyze the dynamic responses of FWTSs under various conditions to assess the operating, fatigue, and extreme loads correctly. These models are also excellent for the control design of FWTSs to reduce the structural loads and platform motions. The complex aerodynamic behavior of FWTS is better captured by the FVW method than by the BEM method. This is because the FVW method can characterize the wake evolution of a wind turbine over time, which may give more reliable predictions in the case of FWTSs due to the possibility of rotor movement into its own wake. Additionally, the accuracy of hydrodynamic modeling is increased by accounting for second-order wave loads using full sum- and difference-frequency QTFs. The QTFs can be calibrated using data from physical tests or high-fidelity CFD simulations to enhance the low-frequency predictions further. For the dynamic structural assessment of FWTSs, using nonlinear beam theories is preferred over the modal analysis in the case of large blade deformations.
The high-fidelity coupled CFD-FEA methods are used at the last design phases, where more in-depth investigations are required for extreme conditions and intricate flow conditions. These methods are suitable for fine-tuning the design, as well as the calibration of the low- and mid-fidelity models. However, due to the high computational demand of a coupled CFD-FEA method, the high-fidelity analyses of FWTSs are mainly restricted to aeroelastic and hydro-aerodynamic studies. In this regard, little attention has been given to the impact of the near-wall grid resolution on CFD simulations of FWTSs. It is common to couple high-fidelity CFD and FEA methods with low- and medium-fidelity models such as PF, MBD, or BEM to reduce the computational demand.
Modeling the mooring system is also part of all numerical modeling of FWTSs. In this regard, during a coupled analysis, the dynamic effects of mooring cables for floating wind turbine systems must be accounted for through the use of dynamic models such as lumped mass, FEA, and FD methods for a more reliable estimation of the ultimate and fatigue loads in a mooring line and correct modeling of the peak tension in extreme events.
Finally, the physical tests are used to validate the numerical models to gain more confidence in these numerical tools. However, the shortage of full-scale field measurements for FWTSs leads to a partial validation study of simulation tools. The physical tests also enhance our understanding of the physical aspect of the problem by revealing complex phenomena that may only be recognized using physical modeling techniques. This enhanced understanding eventually leads to an improvement in the low- and mid-fidelity numerical models. In the full physical testing to solve the issue of Reynold-number dissimilarity between the model and prototype, several solutions are outlined. Hybrid testing is an intriguing option to solve this issue, which can be categorized into numerically modeled aerodynamics and hydrodynamics.
Finally, based on the review carried out in this article, the following possible future research is identified to address challenges in modeling FWTSs dynamics that persist to date:
  • The accuracy of the mid-fidelity tools can be improved by incorporating the effect of vortex-induced vibration (VIV). This effect originates from currents or low-frequency waves and results in time-varying loading emanating from pressure fluctuations owing to vortex shedding from the platform components or mooring lines. The problem arises once the vortex shedding occurs at a frequency close to the structure’s natural frequency, which leads to the resonation of the two frequencies and large oscillation amplitudes.
  • The computational cost of CFD simulations of an FWTS in waves can be reduced by coupling a fully nonlinear potential solver capable of describing the nonlinear, three-dimensional wave field with CFD solvers governing the flow field in the FWTS vicinity. Using this strategy, it is possible to account for inherently nonlinear second-order effects.
  • A more systematic study is required to assess the impact of different materials for mooring lines on the platform’s motions and overall power production.
  • Due to wave second-order effects, more research is required to evaluate the structural fatigue damage for ultra-large FWTSs.
  • Modeling slender offshore structures in waves as rigid might lead to overestimating fluid forces. For example, modeling an offshore wind turbine foundation as completely rigid, commonly adopted in numerical and experimental analyses, may give very conservative wave forces. The size of offshore wind turbines has grown over the last few years, but the size of the platforms used to support these huge machines is also increasing. It may be crucial to consider the structural dynamics (hydro-elasticity) of these platforms in numerical and experimental studies, which are generally not considered.
  • During numerically modeled aerodynamics hybrid tests, the aerodynamic loads are typically calculated using a BEM method, which cannot accurately capture the effects of unsteady loading, dynamic inflow, and turbine-wake interactions. However, this issue can be avoided by using an FVW method.
  • One source of error in hybrid tests comes from the numerical models used. One solution to this problem is to avoid using these numerical models by coupling the two types of hybrid tests for an FWTS model via an Internet connection.
  • To gain confidence in the numerical and experimental results, detailed verification and validation studies are essential in quantifying errors and uncertainties. It is also crucial to identify the limitations of the hybrid testing by using the same FWTS model in both methods, i.e., numerically modeled aerodynamics and hydrodynamics. Further, in the case of CFD and FEA, sensitivity studies are required to test different element sizes, spatial and temporal discretization schemes, turbulence models, mooring line models, etc.
  • Artificial intelligence can be used to substitute the numerical subsystem in hybrid testing, thus increasing the efficiency of this type of test.
  • Field measurements about the impact of FWTS motions on their aerodynamic performance and power generation are crucial, especially for validating the numerical models and understanding where improvements are essential for these models.

Author Contributions

Mojtaba Maali Amiri: “Conceptualization, methodology, formal analysis, investigation, data curation, writing—original draft preparation, writing—review and editing, visualization; Milad Shadman: “Conceptualization, writing—review and editing; Segen F. Estefen: Conceptualization, writing—review and editing, supervision, project administration, funding acquisition

Acknowledgments

The first author would like to thank the Human Resources Program PRH-18 from the Agência Nacional do Petróleo, Gás Natural e Biocombustíveis (ANP) and Financiadora de Estudos e Projetos (FINEP) for the financial support. The third author acknowledges the financial support from the Carlos Chagas Filho Foundation – FAPERJ (Grant # E-26/210.796/2021 (262842)) and the Brazilian Research Council – CNPq (Grant # 303182/2022-9) to the research activities conducted at the Subsea Technology Lab, COPPE – Federal University of Rio de Janeiro. The authors also would like to acknowledge the financial support from the Center of Excellence in Digital Transformation and Artificial Intelligence of the Rio de Janeiro State - Network in Renewable Energy and Climate Change, Carlos Chagas Filho Foundation – FAPERJ (Grant # E-26/290.023/2021). The authors also would like to thank the CNOOC Petroleum Brasil Ltda for its financial support of the research on floating wind turbine.

Conflicts of Interest

“The authors declare no conflict of interest.”

References

  1. Musial, W.; Spitsen, P.; Duffy, P.; Beiter, P.; Marquis, M.; Hammond, R.; Shields, M. Offshore Wind Market Report: 2022 Edition. Technical report, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2022.
  2. Europe, W. Floating offshore wind vision statement. Wind Europe: Brussels, Belgium 2017.
  3. C, O.M.H.; Shadman, M.; Amiri, M.M.; Silva, C.; Estefen, S.F.; La Rovere, E. Environmental impacts of offshore wind installation, operation and maintenance, and decommissioning activities: A case study of Brazil. Renewable and Sustainable Energy Reviews 2021, 144, 110994. [Google Scholar] [CrossRef]
  4. Sánchez, S.; López-Gutiérrez, J.S.; Negro, V.; Esteban, M.D. Foundations in offshore wind farms: Evolution, characteristics and range of use. Analysis of main dimensional parameters in monopile foundations. Journal of Marine Science and Engineering 2019, 7, 441. [Google Scholar] [CrossRef]
  5. Faraggiana, E.; Giorgi, G.; Sirigu, M.; Ghigo, A.; Bracco, G.; Mattiazzo, G. A review of numerical modelling and optimisation of the floating support structure for offshore wind turbines. Journal of Ocean Engineering and Marine Energy 2022, 8, 433–456. [Google Scholar] [CrossRef]
  6. Liu, Y.; Li, S.; Yi, Q.; Chen, D. Developments in semi-submersible floating foundations supporting wind turbines: A comprehensive review. Renewable and Sustainable Energy Reviews 2016, 60, 433–449. [Google Scholar] [CrossRef]
  7. Roddier, D.; Cermelli, C.; Weinstein, A. WindFloat: a floating foundation for offshore wind turbines—part I: design basis and qualification process. International Conference on Offshore Mechanics and Arctic Engineering, 2009, Vol. 43444, pp. 845–853.
  8. Subbulakshmi, A.; Verma, M.; Keerthana, M.; Sasmal, S.; Harikrishna, P.; Kapuria, S. Recent advances in experimental and numerical methods for dynamic analysis of floating offshore wind turbines—An integrated review. Renewable and Sustainable Energy Reviews 2022, 164, 112525. [Google Scholar] [CrossRef]
  9. Yagihashi, K.; Tateno, Y.; Sakakibara, H.; Manabe, H. Dynamic cable installation for Fukushima floating offshore wind farm demonstration project. Proceeding Jicable, 2015.
  10. Umoh, K.; Lemon, M. Drivers for and barriers to the take up of floating offshore wind technology: A comparison of Scotland and South Africa. Energies 2020, 13, 5618. [Google Scholar] [CrossRef]
  11. Robertson, A.; Jonkman, J.; Vorpahl, F.; Popko, W.; Qvist, J.; Frøyd, L.; Chen, X.; Azcona, J.; Uzunoglu, E.; Guedes Soares, C. ; others. Offshore code comparison collaboration continuation within IEA wind task 30: Phase II results regarding a floating semisubmersible wind system. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2014, Vol. 45547, p. V09BT09A012.
  12. Mahfouz, M.Y.; Molins, C.; Trubat, P.; Hernández, S.; Vigara, F.; Pegalajar-Jurado, A.; Bredmose, H.; Salari, M. Response of the International Energy Agency (IEA) Wind 15 MW WindCrete and Activefloat floating wind turbines to wind and second-order waves. Wind Energy Science 2021, 6, 867–883. [Google Scholar] [CrossRef]
  13. Allen, C.; Viscelli, A.; Dagher, H.; Goupee, A.; Gaertner, E.; Abbas, N.; Hall, M.; Barter, G. Definition of the UMaine VolturnUS-S reference platform developed for the IEA Wind 15-megawatt offshore reference wind turbine. Technical report, National Renewable Energy Lab.(NREL), Golden, CO (United States); Univ. of …, 2020.
  14. Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. WindFloat: A floating foundation for offshore wind turbines. Journal of renewable and sustainable energy 2010, 2, 033104. [Google Scholar] [CrossRef]
  15. Sauder, T.; Chabaud, V.; Thys, M.; Bachynski, E.E.; Sæther, L.O. Real-time hybrid model testing of a braceless semi-submersible wind turbine: Part I—The hybrid approach. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2016, Vol. 49972, p. V006T09A039.
  16. Cermelli, C.; Roddier, D.; Aubault, A. WindFloat: a floating foundation for offshore wind turbines—part II: hydrodynamics analysis. International conference on offshore mechanics and arctic engineering, 2009, Vol. 43444, pp. 135–143.
  17. Luan, C. Design and analysis for a steel braceless semi-submersible hull for supporting a 5-MW horizontal axis wind turbine 2018.
  18. Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the semisubmersible floating system for phase II of OC4. Technical report, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2014.
  19. Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW reference wind turbine for offshore system development. Technical report, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2009.
  20. Liu, Z.; Fan, Y.; Wang, W.; Qian, G. Numerical study of a proposed semi-submersible floating platform with different numbers of offset columns based on the DeepCwind prototype for improving the wave-resistance ability. Applied Sciences 2019, 9, 1255. [Google Scholar] [CrossRef]
  21. James, R.; Ros, M.C. Floating offshore wind: market and technology review. The Carbon Trust 2015, 439. [Google Scholar]
  22. Viselli, A.M.; Goupee, A.J.; Dagher, H.J. Model test of a 1: 8-scale floating wind turbine offshore in the gulf of maine. Journal of Offshore Mechanics and Arctic Engineering 2015, 137. [Google Scholar] [CrossRef]
  23. Mathern, A.; von der Haar, C.; Marx, S. Concrete support structures for offshore wind turbines: Current status, challenges, and future trends. Energies 2021, 14, 1995. [Google Scholar] [CrossRef]
  24. Johansen, T.; Nissen-Lie, T.; Aaberg Midtsund, M.; Wiley, T.; Bayat, A.; Fulger, S.; O’Malley, J.; Færøy Sæbo, E. Comparative study of concrete and steel substructures for FOWT. Technical report, Det Norske Veritas (DNV), 2022.
  25. Lamei, A.; Hayatdavoodi, M. On motion analysis and elastic response of floating offshore wind turbines. Journal of Ocean Engineering and Marine Energy 2020, 6, 71–90. [Google Scholar] [CrossRef]
  26. Shi, W.; Liu, Y.; Wang, W.; Cui, L.; Li, X. Numerical study of an ice-offshore wind turbine structure interaction with the pile-soil interaction under stochastic wind loads. Ocean Engineering 2023, 273, 113984. [Google Scholar] [CrossRef]
  27. Musial, W.; Butterfield, S.; Boone, A. Feasibility of floating platform systems for wind turbines. 42nd AIAA aerospace sciences meeting and exhibit, 2004, p. 1007.
  28. Veers, P.; Bottasso, C.; Manuel, L.; Naughton, J.; Pao, L.; Paquette, J.; Robertson, A.; Robinson, M.; Ananthan, S.; Barlas, A.; others. Grand Challenges in the Design, Manufacture, and Operation of Future Wind Turbine Systems. Wind Energy Science Discussions 2022, pp. 1–102.
  29. Sebastian, T. The aerodynamics and near wake of an offshore floating horizontal axis wind turbine 2012.
  30. Matha, D.; Cruz, J.; Masciola, M.; Bachynski, E.E.; Atcheson, M.; Goupee, A.J.; Gueydon, S.M.; Robertson, A.N. Modelling of Floating Offshore Wind Technologies. Floating Offshore Wind Energy: The Next Generation of Wind Energy 2016, pp. 133–240.
  31. Henderson, A.; Collu, M.; Masciola, M. Floating offshore wind energy: The next generation of wind energy, chapter Overview of floating offshore wind technologies. Springer 2016, 15, 124. [Google Scholar]
  32. Catapult, O. Floating offshore wind: Cost reduction pathways to subsidy free. ORE CATAPULT report 2022.
  33. Sykes, V.; Collu, M.; Coraddu, A. A review and analysis of optimisation techniques applied to floating offshore wind platforms. Ocean Engineering 2023, 285, 115247. [Google Scholar] [CrossRef]
  34. Viré, A.; Xiang, J.; Piggott, M.; Cotter, C.; Pain, C. Towards the fully-coupled numerical modelling of floating wind turbines. Energy Procedia 2013, 35, 43–51. [Google Scholar] [CrossRef]
  35. Li, Y.; Castro, A.; Sinokrot, T.; Prescott, W.; Carrica, P. Coupled multi-body dynamics and CFD for wind turbine simulation including explicit wind turbulence. Renewable Energy 2015, 76, 338–361. [Google Scholar] [CrossRef]
  36. Campanile, A.; Piscopo, V.; Scamardella, A. Mooring design and selection for floating offshore wind turbines on intermediate and deep water depths. Ocean Engineering 2018, 148, 349–360. [Google Scholar] [CrossRef]
  37. Collu, M.; Brennan, F.; Patel, M. Conceptual design of a floating support structure for an offshore vertical axis wind turbine: the lessons learnt. Ships and Offshore Structures 2014, 9, 3–21. [Google Scholar] [CrossRef]
  38. Dou, S.; Pegalajar-Jurado, A.; Wang, S.; Bredmose, H.; Stolpe, M. Optimization of floating wind turbine support structures using frequency-domain analysis and analytical gradients. Journal of Physics: Conference Series. IOP Publishing, 2020, Vol. 1618, p. 042028.
  39. Lemmer, F.; Yu, W.; Luhmann, B.; Schlipf, D.; Cheng, P.W. Multibody modeling for concept-level floating offshore wind turbine design. Multibody System Dynamics 2020, 49, 203–236. [Google Scholar] [CrossRef]
  40. Tran, T.T.; Kim, D.H. The aerodynamic interference effects of a floating offshore wind turbine experiencing platform pitching and yawing motions. Journal of Mechanical Science and Technology 2015, 29, 549–561. [Google Scholar] [CrossRef]
  41. Bauchau, O.A. Computational schemes for flexible, nonlinear multi-body systems. Multibody System Dynamics 1998, 2, 169–225. [Google Scholar] [CrossRef]
  42. Otter, A.; Murphy, J.; Pakrashi, V.; Robertson, A.; Desmond, C. A review of modelling techniques for floating offshore wind turbines. Wind Energy 2022, 25, 831–857. [Google Scholar] [CrossRef]
  43. Jonkman, J.; Wright, A.; Barter, G.; Hall, M.; Allison, J.; Herber, D.R. Functional requirements for the WEIS toolset to enable controls co-design of floating offshore wind turbines. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2021, Vol. 84768, p. V001T01A007.
  44. Rathod, U.H.; Kulkarni, V.; Saha, U.K. On the application of machine learning in savonius wind turbine technology: an estimation of turbine performance using artificial neural network and genetic expression programming. Journal of Energy Resources Technology 2022, 144. [Google Scholar] [CrossRef]
  45. Jiang, X.; Day, S.; Clelland, D.; Liang, X. Analysis and real-time prediction of the full-scale thrust for floating wind turbine based on artificial intelligence. Ocean Engineering 2019, 175, 207–216. [Google Scholar] [CrossRef]
  46. Lemmer, F.; Yu, W.; Steinacker, H.; Skandali, D.; Raach, S. Advances on reduced-order modeling of floating offshore wind turbines. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2021, Vol. 85192, p. V009T09A034.
  47. O’Donnell, D.; Murphy, J.; Desmond, C.; Jaksic, V.; Pakrashi, V. Tuned liquid column damper based reduction of dynamic responses of scaled offshore platforms in different ocean wave basins. Journal of Physics: Conference Series. IOP Publishing, 2017, Vol. 842, p. 012043.
  48. Lackner, M.A. An investigation of variable power collective pitch control for load mitigation of floating offshore wind turbines. Wind energy 2013, 16, 435–444. [Google Scholar] [CrossRef]
  49. Savenije, F.; Peeringa, J. Control development for floating wind. Journal of Physics: Conference Series. IOP Publishing, 2014, Vol. 524, p. 012090.
  50. Han, D.; Li, X.; Wang, W.; Su, X. Dynamic modeling and vibration control of barge offshore wind turbine using tuned liquid column damper in floating platform. Ocean Engineering 2023, 276, 114299. [Google Scholar] [CrossRef]
  51. Salic, T.; Charpentier, J.F.; Benbouzid, M.; Le Boulluec, M. Control strategies for floating offshore wind turbine: challenges and trends. Electronics 2019, 8, 1185. [Google Scholar] [CrossRef]
  52. Jonkman, J.M.; Buhl, M. FAST User’s Guide, Nat. Renew. Energy Lab., Golden, CO, USA, Rep. NREL/EL-500-38230 (previously NREL/EL-500-29798) 2005.
  53. Jonkman, J.M.; Wright, A.D.; Hayman, G.J.; Robertson, A.N. Full-system linearization for floating offshore wind turbines in OpenFAST. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2018, Vol. 51975, p. V001T01A028.
  54. Liu, Y.; Ge, D.; Bai, X.; Li, L. A CFD Study of Vortex-Induced Motions of a Semi-Submersible Floating Offshore Wind Turbine. Energies 2023, 16, 698. [Google Scholar] [CrossRef]
  55. Li, H.; Bachynski-Polić, E.E. Experimental and numerically obtained low-frequency radiation characteristics of the OC5-DeepCwind semisubmersible. Ocean Engineering 2021, 232, 109130. [Google Scholar] [CrossRef]
  56. Li, H.; Bachynski-Polić, E.E. Validation and application of nonlinear hydrodynamics from CFD in an engineering model of a semi-submersible floating wind turbine. Marine Structures 2021, 79, 103054. [Google Scholar] [CrossRef]
  57. Li, H.; Bachynski-Polić, E.E. Analysis of difference-frequency wave loads and quadratic transfer functions on a restrained semi-submersible floating wind turbine. Ocean Engineering 2021, 232, 109165. [Google Scholar] [CrossRef]
  58. Zhang, D.; Paterson, E. A study of wave forces on an offshore platform by direct CFD and Morison equation. E3S Web of Conferences. EDP Sciences, 2015, Vol. 5, p. 04002.
  59. Chen, P.; Chen, J.; Hu, Z. Review of experimental-numerical methodologies and challenges for floating offshore wind turbines. Journal of Marine Science and Application 2020, 19, 339–361. [Google Scholar] [CrossRef]
  60. Hmedi, M.; Uzunoglu, E.; Soares, C.G. Review of hybrid model testing approaches for floating wind turbines. Trends in Maritime Technology and Engineering Volume 2 2022, pp. 421–428.
  61. Chen, C.; Ma, Y.; Fan, T. Review of model experimental methods focusing on aerodynamic simulation of floating offshore wind turbines. Renewable and Sustainable Energy Reviews 2022, 157, 112036. [Google Scholar] [CrossRef]
  62. Gueydon, S.; Bayati, I.; de Ridder, E. Discussion of solutions for basin model tests of FOWTs in combined waves and wind. Ocean Engineering 2020, 209, 107288. [Google Scholar] [CrossRef]
  63. Benitz, M.A.; Schmidt, D.P.; Lackner, M.A.; Stewart, G.M.; Jonkman, J.; Robertson, A. Validation of hydrodynamic load models using CFD for the OC4-DeepCwind semisubmersible. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2015, Vol. 56574, p. V009T09A037.
  64. Benitz, M.A.; Schmidt, D.P.; Lackner, M.A.; Stewart, G.M.; Jonkman, J.; Robertson, A. Comparison of hydrodynamic load predictions between reduced order engineering models and computational fluid dynamics for the oc4-deepcwind semi-submersible. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2014, Vol. 45547, p. V09BT09A006.
  65. Tran, T.T.; Kim, D.H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine. Journal of wind engineering and industrial aerodynamics 2015, 147, 104–119. [Google Scholar] [CrossRef]
  66. Bruinsma, N.; Paulsen, B.; Jacobsen, N. Validation and application of a fully nonlinear numerical wave tank for simulating floating offshore wind turbines. Ocean Engineering 2018, 147, 647–658. [Google Scholar] [CrossRef]
  67. Burmester, S.; Vaz, G.; Gueydon, S.; el Moctar, O. Investigation of a semi-submersible floating wind turbine in surge decay using CFD. Ship Technology Research 2020, 67, 2–14. [Google Scholar] [CrossRef]
  68. Zhao, W.; Wan, D. Numerical study of interactions between phase II of OC4 wind turbine and its semi-submersible floating support system. J. Ocean Wind Energy 2015, 2, 45–53. [Google Scholar]
  69. Ferziger, J.H.; Perić, M.; Street, R.L. Computational methods for fluid dynamics; Vol. 3, Springer, 2002.
  70. Davidson, P.A. Turbulence: an introduction for scientists and engineers; Oxford university press, 2015.
  71. Boussinesq, J. Theorie de l’ecoulement tourbillant. Mem. Acad. Sci. 1877, 23, 46. [Google Scholar]
  72. Prandtl, L. Bemerkungen zur Theorie der freien Turbulenz. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik 1942, 22, 241–243. [Google Scholar] [CrossRef]
  73. Ammara, I.; Leclerc, C.; Masson, C. A viscous three-dimensional differential/actuator-disk method for the aerodynamic analysis of wind farms. J. Sol. Energy Eng. 2002, 124, 345–356. [Google Scholar] [CrossRef]
  74. Burmester, S.; Vaz, G.; el Moctar, O. Towards credible CFD simulations for floating offshore wind turbines. Ocean Engineering 2020, 209, 107237. [Google Scholar] [CrossRef]
  75. Liu, Y.; Xiao, Q. Development of a fully coupled aero-hydro-mooring-elastic tool for floating offshore wind turbines. Journal of Hydrodynamics 2019, 31, 21–33. [Google Scholar] [CrossRef]
  76. Zhou, Y.; Xiao, Q.; Liu, Y.; Incecik, A.; Peyrard, C.; Li, S.; Pan, G. Numerical modelling of dynamic responses of a floating offshore wind turbine subject to focused waves. Energies 2019, 12, 3482. [Google Scholar] [CrossRef]
  77. Muzaferija, S. Computation of free surface flows using interface-tracking and interface-capturing methods. Nonlinear water-wave interaction. Computational Mechanics, Southampton 1998.
  78. Bertram, V. Practical ship hydrodynamics; Elsevier, 2011.
  79. Calderer, A.; Guo, X.; Shen, L.; Sotiropoulos, F. Coupled fluid-structure interaction simulation of floating offshore wind turbines and waves: a large eddy simulation approach. Journal of Physics: Conference Series. IOP Publishing, 2014, Vol. 524, p. 012091.
  80. Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of computational physics 1981, 39, 201–225. [Google Scholar] [CrossRef]
  81. Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. Journal of Computational physics 1994, 114, 146–159. [Google Scholar] [CrossRef]
  82. Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C.; Wan, D. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines. Renewable Energy 2017, 112, 280–301. [Google Scholar] [CrossRef]
  83. Yan, J.; Korobenko, A.; Deng, X.; Bazilevs, Y. Computational free-surface fluid–structure interaction with application to floating offshore wind turbines. Computers & Fluids 2016, 141, 155–174. [Google Scholar]
  84. Vaz, G.; Jaouen, F.; Hoekstra, M. Free-surface viscous flow computations: Validation of URANS code FRESCO. International Conference on Offshore Mechanics and Arctic Engineering, 2009, Vol. 43451, pp. 425–437.
  85. Rapuc, S.; Crepier, P.; Jaouen, F.; Bunnik, T.; Regnier, P. Towards guidelines for consistent wave propagation in CFD simulations. In Technology and Science for the Ships of the Future; IOS Press, 2018; pp. 515–524.
  86. Park, J.C.; Kim, M.H.; Miyata, H. Fully non-linear free-surface simulations by a 3D viscous numerical wave tank. International Journal for Numerical Methods in Fluids 1999, 29, 685–703. [Google Scholar] [CrossRef]
  87. Porté-Agel, F.; Lu, H.; Wu, Y.T. A large-eddy simulation framework for wind energy applications. The fifth international symposium on computational wind engineering. Chapel Hill North Carolina, 2010, Vol. 23, p. 27.
  88. Mehta, D.; Van Zuijlen, A.; Koren, B.; Holierhoek, J.; Bijl, H. Large Eddy Simulation of wind farm aerodynamics: A review. Journal of Wind Engineering and Industrial Aerodynamics 2014, 133, 1–17. [Google Scholar] [CrossRef]
  89. Zhang, W.; Markfort, C.D.; Porté-Agel, F. Near-wake flow structure downwind of a wind turbine in a turbulent boundary layer. Experiments in fluids 2012, 52, 1219–1235. [Google Scholar] [CrossRef]
  90. Sanderse, B.; Van der Pijl, S.; Koren, B. Review of computational fluid dynamics for wind turbine wake aerodynamics. Wind energy 2011, 14, 799–819. [Google Scholar] [CrossRef]
  91. Porté-Agel, F.; Lu, H.; Wu, Y.T. Interaction between large wind farms and the atmospheric boundary layer. Procedia Iutam 2014, 10, 307–318. [Google Scholar] [CrossRef]
  92. Leonard, A. Energy cascade in large-eddy simulations of turbulent fluid flows. In Advances in geophysics; Elsevier, 1975; Vol. 18, pp. 237–248.
  93. Nakhchi, M.; Naung, S.W.; Rahmati, M. A novel hybrid control strategy of wind turbine wakes in tandem configuration to improve power production. Energy Conversion and Management 2022, 260, 115575. [Google Scholar] [CrossRef]
  94. Wu, C.; Wang, Q.; Yuan, R.; Luo, K.; Fan, J. Large Eddy Simulation of the Layout Effects on Wind Farm Performance Coupling With Wind Turbine Control Strategies. Journal of Energy Resources Technology 2022, 144, 051304. [Google Scholar] [CrossRef]
  95. Lilly, D.K. The representation of small-scale turbulence in numerical simulation experiments. IBM Form 1967, pp. 195–210.
  96. Amiri, M.M.; Shadman, M.; Estefen, S.F. URANS simulations of a horizontal axis wind turbine under stall condition using Reynolds stress turbulence models. Energy 2020, 213, 118766. [Google Scholar] [CrossRef]
  97. Abdulqadir, S.A.; Iacovides, H.; Nasser, A. The physical modelling and aerodynamics of turbulent flows around horizontal axis wind turbines. Energy 2017, 119, 767–799. [Google Scholar] [CrossRef]
  98. Porté-Agel, F.; Meneveau, C.; Parlange, M.B. A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. Journal of Fluid Mechanics 2000, 415, 261–284. [Google Scholar] [CrossRef]
  99. Sørensen, J.N.; Mikkelsen, R.F.; Henningson, D.S.; Ivanell, S.; Sarmast, S.; Andersen, S.J. Simulation of wind turbine wakes using the actuator line technique. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2015, 373, 20140071. [Google Scholar] [CrossRef]
  100. Abkar, M.; Moin, P. Large-eddy simulation of thermally stratified atmospheric boundary-layer flow using a minimum dissipation model. Boundary-layer meteorology 2017, 165, 405–419. [Google Scholar] [CrossRef]
  101. Ivanell, S.; Sørensen, J.N.; Mikkelsen, R.; Henningson, D. Analysis of numerically generated wake structures. Wind Energy: An International Journal for Progress and Applications in Wind Power Conversion Technology 2009, 12, 63–80. [Google Scholar] [CrossRef]
  102. Sorensen, J.N.; Shen, W.Z. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
  103. Whale, J.; Anderson, C.; Bareiss, R.; Wagner, S. An experimental and numerical study of the vortex structure in the wake of a wind turbine. Journal of Wind Engineering and Industrial Aerodynamics 2000, 84, 1–21. [Google Scholar] [CrossRef]
  104. Lundquist, J.K.; Xiaoxia, G.; Aitken, M.; Quelet, P.T.; Rana, J.; Rhodes, M.E.; St Martin, C.; Tay, K.; Worsnop, R.; Irvin, S. ; others. Wind turbine wake variability in a large wind farm, observed by scanning lidar. AGU Fall Meeting Abstracts, 2014, Vol. 2014, pp. A11G–3076.
  105. Thé, J.; Yu, H. A critical review on the simulations of wind turbine aerodynamics focusing on hybrid RANS-LES methods. Energy 2017, 138, 257–289. [Google Scholar] [CrossRef]
  106. Lei, H.; Zhou, D.; Bao, Y.; Chen, C.; Ma, N.; Han, Z. Numerical simulations of the unsteady aerodynamics of a floating vertical axis wind turbine in surge motion. Energy 2017, 127, 1–17. [Google Scholar] [CrossRef]
  107. Li, Y.; Castro, A.; Martin, J.; Sinokrot, T.; Prescott, W.; Carrica, P. Coupled computational fluid dynamics/multibody dynamics method for wind turbine aero-servo-elastic simulation including drivetrain dynamics. Renewable Energy 2017, 101, 1037–1051. [Google Scholar] [CrossRef]
  108. Weihing, P.; Meister, K.; Schulz, C.; Lutz, T.; Krämer, E. CFD simulations on interference effects between offshore wind turbines. Journal of Physics: Conference Series. IOP Publishing, 2014, Vol. 524, p. 012143.
  109. O’Brien, J.; Young, T.; O’Mahoney, D.; Griffin, P. Horizontal axis wind turbine research: A review of commercial CFD, FE codes and experimental practices. Progress in Aerospace Sciences 2017, 92, 1–24. [Google Scholar] [CrossRef]
  110. Bai, C.J.; Wang, W.C. Review of computational and experimental approaches to analysis of aerodynamic performance in horizontal-axis wind turbines (HAWTs). Renewable and Sustainable Energy Reviews 2016, 63, 506–519. [Google Scholar] [CrossRef]
  111. Naderi, S.; Parvanehmasiha, S.; Torabi, F. Modeling of horizontal axis wind turbine wakes in Horns Rev offshore wind farm using an improved actuator disc model coupled with computational fluid dynamic. Energy Conversion and Management 2018, 171, 953–968. [Google Scholar] [CrossRef]
  112. O’brien, J.; Young, T.; Early, J.; Griffin, P. An assessment of commercial CFD turbulence models for near wake HAWT modelling. Journal of Wind Engineering and Industrial Aerodynamics 2018, 176, 32–53. [Google Scholar] [CrossRef]
  113. Politis, E.S.; Prospathopoulos, J.; Cabezon, D.; Hansen, K.S.; Chaviaropoulos, P.; Barthelmie, R.J. Modeling wake effects in large wind farms in complex terrain: the problem, the methods and the issues. Wind Energy 2012, 15, 161–182. [Google Scholar] [CrossRef]
  114. Alinot, C.; Masson, C. Aerodynamic simulations of wind turbines operating in atmospheric boundary layer with various thermal stratifications. Wind Energy Symposium, 2002, Vol. 7476, pp. 206–215.
  115. Vogel, C.R.; Willden, R.H. Investigation of wind turbine wake superposition models using Reynolds-averaged Navier-Stokes simulations. Wind Energy 2020, 23, 593–607. [Google Scholar] [CrossRef]
  116. Rezaeiha, A.; Micallef, D. Wake interactions of two tandem floating offshore wind turbines: CFD analysis using actuator disc model. Renewable Energy 2021, 179, 859–876. [Google Scholar] [CrossRef]
  117. Rezaeiha, A.; Montazeri, H.; Blocken, B. On the accuracy of turbulence models for CFD simulations of vertical axis wind turbines. Energy 2019, 180, 838–857. [Google Scholar] [CrossRef]
  118. Pinto, M.L.; Franzini, G.R.; Simos, A.N. A CFD analysis of NREL’s 5MW wind turbine in full and model scales. Journal of Ocean Engineering and Marine Energy 2020, 6, 211–220. [Google Scholar] [CrossRef]
  119. Antonini, E.G.; Romero, D.A.; Amon, C.H. Improving CFD wind farm simulations incorporating wind direction uncertainty. Renewable Energy 2019, 133, 1011–1023. [Google Scholar] [CrossRef]
  120. Zang, Y.; Street, R.L.; Koseff, J.R. A dynamic mixed subgrid-scale model and its application to turbulent recirculating flows. Physics of Fluids A: Fluid Dynamics 1993, 5, 3186–3196. [Google Scholar] [CrossRef]
  121. Bardina, J. Improved turbulence models based on large eddy simulation of homogeneous, incompressible, turbulent flows; Stanford University, 1983.
  122. Schumann, U. Realizability of Reynolds-stress turbulence models. The Physics of Fluids 1977, 20, 721–725. [Google Scholar] [CrossRef]
  123. Réthoré, P.E. Wind turbine wake in atmospheric turbulence 2009.
  124. Taulbee, D.B. An improved algebraic Reynolds stress model and corresponding nonlinear stress model. Physics of Fluids A: Fluid Dynamics 1992, 4, 2555–2561. [Google Scholar] [CrossRef]
  125. Gomez-Elvira, R.; Crespo, A.; Migoya, E.; Manuel, F.; Hernández, J. Anisotropy of turbulence in wind turbine wakes. Journal of wind engineering and industrial aerodynamics 2005, 93, 797–814. [Google Scholar] [CrossRef]
  126. Cabezón Martínez, D.; Sanz Rodrigo, J.; Martí Pérez, I.; Crespo Martínez, A. CFD modelling of the interaction between the Surface Boundary Layer and rotor wake. Comparison of results obtained with different turbulence models and mesh strategies 2009.
  127. Cabezón, D.; Migoya, E.; Crespo, A. Comparison of turbulence models for the computational fluid dynamics simulation of wind turbine wakes in the atmospheric boundary layer. Wind Energy 2011, 14, 909–921. [Google Scholar] [CrossRef]
  128. Yang, X.; Sotiropoulos, F. On the predictive capabilities of LES-actuator disk model in simulating turbulence past wind turbines and farms. 2013 American Control Conference. IEEE, 2013, pp. 2878–2883.
  129. Arabgolarcheh, A.; Jannesarahmadi, S.; Benini, E. Modeling of near wake characteristics in floating offshore wind turbines using an actuator line method. Renewable Energy 2022, 185, 871–887. [Google Scholar] [CrossRef]
  130. Shourangiz-Haghighi, A.; Haghnegahdar, M.A.; Wang, L.; Mussetta, M.; Kolios, A.; Lander, M. State of the art in the optimisation of wind turbine performance using CFD. Archives of Computational Methods in Engineering 2020, 27, 413–431. [Google Scholar] [CrossRef]
  131. Reddy, J.N. Introduction to the finite element method; McGraw-Hill Education, 2019.
  132. Santo, G. Fluid-structure interaction simulations of wind turbines with composite blades. PhD thesis, Ghent University, 2019.
  133. Rajamohan, S.; Vinod, A.; Aditya, M.P.V.S.; Vadivudaiyanayaki, H.G.; Arıcı, M.; Nižetić, S.; Le, T.T.; Hidayat, R.; Nguyen, D.T.; others. Approaches in performance and structural analysis of wind turbines–A review. Sustainable Energy Technologies and Assessments 2022, 53, 102570. [Google Scholar] [CrossRef]
  134. Nikishkov, G. Introduction to the finite element method. University of Aizu 2004, pp. 1–70.
  135. Jonkman, J.; Musial, W. Offshore code comparison collaboration (OC3) for IEA Wind Task 23 offshore wind technology and deployment. Technical report, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2010.
  136. Lienard, C.; Boisard, R.; Daudin, C. Aerodynamic behavior of a floating offshore wind turbine. AIAA Journal 2020, 58, 3835–3847. [Google Scholar] [CrossRef]
  137. Li, P.; Cheng, P.; Wan, D.; Xiao, Q. Numerical simulations of wake flows of floating offshore wind turbines by unsteady actuator line model. Proceedings of the 9th international workshop on ship and marine hydrodynamics, Glasgow, UK, 2015, pp. 26–28.
  138. Cheng, P.; Wan, D.; Hu, C. Unsteady aerodynamic simulations of floating offshore wind turbines with overset grid technology. The 26th International Ocean and Polar Engineering Conference. OnePetro, 2016.
  139. Tran, T.T.; Kim, D.H. A CFD study into the influence of unsteady aerodynamic interference on wind turbine surge motion. Renewable Energy 2016, 90, 204–228. [Google Scholar] [CrossRef]
  140. Tran, T.T.; Kim, D.H. The platform pitching motion of floating offshore wind turbine: A preliminary unsteady aerodynamic analysis. Journal of Wind Engineering and Industrial Aerodynamics 2015, 142, 65–81. [Google Scholar] [CrossRef]
  141. Wu, C.H.K.; Nguyen, V.T. Aerodynamic simulations of offshore floating wind turbine in platform-induced pitching motion. Wind Energy 2017, 20, 835–858. [Google Scholar] [CrossRef]
  142. Arabgolarcheh, A.; Rouhollahi, A.; Benini, E. Analysis of middle-to-far wake behind floating offshore wind turbines in the presence of multiple platform motions. Renewable Energy 2023, 208, 546–560. [Google Scholar] [CrossRef]
  143. Sayed, M.; Lutz, T.; Krämer, E.; Shayegan, S.; Wüchner, R. Aeroelastic analysis of 10 MW wind turbine using CFD–CSD explicit FSI-coupling approach. Journal of fluids and structures 2019, 87, 354–377. [Google Scholar] [CrossRef]
  144. Jahani, K.; Langlois, R.G.; Afagh, F.F. Structural dynamics of offshore Wind Turbines: A review. Ocean Engineering 2022, 251, 111136. [Google Scholar] [CrossRef]
  145. Ebrahimi, A.; Sekandari, M. Transient response of the flexible blade of horizontal-axis wind turbines in wind gusts and rapid yaw changes. Energy 2018, 145, 261–275. [Google Scholar] [CrossRef]
  146. Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Fluid–structure interaction simulations of a wind gust impacting on the blades of a large horizontal axis wind turbine. Energies 2020, 13, 509. [Google Scholar] [CrossRef]
  147. Hsu, M.C.; Bazilevs, Y. Fluid–structure interaction modeling of wind turbines: simulating the full machine. Computational Mechanics 2012, 50, 821–833. [Google Scholar] [CrossRef]
  148. Yeh, M.K.; Wang, C.H. Stress analysis of composite wind turbine blade by finite element method. IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2017, Vol. 241, p. 012015.
  149. Wang, L.; Quant, R.; Kolios, A. Fluid structure interaction modelling of horizontal-axis wind turbine blades based on CFD and FEA. Journal of Wind Engineering and Industrial Aerodynamics 2016, 158, 11–25. [Google Scholar] [CrossRef]
  150. Miao, W.; Li, C.; Wang, Y.; Xiang, B.; Liu, Q.; Deng, Y. Study of adaptive blades in extreme environment using fluid–structure interaction method. Journal of Fluids and Structures 2019, 91, 102734. [Google Scholar] [CrossRef]
  151. Tran, T.T.; Kim, D.H. A CFD study of coupled aerodynamic-hydrodynamic loads on a semisubmersible floating offshore wind turbine. Wind Energy 2018, 21, 70–85. [Google Scholar] [CrossRef]
  152. Cheng, P.; Huang, Y.; Wan, D. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Engineering 2019, 173, 183–196. [Google Scholar] [CrossRef]
  153. Li, P.; Wan, D.; Hu, C. Fully-coupled dynamic response of a semi-submerged floating wind turbine system in wind and waves. The 26th International Ocean and Polar Engineering Conference. OnePetro, 2016.
  154. Tran, T.T.; Kim, D.H. Fully coupled aero-hydrodynamic analysis of a semi-submersible FOWT using a dynamic fluid body interaction approach. Renewable energy 2016, 92, 244–261. [Google Scholar] [CrossRef]
  155. Zhang, Y.; Kim, B. A fully coupled computational fluid dynamics method for analysis of semi-submersible floating offshore wind turbines under wind-wave excitation conditions based on OC5 data. Applied sciences 2018, 8, 2314. [Google Scholar] [CrossRef]
  156. Feng, X.; Fang, J.; Lin, Y.; Chen, B.; Li, D.; Liu, H.; Gu, Y. Coupled aero-hydro-mooring dynamic analysis of floating offshore wind turbine under blade pitch motion. Physics of Fluids 2023. [Google Scholar]
  157. Munters, W.; Meyers, J. Dynamic strategies for yaw and induction control of wind farms based on large-eddy simulation and optimization. Energies 2018, 11, 177. [Google Scholar] [CrossRef]
  158. Englberger, A.; Dörnbrack, A. Impact of neutral boundary-layer turbulence on wind-turbine wakes: a numerical modelling study. Boundary-Layer Meteorology 2017, 162, 427–449. [Google Scholar] [CrossRef]
  159. Hsieh, A.S.; Brown, K.A.; DeVelder, N.B.; Herges, T.G.; Knaus, R.C.; Sakievich, P.J.; Cheung, L.C.; Houchens, B.C.; Blaylock, M.L.; Maniaci, D.C. High-fidelity wind farm simulation methodology with experimental validation. Journal of Wind Engineering and Industrial Aerodynamics 2021, 218, 104754. [Google Scholar] [CrossRef]
  160. Richards, P.; Hoxey, R. Appropriate boundary conditions for computational wind engineering models using the k-ϵ turbulence model. Journal of wind engineering and industrial aerodynamics 1993, 46, 145–153. [Google Scholar] [CrossRef]
  161. Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: wall function problems. Atmospheric environment 2007, 41, 238–252. [Google Scholar] [CrossRef]
  162. Richards, P.; Norris, S. Appropriate boundary conditions for computational wind engineering models revisited. Journal of Wind Engineering and Industrial Aerodynamics 2011, 99, 257–266. [Google Scholar] [CrossRef]
  163. Yang, Y.; Xie, Z.; Gu, M. Consistent inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer for the SST k-ω model. Wind and Structures 2017, 24, 465–480. [Google Scholar] [CrossRef]
  164. Liu, Y.; Chen, D.; Li, S. The artificial generation of the equilibrium marine atmospheric boundary layer for the CFD simulation of offshore wind turbines. Journal of Wind Engineering and Industrial Aerodynamics 2018, 183, 44–54. [Google Scholar] [CrossRef]
  165. Wang, L.; Robertson, A.; Kim, J.; Jang, H.; Shen, Z.R.; Koop, A.; Bunnik, T.; Yu, K. Validation of CFD simulations of the moored DeepCwind offshore wind semisubmersible in irregular waves. Ocean Engineering 2022, 260, 112028. [Google Scholar] [CrossRef]
  166. Zhang, Y.; Xu, H.; Law, Y.; Santo, H.; Magee, A. Hydrodynamic analysis and validation of the floating DeepCwind semi-submersible under 3-h irregular wave with the HOS and CFD coupling method. Ocean Engineering 2023, 287, 115701. [Google Scholar] [CrossRef]
  167. Weihing, P.; Schulz, C.; Lutz, T.; Krämer, E. Comparison of the actuator line model with fully resolved simulations in complex environmental conditions. Journal of Physics: Conference Series. IOP Publishing, 2017, Vol. 854, p. 012049.
  168. Chakrabarti, S.K. Hydrodynamics of offshore structures; WIT press, 1987.
  169. Xu, K.; Shao, Y.; Gao, Z.; Moan, T. A study on fully nonlinear wave load effects on floating wind turbine. Journal of Fluids and Structures 2019, 88, 216–240. [Google Scholar] [CrossRef]
  170. Veritas, N. Environmental conditions and environmental loads; Det Norske Veritas Oslo, Norway, 2000.
  171. Faltinsen, O. Sea loads on ships and offshore structures; Vol. 1, Cambridge university press, 1993.
  172. Newman, J.N. Marine hydrodynamics; The MIT press, 2018.
  173. Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Dagher, H.; Gueydon, S.; Qvist, J.; Vittori, F.; Azcona, J.; Uzunoglu, E.; others. OC5 project phase II: validation of global loads of the DeepCwind floating semisubmersible wind turbine. Energy Procedia 2017, 137, 38–57. [Google Scholar] [CrossRef]
  174. Hu, C.; Sueyoshi, M.; Liu, C.; Liu, Y. Hydrodynamic analysis of a semi-submersible type floating wind turbine. The Eleventh ISOPE Pacific/Asia Offshore Mechanics Symposium. OnePetro, 2014.
  175. Lee, C.H.; Newman, J. Computation of wave effects using the panel method. WIT Transactions on State-of-the-art in Science and Engineering 2005, 18. [Google Scholar]
  176. Uçar, M.; Uzunoğlu, E.; Oğuz, E. Comparison and Evaluation of Open-Source Panel Method Codes against Commercial Codes 2021.
  177. Shokouhian, M.; Head, M.; Seo, J.; Schaffer, W.; Adams, G. Hydrodynamic response of a semi-submersible platform to support a wind turbine. Journal of Marine Engineering & Technology 2021, 20, 170–185. [Google Scholar]
  178. Bussemakers, P.J.M. Validation of aero-hydro-servo-elastic load and motion simulations in BHawC/OrcaFlex for the Hywind Scotland floating offshore wind farm. Master’s thesis, NTNU, 2020.
  179. Jonkman, J.M.; Robertson, A.; Hayman, G.J. HydroDyn user’s guide and theory manual. National Renewable Energy Laboratory 2014. [Google Scholar]
  180. Matha, D.; Schlipf, M.; Pereira, R.; Jonkman, J. Challenges in simulation of aerodynamics, hydrodynamics, and mooring-line dynamics of floating offshore wind turbines. ISOPE International Ocean and Polar Engineering Conference. ISOPE, 2011, pp. ISOPE–I.
  181. Duarte, T.M.; Sarmento, A.J.; Jonkman, J.M. Effects of second-order hydrodynamic forces on floating offshore wind turbines. 32nd ASME Wind Energy Symposium, 2014, p. 0361.
  182. Servan-Camas, B.; Gutierrez-Romero, J.E.; Garcia-Espinosa, J. A time-domain second-order FEM model for the wave diffraction-radiation problem. Validation with a semisubmersible platform. Marine Structures 2018, 58, 278–300. [Google Scholar] [CrossRef]
  183. Gutiérrez-Romero, J.E.; García-Espinosa, J.; Serván-Camas, B.; Zamora-Parra, B. Non-linear dynamic analysis of the response of moored floating structures. Marine Structures 2016, 49, 116–137. [Google Scholar] [CrossRef]
  184. Lucas, J. Comparison of first and second-order hydrodynamic results for floating offshore wind structures. GL Garrad Hassan, Report Ref: 11594br02a 2011.
  185. Bayati, I.; Gueydon, S.; Belloli, M. Study of the effect of water depth on potential flow solution of the OC4 semisubmersible floating offshore wind turbine. Energy Procedia 2015, 80, 168–176. [Google Scholar] [CrossRef]
  186. Zhang, L.; Shi, W.; Karimirad, M.; Michailides, C.; Jiang, Z. Second-order hydrodynamic effects on the response of three semisubmersible floating offshore wind turbines. Ocean Engineering 2020, 207, 107371. [Google Scholar] [CrossRef]
  187. Pinkster, J.A. Low frequency second order wave exciting forces on floating structures 1980.
  188. Cao, Q.; Xiao, L.; Guo, X.; Liu, M. Second-order responses of a conceptual semi-submersible 10 MW wind turbine using full quadratic transfer functions. Renewable Energy 2020, 153, 653–668. [Google Scholar] [CrossRef]
  189. Bayati, I.; Jonkman, J.; Robertson, A.; Platt, A. The effects of second-order hydrodynamics on a semisubmersible floating offshore wind turbine. Journal of Physics: Conference Series. IOP Publishing, 2014, Vol. 524, p. 012094.
  190. Coulling, A.J.; Goupee, A.J.; Robertson, A.N.; Jonkman, J.M. Importance of second-order difference-frequency wave-diffraction forces in the validation of a fast semi-submersible floating wind turbine model. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2013, Vol. 55423, p. V008T09A019.
  191. DNV, G. SESAM User Manual, WADAM, Wave Analysis by Diffraction and Morison theory. Høvik, Norway 2019.
  192. Ansys, A. AQWA theory manual. AQWA: Canonsburg, PA, USA 2013.
  193. Wendt, F.F.; Robertson, A.; Jonkman, J.M.; Hayman, G. Verification of new floating capabilities in FAST v8. 33rd Wind Energy Symposium, 2015, p. 1204.
  194. Lee, C.; Newman, J. WAMIT user manual, version 7.0. WAMIT Inc, Chestnut Hill, Massachusetts 2013.
  195. Lin, Y.H.; Yang, C.H. Hydrodynamic simulation of the semi-submersible wind float by investigating mooring systems in irregular waves. Applied Sciences 2020, 10, 4267. [Google Scholar] [CrossRef]
  196. Zhao, Z.; Wang, W.; Shi, W.; Li, X. Effects of second-order hydrodynamics on an ultra-large semi-submersible floating offshore wind turbine. Structures. Elsevier, 2020, Vol. 28, pp. 2260–2275.
  197. Kim, H.; Choung, J.; Jeon, G.Y. Design of mooring lines of floating offshore wind turbine in Jeju offshore area. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2014, Vol. 45530, p. V09AT09A042.
  198. López-Pavón, C.; Watai, R.A.; Ruggeri, F.; Simos, A.N.; Souto-Iglesias, A. Influence of wave induced second-order forces in semisubmersible FOWT mooring design. Journal of Offshore Mechanics and Arctic Engineering 2015, 137. [Google Scholar] [CrossRef]
  199. Niranjan, R.; Ramisetti, S.B. Insights from detailed numerical investigation of 15 MW offshore semi-submersible wind turbine using aero-hydro-servo-elastic code. Ocean Engineering 2022, 251, 111024. [Google Scholar] [CrossRef]
  200. Newman, J.N. Second-order slowly varying forces on vessels in irregular waves. Proceedings of the international symposium on dynamics of marine vehicles and structures in waves. London, UK, 1974, 1974.
  201. Simos, A.N.; Ruggeri, F.; Watai, R.A.; Souto-Iglesias, A.; Lopez-Pavon, C. Slow-drift of a floating wind turbine: An assessment of frequency-domain methods based on model tests. Renewable energy 2018, 116, 133–154. [Google Scholar] [CrossRef]
  202. Matos, V.; Simos, A.N.; Sphaier, S. Second-order resonant heave, roll and pitch motions of a deep-draft semi-submersible: Theoretical and experimental results. Ocean Engineering 2011, 38, 2227–2243. [Google Scholar] [CrossRef]
  203. Robertson, A.N.; Gueydon, S.; Bachynski, E.; Wang, L.; Jonkman, J.; Alarcon, D.; Amet, E.; Beardsell, A.; Bonnet, P.; Boudet, B. ; others. OC6 Phase I: Investigating the underprediction of low-frequency hydrodynamic loads and responses of a floating wind turbine. Journal of Physics: Conference Series. IOP Publishing, 2020, Vol. 1618, p. 032033.
  204. Wang, L.; Robertson, A.; Jonkman, J.; Yu, Y.H. OC6 phase I: Improvements to the OpenFAST predictions of nonlinear, low-frequency responses of a floating offshore wind turbine platform. Renewable Energy 2022, 187, 282–301. [Google Scholar] [CrossRef]
  205. Journée, J.M.; Massie, W. Offshore hydromechanics 2000.
  206. Qu, X.; Li, Y.; Tang, Y.; Hu, Z.; Zhang, P.; Yin, T. Dynamic response of spar-type floating offshore wind turbine in freak wave considering the wave-current interaction effect. Applied Ocean Research 2020, 100, 102178. [Google Scholar] [CrossRef]
  207. Li, Y.; Qu, X.; Liu, L.; Xie, P.; Yin, T.; Tang, Y. A numerical prediction on the transient response of a spar-type floating offshore wind turbine in freak waves. Journal of Offshore Mechanics and Arctic Engineering 2020, 142. [Google Scholar] [CrossRef]
  208. Chang, S.; Huang, W.; Liu, F.; Song, H. Influence of second-order wave force and focusing position on dynamic responses of tension leg platform under a freak wave. Ocean Engineering 2021, 242, 110126. [Google Scholar] [CrossRef]
  209. Cummins, W. The impulse response function and ship motions. Technical report, David Taylor Model Basin Washington DC, 1962.
  210. Gueydon, S.; Weller, S. Study of a floating foundation for wind turbines. Journal of Offshore Mechanics and Arctic Engineering 2013, 135. [Google Scholar] [CrossRef]
  211. Jeon, M.; Lee, S.; Lee, S. Unsteady aerodynamics of offshore floating wind turbines in platform pitching motion using vortex lattice method. Renewable Energy 2014, 65, 207–212. [Google Scholar] [CrossRef]
  212. Khan, M.A. Dynamic stall modeling for wind turbines 2018.
  213. Jeon, M.; Lee, S.; Kim, T.; Lee, S. Wake influence on dynamic load characteristics of offshore floating wind turbines. Aiaa Journal 2016, 54, 3535–3545. [Google Scholar] [CrossRef]
  214. Snel, H.; Schepers, J. Joint investigation of dynamic inflow effects and implementation of an engineering method 1995.
  215. Ferreira, C.; Yu, W.; Sala, A.; Viré, A. Dynamic inflow model for a floating horizontal axis wind turbine in surge motion. Wind Energy Science 2022, 7, 469–485. [Google Scholar] [CrossRef]
  216. Leishman, J.G. Challenges in modelling the unsteady aerodynamics of wind turbines. Wind Energy: An International Journal for Progress and Applications in Wind Power Conversion Technology 2002, 5, 85–132. [Google Scholar] [CrossRef]
  217. Leishman, J.G.; Beddoes, T. A Semi-Empirical model for dynamic stall. Journal of the American Helicopter society 1989, 34, 3–17. [Google Scholar]
  218. Suzuki, A. Application of dynamic inflow theory to wind turbine rotors; The University of Utah, 2000.
  219. Moriarty, P.J.; Hansen, A.C. AeroDyn theory manual. Technical report, National Renewable Energy Lab., Golden, CO (US), 2005.
  220. Sebastian, T.; Lackner, M.A. Development of a free vortex wake method code for offshore floating wind turbines. Renewable Energy 2012, 46, 269–275. [Google Scholar] [CrossRef]
  221. Robertson, A.; Jonkman, J.; Musial, W.; Vorpahl, F.; Popko, W. Offshore code comparison collaboration, continuation: Phase II results of a floating semisubmersible wind system. Technical report, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2013.
  222. Chuang, Z.; Liu, S.; Lu, Y. Influence of second order wave excitation loads on coupled response of an offshore floating wind turbine. International Journal of Naval Architecture and Ocean Engineering 2020, 12, 367–375. [Google Scholar] [CrossRef]
  223. Veritas, D.N. Sesam user manual. Hovik, Norway 2011.
  224. Heinz, J.C.; Sørensen, N.N.; Zahle, F. Fluid–structure interaction computations for geometrically resolved rotor simulations using CFD. Wind Energy 2016, 19, 2205–2221. [Google Scholar] [CrossRef]
  225. Lee, H.; Lee, D.J. Effects of platform motions on aerodynamic performance and unsteady wake evolution of a floating offshore wind turbine. Renewable Energy 2019, 143, 9–23. [Google Scholar] [CrossRef]
  226. Shaler, K.; Branlard, E.; Platt, A.; Jonkman, J. Preliminary introduction of a free vortex wake method into OpenFAST. Journal of Physics: Conference Series. IOP Publishing, 2020, Vol. 1452, p. 012064.
  227. Lee, H.; Sengupta, B.; Araghizadeh, M.; Myong, R. Review of vortex methods for rotor aerodynamics and wake dynamics. Advances in Aerodynamics 2022, 4, 20. [Google Scholar] [CrossRef]
  228. Winckelmans, G.; Leonard, A. Contributions to vortex particle methods for the computation of three-dimensional incompressible unsteady flows. Journal of Computational Physics 1993, 109, 247–273. [Google Scholar] [CrossRef]
  229. Rosenhead, L. The formation of vortices from a surface of discontinuity. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 1931, 134, 170–192. [Google Scholar]
  230. Branlard, E. Wind turbine aerodynamics and vorticity-based methods: Fundamentals and recent applications 2017.
  231. Van Garrel, A. Development of a wind turbine aerodynamics simulation module 2003.
  232. Martín-San-Román, R.; Benito-Cia, P.; Azcona-Armendáriz, J.; Cuerva-Tejero, A. Validation of a free vortex filament wake module for the integrated simulation of multi-rotor wind turbines. Renewable Energy 2021, 179, 1706–1718. [Google Scholar] [CrossRef]
  233. Sebastian, T.; Lackner, M. Analysis of the induction and wake evolution of an offshore floating wind turbine. Energies 2012, 5, 968–1000. [Google Scholar] [CrossRef]
  234. Leishman, G.J. Principles of helicopter aerodynamics with CD extra; Cambridge university press, 2006.
  235. Leishman, J.G.; Bhagwat, M.J.; Bagai, A. Free-vortex filament methods for the analysis of helicopter rotor wakes. Journal of aircraft 2002, 39, 759–775. [Google Scholar] [CrossRef]
  236. Rodriguez, S.N.; Jaworski, J.W. Strongly-coupled aeroelastic free-vortex wake framework for floating offshore wind turbine rotors. Part 2: Application. Renewable Energy 2020, 149, 1018–1031. [Google Scholar] [CrossRef]
  237. Gupta, S. Development of a time-accurate viscous Lagrangian vortex wake model for wind turbine applications; University of Maryland, College Park, 2006.
  238. Ribera, M. Helicopter flight dynamics simulation with a time-accurate free-vortex wake model; University of Maryland, College Park, 2007.
  239. Rodriguez, S.N.; Jaworski, J.W. Strongly-coupled aeroelastic free-vortex wake framework for floating offshore wind turbine rotors. Part 1: Numerical framework. Renewable Energy 2019, 141, 1127–1145. [Google Scholar] [CrossRef]
  240. Hansen, M.O. Aerodynamics of wind turbines; Routledge, 2015.
  241. Vatistas, G.H.; Kozel, V.; Mih, W. A simpler model for concentrated vortices. Experiments in Fluids 1991, 11, 73–76. [Google Scholar] [CrossRef]
  242. Scully, M. Computation of helicopter rotor wake geometry and its influence on rotor harmonic airloads. PhD thesis, Massachusetts Institute of Technology, 1975.
  243. Rankine, W. A Manual of Applied Mechanics, ; Griffin, C., Ed, 1858.
  244. Marten, D.; Wendler, J.; Pechlivanoglou, G.; Nayeri, C.N.; Paschereit, C.O. QBLADE: an open source tool for design and simulation of horizontal and vertical axis wind turbines. International Journal of Emerging Technology and Advanced Engineering 2013, 3, 264–269. [Google Scholar]
  245. Borg, M.; Bredmose, H. Overview of the numerical models used in the consortium and their qualification. LIFES50+ Deliverable 2015, 4. [Google Scholar]
  246. Collier, W.; Sanz, J.M. Comparison of linear and non-linear blade model predictions in Bladed to measurement data from GE 6MW wind turbine. Journal of Physics: Conference Series. IOP Publishing, 2016, Vol. 753, p. 082004.
  247. Wang, Q.; Sprague, M.A.; Jonkman, J.; Johnson, N.; Jonkman, B. BeamDyn: A high-fidelity wind turbine blade solver in the FAST modular framework. Wind Energy 2017, 20, 1439–1462. [Google Scholar] [CrossRef]
  248. Larsen, T.J.; Hansen, A.M. How 2 HAWC2, the user’s manual; Risø National Laboratory, 2007.
  249. Jonkman, J.; Musial, W. IEA wind task 23 offshore wind technology and deployment. National Renewable Energy Laboratory, Golden, CO, December, Technical Report No. NREL/TP-5000-48191, https://www. nrel. gov/docs/fy11osti/48191. pdf 2010.
  250. Popko, W.; Vorpahl, F.; Zuga, A.; Kohlmeier, M.; Jonkman, J.; Robertson, A.; Larsen, T.J.; Yde, A.; Sætertrø, K.; Okstad, K.M. ; others. Offshore Code Comparison Collaboration Continuation (OC4), Phase 1-Results of Coupled Simulations of an Offshore Wind Turbine With Jacket Support Structure. The twenty-second international offshore and polar engineering conference. OnePetro, 2012.
  251. Tasora, A.; Serban, R.; Mazhar, H.; Pazouki, A.; Melanz, D.; Fleischmann, J.; Taylor, M.; Sugiyama, H.; Negrut, D. Chrono: An open source multi-physics dynamics engine. High Performance Computing in Science and Engineering: Second International Conference, HPCSE 2015, Soláň, Czech Republic, May 25-28, 2015, Revised Selected Papers 2. Springer, 2016, pp. 19–49.
  252. Prescott, W.C.; Liu, J. Numerical Integration Techniques for Multibody Dynamic System Software. Technical report, SAE Technical Paper, 1999.
  253. Marten, D.; Wendler, J. QBlade short manual, 2018.
  254. Beardsell, A.; Alexandre, A.; Child, B.; Harries, R.; McCowen, D. Beyond OC5–Further advances in floating wind turbine modelling using Bladed. Journal of Physics: Conference Series. IOP Publishing, 2018, Vol. 1102, p. 012023.
  255. GL, D. Bladed Theory Manual Version 4.8 2016.
  256. Craig Jr, R.R.; Bampton, M.C. Coupling of substructures for dynamic analyses. AIAA journal 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
  257. Jonkman, J.; Buhl, M. New developments for the NWTC’s fast aeroelastic HAWT simulator. 42nd AIAA Aerospace Sciences Meeting and Exhibit, 2004, p. 504.
  258. Moriarty, P.J.; Butterfield, S.B. Wind turbine modeling overview for control engineers. 2009 American Control Conference. IEEE, 2009, pp. 2090–2095.
  259. Lennie, M. Development of the qfem solver: The development of modal analysis code for wind turbine blades in qblade, 2013.
  260. Al-Solihat, M.K.; Nahon, M. Flexible multibody dynamic modeling of a floating wind turbine. International Journal of Mechanical Sciences 2018, 142, 518–529. [Google Scholar] [CrossRef]
  261. Chen, J.; Shen, X.; Liu, P.; Zhu, X.; Du, Z. Design tool for aeroelastic analysis of wind turbine blades based on geometrically exact beam theory and lifting surface method. 35th Wind Energy Symposium, 2017, p. 0450.
  262. Borg, M.; Hansen, A.M.; Bredmose, H. Floating substructure flexibility of large-volume 10MW offshore wind turbine platforms in dynamic calculations. Journal of physics: Conference series. IOP Publishing, 2016, Vol. 753, p. 082024.
  263. Rinker, J.; Gaertner, E.; Zahle, F.; Skrzypiński, W.; Abbas, N.; Bredmose, H.; Barter, G.; Dykes, K. Comparison of loads from HAWC2 and OpenFAST for the IEA Wind 15 MW Reference Wind Turbine. Journal of Physics: Conference Series. IOP Publishing, 2020, Vol. 1618, p. 052052.
  264. Wen, B.; Tian, X.; Dong, X.; Peng, Z.; Zhang, W. Influences of surge motion on the power and thrust characteristics of an offshore floating wind turbine. Energy 2017, 141, 2054–2068. [Google Scholar] [CrossRef]
  265. Wen, B.; Tian, X.; Dong, X.; Peng, Z.; Zhang, W. On the power coefficient overshoot of an offshore floating wind turbine in surge oscillations. Wind Energy 2018, 21, 1076–1091. [Google Scholar] [CrossRef]
  266. Ramos-García, N.; Kontos, S.; Pegalajar-Jurado, A.; González Horcas, S.; Bredmose, H. Investigation of the floating IEA Wind 15 MW RWT using vortex methods Part I: Flow regimes and wake recovery. Wind Energy 2022, 25, 468–504. [Google Scholar] [CrossRef]
  267. Shao, Y.L.; Faltinsen, O.M. Towards efficient fully-nonlinear potential-flow solvers in marine hydrodynamics. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2012, Vol. 44915, pp. 369–380.
  268. Hansen, M.H.; Gaunaa, M.; Madsen, H.A. A Beddoes-Leishman type dynamic stall model in state-space and indicial formulations; 2004.
  269. Karimirad, M.; Moan, T. A simplified method for coupled analysis of floating offshore wind turbines. Marine Structures 2012, 27, 45–63. [Google Scholar] [CrossRef]
  270. Huijs, F.; de Ridder, E.J.; Savenije, F. Comparison of model tests and coupled simulations for a semi-submersible floating wind turbine. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2014, Vol. 45530, p. V09AT09A012.
  271. Borisade, F.; Koch, C.; Lemmer, F.; Cheng, P.W.; Campagnolo, F.; Matha, D. Validation of INNWIND. EU scaled model tests of a semisubmersible floating wind turbine. International Journal of Offshore and Polar Engineering 2018, 28, 54–64. [Google Scholar] [CrossRef]
  272. Yang, J.; He, Y.P.; Zhao, Y.S.; Shao, Y.L.; Han, Z.L. Experimental and numerical studies on the low-frequency responses of a spar-type floating offshore wind turbine. Ocean Engineering 2021, 222, 108571. [Google Scholar] [CrossRef]
  273. Campos, A.; Molins, C.; Gironella, X.; Trubat, P. Spar concrete monolithic design for offshore wind turbines. Proceedings of the Institution of Civil Engineers-Maritime Engineering. Thomas Telford Ltd, 2016, Vol. 169, pp. 49–63.
  274. Mahfouz, M.; Salari, M.; Hernández, S.; Vigara, F.; Molins, C.; Trubat, P.; Bredmose, H.; Pegalar-Jurado, A. Public design and FAST models of the two 15MW floater-turbine concepts. Technical report, tech. rep., Stuttgart, University of Stuttgart, 2020.
  275. Cutler, J.; Bashir, M.; Yang, Y.; Wang, J.; Loughney, S. Preliminary development of a novel catamaran floating offshore wind turbine platform and assessment of dynamic behaviours for intermediate water depth application. Ocean Engineering 2022, 258, 111769. [Google Scholar] [CrossRef]
  276. Huijs, F.; de Bruijn, R.; Savenije, F. Concept design verification of a semi-submersible floating wind turbine using coupled simulations. Energy Procedia 2014, 53, 2–12. [Google Scholar] [CrossRef]
  277. Robertson, A.N.; Jonkman, J.M. Loads analysis of several offshore floating wind turbine concepts. The twenty-first international offshore and polar engineering conference. OnePetro, 2011.
  278. Kvittem, M.I.; Bachynski, E.E.; Moan, T. Effects of hydrodynamic modelling in fully coupled simulations of a semi-submersible wind turbine. Energy Procedia 2012, 24, 351–362. [Google Scholar] [CrossRef]
  279. Karimirad, M.; Michailides, C. Dynamic analysis of a braceless semisubmersible offshore wind turbine in operational conditions. Energy Procedia 2015, 80, 21–29. [Google Scholar] [CrossRef]
  280. Karimirad, M.; Michailides, C. V-shaped semisubmersible offshore wind turbine subjected to misaligned wave and wind. Journal of Renewable and Sustainable Energy 2016, 8, 023305. [Google Scholar] [CrossRef]
  281. Karimirad, M.; Michailides, C. V-shaped semisubmersible offshore wind turbine: An alternative concept for offshore wind technology. Renewable Energy 2015, 83, 126–143. [Google Scholar] [CrossRef]
  282. Ormberg, H.; Bachynski, E.E. Global analysis of floating wind turbines: Code development, model sensitivity and benchmark study. The Twenty-second International Offshore and Polar Engineering Conference. OnePetro, 2012.
  283. Bae, Y.; Kim, M. Coupled dynamic analysis of multiple wind turbines on a large single floater. Ocean Engineering 2014, 92, 175–187. [Google Scholar] [CrossRef]
  284. Bae, Y.; Kim, M.; Kim, H. Performance changes of a floating offshore wind turbine with broken mooring line. Renewable Energy 2017, 101, 364–375. [Google Scholar] [CrossRef]
  285. Luan, C.; Gao, Z.; Moan, T. Design and analysis of a braceless steel 5-mw semi-submersible wind turbine. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2016, Vol. 49972, p. V006T09A052.
  286. Luan, C.; Gao, Z.; Moan, T. Development and verification of a time-domain approach for determining forces and moments in structural components of floaters with an application to floating wind turbines. Marine Structures 2017, 51, 87–109. [Google Scholar] [CrossRef]
  287. Wendt, F.F.; Robertson, A.N.; Jonkman, J.M. FAST model calibration and validation of the OC5-DeepCwind floating offshore wind system against wave tank test data. International Journal of Offshore and Polar Engineering 2019, 29, 15–23. [Google Scholar] [CrossRef]
  288. Liu, Y.; Yoshida, S.; Yamamoto, H.; Toyofuku, A.; He, G.; Yang, S. Response characteristics of the DeepCwind floating wind turbine moored by a single-point mooring system. Applied Sciences 2018, 8, 2306. [Google Scholar] [CrossRef]
  289. Liu, J.; Thomas, E.; Goyal, A.; Manuel, L. Design loads for a large wind turbine supported by a semi-submersible floating platform. Renewable Energy 2019, 138, 923–936. [Google Scholar] [CrossRef]
  290. Chen, J.; Hu, Z.; Liu, G.; Wan, D. Coupled aero-hydro-servo-elastic methods for floating wind turbines. Renewable energy 2019, 130, 139–153. [Google Scholar] [CrossRef]
  291. Li, Y.; Le, C.; Ding, H.; Zhang, P.; Zhang, J. Dynamic response for a submerged floating offshore wind turbine with different mooring configurations. Journal of Marine Science and Engineering 2019, 7, 115. [Google Scholar] [CrossRef]
  292. Zhang, L.; Michailides, C.; Wang, Y.; Shi, W. Moderate water depth effects on the response of a floating wind turbine. Structures. Elsevier, 2020, Vol. 28, pp. 1435–1448.
  293. Thomsen, J.B.; Bergua, R.; Jonkman, J.; Robertson, A.; Mendoza, N.; Brown, C.; Galinos, C.; Stiesdal, H. Modeling the TetraSpar floating offshore wind turbine foundation as a flexible structure in OrcaFlex and OpenFAST. Energies 2021, 14, 7866. [Google Scholar] [CrossRef]
  294. Barooni, M.; Ali, N.A.; Ashuri, T. An open-source comprehensive numerical model for dynamic response and loads analysis of floating offshore wind turbines. Energy 2018, 154, 442–454. [Google Scholar] [CrossRef]
  295. de Souza, C.E.S.; Bachynski-Polić, E.E. Design, structural modeling, control, and performance of 20 MW spar floating wind turbines. Marine Structures 2022, 84, 103182. [Google Scholar] [CrossRef]
  296. Johlas, H.M.; Martínez-Tossas, L.A.; Churchfield, M.J.; Lackner, M.A.; Schmidt, D.P. Floating platform effects on power generation in spar and semisubmersible wind turbines. Wind Energy 2021, 24, 901–916. [Google Scholar] [CrossRef]
  297. Churchfield, M.; Lee, S. SOWFA: Simulator for Wind Farm Applications: National Renewable Energy Laboratory; 2020, 2020.
  298. Shi, W.; Zhang, L.; Karimirad, M.; Michailides, C.; Jiang, Z.; Li, X. Combined effects of aerodynamic and second-order hydrodynamic loads for floating wind turbines at different water depths. Applied Ocean Research 2023, 130, 103416. [Google Scholar] [CrossRef]
  299. Zhang, C.; Wang, S.; Xie, S.; He, J.; Gao, J.; Tian, C. Effects of mooring line failure on the dynamic responses of a semisubmersible floating offshore wind turbine including gearbox dynamics analysis. Ocean Engineering 2022, 245, 110478. [Google Scholar] [CrossRef]
  300. Simpack, A. SIMPACK documentation, 2016.
  301. Yang, R.Y.; Chuang, T.C.; Zhao, C.; Johanning, L. Dynamic response of an offshore floating wind turbine at accidental limit states—mooring failure event. Applied Sciences 2022, 12, 1525. [Google Scholar] [CrossRef]
  302. Yang, Y.; Bashir, M.; Li, C.; Wang, J. Investigation on mooring breakage effects of a 5 MW barge-type floating offshore wind turbine using F2A. Ocean Engineering 2021, 233, 108887. [Google Scholar] [CrossRef]
  303. Hall, M.; Housner, S.; Zalkind, D.; Bortolotti, P.; Ogden, D.; Barter, G. An open-source frequency-domain model for floating wind turbine design optimization. Journal of physics: conference series. IOP Publishing, 2022, Vol. 2265, p. 042020.
  304. Pollini, N.; Pegalajar-Jurado, A.; Bredmose, H. Design optimization of a TetraSpar-type floater and tower for the IEA Wind 15 MW reference wind turbine. Marine Structures 2023, 90, 103437. [Google Scholar] [CrossRef]
  305. Pegalajar-Jurado, A.; Borg, M.; Bredmose, H. An efficient frequency-domain model for quick load analysis of floating offshore wind turbines. Wind Energy Science 2018, 3, 693–712. [Google Scholar] [CrossRef]
  306. Al-Solihat, M.K.; Nahon, M. Stiffness of slack and taut moorings. Ships and Offshore Structures 2016, 11, 890–904. [Google Scholar] [CrossRef]
  307. Hegseth, J.M.; Bachynski, E.E. A semi-analytical frequency domain model for efficient design evaluation of spar floating wind turbines. Marine Structures 2019, 64, 186–210. [Google Scholar] [CrossRef]
  308. Ferri, G.; Marino, E.; Bruschi, N.; Borri, C. Platform and mooring system optimization of a 10 MW semisubmersible offshore wind turbine. Renewable Energy 2022, 182, 1152–1170. [Google Scholar] [CrossRef]
  309. Karimi, M.; Hall, M.; Buckham, B.; Crawford, C. A multi-objective design optimization approach for floating offshore wind turbine support structures. Journal of Ocean Engineering and Marine Energy 2017, 3, 69–87. [Google Scholar] [CrossRef]
  310. Yu, W.; Müller, K.; Lemmer, F.; Bredmose, H.; Borg, M.; Sanchez, G.; Landbo, T. Public definition of the two LIFES50+ 10MW floater concepts. LIFES50+ deliverable 2017, 4. [Google Scholar]
  311. Hopstad, A.L.H.; Argyriadis, K.; Manjock, A.; Goldsmith, J.; Ronold, K.O. Dnv gl standard for floating wind turbines. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2018, Vol. 51975, p. V001T01A020.
  312. West, W.M. Optimization of Synthetic Mooring Systems for Floating Offshore Wind Turbines; The University of Maine, 2022.
  313. Pham, H.D.; Cartraud, P.; Schoefs, F.; Soulard, T.; Berhault, C. Dynamic modeling of nylon mooring lines for a floating wind turbine. Applied Ocean Research 2019, 87, 1–8. [Google Scholar] [CrossRef]
  314. Utsunomiya, T.; Sato, I.; Tanaka, K. At-sea experiment on durability and residual strength of polyester rope for mooring of floating wind turbine. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2019, Vol. 58882, p. V009T13A017.
  315. Verde, S.; Lages, E.N. A comparison of anchor loads, planar displacement, and rotation for nylon and polyester moored systems for a 15 MW floating wind turbine in shallow water. Ocean Engineering 2023, 280, 114404. [Google Scholar] [CrossRef]
  316. Weller, S.; Johanning, L.; Davies, P.; Banfield, S. Synthetic mooring ropes for marine renewable energy applications. Renewable energy 2015, 83, 1268–1278. [Google Scholar] [CrossRef]
  317. Ma, K.T.; Luo, Y.; Kwan, C.T.T.; Wu, Y. Mooring system engineering for offshore structures; Gulf Professional Publishing, 2019.
  318. Ikhennicheu, M.; Lynch, M.; Doole, S.; Borisade, F.; Matha, D.; Dominguez, J.; Vicente, R.; Habekost, T.; Ramirez, L.; Potestio, S.; others. D2. 1 Review of the state of the art of mooring and anchoring designs, technical challenges and identification of relevant DLCs. Technical report, Technical Report. CoreWind Project. 2020. Available online: https://corewind …, 2020.
  319. Trust, C. Floating Wind Joint Industry Project, Phase I Summary Report, Key findings from Electrical Systems, Mooring systems and Infrastructures and Logistics studies 2018.
  320. Xu, K.; Larsen, K.; Shao, Y.; Zhang, M.; Gao, Z.; Moan, T. Design and comparative analysis of alternative mooring systems for floating wind turbines in shallow water with emphasis on ultimate limit state design. Ocean Engineering 2021, 219, 108377. [Google Scholar] [CrossRef]
  321. Alexandre, A.; Percher, Y.; Choisnet, T.; Buils Urbano, R.; Harries, R. Coupled analysis and numerical model verification for the 2MW Floatgen demonstrator project with IDEOL platform. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2018, Vol. 51975, p. V001T01A032.
  322. Pillai, A.; Gordelier, T.; Thies, P.; Cuthill, D.; Johanning, L. Anchor loads for shallow water mooring of a 15 MW floating wind turbine—Part II: Synthetic and novel mooring systems. Ocean Engineering 2022, 266, 112619. [Google Scholar] [CrossRef]
  323. Hordvik, T. Design analysis and optimisation of mooring system for floating wind turbines. Master’s thesis, Norges teknisk-naturvitenskapelige universitet, Fakultet for …, 2011.
  324. Connolly, P.; Hall, M. Comparison of pilot-scale floating offshore wind farms with shared moorings. Ocean Engineering 2019, 171, 172–180. [Google Scholar] [CrossRef]
  325. Liang, G.; Jiang, Z.; Merz, K. Dynamic analysis of a dual-spar floating offshore wind farm with shared moorings in extreme environmental conditions. Marine Structures 2023, 90, 103441. [Google Scholar] [CrossRef]
  326. Hall, M.; Connolly, P. Coupled dynamics modelling of a floating wind farm with shared mooring lines. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2018, Vol. 51319, p. V010T09A087.
  327. Strivens, S.; Northridge, E.; Evans, H.; Harvey, M.; Camp, T.; Terry, N. Floating Wind Joint Industry Project Phase III Summary Report. The Carbon Trust: London, UK 2021.
  328. Ozan, G.; Stavros, K.; Henrik, B.; Tom, B.; Friedemann, B.R. Deliverable1.4 of COREWIND project: Methods for multiple floaters and dynamic cables at farm level, 2021.
  329. Masciola, M.; Jonkman, J.; Robertson, A. Implementation of a multisegmented, quasi-static cable model. The Twenty-third International Offshore and Polar Engineering Conference. OnePetro, 2013.
  330. Davidson, J.; Ringwood, J.V. Mathematical modelling of mooring systems for wave energy converters—A review. Energies 2017, 10, 666. [Google Scholar] [CrossRef]
  331. Azcona, J.; Palacio, D.; Munduate, X.; Gonzalez, L.; Nygaard, T.A. Impact of mooring lines dynamics on the fatigue and ultimate loads of three offshore floating wind turbines computed with IEC 61400-3 guideline. Wind Energy 2017, 20, 797–813. [Google Scholar] [CrossRef]
  332. Hall, M.; Buckham, B.; Crawford, C. Evaluating the importance of mooring line model fidelity in floating offshore wind turbine simulations. Wind energy 2014, 17, 1835–1853. [Google Scholar] [CrossRef]
  333. Wendt, F.F.; Andersen, M.T.; Robertson, A.N.; Jonkman, J.M. Verification and validation of the new dynamic mooring modules available in FAST v8. The 26th International Ocean and Polar Engineering Conference. OnePetro, 2016.
  334. Hall, M.; Goupee, A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean Engineering 2015, 104, 590–603. [Google Scholar] [CrossRef]
  335. Kreuzer, E.; Wilke, U. Mooring systems–A multibody dynamic approach. Multibody System Dynamics 2002, 8, 279–296. [Google Scholar] [CrossRef]
  336. Ma, G.; Zhong, L.; Zhang, X.; Ma, Q.; Kang, H.S. Mechanism of mooring line breakage of floating offshore wind turbine under extreme coherent gust with direction change condition. Journal of Marine Science and Technology 2020, 25, 1283–1295. [Google Scholar] [CrossRef]
  337. Masciola, M.; Jonkman, J.; Robertson, A. Extending the capabilities of the mooring analysis program: A survey of dynamic mooring line theories for integration into FAST. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2014, Vol. 45530, p. V09AT09A032.
  338. Kreuzer, E.; Wilke, U. Dynamics of mooring systems in ocean engineering. Archive of Applied Mechanics 2003, 73, 270–281. [Google Scholar] [CrossRef]
  339. Leonard, J.W.; Nath, J.H. Comparison of finite element and lumped parameter methods for oceanic cables. Engineering structures 1981, 3, 153–167. [Google Scholar] [CrossRef]
  340. Bergua, R.; Robertson, A.; Jonkman, J.; Branlard, E.; Fontanella, A.; Belloli, M.; Schito, P.; Zasso, A.; Persico, G.; Sanvito, A.; others. OC6 project Phase III: validation of the aerodynamic loading on a wind turbine rotor undergoing large motion caused by a floating support structure. Wind Energy Science Discussions 2022, 2022, 1–33. [Google Scholar] [CrossRef]
  341. Yu, Z.; Hu, Z.; Zheng, X.; Ma, Q.; Hao, H. Aeroelastic performance analysis of wind turbine in the wake with a new Elastic Actuator Line model. Water 2020, 12, 1233. [Google Scholar] [CrossRef]
  342. Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW reference wind turbine. Danish wind power research 2013, 2013.
  343. Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C. Aeroelastic analysis of a floating offshore wind turbine in platform-induced surge motion using a fully coupled CFD-MBD method. Wind Energy 2019, 22, 1–20. [Google Scholar] [CrossRef]
  344. Campaña-Alonso, G.; Martin-San-Román, R.; Méndez-López, B.; Benito-Cia, P.; Azcona-Armendáriz, J. OF 2: coupling OpenFAST and OpenFOAM for high fidelity aero-hydro-servo-elastic FOWT simulations. Wind Energy Science Discussions 2023, 2023, 1–21. [Google Scholar] [CrossRef]
  345. Xu, S.; Zhuang, T.; Zhao, W.; Wan, D. Numerical investigation of aerodynamic responses and wake characteristics of a floating offshore wind turbine under atmospheric boundary layer inflows. Ocean Engineering 2023, 279, 114527. [Google Scholar] [CrossRef]
  346. Churchfield, M.; Lee, S.; Moriarty, P. Overview of the simulator for wind farm application (SOWFA). National Renewable Energy Laboratory 2012. [Google Scholar]
  347. Zhang, Y.; Hu, Z. An aero-hydro coupled method for investigating ship collision against a floating offshore wind turbine. Marine Structures 2022, 83, 103177. [Google Scholar] [CrossRef]
  348. Lamei, A.; Hayatdavoodi, M.; Wong, C.; Tang, B. On Motion and Hydroelastic Analysis of a Floating Offshore Wind Turbine. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2019, Vol. 58899, p. V010T09A070.
  349. Stewart, G.; Muskulus, M. A review and comparison of floating offshore wind turbine model experiments. Energy Procedia 2016, 94, 227–231. [Google Scholar] [CrossRef]
  350. Müller, K.; Sandner, F.; Bredmose, H.; Azcona, J.; Manjock, A.; Pereira, R. Improved tank test procedures for scaled floating offshore wind turbines 2014.
  351. Duan, F.; Hu, Z.; Niedzwecki, J. Model test investigation of a spar floating wind turbine. Marine Structures 2016, 49, 76–96. [Google Scholar] [CrossRef]
  352. Make, M.; Vaz, G. Analyzing scaling effects on offshore wind turbines using CFD. Renewable Energy 2015, 83, 1326–1340. [Google Scholar] [CrossRef]
  353. Martin, H.R.; Kimball, R.W.; Viselli, A.M.; Goupee, A.J. Methodology for wind/wave basin testing of floating offshore wind turbines. Journal of Offshore Mechanics and Arctic Engineering 2014, 136. [Google Scholar] [CrossRef]
  354. Tomasicchio, G.R.; D’Alessandro, F.; Avossa, A.M.; Riefolo, L.; Musci, E.; Ricciardelli, F.; Vicinanza, D. Experimental modelling of the dynamic behaviour of a spar buoy wind turbine. Renewable energy 2018, 127, 412–432. [Google Scholar] [CrossRef]
  355. Coulling, A.J.; Goupee, A.J.; Robertson, A.N.; Jonkman, J.M.; Dagher, H.J. Validation of a FAST semi-submersible floating wind turbine numerical model with DeepCwind test data. Journal of Renewable and Sustainable Energy 2013, 5, 023116. [Google Scholar] [CrossRef]
  356. Li, L.; Gao, Y.; Hu, Z.; Yuan, Z.; Day, S.; Li, H. Model test research of a semisubmersible floating wind turbine with an improved deficient thrust force correction approach. Renewable energy 2018, 119, 95–105. [Google Scholar] [CrossRef]
  357. Ahn, H.; Shin, H. Experimental and numerical analysis of a 10 MW floating offshore wind turbine in regular waves. Energies 2020, 13, 2608. [Google Scholar] [CrossRef]
  358. de Ridder, E.J.; Otto, W.; Zondervan, G.J.; Huijs, F.; Vaz, G. Development of a scaled-down floating wind turbine for offshore basin testing. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2014, Vol. 45530, p. V09AT09A027.
  359. Bayati, I.; Belloli, M.; Bernini, L.; Mikkelsen, R.; Zasso, A. On the aero-elastic design of the DTU 10MW wind turbine blade for the LIFES50+ wind tunnel scale model. Journal of Physics: Conference Series. IOP Publishing, 2016, Vol. 753, p. 022028.
  360. Connolly, A.; Guyot, M.; Le Boulluec, M.; Héry, L.; O’Connor, A. Fully coupled aero-hydro-structural simulation of new floating wind turbine concept. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2018, Vol. 51975, p. V001T01A027.
  361. Russo, S.; Contestabile, P.; Bardazzi, A.; Leone, E.; Iglesias, G.; Tomasicchio, G.R.; Vicinanza, D. Dynamic loads and response of a spar buoy wind turbine with pitch-controlled rotating blades: An experimental study. Energies 2021, 14, 3598. [Google Scholar] [CrossRef]
  362. Goupee, A.J.; Kimball, R.W.; Dagher, H.J. Experimental observations of active blade pitch and generator control influence on floating wind turbine response. Renewable Energy 2017, 104, 9–19. [Google Scholar] [CrossRef]
  363. Hara, N.; Tsujimoto, S.; Nihei, Y.; Iijima, K.; Konishi, K. Experimental validation of model-based blade pitch controller design for floating wind turbines: system identification approach. Wind energy 2017, 20, 1187–1206. [Google Scholar] [CrossRef]
  364. Bredmose, H.; Lemmer, F.; Borg, M.; Pegalajar-Jurado, A.; Mikkelsen, R.F.; Larsen, T.S.; Fjelstrup, T.; Yu, W.; Lomholt, A.K.; Boehm, L.; others. The Triple Spar campaign: Model tests of a 10MW floating wind turbine with waves, wind and pitch control. Energy Procedia 2017, 137, 58–76. [Google Scholar] [CrossRef]
  365. Ward, J.C.; Fowler, M.J.; Viselli, A.M.; Goupee, A.J.; Dagher, H.J. Design and validation of a multi-scale model floating offshore test wind turbine. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2018, Vol. 51975, p. V001T01A014.
  366. Nielsen, F.G.; Hanson, T.D.; Skaare, B. Integrated dynamic analysis of floating offshore wind turbines. International conference on offshore mechanics and arctic engineering, 2006, Vol. 47462, pp. 671–679.
  367. Skaare, B.; Hanson, T.D.; Nielsen, F.G.; Yttervik, R.; Hansen, A.M.; Thomsen, K.; Larsen, T.J. Integrated dynamic analysis of floating offshore wind turbines. European wind energy conference and exhibition. Hamburg, Germany, 2007, Vol. 3, pp. 1929–1939.
  368. Chen, J.; Hu, Z.; Wan, D.; Xiao, Q. Comparisons of the dynamical characteristics of a semi-submersible floating offshore wind turbine based on two different blade concepts. Ocean Engineering 2018, 153, 305–318. [Google Scholar] [CrossRef]
  369. Chen, J.; Hu, Z. Experimental investigation of aerodynamic effect–induced dynamic characteristics of an OC4 semi-submersible floating wind turbine. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment 2018, 232, 19–36. [Google Scholar] [CrossRef]
  370. Pham, T.D.; Shin, H. Validation of a 750 kW semi-submersible floating offshore wind turbine numerical model with model test data, part I: Model-I. International Journal of Naval Architecture and Ocean Engineering 2019, 11, 980–992. [Google Scholar] [CrossRef]
  371. Kim, J.; Shin, H. Validation of a 750 kW semi-submersible floating offshore wind turbine numerical model with model test data, part II: Model-II. International Journal of Naval Architecture and Ocean Engineering 2020, 12, 213–225. [Google Scholar] [CrossRef]
  372. Hao, H.; Liao, K.; Ma, Q.; Zheng, X.; Sun, H.; Khayyer, A. Wind turbine model-test method for achieving similarity of both model-and full-scale thrusts and torques. Applied Ocean Research 2023, 130, 103444. [Google Scholar] [CrossRef]
  373. Lei, Y.; Zheng, X.Y.; Li, W.; Zheng, H.; Zhang, Q.; Zhao, S.; Cai, X.; Ci, X.; He, Q. Experimental study of the state-of-the-art offshore system integrating a floating offshore wind turbine with a steel fish farming cage. Marine Structures 2021, 80, 103076. [Google Scholar] [CrossRef]
  374. Cao, Q.; Xiao, L.; Cheng, Z.; Liu, M. Dynamic responses of a 10 MW semi-submersible wind turbine at an intermediate water depth: A comprehensive numerical and experimental comparison. Ocean Engineering 2021, 232, 109138. [Google Scholar] [CrossRef]
  375. Cao, Q.; Xiao, L.; Cheng, Z.; Liu, M.; Wen, B. Operational and extreme responses of a new concept of 10MW semi-submersible wind turbine in intermediate water depth: An experimental study. Ocean Engineering 2020, 217, 108003. [Google Scholar] [CrossRef]
  376. Cao, Q.; Bachynski-Polić, E.E.; Gao, Z.; Xiao, L.; Cheng, Z.; Liu, M. Experimental and numerical analysis of wind field effects on the dynamic responses of the 10 MW SPIC floating wind turbine concept. Ocean Engineering 2022, 261, 112151. [Google Scholar] [CrossRef]
  377. Hall, M.; Goupee, A.J. Validation of a hybrid modeling approach to floating wind turbine basin testing. Wind Energy 2018, 21, 391–408. [Google Scholar] [CrossRef]
  378. Hall, M.; Goupee, A.; Jonkman, J. Development of performance specifications for hybrid modeling of floating wind turbines in wave basin tests. Journal of Ocean Engineering and Marine Energy 2018, 4, 1–23. [Google Scholar] [CrossRef]
  379. Chabaud, V.; Steen, S.; Skjetne, R. Real-time hybrid testing for marine structures: challenges and strategies. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2013, Vol. 55393, p. V005T06A021.
  380. Hall, M.; Moreno, J.; Thiagarajan, K. Performance specifications for real-time hybrid testing of 1: 50-scale floating wind turbine models. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2014, Vol. 45547, p. V09BT09A047.
  381. Bachynski, E.E.; Chabaud, V.; Sauder, T. Real-time hybrid model testing of floating wind turbines: sensitivity to limited actuation. Energy Procedia 2015, 80, 2–12. [Google Scholar] [CrossRef]
  382. Bachynski, E.E.; Thys, M.; Sauder, T.; Chabaud, V.; Sæther, L.O. Real-time hybrid model testing of a braceless semi-submersible wind turbine: Part II—Experimental results. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2016, Vol. 49972, p. V006T09A040.
  383. Berthelsen, P.A.; Bachynski, E.E.; Karimirad, M.; Thys, M. REAL-TIME HYBRID MODEL TESTS OF A BRACELESS SEMI-SUBMERSIBLE WIND TURBINE. PART III: CALIBRATION OF A NUMERICAL MODEL: OMAE2016, Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, June 19-24, 2016, Busan, South Korea, OMAE2016-54640. International Conference on Ocean, Offshore and Arctic Engineering: ASME (American Society of Mechanical Engineers), 2016.
  384. Azcona, J.; Bouchotrouch, F.; González, M.; Garciandía, J.; Munduate, X.; Kelberlau, F.; Nygaard, T.A. Aerodynamic thrust modelling in wave tank tests of offshore floating wind turbines using a ducted fan. Journal of Physics: Conference Series. IOP Publishing, 2014, Vol. 524, p. 012089.
  385. Vittori, F.; Bouchotrouch, F.; Lemmer, F.; Azcona, J. Hybrid scaled testing of a 5MW floating wind turbine using the SIL method compared with numerical models. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2018, Vol. 51319, p. V010T09A082.
  386. Amaral, G.A.; Mello, P.C.; do Carmo, L.H.; Alberto, I.F.; Malta, E.B.; Simos, A.N.; Franzini, G.R.; Suzuki, H.; Gonçalves, R.T. Seakeeping tests of a FOWT in wind and waves: an analysis of dynamic coupling effects and their impact on the predictions of pitch motion response. Journal of Marine Science and Engineering 2021, 9, 179. [Google Scholar] [CrossRef]
  387. Desmond, C.J.; Hinrichs, J.C.; Murphy, J. Uncertainty in the physical testing of floating wind energy platforms’ accuracy versus precision. Energies 2019, 12, 435. [Google Scholar] [CrossRef]
  388. Urbán, A.M.; Guanche, R. Wind turbine aerodynamics scale-modeling for floating offshore wind platform testing. Journal of Wind Engineering and Industrial Aerodynamics 2019, 186, 49–57. [Google Scholar] [CrossRef]
  389. Otter, A.; Murphy, J.; Desmond, C. Emulating aerodynamic forces and moments for hybrid testing of floating wind turbine models. Journal of Physics: Conference Series. IOP Publishing, 2020, Vol. 1618, p. 032022.
  390. Pires, O.; Azcona, J.; Vittori, F.; Bayati, I.; Gueydon, S.; Fontanella, A.; Liu, Y.; De Ridder, E.; Belloli, M.; Van Wingerden, J. Inclusion of rotor moments in scaled wave tank test of a floating wind turbine using SiL hybrid method. Journal of Physics: Conference Series. IOP Publishing, 2020, Vol. 1618, p. 032048.
  391. Hall, M.T. Hybrid modeling of floating wind turbines; The University of Maine, 2016.
  392. Bayati, I.; Belloli, M.; Facchinetti, A. Wind tunnel 2-DOF Hybrid/HIL tests on the OC5 floating offshore wind turbine. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2017, Vol. 57786, p. V010T09A076.
  393. Bayati, I.; Belloli, M.; Bernini, L.; Zasso, A. Wind tunnel validation of AeroDyn within LIFES50+ project: imposed Surge and Pitch tests. Journal of Physics: Conference Series. IOP Publishing, 2016, Vol. 753, p. 092001.
  394. Bayati, I.; Belloli, M.; Bernini, L.; Zasso, A. A formulation for the unsteady aerodynamics of floating wind turbines, with focus on the global system dynamics. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2017, Vol. 57786, p. V010T09A055.
  395. Mancini, S.; Boorsma, K.; Caboni, M.; Cormier, M.; Lutz, T.; Schito, P.; Zasso, A. Characterization of the unsteady aerodynamic response of a floating offshore wind turbine to surge motion. Wind Energy Science 2020, 5, 1713–1730. [Google Scholar] [CrossRef]
  396. Hu, H.; Morteza Khosravi, M.; Sarkar, P. An experimental investigation on the performance and the wake characteristics of a wind turbine subjected to surge motion. 33rd Wind Energy Symposium, 2015, p. 1207.
  397. Rockel, S.; Camp, E.; Schmidt, J.; Peinke, J.; Cal, R.B.; Hölling, M. Experimental study on influence of pitch motion on the wake of a floating wind turbine model. Energies 2014, 7, 1954–1985. [Google Scholar] [CrossRef]
  398. Meng, H.; Su, H.; Guo, J.; Qu, T.; Lei, L. Experimental investigation on the power and thrust characteristics of a wind turbine model subjected to surge and sway motions. Renewable Energy 2022, 181, 1325–1337. [Google Scholar] [CrossRef]
  399. Bayati, I.; Belloli, M.; Facchinetti, A.; Giappino, S. Wind tunnel tests on floating offshore wind turbines: A proposal for hardware-in-the-loop approach to validate numerical codes. Wind Engineering 2013, 37, 557–568. [Google Scholar] [CrossRef]
  400. Bayati, I.; Facchinetti, A.; Fontanella, A.; Taruffi, F.; Belloli, M. Analysis of FOWT dynamics in 2-DOF hybrid HIL wind tunnel experiments. Ocean Engineering 2020, 195, 106717. [Google Scholar] [CrossRef]
  401. Bottasso, C.L.; Campagnolo, F.; Petrović, V. Wind tunnel testing of scaled wind turbine models: Beyond aerodynamics. Journal of wind engineering and industrial aerodynamics 2014, 127, 11–28. [Google Scholar] [CrossRef]
  402. Bayati, I.; Belloli, M.; Ferrari, D.; Fossati, F.; Giberti, H. Design of a 6-DoF robotic platform for wind tunnel tests of floating wind turbines. Energy Procedia 2014, 53, 313–323. [Google Scholar] [CrossRef]
  403. Bayati, I.; Facchinetti, A.; Fontanella, A.; Belloli, M. 6-DoF hydrodynamic modelling for wind tunnel hybrid/HIL tests of FOWT: the real-time challenge. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2018, Vol. 51319, p. V010T09A078.
  404. Fontanella, A.; Bayati, I.; Taruffi, F.; La Mura, F.; Facchinetti, A.; Belloli, M. A 6-DOFs hardware-in-the-loop system for wind tunnel tests of floating offshore wind turbines. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2019, Vol. 58899, p. V010T09A055.
  405. Bayati, I.; Facchinetti, A.; Fontanella, A.; Giberti, H.; Belloli, M. A wind tunnel/HIL setup for integrated tests of Floating Offshore Wind Turbines. Journal of Physics: Conference Series. IOP Publishing, 2018, Vol. 1037, p. 052025.
  406. Stiesdal, H. Hywind: The world’s first floating MW-scale wind turbine. Wind Directions 2009, 31, 52–53. [Google Scholar]
  407. Aubault, A.; Cermelli, C.; Roddier, D. WindFloat: A floating foundation for offshore wind turbines—Part III: Structural analysis. International Conference on Offshore Mechanics and Arctic Engineering, 2009, Vol. 43413, pp. 213–220.
  408. Driscoll, F.; Jonkman, J.; Robertson, A.; Sirnivas, S.; Skaare, B.; Nielsen, F.G. Validation of a FAST model of the statoil-hywind demo floating wind turbine. Energy Procedia 2016, 94, 3–19. [Google Scholar] [CrossRef]
  409. Skaare, B.; Nielsen, F.G.; Hanson, T.D.; Yttervik, R.; Havmøller, O.; Rekdal, A. Analysis of measurements and simulations from the Hywind Demo floating wind turbine. Wind Energy 2015, 18, 1105–1122. [Google Scholar] [CrossRef]
  410. Tanaka, K.; Sato, I.; Utsunomiya, T.; Kakuya, H. Validation of dynamic response of a 2-MW hybrid-spar floating wind turbine during typhoon using full-scale field data. Ocean Engineering 2020, 218, 108262. [Google Scholar] [CrossRef]
  411. Utsunomiya, T.; Sato, I.; Kobayashi, O.; Shiraishi, T.; Harada, T. Numerical modeling and analysis of a hybrid-spar floating wind turbine. Journal of Offshore Mechanics and Arctic Engineering 2019, 141. [Google Scholar] [CrossRef]
  412. Hanson, T.D.; Skaare, B.; Yttervik, R.; Nielsen, F.G.; Havmøller, O. Comparison of measured and simulated responses at the first full scale floating wind turbine Hywind. Proceedings of the European Wind Energy Association Annual Event 2011. [Google Scholar]
  413. Nakamura, A.; Hayashi, Y.; Ichinose, H. VERIFICATION OF LOAD CALCULATION BASED ON SITE MEASUREMENTS OF A 7MW OFFSHORE WIND TURBINE ON V-SHAPED SEMI-SUBMERSIBLE FLOATING STRUCTURE. Grand Renewable Energy proceedings Japan council for Renewable Energy (2018). Japan Council for Renewable Energy, 2018, p. 155.
  414. Choisnet, T.; Percher, Y.; Adam, R.; Favré, M.; Harries, R. On the Correlation Between Floating Wind Turbine Accelerations, Rotor and Tower Loads. International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2020, Vol. 84416, p. V009T09A060.
  415. Choisnet, T.; Rogier, E.; Percher, Y.; Courbois, A.; Le Crom, I.; Mariani, R. Performance and mooring qualification in Floatgen: the first French offshore wind turbine project. 16ième Journées de l’Hydrodynamique 2018, 1, 1–10. [Google Scholar]
  416. Couto, A.; Justino, P.; Simões, T.; Estanqueiro, A. Impact of the wave/wind induced oscillations on the power performance of the WindFloat wind turbine. Journal of Physics: Conference Series. IOP Publishing, 2022, Vol. 2362, p. 012010.
Preprints 91703 g001
Figure 1. Some popular semisubmersible configurations
Figure 1. Some popular semisubmersible configurations
Preprints 91703 g001
Preprints 91703 g002
Figure 2. Two examples of semisubmersible platforms with three offset columns
Figure 2. Two examples of semisubmersible platforms with three offset columns
Preprints 91703 g002
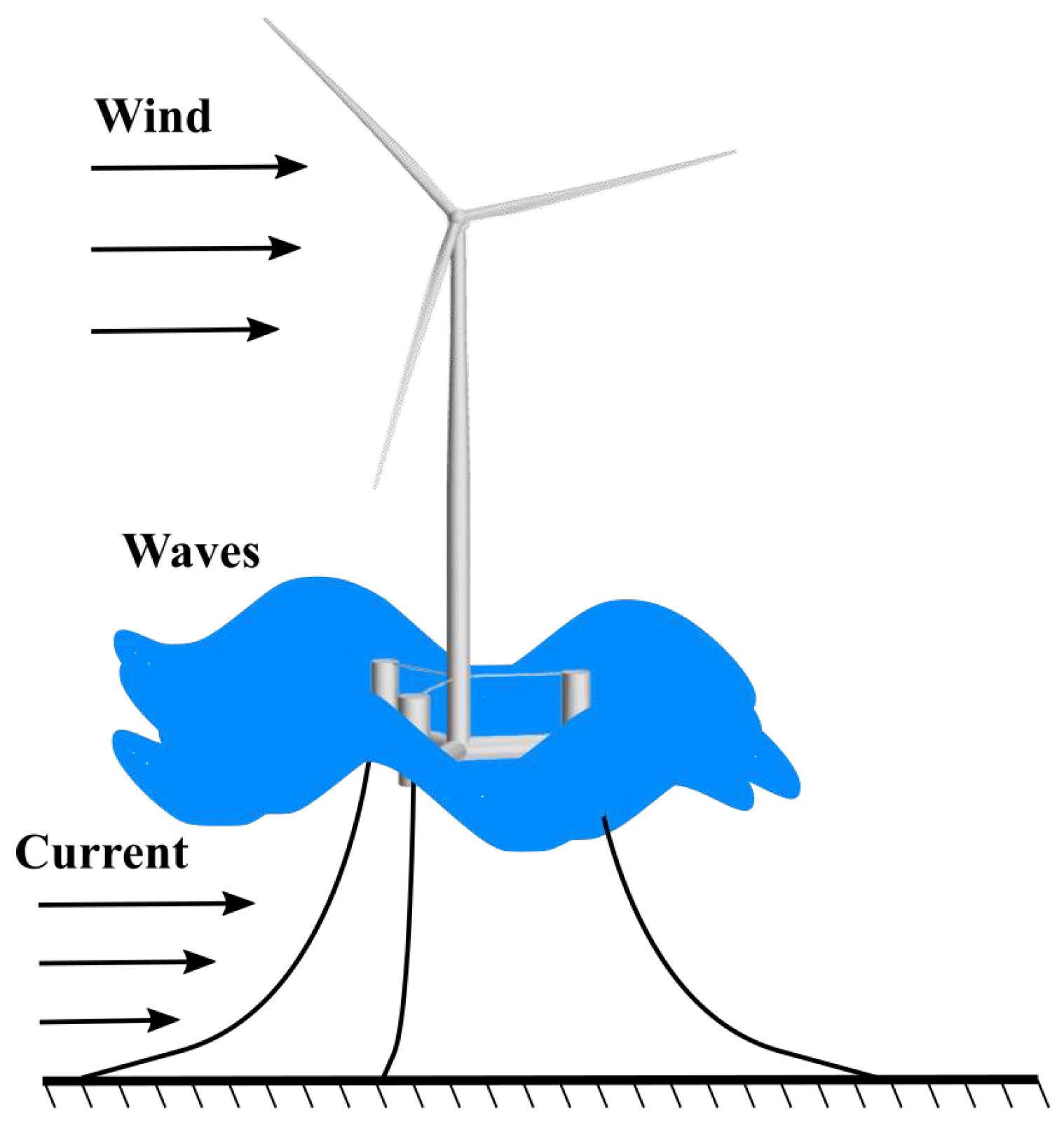
Preprints 91703 g003
Figure 3. An FWTS subject to loads emanating from several sources, such as waves, current and wind
Figure 3. An FWTS subject to loads emanating from several sources, such as waves, current and wind
Preprints 91703 g003
Preprints 91703 g004
Figure 4. Methods for evaluating the coupled hydro-aero-structural dynamic behavior of FWTSs
Figure 4. Methods for evaluating the coupled hydro-aero-structural dynamic behavior of FWTSs
Preprints 91703 g004
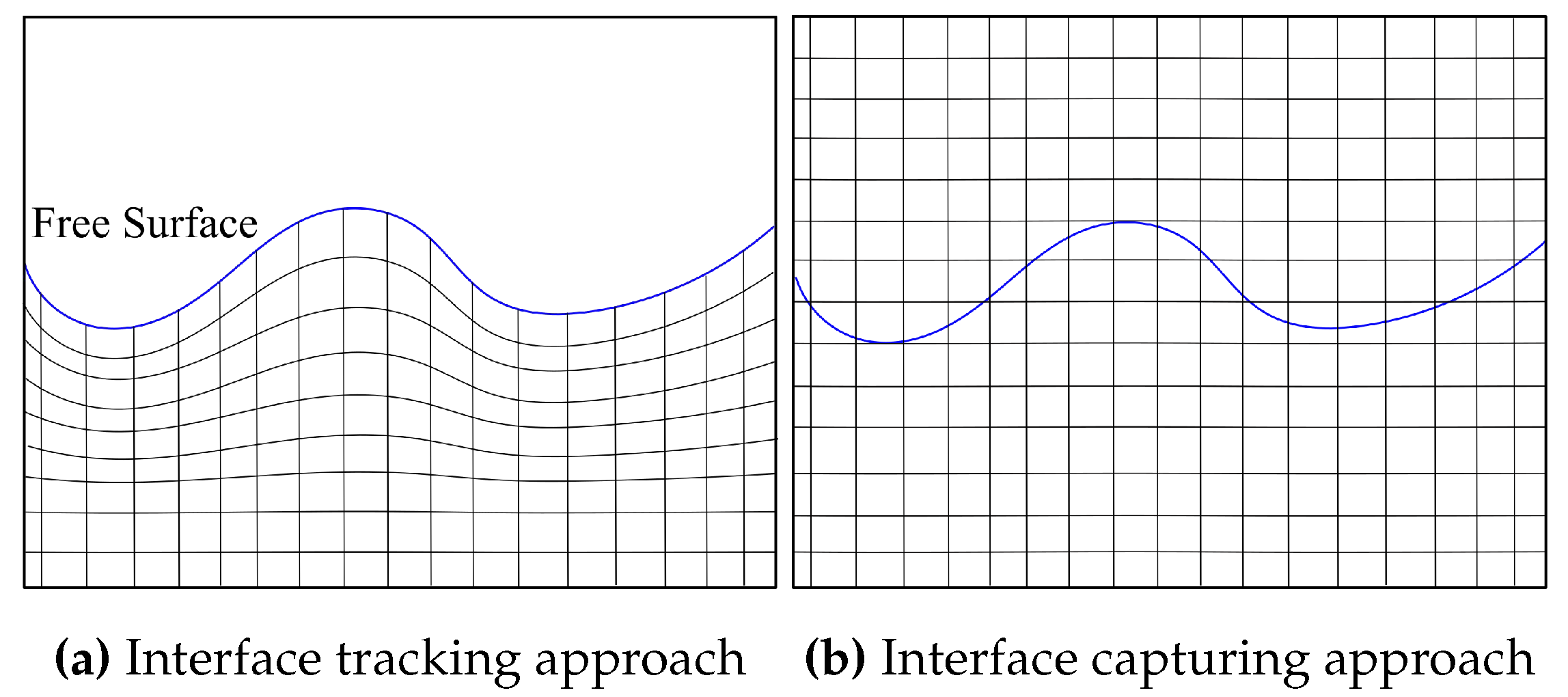
Preprints 91703 g005
Figure 5. Free surface modeling in CFD
Figure 5. Free surface modeling in CFD
Preprints 91703 g005
Preprints 91703 g006
Figure 6. From left to right: wind turbine geometry, actuator disk, actuator line and actuator surface
Figure 6. From left to right: wind turbine geometry, actuator disk, actuator line and actuator surface
Preprints 91703 g006
Preprints 91703 g007
Figure 7. Percentage of CFD software used to study the coupled behavior of an FWTS
Figure 7. Percentage of CFD software used to study the coupled behavior of an FWTS
Preprints 91703 g007
Preprints 91703 g008
Figure 8. Percentage of turbulence models used in CFD codes
Figure 8. Percentage of turbulence models used in CFD codes
Preprints 91703 g008
Preprints 91703 g009
Figure 9. Percentage of methods used to model the turbulent boundary layer close to the blades: wall functions (WF), without WF, and actuator methods
Figure 9. Percentage of methods used to model the turbulent boundary layer close to the blades: wall functions (WF), without WF, and actuator methods
Preprints 91703 g009
Preprints 91703 g010
Figure 10. Linearized boundary conditions typically used in the linear potential flow theory
Figure 10. Linearized boundary conditions typically used in the linear potential flow theory
Preprints 91703 g010
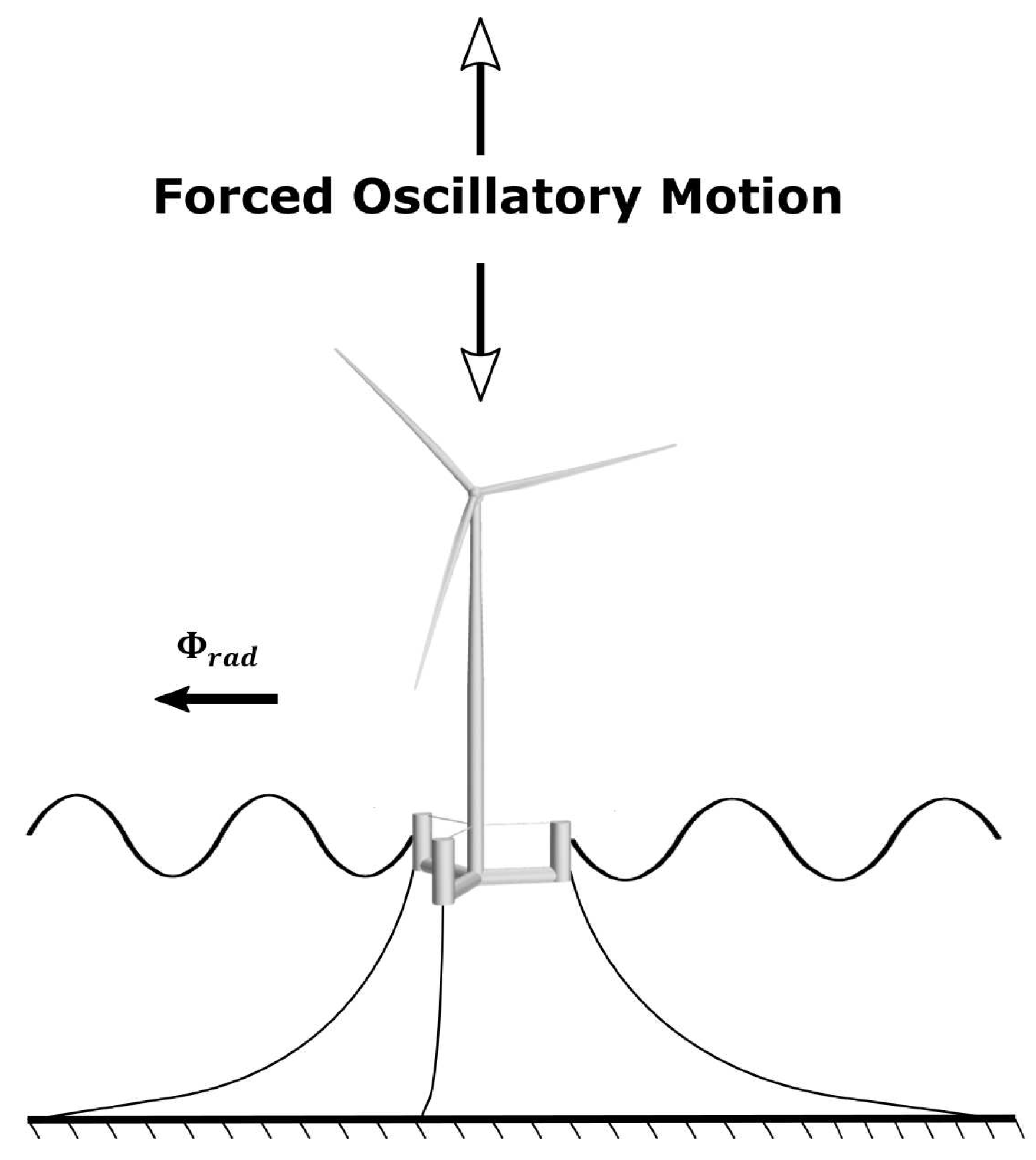
Preprints 91703 g011
Figure 11. The radiation problem related to an FWTS
Figure 11. The radiation problem related to an FWTS
Preprints 91703 g011
Preprints 91703 g012
Figure 12. velocity potential related to the diffraction of the incident waves to an FWTS
Figure 12. velocity potential related to the diffraction of the incident waves to an FWTS
Preprints 91703 g012
Preprints 91703 g013
Figure 13. Elements along the blade span located at the radial position of r, which extend to r + δ r affect the airflow momentum that travels across the circular ring area covered by these rotating elements due to their aerodynamic loads.
Figure 13. Elements along the blade span located at the radial position of r, which extend to r + δ r affect the airflow momentum that travels across the circular ring area covered by these rotating elements due to their aerodynamic loads.
Preprints 91703 g013
Preprints 91703 g014
Figure 14. α : angle of attack, β : pitch angle, ϕ : angle enclosed by the rotor plane and the total incident wind speed W
Figure 14. α : angle of attack, β : pitch angle, ϕ : angle enclosed by the rotor plane and the total incident wind speed W
Preprints 91703 g014
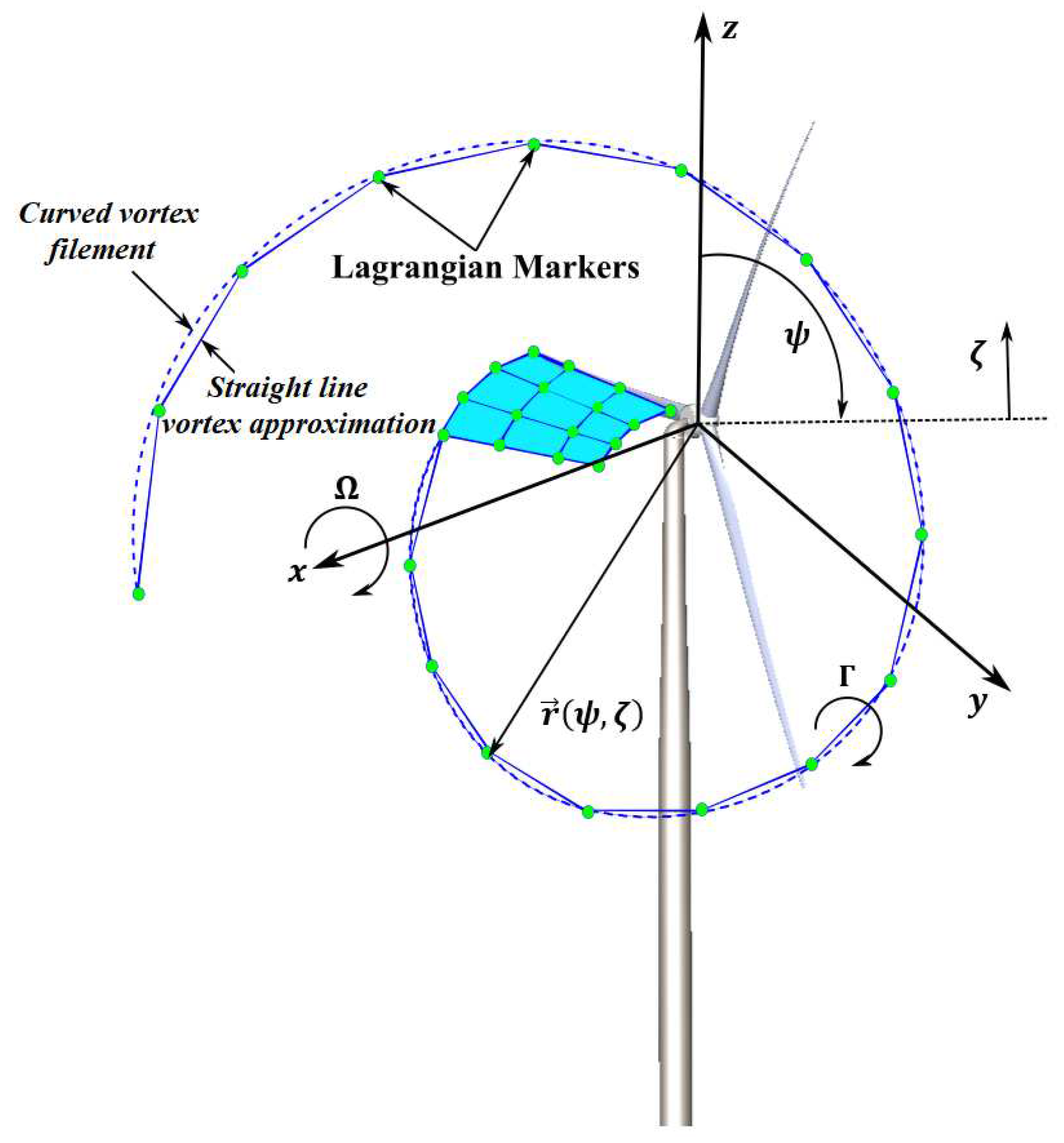
Preprints 91703 g015
Figure 15. FVW method explanation
Figure 15. FVW method explanation
Preprints 91703 g015
Preprints 91703 g016
Figure 16. Multi-body representation of a wind turbine
Figure 16. Multi-body representation of a wind turbine
Preprints 91703 g016
Preprints 91703 g017
Figure 17. Mooring line systems: catenary and taut
Figure 17. Mooring line systems: catenary and taut
Preprints 91703 g017
Preprints 91703 g018
Figure 18. Cost evolution of a traditional steel chain catenary system regarding water depth [319]
Figure 18. Cost evolution of a traditional steel chain catenary system regarding water depth [319]
Preprints 91703 g018
Preprints 91703 g019
Figure 19. A catenary mooring system with clump weights and buoyancy modules [323]
Figure 19. A catenary mooring system with clump weights and buoyancy modules [323]
Preprints 91703 g019
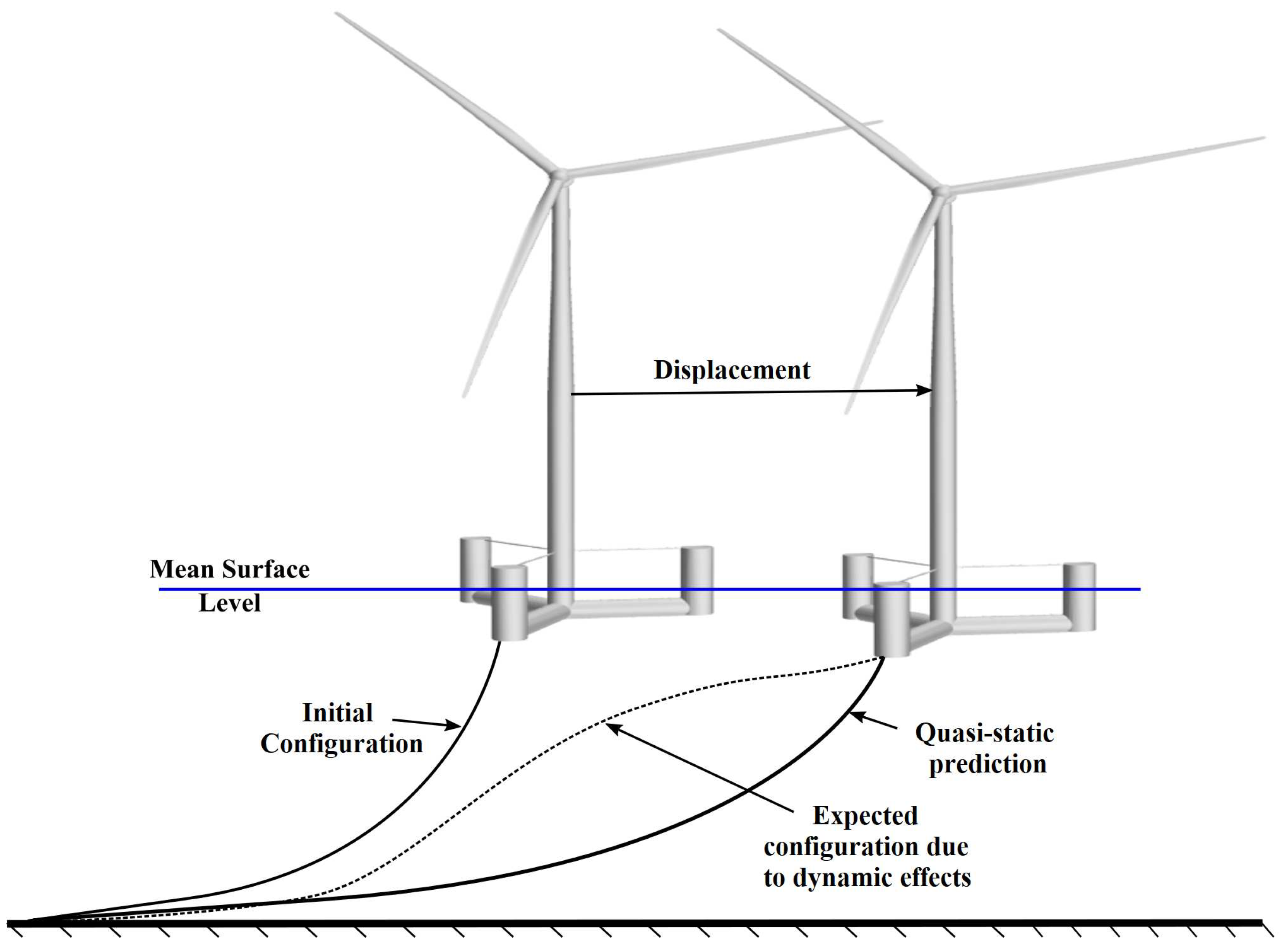
Preprints 91703 g020
Figure 20. Possible response of a mooring line under quasi-static and dynamic assumptions
Figure 20. Possible response of a mooring line under quasi-static and dynamic assumptions
Preprints 91703 g020
Preprints 91703 g021
Figure 21. The measured and calculated (using a wide range of modeling approaches, such as BEM, DBEM, GDW, FVW, and CFD) torque moment and thrust force of a scaled turbine model during one harmonic surge motion of the platform with a frequency of 1 Hz and an amplitude of 0.035 of rotor diameter (Figure reproduced using the data given by [340])
Figure 21. The measured and calculated (using a wide range of modeling approaches, such as BEM, DBEM, GDW, FVW, and CFD) torque moment and thrust force of a scaled turbine model during one harmonic surge motion of the platform with a frequency of 1 Hz and an amplitude of 0.035 of rotor diameter (Figure reproduced using the data given by [340])
Preprints 91703 g021
Preprints 91703 g022
Figure 22. The phases and magnitudes of the QTFs related to force in surge direction and moment in pitch direction obtained from both CFD and potential flow theory using the commercial code WAMIT (Figure reproduced using the data given by [57])
Figure 22. The phases and magnitudes of the QTFs related to force in surge direction and moment in pitch direction obtained from both CFD and potential flow theory using the commercial code WAMIT (Figure reproduced using the data given by [57])
Preprints 91703 g022
Preprints 91703 g023
Figure 23. Numerically modeled aerodynamics hybrid tests
Figure 23. Numerically modeled aerodynamics hybrid tests
Preprints 91703 g023
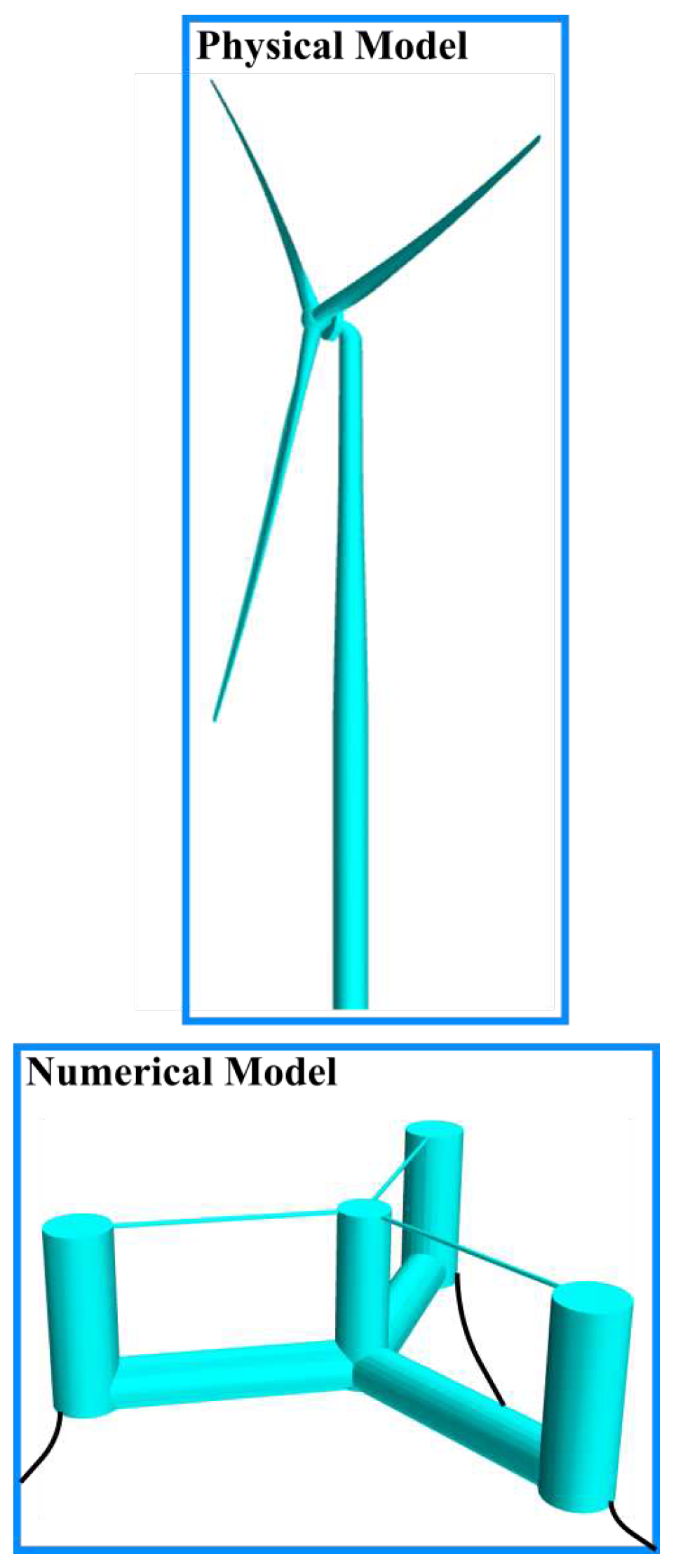
Preprints 91703 g024
Figure 24. numerically modeled hydrodynamics hybrid tests
Figure 24. numerically modeled hydrodynamics hybrid tests
Preprints 91703 g024
Table 1. Summary of the capabilities of coupled numerical tools
Table 1. Summary of the capabilities of coupled numerical tools
Code Hydrodynamics Aerodynamics Structural dynamics Mooring system dynamics
WAMIT Potential flow theory (Frequency domain) - Rigid Body/ Modal Quasi-static method
AQWA Potential flow theory (Frequency/time domain) - Rigid body/ FEA Quasi-static/ Dynamic methods
WINDOPT Potential flow theory (Frequency domain) - Rigid body Quasi-static/ Dynamic methods
OpenFAST Potential flow theory/ Morison Equation (Time domain) BEM, GDW and FVW methods MBD, modal/FEA Quasi-static/ Dynamic methods
BLADED Potential flow theory/ Morison Equation (Time domain) BEM method MBD, modal/FEA Quasi-static/ Dynamic methods
OrcaFlex Potential flow theory/ Morison Equation (Time domain) BEM method MBD, modal/FEA Quasi-static/ Dynamic methods
3DFloat Potential flow theory/ Morison Equation (Time domain) BEM method FEA Quasi-static/ Dynamic methods
HAWC2 Potential flow theory/ Morison Equation (Time domain) BEM method MBD, modal/FEA Quasi-static/ Dynamic methods
SIMA (SIMO/ RIFLEX) Potential flow theory/ Morison Equation (Time domain) BEM method MBD, modal/FEA Quasi-static/ Dynamic methods
QBlade Potential flow theory/ Morison Equation (Time domain) BEM and FVW methods MBD, modal/FEA Quasi-static/ Dynamic methods
Sesam/ Wadam Potential flow theory (Frequency domain) - Rigid body Quasi-static method
Simpack Potential flow theory/ Morison Equation (Time domain) BEM, GDW, and FVW methods MBD, modal/FEA Quasi-static/ Dynamic methods
SLOW Reduced potential flow theory/ Morison Equation (Time domain) Actuator model MBD, modal Quasi-static method
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated