Prerpints.org logo
Preprint
Article

Analyzing Twin Primes, Goldbach’s Strong Conjecture and Polignac’s Conjecture

Altmetrics

Downloads

194

Views

157

Comments

0

Submitted:

23 November 2023

Posted:

27 November 2023

You are already at the latest version

Alerts
Abstract
Here we analyze three well-known conjectures: (i) the existence of infinitely-many twin primes, (ii) Goldbach’s strong conjecture, and (iii) Polignac’s conjecture. We show that the three conjectures are related to each other. In particular, we see that in analysing the validity of the Goldbach’s strong conjecture, one must consider also the existence of an infinite number of twin primes. As a consequence of how we approach this analysis, we also observe that if this conjecture is true, then so is Polignac’s conjecture. Our first step is an analysis of the existence of infinitely-many twin primes numbers. For this, using the formula 4((n−1)!+1) ≡ −n (mod n(n + 2)) – satisfied if and only if (n, n + 2) are twin primes –, together with Wilson’s theorem, we obtain conditions that must be met for two numbers to be twin primes. Our results, obtained from an analytic and functional study, lead us to conclude that there may exist infinitely-many twin primes. Next, we consider the validity of the Goldbach’s strong conjecture. After showing that the conjecture is true for the first even numbers, we notice a pattern that we analyze for any even number, reducing it to three cases: (i) when the even number 2n is two times a prime number n; (ii) when the even number 2n is such that n = 2m, with 2m − 1 and 2m + 1 twin primes; (iii) all other cases, i.e., for any 2n even number ∀n ∈ N with n > 1, n prime or not, with independence of n = 2m being 2m−1 and 2m+1 twin primes or not. In this last case we show that one can always find a certain r ∈ N such that 1 < r < n satisfying that n−r and n+r are primes, so that their sum is 2n. In this case we use the reduction to absurd method, and our results lead us to conclude that Goldbach’s strong conjecture is true to the best of our calculations, as well as the Polignac’s conjecture.
Keywords: 
Subject: Computer Science and Mathematics  -   Algebra and Number Theory

MSC:  11–02

1. Introduction and background

In this paper we analyze three well known mathematical conjectures: the existence of infinite Twin Prime numbers, Goldbach’s Strong Conjecture, and Polignac’s Conjecture.
Although it is not usual, and not normally expected for three conjectures so relevant, with so much historical value, and said independently by different mathematicians (Christian Goldbach in 1742, Alphonse de Polignac in 1826), sometimes it can occur that different events are related to each other. This can be either because for A to happen it is necessary for B and C and D to happen (If B and C and D are true then is A true), or simply because one event can be a direct consequence of another (If A is true then is B true), and this is our case.
Specifically, and as this analysis is approached, it is observed that in order to be able to analyze the validity of Goldbach’s Strong Conjecture, one of the cases to be analyzed is nothing more nor less than the validity of the existence of infinite twin primes. As a consequence of the way in which the analysis of Goldbach’s Strong Conjecture is approached, it is observed that if this conjecture is true, then Polignac’s conjecture is also true.
For this reason, similar to the way in which C. Jouis in 2013 created the Neo-topology from the definition of a “thickness border" in a set A to measure the appropriate degree of typicality [1,2], in our case, and even though we will not use topological concepts for this analysis, we believe it is appropriate to categorize the three conjectures with a common property, and analyze them together in a single article. Note that all three conjectures state that the number 2, or an even number greater than 2, can be written as the subtraction (Twin primes or Polignac’s Conjecture) or the sum (Goldbach’s Strong Conjecture) of two prime numbers.
Twin primes and Goldbach’s conjecture have also deep implications in other fields of science. For instance, in physics it is well known that certain quantum states can codify interesting functions of prime numbers [3], and that these can also be computed with quantum computers [4]. In fact, the dynamics of entangled quantum systems has also been used to identify prime numbers [5]. Goldbach’s conjecture has also proven relevant in high-energy physics [6], and in the calculation of expectation values of the number operator in Fock states [7].
In addition to this, prime numbers and their relations (theorems and conjectures) can be seen as a whole as an ontology. In fact, ontologies are static because the class hierarchy and the relationships between these classes are fixed. They describe conceptual fields without a beginning or an end, without any class change and without any re-arrangement of the relationships between classes. Transitions from one state of knowledge to another one only concerns individual entities which may emerge, become extinct or for which properties may change. As an interesting recent example, in paleontology, systematics, that is the inventory and the organization of the species diversity over time, is complicated by the evolution: the graph of relations between classes may no longer be static; it must consider the temporal dimension. To specify whether a subclass is atypical or not, we borrow topological concepts of interior, exterior, border and closure. Then, we may represent atypical entities in ontologies, by defining a system of relations of inclusion and belonging that are inspired from standard topological operators [8].
Let us then begin by introducing Twin Prime numbers.
It is well known in mathematics, and more specifically in number theory, that two prime numbers (p, q) are twin primes numbers if being q > p , then q = p + 2 .
Hence, primes numbers 3 and 5 form a pair of twin primes. Other examples are (5, 7), (11, 13), (29, 31), etc.
The twin primes conjecture states the existence of infinite pairs of twin primes.
Most mathematicians believe the conjecture is true, and this is based on numerical evidence and heuristic reasoning about the probabilistic distribution of prime numbers.
In 1849, de Polignac made the more general conjecture that for every natural number k, there are infinitely many primes p such that p + 2 k is also prime [9].The case k = 1 of de Polignac’s conjecture is the twin prime conjecture.
It is unknown whether there are infinitely many twin primes or there is a largest pair. The work of Yitang Zhang in 2013, as well as work by James Maynard, Terence Tao and others, has made substantial progress towards proving that there are infinitely many twin primes, but at present this remains essentially unsolved [10].
On April 17th 2013, Yitang Zhang announced a proof that for some integer N less than 70 million, there are infinitely many pairs of primes that differ by N [11]. Zhang paper was accepted by Annals of Mathematics in early May 2013 [12]. Terence Tao subsequently proposed a Polymath Project collaborative effort to optimize Zhang bound [13]. As of April 14, 2014, one year after Zhang announcement, the bound had been reduced to 246 [14].
Some important properties to mention are:
  • Every twin primes pair except ( 3 , 5 ) is of the form ( 6 n − 1 , 6 n + 1 ) for some natural number n; that is, the number between the two primes is a multiple of 6 [15].
  • Brun’s theorem: In 1915, Viggo Brun showed that the sum of reciprocals of the twin primes was convergent [16].
  • It has been proven that the pair ( n , n + 2 ) is a pair of twin primes if and only if 4 ( ( n − 1 ) ! + 1 ) ≡ − n (mod n ( n + 2 ) ).
The last property is a direct consequence of the Wilson’s theorem applied to n and n + 2 if they both are prime numbers. Wilson’s theorem is an old theorem stated by first time by Ibn al-Haytham (c. 1000 AD) [17]. Many years later, in 1770 it was found by John Wilson[18] and Edward Waring announced the theorem, although neither he nor Wilson could prove it. It was Lagrange who gave the first proof in 1771 [19], and it seems that Leibniz was also aware of this result a century earlier, but he never published it [20].
In addition to the references cited above, it is also important to cite some of the most recent works published on the topic. For example, Marc Wolf, François Wolf and François-Xavier Villemin studied in 2019 the distribution of consecutive composite odd numbers and twin primes [34], in 2020 Berndt Gensel for twin primes greater or equal to 4 . 5 presented a new approach to prove the Twin Prime Conjecture by a sieve method to extract all Twin Primes on the level of the Twin Prime Generators [35], and in 2021 Madieyna Diouf also presented a study to analyze the distribution of twin primes numbers [36].
In this paper we analyze the possibility of the existence of infinite twin prime numbers, or on the contrary, if we can guarantee that there is a finite number of them. Using the formula 4 ( ( n − 1 ) ! + 1 ) ≡ − n (mod n ( n + 2 ) ) and Wilson’s Theorem, we show which conditions are met by twin primes, and what would happen if we assume that there is a finite number of them.
Next, we consider Goldbach’s Strong Conjecture, one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states:
“Every even integer greater than 2 can be expressed as the sum of two primes [21]".
The conjecture has been shown for all integers less than 4 × 10 18 [22].
On 7th June 1742, Christian Goldbach wrote a letter to Leonhard Euler [23] in which he proposed the following conjecture:
“Every integer which can be written as the sum of two primes, can also be written as the sum of as many primes as one wishes, until all terms are units".
He then proposed a second conjecture (the weak conjecture) in the margin of his letter:
“Every integer greater than 5 can be written as the sum of three primes"
Euler replied and reminded Goldbach of an earlier conversation they had, in which Goldbach remarked his original conjecture followed from the following statement:
“Every even integer greater than 2 can be written as the sum of two primes".
Which is actually known as Goldbach’s strong conjecture.
Many mathematicians have obtained important results about both conjectures.
Using Vinogradov’s method, Chudakov [24], Van der Corput [25] and Estermann [26] proved that almost all even numbers can be written as the sum of two primes.
Lev Schnirelmann [27,28] proved that any natural number greater than 1 can be written as the sum of not more than C prime numbers, where C is a computable constant. This result was enhanced by many authors, such as Olivier Ramaré, and the best known result currently stems from the proof of the weak Goldbach conjecture by Harald Helfgott [29] which directly implies that every even number n ≥ 4 is the sum of at most four primes.
Chen Jingrun showed in 1973 using the methods of sieve theory that every sufficiently-large even number can be written as the sum of either two primes, or a prime and a semiprime [30].
Hugh Montgomery and Robert Charles Vaughan showed that most even numbers are expressible as the sum of two primes.
Linnik proved the existence of a constant K such that every sufficiently large even number is the sum of two primes and at most K powers of 2. Roger Heath-Brown and Jan-Christoph Schlage-Puchta found that K = 13 works [29]. This was improved to K = 8 by Pintz and Ruzsa [31].
Harald Helfgott [32,33] did a considerable work on Goldbach’s weak conjecture, culminating in 2013, being the weak conjecture fully proved for all odd integers greater than 7.
In addition to the references cited above, it is also important to cite some of the most recent works published about this. For example, Andrei-Lucian Drăgoi published an article about a "vertical" generalization of the binary Goldbach’s Conjecture as applied on primes with prime indexes of any order i (i-primes) [37], and Salman Mahmud in 2020 demonstrated a probabilistic heuristic justification for the Goldbach’s strong conjecture [38].
In this article we analyze it for any even number using for this purpose the study of 3 cases. First case, when the even number 2 n is two times a prime number n. Second case, when the even number 2 n is such that n = 2 m and 2 m − 1 and 2 m + 1 are primes numbers (more exactly twin prime numbers). Third case, in general ∀ n ∈ N when n > 1 is prime or not and with independence of the case n = 2 m being 2 m − 1 and 2 m + 1 twin primes or not. In this last case, we can always find a certain r ∈ N such that 1 < r < n satisfying that n − r and n + r are prime numbers, and adding them of course we obtain 2 n . To analyze the general case we use the reduction to absurd method, and the results obtained lead us to conclude that Goldbach’s Strong Conjecture is true to the best of our calculations, as well as Polignac’s Conjecture.
The paper is organized as follows: in Section 2 we show if it is possible or not that there exist infinitely-many twin prime numbers. In Section 3 we analyze the validity of Goldbach’s Strong Conjecture and as a consequence of this result we analyze also the validity of Polignac’s Conjecture. Finally, in Section 4 we present our conclusions.

2. Is there an infinite number of twin primes?

In this section we analyze if the number of twin primes could be infinite or not.
First, using one property mentioned in the Introduction, we know that:
( n , n + 2 ) are twin prime numbers if and only if 4 ( ( n − 1 ) ! + 1 ) ≡ − n (mod ( n ( n + 2 ) ) ).
That is, if and only if ∃ A ∈ N such that:
4 ( ( n − 1 ) ! + 1 ) + n = A n ( n + 2 )
The value of A is not bounded, that is, when n increases then A increases. For instance:
  • For the pair ( 3 , 5 ) , we obtain A = 1
  • For the pair ( 5 , 7 ) , we obtain A = 3
  • For the pair ( 11 , 13 ) , we obtain A = 101505
  • For the pair ( 17 , 19 ) , we obtain A = 259105757127
  • etc.
That is A ≥ 1 .
Additionally, Wilson’s theorem states that if n is a prime number then ( n − 1 ) ! ≡ − 1 (mod n), that is, ∃ B ∈ N such that:
( n − 1 ) ! = B n − 1
The value of B is not bounded, that is, when n increases then B increases. For instance:
  • For the pair ( 3 , 5 ) , we obtain B = 1
  • For the pair ( 5 , 7 ) , we obtain B = 5
  • For the pair ( 11 , 13 ) , we obtain B = 329891
  • For the pair ( 17 , 19 ) , we obtain B = 1230752346353
  • etc.
That is B ≥ 1 .
If we compare the values of A and B, for each pair of twin prime numbers we observe that B ≥ A for those twin primes that we have analyzed. And it also happens for all ( n , n + 2 ) twin prime numbers, that is, A = 4 ( ( n − 1 ) ! + 1 ) + n n ( n + 2 ) ≤ ( n − 1 ) ! + 1 n = B , because:
( n + 2 ) ( ( n − 1 ) ! + 1 ) = ( n + 1 + 1 ) ( ( n − 1 ) ! + 1 ) = ( n + 1 ) ( ( n − 1 ) ! + 1 ) + ( n − 1 ) ! + 1 ≥ 4 ( ( n − 1 ) ! + 1 ) + n .
That is:
( n + 2 ) ( ( n − 1 ) ! + 1 ) ≥ 4 ( ( n − 1 ) ! + 1 ) + n .
Multiplying the above inequality by n, we have:
n ( n + 2 ) ( ( n − 1 ) ! + 1 ) ≥ n ( 4 ( ( n − 1 ) ! + 1 ) + n ) .
Dividing the above inequality by n ( n + 2 ) , we have:
( n − 1 ) ! + 1 ≥ 4 ( ( n − 1 ) ! + 1 ) + n n + 2 .
Dividing the above inequality by n, we have:
B = ( n − 1 ) ! + 1 n ≥ 4 ( ( n − 1 ) ! + 1 ) + n n ( n + 2 ) = A .
That is, B ≥ A , as we want to prove.
Hence, if we substitute ( n − 1 ) ! in Eq.(1) by B n − 1 , we have:
4 ( B n − 1 + 1 ) + n = A n ( n + 2 ) , 4 B n + n = A n ( n + 2 ) , 4 B + 1 = A ( n + 2 ) , n + 2 = 4 B + 1 A .
Note that, from the above equation, we get n = 4 B + 1 − 2 A A , and since n ∈ N , and n ≥ 3 , this implies:
  • A is an odd number.
  • 4 B + 1 − 2 A ≥ 3 A , that is, B ≥ 5 A − 1 4
So now, if we consider n + 2 as a function of A and B, we will analyze if the function n + 2 ≡ f ( A , B ) = 4 B + 1 A can have a maximum under the constraints, A ≥ 1 (A odd number), B ≥ 1 , B ≥ A and B ≥ 5 A − 1 4 .
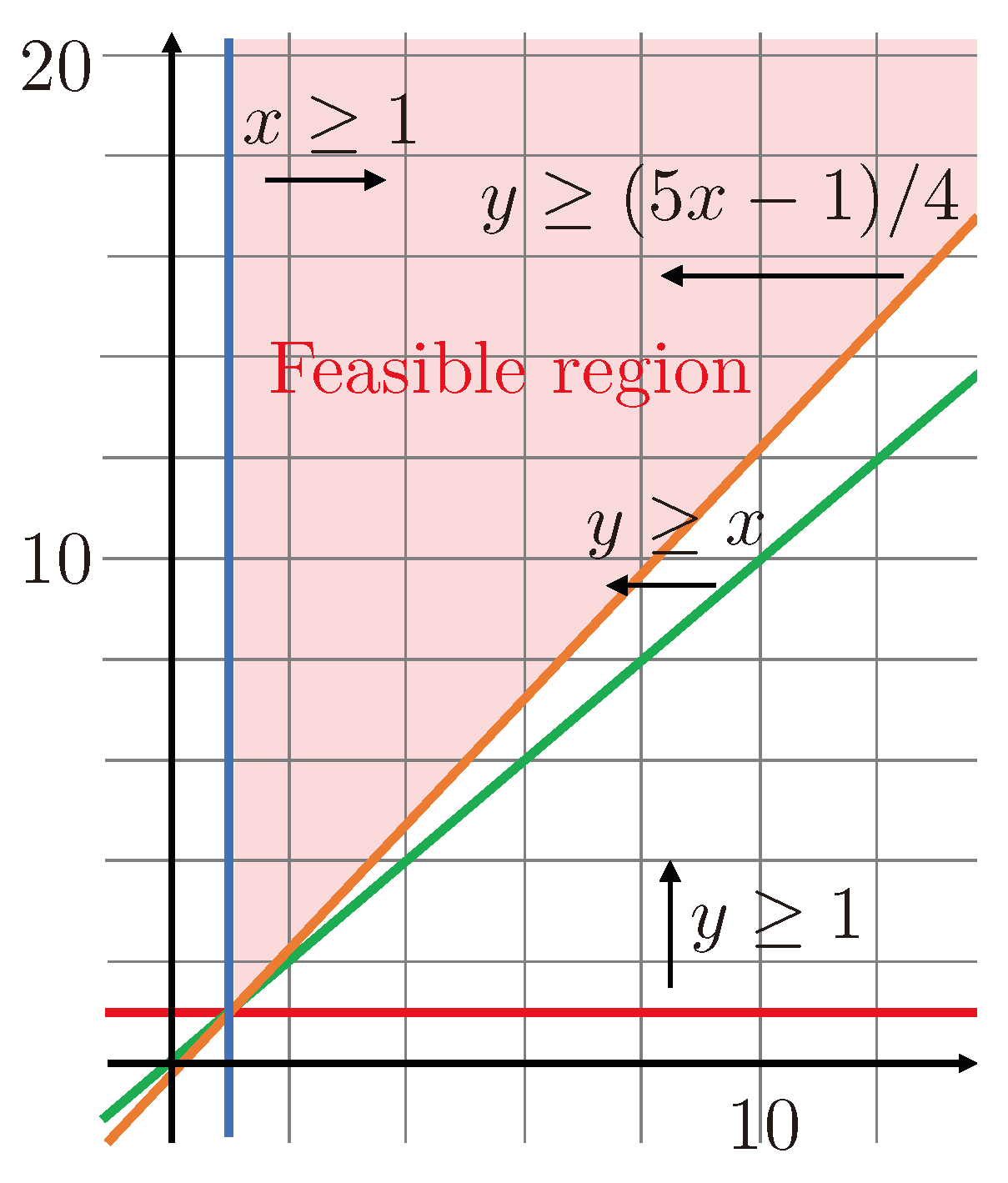
First, we analyze the function z = f ( x , y ) = 4 y + 1 x over the real numbers, and in the feasible region according to the constraints that we have obtained, which can be written in terms of x and y as x ≥ 1 , y ≥ 1 , y ≥ x and y ≥ 5 x − 1 4 . We can see how the feasible region looks like in the next figure:
Preprints 91286 g001
Figure 1. Feasible region of f ( x , y ) according to the constraints.
Figure 1. Feasible region of f ( x , y ) according to the constraints.
Preprints 91286 g001
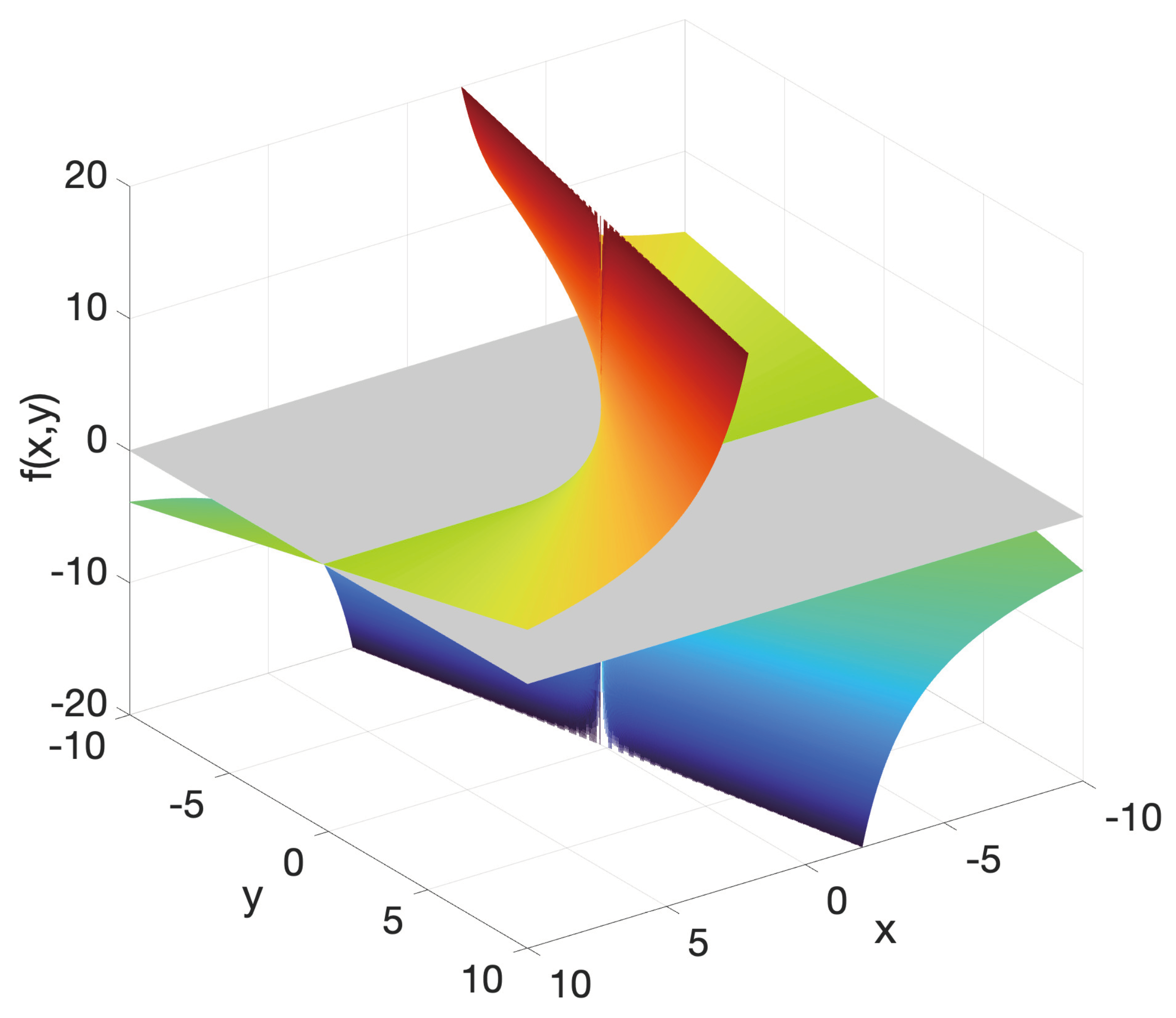
Then, if we calculate the gradient vector of the function z = f ( x , y ) = 4 y + 1 x , we realize that it is never equal to ( 0 , 0 ) , and this implies that this function has neither maximum nor minimum. We can see how this function looks like in the next figure.
Preprints 91286 g002
Figure 2. Function z = f ( x , y ) over the real numbers.
Figure 2. Function z = f ( x , y ) over the real numbers.
Preprints 91286 g002
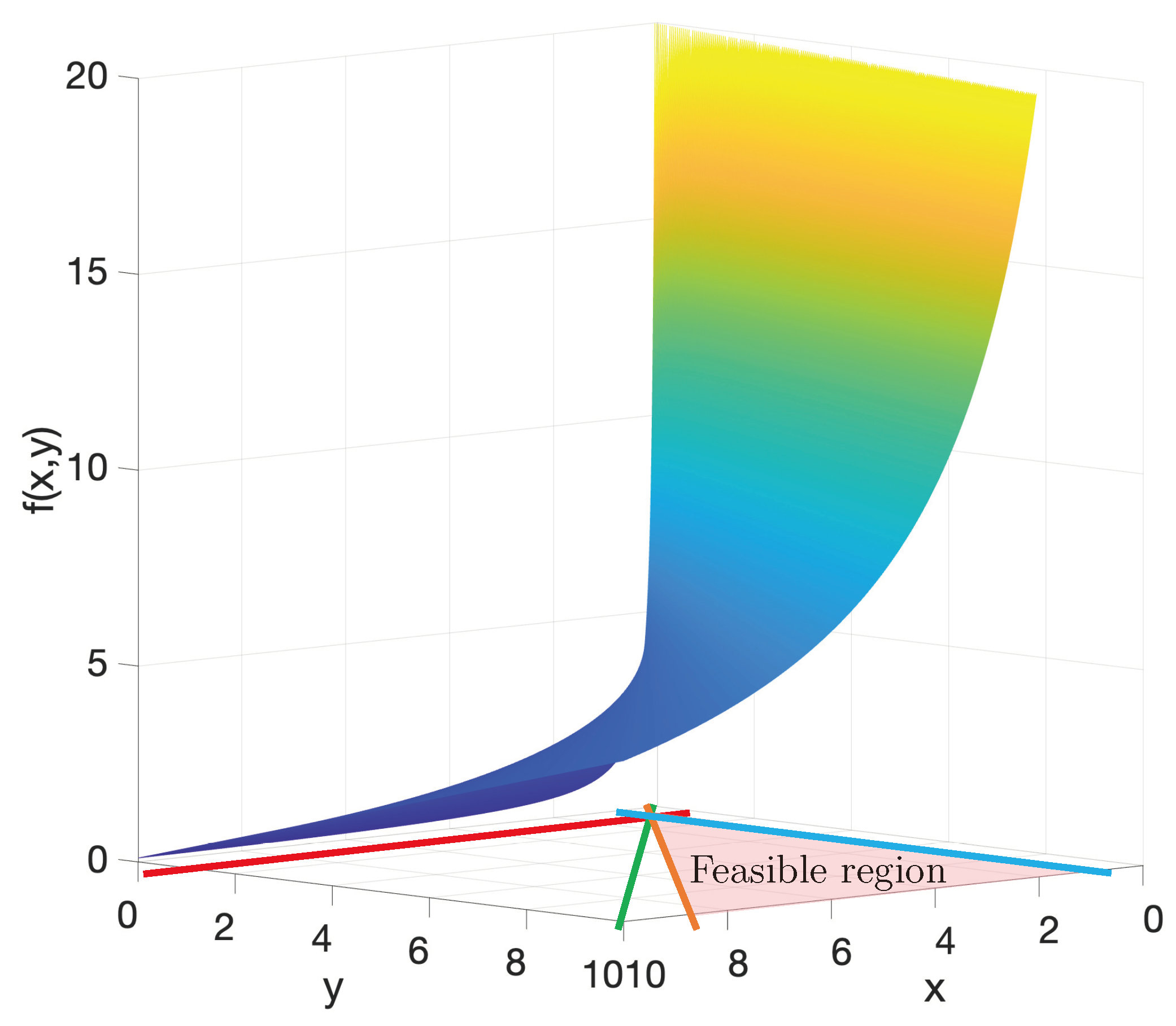
Hence, if we consider this function only over natural numbers and using the above constraints, then over the feasible region (not bounded) this function has neither a maximum, and only for ( A , B ) = ( 1 , 1 ) we obtain the minimum value equal to 5. See the graph in the next figure:
Preprints 91286 g003
Figure 3. Function z = f ( x , y ) directly over the feasible region.
Figure 3. Function z = f ( x , y ) directly over the feasible region.
Preprints 91286 g003
Therefore, we cannot guarantee that there is a finite number of twin primes. On the contrary: these results lead us to conclude that there are infinite twin prime numbers, to the best of our calculations.

3. Goldbach’s Strong Conjecture and Polignac’s Conjecture

Let us now use the previous results on twin prime numbers to assess Golbach’s (strong) and Polignac’s conjectures.

3.1. Analysis for the first even numbers

If we analyze Goldbach’s strong conjecture for the first even numbers 2 n , we find these prime numbers, and we realize that all them are of the form n − r and n + r for r ∈ N .
Let us show this for these first even numbers:
2 · 2 = 2 + 2 ( r = 0 ) 2 · 3 = 3 + 3 ( r = 0 ) 2 · 4 = 3 + 5 ( r = 1 ) 2 · 5 = 3 + 7 = 5 + 5 ( r = 2 , r = 0 ) 2 · 6 = 5 + 7 ( r = 1 ) 2 · 7 = 3 + 11 = 7 + 7 ( r = 4 , r = 0 ) 2 · 8 = 3 + 13 = 5 + 11 ( r = 5 , r = 3 ) 2 · 9 = 5 + 13 = 7 + 11 ( r = 4 , r = 2 ) 2 · 10 = 3 + 17 = 7 + 13 ( r = 7 , r = 3 ) 2 · 11 = 3 + 19 = 5 + 17 = 11 + 11 ( r = 8 , r = 6 , r = 0 ) 2 · 12 = 5 + 19 = 7 + 17 = 11 + 13 ( r = 7 , r = 5 , r = 1 ) 2 · 13 = 3 + 23 = 7 + 19 = 13 + 13 ( r = 10 , r = 6 , r = 0 ) 2 · 14 = 5 + 23 = 11 + 17 ( r = 9 , r = 3 ) 2 · 15 = 7 + 23 = 11 + 19 = 13 + 17 ( r = 8 , r = 4 , r = 2 ) 2 · 16 = 3 + 29 = 13 + 19 ( r = 13 , r = 3 ) .
As we can observe, it seems that they follow a pattern.
For instance:
  • For the cases 2 · 2 or 2 · 3 and all the cases where 2 n is the result for n a prime number, then the sum of n + n is always valid, and for certain cases like 2 · 5 not only 5 + 5 = 10 is valid, we can observe that adding 3 and 7 (both primes) we obtain also 10.
  • There are cases for which n is an even number like 2 · 6 , where 5 = 6 − 1 and 7 = 6 + 1 are just the numbers above and below number 6 and these are prime numbers, more exactly they are twin primes, such that adding them we obtain in this case 12. Another similar case is 2 · 12 , where 11 and 13 are both twin primes such that the sum is 24, but in this case there are also other prime numbers giving their sum also equal to 24.
  • In general, ∀ n ∈ N , when n > 1 is prime or not, or n − 1 and n + 1 are twin primes or not, we observe that it seems that we can always find a certain r ∈ N such that 1 < r < n satisfying that n − r and n + r are prime numbers, and adding them we obtain 2 n .
We will analyze in detail these three cases in the next section.

3.2. Analysis in general

We need to prove that for n ≥ 2 , ∃ p , q both prime numbers, such that 2 n = p + q .
There are two cases where this is satisfied directly. These cases are:
  • If n is prime then 2 n = n + n , that is 2 n can be written as the sum of two primes, both primes being the same n.
  • If n is an even number n = 2 m for m ∈ N , such that 2 m − 1 and 2 m + 1 are twin primes, then 2 m − 1 + 2 m + 1 = 4 m = 2 · 2 m = 2 n . That is, 2 n = 4 m is the sum of 2 m − 1 and 2 m + 1 , both twin primes, and since there exist infinite twin prime numbers, this implies that there are many cases similar to this.
Additionally, in the previous section we have observed that, in general, ∀ n ∈ N when n is prime or not, and with independence of the case n = 2 m being 2 m − 1 and 2 m + 1 twin primes or not, we observe that ∃ r ∈ N such that 1 < r < n satisfying that n − r and n + r are prime numbers and adding them we obtain 2 n . Therefore, we analyze this case with respect to what follows.
We will assume n > 3 because for n = 2 or n = 3 , 2 · 2 = 2 + 2 and 2 · 3 = 3 + 3 , that is, 2 and 3 are the prime numbers, and also that there are no other prime numbers such that adding them the result will be 4 or 6.
We will use also the reduction to absurd method.
Then let us assume that it is not true the statement ∀ n ∈ N n > 3 ∃ r ∈ N 1 < r < n such that n − r and n + r are prime numbers.
Applying the logic rules to negate a quantifier and the corresponding Morgan law to negate a conjunction, we must then analyze if it can be true or not that ∃ n ∈ N n > 3 such that ∀ r ∈ N 1 < r < n , n − r or n + r are not prime numbers.
Hence, let us assume that this n = m , then:
  • If m − r is not prime ∀ r ∈ N 1 < r < n , then this implies that there are not any prime numbers less than m − 1 , but then this is only possible if m = 3 , however we were assuming n > 3 . Therefore this case cannot be possible.
  • If m + r is not prime ∀ r ∈ N 1 < r < n , this implies that there are no prime numbers greater than m + 1 , that is, there would exist a finite number of prime numbers. However this is not true because there exists infinite prime numbers. Therefore this case is not possible.
Hence, we arrive to a contradiction, and therefore it is satisfied that ∀ n ∈ N n > 3 ∃ r ∈ N 1 < r < n such that n − r and n + r are prime numbers. Then for all even number 2 n we can write this as the sum of these prime numbers n − r and n + r .
Additionally, to prove this last case in which we are saying that the primes p and q are obtained by adding and subtracting a certain r to n, we could also prove it in the following way:
If 2 n is such that n is a prime number or not, and there exist two prime numbers p and q such that 2 n = p + q for p ≠ n and q ≠ n , then p and q must be less than 2 n .
Hence, let us assume that p = 2 n − t for t ∈ N t < 2 n . Then, since p ≠ n and q ≠ n , this implies t ≠ n , and then t < n or t > n .
Let us assume that t < n , then p = 2 n − t > n , therefore, since p > n this implies that p = n + r for any r ∈ N r < n , and q should be less than n, because if q > n then p + q > n + n = 2 n . However we were assuming that 2 n = p + q , therefore q must be less than n, that is, q = n − s for any s ∈ N s < n .
Then, since 2 n = p + q this implies that 2 n = n + r + n − s = 2 n + r − s . Then r − s = 0 , that is, r = s and this implies that the primes p and q are obtained adding and subtracting a certain r ∈ N r < n , so that p = n + r and q = n − r .
A possible question now could be how to compute these r values. In this sense, since a prime number is an odd number, this implies that if n is an odd number then r must be an even number, and if n is an even number then r must be an odd number.
In addition, and applying Wilson’s theorem, which states that n is a prime number if and only if ( n − 1 ) ! ≡ − 1 (mod n), then as n − r and n + r must be prime numbers, then the possible values of r must satisfy the next two congruence equations:
( n − r − 1 ) ! ≡ − 1 ( mod n − r ) , ( n + r − 1 ) ! ≡ − 1 ( mod n + r ) .
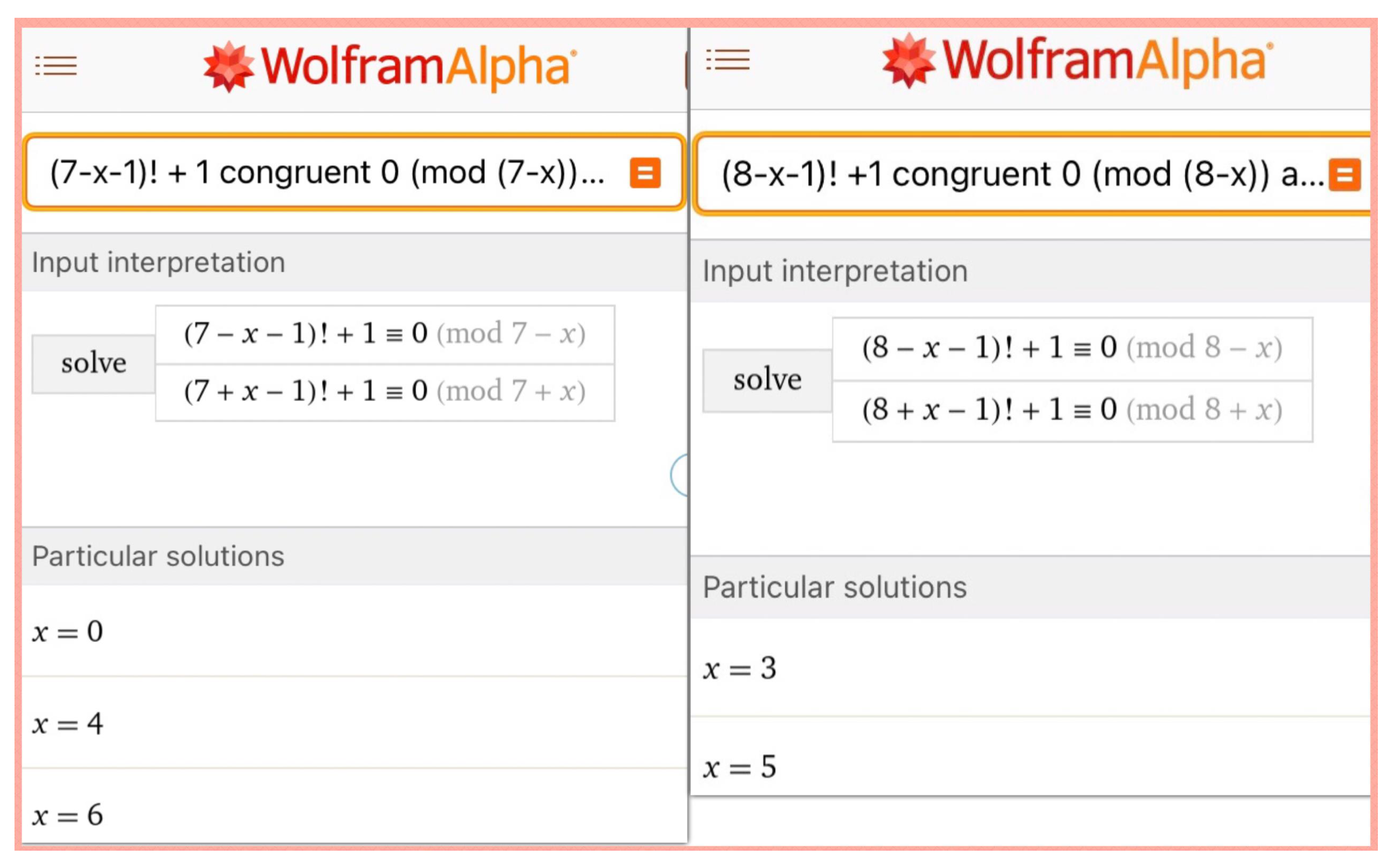
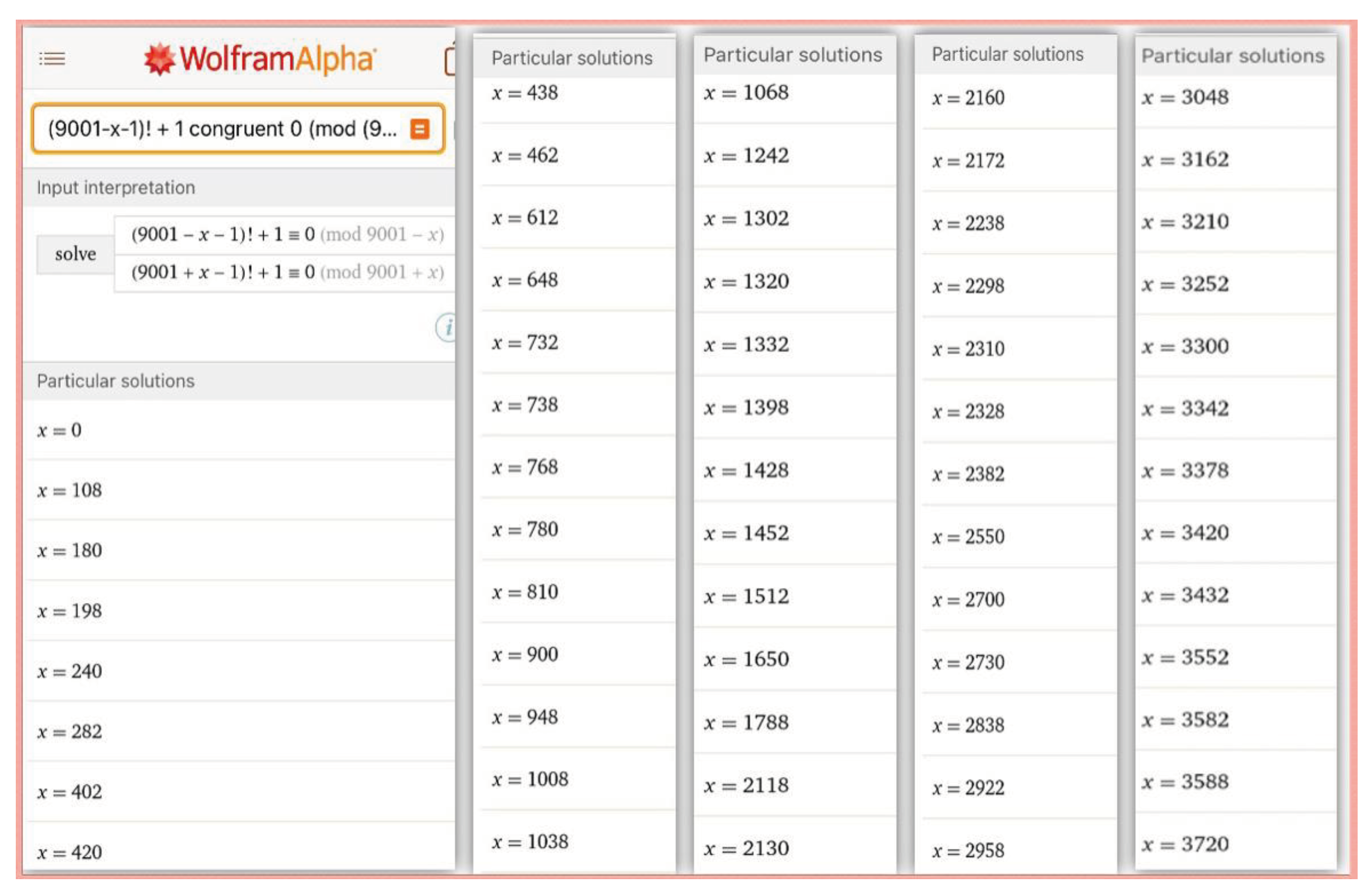
This system of congruence equations can be solved writing any software code, or for example by using Wolfram Alpha to yield solutions, maybe not for very big natural numbers, but below are results that show the possible r values (r is denoted x in Wolfram) to subtract and add to 7 to obtain 14, or the ones to subtract and add to 8 to obtain 16, and the ones to subtract and add to 9001 to obtain 18002.
Preprints 91286 g004
Figure 4. Solutions of x (r) to obtain 14 and 16.
Figure 4. Solutions of x (r) to obtain 14 and 16.
Preprints 91286 g004
Note that for the case of 14, r = 0 is computed because 7 is a prime number and 7 + 7 = 14 , which is correct, as well as the value r = 6 is computed because 1 and 13 are satisfying the equations, however we discard the value r = 6 because 1 is not a prime number.
Preprints 91286 g005
Figure 5. Solutions of x (r) to obtain 18002 (picture 1 of 3).
Figure 5. Solutions of x (r) to obtain 18002 (picture 1 of 3).
Preprints 91286 g005
Preprints 91286 g006
Figure 6. Solutions of x (r) to obtain 18002 (picture 2 of 3).
Figure 6. Solutions of x (r) to obtain 18002 (picture 2 of 3).
Preprints 91286 g006
Preprints 91286 g007
Figure 7. Solutions of x (r) to obtain 18002 (picture 3 of 3).
Figure 7. Solutions of x (r) to obtain 18002 (picture 3 of 3).
Preprints 91286 g007
Therefore, the results lead us to conclude that the Goldbach Strong Conjecture is true, to the best of our observations.
Additionally, with the last result, it is also being proved that there are infinitely-many primes like p and p + 2 r , because we can say that n − r = p and then n + r = p + 2 r . That is, there exist infinite pairs of primes (p, p + 2 r ) for r ∈ N r > 1 , which is equivalent to stating that for all n even natural numbers greater than 2 there exist p and q prime numbers, such that q > p and n = q − p , which is the well known Polignac’s Conjecture. Therefore, these results lead us also to conclude that the Polignac’s Conjecture is also true, again to the best of our observations.

3.3. Corollary: consequence of the validity of Goldbach’s Strong Conjecture

Since ∀ n ∈ N n > 2 even number, can be written as the sum of two prime numbers p and q, then ∀ n ∈ N n > 5 odd number, can be written as the sum of three prime numbers: 3, p and q.
Proof
If n is an odd number greater than 5, then n = 2 ( m + 1 ) + 1 for m ∈ N m ≥ 2 , that is, n = 2 m + 2 + 1 = 2 m + 3 .
Since 2 m is an even number, then there exist p and q prime numbers such that 2 m = p + q .
Therefore:
n = 2 m + 3 = p + q + 3
As we want to prove.
This consequence proves also the weak conjecture of Goldbach, which states that all odd numbers greater than 5 can be expressed as the sum of three primes, but adding something else, because one of these primes can always be the number 3.

4. Conclusions

In this article we analyzed three well-known mathematical conjectures: the conjecture concerning the existence of infinite Twin Primes, Goldbach’s Strong Conjecture, and Polignac’s Conjecture.
Although it is not usual, or what one might expect for three conjectures so relevant and with so much historical value (and also said independently and by different mathematicians), we realized that the three of them are related to each other. In particular, and as a consequence of how our analysis is approached, it is observed that in order to be able to analyze the validity of Goldbach’s Strong Conjecture, one of the cases to be considered is related to the validity of the existence of infinitely-many twin primes. In addition, it is also observed that if this conjecture is true, then Polignac’s conjecture is also true.
Therefore, first we began analyzing the validity or or non - validity of the existence of infinite twin primes.
To do this we used the property 4 ( ( n − 1 ) ! + 1 ) ≡ − n (mod n ( n + 2 ) , which we know to be true for any pair of twin primes ( n , n + 2 ) , as well as Wilson’s Theorem.
In this way we obtained certain conditions that these twin primes must satisfy, and which in turn, only depend on two natural numbers which we call A and B.
These natural numbers A and B are subject to certain restrictions. By extending them to all the real numbers and drawing the feasible region in the plane, we observed that this feasible region is not bounded.
Additionally, if ( n , n + 2 ) is a pair of twin primes, n + 2 and n can be expressed as a function that depends only on these A and B (we call it f ( A , B ) ). That is, it was observed that n + 2 = f ( A , B ) .
Consequently, the next question we asked ourselves next is whether the said function f ( A , B ) extended to the whole real plane and within the feasible region, has a maximum or not. We observed that this function has no maximum in the real numbers, and therefore not in the natural numbers either.
Therefore, from all the above, only one conclusion is valid, which is the existence of infinitely-many twin primes numbers.
Secondly, we followed with the study of the validity of the Goldbach’s Strong Conjecture.
We initially showed that the conjecture is true for those even numbers 2 n such that n is a prime number.
Then, we showed that it is also true for those even numbers 2 n such that n is an even number equal to 2 m and satifying that 2 m − 1 and 2 m + 1 are twin primes numbers. Therefore, since there are infinitely-many twin prime numbers, this fact is important.
Finally, we analyzed in detail that the conjecture is also true ∀ n ∈ N , n > 2 prime or not, and with independence of the case n = 2 m being 2 m − 1 and 2 m + 1 twin primes or not. To analyze this general case we used the reduction to absurd method, and the results obtained lead us to conclude that Goldbach’s Strong Conjecture is true, as well as, Polignac’s Conjecture as a direct consequence of the validity of Goldbach’s Strong Conjecture, to the best of our observations.
The results presented in this paper show also how different conjectures, formulated independently, are actually related to each other, in the sense that proving one of them implies that the other follow. Our findings are relevant beyond pure mathematics, given the impact of prime numbers in other fields of science, such as physics, computer science, cryptography, and more. Exploring the implications of our results in these fields is an interesting research line that we leave for future works.

Acknowledgments

We acknowledge the fruitful discussions over the years with many mathematicians, physicists and computer scientist colleagues regarding validity and applications of these conjectures. We also acknowledge James Peterson for his appreciation of mathematics in all its branches and for reviewing the English spelling. Finally, we also acknowledge computational support from Mathworks and Wolfram Alpha.

References

  1. Jouis, C., Rahman, MY., Ganascia, J–G. (2013). "Neo-Topological Approach to Reasoning on Ontologies with Exceptions and Comparison with Defeasible Description Logics". Proceedings of the Twenty Sixth International Florida Artificial Intelligence Research Society Conference (FLAIRS 2013).
  2. Jouis, C., Guy, F., Habib, B., Ganascia, J–G., (Jun. 2013). "Combination of Topology and Nonmonotonic Logics for Typicality in a Scientific Field: Paleoanthropology". Proceedings of the Twenty-Fourth International Florida Artificial Intelligence Research Society Conference, Miami, Florida, USA.
  3. Latorre, J. I., Sierra, G. “There is entanglement in the primes", arXiv:1403.4765 (2014). [CrossRef]
  4. Latorre, J. I., Sierra, G. “Quantum computation of prime number functions", Quantum Information and Computation, Vol. 14, 0577 (2014). [CrossRef]
  5. Southier, A. L. M., Santos, L. F., Souto Ribeiro, P. H., Ribeiro, A. D., “Identifying primes from entanglement dynamics", Phys. Rev. A 108, 042404 (2023). [CrossRef]
  6. Sanchis-Lozano, M. A., Barbero G., A. F., Navarro-Salas, J. “Prime numbers, quantum field theory and the Goldbach conjecture", International Journal of Modern Physics A, Vol. 27, No. 23, 1250136 (2012). [CrossRef]
  7. Prudencio, T., Silva, E. O., “Goldbach conjecture sequences in quantum mechanics", arXiv:1303.6476 (2013). [CrossRef]
  8. Jouis, C., et al., “Dealing with Atypicality using neo-Topology: Application to Paleontology", Conference Toth 2012, Terminology and Ontology: Theories and applications, At: Chambery, France, Volume: 1 (2012).
  9. de Polignac, A. (1849). "Recherches nouvelles sur les nombres premiers" [New research on prime numbers]. Comptes rendus (in French). 29: 397–401. From p. 400: "1er Théorème. Tout nombre pair est égal à la différence de deux nombres premiers consécutifs d’une infinité de manières … " (1st Theorem. Every even number is equal to the difference of two consecutive prime numbers in an infinite number of ways … ).
  10. Terry Tao. (7 October 2014). “Small and Large Gaps Between the Primes". Video lecture. UCLA Department of Mathematics. [CrossRef]
  11. McKee, Maggie (14 May 2013). "First proof that infinitely many prime numbers come in pairs". Nature. doi:10.1038/nature.2013.12989. ISSN 0028-0836. [CrossRef]
  12. Zhang, Yitang (2014). "Bounded gaps between primes". Annals of Mathematics. 179 (3): 1121–1174. doi:10.4007/annals.2014.179.3.7. MR 3171761. [CrossRef]
  13. Tao, Terence (June 4, 2013). "Polymath proposal: bounded gaps between primes".
  14. Xhang, Y. (2014). “Bounded gaps between primes". Annals of Mathematics, 14 (8): 1121-1174.
  15. Caldwell, Chris K. "Are all primes (past 2 and 3) of the forms 6n+1 and 6n-1?". The Prime Pages. The University of Tennessee at Martin. Retrieved 2018-09-27.
  16. Brun, V. (1915), "Über das Goldbachsche Gesetz und die Anzahl der Primzahlpaare", Archiv for Mathematik og Naturvidenskab (in German), 34 (8): 3–19, ISSN 0365-4524, JFM 45.0330.16.
  17. O’Connor, John J., Robertson, Edmund F., "Abu Ali al-Hasan ibn al-Haytham", MacTutor History of Mathematics Archive, University of St Andrews.
  18. Waring, E. "Meditationes Algebraicae" (Cambridge, England: 1770), page 218 (in Latin).
  19. Lagrange, Joseph L. "Demonstration d’un théorème nouveau concernant les nombres premiers" (Proof of a new theorem concerning prime numbers), Nouveaux Mémoires de l’Académie Royale des Sciences et Belles-Lettres (Berlin), vol. 2, pages 125–137 (1771).
  20. Vacca, G. (1899) "Sui manoscritti inediti di Leibniz”, Bollettino di bibliografia e storia delle scienze matematiche,, vol. 2, pages 113–116. Manuscripts kept at the Royal Public Library in Hanover (Germany), vol. 3 B, bundle 11, page 1.
  21. Weisstein, Eric W. (2002). "Goldbach Conjecture." From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/GoldbachConjecture.html.
  22. Oliveira e Silva, T., Herzog, S., and Gardi, S.(July 2014) “Empirical verification of the even Goldbach conjecture and computation of prime gaps up to 4x1018". Mathematics of Computation, 83 (288): 2033-2060.
  23. Zenil, H. (2007) “Goldbach’s Conjecture". Wolfram Demonstrations Project.
  24. Chudakov, Nikolai G. (1937). "On the Goldbach problem". Doklady Akademii Nauk SSSR. 17: 335–338.
  25. Van der Corput, J. G. (1938). "Sur l’hypothèse de Goldbach" (PDF). Proc. Akad. Wet. Amsterdam (in French). 41: 76–80.
  26. Estermann, T. (1938). "On Goldbach’s problem: proof that almost all even positive integers are sums of two primes". Proc. London Math. Soc. 2. 44: 307–314. doi:10.1112/plms/s2-44.4.307. [CrossRef]
  27. Schnirelmann, L.G. (1930). "On the additive properties of numbers", first published in "Proceedings of the Don Polytechnic Institute in Novocherkassk" (in Russian), vol XIV (1930), pp. 3-27, and reprinted in "Uspekhi Matematicheskikh Nauk" (in Russian), 1939, no. 6, 9–25.
  28. Schnirelmann, L.G. (1933). First published as "Über additive Eigenschaften von Zahlen" in "Mathematische Annalen" (in German), vol 107 (1933), 649-690, and reprinted as "On the additive properties of numbers" in "Uspekhi Matematicheskikh Nauk" (in Russian), 1940, no. 7, 7–46.
  29. Helfgott, H. A. (2013). "The ternary Goldbach conjecture is true". arXiv:1312.7748, [math.NT].
  30. Chen, J. R. (1973). "On the representation of a larger even integer as the sum of a prime and the product of at most two primes". Sci. Sinica. 16: 157–176.
  31. Heath-Brown, D. R.; Puchta, J. C. (2002). "Integers represented as a sum of primes and powers of two". Asian Journal of Mathematics. 6 (3): 535–565. arXiv : math.NT/0201299.
  32. Helfgott, H.A. (2013). "Major arcs for Goldbach theorem". arXiv:1305.2897, [math.NT].
  33. Helfgott, H.A. (2012). "Minor arcs for Goldbach problem". arXiv:1205.5252, [math.NT].
  34. Wolf, M., Wolf, F., Villemin, F–X.”On the distribution of consecutive composite odd numbers and twin primes”. Fundamental Journal of Mathematics and Mathematical Sciences, Volume 11, Issue 1, 2019, Pages 1 to 24.
  35. Gensel, B. “An Elementary Proof of the Twin Prime Conjecture”. Turkish Journal of Analysis and Number Theory. 2020, 8(3), 52-56.
  36. Diouf, M. “On the distribution of twin primes”. International Journal of Contemporary Mathematical Sciences 16.4 (2021): 173-186.
  37. Drăgoi, A–L. “A Matricial Aspect of Goldbach’s Conjecture”. JAMCS 25(2): 1-32, 2017; JAMCS.36895; ISSN: 2456-9968.
  38. Mahmud, A. "The Probabilistic Heuristic Justification for the Goldbach’s Strong Conjecture". International Journal of Scientific and Innovative Mathematical Research(IJSIMR) Volume 8, Issue 4, 2020, PP 47-50.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated