Article
Version 1
Preserved in Portico This version is not peer-reviewed
Variable Selection for Sparse Logistic Regression with Grouped Variables
Version 1
: Received: 16 November 2023 / Approved: 16 November 2023 / Online: 16 November 2023 (15:30:02 CET)
A peer-reviewed article of this Preprint also exists.
Zhong, M.; Yin, Z.; Wang, Z. Variable Selection for Sparse Logistic Regression with Grouped Variables. Mathematics 2023, 11, 4979. Zhong, M.; Yin, Z.; Wang, Z. Variable Selection for Sparse Logistic Regression with Grouped Variables. Mathematics 2023, 11, 4979.
Abstract
We present a new penalized method for estimation in sparse logistic regression models with group structure. Group sparsity suggests us to consider the Group Lasso penalty. Being different from penalized log-likelihood estimation, our method can be viewed as a penalized weighted score function method. Under some mild conditions, we provide non-asymptotic oracle inequalities promoting group sparsity of predictors. A modified block coordinate descent algorithm based on a weighted score function is also employed. The net advantage of our algorithm over the existing Group Lasso-type procedures is that the tuning parameter can be pre-specified. The simulations show that this algorithm is considerably faster and more stable than competing methods. 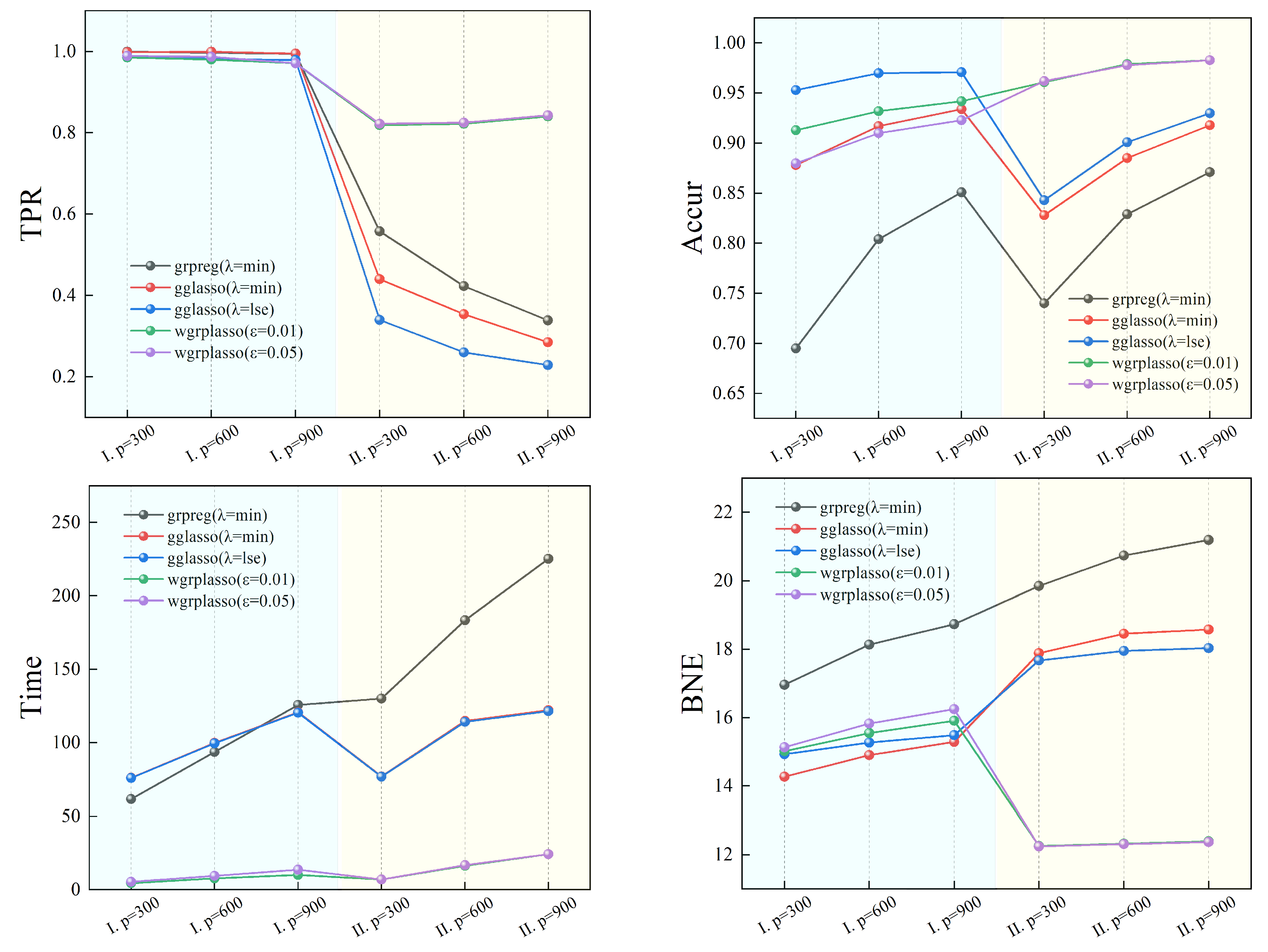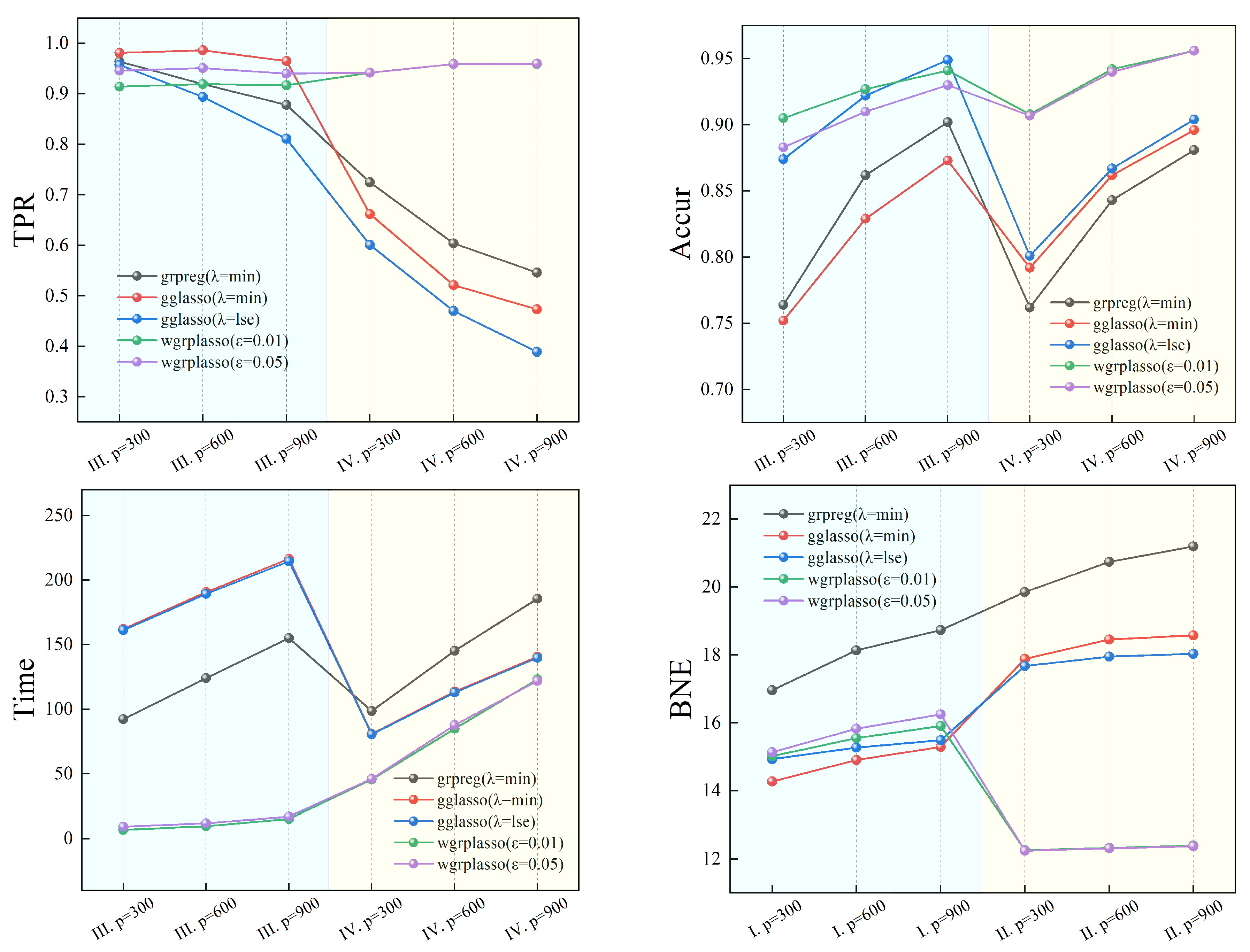Finally, we illustrate our methodology with two real data sets.
Keywords
high-dimensional data; non-asymptotic inequality; logistic regression; variable selection; block coordinate descent algorithm
Subject
Computer Science and Mathematics, Probability and Statistics
Copyright: This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Comments (0)
We encourage comments and feedback from a broad range of readers. See criteria for comments and our Diversity statement.
Leave a public commentSend a private comment to the author(s)
* All users must log in before leaving a comment
