Submitted:
07 November 2023
Posted:
08 November 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- We present a novel modification to the R/S approach, highlighting the distinctions between fractional Lévy motions, fractional Brownian motions, and stock market data.
- We introduce a method for continuously estimating a scaling parameter via machine learning from time series data without employing sophisticated preprocessing methods.
- We propose a new technique for estimating the scaling exponent of fractional Lévy motion using machine learning models, demonstrating its effectiveness through extensive experiments.
- We show that traditional techniques like DFA and other traditional methods do not accurately depict the scaling parameter for time series that are close to fractional Lévy motion, emphasizing the potential for machine learning approaches in this realm.
2. Related Work
3. Methodology
3.1. Random Walks
3.2. Estimating the Hurst Exponent
3.2.1. R/S analysis
3.2.2. Detrended Fluctuation Analysis(DFA)
- Integrate the time series: Calculate the cumulative sum of the deviations of the data points from their mean.
- Divide the integrated time series into non-overlapping segments of equal length n.
- Detrend the data: In each segment, fit a polynomial function (usually a linear function) and subtract it from the integrated time series.
- Calculate the root-mean-square fluctuations for each segment.
- Average the fluctuations over all segments and obtain the fluctuation function .
- Repeat steps 2-5 for various time scales (segment lengths) n.
- Analyze the scaling behavior of F(n) by plotting it against the time scale n on a log-log scale. A linear relationship indicates the presence of long-range correlations in the original time series.
- The Hurst exponent can be estimated from the slope of the log-log plot, providing information about the persistence or anti-persistence in the time series.
3.3. Machine Learning
3.3.1. Linear Models
3.3.2. Boost Regressors
-
AdaBoost:AdaBoost, short for "Adaptive Boosting," is a popular ensemble learning algorithm used in machine learning. It was developed to improve the performance of weak classifiers by combining them into a single, more accurate and robust classifier. The main idea behind AdaBoost is to iteratively train a series of weak classifiers on the data, assigning higher weights to misclassified instances at each iteration. This process encourages the subsequent classifiers to focus on the more challenging instances, ultimately leading to an ensemble model with improved overall performance. [13]
-
CatBoost:CatBoost is a gradient boosting algorithm specifically designed to handle categorical features effectively. It was developed by Yandex researchers and engineers, and it is known for its high performance and accuracy in various machine learning tasks. CatBoost addresses the common challenges associated with handling categorical features, such as one-hot encoding, by employing an efficient, target-based encoding scheme called "ordered boosting." This method reduces overfitting and improves generalization, leading to better results in many applications, [29].
-
LightGBM:LightGBM (Light Gradient Boosting Machine) is a gradient boosting framework developed by Microsoft that is designed to be more efficient and scalable than traditional gradient boosting methods. It is particularly well-suited for large-scale and high-dimensional data. LightGBM incorporates several key innovations, such as Gradient-based One-Side Sampling (GOSS) and Exclusive Feature Bundling (EFB), which significantly reduce memory usage and computational time while maintaining high accuracy.[12]
3.3.3. Multi Layer Perceptron
3.3.4. Error Analysis
4. Machine Learning Training/Validation
4.1. Training Data
4.2. Training the Machine Learning Models
4.3. Validating the trained Models
4.3.1. fractional Brownian motion
4.3.2. Fractional Lévy Motion, α=0.5
4.3.3. Fractional Lévy Motion, α=1.0
| window length | alg. nolds Hurst | alg. nolds DFA | alg. Hurst Hurst | alg. Hurst Hurst simplified |
|---|---|---|---|---|
| 10 | 0.28169 ± 0.01582 | 0.14867 ± 0.24577 | - | - |
| 25 | 0.26134 ± 0.02507 | 0.16672 ± 0.04256 | - | - |
| 50 | 0.29846 ± 0.01826 | 0.15482 ± 0.02765 | - | - |
| 100 | 0.34383 ± 0.01472 | 0.15946 ± 0.01826 | 0.11358 ± 0.01295 | 0.09771 ± 0.0146 |
| 200 | 0.37387 ± 0.00979 | 0.15343 ± 0.01281 | 0.09689 ± 0.00983 | 0.09633 ± 0.01395 |
| 350 | 0.40277 ± 0.00817 | 0.14777 ± 0.00979 | 0.08666 ± 0.0082 | 0.08423 ± 0.01146 |
| window length | Ridge fBm | Ridge fLm | Ridge both |
|---|---|---|---|
| 10 | 0.28117 ± 0.00027 | 0.28126 ± 0.00072 | 0.28145 ± 0.00048 |
| 25 | 0.28131 ± 0.00043 | 0.28134 ± 0.00046 | 0.2813 ± 0.00027 |
| 50 | 0.2812 ± 0.00069 | 0.28136 ± 0.00067 | 0.28124 ± 0.00051 |
| 100 | 0.28138 ± 0.00121 | 0.28139 ± 0.00133 | 0.28141 ± 0.00101 |
| 200 | 0.28127 ± 0.00013 | 0.28133 ± 0.00081 | 0.28124 ± 0.0006 |
| 350 | 0.28129 ± 0.00011 | 0.28135 ± 0.00052 | 0.28129 ± 0.00039 |
| window length | Lasso fBm | Lasso fLm | Lasso both |
| 10 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 25 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 50 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 100 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 200 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 350 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| window length | AdaBoost fBm | AdaBoost fLm | AdaBoost both |
| 10 | 0.22433 ± 0.0129 | 0.22269 ± 0.01196 | 0.21992 ± 0.01335 |
| 25 | 0.18802 ± 0.01813 | 0.20001 ± 0.01125 | 0.19137 ± 0.01486 |
| 50 | 0.18038 ± 0.0187 | 0.19031 ± 0.0111 | 0.17882 ± 0.01649 |
| 100 | 0.17227 ± 0.01964 | 0.1828 ± 0.00976 | 0.17062 ± 0.01527 |
| 200 | 0.19107 ± 0.01682 | 0.19405 ± 0.00888 | 0.18627 ± 0.01331 |
| 350 | 0.1832 ± 0.01297 | 0.18972 ± 0.00662 | 0.17945 ± 0.01015 |
| window length | CatBoost fBm | CatBoost fLm | CatBoost both |
| 10 | 0.16251 ± 0.0228 | 0.1735 ± 0.0155 | 0.16663 ± 0.01876 |
| 25 | 0.10053 ± 0.02435 | 0.12608 ± 0.01514 | 0.11452 ± 0.01884 |
| 50 | 0.08678 ± 0.0223 | 0.10853 ± 0.0148 | 0.09634 ± 0.01796 |
| 100 | 0.0805 ± 0.01776 | 0.09093 ± 0.0143 | 0.08429 ± 0.01576 |
| 200 | 0.09697 ± 0.01578 | 0.11339 ± 0.01109 | 0.10593 ± 0.01341 |
| 350 | 0.08847 ± 0.01262 | 0.10591 ± 0.009 | 0.09767 ± 0.01095 |
| window length | LightGBM fBm | LightGBM fLm | LightGBM both |
| 10 | 0.16298 ± 0.02281 | 0.17226 ± 0.0156 | 0.1669 ± 0.01887 |
| 25 | 0.10358 ± 0.02465 | 0.12709 ± 0.01515 | 0.11801 ± 0.01879 |
| 50 | 0.08901 ± 0.02287 | 0.11128 ± 0.01457 | 0.0991 ± 0.01792 |
| 100 | 0.08219 ± 0.01884 | 0.09293 ± 0.01406 | 0.08662 ± 0.01601 |
| 200 | 0.10263 ± 0.01659 | 0.11551 ± 0.01118 | 0.10916 ± 0.01362 |
| 350 | 0.09302 ± 0.01335 | 0.10787 ± 0.00902 | 0.10049 ± 0.01107 |
| window length | MLP fBm | MLP fLm | MLP both |
| 10 | 0.16992 ± 0.02453 | 0.17416 ± 0.01483 | 0.1626 ± 0.01924 |
| 25 | 0.0989 ± 0.02508 | 0.12536 ± 0.01521 | 0.11192 ± 0.01802 |
| 50 | 0.087 ± 0.02189 | 0.10809 ± 0.01586 | 0.09365 ± 0.01821 |
| 100 | 0.08741 ± 0.01875 | 0.09523 ± 0.01581 | 0.09705 ± 0.01728 |
| 200 | 0.10958 ± 0.01624 | 0.11189 ± 0.01236 | 0.12114 ± 0.01475 |
| 350 | 0.10021 ± 0.01313 | 0.10521 ± 0.00936 | 0.11197 ± 0.01189 |
4.3.4. Fractional Lévy Motion, α=1.5
| window length | alg. nolds Hurst | alg. nolds DFA | alg. Hurst Hurst | alg. Hurst Hurst simplified |
|---|---|---|---|---|
| 10 | 0.27084 ± 0.01484 | 0.23363 ± 0.21841 | - | - |
| 25 | 0.28817 ± 0.02327 | 0.23679 ± 0.0342 | - | - |
| 50 | 0.33359 ± 0.01618 | 0.25416 ± 0.01981 | - | - |
| 100 | 0.3782 ± 0.01311 | 0.25933 ± 0.01619 | 0.21506 ± 0.01824 | 0.21175 ± 0.02937 |
| 200 | 0.40683 ± 0.00869 | 0.23166 ± 0.01267 | 0.20716 ± 0.01488 | 0.20741 ± 0.02327 |
| 350 | 0.43147 ± 0.00722 | 0.21754 ± 0.01074 | 0.20099 ± 0.01288 | 0.20322 ± 0.02032 |
| window length | Ridge fBm | Ridge fLm | Ridge both |
|---|---|---|---|
| 10 | 0.28124 ± 0.00023 | 0.2811 ± 0.00061 | 0.28131 ± 0.00042 |
| 25 | 0.28142 ± 0.0004 | 0.2813 ± 0.0004 | 0.28145 ± 0.00026 |
| 50 | 0.28148 ± 0.00062 | 0.28155 ± 0.00058 | 0.28168 ± 0.00045 |
| 100 | 0.28118 ± 0.00108 | 0.28203 ± 0.00117 | 0.28168 ± 0.00088 |
| 200 | 0.28143 ± 0.00013 | 0.28202 ± 0.00069 | 0.28194 ± 0.00052 |
| 350 | 0.28158 ± 9e-05 | 0.28202 ± 0.00046 | 0.28208 ± 0.00034 |
| window length | Lasso fBm | Lasso fLm | Lasso both |
| 10 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 25 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 50 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 100 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 200 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 350 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| window length | AdaBoost fBm | AdaBoost fLm | AdaBoost both |
| 10 | 0.17954 ± 0.00739 | 0.17841 ± 0.00603 | 0.17501 ± 0.0072 |
| 25 | 0.13308 ± 0.00729 | 0.16829 ± 0.00594 | 0.15288 ± 0.00664 |
| 50 | 0.11901 ± 0.00597 | 0.16298 ± 0.00575 | 0.13967 ± 0.00629 |
| 100 | 0.10492 ± 0.00603 | 0.16836 ± 0.0062 | 0.13647 ± 0.00699 |
| 200 | 0.10557 ± 0.00475 | 0.1677 ± 0.00428 | 0.13728 ± 0.00471 |
| 350 | 0.10388 ± 0.00248 | 0.16646 ± 0.00301 | 0.13614 ± 0.00312 |
| window length | CatBoost fBm | CatBoost fLm | CatBoost both |
| 10 | 0.12585 ± 0.01533 | 0.13493 ± 0.01381 | 0.12543 ± 0.01354 |
| 25 | 0.09966 ± 0.02066 | 0.11572 ± 0.01648 | 0.10284 ± 0.01716 |
| 50 | 0.09861 ± 0.01676 | 0.10646 ± 0.0161 | 0.09885 ± 0.0167 |
| 100 | 0.11132 ± 0.01521 | 0.10493 ± 0.01517 | 0.10261 ± 0.01542 |
| 200 | 0.10422 ± 0.01406 | 0.10233 ± 0.01111 | 0.09901 ± 0.01235 |
| 350 | 0.10423 ± 0.01236 | 0.10089 ± 0.00847 | 0.09761 ± 0.00979 |
| window length | LightGBM fBm | LightGBM fLm | LightGBM both |
| 10 | 0.12474 ± 0.01531 | 0.13449 ± 0.01421 | 0.12653 ± 0.01365 |
| 25 | 0.09164 ± 0.02074 | 0.11827 ± 0.01639 | 0.10419 ± 0.01662 |
| 50 | 0.09421 ± 0.01709 | 0.1128 ± 0.01605 | 0.1014 ± 0.01649 |
| 100 | 0.10036 ± 0.01603 | 0.10926 ± 0.0156 | 0.10413 ± 0.01581 |
| 200 | 0.09374 ± 0.0143 | 0.10574 ± 0.01141 | 0.09917 ± 0.01238 |
| 350 | 0.0929 ± 0.01228 | 0.10395 ± 0.00866 | 0.09765 ± 0.00978 |
| window length | MLP fBm | MLP fLm | MLP both |
| 10 | 0.10349 ± 0.01432 | 0.13397 ± 0.01323 | 0.12935 ± 0.01348 |
| 25 | 0.09597 ± 0.02127 | 0.11178 ± 0.01572 | 0.11672 ± 0.01739 |
| 50 | 0.08883 ± 0.01777 | 0.11371 ± 0.0167 | 0.12015 ± 0.018 |
| 100 | 0.09425 ± 0.01593 | 0.13946 ± 0.01676 | 0.09106 ± 0.01621 |
| 200 | 0.08884 ± 0.01365 | 0.13815 ± 0.01241 | 0.0876 ± 0.01283 |
| 350 | 0.08686 ± 0.01138 | 0.1367 ± 0.00935 | 0.08641 ± 0.01017 |
5. Finance experiments
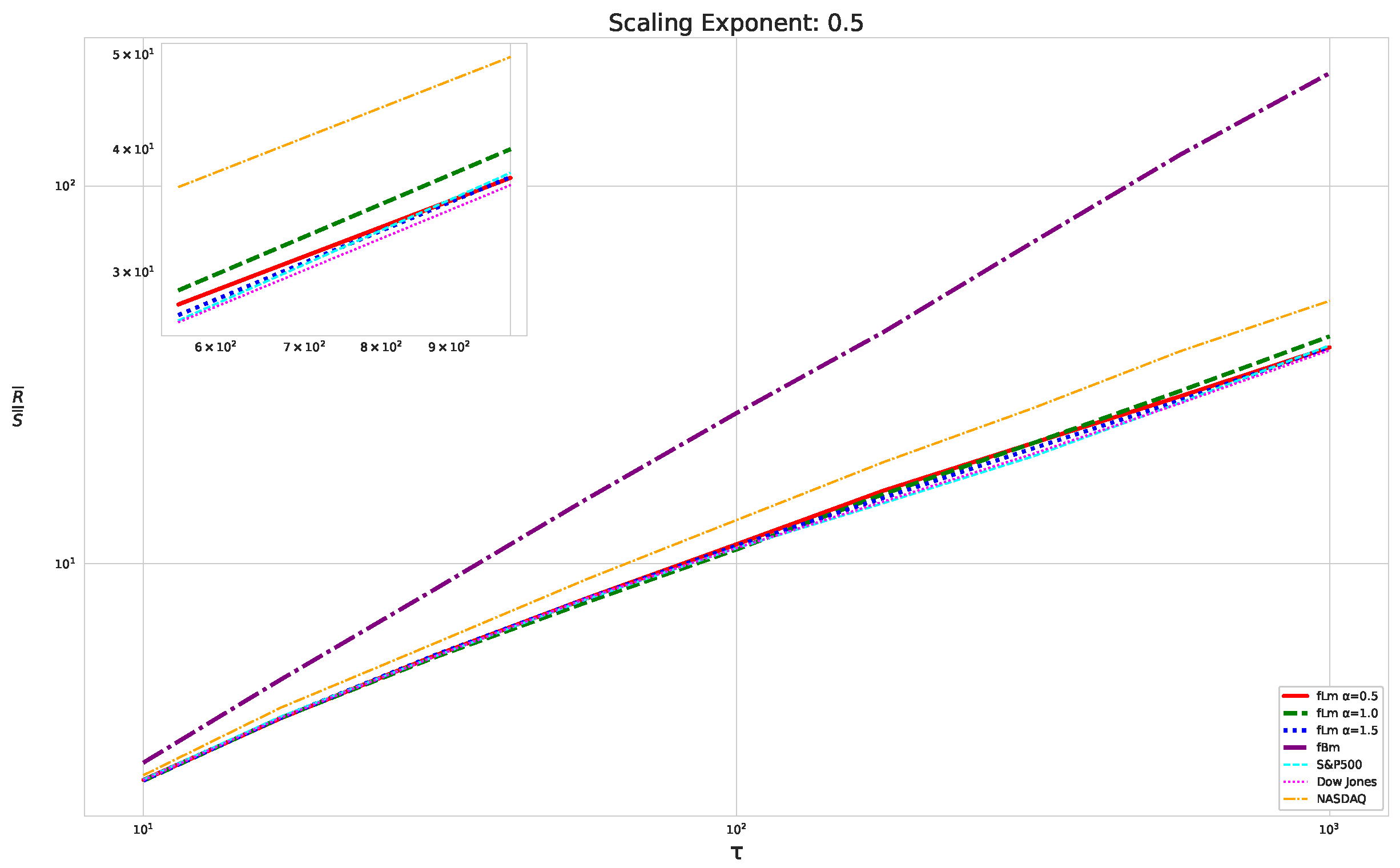
5.1. The Scaling Exponent of financial data
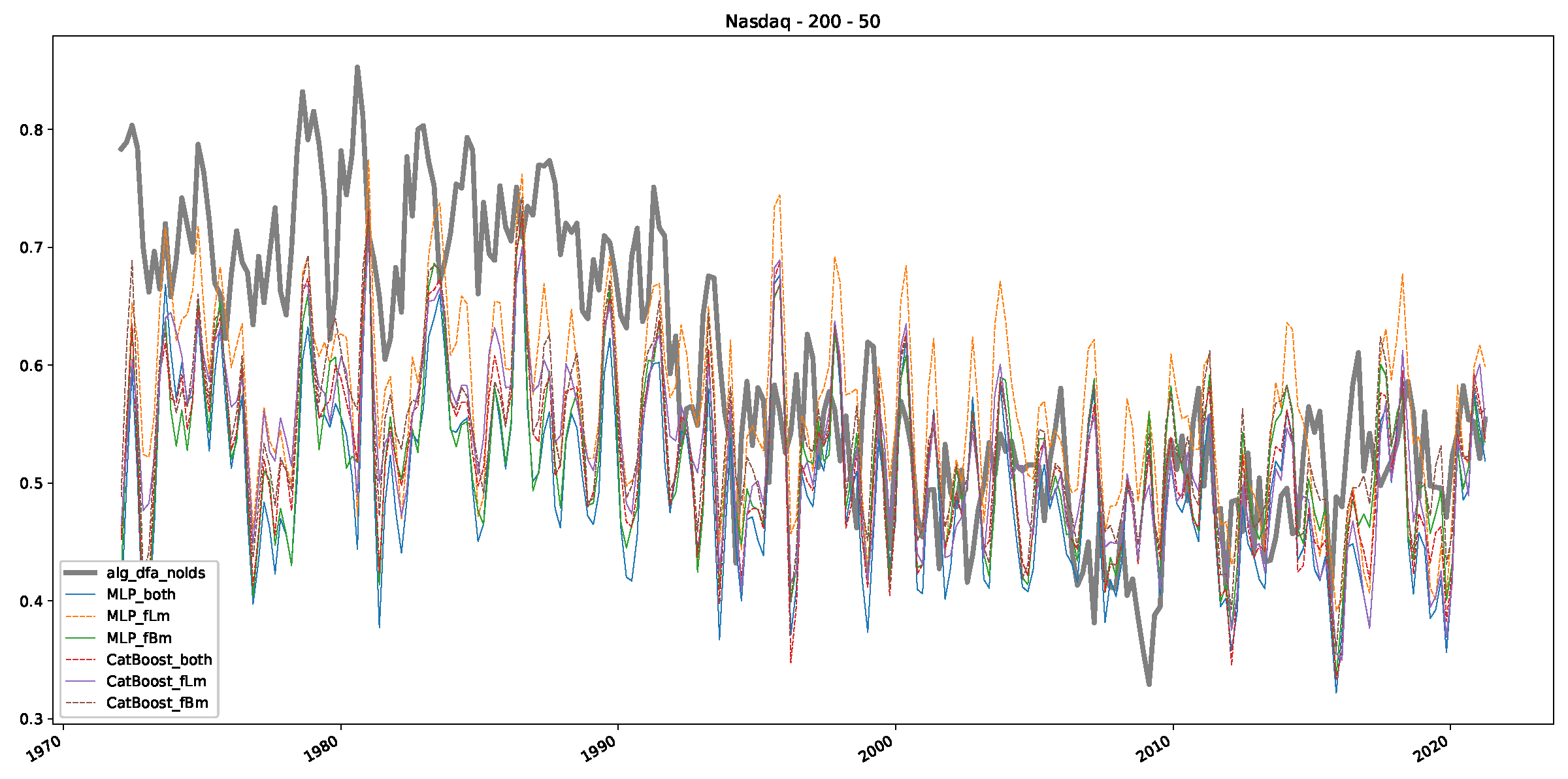
5.2. Results
5.3. Summary & Discussion
6. Conclusions
- We trained a range of machine learning models on both fractional Brownian and fractional Lévy motions with different Hurst/scaling exponents and different Lévy indices. We used the known scaling exponent as the ground truth for the value to be predicted by the machine learning algorithms, i.e., the output of the models. The features, or the input, are time series data from the discussed stochastic processes scaled to the unit interval .
- We validated the trained models for different lengths of input windows using, again, fractional Brownian and fractional Lévy motions. The results show that in most cases the trained machine learning models outperform classical algorithms (such as R/S analysis) to estimate the scaling exponent of both fractional Brownian and fractional Lévy motions.
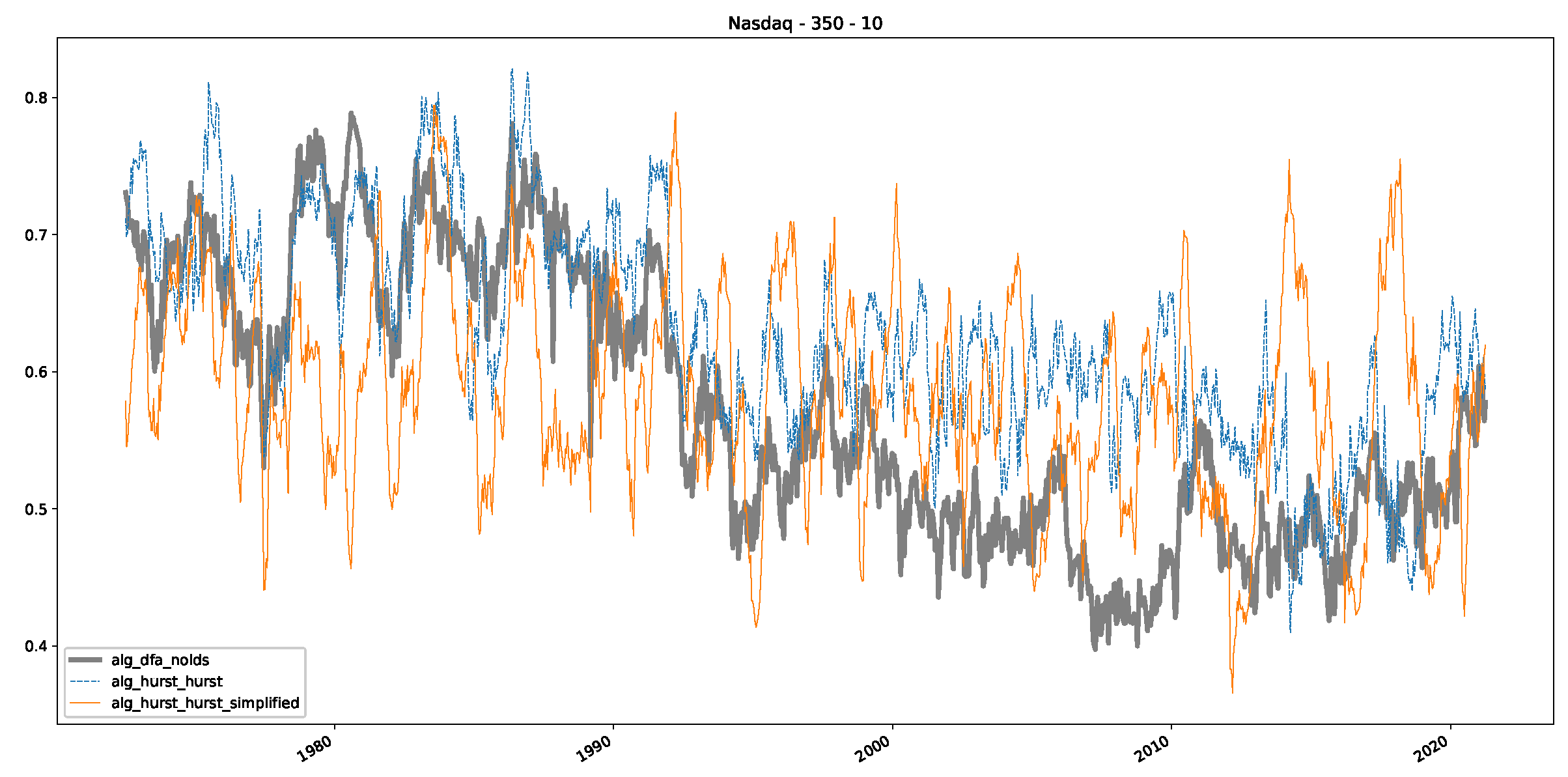
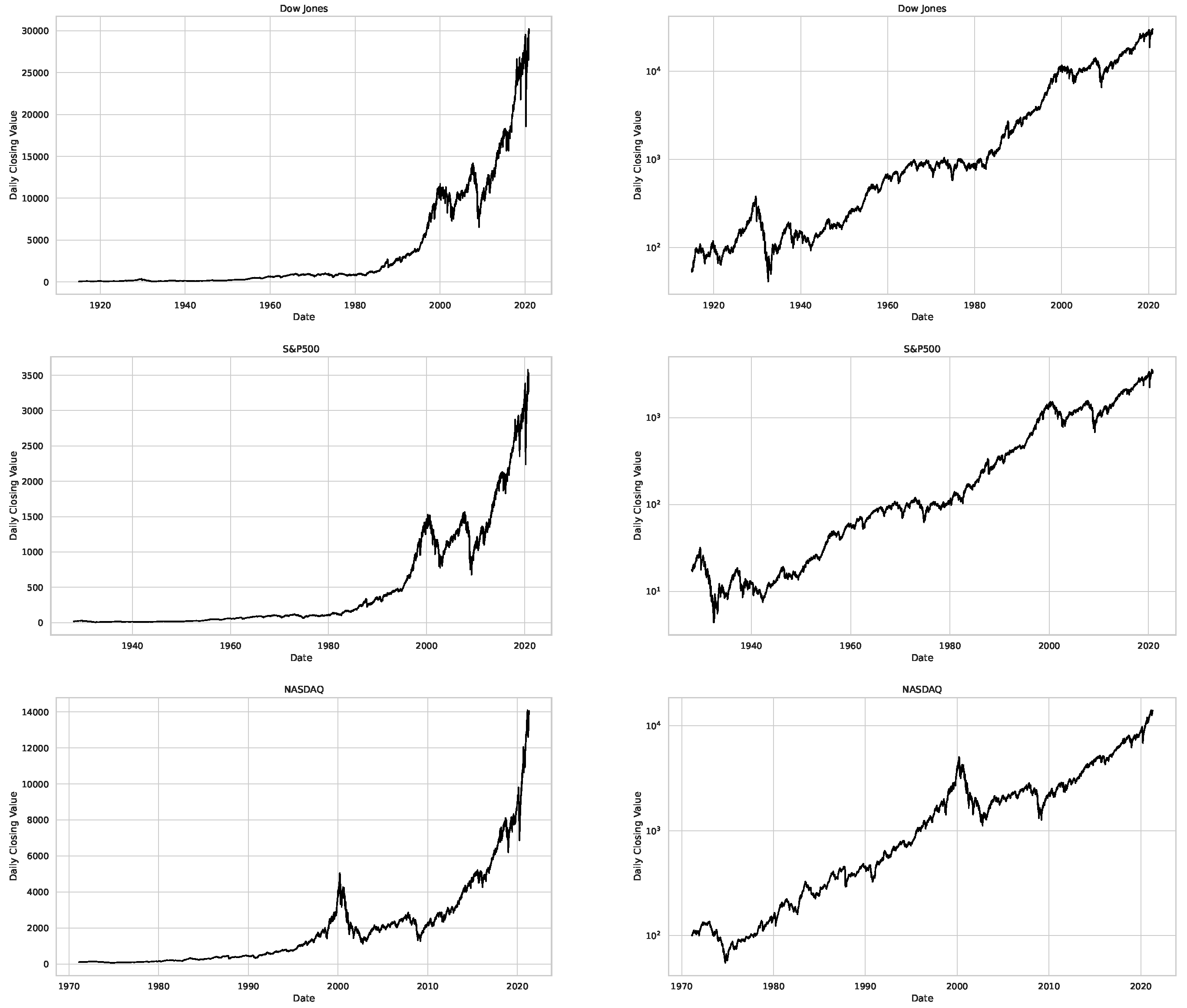
- We then took three asset time series, i.e., Dow Jones, S&P500, and NASDAQ, and applied a slightly modified version of R/S analysis to these data sets to show that these data signals are more akin to fractional Lévy motions than fractional Brownian motions in nature. The reason for doing this was to argue that certain classical algorithms cannot correctly estimate the scaling exponents of these data sets because, as shown in the previous step, compared to the trained models, they suffer from large errors in estimating the scaling exponent of fractional Lévy motions.
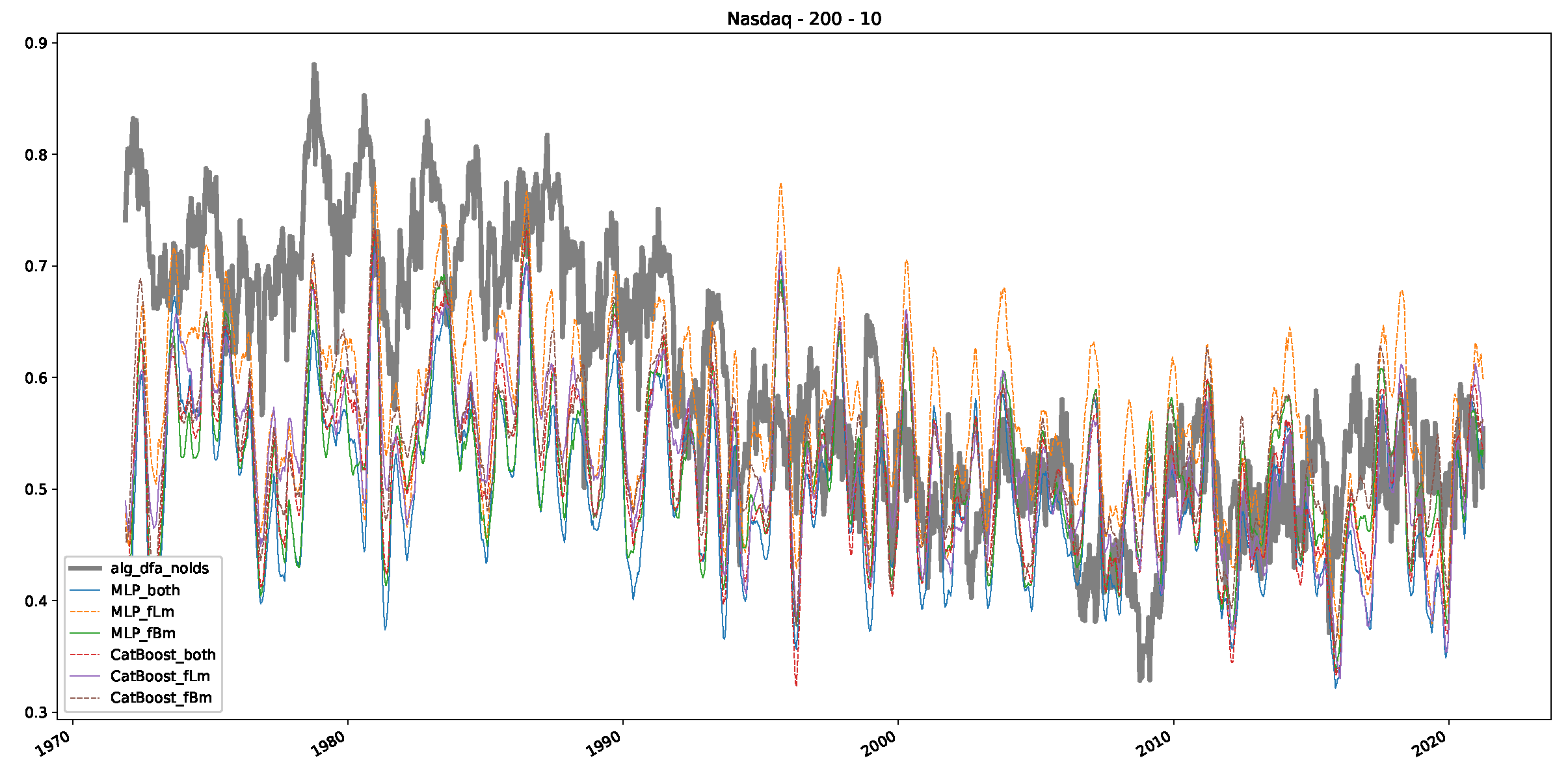
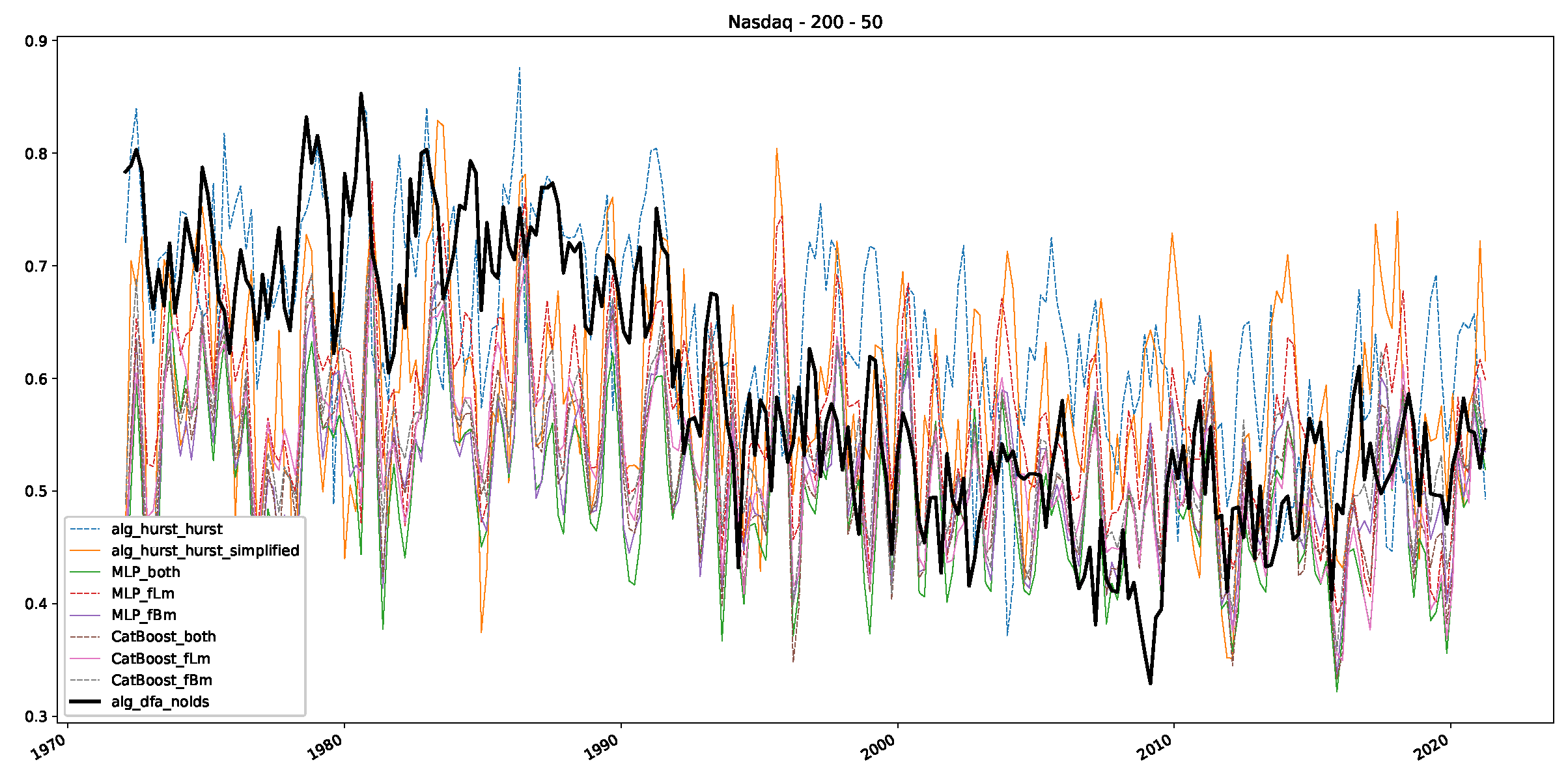
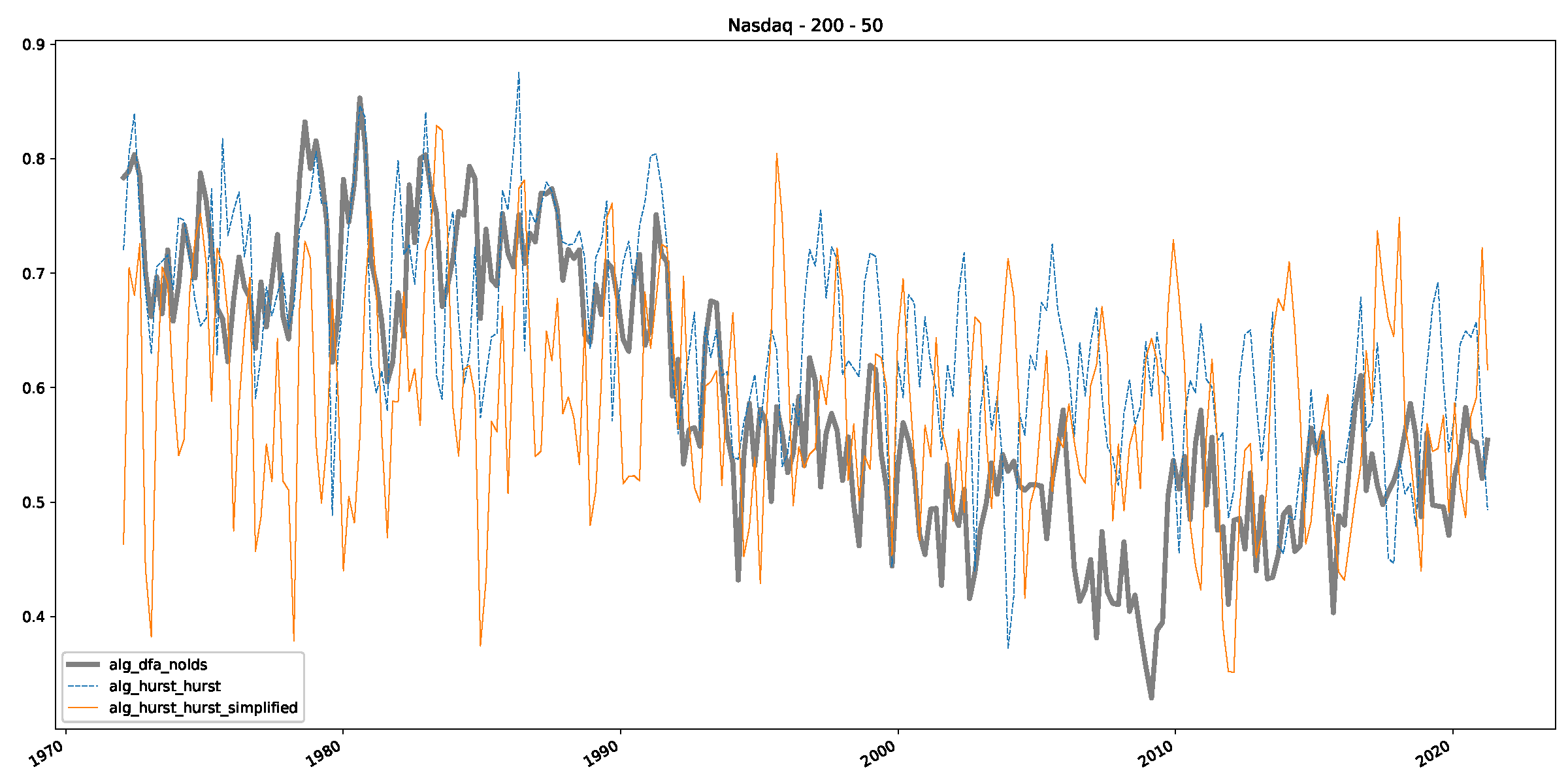
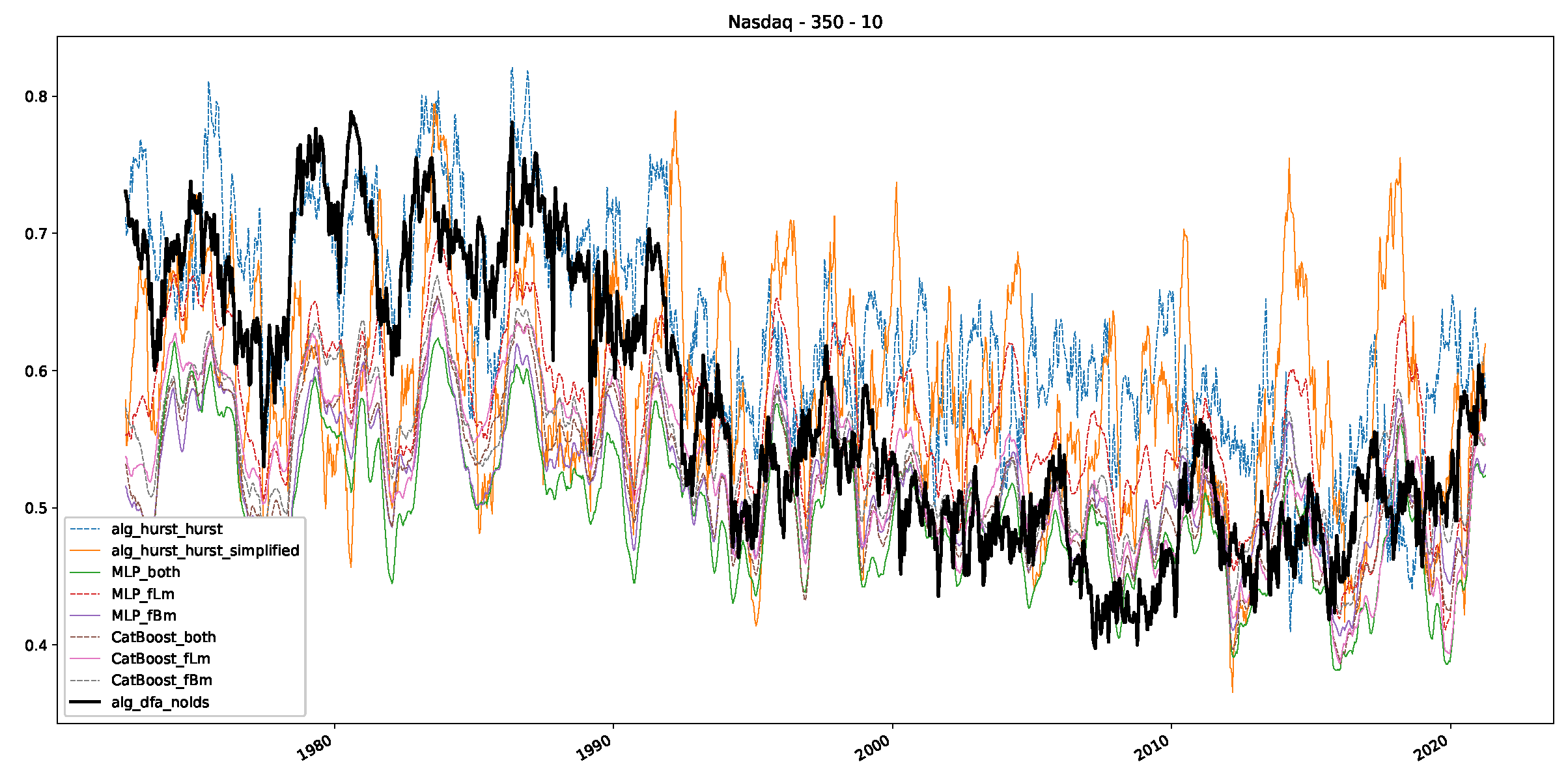
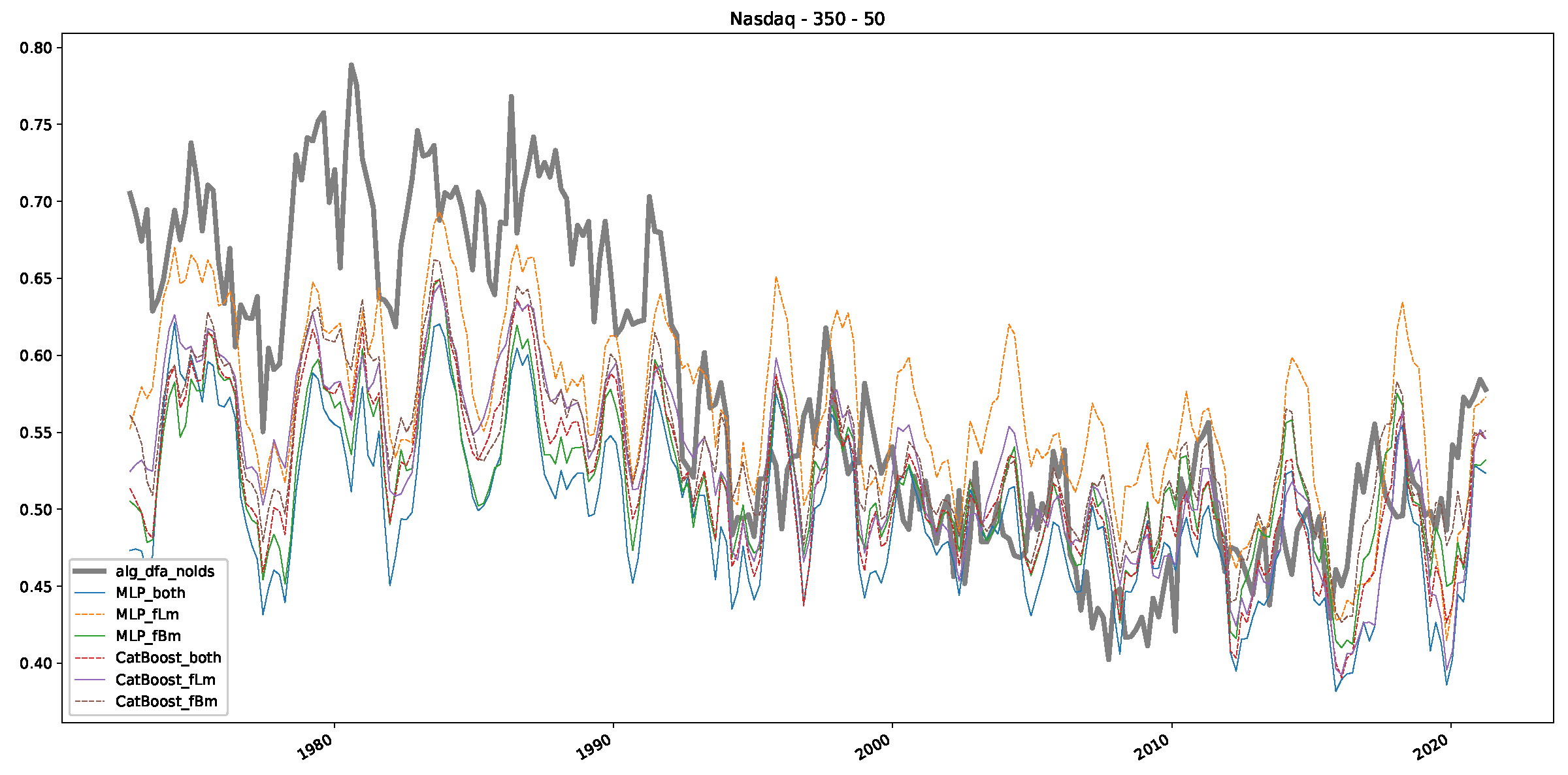
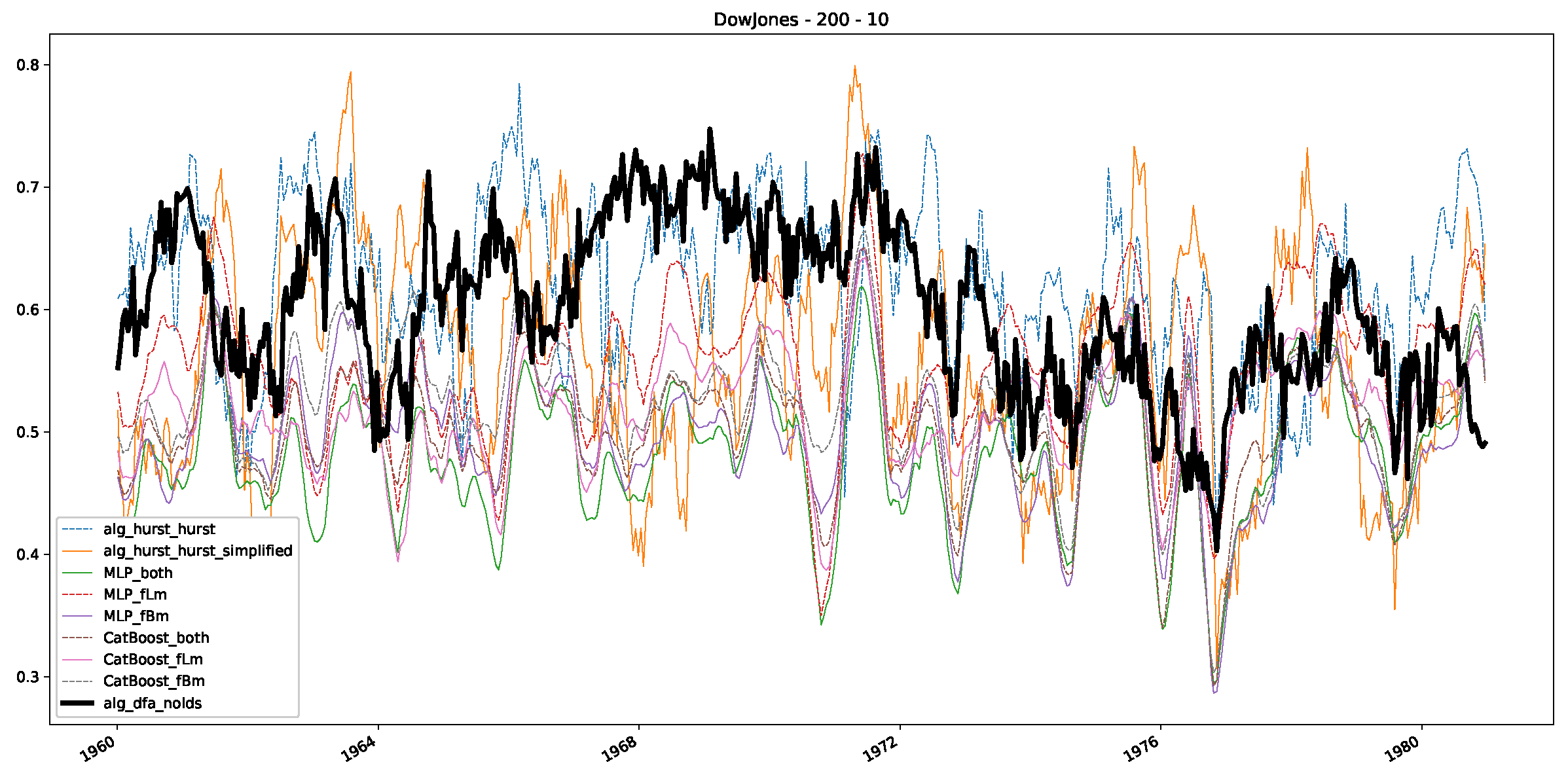
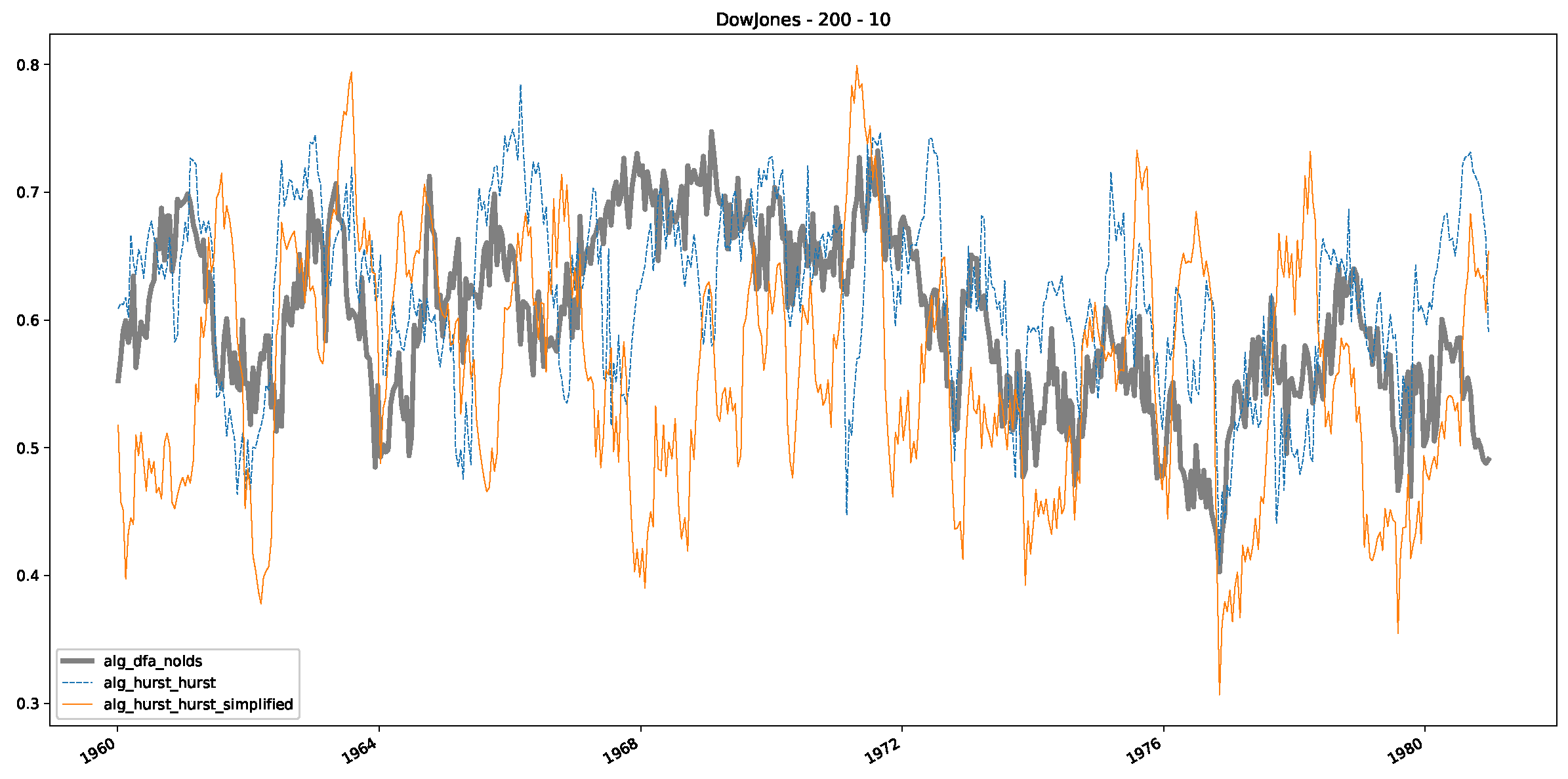
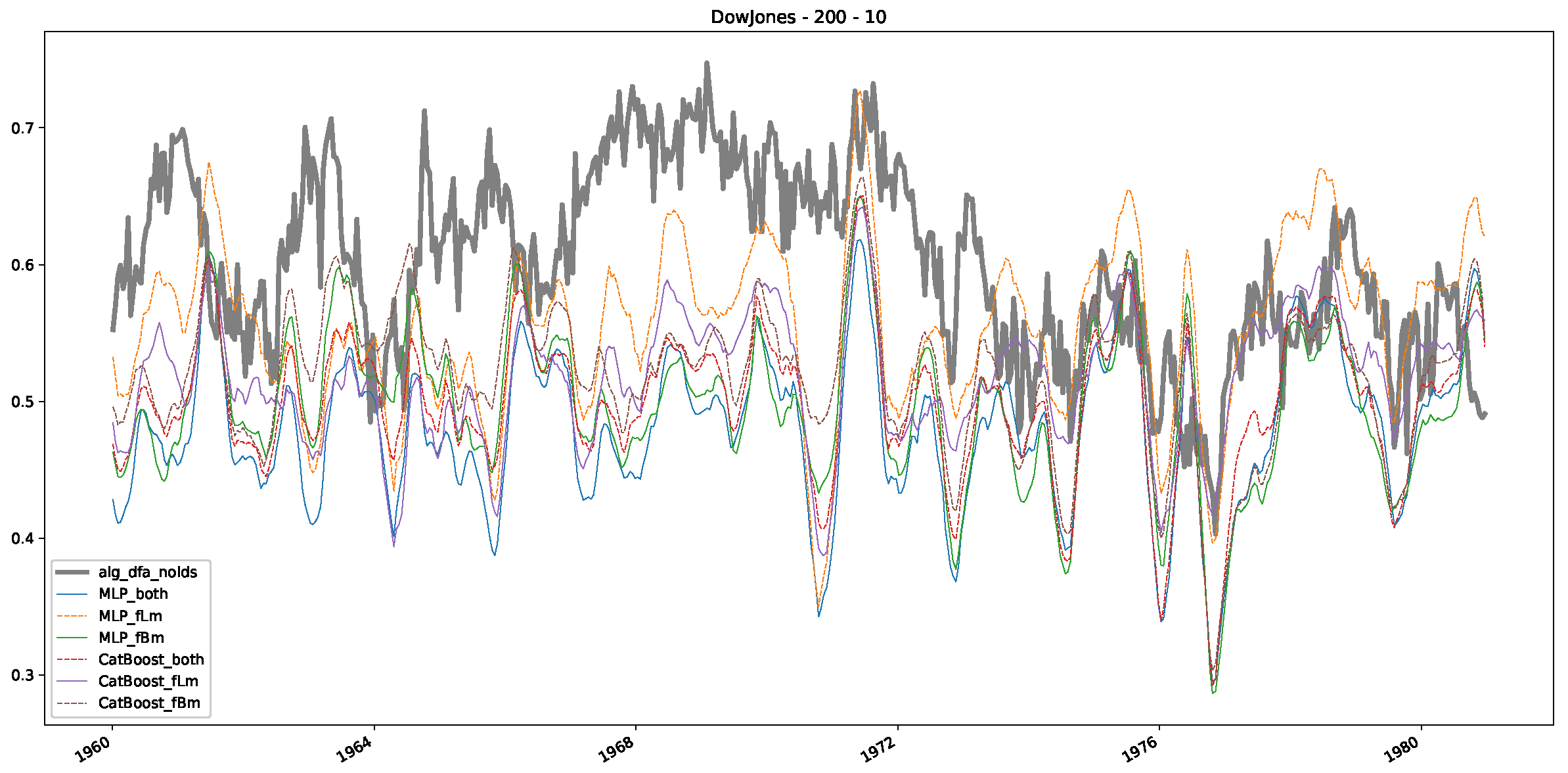
- In a final step, we analyzed the scaling exponent of the previously named three assets in a sliding window manner, to show and discuss the applicability of the trained models and classical algorithms to estimate the scaling behavior of time series data. Our research shows that results from the literature might be wrong in estimating the scaling exponent using detrended fluctuation analysis (DFA) and drawing conclusions from it. To do this, we first reconstructed the scaling behavior using DFA, which coincides with the results from the literature. We then found that the trained machine learning algorithms do not reproduce the scaling behavior from the literature, even though we showed that the assets under study are closer to a fractional Lévy motion, and that our trained models can better estimate the scaling exponent of stochastic processes like these.
Acknowledgments
Appendix A. Fractional Lévy motion and it’s sclaing behavior
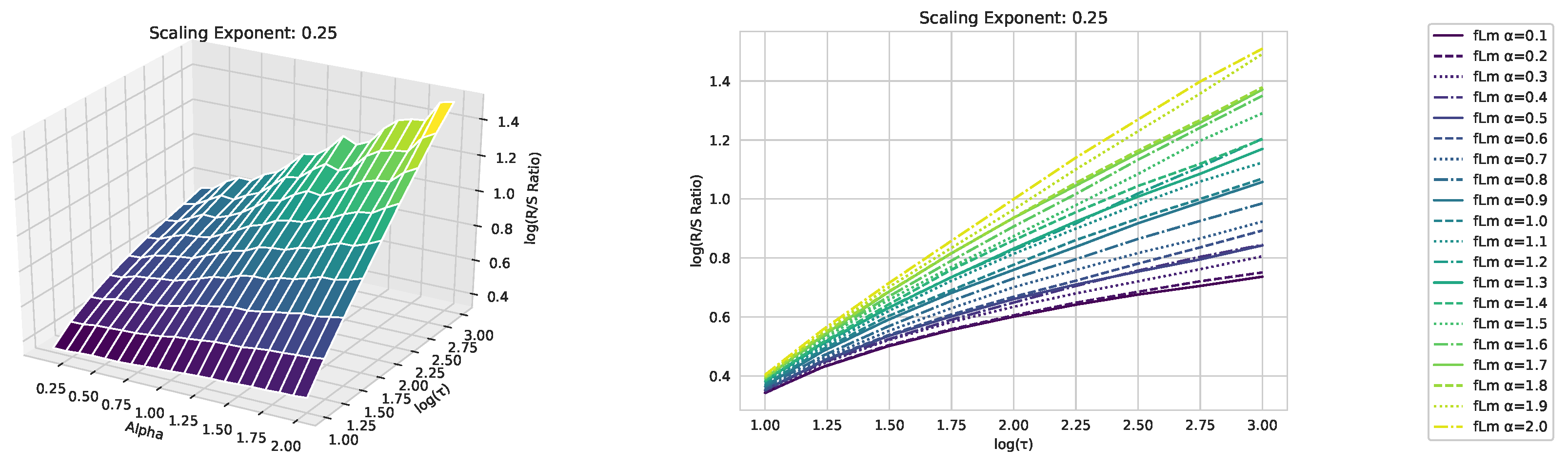
| [H]0.3875 | [H]0.3875 | [H]0.15725 |
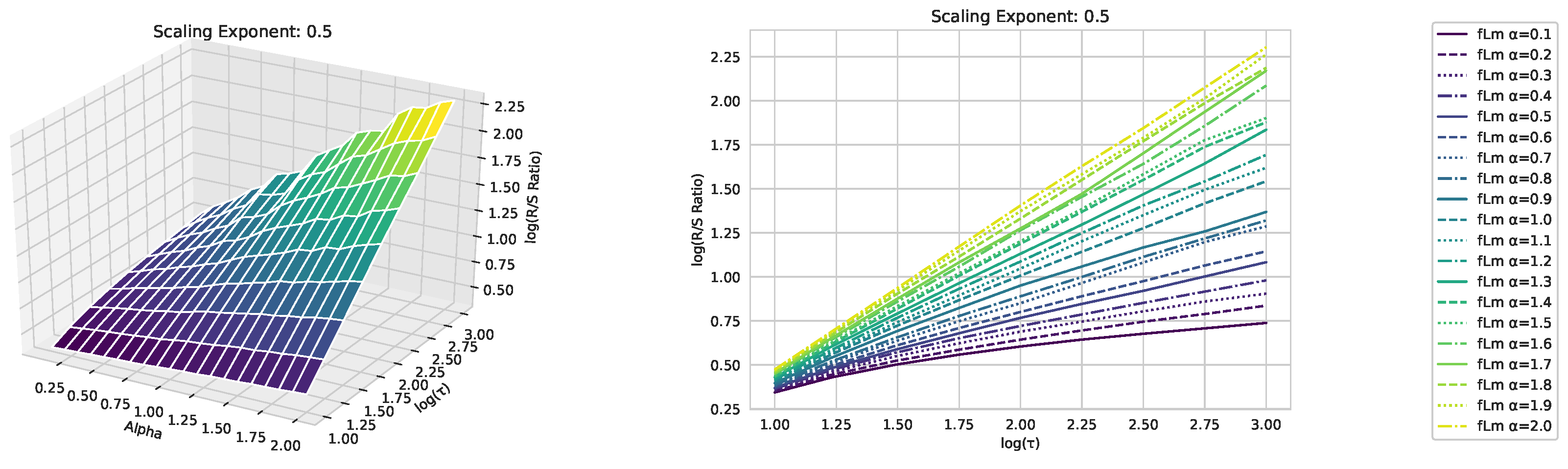
| [H]0.3875 | [H]0.3875 | [H]0.15725 |
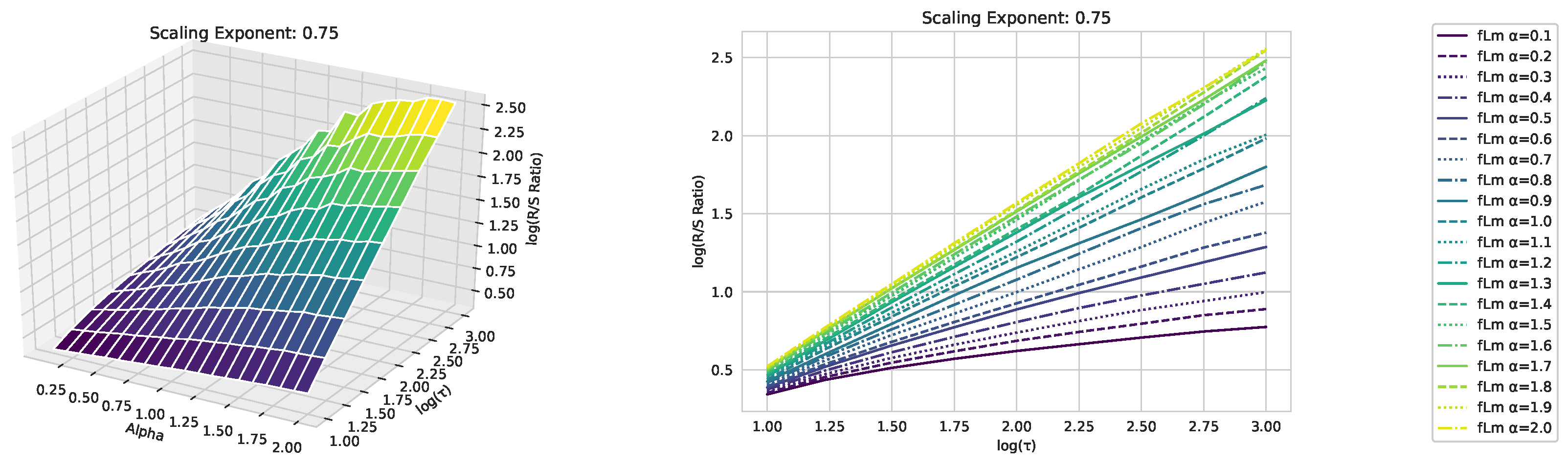
| [H]0.3875 | [H]0.3875 | [H]0.15725 |
Appendix B. Additional Plots, Finance Experiments
Appendix B.1. Additional Plots Dow Jones
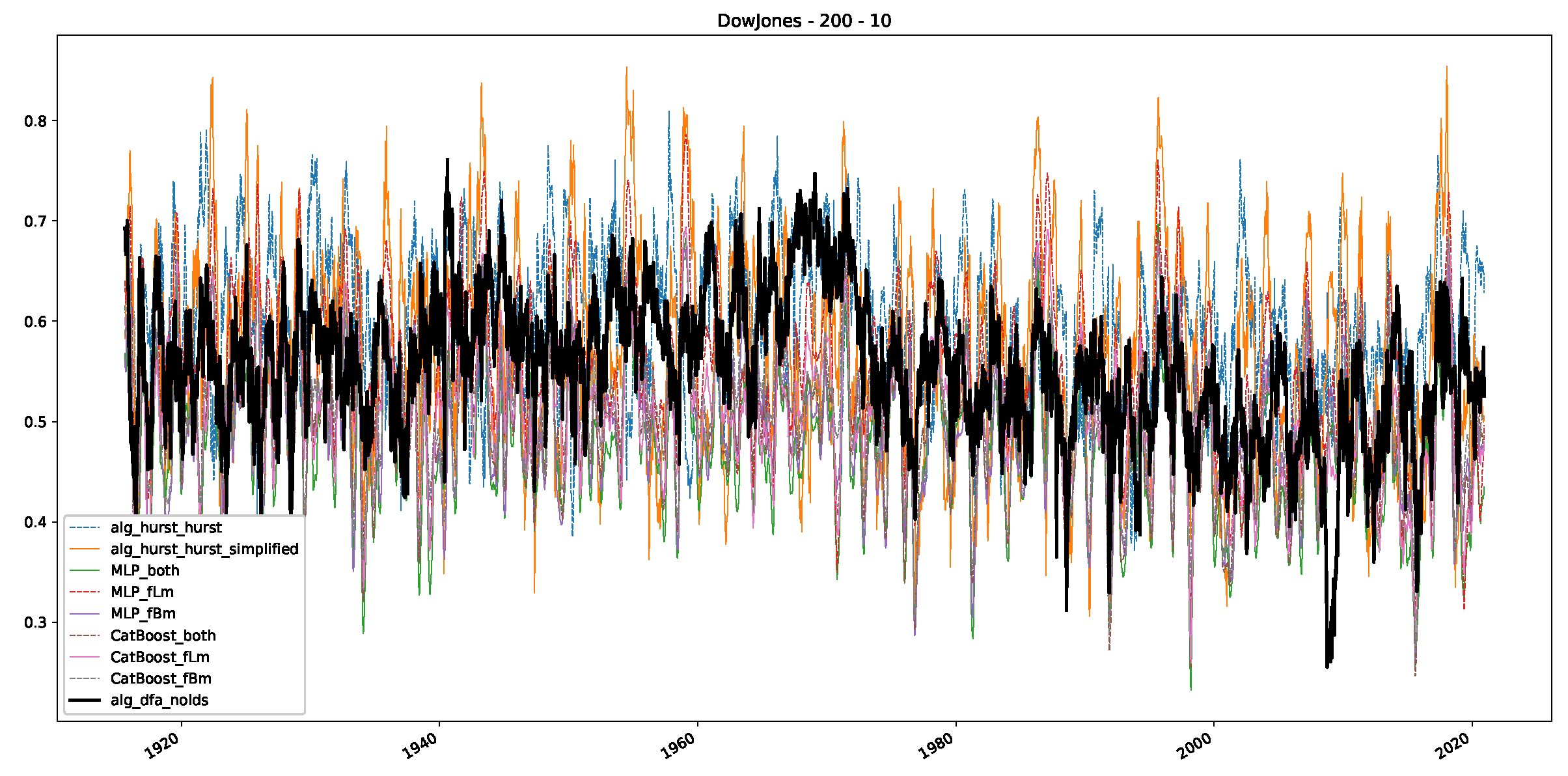
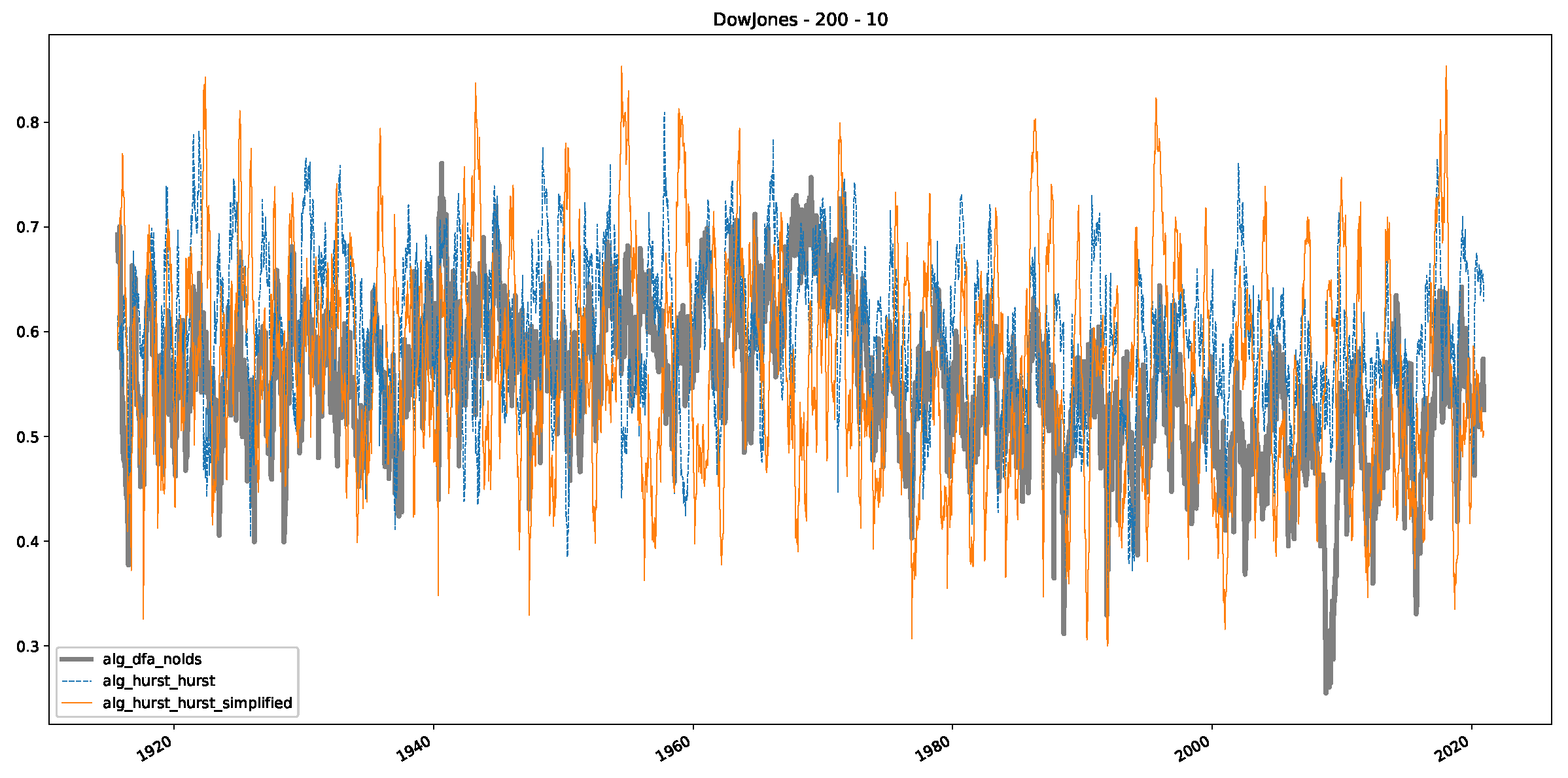
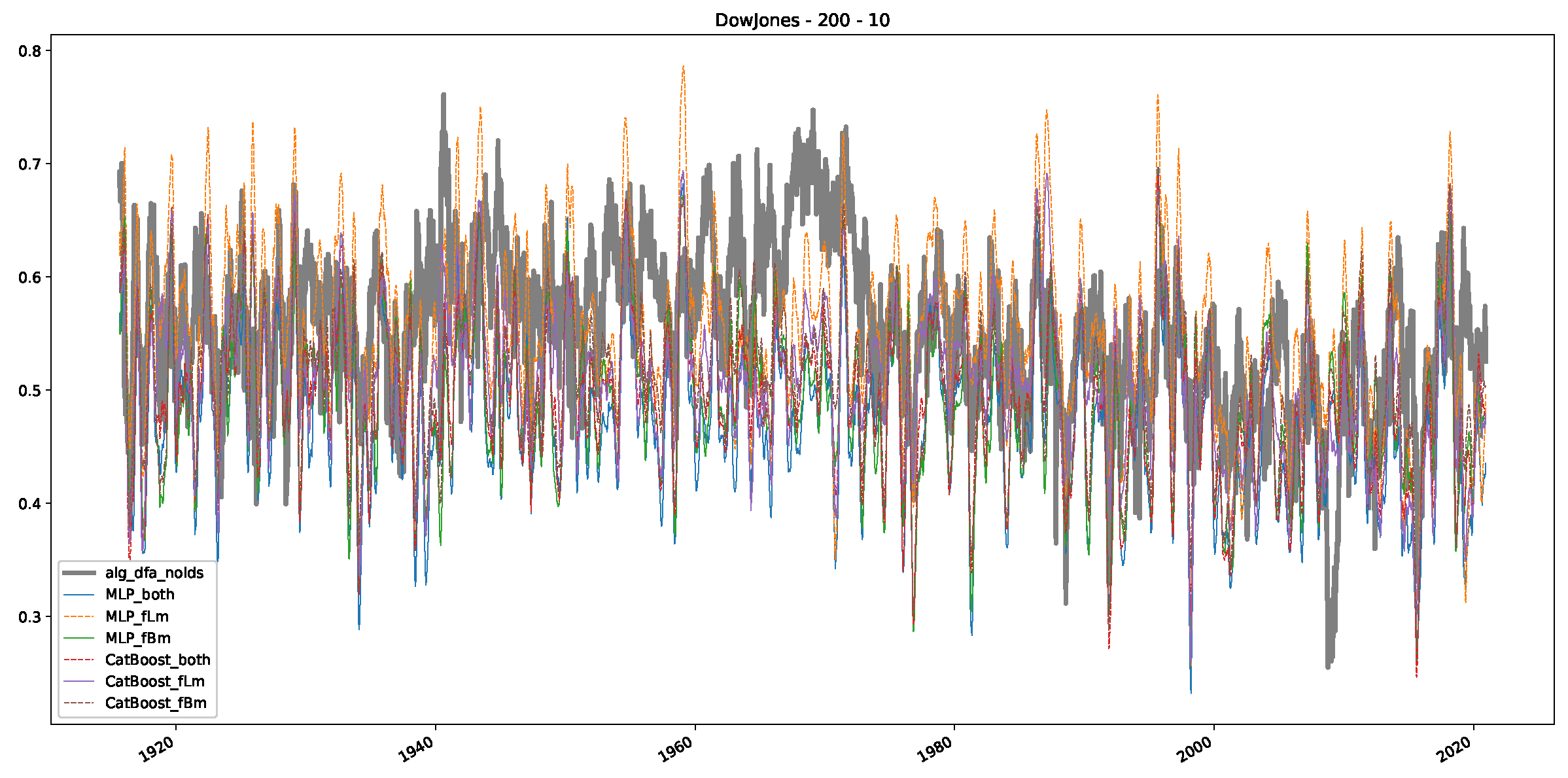
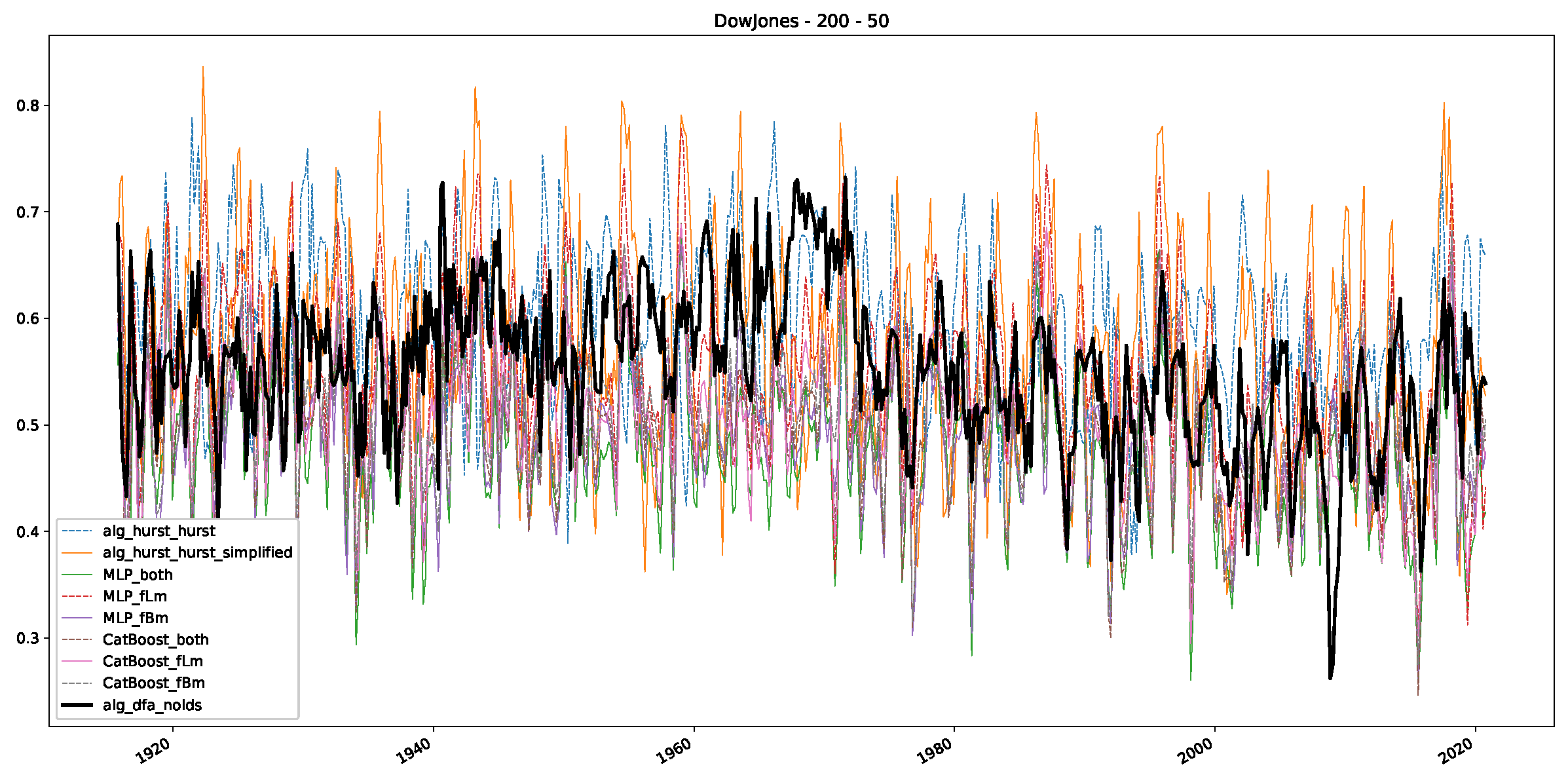
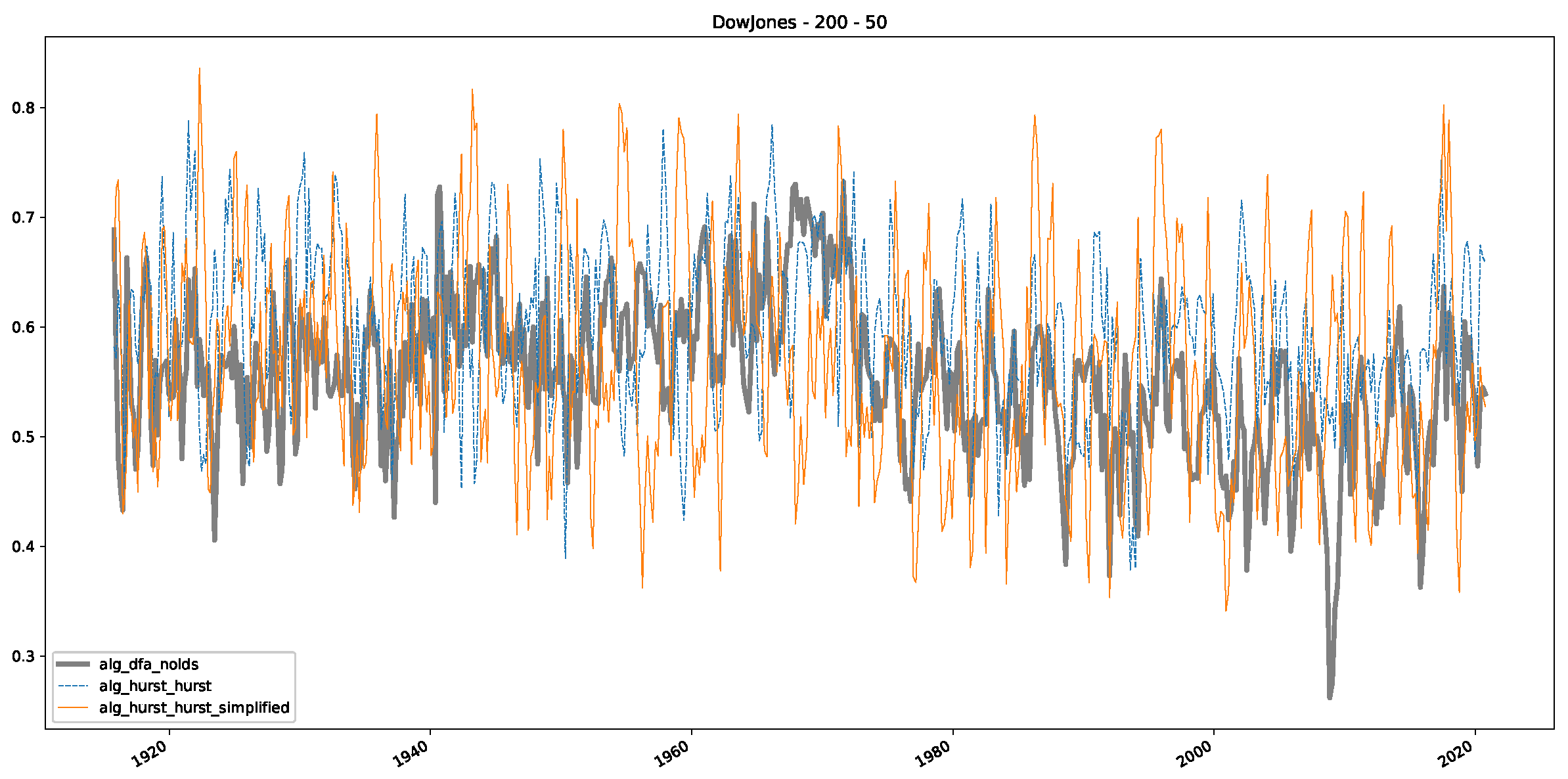
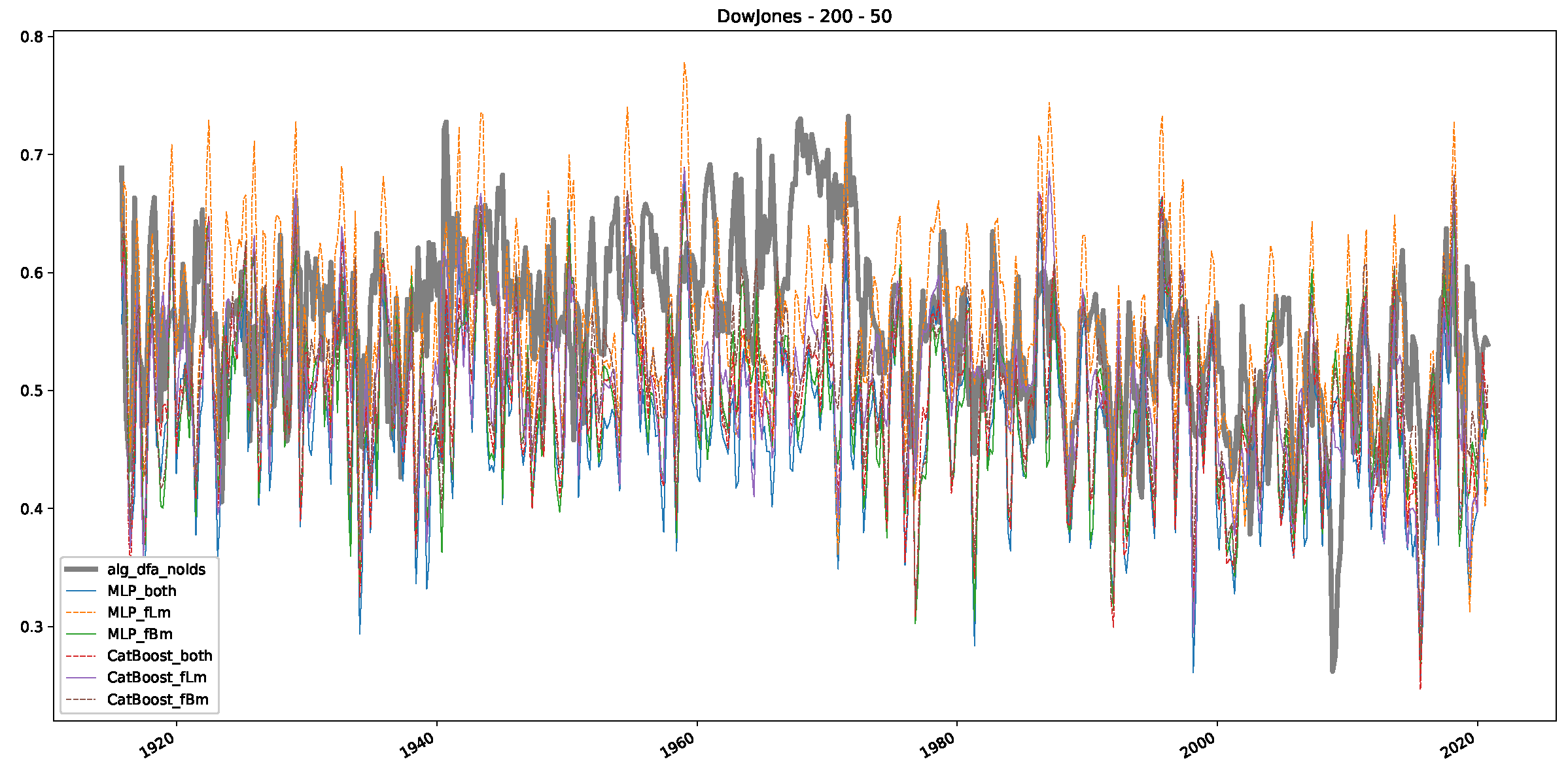
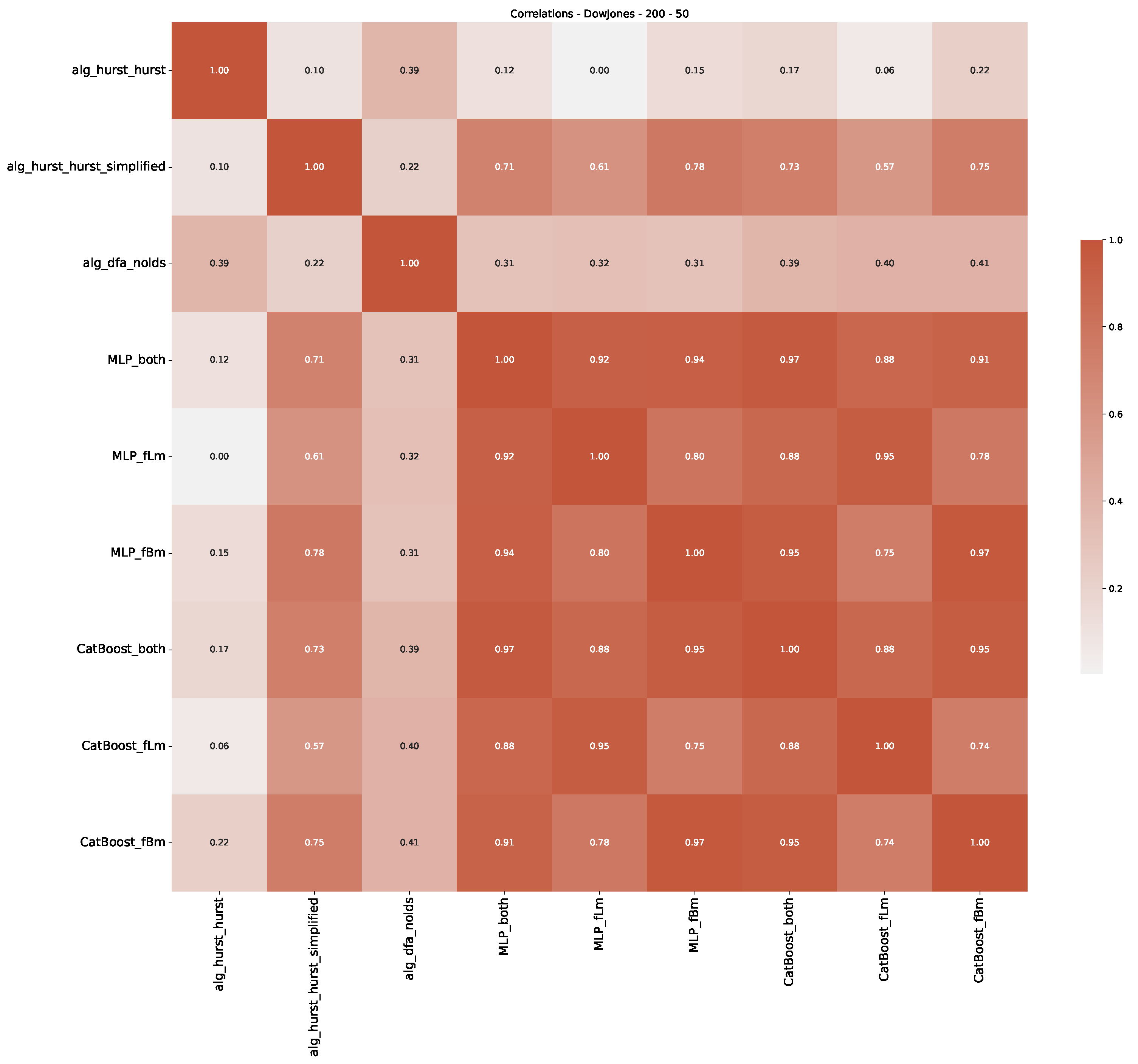
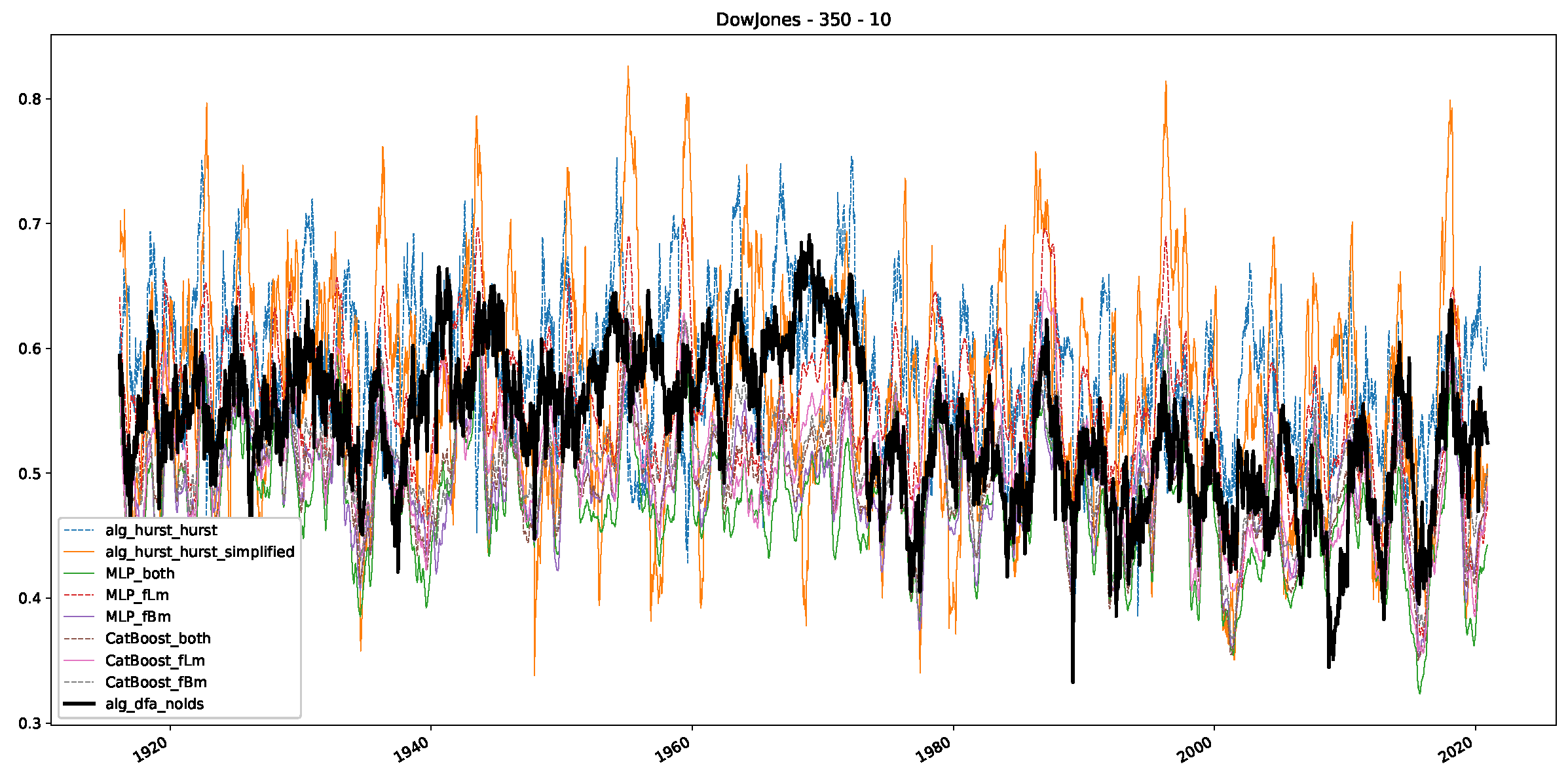
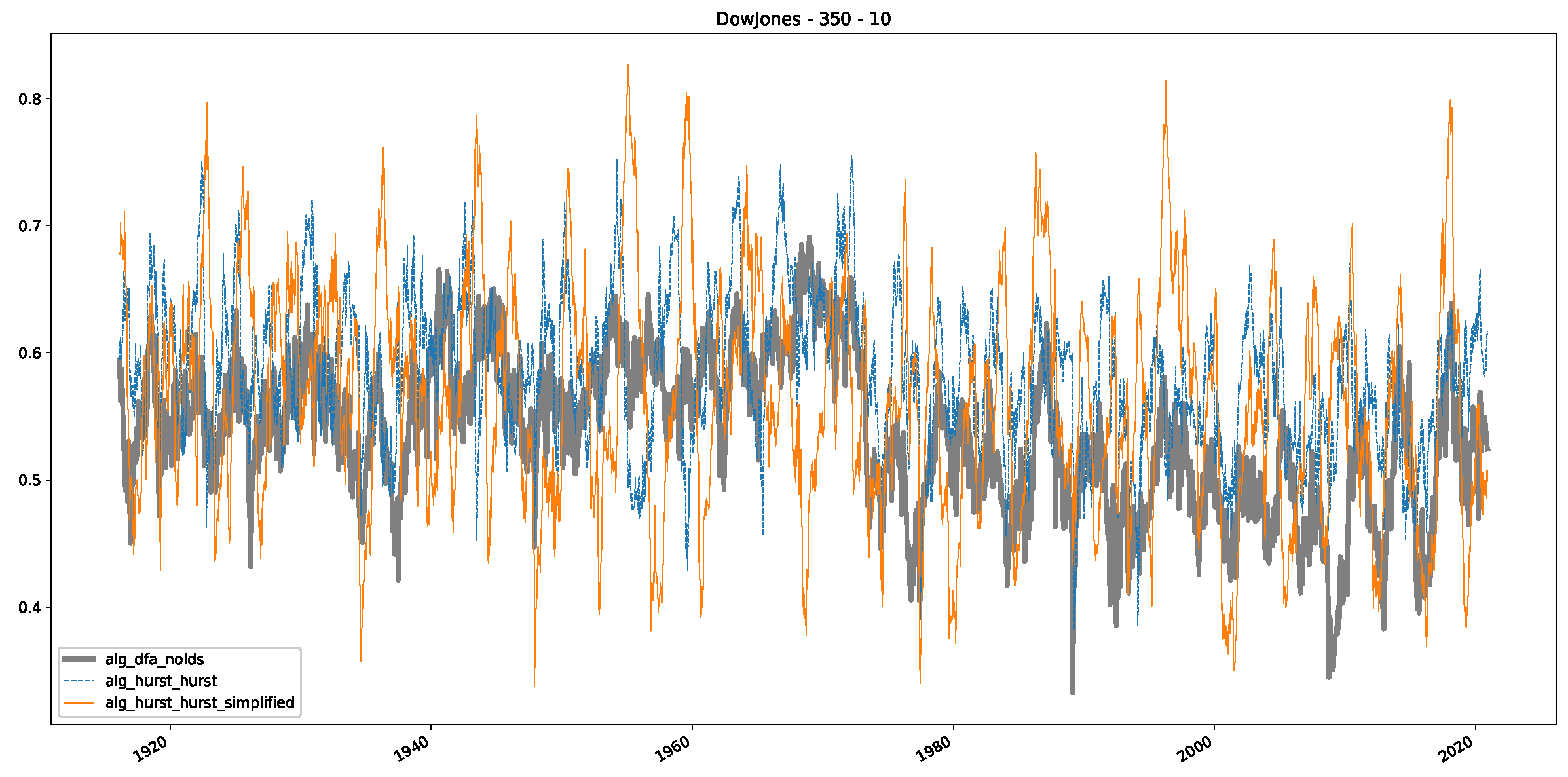
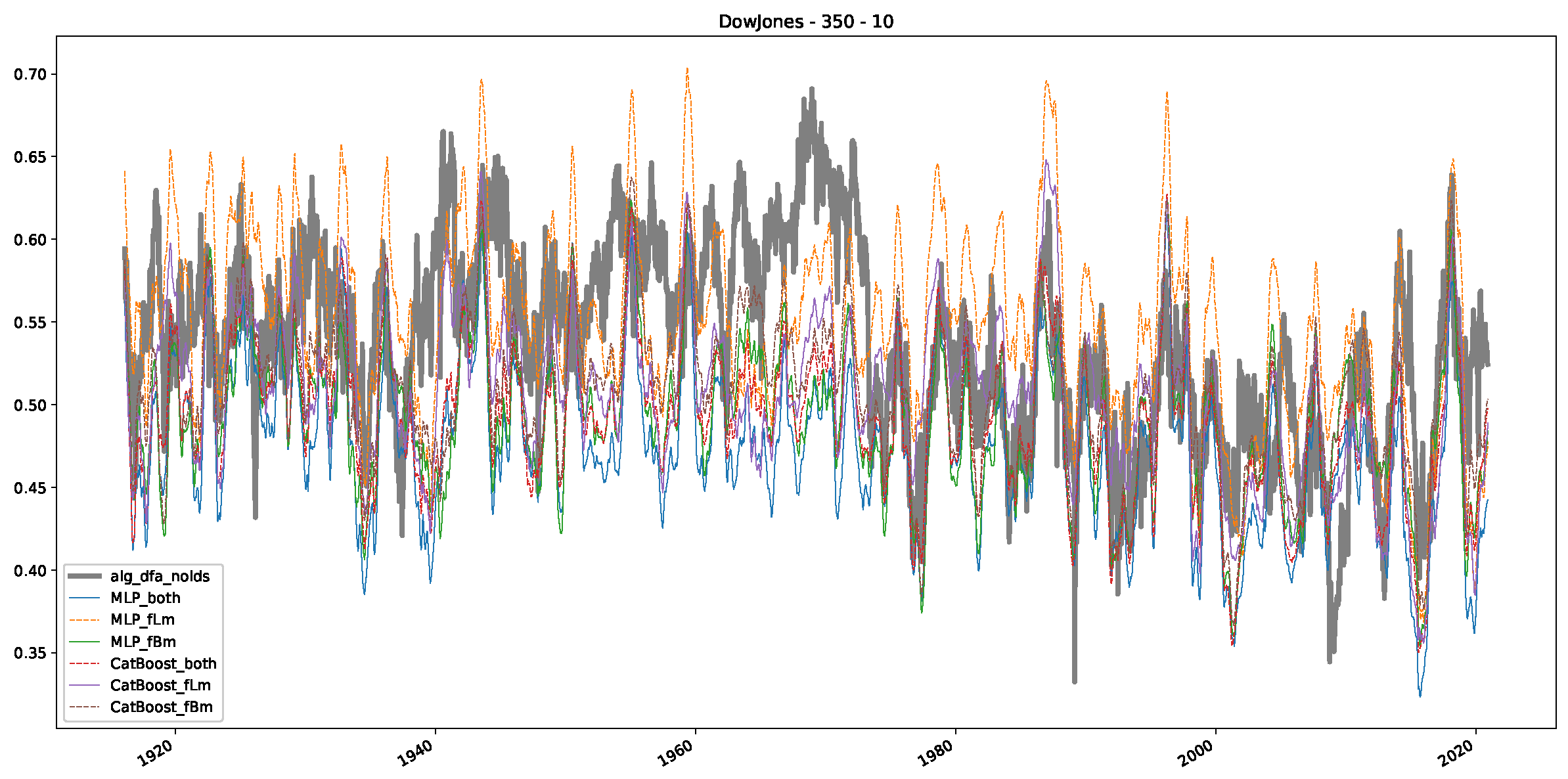
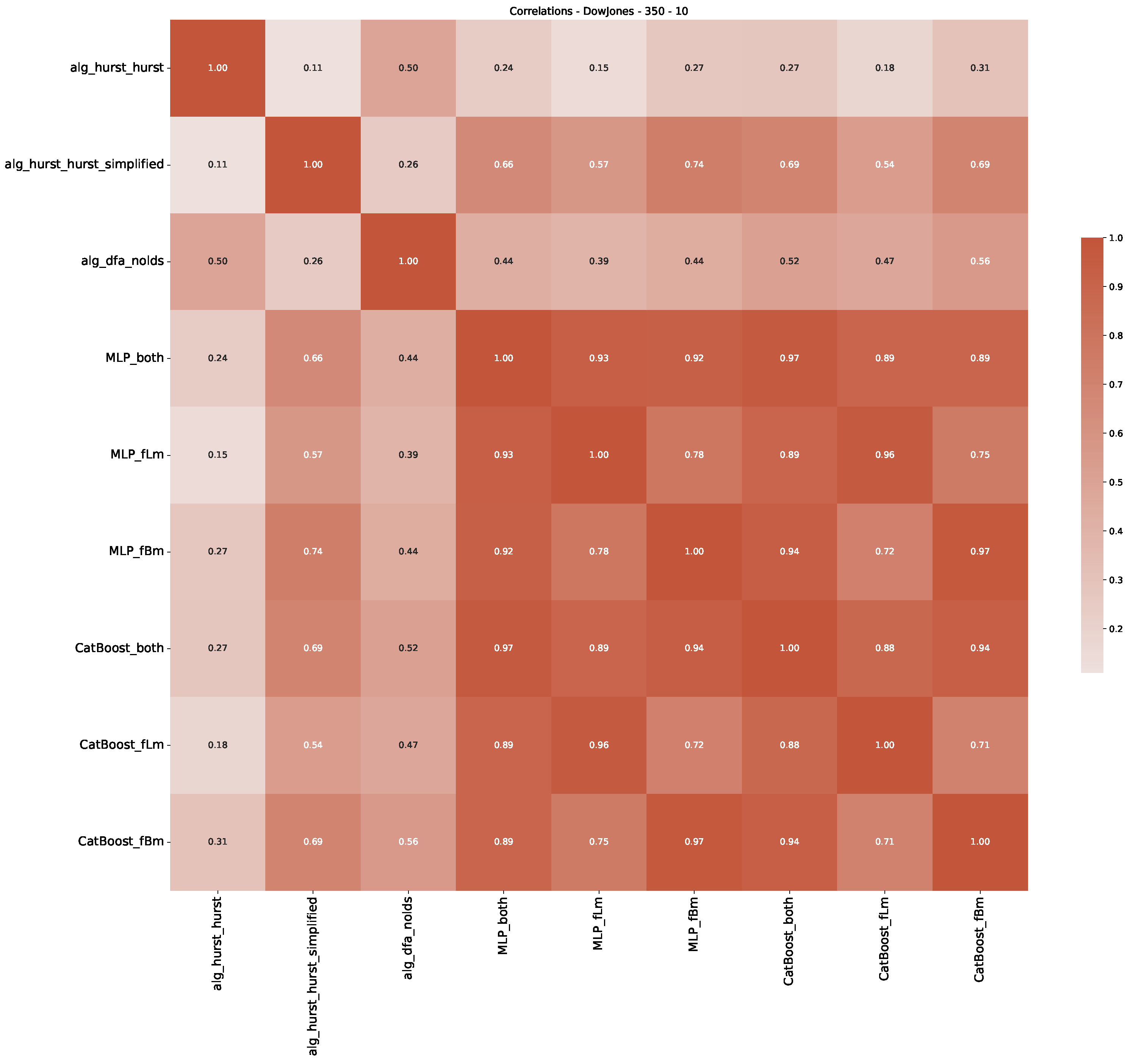
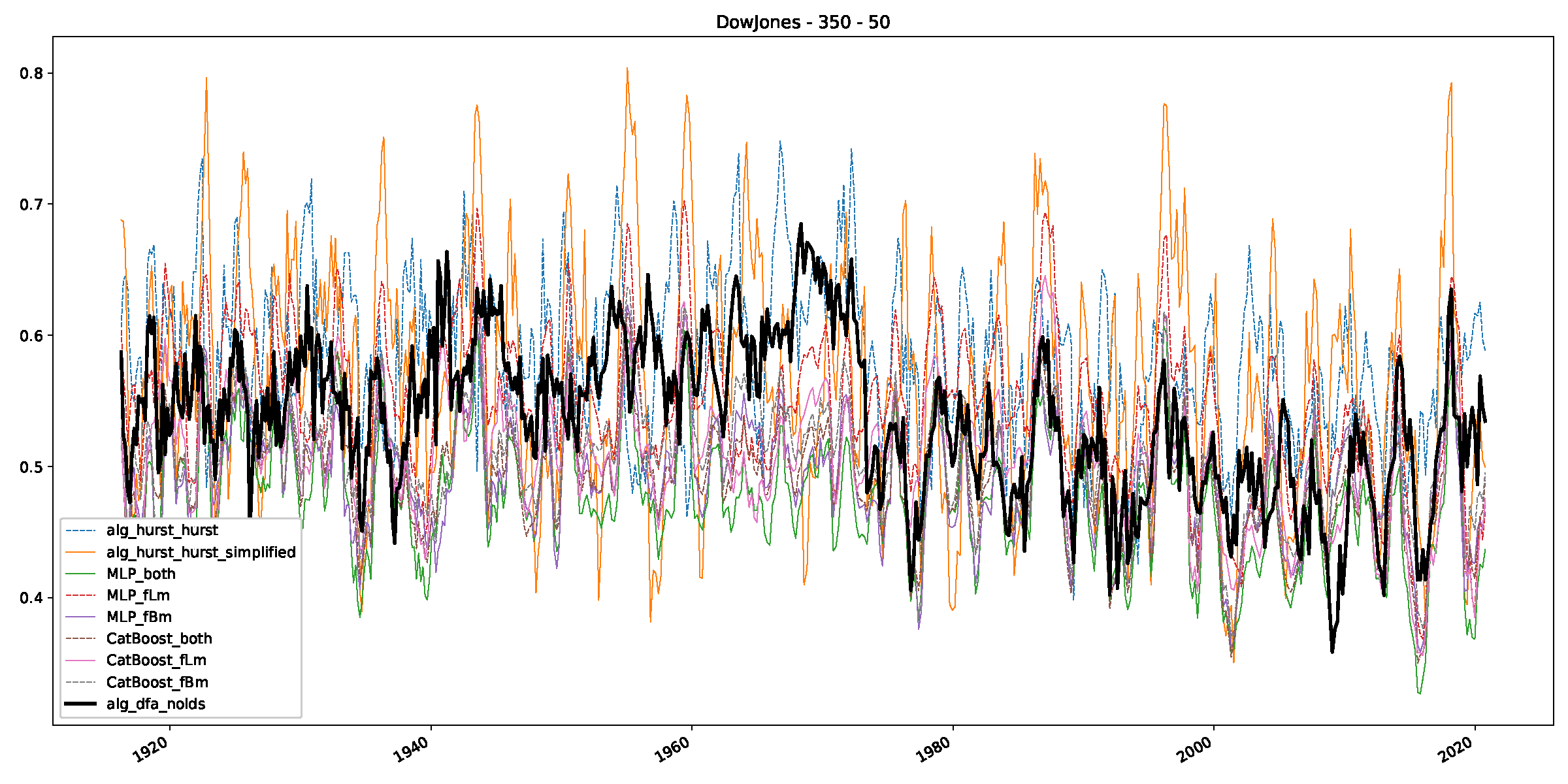
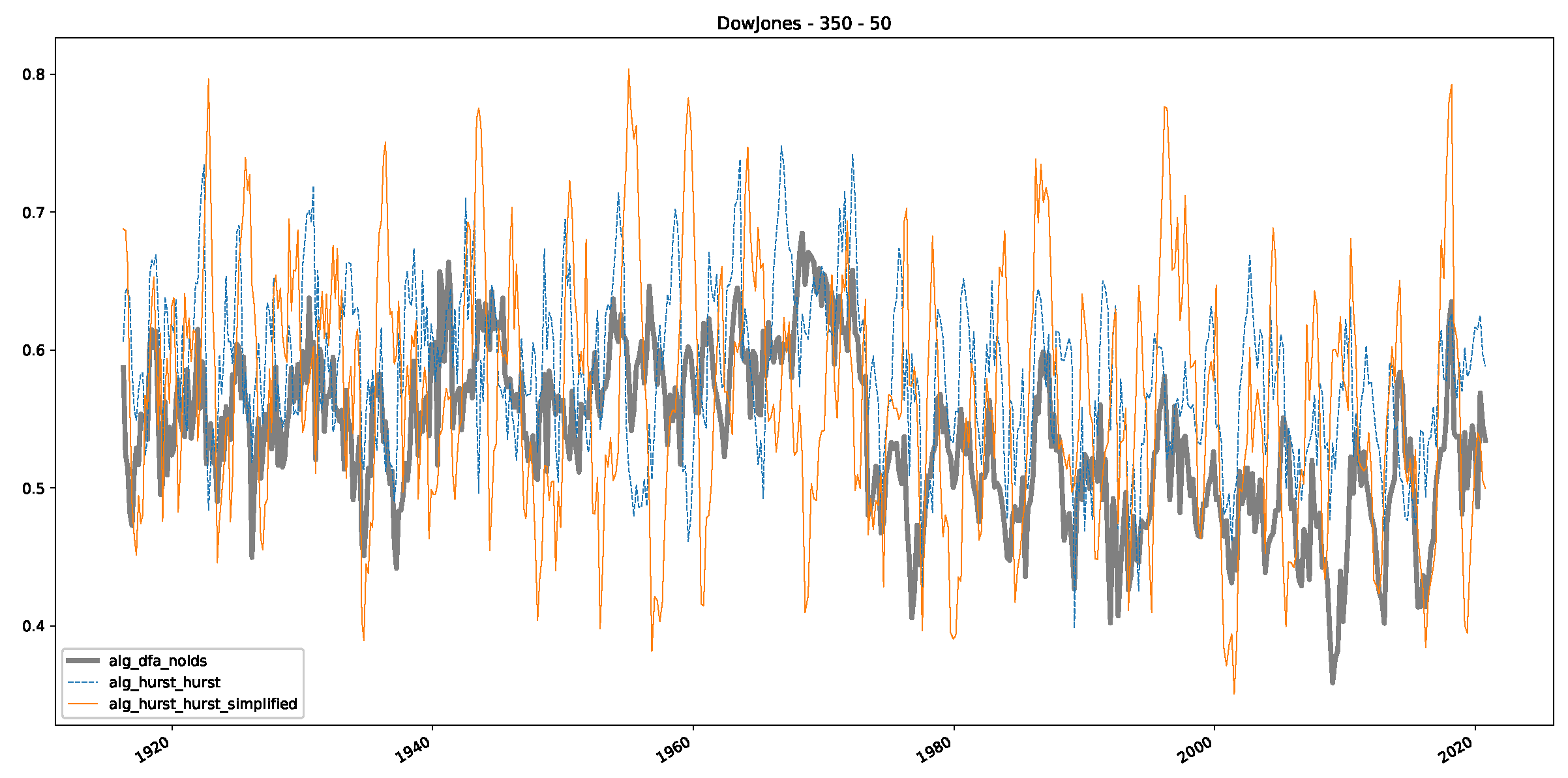
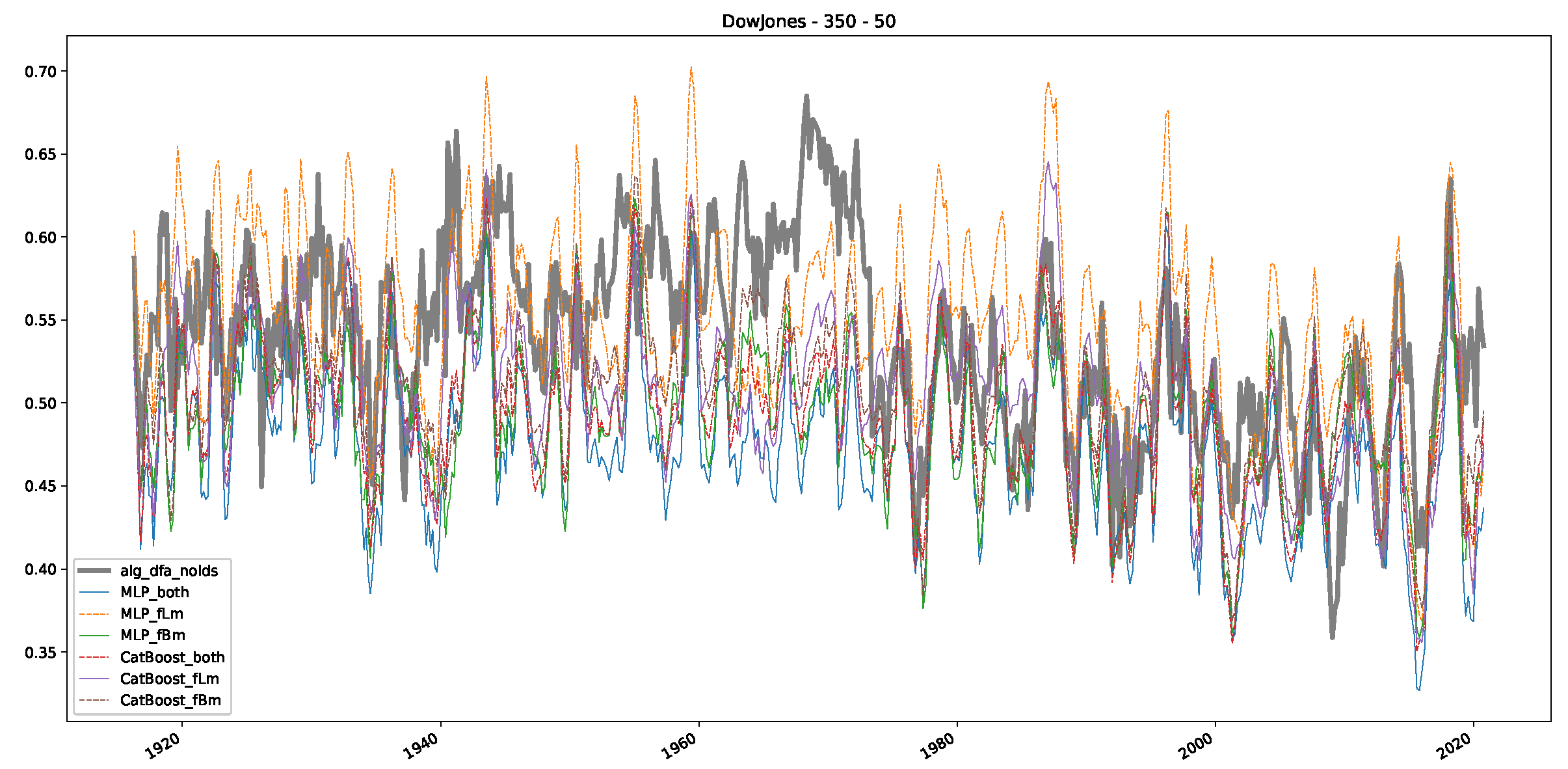
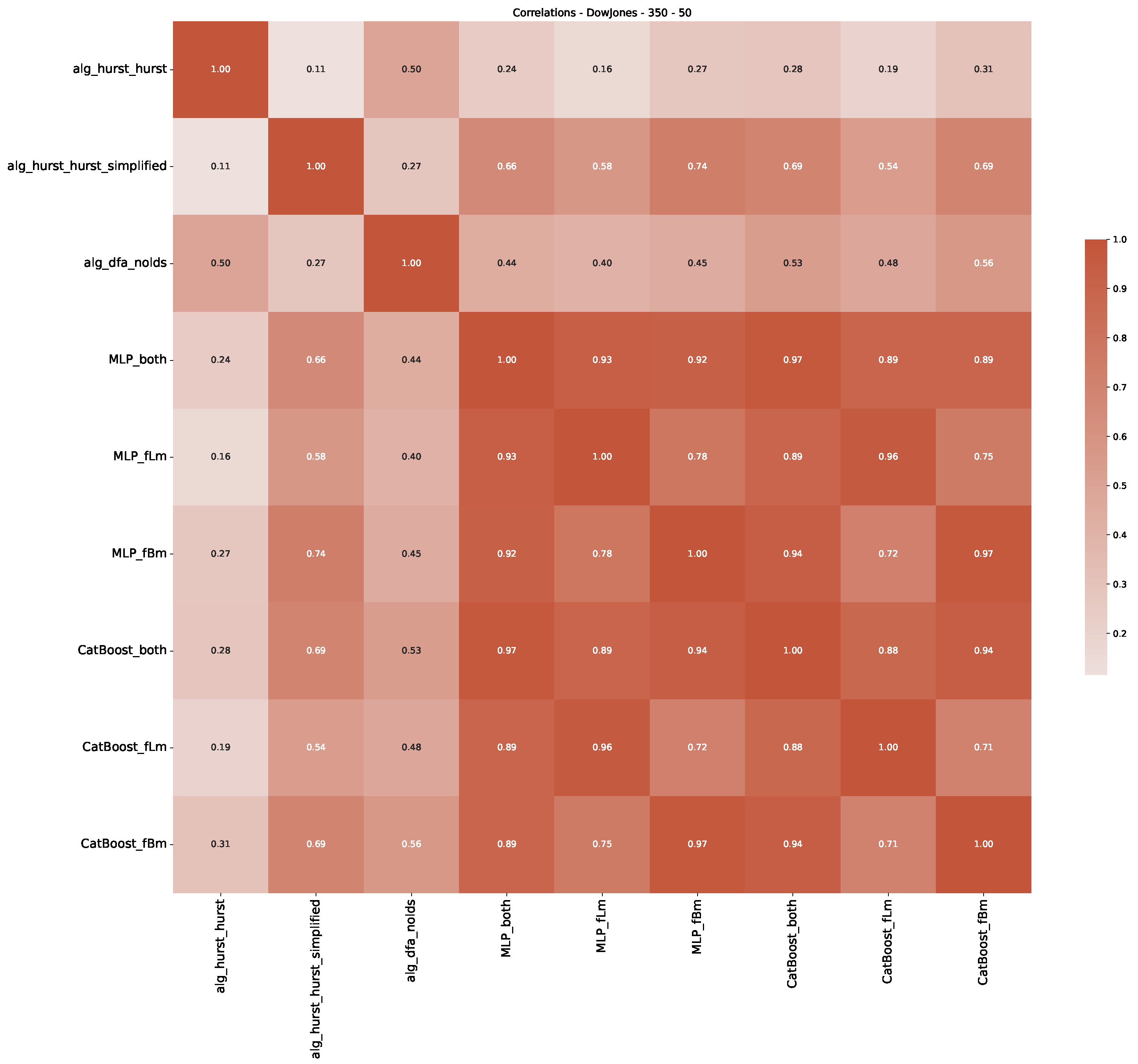
Appendix B.2. Additional Plots S&P500
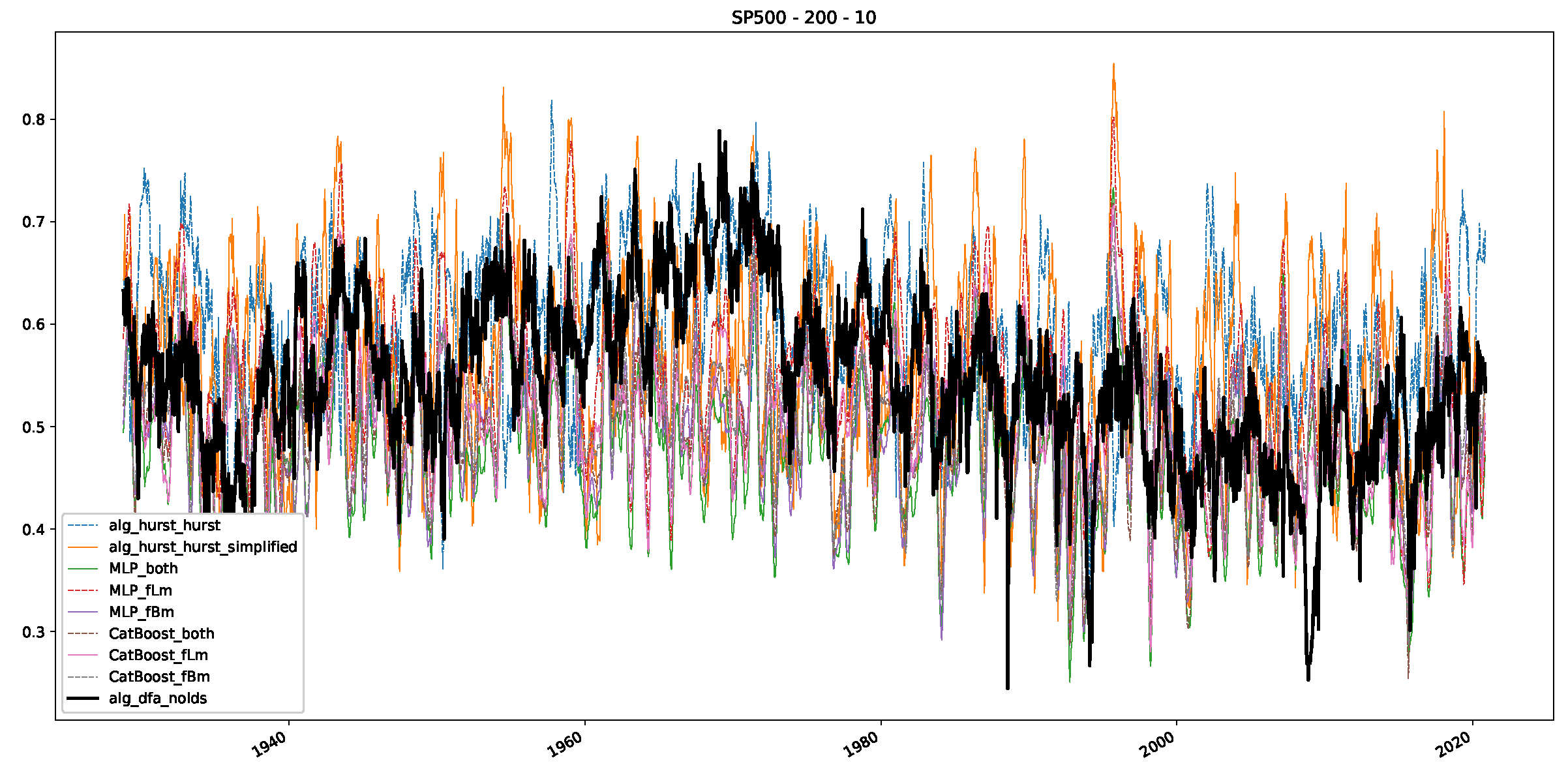
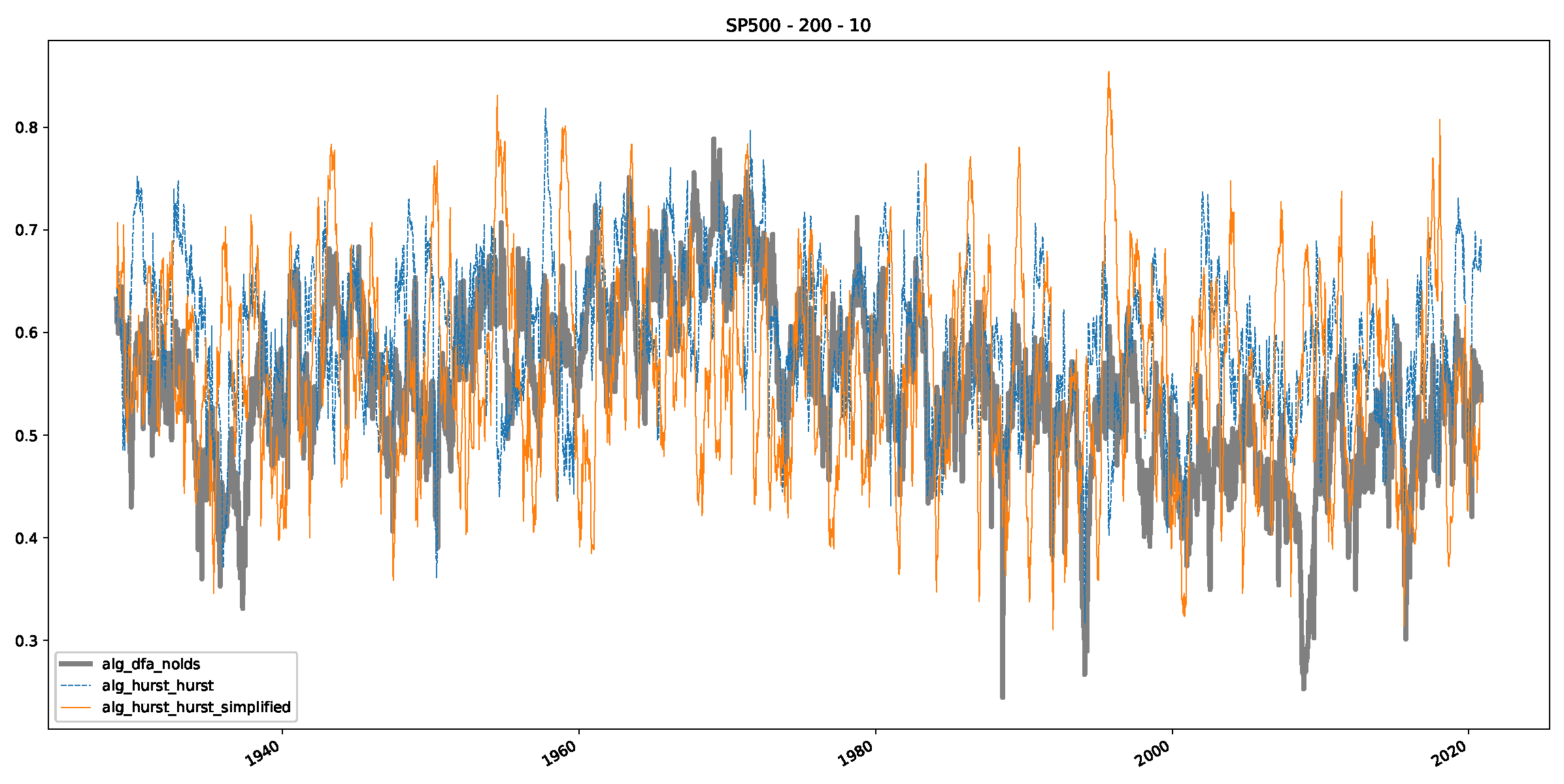
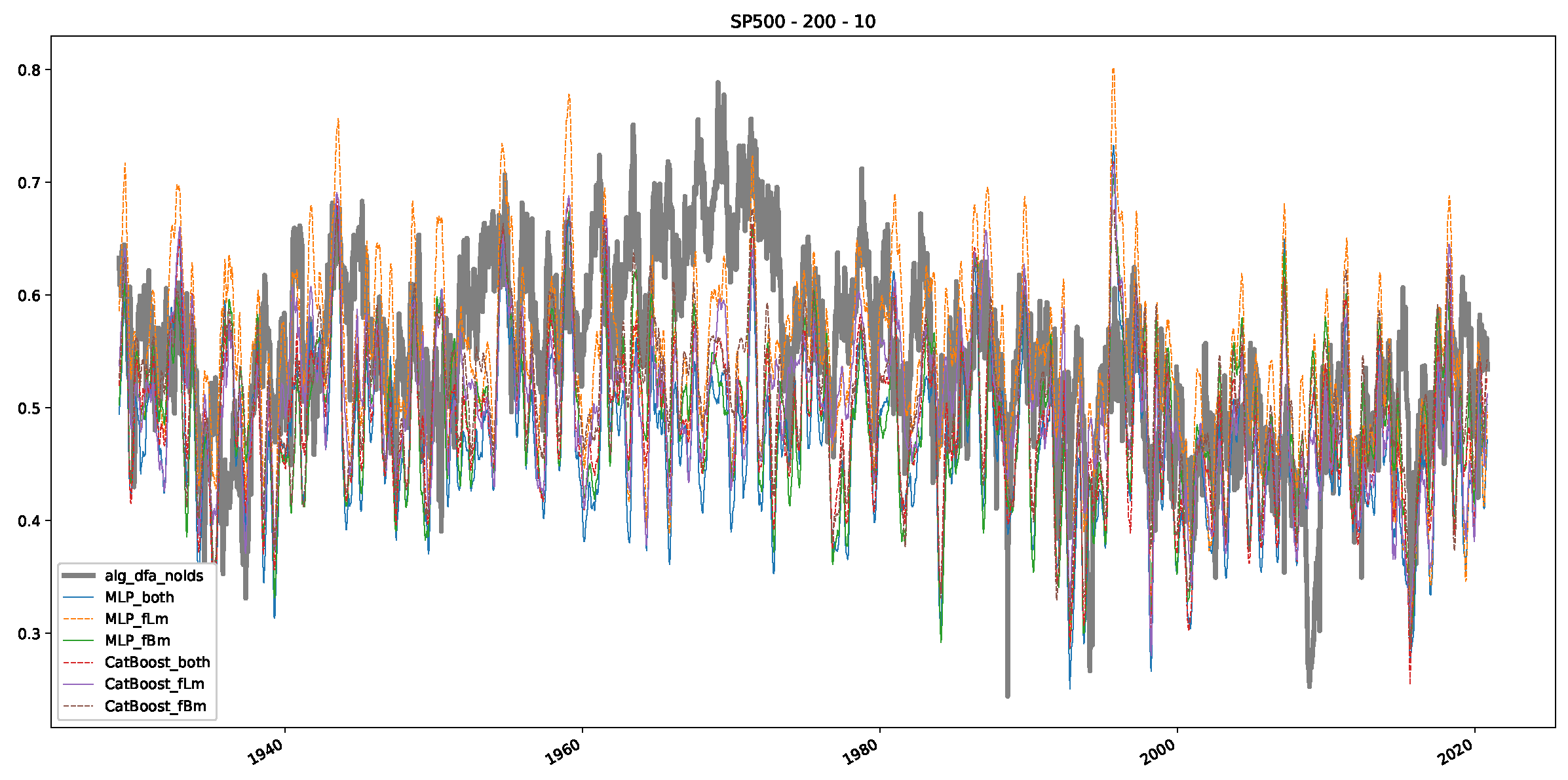
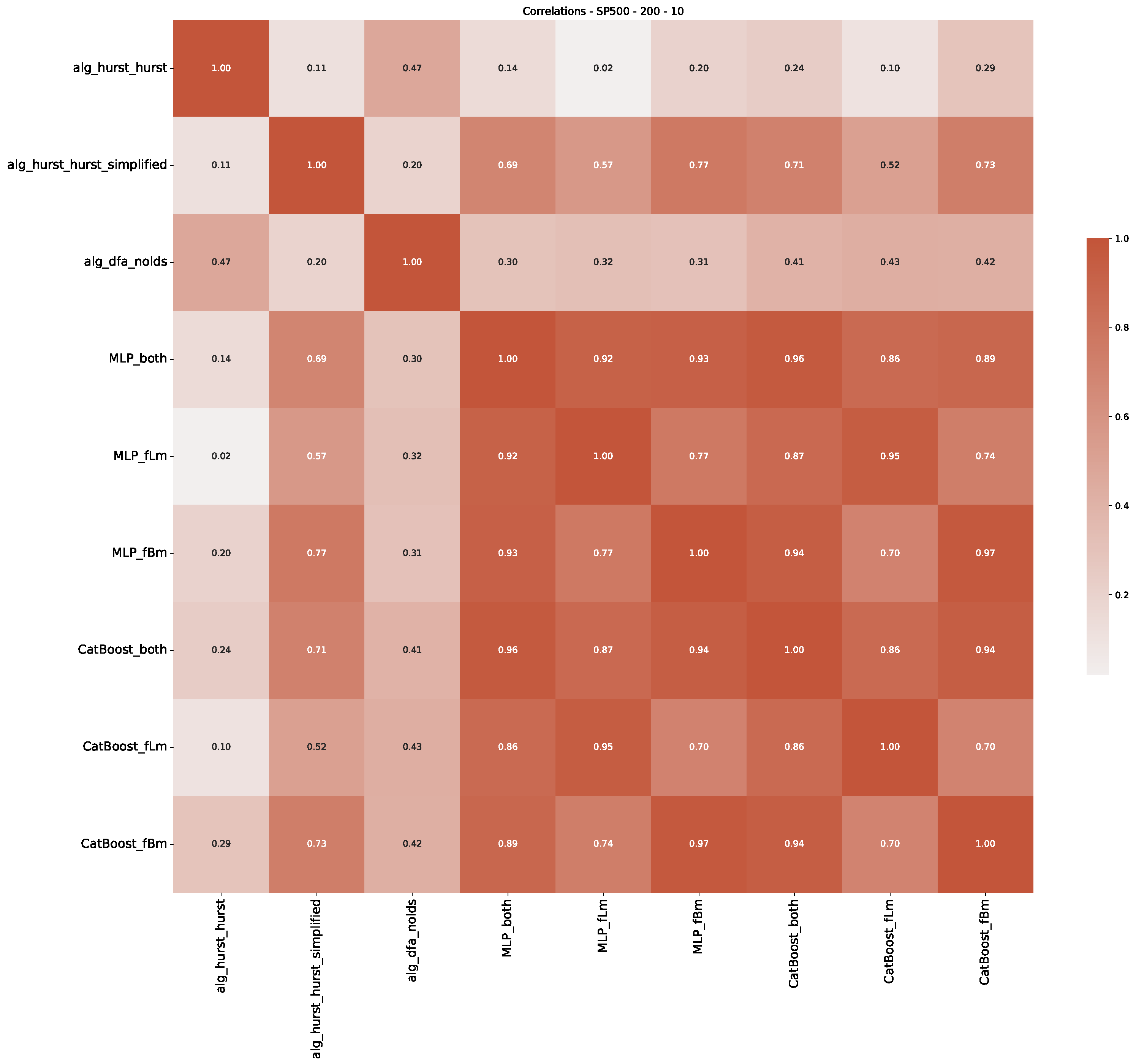
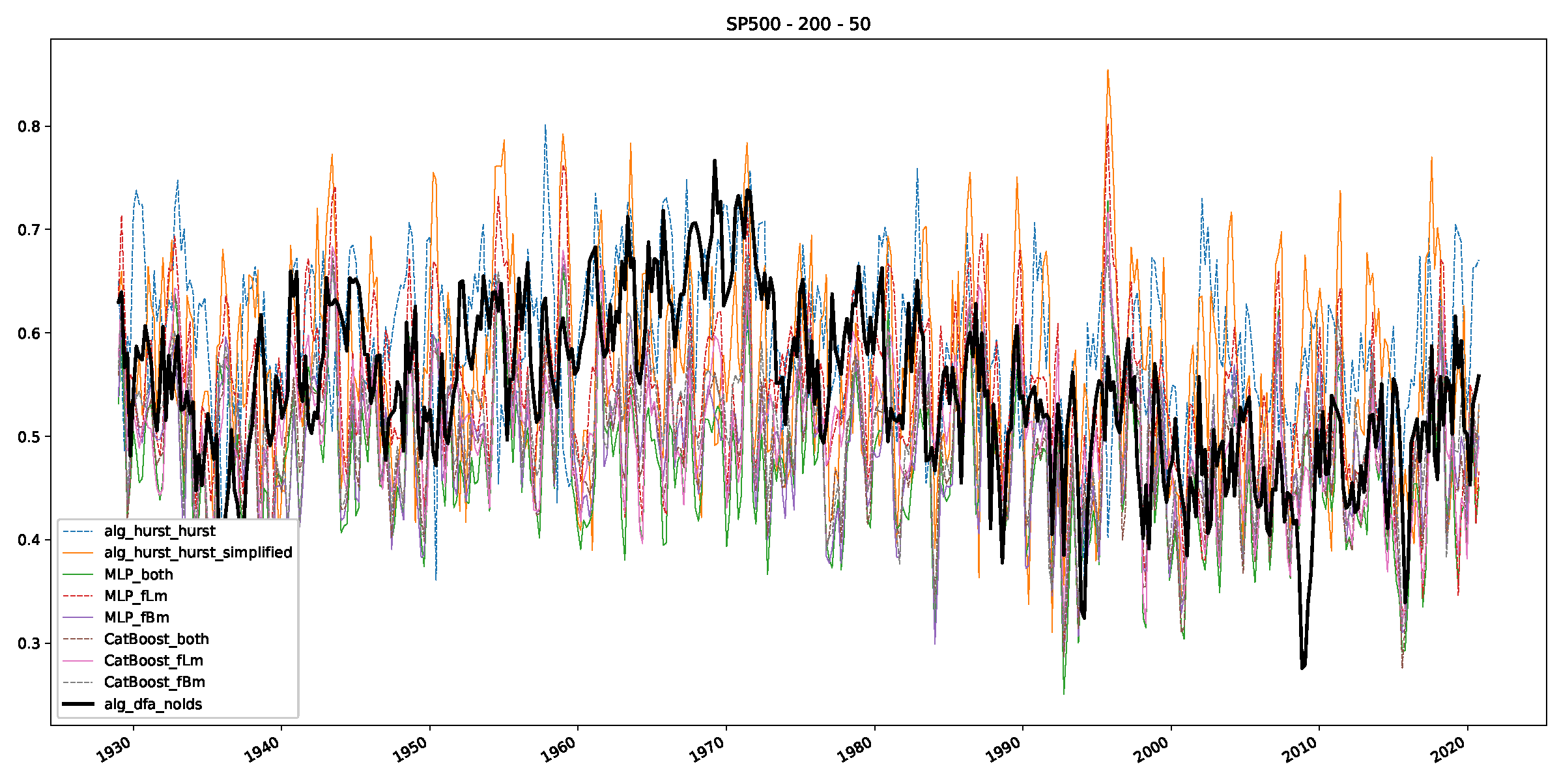
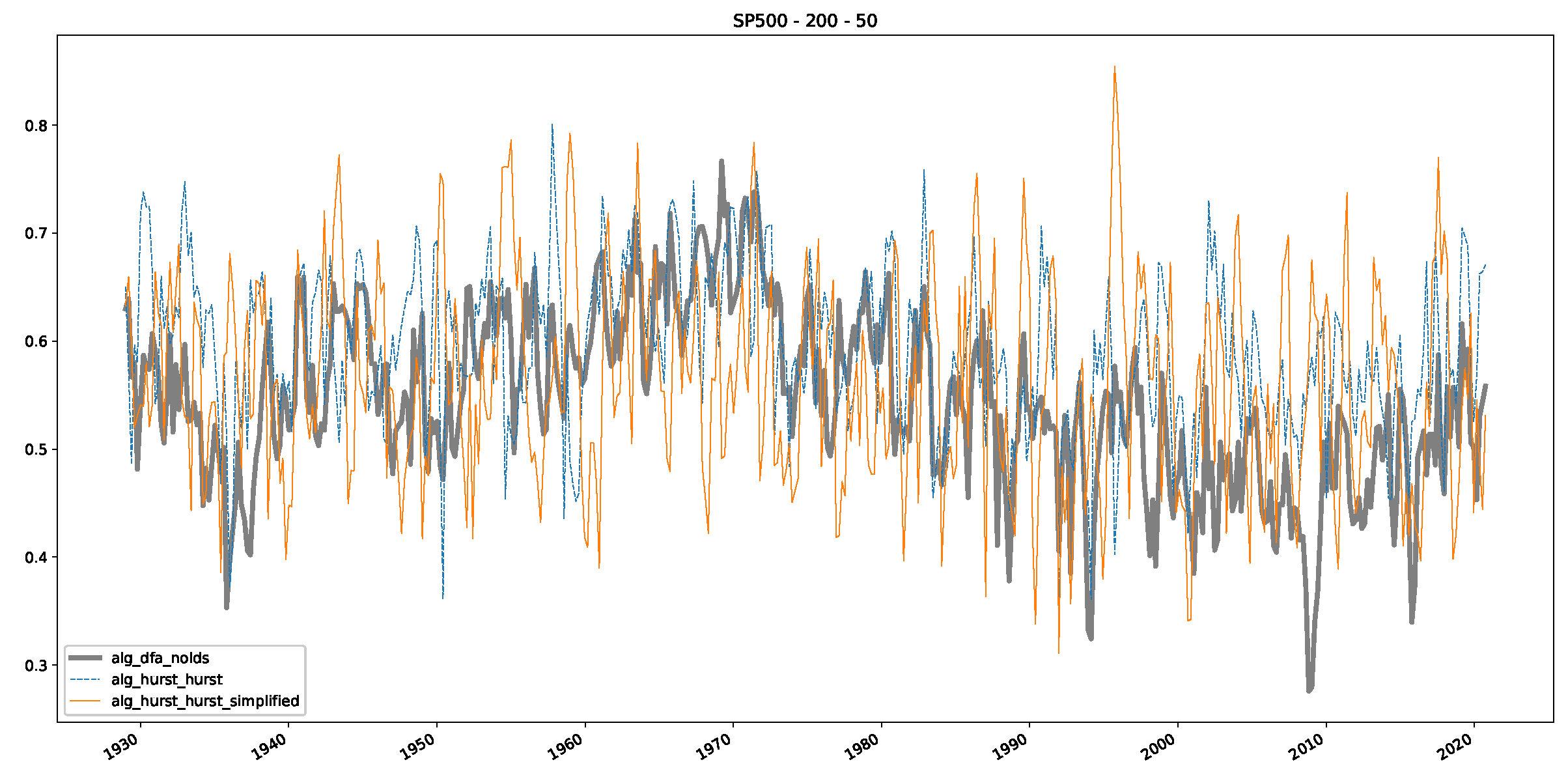
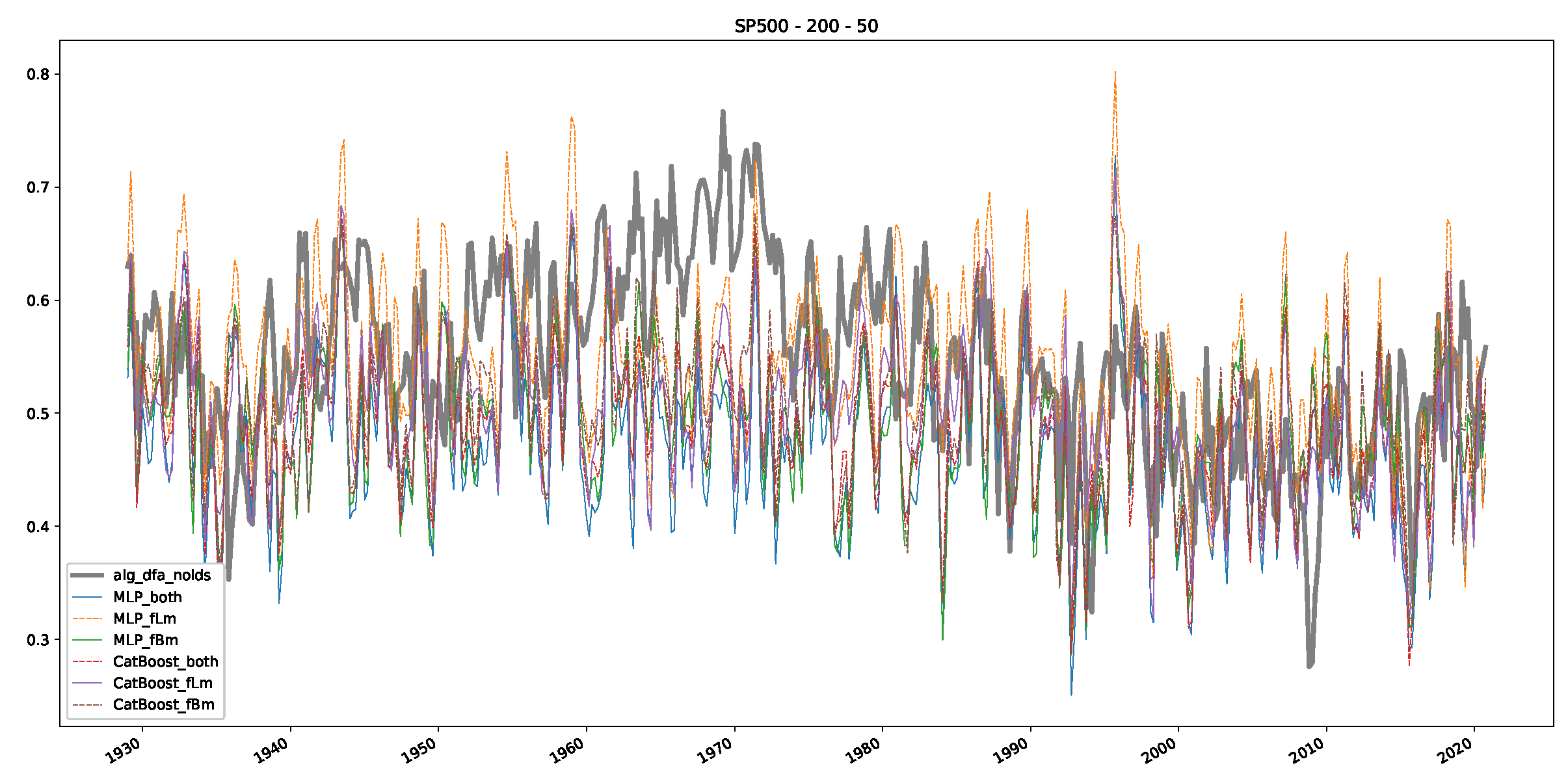
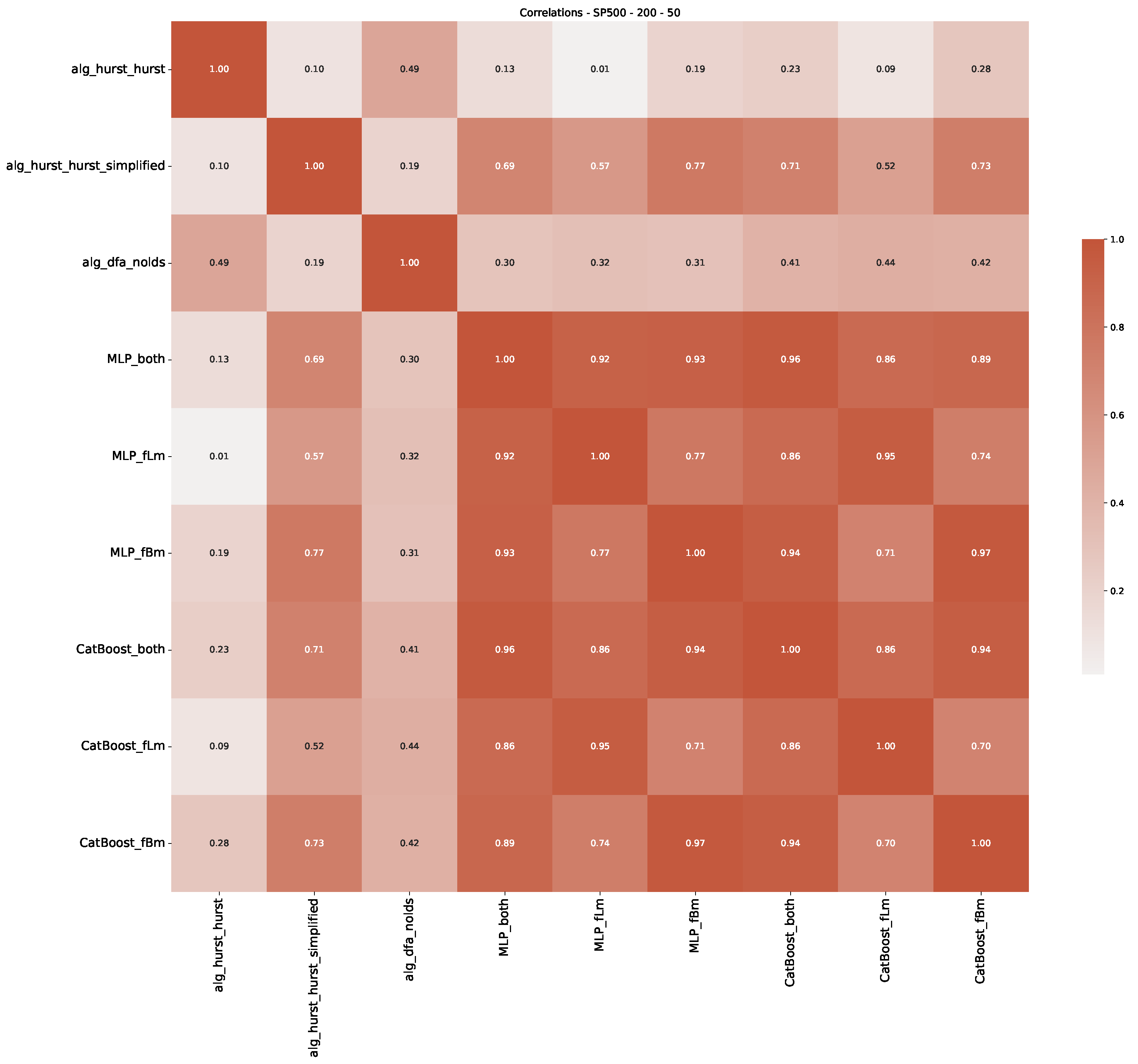
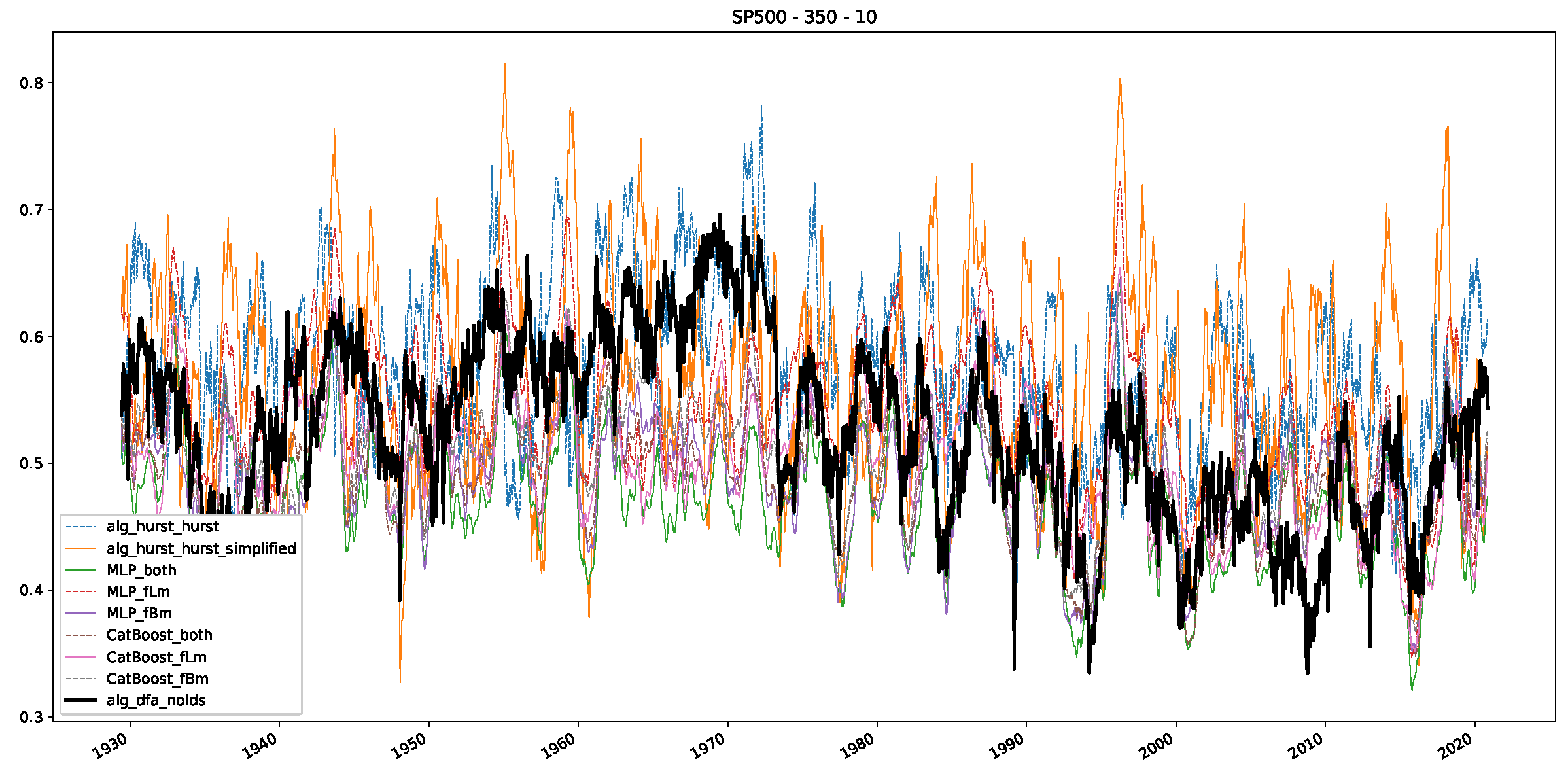
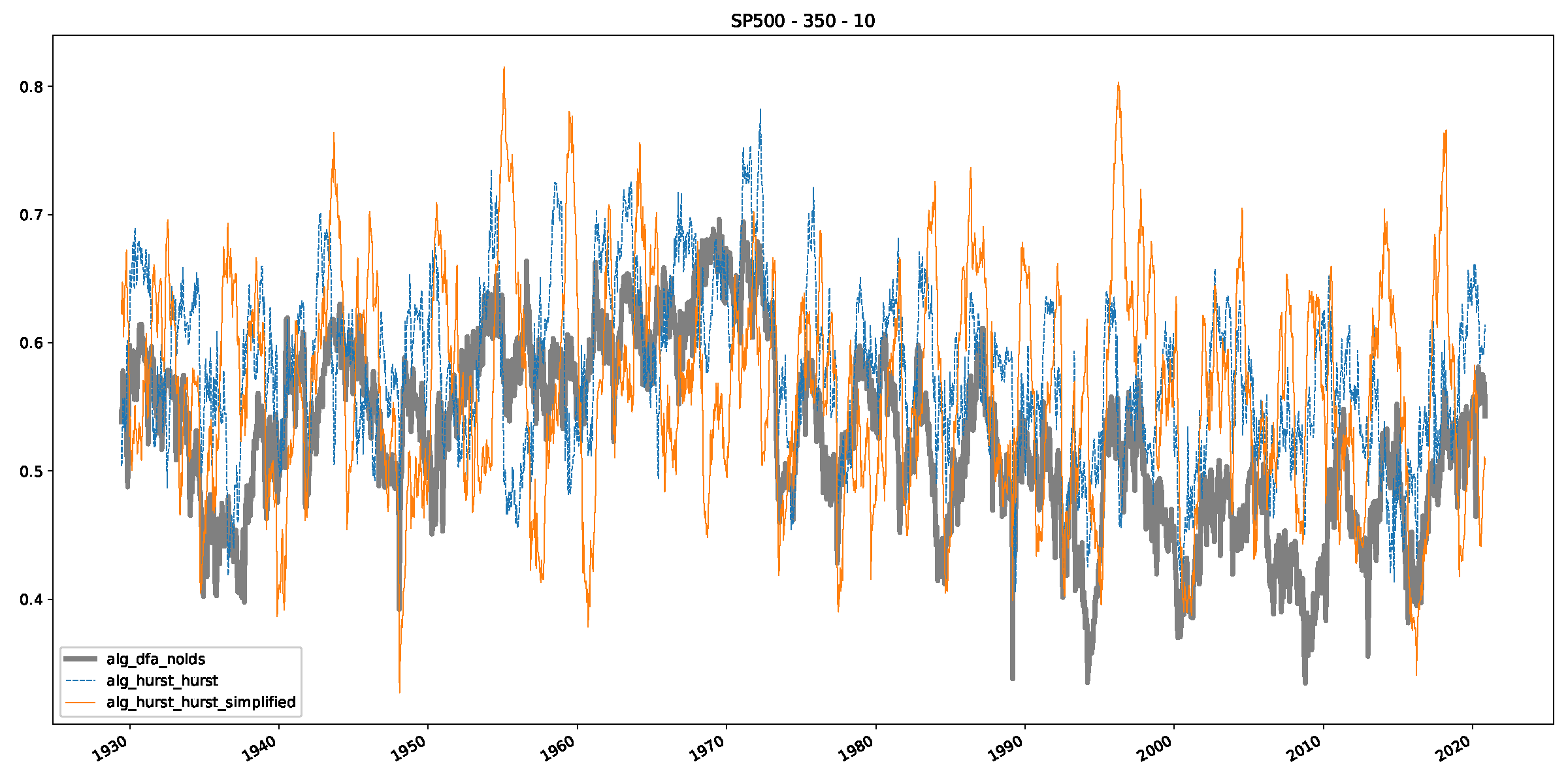
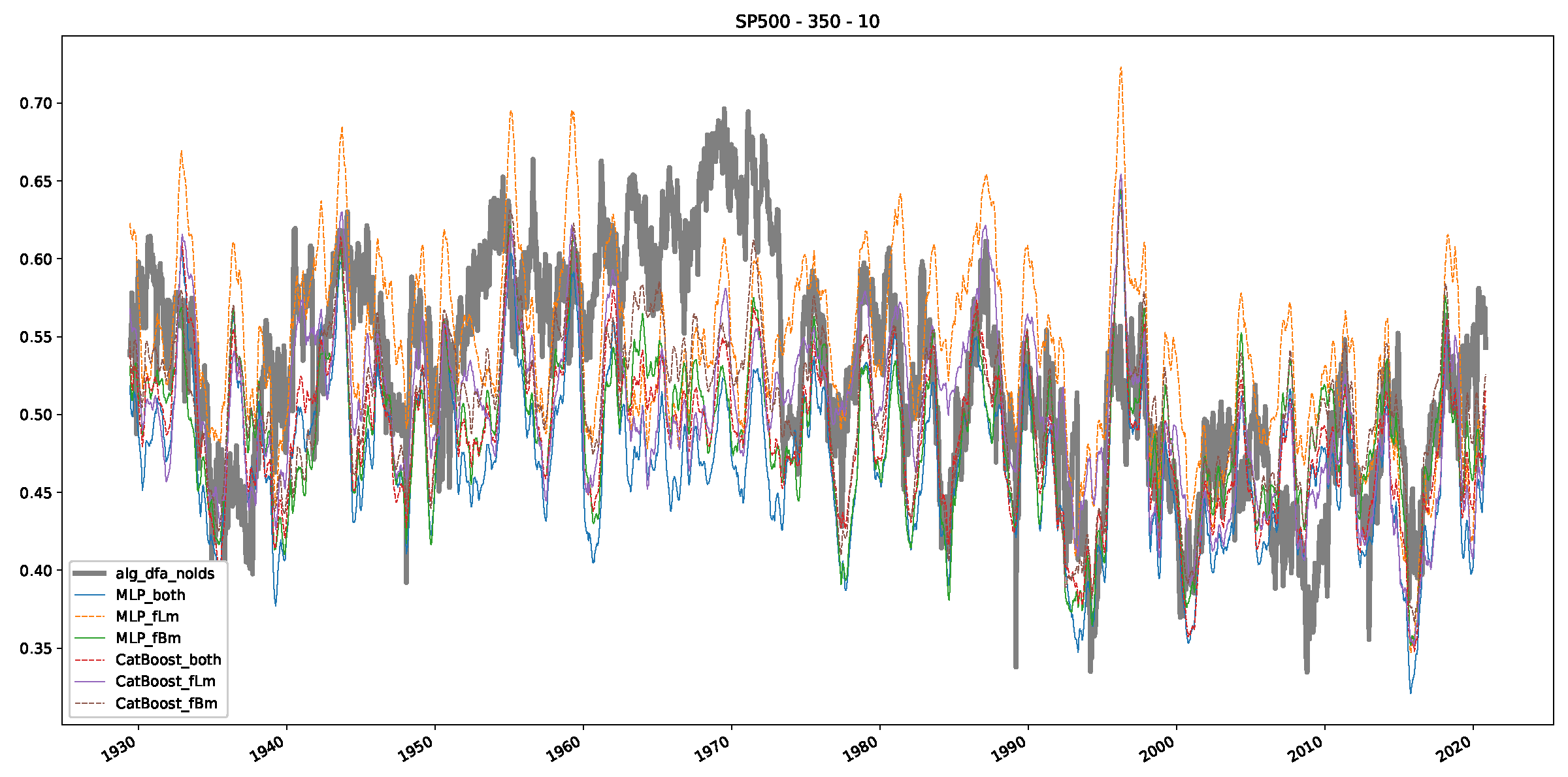
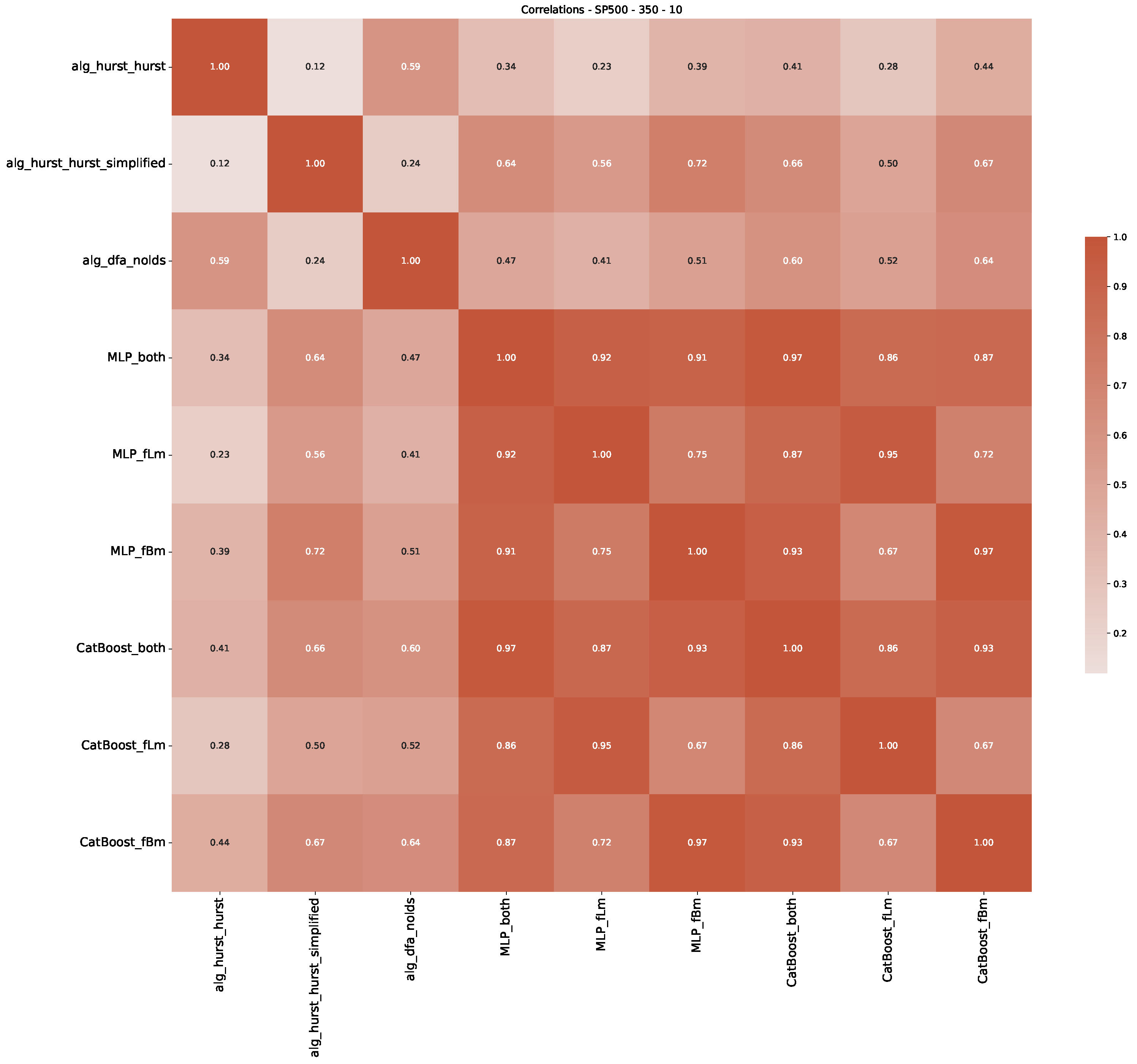
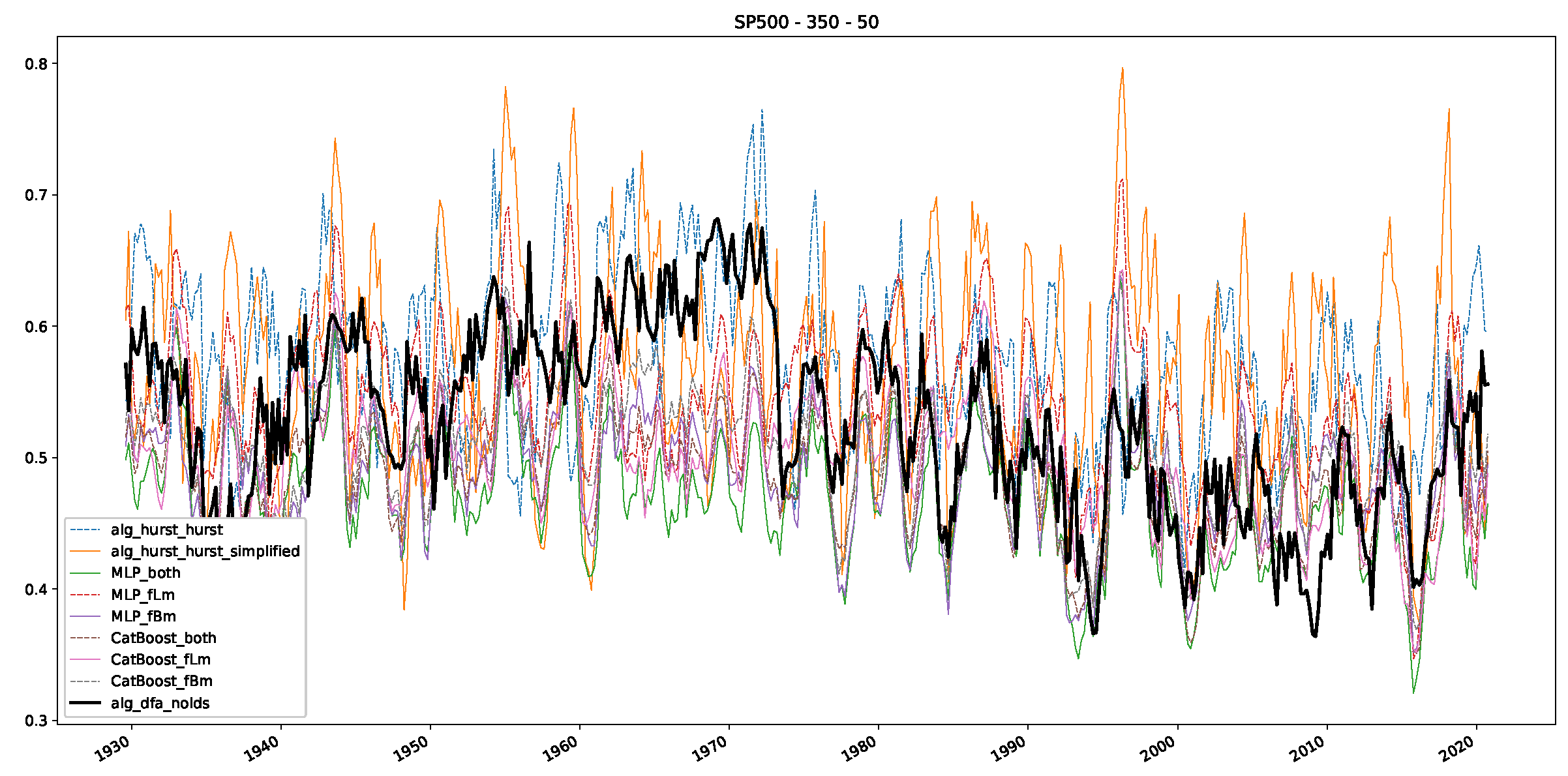
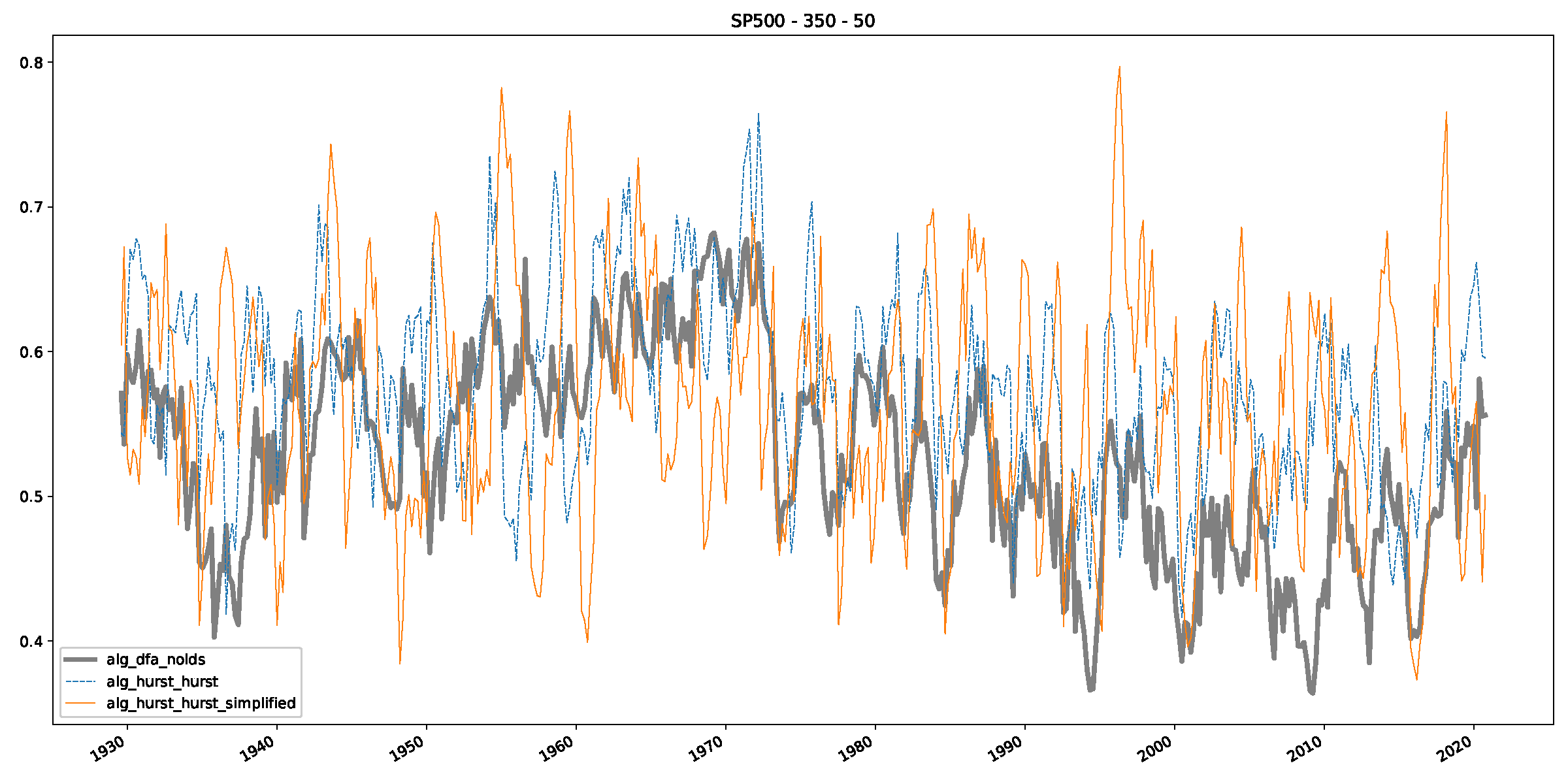
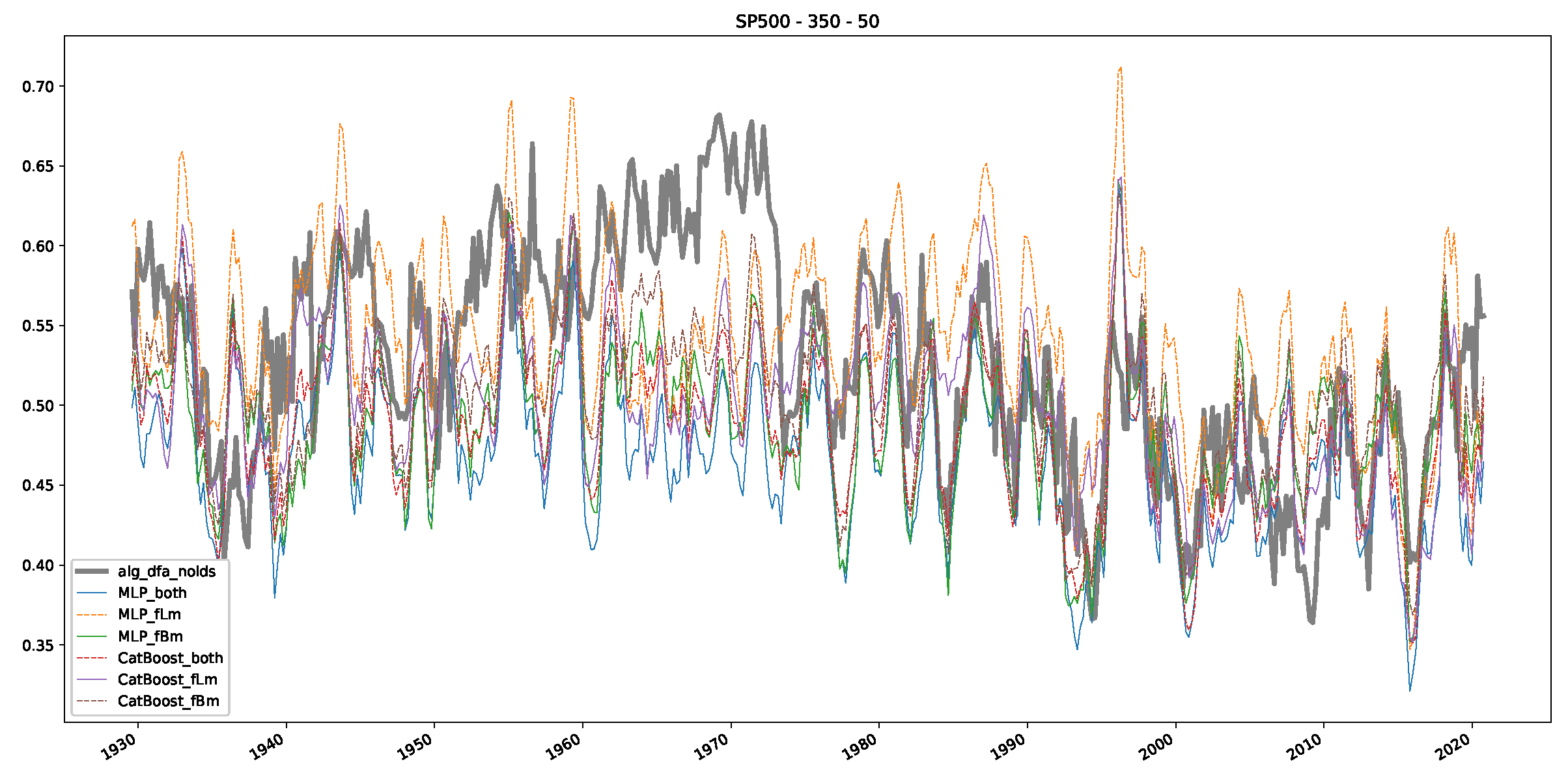
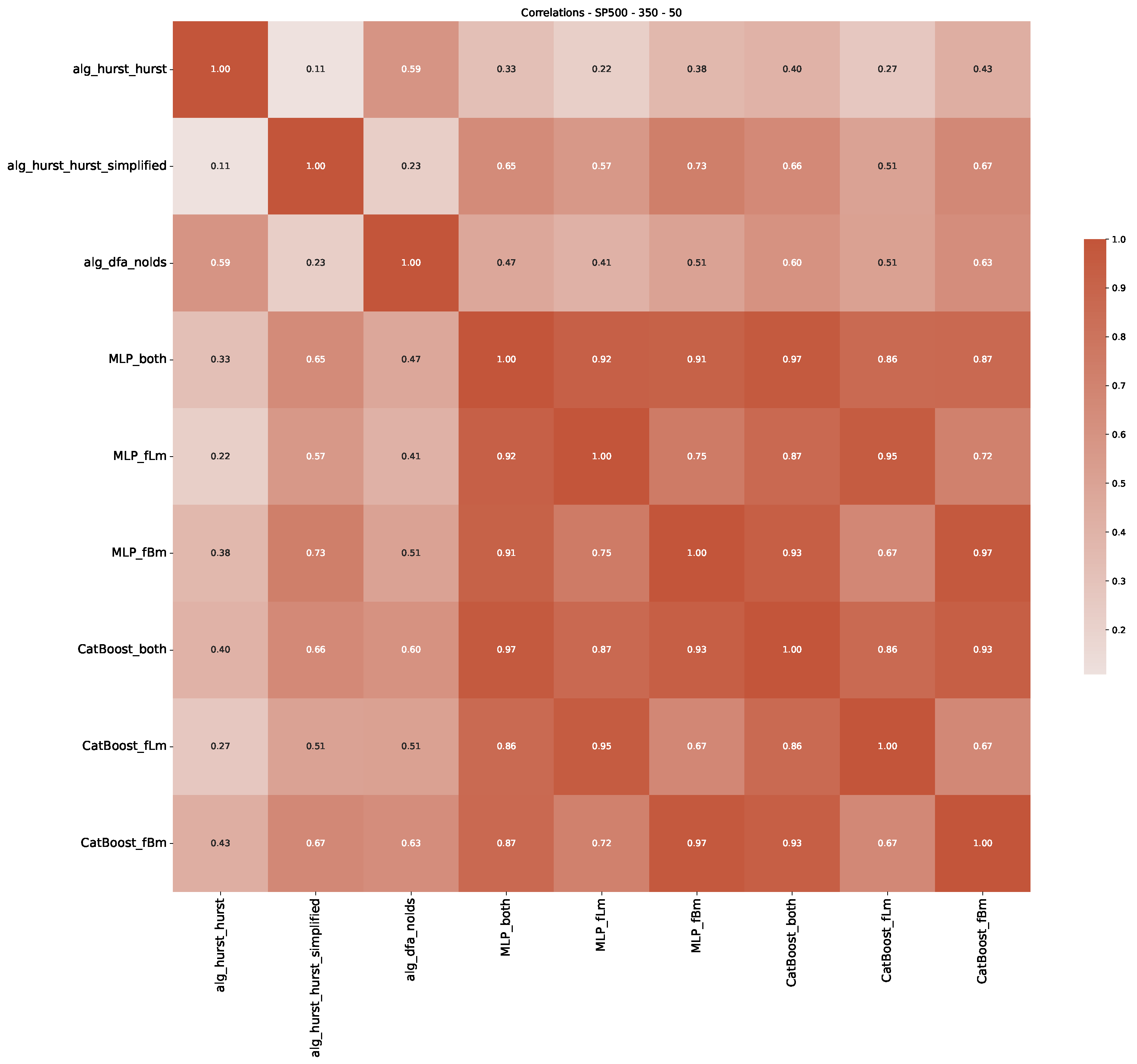
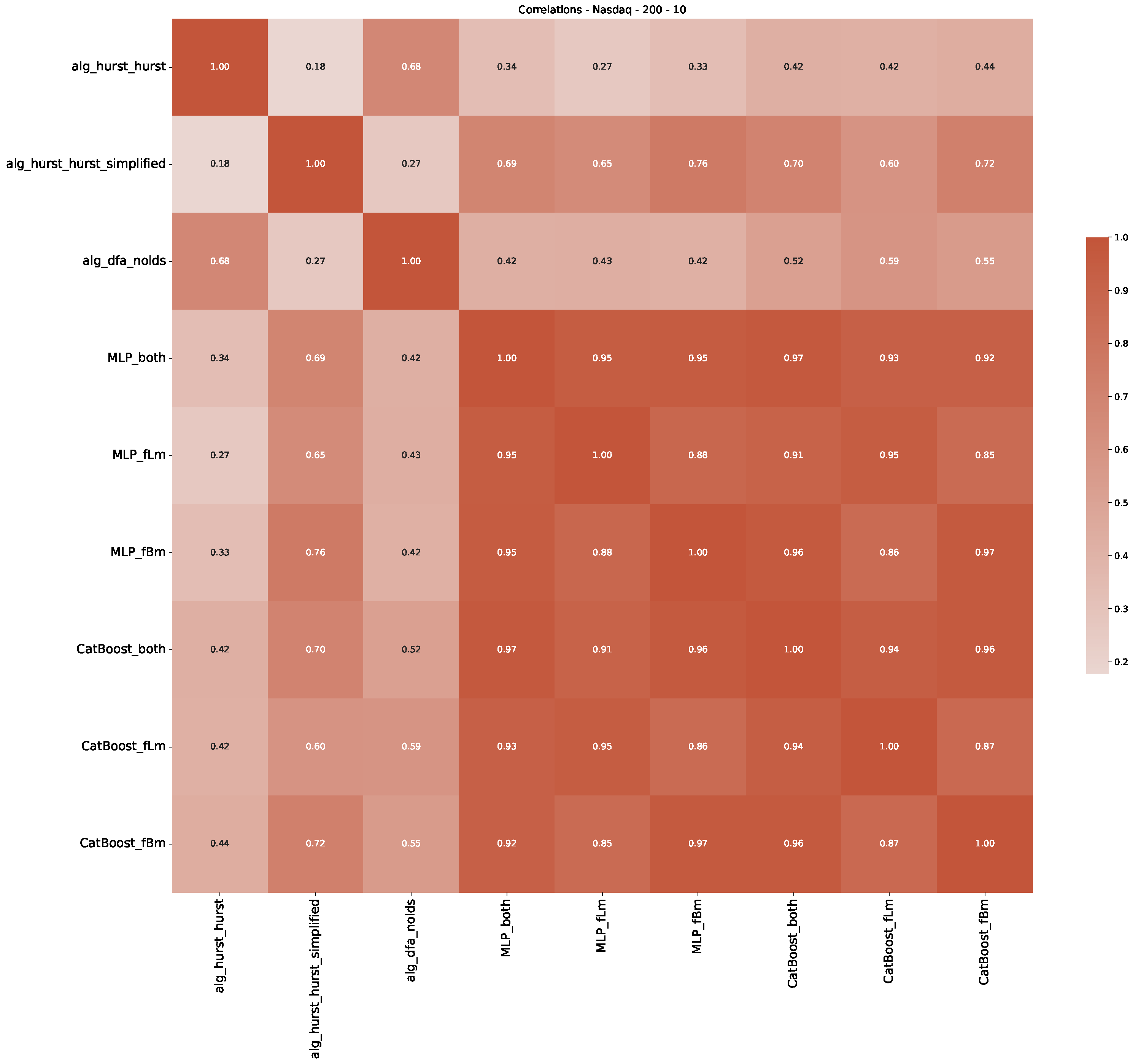
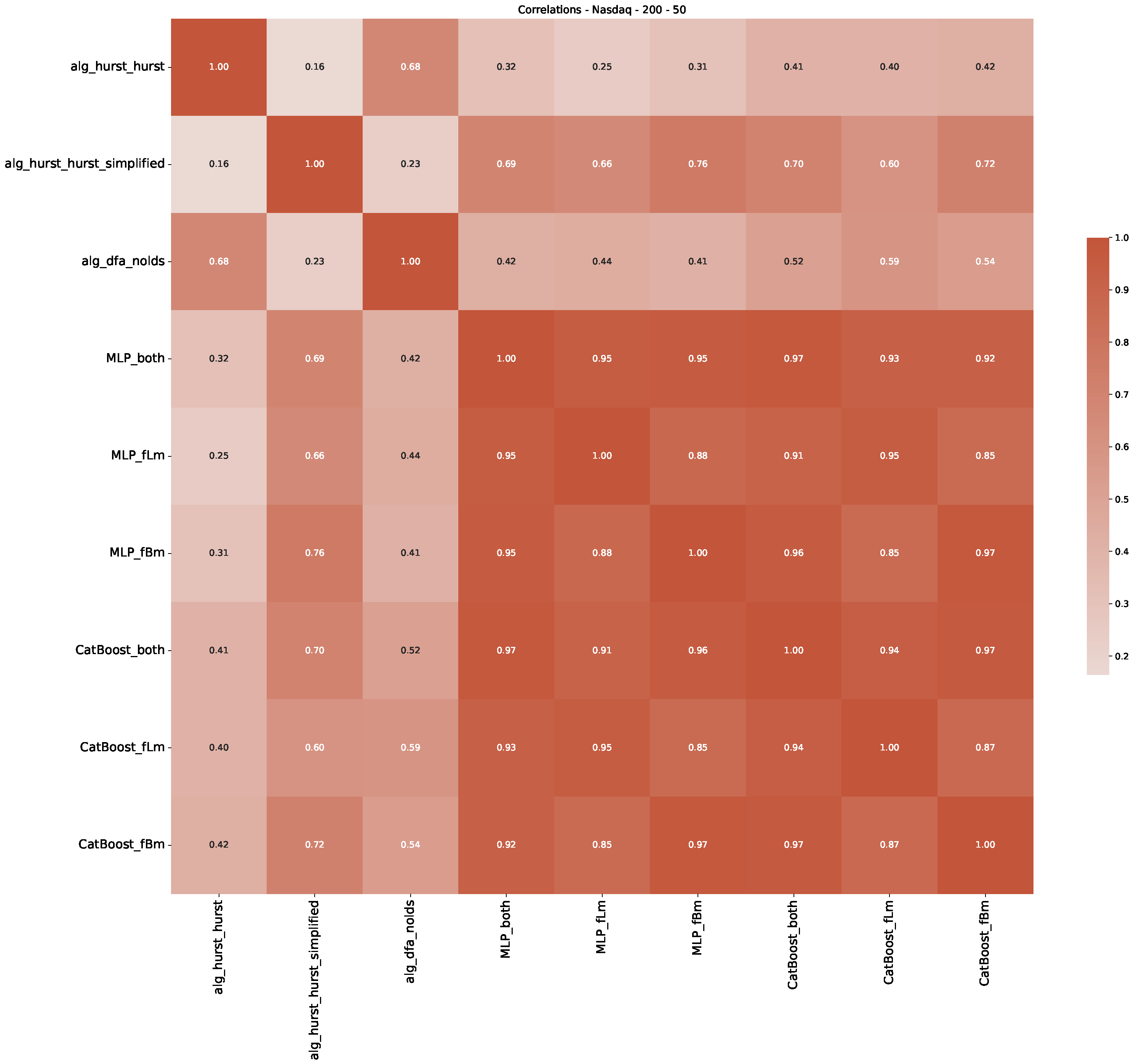
Appendix B.3. Additional Plots NASDAQ
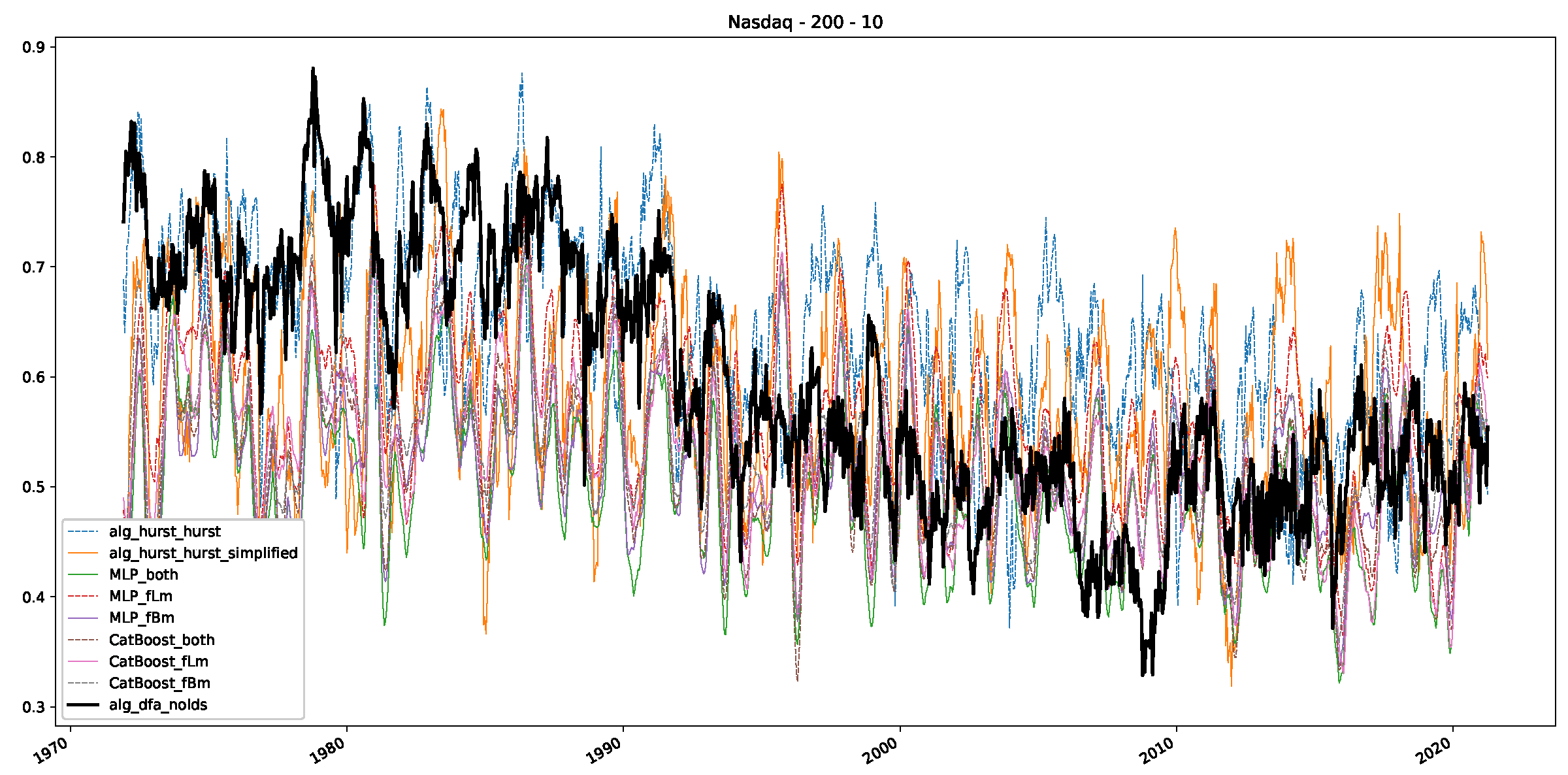
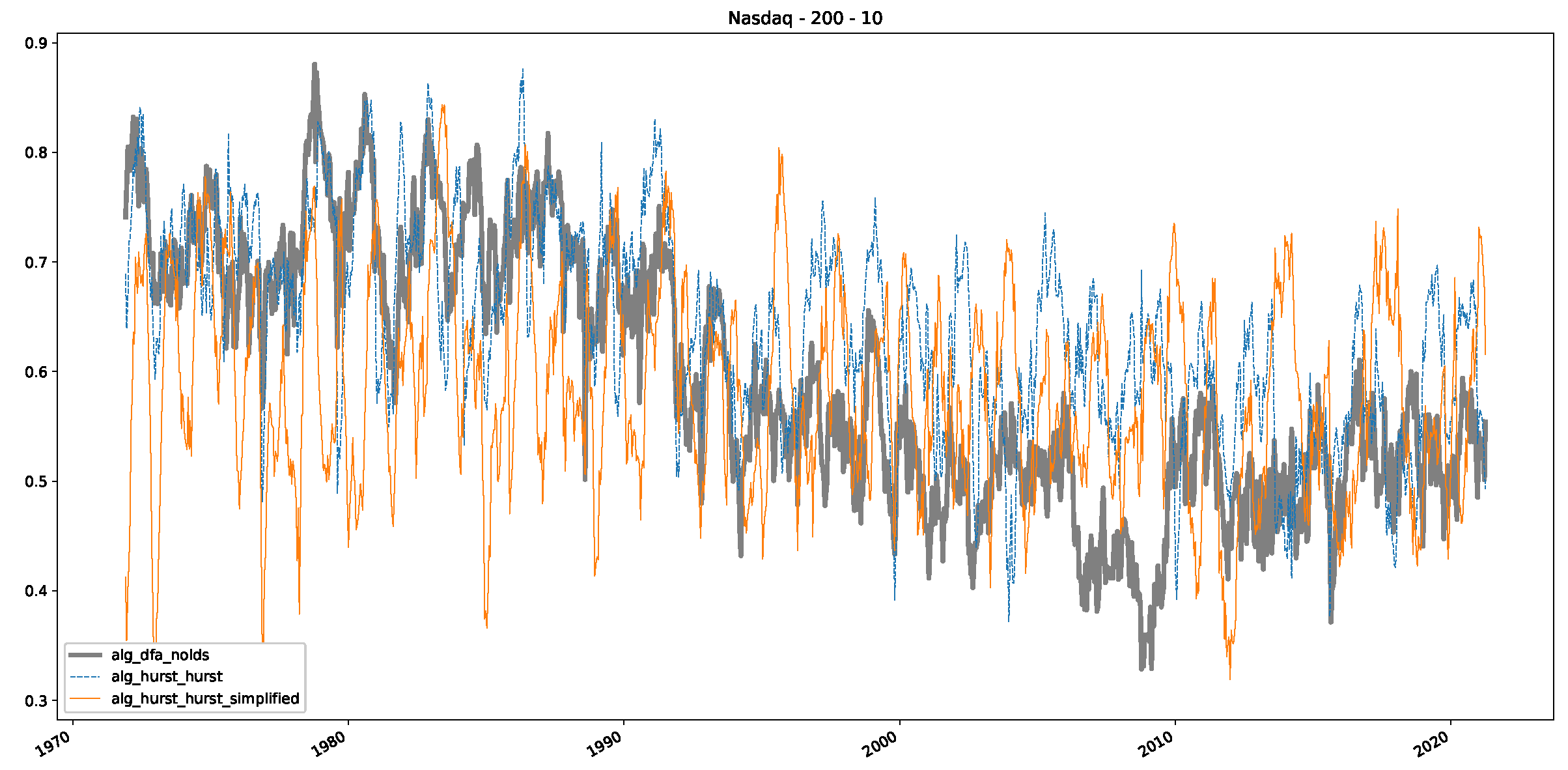
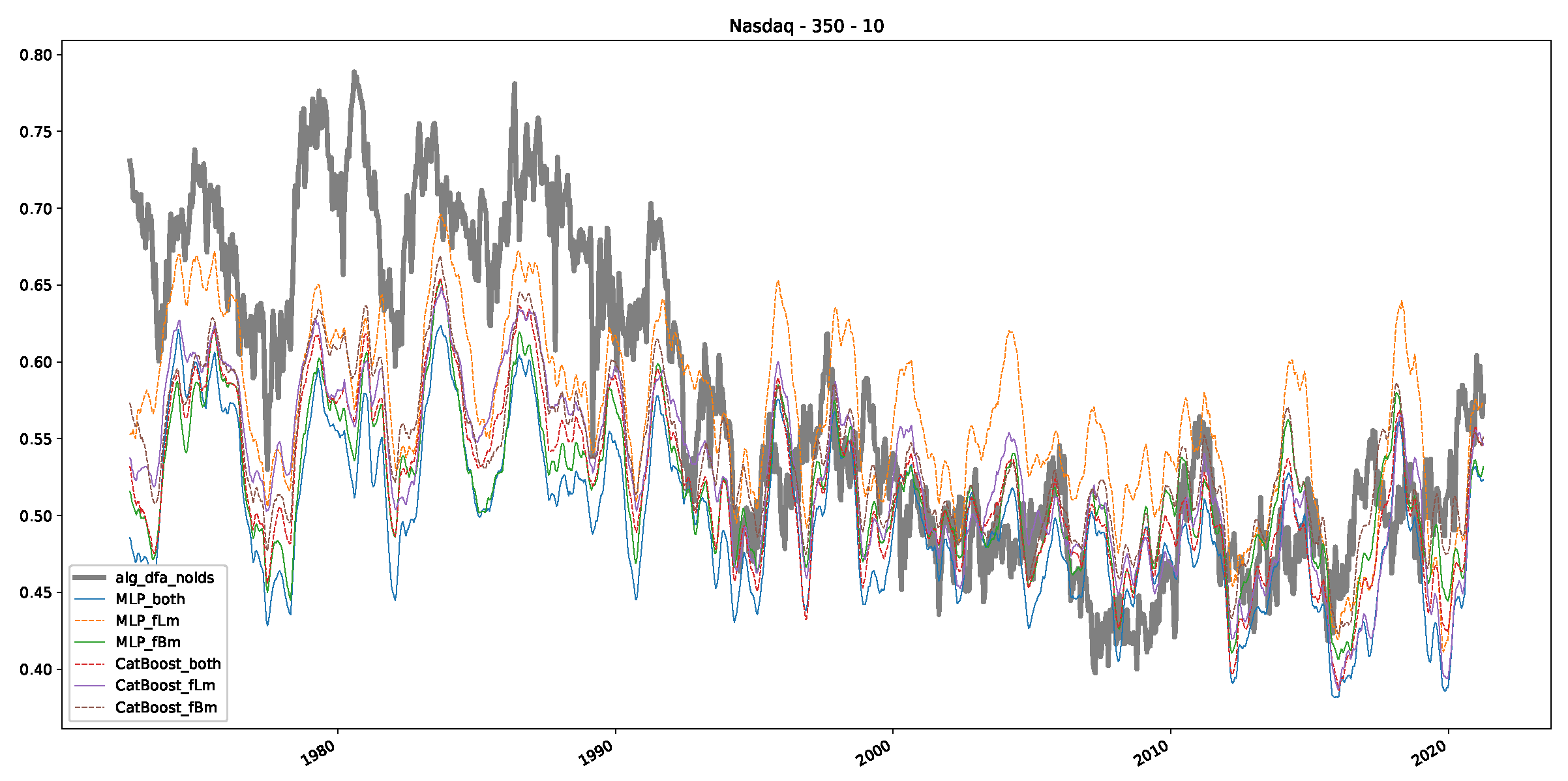
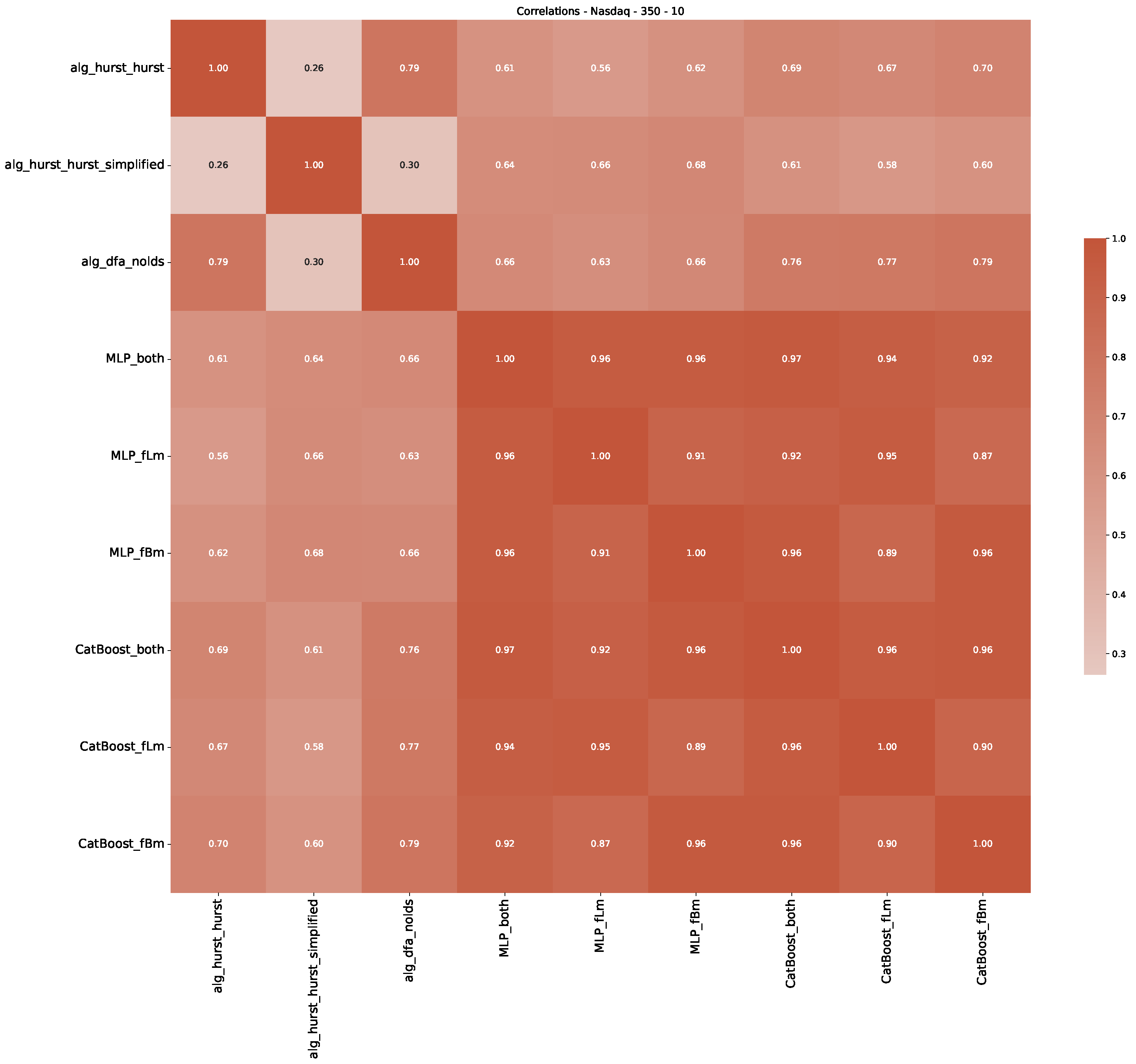
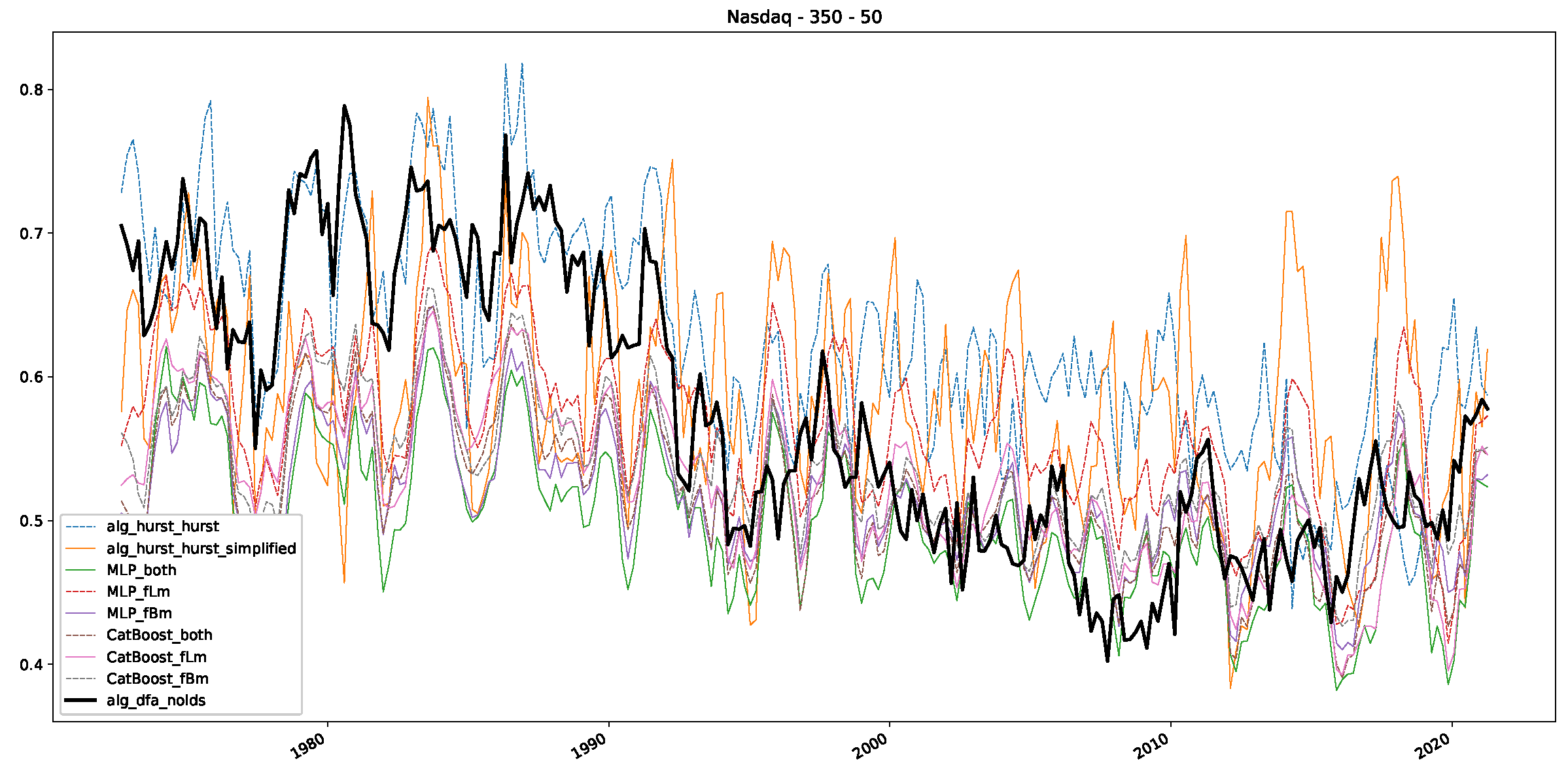
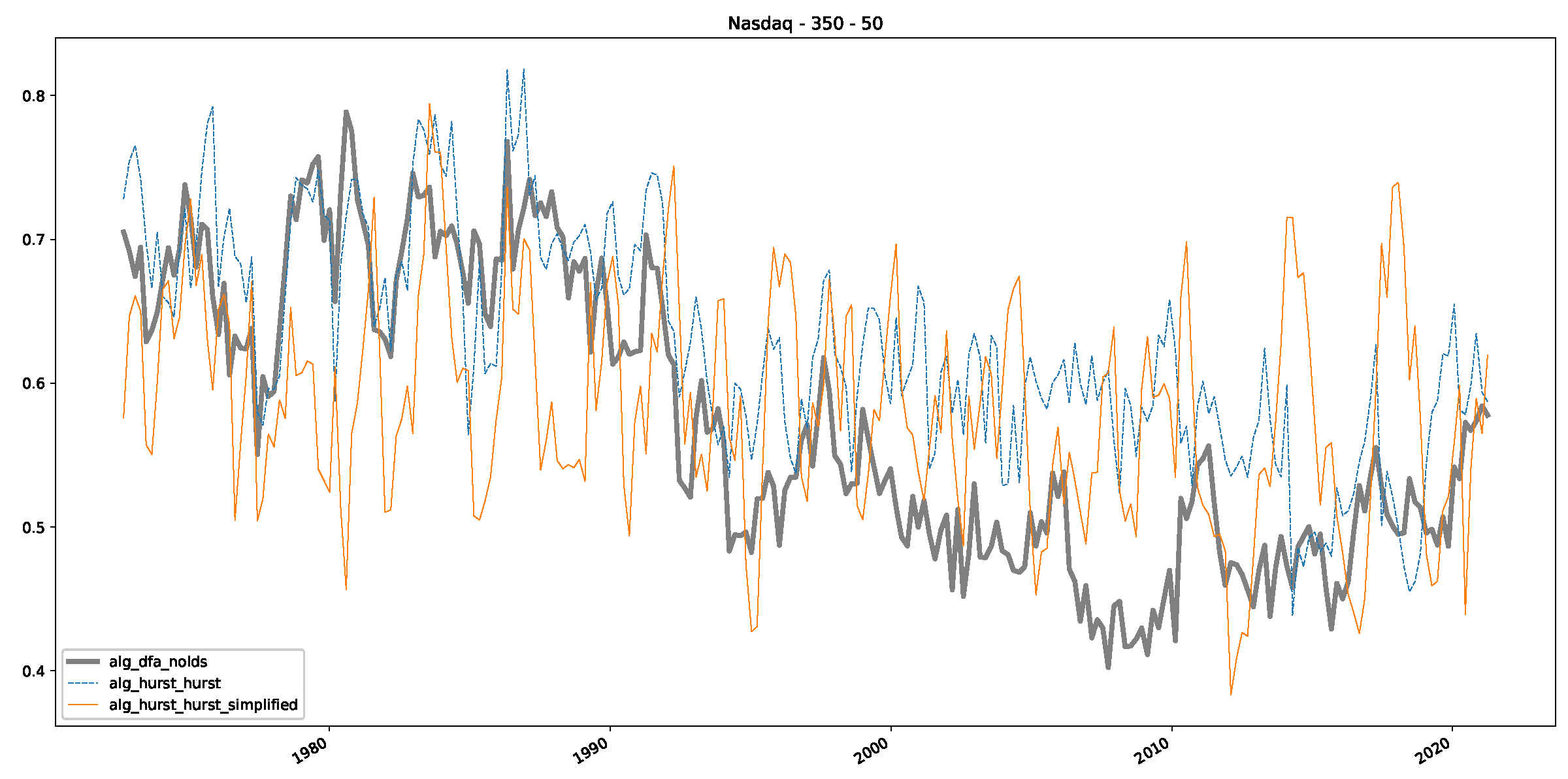
References
- Mandelbrot, B.B.; Wallis, J.R. Robustness of the rescaled range R/S in the measurement of noncyclic long run statistical dependence. Water Resources Research 1969, 5, 967–988.
- Peters, E.E. Fractal market analysis: applying chaos theory to investment and economics; Wiley finance editions, J. Wiley & Sons: New York, 1994. OCLC: 28508185.
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics, 2 ed.; Cambridge University Press, 1997. [CrossRef]
- Ivanov, P.C.; Amaral, L.A.N.; Goldberger, A.L.; Havlin, S.; Rosenblum, M.G.; Struzik, Z.R.; Stanley, H.E. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461–465. [CrossRef]
- Hurst, H.; Black, R.; Sinaika, Y. Long-term Storage in Reservoirs: An experimental Study. Constable: London 1965.
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. Visited on 2022-06-20. [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A: Statistical Mechanics and its Applications 2002, 316, 87–114. [CrossRef]
- Teverovsky, V.; Taqqu, M.S.; Willinger, W. A critical look at Lo’s modified R/S statistic. Journal of Statistical Planning and Inference 1999, 80, 211–227. [CrossRef]
- Ledesman, S.; Ruiz, J.; Garcia, G.; Avina, G.; Hernandez, H. Analysis of self-similar data by artificial neural networks. International Conference on Networking, Sensing and Control 2011, 00, 480–485, [https://ieeexplore.ieee.org/document/5874873]. [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: Results, findings, conclusion and way forward. International Journal of Forecasting 2018, 34, 802–808. [CrossRef]
- Bagnall, A.; Lines, J.; Bostrom, A.; Large, J.; Keogh, E. The great time series classification bake off: a review and experimental evaluation of recent algorithmic advances. Data Mining and Knowledge Discovery 2017, 31, 606–660. [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Advances in Neural Information Processing Systems; Guyon, I.; Luxburg, U.V.; Bengio, S.; Wallach, H.; Fergus, R.; Vishwanathan, S.; Garnett, R., Eds. Curran Associates, Inc., 2017, Vol. 30.
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. Journal of Computer and System Sciences 1997, 55, 119–139. [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Review 1968, 10, 422–437. [CrossRef]
- Mandelbrot, B.; Fisher, A.; Calvet, L. A Multifractal Model of Asset Returns. Cowles Foundation Discussion Papers 1164, Cowles Foundation for Research in Economics, Yale University, 1997.
- Barunik, J.; Aste, T.; Di Matteo, T.; Liu, R. Understanding the source of multifractality in financial markets. Physica A: Statistical Mechanics and its Applications 2012, 391, 4234–4251. [CrossRef]
- Mukherjee, S.; Sadhukhan, B.; Das, K.A.; Chaudhuri, A. Hurst exponent estimation using neural network. International Journal of Computational Science and Engineering 2023, 26, 157–170. [CrossRef]
- Sadhukhan, B.; Mukherjee, S. Undermining the Fractal and Stationary Nature of Earthquake. International Journal of Computer Sciences and Engineering 2018, 06, 670–678, [https://www.researchgate.net/publication/332114260]. [CrossRef]
- Tarnopolski, M. Correlation Between the Hurst Exponent and the Maximal Lyapunov Exponent: Examining Some Low-Dimensional Conservative Maps. Physica A: Statistical Mechanics and its Applications 2018, 490, 834–844. [CrossRef]
- Tyralis, H.; Koutsoyiannis, D.; Dimitriadis, P.; O’Connell, E. On the long-range dependence properties of annual precipitation using a global network of instrumental measurements. Advances in Water Resources 2018, 00, 0–0, [https://www.researchgate.net/publication/321228968]. [CrossRef]
- Bulkah, V.; Kirichenko, L.; Radivilova, T. Machine Learning in Classification Time Series with Fractal Properties. Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining and Processing (DSMP) 2018, 04, 198–201. [CrossRef]
- Liu, H.; Song, W.; Li, M.; Kudreyko, A.; Zio, E. Fractional Lévy stable motion: Finite difference iterative forecasting model. Chaos, Solitons & Fractals 2020, 133, 109632. [CrossRef]
- Huillet, T. Fractional Lévy Motions and Related Processes. Journal of Physics A: Mathematical and General 1999, 32, 7225. [CrossRef]
- Nualart, D. Stochastic Calculus with Respect to Fractional Brownian Motion and Applications. Annales de la faculté des sciences de Toulouse Mathématiques 2006, 15, 63–78. [CrossRef]
- Green, C. flm: Fractional Levy motion, 2018. Calculated using the algorithm in Liu et al, A corrected and generalized successive random additions algorithm for simulating Fractional Levy Motion, Mathematical Geology, 36 (2004).
- Liu, H.H.; Bodvarsson, G.S.; Lu, S.; Molz, F.J. A Corrected and Generalized Successive Random Additions Algorithm for Simulating Fractional Levy Motions. Mathematical Geology 2004, 36, 361–378. [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67, [https://www.tandfonline.com/doi/pdf/10.1080/00401706.1970.10488634]. [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. Journal of the Royal Statistical Society: Series B (Methodological) 1996, 58, 267–288, [https://rss.onlinelibrary.wiley.com/doi/pdf/10.1111/j.2517-6161.1996.tb02080.x]. [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: unbiased boosting with categorical features. Advances in Neural Information Processing Systems; Bengio, S.; Wallach, H.; Larochelle, H.; Grauman, K.; Cesa-Bianchi, N.; Garnett, R., Eds. Curran Associates, Inc., 2018, Vol. 31.
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; Perrot, M.; Duchesnay, E. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research 2011, 12, 2825–2830.
- Raubitzek, S. Estimating the Hurst Exponent via Machine Learning, Full Experiment, 2023.
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; others. Scikit-learn: Machine learning in Python. Journal of machine learning research 2011, 12, 2825–2830.
- Alvarez-Ramirez, J.; Alvarez, J.; Rodriguez, E.; Fernandez-Anaya, G. Time-varying Hurst exponent for US stock markets. Physica A: Statistical Mechanics and its Applications 2008, 387, 6159–6169. [CrossRef]
- Sanyal, M.K.; Ghosh, I.; Jana, R.K. Characterization and Predictive Analysis of Volatile Financial Markets Using Detrended Fluctuation Analysis, Wavelet Decomposition, and Machine Learning. International Journal of Data Analytics (IJDA) 2021, 2, 1–31.
- Skjeltorp, J.A. Scaling in the Norwegian stock market. Physica A: Statistical Mechanics and its Applications 2000, 283, 486–528. [CrossRef]
- Tiwari, A.K.; Albulescu, C.T.; Yoon, S.M. A multifractal detrended fluctuation analysis of financial market efficiency: Comparison using Dow Jones sector ETF indices. Physica A: Statistical Mechanics and its Applications 2017, 483, 182–192. [CrossRef]
- Zunino, L.; Figliola, A.; Tabak, B.M.; Pérez, D.G.; Garavaglia, M.; Rosso, O.A. Multifractal structure in Latin-American market indices. Chaos, Solitons & Fractals 2009, 41, 2331–2340. [CrossRef]
- Ivanova, K.; Ausloos, M. Low q-moment multifractal analysis of Gold price, Dow Jones Industrial Average and BGL-USD exchange rate. The European Physical Journal B - Condensed Matter and Complex Systems 1999, 8, 665–669. [CrossRef]
- Bertrand, P.R.; Hamdouni, A.; Khadhraoui, S. Modelling NASDAQ Series by Sparse Multifractional Brownian Motion. Methodology and Computing in Applied Probability 2012, 14, 107–124. [CrossRef]
- Di Matteo, T. Multi-scaling in finance. Quantitative Finance 2007, 7, 21–36. [CrossRef]
- Fama, E.F. The Behavior of Stock-Market Prices. The Journal of Business 1965, 38, 34–105.
- Peters, E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics; John Wiley & Sons, Inc.: Hoboken, NJ, 1994. Published: 26 January 1994 (Hardcover).
- Mandelbrot, B.B. Fractals and Scaling in Finance: Discontinuity, Concentration, Risk. Selecta Volume E, 1 ed.; Springer: New York, NY, 1997. Published: 18 September 1997 (Hardcover), 01 December 2010 (Softcover), 09 March 2013 (eBook). [CrossRef]
- Samuelson, P.A. Proof That Properly Discounted Present Values of Assets Vibrate Randomly. The Bell Journal of Economics and Management Science 1973, 4, 369–374.
- Tzouras, S.; Anagnostopoulos, C.; McCoy, E. Financial time series modeling using the Hurst exponent. Physica A: Statistical Mechanics and its Applications 2015, 425, 50–68. [CrossRef]
- Alvarez-Ramirez, J.; Rodriguez, E.; Carlos Echeverría, J. Detrending fluctuation analysis based on moving average filtering. Physica A: Statistical Mechanics and its Applications 2005, 354, 199–219. [CrossRef]
- Lu, X.; Tian, J.; Zhou, Y.; Li, Z. Multifractal detrended fluctuation analysis of the Chinese stock index futures market. Physica A: Statistical Mechanics and its Applications 2013, 392, 1452–1458. [CrossRef]
- Karaca, Y.; Zhang, Y.D.; Muhammad, K. Characterizing Complexity and Self-Similarity Based on Fractal and Entropy Analyses for Stock Market Forecast Modelling. Expert Systems with Applications 2020, 144, 113098. [CrossRef]
- Karaca, Y.; Baleanu, D. A Novel R/S Fractal Analysis and Wavelet Entropy Characterization Approach for Robust Forecasting Based on Self-Similar Time Series Modelling. Fractals 2020, 28. [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [CrossRef]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP); Association for Computational Linguistics: Doha, Qatar, 2014; pp. 1724–1734. [CrossRef]
- Raubitzek, S.; Neubauer, T. An Exploratory Study on the Complexity and Machine Learning Predictability of Stock Market Data. Entropy 2022, 24. [CrossRef]
| 1 | The algorithms that perform R/S analysis find a subset of possible intervals and perform the procedure on this subset. |
| 2 | For consistency, our data is restricted to the timeframe from January 3, 1972, to October 30, 2020, which is common to all datasets. |
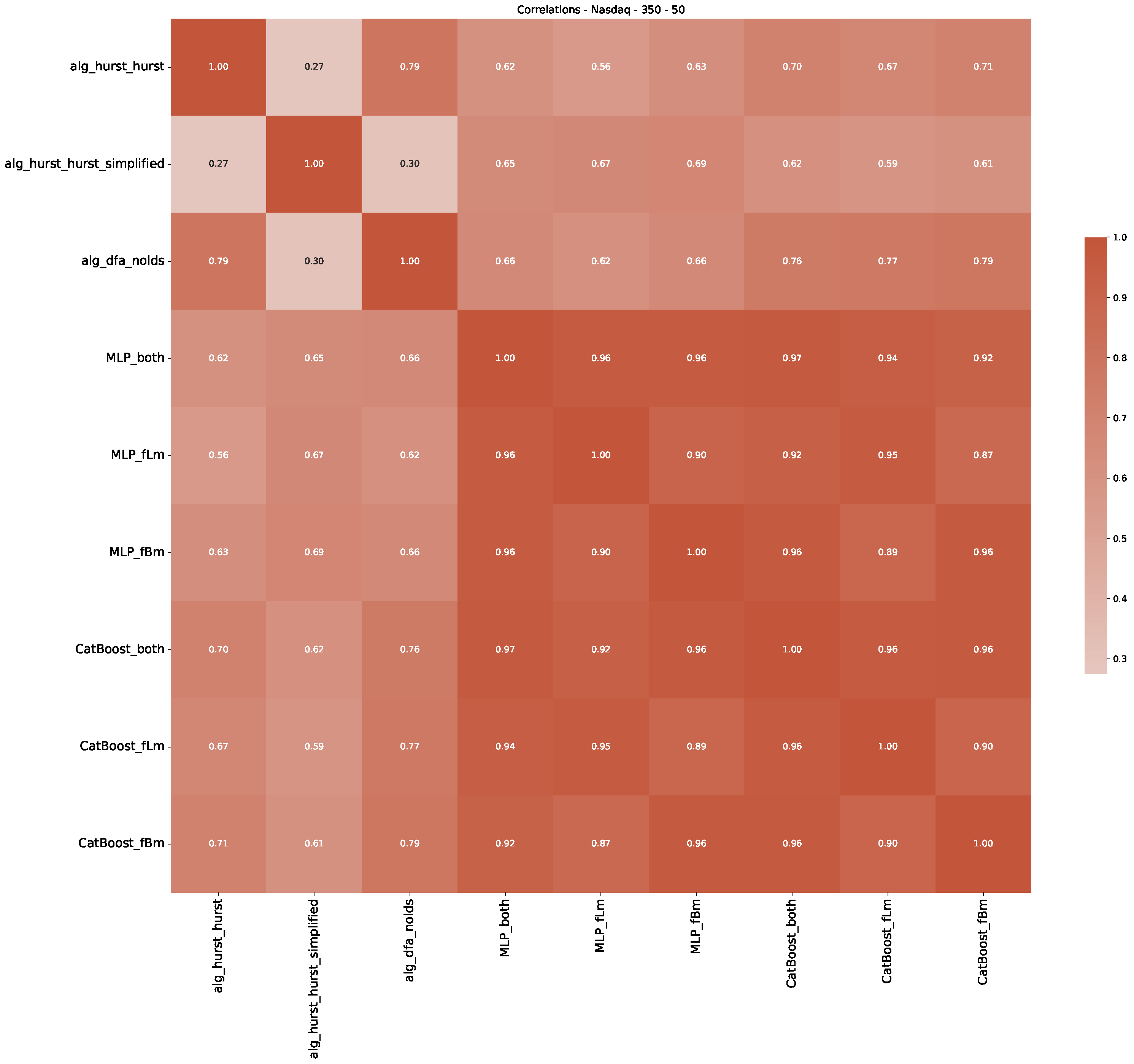
| 3 | This correlation matrix takes into account all available years for the Dow Jones index, not only the interval 1960 to 1980 |
| 4 | We should note that for this comparison, we disregarded the variability of the error and compared only the average errors. When considering the corresponding variability, we find that the best machine learning algorithms and the simplified version of R/S analysis perform very similarly. |
| 5 | All our trained models are available in a corresponding GitHub repository using Python. |

| Window Length and Type of Training Data |
CV-Score Ridge Regressor |
CV-Score Lasso Regressor |
CV-Score AdaBoost Regressor |
CV-Score CatBoost Regressor |
CV-Score LightGBM Regressor |
CV-Score MLP Regressor |
|---|---|---|---|---|---|---|
| 10, fBm | <0.0001 | <0.0001 | 0.29876 | 0.47271 | 0.47396 | 0.45155 |
| 25, fBm | <0.0001 | <0.0001 | 0.53221 | 0.73295 | 0.72234 | 0.69416 |
| 50, fBm | <0.0001 | <0.0001 | 0.66082 | 0.84480 | 0.84369 | 0.82256 |
| 100, fBm | <0.0001 | <0.0001 | 0.73564 | 0.91811 | 0.91329 | 0.90260 |
| 10, fLm | <0.0001 | <0.0001 | 0.29913 | 0.41482 | 0.42049 | 0.41858 |
| 25, fLm | <0.0001 | <0.0001 | 0.36256 | 0.53270 | 0.52886 | 0.52027 |
| 50, fLm | <0.0001 | <0.0001 | 0.40205 | 0.60694 | 0.59713 | 0.56785 |
| 100, fLm | <0.0001 | <0.0001 | 0.42368 | 0.65468 | 0.64698 | 0.60597 |
| 10, both | <0.0001 | <0.0001 | 0.29751 | 0.41519 | 0.41749 | 0.41090 |
| 25, both | <0.0001 | <0.0001 | 0.43414 | 0.59296 | 0.58660 | 0.55943 |
| 50, both | <0.0001 | <0.0001 | 0.51247 | 0.69218 | 0.68393 | 0.64834 |
| 100, both | <0.0001 | <0.0001 | 0.56500 | 0.76081 | 0.75103 | 0.73408 |
| window length | alg. nolds Hurst | alg. nolds DFA | alg. Hurst Hurst | alg. Hurst Hurst simplified |
|---|---|---|---|---|
| 10 | 0.2916 ± 0.01531 | 0.0751 ± 0.24194 | - | - |
| 25 | 0.3302 ± 0.01983 | 0.09547 ± 0.04252 | - | - |
| 50 | 0.36642 ± 0.01355 | 0.10151 ± 0.02645 | - | - |
| 100 | 0.40063 ± 0.01175 | 0.10392 ± 0.019 | 0.21317 ± 0.01494 | 0.114 ± 0.01291 |
| 200 | 0.41373 ± 0.00816 | 0.06301 ± 0.01224 | 0.19125 ± 0.01136 | 0.10718 ± 0.00966 |
| 350 | 0.42249 ± 0.00697 | 0.04495 ± 0.0069 | 0.18045 ± 0.01012 | 0.10363 ± 0.00875 |
| window length | Ridge fBm | Ridge fLm | Ridge both |
|---|---|---|---|
| 10 | 0.28137 ± 0.00024 | 0.28134 ± 0.00071 | 0.28136 ± 0.00045 |
| 25 | 0.28157 ± 0.00033 | 0.28144 ± 0.0004 | 0.28161 ± 0.00022 |
| 50 | 0.28125 ± 0.00051 | 0.28137 ± 0.00056 | 0.28124 ± 0.00043 |
| 100 | 0.28144 ± 0.00088 | 0.28123 ± 0.00122 | 0.28138 ± 0.00089 |
| 200 | 0.28126 ± 0.00011 | 0.28131 ± 0.00071 | 0.28122 ± 0.00053 |
| 350 | 0.2814 ± 0.00012 | 0.28132 ± 0.0005 | 0.28137 ± 0.00038 |
| window length | Lasso fBm | Lasso fLm | Lasso both |
| 10 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 25 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 50 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 100 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 200 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 350 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| window length | AdaBoost fBm | AdaBoost fLm | AdaBoost both |
| 10 | 0.22244 ± 0.01316 | 0.2262 ± 0.013 | 0.21941 ± 0.01388 |
| 25 | 0.16691 ± 0.01471 | 0.19494 ± 0.00965 | 0.17723 ± 0.01186 |
| 50 | 0.14028 ± 0.01172 | 0.17266 ± 0.00652 | 0.14778 ± 0.00961 |
| 100 | 0.11962 ± 0.01022 | 0.16265 ± 0.00337 | 0.13449 ± 0.00574 |
| 200 | 0.12036 ± 0.00652 | 0.16359 ± 0.00161 | 0.1346 ± 0.00317 |
| 350 | 0.12079 ± 0.00461 | 0.16256 ± 0.00117 | 0.13533 ± 0.00224 |
| window length | CatBoost fBm | CatBoost fLm | CatBoost both |
| 10 | 0.16014 ± 0.02044 | 0.21121 ± 0.01504 | 0.1782 ± 0.01751 |
| 25 | 0.08767 ± 0.01857 | 0.1851 ± 0.01472 | 0.11832 ± 0.01546 |
| 50 | 0.05087 ± 0.01546 | 0.16244 ± 0.01481 | 0.07659 ± 0.0142 |
| 100 | 0.02484 ± 0.01112 | 0.13197 ± 0.01461 | 0.04776 ± 0.01179 |
| 200 | 0.026 ± 0.00839 | 0.13222 ± 0.0105 | 0.04831 ± 0.00879 |
| 350 | 0.0257 ± 0.00625 | 0.13197 ± 0.00765 | 0.0479 ± 0.00651 |
| window length | LightGBM fBm | LightGBM fLm | LightGBM both |
| 10 | 0.16011 ± 0.02052 | 0.21073 ± 0.01527 | 0.17831 ± 0.01753 |
| 25 | 0.09248 ± 0.01834 | 0.18331 ± 0.01444 | 0.12301 ± 0.01514 |
| 50 | 0.05323 ± 0.01538 | 0.15624 ± 0.01414 | 0.08313 ± 0.01379 |
| 100 | 0.02802 ± 0.01073 | 0.12563 ± 0.01423 | 0.05224 ± 0.01161 |
| 200 | 0.02904 ± 0.00821 | 0.12482 ± 0.01025 | 0.05178 ± 0.00821 |
| 350 | 0.02863 ± 0.00605 | 0.12465 ± 0.0075 | 0.05151 ± 0.00608 |
| window length | MLP fBm | MLP fLm | MLP both |
| 10 | 0.1656 ± 0.02182 | 0.21432 ± 0.01481 | 0.17702 ± 0.01761 |
| 25 | 0.09959 ± 0.01788 | 0.17948 ± 0.01469 | 0.1326 ± 0.01475 |
| 50 | 0.06085 ± 0.01463 | 0.14635 ± 0.01535 | 0.08806 ± 0.01467 |
| 100 | 0.03473 ± 0.00988 | 0.12899 ± 0.01635 | 0.05588 ± 0.01101 |
| 200 | 0.03578 ± 0.00755 | 0.12915 ± 0.01183 | 0.05784 ± 0.00798 |
| 350 | 0.03586 ± 0.00541 | 0.12858 ± 0.00873 | 0.05516 ± 0.00615 |
| window length | alg. nolds Hurst | alg. nolds DFA | alg. Hurst Hurst | alg. Hurst Hurst simplified |
|---|---|---|---|---|
| 10 | 0.28517 ± 0.01622 | 0.42035 ± 0.2706 | - | - |
| 25 | 0.26316 ± 0.02612 | 0.47115 ± 0.0471 | - | - |
| 50 | 0.26357 ± 0.01986 | 0.45586 ± 0.03011 | - | - |
| 100 | 0.28779 ± 0.01684 | 0.45104 ± 0.02172 | 0.21913 ± 0.01621 | 0.24127 ± 0.01786 |
| 200 | 0.31121 ± 0.01129 | 0.46071 ± 0.01456 | 0.22713 ± 0.01267 | 0.24231 ± 0.01428 |
| 350 | 0.33902 ± 0.00942 | 0.44371 ± 0.01141 | 0.23226 ± 0.01066 | 0.24178 ± 0.01233 |
| window length | Ridge fBm | Ridge fLm | Ridge both |
|---|---|---|---|
| 10 | 0.28139 ± 0.0003 | 0.28116 ± 0.00077 | 0.28123 ± 0.00053 |
| 25 | 0.28133 ± 0.00053 | 0.28131 ± 0.00052 | 0.28135 ± 0.00032 |
| 50 | 0.28134 ± 0.00085 | 0.28135 ± 0.00079 | 0.28131 ± 0.00057 |
| 100 | 0.28141 ± 0.0015 | 0.28124 ± 0.00148 | 0.28122 ± 0.00111 |
| 200 | 0.28136 ± 8e-05 | 0.28122 ± 0.00079 | 0.28121 ± 0.00058 |
| 350 | 0.28133 ± 6e-05 | 0.28109 ± 0.00055 | 0.28109 ± 0.00041 |
| window length | Lasso fBm | Lasso fLm | Lasso both |
| 10 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 25 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 50 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 100 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 200 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| 350 | 0.28137 ± 0.0 | 0.28137 ± 0.0 | 0.28137 ± 0.0 |
| window length | AdaBoost fBm | AdaBoost fLm | AdaBoost both |
| 10 | 0.28501 ± 0.00965 | 0.27944 ± 0.00736 | 0.28093 ± 0.0092 |
| 25 | 0.2994 ± 0.0117 | 0.27436 ± 0.00838 | 0.2817 ± 0.01012 |
| 50 | 0.30762 ± 0.01202 | 0.26953 ± 0.00996 | 0.28504 ± 0.01142 |
| 100 | 0.32061 ± 0.01262 | 0.26418 ± 0.01149 | 0.28198 ± 0.01247 |
| 200 | 0.3201 ± 0.00709 | 0.26357 ± 0.00652 | 0.28126 ± 0.00638 |
| 350 | 0.31737 ± 0.00536 | 0.26173 ± 0.0047 | 0.27918 ± 0.00468 |
| window length | CatBoost fBm | CatBoost fLm | CatBoost both |
| 10 | 0.29105 ± 0.01685 | 0.26013 ± 0.01451 | 0.27373 ± 0.01506 |
| 25 | 0.31954 ± 0.02005 | 0.22098 ± 0.01589 | 0.25413 ± 0.01666 |
| 50 | 0.32883 ± 0.01971 | 0.19311 ± 0.01505 | 0.22873 ± 0.01656 |
| 100 | 0.32947 ± 0.01705 | 0.18257 ± 0.01354 | 0.21623 ± 0.01513 |
| 200 | 0.3283 ± 0.01265 | 0.18206 ± 0.00866 | 0.21506 ± 0.01052 |
| 350 | 0.3265 ± 0.00934 | 0.18128 ± 0.00607 | 0.21404 ± 0.00751 |
| window length | LightGBM fBm | LightGBM fLm | LightGBM both |
| 10 | 0.28999 ± 0.01713 | 0.25899 ± 0.01505 | 0.2733 ± 0.01536 |
| 25 | 0.31583 ± 0.02002 | 0.22418 ± 0.016 | 0.25836 ± 0.01676 |
| 50 | 0.32294 ± 0.02003 | 0.1996 ± 0.01483 | 0.23572 ± 0.01697 |
| 100 | 0.30969 ± 0.01737 | 0.18867 ± 0.01346 | 0.2209 ± 0.01607 |
| 200 | 0.30965 ± 0.0128 | 0.1884 ± 0.00876 | 0.22123 ± 0.01096 |
| 350 | 0.30776 ± 0.00946 | 0.18759 ± 0.00615 | 0.22019 ± 0.00783 |
| window length | MLP fBm | MLP fLm | MLP both |
| 10 | 0.30555 ± 0.01746 | 0.26038 ± 0.01426 | 0.27412 ± 0.0149 |
| 25 | 0.33234 ± 0.01994 | 0.23591 ± 0.01552 | 0.25557 ± 0.01708 |
| 50 | 0.33114 ± 0.02127 | 0.20713 ± 0.01606 | 0.23219 ± 0.01847 |
| 100 | 0.29554 ± 0.01763 | 0.18192 ± 0.01455 | 0.23114 ± 0.01596 |
| 200 | 0.29431 ± 0.01297 | 0.18123 ± 0.00948 | 0.2301 ± 0.01107 |
| 350 | 0.29222 ± 0.00954 | 0.18008 ± 0.00668 | 0.22919 ± 0.00788 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





