Theoretical and Numerical Simulations on The Hepatitis B Virus Model Through a Piecewise Fractional Order

1. Introduction

Hepatitis B is a severe liver infection caused by a virus. This inflammation poses a significant global health challenge. The viral infection, known as hepatitis B, can lead to both acute and chronic illnesses. The primary mode of transmission is from an infected mother to her child during pregnancy, childbirth, or delivery. It can also spread through contact with infected individuals’ blood or other bodily fluids, such as through sexual contact, unsafe injections, or exposure to contaminated medical or public objects. Individuals who inject drugs are also at risk.

According to estimates from the World Health Organization (WHO), approximately 296 million individuals worldwide have chronic hepatitis B, as indicated by the presence of hepatitis B surface antigen. In 2019 alone, around 820,000 people died from hepatitis B, with most deaths attributed to cirrhosis and primary liver cancer (hepatocellular carcinogenesis). Only 6.6 million individuals (22% of those diagnosed) were receiving treatment, accounting for approximately 10% of the total infected population.

The WHO reports a significant decline in the prevalence of chronic hepatitis B virus infection among children under the age of five. In the pre-vaccine era (1980s to early 2000s), the estimated rate was around 5%, whereas in 2019, it dropped to less than 1%. However, despite the availability of highly effective vaccines, the WHO still predicts approximately 1.5 million new cases of hepatitis B infection per year.

Preventive measures for hepatitis B encompass antiviral prophylaxis during pregnancy as well as accessible, safe, and effective vaccinations. These interventions are of paramount importance in the prevention and control of hepatitis B. The HBV models discussed earlier rely on integer-order derivatives, which fail to capture the genetic and memory characteristics observed in fractional-order models.

Fractional calculus, a branch of mathematics concerned with derivatives and integrals of real or complex orders, has gained significant popularity among researchers due to its applicability in modeling real-world phenomena. Consequently, researchers in mathematical biology have increasingly turned their attention to utilizing fractional-order derivatives for more accurate mathematical modeling (see [1,2,3,4,5,6,7] and references therein).

The subject of fractional calculus [8,9] is continually being developed to better understand the properties of real-world problems. This field of study allows researchers to explore and analyze phenomena that cannot be accurately described by traditional integer-order calculus. By incorporating fractional derivatives and integrals, researchers can gain deeper insights into complex systems and phenomena, leading to more comprehensive and accurate modeling approaches.

The ongoing development of fractional calculus offers promising opportunities for advancing our understanding of real-world problems. Several recent studies have explored various types of fractional derivatives and their associated integral operators. Caputo and Fabrizio [10] investigated a new fractional derivative with an exponential kernel. Atangana and Baleanu [11] examined fractional derivatives with Mittag-Leffler kernels, extending them to higher arbitrary orders and formulating their integral operators. Abdeljawad [12] proposed a new nonsingular fractional derivative in Atangana-Baleanu settings, incorporating a multi-parameter Mittag-Leffler function and its discrete version [13,14,15].

For further theoretical works on Atangana-Baleanu fractional differential equations (FDEs), the reader is referred to a series of papers [16,17,18,19,20,21,22,23,24]. In this context, we adopt a novel technique involving piecewise differential and integral operators developed by Atangana-Seda for the Caputo-Fabrizio fractional derivative [25].

Our paper is structured as follows: In Section 2, we present basic definitions and results that will be necessary for later discussions. Section 3 is dedicated to describing the piecewise model. In Section 4, we examine the extinction scenario of the deterministic model in terms of the basic reproduction number. Moving on to Section 5, we analyze the fractional-order system, demonstrating the existence and uniqueness of the solution, along with results regarding the asymptotic behavior of the solution. Section 6 presents the numerical solutions of the piecewise fractional-order model. Section 7 focuses on providing graphical representations of the HBV model. Finally, we conclude the paper with some concluding remarks.

2. Preliminary results

In this part, we present some definitions and basic auxiliary results of piecewise derivative and integral with classical and Mittag-Leffler kernel that are required throughout our paper.

Definition 1.

[25] The piecewise derivative with classical and Mittag–Leffler kernel is given as

$${}_0{}^{PAB}\mathbf{D}_t^{\varsigma }\eta \left(\iota \right)=\left\{\begin{array}{c}{\mathbf{D}}^1\eta \left(\iota \right),\iota \in \left[0,{\iota }_1\right],\\ {}^{PAB}\mathbf{D}_0^{\varsigma }\eta \left(\iota \right),\iota \in \left[{\iota }_1,T\right]\end{array}\right.$$

where

ii) ${\mathbf{D}}^1\eta \left(\iota \right)={\eta }^{\prime }\left(\iota \right)$ is the classical derivative,

iii) ${}^{PAB}\mathbf{D}_0^{\varsigma }\eta \left(\iota \right)$ is the Atangana–Baleanu fractional derivative.

Definition 2.

[25] Let f be continuous. A piecewise integral of f is given as

$${}_0{}^{PAB}\mathbf{I}_t^{\varsigma }\eta \left(\iota \right)=\left\{\begin{array}{c}{\mathbf{I}}^1\eta \left(\iota \right),\iota \in \left[0,{\iota }_1\right],\\ {}^{AB}\mathbf{I}^{\varsigma }\eta \left(\iota \right),\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

where

ii) ${\mathbf{I}}^1\eta \left(\iota \right)={\int }_0^{{\iota }_1}\eta \left(s\right)ds$ is the classical integral,

iii) ${}^{AB}\mathbf{D}^{\varsigma }\eta \left(\iota \right)=\frac{1-\varsigma }{▿\left(\varsigma \right)}\eta \left(\iota \right)+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\mathbb{S})}^{\varsigma -1}\eta \left(s\right)ds$ is the Atangana–Baleanu integral.

Theorem 1.

Let $\mathcal{X}$ be a Banach space. The operator $\Phi :C\left(\mathcal{J},{\mathbb{R}}^{+}\right)\to C\left(\mathcal{J},{\mathbb{R}}^{+}\right)$ is Lipschitzian if there exists a constant $0<L<1$ such that i.e., $∥\Phi (\wp )-\Phi \left({\wp }^{*}\right)∥\le L∥\wp -{\wp }^{*}∥$ for all $\wp ,{\wp }^{*}\in C\left(\mathcal{J},{\mathbb{R}}^{+}\right).$ Then Φ is a contraction.

3. Mathematical model

Here, we will considered generalize the HBV model with class of asymptomatic carriers [26] in the frame of piecewise derivative with classical and Mittag–Leffler kernel as follows

$$\left\{\begin{array}{c}{}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\mathbb{S}\left(\iota \right)=\varrho -\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\Lambda \mathbb{S},\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\mathbb{E}\left(\iota \right)=\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\left(\Lambda +{\psi }_1\right)\mathbb{E},\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\mathbb{A}\left(\iota \right)={\psi }_1\gamma \mathbb{E}-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A},\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }{\mathbb{A}}_c\left(\iota \right)={\psi }_1\left(1-\gamma \right)\mathbb{E}-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c,\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\mathbb{C}\left(\iota \right)={\eta }_1\mathbb{A}+{\tau }_1{\mathbb{A}}_c-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C},\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }{\mathbb{R}}_p\left(\iota \right)={\kappa }_1\mathbb{A}+{\sigma }_1\mathbb{C}+\theta {\mathbb{A}}_c-\Lambda {\mathbb{R}}_p,\end{array}\right.$$

(1)

with the initial conditions

$$\begin{array}{ccc}\hfill \mathbb{S}\left(0\right)& >& 0,\mathbb{E}\left(0\right)>0,\mathbb{A}\left(0\right)>0,\hfill \\ \hfill {\mathbb{A}}_c\left(0\right)& >& 0,\mathbb{C}\left(0\right)>0,{\mathbb{R}}_p\left(0\right)>0.\hfill \end{array}$$

The parameter $\varrho$ represents the birth rate of susceptible individuals, while the effective contact rate and natural fatality rate are denoted by $\omega$ and $\Lambda$, respectively. The rate at which exposed individuals become infected is described as ${\psi }_1\left(1-\gamma \right)$, with a portion of ${\psi }_1\left(1-\gamma \right)$ moving to class $\mathbb{A}$ at a rate of ${\psi }_1\gamma$. Another portion enters class ${\mathbb{A}}_c$ and becomes asymptomatically infected. The rates at which individuals in the acute and asymptomatic classes become carriers are ${\eta }_1$ and ${\tau }_1$, respectively. The recovery rates for acute, asymptomatic, and carrier individuals are denoted as ${\kappa }_1$, $\theta$ and ${\sigma }_1$, respectively. The death rates due to the disease in the acute and chronic classes are represented by $\mu$ and $\nu$, respectively. The coefficients for asymptomatic and carrier individuals are indicated as ${\varphi }_1$ (representing the infectiousness of asymptomatic infections relative to acute infections) and ${ϵ}_1$ (representing the infectiousness of carrier infections relative to acute infections), respectively. The total population represented by $\mathcal{N}\left(\iota \right)$ divided into six classes as followes

(1) susceptible individuals $\mathbb{S}\left(\iota \right)$,

(2) exposed population $\mathbb{E}\left(\iota \right)$,

(3) acute infected population $\mathbb{A}\left(\iota \right)$,

(4) asymptomatic carrier ${\mathbb{A}}_c\left(\iota \right)$,

(5) chronic infected individuals $\mathbb{C}\left(\iota \right)$,

(6) recovered population ${\mathbb{R}}_p\left(\iota \right)$.

So $\mathcal{N}\left(\iota \right)=\mathbb{S}\left(\iota \right)+\mathbb{E}\left(\iota \right)+\mathbb{A}\left(\iota \right)+{\mathbb{A}}_c\left(\iota \right)+\mathbb{C}\left(\iota \right)+{\mathbb{R}}_p\left(\iota \right)$.

4. Equilibrium point and basic reproduction number

The disease free equilibrium point of model (1) obtained by putting equations equal to zero

$$\left\{\begin{array}{c}\varrho -\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\Lambda \mathbb{S}=0\\ \omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\left(\Lambda +{\psi }_1\right)\mathbb{E}=0\\ {\psi }_1\gamma \mathbb{E}-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}=0\\ {\psi }_1\left(1-\gamma \right)\mathbb{E}-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c=0\\ {\eta }_1\mathbb{A}+{\tau }_1{\mathbb{A}}_c-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}=0\\ {\kappa }_1\mathbb{A}+{\sigma }_1\mathbb{C}+\theta {\mathbb{A}}_c-\Lambda {\mathbb{R}}_p=0\end{array}\right.$$

In view of the above equations, the disease free equilibrium point of model (1) is given as

$${\ell }_0=\left(\mathbb{S}\left(0\right),\mathbb{E}\left(0\right),\mathbb{A}\left(0\right),{\mathbb{A}}_c\left(0\right),\mathbb{C}\left(0\right),{\mathbb{R}}_p\left(0\right)\right)=\left(\frac{\varrho }{\Lambda },0,0,0,0,0\right),$$

where $\varrho$ is birth rate of the susceptible individuals and $\Lambda$ is the natural fatality rate. From [27] the nonnegative matrix F and the nonsingular matrix V for the new infection terms and the remaining transfer, terms are given by

$$F=\left(\begin{array}{cccc}0& \frac{\omega \varrho }{\Lambda }& \frac{\omega {\varphi }_1\varrho }{\Lambda }& \frac{\omega {ϵ}_1\varrho }{\Lambda }\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right),$$

$$V=\left(\begin{array}{cccc}{m}_1& 0& 0& 0\\ -\gamma {\psi }_1& m_2& 0& 0\\ -\left(1-\gamma \right){\psi }_1& 0& m_3& 0\\ 0& -{\eta }_1& -{\tau }_1& m_4\end{array}\right).$$

Therefore, using the fact that $R_0=\rho \left(F{V}^{-1}\right)$, we obtaine the basic reproduction number $R_0$ for the model (1)

$$R_0=\frac{\omega \varrho \gamma {\psi }_1}{\Lambda m_2{m}_1}+\frac{\omega {\varphi }_1\varrho {\psi }_1\left(1-\gamma \right)}{\Lambda m_3{m}_1}+\frac{\omega {ϵ}_1\varrho {\eta }_1\gamma {\psi }_1}{\Lambda m_4{m}_1{m}_2}+\frac{\omega {\tau }_1\varrho {\psi }_1{ϵ}_1\left(1-\gamma \right)}{\Lambda m_4{m}_3{m}_1},$$

where

$$\begin{array}{ccc}\hfill m_1& =& \left(\Lambda +{\psi }_1\right),m_2=\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right),\hfill \\ \hfill m_3& =& \left(\Lambda +{\tau }_1+\theta \right),m_4=\left(\Lambda +\nu +{\sigma }_1\right).\hfill \end{array}$$

The endemic equilibria point ${\ell }_1$ of the model (1) is given by

$${\ell }_1=\left({\mathbb{S}}^{*},{\mathbb{E}}^{*},{\mathbb{A}}^{*},{\mathbb{A}}_c,{\mathbb{C}}^{*},{\mathbb{R}}_p^{*}\right),$$

where

$${\mathbb{S}}^{*}=\frac{m_1{\mathbb{A}}^{*}}{\omega \left({\mathbb{A}}^{*}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1{\mathbb{C}}^{*}\right)},$$

$${\mathbb{E}}^{*}=\frac{m_2{\mathbb{E}}^{*}}{\gamma {\psi }_1},$$

$${\mathbb{A}}_c^{*}=\frac{{\psi }_1\left(1-\gamma \right){\mathbb{E}}^{*}}{m_3},$$

$${\mathbb{C}}^{*}=\frac{{\eta }_1{\mathbb{A}}^{*}+{\tau }_1{\mathbb{A}}_c}{m_4},$$

$${\mathbb{R}}_p^{*}=\frac{{\kappa }_1{\mathbb{A}}^{*}+{\sigma }_1{\mathbb{C}}^{*}+\theta {\mathbb{A}}_c}{\Lambda }.$$

using these in first equation of model (1), we get

$${\mathbb{A}}^{*}=-\frac{\Lambda m_1{m}_2{m}_3{m}_4\gamma \left(1-R_0\right)}{\omega m_1{m}_2\left[\gamma m_3\left(m_4+{\eta }_1{ϵ}_1\right)+\left(1-\gamma \right)m_2\left(m_4{\varphi }_1+{\tau }_1{ϵ}_1\right)\right]}.$$

The proposed HBV model (1) has a unique positive endemic equilibria provided $R_0>1$.

5. Qualitative Analysis of PAB – Fractional model 1

In this part, we address the existence, uniqueness and stability results of the solution for model (1) by utilizing the fixed point technique. Let $\mathcal{J}=\left[0,T\right]\subset {\mathbb{R}}^{+},$ we are defining Banach space $\mathcal{E}=C\left(\mathcal{J},{\mathbb{R}}^{+}\right)\times C\left(\mathcal{J},{\mathbb{R}}^{+}\right)\times C\left(\mathcal{J},{\mathbb{R}}^{+}\right)\times C\left(\mathcal{J},{\mathbb{R}}^{+}\right)\times C\left(\mathcal{J},{\mathbb{R}}^{+}\right)\times C\left(\mathcal{J},{\mathbb{R}}^{+}\right)$ under the norm

$$∥\wp ∥=∥\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_P∥=sup\left\{\left|\mathbb{S}\left(\iota \right)\right|+\left|\mathbb{E}\left(\iota \right)\right|+\left|\mathbb{A}\left(\iota \right)\right|+\left|{\mathbb{A}}_c\left(\iota \right)\right|+\left|\mathbb{C}\left(\iota \right)\right|+\left|{\mathbb{R}}_P\left(\iota \right)\right|\right\},$$

where $\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_P\in C\left(\mathcal{J},{\mathbb{R}}^{+}\right).$

Lemma 1.

[25] The solution of the following piecewise Atangana–Baleanu problem

$${}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\wp \left(\iota \right)=G(\iota ,\wp \left(\iota \right)),$$

is given by

$$\wp \left(\iota \right)=\left\{\begin{array}{c}\wp \left(0\right)+{\int }_0^{{\iota }_1}G(\sigma ,\wp \left(\sigma \right))d\sigma ,if\iota \in \left[0,{\iota }_1\right],\\ \wp \left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\wp \left(\iota \right))+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\wp \left(\sigma \right))d\sigma ,if\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

Now, let us reformulate the model (1) in the following form

$$\left\{\begin{array}{c}{}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\mathbb{S}\left(\iota \right)=W_1(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p),\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\mathbb{E}\left(\iota \right)=W_2(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_{\mathbb{C}},\mathbb{C},{\mathbb{R}}_p),\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\mathbb{A}\left(\iota \right)=W_3(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_{\mathbb{C}},\mathbb{C},{\mathbb{R}}_p),\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }{\mathbb{A}}_{\mathbb{C}}\left(\iota \right)=W_4(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_{\mathbb{C}},\mathbb{C},{\mathbb{R}}_p),\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\mathbb{C}\left(\iota \right)=W_5(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p),\\ {}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }{\mathbb{R}}_p\left(\iota \right)=W_6(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p),\end{array}\right.$$

(2)

where

$$\left\{\begin{array}{c}{W}_1(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)=\varrho -\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\Lambda \mathbb{S},\\ W_2(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)=\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\left(\Lambda +{\psi }_1\right)\mathbb{E},\\ W_3(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)={\psi }_1\gamma \mathbb{E}-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A},\\ W_4(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)={\psi }_1\left(1-\gamma \right)\mathbb{E}-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c,\\ W_5(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)={\eta }_1\mathbb{A}+{\tau }_1{\mathbb{A}}_c-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C},\\ W_6(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)={\kappa }_1\mathbb{A}+{\sigma }_1\mathbb{C}+\theta {\mathbb{A}}_c-\Lambda {\mathbb{R}}_p,\end{array}\right.$$

We take our model as

$$\left\{\begin{array}{c}{}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\wp \left(\iota \right)=G(\iota ,\wp \left(\iota \right)),\\ \wp \left(0\right)={\wp }_0>0\end{array}\right.$$

(3)

In view of definition 2 and Lemma 1, the model (3) can be converted into the following fractional form

$$\wp \left(\iota \right)=\left\{\begin{array}{c}\wp \left(0\right)+{\int }_0^{{\iota }_1}G(\sigma ,\wp \left(\sigma \right))d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \wp \left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\wp \left(\iota \right))\hfill \\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\wp \left(\sigma \right))d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

(4)

where

$$\wp \left(\iota \right)=\left(\begin{array}{c}\mathbb{S}\left(\iota \right)\\ \mathbb{E}\left(\iota \right)\\ \mathbb{A}\left(\iota \right)\\ {\mathbb{A}}_c\left(\iota \right)\\ \mathbb{C}\left(\iota \right)\\ {\mathbb{R}}_p\left(\iota \right)\end{array}\right),\wp \left(0\right)=\left(\begin{array}{c}{\mathbb{S}}_0\\ {\mathbb{E}}_0\\ {\mathbb{A}}_0\\ {\mathbb{A}}_c\\ {\mathbb{C}}_0\\ {\mathbb{R}}_{p0}\end{array}\right),\wp \left({\iota }_1\right)=\left(\begin{array}{c}{\mathbb{S}}_{{\iota }_1}\\ {\mathbb{E}}_{{\iota }_1}\\ {\mathbb{A}}_{{\iota }_1}\\ {\mathbb{A}}_c\\ {\mathbb{C}}_{{\iota }_1}\\ {\mathbb{R}}_{p{\iota }_1}\end{array}\right).$$

and

$$G(\iota ,\wp \left(\iota \right))=\left(\begin{array}{c}{W}_1(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)\\ W_2(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)\\ W_3(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)\\ W_4(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)\\ W_5(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)\\ W_6(\iota ,\mathbb{S},\mathbb{E},\mathbb{A},{\mathbb{A}}_c,\mathbb{C},{\mathbb{R}}_p)\end{array}\right).$$

Now, transform the problem (3) into the fixed point problem. Define the operator $\Phi :\mathcal{E}\to \mathcal{E}$ by

$$\Phi \left(\wp \left(\iota \right)\right)=\left\{\begin{array}{c}\wp \left(0\right)+{\int }_0^{{\iota }_1}G(\sigma ,\wp \left(\sigma \right))d\sigma ,\iota \in \left[0,{\iota }_1\right],\hfill \\ \wp \left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\wp \left(\iota \right))\hfill \\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\wp \left(\sigma \right))d\sigma ,\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

In the following theorem, we will prove that the operator $\Phi$ is compact. The following assumptions must be fulfilled for the analysis of existence and uniqueness:

$\left(H_1\right):$$G:J\times \mathcal{E}\to \mathbb{R}$ is continuous and there exist two constants $\tau ,\eta >0$ such that

$$\left|G(\iota ,\wp (\iota \left)\right)\right|\le \tau +\left|\wp \left(\iota \right)\right|\eta ,\mathrm{for}\sigma \in J\mathrm{and}\mathcal{Y}\in F.$$

$\left(H_3\right):$ There exists constant number $\mathcal{L}>0$ such that

$$\left|G(\iota ,{\wp }_1\left(\iota \right))-G(\iota ,{\wp }_2\left(\iota \right))\right|\le \mathcal{L}\left|{\wp }_1\left(\iota \right)-{\wp }_2\left(\iota \right)\right|,\mathrm{for}\iota \in J\mathrm{and}{\wp }_1,{\wp }_2\in \mathcal{E}.$$

Theorem 2.

Suppose $\left(H_1\right)$-$\left(H_2\right)$ are satisfied. Then, the system (2) has a solution, provided thatand

$$0<max\left\{{\iota }_1\eta ,\left(\frac{1-\varsigma }{▿\left(\varsigma \right)}+\frac{{(T-{\iota }_1)}^{\varsigma }}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\right)\eta \right\}<1.$$

(5)

Proof. 

We are transforming the fractional system (2) into a fixed point problem as the following equation

$$\wp =\Phi \left(\wp \left(\iota \right)\right),\wp \in \mathcal{E}.$$

where the operator $\Phi :\mathcal{E}\to \mathcal{E}$ defined by

$$\Phi \left(\wp \left(\iota \right)\right)=\left\{\begin{array}{c}\wp \left(0\right)+{\int }_0^{\iota }G(\sigma ,\wp \left(\sigma \right))d\sigma ,\iota \in \left[0,{\iota }_1\right],\hfill \\ \wp \left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\wp \left(\iota \right))\hfill \\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\wp \left(\sigma \right))d\sigma ,\iota \in \left[{\iota }_1,T\right].\end{array}\right..$$

(6)

Let ${\Psi }_{\zeta }=\left\{\wp \in \mathcal{E}:∥\wp ∥\le \zeta \right\}$ be a closed ball with

$$\zeta \ge \left\{\begin{array}{c}\frac{\left|\wp \left(0\right)\right|+{\iota }_1\tau }{1-{\iota }_1\eta },\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \frac{\left|\wp \left({\iota }_1\right)\right|+\left(\frac{1-\varsigma }{▿\left(\varsigma \right)}+\frac{{(T-{\iota }_1)}^{\varsigma }}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\right)\tau }{1-\left(\frac{1-\varsigma }{▿\left(\varsigma \right)}+\frac{{(T-{\iota }_1)}^{\varsigma }}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\right)\eta },\mathrm{if}\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

Define the operators ${\Phi }_1$ and ${\Phi }_2$ such that $\Phi ={\Phi }_1+{\Phi }_2$ as

$${\Phi }_1\wp \left(\iota \right)=\left\{\begin{array}{c}\wp \left(0\right)+{\int }_0^{\iota }G(\sigma ,\wp \left(\sigma \right))d\sigma ,if\iota \in \left[0,{\iota }_1\right],\\ \wp \left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\wp \left(\iota \right)),\mathrm{if}\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

and

$${\Phi }_2\wp \left(\iota \right)=\left\{\begin{array}{c}0,if\iota \in \left[0,{\iota }_1\right],\\ \frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\wp \left(\sigma \right))d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

Now, we will divide the proof into several steps as follows

Step (1) ${\Phi }_1\wp \left(\iota \right)+{\Phi }_2\wp \left(\iota \right)\in {\Psi }_{\zeta }.$ For if $\iota \in \left[0,{\iota }_1\right],$$\wp \in {\Psi }_{\zeta },$ with (H₁), we have

$$\begin{array}{ccc}\hfill \left|{\Phi }_1\wp \left(\iota \right)+{\Phi }_2\wp \left(\iota \right)\right|& =& \underset{\iota \in \left[0,{\iota }_1\right]}{sup}\left|\wp \left(0\right)+{\int }_0^{\iota }G(\sigma ,\wp \left(\sigma \right))d\sigma \right|\hfill \\ & \le & \left|\wp \left(0\right)\right|+{\int }_0^{\iota }\left|G(\sigma ,\wp (\sigma \left)\right)\right|d\sigma \hfill \\ & \le & \left|\wp \left(0\right)\right|+\iota \left[\tau +\left|\wp \left(\iota \right)\right|\eta \right].\hfill \end{array}$$

Hence

$$\begin{array}{ccc}\hfill ∥{\Phi }_1\wp +{\Phi }_2\wp ∥& \le & \left|\wp \left(0\right)\right|+{\iota }_1\left[\tau +∥\wp ∥\eta \right]\hfill \\ & \le & \left|\wp \left(0\right)\right|+{\iota }_1\tau +{\iota }_1∥\wp ∥\eta \hfill \\ & \le & \left|\wp \left(0\right)\right|+{\iota }_1\tau +{\iota }_1\eta \zeta \hfill \\ & \le & \zeta .\hfill \end{array}$$

For $\iota \in \left[{\iota }_1,T\right],$$\wp \in {\Psi }_{\zeta },$ with (H₁), we have

$$\begin{array}{ccc}\hfill \left|{\Phi }_1\wp \left(\iota \right)+{\Phi }_2\wp \left(\iota \right)\right|& =& \underset{\iota \in \left[{\iota }_1,T\right]}{sup}\left|\wp \left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\wp \left(\iota \right))+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\wp \left(\sigma \right))d\sigma \right|\hfill \\ & \le & \left|\wp \left({\iota }_1\right)\right|+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left|G(\iota ,\wp (\iota \left)\right)\right|+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left|G(\sigma ,\wp (\sigma \left)\right)\right|d\sigma \hfill \\ & \le & \left|\wp \left({\iota }_1\right)\right|+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left[\tau +\left|\wp \left(\iota \right)\right|\eta \right]+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left[\tau +\left|\wp \left(\sigma \right)\right|\eta \right]d\sigma .\hfill \end{array}$$

Hence

$$\begin{array}{ccc}\hfill ∥{\Phi }_1\wp +{\Phi }_2\wp ∥& \le & \left|\wp \left({\iota }_1\right)\right|+\left(\frac{1-\varsigma }{▿\left(\varsigma \right)}+\frac{{(T-\sigma )}^{\varsigma }}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\right)\left[\tau +∥\wp ∥\eta \right]\hfill \\ & \le & \left|\wp \left({\iota }_1\right)\right|+\left(\frac{1-\varsigma }{▿\left(\varsigma \right)}+\frac{{(T-{\iota }_1)}^{\varsigma }}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\right)\tau \hfill \\ & & +\left(\frac{1-\varsigma }{▿\left(\varsigma \right)}+\frac{{(T-{\iota }_1)}^{\varsigma }}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\right)\eta \zeta \hfill \\ & \le & \zeta .\hfill \end{array}$$

This demonstrates that ${\Phi }_1\wp \left(\iota \right)+{\Phi }_2\wp \left(\iota \right)\in {\Psi }_{\zeta }.$

Step (2) ${\Phi }_1$ is contraction.

For $\iota \in \left[0,{\iota }_1\right],$${\wp }_1,{\wp }_2\in {\Psi }_{\zeta }$. Then via $\left(H_2\right),$ we get

$$\begin{array}{ccc}\hfill \left|{\Phi }_1{\wp }_1\left(\iota \right)-{\Phi }_1{\wp }_2\left(\iota \right)\right|& \le & \underset{\iota \in \left[0,{\iota }_1\right]}{sup}{\int }_0^{\iota }\left|G(\sigma ,{\wp }_1\left(\sigma \right))-G(\sigma ,{\wp }_2\left(\sigma \right))\right|d\sigma \hfill \\ & \le & \mathcal{L}{\int }_0^{\iota }\left|{\wp }_1\left(\sigma \right)-{\wp }_2\left(\sigma \right)\right|d\sigma .\hfill \end{array}$$

Hence

$$∥{\Phi }_1{\wp }_1-{\Phi }_1{\wp }_2∥\le \mathcal{L}{\iota }_1∥{\wp }_1-{\wp }_2∥.$$

For $\iota \in \left[{\iota }_1,T\right],$${\wp }_1,{\wp }_2\in {\Psi }_{\zeta }$. Then via $\left(H_2\right),$ we get

$${\Phi }_1\wp \left(\iota \right)=\left\{\begin{array}{c}\wp \left(0\right)+{\int }_0^{\iota }G(\sigma ,\wp \left(\sigma \right))d\sigma ,if\iota \in \left[0,{\iota }_1\right],\\ \wp \left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\wp \left(\iota \right)),if\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

$$\begin{array}{ccc}\hfill \left|{\Phi }_1{\wp }_1\left(\iota \right)-{\Phi }_1{\wp }_2\left(\iota \right)\right|& \le & \underset{\iota \in \left[{\iota }_1,T\right]}{sup}\left|\frac{1-\varsigma }{▿\left(\varsigma \right)}\left|G(\iota ,{\wp }_1\left(\iota \right))-G(\iota ,{\wp }_2\left(\iota \right))\right|\right|\hfill \\ & \le & \frac{1-\varsigma }{▿\left(\varsigma \right)}\mathcal{L}.\hfill \end{array}$$

Hence

$$∥{\Phi }_1{\wp }_1-{\Phi }_1{\wp }_2∥\le \frac{1-\varsigma }{▿\left(\varsigma \right)}\mathcal{L}.$$

Due to (5), we conclude that ${\Phi }_1$ is contraction mapping.

Step (3) ${\Phi }_2$ is relatively compact (i.e continuous, uniform bounded, and equicontinuous).

Part (1): ${\Phi }_2$ is continuous:

Since $G(\iota ,\wp (\iota \left)\right)$ is continuous, then ${\Phi }_2$ is continuous.

Part (2): ${\Phi }_2$ is uniformly bounded on ${\Psi }_{\zeta }:$

For $\iota \in \left[0,{\iota }_1\right],$$\wp \in {\Psi }_{\zeta }$. Then via $\left(H_1\right),$ we get directly that ${\Phi }_2$ is uniformly bounded on ${\Psi }_{\zeta }.$

For $\iota \in \left[{\iota }_1,T\right],$$\wp \in {\Psi }_{\zeta }$. Then via $\left(H_1\right),$ we get

$$\begin{array}{ccc}\hfill \left|{\Phi }_2\wp \left(\iota \right)\right|& \le & \underset{\iota \in \left[{\iota }_1,T\right]}{sup}\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left|G(\sigma ,\wp (\sigma \left)\right)\right|d\sigma \hfill \\ & \le & \frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left[\tau +\left|\wp \left(\sigma \right)\right|\eta \right]d\sigma .\hfill \end{array}$$

Hence

$$∥{\Phi }_2\wp ∥\le \frac{{(T-{\iota }_1)}^{\varsigma }}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\left[\tau +\zeta \eta \right].$$

Hence ${\Phi }_2$ is uniformly bounded on ${\Psi }_{\zeta }$.

Part (3): ${\Phi }_2$ equicontinuous. We have two cases as follows

Case (1) For any ${\iota }_a,{\iota }_b\in \left(0,{\iota }_1\right],{\iota }_a<{\iota }_b$ and $\wp \in {\Psi }_{\zeta }$, we have

$$∥{\Phi }_2\wp \left({\iota }_b\right)-{\Phi }_2\wp \left({\iota }_a\right)∥=0.$$

Case (2) For any ${\iota }_a,{\iota }_b\in \left({\iota }_1,T\right],{\iota }_a<{\iota }_b$ and $\wp \in {\Psi }_{\zeta }$, we have

$$\begin{array}{ccc}\hfill ∥{\Phi }_2\wp \left({\iota }_b\right)-{\Phi }_2\wp \left({\iota }_a\right)∥& \le & \frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{{\iota }_b}{({\iota }_b-\sigma )}^{\varsigma -1}\left|G(\sigma ,\wp (\sigma \left)\right)\right|d\sigma \hfill \\ & & -\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{{\iota }_a}{({\iota }_a-\sigma )}^{\varsigma -1}\left|G(\sigma ,\wp (\sigma \left)\right)\right|d\sigma \hfill \\ & \le & \frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{{\iota }_a}\left[{({\iota }_b-\sigma )}^{\varsigma -1}-{({\iota }_a-\sigma )}^{\varsigma -1}\right]\left|G(\sigma ,\wp (\sigma \left)\right)\right|d\sigma \hfill \\ & & +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_a}^{{\iota }_b}{({\iota }_b-\sigma )}^{\varsigma -1}\left|G(\sigma ,\wp (\sigma \left)\right)\right|d\sigma \hfill \\ & =& \frac{1}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\left[{({\iota }_b-{\iota }_1)}^{\varsigma }-{({\iota }_b-{\iota }_a)}^{\varsigma }-{({\iota }_a-{\iota }_1)}^{\varsigma }\right]\left[\tau +∥\wp ∥\eta \right]\hfill \\ & & +\frac{1}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{({\iota }_b-{\iota }_a)}^{\varsigma }\left[\tau +\zeta \eta \right]\hfill \\ & \to & 0as{\iota }_b-{\iota }_a.\hfill \end{array}$$

Thus, ${\Phi }_2$ is equicontinuous. According to the above analysis together with Arzela-Ascoli theorem, we deduce that $\Phi$ is relatively compact and so completely continuous. Thus by Krasnoselskii fixed point theorem, the equation (2) has at least one solution □

Theorem 3.

Assume that $\left(H_2\right)$ holds. If $0<max\left\{\mathcal{L}{\iota }_1,\frac{\mathcal{L}}{▿\left(\varsigma \right)}\left(\left(1-\varsigma \right)+\frac{{(T-{\iota }_1)}^{\varsigma }}{\Gamma \left(\varsigma \right)}\right)\right\}<1,$ then, the model (2) has unique result.

Proof. 

Taking the operator $\Phi :\mathcal{E}\to \mathcal{E}$ defined by (6). For $\iota \in \left[0,{\iota }_1\right],$${\wp }_1,{\wp }_2\in {\Psi }_{\zeta }$ with (H₂), we have

$$\begin{array}{ccc}\hfill \left|\Phi {\wp }_1\left(\iota \right)-\Phi {\wp }_2\left(\iota \right)\right|& \le & \underset{\iota \in \left[0,{\iota }_1\right]}{sup}{\int }_0^{\iota }\left|G(\sigma ,{\wp }_1\left(\sigma \right))-G(\sigma ,{\wp }_2\left(\sigma \right))\right|d\sigma \hfill \\ & \le & \mathcal{L}{\int }_0^{\iota }\left|{\wp }_1\left(\sigma \right)-{\wp }_2\left(\sigma \right)\right|d\sigma .\hfill \end{array}$$

Thus

$$∥\Phi {\wp }_1-\Phi {\wp }_2∥\le \mathcal{L}{\iota }_1∥{\wp }_1-{\wp }_2∥.$$

For $\iota \in \left[{\iota }_1,T\right],$${\wp }_1,{\wp }_2\in {\Psi }_{\zeta }$ with (H₂), we have

$$\begin{array}{ccc}\hfill \left|\Phi {\wp }_1\left(\iota \right)-\Phi {\wp }_2\left(\iota \right)\right|& \le & \underset{\iota \in \left[{\iota }_1,T\right]}{sup}\left\{\frac{1-\varsigma }{▿\left(\varsigma \right)}\left|G(\iota ,{\wp }_1\left(\iota \right))-G(\iota ,{\wp }_2\left(\iota \right))\right|\right.\hfill \\ & & \left.+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left|G(\sigma ,{\wp }_1\left(\sigma \right))-G(\sigma ,{\wp }_2\left(\sigma \right))\right|d\sigma \right\}\hfill \\ & \le & \frac{1-\varsigma }{▿\left(\varsigma \right)}\mathcal{L}\left|{\wp }_1\left(\iota \right)-{\wp }_2\left(\iota \right)\right|\hfill \\ & & +\frac{\varsigma \mathcal{L}}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left|{\wp }_1\left(\sigma \right)-{\wp }_2\left(\sigma \right)\right|d\sigma .\hfill \end{array}$$

Hence

$$∥\Phi {\wp }_1-\Phi {\wp }_2∥\le \frac{\mathcal{L}}{▿\left(\varsigma \right)}\left(\left(1-\varsigma \right)+\frac{{(T-{\iota }_1)}^{\varsigma }}{\Gamma \left(\varsigma \right)}\right)∥{\wp }_1-{\wp }_2∥.$$

Thus, $\Phi$ is contraction. Consequently, the model (2) has a unique solution. □

5.1. Ulam-Hyers stability

Definition 3.

The model (2) is Ulam-Hyers UH stable if there exists a real number $\mathfrak{M}=max\left\{{\mathfrak{M}}_1,{\mathfrak{M}}_2,{\mathfrak{M}}_3,{\mathfrak{M}}_4,{\mathfrak{M}}_5,{\mathfrak{M}}_6\right\}>0$ such that for each $\epsilon =max\left\{\nu ,{\epsilon }_2,{\epsilon }_3,{\epsilon }_4,{\epsilon }_5,{\epsilon }_6\right\}>0$ there exists a solution $\tilde{\wp }\in \mathcal{E}$ of the inequality

$$\left|{}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\wp \left(\iota \right)-G(\iota ,\wp \left(\iota \right))\right|\le \epsilon ,\iota \in J,$$

corresponding to a solution $\mathcal{Y}\in F$ of model (2) with the following condition

$$\wp \left(0\right)=\tilde{\wp }\left(0\right)$$

such that

$$∥\tilde{\wp }-\wp ∥\le \mathfrak{M}\epsilon ,\iota \in J,$$

where

$$\widehat{\wp }\left(\iota \right)=\left(\begin{array}{c}\widehat{\mathbb{S}}\left(\iota \right)\\ \widehat{\mathbb{E}}\left(\iota \right)\\ \widehat{\mathbb{A}}\left(\iota \right)\\ \widehat{{\mathbb{A}}_c}\left(\iota \right)\\ \widehat{\mathbb{C}}\left(\iota \right)\\ \widehat{{\mathbb{R}}_p}\left(\iota \right)\end{array}\right),\widehat{\wp }\left(0\right)=\left(\begin{array}{c}\widehat{\mathbb{S}}\left(0\right)\\ \widehat{\mathbb{E}}\left(0\right)\\ \widehat{\mathbb{A}}\left(0\right)\\ \widehat{{\mathbb{A}}_c}\left(0\right)\\ \widehat{\mathbb{C}}\left(0\right)\\ \widehat{{\mathbb{R}}_p}\left(0\right)\end{array}\right),G(\iota ,\widehat{\wp }\left(\iota \right))=\left(\begin{array}{c}{W}_1(\iota ,\widehat{\mathbb{S}},\widehat{\mathbb{E}},\widehat{\mathbb{A}},\widehat{{\mathbb{A}}_c},\widehat{\mathbb{C}},\widehat{{\mathbb{R}}_p})\\ W_2(\iota ,\widehat{\mathbb{S}},\widehat{\mathbb{E}},\widehat{\mathbb{A}},\widehat{{\mathbb{A}}_c},\widehat{\mathbb{C}},\widehat{{\mathbb{R}}_p})\\ W_3(\iota ,\widehat{\mathbb{S}},\widehat{\mathbb{E}},\widehat{\mathbb{A}},\widehat{{\mathbb{A}}_c},\widehat{\mathbb{C}},\widehat{{\mathbb{R}}_p})\\ W_4(\iota ,\widehat{\mathbb{S}},\widehat{\mathbb{E}},\widehat{\mathbb{A}},\widehat{{\mathbb{A}}_c},\widehat{\mathbb{C}},\widehat{{\mathbb{R}}_p})\\ W_5(\iota ,\widehat{\mathbb{S}},\widehat{\mathbb{E}},\widehat{\mathbb{A}},\widehat{{\mathbb{A}}_c},\widehat{\mathbb{C}},\widehat{{\mathbb{R}}_p})\\ W_6(\iota ,\widehat{\mathbb{S}},\widehat{\mathbb{E}},\widehat{\mathbb{A}},\widehat{{\mathbb{A}}_c},\widehat{\mathbb{C}},\widehat{{\mathbb{R}}_p})\end{array}\right).$$

Remark 1.

A function $\widehat{\wp }\in \mathcal{E}$ is a solution of the inequality

$$\left|{}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\wp \left(\iota \right)-G(\iota ,\wp \left(\iota \right))\right|\le \epsilon$$

if and only if there exist a small perturbation $z\in F$ such that

(i)$\left|z\left(\iota \right)\right|\le \epsilon ,$$\iota \in J;$

(ii)${}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\widehat{\wp }\left(\iota \right)=G(\iota ,\widehat{\wp }\left(\iota \right))+z\left(\iota \right),$$\iota \in J,$ where

$$z\left(\iota \right)={\left(z_1\left(\iota \right),z_2\left(\iota \right),z_3\left(\iota \right),z_4\left(\iota \right),z_5\left(\iota \right),z_6\left(\iota \right)\right)}^T.$$

Lemma 2.

Let $\widehat{\wp }\in \mathcal{E}$ be a function satisfies the inequalities

$$\left|{}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\widehat{\wp }\left(\iota \right)-G(\iota ,\widehat{\wp }\left(\iota \right))\right|\le \epsilon ,$$

then $\widehat{\wp }$ satisfies the following integral inequalities

$$\left|\widehat{\wp }\left(\iota \right)-\widehat{\wp }\left(0\right)-{\int }_0^{\iota }G(\sigma ,\widehat{\wp }\left(\sigma \right))d\sigma \right|\le k_1\epsilon ,if\iota \in \left[0,{\iota }_1\right],$$

and

$$\left|\widehat{\wp }\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\widehat{\wp }\left(\iota \right))+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\widehat{\wp }\left(\sigma \right))d\sigma \right|\le k_2\epsilon ,if\iota \in \left[{\iota }_1,T\right]$$

where

$$k_1={\iota }_1,$$

and

$$k_2=\frac{1}{▿\left(\varsigma \right)}\left(\left(1-\varsigma \right)+\frac{{(T-{\iota }_1)}^{\varsigma }}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\right).$$

Proof. 

Indeed by Remark 1, we have

$${}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\widehat{\wp }\left(\iota \right)=G(\iota ,\widehat{\wp }\left(\iota \right))+z\left(\iota \right),\iota \in J.$$

Then

$$\widehat{\wp }\left(\iota \right)=\left\{\begin{array}{l}\widehat{\wp }\left(0\right)+{\int }_0^{{\iota }_1}\left(G(\sigma ,\widehat{\wp }\left(\sigma \right))+z\left(\sigma \right)\right)d\sigma ,if\iota \in \left[0,{\iota }_1\right],\\ \widehat{\wp }\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left(G(\iota ,\widehat{\wp }\left(\iota \right))+z\left(\iota \right)\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left(G(\sigma ,\widehat{\wp }\left(\sigma \right))+z\left(\sigma \right)\right)d\sigma ,if\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

For $\iota \in \left[0,{\iota }_1\right]$, $\widehat{\wp }\in \mathcal{E}$, it follows that

$$\begin{array}{ccc}\hfill \left|\widehat{\wp }\left(\iota \right)-\widehat{\wp }\left(0\right)-{\int }_0^{\iota }G(\sigma ,\widehat{\wp }\left(\sigma \right))d\sigma \right|& \le & {\int }_0^{\iota }\left|z\left(\sigma \right)\right|d\sigma \hfill \\ & \le & {\iota }_1\epsilon =k_1\epsilon .\hfill \end{array}$$

For $\iota \in \left[{\iota }_1,T\right]$, $\widehat{\wp }\in \mathcal{E}$, it follow that

$$\begin{array}{ccc}& & \left|\widehat{\wp }\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\widehat{\wp }\left(\iota \right))+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\widehat{\wp }\left(\sigma \right))d\sigma \right|\hfill \\ & \le & \frac{1-\varsigma }{▿\left(\varsigma \right)}\left|z\left(\iota \right)\right|+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left|z\left(\sigma \right)\right|d\sigma \hfill \\ & \le & \frac{1}{▿\left(\varsigma \right)}\left(\left(1-\varsigma \right)+\frac{{(T-{\iota }_1)}^{\varsigma }}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}\right)\epsilon \hfill \\ & \le & k_2\epsilon \hfill \end{array}$$

□

Theorem 4.

Assume that the conditions of Theorem 3 hold . Then the model (2) is UH stable provided that

$$0<\left\{{\iota }_1\mathcal{L},\frac{\mathcal{L}}{▿\left(\varsigma \right)}\left(\left(1-\varsigma \right)+\frac{{(T-{\iota }_1)}^{\varsigma }}{\Gamma \left(\varsigma \right)}\right)\right\}<1.$$

Proof. 

Let $\epsilon =max\{{\epsilon }_1,{\epsilon }_2,{\epsilon }_3,{\epsilon }_4,{\epsilon }_5,{\epsilon }_6\}>0$ and $\widehat{\wp }\in \mathcal{E}$ be a functions satisfying the inequalities

$$\left|{}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\widehat{\wp }\left(\iota \right)-G(\iota ,\widehat{\wp }\left(\iota \right))\right|\le \epsilon ,$$

and let $\wp \in \mathcal{E}$ be the unique solution of the following model

$${}_0{}^{PAB}\mathbf{D}_{\iota }^{\varsigma }\wp \left(\iota \right)-G(\iota ,\wp \left(\iota \right))$$

Now, in the light of Theorem 3, we have

$$\wp \left(\iota \right)=\left\{\begin{array}{l}\wp \left(0\right)+{\int }_0^{\iota }G(\sigma ,\wp \left(\sigma \right))d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \wp \left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\wp \left(\iota \right))\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\wp \left(\sigma \right))d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

Hence, from (H₂) and Lemma 2, then for $\iota \in \left[0,{\iota }_1\right],$ we have

$$\begin{array}{ccc}\hfill \left|\widehat{\wp }\left(\iota \right)-\wp \left(\iota \right)\right|& \le & \left|\widehat{\wp }\left(\iota \right)-\wp \left(0\right)-{\int }_0^{\iota }G(\sigma ,\wp \left(\sigma \right))d\sigma \right|\hfill \\ & \le & \left|\widehat{\wp }\left(\iota \right)-\widehat{\wp }\left(0\right)-{\int }_0^{\iota }G(\sigma ,\widehat{\wp }\left(\sigma \right))d\sigma \right|\hfill \\ & & +{\int }_0^{\iota }\left|G(\sigma ,\widehat{\wp }\left(\sigma \right))-G(\sigma ,\wp \left(\sigma \right))\right|d\sigma \hfill \\ & \le & k_1\epsilon +\mathcal{L}{\int }_0^{\iota }\left|\widehat{\wp }\left(\sigma \right)-\wp \left(\sigma \right)\right|d\sigma .\hfill \end{array}$$

Hence

$$∥\widehat{\wp }-\wp ∥\le k_1\epsilon +\mathcal{L}{\iota }_1∥\widehat{\wp }-\wp ∥.$$

For $\iota \in \left[{\iota }_1,T\right],$ we have

$$\begin{array}{ccc}\hfill \left|\widehat{\wp }\left(\iota \right)-\wp \left(\iota \right)\right|& \le & \left|\widehat{\wp }\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\wp \left(\iota \right))+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\wp \left(\sigma \right))d\sigma \right|\hfill \\ & \le & \left|\widehat{\wp }\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}G(\iota ,\widehat{\wp }\left(\iota \right))+\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}G(\sigma ,\widehat{\wp }\left(\sigma \right))d\sigma \right|\hfill \\ & & +\frac{1-\varsigma }{▿\left(\varsigma \right)}\left|G(\iota ,\widehat{\wp }\left(\iota \right))-G(\iota ,\wp \left(\iota \right))\right|\hfill \\ & & +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left|G(\sigma ,\widehat{\wp }\left(\sigma \right))-G(\sigma ,\wp \left(\sigma \right))\right|d\sigma \hfill \\ & \le & k_2\epsilon +\frac{1-\varsigma }{▿\left(\varsigma \right)}\mathcal{L}\left|\widehat{\wp }\left(\iota \right)-\wp \left(\iota \right)\right|+\frac{\varsigma \mathcal{L}}{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left|\widehat{\wp }\left(\sigma \right)-\wp \left(\sigma \right)\right|d\sigma .\hfill \end{array}$$

Thus

$$∥\widehat{\wp }-\wp ∥\le k_2\epsilon +\frac{\mathcal{L}}{▿\left(\varsigma \right)}\left(\left(1-\varsigma \right)+\frac{{(T-{\iota }_1)}^{\varsigma }}{\Gamma \left(\varsigma \right)}\right)∥\widehat{\wp }-\wp ∥.$$

Since $0<\mathcal{L}{\iota }_1<1$ and $0<\frac{\mathcal{L}}{▿\left(\varsigma \right)}\left(\left(1-\varsigma \right)+\frac{{(T-{\iota }_1)}^{\varsigma }}{\Gamma \left(\varsigma \right)}\right)<1.$ Then, by choosing $\mathfrak{M}>0$ such that

$$\mathfrak{M}=\left\{\begin{array}{c}\frac{k\epsilon }{1-\mathcal{L}{\iota }_1},\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \frac{k\epsilon }{1-\frac{\mathcal{L}}{▿\left(\varsigma \right)}\left(\left(1-\varsigma \right)+\frac{{(T-{\iota }_1)}^{\varsigma }}{\Gamma \left(\varsigma \right)}\right)},\mathrm{if}\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

Thus

$$∥\widehat{\wp }-\wp ∥\le \mathfrak{M}\epsilon .$$

This prove that the model (2) is U-H stable. □

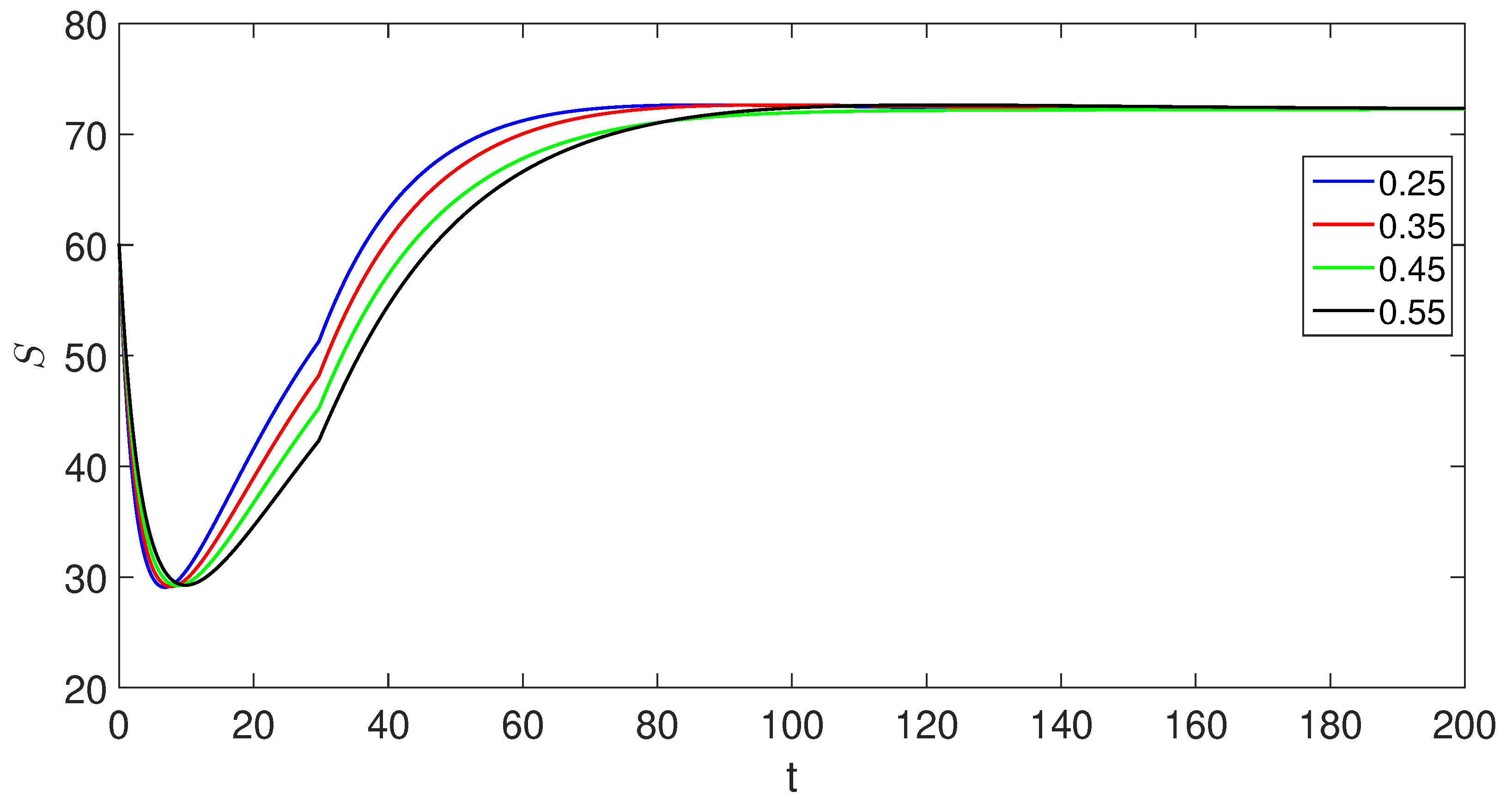
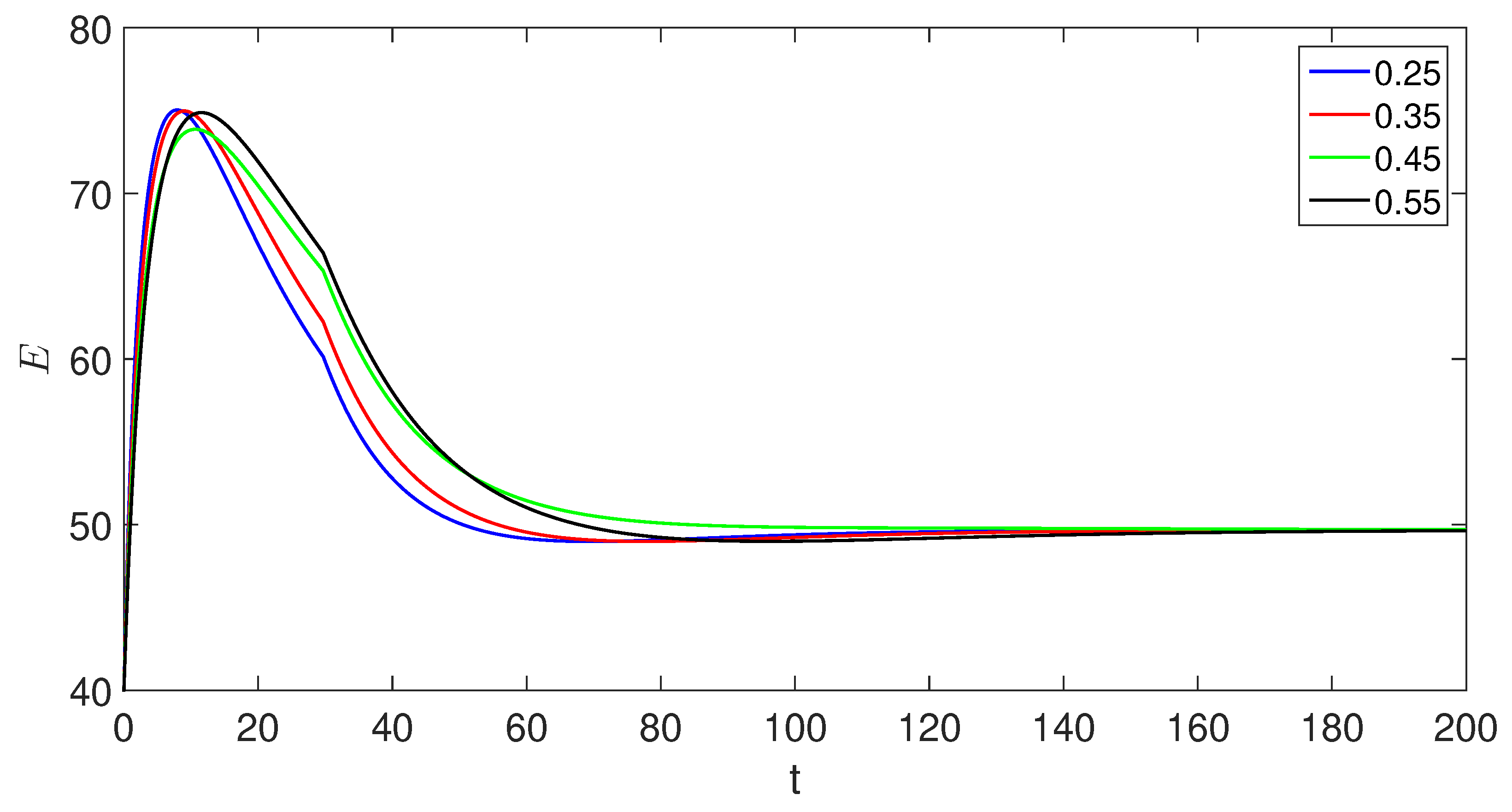
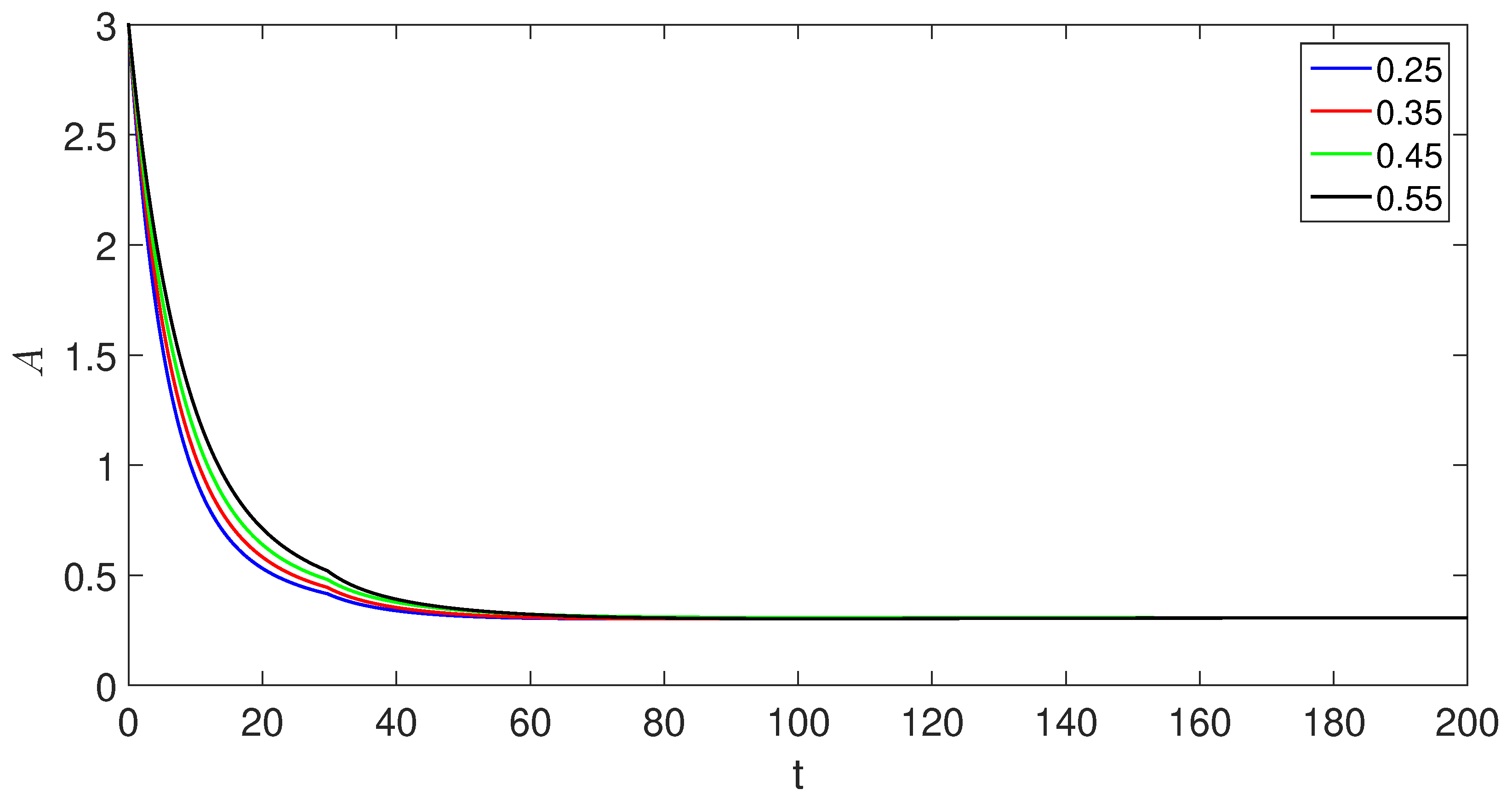
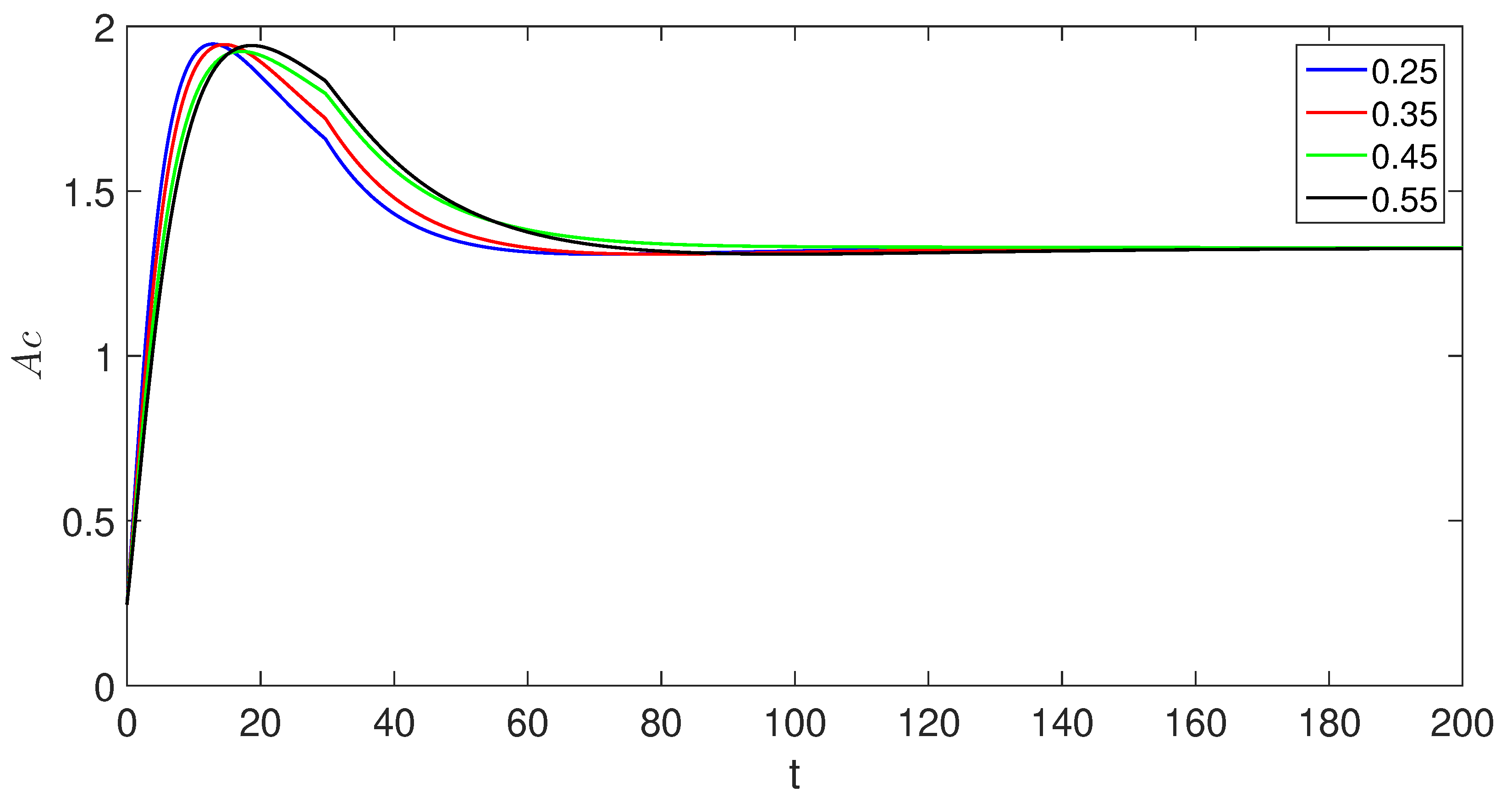
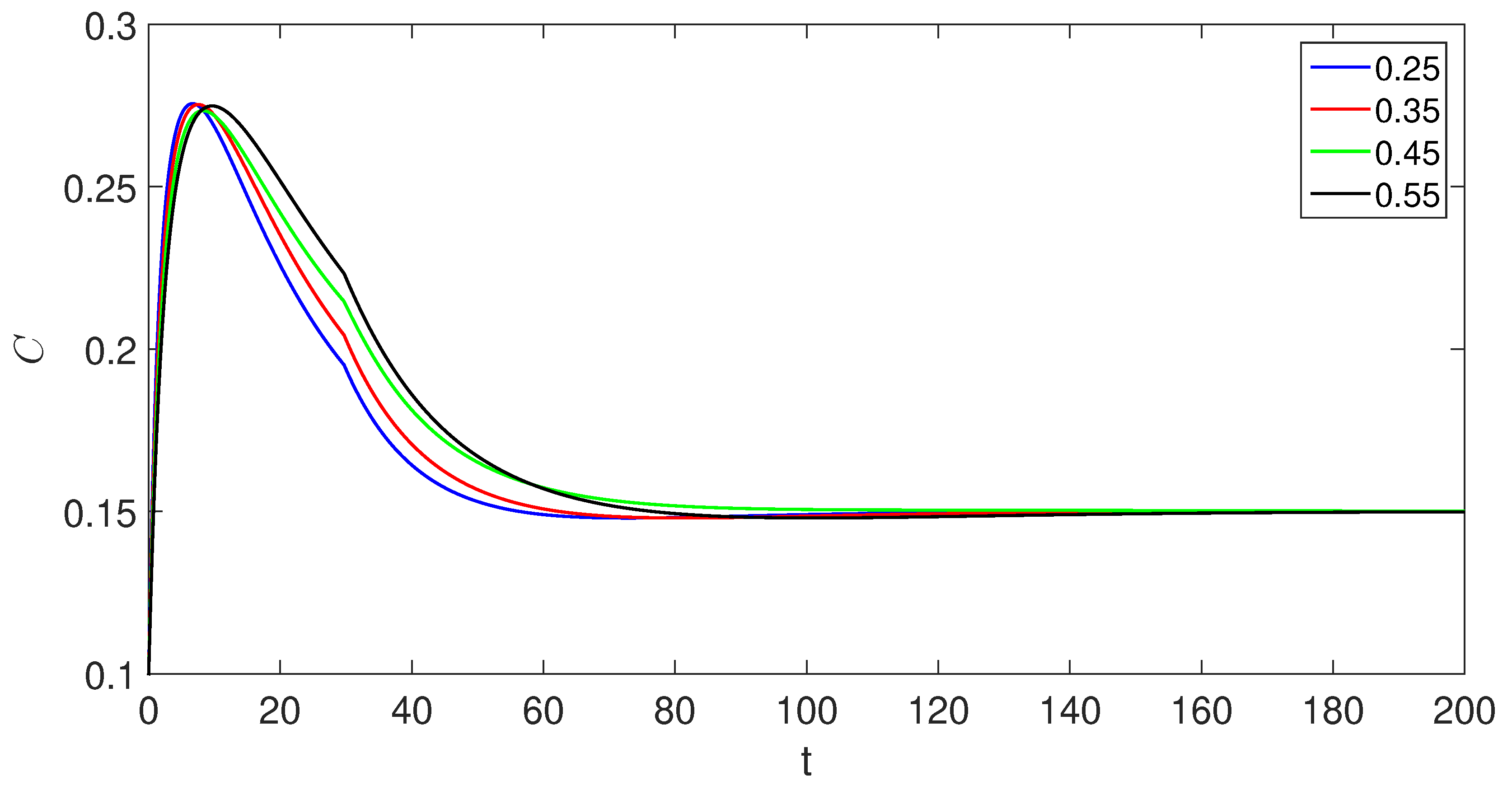
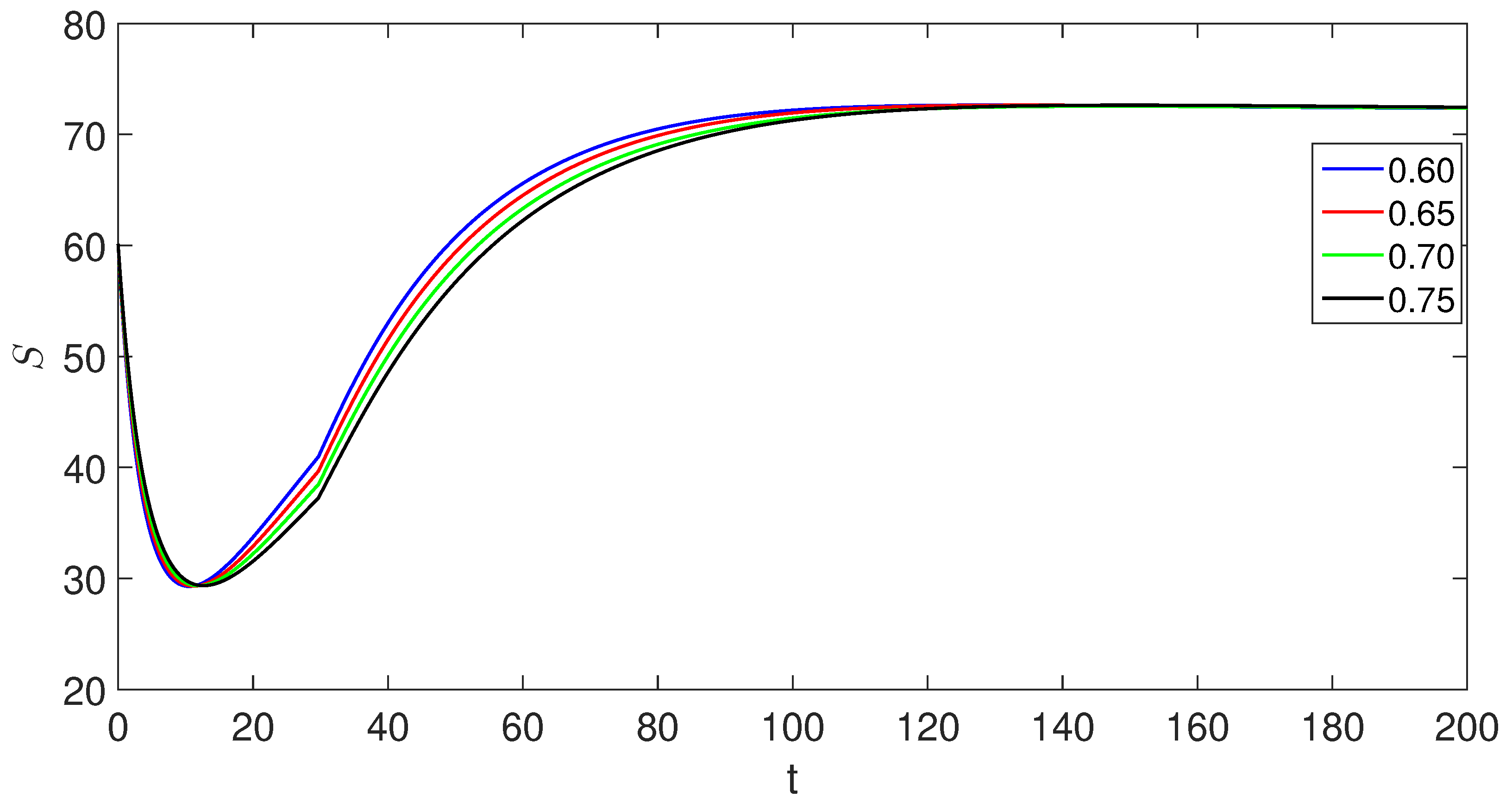
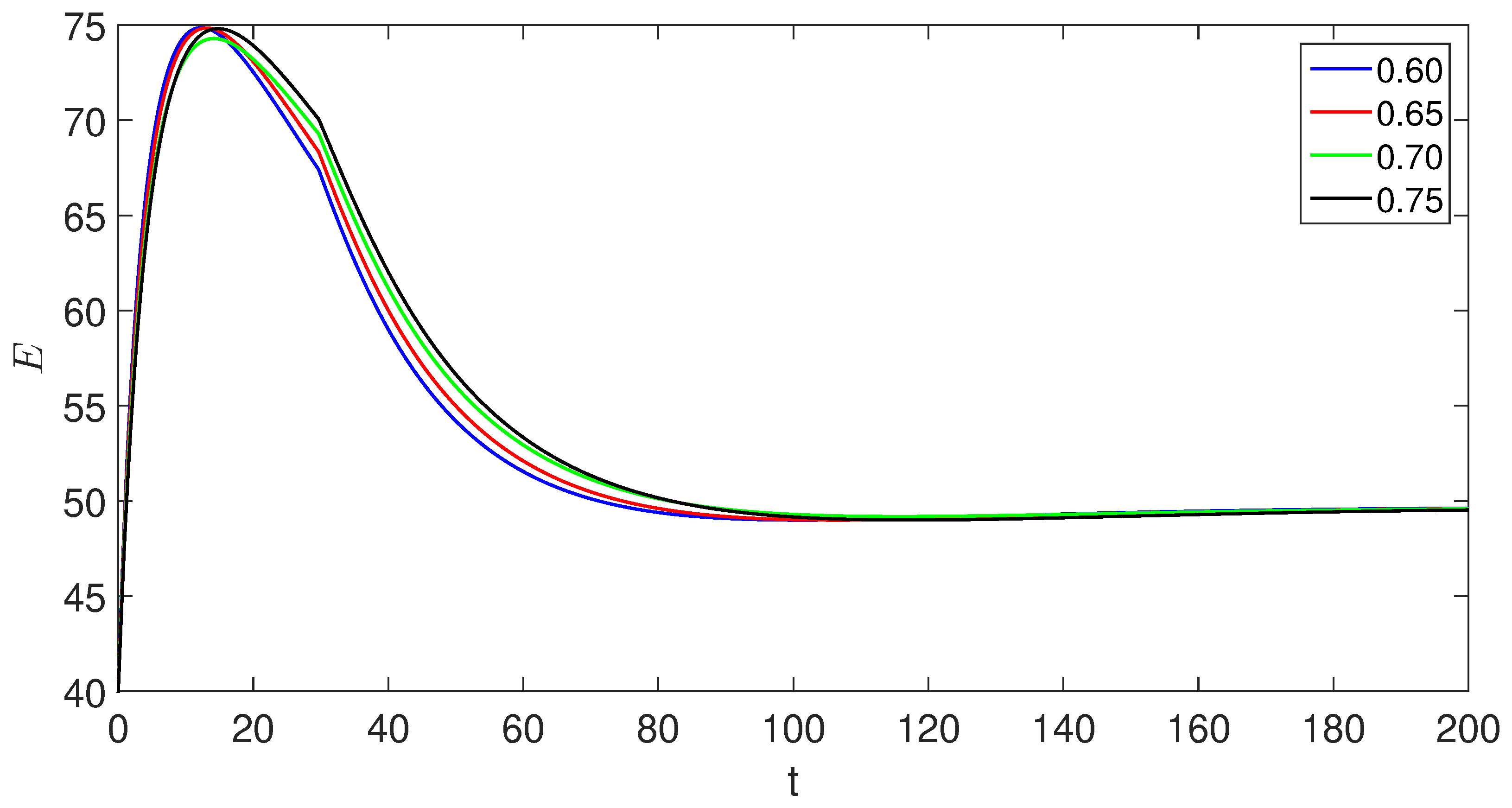
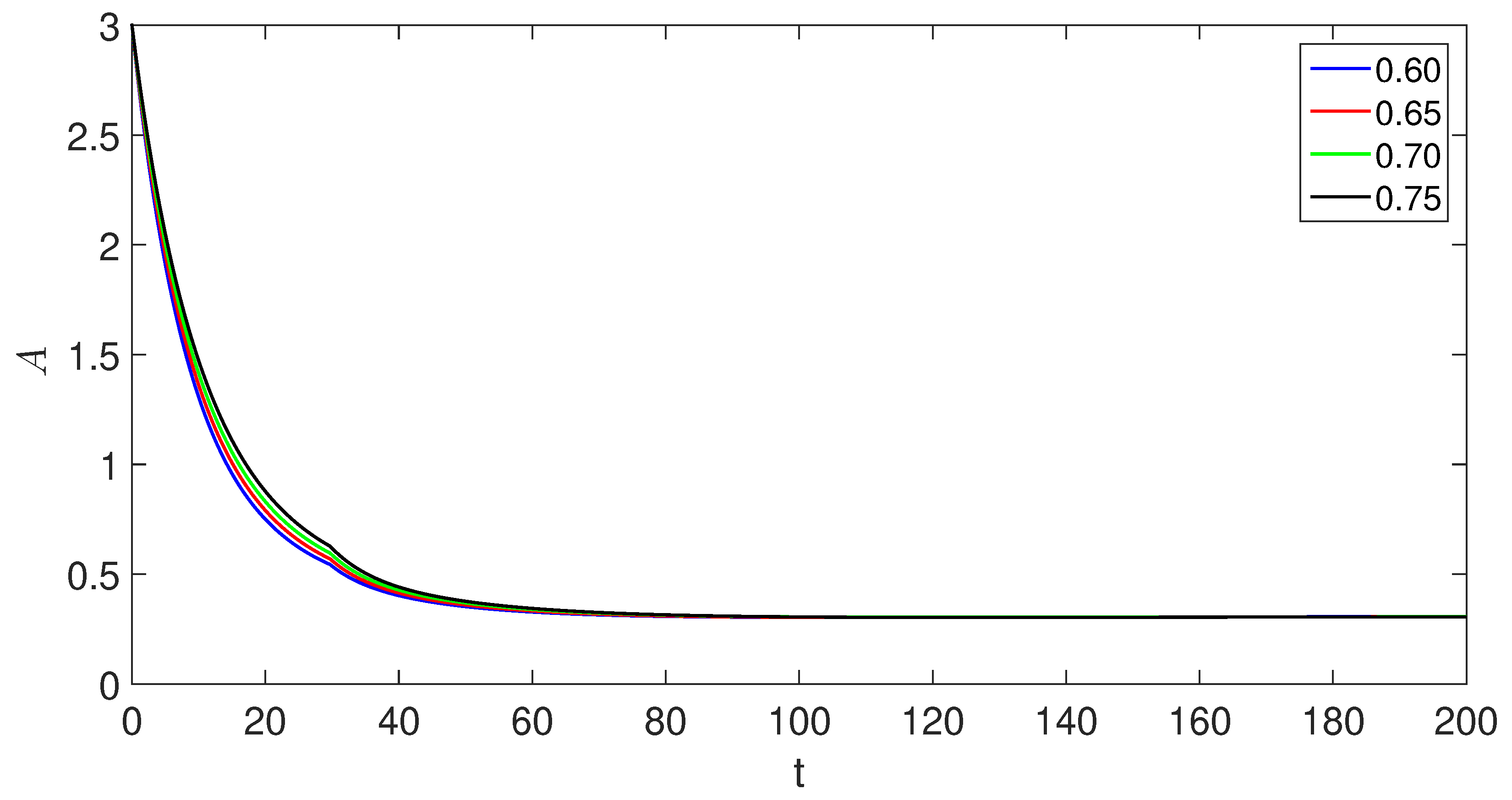
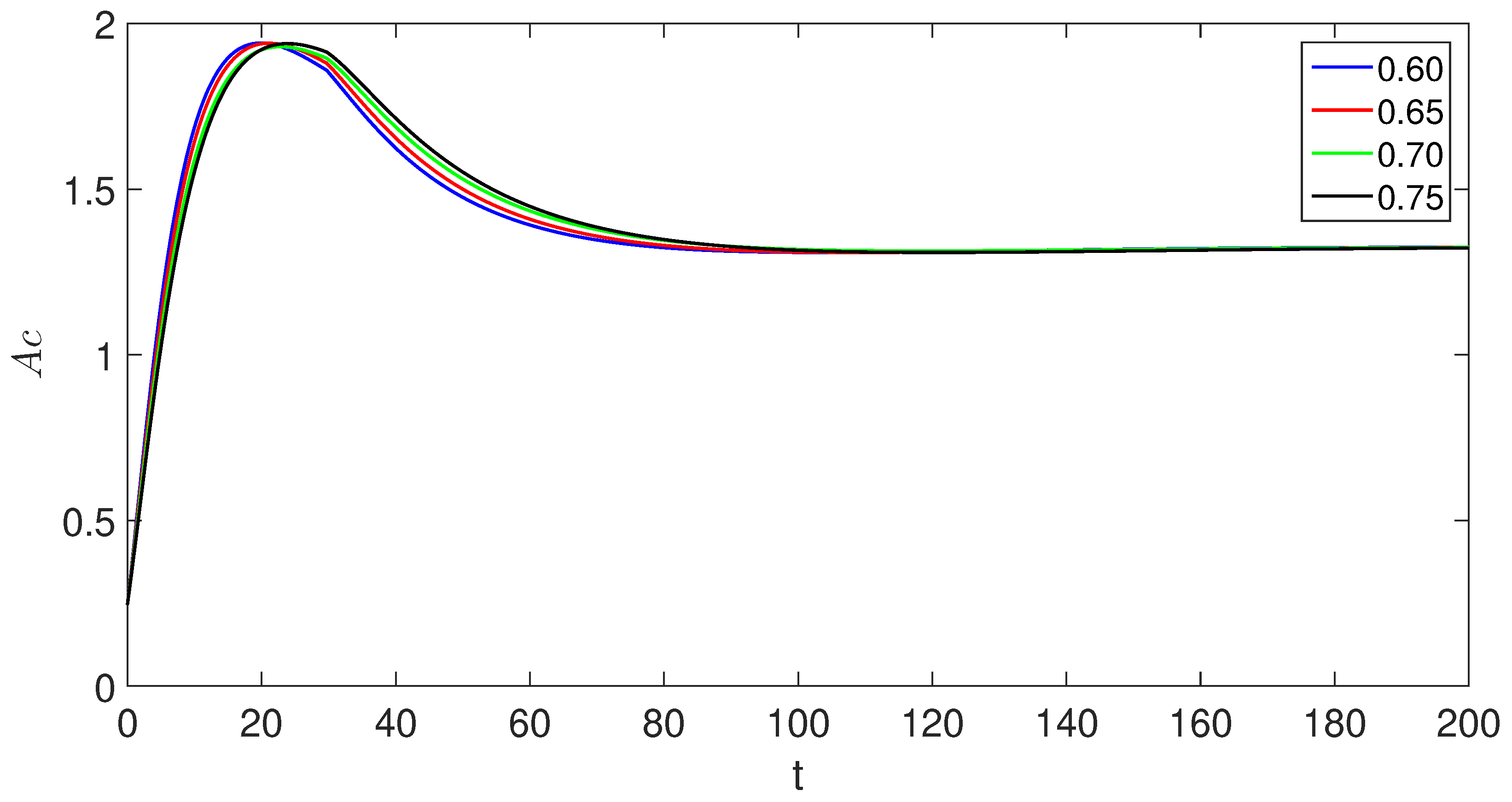
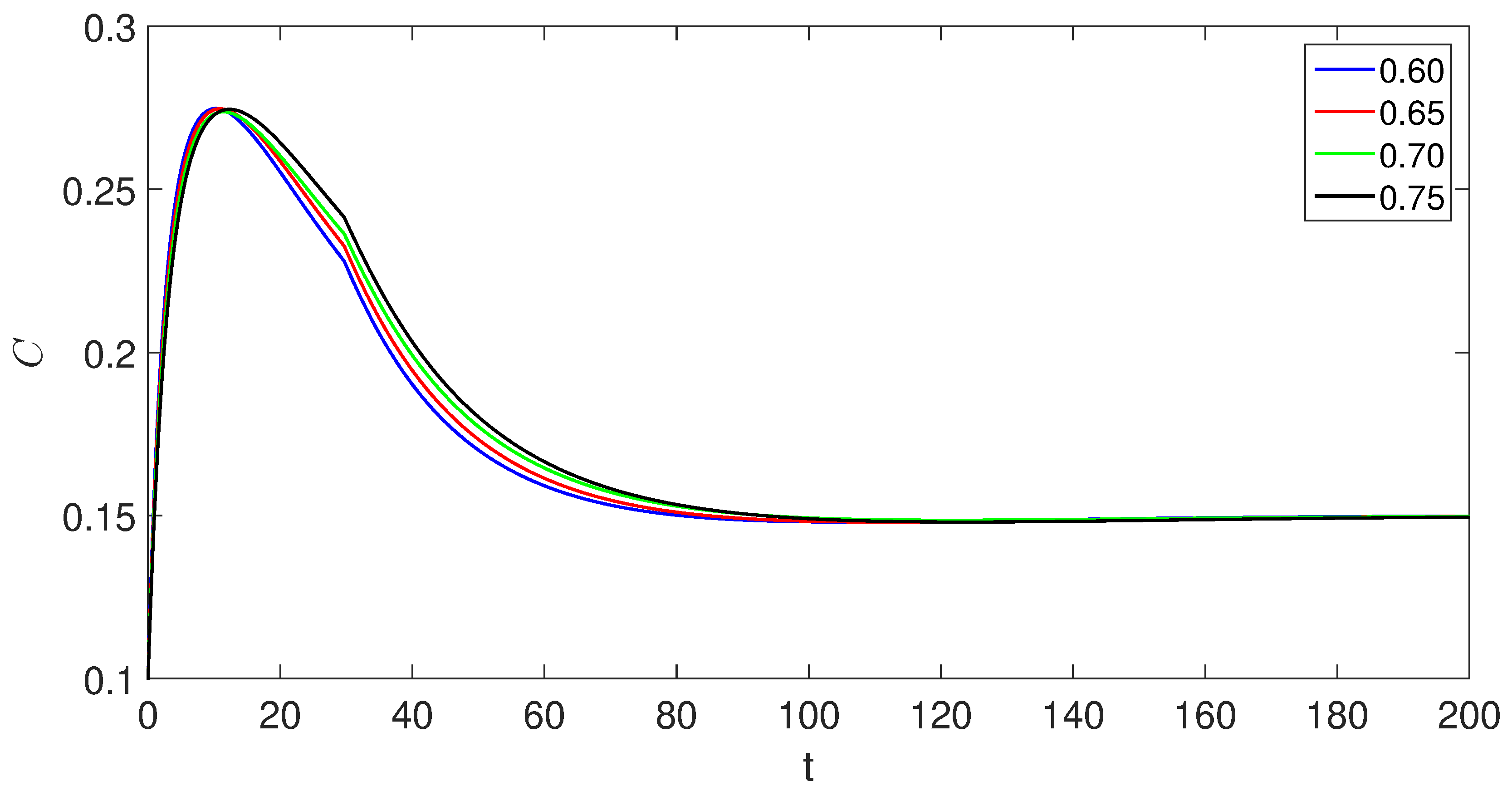
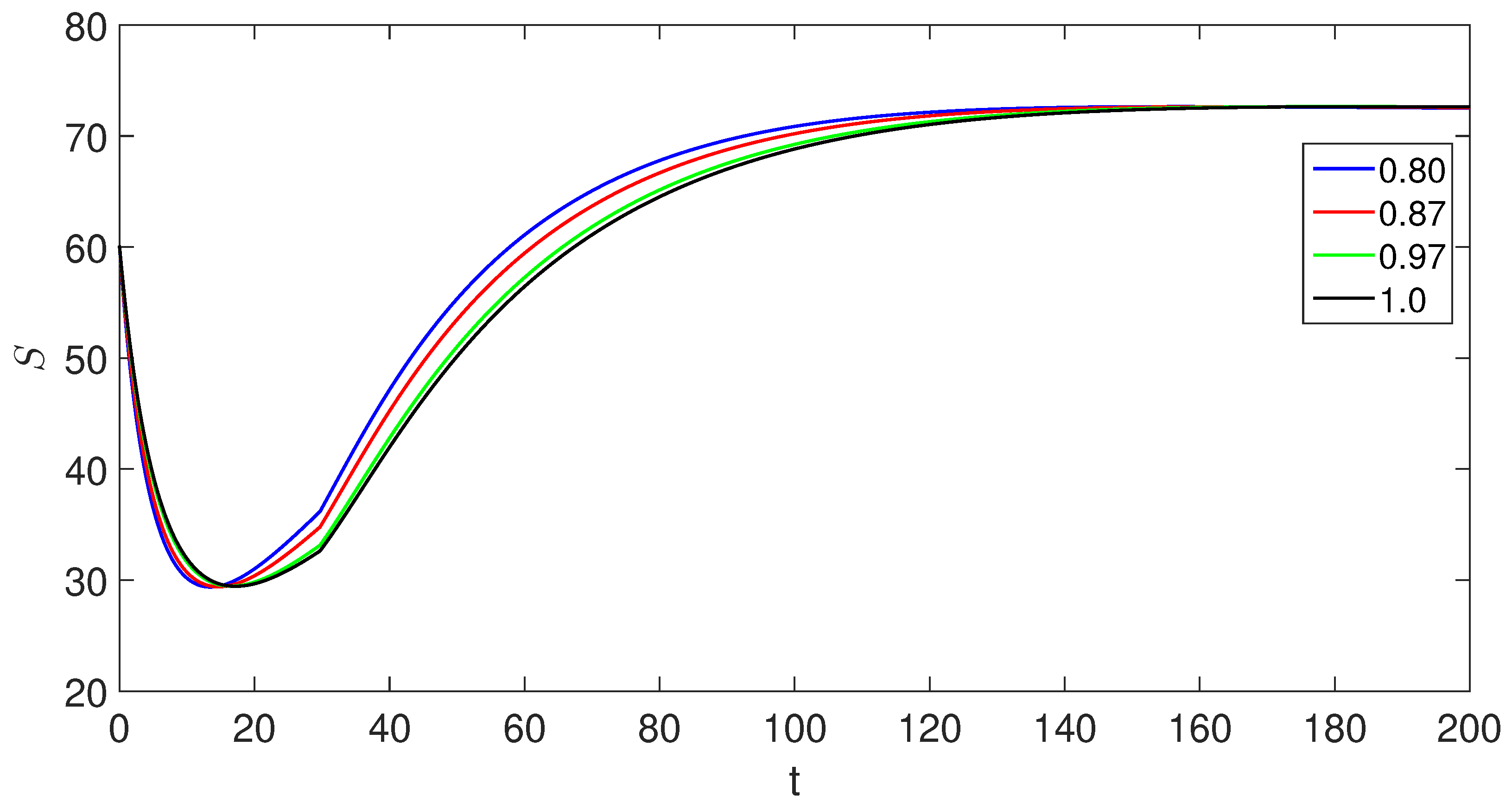
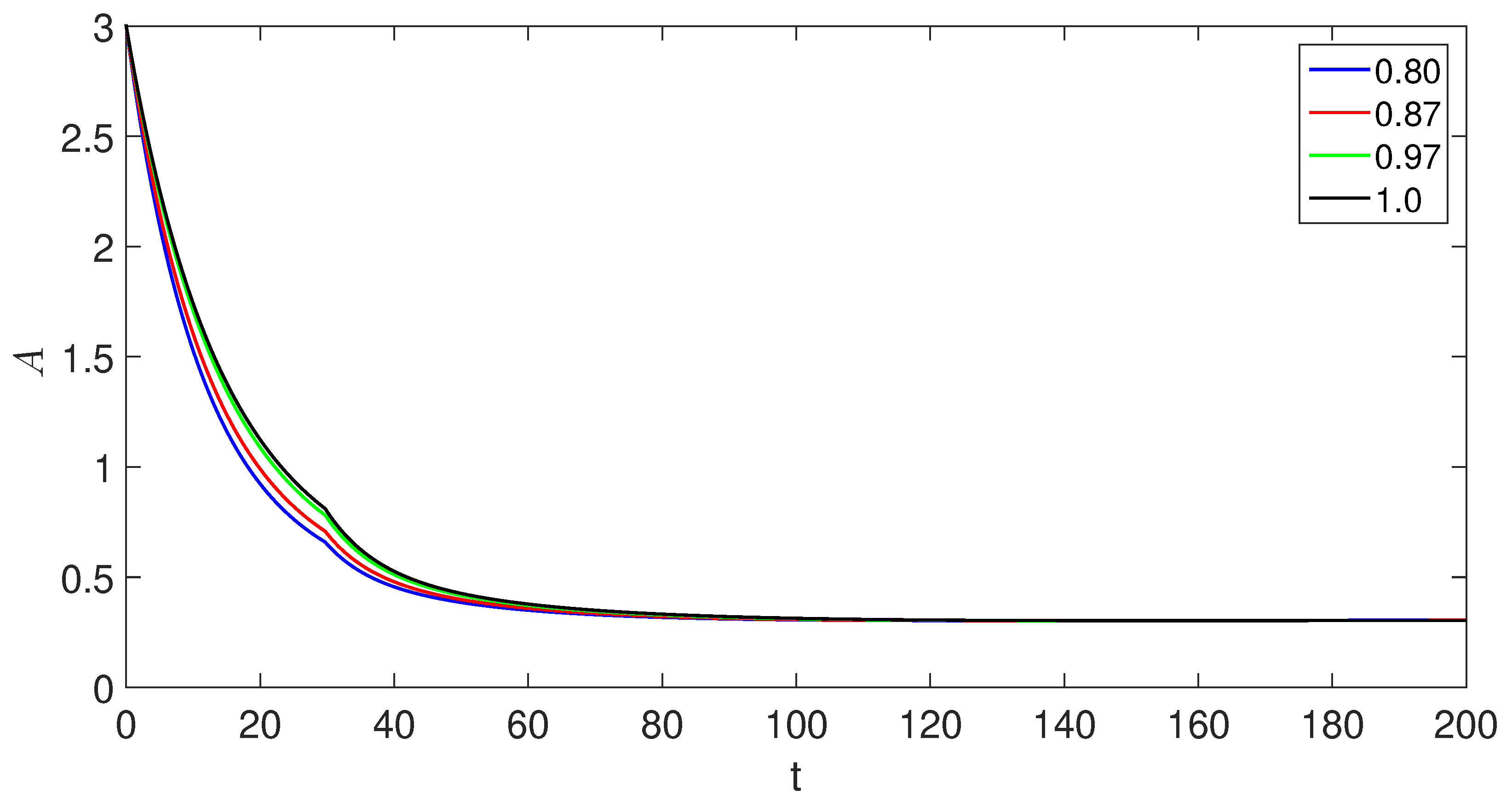
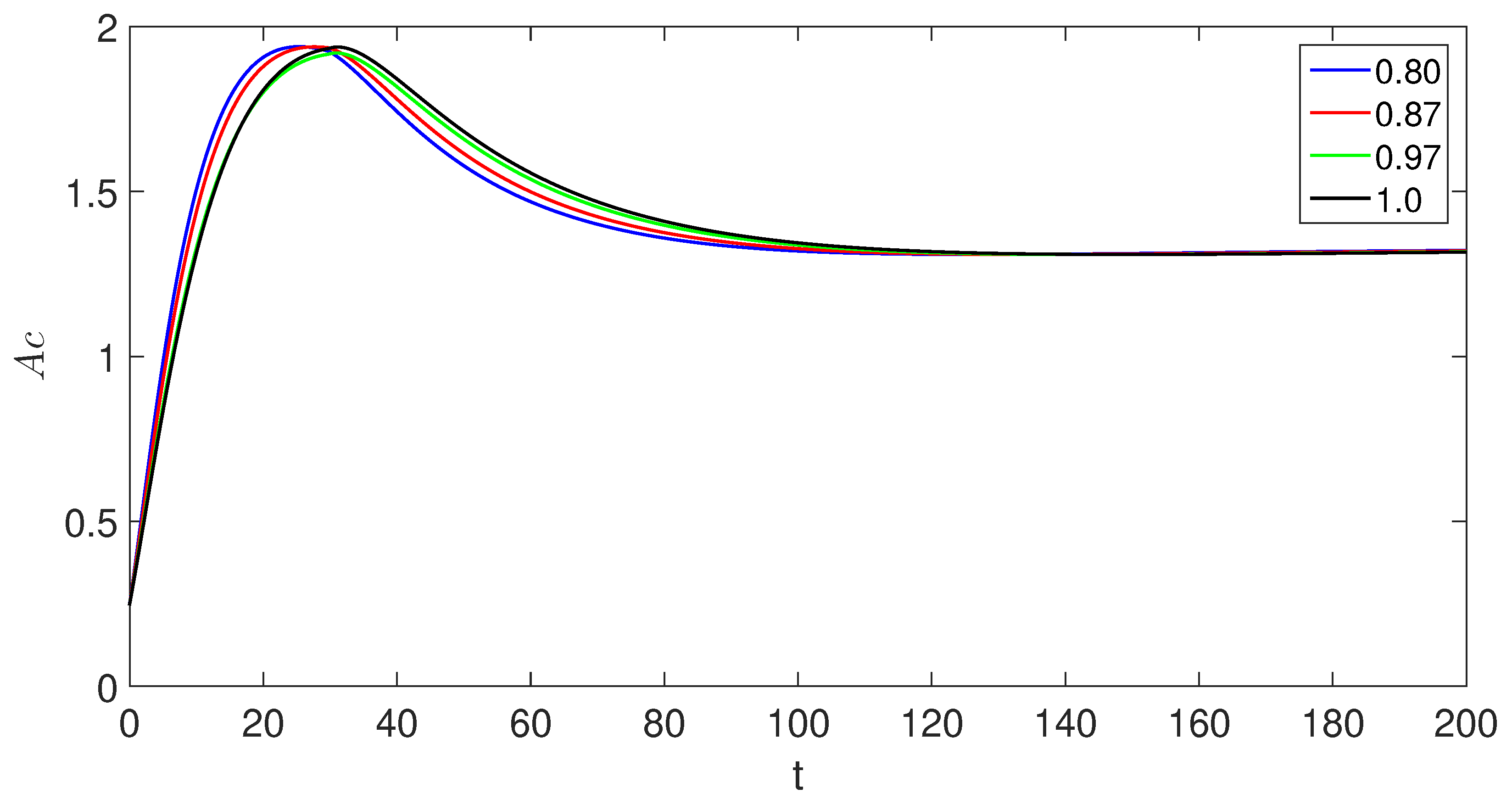
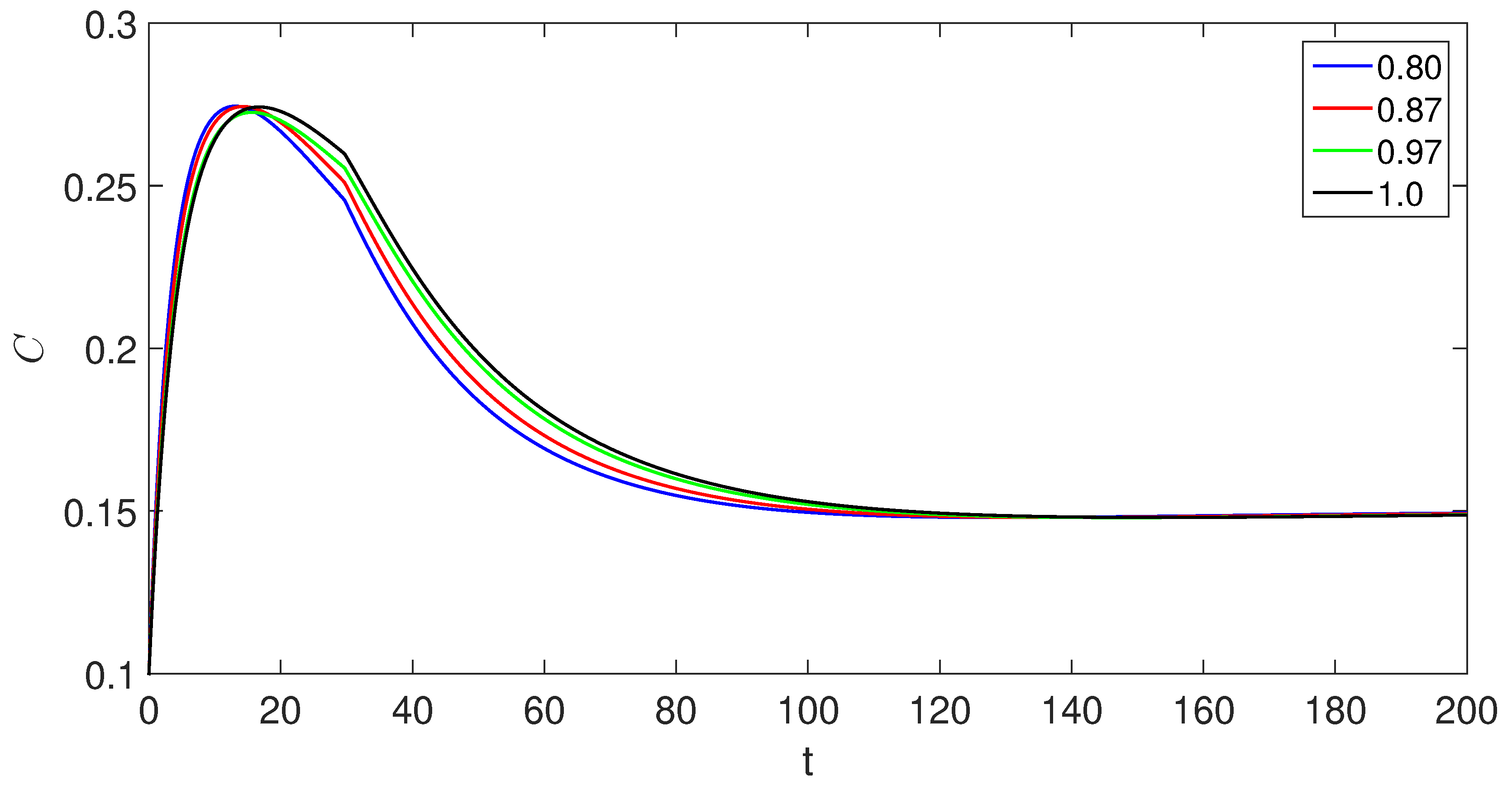
6. Numerical scheme with piecewise derivative

This section presents the numerical resolution of the adopted fractional order model. By applying the piecewise integral local and Atangana-Baleanu derivative, we have

$$\mathbb{S}\left(\iota \right)=\left\{\begin{array}{c}\mathbb{S}\left(0\right)+{\int }_0^{{\iota }_1}\left(\varrho -\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\Lambda \mathbb{S}\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \mathbb{S}\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left(\varrho -\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\Lambda \mathbb{S}\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left(\varrho -\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\Lambda \mathbb{S}\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

$$\mathbb{E}\left(\iota \right)=\left\{\begin{array}{c}\mathbb{E}\left(0\right)+{\int }_0^{{\iota }_1}\left(\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\left(\Lambda +{\psi }_1\right)\mathbb{E}\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \mathbb{E}\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left(\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\left(\Lambda +{\psi }_1\right)\mathbb{E}\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left(\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\left(\Lambda +{\psi }_1\right)\mathbb{E}\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

$$\mathbb{A}\left(\iota \right)=\left\{\begin{array}{c}\mathbb{A}\left(0\right)+{\int }_0^{{\iota }_1}\left({\psi }_1\gamma \mathbb{E}-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \mathbb{A}\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\psi }_1\gamma \mathbb{E}-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left({\psi }_1\gamma \mathbb{E}-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

$${\mathbb{A}}_c\left(\iota \right)=\left\{\begin{array}{c}{\mathbb{A}}_c\left(0\right)+{\int }_0^{{\iota }_1}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ {\mathbb{A}}_c\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

$$\mathbb{C}\left(\iota \right)=\left\{\begin{array}{c}\mathbb{C}\left(0\right)+{\int }_0^{{\iota }_1}\left({\eta }_1\mathbb{A}+{\tau }_1{\mathbb{A}}_c-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \mathbb{C}\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\eta }_1\mathbb{A}+{\tau }_1{\mathbb{A}}_c-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left({\eta }_1\mathbb{A}+{\tau }_1{\mathbb{A}}_c-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

and

$${\mathbb{R}}_p\left(\iota \right)=\left\{\begin{array}{c}{\mathbb{R}}_p\left(0\right)+{\int }_0^{{\iota }_1}\left({\kappa }_1\mathbb{A}+{\sigma }_1\mathbb{C}+\theta {\mathbb{A}}_c-\Lambda {\mathbb{R}}_p\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ {\mathbb{R}}_p\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\kappa }_1\mathbb{A}+{\sigma }_1\mathbb{C}+\theta {\mathbb{A}}_c-\Lambda {\mathbb{R}}_p\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{\iota }{(\iota -\sigma )}^{\varsigma -1}\left({\kappa }_1\mathbb{A}+{\sigma }_1\mathbb{C}+\theta {\mathbb{A}}_c-\Lambda {\mathbb{R}}_p\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

Now, put $\iota ={\iota }_{n+1}$, we get

$$\mathbb{S}\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}\mathbb{S}\left(0\right)+{\int }_0^{{\iota }_1}\left(\varrho -\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\Lambda \mathbb{S}\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \mathbb{S}\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left(\varrho -\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\Lambda \mathbb{S}\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{{\iota }_{n+1}}{({\iota }_{n+1}-\sigma )}^{\varsigma -1}\left(\varrho -\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\Lambda \mathbb{S}\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

$$\mathbb{E}\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}\mathbb{E}\left(0\right)+{\int }_0^{{\iota }_1}\left(\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\left(\Lambda +{\psi }_1\right)\mathbb{E}\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \mathbb{E}\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left(\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\left(\Lambda +{\psi }_1\right)\mathbb{E}\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{{\iota }_{n+1}}{({\iota }_{n+1}-\sigma )}^{\varsigma -1}\left(\omega \left(\mathbb{A}+{\varphi }_1{\mathbb{A}}_c+{ϵ}_1\mathbb{C}\right)\mathbb{S}-\left(\Lambda +{\psi }_1\right)\mathbb{E}\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

$$\mathbb{A}\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}\mathbb{A}\left(0\right)+{\int }_0^{{\iota }_1}\left({\psi }_1\gamma \mathbb{E}-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \mathbb{A}\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\psi }_1\gamma \mathbb{E}-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{{\iota }_{n+1}}{({\iota }_{n+1}-\sigma )}^{\varsigma -1}\left({\psi }_1\gamma \mathbb{E}-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

$${\mathbb{A}}_c\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}{\mathbb{A}}_c\left(0\right)+{\int }_0^{{\iota }_1}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ {\mathbb{A}}_c\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{{\iota }_{n+1}}{({\iota }_{n+1}-\sigma )}^{\varsigma -1}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

$$\mathbb{C}\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}\mathbb{C}\left(0\right)+{\int }_0^{{\iota }_1}\left({\eta }_1\mathbb{A}+{\tau }_1{\mathbb{A}}_c-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ \mathbb{C}\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\eta }_1\mathbb{A}+{\tau }_1{\mathbb{A}}_c-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{{\iota }_{n+1}}{({\iota }_{n+1}-\sigma )}^{\varsigma -1}\left({\eta }_1\mathbb{A}+{\tau }_1{\mathbb{A}}_c-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right],\end{array}\right.$$

and

$${\mathbb{R}}_p\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}{\mathbb{R}}_p\left(0\right)+{\int }_0^{{\iota }_1}\left({\kappa }_1\mathbb{A}+{\sigma }_1\mathbb{C}+\theta {\mathbb{A}}_c-\Lambda {\mathbb{R}}_p\right)d\sigma ,\mathrm{if}\iota \in \left[0,{\iota }_1\right],\\ {\mathbb{R}}_p\left({\iota }_1\right)+\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\kappa }_1\mathbb{A}+{\sigma }_1\mathbb{C}+\theta {\mathbb{A}}_c-\Lambda {\mathbb{R}}_p\right)\\ +\frac{\varsigma }{▿\left(\varsigma \right)\Gamma \left(\varsigma \right)}{\int }_{{\iota }_1}^{{\iota }_{n+1}}{({\iota }_{n+1}-\sigma )}^{\varsigma -1}\left({\kappa }_1\mathbb{A}+{\sigma }_1\mathbb{C}+\theta {\mathbb{A}}_c-\Lambda {\mathbb{R}}_p\right)d\sigma ,\mathrm{if}\iota \in \left[{\iota }_1,T\right].\end{array}\right.$$

By applying Newton Polynomial interpolation scheme we have

$$\mathbb{S}\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}\mathbb{S}\left(0\right)+\sum _{k=2}^i\left\{\begin{array}{c}\frac{5}{12}\left(\begin{array}{c}\varrho -\omega \left(\mathbb{A}\left({\iota }_{k-2}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-2}\right)\right)\\ \mathbb{S}\left({\iota }_{k-2}\right)-\Lambda \mathbb{S}\left({\iota }_{k-2}\right)\end{array}\right)\Delta \iota \\ -\frac{4}{3}\left(\begin{array}{c}\varrho -\omega \left(\mathbb{A}\left({\iota }_{k-1}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-1}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-1}\right)\right)\\ \mathbb{S}\left({\iota }_{k-1}\right)-\Lambda \mathbb{S}\left({\iota }_{k-1}\right)\end{array}\right)\Delta \iota \\ +\frac{23}{12}\left(\begin{array}{c}\varrho -\omega \left(\mathbb{A}\left({\iota }_k\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_k\right)+{ϵ}_1\mathbb{C}\left({\iota }_k\right)\right)\\ \mathbb{S}\left({\iota }_k\right)-\Lambda \mathbb{S}\left({\iota }_k\right)\end{array}\right)\Delta \iota \end{array}\right.,\\ \\ \mathbb{S}\left({\iota }_1\right)+\left\{\begin{array}{c}\frac{1-\varsigma }{▿\left(\varsigma \right)}\left(\varrho -\omega \left(\mathbb{A}\left({\iota }_n\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_n\right)+{ϵ}_1\mathbb{C}\left({\iota }_n\right)\right)\mathbb{S}\left({\iota }_n\right)-\Lambda \mathbb{S}\left({\iota }_n\right)\right)\\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left(\begin{array}{c}\varrho -\omega \left(\mathbb{A}\left({\iota }_{k-2}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-2}\right)\right)\\ \mathbb{S}\left({\iota }_{k-2}\right)-\Lambda \mathbb{S}\left({\iota }_{k-2}\right)\end{array}\right)\Phi \\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left[\left(\begin{array}{c}\varrho -\omega \left(\mathbb{A}\left({\iota }_{k-1}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-1}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-1}\right)\right)\\ \mathbb{S}\left({\iota }_{k-1}\right)-\Lambda \mathbb{S}\left({\iota }_{k-1}\right)\end{array}\right)\right.\\ \left.-\left(\varrho -\omega \left(\mathbb{A}\left({\iota }_{k-2}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-2}\right)\right)\mathbb{S}\left({\iota }_{k-2}\right)-\Lambda \mathbb{S}\left({\iota }_{k-2}\right)\right)\right]\Sigma \\ +\frac{\varsigma }{▿\left(\varsigma \right)}+\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{2\Gamma (\varsigma +3)}\sum _{k=i+3}^n\left[\left(\begin{array}{c}\varrho -\omega \left(\mathbb{A}\left({\iota }_k\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_k\right)+{ϵ}_1\mathbb{C}\left({\iota }_k\right)\right)\\ \mathbb{S}\left({\iota }_k\right)-\Lambda \mathbb{S}\left({\iota }_k\right)\end{array}\right)\right.\\ -2\left(\varrho -\omega \left(\mathbb{A}\left({\iota }_{k-1}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-1}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-1}\right)\right)\mathbb{S}\left({\iota }_{k-1}\right)-\Lambda \mathbb{S}\left({\iota }_{k-1}\right)\right)\\ \left.+\left(\varrho -\omega \left(\mathbb{A}\left({\iota }_{k-2}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-2}\right)\right)\mathbb{S}\left({\iota }_{k-2}\right)-\Lambda \mathbb{S}\left({\iota }_{k-2}\right)\right)\right]\Delta ,\end{array}\right.\end{array}\right.$$

$$\mathbb{E}\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}\mathbb{E}\left(0\right)+\sum _{k=2}^i\left\{\begin{array}{c}\frac{5}{12}\left(\begin{array}{c}\omega \left(\mathbb{A}\left({\iota }_{k-2}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-2}\right)\right)\mathbb{S}\\ -\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_{k-2}\right)\end{array}\right)\Delta \iota \\ -\frac{4}{3}\left(\begin{array}{c}\omega \left(\mathbb{A}\left({\iota }_{k-1}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-1}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-1}\right)\right)\mathbb{S}\left({\iota }_{k-1}\right)\\ -\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_{k-1}\right)\end{array}\right)\Delta \iota \\ +\frac{23}{12}\left(\omega \left(\mathbb{A}\left({\iota }_k\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_k\right)+{ϵ}_1\mathbb{C}\left({\iota }_k\right)\right)\mathbb{S}\left({\iota }_k\right)-\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_k\right)\right)\Delta \iota \end{array}\right.,\\ \\ \mathbb{E}\left({\iota }_1\right)+\left\{\begin{array}{c}\frac{1-\varsigma }{▿\left(\varsigma \right)}\left(\omega \left(\mathbb{A}\left({\iota }_n\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_n\right)+{ϵ}_1\mathbb{C}\left({\iota }_n\right)\right)\mathbb{S}\left({\iota }_n\right)-\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_n\right)\right)\\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left(\begin{array}{c}\omega \left(\mathbb{A}\left({\iota }_{k-2}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-2}\right)\right)\mathbb{S}\left({\iota }_{k-2}\right)\\ -\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_{k-2}\right)\end{array}\right)\Phi \\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left[\left(\begin{array}{c}\omega \left(\mathbb{A}\left({\iota }_{k-1}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-1}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-1}\right)\right)\mathbb{S}\left({\iota }_{k-1}\right)\\ -\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_{k-1}\right)\end{array}\right)\right.\\ \left.-\left(\omega \left(\mathbb{A}\left({\iota }_{k-2}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-2}\right)\right)\mathbb{S}\left({\iota }_{k-2}\right)-\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_{k-2}\right)\right)\right]\Sigma \\ +\frac{\varsigma }{▿\left(\varsigma \right)}+\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{2\Gamma (\varsigma +3)}\sum _{k=i+3}^n\left[\left(\begin{array}{c}\omega \left(\mathbb{A}\left({\iota }_k\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_k\right)+{ϵ}_1\mathbb{C}\left({\iota }_k\right)\right)\mathbb{S}\left({\iota }_k\right)\\ -\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_k\right)\end{array}\right)\right.\\ -2\left(\omega \left(\mathbb{A}\left({\iota }_{k-1}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-1}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-1}\right)\right)\mathbb{S}\left({\iota }_{k-1}\right)-\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_{k-1}\right)\right)\\ \left.+\left(\omega \left(\mathbb{A}\left({\iota }_{k-2}\right)+{\varphi }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)+{ϵ}_1\mathbb{C}\left({\iota }_{k-2}\right)\right)\mathbb{S}\left({\iota }_{k-2}\right)-\left(\Lambda +{\psi }_1\right)\mathbb{E}\left({\iota }_{k-2}\right)\right)\right]\Delta ,\end{array}\right.\end{array}\right.$$

$$\mathbb{A}\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}\mathbb{A}\left(0\right)+\sum _{k=2}^i\left\{\begin{array}{c}\frac{5}{12}\left({\psi }_1\gamma \mathbb{E}\left({\iota }_{k-2}\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_{k-2}\right)\right)\Delta \iota \\ -\frac{4}{3}\left({\psi }_1\gamma \mathbb{E}\left({\iota }_{k-1}\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_{k-1}\right)\right)\Delta \iota \\ +\frac{23}{12}\left({\psi }_1\gamma \mathbb{E}\left({\iota }_k\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_k\right)\right)\Delta \iota \end{array}\right.,\\ \\ \mathbb{A}\left({\iota }_1\right)+\left\{\begin{array}{c}\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\psi }_1\gamma \mathbb{E}\left({\iota }_n\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_n\right)\right)\\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left({\psi }_1\gamma \mathbb{E}\left({\iota }_{k-2}\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_{k-2}\right)\right)\Phi \\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left[\left({\psi }_1\gamma \mathbb{E}\left({\iota }_{k-1}\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_{k-1}\right)\right)\right.\\ \left.-\left({\psi }_1\gamma \mathbb{E}\left({\iota }_{k-2}\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_{k-2}\right)\right)\right]\Sigma \\ +\frac{\varsigma }{▿\left(\varsigma \right)}+\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{2\Gamma (\varsigma +3)}\sum _{k=i+3}^n\left[\left({\psi }_1\gamma \mathbb{E}\left({\iota }_k\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_k\right)\right)\right.\\ -2\left({\psi }_1\gamma \mathbb{E}\left({\iota }_{k-1}\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_{k-1}\right)\right)\\ \left.+\left({\psi }_1\gamma \mathbb{E}\left({\iota }_{k-2}\right)-\left(\Lambda +\mu +{\eta }_1+{\kappa }_1\right)\mathbb{A}\left({\iota }_{k-2}\right)\right)\right]\Delta ,\end{array}\right.\end{array}\right.$$

$${\mathbb{A}}_c\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}{\mathbb{A}}_c\left(0\right)+\sum _{k=2}^i\left\{\begin{array}{c}\frac{5}{12}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_{k-2}\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_{k-2}\right)\right)\Delta \iota \\ -\frac{4}{3}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_{k-1}\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_{k-1}\right)\right)\Delta \iota \\ +\frac{23}{12}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_k\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_k\right)\right)\Delta \iota \end{array}\right.,\\ {\mathbb{A}}_c\left({\iota }_1\right)+\left\{\begin{array}{c}\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_n\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_n\right)\right)\\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_{k-2}\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_{k-2}\right)\right)\Phi \\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left[\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_{k-1}\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_{k-1}\right)\right)\right.\\ \left.-\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_{k-2}\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_{k-2}\right)\right)\right]\Sigma \\ +\frac{\varsigma }{▿\left(\varsigma \right)}+\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{2\Gamma (\varsigma +3)}\sum _{k=i+3}^n\left[\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_k\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_k\right)\right)\right.\\ -2\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_{k-1}\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_{k-1}\right)\right)\\ \left.+\left({\psi }_1\left(1-\gamma \right)\mathbb{E}\left({\iota }_{k-2}\right)-\left(\Lambda +{\tau }_1+\theta \right){\mathbb{A}}_c\left({\iota }_{k-2}\right)\right)\right]\Delta ,\end{array}\right.\end{array}\right.$$

$$\mathbb{C}\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}\mathbb{C}\left(0\right)+\sum _{k=2}^i\left\{\begin{array}{c}\frac{5}{12}\left({\eta }_1\mathbb{A}\left({\iota }_{k-2}\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_{k-2}\right)\right)\Delta \iota \\ -\frac{4}{3}\left({\eta }_1\mathbb{A}\left({\iota }_{k-1}\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_{k-1}\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_{k-1}\right)\right)\Delta \iota \\ +\frac{23}{12}\left({\eta }_1\mathbb{A}\left({\iota }_k\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_k\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_k\right)\right)\Delta \iota \end{array}\right.,\\ \\ \mathbb{C}\left({\iota }_1\right)+\left\{\begin{array}{c}\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\eta }_1\mathbb{A}\left({\iota }_n\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_n\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_n\right)\right)\\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left({\eta }_1\mathbb{A}\left({\iota }_{k-2}\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_{k-2}\right)\right)\Phi \\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left[\left({\eta }_1\mathbb{A}\left({\iota }_{k-1}\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_{k-1}\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_{k-1}\right)\right)\right.\\ \left.-\left({\eta }_1\mathbb{A}\left({\iota }_{k-2}\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_{k-2}\right)\right)\right]\Sigma \\ +\frac{\varsigma }{▿\left(\varsigma \right)}+\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{2\Gamma (\varsigma +3)}\sum _{k=i+3}^n\left[\left({\eta }_1\mathbb{A}\left({\iota }_k\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_k\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_k\right)\right)\right.\\ -2\left({\eta }_1\mathbb{A}\left({\iota }_{k-1}\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_{k-1}\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_{k-1}\right)\right)\\ \left.+\left({\eta }_1\mathbb{A}\left({\iota }_{k-2}\right)+{\tau }_1{\mathbb{A}}_c\left({\iota }_{k-2}\right)-\left(\Lambda +\nu +{\sigma }_1\right)\mathbb{C}\left({\iota }_{k-2}\right)\right)\right]\Delta ,\end{array}\right.\end{array}\right.$$

and

$${\mathbb{R}}_p\left({\iota }_{n+1}\right)=\left\{\begin{array}{c}{\mathbb{R}}_p\left(0\right)+\sum _{k=2}^i\left\{\begin{array}{c}\frac{5}{12}\left({\kappa }_1\mathbb{A}\left({\iota }_{k-2}\right)+{\sigma }_1\mathbb{C}\left({\iota }_{k-2}\right)+\theta {\mathbb{A}}_c\left({\iota }_{k-2}\right)-\Lambda {\mathbb{R}}_p\left({\iota }_{k-2}\right)\right)\Delta \iota \\ -\frac{4}{3}\left({\kappa }_1\mathbb{A}\left({\iota }_{k-1}\right)+{\sigma }_1\mathbb{C}\left({\iota }_{k-1}\right)+\theta {\mathbb{A}}_c\left({\iota }_{k-1}\right)-\Lambda {\mathbb{R}}_p\left({\iota }_{k-1}\right)\right)\Delta \iota \\ +\frac{23}{12}\left({\kappa }_1\mathbb{A}\left({\iota }_k\right)+{\sigma }_1\mathbb{C}\left({\iota }_k\right)+\theta {\mathbb{A}}_c\left({\iota }_k\right)-\Lambda {\mathbb{R}}_p\left({\iota }_k\right)\right)\Delta \iota \end{array}\right.,\\ \\ {\mathbb{R}}_p\left({\iota }_1\right)+\left\{\begin{array}{c}\frac{1-\varsigma }{▿\left(\varsigma \right)}\left({\kappa }_1\mathbb{A}\left({\iota }_n\right)+{\sigma }_1\mathbb{C}\left({\iota }_n\right)+\theta {\mathbb{A}}_c\left({\iota }_n\right)-\Lambda {\mathbb{R}}_p\left({\iota }_n\right)\right)\\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left({\kappa }_1\mathbb{A}\left({\iota }_{k-2}\right)+{\sigma }_1\mathbb{C}\left({\iota }_{k-2}\right)+\theta {\mathbb{A}}_c\left({\iota }_{k-2}\right)-\Lambda {\mathbb{R}}_p\left({\iota }_{k-2}\right)\right)\Phi \\ +\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{▿\left(\varsigma \right)\Gamma (\varsigma +1)}\sum _{k=i+3}^n\left[\left({\kappa }_1\mathbb{A}\left({\iota }_{k-1}\right)+{\sigma }_1\mathbb{C}\left({\iota }_{k-1}\right)+\theta {\mathbb{A}}_c\left({\iota }_{k-1}\right)-\Lambda {\mathbb{R}}_p\left({\iota }_{k-1}\right)\right)\right.\\ \left.-\left({\kappa }_1\mathbb{A}\left({\iota }_{k-2}\right)+{\sigma }_1\mathbb{C}\left({\iota }_{k-2}\right)+\theta {\mathbb{A}}_c\left({\iota }_{k-2}\right)-\Lambda {\mathbb{R}}_p\left({\iota }_{k-2}\right)\right)\right]\Sigma \\ +\frac{\varsigma }{▿\left(\varsigma \right)}+\frac{\varsigma {\left(\Delta \iota \right)}^{\varsigma -1}}{2\Gamma (\varsigma +3)}\sum _{k=i+3}^n\left[\left({\kappa }_1\mathbb{A}\left({\iota }_k\right)+{\sigma }_1\mathbb{C}\left({\iota }_k\right)+\theta {\mathbb{A}}_c\left({\iota }_k\right)-\Lambda {\mathbb{R}}_p\left({\iota }_k\right)\right)\right.\\ -2\left({\kappa }_1\mathbb{A}\left({\iota }_{k-1}\right)+{\sigma }_1\mathbb{C}\left({\iota }_{k-1}\right)+\theta {\mathbb{A}}_c\left({\iota }_{k-1}\right)-\Lambda {\mathbb{R}}_p\left({\iota }_{k-1}\right)\right)\\ \left.+\left({\kappa }_1\mathbb{A}\left({\iota }_{k-2}\right)+{\sigma }_1\mathbb{C}\left({\iota }_{k-2}\right)+\theta {\mathbb{A}}_c\left({\iota }_{k-2}\right)-\Lambda {\mathbb{R}}_p\left({\iota }_{k-2}\right)\right)\right]\Delta ,\end{array}\right.\end{array}\right.$$

where

$$\Delta =\left\{\begin{array}{c}{\left(n-k+1\right)}^{\varsigma }\left[2{\left(n-k\right)}^2+\left(3\varsigma +10\right)\left(n-k\right)+2{\varsigma }^2+9\varsigma +12\right]\\ -{(n-k)}^{\varsigma }\left[2{\left(n-k\right)}^2+\left(5\varsigma +10\right)\left(n-k\right)+6{\varsigma }^2+18\varsigma +12\right],\end{array}\right.$$

$$\Sigma ={\left(n-k+1\right)}^{\varsigma }\left(n-k+3+2\varsigma \right)-{\left(n-k\right)}^{\varsigma }\left(n-k+3+3\varsigma \right),$$

and

$$\Phi ={\left(n-k+1\right)}^{\varsigma }-{\left(n-k\right)}^{\varsigma }.$$

The numerical solution of the model (1) with a unit of time per year is obtained by using the above-described scheme. We use the parameter values from [26] in the numerical solution are $\varrho =2,\Lambda =\frac{1}{67.7},\omega =0.042,{\varphi }_1={ϵ}_1=0.002,{\psi }_1=0.004,\gamma =0.6,\mu =0.001,{\eta }_1={\kappa }_1={\tau }_1=0.02,\theta =0.1,\nu =0.003$ and ${\sigma }_1=0.2.$ In addition, the initial values are selected as

$$\left({\mathbb{S}}_0,{\mathbb{E}}_0,{\mathbb{A}}_0,{\mathbb{A}}_c,{\mathbb{C}}_0,{\mathbb{R}}_{p0}\right)=(60,40,3,0.25,0.1).$$

We now use the numerical scheme established to simulate our results graphically. Using the mentioned data different compartments have presented graphically in the following three cases.

Case (1) When $\varsigma \in (0,0.55]$

We have used $[0,200]$ and plotted the results graphically in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 for various fractional orders. The concerned transmission dynamics of various compartments has been shown. We see the crossover behaviors in each compartments due to piecewise version of derivatives near the point $t_1<100$. The declines in susceptible class, exposed classes and the concerned changes in other compartments $\mathbb{A},\mathbb{AC},\mathbb{C}$ can be observed easily.

Case (2) When $\varsigma \in [0.60,0.75]$

We have used $[0,200]$ and plotted the results graphically in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 for various fractional orders slighter greater than the first case. The concerned transmission dynamics of various compartments has been shown. We see the crossover behaviors in each compartments due to piecewise version of derivatives near the point $t_1<100$. The declines in susceptible class, exposed classes and the concerned changes in other compartments $\mathbb{A},\mathbb{AC},\mathbb{C}$ can be observed easily.

Case (3) When $\varsigma \in (0.75,1.0]$

We have used $[0,200]$ and plotted the results graphically in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 for various fractional orders which are graters in the first two cases here. The concerned transmission dynamics of various compartments has been shown. We see the crossover behaviors in each compartments due to piecewise version of derivatives near the point $t_1<100$. The declines in susceptible class, exposed classes and the concerned changes in other compartments $\mathbb{A},\mathbb{AC},\mathbb{C}$ can be observed easily.

7. Conclusion

We have studied a dynamics system of a Hepatitis B virus (HBV) with the class of asymptomatic carriers with some new perspectives of fractional calculus. We have used piecewise derivatives of fractional orders with non-local kernel as well as singular kernel. We have established some appropriate conditions for the existence of such models using the tools of nonlinear analysis. In addition, for numerical illustration, we have used Adam Bashforth numerical method. Using the real values of parameters already reported the concerned results have been presented graphically under various fractional orders. The model numerical demonstrated the crossover effect in the dynamics using the time domain for transmission $[0,200]$ near the point where $t_1<100$. The mentioned aspects of fractional calculus has recently recognized a powerful tool to elaborate the sudden or abrupt changes in the real world phenomenon with more brilliant ways. In the future, we will use this methodologies in other complex dynamical models of other diseases.

Age-specific data reveals that acute HBV infection is typically asymptomatic in infants, young children (under the age of 10), and immunocompromised adults. Symptomatic cases are more common among adults and older children, accounting for approximately 30 to 50% of infections. Although research suggests that individuals infected with HBV without symptoms can still transmit the virus and may face the risk of liver damage or even death, particularly if they remain asymptomatic for over six months