Monitoring Mean of INAR(1) Process with Discrete Mixture Exponential Innovations

1. Introduction

In practice, there appears to be a limitless number of count datasets in applied disciplines, indicating the utmost significance of count data modelling. Within this context, discrete probability distributions have assumed a central role in modern data modelling, spanning a diverse spectrum of applied fields. In these practical contexts, count data serve as the fundamental quantification of events occurring within specific intervals. The increasing recognition of the need for more adaptable discrete models is evident, particularly when compared to classical continuous or discrete distributions on the real number line. Although count data modelling has traditionally relied on Poisson and negative binomial distributions, the widespread occurrence of over-dispersion and notable skewness or kurtosis in real-world datasets has emphasized the necessity to create new models. Researchers have responded by introducing innovative discrete distributions through the application of various methodologies and have explored their application in various fields.

Time series models serve as indispensable tools for capturing distinct data features, especially when dealing with count data over time. The first-order integer-valued autoregressive (INAR(1)) process is a significant statistical model for studying auto-correlated count data, excelling in accurately representing counts when compared to Poisson and negative binomial models. Consequently, Al-Osh and Alzaid (1987) introduced the INAR(1) process with binomial thinning having Poisson marginal. Subsequently, other variations, such as the INAR(1) process with Poisson-transmuted exponential innovations proposed by Emrah Altun (2022), and the INAR(1) process with Poisson-extended exponential innovations presented by Maya et al. (2022), have emerged. Researchers are exploring these INAR(1) models to enhance their ability to optimally fit real datasets. This diverse collection of INAR(1) models has garnered substantial interest among researchers, undergoing in-depth exploration and contributing to the evolving landscape of time series modelling.

Statistical quality control primarily focuses on count data and the introduction of control charts has revolutionized this field, making them the primary method for process monitoring. Control charts are designed to maintain process stability and swiftly detect parameter shifts, classifying a process as "in-control" if it adheres to a specified model. Consequently, efficient monitoring is essential to promptly identify shifts in the mean. The cumulative sum (CUSUM) and exponentially weighted moving average (EWMA) control charts, known for their memory capabilities, promptly detect these changes. Conventional control charts, frequently utilized, tend to assume the independence of observations, a premise that may not always be reflected in practical scenarios. This necessitates the utilization of control charts in integer-valued time series models. As a result, Wei and Testik (2009) proposed a CUSUM chart for monitoring the mean of the INAR(1) process with Poisson marginals. Some of the notable works include Li et al. (2022); Kim and Lee (2017); Rakitzis et al. (2017) and Li et al. (2016a). Subsequent to the CUSUM chart, Wei (2011) also discussed the corresponding EWMA chart. Some other works include Wei (2009); Li et al. (2016b) and Li et al. (2019).

Motivated by the aforementioned works, our study introduces a novel discrete mixture exponential (DME) distribution. We utilize survival discretization techniques outlined in Chakraborty (2015) to the mixture exponential (ME) distribution proposed by Mirhossaini and Dolati (2008). In addition to exploring the statistical characteristics of this distribution, our paper presents four distinct parameter estimation approaches. Furthermore, we delve into the application of the DME distribution to an associated INAR(1) process, incorporating DME as innovations.

In the context of process monitoring, we develop control charts tailored for tracking the mean of the proposed process. We investigate the statistical design and performance of CUSUM and EWMA control charts in detecting increasing shifts in process mean levels. Our analysis encompasses the evaluation of control chart properties, particularly their Average Run Length (ARL), which indicates their sensitivity in detecting mean changes within the process. A comparative assessment of both monitoring approaches is also undertaken, providing insights into their effectiveness. Lastly, we assess the practicality of our proposed model by applying it to a real-world data.

The paper is structured as follows: In Section 2, we provide an overview of the construction and characteristics of the DME distribution. Section 3 then introduces the associated statistical properties, including the moment-generating function, moments, skewness, kurtosis, and hazard rate function. Section 4 delves into the discussion of four distinct parameter estimation methods, with an assessment of their performance using Monte Carlo simulations. In Section 5, we evaluate the performance of the proposed distribution using a real dataset. We introduce the INAR(1) process with DME innovations and discuss its properties, including estimation and simulation in Section 6. Section 7 focuses on the statistical process control procedure for INAR(1)DME processes, utilizing the CUSUM and EWMA approaches to detect mean increases, accompanied by numerical simulation and real data analysis. The study is concluded in Section 8.

2. The discrete mixture exponential distribution

The survival discretization method by Chakraborty (2015) is implemented on the continuous mixture exponential distribution, incorporating the reparameterization $\lambda =e^{-\theta }$. As a result, the discrete counterpart is called discrete mixture exponential (DME) distribution. To begin, let us define the continuous ME distribution. The probability density function (pdf) and cumulative distribution function (cdf) of the ME distribution are given by

$$g(x;\alpha ,\theta )=\theta e^{-\theta x}\left\{1+\alpha \left(2e^{-\theta x}-1\right)\right\}x>0$$

(2.1)

and

$$G(x;\alpha ,\theta )=\left(1-e^{-\theta x}\right)\left(1+\alpha e^{-\theta x}\right),x>0,$$

(2.2)

where $\theta >0,-1\le \alpha \le 1$.

The DME distribution is presented in the following proposition:

Proposition 2.1.

Let $X\sim$DME($\alpha ,\lambda )$, then the probability mass function (pmf) is given by

$$P(X=x)={\lambda }^x(1-\lambda )(1-\alpha )+\alpha {\lambda }^{2x}(1-{\lambda }^2),x=0,1,2,...,$$

(2.3)

where $0<\lambda <1$ and $-1\le \alpha \le 1$.

The corresponding cdf is given by,

$$F\left(x\right)=(1-{\lambda }^{(1+x)})(1+\alpha {\lambda }^{(1+x)}).$$

(2.4)

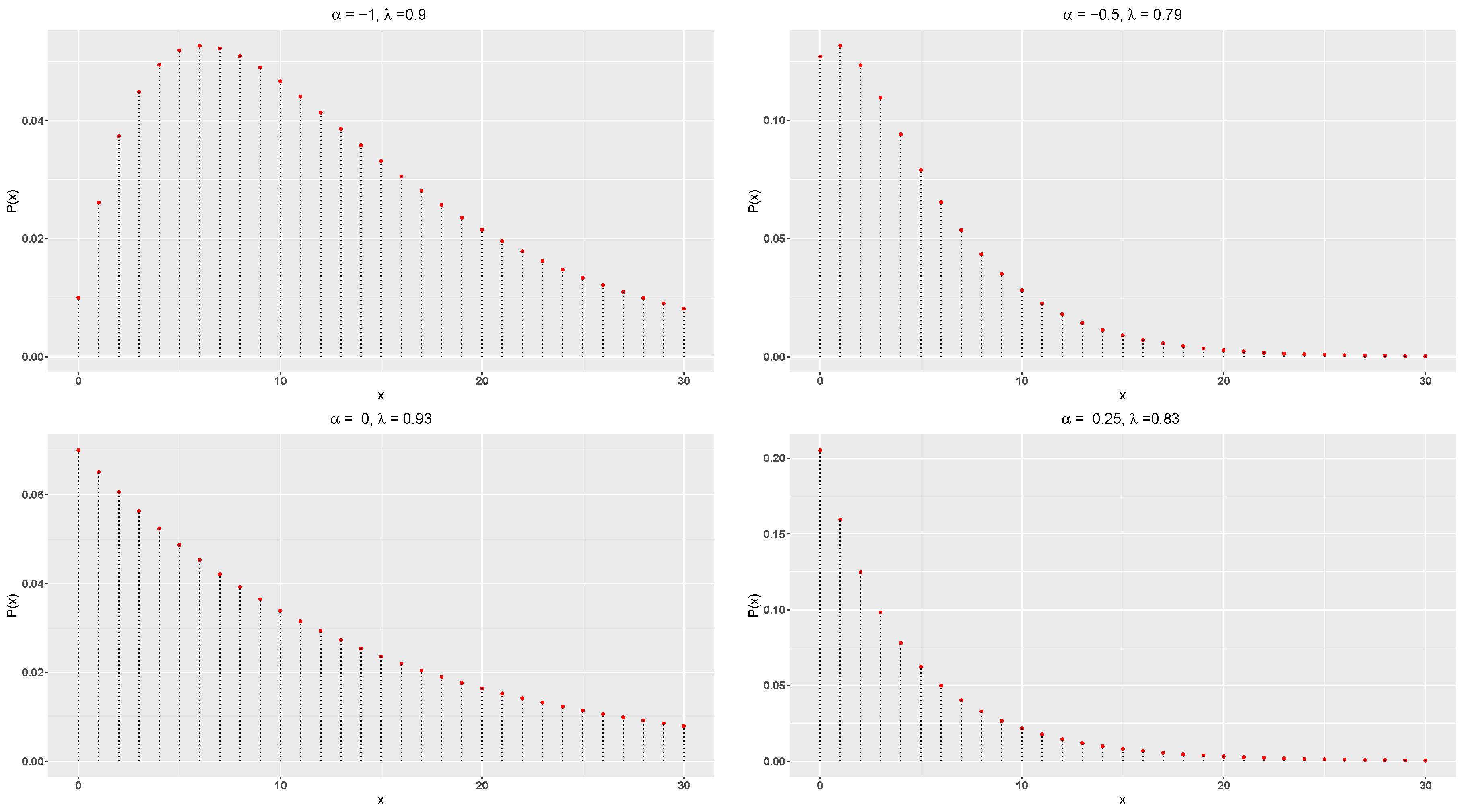
The pmf of the DME distribution always decreases for $-0.3<\alpha <1$ since

$$p^{\prime }\left(x\right)=(1-\alpha )(1-\lambda ){\lambda }^{x}log\left(\lambda \right)+2\alpha {\lambda }^{2x}(1-{\lambda }^2)log\left(\lambda \right)<0.$$

(2.5)

Figure 1 displays the pmf plots of the DME distribution. It can be seen that the DME distribution is rightly skewed and unimodal.

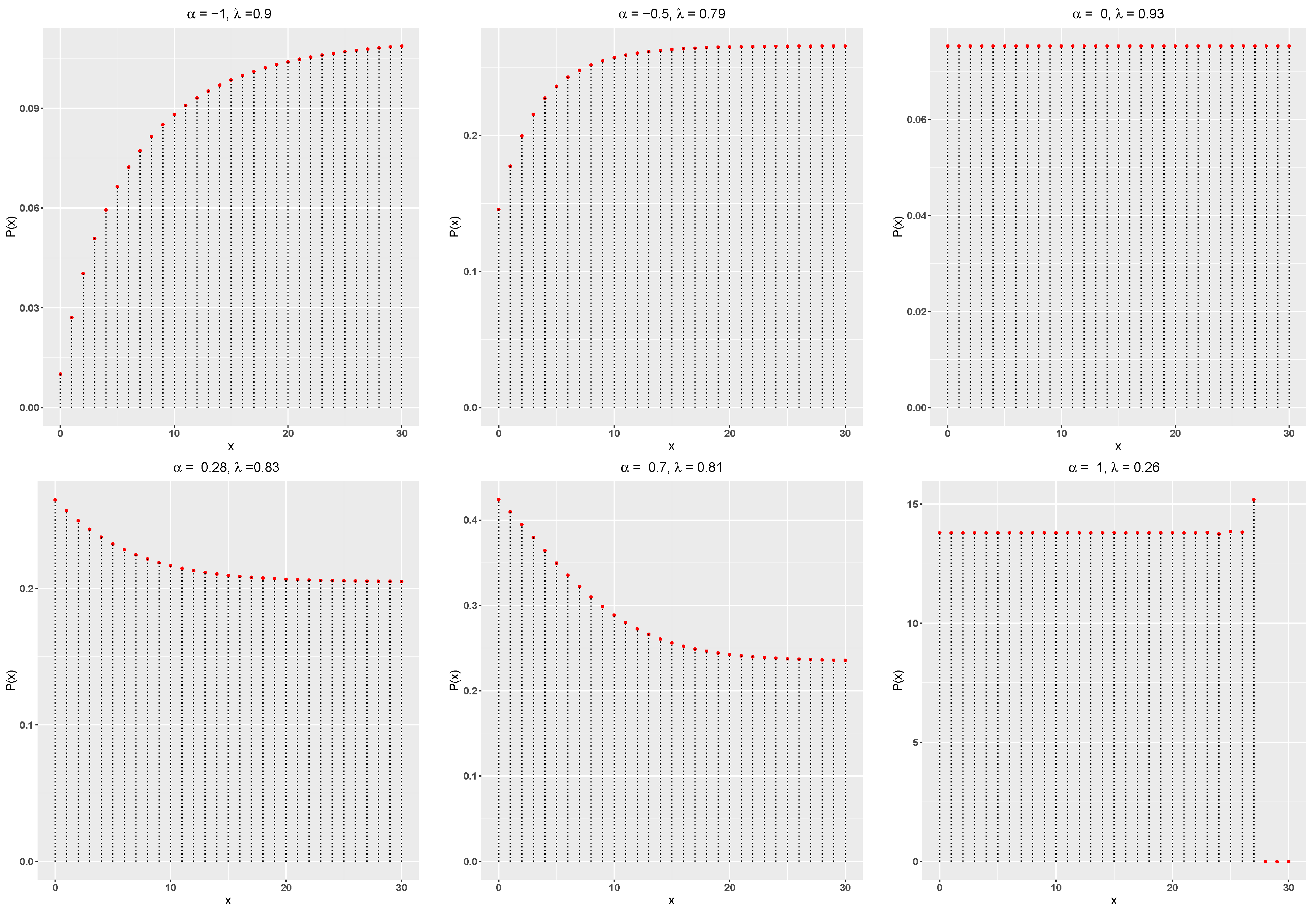
The hazard rate function of the DME distribution is defined as

$$h\left(x\right)=\frac{(1-\lambda )(1+\alpha ({\lambda }^x+{\lambda }^{(1+x)}-1))}{\lambda -\alpha \lambda +\alpha {\lambda }^{(2+x)}}.$$

(2.6)

Figure 2 showcases the DME distribution’s hazard rate function, illustrating its ability to exhibit increasing, decreasing and constant behaviours.

3. Statistical Properties

This section discusses the DME distribution’s moment generating functions, skewness, and kurtosis.

3.1. Moments, Skewness and Kurtosis

Using (2.3), the moment generating function of the DME distribution is given by

$$M_X\left(t\right)=\frac{(1-\lambda )((e^t-1)\alpha \lambda +e^t{\lambda }^2-1)}{\left((1-e^t\lambda )(e^t{\lambda }^2-1)\right)}.$$

(3.1)

The $r^{th}$ moment about the origin of X is given by,

$${\mu }_r^{\prime }=\sum _{x=0}^{\infty }{x}^r{\lambda }^x(1-\lambda )(1-\alpha )+\alpha {\lambda }^{2x}(1-{\lambda }^2),r=1,2,3,..$$

(3.2)

Using (3.2), the first four raw moments of the DME distribution are given by

$$\begin{array}{ccc}\hfill {\mu }_1^{\prime }& =& \frac{(1-\alpha +\lambda )\lambda }{(1-{\lambda }^2)},\hfill \\ \hfill {\mu }_2^{\prime }& =& \frac{\lambda ({(1+\lambda )}^3-\alpha (1+2\lambda +3{\lambda }^2))}{{(1-{\lambda }^2)}^2},\hfill \\ \hfill {\mu }_3^{\prime }& =& \frac{\lambda ({(1+\lambda )}^3(1+4\lambda +{\lambda }^2)-\alpha (1+6\lambda +16{\lambda }^2+12{\lambda }^3+7{\lambda }^4))}{{(1-{\lambda }^2)}^3},\hfill \\ \hfill {\mu }_4^{\prime }& =& \frac{\lambda ({(1+\lambda )}^5(1+10\lambda +{\lambda }^2)-\alpha (1+14\lambda +61{\lambda }^2+104{\lambda }^3+115{\lambda }^4+50{\lambda }^5+15{\lambda }^6))}{{(1-{\lambda }^2)}^4}.\hfill \end{array}$$

(3.3)

Then, the central moments are obtained as,

$$\begin{array}{ccc}\hfill {\mu }_2& =& \frac{\lambda ({(1+\lambda )}^2-{\alpha }^2\lambda -\alpha (1+{\lambda }^2))}{{(1-{\lambda }^2)}^2},\hfill \\ \hfill {\mu }_3& =& \frac{\lambda ({(1+\lambda )}^3(1+3\lambda -4{\lambda }^2)-{\alpha }^2\lambda (1+6\lambda +11{\lambda }^2)-\alpha (1+4\lambda +2{\lambda }^2-16{\lambda }^3-9{\lambda }^4))}{{(1-{\lambda }^2)}^3}.\hfill \end{array}$$

(3.4)

$$\begin{array}{ccc}\hfill {\mu }_4& =& \frac{\lambda ({(1+\lambda )}^4(1+7\lambda +{\lambda }^2)-3{\alpha }^4{\lambda }^3-6{\alpha }^3({\lambda }^2+{\lambda }^4)-2{\alpha }^2\lambda (2+3\lambda +14{\lambda }^2+3{\lambda }^3+2{\lambda }^4))}{{(1-{\lambda }^2)}^4}\hfill \\ \hfill & & -\frac{\lambda \left(\alpha (1+6\lambda +23{\lambda }^2+12{\lambda }^3+23{\lambda }^4+6{\lambda }^5+{\lambda }^6)\right)}{{(1-{\lambda }^2)}^4}.\hfill \end{array}$$

The moment measures of skewness and kurtosis are given by ,

$$\begin{array}{cc}\hfill S\left(x\right)& =\frac{{({(1+\lambda )}^3(-1-3\lambda +4{\lambda }^2)+{\alpha }^2\lambda (1+6\lambda +11{\lambda }^2)+\alpha (1+4\lambda +2{\lambda }^2-16{\lambda }^3-9{\lambda }^4))}^2}{\lambda {({(1+\lambda )}^2-{\alpha }^2\lambda -\alpha (1+{\lambda }^2))}^3}\hfill \end{array}$$

(3.5)

$$\begin{array}{cc}\hfill K\left(x\right)& =\frac{{(1+\lambda )}^4(1+7\lambda +{\lambda }^2)-3{\alpha }^4{\lambda }^3-6{\alpha }^3({\lambda }^2+{\lambda }^4)-2{\alpha }^2\lambda (2+3\lambda +14{\lambda }^2+3{\lambda }^3+2{\lambda }^4)}{\lambda {({\alpha }^2\lambda -{(1+\lambda )}^2+\alpha (1+{\lambda }^2))}^2}\hfill \\ \hfill & -\frac{\alpha (1+6\lambda +23{\lambda }^2+12{\lambda }^3+23{\lambda }^4+6{\lambda }^5+{\lambda }^6)}{\lambda {({\alpha }^2\lambda -{(1+\lambda )}^2+\alpha (1+{\lambda }^2))}^2}.\hfill \end{array}$$

(3.6)

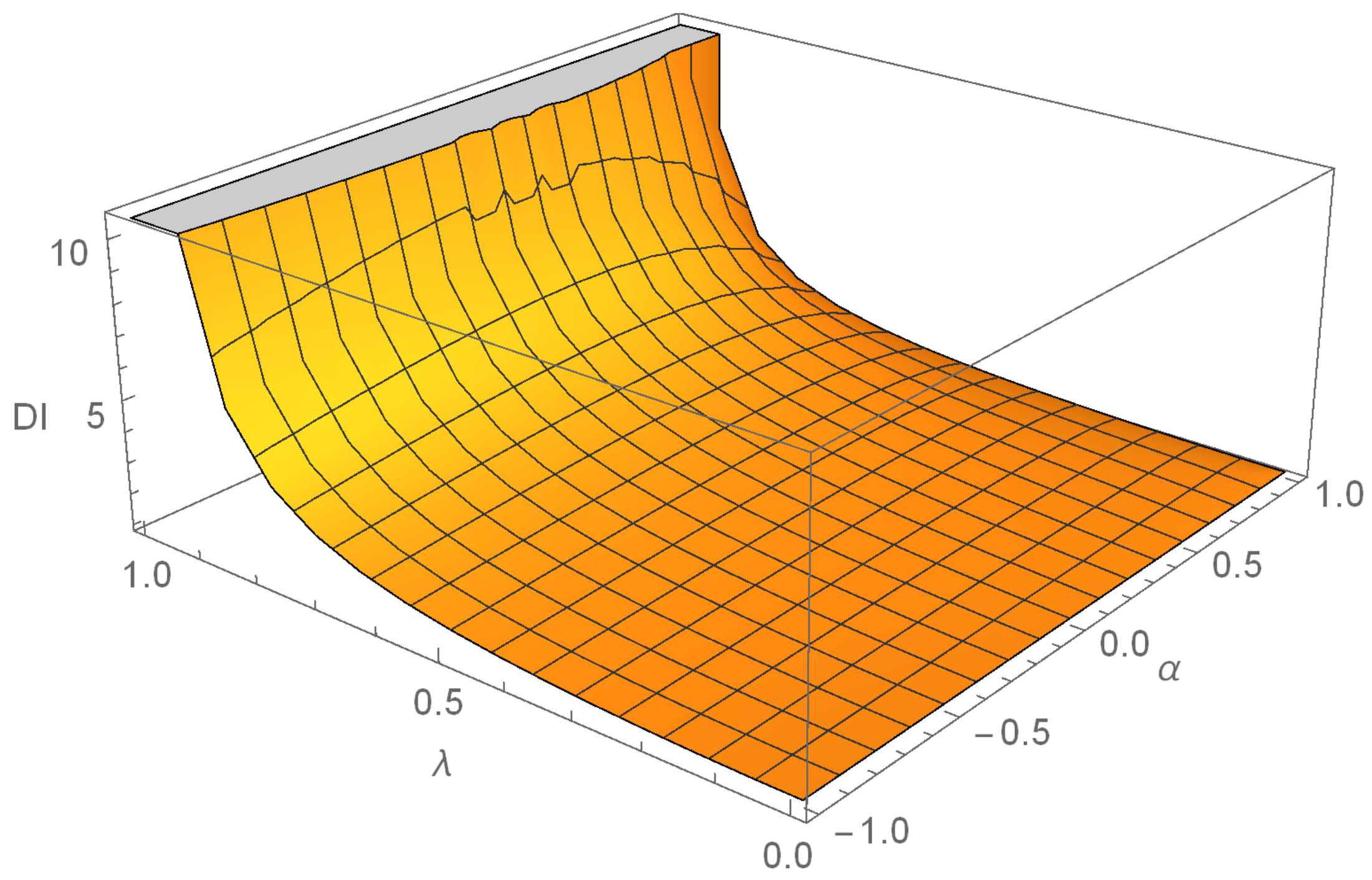
The dispersion index (DI) of the DME distribution is given by,

$$DI=\frac{{\alpha }^2\lambda -{(1+\lambda )}^2+\alpha (1+{\lambda }^2)}{(\lambda -1)(1+\lambda )(1-\alpha +\lambda )}.$$

(3.7)

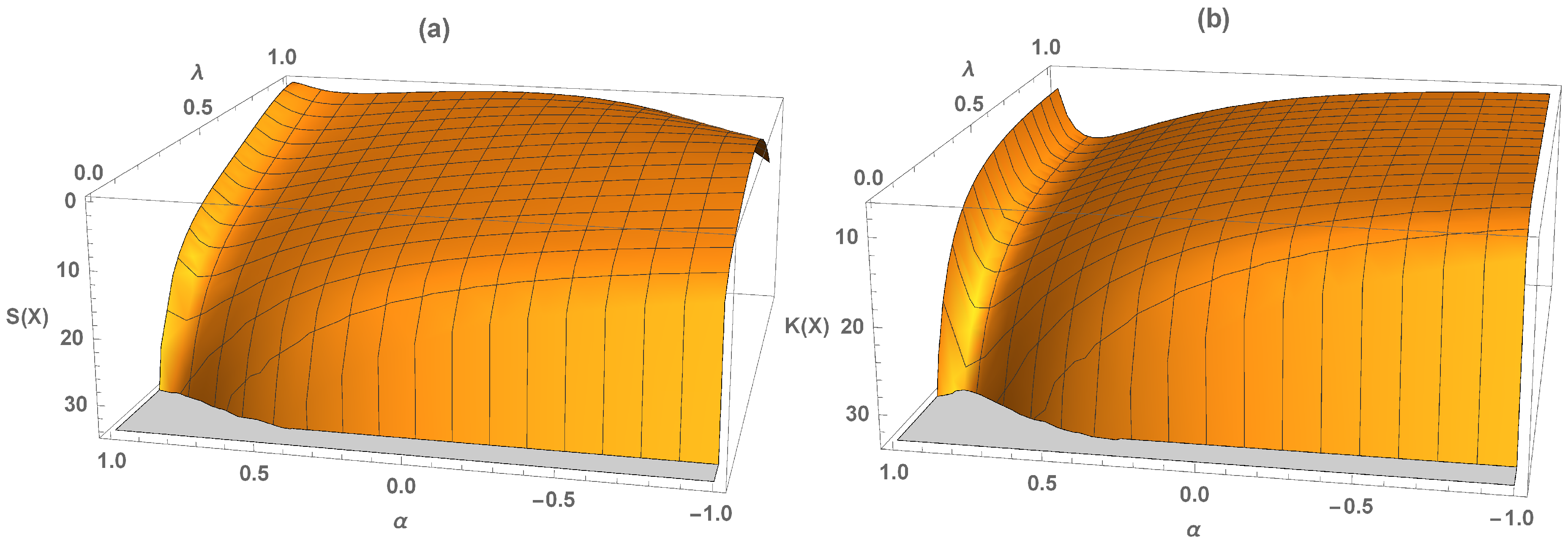
The 3D plots in Figure 3 illustrate the graphical representation of skewness and kurtosis, indicating the right-skewed leptokurtic behavior of the DME distribution. From the 3D plot of DI given in Figure 4, we can see that it is always greater than 1. Table 1 illustrates the variation in mean, variance, DI, skewness and kurtosis with respect to the values of $\alpha$ and $\lambda$.

4. Estimation

This section describes various methods to estimate parameters for the DME distribution. The methods under consideration include maximum likelihood, ordinary least squares, Anderson-Darling and Cramér–von Mises.

4.1. Maximum likelihood estimation

Let $x=(x_1,x_2,x_3,...,x_n)$ be a sample of size n from DME distribution. Then the likelihood function (L) is given by,

$$L(\alpha ,\lambda )=\prod _{i=1}^n\{{\lambda }^{x_i}(1-\lambda )(1-\alpha )+\alpha {\lambda }^{2x_i}(1-{\lambda }^2)\}.$$

(4.1)

Since $\frac{\partial L(\alpha ,\lambda )}{\partial \alpha }=0$ and $\frac{\partial L(\alpha ,\lambda )}{\partial \lambda }=0$ failed to give explicit solutions, the maximum likelihood estimates (MLEs) are obtained by direct maximization of (4.1) using numerical methods.

4.2. Least square estimation

Let $x_{i:n}$ be the $i^{th}$ order statistic of the sample $x=(x_1,x_2,x_3,..,x_n)$. The least square estimates (LSEs) of the parameters are obtained by minimising the following equation:

$$LSE(\alpha ,\lambda )=\sum _{i=1}^n{\left[\left\{(1-{\lambda }^{(1+x_{i:n})})(1+\alpha {\lambda }^{(1+x_{i:n})})\right\}-\frac{i}{n+1}\right]}^2.$$

(4.2)

4.3. Anderson–Darling Estimation

The Anderson–Darling estimates (ADEs) are obtained using minimising the following equation:

$$\begin{array}{cc}\hfill ADE(\alpha ,\lambda )=-n-\frac{1}{n}\sum _{i=1}^n(2i-1)[& log\left((1-{\lambda }^{(1+x_{i:n})})(1+\alpha {\lambda }^{(1+x_{i:n})})\right)\hfill \\ \hfill & +log\left(1(1-{\lambda }^{(1+x_{i:n})})(1+\alpha {\lambda }^{(1+x_{i:n})})\right)].\hfill \end{array}$$

(4.3)

4.4. Cramér–von Mises Estimation

The Cramér–von Mises estimates (CMEs) are obtained by minimising the following equation:

$$CVE(\alpha ,\lambda )=\frac{1}{12n}+{\left[\left\{(1-{\lambda }^{(1+x_{i:n})})(1+\alpha {\lambda }^{(1+x_{i:n})})\right\}-\frac{2i-1}{2n}\right]}^2.$$

(4.4)

4.5. Simulation

The model performance is analysed by means of a simulation study. The simulation is carried out by taking $N=1,000$ replications for sample of sizes n = 100, 200, 300, 400 and 500 with different parameter values. The following quantities are computed.

• Average bias (Bias),
  Bias($\widehat{a}$)=$\frac{1}{N}{\displaystyle \sum _{i=1}^N}({\widehat{a}}_i-a),$ where ${\widehat{a}}_i$ is the $i^{th}$ estimate of the parameter a, $a\in \{\alpha ,\lambda \}$ for $i=1,2,\dots ,N$.
• Root mean square error (RMSE),
  RMSE$\left(\widehat{a}\right)=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{({\widehat{a}}_i-a)}^2}.$

Table 2 lists the Bias and RMSE for the MLEs, LSEs, ADEs and CMEs of the parameters $\alpha$ and $\lambda$. We can see that, as n increases, Bias and RMSE decrease. We can conclude that the ML estimation performs very well and is appropriate for small and large sample sizes.

5. Data analysis

We consider the corn-borer data, consisting of the number of European corn-borer larvae pyrausta in the field (Bodhisuwan and Sangpoom (2016)). This data set is taken to compare the performance of the DME distribution with other competitive distributions such as the Poisson distribution, the discrete Burr (DB) distribution (Krishna and Pundir (2009)), the discrete Gumbel (DG) distribution (Chakraborty and Chakravarty (2014)), the discrete log-logistic (DLL) distribution (Para and Jan (2016)), the discrete Bilal (DBL) distribution (Altun et al. (2022)), the discrete Pareto (DPR) distribution (Krishna and Pundir (2009)) and the discrete Rayleigh (DR) distribution (Roy (2004)).

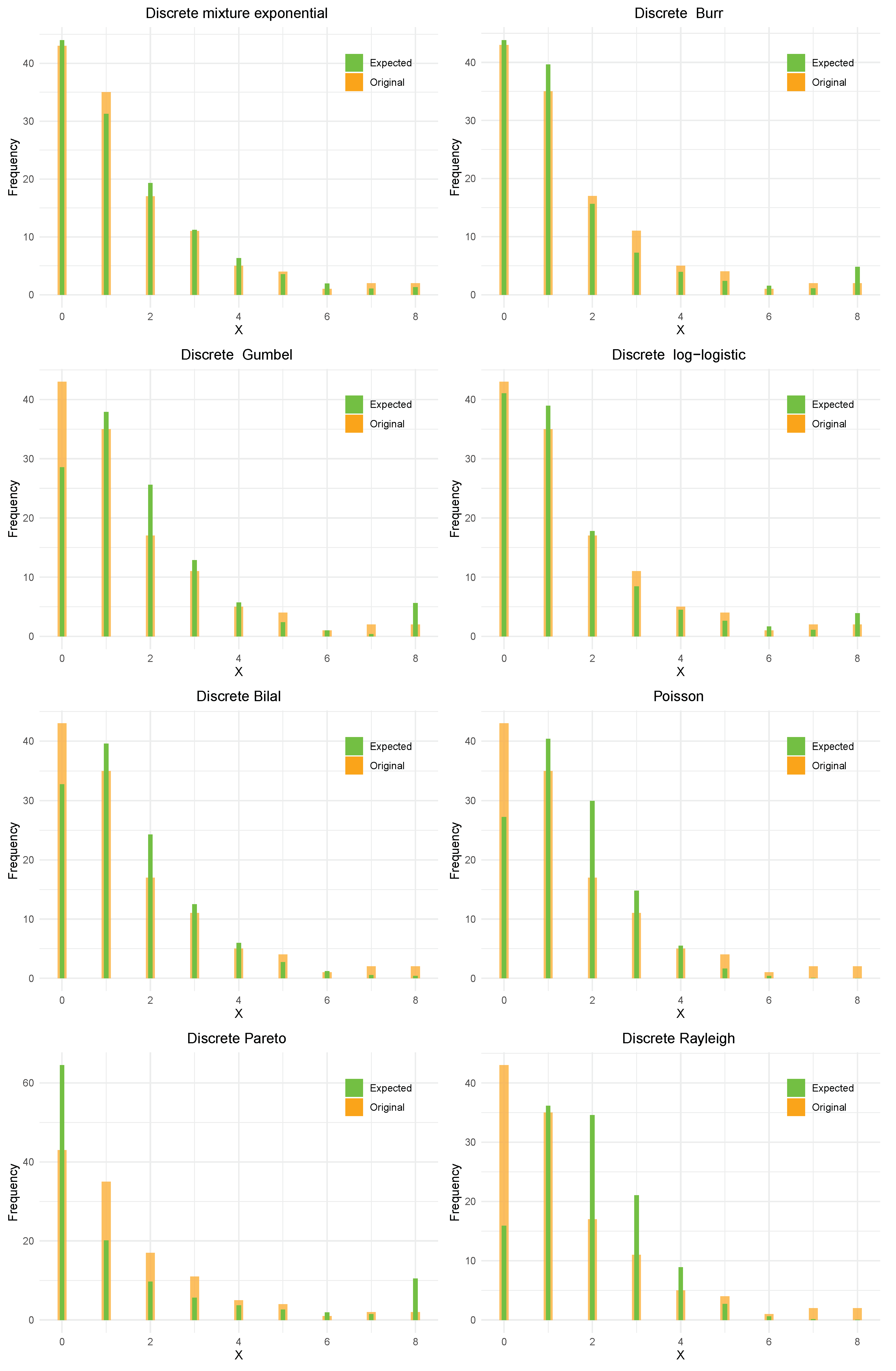
The unknown parameters are obtained using the ML method, along with the standard error (SE) and 95% confidence interval (CI) for various considered models. Model performance is assessed using some widely accepted information criteria and goodness-of-fit statistics. Smaller values of the Akaike information criterion (AIC) and Bayesian information criterion (BIC), as well as larger log-likelihood (log L) values, indicate the adequacy of the model. Furthermore, we employ a ${\chi }^2$ test to evaluate the goodness-of-fit for each fitted distribution, with a small ${\chi }^2$ value and a large p-value indicating a good fit.

Table 3 makes it abundantly clear that the DME distribution is the best of the competitive models under consideration because it has the lowest AIC and BIC, the highest log L and p-value, repectively. Table 4 gives the observed and expected frequencies of corn-borer data under various distributions. Figure 5 indicates better modelling of DME distribution over all the models considered.

6. INAR(1) process with discrete mixture exponential innovations

In this section, we develop the INAR(1) process with innovations following the DME distribution. We consider INAR(1) time series models using the binomial thinning operator with independent Bernoulli counting series random variables. Hereafter, the introduced INAR(1) process with the DME distributed innovations shall be denoted as INAR(1)DME process.

6.1. INAR(1)DME process

The INAR(1)DME process is given by

$$X_t=p\circ X_{t-1}+{ϵ}_t,t\ge 1,$$

(6.1)

where "∘" is the binomial thinning operator, $\left\{{ϵ}_t\right\}$ is a sequence of independent and identically distributed (iid) random variables from DME($\alpha ,\lambda$) distribution and ${ϵ}_t$ is independent of Bernoulli counting process $\left\{B_i\right\}$ and $X_m$ for all $m\le t$. The binomial thinning operator is generated by counting series of independent Bernoulli distributed random variables and is defined as

$$p\circ X=\sum _{i=1}^X{B}_i,p\in (0,1),$$

(6.2)

where X is a non-negative integer-valued random variable and $\left\{B_i\right\}$ is a sequence of independent and identically distributed random variables with Bernoulli $\left(p\right)$ distribution and is independent of X.

The one-step transition probability of the INAR(1) process is given by,

$$P\left(X_t=k\mid X_{t-1}=l\right)=\sum _{i=0}^{min(k,l)}\left(\genfrac{}{}{0pt}{}{l}{i}\right)p^i{(1-p)}^{l-i}P\left({ϵ}_t=k-i\right),k,l\ge 0.$$

(6.3)

The one-step transition probability of the INAR(1)DME process is given by,

$$P\left(X_t=k\mid X_{t-1}=l\right)=\sum _{i=0}^{min(k-l)}\left(\genfrac{}{}{0pt}{}{l}{i}\right)p^i{(1-p)}^{l-i}\{{\lambda }^{k-i}(1-\lambda )(1-\alpha )+\alpha {\lambda }^{2k-i}(1-{\lambda }^2)\}.$$

(6.4)

Also, the stationary marginal density of $\left\{X_t\right\}$ is given by,

$$\begin{array}{cc}\hfill P\left(X_t=k\right)& =\sum _{l=0}^{\infty }P\left(X_t=k\mid X_{t-1}=l\right)P\left(X_{t-1}=l\right)\hfill \\ \hfill & =\sum _{l=0}^{\infty }\sum _{i=0}^{min(k-l)}\left(\genfrac{}{}{0pt}{}{l}{i}\right)p^i{(1-p)}^{l-i}\{{\lambda }^{k-i}(1-\lambda )(1-\alpha )+\alpha {\lambda }^{2k-i}(1-{\lambda }^2)\}.\hfill \end{array}$$

(6.5)

From Wei (2018), the mean and variance of $\left\{X_t\right\}$ can be computed using (3.3) and (3.4) as,

$$\begin{array}{ccc}\hfill E\left(X_t\right)& =& {\mu }_X=\frac{(1-\alpha +\lambda )\lambda }{(1-{\lambda }^2)(1-p)},\hfill \end{array}$$

(6.6)

$$\begin{array}{ccc}\hfill V\left(X_t\right)& =& \frac{\lambda \{\left[(1+p(1-\lambda )){(1+\lambda )}^2\right]-{\alpha }^2\lambda -\alpha (1+p+{\lambda }^2-p{\lambda }^2)\}}{(1-p^2){(1-{\lambda }^2)}^2}.\hfill \end{array}$$

(6.7)

Then, the DI of $\left\{X_t\right\}$ is given by,

$$D{I}_{X_t}=\frac{\left[(1+p(1-\lambda )){(1+\lambda )}^2\right]-{\alpha }^2\lambda -\alpha (1+p+{\lambda }^2-p{\lambda }^2)}{(1+p)(1-{\lambda }^2)(1-\alpha +\lambda )}.$$

(6.8)

Table 5 provides the DI of $\left\{X_t\right\}$ across different parameter configurations, indicating the model’s ability to accommodate over-dispersed data. The one-step-ahead conditional mean and variance of the INAR(1)DME process are given by,

$$\begin{array}{ccc}\hfill E\left(X_t\right|X_{t-1})& =& p{X}_{t-1}+\frac{(1-\alpha +\lambda )\lambda }{(1-{\lambda }^2)},\hfill \end{array}$$

(6.9)

$$\begin{array}{ccc}\hfill V\left(X_t\right|X_{t-1})& =& p(1-p)X_{t-1}+\frac{\lambda ({(1+\lambda )}^2-{\alpha }^2\lambda -\alpha (1+{\lambda }^2))}{{(1-{\lambda }^2)}^2}.\hfill \end{array}$$

(6.10)

6.2. Estimation

6.2.1. Conditional maximum likelihood

The knowledge of the transition probabilities is sufficient for the creation of the likelihood function in the conditional ML (CML) technique. For a given sample $X_1,X_2,...,X_n$ from the INAR(1)DME process, the conditional log-likelihood function is given by,

$$l(p,\alpha ,\lambda )=\sum _{t=2}^{n}P\left(X_t=x_t\mid X_{t-1}=x_{t-1}\right),$$

(6.11)

where $X_1$ is fixed, and $P\left(X_t=x_t\mid X_{t-1}=x_{t-1}\right)$ is given by (6.4). The CML estimates (CMLEs) of the parameters p, $\alpha \mathrm{and}\lambda$ are obtained by maximizing (6.11) using the optim function in R software.

6.2.2. Conditional least square estimation

The conditional least square estimates (CLSEs) of parameters p, $\alpha \mathrm{and}\lambda$ are obtained by minimising the following equation,

$$L(p,\alpha ,\lambda )=\sum _{t=2}^n{(x_t-E\left(X_t\right|X_{t-1}=x_{t-1}))}^2.$$

(6.12)

6.3. Simulation

A simulation study was performed to assess the performance of the CML and CLS estimation methods under the INAR(1)DME process. The simulation is carried out by taking $N=$ 1,000 replications for samples of sizes n = 50, 100, 150, 200, and 250 with different parameter values, and the following quantities were computed.

• Average bias (Bias) of the parameters,
  Bias($\widehat{a}$)=$\frac{1}{N}{\displaystyle \sum _{i=1}^N}({\widehat{a}}_i-a),$ where $a_i$ is the $i^{th}$ estimate of $a\in \{p,\alpha ,\lambda \}.$
• Root mean square error (MSE) of the parameters,
  RMSE$\left(\widehat{a}\right)=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{({\widehat{a}}_i-a)}^2}.$

From Table 6, we can see that as n increases, Bias and RMSE decrease. We can conclude that the CML estimation method performs very well and is appropriate for small and large sample sizes.

7. Control charts for monitoring mean of the INAR(1)DME process

This section explores an efficient control chart for monitoring the INAR(1)DME process. In INAR(1) processes, upward shifts in the process mean indicate a collective rise in associated factors for entities, such as unemployment rate, defect percentage, and disease spread. Identification and timely reporting of such shifts are typically vital. Therefore, with a focus on practical applications, this paper investigates the mean upward shift within the INAR(1)DME process.

We construct the upper-sided control chart to focus exclusively on detecting upward shifts in ${\mu }_X$ as it is directly linked to process deterioration. The main purpose is to detect quickly and accurately a change in the ${\mu }_X$; it is more natural to monitor the process of $\left\{X_t\right\}$ directly by taking care of the impact of autocorrelation. A process is considered in-control when it adheres to a specified model. Conversely, a process is deemed out of control when the parameters within the model change rather than the model itself undergoing a change. When the process is in-control, the parameter values of the INAR(1)DME process will be denoted as $p_0$, ${\alpha }_0$ and ${\lambda }_0$. An increasing shift in ${\mu }_X$ may occur if one of the parameters p, $\alpha$ and $\lambda$ have changed appropriately.

We observe from Table 7 that ${\mu }_X$ is affected by variations in the parameter $\alpha$ within the INAR(1)DME process, resulting in a higher value of ${\mu }_X$. To effectively monitor INAR(1) processes, we employ CUSUM and EWMA control charts and assess the efficiency of these monitoring techniques.

7.1. The CUSUM chart

Initially proposed by Page (1961), the CUSUM chart operates on the fundamental principle of the sequential probability ratio test. Its primary objective is to gather and accumulate information from sample data, thus magnifying the impact of minor process deviations. Numerous studies have extensively demonstrated the effectiveness of the CUSUM chart in monitoring time series comprising of integer values, including Poisson INAR(1) by Wei and Testik (2009) and Wei and Testik (2011), geometrically inflated Poisson INAR(1) by Li et al. (2022), new geometric INAR(1) by Li et al. (2016a) and zero-inflated Poisson INAR(1) by Rakitzis et al. (2017).

Here, we devise the CUSUM control charts due to their sensitivity in detecting small shifts. Furthermore, CUSUM charts also have known optimality properties when detecting a sustained shift from a known in-control distribution to a specified out-of-control distribution (Wei and Testik (2009)).

From Wei and Testik (2009), let $C_0=c_0,c_0\in N_0$. A CUSUM statistic with reference value k is obtained as,

$$C_t=max(0,X_t-k+C_{t-1}),t=1,2,\dots$$

(7.1)

Here $c_o\ge 0$ is the starting value. For ${\mu }_X<k<h$, the monitoring statistics $\left\{C_t\right\}$ are plotted on a CUSUM chart with control region [0, h], where h is the upper control limit. The INAR(1)DME process is considered as being in-control unless $C_t>h$. The reference value k prevents the chart from drifting towards control limits during in-control processes and offers the ability to fine-tune chart sensitivity to specific shifts in the process mean.

7.2. The EWMA chart

Initially proposed by Roberts (2000), the EWMA chart operates on the fundamental principle of giving the highest weight to the nearest samples in the time series, while previous samples contribute minimally. The EWMA chart is useful for detecting persistent shifts for INAR processes (Wei (2009)).

From Wei (2011), let $Q_0=q_0,q_0\in \{0,1,...,u-1\}$ and $\theta \in (0,1]$. An EWMA statistic of the INAR(1) process is given by,

$$Q_t=round(\theta X_t+(1-\theta )Q_{t-1}),t\in N_0,$$

(7.2)

where $round\left(x\right)=z$ if and only if the integer $z\in (x-1/2,x+1/2]$. Let $u\in N$ with $u>1$. The statistics $Q_t$ are plotted on an EWMA chart with control region $[1,u]$, where u is the upper control limit. The process is considered as being in-control unless an out-of-control signal $Q_t\ge u$ is triggered.

7.3. Performance of the INAR(1)DME control charts

The average run length (ARL) is a commonly used measure to evaluate the effectiveness of a control chart in statistical process control. It represents the expected number of data points plotted on the control chart before it signals an out-of-control condition. Two specific types of ARL are considered: ${\mathrm{ARL}}_0$, also known as in-control ARL, measures the number of data points plotted from the beginning of monitoring until a false alarm is triggered. On the other hand, ${\mathrm{ARL}}_1$ referred to as out-of-control ARL, quantifies the number of data points plotted from the start of a process shift until the chart detects that shift. To have an effective control chart, a high ${\mathrm{ARL}}_0$ combined with a small ${\mathrm{ARL}}_1$ is essential.

7.3.1. ARL of CUSUM chart

For a given $C_0=c_0$, the values of $(k,h)$ are chosen to ensure that the ${\mathrm{ARL}}_0$ closely matches a specified value. As $\{X_t,C_t\}$ of the INAR(1)DME process forms a bivariate Markov chain, the Markov chain approach introduced in Wei and Testik (2009) is used here for computing ARL. To offer a comprehensive overview, the computational approach is briefly outlined as follows.

Let us consider the case where $h,k,c_0\in N_0$. Whenever $X_t>k+h$, it leads to an out-of-control signal since $C_t$ exceeds h if and only if $X_t-k+C_{t-1}\ge h$. Hence, the attainable in-control range of $(X_t,C_t)$ needs to be restricted. From Wei and Testik (2009), under the CUSUM chart, the set of attainable in-control values for the bivariate Markov process $\{X_t,C_t\}$ is given by,

$$\mathcal{CR}=\left\{\right(x,i\left)\right|0\le i\le h-1,max(0,i+k-h+1)\le x\le i+k\},$$

(7.3)

which is of size

$$\left|\mathcal{CR}\right|=\frac{1}{2}(h-k)(h+k+1)+hk.$$

(7.4)

The above arguments can also be extended if $h,k$ and $c_0$ are permitted to assume values from the set $\{r/s|r\in {\mathbb{N}}_0\}$, where the common denominator $s\in \mathbb{N},s>1$.

From Li et al. (2022), the transition probability matrix of $(X_t,C_t)$ is expressed as,

$$Q^{\top }\triangleq {\left(p(n,j|m,i)\right)}_{(n,j),(m,i)\in \mathcal{CR}}$$

(7.5)

where

$$\begin{array}{cc}\hfill p(n,j\mid m,i)& \triangleq P\left(X_t=n,Q_t=j\mid X_{t-1}=m,C_{t-1}=i\right)\hfill \\ & =P\left(Q_t=j\mid X_t=n,X_{t-1}=m,C_{t-1}=i\right)P\left(X_t=n\mid X_{t-1}=m,C_{t-1}=i\right)\hfill \\ & ={\delta }_{j,max(0,n-k+i)}P\left(X_t=n\mid X_{t-1}=m\right).\hfill \end{array}$$

The initial probabilities are,

$$\begin{array}{cc}\hfill p\left(m,i\mid c_0\right)& \triangleq P\left(X_1=m,C_1=i\mid C_0=c_0\right)\hfill \\ & =P\left(C_1=i\mid X_1=m,C_0=c_0\right)P\left(X_1=m\mid C_0=c_0\right)\hfill \\ & ={\delta }_{i,max\left(0,m-k+c_0\right)}P\left(X_1=m\right),\hfill \end{array}$$

where ${\delta }_{x,y}$ denotes the Kronecker delta, $P\left(X_t=i\mid X_{t-1}=j\right)$ and $P\left(X_1=m\right)$ are given by (6.4) and (6.5) respectively.

Also, the conditional probability that the run length of $\left\{X_t,Q_t\right\}$ equals r is given by

$$p_{m,i}\left(r\right)\triangleq P\left(\left(X_{r+1},C_{r+1}\right)\notin \mathcal{CR},\left(X_r,C_r\right),\dots ,\left(X_2,C_2\right)\in \mathcal{CR}\mid \left(X_1,C_1\right)=(m,i)\right),$$

where $(m,i)\in \mathcal{CR}$.

Let the vector ${\mu }_{\left(k\right)}$ denote the $k^{th}$ factorial moments, given by,

$${\mu }_{{\left(k\right)}_{m,i}}\triangleq \sum _{r=1}^{\infty }r\cdots (r-k+1)p_{m,i}\left(r\right),k\ge 1,$$

(7.6)

where,

$$\begin{array}{cc}\hfill p_{m,i}\left(r\right)& =\sum _{(n,j)\in \mathcal{CR}}{p}_{n,j}(r-1)p(n,j\mid m,i).\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill {\mu }_{{\left(1\right)}_{m,i}}& =1+\sum _{(n,j)\in \mathcal{CR}}p(n,j\mid m,i){\mu }_{{\left(1\right)}_{n,j}}.\hfill \end{array}$$

That is, ${\mu }_{\left(1\right)}$ is the solution of the linear equation $(I-Q){\mu }_{\left(1\right)}=1$. The dimension of Q and $\mu$ is determined by (7.4). Hence, the ARL depending on the initial choice $C_0=c_0$, is defined as,

$$ARL\left(c_0\right)=1+\sum _{(m,i)\in \mathcal{CR}}{\mu }_{{\left(1\right)}_{m,i}}p\left(m,i\mid c_0\right).$$

7.3.2. ARL of EWMA chart

For a given $Q_0=q_0$, the values of $(\theta ,l,u)$ are chosen to ensure that the ${\mathrm{ARL}}_0$ closely matches a specified value. Subsequently, the ARL values are calculated using the model parameters and EWMA chart designs. As $\{X_t,Q_t\}$ of the INAR(1)DME process forms a bivariate Markov chain, the Markov chain approach introduced in Wei (2011) is used here for computing ARL. To offer a comprehensive overview, the computational approach is briefly outlined as follows.

Let $\left[x\right]$ denote the smallest integer value greater than or equal to x. From Wei (2011), under the EWMA chart, the set of attainable in-control values for the bivariate Markov process $\{X_t,Q_t\}$ is given by,

$$\begin{array}{cc}\hfill \mathcal{I}(u,\theta )=& \left\{(n,q)\in \left\{0,\dots ,\left[\frac{1}{\theta }\left(u-\frac{1}{2}\right)-1\right]\right\}\times \{0,\dots ,u-1\}\mid \right.\hfill \\ \hfill & \left.\left[\frac{1}{\theta }\left(q-\frac{1}{2}-(1-\theta )(u-1)\right)\right]\le n\le \left[\frac{1}{\theta }\left(q+\frac{1}{2}\right)-1\right]\right\}.\hfill \end{array}$$

(7.7)

The transition and initial probabilities of $\{X_t,Q_t\}$ is given by,

$$Q^{\top }\triangleq {\left(p(n,j|m,i)\right)}_{(n,j),(m,i)\in \mathcal{I}(u,\theta )},$$

(7.8)

where

$$\begin{array}{cc}\hfill p(n,j\mid m,i)& \triangleq P\left(X_t=n,Q_t=j\mid X_{t-1}=m,Q_{t-1}=i\right)\hfill \\ & ={\mathbf{I}}_{[j-1/2;j+1/2)}(\theta n+(1-\theta )i)P\left(X_t=n\mid X_{t-1}=m\right).\hfill \end{array}$$

The initial probabilities are,

$$\begin{array}{cc}\hfill p\left(m,i\mid q_0\right)& \triangleq P\left(X_1=m,Q_1=i\mid Q_0=q_0\right)\hfill \\ & ={\mathbf{I}}_{[j-1/2;j+1/2)}(\theta n+(1-\theta )q_0)P\left(X_1=m\right),\hfill \end{array}$$

where ${\mathbf{I}}_A$ denote the indicator function.

Also, the conditional probability that the run length of $\left\{X_t,Q_t\right\}$ equals r is given by

$$p_{m,i}\left(r\right)\triangleq P\left(\left(X_{r+1},Q_{r+1}\right)\notin \mathcal{I}(u,\theta ),\left(X_r,Q_r\right),\dots ,\left(X_2,Q_2\right)\in \mathcal{I}(u,\theta )\mid \left(X_1,Q_1\right)=(m,i)\right),$$

where $(m,i)\in \mathcal{I}(u,\theta )$.

Let the vector ${\mu }_{\left(k\right)}$ denote the $k^{th}$ factorial moments, given by,

$${\mu }_{{\left(k\right)}_{m,i}}\triangleq \sum _{r=1}^{\infty }r\cdots (r-k+1)p_{m,i}\left(r\right),k\ge 1,$$

(7.9)

where

$$\begin{array}{c}{p}_{m,i}\left(r\right)={\displaystyle \sum _{(n,j)\in \mathcal{I}(u,\theta )}}{p}_{n,j}(r-1)p(n,j\mid m,i).\end{array}$$

Then,

$$\begin{array}{c}{\mu }_{{\left(1\right)}_{m,i}}=1+{\displaystyle \sum _{(n,j)\in \mathcal{I}(u,\theta )}}p(n,j\mid m,i){\mu }_{{\left(1\right)}_{n,j}}.\end{array}$$

That is, ${\mu }_{\left(1\right)}$ is the solution of the linear equation $(I-Q){\mu }_{\left(1\right)}=1$.

Hence, the $ARL$ depending on the initial choice $Q_0=q_0$, is defined as,

$$ARL\left(q_0\right)={\displaystyle \sum _{(m,i)\in \mathcal{I}(u,\theta )}}{\mu }_{m,i}p\left(m,i\mid q_0\right).$$

7.4. Numerical simulation

Now, we will assess the performance of both CUSUM and EWMA in detecting changes in the process mean by means of a simulation study. The central aim of our investigation pertains to detecting changes in the parameter ${\mu }_X$. Table 8 presents a comprehensive depiction of the variability observed in ${\mu }_X$ across the various values of the parameter $\alpha$ with respect to ${\alpha }_0$ = -0.1 and 0.9. The deviations are calculated according to $de{v}_{\mu }^{\%}=100\%\times ({\mu }_X-{\mu }_0)/{\mu }_0$, where ${\mu }_0$ is the mean associated with the parameters $p_0,{\alpha }_0\mathrm{and}{\lambda }_0$. We obtain the desired chart designs such that the desired in-control ARL value, ${\mathrm{ARL}}_0$ is 300. Due to the complexity of (6.5), the marginal probabilities are empirically obtained through a simulated process of desirable size at given $(p,\alpha ,\lambda )$. Besides ARL as a performance measure for the control charts, we have also incorporated the usual relative deviation (in %) in the ARL from Wei and Testik (2011), given as $de{v}_{\mathrm{ARL}}^{\%}=100\%\times (\mathrm{ARL}-{\mathrm{ARL}}_0)/{\mathrm{ARL}}_0$ to assess and evaluate the efficacy and performance of the chart.

Under the CUSUM chart, for a given $C_0=c_0$, our focus revolves around possible integer h and k pairs such that the desired in-control ARL is close to ${\mathrm{ARL}}_0$. For the EWMA chart, the design parameters are obtained as follows

• Choose $u\in N$ such that a corresponding one-sided C chart would have an in-control ARL below the desired value ${\mathrm{ARL}}_0$.
• Decrease $\theta \in (0,1]$ to adjust the in-control ARL close to the desired value ${\mathrm{ARL}}_0$. Subsequently, $l=0$ in the combined EWMA chart is calculated accordingly as $l=⌊\frac{1}{2\theta }⌋$.
• Use $q_0\in \{0,...,u-1\}$ for a fine-tuning of the in-control ARL.

Subsequently, the ARL values are calculated using the model parameters and chart designs.

In Table 9 and Table 10, we examine the performance of ARL under CUSUM chart with ${\alpha }_0=(-0.1,0.9)$ with various values of $\alpha$ respectively. The results show the high efficacy of the CUSUM chart in detecting upward shifts in ${\mu }_X$. Specifically, we observed a remarkable decrease in the ARL as ${\mu }_X$ increases. Furthermore, it is important to note that the decline in ARL is significantly greater than the corresponding rise in the magnitude of the shift in ${\mu }_X$.

Hence, it can be concluded that the CUSUM control chart demonstrates effective performance when applied to the INAR(1)DME process. The chart’s ability to efficiently detect upward shifts in ${\mu }_X$ makes it a suitable and beneficial tool for monitoring and controlling the INAR(1)DME process.

In Table 11 and Table 12, we examine the performance of ARL under EWMA chart with

${\alpha }_0=(-0.1,0.9)$ against various values of $\alpha$, respectively. The results show the high efficacy of the EWMA chart in detecting upward shifts in ${\mu }_X$. Specifically, we observed a remarkable decrease in the ARL as ${\mu }_X$ increases. Furthermore, it is important to note that the decline in ARL is significantly greater than the corresponding rise in the magnitude of the shift in ${\mu }_X$. Hence, it can be concluded that the EWMA control chart demonstrates effective performance when applied to the INAR(1)DME process. The chart’s ability to efficiently detect upward shifts in ${\mu }_X$ makes it a suitable and beneficial tool for monitoring and controlling the INAR(1)DME process.

Table 13 provides a comparative analysis of CUSUM and EWMA charts within the context of the INAR(1)DME process, considering specific values of ${\alpha }_0$. Bolded entries indicate instances where the dev(%) is maximized between the two charts sharing the same model parameters. It becomes evident that both charts exhibit a more significant reduction in ARL as ${\mu }_x$ increases. When monitoring data from the INAR(1)DME process and accounting for various shift sizes, the CUSUM chart is the preferred choice for maintaining process control.

7.5. Real data analysis

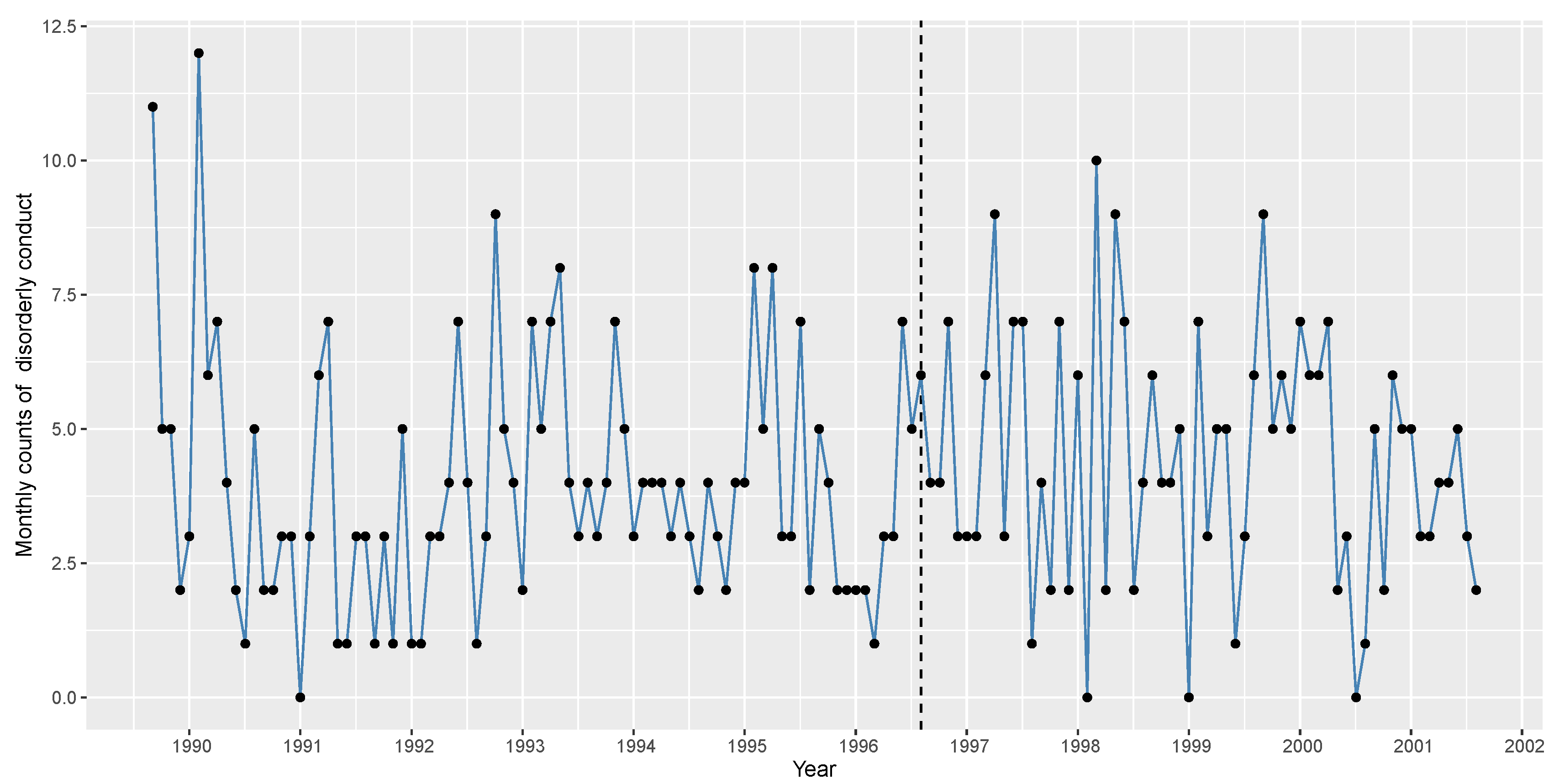
We demonstrate the applicability of the CUSUM control chart by utilizing the disorderly conduct data set obtained from the 44th police car beat in Pittsburgh, which comprises monthly observations from 1990 to 2001. It is used to monitor the mean under the INAR(1)KF process by Kim and Lee (2017). Initially, we use the data from 1990 to 1996 to fit the INAR(1)DME process. Subsequently, we apply the CUSUM control chart to the data from 1997 to detect the presence of any significant mean increase.

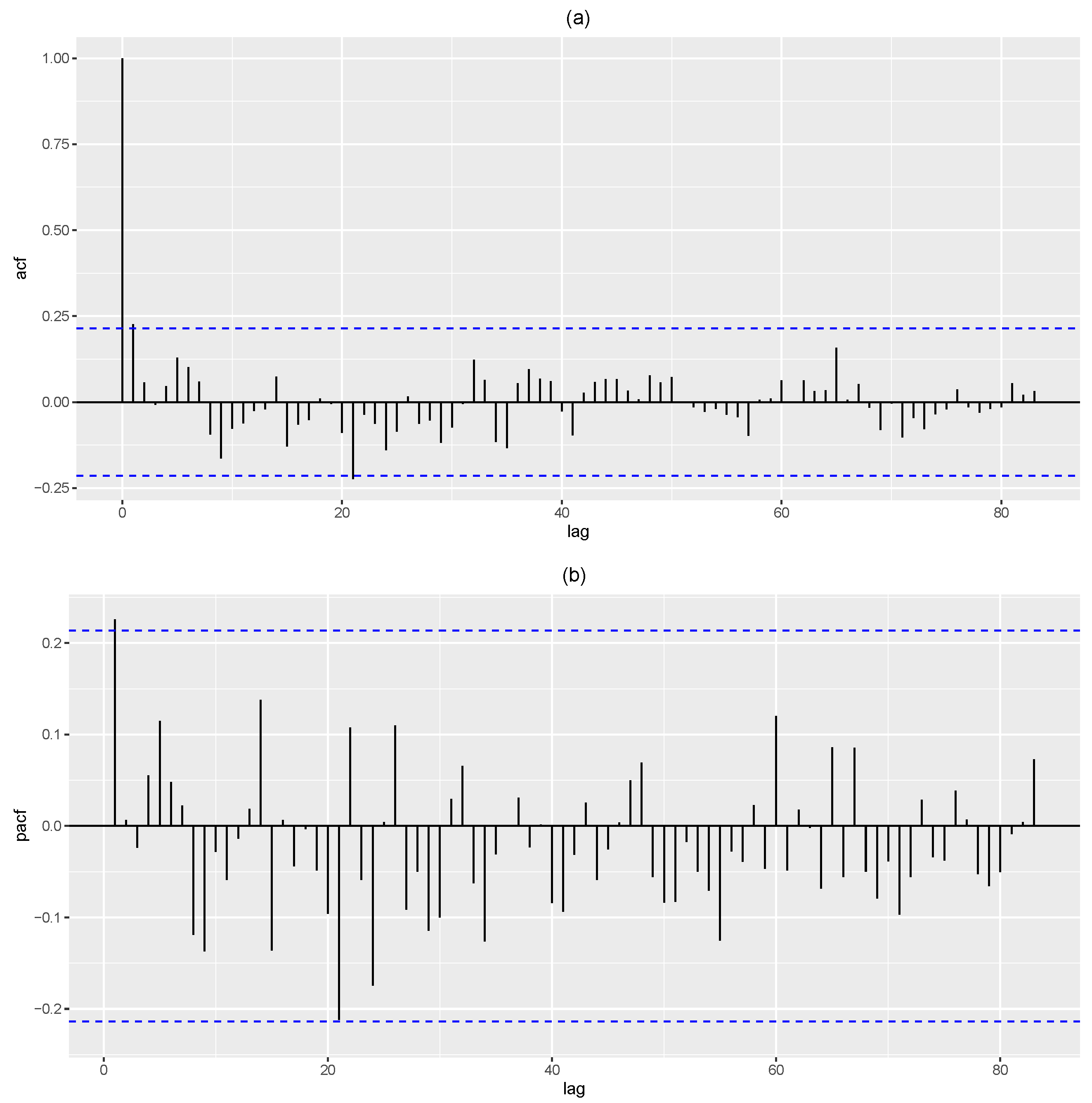
Figure 6 displays the time series plot of the disorderly conduct data set (the dashed line denotes December 1996). Based on the plot, detecting the mean shift after the dashed line is challenging. For the data from 1990 to 1996 (Phase I data), the sample mean, and variance are obtained as 3.9643 and 5.3602, respectively. Figure 7 displays the auto correlation function (ACF) and partial ACF (PACF) plots for the phase I data. Here, only the first lag is significant in the PACF plot, and the ACF plot displays an exponential decay, facilitating to model the data as an INAR(1) process. Hence, we proceed by modelling the data using the INAR(1)DME model and other competing models on the phase I data. The following are considered:

• INAR(1) process with Poisson marginals, Al-Osh and Alzaid (1987) (INARP(1))
• INAR(1) process with negative binomial marginals, McKenzie (1986) (INARNB(1))
• quasi-binomial INAR(1) process with generalized Poisson marginals, Alzaid and Al-Osh (1993) ( QINARGP(1))
• random coefficient INAR(1) process with negative binomial marginals, Wei (2008) (RCINARNB(1))
• iterated INAR(1) process with negative binomial marginals, Al-Osh and Aly (1992) (IINARNB(1))
• negative binomial thinning-based INAR(1) process with geometric marginals, ć et al. (2009) (NBINARG(1))
• INAR(1) process with geometric marginals, Alzaid and Al-Osh (1988) (INARG(1))
• dependent counting INAR(1) process with geometric marginals, ć et al. (2013) (DCINARG(1))
• INAR(1) process with zero-inflated Poisson innovations, Jazi et al. (2012) (INAR(1)ZP)
• INAR(1) process with geometric innovations, Aghababaei Jazi et al. (2012) (INAR(1)G)
• INAR(1) process with Katz family innovations, Kim and Lee (2017) (INAR(1)KF)

Table 14 lists the CMLEs, log L, AIC, BIC and ${\mathrm{RMSE}}^{*}$ for different processes. The maximum log L and minimum AIC and BIC values for the INAR(1)DME process show that it is a better fit than the contending models.

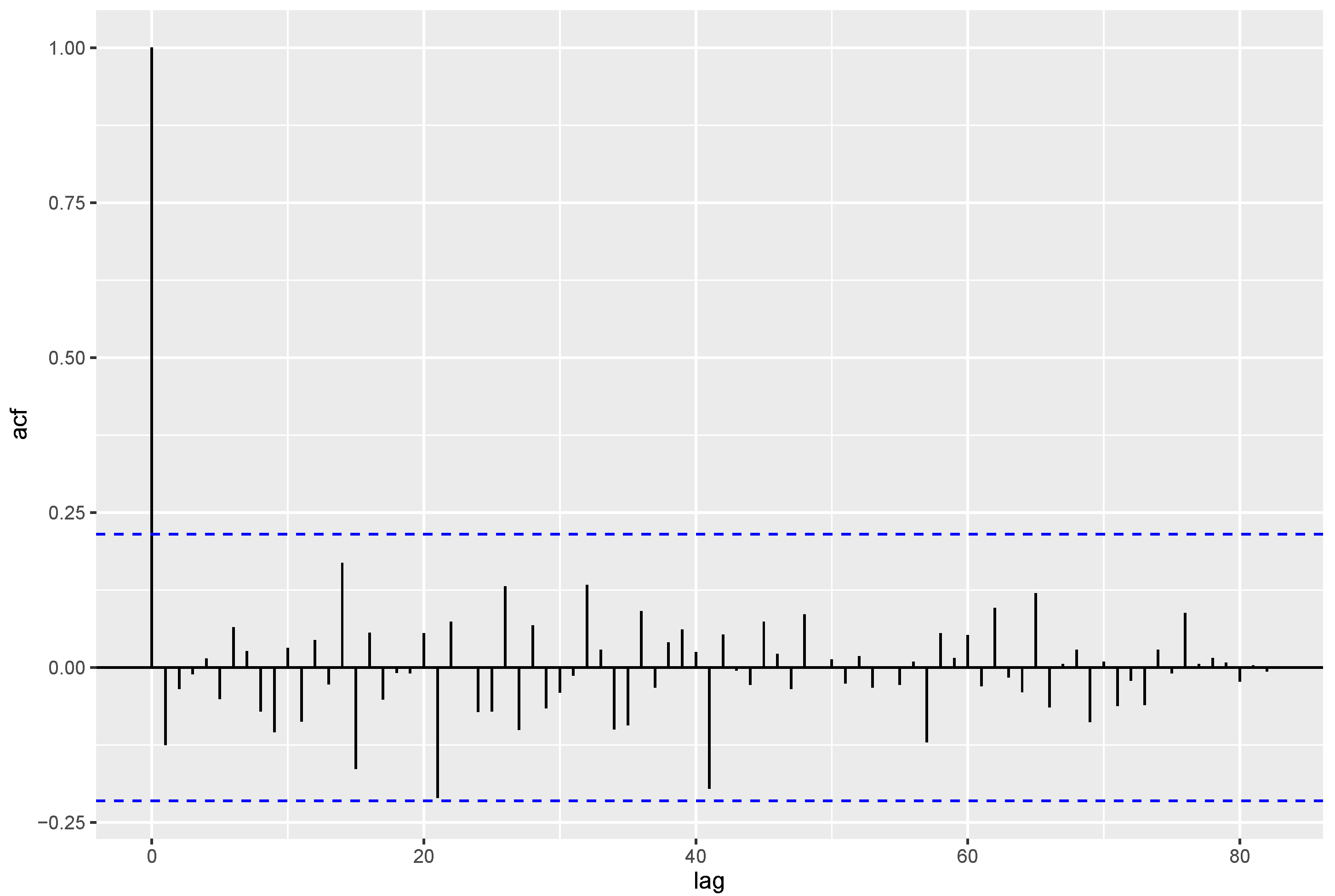
To check whether the fitted INAR(1)DME process is statistically accurate, residual analysis is done with the Pearson residuals. The ACF of the Pearson residuals is displayed in Figure 8, showing that there is no autocorrelation for the Pearson residuals. To ensure this, the Ljung–Box test for the presence of autocorrelation is done with degrees of freedom 10 and has the p-value = 0.957 > 0.05. It indicates that they are uncorrelated. Also, the mean and variance of Pearson residuals are 0.00228 and 0.83, close to the preferred values of 0 and 1, respectively, validating a good fit. Hence, the INAR(1)DME process fits the phase I data well.

The cpgrams of Pearson residuals of phase I is displayed in Figure 9. We can see that the residuals exhibit random behaviour without trend distribution for the phase I data.

The INAR(1)DME model for the phase I data is given by,

$$X_t=0.3789X_{t-1}+{ϵ}_t,$$

(7.10)

where ${ϵ}_t\sim$ DME(-0.9999, 0.5957).

The predicted values can be obtained by,

$$\begin{array}{ccc}\hfill {\widehat{x}}_1& =& 3.8585,\hfill \\ \hfill {\widehat{x}}_t& =& 0.3789{\widehat{x}}_{t-1}+2.3963,t=2,3,\dots n.\hfill \end{array}$$

Figure 10 displays the time series plot of the original versus predicted values for the phase I data.

Now, we consider the CUSUM chart with reference value k=4 (Kim and Lee (2017)) based on the INAR(1)DME process with parameters ($p=0.3789,\alpha =-0.9999,\lambda =0.5957$) and a suitable limit value h is chosen.

Table 15 provides the ARL values with respect to INAR(1)DME, INAR(1)KF and INARP(1) processes for $k=4$ and $c_0=0$ , respectively. Here the INAR(1)DME process outperforms the others since it has less ARL values. Taking $AR{L}_0=200$, the upper control limit CUSUM chart under the INAR(1)DME process is obtained as $h=38$.

The CUSUM chart for disorderly conduct data under INAR(1)DME process is given in Figure 11, where the red horizontal dashed and vertical dashed lines respectively stand for $h=38$ and December 1996.

From the plot, we can see that $C_t\ge h$ occurred in May 2000. The sample mean of the data from January 1997 to May 2000 is 4.7073, which is greater than that of the past observations. Identifying this phenomenon is challenging unless the CUSUM control scheme has been implemented.

8. Conclusion

Our paper presents a novel discrete analogue of the mixture exponential distribution, generated through survival discretization, with a strong emphasis on its statistical properties and the discussion of four distinct estimation methods. These methods play a pivotal role in this research, offering robust tools for parameter estimation. We further explore the application of this distribution in an associated INAR(1) process with DME innovations, conducting a comprehensive investigation into its statistical characteristics and performance through extensive simulation studies. Our work also extends to the domain of process monitoring, where we develop custom control charts tailored to track the process mean. In this context, we meticulously analyze the effectiveness of CUSUM and EWMA control charts in detecting shifts and provide valuable insights through comparative assessments. Additionally, the practical applicability of our proposed model is confirmed through its use with real-world data under the CUSUM chart, showcasing its relevance in both statistical theory and real-world process monitoring and control applications.