Are There Solitonlike Coherent Structure in Boundary Layers ?

1. Introduction

Origins of turbulence is a ubiquitous phenomenon and one of the greatest unsolved mysteries of classical physics [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. After a century of research, although the phenomenon of turbulence is not yet fully understood, some universal structures of turbulence have been discovered, such as, in an incompressible boundary layer, typical coherent structures include $\Lambda$-vortices, solitonlike coherent structure (SCS), hairpin vortices (with their asymmetric and composite variations), pocket structure, typical eddies (TEs), high/low-speed streaks(LSSs), streamwise vortices, ringlike vortices, turbulent spots, dark spots, very large scale motions (VLSMs), and so on.

In particular, CB Lee at Peking University [12,16,21,22], along with his collaborators, have successfully identified solitonlike coherent structure in different types of transitional boundary layers and turbulent boundary layers through experiments. They have utilized Tomographic Particle Image Velocimetry (Tomo-PIV) and their own developed Near-Wall Particle Image Velocimetry (Near-Wall PIV) to capture three-dimensional measurement data of randomly occurring strip-like structures in the turbulent boundary layer. Furthermore, they have employed the Lagrangian tracking method to invert the solitonlike coherent structure, revealing that the fundamental structure of near-wall flow is a solitary-like wave, and concluded that boundary layer flows all possess a common structure, namely solitonlike coherent structure (SCS, which has some typical characteristics as a soliton, such as, traveling downstream at a finite speed with a strong localized pattern and decreases in the later stage of boundary-layer transition, in particular, SCS has the longest living time compared with other coherent structures in wall-bounded flow [12,16].

For the significant discovery of the existence of solitonlike coherent structure or solitary-like wave structures in boundary layer flows, we believe that it is necessary to provide theoretical understanding and explanation. To do so, it is important to investigate whether there exist solitary wave solutions in the Navier-Stokes equations or in the non-steady boundary layer equations derived from the simplification of the Navier-Stokes equations using Prandtl’s boundary layer concept. Ideally, it would be best to find an analytical solution for the non-steady boundary layer equations that clearly includes solitary wave solutions. Unfortunately, to date, an analytical or exact solution to this problem has not been found [1,6].

Regarding water surface waves, researchers have observed the phenomenon of solitary waves and established the equation $u_{,t}+6u{u}_{,x}=\nu u_{,xxx}$ for water waves with a free boundary. They obtained the exact solution $u(x,t)=2\nu c_2^2{tanh}^2(c_1+c_{2}x+c_{3}t)-(8\nu c_2^2+c_3)/\left(6c_2\right)$. However, the Navier-Stokes equations does not include third-order derivatives with respect to spatial coordinates, such as $u_{,xxx}$. Even in the 1D nonlinear Burgers equation $u_{,t}+6u{u}_{,x}=\nu u_{,xx}$, the solution $u(x,t)=-2\nu c_{2}tanh(c_1+c_{2}x+c_{3}t)-c_3/c_2$ is not a solitary wave solution but a shock wave solution.

This naturally raises a question: whether the Navier-Stokes equations or their simplified forms have solitary-like wave solutions? Our belief is that since the Navier-Stokes equations can describe the laws of fluid motion, if there is a common structure of solitonlike coherent structure in boundary layer flows, then the non-steady boundary layer equations of the Navier-Stokes togeth with mass conservation should have solitary-like wave solutions.

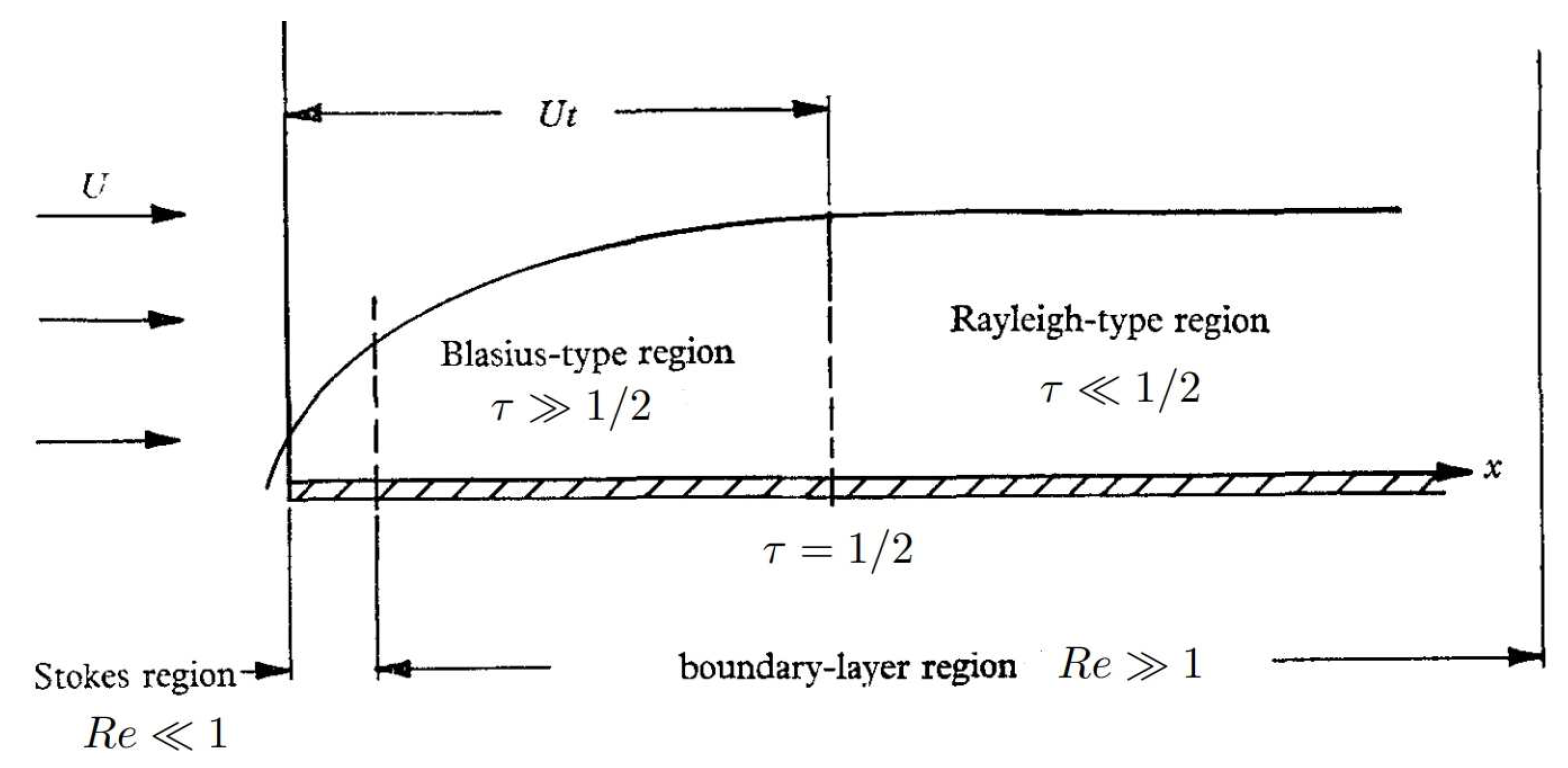
To achieve this belief, the best approach is to obtain exact solutions for the non-steady boundary layer equations of the Navier-Stokes (N-S) equations in certain cases. Due to the complexity of the N-S equations, only a few 1D non-steady problems have obtained exact solutions, such as the exact solution to Stokes’ problem, the flow due to an oscillating infinite plane, which was the first exact solution in fluid dynamics, and the solution to Rayleigh’s problem of an inifinite flat plate started impulsively into motion in its own plane with velocity U, given by $u(y,t)=U\mathrm{erfc}(y/\left(2\sqrt{\nu t}\right))$. Unfortunately, to date, no exact solutions have been obtained for the unsteady boundary layer equations of any 2D problem, and neither the solutions for Stokes nor Rayleigh include solitary-like wave solutions. This shattered our expectation of finding solitary-like wave solutions from historical exact solutions, leaving us with no choice but to face the problem and strive to find new ideas to explore new frontiers.

Lee et al [12,16,21,22] has found that boundary layer flows all exhibit a common structure, namely solitonlike coherent structure. This means that we only need to study one or a few specific cases, as universal laws exist within these special problems. By obtaining an analytical solution for any 2D unsteady boundary layer equations, we can analyze whether it contains solitary-like wave solutions.

In this paper, the author addresses the challenge of finding solitonlike coherent structures (SCS) in boundary layer flows, which are important for understanding turbulence origins and laminar-turbulence transition. The author builds upon their previous work and utilizes a combination of the Navier-Stokes equations and mass conservation to study convergent flow boundary layers.

By incorporating mass conservation, the combined equations now contain third-order derivatives with respect to the coordinate x. This inclusion is crucial, as it allows for the existence of solitonlike coherent structures. Without the mass conservation condition, the Navier-Stokes equations alone do not possess solitonlike coherent structures.

Through their analysis, the author demonstrates that the solution to convergent flow boundary layers encompasses both shock wave and solitary wave solutions. Furthermore, the superposition of these solutions gives rise to solitary-like waves, which are identified as solitonlike coherent structures.

The paper concludes by proving that solitonlike coherent structures exist in all kinds of flows, highlighting the significance of combining the Navier-Stokes equations with mass conservation to obtain these coherent structures. This finding contributes to our understanding of turbulence origins and the transition from laminar to turbulent flow.

After introduction in Section 1, the rest of this paper is organized as follows. In Section 2, based on Sun’s work [31], we formulate the 2D convergent boundary layers. In Section 3, an analytical solution is obtained. In Section 4, convergent turbulent boundary layers is investigated. In Section 5, proved solitonlike coherent structure do exit in all kind of flows. Finally, in Section 6, conclusions and perspectives are drawn.

2. A thin plate immersed in convergent flow

A thin flat plate is immersed at zero incidence in a uniform stream, which flows with speed $U\left(x\right)$ and is assumed not to be affected by the presence of the plate, except in the boundary layer. The fluid is supposed unlimited in extent, and the origin of coordinates is taken at the leading edge, with x measured downstream along the plate and y perpendicular to it. Sun [31] successfully formulated the problem with following single partial differential equation:

$$\begin{array}{cc}\hfill f_{,\eta \eta \eta }& +\alpha f{f}_{,\eta \eta }+\beta [1-{\left(f_{,\eta }\right)}^2]=f_{,\tau \eta }+\gamma \tau (f_{,\tau }{f}_{,\eta \eta }-f_{,\eta }{f}_{\tau \eta }),\hfill \end{array}$$

(1)

where the coefficients are $\alpha =\frac{\delta }{\nu }\frac{dU\delta }{dx}$, $\beta =\frac{{\delta }^2}{\nu }\frac{dU}{dx}$, and $\gamma =\frac{U}{\nu }\frac{d{\delta }^2}{dx}=2(\alpha -\beta )$. If $\alpha$ and $\beta$ are constants, we have main-stream flow $U\left(x\right)=C{x}^n$ and boundary layer thickness $\delta \left(x\right)={\left[\frac{\left|\right(2\alpha -\beta \left)x\right|\nu }{\left|U\right(x\left|\right)}\right]}^{1/2}$.

In case of boundary layer flow in a converging channel flow between two non-parallel planes, the parameters $\alpha =0,\beta =1$ and $\gamma =-2$, we have the convergent channel flow velocity function $U\left(x\right)=\frac{\left|Q\right|}{\rho \theta x}$, which simply expresses the coacervation of the discharge $Q<0$ in the flow, $\theta$ being the angle between the planes. Now we have the boundary layer thickness $\delta \left(x\right)=x{\left(\frac{\nu \rho \theta }{\left|Q\right|}\right)}^{1/2}$, similarity variable $\eta =\frac{y}{\delta }=\frac{y}{x}{\left(\frac{\left|Q\right|}{\nu \rho \theta }\right)}^{1/2}$, and dimensionless diffusion time $\tau =\frac{\left|Q\right|}{\rho \theta }\frac{t}{x^2}$.

Referring to the basic problem is to find a function $f(\eta ,\tau )$ satisfying Sun equation [26] as follows

$$\begin{array}{c}\hfill f_{,\eta \eta \eta }+1-{\left(f_{,\eta }\right)}^2=f_{,\tau \eta }-2\tau (f_{,\tau }{f}_{,\eta \eta }-f_{,\eta }{f}_{\tau \eta }).\end{array}$$

(2)

Eq.2 can be solved numerically, some results are depicted in Figure 1.

3. Solitonlike solution of the first order approximation of Eq.2

Although we can solve the equation 2 numerically and find its solution, we do not know what kind of elements are contained in the solution since the solution is the final composition of those elements. This means that we need to split the solution into some elements. Numerical methods would not be helpful. We need to perform some analytical analysis. Unfortunately, equation 2 cannot be solved exactly, so we have to find its approximate analytical solution.

According to Stewartson [24], Takuda[25] proposed a Figure 2, which can be used to study the

From Figure 2, in the range of $\tau \ll 1/2$, we can expand the function as follows $f=f_0(\eta ,\tau )+\tau f_1(\eta ,\tau )...$, for the first order approximation $f_0$ we have

$$\begin{array}{c}\hfill f_{0,\eta \eta \eta }+1-{\left(f_{0,\eta }\right)}^2=f_{0,\tau \eta }.\end{array}$$

(3)

The exact solution of Eq.3 is obtained as follows

$$\begin{array}{cc}\hfill f_0(\eta ,\tau )& =-\sqrt{3}tanh\zeta -2\sqrt{3}ln(cosh\zeta )-\frac{\sqrt{3}}{2}ln\frac{tanh\zeta -1}{tanh\zeta +1}-\frac{\eta }{2}+g\left(\tau \right),\hfill \end{array}$$

(4)

where $\zeta =\frac{\sqrt{3}}{6}\eta -\frac{5}{6}\tau -c$, and $g\left(\tau \right)$ is an arbitrary function, which can be determined by $f(0,\tau )=0$ and gives

$$\begin{array}{cc}\hfill g\left(\tau \right)& =-\sqrt{3}tanh(\frac{5}{6}\tau +c)+2\sqrt{3}ln(cosh(\frac{5}{6}\tau +c))-\frac{\sqrt{3}}{2}ln\frac{1-tanh(\frac{5}{6}\tau +c)}{1+tanh(\frac{5}{6}\tau +c)}.\hfill \end{array}$$

(5)

Then we can get the first and the second partial derivative of $f(\eta ,\tau )$ respect to $\eta$ as follows $f_{0,\eta }=-tanh\zeta -\frac{1}{2}{\mathrm{sech}}^2\zeta$, and $f_{0,\eta \eta }=-\frac{\sqrt{3}}{6}(1-tanh\zeta ){\mathrm{sech}}^2\zeta$.

The integral constant can be determined by $\frac{\partial f(\eta ,\tau )}{\partial \eta }{|}_{(0,0)}=0$ and leads to $c=\frac{ln(1+\sqrt{2})}{2}$.

The flow velocity component in x coordinate is obtained as follows

$$\begin{array}{cc}\hfill u& =U_{\infty }{f}_{,\eta }=-\frac{\nu Re}{x}\left(\frac{1}{2}{\mathrm{sech}}^2\zeta +tanh\zeta \right),\hfill \end{array}$$

(6)

where $\zeta =\frac{\sqrt{3}}{6}\eta -\frac{5}{6}\tau -\frac{1}{2}ln(1+\sqrt{2})$ and the Reynolds number is $Re=\frac{\left|Q\right|}{\rho \theta \nu }$. The velocity u is depicted in Figure 4 below.

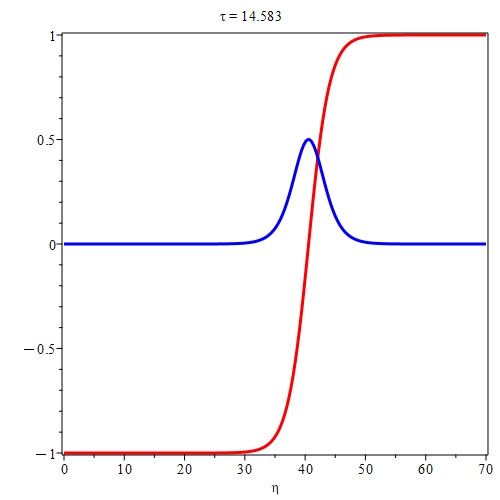
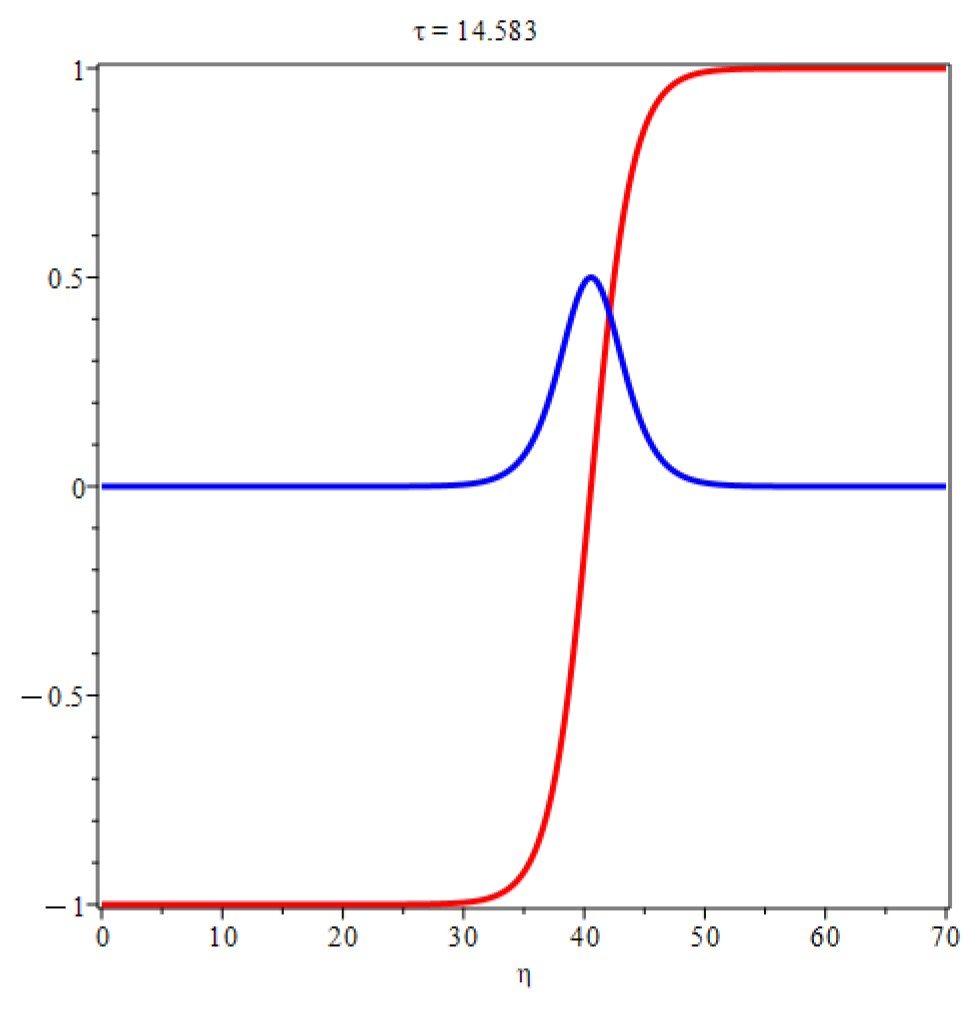
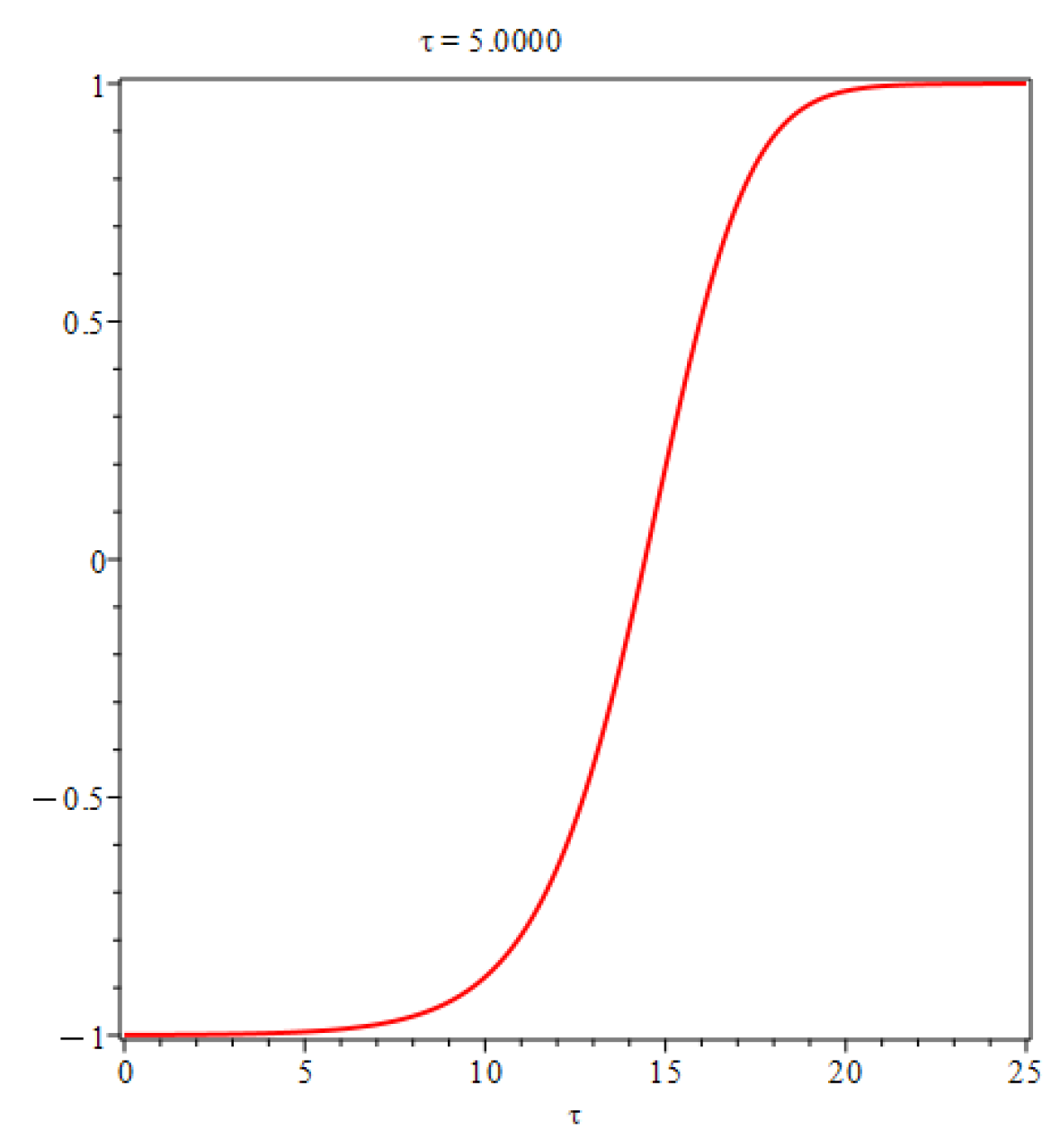
It can see clearly that they contain solitary-like wave solutions ${\mathrm{sech}}^2\zeta$ and shock wave solutions $tanh\zeta$. They compete and suppress each other during different stages of development, eventually forming a solitonlike coherent structure as Lee discovered. The comparing is depicted in Figure 3 below.

In particular, when $\zeta$ is relatively small, such as in the case of $\zeta <0.42$, the solitary wave solution dominates, while when $\zeta >0.42$, the shock wave solution dominates. The velocity u is depicted in Figure 4 below.

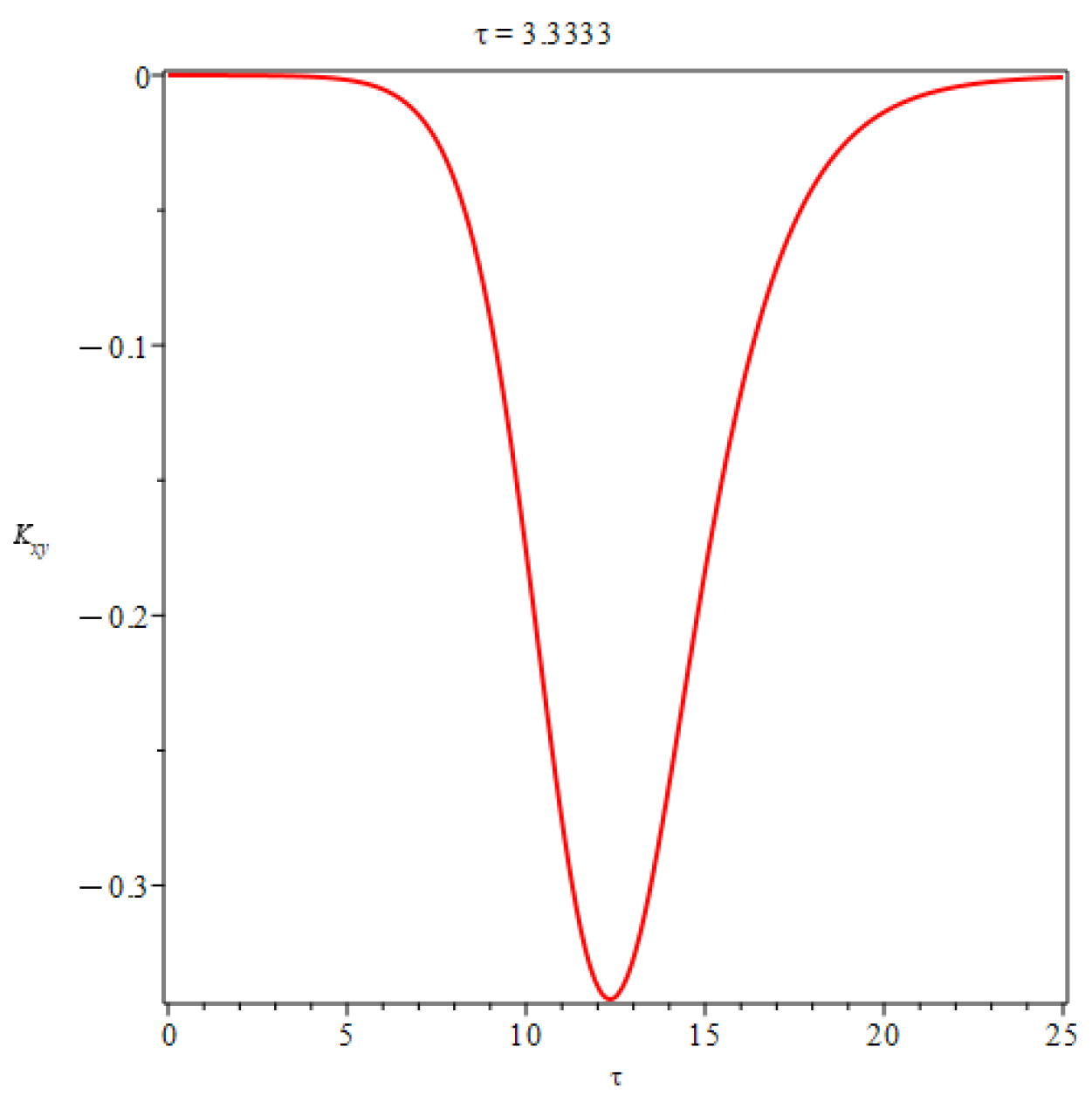
The shear stress is given by

$$\begin{array}{cc}\hfill {\tau }_{xy}& =\mu \frac{\partial u}{\partial y}=\frac{\rho \nu }{\delta }\frac{\partial u}{\partial \eta }={\left(\frac{\nu }{\rho }\right)}^{1/2}{\left(\frac{Q}{\theta }\right)}^{3/2}\frac{1}{x^2}{f}_{0,\eta \eta }\hfill \\ \hfill & =-\frac{\sqrt{3}}{6}{\left(\frac{\nu }{\rho }\right)}^{1/2}{\left(\frac{\left|Q\right|}{\theta }\right)}^{3/2}\frac{1}{x^2}(1-tanh\zeta ){\mathrm{sech}}^2\zeta ,\hfill \end{array}$$

(7)

The shear stress is depicted in Figure 5.

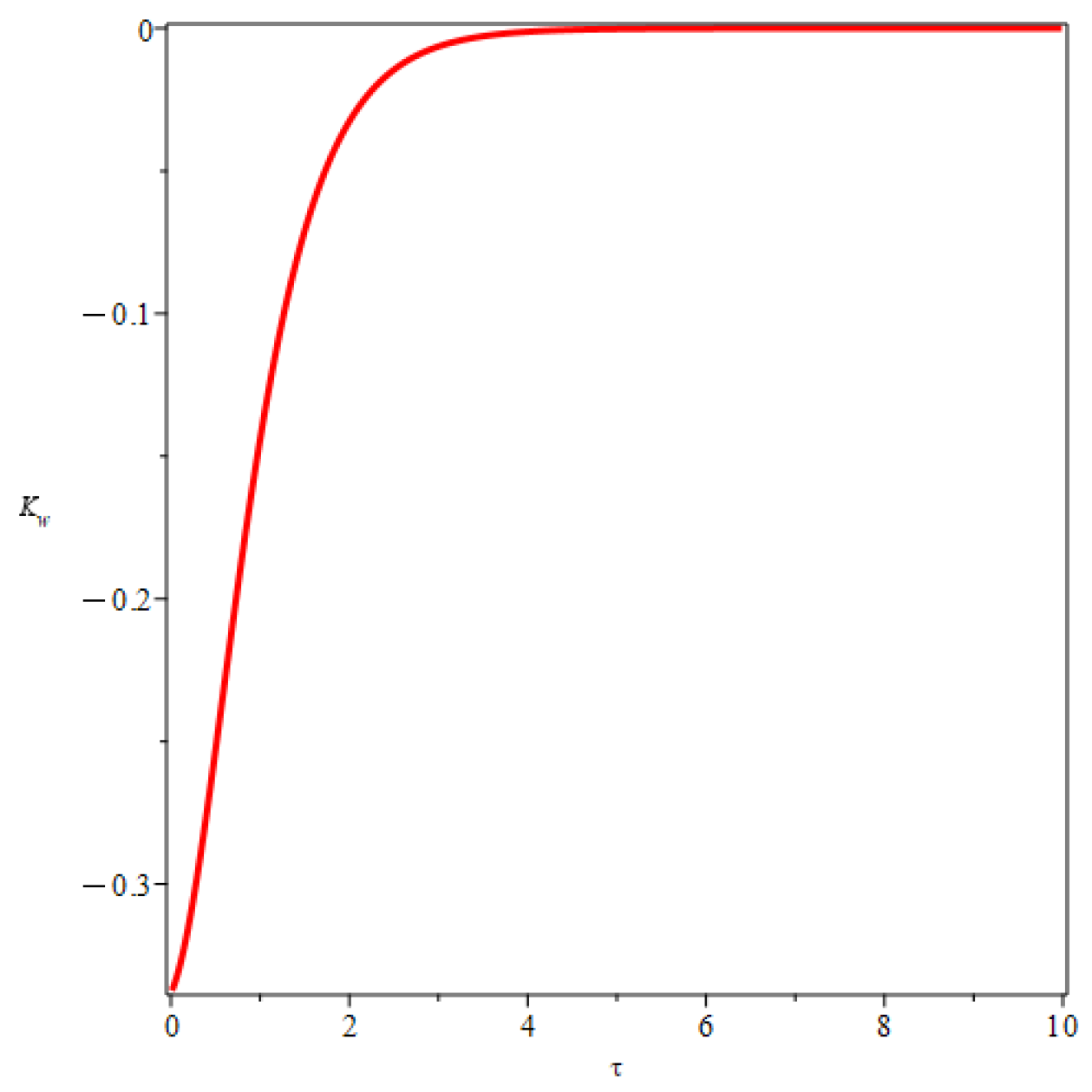
The wall shear stress ${\tau }_w={\tau }_{xy}{|}_{y=0}$, we have

$${\tau }_w=-\frac{\sqrt{3}}{6}{\left(\frac{\nu }{\rho }\right)}^{1/2}{\left(\frac{\left|Q\right|}{\theta }\right)}^{3/2}\frac{1}{x^2}\left[1+tanh(c+\frac{5}{6}\tau )\right]{\mathrm{sech}}^2(c+\frac{5}{6}\tau ),$$

(8)

The wall shear stress is depicted in Figure 6.

The expressions of shear stress in Eq.7 indeed indicate the presence of solitonlike coherent structure solutions. Solitary waves are localized disturbances that maintain their shape and amplitude as they propagate, while solitonlike waves are a superposition of different wave components that resemble solitons but may not exhibit all their characteristics. The identification of solitonlike coherent structure (SCS) in boundary layer flow is a significant step towards understanding turbulence origins.

4. Beyond laminar: Convergent channel turbulent boundary layers

Based on Prandtl mixing length model, we can extend Sun’s laminar formulation to turbulent boundary layes as follows:

$$\begin{array}{cc}\hfill f_{,\eta \eta \eta }& +\alpha f{f}_{,\eta \eta }+\beta [1-{\left(f_{,\eta }\right)}^2]+{\kappa }^2{\eta }^2\sqrt{\underbrace{R{e}_{\delta }}}{\left(|f_{,\eta \eta }|f_{,\eta \eta }\right)}_{,\eta }\hfill \\ \hfill & =f_{,\tau \eta }+\gamma \tau (f_{,\tau }{f}_{,\eta \eta }-f_{,\eta }{f}_{\tau \eta }),\hfill \end{array}$$

(9)

where $\kappa$ is Kaŕmán constant, the Reynolds number is $R{e}_{\delta }=\frac{U\delta }{\nu }$, which is in general, a function of x.

To get rid of the coordinate x, following Sun [30], we need to set $U\delta$=constant, which leads to $\alpha =0$. if we set $\beta =1,\gamma =-2$. Denote $Re=\frac{\left|Q\right|}{\nu \rho \theta }$, hence we have the convergent turbulent boundary layers

$$\begin{array}{cc}\hfill f_{,\eta \eta \eta }& +1-{\left(f_{,\eta }\right)}^2+{\kappa }^2{\eta }^2\sqrt{Re}{\left(|f_{,\eta \eta }|f_{,\eta \eta }\right)}_{,\eta }=f_{,\tau \eta }-2\tau (f_{,\tau }{f}_{,\eta \eta }-f_{,\eta }{f}_{\tau \eta }).\hfill \end{array}$$

(10)

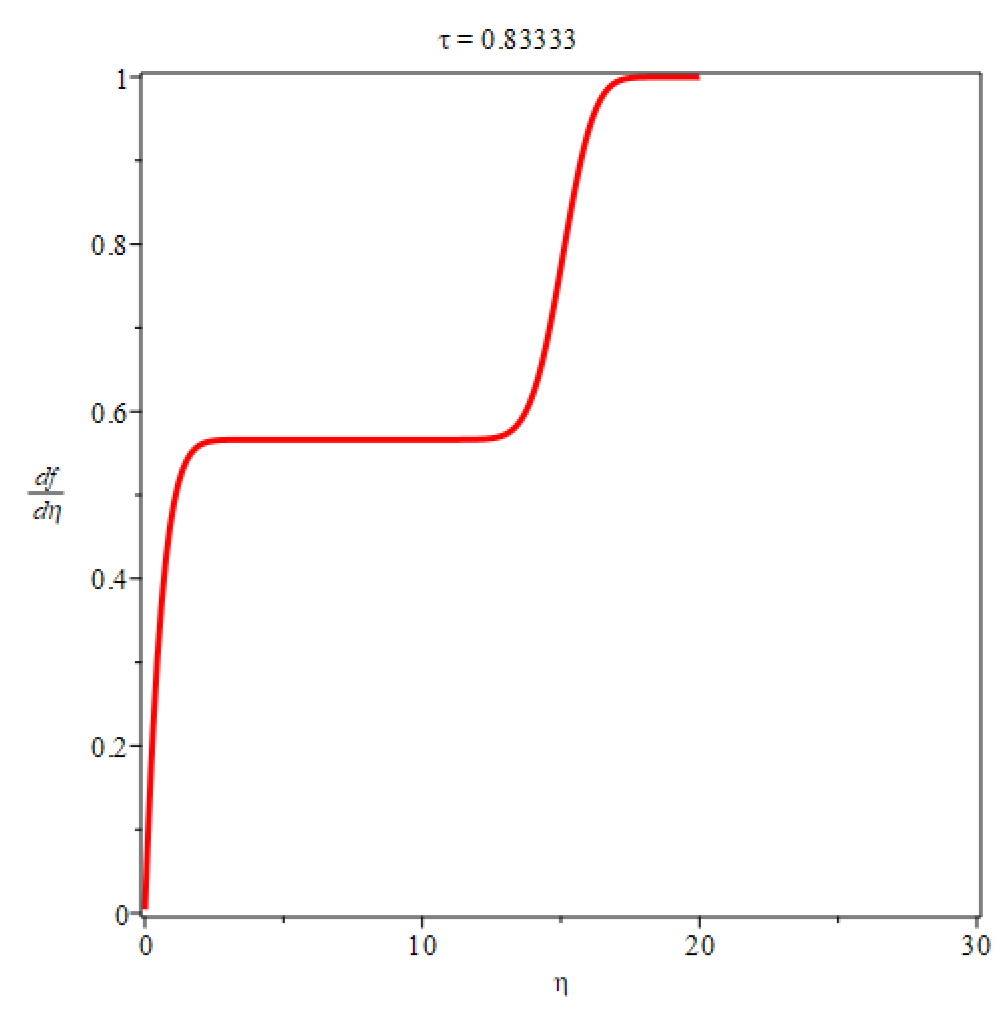
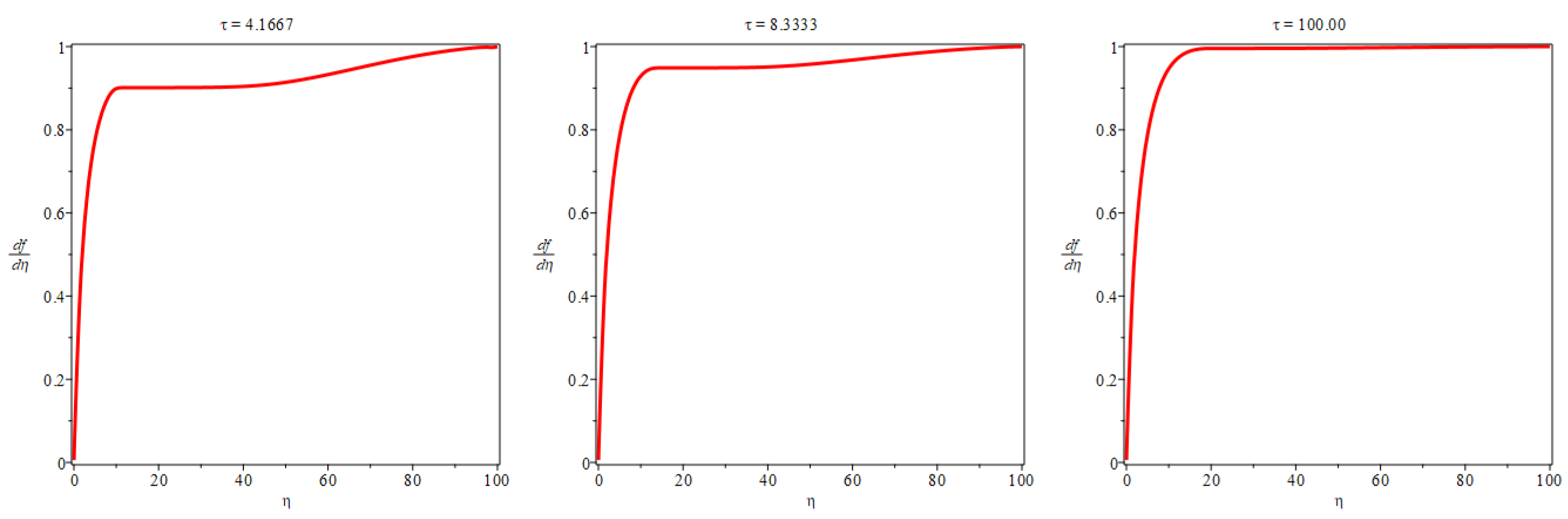
This equation can solved numerically, for $\kappa =0.4$ and $Re=2300$, the results are depicted in Figure 7.

5. Are there solitonlike coherent structures in flows ?

In the previous section, we demonstrated the existence of solitonlike waves through specific examples. However, the question remains as to whether solittonlike waves are universally present in various types of flows. Analyzing specific problems individually is clearly not a viable approach, and therefore, it is necessary to explore this question theoretically in order to gain a rational understanding and obtain general conclusions.

In previous section, by introducing a stream function $\psi (x,y,t)$, the velocity components can be expressed as follows $u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x}$. with the relation, the mass conservation is satisfied, and the momentum conservation of 2D Boundary layers becomes

$$\underbrace{\frac{\partial \psi }{\partial t\partial y}}+\frac{\partial \psi }{\partial y}\frac{\partial \psi }{\partial x\partial y}-\frac{\partial \psi }{\partial x}\frac{\partial \psi }{\partial y^2}=U\frac{dU}{dx}+\nu \underbrace{\frac{{\partial }^3\psi }{\partial y^3}},$$

(11)

We can see that the secret of why this equation has solitonlike solution. The presence of a third-order derivative term in the equation, namely $\frac{{\partial }^3\psi }{\partial y^3}$, is one of the key factors that allows for the existence of soliton-like solutions. This term introduces nonlinearity into the equation, which is essential for the formation and propagation of solitary waves.

In general, solitons arise in nonlinear systems where the nonlinearity counteracts the dispersion effects. Dispersion tends to spread out waves, causing them to disperse and lose their shape over time. However, nonlinearity can balance this dispersion, leading to the formation of solitary waves that maintain their shape as they propagate.

The specific form of the equation and the coefficients of the terms also play a crucial role in determining the existence and properties of solitons. Different types of equations may have different conditions for the existence of soliton-like solutions. Therefore, it is important to analyze the specific equation and its properties to determine if solitons are present.

Overall, the presence of a third-order derivative term is a key factor that allows for the existence of soliton-like solutions, but other factors such as nonlinearity and specific equation properties also contribute to the formation and behavior of solitary waves.

In the same way, we can also check if the general 2D and 3D flows have solitonlike solutions.

5.1. 2D flows

A general 2D flows governing equations are

$$\begin{array}{cc}\hfill \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}& =0,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}& =-\frac{1}{\rho }{p}_{,x}+\nu (\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}& =-\frac{1}{\rho }{p}_{,y}+\nu (\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}),\hfill \end{array}$$

(14)

In similar way, introducing a stream function $\psi (x,y,t)$, the velocity components can expressed as follows

$$u={\psi }_{,y},v=-{\psi }_{,x},$$

(15)

hence we have euqations

$$\begin{array}{cc}\hfill {\psi }_{,yt}+{\psi }_{,y}{\psi }_{,yx}-{\psi }_x{\psi }_{,yy}& =-\frac{1}{\rho }{p}_{,x}+\nu ({\psi }_{,yxx}+\underbrace{{\psi }_{,yyy}}),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill -{\psi }_{,xt}-{\psi }_{,y}{\psi }_{,xx}+{\psi }_x{\psi }_{,xy}& =-\frac{1}{\rho }{p}_{,y}+\nu (-\underbrace{{\psi }_{,xxx}}-{\psi }_{,xyy}).\hfill \end{array}$$

(17)

It is clear to see that the 3rd order differential respect to x and y, therefore the general 2D flows have solitonlike solutions.

5.2. 3D flows

A general 3D flows, whose governing equations are

$$\begin{array}{cc}\hfill \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}& =0,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}& =-\frac{1}{\rho }{p}_{,x}+\nu {\nabla }^{2}u,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}& =-\frac{1}{\rho }{p}_{,y}+\nu {\nabla }^{2}v,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill \frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}& =-\frac{1}{\rho }{p}_{,z}+\nu {\nabla }^{2}w.\hfill \end{array}$$

(21)

where the Laplacian ${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}$.

Introducing two stream functions $\psi (x,y,z,t)$ and $\varphi (x,y,z,t)$, the velocity components can expressed as follows

$$u={\psi }_{,y}-{\varphi }_{,z},v=-{\psi }_{,x}-{\varphi }_{,z},w={\varphi }_{,x}+{\varphi }_{,y}$$

(22)

hence we have

$$\begin{array}{cc}\hfill {\psi }_{,yt}-{\varphi }_{,zt}+\left(\dots \right)& =-\frac{1}{\rho }{p}_{,x}+\nu \underbrace{{\nabla }^2({\psi }_{,y}-{\varphi }_{,z})},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\psi }_{,xt}-{\varphi }_{,zt}+\left(\dots \right)& =-\frac{1}{\rho }{p}_{,y}+\nu \underbrace{{\nabla }^2(-{\psi }_{,x}-{\varphi }_{,z})},\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\varphi }_{,xt}+{\varphi }_{,yt}+\left(\dots \right)& =-\frac{1}{\rho }{p}_{,y}+\nu \underbrace{{\nabla }^2({\varphi }_{,x}+{\varphi }_{,y})}.\hfill \end{array}$$

(25)

It is clear to see that the 3rd order differential respect to x and y, therefore the general 3D flows also have solitonlike solutions.

6. Conclusions and perspectives

The approach of transforming the 2D unsteady laminar boundary layer equations into a single partial differential equation, as described in reference [31], is commendable. This transformation allows for an approximate analytical solution to be obtained for convergent laminar boundary layers.

Through this analysis, it is revealed that the solution for convergent laminar boundary layers includes shock wave solutions and solitary wave solutions. These two types of waves can combine to form solitary-like waves. This analytical prediction of solitary-like waves in boundary layer flow provides evidence for the existence of solitonlike coherent structures in boundary layer flows. It is worth noting that a similar prediction can also be made for turbulent boundary layers.

Furthermore, the study concludes that solitonlike coherent structures exist in all kinds of flows. However, it is important to emphasize that these coherent structures can only be obtained by combining the Navier-Stokes equations with mass conservation. The inclusion of mass conservation results in the presence of third-order derivatives with respect to the coordinate x. Without the mass conservation condition, the Navier-Stokes equations alone do not possess solitonlike coherent structures.

This research significantly contributes to our understanding of solitonlike coherent structures in boundary layer flows and highlights the importance of considering the combined equations of the Navier-Stokes equations and mass conservation in their study.

Availability of data: The data supporting the findings of this study are available from the corresponding author upon reasonable request.

Declaration of Competing Interest: The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.