Prerpints.org logo
Preprint
Article

Improvement in Sizing Constrained Analog IC via Ts-CPD Algorithm

Altmetrics

Downloads

114

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 October 2023

Posted:

10 October 2023

You are already at the latest version

Alerts
Abstract
In this work, we propose a variation of the cellular particle swarm optimization algorithm with differential evolution hybridization (CPSO-DE), to include constrained optimization in it, named Ts-CPD. It is implemented as a kernel of electronic design automation (EDA) tool capable of sizing circuit components considering a single-objective design with restrictions and constraints. The aim is to improve the optimization solutions in the sizing of analog circuits. To evaluate our proposal’s performance, we present the design of three analog circuits: a deferential amplifier, a two-stage operational amplifier, and a folded cascode operational transconductance amplifier. Numerical simulation results indicate that Ts-CPD can find better solutions, in terms of the design objective and the accomplishment of constraints, than those reported in previous works.
Keywords: 
Subject: Computer Science and Mathematics  -   Other

1. Introduction

In recent years, analog circuit design has received much attention, particularly those with Very Large Scale of Integration (VLSI), because optimization is a process that involves many conflicting constraints and a wide range of parameters [1]. Therefore, it is necessary to develop more robust Computer-Aided Design (CAD) and Electronic Design Automation (EDA) tools, which increase productivity and quality and minimize design costs [2].
The design of analog circuits comprises three major stages: selecting a topology, sizing components, and layout extraction [3]. In the case of sizing, it is possible to use the experience when the circuits are small, but manual circuit-sizing in analog design is a time-consuming process [4]. When the circuit grows, it is impossible to size the components solely by experience; thus, mathematical tools are necessary to optimize the circuits. Similarly, component selection is critical in achieving a targeted performance and quality level [5].
The complexity when manually implementing an analog project is usually weeks or months. CAD and EDA tools are used to improve the design process; today’s analog design environment is made of CAD tools for editing, evaluation, and design verification of analog integrated circuits, for example, HSPICE, SMASH, and CADENCE. Automatic analog circuit sizing based on optimization tools is divided into two main subclasses: equation-based and simulation-based circuit optimization. The first uses analytical design equations, while the second takes advantage of simulator circuits, e.g., SPICE, to provide accurate performance figures.
Critical points in optimization-based approaches are the optimization techniques and methods used to evaluate circuit performance. Different optimization techniques are used to dimension and optimize analog integrated circuits, both deterministic and stochastic. In equation-based methods, it is possible to use classical optimization methods. However, when using the circuit simulator, it is necessary to use stochastic heuristic optimization techniques [6].
Many optimization techniques and tools for automation design have been developed over time [7,8]. Also, Geometric Programming was used to design a CMOS op-amp in [9]; the authors used the transistor models called GP0 and GP1, implemented in MATLAB but validated with the HSPICE level-1 models simulation. This method is robust, although it implies using equations for the circuit and each optimization parameter. This technique is updated in [10], where the validation is made using the BSIM3v1 model.
In addition, the fuzzy logic has been used for the circuit design as in [11,12], or in [13], where a multi-objective design is presented, while in [14], a tool for analog synthesis is introduced. In [15], a Neuro-Fuzzy method for analog circuit design is presented; it is of easy implementation, natural understanding, and better performance than static methods of fuzzy optimization; however, it still needs the human experience in the particular circuit to be designed. In [16], the application of an innovative algorithm of the type Customized Genetic Algorithm (CAG) is reported. Its purpose is to improve the optimization process of analog CMOS ICs.
More recently, evolutionary algorithms have been successfully applied to component value selection for analog active filters [17,18] and to the analog integrated circuits design as in [19], where the sizing is achieved using a Particle Swarm Optimization (PSO) algorithm implemented in MATLAB and the results verified at the end with SPICE. In [20], a CMOS differential amplifier and a two stages CMOS op-amp are optimized to occupy the minimal possible area by the circuits and to improve their performances using the gravitational search algorithm in combination with the particle swarm optimization (GSA-PSO). The design is formulated as an optimization problem with a single objective function, although certain manual tuning is necessary to resolve conflicts with either design or performance parameters when using this method. In the work [21], a crazy PSO (CRPSO) is applied to improve the premature convergence to a local minimum of the PSO; the application optimizes the minimization of the total MOS area of two amplifier configurations, a two-stage PMOS type operational amplifier, and an NMOS cascade code amplifier.
A good comparison of several evolutionary methods for the synthesis of analog circuits is presented in [22]; these are Artificial Bee Colony (ABC), PSO, and Chaotic Differential Evolution (CDE). The algorithms are implemented in MATLAB and interfaced with the WINSPICE circuits simulator. In [23], the authors present their tool for the automation design of analog circuits based on the use of a Genetic Algorithm (GA) modified; this is a multi-objective design for CMOS op-amps. Another evolutionary algorithm used for automation design is the New Hybrid Shuffled Frog Leaping Algorithm (NHSFL) implemented in MATLAB linked with the HSPICE circuits simulator [24]. It was tested with two examples of design, but the method can be extended to the general op-amp design according to the authors.
Heuristic techniques are necessary to solve problems with many design criteria [25]. Although they do not guarantee finding the optimal solution exactly, they provide an acceptable approximation to it in an acceptable computation time [26]. Therefore, another challenge for sizing high-performance analog circuits with tight specifications is the need for a powerful enough optimization kernel for EDA tools to handle tighter specifications and improve optimization capability [27]. Different optimization kernels are currently used for EDA tools; among them, we can mention the kernels based on GA [23], PSO [28], ACO in [29], SA in [30], GSA in [20], NSGA-II in [31] and NSGA-II, MOPSO, and MOSA in [32].
Most heuristic methods used in the optimization kernels of the EDA tools are based on multi-objective optimization techniques [6,31] or use a restriction approach with a single objective and static penalty functions. This is due to their simplicity and easy implementation, making it a relatively reliable method [33]. Penalty functions penalize non-feasible solutions by adding a specific value to the objective function as an amount proportional to the violation of the restriction. Thus, the optimization problem is transformed into a restrictionless optimization problem. The main problem with this methodology is choosing the appropriate penalty factor for a particular problem; it is often a complicated task, but if an adequate factor is selected, a premature convergence can occur or solutions outside the feasible region can be obtained [34]. Another approach currently used in problems with restrictions is self-adaptive penalty functions, which significantly improve the results [35]. Unfortunately, many last-generation restricted optimization methods have yet to be introduced into EDA tools. Therefore, advanced restricted optimization methods should be applied to circuit dimensioning tools to address this challenge.
In recent years, algorithms based on cellular automata, such as CPSO [36], CPSO-DE [37], CCAA [38], and MmCAA [39], have shown excellent performance in solving global optimization problems, demonstrating a good balance between exploration and exploitation, as well as a good speed of convergence. Among them, the CPSO-DE has proven to be an excellent design method for identifying adaptive IIR systems due to the use of a differential evolution rule for the neighborhoods of cellular automata of the PSO that improves the balance between exploration and exploitation than the original version of the CPSO.
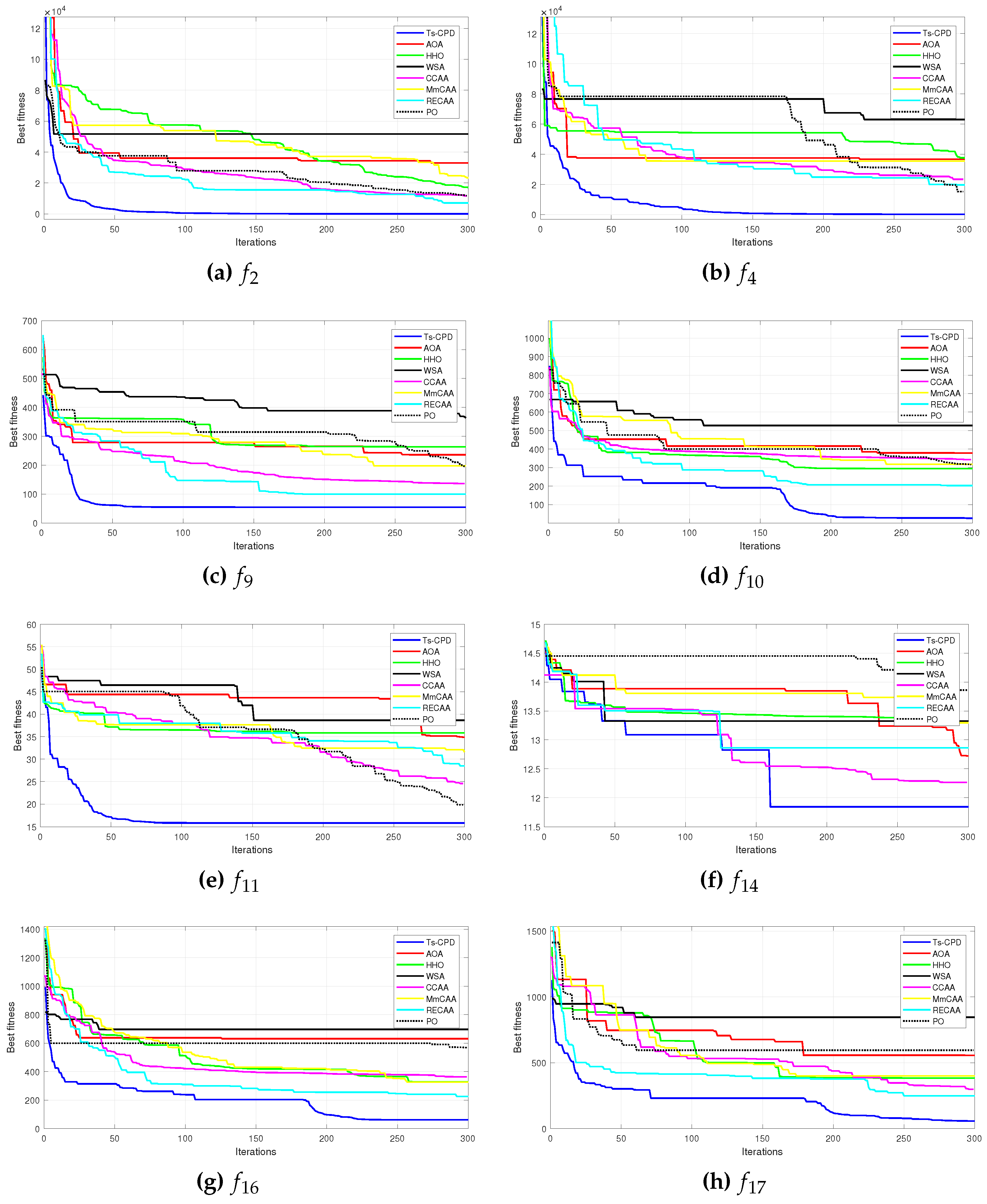
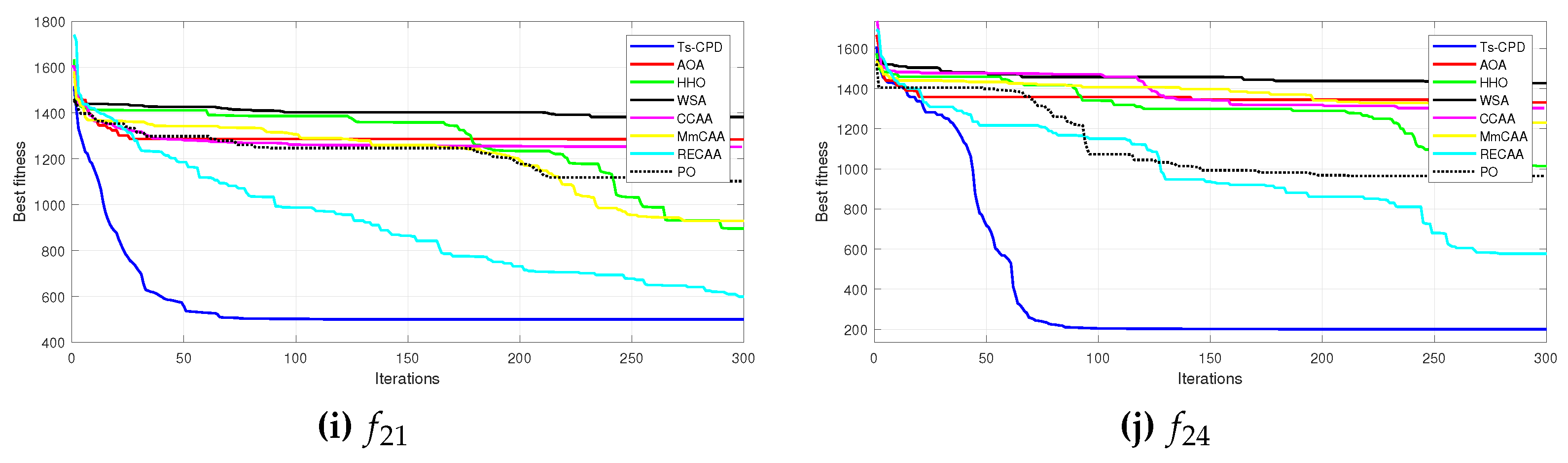
According to the previous observations, this document introduces the hybrid continuous optimization algorithm called CPSO-DE that incorporates cellular automata concepts to improve PSO exploitation capabilities with DE exploitability. The algorithm was tested on established benchmark functions (CEC 2005) [40] against 7 recently published algorithms for global optimization, yielded satisfactory results.
Additionally, Deb’s rules were incorporated into the algorithm to address constrained optimization [41,42]; this algorithm is called Ts-CPD applied in a single design objective problem, for the sizing of analog circuits to improve their performance. The approach is used as the optimization core of an EDA tool to size CMOS analog circuits efficiently. In particular, we focus on diminishing the total component area as the objective. At the same time, other specifications, such as dc gain, bandwidth and power dissipation, are treated as constraints that guarantee good overall performance. The circuits chosen for testing our method are well known, which allows a comparison of results with other proposals. We implemented the optimization in Matlab while the circuit simulation was done in Ngspice. Both optimization and simulation parts are linked.
We compare our proposal with previously published works, including PSO variants such as Particle Swarm Optimization (PSO)[19], Genetic Algorithm (GA)[43], Harmony Search (HS)[44], Differential Evolution (DE)[44], Artificial Bee Colony (ABC)[44], Gravitational Search Algorithm PSO (GSA-PSO)[20], Geometric Programming (GP)[9] and Aging Leader and Challenger PSO (ALC-PSO)[1]. The results show that Ts-CPSO can find a better circuit design solution than the above-listed approaches. In addition, it shows a rapid convergence in all the studied cases.
Overall, the proposed CPSO-DE algorithm is easy to understand, performs exceptionally well for continuous optimization, and is modified with Deb’s rules to define the Ts-CPD algorithm in order to tackle problems with multiple constraints, as demonstrated in the area optimization of CMOS analog circuits.
The rest of the paper is organized as follows: Section 2 gives a review of CPSO-DE, while the hybridization of CPSO-DE with constrained optimization is explained in Section 3. Section 4 describes three circuits in terms of their design variables and constraints. Section 5 validates the proposed Ts-CPD through three cases of study, contrasting the findings against results from previous works. Finally, this article is concluded in section 6.

2. Review of CPSO and CPSO-DE

2.1. Cellular particle swarm optimization

Particle Swarm Optimization (PSO) is one of the most frequently applied swarm intelligence-based algorithms for optimization tasks. PSO simulates the behavior of a bird flock, looking for an equilibrium between exploration and exploitation of the current solutions. Particles in a d-dimensional search space are regarded as candidate solutions. We denote the i-th particle as,
X i = ( x i , 1 , x i , 2 , … , x i , d ) ,
and its velocity as,
V i = ( v i , 1 , v i , 2 , … , v i , d ) .
Each particle evolves in the search space, where P i = ( p i , 1 , p i , 2 , … , p i , d ) is the personal best position of the i-th particle so far and G = ( g 1 , g 2 , … , g d ) is the global best position discovered by the swarm. At each time step t, both the velocity and position of each particle are updated to move it into a new position. Velocity and position are updated as follows:
V i t + 1 = V i t + c 1 r 1 ( P i t − X i t ) + c 2 r 2 ( G t − X i t ) X i t + 1 = X i t + V i t
where c 1 and c 2 are two positive constants (cognitive and social factors), r 1 and r 2 are two uniform random numbers in [ 0 , 1 ] . The fitness h ( X i ) of a particle gives its quality, that is, a better fitness value means a better particle.
Several papers have presented the adaptation, modification, and hybridization of PSO with other techniques to solve a huge variety of problems. Relevant surveys can be consulted in [45,46,47].
One recent variant of PSO is the Cellular-PSO (CPSO). The idea behind CPSO is to apply convenient properties of cellular automata to enhance the performance of PSO [36]. In this reference, it is explained that there are two crucial factors in population-based optimization algorithms: communication mechanisms for the cooperation of the population and information inheriting for the self-adaption of each individual.
The concept of cellular automata (CA) was first proposed by Von Neumann and Ulam, and there are an increasing number of researchers using CA in physics, biology, social science, computer science, and so on [48,49,50]. The implementation of CA is very simple and intuitive, and it consists of interconnected cells that update their states synchronously at discrete time steps. Each cell follows a common local function defined by its neighbors. With this simple local interaction, CA is able to produce complex global behavior.
In this paper, we use the Cellular PSO Outer version (CPSO-outer). In this case, every particle improves its searching capability, generating new solutions not belonging to the swarm. The whole search space is considered the cell space, so every potential candidate solution in the search space can be a cell. Every particle in the swarm is a “smart-cell", defined by (1), able to construct its neighborhood by a local function, enhancing its searching capability.
The neighborhood function makes CPSO-outer differ from common PSO adopting static neighbors. Every particle X i (or “smart-cell") in CPSO-outer generates a set of l neighbors N i + 1 … N i + l taking its current position and the global best position in order to realize a local search, following the next equation[36]:
N i + j = X i t + h ( G ) h ( X i t ) R ∘ V i t h ( X i t ) ≠ 0 , h ( G ) ≥ 0 X i t + h ( X i t ) h ( G ) R ∘ V i t h ( X i t ) ≠ 0 , h ( G ) < 0 X i t + e h ( G ) e h ( X i t ) 2 R ∘ V i t h ( X i t ) = 0 , h ( G ) ≥ 0 X i t + e h ( G ) e h ( X i t ) 2 R ∘ V i t h ( X i t ) = 0 , h ( G ) < 0
for 1 ≤ j ≤ l . R is a vector composed of d uniform random numbers in [ − 1 , 1 ] to obtain random changes in the direction and distance of every new neighbor, and ∘ is the Hadamard product. The idea is that the search range of every particle would be negligible at early iterations when the difference of its fitness value with that of h ( G ) is relatively significant. Then, when particles converge gradually to h ( G ) , a more extensive search range is used.
The neighbors generated by each particle are evaluated, and the neighbor with the best fitness value replaces the particle:
f ( ϕ ) = m i n ( h ( X i ) , h ( N i + 1 ) , … , h ( N i + l ) ) X ϕ = X i i f f ( ϕ ) = h ( X i ) N i + j i f f ( ϕ ) = h ( N i + j ) X i t + 1 = X ϕ t .
This transition rule gives particles new information to explore the search space from an optimal local area to another optimal local area with better fitness value and enhance the diversity of the swarm. So CPSO-outer has more significant potential to search for the global optimum.
The CPSO has been applied and modified to solve a variety of theoretical and practical problems. For instance, in [51], CPSO is used to optimize a milling system. In [52], truss structures are optimized using variants of CPSO, and parameters controlling process planning are tuned by the application of CPSO [53]. Nevertheless, CPSO has not been implemented for sizing analog circuit components.

2.2. Hybrid cellular particle swarm optimization and differential evolution

Hybrid cellular particle swarm optimization and differential evolution (CPSO-DE) is a recent hybrid method that combines the features of PSO, CA, and DE[37], which is an incorporation of local differential search to the CPSO-outer algorithm.
The cellular automata elements used in the CPSO-DE algorithm are,
(a)
configuration: (Q particles or smart-cells);
(b)
cell space: the set of all cells;
(c)
cell state: the particle’s information at time t, S i t = [ X i t ] ;
(d)
neighborhood: Φ ( i ) = { i + δ j } , 1 ≤ j ≤ l (l is the neighborhood size). See Figure 1,
(e)
transition rule: S i t + 1 = φ ( S i t ∪ S Φ ( i ) t ) .
In CPSO-DE, the i-th cell state S i t in the iteration t is updated using the PSO algorithm as follows:
V i t + 1 = w t V i t + c 1 r 1 ( P i t − S i t ) + c 2 r 2 ( P g t − S i t )
S i t + 1 = S i t + V i t + 1
where i = 1 , 2 , ⋯ , Q is the cell index and Q is the number of smart cells, c 1 and c 2 are the cognitive and social acceleration parameters respectively, r 1 and r 2 are two uniform distributed random numbers within [ 0 , 1 ] , w is the inertial weight and decreases linearly. P i is the previous personal best position, P g is the global best position, and X i and V i are the current positions and velocity.
The operators used to determine each smart cell’s neighborhoods are mutation and crossover. The mutation scheme “DE/rand/1”creates a new solution as follows:
O i , k t = S r 1 t + c 3 ( S r 2 t − S r 3 t )
where k = 1 , 2 , ⋯ , l enumerates every neighbor, and l is the neighborhood size. The r 1 , r 2 , r 3 ∈ { 1 , 2 , ⋯ , Q } are randomly chosen integers, distinct from each other and different from i. Factor c 3 is a real value between [ 0 , 2 ] for scaling the difference vector.
The crossover is an introduction to creating l trial vector H i , k , combining the information of the current smart cell with each one of the l mutated vectors, as follows:
H i , j , k = O i , j , k t , i f r i , j ≤ C r o r j = j r a n d , S i , j t , o t h e r w i s e ,
where r i j is a uniformly distributed random number within [ 0 , 1 ] , C r ∈ [ 0 , 1 ] is the crossover probability factor, and j r and ∈ { 1 , 2 , ⋯ , D } is a randomly chosen index, which ensures that H i , k copies at least one component from O i , k . Finally, the transition rule is applied over the trial vectors to update the state of the current smart-cell:
S i t + 1 ( P Φ ) = φ ( f ( S i t + 1 ) , f ( H i , 1 ) , f ( H i , 2 ) , … , f ( H i , l ) )
where the f ( . ) are the fitness functions. In CPSO-outer, the neighborhood function Φ ( i ) generates random neighbors within radius ξ t away from S i t according to its fitness value and the fitness of the best particle. Radius ξ t is small when the smart-cell S i t is far from P g t , so the potential neighbors are close to S i t , and only when S i t converges to an equilibrium point, ξ t would be a uniform random number in [ − 1 , 1 ] . Therefore, the radius of neighborhoods in CPSO-outer increases when the particles stabilize. Therefore, the best results are obtained up to the last iterations.
On the other hand, CPSO-DE generates a random neighbor within radius ξ t = c 3 ( S r 2 t − S r 3 t ) . Thus, the radius of neighborhoods depends on the distribution and the improved information of the swarm as iteration passes, not just from the difference with the best global position. Thus, S i t is more likely to obtain better neighbors in any iteration time.

3. Tournament-selection CPD

The use of cellular automata in heuristic algorithms has been shown to be efficient, more specifically, in the use of adaptive IIR filters through the hybridization of the CPSO and DE algorithms that use a rule based on the use of neighborhoods. However, the CPSO-DE algorithm for the problem with restrictions on the sizing of CMOS circuits has not yet been reported in the literature, hence the motivation for this work.
In this section, we explain the parts that comprise the proposed Ts-CPD algorithm. First, we describe the optimization problem to be solved, which contemplates restrictions. Next, we explain how the initial values are selected, for our algorithm, using tournament selection (Ts), which is a variant of what Deb proposed [41]. We conclude this section by explaining the implementation of the Deb rule in the CPSO-DE, to build the new Ts-CPD algorithm.

3.1. Constrained Optimization Problem

Many optimization problems in science and engineering implicate some constraints that the optimal solution must satisfy. For example, in a generic circuit, the optimization problem consists of finding optimal values of the design parameters. Then, a circuit design problem is usually written as a nonlinear programming (NLP) problem of the following type:
m i n i m i z e f ( X ) X ∈ ( ) n ] S u b j e c t t o : | g p | ≥ s p e c g p p = 1 ⋯ r h q = s p e c h q q = 1 ⋯ s x i , m i n ≤ x i ≤ x i , m a x i = 1 ⋯ n
In the above NLP problem, f is the cost function that maps the input space into the output one, f : ( ) n ] → ( ) , w i t h n=k+m . T h e r e a r e t w o t y p e s o f c o n s t r a i n t s , i n e q u a l i t y c o n s t r a i n t s gp t h a t h a v e t o b e m a j o r o r m i n o r t h a n c e r t a i n specgp , a n d t h e e q u a l i t y c o n s t r a i n t s hq , t h a t h a s t o b e e q u a l t o t h e r e s t r i c t i o n spechq . T h e i t h v a r i a b l e v a r i e s i n t h e r a n g e [xi,min,xi,max].The k independent variables and m dependent ones determine the circuit design represented in a single vector as,
X = ( x 1 , ⋯ , x k , x k + 1 , ⋯ , x k + m ) .
The design variables and constraints for specific circuits studied in this paper are given in the Section 4.

3.2. Tournament-selection

As in the cost function f(X) of the optimization problem expressed in (11), the restrictions are not considered; we need a method that allows us to assess their contribution. In [41], Deb proposes a constraint handling method so that while the cost function is minimized, the constraints in the search for the minimum are considered. We will use Deb’s method in this work, as explained below.
Let’s say that the CPSO-DE algorithm has encountered two solutions for the problem (11), X 1 and X 2 , according to the constrained optimization, solution X 1 is considered better if ([42]):
1.
both solutions are feasible, but X 1 cost ≤ X 2 cost; or,
2.
X 1 is feasible but X 2 is not; or,
3.
both solutions are unfeasible, but X 1 has less overall constraint violations than X 2 .
These rules, implemented as Algorithm 1, are advantageous in finding a better solution for the circuit design, as will be shown in Section 5.
Algorithm 1 Tournament-Selection ( X 1 , X 2 )
1:
if X 1 is feasible X 2 is feasible then
2:
   if  f ( X 1 ) < f ( X 2 )  then
3:
  return  ( X 1 )
4:
   else
5:
  return  ( X 2 )
6:
   end if
7:
else if constraints violation ( X 1 ) < constraints violation ( X 2 )  then
8:
   return ( X 1 )
9:
else
10:
   return ( X 2 )
11:
end if

3.3. Ts-CPD algorithm

This work proposes a new methodology that combines the CPSO-DE algorithm and Deb’s rules for the problem of sizing CMOS analog circuits with constraints. The proposed algorithm, Ts-CPD, incorporates the tournament selection (see Algorithm 1) in the Ψ ( ) function. In this method, a new transition rule is proposed for Ts-CPD, which is applied to the trial vectors to update the state of the current smart-cell:
S i t + 1 ( P Φ ) = Ψ ( … Ψ ( Ψ ( S i t + 1 , H i , 1 ) , H i , 2 ) , … , H i , l )
The transition rule in (13) means that each cell in the neighborhood (including the same smart-cell) competes in a paired tournament (according to Deb criteria), and the winner is chosen to update the state of the smart-cell.
The proposed Ts-CPD method is described in Algorithm 2. First, the algorithm sets the control parameters Q, l, T, x m i n , x m a x y v m a x . Next, the state ( S ) and velocity ( V ) are randomly initialized for each smart-cell. Then, each cell is evaluated, and its number of violated constraints is quantified. In line 9, Algorithm 1 is used to identify the best global position. The process halts according to the stopping criteria of iteration and convergence, according to line 10. Then, the cell state is updated using (6) and (7) in line 12. Later, the neighborhood of size l is generated for each smart-cell, using the DE method. Each neighbor is defined by the mutation and crossover rules in lines 14 and 15 using (8) and (9), respectively. The new transition rule inspired by Deb’s rules and CA behavior, defined in 13, is applied in line 16 to determine the new cell state. Finally, the best local and global positions are updated in lines 18 and 19, respectively, using Algorithm 1. The process is repeated by each smart-cell and neighbor.
Algorithm 2 Ts-CPD
1:
//** Initialization
2:
Set the control parameters: Q, l, T, x m i n , x m a x , v m a x ;
3:
for i = 1 to Q do
4:
   Initialize S i ∈ ( x m i n , x m a x ) randomly;
5:
   Initialize V i ∈ ( − v m a x , v m a x ) randomly;
6:
    P i = S i ;
7:
end for
8:
Evaluate each cell f ( S i ) ;
9:
Identify the best global position ( P g ) : using Algorithm 1;
//*** Loop
10:
while stopping criterion is not satisfied do
11:
   for  i = 1 to Q do
12:
     Update cell state: using equations (6) and (7);
     //***Generate l neighbors using DE method
13:
     for  k = 1 to l do
14:
        Mutation rule: using equation (8);
15:
        Crossover rule: using equation (9);
16:
        New transition rule: using equation (13);
17:
     end for
18:
     Identify the best local position ( P i ) : using Algorithm 1;
19:
     Identify the best global position ( P g ) : using Algorithm 1;
20:
   end for
21:
end while

3.4. Performance of the Ts-CPD algorithm

To test the effectiveness of the Ts-CPD algorithm (without Deb’s rules), we compared it to seven recently published global optimization algorithms, namely AOA [54], HHO [55], WSA [56], CCAA [38], MmCCAA [39], RECAA [57], and PO [58]. We used a total of 25 benchmark functions from CEC 2005 benchmark functions [40], which included five unimodal functions ( f 1 , ⋯ , f 5 ), seven basic multimodal functions ( f 6 , ⋯ , f 12 ), two expanded multimodal functions ( f 13 , f 14 ), and 11 hybrid composition multimodal functions ( f 15 , ⋯ , f 25 ).
We obtained the codes and parameters for these algorithms from the references cited in this study. This ensured that we used the same implementations as the original authors, making the comparison more objective. Table 1 and Table 2 present the average values and standard deviations of the objective function values obtained by each algorithm. We ran each algorithm independently 30 times.
In unimodal problems, the Ts-CPD algorithm showed excellent performance, ranking first among the eight algorithms in terms of average value. Moreover, it surpassed other algorithms in three cases based on standard deviation, highlighting its proficiency in information exploitation.
For the 20 multimodal and hybrid problems, Ts-CPD exhibited the highest average values in 12 instances. It also demonstrated its ability to explore and exploit simultaneously while maintaining robustness, achieving the best standard deviation values in four cases. Figure shows some examples of the convergence curves for different test functions in 30 dimensions.

4. The proposed tool for analog IC sizing

The EDA tool proposed for the designer of analog circuits through the Ts-CPD algorithm allows obtaining a minimum area of the components used while complying with the design specifications. It is handy for designing the frequency response of circuits, such as bandwidth, phase margin, CMRR, or PSRR; only the slew rate can be designed in the time domain. For this purpose, before beginning the design, the designer must introduce the specifications (restrictions) of the circuit and the acceptable ranges and values for the parameters according to the technology used. The parameters to choose are the width and length of the CMOS transistors, capacitance and resistance (if any) values, bias current, and voltage sources.
The tool consists of two main modules: the optimization and synthesis processes. The optimization process contains the Ts-CPD algorithm comprising the CPSO-DE and the Deb rule, with a new transition rule given by (13); this module is implemented in Matlab. The synthesis process uses the specialized Ngspice software, which allows analog circuit simulations without mathematical equations. Instead, the standard configurations necessary to evaluate the performance of circuits are implemented in a netlist format. Both modules, the optimization and synthesis processes, are linked, allowing an automatic circuit design. The flow chart for our EDA tool, using Ts-CPD, is shown in Figure 3.
The following subsection describes three case studies, in terms of their variables and constraints, that will be used to verify the efficiency of the EDA tool.

4.1. Cases of study

To test our algorithm and tool, we chose three case studies, a “CMOS Differential Amplifier" differential amplifier, a “CMOS two-stage operational amplifier," and a “CMOS folded cascode operational transconductance amplifier." These cases were chosen because they have already been studied previously, and therefore, it is possible to compare the results of our algorithm against previous results, which is very interesting. In this sense, case 1 has 5 independent variables and 11 restrictions to meet, case 2 has 5 independent variables and 11 restrictions, while case 3, the most complete, has 9 independent variables and 13 restrictions to meet at the same time.

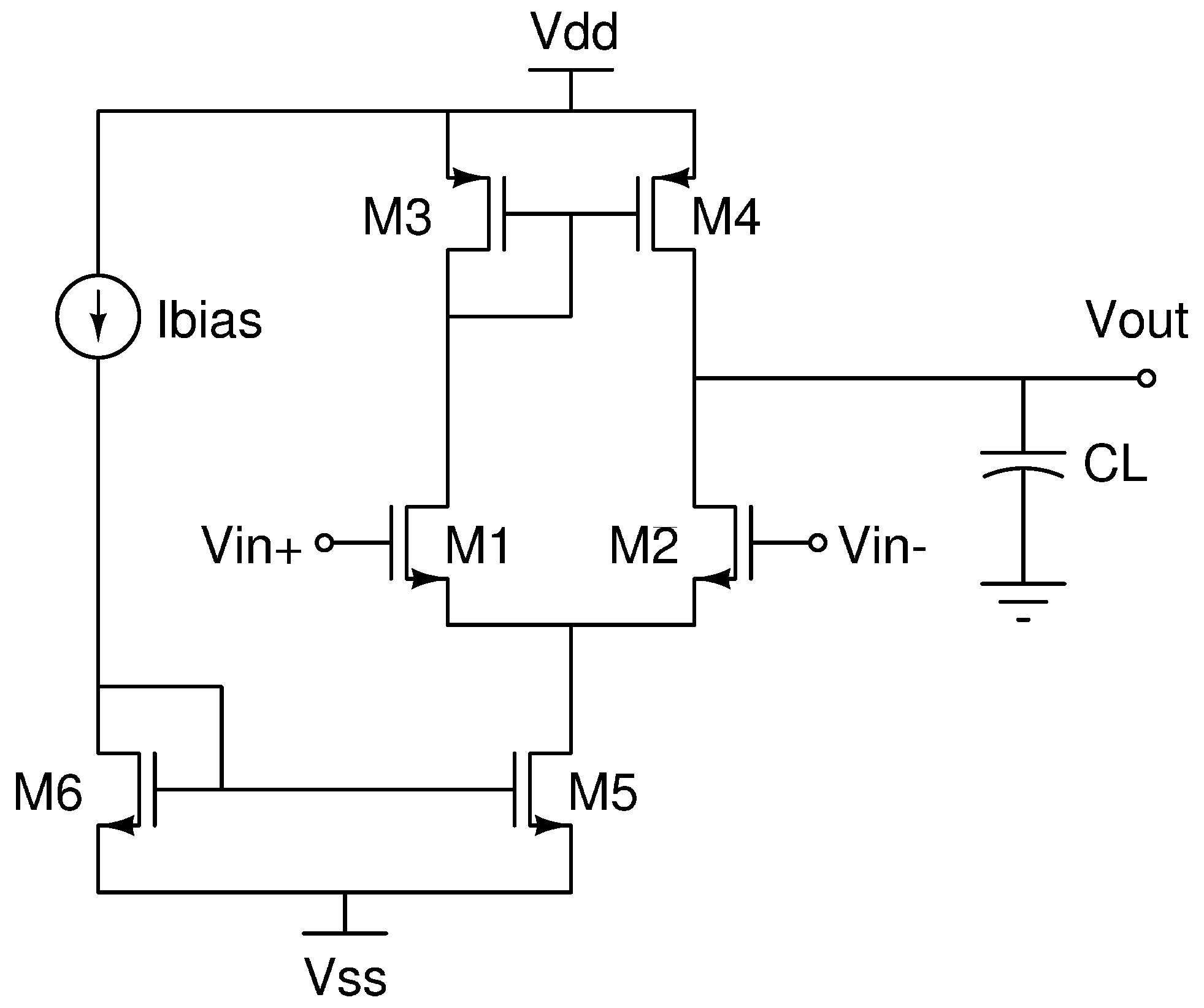
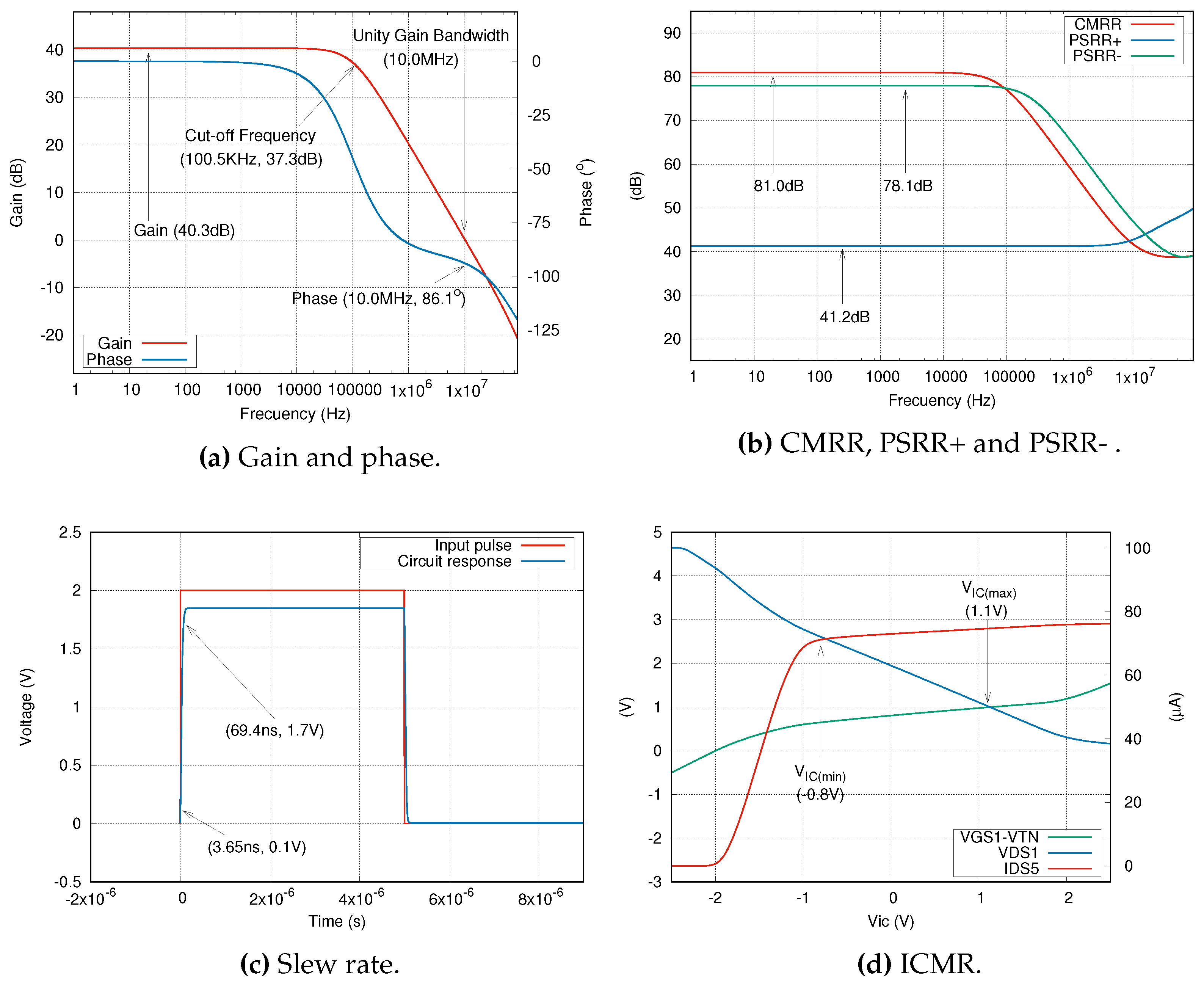
4.1.1. Case 1: CMOS differential amplifier

Figure 4 shows our first case of study, a CMOS differential amplifier. First, M 1 must be equally sized than M 2 ; thus, the following equality restrictions must be satisfied:
W 1 = W 2 and L 1 = L 2 .
Secondly, s of the current source, M 3 and M 4 , must be equally sized, too, thus
W 3 = W 4 and L 3 = L 4 .
We let both W 5 and W 6 be independent variables, and our algorithm selects their values while L 5 = L 6 . That is because the sizes of all s are within a specific range imposed by the technology used for this design:
W n , m i n ≤ W n < W n , m a x , n = 1 , 2 , ⋯ , 6 .
In our case, W n , m i n was fixed to 4 μ m for a better comparison with other works, and W n , m a x was fixed to 120 μ m to have a value large enough. For this example, there are 5 independent variables ( W 1 , W 3 , W 5 , W 6 and I b i a s ) and 2 dependent ones ( W 2 and W 4 ). On the other hand, the design specifications to be met will be treated as constraints. For this case, there are 11 constraints: load capacitance, slew rate, power dissipation, phase margin, cut-off frequency, DC gain, V I C (min), V I C (max), CMRR, PSRR+ and PSRR-.

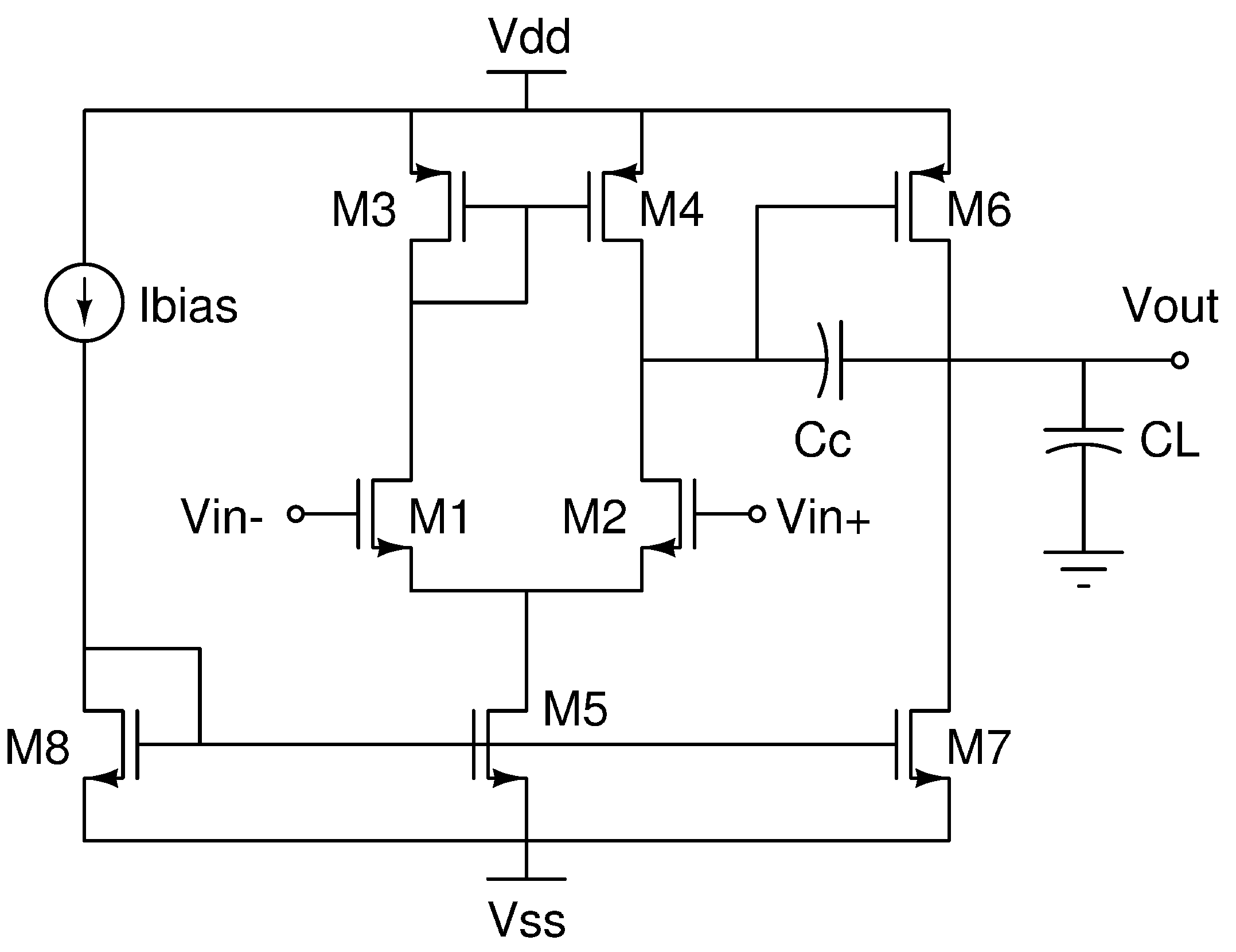
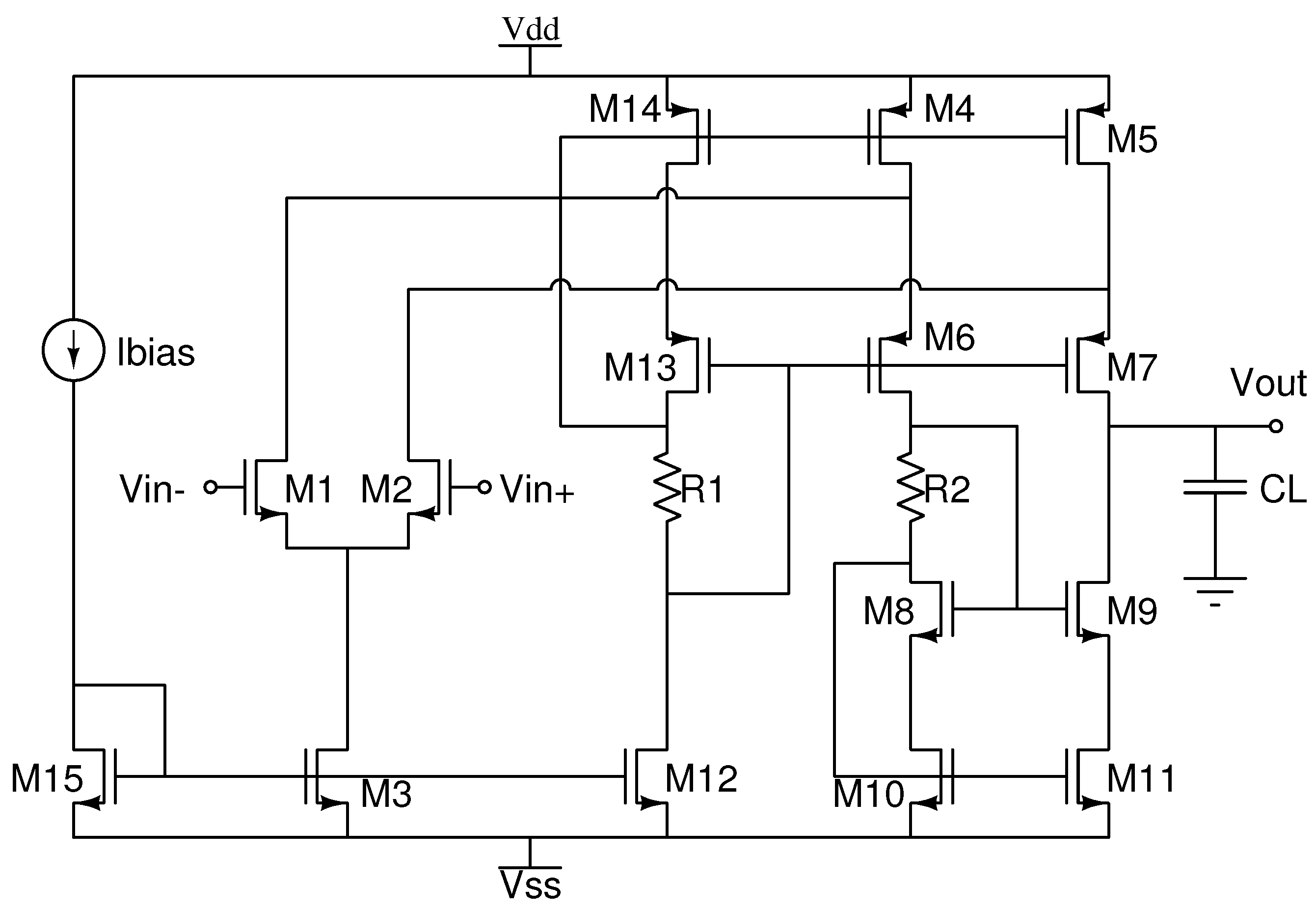
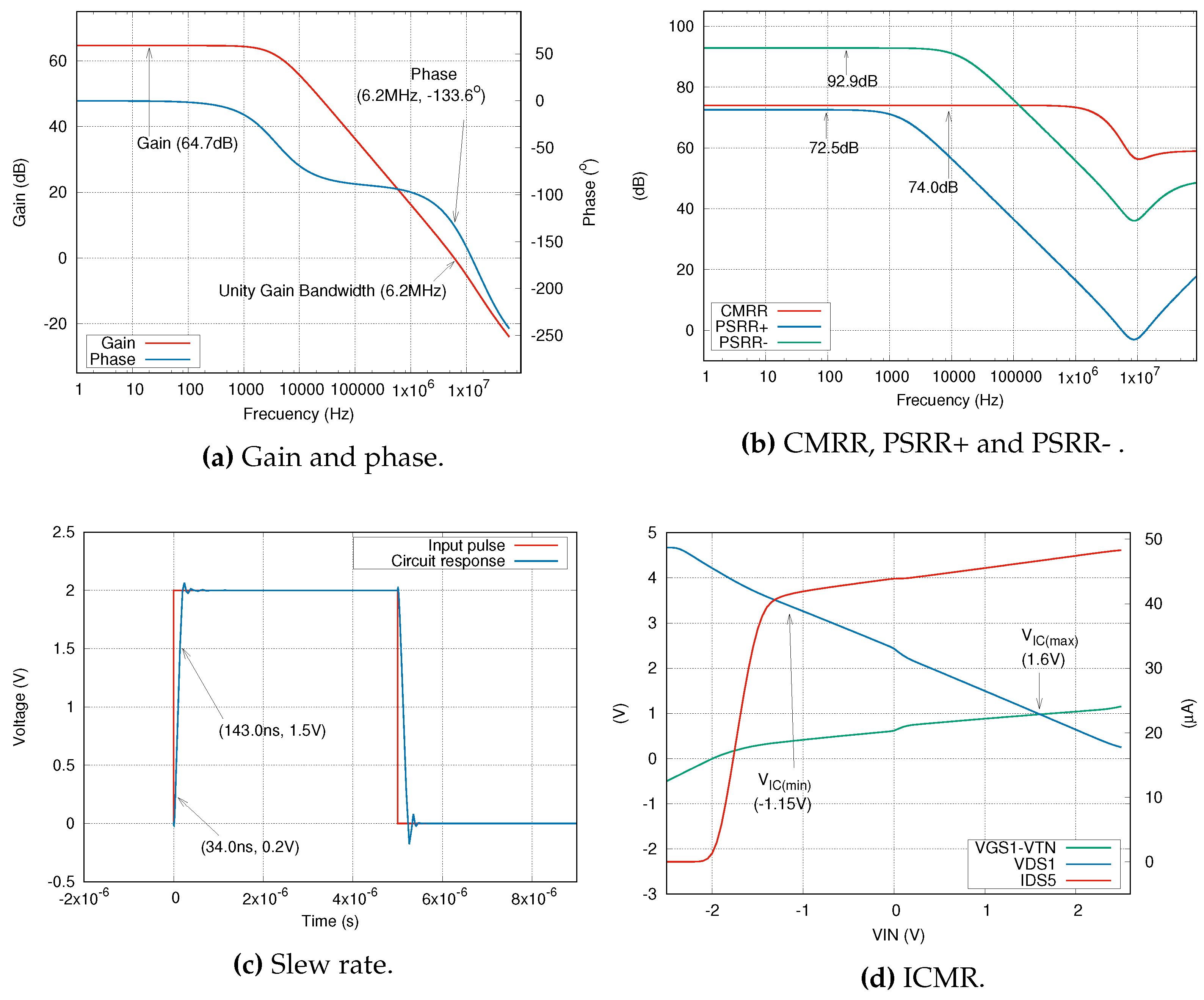
4.1.2. Case 2: CMOS two-stage operational amplifier

Figure 5 shows our second case of study, a CMOS two-stage operational amplifier consisting of 8 s. The first amplification stage, differential input, has the stipulation that M 1 must be equally sized as M 2 , so that equations (14), (15) are still valid, and we add,
W 5 = W 8 and L 5 = L 8 .
Also, to avoid an output offset at the second amplification stage, the following restriction is imposed:
W 7 / L 7 W 5 / L 5 = 2 W 6 / L 6 W 4 / L 4 .
Similarly, as in (16), sizes of the CMOS two-stage operational amplifier are in a specific range, but now n = 8 . Also, the compensation capacitance is within a range of values, between C C , m i n and C C , m a x , which the designer selects:
C C , m i n ≤ C C < C C , m a x .
The C C , m i n and C C , m a x values are fed to the Ts-CPD algorithm through a file in our EDA tool. We choose C C , m i n = 2 pF, because lower values than that are challenging to achieve and C C , m a x = 14 pF to avoid using significant areas, but these values are easily changed.
On the other hand, bias current I B I A S also is within a range o values:
I B I A S , m i n ≤ I B I A S < I B I A S , m a x .
It is clear from equations (14), (15) and (17) that, for the purpose of design, W 2 , W 4 and W 6 can be handled as independent variables, while W 1 , W 3 and W 5 as can be handled as dependent ones. W 7 is deduced from (18), thus, W 7 is also a dependent variable; I B I A S and C C are considered independent variables whose values are bounded by (20) and (19), respectively. Therefore, this example has 5 independent variables, W 2 , W 4 , W 6 , I B I A S and C c , whose values are selected by our algorithm and 5 dependent variables W 1 , W 3 , W 5 , W 7 and W 8 , whose impact over cost function and restrictions is evaluated by our algorithm to determine new values for independent variables, in an iterative process. In this paper, the length of s is considered constant. However, when lengths are considered variables, the minimum and maximum values must be established, as for widths in equation (16). For this case, there are 11 constraints: load capacitance, slew rate, power dissipation, phase margin, unity gain bandwidth, DC gain, V I C (min), V I C (max), CMRR, PSRR+, and PSRR-.

4.1.3. Case 3: CMOS folded cascode operational transconductance amplifier

A third case of study is the folded cascode operational transconductance amplifier (FCOTA) shown in Figure 6. The transistors M 1 and M 2 are equally sized; thus, equation (14) is also valid. We considered the transistor widths W 3 and W 4 independent variables and W 5 and W 14 dependent ones, as follows:
W 4 = W 5 = W 14 and L 4 = L 5 = L 14 .
In addition, W 6 , W 8 , W 12 and W 15 are considered independent variables while W 7 , W 9 , W 10 , W 11 , and W 13 are considered dependent variables, as follows:
W 6 = W 7 = W 13 and L 6 = L 7 = L 13 ,
W 8 = W 9 = W 10 = W 11 and L 8 = L 9 = L 10 = L 11 .
The values of the bias current I B I A S are bounded by (20) and properly selected by our algorithm. For design, we considered R 1 as an independent variable. Thus, our algorithm also selects its value within 1000 < R 1 < 6000 , while R 2 is considered a dependent variable, with R 1 = R 2 . This way, there are 9 independent variables ( W 1 , W 3 , W 4 , W 6 , W 8 , W 12 , W 15 , I B I A S and R 1 ) and 9 dependent variables ( W 2 , W 5 , W 7 , W 9 , W 10 , W 11 , W 13 , W 14 and R 2 ). The constraints for this case are 13: load capacitance, slew rate, power dissipation, phase margin, unity gain bandwidth, DC gain, V I C (min), V I C (max), V o u t (min), V o u t (max), CMRR, PSRR+ and PSRR-.

5. Numerical results and discussion

In order to test our proposed tool, three examples of design are shown in this section. First, the optimization is implemented in MATLAB R2014b, while the simulation of circuits is implemented in the NGSPICE r26 simulator; both are linked, so the design process is completely automated. On the other hand, the model of NMOS and PMOS transistors for 0.35 μ m technology was downloaded from the MOSIS database. Finally, the transistor lengths were set to fixed values close to those in the literature for comparison purposes.
Our design objective is to minimize the area of analog circuits. However, designing an amplifier is always a trade-off, so we introduce the small-signal figure of merit that considers silicon area to assess the designed circuits’ overall performance [61]:
A F O M S S = ( f u · C L / P Q · A r e a )
where f u is the unity gain frequency, C L is the load capacitance, P Q is the power consumption at quiescent, and Area is the component (transistors) area.

5.1. Numerical results for CMOS differential amplifier (Case 1)

As a first example, the differential amplifier of Figure 4 is designed. We aim to minimize the total component area, which is our cost function, below 300 μ m 2 while restrictions are still met. As shown in Table 3, the power dissipation is specified to be < 2 , 200 μ W, DC gain ≥40 dB, slew rate ≥ 10 V/ μ s and the cut-off frequency ≥ 100 KHz. Other specifications are Common Mode Rejection Ratio (CMRR), Positive Power Supply Rejection Ratio (PSRR+), Negative Power Supply Rejection Ratio (PSRR-), and the Input Common-Mode Range (ICMR), all to be > 40 dB, and finally V I C ( m i n ) ≥ − 1.5 V and V I C ( m a x ) ≤ 2 V. The circuit’s load determines load capacitance, but the specification to be satisfied is ≥ 2 pF; we choose 2.1 pF. The AFOM S S is also shown.
For the optimization purpose, some variables are set to a fixed value, and the micro-channel lengths were set to L 1 = L 2 = L 3 = L 4 = 3.5 μ m, L 5 = L 6 = 1.4 μ m, and voltage sources were set to V d d = − V s s = 2.5 V. On the other hand, C c and I b i a s are treated as independent variables with restrictions , i.e. they can run within a specific range of values in our algorithm.
The numerical results for the differential amplifier of Figure 4 are shown in Table 3; it presents a comparison of Ts-CPD with several methods: MOL [59], SOA [60], PSO [19], HS [44], DE [44], Artificial Bee Colony (ABC) [44], and GA [43]. The Ts-CPD obtains the lower total component area for methods that report this design objective and obtains the higher slew rate and PSRR − ; other specifications are also accomplished. Here, the MOL algorithm has the higher AFOM S S value. Table 4 shows the result of the designed differential amplifier for three evolutionary algorithms.
In order to explore the performance of the differential amplifier designed, we show the DC gain and phase margin in Figure 7a; The CMRR, PSRR+, and PSRR- in Figure 7b; Slew rate in Figure 7c; and the ICMR in Figure 7d, which is used for the graphical determination of V I C ( m i n ) and V I C ( m a x ) . These graphics demonstrate that the designed circuit behaves well and is accomplished with all the constraints (Specifications).
Figure 8a shows the convergence of our algorithm for this circuit design, which has an excellent profile. Our algorithm’s behavior was also tested with 50 runs; the corresponding Box and Whisker plot is shown in Figure 8b. The median is 1.4168x 10 − 10 m 2 , which is still below the results reported for other algorithms; see Table 3.

5.2. Numerical results for CMOS two-stage operational amplifier (Case 2)

As a second example, we designed the two-stage operational amplifier in Figure 5. Again, the aim is to minimize the total component area as much as possible while constraints are still met. The total component area is specified to be < 300 μ m 2 , and in this case, the DC gain > 60 dB, unity gain bandwidth ≥ 3 MHz, phase margin ≥ 45 o , slew rate ≥ 10 V/ μ s and load capacitance ≥ 7 pF. In other set of specifications, CMRR > 60 dB, PSRR + > 70 dB, PSRR + > 70 dB, V I C ( m i n ) > − 1.5 V and V I C ( m a x ) ≤ 2 V. At the end, the AFOM S S is shown.
The microchannel lengths of all MOS transistors have been set to a fixed value, L 1 = L 2 ⋯ L 8 = 0.8 μ m, while voltage sources are set to V d d = − V s s = 2.5 V. Here, C c and I b i a s are independent variables. Thus, our algorithm determines its values in concordance with (19) and (20), respectively.
Table 5 shows the complete set of restrictions and design objective for the CMOS operational amplifier of Figure 5, as well as the comparison of methods Ts-CPD, GSA-PSO[20], PSO, and Geometric Programming (GP) [9]. As expected, the Ts-CPD has the lower component area and the highest slew rate and PSRR-. The AFOM S S , on the other hand, is higher for our algorithm. The design parameters of the optimized circuit are shown in Table 6.
The performance of the CMOS two-stage operational amplifier can be evaluated through the gain and phase plot in Figure 9a; the CMRR, PSRR+, and PSRR- plots in Figure 9b; the ICMR in Figure 9c; and the slew rate in Figure 9d. These plots also demonstrate the excellent performance of the designed circuit.
On the other hand, we evaluated the performance of our algorithm with the convergence profile in Figure 10a, and the Box and Whisker plot of Figure 10b. After 16 iterations, the Ts-CPD reached convergence; see Figure 10a. We executed 50 trial runs for the circuit design; Figure 10b shows the corresponding Box and Whisker plot for the total MOS area of transistors. The best value is 4.557 x 10 − 11 m 2 , but the median (6.1738 x 10 − 11 m 2 ) is also lower than others reported for this circuit, as can be seen in Table 5.

5.3. Numerical results for CMOS folded cascode operational transconductance amplifier (Case 3)

Our third example is the folded cascode operational amplifier shown in Figure 6. The total component area specified is < 1315.9 μ m 2 (our design objective). At the same time, specified constraints are gain > 74 dB, unity bandwidth ≥ 10 MHz, phase margin > 60 o , slew rate ≥ 10 V / μ s and load capacitance ≥ 10 pF (we chose exactly 10.0pF). More constraints are CMRR, PSRR+, PSRR- all three ≥ 55 dB, V I C ( m i n ) ≥ − 1.5 , V I C ( m a x ) ≤ 2.5 , and finally V o u t ( m i n ) ≥ − 2 and V o u t ( m a x ) ≤ 2 . And at the end, the AFOM S S is shown.
For all MOS transistors, the lengths have been set to a fixed value, L 1 = L 2 ⋯ L 15 = 1.5 μ m, and the voltage sources are set to V d d = − V s s = 2.5 V. Besides the transistor widths ( W i ), I b i a s , R 1 and R 2 are also variables.
Table 7 shows the numerical results for the FCOTA of Figure 6 and a comparison of methods Ts-CPD and ALC-PSO[1]. Our proposal, Ts-CPD, has the lower total component area (our design objective) and the highest Unity gain bandwidth, phase margin, CMRR, and PSRR-, while other constraints are also met. Additionally, the AFOM S S is greater for our algorithm. The parameters of the optimized circuit for the two proposals are shown in Table 8.
The excellent performance of the CMOS folded cascode operational transconductance amplifier is demonstrated through the plots of gain and phase in Figure 11a; CMRR, PSRR+, and PSRR- in Figure 11b; the ICMR in Figure 11c; and the slew rate, Figure 11d.
The Ts-CPD performance is evaluated with the convergence profile shown in Figure 12a and the Box and Whisker plot of Figure 12b. As can be seen in Figure 12a, the Ts-CPD converges very quickly for this circuit design in just 5 iterations. Figure 12b shows the Box and Whisker plot for 50 trial runs for the total MOS area of transistors. The median is 5.9674 x 10 − 11 m 2 , and the solutions are very clustered towards this value.

6. Conclusions

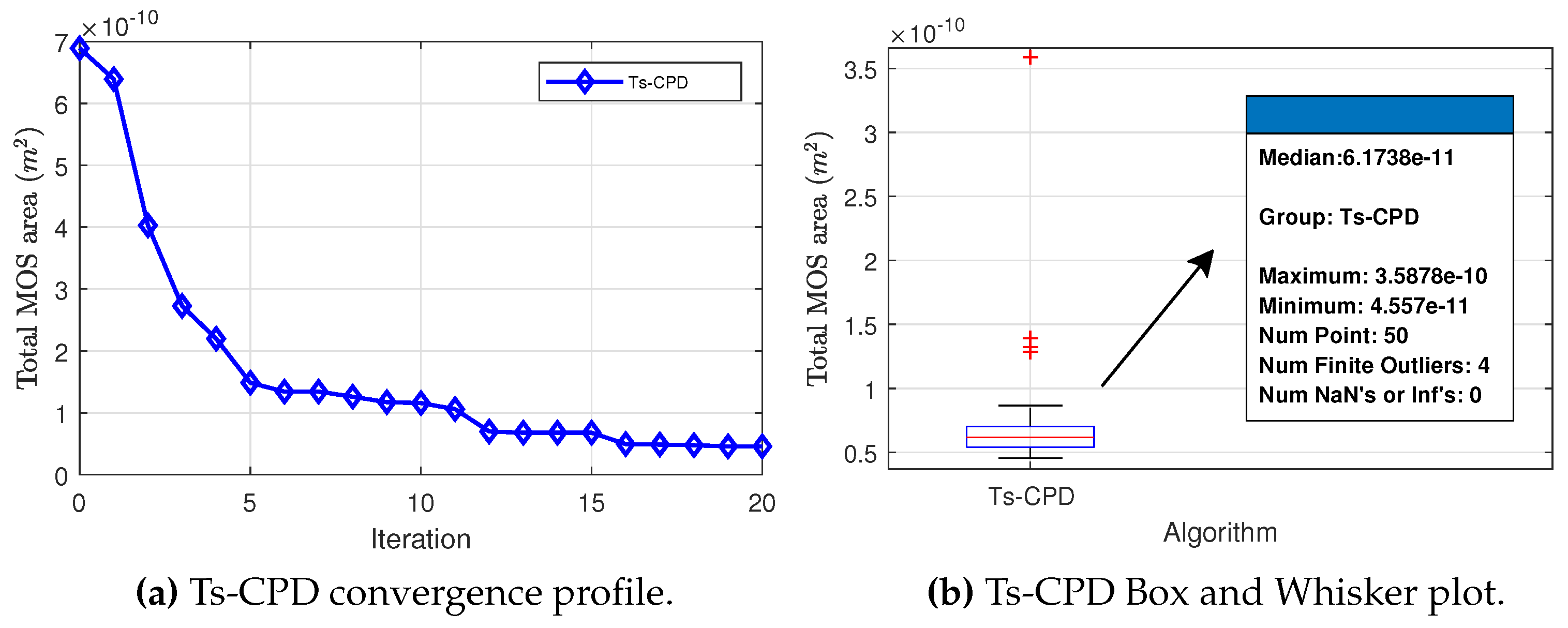
The Ts-CPSO algorithm that was proposed and implemented improves the CPSO by incorporating a way of evaluating the performance of constraints, through the optimization-with-constraints method, with a new rule we proposed. This algorithm has the advantage of not only minimizing the objective function but also ensuring that the constraints are met and then generating the new parameter values. Then the Ts-CPSO algorithm is incorporated into our EDA tool for the optimal sizing of analog circuits, which does not require mathematical equations since the optimization is linked to a simulator that provides the circuit’s behavior.
The Ts-CPD algorithm, as part of our EDA tool, was tested with three cases of study in a 0.35um CMOS technology, a differential amplifier, a two-stage operational amplifier, and a folded cascode operational transconductance amplifier. It was proposed as a design objective to reduce the total area occupied by the transistors while complying with some established constraints. In all cases, our tool found a better solution, for the objective, than previously reported tools, while the constraints were kept within the desired limits.
In future work, we are going to implement a multi-objective algorithm, which we will add as the kernel of our EDA tool. We will also do design tests with analog circuits with more transistors and large-scale analog circuits, such as the ADC, considering the Layout design. As another potential future project, a framework incorporating multiple algorithms for optimizing various analog circuits can be developed. This framework would allow users to customize each algorithm’s parameters to enhance its performance, compare the different methods with convergence plots and identify the optimal design.

Author Contributions

Conceptualization, P. L.-E. and P.M.-R.; methodology, P. L.-E. and P.M.-R.; validation, J.C.S.-T.-M. and N.H.-R.; formal analysis, P. L.-E., P.M.-R. and J.C.S.-T.-M.; investigation, P. L.-E., P.M.-R., J.C.S.-T.-M. and N.H.-R.; resources, P.M.-M. and J.C.S.-T.-M.; writing—original draft preparation, P. L.-E., P.M.-R., J.C.S.-T.-M. and N.H.-R.; writing—review and editing, P.M.-R. and J.C.S.-T.-M. visualization, P. L.-E., P.M.-R. and J.C.S.-T.-M.; supervision, J.C.S.-T.-M. and N.H.-R.; funding acquisition, J.C.S.-T.-M. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the Autonomous University of Hidalgo (UAEH) and the National Council for Humanities, Science and Technology (CONAHCYT) with project number F003-320109.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.

Abbreviations

CPSO-DE Cellular particle swarm algorithm with differential evolution
EDA Electronic design automation
VLSI Very Large Scale of Integration
CAD Computer-Aided Design
Ts-CDP Tournament-selection CPSO-DE

References

  1. De, B.P.; Kar, R.; Mandal, D.; Ghoshal, S.P. An efficient design of CMOS comparator and folded cascode op-amp circuits using particle swarm optimization with an aging leader and challengers algorithm. International Journal of Machine Learning and Cybernetics 2016, 7, 325–344. [Google Scholar] [CrossRef]
  2. Dehbashian, M.; Maymandi-Nejad, M. An enhanced optimization kernel for analog IC design automation using the shrinking circles technique. Engineering Applications of Artificial Intelligence 2017, 58, 62–78. [Google Scholar] [CrossRef]
  3. Cohen, M.W.; Aga, M.; Weinberg, T. Genetic algorithm software for analog circuit design. Procedia CIRP.
  4. Ozenli, D.; Alaybeyoglu, E.; Kuntman, H.; Cicekoglu, O. MOSFET-Only filter design automation based on polynomial regression with exemplary circuits. AEU - International Journal of Electronics and Communications 2018, 84, 342–354. [Google Scholar] [CrossRef]
  5. Durmuş, B. Optimal Components Selection for Active Filter Design with Average Differential Evolution Algorithm. AEU - International Journal of Electronics and Communications 2018, 94, 293–302. [Google Scholar] [CrossRef]
  6. Lourenço, N.; Martins, R.; Horta, N. , Automatic Analog IC Sizing and Optimization Constrained with PVT Corners and Layout Effects; Springer International Publishing: Cham, 2017; chapter PreviousWorks on Automatic Analog IC Sizing; pp. 13–37. [Google Scholar]
  7. Brayton, R.K.; Hachtel, G.D.; Sangiovani-Vicentelli, A.L. A survey of optimization techniques for integrated-circuit design. Proceeding of the IEEE 1981, 69, 1334–1362. [Google Scholar] [CrossRef]
  8. Carley, L.R.; Rutenabar, R. How to automate analog IC designs. IEEE Spectrum 1988, 25, 26–30. [Google Scholar] [CrossRef]
  9. d. Hershenson, M.; Boyd, S.P.; Lee, T.H. Optimal Design of a CMOS op-amp via Geometric Programming. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2001, 20, 1–21. [Google Scholar] [CrossRef]
  10. d. Hershenson, M. Hershenson, M. Analog Circuit Design via Geometric Programming. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 2004, E87-A, 298–310. [Google Scholar]
  11. Fares, M.; Kaminska, B. FPAD: A Fuzzy Nonlinear Programming Aproach to Analog Circuit Design. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 1995, 14, 785–793. [Google Scholar] [CrossRef]
  12. Torralba, A.; Chávez, J.; Franquelo, L.G. Circuit Performance Modeling by Means of Fuzzy Logic. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 1996, 15, 1391–1398. [Google Scholar] [CrossRef]
  13. Oltean, G.; Miron, C.; Mocean, E. Multiobjective Optimization Method for analog circuits design based on fuzzy logic. 9th International Conference on Electronics, Circuits and Systems, 2002, Vol. 2, pp. 770–780.
  14. Torralba, A.; Chávez, J.; Franquelo, L.G. FASY: A fuzzy-Logic Based Tool for Analog Synthesis. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 1996, 15, 705–715. [Google Scholar] [CrossRef]
  15. Miranda-Romagnoli, P.; Hernandez-Romero, N.; Seck-Tuoh-Mora, J.C. A neuro fuzzy solution in the design of analog circuits. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 2011, 94, 434–439. [Google Scholar] [CrossRef]
  16. de Lima Moreto, R.A.; Thomaz, C.E.; Gimenez, S.P. A customized genetic algorithm with in-loop robustness analyses to boost the optimization process of analog CMOS ICs. Microelectronics Journal 2019, 92, 104595. [Google Scholar] [CrossRef]
  17. Vural, R.A.; Yildirim, T. Component Value Selection for Analog Active Filter Using Particle Swarm Optimization. 2010 The 2nd International Conference on Computer and Automation Engineering (ICCAE), 2010, pp. 25–28.
  18. Mostafa, S.S.; Horta, N.; Ravelo-García, A.G.; Morgado-Dias, F. Analog Active Filter Design using a Multi Objective Genetic Algorithm. AEU-International Journal of Electronics and Communications 2018, 93, 83–94. [Google Scholar] [CrossRef]
  19. Vural, R.A.; Yildirim, T. Analog circuit sizing via swarm intelligence. AEU - International Journal of Electronics and Communications 2012, 66, 732–740. [Google Scholar] [CrossRef]
  20. Mallick, S.; Kar, R.; Mandal, D.; Ghoshal, S. Optimal sizing of CMOS analog circuits using gravitational search algorithm with particle swarm optimization. International Journal of Machine Learning and Cybernetics 2017, 8, 309–331. [Google Scholar] [CrossRef]
  21. Ghosh, S.; De, B.P.; Kar, R.; Mandal, D.; Mal, A.K. Optimal design of complementary metal-oxide-semiconductor analogue circuits: An evolutionary approach. Computers & Electrical Engineering 2019, 80, 106485. [Google Scholar]
  22. Sabat, S.L.; Kumar, K.S.; Udgata, S.K. Differential Evolution and Swarm Intelligence techniques for analog Circuit Synthesis. 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC2009), 2009, pp. 469–473.
  23. Barros, M.; Guilherme, J.; Horta, N. Analog circuits optimization based on evolutionary computation techniques. Integration 2010, 43, 136–155. [Google Scholar] [CrossRef]
  24. Jafari, A.; Bijami, E.; Rekabi, B.; Saeed, S. A design automation system for CMOS analog integrated circuits using New Hybrid Shuffled Frog Leaping Algoritm. Microelectronics Journal 2012, 43, 908–915. [Google Scholar] [CrossRef]
  25. Bausser, M.; Talbi, E.G.; Nebro, A.; Alba, E. Metaheuristics for multiobjective combinatorial optimization problems: review and recent issues. Research report, INRIA, 2006.
  26. Chan, F.T.; Tiwari, M.K. Swarm Intelligence; IntechOpen: Rijeka, 2007. [Google Scholar] [CrossRef]
  27. Liu, B.; Gielen, G.; Fernández, F.V. , Automated Design of Analog and High-frequency Circuits: A Computational Intelligence Approach; Springer Berlin Heidelberg, 2014; chapter Basic Concepts and Background, pp. 1–17.
  28. Kumar, P.P.; Duraiswamy, K. An Optimized Device Sizing of Analog Circuits using Particle Swarm Optimization. Journal of Computer Science 2012, 8, 930–935. [Google Scholar]
  29. Gupta, H.; Ghosh, B. Analog Circuits Design Using Ant Colony Optimization. International Journal of Electronics, Computer and Communications Technologies 2012, 2, 9–21. [Google Scholar]
  30. Cheng, Y.; Chan, L.Y.; Chen, Y.L.; Liao, Y.C.; Liu, C.N. A bias-driven approach to improve the efficiency of automatic design optimization for CMOS OP-Amps. 2012 4th Asia Symposium on Quality Electronic Design (ASQED), 2012, pp. 59–63.
  31. Tlelo-Cuautle, E.; Sanabria-Borbon, A.C. Optimising operational amplifiers by evolutionary algorithms and gm/Id method. International Journal of Electronics 2016, 103, 1665–1684. [Google Scholar] [CrossRef]
  32. Lourenço, N.; Martins, R.; Horta, N. Automatic analog IC sizing and optimization constrained with PVT corners and layout effects; Springer, 2017.
  33. Gielen, G.G.E.; Maricau, E.; De Wit, P. Designing reliable analog circuits in an unreliable world. Proceedings of the IEEE 2012 Custom Integrated Circuits Conference, 2012, pp. 1–4. [CrossRef]
  34. Puzzi, S.; Carpinteri, A. A double-multiplicative dynamic penalty approach for constrained evolutionary optimization. Structural and Multidisciplinary Optimization 2008, 35, 431–445. [Google Scholar] [CrossRef]
  35. Dehbashian, M.; Maymandi-Nejad, M. Co-AGSA: An efficient self-adaptive approach for constrained optimization of analog IC based on the shrinking circles technique. Integration 2017, 59, 218–232. [Google Scholar] [CrossRef]
  36. Shi, Y.; Liu, H.; Gao, L.; Zhang, G. Cellular particle swarm optimization. Information Sciences 2011, 181, 4460–4493. [Google Scholar] [CrossRef]
  37. Lagos-Eulogio, P.; Seck-Tuoh-Mora, J.C.; Hernandez-Romero, N.; Medina-Marin, J. A new design method for adaptive IIR system identification using hybrid CPSO and DE. Nonlinear Dynamics 2017, 88, 2371–2389. [Google Scholar] [CrossRef]
  38. Seck-Tuoh-Mora, J.C.; Hernandez-Romero, N.; Lagos-Eulogio, P.; Medina-Marin, J.; niga Peña, N.S.Z. A continuous-state cellular automata algorithm for global optimization. Expert Systems with Applications 2021, 177, 114930. [Google Scholar] [CrossRef]
  39. Seck-Tuoh-Mora, J.C.; Hernandez-Romero, N.; nos, F.S.B.; Volpi-Leon, V.; Medina-Marin, J.; Lagos-Eulogio, P. A majority-minority cellular automata algorithm for global optimization. Expert Systems with Applications 2022, 203, 117379. [Google Scholar] [CrossRef]
  40. Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization. KanGAL report 2005, 2005005, 2005. [Google Scholar]
  41. Deb, K. An efficient constraint handling method for genetic algorithms. Computer Methods in Applied Mechanics and Engineering 2000, 186, 311–338. [Google Scholar] [CrossRef]
  42. Ma, H.; Simon, D. Blended biogeography-based optimization for constrained optimization. Engineering Applications of Artificial Intelligence 2011, 24, 517–525. [Google Scholar] [CrossRef]
  43. Kruiskamp, W.; Leenaerts, D. DARWIN: CMOS opamp Synthesis by means of a Genetic Algorithm. 32nd ACM/IEEE Design Automation Conference, 1995, pp. 433–438.
  44. Vural, R.; Erkmen, B.; Bozkurt, U.; Yildirim, T. CMOS Differential amplifier area optimization with evolutionary algorithms. World Congress on Engineering and Computer Science, WCECS, 2013, Vol. 2, pp. 666–670. San Francisco, USA.
  45. Kameyama, K. Particle Swarm Optimization - A Survey. IEICE Transactions on Information and Systems 2009, E92D, 1354–1361. [Google Scholar] [CrossRef]
  46. Jordehi, A.R. Particle swarm optimisation for dynamic optimisation problems: a review. Neural Computing & Applications 2014, 25, 1507–1516. [Google Scholar]
  47. Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Mathematical Problems in Engineering 2015, 2015, 38. [Google Scholar] [CrossRef]
  48. Wolfram, S. A New Kind of Science; Wolfram Media Inc, 2002.
  49. McIntosh, H.V. One Dimensional Cellular Automata; Luniver Press, 2009.
  50. Adamatzky, A.; Martínez, G.J. Designing Beauty: The Art of Cellular Automata; Vol. 20, Springer, 2016.
  51. Gao, L.; Huang, J.; Li, X. An effective cellular particle swarm optimization for parameters optimization of a multi-pass milling process. Applied Soft Computing 2012, 12, 3490–3499. [Google Scholar] [CrossRef]
  52. Gholizadeh, S. Layout optimization of truss structures by hybridizing cellular automata and particle swarm optimization. Computers & Structures 2013, 125, 86–99. [Google Scholar]
  53. Li, X.; Gao, L.; Wen, X. Application of an efficient modified particle swarm optimization algorithm for process planning. The International Journal of Advanced Manufacturing Technology 2013, 67, 1355–1369. [Google Scholar] [CrossRef]
  54. Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems. Applied Intelligence 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
  55. Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future generation computer systems 2019, 97, 849–872. [Google Scholar] [CrossRef]
  56. Baykasoğlu, A.; Akpinar, Ş. Weighted Superposition Attraction (WSA): A swarm intelligence algorithm for optimization problems–Part 1: Unconstrained optimization. Applied Soft Computing 2017, 56, 520–540. [Google Scholar] [CrossRef]
  57. Seck-Tuoh-Mora, J.C.; Lopez-Arias, O.; Hernandez-Romero, N.; Martínez, G.J.; Volpi-Leon, V. A New Algorithm Inspired on Reversible Elementary Cellular Automata for Global Optimization. IEEE Access 2022, 10, 112211–112229. [Google Scholar] [CrossRef]
  58. Askari, Q.; Younas, I.; Saeed, M. Political Optimizer: A novel socio-inspired meta-heuristic for global optimization. Knowledge-based systems 2020, 195, 105709. [Google Scholar] [CrossRef]
  59. Valencia-Ponce, M.A.; Tlelo-Cuautle, E.; de la Fraga, L.G. On the Sizing of CMOS Operational Amplifiers by Applying Many-Objective Optimization Algorithms. Electronics 2021, 10. [Google Scholar] [CrossRef]
  60. Maji, K.B.; De, B.P.; Kar, R.; Mandal, D.; Ghoshal, S.P. CMOS Analog Amplifier Circuits Design Using Seeker Optimization Algorithm. IETE Journal of Research 2022, 68, 1376–1385. [Google Scholar] [CrossRef]
  61. Paul, A.; Ramírez-Angulo, J.; Sánchez, A.D.; López-Martín, A.J.; Carvajal, R.G.; Li, F.X. An Enhanced Gain-Bandwidth Class-AB Miller op-amp With 23,800 MHz·pF/mW FOM, 11-16 Current Efficiency and Wide Range of Resistive and Capacitive Loads Driving Capability. IEEE Access 2021, 9, 69783–69797. [Google Scholar] [CrossRef]
Preprints 87201 g001
Figure 1. Neighborhood for CPSO-outer and CPSO-DE.
Figure 1. Neighborhood for CPSO-outer and CPSO-DE.
Preprints 87201 g001
Preprints 87201 g002aPreprints 87201 g002b
Figure 2. Convergence curves of the different algorithms for CEC05 functions in 30 dimensions.
Figure 2. Convergence curves of the different algorithms for CEC05 functions in 30 dimensions.
Preprints 87201 g002aPreprints 87201 g002b
Preprints 87201 g003
Figure 3. Flow chart of Ts-CPD as part of an EDA Tool.
Figure 3. Flow chart of Ts-CPD as part of an EDA Tool.
Preprints 87201 g003
Preprints 87201 g004
Figure 4. CMOS differential amplifier.
Figure 4. CMOS differential amplifier.
Preprints 87201 g004
Preprints 87201 g005
Figure 5. CMOS two-stage operational amplifier.
Figure 5. CMOS two-stage operational amplifier.
Preprints 87201 g005
Preprints 87201 g006
Figure 6. CMOS folded cascode operational transconductance amplifier.
Figure 6. CMOS folded cascode operational transconductance amplifier.
Preprints 87201 g006
Preprints 87201 g007
Figure 7. Performance of CMOS differential amplifier.
Figure 7. Performance of CMOS differential amplifier.
Preprints 87201 g007
Preprints 87201 g008
Figure 8. Ts-CPD test for CMOS differential amplifier.
Figure 8. Ts-CPD test for CMOS differential amplifier.
Preprints 87201 g008
Preprints 87201 g009
Figure 9. Performance of CMOS two-stage operational amplifier.
Figure 9. Performance of CMOS two-stage operational amplifier.
Preprints 87201 g009
Preprints 87201 g010
Figure 10. Ts-CPD test for CMOS two-stage operational amplifier.
Figure 10. Ts-CPD test for CMOS two-stage operational amplifier.
Preprints 87201 g010
Preprints 87201 g011
Figure 11. Performance of CMOS folded cascode operational transconductance amplifier.
Figure 11. Performance of CMOS folded cascode operational transconductance amplifier.
Preprints 87201 g011
Preprints 87201 g012
Figure 12. Ts-CPD test for CMOS folded cascode operational transconductance amplifier.
Figure 12. Ts-CPD test for CMOS folded cascode operational transconductance amplifier.
Preprints 87201 g012
Table 1. Performance of metaheuristic algorithms compared with Ts-CPD on 30-dimensional unimodal problems.
Table 1. Performance of metaheuristic algorithms compared with Ts-CPD on 30-dimensional unimodal problems.
Benchmark Ts-CPD AOA HHO WSA CCAA MmCAA RECAA PO
f 1 Avg 1.08e+00 3.54e+04 2.51e+03 7.42e+04 1.99e+04 2.23e+03 8.51e+02 1.88e+04
Std 2.93e+00 5.35e+03 1.22e+03 5.97e+03 7.33e+03 6.25e+02 4.39e+02 7.28e+03
f 2 Avg 1.60e+02 4.11e+04 2.40e+04 1.11e+05 2.44e+04 4.23e+04 1.70e+04 1.92e+04
Std 1.68e+02 5.24e+03 2.82e+03 3.02e+04 4.56e+03 6.21e+03 5.52e+03 4.97e+03
f 3 Avg 2.60e+06 5.23e+08 1.11e+08 1.00e+08 1.19e+08 7.82e+07 3.79e+07 1.68e+08
Std 1.40e+06 1.74e+08 3.41e+07 0.00e+00 5.26e+07 2.80e+07 1.33e+07 1.05e+08
f 4 Avg 9.37e+02 4.83e+04 5.46e+04 1.11e+05 3.49e+04 5.26e+04 2.69e+04 2.89e+04
Std 4.80e+02 7.16e+03 8.20e+03 2.13e+04 6.61e+03 7.99e+03 5.06e+03 6.62e+03
f 5 Avg 5.78e+03 2.97e+04 2.49e+04 4.32e+04 2.17e+04 1.41e+04 8.76e+03 2.52e+04
Std 1.57e+03 3.48e+03 3.38e+03 4.19e+03 3.87e+03 2.32e+03 1.24e+03 2.73e+03
Table 2. Performance of metaheuristic algorithms compared with Ts-CPD on 30-dimensional multimodal problems.
Table 2. Performance of metaheuristic algorithms compared with Ts-CPD on 30-dimensional multimodal problems.
Benchmark Ts-CPD AOA HHO WSA CCAA MmCAA RECAA PO
f 6 Avg 2.40e+03 1.10e+10 1.32e+08 1.00e+08 2.56e+09 4.27e+07 2.00e+06 2.98e+09
Std 4.84e+03 3.16e+09 1.20e+08 0.00e+00 1.93e+09 1.67e+07 1.19e+06 1.98e+09
f 7 Avg 4.72e+00 1.32e+03 3.15e+02 3.61e+03 5.85e+01 1.40e+02 5.57e+01 4.81e+01
Std 7.72e+00 1.68e+02 7.29e+01 5.20e+02 1.47e+01 3.44e+01 1.70e+01 2.70e+01
f 8 Avg 2.10e+01 2.11e+01 2.09e+01 2.11e+01 2.10e+01 2.10e+01 2.10e+01 2.05e+01
Std 5.48e-02 8.26e-02 8.58e-02 5.72e-02 8.31e-02 6.76e-02 6.42e-02 7.97e-02
f 9 Avg 1.02e+02 3.04e+02 3.14e+02 4.01e+02 2.24e+02 2.31e+02 1.63e+02 2.50e+02
Std 2.64e+01 2.18e+01 2.60e+01 1.34e+01 2.52e+01 1.70e+01 2.06e+01 4.29e+01
f 10 Avg 4.89e+01 4.66e+02 4.21e+02 7.25e+02 5.18e+02 3.93e+02 2.54e+02 4.05e+02
Std 1.45e+01 4.68e+01 7.25e+01 5.27e+01 6.17e+01 5.68e+01 2.38e+01 4.22e+01
f 11 Avg 2.16e+01 4.17e+01 4.07e+01 4.37e+01 2.97e+01 3.55e+01 3.27e+01 3.04e+01
Std 2.57e+00 2.49e+00 2.56e+00 2.12e+00 2.07e+00 2.01e+00 1.41e+00 8.22e+00
f 12 Avg 1.29e+06 1.50e+06 7.22e+05 1.50e+06 7.89e+05 6.94e+05 7.14e+05 9.86e+05
Std 1.44e+05 2.46e+05 2.00e+05 1.66e+05 1.39e+05 1.67e+05 1.25e+05 7.79e+03
f 13 Avg 6.45e+00 2.82e+01 3.31e+01 1.27e+02 1.46e+01 2.20e+01 1.76e+01 1.15e+01
Std 4.29e+00 5.82e+00 5.18e+00 3.60e+01 2.80e+00 1.40e+00 1.72e+00 3.09e+00
f 14 Avg 1.30e+01 1.35e+01 1.37e+01 1.39e+01 1.34e+01 1.36e+01 1.34e+01 1.41e+01
Std 3.26e-01 3.42e-01 2.04e-01 2.21e-01 2.90e-01 1.35e-01 2.26e-01 1.43e-01
f 15 Avg 5.69e+02 9.80e+02 7.41e+02 1.24e+03 6.92e+02 5.69e+02 5.13e+02 1.03e+03
Std 1.31e+02 7.26e+01 1.26e+02 8.68e+01 1.08e+02 4.77e+01 5.78e+01 1.16e+02
f 16 Avg 2.91e+02 8.22e+02 4.92e+02 1.17e+03 5.57e+02 4.04e+02 3.07e+02 6.98e+02
Std 1.79e+02 9.05e+01 8.22e+01 1.41e+02 1.05e+02 5.04e+01 4.74e+01 1.03e+02
f 17 Avg 2.90e+02 8.79e+02 5.91e+02 1.18e+03 6.23e+02 4.83e+02 3.52e+02 7.86e+02
Std 1.92e+02 1.40e+02 7.63e+01 1.61e+02 1.21e+02 6.79e+01 5.10e+01 9.67e+01
f 18 Avg 9.77e+02 9.77e+02 9.00e+02 9.00e+02 9.00e+02 9.00e+02 9.00e+02 9.00e+02
Std 6.41e+01 1.44e+02 0.00e+00 3.95e-06 0.00e+00 0.00e+00 0.00e+00 0.00e+00
Std 3.42e+01 1.53e+02 0.00e+00 4.51e-06 0.00e+00 0.00e+00 0.00e+00 0.00e+00
f 20 Avg 9.79e+02 9.73e+02 9.00e+02 9.00e+02 9.00e+02 9.00e+02 9.00e+02 9.00e+02
Std 3.99e+01 1.36e+02 0.00e+00 4.48e-06 0.00e+00 0.00e+00 0.00e+00 0.00e+00
f 21 Avg 9.64e+02 1.31e+03 1.21e+03 1.40e+03 1.33e+03 1.25e+03 8.36e+02 1.14e+03
Std 3.34e+02 1.57e+01 1.09e+02 1.18e+01 3.48e+01 7.07e+01 1.32e+02 1.95e+01
f 22 Avg 9.21e+02 1.42e+03 1.28e+03 1.82e+03 1.24e+03 1.13e+03 1.05e+03 1.09e+03
Std 1.66e+01 7.23e+01 1.20e+02 1.05e+02 9.86e+01 3.48e+01 4.37e+01 8.81e+01
f 23 Avg 1.07e+03 1.31e+03 1.24e+03 1.40e+03 1.35e+03 1.25e+03 9.26e+02 1.15e+03
Std 2.02e+02 1.69e+01 8.21e+01 1.39e+01 2.77e+01 4.86e+01 1.66e+02 2.41e+01
f 24 Avg 2.26e+02 1.37e+03 1.34e+03 1.46e+03 1.39e+03 1.33e+03 9.69e+02 1.07e+03
Std 6.48e+01 1.82e+01 7.33e+01 1.39e+01 4.43e+01 4.04e+01 1.90e+02 1.67e+02
f 25 Avg 1.01e+03 1.38e+03 1.40e+03 1.47e+03 1.40e+03 1.39e+03 1.23e+03 1.28e+03
Std 9.32e+00 2.66e+01 2.99e+01 8.30e+00 3.26e+01 1.90e+01 4.54e+01 1.26e+02
Table 3. Design criteria for CMOS differential amplifier (Case 1) and results obtained with several evolutionary algorithms.
Table 3. Design criteria for CMOS differential amplifier (Case 1) and results obtained with several evolutionary algorithms.
Design criteria Specs. Ts-CPD MOL[59] SOA[60] PSO[19] HS[44] DE[44] ABC[44] GA[43]
Load capacitance (pF) ≥ 2 2.1 5 3.5 5 5 5 5 2
Slew rate (V/ μ s) ≥10 24.3 10 12.28 22.4 14.916 18.451 15.67 3.2
Power dissipation ( μ W) ≤2,000 1,075 863 117 1,260 886 990 830 31
Phase margin ( ∘ ) > 45 86.1 89 83.73 83.8 89.1 88.81 91.248 72
Cut-off frequency (KHz) ≥100 100.5 - 104.8 100 114 129.7 112.367 -
Unity gain bandwidth (MHz) ≥ 1 10 17.87 12.5 12.3 - - - 3.8
DC gain (dB) ≥40 40.3 30 44.02 42 40.98 41.23 42.045 60
V I C ( m i n ) (V) ≥-1.5 -0.8 -0.5 -0.37 -0.8 -0.7 -0.92 -0.97 -1.3
V I C ( m a x ) (V) ≤2 1.1 0.7 1.57 1.4 1.2 1.15 1.2 1.9
CMRR (dB) >40 81.0 59 83.17 84.2 78.5 78.39 79.67 -
PSRR + (dB) >40 41.2 41 60.59 40.1 42.93 43.14 43.857 -
PSRR − (dB) >40 78.1 68 108.6 68 67.64 68.175 68.423 -
Total component area ( μ m 2 ) <300 109 235 236 296 - - - 6,500
AFOM S S (MHz·pF)/( μ W · m m 2 ) 179 457 318 165 - - - 40
Table 4. Design parameters for three algorithms (Case 1).
Table 4. Design parameters for three algorithms (Case 1).
Design parameters Ts-CPD PSO[19] GA[43]
W 1 / L 1 ( μ m/ μ m) 7.6/3.5 29.4/3.5 240/13.2
W 2 / L 2 ( μ m/ μ m) 7.6/3.5 29.4/3.5 240/13.2
W 3 / L 3 ( μ m/ μ m) 4.6/3.5 11.3/3.5 7.3/7.7
W 4 / L 4 ( μ m/ μ m) 4.6/3.5 11.3/3.5 7.3/7.7
W 5 / L 5 ( μ m/ μ m) 5.9/1.4 4.2/1.4 4.6/2.4
W 6 / L 6 ( μ m/ μ m) 11.2/1.4 4.2/1.4 2.4/2.4
I b i a s ( μ A) 141 125 2
Table 5. Design criteria for CMOS two-stage operational amplifier and results obtained with several algorithms.
Table 5. Design criteria for CMOS two-stage operational amplifier and results obtained with several algorithms.
Design criteria Specs. Ts-CPD GSA-PSO[20] PSO[19] GP[9]
Load capacitance (pF) ≥ 7 7.1 7.2 10 3
Slew rate (V/ μ s) ≥ 10 11.9 10.88 11.13 88
Power dissipation ( μ W) ≤ 2,500 1,084 712.8 2,370 5,000
Phase margin ( ∘ ) > 45 46 66.2 66.55 60
Unity gain bandwidth (MHz) ≥3 6.2 5.776 5.32 86
DC gain (dB) >60 64.7 75.43 63.8 89.2
V I C ( m i n ) (V) ≥-1.5 -1.15 -0.886 -0.8 -
V I C ( m a x ) (V) ≤2 1.6 1.9 1.75 -
CMRR (dB) >60 74.0 75.43 63.8 89.2
PSRR + (dB) >70 72.5 83.2 78.27 116
PSRR − (dB) >70 92.9 110.4 93.56 98.4
Total component area ( μ m 2 ) <300 45.6 109.6 265 8,200
AFOM S S (MHz·pF)/( μ W · m m 2 ) 902 532 85 6
Table 6. Design parameters for the four algorithms (Case 2).
Table 6. Design parameters for the four algorithms (Case 2).
Design variables Ts-CPD GSA-PSO[20] PSO[19] GP[9]
W 1 / L 1 ( μ m/ μ m) 4.1/0.8 4/2 4.9/2 232.8/0.8
W 2 / L 2 ( μ m/ μ m) 4.1/0.8 4/2 4.9/2 232.8/0.8
W 3 / L 3 ( μ m/ μ m) 4.0/0.8 4/2 5.9/2 143.6/0.8
W 4 / L 4 ( μ m/ μ m) 4.0/0.8 4/2 5.9/2 143.6/0.8
W 5 / L 5 ( μ m/ μ m) 4.7/0.8 2.8/2 2.1/2 64.6/0.8
W 6 / L 6 ( μ m/ μ m) 19.8/0.8 24/2 90.9/2 588.8/0.8
W 7 / L 7 ( μ m/ μ m) 11.5/0.8 9.2/2 16.3/2 132.6/0.8
W 8 / L 8 ( μ m/ μ m) 4.7/0.8 2.8/2 2.1/2 2/0.8
C C (pF) 3.8 2.8 3 3.5
I b i a s ( μ A) 42.7 28 40.39 10
Table 7. Design criteria for CMOS folded cascode operational transconductance amplifier.
Table 7. Design criteria for CMOS folded cascode operational transconductance amplifier.
Design criteria Specs. Ts-CPD ALC-PSO[1]
Load capacitance (pF) ≥ 10 10.0 10.028
Slew rate (V/ μ s) ≥ 10 13.8 19.37
Power dissipation (mW) ≤ 5 3.3 2.504
Phase margin ( ∘ ) > 60 83.9 63.1
Unity gain bandwidth (MHz) ≥10 17.8 11.11
DC gain (dB) >74 74.1 76.97
V I C ( m i n ) (V) ≥-1.5 -0.69 -1.466
V I C ( m a x ) (V) ≤2.5 2.41 2.486
V o u t ( m i n ) (V) ≥-2 -2.0 -1.936
V o u t ( m a x ) (V) ≤2 1.99 1.996
CMRR (dB) >55 111.8 87.58
PSRR + (dB) >55 82.9 84.21
PSRR − (dB) >55 74.6 61.47
Total component area ( μ m 2 ) <1315.9 600.9 835.2625
AFOM S S (MHz·pF)/( μ W · m m 2 ) 89,764 53,269
Table 8. Design parameters for Case 3.
Table 8. Design parameters for Case 3.
Design variables Ts-CPD ALC-PSO[1]
W 1 / L 1 ( μ m/ μ m) 48.43/1.25 60.46/1.25
W 2 / L 2 ( μ m/ μ m) 48.43/1.25 60.46/1.25
W 3 / L 3 ( μ m/ μ m) 78.66/1.25 35.8/1.25
W 4 / L 4 ( μ m/ μ m) 13.40/1.25 40.1/1.25
W 5 / L 5 ( μ m/ μ m) 13.40/1.25 40.1/1.25
W 6 / L 6 ( μ m/ μ m) 24.26/1.25 45.94/1.25
W 7 / L 7 ( μ m/ μ m) 24.26/1.25 45.1/1.25
W 8 / L 8 ( μ m/ μ m) 25.35/1.25 59.63/1.25
W 9 / L 9 ( μ m/ μ m) 25.35/1.25 59.63/1.25
W 10 / L 10 ( μ m/ μ m) 25.35/1.25 59.63/1.25
W 11 / L 11 ( μ m/ μ m) 25.35/1.25 59.63/1.25
W 12 / L 12 ( μ m/ μ m) 55.60/1.25 14.85/1.25
W 13 / L 13 ( μ m/ μ m) 24.26/1.25 45.94/1.25
W 14 / L 14 ( μ m/ μ m) 13.34/1.25 40.1/1.25
W 15 / L 15 ( μ m/ μ m) 35.23/1.25 -
I b i a s ( μ A) 119.3 -
R 1 ( k Ω ) 4.83 1.89
R 2 ( k Ω ) 4.83 1.89
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated