On Estimation for Reliability of Stress-Strength Model Based on Topp-Leone Distribution

Preprint

Article

On Estimation for Reliability of Stress-Strength Model Based on Topp-Leone Distribution

Altmetrics

Downloads

205

Views

Comments

Taha anwar Taha^*,Abbas najm Salman

This version is not peer-reviewed

Submitted:

08 October 2023

Posted:

09 October 2023

Read the latest preprint version here

Alerts

Abstract

The Paper points at an important point, which is estimate the reliability of system used for stress-strength model when the stress and strength follows Topp-Leone distribution. In this context, this work including two models of stress –strength, the first one when the system has one component with strength subject to one stress, while the another model concern with system has one component which has strength subject for two bounded stresses .The expressions of system reliability of two considered models were derived and estimate using different methods. Comparisons between the considered estimators were made depending on simulation technique based on statistical criterion namely mean squared error.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

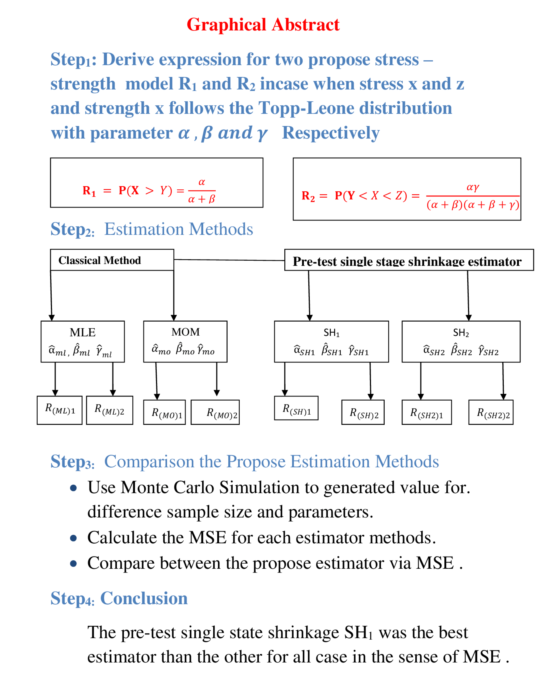
I. Introduction

One of the most popular techniques for data analysis is the stress-strength system, which is employed in a wide range of disciplines like developed engineering, military presentations, healthiness, and useful skills.

The reliability of system in stress-strength model is an assessment of a module's dependability in terms of the random variable X, which stands in for the stress the module is exposed to, and Y, which stands in for the component's capacity to withstand the potential stress.

In stress–strength model of system, the strength X exposed the stress Y. Both random variables X and Y supposed to follows specific probability distribution with definite parameters. The reliability in stress–strength model refers to the probability that strength overdoes stress, i.e. P(X > Y), roughly p. This topic consumes numerous presentations in several ranges. For example, if Y denotes the extreme heaviness produced by overflowing and X signifies the strength of the leg of a bridge on a stream, then p is the probability that the bridge will be hard. Additional instance, if Y and X are respectively symbolize the regulator and conduct groups, then P processes the treatment consequence. Then the estimation of P will be significant in creation interpretations. The system fails when the stress is too great for it to handle.

The stress-strength concept is particularly significant in the research on reliability. Most of the concerns in the statistical approach to the stress-strength model are predicated on the premise that the component strengths are randomly and uniformly distributed and are exposed to a single stress [1].

A system experiences a stress Y and strength X when demonstrated in a conventional reliability stress-strength analysis. Both random variables are considered to follows specific distribution with known or unknown parameters. The probability of strength exceeding stress, or P(X>Y), indicates the reliability of the system. This topic has many applications in many fields

The stress-strength models of the types P(Y<X), P(Y<X<Z), where X, Y and Z are independent random variables refers to strength X and two stress Y and Z, and its follows specific distribution. These two models have wide requests in several of engineering subareas, psychology, genetics, medical trials and others. Kotz [2].

Isaam, K. , Taha, A. and Abbas,N. They Estimated P(Y<X) using different estimation methods[3] .Chandra and Owen [4] derived maximum likelihood estimators (MLEs) and consequent uniform minimum variance unbiased estimators (UMVUEs) for R= P(Y<X< Z).

Singh [5] offered the minimum variance unbiased, maximum likelihood and empirical estimators of R= P(Y<X<Z), where X, Y and Z are independent random variables and follows the normal distribution. Dutta and Sriwastav [6] estimated R when X, Y and Z are exponentially distributed. Ivshin [7] studied the MLE and UMVUE of R when X, Y and Z are either uniform or exponential random variables with unknown location parameters. Wang et al. [8] make statistical inference for P(X<Y<Z) via two methods, the nonparametric normal approximation and the jackknife empirical likelihood.

The Topp-Leone (TL) distribution is therefore J-shaped through its support. Percentage data, rates, particle sizes and specific chemical procedure yield data that can be displayed by this distribution. The TL distribution has a finite support, and various data sets in reliability and life testing are showed using finite support distributions. [9].

Particularly, when the reliability is measured as the proportion of the quantity of effective trials to the amount of whole trials, the TL distribution can well be functional. In stress–strength model the distributions have uses in many spaces. For example, if Y denotes the maximum section elongation and X signifies the tensile strength of a piece of some material, then p processes the quality of the material. Another example, if Y refers the radius of the base of a small cup and X represents the radius of the circular depression in the center of a saucer then P represents the probability of holding the cup. Also, a consumer research organization may want to compare sales percentages of two products with a different advertisement policy each.

Topp and Leone [10] presented the TL distribution and display its properties and also showed its applications for some failure data. Nadarajah and Kotz [11] derive some properties of the TL distribution and provided an expression for its characteristic function. Kotz and Van Dorp [12] given a generalized TL distribution to model some economic facts and they also clear a reflected general TL distribution and studied its properties. Ghitany et al. [13] considered the related of the reliability function of this distribution such as the hazard rate; mean residual life, reversed hazard rate, expected inactivity time and their stochastic orderings.

The topic of the Topp-Leone (TL) distribution dealt with this research, and the probability density function (pdf) is

f (X) = 2 α {(1 - x) x}^{α - 1} {(2 - x)}^{α - 1}

(1)

where 0 < x < 1 and 0 < α < 1.

The distribution function of the TL distribution is given by

F (X) = \{\begin{matrix} 0, & x \leq 0, \\ x^{α} {(2 - x)}^{α} & 0 < x < 1 \\ 1 & x \geq 1 \end{matrix}

(2)

So if u follows uniform distribution, then

X = 1 - \sqrt{1 - U^{1 / α}}

has the TL

(α)

distribution.

Consequently, the hazard rate will be as below

h (x) = \frac{f (x)}{1 - F (x)} = 2 α \frac{(1 - x) {[1 - {(1 - x)}^{2}]}^{α - 1}}{1 - {[1 - {(1 - x)}^{2}]}^{α}}

(3)

The rest of this paper is structured as follows. In Section II, the expression of R₁= P(X > Y) and R₂= P(Y<X< Z) will be derived. Maximum likelihood estimator MLE, the Moment estimator MOM and the Pre-test single stage shrinkage estimator SH of R is obtained in Section III. Monte Carlo Simulation and Numerical Outcomes are laid out in Section IV. Finally, conclusions are presented in Section V.

II. Expression of R₁= P(X > Y) and R₂= P(Y<X< Z)

Derivation of R₁ = P(X > Y)

This Section concentrates on estimating the reliability of when X and Y have independent Topp-Leone distributions. Let n be the number of observations distributed according to the Topp-Leone

Now let X

\sim

TL (α) be independent of Y

\sim

TL (β). Then

R_{1} = P (X > Y) = \int_{0}^{1} F_{Y} (x) f_{x} (x) d x R_{1} = 2 α \int_{0}^{1} x^{α + β - 1} (1 - x) {(2 - x)}^{α + β - 1} d x R_{1} = \frac{α}{α + β}

(4)

Where

α

and

β

are unknown.

Derivation of R2 = P(Y<X<Z)

This Section concentrates on estimating the reliability of R₂ = P(Y<X<Z) when Z, Y and X have independent Topp-Leone distributions such that X, Y and Z are independent and they are distributed Topp-Leone with scale parameters

α

β

γ

respectively such that the p.d.f of the strength X is

f_{x} (x, α) = 2 α {(1 - x) x}^{α - 1} {(2 - x)}^{α - 1} x > 0, α > 0 .

Consequently, the p.d.f of the stresses Y, Z are given respectively by

f_{y} (y, α) = 2 β {(1 - y) y}^{β - 1} {(2 - y)}^{β - 1} y > 0, β > 0 .

f_{Z} (z, γ) = 2 γ {(1 - z) z}^{γ - 1} {(2 - z)}^{γ - 1} z > 0, γ > 0 .

The reliability system of this model P(Y<X<Z) given by

R_{2} = P (Y < X < Z) = \int_{0}^{1} P (Y < X, X < Z) f (x) d x = \int_{0}^{1} F_{Y} (x) {\bar{F}}_{z} (x) f (x) d x = \int_{0}^{1} F_{Y} (x) f (x) - \int_{0}^{1} F_{Y} (x) F_{z} (x) f (x) d x

= \frac{α}{α + β} - \int_{0}^{1} x^{β} {(2 - x)}^{β} x^{γ} {(2 - x)}^{γ} 2 α {(1 - x) x}^{α - 1} {(2 - x)}^{α - 1} d x = \frac{α}{α + β} - \int_{0}^{1} 2 α x^{(α + β + γ)} {(2 - x)}^{(α + β + γ) - 1} {(1 - x) x}^{α - 1} d x = \frac{α}{α + β} - \frac{α}{α + β + γ}

R_{2} = \frac{α γ}{(α + β) (α + β + γ)}

(5)

Where ,

β

and

γ

are unknown.

III. Estimation of R₁ = P(X > Y) and R₂ = P(Y<X<Z)

Maximum Likelihood Estimation of

R_{1}

R_{2}

The Maximum likelihood estimator MLE technique is an important and commonly estimator, since its has a good property for estimate which is known as invariant property [14] .

This Section deals with MLE of reliability

R_{1}

=P(X>Y) and

R_{2}

=P(Y < X < Z) when X, Y and Z are independent Topp-Leone distribution with scale parameters (

α, β, γ)

respectively.

Let x₁, x₂, … . . x_n be a random strength sample of size n with p.d.f. as in (eq.3) then let y_{1 ,}y₂, … y_m. . and z₁, z₂, … . . z_w be the random samples with p.d.f . as in (eq.3) .The Maximum Likelihood function of the observed sample is:

L (α, β, γ, x, y, z) = \prod_{i = 1}^{n} f (x_{i}) \prod_{j = 1}^{m} f (y_{j}) \prod_{k = 1}^{w} f (z_{k}) = \prod_{i = 1}^{n} 2 α {(1 - x_{i}) x_{i}}^{α - 1} {(2 - x_{i})}^{α - 1} \prod_{j = 1}^{m} 2 β {(1 - y_{j}) y_{j}}^{β - 1} {(2 - y_{j})}^{β - 1} \prod_{k = 1}^{w} 2 γ {(1 - z_{k}) z_{k}}^{γ - 1} {(2 - z_{k})}^{γ - 1}

(6)

Taking the logarithm for the above likelihood function eq (6) and the partial derivative for the log-likelihood function with respect to unknown parameters α β

a n d γ

, respectively and equating the partial derivative to zero to solve this equation:

\frac{\partial L n L (x_{i})}{\partial α} = \frac{n}{α} + \sum_{i = 1}^{n} \log [x_{i} (2 - x_{i})] = 0

\frac{\partial L n L (y_{j})}{\partial β} = \frac{m}{β} + \sum_{j = 1}^{m} \log [y_{j} (2 - y_{j})] = 0

\frac{\partial L n L (z_{k})}{\partial γ} = \frac{w}{γ} + \sum_{B = 1}^{w} \log [z_{B} (2 - z_{B})] = 0

The results of the above equations give MLEs of the parameters:

{\hat{α}}_{m l} = \frac{- n}{\sum_{i = 1}^{n} \log [x_{i} (2 - x_{i})]}

(7)

{\hat{β}}_{m l} = \frac{- m}{\sum_{j = 1}^{m} \log [y_{j} (2 - y_{j})]}

(8)

{\hat{γ}}_{m l} = \frac{- w}{\sum_{B = 1}^{w} \log [z_{B} (2 - z_{B})]}

(9)

We obtain the MLE of R₁ and R₂ as

R_{(M L) 1} = \frac{{\hat{α}}_{m l}}{{\hat{α}}_{m l} + {\hat{β}}_{m l}}, R_{(M L) 2} = \frac{{\hat{α}}_{m l} {\hat{γ}}_{m l}}{({\hat{α}}_{m l} + {\hat{β}}_{m l}) ({\hat{α}}_{m l} + {\hat{β}}_{m l} + {\hat{γ}}_{m l})}

(10)

Moment Estimation Method of R₁ and R₂

This section concern with the moment estimator method MOM of R₁ and R₂.The moment estimators of the unknown parameters

α, β

and

γ

will be obtained by equating the population moments with the corresponding sample moments. The population means of random variables X,Y and Z are as below

μ_{x}^{'} = E (x) = 1 - \frac{\sqrt{π}}{2} (\frac{Γ (α + 1)}{Γ (α + \frac{3}{2})})

(11)

μ_{y}^{'} = E (y) = 1 - \frac{\sqrt{π}}{2} (\frac{Γ (β + 1)}{Γ (β + \frac{3}{2})})

(12)

μ_{z}^{'} = E (z) = 1 - \frac{\sqrt{π}}{2} (\frac{Γ (γ + 1)}{Γ (γ + \frac{3}{2})})

(13)

Suppose that X= ( x₁ , x₂ , …x_n ) be a random sample of size n and Y=(y₁ , y₂ …y_m) be a random sample of size m and Z=(z₁ , z₂ …z_w) be a random sample of size w follows Topp-Leone distribution with unknown scales parameter

α, β

and

γ

Then the means of the first and sample moments are given by

μ_{x} = \bar{x} = \frac{1}{n} \sum_{i = 1}^{n} (x_{i}) μ_{y} = \bar{y} = \frac{1}{m} \sum_{j = 1}^{m} (y_{i}) μ_{z} = \bar{z} = \frac{1}{w} \sum_{B = 1}^{w} (z_{i})

By equating the samples moments with the corresponding population moments, then

μ_{x}^{'} = μ_{x}, μ_{y}^{'} = μ_{y}, μ_{z}^{'} = μ_{z}

\bar{x} = 1 - \frac{\sqrt{π}}{2} (\frac{Γ (α + 1)}{Γ (α + \frac{3}{2})}), \bar{y} = 1 - \frac{\sqrt{π}}{2} (\frac{Γ (β + 1)}{Γ (β + \frac{3}{2})}), \bar{z} = 1 - \frac{\sqrt{π}}{2} (\frac{Γ (γ + 1)}{Γ (γ + \frac{3}{2})})

(14)

The moment estimator of

α, β

and

γ

denoted by

{\hat{α}}_{m o}, {\hat{β}}_{m o}

and

{\hat{γ}}_{m o}

can be obtained from (14), respectively as,

{\hat{α}}_{m o} = (\frac{Γ (α_{°} + \frac{3}{2})}{Γ (α_{°})}) . \frac{2}{\sqrt{π}} (1 - \bar{x})

(15)

{\hat{β}}_{m o} = (\frac{Γ (β_{°} + \frac{3}{2})}{Γ (β_{°})}) . \frac{2}{\sqrt{π}} (1 - \bar{y})

(16)

{\hat{γ}}_{m o} = (\frac{Γ (γ_{°} + \frac{3}{2})}{Γ (γ_{°})}) . \frac{2}{\sqrt{π}} (1 - \bar{z})

(17)

Consequently ,we obtain the Moment estimators of R₁ and R₂ as

R_{(M O) 1} = \frac{{\hat{α}}_{m o}}{{\hat{α}}_{m o} + {\hat{β}}_{m o}}, R_{(M O) 2} = \frac{{\hat{α}}_{m o} {\hat{γ}}_{m o}}{({\hat{α}}_{m o} + {\hat{β}}_{m o}) ({\hat{α}}_{m o} + {\hat{β}}_{m o} + {\hat{γ}}_{m o})}

(18)

Pre-test single stage shrinkage estimator (SH) of R₁ and R₂

Some time may we have a prior information value (point guess) of the parameter to be estimated. If this value is in the neighborhood of the accurate value, the shrinkage procedure is valuable to obtain an improved estimator. Thompson in [15], Isaam, K, Taha, A. and Abbas,N.[16] and others suggested shrunken estimators for different distributions when a prior estimate or guess point is available. They indicated that these estimators perform better in the term of mean squared error when a guess value θ₀ close to the true value θ. Pre- test estimator is considered for estimating the parameter θ when a guess point (prior estimate) θ₀ is available about θ due the past knowledge or similar cases. From the empirical studies it has been established that the shrinkage estimators performs better than the usual estimator when the guess point is very close to the true value of the parameter. Therefore to make sure whether θ is closed to θ₀ or not, we may test H₀:θ = θ₀ against H₁: θ ≠ θ₀, so we denote by R to the critical region for above test.

Thompson in 1968 recommended shrinking the usual estimator

\hat{θ}

of θ towards the prior guess point θ₀ and suggested the estimator

\tilde{θ} = K \hat{θ} + (1 - K (\hat{θ})) θ_{°}

, where

(1 - K)

represents the experimenters belief in the guess point θ₀. He found the estimator

\tilde{θ}

which is more efficient than usual estimator

\hat{θ}

if the true value θ is close to θ₀ (H₀ accepted) but may be less efficient otherwise, therefore to resolve the uncertainty that a guess point value is approximately the true value or not, a pre- test of significance may be employed. So he take the usual estimator

\hat{θ}

when θ is far away from θ₀ (H₀ rejected) after he made the pre- test.

Thus, the pre-test shrunken estimator has the following form ; A.N.Salman [17]

\tilde{θ} = \{\begin{matrix} K \hat{θ} + (1 - K) θ_{°} i f \hat{θ} \in R \\ \hat{θ} i f \hat{θ} \notin R \end{matrix}

(19)

Where R may be pre- test region for acceptance the null hypothesis H₀ as we mentioned above,

\hat{θ}

is the usual ML estimator of θ and

K

is a constant shrinkage weight factor such that

0 ≤

K

≤ 1 .

In this research we may assume the region as follow:

R = \{{{(θ}_{°} - θ)}^{2} \leq M S E\}

(20)

R = (θ_{°} - \sqrt{M S E}, θ_{°} + \sqrt{M S E})

(21)

In this research, we suppose

Case 1 Suppose that

K_{n} = {|\frac{S i n n}{n}|}^{2} K_{m} = {|\frac{S i n m}{m}|}^{2} K_{w} = {|\frac{S i n w}{w}|}^{2}, 0 \leq K_{n}, K_{m}, K_{w} \leq 1 a n d θ = θ_{°} .

Where,

θ

may be referred to

α, β a n d γ

Thus, the shrinkage estimator of the scale parameters

α, β

and

γ

of the random variables X,Y, Z that follows Topp-Leone distribution will be as follows:

{\tilde{α}}_{s h 1} = \{\begin{matrix} K_{n} \hat{α} + (1 - K_{n}) α_{°} i f \hat{α} \in R \\ \hat{α} i f \hat{α} \notin R \end{matrix}

(22)

{\tilde{β}}_{s h 1} = \{\begin{matrix} K_{m} \hat{β} + (1 - K_{m}) β_{°} i f \hat{β} \in R \\ \hat{β} i f \hat{β} \notin R \end{matrix}

(23)

{\tilde{γ}}_{s h 1} = \{\begin{matrix} K_{w} \hat{γ} + (1 - K_{w}) γ_{°} i f \hat{γ} \in R \\ \hat{γ} i f \hat{γ} \notin R \end{matrix}

(24)

Case 2 Suppose that

A_{n} = \sqrt{e^{\frac{- n}{10}}}, A_{m} = \sqrt{e^{\frac{- m}{10}}}, A_{w} = \sqrt{e^{\frac{- w}{10}}}, 0 \leq A_{n}, A_{m}, A_{w} \leq 1 a n d θ = θ_{°} .

Where ,

θ

may be referred to

α, β a n d γ

{\tilde{α}}_{s h 2} = \{\begin{matrix} A_{n} \hat{α} + (1 - A_{n}) α_{°} i f \hat{α} \in R \\ \hat{α} i f \hat{α} \notin R \end{matrix}

(25)

{\tilde{β}}_{s h 2} = \{\begin{matrix} A_{m} \hat{β} + (1 - A_{m}) β_{°} i f \hat{β} \in R \\ \hat{β} i f \hat{β} \notin R \end{matrix}

(26)

{\tilde{γ}}_{s h 2} = \{\begin{matrix} A_{w} \hat{γ} + (1 - A_{w}) γ_{°} i f \hat{γ} \in R \\ \hat{γ} i f \hat{γ} \notin R \end{matrix}

(27)

we obtain the Mom of R₁ and R₂ as

R_{(S H) 1} = \frac{{\hat{α}}_{S H 1}}{{\hat{α}}_{S H 1} + {\hat{β}}_{S H 1}}, R_{(S H) 2} = \frac{{\hat{α}}_{S H 1} {\hat{γ}}_{S H 1}}{({\hat{α}}_{S H 1} + {\hat{β}}_{S H 1}) ({\hat{α}}_{S H 1} + {\hat{β}}_{S H 1} + {\hat{γ}}_{S H 1})}

(28)

Consequently , we obtain

R_{(S H 2) 1} = \frac{{\hat{α}}_{S H 2}}{{\hat{α}}_{S H 2} + {\hat{β}}_{S H 2}}, R_{(S H 22} = \frac{{\hat{α}}_{S H 2} {\hat{γ}}_{S H 2}}{({\hat{α}}_{S H 2} + {\hat{β}}_{S H 2}) ({\hat{α}}_{S H 2} + {\hat{β}}_{S H 2} + {\hat{γ}}_{S H 2})}

(29)

IV. Monte Carlo Simulation and Numerical Outcomes

An extensive numerical investigation will be conducted in this section to compare the performance of the various estimators for unlike sample sizes and parameter values for the Topp-Leone distribution. The properties investigated result in mean square errors (MSEs). Matlab 2018 statistical software was used for all computations. A simulation results are conducted to examine and compare the performance of the estimates for shape respecting to the MSE. The best estimator has the smallest value of MSE.

The steps for estimating the parameters, R₁ = P(X > Y) and R₂ = P(Y< X < Z) can be

summarized as follows:

Generate 10000 random samples from Topp-Leone distribution with the sample sizes;(n ,m)= (25,50,75,100) and the parameter values are selected as

α

= (1.2,1.5,3) and

β

=( 3 ,1.5,1.2) for R₁ .Also (n, m ,w )= (25,25,25),(50,50,50),(75,75,75), (100,100,100), (50,25,25), (75,25,25),

(100,25,25), (25,50,25), (50,75,50), (75,100,75), (25,100,25), (25,25,50), (50,50,75),

(75,75,100) and parameter values are selected as

α

= (1.5,1.5,1.5),

β

=( 2.5 ,1.5,3.5) and

γ

=( 3.5 ,1.5,2.5) for R₂.

One can conclude from the simulation results which is used to determine the best consequence of the proposed estimation methods (ML, MO, SH1, SH2) using different samples for the system reliability R₁=p(Y<X) and R₂ = P(Y< X < Z) grounded the Topp-Leone distribution (T-L). The simulation results of the proposed estimation methods are demonstrated in annexed tables and distinguish that Pre-test single stage shrinkage estimator (SH1) of system reliability R₁ , R₂ satisfied the smallest mean squared error in overall; this infers that

{\hat{R}}_{S H 1}

was the best than the others for two considered models.

V. Conclusion

From above results, it observed that in general the best performance of the consider estimators (ML, MO, SH1, SH2,) under the different sample sizes and for the different Parameters of this study is the pre-test single stage shrinkage estimator (SH1) of system reliability R₁ , R₂ for two considered models .This important method has proven its efficiency in estimation as prior estimate approach to real value which depends on classical estimation method and prior information (initial estimate) as a linear combination and make pretest region to know how close the initial value from the actual value .

Appendix A

Table A1. Shown estimates of R₁, when R₁= 0.28571,

α

= 1.2,

β

= 3.

Table A1. Shown estimates of R₁, when R₁= 0.28571,

α

= 1.2,

β

= 3.

n	m	${\hat{R}}_{M L}$	${\hat{R}}_{M O}$	${\hat{R}}_{S H 1}$	${\hat{R}}_{S H 2}$
25	25	0.22795	0.76549	0.26949	0.65166
	50	0.29000	0.69709	0.28616	0.59951
	75	0.25700	0.83259	0.27238	0.71323
	100	0.30891	0.70636	0.29865	0.60523
50	25	0.22768	0.72594	0.26577	0.60214
	50	0.25496	0.79200	0.28253	0.66948
	75	0.31010	0.66498	0.28581	0.59447
	100	0.38670	0.58104	0.29034	0.5384
75	25	0.38350	0.58687	0.30097	0.54219
	50	0.36616	0.64820	0.29003	0.58296
	75	0.27682	0.72916	0.28453	0.62165
	100	0.32255	0.65676	0.28536	0.57684
100	25	0.31769	0.69842	0.28650	0.60441
	50	0.30583	0.72137	0.28373	0.61462
	75	0.34595	0.62115	0.28556	0.55979
	100	0.24077	0.78389	0.28439	0.66114

Table A2. MSE of R₁, when R₁= 0.28571,

α

= 1.2,

β

= 3.

Table A2. MSE of R₁, when R₁= 0.28571,

α

= 1.2,

β

= 3.

n	m	ML	MO	SH1	SH2	Best
25	25	3.3362e-07	2.3018e-05	2.6327e-08	1.3392e-05	SH
	50	1.8372e-09	1.6923e-05	1.9773e-11	9.8467e-06	SH
	75	8.2468e-08	2.9907e-05	1.7781e-08	1.8277e-05	SH
	100	5.3794e-08	1.7695e-05	1.6745e-08	1.0209e-05	SH
50	25	3.3683e-07	1.938e-05	3.9771e-08	1.0012e-05	SH
	50	9.4604e-08	2.5633e-05	1.0121e-09	1.4727e-05	SH
	75	5.9453e-08	1.4384e-05	9.8482e-13	9.5327e-06	SH
	100	1.0197e-06	8.7219e-06	2.1393e-09	6.3848e-06	SH
75	25	9.5616e-07	9.5616e-07	2.3269e-08	6.5779e-06	SH
	50	6.4721e-07	1.314e-05	1.8666e-09	8.8355e-06	SH
	75	7.9146e-09	1.9664e-05	1.3949e-10	1.1286e-05	SH
	100	1.3571e-07	1.3767e-05	1.2546e-11	8.4754e-06	SH
100	25	1.0226e-07	1.7032e-05	6.1133e-11	1.0157e-05	SH
	50	4.0479e-08	1.898e-05	3.926e-10	1.0818e-05	SH
	75	3.6288e-07	1.1252e-05	2.3293e-12	7.5116e-06	SH
	100	2.0201e-07	2.4818e-05	1.7668e-10	1.4095e-05	SH

Table A3. Shown estimation when R1= 0.5, beta1 = 1.5, beta2= 1.5.

n	m	ML	MO	SH1	SH2
25	25	0.52585	0.44398	0.50746	0.47914
	50	0.52351	0.34866	0.50910	0.40764
	75	0.53547	0.52974	0.50933	0.52313
	100	0.52507	0.54220	0.50871	0.53144
50	25	0.47686	0.56972	0.56972	0.53694
	50	0.51562	0.53771	0.50141	0.52235
	75	0.50862	0.52169	0.50146	0.5146
	100	0.53958	0.40917	0.50059	0.44168
75	25	0.51675	0.46870	0.50091	0.47168
	50	0.52847	0.53250	0.50018	0.52059
	75	0.53742	0.42200	0.50086	0.45271
	100	0.55972	0.43488	0.50177	0.46178
100	25	0.47113	0.61394	0.49444	0.55794
	50	0.49079	0.53128	0.50097	0.52011
	75	0.52326	0.53541	0.50074	0.53282
	100	0.53481	0.43170	0.50023	0.45482

Table A4. MSE^s of R₁ when

α

= 1.5,

β

= 1.5.

Table A4. MSE^s of R₁ when

α

= 1.5,

β

= 1.5.

n m ML LS SH1 SH2 Best

25 25 6.6847e-08 3.138e-07 5.561e-09 4.3506e-08 SH1

50 5.5253e-08 2.2904e-06 8.2734e-09 8.5312e-07 SH1

75 1.2578e-07 8.8426e-08 8.6961e-09 5.3482e-08 SH1

100 6.2857e-08 1.7812e-07 7.5812e-09 9.8874e-08 SH1

50 25 5.3536e-08 4.8611e-07 4.537e-10 1.3645e-07 SH1

50 2.4407e-08 1.4221e-07 1.9898e-10 4.9937e-08 SH1

75 7.4261e-09 4.7039e-08 2.1352e-10 2.1311e-08 SH1

100 1.5667e-07 8.2494e-07 3.4689e-11 3.4007e-07 SH1

75 25 2.8048e-08 9.7946e-08 8.2667e-11 8.0202e-08 SH1

50 8.1083e-08 1.0562e-07 3.4017e-12 4.2379e-08 SH1

75 1.4002e-07 6.0841e-07 7.3392e-11 2.2367e-07 SH1

100 3.5666e-07 4.2403e-07 3.1286e-10 1.4606e-07 SH1

100 25 8.332e-08 1.2983e-06 3.0867e-09 3.3573e-07 SH1

50 8.4884e-09 9.7818e-08 9.4062e-11 4.0457e-08 SH1

75 5.4121e-08 1.2542e-07 5.5441e-11 1.0773e-07 SH1

100 1.2119e-07 4.6645e-07 5.3448e-12 2.0412e-07 SH1

Shown estimation when R= 0.71429, beta1 = 3, beta2= 1.2

n m ML MO SH1 SH2

25 25 0.61334 0.34578 0.69064 0.41593

50 0.61151 0.43041 0.69210 0.46764

75 0.72315 0.23630 0.72105 0.35348

100 0.79167 0.21785 0.73058 0.34541

50 25 0.64462 0.22901 0.69405 0.33525

50 0.73712 0.25847 0.71695 0.37117

75 0.67832 0.28617 0.71318 0.38605

100 0.66978 0.27653 0.71211 0.37392

75 25 0.67920 0.24415 0.71638 0.34904

50 0.74174 0.26702 0.71454 0.38343

75 0.74139 0.24329 0.71603 0.36362

100 0.72348 0.27315 0.71518 0.38607

100 25 0.76171 0.42327 0.71933 0.48892

50 0.68467 0.30166 0.71191 0.39779

75 0.73210 0.24035 0.71535 0.35858

100 0.68185 0.31757 0.71511 0.40896

mse

n m ML MO SH1 SH2 Best

25 25 1.0191e-06 1.358e-05 5.5891e-08 8.9014e-06 SH1

50 1.0562e-06 8.0585e-06 4.9205e-08 6.0834e-06 SH1

75 7.8616e-09 2.2847e-05 4.5744e-09 1.3018e-05 SH1

100 5.9891e-07 2.4645e-05 2.6549e-08 1.3607e-05 SH1

50 25 4.853e-07 2.3549e-05 4.095e-08 1.4367e-05 SH1

50 5.2132e-08 2.0777e-05 7.0912e-10 1.1773e-05 SH1

75 1.2934e-07 1.8328e-05 1.2289e-10 1.0774e-05 SH1

100 1.9804e-07 1.9163e-05 4.7435e-10 1.1585e-05 SH1

75 25 1.2307e-07 2.2103e-05 4.3956e-10 1.334e-05 SH1

50 7.5363e-08 2.0004e-05 6.3547e-12 1.0946e-05 SH1

75 7.349e-08 2.2184e-05 3.0541e-10 1.2297e-05 SH1

100 8.4551e-09 1.946e-05 8.0755e-11 1.0773e-05 SH1

100 25 2.6294e-07 1.6149e-05 1.995e-10 9.6001e-06 SH1

50 8.7697e-08 1.7026e-05 5.6266e-10 1.0017e-05 SH1

75 3.174e-08 2.2462e-05 1.1351e-10 1.2653e-05 SH1

100 1.0524e-07 1.5738e-05 6.7611e-11 9.3224e-06 SH1

R= 0.175,

ζ_{1}

=1.5,

ζ_{2}

=2.5,

ζ_{3}

=3.5and q=10000

Method
n,m,w Mle Mom SH1 SH2 Best

(25,25,25) $\hat{R}$
MSE 0.21921
1.9542e-07 0.12232
2.7753e-07 0.18717
1.4807e-08 0.15602
3.6021e-08 SH1

(50,50,50) $\hat{R}$
MSE 0.15329
4.7154e-08 0.15246
5.0796e-08 0.17317
3.3671e-10 0.17118
1.4578e-09 SH1

(75,75,75) $\hat{R}$
MSE 0.16695
6.486e-09 0.15469
4.1266e-08 0.17473
7.4067e-12 0.18071
3.2602e-09 SH1

(100,100,100) $\hat{R}$
MSE 0.20633
9.8161e-08 0.10786
4.5076e-07 0.17513
1.5626e-12 0.13863
1.3226e-07 SH1

(50,25,25) $\hat{R}$
MSE 0.17236
6.9677e-10 0.10592
4.7716e-07 0.17598
9.5917e-11 0.13517
1.5864e-07 SH1

(75,25,25) $\hat{R}$
MSE 0.19945
5.9768e-08 0.11034
4.1811e-07 0.17960
2.119e-09 0.13528
1.5773e-07 SH1

(100,25,25) $\hat{R}$
MSE 0.19819
5.3782e-08 0.10900
4.3554e-07 0.18023
2.733e-09 0.15131
5.6115e-08 SH1

(25,50,25) $\hat{R}$
MSE 0.17935
1.8924e-09 0.12105
2.9108e-07 0.17843
1.1757e-09 0.15127
5.6325e-08 SH1

(50,75,50) $\hat{R}$
MSE 0.18495
9.9087e-09 0.11786
3.2649e-07 0.17604
1.0817e-10 0.15383
4.4799e-08 SH1

(75,100,75) $\hat{R}$
MSE 0.17638
1.9162e-10 0.13235
1.8189e-07 0.1747
8.7569e-12 0.15697
3.2494e-08 SH1

(25,100,25) $\hat{R}$
MSE 0.19069
2.4633e-08 0.11492
3.6099e-07 0.17653
2.3519e-10 0.1392
1.2816e-07 SH1

(25,25,50) $\hat{R}$
MSE 0.23891
4.0841e-07 0.12393
2.6079e-07 0.1901
2.2813e-08 0.15131
5.611e-08 SH1

(50,50,75) $\hat{R}$
MSE 0.16162
1.7909e-08 0.1557
3.7239e-08 0.17367
1.7809e-10 0.16523
9.5422e-09 SH1

(75,75,100) $\hat{R}$
MSE 0.15119
5.6692e-08 0.13748
1.408e-07 0.17433
4.4538e-11 0.16805
4.8245e-09 SH1

R= 0.16667,

ζ_{1}

=1.5,

ζ_{2}

=1.5,

ζ_{3}

=1.5and q=10000

Method
n,m,w Mle Mom SH1 SH2 Best

(25,25,25) $\hat{R}$
MSE 0.15676
9.82e-09 0.18541
3.5124e-08 0.16392
7.5502e-10 0.17445
6.0599e-09 SH1

(50,50,50) $\hat{R}$
MSE 0.1404
6.8985e-08 0.21087
1.9543e-07 0.16415
6.3217e-10 0.18916
5.0602e-08 SH1

(75,75,75) $\hat{R}$
MSE 0.1454
4.3016e-08 0.17792
1.2655e-08 0.16618
2.3994e-11 0.17245
3.3414e-09 SH1

(100,100,100) $\hat{R}$
MSE 0.17169
2.522e-09 0.16521
2.1217e-10 0.1667
1.3565e-13 0.16773
1.1396e-10 SH1

(50,25,25) $\hat{R}$
MSE 0.12897
1.4211e-07 0.29976
1.7713e-06 0.15687
9.5912e-09 0.23538
4.7217e-07 SH1

(75,25,25) $\hat{R}$
MSE 0.1175
2.4171e-07 0.20579
1.5307e-07 0.14959
2.9154e-08 0.18288
2.6288e-08 SH1

(100,25,25) $\hat{R}$
MSE 0.16667
3.7084e-08 0.14741
4.9826e-07 0.23725
4.7221e-09 0.21319
2.1646e-07 SH1

(25,50,25) $\hat{R}$
MSE 0.18239
2.4725e-08 0.12568
1.6795e-07 0.17596
8.6408e-09 0.14649
4.072e-08 SH1

(50,75,50) $\hat{R}$
MSE 0.16269
1.5778e-09 0.15295
1.8804e-08 0.1671
1.907e-11 0.15776
7.9395e-09 SH1

(75,100,75) $\hat{R}$
MSE 0.13608
9.3539e-08 0.20373
1.374e-07 0.1662
2.1631e-11 0.18712
4.1833e-08 SH1

(25,100,25) $\hat{R}$
MSE 0.16371
8.7604e-10 0.2123
2.0823e-07 0.1644
5.1378e-10 0.19272
6.7874e-08 SH1

(25,25,50) $\hat{R}$
MSE 0.13021
1.3291e-07 0.22961
3.9616e-07 0.15341
1.7581e-08 0.2007
1.1581e-07 SH1

(50,50,75) $\hat{R}$
MSE 0.1759
8.5328e-09 0.13769
8.3974e-08 0.16607
3.5792e-11 0.14916
3.0655e-08 SH1

(75,75,100) $\hat{R}$
MSE 0.15083
2.5079e-08 0.18493
3.3366e-08 0.1664
7.1447e-12 0.17714
1.0978e-08 SH1

R= 0.1,

ζ_{1}

=1.5,

ζ_{2}

=3.5,

ζ_{3}

=2.5and q=10000

Method
n,m,w Mle Mom SH1 SH2 Best

(25,25,25) $\hat{R}$
MSE 0.1439
1.9272e-07 0.18133
6.6146e-07 0.11091
1.1897e-08 0.17023
4.9322e-07 SH1

(50,50,50) $\hat{R}$
MSE 0.13639
1.3241e-07 0.14832
2.3344e-07 0.10279
7.8026e-10 0.1621
3.8563e-07 SH1

(75,75,75) $\hat{R}$
MSE 0.10428
1.8297e-09 0.20421
1.0859e-06 0.099843
2.4697e-12 0.18633
7.4528e-07 SH1

(100,100,100) $\hat{R}$
MSE 0.10724
5.2398e-09 0.18486
7.2017e-07 0.099781
4.8049e-12 0.18265
6.8303e-07 SH1

(50,25,25) $\hat{R}$
MSE 0.11243
1.5447e-08 0.18481
7.1931e-07 0.10198
3.9077e-10 0.17709
5.9426e-07 SH1

(75,25,25) $\hat{R}$
MSE 0.11521
2.3139e-08 0.17945
6.3123e-07 0.10323
1.0435e-09 0.17097
5.0368e-07 SH1

(100,25,25) $\hat{R}$
MSE 0.10514
2.6379e-09 0.16091
3.7101e-07 0.10201
4.033e-10 0.16608
4.3671e-07 SH1

(25,50,25) $\hat{R}$
MSE 0.10903
8.1614e-09 0.18471
7.1758e-07 0.10377
1.42e-09 0.19206
8.4754e-07 SH1

(50,75,50) $\hat{R}$
MSE 0.1112
1.2543e-08 0.21963
1.4312e-06 0.10171
2.9161e-10 0.19207
8.4765e-07 SH1

(75,100,75) $\hat{R}$
MSE 0.10183
3.3388e-10 0.21353
1.289e-06 0.099982
3.1663e-14 0.18867
7.8616e-07 SH1

(25,100,25) $\hat{R}$
MSE 0.12711
7.3519e-08 0.19176
8.4195e-07 0.11079
1.1645e-08 0.17787
6.063e-07 SH1

(25,25,50) $\hat{R}$
MSE 0.12573
6.6195e-08 0.19876
9.7531e-07 0.10639
4.0889e-09 0.18526
7.2684e-07 SH1

(50,50,75) $\hat{R}$
MSE 0.11281
1.6403e-08 0.1895
8.0111e-07 0.10081
6.6176e-11 0.18458
7.1541e-07 SH1

(75,75,100) $\hat{R}$
MSE 0.13862
1.4917e-07 0.15759
3.317e-07 0.10038
1.4333e-11 0.16339
4.0187e-07 SH1

R= 0.11667,

ζ_{1}

=3.5,

ζ_{2}

=2.5,

ζ_{3}

=1.5and q=10000

Method
n,m,w Mle Mom SH1 SH2 Best

(25,25,25) $\hat{R}$
MSE 0.11541
1.5718e-10 0.25489
1.9104e-06 0.11629
1.4074e-11 0.21104
8.9072e-07 SH1

(50,50,50) $\hat{R}$
MSE 0.13119
2.1082e-08 0.22845
1.2496e-06 0.11754
7.7031e-11 0.20084
7.0857e-07 SH1

(75,75,75) $\hat{R}$
MSE 0.10116
2.4034e-08 0.25097
1.8038e-06 0.116
4.4505e-11 0.21287
9.256e-07 SH1

(100,100,100) $\hat{R}$
MSE 0.11467
3.9876e-10 0.21453
9.5781e-07 0.1164
7.0629e-12 0.19455
6.0656e-07 SH1

(50,25,25) $\hat{R}$
MSE 0.12773
1.2229e-08 0.22401
1.1522e-06 0.11957
8.4428e-10 0.19822
6.6501e-07 SH1

(75,25,25) $\hat{R}$
MSE 0.14116
5.9999e-08 0.18953
5.3089e-07 0.12366
4.8937e-09 0.18391
4.522e-07 SH1

(100,25,25) $\hat{R}$
MSE 0.13117
2.1028e-08 0.20523
7.8439e-07 0.12032
1.334e-09 0.19259
5.7639e-07 SH1

(25,50,25) $\hat{R}$
MSE 0.11238
1.8361e-09 0.18634
4.855e-07 0.11584
6.8685e-11 0.17234
3.0991e-07 SH1

(50,75,50) $\hat{R}$
MSE 0.12615
8.9875e-09 0.2232
1.1349e-06 0.11812
2.1166e-10 0.19613
6.3138e-07 SH1

(75,100,75) $\hat{R}$
MSE 0.11136
2.8167e-09 0.23389
1.3742e-06 0.11633
1.1273e-11 0.20431
7.682e-07 SH1

(25,100,25) $\hat{R}$
MSE 0.13305
2.6836e-08 0.20444
7.7047e-07 0.1194
7.4595e-10 0.18279
4.3717e-07 SH1

(25,25,50) $\hat{R}$
MSE 0.13803
4.5657e-08 0.15661
1.5957e-07 0.11943
7.6543e-10 0.16303
2.1493e-07 SH1

(50,50,75) $\hat{R}$
MSE 0.12893
1.5035e-08 0.22632
1.2024e-06 0.117
1.1364e-11 0.19254
5.7566e-07 SH1

(75,75,100) $\hat{R}$
MSE 0.13302
2.6751e-08 0.19233
5.7249e-07 0.11656
1.0731e-12 0.18769
5.0448e-07 SH1

R= 0.23333,

ζ_{1}

=3.5,

ζ_{2}

=1.5,

ζ_{3}

=2.5and q=10000

Method
n,m,w Mle Mom SH1 SH2 Best

(25,25,25) $\hat{R}$
MSE 0.21429
3.6267e-08 0.13464 9.7408e-07 0.22908
1.8092e-09 0.15108
6.7651e-07 SH1

(50,50,50) $\hat{R}$
MSE 0.19785
1.2591e-07 0.11743
1.3433e-06 0.2306
7.4572e-10 0.13693
9.2927e-07 SH1

(75,75,75) $\hat{R}$
MSE 0.21823
2.2806e-08 0.10601
1.6212e-06 0.23325
6.592e-13 0.13887
8.9235e-07 SH1

(100,100,100) $\hat{R}$
MSE 0.21461
3.5065e-08 0.12208
1.2378e-06 0.23348
2.1933e-12 0.15091
6.7935e-07 SH1

(50,25,25) $\hat{R}$
MSE 0.2452
1.4077e-08 0.11016
1.5172e-06 0.23601
7.1686e-10 0.14458
7.8772e-07 SH1

(75,25,25) $\hat{R}$
MSE 0.17944
2.9049e-07 0.14782
7.3125e-07 0.2162
2.9371e-08 0.1579
5.6829e-07 SH1

(100,25,25) $\hat{R}$
MSE 0.26793
1.1967e-07 0.10931
1.5382e-06 0.24479
1.3124e-08 0.14556
7.705e-07 SH1

(25,50,25) $\hat{R}$
MSE 0.18239
2.595e-07 0.10106
1.7496e-06 0.22039
1.6755e-08 0.13968
8.7702e-07 SH1

(50,75,50) $\hat{R}$
MSE 0.22786
2.9949e-09 0.10771
1.5781e-06 0.23371
1.3946e-11 0.13791
9.106e-07 SH1

(75,100,75) $\hat{R}$
MSE 0.24163
6.878e-09 0.10018
1.7731e-06 0.23389
3.0849e-11 0.13539
9.5927e-07 SH1

(25,100,25) $\hat{R}$
MSE 0.188
2.0554e-07 0.13646
9.3851e-07 0.22451
7.7868e-09 0.15624
5.943e-07 SH1

(25,25,50) $\hat{R}$
MSE 0.29333
3.6e-07 0.10743
1.5852e-06 0.24206
7.6197e-09 0.14321
8.1225e-07 SH1

(50,50,75) $\hat{R}$
MSE 0.18978
1.8966e-07 0.14026
8.6626e-07 0.23203
1.6882e-10 0.1577
5.7203e-07 SH1

(75,75,100) $\hat{R}$
MSE 0.22703
3.9738e-09 0.10696
1.597e-06 0.23361
7.6452e-12 0.13775
9.1362e-07 SH1

Co-author Information

Abbas N. Salman is a Professor in the Department of Mathematics, College of Education for Pure Sciences (Ibn Al-Haithm), Baghdad University, Baghdad, Iraq, and a Specialist in Mathematics - Mathematical Statistics. P.O. Box: 4150, Al-Adhamiyah, Anter Square, Baghdad, Iraq, Street: 20. https://scholar.google.com/citations?user=Kr2rydcAAAAJ. https://orcid.org/0000-0002-9981-9176. https://www.academia.edu, https://www.growkudos.com/hub/452711/publications , https://www.linkedin.com/feed/, https://repository.uobaghdad.edu.iq/author/abass.najem.ihcoedu,https://www.scopus.com/feedback/results/authorNamesList.uri?origin=searchauthorlookup&src=al&edit=&poppUp=&st1=Salman&st2=Abbas+Najim&OrcidId=0000-0002-9981-9176&authSubject=LFSC&_authSubject=on&authSubject=HLSC&_authSubject=on&authSubject=PHSC&_authSubject=on&authSubject=SOSC&_authSubject=on&s=AUTH--ORCID--ID%280000-0002-9981-9176%29&sdt=&sot=&searchId=&authorIdSearch=&activeFlag=true&showDocument=false&sl=0&exactSearch=off&sid=&carsError=&timeDelay=&redirectURL=&requestFlowType=

References

Hassan A. S. and Basheikh H. M., (2012), "Estimation of Reliability in Multi-Component Stress-Strength Model Following Exponential Pareto Distribution", The Egyptian Statistical Journal, Institute of Statistical Studies Research, Cairo University, Vol. 56, No.2, pp. 82-95.
S. Kotz, Y. Lumelskii, and M. Pensky, The stress- strength model and its generalizations, “Theory and Applications” (World Scientific Publishing Co., 2003). [CrossRef]
Isaam, K, Taha, A. and Abbas,N." Different Estimation Methods of Reliability in Stress -Strength Model under Chen Distribution" AIP Conference Proceedings 2591, 050023, 1-10, 2023.
S. Chandra and D. B. Owen, On estimating the reliability of a component subject to several different stresses (strengths). Naval Research Logistics Quarterly, 22, 1975, 31-39. [CrossRef]
N. Singh, On the estimation of of P=R(X1 < Y < X2). Communication in Statistics Theory & Methods, 9, 1980, 1551-1561. [CrossRef]
K. Dutta, and G. L. Sriwastav, An n-standby system with P(X < Y < Z). IAPQR Transaction, 12, 1986, 95-97.
V. V. Ivshin, On the estimation of the probabilities of a double linear inequality in the case of uniform and two-parameter exponential distributions, Journal of Mathematical Science, 88, 1998, 819-8. [CrossRef]
Z. Wang, W. Xiping, and P. Guangming, "Nonparametric statistical inference for P(X <Y <Z)". The Indian Journal of Statistics, 75-A (1), 2013, 118-138. [CrossRef]
M. Ahsanullah, Record values, "The Exponential Distribution: Theory, Methods and Applications", N. Balakrishnan and A. P. Basu, eds., Gordon and Breach Publishers, New York, New Jersey, 1995b.
C.W. Topp and F.C. Leone."A family of J-shaped frequency functions", J.Amer. Statist.Assoc. 50 (1955), pp. 209–219. [CrossRef]
S. Nadarajah and S. Kotz."Moments of some J-shaped distributions", J. Appl. Statist. 30 (2003), pp. 311–317. [CrossRef]
S. Kotz and J.R. Van Dorp, "Beyond Beta: Other Continuous Families of Distributions with Bounded Support and Applications", World Scientific, Singapore, 2004.
M.E. Ghitany, S. Kotz, and M. Xie." On some reliability measures and their stochastic orderings for the Topp–Leone distribution", J. Appl. Statist. 32 (2005), pp. 715–722. [CrossRef]
TAHA .A "On Reliability Estimation for the RayleighDistribution Based on Monte Carlo Simulation" International Journal of Science and Research (IJSR) ISSN (Online): 2319-7064, 2015.
Thompson, J.R."Some Shrinkage Techniques for Estimating the Mean". J. Amer. Statist. Assoc., 63, 113-122 ,1968. [CrossRef]
Isaam, K, Taha, A. and Abbas,N." Estimation of (S-S) Reliability for Inverted Exponential Distribution" AIP Conference Proceedings 2591, 050006,1-11, 2023. [CrossRef]
A.N.Salman "Pre-test single and double stage shrunken estimators for the mean of normal distribution with known variance". Baghdad Journal for Science, 7(4), (1432–1442),2010.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On Estimation for Reliability of Stress-Strength Model Based on Topp-Leone Distribution

Abstract

I. Introduction

II. Expression of R1= P(X > Y) and R2= P(Y<X< Z)

III. Estimation of R1 = P(X > Y) and R2 = P(Y<X<Z)

IV. Monte Carlo Simulation and Numerical Outcomes

V. Conclusion

Appendix A

Co-author Information

References

MDPI Initiatives

Important Links

Subscribe

II. Expression of R₁= P(X > Y) and R₂= P(Y<X< Z)

III. Estimation of R₁ = P(X > Y) and R₂ = P(Y<X<Z)