Recent Optimization Methods and Techniques for Medical Image Analysis

1. Introduction

Medical images [1] are an important form of data in the medical field; they are used to observe, diagnose and treat diseases. Medical images are usually obtained through a variety of imaging techniques that provide detailed information about the internal structure and state of a patient's tissues. Common types of medical images include: x-ray (X-ray) images [2, 3], computed tomography (CT scan) [4], magnetic resonance imaging (MRI), ultrasound images, radiological images, nuclear medicine images [5-7], pathology slide images [8, 9], ophthalmological images [10], and others. Interpretation and analysis of medical images usually requires highly trained medical professionals such as radiologists, neurologists, surgeons and pathologists. At the same time, the professionalism of the doctors is required to be extremely high. However, with the development of deep learning and computer vision technologies, automated medical image analysis tools are becoming increasingly popular [11], and they can assist doctors in making faster and more accurate diagnoses.

Medical image analysis is a specialised area of computer science and medical imaging [12] that involves the application of advanced algorithms and techniques for processing and interpreting medical images such as X-rays[13, 14], MRI scans[15, 16], CT scans and ultrasound images [17, 18]. Its main goal is to assist healthcare professionals in diagnosing diseases, assessing disease progression and planning treatments by extracting valuable information, detecting abnormalities and quantifying relevant features from medical images. Medical image analysis plays a vital role in improving the accuracy and efficiency of medical diagnosis and treatment planning, and ultimately enhancing patient care. At the same time, medical images greatly improve the accuracy of healthcare professionals in diagnosing and treating various medical conditions. By utilising advanced algorithms and techniques, medical image analysis allows for more precise early detection of diseases, quantification of anatomical and pathological features, and monitoring of disease progression. This not only improves diagnostic accuracy, but also facilitates treatment planning and assessment, leading to more personalised and effective care for patients. In addition, it reduces the need for invasive procedures, minimises healthcare costs and ultimately saves lives by facilitating timely intervention. As medical imaging technology [19] continues to advance, medical image analysis continues to be an important tool in modern healthcare.

Optimisation methods are mathematical techniques used to find the best solution among a set of possible alternatives, usually by minimising or maximising an objective function while observing certain constraints. There are a number of optimisation methods that can be applied to medical image analysis, including gradient descent [20, 21] (where parameters are adjusted iteratively to reach optimal values), linear programming (used in resource allocation and scheduling problems), genetic algorithms [22-24] (inspired by biological evolution to find optimal solutions), and integer programming [25, 26] (which is particularly well suited to discrete decisions). These methods are fundamental in many fields such as engineering, economics, machine learning [22, 27, 28] and operations research for efficient decision making, resource allocation and problem solving in complex systems and processes.

Optimisation algorithms for medical image analysis are key components used to improve the efficiency, accuracy and reliability of medical image processing and interpretation. These algorithms can be applied to various areas of medical imaging including image enhancement, segmentation, feature extraction, classification, alignment and visualisation. Common optimization algorithms for medical image analysis include: image enhancement algorithms [29, 30], image segmentation algorithms [31, 32], feature extraction algorithms [33, 34], classification and recognition algorithms [35], image alignment algorithms [36, 37], visualization algorithms [38, 39], deep learning algorithms [40, 41], uncertainty modelling algorithms, and so on. The development and application of these algorithms have made medical image analysis more accurate, automated and efficient.

Optimisation techniques are crucial in medical image analysis. Firstly, optimisation techniques can be used to fine-tune parameters in image processing algorithms to improve the quality of image enhancement, denoising and segmentation, which are essential for accurate diagnosis and treatment planning. Secondly, optimisation methods help in feature selection and extraction, which can identify relevant information in medical images while reducing noise and irrelevant data. In addition, optimisation plays a key role in optimising the allocation of computational resources (e.g. GPU usage) to speed up the analysis of large datasets and complex algorithms.

This article is about optimisation algorithms related to medical image analysis. The rest of the article is structured as follows: section 2 describes the optimisation algorithms related to medical image analysis. Optimisation methods in fine-tuning are discussed and analysed in Section 3. Section 4 introduces the knowledge about optimisation algorithms in feature selection. Section 5 pair presents the optimisation resource allocation. Section 6 concludes the article.

2. Optimisation algorithms related to medical image analysis

This section presents some optimisation algorithms related to medical image analysis. Figure 1 shows the basic flow of optimization algorithm in image processing.

(1)

Image Enhancement Algorithms

Image enhancement is an important task in the field of digital image processing, which aims to improve the visual quality of an image by improving its quality, clarity, contrast and visualisation. Image enhancement algorithms can be classified into many different types and the exact choice depends on the application scenario and the desired enhancement effect. Common image enhancement algorithms are grey scale stretching, histogram equalisation, adaptive histogram equalisation, sharpening filter, noise filter, bilateral filter, super-resolution reconstruction, colour enhancement and deep learning based enhancement methods.

Different image enhancement algorithms are suitable for different application scenarios and requirements for medical image analysis. Choosing the appropriate algorithm usually requires consideration of the trade-off between medical image quality, computational complexity and enhancement effect. In practical applications, algorithm selection and parameter adjustment are usually required according to specific needs to obtain the best medical image enhancement effect.

(2)

Image Segmentation Algorithms

The goal of image segmentation is to divide the image into different regions or objects to identify different objects or regions in the image. Image segmentation algorithms can be classified into types such as threshold segmentation, region growing, edge detection, watershed segmentation, graph-based segmentation, convolutional neural network (CNN) segmentation, instance segmentation, semantic segmentation etc.

The specific choice of image segmentation algorithm selection depends on the specific requirements of the task, such as image complexity, segmentation accuracy and computational resources. In practical applications, it is usually necessary to consider these factors comprehensively and select the most suitable image segmentation algorithm for the task.

(3)

Feature Extraction Algorithms

Feature extraction is a key step in fields such as machine learning and computer vision, where the goal is to extract the most representative and information-rich features from raw data for subsequent pattern recognition, classification or regression tasks. Traditional feature extraction methods include colour features (including colour histogram, colour moments, colour gradient, etc., which are used to describe the colour information in an image), texture features (such as grey scale covariance matrix, local binary pattern and Gabor filter response, etc., which are used to describe the texture information of an image), shape features (including edge detection, corner detection and contour descriptor, etc., which are used to describe the shape information of an object), optical flow features (for describing the motion information of objects in video sequences, including dense optical flow and sparse optical flow, etc.). Deep learning feature extraction, on the other hand, includes Convolutional Neural Network (CNN) features, Autoencoders features, Generative Adversarial Network (GAN) features, as well as feature selection and dimensionality reduction, among others. In deep learning, the different layers of a neural network can often be viewed as feature extractors from lower to higher levels. Lower layers typically extract low-level features such as edges and textures, while higher layers extract more abstract and semantic features.

The choice of feature extraction method depends on the specific task and data type. In the era of deep learning, the use of pre-trained convolutional neural networks is often the method of choice for many computer vision tasks because of the strong generalisation ability of these networks on large-scale datasets. However, in some cases, traditional feature extraction methods can still be useful, especially if the data is limited or needs to be interpretive.

(4)

Classification and Recognition Algorithms

Classification and recognition algorithms are used to classify the input data into different categories or to identify objects. The common classification algorithms are K Nearest Neighbour Algorithm, Decision Tree, Support Vector Machine, Plain Bayesian Classifier, Neural Network. The common recognition algorithms are Target Detection, Face Recognition, Pose Estimation, Image Semantic Segmentation, Optical Character Recognition (OCR). Deep learning methods perform well in many recognition tasks, but they usually require large amounts of labelled data and computational resources for training. Therefore, factors such as data availability, algorithm complexity, and performance requirements need to be considered when selecting an algorithm.

(5)

Image Registration Algorithm

Image Registration aims to align multiple images or images acquired by different sensors to a common coordinate system. Image registration has a wide range of applications in fields such as medical imaging, remote sensing, computer vision and geographic information systems. Common image alignment algorithms and methods include feature-based alignment, mutual information-based alignment, local transformation-based alignment (Local Transformations), deep learning-based alignment, and so on. Among them, feature-based alignment includes point feature alignment and feature matching. Mutual information-based alignment includes mutual information metric and normalised mutual correlation. Local transformation-based alignment includes B-spline alignment and local affine or nonlinear transformation. Deep learning based alignment includes convolutional neural networks and generative adversarial networks.

The choice of an image alignment algorithm depends on the application area, data type, noise level and computational resources. In practical applications, parameter tuning and performance evaluation are usually required to ensure that accurate alignment results are obtained. Image alignment is the basis of many image processing and analysis tasks and is important for subsequent image analysis and processing.

(6)

Visualisation algorithms

Visualisation algorithms are a set of techniques and methods used to visualise data as graphs or images. They help in understanding data, discovering patterns, demonstrating relationships and conveying information. Some of the common visualisation algorithms and methods are scatter plots, line graphs, histograms and histograms, heat maps, box and line plots, scatter matrices, tree diagrams, network diagrams, map visualisations, 3D visualisations.

These visualisation algorithms can be selected and customised according to the type of data, task requirements and target audience. In the field of data science and information visualisation, choosing the right visualisation methods and tools is important for deeper understanding of the data, decision making and communicating the results.

(7)

Deep Learning Algorithms

Deep learning is a branch of machine learning that is based on the idea of artificial neural networks, where data is modelled and interpreted through multi-layer neural networks to achieve various machine learning tasks. Common deep learning algorithms and methods are Multilayer Perceptron (MLP), Convolutional Neural Networks (CNN), Recurrent Neural Networks (RNN), Self-Encoders, Generative Adversarial Networks (GAN), Reinforcement Learning, Attentional Mechanisms, and Transfer Learning.

These deep learning algorithms have a wide range of applications in a variety of fields, including natural language processing, computer vision, speech recognition, recommender systems, medical image analysis, and autonomous driving. The success of deep learning is due to the availability of large-scale datasets and high-performance computing hardware (e.g., GPUs), making it a powerful tool for solving complex problems. At the same time, deep learning also requires careful parameter tuning and significant computational resources to train complex models.

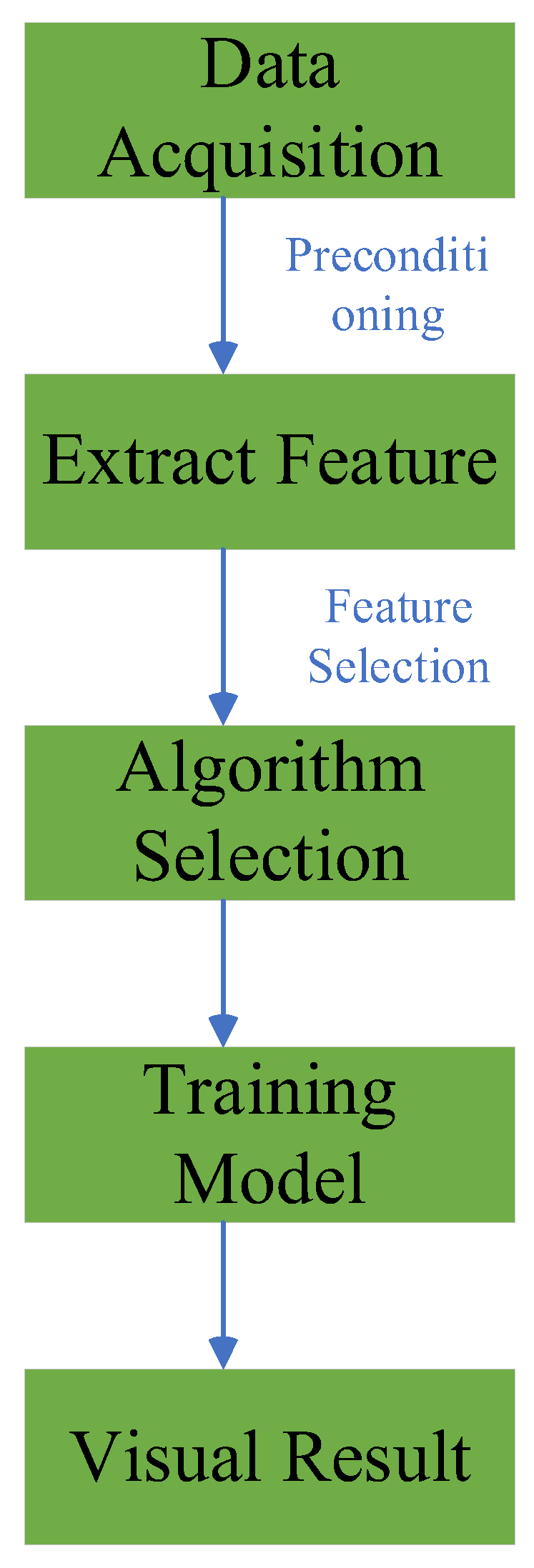
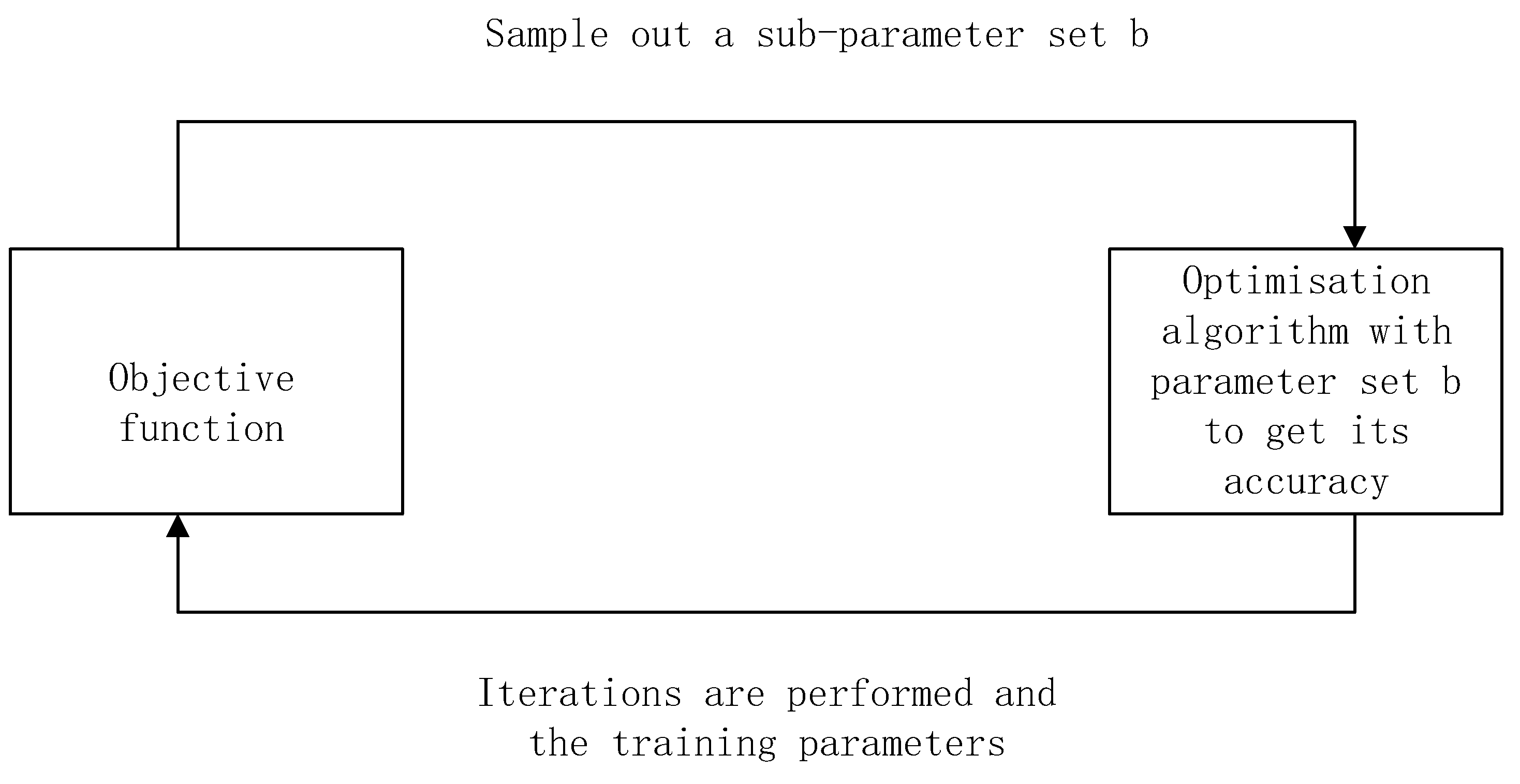
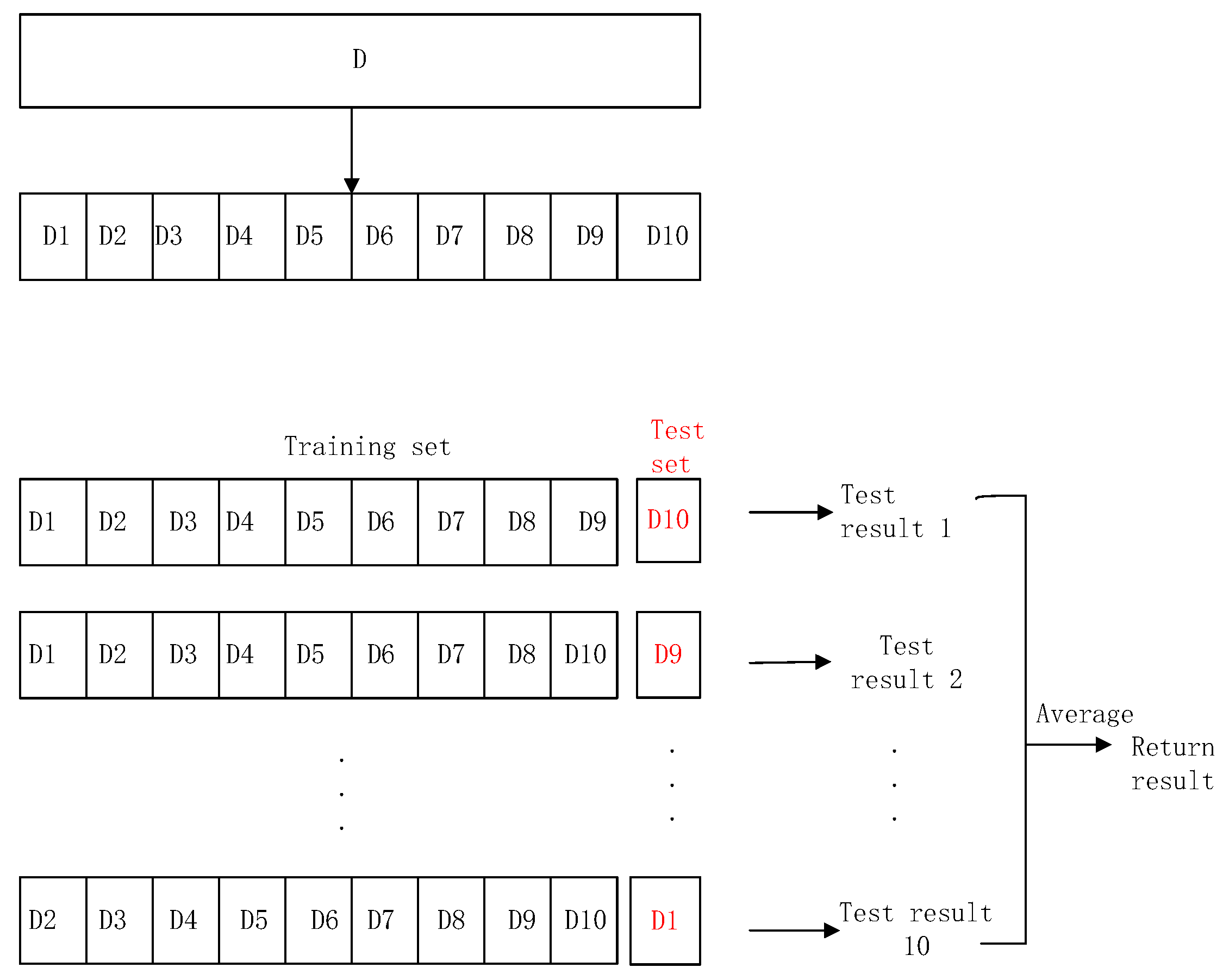
3. Optimization in Fine-tuning

By fine-tuning certain parameters in image processing algorithms during medical image analysis, it is possible to produce an optimal set of parameters for a particular task and improve the accuracy of medical image analysis [42]. Fine-tuning the parameters of an image processing algorithm is a critical step in improving the performance of image processing. Fine-tuning is usually an iterative process that requires careful selection of parameters, monitoring of performance, and adjustments based on results.

Figure 1 illustrates the overall process for parameter optimisation in fine-tuning. The main optimisations in fine-tuning are (1) determining the objective function. In image processing, the objective function is defined as a way to measure the quality or performance of an algorithm under a particular parameter configuration. The function quantifies the effectiveness of the algorithm in accomplishing a specific task such as image enhancement, denoising, or segmentation. Typically, the objective function generates a numerical value that is used as a criterion for evaluating the success of the algorithm. (2) Parameter space generation. Image processing algorithms usually have several tunable parameters, such as filter kernel size, threshold or scaling factor. Different combinations of these parameters form a parameter space that represents all possible configurations of the algorithm. (3) Optimisation algorithms. Optimisation algorithms perform a systematic search of the parameter space using techniques such as gradient descent, genetic algorithms or Bayesian optimisation. The aim is to find parameter values that minimise or maximise the objective function, depending on whether the minimisation or maximisation problem is being solved. (4) Iterative search. The optimisation algorithm iteratively explores the parameter space by evaluating the objective function for different parameter values. Then based on these evaluations, the algorithm adjusts the parameters to bring them closer to the optimal configuration. This process continues until a stopping criterion (e.g., a convergence threshold or a predetermined number of iterations) is met. (5) Parameter tuning. Once the optimisation process has converged or the stopping criteria are met, the algorithm determines a set of parameters that produce the best results based on the defined objective function. These tuned parameters can be used in image processing algorithms to improve performance.

In medical image analysis, optimisation techniques save the time and effort required for manual parameter adjustment by automatically searching for optimal parameter values. This not only improves the efficiency and effectiveness of image processing, but also ensures that the performance of the algorithms is continually optimised across a wide range of medical image analysis tasks, ultimately helping medical professionals to make accurate diagnostic and treatment decisions.

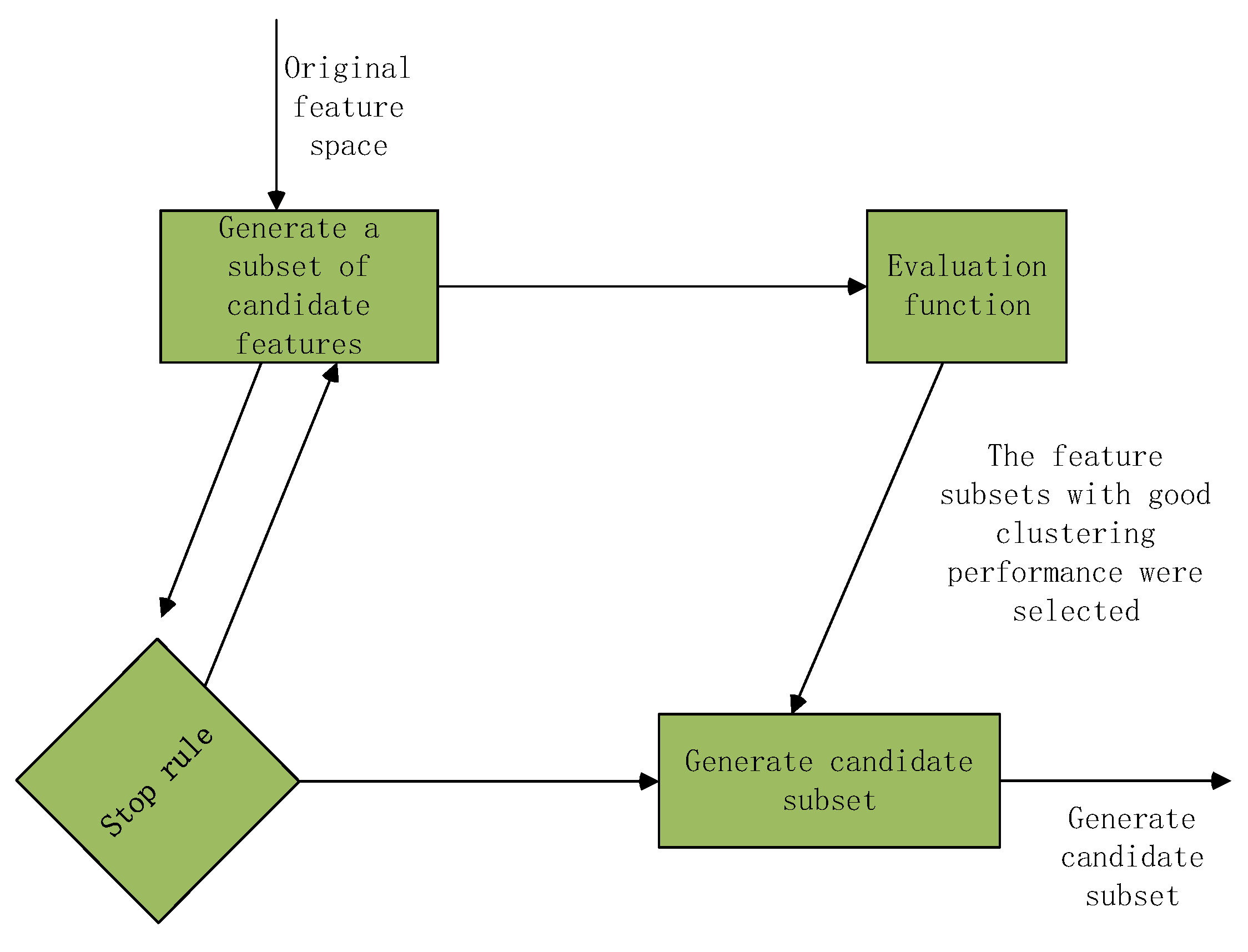
4. Optimization in Feature Selection

Optimisation of feature selection in medical image analysis is of great significance and impact. The structure of the feature selection algorithm is shown in Figure 2. Medical images usually contain a large number of pixels or features, which without feature selection will result in high dimensional data. High dimensional data not only increases the computational and memory requirements, but may also lead to dimensional catastrophe. By optimising feature selection, computational cost and memory requirements can be reduced and the training and inference process can be accelerated.

Optimisation of feature selection can model helps to identify and select the most relevant features, thus improving the performance and accuracy of machine learning models [43, 44]. By eliminating irrelevant or redundant features, the model focuses more on key information, reducing the risk of overfitting and improving generalisation [45]. In medical image analysis, interpretability [46] is critical because medical decisions require trustworthy interpretations [47]. Optimised feature selection helps to identify which features have the most impact on decision making and helps healthcare professionals to understand the decision making process of the model [48]. Also, optimised feature selection helps to reduce the influence from noisy or unstable features. Medical images can be affected by a variety of factors, including image quality, instrument noise, etc., and feature selection can reduce the negative impact of these factors on the model [49]. Optimised feature selection also helps to reduce data privacy and security risks [50]. By reducing the use of sensitive information, the risk of patient data leakage is reduced.

In the feature selection process for medical image analysis, optimisation allows for the systematic identification of the most informative and relevant features while minimising redundancy and noise. The process of optimising features includes (1) feature evaluation metrics. In order to assess the importance of individual features or subsets of features, a quantitative assessment metric (e.g., classification accuracy, information gain, or relevance) needs to be defined. The metric quantifies the ability of a set of features in distinguishing between different medical conditions or accurately describing relevant image attributes. Table 1 gives some indicators for character evaluation. (2) Feature subset search. Feature selection typically involves a combinatorial search of a space of possible feature subsets. This space can be very large, especially when dealing with high-dimensional medical image data. Optimisation techniques such as genetic algorithms, sequential forward selection or recursive feature elimination can be used to efficiently explore this space and select the most informative features. (3) Objective function. The objective function is used to quantify the value of the evaluation metrics for each feature subset. This function can be used to measure the performance of a particular feature set in a given medical image analysis task. (4) Optimisation algorithm. Optimisation algorithms are used to search for subsets of features that maximise or minimise the objective function, depending on whether the objective is feature selection or feature elimination. These algorithms iteratively evaluate different feature subsets and adjust their composition based on performance metrics. (5) Cross-validation[19]. To ensure that the selected features generalise the unseen data well, cross-validation techniques are usually combined with the optimisation process. This helps prevent overfitting and ensures that the selected feature subset is robust and reliable. Figure 3 illustrates the 10-fold cross-validation method. (6) Final feature subset. Once the optimisation process converges or reaches a predefined criterion, it identifies a subset of features that optimise the selected evaluation metrics. This subset can be used as input for subsequent medical image analysis tasks such as classification, segmentation or disease diagnosis.

Optimisation-driven feature selection improves the efficiency and effectiveness of medical image analysis by reducing data dimensionality, improving model interpretability and potentially leading to more accurate and robust results. It also helps mitigate the "curse of dimensionality" often encountered in high-dimensional medical image datasets, where the selection of the right features is critical for improving diagnostic and predictive performance.

5. Optimization in Resource Allocation

Optimisation[51, 52] is also crucial for the efficient allocation of healthcare resources, ensuring that healthcare organisations provide the best possible care to patients while effectively managing limited resources. Optimisation[53] plays an important role in resource planning for healthcare resources, disease detection [54], staff scheduling, patient triage, supply chain management [55], operating theatre scheduling, telemedicine and remote monitoring, emergency response, and resource allocation for rare diseases. Details are described below.

(1)

Resource planning. Optimisation can assist healthcare organisations in long-term resource planning by analysing historical data, patient demographics and forecasting demand. It can help determine the optimal allocation of resources such as hospital beds, medical staff, equipment and medications to meet expected demand while minimising waste and reducing costs.

(2)

Employee Scheduling. For hospitals and clinics, optimisation can be used to create efficient staff schedules that take into account factors such as staff availability [56], skill levels and patient needs. This ensures that the right people are on duty at the right time to provide quality care while maintaining a reasonable workload [57].

(3)

Patient triage. During a surge in patient demand, such as during a pandemic or natural disaster, optimisation algorithms can help healthcare providers prioritise patients based on the severity of their condition and available resources. This ensures that critically ill patients receive immediate attention and appropriate care.

(4)

Supply Chain Management. Optimisation techniques can be used to manage the supply chain [58] of healthcare resources such as medicines, personal protective equipment (PPE) and medical devices. This helps maintain adequate stock levels, minimise waste and avoid shortages.

(5)

Operating theatre scheduling. In the surgical sector, optimisation can optimise surgery scheduling, OR utilisation and staff allocation. This reduces patient wait times, optimises the use of expensive operating theatres and improves overall surgical workflow.

(6)

Telemedicine and remote monitoring. Optimisation can be used to determine the most efficient allocation of resources for telemedicine services and remote patient monitoring, ensuring that patients can access care remotely while minimising pressure on on-site resources.

(7)

Emergency Response. During an emergency or disaster, optimisation models can help emergency responders allocate medical resources efficiently. This includes deploying medical teams, ambulances, and supplies to a disaster area based on real-time data and predicted needs.

(8)

Resource allocation for rare diseases. For diseases with low prevalence, optimisation can help to allocate specialised resources, such as rare disease specialists or specialised equipment, to areas of greatest need [59], ensuring equitable access to care.

(9)

Budget allocation. Healthcare organisations and government agencies can use optimisation to allocate budgets efficiently, ensuring that funds are allocated to the areas of healthcare that are most in need, while meeting the needs of the population.

Optimising healthcare resource allocation [60] helps healthcare organisations make data-driven decisions to maximise the use of available resources, improve patient outcomes and enhance the overall quality and efficiency of healthcare services [61]. It can also play a key role in addressing unforeseen challenges such as pandemics or disasters by rapidly adjusting resource allocation strategies in response to changing circumstances.

6. Conclusion and Future Directions

The field of optimisation is constantly evolving and there are several exciting research directions that may influence its development in the future. These include (1) Robust and uncertainty-aware optimisation. Future research may focus on developing optimisation techniques that are robust to uncertainty and change in real-world data. This is critical in applications such as supply chain management [62], healthcare [63], and finance, where unexpected events can have a significant impact on outcomes. (2) Meta-heuristic and hybrid algorithms. Progress is expected in the development of meta-heuristic algorithms (e.g., genetic algorithms, simulated annealing, particle swarm optimisation) and hybrid methods that combine multiple optimisation techniques. These methods can improve the performance of complex, multi-objective [64] and high-dimensional optimisation problems [65].

Medical image analysis is a key area in the field of medicine that continues to evolve and introduce new technologies to improve the efficiency and accuracy of diagnosis, treatment and disease prevention. Future research directions will continue to drive innovation and development in this field [66]. For the future we can incorporate deep learning to tailor robust and interpretable deep learning models for medical image analysis. At the same time, uncertainty quantification techniques are being incorporated into optimisation-driven analyses to improve diagnosis and treatment planning, advancing real-time and interactive optimisation. In addition, there is an increasing focus on addressing privacy concerns in medical data while optimising the image analysis process, as well as exploring novel optimisation-driven approaches for multimodal and multiscale medical image fusion [67] and analysis to improve the accuracy of disease detection and characterisation. The future of medical image analysis optimisation will be marked by innovations that improve both the clinical utility of image-based healthcare applications and ethical considerations.