Fuzzy Transform Image Compression in the YUV Space

1. Introduction

YUV is a color model used in the NTSC, PAL, and SECAM color encoding systems., describing the color space in terms of a brightness component (the Y band called luma) and the two chrominance components (the U and V bands called chroma).

The YUV model has been used to advantage in image processing; its main advantage is that, unlike the three Red, Green and Blue (RGB) bands, which are equally perceived by the human eye, in YUV space, most of the color image information is contained in the Y band, as opposed to the U and V bands. main applications of the YUV model in image processing, is then the lossy compression of images, which can be performed mainly in the U and V bands, with slight loss of information.

YUV is used in the JPEG color image compression method [1,2] where the Discrete Cousine Transform (DCT) algorithm is executed on the YUV space, sub-sampling and reducing in dynamic range the UV channels in order to balance the reduction of data and the feel of human eyes. In [3] the DCT algorithm is executed in the YUV space for wireless capsule endoscopy application; the results show that the quality of the reconstructed images is better than that obtained by applying the DCT image compression method in the RGB space.

Many authors proposed image compression and reconstruction algorithms applied on the YUV space in order to improve the quality of the reconstructed images.

In [4,5] an image compression algorithm based on fuzzy relation equations is applied in the YUV space to compress color images; the image is divided in blocks of equal sizes, coding the blocks in the UV channels more strongly than the blocks in the Y band. In [6] the Fuzzy Transform technique (for short, F-transform) [7,8] is applied to coding color images in the YUV space; the author show that the quality of color images coded and decoded via F-transform in the YUV space is better than the one obtained using the F-transform method in the RGB space and comparable with the one obtained using the JPEG method.

A fractal image compression technique applied on the YUV space is proposed in [9]; the authors show that the quality of color images coded/decoded using this approach is better than the one obtained applying the fractal image compression method in the RGB space.

Furthermore, comparison tests between RGB and YUV perception-oriented properties performed in [10] show that compressed images in the YUV space provide better quality than images compressed in the RGB spaces in a human-computer interaction and machine vision applications.

In [11] is applied a technique using Tchebichef bit allocation to compress images in the YUV space; the results shown that this method improves the visual quality of color images compressed via JPEG by 42%. A color image compression method applying a subsampling process to the two chroma channels and a modification algorithm to the Y channel is applied to color images in [12] to improve the JPEG performances.

An image compression method with learning-base filter is applied in [13] on color images constructing the filter in YUV space instead of RGB space; author shows that the quality of the coded images is better than the one obtained using the filter in the RGB space. In [14] an image lossy compression algorithm in which quantization and subsampling are executed in the YUV space is applied for wireless capsule endoscopy; the quality of the coded images results better than the one obtained executing quantization and subsampling in the RGB space. In [15] a wavelet-based color image compression method using trained convolutional neural network are used in the lifting scheme is applied on the YUV executing the trained CNN on the Y, U, V channels separately; this method improves the quality of the coded images obtained applying traditional wavelet-based color image compression algorithms; however, execution times are much higher than those adopted by applying traditional color image compression algorithms.

In [16] an image reconstruction method performed on the YUV space is applied to prevent from corruption of data performed using adversarial perturbation of the image; the results show that the image can be recovered on the YUV space without distortions and with a high visual quality.

In this paper we propose a novel image compression algorithm in which the bidimensional First-Degree F-Transform algorithm [17,18] is applied for coding/decoding color images in the YUV space.

A generalization of the F-transform, called high order F^m-transform, has been proposed in [19] in order to reduce the approximation error of the original function approximated with the inverse F-transform. In the F^m -transform the components of the direct high order fuzzy transforms consist of polynomials of degree s, unlike the components of the direct F-transform (labelled as F°-transform), where they were constant values. The greater the degree of the polynomial, the smaller the error of the approximation; however, as the degree of the polynomial increases, the computational complexity of the algorithm increases.

In [18] the bi-dimensional first-order degree F-transform (F¹-transform) is used to compress images; authors show that the quality of the coded/decoded images is better than the one obtained executing F-transform, with negligible augments in CPU time. The critical point of this method consists of the fact that, unlike the F-transform and JPEG methods, it requires not the compressed image to be saved in memory, but matrices of three coefficients of the same size as the compressed image; therefore, it needs a memory area three times greater than that necessary to archive the compressed image.

To solve this problem, we propose a new lossy color image compression algorithm in which is executed the F¹-transform algorithm to code/decode color images transformed in the YUV space. The transformed image in each of the three channels is partitioned into blocks and each block is compressed by the bi-dimensional direct F¹-transform, compressing the blocks of the chroma channels more. The image is subsequently reconstructed by decomposing the single blocks with the use of the bi-dimensional inverse F¹-transform.

The main benefits of this method are as follows:

• the use of the bi-dimensional F¹-transform represents a trade-off between the quality of the compressed image and the CPU times. It reduces the information loss obtained by compressing the image with the same compression rate using the F-transform algorithm with acceptable coding/decoding CPU time;
• the compression of the color images is carried out in the YUV space to guarantee a high visual quality of the color images and solve the criticality of the F¹-transform color image compression method on the RGB space [18] which needs a larger memory to allocate the information of the compressed image. In fact, by performing a high compression of the two chrominance channels, the size of the matrices in which the information of the compressed image is contained, is reduced in these two channels, and this allows to reduce the memory allocation and CPU times.

We compare our color lossy image compression method with the JPEG method and with the image compression methods based on the bi-dimensional F-transform [7,8] and F¹-transform [19] on the RGB space and on the bi-dimensional F-transform on the YUV space [6].

In the next Section the concepts of F-transform and F¹-transform are briefly presented, and the F-transform lossy color image compression method applied in YUV space is shown as well. Our method is presented in Section 3. In Section 4 the comparative results obtained on datasets of color images are shown and discussed; concluding discussions are contained in Section 5.

2. Preliminaries

2.1. The bi-dimensional F-Transform

Let [a,b] be a closed real interval and let {x₁, x₂, …, x_n} be a set of points of [a,b], called nodes, such that x₁ = a < x₂ <…< x_n = b.

Let {A₁,…,A_n} be a family of fuzzy sets of X, where A_i : [a,b] → [0,1: it forms a fuzzy partition of X if the following conditions hold:

(1) A_i(x_i) = 1 for every i =1,2,…,n;

(2) A_i(x) = 0 if x∉(x_i-1, x_i+1), by setting x₀ = x₁ = a and x_n+1 = x_n = b;

(3) A_i(x) is a continuous function over [a,b];

(4) A_i(x) is strictly increasing over [x_i-1, x_i] for each i = 2, …, n ;

(5) A_i(x) is strictly decreasing over [x_i, x_i+1] for each i = 1,…, n-1;

(6) ${\sum }_{i=1}^n{A}_i\left(x\right)=1$ for every x∈[a,b].

Let $\mathrm{h}=\frac{\mathrm{b}-\mathrm{a}}{\mathrm{n}-1}$. The fuzzy partition {A₁,…, A_n} is an uniform fuzzy partition if:

(7) n≥3;

(8) x_i =a+h∙(i-1), for every i = 1, 2, …, n;

(9) A_i(x_i – x) = A_i(x_i + x) for every x $\in$ [0,h] and i = 2,…, n-1;

(10) A_i+1(x) = A_i(x - h) for every x$\in$ [x_i, x_i+1] and i = 1,2,…, n-1.

Let f(x) be a continuous function over [a,b] and {A₁, A₂, …, A_n} be a fuzzy partition of [a,b]. The n-tuple F =$[{\mathrm{F}}_1,{\mathrm{F}}_2,...,{\mathrm{F}}_{\mathrm{n}}]$ is called unidimensional direct F-transform of f with respect to {A₁, A₂, …, A_n} if the following hold:

$${\mathrm{F}}_{\mathrm{i}}=\frac{{\int }_{\mathrm{a}}^{\mathrm{b}}\mathrm{f}\left(\mathrm{x}\right){\mathrm{A}}_{\mathrm{i}}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}}{{\int }_{\mathrm{a}}^{\mathrm{b}}{\mathrm{A}}_{\mathrm{i}}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}} \mathrm{i}=1,2,\dots ,\mathrm{n}$$

(1)

The following function $f_{F,n}$ defined in [a,b]:

$$f_{F,n}\left(\mathrm{x}\right)={\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{F}}_{\mathrm{i}}{\mathrm{A}}_{\mathrm{i}}\left(\mathrm{x}\right)$$

(2)

is called uni-dimensional inverse F-transform of the function f.

The following theorem holds (cfr. [7, Theorem 2]):

Theorem 1.

Let f(x) be a continuous function over [a,b]. For every ε > 0 there exist an integer n(ε) and a fuzzy partition {A₁, A₂, …, A_n(ε)} of [a,b] such that for all x$\in$[a, b]$\left|{f\left(x\right)-f}_{F,n\left(\epsilon \right)}\left(x\right)<ϵ\right|$.

Now consider the discrete case where the function f is known in a set of N points P = {p₁,...,p_N}, where p_j∈[a,b] j = 1,2,…,m. The set {p₁,...,p_N} is called sufficiently dense with respect to the fixed fuzzy partition {A₁, A₂, …, A_n} if for every i = 1,…,n, there exists at least an index j$\in${1,…,m} such that A_i(p_j) > 0.

If the set P is sufficiently dense with respect to the fuzzy partition, we can define the discrete direct F-transform with components:

$${\mathrm{F}}_{\mathrm{i}}=\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{N}}f\left({\mathrm{p}}_{\mathrm{j}}\right){\mathrm{A}}_{\mathrm{i}}\left({\mathrm{p}}_{\mathrm{j}}\right)}{{\sum }_{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{A}}_{\mathrm{i}}\left({\mathrm{p}}_{\mathrm{j}}\right)} \mathrm{i}=1,2,\dots ,\mathrm{n}$$

(3)

and the discrete inverse F-transform:

$$f_{F,n}\left({\mathrm{p}}_j\right)={\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{F}}_{\mathrm{i}}{\mathrm{A}}_{\mathrm{i}}\left({\mathrm{p}}_j\right) \mathrm{j}=1,2,\dots ,\mathrm{N}$$

(4)

The following theorem applied to the discrete inverse F-transform holds (cfr. [7, Theorem 5]):

Theorem 2.

Let f(x) be a continuous function over [a,b], known in a discrete set of points {p₁,...,p_m}. For every ε > 0 there exist an integer n(ε) and a fuzzy partition {A₁, A₂, …, A_n(ε)} of [a,b], with respect to which P is sufficiently dense, that is such that for every j = 1,…,N,$\left|{f\left(p_j\right)-f}_{F,n\left(\epsilon \right)}\left(p_j\right)<ϵ\right|$.

By Theorem 2, the inverse fuzzy transform (4) can be used to approximate the function f in a point.

Now we consider functions in two variables. Let x₁, x₂, …, x_n be a set of n nodes in [a,b] , where n > 2 and x₁ = a < x₂ <…< x_n = b, and let y₁, y₂, …, y_m be a set of n nodes in [c,d], where m > 2 and and y₁ = c < y₂ <…< y_m = d. Moreover, let A₁,…,A_n : [a,b] → [0,1] be a fuzzy partition of [a,b], B₁,…,B_m : [c,d] → [0,1] be a fuzzy partition of [c,d] and let f(x,y) be a function defined in the closed set [a,b]×[c,d].

We suppose that f assumes known values in a set of points (p_j,q_j) ∈[a,b]×[c,d], where i = 1,…,N and j = 1,…,M, where the set P={p₁, … , p_N} is sufficiently dense with respect to the fuzzy partition {A₁,…, A_n} and the set Q={q₁, … ,q_M} is sufficiently dense with respect to the fuzzy partition {B₁,…,B_m}.

In this case, we can define the bi-dimensional discrete F-transform of f, given by matrix [F_hk] h = 1,…,n and k = 1,…,m with components:

$${\mathrm{F}}_{\mathrm{hk}}=\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{M}}{\sum }_{\mathrm{i}=1}^{\mathrm{N}}f({\mathrm{p}}_{\mathrm{i}},{\mathrm{q}}_{\mathrm{j}}){\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{i}}\right){\mathrm{B}}_{\mathrm{k}}\left({\mathrm{q}}_{\mathrm{j}}\right)}{{\sum }_{\mathrm{j}=1}^{\mathrm{M}}{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{i}}\right){\mathrm{B}}_{\mathrm{k}}\left({\mathrm{q}}_{\mathrm{j}}\right)} \mathrm{h}=1,2,\dots ,\mathrm{n} \mathrm{k}=1,2,\dots ,\mathrm{m}$$

(5)

and the bi-dimensional discrete inverse F-transform of f with respect to {A₁, A₂, …, A_n} and {B₁,…,B_m} given by

$$f_{nm}^F\left({\mathrm{p}}_{\mathrm{i}},{\mathrm{q}}_{\mathrm{j}}\right)={\sum }_{\mathrm{h}=1}^{\mathrm{n}}{\sum }_{\mathrm{k}=1}^{\mathrm{m}}{\mathrm{F}}_{\mathrm{h}\mathrm{k}}{\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{i}}\right){\mathrm{B}}_{\mathrm{k}}\left({\mathrm{q}}_{\mathrm{j}}\right), \mathrm{i}=1,2,\dots ,\mathrm{N} \mathrm{j}=1,2,\dots ,\mathrm{M}$$

(6)

2.2. The bi-dimensional F¹-Transform

This paragraph introduces the concept of higher degree fuzzy transform or F^r-transform. One-dimensional square-integrable functions will now be considered.

Let A_h, h = 1,…,n, be the hth fuzzy set of the fuzzy partition {A₁,…,A_n} defined on [a,b] and L₂([x_h−1,x_h+1]) be the Hilbert space of square-integrable functions f,g: [x_h−1,x_h+1] ⟶ R with the inner product:

$${⟨f,g⟩}_h=\frac{{\int }_{{\mathrm{x}}_{\mathrm{h}-1}}^{{\mathrm{x}}_{\mathrm{h}+1}}f\left(\mathrm{x}\right)g\left(\mathrm{x}\right){\mathrm{A}}_{\mathrm{h}}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}}{{\int }_{{\mathrm{x}}_{\mathrm{h}-1}}^{{\mathrm{x}}_{\mathrm{h}+1}}{\mathrm{A}}_{\mathrm{h}}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}}$$

(7)

Given a positive integer r, we denote with $L_2^r$([x_h−1,x_h+1]) a linear subspace of the Hilbert space L₂([x_h−1,x_h+1]) having as orthogonal basis the polynomials {$P_h^0$, $P_h^1$,…,$P_h^r$} constructed applying the Gram-Schmidt ortho-normalization defined as:

$$\left\{\begin{array}{l}{\mathrm{P}}_{\mathrm{h}}^0=1\\ {\mathrm{P}}_{\mathrm{h}}^{\mathrm{s}+1}={\mathrm{x}}^{\mathrm{s}+1}-{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{s}}}\frac{⟨{\mathrm{x}}^{\mathrm{s}+1},{\mathrm{P}}_{\mathrm{h}}^{\mathrm{j}}⟩}{⟨{\mathrm{P}}_{\mathrm{h}}^{\mathrm{j}},{\mathrm{P}}_{\mathrm{h}}^{\mathrm{j}}⟩}\end{array}\right.\mathrm{s}=1,...,\mathrm{r}-1$$

(8)

The following Lemma holds (Cfr. 7, Lemma 1):

Lemma 1.

Let $F_k^r$ be the orthogonal projection of the function f on $L_2^r$ ([x_h−1,x_h+1]). Then:

$$F_h^r(x)={\displaystyle \sum _{s=1}^r}{c}_{h,i}{P}_h^s\left(x\right)$$

(9)

where

$${\mathrm{c}}_{\mathrm{h},\mathrm{s}}=\frac{{⟨\mathrm{f},{\mathrm{P}}_{\mathrm{k}\mathrm{h}}^{\mathrm{s}}⟩}_{\mathrm{k}}}{{⟨{\mathrm{P}}_{\mathrm{h}}^{\mathrm{s}},{\mathrm{P}}_{\mathrm{h}}^{\mathrm{s}}⟩}_{\mathrm{h}}}=\frac{{\int }_{{\mathrm{x}}_{\mathrm{k}-1}}^{{\mathrm{x}}_{\mathrm{k}+1}}f\left(\mathrm{x}\right){\mathrm{P}}_{\mathrm{h}}^{\mathrm{s}}(\mathrm{x}\left){\mathrm{A}}_{\mathrm{h}}\right(\mathrm{x})\mathrm{d}\mathrm{x}}{{\int }_{{\mathrm{x}}_{\mathrm{k}-1}}^{{\mathrm{x}}_{\mathrm{k}+1}}{\left({\mathrm{P}}_{\mathrm{h}}^{\mathrm{s}}(\mathrm{x})\right)}^2{\mathrm{A}}_{\mathrm{h}}\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}}$$

(10)

${\mathrm{F}}_{\mathrm{h}}^{\mathrm{r}}$ it is the hth component of the direct F^r-transform of f . The inverse F^r-transform of f in a point x ∊ [a,b] is:

$$f_{\mathrm{F},\mathrm{n}}^{\mathrm{r}}(\mathrm{x})=\sum _{\mathrm{k}=1}^{\mathrm{n}}{{\mathrm{F}}_{\mathrm{h}}^{\mathrm{r}}\mathrm{A}}_{\mathrm{k}}\left(\mathrm{x}\right)$$

(11)

For r = 0, we have $P_h^0$ = 1 and the F⁰-transform is given by the F-transform in one variable ($F_h^0$(x) = c_h,0).

For r = 1, we have $F_h^1$(x) = (x − x_h) and the hth component of the F¹-transform is given by the formula:

$$F_h^1\left(\mathrm{x}\right)={\mathrm{c}}_{\mathrm{h},0}+{\mathrm{c}}_{\mathrm{h},1}(\mathrm{x}-{\mathrm{x}}_{\mathrm{h}})=F_h^0\left(\mathrm{x}\right)+{\mathrm{c}}_{\mathrm{h},1}(\mathrm{x}-{\mathrm{x}}_{\mathrm{h}})$$

(12)

If the function f is known in a set of N points P ={p₁,…p_N}, c_h,0 and c_h,1 can be discretized in the form:

$${\mathrm{c}}_{\mathrm{h},0}=\frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}f\left({\mathrm{p}}_{\mathrm{i}}\right){\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{i}}\right)}{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{i}}\right)}$$

(13)

$${\mathrm{c}}_{\mathrm{h},1}=\frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}f\left({\mathrm{p}}_{\mathrm{i}}\right){\left({\mathrm{p}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{h}}\right)\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{i}}\right)}{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{i}}\right){\left({\mathrm{p}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{h}}\right)}^2}$$

(14)

The F¹-tranform can be extended in a bi-dimensional space. Let L₂ ([x_h−1, x_h+1] × [y_k−1, y_k+1]) be the Hilbert space of square- integrable functions f: [x_h−1, x_h+1] × [y_k−1,y_k+1]→ R with the weighted inner product:

$${⟨f,g⟩}_{hk}=\underset{{\mathrm{x}}_{h-1}}{\overset{{\mathrm{x}}_{\mathrm{h}+1}}{\int }}\underset{{\mathrm{y}}_{\mathrm{k}-1}}{\overset{{\mathrm{y}}_{\mathrm{k}+1}}{\int }}f\left(x,y\right)g\left(\mathrm{x},\mathrm{y}\right){\mathrm{A}}_{\mathrm{h}}\left(\mathrm{x}\right){\mathrm{B}}_{\mathrm{k}}\left(\mathrm{y}\right)\mathrm{d}\mathrm{x}\dots \mathrm{d}\mathrm{y}$$

(15)

Two functions $f,g\in$ L₂ ([x_h−1, x_h+1] × [y_k−1, y_k+1]) are orthogonal if ${⟨f,g⟩}_{hk}=0$.

Let f: X ⊆ R² → Y⊆ R be a continuous bi-dimensional function defined in a closed set [a,b] × [c,d]. Let {A₁, A₂,…, A_n} be a fuzzy partition of [a,b], and let {B₁, B₂,…, B_m} be a fuzzy partition of [c,d].

Moreover, let {(p₁,q₁),…, (p_N,q_jN)} a set of N points in which is known the function f, where (p_j,q_j)$\in$ [a,b]×[c,d]. Let the set P={p₁, … , p_N} be sufficiently dense with respect to the fuzzy partition {A₁,…, A_n} and let the set Q={q₁, … ,q_M} be sufficiently dense with respect to the fuzzy partition {B₁,…,B_m}.

We can define the bi-dimensional direct F¹-transform of f, with components:

$${\mathrm{F}}_{\mathrm{h}\mathrm{k}}^1\left(\mathrm{x},\mathrm{y}\right)={\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{00}+{\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{10}\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{h}}\right)+{\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{01}\left(\mathrm{y}-{\mathrm{y}}_{\mathrm{k}}\right)$$

(16)

where ${\mathrm{c}}_{hk}^{00}$ is the component ${\mathrm{F}}_{hk}$of the bi-dimensional discrete direct F transform of f, given by (5). The three coefficients in (17) are given by:

$${\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{00}={\mathrm{F}}_{\mathrm{h}\mathrm{k}}=\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{N}}f({\mathrm{p}}_{\mathrm{j}},{\mathrm{q}}_{\mathrm{j}})\cdot {\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{j}}\right)\cdot {\mathrm{B}}_{\mathrm{k}}\left({\mathrm{q}}_{\mathrm{j}}\right)}{{\sum }_{j=1}^N{\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{j}}\right)\cdot {\mathrm{B}}_{\mathrm{k}}\left({\mathrm{q}}_{\mathrm{j}}\right)}$$

(17)

$${\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{10}=\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{N}}f({\mathrm{p}}_{\mathrm{j}},{\mathrm{q}}_{\mathrm{j}})\cdot \left({\mathrm{p}}_{\mathrm{j}}-{\mathrm{x}}_{\mathrm{h}}\right)\cdot {\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{j}}\right)\cdot {\mathrm{B}}_{\mathrm{k}}\left({\mathrm{q}}_{\mathrm{j}}\right)}{{\sum }_{\mathrm{j}=1}^{\mathrm{N}}{\left({\mathrm{p}}_{\mathrm{j}}-{\mathrm{x}}_{\mathrm{h}}\right)}^2\cdot {\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{j}}\right)\cdot {\mathrm{B}}_{\mathrm{k}}\left({\mathrm{q}}_{\mathrm{j}}\right)}$$

(18)

$${\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{01}=\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{N}}f({\mathrm{p}}_{\mathrm{j}},{\mathrm{q}}_{\mathrm{j}})\cdot \left({\mathrm{q}}_{\mathrm{j}}-{\mathrm{y}}_{\mathrm{k}}\right)\cdot {\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{j}}\right)\cdot {\mathrm{B}}_{\mathrm{k}}\left({\mathrm{q}}_{\mathrm{j}}\right)}{{\sum }_{\mathrm{j}=1}^{\mathrm{N}}{\left({\mathrm{q}}_{\mathrm{j}}-{\mathrm{y}}_{\mathrm{k}}\right)}^2\cdot {\mathrm{A}}_{\mathrm{h}}\left({\mathrm{p}}_{\mathrm{j}}\right)\cdot {\mathrm{B}}_{\mathrm{k}}\left({\mathrm{q}}_{\mathrm{j}}\right)}$$

(19)

The inverse F¹-transform of f in a point (x,y) ∊ [a,b] × [c,d] is:

$$f_{\mathrm{F},\mathrm{n}}^1(\mathrm{x},\mathrm{y})=\sum _{h=1}^n\sum _{k=1}^m{\mathrm{F}}_{\mathrm{h},\mathrm{k}}^1{\mathrm{A}}_{\mathrm{h}}\left(\mathrm{x}\right){\mathrm{B}}_{\mathrm{k}}\left(\mathrm{y}\right)$$

(20)

where ${\mathrm{F}}_{\mathrm{h},\mathrm{k}}^1(\mathrm{x},\mathrm{y})$ is the (h,k)th component of the bi-dimensional direct F¹-transform, given by the formula (16).

2.3. Coding/decoding images using the bi-dimensional F and F¹-Transforms

Let I be a grey N × M image. A pixel can be considered a data point with coordinates (i,j), where i = 1,2,…,N and j = 1,2,…M; the value of this data point is given by the pixel value I(i,j). In [8] the image is normalized in [0,1] according with the formula R(i,j) = I(i,j)/(L-1) where L is the number of grey levels, partitioned in blocks of equal sizes N(B)×M(B), coded to a block F_B of sizes n(B) × m(B) with n(B) << N(B) and m(B) << M(B), using the bi-dimensional direct F-transform.

Let {A₁,…,A_n(B)} be a fuzzy partition of [1,N(B)] and let {B₁,…,B_m(B)} be a fuzzy partition of [1,M(B))], each block is compressed by the bi-dimensional direct F-transform:

$${\mathrm{F}}_{\mathrm{h}\mathrm{k}}^{\mathrm{B}}=\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{M}\left(\mathrm{B}\right)}{\sum }_{\mathrm{i}=1}^{\mathrm{N}\left(\mathrm{B}\right)}\mathrm{R}(\mathrm{i},\mathrm{j}){\mathrm{A}}_{\mathrm{h}}\left(\mathrm{i}\right){\mathrm{B}}_{\mathrm{k}}\left(\mathrm{j}\right)}{{\sum }_{\mathrm{j}=1}^{\mathrm{M}\left(\mathrm{B}\right)}{\sum }_{\mathrm{i}=1}^{\mathrm{N}\left(\mathrm{B}\right)}{\mathrm{A}}_{\mathrm{h}}\left(\mathrm{i}\right){\mathrm{B}}_{\mathrm{k}}\left(\mathrm{j}\right)}$$

(21)

The coded image is reconstructed by merging all compressed blocks.

Each block is decompressed by using the bi-dimensional inverse F-transform. The pixel value I(i,j) in the block is approximated by the value:

$$f_{n_B{m}_B}^{F^B}(\mathrm{i},\mathrm{j})=\sum _{\mathrm{h}=1}^{\mathrm{n}\left(\mathrm{B}\right)}\sum _{\mathrm{k}=1}^{\mathrm{m}\left(\mathrm{B}\right)}{\mathrm{F}}_{\mathrm{h}\mathrm{k}}^{\mathrm{B}}{\mathrm{A}}_{\mathrm{h}}(\mathrm{i}){\mathrm{B}}_{\mathrm{k}}(\mathrm{j})$$

(22)

The decoded image is reconstructed by merging the decompressed blocks.

The F-transform compression and decompression algorithms are shown in pseudocode in Algorithms 1a and 1b.

Algorithm 1a. F1-transform image compression

Input: N×M Image I with L grey levels     Size of the blocks of the source image N(B)×M(B)     Size of the compressed blocks n(B)× m(B)

Output: n×m compressed image IC

Normalize the source image I in [0,1] Partition the source image in blocks of size N(B)×M(B) For each block  For h = 1 to n(B)   For k = 1 to m(B)    Compute the (hk)th component of the bidimensional direct F-transform by (21)   Next k  Next h Next block Merge the compressed blocks De-normalize the image Return the compressed n×m image IC

Algorithm 1b. F-transform image decompression

Input: n×m compressed image Ic

Output: N×M decoded image ID

Normalize the compressed image in [0,1] Partition the compressed image Ic in blocks of size n(B)×m(B) For each compressed block  For i = 1 to N(B)   For j = 1 to M(B)    Compute the (i,j)th pixel of the decoded block by the bidimensional inverse F-transform (22)   Next j  Next i Next compressed block Merge the decompressed blocks De-normalize the decompressed image Return the decompressed N×M image ID

In [17] an improvement of the quality of the decompressed image is accomplished using the bi-dimensional F¹-transform.

The blocks are compressed by using the bi-dimensional direct F¹-transform:

$${\mathrm{F}}_{\mathrm{h}\mathrm{k}}^{1\mathrm{B}}={\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{00}+{\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{10}\left(\mathrm{i}-\mathrm{h}\right)+{\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{01}\left(\mathrm{j}-\mathrm{k}\right)$$

(23)

where:

$${\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{00}={\mathrm{F}}_{\mathrm{h}\mathrm{k}}^{\mathrm{B}}=\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{M}\left(\mathrm{B}\right)}{\sum }_{\mathrm{i}=1}^{\mathrm{N}\left(\mathrm{B}\right)}\mathrm{R}(\mathrm{i},\mathrm{j}){\mathrm{A}}_{\mathrm{h}}\left(\mathrm{i}\right){\mathrm{B}}_{\mathrm{k}}\left(\mathrm{j}\right)}{{\sum }_{\mathrm{j}=1}^{\mathrm{M}\left(\mathrm{B}\right)}{\sum }_{\mathrm{i}=1}^{\mathrm{N}\left(\mathrm{B}\right)}{\mathrm{A}}_{\mathrm{h}}\left(\mathrm{i}\right){\mathrm{B}}_{\mathrm{k}}\left(\mathrm{j}\right)}$$

(24)

$${\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{10}==\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{M}\left(\mathrm{B}\right)}{\sum }_{\mathrm{i}=1}^{\mathrm{N}\left(\mathrm{B}\right)}I(\mathrm{i},\mathrm{j}){\left|i-h\right|\mathrm{A}}_{\mathrm{h}}\left(\mathrm{i}\right){\mathrm{B}}_{\mathrm{k}}\left(\mathrm{j}\right)}{{\sum }_{\mathrm{i}=1}^{\mathrm{N}\left(\mathrm{B}\right)}{\mathrm{A}}_{\mathrm{h}}\left(\mathrm{i}\right){(\mathrm{i}-\mathrm{h})}^2{\sum }_{\begin{array}{c}j=1\end{array}}^{\mathrm{M}\left(\mathrm{B}\right)}{\mathrm{B}}_{\mathrm{k}}\left(\mathrm{j}\right)}$$

(25)

$${\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{01}==\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{M}\left(\mathrm{B}\right)}{\sum }_{\mathrm{i}=1}^{\mathrm{N}\left(\mathrm{B}\right)}I(\mathrm{i},\mathrm{j}){\left|j-k\right|\mathrm{A}}_{\mathrm{h}}\left(\mathrm{i}\right){\mathrm{B}}_{\mathrm{k}}\left(\mathrm{j}\right)}{{\sum }_{\mathrm{j}=1}^{\mathrm{M}\left(\mathrm{B}\right)}{\mathrm{B}}_{\mathrm{k}}\left(\mathrm{j}\right){(\mathrm{j}-\mathrm{k})}^2{\sum }_{\mathrm{i}=1}^{\mathrm{N}\left(\mathrm{B}\right)}{\mathrm{A}}_{\mathrm{h}}\left(\mathrm{i}\right)}$$

(26)

The above three coefficients are constructed merging the coefficients of each block and finally stored, forming the output of coding process.

In the inverse process the image is reconstructed by decompressing the block with the bi-dimensional inverse F¹-transform:

$$f_{n_B{m}_B}^{{1F}^B}(\mathrm{i},\mathrm{j})=\sum _{\mathrm{h}=1}^{\mathrm{n}\left(\mathrm{B}\right)}\sum _{\mathrm{k}=1}^{\mathrm{m}\left(\mathrm{B}\right)}{\mathrm{F}}_{\mathrm{h}\mathrm{k}}^{\mathrm{B}}{\mathrm{A}}_{\mathrm{h}}(\mathrm{i}){\mathrm{B}}_{\mathrm{k}}(\mathrm{j})$$

(27)

where the bi-dimensional direct F¹-transform of the block ${\mathrm{F}}_{\mathrm{h}\mathrm{k}}^{\mathrm{B}}$ is calculated by (23).

The decompressed blocks are merged to form the decompressed image.

The F¹-transform compression and decompression algorithms are shown in pseudocode in Algorithms 2a and 2b.

Algorithm 2a. F1-transform image compression

Input: N×M Image I with L grey levels     Size of the blocks of the source image N(B)×M(B)     Size of the compressed blocks n(B)× m(B)

Output: n×m matrices of the direct F1-transform coefficients ${\mathrm{c}}^{00}$$,{\mathrm{c}}^{10}$$\mathrm{and}{\mathrm{c}}^{01}$

1. Normalize the source image I in [0,1] 2. Partition the source image in blocks of size N(B)×M(B) 3. For each block 4.  For h = 1 to n(B) 5.   For k = 1 to m(B) 6.    Compute the component ${\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{00}$ by (24) 7.    Compute the component ${\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{10}$ by (25) 8.    Compute the component ${\mathrm{c}}_{\mathrm{h}\mathrm{k}}^{01}$ by (26) 9.    Compute the (hk)th component of the bidimensional direct F1-transform by (26) 10.   Next k 11.  Next h 12. Next block 13. Merge the compressed blocks to obtain the n×m matrices of the coefficients ${\mathrm{c}}^{00}$$,{\mathrm{c}}^{10}$$\mathrm{and}{\mathrm{c}}^{01}$ 14. Return the compressed n×m matrices of the coefficients ${\mathrm{c}}^{00}$$,{\mathrm{c}}^{10}$$\mathrm{and}{\mathrm{c}}^{01}$

Algorithm 2b. F1-transform image decompression

Input: n×m matrices of the direct F1-transform coefficients coefficients ${\mathrm{c}}^{00}$$,{\mathrm{c}}^{10}$$\mathrm{and}{\mathrm{c}}^{01}$     Size of the blocks of the decoded image N(B)×M(B)     Size of the blocks of the coded image n(B)×m(B)

Output: N×M decoded image ID

1. $\mathrm{Partition}\mathrm{the}{\mathrm{F}}^1-\mathrm{transform}\mathrm{coefficients}{\mathrm{c}}^{00}$$,{\mathrm{c}}^{10}$$\mathrm{and}{\mathrm{c}}^{01}$in blocks of size n(B)×m(B) 2. For each compressed block 3.  For i = 1 to N(B) 4.   For j = 1 to M(B) 5.    Compute the (i,j)th pixel of the decoded block by the bidimensional inverse F1-transform (27) 6.   Next j 7.  Next i 8. Next compressed block 9. Merge the decompressed blocks 10. De-normalize the decompressed image 11. Return the decompressed N×M image ID

3. The YUV-based F¹-transform color image compression method

Let I be a N×M color image in L grey levels. All pixel values in the three bands R, G and B are normalized in [0,1].

Considering a 256 grey levels color image and the scaled and offset version of the YUV color space, the source image is transformed in the YUV space via the formula [20]:

$$\left[\begin{array}{c}\mathrm{Y}\\ \mathrm{U}\\ \mathrm{V}\end{array}\right]=\left[\begin{array}{ccc}0.299& 0.587& 0.114\\ -0.169& -0.332& 0.500\\ 0.500& -0.419& -0.813\end{array}\right]\left[\begin{array}{c}\mathrm{R}\\ \mathrm{G}\\ \mathrm{B}\end{array}\right]+\left[\begin{array}{c}16\\ 128\\ 128\end{array}\right]$$

(28)

Then, the F¹-transform image compression algorithm is executed separately to the three normalized images Y, U and V, using a strong compression for the chroma images U and V.

If N(B) and M(B) are the sizes of each block in the three channels, the blocks in the brightness channel are compressed with rate ${\mathsf{\varrho }}_{\mathrm{Y}}=\frac{n_Y\left(\mathrm{B}\right)\times m_Y\left(\mathrm{B}\right)}{\mathrm{N}\left(\mathrm{B}\right)\times \mathrm{M}\left(\mathrm{B}\right)}$ and the blocks in the two chroma channels are compressed with rate ${\mathsf{\varrho }}_{\mathrm{U}\mathrm{V}}=\frac{n_{UV}\left(\mathrm{B}\right)\times m_{UV}\left(\mathrm{B}\right)}{\mathrm{N}\left(\mathrm{B}\right)\times \mathrm{M}\left(\mathrm{B}\right)}$ , where n_UV(B) << n_Y(B) and m_UV(B) << m_Y(B), so that ρ_UV << ρ_Y .

The F¹-transform image compression algorithm will store, in output for each channel, the three matrixes of the coefficients of the bi-dimensional direct F¹-transform: ${\mathrm{c}}^{00}$, ${\mathrm{c}}^{10}$and ${\mathrm{c}}^{01}$. The size of the three matrices in the brightness channel is ρ_Y(N×M) and the size of the three matrices in each of the two chroma channels is ρ_UV(N×M).

By suitably choosing the brightness and chroma compression rates, it is possible to reduce the memory capacity needed to store the direct F¹-transform coefficients in the RGB space.

For example, suppose we execute the F¹-transform image compression algorithm in the RGB space to compress a 256×256 color image, by partitioning the image into 16x16 blocks compressed into 4×4 blocks. The compression rate will be ρ_RGB = 0.0625 and the size of the matrix of each coefficient is 64×64. Executing the F¹-transform algorithm in the YUV space and compressing the 16×16 blocks in the two chroma channels in 2×2 blocks (ρ_UV = 0.016) and the 16×16 blocks in the brightness channel in 8×8 blocks (ρ_UV = 0.25), the size of the matrix of each coefficient in the U and V channels will be 32×32, and the size of the matrix of each coefficient in the Y channel will be 128×128. So, by carrying out the compression of the source image in the YUV space in this way, an advantage is obtained both in terms of visual quality of the reconstructed image and in terms of available memory necessary to archive the coefficients of the direct F¹-transforms in the three channels.

Below we show in pseudocode the YUV F¹-transform color image compression algorithm (Algorithm 3a).

Algorithm 3a. YUV F1-transform color image compression

Input: N×M color image I with L grey levels     Size of the blocks of the source image N(B)×M(B)     Size of the compressed blocks in the Y channel nY(B)× mY(B)     Size of the compressed blocks in the U and V channels nUV(B)×mUV(B)

Output: n×m matrices of thedirect F1-transform coefficients ${\mathrm{c}}^{00}$$,{\mathrm{c}}^{10}$$\mathrm{and}{\mathrm{c}}^{01}$ in the Y, U and channels

1. Extract the single band images IR, IG and IB 2. Transform the RGB images IR, IG and IB in the YUV images IY, IU and IV by (28) 3. Execute F1-transform image compression (IY, N(B), M(B), nY(B), mY(B) ) //compress IY 4. Execute F1-transform image compression (IU, N(B), M(B), nUV(B), mUV(B) ) //compress IU 5. Execute F1-transform image compression (IV, N(B), M(B), nUV(B), mUV(B) ) //compress IV 6. Return the compressed matrices of the coefficients ${\mathrm{c}}^{00}$$,{\mathrm{c}}^{10}$$\mathrm{and}{\mathrm{c}}^{01}$ in the bands Y, U and V

The decompression process is performed by executing the F¹-transform image decompression algorithm in the brightness and chroma channels. The F¹-transform image decompression algorithm is executed separately for each of the channels Y, U and V, by assigning as input both the three coefficient matrices of the direct F¹-transform and the dimensions of the original and compressed blocks.

Then the three decoded images I_DY, I_DU, and I_DV are transformed in the RGB space, by the formula [20]:

$$\left[\begin{array}{c}R\\ G\\ B\end{array}\right]=\left[\begin{array}{ccc}1.164& 0& 1.596\\ 1.164& -0.813& -0.392\\ 1.164& 2.017& 0\end{array}\right]\left[\begin{array}{c}Y-16\\ U-128\\ V-128\end{array}\right]$$

(29)

Finally, the decoded image in the RGB band (I_DR, I_DG, I_DB) is returned.

Below is shown in pseudocode the YUV F¹-transform color image decompression algorithm (Algorithm 3b).

Algorithm 3b. YUV F1-transform image decompression

Input: n×m matrices of the direct F1-transform coefficients coefficients ${\mathrm{c}}^{00}$$,{\mathrm{c}}^{10}$$\mathrm{and}{\mathrm{c}}^{01}$ in the Y, U and V channels     Size of the blocks of the decoded image N(B)×M(B)     Size of the compressed blocks in the Y channel nY(B)× mY(B)     Size of the compressed blocks in the U and V channels nUV(B)×mUV(B)

Output: N×M decoded image ID

1. ${\mathrm{c}}^{00}$$,{\mathrm{c}}^{10}$$\mathrm{and}{\mathrm{c}}^{01}$in blocks of size nY(B)×mY(B) 2. IDY = ${\mathrm{F}}^1-\mathrm{transform}\mathrm{image}\mathrm{decompression}({\mathrm{c}}_Y^{00}$, ${\mathrm{c}}_Y^{10},{\mathrm{c}}_Y^{01}$, N(B), M(B), nY(B), mY(B) ) //Y ch. decomp. 3. IDU = ${\mathrm{F}}^1-\mathrm{transform}\mathrm{image}\mathrm{decompression}({\mathrm{c}}_{\mathrm{U}}^{00}$, ${\mathrm{c}}_{\mathrm{U}}^{10},{\mathrm{c}}_{\mathrm{U}}^{01}$, N(B), M(B), nUV(B), mUV(B) ) //U ch. decomp. 4. IDV = ${\mathrm{F}}^1-\mathrm{transform}\mathrm{image}\mathrm{decompression}({\mathrm{c}}_V^{00}$, ${\mathrm{c}}_{\mathrm{V}}^{10},{\mathrm{c}}_{\mathrm{V}}^{01}$, N(B), M(B), nUV(B), mUV(B) ) //V ch. decomp. 5. Transform the YUV images IDY, IDU and IDV in the RGB images IDR, IDG and IDB by (29) 6. Return the decompressed N×M color image in the RGB space (IDR, IDG and IDB)

We compare our lossy color image compression report with the JPEG algorithms and the color image compression methods based on F-transform in the RGB space [8], and F-transform on the YUV space [6] and F¹-transform on the RGB space [17].

The Peak Signal to Noise index (PSNR) used to measure the quality of the decoded images. To measure the gain obtained executing the YUV F¹-transform algorithm with respect to another color image compression method, we measure the PSNR gain, expressed in percentage and given by the formula

$$\mathrm{Gain}(\mathrm{YUV}{F}^1-\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m})=\frac{\left[\right(\mathrm{PSNR}\mathrm{YUV}{F}^1-\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\left)-\right(\mathrm{PSNR}\mathrm{other}\mathrm{method}\left)\right]\cdot 100}{\left(\mathrm{PSNR}\mathrm{other}\mathrm{method}\right)}$$

(30)

In next Section the results applied to color image dataset are shown and discussed.

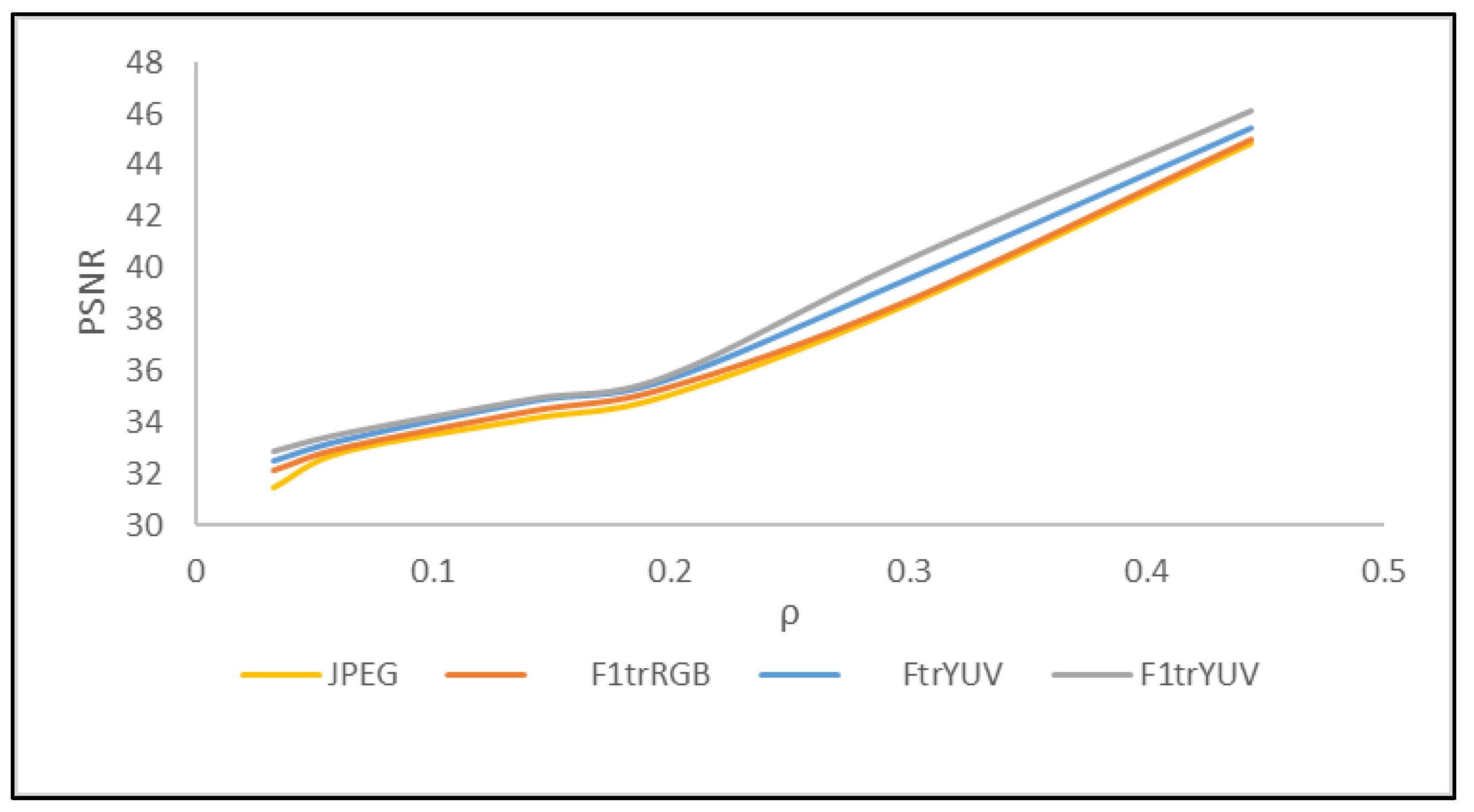
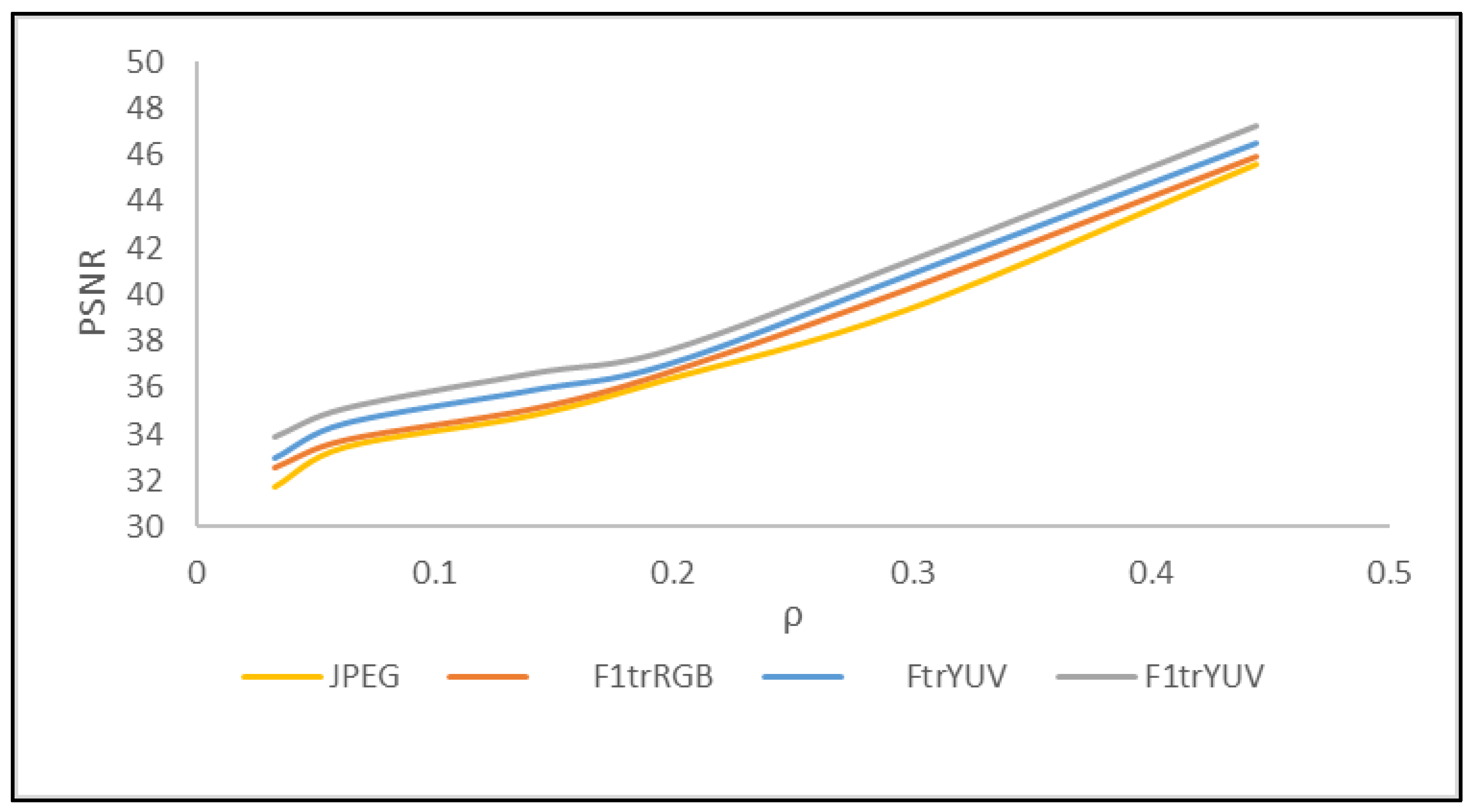
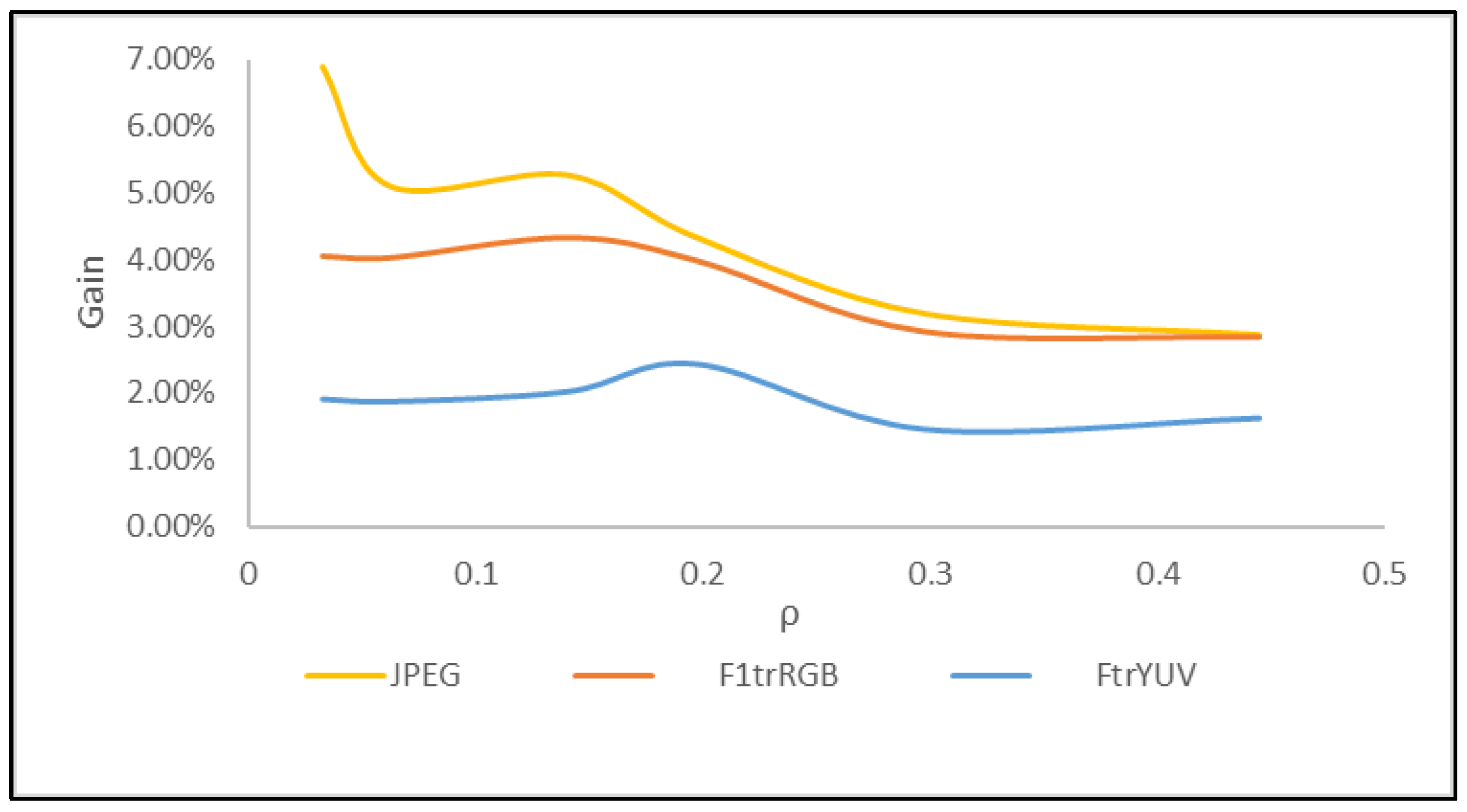
4. Results

We test the YUV F1-transform lossy color image compression algorithm on the color image dataset provided by the University of Southern California Signal and Image Processing Institute (USC SIPI) and published on the website http://sipi.usc.edu/database.

The dataset is made up of over 50 color images of different sizes. For brevity, we show in detail the results obtained for the 256x256 source images 4.1.04 and the 412x512 source image 4.2.07; they are shown in Figure 1.

Each image was compressed and decompressed by performing JPEG, YUV F-transform, F¹-transform and YUV F¹-transform lossy image compression algorithms.

We compare the four image compression methods measuring the quality of the reconstructed image as the compression rate change. The compression rate used by executing YUV F-transform and YUV F¹-transform is the mean compression rate set for each channel Y, U and V.

In Figure 2 we show, for the original image 4.1.04, the decoded images obtained by executing the four algorithms with a compression rate ρ ≈ 0.10.

Figure 3 shows, for the original image 4.1.04, the decoded images obtained by executing the four algorithms setting a compression rate ρ ≈ 0.25.

Figure 4 shows the trend of the PSNR index obtained varying the compression rate. The trends obtained by executing JPEG and F¹-transform are similar. However, for strong compressions (ρ < 0.1), the PSNR value calculated by executing JPEG decreases exponentially as the compression increases: this result shows that the quality of the decoded image obtained by JPEG drops quickly for very high compressions. The highest PSNR values are obtained by performing YUV F-transform and YUV F¹-transform. In particular, the PSNR values obtained with the two methods are similar for ρ < 0.2, while, for lower compressions, YUV F¹-transform provides decompressed images of better quality than those obtained with YUV F-transform.

Now we show the results obtained for the color image 4.2.07. In Figure 5 we give the decoded images obtained by executing the four algorithms with compression rate ρ ≈ 0.10.

Figure 6 shows the decoded images of 4.2.07 obtained by executing the four algorithms with a compression rate ρ ≈ 0.25.

Figure 7 shows the trend of the PSNR index obtained by varying the compression rate. The best values of PSNR are obtained by executing YUV F¹-transform. The trend of the PSNR obtained by executing YUV F-transform is better than the one obtained by executing F-transform and JPEG. As the results obtained for the color image 4.1.04 show, the trend of PSNR obtained by executing JPEG for the image 4.2.07 decays rapidly as compression increases (ρ < 0.1).

In Figure 8 we show the trends of the gain of the YUV F¹-transform algorithm with respect to the other three color image compression algorithms, where the gain index is calculated by (30) and is averaged for all the images of the dataset used in the comparative tests. The gain of the proposed method with respect to YUV F-transform is approximately equal to 2% regardless of the compression rate. The gain of YUV F¹-transform with respect to F¹-transform varies from 3%, for small compressions, to 4% for high compressions (ρ < 0.2). The gain of YUV F¹-transform with respect to JPEG varies from 3%, for small compressions, to 5% for medium-high compressions (0.1 < ρ < 0.2); for compression rates lower than 0.1 the gain index increases quickly as the compression increases until it reaches 7%.

These results shown that the quality of the images coded/decoded by YUV-F¹transform is higher than that obtained using YUV-Ftransform, F¹transform and JPEG, regardless of the compression level.

Finally, in Table 1 we show the mean coding and decoding CPU time obtained by executing the four color image compression algorithms: the average values refer to the CPU times measured for all images of the same size and for all compression rates: we see that both the coding and decoding CPU times measured by executing YUV F1-transform are comparable with those obtainedwith the other four image compression methods. Therefore, YUV-F¹-transform improves the quality of the reconstructed images obtained by executing JPEG, F¹-transform and YUV F-transform and provides CPU times similar to those obtained by executing the other image compression three methods at same time.

5. Conclusions

A lossy color image compression process employing the bi-dimensional F¹_-transform in YUV space is proposed. The benefit of this approach is to improve the quality of the reconstructed image, with acceptable CPU coding/decoding times. In fact, the F1-transform method manages to retain more information of the original image than other image compression methods, but with memory to be allocated and execution times. The proposed method on the YUV space allows to obtain a high quality of the decompressed image, without increasing the allocated memory and the CPU times. The results show that this method improves the quality of the decompressed image compared to that obtained with the use of JPEG, F-transform applied in YUV space and F¹_-transform applied in RGB space. Moreover the execution times are compatible with those obtained by executing the other three color image compression methods.

In the future we intend to adapt the YUV F¹-transform algorithm to the compression of large color images