Submitted:
12 September 2023
Posted:
14 September 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Goals, Organization and Contributions
1.2. Notation
2. Preliminary
2.1. Graph Representation Learning
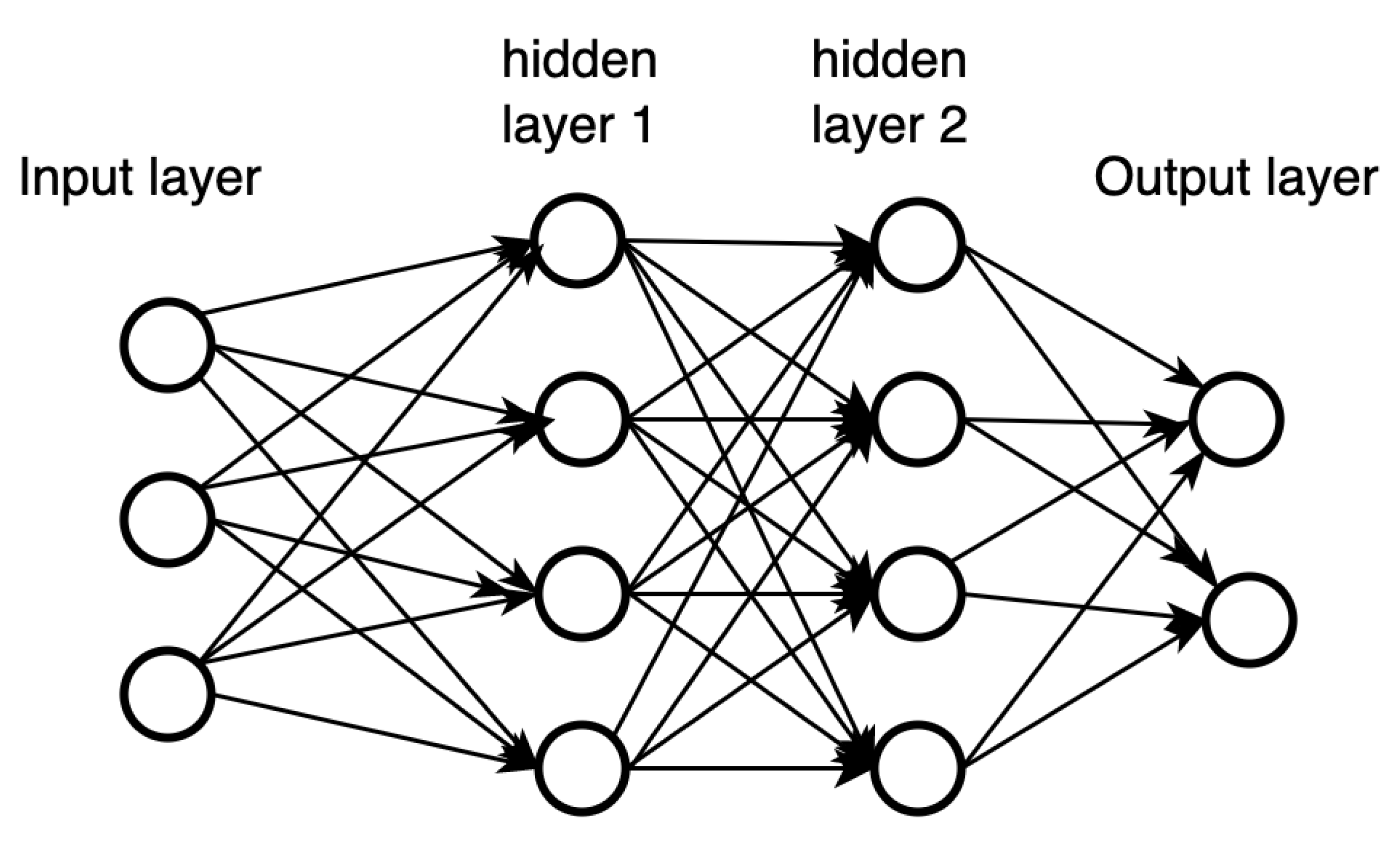
2.2. Neural Network Basics
2.2.1. Neural networks
- Hyperbolic tangent () is defined as . It is non-linear, continuously differentiable, and has a fixed output range (between -1 and 1) [18]. The biggest problem activation gives rise to is the “vanishing gradients” problem, which causes weights stop updating, this concept will be further explained in the next section.
- Rectied Linear Unit function (ReLU) is defined as ReLU [19]. It avoids the vanishing-gradient issue and can be evaluated quickly. However, it suffers from the “dead neurons” problem, in which the neurons with stop outputting anything other than 0.
- LeakyReLU is defined as LeakyReLU, where is a hyperparameter that represents the slope of the function for (see [20]) It addresses the “dead neurons” problem by making a small variations.
-
The softmax function is a function that takes an n-dimensional column (resp. row) vector and outputs an n-dimensional column (resp. row) vector :Note that each and . Thus, these elements can be interpreted as probabilities.
2.2.2. Back-propagation
2.3. Structured Neural Networks for Grids and Sequences
2.3.1. Convolutional neural networks
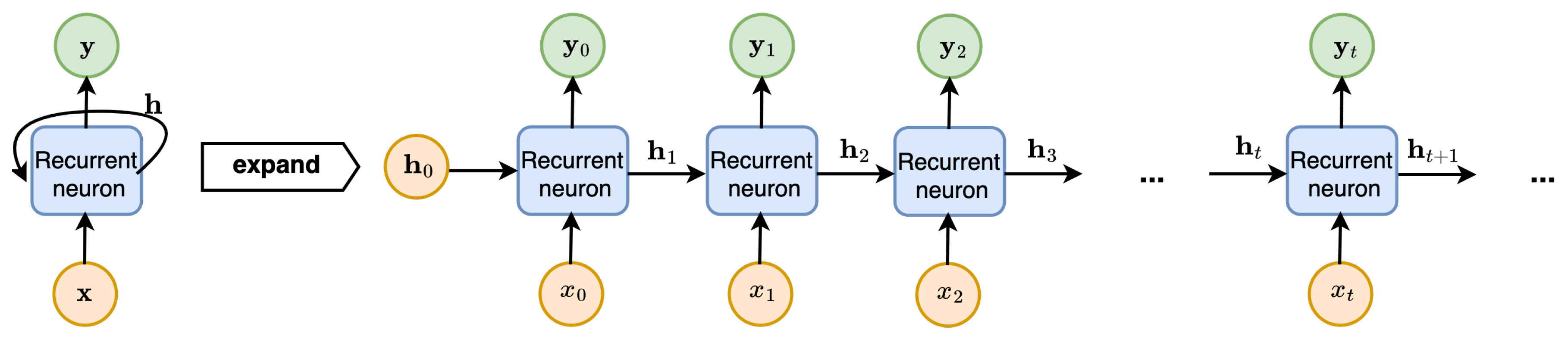
2.4. Recurrent neural networks
2.5. Graph Neural Networks
2.6. The message-passing framework
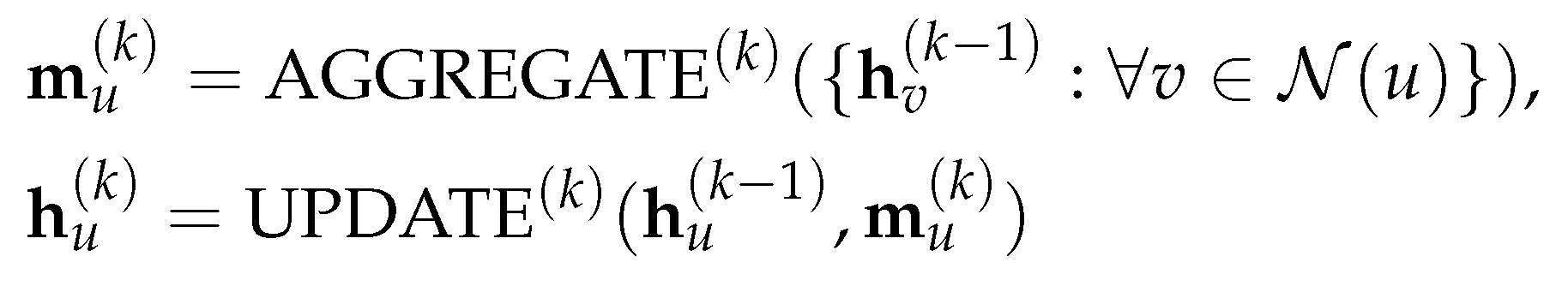
2.7. Different types of graph learning tasks
2.8. Homophilic vs. heterophilic graphs
3. Related Work
3.1. Graph Convolutional Networks
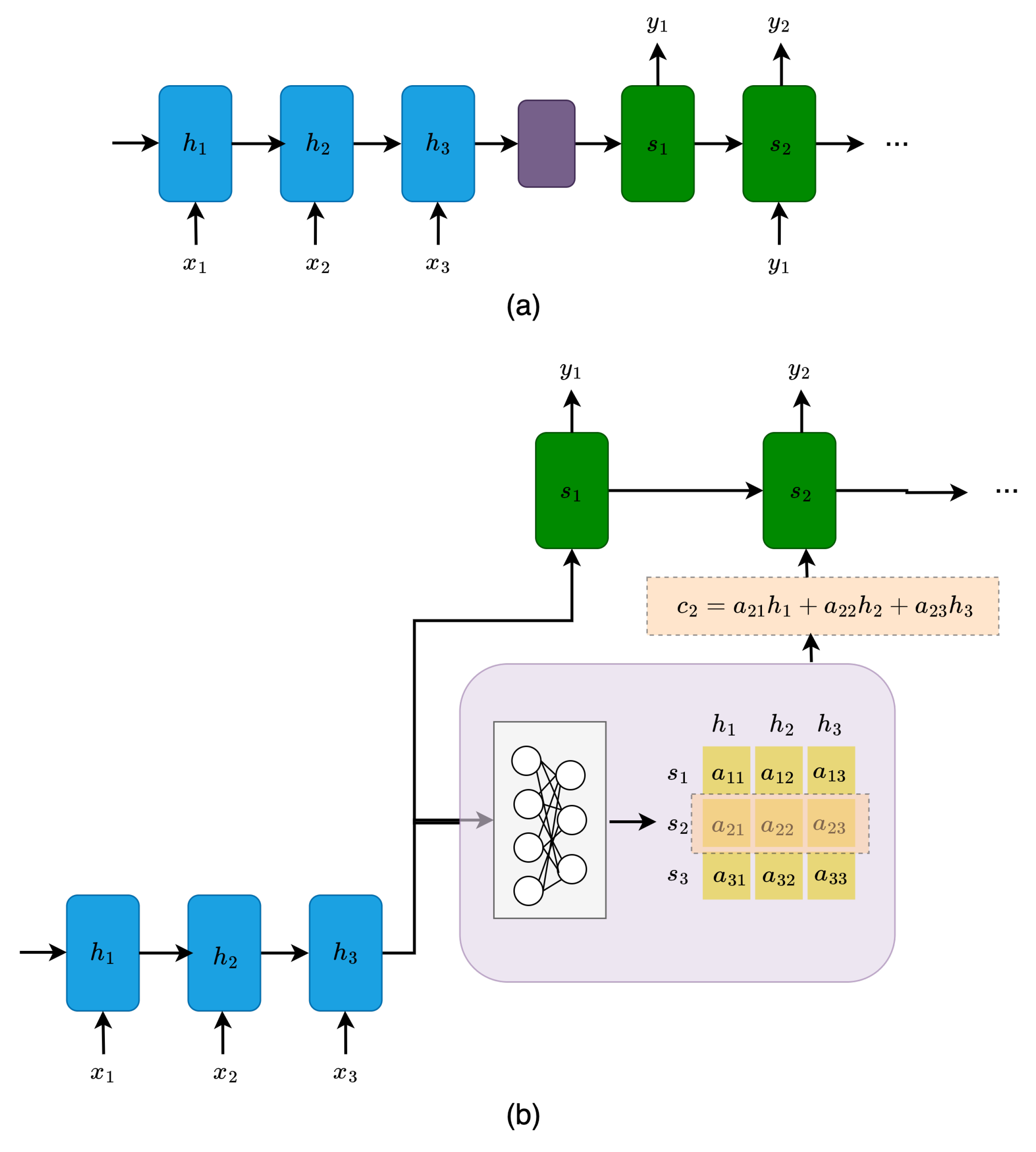
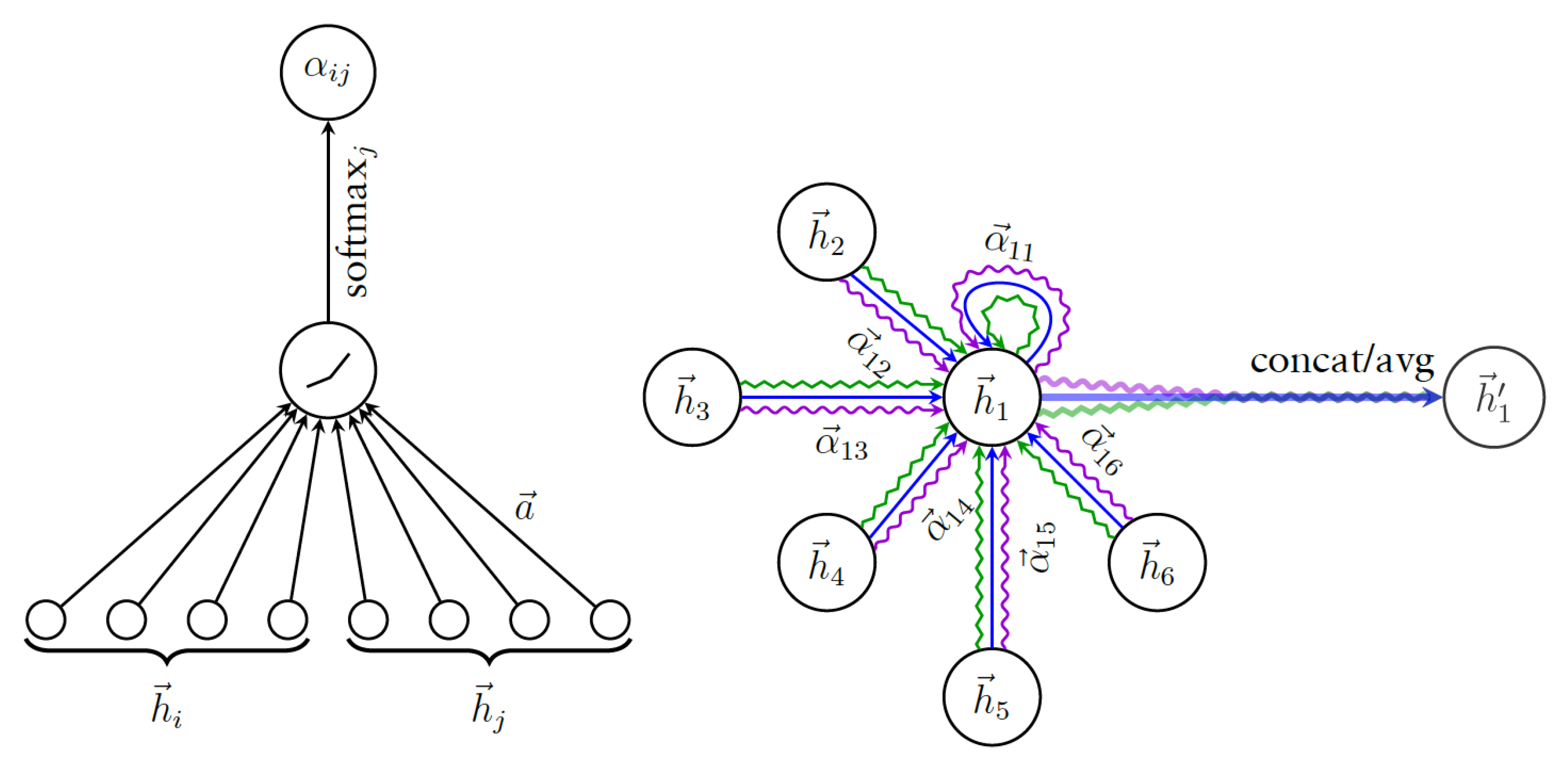
3.2. Attention Mechanism
3.3. Graph Attention Network
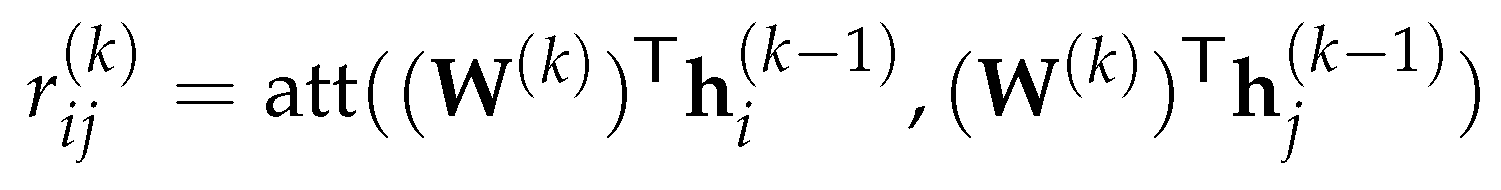
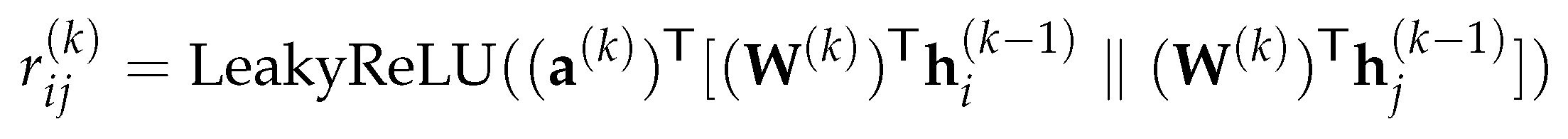
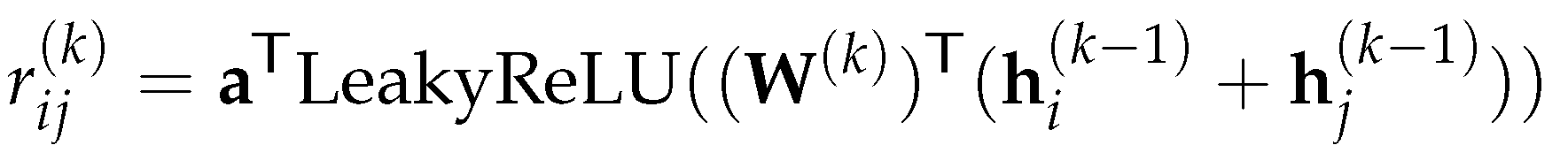
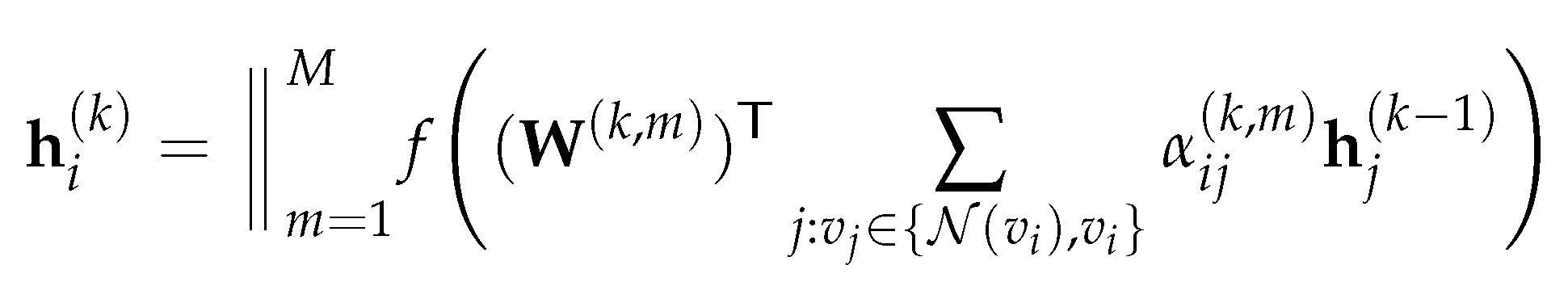

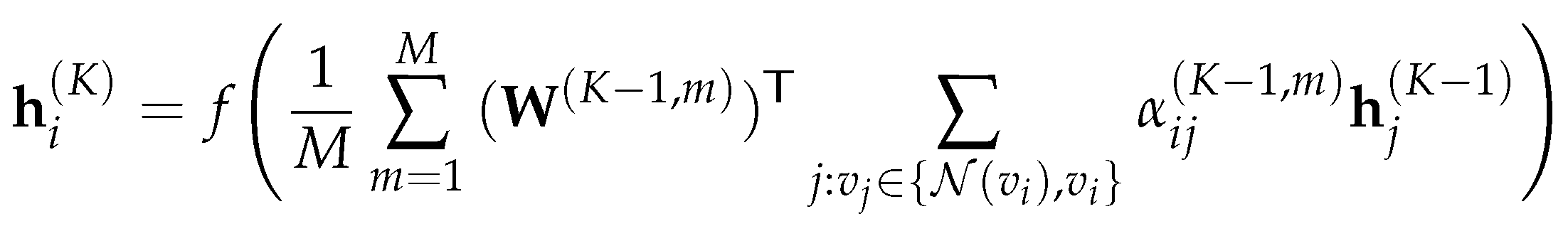
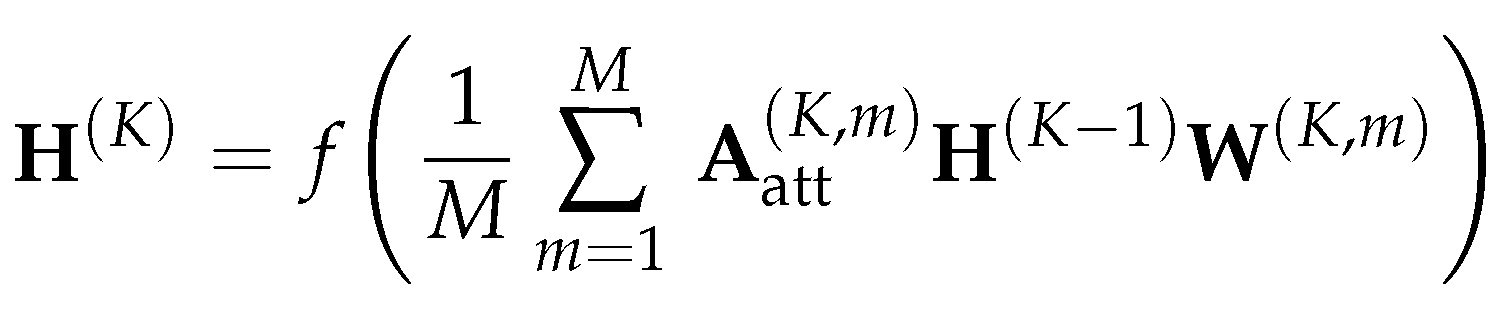
3.4. Direction in Graph Neural Network
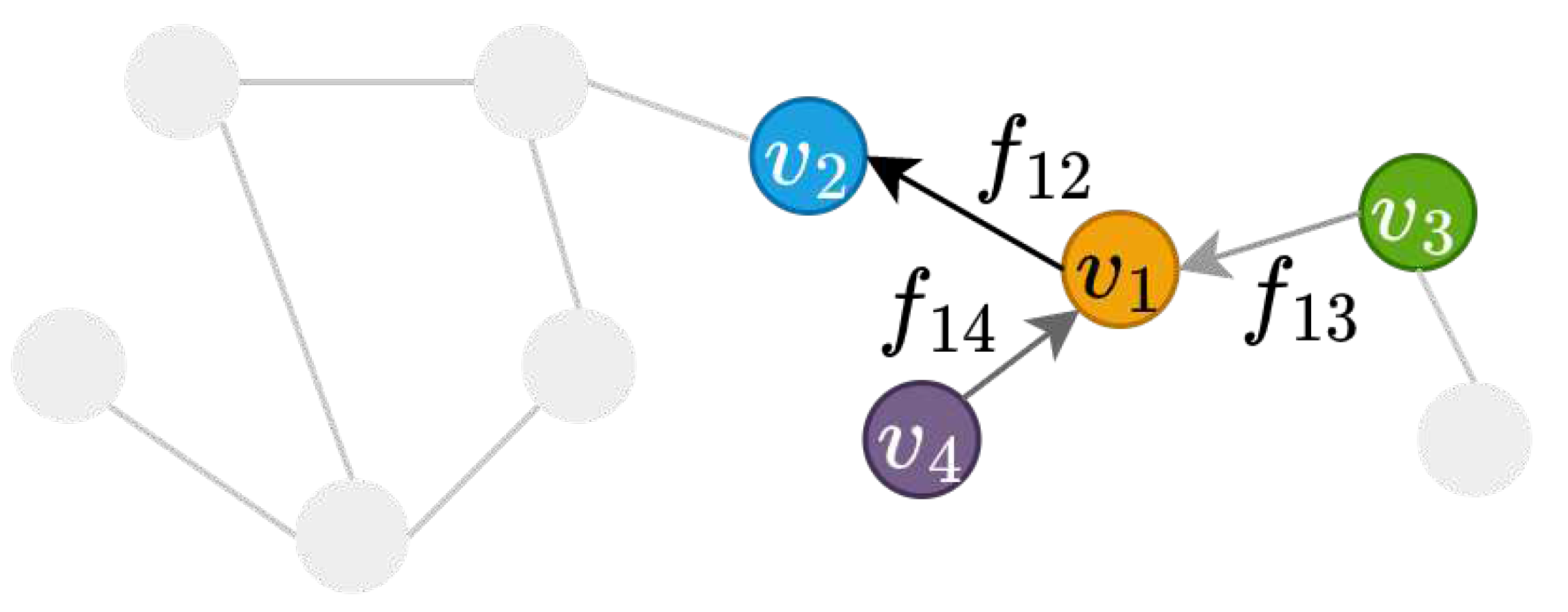
3.4.1. Vector fields in a graph
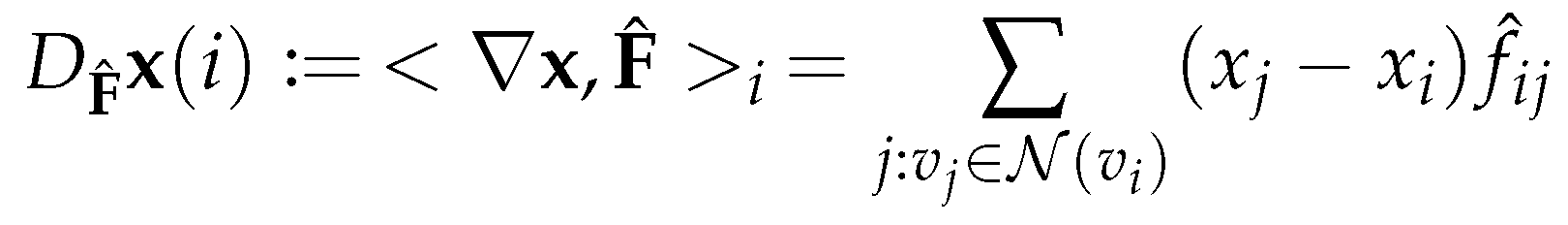
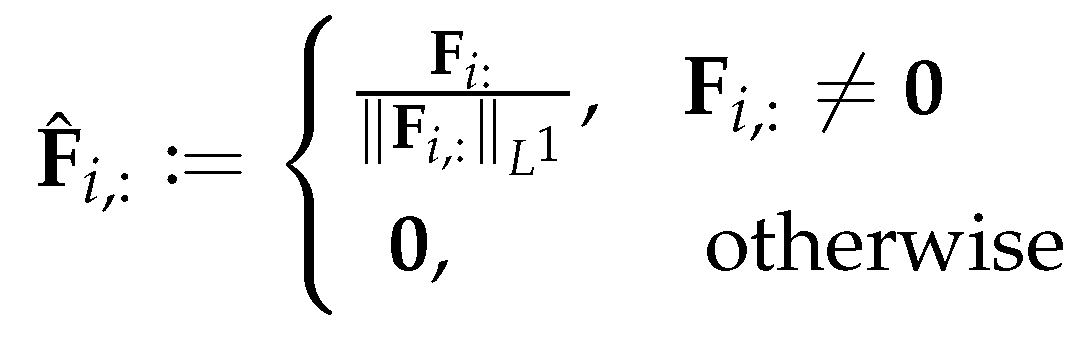
3.4.2. Directional smoothing and derivatives operation
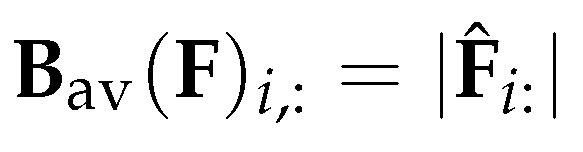
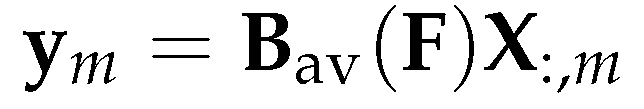
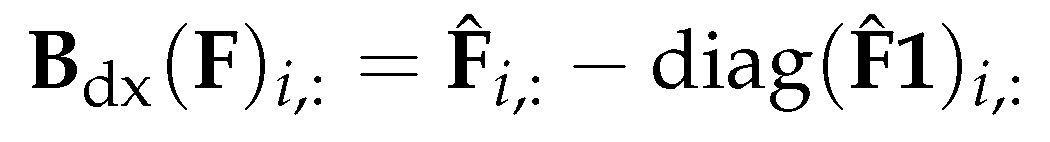
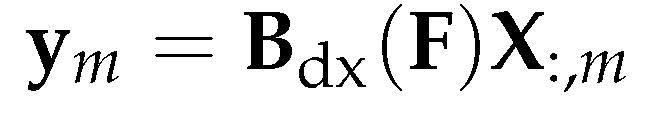
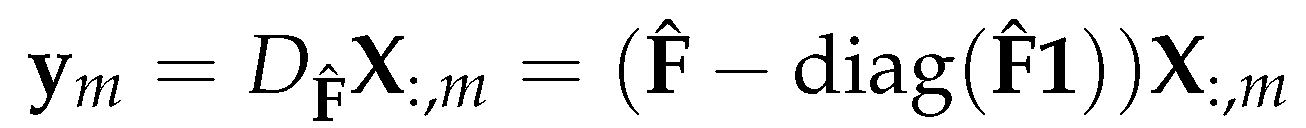
3.4.3. Using gradient of the Laplacian eigenvectors as vector fields
3.4.4. Directional Graph Network
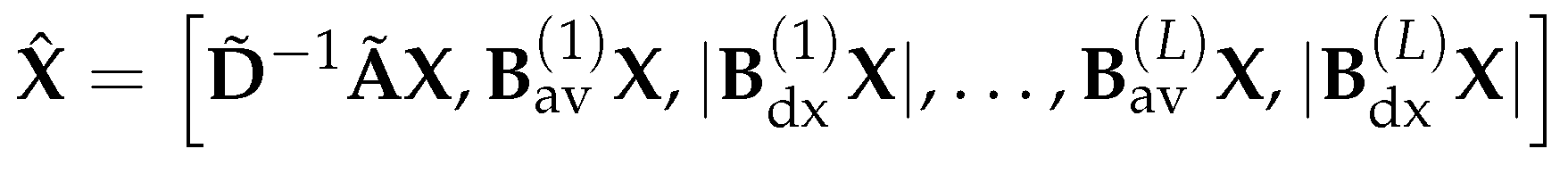
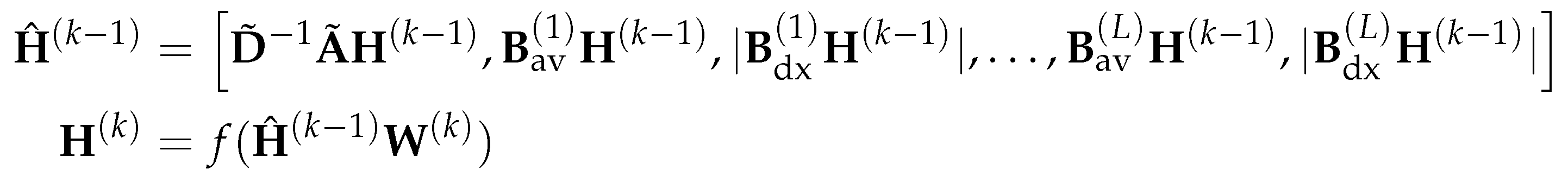
3.4.5. Theoretical Analysis
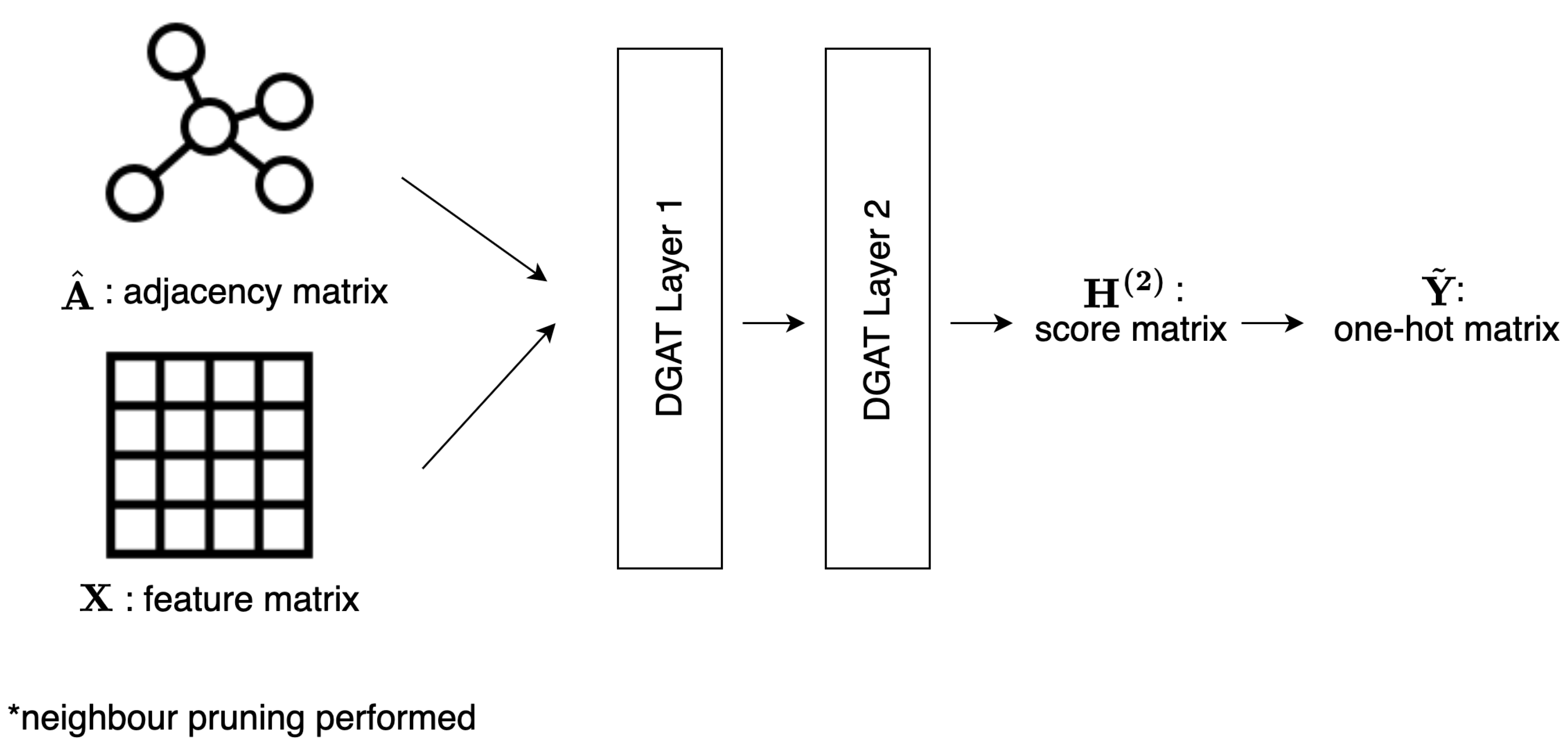
4. Directional Graph Attention Network
4.1. Problem Statement
4.2. Methodology
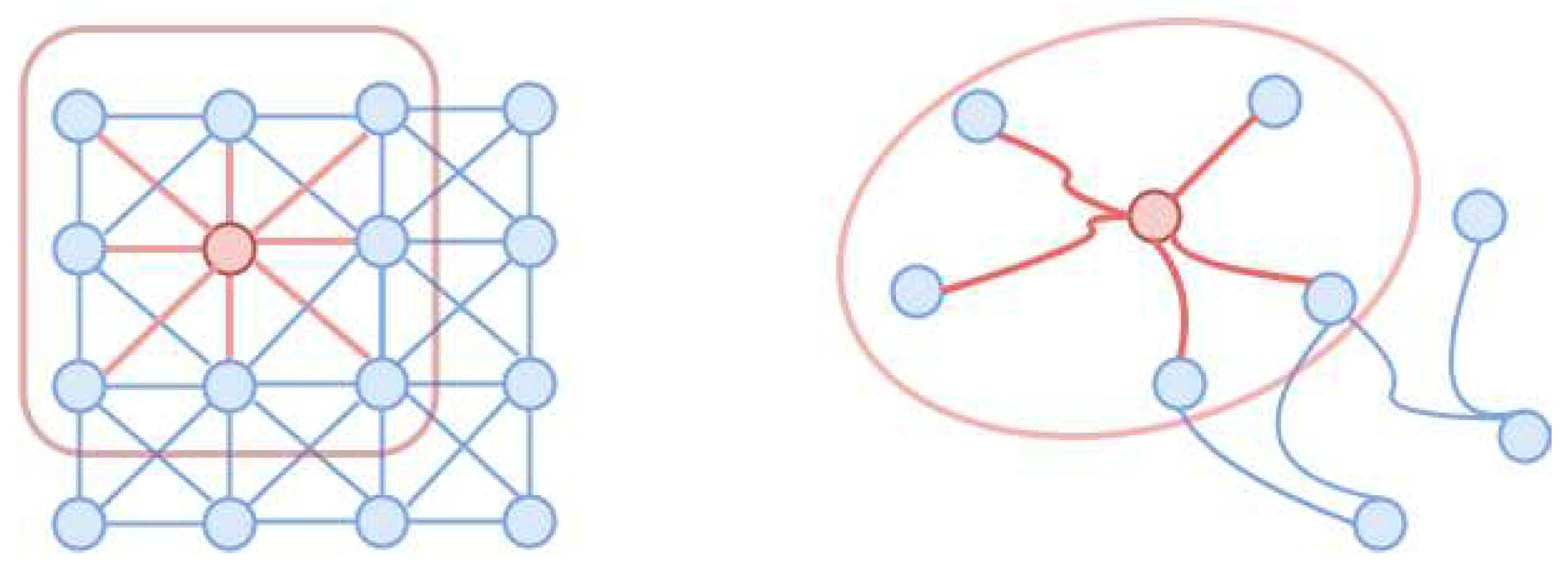
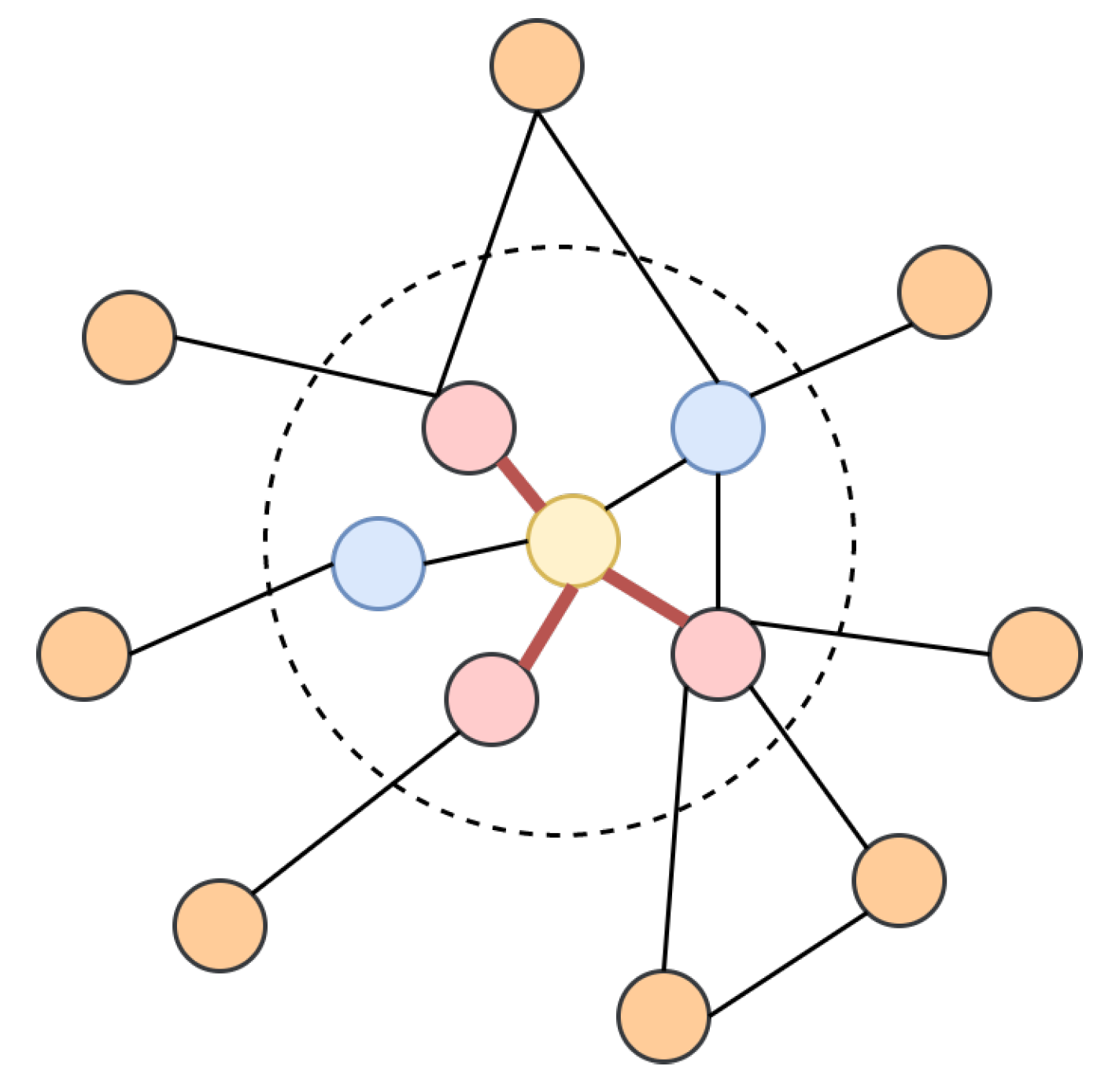
4.2.1. Neighbour pruning
4.2.2. Global Directional Aggregation Mechanism
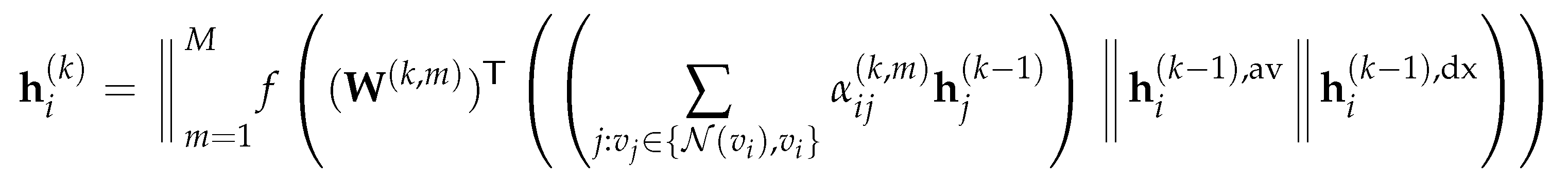
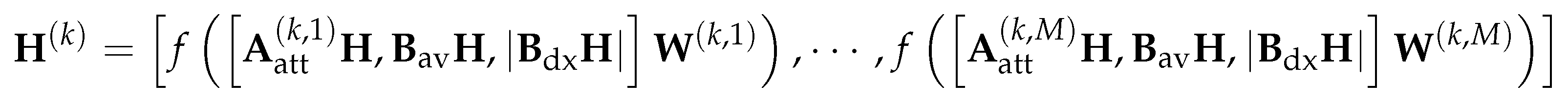
4.2.3. Parameterized normalized Laplacian and Adjacency Matrices
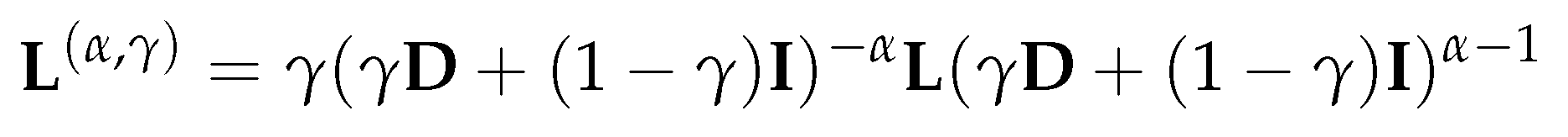
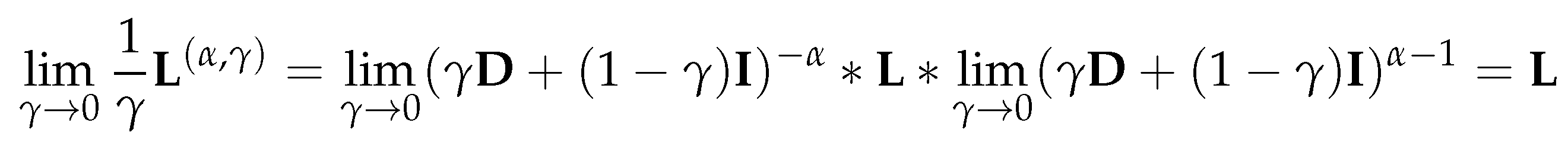
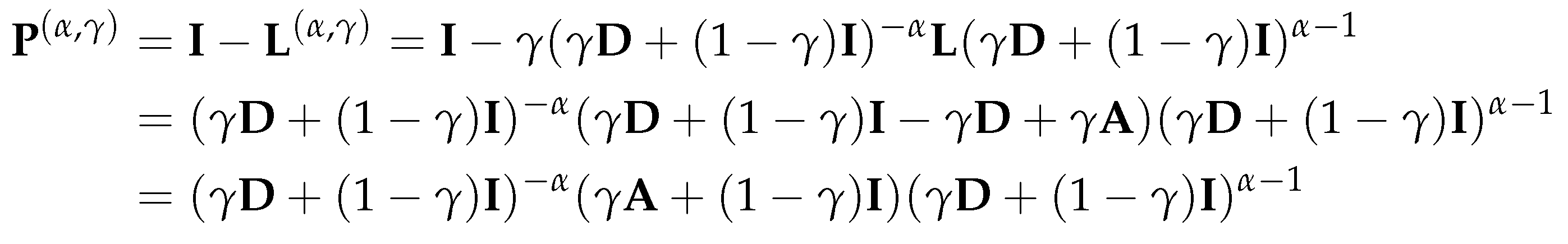
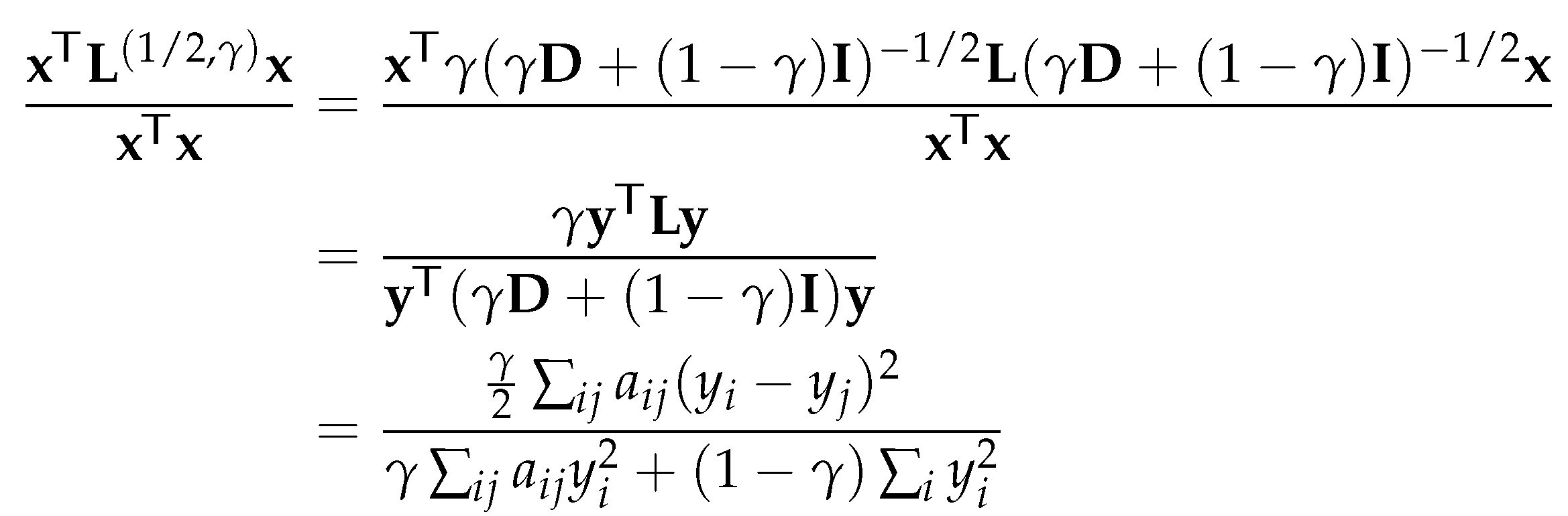
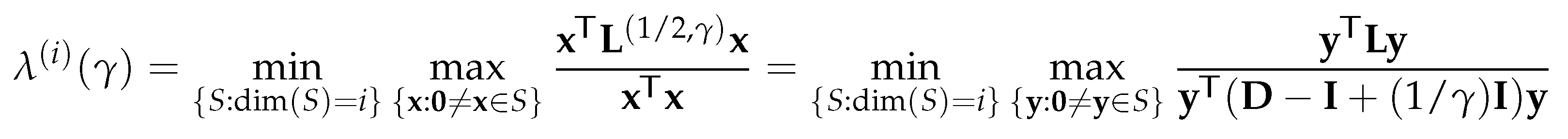
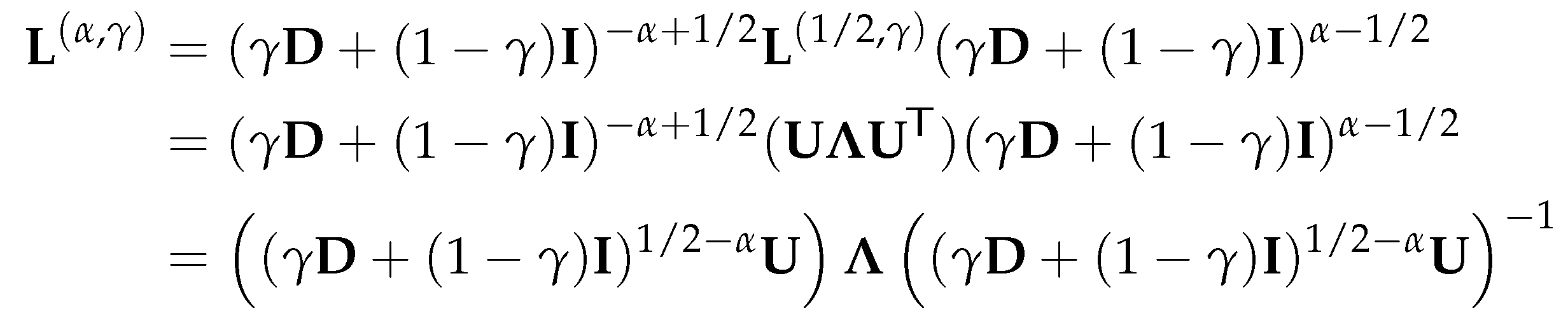 Thus, is also an eigenvalue of for , and column i of is a corresponding eigenvector. □
Thus, is also an eigenvalue of for , and column i of is a corresponding eigenvector. □
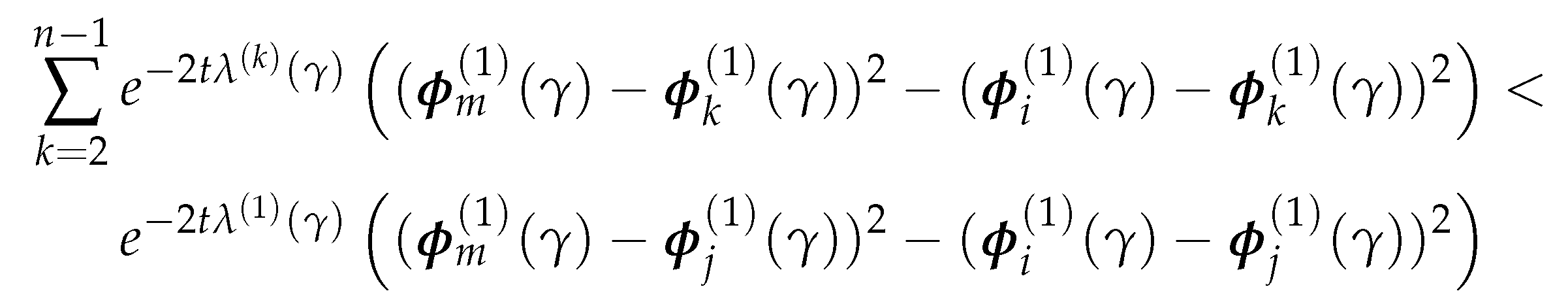
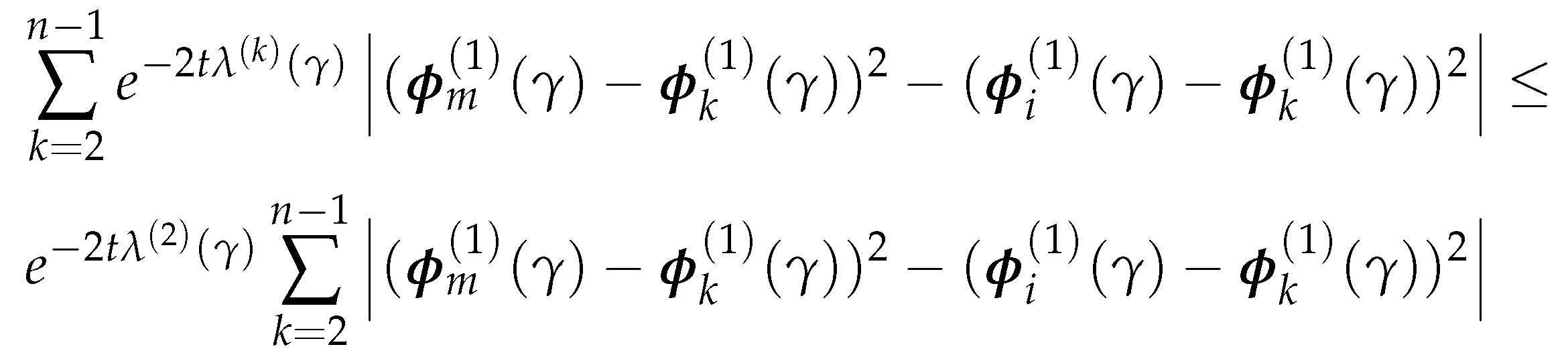
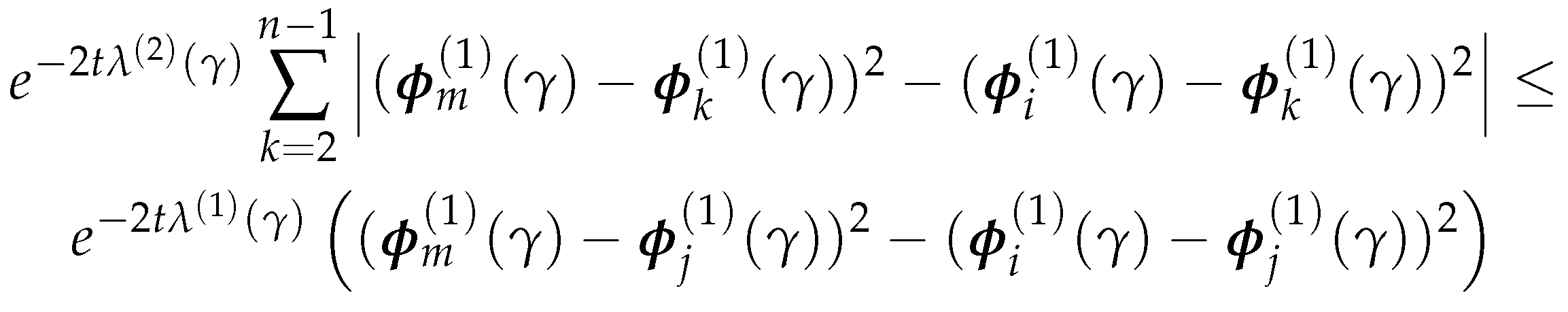
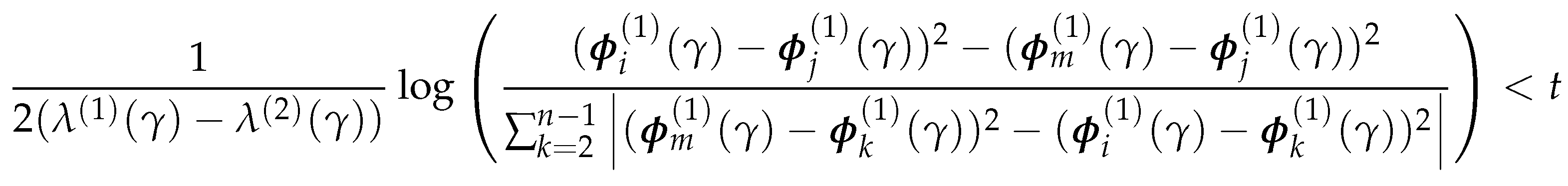
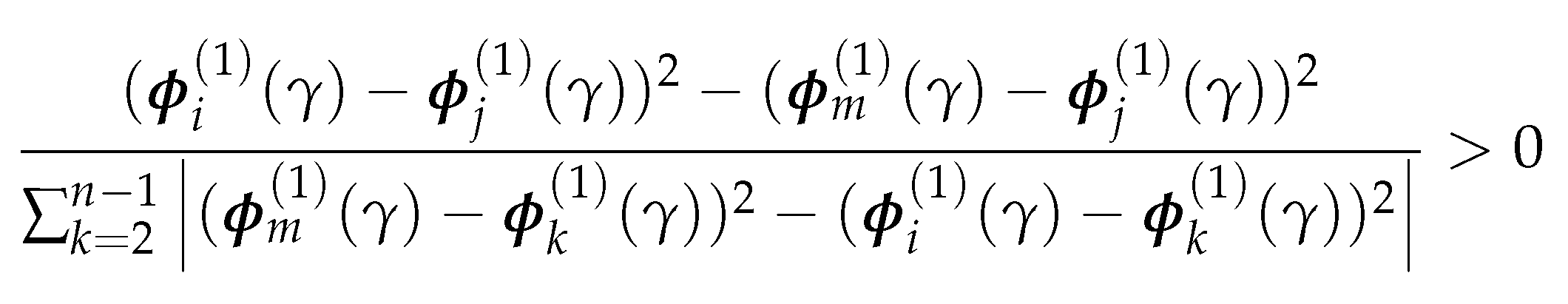
4.3. Vectorized Implementation
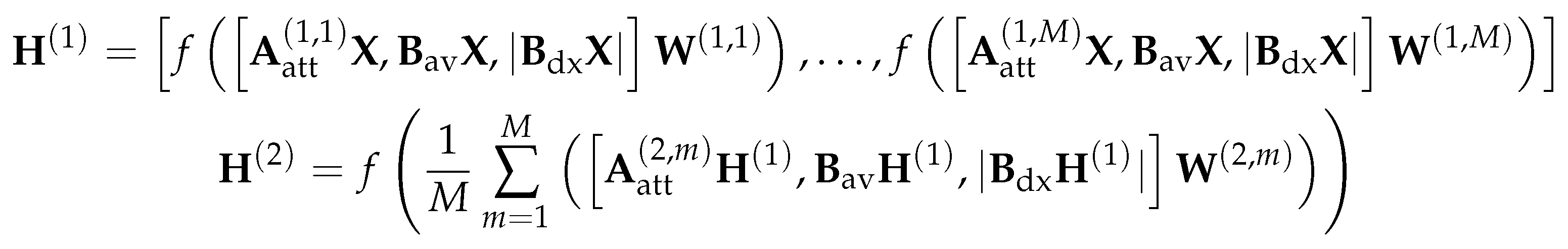
- The GAT model is the first graph model that adopts the attention mechanism. Although the GATv2 model is better, its attention mechanism is still feature-based and there is no essential difference between the two models.
- The mechanisms we proposed are immune to the type of attention mechanisms they can combine with and can be used to enhance any attention mechanism.
- The experiment results in Section 5.4.2 indicate that our DGAT model outperforms GATv2 by a large margin on all synthetic benchmarks. Thus, we believe that there will also be a significant enhancement when applying our mechanisms to the GATv2 model. We will leave the empirical experiments to future work
4.4. Training
- Transductive learning: The model has access to features of all the nodes during the training, including the nodes in . Note that the labels of nodes in are not visible to the model, and they are not used in the loss computation; however, the nodes in will be involved in the message-passing step, and the model will generate the intermediate representations for them.
- Inductive learning: The model only has access to features of nodes in and during training. In this case, the nodes are used in neither the loss computation nor the message-passing step; they are entirely invisible to the model.
4.5. Testing
4.6. Summary
5. Experimental Studies
5.1. Real-World Datasets
5.1.1. Wikipedia networks
5.1.2. Actor co-occurrence network
5.1.3. WebKB
5.1.4. Citation networks
5.2. Synthetic Datasets
5.3. Experimental Setup
5.4. Results and Analysis
5.4.1. Real-world Dataset
Ablation Tests
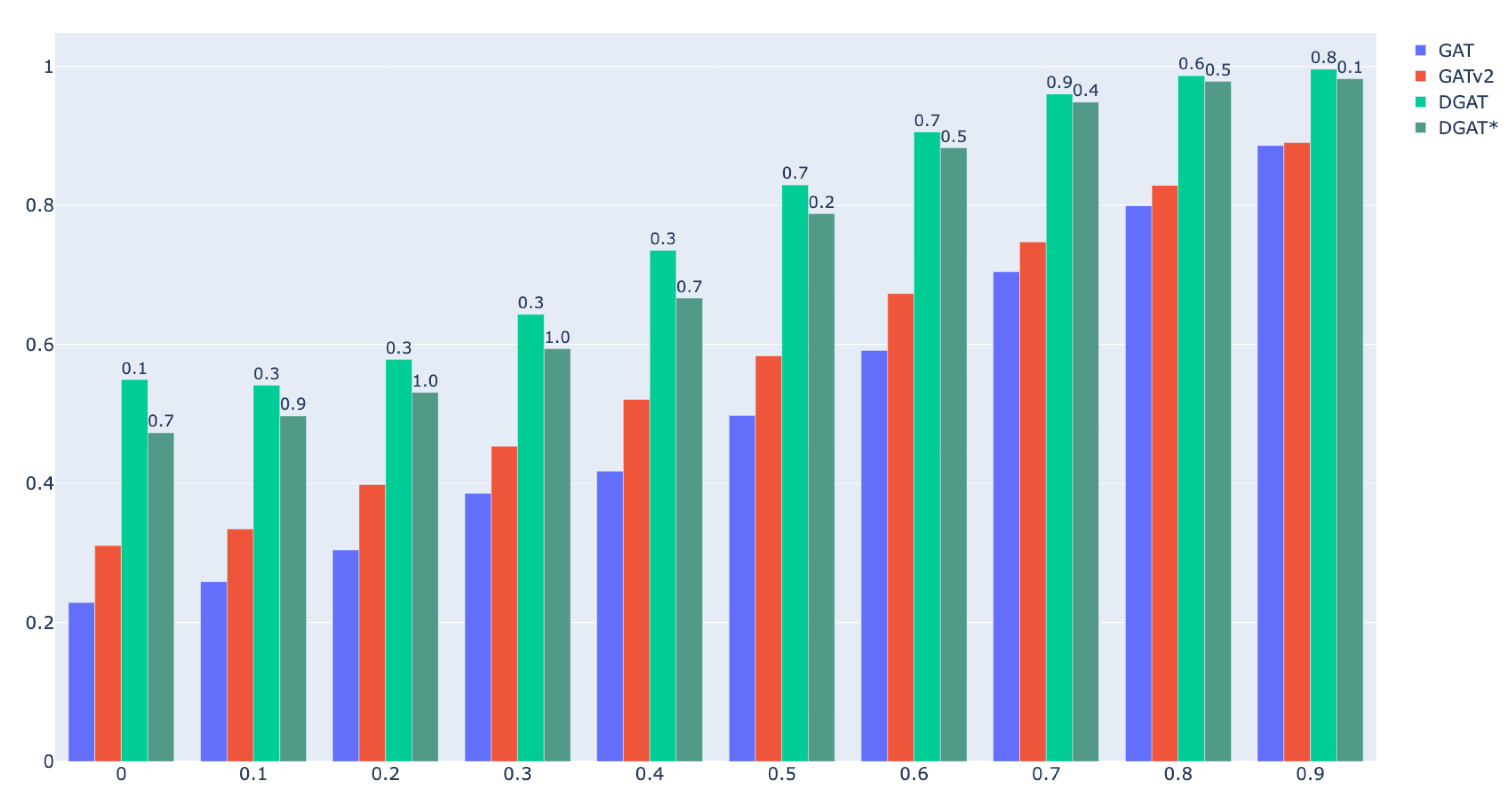
5.4.2. Synthetic Dataset
6. Conclusion and Future Work
6.1. Summary of Contributions
- We have introduced a novel class of normalized Laplacian matrices, referred to as parameterized normalized Laplacians, encompassing both the normalized Laplacian and the combinatorial Laplacian.
- Utilizing the newly proposed Laplacian, we have introduced a more refined global directional flow for enhancing the original Graph Attention Network (GAT) on a general graph.
- Building upon the global directional flow, we have proposed the Directional Graph Attention Network (DGAT), which is an attention-based graph neural network enriched with embedded global directional information. More specially, we have proposed two mechanisms on top of the GAT: the neighbour pruning and the global attention head. The experiments conducted in Chapter 5 demonstrate the effectiveness of the DGAT model for both real-world and synthetic datasets. In particular, the DGAT model exhibited significantly superior performance compared to the original GAT model across all real-world heterophilic datasets. Additionally, the results from the synthetic dataset experiments further demonstrated the DGAT model’s advantage over the GAT model across graphs with varying levels of homophily, encompassing both heterophilic and homophilic datasets.
6.2. Future Work
- Now we have a qualitative guidance on how to select the range of hyperparameter for graph with different homophily level. Can we find quantitative guidance instead?
- What is the correlation between and the homophily level of graphs? This relationship might enable us to more efficiently identify an optimal value.
Acknowledgments
References
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proceedings of the IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Transactions on Neural Networks 2008, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, 2017; pp. 1025–1035. [Google Scholar]
- Velickovi’c, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Luan, S.; Zhao, M.; Chang, X.W.; Precup, D. Break the ceiling: Stronger multi-scale deep graph convolutional networks. Advances in neural information processing systems 2019, 32. [Google Scholar]
- Beaini, D.; Passaro, S.; L’etourneau, V.; Hamilton, W.; Corso, G.; Li`o, P. Directional Graph Networks. In Proceedings of the International Conference on Machine Learning, 2021; PMLR, 2021; pp. 748–758. [Google Scholar]
- Luan, S.; Hua, C.; Lu, Q.; Zhu, J.; Zhao, M.; Zhang, S.; Chang, X.W.; Precup, D. Revisiting heterophily for graph neural networks. Advances in neural information processing systems 2022, 35, 1362–1375. [Google Scholar]
- Zhu, J.; Yan, Y.; Zhao, L.; Heimann, M.; Akoglu, L.; Koutra, D. Beyond Homophily in Graph Neural Networks: Current Limitations and Effective Designs. Advances in Neural Information Processing Systems 2020, 33, 7793–7804. [Google Scholar]
- Ma, Y.; Liu, X.; Shah, N.; Tang, J. Is Homophily a Necessity for Graph Neural Networks? arXiv 2021, arXiv:2106.06134. [Google Scholar]
- Luan, S.; Hua, C.; Lu, Q.; Zhu, J.; Zhao, M.; Zhang, S.; Chang, X.W.; Precup, D. Is heterophily a real nightmare for graph neural networks to do node classification? arXiv 2021, arXiv:2109.05641. [Google Scholar]
- Stankovic, L.; Mandic, D.; Dakovic, M.; Brajovic, M.; Scalzo, B.; Constantinides, T. Graph Signal Processing Part 1: Graphs, Graph Spectra, and Spectral Clustering. arXiv 2019, arXiv:1907.03467. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Representation Learning on Graphs: Methods and Applications. arXiv 2017, arXiv:1709.05584. [Google Scholar]
- Hamilton, W.L. Graph Representation Learning. Synthesis Lectures on Artifical Intelligence and Machine Learning 2020, 14, 1–159. [Google Scholar]
- Cao, S.; Lu, W.; Xu, Q. Deep Neural Networks for Learning Graph Representations. In Proceedings of the AAAI Conference on Artificial Intelligence, 2016; Vol. 30. [Google Scholar]
- Wang, D.; Cui, P.; Zhu, W. Structural Deep Network Embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016; pp. 1225–1234. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. The Bulletin of Mathematical Biophysics 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. ICML, 2010.
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Amari, S.i. Backpropagation and Stochastic Gradient Descent Method. Neurocomputing 1993, 5, 185–196. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics. JMLR Workshop and Conference Proceedings, 2010; pp. 249–256. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision, 2015; pp. 1026–1034. [Google Scholar]
- Gori, M.; Monfardini, G.; Scarselli, F. A New Model for Learning in Graph Domains. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, 2005; IEEE; Vol. 2, pp. 729–734. [Google Scholar]
- Gallicchio, C.; Micheli, A. Graph Echo State Networks. The 2010 International Joint Conference on Neural Networks (IJCNN). IEEE, 2010, pp. 1–8.
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A Comprehensive Survey on Graph Neural Networks. IEEE Transactions on Neural Networks and Learning Systems 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral Networks and Locally Connected Networks on Graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Vinyals, O.; Bengio, S.; Kudlur, M. Order Matters: Sequence to Sequence for Sets. arXiv 2015, arXiv:1511.06391. [Google Scholar]
- Cangea, C.; Velickovi’c, P.; Jovanovi’c, N.; Kipf, T.; Li`o, P. Towards Sparse Hierarchical Graph Classifiers. arXiv 2018, arXiv:1811.01287. [Google Scholar]
- Ying, R.; You, J.; Morris, C.; Ren, X.; Hamilton, W.L.; Leskovec, J. Hierarchical Graph Representation Learning with Differentiable Pooling. arXiv 2018, arXiv:1806.08804. [Google Scholar]
- McPherson, M.; Smith-Lovin, L.; Cook, J.M. Birds of a Feather: Homophily in Social Networks. Annual Review of Sociology 2001, 415–444. [Google Scholar] [CrossRef]
- Pei, H.; Wei, B.; Chang, K.C.C.; Lei, Y.; Yang, B. Geom-GCN: Geometric Graph Convolutional Networks. arXiv 2020, arXiv:2002.05287. [Google Scholar]
- Monti, F.; Boscaini, D.; Masci, J.; Rodola, E.; Svoboda, J.; Bronstein, M.M. Geometric Deep Learning on Graphs and Manifolds Using Mixture Model CNNs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017; pp. 5115–5124. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. Advances in Neural Information Processing Systems 2016, 29. [Google Scholar]
- Lindsay, G.W. Attention in Psychology, Neuroscience, and Machine Learning. Frontiers in Computational Neuroscience 2020, 14. [Google Scholar] [CrossRef]
- Chorowski, J.K.; Bahdanau, D.; Serdyuk, D.; Cho, K.; Bengio, Y. Attention-Based Models for Speech Recognition. Advances in Neural Information Processing Systems 2015, 28. [Google Scholar]
- Chaudhari, S.; Mithal, V.; Polatkan, G.; Ramanath, R. An Attentive Survey of Attention Models. ACM Transactions on Intelligent Systems and Technology (TIST) 2021, 12, 1–32. [Google Scholar] [CrossRef]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention Mechanisms in Computer Vision: A Survey. Computational Visual Media 2022, 1–38. [Google Scholar] [CrossRef]
- Ying, H.; Zhuang, F.; Zhang, F.; Liu, Y.; Xu, G.; Xie, X.; Xiong, H.; Wu, J. Sequential Recommender System Based on Hierarchical Attention Network. IJCAI International Joint Conference on Artificial Intelligence, 2018.
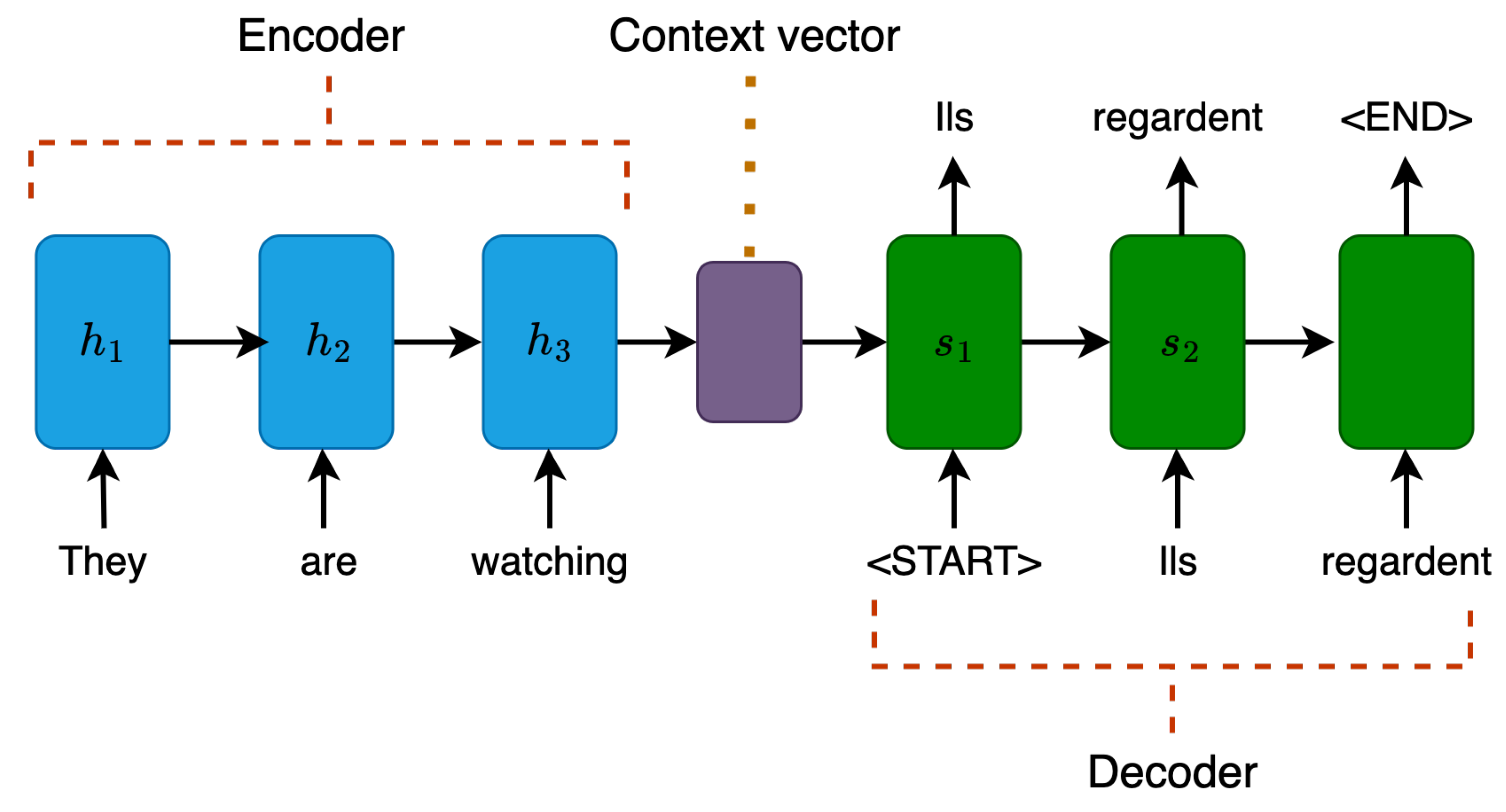
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. Advances in Neural Information Processing Systems 2014, 27. [Google Scholar]
- Cho, K.; Van Merri"enboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Young, T.; Hazarika, D.; Poria, S.; Cambria, E. Recent Trends in Deep Learning Based Natural Language Processing. IEEE Computational Intelligence Magazine 2018, 13, 55–75. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. Advances in Neural Information Processing Systems 2017, 30. [Google Scholar]
- Lee, J.B.; Rossi, R.; Kong, X. Graph Classification Using Structural Attention. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2018; pp. 1666–1674. [Google Scholar]
- Choi, E.; Bahadori, M.T.; Song, L.; Stewart, W.F.; Sun, J. GRAM: Graph-Based Attention Model for Healthcare Representation Learning. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2017; pp. 787–795. [Google Scholar]
- Lee, J.B.; Rossi, R.A.; Kim, S.; Ahmed, N.K.; Koh, E. Attention Models in Graphs: A Survey. ACM Transactions on Knowledge Discovery from Data (TKDD) 2019, 13, 1–25. [Google Scholar] [CrossRef]
- Brody, S.; Alon, U.; Yahav, E. How Attentive Are Graph Attention Networks? arXiv 2021, arXiv:2105.14491. [Google Scholar]
- Luan, S.; Hua, C.; Lu, Q.; Zhu, J.; Chang, X.W.; Precup, D. When Do We Need GNN for Node Classification? arXiv 2022, arXiv:2210.16979. [Google Scholar]
- Alon, U.; Yahav, E. On the Bottleneck of Graph Neural Networks and Its Practical Implications. arXiv 2020, arXiv:2006.05205. [Google Scholar]
- Chung, F.R.; Graham, F.C. Spectral Graph Theory; American Mathematical Soc, 1997. [Google Scholar]
- Ortega, A.; Frossard, P.; Kovacevi’c, J.; Moura, J.M.; Vandergheynst, P. Graph Signal Processing: Overview, Challenges, and Applications. Proceedings of the IEEE 2018, 106, 808–828. [Google Scholar] [CrossRef]
- Coifman, R.R.; Lafon, S. Diffusion Maps. Applied and Computational Harmonic Analysis 2006, 21, 5–30. [Google Scholar] [CrossRef]
- Beaini, D.; Passaro, S.; L’etourneau, V.; Hamilton, W.; Corso, G.; Lio, P. DGN, 2020. Available at https://github.com/Saro00/DGN.
- Luan, S.; Zhao, M.; Hua, C.; Chang, X.W.; Precup, D. Complete the missing half: Augmenting aggregation filtering with diversification for graph convolutional networks. arXiv 2020, arXiv:2008.08844. [Google Scholar]
- Luan, S.; Hua, C.; Xu, M.; Lu, Q.; Zhu, J.; Chang, X.W.; Fu, J.; Leskovec, J.; Precup, D. When do graph neural networks help with node classification: Investigating the homophily principle on node distinguishability. arXiv 2023, arXiv:2304.14274. [Google Scholar]
- Topping, J.; Di Giovanni, F.; Chamberlain, B.P.; Dong, X.; Bronstein, M.M. Understanding Over-Squashing and Bottlenecks on Graphs via Curvature. arXiv 2021, arXiv:2111.14522. [Google Scholar]
- Rong, Y.; Huang, W.; Xu, T.; Huang, J. DropEdge: Towards Deep Graph Convolutional Networks on Node Classification. arXiv 2019, arXiv:1907.10903. [Google Scholar]
- Papp, P.A.; Martinkus, K.; Faber, L.; Wattenhofer, R. DropGNN: Random Dropouts Increase the Expressiveness of Graph Neural Networks. Advances in Neural Information Processing Systems 2021, 34, 21997–22009. [Google Scholar]
- Kim, Y.; Upfal, E. Algebraic Connectivity of Graphs, with Applications. Bachelor’s thesis, Brown University, 2016. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. The Journal of Machine Learning Research 2014, 15, 1929–1958. [Google Scholar]
- Reed, R.; Marks II, R.J. Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks; MIT Press, 1999. [Google Scholar]
- Rozemberczki, B.; Allen, C.; Sarkar, R. Multi-Scale Attributed Node Embedding. Journal of Complex Networks 2021, 9, Cnab014. [Google Scholar] [CrossRef]
- Tang, J.; Sun, J.; Wang, C.; Yang, Z. Social Influence Analysis in Large-Scale Networks. In Proceedings of the Fifteenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2009; pp. 807–816. [Google Scholar]
- Craven, M.; McCallum, A.; PiPasquo, D.; Mitchell, T.; Freitag, D. Learning to Extract Symbolic Knowledge from the World Wide Web. In Proceedings of the Fifteenth National/Tenth Conference on Artificial intelligence/Innovative applications of artificial intelligence, 1998; pp. 509–516. [Google Scholar]
- McCallum, A.K.; Nigam, K.; Rennie, J.; Seymore, K. Automating the Construction of Internet Portals with Machine Learning. Information Retrieval 2000, 3, 127–163. [Google Scholar] [CrossRef]
- Giles, C.L.; Bollacker, K.D.; Lawrence, S. CiteSeer: An Automatic Citation Indexing System. In Proceedings of the Third ACM Conference on Digital Libraries, 1998; pp. 89–98. [Google Scholar]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Galligher, B.; Eliassi-Rad, T. Collective Classification in Network Data. AI Magazine 2008, 29, 93–93. [Google Scholar] [CrossRef]
- Abu-El-Haija, S.; Perozzi, B.; Kapoor, A.; Alipourfard, N.; Lerman, K.; Harutyunyan, H.; Ver Steeg, G.; Galstyan, A. MixHop: Higher-Order Graph Convolutional Architectures via Sparsified Neighborhood Mixing. International Conference on Machine Learning. PMLR, 2019, pp. 21–29.
| 1 | neighour pruning |
| 2 | global directional aggregation |
| 3 | parameterized random-walk Laplacian matrix |


| Cham. | Squi. | Actor | Corn. | Wisc. | Texas | Cora | Cite. | Pubm. | |
|---|---|---|---|---|---|---|---|---|---|
| # Nodes | 2,277 | 5,201 | 7,600 | 183 | 251 | 183 | 2,708 | 3,327 | 19,717 |
| # Edges | 36,101 | 217,073 | 33,544 | 295 | 499 | 309 | 5,429 | 4,732 | 44,324 |
| # Features | 2,325 | 2,089 | 931 | 1,703 | 1,703 | 1,703 | 1,433 | 3,703 | 500 |
| # Classes | 5 | 5 | 5 | 5 | 5 | 5 | 7 | 6 | 3 |
| 0.23 | 0.22 | 0.22 | 0.30 | 0.21 | 0.11 | 0.81 | 0.74 | 0.80 |
| Dataset () | learning rate | weight decay | dropout rate | |||
|---|---|---|---|---|---|---|
| Chameleon | 0.4 | 0.0 | 0.9 | |||
| Squirrel | 0.2 | 0.2 | 0.1 | |||
| Actor | 0.3 | 0.2 | 0.2 | |||
| Cornell | 0.2 | 0.3 | 0.8 | |||
| Wisconsin | 0.5 | 0.3 | 0.7 | |||
| Texas | 0.4 | 0.2 | 0.8 | |||
| Cora | 0.4 | 0.9 | 0.8 | |||
| Citeseer | 0.6 | 0.5 | 0.2 | |||
| PubMed | 0.6 | 1 | 0.3 |
| Cham. | Squi. | Actor | Corn. | Wisc. | Texas | Cora | Cite. | Pubm. | |
|---|---|---|---|---|---|---|---|---|---|
| 42.93 | 30.03 | 28.45 | 54.32 | 49.41 | 58.38 | 86.37 | 74.32 | 87.62 | |
| 50.48 | 37.46 | 35.47 | 77.03 | 82.75 | 78.11 | 84.69 | 73.87 | 84.29 | |
| DGAT | 52.47 | 34.82 | 35.68 | 85.14 | 84.71 | 79.46 | 88.05 | 76.41 | 87.93 |
| 0.23 | 0.22 | 0.22 | 0.30 | 0.21 | 0.11 | 0.81 | 0.74 | 0.80 |
| Ablation Study on Different Components in DGAT (%) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model Components | Chameleon | Squirrel | Actor | Cornell | Wisconsin | Texas | Cora | CiteSeer | PubMed | |||
| n.p. 1 | d.a.2 | p.Laplacian3 | Acc ± Std | Acc ± Std | Acc ± Std | Acc ± Std | Acc ± Std | Acc ± Std | Acc ± Std | Acc ± Std | Acc ± Std | |
| DGAT w/ | ✓ | 51.71 ± 1.23 | 32.91 ± 2.26 | 35.24 ± 1.07 | 82.16 ± 5.94 | 83.92 ± 3.59 | 78.38 ± 5.13 | 87.85 ± 1.02 | 74.50 ± 1.99 | 87.78 ± 0.44 | ||
| ✓ | ✓ | 51.91 ± 1.59 | 34.70 ± 1.02 | 35.51 ± 0.74 | 84.32 ± 4.15 | 84.12 ± 3.09 | 78.65 ± 4.43 | 87.83 ± 1.20 | 76.18 ± 1.35 | 87.93 ± 0.36 | ||
| ✓ | 46.69 ± 1.98 | 34.67 ± 0.10 | 29.63 ± 0.52 | 60.27 ± 4.02 | 54.51 ± 7.68 | 60.81 ± 5.16 | 87.95 ± 1.01 | 76.31 ± 1.38 | 87.90 ± 0.40 | |||
| ✓ | ✓ | 46.95 ± 2.50 | 34.71 ± 1.02 | 29.87 ± 0.60 | 60.54 ± 0.40 | 54.71 ± 5.68 | 60.81 ± 4.87 | 87.28 ± 1.53 | 76.41 ± 1.62 | 87.88 ± 0.46 | ||
| ✓ | ✓ | 52.39 ± 2.08 | 33.93 ± 1.86 | 35.64 ± 0.10 | 84.86 ± 5.12 | 84.11 ± 2.69 | 78.92 ± 5.57 | 87.93 ± 0.99 | 73.91 ± 1.62 | 87.82 ± 0.30 | ||
| ✓ | ✓ | ✓ | 52.47 ± 1.44 | 34.82 ± 1.60 | 35.68 ± 1.20 | 85.14 ± 5.30 | 84.71 ± 3.59 | 79.46 ± 3.67 | 88.05 ± 1.09 | 76.41 ± 1.45 | 87.94 ± 0.48 | |
| Baseline | 42.93 | 30.03 | 28.45 | 54.32 | 49.41 | 58.38 | 86.37 | 74.32 | 87.62 | |||
| Homophily Coefficient | GAT | GATv2 | DGAT () | DGAT* () |
|---|---|---|---|---|
| 0.0 | 22.86 | 31.06 | 54.94 (0.1) | 47.51 (0.7) |
| 0.1 | 25.86 | 33.46 | 54.13 (0.3) | 49.72 (0.9) |
| 0.2 | 30.42 | 39.82 | 57.83 (0.3) | 53.11 (1.0) |
| 0.3 | 38.56 | 45.36 | 64.33 (0.3) | 59.37 (1.0) |
| 0.4 | 41.76 | 52.10 | 73.54 (0.3) | 66.71 (0.7) |
| 0.5 | 49.80 | 58.32 | 82.95 (0.7) | 78.81 (0.2) |
| 0.6 | 59.12 | 67.30 | 90.56 (0.7) | 88.30 (0.5) |
| 0.7 | 70.46 | 74.76 | 96.00 (0.9) | 94.85 (0.4) |
| 0.8 | 79.92 | 82.90 | 98.67 (0.6) | 97.84 (0.5) |
| 0.9 | 88.62 | 89.02 | 99.58 (0.8) | 98.21 (0.1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




