Random Number Generators: Principles and Applications

1. Introduction

Is there a method to generate a sequence of truly random numbers? Can we, really, prove that a sequence of numbers is really random? For instance, which of the following two 26-bit sequences is “random”?

• Sequence $S_1$: 10101010101010101010101010
• Secuence $S_2$: 01101011100110111001011010

By what criteria, however? Without a precise definition of “randomness” no mathematical proof of randomness can be attained. “Intuition” is, often, not sufficient while it may, also, be misleading in trying to precisely define “randomness”. Some “randomness” viewpoints that have been proposed in the literature include the following:

• A process generated by some physical or natural process, e.g. radiation, resistor or semiconductor noise (the practitioner’s view).
• A process that cannot be described in a “few words” or succinctly (the instance or descriptional complexity view) - the smaller the description of a sequence of bits can be made, the less random it is (try to apply this to the two sequences above).
• A process that cannot be guessed in a “reasonable” amount of time (the computational complexity view).
• A process that is fundamentally impossible to guess (the “philosophical” view).
• A process possessing certain statistical characteristic of the ideally uniform process (the statistician’s view).

To see that intuition may not be sufficient, observe that each of the two sequences, $S_1$ and $S_2$, has exactly the same probability of appearing as output of a perfect randomness source which outputs 0 or 1 with equal probabilities, i.e., $\frac{1}{2}$. This probability is equal to $\frac{1}{2^{26}}$. Yet, the sequence $S_2$ appears “more random” than the sequence $S_1$, at least under the descriptional complexity view.

John Von Neumann’s verdict is the following: Any one who considers arithmetical methods of producing random digits is, of course, in a state of sin. For, as has been pointed out several times, there is no such thing as a random number — there are only methods to produce random numbers, and a strict arithmetic procedure of course is not such a method. True randomness is a tough task. Ideally, a number generated at a certain time must not be correlated with previous generated numbers in any way. This guarantees that it is computationally infeasible for an attacker to determine the next number that a random number generator will produce.

Whether there, really, exists randomness in the universe (if, indeed, “God plays dice”, a thesis which Albert Einstein famously denounced) is a fascinating, but elusive, scientific and philosophical question that has yet to be definitely answered. Fortunately, the mathematical theory of computational complexity and cryptography bypasses this difficulty and offers an “Apostolic Pardon” to the “sin” described by Von Neumann. In this context, a sequence is considered “random” if its efficient predictability would imply solving, efficiently, a hard computational problem, most often in number theory. Such problems are the factoring and the discrete logarithm in certain finite fields. In this way, the elusive concept of “randomness” acquires a “behavioural” substance, according to which a sequence is judged as random based on its “behavior” as seen by an outside observer. In other words, a sequence is considered random if it is computationally difficult for an observer with reasonable computational resources at his disposal to predict it. The classical concept of randomness is, in contrast, rather “ontological” and focuses the observation of the sequence itself (the “being”, that is) to characterize it as random or non-random. The “behavioristic” approach, however, leads to interesting and very useful results for use in practical applications such as electronic lotteries, where unpredictability is a major requirement. An excellent source of papers focused on philosophical questions about randomness as well as the interplay between randomness and computation theory is the collective volume [25].

On the practical side, with the rapid development of algorithms for generating random numbers used in both software testing, simulations, and mathematical modeling, multiple problems were observed regarding the randomness properties of these algorithms. Thus, another interesting problem in the field of random number generation is how to characterize “randomness”, i.e. how to decide if a given, sufficiently long, sequence of numbers is indeed random according to some well defined and precise criteria. Unfortunately all available mathematical characterizations of randomness, such as descriptive complexity, are formally undecidable. However, a number of statistical tests have been proposed which can be used to, at least, provide a scale of measurement which can rank random number generators according to the statistical characteristics of the sequences they produce. Such tests include the Diehard statistical test suite as well as other similar tests. In particular, George Marsaglia has proposed and implemented the Diehard randomness test suite, which includes several statistical tests which capture different aspects of randomness in sequences of numbers produced by generators (see Section 4.2 and, also, [11] for a complete presentation of the tests and their implementation). These tests are focused, mainly, on rejecting random number generators that exhibit undesirable, for a random sequence of numbers, properties such as short period, patterns within the binary digits, and non-uniform distribution of the numbers. The Diehard tests are considered among the most reliable randomness tests since the algorithms that pass these tests perform, also, well in practice with respect to randomness properties of the produced numbers.

Our goal in this paper is twofold. On the one hand, we will present some random number generation approaches and comment on their strengths and weaknesses. We cover the simple linear congruential generators, which nevertheless are predictable given a sufficiently long sequence they produce as output and the cryptographically secure generators with unpredictability guarantees based on the computational difficulty of number theoretical problems. We then present an application of cryptographically secure generators in domains where unpredictability is one of the major requirements, i.e. eLotteries and cryptographic key generation. We show how different components, such as true random number generators, cryptographically secure generators, seed quality enhancement techniques, post-betting prevention and ciphers can be combined in order to produce long sequence of unpredictable numbers. On the other hand, we provide a coverage of several statistical tests which can be used to, at least, evaluate implementations of the generators in order to identify weak or faulty implementations whose quality is reflected on the results of the tests. Our focus is not on wide coverage of several approaches in random generation and randomness tests but, rather, to try to explain basic principles and the rationale behind the tests we will describe.

2. Physical Sources of Randomness

A physical source of randomness is a physical system which exhibits variations in some of its properties or characteristics. A small change in the system at a certain time, will progressively impact future conditions in the system over time. Such a source can be tapped in order to produce an infinite sequence of bits, e.g. by converting the analogue values of the variations into digital form. For this reason it is necessary that the deployed physical sources have sufficiently varying random fluctuations of the properties used to draw randomness. Physical sources with good properties are Geiger counters and zener diodes. These sources appear to produce bits that do not follow some easily predictable pattern. However, as time progresses, they sometimes appear to produce long streaks of 0s alternating with long streaks of 1s, which is undesirable.

Nowadays, Physical Unclonable Functions (PUFs) that consist of inherently unclonable physical systems are used as source of randomness. Their unclonability arises from their many random constituent components that can not be controlled. When a stimulus C is applied to a PUF, it reacts with a response R. This pair $(C,R)$ is called a challenge-response pair (CRP). Thus, a PUF can be considered as a function that maps challenges to responses. A response $R_i$ to a challenge $C_i$ can not be exploited to discover another response $R_j$ to a different challenge $C_j$ with $i\ne j$ [10]. Moreover, it is impossible to recover the response $R_i$ corresponding to a challenge $C_i$ without having the right PUF that can produce it. If an attacker tries to analyze the PUF in order to learn its structure, the response behavior of the PUF is changed substantially. A PUF is considered as strong if along with the above properties there is a large number of challenge response pairs $(C_i,R_i)$, $i=1,\dots ,N$, available for the PUF [10]. In [21], a Hardware Random Number Generator (HRNG) which is based on these large number of $(C_i,R_i)$ pairs is presented. A classical RNG sends challenges to a PUF which reacts with the corresponding responses while these responses are used for the bit construction of the random number.

However, due to the existence of a noise while a PUF operates, when it is challenged with $C_i$ a response $R_i^{{}^{\prime }}$, which is a noisy version of $R_i$, is obtained. For this reason, each time a PUF produces helper data which can be used by an error correction code to recover $R_i$. On the other hand, random number generators need a non-deterministic source of entropy. Subsequently, the noise from PUF response can be used for that purpose. So, it makes sense to use the noise from a PUF as a source of entropy to extract a true random seed. The National Institute of Standards and Technology (NIST) in its document SP800-90B has established a clear set of specifications for entropy sources of random bit generators.

The question that arises from this discussion is whether we can produce a random (or at least a “seemingly” random) sequence of numbers using physical randomness sources that are not sufficiently random for the purpose in hand (e.g. they do not follow the uniform distribution). John von Neumann was one of the first to attempt to address this question. According to the model he considered, suppose we have a randomness source that produces a sequence of bits $X_i$ with the property that, for all i, $P[X_i=1]=\delta$, for some $0\le \delta \le 1$. Then, from this source, we can generate a random sequence with the following algorithm: for each pair 01 of bits produced by the source we consider, 0 is returned, while 1 is returned for each pair 10. For 00 or 11, no bit is returned. The von Neumann model is limited because the probability value $\delta$ is assumed to be fixed while it also has the disadvantage that from a source that may produce a very large number of bits, several of which are discarded.

The Santha and Vazirani’s model is less restrictive: a source is called an SV source (Santha-Vasirani source) if for some real number $0\le \delta \le \frac{1}{2}$ it holds that $\delta \le P[X_i=1]\le (1-\delta )$ for all i. A pseudorandom sequence is called minimally random if it has been produced by an SV source. When $\delta =\frac{1}{2}$ then the sequence is considered random. Santha and Vazirani proved that if $\delta <\frac{1}{2}$ then a truly random sequence cannot be produced from a minimally random sequence. That is, for every algorithm that produces a sequence X with input a minimally random sequence, there is a corresponding algorithm for which $P[X_i=1]=d$ or $P[X_i=1]=1-d$.

The next question that therefore arises is whether the combination of several SV sources can produce a more random sequence. Before answering this question, we define the concept of a semi-random source. A source is said to be semi-random if for every $t>0$ and every function $f:{\{0,1\}}^{★}\to [0,1]$ the following holds, for all large integers n and for all n-bit sequences $x=x_1\cdots x_n$:

$$\left|\frac{1}{2^n}\sum _{\mid x\mid =n}f\left(x\right)-\sum _{\mid x\mid =n}P[X_1\cdots X_n=x_1\cdots x_n]f\left(x\right)\right|\le \frac{1}{t^n}$$

(1)

Semi-random sources, as defined by (1), are almost indistinguishable from truly random sources. Therefore, if we can produce a semi-random sequence from a minimally random source (or several such sources together, e.g. by XORing their outputs), we have constructed a sufficiently strong randomness source.

Given as input m independent, minimally random, randomness sources $S_1,\cdots ,S_m$, the following algorithm produces a semi-random sequence. We assume that $\delta$ is given and $m=\lceil {\delta }^{-1}(lognlogn)\rceil$, where n a large integer.

This simple algorithm can be used in practical applications using the outputs of several physical sources of randomness. It is a convenient and one of the most efficient algorithms for converting, possibly, minimally random physical random sequences into semi-random sequences.

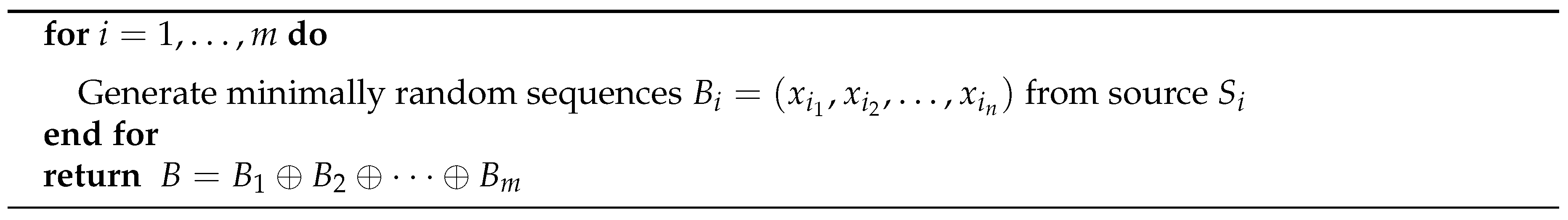
3. Pseudorandom Number Generation

As we discussed in Section 2, using physical sources of randomness may not be convenient in several application domains. One issue is their, potentially, poor randomness properties and another issue is the irreproducibility of their outputs.

In general, the generation of random numbers is very difficult to achieve using physical randomness sources. Fortunately for almost all cryptographic applications, pseudo-random numbers can be used, i.e. numbers that appear to be truly random to someone attempting to interfere, maliciously, with the application. Algorithms that generate pseudorandom numbers, i.e. pseudorandom sequences of bits, are called Pseudorandom Number Generators or PRNGs for short.

The generation of pseudorandom numbers involves the production of long sequences of bits starting from a small, preferably truly random, initial value called a seed. Among the desirable properties that are experted from a PRNG is the generation of uniformly distributed bits, i.e. bits that could have been produced by successive flips of an unbiased coin. Naturally, pseudorandom sequences can never be completely random in the sense of predictability. In particular, given any pseudorandom sequence which has been produced by an algorithm using an initial seed value, an exhaustive search among all possible seed values could identify the seed from which the observed numbers were produced. However, the required time may be prohibitively long. For some classes of PRNGs, however, such as the Linear Congruential Generators discussed in Section 3.1, there are more efficient ways to uncover future values, given an initial segment of the pseudorandom sequence.

This fact leads to the question of how to design PRNGs which are unpredictable in reasonable (i.e. polynomial) time. As an answer to this question, the concept of cryptographically secure PRNGs was, first, proposed by Blum and Micali [4] and Yao [24]. A PRNG is called cryptographically secure if it passes all polynomial-time statistical tests, or in other words if the distribution of bit sequences it produces cannot be separated from truly random sequences by any polynomial-time algorithm. On the other hand, a PRNG is called polynomially predictable if there exists a polynomial time algorithm that, given a sufficiently long sequence of bits produced by the generator, it can predict its next outputs. For example, the Linear Congruence (LCG - see Section 3.1) and $\frac{1}{P}$ generators are polynomially predictable. In contrast, the BBS and RSA (see Section 3.2.1 for a discussion of BBS) are polynomially unpredictable. For this reason, such generators are the generators of choice in applications where unpredictability is a major requirement, such as in the implementation of Electronic Lotteries (see [14,15] and Section 5), key generation and network security protocols.

A key definition in the area of cryptographically secure PRNGs is the following (see [9]):

Definition 1

(Pseudorandom function). A family of functions $F_s:{\{0,1\}}^k\to {\{0,1\}}^l$, indexed by a key $s\in {\{0,1\}}^n$, is said to be pseudorandom if it satisfies the following two properties:

• Easy to evaluate:The value $F_s\left(x\right)$ is efficiently computable given s and x.
• Pseudorandom:The function $F_s$ cannot be efficiently distinguished from a uniformly random function $R:{\{0,1\}}^k\to {\{0,1\}}^l$, given access to pairs $(x_i,F_s\left(x_i\right)$, where the $x_i$’s can be adaptively chosen by the distinguisher.

More specifically, we say that a pseudorandom generator is polynomially unpredictable if and only if for every finite initial part of the sequence produced by that generator and for every bit erased from that part, a probabilistic Turing machine cannot guess this bit in polynomial time. In other words, there is no better way to determine the value of this bit better than flipping an unbiased coin.

In cryptographically secure generators the difficulty of predicting their outputs is based on the difficulty of solving a mathematical problem, most often from algorithmic number theory. For these problems there is no algorithm that solves them in probabilistic polynomial time. The integer factorization (factoring problem), the discrete logarithm problem in finite fields and elliptic curves (discrete logarithm problem), as well as the Quadratic Residuosity Assumption, are among, the most prominent of these problems. Thus, we may say that a generator is cryptographically secure if the solution of a difficult mathematical problem, like the ones listed above is reduced to predicting the next bit of the sequence given the first, polynomially many, bits of the sequence. Formally, a $(k,l)$-PRNG is a polynomial (in k) time function $f:{\left\{0,1\right\}}^k\to {\left\{0,1\right\}}^l$. The input $s_0$ is the seed and $l,k$ are positive integers with $l\ge k+1$. The output $f\left(s_0\right)$ is a sequence of bits $b_0,b_1,b_2,\cdots$ and is called a pseudorandom bit string. The function f is said to be a cryptographically strong PRNG if it has the following properties:

• The bits $b_i$ are easy to calculate (for example in polynomial time in some suitable definition of the size parameter, e.g. size of a modulus).
• The bits $b_i$ are unpredictable in the sense that it is computationally intractable to predict $b_i$ in sequence with probability better than $1/2$, i.e for any computationally feasible next-bit predictor algorithm $B_i$,

  $$P\left[b_i=B\left(b_0...b_{i-1}\right)\right]=1/2$$

  (2)

  for $i=2,\dots ,l$.

3.1. The Linear Congruential Generator

The well known Linear Congruential Generator (LCG) produces a recursively defined sequence of numbers calculated by the following equation:

$$x_{i+1}=(a·x_i+c)modm.$$

(3)

In this equation $x_0$ is the initial state or seed, a is the multiplier, c is the increment and m the modulus. The various choices for the generator parameters a, c and m define the period q of the generator. This is the minimal value q such that $x_q=x_0$ (see the excellent exposition in [12]).

The range of most common LCGs is limited to values of $m\le 2^{64}$ and, thus, they do not have good statistical properties. Therefore, their use in simulations (e.g. Monte-Carlo) is limited. In application where m can be arranged to be of size several hundred or even thousand of bits, this issue can be addressed. However, although current microprocessor technology has progressed significantly and allows the implementation, in hardware, of increased precision integer arithmetic, for such values of m it is necessary to implement, in software libraries, to deploy arbitrary precision integer arithmetic, which may be too expensive for practical purposes.

It is easy to see that the maximum period for an LCG is equal to m. To obtain this upper bound, however, the following conditions should be met (see, e.g., [12]):

• The parameter c should be relatively prime to m.
• If m is a multiple of 4 then $a-1$ should, also, be a multiple of 4.
• For all prime divisors p of m the value of $a-1$ should be a multiple of p.

The reader may consult [12] for more mathematical properties and details of LCGs in the form in Equation (3).

Popular programming languages most often deploy LCGs for the generation of pseudorandom number sequences since strong security properties (mainly unpredictability) are not of concern in customary programming projects where the focus is on randomness (i.e. statistical) properties of the sequences. See, however, Section 5 of this survey paper for the presentation of an application domain, Electronic Lotteries, where unpredictability properties are essential.

There exist several variations of the LCGs as given in (3). It is possible, for instance, to set $c=0$ as the increment value. The resulting generator is termed multiplicative or mixed generator (in short MCG) and has the form

$$x_{n+1}=a{x}_n(modm),n\ge 0.$$

(4)

As a consequence of setting $c=0$, less operations are needed and, thus, the generation of numbers by (4) is faster (albeit slightly) than the generation of numbers by (3) when $c\ne 0$. However, it is not possible to obtain the maximum period (i.e. m) since, for instance, the value 0 cannot appear unless the sequence, itself, is composed of all 0s.

In addition, if $c=0$ and $x_n$ is relatively prime to m for all values of n then the length of the period of the sequence cannot exceed $\phi \left(m\right)$, which is the cardinality of the set of integers between 0 and m that have the property of being relatively prime to m (see, e.g., [12]). Now, if $m=p^e$, where p is a prime number and $e\in \mathbb{N}$, Equation 4 reduces to

$$x_n=a^n{x}_0(mod{p}^e).$$

If a as relatively prime to p then the period of the MCG is the least $\lambda$ such that $x_0=a^{\lambda }{x}_0(mod{p}^e)$. If $p^f$ is the GCD of $x_0$ and $m=p^e$, then this condition reduces to $a^{\lambda }=1(mod{p}^{e-f})$.

If a is relatively prime to m then the smallest integer $\lambda$ for which $a^{\lambda }=1(mod{p}^{e-f})$ is termed the order of $a\mathrm{modulo}m$ and all values a which have maximum possible order modulo m form the set of primitive elements modulo m. Thus, the maximum period possible for MCGs is equal to the order of a primitive element (i.e. maximum possible order) modulo m. This is equal to $m-1$ (see, e.g., [12])) whenever

• m is prime,
• a is a primitive element modulo m,
• $x_0$ is relatively prime to m.

With respect to predictability, the LCGs do not possess good properties. In [6,7,16] efficient algorithms are presented for predicting the next value given past values of the LCG even if some bits of these values are missing (i.e. they have not been given publicly).

3.2. Cryptographically Secure Generators

Since cryptographically secure PRNGs are accompanied by strong security (unpredictability) evidence, we present some of the most powerful cryptographically secure PRNGs and we discuss design directions for the construction of such PRNGs.

3.2.1. The BBS Generator

The BBS generator, proposed by L. Blum, M. Blum and M. Shub in [3], is one of the most often deployed cryptographically strong PRNGs. Its security (unpredictability) is founded on the difficulty of the Quadratic Residue problem.

For every integer N, $\left|N\right|$ is its length in bits and ${\left|N\right|}_b$ its length in base $b>2$. If $\Sigma =\{0,1,\cdots ,b-1\}$, ${\Sigma }^{★}$ is the set of finite sequences with elements from $\Sigma$ and ${\Sigma }^{\infty }$ the set of sequences with an infinite number of elements from $\Sigma$. Also, we define ${\Sigma }^k=\{x\in {\Sigma }^{★}:\left|x\right|=k\}$, i.e. the set of finite sequences of length k. For all sequences $x\in {\Sigma }^{\infty }$, with $x^k$ we denote the initial part of the sequence x of length k (i.e. its first k elements) and with $x_k$ we denote the k-th element of x (its first element is $x_0$).

With $xmodN$ we denote the smallest nonnegative integer remainder from dividing x by the integer N. A quadratic residue $modN$ is any number x for which there exists an integer u such that $x=u^{2}modN$. Recall that $Z_N^{*}=\{$integers $x\mid 0<x<N$ and $gcd(x,N)=1\}$, i.e. the set of integers which are smaller than N and relatively prime with N. The set $Z_N^{*}$ has order, i.e. number of elements, equal to $\varphi \left(N\right)$. The set of quadratic residues $modN$ will be denoted by $QRN$. This is a subset of $Z_N$ and has order $\frac{\varphi \left(N\right)}{4}$. Additionally, with $Z_N^{*}(+1)$ we will denote the subset of $Z_N^{*}$ consisting of its elements which have a Jacobi symbol equal to 1 and with $Z_N^{*}(-1)$ the subset of its elements $Z_N^{*}$ which have Jacobi symbol $-1$. All quadratic residues $modN$ belong in the subset $Z_N^{*}(+1)$.

Each quadratic remainder $u^{2}modN$ has four different roots in $Z_N$, which are $\pm umodN$ and $\pm ymodN$. If, however, we assume that $N\equiv 3mod4$, then every quadratic residue has exactly one square root, which is also a quadratic residue. In other words, the function $f\left(x\right)=x^{2}modN$ is a $1-1$ and onto mapping (i.e. bijection) from $QRN$ to itself.

Finally, we state the definition of Carmichael’s function, which will then also be needed for the concept of special primes. Carmichael’s $\lambda$-function [8] is closely related to Euler’s totient function. However, while Euler’s totient function $\varphi \left(n\right)$ provides the order of the unit group $U(\mathbb{Z}/n\mathbb{Z})$, Carmichael’s function $\lambda \left(n\right)$ provides its exponent. In other words, $\lambda \left(n\right)$ is the smallest positive integer for which it holds that $a^{\lambda \left(n\right)}\equiv 1(modn)$ for any a which is coprime to n. Carmichael’s $\lambda$ function is not multiplicative but has a related property which can be called lcm-multiplicative, as follows:

$$\lambda \left(\mathrm{lcm}\right[m,n\left]\right)=\mathrm{lcm}\left[\lambda \right(m),\lambda (n\left)\right],\mathrm{for}\mathrm{each}\mathrm{pair}\mathrm{of}\mathrm{positive}\mathrm{integers}m,n.$$

(5)

Some special values include $\lambda \left(p^k\right)=\varphi \left(p^k\right)$, for $p^k$ an odd prime power, $\lambda \left(1\right)=\lambda \left(2\right)=1$, $\lambda \left(4\right)=2$, as well as $\lambda \left(2^k\right)=2^{k-2}$ for $k\ge 3$. Based on these special values and Equation (5), $\lambda \left(n\right)$ can be computed for any positive integer n.

A prime number P is called special if $P=2P_1+1$ and $P_1=2P_2+1$, where $P_1,P_2$ are primes greater than 2. A composite number $N=PQ$ is special if and only if P, Q are two distinct special primes and $PQ\equiv 3mod4$.

The set $\mathcal{N}$ of the generator parameters consists of all positive integers $N=PQ$, where P, Q are distinct prime numbers of equal length (i.e. $\left|P\right|=\left|Q\right|$) and $PQ\equiv 3mod4$. For any integer N, the set $X_N=\{x^{2}modN:x\in Z_N^{*}\}$ is the set consisting of the quadratic residues $modN$. The domain of the generator seeds will be $X=\{X_N\mid N\in \mathbb{N}\}$. The seeds should be selected from X according to the uniform distribution for increased generator security.

Given as input a pair $(N,x_0)$, the BBS pseudorandom number generator will output a pseudorandom sequence of bits $b_0{b}_1{b}_2\cdots$ where $b_i=Parity\left(x_i\right)$ and $x_i+1=x_i^{2}modN$. $Parity\left(x\right)$ is the least significant bit of the integer x. The construction of the pseudorandon sequence obviously takes place in polynomial time. As it is shown in [3], the period $\pi$ of the pseudorandom sequence divides or is equal to (under some condition) $\lambda \left(\lambda \right(N\left)\right)$. Given $x_0,N$ and $\lambda \left(N\right)$ we can efficiently calculate $x_i=x_0^{2^i}modN=x_0^{2^{i}mod\lambda \left(N\right)}modN$ for $i>0$. To calculate $x_i$ for $i<0$ we use the equality $x_i=x_{imod\lambda \left(\lambda \right(N\left)\right)}$. As we will see below, if $x_0$ and N are known, but not the values of P and Q, we can construct the pseudorandom sequence forward (i.e. for $i>0$) but not backwards (for $i<0$). thus, it appears that the prediction of the sequence is as hard as factoring a large integer $N=PQ$. Alexi et al. [1] proved that the BBS generator remains cryptographically secure even if it outputs up to $O(loglogN)$ low order bits instead of only one. With this result, the generator’s efficiency is greatly improved. Practically, a BBS generator can be realized as follows:

• Find primes p and q such that $p\equiv q\equiv 3$ mod 4
• Set $N=pq$
• Start with $x_0$ = seed (a truly random value), $i=0$
• Set $x_i=x_{i-1}^2$ mod N
• Output the least significant bit of $x_i$
• Set $i=i+1$, go to step 3

Now regarding the security of this generator, as mentioned above in the introduction, all cryptographically secure generators base their security on the difficulty of solving number theory problems. This problem in the case of the BBS generator is the Quadratic Residuosity Problem. The problem is defined as follows: given N and $x\in Z_N^{*}(+1)$, decide whether x is a quadratic residue $modN$. Recall that exactly half the elements of $Z_N^{*}(+1)$ are quadratic residues.

The Quadratic Residuosity Assumption states that any efficient algorithm for solving the quadratic residuosity problem would give wrong results for at least a percentage of the inputs to the algorithm. More formally, the assumption is as follows: let $poly\left(\right)$ be a polynomial and $P[N,x]$ a polynomial algorithm which when given as input N and x, with $\left|N\right|=\left|x\right|=n$, returns 0 if x is not a quadratic residue $modN$ and 1 otherwise. Also let $0<\delta <1$ be a constant and t a positive integer. Then for n very large and for a fraction d of the numbers N with $\left|N\right|=n$, the probability that the process $P[N,x]$ gives the wrong answer for the integer x (given that x is chosen according to the uniform distribution from $Z_N^{*}(+1)$), exceeds $\frac{1}{n^t}$, that is $\frac{\sum Prob\left(P\right[N,x\left]isnotcorrect\right)}{\frac{\Phi \left(N\right)}{2}}>\frac{1}{n^t}$. The quantity $\frac{1}{n^t}$ can be replaced by $\frac{1}{2}-\frac{1}{n^t}$.

The details of the discussion that follows can be found in [3]. We, also, recall that in what follows, $N=PQ$, with P, Q prime numbers and $PQ\equiv 3mod4$, and that the function $f\left(x\right)=x^{2}modN$ is a $1-1$ mapping from QRN to QRN.

According to the definition of the BBS generator, knowledge of N is sufficient for the efficient generation of the sequence $x_0,x_1,\cdots$ starting from a seed value $x_0$. However, knowing only N and not its two factors P and Q does not suffice for the generation of the sequence in reverse direction, i.e. the sequence $x_0,x_1,x_2,\cdots$ starting from $x_0$. For this purpose, the factors P and Q are needed. This necessity follows from the following argument: Suppose that we can efficiently calculate $x_1$ without knowing the factors of N. Then in order to factor N we choose an $x\in Z_N(-1)$, we set $x_0=x_{2}modN$ and calculate $x_1$. We then compute $gcd(x+x_1,N)=P$ or Q. Therefore, the ability to compute $x_1$ for at least a percentage of the values of x would allow us to factor N efficiently with a high probability of success.

On the other hand, if we could factor N, we could generate the pseudorandom sequence backwards. This fact follows from the following theorem: There exists an efficient deterministic algorithm A which when given as inputs N, the factors P and Q, and any quadratic residue $x_0\in Z_N$, computes the unique quadratic residue $x_{1}modN$ for which $x_1^{2}modN=x_0$. In other words, $A(P,Q,x_0)=x_1$.

Moreover, the factors of N are necessary to have an $ϵ$-advantage in finding the parity bit of $x_1$ in polynomial time, given $x_0$. A probabilistic process P that returns 0 or 1 is said to have $ϵ$-advantage, with $0<{ϵ}^{\frac{1}{2}}$ in guessing the parity bit of $x_1$, if and only if $\frac{\sum Prob(P[N,x_0]=parity\left(x_1\right))}{\frac{\Phi \left(N\right)}{4}}>\frac{1}{2}+ϵ$. Similarly, we can define a probabilistic procedure that would have an $ϵ$-advantage in deciding whether some $x\in Z_N^{*}(+1)$ is a quadratic residue (which is the quadratic residuosity problem). More simply, we would say (according to a lemma of [3]) that, an $ϵ$-advantage in finding the parity bit of $x_1$ can be converted into an $ϵ$-advantage for the quadratic residuosity problem.

In [3] a theorem is given which proves the unpredictability of the BBS generator. By this theorem, for any constant $0<\delta <1$ and any positive integer t, any probabilistic polynomial process P has at most a $\frac{1}{n^t}$ advantage in predicting the sequences generated by BBS backwards (for sufficiently large $n=\mid N\mid$ and for all but a fraction $\delta$ of N). In short, if the BBS generator were predictable, the quadratic residuosity assumption described previously would not hold. For this reason, the generator can be safely assumed to, also, pass every probabilistic, polynomial, statistical test on its long term output.

Having shown that the output of the generator cannot be efficiently predicted, it remains to calculate its period. The fact that the sequence $x_0,x_1,x_2,\cdots$ cannot be predicted shows that the period of $\pi \left(x_0\right)$ should be very large. According to a theorem proved in [3], the period $\pi \left(x_0\right)$ divides $\lambda \left(\lambda \right(N\left)\right)$. However, it would be best for the period to be as long as possible, i.e. equal to $\lambda \left(\lambda \right(N\left)\right)$. The equality $\pi \left(x_0\right)=\lambda \left(\lambda \left(N\right)\right)$ can indeed hold under two conditions. The first is that the integer N is special as defined earlier and the second is to choose a seed $x_0$ so that its order is equal to $\lambda \left(N\right)/2$.

Finally, we define the linear complexity of a sequence of pseudorandom numbers $x_0,x_1,\dots$ the smallest number L for which the linear relationship

$$x_{n+L}=a_{L-1}{x}_{n+L-1}+\dots +a_0{x}_0$$

holds for $n=1,2,\cdots$.

The linear complexity of any pseudorandom sequence does not exceed the period of the sequence. Obviously, the higher the linear complexity of a sequence is, the more cryptographically secure it is with respect to prediction of its output. As demonstrated in [22], the BBS generator does not exhibit any particular form of linear structure, a property which excludes the possibility of applying attacks such as the Lattice Reduction attack on its outputs.

3.2.2. The RSA/Rabin Generator

The second cryptographically secure generator is the RSA/Rabin generator. It is based on the RSA function and it works as follows:

• Find primes p and q as well as a small prime e such that $gcd\left(\right(p-1\left)\right(q-1),e)=1$
• Set $N=pq$
• Start with $x_0$ = seed (a truly random value), $i=0$
• Set $x_i=x_{i-1}^e$ mod N
• Output the least significant bit of $x_i$
• Set $i=i+1$ and repeat from Step 3

The RSA/Rabin generator is cryptographically secure under the RSA function assumption. According to this assumption, given N, e and y, where $y=x^{e}modN$, the problem of determining x is computationally intractable. More details about this generator can be found in [1].

3.2.3. Generators Based on Block-Ciphers

The other two generators that are deployed in the lottery are based on the encryption algorithms DES and AES. The implementations provided by version 2.5.3 of the mcrypt library (available at [17]) was used with key sizes 64 bits for DES and 192 bits for AES.

DES and AES are used in their CFB (Cipher-text Feed-Back) mode and they are operated as follows. An initial random seed is constructed from the combined output of the true random generators and then DES and AES are invoked, using the seed as the Initial Vector (IV), as many times as the values we need to generate. In particular, every time the encryption function is called, a byte with all zeros is encrypted (always in CFB mode) and the encryption result is the output of the corresponding generator.

The cryptographic strength of these two generators is based on the security of the corresponding encryption algorithms and not on a presumed computationally hard mathematical problem, like RSA and BBS. However, both generators have passed, separately, all the Diehard tests and, thus, their output is considered secure.

Bruce Schneier et al. in [18] present the design and analysis of the Yarrow cryptographically secure PRNG. Yarrow relies on a one-way hash function $h\left(x\right)$ with an m-bit digest and a block cipher $E\left(\right)$ with a k-bit key and an n-bit block size. The designer should select an one-way hash function that is collision intractable (e.g. one from the SHA-2 family of hash functions) and a block cipher (e.g. AES) that is highly resistant to known-plaintext and chosen-plaintext attacks.

The major components of Yarrow are an entropy accumulator that collects samples from entropy sources in two pools, a reseed mechanism that periodically reseeds the key with new entropy from the pools, and a block-cipher based generation mechanism that generates random numbers (Figure 1). The basic idea behind the generation mechanism is that if an attacker does not know the block-cipher key he cannot distinguish the generated outputs from a truly random sequence of bits.

The entropy accumulator determines the next unguessable internal state of the PRNG. Each source of entropy sends samples to the entropy accumulator and their hashed values are stored to either a fast pool or a slow pool. The fast pool is used for frequent key reseeding while the slow one for rare reseeding. It is obvious that the collected entropy is no more than the size of the hash digest, i.e m-bit entropy. Initially, the entropy accumulator collects samples until the collected estimated entropy is high enough for reseeding the block cipher with a new key. Recommendations for entropy estimation can be found in [23].

3.2.4. Algorithms M and B

Given two sequences of pseudorandom numbers X and Y, algorithm M will produce a sequence $X^{\prime }$ significantly “more random”. Essentially the numbers in $X^{\prime }$ are the same as those that make up X except that they are in a different positions (i.e. they form a permutation of the original sequence X) in the new sequence. These positions are dictated by the sequence Y.

More specifically, an array N with k elements is formed, where k is an integer depending on the application, often close to 100. The elements in the array N are the first k elements of the sequence X. The steps of the algorithm M (applied iteratively) are the following:

It turns out that in most cases the period of the sequence produced by algorithm M is the least common multiple of the periods of sequences X and Y.

However, there is a more effective way to transpose the elements of a sequence X. The corresponding algorithm is called AlgorithmB. It is similar to M, but it achieves better results in practice. At the same time it has the advantage that only one sequence of pseudorandom numbers is needed and not two, as in the case of M.

Initially (as in M) the first k elements of the sequence X are placed in the array N. Then the variable y takes the value $X_k$ and the following steps are applied iteratively:

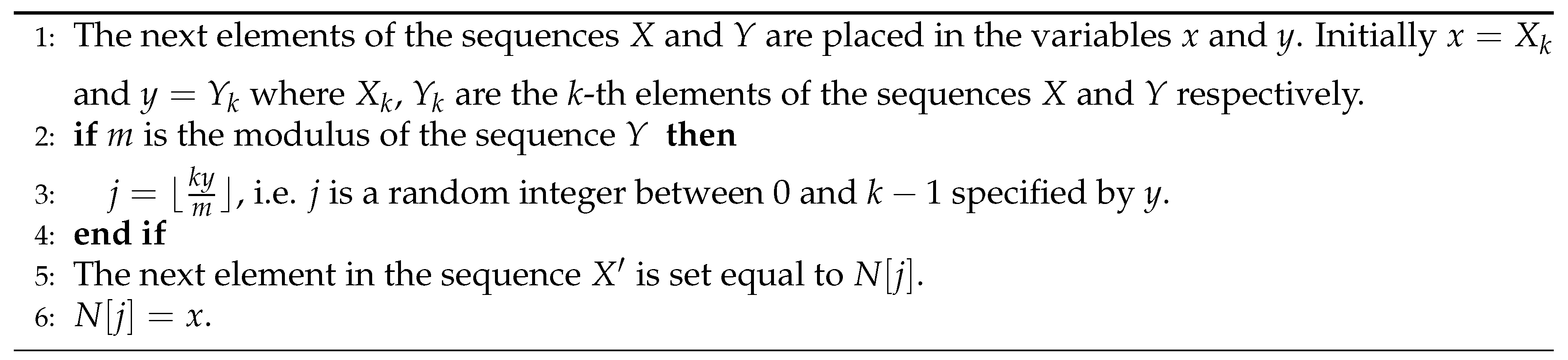
• $j=\lfloor \frac{ky}{m}\rfloor$, where m is the modulus of the sequence X.
• $N\left[j\right]$ is the next new element of the sequence $X^{\prime }$,
• We set $y=N\left[j\right]$ and $N\left[j\right]$ is set to the next element of the sequence X.

Although algorithm M can produce satisfactory pseudorandom number sequences given, as input, even non-random sequences (e.g. the Fibonacci numbers sequence, for example), it is still likely to produce a less random sequence than the original sequences if they are strongly correlated. Such issues do not arise with algorithm B. Algorithm B does not, in any way, reduce the “randomness” of the given sequence of pseudorandom numbers. On the contrary, it increases it with a small computational cost. For these reasons it is recommended to use algorithm B with any PRNG.

A notable disadvantage of algorithm M and B algorithms is that they only modify the order of the numbers in a sequence and not the numbers of the sequences themselves. Although for most applications the ordering of the numbers is important, if the initial generators we choose do not pass some basic statistical tests, permuting their elements with the M and B algorithms will not render them stronger. For this reason, in applications which require pseudorandom number sequences with strong randomness properties with theoretical guarantees that imply unpredictability, it is better to deploy cryptographically secure PRNGs, such as BBS and RSA using, optionally, algorithms M and B.

4. Randomness Tests

In general, the quality of a pseudorandom number generator is based on a specific theoretical framework which provides the assumptions and requirements which lead to a series of theoretical results which demonstrate various quality aspects such as long period and unpredictability.

Although mathematical evidence should be sufficient, a good generator implementation should be able to demonstrate not only in theory but in practice, as well, specific quality aspects. For this reason, the design and implementation of pseudorandom number generation algorithms should, also, be accompanied by the results of statistical or randomness tests which attest to the quality properties of the algorithms or, at least, their specific implementations.

Before we continue, in the probability calculations for some of the tests that follow, the Stirling numbers of the second are needed. These denote the number of ways to partition a set of n elements into k non-empty subsets. The notation for the Stirling numbers of the second kind is $\left\{\begin{array}{c}n\\ k\end{array}\right\}$ and they are defined, algebraically, as follows:

$$\left\{\begin{array}{c}n\\ k\end{array}\right\}=\frac{1}{k!}\sum _{j=0}^k{(-1)}^{k-j}\left(\genfrac{}{}{0pt}{}{k}{j}\right)j^n.$$

(6)

As we discussed in the Introduction section, some quality properties of random number generators are hard to define and evaluate using practical, i.e. finite and computable, approaches. For instance, unpredictability and randomness itself are elusive concepts with various theoretical characterizations most of which not leading to practical, computable, tests. After all, algorithms and computers are deterministic entities whose time evolution follows a well-defined sequence of steps in order to produce results.

On the other hand, the science of Statistics can provide approaches and tools for evaluating, empirically, some measurable properties related to the “randomness” of a number sequence. Using certain statistical tests, the generated sequences are evaluated with respect to their randomness behavior according to the tests’ assumptions and rules.

These tests are designed so that the expected values of a test’s statistical indicators are known to hold for a uniform distribution. Then the generated sequence is subjected to the test and the results are compared with the results that a perfectly uniformly random generated sequence would give. Although a variety tests can be applied on a sequence produced by a PRNG, research in this field has provided guidelines as to which tests are most appropriate and efficient. In general, PRNGs that pass these tests are considered acceptable for generating pseudorandom numbers. For instance, a number of tests are described in [12], several of which are implemented in the Diehard randomness tests suite (see [11]). In what follows, we will describe a number of these tests and discuss the randomness properties they evaluate.

4.1. Practical Statistical Tests

In this section, we will present a number of statistical tests described in Knuth’s book [12]. Most of the tests, however, suit mainly truly random number sequences while some of the test parameters are not provided numerically. Thus, we follow the modifications of these tests as described in [13] which are appropriate for integer number sequences while specific parameter values are provided for the tests.

In particular, the basic theory of tests for real number sequences is provided in [12]. The proposed applicability criteria are, also, suitable for integer sequences as well in some tests. However, integer sequences cannot be tested since the same assumptions as for real number sequences since they may not be applicable to them. For instance, the Permutation Test gives test probabilities based on the premise that no two consecutive terms of the tested sequence can be equal. However, for integer sequences, equality of consecutive terms may occur with a non-negligible probability. Thus, in [13] new combinatorial calculations were developed in order to adapt Knuth’s test suite to integer and binary sequences. Additionally, some of the required parameters for the tests, such as sequence length, alphabet size, block size, and other similar parameters, are, also, provided in [13]. Taking into account the aforementioned issues, the authors of [13] provide the test details and required probability calculations for testing binary and integer sequences, which are of interest for our purposes.

Each of the tests is applied, in general, to a sequence $<U_n>=U_0,U_1,\cdots ,U_{n-1}$ of real numbers which, assumedly, have been chosen independently from the uniform distribution in the interval $(0,1)$. However, some of the tests are designed for sequences of integers rather than sequences of real numbers. If this is the case, we form the auxiliary integer sequence $<Y_n>=Y_0,Y_1,\cdots ,Y_{n-1}$, where $Y_n=\lfloor d{U}_n\rfloor$. Accordingly, this sequence has been, assumedly, produced, by independent choices from the uniform distribution over the integers $0,1,\dots d-1$. The parameter d should be sufficiently large so as the tests’ results are meaningful for our PRNGs (e.g. the $Y_i$’s fall in the PRNG’s range) but not so large as to render the test infeasible in practice.

Below, we discuss some of the tests in Knuth’s book [12]. One may, also, consult their modified form provided in [13]. We first discuss two fundamental tests which are used in combination with other empirical test that we describe afterwards.

4.1.1. The “Chi-Square” Test

In probability theory and statistics, the “chi-squared” distribution, also called “chi-square” and denoted by ${\chi }^2$, with k degrees of freedom is defined as the distribution of the sum of the squares of k standard normal random variables. The “chi-square” distribution of k degrees of freedom is, also, denoted by ${\chi }^2\left(k\right)$ or ${\chi }_k^2$. The “chi-squared” distribution is one of the most frequently used probability distributions in statistics, e.g. in hypothesis testing and in the construction of confidence intervals.

In our case, the “chi-square” distribution is used to evaluate the “goodness-of-fit” of the monitored frequencies of a sequence of observations to the expected frequencies of the distribution under test (this is the hypothesis). The test statistic (stochastic distribution) is of the form ${\chi }^2=\sum {((o_i-e_i)}^2/e_i)$, where $o_i$ and $e_i$ are the observed and expected frequencies of occurrence, correspondingly, of the observations. This Chi-Square test is one of the most widespread statistical tests of a sequence of data derived from observations of a phenomenon, in general. In our case, this phenomenon is the source of pseudorandom numbers and our data is the generated numbers.

We assume the following:

• Each observation can belong to one of k categories.
• We have obtained n independent measurements.

According to this test, we perform n independent observations from the source of data (n should be large enough). In our case, the observations will be the pseudorandom numbers. Then, we count how many times each number appeared. Let us assume that the number s appeared $Y_s$ times. Also, let $p_s$ be the probability of appearance of the number s. We calculate the following statistical indicator (we assume that the numbers generated by the pseudorandom number generator are within the range $1,\dots ,m$):

$$\begin{array}{c}\hfill V=\sum _{1\le s\le m}\frac{{(Y_s-n{p}_s)}^2}{n{p}_s}=\frac{1}{n}\sum _{1\le s\le m}\left(\frac{Y_s^2}{p_s}\right)-n.\end{array}$$

(7)

Next, we compare V to the entries of the distribution tables of ${\chi }^2$ with the parameter k (the degree of freedom) equal to $m-1$. If V is less than the table entry corresponding to 99% or greater than the entry corresponding to 1%, then we do not have sufficient randomness. If it is between the entries of 99% and 95%, then insufficient randomness may exist. A value below 95% is a good indication that the numbers under testing are close to random.

Knuth suggests applying the test for a sufficiently large values of n. Also, for test reliability purposes, he suggests, as a rule of thumb, that n should be sufficiently large to render the expected values of $n{p}_s$ greater than 5. However, a large value of n presents some undesirable properties, such as locally non-random behavior through, for instance, an entrance into a cycle in the sequence. This fact is addressed not by using smaller value for n but by applying the test for several different large values of n.

4.1.2. The Kolmogorov-Smirnov Test

The “Kolmogorov-Smirnov” test measures the maximum difference between the expected and the actual distribution of the given number sequence. In simple terms, the test checks whether a dataset (a PRNG sequence in our case) comes from a particular probability distribution.

In order to approximate the distribution of a random variable X, we target the distribution function $F\left(x\right)$, where $F\left(x\right)=Pr(X\le x)$. If we have n different independent observations of X then from the values corresponding to these observations $X_1,X_2,\cdots ,X_n$ we can, empirically, approximate the function $F_n\left(x\right)$ as follows:

$$F_n\left(x\right)=\frac{\mathrm{The}\mathrm{number}\mathrm{of}{X}_1,X_2,\cdots ,X_n\mathrm{that}\mathrm{is}\le x}{n}.$$

To apply the “Kolmogorov-Smirnov” test we use the following statistical quantities:

$$K_n^{+}=\sqrt{n}\underset{-\infty <x<\infty }{max}(F_n\left(x\right)-F\left(x\right))$$

$$K_n^{-}=\sqrt{n}\underset{-\infty <x<\infty }{max}(F\left(x\right)-F_n\left(x\right))$$

where $K_n^{+}$ measures the maximum deviation when $F_n$ is greater than F and $K_n^{-}$ measures the maximum deviation when $F_n$ is less than F.

The test applies, subsequently, the following steps, based on these functions:

• First, we take n independent observations $X_1,X_2,\cdots ,X_n$ corresponding to a certain continuous distribution function $F\left(x\right)$.
• We rearrange the observations so that they occur in non-descending order $X_{i_1}{X}_{i_2}\cdots X_{i_n}$.
• The desired statistical quantities are given by the following formulas:

  $$K_n^{+}=\sqrt{n}\underset{1\le j\le n}{max}\left(\frac{j}{n}-F\left(X_{i_j}\right)\right)$$

  $$K_n^{-}=\sqrt{n}\underset{1\le j\le n}{max}\left(F\left(X_{i_j}\right)-\frac{j-1}{n}\right)$$

After we have calculated the quantities $K_n^{+}$ and $K_n^{-}$,we compare them to the values in the test’s tables in order to decide whether the given sequence is uniformly random or not. Knuth recommends to apply the test with $n=1000$ using only two decimal places of precision.

Further to these two fundamental tests, we give below some more empirical tests which are used in conjunction with them.

4.1.3. Equidistribution or Frequency (Monobit) Test

This test checks if number of occurrences of each element, i.e. number produced by the PRNG, a is as it would be expected from a random sequence of elements. The Monobit case examines bits, i.e. it is applied on bit sequences but it can, also, be applied to any number range. Knuth suggests two methods for applying the test:

• Using the “Kolmogorov-Smirnov” test with distribution function $F\left(x\right)=x$, for $0\le x<d$.
• For each element a, $0\le a<d$, we count the number of occurrences of a in the given sequence and then we apply the “chi-square” test with degree of freedom $k=d-1$, and probability $p_a=\frac{1}{d}$ for each element (“bin”).

4.1.4. Serial Test

The serial test is, actually, an Equidistribution test for pairs of elements of the sequence, i.e. for alphabet (element) size $d^2$. Thus, the serial test checks that the pairs of numbers are uniformly distributed. For PRNGs with binary output, for instance, where $d=2$, the test checks whether the distribution of the pairs of bits, i.e. $(00,01,10,11)$ is as expected.

The test is applied in the following way:

• We count the number of times that pairs $(Y_{2j},Y_{2j+1})=(q,r)$ occur, for $0\le j\le n$, $0\le q,r<d$.
• We apply the “Chi-Square” test with $d^2-1$ degrees of freedom and probability $\frac{1}{d^2}$ for each category (i.e. $(q,r)$ pair).

For the application of the test, the following considerations apply:

• The value of n should be, at least, $10d^2$.
• The test can also be applied to groups of triples, quadruples, etc. of consecutive generator values.
• The value of d must be limited in order to avoid the formation of many categories.

4.1.5. Gap Test

This test counts the number of elements, or gap, that appear between successive appearances of particular elements in the sequence and then uses the Kolmogorov-Smirnov test to compare with the expected, from a random sequence, number of gaps. In other words, the test checks whether the gaps between specific numbers follows the expected distribution. In Knuth’s book, the test is defined for sequences of real numbers by examining the length of gaps between occurrences of $U_j$ over a specific range of these elements. As we discussed above, the test can easily transformed into a test for integer values.

In particular, if a, b two real numbers with $0\le a<b\le 1$, our goal is to examine the lengths of consecutive subsequences $U_j,U_{j+1},\cdots ,U_{j+r}$ such that $U_{j+r}$ is between a and b while all the other values are not. Thus, this subsequence of $r+1$ exhibits a gap of length r. In what follows, we give the algorithm that, given a, b and a sequence $U_0,U_1,\dots$ of real numbers, counts the number of gaps, as defined above, with lengths ranging over $0,\dots ,t-1$ as well as the number of gaps of length at least t, until n gaps have been computed.

Note that the algorithm terminates only when n gaps have been located (see step 6).

After the algorithm has terminated, we will have calculated the number of gaps of lengths $0,1,\dots ,t-$ and and of lengths at least t, in the array variables

$$COUNT\left[0\right],COUNT\left[1\right],\dots ,COUNT\left[t\right].$$

We can, now, apply the “Chi-Square” test with $k=t+1$ degrees of freedom using the, expected from a random sequence, probabilities below:

$$p_r=p{(1-p)}^r,0\le r\le t-1,p_t={(1-p)}^t.$$

(8)

In the probabilities in (8), we set $p=b-a$ which is the probability of the event $a\le U_j<b$. As stated in [12], the values $n,t$ are selected so that $COUNT\left[r\right]$ is expected to be at least 5 (preferably more than 5).

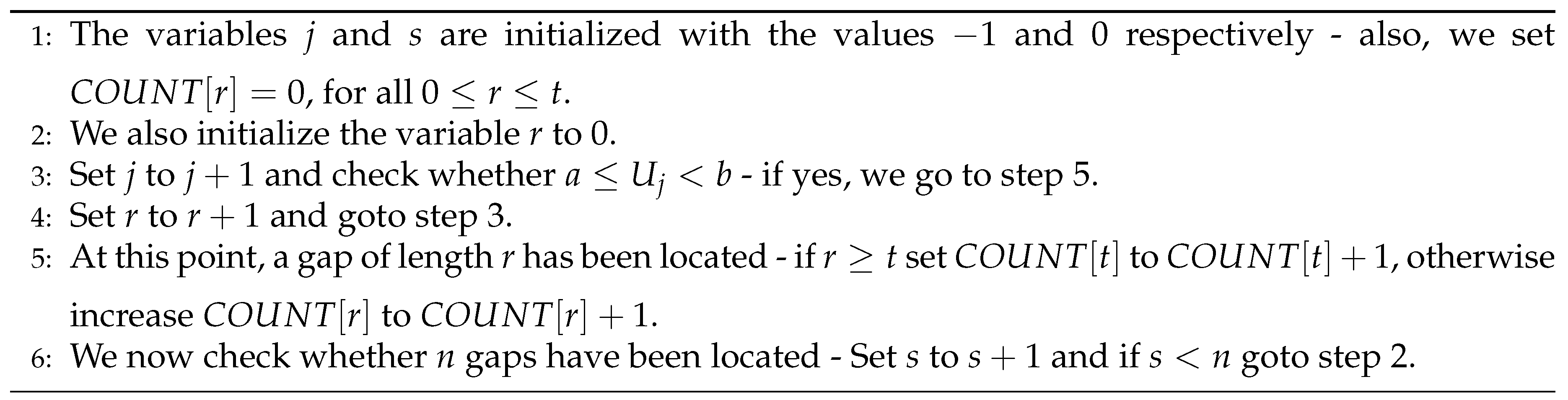
4.1.6. Poker Test

The Poker test proposed by Knuth involves checking n groups of five successive elements $\{Y_{5j},Y_{5j+1},Y_{5j+2},Y_{5j+3},Y_{5j+4}\}$, $0\le j<n$, with respect to whether one of the following seven element patters appears in them, where ordering does not matter:

• All 5 elements are distinct.
• There is only one pair of equal elements.
• There are two distinct pairs of equal elements each.
• There is only one triple of equal elements.
• There is a triple of equal elements and a pair of equal elements, different from the element in the triple.
• There is one one quadruple of equal elements.
• There is a quintuple of equal elements.

In other words, we study the distinctness of the numbers in each group of five elements. Next, we apply the “Chi-Square” test for the number of quintuples in the n groups 5 consecutive elements that fall within each of the 7 categories defined above.

We can generalize the reasoning of the test discussed above by considering n groups of k successive elements, instead of 5. Then we can calculate the number of k-tuples of successive elements which have rdistinct values. The probability $p_r$ for this event is given by the following equation (see [12] for the proof):

$$p_r=\frac{d(d-1)\cdots (d-r+1)}{d^k}\left\{\begin{array}{c}k\\ r\end{array}\right\}.$$

See Equation 6 for the computation of $\left\{\begin{array}{c}k\\ r\end{array}\right\}$, i.e. the Stirling numbers of the second kind.

4.1.7. Coupon Collector’s Test

Using the sequence $Y_0,Y_1,\cdots ,Y_n$, the Coupons collector’s test computes the lengths of the segments $Y_{j+1},\cdots ,Y_{j+r}$ required to obtain the complete set of integers from 0 up to $d-1$.

• Given the PRNG sequence $Y_0,Y_1,\cdots$, where $0\le Y_j\le d-1$, we count the lengths of n consecutive “coupon collector” samplings using the algorithm that follows. In the algorithm, $COUNT\left[r\right]$ is the number of segments of length r, $d\le r<t$, while $COUNT\left[t\right]$ is the number of segments of length at least t.
  Algorithm description:
  
• After the algorithm has counted n lengths, we apply the “Chi-Square” test to
  $COUNT\left[d\right],COUNT[d+1],\cdots ,COUNT\left[t\right]$ (i.e. the number of coupon collection steps of length r) with $k=t-d+1$ (degrees of freedom). The propabilities that correspond to these events are the following (see [12] for the derivation):

  $$p_r=\frac{d!}{d^r}\left\{\begin{array}{c}r-1\\ d-1\end{array}\right\}\mathrm{where}d\le r<t\mathrm{and}{p}_t=1-\frac{d!}{d^{t-1}}\left\{\begin{array}{c}t-1\\ d\end{array}\right\}.$$

4.1.8. Permutation Test

The Permutation test calculates the frequency of appearance of em permutations, i.e. different arrangements, of successive elements in a given number sequence.

More specifically, we divide the numbers of the given sequence into n groups of t elements each, i.e. we form the sets of t-tuples $U_{jt},U_{jt+1},\cdots ,U_{jt+t-1}$, $0\le j<n$. For each t-tuple we may have $t!$ possible permutations or categories. The test counts the frequency of appearance of each such permutation.

Note that for this test it is assumed that all numbers are distinct. This is justifiable if the $U_i$’s are real numbers (since the probability of equality of two real numbers is zero) but not justifiable for integer sequences. See [13] for a discussion of how to alleviate this assumption for the integer sequences of PRNGs.

The frequency of appearance of each permutation or category is calculated by the algorithm P below (see [12] for more details). The algorithm is given a sequence $U_1,U_2,\cdots ,U_t$ of distinct elements. Then it computes an integer $f(U_1,U_2,\cdots ,U_t)$ for which the following is satisfied: $0\le f(U_1,U_2,\cdots ,U_t)\le t!$ and $f(U_1,U_2,\cdots ,U_t)=f(V_1,V_2,\cdots ,V_t)$ if and only if $U_1,U_2,\cdots ,U_t$ and $V_1,V_2,\cdots ,V_t$ have the same relative ordering.

The steps of the algorithm are the following:

Finally, we apply the “Chi-Square” test for $k=t!$ degrees of freedom with probability of each permutation (category) equal to $\frac{1}{t!}$ (see [12] for more details).

4.1.9. Run Test

The Run test checks the lengths of maximal monotone subsequence of the given sequence, i.e. monotonically increasing or decreasing or “runs-up” and “runs-down” respectively. In other words, we consider the length of these monotone runs.

Note, however, that in the Run test we cannot not apply the “Chi-Square” test to the lengths of the monotone runs since they are, in general, not independent. Usually, a long run is followed by a short run etc. In order to handle this difficulty we apply the following procedure, which takes as input a sequence $(U_0,U_1,\cdots ,U_{n-1})$ of distinct real numbers:

• We use an algorithm that measures the lengths of the monotone runs (this is easy to accomplish).
• After the lengths have been computed, we calculate the statistical indicator V as follows:

  $$V=\frac{1}{n-6}\sum _{1\le i,j\le 6}(COUNT\left[i\right]-n{b}_i)(COUNT\left[j\right]-n{b}_j)a_{ij}.$$
  The values $a_{ij},b_i$ and $b_j$ are specific constants, which are given in [12] in matrix form. The value of V is expected to obey the “Chi-Square” distribution with six degrees of freedom and sufficiently large n, e.g. $n>4000$.

The same test can be applied to “runs-down”.

4.1.10. The Maximum t Test

The Maximum t test checks if the distribution of the maximum of t random numbers is as expected. The test works as follows, iterating over n subsequences of t values:

• We take the maximum value of the given t numbers, i.e. for all n subsequences, $0\le j<n$, $V_j=max(U_{jt},U_{jt+1},\cdots ,U_{jt+t-1})$.
• We apply the “Kolmogorov-Smirnov” test to the sequence of maximums $V_0,V_1,\cdots ,V_{n-1}$ with distribution function $F\left(x\right)=x^t$, $x\in [0,1]$. As an alternative, we can apply the Equidistribution test to the sequence $V_0^t,V_1^t,\cdots ,V_{n-1}^t$.

The verification of the test is to show that the distribution function of the $V_j$’s is $F\left(x\right)=x^t$. This is beacause the probability of the event $max(U_1,U_2,\cdots ,U_t)\le x$ is equal to the probability of the independent events $U_1\le x,U_2\le x,\dots ,U_t\le x$ which is equal to the product of the individual probabilities, all equal to x, which gives $x^t$.

4.1.11. Collision Test

The Collision test checks the number of collisions produced by the elements of a given number sequence. We want the number of collisions to be neither too high nor too low. Below, we explain the term collision and highlight the workings of the tetst.

The general experiment we consider is throwing balls in bins at random. When two balls appear in a single bin, we have a collision. In our case, the bins are the test categories and the balls are the sequence elements or observations to be placed into the bins or categories. In the Collision test the number of categories is assumed to be much larger than the number of observations (i.e. distinct numbers in the sequence). Otherwise, we can use direct “Chi-square” tests on the categories as before.

More specifically (see [12]) let us fix, for concreteness, the number of bins or categories m to be $2^{20}$ and the number of balls or observations n to be equal to $2^{14}$. In our experiment, we throw at random these n balls into the m bins. To this end, we will convert the U sequence of real numbers into a corresponding Y sequence of integers for an appropriate choice of d (see discussion in the beginning of Section 4.1).

In this example, we will evaluate the generator’s sequence in a 20-dimensional space using $d=2$, i.e. forming vectors of 20 elements 0 or 1. Each vector j has the form $V_j=Y_{20j},Y_{20j+1},\cdots ,Y_{20j+19}$, with $0\le j<n$.

Given m and n, the test uses an algorithm (see [12] to determines the distribution of the number of collisions caused by the n balls (20-dimensional vectors) when they are placed, at random, into the m bins. The corresponding probabilities are provided similarly as in the Poker test. The probability that c collisions occur in a bin is the probability that $n-c$ bins are occupied, which is given by

$$\frac{m(m+1)\cdots (m-n+c+1)}{m^n}\left\{\begin{array}{c}n\\ n-c\end{array}\right\}.$$

Since n and m are very large, it is not easy to compute these probabilities using the definition of the Stirling numbers of the second kind as given by Equation 6. Knuth has proposed a simple algorithm, called Algorithm S (see [12]) to approximate these probabilities through a process which simulates the placement of the balls into the bins.

4.1.12. Birthday Spacings Test

This test was proposed by G. Marsaglia in 1984 and it is included in the Diehard suite of tests. As in the Collision test, in the Birthday spacings test we randomly throw n balls into m bins. However, in this test the parameter m, the bins, represents the number of available “days in a year” and the parameter n represents “birthdays”, i.e. choices of days in a year.

We start by arranging the dates given n birthdays into of birth in non-descending order. That is, if the birthdays are $(Y_1,Y_2,\cdots ,Y_n)$, where $0\le Y_k<m$, they are sorted into non-decreasing order, say $Y_{\left(1\right)}\le Y_{\left(2\right)}\le \cdots \le Y_{\left(n\right)}$. Then we define the successive spacings between birthdays $S_1=Y_{\left(2\right)}-Y_{\left(1\right)},\cdots ,S_{n-1}=Y_{\left(n\right)}-Y_{(n-1)},S_n=Y_{\left(1\right)}+m-Y_{\left(n\right)}$ We, subsequently, rearrange the spacings into non-decreasing order, say $S_{\left(1\right)}\le S_{\left(2\right)}\le \cdots \le S_{\left(n\right)}$. Finally, we compute the distribution of the random variable R which counts the number these spacings which are equal: it is defined as the number of indices j, $1<j\le n$, such that $S_{\left(j\right)}=S_{(j-1)}$. This distribution of R depends on the specific values of m and n and we can focus on the cases $R=0,1,2$ and at least 3 (see [12]).

As suggested by Knuth, we repeat the test 1000 times and compare the distribution of R found empirically with this procedure with the theoretical distribution using the “Chi-square” test with $k=3$ degrees of freedom.

4.1.13. Serial Correlation Test

The idea behind the Serial Correlation test is to calculate the serial correlation coefficient, which is a statistical indicator of the degree to which the value of $U_{j+1}$, of a real number sequence, depends on the previous value $U_j$.

For a given sequence of numbers $U_1,U_2,\dots ,U_{n-1}$, the serial correlation coefficient is given by the formula below:

$$C=\frac{n(U_0{U}_1+U_1{U}_2+\cdots +U_{n-2}{U}_{n-1}+U_{n-1}{U}_0)-{(U_0+U_1+\cdots +U_{n-1})}^2}{n(U_0^2+U_1^2+\cdots +U_{n-1}^2)-{(U_0+U_1+\cdots +U_{n-1})}^2}$$

The correlation coefficient always ranges from $-1$ to 1. When C is 0 or close to 0, it indicates $U_{j+1}$ and $U_j$ are independent. If $C=\pm 1$, $U_{j+1}$ and $U_j$ are totally linearly dependent. Thus, it is desirable to have C equal or close to 0.

However, since the values $U_0$ and $U_1$ are not, in fact, entirely independent of the values of $U_1$ and $U_2$, C is not expected to be exactly zero. As suggested by Knuth, a good value for C is any value between ${\mu }_n-2{\sigma }_n$ and ${\mu }_n+2{\sigma }_n$ where

$${\mu }_n=-\frac{1}{n-1},{\sigma }_n^2=\frac{n^2}{{(n-1)}^2(n-2)}\mathrm{with}n>2.$$

For a good PRNG, we expect C to lie between these values around $95\%$ of the time.

4.2. The Diehard Suite of Statistical Tests

As we discussed in the introduction, George Marsaglia of the University of Florida has proposed the Diehard statistical test suite for testing PRNGs for randomness. This suite includes a series of statistical tests, similar in spirit as the tests described in Section 4.1, aiming at rejecting PRNGs that exhibit short period, patterns within the binary digits, and non-uniform distribution of numbers. Today the Diehard tests are considered among the most reliable since the algorithms that pass these tests unequivocally certify the random generation of numbers.

The Diehard tests include fifteen statistical tests information about these tests can be found in [11] (implementation and source code). Below, we provide a very brief description of the tests since they are close to the spirit of the tests in Knuth’s book [12] (see, also, Section 4.1):

• Birthday spacings: We select random points on a large interval. The spacings between the selected points should be, asymptotically, exponentially distributed (test connected with the Birthday Paradox in probability theory).
• Overlapping permutations: We analyze sequences of five consecutive numbers from the given sequence. The 120 possible orderings are expected to occur with, approximately, equal probabilities.
• Ranks of matrices: We choose a certain number of bits from the numbers in the given sequence and form a matrix over the elements $\{0,1\}$. We then determine the rank of the matrix and compare with the expected rank of a fully random 0-1 matrix.
• Monkey tests: We view the given numbers as “words” in a language. We count the overlapping words in the sequence of the numbers. The number of such “words;; that do not appear should follow the expected distribution (test based on the Infinite Monkey Theorem in probability theory).
• Count the 1’s: We count the 1’s in either successive or chosen numbers from the given sequence. We then convert the counts to “letters” and count the occurrence of 5-letter such “words”.
• Parking lot test: We randomly place unit radius circles in a 100×100 square area. We say that such a circle is successfully parked if it does not overlap with another already successfully parked circle. After 12000 such parking trials, the number of successfully parked circles should follow an expected normal distribution.
• Minimum distance test: We randomly place 8000 points in a 10000×10000 square area. We, then, calculate the minimum distance between all the point pairs. It is expectet that the square of this distance should follow the exponential distributed for a specific mean value.
• Random spheres test: We randomly select 4000 points in a cube of edge 1000. We, then, center a sphere on each of these points, where the sphere radius is the minimum distance to the other points. It is expected the the minimum sphere volume should follow the exponential distribution for a specific mean value.
• The squeeze test: We multiply 231 by random floating numbers in the range $(0,1)$ until we obtain as a result 1. We repeat this experiment 100000 times. The number of floating points required to obtain 1 should follow an expected distribution.
• Overlapping sums test: We produce a sufficiently long sequence of random floating points in the range $(0,1)$. We add the sequence formed by 100 successive floating point numbers. It is expected that these sums follow the normal distribution with a specific variance and mean values.
• Runs test: We generate a sufficiently long sequence of random floating points in the range $(0,1)$. We count ascending and descending runs. These counts should follow an expected, from random values, distribution.
• The craps test: We play 200000 games of “craps”, counting the winning games and the number of dice throws for each of these games. These counts should follow an expected distribution.

5. Application Domains Where Unpredictability Is Essential

In this section, we present the application of cryptographically secure generators in two domains where unpredictability is one of the major requirements, i.e. eLotteries and cryptographic key generation.

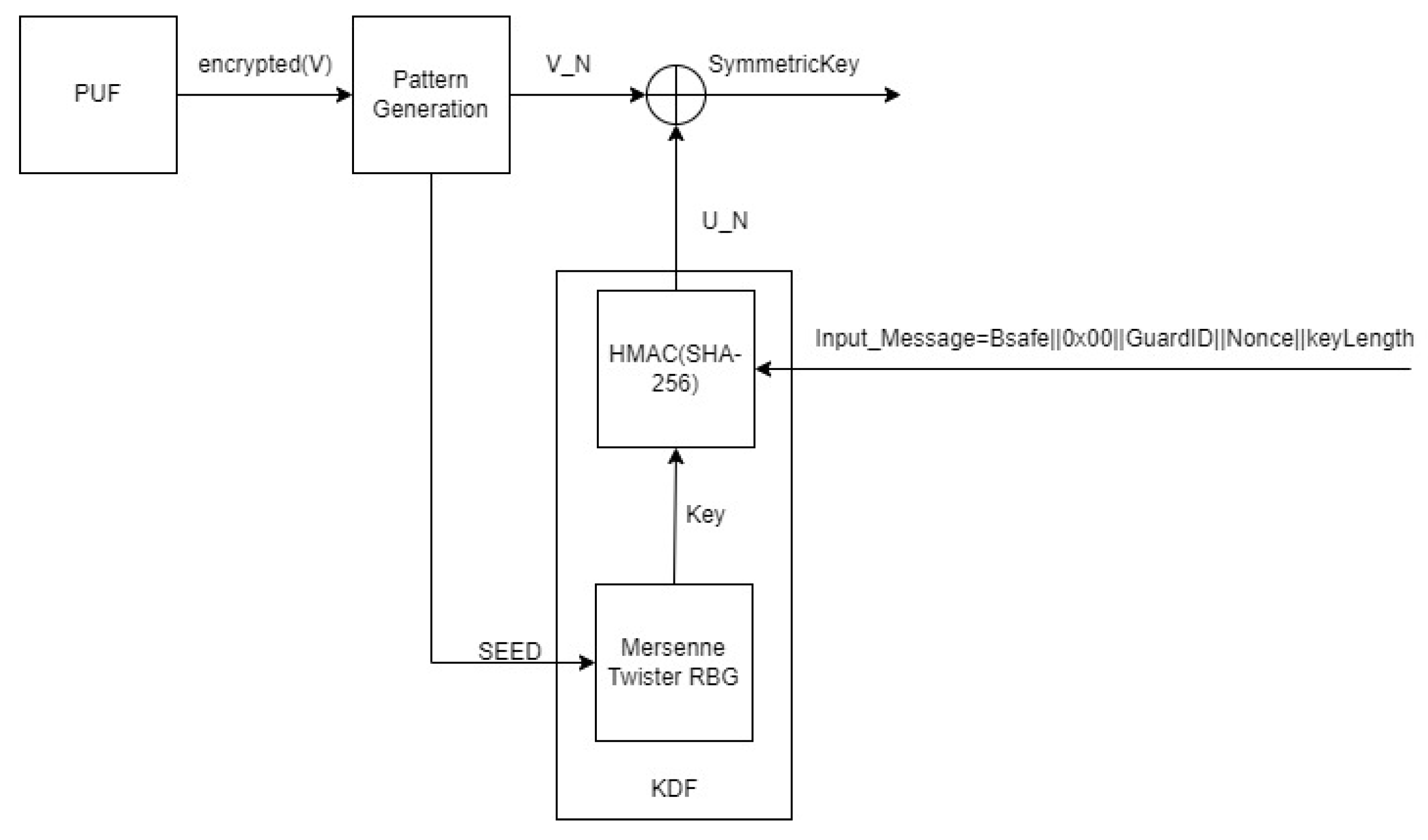
5.1. Cryptographic Key Generation

In cryptography there are many cases where random numbers are used. They are inputs in the generation of session and message keys for symmetric ciphers, and the generation of large prime numbers for RSA and ElGamal-style cryptosystems for asymmetric key generation. There are also multiple uses in network security where random numbers are used as nonces and challenges in various network protocols.

In this section, we present a mechanism for key generation of a symmetric cipher. In [2], various recommendations for the generation of either a symmetric key or asymmetric key pairs can be found. Let B be the key of a symmetric cipher of k-bit length. Then B shall be determined by

$$B=U\oplus V$$

where U is random bit sequence and V is a number determined independently of U. The only restriction is that the process used to create U should provide an entropy less than k-bit, i.e. the size of the key. There i no restriction for V. Its bits could be all zeros which means that U is used as a key straightforward, i.e. $B=U$.

In Figure 2, the structure of the PUF-based symmetric key generator that was developed under the project SafeIT (Section 6) is depicted. Random bit sequences were created by a PUF device. Then the sequence were transmitted to the key generator encrypted (RSA) using the TLS protocol. The entropy of the random bit sequence were greater than 1024-bit. The pattern generation module of the generator selects from this random bit sequence the seed for the key derivation function (KDF) and the value of $V_N$ where the index $N\le 1024$ determines the size of the key. The KDF generates the value of $U_N$ and the symmetric key is generated by $B=U_N\oplus V_N$. The size of the key is N. The KDF is based on the Mersenne Twister random bit generator and the one-way hash function SHA-256 which is a SHA-2 hash function. The input message of the hash function was constructed by the process that requests the symmetric key. Its format is the name of the module (e. g. BSafe in Figure 2) followed by $0x00$, the identification number of a guard, a nonce and the size of the requested key. We selected the hash function SHA-256 because the symmetric algorithm that we used was AES which operates for $128/192/256$-bit key size. Thus, the KDF could provide a key up to 256-bit.

5.2. Online Electronic Lotteries

Online elotteries is an application area where unpredictability of the produced numbers of each draw is an essential requirement. Naturally, in this application field where high financial stakes exist, more requirements are necessary to ensure the validity of each draw, such as the following:

• The produced numbers should obey the uniform distribution over the required number range.
• It should be infeasible for anyone (even the lottery owner and operator) to predict the numbers of the next draw, given the draw history, with a prediction probability “better” than the uniform over the range of the lottery numbers.
• It should be infeasible for anyone (even the lottery owner and operator) to interfere with the draw mechanism in any way.
• The draw mechanism should be designed so as to obey a number of standards and, in addition, there should also be a process through which it can be officially certified (by a lottery designated body) that these standards are met by the lottery operator.
• The draw mechanism should be under constant monitoring (by a lottery designated body) so as to detect and rectify possible deviations from the requirements.
• The details of the operation of the lottery draw mechanism should be publicly available for inspection in order to build trust and interest towards the lottery. In addition, this publicity facilitates auditing (which may be required by a country’s regulation about electronic lotteries).

One such lottery design has been proposed in [14,15]. A high-level description of the system components as well as their roles is shown in Figure 3.

The Generator and Verifier are the two fundamental interacting agents around which the protocol is built. In a high availability configuration, the Generator can be duplicated, although this is a system architecture-related decision, not necessary for the protocol we shall discuss.

To enable pair-wise secure communication, the Generator and the Verifier first execute a key-exchange protocol in order end up sharing a secret key. Additionally, each of them creates a private/public key pair for signing the exchanged communication messages. The Generator then enters an idle state and generates a packet of random numbers only upon the Verifier’s request for the next draw, continuing from the last produced draw.

From the Generator’s pool of truly random bits, drawn from physical sources like semiconductor elements (e.g shot noise), a series of random bits are chosen as seeds for the deployed software PRNGs.

As an alternative, the Generator may use its current internal state to construct the next state deterministically without utilizing any fresh truly random bits for reseeding the generators.

Next, in order to irrevocably link the seed and/or internal state with the coupon file, the Generator combines the drawn genuinely random bits and/or its current state (using the XOR operation) with the "em hash value" of the coupon file. As a result, the coupon file is effectively “frozen”, making it impossible to compare any future, unauthorized modifications to the internal state of the generator, which was committed and signed in the logs at the time the draw was initiated.

The Naor-Reingold function see [20]), which is a one-way pseudorandom function, is then applied to the created bit-sequence as a post-processing safety measure for additional randomization. Then, the software-based random number generators are seeded using this bit sequence. There are currently two block cipher-based generators (DES and AES) and two cryptographically secure pseudorandom number generators (RSA and BBS) that are utilized in our protocol, but any number of software-based generators can be employed in different output configurations. After that, the Generator signs the numbers generated using the final seed sequence using a bit-commitment mechanism. The Verifier receives the encrypted packet containing the committed to seeds and signed random numbers, and the Generator shuts down. The Verifier initially decrypts the received packet in order to get the signed numbers as well as the seed that the Generator is said to have used to generate these numbers. The Verifier then utilizes the seed to replicate the generator’s creation process after confirming that the generator has committed to the provided seed. The draw is deemed successful and is finished by the announcement of the winning numbers if the numbers produced match the numbers supplied by the generator. A warning is issued, the draw is canceled, and the Verifier starts it again (or takes some other step to ensure integrity and continuity) if the numbers received do not match the numbers supplied. Notice that the Verifier function performs an audit of the full drawing process, including the independent computation of the hashed version of the participating coupons and the internal generation of truly random bits (seeds).

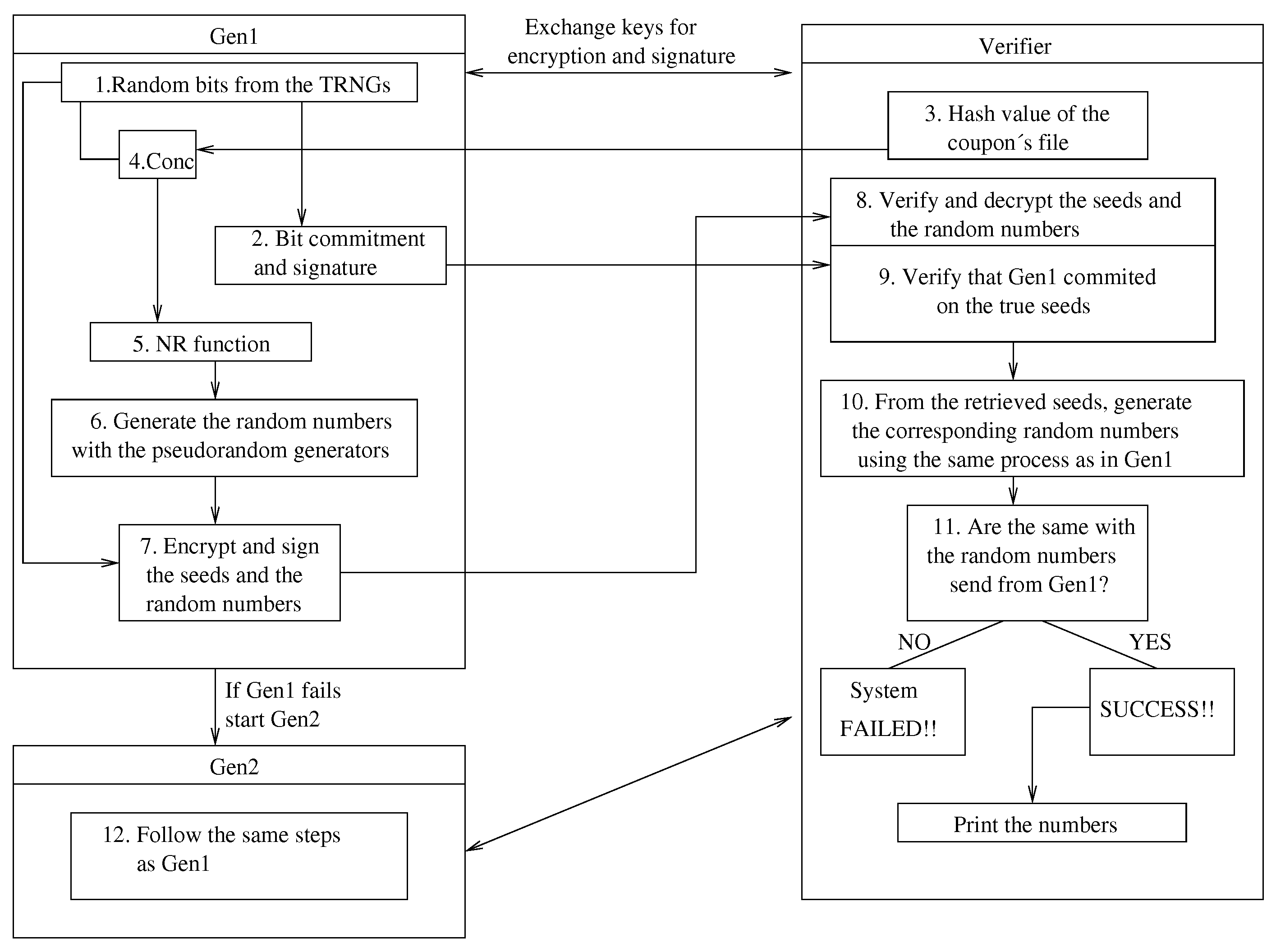
5.3. The Protocol Components

5.3.1. Prevention of Post-Betting

The ability to detect post-betting, i.e. to detect whether a coupon was placed into the coupon database after the winning numbers were produced by the generators, is an important requirement from the protocol. If such an illegal event is detected, the protocol must be stopped immediately and the current draw must be canceled without announcing the winning numbers.

This requirement can be easily satisfied by combining information characterizing the state of the coupon file just before the winning numbers are produced. The state can, also, include information about the truly random seeds obtained from physical sources in order to start the PRNGs of the lottery. For instance, we can use the coupon file’s hash value as the file’s state indicator for ensuring integrity and detecting subsequent, to the draw, efforts to modify it by inserting a new coupon. Then the has value of the coupon file along with the used seeds become input to a pseudorandom functions commonly used in cryptography such as the Naor-Reingold function. In this way, we can also detect insider attacks from corrupted lottery employees who have access to the winning numbers just shortly after they have been generated and before they are announced.

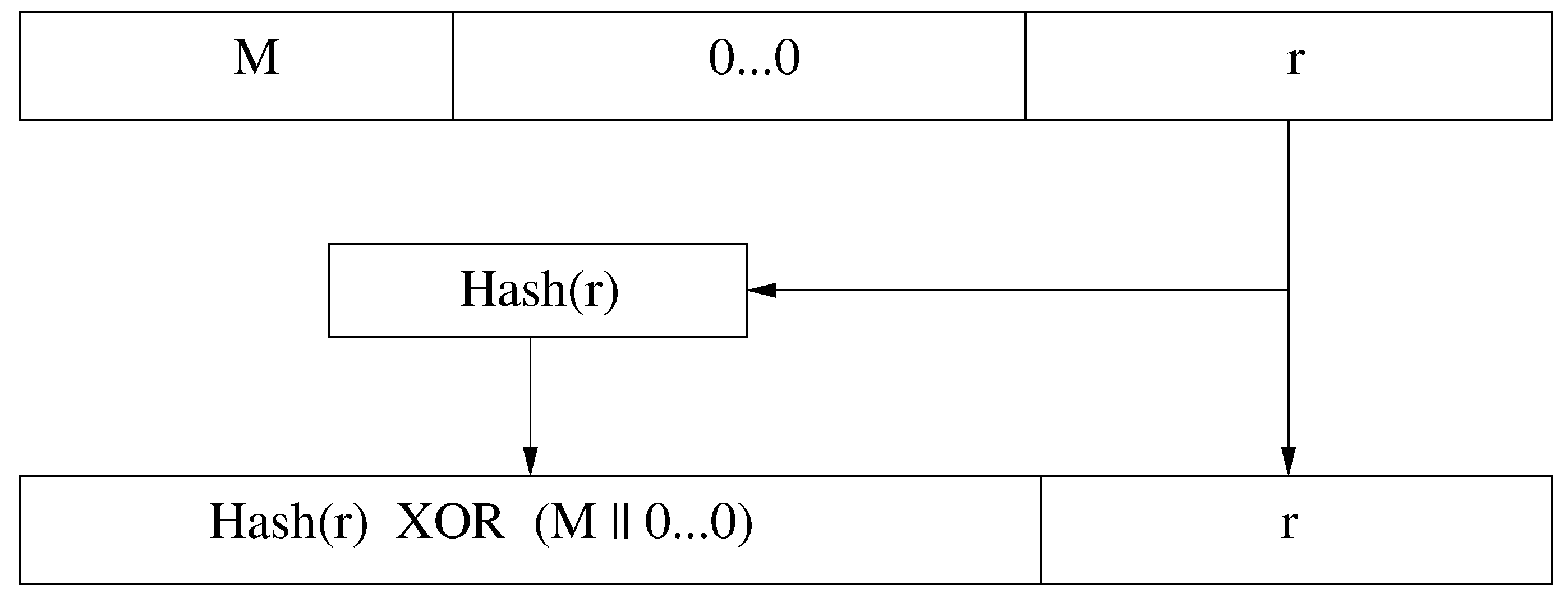
5.3.2. Signing the Numbers and Authenticating Their Source

Both the Generator and the Verifier create, during the lottery initialization process, their own RSA key pair and then exchange their public keys. Using their public keys, they create, jointly, a shared key which they, also, exchange.

Using the shared secret key the winning numbers and seeds from the Generator are encrypted and then signed with the Generator’s public key. After receiving this signed packet, the Verifier verifies the signature of the Generator and uses the shared key to decrypt the winning numbers and seeds. This encryption and signing process eliminates the risks inherent in authentication methods like verifying IP addresses of servers, exchanging password phrases, etc.

Finally, the RSA key pairs van be refreshed, periodically, as an additional security precaution.

5.3.3. Seed Commitment and Reproduction of Received Numbers

An issue that arises after the Verifier receives the winning numbers of the current draw is whether the numbers were, indeed, generated taking into consideration the coupon file’s hash value in order to avoid post-betting, as we explained earlier.

To accomplish this, after receiving the hash value from the Verifier (who has obtained the coupon file after the betting period is closed), the Generator draws a seed from the true random number generators, securely combines it with the hash value (e.g., XORs them together) and then em commits to the result using the Naor-Reingold function (see [20]) discussed below. This function is used to process the mixture of seeds derived from the truly random number generators as combined with the hash value of the coupons file. The result of this processing is given as input to the PRNGs deployed by the lottery (four in the case we study). Moreover, the quality of the seeding process is enhanced and the overall security of the random number generation protocol is enhanced with the employment of the NR function.

Following this processing, the result is transmitted, as a commitment from the Generator, to the Verifier. Then when the Generator produces the numbers of the current draw, the Verifier is able to recreate the numbers using the commitment from the Generator. If the numbers are the same then the verification process is successful. In this case, the current draw is considered valid and the winning numbers can be publicized. Otherwise, an alert is issued for investigating potential malfunction of the generators or an effort to interfere, maliciously, with the lottery operation.

With respect to the Naor-Reingold, or NR function for short, a key is a tuple $〈P,Q,g,\overrightarrow{a}〉$, with P a large prime, Q is a large prime divisor of $P-1$, g an element of order Q in $Z_P^{*}$ and $\overrightarrow{a}=〈a_0,a_1,\dots a_n〉$ a uniformly distributed sequence of $n+1$ elements in $Z_Q$. Given an input x of n bits, $x=x_1\dots x_n$, the NR function is defined as follows:

$$\begin{array}{c}\hfill {\tilde{f}}_{P,Q,g,\overrightarrow{a}}={\left(g^{a_0}\right)}^{{\prod }_{x_i=1}{a}_i}modP.\end{array}$$

In the specific implementation in [14,15], the sizes of P and Q were 1000 bits and 200 bits respectively. Note that, in general, a pseudorandom function is applied both for randomizing, further, the input value and serving as a commitment for the generation of the next winning number sequence, in the case of the lottery. This commitment is based on the Generator’s inputs, i.e. seeds from physical sources and coupon file’s hash value, so that its output (i.e. winning numbers) can be checked for validity. Since the NR function is pseudorandom, revealing input-output relationships does not affect its security. An alternative approach is the use of another “verifiable (pseudo)random function” as defined in [19].

Finally, the Simplified Optimal Asymmetric Encryption Padding, or SAEP protocol (see [5]) can be applied before passing the seeds from the NR function to the Generator. Using this protocol, a padding on the NR function’s output is computed towards security enhancement. More specifically, if M is the message to be encrypted, the SAEP protocol concatenates M with a sequence of 0s and, then, it appends to it a random number r. Then the hash value of r is computed which is XOR-ed with the message M and the 0s. The final message, for encryption,is the concatenation of the result of the XOR operation with the random number r. Finally, the message M is recovered by the receiving party using the reverse process. The SAEP protocol is summarized in Figure 4.

In the random number generation protocol examined in this section, the message M is composed of the seeds that must be sent from the Generator to the Verifier. After the SAEP protocol has been applied all the information is encrypted and signed with the Generator’s private RSA key. The result of this process is transmitted to the Verifier for the verification process.

After receiving the encrypted and signed packet from the Generator, the Verifier first validates the signature and then decrypts the message using the shared key with the Generator. Finally, the Verifier applies the reverse SAEP process retrieving the commitment (seeds).

An indicative key size for the encryption process is 1000 bits and for the signature 2000 bits. The number of 0s used in the SAEP protocol can be, approximately, 100. Also, the size of the random number r can be approximately 100. Finally, the rmd160 algorithm can be used as the hash function, among other suitable choices.

5.3.4. Incorporation of Several True Randomness Sources

The initial randomness, or seed, of a software PRNG must, eventually, be drawn from a source of true randomness or physical source. After considering the various sources of true randomness within a computer (e.g. /dev/random in LINUX, fluctuations in hard disk access times, motherboard clock frequency drift, etc.) and evaluating the trade-offs between ease of use and quality of output, it was decided to use commercial hardware generators known to pass a number of demanding statistical tests (e.g. Diehard - see Section 4.2 for a brief presentation of the tests).

Moreover, it was important to use several such true randomness sources (see Section 2) with their outputs XORed, since it is not uncommon to have, after some time, risky deviations in the physical characteristics of the devices from which the initial randomness (seed) is drawn. These fluctuations, in turn, may cause the appearance of detectable biases or patterns in the produced number sequences.

5.3.5. Mixing the Outputs of the Generators: Algorithms M and B

As we discussed in Section 3.2.4, algorithm M takes as input two sequences $X_n$ and $Y_n$ and combines them in order to produce a sequence of enhanced randomness properties. The algorithm, actually, shuffles the elements of the sequence $X_n$ using as indices the elements of the sequence $Y_n$. Thus, the elements of the new sequence are the elements of $X_n$ but in different order. Algorithm B is similar to M, but it requires only one sequence as input. The output is, again, a shuffled version of the input sequence. Both algorithms are described in detail in Knuth’s book [12].

In the lottery application we examine, however, the involved sequences are composed of 0s and 1s and, thus, we have implemented slightly different variants of M and B. Now algorithm M takes as inputs two bit sequences X and Y while algorithm B takes as input one bit sequence X. In what follows, $X_{out}$ is the output sequence.

Returning to the generators that the protocol uses, the BBS, RSA/Rabin, DES and AES generators, we can combine them in many ways so that the protocol can swap, periodically and (optionally) unpredictably, to different combinations for the generation of the winning numbers. For instance, at one moment we can use the BBS and DES generators, combined with the M algorithm, and at a later time RSA/Rabin with the B algorithm. This will make the lottery protocol more secure and less vulnerable to guessing attacks. Each of the four generators can be used alone or with the B algorithm. In addition, all four generators can be used in groups of two using the M algorithm and in groups of two, three and four, using the XOR operation on their outputs.

5.3.6. Capability for Dynamic, On-Line, Reconfiguration

The electronic lottery protocol deploys four software PRNGs based on RSA, BBS, DES and AES. It was desirable to implement the option of modifying periodically (or through an external signal from the Verifier) the subset of generators whose combined output is used for the lottery draws. This creates additional difficulty to an observer as the output number sequences will originate from different types of generators at different times of the lottery operation.

6. Conclusions

Is it possible to find a method for generating or simulating truly random phenomena, such as a sequence of bits corresponding to the flip of a fair coin, through a systematic procedure or algorithm? According to John von Neumann this question is contradictory and without meaning considering anyone who tries to construct random numbers using some algorithmic method is a sinner. The concept of “method” or systematic procedure appears to be incompatible with randomness at least with respect to a property of randomness which is essential in characterizing a sequence of observations as “randomness”: unpredictability. Through patient observation, the method can be, ultimately, revealed before the eyes of an observer, of sufficient time at her/his disposal, as in the famous game of Eleusis, the game of observation and deductive reasoning. Then, predicting the future workings of the method becomes trivial: just apply the method and obtain its outputs.

Thus, it appears that true randomness, in the sense of unpredictability at least, cannot be achieved by a systematic procedure or algorithm. Moreover, it is still not known whether true randomness exists since the universe may expand fully deterministically and its unpredictability may be simply due to the chaotic behavior of our modeling tools (e.g. non-linear differential equations). What is next, then, even if true randomness does not really exist?

The answer lies in the construction unpredictable, in some precise sense, pseudo-random number generators. The modern science of cryptography, which has its foundations in the science of complexity theory, provides us with tools for building methods which, iteratively, produce numbers whose observation gives absolutely no evidence of what the subsequent numbers will be, unless an extremely enormous amount of time is expended, which is prohibitive even for the fasted supercomputers that exist today or in the near and far future. In cryptography’s toolbox we have PRNGs based on the famous RSA public encryption scheme whose unpredictability is founded on the computational difficulty of the problem of finding prime factors of large integers, the BBS scheme based on the quadratic residuosity assumptions and its computational complexity repercussions, schemes based on other problems such as that of finding the discrete logarithm in a number field, the AES encryption algorithm as well as other “one-way” (i.e. easy to compute but difficult to invert) functions such as the SHA (Secure Hash Algorithms) class of hash functions.

Space limitations, however, do not allow us to continue any further. Our tour of the world of randomness was admittedly short and certainly not detailed or deep enough. What we would be glad to conclude, however, is that the introduction of computational complexity into fields of application where the word “method” suggests the commission of a “sin”, such as in the implementation of electronic lotteries, is possible thanks to the availability of a multitude of methods whose workings can be seen as the evolution of a fully deterministic phenomenon whose prediction becomes practically impossible due to the enormous computing power required.