Submitted:
29 August 2023
Posted:
29 August 2023
You are already at the latest version
Abstract
Keywords:
MSC: 05C17; 05C22; 05E45
1. Scientific Research
References
- Henry Garrett, “New Ideas In Recognition of Cancer And Neutrosophic SuperHyperGraph As Hyper Tool On Super Toot”, Curr Trends Mass Comm 2(1) (2023) 32-55. Available online: https://www.opastpublishers.com/open-access-articles/new-ideas-in-recognition-of-cancer-and-neutrosophic-super-hypergraph-as-hyper-tool-on-super-toot.pdf.
- Henry Garrett, “New Ideas In Recognition of Cancer And Neutrosophic SuperHyperGraph As Hyper Tool On Super Toot”, Curr Trends Mass Comm 2(1) (2023) 32-55. Available online: https://www.opastpublishers.com/open-access-articles/new-ideas-in-recognition-of-cancer-and-neutrosophic-super-hypergraph-as-hyper-tool-on-super-toot.pdf.
- Henry Garrett, “Some Super Hyper Degrees and Co-Super Hyper Degrees on Neutrosophic Super Hyper Graphs And Super Hyper Graphs Alongside Applications in Cancer’s Treatments”, J Math Techniques Comput Math 2(1) (2023) 35-47. Available online: https://www.opastpublishers.com/open-access-articles/some-super-hyper-degrees-and-cosuper-hyper-degrees-on-neutrosophic-super-hyper-graphs-and-super-hyper-graphs-alongside-a.pdf.
- Henry Garrett, “A Research on Cancer’s Recognition and Neutrosophic Super Hypergraph by Eulerian Super Hyper Paths and Hamiltonian Sets as Hyper Covering Versus Super separations”, J Math Techniques Comput Math 2(3) (2023) 136-148. Available online: https://www.opastpublishers.com/open-access-articles/a-research-on-cancers-recognition-and-neutrosophic-super-hypergraph-by-eulerian-super-hyper-Paths-and-hamiltonian-sets-.pdf.
- Henry Garrett, “Neutrosophic 1-Failed SuperHyperForcing in the SuperHyperFunction to Use Neutrosophic SuperHyperGraphs on Cancer’s Neutrosophic Recognition and Beyond”, J Math Techniques Comput Math 2(6) (2023) 221-307. Available online: https://www.opastpublishers.com/open-access-articles/neutrosophic-1failed-superhyperforcing-in-the-superhyperfunction-to-use-neutrosophic-superhypergraphs-on-cancers-neutros.pdf.
- Henry Garrett. Neutrosophic Co-degree and Neutrosophic Degree alongside Chromatic Numbers in the Setting of Some Classes Related to Neutrosophic Hypergraphs. J Curr Trends Comp Sci Res 2023, 1, 16–24. [CrossRef]
- Henry Garrett, “Super Hyper Dominating and Super Hyper Resolving on Neutrosophic Super Hyper Graphs and Their Directions in Game Theory and Neutrosophic Super Hyper Classes”. J Math Techniques Comput Math, 2022; 1, 242–263. [CrossRef]
- Garrett, Henry. “0039 | Closing Numbers and Super-Closing Numbers as (Dual)Resolving and (Dual)Coloring alongside (Dual)Dominating in (Neutrosophic)n-SuperHyperGraph.” CERN European Organization for Nuclear Research - Zenodo, Nov. 2022. [CrossRef]
- Garrett, Henry. “0049 | (Failed)1-Zero-Forcing Number in Neutrosophic Graphs.” CERN European Organization for Nuclear Research - Zenodo, Feb. 2022. CERN European Organization for Nuclear Research. [CrossRef]
- Henry Garrett, “Beyond Neutrosophic Graphs”. Dr. Henry Garrett. 2023. [CrossRef]
- Henry Garrett, “Neutrosophic Duality”. Dr. Henry Garrett. 2023. [CrossRef]
- Aaron, D. Aaron D. Gray, and Michael A. Henning, Paired-domination game played on Paths. Discrete Applied Mathematics 2023, 336, 132–146. [Google Scholar] [CrossRef]
- Walter Carballosa, and Justin Wisby. Total k-domination in Cartesian product of complete graphs. Discrete Applied Mathematics 2023, 337, 25–41. [CrossRef]
- R. R. Del-Vecchio, and M. Kouider, New bounds for the b-chromatic number of vertex deleted graphs. Discrete Applied Mathematics 2022, 306, 108–113. [CrossRef]
- M. E. Elaine et al., Bipartite completion of colored graphs avoiding chordless Paths of given lengths. Discrete Applied Mathematics 2022.
- R. Janczewski et al., Infinite chromatic games. Discrete Applied Mathematics 2022, 309, 138–146. [CrossRef]
- L. Li, and X. Li, Edge-disjoint rainbow triangles in edge- colored graphs. Discrete Applied Mathematics 2022, 318, 21–30. [CrossRef]
- W. Li et al., Rainbow triangles in arc-colored digraphs. Discrete Applied Mathematics 2022, 314, 169–180. [CrossRef]
- Z.Lu,andL.Shi,A sufficient condition for edge-colorable planar graphs with maximum degree 6. Discrete Applied Mathematics 2022, 313, 67–70. [CrossRef]
- Masih, and M. Zaker, Some comparative results concerning the Grundy and b-chromatic number of graphs. Discrete Applied Mathematics 2022, 306, 1–6. [CrossRef]
- F. Wu et al., Color neighborhood union conditions for proper edge-pancyclicity of edge-colored complete graphs. Discrete Applied Mathematics 2022, 307, 145–152. [CrossRef]
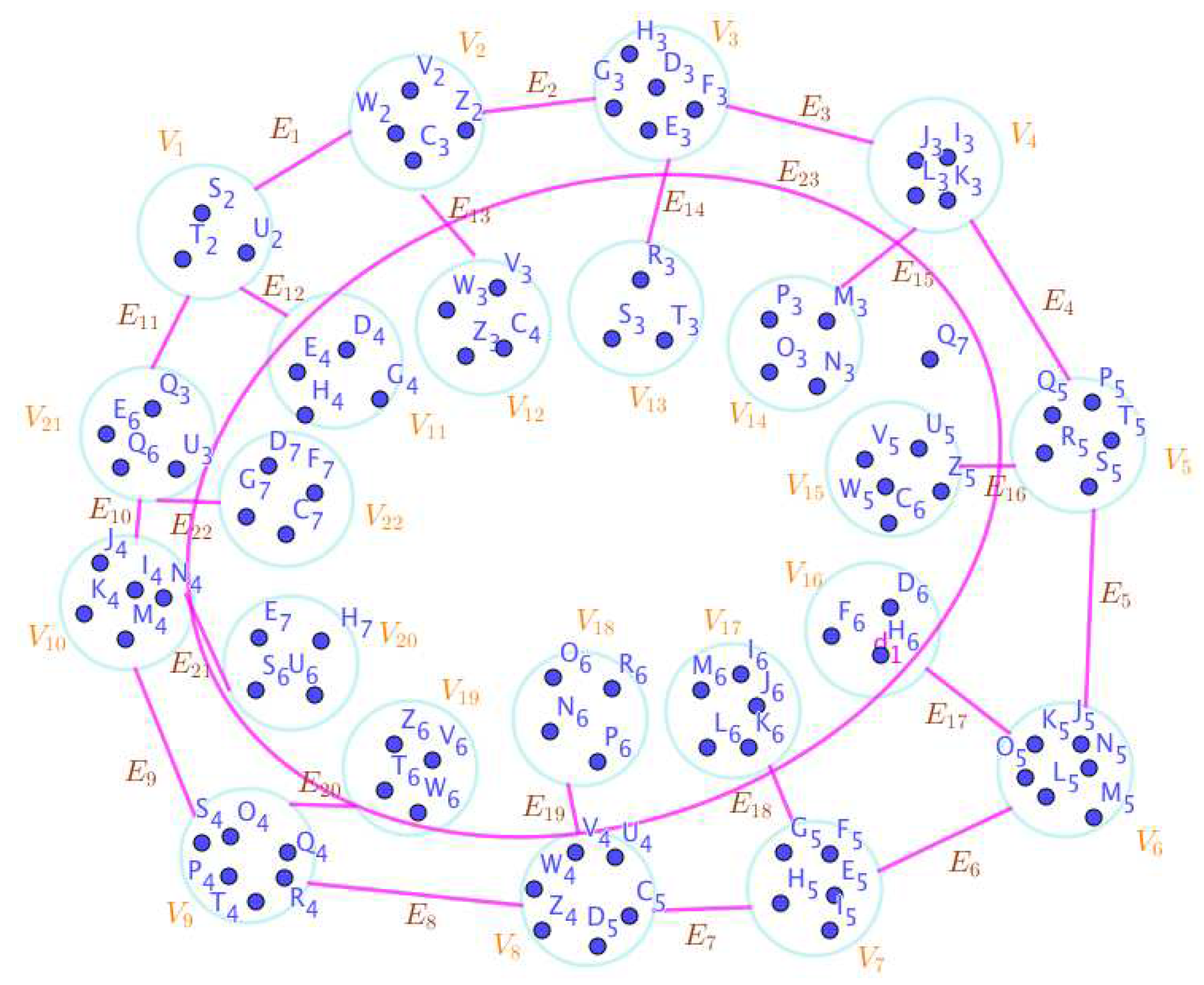
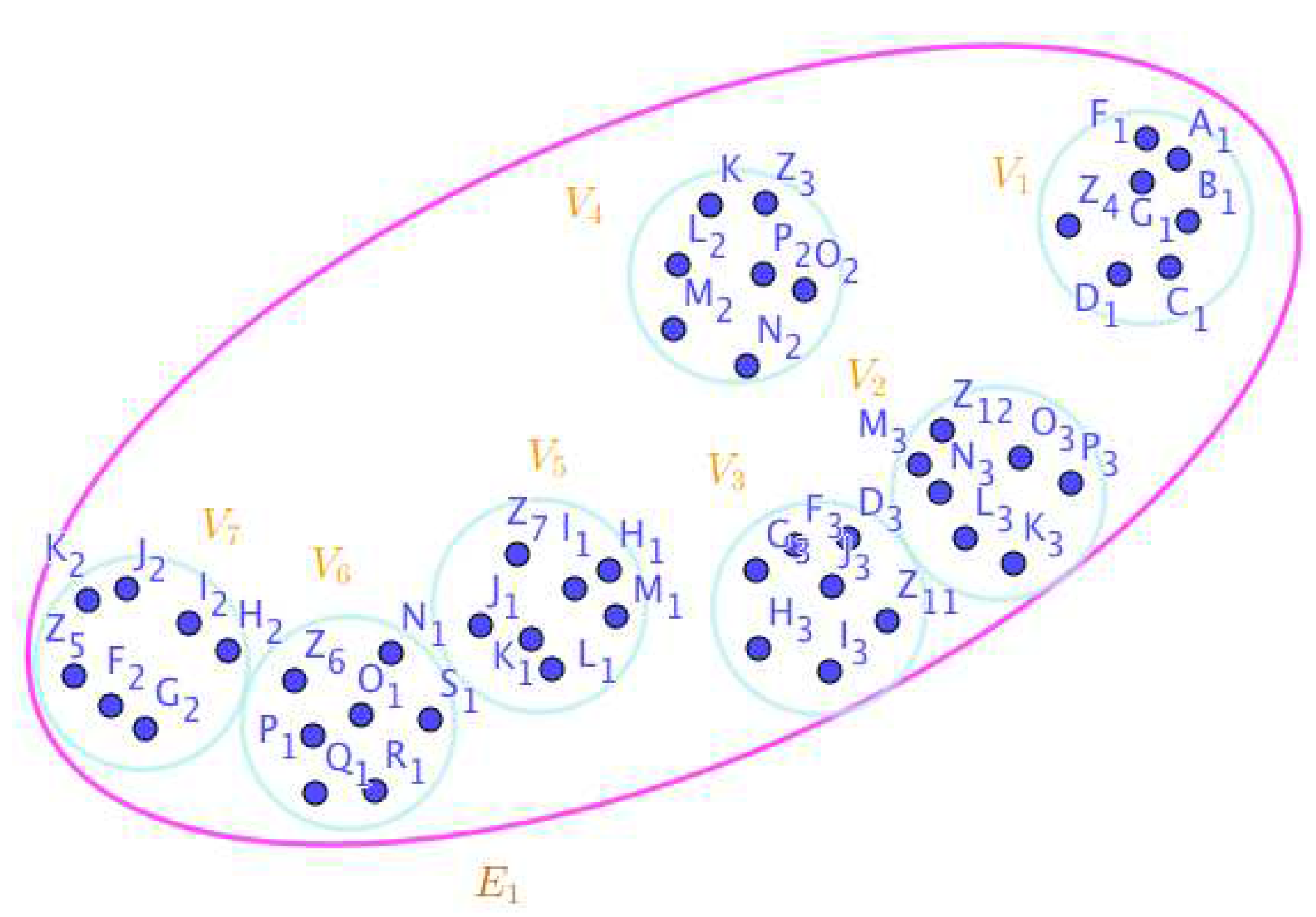
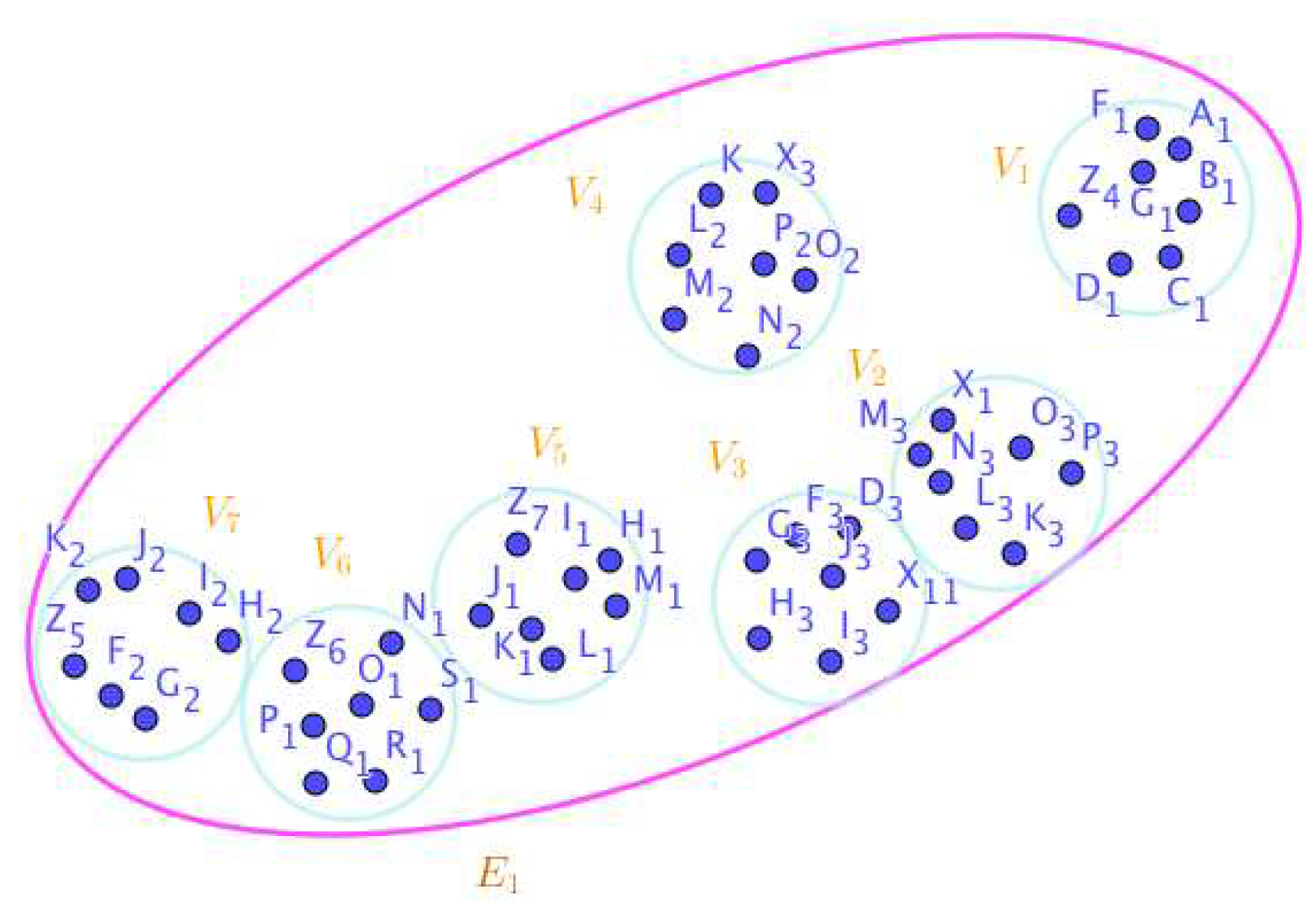

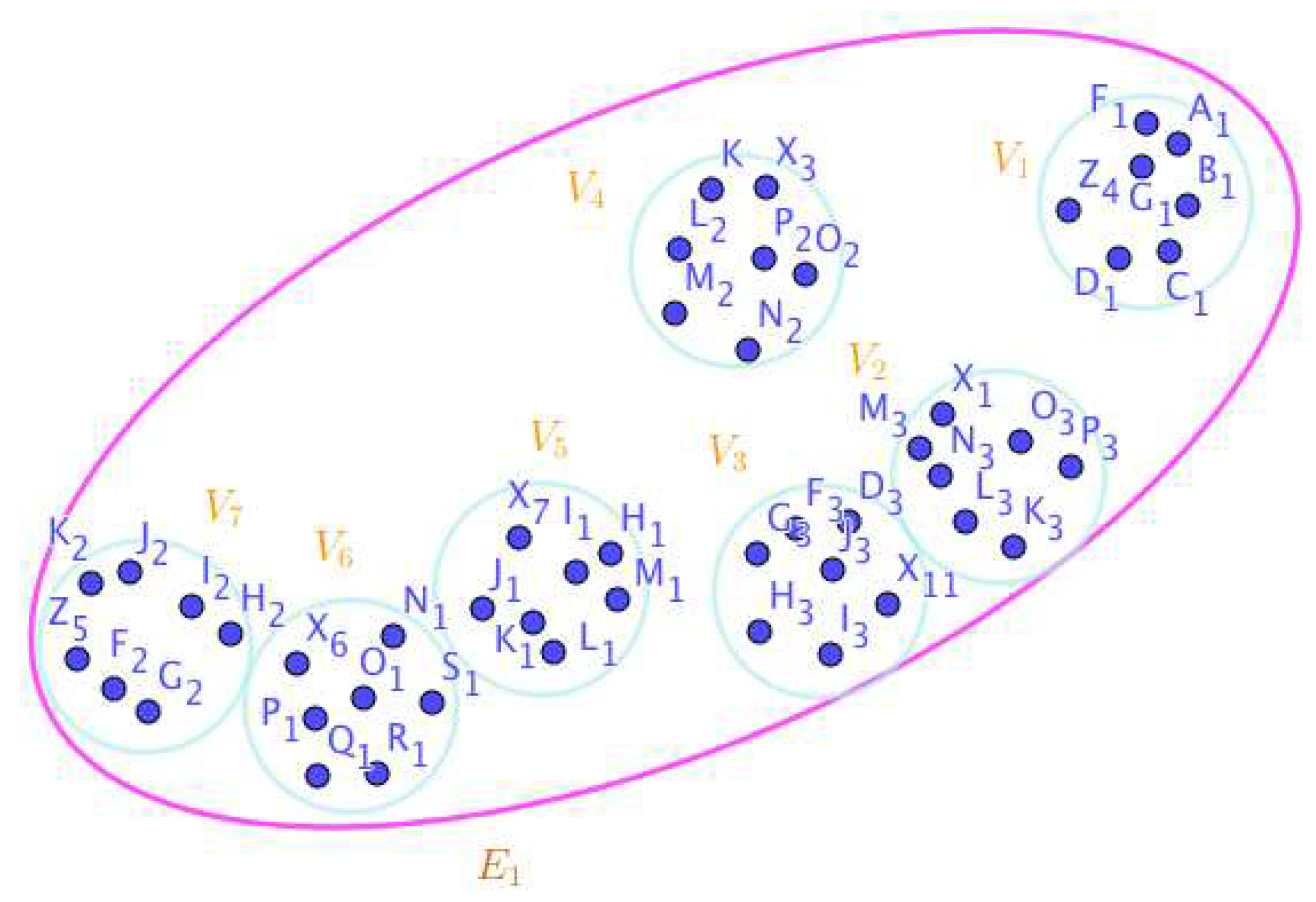
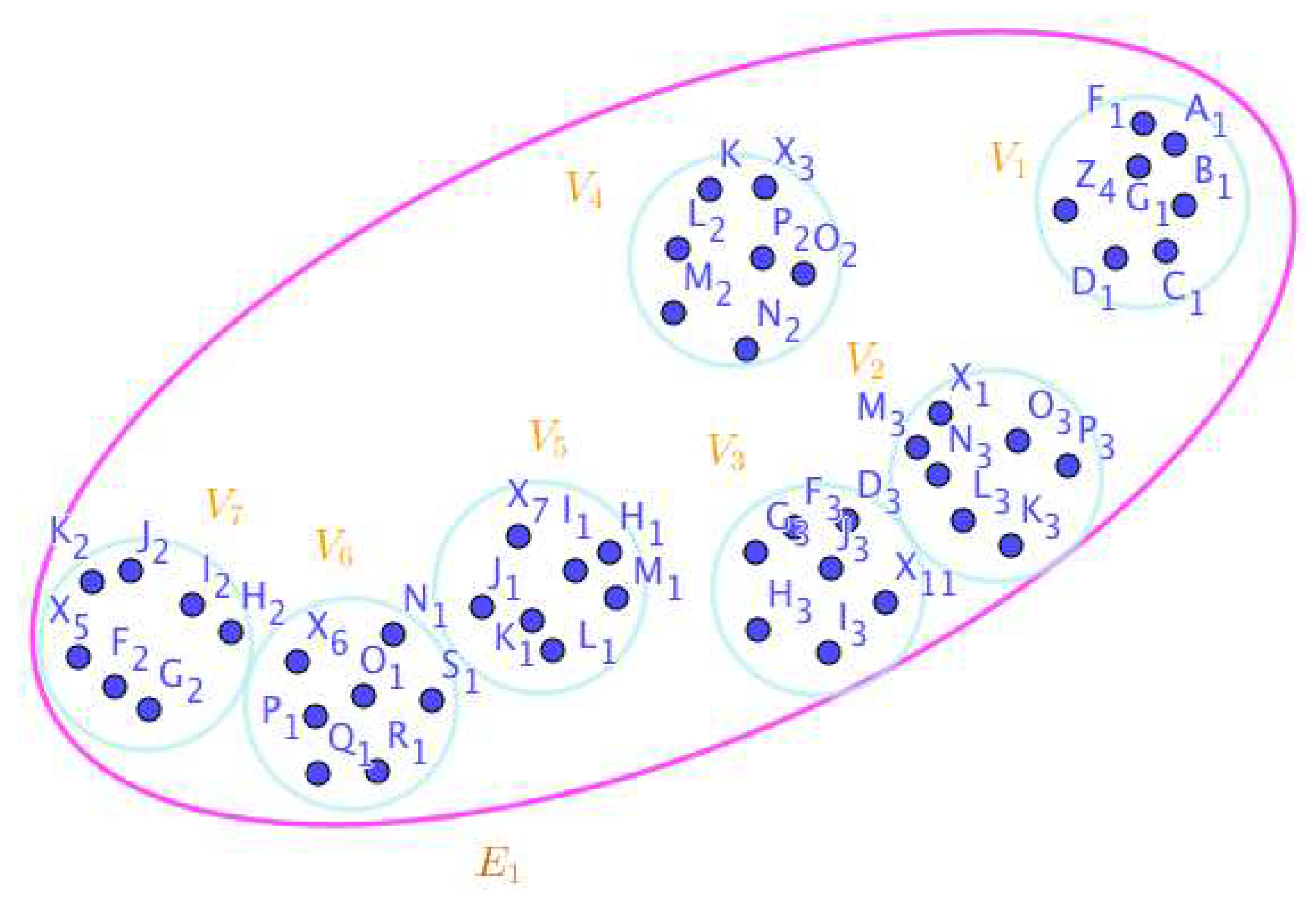
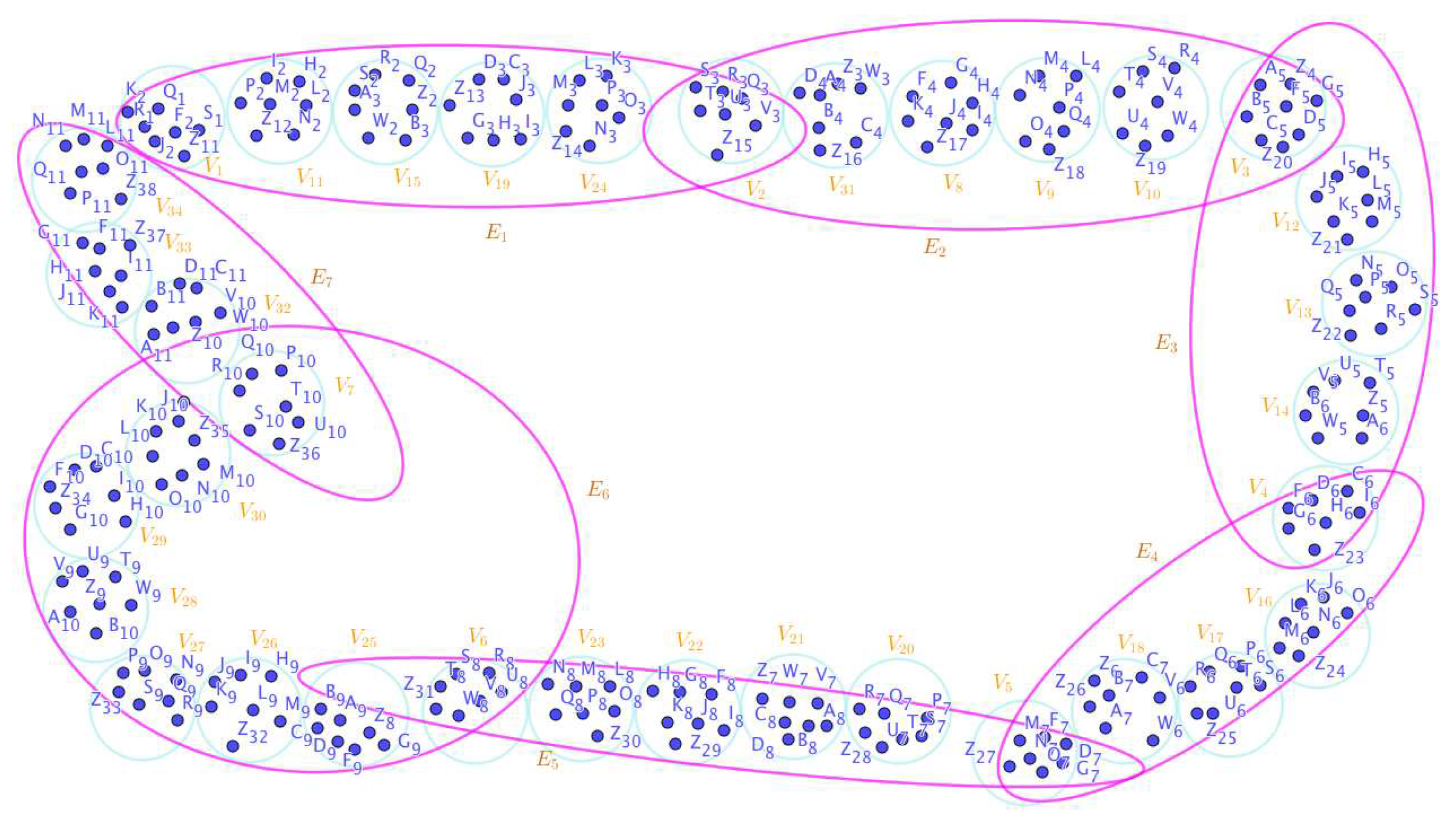
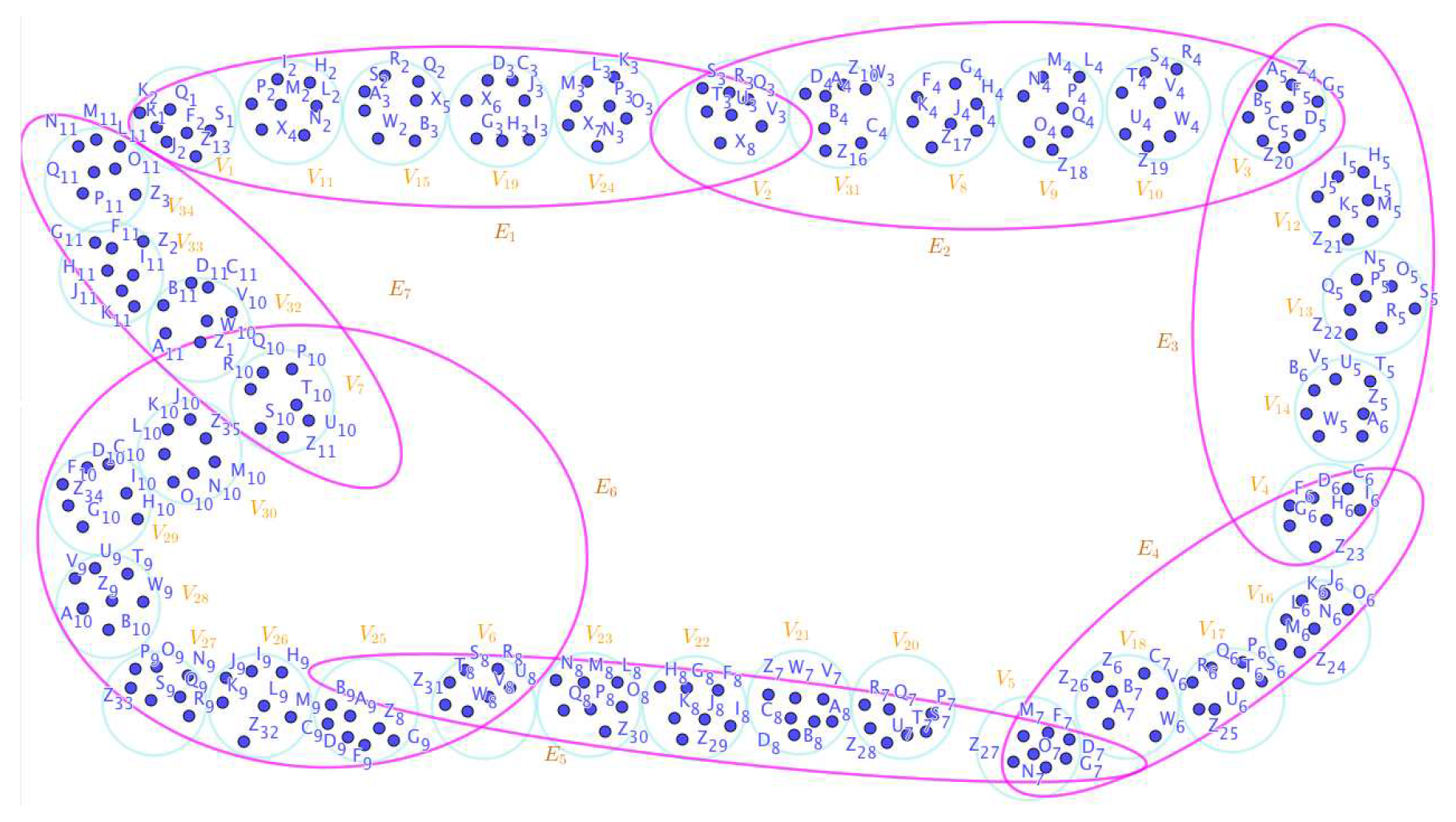
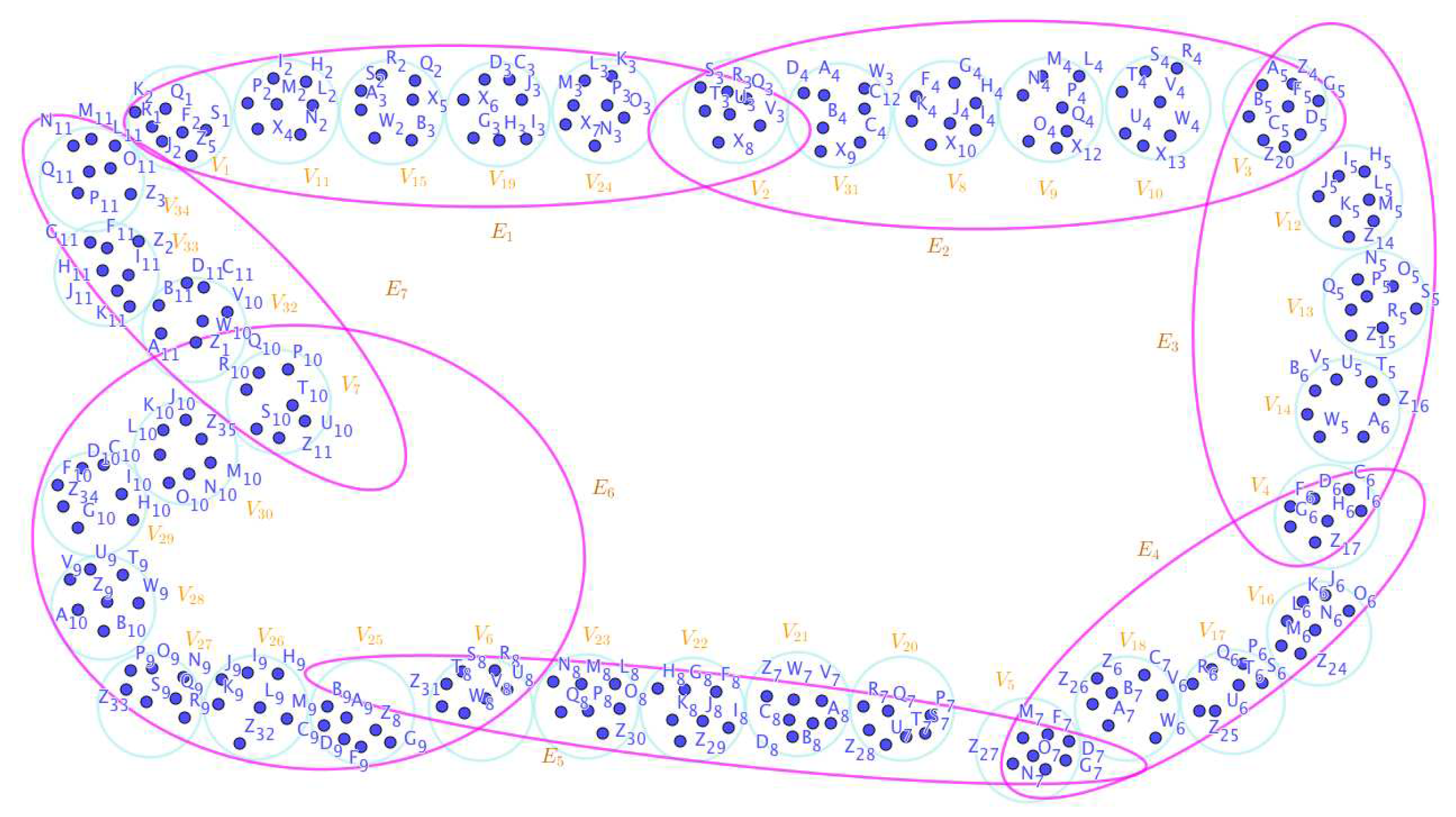
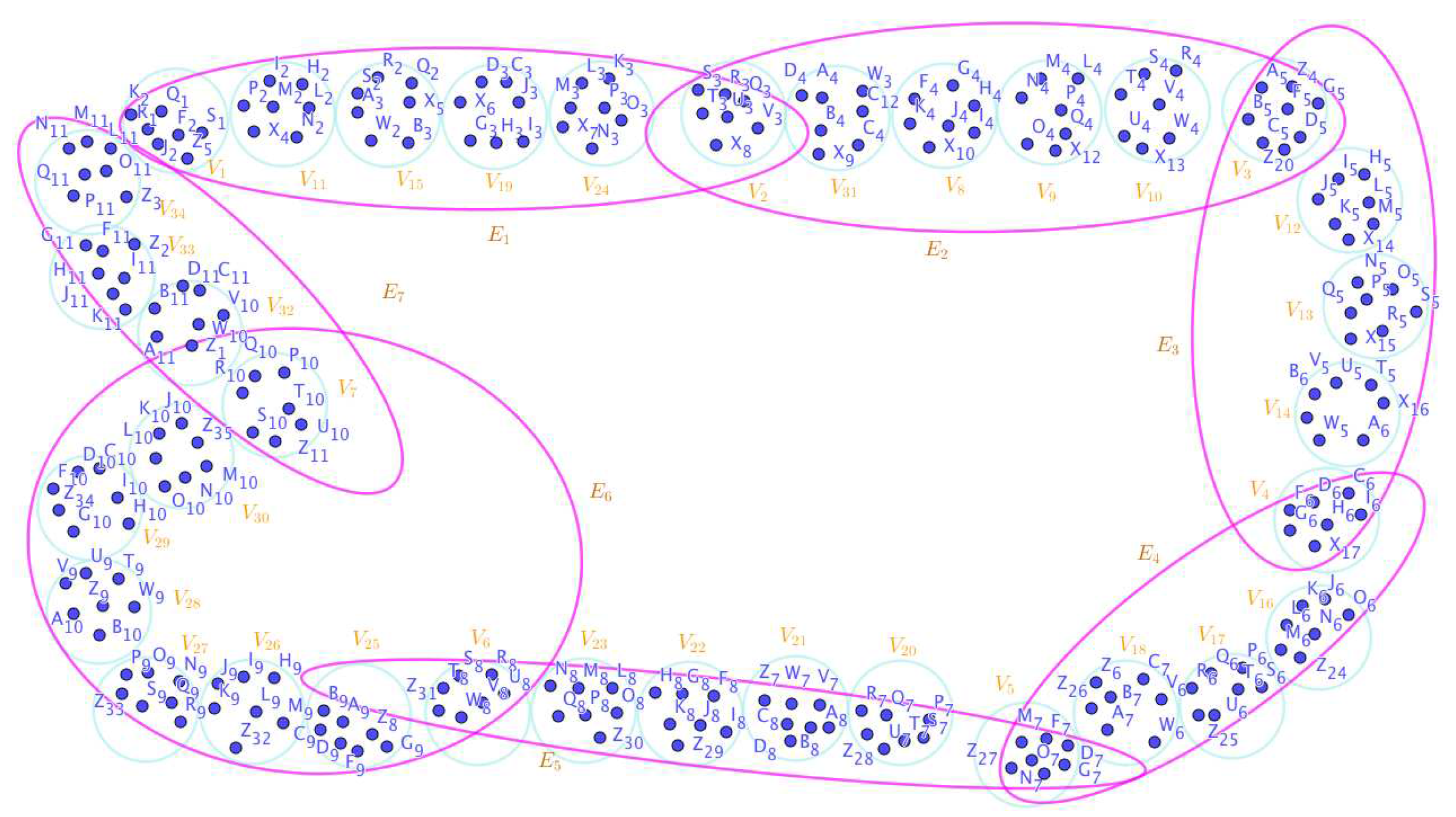
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




