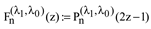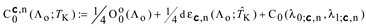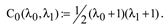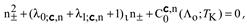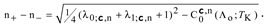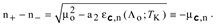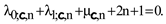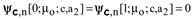Use of Normalizable Seed Solutions for Constructing

Preprint

Article

Use of Normalizable Seed Solutions for Constructing

Altmetrics

Downloads

Views

Comments

Gregory Natanson^*

This version is not peer-reviewed

Submitted:

15 August 2023

Posted:

17 August 2023

You are already at the latest version

Alerts

Abstract

The paper examines rational Darboux-Crum transforms (RDCTs) of the Jacobi-reference (JRef) potential on the line, with an emphasis on the transformations using only normalizable seed solutions. The Cooper-Ginocchio-Khare (CGK) potential constitutes the simplest example of this rich family of exactly solvable one-dimensional (1D) potentials. It was explicitly confirmed that that an arbitrary Darboux-Crum transformation (DCT) of the given Sturm-Liouville equation (SLE) can be represented as a chain of sequential Darboux deformations of the associated Liouville potentials. If the rational SLE (RSLE) under consideration is exactly solvable and the transformation function (TF) used at each step is nodeless then each RSLE constructed in such a way was proven being exactly solvable itself. The exact solvability of RDCTs of the JRef canonical SLE (CSLE) was also confirmed for the DCTs using pairs of juxtaposed eigenfunctions (an extension of the renowned Adler theorem to the RCSLEs of our interest). By re-expressing the reference polynomial fraction (RefPF) of the transformed CSLE in terms of the Krein determinant (KD), instead of Crum Wronskian (CW), it was shown that the eigenfunctions under consideration are expressible in terms of polynomial solutions of a generalized Heun equation with positions of the most poles dependent on the exponent parameters. The outlined technique was extended to two isospectral SUSY partners of the JRef potential (as well as to its third sibling with the inserted new lowest-energy level) which, by analogy with the CGK potential, are quantized by polynomial solutions of the 2-Heun equation with all four poles at some fixed positions on the real axis.

Keywords:

Subject: Computer Science and Mathematics - Analysis

1. Introduction

About thirty years ago Cooper, Ginocchio, and Khare [1] presented a counter-example to Gendenshtein’s famous claim [2] that any exactly solvable potential is necessarily shape-invariant. To counter Gendenshtein’s conjecture, these authors applied the state-erasing Darboux transformation (DT) to the generic (implicit) rational potential [3] exactly quantized in terms of classical Jacobi polynomials with degree-dependent indexes. Since the corresponding canonical Sturm-Liouville equation (CSLE) can be converted by an energy-dependent gauge transformation to the Jacobi differential equation with the exponent parameters depending on the polynomial degree we refer to it as ‘Jacobi-reference’ (JRef) and use the same epithet for the aforementioned potential obtained from this CSLE by the Liouville transformation [4] on the finite interval (0, 1). As it was realized more recently by the author [5] the signature feature of the ‘quasi-rational’ [6] transformation function (TF) used in [1] to generate the corresponding Liouville potential (referred to below by the acronym ‘CGK’) is that its analytical continuation into the complex plane remains finite at any regular singular point of the JRef CSLE so new poles arise only at zeros of the density function in question.

Concurrently with [1] Rudyak and Zakhariev published their pioneering study [7] on the so-called ‘generalized’ DTs of the generic CSLE. In [8] we re-interpreted the transformations introduced by Rudyak and Zahariev as three-step operations:

(i): the Liouville transformation from the CSLE to the Schrödinger equation;
(ii): the Darboux deformation of the corresponding Liouville potential;
(iii): the reverse Liouville transformation from the Schrödinger equation to the new CSLE using the same change of variable as at Step (i).

Thereby we termed these operations as the canonical Liouville-Darboux transformations (CLDTs). It was however understood by us later [9] that one can apply this three-step definition of the generalized DT to any SLE obtained from the given CSLE by a gauge transformation provided the three-step operation in question preserves both leading coefficient function and weight function of the original SLE. For this reason we refer to these transformations of SLEs simply by the acronym ‘LDTs’.

As originally proved by the author in [5] and them more thoroughly analysed in [10] the lowest energy eigenfunction c0 is always accompnaied by the three other basic non-normalizable solutions t0 of the distinct types t =a, b, and d (types I, II, and III in Quesne’s terms [11,12,13]) as far as the so-called [10] ‘tangent polynomial’ (TP)

T_{K} [z]

in the numerator of the rational density function

ρ [z; T_{K}]

has two simple real roots. Here, in following our early study [14] on DTs of centrifugal-barrier potentials (long before the birth of the SUSY quantum mechanics [15,16,17] , the labels a and b are used to identify principal Frobenius solutions (PFSs) near the lower and upper ends of the quantization interval [0, 1] whereas the quasi-rational solution (q-RS) of type d is irregular near both singular endpoints. Note that Sukumar in his pioneering study [17] on SUSY partner of radial potentials a nearly decade later arranged these four types of FFs in a slightly different order: a= T₃, b = T₄, c= T₁, d = T₂.

As illustrated in Appendix A the existence of the quartet of the basic solutions t,0 (t = a, b, c, and d) for the density function with two simple zeros on the real axis outside the interval [0, 1] can be explicitly confirmed for the so-called [10] ‘asymptotically levelled’ (AL) JRef potential with the energy spectrum expressible in an algebraic form. The use of non-normalizable TFs from this quartet in addition to the nodeless eigenfunction c,0 brings us to four Fuschian CSLEs with two extra second-order poles at the TP zeros (besides the two persistent second-order poles at 0 and 1). Each CSLE thus represents the canonical forms of ‘2-Heun equations’ (in Hounkonnou and Ronveaux’s terms [18]). Each of the four CSLEs can be then converted by energy-dependent gauge transformations to the 2-Heun equation with polynomial solutions at the energies of all the possible real q-RSs of the JRef CSLE.

In [9] we introduced the concept of the so-called ‘prime’ form of the CSLE chosen in such a way that that the chacteristic exponents (ChExps) of the Frobenius solutions near the singular endpoints have exactly the same absolute value but opposite signs. As a result the the Dirichlet boundary condition (DBC) imposed on the general solution of the prime SLE automatically selects the PFS near the endpolint in question. One of the advantages of formulating the spectral problem as the Dirichlet problem for the prime SLE is that we can automatically adopt the rigorous theorems proven in [19] for SLEs solved under the DBCs.

As pointed to in [9] the requirement for the TP to remain finite at both endpoints assures that the density function has second-order poles at these points and as a result the corresponding Liouville transformation leads to the one-dimensional (1D) Schrödinger equation on the line. It is worth mentioning in this context that the Liouville-Darboux transforms (LDTs) of the exactly solvable prime SLE are not necessarily exactly solvable if the endpoint is a limit-circle (LC) singularity [20]. In particular the LC endpoints exist if the density function has a simple pole at one of the endpoints so [3] the corresponding Liouville transformation results in the radial Schrödinger equation. As a result some of DTs may violate the conventional rules of the SUSY quantum mechanics [21].

It should be stressed that we make persistent references to the Schrödinger equation with solvable rational potentials solely because the RCSLEs represented in their Liouville form have broad applications in quantum mechanics so the results can be formulated in more familiar terms. However our current study is mostly devoted to exactly solvable rational Sturm-Liouville problems. Note also that Everitt’s catalogue of Sturm–Liouville differential equations [20] includes only some samples of exactly solvable CSLEs (renowned due to their quantum-mechanical analogs), while disregarding their generalizations presented in our paper [3] as well as the extension of our technique to the Fuchsian RCSLE with two poles on the imaginary axis [22].

The paper is structured as follows. In Section 2 we convert the JRef CSLE to its prime form and show that the solutions of the latter SLE obey the DBCs iff the corresponding solutions of the CSLE are squarely integrable with the weight

ρ [z; T_{K}]

In Section 3 we prove that the LDT of a PFS of the prime SLE near each endpoint obeys the DBC for the given end and as a result is itself the PFS of the transformed prime equation at the given energy unless the TF is a PFS on its own and thereby is nullified by the LDT in question. Assuming that the LDT is admissible (i.e. the given TF preserves its sign inside the quantization interval) it directly follows from the proven theorem that the LDT of any eigenfunction of the SLE under consideration is an eigenfunction of the transformed SLE (again putting aside the case when the TF for the given LDT represents the nodeless eigenfunction). Since the same assertion holds for the reverse LDT we conclude that any admissible LDT of any exactly solvable SLE is itself exactly solvable.

In Section 4 we apply the formulated theorem to the CGK potential and its three siblings constructed by the LDTs using as their TFs the three unnormalizable basic solutions t,0 with t =a, b, and d. It is proven that the eigenfunctions of the corresponding CSLEs are expressible in terms of polynomial solutions of four 2-Heun equations with two of the four exponent parameters dependent of the polynomial degree.

In Section 5 we analyze the transformations of the JRef CSLEs defined via Schulze-Halberg’s generic extention [23] of Crum’s [24] renowned formalism. As shown in Appendix B each CSLE constructed in such a way can be allternatively obtained by applying a LDT to the CSLE generated at the previous step. We then convert the CSLEs in question to the Krein form [25] and then take advantage of the fact that the Krein determinant (KD) is formed by seed functions and their first derivatives, in contrast with the Crum Wronskian (CW) requring computation of higher derivatives of the seed functions in question. We refer the reader to Appendix C and D below for more details on this non-conventional representation of the Darboux-Crum transforms (DCTs) of CSLEs. Making advantage of the Krein representation of the CWs formed by q-RSs we express the eigenfunctions of our interest in terms of the so-called ‘polynomials determinants’ (PDs) originally introduced by us in [9] and prove that the latter polynomials represent solutions of Heine-type differential equations. Again the anomalous feature of the derived equations is that two exponent parameters for the poles at 0 and 1 as well as the poistions of all othere poles (excluding the TP zeros) depend on the polynomial degree. In Appendix E we illustrate some results of this Section for the double-step Darboux-Crum transformation (DCT) using two basic solutions as its seed functions. In following [26] we term a LDT of a RCSLE as ‘rational LDT’ (RLDT) if its TF has a quasi-rational form so the given transformation leads to a rational CSLE.

The outlined technique was used to construct the Crum chain of exactly solvable Fuchsian RCSLEs using the nodeless eigenfunction as the TF for each LDT in the chain. The same procedure was also applied to two sibling potentials obtained from the JRef potential by the LDTs using the basic solutions a,0 and b,0 as their TFs. The Liouville transformations of the RCSLEs constructed in such a way thus result in the new SUSY family of the exactly solvable multi-indexed rational potentials formed by isospectral triplets.

In Section 6 we extend Adler’s arguments [27] to the DCT of an exactly solvable RCSLE using as seed solutions a pair of ‘juxtaposed’ [28,29,30] eigenfunctions with overlacing zeros between 0 and 1. Since the first eigenfunction used as the TF has at least one node inside the quantization interval the corresponding LDT results in a RCSLE with an interior singularity at this node so the corresponding Dirichlet problem cannot be analytically solved. However, as proven here, the second LDT brings us back to the exactly solvable CSLE with no interior singularities.

Finally we summarize the main results of our analysis in Section 7. The paper is accompanied by the five Appendicesmentioned above,

2. Exactly Solvable Fuchsian SLE with Two Second-Order Poles on Real Axis

As originally demonstrated by the author [3] the eigenfunctions of the Fuchsian SLE

{\frac{d^{2}}{d z^{2}} + I [z; Λ_{o}; T_{K}; ε]} Φ [z; Λ_{o}; T_{K}; ε] = 0,

(1)

with the energy-dependent polynomial fraction (PF)

I [z; Λ_{o}; T_{K}; ε] : = I^{o} [z; Λ_{o}] + ε ρ [z; T_{K}]

(2)

(named ‘Bose invariant’ by Milson [20] to give credit to the renowned paper by Bose [31]) are formed by classical Jacobi polynomials with positive degree-dependent indexes:

ϕ_{c, n} [z; Λ_{o}; T_{K}] = ϑ_{c, n} [z; Λ_{o}; T_{K}] P_{n}^{(λ_{0; c, n}, λ_{1; c, n})} (2 z - 1)

(3)

and the weight

ϑ_{c, n} [z; Λ_{o}; T_{K}] : = z^{\frac{1}{2} λ_{0; c, n} + \frac{1}{2}} {(1 - z)}^{\frac{1}{2} λ_{1; c, n} + \frac{1}{2}}

(4)

as far as the numerator of the density function

ρ [z; T_{K}] = \frac{T_{K} [z]}{4 z^{2} {(1 - z)}^{2}} ​ ​ (K \leq 2),

(5)

represented by the ‘tangent polynomial’ (TP) of degree K has no zeros inside the interval (0 , 1). In following [10] we parametrize the reference polynomial fraction (RefPF) in superposition (2) as follows

I^{o} [z; Λ_{o}] = \frac{1 - λ_{o}^{2}}{4 z^{2}} + \frac{1}{4 {(1 - z)}^{2}} - \frac{O_{0}^{o} (λ_{o}, μ_{o})}{4 z {(1 - z)}^{}},

(6)

where

O_{0}^{o} (Λ_{o}) = λ_{o}^{2} - μ_{o}^{2} - 1,

(7)

with

Λ_{o} \equiv λ_{o}, μ_{o}

for briefness. It directly follows from the structure of PF (6) that the parameter

λ_{o}

represents the zero-energy exponent difference (ExpDiff) for the pole of CSLE (1) at the origin. Similarly re-writing (6) as

I^{o} [z; Λ_{o}] = \frac{1 - λ_{o}^{2}}{4 z^{2} (1 - z)} + \frac{1}{4 z {(1 - z)}^{2}} + \frac{μ_{o}^{2} - 1}{4 z {(1 - z)}^{}}

(8)

one can verify that the second parameter

μ_{o}

constitutes the zero-energy ExpDiff for the pole of CSLE (1) at infinity.

It has been proven in [10] that the the Jacobi indexes in quesion coincide with positive roots of the two companion quartic equations. In Appendix A below we illustrate these results in the limiting case of the AL potential associated (

λ_{o} = 0

) when both quartic equations can be analytically decomposed into pairs of quadratic equations so the sought-for positive roots become explicitly expressible in radicals and as a result the JRef CSLE in question has an algebraic energy spectrum specified in the mentioned appendix.

Examination of the indicial equation for the pole of JRef CSLE (1) at infinity:

ρ_{\infty; \pm} (Λ_{o}; T_{K}; ε) [ρ_{\infty; \pm} (Λ_{o}; T_{K}; ε) - 1] + \frac{1}{4} [1 - μ^{2} (Λ_{o}; T_{K}; ε)] = 0,

(9)

Where

μ (Λ_{o}; T_{K}; ε) : = \sqrt{1 - 4 \underset{z \to \infty}{l i m} {z^{2} I [z; Λ_{o}; T_{K}; ε]}} = \sqrt{μ_{o}^{2} - a_{2} ε},

(10)

reveals that the latter ε-dependent parameter represents the ExpDiff for the pole in question:

ρ_{\infty; +} (Λ_{o}; T_{K}; ε) - ρ_{\infty; -} (Λ_{o}; T_{K}; ε) = \sqrt{μ_{o}^{2} - a_{2} ε} > 0,

(11)

with

a_{2}

standing for the leading coefficient of the second-degree TP (K=2) so

a_{2} = 0

for K = 0 or 1. This confirms the above assertion that the parameter

μ_{o}

represents the zero-energy ExpDiff for the pole of CSLE (1) at infinity.

If we require for the TP

T_{K} [z] = c_{1} z + c_{0} (1 - z) - a_{2} z (1 - z)

(12)

to remain finite at the ends of the quantization interval [0, 1]:

T_{K} [r] = c_{r} > 0 f o r r = 0, 1

(13)

then density function (5) has the second-order poles at both endpoints i.e.,

0 < \underset{z \to r}{l i m} {{(z - r)}^{2} ρ [z; T_{K}]} = \frac{1}{4} c_{r} < \infty (r = 0, 1) .

(14)

In addition to (12) it is convenient to decompose the numerator of PF (5) in a different way:

T_{K} [z] = c_{0} {(z - 1)}^{2} + c_{1} z^{2} + d z (z - 1)

(15)

where

d = a_{2} - c_{0} - c_{1} .

(16)

The ExpDiffs for the poles of CSLE (1) in the finite plane at

ε = ε_{c, n} (Λ_{o}; T_{K})

can be thus expressed in terms of the eigenvalue in question as

λ_{0; c, n}^{2} = λ_{o}^{2} - c_{0} ε_{c, n} (Λ_{o}; T_{K})

(17)

and

λ_{1; c, n}^{2} = - c_{1} ε_{c, n} (Λ_{o}; T_{K}) .

(18)

Substituting q-RSs (3) into CSLE (1) and making use of (15), (17), and (18), we can represent the resultant hypergeometric equation as

{z (z - 1) \frac{d^{2}}{d z^{2}} + 2 F_{1}^{(λ_{1; c, n}, λ_{0; c, n})} (z) \frac{d}{d z} + C_{0}^{c, n} (Λ_{o}; {\hat{T}}_{K})} F_{n}^{(λ_{1; c, n}, λ_{0; c, n})} (z) = 0,

(19)

where

(20)

and

(21)

with

(22)

The indicial equation for the of the hypergeometric equation at infinity thus takes form:

(23)

(24)

On the other hand, since gauge transformation from CSLE (1) to hypergeometric equation (19) may not change the ExpDiff for the given pole we conclude that

(25)

One can directly verify that two representations the ExpDiff in question are equivalent by substituting (16)-(18), (21) and (22) into the right-hand side of (24). Examination of the roots of quadratic equation (23) also reveals that

n = \frac{1}{2} [μ_{c, n} (Λ_{o}; T_{K}) - λ_{1; c, n} - λ_{0; c, n} - 1] \geq 0,

(26)

i.e., [3, 10]

(27)

In [9] we introduced the concept of the prime SLEs

{\frac{d}{d z} ρ [z] \frac{d}{d z} - q [z; Λ_{o}] + ε w [z; T_{K}]} Ψ [z; Λ_{o}; T_{K}; ε] = 0

(28)

which is obtained from the given RCSLE by the gauge transformation

Ψ [z; Λ_{o}; T_{K}; ε] = ρ^{- \frac{1}{2}} [z] Φ [z; Λ_{o}; T_{K}; ε]

(29)

chosen in such a way that that the chacteristic exponents (ChExps) of the Frobenius solutions of SLE (28) near each singular endpoint have exactly the same absolute value but opposite signs. Note that the weight function for SLE (28) has form:

w [z; T_{K}] \equiv ρ [z; T_{K}] ρ [z]

(30)

regardless of the particular choice of the leading coefficient function

ρ [z] .

In our case we choose

ρ [z] = z (1 - z) .

(31)

To prove that the sum of the ChExps for each pole in the finite plane is equal to 0, first note that [9]

q [z; Λ_{o}] = - ρ [z] I^{o} [z; Λ_{o}] + I {ρ [z]},

(32)

where

\tilde{I} {f [z]} \equiv \frac{1}{4} \overset{•}{f}^{2} [z] / f [z] - \frac{1}{2} \overset{• •}{f} [z],

(33)

with dot standing for the derivative with respect to z. Substituting (8), (31), and

\tilde{I} {z (1 - z)} = \frac{1}{4 z} + \frac{1}{4 (1 - z)}

(34)

into the right hand side of (32) one finds

q [z; λ_{o}, μ_{o}] = \frac{λ_{o}^{2}}{4 z} + \frac{1}{4} (μ_{o}^{2} - 1) .

(35)

On the other hand the PFSs of prime SLE (28) near the singular endpoints can be written as

Ψ_{r} [z; Λ_{o}; T_{K}; ε] : = | z - 1 |^{ρ_{r} (ε; Λ_{o}; T_{K})} F_{r}^{+} [z; Λ_{o}; T_{K}; ε] (r = 0, 1),

(36)

where we choose

F_{r}^{+} [r; Λ_{o}; T_{K}; ε] = 1.

(37)

By definition their ChExps coincide with the positive roots of the indicial equations:

ρ_{0}^{2} (ε; λ_{o}; c_{0}) = \underset{z \to 0}{l i m} {z (q^{o} [z; Λ_{o}] - ε w [z; T_{K}])} = \frac{1}{4} (λ_{o}^{2} - c_{0} ε)

(38)

and

ρ_{1}^{2} (ε; c_{1}) = - \frac{1}{4} c_{1} ε .

(39)

It is crucial that both quadratic equations do not have linear terms which confirms our assertion that the ChExps of two Frobenius solutions near each singular endpoint differ only by sign for any negative energy ε. □

We thus assert that the PFSs in question are unambiguosly selected by the DBCs:

\underset{z \to r}{l i m} Ψ_{r} [z; Λ_{o}; T_{K}; ε] = 0.

(40)

Our last step is to confirm that any eigenfunction detemined by the DBCs

\underset{z \to 0}{l i m} Ψ [z; Λ_{o}; T_{K}; ε_{n}] = \underset{z \to 1}{l i m} Ψ [z; Λ_{o}; T_{K}; ε_{n}] = 0

(41)

is squarely intergrable with weight (30):

0 < \int_{0}^{1} Ψ^{2} [z; Λ_{o}; T_{K}; ε_{n}] w [z; T_{K}] d z < \infty

(42)

or, in other words, that the eigenfunctions of CSLE (1) are normalizable with weight (5):

0 < \int_{0}^{1} ϕ_{c, n}^{2} [z; Λ_{o}; T_{K}] ρ [z; T_{K}] d z < \infty .

(43)

Indeed keeping in mind (36) one can verify that integrals (43) may converge iff the solutions in questions obey DBCs (41).

We thus came to the following theorem originally proven by us in [9]:

Theorem 1.If the density function

ρ [z; T_{K}]

of the given RCSLE has second-order poles at both endpoints then the corresponding Dirichlet problem formulated for the prime SLE is fully equivalent to the requirement that the eigenfunctions of RCSLE are square integrable with the weight

ρ [z; T_{K}]

One of the advantages of formulating the given spectral problem in the form of the prime SLE solved under the DBCs is that we can automatically adopt the rigorous theorems proven in [19] for SLEs solved under the DBCs.

Examination of the asymptotic behavior of PFSs (36) near the corresponding endpoints reveals that

\underset{z \to r}{l i m} (ρ [z] {\overset{\cdot}{Ψ}}_{r} [z; Λ_{o}; T_{K}; ε]) = 0 (r = 0, 1)

(44)

and therefore the so-called [32] ‘generalized’ Wronskian (g-W) of two PFSs near the endpoint 0 or 1 accordingly,

W_{r} [z; Λ_{o}; T_{K}; ε^{'}, {ε^{'}}^{'}] \equiv ρ [z] W {Ψ_{r} [z; Λ_{o}; T_{K}; ε^{'}], Ψ_{r} [z; Λ_{o}; T_{K}; {ε^{'}}^{'}]} (r = 0, 1)

(45)

vanishes at the endpoint in question [19]:

\underset{z \to 0}{l i m} W_{0} [z; Λ_{o}; T_{K}; ε^{'}, {ε^{'}}^{'}] = \underset{z \to 1}{l i m} W_{1} [z; Λ_{o}; T_{K}; ε^{'}, {ε^{'}}^{'}] = 0 .

(46)

Another important relation pointed to in [19]:

{\overset{•}{W}}_{r} [z; Λ_{o}; T_{K}; ε, ε_{c, 0} (Λ_{o}; T_{K})] = [ε_{c, 0} (Λ_{o}; T_{K}) - ε] w [z; T_{K}] ψ_{c, 0} [z; Λ_{o}; T_{K}] \times Ψ_{r} [z; Λ_{o}; T_{K}; ε] (r = 0, 1)

(47)

reveals that the g-W is a monotonic function of z as far as both solutions remain positive and

ε < ε_{c, 0} (Λ_{o}; T_{K})

Selecting the PFS by the DBC allows one to prove that any PFS below the lowest energy level keeps its sign inside the quantization interval

(0, 1)

Theorem 2.

No PFS below the lowest eigenvalue may have nodes inside the quantization interval.

Proof of Theorem 2. Suppose that that

W_{r} [z; Λ_{o}; T_{K}; ε^{'}, {ε^{'}}^{'}]

for

ε < ε_{c, 0} (Λ_{o}; T_{K})

vanishes at

z = z_{r} \in (0, 1)

, i.e.

Ψ_{r} [z_{r}; Λ_{o}; T_{K}; ε] = 0 .

(48)

Without loss of generality we can assume that lowest-energy eigenfunction and the PFS near the singular endpoint z=

r

at an energy

ε < ε_{c, 0} (Λ_{o}; T_{K})

are both positive for

0 < z < z_{0} < 1

0 < z_{1} < z < 1

accordingly (flopping signs if necessary). Under the latter constraint the g-W must be either positive or respectively negative at this point:

W_{0} [z_{0}; Λ_{o}; T_{K}; ε, ε_{c, 0} (Λ_{o}; T_{K})] > 0

(49)

and

W_{1} [z_{1}; Λ_{o}; T_{K}; ε, ε_{c, 0} (Λ_{o}; T_{K})] < 0

(50)

in contradiction with the relations

W_{0} [z_{0}; Λ_{o}; T_{K}; ε, ε_{c, 0} (Λ_{o}; T_{K})] = ρ [z_{0}] ψ_{c, 0} [z_{0}; Λ_{o}; T_{K}] \times {\overset{•}{Ψ}}_{0} [z_{0}; Λ_{o}; T_{K}; ε] < 0

(51)

and accordingly

W_{1} [z_{1}; Λ_{o}; T_{K}; ε, ε_{c, 0} (Λ_{o}; T_{K})] = ρ [z_{1}] ψ_{c, 0} [z_{1}; Λ_{o}; T_{K}] {\overset{•}{Ψ}}_{1} [z_{1}; Λ_{o}; T_{K}; ε] > 0

(52)

keeping in mind that

{\overset{•}{Ψ}}_{0} [z_{0}; Λ_{o}; T_{K}; ε] < 0

(53)

and

{\overset{•}{Ψ}}_{1} [z_{1}; Λ_{o}; T_{K}; ε] > 0 .

(54)

We thus confirmed that the PFS at any energy

ε < ε_{c, 0} (Λ_{o}; T_{K})

is necessarily nodeless. □

Let us also point to another important constraint for the leading coefficient functions of prime SLE (28):

0 \leq ρ^{\frac{1}{2}} [z; T_{K}] ρ [z] < \infty

(55)

which plays a crucial role in our proof in Section 3 that the rational Liouville-Darboux transform (RLDT) of a PFS is itself a PFS of the transformed CSLE unless the PFS in questioncoincides with the transformation function (TF) in question.

3. Liouville-Darboux Transformation of Fuchsian CSLE with Second-Order Poles

Let

Φ_{τ} [z; Λ_{o}; T]

be a nodeless q-RS of a CSLE

{\frac{d^{2}}{d z^{2}} + {\tilde{I}}^{o} [z; Λ_{o}; T] + ε ρ [ξ; T]} Φ_{τ} [z; Λ_{o}; T; ε] = 0

(56)

at the energy

ε = ε_{τ} (Λ_{o}; T) .

(57)

We mark the zero-energy free term by tilde to indicate that we deal with the generic (not necessary rational) CSLE. Note that it generally depends on the parameters

T

in addition to

Λ_{o}

. The selected solution can be used as the TF for the LDT such that Rudyak and Zahariev’s reciprocal function [8]

* Φ_{τ} [z; Λ_{o}; T] = \frac{ρ^{- \frac{1}{2}} [z; T]}{Φ_{τ} [z; Λ_{o}; T]}

(58)

represents a solution of the transformed RCSLE:

{\frac{d^{2}}{d z^{2}} + {\tilde{I}}^{o} [z; Λ_{o}; T | τ] + ε ρ [z; T]} Φ [z; Λ_{o}; T; ε | τ] = 0

(59)

at the same energy (57):

{\frac{d^{2}}{d z^{2}} + {\tilde{I}}^{o} [z; Λ_{o}; T | τ] + ε_{τ} (Λ_{o}; T) ρ [ξ; T]} * Φ_{τ} [z; Λ_{o}; T] = 0

(60)

or, in the Riccati form:

{\tilde{I}}^{o} [z; Λ_{o}; T | τ] \equiv - l d^{2} * Φ_{τ} [z; Λ_{o}; T] - \overset{•}{l d} * Φ_{τ} [z; Λ_{o}; T] - ε_{τ} (Λ_{o}; T) ρ [z; T],

(61)

where the symbolic expression ld f[ξ] denotes the logarithmic derivative of the function f[z] with respect to z. As mentioned in Introduction the author [8] suggested to refer to the aforementioned transformation as ‘LDT’ to stress that we deal with the three-step operation:

the Liouville transformation of the generic CSLE with a density function

ρ [z; T]

to the Schrödinger equation using the change of variable

z (x; T)

defined by the first-order ordinary differential equation (ODE)

z^{'} (x; T) = ρ^{- \frac{1}{2}} [z; T]

(62)

with prime standing for the derivative with respect to x;

the Darboux deformation of the Liouville potential with the TF

Ψ_{τ} [z (x; T); Λ_{o}; T] = ρ^{\frac{1}{2}} [z (x; T); T] Φ_{τ} [z (x; T); Λ_{o}; T]

(63)

the reverse Liouville transformation of the Schrödinger equation with the deformed potential to new CSLE (60) with the original density function

ρ [z; T]

Subtracting

{\tilde{I}}^{o} [z; Λ_{o}; T] = - l d^{2} Φ_{τ} [z; Λ_{o}; T] - \overset{•}{l d} Φ_{τ} [z; Λ_{o}; T] - ε_{τ} (Λ_{o}; T) ρ [z; T]

(64)

from (62) and also taking into account that

l d * Φ_{τ} [ξ; Λ; T] = - l d Φ_{τ} [ξ; Λ; T] - \frac{1}{2} l d ρ [η; T]

(65)

one finds [33]

{\tilde{I}}^{o} [z; Λ_{o}; T | τ] = {\tilde{I}}^{o} [z; Λ_{o}; T] + 2 \sqrt{ρ [z; T]} \frac{d}{d z} \frac{l d Φ_{τ} [z; Λ_{o}; T]}{\sqrt{ρ [z; T]}} + J {ρ [z; T]},

(66)

where the last summand represents the so-called [9] ‘universal correction’ defined via the generic formula

J {f [z]} : = \frac{1}{2} \sqrt{f_{} [z]} \frac{d}{d z} \frac{l d f [z]}{\sqrt{f [z]}} .

(67)

Let

{\frac{d^{2}}{d z^{2}} + I [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}]} Φ [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] = 0

(68)

with the Bose invariant

I [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] = I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}] + ε ρ [z; T_{K}]

(69)

be the CSLE obtined from JRef CSLE (1) via a sequence

{\bar{Σ}}_{k}

of k LDTs, When selecting the LDTs in question we allow their TFs to have seros beteen 0 and 1 so CSLE (69) may have poles inside the quantization interval. If we do use only ‘admissible’ TFs with no zeros between 0 and 1 then we explicitly replace

{\bar{Σ}}_{k}

for

{\bar{Σ}}_{k}

so any of CSLEs

{\frac{d^{2}}{d z^{2}} + I [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}]} Φ [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] = 0 (k = 1, ..., p)

(70)

does not have poles inside the quantization interval and therefote, as explained below, the corresponding Sturm-Liouville problem is exactly solvable.

Let us assume that

\underset{z \to r}{l i m} {{(z - r)}^{2} I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}]} = \underset{z \to r}{l i m} {{(z - r)}^{2} I^{o} [z; Λ_{o}]}

(71)

for

k = 1, ..., p - 1

and then prove that both asymptotic relations hold for

k = p

, i.e.,

\underset{z \to 0}{l i m} {z^{2} I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p}]} = \frac{1}{4} (1 - λ_{o}^{2})

(72)

and

\underset{z \to 1}{l i m} {{(1 - z)}^{2} I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p}]} = \frac{1}{4} .

(73)

First representing universal correction (67) in the explicitly rational form

J {ρ [z; T_{K}]} = \frac{1}{2} \overset{•}{l d} ρ [z; T_{K}] - \frac{1}{4} l d^{2} ρ [z; T_{K}]

(74)

= 2 \overset{⌢}{Q} [z; T_{K}; \frac{1}{2}] + \frac{(2 z - 1) l d T_{K} [z] - 2}{z (z - 1)},

(75)

where

\overset{⌢}{Q} [z; T_{K}; \frac{1}{2}] : = - \frac{1}{2} T_{K}^{\frac{1}{2}} [z] \frac{d^{2}}{d^{2} z} T_{K}^{- \frac{1}{2}} [z]

(76)

= \frac{1}{4} \overset{•}{l d} T_{K} [z] - \frac{1}{8} l d^{2} T_{K} [z],

(77)

one finds that it does not have the second-order poles at z = 0, 1 provided that the TP remains positive at these points (

c_{r} > 0

for

r = 0, 1

For any negative ε the general solution

Φ [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}]

of CSLE (68) can be represented as a suporposition of two Frobenius solutions

Φ_{r}^{\pm} [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] : = | z - r |^{\pm ρ_{r} (ε; λ_{o}; c_{0}) + \frac{1}{2}} F_{r}^{\pm} [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] .

(78)

with

r

= 0 or 1 and

F_{r}^{\pm} [r; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] = 1 .

(79)

It is crucial that the ChExps of the latter solutions are determined by the same indicial equations (38) ans (39) as the ChExps of PFSs (36). Examinations of the asymptotic behavior of Frobenius solutions (78) near the endpont z =

r

thus reveals that

0 < | (z - r) l d Φ [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] | < \infty (r = 0, 1

(80)

In particular this is true for the TF

Φ_{τ_{k + 1}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}]

0 < | (z - r) l d Φ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}] | < \infty (r = 0, 1)

(81)

if the latter is a solution of CSLE (68) at a negative energy

ε_{τ_{k + 1}} (Λ_{o}; T_{K} | {\bar{Σ}}_{k}) < 0,

(82)

where by definition

{\bar{Σ}}_{k + 1} : = {\bar{Σ}}_{k}, τ_{k + 1} .

(83)

Keeping in mind (81) with k = p1 we conclude that the second summand in the RefPF

I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p}] = I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 1}] +

(84)

2 \frac{\sqrt{T_{K} [z]}}{z (z - 1)} \frac{d}{d z} \frac{z (z - 1) l d Φ_{τ_{p}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 1}]}{\sqrt{T_{K} [z]}} + J {ρ [z; T_{K}]},

similarly to universal correction (74), has only simple poles in the finite plane which brings us back to asymptotic relation (71) with k = p. We thus proved

Theorem 3.

The LDT preserves the ExpDiffs for the persitent second-order poles of CSLE (68) at z = 0 ans 1 as far as the TP stays positive at both points.

A similar assertion can be extended to the second-order pole at infinity for a second-degree TP (K=2).

Theorem 4.

The LDT using a quasi-rational TF preserves the ExpDiff for the pole of CSLE (68) at infinity if the TP has the degree of 2.

Proof of Theorem 4. Let us first remind the reader that

\underset{z \to \infty}{l i m} (z^{2} ρ [z; T_{2}]) > 0

(85)

for K=2 and also assume that the asymptotic relations

\underset{z \to \infty}{l i m} (z^{2} I^{o} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{k}]) = \underset{z \to \infty}{l i m} (z^{2} I^{o} [z; Λ_{o}])

(86)

holds for any k < p. Suppose that the logarithmic derivative of the function f[z] in (67) behaves at large z as

l d f [z] = f_{- 1} z^{- 1} + f_{- 2} z^{- 2} + 0 (z^{- 3})

(87)

\frac{1}{z} \frac{d}{d z} (z l d f [z]) \approx f_{- 2} z^{- 3} + 0 (z^{- 4}) .

(88)

In particular choosing

f [z] = ρ [z; T_{2}]

and denoting the average of two TP root

{\bar{z}}_{T}

z_{T} : = \frac{1}{2} (z_{T; 1} + z_{T; 2})

gives

l d f [z] = \frac{2 a_{2} (z - z_{T})}{T_{2} [z]} - \frac{2}{z} - \frac{2}{z - 1}

(89)

with

f_{- 1} = - 2

. Making use of the definition of the universal correction via (67) thus shows that

\underset{z \to \infty}{l i m} (z^{2} J {ρ [z; T_{2}]}) = 0

(90)

The logarithmic derivative of the TF

Φ_{τ_{k + 1}} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{k}]

obeys asymptotic formula (87) if the TF is a q-RS of CSLE (68) and therefore the magnitude of the second summand in sum (84) diminishes at large z as

z^{- 3} .

Multiplying (84) by

z^{2},

making z →∞, and taking into account (90) shows that the last two summands disappear in the specified limit which brings us to the sought-for asymptotic formula

\underset{z \to \infty}{l i m} (z^{2} I^{o} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{p}]) = \frac{1}{4} (1 - μ_{o}^{2})

(91)

The only thing left is to show that the ExpDiff for the pole of CSLEs (68) at infinity is determined by the following radical expressions

μ (Λ_{o}; T_{2}; ε | {\bar{Σ}}_{k}) = \sqrt{4 {}_{ι}a_{2} ε + 1 - 4 \underset{z \to \infty}{l i m} {z^{2} I^{o} [z; Λ_{o}; T_{2}; ε | {\bar{Σ}}_{k}]}} .

(92)

Indeed examination of the indicial equations for the mentioned poles:

ρ_{\infty; \pm} (Λ_{o}; T_{2}; ε | {\bar{Σ}}_{k}) [ρ_{\infty; \pm} (Λ_{o}; T_{2}; ε | {\bar{Σ}}_{k}) - 1] + \frac{1}{4} [1 - μ^{2} (Λ_{o}; T_{2}; ε | {\bar{Σ}}_{k})] = 0

(93)

confirms that

ρ_{\infty; +} (Λ_{o}; T_{2}; ε | {\bar{Σ}}_{k}) - ρ_{\infty; -} (Λ_{o}; T_{2}; ε | {\bar{Σ}}_{k}) = μ (Λ_{o}; T_{2}; ε | {\bar{Σ}}_{k}) .

(94)

Substituting (91) into (92) completes the proof.□

Let us now come back to CSLE (70) with no poles inside the quantization interval and study more carefully the prime SLE

{\frac{d}{d z} ρ [z] \frac{d}{d z} - q [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}] + ε w [z; T_{2}]} Ψ [ξ; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] = 0

(95)

obtained from its canonical form (70) by the gauge transformation

Ψ [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] = ρ^{- \frac{1}{2}} [z] Φ [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}]

(96)

As originally proven in [7] the function

Φ [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] = \frac{W {Φ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}], Φ [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k - 1}]}}{ρ^{\frac{1}{2}} [z; T_{K}] Φ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]}

(97)

is a solution of CSLE (70) if

Φ [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k - 1}]

is a solution of the preceding CSLE in the given chain. The natural question to ask is whether the function

Φ [z; Λ_{o}; T_{K}; ε_{c, n} | {\bar{Σ}}_{k}] =

\frac{W {Φ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}], ϕ_{c, n} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]}}{ρ^{\frac{1}{2}} [z; T_{K}] Φ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]}

(98)

is square-integrable with the weight

ρ [z; T_{K}]

if this is true for the function

Φ [z; Λ_{o}; T_{K}; ε_{c, n} | {\bar{Σ}}_{k - 1}] \equiv ϕ_{c, n} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]

(99)

. (99)

In other words we need to prove that the function

Ψ [z; Λ_{o}; T_{K}; ε_{c, n} | {\bar{Σ}}_{k}] =

(100)

\frac{W {Ψ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}], ψ_{c, n} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]}}{ρ^{\frac{1}{2}} [z; T_{K}] Ψ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]}

where

Ψ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}] = ρ^{- \frac{1}{2}} [z] Φ [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}],

(101)

vanishes at 0 and 1 if the function

ψ_{c, n} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]

obeys the DBCs at these points.

To confirm the above assertion let us first prove

Theorem 5.

Any LDT of the PFS of the CSLE near an endpoint is itself the PFS of the transformed CSLE near the given singular end if the common density function of these CSLEs has the second-order pole at the end in question.

Proof of Theorem 5. Representing the transformed PFS as

Ψ_{r}^{\pm} [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k}] = Τ_{K}^{\frac{1}{2}} [z] Ψ_{r}^{\pm} [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k - 1}] \times

(102)

{(z - r) l d Ψ_{r}^{\pm} [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{k - 1}] - (z - r) l d Ψ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]}

and taking into account that, as a result of (80) and (81), the magnitude of the term in the curly brackets remains bounded in the limit

z \to r

for

r

= 0 or 1, we conlude that solutions (102) must satisfy the DBC at the corresponding endpoint which completes the proof. □

Since any eigenfunction constitutes the PFS at each endpoint we can formulate the main result of this Section as the following proposition:

Theorem 6

If the density function of CSLE (70) has second-order poles at both endpoints then any nonzero LDT of the eigenfunction is itself the eigenfunction of the transformed CSLE

assuming that the LDT is admissible, i.e., the TF in question does not have zeros inside the given quantization interval.

Corollary 1.

Keeping in mind that the lowest-energy eigenfunction is necessarily nodeless [19] one can always use it as the TF for the LDT of the exactly quantized Fuchsian CSLE with second-order poles to formulate the new analytically solvable SL problem.

In Section 4 we apply this prescription to CSLE (1) and show that the LDT in question results in the exactly solvable Fuchsian Sturm-Liouville problem with five second-order poles (including infinity). The corresponding Liouville potential was originally constructed by Cooper, Ginocchio, and Khare [1] as a counter-example to Gendenshtein’s claim [2] that any exactly solvable potential is necessarily shape-invariant. Their pioneering study served a stimulus for author’s own interest in this broad class of RCSLEs solvable by polynomials.

In addition to the normalizable TF c0 one can also use as TFs the three other basic non-normalizable solutions t0 of the distinct types t =a, b, or d (assuming that the TP has a positive discriminant or two of them for the DRtTP). Each of these LDTs results in the 2 Heun equation analytically solvable by polynomials. The common remarkable feature of these equations is that the positions of the poles outside the interval [0, 1] are unambiguously determined by the TP coefficients and thereby are independent of the exponential parameters, in a sharp contrast with more complicated DCTs of CSLE (1) descussed in Section 5, Section 6 and Section 7.

4. RLDTs of JRef CSLE Using Basic TFs

As shown in Appendix A the number of the normalizable eigenfunctions for CSLE

(1) with the zero value of the parameter

λ_{o}

is equal to

n_{o} = ⌊ \frac{1}{2} μ_{o} + \frac{1}{2} ⌋

(103)

In [10] this formula was also extended to non-zero values of

λ_{o}

n_{o} = ⌊ (μ_{o} - λ_{o} + 1) / 2 ⌋

(104)

While examining the details of the analysis presented in [1] the author realized [5] that each lowest-energy eigenfunction

ϕ_{c, 0} [z; Λ_{o}; T_{K}] = ϑ_{c 0} [z; Λ_{o}; T_{K}]

(105)

was necessarily accompanied by three other ‘basic’ solutions of distinguished types a, b, and d:

ϕ_{t, 0} [z; Λ_{o}; T_{K}] = ϑ_{t 0} [z; Λ_{o}; T_{K}]

(106)

iff the TP has a positivie discriminant

Δ_{T}

(see appendix A for the illustration of this proposition for the limiting case of the AL potential).

We can thus perform the four LDTs with TFs (106) for t= a, b, c, or d such that the quasi-rational function

* ϕ_{t, 0} [z; Λ_{o}; T_{K}] = T_{K}^{- \frac{1}{2}} [z] z^{\frac{1}{2} - \frac{1}{2} λ_{0; t, 0}} {(1 - z)}^{\frac{1}{2} - \frac{1}{2} λ_{1; t, 0}}

(107)

is the solution of the new exactly solvable CSLE

{\frac{d^{2}}{d z^{2}} + I^{o} [z; Λ_{o}; T_{K}; ε | t, 0]} Φ [z; Λ_{o}; T_{K}; ε] = 0

(108)

with the Bose invariant

I^{o} [z; Λ_{o}; T_{K}; ε | t, 0] : = I^{o} [z; Λ_{o}; T_{K} | t, 0] + ε ρ [z; T_{K}]

(109)

at the energy

ε = ε_{t, 0} (Λ_{o}; T_{K})

It is essential that TFs (106) of the LDTs in question and therefore TFs (107) of the reverse LDTs have the rational logarithmic derivatives, namely,

l d ϕ_{t, 0} [z; Λ_{o}; T_{K}] = \frac{1 + λ_{0; t, 0}}{2 z} + \frac{​ 1 + λ_{1; t, 0}}{2 (z - 1)}

(110)

and

l d * ϕ_{t, 0} [z; Λ_{o}; T_{K}] = - \frac{1}{2} l d T_{K} [z] + \frac{1 - λ_{0; t, 0}}{2 z} + \frac{​ 1 - λ_{1; t, 0}}{2 (z - 1)},

(111)

which assures that the resultant CSLEs are rational, with K+2 second-order poles in the finite plane.

Representing the monic second-degree TP with two simple zeros at

z_{T; 1}

and

z_{T; 2}

as the monomial product

{\hat{T}}_{2} [z] \equiv Π_{2} (z; {\bar{z}}_{T}) : = (z - z_{T; 1}) (z - z_{T; 2})

(112)

(with hut here and below used to indicate that we deal with a monic polynomial), substituting (75) and (110) into (66), and taking into account that

z (z - 1) l d ϕ_{t, 0} [z; Λ_{o}; T_{2}] = B_{1} [z; {\overset{⇀}{λ}}_{t, 0}]

(113)

with

B_{1} [z; \overset{⇀}{λ}] : = F_{1}^{(λ_{1}, λ_{0})} (z)

(114)

we can represent the RefPF in question as

I^{o} [z; Λ_{o}; {\bar{z}}_{T} | t, 0] = \frac{1 - λ_{o}^{2}}{4 z^{2} (1 - z)} + \frac{1}{4 z {(1 - z)}^{2}} + 2 \overset{⌢}{Q} [z; {\hat{T}}_{2}, \frac{1}{2}] + \frac{{\overset{⌢}{O}}_{2}^{o} [z; Λ_{o}; {\bar{z}}_{T} | t, 0]}{4 z (z - 1) Π_{2} [z; {\bar{z}}_{T}]},

(115)

where

\overset{⌢}{Q} [z; {\bar{z}}_{T}, \frac{1}{2}] \equiv \overset{⌢}{Q} [z; T_{2}, \frac{1}{2}] = \frac{1}{2 Π_{2} [z; {\bar{z}}_{T}]} - \frac{3}{8} \frac{\overset{•}{Π}_{2}^{2} [z; {\bar{z}}_{T}]}{Π_{2}^{2} [z; {\bar{z}}_{T}]}

(116)

Taking into account that

2 z - 1 - F_{1}^{(λ_{1}, λ_{0})} (z) = F_{1}^{(- λ_{1}, - λ_{0})} (z)

(117)

the numerator of the last PF in sum (115) can be convniently represented as

{\overset{⌢}{O}}_{2}^{o} [z; Λ_{o}; {\bar{z}}_{T} | t, 0] = [O_{0}^{o} (Λ_{o}) + 4 (λ_{0} + λ_{1})] {\hat{T}}_{2} [z]

+ 8 (z - z_{T}) F_{1}^{(- λ_{1}, - λ_{0})} (z) .

(118)

We thus proved that the the LDTs using four basic solutions (106) with t= a, b, c, or d as their TFs convert CSLE (1) into the Fuchsian SLEs with the 5 second-order poles.

Taking into account that

\underset{| z \to \infty}{l i m} (z^{2} \overset{⌢}{Q} [z; {\bar{z}}_{T}, \frac{1}{2}]) = - 1

(119)

and re-writing (118) as

{\overset{⌢}{O}}_{2}^{o} [z; Λ_{o}; {\bar{z}}_{T} | t, 0] = O_{0}^{o} (Λ_{o}) {\hat{T}}_{2} [z] + Δ {\overset{⌢}{O}}_{2}^{o} [z; {\overset{⇀}{λ}}_{t, 0}; {\bar{z}}_{T}]

(120)

where

Δ {\overset{⌢}{O}}_{2}^{o} [z; {\overset{⇀}{λ}}_{t, 0}; {\bar{z}}_{T}] = 8 {\hat{T}}_{2} [z] + 4 Δ C_{1} [z; \overset{⇀}{λ}; {\bar{z}}_{T}],

(121)

with the second summand represented by the first-degree polynomial:

Δ C_{1} [z; \overset{⇀}{λ}; {\bar{z}}_{T}] : = (λ_{0} + λ_{1} - 2) {\hat{T}}_{2} [z] + 2 (z - z_{T}) F_{1}^{(- λ_{1}, - λ_{0})} (z)

= (λ_{0} + λ_{1} - 2) {{\hat{T}}_{2} [z] - z (z - z_{T})} - (1 - λ_{0}) (z - z_{T})

(122)

we thus explicitly confirm that

\underset{| z \to \infty}{l i m} (z^{2} I^{o} [z; Λ_{o}; {\bar{z}}_{T} | t, 0]) = O_{0}^{o} (Λ_{o}),

(123)

in agreement with the proof presented in Section 3. One can also verify that the LDTs in question keep unchanged the ExpDiffs for the poles of the CSLE at 0 and 1, as expected.

RSubstituting (3) into (98) with k=1 and

τ_{1} = t, 0

shows that the eigenfunctions in question have the quasi-rational form:

ϕ_{c, n + δ_{t}} [z; Λ_{o}; {\hat{T}}_{2} | t 0] = {\hat{T}}_{2}^{- \frac{1}{2}} [z] ϑ_{c, n} [z; Λ_{o}; {\hat{T}}_{2}] D_{n + 1} [z; Λ_{o}; {\hat{T}}_{2} | t 0; c n],

(124)

where the PDs of degree n+1 are defined as follows

D_{n + 1} [z; Λ_{o}; {\hat{T}}_{2} | t, 0; c, 0] : = |_{S_{1}^{(λ_{1; t, 0}, λ_{0; t, 0})} (z) S_{n + 1}^{(λ_{1; c, n}, λ_{0; c, n})} (z)}^{1 F_{n}^{(λ_{1; c, n}, λ_{0; c, n})} (z)} |

(125)

with the second row formed by the so-called [8,9] ‘supplementary’ Jacobi-seed (JS) polynomials:

S_{m + 1}^{(λ_{1}, λ_{0})} (z) : = F_{1}^{(λ_{1}, λ_{0})} (z) {\hat{F}}_{m}^{(λ_{1}, λ_{0})} (z) + z (z - 1) \overset{•}{\hat{F}}_{m}^{(λ_{1}, λ_{0})} (z) .

(126)

The shift

δ_{t} : = {{- 1 i f t = c;}_{+ 1 i f t = d}^{0 i f t = a o r b,}

(127)

in the index of eigenfunction (124) was introduced due to the fact that the LDTs with the TFs

c, 0

d, 0

either erase the lowest-energy eigenfunction or inserts the new one below the lowest eigenvalue of CSLE (1) while the two other LDTs keep the energy spectrum unchanged.

Substituting (124) into RCSLE (108) with

ε = ε_{c, n} (Λ_{o}; {\hat{T}}_{2})

and decomposing the TP via (15) we conclude that the PDs in question satisfy the differential equation of Heine-type:

(D {{\overset{⇀}{λ}}_{c, n}; {\bar{z}}_{T}} + C_{2}^{c, n} [z; Λ_{o}; {\bar{z}}_{T} | t, 0]) D_{n + 1} [z; Λ_{o}; {\hat{T}}_{2} | t, 0; c, n] = 0,

(128)

where the second-order differential operator is defined via the conventional formula:

D {\overset{⇀}{λ}; {\bar{z}}_{T}} \equiv Π_{2} (z; {\bar{z}}_{T}) z (z - 1) \frac{d^{2}}{d z^{2}} + B_{3} [ξ; \overset{↼}{λ}; {\bar{z}}_{T}] \frac{d}{d z}

(129)

with the linear coefficient function represented by the cubic polynomial

B_{3} [z; \overset{↼}{λ}; {\bar{z}}_{T}] : = 2 F_{1}^{(λ_{1}, λ_{0})} (z) Π_{2} (z; {\bar{z}}_{T}) - 2 z (z - 1) (z - z_{T}) .

(130)

Making use of (21) coupled with (120) it is convenient to write the free-term of Heine-type differential equation (128),

C_{2}^{c, n} [z; Λ_{o}; {\bar{z}}_{T} | t, 0] = \frac{1}{4} {\overset{⌢}{O}}_{2}^{o} [z; Λ_{o}; {\bar{z}}_{T} | t, 0] +

(131)

{\frac{1}{4} d ε_{c, n} (Λ_{o}; T_{2}) + C_{0} ({\overset{⇀}{λ}}_{c, n})} Π_{2} [z; {\bar{z}}_{T}] - F_{1}^{(λ_{1; c, n}, λ_{0; c, n})} (z) (z - z_{T}),

in a slightly different form:

C_{2}^{c, n} [z; Λ_{o}; T_{2} | t, 0] = \frac{1}{4} Δ {\overset{⌢}{O}}_{2}^{o} [z; {\overset{⇀}{λ}}_{t, 0}; {\bar{z}}_{T}] +

C_{0}^{c, n} (Λ_{o}; T_{2}) Π_{2} [z; {\bar{z}}_{T}] - F_{1}^{(λ_{1; c, n}, λ_{0; c, n})} (z) (z - z_{T}) .

(132)

An analysis of the indicial equation for the pole of differential equation (128) at infinity [34,35]:

N_{\pm}^{2} + [B_{3; 3} (\overset{⇀}{λ}; {\bar{z}}_{T}) - 1] N_{\pm} + C_{2; 2}^{c, n} (Λ_{o}; {\hat{T}}_{2} | t, 0) = 0

(133)

with

B_{3; 3} (\overset{⇀}{λ}; {\bar{z}}_{T}) = λ_{1} + λ_{0}

(134)

reveals that

N_{+} - N_{-} = \sqrt{\frac{1}{4} {[B_{3; 3} ({\overset{⇀}{λ}}_{c, n}; {\bar{z}}_{T}) - 1]}^{2} - C_{2; 2}^{c, n} (Λ_{o}; {\hat{T}}_{2} | t, 0)}

(135)

On other hand, since gauge transformation (124) from RCSLE (108) to Heine-type differential equation (128) may not change the ExpDiff for the given pole one finds

N_{+} - N_{-} = μ_{c, n} (Λ_{o}; {\hat{T}}_{2} | t, 0) : = μ (Λ_{o}; {\hat{T}}_{2}; ε_{c, n} (Λ_{o}; {\hat{T}}_{2}) | t, 0)

(136)

with the right-hand side representing ExpDiff for the pole of the RCSLE at infinity at

ε = ε_{c, n} (Λ_{o}; {\hat{T}}_{2})

. To explicitly confirm that

\frac{1}{4} {[B_{3; 3} ({\overset{⇀}{λ}}_{c, n}; {\bar{z}}_{T}) - 1]}^{2} - C_{2; 2}^{c, n} (Λ_{o}; T_{2} | t, 0) = μ_{c, n}^{2} (Λ_{o}; T_{2} | t, 0)

(137)

let us remind the reader that

μ_{c, n} (Λ_{o}; T_{2} | t, 0) = μ_{c, n} (Λ_{o}; T_{2}) : = \sqrt{μ_{o}^{2} - a_{2} ε_{c, n} (Λ_{o}; {\hat{T}}_{2})}

(138)

while, as a direct consequence of (24) and (25),

\frac{1}{4} {(λ_{1; c, n} + λ_{0; c, n})}^{2} - C_{0}^{c, n} (Λ_{o}; T_{2}) = μ_{c, n}^{2} (Λ_{o}; T_{2})

(139)

Bearing in mind that

{(λ_{1} + λ_{0} + 1)}^{2} - {[B_{3; 3} (\overset{⇀}{λ}; {\bar{z}}_{T}) - 1]}^{2} = 4 (λ_{1} + λ_{0}) .

(140)

we thus need to verify that

C_{0}^{c, n} (Λ_{o}; T_{2}) - C_{2; 2}^{c, n} (Λ_{o}; T_{2} | t, 0) = λ_{1; c, n} + λ_{0; c, n}

(141)

The sought-for relation can be then directly obtained by evaluating the leading coefficient of second-order polynomial (132), coupled with (120) and (121). □

Comparing

N = \frac{1}{2} [μ_{c, n} (Λ_{o}; T_{2}) - λ_{+; c, n} - λ_{-; c, n} + 1]

(142)

with (26) we conclude that

N = n+1

(143)

and therefore the leading coefficient of PD (125),

D_{n + 1; n + 1} (Λ_{o}; T_{2} | t, 0; c, n) = \frac{1}{2} (λ_{1; c, n} + λ_{0; c, n} - λ_{1; t, 0} - λ_{0; t, 0} + 2 n)

(144)

must differ from 0.

If we vary the free term of differential equation (128) while keeping fixed the exponent parameters

λ_{0; c, n}

and

λ_{1; c, n}

, then as proven in Heine’s celebrated treatise [36], there are exactly C(n+3, 2) ‘characteristic polynomials’ such that the mentioned differential equation has a polynomial solution of degree

n + 1

. Polynomial (131) thus represents one of these polynomials and as a result the PD in question coincides with the corresponding Heine polynomial and for this reason it is termed by us ‘JS-Heine polynomial’. Note that we use the term ‘characteristic polynomials’ originally introduced by Marden [37] for the free term of the Heine-Stieltjes [36,38] equation with all positive exponent parameters (instead of widely embraced nickname ‘Van Vleck polynomial’ suggested in his later papers [39,40]) to stress that there is no limitation on signs of the exponent parameters in our case so polynomial (131) does not obey the renowned theorems for Van Vleck polynomials (see, i.g., [34,41] and references therein for more recent results).

The crucial difference compared with the conventional theory [36,41,42] is that the coefficient function of the first derivative for differential equation (128) depends on the polynomial degree so the PDs in question represent polynomial solutions for different Heine problems.

Finally if the TP

{\hat{T}}_{2} [z]

has the zero discriminant then

T_{2} [z; z_{T}] : = a_{2} {(z - z_{T})}^{2}

(145)

and the corresponding RefPf has only three poles

I^{o} [z; Λ_{o}; z_{T} | t, 0] = \frac{1 - λ_{o}^{2}}{4 z^{2} (1 - z)} + \frac{1}{4 z {(1 - z)}^{2}} + 2 \overset{⌢}{Q} [z; z_{T}] +

(146)

\frac{{\overset{⌢}{O}}_{1}^{o} [z; Λ_{o}; z_{T} | t, 0]}{4 z (z - 1) (z - z_{T})}

where

\overset{⌢}{Q} [z; z_{T}] : = - \frac{1}{2} (z - z_{T}) \frac{d^{2}}{d^{2} z} \frac{1}{z - z_{T}} = - \frac{1}{{(z - z_{T})}^{2}}

(147)

so the CSLE with RefPF (146) and density function

ρ [z; z_{T}] = \frac{{(z - z_{T})}^{2}}{4 z (z - 1)} ​ ​ ​ ​

(148)

represents the canonical form of the conventional Heun equation [43]. We refer the reader to [44} for a detailed analysis of this limiting case. Though one of four basic solutions disappears in the limit

Δ_{T} \to 0

the disappearing q-RS has either type a or type b (depending on the sign of the root

z_{T}

) so all the arguments presented in next Sections hold except that they should be applied to the corresponding triplet of basic solutions (except of the quartet of q-RSs of four distinct types existing for a positive TP discriminant

Δ_{T})

5. Representation of TFs in Quasi-Rational Form

As outlined in Appendix B sequential LDTs of JRef CSLE (1) result in the CSLE with zero-energy free term (B10). To demonstrate that the eigenfunctions of this CSLE have a quasi-rational form it is convenient to replace the CW for the KD via (C1) in Appendix C. The zero-energy free term for the transformed CSLE just takes form (D1) in Appendix D.

Let us now consider a DCT using as its seed functions 2j +

ℓ

q-RSs

ϕ_{t_{k} {, m}_{k}} [z; Λ_{o}; T_{K}] \propto ϑ_{t_{k} {, m}_{k}} [z; Λ_{o}; T_{K}] {\hat{F}}_{m_{k}}^{(λ_{1; t_{k} {, m}_{k}}, λ_{0; t_{k} {, m}_{k}})} (z)

(149)

with

ϑ_{t, m} [z; Λ_{o}; T_{K}] : = z^{\frac{1}{2} λ_{0; t, m} + \frac{1}{2}} {(1 - z)}^{\frac{1}{2} λ_{1; t, m} + \frac{1}{2}}

(150)

Setting

\bar{Σ}_{2 j + ℓ} : = t_{1} {, m}_{1}; ...; t_{2 j + ℓ} {, m}_{2 j + ℓ},

Θ [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}] : = {[z (1 - z)]}^{- \frac{1}{2} j (j + 1)} \prod_{k = 1}^{2 j + ℓ} ϑ_{t_{k} m_{k}} [z; Λ_{o}; T_{K}],

(151)

and introducing the PDs [9]

D_{n | \bar{Σ}_{2 j})} [z; Λ_{o}; T_{K} | \bar{Σ}_{2 j}] : =

(152)

| {...}_{ε_{1}^{j - 1} {\hat{F}}_{m_{1}}^{(λ_{1; 1}, λ_{0; 1})} (z) ... ε_{2 j}^{j - 1} {\hat{F}}_{m_{2 j}}^{(λ_{1; 2 j}, λ_{0; 2 j})} (z)}^{S_{m_{1} + 1}^{(λ_{1; 1}, λ_{0; 1})} (z) ... S_{m_{2 j} + 1}^{(λ_{1; 2 j}, λ_{0; 2 j})} (z)}_{ε_{1}^{j - 1} S_{m_{1} + 1}^{(λ_{1; 1}, λ_{0; 1})} (z) ... ε_{2 j}^{j - 1} S_{m_{2 j} + 1}^{(λ_{1; 2 j}, λ_{0; 2 j})} (z)}^{{\hat{F}}_{m_{1}}^{(λ_{1; 1}, λ_{0; 1})} (z) ... {\hat{F}}_{m_{2 j}}^{(λ_{1; 2 j}, λ_{0; 2 j})} (z)} |

D_{n | \bar{Σ}_{2 j + 1})} [z; Λ_{o}; T_{K} | \bar{Σ}_{2 j + 1}] : =

(153)

{(- 1)}^{j} | {_{ε_{1}^{j - 1} {\hat{F}}_{m_{1}}^{(λ_{1; 1}, λ_{0; 1})} (z) ... ε_{2 j + 1}^{j - 1} {\hat{F}}_{m_{2 j + 1}}^{(λ_{1; 2 j + 1}, λ_{0; 2 j + 1})} (z)}^{...}}_{ε_{1}^{j - 1} S_{m_{1} + 1}^{(λ_{1; 1}, λ_{0; 1})} (z) ... ε_{2 j + 1}^{j - 1} S_{m_{2 j + 1} + 1}^{(λ_{1; 2 j + 1}, λ_{0; 2 j + 1})} (z)}^{S_{m_{1} + 1}^{(λ_{1; 1}, λ_{0; 1})} (z) ... S_{m_{2 j + 1} + 1}^{(λ_{1; 2 j + 1}, λ_{0; 2 j + 1})} (z)}_{ε_{1}^{j} {\hat{F}}_{m_{1}}^{(λ_{1; 1}, λ_{0; 1})} (z) ... ε_{2 j + 1}^{j} {\hat{F}}_{m_{2 j + 1}}^{(λ_{1; 2 j + 1}, λ_{0; 2 j + 1})} (z)}^{\overset{{\hat{F}}_{m_{1}}^{(λ_{1; 1}, λ_{0; 1})} (z) ... {\hat{F}}_{m_{2 j + 1}}^{(λ_{1; 2 j + 1}, λ_{0; 2 j + 1})} (z)}{}} |

for an even or respectively odd number of the sequential LDTs we can represent the given KD in the following quasi-rational form:

K [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}] = Θ [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}] D_{n | \bar{Σ}_{2 j + ℓ})} [z; Λ_{o}; T_{K} | \bar{Σ}_{2 j + ℓ}] .

(154)

Substituting KD (154) into zero-energy free-term (D1) and taking into account that, by analogy with (113),

z (z - 1) l d Θ [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}] = B_{1} [z; \overset{⇀}{Λ} | {\bar{Σ}}_{2 j + ℓ})],

(155)

where the first-degree polynomial on the right is defined via (114) and

Λ_{r} | {\bar{Σ}}_{2 j + ℓ}) : = \sum_{k = 1}^{2 j + ℓ} λ_{r; t_{k} {, m}_{k}} - j (j - 1) + ℓ - 1

(156)

one finds

I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}] = I^{o} [z; Λ_{o}] + ℓ J {ρ [z; T_{K}]} +

(157)

\frac{2 \sqrt{T_{K} [z]}}{z (z - 1)} \frac{d}{d z} \frac{z (z - 1) l d D_{n | \bar{Σ}_{2 j + ℓ})} [z; Λ_{o}; T_{K} | \bar{Σ}_{2 j + ℓ}]}{\sqrt{T_{K} [z]}} + + \frac{2 \sqrt{T_{K} [z]}}{z (z - 1)} \frac{d}{d z} \frac{B_{1} [z; \overset{⇀}{Λ} | {\bar{Σ}}_{2 j + ℓ})]}{\sqrt{T_{K} [z]}} .

Examination of the last two summands in (157) confirms that they have only simple poles at 0, 1, and ∞ as far as the second-order TP in question remains finite at the endpoints.

Substituting (154) into (D3) we can represent the TFs of our interest in the following quasi-rational form:

Φ_{t, m} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}] = ϑ_{t, m} [z; Λ_{o}; T_{K}] T_{K}^{- \frac{1}{2} ℓ} [z] \times

(158)

\frac{D_{n | \bar{Σ}_{2 j + ℓ}; t, m)} [z; Λ_{o}; T_{K} | \bar{Σ}_{2 j + ℓ}; t, m]}{D_{n | \bar{Σ}_{2 j + ℓ})} [z; Λ_{o}; T_{K} | \bar{Σ}_{2 j + ℓ}]}

It is essential that the exponents of the powers of z and 1z forming function (150) coincide with the ChExps for the poles of the given CSLE at 0 and 1. We thus assume that the PDs remain finite at 0 and 1 except some exotic cases of integer ExpDiffs which will be simply disregarded in the current analysis.

We also assume that

Conjecture

1. The PDs in the numerator and denominator of the PF in the right-hand side of (150) do not have common zeros;

Conjecture 2. Any PD remains finite at the TP zeros

{\bar{z}}_{T}

As the direct consequence of Conjecture 2 TF (158) for

ℓ

= 1 represents a non-principal Frobenius near the poles of CSLE (68) at the TP zeros. We thus exclude the possibility for this TF to be a PFS. Furthermore keeping in mind that function

* Φ_{t, m} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j - 1}] = ϑ_{t, m}^{- 1} [z; Λ_{o}; T_{K}] z (z - 1) \times

(159)

\frac{D_{n | \bar{Σ}_{2 j - 1})} [z; Λ_{o}; T_{K} | \bar{Σ}_{2 j - 1}]}{D_{n | \bar{Σ}_{2 j - 1}; t, m)} [z; Λ_{o}; T_{K} | \bar{Σ}_{2 j - 1}; t, m]}

is the solution of CSLE (68) for k =2j we conclude that the latter equation has poles at the TP zeros only for odd k.

Under the formulated assumptions the PD in the numerator of the PF in the right-hand side of (158) may have zeros only at regular points of CSLE (68) with k = 2j +1 and therefore all its zeros are necessarily simple.

Introducing the rational function

Q [z; {\bar{z}}_{N}] : = l \overset{•}{d} Π_{N} [z; {\bar{z}}_{N}]

(160)

= - \sum_{k = 1}^{N} \frac{1}{{(z - z_{N; k})}^{2}}

(161)

representing the monic PD as the monomial product

{\hat{D}}_{n | \bar{Σ}_{2 j + ℓ})} [z; Λ_{o}; T_{K} | \bar{Σ}_{2 j + ℓ}] \equiv Π_{n | \bar{Σ}_{2 j + ℓ})} [z; \bar{z} | {\bar{Σ}}_{2 j + ℓ})],

(162)

and also making use of (75) we can represent RefPF (157) as

I^{o} [z; Λ_{o}; {\hat{T}}_{K} | {\bar{Σ}}_{2 j + ℓ}] = I^{o} [z; Λ_{o}] + 2 Q [z; \bar{z} | {\bar{Σ}}_{2 j + ℓ})] +

(163)

\frac{Λ_{0} | {\bar{Σ}}_{2 j + ℓ}) + Λ_{1} | {\bar{Σ}}_{2 j + ℓ}) + 2 (1 - ℓ)}{z (z - 1)} + \frac{2 (2 z - 1) {\overset{•}{Π}}_{n | \bar{Σ}_{2 j + ℓ})} [z; \bar{z} | {\bar{Σ}}_{2 j + ℓ})]}{z (z - 1) Π_{n | \bar{Σ}_{2 j + ℓ})} [z; \bar{z} | {\bar{Σ}}_{2 j + ℓ})]} + Δ I^{o} [z; Λ_{o}; {\hat{T}}_{K} | {\bar{Σ}}_{2 j + ℓ}],

with the last summand selected by the requirement that it disappers in the const-TP limit (K=0) associated with the translationally shape-invariant Rosen-Morse (RM) potential [45],

V_{R M} [z; λ_{o}, μ_{o}; T_{0}]

. Namely

Δ I^{o} [z; Λ_{o}; {\hat{T}}_{K} | {\bar{Σ}}_{2 j + ℓ}] : = 2 ℓ \overset{⌢}{Q} [z; T_{K}; \frac{1}{2}] +

(164)

\frac{{\overset{•}{T}}_{K} [z] D_{n | \bar{Σ}_{_{2 j + ℓ}}) + 1}^{(ℓ)} [z; \overset{⇀}{Λ} | {\bar{Σ}}_{_{2 j + ℓ}}); \bar{z} | {\bar{Σ}}_{_{2 j + ℓ}})]}{z (z - 1) T_{K} [z] Π_{n | \bar{Σ}_{2 j + ℓ})} [z; \bar{z} | {\bar{Σ}}_{2 j + ℓ})]},

where we set

D_{N + 1}^{(ℓ)} [z; \overset{⇀}{Λ}; {\bar{z}}_{N}] : = {ℓ (2 z - 1) - F_{1}^{(Λ_{1}, Λ_{0})} (z)} Π_{N} [z; {\bar{z}}_{N}] - z (z - 1) {\overset{•}{Π}}_{N} [z; {\bar{z}}_{N}] .

(165)

As asserted above RefPF (163) may not have poles at the TP zeros for even numbers of the sequential LDTs. This implies that polynomial (165) with

ℓ

= 0 must vanish at both zeros of the second-degree TP

T_{2} [z]

D_{n | \bar{Σ}_{_{2 j}}) + 1}^{(0)} [z_{T; k}; \overset{⇀}{Λ} | {\bar{Σ}}_{_{2 j}}); \bar{z} | {\bar{Σ}}_{_{2 j}})] = 0

(166)

and therefore it can be decomposed as

D_{n | \bar{Σ}_{_{2 j}}) + 1}^{(0)} [z; \overset{⇀}{Λ} | {\bar{Σ}}_{_{2 j}}); \bar{z} | {\bar{Σ}}_{_{2 j}})] = Π_{2} [z; {\bar{z}}_{T}] Ξ_{n | \bar{Σ}_{2 j}) - 1} [z; Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{_{2 j}}]

(167)

for K=2. In Appendix E we illustrate the above decomposition for the double-step DCT using two different basic solutions

t, 0

and

t^{'}, 0

(

t \neq

t^{'})

as its seed functions (i.e.,

{\bar{Σ}}_{_{2}} = t, 0; t^{'}, 0

One can easily verify that rational function (160) is nothing but an alternative form of Quesne’s superposition of two PFs

Q [z; {\bar{z}}_{N}] = \frac{{\overset{• •}{Π}}_{N} [z; {\bar{z}}_{N}]}{Π_{N} [z; {\bar{z}}_{N}]} - \frac{\overset{•}{Π}_{N}^{2} [z; {\bar{z}}_{N}]}{Π_{N}^{2} [z; {\bar{z}}_{N}]}

(168)

(see i.g. (2.16) in [13]). In our earlier works we have overlooked the fact that the latter rational function can be represented in form (161) and thereby has only second order poles at zeros of the PD in question. As a result of this confusion we mistakenly referred to (3.25a′) in [8] as the Quesne partial decomposition.

The RefPFs of the exactly solvable CSLEs with the Liouville potentials representing the RDCTs of the RM potential,

V [z; λ_{o}, μ_{o}; T_{0} | {\bar{Σ}}_{2 j + ℓ}] = V_{R M} [z; λ_{o}, μ_{o}; T_{0}] - ρ^{- 1} [z; T_{0}] I^{o} [z; λ_{o}, μ_{o} | {\bar{Σ}}_{2 j + ℓ}]

(169)

thus take form

I^{o} [z; λ_{o}, μ_{o}; T_{0} | {\bar{Σ}}_{2 j + ℓ}] = \frac{1 - λ_{o}^{2}}{4 z^{2}} + \frac{1}{4 {(1 - z)}^{2}} + 2 Q [z; \bar{z} | {\bar{Σ}}_{2 j + ℓ})] +

(170)

\frac{O_{0}^{o} (λ_{o}, μ_{o}) + Λ_{0} | {\bar{Σ}}_{2 j + ℓ}) + Λ_{1} | {\bar{Σ}}_{2 j + ℓ}) + 2 (1 - ℓ)}{4 z (z - 1)} +

with

A = \frac{1}{2} (μ_{o} - 1) > 0, B = \frac{1}{4} λ_{o}^{2}

(171)

in Quesne’s notation [13].

Multiplying (164) by

z^{2}

, setting

D_{N + 1; N + 1}^{(ℓ)} (\overset{⇀}{Λ}; {\bar{z}}_{N}) = D^{(ℓ)} (\overset{⇀}{Λ}; N) : = 2 ℓ - 1 - \frac{1}{2} (Λ_{0} + Λ_{1}) - N,

(172)

in (164), making

z \to \infty

, coupled with (119), thus gives

\underset{z \to \infty}{l i m} (z^{2} Δ I^{o} [z; Λ_{o}; {\hat{T}}_{K} | {\bar{Σ}}_{2 j + ℓ}]) = K [D^{(ℓ)} (\overset{⇀}{Λ} | {\bar{Σ}}_{2 j + ℓ}); n | \bar{Σ}_{2 j + ℓ})) - ℓ] .

(173)

On the other hand taking into account that

\underset{z \to \infty}{l i m} (z^{2} Q [z; {\bar{z}}_{N}]) = - N

(174)

one finds

\underset{z \to \infty}{l i m} (z^{2} I^{o} [z; Λ_{o}; {\hat{T}}_{0} | {\bar{Σ}}_{2 j + ℓ}] - I^{o} [z; λ_{o}, μ_{o}] - Δ I^{o} [z; Λ_{o}; {\hat{T}}_{K} | {\bar{Σ}}_{2 j + ℓ}]) = Λ_{0} | {\bar{Σ}}_{2 j + ℓ}) + Λ_{1} | {\bar{Σ}}_{2 j + ℓ}) + 2 (1 - ℓ) + 2 n | \bar{Σ}_{2 j + ℓ})

(175)

We thus assert that

\underset{z \to \infty}{l i m} (z^{2} I^{o} [z; Λ_{o}; {\hat{T}}_{K} | {\bar{Σ}}_{2 j + ℓ}]) - \underset{z \to \infty}{l i m} (z^{2} I^{o} [z; λ_{o}, μ_{o}]) = (2 - K) [D^{(ℓ)} (\overset{⇀}{Λ} | {\bar{Σ}}_{2 j + ℓ}); n | \bar{Σ}_{2 j + ℓ})) - ℓ]

(176)

As expected the DCTs in question preserve the ExpDiff for the pole of the CSLE at infinity only for second-degree TPs.

To convert CSLE (68) to the second-order ODE solvable by polynomials it is convinient to re-write RefPF (163) in a slightly different form

I^{o} [z; Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{2 j + ℓ}] = \frac{1 - λ_{o}^{2}}{4 z^{2}} + \frac{1}{4 {(1 - z)}^{2}} + 2 \overset{⌢}{Q} [z; \bar{z} | {\bar{Σ}}_{2 j + ℓ}), 1; ℓ {\bar{z}}_{T}, \frac{1}{2}] +

(177)

\frac{{\overset{⌢}{O}}_{n (\bar{Σ}_{2 j + ℓ}) + 2 ℓ}^{o} [z; Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{2 j + ℓ}]}{4 z (z - 1) Π_{2}^{ℓ} [z; {\bar{z}}_{T}] Π_{n (\bar{Σ}_{2 j + ℓ})} [z; \bar{z} | {\bar{Σ}}_{2 j + ℓ})]}

Where

\overset{⌢}{Q} [z; {\bar{z}}_{N}, 1; ℓ {\bar{z}}_{T}, \frac{1}{2}] : = - \frac{\overset{• •}{χ} [z; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}]}{2 χ [z; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}]}

(178)

\equiv - \frac{1}{2} l d^{2} χ [z; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}] - \frac{1}{2} \overset{•}{l d} χ [z; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}]

(179)

With

χ [z; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}] : = Π_{2}^{\frac{1}{2} ℓ} [z; {\bar{z}}_{T}] Π_{N} [{\bar{z}}_{N}]

(180)

Taking into account that

Q [z; {\bar{z}}_{N}] = \overset{⌢}{Q} [z; {\bar{z}}_{N}, 1] + \frac{{\overset{• •}{Π}}_{N} [{\bar{z}}_{N}]}{2 Π_{N} [{\bar{z}}_{N}]}

(181)

we can alternatively represent rational function (178) as

\overset{⌢}{Q} [z; {\bar{z}}_{N}, 1; ℓ {\bar{z}}_{T}, \frac{1}{2}] = Q [z; {\bar{z}}_{N}] + ℓ \overset{⌢}{Q} [z; {\bar{z}}_{T}; \frac{1}{2}] - \frac{{\overset{• •}{Π}}_{N} [{\bar{z}}_{N}]}{2 Π_{N} [{\bar{z}}_{N}]} + ℓ \frac{(z - z_{T}) {\overset{•}{Π}}_{N} [{\bar{z}}_{N}]}{Π_{2} [z; {\bar{z}}_{T}] Π_{N} [{\bar{z}}_{N}]}

(182)

Making use of (117) let us represent polynomial (165) for

ℓ

=1 as

D_{N + 1}^{(1)} [z; \overset{⇀}{Λ}; {\bar{z}}_{N}] = F_{1}^{(- Λ_{1}, - Λ_{0})} (z) Π_{N} [z; {\bar{z}}_{N}] - z (z - 1) {\overset{•}{Π}}_{N} [z; {\bar{z}}_{N}]

(183)

so summand (164) in RefPF (163) takes form

Δ I^{o} [z; Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{2 j + 1}] : = 2 \overset{⌢}{Q} [z; T_{2}; \frac{1}{2}] + \frac{2 (z - z_{T}) B_{1} [z; - \overset{⇀}{Λ}]}{z (z - 1) T_{2} [z]} - \frac{2 (z - z_{T}) {\overset{•}{Π}}_{n | \bar{Σ}_{2 j + 1})} [z; \bar{z} | {\bar{Σ}}_{2 j + 1})]}{{\hat{T}}_{2} [z] Π_{n | \bar{Σ}_{2 j + 1})} [z; \bar{z} | {\bar{Σ}}_{2 j + 1})]} .

(184)

Substituting (182) into the right-hand side of (177) and comparing the resultant expression with (170) gives

{\overset{⌢}{O}}_{n (\bar{Σ}_{2 j + 1}) + 2}^{o} [z; Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{2 j + 1}] = {\overset{⌢}{O}}_{2}^{o} [z; Λ_{o}; {\bar{z}}_{T}; \overset{⇀}{Λ} | {\bar{Σ}}_{2 j + 1})] + 8 (2 z - 1) Π_{2} [z; {\bar{z}}_{T}] {\overset{•}{Π}}_{n | \bar{Σ}_{2 j + 1})} [z; \bar{z} | {\bar{Σ}}_{2 j + 1})] + 4 z (z - 1) Π_{2} [z; {\bar{z}}_{T}] {\overset{• •}{Π}}_{n (\bar{Σ}_{2 j + ℓ})} [z; \bar{z} | {\bar{Σ}}_{2 j + ℓ})],

(185)

where the first summand is defined via (120). One can directly verify that the leading coefficient of polynomial (185) is equal to

{\overset{⌢}{O}}_{n (\bar{Σ}_{2 j + 1}) + 2; n (\bar{Σ}_{2 j + 1}) + 2}^{o} (Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{2 j + 1}) = O_{0}^{o} (Λ_{o}) + (N + 1) (N + 2)

(186)

in agreement with the asymptotic relation:

2 \underset{z \to \infty}{l i m} (z^{2} \overset{⌢}{Q} [z; {\bar{z}}_{N}; {\hat{T}}_{2}]) = - (N + 1) (N + 2) .

(187)

For j = 0,

ℓ

=1, and

{\bar{Σ}}_{1} = t, m

the monic polynomial

Π_{m} [z; {\bar{z}}_{t, m}] = {\hat{F}}_{m}^{(λ_{1; t, m}, λ_{0; t, m})} (z)

(188)

satisfies hypergeometric equation (19) with

c, n

replaced for

t, m :

{z (z - 1) \frac{d^{2}}{d z^{2}} + 2 F_{1}^{(λ_{1; t, m}, λ_{0; t, m})} (z) \frac{d}{d z} + C_{0}^{t, m} (Λ_{o}; {\hat{T}}_{2})} {\hat{F}}_{m}^{(λ_{1; t, m}, λ_{0; t, m})} (z) = 0,

(189)

where

C_{0}^{t, m} (Λ_{o}; T_{2}) : = \frac{1}{4} O_{0}^{o} (Λ_{o}) + \frac{1}{4} d ε_{t, m} (Λ_{o}; {\hat{T}}_{2}) + C_{0} (λ_{0; t, m}, λ_{1; t, m}),

(190)

Taking into account (118) and also representing

\overset{⇀}{λ}

–dependent parameter (22) as

C_{0} (λ_{0}, λ_{1}) = C_{0} (- λ_{0}, - λ_{1}) + λ_{0} + λ_{1}

(191)

we can re-write polynomial (185) for

{\bar{Σ}}_{1} = t, m

as [8]

{\overset{⌢}{O}}_{m + 2}^{o} [z; Λ_{o}; {\hat{T}}_{2} | t, m] = - [d ε_{t, m} (Λ_{o}; {\hat{T}}_{2}) + 4 C_{0} (- λ_{0; t, m}, - λ_{1; t, m})] Π_{2} [z; {\bar{z}}_{T}] Π_{m} [z; {\bar{z}}_{t, m}] + 8 F_{1}^{(- λ_{1; t, m}, - λ_{0; t, m})} (z) {(z - z_{T}) Π_{m} [z; {\bar{z}}_{t, m}] + Π_{2} [z; {\bar{z}}_{T}] {\overset{•}{Π}}_{m} [z; {\bar{z}}_{t, m}]} .

(192)

The author [8] originally came to representation (192) of polynomial (185) with j =0,

ℓ = 1

by formally replacing

Φ_{τ} [ξ; Λ_{o}; T]

in (58) for TF (149) and then substituting the resultant expression into (61).

Replacing the denominator of the PF in the right-hand side of (158) by monic polynomial (162) shows that the power exponent of the corresponding power function near each pole in the finite plane coincides with one of two ChExps for the given pole. We thus conclude that the numerator of the mentioned PF must satisfy the Heine-type differential equation:

(D {{\overset{⇀}{λ}}_{t, m}; \bar{z} ({\bar{Σ}}_{2 j + ℓ}); ℓ {\bar{z}}_{T}} + C_{n | {\bar{Σ}}_{2 j + ℓ}) + 2 ℓ}^{t, m} [z; Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{2 j + ℓ}]) \times D_{n | {\bar{Σ}}_{2 j + ℓ}, m)} [z; Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{2 j + ℓ}; t, m] = 0,

(193)

with the second-order differential operator

D {λ_{\pm; c, n}; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}} : = z (z - 1) Π_{2}^{ℓ} [z; {\bar{z}}_{T}] Π_{N} [z; {\bar{z}}_{N}] \frac{d^{2}}{d z^{2}} + + B_{N + 2 ℓ + 1} [z; λ_{\pm}; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}] \frac{d}{d z}

(194)

Where

B_{N + 2 ℓ + 1} [z; \overset{⇀}{λ}; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}] : = 2 [F_{1}^{(λ_{1}, λ_{0})} (z) Π_{2}^{ℓ} (z; {\bar{z}}_{T}) - ℓ z (z - 1) (z - z_{T})] Π_{N} (z; {\bar{z}}_{N}) - z (z - 1) Π_{2}^{ℓ} (z; {\bar{z}}_{T}) {\overset{•}{Π}}_{N} (z; {\bar{z}}_{N})

(195)

In a sharp contrast with Heine-type differential operators (129) introduced in Section 4, the positions of

n ({\bar{M}}_{2 j + ℓ}, m)

second-order poles at

{\bar{z}}_{t, m}

depend on the degree-dependent exponent parameters of the ‘generalized Heun operator’ [18]

H {{\overset{⇀}{λ}}_{t, m}; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}} : = \frac{d^{2}}{d z^{2}} + \frac{B_{N + 2 ℓ + 1} [z; \overset{⇀}{λ}; {\bar{z}}_{N}; ℓ {\bar{z}}_{T}]}{z (z - 1) Π_{2}^{ℓ} [z; {\bar{z}}_{T}] Π_{N} [z; {\bar{z}}_{N}]} \frac{d}{d z}

(196)

Despite this distinguished difference we [8,9] still refer to polynomial solutions of second-order differential equation (193) as ‘JS Heine polynomials’.

It should be stressed that the derivation of Heine-type ODE (193) for PDs essentially relies on the assertion that the LDTs in question do not affect the ExpDiffs for the poles of CSLEs (68) at 0 and 1. On the contrary, the PDs generally vanish at these points for the TP

T_{2} [z] = z (1 - z)

(197)

associated with the limiting case

c_{0}, c_{1} \to 0

and as a result they can be decomposed as follows

D_{n ({\bar{M}}_{2 j + ℓ}, m)} [z; Λ_{o}; - 1, 1, 0 | {\bar{Σ}}_{2 j + ℓ}; t m] \propto z^{k_{0} | {\bar{Σ}}_{2 j + ℓ}; t m)} {(z - 1)}^{k_{1} | {\bar{Σ}}_{2 j + ℓ}; t m)} \times P_{n ({\bar{M}}_{2 j + ℓ}; t, m)} [z; Λ_{o} | {\bar{Σ}}_{2 j + ℓ}; t, m]

(198)

where the infinitely many polynomials appearing in decomposition (198) form the so-called [46,47,48] exceptional differential polynomial system (X-DPS). Furthermore if we consider exactly solvable CSLE (70) and choose

t, m = c, n

then the corresponding infinite polynomial sequence constitutes a multi-indexed X-Jacobi orthogonal polynomial system [26,49,50].

Replacing

c, n

in (21) for

t, m

we can represent the free term in differential equation (193) as

C_{n ({M ¯}_{2 j + ℓ}) + 2 ℓ}^{t, m} [z; Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{2 j + ℓ}] = \frac{1}{4} {\overset{⌢}{O}}_{n ({M ¯}_{2 j + ℓ}) + 2 ℓ}^{o} [z; Λ_{o}; {\hat{T}}_{2} | {\bar{Σ}}_{2 j + ℓ}] + [\frac{1}{4} d ε_{t, m} (Λ_{o}; T_{2}) + C_{0} ({\overset{⇀}{λ}}_{t, m})] Π_{2} [z; {\bar{z}}_{T}] Π_{n (M ¯_{2 j + ℓ})} [z; \bar{z} ({\bar{Σ}}_{2 j + ℓ})] - ℓ F_{1}^{(λ_{1; t, m}, λ_{0; t, m})} (z) (z - z_{T}) Π_{n ({M ¯}_{2 j + ℓ})} [z; \bar{z} ({\bar{Σ}}_{2 j + ℓ})] - F_{1}^{(λ_{1; t, m}, λ_{0; t, m})} (z) Π_{2}^{ℓ} [z; {\bar{z}}_{T}] {\overset{•}{Π}}_{n ({M ¯}_{2 j + ℓ})} [z; \bar{z} ({\bar{Σ}}_{2 j + ℓ})] .

(199)

Starting from this point we shall focus solely on sequential LDTs generating the chains of exactly solvable CSLEs (70) by using the lowest-energy eigenfunctions. We will apply the corresponding DCTs either to JRef CSLE (1) itself or to its isospectral RDTs using the basic TFs (106) with

t = a, b

as well as to its double-step RDCTs using both of these basic solutions as seed functions. In other words we discuss the quartets of the isospectral RCSLEs constructed using the seed functions:

{\bar{Σ}}_{k} = c ⋮ 0 : k - 1, {\bar{Σ}}_{k + 1} = t, 0; c ⋮ 0 : k - 1 (t = a o r b), {\bar{Σ}}_{k + 2} = a, 0; b, 0; c ⋮ 0 : k - 1.

(200)

6. Enhanced Adler Theorem

Let us now show that each of the four sequences of the exactly solvable CSLEs (70) with

{\bar{Σ}}_{k}

represented by one of four finite sets of seed functions (200) can be further expanded using pairs of juxtaposed eigenfunctions with nodes. The crucial difference compared with the DCTs using seed solutions (200) is that CSLE (68) constructed by means of the LDT using the TF with nodes inside the quantization interval has a second-order pole at each of these nodes so the corresponding Sturm-Liouville problem is not exactly solvable anymore.

Let us first reproduce Adler’s arguments [27] to prove that the Wronskian of two

sequential eigenfunctions

ψ_{c, N} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

and

ψ_{c, N + 1} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

of the prime SLE

{\frac{d}{d z} ρ [z] \frac{d}{d z} - q [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] + ε_{c, n} (Λ_{o}; T_{2}) w [z; T_{2}]} \times ψ_{c, n} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] = 0

(201)

exactly solvable under the DBCs

\underset{z \to 0}{l i m} ψ_{c, n} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] = \underset{z \to 1}{l i m} ψ_{c, n} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] = 0

(202)

does not have zeros inside the quantization interval (0, 1). It is assumed that SLE (201) is obtained by a RDCT of prime JRef SLE (28) so

\underset{z \to \infty}{l i m} | z q [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] | < \infty

(203)

and all the eigenfunction have the following quasi-rational form

ψ_{c, n} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] = z^{\frac{1}{2} Λ_{0; c, n}} {(1 - z)}^{\frac{1}{2} Λ_{1; c, n}} T_{2}^{- \frac{1}{2} ℓ} [z] \times

(204)

\frac{Π_{n | {\bar{Σ}}_{2 j + ℓ}; c, n)} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}; c, n]}{Π_{n | {\bar{Σ}}_{2 j + ℓ})} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}]}

for n = 0,...,

n_{o} - 1

(Λ_{0; c, n}, Λ_{1; c, n} > 0)

and therefore obey the constraints:

\underset{z \to 0}{l i m} (ρ [z] {\overset{\cdot}{ψ}}_{c, n} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]) = \underset{z \to 1}{l i m} (ρ [z] {\overset{\cdot}{ψ}}_{c, n} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]) = 0

(205)

bearing in mind that the leading coefficient function of prime SLE (201) coincides by definition with leading coefficient function (31) of prime SLE (28). Howerver we do not require the RDCTs in question to represent a sequence of the RLTs admissible at each step.

Since SLE (201) is assumed to be exactly solvable under the DBCs it directly follows from the arguments presented in Section 3 that this is also true for the chain of prime SLEs obtained from SLE (201) by sequential RLDTs using the nodeless eigenfunctions

ψ_{c, 0} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ 0 : k]

as their TFs.

Let us set

W_{N, N + 1} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}] : = W r {ψ_{c, N} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}], ψ_{c, N + 1} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]}

(206)

and prove the following extension of Adler’s renowned proposition [27]:

Theorem 7. Wronskian (206) does not have zeros inside the quantization interval (0, 1).

Proof of Theorem 7. In following [19] we first introduce the g-W

W_{N, N + 1} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] \equiv ρ [z] W_{N, N + 1} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

(207)

and then apply Adler’s arguments to g-W (207) instead of Wronskian (206) keeping in mind that the leading coefficient function

ρ [z]

remains positive inside the quantization interval. We thus need to confirm that g-W (207) preserves its sign between 0 and 1.

It has been already proven in [19] that the eigenfunctions in question have the interlacing zeros

z_{N, k}

and

z_{N + 1, k^{'}}

(k=1,…,N and k'=1,…,

N

+1 accordingly), i.e.,

0 < z_{N + 1, 1} < z_{N, 1} < z_{N + 1, 2} < ... < z_{N + 1, N} < z_{N, N} < z_{N + 1, N + 1} < 1.

(208)

The common important feature of all solutions of second-order ODEs is that the solution itself and its first derivative may not vanish at the same regular point. This implies that the eigenfunctions

ψ_{c, N} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

and

ψ_{c, N + 1} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

have nonzero first derivatives at their nodes. Furthermore each derivative must have opposite sings at two sequential nodes:

{\overset{•}{ψ}}_{c, N + κ} [z_{N + κ, k}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] {\overset{•}{ψ}}_{c, N + κ} [z_{N + κ, k + 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] < 0 (κ = 0, 1)

(209)

and similarly

ψ_{c, N + κ} [z_{N + κ - 1, k}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] ψ_{c, N + ℓ} [z_{N + κ - 1, k + 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] < 0 (κ = 0, 1)

(210)

One can also easily verify that

ψ_{c, N} [z_{N + 1, k}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] {\overset{•}{ψ}}_{c, N} [z_{N, k}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] < 0, ψ_{c, N} [z_{N + 1, k + 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] {\overset{•}{ψ}}_{c, N} [z_{N, k}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] > 0

(211)

and

ψ_{c, N + 1} [z_{N, k}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] {\overset{•}{ψ}}_{c, N + 1} [z_{N + 1, k + 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] < 0 ψ_{c, N + 1} [z_{N, k + 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] {\overset{•}{ψ}}_{c, N + 1} [z_{N + 1, k + 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] > 0.

(212)

As a direct consequence of DBCs (202) coupled with constraints (204), g-W (207) vanishes at both singular ends:

W_{N, N + 1} [0; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] = W_{N, N + 1} [1; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] = 0

(213)

Keeping in mind (211) and settting

c = 0,

d = z_{N + 1, 1}

c = z_{N + 1, N + 1}

d = 1

in the prepositions for the Corollary 2.3 in [19] one finds that the Wronskian in question may not vanish inside these intervals.

Since the derivative of the g-W,

{\overset{•}{W}}_{N, N + 1} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] = [ε_{c, N} (Λ_{o}; T_{2}) - ε_{c, N + 1} (Λ_{o}; T_{2})] w [z; T_{2}] \times ψ_{c, N} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] ψ_{c, N + 1} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

(214)

must preserve its sign between any two sequential points (208) the g-W may not vanish inside the given interval if it has the same sign at its ends. We thus need to prove that the g-W has the same sign at all the points (208) other than 0 and 1 where it vanishes.

To verify this assertion let us remind the reader that

W_{N, N + 1} [z_{N + 1, 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] = ρ [z_{N + 1, 1}] \times ψ_{c, N} [z_{N + 1, 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] {\overset{•}{ψ}}_{c, N + 1} [z_{N + 1, 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] < 0

(215)

and therefore the eigenfunction

ψ_{c, N + 1} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

has a negative derivative at

z = z_{N + 1, 1}

assuming that both eigenfunctions are chosen to be positive inside the interval

(0, z_{N + 1, 1})

. It then directly follows from (209) and (210) with

κ = 1

that the g-W is negative at each of the nodes

z_{N + 1, k}

. On the other hand, according to (211) with k=1 the eigenfunction

ψ_{c, N} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

must have a negative derivative at its first node

z = z_{N, 1}

and hence the g-W must be also negative at this point

W_{N, N + 1} [z_{N, 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] = - ρ [z_{N, 1}] ψ_{c, N + 1} [z_{N, 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] {\overset{•}{ψ}}_{c, N} [z_{N, 1}; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}] < 0

(216)

keeping in mind that the eigenfunction

ψ_{c, N + 1} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

changes its sign at

z = z_{N + 1, 1}

. Making use of (209) and (210) once again, but this time with

κ = 0,

we finally confirm that g-W is also negative at each of the nodes

z_{N, k}

which completes the proof. □

Let us now show that any eigenfunction of the prime SLE

{\frac{d}{d z} ρ [z] \frac{d}{d z} - q [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ N, N + 1] + ε w [z; T_{2}]} \times Ψ [z; Λ_{o}; T_{2}; ε | {\bar{Σ}}_{2 j + ℓ}; c ⋮ N, N + 1] = 0

(217)

with the zero-energy free term restricted by the constraint

\underset{z \to \infty}{l i m} | z q [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ N, N + 1] | < \infty

(218)

can be represented in the form

Ψ_{c, n_{N} (n)} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ N, N + 1] = \times z^{\frac{1}{2} Λ_{0; c, n}} {(1 - z)}^{\frac{1}{2} Λ_{1; c, n}} \times \frac{D_{n | {\bar{Σ}}_{2 j + ℓ}; c ⋮ N, N + 1, n)} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ N, N + 1, n]}{T_{2}^{\frac{1}{2} ℓ} [z] D_{n | {\bar{Σ}}_{2 j + ℓ}; c ⋮ N, N + 1)} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ N, N + 1]} (n \neq N, N + 1),

(219)

Where

n_{N} (n) : = n - θ (n - N) - θ (n - N - 1)

(220)

with

θ (x)

standing for the Heaviside step function. In the orther word we want to prove the following extension of Adler’s results:

Theorem 8.

The DCT of exactly-solvable prime SLE using a pair of juxtaposed eigenfunctions as its seed solutions results in the new exactly solvable Sturm-Liouville problem with the holes at the energies of the seed solutions.

Proof of Theorem 8. By applying Theorem 7 to the LDT of SLE (201) with the TF

ψ_{c, 0} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}]

one finds that the Wronskian

W [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ 0, N, N + 1]

and therefore the coresponding PD may not have nodes inside the quantization interval and hence SLE (217) may not have eigenvalues below the energy

ε_{c, 0} (Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ})

Suppose that SLE (217) has an additional eigenvalue

\tilde{ε}

between the energies

ε_{c, n} (Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ})

and

ε_{c, n + 1} (Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ})

for n < N1. By eliminating one-by-one the lowest eigenvalue via the n+1 sequential LDTs we come to the SLE having the extra eigenvalue

\tilde{ε}

below the energy level

ε_{c, 0} (Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ 0 : n) = ε_{c, n + 1} (Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ})

(221)

which contradicts to the fact that the eigenfunction associated with this level is necessarily nodeless.

One can then continue to eliminate one-by-one the lowest eigenvalue via N-n-1 sequential LDTs which brings us to the exactly solvable LDT of SLE (201) using the set

of the N+2 sequential eigenfunctions

ε_{c, 0} (Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ 0 : k)

with k = 0,1,...,N+1. The complete set of the eigenvalues is thus composed of the energies

ε_{c, n} (Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ})

with N+2 ≤ n ≤

n_{o}

. We thereby assert that the energy spectrum of SLE (217) solved under the DBCs can be obtained from the energy spectrum of SLE (201) by eliminating the eigenvalues

ε_{c, N + κ} (Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ})

for

κ = 0, 1

which completes the proof.□

After proving that any eigenfunction of SLE (217) has form (219) we can apply the Theorems 7 and 8 to the double-step DCT of this SLE using another pair of juxatposed eigenfunctions

ψ_{c, N ′ + κ} [z; Λ_{o}; T_{2} | {\bar{Σ}}_{2 j + ℓ}; c ⋮ N, N + 1]

with

N^{'} > N + 1

and

κ = 0, 1

. By continuing this procedure we prove the exact solvability of any DCT of this SLE (201) using an arbitrary number number J of juxtaposed pairs of egeinfunctions

{\bar{N}}_{2 J} : = N_{1}, N_{1} + 1, ..., N_{J}, N_{J} + 1 < n_{o}

(222)

(the subsequence ii) of segments of consecutive positive integers of even length cited by Garcia-Ferrero and Gómez-Ullate [51] in their recent re-formulation of Adler’s fundanenntal THEOREM).

We thus confirmed that the Wronskian

W [z; Λ_{o}; T_{2} | c ⋮ {\bar{N}}_{2 J}]

and therefore the corresponding Krein determinant [25],

K [z; Λ_{o}; T_{2} | c ⋮ {\bar{N}}_{2 J}],

may not have zeros in the quantization interval [0, 1]. Note that Krein himself [25] came to this conclusion by introducing the spectral function for the corresponding DCT of the radial Schrödinger equation and then stating that the associated potential may not have singularities on the semi-axis. We could not find any further discussions of his arguments in the following literature. The author himself was unable to extend Krein’s argumentation to the Schrödinger equation on the line which could represent an alternative way for the ‘more traditional’ [19,27] proof presented above.

By applying the DCT with the set of seed functions

{\bar{N}}_{2 J}

to CSLE (70) with

{\bar{Σ}}_{k}

represented by one of four finite sets of seed functions (200) we can then generate the quartets of the isospectral SLEs using the following sets of seed functions

c ⋮ 0 : k, {\bar{N}}_{2 J}, a, 0; c ⋮ 0 : k, {\bar{N}}_{2 J}, b, 0; c ⋮ 0 : k, {\bar{N}}_{2 J}, a, 0; b, 0; c ⋮ 0 : k, {\bar{N}}_{2 J}

with

{\bar{N}}_{2 J}

> k+1. In addition we can construct the exactly solvable SLEs using the sets of seed functions

d, 0; c ⋮ {\bar{N}}_{2 J} ({\bar{N}}_{2 J} > 1)

and

d, 0; c ⋮ 0, 1, {\bar{N}}_{2 J} ({\bar{N}}_{2 J} > 1)

with the common lowest eigenvalue

ε_{d, 0} (Λ_{o}; T_{2}) .

7. Discussion

We have examined exactly solvable RDCTs of JRef CSLE (1) using its eigenfunctions as seed functions. Our analysis was mostly focused on the CSLEs with the common density function having two distinct real zeros outside the quantization interval [0, 1]. The simplest representative of this subnet of analytically solvable Fuchsian SLEs was initially introduced by Cooper, Ginocchio, and Khare [1] so we refer to the corresponding Liouville potential as ‘CGK’. The important innovative element of our approach is that we (in following the nearly forgotten paper by Rudyak and Zakhariev [7]) define the ‘Darboux transformation’ of the generic CSLE with no relation to the Liouville transformation converting this CSLE into the Schrödinger equation. On the other hand, it was shown that the transformation introduced in [7] results in the Darboux deformation of the corresponding Liouville potential which allows one to easily relate the properties of the LDTs (as we term these operations) to the renowned results of the conventional SUSY quantum mechanics [52,53,54].

Since we deal with singular SLEs one has to more thoroughly examine the conventional theorems for the 1D Schrödinger equation which are often based on the regular Sturm-Liouville theory [55]. To be able to by-pass the complications associated with the singular endpoints the author [9] introduced the concept of the primary SLEs solved under the DBCs which unambiguously select the PFS near each singular end. After the spectral theory of the given SLE is reformulated as the Dirichlet problem we could take advantage of the scrupulous theory developed in [19] for SLEs solved under the DBCs. Theorem 5 proven in Section 3 represents one of the most important results of this study since it allows us to assert that any LDT of an exactly solvable prime SLE using a nodeless TF results in the exactly solvable prime SLE with the same leading coefficient and weight functions.

As it has been already demonstrated by the author [10] the nodeless eigenfunction of JRef CSLE (1) with the density function constrained in the aforementioned way is accompanied by three basic q-RSs, i.e., such that their analytical continuation into the complex plane remains finite everywhere except the endpoints 0 and 1. In Section 4 we used each of these four basic solutions to construct the exactly solvable RCSLEs with the Liouville potentials represented by the CGK potential and its three ‘siblings’. Namely, two of the mentioned SUSY partners have exactly the same energy spectrum as the JRef potential while the third sibling potential has an extra energy level inserted below the common lowest energy level of the mentioned isospectral potentials.

In Section 5 we study RDCTs of JRef CSLE (1) realized by chains of sequential LDTs. To represent the eigenfunctions of the generated SLEs in the quasi-rational form we converted CWs [24] into the KDs [25] and then expressed the latter in terms of the corresponding PDs [9]. It was demonstrated that the PDs constructed in such a way satisfy the Heine-type differential equations with positions of the most poles dependent on exponent parameters of the corresponding ‘generalized Heun’ [18] operators. Since the latter parameters depend on the degree of the given polynomial solution the PDs are not Heine polynomials in the conventional sense [36,41,42]; however we still refer to them as ‘JS Heine polynomials’ to stress their relationship to differential equations of Heine type.

Based on the proven theorems we have generated four finite chains of exactly solvable RSLEs by eliminating step-by-step the lowest eigenvalue from the common energy spectrum of JRef CSLE (1), of its two isospectral LDTs using TFs a,0 and b,0, as well as of its double-step isospectral DT using the latter solutions as the seed functions.

In Section 6 we extended the Adler theorem [27] to the DCTs of the aforementioned SLEs using the juxtaposed pairs of eigenfunctions which resulted in the four Darboux-Crum subnets of exactly solvable RSLEs.

In future studies we will show that one can extend these results by using as seed functions the quasi-rational PFSs of CSLE (1) near one and only one singular endpoint at energies below its lowest eigenvalue. The existence of such q-RSs, in addition to the basic solutions utilized in this paper, can be directly confirmed by analyzing the q-RSs of the CSLE with the AL Liouville potential [10]. The explicit radical formulas for the energies of these solutions sketched in Appendix A allows one to easily select the quasi-rational PFSs below the lowest eigenvalue. Any of these PFSs can be then used as the seed function for a DCT. One can extend these arguments to Liouville potentials with almost identical asymptotic values.

It should be stressed that the most results of this paper were obtained for the numerator of density function (5) to be a second-degree polynomial with a positive discriminant. In the limiting case of the TP with a double root

z_{T} < 0

z_{T} > 1

one of the basic solutions a,0 or b,0 disappears [44] and the resultant CGK potential has only a single isospectral sibling. It can be shown that both CGK potential and its two remaining siblings constitute the reductions of the Lemieux-Bose potential [56] of type

(1, 1, - 1)

exactly solvable by polynomial solutions of the Heun equation using Ishkhanyan’s classification scheme [57] for this very special subclass of the Liouville potentials of Heun class [58] under assumption that the DBCs are imposed at the ends of the interval (0,1). (As pointed to by the author [59] the Liouville transformation of the given CSLE can be also performed either on the infinite interval (-∞,

z_{T}

) or on the finite interval (

z_{T}

, 0) which have to be considered separately.)

If density function (5) has a single simple zero on the real axis (the so-called ‘linear tangent polynomial’ (LTP) limit [10]) then the ExpDiff for the pole of JRef CSLE (1) at infinity and similarly the corresponding pole of any of its DCTs become energy-independent and as a result LDTs do not preserve this ExpDiff anymore. One thus has to trace these changes more cautiously to determine degrees of the corresponding PDs which will be a subject of a separate publication.

It will be shown that JRef CSLE (1) in the LTP limit preserves its form under the double-step DCT using specific pairs of the basic solutions as seed functions and that a similar double-step ‘shape-invariance’ [2] takes place for the corresponding CGK potential and its siblings. By definition the four potentials constructed in such a way constitute the solvable-by-polynomial reductions of the Lemieux-Bose potential of type (1, 1, 

\frac{1}{2}

) in Ishkhanyan’s classification scheme [57], again assuming that the quantization of the corresponding RCSLE is done on the interval (0,1).

The common remarkable feature of all the CSLEs mentioned so far is that the Liouville transformation of any of them converts it to the Schrödinger equation on the line, On the contrary the Liouville transformation converts JRef CSLE (1) to the radial Schrödinger equation [59,60,61,62,63,64,65] if the TP vanishes at the origin and as a result the ExpDiff for the pole at z=0 becomes energy-independent. Again (similar to the LTP potentials) one has to trace these changes more cautiously to determine degrees of the corresponding PDs.

Another complicating feature of the CSLE with the energy-independent ExpDiff for the pole at z=0 is that there is the region where the singularity at this point becomes LC [21] which results in the breakup of the conventional rules of the SUSY quantum mechanics [20].

It has been demonstrated in [60] that, similar to the LTP JRef potential on the line, the radial JRef potential also preserves its form under the double-step DCT using specific pairs of the basic solutions as seed functions and that a similar double-step ‘shape-invariance’ [2] takes place for the radial counter-parts of the CGK potential and its siblings. Again the four radial potentials constructed in such a way constitute the reductions of the Lemieux-Bose potential [56] of type (

1, \frac{1}{2}

, 

\frac{1}{2}

) exactly solvable by polynomial solutions of the Heun equation [59] provided that the Liouville transformation is done on the interval (0,1).

Funding

This research received no external funding.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A. Algebraic Formulas for Eigenvalues of JRef CSLE in Limiting Case of AL Liouville Potential

Let us consider CSLE (1) with RefPF (8) in the limiting case

λ_{o} = 0

{\overset{⌣}{I}}^{o} [z;, μ_{o}] : = \frac{1}{z^{2} (1 - z^{2})} + \frac{μ_{o}^{2} - 1}{4 z {(1 - z)}^{}}

(A1)

associated with the AL Liouville potential

\overset{⌣}{V} [z; μ_{o}; T_{K}]

such that [10]

\underset{x \to \pm \infty}{l i m} \overset{⌣}{V} [z (x); μ_{o}; T_{K}] = 0

(A2)

Without loss of generality one can choose

c_{1} > c_{0} > 0

changing z for 1-z if necessary. However one still has to consider both cases

c_{1} > c_{0} > 0

and

c_{0} > c_{1} > 0

when the ExpDiff

λ_{o}

increases toward positive values.

Setting

λ_{o} = 0

in (17) and comparing the resultant expression with (18) we conclude that the indexes of the Jacobi polynomials in the right-hand side of (3) are interrelated related via the simple formulas

{\overset{⌣}{λ}}_{0; c, n} = \sqrt{c_{0} / c_{1}} {\overset{⌣}{λ}}_{1; c, n} > 0 .

(A3)

Note the eigenfunctions of prime SLE (28),

ψ_{c, n} [z; μ_{o}; T_{K}] = z^{\frac{1}{2} {\overset{⌣}{λ}}_{0; c, n}} {(1 - z)}^{\frac{1}{2} {\overset{⌣}{λ}}_{1; c, n}} P_{n}^{({\overset{⌣}{λ}}_{1; c, n}, {\overset{⌣}{λ}}_{0; c, n})} (2 z - 1),

(A4)

satisfiy the DBCs

(A5)

as expected.

Substituting (A3) and (18) into (27) brings us to the chain of the quadratic equations [10]

{[{\overset{⌣}{λ}}_{1; c, n} (1 + \sqrt{c_{0} / c_{1}}) + 2 n + 1]}^{2} = μ_{o}^{2} + (a / c_{1}) {\overset{⌣}{λ}}_{1; c, n}^{2}

(A6)

with the positive roots specifying the discrete energy spectrum of CSLE (1) via (18).

It is convenient to convert quadratic equation (A6) to its standard form:

[{(\sqrt{c_{1}} + \sqrt{c_{0}})}^{2} - a_{2}] {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{+}, n}^{2} + 2 (2 n + 1) {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{+}, n} (\sqrt{c_{1}} + \sqrt{c_{0}}) + c_{1} [{(2 n + 1)}^{2} - μ_{o}^{2}] = 0,

(A7)

with the label

{\overset{⌣}{t}}_{+}

indicatings that the second Jacobi index for the corresponding q-RS is determined by the elementary formula

{\overset{⌣}{λ}}_{0; {\overset{⌣}{t}}_{+}, n} = \sqrt{c_{0} / c_{1}} {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{+}, n} ({\overset{⌣}{t}}_{+} = c, d)

(A8)

which extends (A3) to the second q-RS

d, n

ψ_{d, n} [z; μ_{o}; T_{K}] = z^{\frac{1}{2} {\overset{⌣}{λ}}_{0; d, n}} {(1 - z)}^{\frac{1}{2} {\overset{⌣}{λ}}_{1; d, n}} P_{n}^{({\overset{⌣}{λ}}_{1; d, n}, {\overset{⌣}{λ}}_{0; d, n})} (2 z - 1)

(A9)

diverging at both ends (

{\overset{⌣}{λ}}_{0; d, n}, {\overset{⌣}{λ}}_{1; d, n} < 0

One can easily verify that the leading coefficient of quadratic equation (A7) is positive unless both TP zeros lie between 0 and 1. Indeed the leading coefficient in question is trivially positive if

a_{2} \leq 0

(while tthe TP roots must have the opposite signs

a_{2} < 0

keeping in mind that

c_{0} > 0

). We thus need to consider only positive values of

a_{2} .

Setting [3]

b_{r} : = {(- 1)}^{r} (c_{1 - r} - a_{2} - c_{r}) = - 2 a_{2} (z_{T} - r)

(A10)

one finds that

z_{T}

lies beteen 0 and 1 only if

a_{2} > 0, b_{0} > 0, b_{1} > 0

(A11)

i.e. if

a_{2} > | c_{0} - c_{1} | r

(A12)

= 0,1.

On the other hand examination of the TP discriminant

Δ_{T} = b_{r}^{2} - 4 c_{r} a = = [{(\sqrt{c_{0}} + \sqrt{c_{1}})}^{2} - a] \times [{(\sqrt{c_{0}} - \sqrt{c_{1}})}^{2} - a]

(A13)

reveals that condition (A12) holds for the TP with a positive discriminant iff

a_{2} > {(\sqrt{c_{1}} + \sqrt{c_{0}})}^{2}

(A14)

which is nothing but the necessary and sufficient condition for quadratic equation (A7) to have a negative leading coefficient.

Keeping in mind that the quartic equation has a positive linear coefficient it may have a positive root iff

n < \frac{1}{2} (μ_{o} - 1)

(A15)

We thus assert that the number of the bound energy levels in the AL Liouville potential,

n_{o} = ⌊ \frac{1}{2} μ_{o} + \frac{1}{2} ⌋

(A16)

is independent of the TP coefficients as far as the 1D potential does not have singularities at finite points.

In the limiting case of the TP symmetric under the reflection about the point z =

\frac{1}{2}

(

c_{0} = c_{1} = c

) we come to the (symmetric) Ginocchio potential on the line [66,67,68,69], with the eigenfunctions of prime SLE (28) expressible in terms of classical Gegenbauer

polynomials with degree dependent indexes:

ψ_{c, n} [z; μ_{o}; {c, a}_{2}] = {[z (1 - z)]}^{\frac{1}{2} {\overset{⌣}{ω}}_{c, n}} C_{n}^{({\overset{⌣}{ω}}_{c, n} + \frac{1}{2})} (2 z - 1) .

(A17)

If the TP has two simple real zeros outside the interval [0, 1] then the pair of q-RSs

c, n

and

d, n

is accompanied by a pair of the PFSs

a, n

and

b, n

of prime SLE (28) near the singular ends 0 and 1 accordingly:

ψ_{{\overset{⌣}{t}}_{-}, n} [z; μ_{o}; T_{K}] = z^{\frac{1}{2} {\overset{⌣}{λ}}_{0; {\overset{⌣}{t}}_{-}, n}} {(1 - z)}^{\frac{1}{2} {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, n}} P_{n}^{({\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, n}, {\overset{⌣}{λ}}_{0; {\overset{⌣}{t}}_{-}, n})} (2 z - 1),

(A18)

where

{\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, n}

is one of the roots of the quadratic equation

[{(\sqrt{c_{1}} - \sqrt{c_{0}})}^{2} - a_{2}] {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, n}^{2} + 2 (2 n + 1) {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, n} (\sqrt{c_{1}} - \sqrt{c_{0}}) + c_{1} [{(2 n + 1)}^{2} - μ_{o}^{2}] = 0

(A19)

And

{\overset{⌣}{λ}}_{0; {\overset{⌣}{t}}_{-}, n} = - \sqrt{c_{0} / c_{1}} {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, n} ({\overset{⌣}{t}}_{-} = a, b) .

(A20)

Indeed since both quadratic equations (A7) and (A19) share the same free term (which is negative if the SLE has at least n+1 eigenvalues) then the second quadratic equation must have two real roots of the oposite sign as far as the equation has a positive leading coefficient. We thus explicitly confirmed the general theorem proven in [10]:

Theorem 9.The n-th eigenfuncion of CSLE (1) is accompanied by three distint-type q-RSs formed by Jacobi polynomials of degree n1 provided the TP has two simple zeros outside the interval [0, 1].

Since the q-RS

d, 0

and

{\overset{⌣}{t}}_{-}, 0

are all nodeless they must lie below the lowest eigenvalue. In fact

{\overset{⌣}{λ}}_{1; c, 0} - | {\overset{⌣}{λ}}_{1; d, 0} | = - 2 (\sqrt{c_{1}} + \sqrt{c_{0}}) < 0

(A21)

while, as shown below,

{\overset{⌣}{ε}}_{{\overset{⌣}{t}}_{-}, 0} (μ_{o}, T_{2}) < {\overset{⌣}{ε}}_{d, 0} (μ_{o}, T_{2}) < {\overset{⌣}{ε}}_{c, 0} (μ_{o}, T_{2})

(A22)

One can directly verify (A22) by representing the difference between quadratic equations (A7) and (A19) as

({\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{+}, 0} - {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, 0}) [- d ({\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, 0} + {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, 0}) + 2 \sqrt{c_{1}}] + 4 \sqrt{c_{0} c_{1}} ({\overset{⌣}{λ}}_{1; \overset{⌣}{t} +, 0} + {\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, 0}) = 0

(A23)

which gives

(| {\overset{⌣}{λ}}_{1; a, 0} | - | {\overset{⌣}{λ}}_{1; d, 0} |) [2 \sqrt{c_{1}} - d (| {\overset{⌣}{λ}}_{1; a, 0} | + | {\overset{⌣}{λ}}_{1; d, 0} |)] = 4 \sqrt{c_{0} c_{1}} (| {\overset{⌣}{λ}}_{1; d, 0} | + | {\overset{⌣}{λ}}_{1; a, 0} |) > 0

(A24)

And

({\overset{⌣}{λ}}_{1; b, 0} - | {\overset{⌣}{λ}}_{1; d, 0} |) [4 \sqrt{c_{0} c_{1}} - d (| {\overset{⌣}{λ}}_{1; d, 0} | + {\overset{⌣}{λ}}_{1; b, 0}) = 2 \sqrt{c_{1}} (| {\overset{⌣}{λ}}_{1; d, 0} | + {\overset{⌣}{λ}}_{1; b, 0}) > 0

(A25)

The general interrelation formula

λ_{1; t, n}^{2} = - c_{1} ε_{t, n} (Λ_{o}; T_{K})

(A26)

between the energies of the q-RSs and the Jacobi index

λ_{1; t, n}

then brings us directly to (A22) keeping in mind that parameter (16) is negative if

Δ_{T} \geq 0

The most important corollary of proven inequality (A22) is that the LDT using as its TF the basic solution

d, 0

inserts the new lowest eigenvalue above the energies

{\overset{⌣}{ε}}_{a, 0} (μ_{o}, T_{2})

and

{\overset{⌣}{ε}}_{b, 0} (μ_{o}, T_{2})

which implies that the LDTs of the PFSs

a, 0

and

b, 0

remain below the lowest eigenvalue of the transformed SLE. We thus conclude that transformed PFS are both nodeless and thereby can be used for constructing the new exactly solvable CSLE (70) with

Λ_{o} = 0, μ_{o}

and

{\bar{Σ}}_{2} = d, 0; {\overset{⌣}{t}}_{-}, 0

({\overset{⌣}{t}}_{-} = a, b)

The Liouville potential for the limiting case of the TP with a double root was initially studied by Williams and Lévai [70]. Examination of TP discriminant (A13) reveals that the leading coefficient of quadratic equation (A19) vanishes for

Δ_{T} = 0

and as a result the given CSLE has only one basic solution of type

{\overset{⌣}{t}}_{-}

, with

{\overset{⌣}{λ}}_{1; {\overset{⌣}{t}}_{-}, n} = \frac{2 (2 n + 1) c_{1}}{(\sqrt{c_{1}} - \sqrt{c_{0}})} [μ_{o}^{2} - {(2 n + 1)}^{2}]

(A27)

To be more precise, it is the solution of type

a

b

c_{1} < c_{0}

c_{1} > c_{0}

accordingly. As mentioned above one can choose

c_{1} > c_{0}

λ_{o} = 0

(changing z for 1-z if necessary). However when the ExpDiff

λ_{o}

increases toward positive values one has to distinguish between the two branches of the double-root TP (DRtTP) potential [44] with the triplets

c 0, a 0, d 0

c 0, a 0, d 0

depending on the choice of the sign of the difference between the TP coefficients

c_{0}

and

c_{1}

. The branches overlap along the Williams-Lévai’s AL potential curves.

Appendix B. Sequential LDTs of CSLE and Associated Crum Wronskians of Seed Solutions

Let us first demonstrate that the TFs

Φ_{τ_{k + 1}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}] = \frac{W {Φ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}], Φ_{τ_{k + 1}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]}}{ρ^{\frac{1}{2}} [z; T_{K}] Φ_{τ_{k}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k - 1}]}

(B1)

can be alternatively represented in the generalized Crum form [24]:

Φ_{τ_{k + 1}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}] = \frac{W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k + 1}]}{ρ^{\frac{1}{2} k} [z; T_{K}] W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}]}

(B2)

Where

W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k + 1}] : = W r {ϕ_{τ_{1}} [z; Λ_{o}; T_{K}], ..., ϕ_{τ_{k}} [z; Λ_{o}; T_{K}], ϕ_{τ_{k + 1}} [z; Λ_{o}; T_{K}]}

(B3)

First setting

W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{0}] : = ϕ_{τ_{1}} [z; Λ_{o}; T_{K}]

(B4)

one can verify that (B2) trivially holds for k=1. Let us now assume that the right-hand sides of (B1) and (B2) coincide for solution of CSLE (68) with any k < p and show that this should be also true for the LDT using an arbitrary solution of CSLE (68) with k = p,

Φ_{τ_{p}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 1}] = \frac{W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 1}, τ_{p}]}{ρ^{\frac{1}{2} (p - 1)} [z; T_{K}] W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 1}]}

(B5)

as its TF. To confirm the latter assertion we, in following Crum [24], start from the conventional chain formula for Wronskians

W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p}] : = \frac{W r {W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 1}], W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 2}, τ_{p}]}}{W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 1}]}

(B6)

(see §198 in [71]), divide it by

ρ^{\frac{1}{2} (p - 1)} [z; T_{K}] W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 1}]

and then make use of (B1) and (B2) for k = p -1. This gives

\frac{W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p}]}{ρ^{\frac{1}{2} (p - 1)} [z; T_{K}] W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 1}]} = \frac{W {Φ_{τ_{p - 1}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 2}], Φ_{τ_{p}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 2}]}}{ρ^{\frac{1}{2}} [z; T_{K}] Φ_{τ_{p - 1}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{p - 2}]}

(B7)

as asserted.

Let us also prove that the zero-energy free terms in CSLEs (68) obtained by sequential LDTs with TFs (B1):

I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}_{k + 1}] = I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}_{k}] + 2 \sqrt{ρ [z; T_{K}]} \frac{d}{d z} \frac{l d Φ_{τ_{k + 1}} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}_{k}]}{\sqrt{ρ [z; T_{K}]}} + J {ρ [z; T_{K}]},

(B8)

can be re-written as [23]

I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}_{k + 1}] = I^{o} [z; Λ_{o}] + 2 \sqrt{ρ [z; T_{K}]} \frac{d}{d z} \frac{l d W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}_{k + 1}]}{\sqrt{ρ [z; T_{K}]}} - (k^{2} - 1) J {ρ [z; T_{K}]} .

(B9)

Indeed substituting (B2) into the right-hand side of (B8) and also making use of definition (67) of the universal correction we come to the following chain of the recurrence relations:

I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}_{k + 1}] - 2 \sqrt{ρ [z; T_{K}]} \frac{d}{d z} \frac{l d W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}_{k + 1}]}{\sqrt{ρ [z; T_{K}]}} + k^{2} J {ρ [z; T_{K}]} = I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}_{k}] - 2 \sqrt{ρ [z; T_{K}]} \frac{d}{d ξ} \frac{l d W [z; Λ_{o}; T_{K} | {\bar{Σ}}_{k}]}{\sqrt{ρ [z; T_{K}]}} - {(k - 1)}^{2} J {ρ [z; T_{K}]},

(B10)

starting from

I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{1}] - 2 \sqrt{ρ [z; T_{K}]} \frac{d}{d z} \frac{l d ϕ_{τ_{1}} [z; Λ_{o}; T_{K}]}{\sqrt{ρ [z; T_{K}]}} = I^{o} [z; Λ_{o}; T_{K}] + J {ρ [z; T_{K}]}

(B11)

Summing up these recurrence relations brings us to sought-for expression (B9) which completes the proof. □

Appendix C. Krein Representation for CWs Formed by Solutions of Generic CSLE

The representation of the DCTs of a principal solution the Schrödinger equation in terms of the ratio of two KDs [25] was initially studied by Bagrov and Samsonov [72]. They took advantage of this representation to show that DCT can be represented as a linear differential operator acting on solutions of the Schrödinger equation under consideration. In particular making use of the chain relations for Krein determinants allowed the cited authors to prove the equivalence of the mentioned linear operators to integral transformations in the Gelfand-Levitan formalism (see [28] for details and the references therein).

The purpose of this appendix is to obtain the explicit relation between the CW and KD formed by seed solutions

ϕ_{k} [z]

of generic CSLE (56) at the energies

ε_{k}

, where we disregard the dependence of both solutions and energies on the parameters

Λ_{o}; T_{K}

. Namely we prove that

W r {ϕ_{1} [z], ..., ϕ_{2 j + ℓ} [z]} = ρ^{j (j + ℓ - 1)} [z] K {ϕ_{k = 1, ..., 2 j + ℓ} [z]; ε_{k = 1, ..., 2 j + ℓ}}

(C1)

where

K {ϕ_{k = 1, ..., 2 j} [z]; ε_{k = 1, ..., 2 j}} : = | {...}_{}^{ε_{1} ϕ_{1} [z] ... ε_{2 j} ϕ_{2 j} [z]}_{ε_{1}^{j - 1} ϕ_{1} [z] ... ε_{2 j}^{j - 1} ϕ_{2 j} [z]}^{{\overset{•}{ϕ}}_{1} [z] ... {\overset{•}{ϕ}}_{2 j} [z]}_{ε_{1}^{j - 1} {\overset{•}{ϕ}}_{1} [z] ... ε_{2 j}^{j - 1} {\overset{•}{ϕ}}_{2 j} [z]}^{ϕ_{1} [z] ... ϕ_{2 j} [z]} |

(C2)

and

K {ϕ_{k = 1, ..., 2 j + 1} [z]; ε_{k = 1, ..., 2 j + 1}} : = {(- 1)}^{j} | {...}_{}^{ε_{1} ϕ_{1} [z] ... ε_{_{2 j + 1}} ϕ_{_{2 j + 1}} [z]}_{ε_{1}^{j - 1} {\overset{•}{ϕ}}_{1} [z] ... ε_{2 j + 1}^{j - 1} {\overset{•}{ϕ}}_{_{2 j + 1}} [z]}^{{\overset{•}{ϕ}}_{1} [z] ... {\overset{•}{ϕ}}_{2 j + 1} [z]}_{ε_{1}^{j} ϕ_{1} [z] ... ε_{2 j + 1}^{j} ϕ_{_{2 j + 1}} [z]}^{ϕ_{1} [z] ... ϕ_{2 j + 1} [z]} | .

(C3)

To confirm (C1) we formally represent the

(2 j + ℓ)

-th derivative of each seed solution

ϕ_{k} [z]

with respect to its argument z as a superposition of

ϕ_{k} [z]

and its first derivative

\frac{d^{2 j^{'}} ϕ_{k}}{d^{2 j^{'}} z} = {(- ε_{k} ρ [z])}^{j^{'}} ϕ_{k} [z] + F_{j^{'} - 1}^{(0)} [z; ε_{k}] ϕ_{k} [z] + G_{j^{'} - 1}^{(0)} [z; ε_{k}] {\overset{•}{ϕ}}_{k} [z]

(C4)

\frac{d^{2 j^{'} + 1} ϕ_{k}}{d^{2 j^{'} + 1} z} = {(- ε_{k} ρ [z])}^{j^{'}} {\overset{•}{ϕ}}_{k} [z] + F_{j^{'}}^{(1)} [z; ε_{k}] ϕ_{k} [z] + G_{j^{'} - 1}^{(1)} [z; ε_{k}] {\overset{•}{ϕ}}_{k} [z],

(C5)

where the z-dependent polynomials in ε are defined via the following mixed recurrence relations:

F_{j^{'}}^{(1)} [z; ε] = j^{'} l d ρ [z] {(- ρ [z] ε)}^{j^{'}} + \overset{•}{F}_{j^{'} - 1}^{(0)} [z; ε] - G_{j^{'} - 1}^{(0)} [z; ε] (I^{o} [z] + ρ [z] ε), G_{j^{'} - 1}^{(1)} [z; ε] = \overset{•}{G}_{j^{'} - 1}^{(0)} [z; ε_{k}]

(C6)

and

F_{j^{'} - 1}^{(0)} [z; ε] = - {G_{j^{'} - 2}^{(1)} [z; ε] + {(- ρ [z] ε)}^{j^{'} - 1}} I^{o} [z] - ρ [z] ε G_{j^{'} - 2}^{(1)} [z; ε], G_{j^{'} - 1}^{(0)} [z; ε] = (j^{'} - 1) l d ρ [z] {(- ρ [z] ε)}^{j^{'} - 1} + F_{j^{'} - 1}^{(1)} [z; ε] + \overset{•}{G}_{j^{'} - 2}^{(1)} [z; ε]

(C7)

starting from

F_{0}^{(1)} [z; ε] = G_{- 1}^{(1)} [z; ε] \equiv 0

(C8)

and

F_{1}^{(0)} [z; ε] = - I^{o} [z] - ε ρ [z], G_{0}^{(0)} [ξ; ε] \equiv 0

(C9)

Substituting (C6) and (C7) into the CW and eliminating all the summands which contain the monomials

ε_{k}^{{j^{'}}^{'}} ϕ_{k} [z]

ε_{k}^{{j^{'}}^{'}} {\overset{•}{ϕ}}_{k} [z]

appearing in the upper rows we come to (C1), where we also took into account that

2 \sum_{j^{'} = 1}^{j - 1} j^{'} + ℓ j = j (j - ℓ - 1)

(C10)

Appendix D. DCTs of Generic CSLE in Krein Representation

To represent the eigenfunctions in questions in a quasi-rational form it is convenient to express the CWs in terms of Krein determinants (KD) via (C1). Let us set

k = 2 j + ℓ - 1

in (B10) and then replace the CW by KD using (C1). Making use of definition (67) of the universal correction we can re-write the zero-energy term of CSLE (68) as [9]

I^{o} [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}] = I^{o} [z; Λ_{o}] + ℓ J {ρ [z; T_{K}]} 2 \sqrt{ρ [z; T_{K}]} \frac{d}{d z} \frac{l d K [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}]}{\sqrt{ρ [z; T_{K}]}}

(D1)

where

K [z; Λ_{o}; T_{K} | τ_{1}, τ_{2}, ..., τ_{2 j + ℓ}] : = K {ϕ_{τ_{k = 1, ..., 2 j + ℓ}} [z; Λ_{o}; T_{K}]; ε_{τ_{k = 1, ..., 2 j + ℓ}} (Λ_{o}; T_{K})}

(D2)

Note that the universal correction appears in the right-hand side of this expression only for an odd number of sequential LDTs.

Finally the TFs of our interest take the form

Φ_{τ_{2 j + ℓ + 1}} [z; Λ_{o}; T_{K}; ε | {\bar{Σ}}_{2 j + ℓ}] = \frac{K [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}; τ_{2 j + ℓ + 1}]}{ρ^{\frac{1}{2} ℓ} [z; T_{K}] K [z; Λ_{o}; T_{K} | {\bar{Σ}}_{2 j + ℓ}]}

(D3)

Appendix E. Canonical Heun Equation Generated via Two-Step DCT Using Basic Seed Solutions

As the simplest illustration of the derived expresions for

ℓ = 0

let us consider the DCT of JRef CSLE (1) using two different basic solutions

t, 0

and

t^{'}, 0

(

t \neq

t^{'}

). The remarkable feature of this case is that the polynomial denominator of the last PF in sum (177) has degree of 1:

D_{1} [z; Λ_{o}; T_{2} | t, 0; t^{'}, 0] = Δ λ_{1; t t^{'}} z + Δ λ_{0; t t^{'}} (z - 1),

(E1)

where

Δ λ_{r; t t^{'}} : = λ_{r; t, 0} - λ_{r; t^{'}, 0} (r = 0, 1)

(E2)

and as a result CSLE (68) becomes the canonical form of the Heun equation [43] with the poisition

z_{t, t^{'}}

of the extarneous pole dependent on the exponent parameters [5]:

z_{t t^{'}} = \frac{Δ λ_{0; t t^{'}}}{Δ μ_{t t^{'}}},

(E1)

Where

Δ μ_{t t^{'}} : = μ_{t, 0} - μ_{t^{'}, 0}

(E4)

With

μ_{\tilde{t}, 0} : = - λ_{0; \tilde{t}, 0} - λ_{1; \tilde{t}, 0} - 1.

(E5)

PD (E1) thereby takes form

D_{1} [z; Λ_{o}; T_{2} | t, 0; t^{'}, 0] = Δ μ_{t t^{'}} (z - z_{t t^{'}}) .

(E6)

Setting

Λ_{r} | t, 0; t^{'}, 0) : = λ_{r; t, 0} + λ_{r; t^{'}, 0} - 1,

(E7)

representing polynomial (165) as

D_{2}^{(0)} [z; \overset{⇀}{Λ} | t, 0; t^{'}, 0); z_{t t}] = - F_{1}^{(Λ_{1}, Λ_{0})} (z) (z - z_{t t^{'}}) - z (z - 1)

(E8)

and taking into account that

D_{2; 2}^{(0)} (\overset{⇀}{Λ} | t, 0; t^{'}, 0); z_{t t}) = - \frac{1}{2} [Λ_{0} | t, 0; t^{'}, 0) + Λ_{1} | t, 0; t^{'}, 0)]

(E9)

= - \frac{1}{2} (μ_{t, 0} + μ_{t^{'}, 0})

(E10)

we thus need to confirm that according (167):

Δ μ_{t t^{'}} D_{2}^{(0)} [z; \overset{⇀}{Λ} | t, 0; t^{'}, 0); z_{t t}] = - F_{1}^{(Λ_{1}, Λ_{0})} (z) D_{1} [z; Λ_{o}; T_{2} | t, 0; t^{'}, 0] -

(E11)

= - \frac{1}{2} (μ_{t, 0}^{2} - μ_{t^{'}, 0}^{2}) Π_{2} [z; {\bar{z}}_{T}] .

(E12)

In fact keeping in mind that

(λ_{0; t, 0} + λ_{0; t^{'}, 0}) (λ_{1; t, 0} - λ_{1; t^{'}, 0}) + (λ_{0; t, 0} - λ_{0; t^{'}, 0}) (λ_{1; t, 0} + λ_{1; t^{'}, 0}) = 2 λ_{0; t, 0} λ_{1; t, 0} - 2 λ_{0; t^{'}, 0} λ_{1; t^{'}, 0}

(E13)

we can rewrite (E11) as

Δ μ_{t t^{'}} D_{2}^{(0)} [z; \overset{⇀}{Λ} | t, 0; t^{'}, 0); z_{t t}] = - \frac{1}{2} (λ_{0; t, 0}^{2} - λ_{0; t^{'}, 0}^{2}) {(z - 1)}^{2} - \frac{1}{2} (λ_{1; t, 0}^{2} - λ_{1; t^{'}, 0}^{2}) z^{2} - (Δ μ_{t t^{'}} + λ_{0; t, 0} λ_{1; t, 0} - λ_{0; t^{'}, 0} λ_{1; t^{'}, 0}) z (z - 1) .

(E14)

Re-expressing (E14) in terms of the first-degree polynomial

(λ_{0; t, 0}^{2} - λ_{0; t^{'}, 0}^{2}) (1 - z) + (λ_{1; t, 0}^{2} - λ_{1; t^{'}, 0}^{2}) z = (λ_{0; t, 0}^{2} - λ_{0; t^{'}, 0}^{2}) {(z - 1)}^{2} + (λ_{1; t, 0}^{2} - λ_{1; t^{'}, 0}^{2}) z^{2} - [{(μ_{t, 0} + 1)}^{2} - {(μ_{t^{'}, 0} + 1)}^{2} - 2 λ_{0; t, 0} λ_{1; t, 0} + 2 λ_{0; t^{'}, 0} λ_{1; t^{'}, 0}] z (z - 1)

(E15)

then gives

Δ μ_{t t^{'}} D_{2}^{(0)} [z; \overset{⇀}{Λ} | t, 0; t^{'}, 0); z_{t t}] = - \frac{1}{2} (λ_{0; t, 0}^{2} - λ_{0; t^{'}, 0}^{2}) (1 - z) - \frac{1}{2} (λ_{1; t, 0}^{2} - λ_{1; t^{'}, 0}^{2}) z + \frac{1}{2} (μ_{t, 0}^{2} - μ_{t^{'}, 0}^{2}) z (z - 1) .

(E16)

On the other hand multiplying polynomial (12) by

Δ ε_{t t^{'}} : = ε_{t, 0} - ε_{t^{'}, 0}

(E17)

and making use of (17), (18), and (25) with

c

replaced for

t

and

t^{'}

respectively one finds

(μ_{t^{'}, 0}^{2} - μ_{t, 0}^{2}) Π_{2} [z; {\bar{z}}_{T}] = (λ_{0; t, 0}^{2} - λ_{0; t^{'}, 0}^{2}) (1 - z) + (λ_{1; t, 0}^{2} - λ_{1; t^{'}, 0}^{2}) z + (μ_{t, 0}^{2} - μ_{t^{'}, 0}^{2}) z (z - 1) .

(E18)

Comparing (E18) with (E16) brings us directly to (E12) as asserted.

We thus proved that that the RefPF of the CSLE constructed using two different basic solutions

t, 0

and

t^{'}, 0

(

t \neq

t^{'}

) has three second-order poles in the finite plane:

I^{o} [z; Λ_{o}; {\hat{T}}_{2} | t, 0; t^{'}, 0] = \frac{1 - λ_{o}^{2}}{4 z^{2}} + \frac{1}{4 {(1 - z)}^{2}} - \frac{2}{{[z - z_{t t^{'}} (Λ_{o}; {\hat{T}}_{2})]}^{2}} + \frac{{\overset{⌢}{O}}_{1}^{o} [z; Λ_{o}; {\hat{T}}_{2} | t, 0; t^{'}, 0]}{4 z (z - 1) [z - z_{t t^{'}} (Λ_{o}; {\hat{T}}_{2})]}

(E19)

with the position of the third pole dependent on the parameter

Λ_{o}; {\hat{T}}_{2}

References

Cooper, F.; Ginocchio, J.N.; Khare, A. , Relationship between supersymmetry and solvable potentials. Phys. Rev. D 1987, 36, 2458–2473. [Google Scholar] [CrossRef] [PubMed]
Gendenshtein, L.E. Derivation of exact spectra of the Schrödinger equation by means of supersymmetry. JETP Lett. 1983, 38, 356–359. [Google Scholar]
Natanzon, G.A.; Study of the one-dimensional Schrödinger equation generated from the hypergeometric equation. Vestn. Leningr. Univ. 1971, No. 10, 22–28. Available online: arxiv.org/PS_cache/physics/pdf/9907/9907032v1.pdf (accessed on 20 July 1999).
Erdelyi, A.; Bateman, H. Transcendental Functions; McGraw Hill: New York, NY, USA, 1953; Volume 1. [Google Scholar]
Natanson, G.A. Supersymmetry of algebraic-fraction potentials analytically quantized in terms of Heine polynomials II. Generalized Darboux transformations with basic quasi-algebraic kernels, 2011, p. 1. Available online: researchgate.net/publication/326678021 (accessed on 29 March 2011).
Gibbons, J.; Veselov, A.P. On the rational monodromy-free potentials with sextic growth. J. Math. Phys. 2009, 50, 013513–25. [Google Scholar] [CrossRef]
Rudyak, B.V.; Zakhariev, B.N. New exactly solvable models for Schrödinger Equation. Inverse Problems 1987, 3, 125–133. [Google Scholar]
Natanson, G.; Single-source nets of algebraically-quantized reflective Liouville potentials on the line I. Almost-everywhere holomorphic solutions of rational canonical Sturm-Liouville equations with second-order poles. arXiv 2015, pp. 1–112. Available online: arXiv:1503.04798v2 (accessed on 9 Dec 2015).
Natanson, G.; Darboux-Crum Nets of Sturm-Liouville Problems Solvable by Quasi-Rational Functions I. General Theory. 2018, p. 1. Available online: researchgate.net/publication/323831953 (accessed on 1 March 2018).
Natanson, G.; Survey of nodeless regular almost-everywhere holomorphic solutions for exactly solvable Gauss-reference Liouville potentials on the line I. Subsets of nodeless Jacobi-seed solutions co-existent with discrete energy spectrum. arXiv 2016, pp. 1–86. Available online: arXiv:1606.08758 (accessed on 29 Oct 2016).
Quesne, C. Exceptional orthogonal polynomials, exactly solvable potentials and supersymmetry,” J. Phys. A 2008, 41, 392001, 6 pages. 41.
Quesne, C. Solvable Rational Potentials and Exceptional Orthogonal Polynomials in Supersymmetric Quantum Mechanics. SIGMA 2009, 5, 084–24. [Google Scholar] [CrossRef]
Quesne, C. Rational Extensions of the Rosen-Morse II and Eckart Potentials. SIGMA 2012, 8, 080–19. [Google Scholar]
Natanzon, GA. Use of the Darboux theorem for constructing the general solution of the Schrödinger equation with the Pöschl-Teller potential. Vestn Leningr Univ. 1977;No16: 33-39.
Andrianov, A.A.; Borisov, N.V.; Ioffe, M.V. The factorization method and quantum systems with equivalent energy spectra. Phys Lett 1984, 105, 19–22. [Google Scholar] [CrossRef]
Sukumar C., V. Supersymmetric quantum mechanics of one-dimensional system. J Phys A. 1985, 18, 2917–2936. [Google Scholar] [CrossRef]
Sukumar C., V. Supersymmetric quantum mechanics and the inverse scattering method. J. Phys. A 1985, 18, 2937–2955. [Google Scholar] [CrossRef]
Hounkonnou, M.N.; Ronveaux, A. Factorization of generalized Lame and Heun’s differential equations,” Comm. Math. Analysis 2011, 11, 121–136. [Google Scholar]
Gesztesy, F.; Simon, B.; Teschl, G. Zeros of the Wronskian and renormalize oscillation theory. Am. J. Math. 1996, 118, 571–594. [Google Scholar]
Everitt, W.N. A Catalogue of Sturm-Liouville Differential Equations. In Sturm-Liouville Theory, Past and Present; Amrein, W.O., Hinz, A.M., Pearson, D.B., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2005; pp. 271–331. [Google Scholar]
Natanson, G.; Breakup of SUSY quantum mechanics in the Limit-Circle region of the reflective Kratzer oscillator. arXiv 2014, 114 pp. Available online: arXiv:1405.2059v1 (accessed on 7 May 2014).
Milson, R. Liouville transformation and exactly solvable Schrödinger equations. Int. J. Theor. Phys. 1998, 37, 1735–1752. [Google Scholar] [CrossRef]
Schulze-Halberg, A. Higher-order Darboux transformations with foreign auxiliary equations and equivalence with generalized Darboux transformations. Appl. Math. Lett. 2012, 25, 1520–1527. [Google Scholar] [CrossRef]
Crum, M.M. Associated Sturm-Liouville systems,” Quart. J. Math. Oxford (2) 1955, 6, 121–127. [Google Scholar] [CrossRef]
Krein, M. On a continuous analogue of the Christoffel formula from the theory of orthogonal polynomial. Dokl. Akad. Nauk SSSR 1957, 113, 970–973. [Google Scholar]
Garcia-Ferrero, M.; Gȯmez-Ullate, D.; Milson, R. A Bochner type classification theorem for exceptional orthogonal polynomials. J. Math. Anal. Appl. 2019, 472, 584–626. [Google Scholar] [CrossRef]
Adler, V.E. A modification of Crum’s method, Theor. Math. Phys. 1994, 101, 1381–1386. [Google Scholar]
Samsonov, B.F. On the equivalence of the integral and the differential exact solution generation methods for the one-dimensional Schrodinger equation. J. Phys. A 1995, 28, 6989–6998. [Google Scholar] [CrossRef]
Samsonov, B.F. New features in supersymmetry breakdown in quantum mechanics,” Mod. Phys. Lett. A 1996, 11, 1563–1567. [Google Scholar]
Bagrov, V.G.; Samsonov, B.F. Darboux transformation and elementary exact solutions of the Schrödinger equation, Pramana J. Phys. 1997, 49, 563–580. [Google Scholar]
Bose, A.K. A class of solvable potentials. Nuovo Cim. 1964, 32, 679–688. [Google Scholar] [CrossRef]
Weidmann, J. Spectral Theory of Sturm-Liouville Operators Approximation by Regular Problems. In Sturm-Liouville Theory, Past and Present, Amrein, W.O., Hinz, A.M., Pearson, D.B., Eds.; Publisher: Birkhäuser Verlag, Basel, 2005. [Google Scholar]
Schnizer, W.A.; Leeb, H. , Exactly solvable models for the Schrödinger equation from generalized Darboux transformations. J. Phys. A 1993, 26, 5145–5156. [Google Scholar] [CrossRef]
Martínez-Finkelshtein, A; Rakhmanov, E. A. On asymptotic behavior of Heine-Stieltjes and Van Vleck polynomials. Contemp. Math., 2010, 507, 209–232. [Google Scholar]
Martínez-Finkelshtein, A; Rakhmanov, E. A. Critical Measures, Quadratic Differentials, and Weak Limits of Zeros of Stieltjes Polynomials. Comm. Math. Phys. 2011, 302, 53–111. [Google Scholar] [CrossRef]
Heine, E. Handbuch der Kugelfunctionen, Theorie und Anwendungen, vol. 1. Berlin, G. Reimer, 1878. p. 172.
Marden, M. On Stieltjes polynomials, Trans. Amer. Math. Soc. 1931, 33, 934–944. [Google Scholar] [CrossRef]
Stieltjes, T.J. Sur certains polynômes: Qui vérifient une équation différentielle linéaire du second ordre et sur la theorie des fonctions de Lamé. Acta Math. 1885, 6, 321–326. [Google Scholar] [CrossRef]
Marden, M. The geometry of the zeros of a polynomial in a complex variable, Mathematical Surveys, no. 3. New York, American Mathematical Society, 1949.
Marden, M. On the Polynomial Solutions of the Generalized Lamé Differential Equation. Proc. Amer. Math. Soc. 1950, 1, 492–497. [Google Scholar]
Shapiro, B. Algebro-geometric aspects of Heine-Stieltjes theory,” J. London Math. Soc. 2011, 83, 36–56. [Google Scholar] [CrossRef]
Szegȍ, G. Orthogonal Polynomials. New York: American Mathematical Society, 1959.
Sleeman, B.D.; Kuznetsov, V.B. Heun functions: Normal form of Heun equation. In The NIST Handbook of Mathematical Functions. Editor Olver, F.W. J., Lozier, D.W., Boisvert, R.F., Clark, C.W., Eds.; Cambridge University Press: Cambridge. U.K, 2010. [Google Scholar]
Natanson, G.; Dutt-Khare-Varshni potential and its quantized-by-Heun-polynomials SUSY partners as nontrivial examples of solvable potentials explicitly expressible in terms of elementary functions. arXiv 2015, 51 pp. Available online: arXiv:1508.04738v1 (accessed on 11 Aug 2015).
Rosen, N.; Morse P., M. On the vibrations of polyatomic molecules. Phys. Rev. 1932, 42, 210–217. [Google Scholar] [CrossRef]
Natanson, G.; Use of Wronskians of Jacobi polynomials with common complex indexes for constructing XDPSs and their infinite and finite orthogonal subsets. 2019, 1-57. Available online: researchgate.net/publication/331638063 (accessed on 1 Mar 2019).
Natanson, G. Routh polynomials: hundred years in obscurity. Available online: researchgate.net/publication/326522529 2022, 1-61 (accessed on 1 Nov 2022).
Natanson, G. Rediscovery of Routh Polynomials after Hundred Years in Obscurity, in Recent Research in Polynomials. Özger F., Ed. (IntechOpen, London, 2023), 27 pages (Available online: intechopen.com/onlinefirst/1118656).
Gomez-Ullate, D.; Grandati, Y.; Milson, R. Extended Krein-Adler theorem for the translationally shape invariant potentials. J. Math. Phys. 0435; 10. [Google Scholar]
50. Odake, S; Sasaki, R. Krein–Adler transformations for shape-invariant potentials and pseudo virtual states. J. Phys. 5201.
Garcia-Ferrero, M.; Gómez -Ullate, D. Oscillation Theorems for the Wronskian of an Arbitrary Sequence of Eigenfunctions of Schrödinger’s Equation, Lett. Math. Phys. 2014, 105, 551–573. [Google Scholar]
Cooper, F.; Khare, A.; Sukhatme U., P. Supersymmetry and quantum mechanics. Phys. Rep. 1995, 251, 267–385. [Google Scholar] [CrossRef]
Cooper, F.; Khare, A.; Sukhatme U., P. Supersymmetry in Quantum Mechanics. Publisher: Denver, World Scientific, 2001.
Gangopadhyaya, A.; Mallow, J.V.; Rasinariu, C. Supersymmetric Quantum Mechanics. An Introduction. Publisher: London, World Scientific Publishing, 2019.
55. Courant R,; Hilbert D. Methods of Mathematical Physics, 1953.
56. Lemieux, A,; Bose, A.K. Construction de potentiels pour lesquels l’équation de Schrödinger est soluble. Ann. Inst. Henri Poincaré.
Ishkhanyan, A.M. Schrödinger potentials solvable in terms of the general Heun functions", Ann. Phys. 2018, 388, 456–471. [Google Scholar]
Batic, D, Williams, R. ; Nowakowski, M. Potentials of the Heun class. J. Phys. A 2013, 46, 245204–21. [Google Scholar] [CrossRef]
Natanson, G. Radial Lemieux-Bose Potential Conditionally Exactly Quantized by Polynomials. 2022, p. 1. Available online: researchgate.net/publication/359348797 (accessed on 1 April 2022).
Natanson, G. Double-step shape-invariance of 'implicit' radial potential solvable via hypergeometric functions. 2022, p. 1. Available online: researchgate.net/publication/358520011 (accessed on 1 Feb 2022).
Natanzon, G.A. Construction of the Jost function and the S-matrix for a general potential allowing solution of the Schrödinger equation in terms of hypergeometric functions. Sov. Phys. J. 1978, 21, 855–859. [Google Scholar] [CrossRef]
Natanzon, G.A. General properties of potentials for which the Schrödinger equation can be solved by means of hypergeometric functions,” Theor. Math. Phys. 1979, 38, 146–153. [Google Scholar]
Ginocchio, J. A Class of Exactly Solvable Potentials II. The Three-Dimensional Schrodinger Equation,” Ann. Phys. (N.Y.) 1985, 159, 467–480. [Google Scholar]
Wu, J.; Alhassid, Y.; Gùrsey, F. Group theory approach to scattering. IV. Solvable potentials associated with SO(2,2). Ann. Phys. 1989, 196, 163–181. [Google Scholar] [CrossRef]
Lévai, G.; Baye, D.; Sparenberg, J.-M. Phase-equivalent potentials from supersymmetry: analytical results for a Natanzon-class potential, J. Phys. A 1997, 30, 8257–8271. [Google Scholar] [CrossRef]
Ginocchio, J. A class of exactly solvable potentials: I. One-dimensional Schrödinger equation. Ann. Phys. 1984, 152, 203–219. [Google Scholar] [CrossRef]
Lévai, G. Non-compact groups and solvable potentials. In Proceedings of the XXI International Colloquium on Group Theoretical Methods in Physics, Goslar, Germany, 15–20 July 1996; Doebner, H.-D., Nattermann, P., Scherer, W., Eds.; World Scientific: Singapore, 1997; Volume 1, pp. 461–466. [Google Scholar]
Natanson, G. Quantization of one-dimensional Ginocchio potential by Masjed-Jamei polynomials with degree-dependent indexes. 2022, p. 1. Available online: researchgate.net/publication/360950671 (accessed on 1 May 2022).
Natanson, G. Overlapping of Lévai’s and Milson’s e-tangent-polynomial potentials along symmetric curves. Axioms 2023, 12, 584–27. [Google Scholar] [CrossRef]
Williams, B.W.; Lévai, G. An asymmetric "implicit" potential on the real line. Mod. Phys. Lett. 2003, 18, 1901–1909. [Google Scholar] [CrossRef]
Muir, T. A Treatise on the Theory of Determinants; Dover Publications: New York, USA, 1960 (revised and enlarged by W. H. Metzler).
Bagrov, V.G.; Samsonov, B.F. Darboux transformation, factorization and supersymmetry in one-dimensional quantum mechanics,” Theor. Math. Phys. 1995, 104, 1051–1060. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Use of Normalizable Seed Solutions for Constructing

Abstract

1. Introduction

2. Exactly Solvable Fuchsian SLE with Two Second-Order Poles on Real Axis

3. Liouville-Darboux Transformation of Fuchsian CSLE with Second-Order Poles

4. RLDTs of JRef CSLE Using Basic TFs

5. Representation of TFs in Quasi-Rational Form

6. Enhanced Adler Theorem

7. Discussion

Funding

Conflicts of Interest

Appendix A. Algebraic Formulas for Eigenvalues of JRef CSLE in Limiting Case of AL Liouville Potential

Appendix B. Sequential LDTs of CSLE and Associated Crum Wronskians of Seed Solutions

Appendix C. Krein Representation for CWs Formed by Solutions of Generic CSLE

Appendix D. DCTs of Generic CSLE in Krein Representation

Appendix E. Canonical Heun Equation Generated via Two-Step DCT Using Basic Seed Solutions

References

MDPI Initiatives

Important Links

Subscribe