Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

LCAG ：A Lightweight Consensus Algorithm Based on Graph for the Internet of Things

Submitted:

14 August 2023

Posted:

16 August 2023

You are already at the latest version

Abstract
Consensus algorithms are the core technology of blockchain and a focus in the current distributed system research. The consensus algorithms are widely used in distributed systems, it has solved the decentralization problem. The traditional consensus algorithm needs the process of node legitimacy checking, identity authentication, and primary node view change, so the time cost of reaching an agreement between nodes is still exponential. In response to the problem, a lightweight consensus algorithm based on graph (LCAG) is proposed for the Internet of Things (IoT) in this paper, which is proposes an access control table, and reaches an agreement among nodes by calculating the probability of nodes in the control table, and reduces the time overhead of the reaching an agreement in distributed systems. We have carried out simulation experiments for the new algorithm, and the experiments show that: the new algorithm needs less time overhead than the classical Byzantine algorithm need, as well as Byzantine Generals problem (BGP), practical Byzantine fault-tolerant algorithm (PBFT) and directed acyclic graph (DAG) algorithm, and so on. The new algorithm can be applied to the devices of IoT, which have limited computing power.
Keywords: 
Byzantine agreement
;  
graph theory
;  
lightweight consensus algorithm
Subject: 
Computer Science and Mathematics  -   Computer Networks and Communications

I. Introduction

Consensus algorithms are the core technology of blockchain, and in a distributed system and an untrusty or complex environment, all the nodes will reach an agreement although communication entities may not trust each other. That is, decentration is a very important feature of consensus algorithms, for example, the Bitcoin [1]. During the process of reaching an agreement, all the nodes can be deleted or added in the system at any time, can’t be falsified and are anonymous. Consensus algorithms decide blockchain’s security, usability and extensibility, and are crucial to the applicability of blockchain technology. The study and the development of consensus algorithms influent the development and vicissitudes of blockchain [2]. The development of blockchain technology accelerates the development of the Internet of Things [3], which has become a focus of the academic and industrial circles.
Blockchain can be defined as a distributed ledger technology that allows the storing and sharing of data in a decentralized and immutable manner through a network of distributed peer-to-peer members. A blockchain can be considered a decentralized architecture with built-in security to increase the trust and integrity of transactions. That is to say: its advantages are decentralization, openness, independence and anonymity, etc.
In 2008, Satoshi Nakamoto proposed Bitcoin, which is a kind of decentralized cryptocurrency. It is a successful case of decentralized application. Based on a specific cryptographic algorithm, blockchain connects many chains into a big chain, which is decentralized, untrusty, open, anonymous and can’t be falsified. Therefore, it has been widely used in network security field, financial field, government management, public services and so on. The appearance of Bitcoin marked that consensus algorithms started practical application. Consensus algorithms emerged from “the two-army problem”, and were applied in “the Byzantine Generals Problem” [4]. BGP was used to study that when there are attacks in the system from fault nodes or malicious nodes, non-fault nodes can still reach an agreement on a certain event. Many researchers carried out studies on the base of BGP. There have been abundant achievements [5] so far on the base of BGP. A typical example is Practical Byzantine Fault-Tolerance [6] protocol. It studied the relation between the number of fault nodes or malicious nodes and the number of all the nodes. It is believed that if in the system the number of fault nodes or malicious nodes is less than 1/3 of that of all the nodes, non-fault nodes can still reach an agreement without the help of trusty third party. In that case, decentration are guaranteed in the system. Over recent years, a new blockchain based on DAG [7] structure was proposed, it adopts asynchronous communication mechanism and concurrent processing algorithm.
As the core technology of the decentralization, BGP is crucial and superior in the application of blockchain. If the information is to be transmitted between generals and lieutenants, or among lieutenants, or if generals are to be changed, cryptographic techniques will be applied, such as integrity of digital digest, signature and authentication, and encryption and decryption of information. Therefore, generals and lieutenants need much time overhead to reach an agreement. Due to its massive time overhead, BGP, PBFT and DAG haven’t been widely applied. To reduce time overhead when the consensus algorithms are reached an agreement, LCAG is proposed in this paper. Here are the steps of LCAG: at first, the probability of out-degree and in-degree of a certain node is computed. According to the computed probability, the node will make a decision. Secondly, the table of node-accessing-control is made. Finally, all the nodes access the table and make a final decision. Since time overhead of the LCAG is only based on the polynomial time when all the nodes reach an agreement. Therefore, the LCAG can be widely used the devices of IoT is a computing concept that describes the idea of everyday physical objects being connected to the internet and being able to identify themselves to other devices and send and receive data), which have limited computing power.
The main contributions of this paper are as follows:
1) The out-degree and in-degree in the graph theory are introduced for the nodes reach an agreement.
2) First proposes the accessing-control table of consensus algorithm.
3) It takes less time for nodes to reach an agreement, which accelerates the application of blockchain technology in IoT devices. Our contributions in this paper are given as following Table I.
Table I. Performance comparison table of four consensus algorithms.
Table I. Performance comparison table of four consensus algorithms.
consensus algorithm tasks of reaching agreements time overhead to reach agreements
BGP 4 exponential
PBFT 4 exponential
DAG 3 polynomial
LCAG 2 polynomial
The BGP algorithm, the PBFT algorithm and DAG algorithm are the basic theories of decentralization, which accelerate the development of blockchain technology. A number of cryptographic primitives and gossip protocol[8] (the anti-entropy is used in the gossip protocol, in worst case scenario, the time overhead for the nodes of the gossip protocol to reach an agreement is polynomial O ( n 2 ) ) are used, which leads to a great mass of time overhead in the process of the nodes reaching an agreement. Therefore, they cannot be widely used in the devices of IoT, which have limited computing power.
When nodes reach an agreement, LCAG only uses a small number of cryptographic primitives, which not only guarantees its security but also needs a little of time overhead. Therefore, it can be applied in the devices of IoT with limited computing power.
The remainder of this paper is organized as follows. In Section II, we discuss related work concerning a consensus algorithm in the distributed system. In Section III, we provide a description of the novel LCAG algorithm. The experiments of the BGP, PBFT, DAG and LCAG are introduced, their experimental results are discussed In Section IV, while Section V concludes the paper.

II. Related Work

Through a consensus algorithm, nodes can reach an agreement in the distributed system. This is the essential attribute and the core technology of blockchain. Aimed at consensus algorithms of blockchain, researchers have proposed many new algorithms. Literature [9] summarized in details 32 algorithms of blockchain’s technology, and proposed the basic algorithm model of blockchain’s consensus algorithms and classifying methods. It also summarized the development and the performance evaluation of present consensus algorithms.
In order to apply the Byzantine Generals Problem to the distributed system, Lamport proposed Paxous [10] algorithm to realize it that there are some fault nodes in the distributed system, but the system can still reach an agreement on a specific viewpoint. In 1999, Castro and Liskov first proposed PBFT protocol to solve the Byzantine Generals Problem. PBFT quantified the relation between fault nodes and non-fault nodes in the distributed system, and judged whether non-fault nodes can reach an agreement on a specific viewpoint. Only when N ≥ 3 f + 1 , an agreement can be reached. Here, N denotes the total number of nodes, f denotes the total number of disloyal nodes. PBFT has many advantages, but when nodes are deleted or added in the distributed system, time overhead will increase. PBFT performs a lot of tasks in the server-side. PBFT’s consensus algorithm is very complex, and servers need to interact with each other, which results in a mess of data and complex calculation. To reduce calculation and time overhead, many researches have been carried out so far, and there are a lot of achievements.
In 2006, Cowling et al. proposed HQ to improve PBFT. Compared with PBFT, HQ [11] doesn’t need the servers to interact with each other to reach an agreement. Literature [12] proposed a dynamic PBFT algorithm, which needs less time overhead to reach an agreement. Based on it, the system needn’t to be off in the whole process, even when duplicates and nodes access or exit the network. To reduce time overhead, Abraham, Gueta and Malkhi proposed Hot-Stuff [13] algorithm on the base of PBFT. Hot-Stuff algorithm reduces the complexity of communication by applying linear view change. However, Hot-Stuff algorithm is based on LVC and threshold signature, so the communication complexity of each round is still exponential. Based on the extending research of PBFT, Golan-Gueta et al. proposed Scalable Byzantine Fault-Tolerance (SBFT for short) [14] to solve the problem of decentration and extension of the blockchain. But SBFT still uses signature to realize authentication. The problems of extension, such as inadequate throughput, the slow transaction authentication and so on, are considered to be the bottleneck of blockchain’s extendibility, which limit the development of blockchain. To solve these problems, literature [15] discussed the distributed account book consensus algorithm on the base of Directed Acyclic Graph [16]. DAG was introduced based on Gossip protocol, which promoted the development of IOTA (IOTA is a revolutionary type of transaction settlement and data transfer layer designed for the Internet of Things. It is a new type of digital encryption currency that focuses on solving machine-to-machine transaction problems). DAG ensures blockchain’s throughput of high concurrency and is expected to break through the bottleneck of performance in the traditional blockchain. However, in the process of implementing Gossip protocol, a lot of redundant messages are produced and DAG need validate the parent transaction of the parent transaction indirectly, so the time overhead of Gossip protocol in coordinating node consistency is logarithmic. Therefore, the consensus algorithm of DAG can’ be applied to the devices of IoT. In the consensus algorithms of blockchain, the authentication and the legality of transactions among nodes are the basic technology for applying blockchain. Based on security of the transacting nodes of blockchain, literature [17] discussed the security and privacy of blockchain, including classical consensus algorithms, Hash chain storage, mixed protocols, anonymous signature, non-interactive Zero-knowledge Proof and so on. Literature [18] also studied the security and the privacy of blockchain’s conception, attributes, technology and systems.
Blockchain is new technology based on consensus algorithms. It has the characteristics of decentralization and resistance to the falsification. Thanks to its characteristics, blockchain technology has been widely applied to the network. The literature [19] introduced Stackelberg game rules to formulate the interaction among nodes, and balance privacy and data application. In order to meet the fast-growing security requirements of IoT and the delay of Hyperledger Fabric (HLF), literature [20] proposed a HLF latency model for HLF-based IoT networks based on probability distribution fitting, by which mean latency prediction is facilitated once probable configuration environments are determined, in terms of the block size, block generation timeout, and transaction generation rate parameters. Blockchain technology based on consensus algorithms has been widespread applied in the Internet-of-Vehicles, involving the mobile crowdsensing [21] and the Software-Defined Vehicular Networks [22] and the automatic driving [23]. Blockchain technology also involves the research on information security filed, such as the attribute encryption in IoT devices and the key leakage [24], the application and the security of big data in IoT [25], the identity authentication of IoT devices in smart cities [26] and so on.
Consensus algorithms have driven the development of blockchain. But it is still paradoxical to ensure both secure blockchain’s node transaction and little time overhead. How to design efficient and novel consensus algorithms is a challenge that blockchain’s development and application have to face [27]. In order to understand the consensus algorithms is applicated in IoT, we may further refer to the literatures [28,29,30].

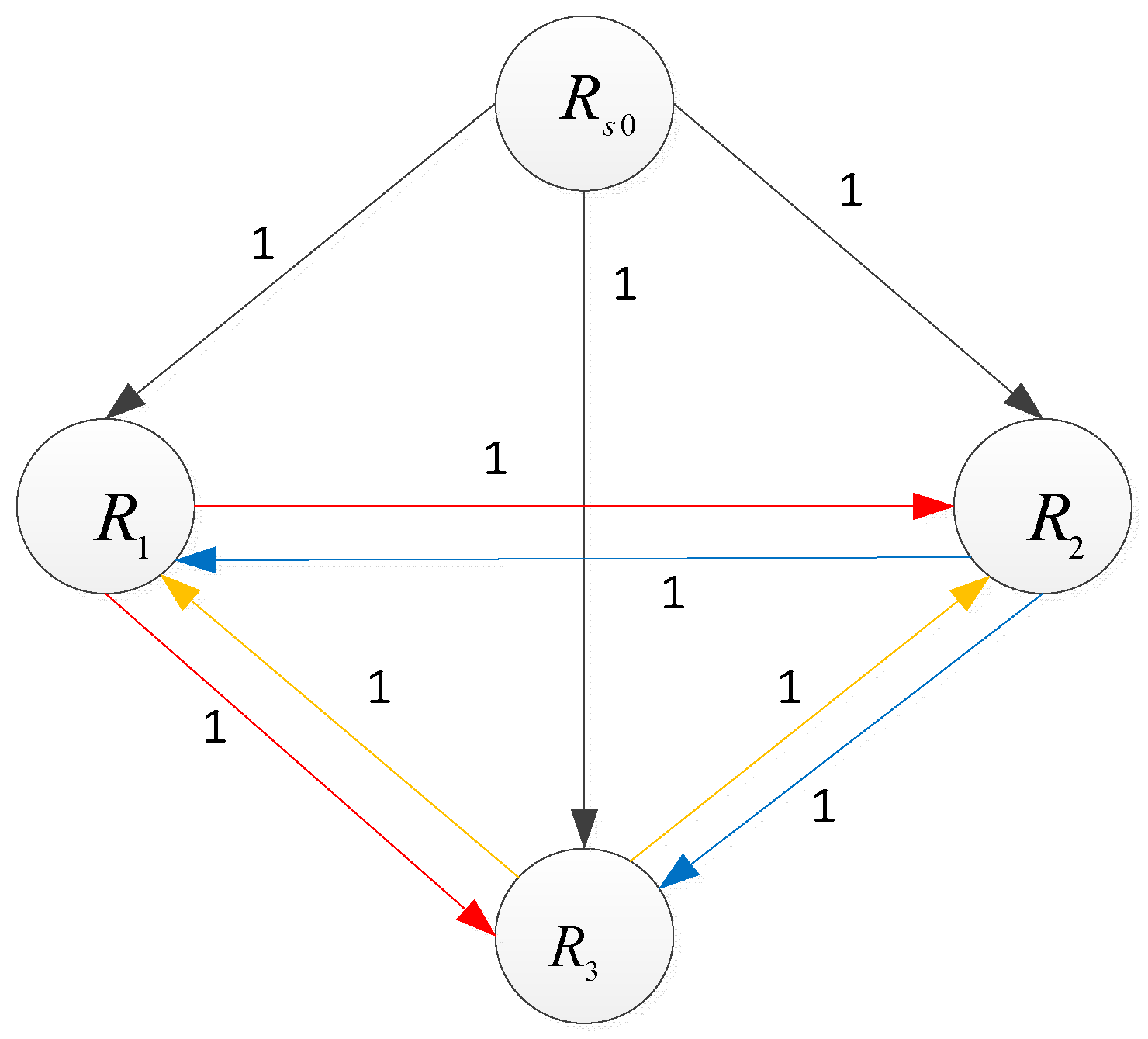
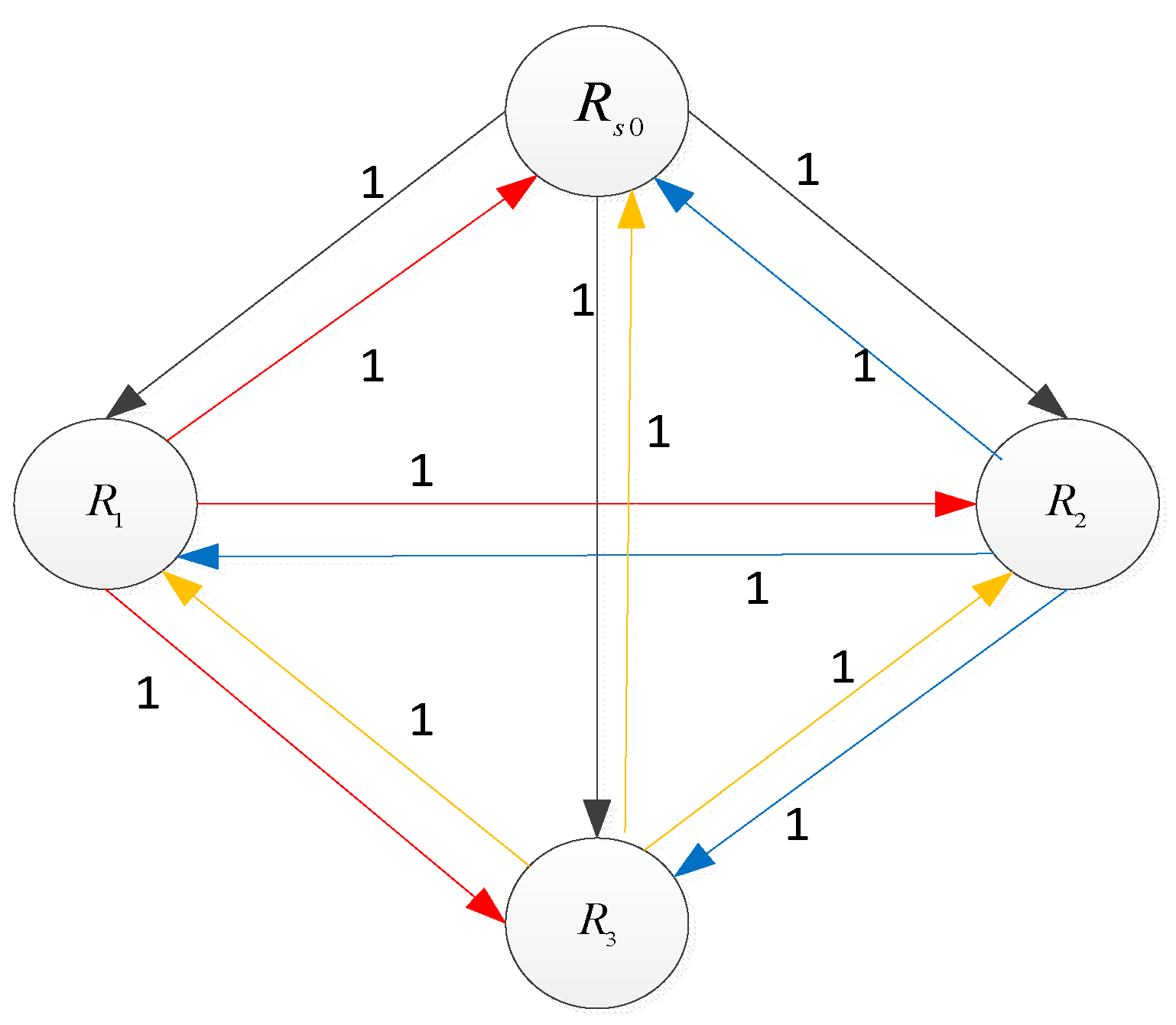
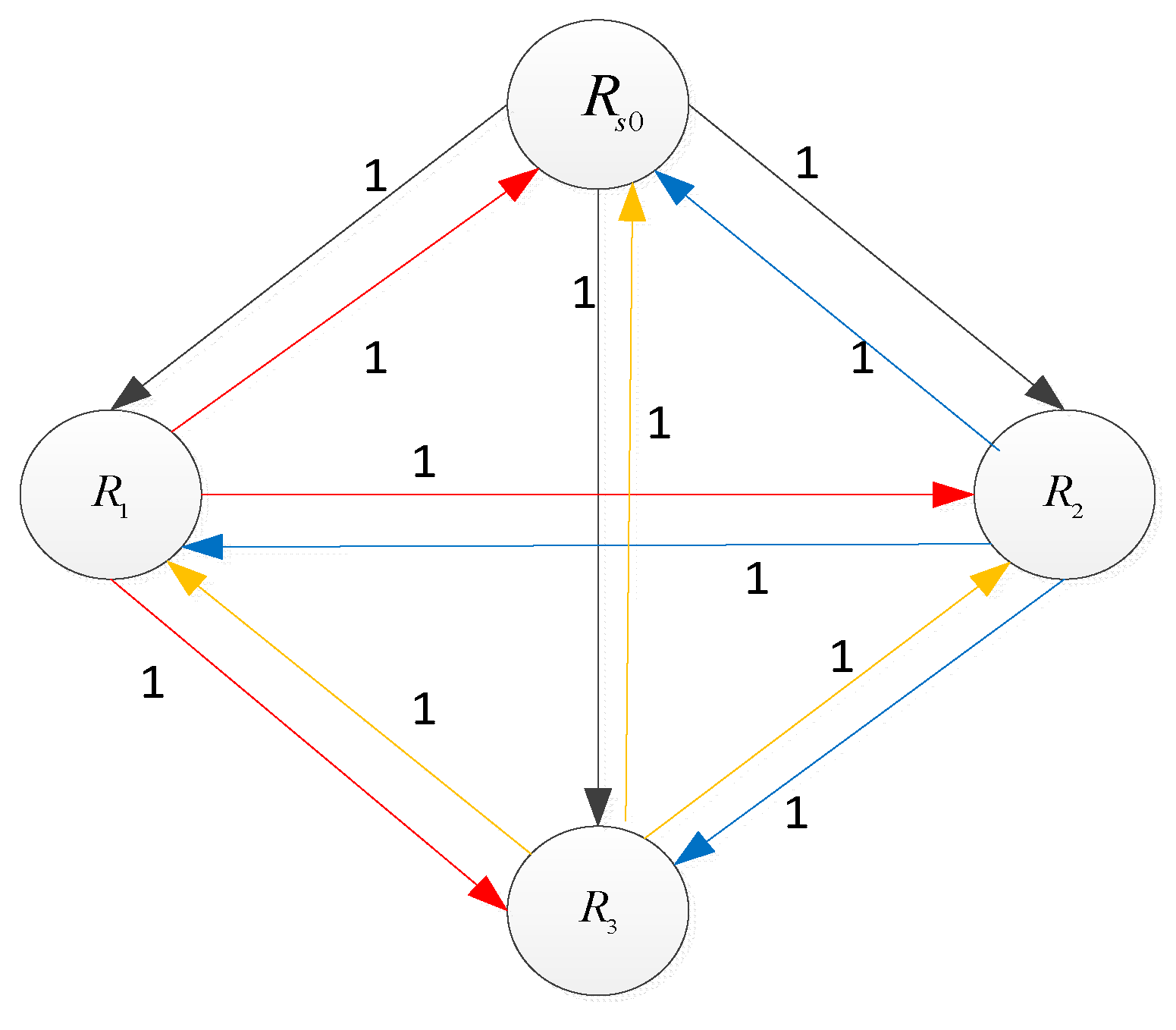
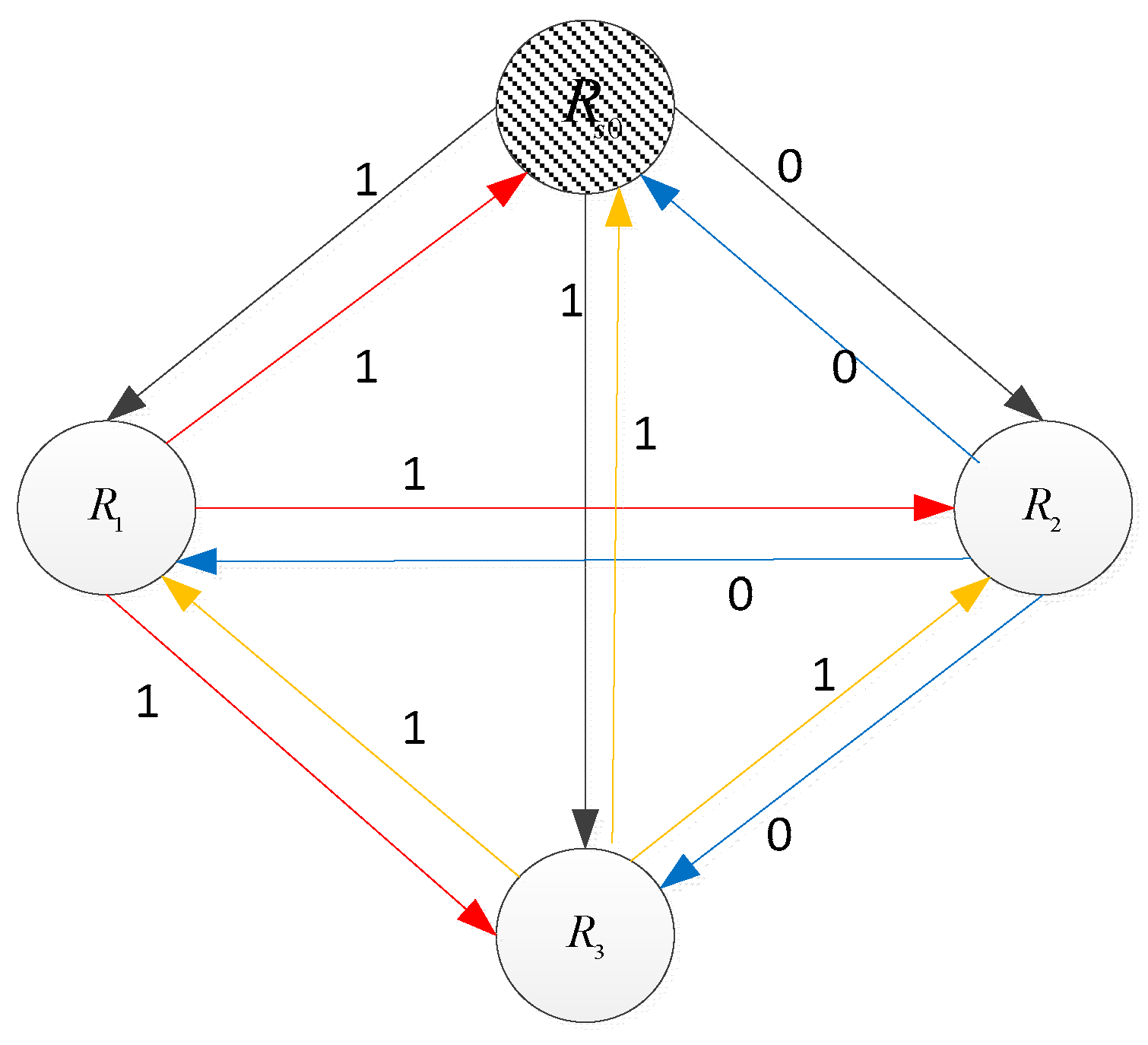
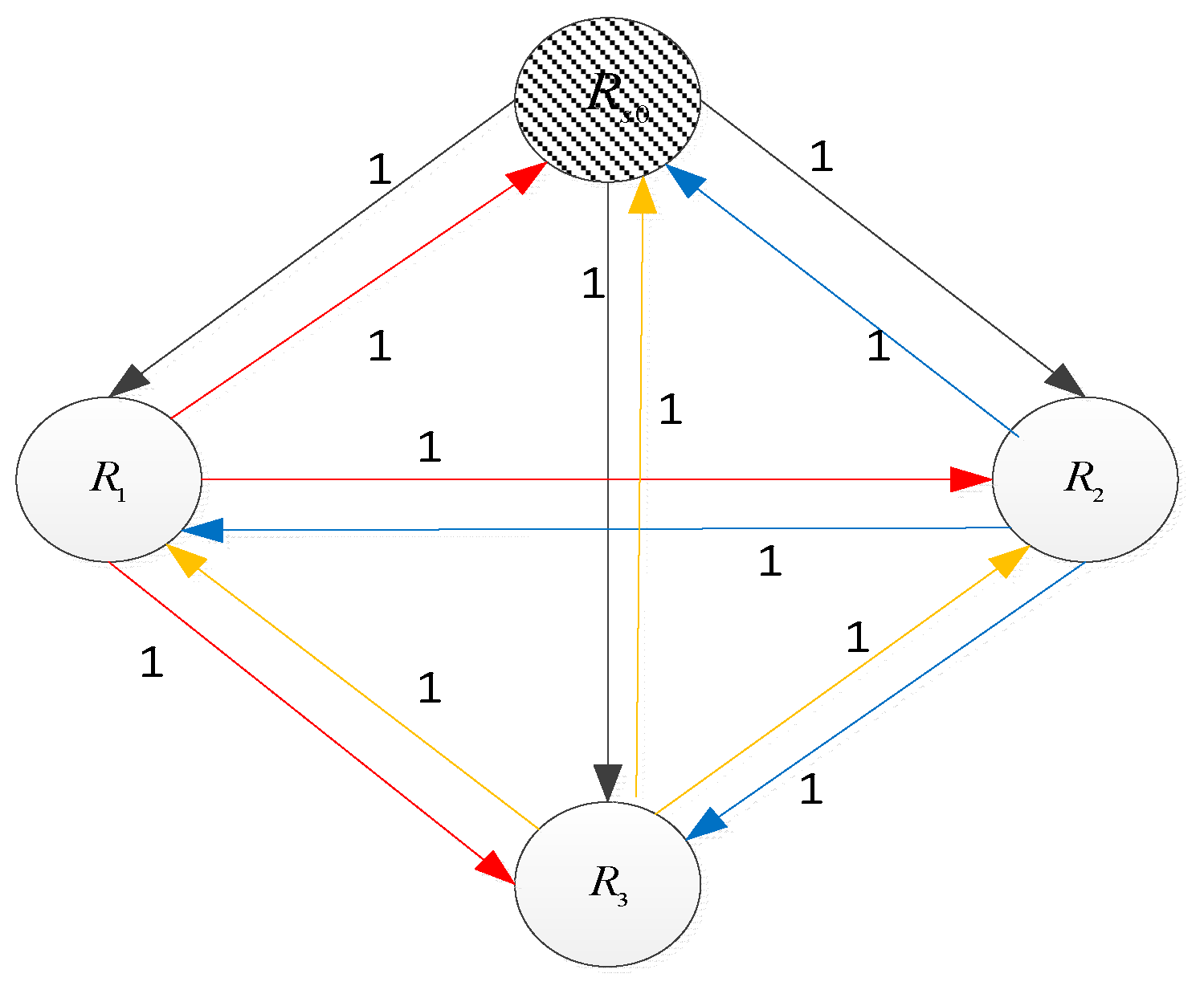
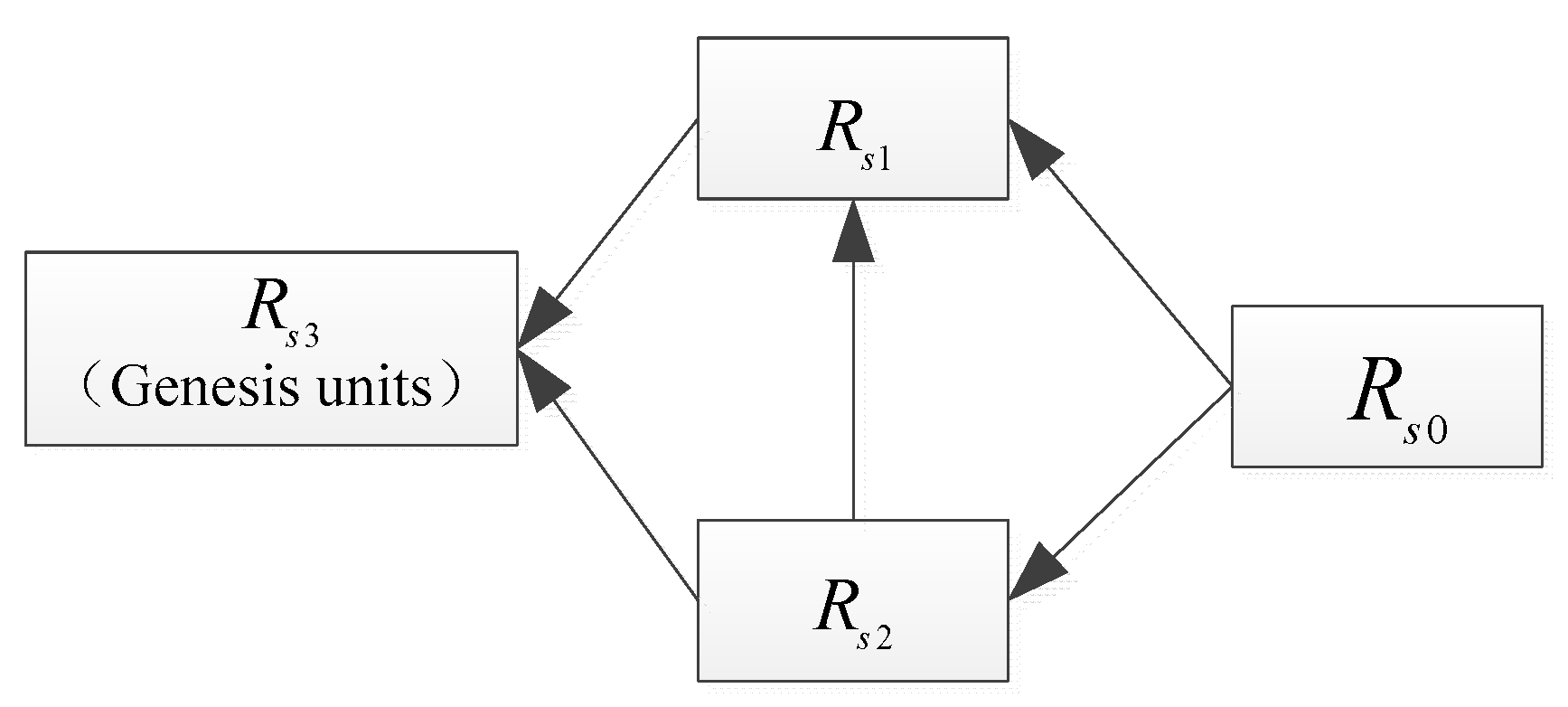
III. The Lcag Algorithm

Traditional consensus mechanisms of blockchain are involved in Hash, signature and authentication, view change and so on, which leads to much time overhead, and restrains blockchain’s development and extension. To reduce time overhead when reaching agreements, LCAG is built based on graph theory.
There , R denotes vertex， R i denotes the ith vertex, e denotes edge or arc， n denotes the counts of the edge or the arc I D ( R ) denotes in-degree of the R vertex， O D ( R ) denotes out-degree of the R vertex， T D ( R ) denotes the sum of I D ( R ) and O D ( R ) .

A. The Related Graph Theory

Graph is a kind of data structure, including directed graph and undirected graph. Its structure includes edge or arc, vertex and so on. The basic knowledge needed in this paper is represented as follows:
1) The degree of Vertex R indicates the number of edges or arcs related to R , denoted as T D R .
2) The in-degree is the number of the arcs, whose head is Vertex R , denoted as I D R . The out-degree is the number of the arcs, whose end is Vertex R , denoted as O D R .
3) The degree of Vertex R is equal to the sum of in-degree and out-degree in the directed graph, as shown in equation (3-1):
T D ( R ) = I D ( R ) + O D ( R )
The purpose of equation (3-1) is to calculate each node’s degrees. This method can quantitate the process of reaching an agreement.
4) The graph’s vertexes n and edges or arcs e satisfy equation (3-2):
e = 1 2 ∑ i = 1 n T D ( R i )
Graph is an important data structure theory in computer science subject, due to its unique topological structure. In the LCAG algorithm, graph is applied as a fundamental theory and provided a framework for the nodes reaching an agreement in distributed systems.

B. LCAG’s Design

LCAG is a lightweight consensus algorithm. Its purpose is to reduce time overhead for nodes to reach an agreement in distributed systems, so it can be widely used in the devices of IoT and the mobile devices.
In LCAG, suppose that there are n nodes, that there might exist fault-nodes or malicious nodes among these nodes and that R s 0 is the initial node, that is, it may regard as a primary node. These nodes communicate with each other, and all of them can send and receive commands. When these nodes send or receive messages, only two kinds of results come out--“true” (denoted as “1”) or “false” (denoted as “0”). LCAG takes nodes as the graph’s vertexes, denoted as R i , i ∈ N . Edges or arcs between two vertexes are denoted as < R i , R j > ， i , j ∈ N . < R i , R j > means that there is communication between Vertex R i and Vertex R j . These nodes constitute a connected complete directed graph in the system, denoted as D G ( < R i , R j > , i , j ∈ n ) . There, T denotes a table of the record structure , m s g and m s g ′ are denoted as sending messages and receiving messages, δ and δ ′ are denoted the result of hash function calculation. LCAG is designed as follow:
1) Build a table T to record nodes’ data, and T has 3 storage components, shown in Figure1.
Preprints 82374 g001
Figure 1. three storage components of T.
Figure 1. three storage components of T.
Preprints 82374 g001
Here, OD is used to save the out-degree of nodes (the number of digits “1” or “0”), and ID is used to save the in-degree of nodes (the number of digits “1” or “0”). OP is used to save the final results decided by each node: “yes” or “no”.
2) The initial node saves the message m s g (“ m s g ” is composed of the number of digits "1" or "0") to be sent into the corresponding storage component ( O D ) of T , calculates H a s h ( m s g ) = δ , and sends the message { m s g | | H a s h ( m s g ) = δ } to the rest n − 1 nodes. At the same time, the initial node saves the message m s g ′ ( “ m s g ′ ” is composed of the number of digits "1" or "0") to be receive into the corresponding storage component ( I D ) of T , and calculates H a s h ( m s g ′ ) = δ ′ .
3）Among the rest n − 1 nodes, one receives the message { m s g | | H a s h ( T ) = δ } sent by the initial node, and then verifies whether the equation H a s h ( m s g ) = δ is satisfied. If it is not satisfied, the initial node will be abandoned. If it is satisfied, this node will send the message to other n − 1 nodes according to the following rules:
a) If this node is loyal, it will obey the initial node`s commands and send the same message received from the initial node to other n − 1 nodes.
b) If this node is disloyal, it will send a message contrary to what sent by the initial node to other n − 1 nodes.
Note：
It was hard to draw clear lines of demarcation between the message { m s g | | H a s h ( m s g ) = δ } sent and the messages { m s g ′ | | H a s h ( m s g ′ ) = δ ′ } received in the processes, when nodes are reaching an agreement. That is, the messages { m s g | | H a s h ( m s g ) = δ } and { m s g ′ | | H a s h ( m s g ′ ) = δ ′ } may be exchanged with each other.
4) The node respectively counts the number of O D ( R ) and the number I D ( R ) (the number of “1” or “0”), and then calculates the probability of “1” (denoted as p ( 1 )   ) and the probability of “0” (denoted as p ( 0 ) ). If p ( 1 )   > p ( 0 ) , the node will output “yes”. Otherwise, the node will output “no”. The final output will be saved into the corresponding storage component “ O P ” of Table T .
5) Repeat 2), 3) and 4) until all the nodes finish sending and receiving messages (“1” or “0”), and complete counting the number of “1” or “0”.
6) The system counts the final “ O P ” data (“yes” and “no”) in T , and calculates the probability of “yes” (denoted as p ( y e s )   ) and the probability of “no” (denoted as p ( n o )   ) in “ O P ” of T .
7) According to e = 1 2 ∑ i = 1 n T D ( R i ) , p ( y e s )   and p ( n o )   , the system reaches an agreement of “Yes” or “No”. If p ( y e s )   > p ( n o ) , the system will reach an agreement of “Yes”. Otherwise, the system will reach an agreement of “No”.
LCAG’s algorithm as follow：
Preprints 82374 i001

C. LCAG’s Provable Security Analysis

The security of LCAG algorithm is one of the basic conditions to guarantee nodes reaching an agreement. During the process of reaching an agreement in the system, LCAG only need to calculate H a s h , and its aim is to ensure the information’s integrity and protect the information from attacks, such as falsifying, man-in-the-middle attack and so on. Its security analysis is given as follows:
1) The security analysis based on standard model
Suppose that when the message { m s g | | H a s h ( m s g ) = δ } is sent, the third party E steals it. E falsifies the message { m s g | | H a s h ( m s g ) = δ } into { m s g ″ | | H a s h ( m s g ) = δ } and then send the falsified message { m s g ″ | | H a s h ( m s g ) = δ } to the next node. When the next node receives the falsified message { m s g ″ | | H a s h ( m s g ) = δ } , it verifies { m s g ″ | | H a s h ( m s g ) = δ } and calculates H a s h ( m s g ″ ) = δ ″ . If δ ′ = δ , the message communicated between nodes is believed not to be falsified, and nodes’ identities of both sides of communication are trusted. Otherwise, it is believed to be falsified, and nodes’ identities of both sides of communication are not trusted. The received message m s g ″ will be discarded, and nodes continue new communication. According to the characteristics of H a s h , because m s g ″ ≠ m s g , δ ″ ≠ δ . In that case, the data’s integrity is destroyed and the messages are attacked by man-in-the-middle attacks. LCAG doesn’t need massive computation, which reduces time overhead for the nodes to reach an agreement in the system.
2) The security analysis based on RO (Random Oracle) model
based on the random oracle (short for RO) model, a provable security analysis scheme of LCAG’s algorithm is proposed to illustrate its algorithm is safe in this paper. LCAG’s algorithm involves only the Hash function which is a one-way function, so the provable security analysis of LCAG’s algorithm is given according to the definition of one-way function and the characteristic of Hash function. The security of LCAG’s algorithm is reduced to the difficult problem of inversion about to one-way function and the difficult problem of collision about to Hash function. LCAG’s provably security scheme illustrates as follow:
a) According to the definition of one-way function, there exists a negligible function ε and any probability polynomial time algorithm A , which satisfies equation (3-3):
Pr [ I n v e r t A , f ( x ) = 1 ] ≤ ε
There, Pr [ I n v e r t A , f ( x ) = 1 ] denotes a successful probability of the inversion about to one-way function, f ( x ) denotes a one-way function.
According to (3-3), when the δ `s value has been obtained, it is impossible that the m s g is successfully calculated by the attacker. Because f ( x ) is a one-way function.
b) In the RO model, the successfully probability is 1 2 that the attacker get the correct answer every time querying the RO. When the number of the attacker asks the RO is n, equation (3-4) is satisfied:
Pr ( A s u c c e e ) = 1 2 n ( n − 1 )
Here Pr ( A s u c c e e ) denotes the probability of the correct answer query the RO. When n → ∞ , equation (3-4) is converged to zero.
In the LCAG algorithm, when n → ∞ , equation (3-5) is satisfied:
Pr ( A ( H a s h ( m s g ′ ) = H a s h ( m s g ) ) | ( δ ′ ≠ δ ) ) ≤ ε
There, A is a probability polynomial time algorithm, ε denotes is a negligible function. That is, when ( δ ′ ≠ δ ) has been know, it is impossible that the m s g ′ = m s g is successfully calculated by the attacker. Because H a s h is a resistant collision function.
According to 1) and 2). LCAG ’s consensus algorithm is secure, so it can resist to the Sybil’ s attack and Double Spend attack.

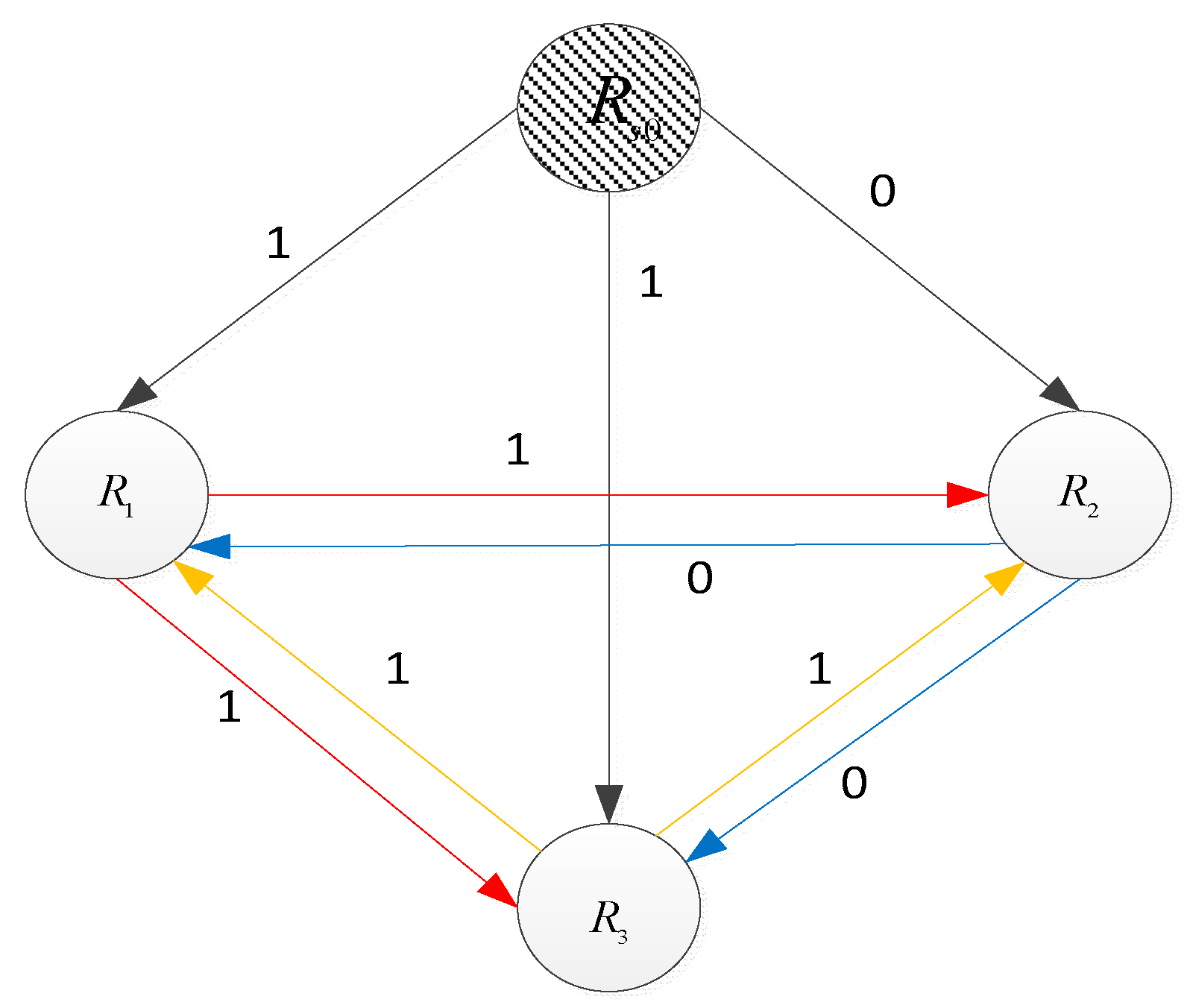
IV. Experiment

Simulation experiments are executed to compare LCAG and classical consensus algorithms with BGP, PBFT and DAG as representatives by choosing 4 nodes (Notice: in LCAG, the initial node is regarded as the primary node. In this paper, choosing at least 4 nodes can satisfy the minimum number requirement of nodes for the BGP algorithm, PBFT algorithm, DAG algorithm and LCAG algorithm). The experiments consist of two parts: one is the ideal situation, or the situation free from disloyal nodes. The other is the situation with disloyal nodes. In the experiments, the adversary model N ≥ 3 f + 1 is discussed. Here N is the number of all the nodes, f is the number of disloyal lieutenant nodes.
BGP, PBFT, DAG and LCAG are implemented in the environment: macOS Big Sur 11.6, Intel Core i5,6 cores and 8GB RAM. Python (3.10) language and Socket interface. The steps for executing the experiments are given as follows.

A. The Ideal Situation

In the ideal situation, there is not any disloyal node. Consensus algorithms satisfy the condition: all the lieutenant nodes observe the commands sent by the primary node, and forward the commands with each other. The ideal situation only discusses the time overhead of BGP, PBFT and LCAG. In Figure 2, Figure 3 and Figure 4, R s 0 is the primary node (that is the initial node), and R i ( 1 ≤ i ≤ 3 , i ∈ Ν ) are lieutenant nodes.
BGP and PBFT in the ideal situation are shown in Figure 2 and Figure 3. According to Figure 2 and Figure 3, R s 0 reaches an agreement with R 1 、 R 2 、 R 3 , and the consensus message is { 1 ， 1 ， 1 } . In the process of reaching an agreement, to ensure the integrity and confidentiality of sent information, nodes execute following process in pairs: ①calculating H a s h value; ②transmitting messages; ③signature and authentication.
LCAG in the ideal situation is shown in Figure 4. According to Figure 4 and LCAG, R s 0 reaches an agreement with R 1 , R 2 , R 3 and the consensus message is { 1 } . Based on graph theory, during the process of reaching an agreement, nodes execute the following process in pairs: ①calculating H a s h value; ②calculating O D ( R ) value and I D ( R ) value of each node. In this process, LCAG doesn’t need the exponential signature and authentication, and only Hash calculation is involved.

B. The Situation with Disloyal Nodes

Let the primary node be disloyal node. BGP, PBFT, DAG and LCAG are discussed. The consensus algorithms satisfy the conditions: ① all the loyal lieutenant nodes observe the commands sent by the primary node; ② disloyal lieutenant nodes forward the commands, which are contrary to what sent by the primary node, to each other; ③ the adversary model is N ≥ 3 f + 1 . Here, N is the number of all the nodes, and f is the number of disloyal lieutenant nodes. According to ③, among the chosen 4 nodes, the number of disloyal lieutenant nodes is 1 at most. In Figure 4, Figure 5 and Figure 6, R s 0 is the disloyal primary node and R i , 1 ≤ i ≤ 3 , i ∈ Ν are lieutenant nodes.
BGP and PBFT in the situation with disloyal nodes are shown in Figure 5 and Figure 6. According to Figure 5 and Figure 6, R s 0 reaches an agreement with R 1 , R 2 and R 3 , and the consensus message is { 1 ， 1 ， 0 } . In the process of reaching an agreement, to ensure the availability of the primary node as well as the integrity and the confidentiality of the information transmitted among nodes, nodes execute the following process in pairs: calculating H a s h value；transmitting messages; signature and authentication; view change of the primary node.
LCAG in the situation with disloyal nodes are shown in Figure 7. According to Figure 7 and LCAG, R s 0 reaches an agreement with R 1 , R 2 and R 3 , and the consensus message is { 1 } . Based on graph theory, in the process of reaching an agreement, nodes execute the following process in pairs: ① calculating H a s h value；② calculating O D ( R ) value and I D ( R ) value of each node. In this process, LCAG doesn’t need the exponential signature and authentication, as well as view change of the primary node.
DAG algorithm’s principle is involved to the gossip protocol, which is used in DAG network to ensure the final consistency of states between different transactions. So, we select the 4 transactions for simulation experiment. Here, R s i ( 0 ≤ i ≤ 4 , i ∈ Ν ) denotes transactions (Also called nodes), genesis unit leftmost can be reached. Each transaction contains the hash value from the genesis unit to its father unit. The structure of 4 nodes DAG is shown in Figure 8 below.
When the gossip protocol is used for the nodes reaching an agreement. It need accomplish three operations: push-gossip, pull-gossip, and push-pull gossip. At same time, in the DAG network, each new transaction validates its parent transaction directly, and validates the parent transaction of the parent transaction indirectly.

C. Experiment Analysis

The tasks finished by BGP, PBFT, DAG and LCAG during the process of reaching an agreement are compared, and the time overhead of BGP, PBFT and LCAG during the process of reaching an agreement is analyzed.
1) The tasks finished by BGP, PBFT, DAG and LCAG during the process of reaching an agreement are presented in Table II. “√” denotes the task needed in the process of reaching an agreement.
As is shown in Table II, in the process of reaching an agreement, DAG and LCAG only needs to finish two tasks (transmitting messages and calculating Hash), while BGP and PBFT need to finish more tasks: transmitting messages, calculating Hash, signature and authentication, view change of the primary node. There, DAG need validate the parent transaction of the parent transaction indirectly, LCAG doesn’t.
Table II. The tasks finished by BGP, PBFT and LCAG.
Table II. The tasks finished by BGP, PBFT and LCAG.
Consensus algorithm Transmitting messages Calculating Hash Signature and authentication View change
BGP √ √ √ √
PBFT √ √ √ √
DAG √ √
LCAG √ √
2) Time overhead of BGP, PBFT,DAG and LCAG is analyzed. There are two parts in this process: one is the ideal situation, or the situation free from disloyal nodes; The other is the situation with disloyal nodes. The number of nodes satisfies the condition: only when N ≥ 3 f + 1 , an agreement can be reached.
a) Time overhead of BGP, PBFT, DAG and LCAG in the ideal situation is shown in Table III.
Table III. Time overhead of BGP, PBFT, DAG and LCAG in the ideal situation (ms).
Table III. Time overhead of BGP, PBFT, DAG and LCAG in the ideal situation (ms).
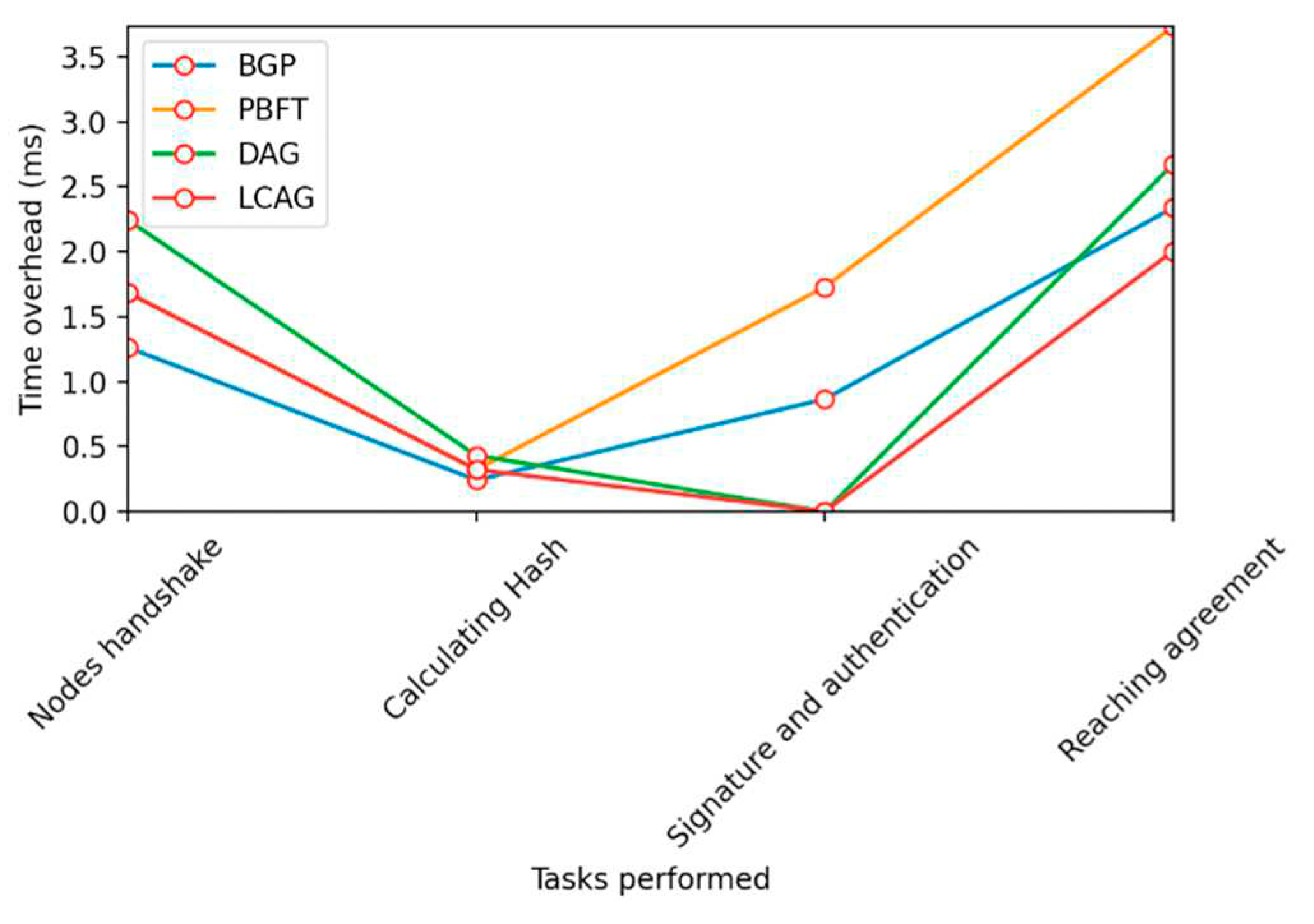
Consensusalgorithm Nodes handshake Calculating Hash Signature and authentication Reachingagreement
BGP 1.2609 0.2421 0.8637 2.3667
PBFT 1.6812 0.3228 1.7274 3.7314
DAG 2.2416 0.4304 0 2.672
LCAG 1.6812 0.3228 0 2.004
As is shown in Table III, in the ideal situation, there is little difference among BGP, PBFT, DAG and LCAG when finish Nodes handshake and calculating Hash. However, BGP and PBFT need time overhead to finish signature and authentication when reaching an agreement, while DAG and LCAG aren’t need time overhead on the exponential signature and authentication when reaching an agreement. Time overhead of BGP, PBFT,DAG and LCAG is clearly shown in Figure 9.
As is shown in Figure 9, time overhead of BGP and PBFT increases faster than that of DAG and LCAG during the process of reaching an agreement. What’s more, BGP and PBFT need much more time overhead than ADG and LCAG . DAG takes more time than LCAG in the process of nodes reaching an agreement, the reasons are: DAG need validate the parent transaction of the parent transaction indirectly, LCAG doesn’t.
b) Time overhead of BGP, PBFT,ADG and LCAG in the situation with disloyal nodes is shown in Table V. When the primary node is disloyal, it needs to change view through a view-change protocol. The process consists of two steps: first, the system sends < V I E W − C H A N G E , v + 1 , n , C , P , i > to inform all the nodes that the primary node must change. Second, when view has been successfully changed, the system sends ( < NEW - V I E W , v + 1 , V , O > ) to inform all the nodes that the primary node has already been changed successfully.
The symbols used in the view-change protocol are shown in Table IV.
Table IV. The symbols denote in the view changed protocol.
Table IV. The symbols denote in the view changed protocol.
Preprints 82374 i002
Time overhead massively increases when the view-change protocol is performed. Time overhead of BGP, PBFT, DAG and LCAG in the process of view-changing is shown in Table V.
Table V. Time overhead of BGP, PBFT and LCAG in the situation with disloyal nodes (ms).
Table V. Time overhead of BGP, PBFT and LCAG in the situation with disloyal nodes (ms).
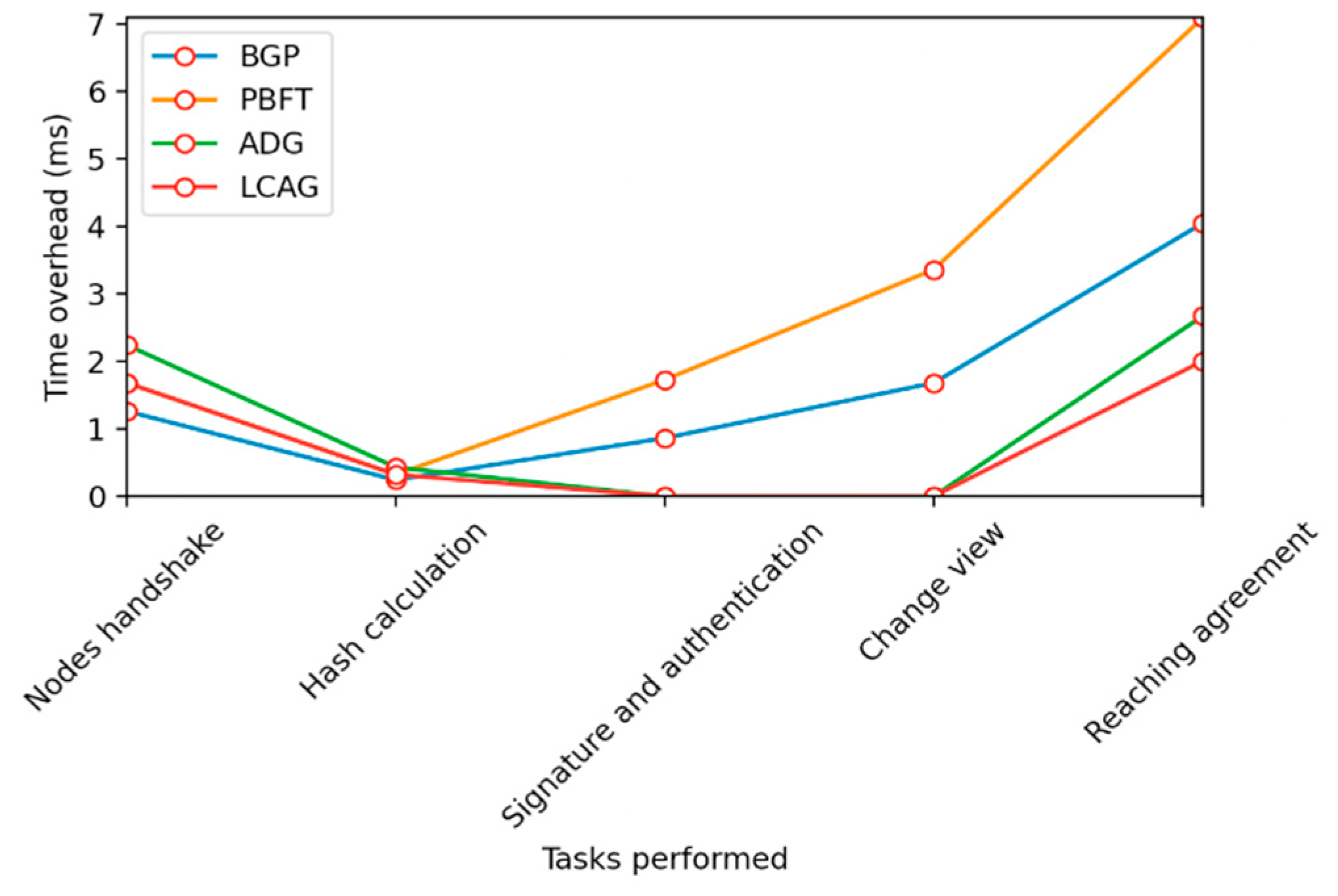
Consensusalgorithm Nodes handshake Calculating Hash Signature and authentication View change Reaching agreement
GP 1.2609 0.2421 0.8637 1.6812 4.0479
PBFT 1.6812 0.3228 1.7274 3.3624 7.0938
DAG 2.2416 0.4304 0 0 2.672
LCAG 1.6812 0.3228 0 0 2.004
As is shown in Table V, if the primary node is disloyal, when BGP and PBFT reach an agreement, it costs them a lot of time overhead to finish signature verification and view change, while DAG and LCAG doesn’t need time overhead to finish these two tasks. Time overhead of BGP, PBFT, DAG and LCAG is shown in Figure10 to compare their time performance in the situation with disloyal nodes.
As is shown in Figure 10, in the situation with disloyal nodes, BGP and PBFT need much more time overhead than DAG and LCAG. DAG and LCAG aren’t involved in the exponential signature and authentication, and it needs least time overhead among the three consensus algorithms. In conclusion, in the situation with disloyal nodes, LCAG is superior than BGP, PBFT and DAG in terms of time overhead.
The consensus algorithms are the core technology of the blockchain, which determine the security and application of the blockchain. Through the experiments above, it is shown that the new consensus algorithm LCAG is superior to the classic BGP, DAG and PBFT in terms of time overhead. Therefore, the blockchain technology based on the new consensus algorithm LCAG can meet the application of IoT devices with limited computing power, such as the BP protocol for reliable transmission of asymmetric channel data [31], the PDP protocol for smart cities [32], and the mobile edge computing on IoT, etc.

V. Conclusion and Future Work

Classical consensus algorithms need a lot of time overhead to reach an agreement, which is an important problem. How to reduce time overhead in the process of reaching an agreement decides the developments of blockchain’s technology and IoT. GBP, PBFT, and ADG needs too much time overhead to reach an agreement, so they are not widely applied. Based on GBP, PBFT is improved and reduces time overhead to reach an agreement. As a result, Byzantium consensus algorithms are applied in blockchain. However, when nodes reach an agreement, massive cryptographic calculation and view change are involved. Therefore, PBFT can’t promote the development of blockchain effectively. Based on gossip protocol, DAG needs DAG need validate the parent transaction of the parent transaction indirectly, which is spend a lot of time in the process of nodes reaching an agreement. Based on graph theory, LCAG simplifies the process of reaching an agreement, only involving information transmitting and calculating Hash, and reduces time overhead to reach an agreement effectively.
Due to innovation and improvement, consensus algorithms have been applied in the blockchain, but they are still deficient. Future work is: ① focusing on the behavior’s provable logical security analysis during the process of reaching an agreement; ②further optimizing the consensus algorithm and reducing time overhead to reach an agreement; ③ ensuring that consensus algorithms are applied in the blockchain technology and the IoT devices.

References

  1. NAKAMOTO, S. Bitcoin: A peer-to-peer electronic cash system[EB/OL]. 2008. https://bitcoin.org/bitcoin.
  2. Cheng CF, et al. Reaching Consensus with Byzantine Faulty Controllers in Software-Defined Networks. Wireless Communications and Mobile Computing. 2021 Apr 12;2021.
  3. Yazdinejad A, et al. Slpow: Secure and low latency proof of work protocol for blockchain in green iot networks. In2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring) 2020 (pp. 1-5). IEEE. 25 May.
  4. LAMPORT L, SHOSTAK R E, PEASE M C. The Byzantine Generals Problem[J]. ACM Transactions on Programming Languages and Systems (TOPLAS) 1982, 4, 382–401. [Google Scholar] [CrossRef]
  5. LIU Yi-Zhong, LIU Jian-Wei,ZHANG Zong-Yang,XU Tong-Ge,YU Hui1. Overview on Blockchain Consensus Mechanisms. Journal of Cryptologic Research 2019, 6, 395–432. [Google Scholar]
  6. CASTRO M, LISKOV B. Practical Byzantine fault tolerance[C]. In: Proceedings of the Third USENIX Symposium on Operating Systems Design and Implementation (OSDI). 1: New Orleans, LA, USA, –25, 1999, 22 February 1999; 25.
  7. Sergio, D.L. : DagCoin: a cryptocurrency without blocks. https://bitslog.wordpress.
  8. Demers, Alan, et al. "Epidemic algorithms for replicated database maintenance." Acm Sigops Operating Systems Review 22.
  9. YUAN Yong, NI Xiao-Chun, ZENG Shuai,WANG Fei-Yue. Blockchain Consensus Algorithms: The State of the Art and Future Trends. ACTA AUTOMATICA SINICA. 2018, 44, 2011−2022.
  10. LAMPORT, L. The part-time parliament[J]. ACM Transactions on Computer Systems (TOCS) 1998, 16, 133–169. [Google Scholar] [CrossRef]
  11. Cowling J, Myers D, Liskov B, Rodrigues R, Shrira L. HQ replication: A hybrid quorum protocol for Byzantine fault tolerance. In: Proc. of the 7th Symp. on Operating Systems Design and Implementation. Berkeley: USENIX Association, 2006.
  12. Xu Hao, Long Yu, Liu Zhiqiang, Liu Zhen, Gu Dawu. Dynamic Practical Byzantine Fault Tolerance. 2018.
  13. ABRAHAM I, GUETA G, MALKHI D. Hot-stuff the linear, optimal-resilience, one-message BFT devil[EB/OL]. 2018. https://arxiv.org/pdf/1803.05069.pdf.
  14. GOLAN-GUETA G, ABRAHAM I, GROSSMAN S, et al. SBFT: A scalable decentralized trust infrastructure for Blockchains[EB/OL]. 2018. https://arxiv.org/pdf/1804.01626.pdf.
  15. GAO Zheng-Feng, ZHENG Ji-Lai,TANG Shu-Yang,LONG Yu,LIU Zhi-Qiang, LIU Zhen,GU Da-Wu. State-of-the-art Survey of Consensus Mechanisms on DAG-based Distributed Ledger. Journal of Software, 2020, 31, 1124−1142.
  16. Chong B. State-of-the-Art and Future Trends of Blockchain Based on DAG Structure[C]// International Workshop on Structured Object-Oriented Formal Language and Method. 2018.
  17. RUIZHANG，RUIXU，LING LIU. Security and Privacy on Blockchain. ACM Comput. Surv. 5: Article 51 (19), 20 July 5111.
  18. Yang R, Yu F R, Si P, et al. Integrated Blockchain and Edge Computing Systems: A Survey, Some Research Issues and Challenges[J]. 1: IEEE Communications Surveys & Tutorials 2019, PP(99), 2019.
  19. Liu W, Cao B, Zhang L, et al. A Distributed Game Theoretic Approach for Blockchain-based Offloading Strategy[C]// IEEE International Conference on Communications. IEEE, 2020.
  20. S Lee, M Kim, J Lee, RH Hsu, TQS Quek. Latency Modeling of Hyperledger Fabric for Blockchain-based IoT (BC-IoT) Networks. https://arxiv.org/abs/2102.09166.
  21. Yin B, Wu Y, Hu T, et al. An Efficient Collaboration and Incentive Mechanism for Internet of Vehicles (IoV) With Secured Information Exchange Based on Blockchains[J]. IEEE Internet of Things Journal 2019, PP(99):1-1.
  22. Qiu C, Yu F R, Xu F, et al. 28 October 2018; 18.
  23. Jiang X, Yu F R, Song T, et al. Blockchain-Enabled Cross-Domain Object Detection for Autonomous Driving: A Model Sharing Approach[J]. IEEE Internet of Things Journal 2020, PP(99):1-1.
  24. Niu J, Li X, Gao J, et al. Blockchain-Based Anti-Key-Leakage Key Aggregation Searchable Encryption for IoT[J]. IEEE Internet of Things Journal 2020, 7, 1502–1518.
  25. Ma Zhaofeng，Wang Lingyun，Wang Xiaochang，Wang Zhen，Zhao Weizhe. Blockchain-Enabled Decentralized Trust Management and Secure Usage Control of IoT Big Data. 1: IEEE Internet of Things Journal PP(99).
  26. Hamdaoui B, Alkalbani M, Rayes A, et al. IoTShare: A Blockchain-Enabled IoT Resource Sharing On-Demand Protocol for Smart City Situation-Awareness Applications[J]. IEEE Internet of Things Journal 2020, PP(99):1-1.
  27. Cao B, Wang R, Sabbagh A, et al. Expected File-Delivery Time of DTN Protocol over Asymmetric Space Internetwork Channels[C]// 2018 6th IEEE International Conference on Wireless for Space and Extreme Environments (WiSEE). IEEE, 2018.
  28. Stefano Savazzi, Monica Nicoli and Vittorio Rampa. Federated Learning With Cooperating Devices: AConsensus Approach for Massive IoT Networks. IEEE INTERNET OF THINGS JOURNAL. 2022, 7, 4641–4654.
  29. Sujit Biswas, Kashif Sharif, Fan Li,et al. PoBT: A Lightweight Consensus Algorithm for Scalable IoT Business Blockchain. IEEE INTERNET OF THINGS JOURNAL. 2020, 7, 2343–2355.
  30. Zhiyuan Jiang, Zixu Cao, Bhaskar Krishnamachari,et al. SENATE: A Permissionless Byzantine Consensus Protocol in Wireless Networks for Real-Time Internet-of-Things Applications. IEEE INTERNET OF THINGS JOURNAL. 2020, 7, 2343–2355.
  31. R Chen, Y Li, Y Yu, H Li, W Susilo. Blockchain-based Dynamic Provable Data Possession for Smart Cities. IEEE Internet of Things Journal (Volume: 7, Issue: 5, 20),P: Page(s): 6576-6588. 20 May.
  32. Mehrdad Salimitari,,Mainak Chatterje,Yaser P.Fallah. A survey on consensus methods in blockchain for resource-constrained IoT networks. Internet of Things.Volume 11, 20, 100212. 20 September.
Preprints 82374 g002
Figure 2. BGP in the ideal situation.
Figure 2. BGP in the ideal situation.
Preprints 82374 g002
Preprints 82374 g003
Figure 3. PBFT in the ideal situation.
Figure 3. PBFT in the ideal situation.
Preprints 82374 g003
Preprints 82374 g004
Figure 4. LCAG in the ideal situation.
Figure 4. LCAG in the ideal situation.
Preprints 82374 g004
Preprints 82374 g005
Figure 5. BGP in the situation with disloyal nodes.
Figure 5. BGP in the situation with disloyal nodes.
Preprints 82374 g005
Preprints 82374 g006
Figure 6. PBFT in the situation with disloyal nodes.
Figure 6. PBFT in the situation with disloyal nodes.
Preprints 82374 g006
Preprints 82374 g007
Figure 7. LCAG in the situation with disloyal nodes.
Figure 7. LCAG in the situation with disloyal nodes.
Preprints 82374 g007
Preprints 82374 g008
Figure 8. DAG structure diagram of the 4 nodes.
Figure 8. DAG structure diagram of the 4 nodes.
Preprints 82374 g008
Preprints 82374 g009
Figure 9. Time overhead of BGP, PBFT, DAG and LCAG in the ideal situation.
Figure 9. Time overhead of BGP, PBFT, DAG and LCAG in the ideal situation.
Preprints 82374 g009
Preprints 82374 g010
Figure 10. Time overhead of BGP, PBFT,ADG and LCAG in the situation with disloyal nodes.
Figure 10. Time overhead of BGP, PBFT,ADG and LCAG in the situation with disloyal nodes.
Preprints 82374 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated