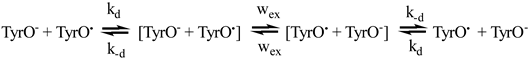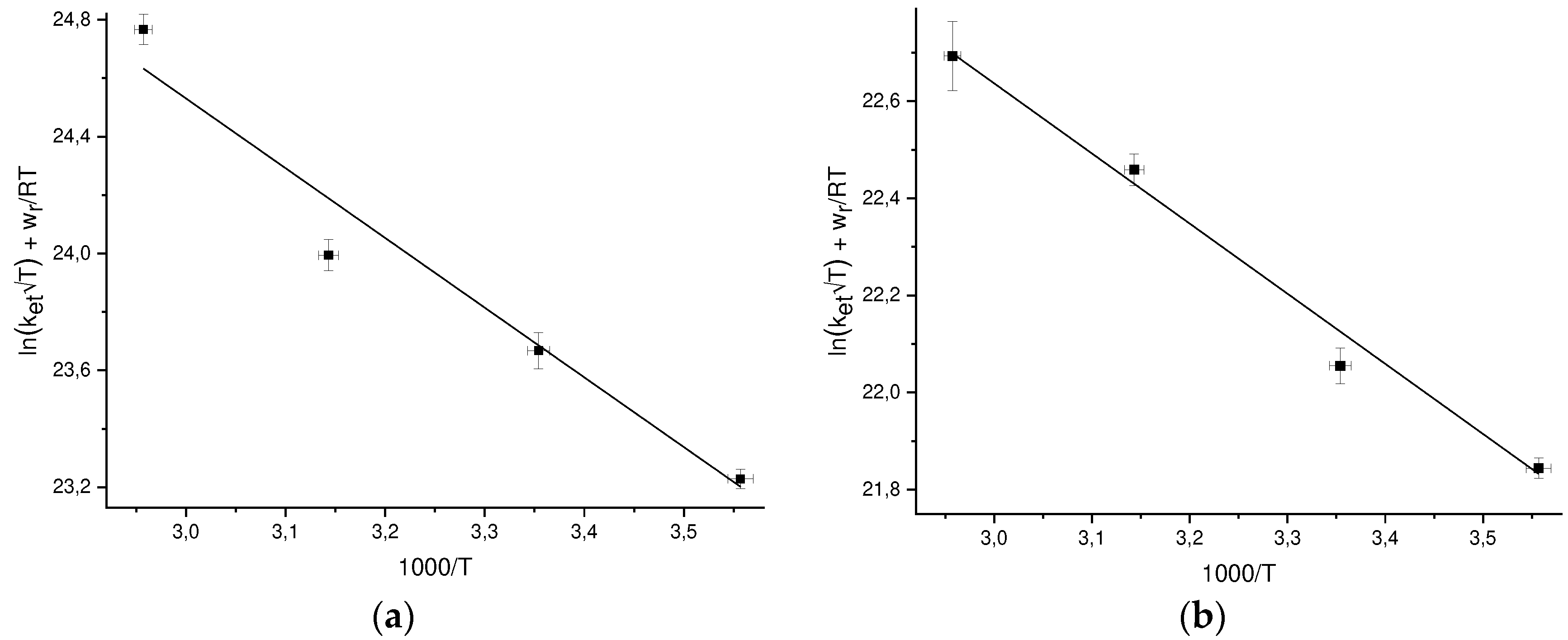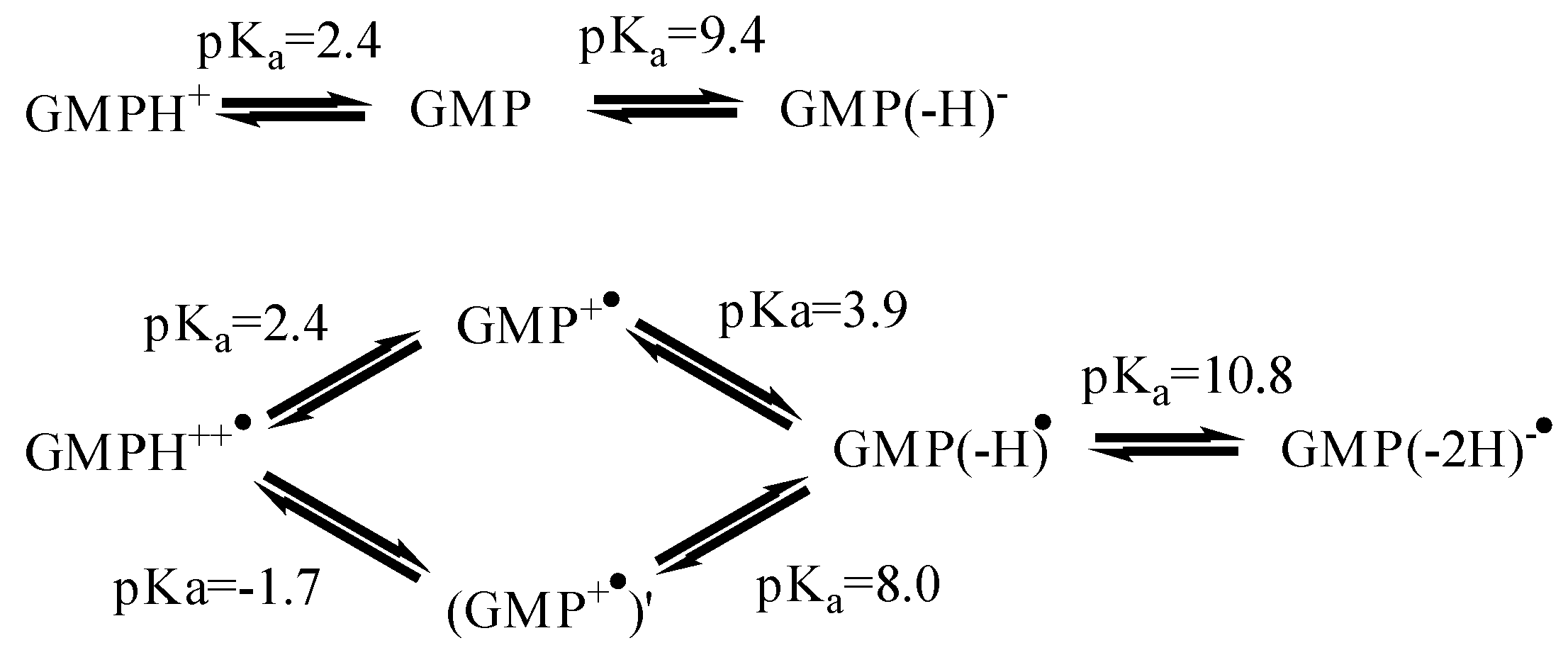1. Introduction
The kinetics of electron transfer reactions is described by Marcus' theory [
1]. According to this theory, the rate constant of the electron transfer reaction is expressed as follows:
where λ is the reorganization energy, ΔG° is the driving force of the reaction.
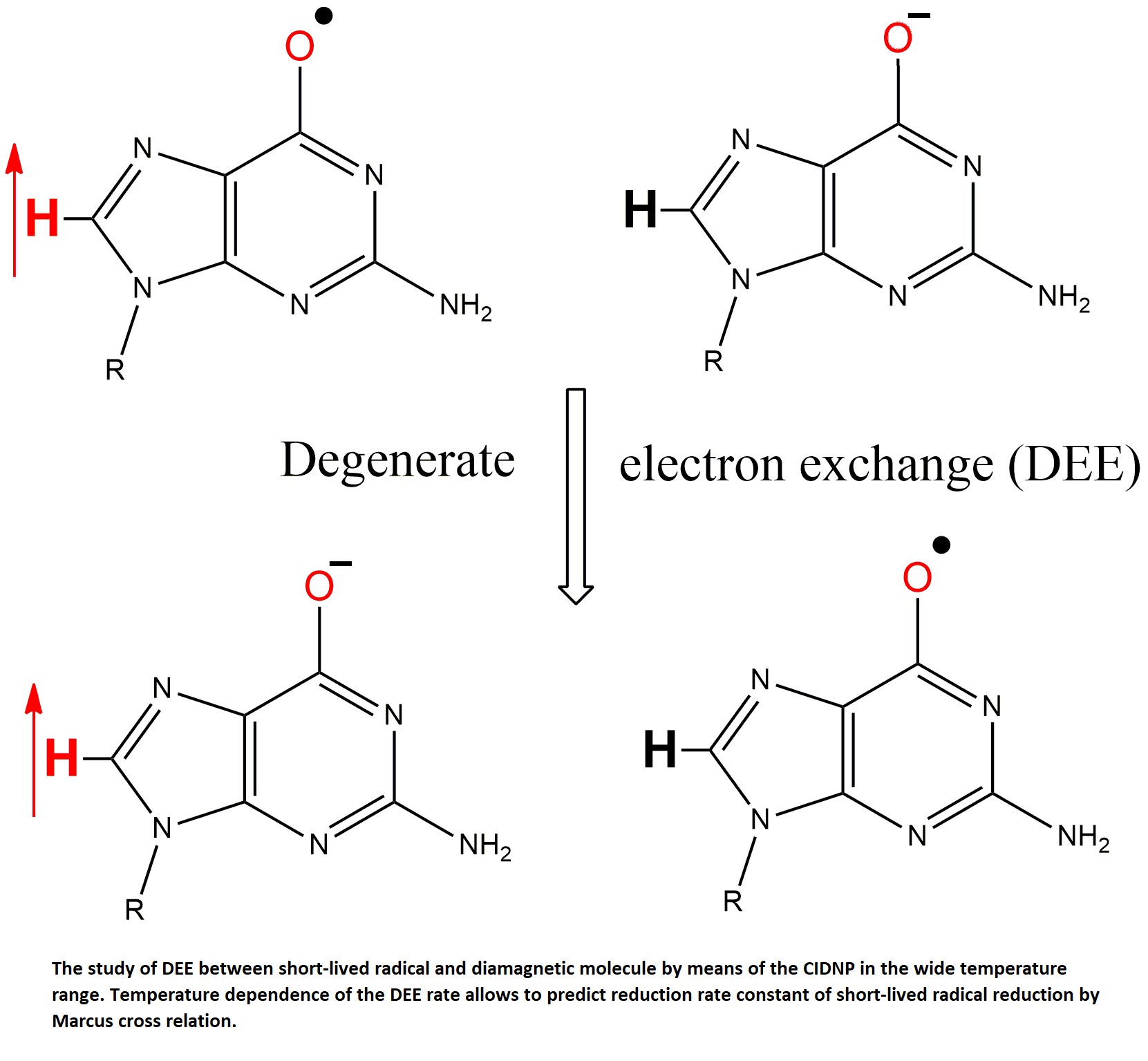
The electron transfer reaction is called degenerate if the donor and acceptor differ by only one electron. Degenerate reactions of electron exchange constitute a special section of Marcus theory because the rate constant k
12 and the reorganization energy λ
12 of an arbitrary electron transfer reaction can be estimated through the equilibrium constant of the cross-reaction K
12 and the rate constants k
11, k
22 and the reorganization energies λ
11, λ
22 of the corresponding degenerate electron exchange (DEE) reactions [
1]:
where A
11, A
22 are the pre-exponents of the DEE rate constants. If both reactants are charged, the terms should be added to the equations 3-4 to account for the work of bringing the charged particles closer together.
Equations 2-4 are used to estimate the DEE rate constants if the cross-reaction rate constant and one of the DEE rate constants are known [
2,
3,
4]. When the rate constants are known only at a single temperature then A
11 = A
22 = 10
11 M
-1s
-1 is often assumed, that introduce an error in the value being determined.
The purpose of this work is to probe the applicability of the Marcus cross-relation with the better accuracy that is provided by knowing of the temperature dependences of the corresponding DEE rate constants. In this case the value of the rate constant of reductive electron transfer to short-lived radical calculated from the cross-relation does not contain the errors due to the uncertainty of the pre-exponent values of the DEE rate constants, since the latter are determined from the temperature dependences of the rates.
To test the Marcus cross-relation, we chose the reduction reactions of the short-lived GMP(-H)
• radical by tyrosine (TyrO
-) and N-acetyl tyrosine (NacTyrO
-) anions. The DEE reactions cannot be studied using optical methods, since there is no change of reactants concentration in course of the reaction, thus the total optical density does not change. The methods for studying DEE reactions between stable reactants (transition metal complexes in different oxidation states, long-lived radicals with the corresponding diamagnetic molecules) usually employ modification one of the reactants. Such methods include the use of deuterated ligands [
5], optical isomers [
6], and radioactive isotopes [
7]. All these methods are not suitable for studying DEE involving short-lived radicals. The DEE reactions between stable reagents can also be studied using line broadening in EPR spectrum [
8,
9,
10,
11] or in NMR spectra [
12,
13,
14]. These methods are also not applicable to short-lived radicals, when the lifetime of the radicals is so short that it is impossible to record their EPR or NMR spectra under normal conditions.
The photoinduced time-resolved chemical induced nuclear polarization (tr-CIDNP) method [
15,
16,
17,
18,
19,
20,
21,
22,
23] fortunately allows to study degenerate exchange reactions involving short-lived radical intermediates [
24,
25,
26]. It is an indirect way of radical intermediates detection that are formed by short laser pulse via quantitative analysis of anomalous enhancement or emission of NMR lines of the diamagnetic reaction products and their dependence on time after a laser pulse.
The reduction reaction of the neutral radical GMP(-H)
• by the anions of tyrosine TyrO
- and N-acetyltyrosine NacTyrO
-, was studied by the tr-CIDNP method; dipyridyl (DP) was used as a dye. The CIDNP kinetics for the systems GMP + DP [
27], NacTyrOH + DP [
28] and GMP + NacTyrOH + DP [
29] were previously studied at t = 25ºC in a wide pH range. The temperature dependence for the DEE rate constant in the GMPH
+/GMPH
++• pair was also measured earlier [
30]. In the temperature range 8-65ºC we measured the DEE rate constants in the pairs GMP(-H)
-/GMP(-H)
•, TyrO
-/TyrO
• and NacTyrO
-/NacTyrO
•. From these temperature dependences of the rate constants the reorganization energies were determined; and with use of their values and Marcus cross relation, the rate constants of the GMP(-H)
• radical reduction reaction by TyrO
- and NacTyrO
- anions were calculated. We compared the calculated rate constants with the measured at t = 25ºC electron transfer reaction rate constant for GMP(-H)
• + TyrO
- and the previously determined reaction rate constant for the reactants GMP(-H)
• + NacTyrO
- [
29].
2. Results
2.1. Mechanism of CIDNP effect
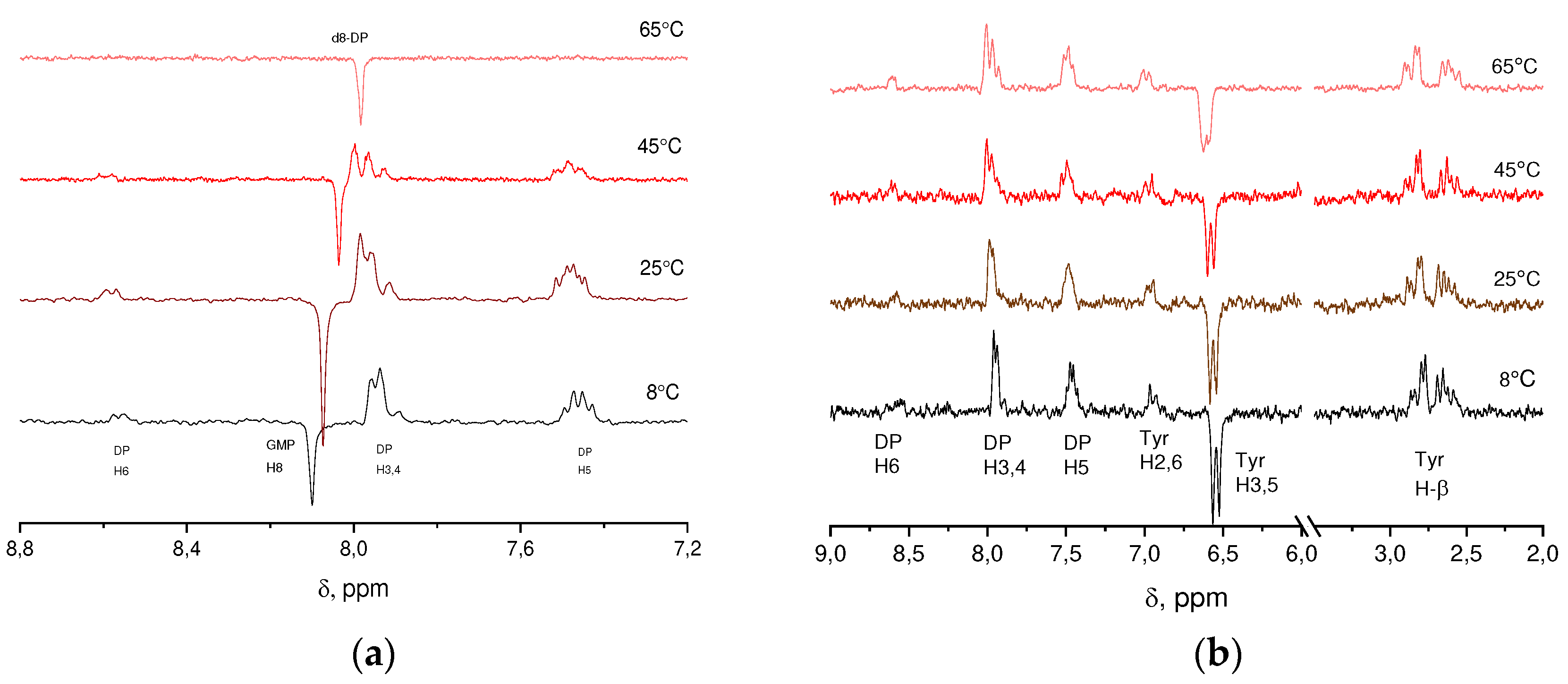
The CIDNP spectra recorded during irradiation of solutions containing DP + GMP(-H)
-, DP + TyrO
- with signal attribution are shown in
Figure 1. The spectra were recorded with zero delay after the laser pulse, without internal standard, the dependence of water chemical shifts on temperature was used: δ(HDO) = 5.060 – 0.0122t + (2.11*10
-5)t
2 (t in ºC) [
31] to relate the chemical shifts.
The CIDNP signal origins as follows. The dye molecule D absorbs a quantum of light and transition from the ground singlet state S0 to the excited singlet state S1 occurs. Due to inter system crossing (ISC) the S1 molecule state converts to the triplet electronic state. Then, as a result of diffusion motion, the dye molecule D in the triplet state encounter the quencher Q, which quenches the dye triplet state by means of electron transfer with a rate constant kq. The radical pair formed in course of this reaction preserves the triplet electron state of the precursor. At the instant of their formation, the radicals are situated in the solvent “cage”. They cannot react back to the ground diamagnetic states due to the conservation of the total electron spin. In order for this to happen, the radical pair must change to the singlet state. Such a transition from the triplet to singlet state (and vice versa) can happen due to the difference of Larmor frequencies of the radicals in the field of the NMR spectrometer (at different g- factors) and due to hyperfine couplings of electron spins of the radicals with magnetic nuclei. Thus, in the high field of NMR spectrometer the rate of singlet-triplet transitions depends, besides of g-factor difference, on the nuclear spin projections along the magnetic field, configuration of nuclei spins (S-T0 mechanism of CIDNP formation in strong magnetic fields). Therefore, the in-cage, geminate, recombination products are enriched in those nuclear spin states that have a higher singlet-triplet interconversion rate. However, the total polarization of nuclear spins does not change since the geminate reaction gives rise only to the sorting between the nuclear polarization of geminate diamagnetic products and the polarization of the radicals which escaped into the bulk of solution. Consequently, at the initial instant of time (on the scale of T1 nuclear relaxation time in radicals) the nuclear polarization of radicals escaped in the bulk of solution is equal in magnitude and opposite in sign to the polarization of diamagnetic products formed in the course of geminate recombination.
The sign of CIDNP signal Г of geminate diamagnetic products is determined by the Kaptein rule [
32] Г = μ•sgn(Δg)•sgn(A), where μ = +1 in the case of a triplet precursor and μ = –1 in the case of a singlet one; sgn(Δg) is the sign of the g-factor difference of the radicals; sgn(A) is the sign of the hfi-coupling constant of the corresponding nucleus. The value of the g-factor of the neutral GMP(-H)
• radical is equal to 2.0034 [
33], g-factors for the TyrO
• and NacTyrO
• radicals are 2.0041 [
34] and 2.0055 [
35], respectively. The sign of the hfi-coupling constant of the H-8 proton of the GMP(-H)
• radical is negative [
33], for TyrO
• and NacTyrO
• the sign of the hfi-coupling constants of the H-3,5 protons is also negative, and of the H-2,6,β protons is positive [34, 35]. There are no experimental data for the DPH
• radical, the calculated hfi-coupling constants of the H-3,4,5,6 protons are negative [
32], and the value of the g-factor of the DP
-• radical anion is equal to 2.0030 [
33]. Kaptein's rule holds for all signals in all
1H CIDNP spectra obtained in this work.
2.2. Experimental data processing
Theoretical fitting of the CIDNP kinetics measured for the systems GMP(-H)
- + DP, NacTyrO
- + DP, TyrO
- + DP was performed within the Fisher model [
36]. The model takes into account the nuclear polarization transfer from radical into diamagnetic molecule due to the second-order radical recombination, paramagnetic nuclear relaxation in radicals, arising of polarization within re-contacts of radicals in the bulk, and polarization transfer from radical to molecule as a result of DEE. The system of three Eqns. (5-7) describes the time evolution of the radical pair concentration R(t), the nuclear polarization in radicals P
R(t), and the experimentally registered nuclear polarization in diamagnetic molecules P
Pr(t):
with initial condition: PPr(t=0) = –PR(t=0) = PG.
here R
0 is the initial concentration of radical pairs; k
R is the rate constant for the second-order radical recombination; T
1 is the nuclear spin relaxation time in radicals; k
obs is the rate constant for DEE; C
q is the concentration of diamagnetic quencher molecules; parameter β = γP
G/R
0 shows the amount of polarization arising in one secondary radical pair (the radical pairs formed by radicals escaped from different geminate pairs, so-called F-pairs); γ is the ratio of CIDNP polarization formed in the secondary radical pair to the polarization in the geminate pair, in the case of a triplet precursor one has γ ≈ 3, usually is taken γ = 2.8 [
27]; P
G is the geminate polarization.
The system of Eqns. (5-7) is written assuming that the fraction of geminate recombination of radical pairs is negligible and that the radical formation due to quenching of the triplet state of the dye occurs instantaneously. Eq. (5) describes the time dependence of the radical concentration, which decreases according to the second-order recombination kinetics. The first terms in Eqns. (6-7) describe transfer of polarization from radicals to diamagnetic molecules due to the recombination of radicals, the third terms in both Eqns. (6-7) describe transfer of polarization from radicals to diamagnetic molecules due to DEE process. The second terms in Eqns. (6-7) describe the polarization forming as a result of radicals encounter in the bulk, i.e. in F-pairs. The fourth term in Eq. (6) describes the decay of nuclear polarization in radicals as a result of nuclear paramagnetic relaxation.
Under experimental conditions, there is a DPH
•/DP pair (pKa(DPH
•) > 14, [
37]) . The possible electron and proton transfer (PCET) is much slower than the electron transfer and cannot affect the CIDNP kinetics of DP protons. Therefore, when modeling the kinetic curves for nuclear polarization of DP, we took k
obs = 0.
In the system GMP(-H)- + TyrO- + DP, the kinetics of nuclear polarization is also affected by the reduction reaction of the GMP(-H)• radical by the TyrO- anion. Then, the time evolution of the concentrations of GMP(-H)•, TyrO• and DPH• radicals and the polarizations of the nuclei in PRGMP, PRTyr radicals, and PPrGMP, PPrTyr diamagnetic molecules are described by the following equations:
with initial conditions: PPrGMP(t=0) = –PRGMP(t=0) = PGGMP, PPr Tyr(t=0) = –PRTyr(t=0) = PGTyr, here kRGMP, kRTyr are the recombination rate constants of the radicals DPH• with GMP(-H)• and TyrO• radicals respectively, kobsred is the observed rate constant of reduction of the GMP(-H)• radical by tyrosinate-anion, βGMP = γPGGMP/R0GMP, βTyr = γPGTyr/R0Tyr .
In the process of solving this system of equations, the parameters kRGMP/kRTyr and kqGMP/kqTyr are introduced, through the latter the ratio of initial concentrations of GMP(-H)• and TyrO• radicals is expressed.
The initial concentration of radical pairs R0 is proportional to the fraction of light absorbed by the dye. The TyrO-, NacTyrO- compounds absorb at λ = 308 nm, as the concentration of tyrosine in the solution increases, the fraction of light absorbed by DP decreases and, accordingly, the initial concentration of radical pairs decreases as well. The ratio of initial concentrations of radical pairs in two experiments with different concentrations of tyrosine is as follows:
In Eq. (15) ε
DP, ε
Tyr are the extinction coefficients at λ = 308 nm; C
DP is DP concentration; C
1Tyr, C
2Tyr are tyrosine concentrations; ε
DP = 1.2*10
3 M
-1cm
-1 [
38], ε
TyrOˉ = ε
NacTyrOˉ = 790±8 M
-1cm
-1 was determined in this work. This effect was taken into account when modeling CIDNP kinetics in systems containing TyrO
- and NacTyrO
-.
The duration of the RF pulse (1-2 μs) is comparable with the characteristic time of the CIDNP decay, so it is necessary to take into account the polarization evolution during the RF pulse. Consideration of the CIDNP kinetics during the RF pulse for the special case of an ideal rectangular pulse is considered in [
39], the case of an RF pulse of arbitrary shape is considered in [
40]. The similar approach was used in the works of Morozova and Yurkovskaya [
41,
42,
43,
44,
45,
46,
47,
48].
To take into account the CIDNP kinetics during the application of the RF pulse along the x-axis, we considered the following system of equations that takes into account the polarization of the nuclei along the y, z axes:
where w(t) is the pulse shape, the equation for dP
Pr/dt is given by Eq. (7), before the pulse P
Pry = 0. The signal observed in the experiment is proportional to the after pulse value of P
Pry. The expression for polarization along the y-axis after the pulse is as follows [
39]:
where t0 is the start time of the RF pulse, T is its duration.
The duration of the π pulse is equal to tπ = 12.70 µs. The shapes of RF pulses of 1 and 2 µs duration used in this work were determined using an oscilloscope.
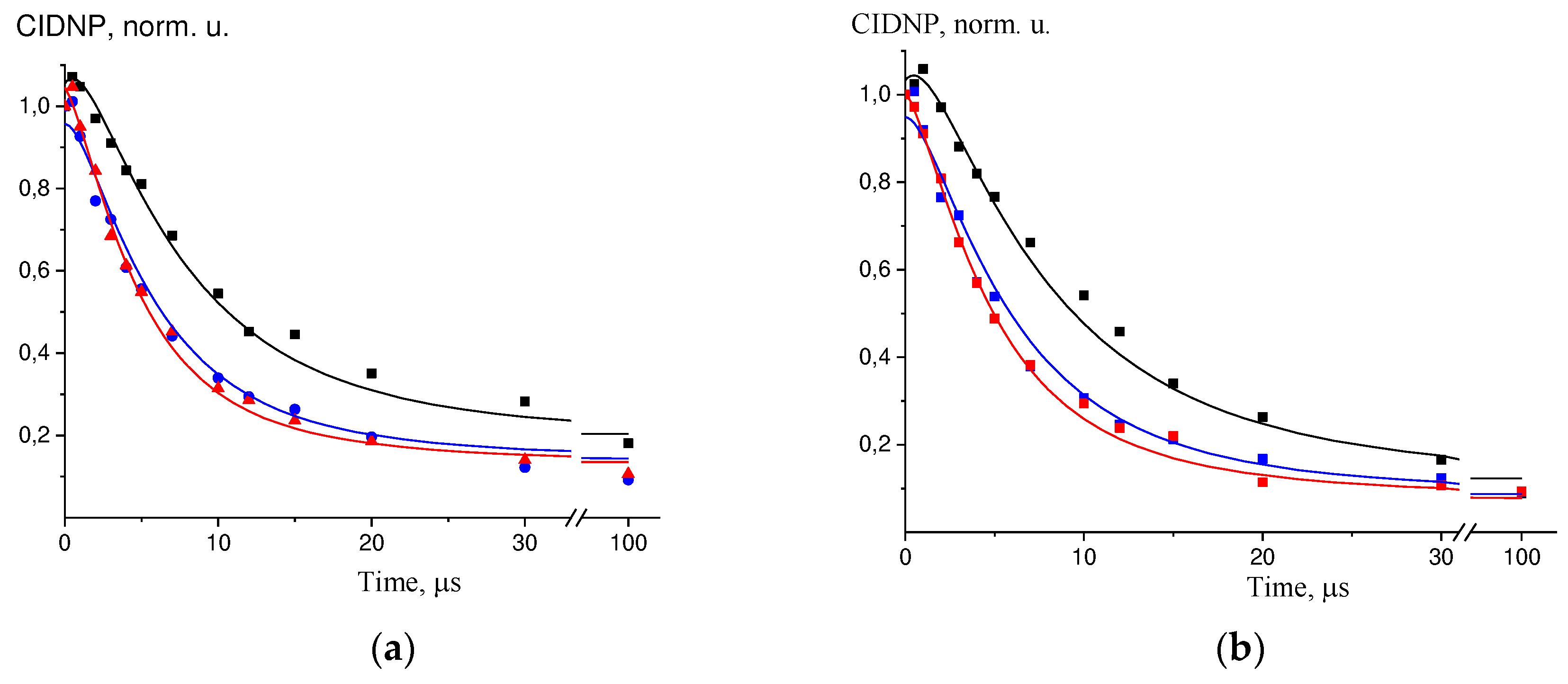
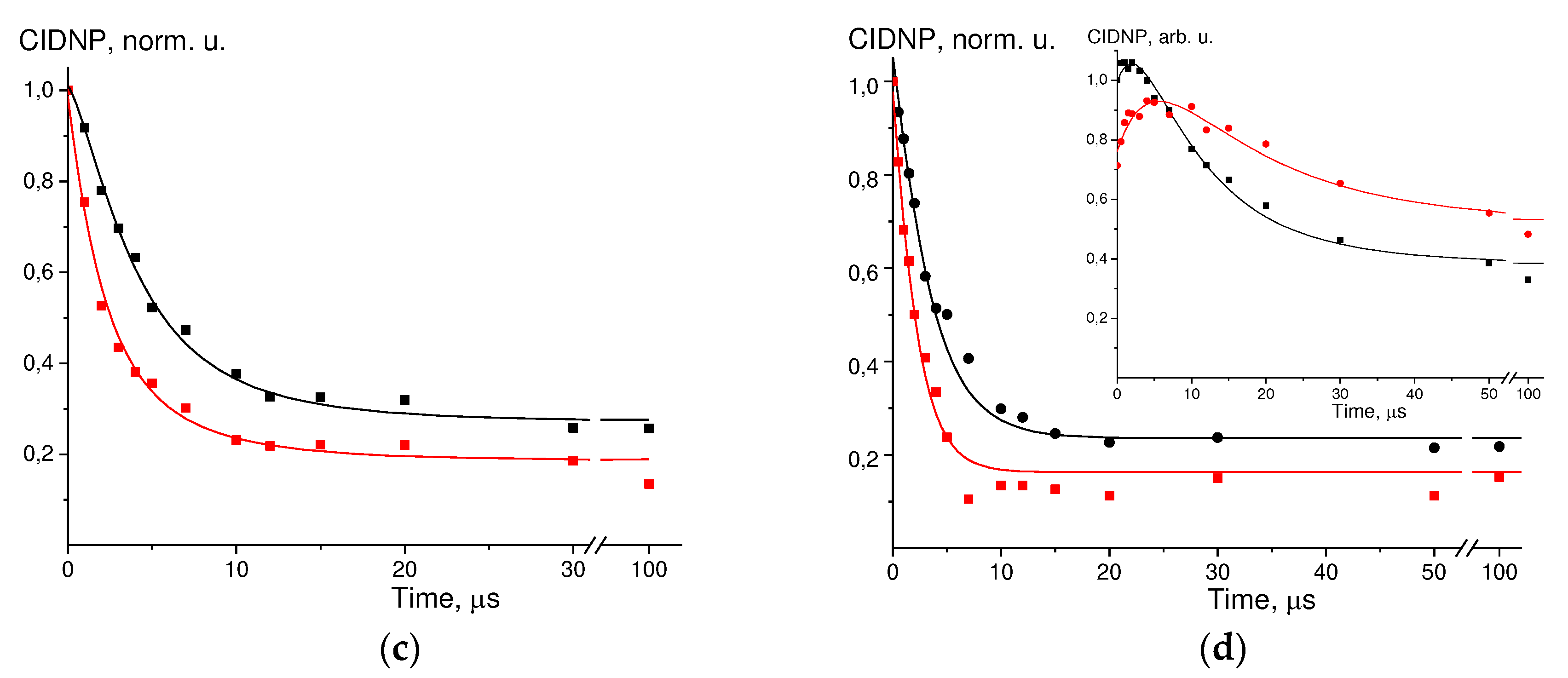
2.3. Results of CIDNP kinetics treatment
In the GMP(-H)
- + DP system, the polarization-time dependences were modeled for 8-th GMP protons and 3,4 DP protons. In the TyrO
- + DP, NacTyrO
- + DP systems, the dependences were modeled for 3,5 and β-protons of tyrosine, and 3,4 protons of DP – the other signals have too low signal-to-noise ratio. In the GMP(-H)
- + TyrO
- + DP system, CIDNP polarization time dependences were modeled for 8-th GMP protons and 3,5 tyrosine protons. Values of the degenerate electron exchange rate constants and paramagnetic nuclear relaxation times obtained from the best agreement between the calculated and experimental curves are given in
Table 1,
Table 2 and
Table 3;
Figure 2(a-c) shows the examples of simulations of these experimental data.
For the GMP(-H)- + DP we did not determine T1 for 3,4 protons of DP at 65°C because perdeuterated d8-DP was used due to the overlapping the 1H NMR signals of H-8 of GMP and H-3,4 of DP. For NacTyrO- + DP at 65°C and TyrO- + DP at 45°C we failed to determine T1 for H-β.
For GMP(-H)
- + DP at 25ºC, the value of the DEE rate constant differs from the literature data, while the paramagnetic relaxation time of the 8-th proton in the GMP(-H)
• radical coincides well with the literature data: k
obs = 4.0*10
7 M
-1s
-1, T
1 =20 μs [
27]. Moreover, the T
1 for the 8-th proton in the GMP(-H)
• radical coincides with the previously found T
1 for the 8-th proton in the GMPH
++• radical over the entire temperature range [
30]. For the NacTyrO
- + DP at t = 25ºC the values of the DEE rate constant and paramagnetic relaxation time of 3,5 protons coincide with the literature data: k
obs = 6.0*10
7 M
-1s
-1, T
1 =63 µs [
29]; = 4*10
7 M
-1s
-1, T
1 = 60 µs [
49]. However, the best fit values of nuclear paramagnetic relaxation times for 3,4 protons in the DPH
• radical do not coincide with the literature data T
1 = 44 µs [28, 38, 50] and T
1 = 45 µs [
49].
Simulation of the experimental data for DP + GMP(-H)
- + TyrO
- is shown in
Figure 2-d, the parameters found are: k
obsred = 1.5*10
8 M
-1s
-1, k
qGMP/k
qTyr = 0.3, k
RGMP/k
RTyr = 1.3. The parameters k
obsGMP, k
obsTyr, T
1GMP, and T
1Tyr found in this work were used in the calculation. There are literature data for the reduction of GMP(-H)
• radical by NacTyrO
- anion: k
obsred = 1.6*10
8 M
-1s
-1, k
qGMP/k
qTyr = 0.56, k
RGMP/k
RTyr = 0.9 [
29].
a) TyrO- + DP at t = 65°C, kinetics for H-3.5 TyrO-, black – C(TyrO-) = 1.5 mM, blue – C(TyrO-) = 2.5 mM, red – C(TyrO-) = 3.5 mM;.
b) TyrO- + DP at t = 65°C, kinetics for H-β TyrO-, black – C(TyrO-) = 1.5 mM, blue – C(TyrO-) = 2.5 mM, red – C(TyrO-) = 3.5 mM;.
c) GMP(-H)- + DP at t = 45°C, kinetics for H-8 GMP(-H)-, black – C(GMP) = 6.5 mM, red – C(GMP) = 13 mM;.
d) GMP(-H)- + TyrO- + DP at t = 25ºC, kinetics for H-8 GMP(-H)-, black – C(TyrO-) = 1.3 mM, red – C(TyrO-) = 2.5 mM, insert – kinetics for H-3.5 TyrO-, black – C(TyrO-) = 1.3 mM, red – C(TyrO-) = 2.5 mM.
2.4. Temperature dependence of the DEE rate constants
For the estimation of the effect of diffusion the following DEE kinetic scheme was considered (using tyrosine as an example):
where the first-order DEE rate wex is related to the second-order rate constant ket as:
kobs is the observable DEE rate constant, kobs it is expressed through ket and kd as follows:
The diffusion rate constant kd was estimated by the Smoluchowski equation, taking into account the charges of the reactants:
where r1, r2 are the radii of the reagents; wr is the work function of approach charged reactants to each other:
we assume that the reactants approaches to the distance equal to the sum of their radii. The factor takes into account the ionic strength of the solution:
where B = (2NAe2/(ε0k))1/2 = 50.345 l1/2K1/2Å-1M-1/2.
The viscosity values of D
2O were taken from [51, 52], dielectric permittivity from [
53]. The average elliptical radii of the reactants were used to estimate r
1 and r
2. An ellipsoid of the smallest volume was described around the molecule and the radius was expressed as [
54]:
where F(φ,α) is an elliptic integral of the first kind; φ = arcsin((a2 – c2)1/2/a); α = ((a2 – c2)/(a2 – b2))1/2; a, b, c are the semiaxes of the ellipsoid, a ≥ b ≥ c.
The ellipsoid semiaxes were calculated using the algorithm N. Shor [
55] with the molecular geometries of the crystal structures of DL-tyrosine [
56], N-acetyl-L-tyrosine and guanosine-5'-monophosphate trihydrate [
57]. The molecular radii found: r(GMP(-H)
-) = 4.18 Å, r(NacTyrO
-) = 3.82 Å, r(TyrO
-) = 3.06 Å, we assumed that the radii of the radicals do not differ from those of the corresponding diamagnetic particles.
When calculating wr, the negatively charged carboxyl and phosphate groups in the reactants were taken into account: z(GMP(-H)-) = -3, z(TyrO-) = -2.
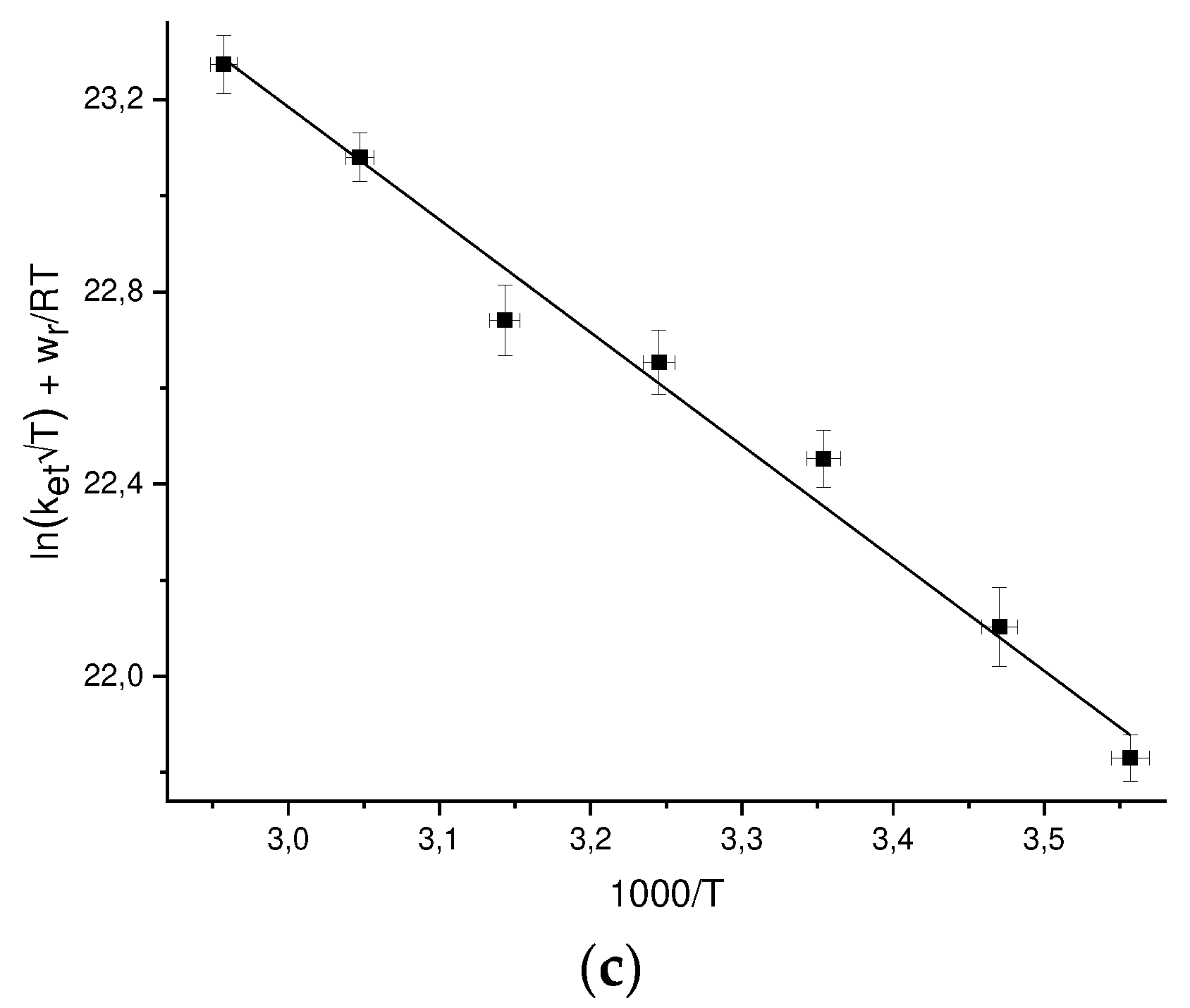
The ket values calculated by Eq.(20) are given in the last columns of Table Error! Reference source not found.-Error! Reference source not found..
The first-order DEE rate constant w
ex depends on temperature as [
1]:
The second-order DEE rate constant ket is expressed as follows:
The K
A in Eq. (26) is the equilibrium constant of pre-reaction complex formation; it depends on temperature as follows [
58] :
where is the reaction zone thickness. Then the second-order rate constant ket depends on temperature as:
The work function w
r depends on the temperature through dependence on temperature of the D
2O dielectric permittivity, at each temperature w
r can be calculated by Eq. (22). To find the pre-exponent A and the reorganization energy λ, we plot the values of ln[k
et√Texp(w
r/RT)], where the k
et values are experimental ones, versus 1/T (
Figure 3) and and approximated these points by linear dependence. The values of A and λ found from the approximation are given in
Table 4.
Previously we studied [
30] the temperature dependence of the DEE rate constant between the GMPH
+ cation and the GMPH
++•, dication radical, the reorganization energy found for this reaction is λ = 0.79 ± 0.11 eV [
21] and coincides with the value for GMP(-H)
- + GMP(-H)
• (see Table
Error! Reference source not found.).
2.5. The Marcus cross-relation equation
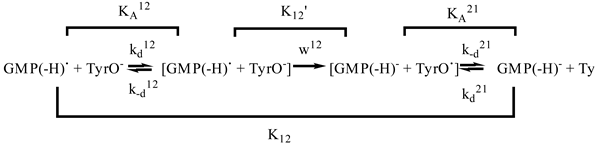
To account for the effects of diffusion the following kinetic scheme of electron transfer was considered (for the radical GMP(-H)• reduction by anion TyrO- as an example):
where the first-order rate w12 is related to the second-order rate constant k12 as:
The observable second-order rate constant kobs12 is expressed through k12 and kd12 as follows:
The rate constants k
12(TyrO
-) and k
12(NacTyrO
-) of GMP(-H)
• reduction by TyrO
- and NacTyrO
- respectively after correction for diffusion (k
d was calculated according Eq. (21)) are the following: k
12(TyrO-) = 1.7*10
8 M
-1s
-1 and k
12(NacTyrO
-) = 1.8*10
8 M
-1s
-1 [
29]. Thus, the values of the reduction rate constants are very close.
The rate constant w12 depends on the temperature as follows:
where ΔG12º’ is the driving force of the first-order redox reaction.
The equilibrium constant between the initial reactants and reaction products K12 is expressed as:
here KA12 and KA21 are the equilibrium constants of the formation of pre-reaction and post-reaction complexes, expressed by Eq. (27). Assuming the radii of radicals and corresponding diamagnetic particles are the same, the pre-exponents in Eq. (32) the factors KA12 and KA21 can be shortened (reduced). The ΔG12º value is expressed through standard electrode potentials, thus, ΔG12º’ can be calculated.
The expression for the second-order electron transfer rate constant k12 is given as follows:
If the electron transfer occurs over a relatively long distance with a weak force interaction between the reactants, then one can assume that λ12 = (λ11 + λ22)/2 that is the Marcus cross relation, where λ11, λ22 are the reorganization energies for the respective DEE reactions.
If we additionally assume the following ratio between the pre-exponents: A12 = (A11A22)1/2, then we can express k12 through the temperature dependence parameters of the DEE rate constants. Thus, the cross-reaction rate constant kcalc12 was calculated employing the following formula:
2.5.1. Reactants parameters for the Marcus cross-relation calculations
The cross-relation calculations require the values of the difference of standard electrode potentials, the reorganization energy and the pre-exponent for the corresponding DEE reactions, as well as the radii of all reactants and products to calculate the work function. In all the cases, we assume that the radii of radicals and corresponding diamagnetic particles are the same.
If only the DEE rate constant at a certain temperature is known, we estimate the pre-exponent as: A11 = 1011 M-1s-1 and calculate the reorganization energy by Eq. (35).
All the parameters of the reactants are given in
Table 5. The Z
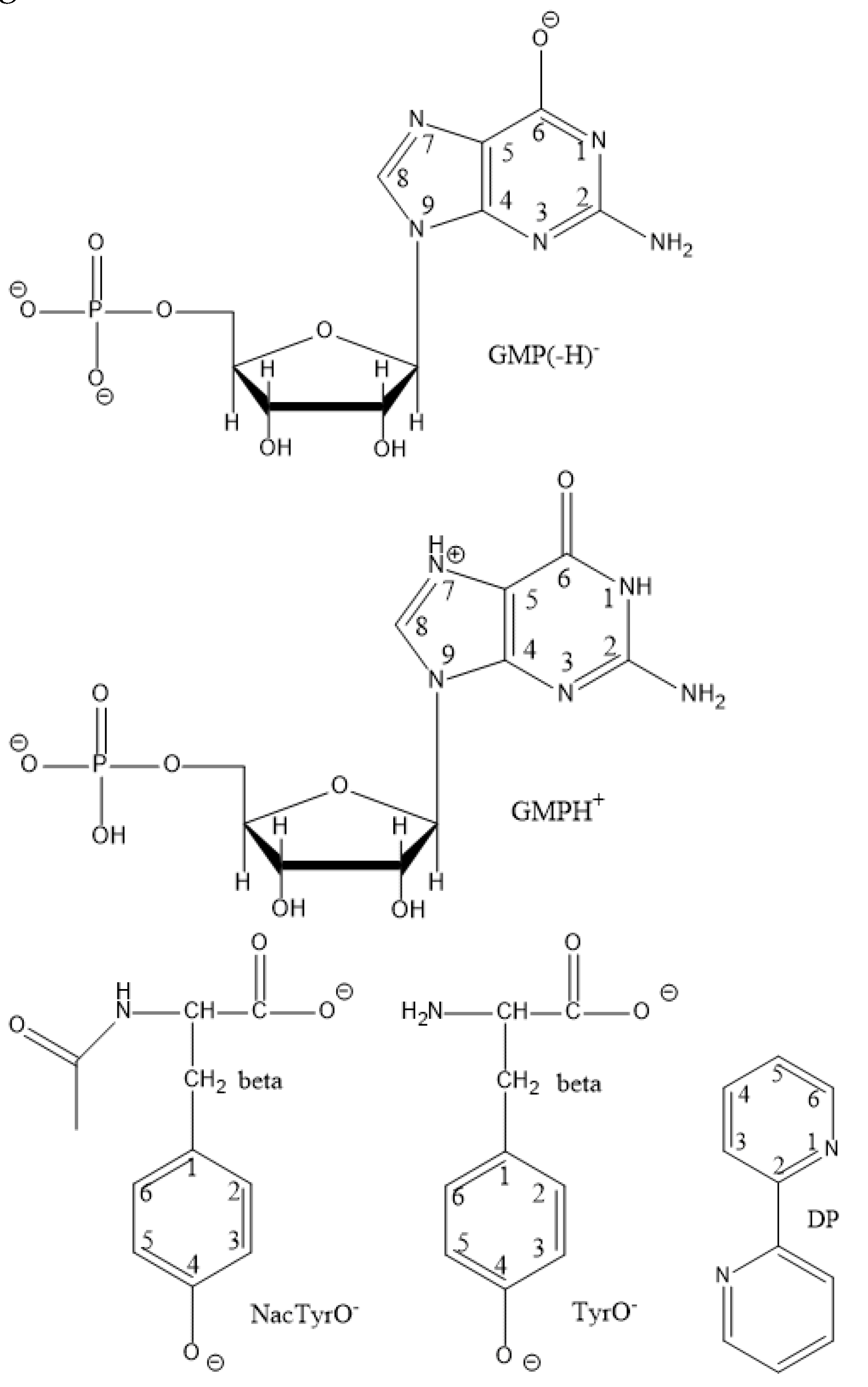
red column shows the charge of the reduced form of each reactant. The structures of some reactants are shown in
Figure 4.
The TyrO
•/TyrO
- case. The standard electrode potential is E° = 0.72 V [
59]. The radius calculation is described above, the pre-exponent and reorganization energy for the DEE reaction were found experimentally in this work.
The NacTyrO
•/NacTyrO
- case. We use the value of the standard electrode potential for N-acetyltyrosine methyl ester at pH = 7, E
7 = 0.97 V [
60]. pK
a(NacTyrOH) = 10.1, then Eº = 0.79 V. The calculation of the radius is described above; the pre-exponent and reorganization energy for the DEE reaction were found experimentally in this work.
The GMP(-H)
•/GMP(-H)
- case. The standard electrode potential of GMP at pH = 7, E
7 = 1.31 V [
61], determined from photoinduced electron transfer reaction rates, that agrees well with that of guanosine at pH = 7, E
7 = 1.29 V [
62], determined by pulsed radiolysis. The acidity constants of GMP [
63] and its radical [
64,
65,
66] are shown in
Figure 4. For GMP(-H)
•/GMP(-H)
- the calculated potential is: Eº = 1.23 V.
The GMPH
++•/GMPH
+ case. The standard electrode potential E° = 1.55 V, calculated from E
7 = 1.29 V [
62]. The pre-exponent and reorganization energy for the DEE reaction were found earlier [
30]. Average elliptical radius r = 4.19 Å, calculated by the method described above, the geometry was taken from the crystal structure of guanosine-5'-monophosphate trihydrate [
57]
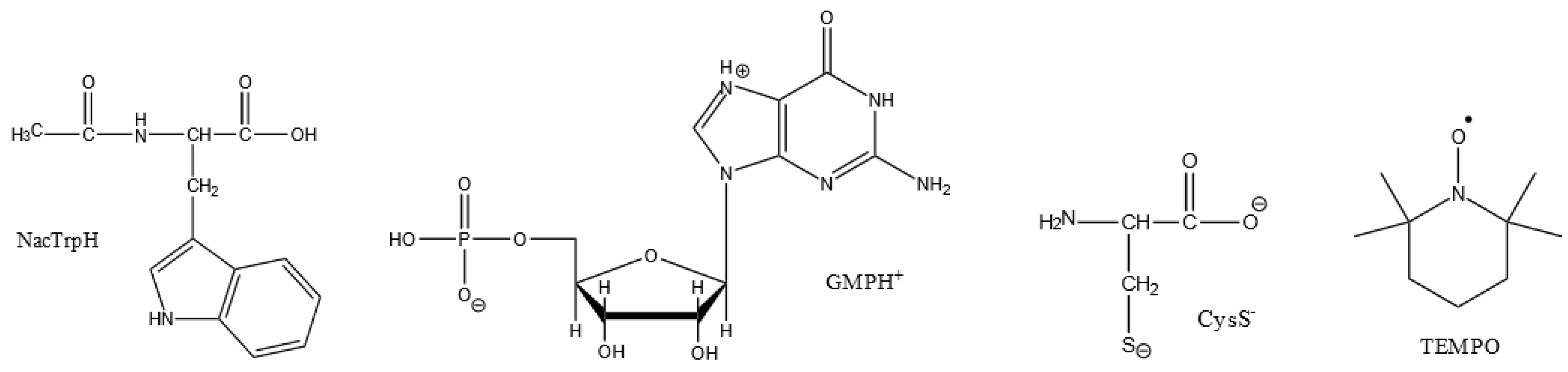
The NacTrpH
+•/NacTrpH case, we use the value of the standard electrode potential for tryptophan, E° = 1.15 V [
59]. The DEE rate constant at 25°C is k
11 = 9*10
8 M
-1s
-1 was determined experimentally by CIDNP with microsecond resolution [
38]. After correction for diffusion by Eq. (20) one has: k
11 = 1.3*10
9 M
-1s
-1. The mean elliptical radius r = 3.83 Å was calculated by the method described above, geometry from was taken from the NacTrpH crystal structure [
67]. We assume that A
11/√T = 10
11 M
-1s
-1, then λ = 0.45 eV.
The ClO
2•/ClO
2- case. The standard electrode potential E° = 0.934 V [
68]. The DEE constant at 25°C is k
11 = 3.3*10
4 M
-1s
-1, determined from a cross relation with parameters A
11/√T = 10
11 M
-1s
-1, r = 1.5 Å [
69]. Then λ
11 = 1.53 eV.
The N
3•/N
3- case. The standard electrode potential E° = 1.33 V [
68]. The DEE rate constant at 25°C k
11 = 3.7*10
6 M
-1s
-1, determined from a cross relation with parameters A
11/√T = 10
11 M
-1s
-1, r = 2 Å [
69]. Then λ
11 = 1.05 eV.
The NO
2•/NO
2- case. The standard electrode potential E° = 1.04 V [
68]. The DEE rate constant at 25°C k
11 = 580 M
-1s
-1, determined experimentally by isotopic substitution [
70]. We assume that A
11/√T = 10
11 M
-1s
-1, then λ = 1.95 eV. The radius r = 1.9 Å [
69].
The [IrCl
6]
2-/[IrCl
6]
3- case. The standard electrode potential E° = 0.892 V [
71]. The DEE constant at 25°C k
11 = 2.3*10
5 M
-1s
-1, determined experimentally by isotopic substitution [
72]. We assume that A
11/√T = 10
11 M
-1s
-1. Radius r = 4.4 Å [
73], DEE rate constant measured at μ = 0.1 M. Then λ = 1.04 eV.
The CysS
•/CysS
- case. The standard electrode potential E° = 0.76 V [
74]. The DEE rate constant at 25°C k
11 = 5.4*10
3 M
-1s
-1, determined from the Marcus cross relation with parameters A
11/√T = 10
11 M
-1s
-1, r = 3.0 Å, the k
12 cross-reaction rate constant was measured at μ = 0.1 M [
74]. Then λ = 1.48 eV.
The TEMPO
+/TEMPO
• case. The standard electrode potential E° = 0.745 V [
75]. The DEE rate constant at 25°C k
obs = 8.6*10
7 M
-1s
-1, determined experimentally by line broadening in the EPR spectrum [
76]. After correction for diffusion by Eq. (20), k
11 = 8.8*10
7 M
-1s
-1. We assume that A
11/√T = 10
11 M
-1s
-1. Then λ = 0.72 eV. The radius r = 3.67 Å [
76].
Figure 5.
Structures of N-acetyltryptophan (NacTrpH), guanosine-5'-monophosphate cation (GMPH+), cysteine anion (CysS-), stable free radical TEMPO – (2,2,6,6-tetramethylpiperidin-1-yl)oxyl.
Figure 5.
Structures of N-acetyltryptophan (NacTrpH), guanosine-5'-monophosphate cation (GMPH+), cysteine anion (CysS-), stable free radical TEMPO – (2,2,6,6-tetramethylpiperidin-1-yl)oxyl.
Table 5.
Parameters of the reactants for the Marcus cross-relation calculations.
Table 5.
Parameters of the reactants for the Marcus cross-relation calculations.
| DEE reaction |
E°, V |
ln(A) |
λ, eV |
r, Å |
Zred
|
| GMP(-H)- + GMP(-H)•
|
1.23 |
31.7 |
0.82 |
4.18 |
-3 |
| GMPH+ + GMPH++•
|
1.55 |
29.2 |
0.79 |
4.19 |
0 |
| NacTyrO- + NacTyrO•
|
0.79 |
27.0 |
0.50 |
3.82 |
-2 |
| TyrO- + TyrO•
|
0.72 |
30.2 |
0.81 |
3.06 |
-2 |
| ClO2- + ClO2•
|
0.934 |
28.2 |
1.53 |
1.5 |
-1 |
| N3- + N3•
|
1.33 |
28.2 |
1.05 |
2.0 |
-1 |
| NO2• + NO2-
|
1.04 |
28.2 |
1.95 |
1.9 |
-1 |
| [IrCl6]2- + [IrCl6]3-
|
0.892 |
28.2 |
1.04 |
4.4 |
-3 |
| TEMPO• + TEMPO+
|
0.745 |
28.2 |
0.72 |
3.67 |
0 |
| CysS- + CysS•
|
0.76 |
28.2 |
1.57 |
3.0 |
-2 |
| NacTrpH + NacTrpH+•
|
1.15 |
28.2 |
0.45 |
3.83 |
0 |
2.6. The T1 temperature dependence.
The temperature dependences of the nuclear paramagnetic relaxation times T1 were obtained by means of the CIDNP kinetics simulation. We assume that the main mechanism of relaxation is modulation of the hyperfine interaction (hfi) tensor due to the stochastic rotation of the molecule as a whole. Then the nuclear paramagnetic relaxation time T1 should depend on the magnetic field B and the rotational correlation time of the molecule as follows:
If the diffusive stochastic rotation of the radical is fast, , then the nuclear paramagnetic relaxation rate 1/T1 is proportional to ; the value of can be estimated from the Stokes-Einstein-Debye equation:
According to [51, 52], the temperature dependence of D2O viscosity in the temperature range 8 - 65ºC is well described by the following equation:
where E/R = 2059 K, η0 = 1.14*10-6 Pa*s.
Then the T1 temperature dependence should be described by the following equation:
where C, E/R are parameters, E/R = 2059 K.
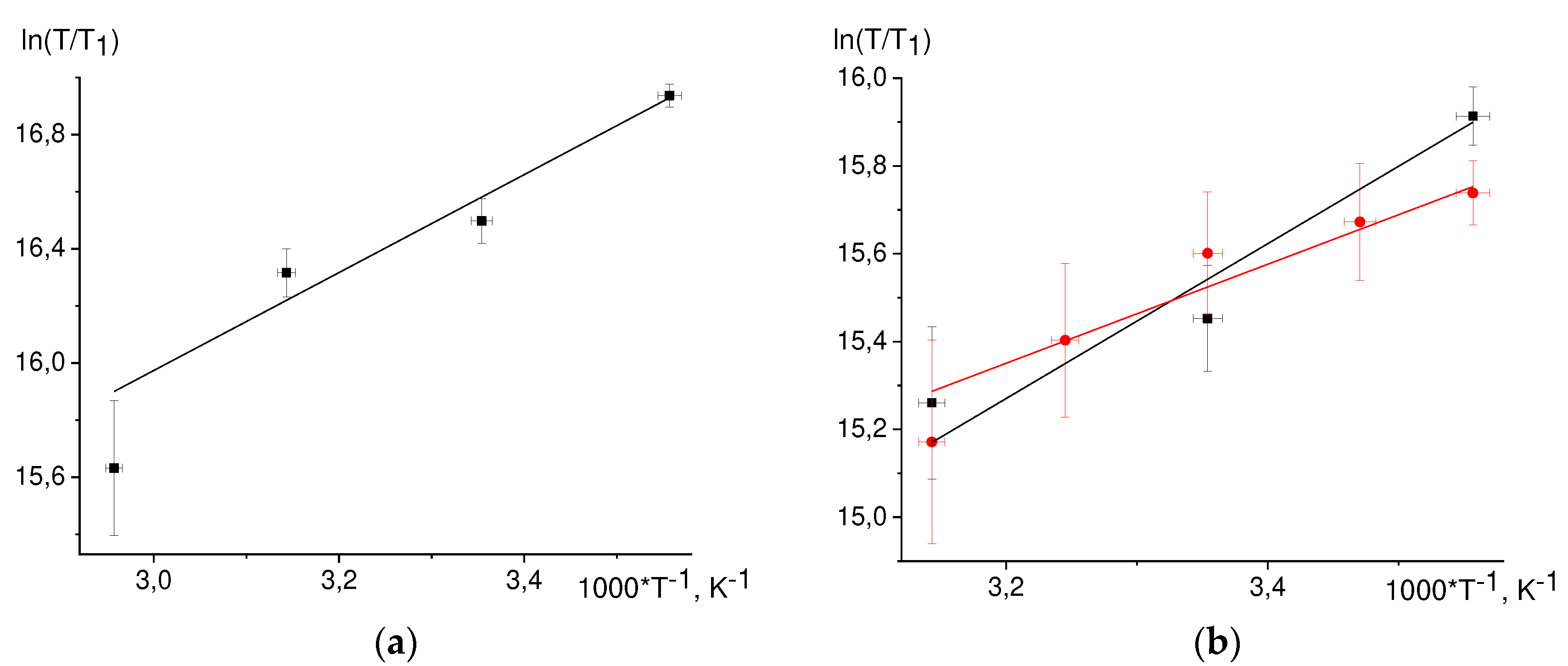
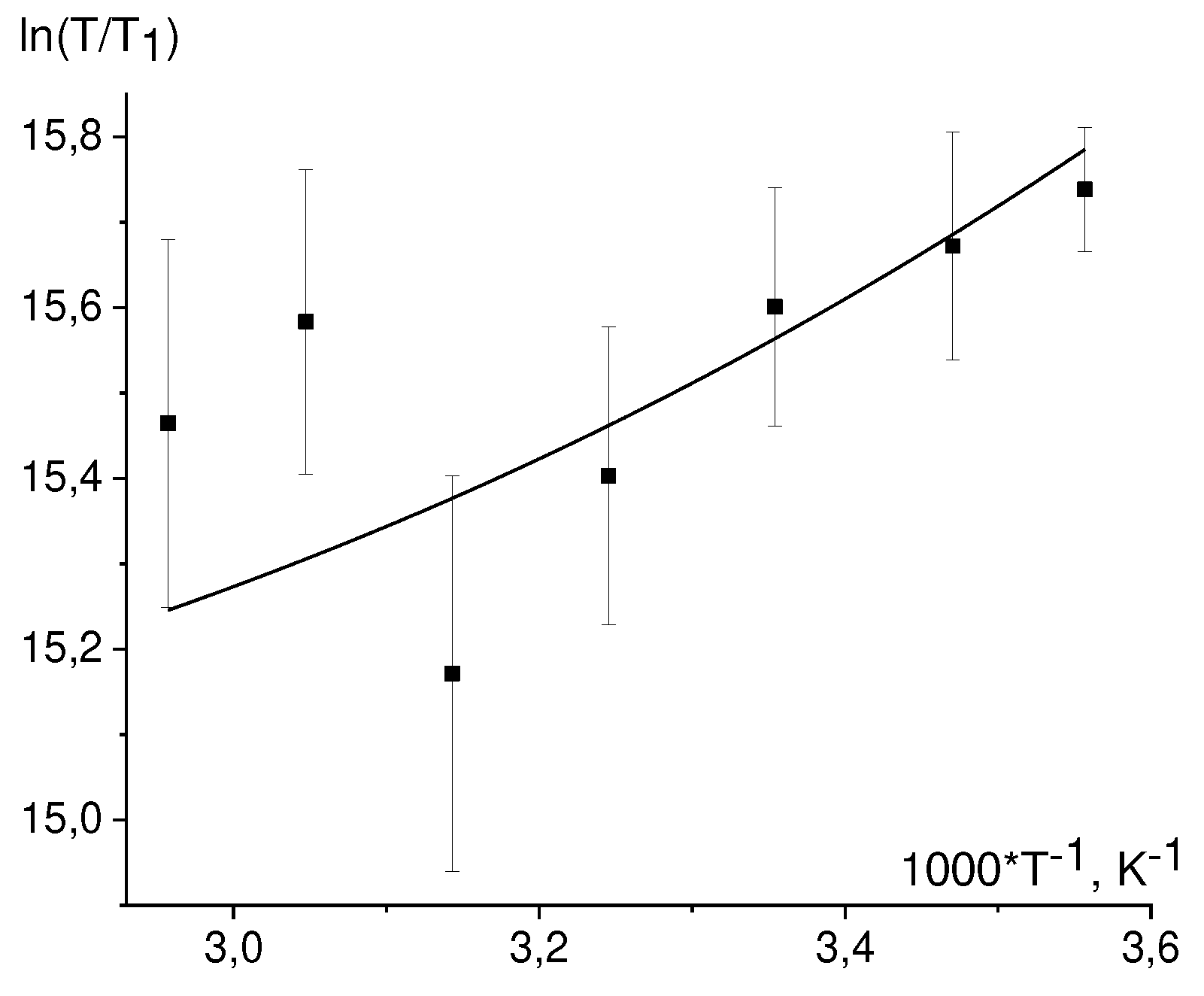
The T
1 temperature dependence, Eq. (39) is linearized in the coordinates ln(T/T
1) vs 1/T (
Figure 6).
While fitting by straight lines we discarded by the dropout values. Found values from the slopes of the straight lines E/R are summarized in
Table 6. For 3,5 protons NacTyrO
•, 8-th proton GMP(-H)
•, H3,4 DPH
• protons the slopes coincide within an error with the slope from viscosity dependence. The slope for ТyrO
• 3,5 protons is almost twice as different from that for viscosity. Earlier we found the slope for the 8-th proton GMPH
++•, it also coincides with the slope from viscosity dependence.
For the H-3,5 of NacTyrO•, H-8 of GMP(-H)•, and H-3,4 of DPH• the slopes of the fitted straight lines coincide with the slope for viscosity within an error margin, indicating that rotational modulation of the hfi tensor is the main mechanism of nuclear paramagnetic relaxation of these protons.
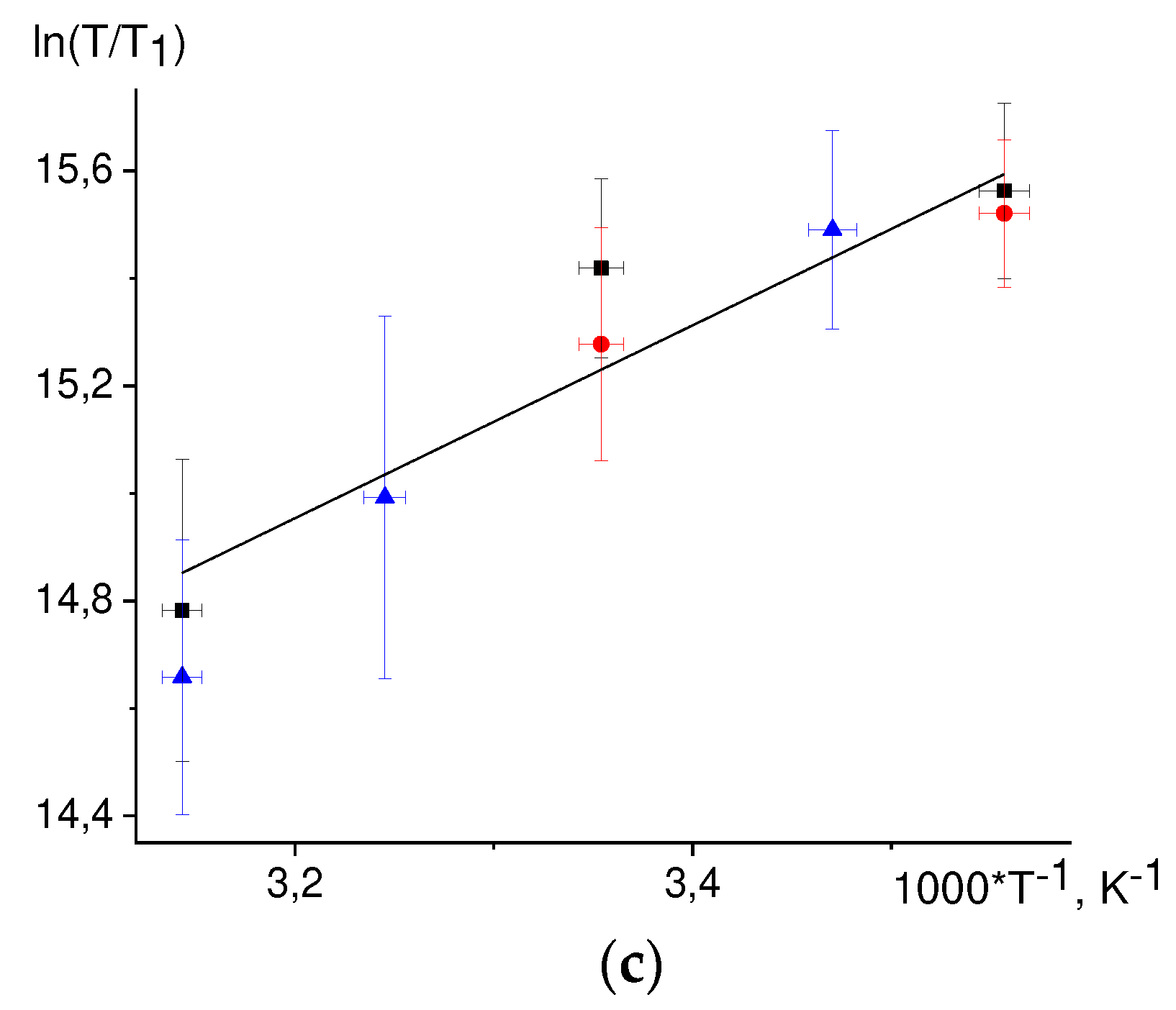
The defined energy value E for the 3,5 TyrO• protons is notably different from that for the viscosity dependence. This result can be rationalized assuming that for these protons two mechanisms gives rise to paramagnetic relaxation: modulation of the hfi tensor due to stochastic rotation of the molecule as a whole and modulation of the hfi tensor due to stochastic rotation of the phenolic ring. Assuming that the ring rotation has a small activation energy, the temperature dependence of the correlation time τe for this rotation is as follows:
while the temperature dependence of the rotational correlation time τM is:
Then the nuclear relaxation time T1 can be expressed employing Lipari-Szabo [77, 78] equation:
where S2 is an order parameter, playing the role of the dimensionless amplitude of molecular motion: the smaller S2, the larger the amplitude; Th is the temperature when the correlation times τe and τM coincide, C2 = C1exp(E/(R·Th).
The temperature dependence of the ln(T/T1) on 1/T has the form:
here E/R = 2059 K is the activation energy for D
2O viscosity. There are three fit parameters: C, S
2, T
h. The value S
2 = 0.01 was taken for the fit. The best fit of the experimental data is then achieved at T
h = 850 K, see
Figure 7.
The paramagnetic relaxation time T1 of the methylene protons (β-CH2 protons) in the NacTyrO• and ТyrO• radicals is almost independent on temperature (Tables Error! Reference source not found.-Error! Reference source not found.). We assume that probably the paramagnetic relaxation of β-CH2 protons occurs also due to the modulation of hfi tensor by intramolecular rotations around the aliphatic bonds. These rotations can have low activation energy, so in a small range of temperatures the rotational frequency changes weakly, which causes the apparent independence of the relaxation time T1 on the temperature.
3. Discussion
3.1. Comparison of the calculation and experiment
A comparison of the electron transfer reaction rate constants calculated from the Marcus cross relation and those found in the experiment are shown in
Table 7 The experimental rate constants were corrected for diffusion by Eq. (30).
Rate constants were calculated by Eq. (34) with parameters from the
Table 7. All experimental rate constants were measured at 25°C. We assume that parameters of the dipeptide Gly-TyrO
- do not differ from those of the NacTyrO
- and parameters of the amide N-acetyltyrosine NacTyrO
--NH
2 differ from those of NacTyrO
- only in charge.
The agreement with the experiment for reactions involving GMPH+/++•, GMP(-H)-/• is noticeably worse than for reactions involving TyrO-/•, NacTyrO-/•. If GMP is an oxidizing agent, the calculated rate value is overestimated, and when GMP is a reducing agent, the calculated value is underestimated. Perhaps the values of standard potentials for GMPH+/++•, GMP(-H)-/• are overestimated, if the error would be in the pre-exponent or in the reorganization energy of GMP, the values would be overestimated or underestimated in all reactions involving GMP, regardless of whether it is oxidation or reduction.
For the reactions TyrO- + GMP(-H)•, NacTyrO- + GMP(-H)• the calculated rate values notably differ from the experimental values than in other GMP involving reactions. Probably this difference can be explained not only by the overestimation of potential of GMP(-H)-/•, but also by other causes.
For reactions involving TyrO-/•, NacTyrO-/• the calculated values agree well with the experimental values. In the case of the reaction TyrO- + N3•, the experimental rate constant is close to the diffusion rate constant; the calculation shows that the reaction occurs in the diffusion control limit; the calculation shows good agreement with the experiment.
3.2. The possible reasons for the failure of the Marcus cross-relation in the reactions of GMP(-H)• radical reduction by TyrO-, NacTyrO- anions.
The Marcus cross-relation is fulfilled under the following conditions: the value of ΔG
12° is not too large, the reaction is far from the inverted region; the reactants and products are in the ground state; the electron transfer is adiabatic [1, 88]. Also the size difference of the reactants should not be very large (2λ
12 ≈ λ
11 + λ
22 requires 2(r
11r
22)
1/2 ≈ r
11 + r
22), otherwise the expression for the cross relation should be modified [
89] .
The Marcus cross-relation for reactions of transition metal complexes was verified in [
90,
91,
92] and for reactions of organic molecules in [93, 94]. The Marcus cross-relation for redox reactions between organic TMPPD and various inorganic oxidating ions was tested in [
95]. A good linear relation over a range of seven orders of magnitudes was found. As a rule, the calculated according to the cross-relation reaction rate constant turns out to be greater than the experimental one; the error increases with the growth of K
12. In the above-mentioned works, verification of the cross-relation was done for rate constants measured only at one temperature with the employment of Eqns. (2-4). In these equations, the parameter ln(f
12) = -(ΔG
12°)
2/(2RTλ
12), f
12 ≈ 1 at ΔG
12° << λ
12. But at large ΔG
12° this parameter contributes significantly, and its calculation requires values of the pre-exponents for DEE reactions. In these works, estimates on the order of 10
11 were taken for the values of the pre-exponents. We believe that this can introduce an error when K
12 is large. In this work, the values of the pre-exponents and reorganization energies of DEE were determined experimentally; that allows to exclude this error. In particular, it turned out that the pre-exponent in the case of GMP is two orders of magnitude greater than the 10
11 M
-1s
-1.
In the course of reactions no any isomer product is formed since as it is seen from the CIDNP spectra the electron is transferred only within the aromatic π-systems of the reactants.
When describing the kinetics of electron transfer, the pre-exponent includes the factor κ, which has the meaning of the probability of electron transfer while passing into transition state. For adiabatic reactions κ = 1, the parameter κ is close to unity if there is substantial overlap of the reactant orbitals [
96]. For reactions of organic molecules, κ = 1 is usually assumed [93, 97]. In addition, possible nonadiabaticity is taken into account in the cross relation as κ
12 = (κ
11κ
22)
1/2.
The steric cross-reacting factor is included in the pre-exponent A12 and is estimated as the geometric mean of the steric factors of the DEE, i.e. A12 = (A11A22)1/2.
Another possible reason for the failure of the Marcus cross-relation can be effect of non-electrostatic interactions between the reactants. In the pairs TyrO-/TyrO•, GMP(-H)-/GMP(-H)•, TyrO-/GMP(-H)• the stacking interactions increasing the stability of pre-reaction complexes are possible. Assume that contribution ΔHº of the stacking-interaction to the enthalpy change of the pre-reaction complex formation is independent of temperature and ΔHº < 0. Then the expressions for the DEE and cross-reaction rate constants taking into account the stacking-interaction are as follows:
In Eq. (47), we assume that ΔH12º ≈ ΔH21º. The Eq.(46) shows that when treating the temperature dependence of the DEE rate constants by the method described above (i.e. considering only the electrostatic interactions), the found values of the reorganization energies λ11obs will be underestimated: λ11obs = λ11 + 4ΔH11º.
Consideration of the stacking-interaction on the one hand increases the calculated cross-reaction rate constant kcalcred due to the factor exp(-ΔH 12º/RT), on the other hand it decreases, as the calculated reorganization energy increases. The final result depends on the values of ΔH11º, ΔH22º, ΔH12º. When ΔH11º = ΔH22º = ΔH12º = -RT the calculated value of kcalcred increases by 1.4 times, when ΔH11º = ΔH22º = -RT, ΔH12º = 0 it decreases by 2 times.
Marcus cross-relation fails if the electron transfer reaction produces products in the vibrationally-excited state.
When we assume that the overlap of the orbitals in the TyrO-/GMP(-H)• pair is less than in the TyrO-/TyrO•, GMP(-H)-/GMP(-H)• pairs, then the electronic factor of the cross-reaction appears to be less than that calculated from the cross relation, κ12 < (κ11κ22)1/2. The enthalpy of the stacking-interaction for the cross-reaction turns out to be lower than for the DEE reactions. This gives rise to the fact that the cross-reaction rate constant is less than the one we calculated without taking these effects into account.
4. Materials and Methods
The set-up for time-resolved CIDNP experiments was based on a Bruker DRX-200 NMR spectrometer (magnetic field 4.7 Tesla, resonance frequency of protons 200 MHz). A detailed scheme of the setup and methodology of the experiment were published in a review devoted to the application of time-resolved CPNR for studying the kinetics and mechanism of reactions of biologically important molecules [
98].
The 1H CIDNP spectra were recorded as follows. First, the sample in a standard 5 mm NMR Pyrex ampule was barbotaged with argon for 7 min to remove dissolved oxygen. Then, the sample was placed in the NMR spectrometer sensor and broadband homonuclear de-coupler pulses were applied for a few seconds on channel 1H to suppress the thermal magnetization of the sample. The pulse sequence WALTZ16 was used. The parameters of the sequence were chosen so that the 1H NMR signals were completely absent from the spectrum without laser irradiation. After that, the sample in the ampoule was irradiated with a single laser pulse of the excimer XeCl-laser COMPEX Lambda Physik (wavelength 308 nm, pulse energy up to 120 mJ, pulse duration ~15 ns), and after time interval τ a registering radiofrequency (RF) pulse with a maximum allowable power -4 dB and duration 1 or 2 μs was applied. After the pulse was applied, the decay of the free induction signal was recorded in the same way as in the conventional NMR experiment. The delay τ was varied in the range from 0 to 100 µs.
The temperature was calibrated by the difference of chemical shifts in the
1H NMR spectrum of methanol, the temperature measurement error 1K [
99].
The pH of the NMR samples was adjusted by addition of NaOD. No correction was made for the deuterium isotope effect on the pH. Experiments with TyrO
- and NacTyrO
- were performed at pH = 11.7, with GMP(-H)
- and GMP(-H)
- + TyrO
- at pH = 11.3. At t = 25ºC the pK
a of phenol groups TyrOH and NacTyrOH are 10.1 and 10.2 [
100], pK
a(GMP) = 9.4 [
63], pK
a(GMP(-H)
•) = 10.8 [
64], but deprotonation is slow and the GMP(-H)
- radical is stable at pH = 11.8 for at least 1000 µs [
27]. The 2,2'-dipyridyl (DP) was used as a dye (photosensitizer); its concentration was 15 mM in all experiments. The concentrations of quencher C
q were chosen so that the characteristic quenching time k
q-1C
q-1 was shorter than the duration of the recording RF pulse (1-2 μs), and so that a rapid decline in polarization due to too high a product of the observed DEE rate constant and the quencher concentration, k
obsC
q, was avoided. The compositions of all samples are given in supplementary information.
The GMP in the form of sodium salt hydrate (mass fraction of water 23.4% was determined by
1H NMR), NacTyrOH, TyrOH, D
2O from "Sigma-Aldrich" were used without additional purification, DP was recrystallized from hexane. For the experiment GMP(-H)
- + DP at 65ºC, d8-DP was used because the signals from DP and GMP overlapped each other. The structures of the studied diamagnetic particles GMP(-H)
-, NacTyrO
-, TyrO
-, DP, and the previously studied GMPH
+ are shown in
Figure 8.
At each temperature, two or three kinetic curves differing in the quencher concentration were recorded. To record each kinetic curve, 4 samples were used for the GMP(-H)- + DP, NacTyrO- + DP, TyrO- + DP systems and 8 samples for the GMP(-H)- + TyrO- + DP system. Each sample was used twice, the delays were followed in increasing order and in decreasing order to reduce the error from depletion. At each time delay, 4 scans (6 for TyrO- + DP at 55°C and 65°C) were taken, so each point of the kinetic curve corresponds to 64 signal accumulations for GMP(-H)- + TyrO- + DP, 48 signal accumulations for TyrO- + DP at T = 55°C, 65°C, 32 signal accumulations for GMP(-H)- + DP, NacTyrO- + DP, TyrO- + DP at T = 8-45°C. A 2 μs RF pulse was used for GMP(-H)- + TyrO- + DP and TyrO- + DP at T = 55°C, 65°C; otherwise, a 1 μs RF pulse was used.
All standard electrode potentials Eo used are reported versus NHE.
5. Conclusions.
The CIDNP technique with microsecond time resolution makes it possible to study the kinetics of DEE reactions for the short-lived radicals and determine the DEE reaction rate constant by performing the reaction at different concentrations of the diamagnetic reactant.
The degenerate electron exchange reactions of the neutral radicals GMP(-H)•, TyrO•, NacTyrO• with anions GMP(-H)-, TyrO-, NacTyrO- in alkaline aqueous media were studied by CIDNP in the temperature range 8-65ºC.
At each temperature chosen in this range, all parameters of CIDNP kinetics were determined, and the experimental values of reorganization energies for the DEE rate constants were found. At the t = 25ºC the rate constant of GMP(-H)• reduction by TyrO- anion was measured.
The agreement of the calculated rate constants employing Marcus cross relation approach with the experimental ones for the reactions involving GMPH+/++•, GMP(-H)-/• is poor, perhaps an overestimated values of the standard electrode potentials for GMPH+/++•, GMP(-H)-/• are used.
The rate constants of GMP(-H)• radical reduction by tyrosine and N-acetyltyrosine anions calculated from the cross relation differ by almost two orders of magnitude from those found experimentally, which is a notably greater difference than that for the other reactions involving GMP-• species. Possible causes for this difference are the not taking into account the nonadiabaticity of the cross-reaction and the enthalpy of the stacking interaction between the reactants in the calculation.
At the same time, the calculated rate constants according to the cross-relation of electron transfer reactions involving TyrO-/•, NacTyrO-/• coincide well with the literature values.
It was also found that the dependences of the nuclear paramagnetic relaxation rate T1 on temperature are described by the Arrhenius dependence; for the methylene protons in the tyrosine and N-acetyltyrosine radicals TyrO• and NacTyrO• these dependencies are almost activationless, while for the NacTyrO• 3,5 protons, GMP(-H)• 8-th proton and 3,4 protons of DPH• the activation energy value coincides with the solvent (D2O) activation energy. This indicates a difference in relaxation mechanisms for these protons: relaxation in the methylene protons of the TyrO• and NacTyrO• radicals occurs due to the modulation of the hfi tensor due to ring inversion, while relaxation in the 3,5 protons of NacTyrO• and 8-th proton of the GMP(-H)• occurs due to modulation of the hfi tensor due to stochastic rotation of the molecule as a whole. The intermediate type of the temperature dependence of the nuclear paramagnetic relaxation rate T1 is observed for the 3,5 protons of the TyrO• radical: the activation energy was about half the activation energy for the solvent viscosity. We assume that the both relaxation mechanisms manifest themselves in this case.
Figure 1.
The 1H CIDNP spectra obtained by photo-irradiation of solutions containing a) 15 mM DP and 9, 7.5, 6.5, 4 mM GMP(-H)- at 8, 25, 45, 65ºC and pH = 11.3; b) 15 mM DP and 6.5, 6, 6, 2.5 mM TyrO- at 8, 25, 45, 65ºC and pH = 11.7.
Figure 1.
The 1H CIDNP spectra obtained by photo-irradiation of solutions containing a) 15 mM DP and 9, 7.5, 6.5, 4 mM GMP(-H)- at 8, 25, 45, 65ºC and pH = 11.3; b) 15 mM DP and 6.5, 6, 6, 2.5 mM TyrO- at 8, 25, 45, 65ºC and pH = 11.7.
Figure 2.
Experimental data (dots) and simulation curves (solid lines) for:.
Figure 2.
Experimental data (dots) and simulation curves (solid lines) for:.
Figure 3.
Temperature dependences of the DEE rate constants ket in the coordinates ln[ket√Texp(wr/RT)] vs 1/T for: a) GMP(-H)• + GMP(-H)- b) NacTyrO• + NacTyrO- c) TyrO• + TyrO-.
Figure 3.
Temperature dependences of the DEE rate constants ket in the coordinates ln[ket√Texp(wr/RT)] vs 1/T for: a) GMP(-H)• + GMP(-H)- b) NacTyrO• + NacTyrO- c) TyrO• + TyrO-.
Figure 4.
Acid-base equilibria for GMP and radical GMP•.
Figure 4.
Acid-base equilibria for GMP and radical GMP•.
Figure 6.
Temperature dependences of the nuclear relaxation time T1 in coordinates ln(T/T1) vs 1/T for: a) H-8 in the radical GMP(-H)• b) H-3,5 in the radical NacTyrO• (black dots) and ТyrO• (red dots); c) H-3,4 in the radical DPH• according to the data for systems GMP(-H)- + DP (black dots), NacTyrO- + DP (red dots), TyrO- + DP (blue dots).
Figure 6.
Temperature dependences of the nuclear relaxation time T1 in coordinates ln(T/T1) vs 1/T for: a) H-8 in the radical GMP(-H)• b) H-3,5 in the radical NacTyrO• (black dots) and ТyrO• (red dots); c) H-3,4 in the radical DPH• according to the data for systems GMP(-H)- + DP (black dots), NacTyrO- + DP (red dots), TyrO- + DP (blue dots).
Figure 7.
Fitting of the nuclear paramagnetic relaxation temperature dependence of 3,5 protons of radical TyrO• according to the Eq. (44) with a fixed value of S2 = 0.01.
Figure 7.
Fitting of the nuclear paramagnetic relaxation temperature dependence of 3,5 protons of radical TyrO• according to the Eq. (44) with a fixed value of S2 = 0.01.
Figure 8.
The structures of diamagnetic reactants and products and GMPH+.
Figure 8.
The structures of diamagnetic reactants and products and GMPH+.
Table 1.
Fitting parameters for the GMP(-H)- + DP system.
Table 1.
Fitting parameters for the GMP(-H)- + DP system.
| t°C |
kobs, M-1s-1
|
T1(H8), µs |
T1(H3,4 DP), µs |
ket, M-1s-1
|
| 8 |
(3.77±0.11)*107
|
12.4±0.5 |
49±8 |
(4.27±0.14)*107
|
| 25 |
(4.91±0.27)*107
|
20.4±1.6 |
60±10 |
(5.50±0.32)*107
|
| 45 |
(5.78±0.28)*107
|
26.1±2.2 |
121±34 |
(6.32±0.32)*107
|
| 65 |
(8.12±0.38)*107
|
55±13 |
-- (d8-DP) |
(9.04±0.45)*107
|
Table 2.
Fitting parameters for the NacTyrO- + DP system.
Table 2.
Fitting parameters for the NacTyrO- + DP system.
| t°C |
kobs, M-1s-1
|
T1(H3,5), µs |
T1(Hβ), µs |
T1(H3,4 DP), µs |
ket, M-1s-1
|
| 8 |
(4.46±0.09)*107
|
34.5±2.3 |
111±16 |
51.1±7 |
(4.71±0.10)*107
|
| 25 |
(5.07±0.18)*107
|
58±7 |
119±24 |
69.1±15 |
(5.27±0.19)*107
|
| 45 |
(6.95±0.22)*107
|
75±13 |
129±35 |
73.2±24 |
(7.19±0.23)*107
|
| 65 |
(8.24±0.57)*107
|
50±9 |
-- |
42.1±19 |
(8.46±0.60)*107
|
Table 3.
Fitting parameters for the TyrO- + DP system.
Table 3.
Fitting parameters for the TyrO- + DP system.
| t°C |
kobs, M-1s-1
|
T1(H3,5), µs |
T1(Hβ), µs |
T1(H3,4 DP), µs |
ket, M-1s-1
|
| 8 |
(2.81±0.13)*107
|
41.1±3 |
118±25 |
98±22 |
(2.94±0.14)*107
|
| 15 |
(3.59±0.28)*107
|
45±6 |
138±21 |
54±10 |
(3.76±0.30)*107
|
| 25 |
(4.78±0.27)*107
|
50±7 |
139±26 |
199±81 |
(5.02±0.29)*107
|
| 35 |
(5.64±0.36)*107
|
63±11 |
149±36 |
95±32 |
(5.90±0.39)*107
|
| 45 |
(5.96±0.42)*107
|
82±19 |
-- |
137±35 |
(6.19±0.45)*107
|
| 55 |
(7.60±0.37)*107
|
56±10 |
121±32 |
48±16 |
(7.92±0.40)*107
|
| 65 |
(8.53±0.49)*107
|
65±14 |
106±30 |
67±22 |
(8.87±0.52)*107
|
Table 4.
The found pre-exponents and reorganization energies for DEE reactions.
Table 4.
The found pre-exponents and reorganization energies for DEE reactions.
| DEE reaction |
ln(A) |
λ, eV |
| GMP(-H)- + GMP(-H)•
|
31.7 ± 1.0 |
0.82 ± 0.11 |
| NacTyrO- + NacTyrO•
|
27.0 ± 0.4 |
0.50 ± 0.04 |
| TyrO- + TyrO•
|
30.2 ± 0.4 |
0.81 ± 0.04 |
Table 6.
The energy E values (see Eq. (42)) defined from the linear fitting of ln(T/T1) vs 1/T dependencies.
Table 6.
The energy E values (see Eq. (42)) defined from the linear fitting of ln(T/T1) vs 1/T dependencies.
| radical, nucleus |
E/R, K |
| GMPH++•, H-8 [30] |
1993 ± 650 |
| GMP(-H)•, H-8 |
1720 ± 270 |
| NacTyrO•, H-3,5 |
1760 ± 370 |
| TyrO•, H-3,5 |
1130 ± 210 |
| DPH•, H-3,4 |
1790 ± 300 |
| η(D2O) [51, 52] |
2059 ± 81 |
Table 7.
Comparison of the rate constants calculated from the cross relation and those found in the experiment.
Table 7.
Comparison of the rate constants calculated from the cross relation and those found in the experiment.
| Reaction |
k12expt, M-1s-1
|
k12calc, M-1s-1
|
Reference |
| NacTrpH + GMPH++•
|
1.2*109
|
7.9*1010
|
[79] |
| TyrO- + GMP(-H)•
|
1.7*108
|
3.7*1010
|
this work |
| NacTyrO- + GMP(-H)•
|
1.8*108
|
1.6*1010
|
[29] |
| CysS- + GMP(-H)•
|
1.9*108
|
6.4*108
|
[80] |
| GMP(-H)- + ClO2•
|
1.1*105
|
5.6*103
|
[81] |
| GMP(-H)- + N3•
|
3.2*109
|
2.0*108
|
[82] |
| TyrO- + ClO2•
|
1.8*108
|
1.1*108
|
[83] |
| NacTyrO- + ClO2 •
|
7.6*107
|
3.2*107
|
[83] |
| TyrO- + N3•
|
6.7*109
|
8.1*1010
|
[84] |
| Gly-TyrO- + NO2•
|
2.0*107
|
1.9*107
|
[85] |
| NacTyrO--NH2 + [IrCl6]2-
|
3.6*107
|
1.2*108
|
[86] |
| TEMPO• + NacTyrO•-NH2
|
1.5*108 a
|
4.1*108
|
[87] |