Enhancing Cache Robustness in Information-Centric Networks: Per-Face Popularity Approaches

1. Introduction

As the current host-based Internet architecture ages, it is becoming increasingly apparent that it is insufficient to handle the content-driven applications in use today. The original Internet architecture was built largely to accommodate end-to-end communication between mutually trustworthy individuals who wished to share data and expensive resources. Since then, the use of the Internet as a communications network has shifted toward its use as a content delivery apparatus.

Because of these limitations as technology and user needs have changed, overlay patches providing security, privacy, mobility, and content delivery have been created to sit on top of the underlying network. These application overlays provide services that the original Internet architects would have never imagined: mobile communications, banking, shopping, multiplayer gaming, streaming media, and many other services. However, the application overlays are not able to benefit from any optimizations at the network layer, because they simply are not provided.

As a result, many researchers have pushed for a complete redesign of the fundamental architecture of the Internet to focus on content as the primary citizen of the network, instead of location. For many applications, users want specific content, but do not care where it comes from as long as the content is genuine and transmitted reliably and quickly. One architectural paradigm that seeks to accomplish the goals of a future Internet redesign is Information-centric networking (ICN) [1,2].

Several projects within the large umbrella of ICN have sought to achieve these goals, with various approaches and to varying degrees of success. Prominent ICN projects include Data-Oriented Network (DONA) [3], Network of Information (NetInf) [4,5], Content-Centric Networking (CCN) [6,7] and Named Data Networking (NDN) [8].

Many interesting research challenges exist to provide the desired features of ICN. In this paper, we discuss technology related to in-network caching of data, which is a key feature to lowering latency and overall network congestion, using technology at the network layer. While in-network storage devices in ICN seek to provide similar services to that which content distribution (or delivery) networks (CDNs) [9] do today, in-network storage devices do so at the network layer, and take advantage of various optimizations therein.

Given the pervasiveness of in-network storage devices in ICN architectures, these devices are prime targets for malicious users. In terms of in-network caching of popular data, an attacker would seek to reduce or remove any benefit experienced by the presence of in-network storage devices, such as content routers. An attack well suited for this type of service degradation is the cache pollution attack [10]. In this type of attack, the malicious attempts to push truly popular content objects out of the cache in favor of less popular content objects. Ultimately, the goal is to reduce the hit rate experienced by users, such that the content that is genuinely popular is rarely or never in the content store of the in-network storage devices.

These types of attacks are not new – they have been experienced for years in the current IP-based Internet such as in CDNs and other situations involving proxy caching servers [11]. However, these attacks will certainly be even more of a threat in an architecture where in-network storage is part of the fundamental fabric of the network, and not just an overlay.

Several proposed solutions for preventing or reducing the effects of cache pollution attacks in ICN exist. However, most are insufficient for various reasons. Some lack adequate security and can be easily overcome, such as CacheShield [12]. Others assume all abnormal behavior follow uniform distributions [13], and still others require significant computational or memory overhead, such as ANFIS [14]. Most current techniques attempt to detect attacks, which is often difficult when attackers employ various smart attacks. Additionally, these techniques can yield false positives if a user is even a little more aggressive in their request frequencies and may punish them even though they were not being malicious.

In this paper, we present variations of cache replacement techniques as part of larger per-face popularity (PFP) schemes, which seek to normalize the contributions from each face (for our purposes, means simply an interface) on a content storage router. This normalization prevents interest message contributions received on any one face from having more effect on what ends up being cached, than the contributions over any other face.

The three primary algorithms that we have developed as variants of PFP are the original PFP scheme, PFP-DA, and PFP-β. The original PFP scheme involves a list of content object request frequencies for each face. This algorithm is effective, but not very scalable, as these lists are unbounded. Also, our original scheme can be affected by so-called natural cache pollution, wherein a content object may have been very popular at one time, thus having many requests, but has fallen out of being truly popular, but remains in the list due to the incredible frequency achieved once upon a time. To remedy the scalability issues and lack of recency, we developed a variation of PFP with dynamic aging added to the content frequency lists and limited the size of these lists to double the size of the actual cache. This resulted in our second scheme, PFP-DA (PFP with dynamic aging.) This scheme was used for most of the tests in this work. Finally, we developed a third scheme, PFP-β (PFP with Beta Parameterization), wherein the PFP-DA scheme remained, but the contributions themselves were scaled using a β parameter. We tested different values for β to determine the effects, and made many interesting discoveries as a result, including some scenarios with 0% cache pollution and higher hit rates than were experienced with PFP-DA itself, which already outperformed LFU-DA and LRU.

Our experiments demonstrate that PFP-based schemes are not only resistant to the effects of cache pollution attacks but suggest that PFP-based schemes are better at representing the overall popularity of content objects across multiple faces. Therefore, the schemes work well even when there are no active attacks occurring. In terms of more general contribution to the state of the art, our schemes employ a novel approach to cache replacement.

2. Related Work

2.1. Cache Pollution Attacks

Fundamentally, cache pollution attacks come in two different forms: locality disruption and false locality. The term locality refers to a phenomenon in which certain content objects from a given requesting region tend to be more popular in that region than other content objects. Thus, a specific arrangement of content objects by their popularity is representative of a locale, or region.

Therefore, locality disruption refers to an attempt by an attacker to simply churn the cache of a given locale in hopes of knocking some of the popular content objects out of the cache. Thus, the attacker will request many different content objects from across the universe of content (the content space.) A false locality attack, on the other hand, is arguably more aggressive attack, in which an attacker wishes to push even the most popular content objects out of the cache in favor of unpopular items. Thus, the attacker wants the cache full of content objects that are not at all representative of the desires of users utilizing the cache. Hence, the locality expressed by the cache is false relative to the actual users’ desires. It is important to note that most security approaches to cache pollution attacks tend to seek to prevent one (or sometimes both) of these types of attacks [10]. We will discuss these briefly.

2.2. Approaches to Secure against Cache Pollution Attacks

One of the best-known examples in the literature in terms of attempting to fight cache pollution is CacheShield, developed by Xie et al. [12]. This approach records interest frequency of items that are not cached. As the recorded frequency t increases, the probability that a content object will be cached increases as well due to the shielding function. However, a major weakness of this approach is that an attacker need only determine the threshold of t values and request content objects at a frequency beyond the threshold of t. Then, their own content objects will be cached.

A cache pollution detection approach using randomness checks was proposed by Park et al. [15]. The randomness check approach utilizes the fact that attackers launching a locality disruption attack request contents in a nearly uniform manner across the content universe. The authors reason that it is less likely attackers will be able to know what contents are popular, and that this popularity changes with time. Therefore, they consider false locality attacks far less likely than locality disruption attacks, which do not require detailed knowledge of the popularity of contents. The approach performs matrix operations, during which popular contents are more likely to be removed from the matrices due to the Zipf-like distributions, whereas attacker requests will remain. This causes the system to rank content requests as malicious when they remain with a given rank value.

As an attempt to improve upon CacheShield [12], the authors of [13] assume a slightly more intelligent attack scenario. They enhance their threat model such that the attackers only focus on a small subset of the content space, namely the items at the tail end of the Zipf distribution. This approach uses a machine-learning based approach. However, it still suffers from weaknesses, including the assumption that all normal behavior is Zipf-like and attackers are always uniform in their distribution of requests.

A neural network (with fuzzy systems) approach was proposed by Karami et al. in [14]. This approach uses techniques that are used in linguistics to determine the degree to which different inputs and outputs are related. Although this approach is reasonably effective at detecting cache pollution attacks (both false locality and locality disruption), the overhead both in terms of memory and computational complexity are significant. For these reasons, this approach is not considered to be very scalable [10].

3. Enhancing Cache Robustness via Per-Face Popularity

In this section, we discuss three Per-Face Popularity, or PFP approaches to increasing cache robustness by means of normalizing popularity contributions across all faces. Firstly, we discuss the original Per-Face Popularity algorithm, or simply, PFP. Then, we look at a more efficient and scalable approach that also considers recency of requests, known as Per-Face Popularity with Dynamic Aging (PFP-DA.) Finally, we discuss a parameterized approach in which exponentiation is used on contributions to reduce numeric distance among the overall popularity values of ranked contents, known as Per-Face Popularity with Beta-Parameterization, or PFP-β (also, PFP-Beta.)

3.1. Per-Face Popularity (PFP) Scheme

With schemes like LFU-DA, all received interests are used much like votes, regardless of the origin face. For example, if 100 interests for content A arrive on face 1, and 20 interests for content A arrive on face 2, face 1 has contributed five times the number of interests as face 2. Thus, face 1 contributes more to determining whether content A is cached or not, than does face 2. If an attacker managed to overwhelm a router over one face with far more interests than any other face, then the attacker can cache essentially whatever he wants. Although some mechanisms, explored earlier, try to detect an attack based on content request frequency, this is not always appropriate, and can lead to false positive identification of attackers where none exist. A face might simply receive more requests for a given content object than other faces, which does not immediately indicate attacker behavior.

The original PFP scheme we developed was based on the concept of ensuring fairness of contributions across all faces on the content storage router. Therefore, no individual face has any more influence on what content objects are cached than any other face. The frequency with which a content object is requested is normalized such that the interests arriving over face 1 do not contribute any more to the cache replacement decisions than the interests arriving over face 2, and so on.

The reasoning for our design of PFP is twofold. Firstly, the effect an attacker can have on a cache is mitigated, thus reducing cache pollution and increasing hit rate by legitimate users, especially the hit rate of the most popular items. Secondly, a latent benefit of our attack effect mitigation efforts, specifically normalization of contributions across faces, is that it is more likely that content that is truly popular across more faces will remain in the cache.

To implement our scheme, we made relatively significant additions and modifications to the ndnSIM environment. Although this will be discussed in more detail later, it is important to note that several design decisions had to be considered. As far as being implementable, we could have given each face its own cache (as a fair portion of the overall cache size), from a performance and scalability perspective, this would have been a poor design decision. Instead, maintaining a single cache and normalizing the contributions was the best approach.

At the core of our scheme is a class known as the popularity manager (PopMan), which maintains lists of content request frequencies based on each face. The name of the content object being requested is recorded with the initial interest from a given face, and subsequent interests for that content object (on that face) cause the frequency value being recorded to be increased. This naturally creates a ranking of the most popular items for each face.

3.1.1. Cache Replacement Algorithm

When the actual content storage router’s cache is full, a cache replacement algorithm is initiated to determine what must be replaced to make room for new content. In PFP, the cache replacement algorithm uses the normalized contributions for content objects across all faces to determine true overall popularity values, and thus to determine what should be removed from the cache. We make use of an item’s rank by each face, and denote it as r. As the list of most popular items (on a given face) is maintained, essentially sorted by requests (with dynamic aging element), each item therefore has a rank. This is where the value r comes from, that is, from the position within the ranked list of items on a given face. Note that each face contributes to the overall calculation by using r, which is normalized by taking its reciprocal. This results in the per-face popularity contribution. That is, each face contributes the reciprocal of r to overall popularity.

$$PerFacePopularityContribution=\frac{1}{r}$$

(1)

The overall popularity of a content object, C, across all faces is the sum of the per-face popularity contributions from all faces. When a face does not have a given content object ranked, the overall contribution is considered 0. The following equation shows the overall popularity calculation, with r_i being the rank of C from the content frequency list for face i.

That is,

$$P(C)={\sum }_{i=1}^n\frac{1}{r_i}$$

(2)

3.2. Per-Face Popularity with Dynamic Aging (PFP-DA)

Although the original PFP scheme showed promise, a couple lingering issues were identified. Namely, that the scheme did not consider recency at all, and that the content frequency lists maintained by the popularity manager could be arbitrarily large. The first issue is a problem since a content object that might have been popular a significant time ago would remain in the cache, even if it wasn’t currently popular, simply due to the extreme number of requests in received once upon a time. This of course reduces the reflection of true locality for a given cache, and contributes to natural cache pollution, in which there is no attacker, yet content objects continue to reside in the cache even though they no longer improve the hit rate significantly. The second issue, the ever-increasing content frequency list size, is clearly a significant problem when considering performance and scalability issues. Therefore, a revised scheme was needed to address these issues.

Borrowing insight from the least-frequently used with dynamic aging (LFU-DA) [16] algorithm, we modified our original PFP algorithm to include recency considerations, resulting in the per-face popularity with dynamic aging (PFP-DA) scheme. The dynamic aging aspect in LFU-DA directly affects the cache itself. However, in PFP-DA, the dynamic aging aspect affects each of the content frequency lists. Therefore, the aging affects the actual cache, but indirectly. In the PFP-DA scheme, the content frequency lists are limited to a finite size based on the actual cache size. In our implementation, the lists are twice the size of the true cache (e.g., 200-size lists for a 100-size cache.) For the majority of cache sizes, this will essentially solve our first problem, in that the list sizes are no longer theoretically unbounded.

Instead of using the frequency of interests for a given content when determining if it belongs in the cache itself, PFP-DA uses the key, K_i for a given content object i. This key is calculated as follows:

$$K_i=F_i+L$$

(3)

The value F_i is the frequency for the given content object, i, and L is the age factor. L is initialized to 0, and then whenever a content item is to be replaced, L is updated to be equal to the key, K_f of item f, that is, the item being removed. Succinctly, this means L = K_f. With respect to PFP-DA, aging is utilized with the rankings for each of the faces, rather than overall content caching.

3.3. Per-Face Popularity with β-Parameterization

PFP-DA yields very good results, as we will see later in this article. However, even slight improvements on top of PFP-DA would be welcome. Therefore, we take advantage of the fact that the overall popularity calculation looks like the formula for the Zipf distribution. Therefore, we considered that introducing a parameter similar to the α value used in Zipf-like distributions would have on the cache, including pollution and hit rates. Thus, our formula for calculating the overall popularity became:

$$P\left(C,\beta \right)=\sum _{\begin{array}{c}i=1\\ 0\le \beta \le 1\end{array}}^n\frac{1}{{r_i}^{\beta }}$$

(4)

The parameter, β, is introduced as being between 0 and 1, inclusive. Thus, our regular PFP-DA would be considered as a special case of the above equation with β = 1. This new parameterized scheme is designated PFP-Beta, or PFP-β. It still maintains dynamic aging, as PFP-DA, but with the additional introduced parameter.

As we would expect, the numeric distance between the top-ranked item and subsequently ranked items is reduced as β is reduced. To get a more intuitive feel for this behavior, let us consider an example. If we consider the regular PFP-DA case, with β = 1, the top-ranked item from a face will contribute 1/1=1, where the second-ranked item will contribute 1/2=0.50, and the third-ranked item will contribute 1/3≈0.33. So, the respective distances are as follows:

Table 1. Numeric distance between items and top item, β = 1.

Rank	Numeric distancefrom top item
1	0
2	0.5
3	0.67
4	0.75
5	0.80

Table 1. Numeric distance between items and top item, β = 1.

Rank	Numeric distancefrom top item
1	0
2	0.5
3	0.67
4	0.75
5	0.80

The distance is lessened if β is set to 0.5, or 0.1, as is follows:

Table 2. Numeric distance between items and top item, (a) β = 0.5, (b) β = 0.1.

	Rank	Numeric distancefrom top item		Rank	Numeric distance from top item
	1	0		1	0
	2	0.29		2	0.07
	3	0.42		3	0.10
	4	0.50		4	0.13
(a)	5	0.55	(b)	5	0.15

Table 2. Numeric distance between items and top item, (a) β = 0.5, (b) β = 0.1.

	Rank	Numeric distancefrom top item		Rank	Numeric distance from top item
	1	0		1	0
	2	0.29		2	0.07
	3	0.42		3	0.10
	4	0.50		4	0.13
(a)	5	0.55	(b)	5	0.15

As β is reduced thus yielding a small distance between each item and the top item, as seen in the above tables, the overall contributions for the ranked items themselves are larger (e.g., for β = 1, the 4th item contributes 0.25, for β = 0.5, that contribution for the 4th item is 0.50, and for β = 0.1, the contribution is 0.87.) What this means is that the popular items are all contributing more, and the difference between a 4th or a 5th item isn’t as significant for a β = 0.1 as it would be for items ranked with β = 1. Therefore, with these larger numbers, it stands to reason that a PFP scheme using a small β will favor items to be cached that have contributions from multiple faces even more than a PFP scheme using a larger β.

We will see that this holds true as we discuss the experimental results later in this article. However, we will also see that a small β value in a PFP scheme also works best under certain circumstances, and far worse in others, involving situations with a higher percentage of attackers.

4. Results

The PFP-DA and PFP-β schemes were implemented using ndnSIM [17,18],which is an NDN simulator based on ns-3 [19]. The ns-3 simulator is well known for its use with both traditional and experimental networks. Its code is entirely open source, which makes it appealing, as the simulator itself, not just scenarios, can be modified.

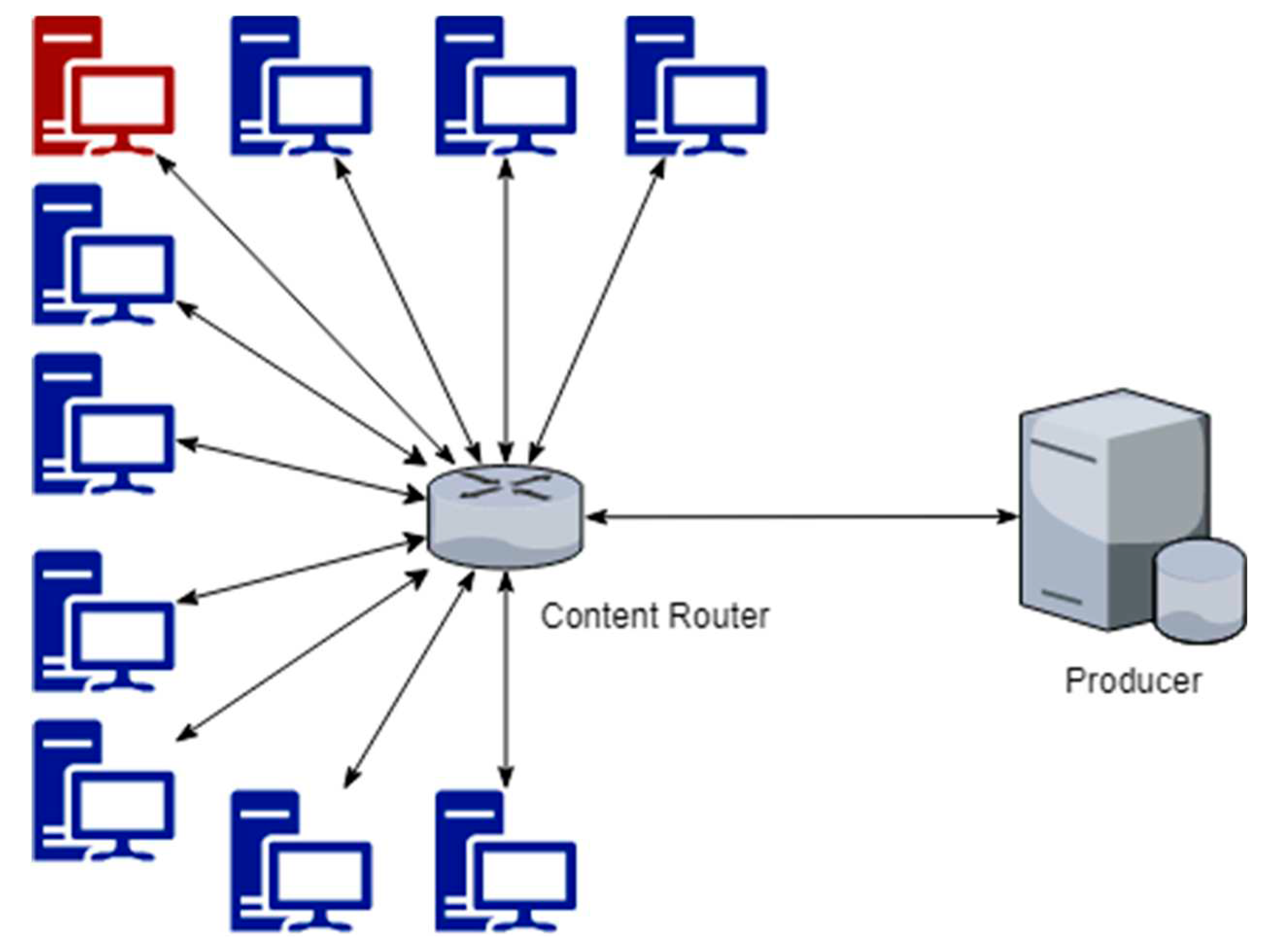
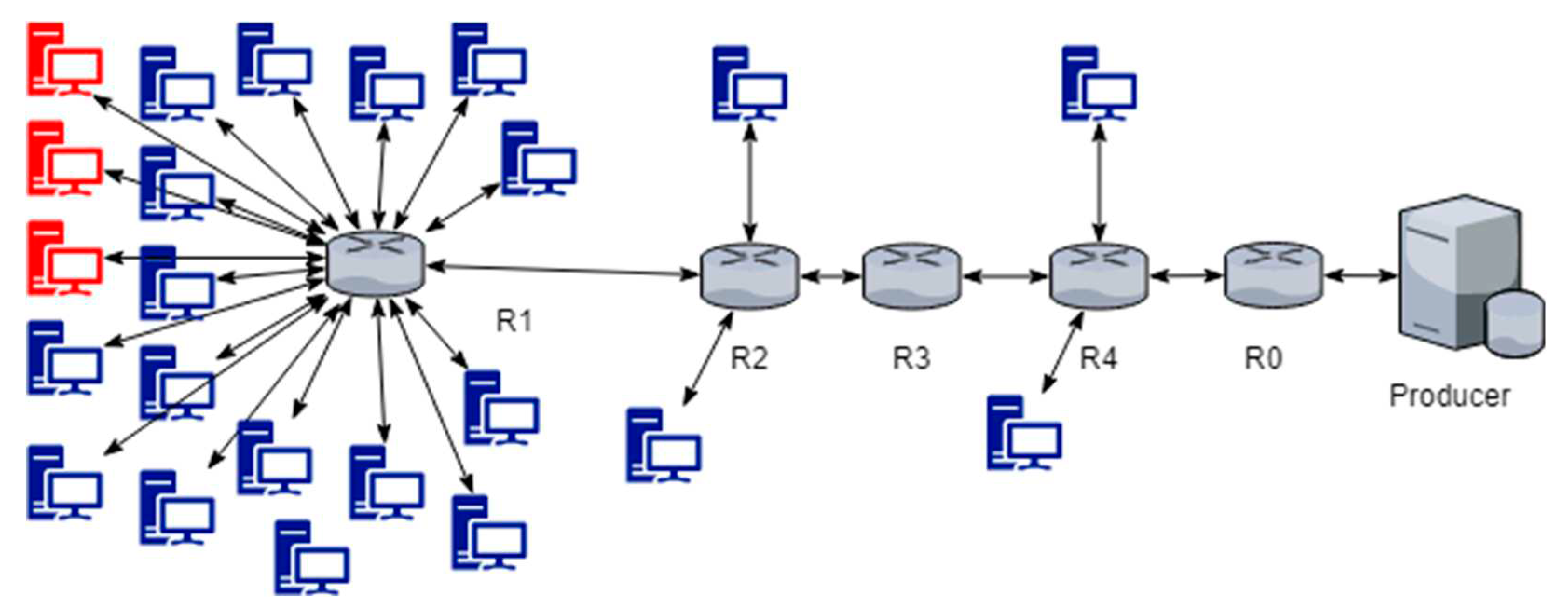
For our hardware setup, we used a System76 Gazelle with quad-core 6 MB cache, 16 GB of DDR4 RAM, and a 3.5 GHz i7-6700HQ CPU. The operating system on this machine is Ubuntu 16.04 LTS.

4.1. Per-Face Popularity with β-Parameterization

The typical workflow with ndnSIM involves creating scenarios, which are implemented in typical C++ source files. The WAF build automation utility [20] is then used to build and run the scenarios and support files. The scenarios are also often accompanied by the use of extensions, which are simply modifications (usually using inheritance from base classes of the simulator) or additional classes needed for the scenarios to function. The scenario file itself is where the entry point for the application lives.

One extension that we created was based on the Policy class. The Policy class in ndnSIM is the actual decision-maker as far as what items remain and what items are removed from the content store’s cache. We created a PopularityPolicy class as a subclass of Policy to define our cache replacement policy. In ndnSIM, data is automatically added to the cache, which is physically slightly bigger than the logical limit of the cache size. In Policy’s doAfterInsert method, a pure virtual function (method), is called immediately after a content object is added to the cache. Then, in this method, the decision can be made to remove any content object according to the cache replacement algorithm.

The PopularityPolicy class that we created maintains a pointer to the popularity manager (PopMan), which is also maintained in the ndnSIM’s NFD Forwarder class, which we modified. Therefore, the PopMan acts as an essential bridge from the forwarding strategy and fabric, to the cache replacement policy. The PopMan records when interests arrive, and over which face, so that ranking can be accomplished. This interest and face data is ultimately maintained in FaceContentFrequency objects, which maintain, as the name suggests, the frequency of requests for content, organized by specific faces. Each FaceContentFrequency object maintains all content requests and a ranked list for its face. This is the class responsible for determining an individual face’s contribution to the overall popularity. The PopMan, in turn, utilizes the contributions from its list of FaceContentFrequency objects, to determine what should be removed when it must decide on the next item to remove from the cache.

So, to summarize, the Policy (PopularityPolicy), in its doAfterInsert method, determines when the cache is full after an insert of a content object obtained from a returned data message. If the cache is full, the PopularityPolicy asks the popularity manager what content object must be removed from the cache. As described earlier, this decision is based on the overall contributions from all faces, normalized such that no single face has more influence than any other face. When this information is obtained, the PopularityPolicy sends an eviction signal to the content store, which evicts the corresponding object from the cache.

4.2. Topologies

We use three topologies in total for the data we have collected. One topology is called the Simple Topology, or ST. Another is the Advanced Topology, or AT. And finally, for testing PFP- β, we used a slightly larger version of the ST called LST, or Larger Simple Topology.

Although Figure 1 implies a single attacker (the red node), the number of attackers was increased during some tests to determine the effect of increasing percentage of attackers. The Large Simple Topology, used with the PFP-β is the same as ST, but with 10 additional consumers, yielding a total of 20 consumers.

The Advanced Topology (AT) seen in Figure 2 is like Xie’s merging scenario in [12]. This topology was used to discover the effects of the different cache replacement schemes on the less busy edge routers (e.g., R2, R4) and intermediate routers (R3, R0.) However, the focus remains on R1, as it has the most attached consumers, and is not on the path from any other router to the producer node and is thus not affected in the same way by interest aggregation and other phenomena inherent to NDN.

4.3. Simulation Results and Analysis

Firstly, we will discuss most of our results, which are derived from tests using the standard PFP-DA scheme. Then, we will discuss some of the early results we’ve obtained from the PFP-β experiments. We will demonstrate that our PFP-based schemes tend to perform substantially better than the current LFU-DA and LRU algorithms under most circumstances. The content space used in these tests consist of 10,000 content objects, using the Zipf-Mandelbrot distribution as implemented in ndnSIM . Unless otherwise noted, the following sections involve the PFP-DA scheme.

It should be noted that regular consumers will generally follow the Zipf-Mandelbrot distribution of requests, across all faces. In other words, the top requested content object would almost certainly be the top request content object on each of the faces. It is possible, however, once the Zipf-Mandelbrot rankings are lower that one face may request one item more than another that has a “higher ranking” based on the probabilities implemented in ndnSIM. In other words, item ranked 150 might be requested on one face more times than item 148, and vice versa. The distribution isn’t truly strict as implemented.

Attackers are expected to have some degree of coordination when spread across multiple faces, and in fact, we have implemented the scenarios so the attackers request in a generally uniform fashion across a small set of less popular items (by the Zipf-Mandelbrot distribution.)

4.3.1. Varying Cache Size

For these tests, one attacker is present for both the simple and advanced topologies, with a request frequency of 720 requests/second. Regular consumers request at 120 requests/second. For these tests in this section, only the cache size was varied, ranging from 100 items (1% of the total content space) to 500 items (5% of the total content space.)

The number of content objects requested by an attacker is equal to the cache size, so it is possible for the attacker to attempt to completely overwhelm the cache. For example, it is clear that if all the consumers attached to a router were attackers, then the cache would be entirely filled with only attacker content. The tests in this section and subsequent sections are to test variations and determine the robustness of the cache replacement algorithms.

The data in Table 3 gives us an interesting picture of how the cache size can affect both the pollution and hit rates. The pollution percentage indicates the percent of the cache at the router occupied by attacker content. The hit percentage (hit rate) is the percentage of legitimate consumer interests that are able to be satisfied by the content store’s cache upon arrival. We also look at the top 100 and top 50 items (according to Zipf-like distribution) to see how stable the algorithms are at maintaining the truly popular contents in the cache.

For all cache sizes, PFP-DA has both the lowest cache pollution percentages, and the highest hit rates. For example, even considering the smallest cache size (100, or 1%), LFU-DA does reasonably well, with an overall hit rate of 12.67%. But, this is over 6% less than PFP-DA. The percentages for the top 100 and top 50 objects are even more remarkable. LFU-DA, for example, maintains 50% to 81.03%, which is good, but PFP-DA maintains percentages from around 75% to nearly 99% for top 50 items. This shows overall excellent performance, and in specific, good resistance to the single attacker.

Now, let us consider the AT (Advanced Topology) results.

Both Table 4 and Table 5 show the data collected and summarized for the Advanced Topology (AT.) The R1 router is the router with most of the consumers attached, and with the single attacker attached as well. The routers R0, R2, R3, and R4 all demonstrate very low hit percentages, and sometimes higher cache pollution.

An interesting discovery is that overall cache pollution percentage is not necessarily an indicator of the hit rate. For example, on R2, PFP-DA maintains higher cache pollution percentages than do LFU-DA or LRU, but the hit rates are still better for PFP-DA than the other algorithms. This is because the cache pollution percentage does not capture information about the quality of items being cached (i.e., what rank in the Zipf-distribution they have.) However, in terms of hit rate, PFP-DA dominates on all hit rate metrics across all routers. Again, we see the top item hit rates on R1 in the 70% to nearly 100% range for PFP-DA.

4.3.2. Varying Attacker Request Frequencies (Single Attacker)

For these tests, one attacker is still present, but the attacker’s aggression is increased. Consumers still have a request frequency of 120, while attacker’s speed (request frequency) is varied from 360 up to 1200. That is to say, the speed varies from three times to ten times that of the normal consumer.

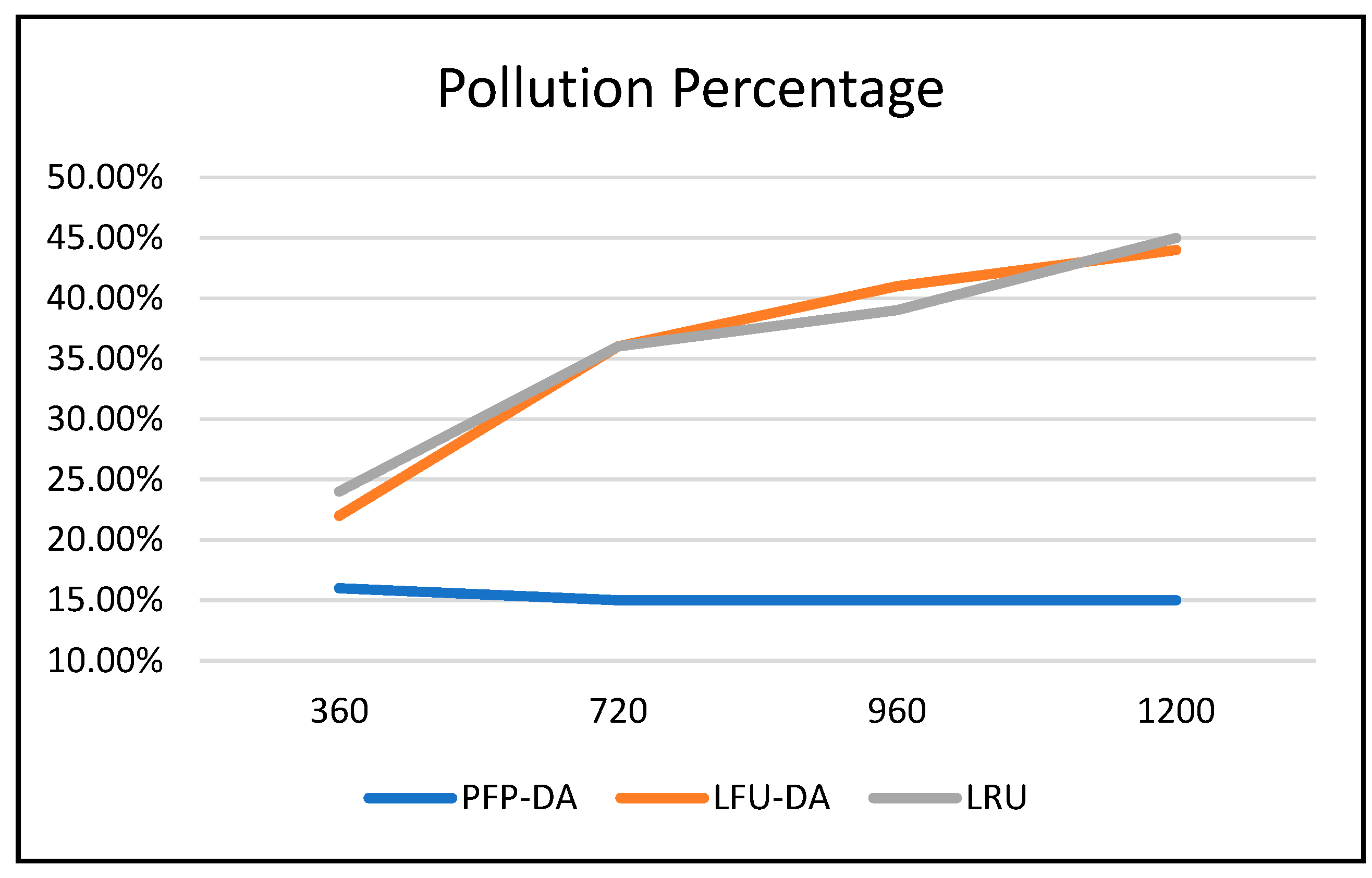
With the Simple Topology (ST), we observe in Table 6 that the pollution percentages of the cache running PFP-DA remains essentially unaffected by the change in attacker request frequency. This is expected behavior, since the contributions from the faces are normalized. Thus, a single attacker (or more correctly, a single face being used as a conduit of attack, or realized attack vector), no matter how aggressive, cannot have any extreme effect on the cache other than what they would normally have if they were minimally, or not at all aggressive. The story is different for LFU-DA and LRU. While the percentage differences are not enormous, it is clear that both algorithms are susceptible to aggressive attacks.

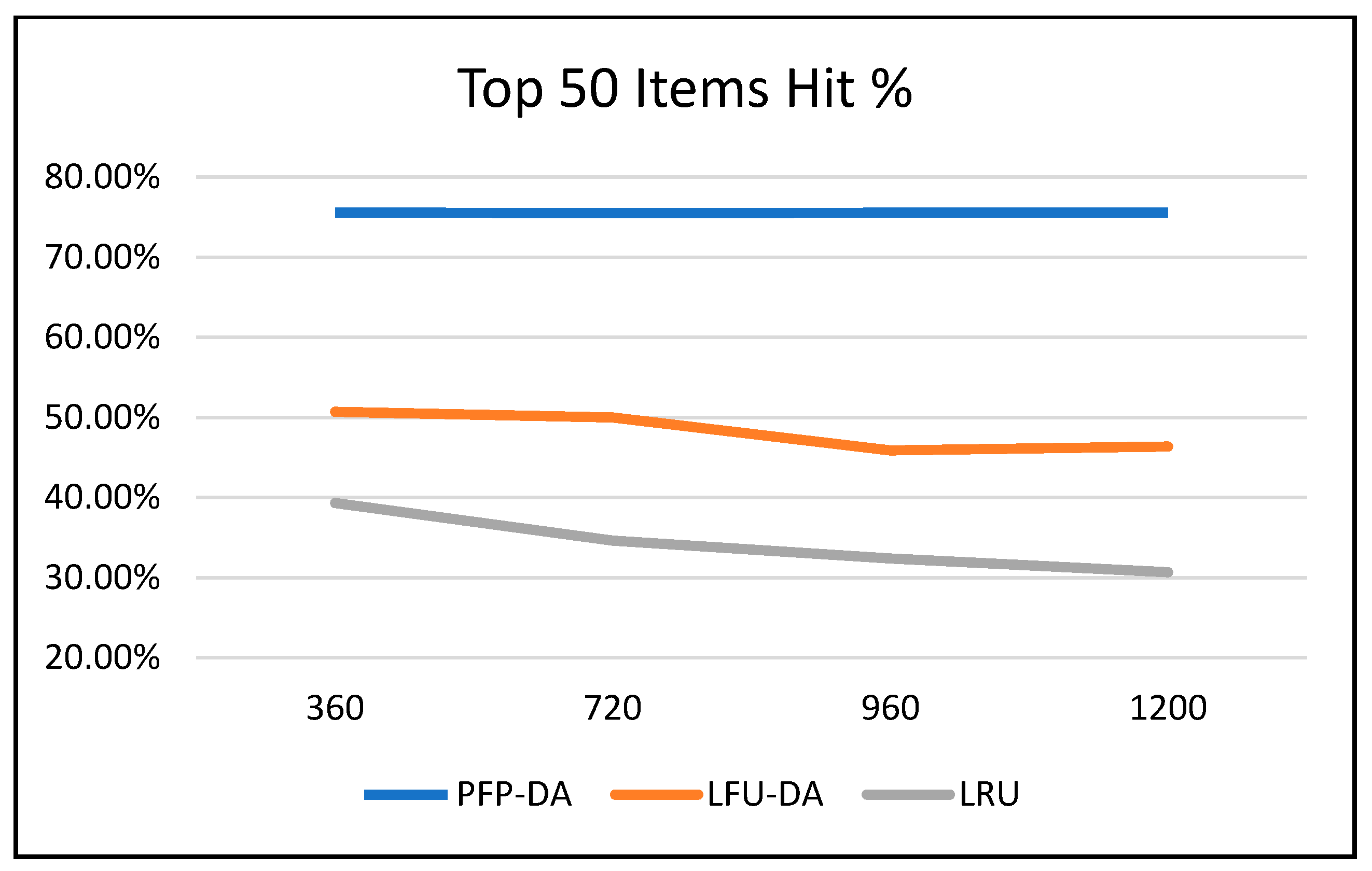
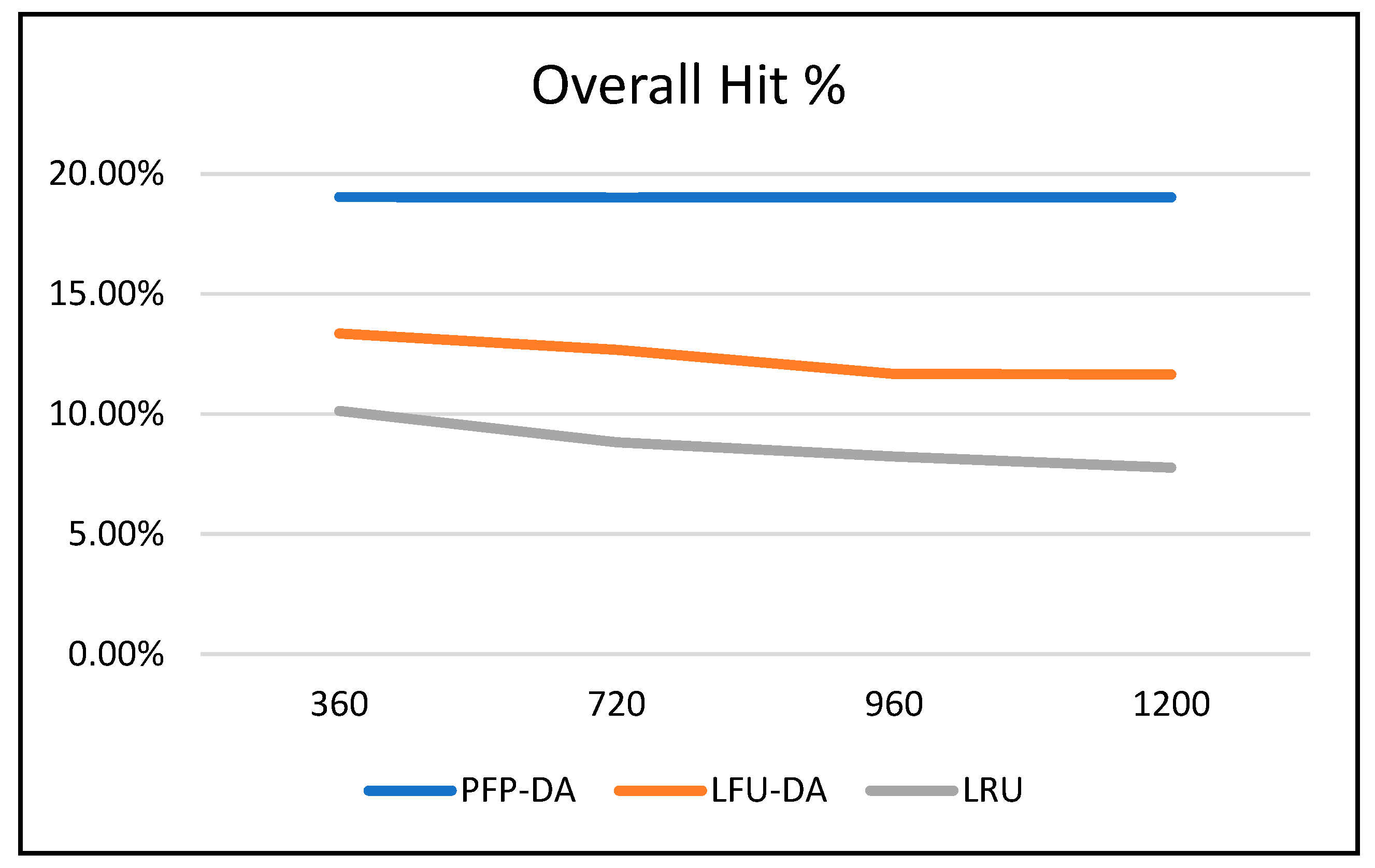
Figure 3, Figure 4, and Figure 5 all graphically demonstrate the data recorded in Table 6. While the LFU-DA and LRU are affected by the increased attacker aggression, PFP-DA remains virtually unaffected. This is clearest when considering the pollution percentage in Figure 3. While PFP-DA maintains a low, steady pollution percentage, both LFU-DA and LRU both increase significantly. And, while LFU-DA does maintain a reasonably good hit rate throughout, the percentage does drop, and interestingly, starts out substantially lower than with PFP-DA.

Let us consider the AT (Advanced Topology) test results, with a single attacker and varying of the request frequency.

Again, with the Advanced Topology in Table 7 and Table 8 we see that PFP-DA dominates the other two algorithms, especially in terms of hit rate. For routers R0, R2, R3, and R4, the hit rates are quite low, as before. This is largely due to them not being connected directly to any, or in the cases of R2 and R4, not many consumers. For a network design perspective, the routers with very low hit rates in such simulations might be good candidates to be regular non-storage routers, since their contributions are mostly negligible for all three algorithms.

We once again turn our attention to router R1. Running PFP-DA, R1 maintains around 16.6% to 16.9% hit rate throughout all attack frequencies. LFU-DA also appears to be reasonable resistant to attack, even increasing overall hit rate at 1200 attack frequency. This seems odd, but largely stems from natural fluctuations between launch scenarios.

There remains no question, however, as to which algorithm performs best. PFP-DA maintains the highest percentage of overall hit rate. Considering the top 50 items, PFP-DA has anywhere from 20-30% better hit rate than LFU-DA.

4.3.3. Varying Number of Attackers

To further understand how these three algorithms work under different conditions, we turn our attention to varying the number of attackers (or more correctly, the number of faces under attack that are dominated by the attackers.) In the scenarios used for these tests, the cache size is 100 (1%), the attackers’ request frequency is 720 requests/second, and the regular consumers request at 120 requests/second. Arguably it is reasonably difficult for attackers to overwhelm many faces on a content storage router, but we wanted to test out the algorithms’ performance under stressful conditions. If any attack variation will have a significant impact on PFP-DA, it would be a larger percentage of attackers. PFP-DA would not benefit from normalizing contributions directly, as it did with the single attacker, varying frequency scenarios.

The data in Table 9 for the Simple Topology gives us insight into the typical performance of algorithms, including when there are no attacks occurring. For ST, since there are 10 total consumers, 1 attacker is 10%, 3 attackers is 30%, and so on. We tested variations from 0 attackers all the way up to 7 attackers, which is 70%.

In Figure 6, the pollution percentages for LFU-DA and LRU remain very similar, with PFP-DA outperforming both from about the 10% up to the 7-attacker (70%) scenarios. At around the higher percentage of attackers, the gap closes substantially, as PFP-DA is overcome with cache pollution.

Important to note, however, is that the quality of content remaining in the cache is not captured by the overall cache pollution percentage data. The hit rates give us a much better picture of this, in Figure 7 and Figure 8. Both the overall and top 50 item hit rates take on very similar shapes, graphically. LRU, largely by coincidence, overtakes LFU-DA around the 50% attacker mark. This is largely because LFU-DA is based on request frequency, while LRU is not. Therefore, LRU depends entirely on recency, and is affected only due to attacker content being more recently accessed as the number of attackers increase. Thus, the LRU data is arguably affected indirectly, whereas LFU-DA and PFP-DA are primarily affected by frequency, which means they are directly affected by incoming frequencies.

The difference between PFP-DA and both LRU and LFU-DA is remarkable. Even as the number of attackers increase, and PFP-DA is affected, it still performs substantially better than LRU and LFU-DA. We note that PFP-DA has a better hit rate (overall) by 5-9% during the increase of attacks. Even more interesting, is that PFP-DA still maintains almost 35% hit rate for the top 50 items, even as LFU-DA is entirely overwhelmed.

Perhaps most remarkable scenario is the 0% (no attacker) scenario. This clearly shows PFP-DA is superior to both LFU-DA and LRU by about 6% better hit rate overall, and around 30% for the top 50 items. This demonstrates that PFP-DA is the best cache replacement algorithm overall, even during periods where no attack is being launched. The explanation for this is that because of the normalization across the multiple faces, the items that remain in the cache give a truer and fair indication of what is popular, not just popular across one or two faces with higher frequencies of request. Depending on the traffic arriving at a given router, the popularity of content arriving at each of the faces are not necessarily homogenous, and in fact, might vary significantly based on origin of requests.

The results for the “no attacker” scenario are displayed graphically in Figure 9, which charts the moving average with an x-axis logarithmic scale. Clearly, PFP-DA outperforms LFU-DA and LRU for the top content objects, maintaining a very strong hit rate until around the item 100, where the results are less clear. Our previous results show that PFP-DA performs better with maintaining the most popular items in the cache, and this figure reinforces that PFP-DA is better, even with no active attack.

4.3.4. PFP-β Results

As discussed earlier, PFP-β (PFP-Beta) takes a β parameter, which acts as the exponent to the denominator for each of the contributions from faces, during the overall popularity calculation. Equation 4 is repeated below and expanded to demonstrate the use of β.

$$P\left(C,\beta \right)=\sum _{\begin{array}{c}i=1\\ 0\le \beta \le 1\end{array}}^n\frac{1}{{r_i}^{\beta }}=\frac{1}{{r_1}^{\beta }}+\frac{1}{{r_2}^{\beta }}+\dots +\frac{1}{{r_{n-1}}^{\beta }}+\frac{1}{{r_n}^{\beta }}$$

The lower the β, the smaller the numeric difference between the per-face contribution for each item and the top item. This causes content objects that have interests received from multiple faces to be favored substantially. The mechanism for this behavior is described in more detail in § 3.3.

The motivation for this variation on PFP-DA is to see if we can further lower cache pollution and increase hit rate. Through our initial tests, we have made some very interesting discoveries.

Table 10. PFP- β with single attacker, cache size of 100, beta of 0.05, varying attack frequency.

Attacker Speed	Pollution %	Hit %	top 100	top 50
720	0.00%	22.76%	87.98%	98.83%
840	0.00%	22.81%	87.97%	98.83%
960	0.00%	22.84%	87.98%	98.83%

Table 10. PFP- β with single attacker, cache size of 100, beta of 0.05, varying attack frequency.

Attacker Speed	Pollution %	Hit %	top 100	top 50
720	0.00%	22.76%	87.98%	98.83%
840	0.00%	22.81%	87.97%	98.83%
960	0.00%	22.84%	87.98%	98.83%

Firstly, we can observe the effects (or lack thereof) of varying the attack speed of the single attacker. The pollution is 0%, which is impressive. The hit rates are substantially better than the single attacker scenarios we tested for PFP-DA (see Table 6.) Of course, with PFP-DA, the regular Simple Topology was used, with 10 nodes attacked to the router, whereas our PFP- β was tested with the Larger Simple Topology (LST), which has 20. However, we will find that even with two attackers (10%) against the LST, considering the coordination and the consistency of percentage, the pollution will remain at 0%, with almost identical hit rates.

Therefore, we can conclude that if we consider the PFP-DA tests from earlier to be a special case of PFP- β where β = 1.0, that the smaller β = 0.05 for essentially the same variations, performs approximately 16% better in terms of cache pollution, approximately 3.7% better for overall hit rate, about 25% better for the top 100 items (by Zipf-like distribution), and about 23% better for top 50 items (98.83% vs 75.53%, for a rate of 720.) Astonishingly, the top 50 items experience just under 99% hit rate with our β = 0.05. Although 75.53% was incredibly good, and totally outperformed LFU-DA (50% top 50 hit rate), our β = 0.05 tests far surpass our previous PFP-DA tests in terms of small attacker percentage with varying attacker frequency.

Secondly, we tested variations of β value, keeping the number of attackers at 2 with attack frequencies of 720 each, a cache size of 100. As we see in Table 11, increasing the β value increases the pollution percentage, and decreases the hit rates in these scenarios. Ceteris paribus, as β moves toward the regular PFP-DA (β = 1.0), the performance drops.

Thirdly, we held the number of attackers at 2 with attack frequencies of 720 each, a constant β = 0.1, and varied the cache size. As more spaces become available, the pollution percentage increases extremely slightly. However, it is negligible, even for a cache size of 500 (5% of the content space), as only a few items, accounting for 0.4% of the entire cache, can make it in to the content store’s cache.

The overall hit rate increases significantly, as would be expected since more items can reside in the cache, overall. The top 100 and top 50 hit rates increase slightly, but they are so close to 100% already, there is little room for improvement.

In Table 13 we see where the PFP-β falls short. Although the performance of PFP-β is better than PFP-DA for small percentages of attackers, PFP-β performs worse than PFP-DA when the number of attackers increases. In other words, it appears that lower β values are resistant to cache pollution under a small percentage of attackers (less than 15%, for example), but higher β values (such as the original PFP-DA, technically holding β = 1.0) allow for more resistance against larger percentages of attackers.

5. Summary, Conclusions, and Future Work

Throughout this work, we have explored the effects of normalizing contributions toward caching influence across faces, yielding our Per-Face Popularity, or PFP schemes. The original PFP scheme showed promise but was not scalable due to overly large (unbounded) lists that needed to be maintained of content object rankings for each face. To mitigate this issue, and to also add a sense of recency to our PFP scheme, we developed PFP-DA. PFP-DA employs a dynamic aging characteristic to ensure that content items that were ranked for a given face do not remain there longer than they should due to extreme popularity at one time. Many of our tests involved PFP-DA. The results clearly demonstrate that PFP-DA performs better than LFU-DA and LRU in nearly all circumstances that were tested. This was especially true in terms of the ability of PFP-DA to maintain the most popular items in the cache, thus yielding much higher hit rates.

To further explore the PFP-DA scheme, a β parameter was added, which, when sufficiently small, reduces the numeric distance between the rank contribution of the top ranked item, and any subsequent item. We can consider our regular PFP-DA as a special case of PFP-β with β = 1.0. The PFP-β tests yielded interesting results. For smaller values of β, the cache pollution tended to be less (even 0%), and hit rates tended to be greater (nearly 100% for top 100 and top 50 items), but only if the percentage of attackers was relatively small.

In conclusion, we have created a new approach to increasing cache robustness by means of normalizing influence on the caching decisions, by a per-face fairness technique called Per-Face Popularity, or PFP. We have improved the original algorithm substantially and created many additional opportunities for future research as well.

For our future research endeavors related to this work, we will explore the applicability of our PFP techniques on current caching technologies, such as those used by CDNs. Even though our original work is geared toward content-centric approaches, specifically NDN, it is possible that our research can yield more immediate benefit to the industry, even if used in application overlays.

Further comparisons with other caching algorithms, such as the Name Popularity Algorithm [21] and CaDaCa [22] are needed. It is possible that the PFP-based algorithms could enhance or be enhanced by, these additional caching techniques in a hybrid strategy.

Furthermore, we will continue to refine our techniques and attempt to arrive at precise mathematical or statistical models to better predict and describe the behavior of our schemes.