Prerpints.org logo
Preprint
Article

Long Memory Cointegration in the Analysis of Maximum, Minimum and Range Temperatures in Africa: Implications for Climate Change

Altmetrics

Downloads

117

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 July 2023

Posted:

24 July 2023

You are already at the latest version

Alerts
Abstract
This paper deals with the analysis of the temperatures in a group of 36 African countries. By looking at the maximum, minimum and the range (the difference between the maximum and the minimum) and using a long memory model based on fractional integration and cointegration, we first show that all series display a long memory pattern, with a significant positive time trend in 29 countries for the maximum temperatures and in 33 for the minimum ones. Looking at the range, the estimated value for the order of integration is smaller than the one based on maximum or minimum temperatures in 17 countries. Performing fractional cointegration tests between the maximum and minimum temperatures, our results indicate that the two series cointegrate in the classical sense (i.e., with a short memory equilibrium relationship) in a group of 11 countries, and there is another group of eight countries displaying cointegration in a fractional sense. The remaining 17 countries with no evidence of cointegration are therefore at the very high risk of climate change due to the absence of long-term comovement in their maximum and minimum temperatures. Findings in this paper are of tremendous interpretations and relevance for the analysis and climate projections in Africa.
Keywords:ย 
Subject:ย Environmental and Earth Sciencesย  - ย  Atmospheric Science and Meteorology

1. Introduction

Temperature is a key indicator of climate change, and monitoring changes in temperature over time can help identify potential impacts on ecosystems, agriculture, and human health (FAO, 2021). In a report by the Intergovernmental Panel on Climate Change (IPCC, 2018), it is mentioned that global warming induced by human activity will produce temperatures around 1.0ยฐC higher than in times of the pre-industrial period, and that if current trends continue, global warming is expected to reach 1.5โ„ƒ between 2030 and 2052. The report also noted that some regions of the globe are experiencing more warming than others due to vegetation cover and other factors (Nicholls et al., 1996; Percival et al., 2001; Caballero et al., 2002; Gil-Alana, 2008; Franzke, 2012; Ludescher et al., 2016; Contractor et al., 2020; etc.). There are also clear evidences to show the dependency of global warming on the diurnal temperature range (DTR), that is, the difference between the maximum and minimum temperature (Karl et al., 1991). The National Oceanic and Atmospheric Administration (NOAA) and National Aeronautics and Space Administration (NASA) have measured-out 2010 to be the warmest year on record when compared to the average baseline of the 20th century and of 1951โ€“1980, respectively. Hansen et al. (2010) and Cahill et al. (2015) have proved that the temperature increase trend would likely continue due to the continuous increases in the greenhouse gas (GHG) concentration, while in the sub-Saharan African region, the warming is likely to be higher compared to global average, and the speed of temperature rise will be more than the rise in the global mean temperature (see, e.g., Shepard, 2019; Ray, 2021). Africa is particularly vulnerable to the effects of climate change due to its dependence on rain-fed agriculture and limited infrastructure to cope with extreme weather events (IPCC AR6, 2021; Ngarukiyimana, Ruhinda and Mupenzi, 2020). Furthermore, the large-scale climate patterns such as El Niรฑo-Southern Oscillation (ENSO), Indian Ocean Dipole (IOD), and Atlantic Multidecadal Oscillation (AMO) often influence Africanโ€™s climate, causing heatwaves, droughts, and floodings in different regions of the continent (Ngarukiyimana, Ruhinda and Mupenzi, 2020).
In the very arid regions of Africa, the temperature is expected to rise faster compared to other parts of the world in the 21st century (CDKN, 2014). Thus, the African continent is very prone to climate variability changes due to its geographical location on the globe. The continent lies between 37oN and 35oS and in this position, the continent lies almost perfectly on the equator, covering a total land area of about 30.2 million square kilometres, which is about one-fifth of the land area of the entire globe (https://www.mapsofworld.com/lat_long/africa.html#:~:text=Africa's%20latitude%20and%20longitude%20lies,of%20the%20world's%20land%20area). Figure 1 shows the map of African showing all countries, and how the equator divides the continent into two parts, that is, the continent lies within the intertropical zone between the Tropic of Cancer and the Tropic of Capricorn, where the tropics are regions of the globe surrounding the equator.
This latitudinal position of Africa around the tropics makes rainfall, temperature and humidity in Africa to be high compared to other continents (https://en.wikipedia.org/wiki/Tropics). There are also different climate types experienced annually. These are the equatorial climate, tropical wet and dry climate, tropical monsoon climate, semi-arid climate, desert climate and subtropical highland climate (https://en.wikipedia.org/wiki/Climate_of_Africa). It is very rare to experience a temperate climate in any part of Africa except at very high elevations and along the fringes. African deserts are the hottest and driest worldwide due to subtropical ridges with hot, dry air masses. As predicted by IPCC AR6 (2021). temperatures in African countries are expected to have increased by 1.5ยฐC - 3ยฐC in 2050. Putting temperature on one side, the total annual greenhouse gasses are also rising fast at the rate of about 1.6% per annum with carbon dioxide emissions alone increasing by about 2% per year. This together with the fast-rising temperature could change the African climate in such a way that urgent intervention would be required coupled with energy issues and poor amenities that most countries are experiencing. Thanks to the IPCC for their efforts in monitoring the African climate (IPCC AR6, 2021).
Focussing specifically on Africa, there are various studies investigating the temperature dynamics and its maximum and minimum ranges on the continent. The mean annual DTR for Ethiopia, Sudan, South Africa and Zimbabwe have been considered by Nicholls et al. (1996). where the authors observed a decrease of 0.5ยฐC to 1.0ยฐC in the mean annual DTR for Sudan and Ethiopia. For countries in the southern part of the continent such as Zimbabwe and South Africa, the DTR reduced during the period 1950 โ€“ 1960. Kruger and Sekele (2012) and Kruger and Nxumalo (2016) find evidence of increasing warming trends in South Africa. Extending the analysis to other countries, New et al. (2006) investigated trends in daily climate extremes over Southern and Western Africa and found a repeating pattern of temperature extremes associated with rising temperatures. Neumann et al. (2007) found that temperature in the Volta basin, West Africa exhibited highly significant positive trends. In a similar vein, Muthoni (2020) studied temperatures in West Africa and also found a strong warming trend.
Meanwhile, there have been controversies in relation to the speed of temperature increase, on the appropriate estimation method to model temperature across time. The most standard approach still recommends incorporating a linear trend in the modelling framework. Using the linear model with fractional integration methods, Gil-Alana et al. (2019) examined issues such as linear trends, seasonality and persistence in Western, Eastern, and Southern regions of Africa and found that time trends are required in most of the countries to explain the climate features in the areas. They also found evidence of structural breaks in some of the countries. Other papers that have applied fractional integration in a linear framework to analyse temperature and rainfall data include Ogunsola and Yaya (2019) and Yaya and Vo (2020).
Closely-related research to the present paper is the one conducted in three African countries, namely, South Africa, Kenya, and Cรดte dโ€™Ivoire by Carcel and Gil-Alana (2015). They check for warming trends and using fractional integration, they showed that only Kenya has experienced a significant temperature increase in the last 30 years as at the time of the research.
In the current paper, we, therefore, investigated persistence and linear trend in the maximum and minimum annual average temperatures in 36 African countries chosen by data availability from Climate Change Knowledge Portal (CCKP). Due to the statistical distribution of maximum and minimum temperature, we also examine the difference between the two series which leads to the diurnal range as this informs climate differences in the study area. High maximum temperatures and low minimum temperatures are experienced in desert or arid climate with scanty vegetation cover, while moderate maximum temperatures and low minimum, temperatures are often recorded in temperature climate regions. The latter is unlikely to be experienced in the sub-Saharan region of Africa. Thus, changes in the distribution of maximum and minimum temperatures over time can indicates climatic changes as the frequency or intensity of extreme temperatures, and its events such as heat waves or cold snaps can be indicative of climate change.
Having obtained the fractional integration estimates based on a linear trend specification, we conducted homogeneity of paired Local Whittle (LW) estimates of fractional orders based on Hausman-type test of Robinson and Yajima (2002) since the statistical equality of the fractional orders is a pre-requisite for cointegration, at least in the bivariate representation as is the case in this paper. We extended the analysis to testing for fractional cointegration using narrow-band frequency domain least square (NBFDLS) estimates of Christensen and Nielsen (2006) in the fractional cointegration framework of Marinucci and Robinson (2001). The NBFDLS estimates for the cointegrating vector were obtained and used to compute the model residuals in models linking each country's maximum and minimum temperatures. Then, fractional integration estimates were obtained on the residuals based on the LW estimator. Note that cointegration is relevant in the present context since it will indicate us if there is a long run equilibrium relationship between maximum and minimum temperatures. On the other hand, lack of this property will suggest that the two series move apart supporting potential extreme changes in temperatures.
In conclusion, the hypothesis to be tested in this paper are the following: we first consider the possibility of long memory or long range dependence in the variables under examination since this is a property widely observed in climatological data. Then, based on this observation, we claim that the estimation of the linear trends in the data is clearly affected by the long memory property, and not to take into account this issue will clearly produce biased estimates of the time trend coefficient to explain CC. As a final issue, the possibility of cointegration is also examined looking at the difference between maximum and minimum temperatures, claiming that under normal circumstances both variables should be linked in a long run equilibrium relationship.

2. Data

Maximum and minimum average annual temperature (0C) datasets for 36 African countries were analysed to provide insights into climate change on the continent. The countries are: Angola, Benin, Botswana, Burkina Faso, Cameroon, Central African Republic, Chad, Congo, Cote dโ€™รvoire, Egypt, Gabon, Ghana, Guinea, Guinea-Bissau, Kenya, Lesotho, Liberia, Libya, Madagascar, Malawi, Mali, Mauritania, Morocco, Namibia, Niger, Nigeria, Rwanda, Sierra Leone, Senegal, South Africa, Sudan, Tanzania, Tunisia, Uganda, Zambia and Zimbabwe. 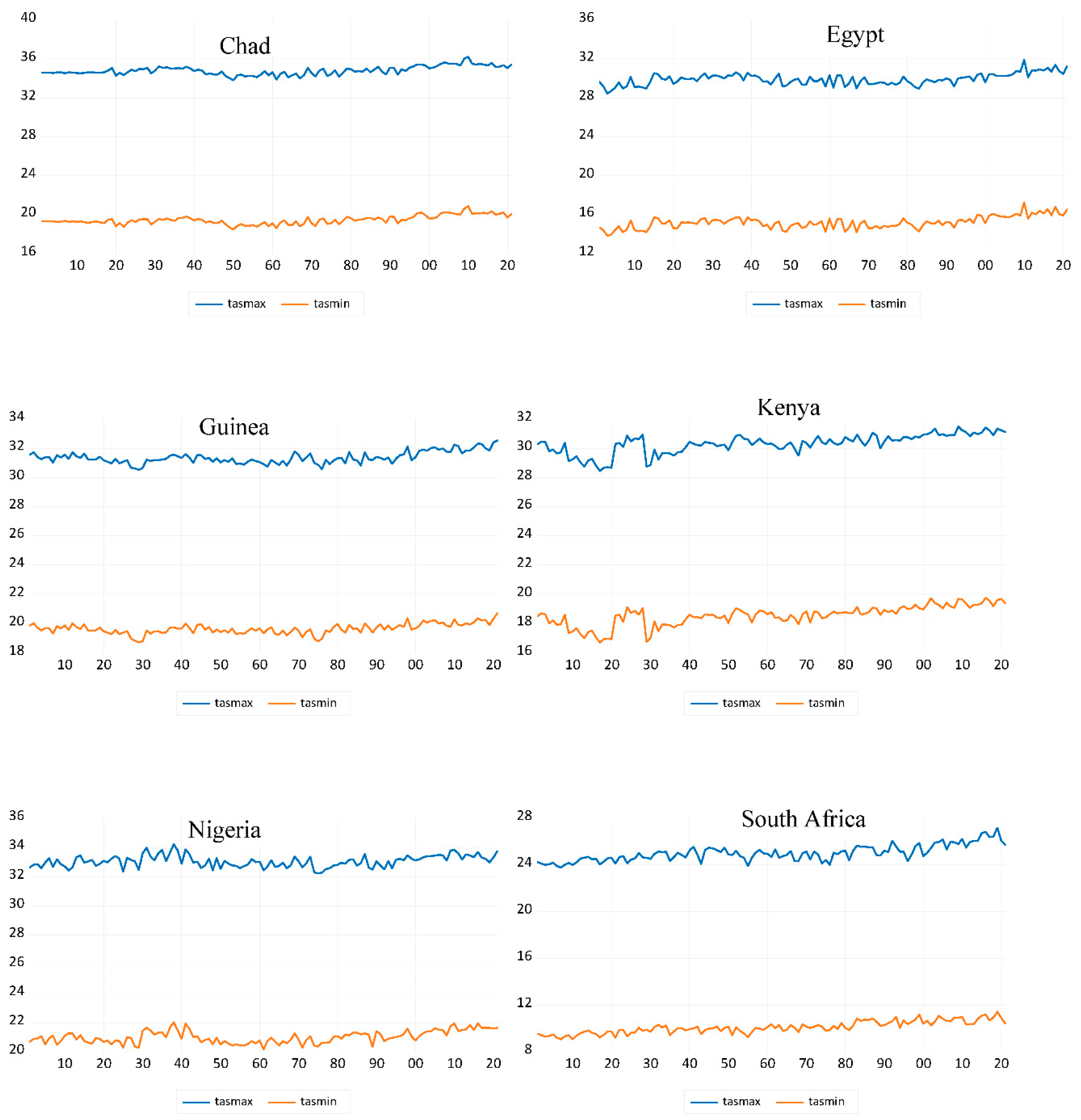The datasets were retrieved from the World Bank Climate Change Knowledge Portal at https://climateknowledgeportal.worldbank.org/. (see World Bank, 2021). This portal has been collecting historical monthly and annual climate data of countries in the world since 1901 till date, and the nature of the analysis to be carried out here required only annual data since monthly datasets could bias our results due to the interference of seasonality. In each of the five geographical zones of Africa, we displayed a graph showing the distribution of maximum and minimum temperature, whereas, in the case of West Africa zone, we have temperature plots for Guinea and Nigeria, others are Chad (Central Africa), Egypt (North Africa), Kenya (East Africa) and South Africa (Southern Africa). In each case, both the maximum and minimum temperatures are plotted on the left vertical axis as shown in Figure 1.
In all the plots, it is obvious to notice shifts in temperature trend, signalling global warming over time. In the case of Chad, the temperature increased consistently from 1950 to reach astronomic thermometric readings in 2010, similarly to Kenya, Nigeria and South Africa. The temperature shift in temperature trends is noticed around 1970 in the case of Egyptian temperature plots, and between 1970-1980 in the case of Nigeria. Table 1, therefore, displays a data summary, showing the starting maximum and starting minimum temperatures in 1901 and corresponding sample ending maximum and minimum temperatures in 2021 for the 36 countries. It is found that ending temperatures in 2021 are quite higher than starting temperatures in 1901, resulting in a positive shift in temperature trend due to global warming. The annual range, the difference between the annual maximum and annual minimum temperature, which is used to proxy the diurnal temperature range (DTR) is also presented in the table for 1901 and 2021 data.

3. Econometric Methods

3.1. Testing for a Linear Trend

The analysis of climatological time series datasets takes its root from the seminal work of Hamilton (1994) where a linear model was employed to fit climate datasets. Hamilton (1994) used a model of the form:
y t   =   ฮฑ     +     ฮฒ   t   +   x t   ,         t     =     1   ,     2   ,     ...   ,
where y t is climatic series under investigation and t is the time trend t = 1, 2, โ€ฆ . Then, x t is the deviation term, derived from the original series y t . The model's parameters are ฮฑ and ฮฒ, which represent the intercept and slope, respectively. The slope, ฮฒ, measures the average change in y t   over time, when t = t 0 . Thus, in the context of climatic research, there is long-run warming if the slope, ฮฒ, is positive and statistically significant, implying that the temperature is rising. The estimation of the deviation term is critical in carrying out this assessment. This is determined by the distribution from which x t   is created, and hence by the overall estimation of the process.
In most early studies, the error term xt in (1) was assumed to be well behaved, i.e., displaying a short-memory (SM) structure, also denominated integrated of order 0 or I(0) process. In this context, the simplest structure was the white noise case where no time dependence is permitted. If that dependenc allowed, the ordinary AutoRegressive Moving Average (ARMA) models were employed. However, the time dependence between the observations may display a higher range. Thus, it may exhibit long-term dependence (LTD) or long memory (LM), as claimed in various climatological data by researchers such as Montanari et al. (1996). Stephenson et al. (2000). Percival et al. (2001). Gil-Alana (2003, 2005) and others. Gil-Alana (2012) then adapted the linear model of Hamilton (1994) to the fractional integration or I(d) framework where the dependency of historical temperature observations of Alaska over long past time periods is investigated. This phenomenon is known as the long-range dependency (LRD) or LTD. Climatic variables often exhibit this property due to the natural variability, from year to year, and to the next. Climatic variables can also vary on much longer time scales such as from decades to centuries, and due to human interference, there may be a shift in the mean state of a particular climatic variable, such as temperature or rainfall. In this study, we will LRD or shift or shift in mean state of climate variables based on fractional integration and cointegration. Note, LRD is an aspect of fractional integration, thus LRD is often explained based on this broader perspective.

3.2. Testing for Fractional Integration

The following is the standard non-seasonal fractional integration model i.e. an integrated of order d or I(d) model:
( 1     โˆ’     L ) d x t     =       u t   ,       t     =     1   ,     2   ,     ....  
where d is any real number (such as integer or fractional values), L is the lag-operator L x t = x t โˆ’ 1 , and u t denotes the white noise process, which is an I(0) process in the context of fractional integration I(d) process (An I(0) process is defined as a covariance stationary process where the infinite sum of its autocovariances is finite. It includes the white noise model but also the stationary ARMA-class of models). The polynomial (1 - L)d in (2) is a Binomial representation, which can be expanded as follows:
( 1     โˆ’     L ) d     =   โˆ‘ j = 0 โˆž ( d j )   ( โˆ’ 1 ) j   L j     =   1     โˆ’     d   L   +     d   ( d   โˆ’   1 ) 2   L 2     โˆ’   ...  
and therefore
( 1     โˆ’     L ) d   x t   =     x t   โˆ’     d   x t โˆ’ 1     +     d   ( d   โˆ’   1 ) 2   x t โˆ’ 2     โˆ’   ...  
depicting that equation (2) can be written as
x t   =     d   x t โˆ’ 1     โˆ’     d   ( d   โˆ’   1 ) 2   x t โˆ’ 2     +       ...     +   u t .    
Intuitively, the role of d in equation (3) is clear as it is a slope coefficient between x t and its lagged values such as x t โˆ’ 1 ,   x t โˆ’ 2 ,   . . .   . Thus, it determines the degree of correlation between x t   and its lagged values. So, regression, or correlation here in explaining fractional integration or LRD processes leads to time series dependency or persistency as they are often used interchangeably. The model in (2) is non-seasonal model type since the dataset at hand in annual temperature series, and testing seasonality in addition, is not of interest in this paper.
Many methods have been used to estimate the fractional dependence parameter d. Some of these methods are semi-parametric, while others are parametric methods. Semiparametric techniques are typically implemented in the frequency domain. In this study, we use a parametric frequency domain Whittle estimation approach (see Dahlhaus, 1989) in conjunction with a testing procedure of Robinson (1994a) that depends on the Lagrange Multiplier (LM) principle. Robinson (1994a) uses the null hypothesis test:
H o :   d   =   d o   ,
for any real value d0 in a model given by the equations (1) and (2), that is,
y t   =   ฮฑ     +     ฮฒ   t   +   x t   ,       ( 1     โˆ’     L ) d x t     =     u t ,       t     =     1   ,     2   ,     ...   ,
where u t is a white noise process. The fundamental advantage of this approach is that, because it depends on the LM principle, all of it is evaluated under the null, and because do can be any actual number, it is valid even in nonstationary situations (i.e., do โ‰ฅ 0.5), with a regular normal limit distribution. In addition, this standard normal distribution holds independently of the inclusion or not of deterministic terms in the model like an intercept and/or a linear time trend, being this method the most efficient one in the Pitman sense against local departures from the null. (See, Robinson, 1994).
In complement to the aforesaid parametric methodology, we also use a semiparametric method to conduct the analysis. It is named semiparametric because no functional form is imposed on the error term, making only the assumption that it is integrated of order zero, i.e., I(0). In other words, it might be a simple white noise process or an ARMA process with a weak dependency autocorrelation. We employ in the paper a "local" Whittle (LW) estimate in the frequency domain, which is based on a frequency band that degenerates to zero. This approach (Robinson, 1995) is defined implicitly by:
d ^     =     arg   min   d   (   log   C * ( d )         โˆ’         2   d   1 m   โˆ‘ j = 1 m   log   ฮป j     )   ,
f o r   d   โˆˆ   ( โˆ’ 1 / 2     ,   1 / 2 )   ;         C ( d )   ยฏ   =     1 m   โˆ‘ j   =   1 m I ( ฮป   j )     ฮป     j     2   d ,         ฮป j     =     2     ฯ€   j T   ,         1 m   +   m T     โ†’     0 ,
where m represents the bandwidth parameter, and I(ฮปj) represents the periodogram of the time series, xt, which is given by:
I ( ฮป j )   =   1 2   ฯ€   T     | โˆ‘ t = 1 n x t   e i   ฮป j   t | 2 .
Robinson (1995) demonstrated under finiteness of the fourth moment and other very mild conditions:
m     ( d ^   โˆ’   d o )     โ†’ d     N ( 0 ,     1 / 4 )         a s   T     โ†’   โˆž ,
where do is the actual value of d and in addition to the requirement that mโ†’โˆž is slower than T.

3.3. Homogeneity of Paired Fractional Integration Parameters

Following from the local Whittle estimate, it is important to do the test of homogeneity of paired integration orders. As earlier argue, this is a necessary condition for testing cointegration in a bivariate system. The following null hypothesis is used to assess the homogeneity of the orders of integration:
H 0 : d y 1 = d y 2 ,
where the orders of integration of the individual series are represented by d y 1 and d y 2 (see Robinson and Yajima, 2002; Yaya, 2022). The test statistic is defined as,
T ^ x y = m 1 / 2 ( d ^ y 1 โˆ’ d ^ y 2 ) { 1 2 [ 1 โˆ’ G ^ y 1. y 2 2 / ( G ^ y 1 G ^ y 1. y 2 ) ] } 1 / 2 + h ( T )
where h ( T ) > 0 and G ^ y 1. y 2 denote the (y1.y2)th element of ฮ› ^ ( ฮป j ) โˆ’ 1 I ( ฮป j ) ฮ› ^ ( ฮป j ) with ฮ› ^ ( ฮป j ) = d i a g { e i ฯ€ d ^ y 1 / 2 ฮป โˆ’ d ^ y 1 ,   e i ฯ€ d ^ y 2 / 2 ฮป โˆ’ d ^ y 2 } .

3.4. Narrow-Band Frequency Domain Least Square Approach

At this juncture, we considered the narrow band frequency domain least square (NBFDLS) estimates in obtaining the cointegrating vector linking the maximum and minimum temperatures. This approach is applied when the cointegrating pairs are deemed to possess long memory, having weakly dependent regressors. Since the regressors and the residuals are of long memory, thus, they are deemed to be correlated even at a very long time span. In that case, both the least squares and generalized least squares estimates will be inconsistent (see Robinson and Hidalgo, 1997). Robinson (1994b) earlier proposed a semi-parametric NBFDLS estimator which uses OLS on a degenerated band of frequencies around the origin. An improved version of the test for the stationary time series is given in Christensen and Nielsen 2006.
In the two-variable case, where y 1 t is for maximum temperature and y 2 t is for minimum temperature series, both of fractional integration order d < 0.5 and residuals of order d e < d , the NBFDLS estimator is given by,
ฮฒ ^ = { 1 m โˆ‘ j = 1 m Re [ I y 1 y 1 ( ฮป j ) ] } โˆ’ 1 ร— 1 m โˆ‘ j = 1 m Re [ I y 1 y 1 ( ฮป j ) ]
which is asymptotically distributed as,
m ฮป m d e โˆ’ d ( ฮฒ ^ โˆ’ ฮฒ 0 ) โ†’ D N [ 0 , g e ( 1 โˆ’ 2 d ) 2 2 g y 1 ( 1 โˆ’ 2 d โˆ’ 2 d e ) ]
where g y 1 and g e are the elements of a G diagonal 2 ร— 2 matrix. From (10), the normality is ensured as long as d + d e < 0.5 (Christensen and Nielsen, 2006).

4. Main Results

Having presented the dataset used in Section 2, we therefore present the main results obtained based on the econometric methods presented in Section 3 above. In Table 2, the results of temperature data stationarity are presented by employing Augmented Dickey-Fuller (ADF, Dickey and Fuller, 1979) unit root test for no deterministic term, intercept only, and intercept with the trend. These are the three options available for the test in the case of a linearly assumed time series process. The choice of the unit root test is motivated by its design in a linear framework which mimics the assumed linear specification of climatological time series as in Hamilton (1994) (see equation (1)). The results, in Table 2 showed non-rejection of the unit root null hypothesis when no deterministic term (none) is assumed for maximum, minimum and range temperature series. The stern acceptance of non-stationarity of the three- time series could be due to the high power of the test when the degree of freedom, as a result of no deterministic term in the test framework leaving only the augmented component, is compromised. By testing with only intercept, very few countries out of the 36 countries showed rejection of unit root null hypotheses in the case of both maximum and minimum temperature, while in the case of temperature range series, null hypotheses of unit root were rejected in almost all the 36 cases. For intercept with trend specification, the results for the range temperature are similar to those from the intercept only. For intercept with trend, as in maximum and minimum temperatures, more rejections of unit root null were observed compared to that of intercept only specification of the test. This mixed decision of the results of the unit root test for temperature series is due to the fact that the unit root test lacks power against trend-stationarity and fractional alternatives (Diebold and Rudebusch, 1991; Hassler and Wolter, 1994; Lee and Schmidt, 1996). Also, when the persistence is likely to fall in long- range dependence range (i.e. 0 < d < 1 ) or long memory range ( 0 < d < 0.5 ), ADF-like unit root tests might find it difficult to detect correctly the stationarity/non-stationarity of the series.
This weakness of the unit root test makes fractional integration (fractional unit root) attractive since the test allows for persistence level (series differencing) in fractional value other than unit differencing as in the unit root test to be determined. Robinson (1994b) can be seen as an ADF test in a fractional sense since it allows testing fractional integration based on no deterministic term, intercept only and intercept with the trend. This test is earlier described above in equations (4)-(6). Here in Table 3, the results are presented for only the case of intercept with trend. Evidences of long memory and long-range dependence, i.e., 0 < d < 1 are found in maximum and minimum temperatures, with d less than 0.5 in a number of countries and fairly above 0.5 in others. The highest bound values for d are 0.72 (Rwanda) and 0.76 (Uganda) in the case of maximum temperature, and these values correspond to d values 0.43 (0.27, 0.60) and 0.48 (0.32, 0.65), respectively for minimum temperatures. In the maximum, temperature, evidence of d fairly above the long memory stationary range (i.e d > 0.5 ) are found in Kenya, Madagascar, Rwanda and Uganda, while in the case of minimum temperature, we have Benin, Burkina Faso, Ghana and Madagascar. These results imply that long memory exists generally in maximum and minimum temperature distributions even though the upper bound of the confidence limit shows that some estimates might be in the long-range dependence range which is still close to 0.5. Differing persistence estimates explain the dynamics of temperature predictions, not in terms of trend often expected in climatological study but in terms of inherent correlations of current observations to past lagged historical values, large enough to compare the present climate with climate of the same regions over many decades. In that case, using only the linear trend approach such as that employed in Hamilton (1994) could lead to bias due to ignorance of exploring the (long memory) time series properties of the climatological observations.
Also, the temperature range series, which is the difference between the maximum and minimum temperature display long memory as well in a number of countries but with an upper bound limit above 0.5 in many cases. Table 3 also indicates 29 cases of significant trends in the case of maximum temperatures, and 33 cases for the minimum temperatures, all them with significant positive coefficients, while only 9 countries show significant trends in the range, three with a positive value (Lesotho, Morocco and Botswana) and five with a negative trend (Sudan, Burkina Faso, Nigeria, Egypt, Kenya, and Central Africa).
For clarity, Table 4, therefore, summarized the results in Table 3 for cases where d value for range series is less than either or both d values for maximum and minimum temperatures. These countries include: Angola, Botswana, Central African Republic, Chad, Congo, Egypt, Gabon, Kenya, Libya, Madagascar, Malawi, Namibia, Nigeria, Sudan, Uganda, and Zimbabwe. These are the countries in which maximum and minimum temperatures are likely to have long-run relationships but the high confidence band for the range series poses suspicion which requires further robust analysis before one concludes the long run relationship existing between the pair.
The framework of fractional integration employed here also allows us to simultaneously test for positive trends in the series under investigation, as we know that significant positive trends in temperature series suggest evidence of global warming induced by temperature increases. In Table 3, positive and significant trend coefficients are found in 29 countries for the case of maximum temperature, and in 33 countries in the case of minimum temperature. Thus, in Table 4, it is put together that evidence of temperature increase is observed in 34 countries, that is, all except Liberia and Sierra Leone.
In order to further establish the long -run relationship between maximum and minimum temperature series, we carried out homogeneity of fractional integration orders, where we ignore the confidence band since the test is defined in the frequency domain using periodogram bands. The estimation of d parameter is based on Local Whittle (LW) estimators and the significant difference in paired values of d are tested based on the approach described earlier in equations (7)-(8). Estimates of T ^ x y statistics, as given in Robinson and Yajima (2002) are presented in Table 5 where none of these estimates are significant at 5% level. Recall that the test is asymptotically normally distributed with 1.96 as its two-sided rejection value, and all these estimates are below the value. Evidence of homogeneity in all the pairs (maximum and minimum temperature pairs) further supports the possibility of long-run relationship, based on fractional cointegration in the comovement of maximum and minimum temperatures in the 36 African countries under investigation.
We further the analysis by using fractional cointegration, and following now, the two-step approach developed in Engle and Granger (1987). Thus, we first conduct the regression of one of the variables (maximum) against the other (minimum). However, instead of using OLS regressions either in the time or in the frequency domain, we follow Nielsen (2015) and perform the narrow band frequency domain least square (NBFDLS) estimation approach, using as bandwidth numbers m = T0.5 and T0.6. The estimated regression coefficients are displayed in Table 6. In the second step, we estimated the order of integration in the residuals of the estimated relationships by using Whittle estimates in the frequency domain. Results are reported across Table 7.
in the cointegrating residuals are 19 less 11 countries.
The results are similar in the two cases in relation with the bandwidth numbers. Evidence of I(0) residuals, supporting thus short memory in the long run equilibrium relationship is found in the cases of Angola, Botswana, Cameroon, Congo, Gabon, Kenya, Madagascar, Mauritania, Namibia and Zimbabwe. If m = T0.5, this hypothesis is also supported by Malawi and Morocco. Thus, for these groups, our results support the hypothesis of cointegration with a rapid reversion of the series to a long run equilibrium relationship. On the other extreme, evidence of nonstationary I(1) is found for Liberia and Sierra Leone for the two bandwidth numbers, and also for Ghana if m = T0.5. In all the other countries, the estimate of the differencing parameter is in the interval (0, 1), and evidence of cointegration (in the sense that the order of integration of the residuals is lower than the minimum of the two individual series) is found in the cases of Angola, Botswana, Cameroon, Central African Republic, Congo, Gabon, Kenya, Madagascar, Malawi, Morocco, Namibia, Nigeria, Tanzania, Uganda and Zimbabwe for the two bandwidth numbers, but also for Benin, Burkina Faso, Mauritania and Tunisia if m = T0.6. Thus, the countries with no evidence of cointegration are Chad, Cote dโ€™Ivoire, Egypt, Ghana, Guinea, Guinea Bissau, Lesotho, Liberia, Libya, Mali, Niger, Rwanda, Sierra Leone, Senegal, South Africa, Sudan and Zambia. Among the 19 countries listed in Table 7 with evidence of cointegration, 11 group of countries display short memory equilibrium relationships between their maximum and minimum temperatures, i.e. I ( 0 ) evidences. These countries include Angola, Botswana, Cameroon, Congo, Gabon, Kenya, Madagascar, Mauritania, Morocco, Namibia, and Zimbabwe, while the remaining eight countries indicate long memory cointegration, i.e. I ( d > 0 ) .

5. Conclusion

This paper investigates persistence and linear trends in the maximum and minimum annual average temperatures in 36 African countries. The statistical distribution of maximum and minimum temperature series, with the diurnal range in the climatological study as they act as an important factors driving global warming, have gingered our interest. Historical datasets from 1901 to 2021 are analysed with the annual range series. The results first establish long term memory in maximum and minimum temperatures over the historic years implying that temperature series is often strongly correlated with its past lag values. This is a persistence property, often measured as fractional integration. It assists in uncover the correlation property of this series, classified as long memory, mean-reverting and non-mean-reverting, and these have implications for erratic and predicted climatic series. Thus, long term memory observed in this paper further indicates the possibility of temperatures in Africa being predicted for future values. The trend analysis shows evidence of trend shifts in the plots and these are revealed further in the positive significant trend coefficients with insignificant positive trend in range series. Note that trend analysis allows one in making future predictions, but the approach used in this paper checking future predictions based on fractional integration is relatively novel and hardly adopted in climatological studies. Few papers along this line are those of Gil-Alana, Yaya and Fagbamigbe, (2019). and Gil-Alana (2003, 2008, 2012), among others.
Our results support the hypothesis of fractional cointegration. This implies that both maximum and minimum temperatures follow a long run equilibrium relationship with shocks in the range displaying transitory effects and not producing permanent discrepancies between the maximum and minimum temperatures. Also, 17 countries among the 36 African countries are at the very high risk of climate change due to the absence of long-term comovement in the maximum and minimum temperatures in those countries, compared to other countries with mild effect. Though, most African countries are prone to the effect of climatic change as the econometric findings reveal, but some regions of the continents are fairer than others.
Findings in this paper are of relevance for climatological studies in a number of ways. It allows for proper understanding of historical temperature patterns in Africa which is crucial for predicting and mitigating the impacts of climate change. Thus, it helps in studying the large-scale climate patterns that influence Africanโ€™s climate in its different regions (see Guo and Wang, 2015; World Bank, 2021). Understanding these patterns and their potential impacts on different parts of Africa is essential for developing effective adaptation and mitigation strategies. Additionally, research on large-scale climate patterns in Africa can contribute to global climate models, improving the accuracy of climate projections and enhancing our understanding of the global climate system.
As a final issue, we should note that the last century was a particularly convulse era of humankind; due to this, issues such as heterogeneity (changes in the variance) and stability (structural breaks) in the data should also be taken into account, noting that some authors have found that long memory and nonlinearities and breaks are issues which are intimately related (Diebold and Inoue, 2001; Granger and Hyung, 2004; etc.). Thus, nonlinear deterministic trend structures, based, for instance, on Chebyshev polynomial in time (Cuestas and Gil-Alana, 2016), Fourier functions (Gil-Alana and Yaya, 2021) or neural networks (Yaya et al., 2021) could be examined in these data still under the assumption of long range dependence. Work in this line is now in progress.

Declarations

Not applicable

Ethics approval/declarations (include appropriate approvals or waivers)

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.

Author Contributions

OSY: conceptualization, methodology, formal analysis, validation, writing original draft, writing review and editing, visualization, and supervision. OAA: conceptualization, methodology, formal analysis, validation, writing original draft, writing review and editing, visualization, and supervision. HAO & OEO: writing-review and editing, visualization, and validation. LAG: methodology, formal analysis, writing original draft, writing-review and editing, and visualization.

Funding

No funding was received

Data availability statement

The data and the codes that support the findings of this study is available from the corresponding author upon request.

Acknowledgments

Comments from the Editor and four anonymous reviewers are gratefully acknowledged.

References

  1. Caballero, Rodrigo; Jewson, S. and Brix, A. Long memory in surface air temperature: detection, modeling, and application to weather derivative valuation. Climate Research 2002, 21, 127โ€“140. [Google Scholar] [CrossRef]
  2. Cahill, Niamh; ahmstorf; tefan; Parnell, Andrew C. Change points of global temperature. Environmental Research Letters 2015, 10, 084002. [Google Scholar] [CrossRef]
  3. Carcel, Hector; Gil-Alana, Luis A. Climate Warming: Is There Evidence in Africa? Advances in Meteorology 2015, 2015, 917603. [Google Scholar] [CrossRef]
  4. CDKN (2014). The IPCCโ€™s Fifth Assessment Report Whatโ€™s in it for Africa?
  5. http://cdkn.org/wp-content/uploads/2014/04/AR5_IPCC_Whats_in_it_for_Africa. 20 June 2016.
  6. Christensen, Bent Jesper; Nielsen, Morten ร˜rregaard. Asymptotic normality of narrow-band least squares in the stationary fractional cointegration model and volatility forecasting. Journal of Econometrics 2006, 133, 343โ€“371. [Google Scholar] [CrossRef]
  7. Contractor, Steefan; onat; G, Markus; Alexander, Lisa V. Changes in Observed Daily Precipitation over Global Land Areas since 1950. Journal of Climate 2021, 34, 3โ€“19. [Google Scholar] [CrossRef]
  8. Dahlhaus, Rainer. Efficient Parameter Estimation for Self-Similar Processes. The Annals of Statistics 1989, 17, 1749โ€“1766. [Google Scholar] [CrossRef]
  9. Dickey, D.A. Dickey, D.A. and W.A. Fuller (1979), Distribution of the estimators for autoregressive time series with a unit root, Journal of the American Statistical Association 74, 366, 427-431.
  10. Diebold Francis X. and Rudebusch Glenn D. (1991). On the power of Dickey-Fuller tests against fractional alternatives.
  11. Diebold, Francis; Inoue, Atsushi. Long Memory and Regime Switching. , 2000. [Google Scholar] [CrossRef]
  12. Engle, R. Engle, R. and Granger, C.W.J. (1987). Cointegration and error correction.
  13. estimation and testing. Econometrica 55, 251โ€“276.
  14. FAO. (2021). Climate change and food security in Africa: A review of the status, challenges and opportunities. Rome, Italy.
  15. Franzke, Christian. Nonlinear Trends, Long-Range Dependence, and Climate Noise Properties of Surface Temperature. Journal of Climate 2012, 25, 4172โ€“4183. [Google Scholar] [CrossRef]
  16. Gil-Alana, L. A. (2003). An application of fractional integration to a long temperature time series. International Journal of Climatology, 23, 1699โ€“1710.
  17. Gil-Alana, Luis A. Statistical Modeling of the Temperatures in the Northern Hemisphere Using Fractional Integration Techniques. Journal of Climate 2005, 18, 5357โ€“5369. [Google Scholar] [CrossRef]
  18. Gil-Alana, L. A. (2008), Time trends with breaks and fractional integration in temperature time series, Climatic Change, 9, 325โ€“337.
  19. Gil-Alana, Luis A. Long memory, seasonality and time trends in the average monthly temperatures in Alaska. Theoretical and Applied Climatology 2011, 108, 385โ€“396. [Google Scholar] [CrossRef]
  20. Gil-Alana, L. Gil-Alana, L.A, & Cuestas, J. (2016). A nonlinear approach with long range sependence based on Chebyshev polynomials. Studies in Nonlinear Dynamics and Econometrics 16, 5, 445-468.
  21. Gil-Alana, Luis A.; Yaya, OlaOluwa S. Testing fractional unit roots with non-linear smooth break approximations using Fourier functions. Journal of Applied Statistics 2020, 48, 2542โ€“2559. [Google Scholar] [CrossRef] [PubMed]
  22. Gil-Alana, Luis A.; aya; S, OlaOluwa; Fagbamigbe, Adeniyi F. Time series analysis of quarterly rainfall and temperature (1900โ€“2012) in sub-Saharan African countries. Theoretical and Applied Climatology 2018, 137, 61โ€“76. [Google Scholar] [CrossRef]
  23. Granger, Clive W.J.; Hyung, Namwon. Occasional structural breaks and long memory with an application to the S&P 500 absolute stock returns. Journal of Empirical Finance 2004, 11, 399โ€“421. [Google Scholar] [CrossRef]
  24. Guo, Y. Guo, Y. And X. Wang (2015), Climate change and its impact of Chinaโ€™s agricultural production, International Journal of Global Warming 7(3), 437-450.
  25. Hamilton, J.D. Hamilton, J.D. (1994). Time Series Analysis Princeton University Press, Princeton, NJ., 820 pages.
  26. Hansen, J., Ruedy, R., Sato, M. and Lo, K. (2010), Global surface temperature change, Reviews of Geophysics, 48(4), RG4004. [CrossRef]
  27. Hassler, Uwe; Wolters, Jรผrgen. On the power of unit root tests against fractional alternatives. Economics Letters 1994, 45, 1โ€“5. [Google Scholar] [CrossRef]
  28. Hausman, J. Hausman, J., Misspecification Tests in Econometrics, 1978, Econometrica, Vol. 46, pp. 1251-1271.
  29. Hosking, J.R.M. Hosking, J.R.M. (1981) Fractional differencing, Biometrika 68(1).
  30. IPCC (2018). Global Warming of 1.5ยฐC. An IPCC Special Report on the impacts of global warming of 1.5ยฐC above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty [Masson-Delmotte, V., P. Zhai, H.
  31. IPCC AR6 (2021). Climate Change 2021: The Physical Science Basis. IPCC Sixth Assessment Report Working Group 1.
  32. Karl, T.R., Kukla, G., Razuvayev, V.N., Changery, M.J., Quayle, R.G., Heim Jr., R.R., Easterling, D.R. and Fu, C.B. (1991). Global Warming: Evidence for asymmetric diurnal temperature change. Geophysical Research Letters, 18(12), 2253-2256.
  33. Kruger, A. C.; Sekele, S. S. Trends in extreme temperature indices in South Africa: 1962-2009. International Journal of Climatology 2012, 33, 661โ€“676. [Google Scholar] [CrossRef]
  34. Kruger, Andries C.; Nxumalo, M. Surface temperature trends from homogenized time series in South Africa: 1931-2015. International Journal of Climatology 2016, 37, 2364โ€“2377. [Google Scholar] [CrossRef]
  35. Lee, Dongin; Schmidt, Peter. On the power of the KPSS test of stationarity against fractionally-integrated alternatives. Journal of Econometrics 1996, 73, 285โ€“302. [Google Scholar] [CrossRef]
  36. Ludescher, Josef; unde; rmin; ranzke; E, Christian L.; Schellnhuber, Hans Joachim. Long-term persistence enhances uncertainty about anthropogenic warming of Antarctica. Climate Dynamics 2015, 46, 263โ€“271. [Google Scholar] [CrossRef]
  37. Marinucci, D; Robinson, P.M. Semiparametric fractional cointegration analysis. Journal of Econometrics 2001, 105, 225โ€“247. [Google Scholar] [CrossRef]
  38. Montanari, Alberto; osso; enzo; Taqqu, Murad S. Some long-run properties of rainfall records in Italy. Journal of Geophysical Research: Atmospheres 1996, 101, 29431โ€“29438. [Google Scholar] [CrossRef]
  39. Muthoni, F. (2020). Spatial-Temporal Trends of Rainfall, Maximum and Minimum Temperatures Over West Africa IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 13, 2960-2973.
  40. New, M., B. Hewitson, D.B. Stephenson, A. Tsiga, A. Kruger, A. Manhique, B. Gomez, C.A.S. Coelho and Co-authors (2006). Evidence of trends in daily climate extremes over southern and west Africa. Journal of Geophyical Researchโ€“Atmosphere., 111, D14102. [CrossRef]
  41. Neumann, Rebekka; ung; erlinde; aux; atrick; Kunstmann, Harald. Climate trends of temperature, precipitation and river discharge in the Volta Basin of West Africa. International Journal of River Basin Management 2007, 5, 17โ€“30. [Google Scholar] [CrossRef]
  42. Ngarukiyimana, J; a review: B., Ruhinda, B., & Mupenzi, J. (2020). Climate change and adaptation strategies for agricultural sector in Rwanda: a review. Environment, Development and Sustainability, 22(1), 209-233.
  43. Nicholls N, Gruza GV, Jouzel J, Karl TR, Ogallo LA, Parker DE (1996). Observed climate variability and change. In: Houghton JT, Meiro Filho LG, Callendar BA, Kattenburg A, Maskell K (eds) Climate change 1995: The Science of Climate Change. Cambridge University Press, Cambridge, p 133โ€“192.
  44. Nielsen, M.O. (2015), Multivariate fractional integration and cointegration, Doctoral thesis, in Economics, University of Aarhus, Denmark.
  45. Ogunsola, O.E.; Yaya, O.S. Maximum and Minimum Temperatures in South-Western Nigeria: Time trends, Seasonality and Persistence. Journal of Physics: Conference Series 2019, 1299, 012057. [Google Scholar] [CrossRef]
  46. Percival, Donald B.; verland; E, James; Mofjeld, Harold O. Interpretation of North Pacific Variability as a Short- and Long-Memory Process*. Journal of Climate 2001, 14, 4545โ€“4559. [Google Scholar] [CrossRef]
  47. Ray, C.A. The Impact of Climate Change on Africaยดs Economies. African Program, Analysis, Foreign Policy Research Institute, Pennsylvania, USA. 2021. Available online: https://www.fpri.org/article/2021/10/the-impact-of-climate-change-on-africas-economies/ (accessed on 16 May 2022).
  48. Robinson, P. M. (1994a). Efficient Tests of Nonstationary Hypotheses. Journal of the American Statistical Association, 89, 1420โ€“1437.
  49. Robinson, P. M. Semiparametric Analysis of Long-Memory Time Series. The Annals of Statistics, 22 1994. [Google Scholar] [CrossRef]
  50. Robinson, P. M. Gaussian Semiparametric Estimation of Long Range Dependence. The Annals of Statistics 1995, 23, 1630โ€“1661. [Google Scholar] [CrossRef]
  51. Robinson, P. M.; Hidalgo, F. J. Time series regression with long-range dependence. The Annals of Statistics 1997, 25, 77โ€“104. [Google Scholar] [CrossRef]
  52. Robinson, Peter M.; Yajima, Yoshihiro. Determination of cointegrating rank in fractional systems. Journal of Econometrics 2002, 106, 217โ€“241. [Google Scholar] [CrossRef]
  53. Shepard, D. Global warming: severe consequences for Africa. United Nations African Renewal. 2019. Available online: https://www.un.org/africarenewal/magazine/december-2018-march-2019/global-warming-severe-consequences-africa (accessed on 16 May 2022).
  54. Stephenson, D.B.; Pavan, V.; ojariu. Is the North Atlantic oscillation a random walk? International Journal of Climatology, 2000, 20, 1โ€“18. [Google Scholar] [CrossRef]
  55. Yaya, O. S. Yaya, O. S. (2022). Compendium of Time Series Econometrics with Applications. Ibadan University Printery, Nigeria.
  56. Yaya, O. S. and Vo, X. V. (2020). Statistical Analysis of Rainfall and Temperature (1901-2016) in South-East Asian Region. Theoretical and Applied Climatology, 142, 287โ€“303.
  57. Yaya, O. Yaya, O., Ogbonna, A.E., Gil-Alana, L.A. and Furuoka, F. (2021). A new unit root analysis for testing hysteresis in unemployment, Oxford Bulletin of Economics and Statistics 83(4), 960-981.
  58. World Bank. Climate change knowledge portal. 2021. Available online: https://climateknowledgeportal.worldbank.org/.
Preprints 80150 g001
Figure 1. Map of Africa showing all countries.
Figure 1. Map of Africa showing all countries.
Preprints 80150 g001
Preprints 80150 g002
Figure 1. Time plots of Maximum and Minimum temperatures in Africa (Chad, Egypt, Guinea, Kenya, Nigeria and South Africa).
Figure 1. Time plots of Maximum and Minimum temperatures in Africa (Chad, Egypt, Guinea, Kenya, Nigeria and South Africa).
Preprints 80150 g002
Table 1. Data Summary.
Table 1. Data Summary.
Country Max.Temp (0C) Min.Temp (0C) Range (0C)
1901 2021 1901 2021 1901 2021
Angola 28.18 28.60 14.51 14.93 13.67 13.67
Benin 33.23 34.47 21.58 22.98 11.65 11.49
Botswana 29.08 29.81 13.16 13.72 15.92 16.09
Burkina Faso 34.46 36.27 21.78 23.81 12.68 12.46
Cameroon 29.51 30.59 18.84 19.87 10.67 10.72
Central Afr. Rep. 31.34 32.16 18.60 19.45 12.74 12.71
Chad 34.58 35.42 19.32 20.06 15.26 15.36
Congo 28.77 29.77 19.72 20.73 9.05 9.04
Cote dโ€™รvoire 31.67 32.54 21.42 22.26 10.25 10.28
Egypt 29.64 31.27 14.69 16.53 14.95 14.74
Gabon 28.69 29.84 20.36 21.51 8.33 8.33
Ghana 32.17 33.4 21.97 23.25 10.2 10.15
Guinea 31.57 32.53 19.86 20.69 11.71 11.84
Guinea-Bissau 33.74 34.99 21.4 22.59 12.34 12.40
Kenya 30.28 31.11 18.51 19.39 11.77 11.72
Lesotho 17.24 19.45 4.35 5.11 12.89 14.34
Liberia 30.38 30.50 21.17 21.30 9.21 9.20
Libya 28.77 29.87 15.21 16.28 13.56 13.59
Madagascar 27.39 27.63 17.92 18.16 9.47 9.47
Malawi 27.23 28.10 16.41 17.54 10.82 10.56
Mali 35.28 36.93 20.99 22.68 14.29 14.25
Mauritania 34.65 36.02 21.27 22.62 13.38 13.40
Morocco 23.26 24.52 11.39 12.49 11.87 12.03
Namibia 27.34 27.62 12.28 12.66 15.06 14.96
Niger 34.77 35.70 19.99 20.52 14.78 15.18
Nigeria 32.63 33.74 20.69 21.65 11.94 12.09
Rwanda 24.88 25.29 12.78 13.19 12.10 12.10
Sierra Leone 31.69 32.25 21.70 22.18 9.99 10.07
Senegal 35.51 36.91 21.09 22.39 14.42 14.52
South Africa 24.25 25.73 9.55 10.44 14.70 15.29
Sudan 35.61 35.89 19.92 20.51 15.69 15.38
Tanzania 27.90 28.50 16.53 17.55 11.37 10.95
Tunisia 25.20 27.07 12.97 15.65 12.23 11.42
Uganda 28.67 29.34 16.55 17.14 12.12 12.20
Zambia 28.50 29.06 14.60 15.22 13.90 13.84
Zimbabwe 27.80 28.64 14.25 15.14 13.55 13.50
Table 2. Results of ADF Unit root test.
Table 2. Results of ADF Unit root test.
Country Max.Temp (0C) Min.Temp (0C) Range (0C)
none Intercept Intercept + Trend none Intercept Intercept + Trend none Intercept Intercept + Trend
Angola 0.3171[2] -3.1469[1] -4.5576[1] 0.3355[2] -3.1752[1] -5.5564[0] 0.0020[4] -5.6877[1] -5.7386[1]
Benin 0.3490[2] -3.9137[1] -3.9400[1] 0.4778[3] -2.6479[1] -5.0183[0] -0.1613[1] -3.3023[1] -5.7028[0]
Botswana 0.3105[2] -2.5926[2] -7.6741[0] 0.2941[2] -4.6700[0] -7.1066[0] 0.1823[4] -8.9667[0] -9.3857[0]
Burkina Faso 0.3541[1] -5.7067[0] -6.3192[0] 0.5060[3] -3.4801[0] -5.3749[0] -0.2151[2] -2.8794[1] -4.1499[1]
Cameroon 0.5978[3] -6.8662[0] -7.5844[0] 0.6235[2] -2.2884[2] -2.7278[2] -0.1049[3] -8.0343[0] -8.0094[0]
Central Afr. Rep. 0.5203[2] -2.4402[2] -3.2942[2] 0.5388[2] -2.1126[2] -3.0607[2] -0.4083[4] -2.7591[2] -3.2665[2]
Chad 0.4917[2] -1.5969[2] -2.1705[2] 0.4425[2] -1.5745[2] -2.4938[2] 0.0663[2] -3.2194[2] -6.7898[0]
Congo 0.7671[2] -1.5726[2] -2.5181[2] 0.7625[2] -1.5746[2] -2.5178[2] -0.3702[7] -10.4267[0] -10.3999[0]
Cote dโ€™รvoire 0.6385[3] -2.2845[2] -2.9577[2] 0.4687[3] -4.2075[0] -5.5144[0] 0.0725[1] -3.8767[1] -4.3940[1]
Egypt 1.3401[5] -2.4317[2] -2.8386[2] 0.8076[2] -2.2244[2] -2.9386[2] -0.1216[3] -2.2496[3] -7.6871[0]
Gabon 0.8330[2] -1.4901[2] -2.3948[2] 0.8256[2] -1.4763[2] -2.3920[2] 0.1416[3] -10.1007[0] -10.1330[0]
Ghana 0.5132[2] -3.4754[1] -3.7306[1] 0.4655[3] -3.8136[0] -5.1423[0] -0.0556[2] -.34082[1] -4.4562[1]
Guinea 0.6804[3] -1.4924[2] -2.5401[2] 0.3832[2] -1.9008[2] -5.5536[0] 0.1458[1] -3.4493[1] -3.6109[1]
Guinea-Bissau 0.7792[3] -0.6981[3] -1.9087[3] 0.6523[3] -1.6596[2] -2.8914[2] 0.0566[1] -5.5719[0] -5.7066[0]
Kenya 0.2804[2] -1.7647[2] -5.8075[0] 0.3017[2] -1.6298[2] -6.2287[0] -0.1759[2] -9.8508[0] -10.3136[0]
Lesotho 1.2995[4] -1.9224[2] -6.8761[0] 0.6396[3] -1.7927[3] -8.3858[0] 0.9444[4] -3.4123[1] -3.8653[1]
Liberia 0.1592[2] -2.4895[2] -2.88994[2] 0.1373[2] -2.5105[2] -2.9140[2] 0.0055[1] -3.4392[1] -3.43039[1]
Libya 0.8349[3] -1.6497[2] -2.8180[2] 1.0739[4] -1.5606[2] -2.7181[2] 0.0138[3] -3.2888[2] -3.2934[2]
Madagascar 0.0635[2] -2.1187[2] -1.9551[2] 0.0487[2] -2.1117[2] -1.9450[2] 0.3742[4] -11.5073[0] -11.5446[0]
Malawi 0.2509[2] -2.7236[2] -7.6837[0] 0.8124[5] -5.4000[0] -6.7249[0] -0.2075[3] -8.4672[0] -8.4866[0]
Mali 0.3529[1] -3.5324[1] -6.9707[0] 0.3714[1] -2.7152[1] -5.9485[0] -0.0972[2] -3.1696[1] -3.6366[1]
Mauritania 0.5921[3] -1.5369[3] -8.0244[0] 0.5942[3] -1.3504[3] -6.4320[0] -0.0422[1] -5.4342[0] -5.4130[0]
Morocco 0.7185[2] -1.3661[2] -2.9879[2] 0.4502[2] -2.8884[1] -4.5408[1] 0.1326[1] -5.8760[0] -7.1333[0]
Namibia 0.2682[2] -4.3714[0] -5.8074[0] 0.4270[3] -3.8688[0] -5.4211[0] -0.1240[1] -5.3411[1] -5.4117[1]
Niger 0.2721[2] -2.5021[2] -2.6363[2] 0.2250[3] -1.9597[3] -3.1829[2] 0.0795[2] -3.0056[2] -3.1562[2]
Nigeria 0.4313[3] -3.0302[2] -3.1060[2] 0.4166[2] -2.1146[2] -2.6235[2] -0.3924[5] -5.3338[1] -8.1575[0]
Rwanda 0.1542[2] -1.5675[2] -5.2979[0] 0.1774[2] -1.9275[2] -6.3444[0] -0.1543[2] -3.4441[1] -3.5358[1]
Sierra Leone 0.3976[2] -1.5657[2] -2.3501[2] 0.3002[2] -1.9091[2] -2.6355[2] 0.2008[2] -3.2376[1] -3.3123[1]
Senegal 0.7078[3] -1.0306[3] -6.1205[0] 0.4334[2] -2.0313[2] -6.1411[0] 0.0830[1] -5.3179[0] -5.5103[0]
South Africa 0.9217[3] -2.1540[2] -6.4079[0] 0.9368[3] -1.5133[3] -8.3558[0] 0.5516[4] -4.0968[1] -4.2192[1]
Sudan 0.2813[2] -2.0396[2] -2.3404[2] 0.5028[2] -1.2508[2] -2.3882[2] -0.5557[3] -0.9761[3] -6.9848[0]
Tanzania 0.2266[2] -1.7813[2] -6.7236[0] 0.4748[2] -1.4784[2] -6.4684[0] -0.2570[1] -4.5037[1] -4.4851[1]
Tunisia 1.1141[3] -0.6051[3] -4.5628[1] 1.0992[3] -0.9542[3] -3.9033[1] -0.3608[1] -6.2147[0] -6.3774[0]
Uganda 0.2406[2] -1.6153[2] -5.3460[0] 0.2176[2] -1.5610[2] -6.0091[0] -0.0973[2] -8.7951[0] -8.8230[0]
Zambia 0.1086[2] -3.6010[1] -4.7715[1] 0.2810[4] -5.5308[0] -6.4403[0] -0.0471[3] -4.3075[1] -4.5314[1]
Zimbabwe 0.1805[2] -2.5659[2] -8.0439[0] 0.6485[5] -5.6556[0] -7.2592[0] -0.0185[4] -9.1363[0] -9.4686[0]
Note: significant unit root test t-statistics at 5% level are in bold. In squared brackets are optimal lag length of the augmentation component, selected based on minimum information criteria.
Table 3. Results of fractional integration based on linear trend.
Table 3. Results of fractional integration based on linear trend.
Country Max.Temp (0C) Min.Temp (0C) Range (0C)
d Intercept Trend d Intercept Trend d Intercept Trend
Angola 0.31 (0.17, 0.45) -0.2675 (-2.68) 0.0045 (3.45) 0.37 (0.22, 0.52) -0.2532 (-2.39) 0.0043 (3.10) 0.11 (-0.03, 0.26) -0.0131 (-0.61) 0.0002 (0.75)
Benin 0.43 (0.29, 0.58) -0.1435 (-0.47) 0.0034 (0.84) 0.52 (0.37, 0.67) -0.4087 (-1.11) 0.0094 (1.97) 0.49 (0.32, 0.66) 0.2755 (0.97) -0.0057 (-1.54)
Botswana 0.26 (0.11, 0.41) -0.6811 (-3.61) 0.0115 (4.61) 0.30 (0.15, 0.45) -0.5774 (-3.66) 0.0096 (4.64) 0.13 (-0.02, 0.28) -0.1067 (-1.57) 0.0018 (1.90)
Burkina Faso 0.41 (0.25, 0.57) -0.2738 (-0.88) 0.0059 (1.47) 0.50 (0.34, 0.67) -0.5762 (-1.41) 0.0125 (2.40) 0.49 (0.34, 0.64) 0.3700 (1.37) -0.0066 (-1.88)
Cameroon 0.26 (0.11, 0.42) -0.1617 (-1.48) 0.0030 (2.11) 0.35 (0.23, 0.48) -0.1904 (-1.36) 0.0039 (2.16) 0.24 (0.09, 0.39) 0.0350 (0.34) -0.0007 (-0.52)
Central Afr. Rep. 0.40 (0.25, 0.55) -0.2546 (-1.64) 0.0047 (2.34) 0.41 (0.27, 0.55) -0.2927 (-1.76) 0.0056 (2.57) 0.25 (0.13, 0.37) 0.0459 (1.54) -0.0008 (-2.14)
Chad 0.47 (0.34, 0.59) -0.3542 (-1.43) 0.0069 (2.14) 0.47 (0.34, 0.60) -0.3864 (-1.61) 0.0075 (2.42) 0.36 (0.22, 0.51) 0.0398 (0.61) -0.0007 (-0.88)
Congo 0.38 (0.24, 0.52) -0.2349 (-1.71) 0.0047 (2.64) 0.38 (0.24, 0.53) -0.2347 (-1.69) 0.0047 (2.62) 0.03 (-0.14, 0.19) -0.0003 (-1.11) 5.02e-06 (0.47)
Cote dโ€™รvoire 0.38 (0.24, 0.52) -0.2606 (-1.49) 0.0050 (2.17) 0.46 (0.31, 0.62) -0.2986 (-1.32) 0.0063 (2.13) 0.41 (0.26, 0.56) 0.0449 (0.36) -0.0011 (-0.67)
Egypt 0.36 (0.23, 0.49) -0.7025 (-2.48) 0.0110 (3.07) 0.33 (0.21, 0.46) -0.7595 (-2.97) 0.0126 (3.78) 0.28 (0.14, 0.43) 0.0964 (1.57) -0.0018 (-2.29)
Gabon 0.35 (0.22, 0.48) -0.2371 (-1.87) 0.0047 (2.86) 0.35 (0.22, 0.48) -0.2368 (-1.86) 0.0047 (2.89) 0.01 (-0.16, 0.17) 0.0010 (1.24) -1.61e-05 (-0.89)
Ghana 0.43 (0.28, 0.57) -0.2533 (-0.10) 0.0051 (1.53) 0.52 (0.36, 0.69) -0.3394 (-1.00) 0.0082 (1.87) 0.44 (0.29, 0.59) 0.1312 (0.64) -0.0031 (-1.17)
Guinea 0.48 (0.34, 0.61) -0.2960 (-1.20) 0.0069 (2.14) 0.43 (0.29, 0.58) -0.2351 (-1.15) 0.0052 (1.96) 0.50 (0.35, 0.65) -0.0652 (-0.49) 0.0015 (0.88)
Guinea-Bissau 0.43 (0.29, 0.56) -0.3678 (-1.56) 0.0080 (2.62) 0.40 (0.27, 0.54) -0.3134 (-1.48) 0.0068 (2.47) 0.49 (0.32, 0.65) -0.0597 (-0.44) 0.0012 (0.70)
Kenya 0.51 (0.34, 0.69) -0.8421 (-2.04) 0.0138 (2.57) 0.46 (0.29, 0.63) -0.8897 (-2.60) 0.0148 (3.32) 0.01 (-0.15, 0.16) 0.0590 (2.18) -0.0010 (-2.51)
Lesotho 0.33 (0.18, 0.48) -1.2242 (-4.65) 0.0204 (5.91) 0.17 (0.01, 0.34) -0.8300 (-7.89) 0.0133 (9.46) 0.39 (0.26, 0.52) -0.3765 (-1.35) 0.0076 (2.07)
Liberia 0.46 (0.33, 0.60) -0.1529 (-0.79) 0.0033 (1.31) 0.47 (0.33, 0.61) -0.1567 (-0.77) 0.0034 (1.26) 0.52 (0.37, 0.67) 0.0009 (0.02) -1.9E-6 (-3.4E-3)
Libya 0.30 (0.18, 0.41) -0.5191 (-3.56) 0.0088 (4.62) 0.31 (0.19, 0.43) -0.5245 (-3.58) 0.0089 (4.66) 0.29 (0.16, 0.41) 0.0056 (0.18) -0.0001 (-0.27)
Madagascar 0.50 (0.37, 0.63) 0.2853 (1.04) -0.0014 (-0.41) 0.50 (0.37, 0.63) 0.2848 (1.04) -0.0014 (-0.41) 0.09 (-0.05, 0.24) -0.0007 (-2.13) 1.17e-05 (1.02)
Malawi 0.27 (0.14, 0.40) -0.3624 (-2.27) 0.0065 (3.10) 0.34 (0.19, 0.49) -0.3209 (-1.85) 0.0061 (2.74) 0.21 (0.05, 0.36) -0.0315 (-0.34) 0.0005 (0.37)
Mali 0.34 (0.17, 0.50) -0.4459 (-2.03) 0.0082 (2.91) 0.44 (0.28, 0.60) -0.5188 (-1.81) 0.1002 (2.81) 0.47 (0.33, 0.60) 0.1233 (0.84) -0.0022 (-1.14)
Mauritania 0.24 (0.11, 0.38) -0.5051 (-3.45) 0.0089 (4.62) 0.37 (0.23, 0.51) -0.4718 (-2.30) 0.0088 (3.33) 0.54 (0.37, 0.72) 0.0044 (0.02) 0.0001 (0.04)
Morocco 0.31 (0.19, 0.43) -0.7799 (-3.99) 0.0131 (5.12) 0.33 (0.19, 0.47) -0.6570 (-3.10) 0.0110 (3.95) 0.32 (0.16, 0.48) -0.1260 (-1.88) 0.0022 (2.54)
Namibia 0.43 (0.27, 0.59) -0.3729 (-2.03) 0.0063 (2.62) 0.46 (0.30, 0.62) -0.3898 (-2.06) 0.0067 (2.72) 0.16 (0.01, 0.31) 0.0302 (0.63) -0.0005 (-0.82)
Niger 0.38 (0.25, 0.51) -0.2735 (-0.97) 0.0051 (1.37) 0.40 (0.26, 0.54) -0.3080 (-1.20) 0.0059 (1.78) 0.47 (0.32, 0.62) 0.0149 (0.06) -0.0006 (-0.20)
Nigeria 0.34 (0.20, 0.47) -0.1288 (-0.64) 0.0028 (1.05) 0.44 (0.30, 0.58) -0.2389 (-0.93) 0.0055 (1.65) 0.23 (0.08, 0.38) 0.1611 (1.47) -0.0028 (-1.94)
Rwanda 0.56 (0.40, 0.72) -0.7239 (-2.07) 0.0112 (2.45) 0.43 (0.27, 0.60) -0.5405 (-2.36) 0.0092 (3.11) 0.49 (0.35, 0.63) -0.1847 (-0.67) 0.0022 (0.62)
Sierra Leone 0.49 (0.36, 0.63) -0.2284 (-0.98) 0.0054 (1.76) 0.47 (0.33, 0.60) -0.1962 (-0.92) 0.0045 (1.61) 0.54 (0.39, 0.68) -0.0289 (-0.29) 0.0008 (0.60)
Senegal 0.38 (0.24, 0.51) -0.4027 (-1.73) 0.0084 (2.79) 0.38 (0.24, 0.52) -0.3206 (-1.48) 0.0068 (2.44) 0.51 (0.34, 0.67) -0.0793 (-0.50) 0.0016 (0.79)
South Africa 0.37 (0.22, 0.52) -0.9884 (-3.81) 0.0164 (4.85) 0.17 (0.01, 0.33) -0.7896 (-8.70) 0.0129 (10.60) 0.34 (0.21, 0.47) -0.1684 (-0.95) 0.0032 (1.39)
Sudan 0.41 (0.29, 0.54) -0.5250 (-1.55) 0.0085 (1.92) 0.45 (0.32, 0.57) -1.0093 (-2.94) 0.0162 (3.65) 0.35 (0.22, 0.48) 0.4540 (4.03) -0.0075 (-5.12)
Tanzania 0.39 (0.22, 0.56) -0.6903 (-3.13) 0.0113 (3.94) 0.41 (0.24, 0.57) -0.6844 (-2.97) 0.0119 (4.01) 0.40 (0.24, 0.56) -0.0020 (-0.01) -0.0006 (-0.28)
Tunisia 0.30 (0.17, 0.42) -1.0054 (-5.14) 0.0170 (6.60) 0.37 (0.24, 0.50) -0.9363 (-3.78) 0.0162 (5.02) 0.42 (0.27, 0.58) -0.0873 (-0.50) 0.0010 (0.44)
Uganda 0.58 (0.41, 0.76) -0.8968 (-1.93) 0.0141 (2.32) 0.48 (0.32, 0.65) -0.8757 (-2.52) 0.0147 (3.25) 0.48 (0.32, 0.65) 0.0270 (0.34) -0.0006 (-0.52)
Zambia 0.28 (0.15, 0.41) -0.4044 (-2.09) 0.0072 (2.86) 0.37 (0.22, 0.52) -0.2876 (-1.42) 0.0052 (1.97) 0.37 (0.22, 0.52) -0.0920 (-0.54) 0.0019 (0.83)
Zimbabwe 0.24 (0.11, 0.38) -0.5374 (-2.75) 0.0094 (3.66) 0.30 (0.14, 0.45) -0.4260 (-2.30) 0.0076 (3.14) 0.30 (0.14, 0.45) -0.1163 (-1.24) 0.0020 (1.55)
Note, significant linear trend coefficients (intercept or trend) at 5% level one-sided test (t > 1.64) are in bold with t-statistics in parentheses. For fractional d values, standard errors are in parentheses.
Table 4. Summary of Results in Table 3.
Table 4. Summary of Results in Table 3.
Country Evidence of significant trend increase Evidence of dRange < min (dMax.Temp, dMin.Temp)
Angola ๐Ÿ—ธ ๐Ÿ—ธ
Benin ๐Ÿ—ธ
Botswana ๐Ÿ—ธ ๐Ÿ—ธ
Burkina Faso ๐Ÿ—ธ
Cameroon ๐Ÿ—ธ ๐Ÿ—ธ
Central Afr. Rep. ๐Ÿ—ธ ๐Ÿ—ธ
Chad ๐Ÿ—ธ ๐Ÿ—ธ
Congo ๐Ÿ—ธ ๐Ÿ—ธ
Cote dโ€™รvoire ๐Ÿ—ธ
Egypt ๐Ÿ—ธ ๐Ÿ—ธ
Gabon ๐Ÿ—ธ ๐Ÿ—ธ
Ghana ๐Ÿ—ธ ๐Ÿ—ธ
Guinea ๐Ÿ—ธ ๐Ÿ—ธ
Guinea-Bissau ๐Ÿ—ธ ๐Ÿ—ธ
Kenya ๐Ÿ—ธ ๐Ÿ—ธ
Lesotho ๐Ÿ—ธ ๐Ÿ—ธ
Liberia
Libya ๐Ÿ—ธ ๐Ÿ—ธ
Madagascar ๐Ÿ—ธ ๐Ÿ—ธ
Malawi ๐Ÿ—ธ ๐Ÿ—ธ
Mali ๐Ÿ—ธ
Mauritania ๐Ÿ—ธ
Morocco ๐Ÿ—ธ
Namibia ๐Ÿ—ธ ๐Ÿ—ธ
Niger ๐Ÿ—ธ
Nigeria ๐Ÿ—ธ ๐Ÿ—ธ
Rwanda ๐Ÿ—ธ
Sierra Leone
Senegal ๐Ÿ—ธ
South Africa ๐Ÿ—ธ
Sudan ๐Ÿ—ธ ๐Ÿ—ธ
Tanzania ๐Ÿ—ธ
Tunisia ๐Ÿ—ธ
Uganda ๐Ÿ—ธ ๐Ÿ—ธ
Zambia ๐Ÿ—ธ
Zimbabwe ๐Ÿ—ธ ๐Ÿ—ธ
Table 5. Results of Homogeneity of paired persistence parameters for maximum and minimum temperatures.
Table 5. Results of Homogeneity of paired persistence parameters for maximum and minimum temperatures.
Country T 0.5 T 0.6
Angola 0.1315 0.2008
Benin 1.0788 0.3417
Botswana 0.3511 0.2472
Burkina Faso 1.9117 0.7278
Cameroon 0.1519 0.7277
Central Afr. Rep. 0.3209 0.3103
Chad 0.4145 0.4604
Congo 0.0107 0.0224
Cote dโ€™รvoire 0.7076 0.2825
Egypt 0.2899 0.2687
Gabon 0.0356 0.0143
Ghana 1.1170 0.0722
Guinea 0.1387 0.5569
Guinea-Bissau 0.1917 0.0568
Kenya 0.4196 0.0586
Lesotho 0.7969 0.7003
Liberia 0.0343 0.0833
Libya 0.1445 0.3202
Madagascar 0.0066 0.0013
Malawi 0.0669 0.8570
Mali 1.1013 0.6679
Mauritania 0.5987 0.4710
Morocco 0.7275 0.9893
Namibia 0.1210 0.4668
Niger 0.1434 0.4195
Nigeria 0.5054 0.7256
Rwanda 0.2099 0.6325
Sierra Leone 0.0190 0.3437
Senegal 0.0281 0.2062
South Africa 0.4934 0.6006
Sudan 0.4931 0.3506
Tanzania 0.0358 0.6058
Tunisia 0.9987 0.1570
Uganda 0.3072 0.4192
Zambia 0.0084 0.5026
Zimbabwe 0.0262 0.4947
Recall, homogeneity of fractional d is normally distributed, therefore the two-sided test is rejected based on critical value of 1.96 at 5% level.
Table 6. Estimated regression coefficients for the NBFDLS (Narrow Band Frequency Domain Least Square).
Table 6. Estimated regression coefficients for the NBFDLS (Narrow Band Frequency Domain Least Square).
Country T 0.5 T 0.6
Angola 1.0598 1.0343
Benin 0.5121 0.4858
Botswana 1.1830 1.1676
Burkina Faso 0.5179 0.5152
Cameroon 0.5366 0.5421
Central Afr. Rep. 0.8510 0.8574
Chad 0.9659 0.9600
Congo 0.9994 0.9991
Cote dโ€™รvoire 0.7146 0.7051
Egypt 0.9012 0.9053
Gabon 0.9992 0.9996
Ghana 0.5931 0.5708
Guinea 1.1052 1.0813
Guinea-Bissau 1.0649 1.0491
Kenya 0.9676 0.9627
Lesotho 1.2112 1.2209
Liberia 0.9692 0.9693
Libya 0.9775 0.9809
Madagascar 1.0008 1.0007
Malawi 1.0256 0.9424
Mali 0.7598 0.7629
Mauritania 0.8452 0.8394
Morocco 1.1145 1.0847
Namibia 0.9024 0.9077
Niger 0.8349 0.8087
Nigeria 0.6811 0.6637
Rwanda 1.0121 0.9834
Sierra Leone 1.0469 1.0342
Senegal 1.0694 1.0512
South Africa 1.1596 1.1726
Sudan 0.6717 0.6733
Tanzania 0.9103 0.8871
Tunisia 0.9855 0.9785
Uganda 0.9589 0.9506
Zambia 1.0194 0.9536
Zimbabwe 1.1875 1.1152
Table 7. Estimates of d in the NBFDLS regression.
Table 7. Estimates of d in the NBFDLS regression.
Country m = T0.5 m = T0.6 Evidence of d smaller than in individual series
m = T0.5 m = T0.6
Angola 0.14 (-0.05, 0.42) + 0.15 (-0.03, 0.43) + ๐Ÿ—ธ ๐Ÿ—ธ
Benin 0.44 (0.26, 0.75) 0.46 (0.26, 0.75) ๐Ÿ—ธ
Botswana -0.20 (-0.41, 0.11) + 0.11 (-0.16, 0.43) + ๐Ÿ—ธ ๐Ÿ—ธ
Burkina Faso 0.43 (0.19, 0.88) 0.43 (0.19, 0.88) ๐Ÿ—ธ
Cameroon 0.06 (-0.10, 0.31) + 0.06 (-0.12, 0.32) + ๐Ÿ—ธ ๐Ÿ—ธ
Central Afr. Rep. 0.31 (0.13, 0.57) 0.31 (0.15, 0.57) ๐Ÿ—ธ ๐Ÿ—ธ
Chad 0.51 (0.30, 0.82) 0.51 (0.30, 0.81)
Congo 0.00 (-0.19, 0.29) + 0.02 (-0.19, 0.28) + ๐Ÿ—ธ ๐Ÿ—ธ
Cote dโ€™รvoire 0.48 (0.27, 0.80) 0.47 (0.26, 0.79)
Egypt 0.42 (0.29, 0.61) 0.42 (0.29, 0.58)
Gabon -0.10 (-0.28, 0.18) + -0.08 (-0.27, 0.19) + ๐Ÿ—ธ ๐Ÿ—ธ
Ghana 0.42 (0.14, 0.77) 0.42 (0.12, 0.78)
Guinea 0.64 (0.38, 1.00) 0.63 (0.36, 0.98)
Guinea-Bissau 0.53 (0.20, 0.96) 0.57 (0.30, 0.91)
Kenya -0.03 (-0.17, 0.23) + -0.02 (-0.18, 0.23) + ๐Ÿ—ธ ๐Ÿ—ธ
Lesotho 0.57 (0.41, 0.77) 0.56 (0.41, 0.77)
Liberia 0.72 (0.43, 1.20) 0.72 (0.43, 1.19)
Libya 0.56 (0.35, 0.82) 0.56 (0.35, 0.83)
Madagascar -0.13 (-0.32, 0.11) + -0.12 (-0.31, 0.12) + ๐Ÿ—ธ ๐Ÿ—ธ
Malawi 0.22 (-0.02, 0.57) + 0.27 (0.04, 0.58) ๐Ÿ—ธ ๐Ÿ—ธ
Mali 0.46 (0.25, 0.82) 0.48 (0.26, 0.83)
Mauritania 0.26 (-0.01, 0.52) + 0.26 (-0.01, 0.62) + ๐Ÿ—ธ
Morocco 0.17 (-0.02, 0.46) + 0.22 (0.05, 0.47) ๐Ÿ—ธ ๐Ÿ—ธ
Namibia 0.20 (-0.03, 0.59) + 0.20 (-0.04, 0.58) + ๐Ÿ—ธ ๐Ÿ—ธ
Niger 0.51 (0.30, 0.76) 0.50 (0.28, 0.76)
Nigeria 0.24 (0.08, 0.46) 0.25 (0.08, 0.45) ๐Ÿ—ธ ๐Ÿ—ธ
Rwanda 0.59 (0.40, 0.89) 0.60 (0.39, 0.71)
Sierra Leone 0.68 (0.38, 1.08) 0.69 (0.40, 1.11)
Senegal 0.42 (0.14, 0.77) 0.43 (0.16, 0.77)
South Africa 0.54 (0.37, 0.76) 0.55 (0.38, 0.74)
Sudan 0.61 (0.45, 0.83) 0.61 (0.46, 0.83)
Tanzania 0.36 (0.12, 0.71) 0.35 (0.13, 0.72) ๐Ÿ—ธ ๐Ÿ—ธ
Tunisia 0.30 (0.15, 0.57) 0.30 (0.15, 0.59) ๐Ÿ—ธ
Uganda 0.28 (0.02, 0.62) 0.29 (0.03, 0.62) ๐Ÿ—ธ ๐Ÿ—ธ
Zambia 0.44 (0.29, 0.66) 0.46 (0.32, 0.65)
Zimbabwe 0.10 (-0.04, 0.31) + 0.14 (0.00, 0.33) ๐Ÿ—ธ ๐Ÿ—ธ
Note, + indicates evidence of I(d=0) in the cointegrating residuals, and these are 11 countries, while evidence of I ( d > 0 )
Disclaimer/Publisherโ€™s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

ยฉ 2024 MDPI (Basel, Switzerland) unless otherwise stated