Prerpints.org logo
Preprint
Article

Bi-SQUID versus dc SQUID in Flux Driven Traveling-Wave Parametric Amplifier

Altmetrics

Downloads

134

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 July 2023

Posted:

10 July 2023

You are already at the latest version

Alerts
Abstract
Characteristics of artificial waveguide lines composed of finite size artificial cells are analyzed and discussed with relation to designing the travelling wave parametric amplifiers. From this point of view, flux driven amplifier suggested recently can be considered as the most successful amplifier design. To increase dynamic range of the amplifier, dc SQUID cells of the artificial line in use can be substituted for bi-SQUID cells. The 1-dB compression points of the amplifier gain are calculated and compared for both types of the cells.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

Parametric amplifiers (PA) are known as ultimate-low-noise amplifiers; however, such conventional cavity-based amplifiers are burdened with a gain-bandwidth trade-off. To overcome the drawback, travelling-wave parametric amplifiers (TWPA) were suggested. TWPAs are based on using waveguide lines with nonlinear reactive parameters (of capacitive or inductive types) such as a kinetic-inductance microwave line [1] or artificial lines composed of lumped cells with nonlinear capacitors or inductances. As far as the superconducting kinetic inductance of Josephson junctions L J = L J 0 / c o s ⁡ ( φ ) is strongly nonlinear (here L J o = Φ 0 / ( 2 π I c ) , Φ 0 = h / ( 2 e ) , I c is the Josephson-junction critical current and φ is the Josephson-junction phase) the artificial lines composed of superconducting cells containing Josephson junctions are generally used in the designs of Josephson Travelling Wave Parametric Amplifiers (JTWPA) [2,3,4,5,6,7,8,9,10,11,12]. The amplifiers capable of working at low and very low temperatures can provide the extremely high sensitivity approaching quantum limit level. Therefore, JTWPA are currently considered as promising readout devices for use in the field of precision quantum measurements (including single-photon detectors), quantum communications and quantum computing (see [13, 14], and review [15]).
However, when the pump and signal waves propagate in the common artificial Josephson line of JTWPA, the attainable gain is limited by depletion of the pump wave [8, 9, 15] since the initial amplitude of the pump wave is restricted by critical current values of the used Josephson junctions. To overcome the problem, a two-line JTWPA design with magnetic flux drive was suggested [16]. In the design, a separate non-Josephson (linear) transmission line is used for the pump wave propagation. This line is inductively coupled with SQUID-like cells of the signal artificial line and therefore the pump wave produces a travelling wave of magnetic flux applied to the signal line cells. This magnetic flux wave provides modulation of the cell inductances in the travelling-wave fashion.
In this paper, we discuss characteristics of the artificial waveguide lines composed of lumped element cells in connection with designing the Josephson travelling wave parametric amplifiers and consider the increase in dynamic range of the two-line flux-driven amplifier by substitution dc SQUID cells for bi-SQUID cells.

2. Effect of finite size of artificial cells

Usually, the JTWPA designs are based on implementation of the artificial right-handed lines containing Josephson junctions, although the left-handed artificial lines can be also used as recently reported in [17]. The right-handed artificial lines correspond to the existing natural distributed waveguide lines. Therefore, the natural distributed lines are often modelled by the right-handed artificial LC-lines under the stipulation that the length of the distributed line pieces described by the lumped LC-cells goes to zero. The limit processing (when L , C → 0 ) leads to telegrapher’s equations and hence to differential wave equation [18].
However, when the lumped cells of the implemented artificial lines model the continuous line pieces of finite length, one should describe the discrete system using discrete-valued equations as it is realized in [19] (versus continuum approximation in [12]) and partly in [16]. Nevertheless, to simplify analysis of the artificial network, many authors consider the structure as a really distributed continuous waveguide line to describe propagation of the pumping, signal and idler waves in the artificial structure using a wave-type equation for continuous medium. In the approach, wave impedance of the artificial line is considered as a real-value impedance Z0 of the corresponding really-distributed waveguide line. However, this is generally incorrect. 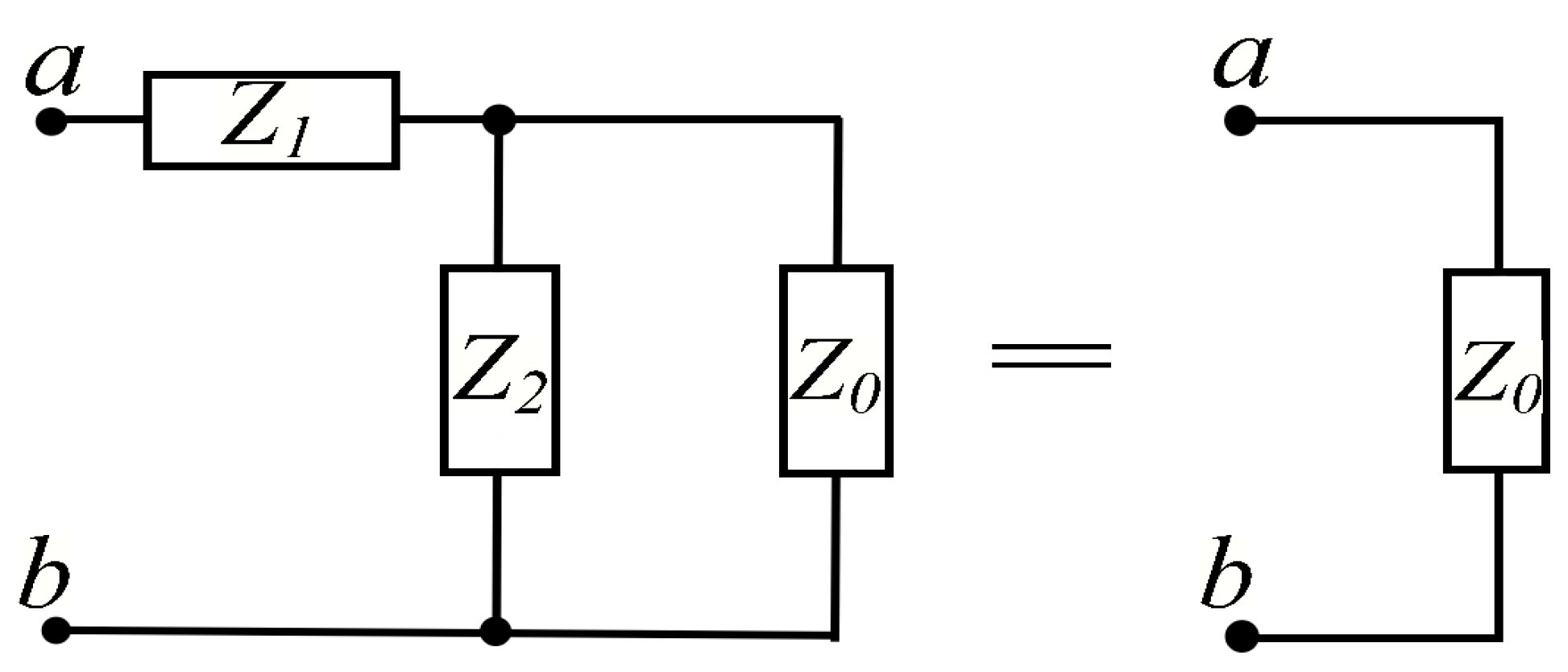Figure 1 illustrates simple reasoning which can be used to calculate wave impedance of the long artificial line, consisting of Z1-Z2 Γ -cells. If Z0 is the wave impedance, then it does not change with connecting same additional cell. This requirement yields in the following equality:
Z 0 = Z 1 / 2 + Z 1 Z 2 + Z 1 2 / 4 .
In case of conventional dissipativeless cell line with the cell element impedances Z 1 = i ω L and Z 2 = ( i ω C ) − 1 , the wave impedance of the artificial line is complex:
Z 0 = i ω L / 2 + L / C − ( ω L ) 2 / 4 = L / C · e i χ ,
χ = a r c s i n ( ω L / 2 ) / L / C = a r c s i n ω / 2 / L C ,
where the angle χ changes from χ = 0 at ω → 0 to χ = π / 2 at cut-off frequency
ω c u t = 2 / L C .
Thus, the wave impedance changes from the real value ρ = L / C at low frequency to imaginary value i ρ at ω → ω c u t . This fact means that the artificial cell line cannot be matched with any constant real-valued impedance over total frequency band up to the cut-off frequency. For example, when the cell line is connected to the real-valued impedance ρ = L / C , reflection factor is imaginary and frequency-dependent:
Γ = ( ρ − Z 0 ) / ( ρ + Z 0 ) = − i · t g ( χ / 2 ) .
Absolute magnitude of the factor changes from Γ = 0 at ω → 0 to Γ = 1 at ω → ω c u t . Of course, the problem vanishes with decreasing the cells size (at L → 0 and C → 0 ), i. e. with limit processing to distributed waveguide line when Z 0 → ρ = L / C .
To mitigate the reflection problem, one could increase the cut-off frequency of the artificial line as compared with frequencies of the pumping, signal and idler signals, however, it leads additionally to intense depleting of the pump wave due to unwanted leak of the pump power to the higher harmonics and intermodulation components occurred in the frequency band ranging up to the cutoff frequency. Besides, the described dependence of the wave impedance on frequency leads automatically to the frequency dependent phase velocity decreasing with frequency.

2.1. One-line amplifier design

In 3-wave operation mode when ω s + ω i = ω p , finding of reasonable trade-off seems very problematic since both the wave reflection and the phase mismatch of the pumping, signal and idler waves enforce setting the cutoff frequency much higher than the wave frequencies, but it does not allow keeping the higher harmonics and the intermodulation components out of the frequency band. The restrictions can be mitigated with using 4-wave operation mode when ω s + ω i = 2 ω p . In this case, all three frequencies ω s , ω i , ω p can be located nearer with each other in the vicinity of ~ ω c u t / 3 so that both the harmonics and the intermodulation components produced by the Kerr nonlinearity are above the cutoff frequency, and reflection factor (at ω c u t / 3 ) is quite moderate: Γ ≃ 0.15 . At the same time, the frequency closeness makes difficulties for efficient filtering out the pump frequency from the amplified signal.

2.2. Two-line amplifier design

The flux driven JTWPA with two-line amplifier design suggested in [16] consists of two coupled separate artificial waveguide lines. The first artificial LC-line, where both the signal and idler waves propagate, is based on using a serial array of dc SQUIDs coupled inductively to the second superconducting LC-transmission line carrying the pumping wave. The latter is linear (non-Josephson) and therefore is free from any limitation on the pump wave amplitude and from energy leakage to higher harmonics as well. The pump signal applies rf magnetic flux Φ r f to the SQUID cells and, due to the cell nonlinear properties, provides modulation of the dipole cell inductances L c e l l (with a depth m) in the wave manner through influence the maximum superconducting current I s m a x of the dc SQUID cell. The inductance modulation can be provided either on the pump frequency when a dc flux bias Φ d c < Φ 0 / 2 is additionally applied:
L c e l l = L c e l l ( Φ d c ≠ 0 ) · 1 + m 1 · cos ⁡ Ω p t − k p x ,
or on the double frequency when no dc flux is applied ( Φ d c = 0 ):
L c e l l = L c e l l ( Φ d c = 0 ) · 1 + m 2 · cos ⁡ 2 Ω p t − 2 k p x .
However, in the latter case, the modulation depth m 2 is considerably less than m 1 due to the approximately c o s -like dependence [20] of the maximum superconducting current I s m a x of dc SQUID on the applied magnetic flux Φ e . At the low loop inductance (as assumed in [16]), I s m a x ≈ 2 I c c o s ⁡ ( φ e / 2 ) , where φ e = 2 π Φ e / Φ 0 , and hence at Φ d c < Φ 0 / 2
I s m a x ≈ 2 I c c o s ⁡ ( φ d c / 2 ) − s i n ⁡ ( φ d c / 2 ) · ( φ r f / 2 ) − 0.5 · c o s ⁡ ( φ d c / 2 ) · ( φ r f / 2 ) 2 ,
where φ d c = 2 π Φ d c / Φ 0 , and φ r f = 2 π Φ r f / Φ 0 is the normalized values of the applied dc and rf magnetic fluxes. This expression shows that dc flux changes the maximum superconducting current (from 2 I c to 2 I c c o s ⁡ ( φ d c / 2 ) ) and hence the dipole inductance of dc SQUID and modulation of the inductance from (7) to (6) with about four times higher modulation depth.
The inductance modulation waves (6) and (7) yield in the signal frequency mixing either to ω p ± ω s or to 2 ω p ± ω s corresponding to 3-wave and 4-wave operation modes, when ω s is the signal frequency and the idler frequency is ω i = ω p − ω s or ω i = 2 ω p − ω s , respectively. In both cases, the signal and idler wave frequencies can be optimally located in the vicinity of ~ ω c u t / 3 , where reflection factor is moderate, Γ ≃ 0.15 , and phase velocities of the waves are quite close to each other: v s ≈ v i ≈ 1 / L C (with using dimensionless coordinate x normalized on the cell length “a”), and therefore can be tuned closely to phase velocity of the pump wave propagating in the second line. For example, when one sets the pump frequency ω p ≃ ( 3 / 4 ) · ω c u t in 3-wave mode or 2 ω p ≃ ( 3 / 4 ) · ω c u t in 4-wave mode, the signal and idler frequency band can be ranged from ω s ≃ ω c u t / 4 to ω s ≃ ω c u t / 2 , that enables eliminating wave components at frequencies ω p + ω s , i > ω c u t and 2 ω p + ω s , i > ω c u t , respectively, and decreasing reflection factor at signal frequency ω s and idler frequency ω i down to Γ ≲ 0.2 . 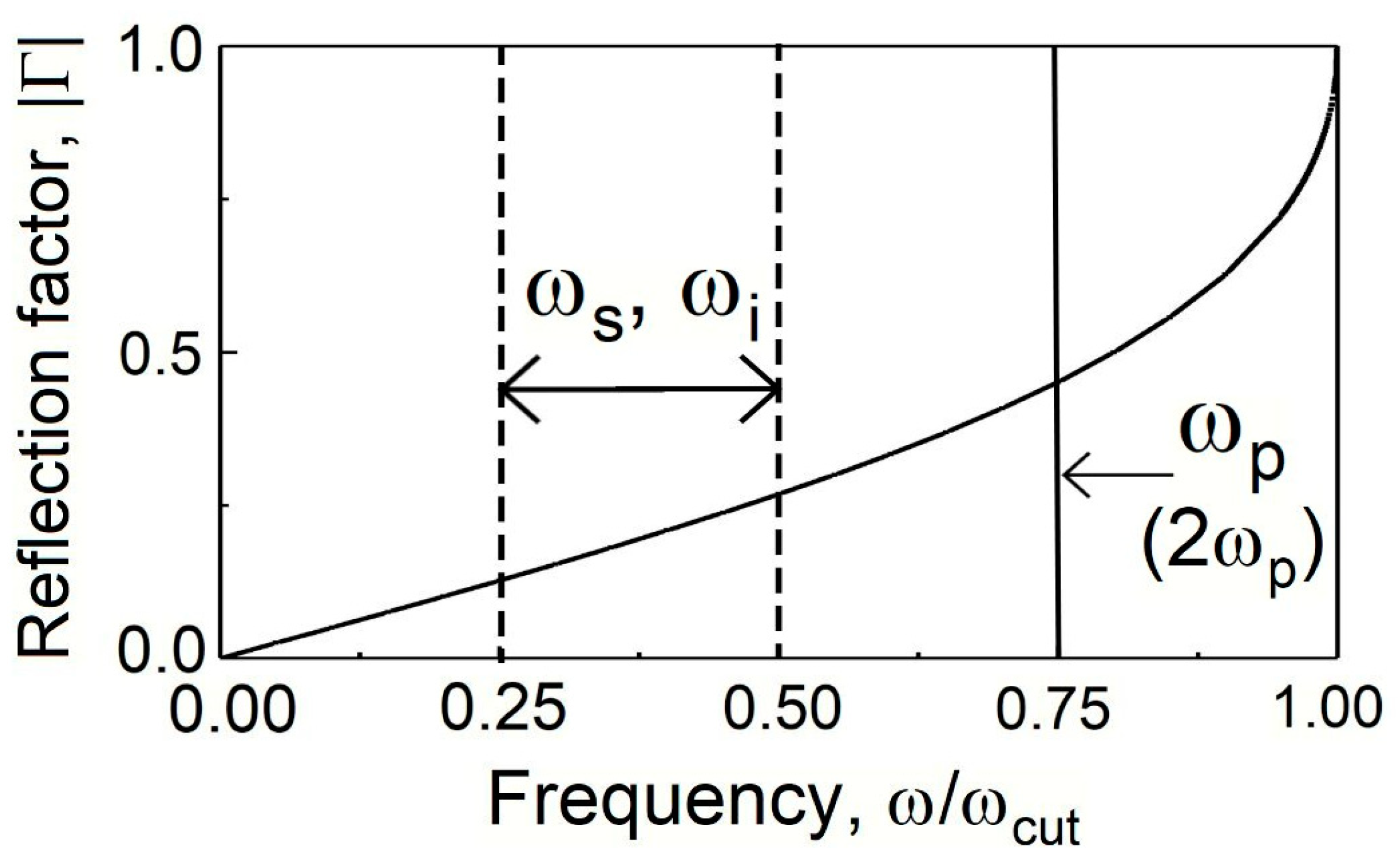Figure 2 shows reflection factor Γ ( ω ) for the artificial waveguide line of lumped L and C elements which is connected to resistor R = ρ ≡ L / C , as well as optimal values of both the pump wave frequency ω p in 3-wave mode (or double frequency 2 ω p in 4-wave mode) and the frequency range for signal and idler waves.

3. Increase in dynamic range with using bi-SQUID cells

Dynamic range (DR) of amplifier can be defined as maximum-to-minimum ratio of the output signal power within the range of linear relation between the output signal and input signal, starting from the minimum value of the output signal amplitude restricted by the root-mean-square (rms) value of the output noise.
Although the gain of the flux driven JTWPA is not restricted by the pump wave depletion, the output signal power is inevitably limited by nonlinear distortions as the rf current amplitude increases and nears the maximum superconducting current of the cells (as inductances) in use, namely dc SQUIDs suggested in [16]. In fact, a linear wave-type equation with a periodically modulated reactive parameter, which was derived in [16] for the magnetic flux Φ ( x , t ) in the frame of distributed line approximation (with using dimensionless coordinate x normalized on the cell spacing “a”) gives an exponential increase in amplitudes with x of both the signal and idle travelling flux waves Φ s x , t and Φ i x , t . However, to obtain an output power, one needs to know the amplitude of the current travelling waves I s x , t and I i x , t . The relation between the flux and current amplitudes, Φ a and I a , is linear at low values: k Φ a = L I a , where k is the wave number (reduced to the reciprocal of the cell spacing), L is the running inductance (dipole inductance of SQUID-cell), and k Φ a is amplitude of the flux per unit length. But this ratio becomes nonlinear with increase in the wave amplitudes and then the current wave amplitude can be written as I a = k Φ a / L − δ I a Φ a . This leads to the power gain reduction by factor η p = δ I a / k Φ a / L 2 rising with nearing the current amplitude to the maximum superconducting current value of the SQUID cells in use. The linear domain limit determines the dynamic range of the amplifier. End point of the linear range can be characterized by the signal amplitude corresponding to the power gain reduction by 1 dB; this is called as 1 dB compression point.
Increase in the critical current I c of the used Josephson junctions to increase the maximum superconducting current of the SQUID-cells cannot be an acceptable solution for extending the linear domain, since the critical current magnitude determines some other normalized parameters answering for the amplifier performance. For example, one has to increase geometric loop inductance in order to increase the flux applied by the pumping wave, but has to decrease normalized value of the loop inductance
l = 2 π I c L / Φ 0
by decreasing the junction critical current to increase both the modulation depth of the maximum superconducting current of the cell and the characteristic Josephson junction inductance
L J 0 = Φ 0 / ( 2 π I c )
and hence the modulation depth of the dipole cell inductance.
In such a way, to increase the linear domain of the flux driven JTWPA at the tradeoff-assigned magnitude of the junction critical current, one needs to modify the cells in use in order to increase the linear domain of the cell characteristic describing relation between transport current via the cell I b produced by the signal and idler waves and the corresponding phase drop Δ φ on the cell. The phase drop answers the flux ( Φ 0 / 2 π ) Δ φ per length of the waveguide line composed of the cells.
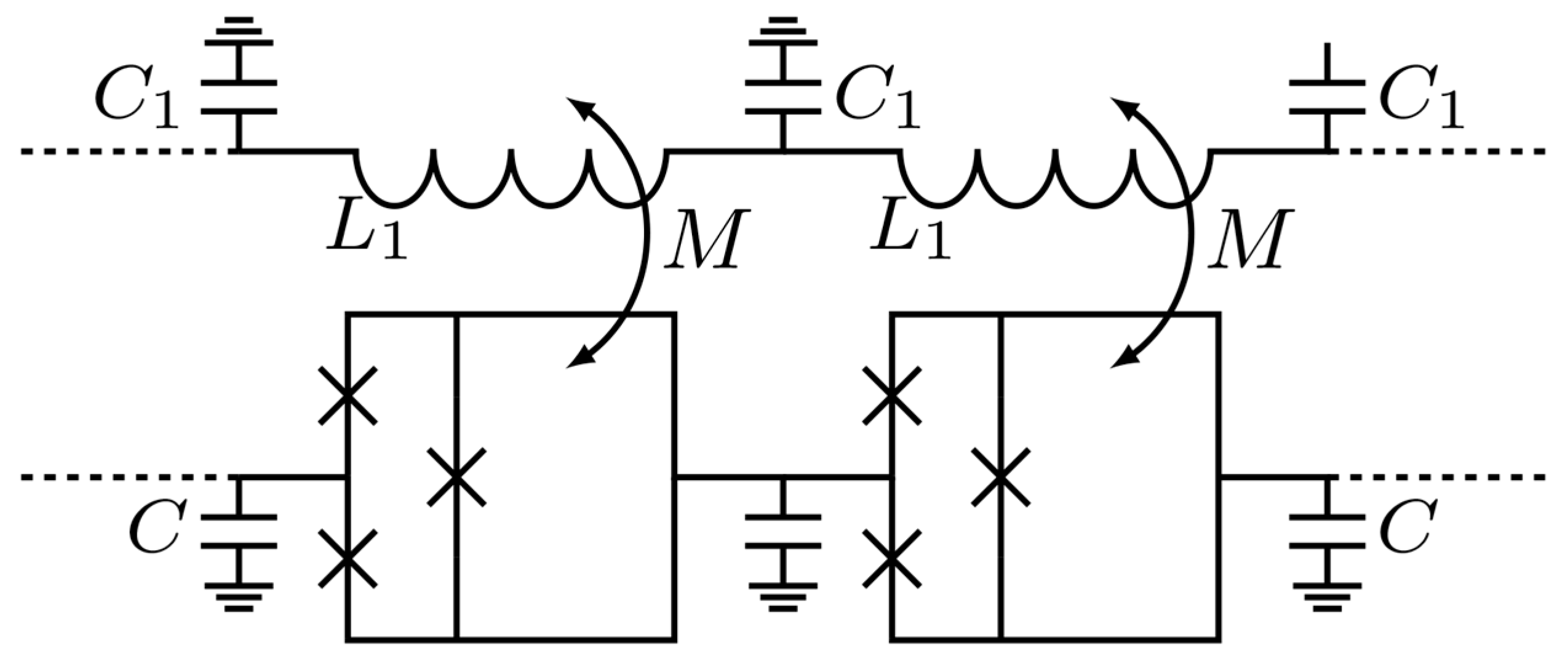
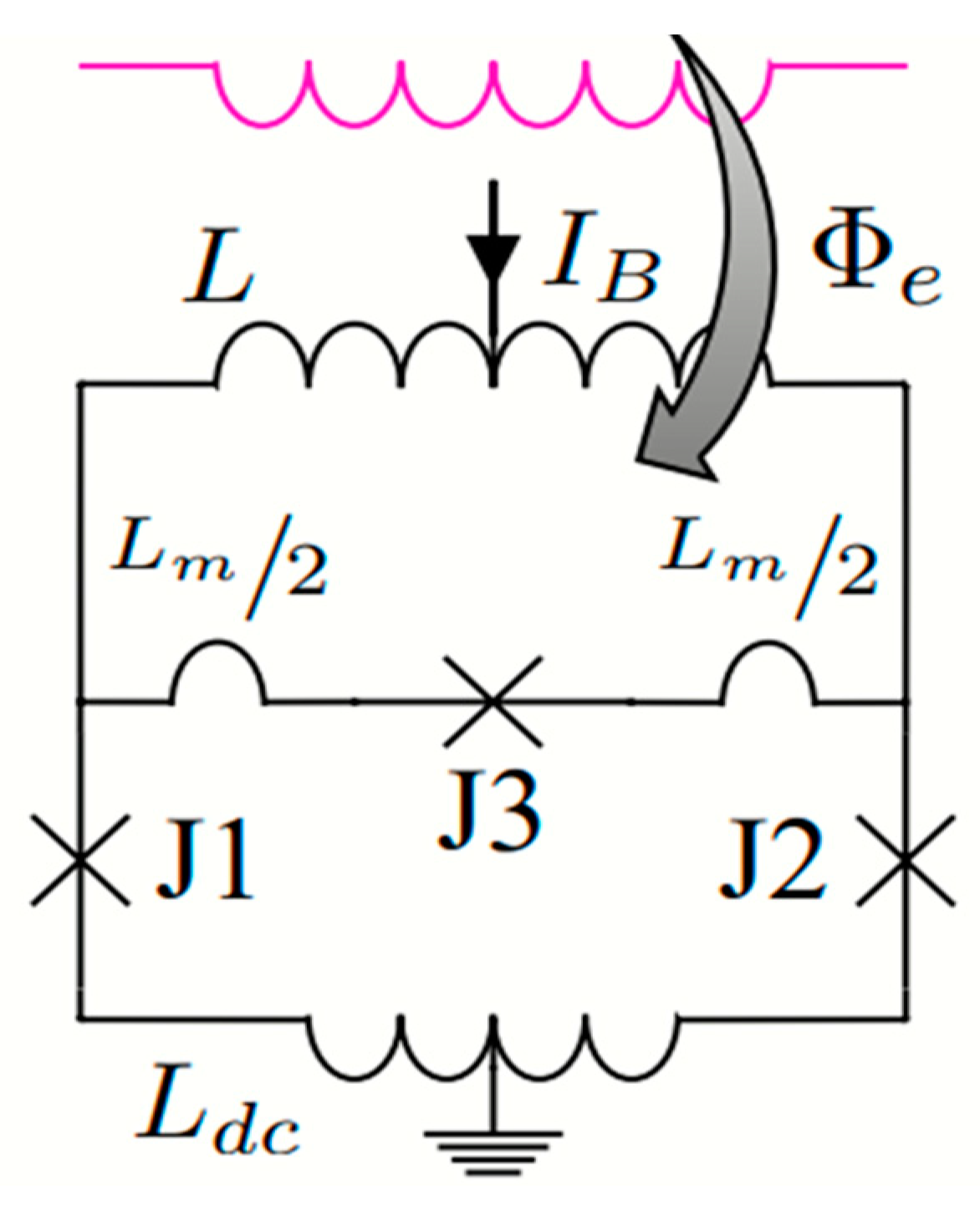
For this purpose, one can substitute the dc SQUID cells for bi-SQUID cells as suggested recently in [21] and shown in Figure 3. In the cell, the required improvement may be achieved through redirection of the currents flowing inside the cell with the current via the added 3-rd Josephson junction. The mechanism can be explained in the following way.
In the absence of both the signal and idler waves (i. e. at I b = 0 ) when the only dc magnetic flux Φ d c is applied to assign operation point, Josephson phases 1 and 2 of the junctions J1 and J2 in symmetric cells of both types, dc SQUID and bi-SQUID, are equal in magnitude and opposite in their signs in regard to direction of transport current, i. e. φ 2 = − φ 1 , due to the induced counterclockwise circular screening supercurrent. 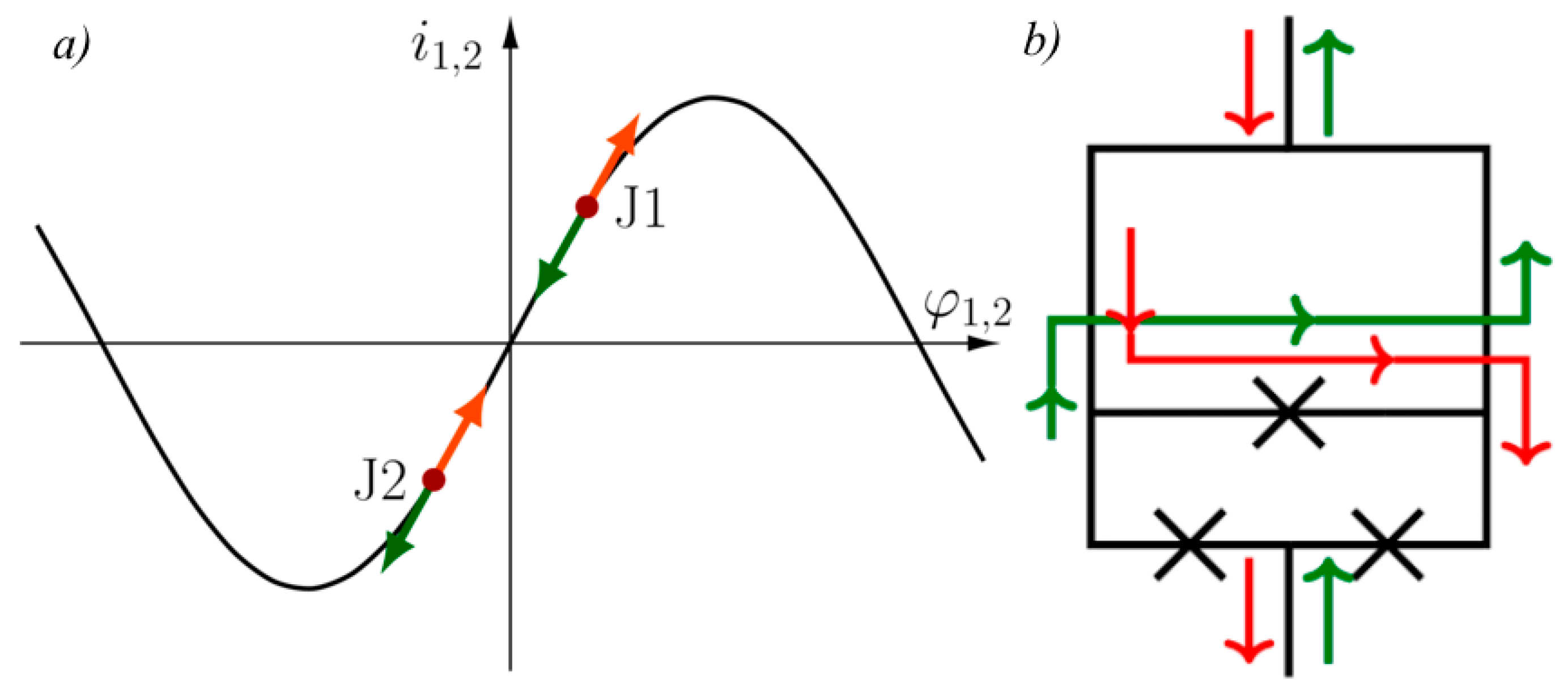Figure 4a shows schematically the phases and the currents flowing through the junctions J1 and J2 when the only dc magnetic flux is applied to the cells. At negligibly small geometric inductance of the device loops, as assumed in [16], φ 1 = − φ 2 = φ d c / 2 = π Φ d c / Φ 0 .
When the waves propagate in artificial line and produce a relatively slow-varying transport current I b flowing via a symmetric dc SQUID and a symmetric bi-SQUID both in superconducting state, this current (when the wave frequencies are much less than both the Josephson characteristic and plasma frequencies ω c = 2 π I c R n / Φ 0 , ω 0 = 2 π I c / ( Φ 0 C j ) ; C j and R n are the junction capacitance and normal resistance) is carried practically by the only superconducting currents through Josephson junctions J1 and J2 and therefore the Josephson phases 1 and 2 of the junctions obey the current relation
i b ≡ I b / I c = i 2 + i 1 = sin φ 2 + sin φ 1
and the phase equation which is
φ 1 − φ 2 = φ e − l ( sin ⁡ φ 1 − sin ⁡ φ 2 ) / 2
for dc SQUID (in detail, see the macroscopic quantum interference effect in [20) and
φ 1 − φ 2 = φ e − l ( sin ⁡ φ 1 − sin ⁡ φ 2 ) / 2 − l i c 3 sin ( φ 1 − φ 2 )
for bi-SQUID in accord with the schematic in Figure 4, where the junctions J1 and J2 are on the left and right sides, respectively, and J3 is above them. In both equations, l is the normalized loop inductance (8), φ e = 2 π Φ e / Φ 0 is normalized value of the applied magnetic flux Φ e = Φ d c + Φ r f , where Φ d c is the applied dc magnetic flux setting operation point, and Φ r f is the rf magnetic flux which is applied by the pump wave to modulate the cell dipole inductance; correspondingly, φ e = φ d c + φ r f .
In dc SQUID, transport current ib causes displacement of both the points 1 and 2 shown in Figure 4a in the sinusoid in direction corresponding to either increase of the junction phases at i b > 0 or decrease of the ones at i b < 0 , and some drop of Josephson phase Δ φ appears on the cell: Δ φ > 0 or Δ φ < 0 respectively. Relation between the phase drop and the transport current is evidently nonlinear. As seen from the sketch (Figure 4a), the nonlinearity results from either the first junction at positive transport current (corresponding to red color of the shown arrows) or the second junction (green arrows) at negative transport current.
In bi-SQUID, the nonlinearity problem is considerably mitigated through the current flowing via the added Josephson junction J3. As follows from numerical simulation (see [21]), this current flows through the third junction always in the same direction independently on the transport current direction, however on different paths through the other circuit elements in dependence on the transport current direction and therefore changes division of the transport current between the main junctions J1 and J2. These two possible paths of the current I 3 are shown in Figure 4b by the red lines and red arrows for the positive transport current and by the green lines and arrows for the negative transport current. In both cases, the current I 3 provides decrease in the current flowing through that junction which is responsible for nonlinearity in the relation between the phase drop Δ φ and transport current i b (i. e. for nonlinearity of the dipole inductance of the cell).
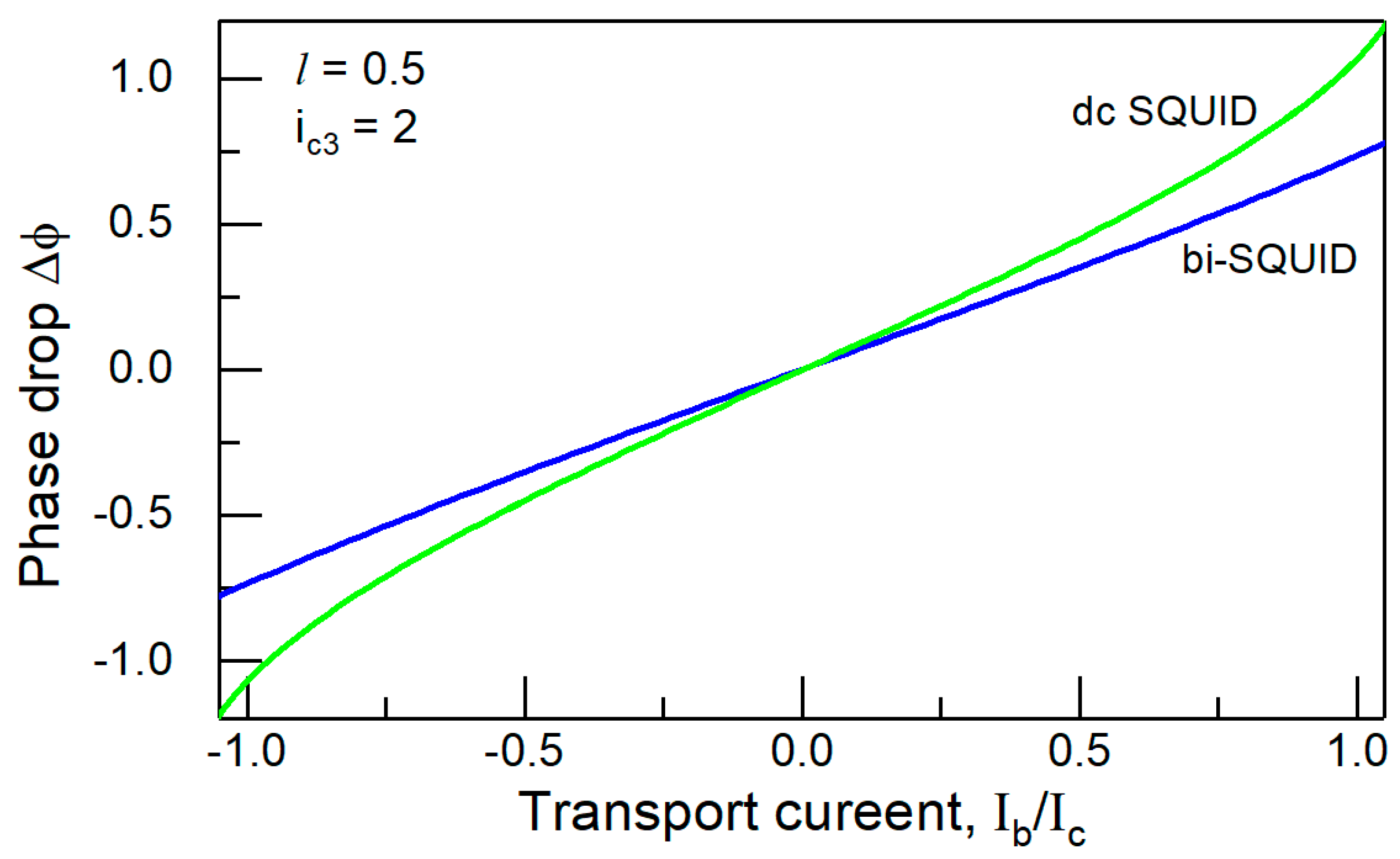
As an example, Figure 5 shows phase drops Δ φ on both dc SQUID (green line) and bi-SQUID (blue line) having the same critical current I c of the basic junctions J1, J2 and the same normalized geometric inductance l = 0.5 versus transport current i b = I b / I c created by both the signal and idler waves. The same dc magnetic flux Φ d c = Φ 0 / 3 is applied to both devices to set operation point. In bi-SQUID, normalized critical current of the 3-rd junction i c 3 ≡ I c 3 / I c = 2 . The presented dependences evidence appreciable increase in the linearity range with using bi-SQUID cells and hence increase in dynamic range of the flux driven JTWPA.
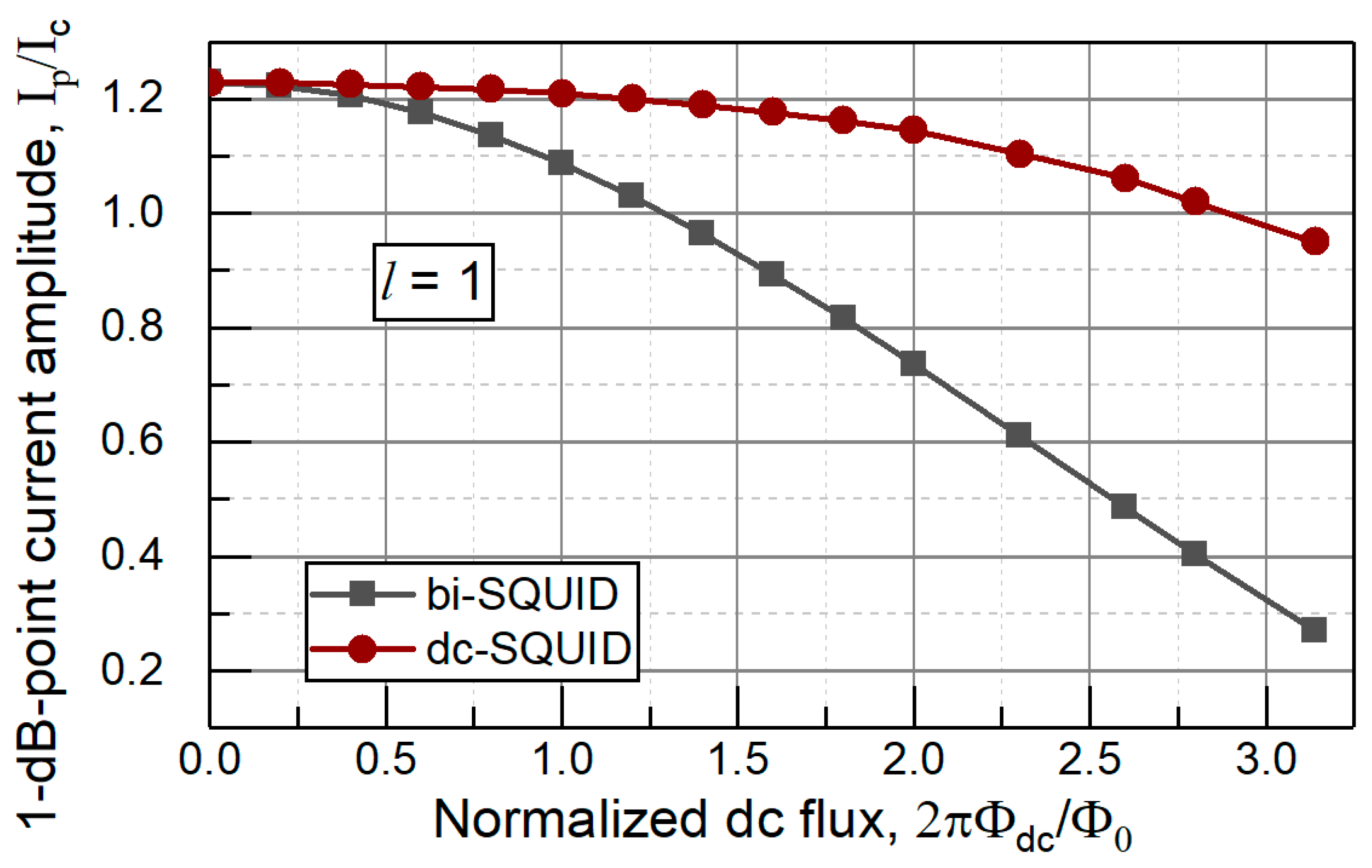
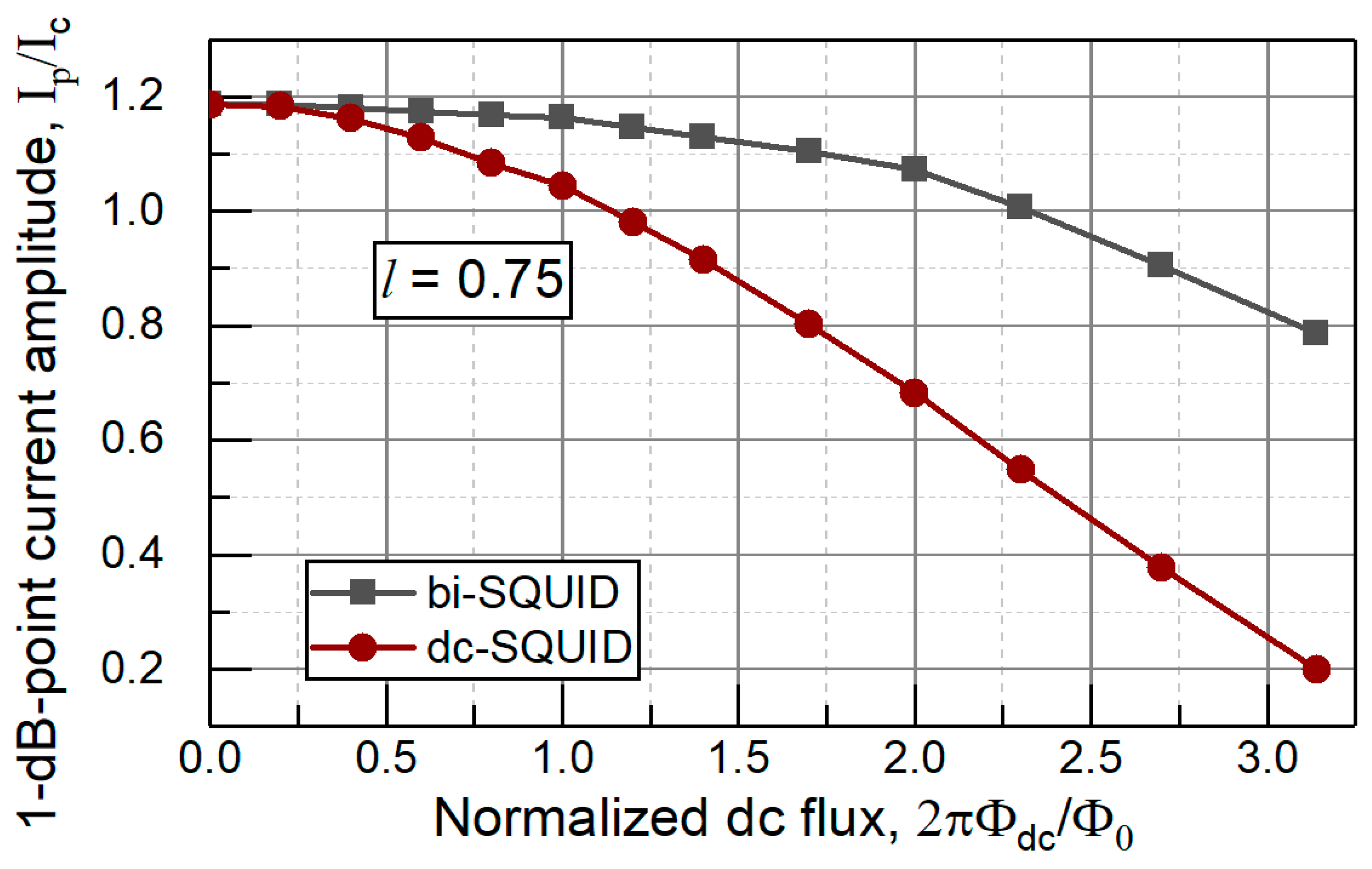
Quantitative characterization of the linearity domain increase can be done through considering the one dB compression points of the power gain. Figure 6 and Figure 7 present the calculated one dB compression points as function of the applied dc bias flux φ d c = 2 π Φ d c / Φ 0 setting operation point for both the dc SQUID cell and the bi-SQUID cell at the same values l = 1 and l = 0.75 of the normalized cell inductances. It is evidenced that dynamic range of the flux driven JTWPA can be increased by 2 to 3 times with using bi-SQUID cells.

4. Bi-SQUID cell parameters

The observed increase in dynamic range with using bi-SQUID cells depends first of all on magnitudes of main parameters which are the normalized cell inductance l and the normalized critical current of the third Josephson junction i c 3 = I c 3 / I c . Both the parameters influence on the current redirection inside the cell. Increase of the inductive parameter l, on the one hand, improves the redirection, but on the other hand, a high value of l decreases the fractional Josephson-junction contribution to the cell inductance and hence essentially restricts the obtainable modulation of the reactive parameter. Therefore, the magnitude l ~ 1 can be considered as a tradeoff value of this parameter.
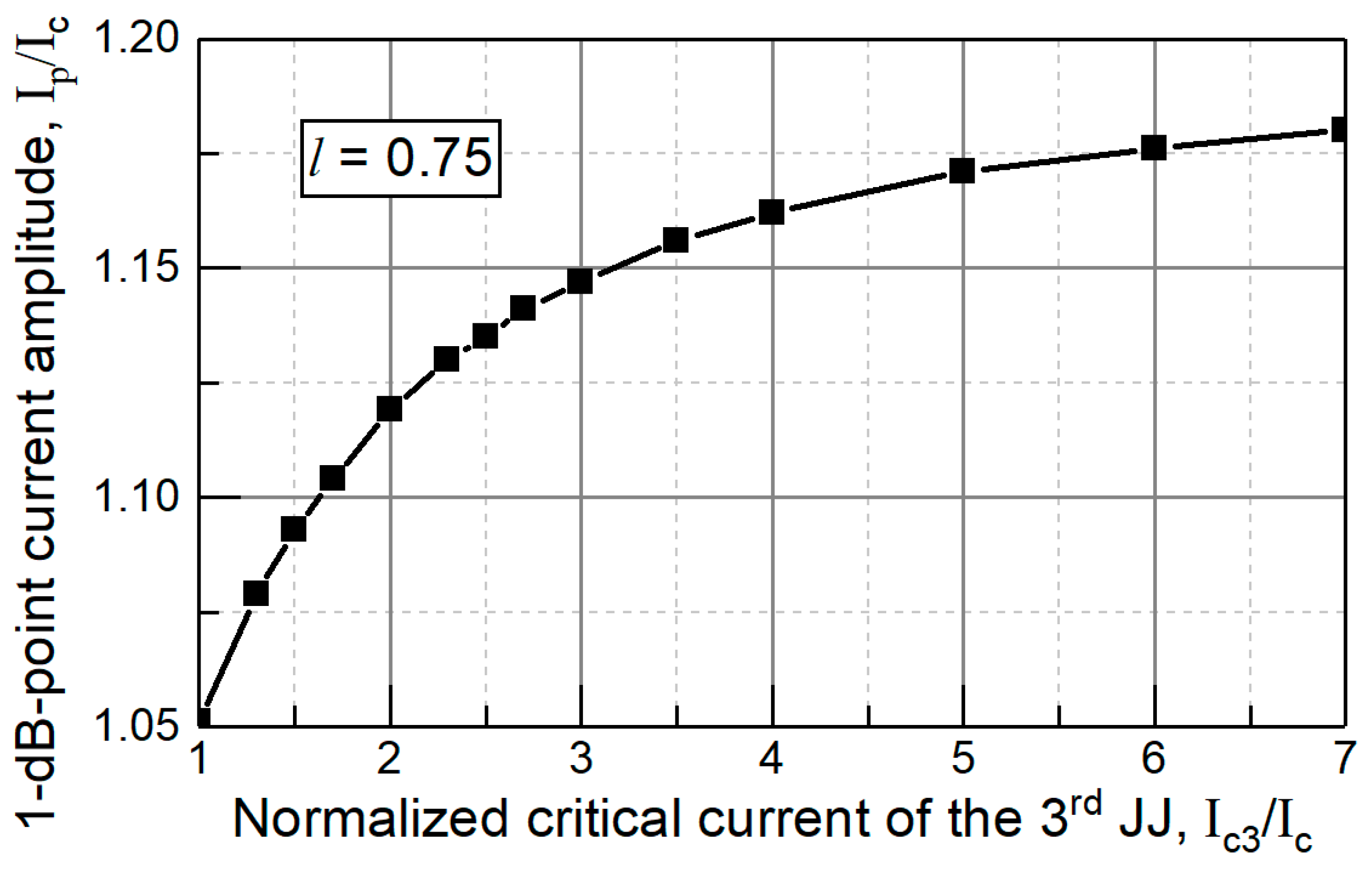
Next, Figure 8 shows the 1 dB compression point of the gain of the flux driven JTWPA with bi-SQUID cells versus normalized value of the 3-rd Josephson junction i c 3 . An increase in critical current of this junction results in monotonic rise of the point, i. e. improvement of the linearity. However, most of the improvement can be achieved with i c 3 ~ 2 to 3.
Except the discussed main parameters, one has to consider satellite parameters which can also influence the linear domain of the bi-SQUID cell and hence the gain reduction. These are the second loop inductance and the magnetic flux which can be applied to the loop. Figure 9 shows schematically all inductances in the bi-SQUID cell, where L is the main part of the principal loop inductance of the cell, and L d c and L m are parts of the second loop inductance with the normalized values:
l d c = 2 π I c L d c / Φ 0
l m = 2 π I c L m / Φ 0
Unfortunately, inductance of the second loop cannot be decreased exactly down to zero, and some flux can occur in the loop as well. In a rough way, the latter can be considered as the flux Φ 2 of a locally homogeneous magnetic field applied to the bi-SQUID in order to apply to its principal loop dc magnetic flux Φ d c needed to set operation point. In this case, ratio of the fluxes, κ = Φ 2 / Φ d c , can be estimated by ratio of the loop areas and hence roughly by ratio of the loop geometric inductances in square (believing roughly that the loop inductance is proportional to linear size r, while the loop area S ~ r2).
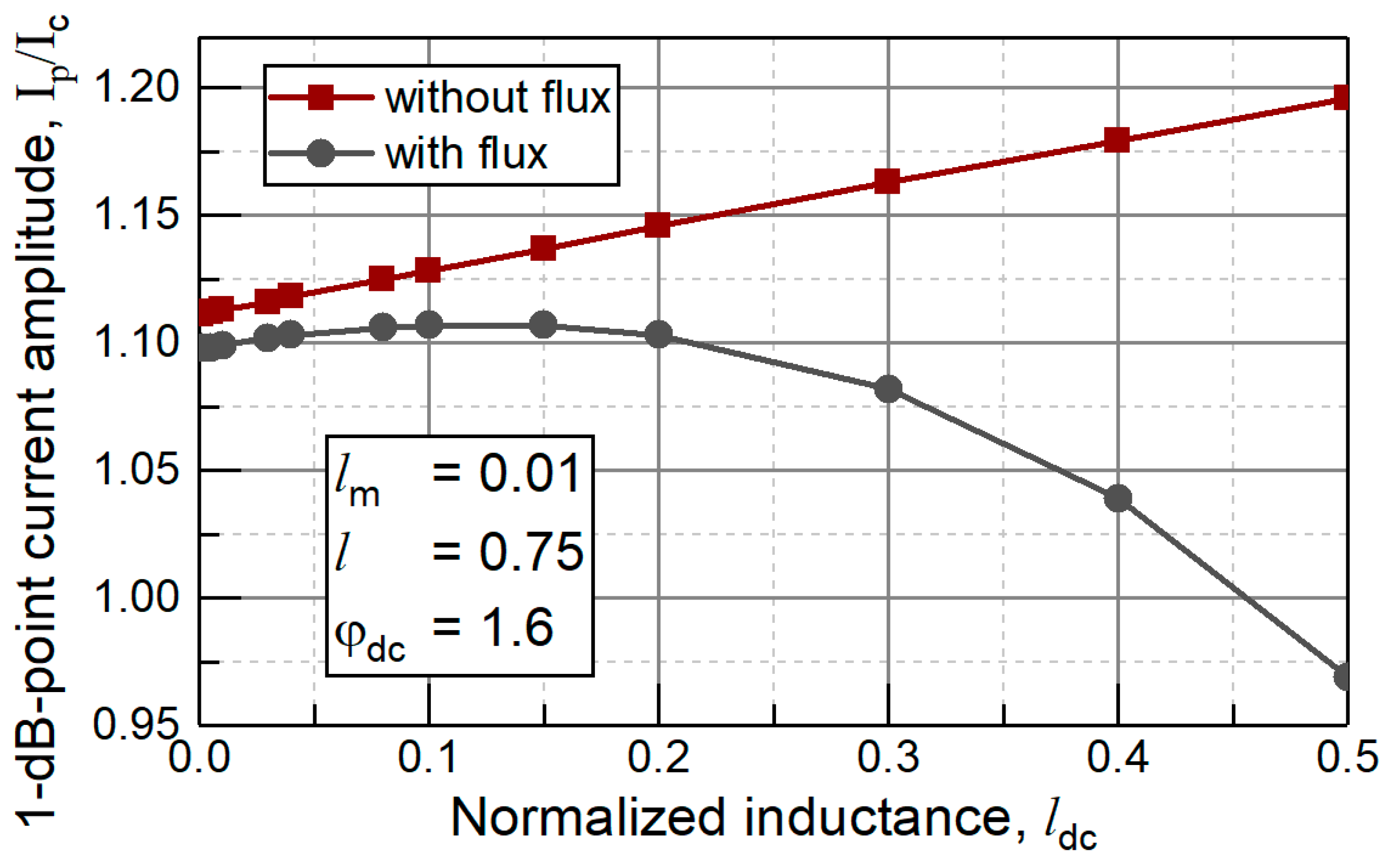
Interestingly, the moderate normalized inductance component l d c even slightly rises the 1 dB gain compression points (up to ≲ 10 % ) as shown in Figure 10, but the applied dc flux influences inversely and causes reduce overpowering positive impact of the inductance component l d c as seen from Figure 10.
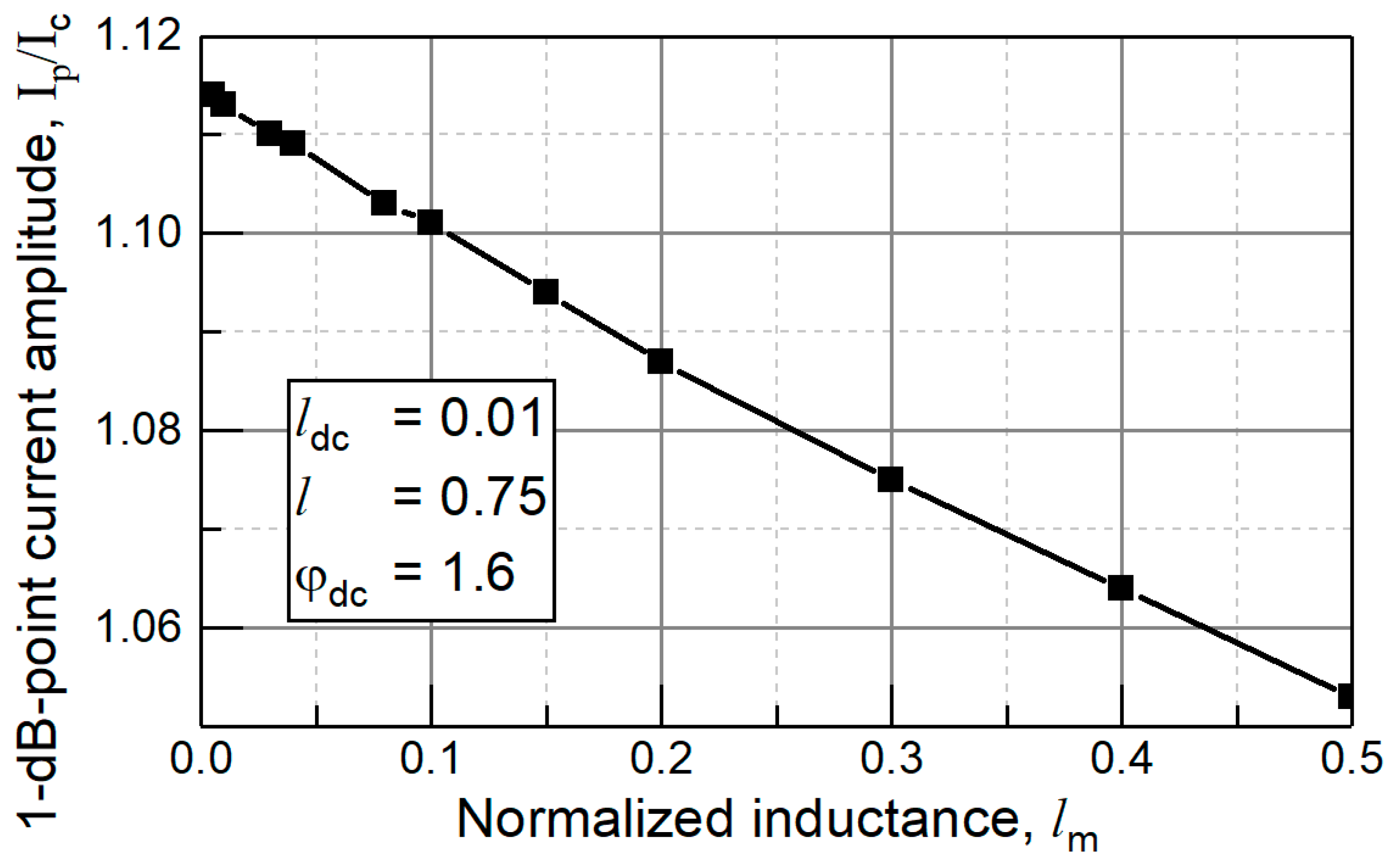
As for the other inductance part l m , its increase reduces the 1 dB gain compression points (up to ≲ 10 % ) as seen from Figure 11. These effects can be explained as follows. Inductance L m is connected in series with the third junction J3 and therefore increases inductive impedance of the branch as compared to the parallel branch containing junctions J1 and J2. On the contrary, the second inductance part L d c changes the inductive impedance ratio in reverse direction through increasing inductive impedance of the J1-J2 branch. Therefore, the inductance parts influence oppositely on the current redirection mechanism inside the bi-SQUID cell and hence on the one dB gain compression points.
Minimum value of the output signal of the flux driven JTWPA actually does not change with substituting the dc SQUID cells for bi-SQUID cells. In fact, fluctuations arising in Josephson junctions can be described using Langevin method [20,22,23], i. e. by adding noise current sources connected in parallel to the junctions. The in-phase current fluctuations (in regard to direction of transport current) arising in the basic junctions J1 and J2 yield in fluctuations of both the transport current and the phase drop Δ φ on the cell. These are the fluctuations forming output noise of the flux driven JTWPA. The antiphase current fluctuations arising in the junctions J1, J2 cause circular noise current in the cell loop and hence some small fluctuations of the dc flux setting operation point of the cell. The added Josephson junction J3 can give contribution to the only circular noise current, however, this contribution is about compensated by shunting impact of the junction on the antiphase current fluctuations produced by the junctions J1, J2. In such a way, influence of the added junction J3 on the noise characteristics of JTWPA can be considered as negligibly small.

5. Conclusions

In such a way, with the substitution of dc SQUID cells for bi-SQUID cells, the dynamic range of the flux-driven JTWPA increases by a factor of 2 to 3 due to the current redirection mechanism inside the cells. To achieve this, it suffices to set the normalized value of the cell loop l ~ 1 and two to three times as much critical current of the third junction as compared to the basic junctions provide sufficiency of the mechanism. Negative contribution of satellite parameters, inductance of the second low-inductance loop and magnetic flux occurred in the loop, can be reduced down to several percent when the inductance is three to four times less than the main inductance of the cell.
Moreover, the two-line design of the flux driver JTWPA allows maximal mitigating the restrictions followed from the complex-valued frequency-dependent wave impedance of the used artificial waveguide lines composed of lumped elements.

Author Contributions

All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Russian Science Foundation (RSCF) grant number 19-72-10016-P.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. M. R. Vissers, R. P. Erickson, et al., “Low-noise kinetic inductance traveling-wave amplifier using three-wave mixing, Appl. Phys. Lett. 108, p. 012601, 2016. [CrossRef]
  2. M. Sweeny and R. Mahler, "A travelling-wave parametric amplifier utilizing Josephson junctions," IEEE Trans. Magn., vol 21, no. 2, pp. 654-655, Mar. 1985.
  3. Yaakobi, L. Friedland, C. Macklin, and I. Siddiqi, “Parametric amplification in Josephson junction embedded transmission lines, ”Phys. Rev. B, vol. 87, 144301, 2013. https://journals.aps.org/prb/export/10.1103/PhysRevB.87.144301.
  4. Cl. Bockstiegel, et al., "Development of a broadband NbTiN traveling wave parametric amplifier for MKID readout," Journal of Low Temperature Physics, vol. 176, no. 3, pp. 476-482, 2014.
  5. K. O’Brien, C. Macklin, I. Siddiqi, and X. Zhang, "Resonant phase matching of Josephson junction traveling wave parametric amplifiers," Phys. Rev. Lett., vol. 113, Art no. 157001, 2014.
  6. T. C. White, et al., "Traveling wave parametric amplifier with Josephson junctions using minimal resonator phase matching," Appl. Phys. Lett., vol. 106, no 24, Art no. 242601, 2015,.
  7. M. T. Bell, and A. Samolov, “Traveling-wave parametric amplifier based on a chain of coupled asymmetric SQUIDs,” Phys. Rev. Appl., vol. 4, no. 2, Art no. 024014, 2015.
  8. B. Zorin, Josephson “Traveling-Wave Parametric Amplifier with Three-Wave Mixing,” Phys. Rev. Appl., vol 6, Art. no. 034006, 2016.
  9. B. Zorin, et al. "Traveling-wave parametric amplifier based on three-wave mixing in a Josephson metamaterial," 2017 16th Int. Supercond. Electronics Conf., IEEE, 2017.
  10. Miano, O. Mukhanov, “Symmetric traveling-wave parametric amplifier,” IEEE Trans. Appl. Supercond., vol. 29, Art no.1501706, 2019.
  11. Ranadive, M. Esposito, L. Planat, E. Bonet, C. Naud, O. Buisson, W. Guichard, N. Roch, “Kerr reversal in Josephson meta-material and traveling wave parametric amplification,” Nature Communications, Vol. 13, Art. no. 1737, 2022. [CrossRef]
  12. E. Kogan, “On parametric amplification in Josephson transmission line,” Basic Sol. Stat. Phys., vol. 260, p. 2300005, 2023; arXiv:2301.09644v1 [cond-mat.supr-con] .22 Jan. 2023.
  13. Ch. Macklin, et al., "A near–quantum-limited Josephson traveling-wave parametric amplifier," Science, vol. 350, no. 6258, pp. 307-310, 2015.
  14. M. Haider, et al., "A Josephson Traveling Wave Parametric Amplifier for Quantum Coherent Signal Processing," 2019 IEEE MTT-S Int. Microwave Symp. (IMS), IEEE, 2019.
  15. M. Esposito, A. Ranadive, L. Planat, and N. Roch, “Perspective on traveling wave microwave parametric amplifiers,” Appl. Phys. Lett., 119, 120501, 2021. [CrossRef]
  16. B. Zorin, “Flux-driven Josephson traveling-wave parametric amplifier,” Phys. Rev. Appl., vol.12, no. 4, Art no.044051, 2019.
  17. Kow, V. Podolskiy, and A. Kamal , “Self-phase-matched broadband amplification with a left-handed Josephson transmission line,” arXiv:2201.04660v1 [quant-ph] 12 Jan. 2022.
  18. K. K. Likharev, Essential Graduate Physics. EM: Classical Electrodynamics, part 7. http://commons.library.stonybrook.edu/egp/.
  19. E. Kogan, “On parametric amplification in discrete Josephson transmission line,” arXiv:2301.09644v5 [cond-mat.supr-con] 28 June 2023.
  20. K. K. Likharev, Dynamics of Josephson junctions and circuits, Gordon and Breach, 1986.
  21. Yusupov, L. V. Filippenko, D. E. Bazulin, N. V. Kolotinskiy, M. A. Tarasov, E. Goldobin, V. P. Koshelets, V. K. Kornev, "Flux-pumped Josephson Travelling-Wave Parametric Amplifiers Based on Bi-SQUID Cells,” IEEE Transactions on Applied Superconductivity, vol. 32, no. 4, pp. 1-5, June 2022, Art. no. 1700105. [CrossRef]
  22. R. L. Stratonovich, Selected topics in the theory of random noise, New York: Gordon and Breach, 1967.
  23. D. Whalen, Detection of signals in noise, New York: Academic Press, 1971.
Preprints 78966 g001
Figure 1. If Z0 is a wave impedance of a long artificial line of Γ -cells, the value Z0 does not change with the cell adding.
Figure 1. If Z0 is a wave impedance of a long artificial line of Γ -cells, the value Z0 does not change with the cell adding.
Preprints 78966 g001
Preprints 78966 g002
Figure 2. Reflection factor Γ ( ω ) for the artificial waveguide of lumped L and C elements which is connected to resistor R = ρ ≡ L / C ; optimal values of both the pump wave frequency ω p in 3-wave mode (or double frequency 2 ω p in 4-wave mode) and the frequency range for signal and idler waves.
Figure 2. Reflection factor Γ ( ω ) for the artificial waveguide of lumped L and C elements which is connected to resistor R = ρ ≡ L / C ; optimal values of both the pump wave frequency ω p in 3-wave mode (or double frequency 2 ω p in 4-wave mode) and the frequency range for signal and idler waves.
Preprints 78966 g002
Preprints 78966 g003
Figure 3. After [21]. The inductively-coupled elementary cells of the pump and signal transmission lines of JTWPA based on using bi-SQUIDs. C and C1 are ground capacitances of the two lines: L 1 C 1 -line for the pump wave and L C -line for the signal and idler waves, where L is inductance of the bi-SQUID cell.
Figure 3. After [21]. The inductively-coupled elementary cells of the pump and signal transmission lines of JTWPA based on using bi-SQUIDs. C and C1 are ground capacitances of the two lines: L 1 C 1 -line for the pump wave and L C -line for the signal and idler waves, where L is inductance of the bi-SQUID cell.
Preprints 78966 g003
Preprints 78966 g004
Figure 4. After [21]. (a) Josephson phases and currents through the junctions J1 and J2 described by two points in sinusoid on the current-phase plane when some dc magnetic flux is applied to the cell, dc SQUID or bi-SQUID, inducing counterclockwise circular screening supercurrent, and bias current is absent. The red and green arrows show directions of displacement of the points at positive (red color) and negative (green color) bias current. (b) Paths of the current flowing through the additional junction in bi-SQUID at positive (red lines and red arrows) and negative (green lines and arrows) bias currents. The junctions J1 and J2 are on the left and right sides, respectively, and J3 is above them.
Figure 4. After [21]. (a) Josephson phases and currents through the junctions J1 and J2 described by two points in sinusoid on the current-phase plane when some dc magnetic flux is applied to the cell, dc SQUID or bi-SQUID, inducing counterclockwise circular screening supercurrent, and bias current is absent. The red and green arrows show directions of displacement of the points at positive (red color) and negative (green color) bias current. (b) Paths of the current flowing through the additional junction in bi-SQUID at positive (red lines and red arrows) and negative (green lines and arrows) bias currents. The junctions J1 and J2 are on the left and right sides, respectively, and J3 is above them.
Preprints 78966 g004
Preprints 78966 g005
Figure 5. After [21]. Phase drops on both dc SQUID (green line) and bi-SQUID (blue line) with i c 3 = 2 and same value l = 0.5 of the normalized geometric inductance versus transport current. The same dc magnetic flux Φ d c = Φ 0 / 3 is applied to both devices.
Figure 5. After [21]. Phase drops on both dc SQUID (green line) and bi-SQUID (blue line) with i c 3 = 2 and same value l = 0.5 of the normalized geometric inductance versus transport current. The same dc magnetic flux Φ d c = Φ 0 / 3 is applied to both devices.
Preprints 78966 g005
Preprints 78966 g006
Figure 6. The current wave amplitude I p / I c corresponding to the 1 dB compression point of the gain of JTWPA vs. normalized value of the applied dc bias flux φ d c = 2 π Φ d c / Φ 0 with dc SQUID cells (red line) and bi-SQUID cells (black line) at the same value l = 1 of the normalized cell inductances.
Figure 6. The current wave amplitude I p / I c corresponding to the 1 dB compression point of the gain of JTWPA vs. normalized value of the applied dc bias flux φ d c = 2 π Φ d c / Φ 0 with dc SQUID cells (red line) and bi-SQUID cells (black line) at the same value l = 1 of the normalized cell inductances.
Preprints 78966 g006
Preprints 78966 g007
Figure 7. The current wave amplitude I p / I c corresponding to the 1 dB compression point of the gain of JTWPA vs. normalized value of the applied dc bias flux φ d c = 2 π Φ d c / Φ 0 with dc SQUID cells (red line) and di-SQUID cells (black line) at the same value l = 0.75 of the normalized cell inductances.
Figure 7. The current wave amplitude I p / I c corresponding to the 1 dB compression point of the gain of JTWPA vs. normalized value of the applied dc bias flux φ d c = 2 π Φ d c / Φ 0 with dc SQUID cells (red line) and di-SQUID cells (black line) at the same value l = 0.75 of the normalized cell inductances.
Preprints 78966 g007
Preprints 78966 g008
Figure 8. The current wave amplitude I p / I c corresponding to the 1 dB compression point of the gain of JTWPA with bi-SQUID cells versus normalized value of the 3-rd Josephson junction i c 3 = I c 3 / I c at l = 0.75 and φ d c = 2 π Φ d c / Φ 0 .
Figure 8. The current wave amplitude I p / I c corresponding to the 1 dB compression point of the gain of JTWPA with bi-SQUID cells versus normalized value of the 3-rd Josephson junction i c 3 = I c 3 / I c at l = 0.75 and φ d c = 2 π Φ d c / Φ 0 .
Preprints 78966 g008
Preprints 78966 g009
Figure 9. Bi-SQUID cell schematic, where L is the main part of the principal loop inductance of the cell, and L d c and L m are parts of the second loop inductance.
Figure 9. Bi-SQUID cell schematic, where L is the main part of the principal loop inductance of the cell, and L d c and L m are parts of the second loop inductance.
Preprints 78966 g009
Preprints 78966 g010
Figure 10. The one dB gain compression points versus the normalized inductance component l d c of the second loop inductance of bi-SQUID cell when no magnetic flux is applied to the loop (red line) and when magnetic flux Φ 2 = κ Φ d c is applied to the loop (black line). In both cases, the normalized value of the main loop inductance l = 0.75 , and the normalized dc flux applied to the main loop φ d c = 2 π Φ d c / Φ 0 = 1.6 , and l m = 0.01 ( normalized value of   L m ) . Factor κ = l d c 2 / l 2 corresponds approximately to the loop square ratio.
Figure 10. The one dB gain compression points versus the normalized inductance component l d c of the second loop inductance of bi-SQUID cell when no magnetic flux is applied to the loop (red line) and when magnetic flux Φ 2 = κ Φ d c is applied to the loop (black line). In both cases, the normalized value of the main loop inductance l = 0.75 , and the normalized dc flux applied to the main loop φ d c = 2 π Φ d c / Φ 0 = 1.6 , and l m = 0.01 ( normalized value of   L m ) . Factor κ = l d c 2 / l 2 corresponds approximately to the loop square ratio.
Preprints 78966 g010
Preprints 78966 g011
Figure 11. The one dB gain compression points versus the normalized inductance component l m of the second loop inductance of bi-SQUID cell when no magnetic flux is applied to the loop. Normalized value of the main inductance l = 0.75 , normalized dc flux applied.
Figure 11. The one dB gain compression points versus the normalized inductance component l m of the second loop inductance of bi-SQUID cell when no magnetic flux is applied to the loop. Normalized value of the main inductance l = 0.75 , normalized dc flux applied.
Preprints 78966 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated