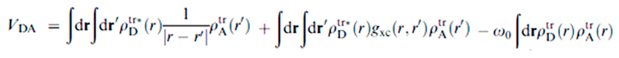Photoswitchable Molecular Units with Tunable Non-Linear Optical Activity: A Theoretical Investigation

Aggelos Avramopoulos; Heribert Reis; Demeter Tzeli; Robert Zaleśny; Manthos Papadopoulos

doi:10.20944/preprints202307.0483.v1

Submitted:

06 July 2023

Posted:

07 July 2023

You are already at the latest version

Abstract

A series of derivatives, involving two dithienylethene (DTE), groups, connected by several molecular linkers (bis(ethylene-1,2-dithiolato)Ni- (NiBDT), naphthalene, quasilinear oligothiophene chains) are investigated with the aid of computational quantum chemistry methods. This involves the computation of the second- and third-order nonlinear optical properties, i.e. molecular hyperpolarizabilities of the designed/selected derivatives. These properties can be efficiently controlled by DTE switches, in connection with light of appropriate frequency. We found that NiBDT, as a linker, is associated with a greater contrast, in comparison to naphthalene, between the first and second hyperpolarizabilities of the “open-open” and the “closed-closed” isomers. This is explained by invoking the low lying excited states of NiBDT. It has been found that the second hyperpolarizability can be used as an index, which follows the structural changes induced by photochromism. The two-photon absorption, which is related to the imaginary part of second hyperpolarizability, has also been investigated for the S0S1 transition. Furthermore, the intramolecular excited-state energy transfer (EET) is studied as well as the overlap between the absorption and emission spectra of the donor and acceptor groups of the molecules. The electronic coupling, VDA, between the donor and acceptor fragments, as well as the emission spectrum of the donor and the absorption spectrum of the acceptor have been computed, assuming a Förster type transfer mechanism. EET is a critical factor governing the photochromism. Two methods were used to compute VDA, one based on linear response and one based on the distributed multipole analysis (DMA); both techniques give very similar results for the dominating Coulomb contribution. For NiBDT as the linker a low VDA value has been computed. We found that VDA is affected by the molecular geometry. Our results clearly show that the linker strongly influences the communication between the open-closed DTE groups and thus, photochromism. The present computations show that full photochromism is attained in derivatives where two DTE groups are linked by a tetrathiophene chain, in agreement with experiment. The sensitivity of molecular linear and nonlinear optical properties upon photochromism can assist with the identification of the molecular isomers.

Keywords:

(Hyper)polarizability

;

Density Functional Theory

;

Molecular Switches

;

Photochromism

;

Two-Photon absorption

;

Dithienylethene

;

bis(ethylene-1

;

2-dithiolato

;

Excited-state Energy Transfer

Subject:

Chemistry and Materials Science - Theoretical Chemistry

Introduction

Multi-photochromic molecules are of current interest, since such systems allow to access up tp 2ⁿ molecular states, if n photochromic units are distinguishable, while molecules involving one photochromic unit are bistable [1,2]. For example, a derivative which involves two similar photochromic switches, may have the following states: “open-open” (oo), “open-closed” (oc), “closed-closed” (cc). However, in several cases involving DTE switches, the “closed-closed” isomer is not observed. This has been attributed to Excitation Energy Transfer (EET) as an efficient competition process to the photoinduced cyclisation. The photo-activity of the involved photochromic groups depends on the linker or molecular bridge, which connects them.[2] It is understood that a saturated linker may allow the photochromic groups to retain their photo-activity.

EET is a process of great importance in many areas of research (e.g. biological systems, opto-electronic devices).[3] Of particular relevance to the present work, and the most frequent observed EET, is singlet excitation energy transfer (SEET). SEET has been used to rationalize several important processes (e.g. the light-harvesting in photosynthesis)[4]

An important parameter for the understanding of EET is the electronic coupling factor, between the two switching units; this is an off-diagonal Hamiltonian matrix element between the initial and final diabatic states in the transfer processes.[3] This coupling involves a Coulomb and a short-range term[3],[5]. At large separations the former reduces to the Förster dipole-dipole coupling.[5] The latter involves Dexter’s exchange coupling[6] and an overlap term.[7] In solution, a further term related with the effect of the solvent may also be play a role[8] .

It has been established by early work that overlap of the donor fluorescence spectrum with the acceptor absorption spectrum ensures the energy conservation, in the weak coupling limit [9] . Kaieda et al[10]. studied the photocyclization of dithienylethene multimers and reported that the overlap of the fluorescence spectrum of the (oo) dimer and the absorption spectrum of the (oc) form, suggests that intramolecular energy transfer, from the excited open-ring fragment to the closed-ring unit, is possible.

The effect of the bridge on the electronic coupling

The significant role of the bridge on EET has been studied by several authors, in particular, Chen et al. [11] investigated the effect of the bridge on the Coulomb coupling, which makes the major contribution to the electronic coupling. They found that the EET rate increases, in comparison through-space models, when the donor and acceptor transition dipoles are arranged longitudinally and linked by a polarizable bridge (e.g. involving aromatic groups).

Scholes et al. [12] studied the through-space and through-bond effects on exciton interactions in a series of dinaphthyl molecules, in which the naphthyl units are connected by a polynorbornyl bridge. The enhancement of the energy delocalization by the through-bond interactions has been noted. Electronic coupling through rigid saturated spacers, involving up to 12 σ bonds has been reported[12,13].

Energy transfer rates have been studied in donor-bridge-acceptor (D-B-A) systems[14]; several factors have been considered e.g. the bridge length[15,16], conformation[17], electronic properties[18]. McConnell’s super-exchange theory for electron transfer[19] has also been frequently applied to energy transfer[14].

Kudernac et al.[20], in their study of uni- and bi-directional light-induced switching of DTEs, linked to the surface of gold nanoparticles, found that the ring-closure process, depends on the spacer.

If several DTE units are present in a molecule, a stepwise photo-cyclization process is significant. Non-conjugated linkers are associated with a fully ring-closed isomer,[21] because no SEET takes place. However, if π-conjugated linkers are involved, usually, a partial photochromism is observed, due to SEET.

Computation of EET

EET has been approximated by Förster’s theory[9,22]. This approach has been successfully applied in many cases (e.g. in predicting EET rates)[22], however, there are several cases where it has failed)[23,24]. This method assumes that there is a very weak coupling between an open DTE unit (D) and a closed one (A) and that their spatial extensions are much smaller than R_DA (the distance between D and A), so that the point-dipole approximation can be employed[22]. Several methods have been proposed for a more accurate description of EET[24,25] (e.g. transition monopole approximation[26] transition density cubes[27] and the fragment excitation difference (FED) method[3]).

Perhaps the simplest approach to calculate the electronic coupling between chromophores is to approximate it by the Coulomb interaction and to compute it by employing the transition dipole moments, that is, the point dipole approximation (PDA), which is an easy way to calculate the coupling, but it fails at short distances.[28] One may go beyond the dipole-dipole approximation to involve multipole couplings. For short distances these have been found to have significant contributions.[29] A less approximate approach to compute the Coulomb coupling is to use the density cube method.[27] The point dipole approximation (PDA) is frequently used, giving satisfactory results, when the distance between the donor and the acceptor (R_DA) is much larger than their dimensions. Overestimated results may be received at short distances. [30]

The study of molecular optical properties provides valuable information in several important areas (e.g. nano-structures).[31] Studies of single-molecules itself help us to probe and to understand mechanisms in a deeper detail and could be used to obtain information on what is happening at the nanoscale[31] The third-order nonlinear optical response of energy transfer systems has been studied theoretically by Young and Fleming. [32] The effect of molecular switching on the NLO properties has also been studied by several research groups. [33,34,35]. The stimuli (e.g. light irradiation, pH variation), which were used to induce the molecular transformation have also been discussed.³⁴ The DTE switches, in connection with light of appropriate frequency (which leads to “open” or “closed” DTE units) allow to control the molecular linear and nonlinear optical (L&NLO) properties efficiently, since the cyclization reaction increases the conjugation and thus polarization DTE multistate molecular materials have been considered as a research field of significant interest.[36] This is of great importance for several applications (e.g., data processing, photonic communication).[37] In addition, EET is a significant property of excited states and these states provide an important tool for the rationalization of the L&NLO properties. Thus, the photochromic properties of DTEs, their L&NLO and EET provide complementary information about the molecular structure.

Taking into account the aforementioned challenging issues, the following topics have been addressed here:

(i) The relationship between the molecular (hyper)polarizabilities of several derivatives consisting of 2 DTE units, with and without different substituents, and connected by different conjugated linkers, and the changes induced by photochromism on these properties. It is a major objective to find those structures and linkers, in particular, which lead to a significant contrast between the hyperpolarizabilities of the “open” and the “closed” isomers. A detailed discussion on the selection of the molecular linkers (molecular bridges ) used in this study is given in the Results and Discussion method.

(ii) The effect of the linker on the electronic communication of the DTE units and the photochromism as well as the intramolecular EET. A series of linkers has been selected in order to tune EET and eventually to minimize it, to attain full photochromism.

II. Methods

We shall discuss the following topics in this section: (i) a definition of the hyperpolarizabilities, (ii) the functionals we have employed, (iii) the validation procedures we have used, (iv) the method used to compute the transition energies, (v) the computational approach employed to calculate the emission spectrum of the donor, the absorption spectrum of the acceptor and their overlap, (vi) the procedure used to compute two-photon absorption, (vii) the methods employed for the computation of the electronic coupling.

II.1. Definitions

A Taylor series may be used for the expansion of the energy (E) of a molecule, which is placed in a static, uniform electric field (F_i) :[38]

E (F) = E^{0} - μ_{i} F_{i} - (1 / 2) α_{i j} F_{i} F_{j} - (1 / 6) β_{i j k} F_{i} F_{j} F_{k} - (1 / 24) γ_{i j k l} F_{i} F_{j} F_{k} F_{l} - \dots

(1)

where, E⁰ is the field free energy and μ_i α_ij β_ijk γ_ijkl, are the dipole moment, polarizability, first and second hyperpolarizability components, respectively; a summation over repeated indices is implied. The average (hyper)polarizabilities are defined by:

(2)

(3)

where β_ι

(4)

(5)

The finite field perturbation theory (FPT) has been used for the calculation of the static (hyper)polarizabilities.[39] The Romberg-Rutishauer method[40,41,42] has been employed in order to safeguard the numerical stability of the computed (hyper)polarizability values. The computed static (hyper)polarizabilities values are expected to be useful for a relative comparison of the NLO properties of the studied photoswitchable compounds, since these are a good approximation to dynamic ones (frequency-dependent) in the off-resonant region.[43] The following field strengths have been used: 2^mF, m=1-4 and F=0,0005 a.u.. The GAUSSIAN 16 software has been employed for the DFT computations (see below).[44]

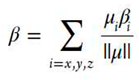
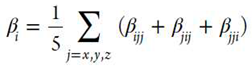
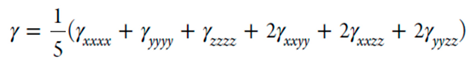
II.2. Functionals and Basis sets

The following functionals have been used for the computation of the reported molecular properties:

(i) B3LYP. This functional has been used to calculate the structure of the considered compounds. For all the molecular structures vibrational analysis was performed to verify that a real minimum has been found on the potential energy hyper-surface. B3LYP is a well-tested functional[45] which has been used for the determination of the structure of several other NiBDT derivatives.[46,47,48,49]. Its satisfactory performance has been also demonstrated in the literature.[50,51,52] For the case of the sexithiophene derivatives the conjugated skeleton is essentially planar, as shown experimentally in the crystal,[53] and this conformation is used in our computations. In order to further examine the performance of the B3LYP functional on the oligothiophene structures, we made geometry optimization of 1cc and 1oo molecules, R=Cl (Fig. 1)by employing the M062-X functional, since the latter has been shown to predict satisfactorily the geometries of π-conjugated systems, due to the appropriate amount (28%) of the included HF exchange. [54] The comparison between the geometries is shown in S.I material (Figure S1).

(ii) CAM-B3LYP. This long range corrected version of B3LYP[55] has been employed to compute the (hyper)polarizabilities of the considered derivatives. Detailed justification for its use has been reported in ref. [49]. The CAM-B3LYP functional[55] has also been used for the two-photon absorption calculations (II.6). We have employed the 6-31G* and cc-pVTZ basis set for H, C, O, F, and S atoms[56,57,58,59] and the quasi-relativistic effective core potential ECP28MWB(SDD) for the Ni atoms.[60] .

The adequacy of the CAM-B3LYP/6-31G* approach for the computation of the NiBDT properties is well documented.[46,48] NiBDT derivatives, having a singlet diradical character, should in principle be studied with a multiconfigurational wave function. However, it has been shown that broken-symmetry DFT [(U)DFT] gives satisfactoty property values.[46,49,61]

The electronic structure of the NiBDT derivatives, see Figure 5, have been studied via density functional theory (DFT) and time-dependent DFT (TD-DFT). The geometries of the structures are energetically optimized using the B3LYP[45] and the CAM-B3LYP[55] functionals and the 6-31G* basis set for H, C, O, F, and S atoms and the quasi-relativistic effective core potential ECP28MWB(SDD) for the Ni atoms.⁵² The absorption and emission spectra of the studied structures were calculated via the TD-DFT. TD-DFT can predict absorption and emission spectra of molecules in very good agreement with experimental spectra.[62,63] Particularly, CAM-B3LYP functional has been developed to correct for the long-range behavior and it is regarded as appropriate for the computation of the absorption spectra when charge transfer states are involved. [64] Four main excited states were energetically optimized. In all cases, the absorption and emission spectra of the studied systems were calculated including up to 130 singlet-spin excited electronic states. All calculations were carried out with the Gaussian16 code. Time-dependent density functional theory (TD-DFT)[65,66] in connection with the CAM-B3LYP functional[55] has been used to compute the transition energies. It has been reported that this approach give satisfactory results.[67,68] All the reported computations were employed in the gas phase.

II.3 Two-photon absorption

The two-photon absorption (2PA) process is described by the imaginary part of the frequency-dependent second hyperpolarizability.[69,70,71] At the molecular scale, the two-photon absorption process is characterized by the second-order transition moment S_ab that can be computed from the single residue of the quadratic response function.[72] In this work we assumed one source of photons and linearly polarized light. In such case, the orientationally averaged two-photon absorption strength for an isotropic medium can computed as :[73]

< δ 2^{PA} > = \frac{1}{15} \sum_{a b} (S_{a a} S_{b b}^{*} + {2 S}_{a b} S_{b a}^{*})

(6)

<δ^2PA>, in what follows given in atomic units, is directly related to the two-photon absorption cross section (σ^2PA), which can be determined experimentally. The interested reader is referred to other work for conversion to macroscopic units (cross section is commonly expressed in Goppert-Mayer (GM) units).[74] The two-photon absorption calculations were performed using GAMESS US program [75,76] using CAM-B3LYP functional[55] and 6-31G(d) basis set. The choice of the CAM-B3LYP functional requires a proper justification. In the case of 2PA process, there are several striking reports regarding unsatisfactory performance of exchange–correlation functionals in predicting the magnitude of two-photon strengths.[55,74,75,76,77] For example, the CAM-B3LYP functional gives 2PA strengths that are often underestimated in comparison with the reference coupled-cluster values,[74] even though it improves upon conventional functionals in predicting excitation energies to charge-transfer states, as explained above. However, as recently demonstrated for a series of organic molecules, only range-separated functionals (CAM-B3LYP and LC-BLYP) correctly predict changes in δ^2PA upon chemical modifications and reproduce experimental trends. [78,79] The functionals with fixed amount of exact exchange fail to predict key parameters such as the transition moments between electronic states and excitation energies, such that their agreement with RI-CC2 reference data is due to error cancellations. Moreover, range-separated functionals such as CAM- B3LYP and LC-BLYP yield 2PA strengths which substantially deviate from reference values and this can be linked to underestimated excited-state dipole moments. However, the errors are rather systematic and these functionals nicely reproduce the chemical trends.

ΙΙ.4 Computation of the Electronic Coupling:

The electronic coupling between the excitation of the donor (D) and the acceptor (A), V_DA, is of major importance for understanding EET; it appears in the energy transfer rate, k_EET,

k_EET = (2π/ћ)| V_DA|²J,

(7)

where J is the spectral overlap (i.e. the overlap integral) between the emission band of the donor and the absorption band of the acceptor.[1] We have computed V_DA by two methods: one based on the linear response method and the other based the distributed multipole approach.

Linear response method. According to this approach V_DA is given by:[80]

(8)

ρ^tr gives the transition density of the donor and the acceptor. The Coulomb interaction between the transition densities is given by the first term, g_xc is the exchange-correlation kernel, and the second term gives the exchange-correlation interaction; ω₀ is the average resonance transition energy of the dimer, while the third term gives a correction contribution.

Distributed multipole analysis. For very large molecules the computational cost of the analytical calculation of the EET terms may be prohibitively large and a more economic method would be useful. For the Coulomb term, which is generally the largest contribution to the EET coupling, several schemes based on a more sophisticated treatment of the transition densities have been published (see, e.g. the literature cited in Ref. [81] to overcome the shortcomings of the original point dipole treatment using molecular transition dipole moments by Förster.[82] A particularly accurate and computationally economical method, based on the distributed multipole expansion of the transition densities, has been published by Błasiak et al.[81] In this approach, the electrostatic part of the EET coupling between two excited molecules is computed using transition-density derived cumulative atomic multipole moments (TrCAMM). We have here applied a similar method, replacing TrCAMM by the distributed multipole analysis (DMA), pioneered by Stone.[83,84] Apart from this change, the approach was used as described in Ref. [81], to which we refer for further details. The transition densities required where computed using Multiwfn 3.7 ,[85] and the distributed multipole analysis was performed with the GDMA 2.3.3 program. [86] Preliminary tests using several ethylene and naphthalene dimers in the same configuration as used in Ref. [81] have been performed to ensure that the substitution of TrCAMM by DMA still leads to viable results; the differences to the values reported in Ref. [81] were smaller than 5%.

III. Results and Discussion

In this section we shall consider: (i) the static (hyper)polarizabilities of 2 DTE units with and without different substituents and connected by a quasilinear tetrathiophene chain as well as 2 DTE units connected by NiBDT and naphthalene as linkers, (ii) the two-photon absorption of selected thiophenes and (iii) the excited energy transfer (EET).

As mentioned in the introduction, the linker is of crucial importance for the communication between the open-closed DTE units and for the modulation of the molecular NLO properties. Three types of molecular bridges were selected: (a) a quasilinear tetrathiophene chain (see Figure 1), which is known for its remarkable electronic and optoelectronic properties[53] (b) NiBDT which provides an excellent basis for the formation of molecular materials with exceptional optical, electronic and conductive properties[87] and finally naphthalene, which involves two fused benzene rings; this is a 10π electron system similar to NiBDT. It is also noted that two derivatives of molecule 1 (Figure 1) with R=Cl and R=Phenyl, have been synthesized and their photochromism studied , thus allowing to compare the predicted ring closure of both DTE groups with the corresponding experimental finding. A 1D π-conjugated NiBDT nanosheet has also been synthesized.[88]

The main reasons for selecting the above bridges are, first, the expected significant contrast in the NLO properties of the three isomers (oo, oc and cc) and second, the interesting and challenging properties associated with the low-lying excited states of NiBDT, in connection with EET. It is also noted that each molecular structure (cc,co,cc) is studied separately, in its lowest energy conformation, since we are interested in probing and understanding the relationship EET-NLO activity mechanism in more detail. Eventually, we want to understand how to attain full photochromism by modifying the molecular structure.

III.1 (Hyper)polarizabilities

The photochemical process leads to a large change of the structure, which is accompanied by very structure sensitive first and second hyperpolarizability properties (Table 1 and Table 2).

Table 1. The (hyper)polarizabilities of the 1cc, 1oc and 1oo (Figure 1). The structures have been computed with the B3LYP/6-31G* method and the (hyper)polarizabilities with the CAM-B3LYP/6-31G*. All values are given in a.u.

	α			β			γ (x10³)
R	1cc	1co	1oo	1cc	1co	1oo	1cc	1co	1oo
H	972.6 1049.5³	882.3	796.9	680 790³	14860	150	14111 14660³	8476	4078
Cl	1025.4 1108.0³ 914.0⁴	926.0 824.6⁴	827.2 776.7⁴	1200 1250³ 1960⁴	20860 11700⁴	243 144⁴	15635 16270³ 8654⁴	9299 4719⁴	4185 2837⁴
NO2	1123.8	988.8	842.5	257	48040	773	22841	13260	4284
NH2	1024.4	918.9	822.2	530	401	486	16212	8949	4208
Ph	1239.1	1096.1	960.8	-310	10140	150	23611	12378	4692
NO2/ NH21	1094	930.0	832.4	71350	2950	4950	25370	9049	4272
NO2/NH22	1094	988.0	832.4	71350	61260	4950	25370	14861	4272

¹ NO2/NH2 groups are anchored on open/closed unit. ² NO2/NH2 groups are anchored on closed/open unit. ³ Basis Set: C,S,F,Cl,H: cc-pVTZ, ⁴ Properties have been computed at the M062-X optimized geometry.

Table 2. The absorption wavelength (λ;nm) of the lowest lying allowed transition and the (hyper)polarizabilities (a.u.) of 2oo, 2oc, 2cc, 3oo and 3cc (Figure 2).

Derivative	λ	α	β	γ(x10³)
2oo	622.3¹	880.3¹	-410¹	2741¹
2oc	884.1¹	1163¹ 1225²	1349¹ 1330²	17400¹ 19236²
2cc	994.3¹	1576.9¹ 1652.5²	-14076¹ -13080²	67870¹ 68890²
3oo	614.0¹	792.9¹	432¹	1416¹
3cc	878.9¹	1129.6¹	5800¹	13971¹

1 (U) CAMB3LYP/6-31G*. ³² Basis Set: C,S,F,H: cc-pVTZ, Ni: SDD.

A. Oligothiophenes

A series of derivatives with two DTE groups connected by a tetrathiophene group have been studied (Table 1; Figure 1), with different substituents R/R: H/H, Cl/Cl, NO₂/NO₂, NH₂/NH₂, Ph/Ph and NO₂/NH₂ on the DTE groups. We note that these derivatives may also be considered as alkene, methyl end-capped sexithiophenes, which may be a more adequate characterization at least for the open-open isomers.[87]

Polarizabilities. The average polarizabilities of the “open-open” (oo) isomers are: 879±82 a.u. (Table 1), where the limits denote the maximum and minimum average polarizability values among the oo isomers. For the “open-closed” (oc) and “closed-closed” (cc) isomers the corresponding values are 989±107 a.u. and 1106±133 a.u., respectively. The observed trend is α(cc)> α(oc)> α(oo); this is explained by the increased conjugation associated with the closed DTE thus increasing the electron mobility. For R=Ph, as expected, we observe the larger polarizability.

First hyperpolarizabilities. The largest β value is observed for the pair ,R: NO₂/NH₂ of 1cc (71350 a.u.) and 1co (61250 a.u.) isomers (Figure 1). This pair of substituents gives very different first hyperpolarizability values depending heavily on the state of the DTE unit (closed or open) to which they are bonded. For the 1co isomer the larger β value is observed when NO₂ is bonded to the closed DTE unit and NH₂ is bonded to the open one. The tetrathiophene unit is conjugated (Figure 1). We shall now consider the effect of the extension of the conjugation path due to the closed DTE unit(s). The effect of extending the conjugation path on β may be seen when R: H/H (Table 1); the maximum β value (14860 a.u.) is observed for 1co.

The impact of extending the conjugation path on the first hyperpolarizability may also be seen when R: Cl/Cl, NO₂/NO₂. NH₂/NH₂ or Ph/Ph, but in these cases charge-transfer may also affect the results. The effect of charge-transfer on β, may be seen by the difference:

Δ1 = β(Is; R:NO₂/NH₂) – (β(Is; R:NO₂/NH₂)+ β(Is; R:NH₂/NO₂))/2,

(9)

where, Is: 1cc, 1oc or 1oo.

This difference takes the values 70956 a.u., [-21270], 37040 a.u., and 4321 a.u. for 1cc, [1co], 1oc or 1oo, respectively (Table 1). The effect of charge-transfer, as a function of conjugation, upon photoswitching, may be expressed by the above sequence of values. We observe that the molecular state, the conjugation and the charge transfer have a very significant effect on the first hyperpolarizability (β).

Second hyperpolarizabilities. Larger property values are observed for the cc isomer, as it would be expected due to the conjugation; the following trend is observed: γ(cc)> γ(oc)> γ(oo) (Table 1). In particular we note, the effect of extending the conjugation path on γ may be seen by comparison with R,R’:H/H; the maximum second hyperpolarizability value is observed for 1cc (14111x10³ a.u.). The effect of charge-transfer on γ, may be estimated by the difference:

Δ2 = γ(Is; R,R’:NO2/NH2) – (γ(Is; R,R’:NH2/NO2) + γ(Is; R,R’:NO2/NH2))/2,

(10)

where, Is: 1cc, 1co, [1oc] or 1oo. This difference takes the values 5844 x10³ a.u., [-2056], 3757 x10³ a.u., and 26 x10³ a.u. for 1cc, [1co], 1oc and 1oo, respectively (Table 1). Again, the effect of charge-transfer, as a function of the conjugation length may be expressed by the above sequence of values. We observe that both conjugation enhancement, upon photoswithing, and charge transfer have a very significant effect on the second hyperpolarizability (γ).

Taking the ratios Δ1(1cc)/Δ1(1oo) = 16.9 ( (eq. 9) and Δ2(1cc)/Δ2(1oo) = 224.8 (eq. 10), we observe that the effect of charge-transfer, as a function of conjugation has a much greater effect on γ than on β. The corresponding ratio for the polarizability (α) is 3.4. In general α obeys most of the trends of γ, but in a less pronounced way. Finally let us also note that for the case of α and γ, change of the geometry (B3LYP/M062-X) has s small effect on the contrast ratios, k=P_1cc/P_1oo and λ= P_1cc/P_1co (Table 1;R=Cl). It is observed that k=1,24/1.17(α), 3.74/3.05 (γ) , while λ=1.11/1.11 (α), 1,68/1.83(γ). The notation A/B(P) stands for the ratio computed at the B3LYP/M062-X optimized geometry and P=α,γ denotes the property. For the case of β the effect was found to be larger and stands for k=4.9/13.6 and λ=0.06/0.17.

B. Derivatives Having NiBDT and Naphthalene as Linkers

A series of derivatives have been studied, which involve two DTE groups, connected by either NiBDT or naphthalene (Figure 2; Table 2). Both linkers have 10π electrons.

NiBDT. We observe that the cc isomer lies lower in total energy compared with oc and oo ones (Table S1):

E(2oo)> E(2oc)> E(2cc),

We also observe that an increase of conjugation, upon photoswitching, leads to a decrease of the |HOMO-LUMO| (=Δ_HL) gap (Table S1), due to destabilization of HOMO; for 2oo, 2oc and 2cc the corresponding Δ_HL values are 0.059 a.u., 0.050 a.u. and 0.042 a.u., respectively. Let us note that a similar trend was found for the sexithiophene derivatives (Table S1)

These results are in agreement with those reported in the literature.[89] A red-shift of λ_max is also noted, upon changing the structure of the isomer: λ(2cc)> λ(2oc) λ(2oo) (Table 2).

For the (hyper)polarizabilities we observe the trend (Table 2): P(2cc)> P(2oc)> P(2oo), where P: α, |β|, γ. The cc isomer has remarkably larger properties (α, |β|, γ) values than the other isomers.

Naphthalene. For the total energy we also observe that: E(3oo)> E(3cc) (Table 2). A similar trend was found for NiBDT as a linker. For the (hyper) polarizabilities, we found: P(cc)> P(oo), P=α,β,γ. A significant change for β and γ of oo and cc isomers is also observed.

NiBDT and Naphthalene have both 10π electrons, however their effect on α, β, and γ is very different. For NiBDT, as a bridge, the ratio of P_2cc/P_2oo, where P= α, β, or γ is 1.8, 34.3 and 24.7, respectively, while for napthalene the corresponding ratios for 3cc/3oo are 1.42(α), 13.4(β) and 9.9(γ). The ratio P_2cc/P_3cc, which shows the effect of the type of the bridge on the L&NLO molecular properties is 1.4, -2.4 and 4.9 for α, β, and γ, respectively. As it has been shown, the existence of low lying excited states, due to the presence of NiBDT, significantly enhances the polarization character.[90]

In the previous article [49] we have investigated the contrast between the L&NLO properties of the “open” and “closed” isomer of the derivatives involving one DTE unit. [49] We found that P(c)>P(o), where P: α or γ. In this work, the considered molecules involve two DTE groups. We observe, in general, P(cc)>P(co)>P(oo), where P: α or γ. This trend is due to an increase of conjugation, upon photoswitching, in the order cc>oc>oo. As shown in Ref [49] increasing the conjugation path increases the positive contribution of the density of the second hyperpolarizability much more than the negative one, thus reinforcing the γ values. The trends observed in the first hyperpolarizability are less regular.

Summarizing the findings from Table 1 and Table 2, we note that the molecular L&NLO optical properties follow the structural changes induced by photochromism. The first hyperpolarizability (β) shows a less regular dependence in comparison to polarizability (α) and second hyperpolarizability (γ). There is a significant contrast between the computed values, for the first and second hyperpolarizabilities of the open-open and closed-closed isomers of the considered derivatives. NiBDT as a linker leads to a greater contrast, in comparison to naphthalene and oligothiophene. The great effect of conjugation on the hyperpolarizabilities is clearly demonstrated by the closed-closed isomers. The results (Table 1 and Table 2) show that the hyperpolarizabilities and in particular γ can be used as an index, which follows the structural changes induced by photochromism. Therefore, the sensitivity of the polarization character upon photoswitching can assist to the identification of the molecular isomers (oo-oc-cc) upon light irradiation. To reinforce the validity of the basis set 6-31G* for the properties considered here, we have computed selected cases with the larger basis set cc-pVTZ. As shown in Table 1 and Table 2 there is a reasonable agreement between the two sets of data.

HOMA analysis. To obtain a further insight into the reasons for the differences of the hyperpolarizabilities for the different isomers, we computed a measure for the conjugation along the quasilinear conjugated [-C=C-]_n chain, following the prescription of the Harmonic Oscillator Model of Aromaticity (HOMA) index I_HOMA [91]:

I_{H O M A} = 1 - \frac{α}{n} \sum_{i = 1}^{n} {(R_{i} - R_{O p t})}^{2}

(11)

where n is the number of CC bonds, R_i is the i-th bond length of the conjugated chain, R_Opt is the reference bond length in benzene, chosen as an optimally conjugated system and computed at the same level of theory (1.397 Å at B3LYP/6-31G*), and 257.7 Å^-2 is a normalization factor chosen such that I_HOMA of an aromatic compound approaches 1 and that of its Kekulé non-aromatic structure becomes 0.

The HOMA index was computed for two of the R₁-1xy-R₂ series of isomers (x,y=c,o); a) with R₁=NO_2, R₂=NH_2, and b) with R₁=R₂=H. For the internal [-C=C-]₂₁ chain, which can be written as a neutral, fully conjugated pseudolinear structure in all isomers, the calculated HOMA indices using eq. 11, with n=21, are shown in Table 3. For both molecules the conjugation as measured by the HOMA index increases with the number of closed ring structures.

III.2 Two-photon Absorption

The electronic structure parameters (excitation energies, oscillator strengths and two-photon transition strengths) corresponding to five lowest-energy electronic excitations of 1cc,1co,1oo molecules(Fig. 1, R=H) are shown in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. Note that the values of two-photon absorption (2PA) strengths for higher lying states (S₄-S₅) are not very accurate due to resonance effects (they are overestimated). In order to obtain more realistic values on should employ damped response theory,[92] but given the size of the studied systems such calculations were not feasible. We will start with the analysis of one-photon absorption properties. The data shown in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 allow to draw a few general comments.

First, for all considered substituents, the S₀→S₁ transition is characterized by very large values of oscillator strengths (spanning the range 1.18 (R=NO₂, oc) – 2.54 (R=NO₂, oo)).

Second, there is a common pattern for all compounds for this transition:

∆E(cc) < ∆E(oc) < ∆E(oo) and

f(oc) < f(cc) < f(oo)

Third, for cc and oc isomers with R=NO₂ and R=NO₂, NH₂ substituents there is a moderate change in S₀→S₁ excitation energy in comparison to other derivatives (R=Cl, R=H, R=NH₂). However, for oo we note that the S₀→S₁ excitation energy is insensitive to the change of substituent, i.e. it is roughly 2.8 eV. The 2PA properties corresponding to the S₀→S₁ transition are negligible (i.e. less than 10⁴ au) for most of the compounds. There are only three exceptions, i.e. oc isomer (R=NO₂; Table 7)), cc and oc with R=NO₂, R’=NH₂ (Table 8 and Table 9). The corresponding values for all three cases exceed 5×10⁴ and reach up to 12×10⁴ (cc isomer). Taken together, these results demonstrate that in the case of bright S₀→S₁ transition it is possible to tune the excitation energies and 2PA transition strengths by changing substituents only for cc and oc isomers. The most pronounced change in properties is achieved by using asymmetric substitution by NO₂ and NH₂ and 2PA strengths can be increased by two orders of magnitude.

ΙΙΙ. 3 Excitation Energy Transfer

The intra-molecular EET and the overlap between absorption and emission spectra of the studied systems will be analyzed. The intra-molecular process depends on a number of factors (e.g. V_DA – the electronic coupling between the donor and the acceptor-, the overlap of the emission spectrum of the donor and the absorption spectrum of the acceptor). By necessity this study has to be selective. Thus, analysis of the intra-molecular EET will rely on V_DA. Additionally, the overlap of the emission spectrum of the donor and the absorption spectrum of the acceptor will be studied.

The selected bridges, between the DTE units (Figure 1, Figure 2 and Figure 3), allow to tune V_DA and eventually EET. In this context, it is useful to find out how the modification of structure affects V_DA. In particular, it is important to specify rules to minimize EET and thus to attain full photochromism. This is a central question of our study.

ΙΙΙ. 3A. Intra-molecular excited energy transfer

For the study of the intra-molecular EET (excited energy transfer) we have employed the following approaches:

(i)Two methods have been used for the computation, of V_DA of several models, that is the coupling between the donor (open unit) and the acceptor (closed unit). (ii) For the case of 1oc isomer, the emission spectrum of the donor andthe absorption spectrum of the acceptor have been analyzed.

A. In the following section we will discuss the results, obtained by the two methods we have used to calculate V_DA.

Linear response method. The ground state equilibrium geometries have been used to compute V_DA.[1] We have employed three types of molecular bridges, NiBDT, naphthalene and an oligothiophene (Figure 1, Figure 2 and Figure 3). For NiBDT and naphthalene, the cis and trans isomers of the corresponding derivative have been considered. For the trans isomer of naphthalene, as a bridge, we have used two conformations, one is planar and in the other, the plane of naphthalene is vertical to the plane of DTE groups. NiBDT is bonded with the two switches with two different ways: (i) NiBDT is fused with the two DTE units (2oc; Figure 2) and (ii) it is bonded with the switches with single bonds (7oc & 8oc; Figure 3). Each molecule is decomposed into two fragments: D (donor; the open DTE) and A (acceptor; the closed DTE bonded with the bridge ). The bond, which is cut is capped with a hydrogen atom at both ends. Thus, a well-defined fragment results. The employed models are given in Figure 3. The linker (or bridge), i.e naphthalene, NiBDT, oligothiophene is bonded to the closed DTE unit (acceptor). This model corresponds to the M2 one employed by Fihey et al.[1] It has been selected because it was found in ref [1] when the bridge is bonded to the acceptor unit the Coulomb interaction is enhanced and thus a significant EET process takes place. A detailed discussion of this and several other models is given in the above reference. For the computation of V_DA one needs to find the excited states, which participate in the EET process.[1] For the open DTE moiety, which is the donor fragment, the excited state involves, in most cases, a HOMO-LUMO transition; this is connected with the photocyclization process. Thus, the selected relevant transition energy should lie in the UV region. The relevant excited state of the closed DTE unit, which is the acceptor -fragment, is selected by taking into account two criteria: (i) its energy should be close and lower than the energy of the donor and (ii) it should have a non-negligible oscillator strength. It has been shown, based on the Förster’s theory that a significant suppression of the EET rate takes place, when the excitation energy difference between the donor and the acceptor is large, in comparison with other relevant energy properties of the interacting molecules.[93] Table 10 reports two contributions to V_DA: the coulombic (V_c) and the exchange (V_xc).

Areephong et al.[53] observed ring closure of both photochromic units for the sexithiophenes they studied (1oc; Figure 1; R: Cl). In agreement with the experimental observation, a low value of V_DA was computed for R=Cl, (8.3 cm^-1; Table 11) suggesting ring closure,. In the second derivative considered (2oc; Figure 2), each DTE group is fused with two NiBDT molecules, while the Ni compound also operates as a bridge. A rather low V_DA has been computed for this (10.3 cm^-1). Therefore, if we consider this value of V_DA (8.3 cm^-1) as a reference, it is likely that NiBDT bridge allows the switching between the three states, although for a more complete answer other factors should also be considered (e.g energy transfer speed, cyclisation time).[1]

We observe that for 2oc the relevant excited state of the donor is the 22^nd (268 nm; Table 11). This is, of course, quite high and reinforces the conjecture of a very low probability of EET. Nevertheless, although it is known that the higher-energy emission bands in the UV would violate Kasha’s rule and Kasha−Vavilov rule for fluorescence, violations of these rules are reported specifically in connection with intramolecular EET.[94,95,96,97] Figure 4 presents the emission spectrum of the fragment, which operates as donor, the absorption spectrum of the fragment, which acts as acceptor and their overlap. The emission, which is relevant for EET is found in the area 230-300nm. We observe two peaks at 250 nm and 270 nm. However, two antagonistic processes are likely to take place before EET proceeds: internal conversion to S₁ and photo-cyclization of the open DTE group. In addition, all the oscillator strength (f) values, associated with the emission in UV, except that of the 22^nd state are negligible (Table S3). Taking into account these considerations and the corresponding small value of V_AD (10.3 cm^-1), we believe that EET is unlikely to take place and thus the open DTE unit of 2oc is likely to close.

4oc, 5oc and 6oc have naphthalene as a linker; 4oc involves the DTE groups in cis orientation, while 5oc and 6oc have the DTE units in trans orientations. In 5oc and 6oc the naphthalene groups have a different arrangement (Figure 3). In all considered cases V_xc is very small. We observe that V_DA is very large for 4oc-6oc, where naphthalene is the linker. This suggests significant EET and thus, partial photochromic activity (i.e. the closing of only one photochromic unit is likely to be observed). The significant effect of geometry on V_DA is clearly demonstrated by these results (Table 10).

7oc and 8oc involve NiBDT as a linker. 7oc and 8oc have the DTE groups in cis and trans orientation, respectively. We observe that for 7oc and 8oc the excited states, S₁ – S₃ , of the donor have for emission f=0. Thus S₄ was considered. The smaller V_DA is observed for the trans isomer, 8oc (12.8cm^-1). This low V_DA suggests that no significant EET takes place, therefore, both DTE groups are likely to close.

It is interesting to compare the V_DA (Coulomb contribution, V_C) value of naphthalene as a linker with that of a biphenyl group as a bridge. In the first case V_C = 101.6-120.9 cm^-1, depending on the orientation of the open/closed units of the linker; in naphthalene the two phenyl groups are fused. In the second case, V_DA = 3.1cm^-1; the two phenyl groups are connected with a single bond. The great effect of the structure on V_DA is clearly seen.

We observe that for 5oc (Table 11, Figure 3) the transition energy for the acceptor, 4.209eV is associated with the 4^th excited state, S₄. However, for 8oc, the corresponding transition energy 4.136 eV is associated with the excited state S₅₀. This very large number of intervening excited states is due to the presence of NiBDT.[90] The unusually large NLO properties of NiBDT derivatives (Table 2) are also due to the significant number of low-lying excited states.

The calculation of V_DA, by the linear response method, illuminates some aspects of EET, that is the excitation of the open DTE and the absorption of the closed DTE, which is due to the de-excitation of the open DTE.

Our results clearly show that the linker strongly influences the communication between the DTE groups and thus, photochromism. The molecular geometry has a significant effect on V_DA. NiBDT, as a linker, is associated with, relatively, low V_DA values; therefore both DTE groups are likely to close. This low V_DA is due to the near-IR absorption spectrum of NiBDT. Our computations have shown that the considered oligothiophene, as a linker, is associated with low V_DA and thus allows both DTE groups to close. This is in agreement with the experimental observation.[53]

Distributed multipole analysis (DMA). To gain a further understanding of the EET process we have also computed the V_c contribution of V_DA by the method proposed by Błasiak, et al.,[81] which relies on the distributed multipole expansion of the transition densities. The results for the DMA treatment, as a function of the limiting value of the sum of the interacting multipole moments l+l’ (where l,l’=0 (charge), ... , 4 (hexadekapole)) are given in Table 12. It has been shown in Ref. [[81]], and was also found here, that limiting the sum of the ranks yields better results than the alternative approach of using all multipoles up to a limiting rank l. As the values show, the electrostatic contribution computed using the multipole expanded transition density employing the highest limiting rank l+l’ = 4 compare quite well with the analytically computed values (linear response method); the differences are in the range of 10^-4 eV (̴ 0.8cm^-1). We note that both the added terminal hydrogen H_term as well as the carbon atom connected with it were not used as explicit expansion centers in the DMA treatment. The remaining differences between the multipole-expanded method and the analytical values may be caused at least in part by a not yet converged expansion series and/or by the charge density of H_term, which has not been removed. Although H_term was not used as an expansion center, its associated charge density is still taken into account in the DMA treatment.

We concluded that the results for V_c, computed with the DMA method, are in satisfactory agreement with those calculated with the linear response approach (Table 10 and Table 12).

ΙΙΙ. 3.Β Overlap of the emission spectrum of the donor and the absorption spectrum of the acceptor

In this section we shall discuss the overlap of the emission spectrum of the donor and the absorption spectrum of the acceptor. The considered systems involve 2oo, 2oc and 2cc (Figure 2), where for the pair 2oo/2oc, 2oo is the donor and 2oc is the acceptor, i.e., 2oo absorbs photons and then emits, while the 2oc absorbs the emitted photons. Similarly, for the pair 2oc/2cc, 2oc is the donor and 2cc is the acceptor, i.e., 2oc which had absorbed photons, it emits, while the 2cc absorbs the emitted photons. This overlap is an indication that EET phenomenon may occurs between different molecules. Of particular relevance for this work is overlap in the UV area, because photo-cyclization takes place at this area. One of our major themes is whether EET will allow the open DTE unit of 2oc to close leading to 2cc.

For the case of the 2oo structure, two conformers a and b have been obtained. Rotations around C-C bond convert a isomer to b, see Figure 5. The a conformer is lowest in energy than b by 0.18 eV because weak π-π interactions are formed between the rings of the central NiBDT and the rings of the other NiBDT groups. However, both present similar absorption spectra, i.e., their peaks differ less than 6 nm and up to 0.03 eV, see below. Finally, it should be mentioned that the optimized geometry of the excited states of 2oo, that corresponds to the main peaks of the emission spectra, have similar geometry with b.

The absorption spectrum of 2oo has a main peak in the visible range at ~600 nm, an intense peak in UV area at ~310 nm and small overlapping peaks at ~700 nm and ~900 nm in NIR area. On the contrary, the main peak of the absorption spectra of 2oc and 2cc is found at 807 and 862 nm in NIR area. At 650 and 600 nm there are some overlapping peaks for the 2oc and at 670 nm for the 2cc. Finally, both present small peaks in the UV area of 400-300 nm, see Figure 6 and Figure S4-S5, Table 13 and Table S4 of SI. The emission spectrum of 2oo presents two peaks of similar intensity at 670 nm and 313 nm in the vis and UV regions, respectively. The emission spectrum of 1oc presents three peaks: an intent at 917 nm in the NIR region and two peaks of similar intensity at 662 nm and 326 nm in vis and UV area.

The vertical and adiabatic excitation energies with respect to the ground state and the vertical emission de-excitation are shown in Table 14. We found that the absorption spectra of 2oo presents two main peaks that correspond to excitations of 2.07 and 4.01 eV and a small peak that corresponds to excitations of 1.81. As new rings are formed (2oo→2oc→2cc), less energy is needed for these three vertical excitations, i.e., the excitations are red shifted for the 2oc structure up to 0.3 eV and further red shifted for 2cc. The most intense red shifted excitation is for the small peak at 1.81 eV and the least red shifted excitation is for the main peak of the 4.01 eV. Similarly, the vertical emission and the adiabatic excitation is similar or less for the 2oc comparing to 2oo.

It is of interest that the vertical main emitting peaks of the 2oo are at 1.44, 1.85, and 3.97 eV, very similar to the absorption peaks of the 2oc which are at 1.54, 1.87, and 3.92 eV, see Table 14. This shows that energy transfer is possible from the excited open-ring unit to the closed-ring unit, i.e., 2oo→2oc. Similarly, the vertical main emitting peaks of the 2oc are at 1.35, 1.86, and 3.81 eV and the adiabatic de-excitation energies are at 1.40, 1.87, and 3.88 eV; and thus, they are very similar to the absorption peaks of the 2cc which are at 1.44, 1.84, and 3.92 eV. Again, energy transfer is possible from the excited open-ring (2oc→2cc) unit to the closed-ring unit. Conclusively, energy transfer is possible through this 2oo→2oc→2cc process.

The findings of the reported excited state computations are in agreement with the conclusions presented in Ref. 87. The authors there reported that excited-state quenching is responsible for the absence of photochemistry in dithienylethene/sexithiophene-based polymer while intramolecular quenching is observed for the dithienylethene units by the sexithiophene unit.

Finally, the frontier molecular orbitals (MO) involving in the main excitations are depicted in Figure 7, Figure 8 and Figure 9. It is of interest that many MO orbitals are involved in the main excitations, see Table S4 and Table 13. The main absorption peaks of the a conformer in vis and UV area are at 599 nm and 310 nm and they present a small charge transfer (CT) character. This results from the fact that in a conformer π-π interactions exist, which are observed in the occupied orbitals, see for instance HOMO and HOMO-6 in Figure 7. In the unoccupied LUMO and LUMO+2 orbitals, where the electron is transferred via the excitation, it is in the peripheral NiBDT group. On the contrary, in the b conformer no CT character is observed due to the absence of the π-π interactions. The fluorescence peaks of the 2oo at 859 nm and 670 nm have not a CT character, however, the peak at 312 nm does, see Figure 7. The three peaks of the absorption spectrum of 2oc at 807, 664, and 316 nm have only a small partially CT character. The emitting peak at 326 nm is a CT de-excitation from d orbitals of Ni to p electrons of S, see Figure 8. Finally, regarding the 1cc, where additional aromatic rings are formed, the absorption peak at 317 nm has a clear CT character, with a significant f coefficient of 0.14, from the peripheral C₂H₂S₂Ni group to the whole molecule, i.e., the electron density is delocalized in all 2cc structure, see Figure 9.

Conclusions

A significant contrast of the hyperpolarizabilities has been observed between the open-open, open-closed and the closed-closed isomers of the studied compounds. NIBDT, as a linker, is associated with a greater contrast, in comparison to naphthalene, in the properties of interest. This has been attributed to the low lying excited states of NiBDT. As it has been shown, the existence of low lying excited states, due to the presence of NiBDT, significantly enhances the polarization character.

The closed-closed isomer clearly demonstrates the great effect of the conjugation on the hyperpolarizabilities. The structural changes induced by photochromism can be closely followed by the second hyperpolarizability, and thus this property can be used as an index to monitor the molecular changes, which are due to photochromism. A similar trend, although to a lesser extent, has also been found for the first hyperpolarizability. Overall, it is observed that the NLO molecular properties can be used as probes for detection of the possible molecular states.

As expected, we found that the linker greatly affects the communication between the DTE groups and thus, photochromism. It was found that a low V_DA is associated with NiBDT as a linker, therefore both DTE groups are likely to close. The near-IR absorption spectrum of NiBDT could be associated with the observed low V_DA and the diminished communication. We found that V_DA is also affected by the molecular geometry. The computed low V_DA value for the case of the sexithiophene, R=Cl, molecular switch is in agreement with the experimentally observed full photochromism [84]. The linear response and the DMA methods give very close electrostatic contributions to V_DA.

Εnergy transfer may occur via the oo→oc→cc process. The vertical main emitting peaks of the oo are very similar to the absorption peaks of the oc. Similarly, the vertical main emitting peaks of the oc and the adiabatic de-excitation energies are very similar to the absorption peaks of cc.

Intramolecularly, the cc fragment, presents major absorption peaks at ~650 nm, while the oo fragment does not present significant emission in this area. Thus, the bridge does not ease the charge transfer intramolecular from the o fragment.

An overlap is observed between the fluorescence spectrum of oc with the absorption spectrum of cc and between the fluorescence spectrum of oο with the absorption spectrum of οc. The absorption and emission peaks at ~310 nm in all cases present charge transfer character.

The results of the present study clearly reveal that the electronic nature of the NiBDT molecular bridge, connecting the open-closed DTE units, could allow the photoswitching between molecular states with tunable polarization characteristics. The sensitivity of the L&NLO properties could be used as a probe for the identification of the photoswitching process and the existence of the possible isomers.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Conceptualization: A.A., M.G.P.; investigation: A.A.,D.T. H.R.,R.Z and M.G.P, data curation: : A.A.,D.T. H.R.,R.Z and M.G.P.; writing—original draft: M.G.P.,A.A.,D.T. H.R.,R.Z; writing—review & editing: M.G.P.,A.A., D.T All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The authors wish to acknowledge Prof. Denis Jacquemin, Prof. Wesley Browne, Prof. Jan Cz Dobrowolski and Prof. Seiya Kobatake for some helpful and constructive discussions.

References

Fihey, A., R. Russo, L. Cupellini, D. Jacquemin, and B. Mennucci. "Is Energy Transfer Limiting Multiphotochromism? Answers from Ab Initio Quantifications." Physical Chemistry Chemical Physics 2017, 19, 2044-52. [CrossRef]
Galanti, A., J. Santoro, R. Mannancherry, Q. Duez, V. Diez-Cabanes, M. Valasek, J. De Winter, J. Cornil, P. Gerbaux, M. Mayor, and P. Samori. "A New Class of Rigid Multi(Azobenzene) Switches Featuring Electronic Decoupling: Unravelling the Isomerization in Individual Photochromes." Journal of the American Chemical Society 2019, 141, 9273-83. [CrossRef]
Hsu, C. P. "The Electronic Couplings in Electron Transfer and Excitation Energy Transfer." Accounts of Chemical Research 2009, 42, 509-18. [CrossRef]
Nakamura, Y., N. Aratani, and A. Osuka. "Cyclic Porphyrin Arrays as Artificial Photosynthetic Antenna: Synthesis and Excitation Energy Transfer." Chemical Society Reviews 2007, 36, 831-45. [CrossRef]
Zhang, L. Y., R. A. Friesner, and R. B. Murphy. "Ab Initio Quantum Chemical Calculation of Electron Transfer Matrix Elements for Large Molecules." Journal of Chemical Physics 1997, 107, 450-59. [CrossRef]
Headgordon, M., A. M. Grana, D. Maurice, and C. A. White. "Analysis of Electronic-Transitions as the Difference of Electron-Attachment and Detachment Densities." Journal of Physical Chemistry 1995, 99, 14261-70. [CrossRef]
You, Z. Q., C. P. Hsu, and G. R. Fleming. "Triplet-Triplet Energy-Transfer Coupling: Theory and Calculation." Journal of Chemical Physics 2006, 124. [CrossRef]
Iozzi, M. F., B. Mennucci, J. Tomasi, and R. Cammi. "Excitation Energy Transfer (Eet) between Molecules in Condensed Matter: A Novel Application of the Polarizable Continuum Model (Pcm)." Journal of Chemical Physics 2004, 120, 7029-40. [CrossRef]
Scholes, G. D. "Long-Range Resonance Energy Transfer in Molecular Systems." Annual Review of Physical Chemistry 2003, 54, 57-87. [CrossRef]
Kaieda, T., S. Kobatake, H. Miyasaka, M. Murakami, N. Iwai, Y. Nagata, A. Itaya, and M. Irie. "Efficient Photocyclization of Dithienylethene Dimer, Trimer, and Tetramer: Quantum Yield and Reaction Dynamics." Journal of the American Chemical Society 2002, 124, 2015-24.
Chen, H. C., Z. Q. You, and C. P. Hsu. "The Mediated Excitation Energy Transfer: Effects of Bridge Polarizability." Journal of Chemical Physics 2008, 129. [CrossRef]
Scholes, G. D., K. P. Ghiggino, A. M. Oliver, and M. N. Paddonrow. "Through-Space and through-Bond Effects on Exciton Interactions in Rigidly Linked Dinaphthyl Molecules." Journal of the American Chemical Society 1993, 115, 4345-49. [CrossRef]
Oevering, H., M. N. Paddonrow, M. Heppener, A. M. Oliver, E. Cotsaris, J. W. Verhoeven, and N. S. Hush. "Long-Range Photoinduced through-Bond Electron-Transfer and Radiative Recombination Via Rigid Nonconjugated Bridges - Distance and Solvent Dependence." Journal of the American Chemical Society 1987, 109, 3258-69. [CrossRef]
Pettersson, K., A. Kyrychenko, E. Ronnow, T. Ljungdahl, J. Martensson, and B. Albinsson. "Singlet Energy Transfer in Porphyrin-Based Donor-Bridge-Acceptor Systems: Interaction between Bridge Length and Bridge Energy." Journal of Physical Chemistry A 2006, 110, 310-18. [CrossRef]
Cho, H. S., D. H. Jeong, M. C. Yoon, Y. H. Kim, Y. R. Kim, D. Kim, S. C. Jeoung, S. K. Kim, N. Aratani, H. Shinmori, and A. Osuka. "Excited-State Energy Transfer Processes in Phenylene- and Biphenylene-Linked and Directly-Linked Zinc(Ii) and Free-Base Hybrid Diporphyrins." Journal of Physical Chemistry A 2001, 105, 4200-10. [CrossRef]
Smith, T. A., N. Lokan, N. Cabral, S. R. Davies, M. N. Paddon-Row, and K. P. Ghiggino. "Photophysics of Novel Donor-{Saturated Rigid Hydrocarbon Bridge}-Acceptor Systems Exhibiting Efficient Excitation Energy Transfer." Journal of Photochemistry and Photobiology a-Chemistry 2002, 149, 55-69.
Kroon, J., A. M. Oliver, M. N. Paddonrow, and J. W. Verhoeven. "Observation of a Remarkable Dependence of the Rate of Singlet Singlet Energy-Transfer on the Configuration of the Hydrocarbon Bridge in Bichromophoric Systems." Journal of the American Chemical Society 1990, 112, 4868-73. [CrossRef]
El-ghayoury, A., A. Harriman, A. Khatyr, and R. Ziessel. "Intramolecular Triplet Energy Transfer in Metal Polypyridine Complexes Bearing Ethynylated Aromatic Groups." Journal of Physical Chemistry A 2000, 104, 1512-23. [CrossRef]
McConnell, H. M. "Intramolecular Charge Transfer in Aromatic Free Radicals." Journal of Chemical Physics 1961, 35, 508-15. [CrossRef]
Kudernac, T., S. J. van der Molen, B. J. van Wees, and B. L. Feringa. "Uni- and Bi-Directional Light-Induced Switching of Diarylethenes on Gold Nanoparticles." Chemical Communications 2006, 34, 3597-99.
Chen, J. X., J. Y. Wang, J. R. He, and X. F. Peng. "Photochromic Properties of Ruthenium Complexes with Dithienylethene-Ethynylthiophene." Dyes and Pigments 2021, 184.
Chergui, M. "Ultrafast Molecular Photophysics in the Deep-Ultraviolet." Journal of Chemical Physics 2019, 150. [CrossRef]
Munoz-Losa, A., C. Curutchet, B. P. Krueger, L. R. Hartsell, and B. Mennucci. "Fretting About Fret: Failure of the Ideal Dipole Approximation." Biophysical Journal 2009, 96, 4779-88. [CrossRef]
Beljonne, D., C. Curutchet, G. D. Scholes, and R. J. Silbey. "Beyond Forster Resonance Energy Transfer in Biological and Nanoscale Systems." Journal of Physical Chemistry B 2009, 113, 6583-99. [CrossRef]
Kenny, E. P., and I. Kassal. "Benchmarking Calculations of Excitonic Couplings between Bacteriochlorophylls." Journal of Physical Chemistry B 2016, 120, 25-32. [CrossRef]
Sauer, K., R. J. Cogdell, S. M. Prince, A. Freer, N. W. Isaacs, and H. Scheer. "Structure-Based Calculations of the Optical Spectra of the Lh2 Bacteriochlorophyll-Protein Complex from Rhodopseudomonas Acidophila." Photochemistry and Photobiology 1996, 64, 564-76. [CrossRef]
Krueger, B. P., G. D. Scholes, and G. R. Fleming. "Calculation of Couplings and Energy-Transfer Pathways between the Pigments of Lh2 by the Ab Initio Transition Density Cube Method." Journal of Physical Chemistry B 1998, 102, 5378-86.
Kistler, K. A., F. C. Spano, and S. Matsika. "A Benchmark of Excitonic Couplings Derived from Atomic Transition Charges." Journal of Physical Chemistry B 2013, 117, 2032-44. [CrossRef]
Scholes, G. D., and K. P. Ghiggino. "Electronic Interactions and Interchromophore Excitation Transfer." Journal of Physical Chemistry 1994, 98, 4580-90. [CrossRef]
Munoz-Losa, A., C. Curutchet, B. P. Krueger, L. R. Hartsell, and B. Mennucci. "Fretting About Fret: Failure of the Ideal Dipole Approximation." Biophysical Journal 2009, 96, 4779-88. [CrossRef]
Moerner, W. E. "Viewpoint: Single Molecules at 31: What's Next?" Nano Lett 2020, 20, 8427-29.
Yang, Mino, and Graham R. Fleming. "Third-Order Nonlinear Optical Response of Energy Transfer Systems." The Journal of Chemical Physics 1999, 111, 27-39. [CrossRef]
Coe, Benjamin J. "Molecular Materials Possessing Switchable Quadratic Nonlinear Optical Properties." Chemistry – A European Journal 1999, 5, 2464-71. [CrossRef]
Castet, Frédéric, Vincent Rodriguez, Jean-Luc Pozzo, Laurent Ducasse, Aurélie Plaquet, and Benoît Champagne. "Design and Characterization of Molecular Nonlinear Optical Switches." Accounts of Chemical Research 2013, 46, 2656-65. [CrossRef]
Beaujean, Pierre, Lionel Sanguinet, Vincent Rodriguez, Frédéric Castet, and Benoît Champagne. "Multi-State Second-Order Nonlinear Optical Switches Incorporating One to Three Benzazolo-Oxazolidine Units: A Quantum Chemistry Investigation." Molecules 2022, 27, 2770.
Zhang, J. J., Q. Zou, and H. Tian. "Photochromic Materials: More Than Meets the Eye." Advanced Materials 2013, 25, 378-99. [CrossRef]
Boixel, J., A. Colombo, F. Fagnani, P. Matozzo, and C. Dragonetti. "Intriguing Second-Order Nlo Switches Based on New Dte Compounds." European Journal of Inorganic Chemistry 2022, 2022. [CrossRef]
Buckingham, A.D. "Permanent and Induced Molecular Moments and Long-Range Intermolecular Forces." In Advances in Chemical Physics 1967, 107-42.
Cohen, H. D., and C. C. Roothaan. "Electric Dipole Polarizability of Atoms by Hartree-Fock Method .I. Theory for Closed-Shell Systems." Journal of Chemical Physics 1965, 43, S034-+.
Romberg, W. "Vereinfachte Numerische Intergration." Kgl. Norske Vid. Selsk. Forsk 1955, 28, 30-36.
Rutishauser, H. Ausdehnung Des Rombergschen Prinzips." Num. Math 1963, 5, 48-54. [CrossRef]
Davis, P. J., and P. Rabinowitz. Numerical Intergration. London: Blaisdell, 1967.
Takamuku, Shota, and Masayoshi Nakano. "Theoretical Study on Second Hyperpolarizabilities of Intramolecular Pancake-Bonded Diradicaloids with Helical Scaffolds." ACS Omega 2019, 4, 2741-49. [CrossRef]
Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox. Gaussian 16 Rev. B.01,Gaussian, Inc., Wallingford CT, 2016.
Becke, A. D. "A New Mixing of Hartree-Fock and Local Density-Functional Theories." Journal of Chemical Physics 1993, 98, 1372-77. [CrossRef]
Serrano-Andres, L., A. Avramopoulos, J. Li, P. Labeguerie, D. Begue, V. Kello, and M. G. Papadopoulos. "Linear and Nonlinear Optical Properties of a Series of Ni-Dithiolene Derivatives." Journal of Chemical Physics 2009, 131, 134312. [CrossRef]
Avramopoulos, A., H. Reis, G. A. Mousdis, and M. G. Papadopoulos. "Ni Dithiolenes - a Theoretical Study on Structure-Property Relationships." European Journal of Inorganic Chemistry 2013, 4839-50. [CrossRef]
Avramopoulos, A., H. Reis, N. Otero, P. Karamanis, C. Pouchan, and M. G. Papadopoulos. "A Series of Novel Derivatives with Giant Second Hyperpolarizabilities, Based on Radiaannulenes, Tetrathiafulvalene, Nickel Dithiolene, and Their Lithiated Analogues." Journal of Physical Chemistry C 2016, 120, 9419-35. [CrossRef]
Avramopoulos, Aggelos, Robert Zaleśny, Heribert Reis, and Manthos G. Papadopoulos. "A Computational Strategy for the Design of Photochromic Derivatives Based on Diarylethene and Nickel Dithiolene with Large Contrast in Nonlinear Optical Properties." The Journal of Physical Chemistry C 2020, 124, 4221-41. [CrossRef]
Sutradhar, T., and A. Misra. "The Role of Pi-Linkers and Electron Acceptors in Tuning the Nonlinear Optical Properties of Bodipy-Based Zwitterionic Molecules." Rsc Advances 2020, 10, 40300-09. [CrossRef]
Cao, L. L., and U. Ryde. "Influence of the Protein and Dft Method on the Broken-Symmetry and Spin States in Nitrogenase." International Journal of Quantum Chemistry 2018, 118. [CrossRef]
Garcia-Borras, M., M. Sola, J. M. Luis, and B. Kirtman. "Electronic and Vibrational Nonlinear Optical Properties of Five Representative Electrides." Journal of Chemical Theory and Computation 2012, 8, 2688-97. [CrossRef]
Areephong, Jetsuda, Johannes H. Hurenkamp, Maaike T. W. Milder, Auke Meetsma, Jennifer L. Herek, Wesley R. Browne, and Ben L. Feringa. "Photoswitchable Sexithiophene-Based Molecular Wires." Organic Letters 2009, 11, 721-24. [CrossRef]
Jacquemin, Denis, Antoine Femenias, Henry Chermette, Ilaria Ciofini, Carlo Adamo, Jean-Marie André, and Eric A. Perpète. "Assessment of Several Hybrid Dft Functionals for the Evaluation of Bond Length Alternation of Increasingly Long Oligomers." The Journal of Physical Chemistry A 2006, 110, 5952-59. [CrossRef]
Yanai, T., D. P. Tew, and N. C. Handy. "A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (Cam-B3lyp)." Chemical Physics Letters 2004, 393, 51-57. [CrossRef]
Francl, M.M., W.J. Pietro, W.J. Hehre, M.S Gordon, DeFees D.J., and J.A Pople. "Self-Consistent Molecular Orbital Methods. Xxiii. A Polarization-Type Basis Set for Second-Row Elements " Journal of Chemical Physics 1982, 77, 3654-65. [CrossRef]
Hariharan, P.C., and J.A. Pople. "The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies." Theoretica Chimica Acta 1973, 28, 213-22. [CrossRef]
Dunning, T. H. "Gaussian-Basis Sets for Use in Correlated Molecular Calculations .1. The Atoms Boron through Neon and Hydrogen." Journal of Chemical Physics 1989, 90, 1007-23. [CrossRef]
Woon, D. E., and T. H. Dunning. "Gaussian-Basis Sets for Use in Correlated Molecular Calculations .3. The Atoms Aluminum through Argon." Journal of Chemical Physics 1993, 98, 1358-71. [CrossRef]
Dolg, M., U. Wedig, H. Stoll, and H. Preuss. "Energy-Adjusted Abinitio Pseudopotentials for the 1st-Row Transition-Elements." Journal of Chemical Physics 1987, 86, 866-72.
Bachler, V., G. Olbrich, F. Neese, and K. Wieghardt. "Theoretical Evidence for the Singlet Diradical Character of Square Planar Nickel Complexes Containing Two Omicron-Semiquinonato Type Ligands." Inorganic Chemistry 2002, 41, 4179-93. [CrossRef]
Tzeli, Demeter, Giannoula Theodorakopoulos, Ioannis D. Petsalakis, Dariush Ajami, and Julius Rebek, Jr. "Conformations and Fluorescence of Encapsulated Stilbene." Journal of the American Chemical Society 2012, 134, 4346-54. [CrossRef]
Tzeliou, Christina Eleftheria, and Demeter Tzeli. "3-Input and Molecular Logic Gate with Enhanced Fluorescence Output: The Key Atom for the Accurate Prediction of the Spectra." Journal of Chemical Information and Modeling 2022, 62, 6436-48. [CrossRef]
Peach, Michael J. G., Peter Benfield, Trygve Helgaker, and David J. Tozer. "Excitation Energies in Density Functional Theory: An Evaluation and a Diagnostic Test." The Journal of Chemical Physics 2008, 128, 044118. [CrossRef]
Dreuw, A., and M. Head-Gordon. "Single-Reference Ab Initio Methods for the Calculation of Excited States of Large Molecules." Chemical Reviews 2005, 105, 4009-37. [CrossRef]
Casida, M. E., and M. Huix-Rotllant. "Progress in Time-Dependent Density-Functional Theory." Annual Review of Physical Chemistry, 2012, 63, 287-323. [CrossRef]
Jacquemin, D., E. A. Perpete, G. E. Scuseria, I. Ciofini, and C. Adamo. "Td-Dft Performance for the Visible Absorption Spectra of Organic Dyes: Conventional Versus Long-Range Hybrids." Journal of Chemical Theory and Computation 2008, 4, 123-35. [CrossRef]
Jacquemin, D., A. Planchat, C. Adamo, and B. Mennucci. "Td-Dft Assessment of Functionals for Optical 0-0 Transitions in Solvated Dyes." Journal of Chemical Theory and Computation 2012, 8, 2359-72. [CrossRef]
Mahr, H. "Two-Photon Absorption Spectroscopy." In Quantum Electronics, edited by H. Rabin and C. L. Tang, 494. New York: Academic Press, 1975.
R L Swofford, and, and A C Albrecht. "Nonlinear Spectroscopy." Annual Review of Physical Chemistry 1978, 29, 421-40.
Bloembergen, Nicolaas. Nonlinear Optics, Nonlinear Optics, 1996.
Olsen, Jeppe, and Poul Jo/rgensen. "Linear and Nonlinear Response Functions for an Exact State and for an Mcscf State." The Journal of Chemical Physics 1985, 82, 3235-64. [CrossRef]
Monson, P. R., and W. M. McClain. "Polarization Dependence of the Two-Photon Absorption of Tumbling Molecules with Application to Liquid 1-Chloronaphthalene and Benzene." The Journal of Chemical Physics 1970, 53, 29-37. [CrossRef]
Beerepoot, Maarten T. P., Daniel H. Friese, Nanna H. List, Jacob Kongsted, and Kenneth Ruud. "Benchmarking Two-Photon Absorption Cross Sections: Performance of Cc2 and Cam-B3lyp." Physical Chemistry Chemical Physics 2015, 17, 19306-14. [CrossRef]
Schmidt, Michael W., Kim K. Baldridge, Jerry A. Boatz, Steven T. Elbert, Mark S. Gordon, Jan H. Jensen, Shiro Koseki, Nikita Matsunaga, Kiet A. Nguyen, Shujun Su, Theresa L. Windus, Michel Dupuis, and John A. Montgomery Jr. "General Atomic and Molecular Electronic Structure System." Journal of Computational Chemistry 1993, 14, 1347-63. [CrossRef]
Zahariev, F., and M. S. Gordon. "Nonlinear Response Time-Dependent Density Functional Theory Combined with the Effective Fragment Potential Method." J Chem Phys 2014, 140, 18A523. [CrossRef]
Zaleśny, Robert, N. Arul Murugan, Guangjun Tian, Miroslav Medved’, and Hans Ågren. "First-Principles Simulations of One- and Two-Photon Absorption Band Shapes of the Bis(Bf2) Core Complex." The Journal of Physical Chemistry B 2016, 120, 2323-32. [CrossRef]
Beerepoot, Maarten T. P., Md Mehboob Alam, Joanna Bednarska, Wojciech Bartkowiak, Kenneth Ruud, and Robert Zaleśny. "Benchmarking the Performance of Exchange-Correlation Functionals for Predicting Two-Photon Absorption Strengths." Journal of Chemical Theory and Computation 2018, 14, 3677-85. [CrossRef]
Choluj, M., M. M. Alam, M. T. P. Beerepoot, S. P. Sitkiewicz, E. Matito, K. Ruud, and R. Zalesny. "Choosing Bad Versus Worse: Predictions of Two-Photon-Absorption Strengths Based on Popular Density Functional Approximations." J Chem Theory Comput 2022, 18, 1046-60. [CrossRef]
Iozzi, M. F., B. Mennucci, J. Tomasi, and R. Cammi. "Excitation Energy Transfer (Eet) between Molecules in Condensed Matter: A Novel Application of the Polarizable Continuum Model (Pcm)." J Chem Phys 2004, 120, 7029-40. [CrossRef]
Blasiak, B., M. Maj, M. Cho, and R. W. Gora. "Distributed Multipolar Expansion Approach to Calculation of Excitation Energy Transfer Couplings." J Chem Theory Comput 2015, 11, 3259-66. [CrossRef]
Förster, Th. "Zwischenmolekulare Energiewanderung Und Fluoreszenz." Annalen der Physik 1948, 437, 55-75. [CrossRef]
Stone, A. J. "Distributed Multipole Analysis, or How to Describe a Molecular Charge Distribution." Chemical Physics Letters 1981, 83, 233-39. [CrossRef]
Stone, Anthony. The Theory of Intermolecular Forces: Oxford University Press, 2013.
Lu, Tian, and Feiwu Chen. "Multiwfn: A Multifunctional Wavefunction Analyzer." Journal of Computational Chemistry 2012, 33, 580-92. [CrossRef]
Stone, Anthony J. "Distributed Multipole Analysis: Stability for Large Basis Sets." Journal of Chemical Theory and Computation 2005, 1, 1128-32. [CrossRef]
Oliver, S., and C. Winter. "Metal Dithiolene Complexes for All-Optical Switching Devices." Advanced Materials 1992, 4, 119-21. [CrossRef]
Matsuoka, R., R. Sakamoto, T. Kambe, K. Takada, T. Kusamoto, and H. Nishihara. "Ordered Alignment of a One-Dimensional Pi-Conjugated Nickel Bis(Dithiolene) Complex Polymer Produced Via Interfacial Reactions." Chemical Communications 2014, 50, 8137-39.
Lei Zhang, Gilles H. Peslhebre, and Heidi M. Muchall. "A General Measure of Conjugation in Biphenyls and Their Radical Cations." Canadian Journal of Chemistry 2010, 88, 1175-85. [CrossRef]
Serrano-Andres, L., A. Avramopoulos, J. Li, P. Labeguerie, D. Begue, V. Kello, and M. G. Papadopoulos. "Linear and Nonlinear Optical Properties of a Series of Ni-Dithiolene Derivatives." J Chem Phys 2009, 131, 134312. [CrossRef]
Dobrowolski, Jan Cz, and Sławomir Ostrowski. "On the Homa Index of Some Acyclic and Conducting Systems." Rsc Advances 2015, 5, 9467-71. [CrossRef]
Kauczor, Joanna, Patrick Norman, Ove Christiansen, and Sonia Coriani. "Communication: A Reduced-Space Algorithm for the Solution of the Complex Linear Response Equations Used in Coupled Cluster Damped Response Theory." The Journal of Chemical Physics 2013, 139, 211102. [CrossRef]
Thanh Phuc, Nguyen, and Akihito Ishizaki. "Control of Excitation Energy Transfer in Condensed Phase Molecular Systems by Floquet Engineering." The Journal of Physical Chemistry Letters 2018, 9, 1243-48.
Escudero, D., and K. Veys. "Anti-Kasha Fluorescence in Molecular Entities: Central Role of Electron-Vibrational Coupling." Accounts of Chemical Research 2022. [CrossRef]
Veys, K., and D. Escudero. "Computational Protocol to Predict Anti-Kasha Emissions: The Case of Azulene Derivatives." Journal of Physical Chemistry A 2020, 124, 7228-37. [CrossRef]
Escudero, D. "Revising Intramolecular Photoinduced Electron Transfer (Pet) from First-Principles." Accounts of Chemical Research 2016, 49, 1816-24. [CrossRef]
Rohrs, M., and D. Escudero. "Multiple Anti-Kasha Emissions in Transition-Metal Complexes." Journal of Physical Chemistry Letters 2019, 10, 5798-804. [CrossRef]

Figure 1. The structures of 1cc, 1co and 1oo computed with the B3LYP/6-31G* method.

Figure 2. The structures of 2oo, 2oc, 2cc, 3oo and 3oc, computed with the B3LYP/6-31G* method.

Figure 3. The considered dimers (left fragment: donor; right fragment: acceptor.

Figure 4. The absorption (black line) and the emission spectra (red, green, blue lines) of the 2oc fragments (left fragment: Donor, right fragment: Acceptor). The CAMB3LYP/6-31G* method was used.

Figure 5. Calculated open-open (2oo), open-closed (2oc) and closed-closed (2cc) structures at CAM-B3LYP/6-31G*_H,C,O,F,S ECP28MWB(SDD)_Ni.

Figure 6. NIR-vis-UV absorption (solid line) and emission (dotted line) spectra of the 2oo, 2oc, and 2cc structures at CAM-B3LYP/6-31G*_H,C,O,F,S ECP28MWB(SDD)_Ni level of theory. (Peak half-width at half height: 0.09 eV).

Figure 7. Frontier molecular orbitals (MO) involving in the main absorption and emission excitations of 2oo.

Figure 8. Frontier molecular orbitals (MO) involving in the main absorption and emission excitations of 2oc.

Figure 9. Frontier molecular orbitals (MO) involving in the main absorption excitations of 2cc.

Table 3. Computed HOMA index of NO₂ -1AB-NH₂ and H-1AB-H, A,B = c,o.

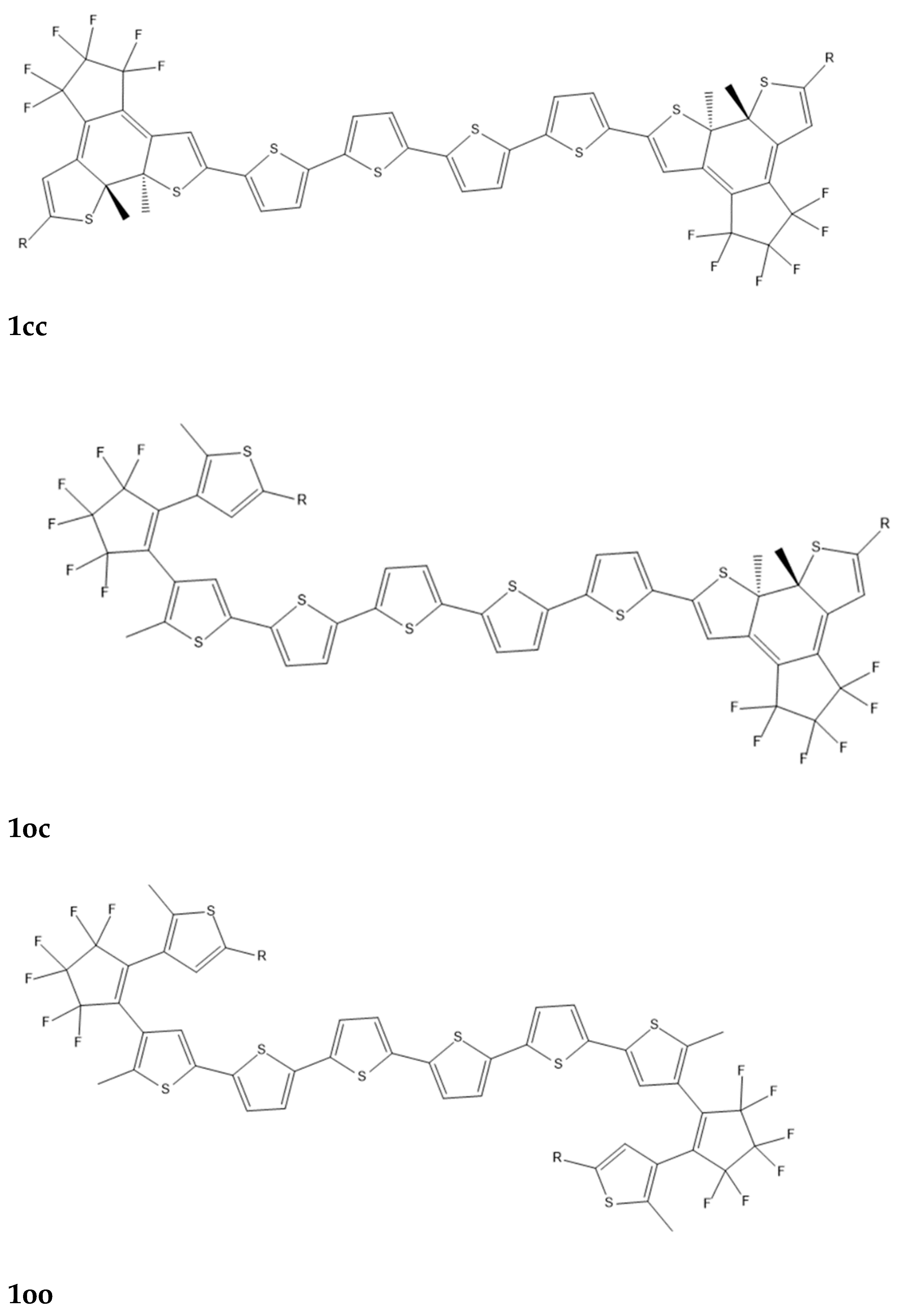
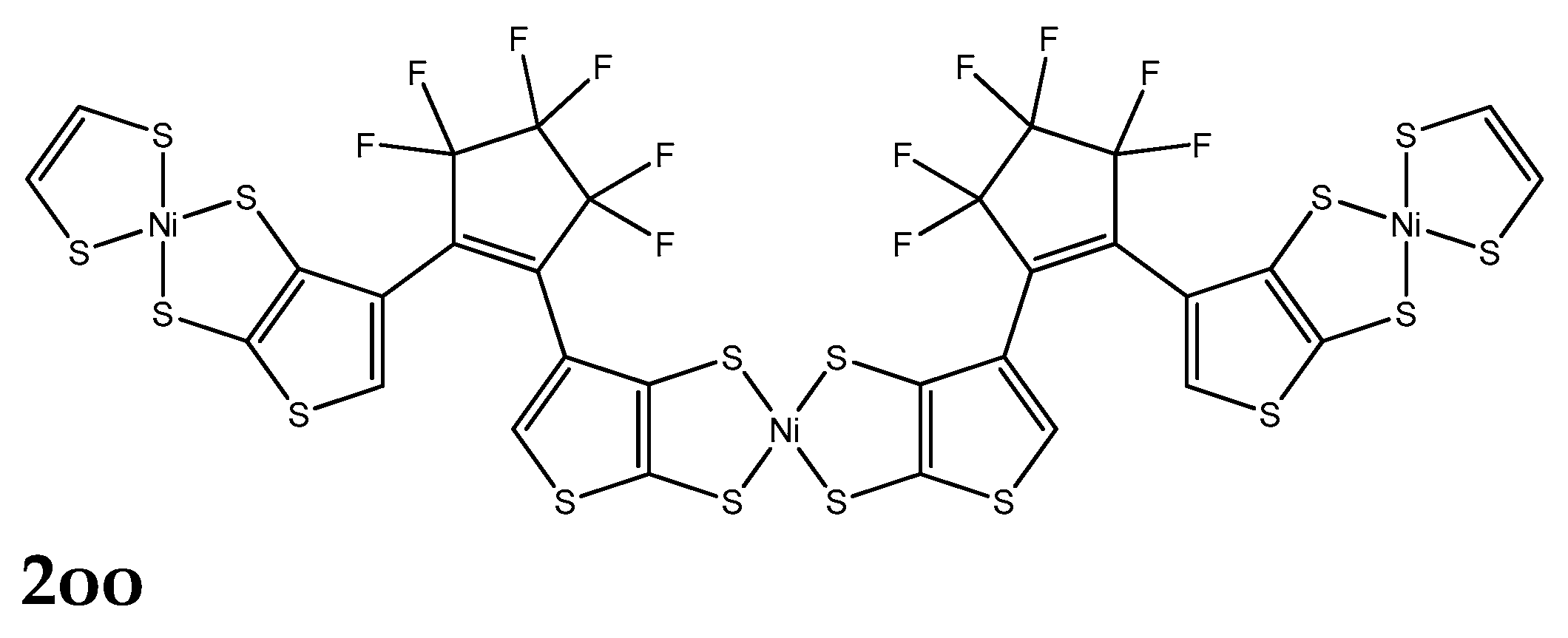
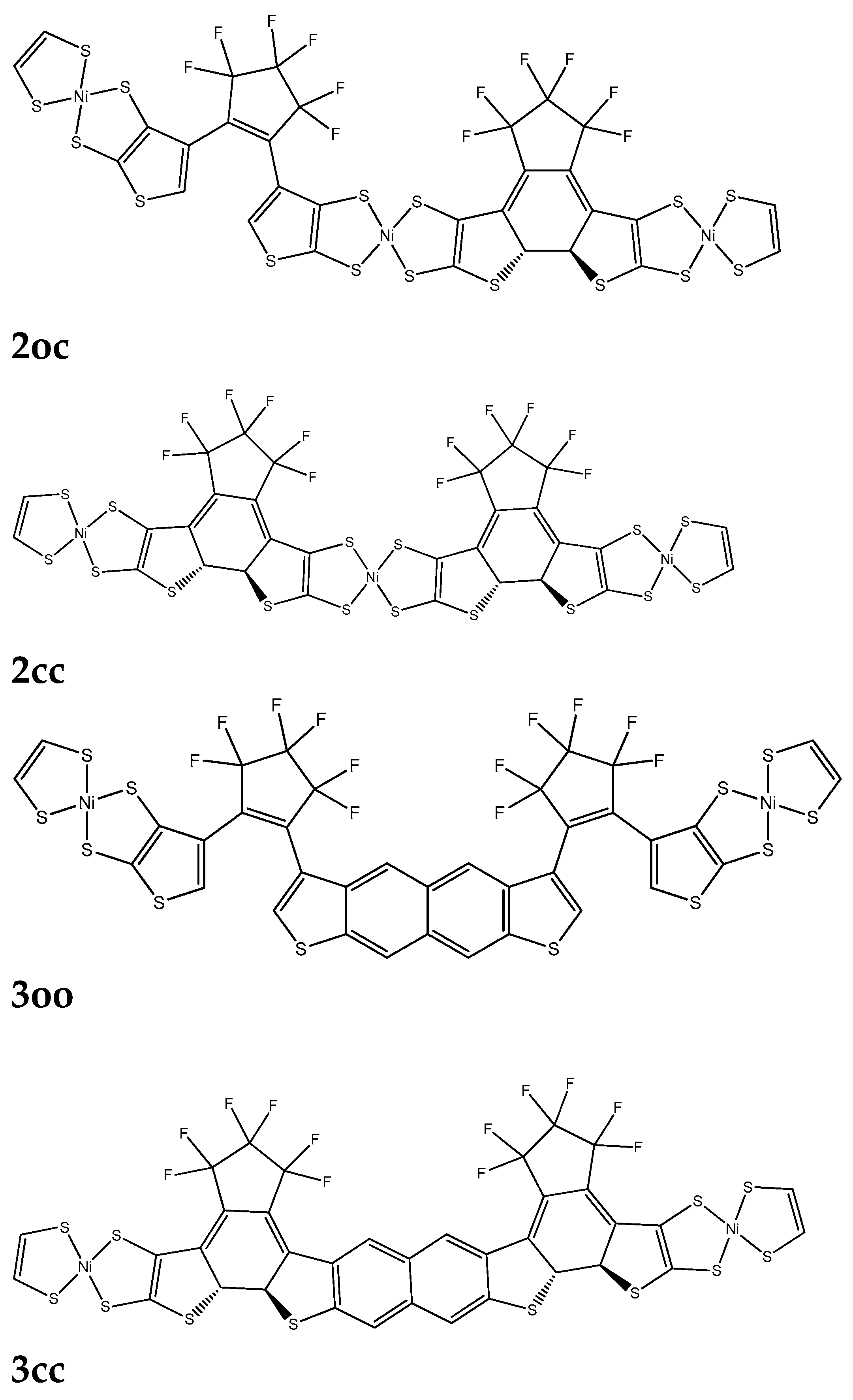
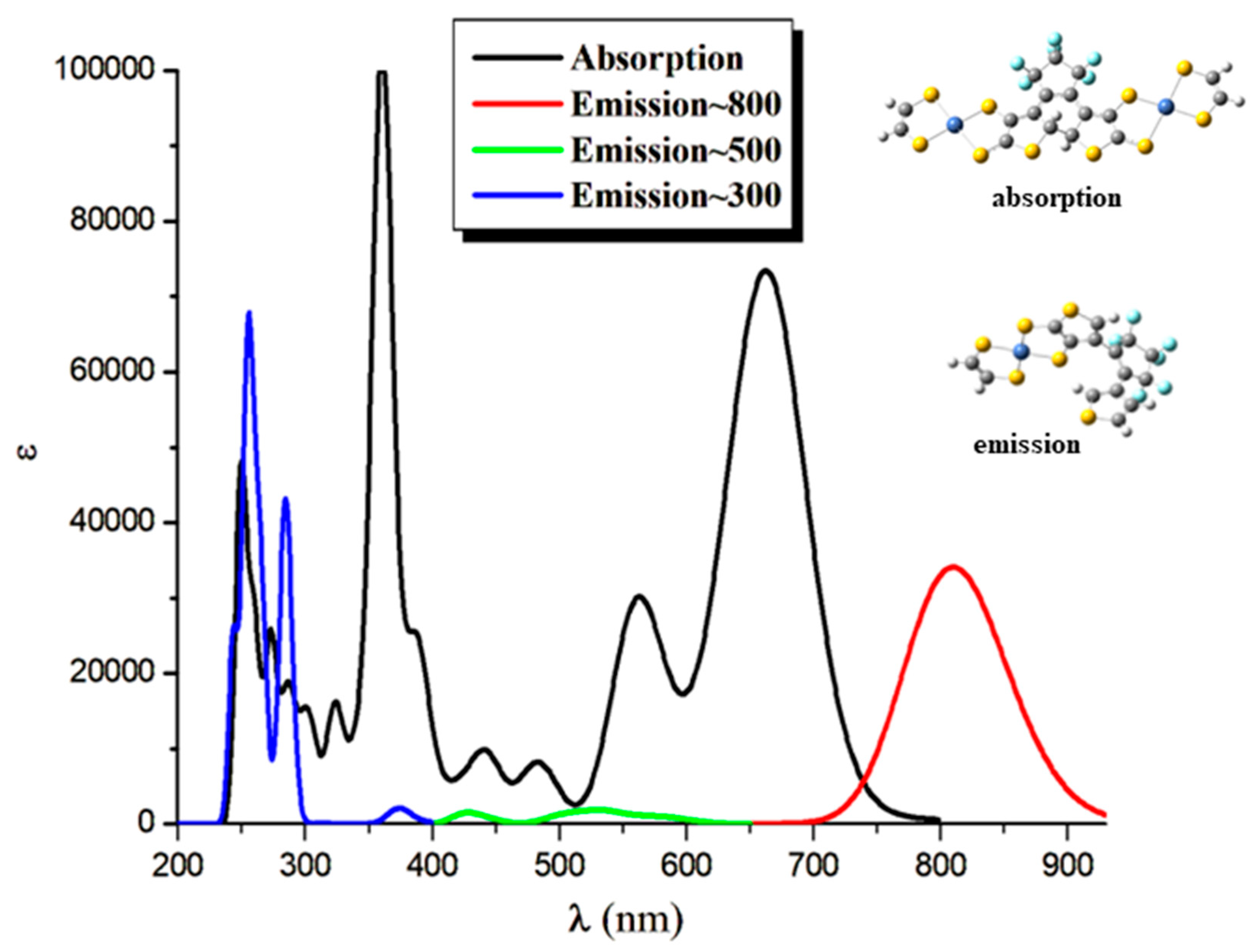
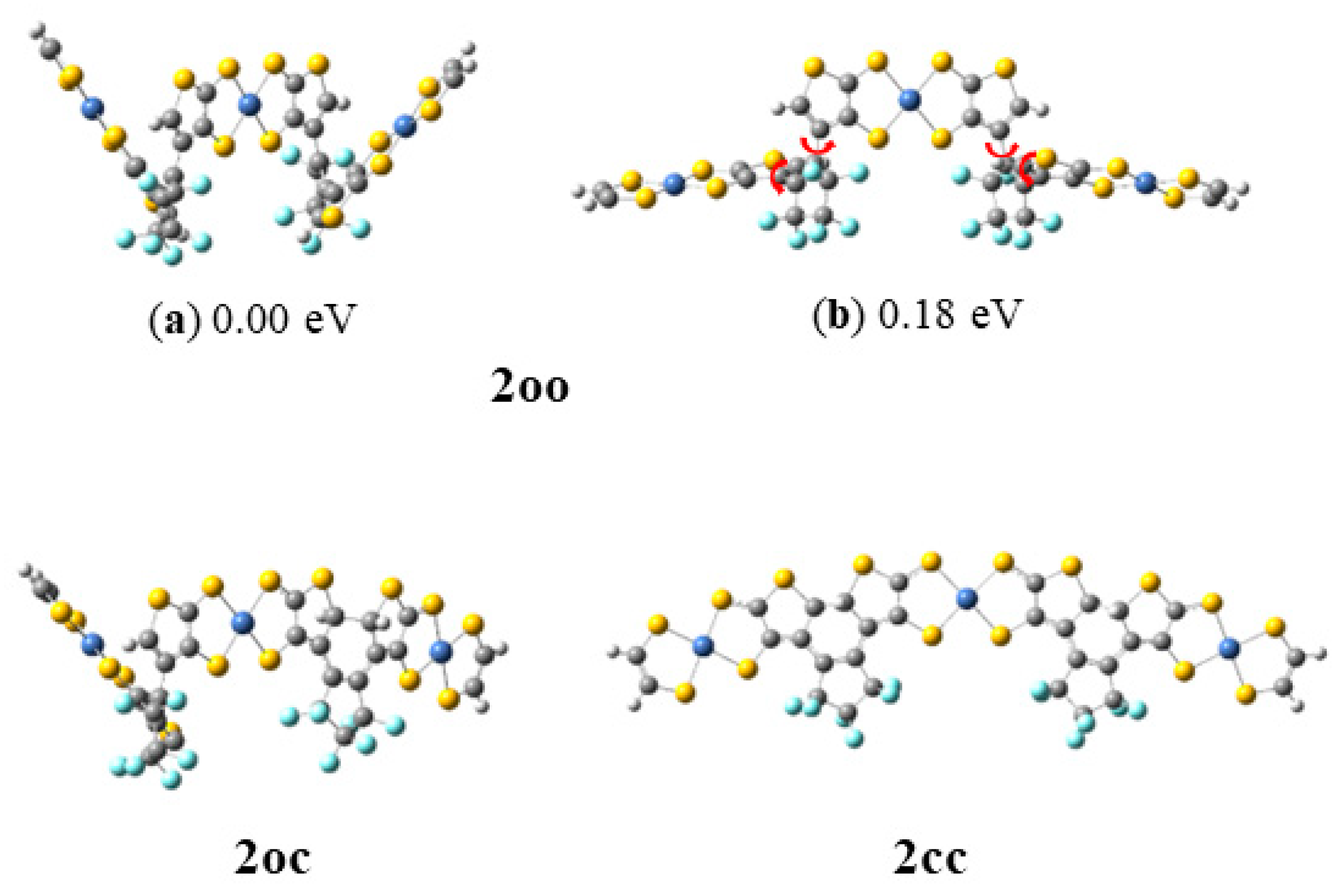
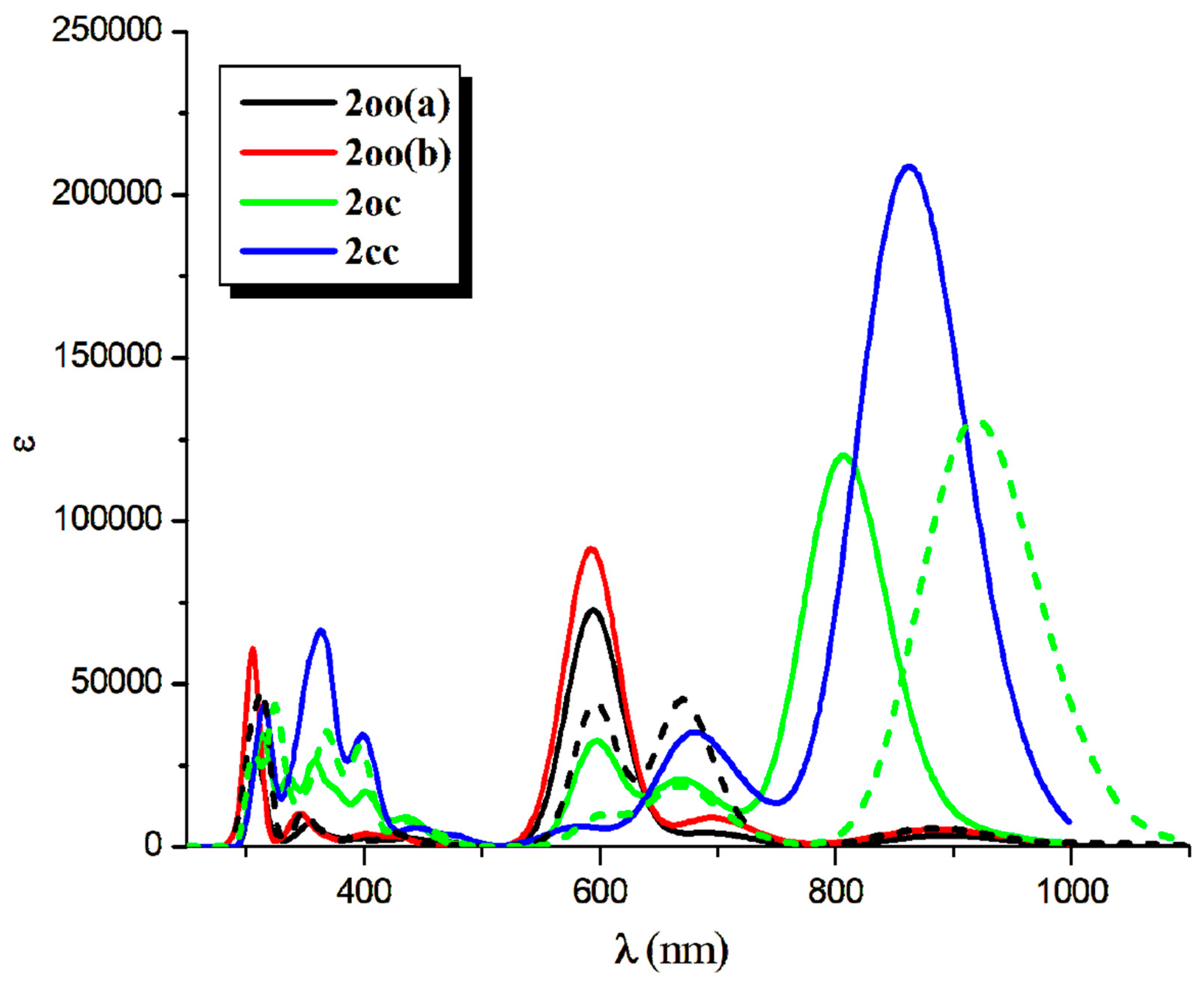
	1cc			1oc			1oo
	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³
S₀→S₁	2.162	2.3537	<0.1	2.243	1.4665	7.0	2.820	2.5150	<0.1
S₀→S₂	2.344	0.0159	0.2	2.843	1.2518	113.3	3.543	0.0226	8.6
S₀→S₃	2.885	0.6755	0.4	3.436	0.0660	1512.2	3.994	0.0236	<0.1
S₀→S₄	3.340	0.0008	6690.7	3.648	0.0164	2358.2	4.023	0.0380	126.0
S₀→S₅	3.577	0.0002	3105.5	3.793	0.0868	19.5	4.156	0.0030	2023.3

Table 4. Excitation energy (∆E, [eV]), oscillator strength (f) and two-photon transition strength (⟨δ2PA⟩, [au]) corresponding to five lowest-energy electronic transitions for molecule R=Cl (Figure 1).

	NO₂ -1AB-NH₂				H-1AB-H
AB	cc	co	oc	oo	cc	oc	oo
I_HOMA	0.827	0.806	0.807	0.778	0.843	0.812	0.790

Table 5. Excitation energy (∆E, [eV]), oscillator strength (f) and two-photon transition strength (⟨δ2PA⟩, [au]) corresponding to five lowest-energy electronic transitions for molecule R=H (Figure 1).

	1cc			1oc			1oo
	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³
S₀→S₁	2.169	2.1698	<0.1	2.252	1.3319	3.2	2.819	2.4780	<0.1
S₀→S₂	2.344	0.0114	1.8	2.844	1.3222	94.1	3.544	0.0208	5.2
S₀→S₃	2.878	0.7472	0.3	3.450	0.0534	1192.0	4.045	0.0252	<0.1
S₀→S₄	3.353	0.0002	5802.2	3.643	0.0144	2168.1	4.080	0.0337	431.2
S₀→S₅	3.556	0.0002	2516.0	3.748	0.0822	25.3	4.162	0.0106	1657.9

Table 6. Excitation energy (∆E, [eV]), oscillator strength (f) and two-photon transition strength (⟨δ2PA⟩, [au]) corresponding to five lowest-energy electronic transitions for molecule R=NH₂ (Figure 1).

	1cc			1oc			1oo
	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³
S₀→S₁	2.161	2.4581	<0.1	2.253	1.5232	2.8	2.817	2.5106	<0.1
S₀→S₂	2.353	0.0150	31.9	2.885	1.2299	41.8	3.540	0.0226	2.6
S₀→S₃	2.935	0.5549	0.3	3.526	0.0218	1966.6	3.940	0.0263	1.0
S₀→S₄	3.382	0.0005	9561.7	3.562	0.0402	1807.8	3.949	0.0974	13.5
S₀→S₅	3.544	0.0002	1.6	3.905	0.0294	25.9	4.128	0.0018	1927.5

Table 7. Excitation energy (∆E, [eV]), oscillator strength (f) and two-photon transition strength (⟨δ2PA⟩, [au]) corresponding to five lowest-energy electronic transitions for molecule R=NO₂ (Figure 1).

	1cc			1oc			1oo
	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³
S₀→S₁	1.932	2.0938	<0.1	1.984	1.1765	49.1	2.820	2.5449	<0.1
S₀→S₂	2.068	0.0024	39.1	2.691	1.4493	367.0	3.539	0.0248	20.3
S₀→S₃	2.696	1.0551	<0.1	3.229	0.1597	3058.4	3.840	0.0130	0.4
S₀→S₄	3.089	0.0009	10167.0	3.374	0.1308	715.1	3.853	0.0056	20.2
S₀→S₅	3.322	0.0006	4760.5	3.468	0.0753	9.2	3.912	0.0003	<0.1

Table 8. Excitation energy (∆E, [eV]), oscillator strength (f) and two-photon transition strength (⟨δ2PA⟩, [au]) corresponding to five lowest-energy electronic transitions for molecule R=NO₂, R’=NH₂ (Figure 1).

	1cc			1oc^a)			1oo
	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³	ΔE	f	<δ^2PA> ×10³
S₀→S₁	1.951	1.7422	118.4	2.249	1.5157	8.3	2.817	2.5218	3.5
S₀→S₂	2.243	0.6864	85.5	2.886	1.2587	9.6	3.538	0.0245	9.3
S₀→S₃	2.704	0.3358	1286.2	3.528	0.0035	3251.3	3.799	0.0068	9.3
S₀→S₄	3.002	0.3582	2916.7	3.542	0.0658	557.8	3.912	0.0002	0.2
S₀→S₅	3.253	0.0042	1586.6	3.777	0.0015	0.6	3.951	0.0583	5.3

^a NO2 group attached to “open” moiety.

Table 9. Excitation energy (∆E, [eV]), oscillator strength (f) and two-photon transition strength (⟨δ2PA⟩, [au]) corresponding to five lowest-energy electronic transitions for molecule R=NO₂, R’=NH₂. (Figure 1).

	1oc^a
	ΔE	f	<δ^2PA> ×10³
S₀→S₁	1.972	1.2258	70.5
S₀→S₂	2.650	1.3286	541.5
S₀→S₃	3.195	0.2143	3036.5
S₀→S₄	3.360	0.1164	743.6
S₀→S₅	3.460	0.0732	11.5

^a NO2 group attached to “closed” moiety.

Table 10. Electronic couplings (V_DA) and different contributions (V_c, V_xc) for the considered dimers. All values are given in cm^-1. All values were computed with CAM-B3LYP/6-31G* method.

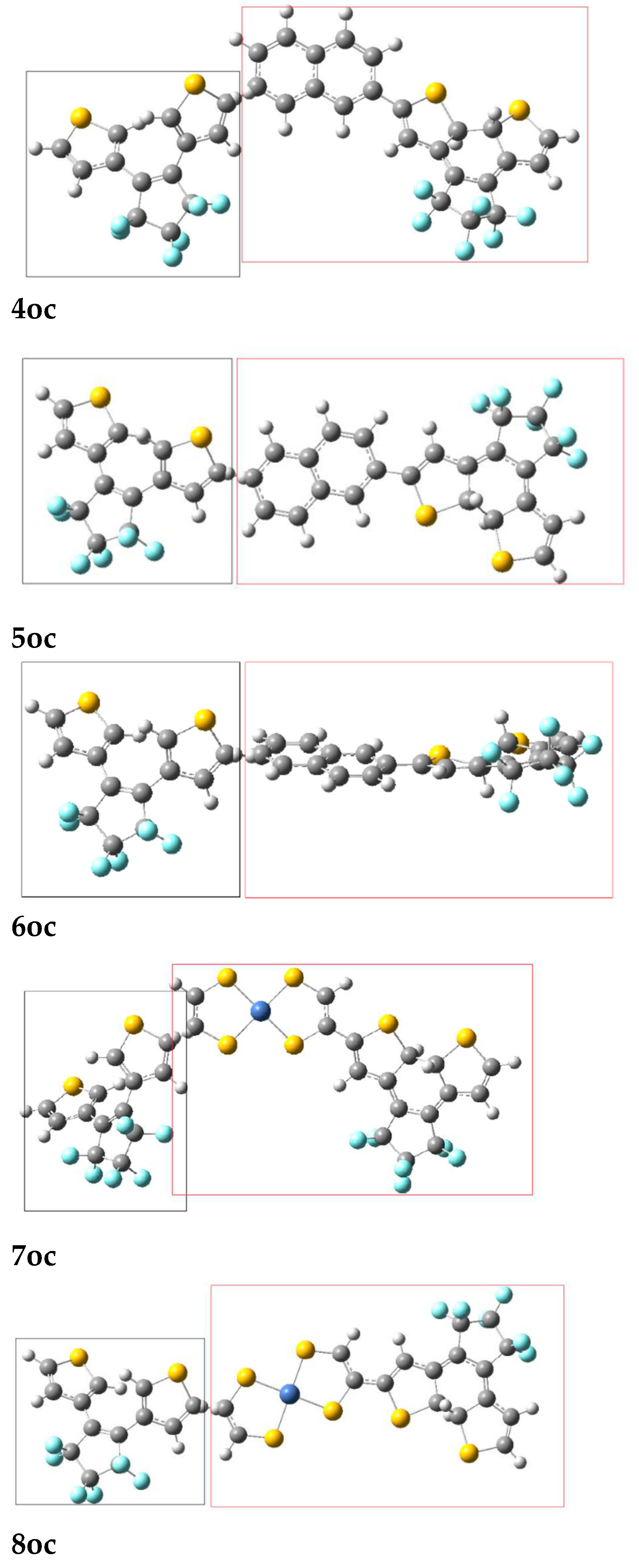
Dimer	V_DA	V_c	V_xc
1oc^a	8.3	8.1 9,7^b	0.2 0.25^b
2oc	10,3	9,7	0,6
4oc	101.5	101.6	-0.1
5oc	113.0	111.3	1.7
6oc	120.4	120.9	-0.5
7oc	32.3	30.9	1.4
8oc	12.8	12.1	0.7

^a R=Cl (Fig. 1).^b Properties have been computed at the M062-X optimized geometry.

Table 11. Electronic transition energies(E;eV) and oscillator strengths (f).

Dimer	D_n^a	E/f^b	Transition/(%)	A_n^a	E/f^b	Transition/(%)
1oc^c	D₁	4.433/0.139 4.450/0.111^d	HOMO->LUMO/(100)	A₇	4.233/0.04 4.320/0.01^d	HOMO-2->LUMO/21 HOMO-1->LUMO+4/19 HOMO->LUMO+4/27
2oc	D₂₂	4,619/0,22	HOMO-14->LUMO (50%) HOMO->LUMO+2 (12.5%) HOMO-5->LUMO+1 (14.5%)	A₅₅	4,607/0,04	HOMO->LUMO+9(22%) HOMO-9->LUMO+4 (11%) HOMO-7->LUMO+3(5,8%) HOMO-1->LUMO+5(8%)
4oc	D₁	4.226/0.702	HOMO->LUMO/(98)	A₄ A₁ A₂	4.176/0.124 2.628/0.458 3.892/0.121	HOMO->LUMO+1/67 HOMO->LUMO/95 HOMO-1->LUMO/54 HOMO-2->LUMO+1/32
5oc	D₁	4.217/0.181	HOMO->LUMO/(98)	A₄ A₁ A₂ A₃	4.209/0.356 2.607/0.470 3.908/0.108 3.921/0.136	HOMO->LUMO+1/63 HOMO->LUMO/100 HOMO-2->LUMO/84 HOMO-1->LUMO/77
6oc	D₁	4.217/0.702	HOMO->LUMO/(98)	A₄ A₁ A₂ A₃	4.210/0.356 2.607/0.689 3.909/0.108 3.921/0.136	HOMO->LUMO+1/63 HOMO->LUMO/100 HOMO-2->LUMO/84 HOMO-1->LUMO/77
7oc	D₁ D₂ D₃ D₄	2.482/0 3.147/0 3.627/0 4.231/0.174	HOMO->LUMO/(100)	A₆ A₂₄ A₄₂ A₄₆ A₅₀	1.345/0.37 2.650/0.28 3.770/0.15 4.040/0.06 4.160/0.06	HOMO->LUMO/92 HOMO->LUMO+1/84 HOMO-1->LUMO+1/79 HOMO-2->LUMO+1/84 HOMO-6->LUMO/29 HOMO-14->LUMO/25 HOMO-3->LUMO/8
8oc	D₁ D₂ D₃ D₄	2.456/0 3.140/0 3.620/0 4.205/0.173	HOMO->LUMO/(100)	A₆ A₇ A₂₄ A₃₂ A₄₀ A₄₇ A₅₀	1.383/0.51 2.607/0.02 2.600/0.215 3.109/0.04 3.730/0.141 4.095/0.06 4.136/0.01	HOMO->LUMO/92 HOMO-1->LUMO/79 HOMO->LUMO+1/87 HOMO-2->LUMO/44 HOMO-1->LUMO+1/79 HOMO-2->LUMO+1/40 HOMO->LUMO+2/37

^a D_n /A_n: n denotes the number of Donor/Acceptor state for the transition S₀->S_{n .}^b E/f: Electronic Transition Energy(eV)/Oscillator Strength. ^c R=Cl (Figure 1). ^d Properties have been computed at the M062-X optimized geometry.

Table 12. Comparison of the Coulomb-term contribution to the total EET, computed using a multipole expansion of the transition density, with analytically computed values; all values are in cm^-1( ̴10^-4eV).

l+l’ Bridge	0	1	2	3	4	Analyt. Coulomb^a	Analyt. EET^a.
Naphthalene	82.3	137.1	143.6	127.4	117.8	111.3	112.9
NiBDT	4.8	8.1	13.7	12.1	15.3	12.1	12.9

^a The distributed multipole moments are computed analytically (using, in our case, Stones' GDMA method) in contrast to the 'fitting' procedures used by other approaches, which fit the multipole moments to the external charge density.

Table 13. Excitation energies, ΔE (eV), λ_max (nm), and f-values for the main peak of the absorption and emission spectra and the corresponding main excitations of the 2oo, 2oc, and 2cc structures at CAM-B3LYP/6-31G*_H,C,O,F,S ECP28MWB(SDD)_Ni level of theory.

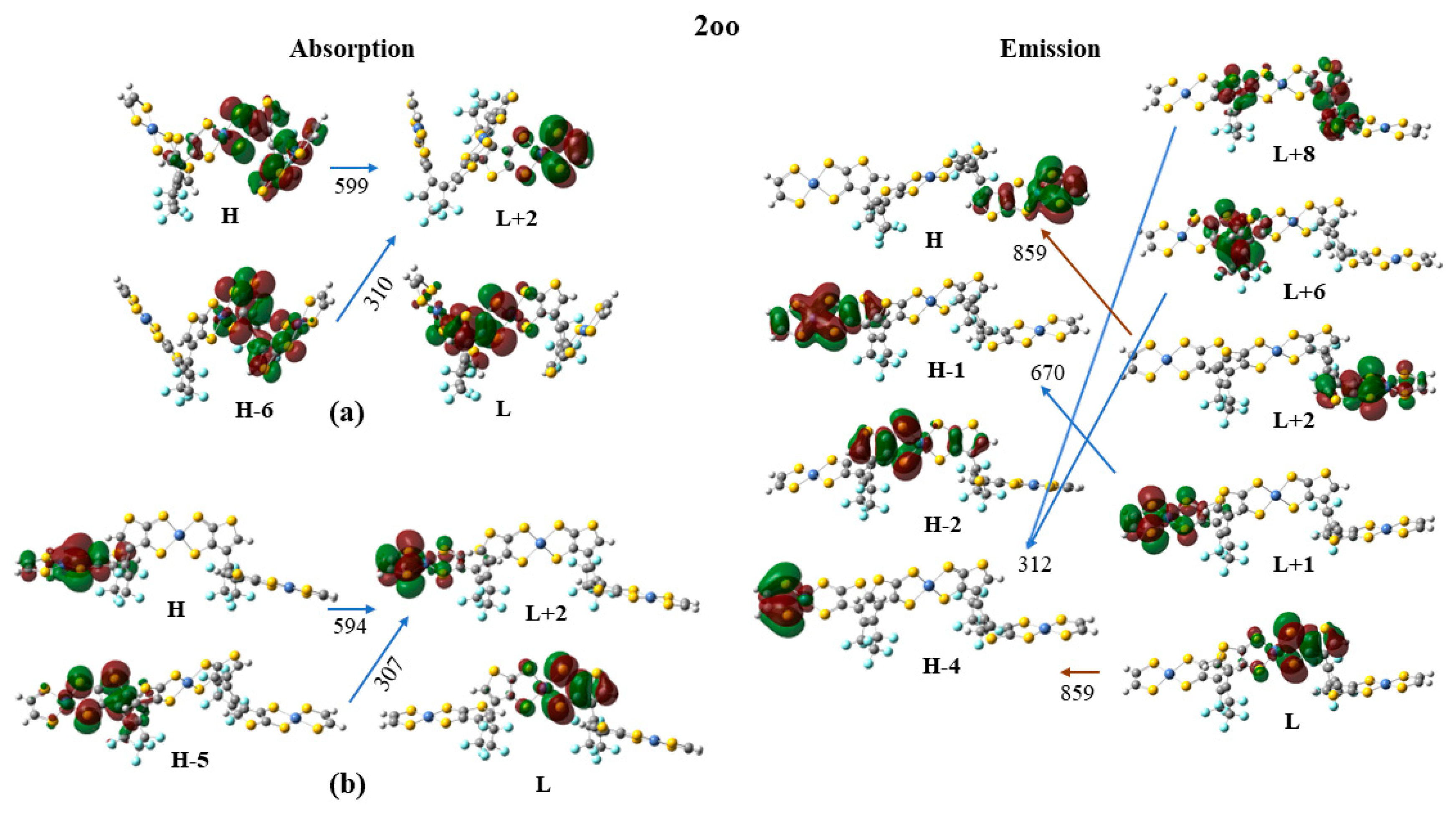
Struct	ΔΕ	λ_max	f	Excitations
Absorption
2oo(a)	1.805	686.9	0.0115	0.35\|H-2 L+1> − 0.29\|H L+2> + 0.28\|H-1 L+1> + 0.26\|H-2 L>
	2.071	598.7	0.1141	0.20\|H L+2> + 0.16\|H-1 L+2> − 0.21\|H-10 L+5>
	4.006	309.5	0.1252	0.19\|H-6 L+2> − 0.13\|H-1 L+6>
2oo(b)	1.791	692.2	0.0447	0.56\|H-1 L+1> − 0.36\|H L+2>
	2.088	593.7	0.4031	0.42\|H L+2> + 0.23\|H-1 L+1> − 0.18\|H-2 L>
	4.044	306.6	0.2014	0.18\|H-2 L+8> + 0.20\|H-5 L+2> − 0.22\|H-35 L> − 0.20\|H-19 L+3>

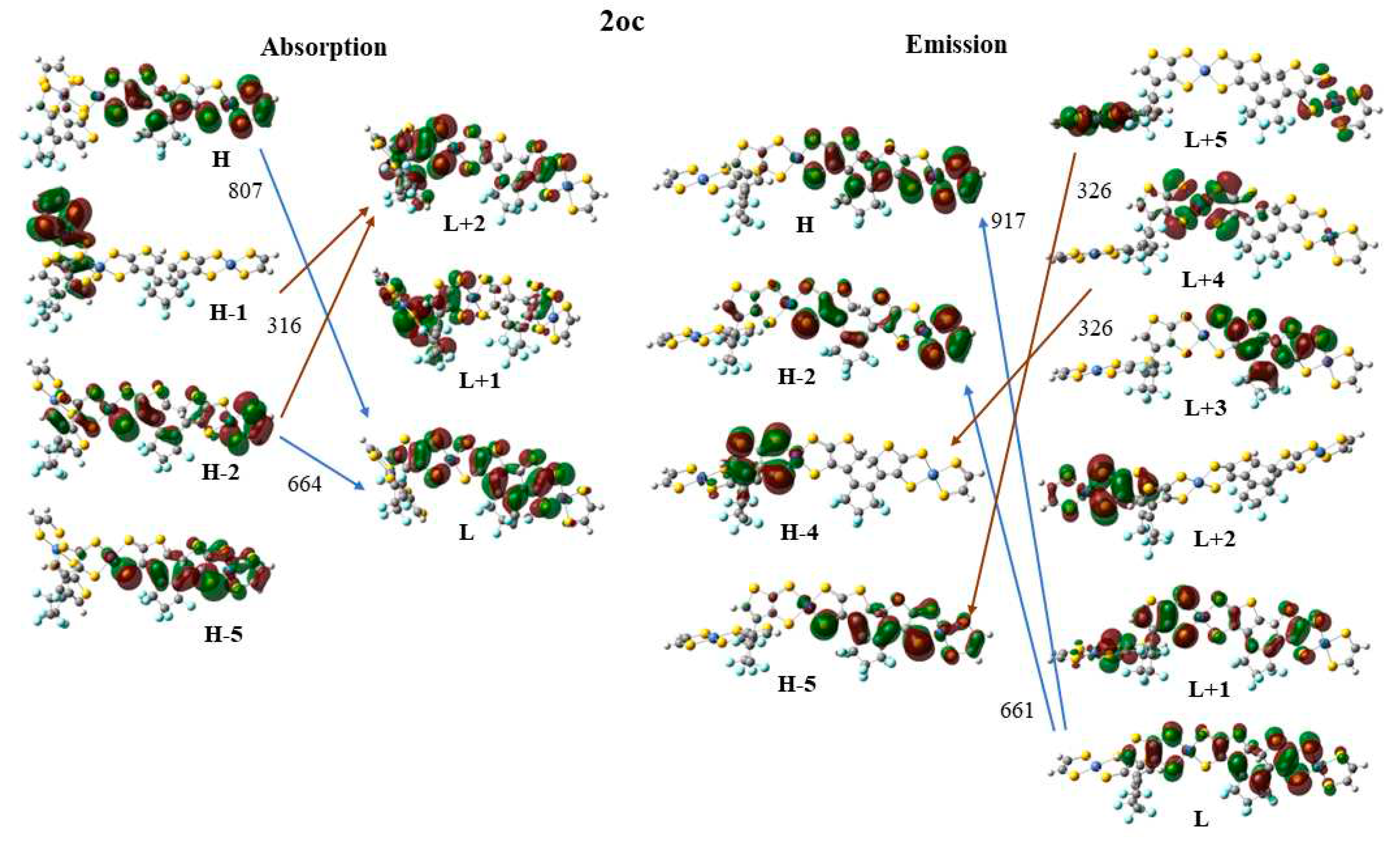
2oc	1.537	806.9	0.7112	0.58\|H L> − 0.23\|H-5 L>
	1.868	663.7	0.0926	0.38\|H-2 L> − 0.27\|H-5 L>
	3.925	315.9	0.0983	0.39\|H-17 L> + 0.22\|H-26 L> +0.31\|H-26 L+2>

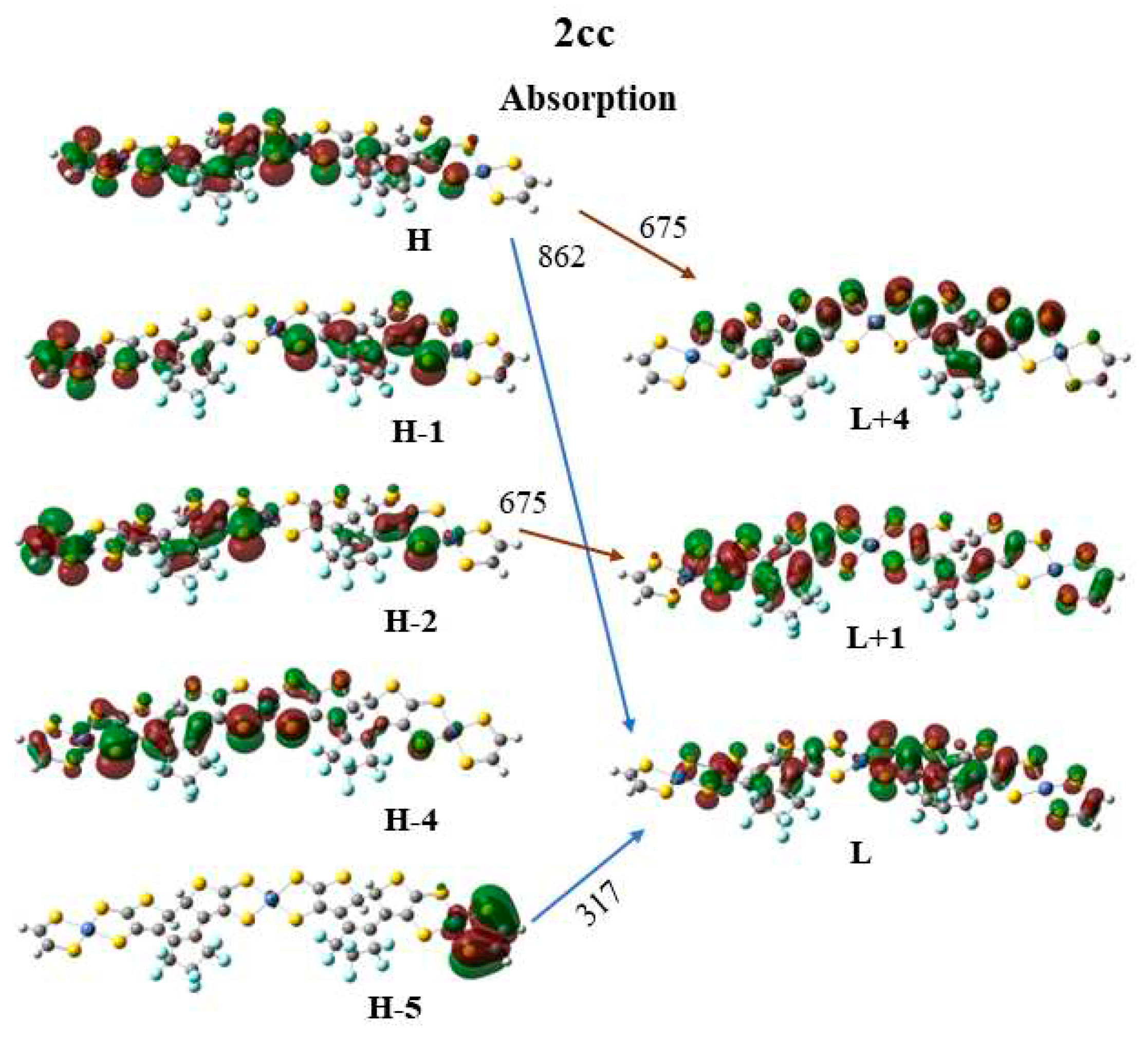
2cc	1.438	862.3	1.3931	0.51\|H L> + 0.30\|H-1 L+1>
	1.837	675.1	0.1866	0.23\|H L+4> + 0.20\|H-4 L> − 0.23\|H-2 L+1> + 0.18\|H-1 L>
	3.107	399.0	0.1077	0.28\|H-1 L+1> + 0.21\|H L+4> − 0.21\|H-4 L+1>− 0.18\|H-4 L>
	3.369	368.0	0.1701	0.29\|H-17 L> − 0.16\|H-18 L> + 0.15\|H-8 L>
	3.519	352.4	0.1073	0.27\|H-19 L+1> + 0.19\|H-19 L> − 0.18\|H-9 L+1>− 0.11\|H-2 L+1>
	3.917	316.5	0.1402	0.27\|H-16 L+1> + 0.21\|H-16 L>− 0.19\|H-13 L>+ 0.26\|H-5 L>
Emission
2oo	1.444	858.7	0.0170	0.65\|H-4 L> − 0.15\|H-2 L>
	1.851	669.7	0.1938	0.47\|H-1 L+2> − 0.51\|H-1 L+1> − 0.39\|H-14 L+2>+ 0.27\|H-12 L+2> + 0.21\|H-14 L+1>
	2.074	597.8	0.1588	0.52\|H L+2> + 0.40\|H-9 L+4>
	3.966	312.6	0.2401	0.33\|H-2 L+8> + 0.14\|H-2 L+6> − 0.36\|H-34 L>

2oc	1.353	916.5	0.7071	0.57\|H L> − 0.24\|H-4 L>
	1.874	661.6	0.0774	0.32\|H-5 L> + 0.29\|H L+1> − 0.43\|H-2 L>− 0.25\|H H-19>
	3.806	325.8	0.0748	0.31\|H-15 L> + 0.23\|H-4 L+4> − 0.25\|H-5 L+5>

Table 14. Vertical and adiabatic excitation energies in eV of the main peaks of the 2oo, 2oc, and 2cc structures at CAM-B3LYP/6-31G*_H,C,O,F,S ECP28MWB(SDD)_Ni.

2oo	2oc	2cc	2oo	2oc	2oo	2oc
S₀ → S_i ^a			S_i→ S₀ ^b		S₀ → S_i ^c
1.81 (1.79)^d	1.54	1.44	1.44	1.35	1.67	1.40
2.07 (2.09)^d	1.87	1.84	1.85	1.86	1.98	1.87
4.01 (4.04)^d	3.92	3.11	3.97	3.81	4.00	3.88
		3.37
		3.52
		3.92

^a Vertical absorption at the geometry of the ground state. ^b Vertical emission at the geometry of the emitted state. ^c Adiabatic excitation. ^d Main peaks of the b structure in parenthesis.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.