Towards Action + State Process Model Discovery

Preprint

Article

Towards Action + State Process Model Discovery

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 June 2023

Posted:

28 June 2023

You are already at the latest version

Alerts

Abstract

Process model discovery covers different methodologies to mine a process model from traces of process executions, and is gaining an important role in Artificial Intelligence research. Current approaches in the area, with few exceptions, focus on determining a model of the flow of actions only. However, in several contexts, (i) restricting the attention to actions is quite limitative, since the effects of such actions have to be analysed, too, and (ii) traces provide additional pieces of information, in the form of states (i.e., values of parameters possibly affected by the actions): for instance, in several medical domains traces include both actions and measurements of patients’ parameters. In this paper, we propose AS-SIM (Action-State SIM), the first approach able to mine a process model which comprehends two distinct classes of nodes, to capture both actions and states.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Process Mining (PM) [1] consists of different methodologies for a-posteriori analysis, able to take as input a repository (termed event log) storing the sequences of actions (traces henceforth [1]) that have been executed at a given organization, to extract non-trivial information from it. Process model discovery is one of the main sub-areas of PM, and aims at mining a process model from the event log. The process model is an oriented graph, where nodes represent actions in the traces and arcs represent the ordering relation between them. Many different process discovery methodologies have been proposed in the literature, obtaining successful results in many application domains, such as, e.g., business or production processes.

However, while in many contexts a “traditional” process model, representing the flow of actions, suffices to include all the key elements for further analysis, in other cases the actions cover only one part of the useful information, since their enactment depends on the current state of affairs and their effect (in terms of the variations they produce on such a state) is not strictly predictable/deterministic. It is therefore essential to include a description of the evolution of the state in the model, too. In all such applications, event logs usually contain also state information. For instance, in the medical context, actions are poorly meaningful if they are not related to the current state of the patient, and considering their effects (in terms of modifications to the previous state of the patient) is a crucial issue. In fact, patient traces log sequences of (timestamped) actions and states (where a state is the recording of patient’s parameters), or the information stored in the hospital information system can be converted into this format (see e.g. [2]).

In these domains, mining a model considering only the flow of actions is limitative, since:

i.: The model would be incomplete, as it would neglect the state where actions are performed, and actions’ effects on such a state, and
ii.: state information are indeed available in the input traces – and can therefore be exploited.

In this paper, we aim at introducing a new line of research in process model discovery, that we term action+state process model discovery, to extend “traditional” process model discovery techniques to cope also with state-related pieces of information. The key contributions of our proposal are general, and could be applied to extend different process miners in the literature. However, for the sake of concreteness, in this paper, we specifically work to extend SIM (Semantic Interactive Miner), a mining algorithm we have recently developed [3]. With respect to other miners in the literature, SIM is characterized by the fact that it supports highly interactive (with analysts/domain experts) step-by-step sessions of work to discover the process model, starting from a basic automatically-mined model with maximal precision [4] (i.e., fully adherent to the event log content), and then progressively generalizing/simplifying it through the application of merge and abstraction operations (see Section 2).

In the following, we thus present AS-SIM (Action-State SIM), which extends SIM to deal with state mining as well. In particular, in Section 2 we briefly overview SIM. In Section 3, we present our representation formalism: a bipartite graph consisting of both action nodes and state nodes. In Section 4, we outline the general behavior of AS-SIM, and its basic functionalities. In Section 5, we describe our approach to mine the initial action-state process model. In Section 6, we propose a methodology to achieve a compact representation of state nodes (possibly interacting with analysts). In Section 7, we discuss the related work. The extensions of SIM’s merge and abstraction facilities to operate on the new bipartite process model are left as future work, as discussed in Section 8.

2. Overview of SIM

In this section, we will provide an overview of the main features of SIM. For more details, please refer to our previous works [3,5]

In the area of process discovery, many systems are designed as "black boxes," where an event log is inputted, and a model is outputted based on specific parameters. If the analysts are unsatisfied with the outputted model, they can only re-run the system using different parameters, resulting in a "blind search" as they are unaware of the effect of parameter values on the output model. Instead, SIM seeks to provide a solution by enabling analysts to leverage their knowledge in model discovery and use also pre-encoded domain knowledge (where possible).

SIM provides the possibility to refine (ISA relations) and to compose (Part-Of relations) process actions through (taxonomic) a-priori domain knowledge. It begins by automatically mining an initial process model from the event log with precision and replay-fitness [4] set to 1. Although generalizations may be required due to incomplete logs, SIM aims to ensure that these generalizations are driven by analysts via an interactive and incremental process. This is achieved by applying a set of operations to generalize the initial model in different steps.

In synthesis, four main aspects characterize SIM’s definition and behaviour:

Initial model: SIM starts by mining an initial model from the log with precision = 1 and replay-fitness = 1. This model exactly covers all the behaviour described by the input traces in the logs. However, since logs are incomplete, some forms of generalizations are needed. Thus, generalizations are directly driven by the analyst through an interactive and incremental process to avoid losing precision and/or replay-fitness.
Generalizations: in SIM, generalizations can be obtained by applying two types of operations: merge operations and abstraction operations. Merge operations merge the instances of some paths occurring in the model, and SIM provides facilities to specify paths, search their occurrences in the model, and merge them. Abstraction operations move from a process description, where actions are reported at the ground level to more user-interpretable/compact descriptions, in which sets of actions are abstracted into "macro-actions" subsuming them (ISA relations) or constituted by them (Part-Of relations).
Incremental and selective application of generalization operators: SIM provides analysts with the possibility of selectively applying generalization (e.g., the analyst can decide what occurrences of the path to merge or what instances of the actions composing a macro-action to abstract) and operating step-by-step. In this way, the final model can be built by applying subsequent merge and abstraction steps, leading to a progressively more generalized version.
Model evaluation and versioning: SIM enables analysts to perform a quantitative evaluation of the model, considering parameters such as replay-fitness, precision, and generalization. It also allows analysts to backtrack to previous versions of the model (versioning).

3. Action-state log-tree: representation formalism

In AS-SIM we extend SIM to cope with input traces containing both actions and state information. The starting point of AS-SIM is the definition of an extended formalism to represent the process model. Besides action nodes (to represent actions), the new formalism must also include state nodes, to represent the state of affairs, and arcs, that can connect two (action or state) nodes, to represent the control flow of action execution and/or state evaluations.

The starting point in the definition of the AS-SIM formalism is the definition of the domain of actions and of states.

As in SIM, the domain

A

of actions is simply the set

{a_{1}, \dots, a_{n}}

of all the actions appearing in the input traces (possibly, a preprocessing phase can be adopted to filter out actions appearing below a given threshold frequency). On the other hand, in AS-SIM states are described in terms of the values assumed by a set of parameters (i.e., features) measured at a given point of time as reported in the traces, and describing (possibly in a partial way) the context where actions are executed. In the following, we denote by

P

the set

{p_{1}, \dots, p_{m}}

of all the parameters appearing in the input traces (possibly filtered using frequency). For the sake of generality, in AS-SIM we distinguish parameters along two different dimensions:

along the temporal dimension, a parameter may be constant (in case the value of the parameter cannot vary in time) or changing; in this case, the parameter assumes the form of a time series;
along the value-type dimension, a parameter may be numeric (in such a case, the measure unit adopted for the parameter must be part of the domain description), symbolic (i.e., assume a finite set of non-numeric values that cannot be ordered along a scale; e.g., true/false) or categorical (i.e., assume non-numeric values that are ordered along a scale; e.g., low<medium<high).

Independently of the value-types, each single value for a parameter represents a measurement/observation on the parameter, and is modeled by a pair <value, timestamp>. Each state is characterized by the values assumed by a subset of the parameters in

P

. For instance, in the context of medical traces, “states describe clinical situations in terms of a set of state variables with a clinical sense” [6]. In real contexts, some state variables may be unavailable at the time of measurement – so that only a subset of parameters in

P

is considered. For the sake of clarity, we assume the conventions that:

the (unique) value of constant parameters is collected in the initial state (which may possibly contain also values for some of the changing parameters);
each state (except the initial one) follows a source action (or set of actions) and precedes a destination action (or set of actions), and contains, for each observed parameter, all the <value, timestamp> observations collected for the parameter in the slice of time between the execution of the source action and of the destination action.

AS-SIM adopts two types of nodes: action nodes and state nodes. As in SIM, an action node represents a pair

< {a_{1}, \dots, a_{k}}, T_{s} >

, where

{a_{1}, \dots, a_{k}}

is a set of actions in

A

. Actions in the same node are in any-order relation.

T_{s}

is the set of support traces in the log, that we will explain below.

On the other hand, a state node represents a pair

< {S_{p_{1}}, \dots, S_{p_{k}}}, T_{s} >

, where

S_{p_{i}}

1 \leq i \leq k,

k > 0

is a pair

< p_{i}, < < v_{1}, t_{1} >, \dots, < v_{j}, t_{j} > > >

in which

p_{i} \in P

represents a parameter, and

< < v_{1}, t_{1} >, \dots, < v_{j}, t_{j} > >

, with

j > 0

is a time series with the observed timestamped values for

p_{i}

. Again,

T_{s}

is the set of support traces in the log (see below).

Action nodes thus support a compact representation of sets of actions which can be executed in any order, and state nodes a compact representation of a timestamped sequence of parameters observations into a unique node.

Oriented arcs connect a source node and a destination node to model a temporal sequence relation (i.e., ordering) between them. However, since, for the sake of compactness, we model series of observations of parameter values (with no action interleaved between them) into a unique state node, in the AS-SIM formalism we admit arcs connecting:

two actions nodes $N 1$ and $N 2$ (to represent the fact that the action(s) in $N 1$ precede(s) those in $N 2$ );
an action node $N 1$ to a state node N2 (to represent the fact that the action(s) in $N 1$ precede(s) the state described in $N 2$ );
a state node $N 1$ to an action node $N 2$ (to represent the fact that the state in $N 1$ precedes the action(s) in $N 2$ ).

On the other hand, arcs starting from a state node and ending into a state node are not allowed.

Thus, in AS-SIM, a process model graph consists of an oriented graph, in which two classes of nodes (action nodes and state nodes) are connected by oriented arcs, as discussed above. In the graph, an initial node can be distinguished.

In particular, the initial process model (which is automatically mined by AS-SIM, as discussed in Section 5.2) has the form of a tree, and is called action-state log-tree.

Notably, each path from the root of the action-state log-tree to a given node N denotes a set of possible action+state patterns (called support patterns of N henceforth), obtained by following the ordering represented by the arcs in the path to visit the action-state log-tree, ordering in every possible way the actions in each action-node, and considering the parameter values in state-nodes. For instance, the path

N 1 : {a, b} \to

N 2 : {< p_{i}, < < v_{1}, t_{1} >, \dots, < v_{k}, t_{k} > > > < p_{j}, < < v_{1}, t_{1} >, \dots, < v_{h}, t_{h} > > >} \to N 3 : {c}

where

N 1

and

N 3

are action nodes (

a, b, c

are actions in

A

) and

N 2

is a state node, represents the support patterns ab

{< p_{i}, < < v_{1}, t_{1} >, \dots, < v_{k}, t_{k} > > > < p_{j} < < v_{1}, t_{1} >, \dots, < v_{h}, t_{h} > > >}

c and ba

{< p_{i}, < < v_{1}, t_{1} >, \dots, < v_{k}, t_{k} > > > < p_{j}, < < v_{1}, t_{1} >, \dots, < v_{h}, t_{h} > > >}

As in SIM, also in AS-SIM each node contains a set of pointers to all and only those traces (called support traces) in the log whose prefixes exactly match the one of the support patterns of the node.

Besides the process model graph, a process model in AS-SIM should also account for the description(s) of the properties of the parameters used to describe states. Thus, a set of parameter tables is also introduced. Notably, as we will detail in the following, certain properties of parameter representation can be changed (interactively with the analysts) during the mining process. As a consequence, multiple parameter tables are defined in our process model representation.

Each parameter table is linked to one or more state nodes, and details the properties of parameters. For each parameter, it contains the following properties:

Temporal Type: constant, changing;
Value Type: numeric, symbolic, categorical;
Parameter Operator (having as value NULL, if no discretization/time series reduction has been performed, or the list of the applied operators – see Section 6.1 – otherwise).

Additional properties depend on the value-type of parameters:

numeric parameters have properties: range, measure unit;
symbolic parameters have the valueset property, specifying the set of the possible values they may assume;
categorical parameters have properties range, measure unit, discretization function (see Section 5.1).

4. An overview of AS-SIM

Overall, the architecture of AS-SIM is depicted in Figure 1, and relies on the following workflow (where each number denotes a phase of the workflow):

the event log is inputted to the “log pre-processing” phase, where it undergoes Trace Standardization (see Section 5.1);
then, with the help of the domain expert(s), in the second step of log pre-processing, the standardized process traces can be transformed (optionally) by applying parameter discretization (for constant parameters) and dimensionality reduction (for changing parameters), see Section 5.1;
the parameter table, which contains the details of parameter properties, as described in Section 3, is built as output of the pre-processing phase and properly updated on the basis of the pre-processing operations illustrated at phases 1 and 2. In this phase, the parameter table includes parameters and characteristics of the process model at the global level; it will then be linked to the root of the versioning tree in phase 4 (see below);
the Build-Tree Algorithm (Algorithm 1) constructs the initial action+state process model, starting from the pre-processed log, and the versioning tree root is created;
on the basis of medical knowledge and by using a set of facilities described in Section 6, the expert can collapse a set of states, occurring between the same two actions A and B, thus improving the readability and simplicity of the model. In particular, s/he can take advantage of the same parameter operations (divided into parameter discretization and dimensionality reduction) adopted in phase 2; additionally, s/he can rely on filtering and clustering operations. Finally, aggregation operations realize the actual fusion of state nodes and allow the user to aggregate the different values of the parameters collected in different state nodes into single summary representations. These (optional) facilities can be differently combined, acting as the building blocks of the overall model generalization strategy;
each state fusion step provides a new process model, i.e., a new node in the versioning tree capturing the evolution of the process model from the initial action-state log-tree; possibly, backtracking can be applied, and a different model generalization strategy can be tested;
each node of the versioning tree (e.g., node M4 in Figure 1) is associated with a process model, and with a parameter table for every state node in the model, which is properly updated in the state fusion step.

In the following, a more detailed description will be provided about the workflow architecture phases presented above.

5. Pre-processing of the log and Mining the action-state log-tree

The initial process mining step in AS-SIM takes as input an event log (i.e., a set of traces), and provides as an output a tree, containing action nodes and state nodes. In general, input logs may assume quite different formats. To facilitate the definition of the algorithm to mine the action-state log-tree (Section 5.2), we first pre-process the log, to “normalize” it (Section 5.1).

5.1. Log pre-processing

Given the variety of the formats for parameters in organization event logs, we introduce a compulsory pre-processing phase, to “standardize” them.

Then, optionally, the traces in the log can be transformed by applying:

discretization of constant parameters;
dimensionality reduction of changing parameters (i.e., time series).

Discretization is achieved through the definition and application of a set of discretization functions. Specifically, for each numeric parameter

p_{i} \in P

(with domain

D_{p}

) we define a discrete domain of values

D_{p}^{'}

and a total discretization function

f_{p_{i}} : D_{p} \to D_{p}^{'}

that maps any value in

D_{p}

into a corresponding value in

D_{p}^{'}

In this paper we assume that discrete domains and discretization functions for the parameters in the model are provided as an input to AS-SIM. Notably, however, such functions can be either provided by analysts and domain experts, or pre-computed on the basis of the (values of the parameters in the) input traces (e.g., considering the values probability distributions).

When working on time series, on the other hand, keeping all the sampled parameter values may be useless: more summarized information would save storing space, while at the same time clarifying the series behavior. To this end, SIM incorporates a set of dimensionality reduction techniques. Currently, we provide a set of mathematical transforms that move from the time domain to the time domain, but reduce dimensionality, namely the Wavelet Transform [7] and Piecewise Constant Approximation (PCA) [8].

Wavelets are basis functions used to represent other functions, which are local both in time and in frequency. The Wavelet Transform can be repeatedly applied to the data: each application brings out a higher resolution of the data, while at the same time it smooths the remaining data.

Through PCA, on the other hand, the original time series is divided into intervals of equal length, and is transformed in a piecewise constant function, where all the time points within the same interval assume as a value the average of the original time series values in the interval itself.

In addition to such transforms, we provide a more qualitative dimensionality reduction technique as well, namely Temporal Abstractions (TA) [9].

TA is an Artificial Intelligence technique that derives high-level concepts from time stamped data. It allows one to move from a point-based representation of the time series data to an interval-based one, where the input points are the sampled measurements, and the output intervals aggregate adjacent points sharing a common behavior, persistent over time. Such a behavior is identified by a proper qualitative symbol. Basic Temporal Abstractions can be further subdivided into state TAs and trend TAs. State TAs are exploited to extract intervals associated with qualitative levels, such as low and high parameter values; trend TAs are used to detect intervals of increasing or decreasing behavior. Through TA, huge amounts of temporal information can be effectively mapped to a compact symbolic representation, which not only summarizes the original longitudinal data, but also maps them to a qualitative domain with a clear semantics.

Such operations can also be applied on parameters in the phase of fusion of state nodes (see Section 6).

Example

To clarify the concepts exposed, we consider the domain of stroke treatment, focusing in particular on patients eligible for the Thrombolysis treatment (TPA). Even if this treatment is particularly effective in breaking down the blood clots which cause the ischemic attack, it can be dangerous for patients, who need a continuous monitoring of their vital signs before and after the administration of the TPA drug. In particular, among the parameters to be taken into account to define the patients’ states, the most important ones are the age and the time since the Stroke Onset (TSO). For these paramenters, the domain-discretization function is defined in terms of discretization levels provided by domain experts and is reported in Table 1.

Among the monitoring parameters, particular attention is paid to assess the patients’ cardiac and respiratory status, therefore we focus on the Arterial Pressure (AP), Cardiac Frequency (CF) and Respiratory Frequency (RF), which are collected in the form of time series.

5.2. Mining the action-state log-tree

Algorithm 1 describes (as pseudo-code) how AS-SIM builds the initial action+state process model, starting from a “standardized” log. The output of Algorithm 1 is a model with the form of a tree, and we call it action-state log-tree. Algorithm 1 is an extension of SIM’s algorithm to build log-trees [3] and works fully automatically. The inputs of Algorithm 1 are:

log is a variable representing the “standardized” log,
index is a variable that depicts a given position in the traces,
$〈 P, T 〉$ is a node (either an action-node or a state-node), and
two user-defined thresholds $α$ and $β$ (for details, see below).

Algorithm 1: Build-Tree pseudocode

1:: $B u i l d - T r e e (l o g, i n d e x, 〈 P, T 〉, α, β)$
2:: $〈 {n e x t P}_{S}, {n e x t P}_{A} 〉 \leftarrow g e t N e x t (i n d e x + 1, T, α)$
3:: if $({n e x t P}_{S} \cup {n e x t P}_{A})$ not empty then
4:: $n e x t N o d e s \leftarrow n e x t N o d e s \cup X O R v s A N Y (〈 {n e x t P}_{S}, {n e x t P}_{A} 〉, T, β)$
5:: foreach $n o d e 〈 P ’, T ’ 〉 \in n e x t N o d e s$ do
6:: $A p p e n d S o n (〈 P ’, T ’ 〉, 〈 P, T 〉)$
7:: $B u i l d - T r e e (l o g, i n d e x + | P ’ |, 〈 P ’, T^{'} 〉, α, β)$
8:: end for
9:: end if

Notably, the component T of the nodes is a set of traces (the support traces for the node), and is initially the set of all the traces in the log. For the sake of simplicity, Algorithm 1 assumes that the dummy action # is the first action in all the traces start. A dummy action-node, corresponding to such action #, and having as support traces T the set of all the traces in the log, is built to model the root of the log-tree. Thus, initially, Algorithm 1 is invoked on the first position (

index = 0

) in the traces, on the root node

〈 {#}, T 〉

(where T is the set of all the traces), and on the threshold

α

and

β

set by the analysts. The algorithm processes “in parallel” the traces in the log, position-by-position.

The function getNext (see line 2) analyses the traces in T to discover all candidates to be the next elements (either actions or states). At this step, “rare” patterns can be excluded. In particular, if

P = {X}

, and Y is a possible next element, The function getNext will give Y as output only if the edge frequency

E_{F}

of the sequence

X > Y

is higher than the value of (user-defined) threshold

α

, where:

E_{F} (X > Y) = \frac{| X > Y |}{| T |}

(1)

being

| X > Y |

the number of traces in T where Y immediately follows X (i.e., the cardinality of the support traces of Y), and being

| T |

the cardinality of the support traces of X. Setting

α > 0

allows to exclude the noisy patterns. Notably, if rare/noisy patterns are excluded, the resulting action-state log-tree does not guaranteed that precision and replay-fitness are equal to 1 (see [4]). In this paper,

α

is set to 0, and thus all the traces are given as input of Algorithm 1 to build the initial model. On the remaining next states

{nextP}_{S}

and next actions

{nextP}_{A}

, the function XORvsANY picks out the possible sets of actions in any-order (see line 4). Let us point out our assumption:

i.: the states can not be in any-order (so they are directly managed as XOR sons of the current node);
ii.: the same action may appear more than once as a son of the current node (e.g., as a “unitary” action-node and/or in one or more “any-order” action-nodes).

To identify any-order sets of actions appearing in

{nextP}_{A}

, support traces in T are inspected at positions

index + 2

(binary any-order),

index + 3

(ternary any-order) and so on, until no “wider” any-order can be determined. For the sake of simplicity, let us describe the case of binary any-orders: XORvsANY evaluates the dependency frequency

A \to B

between every action pair

〈 A, B 〉

{nextP}_{A} \times {nextP}_{A}

by considering sequences of two actions A (at position

index + 1

) and B (at position

index + 2

) following P in the traces T as follows:

A \to B = \frac{1}{2} (\frac{| A > B |}{\sum_{C \in A} | A > C |} + \frac{| A > B |}{\sum_{D \in A} | D > B |})

(2)

where, always considering the traces in T,

| A > B |

is the number of traces in which A is immediately followed by B,

| A > C |

is the number of traces in which A is immediately followed by some action

C \in A

, and

| D > B |

is the number of traces in which B is immediately preceded by some action

D \in A

. If both the dependency frequencies of

A \to B

and

B \to A

are higher than the (user-defined) threshold

β

, this means that A and B happen frequently in any-order in the same traces. XORvsANY picks out an any-order relation between A and B, and builds a new node

A & B

with the associated support traces. Thus, the function XORvsANY provides as output the variable nextNodes, which is a set of nodes

〈 P^{'}, T^{'} 〉

. Each node is appended to the action-state log-tree (function AppendSon; see line 6), and Build-Tree is recursively called on them (i.e. the first parameter index is properly set according to the cardinality of

P^{'}

; see line 7).

As last step, a dummy node $ is built, and all the leaves are connected to such node.

5.3. Properties of the action-state log-tree model

The action-state log-tree is a tree with precision (i.e., each path in the action+state log-tree corresponds to at least one trace in the log), and replay-fitness (i.e., each trace in the log can be replayed in the action+state log-tree with no errors) equals to 1 (see [4]).

6. Fusion over state nodes

As discussed above, the action-state log-tree may often be quite wide. In particular, in many cases, a wide set of state-nodes

S_{1}, \dots S_{k}

may lay between an “origin” action node A and the same “destination” action node B: in the log-tree, different instances of B, one per branch, are represented. This makes the log tree redundant and difficult to read. Therefore, in this case, a simple post-processing step is adopted, to merge all such instances of B in a single action-node, technically transforming the log-tree into a graph (action-state base-graph henceforth).

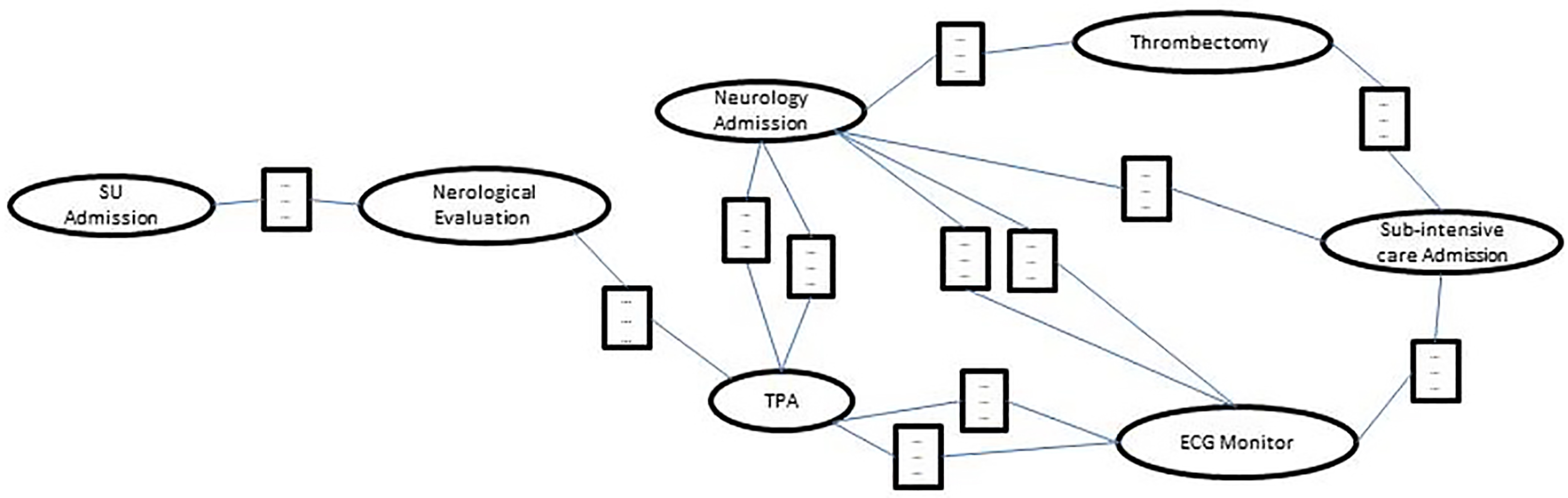
Figure 2 shows the action-state base-graph, based on traces from the stroke domain focusing on the TPA administration procedure, described in Section 5.1. Here, the states are represented by rectangles, while the actions by ellipses. In the process in Figure 2, after admission in the Stroke Unit (SU), the patients are evaluated by experts and the TPA drug is administered. At the conclusion of the TPA infusion, the patients are monitored and sent to the neurological ward, or further examined through the installation of a continuous ECG monitor before being discharged to the Sub-intensive care ward. In the neurology ward, the model in Figure 2 suggests that patients can undergo to an additional treatment (Thrombectomy) or discharged to the Sub-intensive care ward. For brevity and readability, we do not specify the contents of the state nodes in Figure 2.

Given the action-state base-graph, the user may also wish to fuse (some of) the different states laying between action nodes A and B into one.

In this Section, we provide different facilities and operations to summarize state information and to facilitate the fusion of state nodes

S_{1}, \dots, S_{k}

into a unique state node, or into a certain number (less than k) of state nodes. We categorize such facilities/operations into four different types, applicable to sets

S_{1}, \dots, S_{k}

of states-nodes between two action-nodes A and B:

Parameters operations, acting on the values of a specific parameter (Section 6.1);
Filtering operations, to ignore one or more parameters (Section 6.2);
Clustering operations, to partition the set $S_{1}, \dots, S_{k}$ of states-nodes into subsets of state-nodes, each one to be fused into a unique state-node (Section 6.3);
Aggregation operations, aggregating the values of a given parameter taken from different state-nodes (Section 6.4).

As we will see, such operations can be combined in different ways, for the sake of simplifying the AS-process-model (see Section 6.5). However, the basic idea is that filtering operations rule-out non-interesting parameters, parameters operations simplify the values of a given parameter in each considered node, clustering fixes the state-nodes to be fused (if no clustering is performed,

S_{1}, \dots, S_{k}

can be fused all together into a unique state-node), and, once fixed a set of state-nodes to be fused, aggregation operators are applied to each parameter to aggregate the parameter values taken from such nodes.

In the following, we present such operations.

6.1. Parameter Operations

Parameter operations allow to simplify/summarize the representation of a single parameter.

In some situations, experts may not be interested in raw parameter values, but could prefer a more abstract and summarized information.

Specifically, as regards constant parameters, we support the use of discretization (see Section 5.1); when dealing with changing parameters, which assume the form of time series, different dimensionality reduction approaches are made available. All of these facilities are optional, and can be applied not only at the time of generalization over state nodes, but also as a pre-processing step, and have therefore been introduced in Section 5.1.

It is worth noting that parameter operations may produce, as a side effect, state coalescing: e.g., if all parameters assume the same values after discretization, they will be identical over two or more states. In this case, the corresponding state nodes are automatically fused.

Parameter operations modify the parameters tables associated with the state-nodes at hand, which explicitly keep track of discretizations and dimensionality reductions.

6.2. Filtering operations

An analyst, interacting with our system, may wish to restrict her/his analysis to a subset of parameters.

To this end, we provide an optional filtering facility, which allows the expert to check what parameters s/he wants to keep in the fused state node that will be generated. On the basis of domain knowledge, in fact, the expert may be aware that certain parameters are not particularly interesting for the problem at hand, but they might have been recorded in all traces as a routine. A graphical interface allows the user to select the parameters to be filtered away.

It is worth noting that filtering operations may produce, as a side effect, state coalescing: in fact, if some parameters have been filtered away, the remaining ones could be identical over two or more states. In this case, the corresponding state nodes are automatically fused.

Filtering operations modify the parameters tables associated with the state-nodes at hand, since they eliminate some parameters.

6.3. Clustering operations

An analyst may also want to cluster input states into more homogeneous groups, in order to build a more focused model. If this facility is not used, a single state node will be created through fusion, by generalizing over all the states between action nodes A and B in the input model; otherwise, fusion will be applied to each subset of state-nodes (between A and B) obtained by clustering, to generate different state nodes, which will be drawn as parallel branches in the resulting process model. Of course, there is a trade off between the richer information carried by the state separation, and the greater readability of a model with a single state node. The interactivity of AS-SIM, and the possibility of backtracking, provides a very large flexibility in dealing with this issue.

This clustering operation is currently realized via the k-means algorithm [10]. Other algorithms may be integrated as well, in the future.

6.4. Aggregation Operations

Given a set of nodes (i.e. all the states nodes between two actions A and B, or all the nodes in one cluster), their fusion into a unique “summary” state-node can be obtained by applying aggregation operations to each parameter in the state node description. Notably, different aggregation operations can be used for different parameters.

Non discretized numeric constant parameters can be aggregated resorting to a whole set of statistical techniques provided by AS-SIM. Namely, the user can calculate mean, variance, standard deviation, quartiles, median, and all the other basic statistical operators on numeric values.

Non dimensionality-reduced changing parameters (i.e., time series), can be treated similarly: indeed, if all the time series samples have been kept, AS-SIM allows the user to align in time the different series belonging to different state nodes, cutting longer series in order to work with data of the same length. Missing data within a time series are completed resorting to interpolation techniques. Once two or more time series are aligned sample by sample, AS-SIM allows to apply the statistical operators mentioned above on every single sample, generating, e.g., the time series of the mean values.

As regards discretized constant parameters, two strategies are possible. In the first case, the most frequent discretized value is used to substitute the set of discretized values belonging to the different state-nodes. This aggregation strategy can be applied to numeric, symbolic or categorical parameters.

In the case of numeric and categorical parameters, an alternative approach is also possible: each discretization interval/qualitative level is mapped to a number on an ordered scale; the statistical operations mentioned above are applied to such numbers for aggregation; then, the resulting number is mapped back to the original domain.

As regards dimensionality-reduced time series numeric parameters, if a Wavelet Transform or a PCA technique has been adopted as a first step, the parameter is still represented as a sequence of values in time – simply, the number of these values is much lower than the number of the original samples. Therefore, all the aggregation operations working on raw time series can still be applied. On the other hand, if Temporal Abstractions have been adopted, the time series have been transformed into sequences of symbols, where every symbol corresponds to an interval of a fixed duration (set at the time of reducing dimensionality, and specified in the parameter table), and qualitatively summarizes the behavior of the series in that interval. The different sequences of symbols (one per state) can be further collapsed into a single sequence, by selecting the most frequent symbol interval by interval. Alternatively, complex TAs [9] can be adopted. Complex TAs are Temporal Abstraction able to aggregate two series of intervals into a series of higher level intervals, in order to identify more complex patterns (e.g., an interval of increasing trend followed by an interval of decreasing trend, thus determining a peak). Such a method can be used when the original time series parameters have already been abstracted by means of basic TAs in the pre-processing phase. The two last approaches can be adopted also on changing parameters that are symbolic or categorical in nature, and can be therefore expressed as time series of qualitative values.

Aggregation operations modify the parameter table associated with the unique state-node that is generated, since they put together all the parameters of the original state nodes they fuse.

6.5. Combining the basic operations

Different possibilities of combining the basic operations illustrated above are also provided.

Specifically, parameter operations can be optionally adopted as a first step, either in pre-processing, or in the fusion of state nodes, or both. Then, filtering and partitioning operations can be optionally applied.

The final step will be the application of the proper aggregation operation, working either on raw parameters, or on discretized/dimensionality reduced ones, as already explained in Section 6.4.

Example

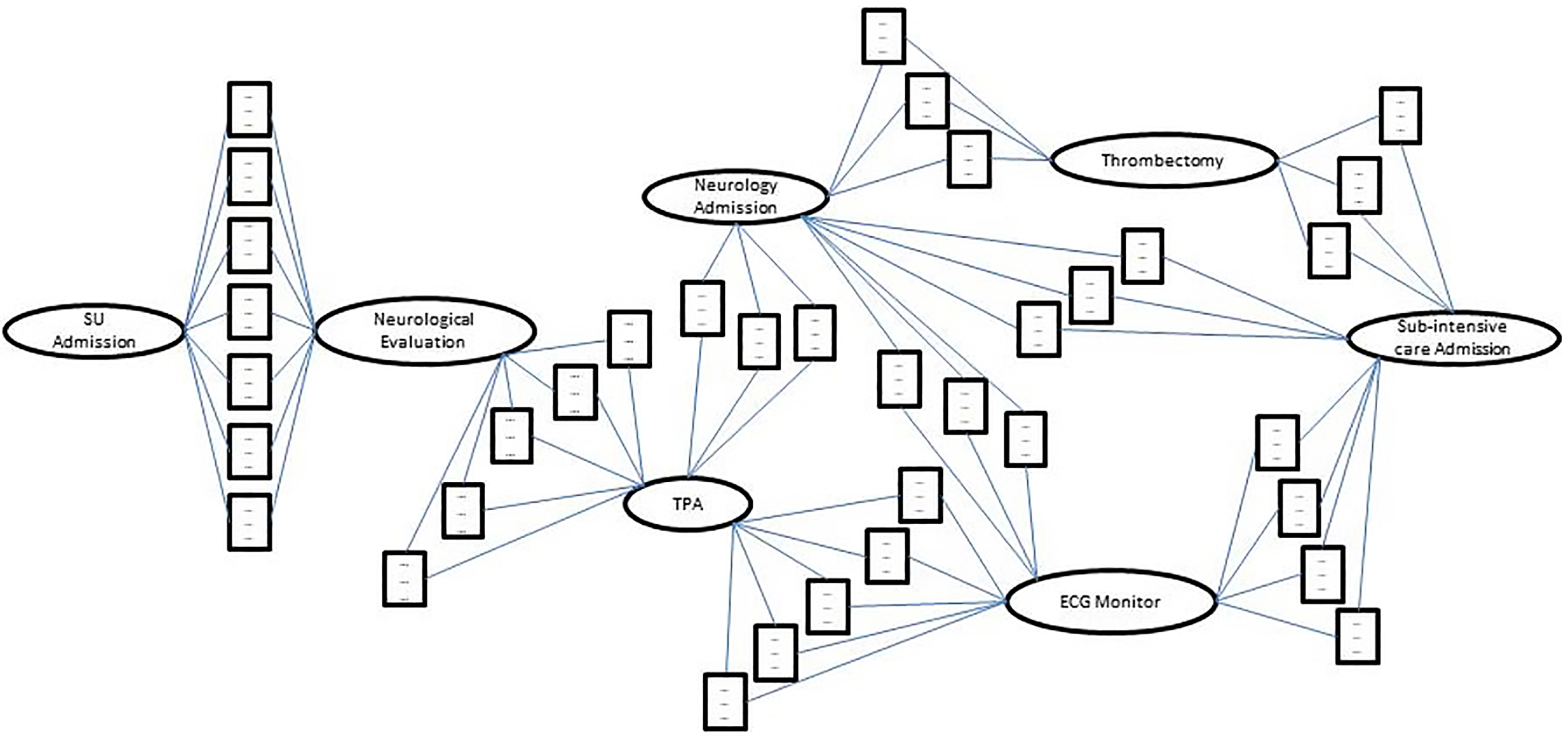
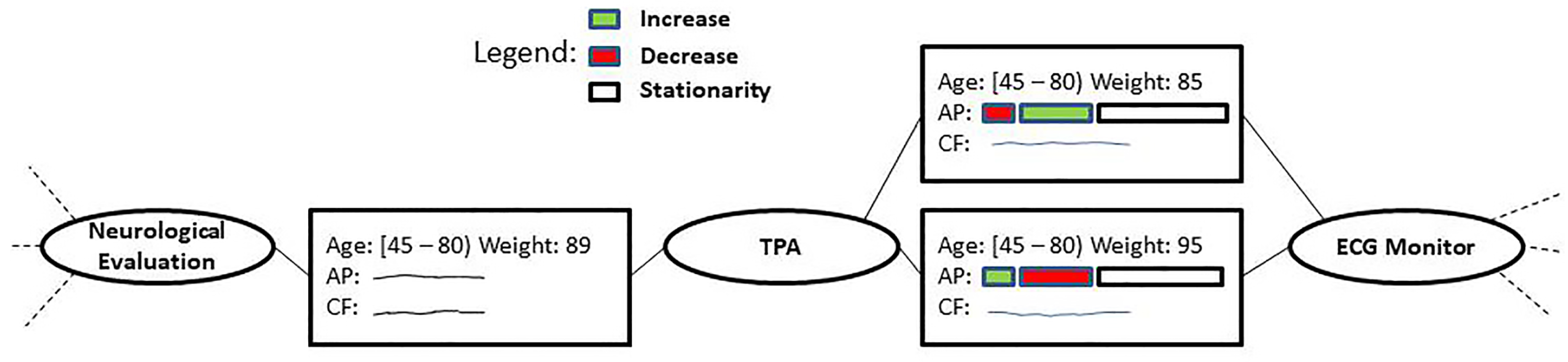
Reverting back to the example described in Section 5.1, we describe the flow of work a user performs to manage the initial complexity of the Action-State log tree in Figure 2, to obtain a more manageable version using the parameter and state node operators described above. We focus on a particular section of the model, which is shown in Figure 3. In the latter, after admission in SU and evaluation by the neurologist (first action of this process excerpt), patients are treated with TPA to dissolve the thrombus obstructing the blood flow to the brain. Before and after this treatment, the patient’s vital parameters are checked through continuous monitoring (see the state-nodes (rectangles) in Figure 3). Before the therapy, monitoring is performed to guarantee the administration of the TPA under controlled conditions, while after the therapy it is necessary to monitor the evolution of the patient’s conditions to guide the next steps to be taken. After post-TPA monitoring, the installation of an ECG device for continuous cardiac monitoring may suggest the need for further investigations for patients who experienced post-TPA issues.

As a first consideration, the states between Neurological Evaluation and TPA are all related to patients eligible for TPA administration. Therefore, there is no need to differentiate patients with different conditions, since all of them are equally fit for receiving the thrombolysis treatment. In order to simplify the states contents, it is possible to filter out features which, in the clinical practice, can be considered marginally important with respect to the others in the current context. For example, the stability of the patients’ conditions is mainly checked by monitoring AP and CF trends, therefore the RF can be filtered out using the filtering operator on each of the states between Neurological Evaluation and TPA. The user can then decide to fuse all the latter states into one. The mean operator is applied for age and weight, while a point-to-point average operator is applied for the time series present in the fused states. The result of the fusion can be seen in Figure 4

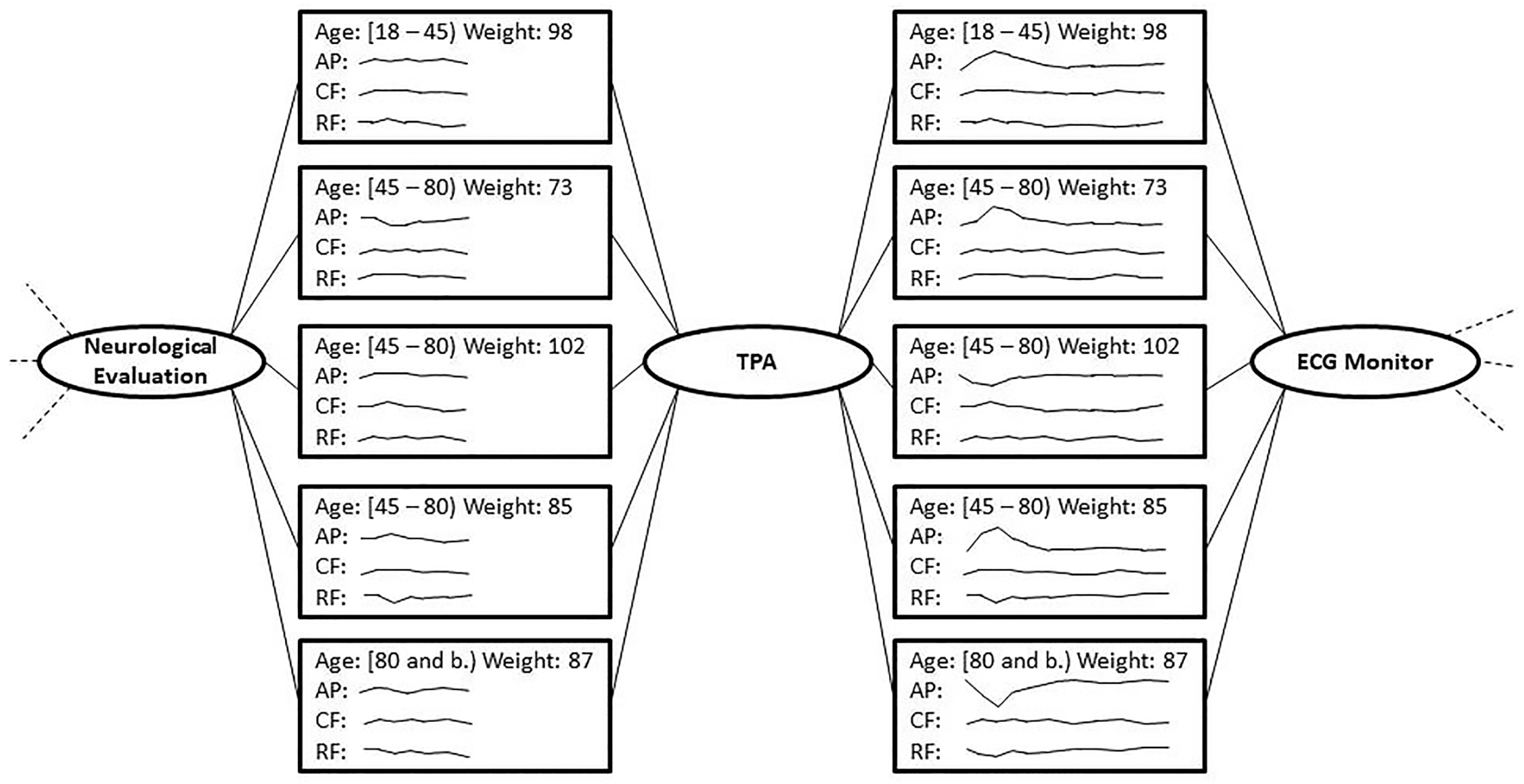
Suppose that, later, the user decides to further reduce the complexity by fusing the states between TPA and ECG Monitor installation. As in the previous strategy, the user decides to filter out the RF feature, and simply fuse all the states into one. Before fusing, it is worth considering that the vital signs monitoring after TPA lasts much longer than in the previous situation. Therefore the user decides to apply a dimensionality reduction technique to the remaining time series (AP and CF) before performing the fusion. The temporal abstraction operator is then applied to the AP and CF series of each state, in order to highlight the trends of their evolution. As a final step, s/he fuses of all the states, using the median operator on Age and Weight, and resorts to complex TAs for trends for AP and CF. Based on the medical knowledge, an increasing trend and a decreasing one are aggregated into a stationary trend.

Analyzing the result in Figure 5, it appears that AP is aggregated as a stationary trend for the whole monitoring duration. However, this does not match any of the situations described in the original states, where the AP of each patient has an unstable and never stationary trend. This fact should suggest problematic situations of patients facing issues that could be investigated. The described fusion, instead, completely hides these problems, and prevents the physicians from further monitoring these patients for cardiac problems after undergoing TPA.

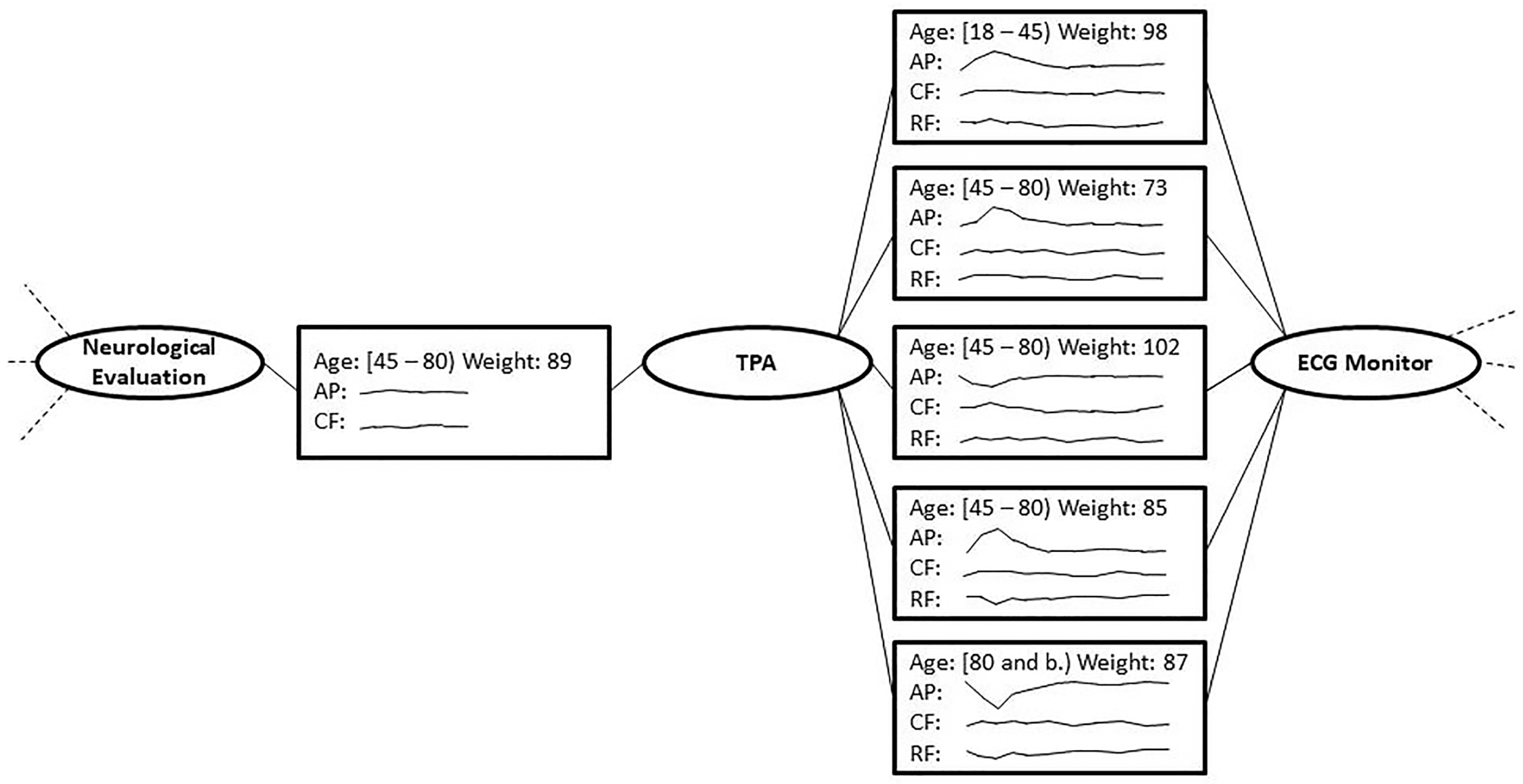
Considering the issues above, the user decides to backtrack to the previous situation (see Figure 4) to try a different strategy, in order to maintain the patients’ peculiarities in this context. As in the previous cases, the user acts for each state, filtering out RF, abstracting PA using the trend operator for TAs and leaving CF unchanged, to decide how to treat it after the aggregation. In order to identify sub-groups of homogeneous states sharing particular trend distributions, the user applies the clustering operator to the states in this context. The system divides these states into two distinct groups, A and B. The user then fuses all the states belonging to cluster A into a single state and does the same operation to fuse all the states of cluster B into one. In both cases, the operators are the mean for Age and Weight, the complex abstractions of the abstracted trends for AP and the point-to-point average for CF. The two obtained fused states are shown in Figure 6.

Comparing the two fused states between TPA and ECG Monitor, it can be observed for both an unstable behavior of AP for the entire post-TPA monitoring, but with two very different evolution of the relative trends. These differences could be useful for physicians for a more in-depth analysis. As a last step, considering the prolonged monitoring time of the CF parameter, the user considers a dimensionality reduction strategy for it, performing a PCA to reduce the measurement frequency, while maintain the signal’s shape.

Thanks to the techniques used above, the user can simplify the complete model, shown in Figure 2, by appropriately addressing each context in the model. At the end of this work, it is possible to obtain a more general and easily interpretable model, like the one shown in Figure 6.

Figure 7. Action-state base-graph for thrombolysis treatment in stroke disease after states processing and fusion

7. Related work

To the best of our knowledge, only few prior works have addressed the explicit representation of the flow of both actions and states in the process model discovery.

In particular, in the area of medical data mining, authors of [11,12] tackle the problem of medical knowledge formalization and propose an approach to derive (manually or automatically) a model from medical data representing sequences of patient visits. Each visit determines the state of a patient, and is followed by a prescription of therapies to be followed until the next visit. From these input medical data, authors extract a graph where nodes represent patient’ states, and arcs (representing the evolution between pairs of states) are labelled by the therapies leading from the input to the output states. Unlike our approach, the above works focus only on states and on their transitions, rather than on the overall action-state process model.

In the area of PM, data-flow discovery has been considered in [13,14], to identify decision points or to learn the rules that govern the decisions themselves. The authors in [13,14] adopt methods from the area of conformance checking to align the event log (that incorporates data measurements) to the process model, and generate a decision tree for every decision point, in order to select the correct alternative on the basis of the data. The output is an extended Petri Net where guards are introduced to describe the effect of data on transitions (i.e., what actions have to be executed based on data values).

Unlike our approach, none of the above works explicitly tackles the general problem of discovering a process model that explicitly distinguish between action and state nodes from input traces that contain both action and state information. In our opinion, such a model would be very useful in all domains where the state preconditions and/or the effects of actions on states have to be analysed. Therefore, we think that our approach may become the starting point of a new line of research in the area of process model discovery.

To improve the quality of discovered process models, approaches that leverage domain knowledge in the process model discovery have appeared in the PM literature [15].

Preliminary works considered exploiting domain knowledge only in an automated fashion. For instance, the work in [16] presents an automated process discovery algorithm that exploits prior knowledge in the form of augmented Information Control Nets, using ideas from Bayesian statistics. In [17], authors focus on declarative process model discovery and propose various automated techniques to remove redundant or not interesting constraints from the discovered process models as well as to guide the discovery approach by leveraging domain knowledge to identify the most relevant constraints from the domain point of view. The work in [18] presents an automated hybrid approach to process model discovery where domain knowledge is encoded in the form of precedence constraints (over the topology of the resulting process models) and mining algorithms are formulated in terms of reasoning problems over such precedence constraints. It is, however, worth noting that, in all of these contributions, domain knowledge must necessarily be expressed in the form of rules or constraints, and the user cannot control the discovery of the process, which, in the end, can be very complex.

Recently, new process model discovery approaches have been emerging that enable users to interactively integrate domain knowledge into the process model under construction. In particular, an interesting approach is the Interactive Process Discovery (IPD) presented in [19], which incrementally combines domain knowledge with the information in the event log so as to improve accuracy and understandability of the discovered process while preserving its soundness. Specifically, starting from an initial process model with no activity from the event log, the user incrementally extends the model by adding new elements and gets feedback from IPD about the positioning of new elements and relations between process activities. IDP uses “synthesized nets” (a type of Petri nets) as the underlying formalism for process models, and “synthesized rules” as a way to extend a process model into a new one by adding a transition and/or a place selected by the user at a time. The suitability and effectiveness of IPD to model real-world processes have been assessed in [20] where authors present an experimental evaluation based on a case study in healthcare. The authors of [21] propose an interactive process mining approach to discover dynamic risk models for patients suffering from chronic diseases based on patients’ dynamic behavior provided by health sensor data. This approach is based on the interactive pattern recognition framework and allows a domain expert to adjust the model under construction interactively and iteratively. The obtained model can be leveraged to customize treatments based on a patient’s unique behaviour. Finally, in [22,23], authors propose an interactive process model discovery approach (and a tool) that allows users to learn a process model by incrementally adding observed process behavior (through new traces) to the process model under construction. A possible drawback of such approach is the complexity of selecting the right traces when the noise in the data is high.

It is important to note that, unlike our approach, none of the above approaches explicitly represents in the discovered process model the flow of both actions and states from input traces and, at the same time, leverages domain knowledge and/or interacts with the user to build more understandable models.

8. Future work and conclusions

In this paper, we have proposed AS-SIM, the first process model discovery approach that mines and provides an explicit representation of the flow of both actions and states from input traces.

As future work, we plan to conduct an extensive experimental evaluation, for instance in the medical context by resorting to the freely-available MIMIC clinical database [24]. Also, we aim at extending AS-SIM with a wide class of merge and abstraction operations that allow experts to move progressively from an action-state log-tree (which is a potentially overfitting process model) to a more generalized graph-based process model. In particular, we will work on the definition of merge and abstraction operations, which generalize and complement the current operations in SIM so as to consider also state-nodes.

Acknowledgments

This research has been partially supported by the INDAM – GNCS Project 2023.

References

van der Aalst, W.M.P. Process Mining - Data Science in Action, Second Edition; Springer, 2016. [CrossRef]
Wang, S.; McDermott, M.B.A.; Chauhan, G.; Hughes, M.C.; Naumann, T.; Ghassemi, M. MIMIC-Extract: A Data Extraction, Preprocessing, and Representation Pipeline for MIMIC-III. CoRR 2019, abs/1907.08322, [1907.08322].
Bottrighi, A.; Canensi, L.; Leonardi, G.; Montani, S.; Terenziani, P. Interactive mining and retrieval from process traces. Expert Syst. Appl. 2018, 110, 62–79. [CrossRef]
Buijs, J.C.A.M.; van Dongen, B.F.; van der Aalst, W.M.P. On the Role of Fitness, Precision, Generalization and Simplicity in Process Discovery. On the Move to Meaningful Internet Systems: OTM 2012, Confederated International Conferences: CoopIS, DOA-SVI, and ODBASE 2012, Rome, Italy, September 10-14, 2012. Proceedings, Part I; Meersman, R.; Panetto, H.; Dillon, T.S.; Rinderle-Ma, S.; Dadam, P.; Zhou, X.; Pearson, S.; Ferscha, A.; Bergamaschi, S.; Cruz, I.F., Eds. Springer, 2012, Vol. 7565, Lecture Notes in Computer Science, pp. 305–322. [CrossRef]
Bottrighi, A.; Guazzone, M.; Leonardi, G.; Montani, S.; Striani, M.; Terenziani, P. Integrating ISA and Part-of Domain Knowledge into Process Model Discovery. Future Internet 2022, 14, 357. [CrossRef]
Bottrighi, A.; Guazzone, M.; Leonardi, G.; Montani, S.; Striani, M.; Terenziani, P. AS-SIM: An Approach to Action-State Process Model Discovery. Foundations of Intelligent Systems - 26th International Symposium, ISMIS 2022, Cosenza, Italy, October 3-5, 2022, Proceedings; Ceci, M.; Flesca, S.; Masciari, E.; Manco, G.; Ras, Z.W., Eds. Springer, 2022, Vol. 13515, Lecture Notes in Computer Science, pp. 336–345. [CrossRef]
Chan, K.; Fu, A.W. Efficient Time Series Matching by Wavelets. Proceedings of the 15th International Conference on Data Engineering, Sydney, Australia, March 23-26, 1999; Kitsuregawa, M.; Papazoglou, M.P.; Pu, C., Eds. IEEE Computer Society, 1999, pp. 126–133. [CrossRef]
Keogh, E.J. Fast Similarity Search in the Presence of Longitudinal Scaling in Time Series Databases. 9th International Conference on Tools with Artificial Intelligence, ICTAI ’97, Newport Beach, CA, USA, November 3-8, 1997. IEEE Computer Society, 1997, pp. 578–584. [CrossRef]
Bellazzi, R.; Larizza, C.; Riva, A. Temporal Abstractions for Interpreting Diabetic Patients Monitoring Data. Intell. Data Anal. 1998, 2, 97–122. [CrossRef]
Hartigan, J.A. Clustering Algorithms; John Wiley & Sons, Inc., 1975.
Kamisalic, A.; Riaño, D.; Welzer, T. Formalization and acquisition of temporal knowledge for decision support in medical processes. Comput. Methods Programs Biomed. 2018, 158, 207–228. [CrossRef]
Kamišalić, A.; Riaño, D.; Kert, S.; Welzer, T.; Nemec Zlatolas, L. Multi-level medical knowledge formalization to support medical practice for chronic diseases. Data & Knowledge Engineering 2019, 119, 36–57. [CrossRef]
de Leoni, M.; Felli, P.; Montali, M. A Holistic Approach for Soundness Verification of Decision-Aware Process Models. Conceptual Modeling - 37th International Conference, ER 2018, Xi’an, China, October 22-25, 2018, Proceedings; Trujillo, J.; Davis, K.C.; Du, X.; Li, Z.; Ling, T.W.; Li, G.; Lee, M., Eds. Springer, 2018, Vol. 11157, Lecture Notes in Computer Science, pp. 219–235. [CrossRef]
de Leoni, M.; van der Aalst, W.M.P. Data-aware process mining: discovering decisions in processes using alignments. Proceedings of the 28th Annual ACM Symposium on Applied Computing, SAC ’13, Coimbra, Portugal, March 18-22, 2013; Shin, S.Y.; Maldonado, J.C., Eds. ACM, 2013, pp. 1454–1461. [CrossRef]
Schuster, D.; van Zelst, S.J.; van der Aalst, W.M. Utilizing domain knowledge in data-driven process discovery: A literature review. Computers in Industry 2022, 137, 103612. [CrossRef]
Rembert, A.J.; Omokpo, A.; Mazzoleni, P.; Goodwin, R.T. Process Discovery Using Prior Knowledge. Proceedings of the 11th International Conference on Service-Oriented Computing (ICSOC 2013); Basu, S.; Pautasso, C.; Zhang, L.; Fu, X., Eds. Springer Berlin Heidelberg, 2013, pp. 328–342. [CrossRef]
Maggi, F.M.; Bose, R.P.J.C.; van der Aalst, W.M.P. A Knowledge-Based Integrated Approach for Discovering and Repairing Declare Maps. Proceedings 25th International Conference on Advanced Information Systems Engineering (CAiSE 2013); Salinesi, C.; Norrie, M.C.; Pastor, Ó., Eds. Springer Berlin Heidelberg, 2013, pp. 433–448. [CrossRef]
Greco, G.; Guzzo, A.; Lupia, F.; Pontieri, L. Process Discovery under Precedence Constraints. ACM Trans. Knowl. Discov. Data 2015, 9. [CrossRef]
Dixit, P.M.; Verbeek, H.M.W.; Buijs, J.C.A.M.; van der Aalst, W.M.P. Interactive Data-Driven Process Model Construction. Proceedings of the 37th International Conference on Conceptual Modeling (ER 2018); Trujillo, J.C.; Davis, K.C.; Du, X.; Li, Z.; Ling, T.W.; Li, G.; Lee, M.L., Eds. Springer International Publishing, 2018, pp. 251–265. [CrossRef]
Benevento, E.; Aloini, D.; van der Aalst, W.M. How Can Interactive Process Discovery Address Data Quality Issues in Real Business Settings? Evidence from a Case Study in Healthcare. Journal of Biomedical Informatics 2022, 130, 104083. [CrossRef]
Valero-Ramon, Z.; Fernandez-Llatas, C.; Valdivieso, B.; Traver, V. Dynamic Models Supporting Personalised Chronic Disease Management through Healthcare Sensors with Interactive Process Mining. Sensors 2020, 20. [CrossRef]
Schuster, D.; van Zelst, S.J.; van der Aalst, W.M.P. Incremental Discovery of Hierarchical Process Models. Research Challenges in Information Science; Dalpiaz, F.; Zdravkovic, J.; Loucopoulos, P., Eds.; Springer International Publishing: Cham, 2020; pp. 417–433. [CrossRef]
Schuster, D.; van Zelst, S.J.; van der Aalst, W.M. Cortado: A dedicated process mining tool for interactive process discovery. SoftwareX 2023, 22, 101373. [CrossRef]
Johnson, A.E.; Pollard, T.J.; Shen, L.; Lehman, L.w.H.; Feng, M.; Ghassemi, M.; Moody, B.; Szolovits, P.; Anthony Celi, L.; Mark, R.G. MIMIC-III, a freely accessible critical care database. Scientific Data 2016, 3, 160035. [CrossRef]

Figure 1. The workflow architecture (circled numbers represent the workflow phases presented in Section 4)

Figure 2. Action-state base-graph for thrombolysis treatment in stroke disease

Figure 3. Excerpt of the action-state base-graph focusing on TPA administration

Figure 4. Excerpt of the action-state base-graph after the fusion of the states between Neurological Evaluation and TPA

Figure 5. Excerpt of the action-state base-graph after the fusion of all the states between TPA and ECG Monitor

Figure 6. Excerpt of the action-state base-graph after fusion of the states between TPA and ECG Monitor after clustering

Table 1. Discretization levels of the selected patients’ parameters.

PARAMETER	MEASURE UNIT	DISCRETIZATION LEVELS
Age	Years	[0 - 18); [18 - 45); [45 - 80); [80 and beyond)
Time since onset (TSO)	Hours	[0 - 4.5); [4.5 and beyond)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Towards Action + State Process Model Discovery

Abstract

1. Introduction

2. Overview of SIM

3. Action-state log-tree: representation formalism

4. An overview of AS-SIM

5. Pre-processing of the log and Mining the action-state log-tree

5.1. Log pre-processing

Example

5.2. Mining the action-state log-tree

5.3. Properties of the action-state log-tree model

6. Fusion over state nodes

6.1. Parameter Operations

6.2. Filtering operations

6.3. Clustering operations

6.4. Aggregation Operations

6.5. Combining the basic operations

Example

7. Related work

8. Future work and conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe