Prerpints.org logo
Preprint
Article

Experimental and Numerical Flexural-Torsional Performance of Thin-Walled Open-Ended Steel Vertical Pile Foundations Subjected to Lateral Loads

Altmetrics

Downloads

108

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 June 2023

Posted:

25 June 2023

You are already at the latest version

Alerts
Abstract
This research investigates the effects of torsional moments on the mechanical behavior of thin-walled open-ended vertical pile foundations subjected to lateral wind loads. The warping and torsion effect generated over the piles due to the resultant lateral load impact outside the shear center is analyzed in-field tests. Complementarily, a two-dimensional finite element model based on the simple bending stress-strain state as well as a three-dimensional finite element model considering torsional effects were implemented and their results analyzed. Finally, a comparative analysis between the in-field lateral loading tests and the finite element model approaches was established and correlations between the errors and the parameters of influence were highlighted. From the results, it has been ascertained that the slender thin-walled open-ended pile foundations are particularly sensitive to small load deviations from their center of gravity, this leads to the fact that the slenderer and the more eccentricity of the load, the more it affects the torsion and warping of the pile. Calculation methodologies usually consider a simple in-plane bending behavior which conducts to errors between 44 and 58% of the experimental results.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Pile foundation systems are widely used in civil engineering applications, where significant and variable loads impact the piles[1,2]. These systems are usually designed to respond elastically to any type of load [3]. Pile foundations in photovoltaic solar panels are characterized by being partially embedded in the ground and thin-walled open-ended steel piles are commonly used [4,5,6]. The pile’s area that is unembedded, has to withstand significant lateral loads, essentially wind loads, which impact randomly on the lateral surface of piles [2]. The mechanical behavior of this type of foundation is normally analyzed by means of in-field pull-out tests (PoT), prior to the design phase [7,8]. The experimental tests consist of applying different levels of lateral loads at a certain height of the pile and measuring the horizontal displacement at a certain distance from the ground level. The analysis of the stress-strain relationship of piles has traditionally been performed by means of a plane state stress approach [8], without considering second-order effects or deformations produced by the torsional moments.
In any analytical or numerical analysis, the correct choice of the soil constitutive model and the calibration of its parameters are of utmost importance. These decisions will invariably be based on material characterization from in-situ testing or laboratory testing on high-quality, representative, undisturbed, or reconstituted soil samples [5,9]. Several strategies have been suggested according to the modeling of the mechanical behavior of the pile-soil system. The Elastic-Beam-on-Winkler-Foundation [10] is the most basic type and offers resistance in direct proportion to pile displacement. Elastic-Beam-on-Nonlinear-Foundation was a notion that was used by several researchers. In that formulation, the beam is considered to be elastic throughout the analysis, while the load-displacement relationship of the foundation is assumed to follow a nonlinear equation. Empirical p-y curves [11,12] having varying values of spring stiffness are used to describe load-deformation relationships. This allows to evaluate a non-proportional connection between the lateral displacement and the soil resistance per unit length of pile p. In engineering practice, this approach is often used to examine how a loaded pile responds. Obtaining accurate p-y curves for a specific location presents the greatest challenge in practice.
Several standardized design procedures are available, for instance, the API design rules [13] or in France, the recommendations of the so-called Fascicule 62 [14]. Many studies have been focused on the fatigue effect of lateral cyclic loads of pile foundations generated by winds [15], tides, or water waves [16] in advanced civil engineering structures [1,9,12,17,18] or subjected to torsion loads [19,20,21,22]. Basack et al. [19] studied the pile degradation factor with increasing number of cycles and proposed a 2D finite element model. Other studies have focused on the lateral loads of pile foundations of close-end piles [2,23,24,25,26,27]. Nevertheless, few studies have focused on the specific behavior of thin-walled open-ended pile foundations under lateral loads [6,28]. He et al. [6] analyzed the effects of vertical dynamic interaction for off-shore thin-walled pipe piles. The different dimensions and properties of thin-walled open-ended piles lead to these types of pile foundations having different mechanical behavior and consequently, the need for a specific calculation methodology. This study arises as a consequence of detecting in numerous in-field tests provided by Auscultia company, a significantly different behavior depending on the pile used, which evidences a poor adjustment to the simple bending behavior model, used for solid section piles when applied to short piles of thin-walled metal sections.
In this research, the torsional susceptibility of a series of the most common standardized steel piles applied as pile foundations of photovoltaic solar panels and its influence on the lateral strain measured during simple bending tests are analyzed and discussed. To this aim, a theoretical-experimental study of the tensile-deformational state that occurs in metal piles of different mechanical characteristics embedded in the soil is carried out, where an essentially elastic behavior is recorded for the applied loads (Winkler's model), as a consequence of the stresses transmitted by the structure. It consists of the following phases: (i) Approach of the theoretical model. Bending in plane stress state and pure torsion. In this chapter the theoretical bases of the behavior of the structural system pile-ground will be established from the point of view of the theory of elasticity and strength of materials. The ground where the test campaign is programmed will be characterized and the geometrical parameters of the different piles susceptible to influence the deflection or twist of the piles will be established. (ii) Field experimentation through traditional lateral load tests, using instrumentation to measure lateral loads and deformations. The objective of the test campaign is to compare the displacement-deformation produced in the test piles with respect to the theoretical one and to carry out a retrospective study to characterize the soil in relation to its capacity to receive horizontal actions. (iii) Analysis of field results. Influence of geometric parameters on the torsion and bending component produced. The study is limited to soils that present an essentially elastic behavior in the range of applied working pressures. Therefore, the stress states reached in the tests that produce permanent deformations of the soil are discarded.

2. Theoretical Background

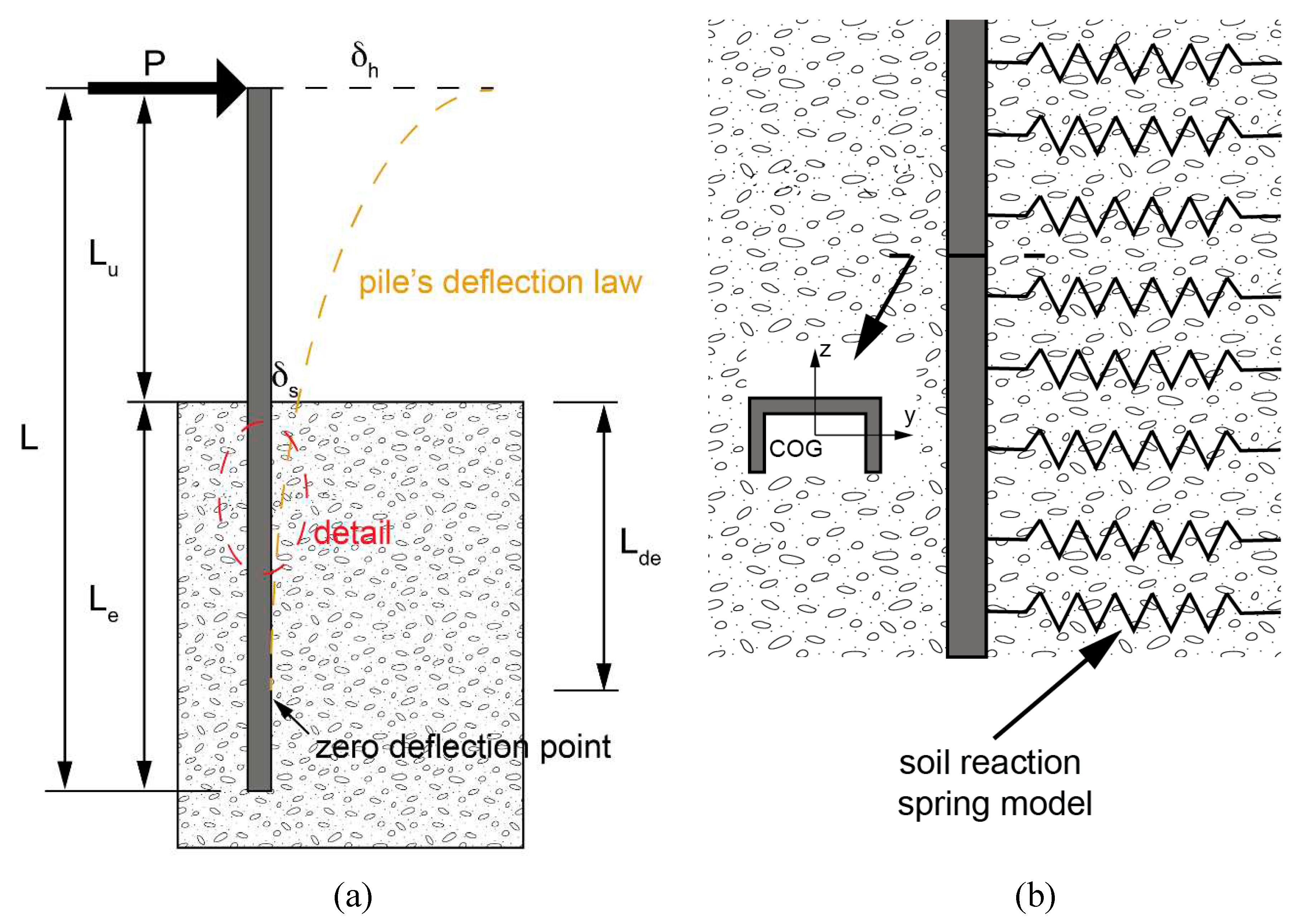
From the traditional analysis approach, pile foundation systems in solar panels are commonly modeled as an Euler beam subjected exclusively to lateral loads. The pile’s total length L is equal to its embedded length Le plus an external length Lu (Figure 1a). In the part of the pile that is unembedded (Lu in Figure 1.a), there is a distribution of shear forces and bending moments. On the other hand, in the zone embedded in the soil (Le in Figure 1a), a distribution of stresses is produced by the pile-soil system, the resultant forces must guarantee the static balance of the pile-soil system. Soil reactions are usually modeled as a discrete distribution of springs along the embedded length of the pile (Figure 1b) in accordance with Winkler [2,3,10,29].
The lateral load-deflection law of springs is normally non-linear and the displacement of the springs is discretized and independent of each other. Since the behavior of the soil is continuous, the model results will strongly depend on the number of springs that discretize the soil. Note that axial friction along the pile is not taken into account in this model.
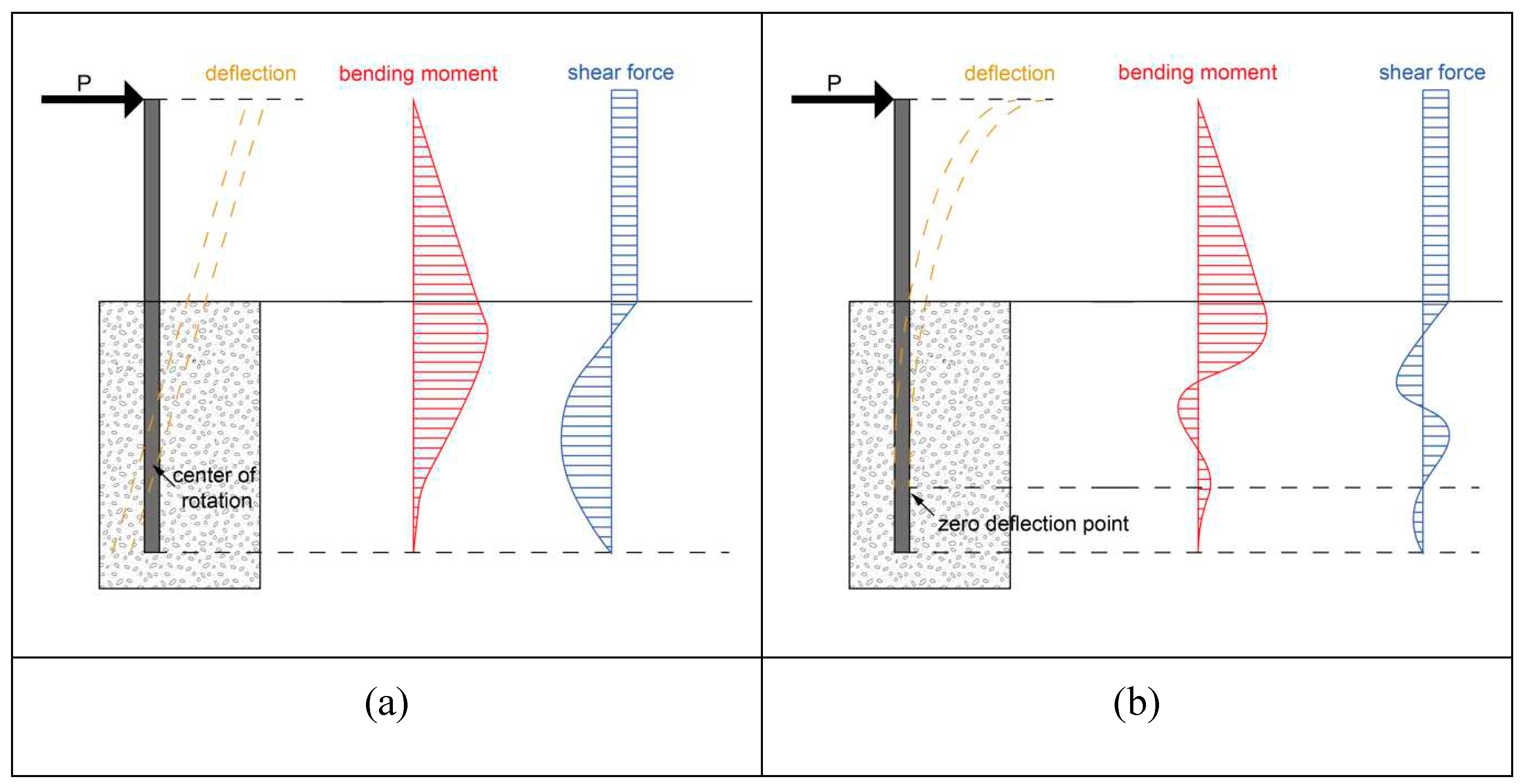
The degree of stress distribution depends on the stiffness of the steel pile and the characteristics of the soil as well as the restraint at the ends of the pile. In general, laterally loaded driven vertical piles are classified into two main types: rigid and elastic piles. Figure 2a,b show the distribution of shear forces and bending moments along the length of laterally loaded rigid and flexible vertical piles, respectively.
Focusing on the characteristics of reduced stiffness of thin-walled open-ended steel piles commonly used in photovoltaic panel foundations, the piles were analyzed as flexible behavior using the Winkler soil model [2,3,10,29]. The fundamental differential equation derived from beam theory is presented in Equation (1)[30].
E P · I P d 4 y d z 4 = − p · b
where p is the lateral load, b is the pile’s width in contact with soil, y is the lateral deflection of the pile, Ep is the elastic modulus of the pile, and Ip moment of inertia of the pile.
As an elastic behavior of the soil is considered, the relationship between the load and lateral displacement will be p=kh∙y, so the elastic equation can be expressed as a function of the horizontal ballast or Winkler modulus of the soil kh:
E P · I P d 4 y d z 4 + k h · y · b = 0

3. Materials and Methods

3.1. Steel pile description and properties

In this study, six different thin-walled open-ended steel piles standardized according to UNE-EN 36526:2018 [31], UNE-EN 36524:2018 [32] and UNE-EN 10025:2020-2 [33] have been used. Table 1 presents the fundamental properties of the structural steel piles analyzed in this research and their designation. The selection criteria of the piles were those most commonly used as foundations for photovoltaic panels. All the piles have the same yield strength of 355 MPa and it is the dimensions of the piles that vary: cross sectional area, bending inertia, torsional inertia, thickness, length, and torsional susceptibility index. Since the transverse deformation modulus of steel (G) is constant for all sections and the equivalent horizontal stresses (H) are compared, the torsional susceptibility index ω is defined as follows:
ω=(Lc×e)/It
which takes into account the main parameters that influence the twist of the sections for a given horizontal action [34].

3.2. Experimental soil characterization and model

A geotechnical study according to the ISO 14688-1:2017 standard [35] was performed on the soil where the driven vertical steel pile subjected to lateral loads were carried out. From the results, it was established the soil was formed by the following geotechnical layers (GL):
  • GL0, topsoil, and anthropic fills: the horizon formed by silty clays with pebbles and plant debris. Average thickness: 22 cm.
  • GL1, Quaternary deposit: it is a fine colluvial deposit formed by silty, silty clayey, clayey material with millimeter-centimeter-sized pebbles. Average thickness: 88 cm.
  • GL2, altered rocky substrate: formed by gypsum that alternates mainly with argillites, or marls or siltstones depending on the different zones. Alteration degree between II-V. Average thickness: 2.19 m.
  • GL3, rocky substrate: made up of gypsum that alternates mainly with argillites or marls, or siltstones depending on the different zones.
Furthermore, dynamic probing super heavy (DPSH) tests were carried out according to ISO 22476-2:2005 [36]. This type of test is simple to perform, customizable, and reasonably affordable. It provides practically continuous information that allows the good formulation of geotechnical models and determines the firm layer of a particular soil. The DPSH test consists of striking a steel cone attached to a pair of rods with a 63.5 kg hammer dropped from a height of 0.75 m, creating a dynamic force, and counting the number of blows (N20) needed to induce the cone to penetrate 20 cm into the ground. In this soil, more than 156 DPSH tests were performed at different locations. Table 2 presents the average results of N20 DPSH tests for each layer. As observed, the hardness of the GL1 is 40% and GL2 160% more than GL0, respectively.
The horizontal ballast modulus of the soil is not an easily measurable magnitude because it depends on a large number of variables: dimensions of the loaded area, heterogeneity of the layer, magnitude and duration of the loads, etc. This study has been experimentally determined from the field tests of each pile. Using the expressions proposed by Terzaghi [37] and Broms [38]:
k h = 0.75 E 0 b
where b is the contact width of the pile with the soil and E0 is Young’s modulus of the soil.

4. Experimental programme

In this study, an experimental campaign that comprises 96 in-field tests was carried out on six different driven steel thin-walled piles (Table 1 and Table 3). All the piles were placed in the ground by direct driving without the need for initial drilling or other techniques that could disturb the ground. The driving was performed by progressive and soft tapping with a 550 kg hammer hitting the free head of the pile. Figure 3 shows the in-field driving of the HEA140 pile. The verticality of the piles was controlled during the driving procedure by means of digital inclinometers of 0.1º ensuring a deviation of less than 2º.
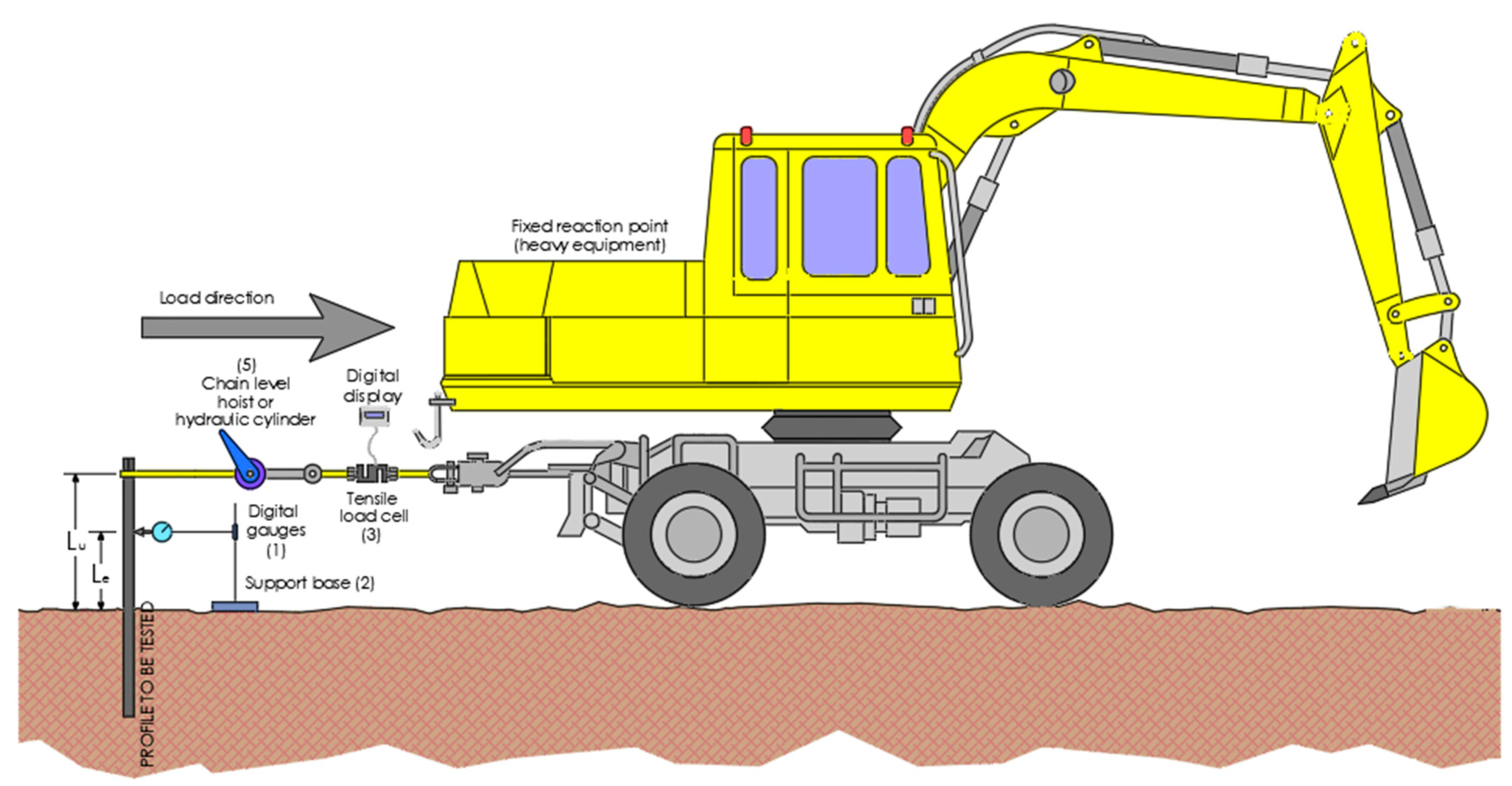
Figure 4 shows the general scheme of the test procedure and setup. A hydraulic cylinder with a maximum load capacity of 100 kN was installed in the upper free-head of the pile, to which was attached a load cell with a maximum load of 150 kN and a digital display with a converter for reading the tensile measurements. The lateral load was applied by means of a hydraulic excavating machine (Figure 4). A dial indicator with 50 mm travel and 0.01 mm accuracy was placed on the pile at a distance of 5 cm from the ground to determine the experimental lateral displacement.
The permanent deformation of each step (unloading) is also measured to establish the elastic deformation field of the soil. Table 3 shows the length of the pile embedded in the soil, Le, the height of load application, Lu, and the load steps as well as the number of tests performed for each type of pile.
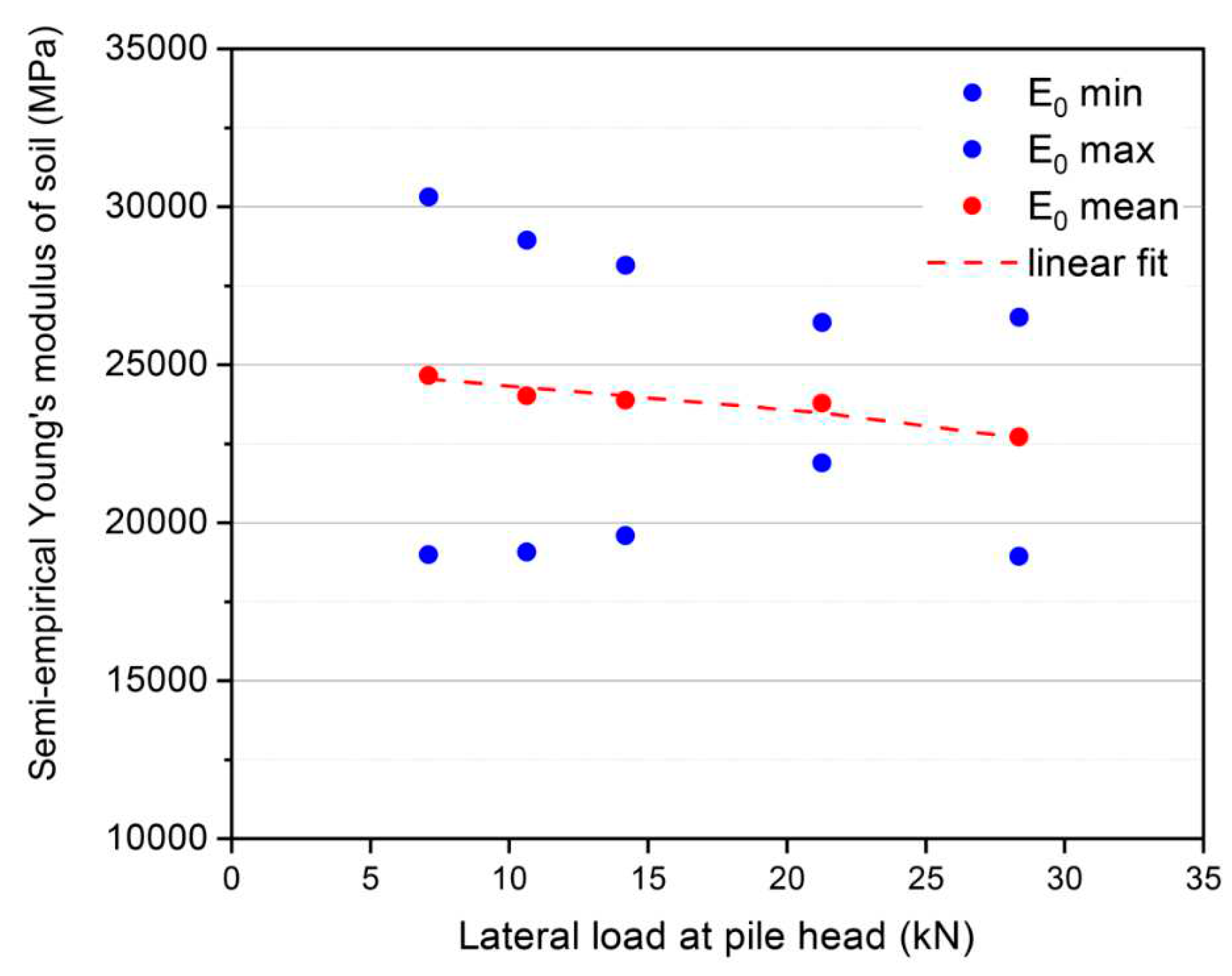
To determine the ballast modulus, the theoretical lateral displacement of the pile was determined according to the universal elastic equation (Equation (2)) for each lateral load applied. The elastic modulus was obtained experimentally through lateral load tests on profiles with greater inertia (HEA-140), at a load application height of 0.4 m above ground level, to reduce the effects of torsion. From the Equation (4), an elastic modulus of 24.1 MPa was obtained from a total of 12 tests carried out. In this way, the theoretical ballast modulus kh was determined as the ratio of force to displacement for each load step from the Equation (2). Knowing this value of the soil stiffness and the geometric data of the pile, the value of Young’ modulus of the soil E0 was obtained according to Equation (4). This calculation was made for each load step and number of tests shown in the Table 5 for the HEA140 pile. The mean of these results with their maximum and minimum values for the pile is presented in Figure 5. In this way, the non-linear soil stiffness law is obtained semi-empirically from Young’s modulus, which is subsequently used in finite element models developed in the next section.

5. Development of the finite element models

5.1. Two-dimensional finite element model

A two-dimensional model was developed using the L-Pile software from Ensoft, Inc. (US). LPILE is an internationally recognized special-purpose computer program based on rational procedures for analyzing a pile under lateral load using the p-y method. LPILE solves the differential equation for a beam column using a finite difference approach. The program calculates the deflection, bending moment, shear force, and soil response along the length of the pile.
For our model, we have considered soils with elastic behavior, based on the characterization of the soil deformation modulus. Cross-sections are characterized based on their geometry, embedment depth, elastic modulus, and moment of inertia. As it is a plane tension model, only the moment of inertia in the plane of application of the loads is introduced. Loads are entered as lateral stress in stages, reproducing the loading sequence of the field test.
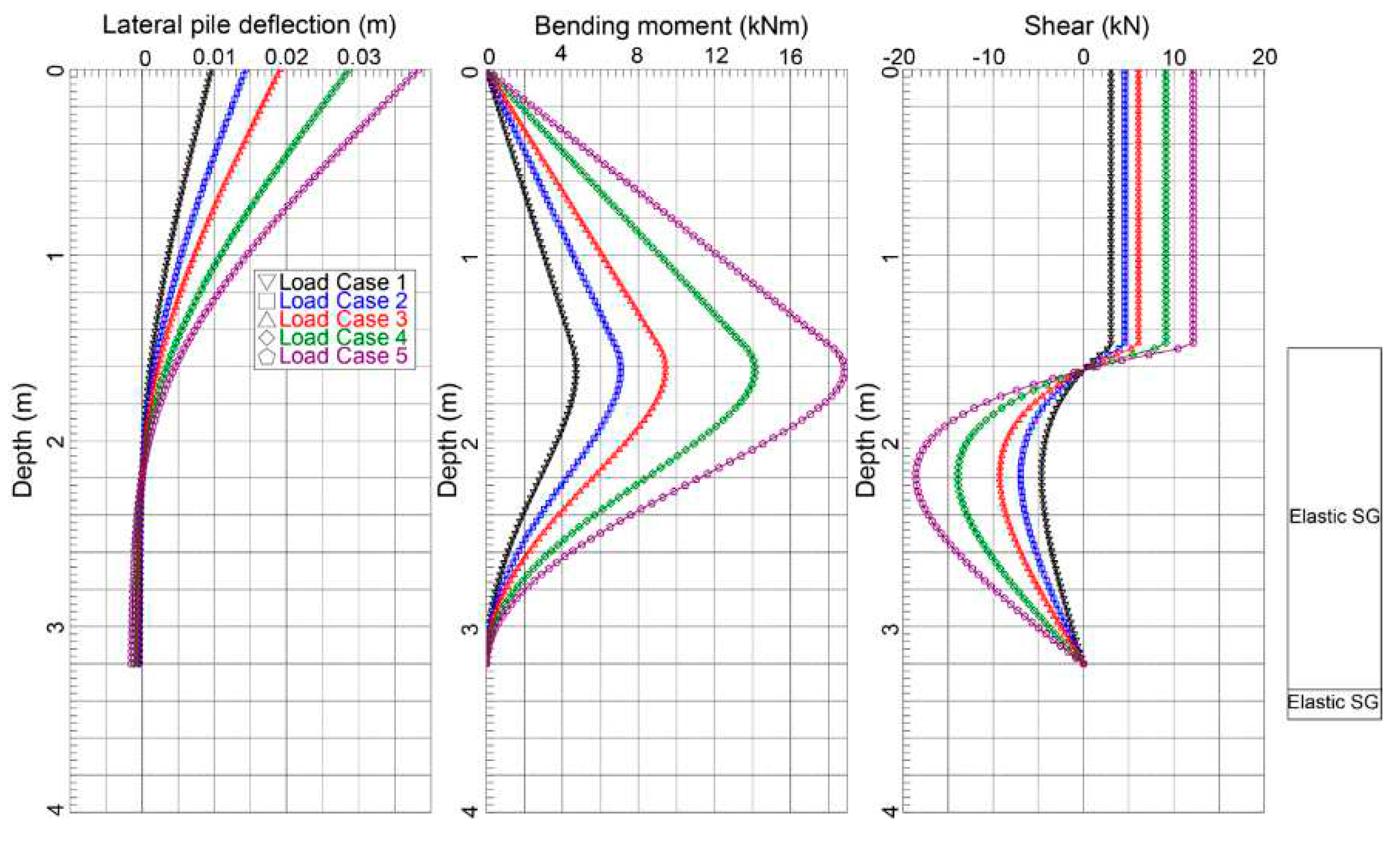
The deflections obtained in the theoretical model (Figure 6) will allow us to compare the expected result under the hypothesis of simple bending with that produced in the field tests and to detect deviations that show an inadequate fit of the theoretical model that does not take into account the susceptibility to torsion and other second-order effects that occur in the field test.

5.2. Three-dimensional finite element model

A three-dimensional model is made with SAP2000 software (Figure 7). The steel profiles have been modeled by shell-type elements, based on the geometry and thicknesses of the wings and webs of each pile. A modulus of elasticity of the steel of 210 GPa was used. The soil is modeled using the horizontal ballast modulus calculated for each pile from the Terzachi-Broms Equation (4) and the deformation modulus obtained in the experimental tests. The ballast modulus is setting in the software as spring shell elements, with linear behavior. It was analyzed using a 5×5 mm mesh size.

6. Results and comparison

In this section, the experimental lateral load at free head pile-displacement as well as the two- and three-dimensional finite element model curves are presented. The experimental results of six steel piles (Table 1 and Table 3) specifically implemented for this work are shown and compared with each other. Between 24 and 12 in-field tests were performed for each pile and their mean values and standard deviation are presented.

6.1. Single-symmetrical thin-walled open-ended cross sections

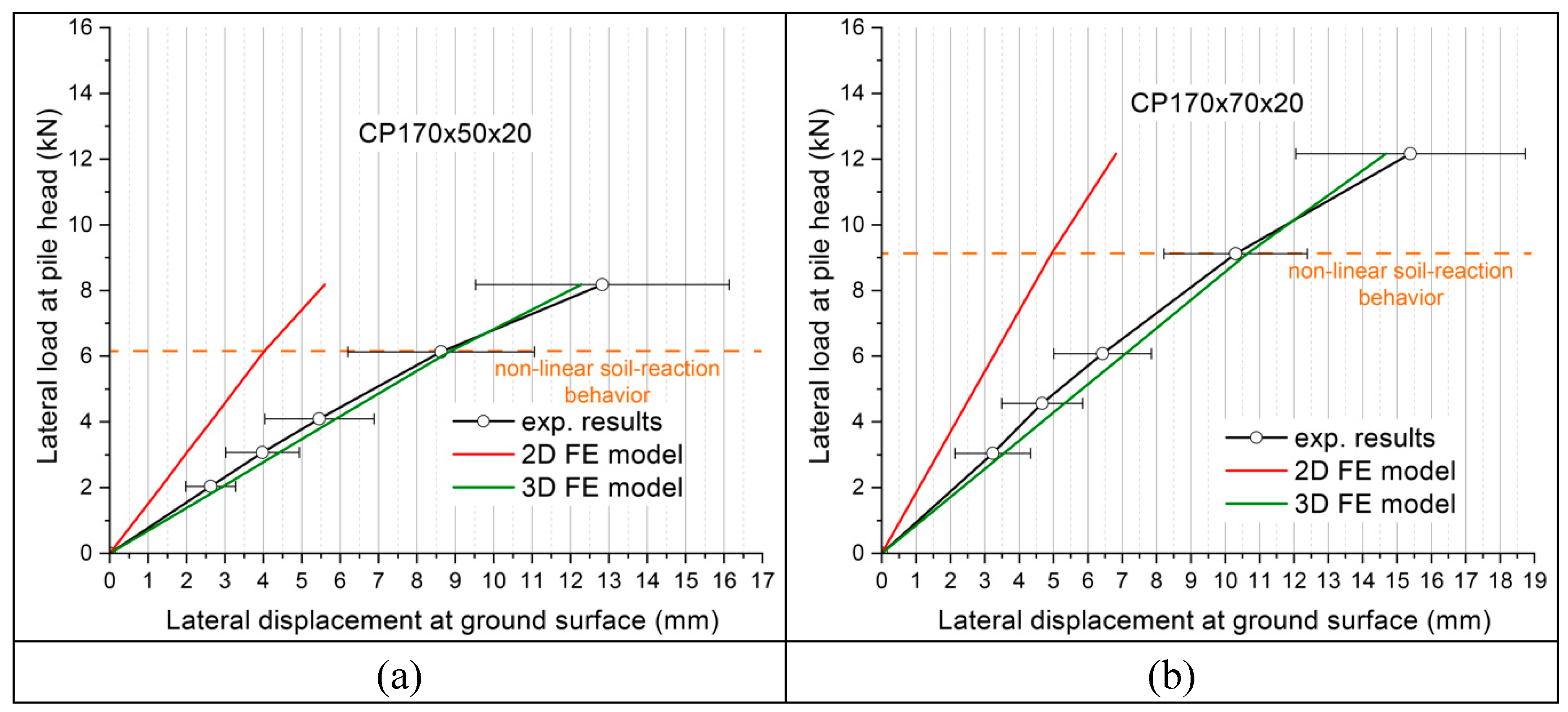
The lateral load-displacement curves for the CP170×50×20 pile are shown in Figure 8a. Mean values and standard deviation of 24 experimental results are shown. The stiffness and maximum lateral capacity of the pile in the 3D finite element model (FEM) are considered to be consistent with experimental measurements in the field. All 3D FEM results are within the measured experimental deviation. The heterogeneous behavior of the soil conducts to the dispersion of the experimental measurements greater as the load values are higher, as we approach the elastic limit of the soil.
Because of this, the stiffness of the 3D FEM is slightly lower than the experimental average values up to the fourth load step (6.13 kN) and upper for higher loads. Estimated values using the 3D FEM that takes into account the coupled effect of torsion range from 3 to 7.6% of the mean displacements and are always within the range of deviation from the results in the field. This shows how the 3D FEM significantly better simulates the real behavior of the driven pile.
Nevertheless, the 2D FEM that takes into account exclusively the lateral displacement due to simple bending is underestimated between 48 to 58% with respect to the average displacement.
A similar behavior was observed in Figure 8b, where the CP170×70×20 results are shown. The lateral load-displacement curve of the 3D FEM shows a stiffness remarkably in agreement with the experimental one. As in Figure 8a, for load levels below the onset of the nonlinear behavior of the soil, the 3D model overestimates the deflection and vice versa for higher levels. The relative errors made in the calculation of the lateral displacements in the 3D model range from 3.8 to 8%. For the 2D model, there is an underestimation of the lateral displacement (it considers the pile much stiffer in bending) with a deviation of the mean results in the field between 49 to 58%.

6.2. Bi-symmetrical thin-walled open-ended cross sections

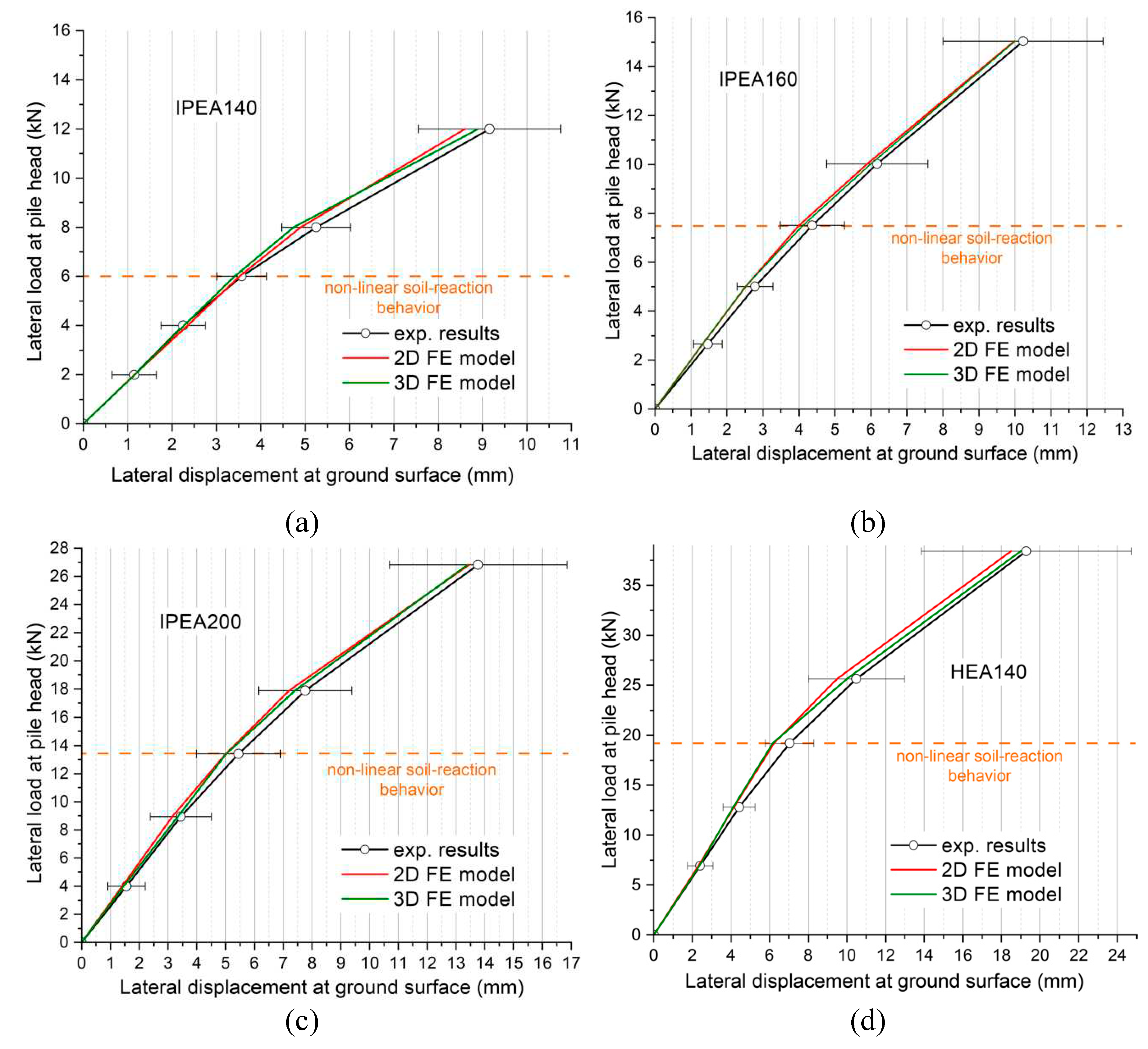
In Figure 9a, the lateral load-displacement curves of an experimental IPEA140 pile and the FEMs are shown. As can be seen, the load-displacement results determined by both two-dimensional and three-dimensional models correspond very closely to the experimental results obtained in the field for any load step. The largest relative difference between the 2D model results with the field results is 8% and for the 3D model 10%. This indicates that both models provide results with admissible accuracy for design and calculation. It is worth noting that the results of the two-dimensional model do match the experimental results remarkably well, unlike what happened for the CP170 piles (Figure 8).
Regards with the IPEA160 pile (Figure 9b), the trend of the results was qualitatively very similar to those of IPEA140. Two-dimensional and three-dimensional model results are obtained very similarly to the average field results with a maximum relative displacement error of 9 and 6%, respectively. All FEM results within the dispersion of the experimental results measurements.
Tests were performed on an IPEA200 pile to have a wider range of piles with different bending inertia, torsional and warping constant (Figure 9c). In this case, a considerable stiffness increase is observed in the experimental results of the lateral load-displacement curve compared to Figure 9a,b. However, the two-dimensional and three-dimensional models still properly simulate the real behavior of the pile ground system. The values of the maximum relative errors made for lateral displacement by the 2D and 3D models were 9% for both models. It is worth noting that the point of highest relative error is around the load from which the nonlinearity of the terrain occurs due to the discretization carried out.
Finally, a HEA140 pile with more similar inertia in both bending axes was tested and the results are shown in Figure 9d. A much higher stiffness than the IPEA piles was observed, which allowed reaching maximum absolute load values of 38 kN. Both two-dimensional and three-dimensional models estimated the bending behavior according to the experimental results. The largest error observed for the 2D and 3D models was 12% for both cases. Again, this error occurred at the transition of the change in soil stiffness.

7. Discussion

Most of the standards [7,8] analyze the behavior of driven vertical piles subjected to lateral loads using simple bending models. Nevertheless, our results of the test in the field performed revealed that the simple bending model does not suitably reproduce the strain distribution that occurs in the steel pile when dealing with thin-walled open-ended steel cross sections. During the experimental tests, significant torsion and warping were observed in the walls of the cross sections, suggesting the existence of torsional moments that cannot be disregarded during the design of foundations.
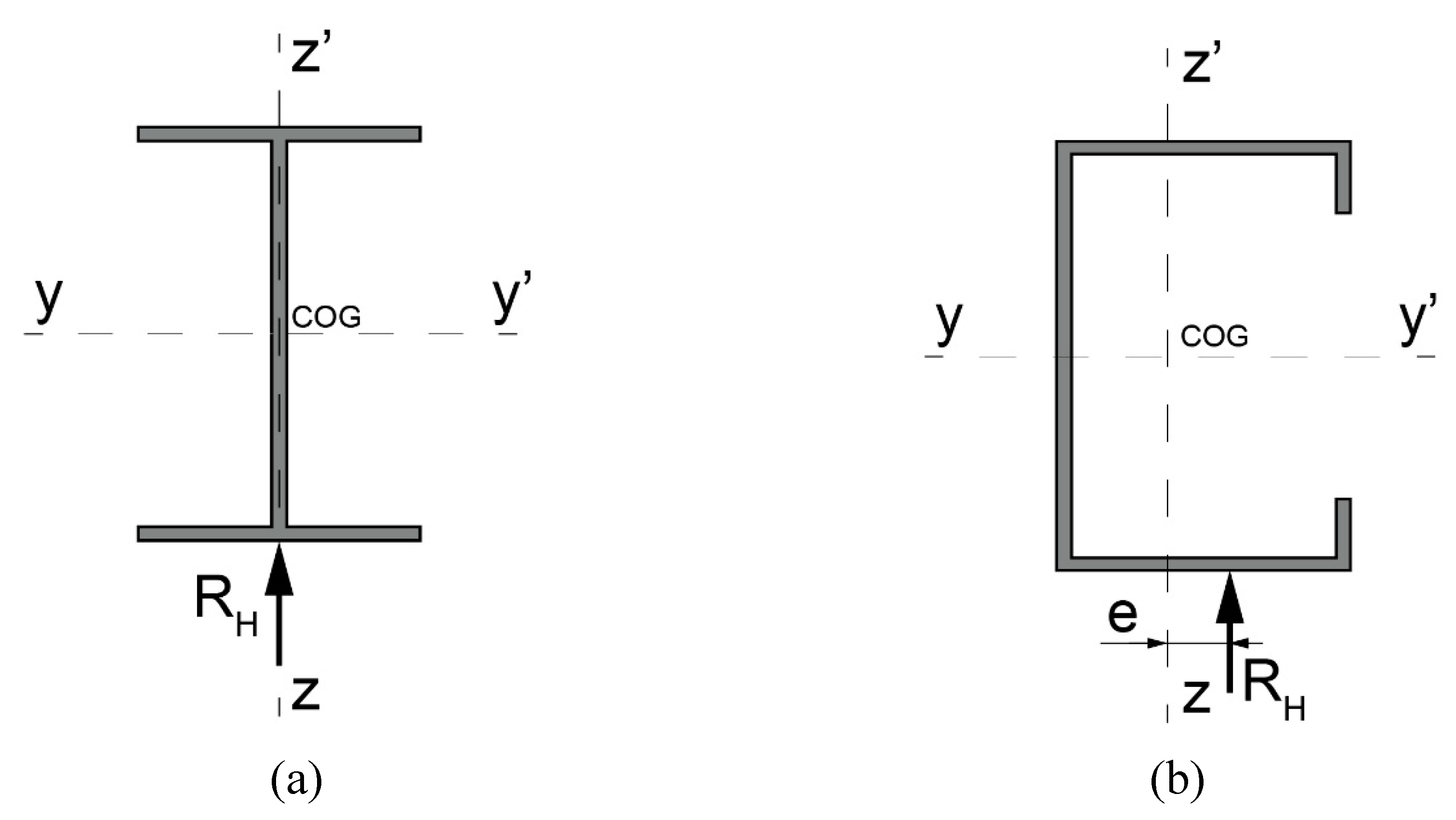
The resultant lateral loads may generate significant eccentricities depending on the wind impact zone with respect to the center of gravity of the pile cross section.
Figure 10a,b show a scheme of the resultant lateral load applied on “H” and “C” piles, respectively. The “H” piles are doubly symmetric cross sections in which the centroid and shear center are at the same point while the “C” piles, single symmetric cross sections, the center of gravity and shear center do not match, they are at different points of the cross section. As observed in Figure 10, the resultant lateral load can impact eccentrically respect to the shear center due to varied reasons such as cross section geometry (case of "C" pile, Figure 10.b), asymmetries of the structure itself supporting the foundations or by geometric deviations during assembly [39]. If the resultant lateral load does not agree on the shear center causes a torsion moment (MT=RH×e) in the cross section pile that can generate important shear strains depending on their torsional capacity and the magnitude of eccentricity.
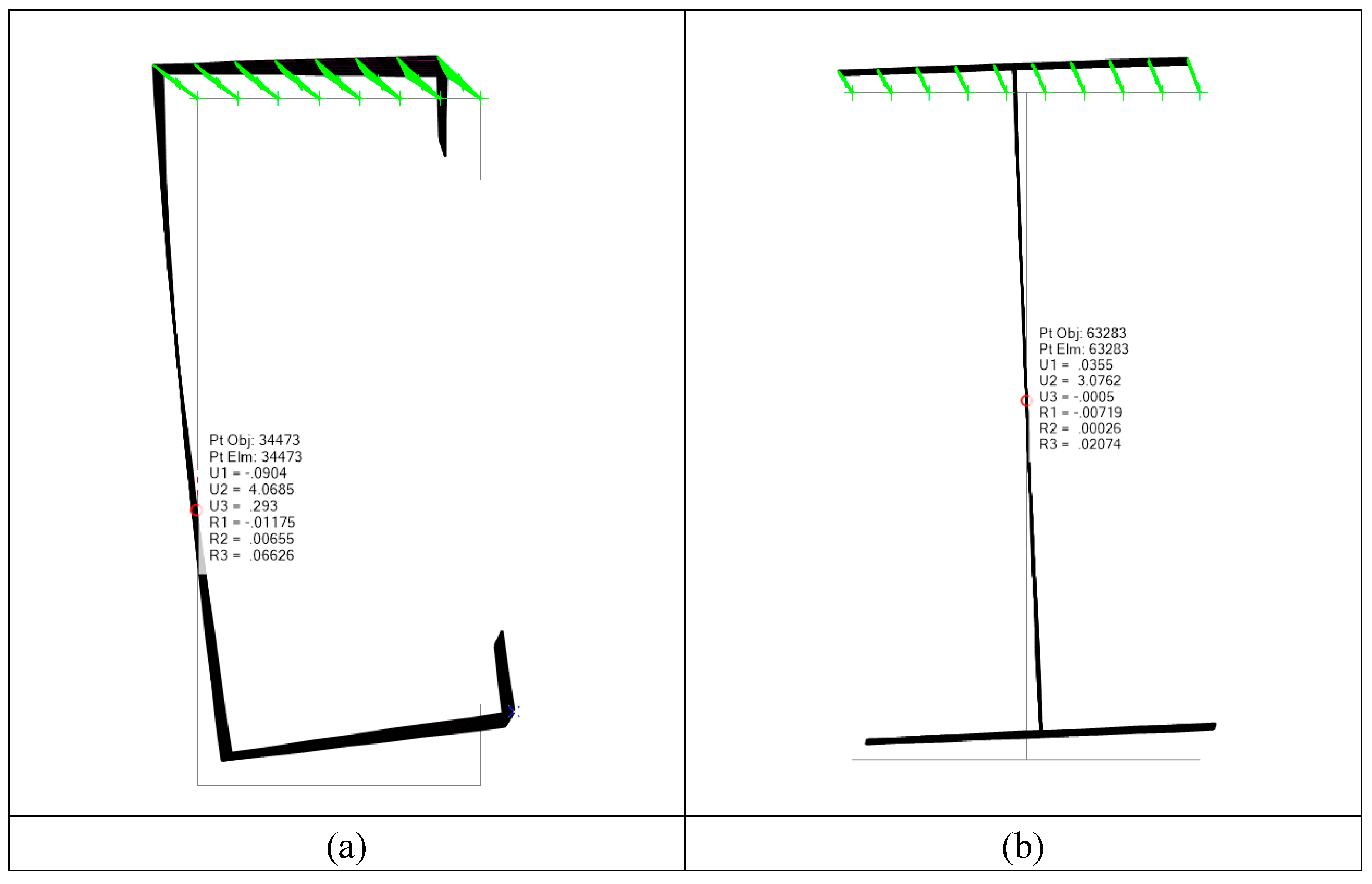
Figure 11.a shows how section C170x50x20 underwent a torsion angle of 3.79º according to the 3D model results for a lateral load value of 6.08 kN (Table 3). However, in the case of the column in IPEA140 (Figure 9b) the twist angle is of 1.18º for 7.51 kN (Table 3) lateral load. This model shows how the torsional effect is not unique to cross sections with an axis of symmetry. However, the fact that the load does not pass through the shear center causes the torsion effect to occur at much lower loads (in this comparison 23%). Therefore, the simple bending model for the design and calculation of thin-walled slender sections is not recommended, especially in profiles with low torsional capacity.

8. Correlations

To study the influence of torsion or deformation of the wings on the deflection measured in the tests, the concept of deviation ε is defined as the percentage error of the deflection measured in field tests, with respect to the theoretical deflection of the 2D and 3D finite element models. This term provides us therefore with a value of the error that occurs when characterizing the bending behavior of the soil without taking into account the effects of torsion in 2D FEM and taking them into account in 3D FEM.
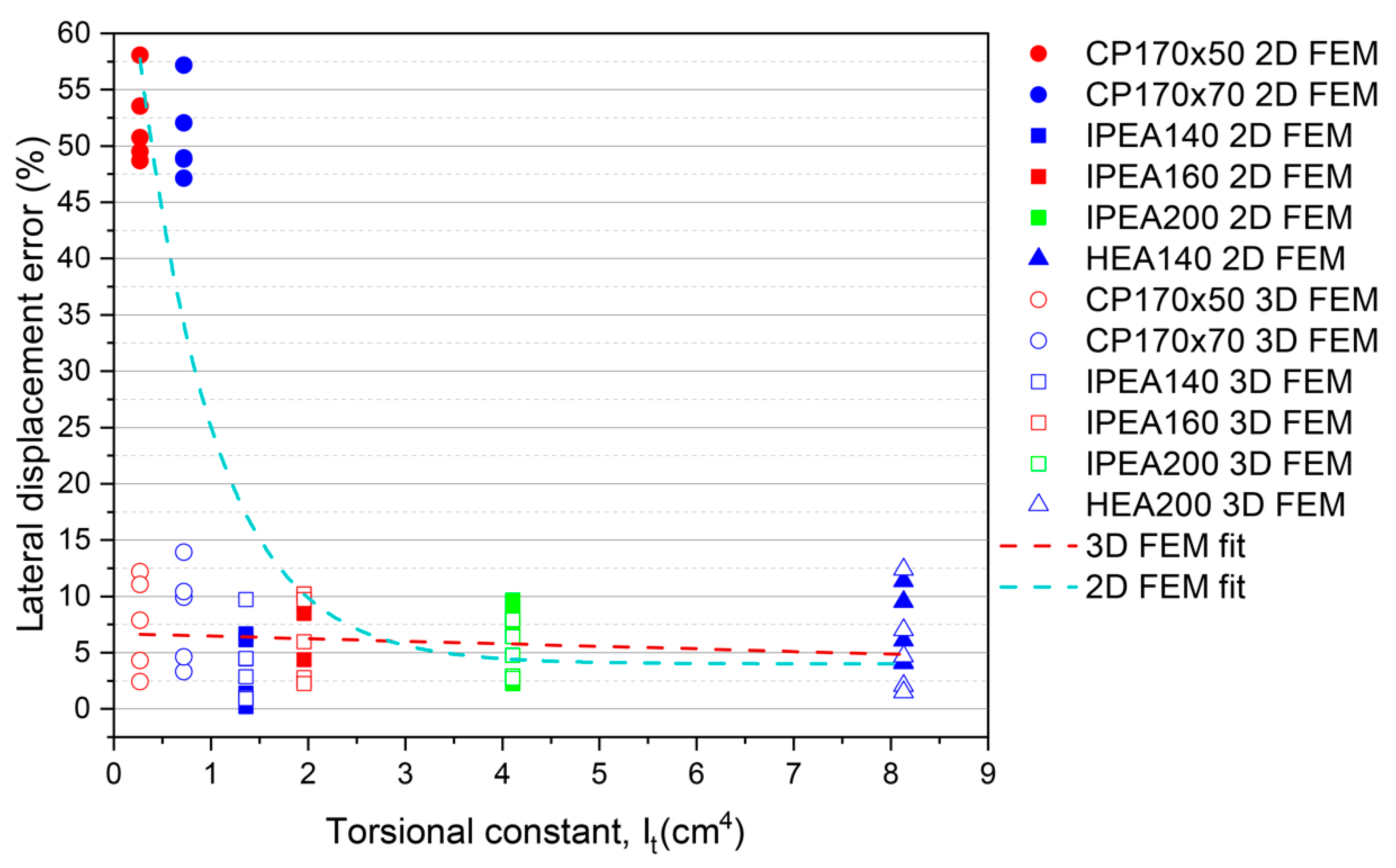
In order to determine the torsional susceptibility of a cross section, the so-called torsional susceptibility index ω described in section 3, and to measure the susceptibility to Saint Venant torsion, the torsional constant It will be plotted versus lateral displacement error. Next, correlations between the ε values obtained for each pile and the torsional and bending susceptibility parameters previously defined are going to be proposed, with the objective of measuring the influence of each of them on the deformation recorded in the tests.
Figure 12 shows on the ordinate axis the error made in the calculation of the lateral displacement of an abutment versus the torsional constant of the cross section of that abutment. This error, in percentage terms, has been calculated and plotted for the 2D and 3D finite element models of the six different cross sections (Table 1) tested in the field. In addition, the best fit found to the trend of the results obtained is plotted.
It is observed that there is a direct relationship between the error made in determining the lateral displacement of the head of the column with the torsional constant of the cross section. The higher the torsional constant, the smaller the error. In fact, the errors made in the 3D FEM are always less than 14%. In the 3D FEM, as the torsional constant increases, the errors decrease with a linear trend reaching a maximum error of 12% for the largest torsional constant of 8.16 cm4 (HEA200). In the 2D FEM, the error trend decreases exponentially with increasing torsional constant. For very low torsional constants and piles with one symmetry axis, not passing the resultant forces through the shear center, the largest error is 58%. This tendency is not only due to the torsional constant but also to other factors such as the length of the pile and the eccentricity of the load, which is why the torsional susceptibility index will be used.
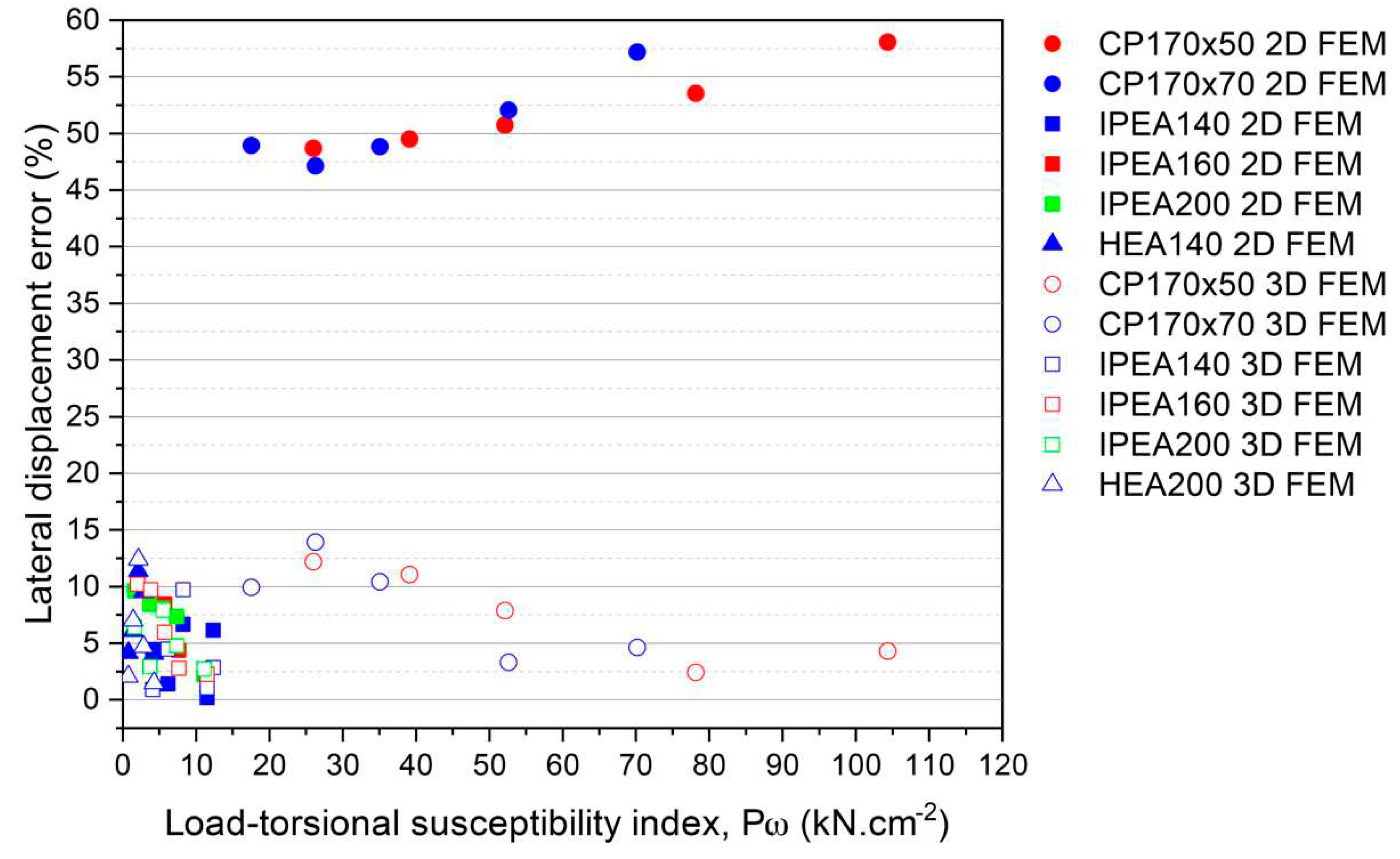
Figure 13 shows the error in the lateral displacement of the column, y-axis, versus the product of the applied lateral load and the torsional susceptibility index in the x-axis.
It can be seen that the IPEA and HEA sections, which have the largest torsional constant of inertia, leading to a load-torsional susceptibility index below 13 kN.cm-2. And the errors of these piles are less than 12%. The CP170 piles, with lower torsional constants of inertia, are more sensitive to the applied load and have a range of values between 17 and 104 kN.cm-2. It should be noted that the trend of both 2D and 3D FEM is linear with error values between 58 and 46%, as well as 14 and 2.5%, respectively.
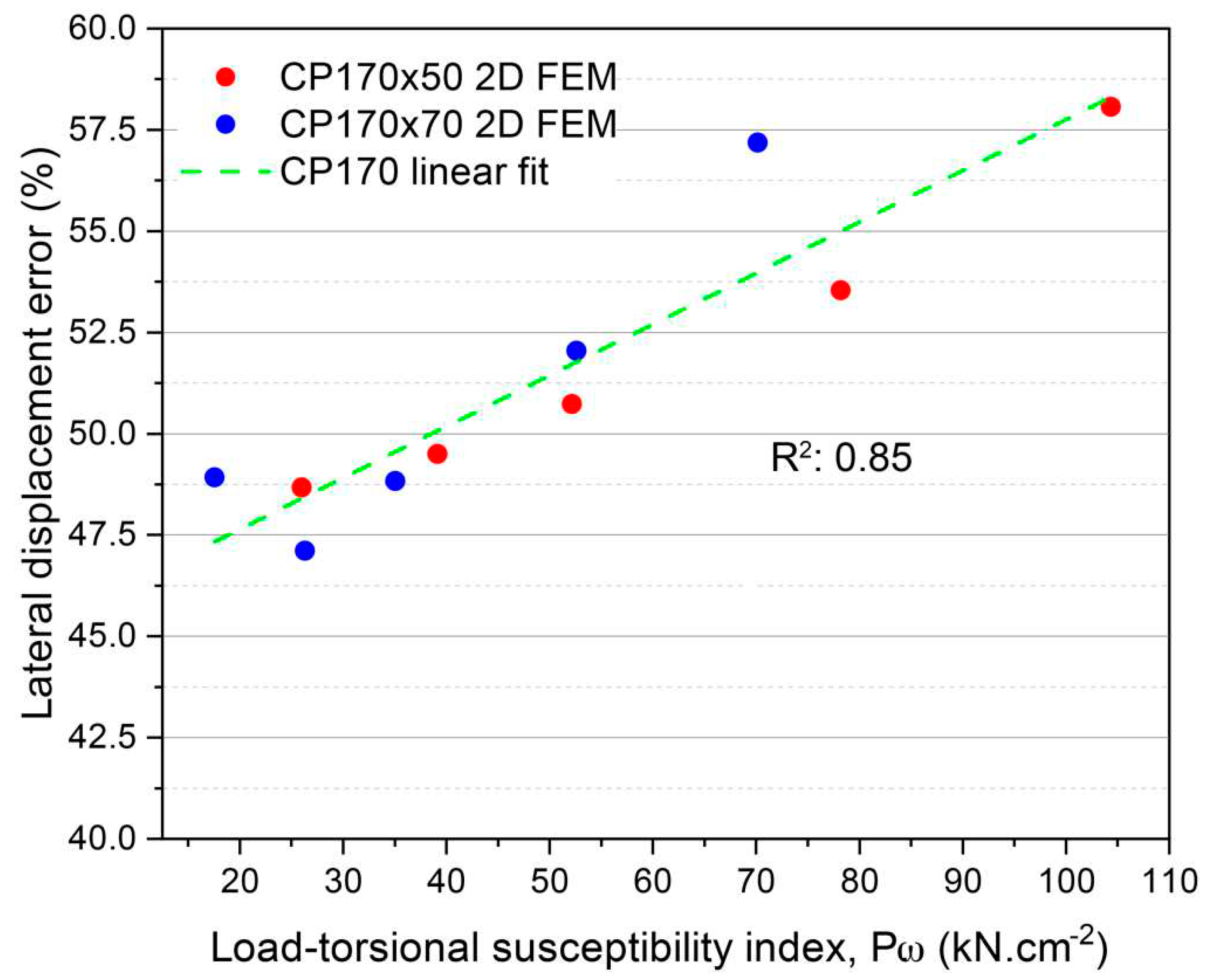
Figure 14 shows the results of lateral displacement error versus load-torsional susceptibility index product for CP170 sections.
As already confirmed by this work, modeling the behavior of a thin-walled cross section subjected to lateral loads considering only the effects of simple bending leads to very significant errors. Figure 14 shows the increasing trend of this error for CP170 cross sections and, therefore, is a useful tool to correct the results obtained by the simple bending theory for CP170 cross sections.

9. Conclussions

This paper has investigated the torsional effect of thin-walled open-ended piles subjected to lateral loads. Three types of cross-sections (IPEA, HEA, and CP) with six different moments of inertia, torsional and warping constant have been analyzed. The following conclusions have been drawn:
  • The traditional analysis considering exclusively simple bending models to predict the thin-walled open-ended steel pile’s behavior under horizontal loading derives in significant displacement inaccuracies, with a maximum of 58% in order to the experimental tests.
  • The fact that the resultant load does not pass through the shear center causes the torsion effect to occur at much lower loads, around 23%.
  • It has been established correlations between the lateral displacement errors taking into account the torsion effects depend on the cross section’s geometry as well as the load application.
  • For thin-walled open-ended piles with low torsional constant and resulting loads acting through the shear center, the maximum lateral displacement errors are less than 15% and follow a horizontal linear trend with decreasing slope as the torsional constant increases.
  • The lateral load behavior of thin-walled open-ended piles is also influenced not only by the torsional constant but also by the horizontal load applied, the height of application and the eccentricity. For this purpose, the torsional susceptibility index ω has been defined.
  • The correlation of lateral displacement errors obtained for any typology of piles is linear. For the most unfavorable case, single symmetrical profiles (CP in this study) the fit with the experimental results is with an R-squared of 0.85. The use of this correlation is proposed to correct the errors made when calculating by traditional methods that consider simple bending exclusively.

Author Contributions

José Antonio Pérez: Conceptualization, Methodology, Formal Analysis, Writing original draft. Antonio Manuel Reyes-Rodríguez: Conceptualization. Estíbaliz Sánchez-González: Conceptualization, Formal Analysis, Writing - Review & Editing, Supervision. José D. Ríos: Conceptualization, Writing - Review & Editing, Supervision.

Funding

This research received no external funding.

Acknowledgments

Authors would like to acknowledge the financial support of the experimental campaign from the Auscultia company.

Conflicts of Interest

“The authors declare no conflict of interest.”

Nomenclature

A Pile cross section
b Width of the pile’s surface in contact with soil
c Width of cross section at top flange
e Eccentricity of the horizontal load respect to the center of gravity of cross section
E0 Elastic modulus of soil
Ep Elastic modulus of steel pile
G Shear modulus of steel pile
Ip Higher moment of inertia of steel pile
It Torsional constant of steel pile
Iw Warping constant of steel pile
Iy Moment of inertia of y-axis
Iz Moment of inertia of z-axis
kh Horizontal modulus of ballast
L Pile length
Lde Length of pile at zero lateral displacement from the ground surface
Le Length of pile embedded in the ground
Lu Height of horizontal load application respect to ground surface
Mt Torsional moment
p Soil reaction
RH Horizontal load at pile head
t Web thickness of cross section
δh Horizontal or lateral displacement of head pile
δs Horizontal or lateral displacement of pile at ground surface
ω Torsional susceptibility index

References

  1. Cao, G.; Wang, X.; He, C. Dynamic analysis of a laterally loaded rectangular pile in multilayered viscoelastic soil. Soil Dyn Earthq Eng 2023, 165. [Google Scholar] [CrossRef]
  2. Abdelaziz, A.Y.; El Naggar, M.H.; Ouda, M. Determination of depth-of-fixity point for laterally loaded vertical offshore piles: A new approach. Ocean Eng 2021, 232. [Google Scholar] [CrossRef]
  3. Kampitsis, A.E.; Giannakos, S.; Gerolymos, N.; Sapountzakis, E.J. Soil-pile interaction considering structural yielding: Numerical modeling and experimental validation. Eng Struct 2015, 99, 319–33. [Google Scholar] [CrossRef]
  4. Hoang, L.T.; Matsumoto, T. Long-term behavior of piled raft foundation models supported by jacked-in piles on saturated clay. Soils Found 2020, 60, 198–217. [Google Scholar] [CrossRef]
  5. Qin, W.; Cai, S.; Dai, G.; Wang, D.; Chang, K. Soil Resistance during Driving of Offshore Large-Diameter Open-Ended Thin-Wall Pipe Piles Driven into Clay by Impact Hammers. Comput Geotech 2023, 153. [Google Scholar] [CrossRef]
  6. He, R.; Zhang, J.; Zheng, J. Vertical dynamic interaction factors for offshore thin-walled pipe piles. Comput Geotech 2022, 145, 104656. [Google Scholar] [CrossRef]
  7. ISO 22477-10; 2016 Geotechnical investigation and testing — Testing of geotechnical structures — Part 10: Testing of piles: rapid load testing n.d.
  8. ASTM D3966-07; Standard Test Methods for Deep Foundations Under Lateral Load 201. 2010.
  9. Basack, S.; Karami, M.; Karakouzian, M. Pile-soil interaction under cyclic lateral load in loose sand: Experimental and numerical evaluations. Soil Dyn Earthq Eng 2022, 162. [Google Scholar] [CrossRef]
  10. Winkler, E. Theory of elasticity and strength. Czechoslov Dominicus 1867, 77–93. [Google Scholar]
  11. Kim, Y.; Jeong, S. Analysis of soil resistance on laterally loaded piles based on 3D soil-pile interaction. Comput Geotech 2011, 38, 248–57. [Google Scholar] [CrossRef]
  12. Bourgeois, E.; Rakotonindriana, M.H.J.; Le Kouby, A.; Mestat, P.; Serratrice, J.F. Three-dimensional numerical modelling of the behaviour of a pile subjected to cyclic lateral loading. Comput Geotech 2010, 37, 999–1007. [Google Scholar] [CrossRef]
  13. American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms, RP2A-WSD. Dallas: API; 2000. n.d.
  14. Ministère de l’Equipement du Logement et des Transports. Fascicule 62, Titre V: Règles techniques de conception et de calcul des fondations des ouvrages de génie civil; 1993 n.d.
  15. Zhang, X.; Liu, C.; Ye, J. Model Test Study of Offshore Wind Turbine Foundation under the Combined Action of Wind Wave and Current. Appl Sci 2022, 12. [Google Scholar] [CrossRef]
  16. Li, C.; Xiao, Y.; Liu, J.; Lin, Q.; Zhang, T.; Liu, J. The Impact of Scour on Laterally Loaded Piles Bored and Socketed in Marine Clay. J Mar Sci Eng 2022, 10. [Google Scholar] [CrossRef]
  17. Rosquoet, F.; Thorel, L.; Garnier, J.; Canepa, Y. Lateral cyclic loading of sand-installed piles. Soils Found 2007, 47, 821–32. [Google Scholar] [CrossRef]
  18. LeBlanc, C.; Houlsby, G.T.; Byrne, B.W. Response of stiff piles in sand to long-term cyclic lateral loading. Geotechnique 2010, 60, 79–90. [Google Scholar] [CrossRef]
  19. Basack, S.; Nimbalkar, S. Numerical Solution of Single Pile Subjected to Torsional Cyclic Load. Int J Geomech 2017, 17, 1–17. [Google Scholar] [CrossRef]
  20. Nimbalkar, S.S.; Punetha, P.; Basack, S.; Mirzababaei, M. Piles subjected to torsional cyclic load: Numerical analysis. Front Built Environ 2019, 5, 1–10. [Google Scholar] [CrossRef]
  21. Georgiadis, K.; Sheil, B. Effect of torsion on the undrained limiting lateral resistance of piles in clay. Geotechnique 2020, 70, 700–10. [Google Scholar] [CrossRef]
  22. Nghiem, H.M.; Chang, N.Y. Efficient solution for a single pile under torsion. Soils Found 2019, 59, 13–26. [Google Scholar] [CrossRef]
  23. Cheng, X.; Ibraim, E.; Liu, H.; Pisanò, F.; Diambra, A. Large diameter laterally loaded piles in sand: Numerical evaluation of soil stress paths and relevance of laboratory soil element testing. Comput Geotech 2023, 154. [Google Scholar] [CrossRef]
  24. Pedone, G.; Kontoe, S.; Zdravković, L.; Jardine, R.J.; Vinck, K.; Liu, T. Numerical modelling of laterally loaded piles driven in low-to-medium density fractured chalk. Comput Geotech 2023, 156, 105252. [Google Scholar] [CrossRef]
  25. Liu, J.; Chen, X.; Liu, X. A test method to study scour effects on the lateral response of rigid piles in sand under real scour conditions. Ocean Eng 2022, 262. [Google Scholar] [CrossRef]
  26. Han, J.; Frost, J.D. Load-deflection response of transversely isotropic piles under lateral loads. Int J Numer Anal Methods Geomech 2000, 24, 509–29. [Google Scholar] [CrossRef]
  27. Li, L.; Sui, G.; Zhou, J.; Oh, E. Parametric Study of Lateral Loaded Blade Pile in Clay. Geosci 2022, 12. [Google Scholar] [CrossRef]
  28. Liyanapathirana, D.S.; Deeks, A.J.; Randolph, M.F. Behaviour of Thin-Walled Open-Ended Piles During Driving. Comput Mech Front New Millenn 2001, 393–398. [Google Scholar] [CrossRef]
  29. Mašín, D.; Tamagnini, C.; Viggiani, G.; Costanzo, D. Directional response of a reconstituted fine-grained soil - Part II : Performance of different constitutive models. Int J Numer Anal Methods Geomech 2006, 30, 1303–36. [Google Scholar] [CrossRef]
  30. Sivaraman, S.; Muthukkumaran, K. Non-linear performance analysis of free headed piles in consolidating soil subjected to lateral loads. Eng Sci Technol an Int J 2021, 24, 449–57. [Google Scholar] [CrossRef]
  31. UNE 36526:2018; Steel products. Hot rolled IPE sections. Dimensions and masses. 2018.
  32. UNE 36524:2018; Steel products. Hot rolled HE sections. Dimensions and masses. 2018.
  33. UNE 10025:2020; Hot rolled products of structural steels - Part 2: Technical delivery conditions for non-alloy structural steels n.d.
  34. Ortiz Berrocal, L. Resistencia de materiales. third edit. 2007.
  35. ISO 14688-1:2017; Geotechnical investigation and testing — Identification and classification of soil — Part 1: Identification and description n.d.
  36. ISO 22476-2:2005; Geotechnical investigation and testing — Field testing — Part 2: Dynamic probing n.d.
  37. Terzaghi, K. Evalution of Conefficients of Subgrade Reaction. Géotechnique 1955, 5, 297–326. [Google Scholar] [CrossRef]
  38. Broms, B.B. Lateral Resistance of Piles in Cohesive Soils. J Soil Mech Found Div 1964, 90, 27–63. [Google Scholar] [CrossRef]
  39. Wang, M.; Wang, M.; Cheng, X.; Lu, Q.; Lu, J. A New p–y Curve for Laterally Loaded Large-Diameter Monopiles in Soft Clays. Sustain 2022, 14. [Google Scholar] [CrossRef]
Preprints 77273 g001
Figure 1. Pile model of a C cross section: (a) lengths and deflection law and (b) detail of Winkler spring model.
Figure 1. Pile model of a C cross section: (a) lengths and deflection law and (b) detail of Winkler spring model.
Preprints 77273 g001
Preprints 77273 g002
Figure 2. Failure modes of a free-head pile: (a) rigid pile and (b) flexible pile.
Figure 2. Failure modes of a free-head pile: (a) rigid pile and (b) flexible pile.
Preprints 77273 g002
Preprints 77273 g003
Figure 3. Driving process for the IPEA-140 pile.
Figure 3. Driving process for the IPEA-140 pile.
Preprints 77273 g003
Preprints 77273 g004
Figure 4. In-field lateral loading test setup.
Figure 4. In-field lateral loading test setup.
Preprints 77273 g004
Preprints 77273 g005
Figure 5. Non-linear ballast modulus semi-empirical estimation for HEA140.
Figure 5. Non-linear ballast modulus semi-empirical estimation for HEA140.
Preprints 77273 g005
Preprints 77273 g006
Figure 6. Lateral deflection, bending moment and shear force of 2D FEM CP170×70.
Figure 6. Lateral deflection, bending moment and shear force of 2D FEM CP170×70.
Preprints 77273 g006
Preprints 77273 g007
Figure 7. Displacement results of the 3D FEM of each pile.
Figure 7. Displacement results of the 3D FEM of each pile.
Preprints 77273 g007
Preprints 77273 g008
Figure 8. In-field and FEM load-deflection curves: (a) CP170×50×20 and (b) CP170×70×20.
Figure 8. In-field and FEM load-deflection curves: (a) CP170×50×20 and (b) CP170×70×20.
Preprints 77273 g008
Preprints 77273 g009
Figure 9. In-field and FEM load-deflection curves: (a) IPEA140, (b) IPEA160, (c) IPEA 200 and (d) HEA140.
Figure 9. In-field and FEM load-deflection curves: (a) IPEA140, (b) IPEA160, (c) IPEA 200 and (d) HEA140.
Preprints 77273 g009
Preprints 77273 g010
Figure 10. Schematic diagram of resultant lateral load applied on “H” and “C” cross sections.
Figure 10. Schematic diagram of resultant lateral load applied on “H” and “C” cross sections.
Preprints 77273 g010
Preprints 77273 g011
Figure 11. Strain after lateral load at head pile of 3D FEM: (a) CP170x50x20 at 6.08 kN and (b) IPEA160 at 7.5 kN.
Figure 11. Strain after lateral load at head pile of 3D FEM: (a) CP170x50x20 at 6.08 kN and (b) IPEA160 at 7.5 kN.
Preprints 77273 g011
Preprints 77273 g012
Figure 12. Plot of lateral displacement error (ε) versus torsional constant for all 2D and 3D FEM.
Figure 12. Plot of lateral displacement error (ε) versus torsional constant for all 2D and 3D FEM.
Preprints 77273 g012
Preprints 77273 g013
Figure 13. Plot of lateral displacement error versus load-torsional susceptibility index for all 2D and 3D FEM.
Figure 13. Plot of lateral displacement error versus load-torsional susceptibility index for all 2D and 3D FEM.
Preprints 77273 g013
Preprints 77273 g014
Figure 14. Plot of lateral displacement error versus load-torsional susceptibility index for single-symmetrical 2D FEM.
Figure 14. Plot of lateral displacement error versus load-torsional susceptibility index for single-symmetrical 2D FEM.
Preprints 77273 g014
Table 1. Designation and structural steel pile properties.
Table 1. Designation and structural steel pile properties.
Pile Cross section
area (cm2)		 Iy (cm4) Iz (cm4) It (cm4) Iw (cm6) e (cm) Lc (cm) ω (cm-2) c/t (-)
CP170x50x20x3 8.40 343.12 26.76 0.27 1769.64 1.96 1.40 10.16 15.67
CP170x70x20x4 12.71 555.58 78.21 0.72 4892.15 2.27 1.50 4.73 16.5
IPEA140 13.39 434.86 36.43 1.36 1980.00 0.50 1.40 0.51 4.93
IPEA160 16.18 689.26 54.43 1.96 3960.00 0.50 1.50 0.38 5.08
IPEA200 23.47 1591.42 117.17 4.11 12990.00 0.50 1.70 0.21 5.11
HEA140 31.42 1033.10 389.33 8.13 15060.00 0.50 0.90 0.06 6.5
Table 2. Average results of N20 DPSH tests in field.
Table 2. Average results of N20 DPSH tests in field.
Geotechnical layer Average N20 DPSH test
GL0 5
GL1 7
GL2 13
GL3 R
Table 3. Load steps and experimental loading test setup.
Table 3. Load steps and experimental loading test setup.
Le (m) Step 1
(kN)		 Step 2
(kN)		 Step 3
(kN)		 Step 4
(kN)		 Step 5
(kN)		 Lu
(m)		 Nº tests
CP170x50x20x3 1.50 2.04 3.07 4.09 6.13 8.18 1.40 24
CP170x70x20x4 1.70 3.04 4.56 6.08 9.12 12.16 1.50 24
IPEA140 1.60 2.00 4.00 6.00 8.00 12.00 1.40 12
IPEA160 1.70 2.65 5.01 7.51 10.02 15.04 1.50 12
IPEA200 2.50 4.00 8.94 13.41 17.88 26.82 1.70 12
HEA140 2.00 6.93 12.81 19.21 25.62 38.43 0.90 12
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated