Prerpints.org logo
Preprint
Review

Alogrithms for the ACD Problem and Cryptanalysis of ACD-based FHE schemes, Revisited

This version is not peer-reviewed.

Submitted:

08 June 2023

Posted:

09 June 2023

Read the latest preprint version here

Abstract
The security of several full homomorphic encryption (FHE) schemes depends on the hardness of the approximate common divisor (ACD) problem. The analysis of attack and defense against the system is one of the frontiers of cryptography research. In this paper, the performance of existing algorithms, including orthogonal lattice, simultaneous diophantine approximation, multivariate polynomial and sample pre-processing are reviewed and analyzed for solving the ACD problem. Orthogonal lattice (OL) algorithms are divided into two categories (OL-$\land$ and OL-$\vee$) for the first time. And an improved algorithm of OL-$\vee$ is presented to solve the GACD problem. This new algorithm works well in polynomial time if the parameter satisfies certain conditions. Compared with Ding and Tao's OL algorithm, the lattice reduction algorithm is used only once, and when the error vector $\mathbf{r}$ is recovered in Ding et al.'s OL algorithm, the possible difference between the restored and the true value of $p$ is given. It is helpful to expand the scope of OL attacks.
Keywords: 
Approximate common divisors
;  
Fully homomorphic encryption
;  
lattice attack
;  
orthogonal lattice
Subject: 
Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

It is well known that the Greatest Common Divisor (GCD) problem has been widely and deeply studied. Euclid algorithm is a classical algorithm for solving the GCD problem, which is called by Knuth [4] as the ancestor of all GCD algorithms. In the last two decades, many improvements to the GCD algorithms have been proposed. And these algorithms have a wide range of applications in computational algebra and cryptography. However, the approximate common divisor (ACD) problem remains a number theory problem. The ACD problem was first studied by Howgrave-Graham [5]. Further interest in this problem was proposed by the homomorphic encryption (FHE) scheme of Van Dijk et al. [16] and its variants [19,24,34]. The security of these cryptosystems depends on the hardness assumption of the ACD problem and its variants.
Fix γ , η , ρ ∈ N * , let p be an η -bit odd integer, define the efficiently sampleable distribution D γ , ρ ( p ) as
D γ , ρ ( p ) = { p q + r | q ←   Z ∩ [ 0 , 2 γ / p ) , r ←   Z ∩ ( − 2 ρ , 2 ρ ) } .
The ACD problem is usually formulated in two ways: general approximate common divisor (GACD) problem and partial approximate common divisor (PACD) problem. Given polynomially many samples x i = p q i + r i from D γ , ρ ( p ) ( r i ≠ 0 for all i), to calculate p, which is the GACD problem. Given polynomially many samples x i = p q i + r i from D γ , ρ ( p ) , as well as a sample x 0 = p q 0 for uniformly chosen q 0 ∈ Z ∩ [ 0 , 2 γ / p ) , to compute p, which is the PACD problem.
By definition, PACD cannot be harder than GACD, and intuitively it seems that it should be easier than GACD. However, Van Dijk et al. ] mentioned that there was no PACD algorithm that did not work for GACD. And the usefulness of PACD was demonstrated by the construction [19], where a much more efficient variant of the scheme [16] was built, whose security relied on PACD rather than GACD. Thus, it is very important to get whether or not PACD is actually easier than GACD. Moreover, ACD problems were divided into computational and decision versions. Coron et al. [32] pointed out that the two versions are equivalent. By definition, PACD cannot be harder than GACD, and intuitively it seems that it should be easier than GACD. However, Van Dijk et al. [16] mentioned that there was no PACD algorithm that did not work for GACD. And the usefulness of PACD was demonstrated by the construction [19], where a much more efficient variant of the scheme [16] was built, whose security relied on PACD rather than GACD. Thus, it is very important to get whether or not PACD is actually easier than GACD. Moreover, ACD problems were divided into computational and decision versions. Coron et al. [32] pointed out that the two versions are equivalent.
The variant problems based on ACD mainly include CRT-ACD and CS-ACD. Cheon et al. [26] and Lepoint [33] call the problem of computing p 1 , ⋯ , p l from the public key the CRT-ACD problem. Cheon and Stehle [34] proposed a FHE scheme whose parameters are set to ( ρ , η , γ ) = ( λ , λ + log λ , Ω ( d 2 λ log λ ) ) , Where d is the depth of the circuit for homomorphism computation. The problem corresponding to this set of parameters is called CS-ACD. Despite the utility of the two variants, the algorithms that secures its security foundation have not been probed well enough.
The original papers [5,16] presented a few possible lattice attacks on this problem, including orthogonal lattices (OL), simultaneous diophantine approximation (SDA) and multivariate polynomial equations (MP). Further cryptanalytic work was done by [23,24,25,30,31,36,37,41,42,43,44]. This paper surveys and compares the known lattice algorithms for the ACD problem.
Our main contribution is to propose an improved algorithm of OL-∨ to reduce both space and time costs for solving the GACD problem. Another contribution is to give the possible difference between the restored and the true value of p when r is recovered, which is helpful to expand the scope of OL attacks. Our third contribution is to analyze the application range and performance of SDA, OL, MP algorithms and pre-processing. These work is very helpful for cryptographic algorithm attacks to achieve better results.

2. Preliminaries

Throughout this paper, capital boldface letters denote matrices, e.g. A , lowercase bold letters denote vectors e.g. a . Let ( · , · ) , ∥ · ∥ be the inner product and the l 2 Euclidean length respectively. A T denote the transpose of matrix A . The notation log refers to the base-2 logarithm. And ⌊ r ⌋ denotes the largest integer not more than real number r.

2.1. Lattice

Definition 1 
(Lattice). A rank-t lattice L in the R n is spanned by t linearly independent vectors
L = { ∑ i = 1 t u i b i | u i ∈ Z } ,
where { b 1 , ⋯ , b t } is a basis for L and
B = ( b 1 , ⋯ , b t )
is the corresponding basis matrix. The rank or dimension and determinant of L are respectively denoted as dim ( L ) = n and
det ( L ) = | det ( B B T ) | .
If B is a square matrix, then
det ( L ) = | det ( B ) | .
In addition, when a set of column vectors u ⊂ Z n is given, the orthogonal lattice is defined as L ⊥ ( u ) = { v ∈ Z n | ( v , u ) = 0 }.
When t = n , the lattice L is called a full rank lattice. In fact, it is only necessary to consider the full rank lattice in Euclidean space. Therefore, the lattices mentioned below are full rank lattice.
The length of the shortest non-zero vector, denoted by λ 1 , is a very important parameter of a lattice. It is expressed as the radius of the smallest zero-centered ball containing a non-zero linearly independent lattice vector. Generally, successive minima was defined as follows:
Definition 2 
(Successive minima). Let L be a lattice of rank t. For 1 ≤ i ≤ t , the i-th successive minima is defined as
λ i ( L ) = i n f { r | dim ( s p a n ( L ∩ B n ( 0 , r ) ) ) ≥ i } ,
where B n ( 0 , r ) = { x ∈ R n | ∥ x ∥ ≤ r } is a ball centered at the origin.
For the shortest vector of a random lattice, the Gaussian hypothesis is expressed as follows:
Gaussian Heuristic (First Minima). Let L be a full rank lattice in R t , then the length of the shortest non-zero vector λ 1 in L is estimated by
λ 1 = t 2 π e ( det L ) 1 / t .

2.2. Lattice basis reduction

Lattice reduction algorithm is employed to transform a lattice basis to another basis, and the latter one is nearly orthongral with each other and relatively shorter. As far, the LLL algorithm [1] and the BKZ algorithm [17] are well-known lattice reduction algorithms.
Definition 3 
(Gram Schmidt Orthogonalization). Given a sequence of t linearly independent vectors b 1 , b 2 , ⋯ , b t , the Gram Schmidt orthogonalization is the sequence of vectors b 1 * , b 2 * , ⋯ , b t * defined by
b i * = b i − ∑ j = 1 i − 1 μ i , j b j * ,
where
μ i , j = ( b i , b j * ) ( b j * , b j * ) , 1 ≤ j < i ≤ t .
Definition 4 
( δ − LLL reduction basis). Given a lattice basis B = ( b 1 , ⋯ , b t ) , the corresponding Gram-Schmidt basis B * = ( b 1 * , ⋯ , b t * ) , B is a reduced basis if and only if the following two conditions are satisfied:
①
(Size condition) μ i , j = ( b i , b j * ) ∥ b j * ∥ 2 ≤ 1 / 2 , for all 1 ≤ j < i ≤ t ;
②
(Lovász condition) ∥ b i * ∥ 2 ≥ ( δ − μ i , i − 1 2 ) ∥ b i − 1 * ∥ 2 , for all 1 < i ≤ t , where 1 / 4 < δ < 1 .
Definition 5 
(Geometric Series Assumption[8],GSA). Given Gram-Schmidt basis ( b 1 * , ⋯ , b t * ) ,
∥ b i * ∥ ∥ b 1 ∥ = θ i − 1 ,
for i = 1 , 2 , ⋯ , t , where 0 < θ < 1 is called GSA constant.
The Geometric Series Assumption (GSA) means the length of Gram-Schmidt basis ∥ b i * ∥ with LLL reduction decays geometrically with quotient θ and indicates ∥ b i * ∥ ≤ ∥ b 1 ∥ for i = 1 , 2 , ⋯ , t .
In the subsections 3.1 and 3.2, the analysis based on the following assumptions:
Assumption 1 ([37]). Let L be a “random” lattice of rank t and b 1 , ⋯ , b t be an LLL-reduced basis for L , then
∥ b 1 ∥ ≤ ( 1.02 ) t det ( L ) 1 / t
and
∥ b 1 ∥ ≤ ( 1.04 ) t λ 1 ( L ) .
Nguyen and Stehlé [9] have studied the performance of LLL on “random” lattices and have hypothesised that an LLL-reduced basis satisfies the improved bound (2). By analogy with the relationship between the worst-case bounds ∥ b 1 ∥ < 2 t / 4 det ( L ) / 1 / t and ∥ b 1 ∥ < 2 t / 2 λ 1 ( L ) , it is natural to suppose that (3) is hold.
Assumption 2([37]). Let L be a “random” lattice of rank t and let b 1 , ⋯ , b t be an LLL-reduced basis for L , then
∥ b i ∥ < i ( 1.02 ) i det ( L ) 1 / t .
Nguyen and Stehlé [9] show that ∥ b i + 1 * ∥ ≤ ∥ b i * ∥ almost always in Figure 4, and certainly ∥ b i + 1 * ∥ ≤ 1.2 ∥ b i * ∥ with overwhelming probability. Galbraith et al. make the heuristic assumption that ∥ b i * ∥ ≤ ∥ b 1 * ∥ for all 2 ≤ i ≤ n , so it is easy to show that, for all 2 ≤ i ≤ n , ∥ b i ∥ ≤ 1 + ( i − 1 ) / 4 ∥ b 1 ∥ . So it leads to Assumption 2 for “random” lattices.
In the subsection 3.2.2, the conclusion of the following theorem will be used.
Theorem 1. 
[29] Given a LLL reduction lattice basis B = ( b 1 , ⋯ , b t ) , ( b 1 * , ⋯ , b t * ) is the corresponding Gram-schmidt basis. The following results were hold:
(1) 
∥ b 1 ∥ ≤ α t − 1 4 | det ( B ) 1 t | ;
(2) 
∥ b j * ∥ ≤ α ( i − j ) 2 ∥ b i * ∥ , for 1 ≤ j < i ≤ n ;
(3) 
∥ b j ∥ ≤ α ( i − 1 ) 2 ∥ b i * ∥ , for 1 ≤ j < i ≤ n ;
where α = 1 δ − 1 4 , δ is the parameter in the Definition 4.
After the LLL algorithm, a number of lattice reduction algorithms emerged. In practice, the Block-Korkine-Zolotarev (BKZ) algorithm proposed by Schnorr and Euchner [3] has a good performance. For the BKZ algorithm, according to [17], the block size β determines how short the output vector is. With the increase of β , the output basis becomes much reduced but the cost significantly increases. Gama and Nguyen [12] identified the Hermite factor of the reduced basis as the dominant parameter in the runtime of the lattice reduction and the quality of the reduced basis. For an t-dimensional lattice L , the Hermite factor
δ 0 t = ∥ b 1 ∥ ( det ( L ) 1 t ,
where b 1 is the first reduced basis vector of L and δ 0 is called as the root-Hermite factor. Chen [27] gave an expression between the root-Hermite factor δ 0 and the block size β :
δ 0 = β 2 π e ( π e ) 1 β 1 2 ( β − 1 ) .
Under the GSA and based on the Hermit factor (5), Xu et al. [42] gave an upper bound on the i-th reduced basis vector
∥ b i ∥ ≤ i + 3 2 · δ 0 t · ( det L ) 1 t .

3. Algorithms to solve ACD problem

In this section, the first three subsections describe and analysis the lattice-based algorithms (SDA, OL, MP) to solve the ACD problem, and the last subsection analyzes the prospects of the pre-processing technology for ACD samples, when sufficiently many samples are available.

3.1. Simultaneous Diophantine approximation (SDA)

Van Dijk et al. [16] showed that the ACD problem can be solved using the SDA method. The basic idea of this attack is to note that if x i = p q i + r i for 1 ≤ i ≤ t , where r i is small, then
x i x 0 ≈ q i q 0
for 1 ≤ i ≤ t , where x 0 = p q 0 + r 0 . That’s what it means the fractions q i / q 0 are an instance of simultaneous diophantine approximation to x i / x 0 . Once q 0 is determined, r 0 can be computed from
r 0 ≡ x 0 ( mod q 0 ) .
Hence,
p = x 0 − r 0 q 0 .
In fact, this attack does not benefit significantly from having an exact sample x 0 = p q 0 , r 0 = 0 , so such a sample can be unknown. As in [16], construct the lattice L of rank t + 1 , which is generated by the basis matrix B , where
B = 2 ρ + 1 x 1 ⋯ x t − x 0 ⋱ − x 0 .
Let v ∈ L , then
v = ( q 0 , q 1 , ⋯ , q t ) B = ( 2 ρ + 1 q 0 , q 0 x 1 − q 1 x 0 , ⋯ , q 0 x t − q t x 0 ) = ( 2 ρ + 1 q 0 , q 0 r 1 − q 1 r 0 , ⋯ , q 0 r t − q t r 0 ) .
Since q i ≈ 2 γ − η , the length of the first entry of v is approximately 2 γ − η + ρ + 1 . The length of the rest of entries of v , which are of the form q 0 r i − q i r 0 for 1 ≤ i ≤ t , is estimated to be | q 0 r i − q i r 0 | ≤ 2 | q 0 r i | ≈ 2 γ − η + ρ + 1 . Therefore, ∥ v ∥ is approximately
2 γ − η + ρ + 1 t + 1 .
The vector ∥ v ∥ satisfying the above conditions is called the target vector.
Hence, if
2 γ − η + ρ t + 1 < ( t + 1 ) / 2 π e det ( L ) 1 / ( t + 1 ) ,
then the target vector v is expected to be the shortest non-zero vector in the lattice. The attack is to run a lattice basis reduction algorithm to get a candidate w for the shortest non-zero vector. The first entry of w divided by 2 ρ + 1 will give a candidate for q 0 , then computes r 0 ≡ x 0 ( mod q 0 ) and p = ( x 0 − r 0 ) / q 0 . Finally test this value for p by checking if x i mod p are small for all 1 ≤ i ≤ t . This is the SDA algorithm.
A better approximation 2 γ − η + ρ t + 1 of tager vector ∥ v ∥ is given by Van Dijk et al. [16], and an exact approximation
0.47 ( t + 1 ) p · 2 ρ + γ
is given by Galbraith et al. [37]. That is to say about twice the above approximation (taking p ≈ 2 η ).
Galbraith et al. [37] applies the Gaussian heuristic and λ 2 ( L ) > 2 t / 2 λ 1 ( L ) to estimate
λ 2 ( L ) ≈ ( t + 1 ) / ( 2 π e ) ( det L ) 1 / ( t + 1 ) ≈ ( t + 1 ) / ( 2 π e ) 2 ( ρ + 1 + γ t ) / ( t + 1 ) .
Hence, the target vector v is the shortest vector in the lattice and is found by LLL if the expression (1) of Gaussian Heuristic is less than ( t + 1 ) / 2 π e det ( L ) t + 1 when multiplied by the factor 1 . 04 t + 1 according to Equation (3). Namely,
0.47 ( t + 1 ) ( 1.04 ) t + 1 2 γ + ρ − η < ( t + 1 ) / ( 2 π e ) 2 ( ρ + 1 + γ t ) / ( t + 1 ) .
Ignoring constants and the ( 1.04 ) t + 1 term (the term ( 1.04 ) t + 1 does not have any significant effect on the performance of the algorithm[37]) in the above equation (8), a necessary (not sufficient) condition for the algorithm to succeed is
t + 1 > γ − ρ η − ρ ≈ γ η .
So t should be greater than γ η to ensure that the target vector v will likely be the shorest vector in the lattice L . This lower bound on t is more advantageous for the analysis of CS-ACD [34]. For CS-ACD, if ρ is close to η , which means that for smaller γ , the dimension of the Lattice L grows rapidly. Concretely speaking, the parameters in CS-ACD are set to
( ρ , η , γ ) = ( λ , λ + d log λ , Ω ( d 2 λ log λ ) ) ,
where d is the circuit depth and λ is the security paremeter. Let’s say λ = 200 , d = 20 , set Ω ( x ) = x , and then ( ρ , η , γ ) = ( 200 , 353 , 611508 ) . For these values, t ≥ 3995 . Therefore, in order to prevent lattice attacks, this ratio ( γ − ρ ) / ( η − ρ ) needs to be large enough. These arguments reconfirm that the method in [34] can provide more efficient parameters for homomorphic encryption.

3.2. Orthogonal Lattice (OL) based approach

Nguyen and Stern ([6]) have demonstrated the usefulness of the orthogonal lattice in cryptanalysis, and this has been used in several ways to attack the ACD problem. The idea is to find u = ( u 1 , u 2 , ⋯ , u t ) ∈ L ⊥ ( q , r ) that is orthogonal to both q = ( q 1 , q 2 , ⋯ , q t ) and r = ( r 1 , r 2 , ⋯ , r t ) . Since x i = p q i + r i , x = ( x 1 , x 2 , ⋯ , x t ) is orthogonal to u . The task is to find t − 1 linearly independent vectors u shorter than any vector in L ⊥ ( x ) to recover q , r and therefore p.
Based on the idea of Nguyen and Stern, the current idea is to find t − 1 linearly independent vectors u only orthogonal to q . The core steps of the current OL algorithm include the following two steps:
First, find t − 1 linearly independent vectors u orthogonal to q , that is,
∑ i = 1 t u i · q i = 0
then establish and solve indefinite equations
∑ j = 1 t u i j · x j = ∑ i = 1 t u i j · r j ,
where u i = ( u i 1 , u i 1 , ⋯ , u i t ) , ( i = 1 , 2 , ⋯ , t − 1 ) .
Let the general solution of (11) be
d = d 0 + t 1 d 1
Where d 0 is a particular solution of (11), d 1 is the basis vector of the solution space of the corresponding homogeneous system of linear equations, and t 1 is the integer parameter.
Second, find small positive integer solutions to (11). At present, the common way to find the small solutions is to construct the lattice L with basis matrix
B = d 0 d 1 .
Next, LLL algorithm is employed to reduce the basis matrix B , and the first output is expected to be the vector r . However, at present, what can meet this expectation are experimental conditions, and there is still a lack of theory. Now, the existing OL methods orthogonal to q are classified. According to the constructed lattice, they are divided into two categories. The first OL algorithm constructs lattice L 1 ( α ) with basis matrix B 1 :
B 1 = x 1 α x 2 α ⋮ ⋱ x t α
and its shape likes ∧, so it is called OL-∧ algorithm. This kind of algorithm can be referred to [GGM16,XSH18].
The second OL algorithm constructs lattice L 2 ( α ) with basis matrix B 2 :
B 2 = α x 1 α x 2 ⋱ ⋮ α x t − 1 N ,
where N is a big integer with γ + η bits . Or construct a lattice L 2 ′ ( α ) with basis matrix is B 2 ′ :
B 2 ′ = α x 1 α x 2   ¨ ⋮ α x t − 1 x t .
Both (15) and (16) are all shaped ∨, so they are called OL-∨ algorithm. This kind of algorithm can be referred to [30,31,41,42].

3.2.1. OL-∧ algorithm

This algorithm uses the lattice L 1 ( α ) mentioned above, and the basis matrix is B 1 , then
B 1 B 1 T = A + x T x , A = α 2 I t , x = ( x 1 , x 2 , ⋯ , x t ) ,
where I t is the identity matrix of order t, and
det ( B 1 B 1 T ) = det ( 1 + x A − 1 x ) = α 2 t − 2 ( α 2 + x 1 2 + x 2 2 + ⋯ + x t 2 ) .
Therefore,
det ( L 1 ( α ) ) = α t − 1 ( α 2 + x 1 2 + x 2 2 + ⋯ + x t 2 ) < t + 1 · α t − 1 · 2 γ .
(I) When =2
Let v = ( ∑ i = 1 t u i x i , u 1 2 ρ , ⋯ , u t 2 ρ ) ∈ L 1 ( α ) , in order to find the condition that u is orthogonal to q (t dimension), it needs to be satisfied
∑ i = 1 t u i x i − ∑ i = 1 t u i r i ≤ p / 2 ,
so it forces the equation
∑ i = 1 t u i x i = ∑ i = 1 t u i r i
to be true. In order to make the equation (18) be established, Galbraith et al. ([37]) gives the bounds of the short vectors in the lattice L 1 :
∥ v ∥ ≤ 2 η − 2 − log ( t + 1 ) .
Next, to show that under condition (19), formulas (17) and (10) hold, the following proof is given. Let ∥ v ∥ = N , then ∑ i = 1 t u i x i ≤ N and u i r i | ≤ | u i 2 ρ ≤ N for 1 ≤ i ≤ n . Thus
∑ i = 1 t u i x i − ∑ i = 1 t u i r i ≤ ∑ i = 1 t u i x i + ∑ i = 1 t u i r i ≤ ( t + 1 ) N .
Because (19) is true and p > 2 η − 1 , ( t + 1 ) N < 2 η − 2 < p / 2 . Hence
∑ i = 1 t u i x i − ∑ i = 1 t u i r i < p / 2 .
To prove that (10) holds, suppose ∑ i = 1 t u i q i ≠ 0 , so
2 η − 1 < p ∑ i = 1 t u i q i = ∑ i = 1 t u i ( x i − r i ) ≤ ∑ i = 1 t u i x i + ∑ i = 1 t u i r i ≤ ( t + 1 ) N < 2 η − 2 ,
this is a contradiction.
To analyse the method, Galbraith et al. [37] use Assumption 2. This shows that LLL algorithm can be used to find t − 1 linearly independent vectors as long as
t ( 1.02 ) t det ( L 1 ( α ) ) 1 / t ≤ 2 η − 2 − log ( t + 1 ) ,
and as well
det ( L 1 ( α ) ) = α t − 1 ( α 2 + x 1 2 + x 2 2 + ⋯ + x t 2 ) ≈ 2 ρ ( t − 1 ) + γ .
Hence, the condition for success is
4 t ( t + 1 ) ( 1.02 ) t 2 ρ + ( γ − ρ ) / t ≤ 2 η .
Ignoring constants and the exponential approximation factor ( 1.02 ) t from the lattice reduction algorithm, Galbraith et al. [37] gives a lower bound on sample t:
t ≥ γ − ρ η − ρ .
Find t − 1 vectors u that satisfies the bound of the short vector by LLL algorithm, then the system of equations can be set up to solve, and then find r .
(II)  α  in the general case
Using the bound of (6), the condition that u is orthogonal to q is constructed. Specific measures are as follows([42]):
①
Let v = ( ∑ i = 1 t u i x i , α u 1 , ⋯ , α u t ) ∈ L 1 ( α ) , then
| ∑ i = 1 t u i q i | ≤ α + t · 2 ρ α · ∥ v ∥ 2 η − 1 ;
②
Using BKZ- β alogrithm, reduce the lattice matrix B 1 . Let v i = ( ∑ j = 1 t u i j x j , α u i 1 , ⋯ , α u i t ) be the i-th reduce basis of L 1 ( α ) , Then
∥ v i ∥ ≤ i + 3 2 · δ 0 t · det ( L 1 ) 1 t   ≤ i + 3 2 · δ 0 t · ( t + 1 · α t − 1 · 2 γ ) 1 / t   ≤ i + 3 2 · ( t + 1 ) 1 2 t · δ 0 t · 2 γ t · α t − 1 t .
Thus
| ∑ j = 1 t u i j q j | < i + 3 · ( t + 1 ) 1 2 t · δ 0 t · 2 γ t − η · α + t · 2 ρ α 1 t .
Let
f ( α ) = α + t · 2 ρ α 1 t ,
then minimize f ( α ) . Xu et al. [42] offer the following conclusion: When
α 0 = t t − 1 · 2 ρ ,
min α > 0 f ( α ) = f ( α 0 ) = t ( t t − 1 ) t − 1 t · 2 t − 1 t · ρ .
Using the minimum of f ( α ) , the tighter bound of | ∑ j = 1 t u i j q j | was found:
| ∑ j = 1 t u i j q j | < i + 3 · g ( t ) · δ 0 t · 2 γ − ρ t − η + ρ ,
where
g ( t ) = t ( t t − 1 ) t − 1 t · ( t + 1 ) 1 2 t ,
As analyzed by Xu et al. [42],
lim t → ∞ g ( t ) t = 1 .
therefore
| ∑ j = 1 t u i j q j | < ( i + 3 ) t · δ 0 t · 2 γ − ρ t − η + ρ .
In order to make ∑ j = 1 t u i j q j = 0 , the right side of the upper bound has to be less than 1:
( i + 3 ) t · δ 0 t · 2 γ − ρ t − η + ρ < 1 ,
thus the condition
γ − ρ t − ( η − ρ ) + t log δ 0 + log t ( i + 3 ) < 0
holds. The dominant calculation of OL attacks is the lattice reduction for finding t − 1 linearly independent homogeneous equations on r 1 , ⋯ , r t or q 1 , ⋯ , q t . Based on the condition (21), it is expected that
γ − ρ t − ( η − ρ ) + t log δ 0 + log t 2 + 2 t < 0 .
Since δ 0 > 1 , the attack can work when
t ≥ γ − ρ η − ρ .
According to (22), it is obtained that
log δ 0 < η − ρ t − γ − ρ t 2 − log t 2 + 2 t t ,
which is equivalent
log δ 0 < − ( γ − ρ ) 1 t − η − ρ 2 ( γ − ρ ) 2 + ( η − ρ ) 2 4 ( γ − ρ ) − log t 2 + 2 t t .
When t = 2 ( γ − ρ ) η − ρ , the above expression is optimized as
log δ 0 < ( η − ρ ) 2 4 ( γ − ρ ) − η − ρ 2 ( γ − ρ ) − η − ρ 4 ( γ − ρ ) log γ − ρ η − ρ 2 + γ − ρ η − ρ .
Also notice that when t ≥ 2 , log t 2 + 2 t ≥ log 4 t , then the logarithm term on t of condition (22) can reduce to get the following condition:
γ − ρ t − ( η − ρ ) + t log δ 0 + log 4 t < 0 .
Similarly, taking t = 2 ( γ − ρ ) η − ρ , the above condition is optimimized as
log δ 0 < ( η − ρ ) 2 4 ( γ − ρ ) − 3 ( η − ρ ) 4 ( γ − ρ ) − η − ρ 4 ( γ − ρ ) log γ − ρ η − ρ .
(III) Using the rounding technique, construct a deformed lattice
Construct a lattice L 1 ( α ) ^ whose lattice basis matrix is B 1 ^ [42]:
B 1 ^ = ⌊ x 1 α ⌋ 1     ⌊ x 2 α ⌋ 1 ⋮ ⋱ ⌊ x t α ⌋ 1
where α > 0 . Similar to the idea of the case (II), the condition for ∑ j = 1 t u i j q j = 0 was found by Xu et al. [XSH18-3.3]. The optimal value of α is:
α 0 = t ( t − 1 ) ( t + 1 ) · 2 ρ ,
and the condition (21) holds as well. As discussed at the end of case (II), this attack can also be performed at
t ≥ γ − ρ η − ρ .

3.2.2. OL-∨ algorithm

This algorithm uses the lattice L 2 ( α ) mentioned above with basis matrix B 2 or the lattice L 2 ′ ( α ) with basis matrix B 2 ′ .
(I) When  α = 1 , B 2 ( t , t ) = N
Let
v = ( u 1 , ⋯ , u t − 1 , ∑ i = 1 t − 1 u i x i + u t N ) ∈ L 2 ,
to find the condition that u is orthogonal to q ( t − 1 dimension), it needs to be satisfied:
∑ i = 1 t − 1 u i x i ≤ N / 2 ,
then it is to force the equation
u t = 0 .
To make the equation u t = 0 true, Ding et al. [30] and Yang et al. [41] gave the bounds of the short vectors of the lattice L 2 ( α ) , they are shown in (28) and (29) respectively,
∥ v ∥ ≤ 2 η − ρ − 1 − log t − 1
∥ v ∥ ≤ 2 η − ρ − 2 − log t − 1
In order to show that under the condition (28) or (29), formulas (26) and (27) hold, the following proof is given. Here, only condition (29) is used to prove.
Let M = 2 η − ρ − 2 − log t − 1 , and ∥ v ∥ = ∑ i = 1 t − 1 u i 2 + ( ∑ i = 1 t − 1 u i x i + u t N ) 2 < M .
Thus
| u i | < M , ∑ i = 1 t − 1 u i x i + u t N < M ( 1 ≤ i ≤ t − 1 ) .
Since 2 γ + η − 1 ≤ N ≤ 2 γ + η ,
∑ i = 1 t − 1 u i x i ≤ 2 γ t − 1 · ∥ u ∥ ≤ 2 γ t − 1 · ∥ v ∥ ≤ 2 γ t − 1 · 2 η − ρ − 2 − log t − 1 = 2 γ + η − ρ − 2 < N / 2 .
Therefore, there is no modular N operation and u t = 0 .
Next, it is easy to obtain that ∑ i = 1 t − 1 u i q i = 0 and ∑ i = 1 t − 1 u i x i = ∑ i = 1 t − 1 u i r i hold.
(II) When  α = 1 , B 2 ′ ( t , t ) = x t
Let
v = ( u 1 , ⋯ , u t − 1 , ∑ i = 1 t u i x i ) ∈ L 2 ’ ,
in order to find the condition that u is orthogonal to q (t dimension), it needs to be satisfied:
∑ i = 1 t u i x i ≤ p / 2 .
In order to make (30) true, Yu et al. [41] and Gebregiyorgis et al. [36] gave the bounds of the short vectors in the lattice L 2 ′ and they were given by the following formulas respectively,
∥ v ∥ ≤ 2 η − ρ − 2 − log t ,
∥ v ∥ ≤ 2 η − ρ − 3 − log t .
After analysis, (32) is tighter than (31). Similarly, it can be proved that (30) holds under the condition (31) or(32). So the equations ∑ i = 1 t − 1 u i q i = 0 and ∑ i = 1 t u i x i = ∑ i = 1 t u i r i can also be obtained.
(III)  α = 1 , lower bound estimating for the number of samples t
Under the GSA, Yu et al. use LLL algorithm to get the upper bound of ( t − 1 ) -th short vector v t − 1 , by Theorem 1:
∥ v t − 1 ∥ 2 ≤ α ( t − 2 ) 2 ∥ v t − 1 * ∥ 2 = 4 3 ( t − 2 ) 2 ∥ v t − 1 * ∥ 2 , ( α = 4 3 ) ≤ 4 3 ( t − 2 ) 2 ∥ v 1 * ∥ 2 ≤ 4 3 ( t − 2 ) 2 4 3 ( t − 1 ) 4 · det ( L 2 ′ ) = 4 3 ( 3 t − 5 ) 4 · 2 γ t .
Due to
4 3 ( 3 t − 5 ) 4 · 2 γ t ≤ 2 η − ρ − 2 − log t ,
the bound of t in [30] is optimized, and the optimization result is given as follows [41]:
t ≥ 5 3 ( η − ρ − ( η − ρ ) 2 − 1.2 γ ) .
Yu et al. also indicates the hypothesis in [36]
λ t − 1 ( L ) = det ( L ) 1 / t t / 2 π e ,
is too strong and unreasonable, and t > γ / ( η − ρ ) is too small, it should be increased by 10 or 20.
For OL algorithm in [31], where − N or N works equally, the idea of this algorithm can be classified as OL-∨, and it is equivalent to the case
α = 1 , B 2 ( t , t ) = N ,
just N is the same as length as x x i , so the algorithm is a little bit more conservative.
In [31], the lattices L 3 and L 3 ′ were defined, their basis matrices were B 3 and B 3 ′ :
B 3 = 1 x 1 1 x 2 ⋱ 1 x t − N ,
B 3 ′ = 1 r 1 1 r 2 ⋱ 1 r t .
Let v ∈ L 3 ∩ L 3 ′ , then
∑ i = 1 t u i · x i − u t + 1 N = ∑ i = 1 t u i · r i .
For the sake of ∑ i = 1 t u i · q i = 0 , it is to force the equation u t + 1 = 0 is true. Find a vector v = ( u 1 , u 2 , ⋯ , u t , ∑ i = 1 t u i · x i ) ∈ L 3 , such that the corresponding vector u = ( u 1 , u 2 , ⋯ , u t ) is orthogonal to q . The experiment in [31] gives the following conditions that LLL algorithm can generate t − z ( z = 1 , 2 ) vectors u (theoretically not proved):
  • condition 1:  N is a large random integer with γ bits;
  • condition 2:  z ≤ 2 ;
  • condition 3:  ρ < η / 2 ;
  • condition 4:  t ≥ ( 4 γ ) 1 / 3 ;
  • condition 5:  ∥ v ∥ ≤ 2 γ / ( t + 1 ) .
Under the above conditions, the equation ∑ i = 1 t u i x i = ∑ i = 1 t u i r i is true. So r can be solved and p is recovered.
(IV)  α in general
Similar to the idea of OL-∧ when α is in general, the condition for ∑ j = 1 t u i j q j = 0 is found by [XSH18-3.2]. The conclusions are as follows: the optimal value of α is
α 0 = t 2 + t t − 1 · 2 ρ ,
and the condition
γ − ρ t − ( η − ρ ) + t log δ 0 + log ( t i + 3 ) < 0 .
holds. The specific steps are below ([42]):
①
Let v = ( α u 1 , ⋯ , α u t − 1 , ∑ i = 1 t u i x i , ) ∈ L 2 ( α ) , Then
| ∑ i = 1 t u i q i | ≤ α + t 2 + t · 2 ρ α · ∥ v ∥ 2 η − 1 ;
②
Using BKZ- β alogrithm, reduce the basic matrix B 2 . Let v i = ( α u i 1 , ⋯ , α u i , t − 1 , ∑ j = 1 t u i j x j ) be the i-th reduce basis of L 2 ( α ) , Then
∥ v i ∥ ≤ i + 3 2 · δ 0 t · det ( L 2 ) 1 t ≤ i + 3 2 · δ 0 t · ( α t − 1 N ) 1 / t ≤ i + 3 2 · δ 0 t · 2 γ t · α 1 − 1 t .
Thus
| ∑ j = 1 t u i j q j | ≤ i + 3 · α + 2 ρ t 2 + t α 1 t · δ 0 t · 2 γ t − η .
A little bit of clarification here. When α = 1 , then the formula
| ∑ j = 1 t u i j q j | ≤ i + 3 · ( 1 + 2 ρ t 2 + t ) · δ 0 t · 2 γ t − η
is true. In order to make ∑ j = 1 t u i j q j = 0 , the formula
i + 3 · ( 1 + 2 ρ t 2 + t ) · δ 0 t · 2 γ t − η < 1
holds, then
γ t − ( η − ρ ) + t log δ 0 + log ( i + 3 ) ( t 2 + t ) < 0 .
For finding t − 1 linearly independent vectors orthogonal to ( q 1 , ⋯ , q t ) , the following condition
γ n − ( η − ρ ) + n log δ 0 + log ( ( t 3 + 3 t 2 + 2 t ) < 0
is established. Next, let
f ( α ) = α + 2 ρ t 2 + t α 1 t ,
then minimize f ( α ) . When
α 0 = t 2 + t t − 1 · 2 ρ ,
min α > 0 f ( α ) = f ( α 0 ) = t t 2 + t t − 1 t − 1 t · 2 t − 1 t · ρ .
Using the minimum of f ( α ) , the tighter bound of | ∑ j = 1 t u i j q j | was found:
| ∑ j = 1 t u i j q j | < i + 3 · g ( t ) · δ 0 t · 2 γ − ρ t − η + ρ ,
where
g ( t ) = t t 2 + t t − 1 t − 1 t .
As analyzed by Xu et al. [42],
lim t → ∞ g ( t ) t = 1 ,
therefore
| ∑ j = 1 t u i j q j | < ( i + 3 ) · t · δ 0 t · 2 γ − ρ t − η + ρ .
In order to make ∑ j = 1 t u i j q j = 0 , the right side of the upper bound has to be less than 1:
( i + 3 ) · t · δ 0 t · 2 γ − ρ t − η + ρ < 1 ,
thus the condition
γ − ρ t − ( η − ρ ) + t log δ 0 + log ( t i + 3 ) < 0
holds. The dominant calculation of OL attacks is the lattice reduction for finding t − 1 linearly independent homogeneous equations on r 1 , ⋯ , r t or q 1 , ⋯ , q t . Based on the condition (34), it is expected that
γ − ρ t − ( η − ρ ) + t log δ 0 + log t 3 + 2 t 2 < 0
Since δ 0 > 1 , the attack can work when
t ≥ γ − ρ η − ρ .
According to (35), It is obtained that
log δ 0 < η − ρ t − γ − ρ t 2 − log t 3 + 2 t 2 t ,
which is equivalent
log δ 0 < − ( γ − ρ ) 1 t − η − ρ 2 ( γ − ρ ) 2 + ( η − ρ ) 2 4 ( γ − ρ ) − log t 3 + 2 t 2 t .
When t = 2 ( γ − ρ ) η − ρ , the above expression is optimized as
log δ 0 < ( η − ρ ) 2 4 ( γ − ρ ) − η − ρ 2 ( γ − ρ ) log 2 ( γ − ρ ) η − ρ − η − ρ 4 ( γ − ρ ) log 2 ( γ − ρ ) η − ρ + 2
Also notice that when t ≥ 2 , log t 3 + 2 t 2 ≥ log ( 2 t ) , then the logarithm term on t of condition (36) can reduce to get the following condition:
γ − ρ t − ( η − ρ ) + t log δ 0 + log ( 2 t ) < 0 .
Similarly, taking t = 2 ( γ − ρ ) ( η − ρ ) , this condition is optimimized as
log δ 0 < ( η − ρ ) 2 4 ( γ − ρ ) − ( η − ρ ) 2 ( γ − ρ ) − η − ρ 2 ( γ − ρ ) log 2 ( γ − ρ ) η − ρ .

3.2.3. Recover r or q

(1) Recover  r by LLL algorithm
Let the general solution formula of (11) be
d = d 0 + t 1 d 1 + ⋯ + d z ,
where d 0 is a particular solution of (11), d 1 , ⋯ , d z are the basis vectors for the solution space of the corresponding homogeneous system of linear equations, and t 1 , ⋯ , t z are the integer parameters.
Next, find small positive integer solutions to (11) to get r . Constract the lattice L with basis matrix
B = d 0 d 1 ⋯ d z .
Let d ′ ∈ L , then
d ′ = k 0 d 0 + k 1 d 1 + ⋯ + k z d z
where k 0 , k 1 , ⋯ , k z are integers. Obviously, when k 0 = 1 , (40) = (38). Reduce the lattice B to B ′ :
B ′ = d 0 ′ d 1 ′ ⋮ d z ′ .
To facilitate finding r , consider the explicit vectors d 0 ′ , d 1 ′ , ⋯ , d z ′ . It’s easy to deduce that only one of them is the solution to (11).
Let d i ′ is the solution to (11), and if d i ′ = d 0 ′ , then d 0 ′ is probably equal to r . With this in mind, Ding and Tao [31] found the conditions that the algorithm can work well (see 3.2.2). In addition, if d i ′ ≠ d 0 ′ , we find an interesting thing that the recovery value p ′ is only 1 or 2 different from the true value p in many cases of our experiment. And our experiments lead to the following general conclusions between p and p ′ :
Let d i ′ = ( u i 1 , u i 2 , ⋯ , u i t ) ≠ d 0 ′ , d r u = gcd ( r 1 − u i 1 , r 2 − u i 2 , ⋯ , r t − u i t ) , then
p ′ − p = d r u ,
where p ′ is the recovered value of p. So, if d i ′ ≠ d 0 , using vector d i ′ , p ′ can be restored. And since d r u is bounded, p can be restored by p ′ .
In summary, one of the outputs d 1 , ⋯ , d z generated by the LLL algorithm can be used to recover r under the appropriate conditions.
(2) Recover  q
Let U = ( u i j ) t × t , which satisfies LLL ( B ) = U B , where B , LLL ( B ) are the lattice basis matrix and LLL reduced lattice basis matrix respectively, then U is a unimodular matrix with | U | = ± 1 . Constract the system
U q T = ( 0 , 0 , ⋯ , 0 , d ) T .
Because ( q 1 , q 2 , ⋯ , q t ) = 1 with probability 1 / ζ ( t ) , where ζ ( t ) = ∑ i = 1 ∞ 1 / k t is the function of Euler-Rieamann zeta, the probability that d = ± 1 is very high. Therefore ( q 1 , q 2 , ⋯ , q t ) is the absolute value of the last column of U − 1 and p = ⌊ x i / q i ⌋ [42]. It can be known from OL algorithm, the first t − 1 row vector of matrix U can be generated by LLL algorithm, but the t-th row vector u t = ( u t 1 , u t 2 , ⋯ , u t t ) has to satisfy the following equation:
u t 1 q 1 + u t 2 q 2 + ⋯ + u t t q t = ± 1 .
If (43) is considered in isolation, it is very possible for (43) to be established. But from the above analysis, it can be seen that the matrix U is a transition matrix from a basis of a lattice to its reduced basis, and U is a unimodular matrix. Furthermore, through our experiments, it is difficult to guarantee that the last row vector u t of U satisfies the equation (43). So finding such a matrix U is still an open question.

3.2.3. An improved algorithm of OL-∨

In this part, an improved algorithm of OL-∨ is proposed. Constract a lattice L with the basis matrix
B = 1 x 1 1 x 2 ⋱ ⋮ 1 x t N ,
where N is an integer with γ + η bits. Using the lower bound of t in [41] and the upper bound of the short vector in [36], the following improved Algorithm 1 is given.
When
η ≥ ρ + 1.1 γ ,
this algorithm can successfully recover p. It is an improvement of Ding and tao’s OL algorithm [31]. Firstly, the lower bound of t and the upper bound of the short vector v are modified. Secondly, the later step using the LLL algorithm has been cancelled in the recovery of r . This is because when the algorithm is implemented with isolve command of Maple, the special solution of the equations (11) is exactly the small positive integer solution under the condition (44). Thirdly, unlike Ding and tao’s OL algorithm [31] which is not proved theoretically, our algorithm is correct theoretically. And it can be seen that the attack range is extended greatly and the efficiency increases quickly.
Algorithm 1  An improved OL algorithm for GACD
Input: An appropriate positive integer t = ⌊ 5 3 ( η − ρ − ( η − ρ ) 2 − 1.2 γ ) ) ⌋ , and ACD samples x 1 , ⋯ , x t .
Output: Integer p.
1. Randomly choose N ∈ ( 2 γ + η − 1 , 2 γ + η ) .
2. Reduce lattice L by LLL algorithm with δ = 3 / 4 . Let the reduced basis be v 1 , ⋯ , v t + 1 , where v i = ( u i 1 , ⋯ , u i t , v i ( t + 1 ) ) , ( i = 1 , ⋯ , t + 1 ) .
3. If ∥ v i ∥ < 2 η − ρ − 3 − log t , ( i = 1 , ⋯ , t − z ) , where z = 1 , 2 , then solve the integer linear system with t unknowns r 1 , ⋯ , r t as follows
∑ j = 1 t u i j r i = ∑ j = 1 t u i j · x i ( i = 1 , ⋯ , t − z ) .
Therefore, the integer solutions can be expressed as follow:
d = d 0 + t 1 d 1 + ⋯ + t z d z ,
where d 0 is a special solution of the linear system, t 1 , ⋯ , t z are integers, d 1 , ⋯ , d z is a basis of integer solution space for the corresponding homogeneous linear equations.
4. d 0 = r .
5. Compute p = gcd ( x 1 − r 1 , x 2 − r 2 ) .
Return p.

3.3. Multivariate polynomial (MP) equations method

Howgrave-Graham ([5]) is the first to consider reducing the PACD problem by giving two ACD sample inputs, N = p q 0 and a = p q 1 + r 1 . The idea is based on finding small roots of modular univariate linear equations of the form a + x ≡ 0 ( mod p ) for unknown p. It is generalized to a multivariate version in [16] which is called MP method. In fact, MP method is an extension of Coppersmith’s method ([Cop96b]). A rigorous analysis of this algorithm was provided by Cohn and Heninger [25] and a variant for the case when the “errors” are not all the same size was given by Takayasu and Kunihiro [28]. It is well-known that MP approach has some advantages if the number of ACD samples is very small, but the application with a large number of samples in actual cryptanalysis needs a great deal of attention. In addition, the MP approach can be applied to both PACD and GACD problems, but it is simpler to explain and analyse the PACD problem. Hence, in the following discussion, only this case will be told.
Notice that some notations change here. let N = p q 0 and let a i = p q i + r i for 1 ≤ i ≤ m be our ACD samples, where | r i | ≤ R for some given bound R. The idea is to construct a polynomial Q ( X 1 , X 2 , ⋯ , X m ) in m variables such that Q ( r 1 , ⋯ , r m ) ≡ 0 ( mod p k ) for some k. The parameters m and k are to be optimized. In [25], such a multivariate polynomial is constructed as integer linear combinations of the products ( X 1 − a 1 ) i 1 · · · ( X 1 − a m ) i m N l where l is chosen such that i 1 + ⋯ + i m + l ≥ k .
Let
f [ i 1 , i 2 , ⋯ , i m ] ( X 1 , X 2 , ⋯ , X m ) = ( R X 1 − a 1 ) i 1 ( R X 2 − a 2 ) i 2 ⋯ ( R X m − a m ) i m N l .
Here, the bound of the polynomial degree t has to be chosen. It doesn’t do any good to talk about k > t , because it leads to the entire matrix being multiplied by the scalar N k − t for the case t = k . Accordingly, Cohn and Heninge [25] consider the lattice L generated by the coefficient row vectors of (45) such that i 1 + ⋯ + i m ≤ t and l = m a x ( k − ∑ j i j , 0 ) . If the occurrence of monomial in f [ i 1 , i 2 , ⋯ , i j ] is sorted in inverse lexicographical order, then the basis matrix for the lattice L is lower triangular. 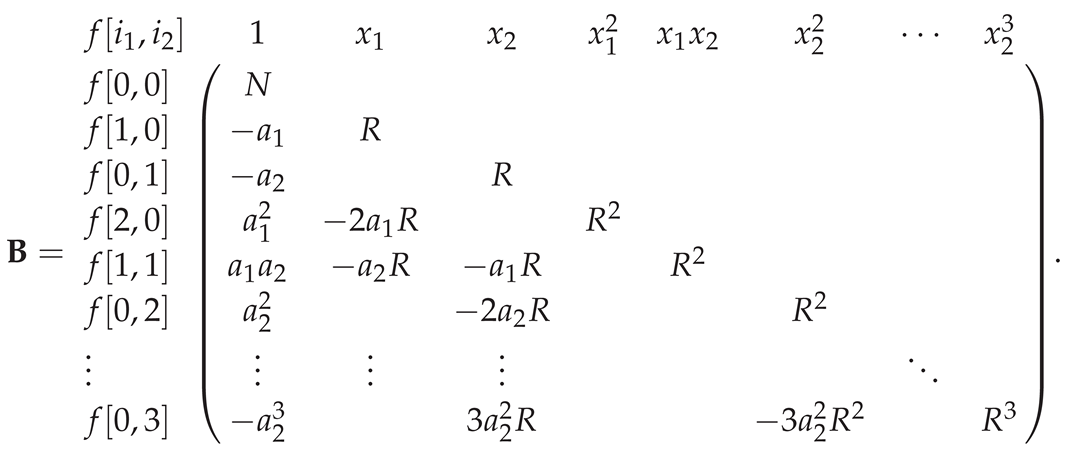For example, when ( t , m , k ) = ( 3 , 2 , 1 ) , the corresponding basis matrix is B : Preprints 76097 i005
It is shown that the dimension of the lattice L is dim ( L ) = d = t + m m , and its determinant is
det ( L ) = R d m t m + 1 N k + m m k m + 1 = 2 d ρ m t m + 1 + k + m m γ k m + 1 ,
where R = 2 ρ , N = 2 γ . The following is a brief proof of dim ( L ) and det ( L ) .
Clearly, dim ( L ) is the number of possible polynomials of the form
( R X 1 − a 1 ) i 1 ( R X 2 − a 2 ) i 2 ⋯ ( R X m − a m ) i m N l
in the variables ( X 1 , X 2 , ⋯ , X m ) . So, count the possible number of combinations of the exponents i j , where i j ≥ 0 , so that 0 ≤ i 1 + ⋯ + i m ≤ t . Assigning t + 1 values ( 0 , 1 , 2 , ⋯ , t ) to m exponents i j can be denoted by t + m m . Equivalently, count the number of non-negative integer solutions to the equation i 1 + ⋯ + i m = t ′ in the variables i j . It has t ′ + m − 1 t ′ possible number of solutions. Note that since
t + m m = t + m − 1 t + t + m − 1 t − 1 ,
and
m − 1 0 + m 1 + ⋯ + t + m − 1 t = t + m m .
Adding all possible number of solutions for 0 ≤ t ′ ≤ t gives the result
dim ( L ) = t + m m .
Next, det ( L ) = N S N R m S R , where S N is the sum of exponents of N and S R is the sum of exponents of R. Because there are in total t + m m monomials with m + i − 1 i of them having exponent i. This implies that R has exponent i m + i − 1 i / m = m + i − 1 i − 1 . Summing up for 1 ≤ i ≤ t gives the total exponent of R. So
S R = m 0 + m + 1 1 + ⋯ + t + m − 1 t − 1 = t + m m t + m t − 1 t + m m = t + m m t m + 1 .
The exponent of N in each monomial expression is l, where l = m a x ( k − ∑ j i j , 0 ) . A similar analysis gives the exponent of N to be
S N = k + m m k m + 1 .
Substituting N and R by their size estimates 2 γ and 2 ρ respectively gives the result
det ( L ) = R d m t m + 1 N k + m m k m + 1 = 2 d ρ m t m + 1 + k + m m γ k m + 1 .
Let v be a vecor in L and
Q ( X 1 , ⋯ , X m ) = ∑ i 1 , i 2 , ⋯ , i m ( Q i 1 m x 1 m i 1 i m ) ,
then
v = ∑ i 1 , i 2 , ⋯ , i m ( Q i 1 m R i 1 + ⋯ + i m ) .
If | Q ( r 1 , ⋯ , r m ) | < p k , clearly the equation Q ( r 1 , ⋯ , r m ) = 0 holds over the integers. So the norm of | Q ( r 1 , ⋯ , r m ) | needs to be bounded. Notice that
| Q ( r 1 , ⋯ , r m ) | ≤ ∑ i 1 , i 2 , ⋯ , i m | r 1 | i 1 + ⋯ + | r m | i m ≤ ∑ i 1 , i 2 , ⋯ , i m R i 1 + ⋯ + R i m = ∥ v ∥ 1 .
where the norm ∥ v ∥ 1 represents the sum of the absolute values of the components for the vector v . Hence, if ∥ v ∥ 1 < p k for some k, then v ∈ L is the target vector found in the MP algorithm. In order to save time and memory, more than m algebraically independent target vectors are usually selected for elimination. By using Gröbner basis method or the existing corresponding results to reduce the system to a univariate polynomial equation and hence solve for ( r 1 , ⋯ , r m ) . Then p = gcd ( N , a 1 − r 1 ) can be determined.
When ( t , k ) = ( 1 , 1 ) , the MP algorithm is the same as the orthogonal lattice attack [DGHV10, CH13, GGM16]. Such parameters ( t , k ) = ( 1 , 1 ) are called “unoptimised”. The question is whether the algorithm is better at t > 1 .

3.3.1 The heuristic analysis results of the MP algorithm in [25]

Cohn and Heninger [25] give a heuristic theoretical analysis of the MP algorithm and suggest optimal parameter choices ( t , m , k ) . Later, Galbraith et al. sketched CH approach in [37]. The main results of the analysis are presented here.
Result 1. Let β = η / γ ≪ 1 , so that p ≈ N β , then the parameters ( t , m , k ) satisfy the relational expression
m t ρ ( m + 1 ) k + γ k m ( m + 1 ) t m < β γ = η .
Proof. Because the MP algorithm is executed successfully, m vectors satisfying ∥ v ∥ 1 < p k need to be generated. Using ∥ v ∥ 1 < d ∥ v ∥ and the bounds from Assumption 2, the LLL-reduced basis satisfying the condition ∥ b i ∥ 1 ≤ d ( 1.02 ) d ( det L ) 1 / d can be found, where d is the dimension of the lattice. If this bound is less than p k ≈ 2 η k , then enough vectors are needed to be obtained. Hence,
d d ( 1.02 ) d det ( L ) < 2 η k d ,
and so
d log d + d d log 1.02 + d ρ m t m + 1 + γ k + m m k m + 1 < k η d .
Let β = η / γ ≪ 1 , so that p ≈ N β . With the first two terms of (46) deleted and approximating k + m m ≈ k m , d = t + m m ≈ t m , the formula (46) can be reduced to
m t ρ ( m + 1 ) k + γ k m ( m + 1 ) t m < β γ = η .
Result 2 (Heuristic). For fixed m, if η 2 ≫ γ and ρ = log R < η ( 1 + o ( 1 ) ) β 1 / m , then the ACD problem can be solved in polynomial time.
Remark 1. 
Result 2 does not imply that the MP approch is better than the SDA or OL approches. When  ρ  is small, all algorithms based on lattices of dimension approximately  γ / η , and the lattice input size is proportional to γ , so they are all polynomial time if they return a correct solution to the problem.

3.3.2 The heuristic analysis results of the MP algorithm in [36]

Gebregiyorgis [36] solved the corresponding polynomial equations in m variables. The following conclusion was obtained.
Result 3. Under the hypothesis
λ m ( L ) = ( det L ) 1 d d 2 π e ,
where d = t + m m , λ m ( L ) is short if d > k + m m γ ( m + 1 ) ( η − ρ ) .
Proof. If λ m ( L ) = ( det L ) 1 d d 2 π e , then λ m ( L ) < p k which implies
log ( det L ) < d k η .
So
d ρ m t m + 1 + γ k + m m k m + 1 < k d η ,
which is implied by
γ k + m m 1 m + 1 < d ( η − ρ ( t / k ) ) .
This is equivalent to
d = t + m m > k + m m γ ( m + 1 ) ( η − ρ ( t / k ) ) ≈ k + m m γ ( m + 1 ) ( η − ρ ) .
For d > k + m m γ ( m + 1 ) ( η − ρ ) , the first m output vectors v i of the LLL algorithm satisfy ∥ v i ∥ 1 < p k giving us polynomial relations between r 1 , ⋯ , r m . Let v = ( u 1 , ⋯ , u d ) and consider the d monomials ( 1 , X 1 , X 2 , X 1 2 , X 1 X 2 , X 2 2 , ⋯ , X m t ) in degree reverse ordering. Then the corresponding polynomial to lattice vector v is
Q ( X 1 , X 2 , ⋯ , X m ) = ∑ i = 1 d u i R j 1 + j 2 + ⋯ + j m X 1 m j 1 j m .
Next, collect m such independent polynomial equations. The system of equations can be solved using the Gröbner basis algorithms to find r 1 , ⋯ , r m ∈ Z . Note that the first m output of the LLL algorithm do not necessarily give an algebraic independent vectors. In this case, subsequent vectors generated by the LLL algorithm with l 1 norm less than p k (if there are any) need to be added. Alternatively, to get algebraic independent polynomial equations, the polynomial equations needs to be factored. Finally, p is recovered with a high probability by computing gcd ( N , a 1 − r 1 , a 2 − r 2 , ⋯ , a m − r m ) .
The drawback of the CH-approach is that enough independent polynomial equations cannot be discovered. Gebregiyorgis’s experiment shows that this is the case. Moreover, the running of the Gröbner basis part is stuck even for small parameters.

3.3.3. The heuristic analysis results of the MP algorithm in [37]

Galbraith et al. [37] analyzed the conclusions of [25] and considered the parameters more generally, where it was assumed that the optimal solution would be to take t , k > 1 . Here are the main results.
Result 4. The condition η 2 ≫ γ in Result 2 means the MP attack can be avoided in practice relatively easily.
Remark 2. 
The OL method does not have any such hard limit on its theoretical feasibility. However, in practice the restriction η 2 ≫ γ is not so different from the usual condition that the dimension must be at least γ / η . If γ > η 2 , then the required dimension would be at least η , which is infeasible for lattice reduction algorithms for the parameters used in practice.
Result 5. For CS-ACD parameters, Galbraith et al. [37] suppose ρ ≈ η (e.g., ρ / η = 0.9 ) and γ = η 1 + δ for some δ > 0 , their experimental condition t ρ < k η implies that t ≈ k in which case k + m m ≈ d = t + m m > γ η k + m m 1 m + 1 . So this bound suggested that MP approach has no advantage over other methods for parameters of CS-ACD. Their experimental results also confirm this.
Result 6. When m is large, the best choices for the MP algorithm are ( t , k ) = ( 1 , 1 ) , and so MP method was not better than the SDA or OL methods by practical experiments.

3.4. Pre-processing of the ACD samples

The most important factor in the hardness of the ACD problem is the ratio γ / η , which is the size of the integers x i relative to the size of p. The main idea of pre-processing method is: for the same p, without changing the size of the errors r i , reduce γ and find an easier set of ACD instances.
The method of preserving the sample size was analysed briefly in [36] and further discussion about preserving and aggressive shortening the sample size was given in [37]. Here is a brief overview and the statistic analysis of Galbraith’s results [37] on the pre-processing method.
The main idea of the pre-processing is the step by taking differences x k − x i for x k > x i and x k ≈ x i ( 1 ≤ i ≤ τ ) . The essence is that if x k ≈ x i then q k ≈ q i but r k and r i are not affected at not. Hence, x k − x i = p ( q k − q i ) + ( r k − r i ) is an ACD sample for the same p but with a smaller q and a similar sized error r. It is natural to want to be able to iterate this process until the sample size is suitable for the OL attack.

3.4.1 Preserving the sample size

Let the original samples x i = p q i + r i , | r i | ≤ 2 ρ , and the samples at iteration k are of the form
x = ∑ i = 1 2 k c i x i , c i = ± 1 ,
so the error terms is a “random” sum of 2 k ρ -bit integers:
r = ∑ i = 1 2 k c i r i , c i = ± 1 .
Since the r i ∈ [ − 2 ρ , 2 ρ ] are uniformly distributed, for large k,
E ( r ) = 0 , Var ( r ) = 1 3 2 2 ρ + k .
So the condition of | r | ≤ 2 2 ρ + k / 2 is expected. The analysis results in [37] are as follows:
Result 7. An absolute upper limit on the number of iterations is 2 ( η − ρ ) , and after the final iteration, the samples are reduced to bitlength no fewer than γ − 2 b ( η − ρ ) bits.
Remark 3. 
Let x 1 , x 2 , ⋯ , x τ be the intial γ -bit ACD samples. Suppose B = 2 b , b is typically 8 or 16. After I iterations, approximately τ − I B samples are generated, each of γ − I b bits. If ρ + k / 2 > η , then the errors have grown so large that all information about p is lost essentially. Hence, an absolute upper limit on the number of iterations is 2 ( η − ρ ) ). This means that after the final iteration the samples are reduced to bitlength no fewer than γ − 2 b ( η − ρ ) bits.
Result 8. The pre-processing approach can make very little effect on the ACD problem.
Remark 4. 
An attack on the original ACD problem requires a lattice of dimension roughly γ / η (assuming ρ ≪ η ). After k iterations of pre-processing, a lattice of dimension γ − b k η − ( ρ + k / 2 ) was needed. Even in the best case when taking k = 2 ( η − ρ ) and keep the denominator constant at ( η − ρ ) , the lattice dimension is lowered from γ / η to ( γ / η ) − 2 b . Since b = 8 or 16, the lattice dimension decreased very little.

3.4.2 Aggressive shortening

The idea of the aggressive shortening method in [37] is to generate new samples (that are still about the same bitlength) by taking sums/differences of the initial list of samples. The steps consist of the following four steps:
Step 1. Let S = ( x 1 , ⋯ , x τ ) be a set of ACD samples, with x k = p q k + r k having mean and standard deviation given respectively by
μ = E ( x k ) = 2 γ − 1 and σ 0 = 1 3 2 2 ( γ − 1 ) ( 1 + 2 − 2 ( γ − ρ − 1 ) ) ≈ 1 3 2 γ − 1 .
Let
S k = ∑ i = 1 l x k i , [ k = 1 , ⋯ , m ] ,
that is to say, the m random sums S 1 , ⋯ , S m of l elements of S were generated. So
E ( S k ) = l · 2 γ − 1 , Var ( S k ) = l 3 2 2 ( γ − 1 ) ( 1 + 2 − 2 ( γ − ρ − 1 ) ) .
Step 2. Sort the new samples S 1 , ⋯ , S m to obtain the list S ( 1 ) ≤ ⋯ ≤ S ( m ) . These are called order statistics and are represented by S ( k ) .
Step 3. Consider the neighbouring differences or spacings T k = S ( k + 1 ) − S ( k ) for k = 1 , ⋯ , m − 1 , and derive the statistical distribution of the spacings.
Step 4. Store the τ = m / 2 spacings as input to the next iteration of the algorithm. After I iterations, OL attacks can be applied.
The following analysis results were presented in [37]:
Result 9. The total number of iterations performed satisfies I < η .
The complexity is proportional to I m l o g ( m ) , since each iteration computes a sorted list of size m. The mean and the standard deviation of the spacings is inversely proportional to m, so m is expected to be very large. Suppose, at the j-th iteration, a list of τ j − 1 values are Y 1 ( j − 1 ) , Y 2 ( j − 1 ) , ⋯ , Y τ j − 1 ( j − 1 ) (so τ 0 = τ ) with standard deviation σ j − 1 . The statistical distribution of such generic spacings have Exponential distributions. Suppose Z 1 , ⋯ , Z m are independent and identically distributed random variables on R with common distribution function F, inverse distribution function F − 1 and density function f = F ′ . If Z ( 1 ) ≤ ⋯ ≤ Z ( m ) denote the order statistics of Z 1 , ⋯ , Z m , then the k-th spacing Z ( k + 1 ) − Z ( k ) is well-approximated for large m as an Exponential random variable with (rate) parameter m f ( F − 1 ( k m ) [37]. In particular, Suppose Z 1 , ⋯ , Z m ∼ N ( μ , σ 2 ) are normally distributed with mean μ and variance σ 2 , then f ( F − 1 ( u ) ) = g ( G − 1 ( u ) ) σ , where G − 1 and g are respectively the inverse distribution function and density function of a standard Normal N ( 0 , 1 ) random variable. Let H ( u ) denote the function g ( G − 1 ( u ) ) − 1 , Galbraith et al. [37] have been graphed and analyzed that H is a moderately small value away from the extreme order statistics, for example H ( u ) ≈ 4 for 0.2 < u < 0.8 . Thus the spacings have an Exponential distribution (with parameter depending on k) given by Z k + 1 − Z k ∼ E x p m σ H ( k m ) with mean σ H ( k m ) m .
Remark 5. 
As noted in [37] that a random sum S k is well-approximated as a Normal random variable with variance l σ j − 1 2 for l > 1 . The k-th spacing in this Normal approximation case essentially has a distribution given by S ( k + 1 ) − S ( k ) ∼ E x p m l σ j − 1 H ( k m ) with mean l H ( k m ) m σ j − 1 . H ( k m ) ≈ 4 when 0.2 m ≤ k ≤ 0.8 m , so by considering the “middle” spacings of T 1 , ⋯ , T m − 1 , τ j = m / 2 random variables can be obtained with approximately the same distribution that are in general independent. Thus at the end of the j-th iteration, random variables Y 1 ( j ) , Y 2 ( j ) , ⋯ , Y τ j ( j ) is obtained, with mean and standrad deviation σ j = 4 l m σ j − 1 . After j iterations, the random variables γ are sums of ( 2 l ) j of the original ACD samples, so the standard deviation of an error term in the output of the j-th has increased by a multiple of ( 2 l ) j 2 . Hence, the total number of iterations performed satisfies I < η .
Result 10. To have samples of size close to η -bits thus required η ≈ i · log ( 4 l / m ) + γ − 1 . Optimistically taking i = η , the number of new samples m should satisfy: log m ≈ γ − 1 η + log l + 1 . In other words, m is close to 2 γ / η .
Remark 6. 
After i iterations, the average size of samples is ( 4 l / m ) i 2 γ − 1 .
Result 11. In practice, m was prohibitively large. For the parameter sizes required for a cryptographic system, the resulting errors grew too rapidly to be useful for the neighbouring difference.

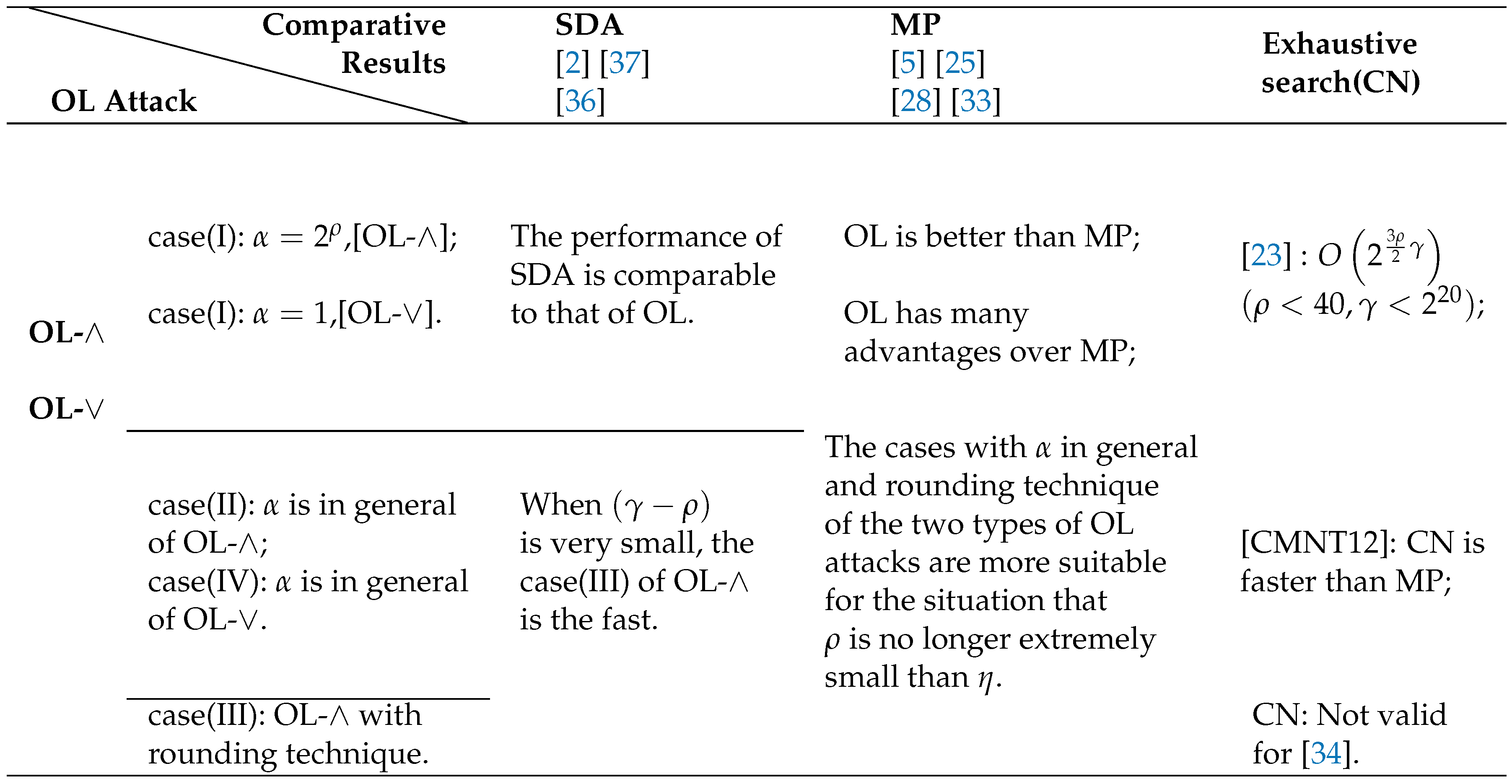
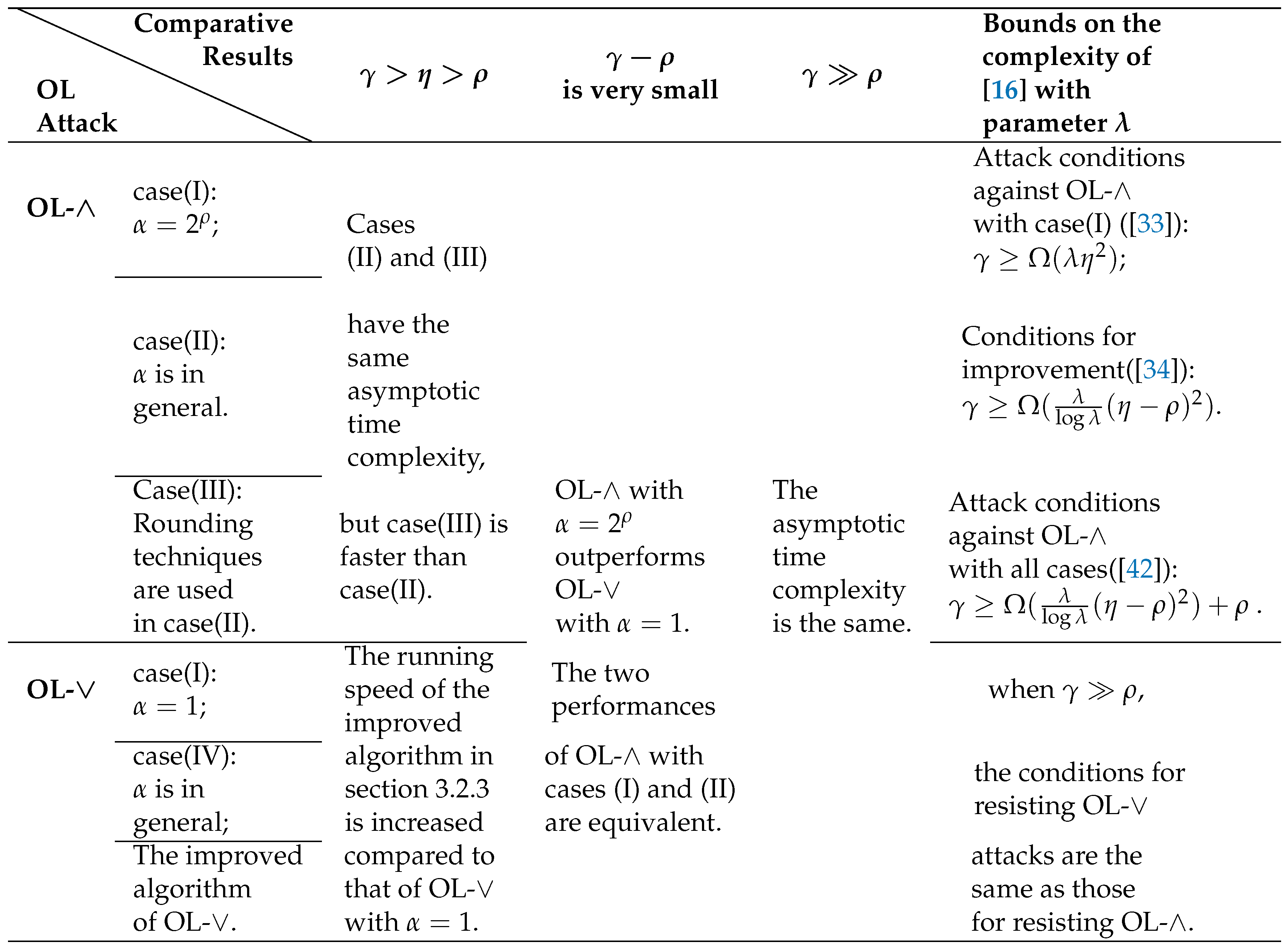
4. Comparisons of OL with SDA and MP algorithms

The ACD problem is currently a hard problem for appropriate parameter settings. Some cryptographic applications exploited the hardness problem of ACD. The homomorphic encryption schemes over the integers are particular examples, such as [16,19,34,35,38]. The security analysis of these schemes was based on the complexity of different algorithms to analyze and solve the ACD calculation problem. These algorithms were in turn based on the worst-case performance of the lattice reduction algorithm. It is important to analyze the current most effective algorithm to solve the ACD problem from practical point of view.

4.1 Comparision with the SDA algorithm

The SDA-approach (see Section 3.1) solves the ACD problem using simultaneous diophantine approximation method. The dimension of the lattice required is greater than ( γ − ρ ) / ( η − ρ ) . As if the proportion of these parameters is too large, the LLL algorithm cannot produce the desired output.
Van Dijk et al. [16] and Galbraith etal. [36] point out that the SDA algorithm is comparable to the performance when α = 2 ρ in the OL-∧ approach. Hence, the OL-∧ attack using the rounding technique is the fastest since it employs the input basis matrix with smaller entries, especially when ( γ − ρ ) is small. This fact is confirmed by experiments of Xu et al. [42].

4.2. Comparison of the two types of OL attacks

At first, the following asymptotic complexity estimatioans are given. Then according to operating conditions that depend on δ 0 , the corrsponding comparion is presented.
Theorem 2. 
([42]) The time complexity for solving ( γ , η , ρ ) -ACD instances is
2 Ω γ − ρ ( η − ρ ) 2 log γ − ρ ( η − ρ ) 2
by running BKZ- β to achieve a root-Hermite factor δ 0 such that (24) holds if one SVP oracle costs 2 O ( β ) .
Theorem 3. 
([42]) For given ( γ , η , ρ ) -ACD instances and some sufficiently large security parameter λ , if the condition
γ ≥ Ω λ log λ ( η − ρ ) 2 + ρ
holds, then the time complexity for solving ( γ , η , ρ ) -ACD instances is 2 λ by running BKZ- β if one SVP oracle costs 2 O ( β ) .
Comparision of the OL-∧ attacks According to the analysis in Section 4.1 of [42], OL-∧ attacks in Section 3.2.1, cases (II) and (III) have the same asymptotic time complexity. Notice that in OL-∧ attack, the entries of input basis matrix in case (III) are approximately reduced by ρ bits compared to that in case (II). Hence, the OL-∧ attack in case (III) will be faster in practical cryptanalysis. In typical scenarios, the OL-∧ attack in case (III) only achieves a constant improvement of the overall attack complexity. Based on the time complexity in the paper [20], the acceleration caused by reducing the number of bits ρ is 1 − ( ρ / γ ) . This improvement may be quite significant in practice.
Comparision with the two types of OL attacks When γ ≫ ρ , all these OL attacks for solving the ( γ , η , ρ ) -ACD problem have the same asymptotic time complexities; the OL-∧ attack is more advantageous than the OL-∨ attack when γ − ρ is relatively small; the case (II) is almost close to the case (III) of OL-∧ attack.
In order to hinder the attack of OL-∧, for the security parameter λ of [16], the following are the asymptotics conditions given by various literature.
condition 1:  γ ≥ Ω ( λ η 2 ) ([16]);
condition 2:  γ ≥ Ω λ log λ ( η − ρ ) 2 ([34]);
condition 3:  γ ≥ Ω λ log λ ( η − ρ ) 2 + ρ ([42]).
Obviously, condition 2 is better than condition 1. Compared to the condition 2 in [34], condition 3 in [42] is better in the case that ( γ − ρ ) is relatively small.
Galbraith et al. [36] showed the success condition of the case (I) of OL-∧ attack based on the LLL algorithm. In [42], when α is in general case, the two OL attacks based on the BKZ- β algorithm, the expression on ACD parameters γ , η , ρ , the number t of ACD samples and the root-Hermite factor δ 0 were given by (24). This expression can be used to evaluate the specific security of ACD-based schemes.

4.3. Comparision with the MP Algorithm

The common drawback of MP Algorithm is that the dimensions and entries of the involved lattices are quite large, which affects the speed of the algorithm. Galbraith et al.([36]) pointed out that the MP approach is not better than the OL-∧ attack for practical cryptanalysis. Hence, the OL-∧ attacks in case (II) and (III) have more advantageous than the MP approach.

4.4. Brief summary

From (22) and (33), the following theorem can be obtained.
Theorem 4. 
([42])The time complexities to solve ( γ , η , ρ ) -ACD instances by running BKZ- β if one SVP oracle costs 2 O ( β ) is given:
①
The OL-∧ with α = 2 ρ : 2 Ω γ − ρ ( η − ρ ) 2 log γ − ρ ( η − ρ ) 2 ;
②
The OL-∨ with α = 1 : 2 Ω γ ( η − ρ ) 2 log γ ( η − ρ ) 2 .
Based on the above analysis and comparison in the first three sections, all the results are presented in Table 1 and Table 2.

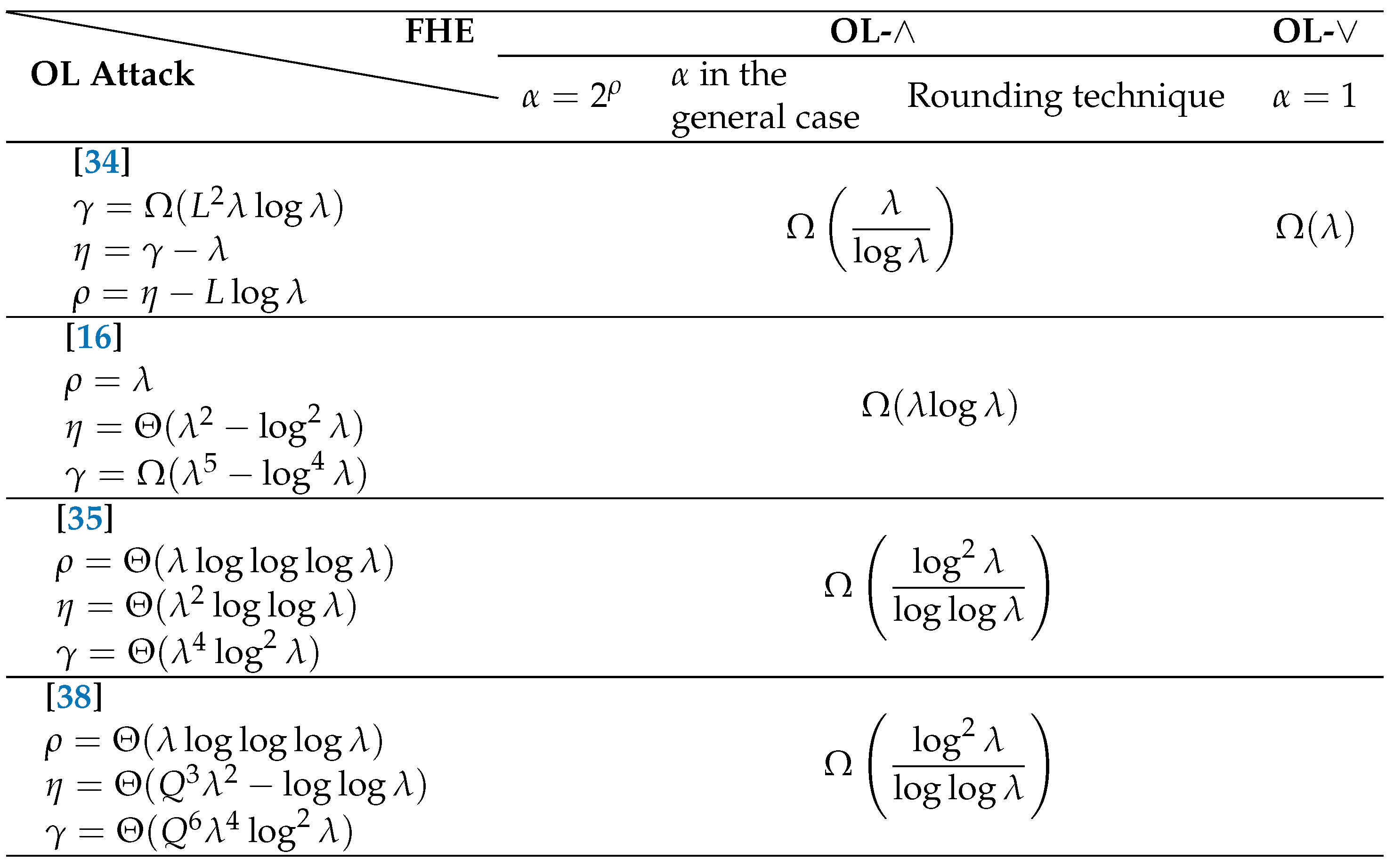
5. Cryptanalysis of OL attacks in ACD-based FHE Schemes

In this section, by using OL attack, the time complexity of the ACD problem in FHE scheme [DGHV10, KN15, CS15, KT16] is analysed and summarized. In particular, Cheon and Stehle [34] proposed a homomorphic encryption scheme whose parameters are
( ρ , η , γ ) = ( λ , λ + l o g λ , Ω ( d 2 λ l o g λ ) ) ,
where d is the depth of the circuit for homomorphic calculation, here ρ ≪ η is no longer satisfied. They also indicated that if the (decision) ACD problem can be solved, then it can be solved LWE. And this set of parameters is obviously difficult.
According to Theorem 2 and Theorem 4, the log of the asymptotic time complexities for solving ( γ , η , ρ ) -ACD instances are summarized as Table 3.
Through the analysis of the Table 3, the following conclusions can be drawn:
①For the scheme of [16], those parameters are conservative to get Ω ( λ ) -bit security for OL attacks. Further, according to Theorem 3, using γ = Ω ( ( λ / log λ ) η 2 ) instead of γ = Ω ( λ η 2 ) in order to achieve λ -bit security;
②For the scheme of [35], those parameters are optimistic to achieve Ω ( λ ) -bit security for the OL attacks. Furthermore, based on 3, taking γ = Θ λ 5 ( log log λ ) 2 log λ instead of γ = Θ ( λ 4 log 2 λ ) for obtaining λ -bit security;
③For the scheme of [38], Q does not effect the asymptotic time complexities of OL attacks compared to the case of the [35] Scheme. The corresponding parameters are also optimistic to achieve Ω ( λ ) -bit security for the OL attacks;
④For the scheme of [34], the asymptotic time complexities of obtainning the ( γ − ρ ) most significant bits of p for OL attacks is presented.

6. Prospects

Based on the above survey of ACD problem attacks , the ACD problem can be solved under certain conditions using the SDA, OL, MP algorithms. These results show that the applicable range of the three algorithms can be expanded even further. To date, several FHE schemes have been designed based on ACD and variant problems. Existing schemes conservatively set the parameters to be secure against these algorithms. Therefore, it is still worth further exploration to improve the existing algorithms for solving the ACD problem.
Although the present survey offers an initial contribution to the literature concerning the algorithms for ACD problem, the following open problems for further research are left. The application of the improved algorithm in section 3.2.3 needs to be considered for achieving cryptanalysis. Whether the algorithm can be improved to reduce parameter constraints.
For future work, our work points to some directions for addressing the ACD problem, which has great potential in term of further improvement in both theory and practice. This improvement is very much related to the Hermit factor of the reduction algorithm.

7. Conclusions

In this paper, known attacks on the ACD problem are investigated. The performance and application range of each algorithm are analyzed. OL algorithms are divided into two categories (OL-∧ and OL-∨) for the first time. This work is very helpful for OL attacks to achieve better results. An improved algorithm of OL-∨ is presented to solve the GACD problem. This algorithm works well in polynomial time if the parameter satisfies certain conditions. Compared with [31], the lattice reduction algorithm is used only once, and when the error term r is recovered in [31], the possible difference between the restored and the true value of p is given. It is helpful to expand the scope of OL attacks.

Author Contributions

Conceptualization, Ran Y. and Wang L.; Methodology, Ran Y. and Wang L.; Validation, Pan Y. and Wang L.; Writing—original draft preparation, Ran Y.; Writing—review and editing, all; Code implementation, Ran Y. and Wang L.; Supervision and project administration, Pan Y.

Funding

This research is partially supported by the National Natural Science Foundation of China (NSFC) (62272040).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. A. K. Lenstra; H. W. Lenstra; and L. Lovász. Factoring polynomials with rational coeffcients. Math. Ann. 1982, 261(4): 515–534.
  2. J. C. Lagarias. The computational complexity of simultaneous Diophantine approximation problems. SIAM J. Comput. 1985, 14(1): 196–209. [CrossRef]
  3. Claus-Peter Schnorr and M. Euchner. Lattice basis reduction: Improved practical algorithms and solving subset sum problems. Math. Program. 1994, 66: 181–199. [CrossRef]
  4. D. E. Knuth. The art of computer programming, seminumerical algorithm[J]. Software: Practice and Experience, 1982, 12(9): 883–884.
  5. N. Howgrave-Graham. Approximate integer common divisors. Cryptography and Lattices. Springer Berlin Heidelberg, 2001: 51–66.
  6. P. Q. Nguyen and Jacques Stern. The Two Faces of Lattices in Cryptology. In J. Silverman (ed.), Cryptography and Lattices, Springer LNCS 2146, 2001: 146–180.
  7. Avrim Blum, Adam Kalai and Hal Wasserman. Noise-tolerant learning, the parity problem, and the statistical query model. Journal of ACM, 2003, 50(4): 506–519. [CrossRef]
  8. Claus-Peter Schnorr. Lattice reduction by random sampling and birthday methods. In STACS 2003, 20th Annual Symposium on Theoretical Aspects of Computer Science, Berlin, Germany, February 27–March 1, Proceedings, 2003: 145-156.
  9. Phong, Q. Nguyen and Damien Stehlé. LLL on the Average. In Florian Hess, Sebastian Pauli and Michael E. Pohst (eds.), ANTS-VII, Springer LNCS 4076, 2006: 238-256.
  10. V. Lyubashevsky. The Parity Problem in the Presence of Noise, Decoding Random Linear Codes, and the Subset Sum Problem. APPROX-RANDOM 2005, Springer LNCS 3624, 2005: 378–389.
  11. C. Gentry, C. Peikert, V. Vaikuntanathan. Trapdoors for hard lattices and new cryptographic constructions[C], Proceedings of the fortieth annual ACM symposium on Theory of computing. ACM, 2008: 197–206. [CrossRef]
  12. N. Gama and P. Q. Nguyen. Predicting lattice reduction. In Advances in Cryptology-EUROCRYPT 2008, 27th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Istanbul, Turkey, April 13–17, 2008. Proceedings, 2008: 31-51.
  13. C. Gentry. A Fully Homomorphic Encryption Scheme. PhD thesis, The department of computer science, Stanford University, Stanford, CA, USA, 2009.
  14. P. Q. Nguyen, Valle B. The LLL algorithm: survey and applications. Springer Publishing Company, Incorporated, 2009.
  15. C. Gentry, Toward basing fully homomorphic encryption on worst-case hardness, in: T. Rabin(ed.), Advances in Cryptology-CRYPTO 2010, Lecture Notes in Comput. Sci. Springer, Berlin, Heidelberg, 2010, 6223: 116–137.
  16. M. Van Dijk, C.Gentry, S. Halevi, V. Vaikuntanathan, Fully homomorphic encryption over the integers, in: H. Gilbert (ed.), Advances in Cryptology—EUROCRYPT 2010, Lecture Notes in Comput. Sci. Springer, Berlin, Heidelberg, 2010, 6110: 24–43.
  17. G. Hanrot, X. Pujol, and D. Stehlé. Terminating bkz. IACR Cryptology ePrint Archive, 2011: 198.
  18. H. Cohn, N. Heninger. Approximate common divisors via lattices. CoRR, abs/1108. 2714, 2011.
  19. J. S. Coron, A. Mandal, D. Naccache, M. Tibouchi, Fully homomorphic encryption over the integers with shorter public keys, in: P. Rogaway (ed.), Advances in Cryptology-CRYPTO 2011, Lecture Notes in Comput. Sci, Springer, Berlin, Heidelberg, 2011, 6841: 487–504.
  20. A. Novocin, D. Stehlé, and G. Villard. An LLL-reduction algorithm with quasi-linear time complexity: extended abstract. In Proceedings of the 43rd ACM Symposium on Theory of Computing, 2011: 403–412.
  21. S. D. Galbraith, Mathematics of Public Key Cryptography. Cambridge University Press, 2012.
  22. Y. Ramaiah, G. Kumari, Efficient public key generation for homomorphic encryption over the integers[C]. Third International conference on advances in communication, network and computing. 2012.
  23. Y. Chen, P. Q. Nguyen. Faster algorithms for approximate common divisors: Breaking fully homomorphic encryption challenges over the integers. Advances in Cryptology-EUROCRYPT 2012. Springer Berlin Heidelberg, 2012: 502–519.
  24. J. S. Coron, D. Naccache, M. Tibouchi. Public Key Compression and Modulus Switching for Fully Homomorphic Encryption over the Integers. In D. Pointcheval and T. Johansson (ed.), EUROCRYPT’12, Springer LNCS, 2012, 7237: 446–464.
  25. H. Cohn, N. Heninger. Approximate common divisors via lattices. In proceedings of ANTS X, vol. 1 of The Open Book Series, 2013: 271–293.
  26. J. H. Cheon, J. S. Coron, J. Kim, M. S. Lee, T. Lepoint, M. Tibouchi, and A. Yun. Batch fully homomorphic encryption over the integers. In Proc. of EUROCRYPT, Springer LNCS, 2013, 7881: 315-335.
  27. Y. Chen. Réduction de réseau et sécurité concrète du chiffrement complètement homomorphe. Ph.d theses, Paris 7, June 2013.
  28. Atsushi Takayasu and Noboru Kunihiro, Better Lattice Constructions for Solving Multivariate Linear Equations Modulo Unknown Divisors, IEICE Transactions 97-A, 2014, 6: 1259-1272.
  29. J. Hoffstein, J. Pipher, and J. H. Silverman. An Introduction to Mathematical Cryptography. Springer Publishing Company, 2nd edition, 2014.
  30. J. Ding, C. Tao. A New Algorithm for Solving the General Approximate Common Divisors Problem and Cryptanalysis of the FHE Based on the GACD problem. Cryptology ePrint Archive, Report 2014/042, 2014.
  31. J. Ding, C. Tao. A New Algorithm for Solving the Approximate Common Divisor Problem and Cryptanalysis of the FHE based on GACD. IACR Cryptol. ePrint Arch, 2014: 42.
  32. J. S. Coron, T. Lepoint, M. Tibouchi, Scale-Invariant Fully Homomorphic Encryption Over the Integers, in: H. Krawczyk (ed.), Public-Key Cryptography—PKC 2014, Lecture Notes in Comput. Sci. Springer, Berlin, Heidelberg, 2014, 8383: 311-328.
  33. T. Lepoint. Design and Implementation of Lattice-Based Cryptography. Cryptography and Security [cs.CR]. Ecole Normale Supérieure de Paris-ENS Paris, 2014.
  34. J. H. Cheon, D. Stehlé. Fully Homomorphic Encryption over the Integers Revisited. In E. Oswald and M. Fischlin (eds.), EUROCRYPT’15, Springer LNCS, 2015, 9056: 513-536.
  35. K. Nuida, K. Kurosawa. (Batch) Fully Homomorphic Encryption over Integers for Non-Binary Message Spaces. Springer, Berlin, Heidelberg, 2015.
  36. S. Gebregiyorgis. Algorithms for the Elliptic Curve Discrete Logarithm Problem and the Approximate Common Divisor Problem. PhD thesis, The University of Auckland, Auckland, New Zealand, 2016.
  37. S. Galbraith, S. Gebregiyorgis, S. Murphy. Algorithms for the approximate common divisor problem. LMS Journal of Computation and Mathematics. 19(A), 2016.: 58-72. [CrossRef]
  38. Eunkyung Kim and Mehdi Tibouchi. FHE over the integers and modular arithmetic circuits. In Cryptology and Network Security-15th International Conference, CANS 2016, Milan, Italy, November 14-16, 2016, Proceedings, 2016: 435–450.
  39. D. Benarroch, Z. Brakerski, T. Lepoint. FHE over the Integers: Decomposed and Batched in the Post-Quantum Regime. Springer, Berlin, Heidelberg, 2017.
  40. J. Dyer, M. Dyer, J. Xu. Order-preserving encryption using approximate integer common divisors,Data Privacy Management, Cryptocurrencies and Blockchain Technology: ESORICS 2017 International Workshops, DPM 2017 and CBT 2017, Oslo, Norway, September 14-15, 2017, Proceedings. Springer International Publishing, 2017: 257–274.
  41. Xiaoling Yu, Yuntao Wang, Chungen Xu, Tsuyoshi Takagi. Studying the Bounds on Required Samples Numbers for Solving the General Approximate Common Divisors Problem. 2018 5th International Conference on Information Science and Control Engineering. [CrossRef]
  42. J. Xu, S. Sarkar, L. Hu, Revisiting orthogonal lattice attacks on approximate common divisor problems and their applications. Cryptology ePrint Archive, 2018.
  43. J. H. Cheon, W. Cho, M. Hhan, Algorithms for CRT-variant of approximate greatest common divisor problem. Journal of Mathematical Cryptology, 2020, 14(1): 397–413. [CrossRef]
  44. W. Cho, J. Kim, C. Lee. Extension of simultaneous Diophantine approximation algorithm for partial approximate common divisor variants. IET Information Security, 2021, 15(6): 417–427. [CrossRef]
Table 1. Compare the effects of SDA, MP, CN and OL algorithms on ACD problem
Table 1. Compare the effects of SDA, MP, CN and OL algorithms on ACD problem
Preprints 76097 i001
Table 2. Comparison of Algorithms OL-∧ and OL-∨
Table 2. Comparison of Algorithms OL-∧ and OL-∨
Preprints 76097 i002
Table 3. Comparison of Algorithms OL-∧ and OL-∨
Table 3. Comparison of Algorithms OL-∧ and OL-∨
Preprints 76097 i003
Table 4. Cryptanalysis of FHE schemes based on ACD.
Table 4. Cryptanalysis of FHE schemes based on ACD.
Preprints 76097 i004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

226

Views

44

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated