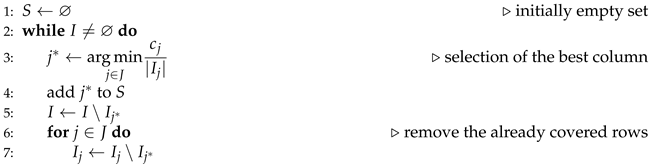Prerpints.org logo
Preprint
Article

A Surprisal-Based Greedy Heuristic for the Set Covering Problem

Altmetrics

Downloads

140

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 June 2023

Posted:

02 June 2023

You are already at the latest version

Alerts
Abstract
In this paper we exploit concepts from Information Theory to improve the classical Chvatal’s greedy algorithm for the Set Covering Problem. In particular, we develop a new greedy procedure, called Surprisal-Based Greedy Heuristic (SBH), incorporating the computation of a “surprisal” measure when selecting the solution columns. Computational experiments, performed on instances from the OR-Library, show that SBH yields a 2.5% improvement in terms of the objective function value over the Chvatal’s algorithm while retaining similar execution times, making it suitable for real-time applications. The new heuristic was also compared with Kordalewski’s greedy algorithm, obtaining similar solutions with much lower times on large instances, and Grossmann and Wool’s algorithm for unicost instances, where SBH obtained better solutions.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

The Set Covering Problem (SCP) is a classical combinatorial optimization problem defined as follows. Let I be a set of m items and J = { S 1 , S 2 … , S n } a collection of n subsets of I where each subset S j ( j = 1 , ⋯ , n ) is associated to a non-negative cost c j . The SCP amounts to find a minimum cost subcollection of J that covers all the elements of I at minimum cost, the cost being defined as the sum of subsets cost.
The SCP finds applications in many fields. One of the most important is Crew Scheduling, where SCP provides a minumum-cost set of crews in order to cover a given set of trips. These problems include Airline Crew Scheduling (see, e.g., Rubin [1] and Marchiori [2]) and Railway Crew Scheduling (see, e.g., Caprara [3]). Other applications are the Winner Determination Problem in combinatorial auctions, a class of sales mechanisms (Abrache et al. [4]) and Vehicle Routing (Foster et al. [5], Cacchiani et al. [6] and Bai et al. [7]). The SCP is also relevant in a number of Production Planning Problems, as described by Vemuganti in [8], where it has often to be solved in real-time.
Garey and Johnson in [9] have proven that the SCP is NP-hard in the strong sense. Exact algorithms are mostly based on branch-and-bound and branch-and-cut techniques. Etcheberry [10] utilizes sub-gradient optimization in a branch-and-bound framework. Balas and Ho [11] present a procedure based on cutting planes from conditional bounds, i.e., valid lower bounds if the constraint set is amended by certain inequalities. Beasley [12] introduces an algorithm which blends dual ascent, subgradient optimization and linear programming. In [13], Beasley and Jornsten incorporate the [12] algorithm into a Lagrangian heuristic. Fisher and Kedia [14] use continuous heuristics applied to the dual of the linear programming relaxation, obtaining lower bounds for a branch and bound algorithm. Finally, we mention Balas and Carrera [15] with their procedure based on a dynamic subgradient optimization and branch and bound. These algorithms were tested on instances involving up to 200 rows and 2000 columns in the case of Balas and Fisher’s algorithms and 400 rows and 4000 columns in [12,13,15]. Among these algorithms the fastest one is the Balas and Carrera’s algorithm, with an average time in the order of 100 seconds on small instances and 1000 seconds on largest ones (on a Cray-1S computer). Caprara [16] compared these methods with the general-purpose ILP solvers CPLEX 4.0.8 and MINTO 2.3, observing that the latter ones have execution times competitive with that of the best exact algorithms for the SCP in literature.
In most industrial applications it is important to rely on heuristic methods, in order to obtain “good” solutions quickly enough to meet the expectations of decision-makers. To this purpose, many heuristics have been presented in the literature. The classical greedy algorithm proposed by Chvatal [17] sequentially inserts the set with a minimum score in the solution. Chvatal proved that the worst case performance ratio does not exceed H ( d ) = ∑ i = 1 d 1 i , where d is the size of the largest set. More recently Kordalewski [18] described a new approximation heuristics for the SCP. His algorithm involves the same scheme of Chvatal’s procedure, but modifies the score by including a new parameter named difficulty. Wang et al. [19] presented the TS-IDS algorithm designed for deep web crawling and then Singhania [20] tested it in a resource management application. Feo and Resende [21] present a Greedy Randomized Adaptive Procedure (GRASP), in which they first construct an initial solution through an adaptive randomized greedy function and then apply a local search procedure. Haouari and Chaouachi [22] introduce PROGRES, a probabilistic greedy search heuristic which uses diversification schemes along with a learning strategy.
Regarding Lagrangian heuristics, we mention the algorithm developed by Beasley [23] and then improved by Haddadi [24], which consists of a subgradient optimization procedure coupled with a greedy algorithm and Lagrangian cost fixing. A similar procedure is designed by Caprara et al. [25], which includes three phases, subgradient, heuristic and column fixing, followed by a refining procedure. Beasley and Chu [26] propose a genetic algorithm in which a variable mutation rate and two new operators are defined. Similarly Aickelin [27] describes an indirect genetic algorithm. In this procedure actual solutions are found by an external decoder function and then an another indirect optimization layer is used to improve the result. Lastly, we mention Meta-Raps, introduced by Lan et al. [28], an iterative search procedure that uses randomness as a way to avoid local optima. All the mentioned heuristics present calculation times not compatible with real contexts. For example Caprara’s algorithm [25] produces solutions with an average computing time of about 400 seconds (on a DECstation 5000/240 CPU), if executed on non-unicost instances from Beasley’s OR Library, with 500 × 5000 and 1000 × 10000 as matrix sizes. Indeed, the difficulty of the problem leads to very high computational costs, which has led academics to research heuristics and meta-heuristics capable of obtaining good solutions, as close as possible to the optimal, in a very short time, in order to tackle real-time applications. To this respect, it is worth noting the paper by Grossman and Wool [29] in which a comparative study of eight approximation algorithms for the unicost SCP is proposed. Among these there were several greedy variants, fractional relaxations and randomized algorithms. Other investigations have been carried out over the years are: Galinier et al. [30], who study a variant of SCP, called the Large Set Covering Problem (LSCP), in which sets are possibly infinite; Lanza-Gutierrez et al. [31], which are interested in the difficulty of applying metaheuristics designed for solving continuous optimization problem to the SCP; Sundar et al. [32] who propose another algorithm to solve the SCP by combining an artificial bee colony (ABC) algorithm with local search.
In this paper, we exploit concepts from Information Theory (see Borda [33]) to improve the Chvatal’s greedy algorithm. Our purpose is to devise a heuristic able to improve the quality of the solution while retaining similar execution times to those of Chvatal’s algorithm, making it suitable for real-time applications. In particular, our algorithm, named Surprisal-Based Greedy Heuristic (SBH), introduces a surprisal measure, also known as self-information, to account partly for the problem structure while constructing the solution. We compare the proposed heuristic with three other greedy algorithms, namely the Chvatal’s greedy procedure [17], the Kordalewski’s algorithm [18] and the Altgreedy procedure [29] for unicost problems. We emphasize that SBH improves the classical Chvatal’s greedy algorithm [17] in terms of objective function and has the same scalability in computation time while the Kordalewski’s algorithm produces slightly better solutions but its computation times are much higher than those of the SBH algorithm, making it impractical for real-time applications.
The reminder of the article is organized as follows: in the Section 2 we describe the three algorithms involved in our analysis and illustrate SBH. Section 3 presents an experimental campaign which compares the greedy algorithms mentioned above. Finally, Section 4 reports some conclusions.

2. Surprisal-Based Greedy Heuristic

2.1. Problem Formulation

The SCP can be formulated as follows. In addition to the notation introduced in Section 1, let a i j be a constant equal to 1 if item i is covered by subset j and 0 otherwise. Moreover, let x j denote a binary variable defined as follows:
x j = 1 if column j is selected , 0 otherwise .
An SCP formulation is:
minimize ∑ j ∈ J c j x j
∑ j ∈ J a i j x j ≥ 1 i ∈ I ,
x j ∈ { 0 , 1 } j ∈ J ,
where (1) aims to minimize the total cost of the selected columns and (2) imposes that every row is covered by at least one column.
Algorithm 1 Chvatal’s greedy algorithm
Preprints 75479 i001

2.2. Greedy Algorithms

As we explained in the previous section, we are interested in greedy procedures in order to produce good solutions in a very short time, suitable for real-time applications. SCP greedy algorithms are sequential procedure that identify the best unselected column w.r.t. to a given score and then insert it in the solution set.
Let I j be the set of rows covered by column j and J i the set of columns covering row i. Figure 1 shows the pseudocode of the Chvatal’s greedy algorithm [17]. Each column j is given a score equal to the column cost c j divided by the number of rows I j covered by j. At each step the algorithm inserts the column j * with the minimum score in the solution set.
A variant of the Chvatal’s procedure for unicost problems was suggested by Grossman and Wool [29] with the name of Altgreedy. This algorithm is composed by two main steps: in a first phase, the column with the highest number of covered rows is inserted in the solution; then some columns are removed from the solution set according to lexicographic order as long as the number of the new uncovered rows remains smaller than the last number of new rows covered.
More recently, Kordalewski [18] proposed a new greedy heuristic which is a recursive procedure that introduces two new terms: valuation and difficulty. In the first step, valuation is computed for all columns j by dividing the number of rows, covered by j, by the column cost, like in Chvatal’s score. For each row i is defined a parameter, difficulty, which is the inverse of the sum of the valuations of the sets covering i, used to indicate how difficult it might be to cover that row. This is based on the observation that a low valuation implies a low probability of selection. Valuation v can be computed as:
v j = ∑ i ∈ I j d i c j
while difficulty d will be only updated with the new valuations.

2.3. The SBH Algorithm

In this section, we describe the Surprisal-Based Greedy Heuristic SBH, that constitutes an improvement on the classic Chvatal’s greedy procedure. As illustrated in Section 2.2, Chvatal’s algorithm assigns each column j a score equal to the unit cost to cover the rows in I j . Then it inserts iteratively the columns with the lowest score in the solution set. However, this approach is flawed when rows in I j are poorly covered. Indeed it does not consider the probability that rows i ∈ I j are covered by other columns j ′ ∈ J i . Our algorithm aims to correct this by introducing an additional term expressing the “surprisal” that a column j is selected. Therefore our score considers two aspects: the cost of a column j and the probability that the rows in I j can be covered by other columns.
To describe formally our procedure, we introduce some concepts from Information Theory. The term information refers to any message which gives details in an uncertain problem and is closely related with the probability of occurrence of an uncertain event. Information is an additive and non-negative measure which is equal to 0 when the event is certain and it grows when its probability decreases. More specifically, given an event A with probability to occur p A , the self-information I A is defined as:
I A = − log p A .
Self-information is also called surprisal because it expresses the “surprise” of seeing event A as the outcome of an experiment. In the SBH algorithm, at each stage we compute the surprisal of each column. The columns containing row i are considered independent of each other, so the probability of selecting one of them (denoted as event A ¯ ) is
p A ¯ = 1 | J i | .
Therefore the opposite event, i.e., select row i with a column different from the current one, is:
p A = 1 − 1 | J i | = | J i | − 1 | J i | .
The self-information measure contained in this event is:
I i = − log | J i | − 1 | J i | .
Thanks to the additivity of the self-information measure, surprisal of a column j can be written as:
I j = ∑ i ∈ I j I i = ∑ i ∈ I j − log | J i | − 1 | J i | .
We modify Chvatal’s cost of column j, i.e., c j | I j | , by introducing the surprisal of j to the denominator, in order to favour columns with a high self-information. In particular, at each step we select the column that minimizes:
min j ∈ J c j | I j | · I j ,
which is equivalent to
min j ∈ J c j | I j | ∏ i ∈ I j | J i | − 1 | J i | .
This formulation is the same of minimizing the probability of the intersection of independent events, each of which is to select a column, other than the current one, covering row i. Two extreme cases can occur:
  • if column j is the only one covering a row i ∈ I j , there is no surprise that it will be selected: in this case I j will be high and the modified cost (9) of column j will be 0 so that column j will be included in the solution;
  • if, on the other hand, all rows i ∈ I j are covered by a high number of other columns j ′ ∈ J i , surprisal I j will be very low. In this case, the cost attributed to column j will be greater than its Chvatal’s cost.
To illustrate this concept, we now present a numerical example. Let
( a i j ) = 1 1 0 0 0 0 0 1 1 1 1 0 1 0 1 1 , ( c j ) = 3 1 2 5
be the coverage matrix and the column cost vector. We denote by C H s c o r e i and S B H s c o r e i Chvatal and SBH score vectors, respectively, at the i-th iteration, where a hyphen is inserted to indicate that the corresponding column has already been selected. The three iterations of the Chvatal’s algorithm produce:
C H s c o r e 1 = 1 ; 1 2 ; 1 ; 5 2 C H s c o r e 2 = 3 ; − ; 2 ; 5 2 C H s c o r e 3 = − ; − ; − ; 5
and columns 2 , 3 , 4 are selected with a total cost equal to 8. On the other hand, our SBH algorithm gives:
S B H s c o r e 1 = 2 9 ; 1 6 ; 4 9 ; 0 S B H s c o r e 2 = 1 2 ; 1 6 ; 4 3 ; −
Hence, our algorithm selects only two columns (4 and 2), with a total cost of 6. Therefore, SBH outperforms Chvatal’s procedure because the latter cannot recognize the column that must necessarily be part of the solution.

3. Experimental Results

The aim of our computational experiments has been to assess the performance of the SBH heuristic procedure with respect to the other greedy heuristics proposed in literature. We implemented the heuristics in C++ and performed our experiments on a stand-alone Linux machine with 4 cores processor clocked at 3 GHz and equipped with 16 GB of RAM. The algorithm has been tested on 77 instances from Beasley’s OR Library [34]. Table 1 describes the main features of the test instances and, in particular, the column density, i.e., the percentage of ones in matrix a and column range, i.e., the minimum and maximum value of objective function coefficients. The remaining column headings are self-explanatory. Instances are divided into sets having sizes ranging from 200 × 1000 to 1000 × 10000 . Set E contains small unicost instances of size 50 × 500 . Sets 4, 5 and 6 were generated by Balas and Ho [11] and consist of small instances with low density while sets A to E come from Beasley [12]. The remaining instances (sets N R E to N R H ) are from [23]. Such instances are significantly larger and optimal solutions are not available. Similarly, Table 2 reports features of seven large scale real-word instances derived from crew-scheduling problem [25].
We compare SBH with the Chvatal’s procedure [17] (CH) and the heuristic by Kordalewski [18] (KORD). Table 3, Table 4 and Table 5 report the computational results for each instance under the following headings:
  • Instance: the name of the instance where the string before “dot” refers to the set which the instance belongs to;
  • BS: objective function value of the best known solution;
  • SOL: the objective function value of the best solution determined by the heuristic;
  • TIME: the execution time in seconds;
  • GAP: percentage gap between BS and the SOL value, i.e.,
    G A P = 100 × S O L − B S B S
Columns “SBH vs CH” and “SBH vs KORD” report the percentage improvement of SBH w.r.t. CH and KORD, respectively. Regarding Table 3 it is worth noting that our heuristic, compared to Chvatal’s greedy procedure, has a smaller gap ranging from 12.65 % to 11.03 % , with an average improvement of 1.42 % . Among these instances, SBH provides a better solution than [17] in 19 out of 24 instances problems. We point out that the best objective function value is given by the Kordalewski’s algorithm which is slightly better than our SBH procedure (by only 0.59 % ), but is slower.
Similar observations can be done for Table 4. Here, SBH performs better even though it differs from the Kordalewski algorithm only by 0.07 % . Comparing SBH with CH, it is worth noting that only in 4 instances out of 45 SBH obtained a worse solution. SBH comes close to the optimal solution with an average gap of 10.69 % and is better than CH by 2.62 % . Execution time of all these instances averages 0.113 seconds for CH, 0.230 seconds for the Kordalewski procedure and 0.564 seconds for SBH. Increasing the size of the instances (which is the case of the rail problems), the Kordalewski’s algorithm becomes much slower. Consequently, on these instances we compare only the CH and SBH heuristics. On these instances, our SBH algorithm provides an average objective function improvement of 5.82 % with comparable execution times.
We now compare the algorithms on unicost instances, obtained by setting the cost of all columns equal to 1, like in Grossman and Wool’s paper [29]. Results are showed in Tables Table 6, Table 7 and Table 8, where the subdivision of instances is the same as before. The additional column “SBH vs ALTG” reports the percentage improvement of SBH w.r.t. ALTG algorithm. Looking at Table 6, it worth noting that the heuristic which performs better is that of Kordalewski. Indeed, our heuristic SBH is worst than KORD of about 3.49 % while it is better then the other two greedy procedures with a gap of 1.15 % . Here, computation times are all comparable and range between 0.002 and 0.007 seconds. SBH improves its performance on larger instances, as shown in Table 7 and Table 8. In particular, it yields an average improvement of 1.50 % on CH and ALTG ([29]) on s c p instances, and respectively 1.39 % and 12.97 % on r a i l instances. Comparing SBH and K O R D on the s c p instances, we observe that they are very similar with a 0.07 % improvement. On the largest instances (Table 8) it emerges that the computational time of KORD makes it impractical for real-time applications.

4. Conclusions

In this paper, we have proposed a new greedy heuristic, SBH, an improvement of the classical greedy algorithm proposed by Chvatal [17]. We showed that in the vast majority of the test instances SBH generates better solutions then other greedy algorithms such as the Kordalewski’s algorithm [18] and Altgreedy [29]. Computational tests have also shown that the Kordalewski’s algorithm is not suitable for real-time application since it presents very large execution times while our SBH algorithm runs in few seconds even on very large instances.

Author Contributions

Conceptualization, G.G. and E.G.; methodology and validation, T.A.; formal analysis and software, D.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

This work was partly supported by Ministero dell’Università e della Ricerca (MUR) of Italy. This support is gratefully acknowledged (“Decreto Ministeriale n. 1062 del 10-08-2021. PON Ricerca e Innovazione 14-20 nuove risorse per contratti di ricerca su temi dell’innovazione" contract number 12-I-13147-10).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rubin, J. A technique for the solution of massive set covering problems, with application to airline crew scheduling. Transp. Sci. 1973, 7, 34–48. [Google Scholar]
  2. Marchiori, E.; Steenbeek, A. An evolutionary algorithm for large scale set covering problems with application to airline crew scheduling. In Proceedings of the Real-World Applications of Evolutionary Computing: EvoWorkshops 2000: EvoIASP, EvoSCONDI, EvoTel, EvoSTIM, EvoRob, and EvoFlight Edinburgh, Scotland, UK, April 17, 2000 Proceedings. Springer, 2000, pp. 370–384.
  3. Caprara, A.; Fischetti, M.; Toth, P.; Vigo, D.; Guida, P.L. Algorithms for railway crew management. Math. Program. 1997, 79, 125–141. [Google Scholar] [CrossRef]
  4. Abrache, J.; Crainic, T.G.; Gendreau, M.; Rekik, M. Combinatorial auctions. Ann. Oper. Res. 2007, 153, 131–164. [Google Scholar] [CrossRef]
  5. Foster, B.A.; Ryan, D.M. An integer programming approach to the vehicle scheduling problem. J. Oper. Res. Soc. 1976, 27, 367–384. [Google Scholar] [CrossRef]
  6. Cacchiani, V.; Hemmelmayr, V.C.; Tricoire, F. A set-covering based heuristic algorithm for the periodic vehicle routing problem. Discret. Appl. Math. 2014, 163, 53–64. [Google Scholar] [CrossRef] [PubMed]
  7. Bai, R.; Xue, N.; Chen, J.; Roberts, G.W. A set-covering model for a bidirectional multi-shift full truckload vehicle routing problem. Transp. Res. Part Methodol. 2015, 79, 134–148. [Google Scholar]
  8. Vemuganti, R.R. Applications of set covering, set packing and set partitioning models: A survey. In Handbook of Combinatorial Optimization: Volume1–3; 1998; pp. 573–746. [Google Scholar]
  9. Garey, M.R.; Johnson, D.S. Computers and intractability; freeman: San Francisco, 1979; Volume 174. [Google Scholar]
  10. Etcheberry, J. The set-covering problem: A new implicit enumeration algorithm. Operations research 1977, 25, 760–772. [Google Scholar] [CrossRef]
  11. Balas, E.; Ho, A. Set covering algorithms using cutting planes, heuristics, and subgradient optimization: a computational study; Springer, 1980. [Google Scholar]
  12. Beasley, J.E. An algorithm for set covering problem. Eur. J. Oper. Res. 1987, 31, 85–93. [Google Scholar]
  13. Beasley, J.E.; Jörnsten, K. Enhancing an algorithm for set covering problems. Eur. J. Oper. Res. 1992, 58, 293–300. [Google Scholar] [CrossRef]
  14. Fisher, M.L.; Kedia, P. Optimal solution of set covering/partitioning problems using dual heuristics. Manag. Sci. 1990, 36, 674–688. [Google Scholar] [CrossRef]
  15. Balas, E.; Carrera, M.C. A dynamic subgradient-based branch-and-bound procedure for set covering. Oper. Res. 1996, 44, 875–890. [Google Scholar]
  16. Caprara, A.; Toth, P.; Fischetti, M. Algorithms for the set covering problem. Ann. Oper. Res. 2000, 98, 353–371. [Google Scholar] [CrossRef]
  17. Chvatal, V. A greedy heuristic for the set-covering problem. Math. Oper. Res. 1979, 4, 233–235. [Google Scholar] [CrossRef]
  18. Kordalewski, D. New greedy heuristics for set cover and set packing. arXiv 2013, arXiv:1305.3584. [Google Scholar]
  19. Wang, Y.; Lu, J.; Chen, J. Ts-ids algorithm for query selection in the deep web crawling. Web Technologies and Applications: 16th Asia-Pacific Web Conference, APWeb 2014, Changsha, China, September 5-7, 2014. Proceedings 16. Springer, 2014, pp. 189–200. 5 September.
  20. Singhania, S. Variations in Greedy Approach to Set Covering Problem. PhD thesis, University of Windsor, Canada, 2019. [Google Scholar]
  21. Feo, T.A.; Resende, M.G. Greedy randomized adaptive search procedures. J. Glob. Optim. 1995, 6, 109–133. [Google Scholar]
  22. Haouari, M.; Chaouachi, J. A probabilistic greedy search algorithm for combinatorial optimisation with application to the set covering problem. J. Oper. Res. Soc. 2002, 53, 792–799. [Google Scholar] [CrossRef]
  23. Beasley, J.E. A lagrangian heuristic for set-covering problems. Nav. Res. Logist. (NRL) 1990, 37, 151–164. [Google Scholar]
  24. Haddadi, S. Simple Lagrangian heuristic for the set covering problem. Eur. J. Oper. Res. 1997, 97, 200–204. [Google Scholar]
  25. Caprara, A.; Fischetti, M.; Toth, P. A heuristic method for the set covering problem. Oper. Res. 1999, 47, 730–743. [Google Scholar] [CrossRef]
  26. Beasley, J.E.; Chu, P.C. A genetic algorithm for the set covering problem. Eur. J. Oper. Res. 1996, 94, 392–404. [Google Scholar] [CrossRef]
  27. Aickelin, U. An indirect genetic algorithm for set covering problems. J. Oper. Res. Soc. 2002, 53, 1118–1126. [Google Scholar]
  28. Lan, G.; DePuy, G.W.; Whitehouse, G.E. An effective and simple heuristic for the set covering problem. Eur. J. Oper. Res. 2007, 176, 1387–1403. [Google Scholar]
  29. Wool, A.; Grossman, T. Computational experience with approxima-tion algorithms for the set covering problem; Technical report, Technical Report CS94-25; Weizmann Institute of Science, 1994. [Google Scholar]
  30. Galinier, P.; Hertz, A. Solution Techniques for the Large Set Covering Problem. Les Cahiers du GERAD, ISSN 2003, 7112440, 1–19. [Google Scholar] [CrossRef]
  31. Lanza-Gutierrez, J.M.; Crawford, B.; Soto, R.; Berrios, N.; Gomez-Pulido, J.A.; Paredes, F. Analyzing the effects of binarization techniques when solving the set covering problem through swarm optimization. Expert Syst. Appl. 2017, 70, 67–82. [Google Scholar] [CrossRef]
  32. Sundar, S.; Singh, A. A hybrid heuristic for the set covering problem. Oper. Res. 2012, 12, 345–365. [Google Scholar] [CrossRef]
  33. Borda, M. Fundamentals in information theory and coding; Springer Science & Business Media, 2011. [Google Scholar]
  34. Beasley, J.E. OR-Library: distributing test problems by electronic mail. J. Oper. Res. Soc. 1990, 41, 1069–1072. [Google Scholar] [CrossRef]
Table 1. Instances features: sets 4-6, A-E and NRE-NRH.
Table 1. Instances features: sets 4-6, A-E and NRE-NRH.
Set |I| |J| Density Range Count
4 200 1000 2% 1-100 10
5 200 2000 2% 1-100 10
6 200 1000 5% 1-100 5
A 300 3000 2% 1-100 5
B 300 3000 5% 1-100 5
C 400 4000 2% 1-100 5
D 400 4000 5% 1-100 5
E 50 500 20% 1-100 5
NRE 500 5000 10% 1-100 5
NRF 500 5000 20% 1-100 5
NRG 1000 10000 2% 1-100 5
NRH 1000 10000 5% 1-100 5
Table 2. Instances features: rail sets.
Table 2. Instances features: rail sets.
Instance |I| |J| Range Density
rail516 516 47311 1-2 1.3%
rail582 582 55515 1-2 1.2%
rail2536 2536 1081841 1-2 0.4%
rail507 507 63009 1-2 1.3%
rail2586 2586 920683 1-2 0.3%
rail4284 4284 1092610 1-2 0.2%
rail4872 4872 968672 1-2 0.2%
Table 3. Results for instance sets 4 − 6
Table 3. Results for instance sets 4 − 6
Instance BS CH KORD SBH SBH vs CH SBH vs KORD
SOL TIME GAP SOL TIME GAP SOL TIME GAP
4.1 429 463 0.002 7.93% 458 0.011 6.76% 471 0.002 9.79% 1.73% 2.84%
4.2 512 582 0.002 13.67% 569 0.010 11.13% 587 0.002 14.65% 0.86% 3.16%
4.3 516 598 0.002 15.89% 576 0.011 11.63% 577 0.003 11.82% -3.51% 0.17%
4.4 494 548 0.002 10.93% 540 0.009 9.31% 542 0.002 9.72% -1.09% 0.37%
4.5 512 577 0.002 12.70% 572 0.009 11.72% 571 0.003 11.52% -1.04% -0.17%
4.6 560 615 0.002 9.82% 603 0.008 7.68% 599 0.002 6.96% -2.60% -0.66%
4.7 430 476 0.003 10.70% 480 0.008 11.63% 474 0.002 10.23% -0.42% -1.25%
4.8 492 533 0.003 8.33% 520 0.009 5.69% 553 0.002 12.40% 3.75% 6.35%
4.9 641 747 0.003 16.54% 721 0.010 12.48% 723 0.003 12.79% -3.21% 0.28%
4.10 514 556 0.002 8.17% 551 0.010 7.20% 548 0.002 6.61% -1.44% -0.54%
5.1 253 289 0.005 14.23% 289 0.016 14.23% 289 0.005 14.23% 0.00% 0.00%
5.2 302 348 0.005 15.23% 345 0.019 14.24% 337 0.006 11.59% -3.16% -2.32%
5.3 226 246 0.004 8.85% 246 0.017 8.85% 243 0.005 7.52% -1.22% -1.22%
5.4 242 265 0.004 9.50% 264 0.016 9.09% 266 0.004 9.92% 0.38% 0.76%
5.5 211 236 0.004 11.85% 228 0.016 8.06% 230 0.004 9.00% -2.54% 0.88%
5.6 213 251 0.004 17.84% 249 0.016 16.90% 245 0.004 15.02% -2.39% -1.61%
5.7 293 326 0.004 11.26% 314 0.017 7.17% 322 0.004 9.90% -1.23% 2.55%
5.8 288 323 0.004 12.15% 316 0.016 9.72% 315 0.005 9.38% -2.48% -0.32%
5.9 279 312 0.004 11.83% 304 0.015 8.96% 304 0.005 8.96% -2.56% 0.00%
5.10 265 293 0.003 10.57% 285 0.016 7.55% 286 0.008 7.92% -2.39% 0.35%
6.1 138 159 0.004 15.22% 156 0.010 13.04% 156 0.006 13.04% -1.89% 0.00%
6.2 146 170 0.004 16.44% 164 0.009 12.33% 167 0.007 14.38% -1.76% 1.83%
6.3 145 161 0.004 11.03% 152 0.009 4.83% 163 0.006 12.41% 1.24% 7.24%
6.4 131 149 0.004 13.74% 147 0.009 12.21% 138 0.007 5.34% -7.38% -6.12%
6.5 161 196 0.004 21.74% 190 0.009 18.01% 194 0.006 20.50% -1.02% 2.11%
Average 0.003 12.65% 0.012 10.42% 0.004 11.03% -1.42% 0.59%
Table 4. Results for instance sets s c p
Table 4. Results for instance sets s c p
Instance BS CH KORD SBH SBH vs CH SBH vs KORD
SOL TIME GAP SOL TIME GAP SOL TIME GAP
A.1 253 288 0.008 13.83% 279 0.033 10.28% 281 0.012 11.07% -2.43% 0.72%
A.2 252 284 0.008 12.70% 276 0.035 9.52% 282 0.011 11.90% -0.70% 2.17%
A.3 232 270 0.008 16.38% 253 0.037 9.05% 253 0.012 9.05% -6.30% 0.00%
A.4 234 278 0.008 18.80% 265 0.037 13.25% 273 0.012 16.67% -1.80% 3.02%
A.5 236 271 0.008 14.83% 255 0.033 8.05% 258 0.012 9.32% -4.80% 1.18%
B.1 69 77 0.019 11.59% 75 0.044 8.70% 75 0.034 8.70% -2.60% 0.00%
B.2 76 86 0.018 13.16% 84 0.036 10.53% 86 0.051 13.16% 0.00% 2.38%
B.3 80 89 0.019 11.25% 85 0.039 6.25% 85 0.038 6.25% -4.49% 0.00%
B.4 79 89 0.021 12.66% 89 0.046 12.66% 87 0.035 10.13% -2.25% -2.25%
B.5 72 78 0.019 8.33% 78 0.037 8.33% 79 0.052 9.72% 1.28% 1.28%
C.1 227 258 0.014 13.66% 254 0.059 11.89% 255 0.028 12.33% -1.16% 0.39%
C.2 219 258 0.017 17.81% 251 0.061 14.61% 249 0.023 13.70% -3.49% -0.80%
C.3 243 276 0.014 13.58% 271 0.059 11.52% 270 0.021 11.11% -2.17% -0.37%
C.4 219 257 0.014 17.35% 252 0.059 15.07% 256 0.030 16.89% -0.39% 1.59%
C.5 215 233 0.013 8.37% 229 0.060 6.51% 230 0.026 6.98% -1.29% 0.44%
D.1 60 74 0.049 23.33% 68 0.066 13.33% 71 0.086 18.33% -4.05% 4.41%
D.2 66 74 0.042 12.12% 70 0.070 6.06% 71 0.088 7.58% -4.05% 1.43%
D.3 72 83 0.037 15.28% 81 0.081 12.50% 79 0.104 9.72% -4.82% -2.47%
D.4 62 71 0.042 14.52% 67 0.071 8.06% 65 0.085 4.84% -8.45% -2.99%
D.5 61 69 0.037 13.11% 70 0.070 14.75% 74 0.098 21.31% 7.25% 5.71%
E.1 5 5 0.002 0.00% 5 0.001 0.00% 5 0.005 0.00% 0.00% 0.00%
E.2 5 5 0.003 0.00% 6 0.002 20.00% 5 0.003 0.00% 0.00% -16.67%
E.3 5 5 0.002 0.00% 5 0.002 0.00% 5 0.003 0.00% 0.00% 0.00%
E.4 5 6 0.002 20.00% 5 0.001 0.00% 5 0.005 0.00% -16.67% 0.00%
E.5 5 5 0.002 0.00% 5 0.002 0.00% 5 0.003 0.00% 0.00% 0.00%
NRE.1 29 30 0.150 3.45% 32 0.217 10.34% 30 0.772 3.45% 0.00% -6.25%
NRE.2 30 36 0.163 20.00% 34 0.202 13.33% 35 0.836 16.67% -2.78% 2.94%
NRE.3 27 31 0.145 14.81% 31 0.204 14.81% 30 0.661 11.11% -3.23% -3.23%
NRE.4 28 32 0.153 14.29% 33 0.211 17.86% 31 0.622 10.71% -3.13% -6.06%
NRE.5 28 33 0.151 17.86% 31 0.202 10.71% 32 0.579 14.29% -3.03% 3.23%
NRF.1 14 16 0.324 14.29% 15 0.312 7.14% 16 2.216 14.29% 0.00% 6.67%
NRF.2 15 16 0.316 6.67% 16 0.369 6.67% 16 2.544 6.67% 0.00% 0.00%
NRF.3 14 17 0.318 21.43% 15 0.328 7.14% 16 2.346 14.29% -5.88% 6.67%
NRF.4 14 17 0.322 21.43% 16 0.318 14.29% 16 2.510 14.29% -5.88% 0.00%
NRF.5 13 16 0.320 23.08% 15 0.312 15.38% 15 2.465 15.38% -6.25% 0.00%
NRG.1 176 203 0.120 15.34% 197 0.545 11.93% 197 0.287 11.93% -2.96% 0.00%
NRG.2 154 182 0.136 18.18% 176 0.512 14.29% 171 0.297 11.04% -6.04% -2.84%
NRG.3 166 192 0.123 15.66% 186 0.549 12.05% 186 0.322 12.05% -3.13% 0.00%
NRG.4 168 191 0.137 13.69% 191 0.518 13.69% 193 0.307 14.88% 1.05% 1.05%
NRG.5 168 194 0.120 15.48% 188 0.528 11.90% 190 0.312 13.10% -2.06% 1.06%
NRH.1 63 76 0.330 20.63% 74 0.826 17.46% 72 1.453 14.29% -5.26% -2.70%
NRH.2 63 74 0.340 17.46% 72 0.824 14.29% 74 1.432 17.46% 0.00% 2.78%
NRH.3 59 65 0.335 10.17% 71 0.785 20.34% 67 1.516 13.56% 3.08% -5.63%
NRH.4 58 69 0.322 18.97% 65 0.784 12.07% 65 1.610 12.07% -5.80% 0.00%
NRH.5 55 63 0.327 14.55% 61 0.779 10.91% 61 1.399 10.91% -3.17% 0.00%
Average 0.113 13.78% 0.230 10.83% 0.564 10.69% -2.62% -0.07%
Table 5. Results for instance set r a i l .
Table 5. Results for instance set r a i l .
Instance BS CH SBH SBH vs CH
SOL TIME GAP SOL TIME GAP
rail507 174 216 0.193 24.14% 199 0.277 14.37% -7.87%
rail516 182 204 0.160 12.09% 196 0.211 7.69% -3.92%
rail582 211 251 0.214 18.96% 240 0.310 13.74% -4.38%
rail2536 691 894 7.276 29.38% 828 10.206 19.83% -7.38%
rail2586 952 1166 5.521 22.48% 1089 8.224 14.39% -6.60%
rail4284 1065 1376 8.284 29.20% 1311 12.165 23.10% -4.72%
rail4872 1538 1902 7.318 23.67% 1790 10.199 16.38% -5.89%
Average 4.138 22.84% 5.942 15.64% -5.82%
Table 6. Results for unicost instance sets 4 − 6
Table 6. Results for unicost instance sets 4 − 6
Instance CH ALTG KORD SBH SBH vs CH SBH vs ALTG SBH vs KORD
SOL TIME SOL TIME SOL TIME SOL TIME
4.1 41 0.003 41 0.001 41 0.005 42 0.003 2.44% 2.44% 2.44%
4.2 41 0.002 41 0.001 38 0.004 42 0.002 2.44% 2.44% 10.53%
4.3 43 0.002 43 0.001 39 0.004 43 0.002 0.00% 0.00% 10.26%
4.4 44 0.002 44 0.001 42 0.005 45 0.002 2.27% 2.27% 7.14%
4.5 44 0.002 44 0.001 40 0.004 41 0.002 -6.82% -6.82% 2.50%
4.6 43 0.003 43 0.001 40 0.006 42 0.002 -2.33% -2.33% 5.00%
4.7 43 0.002 43 0.001 41 0.005 43 0.003 0.00% 0.00% 4.88%
4.8 42 0.002 42 0.001 40 0.005 39 0.003 -7.14% -7.14% -2.50%
4.9 42 0.002 42 0.001 42 0.005 42 0.003 0.00% 0.00% 0.00%
4.10 43 0.002 43 0.001 41 0.006 41 0.002 -4.65% -4.65% 0.00%
5.1 37 0.007 37 0.002 37 0.009 38 0.005 2.70% 2.70% 2.70%
5.2 38 0.005 38 0.004 36 0.008 37 0.007 -2.63% -2.63% 2.78%
5.3 37 0.004 37 0.003 35 0.012 38 0.005 2.70% 2.70% 8.57%
5.4 39 0.003 39 0.002 36 0.008 37 0.004 -5.13% -5.13% 2.78%
5.5 37 0.004 37 0.002 37 0.008 37 0.007 0.00% 0.00% 0.00%
5.6 40 0.004 40 0.002 36 0.008 37 0.005 -7.50% -7.50% 2.78%
5.7 38 0.005 38 0.002 37 0.008 36 0.006 -5.26% -5.26% -2.70%
5.8 39 0.005 39 0.002 37 0.010 39 0.005 0.00% 0.00% 5.41%
5.9 38 0.003 38 0.002 37 0.009 39 0.005 2.63% 2.63% 5.41%
5.10 39 0.003 39 0.002 36 0.009 38 0.004 -2.56% -2.56% 5.56%
6.1 23 0.004 23 0.002 22 0.005 23 0.006 0.00% 0.00% 4.55%
6.2 22 0.005 22 0.003 21 0.005 21 0.006 -4.55% -4.55% 0.00%
6.3 23 0.005 23 0.002 23 0.005 23 0.007 0.00% 0.00% 0.00%
6.4 22 0.004 22 0.002 22 0.005 23 0.008 4.55% 4.55% 4.55%
6.5 23 0.005 23 0.002 22 0.006 23 0.006 0.00% 0.00% 4.55%
Average 0.003 0.002 0.007 0.004 -1.15% -1.15% 3.49%
Table 7. Results for unicost instance sets s c p
Table 7. Results for unicost instance sets s c p
Instance CH ALTG KORD SBH SBH vs CH SBH vs ALTG SBH vs KORD
SOL TIME SOL TIME SOL TIME SOL TIME
A.1 42 0.009 42 0.004 41 0.019 43 0.011 2.38% 2.38% 4.88%
A.2 42 0.008 42 0.005 41 0.020 42 0.011 0.00% 0.00% 2.44%
A.3 43 0.009 43 0.004 41 0.020 42 0.011 -2.33% -2.33% 2.44%
A.4 41 0.008 41 0.005 39 0.018 41 0.011 0.00% 0.00% 5.13%
A.5 43 0.007 43 0.004 41 0.017 41 0.011 -4.65% -4.65% 0.00%
B.1 24 0.019 24 0.010 23 0.027 23 0.044 -4.17% -4.17% 0.00%
B.2 23 0.020 23 0.013 24 0.028 22 0.038 -4.35% -4.35% -8.33%
B.3 23 0.019 23 0.011 23 0.026 23 0.036 0.00% 0.00% 0.00%
B.4 24 0.024 24 0.011 23 0.031 23 0.037 -4.17% -4.17% 0.00%
B.5 25 0.021 25 0.011 24 0.029 24 0.038 -4.00% -4.00% 0.00%
C.1 47 0.015 47 0.008 46 0.041 46 0.023 -2.13% -2.13% 0.00%
C.2 47 0.018 47 0.009 47 0.037 45 0.023 -4.26% -4.26% -4.26%
C.3 47 0.017 47 0.007 46 0.038 46 0.023 -2.13% -2.13% 0.00%
C.4 46 0.013 46 0.008 45 0.036 46 0.023 0.00% 0.00% 2.22%
C.5 47 0.013 47 0.012 46 0.040 46 0.023 -2.13% -2.13% 0.00%
D.1 27 0.036 27 0.020 26 0.047 27 0.078 0.00% 0.00% 3.85%
D.2 26 0.037 26 0.021 26 0.048 27 0.082 3.85% 3.85% 3.85%
D.3 27 0.040 27 0.020 27 0.049 26 0.077 -3.70% -3.70% -3.70%
D.4 26 0.038 26 0.020 26 0.048 27 0.080 3.85% 3.85% 3.85%
D.5 27 0.039 27 0.020 26 0.050 27 0.091 0.00% 0.00% 3.85%
E.1 5 0.002 5 0.001 5 0.001 5 0.003 0.00% 0.00% 0.00%
E.2 5 0.002 5 0.001 6 0.001 5 0.004 0.00% 0.00% -16.67%
E.3 5 0.002 5 0.001 5 0.001 5 0.003 0.00% 0.00% 0.00%
E.4 6 0.002 6 0.001 5 0.001 5 0.004 -16.67% -16.67% 0.00%
E.5 5 0.002 5 0.001 5 0.001 5 0.003 0.00% 0.00% 0.00%
NRE.1 18 0.144 18 0.089 18 0.178 18 0.577 0.00% 0.00% 0.00%
NRE.2 18 0.150 18 0.088 18 0.188 18 0.570 0.00% 0.00% 0.00%
NRE.3 18 0.145 18 0.089 18 0.172 18 0.560 0.00% 0.00% 0.00%
NRE.4 18 0.142 18 0.087 18 0.174 18 0.552 0.00% 0.00% 0.00%
NRE.5 18 0.148 18 0.088 18 0.180 18 0.551 0.00% 0.00% 0.00%
NRF.1 11 0.311 11 0.201 11 0.321 11 2.513 0.00% 0.00% 0.00%
NRF.2 11 0.309 11 0.214 11 0.315 11 2.609 0.00% 0.00% 0.00%
NRF.3 11 0.307 11 0.211 11 0.309 11 2.560 0.00% 0.00% 0.00%
NRF.4 11 0.299 11 0.203 11 0.339 11 2.313 0.00% 0.00% 0.00%
NRF.5 11 0.309 11 0.204 11 0.306 11 2.320 0.00% 0.00% 0.00%
NRG.1 65 0.116 65 0.077 64 0.463 64 0.262 -1.54% -1.54% 0.00%
NRG.2 65 0.115 65 0.125 65 0.402 65 0.258 0.00% 0.00% 0.00%
NRG.3 66 0.125 66 0.110 64 0.442 64 0.273 -3.03% -3.03% 0.00%
NRG.4 66 0.124 66 0.136 65 0.437 65 0.279 -1.52% -1.52% 0.00%
NRG.5 66 0.115 66 0.076 64 0.490 64 0.271 -3.03% -3.03% 0.00%
NRH.1 36 0.340 36 0.217 36 0.712 35 1.460 -2.78% -2.78% -2.78%
NRH.2 36 0.327 36 0.247 35 0.658 35 1.424 -2.78% -2.78% 0.00%
NRH.3 36 0.323 36 0.236 35 0.640 35 1.458 -2.78% -2.78% 0.00%
NRH.4 36 0.334 36 0.216 35 0.653 35 1.436 -2.78% -2.78% 0.00%
NRH.5 36 0.324 36 0.211 35 0.644 35 1.427 -2.78% -2.78% 0.00%
Average 0.110 0.075 0.193 0.544 -1.50% -1.50% -0.07%
Table 8. Results for unicost instance sets r a i l
Table 8. Results for unicost instance sets r a i l
Instance CH ALTG KORD SBH SBH vs CH SBH vs ALTG SBH vs KORD
SOL TIME SOL TIME SOL TIME SOL TIME
rail2536 894 7.263 975 5.561 821 126.091 847 10.030 -5.26% -13.13% 3.17%
rail2586 1166 5.562 1253 4.539 1112 172.448 1139 7.300 -2.32% -9.10% 2.43%
rail4284 1376 8.372 1563 6.637 1285 260.187 1339 12.740 -2.69% -14.33% 4.20%
rail4872 1902 7.399 2137 6.178 1848 315.863 1860 11.312 -2.21% -12.96% 0.65%
rail507 216 0.193 237 0.144 211 1.276 211 0.267 -2.31% -10.97% 0.00%
rail516 204 0.156 259 0.121 232 1.432 211 0.218 3.43% -18.53% -9.05%
rail582 251 0.215 289 0.148 265 1.729 255 0.300 1.59% -11.76% -3.77%
Average 4.166 3.333 125.575 6.024 -1.39% -12.97% -0.34%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated