Complete Bifurcation Analysis of the Vilnius Chaotic Oscillator

The paper is dedicated to the numerical and experimental study of nonlinear oscillations exhibited by the Vilnius chaotic generator. The need for practical applicability of the mentioned generator in chaotic communication systems defined the necessity to study the operation of the circuit in a wide parameter range. The bifurcation maps and corresponding one-parameter diagrams, obtained and analysed utilising the Method of Complete Bifurcation Groups, reveal the complex nonlinear dynamics and regions of robust chaotic oscillations. Laboratory experiments allow the verification of the numerical results and identification of the most practically relevant phenomena.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The Internet of Things (IoT) rapid expansion creates new challenges to electronic circuit design. Numerous applications like environmental sensing and healthcare monitoring impose the need for long-term autonomous operation of electronic modules. In [1,2], the authors conclude that batteries are the most promising energy sources for IoT applications, particularly wireless sensor networks. Energy harvesting techniques suffer from insufficient power levels and are often unpredictable and unable to charge the power elements remotely [2]. This, in turn, implies DC voltage levels available to power electronic circuits may change during the operation of the sensor mode in a relatively wide range. The requirement of long autonomous operation of IoT devices also dictates additional restrictions on the quality of the used components that could deteriorate during long-term operation. Thus, the unsupervised sensors should ensure the data collection functionality while safely keeping and transferring the data for a wide range of parameter values.

The use of chaotic signals generated by various electronic systems has been growing for the last several decades, and it is considered a major candidate for future technologies. Chaotic oscillators have found applications in communications [3,4,5], random number generators [6], chaotic computing [7] and other fields. The main requirements for the practical application of a chaotic oscillator are the circuit’s simplicity, the variety of different chaotic modes, and robustness. When the chaotic oscillators are implemented as part of the embedded communication system, generating signals for data-security applications, they are susceptible to system parameter changes [8]. The “butterfly effect” [9] manifests as a sensitive dependence of the chaotic system’s dynamics on the initial conditions, leading to undesirable transitions from the chaotic to period modes and vice versa. This uncertain behaviour could compromise the security of the whole chaos-based data transmission system. Thus, it is crucial to determine the dynamics of the nonlinear system in a wide parameter range and ensure a robust chaotic operation.

The current study is dedicated to a comprehensive analysis of the Vilnius chaos oscillator. First presented in 2004 [10], this circuit has been intended to become a tool to demonstrate the complex dynamics of simple electronic systems to students in the lab. However, several attempts have been made to adapt this oscillator to practical IoT applications [5,11]. It has been demonstrated that the oscillator could be modified for utilisation as a source of chaotic oscillations in secure data transmission systems. Thus, there is a need to study the nonlinear dynamics of the mentioned system at different voltage levels and consider the possible component variations while ensuring robust chaotic operation.

The numerical study is based on one of the most advanced methodologies for the detailed analysis of the nonlinear dynamics of chaotic systems – The Method of Complete Bifurcation Groups (MCBG), first presented in [12]. The method, based on the concepts of the periodic skeleton, bifurcation groups, and rare attractors [13], allows the numerical detection and continuation of all stable and unstable periodic modes of the dynamical systems. The bifurcation group nT has been defined as a complete set of all interconnected stable and unstable regimes, starting from period n. Introducing the concept of a bifurcation group allows the simplification and structuring of the analysis. The regions of robust chaos are characterised by the appearance of unstable-periodic infinitiums (UPI)- subgroups of only unstable periodic orbits [14]. It has been proved that the MCBG allows the implementation of the most comprehensive analyses of the system’s dynamics, as parameters are varied.

This paper is organised as follows. The second section describes the schematic and analytical model of the Vilnius oscillator. The third section presents the numerical analysis of the system dynamics as various parameters are varied. The fourth section is devoted to experimental verification of the numerically obtained results. The last section provides the conclusions and suggestions on the applicability of this type of chaotic oscillator.

2. Vilnius oscillator model

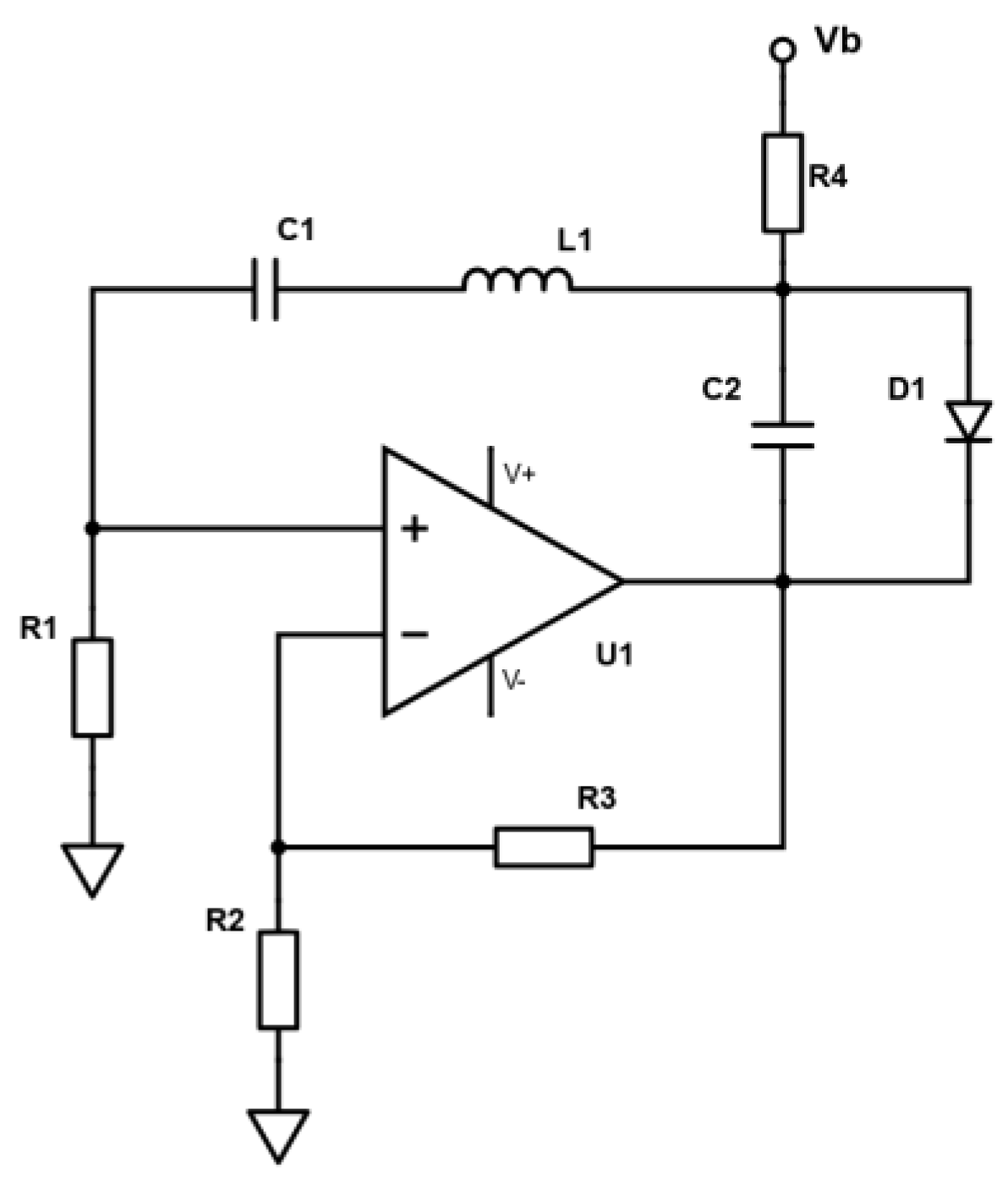
The schematic of the Vilnius chaotic oscillator is depicted in Figure 1. The circuit is easy to implement and modify, as it includes no unique components, just the off-the-shelf operational amplifier, diode, capacitors, inductors and resistors.

This oscillator exhibits complex behaviour under specific component parameters despite being relatively simple. The frequency of the waveforms observed in the circuit is determined by reactive components C₁, L₁, and C₂. Thus, it is possible to adapt the scheme for the frequency range of interest. Diode D₁ is the mandatory nonlinear element needed for the chaotic oscillator. It can be a general-purpose silicon diode like 1N4148 or Schottky diode. Also, no special requirements apply to the operational amplifier. A reader can use, for example, an LTspice computer simulation program to get a quick insight into the circuit’s operation and observe typical waveforms. However, even such a brief study reveals that the number of parameters that affect the system’s dynamics is too large to adopt a trial-and-error approach when the robust chaos is of interest. That is why the study of nonlinear dynamics using bifurcation diagrams must be performed to identify the regions of chaotic behaviour for further practical implementation of the Vilnius oscillator.

In this study, a system of equations initially developed in [10] is used to describe the dynamics of the oscillator:

\frac{d x}{d t} = y,

(1)

\frac{d y}{d t} = a y - x - z,

(2)

ε \frac{d z}{d t} = b + y - c (e^{z} - 1),

(3)

where the dimensionless variables and parameters suggested for conventional numerical analysis are:

x = \frac{V_{C 1} \cdot q}{k_{B} \cdot T}; y = \frac{I_{L 1} \cdot q \cdot \sqrt{\frac{L}{C_{1}}}}{k_{B} \cdot T}; z = \frac{V_{C 2} \cdot q}{k_{B} \cdot T},

(4)

a = \frac{(k - 1) \cdot R_{1}}{\sqrt{\frac{L}{C_{1}}}}; b = \frac{I_{R 4} \cdot q \sqrt{\frac{L}{C_{1}}}}{k_{B} \cdot T}; c = \frac{I_{S} \cdot q \cdot \sqrt{\frac{L}{C_{1}}}}{k_{B} \cdot T}; ε = \frac{C_{2}}{C_{1}} .

(5)

To express the current through R₄, it is assumed that R₄>> R₁_, so according to Ohm’s law:

I_{R 4} = \frac{V_{b}}{R_{4}} .

(6)

The gain of the non-inverting amplifier is expressed as:

k = 1 + \frac{R_{3}}{R_{2}} .

(7)

k_B is Boltzmann’s constant; T is the temperature in Kelvins.

The system’s parameters of interest are a, b and ε, which could be adjusted by input voltage, variable capacitor C₂ and variable resistors R₁, R₂, R₃, and R₄.

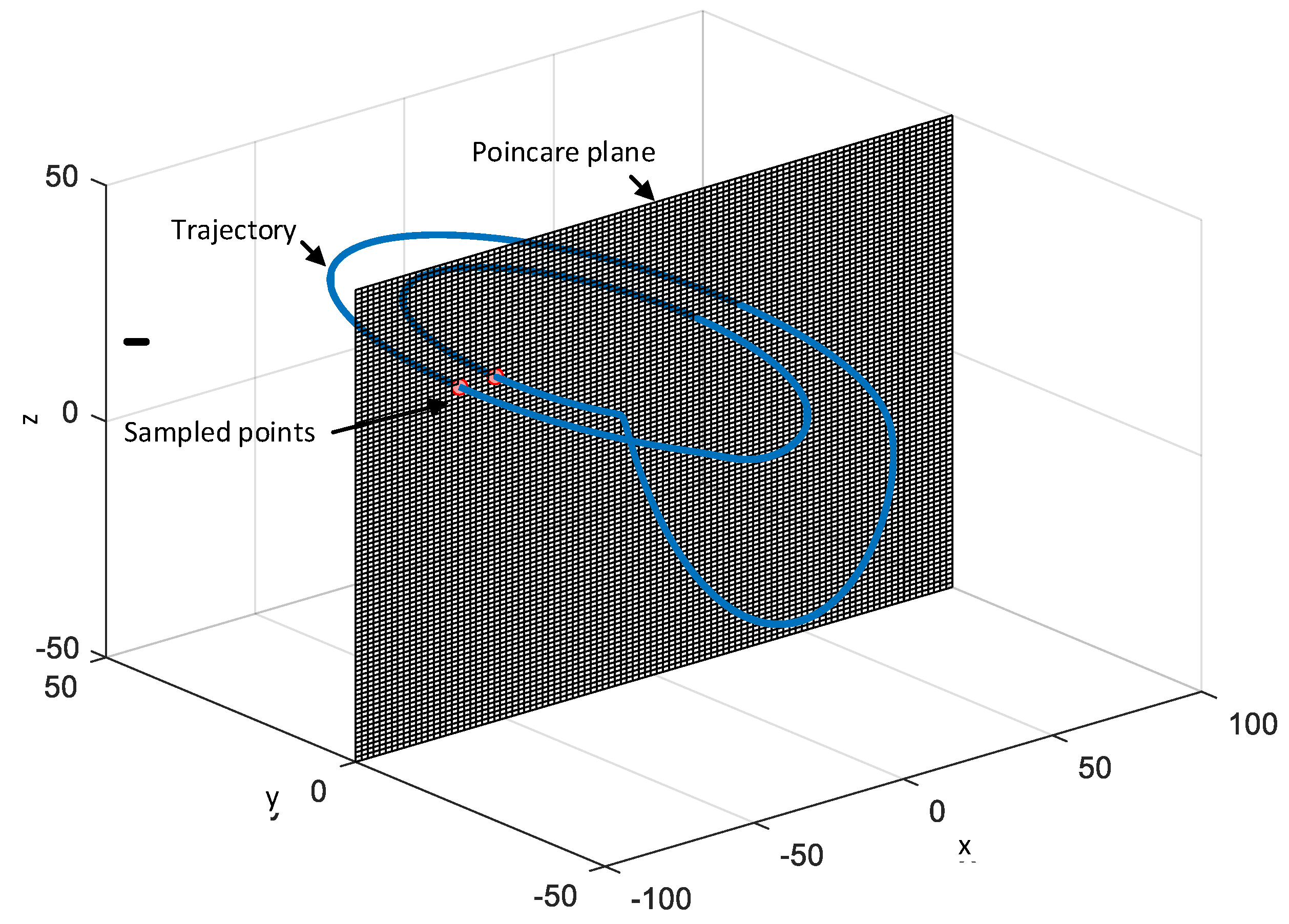
The study of the nonlinear dynamics of the Vilnius oscillator will be provided based on one and two-parameter bifurcation diagrams that allow estimation of the system’s mode of operation for various combinations of component values. However, this approach requires obtaining the discrete-time model of the original oscillator. The models could be constructed by application of the Poincaré map. In the case of the Vilnius oscillator, y=0 is selected as the Poincaré plane. Thus, the trajectories crossing this plane from one side will define the sampled model and provide the required information on the periodicity of the regimes under study (see Figure 2).

All the calculations are made utilising specially prepared MATLAB scripts, including the solution of the equations with the Runge-Kutta (4,5) method, implemented in the ode45 function. As constructing bifurcation maps and complete bifurcation diagrams in the wide range of system parameters is time-consuming, the Parallel Computing Toolbox functionality has been intensively utilised to efficiently distribute the computation tasks between all available physical cores of the computer. The results of the numerical calculations and the analysis of the obtained diagrams are provided in the next section.

3. Complete Bifurcation Analysis

The main goal of the current research is to study the dynamics of the Vilnius oscillator, operating in the parameter range viable for applications in wireless sensor networks. The parameters under study are b- defined by the voltage V_b , a- related to the amplifier gain k, and ε- defined by C₁ and C₂. The task is to provide the study of complex phenomena observed in the chaotic oscillator at different combinations of selected defined parameters.

In the following subsections, the study of nonlinear dynamics of the oscillator is based on the construction of two-parameter bifurcation diagrams (bifurcation maps) and the complete bifurcation analysis of the corresponding one-parameter diagrams as the cross-sections of the map.

3.1. Dynamics of the oscillator in the b-ε plane

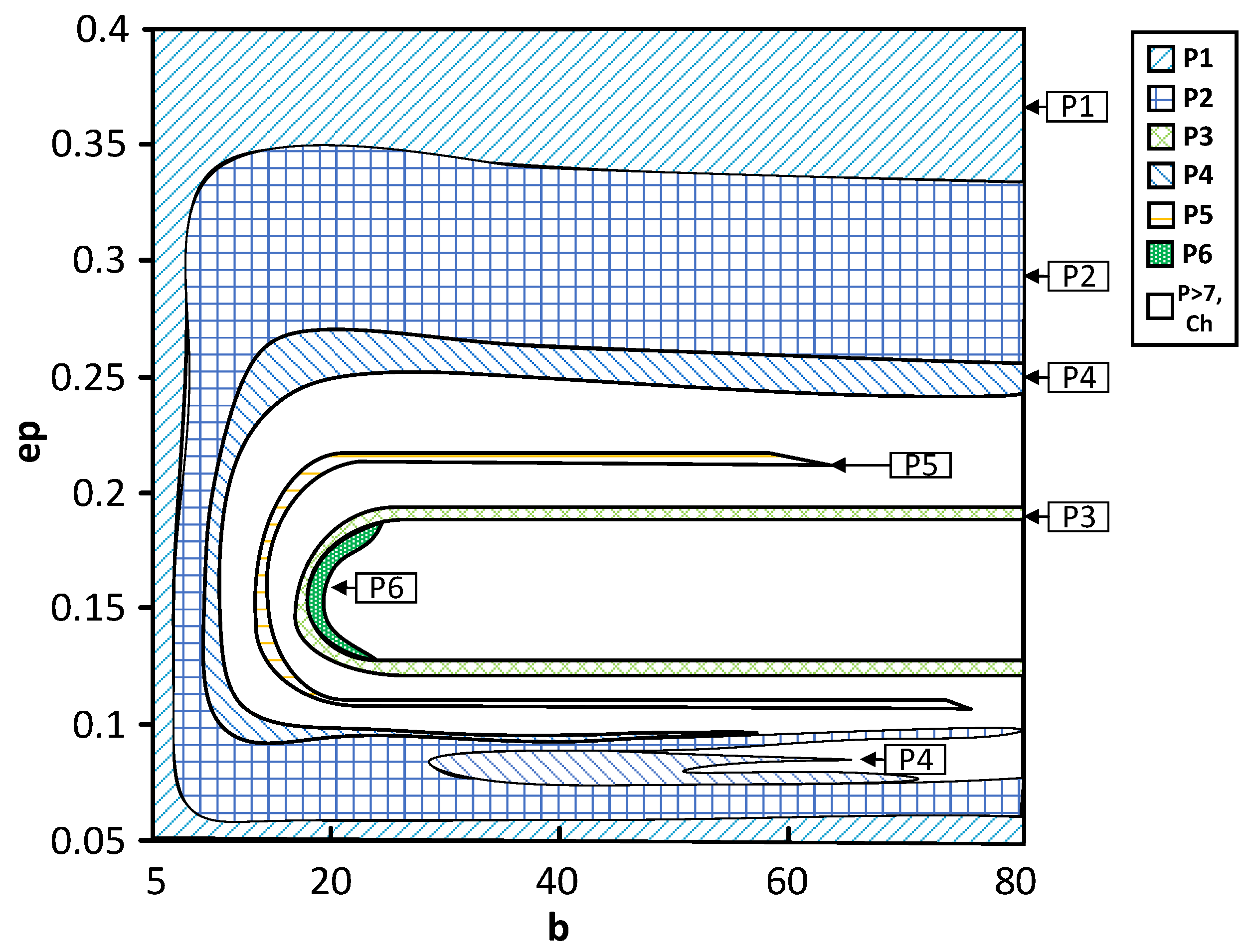
First, the parameter a is fixed at the value 0.3, and the system’s dynamics are studied, varying b and ε. The obtained map for ε=0.05-0.4 and b=5-80 is shown in Figure 3. Periodic operation modes are depicted up to period-6, and other high-periodic regimes and chaos are shown as white regions.

The bifurcation map demonstrates that for low values of b (defined by the input voltage), the system’s dynamics are mainly periodic – exhibiting P1 to P4 oscillations for all values of ε. From a practical point of view, the system could not be used as the generator of chaotic oscillations for low voltages (defined by b<12). This is also illustrated in Figure 4, where stable regimes are depicted in blue and unstable ones in red. The complete bifurcation diagram shows the clear transition from P1 to P4 and back to P1 through subsequent period doublings without any signs of UPIs, defining the chaotic oscillations. The construction of the unstable branches allows the verification that all the regimes represent a single bifurcation group 1T. No coexisting chaotic attractors could be detected either.

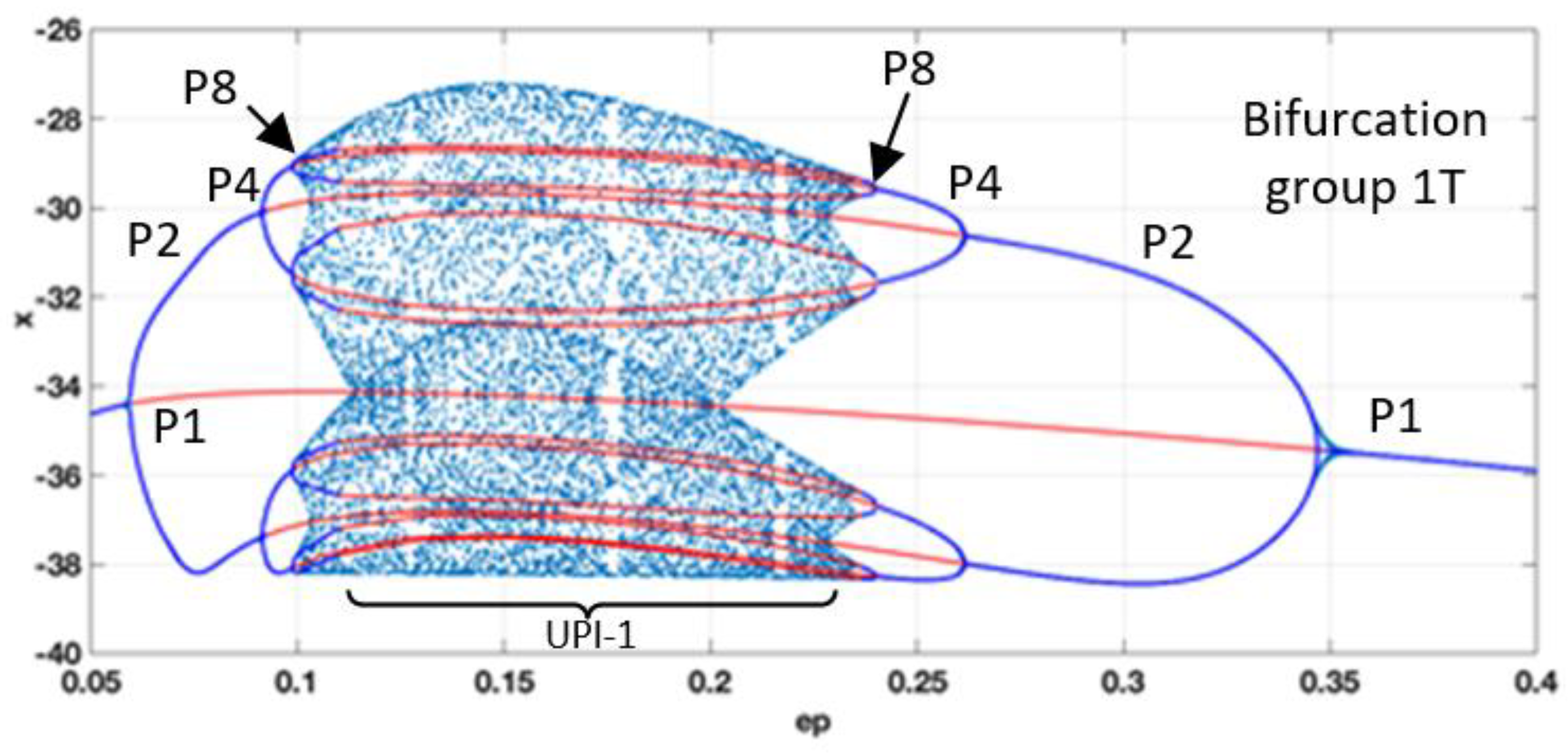
However, there is a definite border (b>12), where the system becomes chaotic for a relatively wide range of ε values. There could be intermittent chaotic dynamics (with various periodic windows) or robust chaos without interrupting periodic modes. Figure 5 shows a classical period-doubling route to chaos enclosing the interval with UPI₁, where only unstable regimes are observed, and the chaotic oscillations could be assumed robust. It can be inferred that setting system parameters within the range ε=0.1-0.23, should guarantee stable chaotic oscillations without the issue of transitioning to some periodic mode due to external noise or fluctuations in the component’s values.

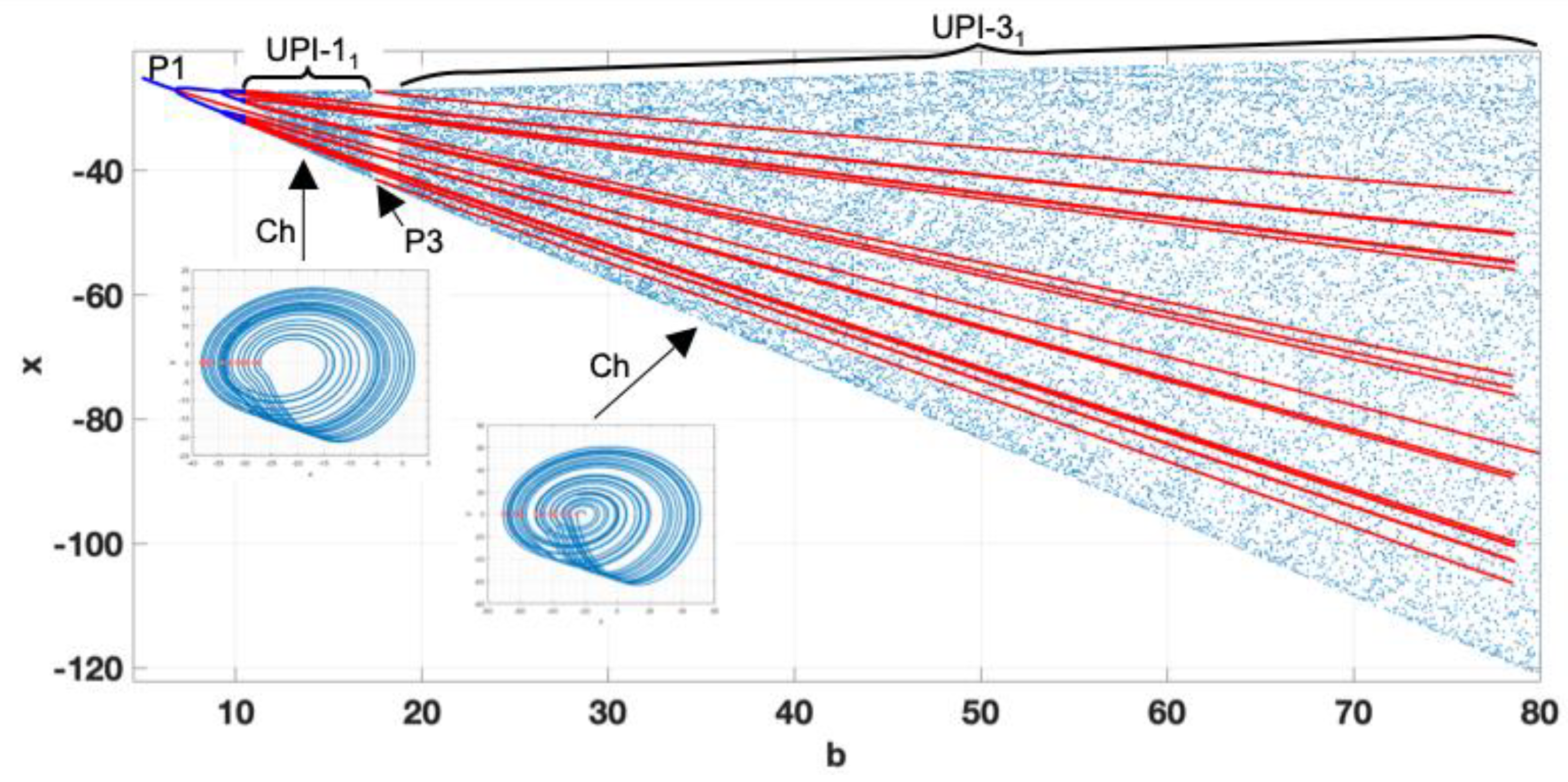
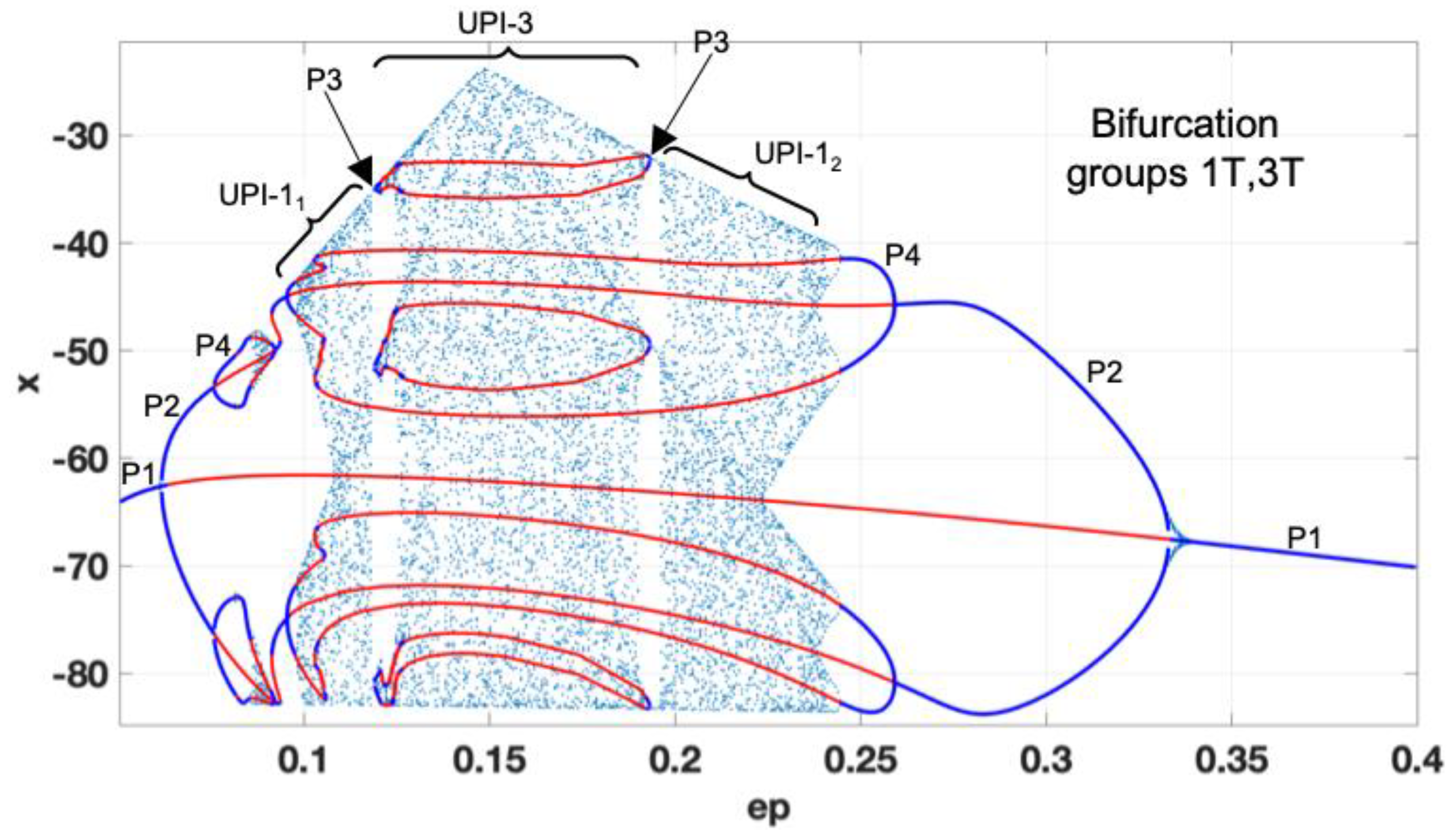
The system’s behaviour remains similar for higher values of b, as shown in Figure 6. However, the amplitude of x (related to V_C1) increases. Compared to the previous diagram, the system exhibits a non-smooth transition to chaos from the left side. This phenomenon could be explained by the presence of a diode in the circuit, defining the non-smooth switchings as the voltage rises and a certain threshold is reached. It has been noticed that the systems with non-smooth bifurcations could exhibit robust chaotic oscillations. However, in this case, we observe the appearance of three separated UPI-1₁ , UPI-3, UPI-1₂ corresponding to the robust chaotic regions. Periodic windows in the chaotic regions appear, forming the P3 modes. The transition to stable periodic regimes is observed as ε>0.24.

The second part of the investigation in the b-ε plane is dedicated to constructing the complete bifurcation diagrams for fixed values of ε and varying the parameter b. For ε < 0.12, a wide diversity of dynamical patterns could be observed, as b is varied. Figure 7 shows period doublings, intermittent chaos and wide periodic windows. These regimes could not be relevant for practical applications, as any slight supply voltage variations could cause unpredicted transitions between different modes, compromising the whole system’s security. Chaotic attractors observed in the corresponding regions (see e.g., Figure 7 Ch attractor) are not dense enough, indicating the insufficient level of diversity required by practical communication systems.

However, the further increase in parameter ε leads to the formation of several robust chaotic regions (see UPI-1₁ and UPI-3₁ in Figure 8) with acceptable characteristics and durability to parameter changes. But all large periodic windows converge to a single wide P3 window (Figure 8). In practice, we are interested in the low-voltage operation of the system, so the region of b=12-28 is the most appropriate.

Setting the ε=0.15 in the middle of the predicted chaotic region in the bifurcation map (see Figure 3), it is possible to obtain the diagram where all periodic windows shrink to a negligible stable P3 mode, and the continuous robust chaotic area (UPI-3₁) is formed. This is demonstrated in Figure 9. The advisable region to operate the oscillator would be in the range of b=20-80.

As it can be deduced from Figure 3, the further increase of ε leads to the deterioration of chaotic dynamics and diagrams, like those shown in Figure 7 and Figure 8, could be obtained.

In the next subsection, we choose the lowest possible value of b (directly connected to the input voltage), which ensures robust chaotic oscillations and provide the complete bifurcation analysis, as ε and a are varied.

3.2. Dynamics of the oscillator in the a-ε plane

The first step is the construction of the bifurcation map, selecting ε and a as primary and secondary bifurcation parameters. The obtained two-parameter bifurcation map, depicting periodic regimes up to P8 and chaos (white regions), is shown in Figure 10.

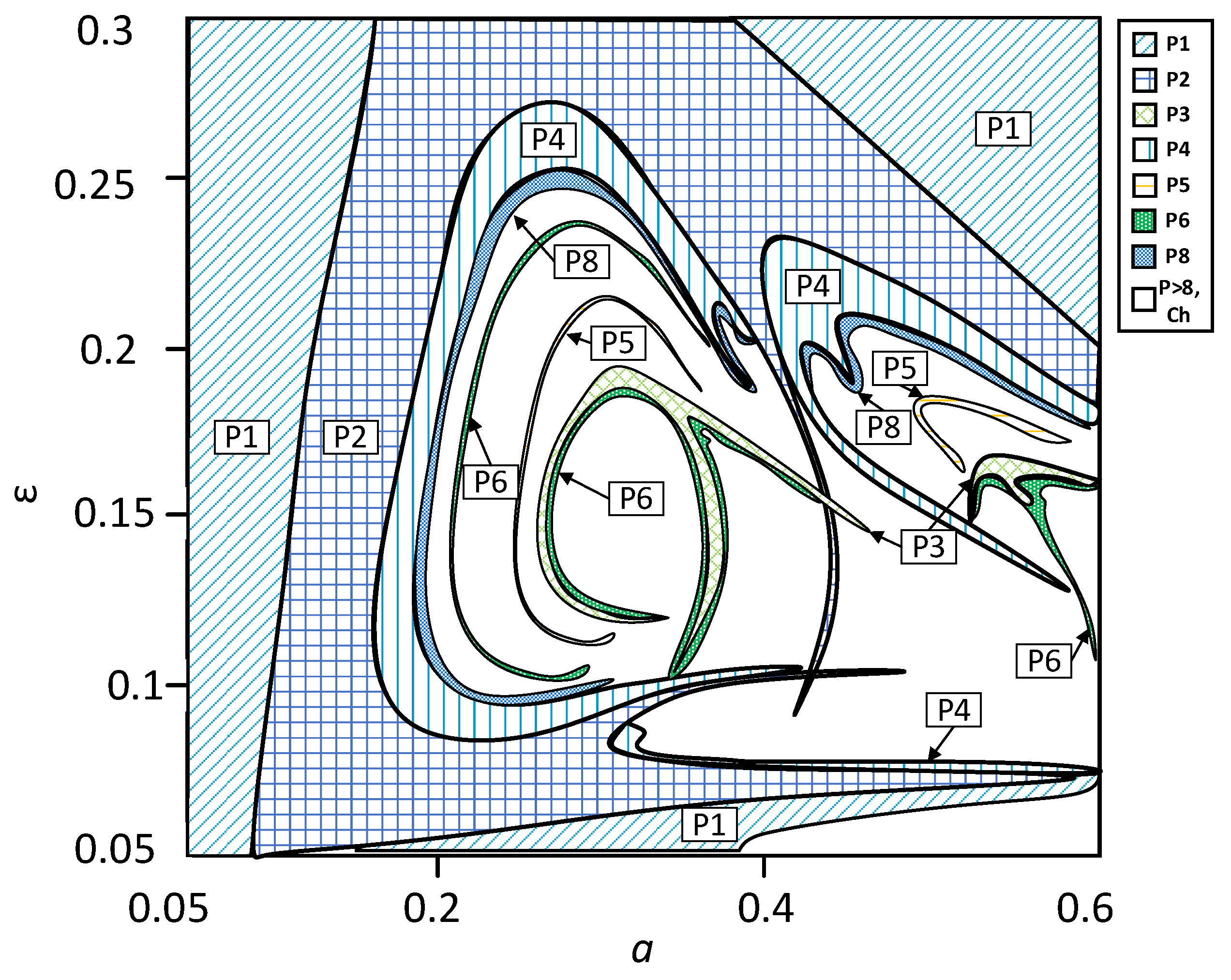
The diagram shows the complex distribution of periodic and chaotic regions in the selected parameter space, including some unusual “spiking patterns” previously observed in other systems and described by Jason Gallas, e.g., in [15]. The map allows making preliminary conclusions on the regions of possible practical interest. For a<0.25 only P1-P8 regimes are observed without any transitions to chaos in the whole range of ε values. As a increases further, more complex transitions between periodic modes and chaos could be observed for different values of ε. It should be noticed that the bifurcation map is obtained by means of brute-force iterations and, thus, sometimes, does not reveal the actual structure of the bifurcation patterns. Therefore, it is necessary to construct the complete bifurcation diagrams as the “cross-sections” of the obtained map. Construction of the periodic skeletons and branch continuation techniques allow the detection of all stable and unstable regimes in the parameter range of interest.

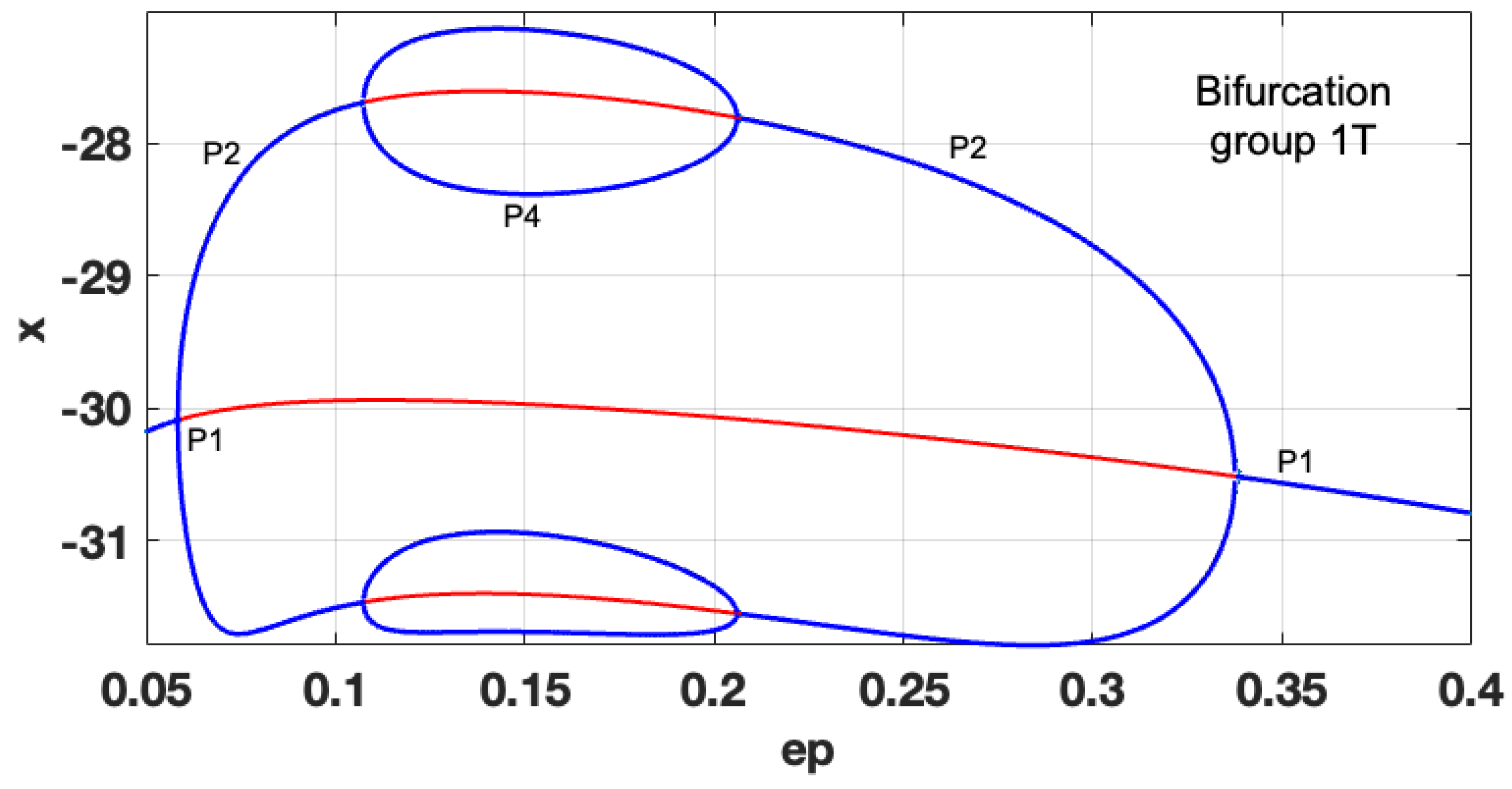
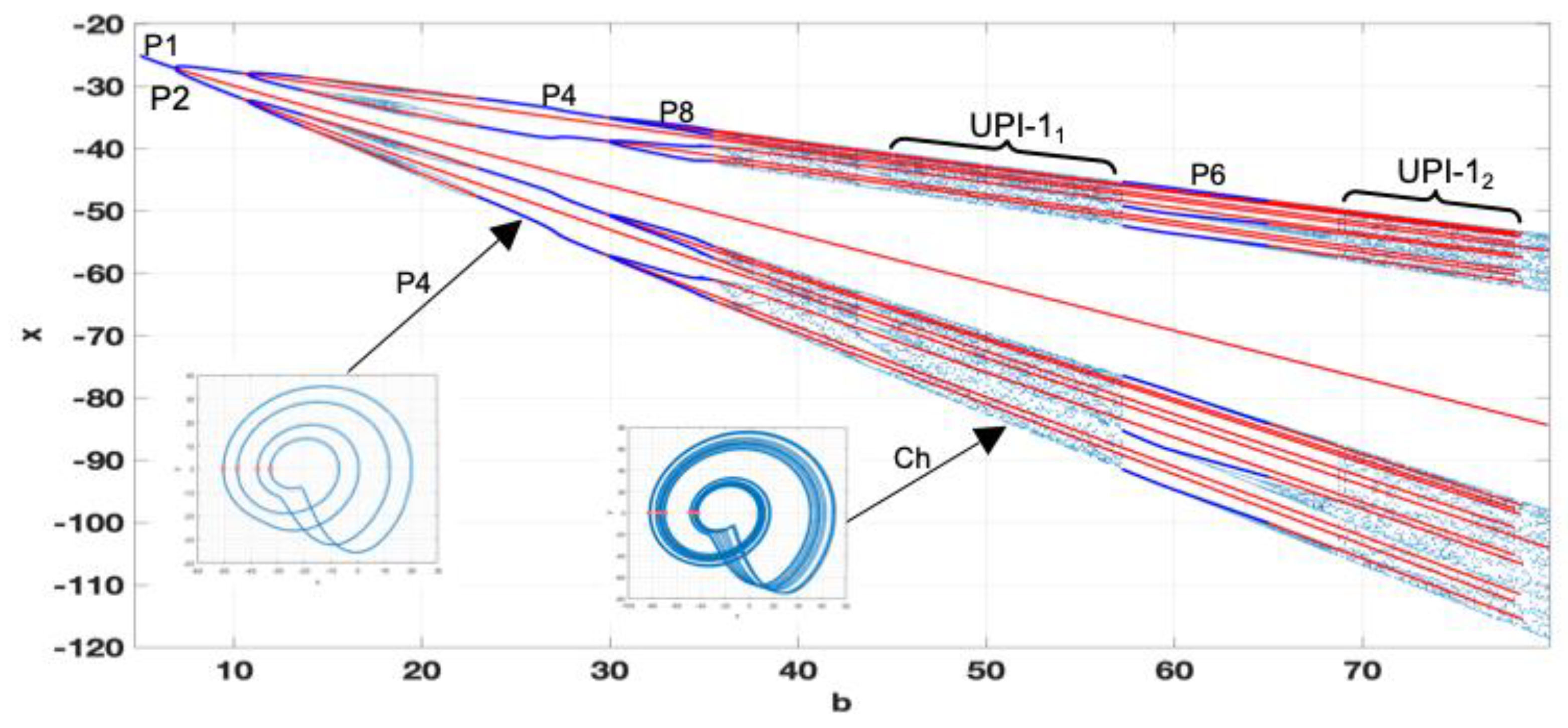
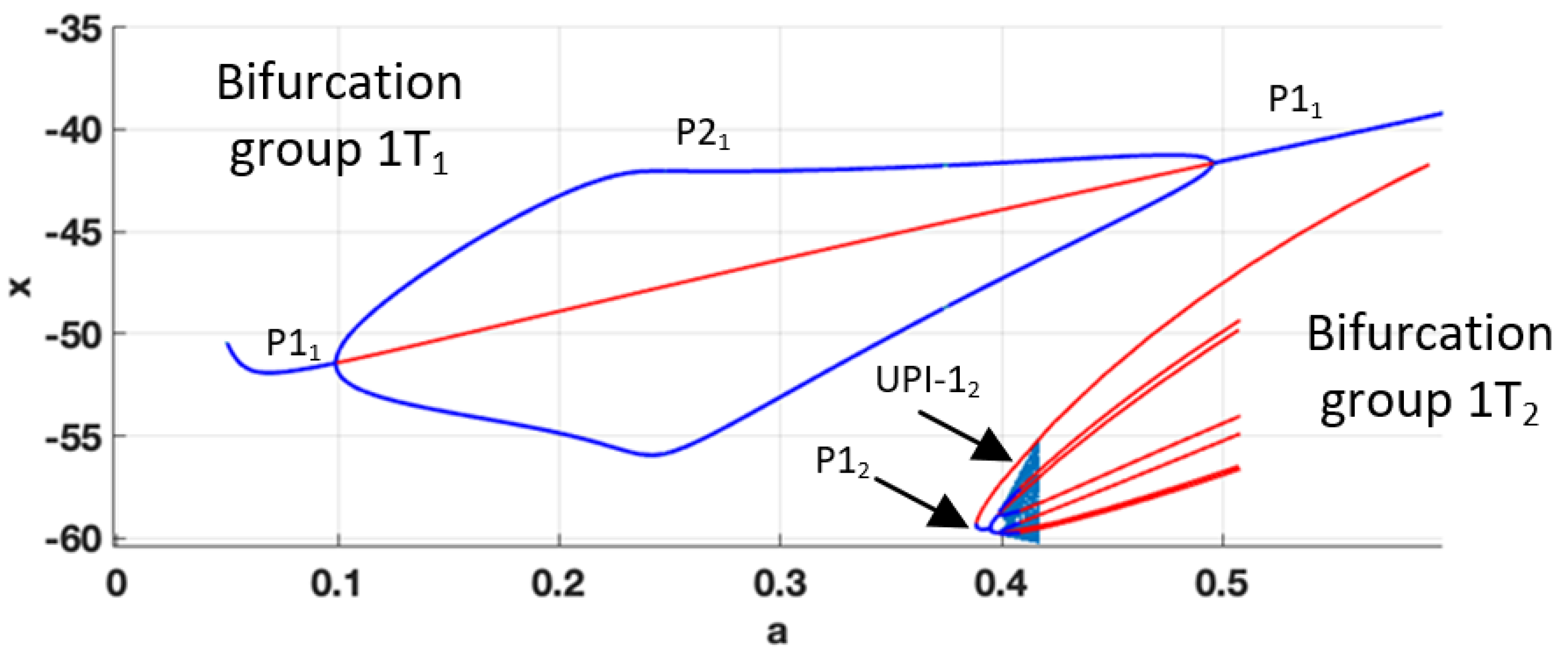
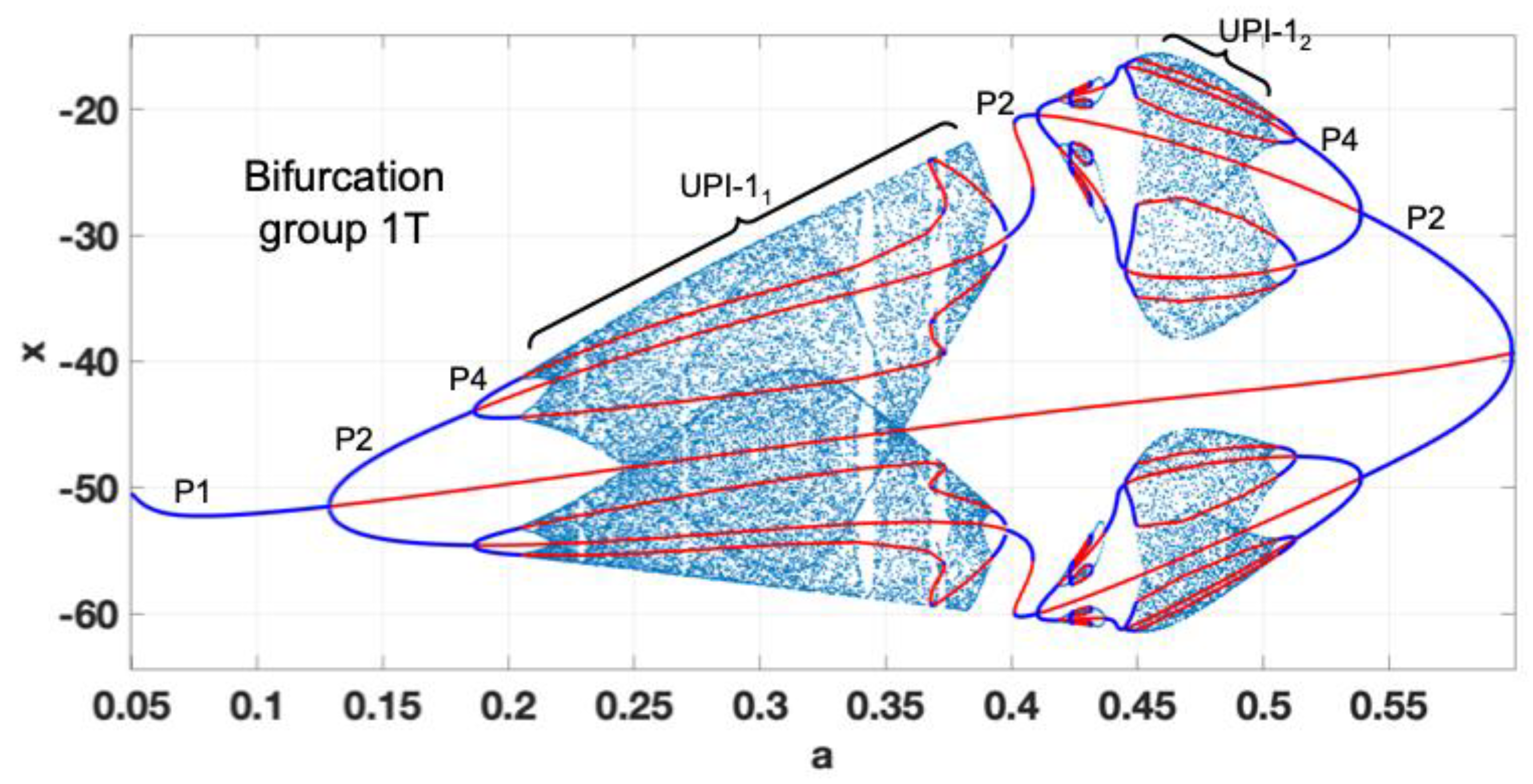
First, we obtain the complete bifurcation diagram for ε=0.07. According to the map (see Figure 10), the transition P1-P2-P1 should be observed. However, the obtained complete bifurcation diagram in Figure 11, shows two coexisting bifurcation groups – 1T₁ and 1T₂. 1T₁ is formed by the predicted P1₁-P2₁-P2₁ cascade. However, 1T₂ coexists with 1T₁, becoming stable for a=0.385 and experiencing the full period-doubling cascade with the formation of UPI-1₂, indicating chaotic dynamics. The chaotic attractor collides with the unstable branch of P1₂ at a=0.415 and is no longer observed. Practically the appearance of two coexisting bifurcation groups with stable regimes could lead to unpredicted “jumps” from stable P2 to chaotic motion due to the inevitable presence of noises in the real circuit. Thus, the use of the detected chaotic regime is not a viable option.

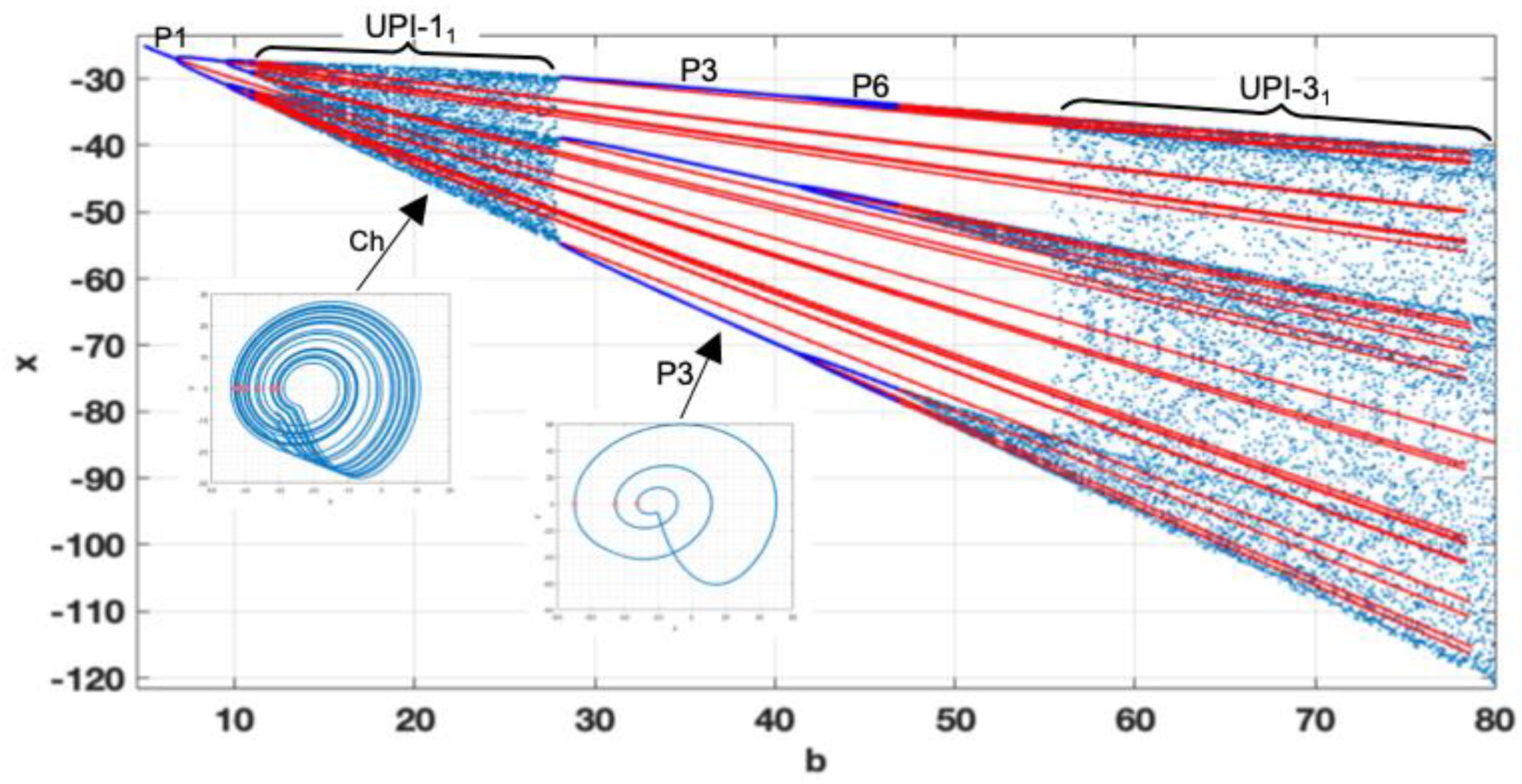
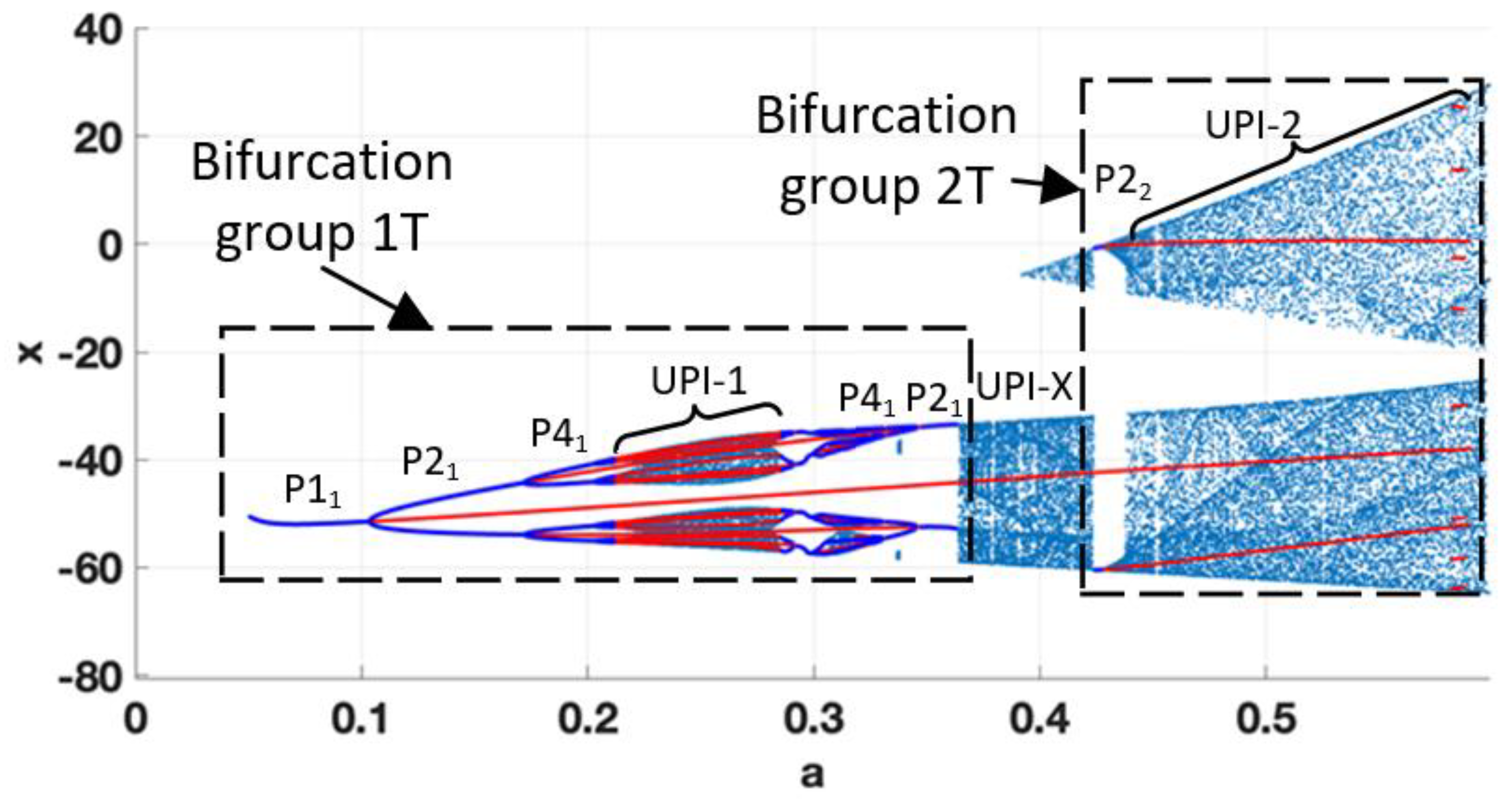
As the value of ε=0.1, the complete bifurcation diagram reveals the appearance of non-smooth phenomena, manifesting as abrupt changes in the system’s dynamics (see Figure 12). The diagram is formed by bifurcation groups 1T and 2T. The first group shows the transition to UPI-1 through the period-doubling cascade and further reverse transition up to P2₁. However, for a=0.36, the non-smooth transition to UPI-X is observed, and the system exhibits robust chaos. The bifurcation group 2T is composed of a narrow region of P2₂ regime with further rapid chaotisation (see UPI-2). For the observed parameters, the recommended values of a, ensuring robust chaotic oscillations, not affected by small perturbations, could be a=0.25, 0.4, 0.5, pointing to the middle parts of the UPIs.

The next diagram obtained for ε=0.2 (see Figure 13) shows a single bifurcation group 1T with a complex structure of transitions from P1 to UPI-1₁, then to P2 with double sided period-doubling cascade, finally leading to the formation of another UPI-1₂, and reverse transition to P2 mode of operation. The observed transitions are smooth; the UPI regions do not include significant periodic windows and could be used as regions of robust chaos.

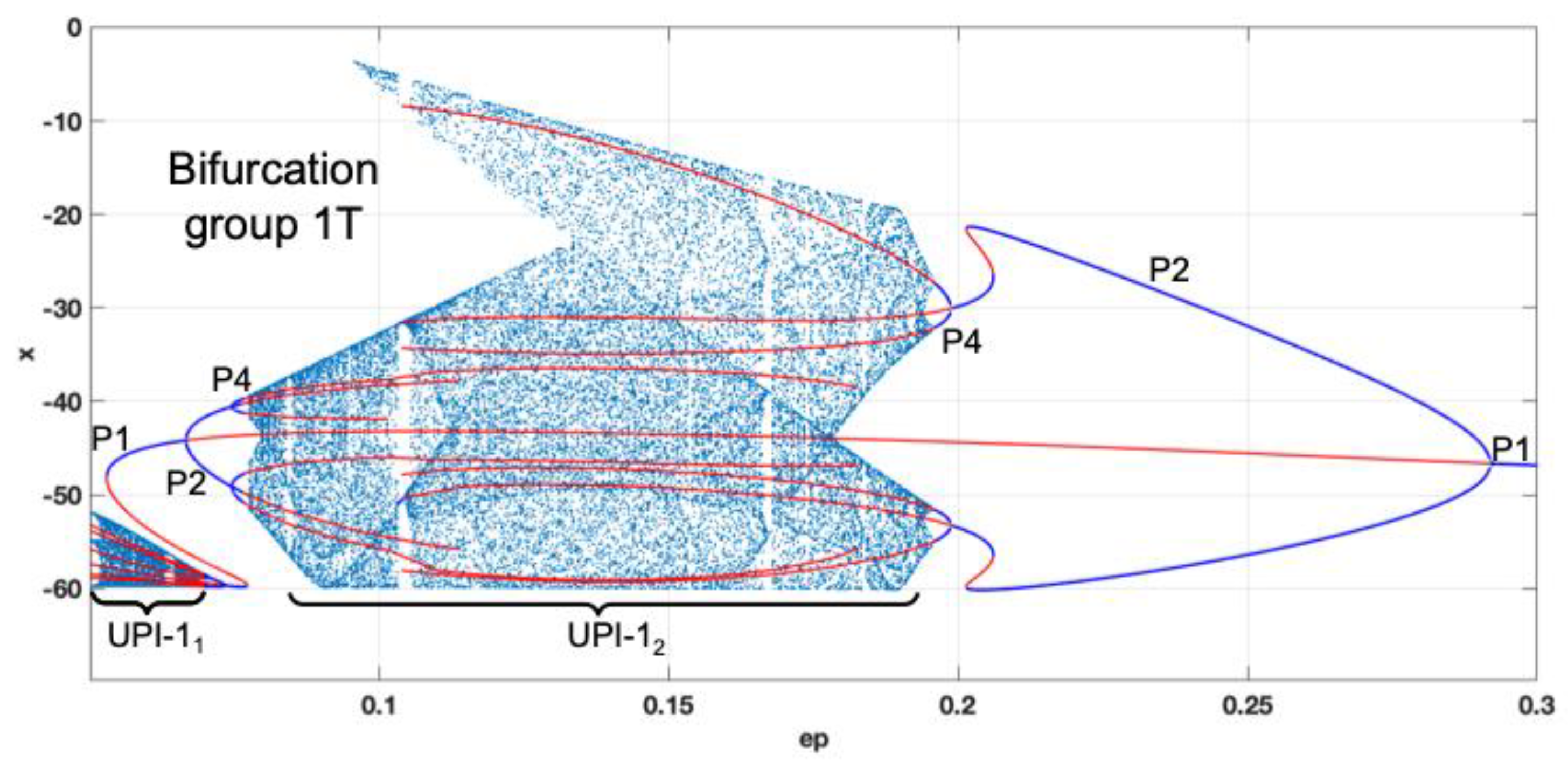
The last bifurcation diagram is obtained by fixing the value of a=0.4 and selecting ε as the bifurcation parameter (Figure 14). If we start from ε=0.3 and decrease the value, we observe the period-doubling route to robust chaos (UPI-1₂). The manifestation of the non-smooth nature of the systems leads to the sudden transitions and disappearance of chaotic attractor for ε=0.06. The UPI-1₁, observed for the values of ε=0.01-0.06, coexists with the stable P1 regimes and could not be used as a reliable source of chaotic oscillations.

3. Experimental verification

This section includes a description of the experimentally obtained results. The most complex diagrams were verified, obtaining the phase portraits and allowing the regime’s periodicity detection. First, we provide a short description of a simple experimental setup. Further, the analysis and compilation of the obtained results are provided.

3.1. Test setup

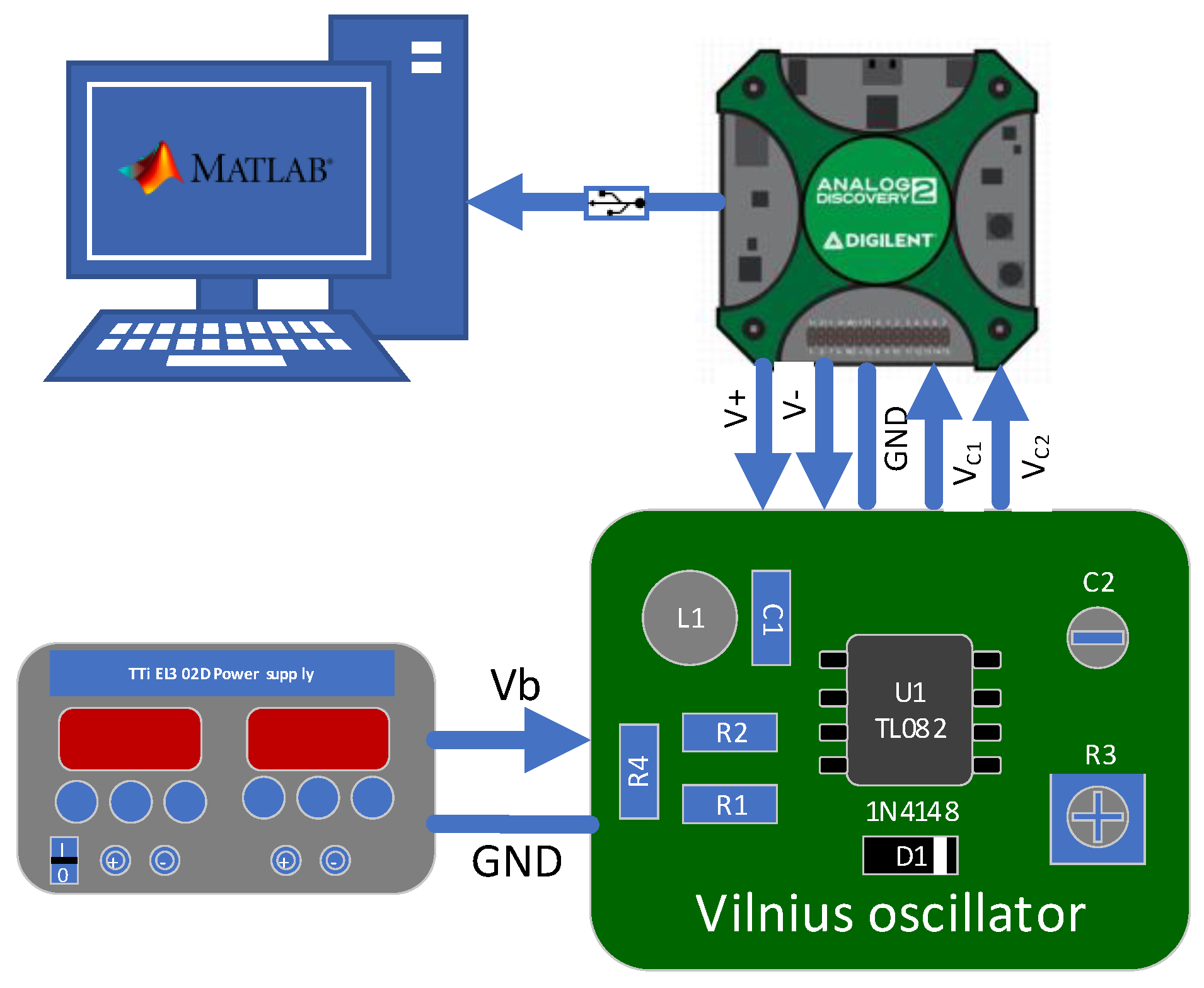
The experimental setup is shown in Figure 15. The Vilnius oscillator is designed from off-the-shelf components, including: operational amplifier U₁ – TL082, diode D₁ – 1N4148, R₁=1kΩ, R₂=10kΩ, R₄=20kΩ, R₃=10kΩ (variable), L₁=1mH, C₁=1nF, C₂=1nF (variable). The TTi EL302D power supply provides the input voltage V_b.

Analog Discovery 2 is used as a universal tool to power the U₁ with +-5V and capture the voltages on C₁ and C₂. Further, the data is transferred to the Digilent WaveForms application and saved for processing in Matlab. The experimental setup allows variations of R₃, C₂ and V_b, that are directly connected to the a, ε and b parameters of the Vilnius oscillator (see equations (4)-(7) ). To reduce the confusion and compare experimental results to the numerically obtained diagrams, the values of a, ε and b will be used in all the graphs.

3.2. Experimental results and analysis

We start with the verification of selected diagrams obtained in Subsection 3.2 where b=30 is fixed, and parameters ε and a are varied (adjusting C₂ and R₃), as the proposed diagrams provide the most complicated structures that would allow us to evaluate the degree of accuracy of the obtained numerical results. The simplest way to verify the validity of theoretical results is to obtain the waveforms and appropriate phase portraits for selected points in the parameter space, also marking the bifurcation points. 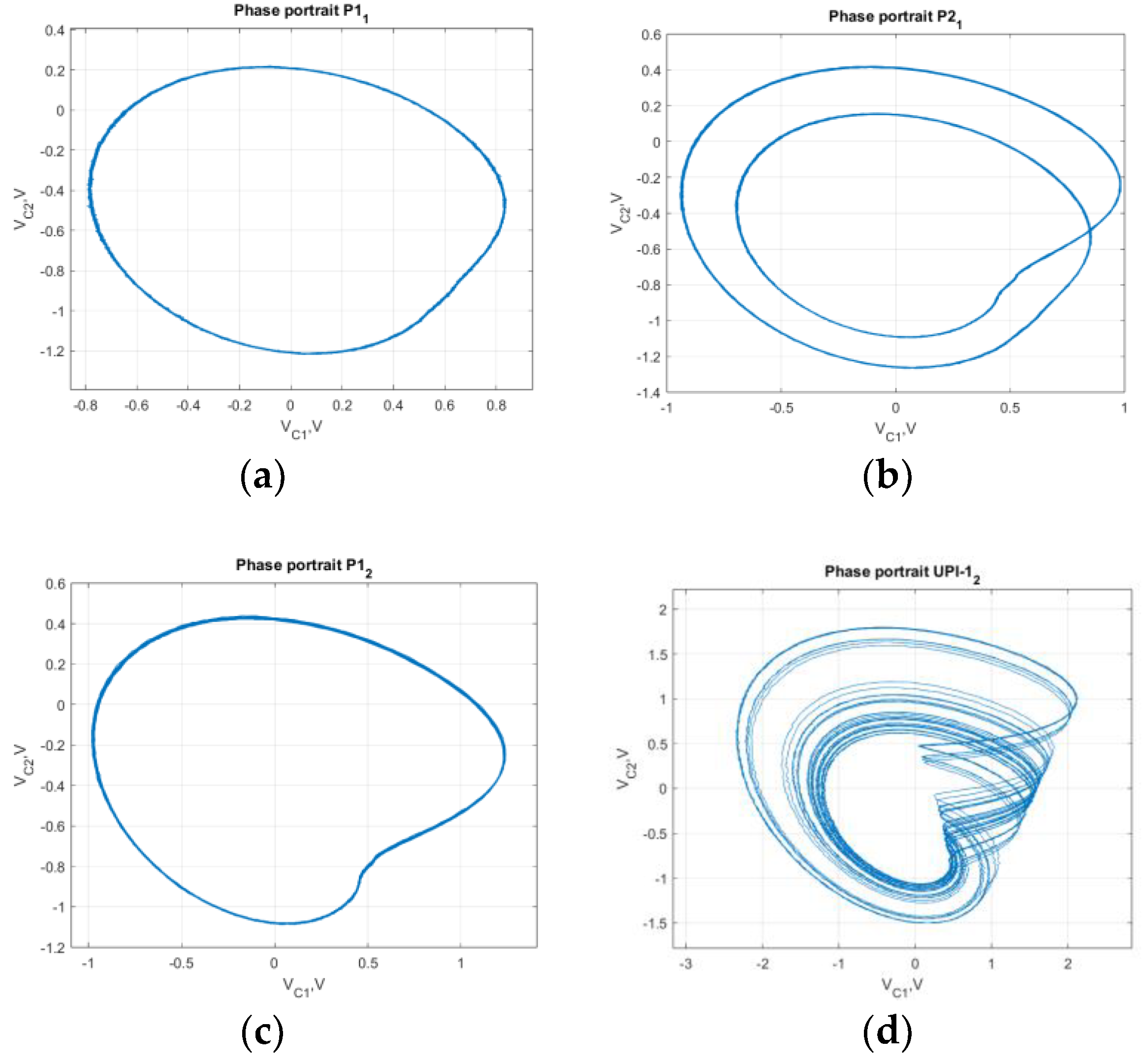Taking the complete bifurcation diagram from Figure 11, as the basis, we capture the phase portraits for different modes, as b=30, ε=0.07, and a varied from 0.05 to 0.6 – see Figure 16.

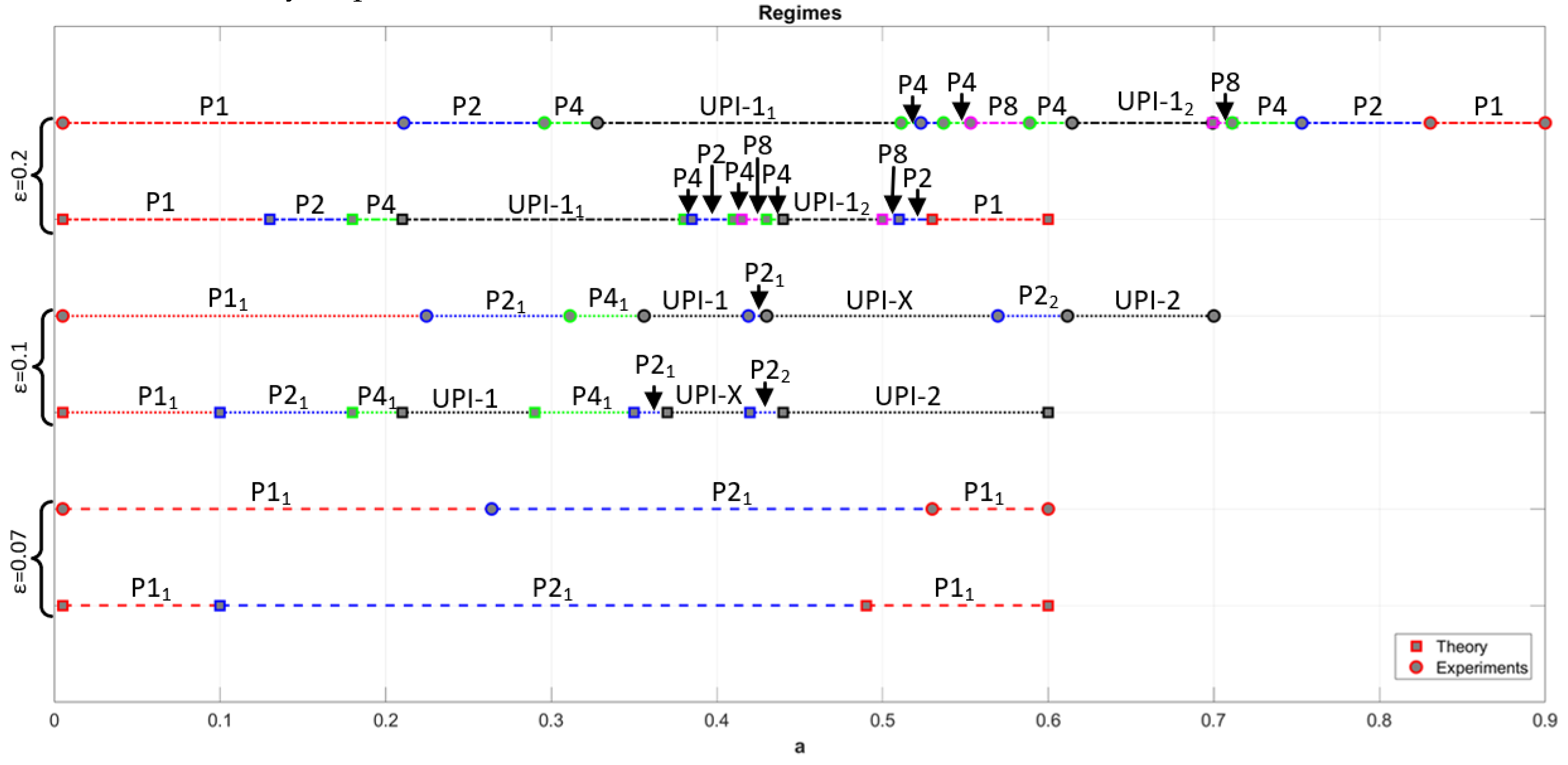
As in Figure 11, the phase portraits show the transition P1-P2-P1 as the value a is increased through the range. The appearance of coexisting chaotic mode was also identified experimentally. Practically, the P1₂ was not “stable” as transient jumps to chaotic mode were observed – the corresponding chaotic attractor is shown in Figure 16d. The jumps were caused by the noise present in the circuit, and even movement of the connecting wires could cause the system to go to/from chaotic mode. These observations allow us to conclude that the MCBG gives reliable information about the predicted modes of operation of the circuit. However, it is impractical to provide phase portraits for every single regime. Still, it would be more beneficiary to aggregate the information about all experimentally observed modes and points of transitions in a single graph. For that purpose, we propose using a mode transition graph – providing data on the ranges for all regimes and depicting transition points. This analogue of the bifurcation diagram also allows the comparison of experimentally and numerically obtained results. The graph, constructed for diagrams, shown in Figure 11, Figure 12 and Figure 13, is presented in Figure 17 and includes theoretical (based on numerical calculations) and experimental results.

The obtained mode transition graphs clearly show that it was possible to verify theoretically obtained results successfully. For each ε value, the pair or graphs show that the sequences of transitions between periodic and chaotic modes of operation remain the same. This is true for relatively simple cases – e.g., for ε=0.07, where the P1-P2-P1 transition is observed, and also for highly complex mode transition structures with multiple forward and reverse period-doubling cascades and chaotisation scenarios – e.g., for ε=0.1 and ε=0.2. It should be mentioned that despite the direct correspondence of the mode transition sequences, the practically obtained ranges of parameter values for each mode differ. One commonly observed pattern is that in experiments P1 mode loses its stability for higher values of a, leading to the general shift of the mode transition graph and corresponding transition (bifurcation) points. The observed mismatches could be explained by experimental component tolerances, parasitic elements, and unavoidable noises in the practically implemented circuit.

It should be noted that the phase portraits could still be used to identify some specific features of the regimes under interest. For example, for ε=0.1, both UPI-1 and UPI-2 define the appearance of the chaotic modes of operation (Figure 17). However, the strange attractors of these regimes differ in the density of orbits and amplitude, which could be of particular interest when applying the obtained signals to actual data security circuitry. 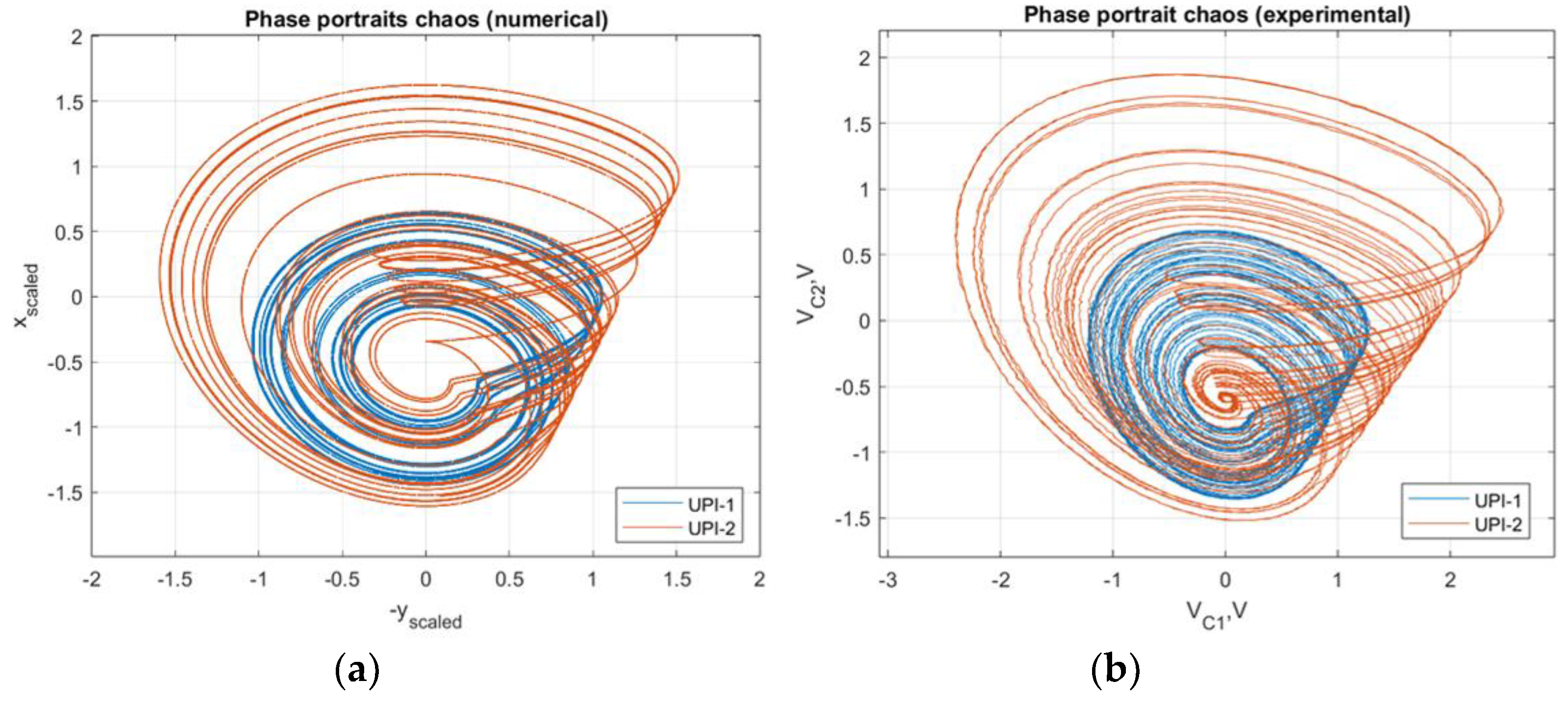Figure 18 compares two chaotic attractors for a=0.25 (UPI-1) and a=0.5 (UPI-2), obtained numerically (scaled for the comparison) and experimentally.

The similarity of theoretical and experimental attractors highlights the validity of numerically obtained results and applicability of the MCBG for prediction, analysis and characterization of complex dynamics of nonlinear systems.

4. Conclusions

One of the key parameters defining the applicability of the chaotic oscillators to secure communication systems is energy efficiency (possibility to operate in low-power modes) and robustness (insusceptibility to slight parameter variations and noise). Thus, investigating the dependence of nonlinear dynamics of these kinds of generators on the operation voltage and component parameter changes is crucial for practical solutions.

The paper demonstrated the numerical study of possible chaotization scenarios and various nonlinear phenomena observed in the Vilnius chaotic oscillator as system parameters vary. It has been shown that the construction of the bifurcation map allows for the convenient identification of the most appropriate parameter ranges to be used for obtaining robust chaotic modes of operation. The consequent construction of complete bifurcation diagrams and application of the MCBG allows for in-depth analysis of transitions between different modes of operation. It identifies the non-smooth phenomena and coexisting attractors that could not be detected by the bifurcation maps. It has been shown that the Vilnius oscillator could exhibit periodic modes of operation, smooth and non-smooth transitions to chaos (defined by UPIs), and the coexistence of various bifurcation groups. The practically relevant regions of robust chaos have been identified for each set of parameter values.

The numerically obtained results’ validity has been verified through laboratory experiments. Phase portraits for a wide range of parameter values have been obtained, and bifurcation points have been marked. The mode transition graphs showed that numerical results qualitatively match the experimental ones, providing the same sequence of bifurcations and periodic or chaotic regimes. However, due to the presence of parasitic elements, limited tolerances of the components and noises, the mismatch in the parameter values, where the transitions between the modes occur, are observed.

The main conclusion is that the Vilnius oscillator could robustly generate chaotic signals required in secure communications in a wide range of appropriately tuned parameters. A numerical investigation utilising MCBG predicts the expected bifurcation and chaotisation patterns. However, experimental verification is still a crucial step in detecting the precise parameters of the system. Further study could contain the laboratory experiments allowing practical estimation of energy efficiency of the proposed robust chaotic regimes and defining the practically relevant criteria for selecting one of the available robust chaotic modes according to the requirements defined by specific applications.

Author Contributions

Formal analysis, A.I., D.P. and A.L; Funding acquisition, A.I.; Investigation, I.C.V. and A.I.; Methodology, D.P. and A.L.; Software, I.C.V. and S.T.; Supervision, D.P.; Validation, D.P. and S.T.; Visualization, I.C.V., D.P.; Writing—original draft, A.I., D.P. and I.C.V.; Writing—review & editing, A.I., D.P. and A.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work has been supported by the European Regional Development Fund within Activity 1.1.1.2 “Post-doctoral Research Aid” of the Specific Aid Objective 1.1.1 “To increase the research and innovative capacity of scientific institutions of Latvia and the ability to attract external financing, investing in human resources and infrastructure” of the Operational Programme “Growth and Employment” (No.1.1.1.2/VIAA/4/20/651).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Mishu, M.K.; Rokonuzzaman, M.; Pasupuleti, J.; Shakeri, M.; Rahman, K.S.; Hamid, F.A.; Tiong, S.K.; Amin, N. Prospective Efficient Ambient Energy Harvesting Sources for IoT-Equipped Sensor Applications. Electronics 2020, 9, 1345. [CrossRef]
Raj, A.; Steingart, D. Review—Power Sources for the Internet of Things. J. Electrochem. Soc. 2018, 165, B3130. [CrossRef]
Litvinenko, A.; Aboltins, A. Chaos Based Linear Precoding for OFDM. In Proceedings of the 2015 Advances in Wireless and Optical Communications (RTUWO); November 2015; pp. 13–17.
Litvinenko, A.; Bekeris, E. Probability Distribution of Multiple-Access Interference in Chaotic Spreading Codes Based on DS-CDMA Communication System. ElAEE 2012, 123, 87–90. [CrossRef]
Babajans, R.; Cirjulina, D.; Grizans, J.; Aboltins, A.; Pikulins, D.; Zeltins, M.; Litvinenko, A. Impact of the Chaotic Synchronization’s Stability on the Performance of QCPSK Communication System. Electronics 2021, 10, 640. [CrossRef]
Dantas, W.G.; Rodrigues, L.R.; Ujevic, S.; Gusso, A. Using Nanoresonators with Robust Chaos as Hardware Random Number Generators. Chaos 2020, 30, 043126. [CrossRef]
Majumder, B.; Hasan, S.; Uddin, M.; Rose, G.S. Chaos Computing for Mitigating Side Channel Attack. In Proceedings of the 2018 IEEE International Symposium on Hardware Oriented Security and Trust (HOST); April 2018; pp. 143–146.
Karimov, T.I.; Druzhina, O.S.; Ostrovskii, V.Y.; Karimov, A.I.; Butusov, D.N. The Study on Multiparametric Sensitivity of Chaotic Oscillators. In Proceedings of the 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus); January 2020; pp. 134–137.
Azar, A.T.; Serranot, F.E.; Vaidyanathan, S. Chapter 10—Sliding Mode Stabilization and Synchronization of Fractional Order Complex Chaotic and Hyperchaotic Systems. In Mathematical Techniques of Fractional Order Systems; Azar, A.T., Radwan, A.G., Vaidyanathan, S., Eds.; Advances in Nonlinear Dynamics and Chaos (ANDC); Elsevier, 2018; pp. 283–317 ISBN 9780128135921.
Tamaševičius, A.; Mykolaitis, G.; Pyragas, V.; Pyragas, K. A Simple Chaotic Oscillator for Educational Purposes. Eur. J. Phys. 2005, 26, 61–63. [CrossRef]
Čirjuļina, D.; Pikulins, D.; Babajans, R.; Anstrangs, D.D.; Chukwuma Victor, I.; Litvinenko, A. Experimental Study of the Impact of Component Nominal Deviations on the Stability of Vilnius Chaotic Oscillator. In Proceedings of the 2020 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW); October 2020; Vol. 1, pp. 231–236.
Zakrzhevsky, M. New Concepts of Nonlinear Dynamics: Complete Bifurcation Groups, Protuberances, Unstable Periodic Infinitiums and Rare Attractors. Journal of Vibroengineering, 2008, Vol. 10, Iss. 4, pp. 421-441, ISSN 1392-8716.
Zakrzhevsky, M.V. Global Nonlinear Dynamics Based on the Method of Complete Bifurcation Groups and Rare Attractors. In Proceedings of the Volume 4: 7th International Conference on Multibody Systems, Nonlinear Dynamics, and Control, Parts A, B and C; ASMEDC: San Diego, California, USA, January 1, 2009; pp. 1411–1418.
Klokov, A.V.; Zakrzhevsky, M.V. Parametrically Excited Pendulum Systems with Several Equilibrium Positions: Bifurcation Analysis and Rare Attractors. Int. J. Bifurcation Chaos 2011, 21, 2825–2836. [CrossRef]
Gallas, J.A.C. The Structure of Infinite Periodic And Chaotic Hub Cascades In Phase Diagrams Of Simple Autonomous Flows. Int. J. Bifurcation Chaos 2010, 20, 197–211. [CrossRef]

Figure 1. The schematic diagram of the Vilnius oscillator.

Figure 2. The introduced Poincaré plane for obtaining a sampled model of the Vilnius oscillator.

Figure 3. Two-parameter bifurcation diagram for a=0.3; b=5-80; ε=0.05-0.4.

Figure 4. Complete bifurcation diagram for b=10; a=0.3; ε=0.05-0.4.

Figure 5. Complete bifurcation diagram for b=15; a=0.3; ε=0.05-0.4.

Figure 6. Complete bifurcation diagram for b=50; a=0.3; ε=0.05-0.4.

Figure 7. Complete bifurcation diagram for a=0.3; ε=0.1; b=5-80.

Figure 8. Complete bifurcation diagram for a=0.3; ε=0.12; b=5-80.

Figure 9. Complete bifurcation diagram for a=0.3; ε=0.15; b=5-80.

Figure 10. Two-parameter bifurcation diagram for b=30; a=0.05-0.6; ε=0.05-0.3.

Figure 11. Complete bifurcation diagram for b=30; ε=0.07; a=0.05-0.6.

Figure 12. Complete bifurcation diagram for b=30; ε=0.1; a=0.05-0.6.

Figure 13. Complete bifurcation diagram for b=30; ε=0.2; a=0.05-0.6.

Figure 14. Complete bifurcation diagram for b=30; ε=0.05-0.3; a=0.4.

Figure 15. The diagram of the test setup.

Figure 16. Phase portraits for b=30, ε=0.07 (a) a=0.21; (b) a=0.31; (c) a=0.53; (d) a=0.67.

Figure 17. Mode transition graphs for b=30; a=0.05-0.9, ε=0.07, 0.1, 0.2.

Figure 18. Chaotic attractors obtained for b=30, ε=0.1, a=0.25 (UPI-1) and a=0.5 (UPI-2), (a) numerical attractor; (b) experimental attractor.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer