Submitted:
12 May 2023
Posted:
17 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- Model theory:
-
In [1] we coined the concept of graph algebra, introduced graph terms and showed that graph term algebras are free graph algebras. There was, however, no model theory in the sense of traditional Universal Algebra. As a kind of “proof of concept”, we generalize therefore some basic model-theoretic concepts and results from traditional algebras to graph algebras. We concentrate on the concept “generated subalgebra” and the related problem of characterizing monomorphic and epimorphic homomorphisms, respectively.To tackle this task, we make some substantial effort in Section 3 to revise and reformulate traditional set-theoretic definitions, constructions and proofs in Universal Algebra by means of more category-theoretic concepts and constructions. Relying on this reformulation, we can in Section 4 smoothly transfer concepts, definitions and results from traditional algebras to graph algebras. Especially, we prove that all monomorphic homomorphisms between graph algebras are regular.In [1] we adapted the original idea of sketch operations [5] and defined the arity of a graph operation as a single graph inclusion. This definition does not allow us, however, to consider projections as legal graph operations. To be closer to the traditional concept of operation in Universal Algebra, and to be able to define an appropriate concept of derived graph operation, we declare therefore in this paper the arity of a graph operation as a span of graph inclusions. In Section 4.2 we clarify the relation between both versions and discuss to what extent they are equivalent.To prove that all monomorphic homomorphisms between graph algebras are regular, we also introduce in Section 4.4 partial graph algebras. We define a so-called term completion procedure transforming partial graph algebras into total graph algebras. This procedure provides for each signature a free functor from the corresponding category of partial graph algebras to the corresponding category of graph algebras. The construction of graph term algebras turns out to be just a special case of this new procedure.
- Derived graph operations:
-
To understand why the strong interconnection between “representation of data” and “representation of derived operations” breaks down in the case of graph operations and to find out how to define derived graph operations in an appropriate way, we include in the paper a more in-depth analysis of the concept term and discuss in Section 3.4 substitution calculi in general.In Section 3.7 we recall the construction of syntactic Lawvere theories as it is described in [8], for example. In Section 5.1 we discuss finite product categories and elucidate that terms can be characterized as normal forms for finite product expressions, thus Lawvere’s original slogan “composition is substitution” can be turned into the slogan “substitution is symbolic composition plus normalization”.Reviewing the relationship between finite products and tensor products, we identify in Section 5.2 copying as the cause of the problem. We argue that, in case of graph operations, “copying of data”, as a computation of its own, has to be replaced by “soldering” of input and (!) output ports of computations.In such a way, we end up in Section 5.3 with three mechanisms to construct new graph operations out of given ones: parallel composition, instantiation (“soldering” of input and output ports), and sequential composition.Finally, we introduce in Section 5.4 graph operation expressions with a structure as close as possible to the structure of terms. We define their semantics, i.e., the derived graph operations we have been looking for, by means of the three mechanisms parallel composition, instantiation and sequential composition.
2. Notations and Preliminaries
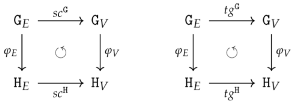
 . On the other side, the adjunction ensures that for any small graph the interpretation category is isomorphic to the functor category and thus a presheaf topos.
. On the other side, the adjunction ensures that for any small graph the interpretation category is isomorphic to the functor category and thus a presheaf topos.- and
- for all .
3. Algebras and Term Algebras
3.1. Signatures, Algebras and Homomorphisms
- a set ofoperation symbols,
- a map assigning to each operation symbol as its arity a pair of finite sets with for some , and .
- a set A, called the carrier of , and
- a family of maps called .
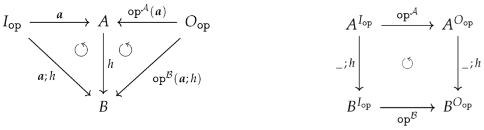
3.2. Subalgebras
“If M is a family of closed subsets in , then its intersection is closed as well”
- isaccessible via a map if.
- If is accessible via an inclusion map , i.e., if, we say also that isgenerated by A.
- is said to be generated if it is generated by the empty set, i.e., accessible via the unique map from the initial object ∅ in to B.
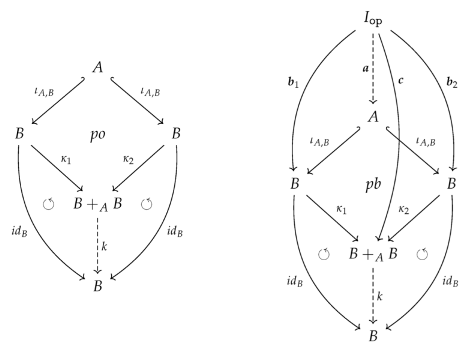
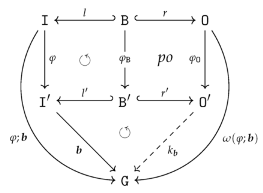
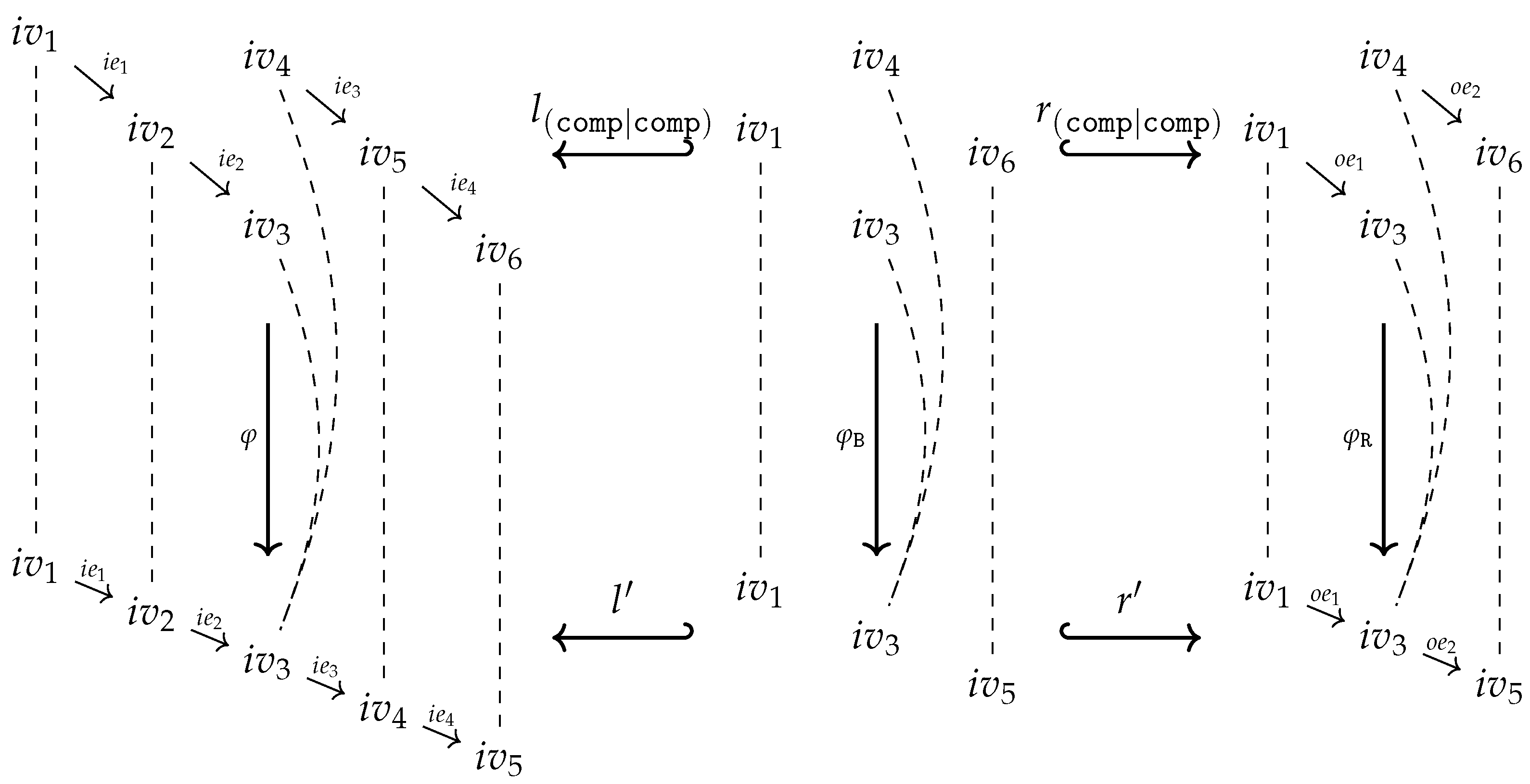
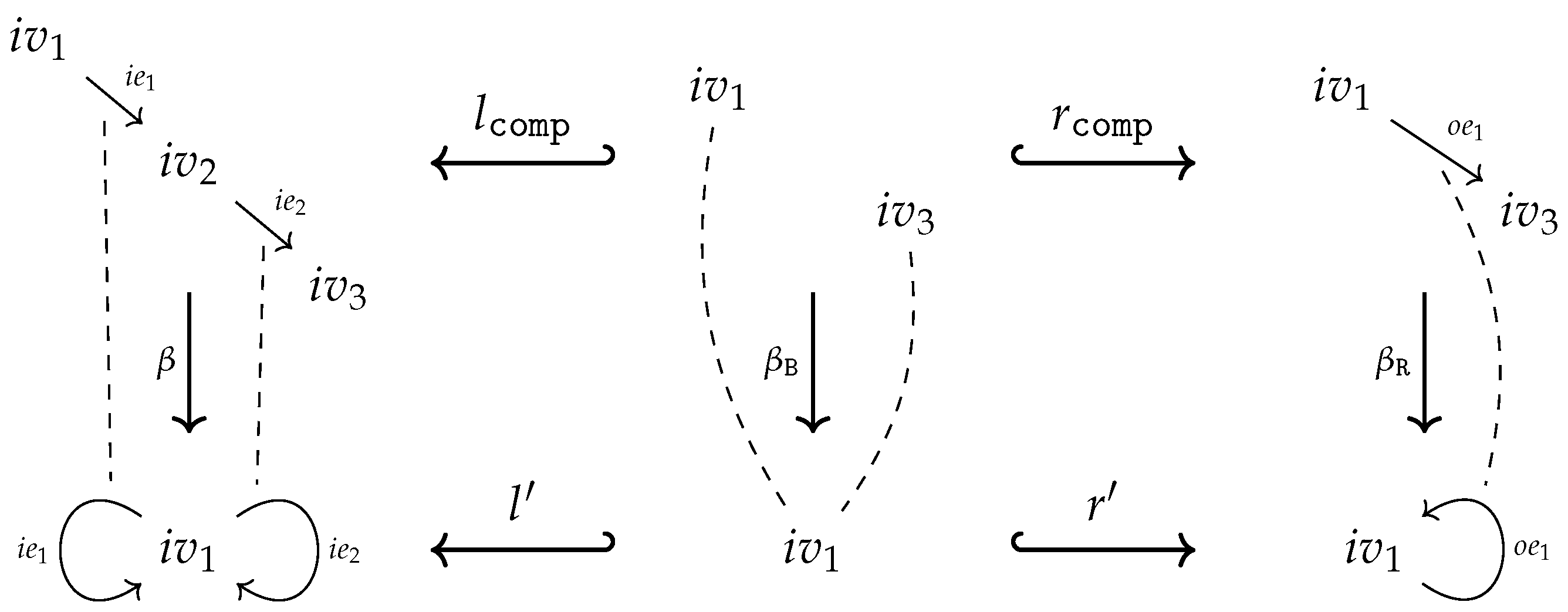
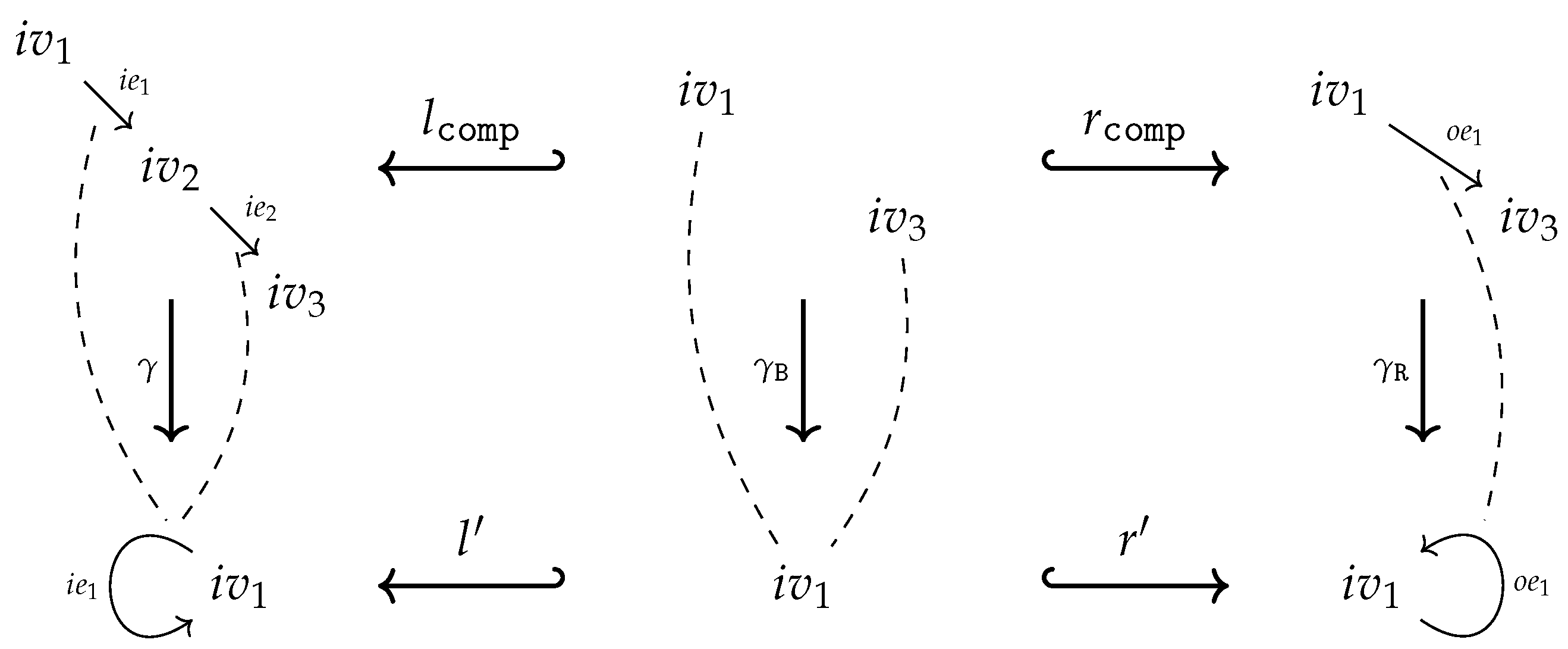
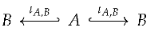 of inclusion maps (see the left diagram below). We set , , and . Since is injective both maps are injective too and, moreover, the pushout square is as well a pullback square. This ensures, especially, that is the equalizer of the maps in . The pushout property of the square provides a unique map such that
of inclusion maps (see the left diagram below). We set , , and . Since is injective both maps are injective too and, moreover, the pushout square is as well a pullback square. This ensures, especially, that is the equalizer of the maps in . The pushout property of the square provides a unique map such that
- Case 1
-
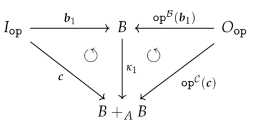
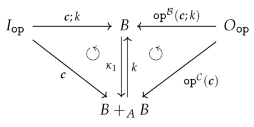
factors through : There exists a map such that (see the right diagram above). is unique since is a monomorphism. We simply set
- Case 2
- factors through : Analogously to Case 1.
- Case 3
- Overlapping of Case 1 and 2: There exist maps such that . Due to the pullback property of the square there exists a unique such that . The homomorphism property of ensures thus we get, finally, . That is, in the event of an overlapping, Case 1 and Case 2 define the same output . Note, that there will always be an overlapping for constant symbols!
- Case 4
-
factors neither through nor through : This can only happen if with . Utilizing the operations in to a maximal extent, Cases 1 and 2 define a partial map from to . However, since we restrict ourselves to total operations, we have to find an ad hoc totalization trick to turn into a total operation. Employing (7), we may decide to utilize the operations in to produce outputs in the left copy of B in . We set
3.3. Terms and Term Algebras
- Variables:
- , for all ;
- Constants:
- , for all with ;
- Operations:
- , for all with , and all maps in .
- Variables:
- , for all ;
- Constants:
- , for all ;
- Operations:
- , for all .
- Constants:
- , for all with , and
- Operations:
- , for all with , and all maps in .
- Constants:
- , for all ;
- Operations:
- , for all where is the map in defined by .
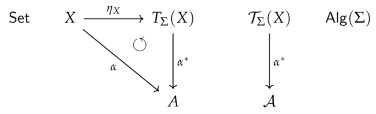
3.4. Substitutions
3.4.1. Substitution Calculi
- (1)
- substitution (declaration), i.e., an assignment of expressions to variables.
- (2)
- substitution application, i.e., the replacement of occurrences of variables in a given expression by the expressions assigned to the variables by a substitution.
- (3)
- preservation of well-formedness, i.e., replacing variables in a well-formed expression by well-formed expressions should result in a well-formed expression.
- (4)
- composition of linkable substitutions.
- (5)
- composition of substitutions is compatible with substitution application.
- (6)
- composition of substitutions is associative.
- (7)
- variable assignments, i.e., assignments of semantic items to variables.
- (8)
- evaluation of expressions, computing for each expression a unique semantic item or truth value, respectively.
- (9)
- composition of substitutions with variable assignments as well as composition of variable assignments with homomorphisms.
- (10)
- compatibility w.r.t. substitution application and/or evaluation, respectively.
- (11)
- associativity for the three new possible combinations of the four kinds of composition, i.e., substitution-substitution-assignment, substitution-assignment-homomorphism, and assignment-homomorphism-homomorphism, respectively.
3.4.2. Substitutions by Algebraic Extensions
- Feature (1):
- Substitutions become simply a special case of variable assignments and
- Feature (2):
- Substitution applications appear as a special case of term evaluations namely as algebraic extensions . Applying a substitution to a -term means nothing but to compute the -term . As mentioned before, it is common to use instead of also the more informative notation in (10) in case of finite sets of variables.
- Feature (3):
- Preservation of well-formedness is implicitly ensured by the fact that the structures, we define in Definition 10 (Term algebra), are indeed -algebras.

substitution; (substitution; assignment) = (substitution; substitution); assignment,
- Variables:
- , for all ;
- Constants:
- , for all ;
- Operations:
- , for all .
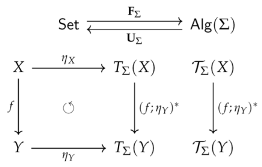
3.5. Two Model-Theoretic Implications of the Existence of a Free Functor
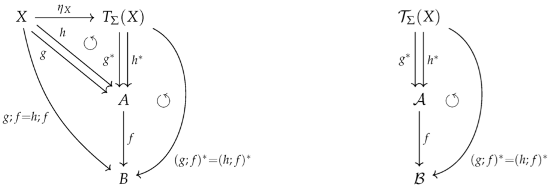
- is accessible via .
- is accessible via .
- is an epimorphisms in .
- is an epimorphism in , i.e., surjective.
3.6. Terms and Derived Operations
- Variables:
- for all the (projection) map is defined by for all ;
- Constants:
- , for all ;
- Operations:
- , for all , .
3.7. Syntactic Lawvere Theories
3.7.1. Construction of Lawvere Theories
- Objects:
-
As objects we chose canonical finite sets of variablesFor all we assume to be equipped with a fixed total order thus we can reuse the tuple notation to represent maps as discussed in Section 2.
- Morphisms:
- Morphisms are all tuples representing a substitution (declaration) .
- Identities:
- The identity on is the tuple representing the substitution .
- Composition:
- The composition of two tuples and is the tuple representing the substitution where is the application of the substitution according to Definition 11 (compare also (11)).
- Laws:
- Identity and associativity law are ensured by feature (5) composition of substitutions is compatible with substitution application (compare also (12))
3.7.2. Properties of Lawvere Theories
- The product of two objects and is defined by with projections and .
- The tuple of two morphisms and in is given by
4. Graph Algebras and Graph Term Algebras
4.1. Graph Signatures, Graph Algebras and Homomorphisms

- Two different kinds of input items.
- This is evident due to working with graphs which consists of both vertices and edges. Instead of a single set, we declare therefore a graph as the input arity.
- Arbitrary many output items.
- A single output is assumed for algebraic operations, but graph operations can produce arbitrarily large finite graphs as output. Similar to the input, the output arity is chosen to be a graph.
- Output is often related to the input.
- In the case of the composition operation above, the relation between the two arity graphs and is clear from the labelling: the output edge ’’ has the same source and target as the input edges ’’ and ’’, respectively. Instead of always requiring coherent labelling, we introduce a third arity graph , called the boundary of , to encompass the connection between input and output in a fitting way.
- a set of operation symbols,
- a map assigning to each operation symbol in its arity span, i.e., a span of inclusion graph homomorphisms between finite graphs such that the sets and as well as the sets and are disjoint. The graphs , , are referred to as theinput arity,boundary arity, and output arity of , respectively.
- by a graph , called the carrier of , and
- a family of maps such that the following diagram commutes for all in and all graph homomorphisms .
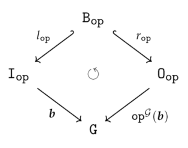
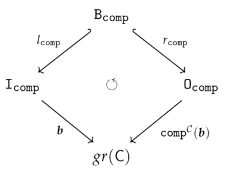

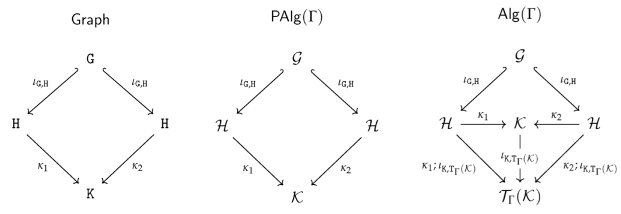
4.2. Comparison with the old definitions
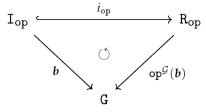
4.2.1. Comparison of Arity Declarations
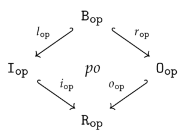
4.2.2. Equivalence of graph operations
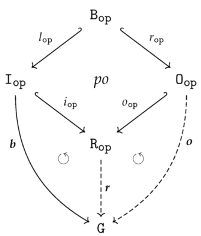
4.2.3. Equivalence of homomorphism conditions
4.3. Graph Subalgebras
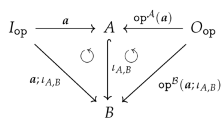
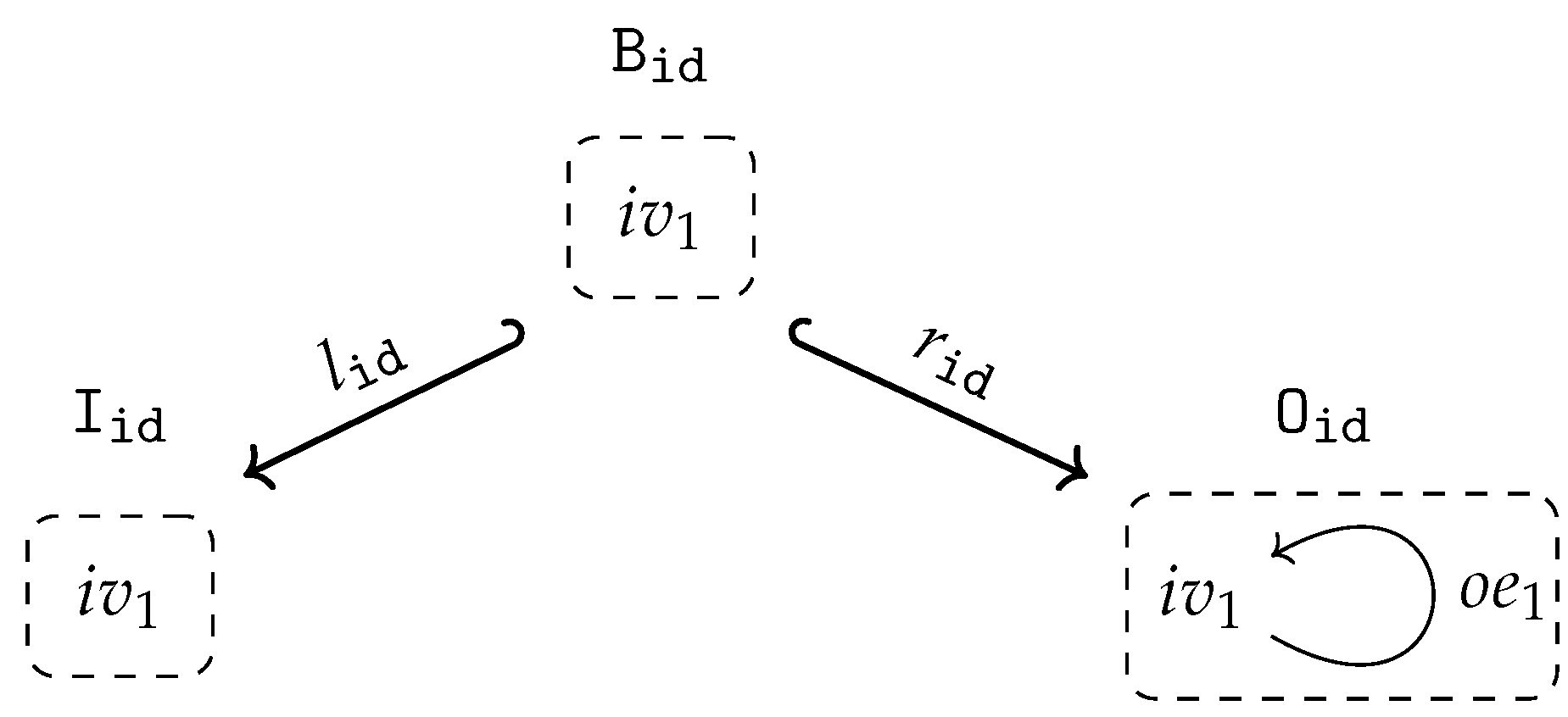
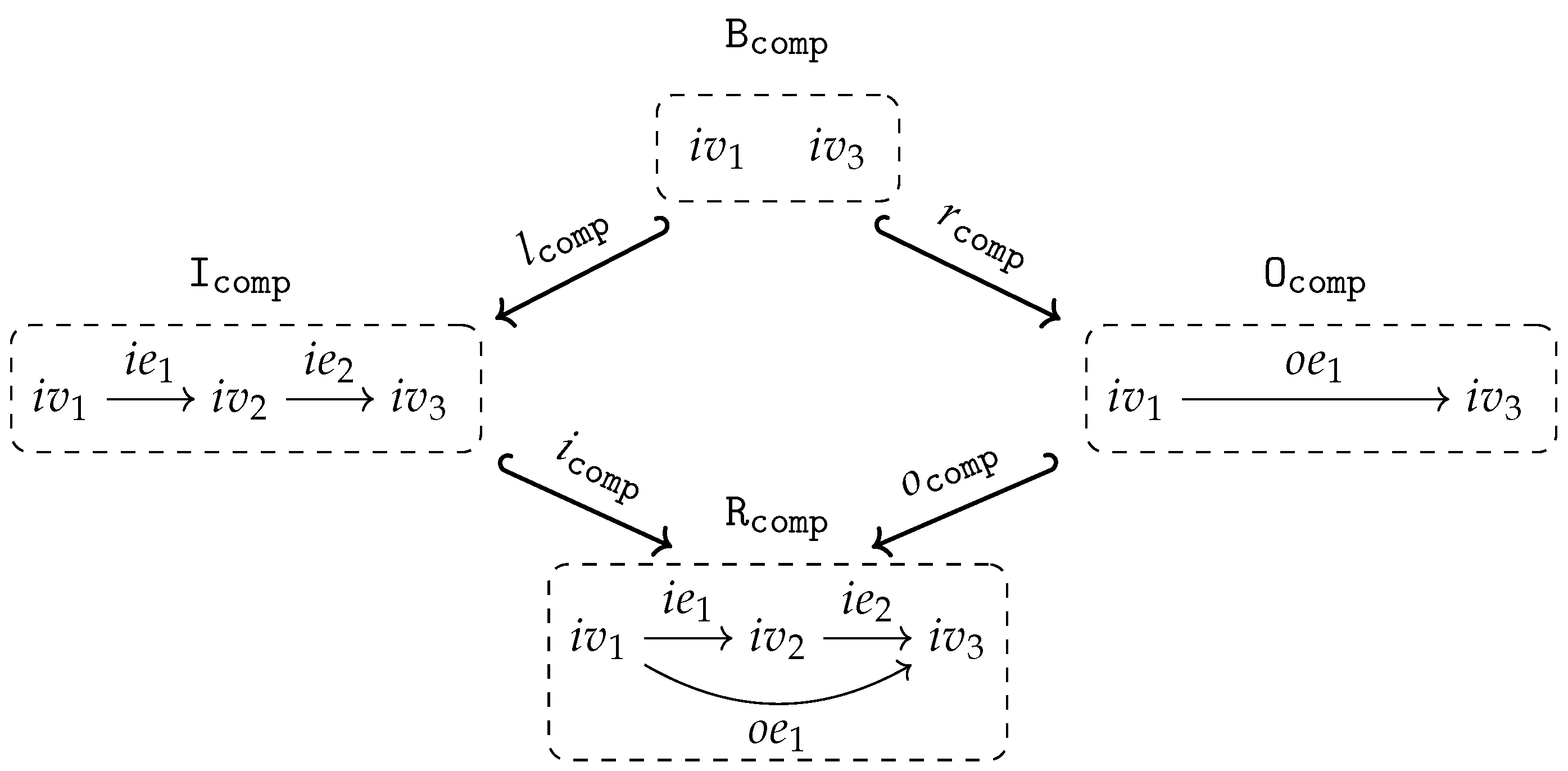
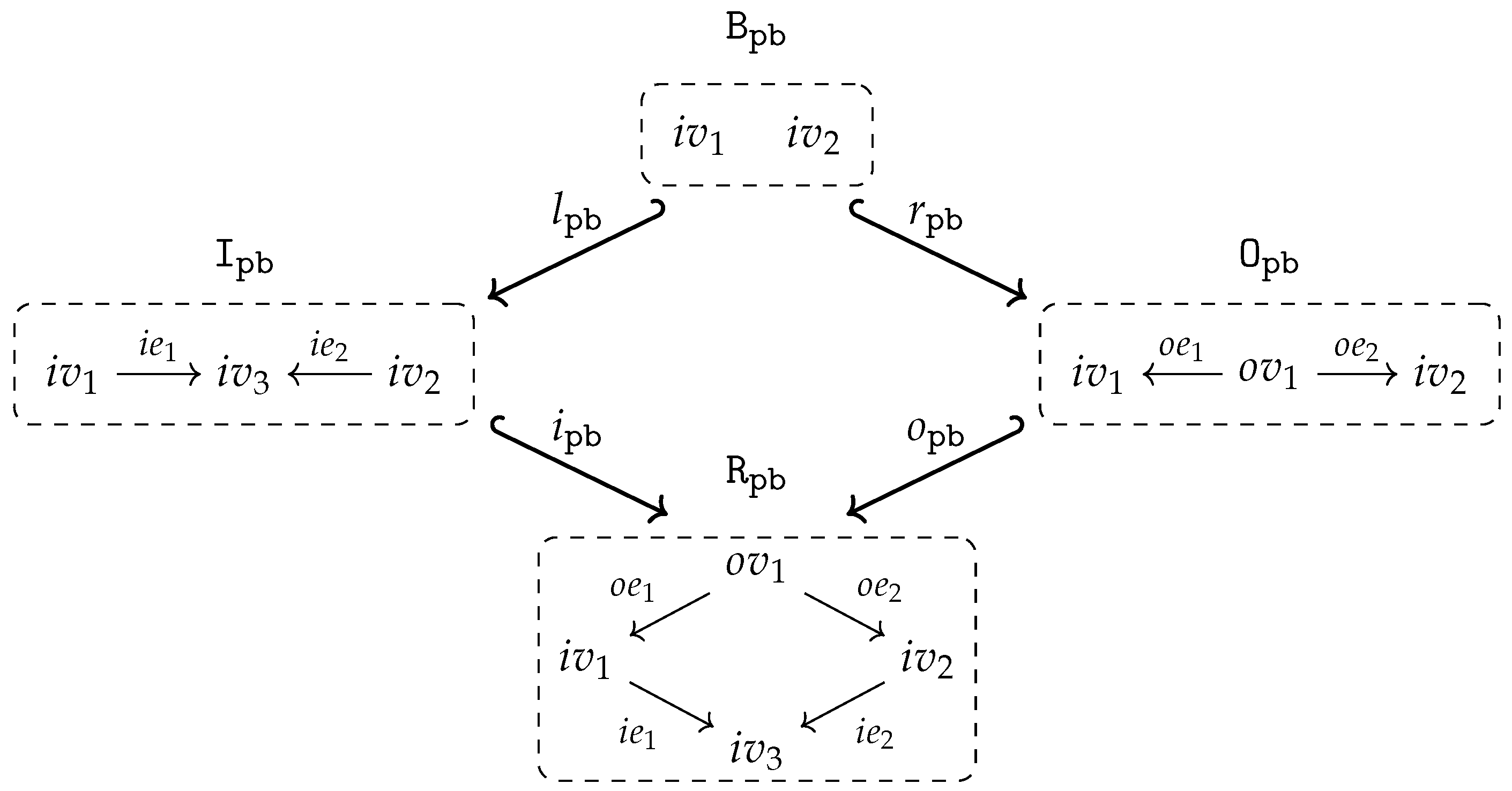
- isaccessible via a graph homomorphism if .
- If is accessible via an inclusion graph homomorphism , i.e., if , we say also that isgenerated by .
- is said to be generated if it is generated by the empty graph, i.e., accessible via the unique graph homomorphism from the initial object in to .
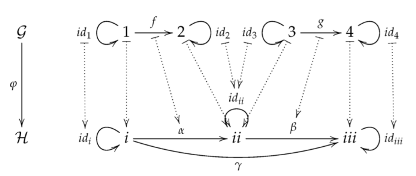
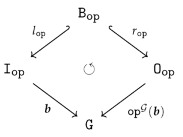
4.4. Partial Graph Algebras and their Term Completion
- by a graph , called the carrier of , and
- a family of partial maps such that the following diagram commutes for all in and all graph homomorphisms .
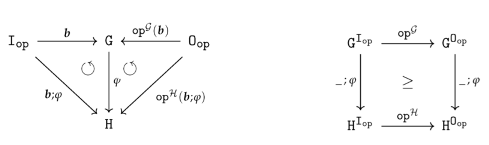
- Generators:
- Constants:
-
For all constants in , such that the graph contains
- as a vertex, for each vertex in ;
-
as an edge, for each edge in ,where and
- Operations:
-
For all in with and any such that there is no with , contains
- as a vertex, for each vertex in ;
- as an edge, for each edge in , where

- The term notation provides a uniform mechanism to create unique identifiers for the new graph items introduced by applying a non-deleting injective graph transformation rule.
- At the same time, the term notation encodes all the information necessary to identify uniquely the pushout that has been creating the new items.
- Constants:
-
For all constants in :
- Utilizing:
- If is defined, we simply reuse it:
- Completion:
-
If is not defined, i.e., we set
- for each vertex in and
- for each edge in .
- Operations:
-
For all in with and any :
- Utilizing:
- If there is a with , we reuse :
- Completion:
- If there is no with , we set
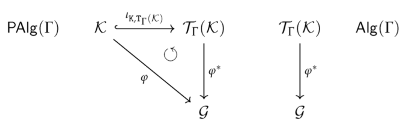
- Generators:
- In this basic case the defining condition forces for all and for all .
- Constants:
-
In the second basic case we have for all constants in :
- Utilizing:
- If is defined, the definition of operations in , the defining condition and the assumption that φ is a Γ-homomorphism ensure that satisfies the homorphism condition for the constant :
- Completion:
-
If is not defined, the definition of operations in and the required homomorphism condition for forces for each vertex inFor each edge in we get, analogously, .
- Operations:
-
We have for all in with and any :
- Utilizing:
- If there is a with , the definition of operations in , the defining condition and the assumption that φ is a Γ-homomorphism ensure that satisfies the homomorphism condition for :
- Completion:
-
If there is no with , the induction hypothesis is that is already defined on a subgraph and that . This ensures . In the induction step we extend to the graph . The definition of operations in and the required homomorphism condition for forces for each vertex inFor each edge in we get, analogously, .
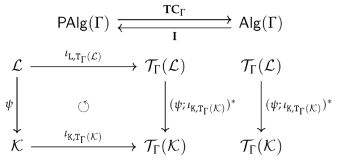
4.5. Graph Terms and Graph Term Algebras
- Graph terms
- We denote the graph , according to Definition 23, also by and call it thegraph of all (graph) -terms on .
- Graph term algebra
- We denote the term completion Γ-algebra , according to Definition 24, also by and call it the-term graph algebra on .
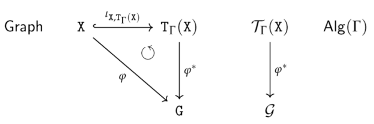
- Substition Calculus:
- Graph term algebras manifest the “internalization approach” in the case of graph algebras. Relying on Proposition 11, we can indeed obtain a fully fledge substitution calculus, meeting the requirements formulated in Section 3.4.1. Based on the idea that a substitution (declaration) is now given by a graph homomorphism and that a variable assignment is a graph homomorphism for a -algebra , we can simply transfer all the discussion, definitions and results from Section 3.4.2 to graph algebras. We will spare the reader this copy-paste exercise.
- No appropriate concept of Derived Operation:
- In traditional Universal Algebra we do have a one-to-one correspondence between the “internal view” of terms as elements of free algebras and the “external view” of terms as an appropriate representation of derived operations (compare Definition 12 and Definition 14). It took us a while to understand that and why this one-to-one correspondence breaks down if it comes to graph algebras. We discuss and address this problem in the next section.
5. Derived Graph Operations
5.1. Reconstruction of syntactic Lawvere Theories
5.1.1. Categories with Finite Products
- has an empty product (terminal object) , i.e., for any object A in there is a morphism such that
- For any family , of objects there is an object together with projections , such that
-
for any object B and any family , of morphisms there is a morphism withMoreover, we have and .
- Finally, for all morphisms the following equation holds
5.1.2. Categories based on Finite Product Expressions
- Objects:
- As objects we choose the same canonical finite sets of variables as for
- Morphisms:
-
Morphisms are all finite product expressions defined inductively as follows
- Symbolic Projections:
- is an fp-expression for all , .
- Constant and Operation Symbols:
- with is an fp-expression if is an n-ary operation symbol in .
- Empty Symbolic Tuples:
- is an fp-expression for all .
- Non-empty Symbolic Tuples:
- is an fp-expression for all , and all families , of fp-expressions.
- Symbolic Sequential Composition:
- is an fp-expression for all and all fp-expressions , .
- Symbolic Identities:
- is the identity on for all and is the identity on .
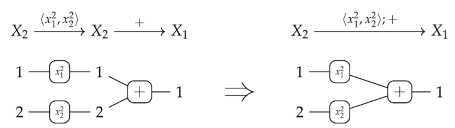
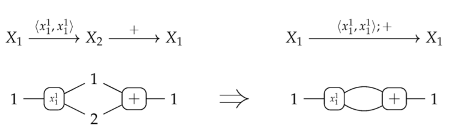

- Variables:
- , for all , .
- Constants:
- , for all ;
- Operations:
- , for all , .
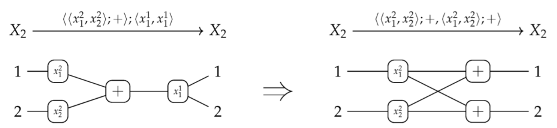
5.1.3. Substitutions Revisited
substitution application ≅ symbolic composition plus normalization.
5.2. Analysis of Finite Product Expressions
5.2.1. Finite Products vs. Tensor Products
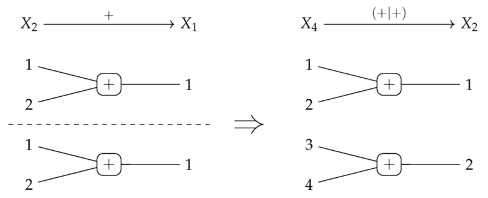
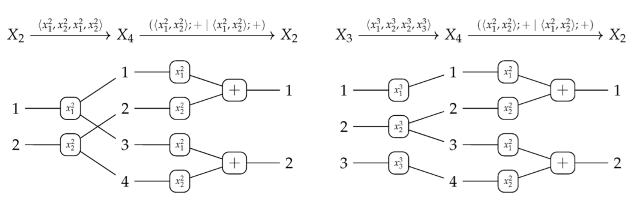
5.2.2. Copying vs. Soldering
5.3. Three Mechanisms to construct new Graph Operations
5.3.1. Parallel Composition
5.3.2. Instantiation
5.3.3. Sequential Composition
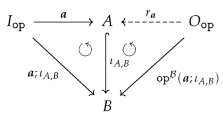
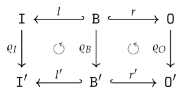
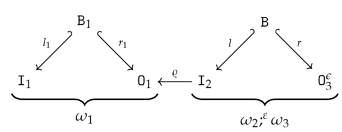
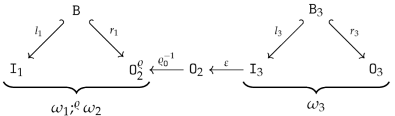
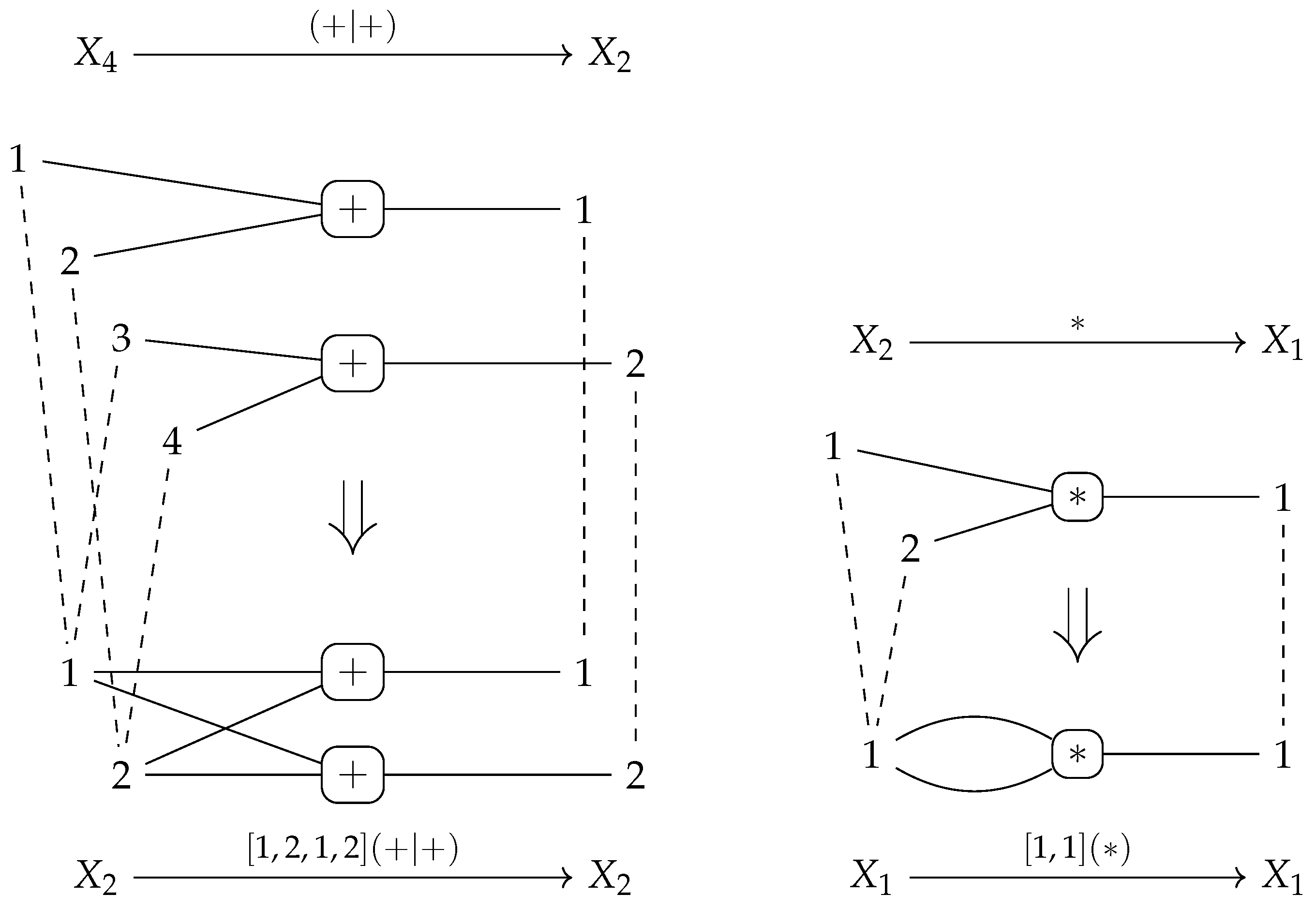
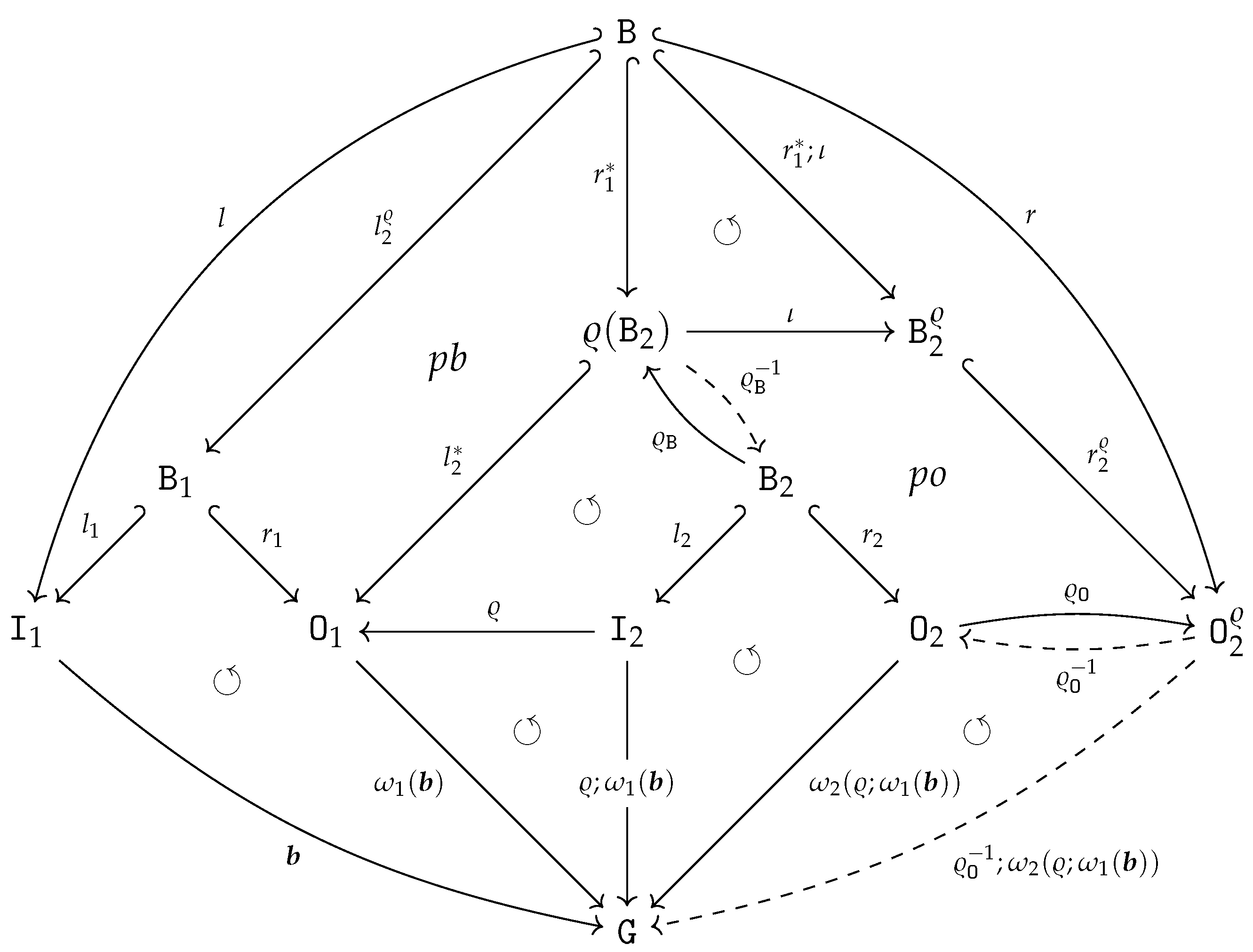
- For canonical arity spans and , we can have an equality only if is a built-in projection.
- There are two kinds of output items produced by the sequential composition of two graph operations. First, the output items produced by . Second, the output items produced by and implicitly transferred by , i.e., the items in . In other words, the resulting arity will not satisfy the disjointness condition in 15 if is non-empty!
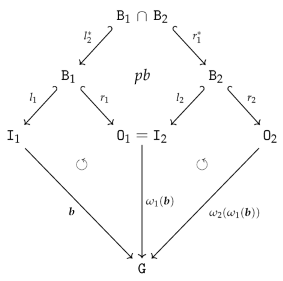
- We obtain an epi-mono factorization of by constructing the image of w.r.t. . The resulting restriction of becomes an isomorphism since is an isomorphism.
- The boundary arity of can now be constructed by simple intersection (pullback): and .
- To be able to define as an extension of such that consists of canonical sets of output vertices and output edges, according to Remark 10, we first have to reindex the output vertices/edges in . We construct a graph , isomorphic to with and where and for and .
- We can define an isomorphism that is the identity on and, in addition, restricted to is an order-preserving map from to while restricted to is an order-preserving map from to . The construction ensures that becomes an inclusion graph homomorphism .
- We construct by a pushout of the span
 with where is constructed by “index shifting” and where is also constructed by “index shifting”.
with where is constructed by “index shifting” and where is also constructed by “index shifting”. - The construction ensures and that becomes an isomorphism. We set and obtain a canonical arity span as required.
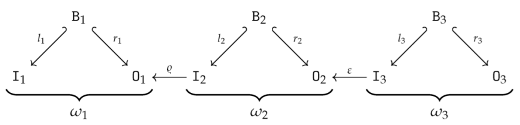
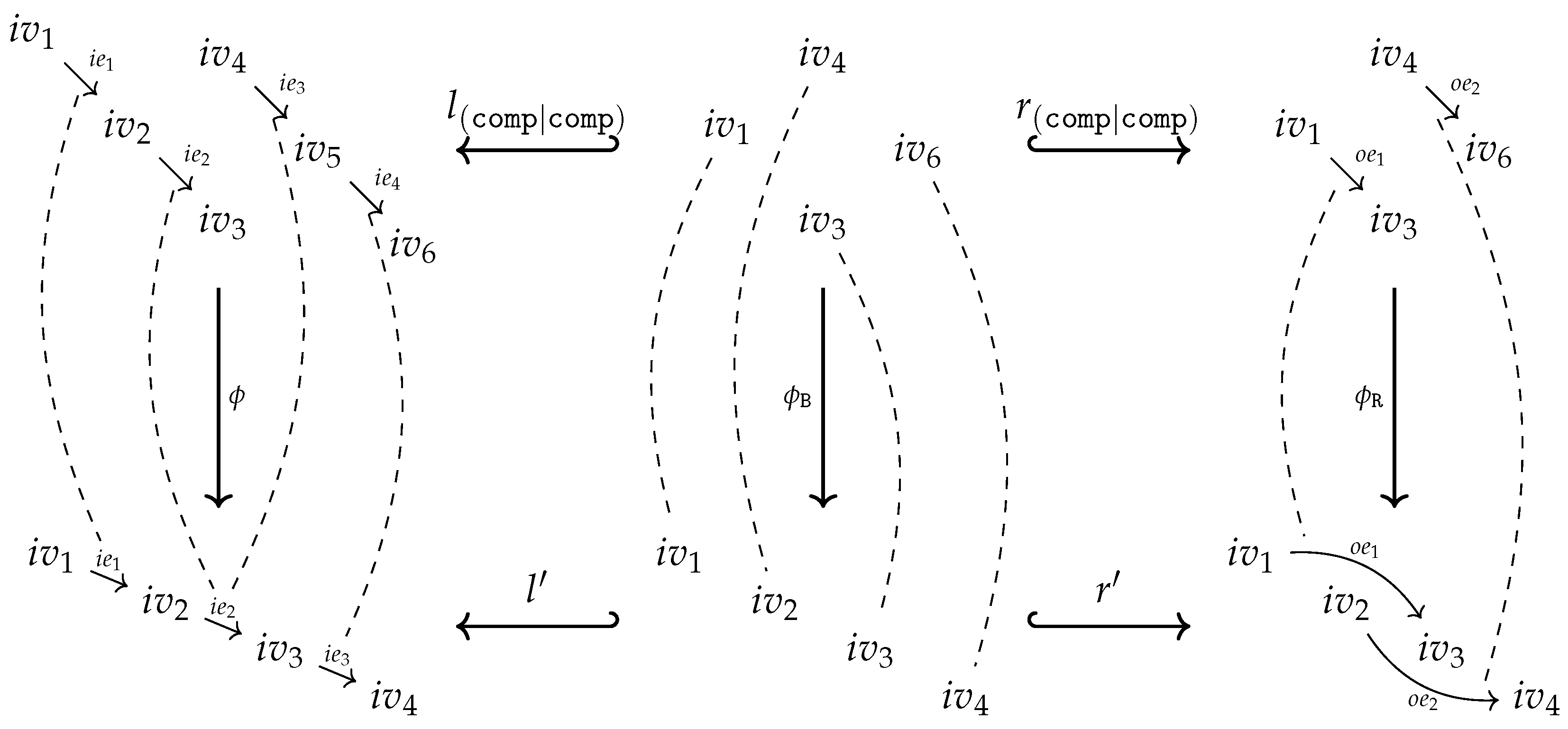
5.4. Graph Operation Expressions and Derived Graph Operations
- Projections:
-
with arity span for any finite canonical input arity graph and any subgraph .is called aprojection expression.
- Constants:
-
with arity for any constant symbol and any finite canonical input arity graph .Moreover, with arity for any non-empty subgraph .Both expressions and are declared assingle -expressions.
- Operations:
-
for any operation symbol , any finite canonical input arity graph , and any graph homomorphism where the arity is constructed as an instance of the arity by means of and a pushout as done in (31).Moreover, for any non-empty subgraph such that non-empty with arity .Both expressions and are calledbasic -expressions and are declared as single -expressions.
- Multi expressions:
-
for any family , , of single Γ-expressions or projection expressions with, at least, one single Γ-expression. The arity is constructed as described in Remark 17.Moreover, for any finite canonical input arity graph , and any graph homomorphism with arity constructed as an instance of the arity by means of and a pushout as done in (31).Both expressions and are declared asmulti -expressions.
- Symbolic composition:
-
for any single or multi Γ-expression with arity , any basic Γ-expression with arity , and any graph isomorphism .The arity with isomorphic to is constructed as described in Section 5.3.3.is declared as asingle -expressions.
- Constants:
- In the case , we will just write instead of and instead of .
- Operations:
- In the case , we will just write instead of and instead of .
- Projections:
- , according to (17), for all .
- Constants:
-
for all .for all .
- Operations:
-
, according to Section 5.3.2, for all .for all .
- Multi expressions:
-
, according to Section 5.3.1, for all ., according to Section 5.3.1 and Section 5.3.2, for all .
- Symbolic composition:
- , according to Section 5.3.3, for all .
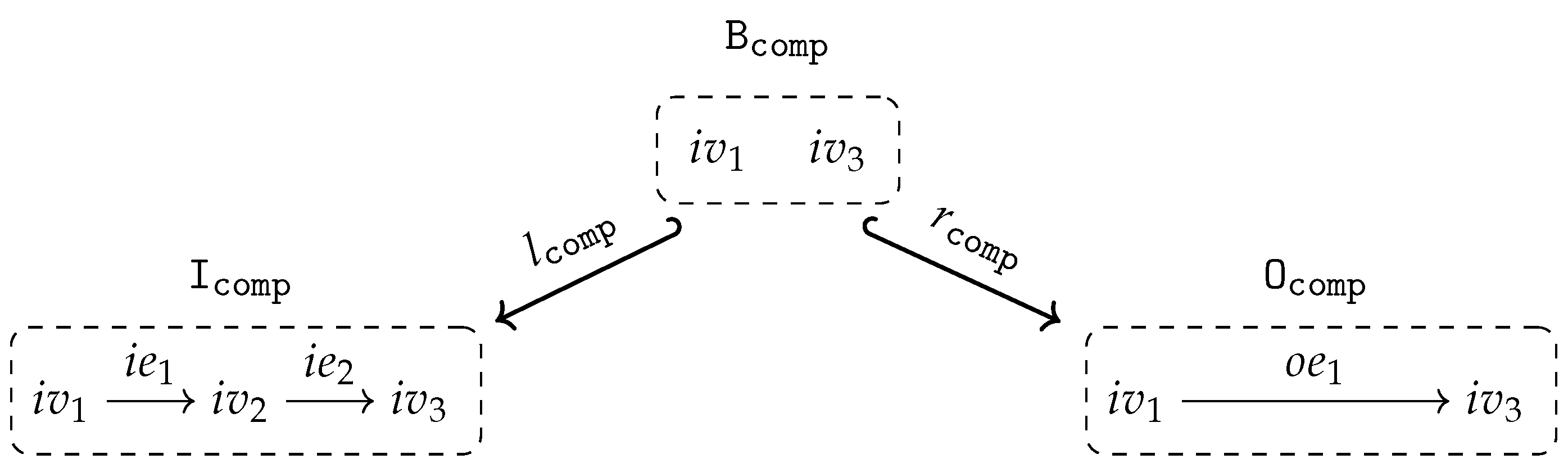
For any finite canonical input arity graph and any finite subgraph there exist a graph operation expression with input arity and an output arity isomorphic to such that for all Γ-algebras we have (up to arity renaming) for the graph operation defined in Lemma 6.
- By means of the restriction expressions and we can simulate the “pseudo operation symbols” , , , and their semantics by chosing to be the single output vertex or the single output edge (together with its source and target), respectively.
- Once, we have been able to represent all the single vertices and edges in a subgraph by corresponding graph operation expressions, we can combine them into one graph operation expression by the trick used in Conjecture 3 to define the graph operation expression . All the single output arities will be soldered together resulting in a graph isomorphic to .
6. Operations in Topoi
7. Related Work
- Input and output arity graphs are not described with concrete syntactic identifiers, but are implicitly considered as being given by “equivalence up to arity renaming”.
- There are no boundaries and thus no systematic treatment of “preservation conditions” as we formalized them by means of the commutativity condition in (16).
- In the examples, preservation conditions are expressed by means of ad-hoc equations between vertices and/or edges, respectively.
- There is no explicit notion of “derived graph operation” and the issue of “graph operation expressions” is not addressed at all.
- Derived graph operations, in our sense, appear only implicit when properties of graph operations are described by means of equations between vertices and/or edges.
- Traditional monoidal categories and string diagrams deal only with single isolated items as input and output of operations.
- This becomes manifested in the absence of boundaries.
- The essential difference is that the presence of boundaries forces us to replace “copying of items” internal in a diagram by “soldering of input and output ports”, i.e., by constructing an instance of a diagram as a whole.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wolter, U.; Diskin, Z.; König, H. Graph Operations and Free Graph Algebras. In Proceedings of the Graph Transformation, Specifications, and Nets - In Memory of Hartmut Ehrig. Springer, LNCS 1 0800, 2018, pp. 313–331. [Google Scholar] [CrossRef]
- Wolter, U. Logics of Statements in Context - Category Independent Basics. Mathematics 2022, 10. [Google Scholar] [CrossRef]
- Makkai, M. Generalized Sketches as a Framework for Completeness Theorems. Journal of Pure and Applied Algebra 1997, 115, 49–79. [Google Scholar] [CrossRef]
- Cadish, B.; Diskin, Z. Heterogeneous View Integration via Sketches and Equations. In Proceedings of the ISMIS; 1996; Vol. 1079, pp. 603–612.
- Diskin, Z. Databases as Diagram Algebras: Specifying Queries and Views Via the Graph-Based Logic of Sketches. Technical Report 9602, Latvia, 1996. [Google Scholar]
- Diskin, Z.; Kadish, B. A Graphical Yet Formalized Framework for Specifying View Systems. In Proceedings of the First East-European Symposium on Advances in Databases and Information Systems. Nevsky Dialect; 1997; pp. 123–132. [Google Scholar]
- Burroni, A. Algèbres graphiques (sur un concept de dimension dans les langages formels). Cahiers de topologie et géométrie différentielle catégoriques 1981, 22, 249–265. [Google Scholar]
- Poigné, A. , Guildford, U.K. September 16–20, 1985 Proceedings; Pitt, D.; Abramsky, S.; Poigné, A.; Rydeheard, D., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 1986; pp. 76–102. https://doi.org/10.1007/3-540-17162-2_118.categorically. In Category Theory and Computer Programming: Tutorial and Workshop, Guildford, U.K. September 16–20, 1985 Proceedings; Pitt, D., Abramsky, S., Poigné, A., Rydeheard, D., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 1986; Springer Berlin Heidelberg: Berlin, Heidelberg, 1986; pp. 76–102. [Google Scholar] [CrossRef]
- Ehrig, H.; Ehrig, K.; Prange, U.; Taentzer, G. Fundamentals of Algebraic Graph Transformation; Monographs in Theoretical Computer Science. An EATCS Series, Springer, 2006.
- Barr, M.; Wells, C. Category Theory for Computing Science; Series in Computer Science; Prentice Hall International: London, 1990. [Google Scholar]
- Pierce, B.C. Basic Category Theory for Computer Scientists; The MIT Press Cambridge, Massachusetts London, England, 1991.
- Wolter, U. Cogenerated Quotient Coalgebras. Technical Report Report No 299, Department of Informatics, University of Bergen, 2005.
- Ehrig, H.; Mahr, B. Fundamentals of Algebraic Specification 1: Equations and Initial Semantics; EATCS Monographs on Theoretical Computer Science 6, Springer, 1985.
- Wolfgang Wechler. Universal Algebra for Computer Scientists. In Proceedings of the Monographs in Theoretical Computer Science. An EATCS Series. Springer-Verlag, Berlin Heidelberg, 1992, Vol. 25, p. 339. [CrossRef]
- MacLane, S. Categories for the Working Mathematician; Springer-Verlag: New York, 1971. [Google Scholar]
- Goldblatt, R. Topoi: The Categorial Analysis of Logic; Dover Publications, 1984.
- Reichel, H. Initial Computability, Algebraic Specifications, and Partial Algebras; Oxford University Press, 1987.
- Wolter, U. An Algebraic Approach to Deduction in Equational Partial Horn Theories. J. Inf. Process. Cybern. EIK 1990, 27, 85–128. [Google Scholar]
- Claßen, I.; Große-Rhode, M.; Wolter, U. Categorical concepts for parameterized partial specifications. Math. Struct. in Comp. Science 1995, 5, 153–188. [Google Scholar] [CrossRef]
- Corradini, A.; Gadducci, F. An Algebraic Presentation of Term Graphs, via GS-Monoidal Categories. Applied Categorical Structures 1999, 7, 299–331. [Google Scholar] [CrossRef]
- Selinger, P. , B., Ed.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2011; pp. 289–355. https://doi.org/10.1007/978-3-642-12821-9_4.Categories. In New Structures for Physics; Coecke, B., Ed.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2011; Springer Berlin Heidelberg: Berlin, Heidelberg, 2011; pp. 289–355. [Google Scholar] [CrossRef]
- Makkai, M. First Order Logic with Dependent Sorts, with Applications to Category Theory. available from Makkai’s homepage http://www.math.mcgill.ca/makkai/.


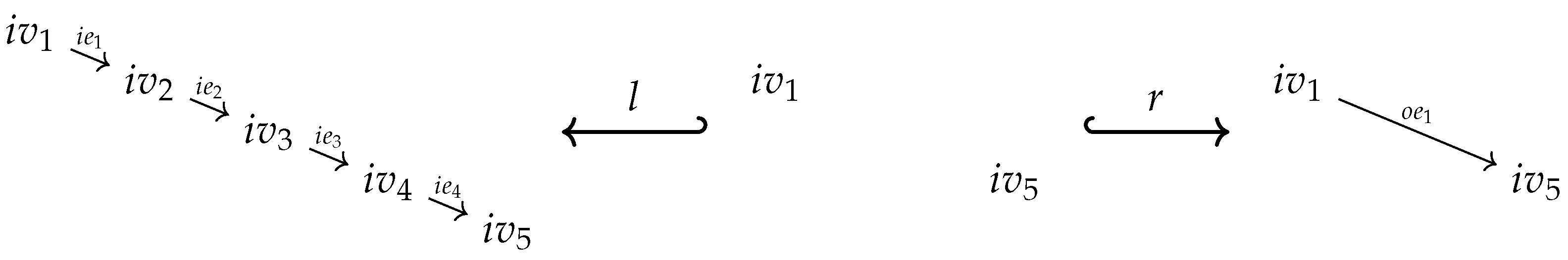
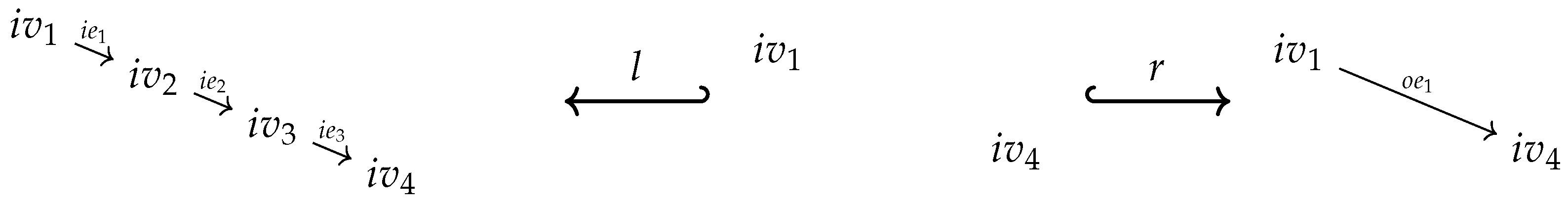
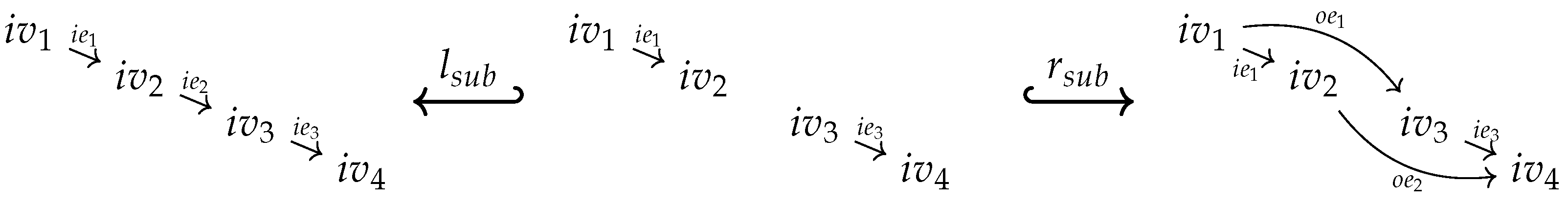
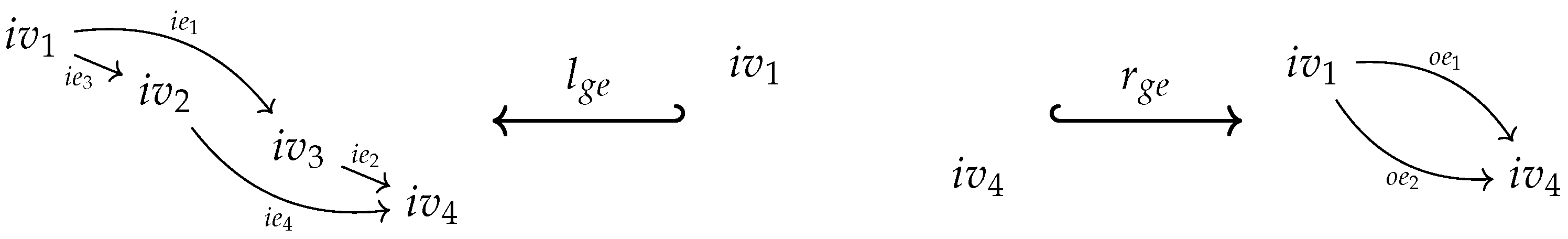
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




