Performance Analysis of CHAID Algorithm for Accuracy

1. Introduction

Since the 1990s, with the rapid development of information technology, the application of database systems has become more widespread, and at the same time database technology has entered a completely new stage, from solely managing some simple data in the past to managing a wide variety of complex data such as images, videos, audio, graphics and electronic files generated by various devices, thereby the amount of data has become larger and larger.

In this era of such advanced information, the vast amount of information may not only bring us benefits but also bring us many negative effects. The most important factor in the influence on negative effects is that effective information is difficult to be refined, and too much meaningless data will inevitably bring about the information distance and the loss of meaningful knowledge. This is what John Nalsbert calls the “information-rich but knowledge-poor” dilemma [1]. With the original functions of the database system, people could not discover the relationships and rules implied in the data, and could not predict future trends based on the existing data. There is a lack of methods to uncover the hidden value behind the data. To solve this problem, there is an urgent need for a technology that can analyze large amounts of information more deeply, get insight into the hidden value, and make the seemingly useless data useful.

Decision trees are an effective way to generate classifiers from data, and decision trees represent the class of the most widely applied logical methods [2,3]. In 1980 Kass first proposed the chi-squared automatic interaction detector (CHAID), a tool used to discover relationships between variables, a decision tree technique based on an adjusted significance test (Bonferroni test) [4,5]. It divides the respondents into several groups according to the relationship between the underlying variable and the dependent variable, and then each group into several groups. Dependent variables are usually some key indicators, such as the level of use, purchase intention, etc. A dendrogram is displayed after each program run. The top is a collection of all respondents, the following is a subset of two or more branches, and the CHAID classification is based on a dependent variable [6].

In practice, CHAID is often used in the context of direct selling, selecting consumer groups and predicting their response, and how some variables affect other variables [7,8], while other early applications are in the research field of medicine and psychiatry. There are also engineering project cost control, financial risk warning, and fire reception and handling analysis [9]. We have been starkly aware of CHAID maps non-linear relationships quite well, and it can empower predictive models with stability [10]. But we don’t know how high its accuracy is precisely. To find out the perfect scope CHAID algorithm fits into, this paper presents the analysis of the accuracy of the CHAID algorithm.

2. CHAID Algorithm and Chi-Square Detection

The core idea of CHAID algorithm is that optimal divide the samples according to the given target variable and the selected feature index (such as predictive variable), and group the contingency table to automatically judge according to the significance of chi-square test. The field selection of the CHAID algorithm is performed by using the chi-square test.

2.1. Classification Process of the CHAID Algorithm

The target variables for categorization are first selected, then cross-categorized with the target variables to produce a series of 2-D taxonomic tables.

The chi-square value of the two-dimensional classification table is calculated separately, and the size of the P-values is compared, and the two-dimensional table with the lowest P-value is used as the best initial classification table, and then the categorical variable is used as the first-level variable of the CHAID decision tree.

Based on the best initial classification table, we will continue to classify the target variables to obtain the second and tertiary variables of the CHAID decision tree.

The process is repeated until the p-value is greater than the set statistically significant alpha value or until the classification stops when all variables are classified.

2.2. Introduction of Chi-Square Detection

2.2.1. The Concept and Significance of Chi-Square Detection

Chi-square detection is the deviation between the theoretical value and the actual value of the statistical sample. The degree of deviation determines the size of the chi-square value. If the degree of deviation is smaller, the chi-square value will be smaller. On the contrary, the larger the chi-square value is, if the actual value and the theoretical value are calculated, the chi-square value is equal to 0.

2.2.2. The Basic Idea of Chi-Square Detection

Chi-square test is a commonly used hypothesis test based on the chi-square distribution.

Firstly, assume that the hypothesis: the expected frequency is not different from the observed frequency’ holds. Under this premise, the chi-squared values of the theoretical and actual values are calculated. The probability that hypothesis holds under the current statistical sample can be determined based on the chi-squared distribution and degrees of freedom. The following figure shows some chi-square value probability tables:

Table 1. A probability table of partial chi-square distributions.

$\mathbf{P}({\mathbf{x}}^2\ge \mathbf{k}$)	k	$\mathbf{P}({\mathbf{x}}^2\ge \mathbf{k}$)	k
0.50	0.455	0.05	3.841
0.40	0.708	0.025	5.024
0.25	1.323	0.010	6.635
0.15	2.072	0.005	7.879
0.10	2.706	0.001	10.828

Table 1. A probability table of partial chi-square distributions.

$\mathbf{P}({\mathbf{x}}^2\ge \mathbf{k}$)	k	$\mathbf{P}({\mathbf{x}}^2\ge \mathbf{k}$)	k
0.50	0.455	0.05	3.841
0.40	0.708	0.025	5.024
0.25	1.323	0.010	6.635
0.15	2.072	0.005	7.879
0.10	2.706	0.001	10.828

If the P-value is small, then the probability of the hypothesis ${\mathrm{H}}_0$ holding is small, the hypothesis ${\mathrm{H}}_0$ should be rejected, indicating a significant difference between the theoretical value and the actual value; if the P-value is large, the hypothesis ${\mathrm{H}}_0$ cannot be rejected and there is a difference between the theoretical value and the actual situation represented by the actual value.

2.2.3. Formula for Chi-Square Detection

$$\begin{gathered} x^2={\displaystyle \sum _{}^{}\frac{{(A-E)}^2}{E}}={\displaystyle \sum _{i=1}^k\frac{{(A_i-E_i)}^2}{E_i}}={\displaystyle \sum _{i=1}^k\frac{{(A_i-n{p}_i)}^2}{n{p}_i}} \\ (i=1,2,3,\dots ,k) \end{gathered}$$

(1)

In this formula,where ${\mathrm{x}}^2$is the chi-square value obtained by the actual and theoretical values, k is the number of cells in the two-dimensional table, ${\mathrm{A}}_{\mathrm{i}}$ is the actual value of i, ${\mathrm{E}}_{\mathrm{i}}$ is the expected value of i, n is the total number of samples,${\mathrm{p}}_{\mathrm{i}}$ is the expected frequency of i, and ${\mathrm{E}}_{\mathrm{i}}$ = (n: the total number of samples) * (${\mathrm{p}}_{\mathrm{i}}$: the expected probability of i).

2.2.4. Steps for Chi-Square Detection

Firstly, assuming that ${\mathrm{H}}_0$holds, determine the degree of freedom (degree of freedom = (row-1) * (column-1), where the row, the column is the number of rows and columns in the two-dimensional table). Then the theoretical frequency number is obtained with the maximum likelihood estimation, At last, substitute it into the formula to solve.

Table 2. Chi-square detection sample data.

	Male	Female
Make up	15 (55)	95 (55)	110
Do not make up	85 (45)	5 (45)	90
	100	100	200

Table 2. Chi-square detection sample data.

	Male	Female
Make up	15 (55)	95 (55)	110
Do not make up	85 (45)	5 (45)	90
	100	100	200

Assume that in the above example “whether or not to make up has no relationship with gender”.

Maximum likelihood estimation yields the expected value ${\mathrm{E}}_{\mathrm{i}}$: ${\mathrm{E}}_1$=100 * 110 / 200=55 (100 is the number of men actually surveyed, 110 / 200 is the number of people in all the surveys, from which the likelihood estimate of men made up).

$${\mathrm{E}}_2=100\ast 110/200=55$$

$${\mathrm{E}}_3=100\ast 90/200=45$$

$${\mathrm{E}}_4=100\ast 90/200=45$$

There is a significant difference between the value obtained in maximum likelihood estimation (inside of parentheses) and the actual value (outside of parentheses).

Generation formula:

$${\mathrm{x}}^2=\sum _{\mathrm{i}=1}^{\mathrm{k}}\frac{{\left({\mathrm{A}}_{\mathrm{i}}-\mathrm{n}{\mathrm{p}}_{\mathrm{i}}\right)}^2}{\mathrm{n}{\mathrm{p}}_{\mathrm{i}}}=\frac{{\left(95-55\right)}^2}{55}+\frac{{\left(15-55\right)}^2}{55}+\frac{{\left(85-45\right)}^2}{45}+\frac{{\left(5-45\right)}^2}{45}=129.3>10.828$$

(2)

Because the desired result, ${\mathrm{x}}^2$> 10.828, means that the null hypothesis of 0.001 might hold, the 99.9% probability is that no makeup is significantly associated with sex;

2.3. The Field Selection Procedure for CHAID Algorithm

After understanding the process of chi-square detection, let’s take a look at the field selection process of CHAID algorithm.

CHAID field is selected using a chi-square statistic. Chi-square distribution is actually whether the two category fields are distributed or not. And the numerical field will help you automatically discrete, into a category field, to analyze whether it is related to the target field. Larger indicates that the more significant the relationship, otherwise not obvious.

The row of the above table is the income level, and the column is whether to buy a computer. The calculation of chi-square statistics should first draw the frequency from the data, and then find their expectations. Then the squared difference between the two is found and summed.

Table 3. Income and actual data.

income	Yes	No	Total
high	2	2	4
medium	4	2	6
low	3	1	4
Total	9	5	14

Table 3. Income and actual data.

income	Yes	No	Total
high	2	2	4
medium	4	2	6
low	3	1	4
Total	9	5	14

Table 4. Income and buying a computer expectation data.

income	Yes	No	Total
high	2.571429	1.428571	4
medium	3.857143	2.142857	6
low	2.571429	1.428571	4
Total	9	5	14

Table 4. Income and buying a computer expectation data.

income	Yes	No	Total
high	2.571429	1.428571	4
medium	3.857143	2.142857	6
low	2.571429	1.428571	4
Total	9	5	14

Table 5. The squared difference between the expected data and the actual data.

income	Yes	No
high	0.126984	0.228571
medium	0.005291	0.009524
low	0.071429	0.128571

Table 5. The squared difference between the expected data and the actual data.

income	Yes	No
high	0.126984	0.228571
medium	0.005291	0.009524
low	0.071429	0.128571

The first table is a table of the actual data, derived from the actual data statistics. The second table is a table of seeking expectations, which is equivalent to thinking that the two are independent, so you can multiply them directly by the probability, and then multiply the total.

The third table is seeking the variance. After summing, ${\mathrm{x}}^2$ is equal to 0.57, and the corresponding probability is 75%, indicating that the two are relatively weak. The full chi-square probabilities show as follows.

Table 6. All chi-square probabilities.

age	student	credit_rating	income
$x^2$=3.54667 P = 0.16977	$x^2$=2.80000 P = 0.09426	$x^2$=0.93333 P = 0.33400	$x^2$=0.57037 P = 0.75188

Table 6. All chi-square probabilities.

age	student	credit_rating	income
$x^2$=3.54667 P = 0.16977	$x^2$=2.80000 P = 0.09426	$x^2$=0.93333 P = 0.33400	$x^2$=0.57037 P = 0.75188

After comparison, we can see that the age feature value is the largest in ${\mathrm{x}}^2$=3.54667 value, indicating that the age is the most closely related to whether to buy a computer, so we chose age variable as the variable of the decision tree to produce the leaf node of the next level.

3. Comparison of Decision Tree Algorithm and Accuracy Analysis of CHAID Algorithm

The three most commonly used decision tree algorithms are CHAID, CART, and ID3, including the latest C4.5, and even C5.0.

CHAID algorithm has a long history. According to the principle of local optimization, CHAID uses the chi-square test to select the independent variables that affects the dependent variable most. Then, because the independent variables may have many different categories, CHAID algorithm will generate equal amounts of leaf nodes according to the number of categories of the independent variable, so CHAID algorithm is a multi-fork tree.

The CHAID method is optimal when the predictor variable is categorical variable. For continuous variables, CHAID automatically divides the continuous variables into 10 segments, but there may be omissions.

CHAID algorithm uses the chi-square detection method in statistics, and because of the chi-square detection method, CHAID has a good mathematical theoretical basis in branch calculation, and its credibility and its accuracy are relatively high.

On this basis the CHAID algorithm uses the pre-pruning method, pre-pruning is pruning before dividing and generating the decision tree under constant pruning, so pre-pruning not only reduces the training time overhead and testing time overhead of CHAID decision tree but also reduces the risk of overfitting. On the other hand, some pre-pruning divisions may not improve the generalization performance, or may even cause a temporary decrease in generalization performance, but subsequent divisions based on this division may lead to a significant improvement in generalization performance, thus posing the risk of underfitting. Therefore, if the number of pruning is maintained in a good interval when the amount of data is sufficient and the types are mostly categorical variables, the risk of underfitting of CHAID algorithm will be further reduced and the accuracy will be further improved.

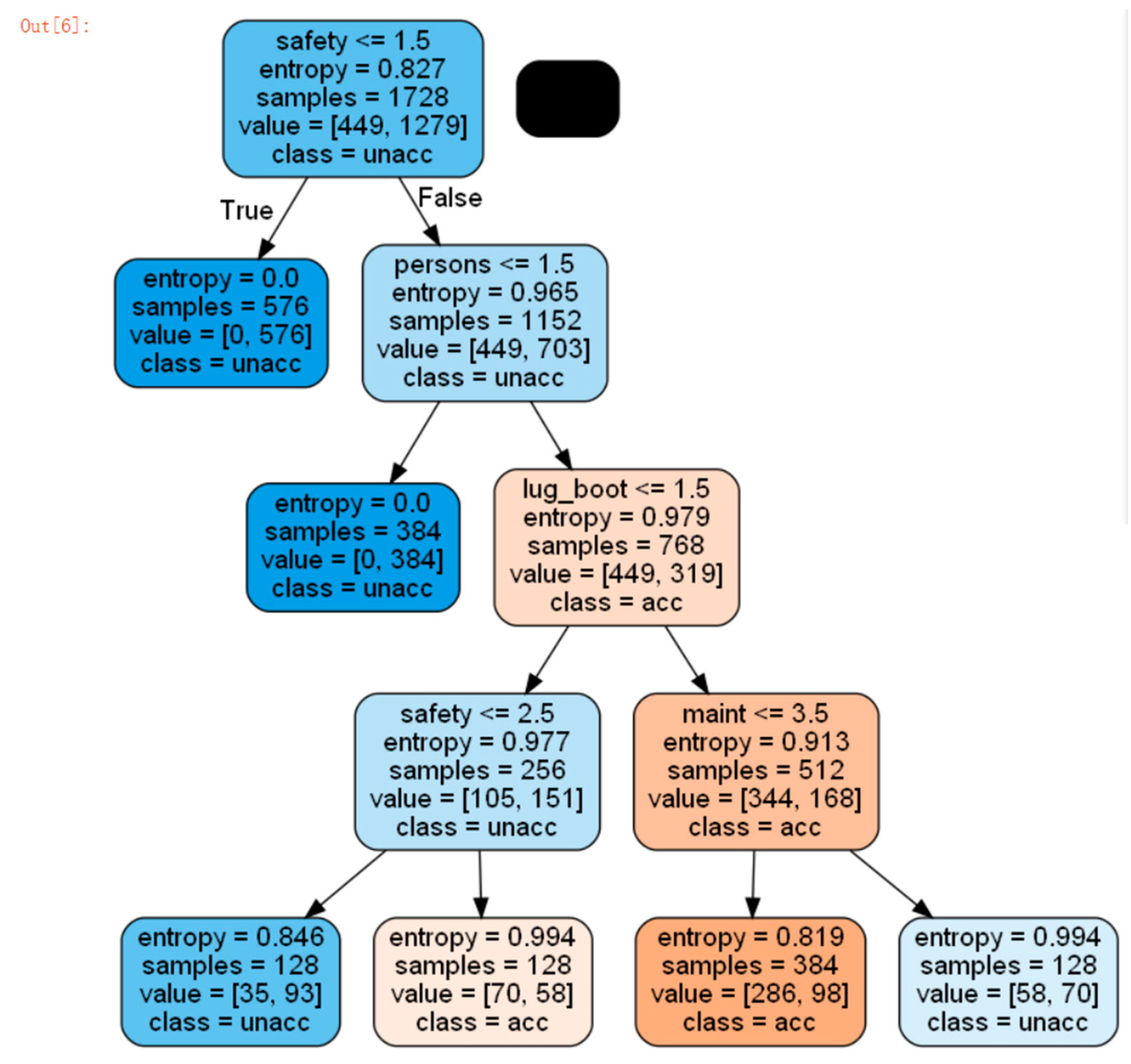
In Figure 1, we can calculate the most significant correlation with the CHAID algorithm, which is the first layer of the decision tree. The other branches are subdivided again on the basis of safety factors, and finally get a high sense of security, 4 or more people, and the medium price has the highest satisfaction and the largest correlation.

As for the CART (Classification and Regression Tree) algorithm, the segmentation logic of CART is the same as that for CHAID, and the division of each layer is based on the test and selection of all independent variables. However, the test standard used by CART is not the chi-square test, but the indicators of impurity, such as the Gini coefficient (Gini). The biggest difference between the two is that CHAID adopts the principle of local optimization, that is, the nodes are irrelevant to each other. After a node is determined, the following growth process is carried out completely within the node. CART, on the other hand, focuses on the overall optimization and adopts the post-pruning method, which makes the tree grow as much as possible, then cuts the tree back, and evaluates the non-leaf nodes in the tree from bottom to top, so the cost of training time is much larger than the pre-pruning decision tree.

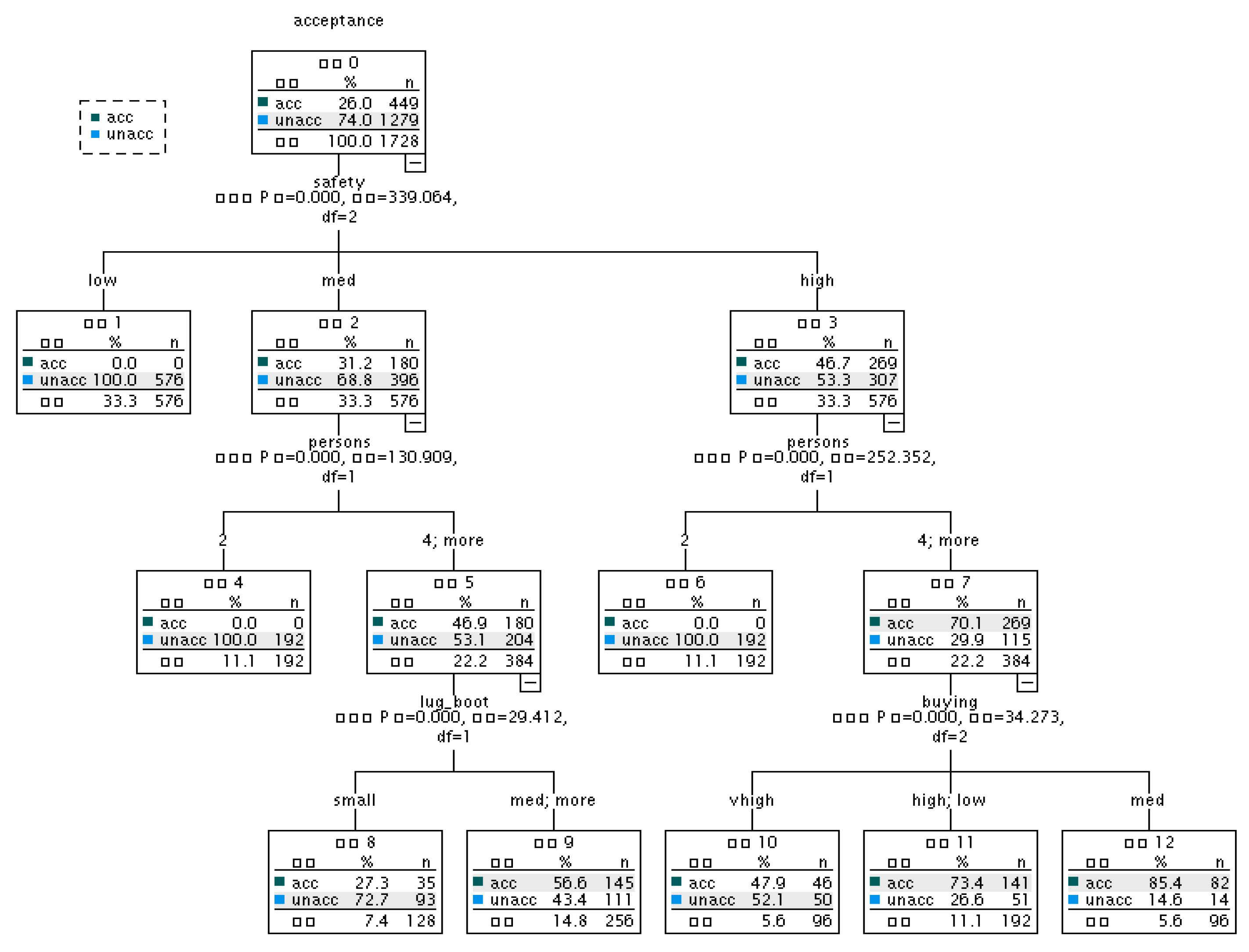
In Figure 2, we can calculate the safety term on the CART algorithm data, which is also the first layer of the decision tree. But the other layers are very different.

If there is missing data in the independent variable, CART will be used to find alternative data to replace the missing value, while CHAID will take the missing value as a separate type of value.

CART and CHAID, one is a binary tree and the other is a multi-fork tree; CART selects the best binary cut in each branch, so a variable is likely to be used multiple times in different trees; CHAID divides multiple statistically significant branches for one variable at a time, which will grow faster, but the support of the sub is rapidly decreases compared with CART, approaching a bloated and unstable tree more quickly.

Therefore, after the number of data categories in the data set increases to a certain extent, the accuracy of the CHAID algorithm will have a large decrease compared with the CART algorithm. The number of features of the data can be reduced by removing some data irrelevant to the target data during the data cleaning, so as to improve the accuracy of the CHAID algorithm.

ID3 (Iterative Dichotomiser) algorithm and CART are in the same period, its biggest feature is that the independent variable selection criteria is that based on the measure of information gain selects the attribute with the highest information gain as the split attribute of the node, the result is the minimum information required to classify the segmented node, which is also an idea of division purity. As for the later development of C4.5, which can be understood as the development version of ID3, the main difference between the two is that C4.5 uses the information gain rate instead of the information gain measure in ID3. The main reason for such a replacement is that the information gain measure has a disadvantage, that is, it tends to choose attributes with a large number of values. Here is an extreme example, for the division of Member_Id, each Id is a purest group, but such a division has no practical significance. The information gain rate adopted by C4.5 can overcome this disadvantage. It adds a piece of split information to normalize constraint on the information gain. And C5.0 is the latest version. Compared to C4.5, C5.0 uses less memory and builds a smaller rule set than C4.5, while being more accurate.

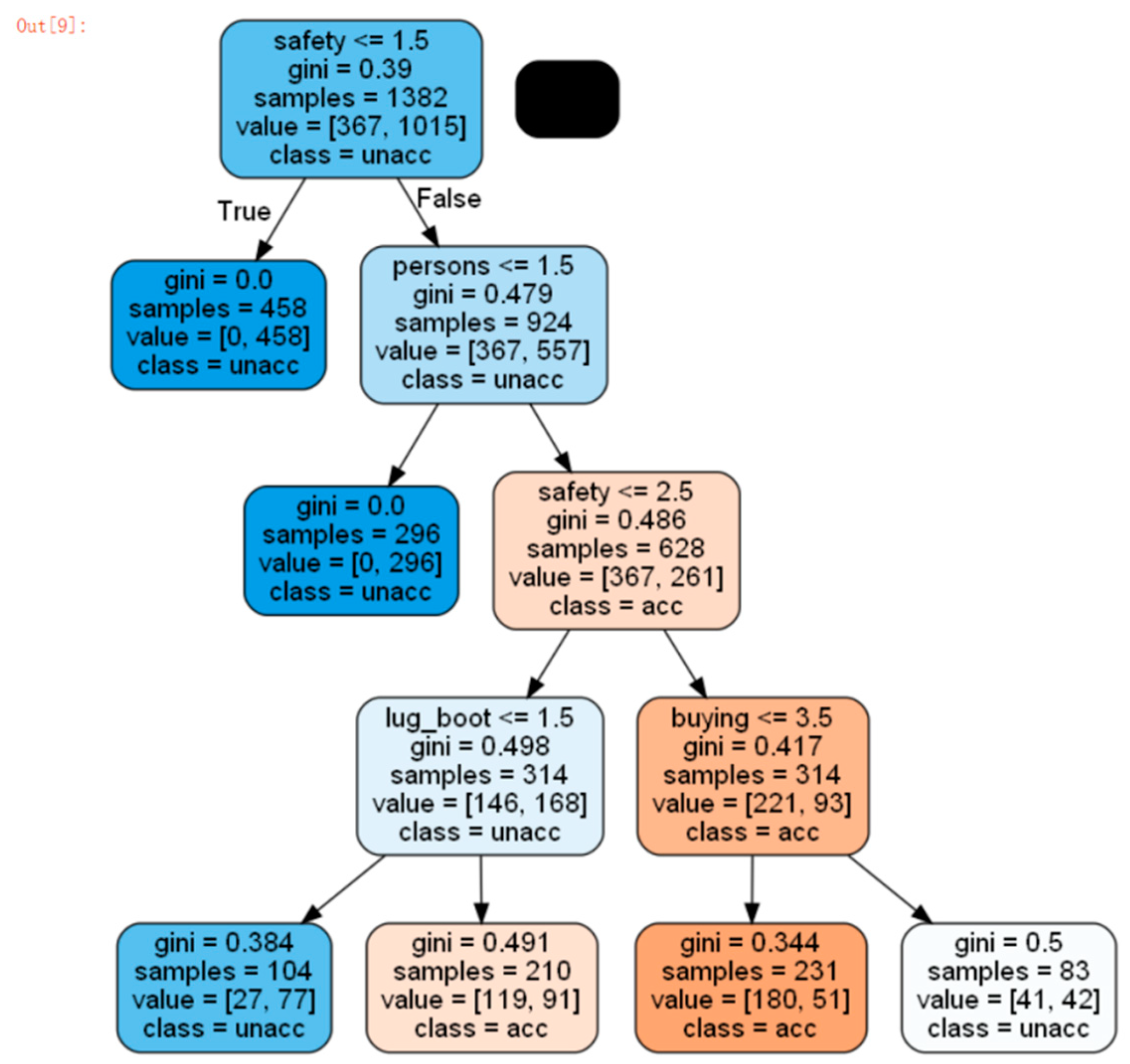
Figure 3. ID3 decision tree.

Figure 3. ID3 decision tree.

We can use the ID3 algorithm on the car purchase factor data and the safety item is also the first layer of the decision tree. But it is very different from CHAID overall.

4. Discussion, Conclusion and Future Work

The decision tree algorithm belongs to the supervised learning machine learning method, and it is a commonly used technology in data mining. It can be used to classify the analyzed data, and it can also be used for prediction. Common algorithms are CHAID, CART, ID3, C4.5, C5.0, and so on. The second part is the study of the core idea of the CHAID decision tree algorithm and the classification process, the specific steps of the classification process, and the principle formula of the CHAID decision tree algorithm in the branching processThe third part is a comparison between the CHAID decision tree algorithm and other commonly used decision tree algorithms, and a partial analysis of the accuracy of the CHAID algorithm. In this study, we also give an example of automobile satisfaction factor analysis, and use multiple decision tree algorithms to implement and make a simple comparison.

The CHAID algorithm uses chi-square detection and pre-pruning in the branch method, the CART is the Gini coefficient (Gini) pruning in the branch method. ID3 is a measure based on information gain; and C4.5 and C5.0 adopt information gain rate. This paper can let us have a basic understanding of these algorithms, let us choose a relatively good decision tree algorithm for data mining according to our specific data. In the application of CHAID algorithm can also make some countermeasures according to some factors affecting accuracy, so more conducive to get a more accurate and better result.

In the next stage of research, I will find more data to compare these several decision tree algorithms, and I will further discuss the accuracy of CHAID algorithm in different data. According to the experimental results, we can specifically summarize the differences between these decision tree algorithms and the influence of different data on the accuracy of CHAID algorithm, as well as the differences between the accuracy of each algorithm. When we choose the decision tree algorithm according to the specific situation of the data, we can have a clearer and more intuitive understanding, and have a better understanding of the accuracy analysis of CHAID algorithm.