1. Introduction
Quantum computing constitutes a critical issue as the impact of theirs advent and development, will be present in every cell of our technology and therefore our life. Quantum computational systems use the qubit (QUantum BIT) instead of the typical bit, which has a unique property; it can be in basic states |0〉, |1〉 or in any linear combination of these two states, such that
,
[
67]. This is an algebraic-mathematical expression of quantum superposition which claims, that two quantum states can be added and their sum can be also a valid quantum state [
57]. Regardless of superposition, quantum computers’ power and capability, are based on quantum mechanics and specifically on the phenomenon of quantum entanglement and the no-cloning system. The odd phenomenon of quantum entanglement states that there are particles that are generated, interact and connected, regardless the distance or the obstacles that separate them [
66]. This fundamental law of quantum physics allows us to know or to measure the state of one particle if we know or measure the other particles.
A programmable quantum device is able to solve and overcome problems that a classical computer is unable to solve in any logical amount of time. A quantum computer can perform operations with enormous speed, in a flash of an eye, process and store an extensive number of information. This huge computational power which makes quantum computers superior than classical computers, was described in 2012 by John Preskill with the term quantum supremacy [
61]. Quantum Mechanics provides us a fascinating theorem, the no-cloning theorem. As an evolution of no-go theorem by James Park, the no-cloning theorem states that the creation of identical copies of an arbitrary unknown quantum state is forbidden [
57]. This is a fundamental theorem of quantum physics and quantum cryptography.
Cryptography is the science of secure communication that implements complex mathematics into cryptographic protocols and algorithms [
62] The cryptosystems, they appear in every electronic transaction and communication in our everyday life. The security, the efficiency and the speed of these cryptographic methods and schemes, are the main issue of interest and study. The contemporary cryptosystems are considered to be vulnerable to a quantum computer attack. In the 1994, the American mathematician and cryptographer professor Peter Shor presented an algorithm [
70], which dumbfound the scientists. Shor in his work argued that with the implementation of the proposed algorithm in a quantum device, there is no more security in current computational systems. This was a real revolution for the science of computing and a great motivator for the design and construction of quantum computational devices. Post-quantum cryptography refers to cryptographic algorithms that are thought to be secure against an attack by a quantum computer. Post-quantum cryptography studies and analyzes the preparation for the era of quantum computing by updating existing mathematical-based algorithms and standards [
12].
Lattice-based cryptographic protocols attract the interest of researchers for an amount of reasons. Firstly, the algorithms that are applied to lattice-based protocols are simple and efficient. Additionally, they have proven to be secure protocols and create a multitude of applications.
In this review, we examine the cryptographic schemes that are developed for a quantum computer. The following research questions were answered:
How much the science of Cryptography is affected by quantum computers ?
What cryptosystems are efficient and secure for the quantum era?
Which are the most known lattice-based cryptographic schemes and how do they function?
How can we evaluate NTRU, LWE and GGH cryptosystem?
Which are their strengths and weaknesses ?
The rest of the paper is organized as follows. In
Section 2 we present the changes and the challenges due to quantum devices in cryptography and in
Section 3 are described the cryptographic schemes in quantum era. In
Section 4 we present some basic issues about lattice theory. In
Section 5 and
Section 6 we present the lattice based cryptographic schemes NTRU, LWE and GGH correspondingly, while is given a discrete implementation of them. In addition, the GGH cryptosystem is described in
Section 7. Results and comparisons are given in
Section 8 while some future work directions are presented in
Section 9. Finally,
Section 10 concludes this work.
2. The evolution of Quantum Computing in Cryptography
Cryptography is an indispensable tool for protecting information in computer systems and modern cryptographic algorithms are based on hard mathematical problems, such as the factorization of large prime numbers and the discrete logarithm problem. We can divide the cryptographic protocols in two broad categories: symmetric cryptosystems and asymmetric (public key cryptosystems) cryptosystems [
62].
Symmetric cryptosystems use the same key for encryption and decryption and despite their speed and their easy implementation, they have certain disadvantages. One main issue of this type of cryptosystems is the secret key distribution between two parties that want to communicate safely. Another drawback of symmetric cryptographic schemes is that, the private keys which are being used must be changed frequently in order not to be known by a fraudulent user. If we can ensure the existence of an efficient method to generate and exchange keys, symmetric encryption and decryption methods are considered to be secure.
Asymmetric cryptographic schemes use a pair of keys, private and public key, for encryption and decryption. This type of cryptosystems relies on mathematical problems that are characterized as hard to be solved. Some of the most widely known and implemented public key cryptosystems are RSA [
63], the Diffie-Helman protocol, ECDSA and others. Since the early 1990’s all these cryptographic schemes were believed to be effective and secure but Shor’s algorithm changed things up.
Peter Shor proved with his algorithm, that a quantum computer could quickly and easily compute the period of a periodic function in polynomial time [
68]. Since 1994, when Shor’s protocol was presented, has been a great amount of study, analysis and implementation of the algorithm both in classical and quantum computing devices. Shor’s method solves the factorization problem and the discrete logarithm problem, that are the basis of the current cryptographic schemes and therefore the public key cryptosystems are insecure and vulnerable to a quantum attack [
70].
2.1. Quantum Cryptography
In 1982, for the first time was recommended the term "Quantum Cryptography" but the idea of quantum information was appeared for the first time in the decade of 1970’s, from Stephen Wiesner and his work about quantum money [
77]. Quantum Cryptography is the science that uses the main principles of quantum physics to transfer or store data in complete security. In general, in Quantum Cryptography the transmission and the encryption procedure is performed with the aid of Quantum Mechanics [
75]. Quantum cryptography exploits the fundamental laws of Quantum Mechanics like superposition and quantum entanglement, and constructs cryptographic protocols advanced and more efficient.
A basic problem in classical cryptographic schemes is the key generation and exchange, as this process is endangered and unsafe when takes place in an insecure environment. When two different parties want to communicate and transfer data, they exchange information (i.e. key, message) and this procedure occurs in a public channel, so their communication could be vulnerable to an attack by a third party [
11]. The most fascinating and also useful discovery and widely used method of Quantum Cryptography is the Quantum Key Distribution.
2.2. Quantum Key Distribution
Quantum Key Distribution (QKD) utilizes the laws of Quantum Physics in the creation of a secret key through a quantum channel. With the principles of Quantum Physics, in QKD a secret key is being generated and a secure communication between two (or more parties) is been established. The inherent randomness of the quantum states and the results accrue from their measurements have as a result a total randomness in the generation of the key. Quantum Mechanics, solves the problem of key distribution - the main challenge in cryptographic schemes - with the aid of quantum superposition, quantum entanglement and the Uncertainty Principle of Heisenberg. Heisenberg’s Principle argues that two quantum states cannot be measured simultaneously [
66] . This principle has as consequence, the detection of someone who tries to eavesdrop the communication between two parties. If a fraudulent user tries to change the quantum system, he will be detected and the users abort the protocol.
Let us suppose that we have two parties that they want to communicate and use a Quantum Key Distribution protocol to generate a secret key. A quantum key distribution scheme has two phases and for its implementation it is necessary the existence of a classical and a quantum channel. In the quantum channel, it is generated and reproduced the private key and in the classical channel takes place the communication of the two parties. Into the quantum channel are sent polarized photons and each one of the photons has a random quantum state. Both the two parties have in their possession a device that collects and measures the polarization of these photons. Due to Heisenberg’s principle, the measurement of the polarized photons can reveal a possible eavesdropper as in his effort to elicit information, the state of the quantum system changes and the fraudulent user is being detected.
In 1984, Charles Bennett and Gilles Brassard proposed the first Quantum Key Distribution protocol, the BB84 protocol, named by its developers and the year it was published [
10]. BB84 is the most studied, analyzed and implemented QKD protocol and since then have been proposed various QKD protocols. B92 and SARG04 that are known as variants of BB84, and E91 that exploits the phenomenon of quantum entanglement, are a few of the widely known quantum key distribution protocols [
67]. All these QKD protocol are in theory well designed and structured and are proved to be secure, but in practice, in their implementation, there are imperfections. Loopholes, as unwell constructed detectors or defective optical fibers, and generally imperfections in devices and the practical QKD system, make the QKD protocols vulnerable to attacks. Exploiting these weaknesses of the system, one can perform certain types of attacks and this is the basic issue of research and study, the QKD security.
3. Cryptographic Schemes in Quantum Era
The advances in computer processing power and the evolution of quantum computers for many people, seem to be a threat in the distant future. On the other hand, researchers and security technologists are anxious about the capabilities of a quantum computational device to threat the security of contemporary cryptographic algorithms. Shor’s algorithm consists of two parts, a classical part and a quantum part and with the aid of a quantum routine could break modern cryptographic schemes, like RSA and the Diffie-Hellman cryptosystem[
23]. These type of cryptosystems are based on hard mathematical problems like the factorization problem and the discrete logarithm problem, the cornerstone of modern cryptographic schemes.
From that moment and after, it is widely known in the scientific and technological community, that with the arrival of a sufficiently large quantum computer there is no more security in ours encryption schemes. Therefore, post-quantum data encryption protocols are the basic topic of research and work, with main goal to construct cryptosystems resistant to quantum computers’ attacks [
12]. Subsequently, we present certain cryptographic schemes that have been developed and there are secure under an attack of a quantum computer.
3.1. Code-Based Cryptosystems
Coding Theory is an important scientific field which study and analyze linear codes that are being used for digital communication. The main subject of research in Coding Theory is finding a secure and efficient data transmission method. In the process of data transmission, often, data are lost due to errors owing to noise, interference or other reasons and the main subject of study of coding theory is to minimize this data loss [
74]. When two discrete parties want to communicate and transfer data, they add extra information to each message which is transferred to enable the message to be decoded despite the existing errors.
Code-based cryptographic schemes are based on the theory of error correcting codes and are considered to be prominent for the quantum computing era. These cryptosystems are considered to be reliable and their hardness relies on hard problems of coding theory, such as the syndrome decoding (SN) and learning parity with noise (LPN).
In 1978 Robert McEliece, proposed the first code-based cryptosystem based on the hardness of decoding random linear codes, a problem which is considered to be NP-hard [
44]. The main idea of McEliece is to use an error-correcting code, for which it is known a decoding algorithm and which is capable to correct up to
t errors to generate the secret key. The public key is constructed by the private key, covering up the selected code as a general linear code. The sender creates a codeword using the public key that is disturbed up to
t errors. The receiver performs error correction and efficient decoding of the codeword and decrypts the message.
McEliece’s cryptosystem and Niederreiter cryptosystem that was proposed by Harald Niederreiter in 1986 [
53], can be suitable and efficient for encryption, hashing and signature generation. McEliece cryptosystem has a basic disadvantage, the large size of the keys and ciphertexts. In modern variants of McEliece cryptosystem has been an effort to reduce the size of the keys. However, these type of cryptographic schemes are considered to be resistant to quantum attacks and this make them prominent for post-quantum cryptography.
3.2. Hash-Based Cryptosystems
Hash based cryptographic schemes in general, generate digital signatures and relies on the security of cryptographic hash functions, like SHA-3. In 1979, Ralph Merkle proposed a public key signature scheme based on one-time signature (OTS) and Merkle signature scheme is considered to be the simplest and the most widely known hash-based cryptosystem [
45]. This digital signature cryptographic scheme converts a weak signature with the aid of a hash function to a strong one.
The Merkle signature scheme is a practical development of Leslie Lamport’s idea of OTS that turn it into a many times signature scheme, a signature process that could be used multiple times. The generated signatures are based on hash functions and their security is guaranteed even against quantum attacks.
Many of the reliable signature schemes based on hash functions have the drawback, that the person who signs must keep a record of the exact number of previously signed messages, and any error in this record will create a gap in their security. Another disadvantage of these schemes is that it can be generated certain number of digital signatures and if this number increases indefinitely, then the size of the digital signatures is very large. However, hash-based algorithms for digital signatures are regarded as safe and strong against a quantum attack and can be used for post-quantum cryptography.
3.3. Multivariate Cryptosystems
In 1988 T. Matsumoto and H. Imai [
42] presented a cryptographic scheme which is based on multivariate polynomials of degree two over a finite field, for encryption and for signature verification. In 1996 J. Patarin [
59] implemented a cryptosystem that relies its security on difficulty of solving systems of multivariate polynomials in finite fields.
The multivariate quadratic polynomial problem states that given m quadratic polynomials in n variables with their coefficients to be chosen from a field , is requested to find a solution such that , for . The choice of the parameters make the cryptosystem reliable and safe against attacks, so this problem is considered to be NP - hard.
This type of cryptographic schemes are believed to be efficient and fast, with high speed computations process and proper for implementation on smaller devices. The need of new, stronger cryptosystems with the evolution of quantum computers created various candidates for secure cryptographic schemes based on the multivariate quadratic polynomial problem [
12]. These type of cryptosystems are considered to be an active issue of research due to their quantum resilience.
3.4. Lattice-Based Cryptosystems
Cryptographic schemes that are based on lattice theory gain the interest of the researchers and perhaps is the most famous of all candidates for post-quantum cryptography. Let imagine a lattice like a set of points in a
n dimensional space with periodic structure. The algorithms which are implemented in lattice based cryptosystems are characterized by simplicity and efficiency and highly parallelizable [
56].
Lattice-based cryptographic protocols are proved to be secure, as rely their strong security on well-known lattice problems such as the Shortest Vector Problem (SVP) and the Learning with Errors problem (LWE). Additionally, they create powerful and efficient cryptographic primitives, such as fully homomorphic encryption and functional encryption [
39]. Moreover, lattice-based cryptosystems create several applications, like key exchange protocols and digital signature schemes. For all these reasons, lattice based cryptographic schemes are believed to be the most active field of research in the post-quantum cryptography and the most prominent and promising one.
4. Lattices
Lattices are considered to be a typical subject in both cryptography and cryptanalysis and an essential tool for future cryptography, especially with the transition to quantum computing era. The study and the analysis of the lattices goes back to the 18th century, when C.F. Gauss and J.L. Lagrange used lattices in number theory and H. Minkowski with his great work "geometry of numbers" arised the study of lattice theory [
60]. In the late 1990s, a lattice was used for the first time in a cryptographic scheme and the latest years the evolution in this scientific field has been enormous, as there are lattice-based cryptographic schemes for encryption, digital signatures, trapdoor functions and much more.
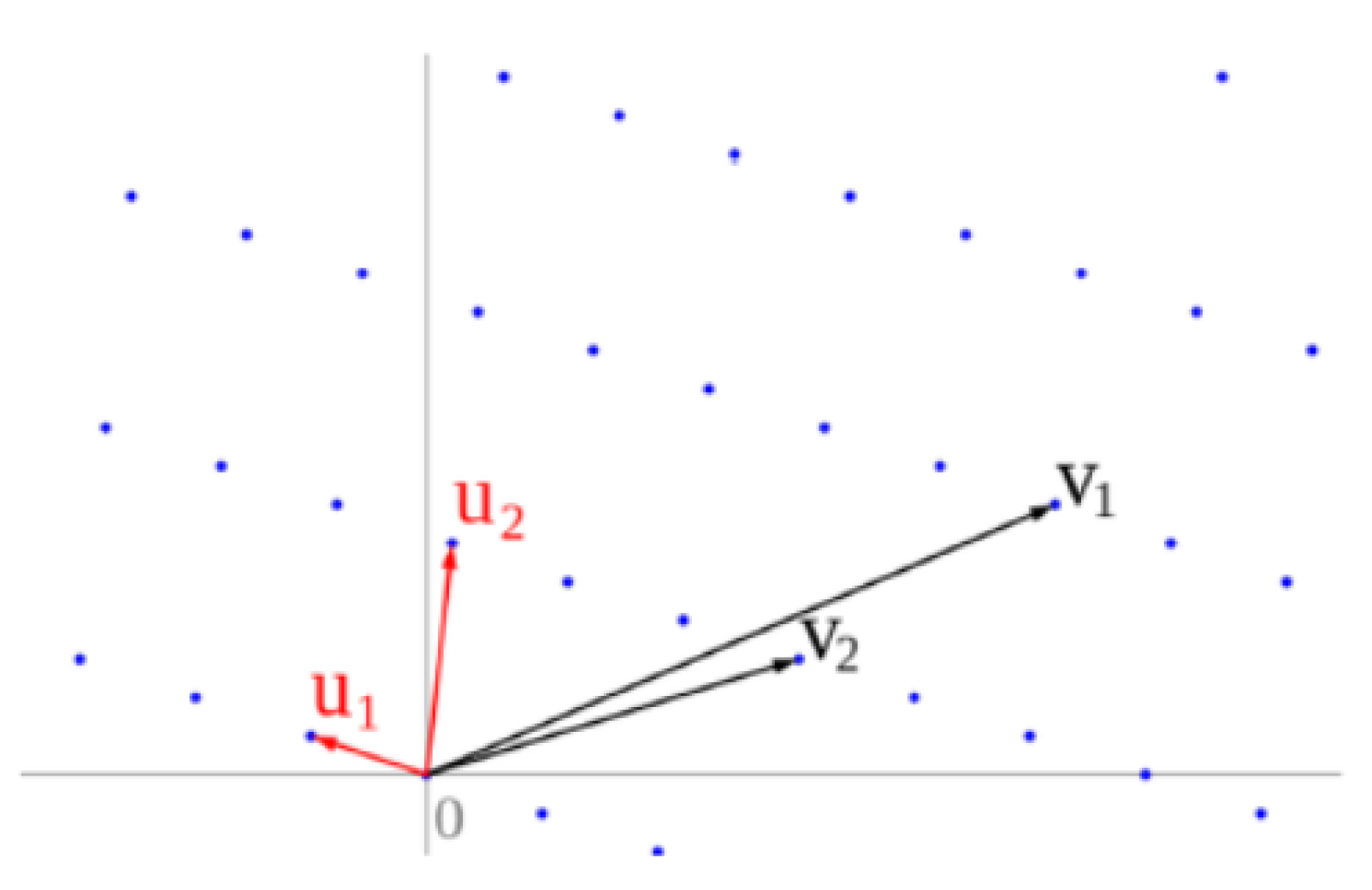
A lattice is a dicrete subgroup of points in n-dimensional space with periodic structure. Any subgroup of
is a lattice, which is called integer lattice. It is appropriate to describe a lattice using its basis [
56]. The basis of a lattice is a set of independent vectors in
and by combining them, the lattice can be generated.
Definition 1. A set of vectors
is linearly independent if the equation
accepts only the trivial solution
.
Definition 2. Given
n linearly independent vectors
, the lattice generated by them is defined as
Therefore, a lattice consists of all integral linear combinations of a set of linearly independent vectors and this set of vectors
is called a lattice basis. So, a lattice can be generated by different bases as it is seems in
Figure 1.
Definition 3. The same number of elements of all the bases of a lattice it is called the dimension (or rank) of the lattice, since it matches the dimension of the vector subspace spanned by .
Definition 4. Let
be a lattice with dimension
n and
a basis of the lattice. We define as fundamental parallelepiped as the set:
Not every given set of vectors forms a basis of a lattice and the following theorem give us a criterion.
Theorem 1. Let be a lattice with rank n and , n linearly independent lattice vectors. The vectors form a basis of if and only if .
Definition 5. A matrix is called unimodular if .
For example, the matrix
with
.
Theorem 2. Two bases generate the same lattice if and only if there is an umimodular matrix such that .
Definition 6. Let be a lattice of rank n and let B a basis of . We define the determinant of denoted , as the n-dimensional volume of .
We can write
and also
An interesting property of the lattices is that the smaller the determinant of the lattice is, so the denser the lattice is.
Definition 7. For any lattice
, the minimum distance of
is the smallest distance between any two lattice points:
It is obvious that the minimum distance can be equivalently defined as the length of the shortest nonzero lattice vector:
4.1. Shortest Vector Problem (SVP)
The Shortest Vector Problem (SVP) is a very interesting and extensively studied computational problem on lattices. The Shorter Vector Problem states that given a lattice should be found the shortest nonzero vector in .
That is to say, given a basis
, the shortest vector problem is to find a vector
satisfying
A variant of Shortest Vector Problem is computing the length of the shortest nonzero vector in
(e.g.
) without necessarily finding the vector.
Theorem 3.
Minkowski’s first theorem. The shortest nonzero vector in any n-dimensional lattice has length at most , where is an absolute constant (approximately equals to ) that depend only of the dimension n and is the determinant of the lattice.
Two great mathematicians J. Lagrange and C.F.Gauss where the first ones that had studied the lattices and knew an algorithm to find the shortest nonzero vector in two dimensional lattices. In 1773, Lagrange proposed an efficient algorithm to find a shortest vector of a lattice and Gauss, working independently, made a publication with his proposal for this algorithm in 1801 [
60].
A
g-approximation algorithm for SVP is an algorithm that on input a lattice
, outputs a nonzero lattice vector of length at most
g times the length of the shortest vector in the lattice. The LLL lattice reduction algorithm is capable to approximate SVP within a factor
where
n is the dimension of the lattice. Micciancio proved that the Shortest Vector Problem is NP-hard even to approximate within any factor less than
[
48]. SVP is considered to be a hard mathemarical problem and can be used as cornerstone for the construction of provably secure cryptographic schemes, like lattice based cryptography.
4.2. Closest Vector Problem (CVP)
The Closest Vector Problem (CVP) is a computational problem on lattices that relates closely to Shortest Vector Problem. CVP states that given a target point , should be found the lattice point closest to the target.
Let
be a lattice and a fixed point
, we define the distance:
CVP can be formulated as following : Given a basis matrix B for the lattice and a , compute a non-zero vector such that is minimal. So, we search a non-zero vector , such that .
Another version of the CVP is computing the distance of the target from the lattice, without finding the closest vector of the lattice and many applications only demand to find a lattice vector that is not too far from the target, not necessarily the closest one.
The most famous polynomial-time algorithms to solve the Chortest Vector Problem are Babai’s algorithm and Kannan’s algorithm which are based on lattice reduction. Below we present the first algorithm which was proposed by Lazlo Babai in 1986 [
4].
|
Algorithm 1: Babai’s Round-off Algorithm |
|
Input: basis , target vector
Output: approximate closest lattice point of c in
1: procedure RoundOff
2: Compute inverse of
3:
4: return v
5: end procedure
|
CVP is considered to be NP-hard to solve approximately within any constant factor and is the cornerstone for many cryptographic schemes of lattice cryptography where the decryption procedure corresponds to a CVP computation [
49]. Besides cryptography, CVP has various applications in computer science and the problem to find a good CVP approximation algorithm with approximation factors that grow as a polynomial in the dimension of a lattice is an active open problem in lattice theory.
4.3. Lattice reduction
Lattice reduction or else Lattice Basis Reduction is about finding an interesting, useful basis of a lattice. Such a requested useful basis, from a mathematical point of view, satisfies a few strong properties. A lattice reduction algorithm is an algorithm that takes as input a basis of the lattice and returns a simpler basis which generates the same lattice. For computing science we are interested in computing such bases in a reasonable time, given an arbitrary basis. In general, a reduced basis is composed from vectors with good properties, such as being short or being orthogonal.
In 1982 Arjen Lenstra, Hendrik Lenstra and Laszlo Lovasz published a polynomial-time basis reduction algorithm, LLL, which took its name from the initials of their surnames [
36]. The basis reduction algorithm approaches the solution of the smallest vector problem in small dimensions, especially in two dimensions, the shortest vector is too small that can be computed in a polynomial time. On the contrary, in large dimensions there is no algorithm known which solves the SVP in a polynomial time. With the aid of the Gram-Schmidt orthonormalization method we define the base reduction method LLL .
5. The NTRU cryptosystem
NTRU is a public key cryptosystem that was presented in 1996 by Jeffrey Hoffstein, Jill Pipher and Joseph H. Silverman [
32]. Until 2013, the NTRU cryptosystem was only commercially available but after, it was released into the public domain for public use. The NTRU is one of the fastest public key cryptographic schemes, it uses polynomials rings for the encryption and decryption of data, and it is based on the shortest vector problem in a lattice. NTRU is more efficient than other current cryptosystems like RSA, and is believed to be resistant to quantum computers attacks and this make it prominent post quantum cryptosystem.
To describe the way NTRU cryptographic scheme operates, firstly we have to give some definitons.
Definition 8. Fix a positive integer N. The ring of convolution polynomials (of rank N) is the quotient ring
Definition 9. The ring of convolution polynomials (modulo q) is the quotient ring
Definition 10. We consider a polynomial
as an element of
by reducing its coefficients mopulo
q. For any positive integers
and
, we let
Polynomials in are called ternary (or trinary) polynomials. They are analogous to binary polynomials, which have only 0’s ans 1’s as coefficients.
We assume we have two polynomials
and
. The product of these two polynomials is given by the formula
We will denote the inverses by
and
, such that
5.1. Description
The NTRU cryptographic scheme is based firstly on three well chosen parameters
, such that
N is a fixed positive large integer,
p and
q, is not necessary to be prime but are relatively prime, e.g.
and
q will be always larger than
p[
32]. Secondly, NTRU depends on four sets of polynomials
,
,
and
with integer coefficients of degree
and works on the ring
.
Every element is written as a polyonomial or as vector . We assume that there are two parties, Alice and Bob, that they want to transfer data, to communicate, with security. A trusted party or the first party selects public parametres such that N,p are prime numbers, and .
Alice chooses randomly two polynomials and . These two polynomials are Alice’s private key.
Alice computes the inverses polynomials
-
Alice computes and the polynomial is Alice’s public key. Alice’s private key is the pair and by only using this key, she can decrypt messages. Otherwise, she can store , which is probably intertible and compute when she needs it.
Alice publishes her key h.
Bob wants to encrypt a message and chooses his plaintext . The is a polynomial with coefficients such that .
Bob chooses a random polynomial
, which is called ephemeral key, and computes
and this is the encrypted message that Bob sends to Alice.
Alice chooses the coefficients of a in the interval from (center lifts to an element of R).
Alice computes
and she recovers the message
m as if the parameters have been chosen correctly, the polynomial
equals to the plaintext
.
Depending on the choise of the ephemeral key the plaintext can be encrypted with many ways, as its possible encryptions are . The ephemeral key should be used one time and only, e.g. it shouldn’t be used to encrypt two different plaintexts. Additionally, Bob shouldn’t encrypt the same plaintext by using two different ephemeral keys.
5.2. Discrete implementation
Assume the trusted party chooses the parametres . As we can see and are prime numbers, and the condition is satisfied as it is .
-
Alice chooses the polynomials
These polynomials, is the private key of Alice.
-
Alice computes the inverses
Alice can store as her private key.
-
Alice computes
and publishes her public key
.
Bob decides to encrypt the message and uses the ephemeral key .
-
Bob computes and sends to Alice the encrypted message
that is
.
-
Alice receive the ciphertext and computes
Therefore Alice centerlifts modulo 61 to obtain
She reduces
modulo 3 and computes
and recovers Bob’s message
5.3. Security
NTRU is one of the most fast public key cryptosystems which is based on lattice theory and it is used for encryption (NTRU-Encrypt) and digital signatures (NTRUSign). For the moment that NTRU was presented, in 1996, NTRU security has been a main issue of interest and research. NTRU hardness relies on the hard mathematical problems in a lattice, such as the Shortest Vector Problem [
56].
The authors of NTRU in their paper [
32] argue that the secret key can de recovered by the public key, by finding a sufficiently short vector of the lattice that is generated in NTRU algorithm. D. Coppersmith and A. Shamir proposed a simple attack against the NTRU cryptosystem. In their work argued that the target vector
(the symbol || denotes vector concatenation) belongs to the natural lattice:
It is obvious that
is a full dimension lattice in
, with volume
. The target vector is the shortest vector of
, so the SVP-oracle should heuristically output the private keys
f and
g. Hoffstein et al. claimed that if one chooses the number
N reasonably, the NTRU is sufficient secure as all these type of attacks are exponential in
N. These type of attacks are based on the difficulty of solving certain lattice problems, such as SVP and CVP. Lattice attacks can be used to recover the private key of an NTRU system, but they are generally considered to be infeasible for the current parameters of NTRU. It is important that the key size of the NTRU protocol is
and this fact makes NTRU a promising cryptographic scheme for post-quantum cryptography.
Furthermore, the cryptanalysis of NTRU is an active area of reasearch and they have been developed other type of attacks against NTRU cryptosystem. We refer to some of them as detailed below.
Brute-Force Attack. In this type of attack, are being tested all possible values of the private key until the correct one is found. Brute-force attacks are generally not practical for NTRU, as the size of the key space is very large.
Key Recovery Attack. This type of attack relies on exploiting vulnerabilities in the key generation process of NTRU. For example, if the random number generator used to generate the private key is weak, a fraudulent user may be able to recover the private key.
Side-channel Attack. This type of attack take advantage of the weaknesses in the implementation of NTRU, such as timing attack, power analysis attack, and fault attack. Side-channel attacks require physical access to the device running the implementation.
To protect NTRU against these types of attacks and avoid the leak of secret data and information, researchers use various techniques to ensure its security, such as parameter selection, randomization, and error-correcting codes.
6. The LWE cryptosystem
In 2005, O. Regev presented a new public key cryptographic scheme, the Learning with Errors cryptosystem and for this work, Regev won in 2018 the Godel Prize [
64]. LWE is one of the most famous lattice-based cryptosystems and one of the most widely studied in recent years. It is based on the Learning with Errors problem and the hardness of finding a random linear function of a secret vector modulo a prime number. The LWE public key cryptosystem is a probabilistic cryptosystem, which relies on a high probability algorithm. Since LWE proved to be secure and efficient, it becomes one of the most contemporary and innovational research topics in both lattice- based cryptography and computer science.
6.1. The Learning with Errors Problem
Firstly, we have to introduce the Learning with Errors problem (LWE). Assuming that we have a secret vector
with coefficients integer numbers and
n linear equations such that
We use the symbol "≈" to claim that the value approaches the real answer to within a certain error. This problem is a difficult one as by multiplying and adding rows together, the errors in every different equation will compound, so the final row reduced state will be worthless and the answer will be faraway from the real value.
Definition 11. Let be a secret vector and be a given distribution on . An LWE distribution generates a sample or where is uniformly distributed and , where and is the inner product of a and s in .
We call the LWE distribution, s is called the private key and e is called the error distribution. If is uniformly distributed, then is called the uniform LWE distribution.
Definition 12. Fix , and an error probability distribution on . Let s be a vector with n coefficients in . Let on be the probability distribution choosing a vector uniformly at random, choosing according to and outputting where additions are performed in . We say an algorithm solves LWE with modulus q and error distribution if for any given enough samples from it outputs s with high probability.
Definition 13. Suppose we have a way of generating samples from as above, and also generating random uniformly distributed samples of from . We call this uniform distribution U. The decision-LWE problem is to determine after a polynomial number of samples, whether the samples are coming from or U .
Simplifying the definition and formulated in more compact matrix notation, if we want to generate a uniformly random matrix A with coefficients between 0 and q and two secret vectors s, e with coefficients drawn from a distribution with small variance, the LWE sample can be calculated as: . The LWE problem states that is hard to recover the secret s from such a sample.
Definition 14. For , the family is the (uncountable) set of all elliptical Gaussian ditributions over a number field in which .
The choise of the parametres is crucial for the hardness of this problem. The distribution is a Gaussian distribution or a binomial distribution with variance 1 to 3, the lenght of the secret vector n is such that and the modulus q is in the range to .
6.2. Description
Assuming , are positive integers and is a given probability distribution in . The LWE cryptographic scheme is based on LWE distribution and is being described below.
The parametres of the LWE cryptosystem are of great importance for the security of the protocol. So, let n be the security parameter of the system, m, q are two integers numbers and is a probability distribution on .
The security and the correctness of the cryptosystem are based on the following parametres, which are be chosen appropriately.
Choose q a prime number between and .
Let for some arbitary constant .
The probability distribution is chosen to be for
We suppose that are two parties, Alice and Bob, who want to transfer informations securily. The LWE cryptosystem has the typical structure of a cryptographic scheme and its steps are the following.
Alice chooses uniformly at random . s is the private key.
-
Alice generates a public key by choosing m vectors independently from the uniform distribution. She also chooses elements (error offsets) independently according to . The public key is , where .
In matrix form, the public key is the LWE sample , where s is the secret vector.
-
Bob in order to encrypt a bit, chooses a random set S uniformly among all subsets of . The encryption is if the bit is 0 and if the bit is 1.
In matrix form, Bob can encrypt a bit m by calculating two LWE problems : one using A as random public element, and one using b. Bob generates his own secret vectors and e and make the LWE samples , . Bob has to add the message that wants to encrypt to one of these samples, where is a random integer between 0 and q. The encrypted message of Bob consists of the two samples , .
-
Alice wants to decrypt Bob’s ciphertext. The decryption of a pair is 0 if is closer to 0 than to modulo q. In other case the decryption is 1.
In matrix form, Alice firstly calculates . As long as is small enough, Alice recovers the message as .
6.3. Discrete implementation
We choose and .
Therefore, the encryption scheme worked correctly.
6.4. Implementations and Variants
The Learning with Errors (LWE) cryptosystem is a popular post-quantum cryptographic scheme that relies on the hardness of solving certain computational problems in lattices. There are several variants of the LWE cryptosystem, including the Ring-LWE, the Dual LWE, the Module-LWE, the Binary-LWE, the Multilinear LWE and others.
6.4.1. The RING-LWE cryptosystem
This variant of LWE uses polynomial rings instead of the more general lattices used in standard LWE. Ring-LWE has a simpler structure, which makes it faster to implement and more efficient in terms of memory usage. In 2013, Lyubashevsky et al [
38] presented a new public key cryptographic scheme that is based in LWE problem.
The Ring-LWE cryptosystem structure.
Lyubachevsky et al proposed a well analyzed a cryptosystem that uses two ring elements for both public key and ciphertext and it is an extension of the public key cryptograsystem on plain lattices.
The two parties that they want to communicate, agree on complexity value of n, the highest co-efficient power to be used. Let be the fixed ring and it is chosen an integer q, such as . The steps of the RING-LWE protocol are described below.
A secret vector s with n length is chosen with modulo q integer entries in ring , where . This is the private key of the system.
-
It is chosen an element and a random small element from the error distribution and we compute .
The public key of the system is the pair .
-
Let m be the n bit message that is for encryption.
The message m is considered as an element of R and the bits are used as coefficients of a polynomial of degree less than n
The elements are generated from error distribution.
It is computed the .
It is computed the and it is send to receiver.
-
The second party receives the payload and computes . It is evaluated each and if then the bits are recovered back to 1, or else 0.
Ring-LWE cryptographic scheme is similar to LWE cryptosystem was proposed by Regev. Their difference is that the inner products are replaced with ring products, so the result is new ring structure, increasing the efficiency of the operations.
6.5. Security
Learning with Errors (LWE) is a computational problem that is the basis for cryptosystems and especially for cryptographic schemes of post-quantum cryptography. It is considered to be a hard mathematical problem and as a consequence the cryptosystems that are based on LWE problem are of high security as well. LWE cryptographic protocols are a contemporary and active field of research and therefore their security is studied and analyzed continually and steadily.
There are a various of attacks can be performed against the cryptosystems which are based in LWE problem. We can say that these types of attacks are in general, those attacks that that exploit weaknesses in the LWE problem itself, and those attacks that exploit weaknesses in the specific implementation of the cryptosystem. Below we present some of these types of attacks that can be launched against LWE-based cryptographic schemes.
-
Dual Attack. This type of attack is based on the dual lattice and is most effective against LWE instances with small size of plaintext messages.
Thus, hybrid dual attacks that are appropriate for spare and small secrets and in a hybrid attack one guesses part of the secret and performs some attacks on the remaining part [
13] Since guessing reduces the dimension of the problem, the cost of the attack on the part of the secret that remains it is reduced. In addition,0 the lattice attack component can be reused for multiple guesses. The optimal attack is achieved when the cost of guessing equals to the cost of the lattice attack and we define where the lattice attack component is a primal attack as the hybrid primal attack, and respectively, the hybrid dual attack.
Shieving Attack. This type of attack is relied on the idea of sieving, which claims to find linear combinations of the LWE samples that reveal information about the secret. Sieving attacks can be used to solve the LWE problem with fewer samples than its original complexity.
Algebraic attack. This type of attack is based on the idea of finding algebraic relations between the LWE samples that let put secret data information. Algebraic attacks can be suitable for solving the LWE problem with fewer samples than the original complexity as well.
Side-channel attack. This type of attack exploits weaknesses in the implementation of the LWE-based scheme, such as timing attack and others. Side-channel attacks are generally easier to mount than attacks against the LWE problem itself, but they require physical access to the device running the implementation.
Attack that use the BKW algorithm. This is a classic attack, is considered to be sub-exponential and is most effective against small or small structured LWE instances.
To mitigate these attacks, LWE-based schemes typically use various techniques such as parameter selection, randomization, and error-correcting codes. These techniques are designed to make the LWE problem harder to solve and to prevent attackers from taking advantage of vulnerabilities in the implementation.
7. The GGH cryptosystem
In 1997 Oded Goldreich, Shafi Goldwasser and Shai Halevi proposed a cryptosystem (GGH) [
30] based on algrebraic coding theory and can be seen as a lattice analogue of the McEliece cryptosystem [
44]. In both GGH and McEliece schemes, a ciphertext is the addition of a random noise vector corresponding to the plaintext [
56]. At GGH cryptosystem the public and the private key is a representation of a lattice and at MCEliece the public and the private key is a representation of a linear code. The basic distinction between these two cryptographic schemes is that the domains in which the operations take place are different. The main idea and structure of GGH cryptographic scheme is characterized by simplicity and it is based on the difficulty to reduce lattices.
7.1. Description
The GGH public key encryption scheme is formed by the key generation algorithm K, the encryption algorithm E and the decryption algorithm D. It is based on lattices in , a key derivation function and a symmetric cryptosystem (), where K is the key generation algorithm, P the set of plain texts, C the set of ciphertexts, the encryption algorithm and the decryption algorithm.
The key generation algorithm K generates a lattice L by choosing a basis matrix V that is nearly orthogonal. An integer matrix U it is chosen which has determinant and the algorithm computes . Then, the algorithm outputs and .
The encryption algorithm E receives as input an encryption key and a plain message . It chooses a random vector and a random noise vector u. Then it computes , and encrypts the message . It outputs the ciphertext .
The decryption algorithm D takes as input a decryption key and a ciphertext . It computes and and decrypts as . If algorithm outputs the symbol ⊥ the decryption fails and then D outputs ⊥, otherwise the algorithm outputs m.
We assume that exist two users, Alice and Bob, that they want to communicate secretly. The main (classical) process of GGH cryptosystem is being decribed below.
Alice chooses a set of linearly independent vectors which form the matrix . Alice, by calculating the Hadamard Ratio of matrix V and verifying that is not too small, checks her vector’s choice. This is Alice’s private key and we let L be the lattice generated by these vectors.
Alice chooses an unimodular matrix U with integer coefficients, that satisfies .
Computes a bad basis for the lattice L, as the rows of , and this is Alice’s public key. Then, she publishes the key .
Bob chooses a plaintext that he wants to encrypt and he chooses a small vector m (e.g. a binary vector) as his plaintext. Then he chooses a small random "noise" vector r which acts as a random element and r is been chosen randomly between and , where is a fixed public parameter.
Bob computes the vector using Alice’s public key and sends the ciphertext e to Alice.
Alice, with the aid of Babai’s algorithm, uses the basis to find vector in L that is close to e. This vector is the , since the "noise" vector r is small and since she uses a good basis. Then, she computes ans she recovers m.
Supposing there is an eavesdropper, Eve, which wants to obtain information of the communication between Alice and Bob. Eve has in her possession the message e that Bob sends to Alice and therefore tries to find the closest vector to e, solving the CVP, using the public basis W. As she uses vectors that are not reasonably orthogonal, Eve will recover a message which probably will not be near to m.
7.2. Discrete implementation
Alice chooses a private basis and that it is a good basis since and are orthogonal vectors, e.g. it is . The rows of the matrix is Alice’s private key. The lattice L spanned by and has determinant and the Hadamard ratio of the basis is
Alice chooses the unimodular matrix U that its determinant is equal to 1, such as with .
Alice computes the matrix W, such that . Its rows are Alice’s bad basis and , since it is and these vectors are nearly parallel and so they are suitable for a public key.
It is very important the noise vector to be selected carefully and that it is not shift where the nearest point is located. For Alice’s basis that generates the lattice L, is chosen that . So, it is choosen the vector to be () with and .
Bob wants to encrypt the message . The message can be seen as a linear combination of the basis , such as and the noise vector can be added.
The corresponding ciphertext is and Bob sends it to Alice.
Alice using the private basis, she applies Babai’s algorithm and finds the closest lattice point. So, she solves the equation and finds and . So, the closest lattice point is and this lattice vector is close to e.
Alice realizes that Bob must have computed as a linear combination of the public basis vectors and then solving the linear combination again she finds and and recovers the message .
Eve has in her possesion the encrypted message that Bob had send to Alice and tries to solve the CVP using the public basis. So, she is solving the equation and finds the incorrect values , and recovers the incorrect encryption .
In 1999 and in 2001 D. Micciancio proposed a simple technique to reduce both the size of the key and size of the ciphertext of GGH cryptosystem without decreasing the level of its security [
46,
50].
7.3. Security
In GGH cryptographic scheme, if a security parameter n is chosen, the key size and the encryption time can take and it is more effiecient than other cryptosystems like AD.
There are some natural ways to perform an attack to the GGH cryptographic scheme.
-
Leak information and obtain the private key V from the public key W.
For this type of attack, it is performed a lattice basis reduction (LLL) algorithm on the public key, the matrix W. It is possible that the output is a basis that is good enough to allow the efficient solution of the required closest vector instances. If the dimension of the lattice is large enough, is very difficult for this attack to succeed.
-
Try to obtain information about the message from the ciphertext e, assuming that the error vector r is small.
For this type of attack, it is useful that in the ciphertext , the error vector r is a vector with small entries. An idea is to compute and try to deduce possible values for some entries of . For example, if the j-th column of has particularly small norm, then one can deduce that the j-th entry of is always small and hence get an accurate estimate for the j-th entry of m. To defeat this attack one should only use some low-order bits of some entries of m to carry information, or use an appropriate randomised padding scheme
Try to solve the Closest Vector Problem of e with respect to the lattice that is being generated by W, for example by performing the Babai’s nearest plane algorithm or the embedding technique.
Moreover, certain types of attacks can be performed against GGH, which are being discussed below like Nguyen’s attack and Lee and Hahn attack.
Goldreich, Goldwasser and Halevi claimed that increasing the key size compensates for the decrease in computation time [
56]. When presented their paper, the three authors, published five numerical challenges corresponding to increase the value of the parameters
n in higher dimensions with the aim to support their algorithm. In each challenge were given a public key and a ciphertext and was requested to recover the plaintext.
In 1999, P.Nguyen exploited the weakness specific to the way the parametres are chosen and developed an attack against the GGH cryptographic scheme [
54]. The first four challenges, for
were broken since then GGH is considered to be broken, partially in its original form. Nguyen argued that the choice of the error vector is its weakness and make it vulnerable to a possible attack. The error vectors used in the encryption of the GGH algorithm must be shorter than the vectors that generate the lattice. This weakness makes Closest Vector Problem instances arising frim GGH easier than general CVP instances [
56].
The other weakness of GGH cryptosystem is the choice of the error vector e in the encryption algorithm procedure. The e vector is in and it is chosen to maximize the Euclidean norm under requirements on the infi
nity norm. Nguyen takes the ciphertext modulo , where m is the plaintext and B the public key, and the e disappears from the equation. This is because and every choice is . So, this leaks information about the message and increasing the modulus to and adding an all vector s to the equation. If this equation is solved for m, it leaks information for . Nyguen also demonstrated that in most cases this equation it could be easily solved for m.
In 2006 Nguyen and Regev performed an attack at GGH signatures scheme, transforming a geometrical problem to a multivariate optimization problem [
55]. The final numerical challenge for
was solved by M.S. Lee and S.G. Hahn in 2010 [
35]. Therefore, GGH has weaknesses and trapdoors such that it is vulnerable to certain type of attacks, as one attack that allows a fraudulent user to recover the secret key using a small amount of information about the ciphertext. Specifically, if an attacker can obtain the two smallest vectors in the lattice, they can give information and recover the secret key using Coppersmith’s algorithm. As a result, GGH has a limited practical use and has been largely superseded by newer and more secure lattice-based cryptosystems. So, while GGH had an important early contribution to the field of lattice-based cryptography, it is not currently considered a practical choice for secure communication due to its limitations in security.
8. Evaluation, Comparison and Discussion
We have presented a few of the main cryptographic schemes that are based on the hardness of lattice problems and especially based on the Closest Vector Problem. GGH is a public key cryptosystem which is based in algebraic coding theory. A plaintext is been added with a vector noise and the result of this addition is a ciphertext. Both the private and the the public key is a depiction of a lattice and the private key has a specific structure. The Nguyen’s attack [
54] revealed the weakness and vulnerability of the GGH cryptosystem and for many researchers, after that considered GGH to be unusable [
52,
54]
Therefore, in 2010, M.S. Lee and S.G. Hahn presented a method that solved the numerical challenge of the highest dimension 400 [
35]. Applying this specific method Lee and Hann, lead to the conclusion that the decryption of the ciphertext can be accomplished using partial information of the plaintext. Thus, this methods requires some knowledge of the plaintext and can’t be performed in actually real cryptanalysis circumstances. At the other side, in M. 2012 Yoshino and N. Kunihiro and C. Gu et al in 2015, have presented a few modifications and improvements in GGH cryptosystem claiming that made it more resistant in these attacks [
78].
The same year C.F. de Barros and L.M. Schechter with their paper "GGH may not be dead after all", proposed certain improvements for GGH and finally a variation of the GGH cryptographic scheme [
8]. De Barros and Schecher by reducing the public key, in order to find a basis with the aid of Babai’s algorithm perform a direct way to attack to GGH. They increase the length of the noise vector
setting a new parameter
k that modified the GGH cryptographic algorithm. Their modifications resulted in a variation of GGH more resistant to cryptanalysis, but with slower decrytpion process of the algorithm. In 2015, Brakerski et al., described certain types of attacks against some variations of GGH cryptosystem and rely on the linearity of the zero-testing procedure [
16].
GGH was a milestone in the evolution of post quantum cryptography, was one of the earliest lattice based cryptographic schemes and it is based on the hardness of the Shortest Vector Problem. Even though is considered to be one of the most important lattice-based cryptosystems and still has a theoretical interest, it is not recommended for practical use due to its security weaknesses. GGH is the less efficient than other lattice-based cryptosystems. The process to encrypt and decrypt a message requires a large amount of computations and this fact makes the GGH cryptosystem obviously slower and less practical than other lattice-based cryptosystems.
Thus, GGH protocol is vulnerable to certain attacks, such as Coppersmith’s attack and Babai’s nearest plane algorithm and it is considered not to be strong enough. These attacks disputed the security of the GGH and make it less preferable than newer, stronger and more secure lattice-based cryptosystems. Evaluating the efficiency of GGH cryptographic protocol, GGH is relatively inefficient to other lattice-based cryptosystems like NTRU, LWE and others and especially in the key generation and for large key length. As GGH cryptosystem is based in multiplications of matrices, when we choose large keys, it requires a computationally expensive basis reduction algorithm for the encryption and decryption procedure.
Moreover, GGH is considered to be a complex crypographic scheme which requires concepts and knowledge of lattices and linear algebra to study, analyze and implement. GGH also has one more drawback that is the lack of standardization and this makes hard the comparison of its functionality, security and connectivity with other cryptographic schemes. GGH was one of the first cryptogrpahic schemes that were developed and are based on lattice theory and cryptography. In spite of the fact that GGH certainly has interesting theoretical basis and properties, GGH is not used in practice due to its limitations in security, efficiency, and complexity.
NTRU is a public key cryptographic scheme that is based on the Shortest Vector Problem in a lattice and was first presented in the 1990s. It is one of the most well studied and analyzed lattice-based cryptosystems and have been many cryptanalysis studies og NTRU algorithms, including NTRU signatures. NTRU has a high level of security and efficiency and it is a promising protocol for the post-quantum cryptography. Moreover, NTRU cryptographic algorithm uses polynomial multiplication as its basic operation and it is notable for its simplicity.
A main advantage of NTRU cryptosystem is its speed and has been used in certain commercial applications, where speed is a priority. NTRU has a fast implementation compared with other lattice-based cryptosystems, such as GGH, LWE and Ajtai-Dwork. For this reason, NTRU is preferable for applications that require fast encryptions and decrytpion, such as in IoT devices or in embedded systems. In addition to its speed, NTRU uses smaller key sizes compared to other public key cryptosystems, while still maintaining the same level of security. This makes it ideal for applications or environments with limited memory and processing power.
NTRU is considered to be a secure cryptographic scheme against various types of attacks. It is designed to be resistant against attacks such as lattice basis reduction, meet-in-the-middle attacks and chosen ciphertext attacks. NTRU is believed to be a strong cryptographic scheme for the quantum era, meaning that is considered to be resistant against attacks by quantum computers.
NTRU has become famous and widely usable after 2017, because since then it was under a patent it was difficult for the researchers to use it and modificate it. Thus, NTRU is not widely used or standardized in the industry, making it difficult to assess its interoperability with other cryptosystems. Furthermore, NTRU is considered to be a public key cryptohraphic protocol with a relative complexity and its analysis and implementation requires a good understanding of lattice-based cryptography and ring theory. NTRU is a promising lattice-based cryptosystem for post quantum cryptography that offers fast implementation and strong security guarantees.
Learning with Errors (LWE) is a widely used and well studied public key cryptographic scheme that is based in lattice theory. LWE is considered to be secure against both classical and quantum attacks and indeed, is consedered to be among the most secure and efficient of these schemes, while NTRU has limitations in terms of its security. LWE depends its hardness on the difficulty of finding a random error vector in a matrix product and this makes it a resistant cryptosytem against various types of attacks, the same types of attacks with NTRU. It considered to be a strongly secure cryptosystem and post-quantum secure which it means, that is resistant to attacks by a quantum computer.
LWE uses keys with small length size comparing with other cryptographic schemes that are designed for the quantum era, like code-based and hash-based cryptosystems. Just like NTRU, LWE is appropriate for implementation in resource-constrained environments, such as in IoT devices or in embedded systems. A basic advantage of LWE cryptosystem is its flexibility as it is a versatile cryptographic scheme that can be suitable in a variety of cryptographic methods such as digital signatures, key exchange and encryption. LWE can also be used as a building block for more complex cryptographic protocols and from LWE were developed other variations of it.
LWE can be vulnerable to certain type of attacks, like side-channel attacks, i.e. timing attacks or power analysis attacks, if we wouldn’t take the right countermeasures. Just like NTRU, LWE is not considered to be standardized and widely adopted by the computing industry and this makes it difficult to assess its interoperability with other cryptosystems and the comparison with them. Moreover, LWE cryptographic protocol is characterized with complexity and its understanding and modification becomes challenging.
Undoubtedly, both NTRU and LWE are fast, efficient and secure cryptographic schemes. NTRU uses smaller keys sizes and that makes it suitabale for applications where memory and computational power are limited. Both LWE and NTRU are considered to be strong and resistant to various types of attacks and are considered to be prominent for post-quantum cryptography. Thus, LWE is an adaptable cryptographic protocol and can be used in a wide range of cryptographic tasks and methods, while NTRU is primarily used for encryption and decryption.
In summary, LWE and NTRU are both promising lattice-based cryptosystems that offer strong security guarantees and are resistant to quantum attacks. NTRU is known for its fast implementation and smaller key sizes, while LWE offers more flexibility in cryptographic primitives and is currently undergoing standardization. Ultimately, the choice between LWE and NTRU will depend on specific use cases and implementation requirements.
Overall, each lattice-based cryptosystem has its own strengths and weaknesses depending on the specific use case. Choosing the right one requires careful consideration of factors such as security, efficiency, and ease of implementation.
9. Lattice-based Cryptographic Implementations and Future Research
Quantum research over the past few years has been particularly transformative, with scientific breakthroughs that will allow exponential increases in computing speed and precision. In 2016, the National Institute of Standards and Technology (NIST) has announced an invitation to researchers to submit their proposals for developed public - key post-quantum cryptographic algorithms. At the end of 2017, when was the initial submission deadline, there were submitted 23 signature schemes and 59 encryption - key encapsulation mechanism (KEM) schemes, in total 82 canditates’ proposals.
In July 2022, the NIST has finished the third round of selection and has chosen a set of encryption tools designed to be secure against attacks by future quantum computers. The four selected cryptographic algorithms are regarded as an important milestone in securing the sensitive data against the possibility of cyberattacks from a quantum computer in the future [
58].
The algorithms are created for the two primary purposes for which encryption is commonly employed: general encryption, which is used to secure data transferred over a public network, and digital signatures, which are used to verify an individual’s identity. Experts from several institutions and nations collaborated to develop all four algorithms which are presented below.
-
CRYSTALS-Kyber
This cryptographic scheme is being selected by NIST, for general encryption and is based on the module Learning with Errors problem. CRYSTALS-Kyber is similar to Ring-LWE cryptographic scheme but it is considered to be more secure and flexibile. The parties that communicate can use small encrypted keys and exchange them easily with high speed.
-
CRYSTALS-Dilithium
This algorithm is recommended for digital signatures and relies its security on the hardness of lattice problems over module lattices. Like other digital signature schemes, the Dilithium signature scheme allows a sender to sign a message with their private key, and a recipient to verify the signature using the sender’s public key but ilithium has the smallest public key and signature size of any lattice-based signature scheme that only uses uniform sampling.
-
FALCON
FALCON is cryptographic protocol which is proposed for digital signatures. Falcon cryptosystem is based on the theoretical framework of Gentry et al [
28]. It is a promising post-quantum algorithm as it provides fast signature generation and verification capabilities. FALCON cryptographic algorithm has strong advantages such as security, compactness, speed, scalability and RAM Economy.
-
SPHINCS+
SPHINCS plus is the third digital signature algorithm that was selected by NIST. SPHINCS + uses hash functions and is considered to be a bit larger and slower than FALCON and Dilithium. It is regarded as an improvement of the SPHINCS signature scheme, which was presented in 2015, as it reduces the size of the signature. One of the key points of interest of SPHINCS+ over other signature schemes is its resistance to quantum attacks, by depending on the hardness of a one-way function.
10. Conclusions
Significant progress has been made in recent years, taking us beyond classical computing and into a new era of data called quantum computing. Quantum research over the past few years has been particularly transformative, with scientific breakthroughs that will allow exponential increases in computing speed and precision. Research on post-quantum algorithms is active and huge sums of money are being invested for this reason, because it is necessary the existence of strong cryptosystems.
It is considered almost certain that both the symmetric key algorithm and hash functions they will continue to be used as tools of post quantum cryptography. A various of cryptographic schemes have been proposed for the quantum era of computing and this is an active research topic. The development and the standardization of an efficient post-quantum algorithm is the challenge of the academic community. What was once considered a science fiction fantasy is now a technological reality. The quantum age is coming, it will bring enormous changes, therefore we have to be prepared.
References
- Albrecht, M.; Ducas, L. Lattice Attacks on NTRU and LWE: A History of Refinements; Cambridge University Press, 2021. [Google Scholar]
- Alkim, E.; Dukas, L.; Pöppelmann, T.; Schwabe, P. Post-quantum Key Exchange – A New Hope. In Proceedings of the USENIX Security Symposium 2016, Austin, TX, USA, 10–12 August 2016; Available online: https://eprint.iacr.org/2015/1092.pdf.
- Ashur, T.; Tromer, E. Key Recovery Attacks on NTRU and Schnorr Signatures with Partially Known Nonces. In Proceedings of the 38th Annual International Cryptology Conference; 2018. [Google Scholar]
- Babai, L. On Lovasz’ lattice reduction and the nearest lattice point problem. Combinatorica 1986, 6, 1–13. [Google Scholar] [CrossRef]
- Bai, S.; Gong, Z.; Hu, L. Revisiting the Security of Full Domain Hash. In Proceedings of the 6th International Conference on Security, Privacy and Anonymity in Computation, Communication and Storage; 2013. [Google Scholar]
- Bai, S.; Chen, Y.; Hu, L. Efficient Algorithms for LWE and LWR. In Proceedings of the 10th International Conference on Applied Cryptography and Network Security; 2012. [Google Scholar]
- Balbas, D. The Hardness of LWE and Ring-LWE: A Survey Cryptology ePrint Archive 2021.
- Barros, C.; Schechter, L.M. GGH may not be dead after all. In Proceedings of the Congresso Nacional de Matemática Aplicada e Computacional; 2015. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Breidbart, S.; Wiesner, S. Quantum cryptography, or Unforgeable subway tokens. In Proceedings of the Advances in Cryptology: Proceedings of Crypto ’82; 1982; pp. 267–275. [Google Scholar]
- Bennett, C.H.; Brassard, G. Quantum Cryptography : Public Key Distribution and Coin Tossing. In Proceedings of the International Conference in Computer Systems and Signal Processing; 1984. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Ekert, A. Quantum cryptography. Scientific American 1992, 50–57. [Google Scholar] [CrossRef]
- Berstein, D.J.; Buchmann, J.; Brassard, G.; Vazirani, U. Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Bi, L.; Lu, X.; Luo, J.; Wang, K.; Zhang, Z. Hybrid dual attack on LWE with arbitrary secrets. Cryptology ePrint Archive 2022. [Google Scholar] [CrossRef]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. New Constructions of Strongly Unforgeable Signatures Based on the Learning with Errors Problem. In Proceedings of the 48th Annual ACM Symposium on Theory of Computing; 2016. [Google Scholar]
- Brakerski, Z.; Langlois, A.; Regev, O.; Stehl, D. Classical Hardness of Learning with Errors. In Proceedings of the 45th Annual ACM Symp. on Theory of Computing (STOC); 2013; pp. 575–584. [Google Scholar]
- Brakerski, Z. , Gentry, C., Halevi, S., Lepoint, T., Sahai, A., Tibouchi, M. Cryptanalysis of the quadratic zero-testing of GGH. IACR Cryptology ePrint Archive, 2015, 845. [Google Scholar]
- Bonte, C.; Iliashenko, I.; Park, J.; Pereira, H.V.; Smart, N. FINAL: Faster FHE instantiated with NTRU and LWE Cryptology ePrint Archive 2022.
- Bos, W.; Costello, C. ; Ducas, L. l; Mironov, I. ; Naehrig, M. ; Nikolaenko, V. ; Raghunathan, A. ; Stebila, D. Frodo: Take off the ring! Practical, quantum-secure key exchange from LWE. In Proceedings of the CCS 2016, Vienna, Austria, 2016; Available online: https://eprint.iacr.org/2016/659.pdf.
- Buchmann, J; Dahmen, E.; Vollmer, U. Cryptanalysis of the NTRU Signature Scheme. In Proceedings of the 6th IMA International Conference on Cryptography and Coding; 1997.
- Buchmann, J.; Dahmen, E.; Vollmer, U. Cryptanalysis of NTRU using Lattice Reduction. Journal of Mathematical Cryptology 2008. [Google Scholar]
- Chunsheng, G. Integer Version of Ring-LWE and its Applications Cryptology ePrint Archive 2017.
- Coppersmith, D.; Shamir, A. Lattice attacks on NTRU. advances in Cryptology—EUROCRYPT’97.
- Diffie, W.; Hellman, M. New Directions in Cryptography. IEEE Transactions in Information Thery 1976, 644–654. [Google Scholar] [CrossRef]
- Dubois, V.; Fouque, P.A.; Shamir, A.; Stern, J. Practical cryptanalysis of sflash. In Advances in Cryptology CRYPTO 2007; 2007; Volume 4622 of Lecture Notes in Computer Science, pp. 1–12. [Google Scholar]
- Faugere, J.; Otmani, A.; Perret, L.; Tillich, J.; Sendrier, N. Cryptanalysis of the Overbeck-Pipek Public-Key Cryptosystem. Advances in Cryptology – ASIACRYPT 2010.
- Faugère, J.C.; Otmani, A.; Perret, L.; Tillich, J.P. On the Security of NTRU Encryption. Advances in Cryptology – EUROCRYPT 2010.
- Galbraith, S. Mathematics of Public Key Cryptography; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for Hard Lattices and New Cryptographic Constructions. Cryptology ePrint Archive 2007. [Google Scholar]
- Gentry, C. Fully Homomorphic Encryption Using Ideal Lattices. In Proceedings of the 41st Annual ACM Symp. on Theory of Computing (STOC); pp. 169–178.
- Goldreich, O.; Goldwasser, S.; Halive, S. Public-Key cryptosystems from lattice reduction problems. Crypto ’97 1997, 10, 112–131. [Google Scholar]
- Gu, C.; Yu, Z.; Jing, Z.; Shi, P.; Qian, J. Improvement of GGH Multilinear Map. In Proceedings of the IEEE Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC); pp. 407–411.
- Hoffstein, J.; Pipher, J.; Silverman, J. NTRU: A ring-based public key cryptosystem. InAlgorithmic Number Theory (Lecture Notes in Com- puter Science; Springer: New York, NY, USA, 1998; Volume 1423, pp. 267–288. [Google Scholar]
- Kannan, R. Algorithmic Geometry of Numbers. In Annual Reviews of Computer Science; Annual Review Inc.: Palo Alto, CA, USA, 1987; pp. 231–267. [Google Scholar]
- Komano, Y.; Miyazaki, S. On the Hardness of Learning with Rounding over Small Modulus. In Proceedings of the 21st Annual International Conference on the Theory and Application of Cryptology and Information Security; 2015. [Google Scholar]
- Lee, M.S.; Hahn, S.G. Cryptanalysis of the GGH Cryptosystem. Mathematics in Computer Science 2010, 201–208. [Google Scholar] [CrossRef]
- Lenstra, A.K.; H. W. Lenstra, Jr. ; L. Lovasz. Factoring polynomials with rational coefficients. Mathematische Annalen 1982, 261, 513–534. [Google Scholar] [CrossRef]
- Lyubashevsky, V.; Micciancio, D. Generalized Compact Knapsacks Are Collision Resistant. In Proceedings of the 33rd International Colloquium on Automata, Languages and Programming; 2006; pp. 144–155. [Google Scholar]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On Ideal Lattices and Learning with Errors over Rings. Advances in Cryptology – EUROCRYPT 2010.
- Lyubashevsky, V. A Decade of Lattice Cryptography. Advances in Cryptology – EUROCRYPT 2015.
- Martinet, G.; Laguillaumie, F.; Fouque, P.A. Cryptanalysis of NTRU using Coppersmith’s Method. Cryptography and Communications 2011. [Google Scholar]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On Ideal Lattices and Learning with Errors over Rings. ACM 2013, 60, 43:1–43:35. [Google Scholar] [CrossRef]
- Matsumoto, T; Imai, H. Public quadratic polynomials-tuples for efficient signature verification and message encryption. Advances in cryptology -EURO-CRYPT ’88 1988, 330, 419–453. [Google Scholar]
- May, A.; Peikert, C. Lattice Reduction and NTRU. In Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science; 2005. [Google Scholar]
- McEliece, R. A public key cryptosystem based on alegbraic coding theory. DSN progress report 1978, 42-44, 114–116. [Google Scholar]
- Merkle, R. A certified digital signature. In Advances in Cryptology – CRYPTO’89; Springer: Berlin/Heidelberg, Germany, 1989; pp. 218–238. [Google Scholar]
- Micciancio, D. Improving Lattice Based Cryptosystems Using the Hermite Normal Form. In Cryptography and Lattices Conference; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Micciancio, D. , O. Lattice-based cryptography. In Post-quantum cryptography; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Micciancio, D. On the Hardness of the Shortest Vector Problem. Ph.D. Thesis, Massachusetts Institute of Technology, USA, 1998. [Google Scholar]
- Micciancio, D. The shortest vector problem is NP-hard to approximate within some constant. In Proceedings of the 39th FOCS IEEE.
- Micciancio, D. Lattice based cryptography: A global improvement. Technical report. Theory of Cryptography Library 1999, 99-05. [Google Scholar]
- Micciancio, D. The hardness of the closest vector problem with preprocessing. IEEE Trans. Inform. Theory 2001, 47. [Google Scholar] [CrossRef]
- Minaud, B. , Fouque, P. A. Cryptanalysis of the New Multilinear Map over the Integers. IACR Cryptology ePrint Archive 2015, 941. [Google Scholar]
- Niederreiter, H. Knapsack-type cryptosystems and algebraic coding theory. Problems of Control and Information Theory. Problemy Upravlenija I Teorii Informacii. 1986, 15, 159–166. [Google Scholar]
- Nguyen, P.Q. Cryptanalysis of the Goldreich-Goldwasser-Halevi cryptosystem from crypto’97. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, USA; 1999; pp. 288–304. [Google Scholar]
- Nguyen P., Q. Regev, O. Learning a parallelepiped: Cryptanalysis of GGH and NTRU signatures. Journal of Cryptology 2009, 22, 139–160. [Google Scholar] [CrossRef]
- Nguyen, P.Q.; Stern, J. The two faces of Lattices in Cryptology. In Proceedings of the International Cryptography and Lattices Conference, Rhode, USA, 29-30 March 2001; pp. 146–180. [Google Scholar]
- Nielsen, M. ,; Chuang, I. Quantum computation and quantum information, Ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Post-Quantum Cryptography. Available online: https://csrc.nist.gov/Projects/post-quantum-cryptography/selected-algorithms-2022.
- Patarin, J. Hidden field equations and isomorphism of polynomials Eurocrypto ’96 1996.
- Peikert, C. Lattice-Based Cryptography: A Primer. IACR Cryptology ePrint Archive 2016. [Google Scholar]
- Preskill, J. Quantum computing and the entanglement frontier. 2012.
- Poulakis, D. Cryptography, the science of secure communication, 1st ed.; Ziti Publications: Thessaloniki, Greece, 2004. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, A. Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Journal of the ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. Journal of the ACM 2009, 56, 1–40. [Google Scholar] [CrossRef]
- Regev, O. The Learning with Errors Problem: Algorithms and Applications. Foundations and Trends in Theoretical Computer Science 2015. [Google Scholar]
- Sabani, M.; Savvas, I.K.; Poulakis, D.; Makris, G.; Butakova, M. The BB84 Quantum Key Protocol and Potential Risks. In , , In Proceedings of the 8th International Congress on Information and Communication Technology (ICICT 2023), London, UK, 20–23 February 2023. [Google Scholar]
- Sabani, M.; Savvas, I.K.; Poulakis, D.; Makris, G. Quantum Key Distribution: Basic Protocols and Threats. In Proceedings of the 256th Pan-Hellenic Conference on Informatics (PCI 2022), Greece, November 2022; pp. 383–388. [Google Scholar]
- Sabani, M.; Galanis, I.P.; Savvas, I.K.; Garani, G. Implementation of Shor’s Algorithm and Some Reliability Issues of Quantum Computing Devices. In Proceedings of the 25th Pan-Hellenic Conference on Informatics (PCI 2021), Volos, Greece, 26–28 November 2021; pp. 392–296. [Google Scholar]
- Scherer, W. Mathematics of Quantum Computing, An Introduction; Springer, 2019. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. J Comput. SIAM 1997, 26, 1484–509. [Google Scholar] [CrossRef]
- Silverman, J.H.; Piher, J.; Hoffstein, J. An introduction to Mathematical Cryptopraphy, 1st ed.; Springer: USA, 2008. [Google Scholar]
- Susilo, W.; Mu, Y. >Information Security and Privacy; Springer, 2014. [Google Scholar]
- Takagi, T.; Kiyomoto, S. Improved Sieving Algorithms for Shortest Lattice Vector Problem and Its Applications to Security Analysis of LWE-based Cryptosystems. In Proceedings of the 23rd Annual International Conference on the Theory and Applications of Cryptographic Techniquesthe Name of the Conference; 2004. [Google Scholar]
- Trappe, W.; Washington, L.C. Introduction to Cryptography with Coding Theory; Pearson Education: USA, 2006. [Google Scholar]
- Van Assche, G. Quantum Cryptography and Secret-Key Distillation, 3rd ed.; Cambridge University Press: New York, 2006. [Google Scholar]
- Wang, Q.; Jin, Z.; Dong, X. Survey of Lattice-based Cryptography: Attacks, Constructions, and Challenges. IEEE Communications Surveys Tutorials 2019. [Google Scholar]
- Wiesner, S. Conjugate coding. Sigact News 1983, 15, 78–88. [Google Scholar] [CrossRef]
- Yoshino, M. ; Kunihiro, Improving GGH Cryptosystem for Large Error Vector. In Proceedings of the International Symposium on Information Theory and its Applications, Honolulu, Hawaii, USA, 28–31 October 2012; pp. 416–420. [Google Scholar]
- Zheng, Z.; Tian, K.; Liu, F. Modern Cryptography Volume 2 A Classical Introduction to Informational and Mathematical Principle; Springer: Singapore, 2023. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).