Gearbox Fault Diagnosis Based on Optimized Stacked Denoising Auto Encoder and Kernel Extreme Learning Machine

Preprint

Article

Gearbox Fault Diagnosis Based on Optimized Stacked Denoising Auto Encoder and Kernel Extreme Learning Machine

Altmetrics

Downloads

107

Views

Comments

A peer-reviewed article of this preprint also exists.

Zhenghao Wu,Hao Yan,Xianbiao Zhan,Liang Wen,

Xisheng Jia^*

Zhenghao Wu,Hao Yan,Xianbiao Zhan,Liang Wen,

Xisheng Jia^*

This version is not peer-reviewed

Submitted:

28 April 2023

Posted:

04 May 2023

You are already at the latest version

Alerts

Abstract

In a complex working environment, the fault signal of the gearbox is greatly affected by the outside world, and fault feature recognition is difficult, so the fault diagnosis accuracy is difficult to meet the expected requirements. To solve this problem, this paper proposes a gearbox fault diagnosis method based on an optimized stacked denoising auto encoder (SDAE) and kernel extreme learning machine (KELM). Firstly, the Particle Swarm Optimization algorithm in Adaptive Weight (SAPSO) was adopted to optimize the SDAE network structure, and the number of hidden layer nodes, learning rate, noise addition ratio and iteration times were adaptively obtained to make SDAE obtain the best network structure. Then, the best SDAE network structure was used to extract the deep feature information of weak faults in the original signal. Finally, the extracted fault features are fed into KELM for fault classification. Experimental results show that, compared with existing commonly used methods of fault diagnosis, the fault diagnosis model proposed in this paper can reduce the influence of noise in the original signal can better learn the deep-level features in the original signal and has higher diagnosis accuracy, faster diagnosis speed and good generalization in fault diagnosis.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The gearbox is a key component of the transmission system of self-propelled artillery, tank, helicopter, and other equipment, and plays an important role in the operation of equipment. These equipment operate in complex and harsh environments such as long-term wind and sand, rain and snow, and plateau hypoxia, which is easy to cause gear wear and broken teeth and other faults. If these faults are not detected and handled as soon as possible, the operation of the equipment may be affected, resulting in the reduction of the working efficiency of the transmission system, or the equipment may be damaged, resulting in casualties and other serious accidents. Vibration signal contains all the information of equipment running state. Fault prognostics and health Management (PHM) technology based on vibration signal can better improve the reliability and safety of equipment and avoid serious faults of equipment. Therefore, the use of vibration signal for gearbox fault diagnosis has important practical value [1,2,3].

Health monitoring and fault diagnosis of equipment by extracting features from vibration signals is a common method used by many scholars [4,5,6]. The purpose of extracting features from vibration signals is to use them as indicators to judge whether a gearbox has failed or deteriorated in function. For example, Li et al. [7] used Pearson correlation coefficient plots and orthogonality to select time-domain features of diesel engines and used the parameters of the best better-correlated correlated time-domain features to input into a generalized regression neural network for fault classification, which could significantly improve the accuracy of fault identification. Meng et al. [8] used time domain and frequency domain features to input into the KELM optimized by quantum particle swarm optimization (QPSO) for fault classification, which could well identify gearbox faults. Zhao et al. [9] used adaptive Variational Time Domain Decomposition (VTDD) to decompose and reconstruct complex multi-shock vibration signals. This method was used to extract features from the vibration signals of engine valve faults with good results. Wang et al. [10] used Pearson correlation coefficients and fault state selection features to be able to diagnose engine faults and damage levels well. Dhamande et al. [11] used continuous and discrete wavelets to extract time-frequency domain features from gear and bearing vibration signals for fault diagnosis, with better results than conventional time-domain and frequency-domain feature parameters. Li et al. [12] generated depth statistical features from the time, frequency, and time-frequency domain signals of rotating machinery and fed them into a Support Vector Machine (SVM) for fault diagnosis with good results.

The above methods using feature extraction can solve some fault diagnosis problems well, but they are often not effective in dealing with complex vibration signals. Complex vibration signals are often mixed with a lot of noise and have non-smooth, non-linear characteristics. In order to solve this problem, the method of signal decomposition was used by many scholars. Examples include Empirical Modal Decomposition (EMD), Variational Modal Decomposition (VMD), Local Mean Decomposition (LMD), Wavelet Transform (WT), etc. Yang et al. [13] combined a hybrid fault diagnosis method of EMD and WT, which can effectively solve the problem of component failure in wind turbine gearboxes. Yan et al. [14] can eliminate the noise in the original signal well by using VMD. Han et al. [15] used LMD to decompose the original signal into a finite number of product functions (PF) and extracted Multi-scale Symbolic Dynamic information Entropy (MSDE) as features for fault diagnosis, and the method was experimentally proven to be good at eliminating noise. Syed et al. [16] used the eight decomposition coefficients of the wavelet family to extract the root-mean-square energy as a feature, which was fed into the classifier with very satisfactory results. These methods can well eliminate the noise in the vibration signal and retain the main fault characteristic signals, effectively improving the fault diagnosis accuracy of complex vibration signals.

Currently, deep learning-based fault diagnosis methods are a hot research topic. Liu et al. [17] used CNN to extract the features of continuous wavelet transform (CWT) to construct the wavelet time-frequency graph, which was input into the ELM classifier optimized by the Sparrow search optimization algorithm (SSA), which could well identify bearing faults. Liu et al. [18] used LMD to eliminate noise from the reciprocating compressor signal and then fed the frequency domain signal into an SDAE network for fault diagnosis, which was more effective than the conventional method. Shao et al. [19] designed a One-dimensional Convolutional Neural Network (1D-CNN) with a self-encoder structure, which can extract deep-level features in the signal for fault diagnosis and has good robustness. Jia et al. [20] used the Sparrow Search Algorithm (SSA) to optimize the SDAE network and input the time-frequency map generated by the CWT into the optimized SDAE for fault diagnosis, with a high accuracy rate.

These methods, although to a certain extent solving the problem of gearbox fault diagnosis, also suffer from the following problems:

Traditional machine learning methods need to extract features manually, which is time-consuming and laborious. Moreover, the selection of features depends on previous experience, which has limitations in practical engineering applications.

Deep learning methods can effectively learn the deep information hidden in the data, but the selection of parameters for commonly used deep learning network models is based on previous experience and personal experimental debugging, which is time-consuming and labor-intensive, and fault diagnosis models require a large amount of labeled data to be trained for a long time to ensure the accuracy of the diagnosis results and the generalization of the diagnosis model.

A diagnostic model with fast diagnostic speed, high diagnostic accuracy, and strong operability is the need for practical engineering applications. Therefore, the following work is done to improve this paper’s time efficiency and fault diagnosis accuracy. Firstly, the PSO algorithm is improved to provide faster and better global optimization capabilities. Fast determination of optimal parameters for SDAE network models using improved PSO. Then, the optimized SDAE network was used to extract the deep features of the original signals. Finally, the fast classification ability of KELM was used to classify the extracted deep features quickly. The major contributions of this paper include the following:

By improving the inertia weights of particles and adopting the PSO with adaptive weights, the parameter optimization of the SDAE network is faster and more effective.
Using the optimized SDAE network structure, deep-level features can be extracted directly from the original signal, avoiding the disadvantages of manual feature extraction.
The SAPSO-SDAE-KELM diagnostic model proposed in this paper solves the problems of noise reduction and dimensional catastrophe of the original signal, avoids the phenomenon of overfitting, and achieves rapid diagnosis of gearbox faults.

The rest of the paper is organized as follows: Section 2 introduces the theory related to the gearbox fault diagnosis method proposed in this paper. Section 3 introduces the SDAE network construction and fault diagnosis process. Section 4 shows the experiments and data set generation. Section 5 shows the comparison of diagnostic methods and noise addition experiments, which validate the method proposed in this paper. Section 6 gives the conclusions of this paper and proposes future research plans.

2. Theoretical Background

2.1 SDAE implements the principle of dimensionality reduction and denoising

SDAE is a deep-learning network composed of multiple denoising autoencoders. SDAE is an unsupervised learning method that can extract deep features of gearbox faults from vibration signals.

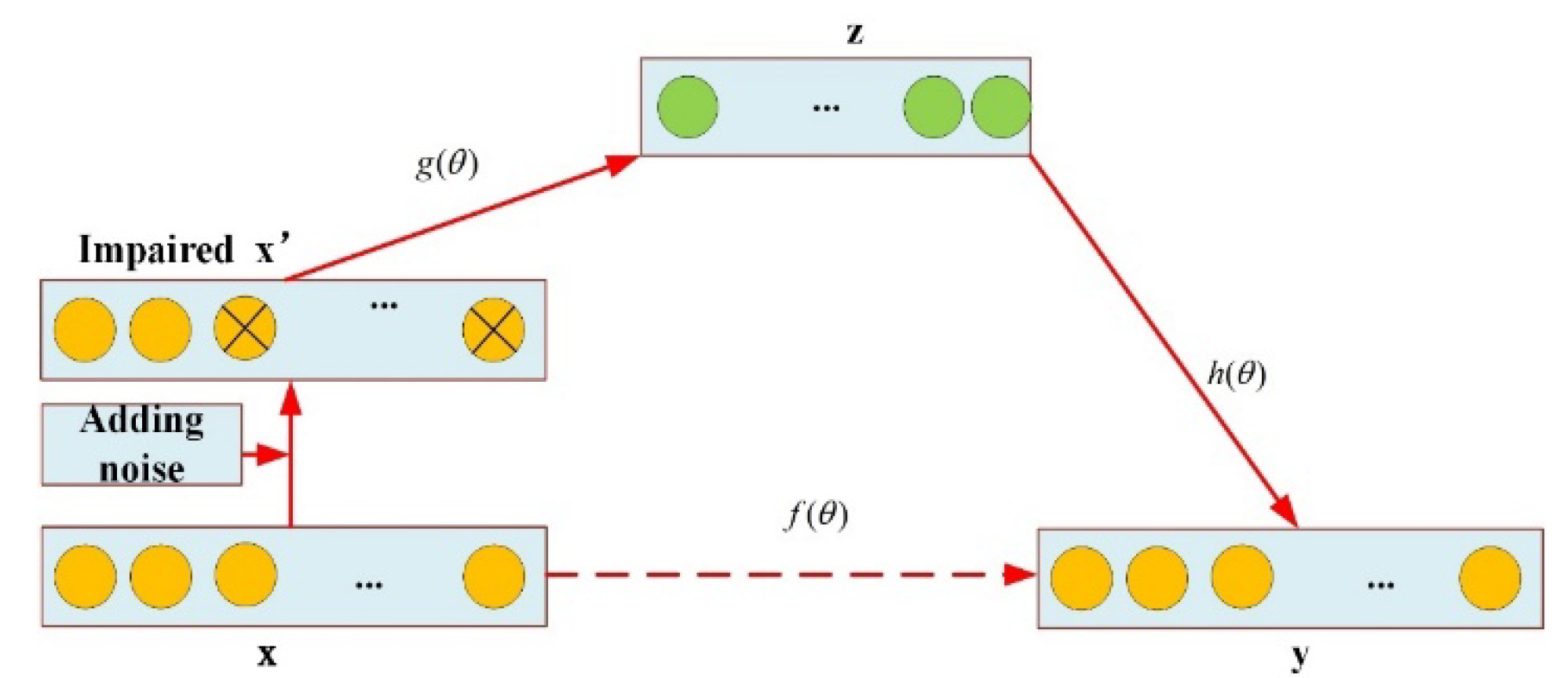
2.1.1. Principle of noise reduction with denoising autoencoder

Denoising Autoencoder (DAE) [21] is an improvement on the Auto encoder (AE) [22]. Noise reduction is achieved by adding noise to the original vibration signal at the input, corrupting the original signal by noise, and then reconstructing a better input without noise using a sample containing noise [23,24]. The structure of the DAE is shown in Figure 1.

The process of noise reduction of the original vibration signal by DAE is as follows:

Input noise to the original vibration signal $x$

to obtain the damaged signal

x^{'}

2): 2. The damaged signal a is used as the input, and the hidden layer Z is obtained through encoding. The encoding formula is as follows:

z = g (w x^{'} + b)

()

3.: After decoding and reconstruction, the reconstructed signal $y$

is obtained, so that reconstructed signal

y

is close to the original signal

x

y = h (w' z + b^{'})

(2)

4.: Train the parameter $θ = \{w, b, w^{'}, b^{'}\}$

in the DAE with minimized reconstruction error:

L_{D A E} = \sum_{i = 1}^{n} {(x_{i} - y_{i})}^{2}

(3)

Where

x

is the original vibration signal,

x^{'}

is the original signal after adding noise,

z

is the hidden layer variable,

y

is the reconstructed signal,

w

is the weight coefficient,

b

is the bias vector,

g (\cdot)

and

h (\cdot)

are the activation functions.

As can be seen from the above process, DAE noise reduction is achieved by adding noise to the original vibration signal, which, together with the noise of the original signal, is eliminated at the time of encoding. The hidden layer decoding provides a good restoration of the original vibration signal, and by minimizing the reconstruction error, the trained DAE model has better robustness.

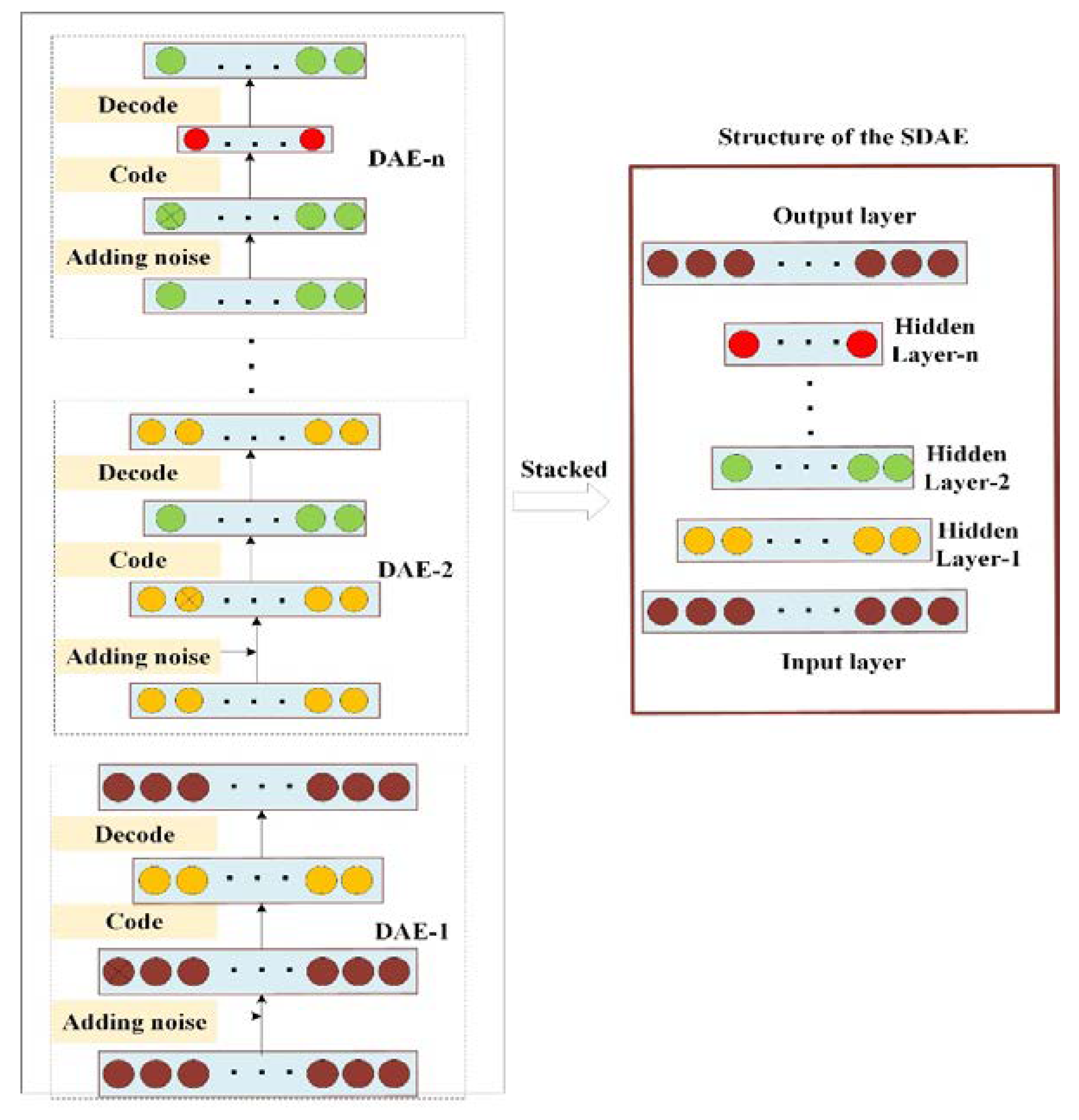
2.1.2. Stacked denoising autoencoder (SDAE)

Although DAEs can achieve the effect of dimensional and noise reduction on the original vibration data, individual DAEs are still shallow neural networks that do not learn the deeper features of the original vibration signal very well. SDAE is a deep neural network made up of multiple DAEs stacked on top of each other. The hidden layer of the previous DAE is used as input to the next DAE, forming a multi-layer DAE model structure, and finally achieving the extraction of feature information layer by layer, so SDAE has better learning ability and expression ability for data features. The structure of the SADE is shown in Figure 2.

The SDAE stacking process is as follows:

1. The first DAE training.

\{\begin{cases} z_{1} = f (x^{'}) = s_{f} (W_{1} x + b_{1} ） \\ y = g (z_{1}) = s_{g} (W_{2} z_{1} + b_{2}) \end{cases}

(4)

The error reconstruction is calculated as:

L_{S D A E} (x, y) = \sum_{i = 1}^{n} {(x_{i} - y_{i})}^{2}

(5)

The weighting and bias update formulae are as follows:

\{\begin{cases} W_{1}^{'} = W_{1} - τ \frac{\partial L_{S D A E}}{\partial y} \times \frac{\partial y}{\partial W_{1}} \\ b_{1}^{'} = b_{1} - τ \frac{\partial L_{S D A E}}{\partial z_{1}} \times \frac{\partial z_{1}}{\partial b_{1}} \end{cases}

(6)

In the above equation,

τ

is the learning rate,

\frac{\partial L_{S D A E}}{\partial W_{1}}

is the partial derivative of

W_{1}

, and

\frac{\partial L_{S D A E}}{\partial b_{1}}

is the partial derivative of

b_{1}

. After the first DAE is trained, the hidden layer is extracted and used as the input layer for the next DAE.

2. The second DAE training

\{\begin{cases} h_{1} = f (x^{'}) = s_{f} (W_{2} x^{'} + b_{2} ） \\ y = g (z_{1}) = s_{g} (W_{3} z_{2} + b_{3}) \end{cases}

(7)

The weights and bias updates are calculated as follows:

\{\begin{cases} W_{2}^{'} = W_{2} - τ \frac{\partial L_{S D A E}}{\partial y} \times \frac{\partial y}{\partial W_{2}} \\ b_{2}^{'} = b_{2} - τ \frac{\partial L_{S D A E}}{\partial z_{2}} \times \frac{\partial z_{2}}{\partial b_{2}} \end{cases}

(8)

The subsequent training process is the same as in steps 1 and 2, and all SDAEs in SDAE are trained in the same way. The weights and biases of the SDAE network are adjusted by a gradient descent algorithm [25] to fine-tune them in reverse.

2.2 An improved PSO algorithm for selecting SDAE network parameters

The particle swarm optimization algorithm [26] is a swarm optimization method that simulates the predatory habits of birds. Before the optimization algorithm begins, a random initialization determines the initial velocity and position of the particles. Set the position of the

i

th particle in

n

-dimensional space to be

X_{i} = [x_{i, 1}, x_{i, 2} ..., x_{i, n}]

and the initial velocity to be

V_{i} = [v_{i, 1}, v_{i, 2} ..., v_{i, n}]

, then for each iteration of training, at moment t, the particle’s velocity and position are expressed as in (12) (13):

v_{i . j} (t + 1) = ω v_{i . j} (t) + c_{1} r_{1} [p_{i . j} - x_{i . j} (t)] + c_{2} r_{2} [p_{1, j} - x_{i . j} (t)]

(9)

x_{i . j} (t + 1) = x_{i . j} (t) + v_{i . j} (t + 1), j = 1, ..., n

(10)

where:

c_{1}

and

c_{2}

are learning factors;

r_{1}

and

r_{2}

are uniformly distributed random numbers between 0 and 1, and

P_{i} = [p_{i, 1}, p_{i, 2} ..., p_{i, n}]

is the best position in the local neighborhood. In the process of optimization, it is also necessary to set particle velocity interval

[v_{\min}, v_{\max}]

and position range

[x_{\min}, x_{\max}]

to realize the control of particle optimization range.

The PSO algorithm is superior in solving complex optimization problems, but has the following drawbacks: the algorithm does not have high search accuracy, has a poor local search capability, tends to fall into local minimal value solutions, and has some dependence on parameters. In view of these drawbacks, the inertia weights

ω

of the particles are improved in this paper [27] by self-adopting the PSO algorithm with adaptive weights. The SAPSO algorithm balances global search capability with local improvement capability by taking non-inertial dynamic inertia weights, which are calculated as shown below:

ω = \{\begin{cases} ω_{\min} - \frac{(ω_{\max} - ω_{\min}) * (f - f_{\min})}{f_{a v g} - f_{\min}}, f \leq f_{a v g} \\ ω_{\max}, f > f_{v g} \end{cases}

(11)

Where:

ω_{\max}

ω_{\min}

denote the maximum and minimum values of

ω

respectively,

f

denote the current objective function value of the particle,

f_{a v g}

and

f_{\min}

denote the current average and minimum objective values of all particles respectively. As can be seen from the above equation, the inertia weights are self-varying with the value of the particle’s objective function and are therefore called adaptive weights.

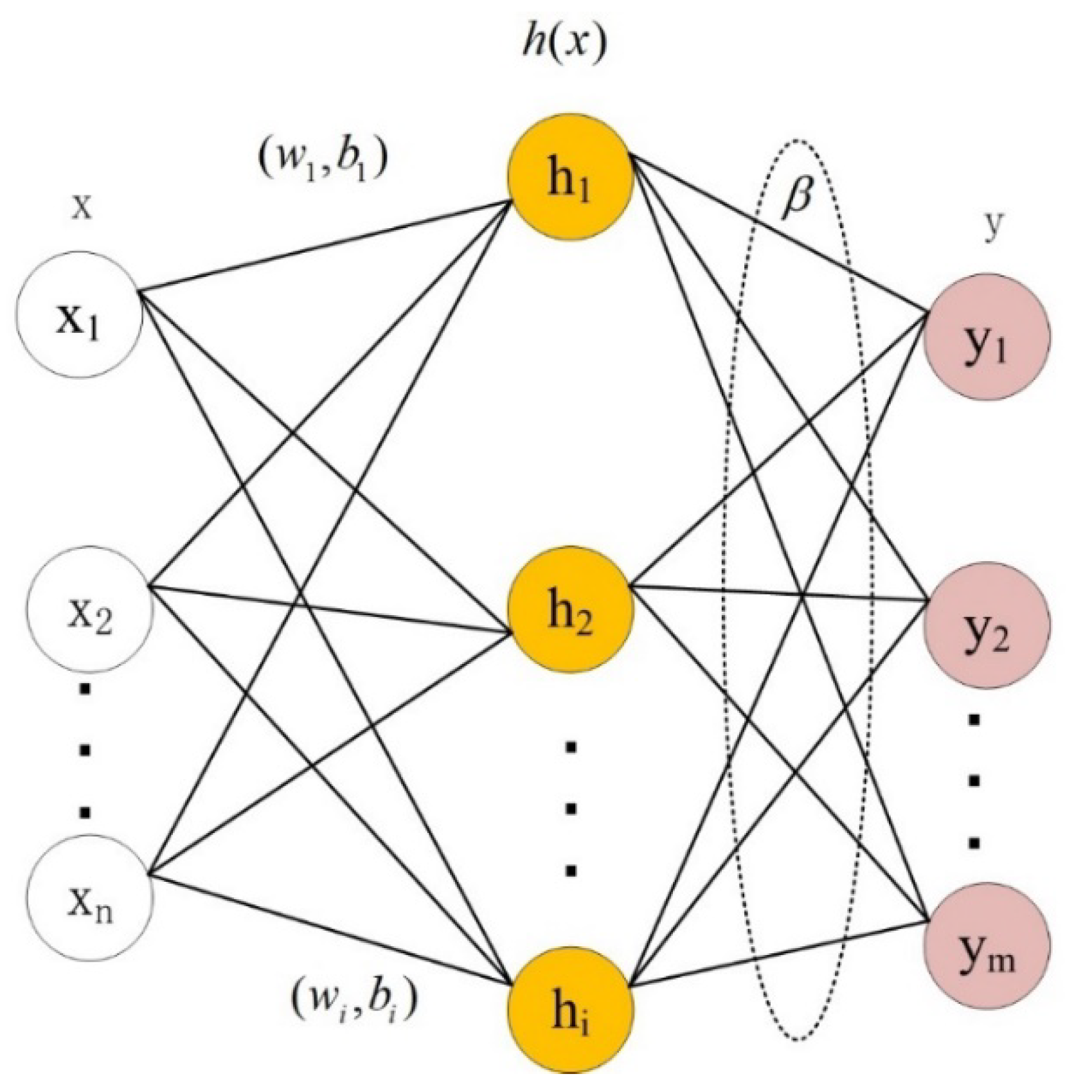
2.3 Kernel Based Extreme Learning Machine（KELM）

The extreme learning machine (ELM) was proposed by Huang [28] and others based on the theory of Moore-Penrose generalized inverse. The main solution to the problems of the slow learning rate, long iteration time, and the need to set learning parameters such as learning step size and learning rate in advance in Single-hidden Layer Feedforward Neural Networks （SLFNs）. The ELM simply sets the appropriate number of nodes, generates all the parameters required for the corresponding implicit layer, and determines the weights of the output layer by means of a least squares method. ELM is widely used in engineering practice due to its advantages of fast learning and approximation of non-linear terms. Kernel based extreme learning machine (KELM) [29] is an improved algorithm based on extreme learning machine and combined with kernel functions, KELM can improve the performance of the model while retaining the benefits of ELM. The basic structure of the Extreme Learning Machine is shown in Figure 3.

The model equation for the extreme learning machine is：

y = h (x) β = H β

where:

x

is the input vector,

y

is the output vector,

h (x)

, H is the hidden layer feature matrix, and

β

is the output weight.

β

is calculated as:

β = H^{T} {(H H^{T} + \frac{I}{C})}^{- 1} T

(13)

Where T is the input vector, C is the canonical factor and I is the unit matrix.

KELM is the introduction of a kernel function to replace the mapping of hidden layer nodes in ELM and its model is calculated as:

y = h (x) H^{T} {(H H^{T} + \frac{I}{C})}^{- 1} T = K (x) H^{T} {(H H^{T} + \frac{I}{C})}^{- 1} T

(14)

Radial basis functions are selected as kernel functions in this paper:

\ker (x, y) = \exp (- \frac{‖x - y‖}{2 σ^{2}})

(15)

where

x

is the input,

y

is the output and

σ

is the width parameter of the kernel function.

Introducing the kernel function into ELM results in the following output:

y = [\begin{array}{l} \ker (x, x_{1}) \\ \begin{matrix} . \\ . \\ . \end{matrix} \\ \ker (x, x_{n}) \end{array}] H^{T} {(H H^{T} + \frac{I}{C})}^{- 1} T

(16)

where:

(x_{1}, x_{2}, ..., x_{n})

is the given training sample, can be

n

the number of samples, and

\ker (\cdot)

is the kernel function.

3. SDAE network construction and SAPSO-SDAE-KELM troubleshooting process

3.1 Construct the optimal SDAE network chat structure

3.1.1 Determine the number of hidden layers

Is it better to have more hidden layers in a SDAE neural network? For this problem, Du et al. [30] conducted simulation experiments and concluded that the network structure of SDAE containing three hidden layers for fault diagnosis works best. Experiments were carried out according to their experimental methodology, using data from the experiments in Section 4. The first thing that should be considered when determining whether SDAE hidden layer is optimal is the principle of SDAE. The essence of SDAE is to minimize the error value between the input data and the reconstructed data by decoding and encoding. The smaller the error between the input condition signal and the reconstructed data signal, the stronger the SDAE fault signal extraction capability, and the larger the error, the weaker the SDAE fault signal feature extraction capability. The smaller error value indicates that the sparse deep-level feature data in the hidden layer can well characterize the original data when the data in the hidden layer is used for fault diagnosis, which better reflects the rigor of the diagnosis method.

The RMSE characterizes the error between the input data and the reconstructed data in a very specific way, and therefore the root mean square error (RMSE) is a good evaluation metric to assess the magnitude of the error between the two vectors. Pearson’s correlation coefficient is the most commonly used statistical measure to describe the extent to which two variables are related to each other. When the inputs and outputs are more similar, the error between the inputs and outputs is smaller, so the Pearson correlation coefficient can be used as an evaluation indicator to measure the variation in inputs and outputs. Therefore, RMSE and Pearson’s correlation coefficient are introduced in this paper as evaluation indicators. The calculation formula is as follows:

R M S E = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (X_{i} - Y_{i}))^{2}}

(17)

ρ_{X Y} = \frac{1}{n} \frac{\sum_{i = 1}^{n} (X_{i} - E (X)) (Y_{i} - E (Y))}{\sqrt{\frac{\sum_{i = 1}^{n} {(X_{i} - E (X))}^{2}}{n}} \sqrt{\frac{\sum_{i = 1}^{n} {(Y_{i} - E (Y))}^{2}}{n}}}

(18)

Where

n

is the number of vibration signal samples,

X_{i}

is the original signal and

Y_{i}

is the corresponding reconstructed signal.

E (X)

is the mean value of the raw signal and

E (Y)

is the mean value of the output signal.

In order to obtain the best-hidden layers for SDAE, SDAE networks containing 2, 3, 4, and 5 hidden layers are designed and verified respectively. The RMSE, Pearson’s correlation coefficient, and fault diagnosis accuracy were calculated respectively. The details are shown in Table 1.

As can be seen from the above table, the SDAE containing 3 hidden layers has a value of 0.0093 for RMSE, a correlation coefficient of 0.996, and a fault diagnosis accuracy of 100.0%. SDAE works best when it contains 3 hidden layers compared to other numb the errors of hidden layers. Therefore, the SDAE network structure with 3 hidden layers is adopted in this paper.

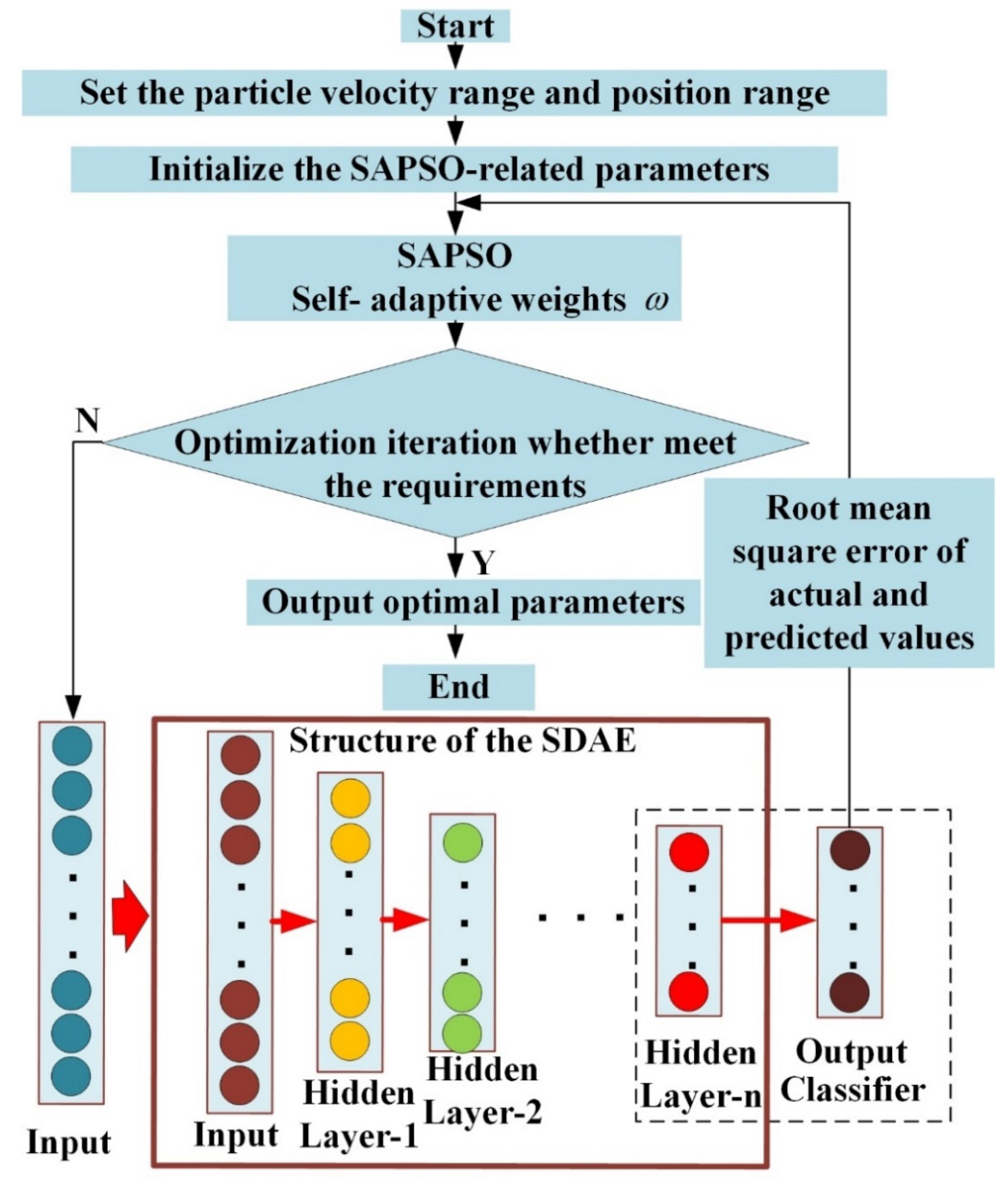
3.1.2. The best parameters of SDAE are selected by improved PSO optimization

The process of selecting parameters for improved PSO optimization of SDAE network structure is shown in Figure 4, and the specific steps are described as follows:

Step 1. Set the particle swarm velocity interval and position range.

Step 2. Initializes the population size and a number of iterations of the particle swarm optimization algorithm.

Step 3. Set the bit initial position of the particles. Calculate the fitness, which is determined by the root mean square error (RMSE) magnitude between the actual and predicted values of the particle population.

Step 4. A particle swarm search algorithm with a self-adaptive inertia factor

ω

is used for iterative optimization. In one iteration, the individual best extreme

p b e s t

of a single particle and the global best

g b e s t

of a population of particles are recorded, while the position and velocity of the particles are updated.

Step 5. Determine whether the current number of iterations exceeds the iteration limit. If yes, the iteration is terminated and the globally optimal result

g b e s t

and the

p b e s t

of individual particles are output; If no, the next step is executed.

Step 6. The optimal parameters are obtained. When the iteration proceeds until the RMSE of the actual and predicted values is reduced to a predetermined value, the search for the best stops. At this point, the relevant parameters corresponding to the best position of the particle swarm are the best parameters in the SDAE network. If the RMSE is greater than the predetermined value, the iterative search continues and returns to step 4.

3.2. Fault diagnosis method and process of SAPSO-SDAE-KELM

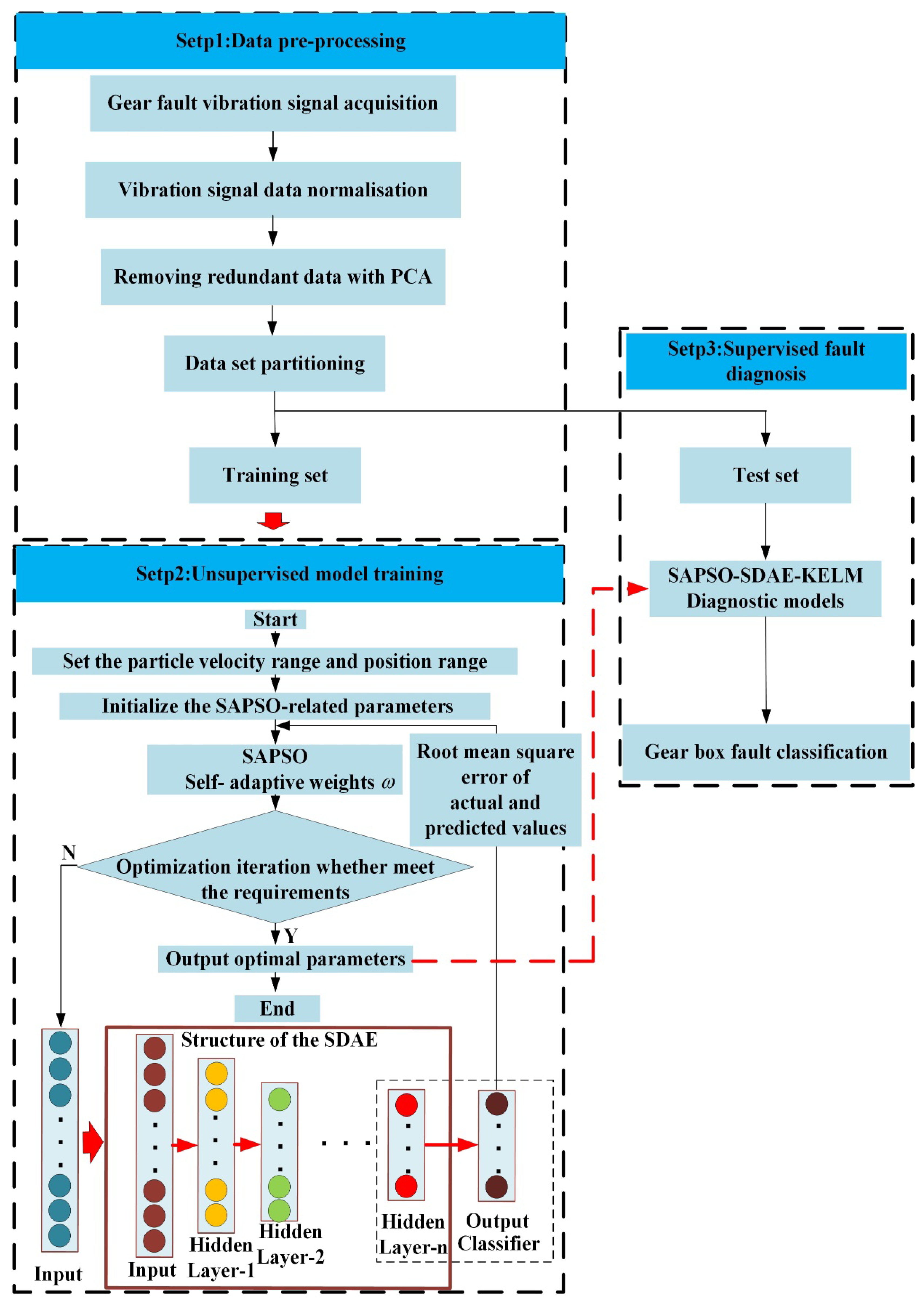
The SAPSO-SDAE-KELM based gearbox fault diagnosis flow chart is shown in Figure 5 and is divided into the following 3 steps.

Step 1: Data pre-training. The vibration signal of the gearbox is obtained by using the experimental platform, the vibration signal is normalized, the redundant signal in the original signal is removed by PCA, and then it is divided into a training set and a test set.

Step 2: Unsupervised model training. The training set divided in step 1 is used to input the SAPSO-SDAE neural network model. The SDAE neural network model and its parameters are first initialized. The hyperparameter in the network model is then optimized by round-robin optimization. If the results of the network training do not meet the requirements, the training is re-iterated until the requirements are met.

Step 3: Supervised fault diagnosis. Using the parameters obtained in Step 2, the optimal SDAE network structure is constructed. The step 1 test set data is labeled and fed into the SDAE network for deep feature extraction. The data from the last hidden layer is extracted and fed into KELM for fault classification to produce fault diagnosis results.

4. Experiments and data pre-processing

4.1. Experimental platform

Figure 6 shows the structure and sensor layout of the test bed. The test bench consists of a base, planetary gear reducer, three-phase asynchronous motor, electromagnetic speed control motor, and magnetic powder brake. The experiments were carried out on a reducer model JZQ175. The vibration sensor model is IEPE general number 14100. Through the CNC machine tool, the gearbox gear preset 2mm crack, 5mm crack, and 2mm broken teeth, and 5mm broken teeth 4 kinds of faults. Figure 7 shows the preset fault.

4.2. Signal acquisition and sample generation

4.2.1. Signal acquisition scheme

After the experimental platform runs smoothly, the signal is collected. The input speed of the motor was 1200 r/min, the magnetic powder brake load current was 1A, the sampling frequency of the vibration sensor was 20000 Hz, and the signal sampling time was 6 seconds. The vibration signals are collected for each of the 5 operating conditions.

4.2.2. Sample construction and data set generation

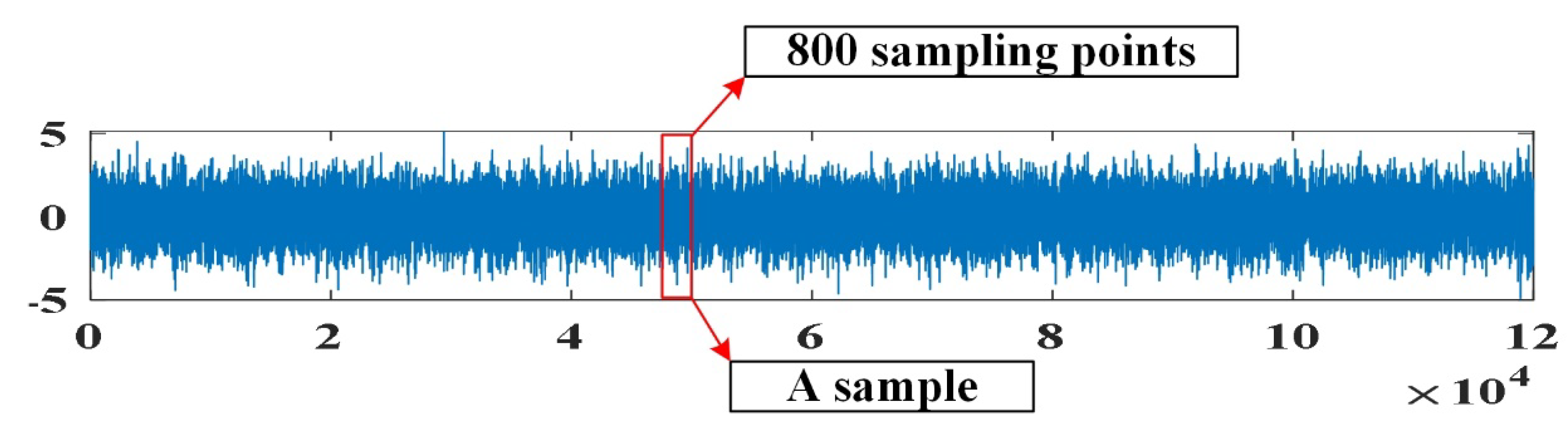
As can be seen from Table 2, 120,000 data points were collected for each operating conditions in this experiment. One sample is taken for every 800 points, so 150 samples can be taken for each working condition, and the sample construction is shown in Figure 8.

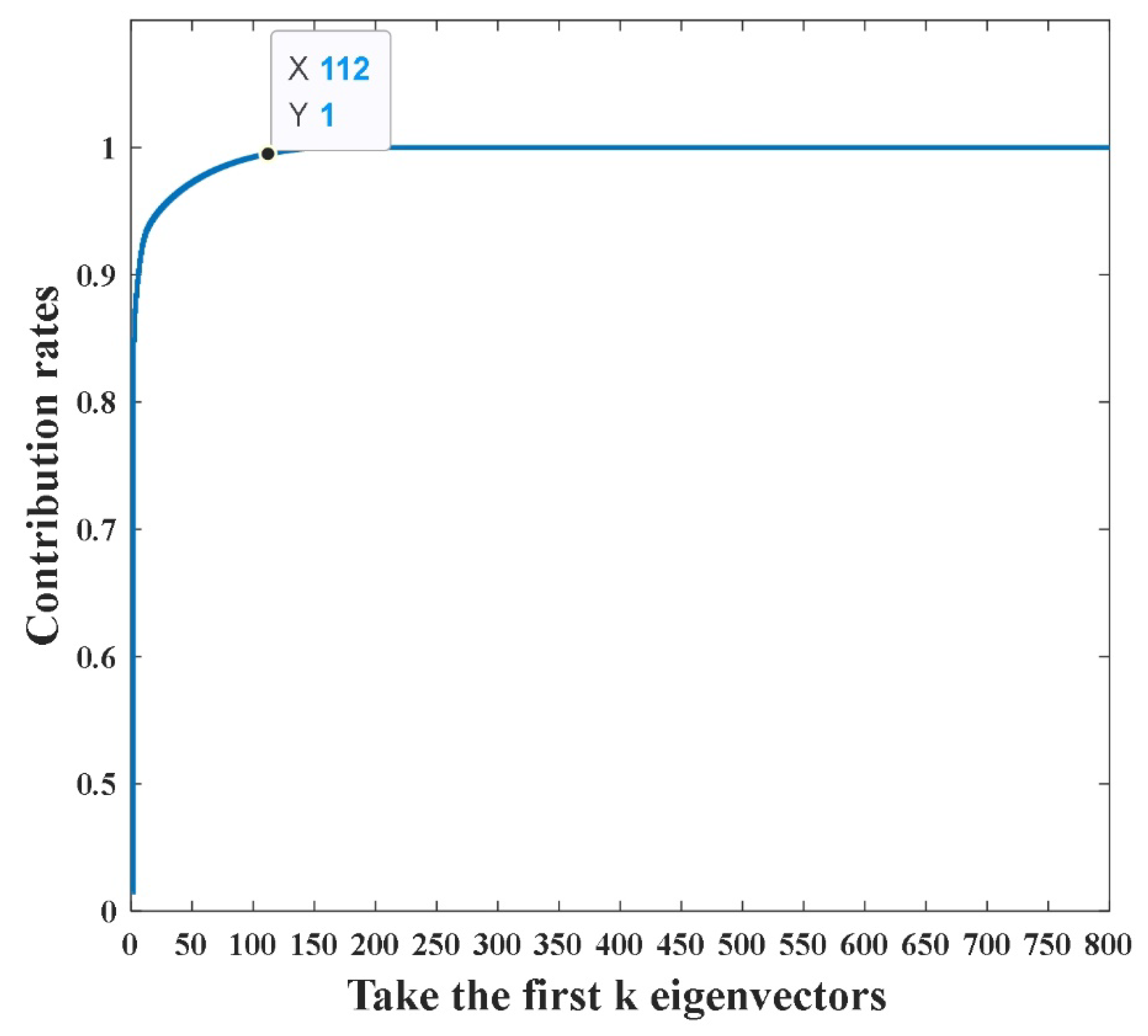
In order to speed up the training, PCA is used to eliminate redundant signals from the original signal. Figure 9 shows the effect of PCA dimensionality reduction. It can be seen from Figure 9 that when the data is reduced to 112 dimensions, the essential characteristics of the original signal can be better retained. The ratio of training set and test set is divided into 8:2, and the details of sample division are shown in Table 3:

Training set and testing set according to the division of 8:2, as shown in Table 3:

5. Method validation and comparison

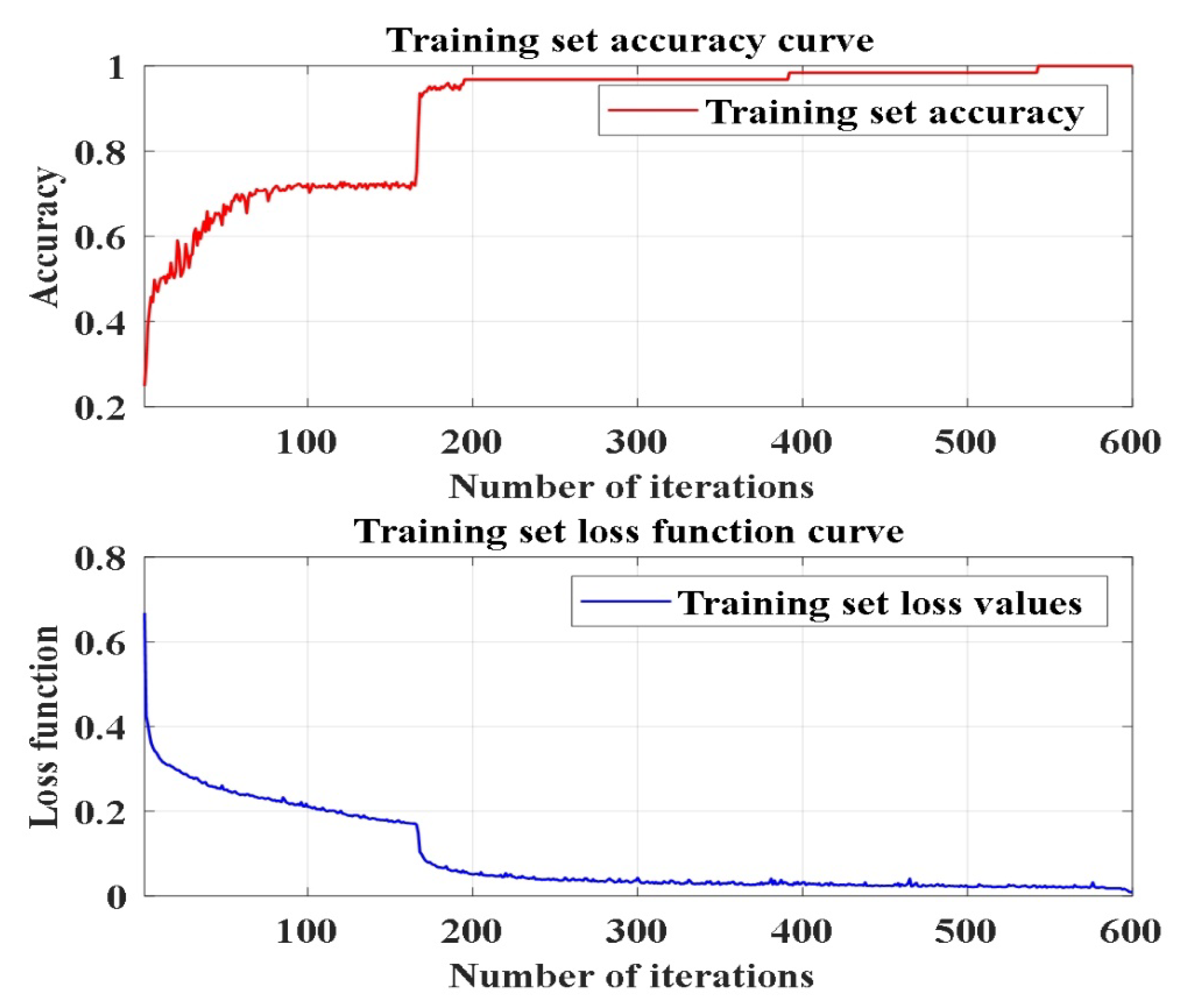
Before the method verification and comparison, the optimal SDAE neural network structure is first clarified. According to 3.1.1, the optimal network structure contains three hidden layers. Using the method in 3.1.2 and the sample data in 4.2, the optimal parameters of SDAE are obtained as follows. The number of iterations is 600, the learning rate is 0.6, the noise addition ratio is 0.3, and the number of hidden layer nodes is 69-55-46. The training curve of SDAE neural network is shown in Figure 11.

5.1. Comparison of Optimization Results after Particle Swarm Improvement

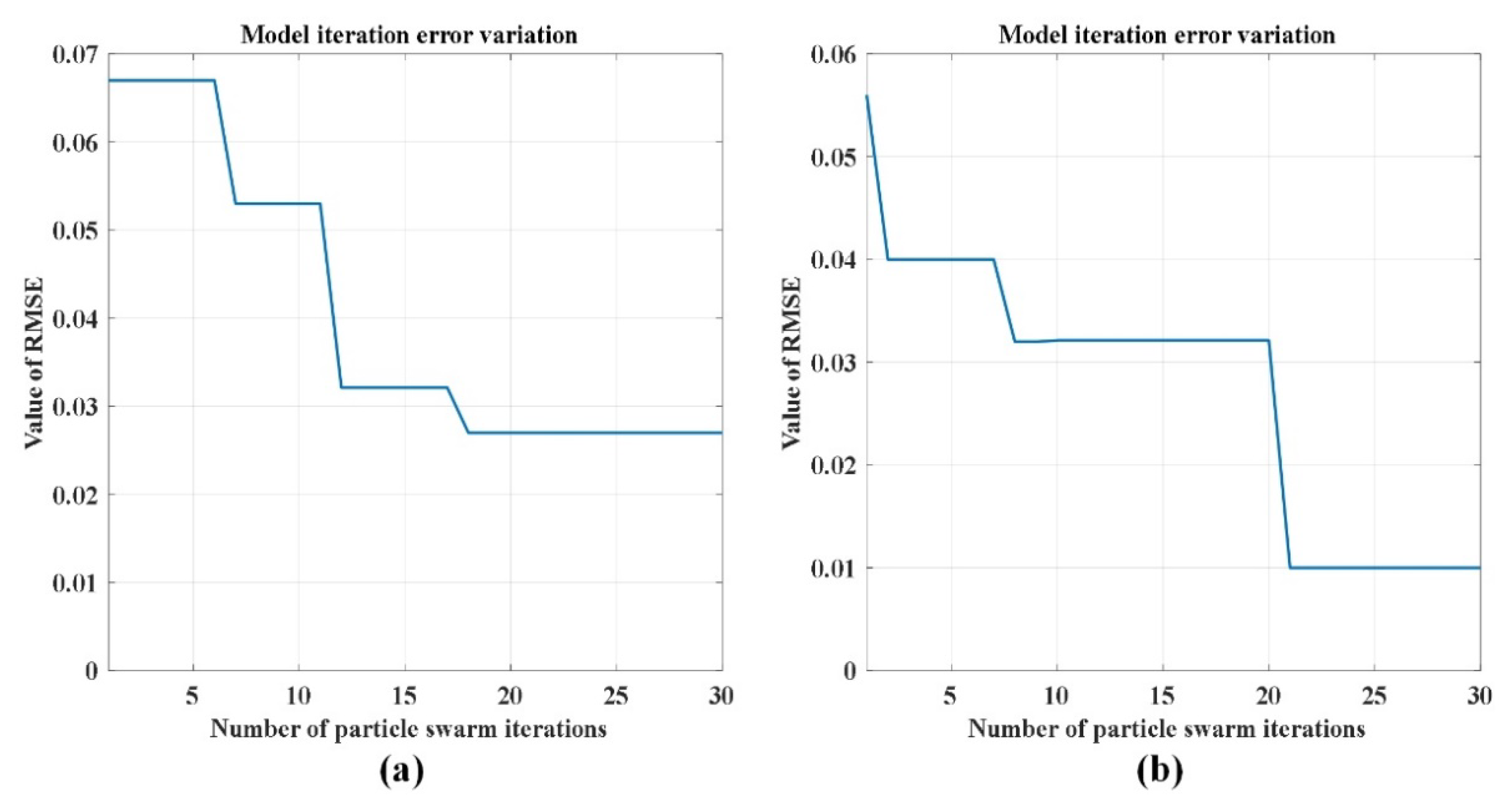
To verify that the improved PSO optimization method proposed in this paper is better, PSO and SAPSO are used to optimize the SDAE neural network respectively. The RMSE of the actual value and the predicted value is used as the fitness value in 2.2, so the size of the fitness value can be used to determine which optimization effect is better. The smaller the fitness value, the better the SDAE network is trained. Figure 11 shows the change of fitness value in the iterative optimization process of PSO and SAPSO. It can be seen from the figure that the final fitness value of PSO is 0.028, while the lowest fitness value of SAPSO is 0.01. The fitness value of SAPSO is less than that of PSO, which can prove that SAPSO has better optimization effect.

5.2. Comparison with other fault diagnosis methods

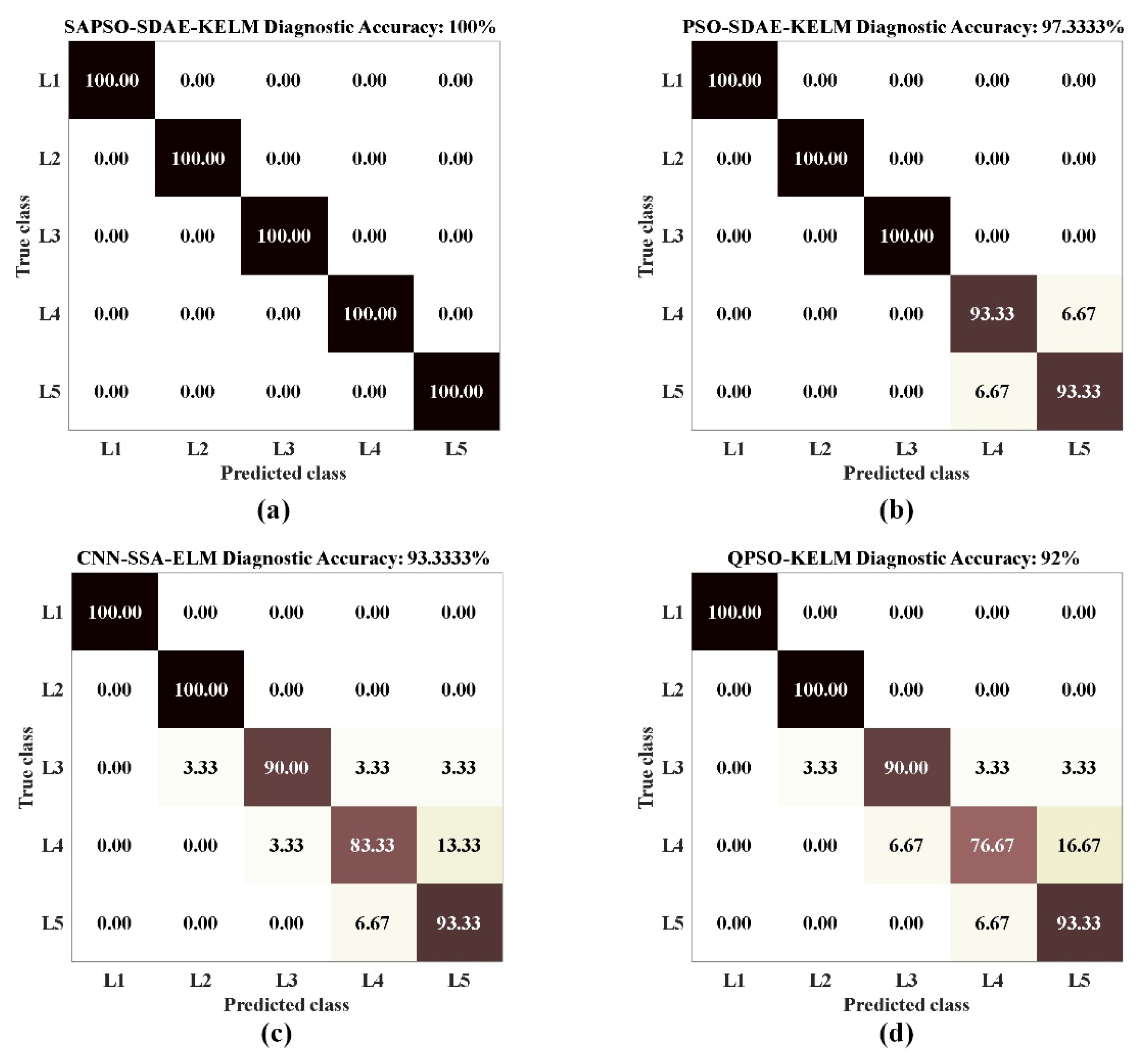
In order to verify the superiority of the SAPSO-SDAE-KELM diagnosis model proposed by the ontology, CNN-SSA-ELM, QPSO-KELM and PSO-SDAE-KELM fault diagnosis methods were selected to compare with it. The vibration data collected by the above testbed were used for testing. These diagnostic methods include deep learning method and machine learning fault diagnosis method based on feature extraction. The diagnosis results are shown in Table 4. It can be seen from the table that the accuracy of the fault diagnosis method in this paper is 100% and the running time is 8.76 seconds. Compared with the other three methods, the fault diagnosis method in this paper has great advantages in diagnosis accuracy and diagnosis time.

It can be seen from Figure 12 that the accuracy of PSO-SDAE-KELM is slightly lower than that of SAPSO-SDAE-KELM, because SDAE feature extraction is greatly affected by parameters, while SAPSO is better than PSO in parameter optimization. The accuracy of CNN-SSA-ELM is 93.33%, and the diagnosis time is 14.36 seconds, which is the longest among these methods. Although CNN has a good effect in the feature extraction method, compared with SDAE, it lacks the effect of noise reduction, which affects the accuracy of fault diagnosis, and the long time of image feature extraction leads to the slow speed of fault diagnosis. The fault diagnosis accuracy of QPSO-KELM is 92%, mainly because the fault features need to be extracted and selected manually in the diagnosis, which has a great impact on the speed and diagnosis results of fault diagnosis. From the above comparison,SAPSO-SDAE-KELM has superior performance in diagnostic accuracy.

5.3. Verification of different signal inputs

To verify the generality of the proposed method in this paper different signals are fed into the diagnostic model presented for validation. In this paper, the input signals are divided into original vibration signals, frequency domain signals and characteristic signals for testing.

The frequency domain signal is the original vibration signal obtained by the fast Fourier transform (FFT). The original vibration has 120000 collection points for each working condition, and 60000 points after transforming into frequency domain signal. Taking 400 points as a sample, there are 150 samples for each condition, so that it is consistent with the original vibration signal data set. After reducing to 78 dimensions using PCA, the training set is 120×78 and the test set is 30×78 for each condition.

The feature signal is to extract the time domain features and frequency domain features of the original vibration signal as input signals. In this paper, 19-time domain features and 4 frequency domain features of the vibration signal are extracted as input signals, and the details are shown in Table 5.

Every 800 points in the original vibration signal is a sample for feature extraction, so as to ensure that the number of samples in each working condition is 150, which is the same as the original vibration signal input samples. After 23 features were extracted, the input vector composed of each condition was 150×23, the training set was 120×23, and the test set was 30×23. After SAPSO optimization, the SDAE network parameters corresponding to the three signal input methods are shown in Table 6.

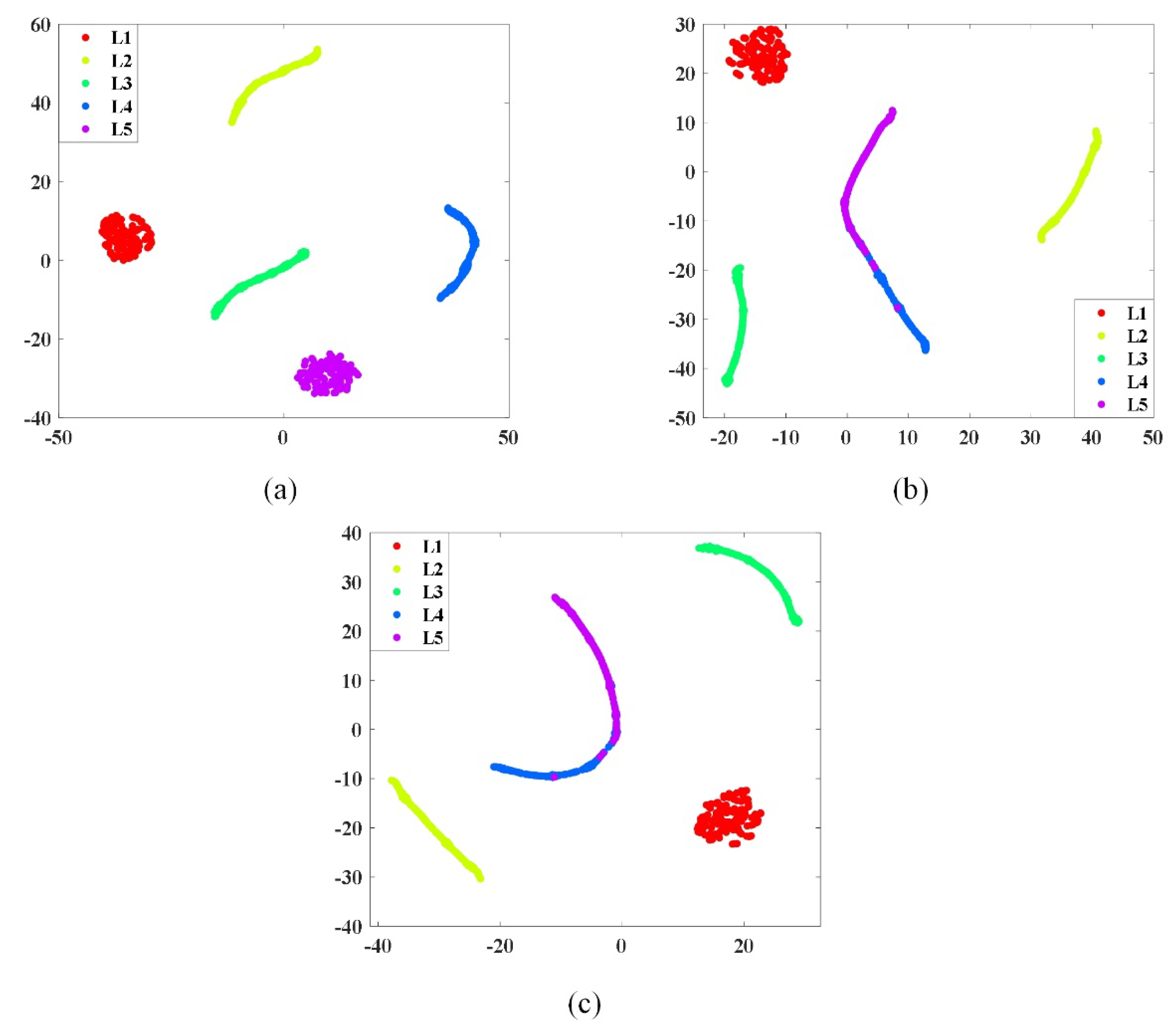
In order to visualize how the SDAE network extracts deeper features from the data, the t- stochastic neighbor embedding (t-SNE) method is adopted to visualize the distribution of features in the last hidden layer of the SDAE neural network. The feature scatter plots of the hidden layers for the three different signal inputs are shown in Figure 13. As can be seen from the figure, the deep features of the 5 different operating conditions of the time domain signal extracted using SDAE can be well separated and there is no cross-mixing. The frequency domain signals and feature signals are fed into the SDAE network for deep feature extraction, from the graph it can be seen that there is a small amount of crossover on the features labelled as L4 and L5, the other features can be well separated.

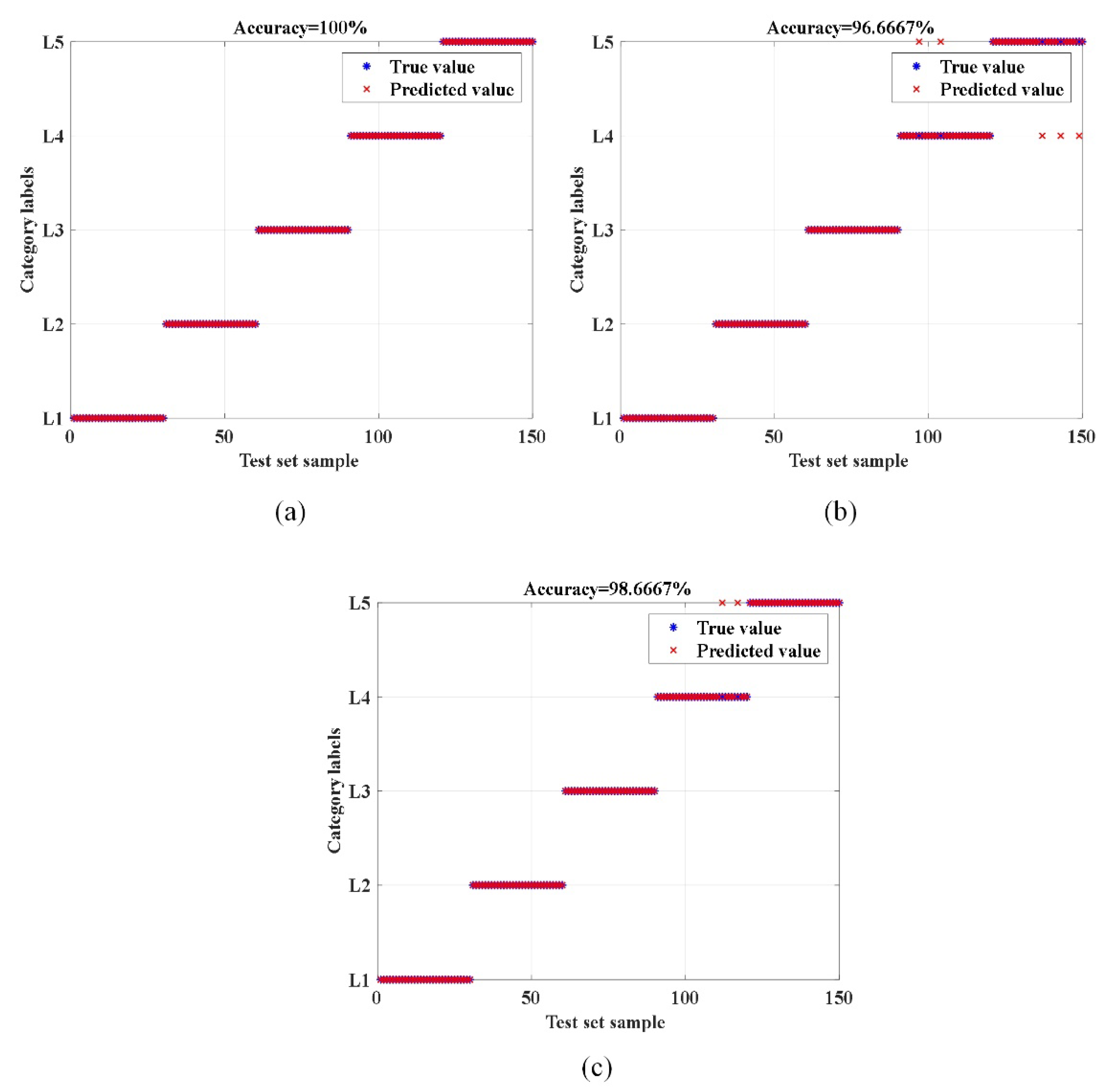
Figure 14 shows the diagnostic results of the time domain signal, frequency domain signal and feature signal input into SAPSO-SDAE-KELM. The accuracy rates were 100%, 96.67% and 98.67% respectively. The diagnostic results nicely validate the results of the feature visualization in Figure 13. The lowest diagnostic accuracy of the three signal inputs is over 96%, indicating that the SDAE network can well extract the features of different signal inputs, and therefore the diagnostic model proposed in this paper has good generalization.

5.4. Verification of the noise reduction effect

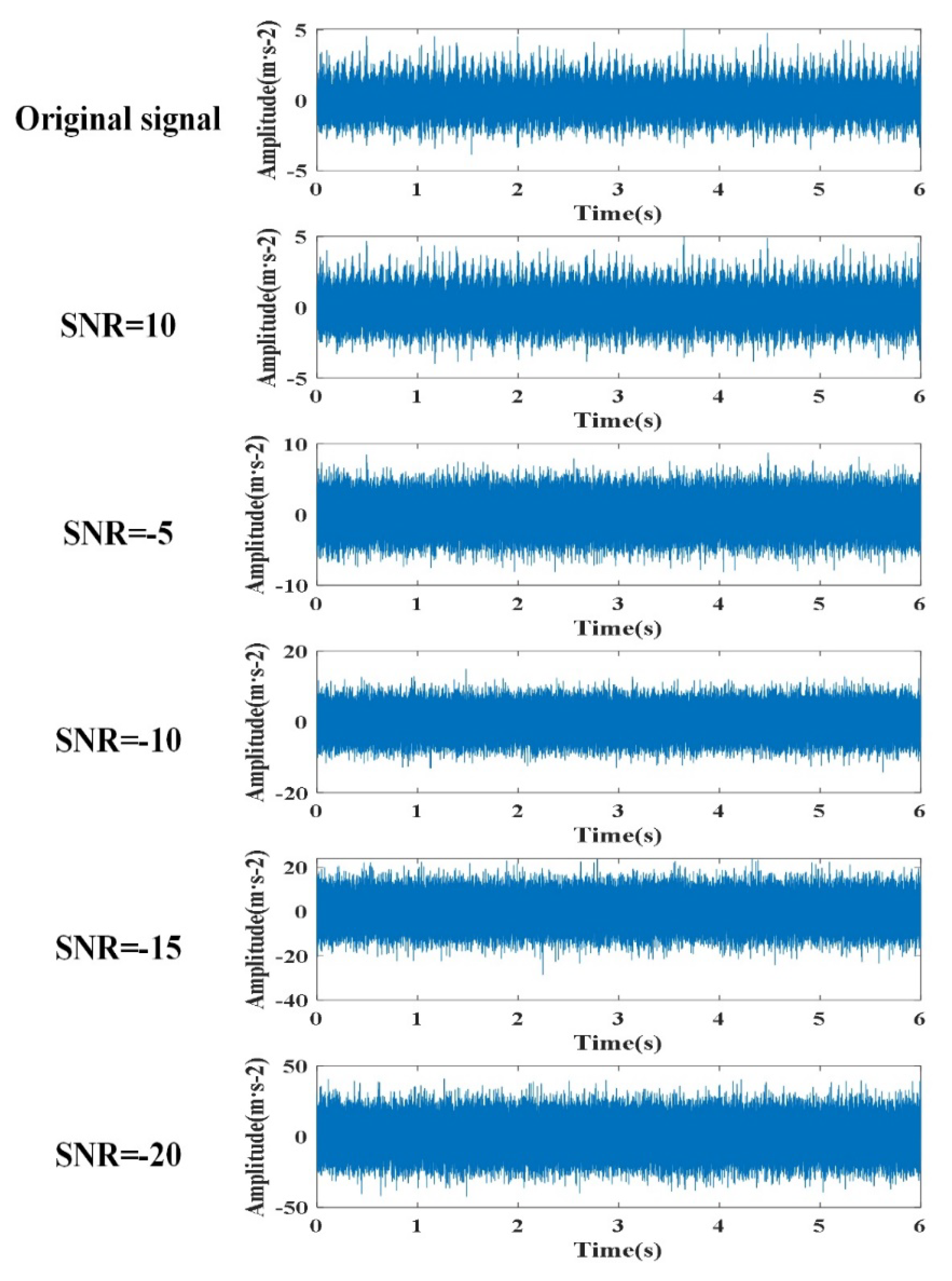
The actual working environment of gearboxes is very complex, facing the effects of different environments such as sand, rain, snow and plateau. The complex operating environment of the gearbox is simulated by adding noise to the original signal. By controlling the size of the input noise to test, add noise to the vibration signal to make the signal-to-noise ratio of -20db, -15db, -10db, -5db, 10db, in order to get different kinds of noise signals. Figure 15 shows the time domain waveform of the vibration signal after adding Gaussian white noise with different signal-to-noise ratios for a 5mm broken tooth condition. The figure shows that with the addition of noise, the amplitude of the vibration signal becomes significantly larger, thus showing that the fault signal is masked by the noise signal. Using signals containing different noises, they are fed into the fault diagnosis model proposed in this paper for fault diagnosis. In order to verify the stability of this model, the signals with added noise are fed into different diagnostic methods for comparison. The results are shown in Table 7.

It can be seen from the table that the accuracy of the four diagnostic methods is affected by the noise, and the diagnostic accuracy decreases with the increase of the noise. The accuracy of PSO-SDAE-KELM is decreased by 4%, CNN-SSA-ELM is decreased by about 15%, QPSO-KELM is decreased by 17%, and SAPSO-SDAE-KELM is only decreased by 2.7%. The accuracy of the method proposed in this paper is still higher than 97% in the case of high noise, which shows that the model has a good anti-noise effect.

6. Conclusions

This paper presents a gearbox fault diagnosis model using SAPSO-SDAE-KELM. Through experimental comparison and analysis, the gearbox fault diagnosis model proposed in this paper outperforms other fault diagnosis models in terms of diagnostic accuracy and diagnostic speed. This paper contributes as follows:

The hyperparameters associated with the structure of the SDAE network have a significant effect on the classification effect of the model. The improved PSO was used to optimize SDAE and other parameters to realize the rapid adaptive adjustment of network structure.

The fault diagnosis is carried out by the optimized SDAE network with different signal inputs, and the diagnosis accuracy is above 96%, which proves that the diagnosis model in this paper has good generalizability corresponding to different signal inputs.

Through noise addition experiments, the method proposed in this paper has a high diagnostic accuracy in the presence of high noise. Compared to other diagnostic models, the method proposed in this paper has better noise immunity.

This paper mainly studies the use of SDAE to extract high-dimensional features of one-dimensional signals for fault diagnosis. In future research, it can use the input of two-dimensional signals or picture signals into SDAE to extract deep fault features for fault diagnosis. Gearbox hybrid fault diagnosis will be further investigated in the future.

References

Feng Z, Gao A, Li K, et al. Planetary gearbox fault diagnosis via rotary encoder signal analysis. Mechanical Systems and Signal Processing, 2021, 149: 107325.
Hendriks J, Dumond P, Knox D A. Towards better benchmarking using the CWRU bearing fault dataset. Mechanical Systems and Signal Processing, 2022, 169: 108732.
Wang, Y. Study on nature of crossover phenomena with application to gearbox fault diagnosis. Mechanical Systems and Signal Processing, 2017, 83: 272-295.
Wang C, Peng Z, Liu R, et al. Research on Multi-Fault Diagnosis Method Based on Time Domain Features of Vibration Signals. Sensors, 2022, 22(21): 8164.
A new hybrid deep signal processing approach for bearing fault diagnosis using vibration signals. Neurocomputing, 2020, 396: 542-555.
Li J, Li X, Li Y, et al. A New Method of Tractor Engine State Identification Based on Vibration Characteristics. Processes, 2023, 11(2): 303.
Zhiyong L, Hongdong Z, Ruili Z, et al. Fault identification method of diesel engine in light of pearson correlation coefficient diagram and orthogonal vibration signals. Mathematical Problems in Engineering, 2019, 2019.
Meng S, Kang J, Chi K, et al. Gearbox fault diagnosis through quantum particle swarm optimization algorithm and kernel extreme learning machine. Journal of Vibroengineering, 2020, 22(6): 1399-1414.
Zhao N, Zhang J, Ma W, et al. Variational time-domain decomposition of reciprocating machine multi-impact vibration signals. Mechanical Systems and Signal Processing, 2022, 172: 108977.
Wang C, Peng Z, Liu R, et al. Research on Multi-Fault Diagnosis Method Based on Time Domain Features of Vibration Signals. Sensors, 2022, 22(21): 8164.
Dhamande L S, Chaudhari M B. Compound gear-bearing fault feature extraction using statistical features based on time-frequency method. Measurement, 2018, 125: 63-77.
Li C, Sánchez R V, Zurita G, et al. Fault diagnosis for rotating machinery using vibration measurement deep statistical feature learning. Sensors, 2016, 16(6): 895.
Yang Q, An D. EMD and wavelet transform based fault diagnosis for wind turbine gear box. Advances in Mechanical Engineering, 2013, 5: 212836.
Yan H, Bai H, Zhan X, et al. Combination of VMD Mapping MFCC and LSTM: A New Acoustic Fault Diagnosis Method of Diesel Engine. Sensors, 2022, 22(21): 8325.
Han M, Wu Y, Wang Y, et al. Roller bearing fault diagnosis based on LMD and multi-scale symbolic dynamic information entropy. Journal of Mechanical Science and Technology, 2021, 35: 1993-2005.
Syed S H, Muralidharan V. Feature extraction using Discrete Wavelet Transform for fault classification of planetary gearbox–A comparative study. Applied Acoustics, 2022, 188: 108572.
Liu X, Zhang Z, Meng F, et al. Fault Diagnosis of Wind Turbine Bearings Based on CNN and SSA–ELM. Journal of Vibration Engineering & Technologies, 2022: 1-17.
Liu Y, Duan L, Yuan Z, et al. An intelligent fault diagnosis method for reciprocating compressors based on LMD and SDAE. Sensors, 2019, 19(5): 1041.
Shao X, Kim C S. Unsupervised Domain Adaptive 1D-CNN for Fault Diagnosis of Bearing. Sensors, 2022, 22(11): 4156.
Jia N, Cheng Y, Liu Y, et al. Intelligent Fault Diagnosis of Rotating Machines Based on Wavelet Time-Frequency Diagram and Optimized Stacked Denoising Auto-Encoder. IEEE Sensors Journal, 2022, 22(17): 17139-17150.
Vincent P, Larochelle H, Lajoie I, et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. Journal of machine learning research, 2010, 11(12).
Bengio Y, Courville A, Vincent P. Representation learning: A review and new perspectives. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(8): 1798-1828.
Yang P, Chen J, Zhang H, et al. A fault identification method for electric submersible pumps based on dae-svm. Shock and Vibration, 2022, 2022.
Shao H, Jiang H, Lin Y, et al. A novel method for intelligent fault diagnosis of rolling bearings using ensemble deep auto-encoders. Mechanical Systems and Signal Processing, 2018, 102: 278-297.
Wang B, Hu T. Distributed pairwise algorithms with gradient descent methods. Neurocomputing, 2019, 333: 364-373.
Kennedy J, Eberhart R. Particle swarm optimization//Proceedings of ICNN’95-international conference on neural networks. IEEE, 1995, 4: 1942-1948.
Han H, Bai X, Han H, et al. Self-adjusting multitask particle swarm optimization. IEEE Transactions on Evolutionary Computation, 2021, 26(1): 145-158.
Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: theory and applications. Neurocomputing, 2006, 70(1-3): 489-501.
Ding S, Zhao H, Zhang Y, et al. Extreme learning machine: algorithm, theory and applications. Artificial Intelligence Review, 2015, 44: 103-115.
Du X, Jia L, Haq I U. Fault diagnosis based on SPBO-SDAE and transformer neural network for rotating machinery. Measurement, 2022, 188: 110545.

Figure 1. Structure of DAE.

Figure 2. Structure of SDAE.

Figure 3. The basic structure of the ELM.

Figure 4. Flowchart of the improved particle swarm optimization algorithm for obtaining the optimal parameters of the SDAE network structure.

Figure 5. SAPSO-SDAE-KELM based gearbox fault diagnosis flow chart.

Figure 6. Test bench structure and sensor placement.

Figure 7. Fault preset condition: (a) 2 mm crack; (b) 5 mm crack; (c) 2 mm break. (c) 5 mm break.

Figure 8. Sample construction.

Figure 9. PCA reduces the dimension of the original signal.

Figure 10. The SDAE training curve.

Figure 11. Variation of RMSE with number of iterations:(a) PSO; (b) SAPSO.

Figure 12. Accuracy of different diagnostic methods: (a) SAP-SO-SDAE-KELM; (b) PSO-SDAE-KELM;(c) CNN-SSSA-ELM; (d) QPSO-KELM.

Figure 13. Feature visualization of hidden layers: (a) Time domain signals; (b) Frequency domain signals;(c) Feature signals.

Figure 14. Diagnostic results for three different signals: (a) Time domain signals; (b) Frequency domain signals;(c) Feature signals.

Figure 15. Time domain waveforms at different signal-to-noise ratios.

Table 1. Evaluation indicator values for different numbers of hidden layers

Number of hidden layers	2	3	4	5
Pearson’s coefficient	0.983	0.996	0.976	0.978
RMSE	0.0125	0.0093	0.0392	0.0534
Diagnostic accuracy	99.33%	100.0%	98.0%	96.67%

Table 2. Vibration signal acquisition solution.

Fault status	Sampling frequency	Sampling time	Input speed	Number of sensors	Load currents
normal	20000Hz	6s	1200r/min	2	1A
2 mm crack	20000Hz	6s	1200r/min	2	1A
5 mm crack	20000Hz	6s	1200r/min	2	1A
2 mm break	20000Hz	6s	1200r/min	2	1A
5 mm break	20000Hz	6s	1200r/min	2	1A

Table 3. Composition of the dataset.

Fault status	Labels	Training Sets	Testing Sets
normal	L1	120×112	30×112
2 mm crack	L2	120×112	30×112
5 mm crack	L3	120×112	30×112
2 mm break	L4	120×112	30×112
5 mm break	L5	120×112	30×112

Table 4. The accuracy and diagnosis time of different fault diagnosis methods.

Labels	SAPSO-SDAE-KELM	PSO-SDAE-KELM	CNN-SSSA-ELM	QPSO-KELM
L1	100.0%	100.0%	100.0%	100.0%
L2	100.0%	100.0%	100.0%	100.0%
L3	100.0%	100.0%	90.0%	90.0%
L4	100.0%	93.33%	83.33%	76.67%
L5	100.0%	93.33%	90.33%	93.33%
Diagnostic time	8.71s	14.62s	10.33s	12.76s
Accuracy	100.0%	97.33%	93.33%	92.0%

Table 5. Vibration signal feature extraction situation.

Feature types	Extracted features	Number of features
Time domain feature	1 maximum value,2 minimum value,3 peak-peak value,4 mean value,5 mean square value,6 root mean square (RMS),7 average amplitude,8 root amplitude,9 variance,10 standard deviation,11 peak value,12 kurtosis,13 skewness,14 energy,15 peak factor,16 pulse factor,17 waveform factor,18 margin factor,19 clearance factor	19
Frequency domain feature	1 frequency mean value,2 frequency center,3 root mean square frequency,4 frequency standard deviation.	4

Table 6. SDAE parameters for different signal inputs.

Input signals	Number of nodes in the hidden layer	Learning Rate	Noise addition rates	Number of iterations
Time domain signals	69-55-46	0.6	0.3	600
Frequency domain signals	56-42-34	0.4	0.1	300
Feature signals	15-11-6	0.5	0.1	200

Table 7. The diagnostic accuracy of different diagnostic methods under different signal-to-noise ratios.

SNR(db)	Diagnostic accuracy
SNR(db)	SAPSO-SDAE-KELM	PSO-SDAE-KELM	CNN-SSSA-ELM	QPSO-KELM
10	100.0%	100.0%	100.0%	100.0%
-5	99.33%	98.67%	96.0%	94.67%
-10	98.67%	97.33%	91.33%	90.0%
-15	98.00%	96.67%	88.67%	85.33%
-20	97.33%	95.33%	84.67%	82.67%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Gearbox Fault Diagnosis Based on Optimized Stacked Denoising Auto Encoder and Kernel Extreme Learning Machine

Abstract

1. Introduction

2. Theoretical Background

2.1 SDAE implements the principle of dimensionality reduction and denoising

2.1.1. Principle of noise reduction with denoising autoencoder

2.1.2. Stacked denoising autoencoder (SDAE)

1. The first DAE training.

2. The second DAE training

3. SDAE network construction and SAPSO-SDAE-KELM troubleshooting process

3.1 Construct the optimal SDAE network chat structure

3.1.1 Determine the number of hidden layers

3.1.2. The best parameters of SDAE are selected by improved PSO optimization

3.2. Fault diagnosis method and process of SAPSO-SDAE-KELM

4. Experiments and data pre-processing

4.1. Experimental platform

4.2. Signal acquisition and sample generation

4.2.1. Signal acquisition scheme

4.2.2. Sample construction and data set generation

5. Method validation and comparison

5.1. Comparison of Optimization Results after Particle Swarm Improvement

5.2. Comparison with other fault diagnosis methods

5.3. Verification of different signal inputs

5.4. Verification of the noise reduction effect

6. Conclusions

References

MDPI Initiatives

Important Links

Subscribe