Proof the Collatz Conjecture in Binary Strings

Jishe Feng

doi:10.20944/preprints202304.0931.v2

Preprint

Article

Proof the Collatz Conjecture in Binary Strings

This version is not peer-reviewed.

Jishe Feng^*

This version is not peer-reviewed.

Downloads

477

Views

455

Comments

Submitted:

19 May 2023

Posted:

19 May 2023

You are already at the latest version

Abstract

The following is the Collatz Conjecture: Suppose we begin with a positive number, multiply it by 3 and add 1 if it is odd, and divide it by 2 if it is even. Then continue doing this as long as you can. Will it matter where you start, whether you end up at the number 1? The Collatz conjecture has been studied for around 85 years. We transform the Collatz function from decimal to binary, then use the binary string's character to prove the Collatz conjecture. In addition, we use mathematics to give another interpretation to chaos, which is the ultimately periodic positive integer sequence.

Keywords:

Collatz conjecture

;

binary number

;

ultimately periodic

;

chaos

Subject:

Computer Science and Mathematics - Algebra and Number Theory

MSC: 11B25; 11B83; 03D20

1. Introduction

The Collatz Conjecture, also known as the Collatz conjecture,

$3 x + 1$ mapping, Ulam conjecture, Kakutani’s problem, Thwaites conjecture, Hasse’s algorithm, or Syracuse problem [1], is one of the unsolved problems in mathematics. Paul Erdos (1913-1996) commented on the intractability of the

$3 x + 1$ problem [2], stating that "Mathematics is not ready for those problems yet".

The Collatz Conjecture states that, for any positive integer x, if x is even, divide it by 2; if x is odd, multiply it by 3 and add 1. Repeating this process continuously leads to the conjecture that no matter which number is initially chosen, the result will always reach 1 eventually.

2. A table and its algebraic expression

We employ the notations found in [6] and provide the following description of a Collatz function:

$T (n) = \{\begin{matrix} 3 n + 1, & if n is odd number, \\ \frac{n}{2} & if n is even number . \end{matrix}$

(1)

Let N denote the set of positive integers. For

$n \in N$ , and

$k = 0, 1, 2, 3, \dots,$

$T^{0} (n)$ and

$T^{k + 1} (n)$ denote n and

$T (T^{k} (n)$ , respectively. Concerning the behavior of the iteration of the Collatz function, for any integer n, there must exist an integer r such that

$T^{r} (n) = 1 .$

(2)

The reduced Collatz function [7,8] is an alternate form of the Collatz function that translates one odd number to the next odd number, so that only odd numbers are included in the Collatz sequence. We use a table that has been modified from the tables in [7], which is the process for iterating the Collatz function (1) on n. For instance, if

$n = 117$ , the table is as follows.

Line 0							117	$\frac{3^{5}}{2^{15}} \cdot 117$
Line 1	117→	352→	176→	88→	44→	22→	11	$\frac{3^{4}}{2^{15}}$
Line 2	11→	34→	17					$\frac{3^{3}}{2^{10}}$
Line 3	17→	52→	26→	13				$\frac{3^{2}}{2^{9}}$
Line 4	13→	40→	20→	10→	5			$\frac{3}{2^{7}}$
Line 5	5→	16→	8→	4→	2→	1		$\frac{1}{2^{4}}$
Line 6	1→	4→	2→	1

The table’s unique feature is that the first and last numbers in each row are all odd numbers. If x is the first odd number, then y in the same row can be represented by the formula

$y = \frac{3 x}{2^{r}} + \frac{1}{2^{r}},$

(3)

where r is the number of the arrows from the even number to last odd number in the same row. For instance, for the table on

$n = 117$ , there are the following,

Line 1	suppose $v = 117,$	there is the expression $\frac{3}{2^{5}} \cdot v + \frac{1}{2^{5}} = 11 = u,$
Line 2	suppose $u = 11,$	there is the expression $\frac{3}{2} \cdot u + \frac{1}{2} = 17 = z,$
Line 3	suppose $z = 17,$	there is the expression $\frac{3}{2^{2}} \cdot z + \frac{1}{2^{2}} = 13 = y,$
Line 4	suppose $y = 13,$	there is the expression $\frac{3}{2^{3}} \cdot y + \frac{1}{2^{3}} = 5 = x,$
Line 5	suppose $x = 5,$	there is the expression $\frac{3}{2^{4}} \cdot x + \frac{1}{2^{4}} = 1,$
Line 6	suppose $a = 1,$	there is the expression $\frac{3}{2^{2}} a + \frac{1}{2^{2}} = a = 1 .$

Substitute the expression in line 1 into the expression in line 2, we obtain

$\frac{3}{2} \cdot (\frac{3}{2^{5}} \cdot v + \frac{1}{2^{5}}) + \frac{1}{2} = \frac{3^{2}}{2^{6}} \cdot v + \frac{3}{2^{6}} + \frac{1}{2} = z$

We substitute this expression into the expression in line 3, get

$\frac{3}{2^{2}} \cdot (\frac{3^{2}}{2^{6}} \cdot v + \frac{3}{2^{6}} + \frac{1}{2}) + \frac{1}{2^{2}} = \frac{3^{3}}{2^{8}} \cdot v + \frac{3^{2}}{2^{8}} + \frac{3}{2^{3}} + \frac{1}{2^{2}} = y$

Using the same method, i.e., the composite function of the reduced Collatz function, we get the following expressions,

$\frac{3}{2^{3}} \cdot y + \frac{1}{2^{3}} = \frac{3}{2^{3}} \cdot (\frac{3^{3}}{2^{8}} \cdot v + \frac{3^{2}}{2^{8}} + \frac{3}{2^{3}} + \frac{1}{2^{2}}) + \frac{1}{2^{3}} = \frac{3^{4}}{2^{11}} \cdot v + \frac{3^{3}}{2^{11}} + \frac{3^{2}}{2^{6}} + \frac{3}{2^{5}} + \frac{1}{2^{3}} = x$

$\frac{3}{2^{4}} \cdot x + \frac{1}{2^{4}} = \frac{3^{5}}{2^{15}} \cdot v + \frac{3^{4}}{2^{15}} + \frac{3^{3}}{2^{10}} + \frac{3^{2}}{2^{9}} + \frac{3}{2^{7}} + \frac{1}{2^{4}} = 1$

Thus, we have an algebraic expression

$T^{20} (117) = \frac{3^{5}}{2^{15}} \cdot 117 + \frac{3^{4}}{2^{15}} + \frac{3^{3}}{2^{10}} + \frac{3^{2}}{2^{9}} + \frac{3}{2^{7}} + \frac{1}{2^{4}} = 1$

(4)

Proposition 1.

For positive integers

$i, j, k, l$ , and

$l_{k}, l_{k - 1}, \dots, l_{1}$ , if

$i > j$ , then there is a recurrence relation

$T^{i} (n) = \frac{3^{k}}{2^{l}} T^{j} (n) + \frac{3^{k - 1}}{2^{l_{k}}} + \dots + \frac{3^{2}}{2^{l_{3}}} + \frac{3}{2^{l_{2}}} + \frac{1}{2^{l_{1}}}$

(5)

where

$k + l = i - j$ , and

$l \geq l_{k} \geq l_{k - 1} \geq \dots \geq l_{1} .$ This is the associativity of the composite function of the reduced Collatz functions.

For example, there are

$T^{3} (97) = \frac{3}{2^{2}} \cdot 97 + \frac{1}{2^{2}} = 73$

$T^{18} (97) = \frac{3^{7}}{2^{11}} \cdot 97 + \frac{3^{6}}{2^{11}} + \frac{3^{5}}{2^{9}} + \frac{3^{4}}{2^{7}} + \frac{3^{3}}{2^{6}} + \frac{3^{2}}{2^{5}} + \frac{3}{2^{2}} + \frac{1}{2} = 107$

We can get the algebraic expression about the Collatz function,

$\begin{matrix} T^{26} (97) & = & \frac{3^{3}}{2^{5}} \cdot T^{18} (97) + \frac{3^{2}}{2^{5}} + \frac{3}{2^{4}} + \frac{1}{2^{2}} \\ = & \frac{3^{10}}{2^{16}} \cdot 97 + \frac{3^{9}}{2^{16}} + \frac{3^{8}}{2^{14}} + \frac{3^{7}}{2^{12}} + \frac{3^{6}}{2^{11}} + \frac{3^{5}}{2^{10}} + \frac{3^{4}}{2^{7}} + \frac{3^{3}}{2^{6}} + \frac{3^{2}}{2^{5}} + \frac{3}{2^{4}} + \frac{1}{2^{2}} \\ = & 91 . \end{matrix}$

The powers of 2 in the denominator are the sum of the numbers of arrows after the even numbers to the end of the line and the power of 2 in its next line. We can see that in the last column of the table from the last row to the first row, the powers of 3 are 0,

$1, 2, 3, \dots$ in the numerator successively.

Example 1.

When the Collatz function is iterated for n=7, we obtain the following sequence:

$7 \to 22 \to 11 \to 34 \to 17 \to 52 \to 26 \to 13 \to 40 \to 20 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1 \to \dots$ .

If we utilize the iteration of the reduced Collatz function, we get the following table and algebraic expression:

7→	22→	11			$\frac{3^{5}}{2^{11}} \cdot 7$	$\frac{3^{4}}{2^{11}}$
11→	34→	17				$\frac{3^{3}}{2^{10}}$
17→	52→	26→	13			$\frac{3^{2}}{2^{9}}$
13→	40→	20→	10→	5		$\frac{3}{2^{7}}$
5→	16→	8→	4→	2→	1	$\frac{1}{2^{4}}$

$T^{16} (7) = T (5, 11, 7) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{11}} + \frac{3^{5}}{2^{11}} \cdot 7 = 1 .$

3. The ultimately periodic sequence and a Diophantine Equation

$a_{k}$ is the first odd number in a table of the Collatz function applied to number n, the formula

$\frac{3 a_{k} + 1}{2^{r}},$ can be used to represent the last odd number in the same row. Thus one obtains a recurrenc relation of the Collatz function,

$\frac{3 a_{k} + 1}{2^{r}} = a_{k + r + 1} .$

(6)

This yields the Collatz function’s sequence

${a_{k}}_{k = 0}^{\infty}$ , which we will refer to as the ultimately periodic sequence [9,10].

For any given positive iteger number n, by the iteration

$\{\begin{matrix} a_{0} = n \\ a_{k} = T (a_{k - 1}), for k > 0 \end{matrix}$

one obtains a positive integer sequence

$a = {a_{i}}_{i = 0}^{+ \infty}$ , where

$T (\cdot)$ is the Collatz function. Thus we give another notation about the Collatz conjecture is:

Conjecture 1.

For any

$n \in Z^{+}$ , there exists a positive integer

$η (a) \in Z^{+}$ , such that sequence

$a_{i} = a_{i + 3}$ , for

$i \geq η (a)$ . In other words, the sequence

$a = {a_{i}}_{i = 0}^{+ \infty}$ must be an ultimately periodic sequence, and its preperiod

$η (S)$ must be the smallest nonnegative integer such that the subsequence

${a_{i}}_{i \geq η (S)}$ is periodic

${4, 2, 1}$ .

Example 2.

For

$a_{0} = 5$ , one obtains the ultimately periodic sequence,

${5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, \dots},$ its preperiod

$η (S) = 3$ , and its periodic is

${4, 2, 1}$ .

Example 3.

For

$S_{0} = 7$ , one obtains the ultimately periodic sequence,

${7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, \dots},$ its preperiod

$η (S) = 14$ , and its periodic also is

${4, 2, 1}$ .

We can get a Diophantine Equation from the relation (6)

$3 x + 1 = 2^{r} y$

(7)

where x and y are any positive odd numbers, r is any positive integer. We have the root:

$x = y = 1, r = 2$ ,

$x = \frac{4^{k} - 1}{3}, y = 1, r = 2 k$ . for

$k = 1, 2, 3, \dots,$ and the other roots are the every row in the table of the Collatz sequence.

As it turns out, if the ring over which the sequence is defined is finite, then the sequence is guaranteed to eventually repeat [10]. This give us a new approach to proof the Collatz Conjecture. We use the division of 2 and multiplication of 3 and addition 1 in binary format get a ring, Thus proof the Collatz Conjecture.

According (6), there are three cases:

(i)

$a_{k} = a_{k + r + 1}$ , this implies that,

$r = 2, a_{k} = 1, a_{k + 1} = 4, a_{k + 2} = 2;$

(ii)

$a_{k} > a_{k + r + 1},$ this implies that

$r > 2$ and

$a_{k} > 1;$

(iii)

$a_{k} < a_{k + r + 1},$ this implies that

$r = 1 .$

For (i), there is an iteration (6), for (ii) and (iii), there is a algebraic expression (5) equals to 1 .

4. Numerical example

Applying the Collatz function on 9, 23, 15, 17, 61, 397 respectively, one obtains the following algebraic expressions,

$T^{19} (9) = T (6, 13, 9) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{11}} + \frac{3^{5}}{2^{13}} + \frac{3^{6}}{2^{13}} \cdot 9 = 1,$

(8)

$T^{15} (23) = T (4, 11, 23) = \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{11}} \cdot 23 = 1,$

(9)

$T^{17} (15) = T (5, 12, 15) = \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{12}} + \frac{3^{5}}{2^{12}} \cdot 15 = 1,$

(10)

$T^{12} (17) = T (3, 9, 17) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{9}} \cdot 17 = 1,$

(11)

$T^{19} (61) = T (5, 14, 61) = \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{14}} + \frac{3^{5}}{2^{14}} \cdot 61 = 1 .$

(12)

$T^{16} (397) = T (5, 11, 397) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{11}} + \frac{3^{5}}{2^{17}} + \frac{3^{6}}{2^{20}} + \frac{3^{7}}{2^{20}} \cdot 397 = 1,$

(13)

For the formula

$T (6, 14, 18) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{11}} + \frac{3^{5}}{2^{13}} + \frac{3^{6}}{2^{14}} \cdot 18 = 1,$

we rewrite it as an integer equation,

$3^{6} \cdot 18 + 3^{5} \cdot 2 + 3^{4} \cdot 2^{3} + 3^{3} \cdot 2^{4} + 3^{2} \cdot 2^{5} + 3 \cdot 2^{7} + 2^{10} = 2^{14} .$

To calculate the power of 3 and the value of 18 using powers of 2,

$\begin{matrix} 3 & = & 2 + 1 \\ 3^{2} & = & 2^{3} + 1 \\ 3^{3} & = & 2^{4} + 2^{3} + 2 + 1 \\ 3^{4} & = & 2^{6} + 2^{4} + 1 \\ 3^{5} & = & 2^{7} + 2^{6} + 2^{5} + 2^{4} + 2 + 1 \\ 3^{6} & = & 2^{9} + 2^{7} + 2^{6} + 2^{4} + 2^{3} + 1 \\ 18 & = & 2^{4} + 2 \end{matrix}$

substituting these expressions into the left-hand side of the above equation, one obtains,

$\begin{matrix} 3^{6} \cdot 18 + 3^{5} \cdot 2 + 3^{4} \cdot 2^{3} + 3^{3} \cdot 2^{4} + 3^{2} \cdot 2^{5} + 3 \cdot 2^{7} + 2^{10} \\ = & (2^{9} + 2^{7} + 2^{6} + 2^{4} + 2^{3} + 1) \cdot (2^{4} + 2) + (2^{7} + 2^{6} + 2^{5} + 2^{4} + 2 + 1) \cdot 2 \\ + (2^{6} + 2^{4} + 1) \cdot 2^{3} + (2^{4} + 2^{3} + 2 + 1) \cdot 2^{4} + (2^{3} + 1) \cdot 2^{5} + (2 + 1) \cdot 2^{7} + 2^{10}, \end{matrix}$

and get the value

$2^{14}$ which is equal to the right value of the equation.

5. Convert an integer number from decimal to binary

Be inspired by the above, we use binary to rewrite the Collatz function (1) as the following formulas (14). We denote a binary number, which is a string of 0s and 1s, as

$n = {(1 \times \dots \times)}_{2}$ , where × is either 1 or 0, e.g.

$3 = {(11)}_{2}$ ,

$T (n) = \{\begin{matrix} {(11)}_{2} \cdot {(1 \times \dots \times 1)}_{2} + 1 = {(1 \times \times \times 10 \dots 0)}_{2}, & if n is odd number, \\ \frac{{(1 \times \dots \times 10 \dots 00)}_{2}}{{(10)}_{2}} = {(1 \times \dots \times 10 \dots 0)}_{2}, & if n is even number . \end{matrix}$

(14)

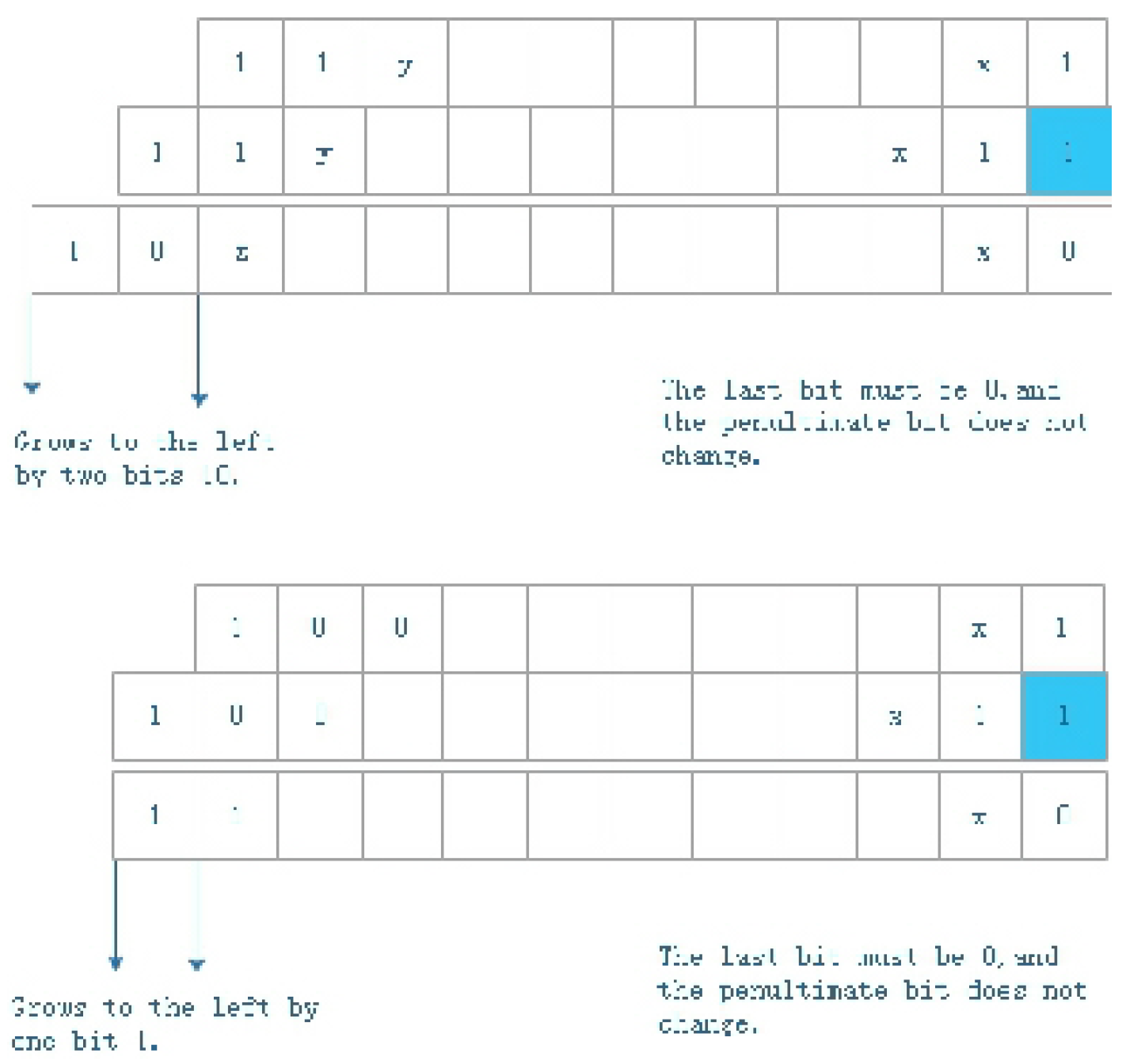
When n is an odd number, as shown in Figure 1, if

$x, y$ , and z are all bits 0 or 1, the result value

$T (n)$ in binary string grows to the left by appending bits 10 or 1, and the penultimate bit x does not change as the penultimate bit x in the binary string of number n.

Figure 1. The Collatz function performs on odd number growing to the left by appending 10 or 1. The last bit must be 0 and the penultimate bit does not change.

When n is an even number, the result value of Collatz function

$T (n)$ is discarding the trailing zero, and the result value of the reduced Collatz function is discarding all r trailing zeroes, and r is also the number of zeroes in trailing of the binary string in the second columns.

We give the iteration of the Collatz function for

$7 = {(111)}_{2}, 67 = {(1000011)}_{2}$ in binary as the following two tables.

111→	10110→	1011			$\frac{3^{5}}{2^{11}} \cdot 7$	$\frac{3^{4}}{2^{11}}$
1011→	100010→	10001				$\frac{3^{3}}{2^{10}}$
10001→	110100→	11010→	1101			$\frac{3^{2}}{2^{9}}$
1101→	101000→	10100→	1010→	101		$\frac{3}{2^{7}}$
101→	10000→	1000→	100→	10→	1	$\frac{1}{2^{4}}$
1000011→	11001010→	1100101				$\frac{3^{7}}{2^{19}}$
1100101→	100110000→	10011000→	1001100→	100110→	10011	$\frac{3^{6}}{2^{18}}$
10011→	111010→	11101→				$\frac{3^{5}}{2^{14}}$
11101→	1011000→	101100→	10110→	1011		$\frac{3^{4}}{2^{13}}$
1011→	100010→	10001→				$\frac{3^{3}}{2^{10}}$
10001→	110100→	11010→	1101			$\frac{3^{2}}{2^{9}}$
1101→	101000→	10100→	1010→	101		$\frac{3}{2^{7}}$
101→	10000→	1000→	100→	10	1	$\frac{1}{2^{4}}$
1

$T^{27} (67) = T (8, 19, 67) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{13}} + \frac{3^{5}}{2^{14}} + \frac{3^{6}}{2^{18}} + \frac{3^{7}}{2^{19}} + \frac{3^{8}}{2^{19}} \cdot 67 = 1$

Example 4.

For10027=(10011100101011)

$_{2}$ , we manipulate the iteration of the Collatz function in binary as the following table and the algebraic expression, we only concentrate the first two columns in binary string.

10027=(10011100101011) $_{2} \to$	(111010110000010) $_{2} \to$	$\frac{3^{30}}{2^{61}} \cdot$ 10027	$\frac{3^{29}}{2^{61}}$
15041=(11101011000001) $_{2} \to$	(1011000001000100) $_{2} \to$		$\frac{3^{28}}{2^{60}}$
11281=(10110000010001) $_{2} \to$	(1000010000110100) $_{2} \to$		$\frac{3^{27}}{2^{58}}$
8461=(10000100001101) $_{2} \to$	(110001100101000) $_{2} \to$		$\frac{3^{26}}{2^{56}}$
3173=(110001100101) $_{2} \to$	(10010100110000) $_{2} \to$		$\frac{3^{25}}{2^{53}}$
595=(1001010011) $_{2} \to$	(11011111010) $_{2} \to$		$\frac{3^{24}}{2^{49}}$
893=(1101111101) $_{2} \to$	(101001111000) $_{2} \to$		$\frac{3^{23}}{2^{48}}$
335=(101001111) $_{2} \to$	(1111101110) $_{2} \to$		$\frac{3^{22}}{2^{45}}$
503=(111110111) $_{2} \to$	(10111100110) $_{2} \to$		$\frac{3^{21}}{2^{44}}$
755=(1011110011) $_{2} \to$	(100011011010) $_{2} \to$		$\frac{3^{20}}{2^{43}}$
1133=(10001101101) $_{2} \to$	(110101001000) $_{2} \to$		$\frac{3^{19}}{2^{42}}$
425=(110101001) $_{2} \to$	(10011111100) $_{2} \to$		$\frac{3^{18}}{2^{39}}$
319=(100111111) $_{2} \to$	(1110111110) $_{2} \to$		$\frac{3^{17}}{2^{37}}$
479=(111011111) $_{2} \to$	(10110011110) $_{2} \to$		$\frac{3^{16}}{2^{36}}$
719=(1011001111) $_{2} \to$	(100001101110) $_{2} \to$		$\frac{3^{15}}{2^{35}}$
1079=(10000110111) $_{2} \to$	(110010100110) $_{2} \to$		$\frac{3^{14}}{2^{34}}$
1619=(11001010011) $_{2} \to$	(1001011111010) $_{2} \to$		$\frac{3^{13}}{2^{33}}$
2429=(100101111101) $_{2} \to$	(1110001111000) $_{2} \to$		$\frac{3^{12}}{2^{32}}$
911=(1110001111) $_{2} \to$	(101010101110) $_{2} \to$		$\frac{3^{11}}{2^{29}}$
1367=(10101010111) $_{2} \to$	(1000000000110) $_{2} \to$		$\frac{3^{10}}{2^{28}}$
2051=(100000000011) $_{2} \to$	(1100000001010) $_{2} \to$		$\frac{3^{9}}{2^{27}}$
3077=(110000000101) $_{2} \to$	(10010000010000) $_{2} \to$		$\frac{3^{8}}{2^{26}}$
577=(1001000001) $_{2} \to$	(11011000100) $_{2} \to$		$\frac{3^{7}}{2^{22}}$
433=(110110001) $_{2} \to$	(10100010100) $_{2} \to$		$\frac{3^{6}}{2^{20}}$
325=(101000101) $_{2} \to$	(1111010000) $_{2} \to$		$\frac{3^{5}}{2^{18}}$
61=(111101) $_{2} \to$	(10111000) $_{2} \to$		$\frac{3^{4}}{2^{14}}$
23=(10111) $_{2} \to$	(1000110) $_{2} \to$		$\frac{3^{3}}{2^{11}}$
35=(100011) $_{2} \to$	(1101010) $_{2} \to$		$\frac{3^{2}}{2^{10}}$
53=(110101) $_{2} \to$	(10100000) $_{2} \to$		$\frac{3}{2^{9}}$
5=(101) $_{2} \to$	(10000) $_{2} \to$		$\frac{1}{2^{4}}$

$\begin{matrix} T^{91} (10027) & = & \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{14}} + \frac{3^{5}}{2^{18}} + \frac{3^{6}}{2^{20}} + \frac{3^{7}}{2^{22}} + \frac{3^{8}}{2^{26}} + \frac{3^{9}}{2^{27}} \\ + \frac{3^{10}}{2^{28}} + \frac{3^{11}}{2^{29}} + \frac{3^{12}}{2^{32}} + \frac{3^{13}}{2^{33}} + \frac{3^{14}}{2^{34}} + \frac{3^{15}}{2^{35}} + \frac{3^{16}}{2^{36}} + \frac{3^{17}}{2^{37}} + \frac{3^{18}}{2^{39}} \\ + \frac{3^{19}}{2^{42}} + \frac{3^{20}}{2^{43}} + \frac{3^{21}}{2^{44}} + \frac{3^{22}}{2^{45}} + \frac{3^{23}}{2^{48}} + \frac{3^{24}}{2^{49}} + \frac{3^{25}}{2^{53}} + \frac{3^{26}}{2^{56}} + \frac{3^{27}}{2^{58}} \\ + \frac{3^{28}}{2^{60}} + \frac{3^{29}}{2^{61}} + \frac{3^{30}}{2^{61}} \cdot 10027 \\ = & 1 \end{matrix}$

The ultimately periodic sequence of the sequence of the Collatz, its preperiod

$η (S) = 89$ , and its periodic also is

${4, 2, 1} .$

6. The character of a binary string

The Collatz function iteration was applied to its binary string of a positive integer number (14), and we highlight its properties below. The research papers on this subject can be found in [6,7]. "A full description of how a bit string’s length will change under application of the reduced Collatz map has yet to appear in the literature⋯, this article provides a way to tell, by inspection, the change in length that a bit string will incur under the reduced Collatz map." Here, we’ll describe the change caused by the application of the reduced Collatz function (3) (

$r \geq 1$ ) or Collatz function (

$r = 1$ ) in binary format, along with an inspection of the change.

We shall discuss the table’s horizontal and vertical aspects in binary string.

6.1. The row character

$i)$ As illustrated in Figure 1, we compare the first binary string of odd number

$a_{k}$ and the second binary string of even number

$3 a_{k} + 1$ in every line. The Collatz function

$3 a_{k} + 1$ in binary grows to the left of the binary string

$a_{k}$ by appending one bit 1 or two bits 10, the last bit must be 0, and the penultimate bit does not change, let

$x, y$ and z in the binary string be 0 or 1.

$a_{k} = {(100 \dots x 1)}_{2}$ , then

$3 a_{k} + 1 =$

${(11 \dots x 0)}_{2}$ , or

$a_{k} = {(11 y \dots x 1)}_{2}$ , then

$3 a_{k} + 1 =$

${(10 z \dots x 0)}_{2} .$

$i i)$ The last binary string is created by discarding all trailing zeroes (one or more integers) from the second column even number in binary string.

6.2. The first column character

The binary string is concentrated in the first column of the table. We concentrate the sub-binary string (which is make of bit 1 and sepereted by at least one bit 0),

$s 1 = (1111)$ , which is to the right of the binary string,

$a_{k} = {(1 \dots 01 \dots 1)}_{2}$ on the ith line. From top to bottom of the table, and sub-binary string,

$s_{2} = (11 \dots 11)$ , which is in the following line,

$(i + 1)$ -th, the binary string,

$a_{k + r} = {(1 \dots 01 \dots 1)}_{2}$ . Let

$s_{1}$ have the length

$l (s_{1})$ and

$s_{2}$ have the length

$l (s_{2})$ .

For positive

$m > 1$ , if

$l (s_{1}) = m,$ then

$l (s_{2}) = m - 1$ , and the next must be

$l (s_{3}) = m - 2$ , and so on, to 1, i.e.,

$l (s_{t}) = 1$ correspondingly,

$a_{k} < a_{k + r} < \dots < a_{t} .$

When

$l (s_{1}) = 1$ , then

$l (s_{2}) = 1$ or

$l (s_{2}) = h > 1$ , correspondingly,

$a_{k} > a_{k + r}$ .

The last line in the table must be 1.

6.3. Hard number

I coined the term hard number to describe the last odd number that any integer can reach before it becomes

$4^{k}$ , which appears in the sequence of the Collatz function and has

$2 k$ trailing zeroes, its formula is

$a_{k} = \frac{4^{k} - 1}{3} = {(101 \dots 101 \dots 101)}_{2}, a_{k + 1} = 4^{k} = 2^{2 k} = {(10 \dots 0)}_{2}, a_{3 k + 1} = 1 .$

where in the binary string

${(101 \dots 101 \dots 101)}_{2}$ , which has k 1s. The first hard numbers are:

$1 = {(1)}_{2}, 5 = {(101)}_{2}, 21 = {(10101)}_{2}, 85 = {(1010101)}_{2}, 341 = {(101010101)}_{2}, 1365 = {(10101010101)}_{2}, 5461 = {(1010101010101)}_{2}, \dots .$

A hard number is in the last second line in the table of the Collatz sequenc.

6.4. Proof the Collatz conjecture

The character shows everything from the tables 10027 and 63 in [7]. As a result of this section, we may provide a universal approach for proving the Collatz conjecture.

For any positive integer n, the sequence of the iteration under the Collatz function (6), is the first column in the table, by the character in row of that growing in the left by appending 10 or 1, discarding all trailing more than two zeroes to make the sequence shrink to a hard number and eventually reach 1, which means that for any positive integer n, the algebraic expression (5) must exist.

Thus, for any positive integer n, there exists an ultimately periodic series resulting from iteration of the Collatz function (6), and the Diophantine equations (7) must have finite roots.

Claim 1.

We give the statement "period three implies chaos" [3] another interpretation: for positive integer n, the sequence of the Collatz is an ultimately periodic sequence, its preperiod

$η (n)$ is an related-to n positive, and the least period

$ρ (n) = 3$ .

7. Conclusions

We transform the Collatz function from decimal to binary, then use the binary string’s character to prove the Collatz conjecture. In addition, we use mathematics to give another interpretation to chaos, which is the ultimately periodic positive integer sequence.

Acknowledgments

Gansu Province Educational Technology Innovation Project, No. 2022A13.

References

Jeffrey C. Lagarias. The 3x + 1 Problem and Its Generalizations. American Mathematical Monthly, Vol. 92, No. 1, pp 3-23.(1985).
Jeffrey C. Lagarias. The 3x+1 Problem: An Overview. arXiv:2111.02635.
Li, T., Yorke, J. A. Period three implies chaos. Am. Mat. Monthly, 82, 985–992 (1975).
TERENCE TAO, Almost all orbits of the Collatz map attain almost bounded values. arXiv:1909.03562v5, 2022,1,15.
Jishe FENG, Xiaomeng WANG, Xiaolu GAO, Zhuo PAN. The research and progress of the enumeration of lattice paths. Frontiers of Mathematics in China, 2022, 17(5): 747-766.
Alf Kimms. The structure of the 3x + 1 problem, Electronic Journal of Graph Theory and Applications. 9(1)(2021), 157–174.
Richard Kaufman. A reduced forward Collatz algorithm: How binary strings change their length under 3x+1. arXiv:2301.07466.
Patrick Chisan Hew. Collatz on the Dyadic rdtional in [0.5,1) with fractals: how bit strings change their length under 3x+1. Experimental Mathematics, 2021, 30(4): 481-488.
G. Ganesan. Linear recurrences over a finite field with exactly two periods. Advances In Applied Mathematics 127(2021)102180.
D. Quijada. Periods of linearly recurring sequences. Bachelor thesis, Washington and LeeUniversity, 2015.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

477

Views

455

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Proof the Collatz Conjecture in Binary Strings

Abstract

Keywords:

Subject:

1. Introduction

2. A table and its algebraic expression

3. The ultimately periodic sequence and a Diophantine Equation

4. Numerical example

5. Convert an integer number from decimal to binary

6. The character of a binary string

6.1. The row character

6.2. The first column character

6.3. Hard number

6.4. Proof the Collatz conjecture

7. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe