Submitted:
21 April 2023
Posted:
21 April 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
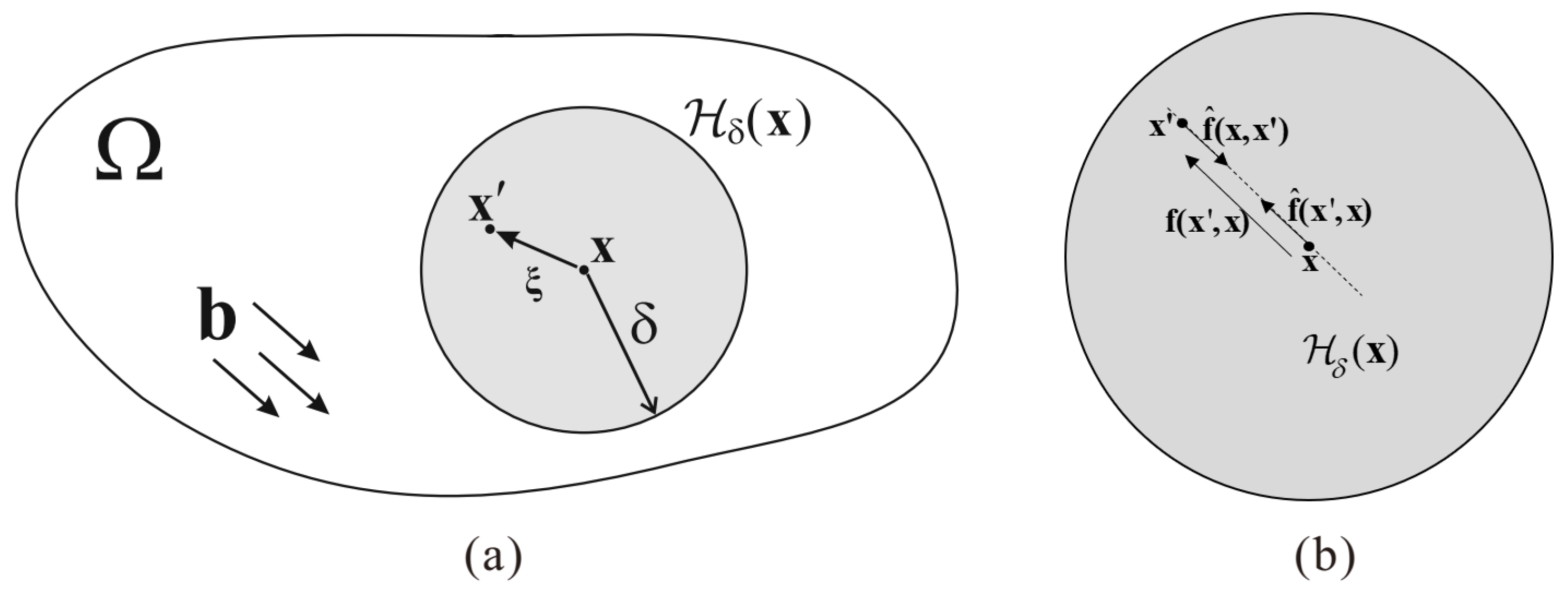
2. Thermal Elastoplastic Bond-based Peridynamic Model
3. Thermoelastic Hybrid Peridynamics and Classical Continuum Mechanics (PD-CCM) Model
3.1. Governing Equations
- Kinematic admissibility and compatibility
- Static admissibility
- Constitutive equations
3.2. Stiffness/Thermal Modulus Constraint Equations
- If and only if , and , , the model is restricted to the pure CCM model at point . Then the elastic energy density at point can be written as
- If and only if , and , , the model is restricted to the pure PD model at point . Considering Equation (4), the elastic energy density at point can be written as
- If and only if , and such that , the hybrid model must be used at point . Considering Equation (4), the elastic energy density at point can be written as
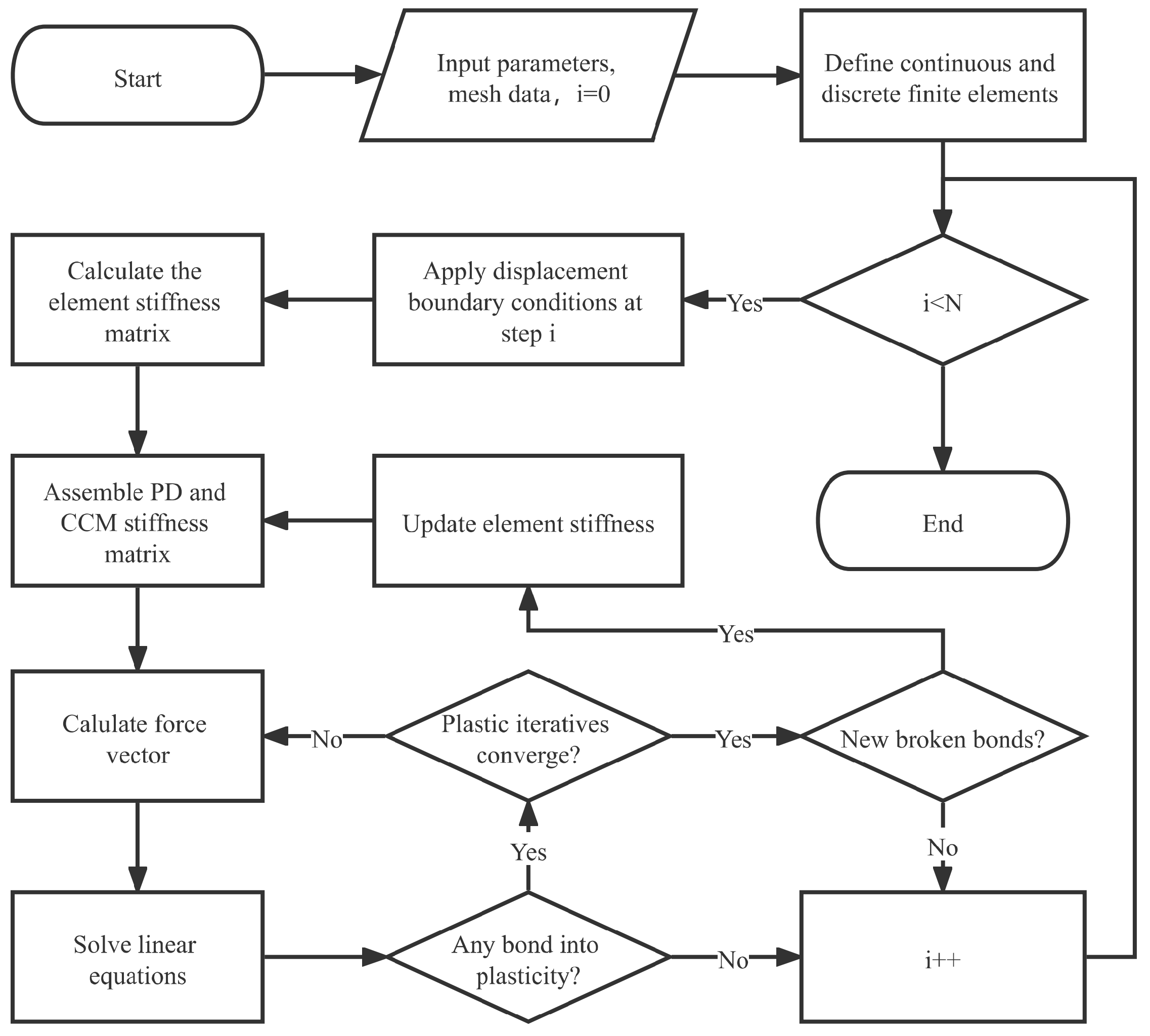
4. Plastic-Fracture Calculations
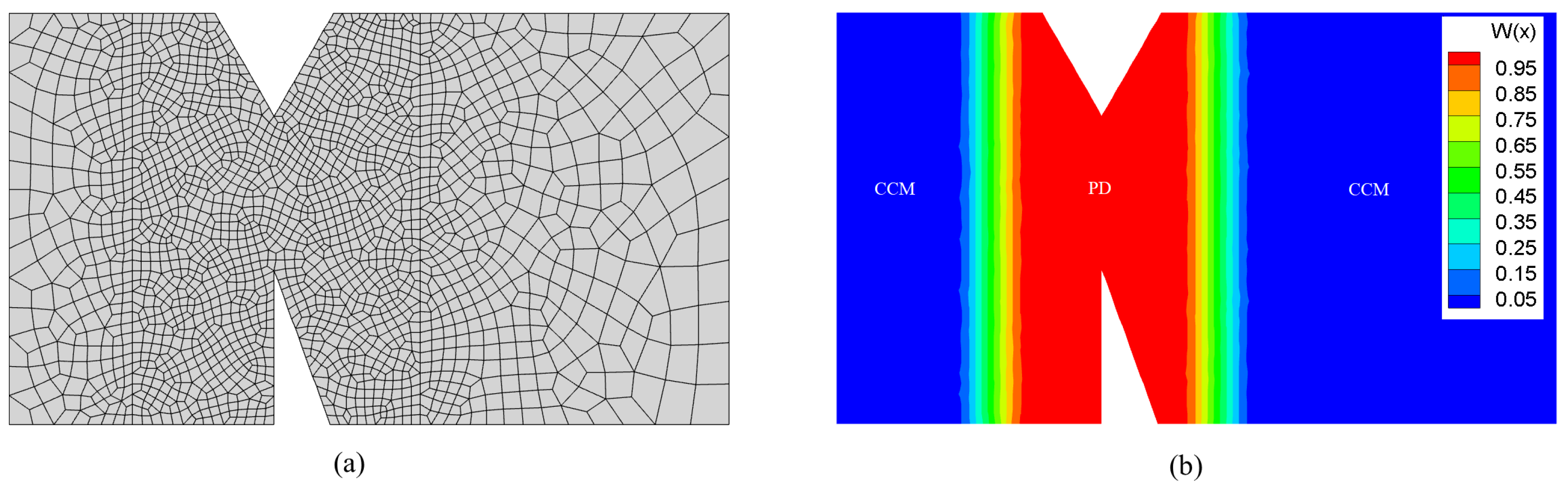
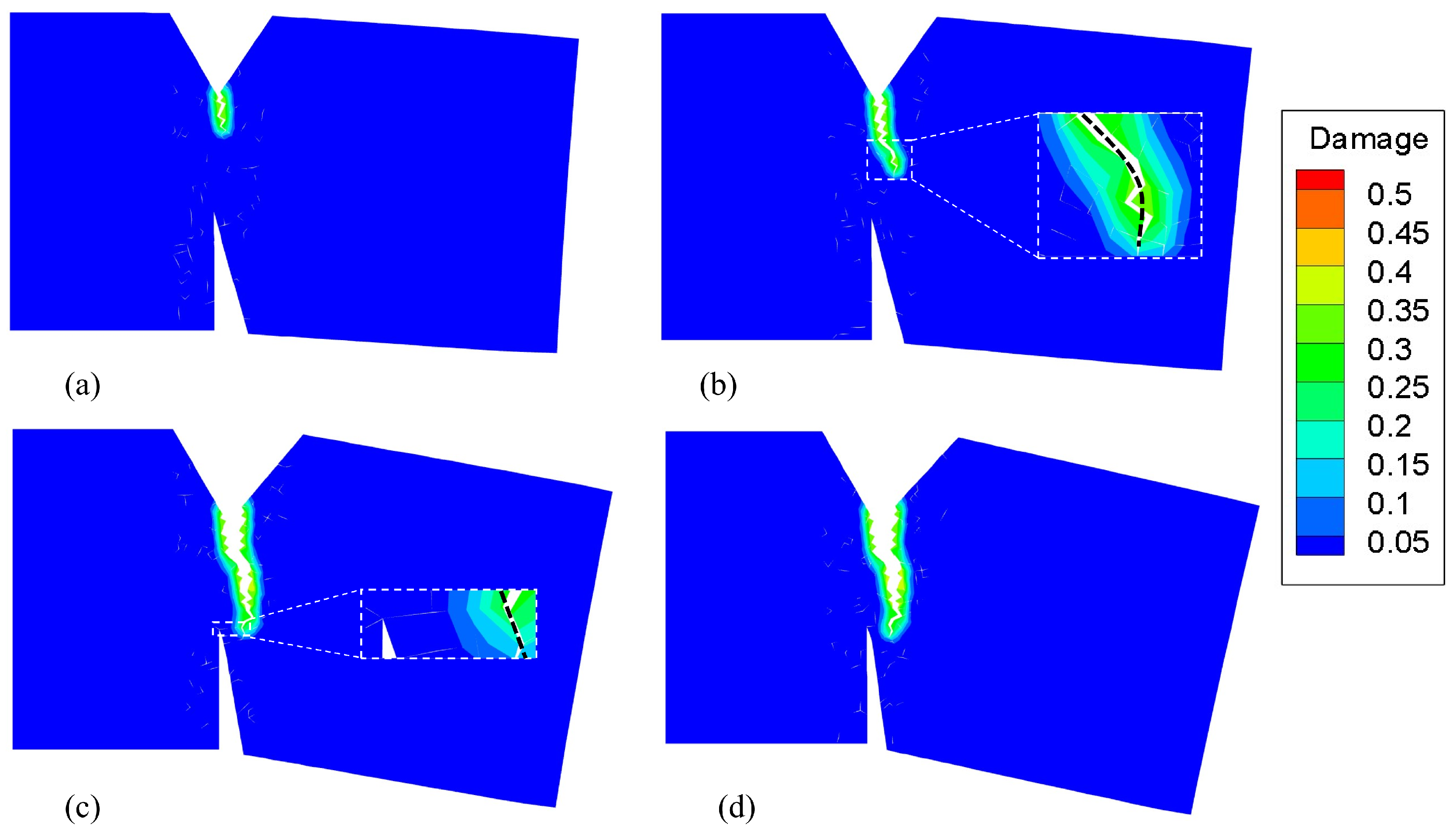
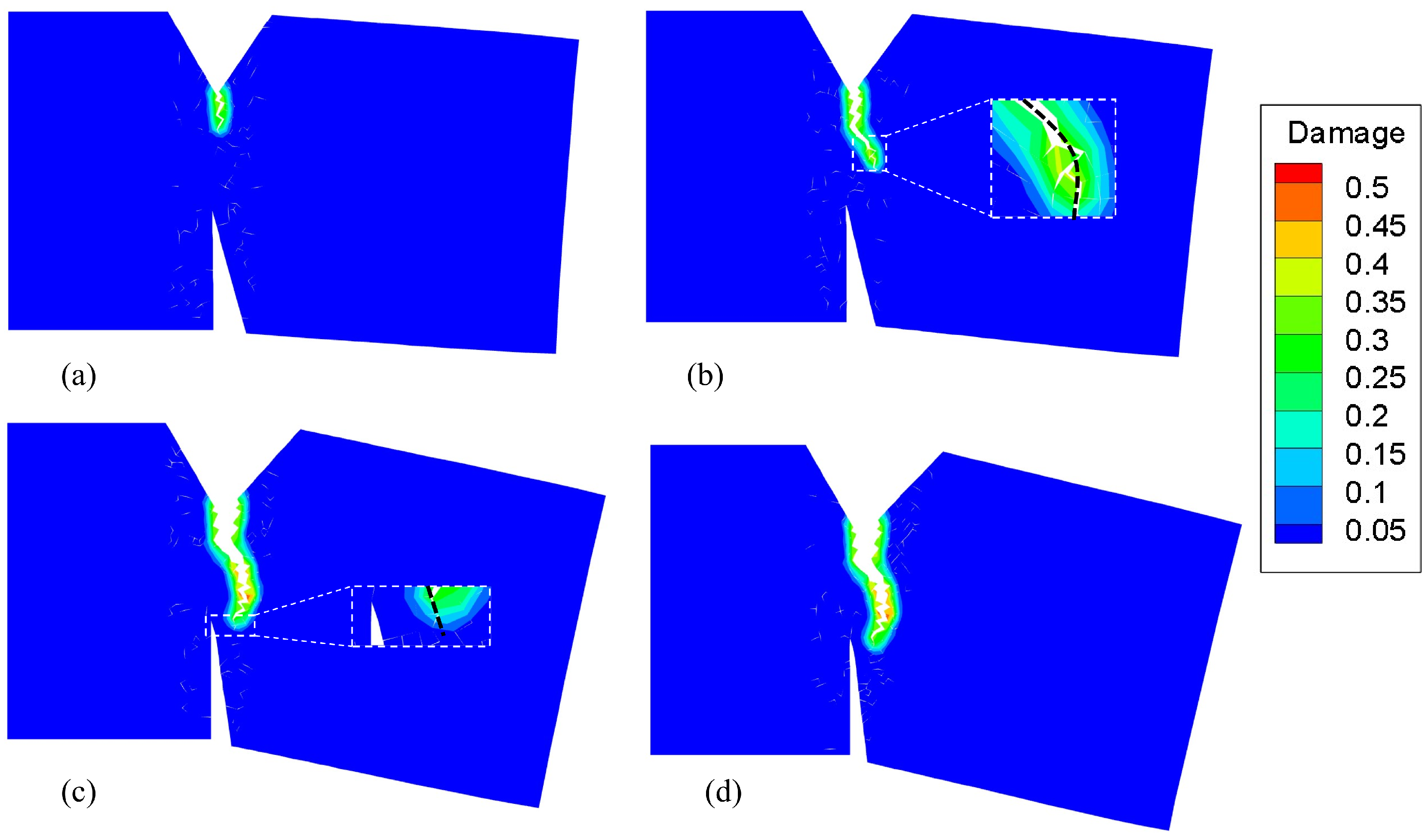
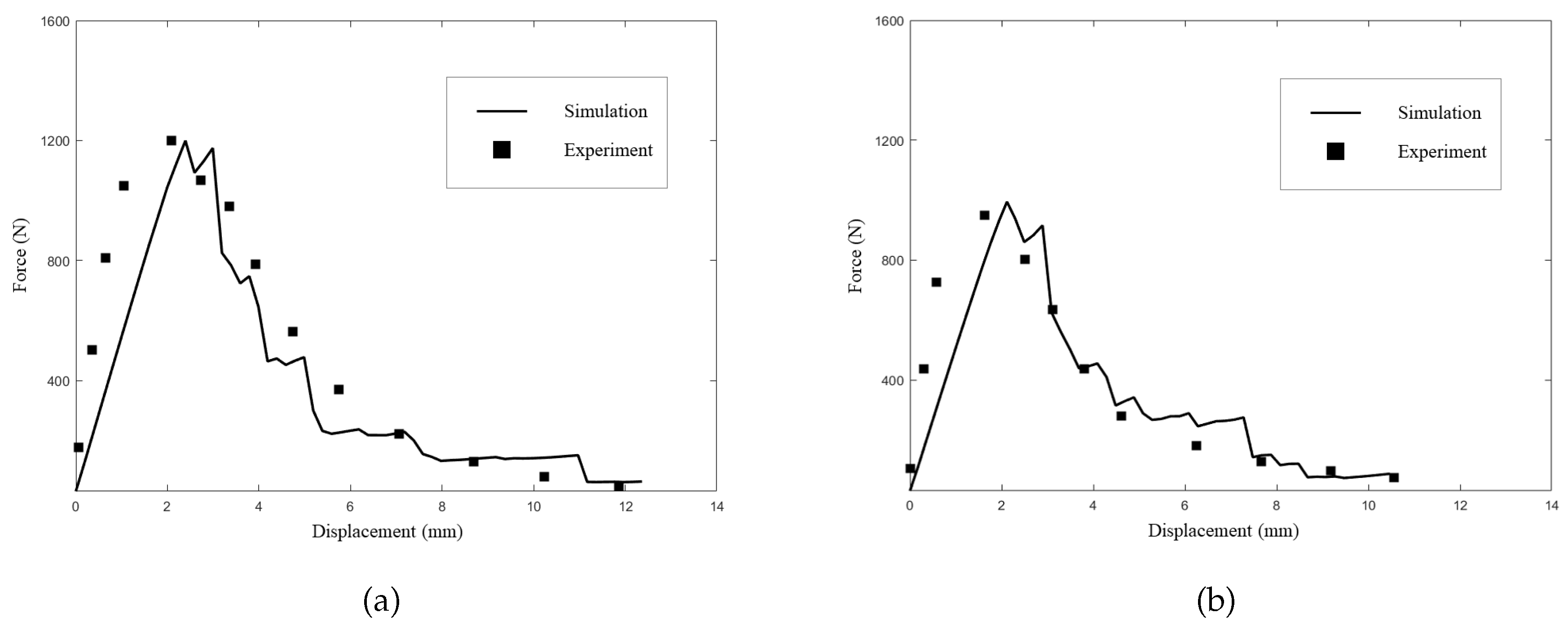
5. Numerical Examples
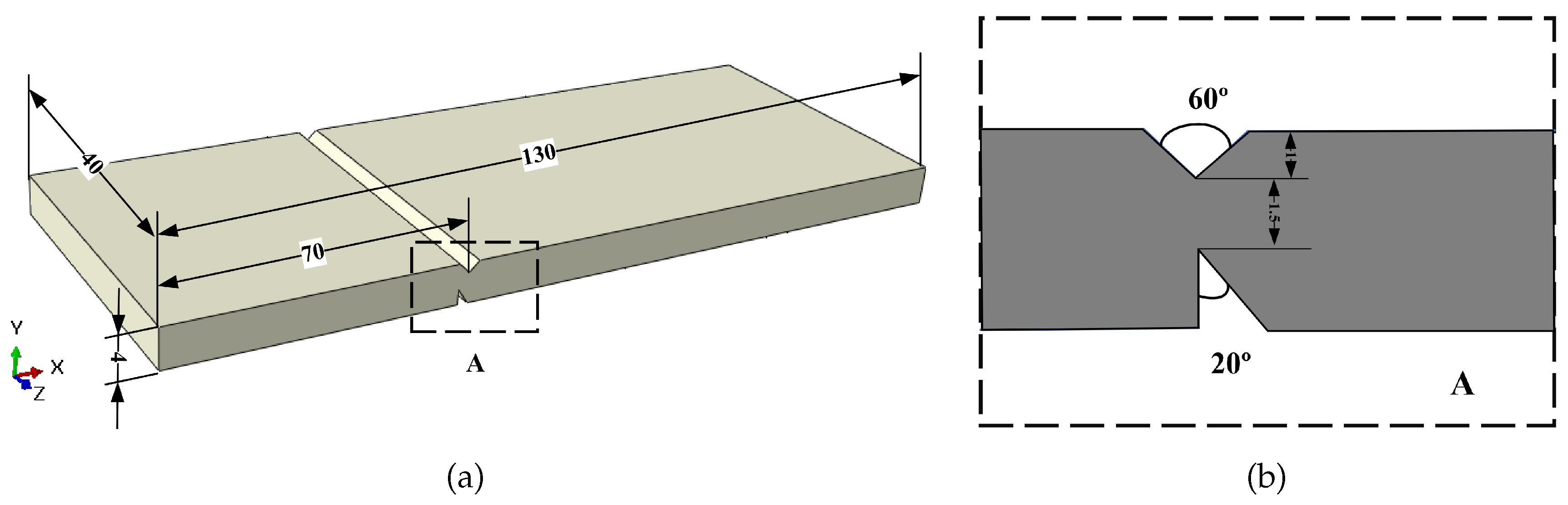
5.1. Example 1: GH4099 Superalloy Structure
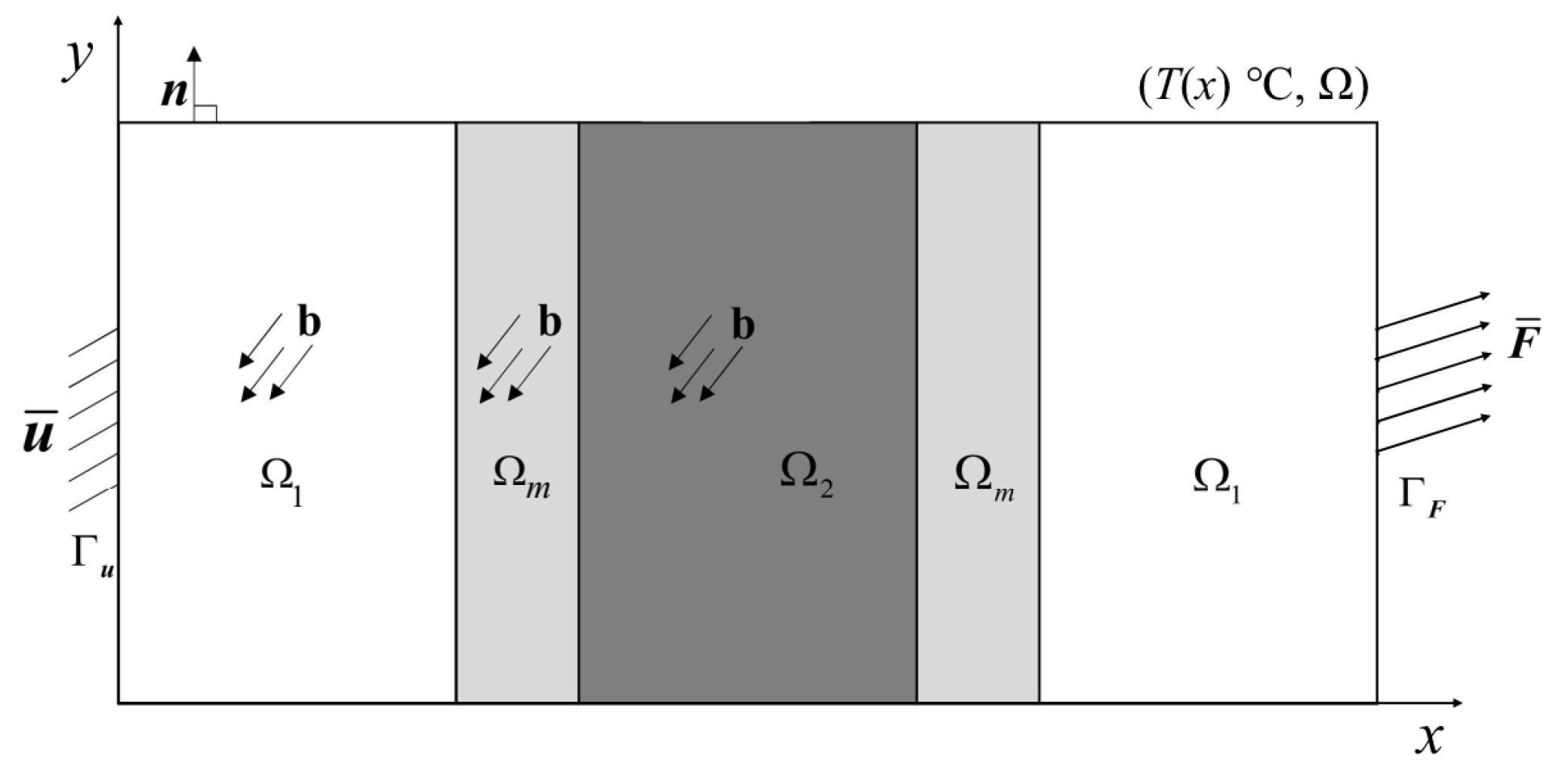
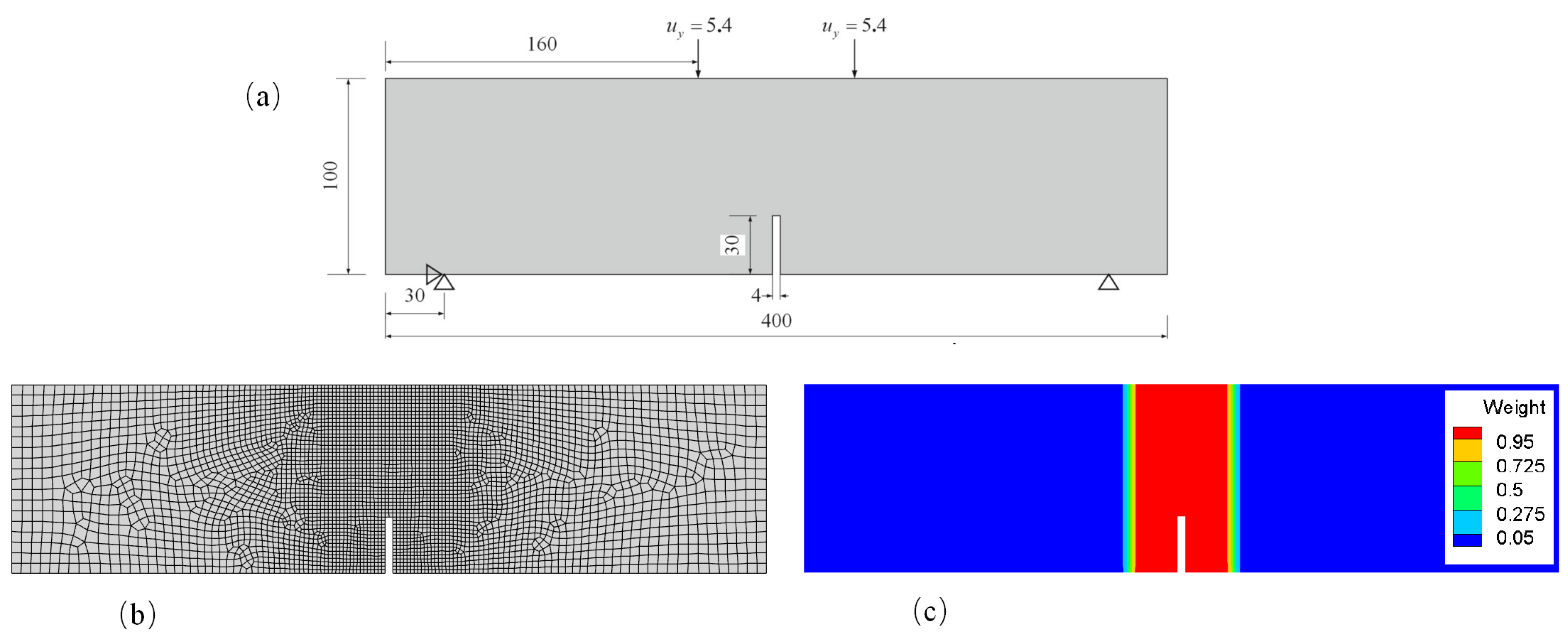
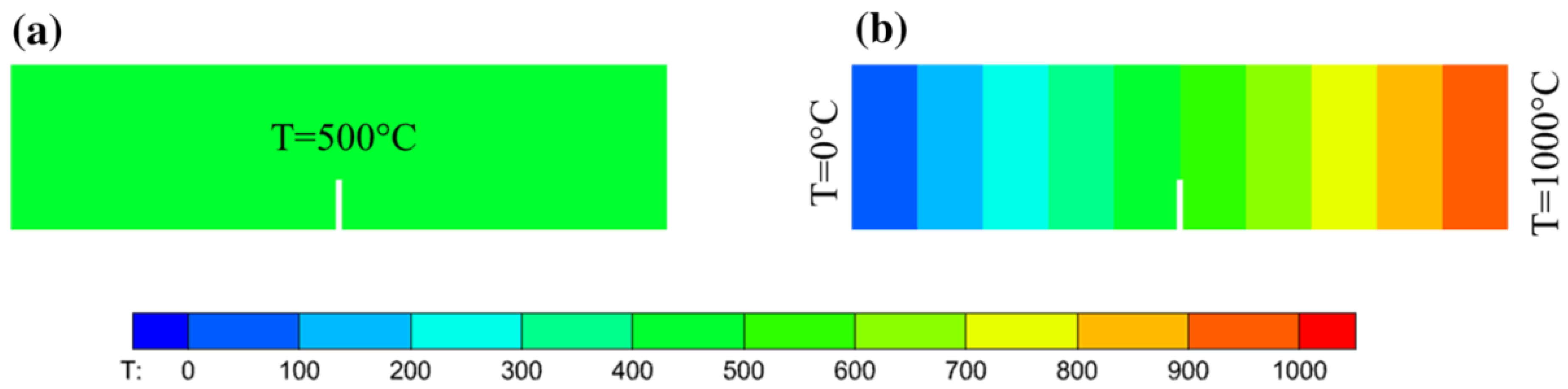
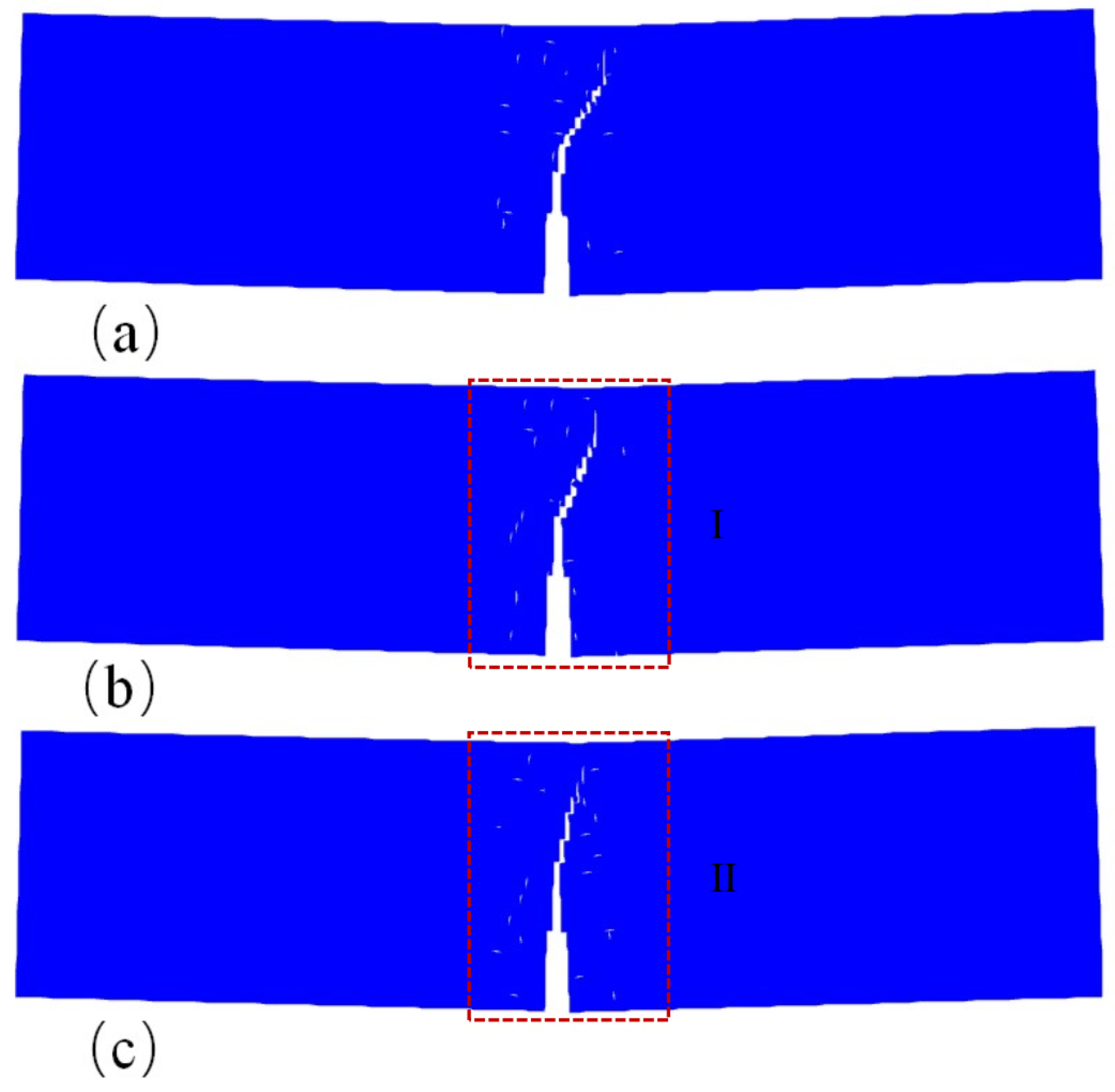
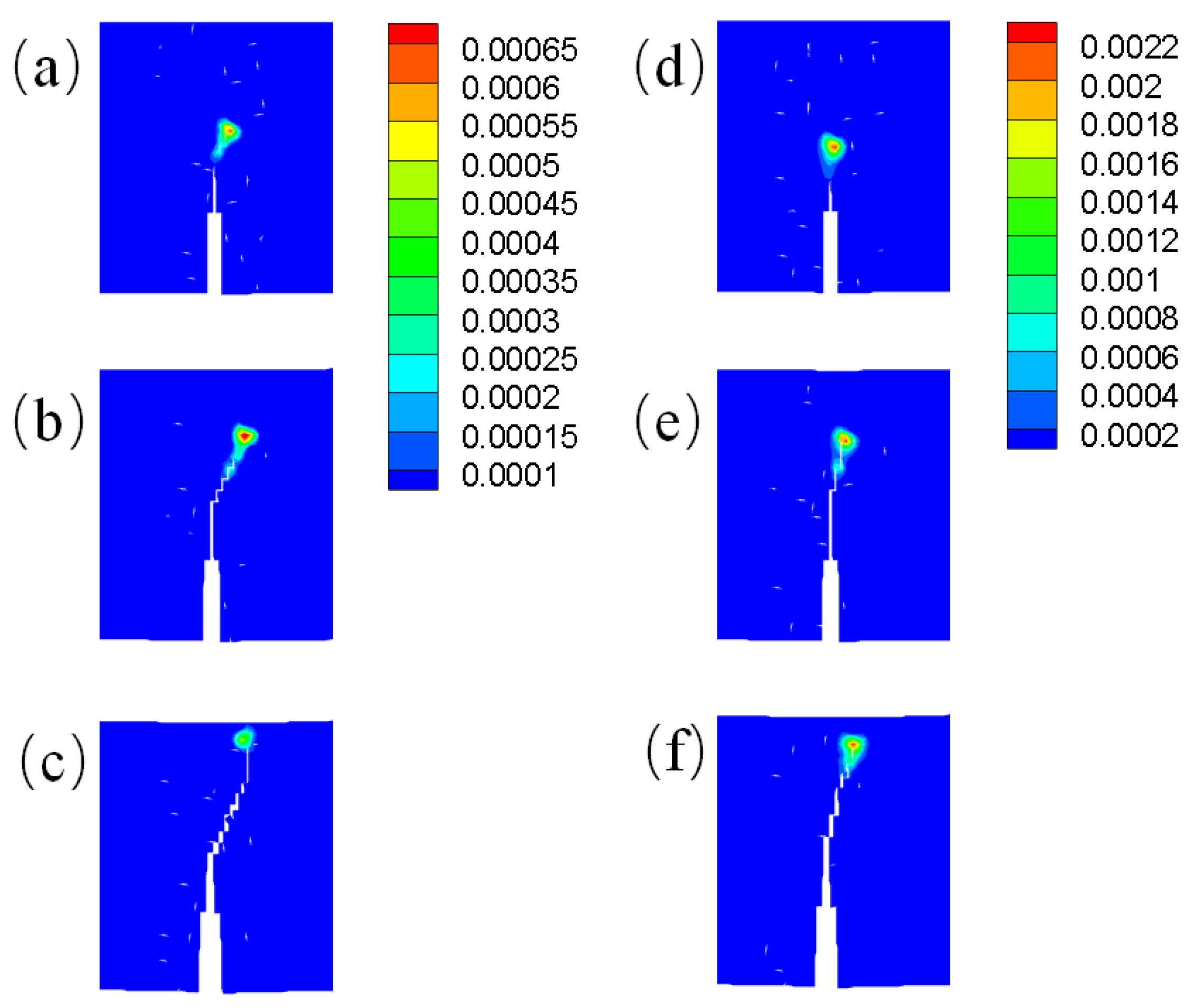
5.2. Example 2: Four-point bending beam
6. Conclusion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.F.; Zeng, X.G.; Chen, H.Y. A Three-dimensional dynamic constitutive model and its finite element implementation for NiTi alloy based on irreversible thermodynamics. Acta Mechanica Solida Sinica 2019, 32, 356–366. [Google Scholar] [CrossRef]
- Liang, W.; Hu, X.; Zheng, Y.; Deng, D. Determining inherent deformations of HSLA steel T-joint under structural constraint by means of thermal elastic plastic FEM. Thin-Walled Structures 2020, 147, 106568. [Google Scholar] [CrossRef]
- Fan, Z.X.; Kruch, S. A comparison of different crystal plasticity finite-element models on the simulation of nickel alloys. Materials at High Temperatures 2020, 37, 328–339. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. Journal of the Mechanics and Physics of Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Wu, C.T.; Ren, B. A stabilized non-ordinary state-based peridynamics for the nonlocal ductile material failure analysis in metal machining process. Computer Methods in Applied Mechanics and Engineering 2015, 291, 197–215. [Google Scholar] [CrossRef]
- Zhan, J.; Yao, X.; Han, F.; Zhang, X. A rate-dependent peridynamic model for predicting the dynamic response of particle reinforced metal matrix composites. Composite Structures 2021, 263, 113673. [Google Scholar] [CrossRef]
- Askari, A.; Azdoud, Y.; Han, F.; Lubineau, G.; Silling, S. 12 - Peridynamics for analysis of failure in advanced composite materials. In Numerical Modelling of Failure in Advanced Composite Materials; Hallett, S.R., Camanho, P.P., Eds.; Woodhead Publishing, 2015; pp. 331–350. [Google Scholar]
- Bobaru, F.; Foster, J.T.; Geubelle, P.H.; Silling, S.A. (Eds.) Handbook of Peridynamic Modeling; Advances in Applied Mathematics, Chapman and Hall/CRC, 2016. [Google Scholar]
- Ha, Y.D.; Bobaru, F. Characteristics of dynamic brittle fracture captured with peridynamics. Engineering Fracture Mechanics 2011, 78, 1156–1168. [Google Scholar] [CrossRef]
- Han, F.; Lubineau, G. Coupling of nonlocal and local continuum models by the Arlequin approach. International Journal for Numerical Methods in Engineering 2012, 89, 671–685. [Google Scholar] [CrossRef]
- Agwai, A.; Guven, I.; Madenci, E. Damage prediction for electronic package drop test using finite element method and peridynamic theory. Electronic Components & Technology Conference, 2009.
- Kilic, B.; Madenci, E. Coupling of peridynamic theory and the finite element method. Journal of mechanics of materials and structures 2010, 5, 707–733. [Google Scholar] [CrossRef]
- Oterkus, E.; Madenci, E.; Weckner, O.; Silling, S.A.; Bogert, P.; Tessler, A. Combined finite element and peridynamic analyses for predicting failure in a stiffened composite curved panel with a central slot. Composite Structures 2012, 94, 839–850. [Google Scholar] [CrossRef]
- Liu, W.Y.; Hong, J.W. A coupling approach of discretized peridynamics with finite element method. Computer Methods in Applied Mechanics and Engineering 2012, 245-246, 163–75. [Google Scholar] [CrossRef]
- Lubineau, G.; Azdoud, Y.; Han, F.; Rey, C.; Askari, A. A morphing strategy to couple non-local to local continuum mechanics. Journal of the Mechanics and Physics of Solids 2012, 60, 1088–1102. [Google Scholar] [CrossRef]
- Azdoud, Y.; Han, F.; Lubineau, G. The morphing method as a flexible tool for adaptive local/non-local simulation of static fracture. Computational Mechanics 2014, 54, 711–722. [Google Scholar] [CrossRef]
- Han, F.; Lubineau, G.; Azdoud, Y. Adaptive coupling between damage mechanics and peridynamics: A route for objective simulation of material degradation up to complete failure. Journal of the Mechanics and Physics of Solids 2016, 94, 453–472. [Google Scholar] [CrossRef]
- Macek, R.W.; Silling, S.A. Peridynamics via finite element analysis. Finite elements in analysis and design 2007, 43, 1169–1178. [Google Scholar] [CrossRef]
- Zhan, J.M.; Yao, X.H.; Han, F.; Zhang, X.Q. A rate-dependent peridynamic model for predicting the dynamic response of particle reinforced metal matrix composites. Composite Structures 2021, 263, 113673. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, S. Ordinary state-based peridynamics for plastic deformation according to von Mises yield criteria with isotropic hardening. Journal of the Mechanics and Physics of Solids 2016, 86, 192–219. [Google Scholar] [CrossRef]
- Liu, Z.M.; Bie, Y.H.; Cui, Z.Q.; Cui, X.Y. Ordinary state-based peridynamics for nonlinear hardening plastic materials’ deformation and its fracture process. Engineering Fracture Mechanics 2020, 223, 106782. [Google Scholar] [CrossRef]
- Kilic, B.; Madenci, E. Peridynamic Theory for Thermomechanical Analysis. IEEE Transactions on Advanced Packaging 2010, 33, 97–105. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Computers & Structures 2005, 83, 1526–1535. [Google Scholar]
- Liu, Z.Y.; Liu, S.K.; Han, F.; Chu, L.S. The Morphing method to couple local and non-local thermomechanics. Computational Mechanics 2022, 1–18. [Google Scholar] [CrossRef]
- Li, Z.B.; Han, F. The peridynamics-based finite element method (PeriFEM) with adaptive continuous/discrete element implementation for fracture simulation. Engineering Analysis with Boundary Elements 2023, 146, 56–65. [Google Scholar] [CrossRef]
- Silling, S.A.; Lehoucq, R.B. Peridynamic Theory of Solid Mechanics. Advances in Applied Mechanics 2010, 44, 73–168. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





