Physical Layer Security Performance Analysis of RIS-aided Cognitive Radio Networks

Preprint

Article

Physical Layer Security Performance Analysis of RIS-aided Cognitive Radio Networks

Altmetrics

Downloads

173

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

20 April 2023

Posted:

21 April 2023

You are already at the latest version

Alerts

Abstract

Abstract- Cognitive radio (CR) play an important role in improving spectral efficiency (SE) of wireless communication, meanwhile, intelligent reflecting surface (IRS) is an effective technology to improve the secrecy performance of wireless communication system by adjusting the phase shift and amplitude of channel. Thus, we consider an IRS-aided multiple-input single-output (MISO) CR systems to enhance secrecy rate, which is consists of a single eavesdropping link, a primary network containing the primary receiver (PR), and secondary network including secondary receiver (SR) and the SR transmitter (SR-TX). Specifically, we minimize the transmit power of SR subject to secrecy capacity constraint and interference temperature (IT) constraint on PR, by jointly optimizing the beamforming vector and artificial noise (AN) constraints matrix at SR-TX as well as the phase shift matrix of IRS. Numerical results show that the different values of transmit antennas at the SR-TX and the number of IRS elements can significantly decrease the transmit power under the condition of ensuring secure communication.

Keywords:

Subject: Engineering - Telecommunications

1. Introduction

Recently, physical layer security (PLS) has been considered to guarantee the information is not eavesdropped. More specifically, beamforming vector is designed at the transmitter of multiple antennas to improve the PLS [1]. Another considering technology was to transmit artificial noise (AN) from the transmitter to enhance the secrecy rate. By analyzing and optimizing the achievable secrecy capacity of the system, the authors in [2] show that the AN can improve the secrecy performance, by designing it to interference the eavesdropping channel, while AN vector into the null space of the legitimate channel. Jointly optimization of beamforming vector and AN vector to minimize the transmit power was proposed in [3] and [4], and the authors also considered the imperfect channel state information (CSI) of the eavesdropper [4]. In addition, it has been designed for various wireless communication at present. The author in [5] introduces AN vector to improve the security performance of cognitive radio (CR) communication scenario.

Moreover, the number of devices serving wireless communication has increased dramatically, the demand for spectral efficiency has also increased. Therefore, cognitive radio networks (CRNs) have been studied widely due to the ability to improve spectral efficiency [6]. Besides, the intelligent reflecting surface (IRS) has attracted wide attention recently since it can actively adjust the phase shifts and amplitude of the channel [7], applying IRS to wireless networks can enhance spectral and energy efficiency. Therefore, many existing literature use RIS to assist secure wireless communication systems in different scenarios, such as the multiple-input signal-output (MISO) case [8], UAV communication [9], the millimeter wave communication [10], and CRNs system [11].

However, few authors have studied IRS-aided CR system until recently, except for a few influential papers that have been published in [12]- [13]. The authors in [12] investigate the IRS can reduce the transmission power of the secondary transmitter (ST). In [13], IRS assisted CR system has been proposed by establishing an optimization to maximize the secrecy rate of ST while exist a static eavesdropper, which the cooperative beamforming was considered, as well as to ensure the quality of service (QoS) of the primary receiver (PR).

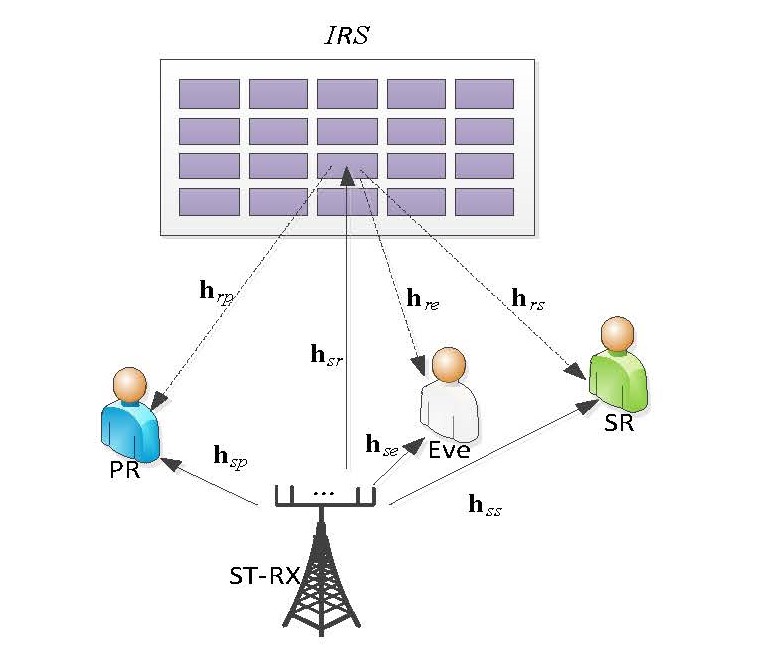
In addition, the RIS has been exploited to assist secure communication by cooperate with other traditional security technologies include the AN [14], cooperative relaying [15] and simultaneous wireless information and power transfer SWIPT [16]. Inspired of CR system and the advantages of IRS, we consider the Physical layer security of IRS-aided CR system with AN as shown in Figure 1. Including a multiple-antennas secondary receiver (SR) transmitter (SR-TX), a signal antenna SR and primary receiver (PR). Moreover, there was a static signal antenna eavesdropper near the SR-TX. More specifically, we introduce AN at SR-TX to interfere with eavesdropper, and the problem of minimize the transmit power of SU was considered, by alternating optimizing the beamforming vector and AN and phase shift matrix of IRS, while subject to the security capacity constraint and the interference temperature constraint at PR and the secrecy rate constraint. In the processing of solving this problem. we use iterative algorithm (AO) base on a block coordinate descent (BCD) method [17] to deal with the non-convex problem, which transform object problem into a two subproblems, and the variables in two subproblems are alternatively optimized. In addition, the method of semidefinite relaxation (SDR) to solve the unit module constraint. A Gaussian randomization scheme in [18] is applied to recover the rank-1 variables until the algorithm converges.

2. System Model

As shown in Figure 1, consider an RIS-aided CR communication system including a multiple antennas SR-TX, a signal antenna SR and PR, an eavesdropper (Eve), and an RIS that is composed of

N

reflecting meta-surfaces.

2.1. Main Link

Let

h_{s p} \in ℂ^{M \times 1}

h_{s s} \in ℂ^{M \times 1}

h_{s e} \in ℂ^{M \times 1}

h_{s r} \in ℂ^{N \times M}

represent the channels from the ST-RX to the PR, the SR, and the IRS, respectively. On the other hand, the channels from the IRS to the PR and the SR are given by

h_{r p} \in ℂ^{N \times 1}

and

h_{r s} \in ℂ^{N \times 1}

, respectively. the diagonal phase shift matrix of the IRS is denoted by

Φ = d i a g (f_{1}, f_{2}, \dots f_{N})

[3], where

f_{n} = e^{j θ_{n}}, n = 1, \dots, N

and

θ_{n} \in [0, 2 π)

represent the phase shift of the signal transmission to each IRS elements.

The transmitted signal

x_{s}

is expressed by

x_{s} = w s + z

(1)

where

w \in ℂ^{M \times 1}

is the beamforming vector,

z \in ℂ^{M \times 1}

is the AN vector with

z ~ C N (0, Z \underline{≻} 0)

The received signal reflected by the IRS at the SR can be expressed as

y_{s} = (h_{s s}^{T} + h_{r s}^{T} Φ h_{s r}) x_{s} + n_{s}

(2)

where

n_{s} ~ C N (0, σ_{s}^{2})

is the complex additive white Gaussian noise (AWGN) at the SR-TX. Thus, the signal-to-interference-plus-noise ratio (SINR) at the SR can be written as

γ_{s} = \frac{{| {\tilde{h}}_{s} w |}^{2}}{{| {\tilde{h}}_{s} z |}^{2} + σ_{s}^{2}}

(3)

where

{\tilde{h}}_{s} = h_{s s}^{T} + h_{r s}^{T} Φ h_{s r}

. Since the primary receiver transmitter (PT-RX) is not considered in our proposed model, PR will not only receive interference from the SR, but also the signal reflected by IRS when the ST-RX broadcasts the signal

x_{s}

. Therefore, the interference signal at the PR can be expressed as

y_{p} = (h_{s p}^{T} + h_{r p}^{T} Φ h_{s r}) x_{s} + n_{p}

(4)

where

n_{p} ~ C N (0, σ_{p}^{2})

is the AWGN at the PR. Then, the interference power is given by

I_{p} = {| {\tilde{h}}_{p} w |}^{2} + {| {\tilde{h}}_{p} z |}^{2}

(5)

where

{\tilde{h}}_{p} = h_{s p}^{T} + h_{r p}^{T} Φ h_{s r}

2.2. Eavesdropping Link

Let

h_{s e} \in ℂ^{M \times 1}

denote the channels from the ST-RX to the Eve, while the transmitted signal from the RIS to the Eve is denoted by

h_{r e} \in ℂ^{N \times 1}

. The received signal reflected by the RIS at the eavesdropper can be expressed as

y_{e} = (h_{s e}^{T} + h_{r e}^{T} Φ h_{s r}) x_{s} + n_{e}

(6)

where

n_{e} ~ C N (0, σ_{e}^{2})

denote the AWGN at the Eve. Thus, SINR at the Eve can be written as

γ_{e} = \frac{{| {\tilde{h}}_{e} w |}^{2}}{{| {\tilde{h}}_{e} z |}^{2} + σ_{e}^{2}}

(7)

where

{\tilde{h}}_{e}^{} = h_{s e}^{T} + h_{r e}^{T} Φ h_{s r}

3. Problem Formulation

In this section, we minimize the transmit power at ST-RX, by jointly optimizing the beamforming vector

w

and AN vector

z

, as well as the reflecting phase

θ

of IRS. In other hand, the constraints are as follows.

3.1. Interference power constraint

Let

ϕ_{p}

denote the upper bound of interference power at the PR. Then the constraint of interference power (IT) can be expressed as

{| {\tilde{h}}_{p} w |}^{2} + {| {\tilde{h}}_{p} z |}^{2} < ϕ_{p}

(8)

3.2. Secrecy rate constraints

To ensure that the SR can correctly decode the transmit signal

s

from the ST-RX, we transform the SR’s achievable rate into the following SINR constraint

\frac{{| {\tilde{h}}_{s} w |}^{2}}{{| {\tilde{h}}_{s} z |}^{2} + σ_{s}^{2}} \geq {\bar{γ}}_{s}

(9)

where

{\bar{γ}}_{s}

represents the minimal required SINR at the SR.

Similarly, the eavesdropper cannot eavesdrop on useful information, thus the Eve’s SINR constraint can be given by

\frac{{| {\tilde{h}}_{e} w |}^{2}}{{| {\tilde{h}}_{e} z |}^{2} + σ_{e}^{2}} \leq {\bar{γ}}_{e}

(10)

where

{\bar{γ}}_{e}

denoted the upper bound of SINR of eavesdropping link to obtain the information from ST-RX.

3.3. Phase constraint

IRS has the advantage of adjusting the phase and amplitude of the channel [3]. However, in this paper, we assume that IRS reflects the signal without changing the amplitude of the signals, the constraint can be written as

| f_{i} | = 1, i = 1, \dots, N

(11)

Based on above constraints, the transmit power minimization problem is expressed as

(P 0) : \min_{z, w, θ} T r (W + Z)

(12)

s . t . (8), (9), (10), (11)

(13)

Z \underline{≻} 0

(14)

W \underline{≻} 0

(15)

rank (W) = 1

(16)

where

W = {ww}^{H}

satisfying (15) and (16),

Z = {zz}^{H}

satisfying (14). To the best of our knowledge, it is hard to solve P0. Firstly, the constraint of unit modulus in (11) is not easy to converted into a tractable convex when we optimize

θ

. Secondly, the objective function (OF) is in a semi-closed form. Lastly, both the OF (11) and constraints (8) contain coupled optimization variables.

4. Proposed Solutions

In this section, proposed method is mainly divided into two steps to solve the P0. Firstly, the beamforming vector

w

and AN vector

z

at the ST-RX are jointly optimized when phase shift

f_{i}

of IRS is given. And then, fixed

w

and

z

, optimize

f_{i}

to minimize the transmit power. Specifically, two subproblems P0-A and P0-B of P0 can be written as follows

(1). P0-A:

\min_{z, w} T r (W + Z)

s.t. (8), (9), (10), (14), (15), (16)

(2). P0-B:

\min_{θ} T r (W + Z)

s.t. (8), (9), (10), (11)

Then, we continuously update the values of

f_{i}

w

and

z

through AO of these two subproblem until the OF

T r (W + Z)

converges.

4.1. Optimization of W and Z

Dealing with the constraints (3), we denote

\begin{array}{l} h_{r s}^{T} Φ h_{s r} = f^{T} d i a g (h_{r s}^{T}) h_{s r} = f^{T} G_{s} \\ h_{r p}^{T} Φ h_{s r} = f^{T} d i a g (h_{r p}^{T}) h_{s r} = f^{T} G_{p} \\ h_{r e}^{T} Φ h_{s r} = f^{T} d i a g (h_{r e}^{T}) h_{s r} = f^{T} G_{e} \end{array}

(17)

where

f ≜ {[f_{1}, \dots, f_{N}]}^{T}

f_{n} ≜ e^{j θ_{n}}, \forall n \in 1, \dots, N

. Then, we denote

{\tilde{G}}_{s} = [G_{s}; h_{s s}^{T}]

{\tilde{G}}_{p} = [G_{p}; h_{s p}^{T}]

{\tilde{G}}_{e} = [G_{s}; h_{s e}^{T}]

\tilde{f} = [f; 1]

and letting

\tilde{F} = \tilde{f} {\tilde{f}}^{H}

satisfying

\tilde{F} \underline{≻} 0

and

r a n k (\tilde{F}) = 1

, we have

\begin{array}{l} {\tilde{h}}_{s} = h_{s s} + h_{r s}^{T} Φ h_{s r} = {\tilde{f}}^{T} {\tilde{G}}_{s} \\ {\tilde{h}}_{p} = h_{s p} + h_{r p}^{T} Φ h_{s r} = {\tilde{f}}^{T} {\tilde{G}}_{p} \\ {\tilde{h}}_{e} = h_{s e} + h_{r e}^{T} Φ h_{s r} = {\tilde{f}}^{T} {\tilde{G}}_{e} \end{array}

(18)

Then, P0 has the same optimal solutions as following

(P 1) : \min_{Z, W, \tilde{F}} Tr (W) + Tr (Z)

(19)

s . t . Z, W, \tilde{F} \underline{≻} 0, r a n k (\tilde{F}) = 1

(20)

\frac{Tr (\tilde{F} {\tilde{G}}_{s} W {\tilde{G}}_{s}^{H})}{Tr (\tilde{F} {\tilde{G}}_{s} Z {\tilde{G}}_{s}^{H}) + σ_{s}^{2}} > {\bar{γ}}_{s}

(21)

\frac{Tr (\tilde{F} {\tilde{G}}_{e} W {\tilde{G}}_{e}^{H})}{Tr (\tilde{F} {\tilde{G}}_{e} Z {\tilde{G}}_{e}^{H}) + σ_{e}^{2}} < {\bar{γ}}_{e}

(22)

Tr (\tilde{F} {\tilde{G}}_{p} W {\tilde{G}}_{p}^{H}) + Tr (\tilde{F} {\tilde{G}}_{p} Z {\tilde{G}}_{p}^{H}) < ϕ_{p}

(23)

Both of problem P1 and all constraints become convex after processing. Fixing either

{Z, W}

\tilde{F}

, the subproblem is easier to solve by using the AO. When an initial value of

\tilde{F}

is given, problem P1 can be rewrite as problem P1a

(P 1 a) : \min_{Z, w} Tr (W) + Tr (Z)

(24)

s . t . Z, W \underline{≻} 0

(25)

\frac{Tr (Ψ_{s} W)}{Tr (Ψ_{s} Z) + σ_{s}^{2}} > {\bar{γ}}_{s}

(26)

\frac{Tr (Ψ_{e} W)}{Tr (Ψ_{e} Z) + σ_{e}^{2}} < {\bar{γ}}_{e}

(27)

Tr (Ψ_{p} W) + Tr (Ψ_{p} Z) < ϕ_{p}

(28)

where

Ψ_{s} = {\tilde{G}}_{s}^{H} \tilde{F} {\tilde{G}}_{s}

Ψ_{p} = {\tilde{G}}_{p}^{H} \tilde{F} {\tilde{G}}_{p}

Ψ_{e} = {\tilde{G}}_{e}^{H} \tilde{F} {\tilde{G}}_{e}

. Thus, we can use CVX tools to find the optimal solution of P1a [19]3. If the rank of the obtained

W

matrix is not 1, Gaussian randomization method can be used to convert the rank to 1, and then

W

can be obtained by eigenvalue decomposition.

4.2. Optimization of phase matrix $\tilde{F}$

In the second step, we fix the variable

{W, Z}

, the subproblem of P0b is easier to handle. We first reformulate the constraint in (9) and (10), respectively. Specifically, it can be simplified as

\begin{array}{l} \frac{{\tilde{h}}_{s}^{H} W {\tilde{h}}_{s}}{{\tilde{h}}_{s}^{H} Z {\tilde{h}}_{s} + σ_{s}^{2}} \geq {\bar{γ}}_{s} \\ \Leftrightarrow Tr ([W - {\bar{γ}}_{s} Z] {\tilde{h}}_{s} {\tilde{h}}_{s}^{H}) \geq {\bar{γ}}_{s} σ_{s}^{2} \\ \Leftrightarrow Tr ([W - {\bar{γ}}_{s} Z] ({\tilde{G}}_{s}^{H} \tilde{f}) ({\tilde{f}}^{H} {\tilde{G}}_{s})) \geq {\bar{γ}}_{s} σ_{s}^{2} \\ \Leftrightarrow Tr ({\tilde{G}}_{s} [W - {\bar{γ}}_{s} Z] {\tilde{G}}_{s}^{H} \tilde{F}) \geq {\bar{γ}}_{s} σ_{s}^{2} \end{array}

(29)

\begin{array}{l} \frac{{\tilde{h}}_{e}^{H} W {\tilde{h}}_{e}}{{\tilde{h}}_{e}^{H} Z {\tilde{h}}_{e} + σ_{e}^{2}} \leq {\bar{γ}}_{e} \\ \Leftrightarrow Tr ([W - {\bar{γ}}_{e} Z] {\tilde{h}}_{e} {\tilde{h}}_{e}^{H}) \leq {\bar{γ}}_{e} σ_{e}^{2} \\ \Leftrightarrow Tr ([W - {\bar{γ}}_{e} Z] ({\tilde{G}}_{e}^{H} \tilde{f}) ({\tilde{f}}^{H} {\tilde{G}}_{e})) \leq {\bar{γ}}_{e} σ_{e}^{2} \\ \Leftrightarrow Tr ({\tilde{G}}_{e} [W - {\bar{γ}}_{e} Z] {\tilde{G}}_{e}^{H} \tilde{F}) \leq {\bar{γ}}_{e} σ_{e}^{2} \end{array}

(30)

Then, by introducing slack variables into the SINR constraint of SR in (29) and Eve in (30), which can be rewritten as following respectively

Tr ({\tilde{G}}_{s} [W - {\bar{γ}}_{s} Z] {\tilde{G}}_{s}^{H} \tilde{F}) \geq {\bar{γ}}_{s} σ_{s}^{2} + δ_{0}, δ_{0} \geq 0

(31)

Tr ({\tilde{G}}_{e} [W - {\bar{γ}}_{e} Z] {\tilde{G}}_{e}^{H} \tilde{F}) \leq {\bar{γ}}_{e} σ_{e}^{2} - δ_{1}, δ_{1} \geq 0

(32)

Finally, the P0b is rewritten as

(P 2) : \max_{\tilde{f}, δ} {‖ δ ‖}_{1}

(33)

s . t . Tr ({\tilde{G}}_{s} [W - {\bar{γ}}_{s} Z] {\tilde{G}}_{s}^{H} \tilde{F}) \geq {\bar{γ}}_{s} σ_{s}^{2} + δ_{0}

(34)

Tr ({\tilde{G}}_{e} [W - {\bar{γ}}_{e} Z] {\tilde{G}}_{e}^{H} \tilde{F}) + δ_{1} \leq {\bar{γ}}_{e} σ_{e}^{2}

(35)

Tr (Λ_{p} \tilde{F}) + Tr (V_{p} \tilde{F}) < ϕ_{p}

(36)

δ \underline{≻} 0

(37)

| {\tilde{f}}_{n} | = 1, n = 1, \dots, N

(38)

where

δ = {[δ_{0}, δ_{1}]}^{H}

Λ_{p} = {\tilde{G}}_{p} W {\tilde{G}}_{p}^{H}

, and

V_{p} = {\tilde{G}}_{p} Z {\tilde{G}}_{p}^{H}

. Therefore, we observed that the constraint of (38) in P3 is the unit modulus constraint. According to [4], we can use semidefinite programming (SDP) method to handle the constraint. Thus, P2 can be rewritten as

(P 2 a) : \max_{F, δ} {‖ δ ‖}_{1}

(39)

s . t . (34), (35), (36), (37)

(40)

d i a g (\tilde{F}) = 1_{N}

(41)

\tilde{F} \underline{≻} 0

(42)

rank (\tilde{F}) = 1

(43)

where the constraints (41), (42) and (43) replace the constraint (38). To the best of our knowledge, all the constraint of P2a is convex except the (43). We can use the semi-definite relaxation (SDR) method to handle constraint (43), but it is not guarantee that all the

\tilde{F}

matrices we obtain have rank 1, so that

{\tilde{f}}_{n}

is failed to solved by using eigenvalue decomposition. To avoid this kind of situations, the most effective way is the Lemma 1 as follows.

Lemma 1: Any positive semidefinite matrix

A

satisfies the inequality [4]

| I + A | \geq 1 + Tr (A)

(44)

and the equality in (44) holds if and only if

rank (A) \leq 1

. Then, the constraint (43) can be recast as

\begin{matrix} (43) & \Leftrightarrow | I + \tilde{F} | \geq 1 + Tr (\tilde{F}) \\ \Leftrightarrow \log \det | I + \tilde{F} | \geq \log (1 + (N + 1)) \end{matrix}

(45)

where

Tr (\tilde{F}) = N + 1

. By using the method of penalty-based, P2a is rewritten as

(P 2 b) : \max_{F, δ} {‖ δ ‖}_{1} + κ [\log (1 + (N + 1)) - \log \det (I + \tilde{F})]

(46)

s . t . (40), (41), (42)

(47)

where

κ

denote penalty factor, which is aim to penalize the case of

rank (\tilde{F}) \neq 1

. However, it is hard to solve because

\log \det (I + \tilde{F})

is concave function about

\tilde{F}

, by utilizing the first-order Taylor to obtain the upper bound approximately

\log \det (I + \tilde{F}) \leq (\log e) T r {{({(I + {\tilde{F}}^{(n)})}^{- 1})}^{*} (\tilde{F} - {\tilde{F}}^{(n)})} + (\log e) \log \det (I + {\tilde{F}}^{(n)})

(48)

where

e

is the natural logarithm. Finally, P2b is recast as

(P 2 c) : \max_{F, δ} {‖ δ ‖}_{1} + κ [- (\log e) T r {{({(I + F^{(n)})}^{- 1})}^{*} (F - F^{(n)})}]

(49)

s . t . (40), (41), (42)

(50)

After above processing, P2c can be solved using CVX tools. The whole AO algorithm is shown in Algorithm 1. The convergence of the transmit power can be guaranteed by iterative optimization P1a and P2c.

Algorithm 1 Alternating Optimization Algorithm

1: Input:

N

M

h

.
2: Output:

{\tilde{F}}^{*}

W^{*}

Z^{*}

.
3: Initialize

{\tilde{F}}_{0}

by random generated.
4: repeat
5: Obtain

W_{i}

and

Z_{i}

by solving (P1a) in (24) for given

{\tilde{F}}_{i}

.
6: if

rank (W) \neq 1

rank (Z) \neq 1

7:      Gaussian randomization algorithm;
8:    end
9:    Obtain

{\tilde{F}}_{i + 1}

by solving (P2c) in (49) for given

W_{i}

and

Z_{i}

.
10: if

rank ({\tilde{F}}_{i + 1}) \neq 1

11:      Gaussian randomization algorithm;
12:    end
13:  compute

P_{i + 1} = Tr (W_{i}) + Tr (Z_{i})

.
14: Update

i \leftarrow i + 1

15: until

P_{i + 1} - P_{i} \leq 1 e - 3

5. Numerical results

We assume that the ST-RX, the SR, the PR, the eavesdropper, and the RIS are located at (0,10), (180,0), (160,0), (170,0), (100,25) in meter (m) in a two-dimensional plane, respectively. The channels of ST-RX -Eve, ST-RX -SR and ST-RX -PR experience Rayleigh fading, while the ST-RX -RIS, RIS-SR, RIS-PR and RIS-Eve links experience Rician fading with a Rician factor of 4. The large-scale fading is defined as

10^{- 3} d^{- c}

, where

d

is the link distance,

c

is the path-loss exponent, which 2.2, 2.2, 2.2, 2, 2, and 2 denote the ST-RIS, the RIS-SR, the RIS-PR, the RIS-Eve, the ST-SR, the ST-PR and the ST-Eve links, respectively. Other default system parameters are set as:

σ_{s}^{2} = σ_{e}^{2} = σ_{p}^{2} = - 65 d B m

{\bar{γ}}_{s} = 8

{\bar{γ}}_{e} = 2

ϕ_{p} = - 35 d B m

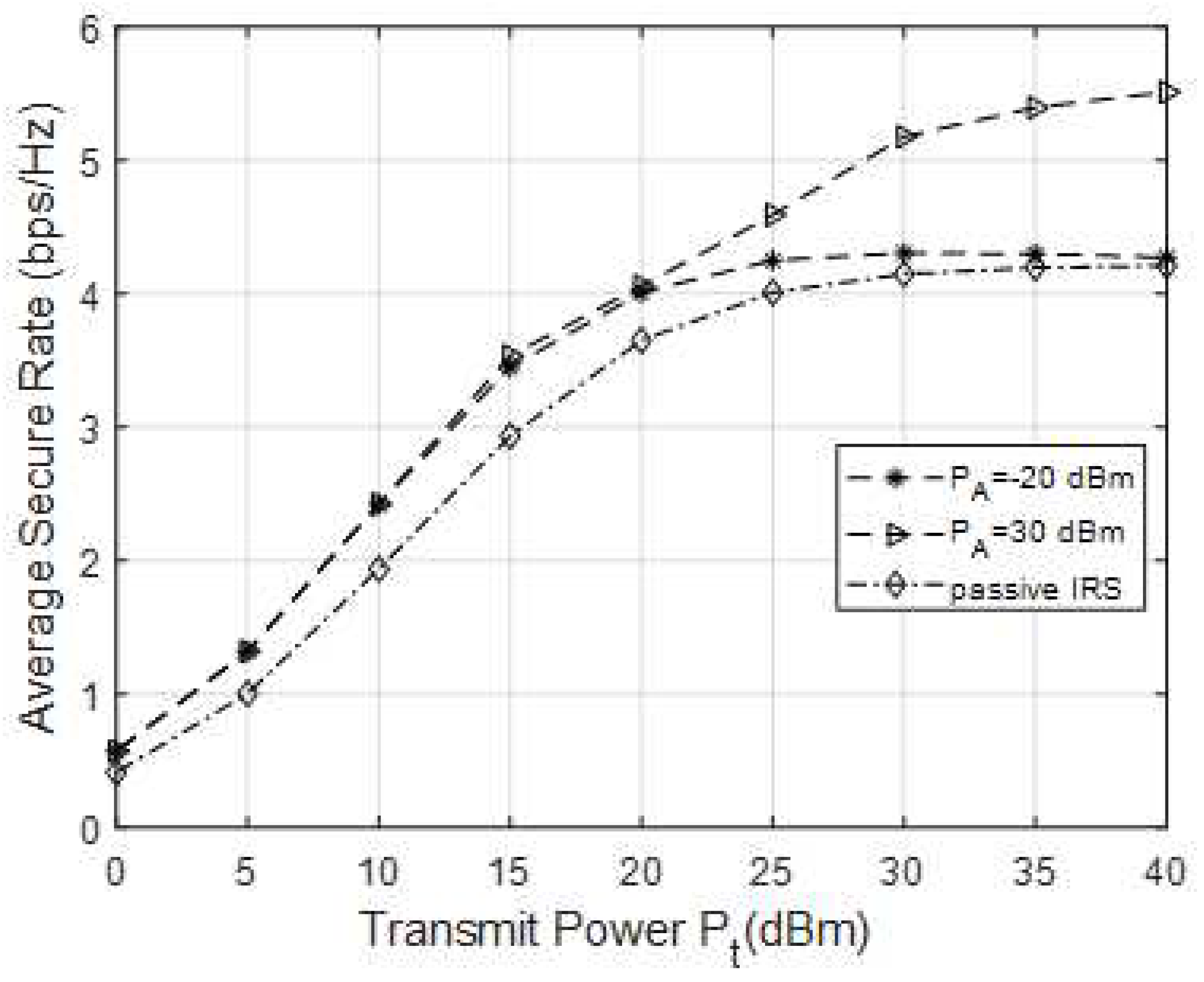
In Figure 2, the relationship curve between different transmission power and average safety rate of ST is shown. Set the number of reflection units for IRS

N = 16

. Among them, "passive IRS" represents the simulation curve in the presence of IRS, and "

P_{A} = 20 d B m

" represents the safety rate simulation curve that can be achieved when the maximum noise amplification power of the active IRS is 20dBm. Compare the safety performance of passive IRS and active IRS assisted CR systems under the same parameter settings. The maximum interference power received by PR is

P_{I} = 10 d B m

. As the

p_{t}

increases, the average security rate of the SR end also continues to increase and shows a trend of convergence. In the case of an active IRS, the maximum amplification amplitude coefficient of each reflection unit is set to

a_{\max}^{2} = 30 d B

. Consider two cases where the maximum noise amplification power of an active IRS is

P_{A} = 30 d B m

and

P_{A} = - 20 d B m

respectively. From the figure, when the transmission power is the same, the safety performance gain brought by active IRS is always better than that of passive IRS. This is because the active IRS can not only adjust the phase of the incident signal, but also amplify the incident signal, and the channel capacity at the SR end will further increase. However, active IRS amplifies the incoming signal while also amplifying the introduced thermal noise. The simulation results show that the average safety rate of different amplified noise power budgets is basically the same when the transmission power is small. This indicates that under low transmission power conditions, the noise power budget of active IRS has little impact on the safety performance of the system. When the transmission power is high, the average safe rate increases with

P_{A}

increasing. Then, as the transmission power increases to a certain value, the safety rate curve gradually smooths out, and even at

P_{t} = 40 d B m

, the average safety rate of the "

P_{A} = - 20 d B m

" and "passive IRS" curves is almost the same. This is because when the threshold value of amplified noise power is low and the transmission power is high, the amplification of the incident signal by the active IRS will also be limited according to the constraints of amplified noise. In addition, in the case of "passive IRS", due to the limitation of the PR end interference power threshold condition

P_{I} = 10 d B m

, when the power increases to a certain value, the channel gain brought by the reflection link will continue to weaken until

P_{I} = 10 d B m

the average safe rate no longer increases.

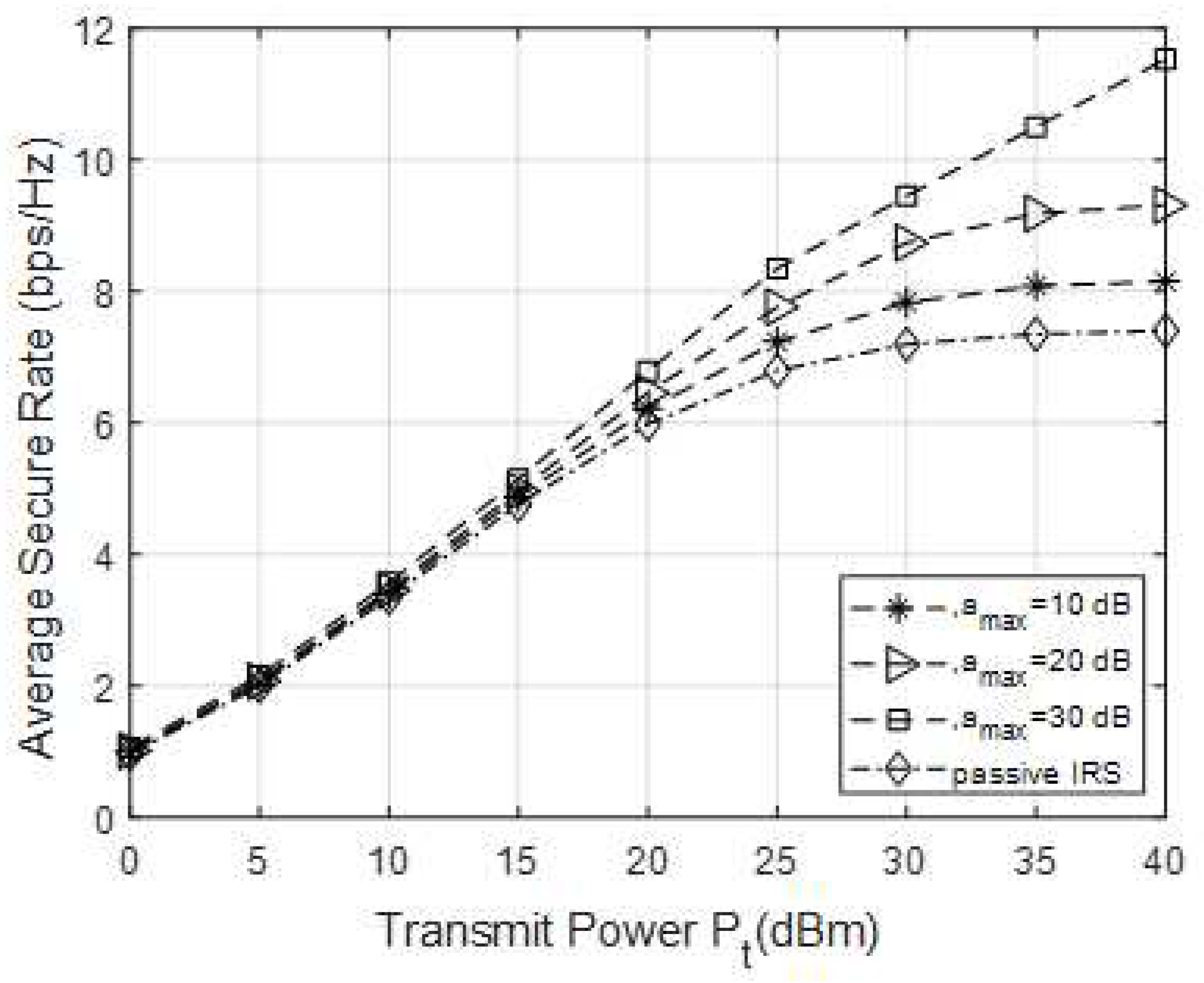
In Figure 3, the average safety rate curves of passive IRS and active IRS assisted CR systems with different amplitudes were compared under different transmission powers of ST. Set

N = 32

P_{A} = 30 d B m

P_{I} = 10 d B m

, and compare the average safety rate under different

a_{\max}^{2}

conditions. As shown in Figure 3, the average safety rate will increase as

a_{\max}^{2}

increases. Especially when the reflection power is less than 15dBm, the safety rate curves of different amplification amplitudes are basically consistent. Under weak power conditions, the safety rate is not sensitive to the amplification gain of active IRS. When the transmission power is greater than 15dBm, as the amplification amplitude increases, the average safety rate also increases. Compared to passive IRS, active IRS can achieve better safety performance.

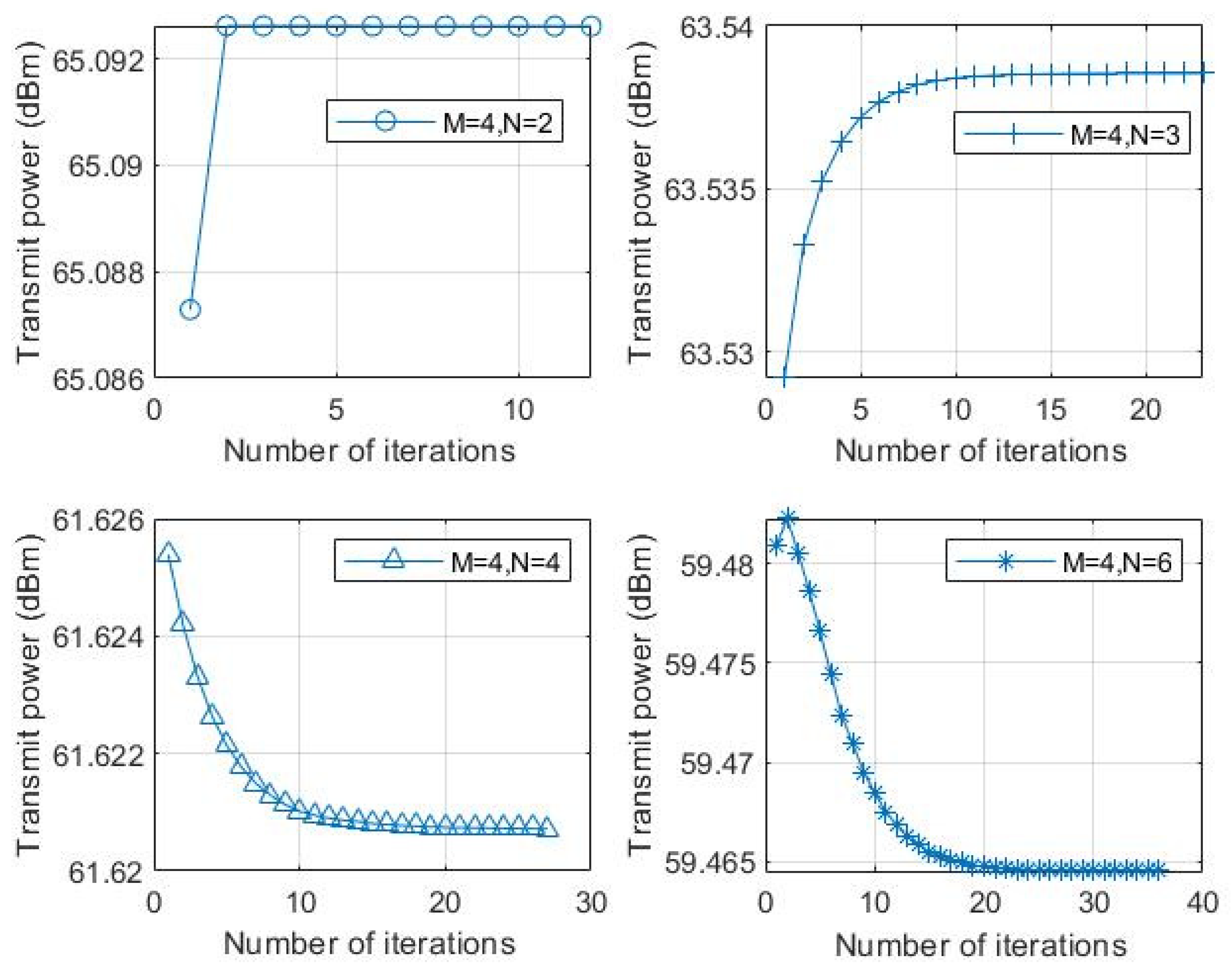
In Figure 4, the transmitted power curves for different numbers of reflection units are given while the number of antennas is

M = 4

. When

N > 3

, the transmitted power decreases with the increase of the number of reflection units, it is shown that IRS can guarantee the security of CR systems with low power consumption. From Figure 2, it is seen that the convergence times of the algorithm increase with the increase of

N

. This is because when the increase of IRS elements will make the dimension of phase matrix

Φ

larger, more computation time and iterations are required to optimization of

Φ

. Therefore, more IRS elements will reduce the transmit power of ST-RX, but increase the time complexity of the algorithm.

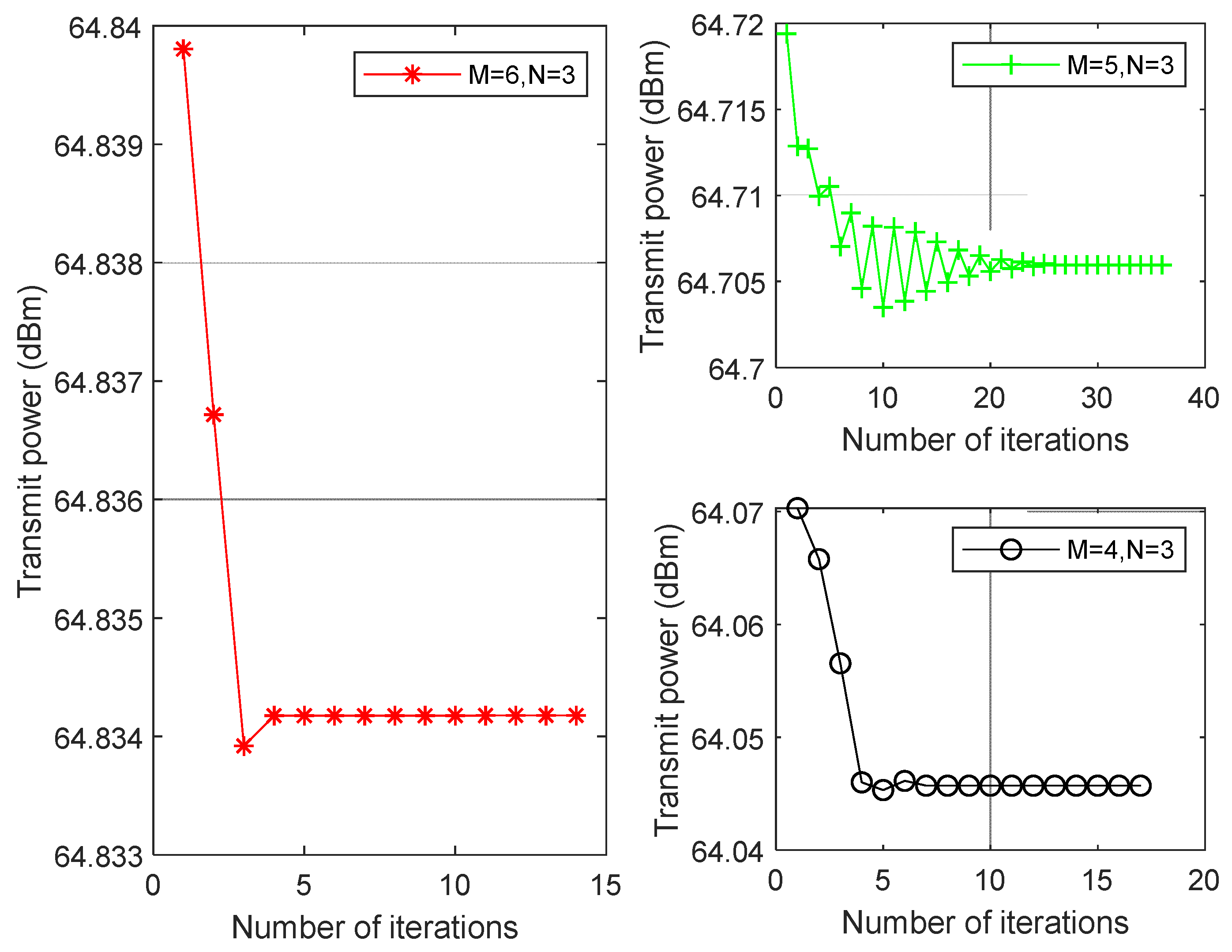
In Figure 5, we have plotted the transmitted power curves for different numbers of antennas while the number of reflection units is

N = 3

. We observed that the number of iterations decreases when proposed algorithm converges with the increase of the number of antennas. Moreover, the less transmit power is required as the number of antennas of ST-RX under fixing the IRS elements. Therefore, the number of IRS elements and transmit antennas can be increased appropriately if the transmit power of ST-RX is limited, while the constraints of secure communication.

6. Conclusion

In this paper, by designing the IRS-aided CR system, we investigated the secrecy performance by introducing AN vector at ST-RX. The OF is minimize the transmit power of the ST-RX by jointly optimizing the

{w, z}

and

θ_{i}

, while subject to secrecy rate constraint and IT constraint of PR. To solve it, the AO algorithm was utilized to solve the challenge constraint. By utilizing the SDR scheme, we have dealt with the

{w, z}

and

θ_{i}

effectively. For the constraint of unit modulus, the penalty function method was applied. Simulation results illustrate that the joint scheme can effectively reduce the transmit power at ST-RX under the condition of ensuring secure communication. on the other hand, the QoS of PR can be satisfied.

References

L. Dong and H. -M. Wang, "Enhancing Secure MIMO Transmission via Intelligent Reflecting Surface," IEEE Trans. Wireless Commun, vol. 19, no. 11, pp. 7543-7556, Nov. 2020. [CrossRef]
S. Hong, C. Pan, H. Ren, K. Wang and A. Nallanathan, "Artificial-Noise-Aided Secure MIMO Wireless Communications via Intelligent Reflecting Surface," IEEE Trans. Commun, vol. 68, no. 12, pp. 7851-7866, Dec. 2020. [CrossRef]
Q. Wu and R. Zhang, “Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network,” IEEE Commun. Mag., vol. 58, no. 1, pp. 106–112, Jan. 2020. [CrossRef]
S. Hong, C. Pan, H. Ren, K. Wang, K. K. Chai and A. Nallanathan, "Robust Transmission Design for Intelligent Reflecting Surface Aided Secure Communication Systems with Imperfect Cascaded CSI," IEEE Trans. Wireless Commun. [CrossRef]
V. Nguyen, T. Q. Duong, O. A. Dobre and O. Shin, "Joint Information and Jamming Beamforming for Secrecy Rate Maximization in Cognitive Radio Networks," IEEE Trans. Inf. Forensics Security, vol. 11, no. 11, pp. 2609-2623, Nov. 2016. [CrossRef]
W. Zhang, C. Wang, X. Ge, and Y. Chen, “Enhanced 5G cognitive radio networks based on spectrum sharing and spectrum aggregation,” IEEE Trans. Commun, vol. 66, no. 12, pp. 6304–6316, 2018. [CrossRef]
A. Almohamad et al., "Smart and Secure Wireless Communications via Reflecting Intelligent Surfaces: A Short Survey," IEEE Open Journal of the Communications Society, vol. 1, pp. 1442-1456, 2020. [CrossRef]
X. Yu, D. Xu and R. Schober, "Enabling Secure Wireless Communications via Intelligent Reflecting Surfaces," 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 2019, pp. 1-6.
S. Fang, G. Chen and Y. Li, "Joint Optimization for Secure Intelligent Reflecting Surface Assisted UAV Networks," IEEE Wireless Commun. Lett. [CrossRef]
X. Lu, W. Yang, X. Guan, Q. Wu and Y. Cai, "Robust and Secure Beamforming for Intelligent Reflecting Surface Aided mmWave MISO Systems," IEEE Wireless Commun. Lett, vol. 9, no. 12, pp. 2068-2072, Dec. 2020. [CrossRef]
X. Guan, Q. Wu and R. Zhang, "Joint Power Control and Passive Beamforming in IRS-Assisted Spectrum Sharing," IEEE Commun. Lett, vol. 24, no. 7, pp. 1553-1557, July 2020. [CrossRef]
L. Zhang, C. Pan, Y. Wang, H. Ren, K. Wang and A. Nallanathan, "Robust Beamforming Optimization for Intelligent Reflecting Surface Aided Cognitive Radio Networks," 2020 IEEE Global Communications Conference (GLOBECOM), Taipei, Taiwan, 2020, pp. 1-6.
Xiao, Haitao; Dong, Limeng; Wang, Wenjie. 2020. "Intelligent Reflecting Surface-Assisted Secure Multi-Input Single-Output Cognitive Radio Transmission" Sensors 20, no. 12: 3480. [CrossRef]
X. Guan, Q. Wu and R. Zhang, "Intelligent Reflecting Surface Assisted Secrecy Communication: Is Artificial Noise Helpful or Not?," IEEE Wireless Commun. Lett, vol. 9, no. 6, pp. 778-782, June 2020. [CrossRef]
Z. Abdullah, G. Chen, S. Lambotharan and J. A. Chambers, "A Hybrid Relay and Intelligent Reflecting Surface Network and Its Ergodic Performance Analysis," IEEE Wireless Commun. Lett, vol. 9, no. 10, pp. 1653-1657, Oct. 2020. [CrossRef]
Q. Wu and R. Zhang, "Weighted Sum Power Maximization for Intelligent Reflecting Surface Aided SWIPT," IEEE Wireless Commun. Lett, vol. 9, no. 5, pp. 586-590, May 2020. [CrossRef]
S. J. Wright, “Coordinate descent algorithms,” Math. Program., vol. 151, no. 1, pp. 3–34, Mar. 2015. [CrossRef]
W.-K. Ma, T. N. Davidson, K. M. Wong, Z.-Q. Luo, and P.-C. Ching, “Quasi-maximum-likelihood multiuser detection using semi-definite relaxation with application to synchronous CDMA,” IEEE Trans. Signal Process., vol. 50, no. 4, pp. 912–922, Apr. 2002. [CrossRef]
S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge, U.K.Cambridge Univ. Press, 2004.

Figure 1. RIS-aided CR system with an eavesdropper.

Figure 2. Average Security Rate with different transmision power

p_{t}

when

N = 16

Figure 2. Average Security Rate with different transmision power

p_{t}

when

N = 16

Figure 3. Average Security Rate with different transmision power

p_{t}

when

N = 32

Figure 3. Average Security Rate with different transmision power

p_{t}

when

N = 32

Figure 4. Convergence of the proposed algorithm with different values of N.

Figure 5. Convergence of the proposed algorithm with different values of M.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Physical Layer Security Performance Analysis of RIS-aided Cognitive Radio Networks

Abstract

1. Introduction

2. System Model

2.1. Main Link

2.2. Eavesdropping Link

3. Problem Formulation

3.1. Interference power constraint

3.2. Secrecy rate constraints

3.3. Phase constraint

4. Proposed Solutions

4.1. Optimization of W and Z

4.2. Optimization of phase matrix F ˜

5. Numerical results

6. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

4.2. Optimization of phase matrix $\tilde{F}$