Quantum Dynamic Approach of B2N(∓,0) and N2B(∓,0) Clusters Study: A Symmetry Breaking due to the JAHN-TELLER Effect

Majid Monajjemi; Fatemeh Mollaamin

doi:10.20944/preprints202304.0504.v1

Preprint

Article

Quantum Dynamic Approach of B₂N^(∓,0)and N₂B^(∓,0)Clusters Study: A Symmetry Breaking due to the JAHN-TELLER Effect

This version is not peer-reviewed.

This version is not peer-reviewed.

Downloads

127

Views

Comments

Submitted:

18 April 2023

Posted:

18 April 2023

You are already at the latest version

Abstract

Boron nitride clusters play an important role as precursors in the formation of ultra-hard thin solid boron nitride films, which have received considerable attention in material science. In this contribution, we investigated the ground and low-lying electronic states of B₂N^(∓,0)and N₂B^(∓,0). Triatomic NBN and BNB have been previously investigated using a variety of spectroscopic and calculational methods, and it is generally agreed that both of them are linear in their ground electronic states. The six ions including B₂N^(-), B₂N⁽⁺⁾, B₂N ⁽⁰⁾ , BN₂^(-), BN₂ ⁽⁺⁾ and BN₂ ⁽⁰⁾have been studied and been also compared with one another in terms of various basis sets and predication of the symmetry breaking (SB) phenomenon. Artifactual symmetry breaking along the v3 coordinate is observed in the ab initio wave functions for the neutral ground state up to the coupled-cluster level of theory, even when Brueckner orbitals are used. In the D_∞h point group of B₂N^(∓,0) and N₂B^(∓,0) variants, the unpaired electrons are delocalized, while in the asymmetric C_∞v point group, they are localized on either one of the B atoms or N atoms of B₂N^(∓,0)and N₂B^(∓,0), respectively. Structures with broken symmetry,C_∞v, can be stable by interaction to the D_∞h point group. In viewpoint of quantum chemistry, the second-order Jahn-Teller effect permits the unpaired electron to localize on boron atom, rather than being delocalized. Finally, from a statistical thermodynamical analysis, we calculated the thermochemical stabilities of those six ions.

Keywords:

Boron nitride

;

B2N(∓

;

N2B(∓

;

JAHN-TELLER

;

Symmetry Breaking.

Subject:

Chemistry and Materials Science - Physical Chemistry

1. Introduction

1.1. The structure of boron nitride clusters

It is generally agreed that BNB and NBN are linear in their electronic states, but the controversy as to whether their geometries are symmetric or asymmetric have not yet been definitively settled [1-10]. Six ions including B₂N ^(-), B₂N ⁽⁺⁾, B₂N ⁽⁰⁾ , BN₂ ^(-), BN₂ ⁽⁺⁾ and BN₂ ⁽⁰⁾ compounds have been studied as the most complex items of (SB), both real and artifactual, due to pseudo second-order Jahn–Teller effect. Although various experimental or theoretical investigations were done for these issues [7-10], there are no quantum reports of this phenomenon through various basis sets calculation [11-19]. Paldus [9] investigated the molecular system of B₂N ⁽⁰⁾ through multi-reference coupled cluster optimization with RMR Hamiltonian & CCSD (T) using cc-pVNZ, (N=2-5). In other approaches of CCSD (T), method, it has been also exhibited an asymmetric configuration of unequal BN bound length [1, 3]. B₂N⁽⁰⁾ structure has been approved by Raman technique [4] which can be also synthesized according to the

{B (}^{2} P) + {N (}^{4}

\to {B N (}^{1} Σ^{+})

and

{B (}^{2} P) + {B N (}^{1} Σ^{+}

)

\to {B N B (}^{2} Σ_{(u)}^{+})

reactions [12]. The mathematical extrapolation suggested by Schlegel for the PMP4 calculation can be arranged as:

E_{P M P 4 \approx} E_{U M P 4} + E_{P M P 3} - E_{U M P 3}

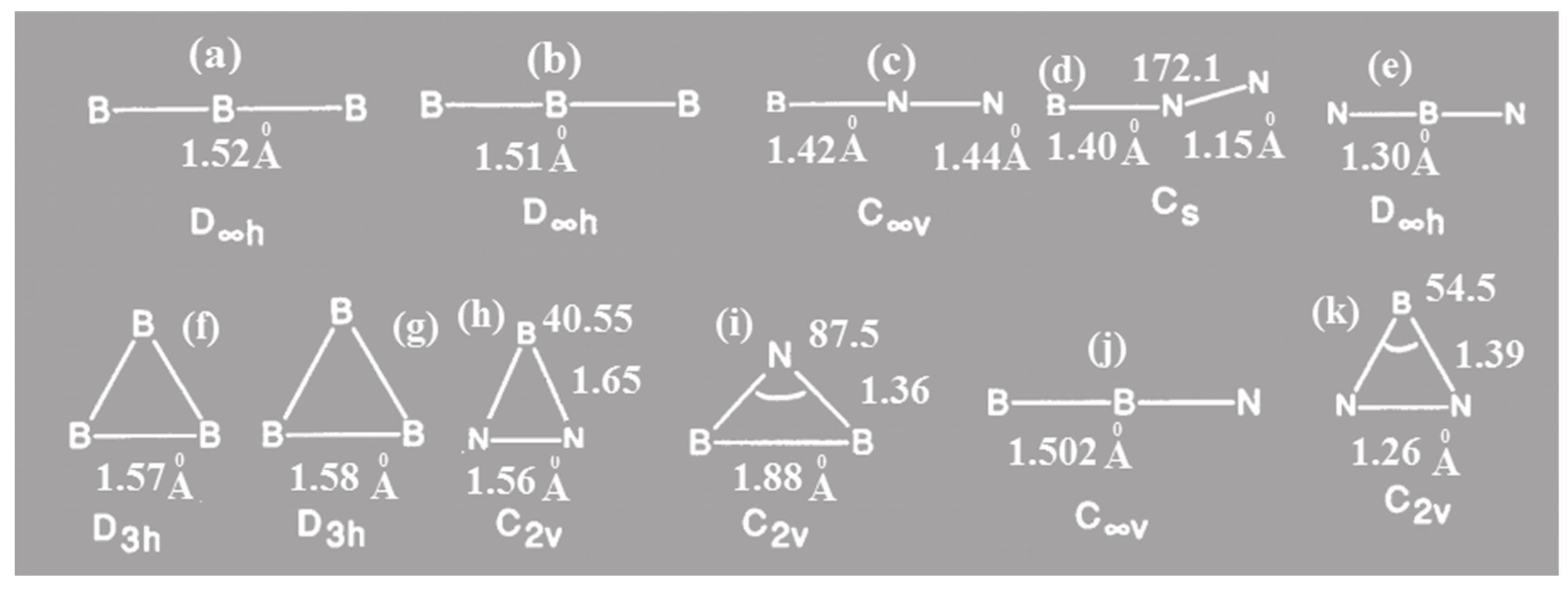
and

E_{\infty} ≅ \frac{E_{2} + E_{3}}{1 - \frac{E_{4}}{E_{2}}}

. The related optimized parameters are also confirmed based on Figure1. The UHF/6-31G* calculation for spin expectation for <S²> are collected in Table 1 and Figure 1.

An accurate work on the electronic structure of B_x N_3-x (x = 1, 2) was exhibited by Martin et al [1, 3, 5, 7 and 10] using both theoretical spectroscopic measurements.

Asmis [2] confirmed the ground state structure of

B_{2} N^{-}

both by photoelectron analysis and theory and indicated its electronic configuration as (

{\tilde{X}}^{1} \sum_{g}^{+}

). He also demonstrated the situation of B₂N ⁽⁰⁾ (

{\tilde{X}}^{2} \sum_{u}^{+}

) and

({\tilde{A}}^{2} \sum_{g}^{+})

in excited state by a linear symmetry combination as reaction as follows;

{\tilde{X}}^{1} \sum_{g}^{+} \to {\tilde{X}}^{2} \sum_{u}^{+} + e^{-}

and

{\tilde{X}}^{1} \sum_{g}^{+} \to {\tilde{A}}^{2} \sum_{g}^{+} + e^{-}

. In other side, the IR data exhibited a spectrum at 6000 cm⁻¹ in

{\tilde{A}}^{2} \sum_{g}^{+} \to {\tilde{X}}^{2} \sum_{u}^{+}

[7, 8]. The Walsh’s idea [17] confirmed all B

N^{(-, 0, +)}

variants of (

{\tilde{X}}^{2} \sum_{u}^{+}

) to

({\tilde{X}}^{1} \sum_{g}^{+})

for B₂N ⁽⁰⁾ and

B_{2} N^{-}

, respectively.

Löwdin [18] exhibited; such broken-symmetry (BS) usually has a lower energy compared with the symmetry-adapted (SA). It is notable the SB phenomenon, is due to the restricted hartree fock or in opposite the ROHF potential energy surfaces (PESs) for the linear ABA type (Such as NB₂ or BN₂). Wigner [19] confirmed that the Pauli principle and being simultaneously an Eigen function of <S²> and <S_Z> can be written as:

ψ_{S, M} (\vec{x_{1}}, \vec{x_{2}}, \dots . . \vec{x_{N}}) = (\sqrt{f_{N}^{S}})^{- 1} \sum_{i = 1}^{f_{N}^{S}} Ф_{i} (\vec{r_{1}}, \vec{r_{2}}, \dots . . \vec{r_{N}}) Θ_{i} (σ_{1}, σ_{1}, \dots . . σ_{N})

Where,

Ф_{i}

is the spinless Schrödinger equation and

Θ_{i}

is spin eigenfunctions, and

f_{N}^{S}

is the number of spin Eigen-functions [19]. In this article, we focus on the <S_z> and <S²> quantum numbers of various BN compounds (Table 1).

1.2 Thermochemical Considerations

Seifert et al.[20] Calculated the physical and chemical properties of boron-nitrogen clusters based on thermochemical studies. For B2N, basically 3 different structures can be written as: BBN → B2 + N; (b) BBN→B + (BN); (c) BNB→(BN) + B. For BN2, the following three fragmentation reactions were considered: (a) BNN→B + N2; (b) BNN→(BN) + N; (c) NBN →(BN) + N. It is confirmed generally, BNN should be stronger than NBN, and in the other side, BNB will be more stable than NBB. This is in agreement with the data, that B2N is appeared in mass spectra, while BN2 is not. We also calculated the thermochemical properties of our model based on Seifert work.

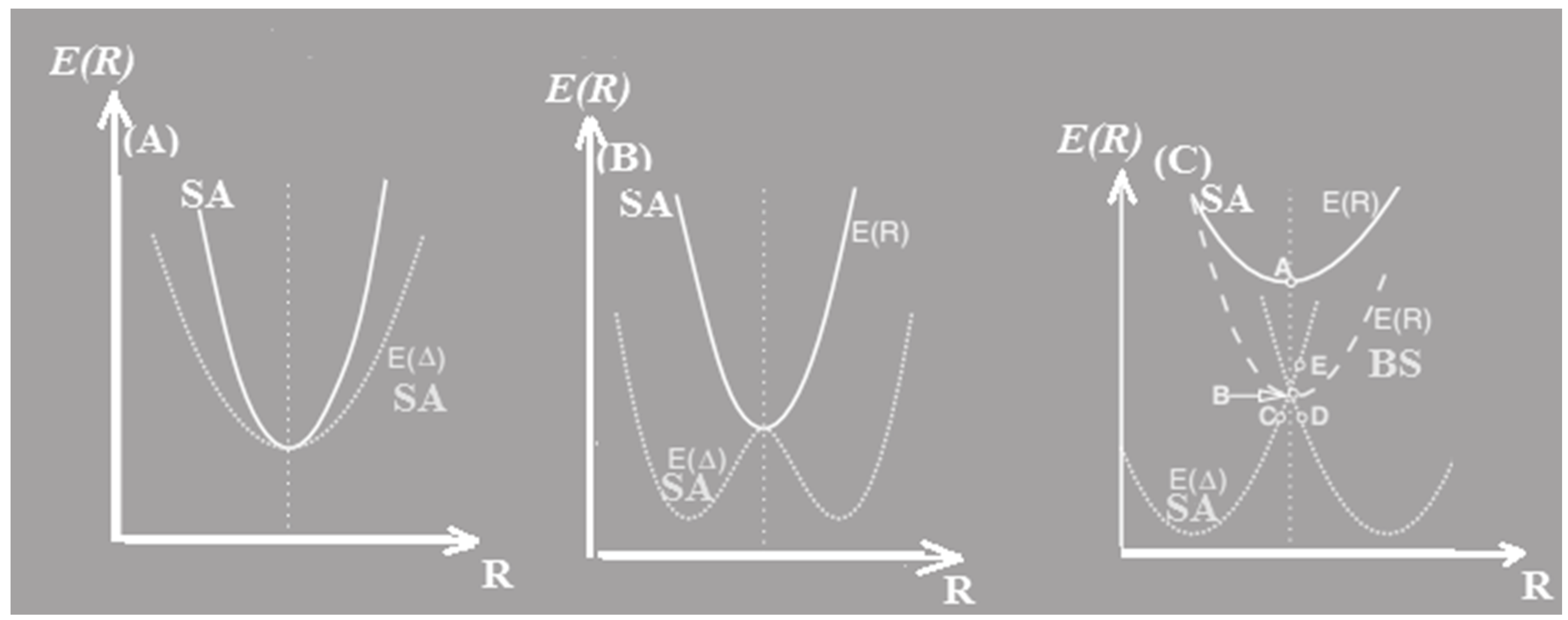
1.2. Potential energies surfaces (PESs)

PESs of linear triatomic XYX has been done for the cutting along the symmetrical and asymmetrical stretching modes. We mentioned the linear of X-Y and Y-X as R1 and R2, respectively. Cutting of the symmetrical stretching is oriented by the parameters same as R =R1=R2, and the energy minimum on the PEC E(R) describes the symmetrical optimized for R=Re. We also define these stretching coordinates as: ∆(R)=R1-R=R-R2. As well as the two PECs, defined by E(R) and E [∆(R)] , along the R and ∆ orientation, respectively. Consequently, the PEC has been labeled as E( R) or V (R) for the symmetrical stretching form and as well as the E [∆(R)] or V [∆(R)] has been defined for the asymmetric al form. (Figure 2).

2. Computational details and Methods

CASSCF wave functions have been accomplished as a basic calculation for estimating the energies along the BN–B coordinating changes. Since the definition of active space is needed for the CASSCF wave function, all the valence orbitals of the constituent atoms, i.e., 2s 12p have been considered clearly. EPR-III (and II) basis sets of Barone’s model [21] shown the most compatible data for electrostatic potential fitting (ESP).

The EPR(II) is a double-ζ basis set with polarization for B to F [21, 22] that is needed for N₂

B^{(\mp, 0)}

B₂

N^{(\mp, 0)}

calculation. EPR(III) is also a triple-ζ including diffuse parameter, of d-orbital, and compared with EPR(II), s-part improved for better energy minimization [20-24].

The correlation of valence basis sets have been investigated by Dunning and coworkers, named by cc-pVxZ, where x =2, 3, 4, 5 & 6 where used in this work. Additionally, these are includes of basically contracted sets of [3s2p1d] (cc-pVDZ), [4s3p2d1f] (cc-pVTZ), [5s4p3d2f 1g] (cc-pVQZ), and [6s5p4d3f 2g1h] (ccpV5Z) that are constructed through adding shell layers orbitals of s,p,d,... to the atomic Hartree–Fock wavefunction. Moreover, the polarization factors, which increase from 1d-cc-pVDZ to 4d-cc-pV5Z are added.

In other sides, the active space for the CASSCF (active electrons / active orbitals) should be defined for all valence orbitals in the post HF methods, such as 11/ 12 for B₂N⁽⁰⁾ and 10/ 12 for B₂N⁽⁺⁾ and so on.

The various basis sets in their effect to symmetry breaking of artifactual or trial wave function, the B₂

N^{(\mp, 0)}

have been optimized through several level of theories such as CASSCF(11/12)/ccPVQZ for B₂

N^{(-)}

, CASSCF(11/12)/AUG-ccPVTZ for B₂

N^{(0)}

and CASSCF (10/12)/ccPVTZ for B₂

N^{(+)}

[25, 26]. For this purpose, the self correlation consistent orbitals are well increased both in size and accuracy to converge systematically. The augmented functional sets are used from cc-pVNZ (N=2-6) by the addition of a single diffuse orbitals for the anions and in other hand for each item, only the polarization orbitals were used. The configuration interaction (CI) including single and double items [27] have been also used for estimating several physical parameters such as natural bounding orbital (NBO), Atoms in molecules by Bader (AIM) [28], NPA or natural population analysis, electrostatic potentials, and electrostatic potential-derived charge using the Merz-Kollman-Singh[29], chelp[30], or chelpG[31]. The Hyperpolarizability has been calculated via CISD, QCISD, MP₂ and CASSCF levels of calculations. The AIM of Bader’s theory was used for measuring the critical point maps to predict the atomic behaviors in B₂

N^{(\mp, 0)}

species [28].

The atomic charges can be computed over several species of N₂

B^{(\mp, 0)}

and

{B_{2} N}^{(\mp, 0)}

using abinitio quantum chemical packages such as Gaussian or GAMESS-US [32]. The potential surfaces(PS) of B₂N and BN₂ have been studied using the post Hartree Fock methods, such as CASSCF, MP4, PMP4, and QCISD. Spin contamination is shown to present severe problems with the MP4SDQ procedure.

3. Results and Discussion

3.1. Molecular orbital description

3.1.1. B₂ $N^{(\mp, 0)}$

Definition of the PS was exhibited to be not entirely enough at the UHF, more not qualitatively. In our calculation B₂N variants mostly are found to have a symmetric linear coordination in its ground state

({\tilde{X}}^{2} \sum_{u}^{+})

. Sometimes the asymmetric linear structure possibly being appeared a small amounts at higher temperatures. The B₂

N^{(0)}

configuration term of ground state (

{\tilde{X}}^{2} \sum_{u}^{+})

with electrons occupancy with the lowest excited state is:

{1 σ}_{g}^{2}, {1 σ}_{u}^{2} {, 2 σ}_{g}^{2}, {3 σ}_{g}^{2} {, 2 σ}_{u}^{2}, {1 π}_{u}^{4}, {4 σ}_{g}^{2}, 3 σ_{u}^{1}

that predicted to be

{\tilde{A}}^{2} Σ_{(g)}^{+}

, with an orbital occupancy of

{1 σ}_{g}^{2}, {1 σ}_{u}^{2} {, 2 σ}_{g}^{2}, {3 σ}_{g}^{2} {, 2 σ}_{u}^{2}, {1 π}_{u}^{4}, {4 σ}_{g}^{1}, 3 σ_{u}^{2}

. In addition,

{\tilde{B}}^{2} П_{g}

exited state can be written

{{1 σ}_{g}^{2}, {1 σ}_{u}^{2} {, 2 σ}_{g}^{2}, {3 σ}_{g}^{2} {, 2 σ}_{u}^{2}, π_{u}^{4}, 4 σ}_{g}^{2}, {1 π}_{g}^{1}

(above the

{\tilde{A}}^{2} Σ_{g}^{+}

) is subject to the Renner-Teller effect and further exited state depends on the

(^{4} П_{g})

of triplet form. The electron Configuration energies of

{B_{2} N}^{(\mp, 0)}

both in ground and exited states, with HOMO/LUMO amounts are listed in Table 2.

Seifert confirmed that BNB molecule (Figure 1e.) is much more stable compared with BBN (Figure 1c), and that BNB will not dissociate automatically in BN + B or N. +B₂. Bent quartet B₂N (²B₄) : (a₁)²(a₁)² (b₂)²(a₁)²(a₁)²(b₂)²(a₁)(b₁)²(b₂)(a₁) is also found much more stable compared to other species due to the effect of polarization orbitals. Inspection of (<S>²) denotes an excessive amount of spin contamination, actually increases, rather than decreases, spin contamination. Since B₂ is known to have a very low-lying

({\tilde{X}}^{5} \sum_{u}^{-})

state besides the ground

({\tilde{X}}^{3} \sum_{g}^{-})

state, this fact can be interpreted from connecting the

({\tilde{X}}^{5} \sum_{u}^{-})

B₂ to the ⁴S nitrogen atom. Indeed, a

({\tilde{X}}^{6} \sum_{g}^{+})

state B₂N(C_∞v) ;{(σ)² (σ)² (σ)² (σ)² (σ)² (σ)² (π)² (σ) (π)²} was found to lie only 23.0 kcal mol^{- 1} above the doublet state with high value of <S>². For the sextuplets contaminating B₂N(C_∞v)

({\tilde{X}}^{6} \sum_{g}^{+})

, the dynamic correlation would be even smaller. Indeed, B₂N (C_∞v)

({\tilde{X}}^{2} \sum_{g}^{+})

lies 44.9 kcal mol^-1 above B₂N(C_∞v)

({\tilde{X}}^{6} \sum_{g}^{+})

at the UMP4 level, and 69.1 kcal mol^{- 1} at the PMP4 level. At this situation, B₂N has a symmetric linear (D_∞h) structure with

({\tilde{a}}^{2} \sum_{u}^{+})

; ground state with bond distance 1.31 angstrom and frequency around 20201 cm^-1 . It is notable that the B₂N (

{\tilde{a}}^{2} \sum_{u}^{+})

; ) can be stabilized by resonance configuration as follows:

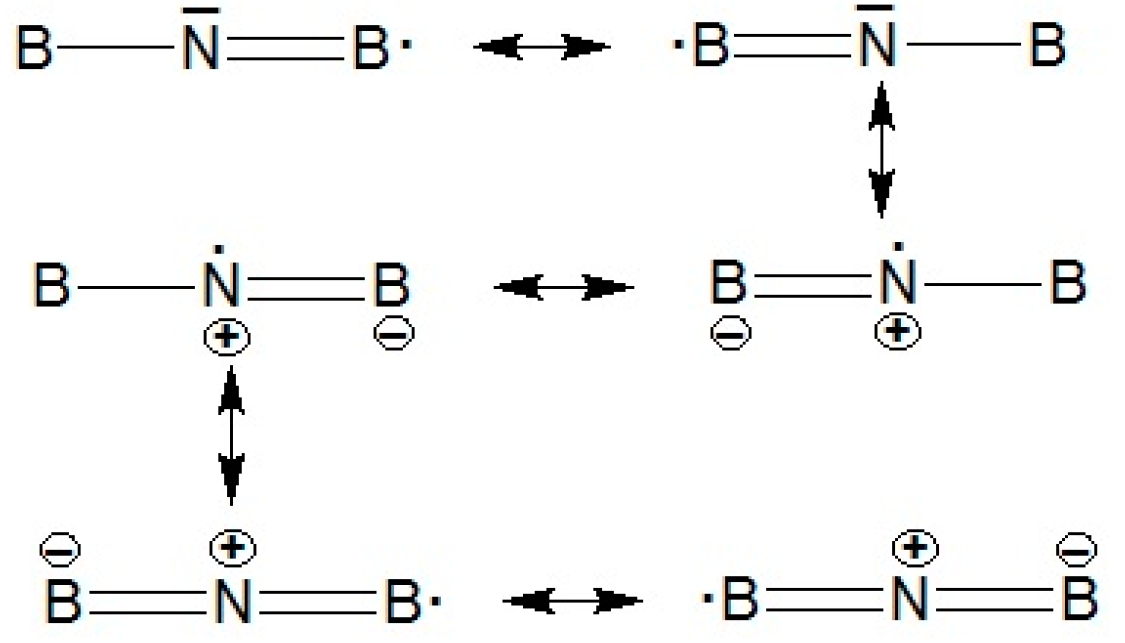
For the quartet state, the C_2v structure B₂N (²B₄) will be most stable. It is isoelectronic with B₃ except for two unpaired ,while B₂N^- is isoelectronic with C₃ ).

3.1.2. N₂ $B^{(\mp, 0)}$

Although our calculations confirm the more stability of BNN than NBN at the global minimum, at the casscf/ccpvxz (x=3, 4) levels, the linear quartet structures of BN₂ (D_∞h) (⁴

Π_{g})

(Tables 1&2) exhibited an symmetrical structure, while (C_∞v) (⁴

Σ_{g}^{-})

shown asymmetrical situation and are predicted to be most stable. At the casscf/cc-pvxz (x=4,5) levels on the other hand, the BN₂ (D_∞h)(⁴

Π_{g})

and (C_∞v)(⁴

Σ_{g}^{-})

is reversed and the bent doublet structure ²B₂(C_2v) is stabilized. During spin rotation, the symmetric linear doublet form of BN₂ (D_∞h)(²

Π_{g})

approaches towards (C_∞v)(⁴

Σ_{g}^{-})

. In addition, an asymmetric linear doublet (C_∞v)(²

Π_{g})

can only be found after considerable amount, even with a lower energy by having a nonzero gradient on the bond angle. At the correlated optimization, BN₂ (C_∞v)(²

Π_{g})

convert to be the most stable structure at this point and through spin rotation, BN₂ (D_∞h)(²

Π_{g})

has only a little different with above items. Both of them are due to RennerTeller effect that theire frequencies are imaginary. As it can be seen in Table 2, a lower energy exists for BN₂ (D_∞h)(²

Π_{g})

at the Hartree-Fock level and also the Hartree fock frequencies may give imaginary variables due to the problem with (C_∞v)(²

Π_{u})

too. At the MP₄SDQ/EPR-II//QCISD/EPR-II levels (Table 2), the bent structure is less stable that the linear one. At the MP₄SDQ/EPR-III//QCISD/EPR-III levels, the Hartree-Fock result is confirmed at the PMP4 level. At both the CASSCF (11, 12)/UHF levels, the linear structure becomes distinctly more stable, by 6.5 and 6.1 kcalmol^-I, respectively. It is remarkable that the BN₂ (D_∞h)(²

Π_{g})

can be stabilized by resonance configuration as follows:

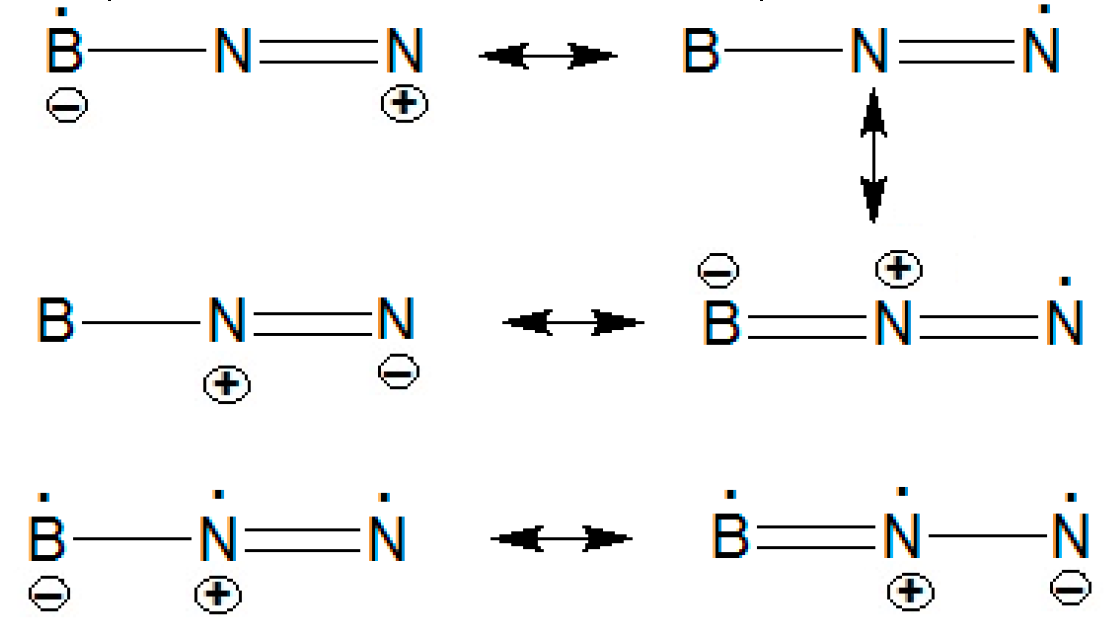
The lowest-lying states Renner-Teller distortions, harmonic frequencies, IR, and Raman are listed in Table 3.

3.2. Thermochemical studies of B2N and BN2

The concerned formulas are exhibited in many textbooks of statistical quantum thermodynamics; expressions may also be found Herzberg book [33, 34] that was used in the present work. Table 4 data exhibit the calculated energies of related reaction at the MP4/6-31G*, PMP4/6-31G*, CCD/6-31G*, and CCD + ST(CCD)/6-31G* levels, along with the LCAO-LDA.

Comparing the quantities optimization of Seifert et al. with our data in this work, it is confirmed that BNB {(D_∞h) (²

Σ_{g}^{-})

} is much more stable than BBN ((C_∞v) (²

Σ_{g}^{+})

), and therefore BNB will not dissociate automatically in either BN + B or B₂ + N.

3.3. Quantum symmetry breaking of N₂ $B^{(\mp, 0)}$ and ${B_{2} N}^{(\mp, 0)}$ and partial charges

One of the targets of this work is to illustrate the difference among the electromagnetic situation of the

{B_{2} N}^{(\mp, 0)}

species due to changing basis sets and methods and also the quantum SB report due to trial wave function. In

D_{\infty h}

position of

{B_{2} N}^{(\mp, 0)}

, the unpaired electron is delocalized, while in the asymmetric

C_{\infty v}

, it is localized on either one of the B atoms. C

\infty

_V by SB structure becomes stronger through changing to

D_{\infty h}

. Based on quantum chemistry theories, the second-order Jahn-Teller effect allows the unpaired electron to localize on boron atom, rather than being delocalized (Table 2 and Figure 3a,b).

The unpaired electron of nitrogen in

{B_{2} N}^{(0)}

(

D_{\infty h}

) is delocalized and it is localized in the asymmetric (

C_{\infty v}

) for both of

{B_{2} N}^{(, 0)}

and

{B_{2} N}^{(-)}

species. Moreover, there is a restriction for the unpaired electron of nitrogen of BNB for delocalization between

D_{\infty h}

and

C_{\infty v}

symmetries states. These limitations between localized and non-localized situations increase the SB effect of the

{B_{2} N}^{(\mp, 0)}

species. Meanwhile, ESP, forces,

γ = {(V}_{B} - V_{N}) / r_{B N}

, attraction and repulsion energies (eV) of

{B_{2} N}^{(\mp, 0)}

in ground and exited states are listed in table 2. The MESP fitting for

{B_{2} N}^{(, 0)}

and the summation of partial charges for two boron and one nitrogen (

B^{{δ q}_{1}} - N^{{δ q}_{2}} - B^{{δ q}_{3}}

) in all models from

∆ = 0.0 t o 0.07

are zero (Table 2). Obviously, the summation of partial charges in

B^{{δ q}_{1}} - N^{{δ q}_{2}} - B^{{δ q}_{3}}

for

{B_{2} N}^{(0)}

radical is not 0.0 and it has changed according to: (0.23+0.23+0.52=0.98) for

∆^{u} = 0.0

, (0.24+0.23+0.52=0.99) for

∆^{u} = 0.02

. The changes among

∆^{u}, ∆^{k}

and

∆^{x}

is due to various methods and basis sets that are used in our work. Certainly, it is related to the the summation of partial charges in

{B_{2} N}^{(0)}

radical that is far from 0.0 and varies between 0.00 and 0.16. It could be due to the fact that the unpaired electron of nitrogen is localized while

{B_{2} N}^{(-)}

is under the influence of the unpaired electron.

Interestingly, for the exited state of

{B_{2} N}^{(0)}

, changing of MESP for both exited and ground states of (

{\tilde{B}}^{4} П_{g}

), (

{\tilde{X}}^{2} \sum_{u}^{+})

, respectively are small. The sum of partial charges (in

B^{{δ q}_{1}} - N^{{δ q}_{2}} - B^{{δ q}_{3}}

) for all items from

∆ = 0.0

∆ = 0.2

are -1, however, the total partial charges of

B^{{δ q}_{1}} - N^{{δ q}_{2}} - B^{{δ q}_{3}}

for

{B_{2} N}^{(-)}

are not -1. The nitrogen of

{B_{2} N}^{(-, +, 0)}

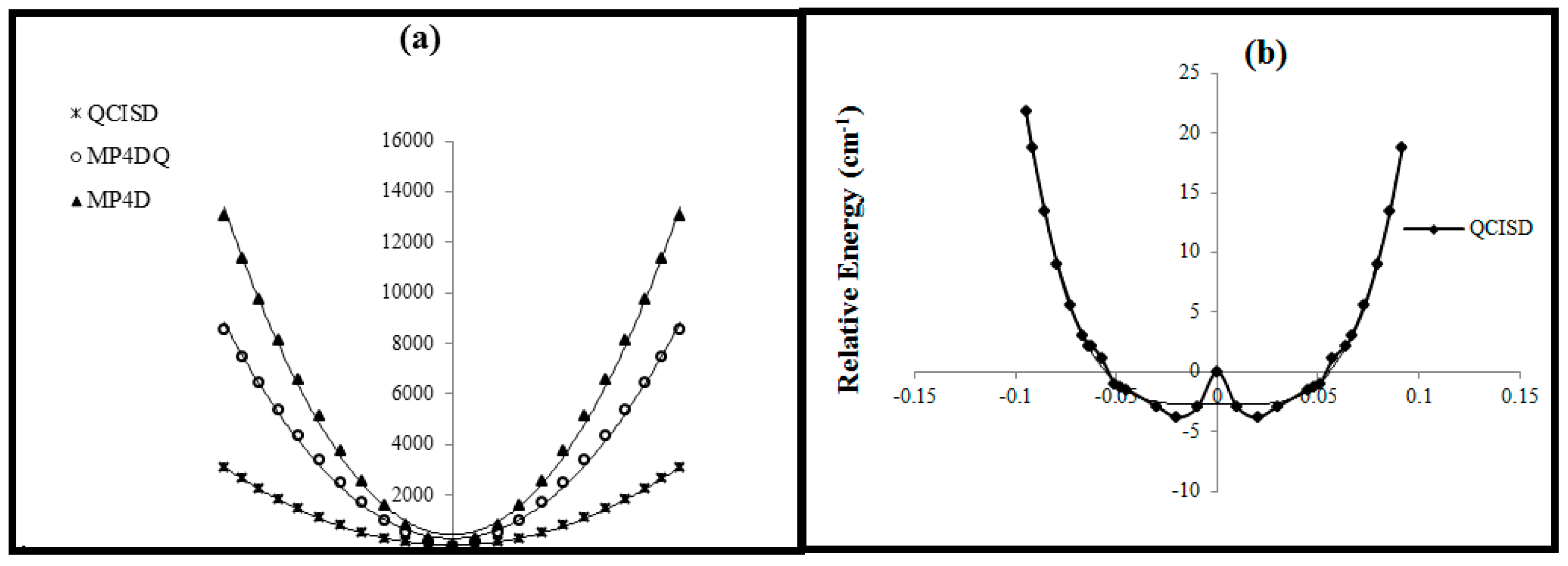
is always positive for radical and anion and negative for cation, while in exited states, the sum of partial atomic charges are positive for all three forms. As it can be seen in Figure 4, radical or anion B₂

N^{(-, 0)}

has not been appeared from these kind calculation, though, for cation, there is a critical point at

90^{°}

for MP₄DQ and MP₄DSQ methods.

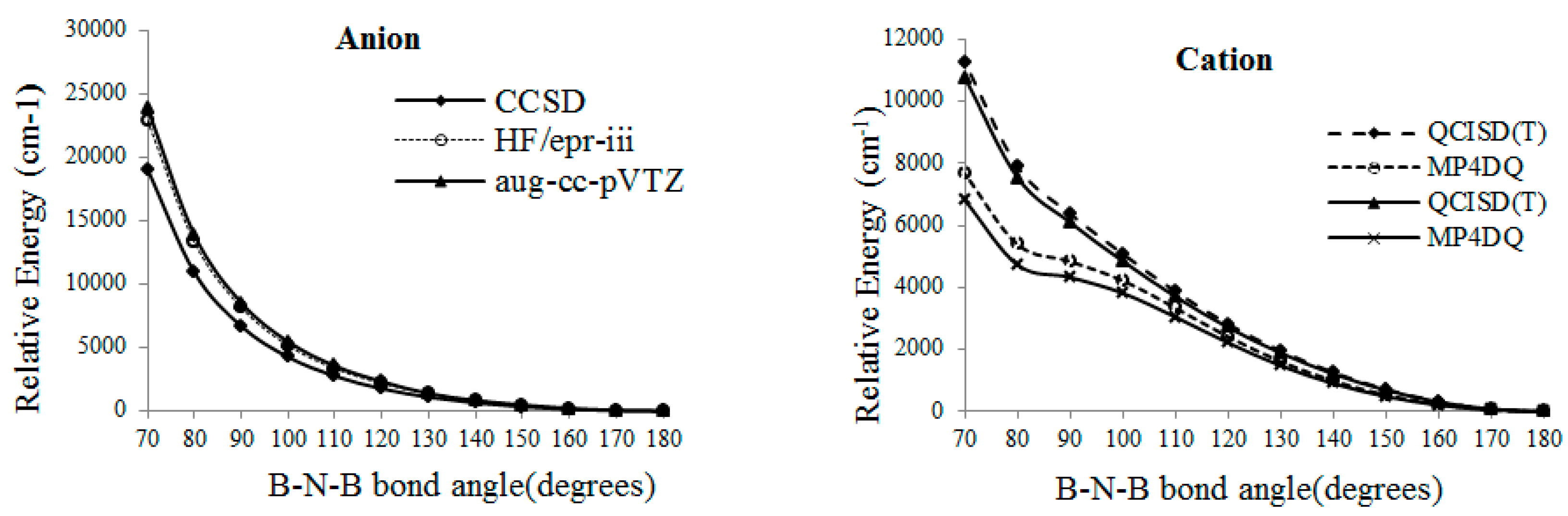
From the SCF calculation, the minimum energy related to a bent structure with an angle around

90^{°}

, however, for the QCISD(T), MP₄DQ, MP₄DSQ and HF/aug-cc-pVTZ calculations (Figure 2), the linear situation has the lowest energies for radical and anion . By consideration wave function, when the BNB has

D_{\infty h}

, the real wave-function might be converting as an irreducible representation of the

D_{\infty h}

. Table 5 presents data for the association enthalpy, entropy, and free energy from the statistical thermodynamic and partition functions, as well as values for the absolute entropy [35-44].

5. Conclusions

The potential surfaces of

{B_{2} N}^{(\mp, 0)}

and

{N_{2} B}^{(\mp, 0)}

, have been studied using several post HF and basis sets methods. CASSCF optimization exhibited SB phenomenon for linear BNB containing an unequal bond length. We found for yielding accurate data doing perturbation theory (CASSCF+PT2) calculation and multi-reference (CI) with (CASSCF+1+2) wave functions are needed. In summary, we have clearly shown , where the SB problem is hidden , usual way to circumvent of peculiarities are the most important feature of this work. In particular, we find the low value for the anti-symmetric stretching fundamental frequency very encouraging, providing an additional support to the idea of actual symmetry breaking in the BNB ground state.

Author Contributions

Majid Monajjemi: Conceptualization and idea, Methodology, , Supervision. Fatemeh Mollaamin: Methodology, Software, Formal analysis, Investigation, Data Curation, Writing-review and editing, Visualization, Resources.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

J.M.L. Martin, J.-P. François, and R. Gijbels, Chem. Phys., 90, 6469 (1989). [CrossRef]
K.R.Asmis, T.R.Taylor, and D.M. Neumark, J. Chem. Phys., 111, 8838 (1999). doi: org/ 10.1063/1.480230.
J.M.L.Martin, J.-P.François, and R. Gijbels, Chem. Phys. Lett., 172, 354 (1990). [CrossRef]
L.B.Knight, Jr.D.W.Hill, T.J.Kirk, and C.A. Arrington, J. Phys. Chem., 96, 5604 (1992). [CrossRef]
J. M. L.Martin, J.-P.François, and R. Gijbels, Chem. Phys. Lett. 193, 243 (1992). [CrossRef]
P. Hassanzadeh, and L. Andrews, J. Phys. Chem. 96, 9177 (1992). [CrossRef]
L. Andrews, P. Hassanzadeh, T. R. Burkholder, and J. M. L. Martin, J.Chem. Phys. 98, 922 (1993). [CrossRef]
C. A. Thompson, and L. Andrews, J. Am. Chem. Soc. 117, 10125 (1995). [CrossRef]
X. Li, and J. Paldus, J. Chem. Phys. 126, 224304 (2007). [CrossRef]
J.M.L. Martin, J. El-Yazal, Mol. Phys. 85,527 (1995). [CrossRef]
G.Meloni, M. Sai Baba, and A. Gingerich, J. Chem. Phys. 113, 8995 (2000). [CrossRef]
W. R. M. Graham, and W. Weltner Jr., J. Chern. Phys. 65, 1516 (1976). [CrossRef]
M. Monajjemi, Chemical Physics. 425, 29 (2013). [CrossRef]
M.Monajjemi, V.S.Lee, M.Khaleghian, B.Honarparvar, F. Mollaamin, J. Phys. Chem. C, 114, 15315 (2010). [CrossRef]
M.Monajjemi, J.E. Boggs, J. Phys. Chem. A, 117, 1670 (2013). [CrossRef]
M. Monajjemi, Struct. Chem. 23, 551 ( 2012). [CrossRef]
L. Mahdavian, M. Monajjemi, Microelectronics journal, 41, 142 (2010). [CrossRef]
Löwdin, P.O. Rev. Mod. Phys. 35, 496 (1963). [CrossRef]
E. P. Wigner, Group Theory and its Application to the Quantum Mechanics of Atomic Spectra, Academic Press, New York, p. 259 (1959).
G. Seifert, B. Schwab, S. Becker, and H. J. Dietze, Int. J. Mass Spectr. Ion Proc. 85, 327 (1988).
V. Barone, Recent Advances in Density functional methods, parts I, Ed. D.P.Chong , world scientific publ. Co, springer, (1996).
X.Blase, A.Rubio, S.G.Louie, and M.L. Cohen, Europhysics Letters (EPL), 28, 335 (1994). [CrossRef]
X. Blase, J.C. Charlier, A.de.Vita, R. Car, Appl. Phys. Lett. 70, 197 (1997). [CrossRef]
W.Han, Y.Bando, K.Kurashima, and T. Sato, Appl. Phys. Lett. 73, 3085 (1998). [CrossRef]
T.E.H. Walker, W. G. Richards, J.chem.phys. 52, 1311 (1970). [CrossRef]
S. Koseki, M.W. Schmidt, and M.S. Gordon, J.phys.chem. 96, 10768 (1992). [CrossRef]
J.A. Pople, M. Head-Gordon, and K. Raghavachari, J.chem.phys., 87, 5968 (1987). [CrossRef]
R.F.W. Bader, Atoms in Molecule: A quantum Theory , Oxford Univ. press, Oxford, (1990).
B.H. Besler, K.M. Merz Jr., and P.A. Kollman, J. comp. Chem. 11, 431 (1990). [CrossRef]
L.E. Chirlian, and M.M. Francl, J.comp.chem. 8, 894 (1987). [CrossRef]
C.M. Breneman, and K.B. Wiberg, J. Comp.Chem. 11, 361 (1990). [CrossRef]
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, (2016).
G. Herzberg, Infrared and Raman Spectra ofPolyatomic Molecules (Van Nostrand Reinhold, New York), p. 521 If. (1945).
Manual ofsymbols and Terminology for Physico-chemical Quantities and Units (prepared by M. L. McGlashan, revision prepared by M. A. Paul, second revision by D. H. Whilfen) , Pure Appl. Chern. 51,1 (1979).
S. Bagheri, M.Monajjemi, A. Ziglari , A. Taghvamanesh ,Russian Journal of Physical Chemistry B, 15, S140-S148 (2021). [CrossRef]
M. A. Ashraf, Z. Liu & M. Najafi , Russian Journal of Physical Chemistry B, 14, 217-221 (2020). [CrossRef]
Yu. Shaulov, L. V. Vladimirov, A. V. Grachev, V. M. Lalayan, E. M. Nechvolodova, R. A. Sakovich, V. K. Skachkova, E. V. Stegno, L. A. Tkachenko, S. A. Patlazhan & A. A. Berlin, Russ. J. Phys. Chem. B, 14, 183-189 (2020). [CrossRef]
E.A. Lebedeva, S.A. Astaf’eva, T.S. Istomina, Russ. J. Phys. Chem. B, 16, 316-322 (2022). [CrossRef]
A.G. Korotkikh, I.V. Sorokin, E.A. Selikhova, V. A. Arkhipov, Russ. J. Phys. Chem. B, 14, 592-600 (2020). [CrossRef]
A.G. Korotkikh, I.V. Sorokin, V.A. Arkhipov, Russ. J. Phys. Chem. B, 16, 253-259 (2022). [CrossRef]
Gerasimov, G. N. ; Gromov,V. F.; Ikim, M. I.; L. I. Trakhtenberg, Effect of Composition and Structure of Metal Oxide Composites Nanostructured on Their Conductive and Sensory Properties, Russ. J. Phys. Chem., 2021, 15, 1072–1083. https://doi.org/ 10.1134/ S199079 31 21310018.
Kablov, V.F., Strakhov, V.L., Kaledin, V.O. et al. Mathematical Modeling of the Physicochemical Properties of a Heat-Shielding Material from Highly Filled Elastomers. Russ. J. Phys. Chem. B 2021, 15, 880–887. https://doi.org/ 10.1134/S199079 3121050043.
Sarvendra Kumar, Surbhi & Yadav, M.K. Optimized Molecular Geometries, Internal Coordinates, Vibrational Analysis, Thermodynamic Properties, First Hyperpolarizability and HOMO–LUMO Analysis of Duroquinone Using Density Functional Theory and Hartree–Fock Method. Russ. J. Phys. Chem. B 2021, 15 (Suppl 1), S22–S31. https://doi.org/ 10.1134/S1990793121090116.
Sakovich, R.A., Shaulov, A.Y., Nechvolodova, E.M. et al. Energy of Intramolecular Interactions and Structure of Metallophosphate Polycomplexes with Water Molecules and Nitrogen-Containing Compounds. Russ. J. Phys. Chem. B 2020, 14, 516–521. [CrossRef]

Figure 1. Stationary points for BN₂, NB₂, and B₃; Bond distances in Angstrom units.

Figure 2. The cuts of the PES along the symmetric ® and asymmetric

(∆)

stretching by E( R) and E(

∆)

, respectively.

Figure 2. The cuts of the PES along the symmetric ® and asymmetric

(∆)

stretching by E( R) and E(

∆)

, respectively.

Figure 3. The B₂

N^{(-, 0, +)}

relative energies versus B-N-B bond distance in (a) for cation, (b), for radical.

Figure 3. The B₂

N^{(-, 0, +)}

relative energies versus B-N-B bond distance in (a) for cation, (b), for radical.

Figure 4. Relative energies of B₂

N^{(-, +)}

versus B-N-B bond angle in various levels of theory.

Figure 4. Relative energies of B₂

N^{(-, +)}

versus B-N-B bond angle in various levels of theory.

Table 1. Electronic configurations and expectation values for <S²> by casscf/cc-pvxz (x=3) level of theory

Item	molecule	Point group	Term	${{< S}^{2} >}^{a}$	$< {S_{1}^{2} >}^{b}$	$< {S_{A}^{2} >}^{c}$	Electronic configuration
(a)	B₃	D_∞h	² $Π_{g}$	1.80	1.80	0.84	(σ_g)²(σ_u)²(σ_g)²(σ_g)²(σ_u)²(σ_g)(σ_u)(π_u)³
(b)	B₃	D_∞h	⁴ $Π_{u}$	3.80	3.75	3.70	(σ_g)²(σ_u)²(σ_g)²(σ_g)²(σ_u)²(σ_g)(σ_u)(π_u)³
(c)	BN₂	C_∞v	² $Π_{g}$	0.85	0.80	0.75	(σ)² (σ)² (σ)² (σ)² (σ)² (σ)² (π)⁴ (σ)² (π)
(d)	BN₂	C_s	⁴ $A_{2}$	1.35	1.30	0.90	(aʹ)² (aʹ)² (aʹ)² (aʹ)² (aʹ)² (aʹ)² (aʹ)² (aʺ)² (aʹ)² (aʹ)² (aʺ)²
(e)	BN₂	D_∞h	² $Π_{g}$	0.90	0.90	0.81	(σ_g)²(σ_u)²(σ_g)²(σ_g)²(σ_u)²(σ_g)²(π_u)⁴ (σ_u)² (π_g)
(f)	B₃	D_∞h	² $Π_{g}$	1.80	1.80	0.85	(σ_g)²(σ_u)²(σ_g)²(σ_g)²(σ_u)²(σ_g) (σ_u) (π_u)³
(g)	B₃	D_∞h	⁴ $Π_{g}$	3.80	3.80	3.70	(σ_g)²(σ_u)²(σ_g)²(σ_g)²(σ_u)²(σ_g) (σ_u) (π_u)³
(h)	BN₂	C_2v	² $A_{g}$	1.40	1.30	1.10	(a₁)² (b₁)²(a₁)²(a₁)²(b₂)²(a₁)²(b₁)² (b₂)²(a₁)²(a₂)
(i)	B₂N	C_∞v	² $Σ_{g}^{+}$	2.30	2.25	2.60	(σ)² (σ)² (σ)² (σ)² (σ)² (σ)² (σ) (π)⁴ (b₁)²(b₂)²(a₁)²
(j)	B₂N	C_∞v	⁴ $Σ_{g}^{+}, Σ_{g}^{-}, ∆$	4.00	4.00	3.74	(σ)² (σ)² (σ)² (σ)² (σ)² (σ)² (π)³ (σ) (π)
(k)	BN₂	C_2v	⁴ $B_{1}$	3.80	3.80	3.70	(a₁)² (b₂)²(a₁)²(a₁)²(b₂)²(a₁)²(b₁)² (a₁)²(a₁) (b₂) (a₂)

Table 2. Geometries and electrical properties of B₂

N^{(0)} = 17 e

, B₂

N^{(-)} = 18 e

and B₂

N^{(+)} = 16 e

in ground and exited states.

Table 2. Geometries and electrical properties of B₂

N^{(0)} = 17 e

, B₂

N^{(-)} = 18 e

and B₂

N^{(+)} = 16 e

in ground and exited states.

State (*N_e)	$E_{e} (H a r t r e e)$	Total Configuration (Energy of $\|α〉 * (H o m o - L u m o)$ **	$β$ Configuration Energy of $\|β〉 $ Beta virtual*	$r_{e} (B_{1} N) r_{e} (N B_{2})$	$A_{1} (2,1, 3, - 2, - 1) A_{2}$ $(2,1, 3, - 1, - 2)$
$\tilde{X}$ ²Σ⁺ ${(C}_{\infty v})$ (*17e)	${- 104.078196}^{a} {- 104.082033}^{a^{'}} {- 104.075492}^{a^{''}}$	${[A], π}^{4}, σ^{2}, σ^{1} \|α〉 = - 0.4464 1^{a} * E (\|α〉) (- 34.87083)^{a} * * (- 0.48614)^{a}$	$[B] σ^{1} \|β〉 = - 0.2618 0^{a} * (- 34.15046)^{a} * * (- 0.17697)^{a}$
${\tilde{X}}^{2} Σ_{u}^{+}$ ( $D_{\infty h})$ (*17e)	$- 103.639678$	${[A^{'}] π_{u}^{4}, 4 σ}_{g}^{2} {, 3 σ}_{u}^{1} \|α〉 = - 0.4247 7^{d} * (- 34.74888)^{d} * * (- 0.49245)^{d}$	$[B^{'}], {4 σ}_{g}^{1} \|β〉$ =-0.24844^d $* (- 34.06924)^{d}$ ** ${(- 0.18742)}^{d}$	$1.317$ 6^d $1.317 6^{d}$	$A_{1} = 180 . 0^{d} A_{2} = {180.0}^{d}$
${\tilde{A}}^{2} Σ_{g}^{+}$ (*17e)	$- 104.10475 9^{k} - 104.07817 3^{K^{'}}$	${[A^{'}] π_{u}^{4}, 4 σ}_{g}^{1} {, 3 σ}_{u}^{2} \|α〉 = - 0.4463 8^{u} * (- 34.8744)^{u} * * (- 0.48626)^{u}$	${[A^{'}] π_{u}^{4}, 4 σ}_{u}^{1}, = - 0.26134 * (- 34.15408) * * (- 0.17666$ )	$1.315 4^{k} 1.315 4^{k}$	$A_{1} = 180 . 0^{k} A_{2} = {180.0}^{k}$
${\tilde{B}}^{4} П_{g}$ (*17e)	$- 104.02970 2^{h} - 104.01411 7^{a}$	${[A^{'}] π}_{u}^{4}, π_{g,}^{2} σ_{g}^{1} \|α〉 = - 0.2689 9^{h} * (- 35.04484)^{h} * (- 0.30125)^{h}$	$[A^{'}], π_{u}^{2} \|β〉 = - 0.496 5^{h} * (- 33.74801) * * (- 0.50595)$	$* 1.307 9^{x} * 1.307 9^{x}$	${* A}_{1} = 180 . 0^{x} {* A}_{2} = 180^{x}$
${\tilde{X}}^{1} Σ_{g}^{+}$ (*18e)	${- 104.196567}^{a} - 104.20191 4^{a^{'}} - 104.19501 7^{a^{''}}$	${[A^{'}] 1 π_{u}^{4}, 4 σ}_{g}^{2} {, 3 σ}_{u}^{2} = - 0.1390 4^{a} * E (\|α〉) = - 32.486 47^{a} * * - 0.36286$		$* 1.33 5^{y} * 1.33 5^{y}$	$A_{1} = * 180 . 0^{y} A_{2} = * {180.0}^{y}$
${\tilde{X}}^{1} Σ_{g}^{+}$ (*18e)	${- 104.196566}^{b}$	$* E (\|α〉) = - 32.4864 4^{b}$		$1.329 1^{b} 1.3291$	$A_{1} = 180 . 0^{b} A_{2} = 180.0$
$\tilde{B}$ ³Σ_g (*16e)	$- 103.76092 2^{a} - 103.77671 1^{h} - 103.76285 5^{a^{'}} - 103.75905 8^{a^{''}}$	${{[A^{'}] 4 σ}_{g}^{1} {, 3 σ}_{u}^{1}, π_{u}^{4},}^{a} π_{u}^{2} \|α〉 = - 0.7432 3^{a} * E (\|α〉) (- 37.33372)^{a} * * (- 0.53385)^{a}$	${[A^{'}], π_{u}^{2} \|β〉 {= - 0.75222}}^{a} * E (\|β〉) (- 35.72475)^{a} * * (- 0.5213 1^{a}$	$* 1.297 6^{w} * 1.297 6^{w}$	$A_{1} = * 180 . 0^{w} A_{2} = * 180 . 0^{w}$

(a)QCISD/EPR-III;(d)CASSCF(11,12)/UHF;(z)b3p86/6-31g*;(a^')MP₄D/EPR-III//QCISD/EPR-III; (m)CASSCF(10,12)/EPR-III(x)b3lyp/6-31g*;(a'')MP₄SDQ/EPR-III//QCISD/EPR-III; (g)CASSCF(10,12)rohfAUG-cc-pvqz;(y)m062x/epr-ii;(b)QCISD/EPR-III(

[A] : {1 σ}^{2}, 2 σ^{2}, 3 σ^{2}, {4 σ}^{2}, {5 σ}^{2}

; :(w)b3lyp/6-31g*;(c) QCISD/EPR-II

[A^{'}] : {1 σ}_{g}^{2}, {1 σ}_{u}^{2} {, 2 σ}_{g}^{2}, {3 σ}_{g}^{2} {, 2 σ}_{u}^{2}

; (v)CASSCF(11,12)/AUG-cc-pvqz;(c')MP₄D/EPR-II//QCISD/EPR-II:

[B] : σ^{1}, σ^{1}, σ^{1} {, σ}^{1}, σ^{1}, π^{2}

; (c'')MP₄SDQ/EPR-II//QCISD/EPR-II; [

B^{'}

{1 σ}_{g}^{1}, {2 σ}_{g}^{1} {, 1 σ}_{u}^{1}, {3 σ}_{g}^{1} {, 2 σ}_{u}^{1}, {1 π}_{u}^{2}

; (f) CBS-lq; (h)QCISD(T)/EPR-III; [C]:

{1 σ}_{g}^{2}, {1 σ}_{u}^{2} {, 2 σ}_{g}^{2}, {3 σ}_{g}^{2} {, 2 σ}_{u}^{2}, {4 σ}_{g}^{2}

; (n)CBS4O; (u) TD/EPR-II ; (k) TD/EPR-III//QCISD (T)/EPR-III;

{(K}^{'})

TD/EPR-III//QCISD /EPR-III;

[C^{'}] : {1 σ}_{g}, {1 σ}_{u} {, 2 σ}_{g} {, 3 σ}_{g} {, 2 σ}_{u}

; [D]:

{1 σ}_{g}^{2}, {2 σ}_{g,}^{2} {1 σ}_{u}^{2}, {3 σ}_{g}^{2} {, 2 σ}_{u}^{2}

Table 3. Harmonic frequencies, IR intensities and Raman activities of the most important clusters.

			ν₃				ν₃			ν₂
Item	Point group	Term	cm^-1	IR	Ram an	cm^-1	IR	Raman	cm^-1	IR	Ra man	E_sp(kcal.mol ^-1₎
B₂N	C_∞ν	² $Σ_{g}^{+}$	229	9	23	229	9	23	1355	12	10	4.08
B₂N	D_∞h	² $Σ_{u}^{+}$	78	4	0	229	9	23	1122	0	4	4.87
BN₂	C_∞ν	² $Π_{u}$	111	12	15	244	10	7	907	12	10	4.45
BN₂	C_s	² $A_{1}^{"}$	109	-	-	287	15	6	944	35	23	4.76
BN₂	C_ν	⁴ $Σ_{u}^{-}$	85	2	3	400	1	3	1132	15	16	4.23
BN₂	D_∞h	² $Π_{g}$	-	-	-	176	19	0	1565	17	9	4.79
BN₂	C_2ν	² $A_{1}^{'}$	-	-	-	102	-	-	1653	78	14	3.54
BN₂	C_2ν	² $A_{2}^{'}$	-	-	-	1088	1	5	1432	14	54	5.01
BN₂	C_2ν	² $B_{1}^{'}$	-	-	-	-	-	-	1343	18	52	3.99

Table 4. Energies (kcal mol^{- 1} )of boron nitried reactions at various levels.

Reaction	MP₄D/EPR-III// QCISD/EPR-III	QCISD/ EPR-III	CASSCF(10,12) /EPR-III	TD/EPR-III// QCISD	QCISD/ EPR-II	CBS-lq
B₂N → BN + B	6.44	5.34	5.74	5.03	4.99	4.87
B₂N → B₂ + N	7.35	7.12	7.24	6.99	6.04	5.99
BN₂ → BN + N	4.91	4.21	4.33	4.38	4.33	4.21
BN₂ → N₂ + B	0.15	0.18	0.16	0.19	0.21	0.09

Table 5. Calculated thermodynamic properties at some selected temperatures.

Temperature (K)	B₂N^(-)	BN₂^(-)	B₂N⁽⁺⁾	BN₂⁽⁺⁾	B₂N⁽⁰⁾	BN₂⁽⁰⁾
Association enthalpy (kcal/mol)
0 300 1000 20000	-266.5 -266.1 -269.1 -269.8	-225.1 -227.1 -228.9 -230.1	-208.5 -211.4 -210.08 -203.05	-199.09 -205.03 -205.96 -202.08	193.07 -201.05 -204.55 -205.01	194.08 -207.02 -203.63 -208.07
Free energy of association (kcal/mol)
0 300 1000 20000	-264.92 -247.97 -203.97 -139.95	-225.04 -206.95 -160.08 -89.92	-206.99 -192.05 -135.95 -65.04	-199.04 -185.09 -131.40 -75.83	200.05 -203.05 -207.95 -204.09	200.49 -200.06 -202.91 -205.06

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

127

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum Dynamic Approach of B2N(∓,0) and N2B(∓,0) Clusters Study: A Symmetry Breaking due to the JAHN-TELLER Effect

Abstract

Keywords:

Subject:

1. Introduction

1.1. The structure of boron nitride clusters

1.2. Potential energies surfaces (PESs)

2. Computational details and Methods

3. Results and Discussion

3.1. Molecular orbital description

3.1.1. B2 N ( ∓ , 0 )

3.1.2. N2 B ( ∓ , 0 )

3.2. Thermochemical studies of B2N and BN2

3.3. Quantum symmetry breaking of N2 B ( ∓ , 0 ) and B 2 N ( ∓ , 0 ) and partial charges

5. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

Quantum Dynamic Approach of B₂N^(∓,0)and N₂B^(∓,0)Clusters Study: A Symmetry Breaking due to the JAHN-TELLER Effect

3.1.1. B₂ $N^{(\mp, 0)}$

3.1.2. N₂ $B^{(\mp, 0)}$

3.3. Quantum symmetry breaking of N₂ $B^{(\mp, 0)}$ and ${B_{2} N}^{(\mp, 0)}$ and partial charges