A Simple Hidden Markov Model Could Prevent Physician Error in Failure To Diagnose Infectious Mononucleosis

Preprint

Article

A Simple Hidden Markov Model Could Prevent Physician Error in Failure To Diagnose Infectious Mononucleosis

Altmetrics

Downloads

277

Views

357

Comments

Vanathi Gopalakrishnan^*

This version is not peer-reviewed

Submitted:

18 April 2023

Posted:

19 April 2023

You are already at the latest version

Alerts

Abstract

Infectious mononucleosis (Mono) is mostly caused by the Epstein-Barr virus (EBV), and can spread through infected people sharing food and drinks with others. Once this virus gets into your system, it is there to stay. The virus can get activated when a person has low immunity and can cause major complications. Furthermore, if physicians miss the diagnosis of this disease, and prescribe penicillin-based antibiotics, it can cause severe rash and adverse reactions that compromise patient safety. This paper develops a simple Hidden Markov Model using which a Viterbi algorithm provides the maximum a posteriori probability estimate for the most likely hidden state path, given a sequence of symptoms arising as observations from a patient with hidden EBV positive or negative states. Apart from bringing awareness to help reduce missed diagnoses and subsequent adverse events, this work provides a tool for health care systems to better incorporate prompts during electronic medical record (EMR) interactions to help physicians catch potential missed diagnoses during a visit. This research demonstrates how statistical models can be used to assess likelihood of underlying conditions that require tests to be offered by physicians in order to make a definitive diagnosis. The model developed and applied herein for estimating likelihood of EBV infection from a series of observations has the potential to alter guidelines within healthcare systems to ensure that the safety of patients, particularly teens, is not compromised due to a lack of definitive diagnosis for Mono at point of care.

Keywords:

Subject: Public Health and Healthcare - Primary Health Care

Key Messages

What is already known on this topic – Infectious mononucleosis (Mono) is a viral syndrome characterized by fever, pharyngitis and posterior cervical lymphadenopathy and most often affects adolescents and young adults 15 to 24 years of age. EBV infection is extremely common worldwide (approximately 90% of adults becoming antibody-positive before the age of 30), and 75% of young adults between the ages of 18 and 22 developing Mono months after being infected by EBV, which stays dormant and can cause major complications in individuals with compromised immunity.

What this study adds – Inspite of EBV infection and Mono being so prevalent, physicians can fail to order the necessary tests to confirm this diagnosis. They may order antibiotics for a pediatric patient without considering Mono as a possibility, and perhaps not realizing that certain antibiotics can cause severe adverse reactions such as a maculopapular rash, that usually arises between 3 and 10 days of taking penicillin and its multi-drug combinations such as Augmentin. This study develops a probabilistic model using which the likelihood of hidden states such as EBV infection can be easily estimated so that physicians can be alerted by building prompts into future EMRs.

How this study might affect research, practice or policy – This research provides a model containing probabilities that describe the EBV infection as a possible hidden state and demonstrates how the likelihood of EBV can be calculated to ensure that Mono is not missed by physicians (via a possible change in policy or practice within healthcare), especially since there exist highly sensitive tests for EBV, which can be readily ordered at the time of clinical visit. This research also highlights the utility of Markov models such as developed herein for estimating and comparing probabilities associated with likelihoods of hidden disease states, which can be used more broadly for medical knowledge engineering.

Introduction

Infectious mononucleosis (Mono), also known as glandular fever or the kissing disease, is caused most often by the Epstein-Barr virus (EBV), and can be diagnosed by serological analysis.[1,2,3,4,5,6,7,8,9,10,11] Blood tests can help diagnose mononucleosis by detecting specific antibodies that the body produces in response to EBV. The two types of antibodies that are typically detected are immunoglobulin M (IgM) and immunoglobulin G (IgG). A positive test for IgM antibodies indicates a recent infection, while a positive test for IgG antibodies indicates a past infection. A complete blood count (CBC) can help diagnose mononucleosis by showing an increased number of white blood cells, particularly lymphocytes, which are the cells targeted by EBV. While the monospot test is a rapid diagnostic test that detects the presence of heterophile antibodies that are produced in response to EBV within a few hours, it may miss infections that are in the beginning stages. The EBV DNA testing is highly reliable and sensitive and can detect the presence of EBV DNA in the blood, enabling accurate diagnosis of current and past infections in a few days, typically around 3 days after the patient provides their blood sample to the testing lab.

The diagnosis of Mono is often made based on a combination of symptoms, physical examination, and laboratory tests.[12] It is well known that if certain antibiotics are prescribed to a patient who was not tested for Mono but was positive, the patient could develop a rash that can spread all over the body and cause swelling and itching that can last for days and weeks.[13,14,15,16,17,18,19,20,21,22] Other complications could potentially arise from failure of a physician to diagnose Mono by ordering appropriate tests.[23,24,25,26,27] This research was motivated by the observation that ordering these tests is rather painless especially given the wide adoption of electronic medical records in current healthcare systems, and once the patient tests negative for Strep throat infections in the clinic. We will also assume that the patient tested negative for other infectious diseases such as COVID-19 which have rapid tests available. Since EBV infection is extremely common worldwide, with approximately 90% of adults becoming antibody-positive before the age of 30, with a recent study determining that 75% of young adults between the ages of 18 and 22 develop typical infectious mononucleosis after primary EBV infection.[28] Mono is a viral syndrome characterized by fever, pharyngitis (“sore throat”), and posterior cervical lymphadenopathy (“swollen neck or glands”) and most often affects adolescents and young adults 15 to 24 years of age.[29] Pediatricians particularly need to avoid missing the Mono diagnosis especially when these primary signs are obvious. This paper presents a reasonably easy tool that can be used for training physicians to think in terms of probabilities and hidden states, using both pen and paper analyses, as well as simple programming that could be taught as part of the Medical curriculum.

Decision theory has been employed by medical practitioners and physician training has included algorithmic approaches to decision making for most of this past century.[30,31] Even though the actual use of these techniques are limited in clinical practice, decision theoretic approaches which combine probabilities with utilities such as cost/risk, enable guidelines for patient management. The work presented in the methods section below demonstrates statistical methods that can be used to assess the probabilities of hidden causes for observed symptoms over time. Such probabilities of observed sequences arising from probable causes can easily be compared computationally and used as input to decision theoretic calculations which can include the other parameters used for risk assessment conveyed numerically as utilities.

Methods

Hidden Markov Models (HMMs) are statistical models that are commonly used in many real-world applications and are also very popular in Bioinformatics.[32] As an artificial intelligence tool, HMMs have been most extensively used in speech recognition. A HMM is a generative model in that it consists of a set of states that are hidden, which emit a sequence of observations with associated probabilities. There are two types of probabilities that comprise a HMM – the state transition probabilities, and the emission probabilities. Apart from these, there is an initial distribution of probabilities for starting in any of the hidden states. Once you are in a state, the transition probabilities inform the model as to how likely it is to remain in the same hidden state, versus transitioning to other states in the model. The emission probabilities provide the distribution for how likely a particular observation arose due to that hidden state in the model. Given an observation sequence, there exist well-known algorithms for HMMs that can estimate the most likely hidden state path (Viterbi algorithm), and the probability of that sequence given the HMM.

The Viterbi algorithm takes as input the following:

and outputs the following:

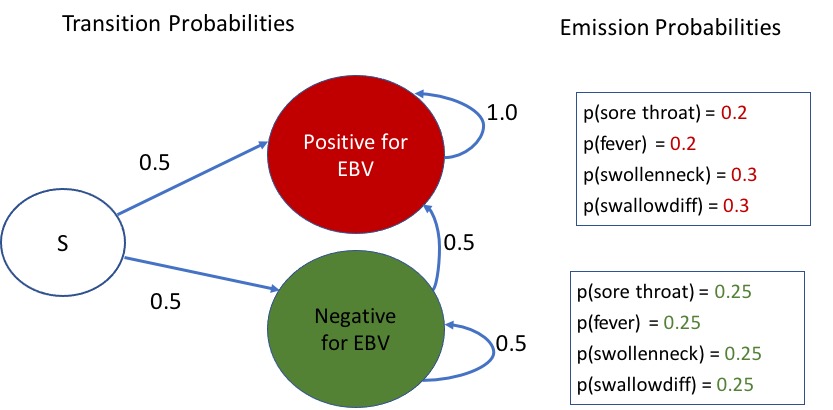
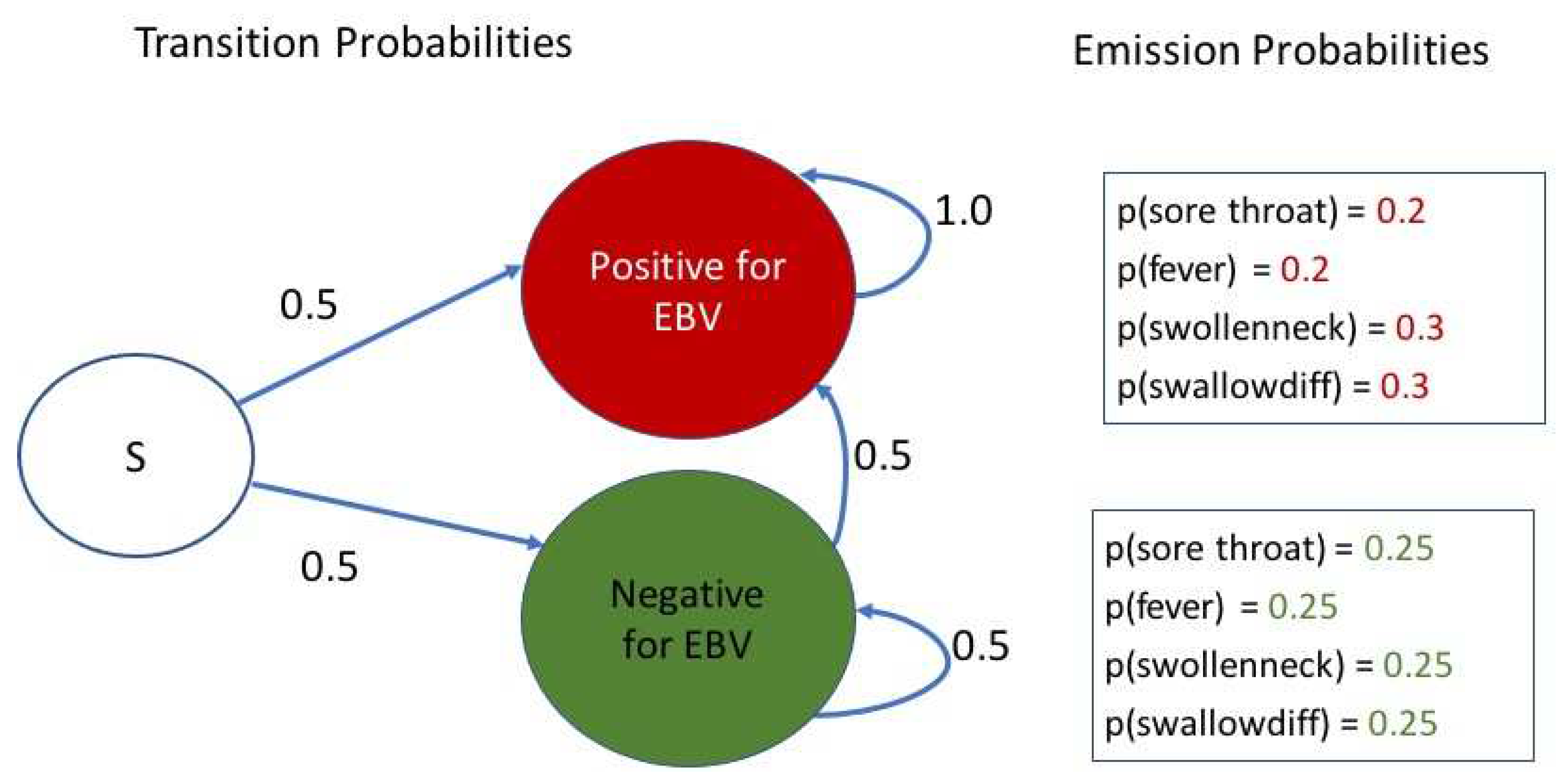
A simple Hidden Markov Model (HMM) for a patient who tests negative for Strep Throat and other infections such as COVID-19, is presented below for considering EBV positive/negative status:

Let the start state (S) represent the Absence of Strep Throat and also that other simple rapid tests such as for COVID-19 were also negative. The HMM in Figure 1 shows the transition probabilities between the start state S, and the two possible hidden states – “Positive for EBV” and “Negative for EBV”. Once someone is in the positive state, since EBV stays on in the body, and the EBV blood test can reveal past infections as well, there is a zero transition probability to the negative state. If one is in the negative state, there is an equal chance of transitioning between negative and positive states, similar to the distribution from start state (initial probabilities).

Apart from the state transition probabilities, a HMM has emission probabilities associated with each hidden state. Let us define the set of possible observations as comprising of “sorethroat”, “fever”, “swollenneck”, and “swallowdiff” to denote the presence of a sore throat, fever, swollen neck or glands, and difficulty swallowing. These can be appropriately optimized by health systems and physicians. For our demonstration of the power of these models for estimating the most probable hidden state sequence from observations, these appear adequate. We next provide equal emission probabilities of 0.25 to each of these four observations when in the EBV negative state, and assign {0.2, 0.2, 0.3, 0.3} as the respective emission probabilities in the EBV positive state. These are also shown in Figure 1.

The famous Viterbi algorithm is used to calculate the most likely sequence of hidden states or state path, given the observed emissions, via calculating the maximum a posteriori probability of that most likely state path. The Viterbi algorithm is a dynamic programming algorithm, and calculations can be done easily even by hand (see Table 1) for a small sequence of observations. There are python implementations of this algorithm that can also be utilized. Using the simple python implementation recommended by ChatGPT, the author was able to verify the calculations that were done by hand using this above simple HMM. Below are some sample observations, and results from application of the Viterbi algorithm to determine the most likely sequence of hidden states and associated probability. It must be noted that probabilities always get smaller as they are multiplied. The maximum probability for the most likely state path for the sequence of observations is calculated keeping track of the most likely hidden state sequence. The >>> refers to the command line prompts used to specify the observations, run the Viterbi python program and observe the outputs opt and max_prob, which are the variables containing the most likely hidden state path and maximum probability for the observation, obs.

>>> obs = ["sorethroat"]
>>> opt, max_prob = viterbi(obs, states, start_p, trans_p, emit_p)
>>> print("Most likely hidden states:", opt)
(’Most likely hidden states:’, [’NegativeforEBV’])
>>> print("Probability of most likely hidden states:", max_prob)
(’Probability of most likely hidden states:’, 0.125)
>>> obs = ["swollenneck"]
>>> opt, max_prob = viterbi(obs, states, start_p, trans_p, emit_p)
>>> print("Most likely hidden states:", opt)
(’Most likely hidden states:’, [’PositiveforEBV’])
>>> print("Probability of most likely hidden states:", max_prob)
(’Probability of most likely hidden states:’, 0.15)
>>> obs=["sorethroat", "fever", "sorethroat", "fever", "swollenneck", "swallowdiff"]
>>> opt, max_prob = viterbi(obs, states, start_p, trans_p, emit_p)
>>> print("Most likely hidden states:", opt)
(’Most likely hidden states:’, [’PositiveforEBV’, ’PositiveforEBV’, ’PositiveforEBV’, ’PositiveforEBV’, ’PositiveforEBV’, ’PositiveforEBV’])
>>> print("Probability of most likely hidden states:", max_prob)
(’Probability of most likely hidden states:’, 7.200000000000002e-05)
>>> obs=["sorethroat", "fever"]
>>> opt, max_prob = viterbi(obs, states, start_p, trans_p, emit_p)
>>> print("Most likely hidden states:", opt)
(’Most likely hidden states:’, [’PositiveforEBV’, ’PositiveforEBV’])
>>> print("Probability of most likely hidden states:", max_prob)
(’Probability of most likely hidden states:’, 0.020000000000000004)
>>> obs = ["sorethroat", "fever", "swollenneck"]
>>> opt, max_prob = viterbi(obs, states, start_p, trans_p, emit_p)
>>> print("Most likely hidden states:", opt)
(’Most likely hidden states:’, [’PositiveforEBV’, ’PositiveforEBV’, ’PositiveforEBV’])
>>> print("Probability of most likely hidden states:", max_prob)
(’Probability of most likely hidden states:’, 0.006000000000000001)
>>> obs = ["sorethroat", "fever", "swollenneck", "swallowdiff"]
>>> opt, max_prob = viterbi(obs, states, start_p, trans_p, emit_p)
>>> print("Most likely hidden states:", opt)
(’Most likely hidden states:’, [’PositiveforEBV’, ’PositiveforEBV’, ’PositiveforEBV’, ’PositiveforEBV’])
>>> print("Probability of most likely hidden states:", max_prob)
(’Probability of most likely hidden states:’, 0.0018000000000000002)

From the above analyses, it is clear that if just sore throat or fever was present as a single observation, the hidden state is more likely to be Negative for EBV. But, even having both or just a single more severe symptom such as swollen neck, would result in the most likely hidden state sequence becoming Positive for EBV. The calculations that are performed by hand to estimate the maximum a posteriori probability of the sequence {“sorethroat”, “fever”, “swollenneck”, “swallowdiff”} are shown in Table 1. In dynamic programming, each previously calculated maximum probability for each previous hidden state is utilized in the computation for observing an emission in the current state, and the state that gives rise to the maximum probability in the current state is then kept track off using the backtrace pointer. Backtracking from the final maximum probability cell at the final observation, provides the hidden state sequence that is most likely as per the HMM and the Viterbi algorithm. The forward algorithm for HMM can also be used as needed to determine the probability of the sequence given the model.

The Viterbi algorithm calculates the maximum of the probabilities of transitioning from each previous hidden state, at each step in the sequence, and emitting that particular symbol in the current state, as represented by the calculations for each cell along each column of Table 1. The emission probabilities for seeing the observation specified in the column header, is multiplied along with the probability of transitioning from each the previous hidden states, and the maximum probability for the observations up to that previous state. Then the maximum of these probabilities and the hidden previous state that gave rise to that maximum probability are stored for each cell. In Table 1, the blue arrows are used to enable backtracking from the maximum probability state, to previous hidden states that yielded the maximum probability observation in the current state. Backtracking via these pointers reconstructs the most likely hidden state sequence for the full set of 4 observations in this example.

Discussion

The above simple HMM model is representative of Markov modeling as a powerful tool for reasoning about hidden states that are important for accurate medical diagnosis and preventing medical errors. If more physicians were educated in these types of reasoning, it is likely that they would consider more possibilities to ensure accurate diagnosis at point of care clinics. Such tools can also be a valuable diagnostic assistant at point of care clinics if prompts could be offered to physicians as they are using electronic medical records to order tests and medications for their patient. For example, a prompt for justification of antibiotic prescription in the absence of a definitive diagnosis would ensure safety of patients who may be EBV positive at time of care. It would be even better if the prompt could alert the physician to the possibility of ordering a Mononucleosis test to rule it out definitively. Given that the EBV blood test could take up to 3 days to yield a result, it may indeed be worthwhile to order the test on the day of the visit if lacking a clear diagnosis of other infections, and signs indicating that Mono is a likely possibility. Thereby, even if an antibiotic was ordered, it could be stopped earlier to prevent adverse events such as a severe maculopapular rash, that usually arises between 3 and 10 days of taking penicillin and its multi-drug combinations such as Augmentin.

Even if there is a possibility of error in using such a tool due to the inherent assumptions that underlie the HMM, such as the first-order Markov condition used herein, which assumes that only the previous state matters in the statistical calculations, the ability to consider all the possibilities before making a diagnosis or providing a therapy is of vital importance to medical practice. Furthermore, such tools can be calibrated by learning the state transition and emission probabilities from real-world evidence via appropriate aggregated data from national resources such as available using the i2b2 system.[33]

Conclusions and Future Work

Simple statistical modeling methods such as the HMM approach presented herein can augment decision making capabilities in clinical practice. For accurate timely diagnosis of EBV which causes infectious mononucleosis, the highly sensitive EBV DNA testing from blood samples which can take around 3 days to detect current infections has the potential to avert undesirable side effects such as maculopapular rash in patients. High school students who receive certain prescription antibiotics are vulnerable to such side effects, if their pediatrician misses the diagnosis for Mono. This can result in extra time taken off from school, and potential trips to the hospital/health care provider for corticosteroids that can cause further harmful side effects to manage. The costs associated with such unnecessary adverse effects are likely to exceed that for the EBV blood test. Therefore, this research aims to bring this awareness to physicians and health care systems that it would be in the best interest of patient safety to prescribe the EBV blood test especially when strep throat and other infectious diseases such as COVID-19 have been ruled out.

Future work will involve further data collection from electronic health records to develop a reasonable cohort of patients who were tested for EBV, to learn the parameters for the HMM using algorithms such as Baum-Welch, which is a special case of the Expectation-Maximization algorithm that iteratively learns the unknown state transition and emission probabilities. The Baum-Welch uses the forward-backward algorithm to compute the statistics for the expectation step from a database of observed sequences. The existence of a well-developed theory and algorithms for HMMs makes them attractive as effective modeling tools for aiding diagnosis.

Acknowledgments

The author gratefully acknowledges the suggestions made by Serena Mani from the Bloomberg School of Public Health at Johns Hopkins University on initial drafts of this manuscript, which helped enhance its relevance in the context of the available literature. The author also gratefully acknowledges the Patient-Like-Mine (PaLM) project in the Department of Family Medicine, at the School of Medicine, University of Pittsburgh, for partial funding that allowed this research to unfold.

References

Gotlieb-Stematsky, T.; Vansover, A.; Rannon, L. [Serological diagnosis of infectious mononucleosis by indirect immunofluorescence with Epstein-Barr virus]. Harefuah 1971, 80, 182–184. [Google Scholar] [PubMed]
Tamarova, L.D.; Filatov, F.P.; Gasparian, M.O.; Barinskii, I.F. [Serological studies of antibodies to Epstein-Barr virus in infectious mononucleosis]. Vopr Virusol 1976, 191–195. [Google Scholar]
Ginsburg, C.M.; Henle, W.; Henle, G.; Horwitz, C.A. Infectious mononucleosis in children. Evaluation of Epstein-Barr virus-specific serological data. JAMA 1977, 237, 781–785. [Google Scholar] [CrossRef] [PubMed]
Gout, J.P.; Seigneurin, D.; Seigneurin, J.M.; Bost, M.; Micoud, M. [Heterophil antibody negative infectious mononucleosis due to Epstein-Barr virus. A clinical, hematological and serological study of 14 cases (author’s transl)]. Sem Hop 1980, 56, 434–438. [Google Scholar] [PubMed]
Takiuchi, Y.; Tatsumi, E.; Shirakawa, S.; Uchino, H. Infectious mononucleosis and Epstein-Barr virus in Japan. I. Clinical and serological aspects. Nihon Ketsueki Gakkai Zasshi 1980, 43, 700–710. [Google Scholar] [PubMed]
Timar, L.; Koller, M.; Budai, J. Serological follow-up of children with infectious mononucleosis caused by Epstein-Barr virus. Acta Paediatr Acad Sci Hung 1981, 22, 243–249. [Google Scholar] [PubMed]
Lamy, M.E.; Favart, A.M.; Cornu, C.; Mendez, M.; Segas, M.; Burtonboy, G. Study of Epstein Barr virus (EBV) antibodies: IgG and IgM anti-VCA, IgG anti-EA and Ig anti-EBNA obtained with an original microtiter technique: --serological criterions of primary and recurrent EBV infections and follow-up of infectious mononucleosis--seroepidemiology of EBV in Belgium based on 5178 sera from patients. Acta Clin Belg 1982, 37, 281–298. [Google Scholar] [CrossRef]
Horwitz, C.A.; Henle, W.; Henle, G.; Rudnick, H.; Latts, E. Long-term serological follow-up of patients for Epstein-Barr virus after recovery from infectious mononucleosis. J Infect Dis 1985, 151, 1150–1153. [Google Scholar] [CrossRef]
de Ory, F. [Serological diagnosis of infectious mononucleosis caused by Epstein-Barr virus]. Enferm Infecc Microbiol Clin 1991, 9, 63–64. [Google Scholar]
Farber, I.; Wutzler, P.; Wohlrabe, P.; Wolf, H.; Hinderer, W.; Sonneborn, H.H. Serological diagnosis of infectious mononucleosis using three anti-Epstein-Barr virus recombinant ELISAs. J Virol Methods 1993, 42, 301–307. [Google Scholar] [CrossRef]
Feng, Z.; Li, Z.; Sui, B.; Xu, G.; Xia, T. Serological diagnosis of infectious mononucleosis by chemiluminescent immunoassay using capsid antigen p18 of Epstein-Barr virus. Clin Chim Acta 2005, 354, 77–82. [Google Scholar] [CrossRef] [PubMed]
Bell, A.T.; Fortune, B.; Sheeler, R. Clinical inquiries. What test is the best for diagnosing infectious mononucleosis? J Fam Pract 2006, 55, 799–802. [Google Scholar] [PubMed]
White, L.R.; Karofsky, P.S. Review of the clinical manifestations, laboratory findings, and complications of infectious mononucleosis. Wis Med J 1985, 84, 19–25. [Google Scholar]
Robinson, R.G. Abdominal complications of infectious mononucleosis. J Am Board Fam Pract 1988, 1, 207–210. [Google Scholar]
Jenson, H.B. Acute complications of Epstein-Barr virus infectious mononucleosis. Curr Opin Pediatr 2000, 12, 263–268. [Google Scholar] [CrossRef] [PubMed]
Hervas Angulo, A.; Arizcuren Domeno, M.A.; Tiberio Lopez, G.; Oteiza Olaso, J. [Clinical and analytic characteristics and complications in patients with infectious mononucleosis referred from primary care to specialists]. Aten Primaria 2003, 32, 311–312. [Google Scholar] [CrossRef]
Orti, A.; Otero, M.C.; Tallon, P.; Merlos, R.; Perez-Tamarit, D.; Morant, A.; Cordoba, J.; Asensi, F. Epstein-Barr virus mononucleosis: neurologic complications. Clin Pediatr (Phila) 2003, 42, 361–364. [Google Scholar] [CrossRef]
Tsai, M.H.; Hsu, C.Y.; Yen, M.H.; Yan, D.C.; Chiu, C.H.; Huang, Y.C.; Lin, S.J.; Lin, T.Y. Epstein-Barr virus-associated infectious mononucleosis and risk factor analysis for complications in hospitalized children. J Microbiol Immunol Infect 2005, 38, 255–261. [Google Scholar]
Nagler, J.; Ruebner, R.L. Suppurative complications and upper airway obstruction in infectious mononucleosis. J Hosp Med 2007, 2, 280–282. [Google Scholar] [CrossRef]
Papadopoulou-Legbelou, K.; Papadopoulou-Alataki, E.; Fleva, A.; Spanou, S.; Pavlitou, A.; Varlamis, G. Cardiac complications and immunophenotypic profile of infectious mononucleosis syndrome in children. Indian Pediatr 2012, 49, 195–198. [Google Scholar] [CrossRef]
van Baarle, D. T-cells and cardiac complications in infectious mononucleosis. Indian Pediatr 2012, 49, 189–190. [Google Scholar] [PubMed]
Zamor, R.; Edmunds, K.; Orscheln, E.; Duma, E. Severe Complications From Infectious Mononucleosis After Prolonged Steroid Therapy. Pediatr Emerg Care 2021, 37, e1741–e1744. [Google Scholar] [CrossRef] [PubMed]
van der Woude, H.J.; van der Werf, T.S.; Verschuuren, E.A.; Tamminga, R.Y.; Rosati, S.; Meertens, J.H.; Zijlstra, J.G. An 18-year-old man with rapidly progressive multiorgan failure after a positive mononucleosis spot test result. Chest 2006, 130, 291–295. [Google Scholar] [CrossRef] [PubMed]
Lennon, P.; JP, O.N.; Fenton, J.E.; T, O.D. Challenging the use of the lymphocyte to white cell count ratio in the diagnosis of infectious mononucleosis by analysis of a large cohort of Monospot test results. Clin Otolaryngol 2010, 35, 397–401. [Google Scholar] [CrossRef] [PubMed]
P, L.; J, E.F.; J, P.O.; T, P.O. Challenging the use of the absolute lymphocyte count in the diagnosis of infectious mononucleosis by analysis of a large cohort of monospot test results. Clin Otolaryngol 2013, 38, 107–108. [Google Scholar] [CrossRef]
Salehi, H.; Salehi, M.; Roghanian, R.; Bozari, M.; Taleifard, S.; Salehi, M.M.; Salehi, M. Comparison of serological and molecular test for diagnosis of infectious mononucleosis. Adv Biomed Res 2016, 5, 95. [Google Scholar] [CrossRef] [PubMed]
Byrne, A.; Bush, R.; Johns, F.; Upadhyay, K. Limited Utility of Serology and Heterophile Test in the Early Diagnosis of Epstein-Barr Virus Mononucleosis in a Child after Renal Transplantation. Medicines (Basel) 2020, 7. [Google Scholar] [CrossRef]
Dunmire, S.K.; Hogquist, K.A.; Balfour, H.H. Infectious Mononucleosis. Curr Top Microbiol Immunol 2015, 390, 211–240. [Google Scholar] [CrossRef]
Sylvester, J.E.; Buchanan, B.K.; Silva, T.W. Infectious Mononucleosis: Rapid Evidence Review. Am Fam Physician 2023, 107, 71–78. [Google Scholar]
Albert, D.A. Decision theory in medicine: a review and critique. Milbank Mem Fund Q Health Soc 1978, 56, 362–401. [Google Scholar] [CrossRef]
Renella, R.; Fanconi, S. Decision-making in pediatrics: a practical algorithm to evaluate complementary and alternative medicine for children. Eur J Pediatr 2006, 165, 437–441. [Google Scholar] [CrossRef] [PubMed]
Mor, B.; Garhwal, S.; Kumar, A. A Systematic Review of Hidden Markov Models and Their Applications. Arch Computat Methods Eng 2021, 28, 1429–1448. [Google Scholar] [CrossRef]
Murphy, S.N.; Weber, G.; Mendis, M.; Gainer, V.; Chueh, H.C.; Churchill, S.; Kohane, I. Serving the enterprise and beyond with informatics for integrating biology and the bedside (i2b2). J Am Med Inform Assoc 2010, 17, 124–130. [Google Scholar] [CrossRef] [PubMed]

Figure 1. A simple HMM for modeling EBV positive and negative hidden states. State transition probabilities are depicted as are the emission probabilities for observing each of the four symptoms for each hidden state with colors in red indicating the distribution for positive for EBV and green indicating negative for EBV.

Table 1. Below is the hand calculation for the Viterbi dynamic programming algorithm. The observation sequence is ”sorethroat”, “fever”, “swollenneck”, and “swallowdiff.” The most likely state path is obtained by backtracking using pointers. The emission probabilities are indicated in red and green fonts for the EBV positive and negative states respectively. The font colors of purple and blue indicate the previously calculated maximum probability thus far for the EBV positive and negative states respectively.

	Sorethroat	Fever	Swollen Neck	Swallowing Difficulty
EBV +ve	0.2 * 0.5 = 0.1 ←	Max {0.20.11.0,0.20.1250.5} = 0.02 ←	Max {0.30.021.0,0.30.0160.5) = 0.006 ←	Max {0.30.0061.0, 0.30.0020.5} = 0.0018
EBV -ve	0.25 * 0.5= 0.125	Max {0.250.1250.5, 0.25 0.10.0) = 0.016	Max {0.250.0160.5,0.250.020.0)=0.002	Max { 0.250.0020.5,0.250.0060.0)= 0.00025

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Simple Hidden Markov Model Could Prevent Physician Error in Failure To Diagnose Infectious Mononucleosis

Abstract

Key Messages

Introduction

Methods

Discussion

Conclusions and Future Work

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe