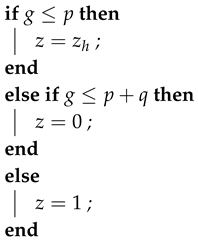1. Introduction
Two seminal papers have profoundly shaped the landscape of the Lot Sizing Problem (LSP). The inaugural paper, known as the Dynamic Economic Lot Sizing model (DLS), was concurrently introduced by [
1,
2], and is widely recognized as the Manne-Wagner-Whitin Model. In its "classical" rendition, the DLS addresses a discrete-time, finite-horizon inventory management challenge involving a singular item. Its primary objective is to efficiently meet deterministic time-varying demands through optimal stock management or procurement strategies, with further elucidation provided in ([
3]). The second pivotal paper, the Economic Lot Scheduling Problem (ELSP), was brought forth by Elmaghraby ([
4]). Both of these works tackle a fundamental issue within production planning determining optimal lot sizes and production schedules for a multitude of items produced on a shared production line or machine. The overarching goal is to minimize expenses associated with production and inventory while simultaneously fulfilling demand requirements and adhering to pertinent production constraints. Supplementary insights can be found in ([
4]). Researchers have further expanded upon the work of Elmaghraby and Manne-Wagner-Whitin to tackle variations and more advanced versions of the ELSP and DLS. These advancements include incorporating uncertainties, time windows, and remanufacturing into the models. For a comprehensive overview of the economic lot sizing problem, readers can consult [
5,
6]. The Economic Lot Scheduling Problem (ELSP) with remanufacturing options (ELSPR) represents an extension of the classical Wagner Whitin model. A notable enhancement is the incorporation of a distinct element: within each time period, predetermined quantities of used products are introduced into the system. These returned items offer the potential for remanufacturing, serving to fulfill demand alongside the conventional manufacturing processes. In recent decades, there has been a growing emphasis on production planning, particularly with regard to incorporating recycling options [
7]. The literature outlines two distinct categories of recycling production planning problems.
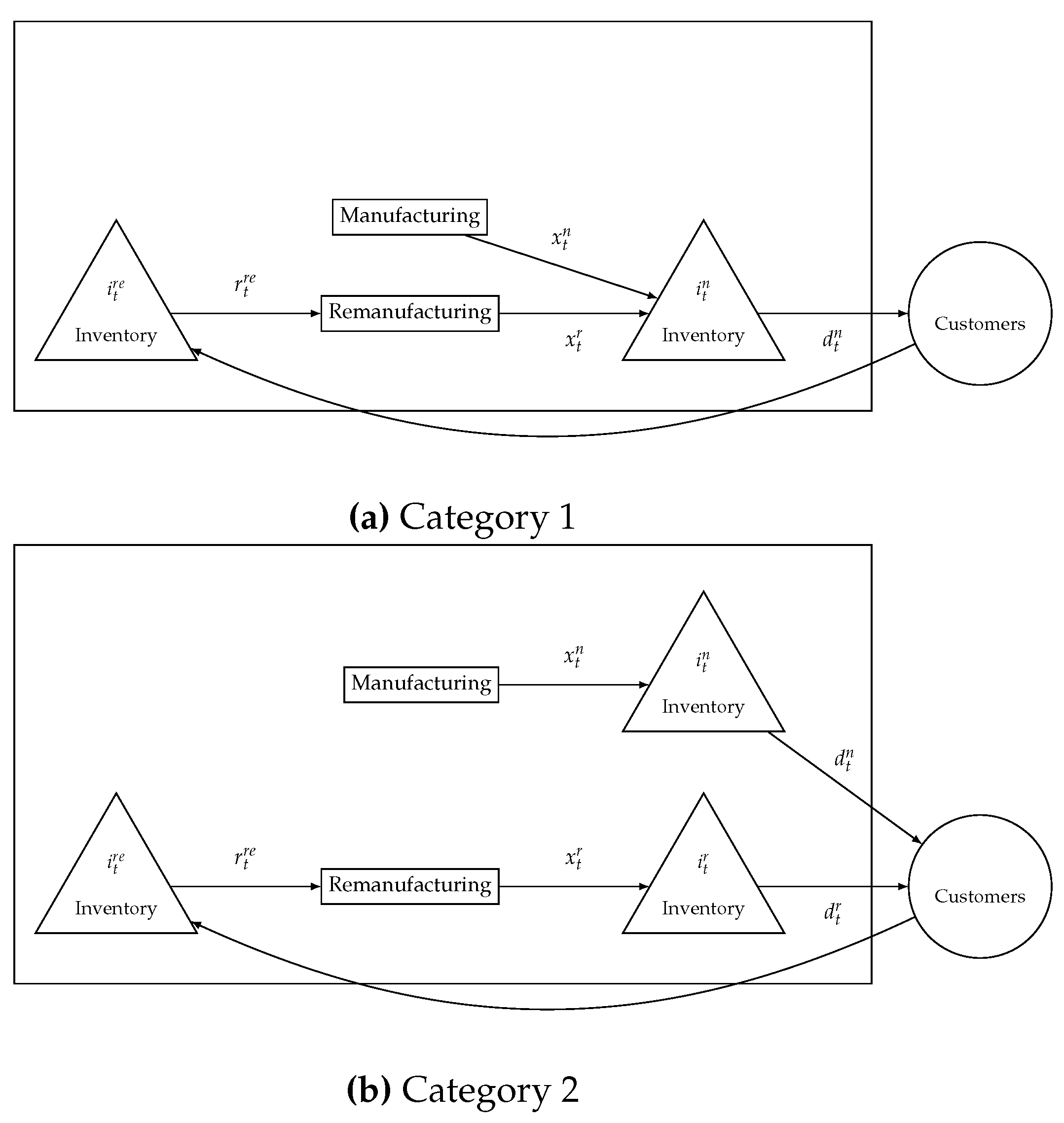
In the first category (Cat. 1), the primary objective is to meet the external demand for products through either remanufactured or newly produced goods
Figure 1. This category focuses on regulating two types of inventories: the inventory of new products and the inventory of remanufactured products. It is assumed that both new and remanufactured products are identical and, thus, considered serviceable entities that can fulfill demands. Numerous authors have extensively studied this category [
8]. This category also encompasses issues related to pricing and lot sizing, wherein demand is fulfilled through various substitution alternatives.
The second category (Cat. 2) deals with two distinct demands: one for new products and the other for recycled products. Additionally, this category introduces a key feature where a deterministic quantity of returned goods enters the system in each period. These returned items can be remanufactured and used to meet the demand for remanufactured products, complementing the regular production of new items. As a result, the inventory includes three types of stocks: new products, remanufactured products, and returned products
Figure 1.
In specific industrial sectors, such as the paper industry, two different types of demand are observed: one for recycled paper and the other for paper made from new fiber. Recycled paper is typically priced lower due to its reduced water and energy consumption during production, compared to virgin fiber papers [
9]. Moreover, recycled paper often benefits from shorter transportation distances as it is sourced locally, while virgin fiber and new fiber papers are imported from other countries in larger quantities. This observation extends to other sectors, including photocopiers, tires, and personal computers see [
10,
11].
Publications regarding Category 1: Building upon Elmaghraby’s groundwork (see [
4]), Tang and Teunter ([
12]) investigated the hybrid production line’s multi-product dynamic lot sizing. This involved manufacturing new products and remanufacturing returns, with a single manufacturing and remanufacturing lot per product synchronized within a common cycle. They constructed a Mixed Integer Linear Programming (MILP) problem for precise resolution. The multi-product dynamic lot sizing problem with distinct manufacturing and remanufacturing sources, each operating on separate dedicated lines, was further examined in [
13].
In a study by [
14], a multi-item economic lot-sizing problem involving remanufacturing and capacitated production was examined. The study drew upon the concept introduced by Garfinkel and Nemhauser (1969), known as the Set Partitioning Problem (SPP). Another contribution, by [
15], delved into the multi-item economic lot-sizing problem with remanufacturing and uncapacitated production. They extended the model initially proposed by [
16] and put forward two innovative variations of the Variable Neighborhood Search (VNS) algorithm. These variants aimed at discovering optimal solutions for the ELSR problem. In a separate work, [
17] introduced an effective Mixed Integer Programming (MIP)-based matheuristic for the multi-item capacitated lot-sizing problem with remanufacturing (CLSP-RM). Notably, this approach addresses capacity constraints individually for new and remanufactured products.
[
18] conducted a comparative analysis of MIP approaches for the economic problem of single-item lot-sizing with remanufacturing (ELSR) and uncapacitated production. They proposed a shortest path formulation. [
19] contributed a polynomial-time heuristic within this category. Their work also includes a comprehensive compilation of methods developed by [
20,
21,
22,
23,
24]. Addressing an extension of the economic problem of single-item lot sizing, [
25] introduced considerations for remanufacturing, final disposal, and distinct demand flows for new and remanufactured products. This extension also accounted for a unidirectional substitution, wherein the demand for remanufactured products can be satisfied by new items, but not vice versa. The authors proposed both a network flow formulation and a pseudopolynomial time dynamic programming algorithm. Notably, the model does not incorporate capacity constraints.
Publications regarding category 2: By [
26] address the production planning problem within a hybrid manufacturing and remanufacturing system (HMRS). They postulate a multi-objective mathematical model (MIP) whose objective is to determine a production plan taking into account the available capacities in each period, which satisfies the demand for new and remanufactured products and minimizes all costs of production, storage and disposal of new products, as well as the minimization of CO2 emissions generated in production. They introduce a solution method based on a non-dominant sorting algorithm (NSGA-II).
[
27] investigates the joint problem of pricing and lot sizing in a hybrid manufacturing and remanufacturing system with a one-way substitution option. Two demand performances, for new and remanufactured items, are considered in this paper. In the case of a shortage of remanufactured items, a one-way substitution option is assumed, so that the demand for these remanufactured items is satisfied with new items. The presented mathematical model is an MIP but without capacity constraints. As a solution method they adapt "the cost and benefit heuristic" (CB-heuristic) introduced by [
28] and also a memetic algorithm which is improved with the help of a local search.
Zhang et al. ([
29]) investigate the capacitated lot sizing problem in closed-loop suply chain considering setup costs, product returns, and remanufacturing. They present a Lagrange relaxation to solve the problem. Based on Zhang’s model we formulate the same problem but taking more general capacity constraints and doing more extensive numerical experiments.
The capacitated lot-sizing problem model is NP-hard. The proof of this statement is to be found in [
30,
31]. [
32] has shown that even the two-item problem with constant capacity is NP-hard. Heuristic methods employed for solving problems within the CLSP class typically rely on a wide range of sorting rules and other criteria derived from factors such as demand, capacity, setup costs, inventory costs, and production costs. Examples of such heuristic methods include those presented in references like [
22,
23,
33,
34]. The achieved solution margin tends to vary within the range of 1% to 10%, as reported in references such as [
29,
34].
1.1. Research Contributions
This study incorporates two significant constraints. The first constraint ensures that the cumulative demand for both new and remanufactured products remains within the cumulative capacity for each period. The second constraint mandates that the cumulative demand for remanufactured products during each period does not surpass the cumulative quantities of used products returned within the same period. No specific relationship is imposed between the existing capacities and the quantities of returned products. This particular characteristic, which is overlooked in certain promoted publications, adds an additional layer of complexity to the problem, rendering it non-standard in nature.
The contribution of this work can be summarized as follows: We examine two overarching problem classes under the framework of the aforementioned capacity constraints. These classes are as follows:
The first class involves production periods where the demand for both new and remanufactured product exceeds the available capacity within those specific time frames. To address this scenario, we propose a linear program devoid of capacity constraints, providing a highly accurate approximation of the optimal solution.
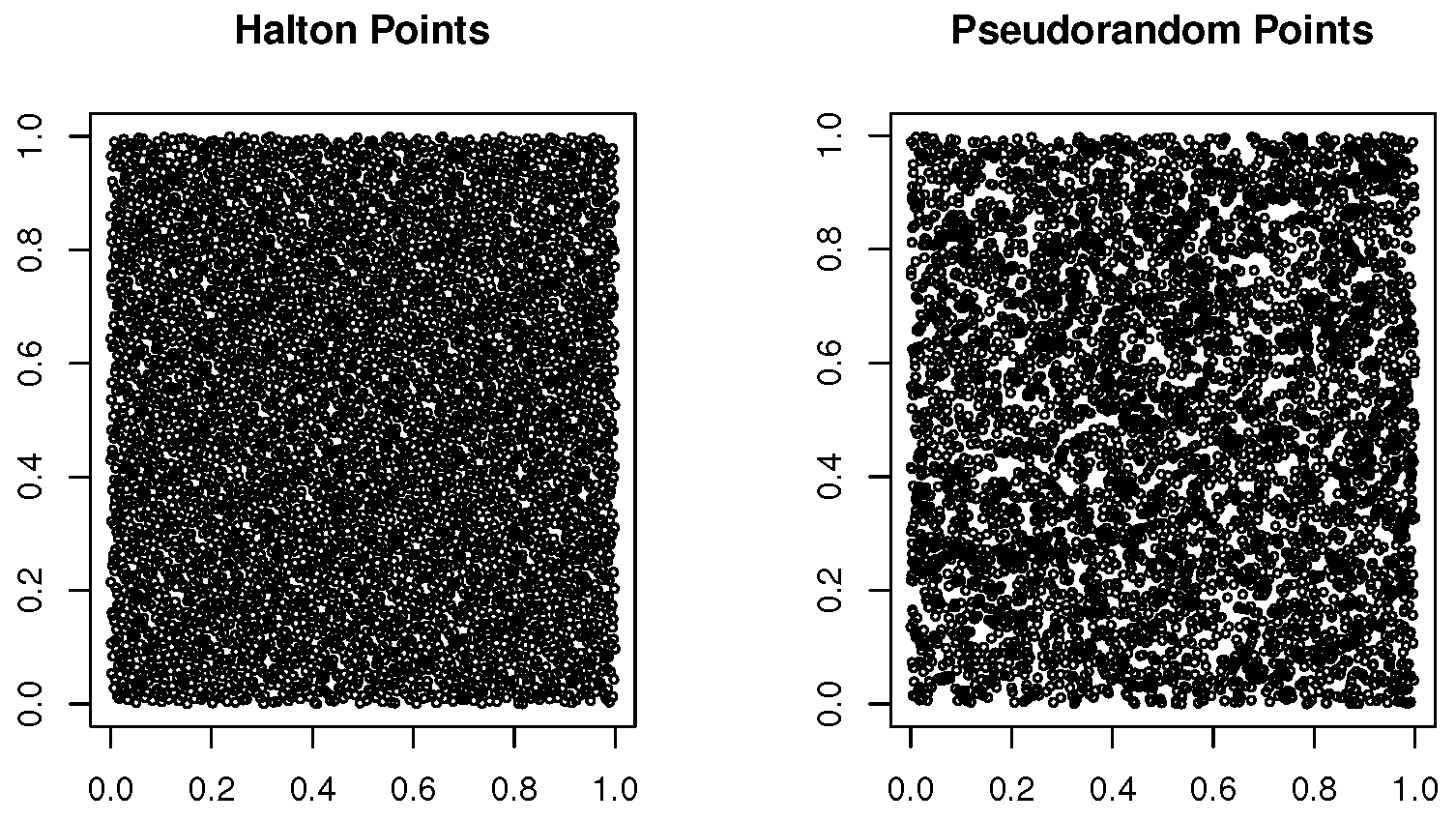
In the second problem class, each period experiences demand that falls short of the existing capacity. This specific problem category exhibits an NP-hard nature, leading us to adopt a direct simulation approach. Additionally, the quasi-random numbers
, introduced by [
35,
36,
37], showcase significant properties, as evidenced by [
38]. Among these characteristics, their uniform distribution stands out. Accordingly, we present a straightforward simulation utilizing these quasi-random numbers (
). Irrespective of the input parameters, we organize production based on both feasibility and randomness. Starting from the initial production period, we define lower and upper limits for viable production ranges of the new product. This production information informs the establishment of production range limits for the remanufactured product. The order in which the new or remanufactured product is produced holds no significance in the algorithm’s execution. These defined limits delineate production intervals that strictly adhere to all problem constraints. Within each interval, a random production quantity is generated using uniform random numbers derived from the Halton sequence. It is imperative to emphasize that the random production process significantly influences the subsequent determination of feasible production intervals.
Moreover, our heuristic approach ensures the generation of a feasible solution whenever the problem is solvable. After simulating N production plans, we select the most cost-effective one. This solution is then compared against numerical solutions obtained through the Gurobi solver. The scheduling process is straightforward, and the results prove to be quite satisfactory given the scale of the presented problems.
1.2. Outline
The rest of the paper is organized as follows:
Section 2 we propose a new mathematical programming formulation for the problem. In
Section 3 we present a relaxation of the problem without capacity constraints (Model A) and we will see that the solution obtained for the chosen class of tasks is very close to the optimal solution of the original problem. In
Section 4, we present a heuristic solution method (Model B) for another class of tasks. In
Section 5, we report the results of computational experiments. In
Section 6 we present some conclusions and suggested directions for further research.
6. Conclusions and Outlook
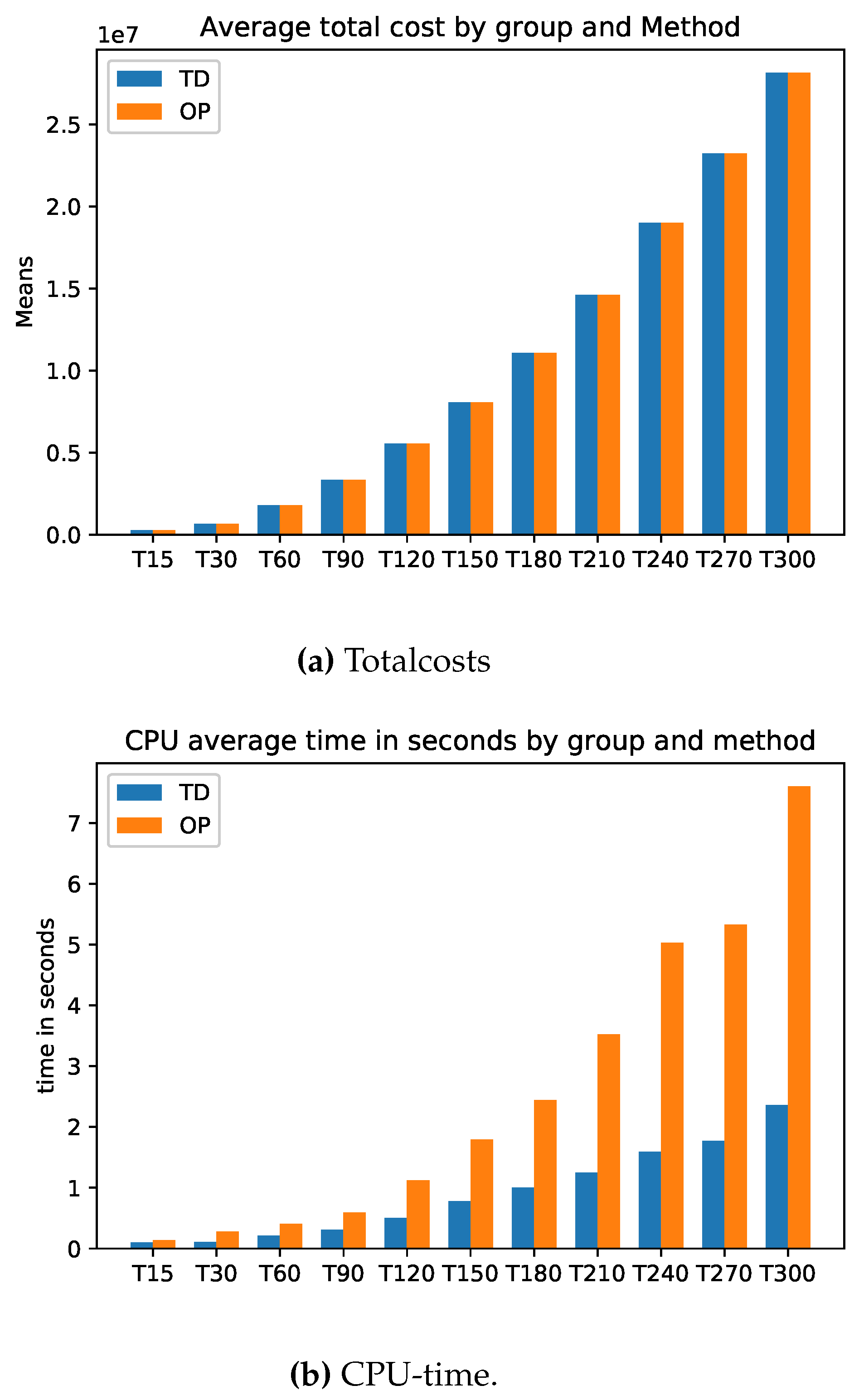
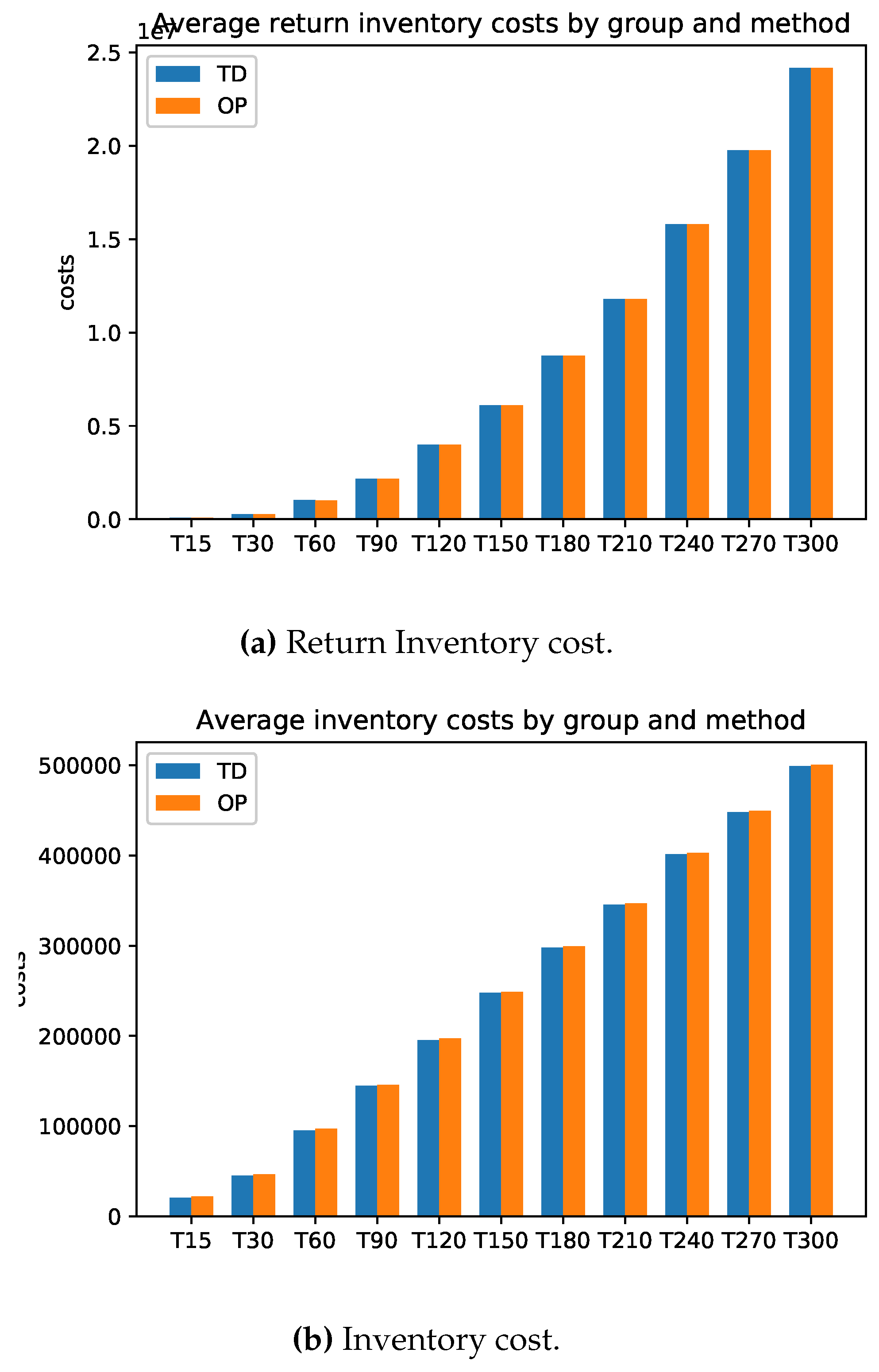
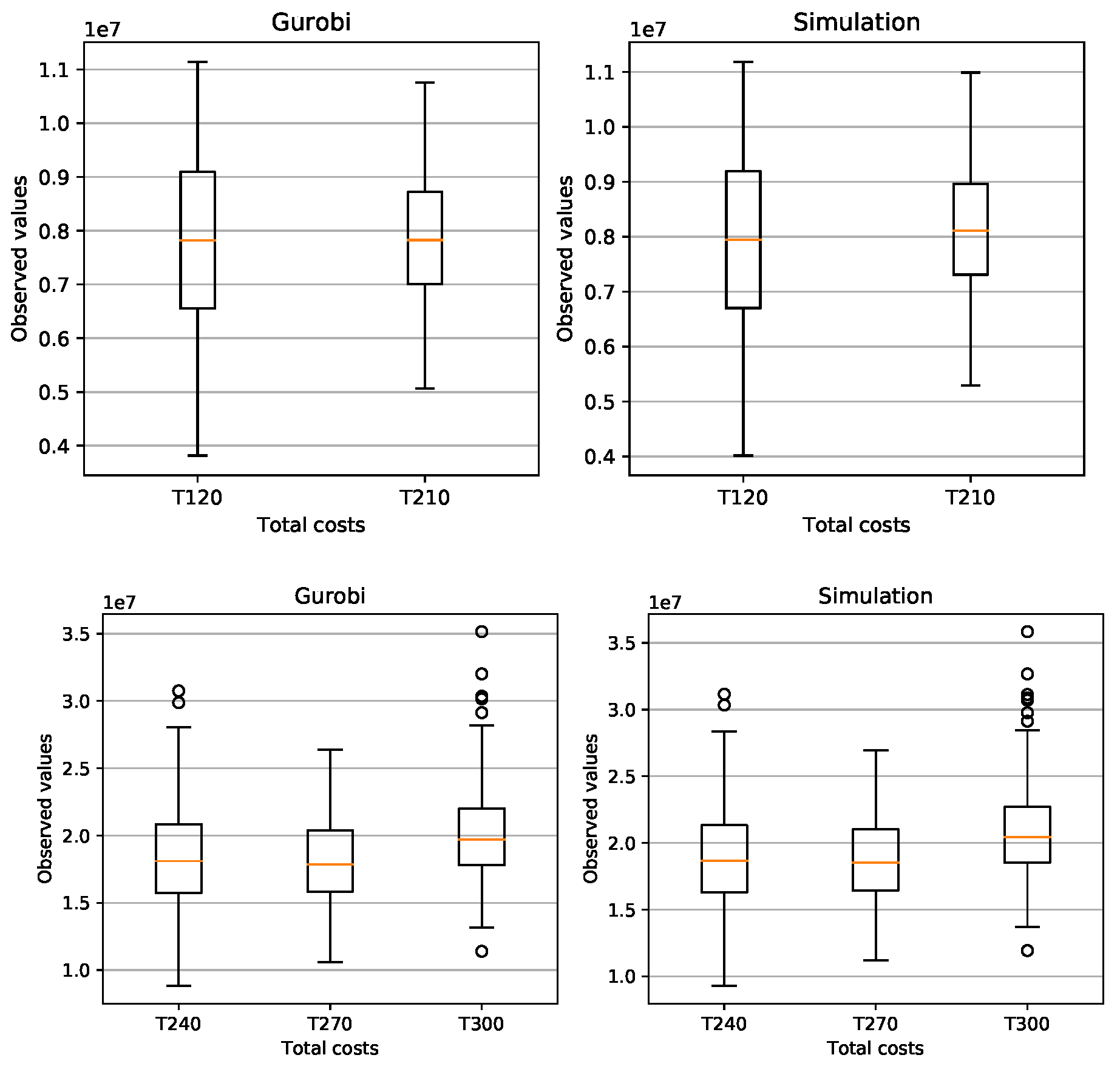
We have analyzed a problem that belongs to the NP-hard class. However, the choice of the parameters is very important to obtain a problem that is really NP-hard. With the choice of parameters made in model A, we see that this class of problems is easily solved with a standard solver. By doing a relaxation of the problem, the solution is found more quickly. The error rate is between 0.02% and 2% (taking into account more than 1800 instances). In addressing more intricate CLSP class problems characterized by Model A, the solution derived from Model A can serve as an initial approximation for tackling the problem. This initial approximation can then be seamlessly integrated into various heuristic or metaheuristic approaches.
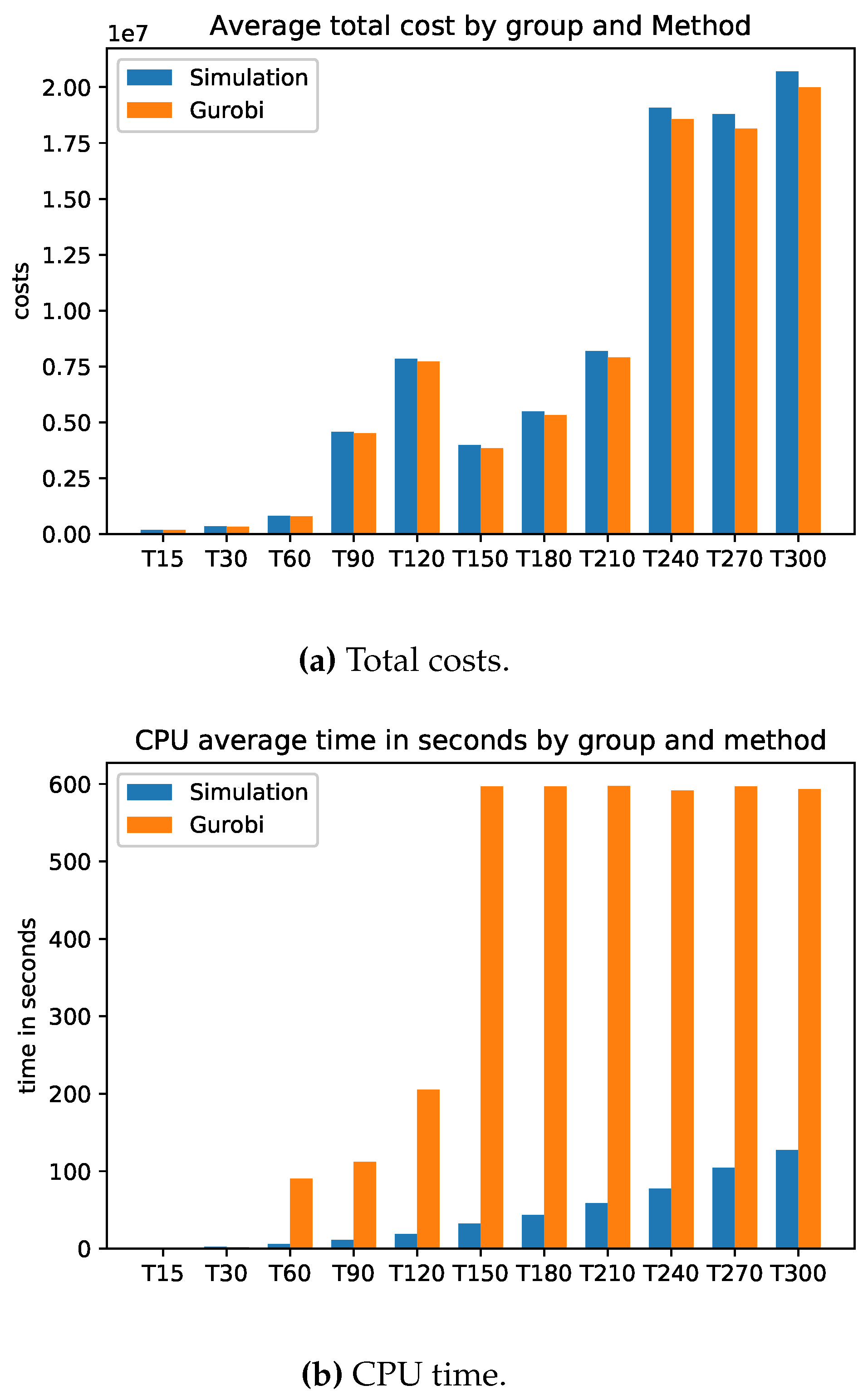
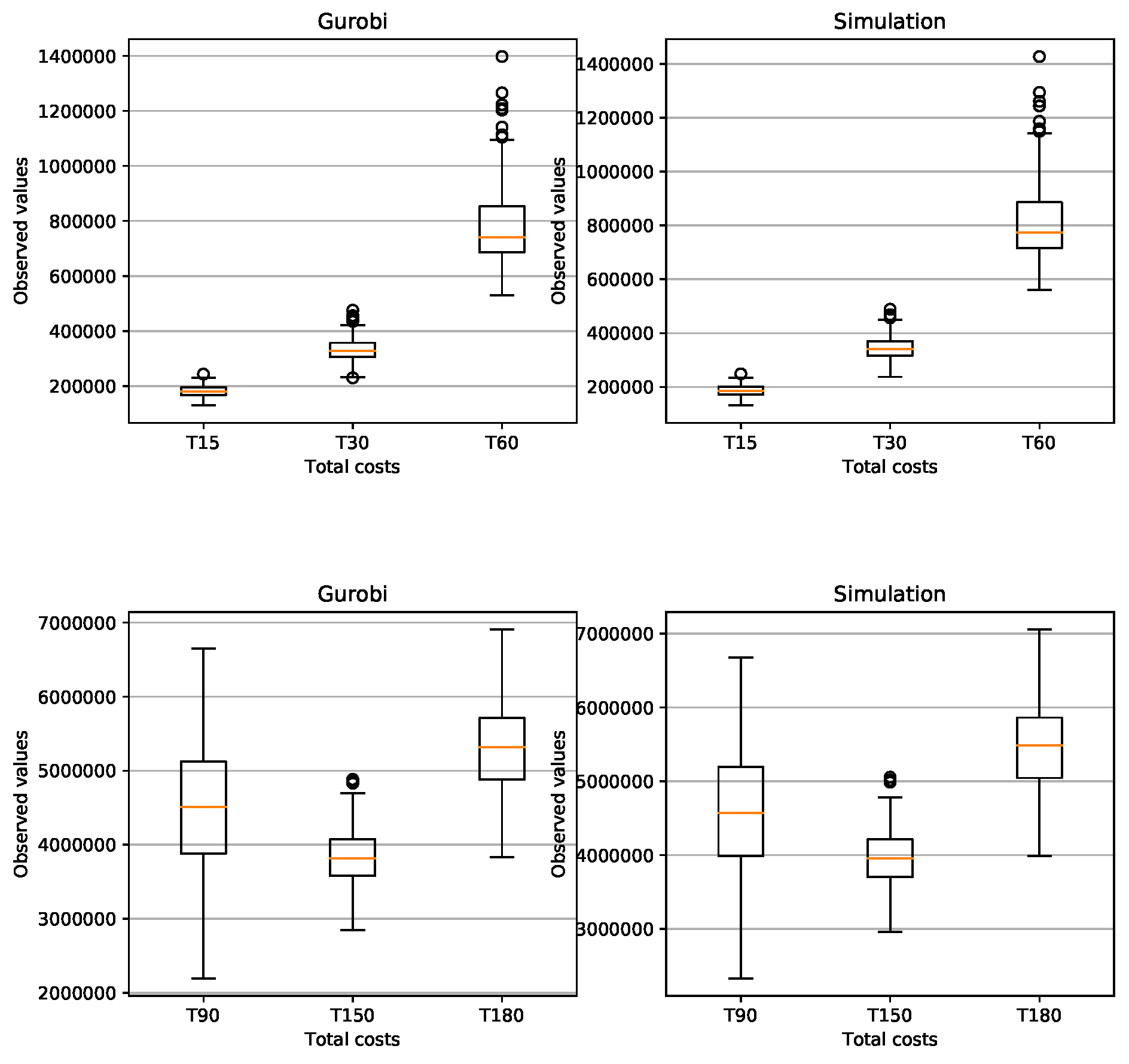
If we choose the parameters according to model B, Gurobi needs a lot of time to find the optimal solution. In this kind of problem, the presented simulation can help a lot in finding a good solution. We have seen that the error rate is between 1.7% and 3.5% (taking into account more than 2000 instances). On average Gurobi solves the problem with a maximum time of 600 seconds better than the simulation. The great advantage of the simulation is that the calculation is extremely fast and easy.Thanks to the Halton numbers, few simulations are needed to obtain a very good approximation of the solution.
The quality of the solutions can be improved by increasing the number of simulations but it is necessary to have a fairly fast computer. In this work we use at most 10 million simulations. Another parameter that influences the quality of the solutions is the correct choice of the probability p (see (35)). Is there an optimal probability? This is a question for further research.
The simulation possesses a broad nature and can be tailored to examine additional, intricate production issues within the NP-hard category. The benefit is readily apparent: it circumvents the necessity for an extensive array of sorting rules and additional criteria stemming from factors like demand, setup expenses, production outlays, or capacities.