Numerical Modelling and Simulation of the Solid Oxide Cell Stacks and Metal Interconnect Oxidation With OpenFOAM

1. Introduction

Transition to the renewable energy system where solar and wind energy prevail leads to a challenge to the grid balance. Applying solid oxide cells (SOCs) as energy storage and conversion devices may be part of the solution to this problems. Their operation at high temperatures provides several advantages such as high efficiencies, possibility of sector coupling on the heat side, the capability of being reversibly operated, and the tolerance to various fuels. In order to increase the lifetime of SOCs, their degradation behaviour should be studied as it obstructs the long-term operation. Significant degradation mechanisms, such as Ni agglomeration and Cr poisoning, are related to the local distribution of the overpotential and chemical species. However, measuring local values for these during the operation of SOCs is not only a technical challenge but also a potentially dangerous task as gas leakages, burns and electric shocks could happen. In contrast, simulation can be an efficient and safe method to visualize the local physical values. Therefore, a three-dimension model that can capture the physical processes in an SOCs is necessary.

Although there was a number of scientific findings due to simulation in the past decade [1,2,3,4,5,6,7,8], simulations are usually steady-state simulations, making it impossible to trace the degradation over time. Besides, it can be seen that many numerical investigations of SOCs were carried out with commercial software, for example, DETCHEM, ANSYS Fluent, COMSOL, etc. Mathematical models used to describe the multiphysical and multiscale transport processes in the SOCs have been incorporated into a ’black-box’. It is usually impossible to visualize the implementation of these models. In addition, the knowledge transfer may be limited within the research community due to the licence issues. In this work, the authors employed a computational code, openFuelCell2 [9,10], which has been implemented with an open-source library, OpenFOAM [11]. The code has witnessed a reliable performance in low temperature electrochemical applications, for example, the proton exchange membrane fuel cells [12,13,14,15]. This work aims to extends the capability of openFuelCell2 to high temperature applications, i.e. SOFC and SOEC. The comparison between the simulation results with openFuelCell2 and COMSOL is conducted for the basic steady-state model. A degradation model to describe the performance degradation with the evolution of time due to metal interconnect (MIC) oxide scale growth is additionally proposed and implemented into openFuelCell2. Effects of different protective coatings on MIC oxidation are discussed. Numerical simulations are performed for the F10 SOC stack design [16] in Forschungszentrum Jülich GmbH (FZJ), the detailed description of which is given in the next section.

2. Geometry of the model

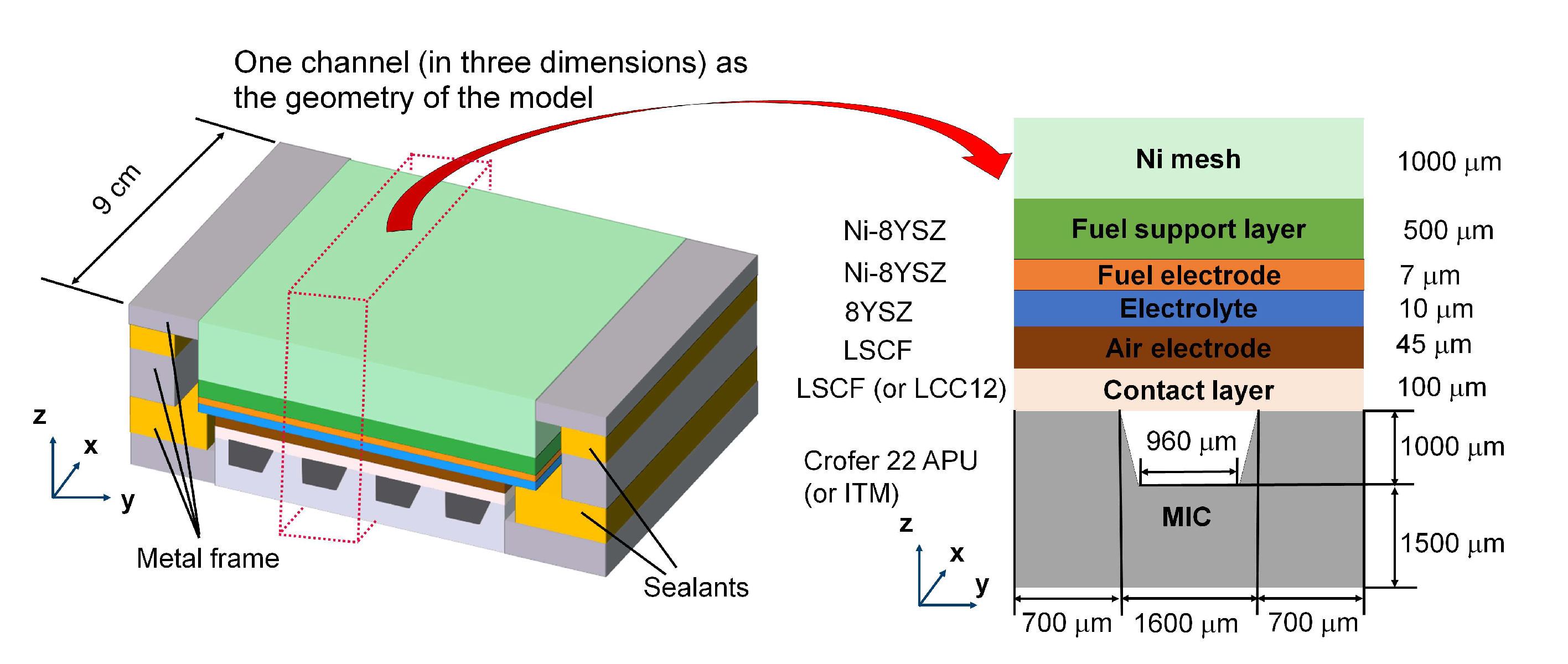
It is helpful to introduce the general information of the F10 SOC stack design in FZJ first. The simplified geometry of the repeating unit of the SOC stack is shown at left-hand side of Figure 1. The standard design is an fuel-electrode supported cell (FESC) where a thick support layer at the fuel side, made of Ni/8YSZ (8mol % yttria-stabilized zirconia), provides necessary mechanical strength. The repeating unit consists of roughly 1000 µm thick Ni-mesh as the distributor and contacting element at the fuel side, a 500 µm thick support layer Ni/8YSZ [17], a 7 µm thick fuel electrode Ni/8YSZ [17], a 10 µm thick 8YSZ electrolyte [17], a 45 µm thick air electrode La_0.58Sr_0.4Co_0.2Fe_0.8O_3- (LSCF) [17] and a 100 µm thick contact layer LSCF (or LCC12, La_0.97Mn_0.4Co_0.3Cu_0.3O_3-). Besides, a barrier layer (GDC, gadolinia-doped ceria) is added between the electrolyte and the air electrode to prevent interfacial reaction. Furthermore, there is a protective coating on the MIC to alleviate issues of metal oxidation and Cr poisoning. In FZJ, the protective coating on the MIC surface is usually made of MnCo_1.9Fe_0.1O₄ (MCF) applied by atmospheric plasma-spraying (APS). Another widely used coating is made of MnO_x and is added onto MIC via wet-powder-spraying (WPS). The drawback of WPS, in contrast to APS, is that it can only generate a porous layer that can not efficiently prevents metal oxidation and chromium poisoning. Consequently, stacks with APS coatings have better performance than stacks with WPS coatings [18]. The MIC is made by either Crofer 22 APU or intermediate temperature metal (ITM). For sealing the stack glass ceramic sealants are used on all bonding surfaces.

Numerical simulation of the whole geometry usually means a rather large calculation effort. With the purpose of accelerating the computation while capturing main features of the repeating unit of a real SOC stack, the following assumptions are made:

• The barrier layer and protective coating are ignored in the geometry of the model. Their effects on the resistance are considered in the electronic conductivity of the air electrode and air side contact layer.
• The metal frame is ignored in the geometry of the model.

Therefore, the computational domain in this study refers to a representative three-dimensional slice of one-channel in a real SOC stack as shown at the right-hand side of Figure 1.

3. Governing equations of the basic model

The SOC stack is a complex electrochemical device that contains different physics processes which are coupled with each other. This interplay strongly affects the performance of SOC stacks. Therefore, suitable mathematical models should be implemented otherwise the results are questionable. Although it is recommended to involve as many details as possible, several plausible simplifications can be made to alleviate the difficulty in multiphysics modelling:

• Properties of materials, such as permeability, porosity and electrical conductivity, are homogeneous and isotropic.
• All fluid is in laminar flow regime.
• Heat transfer is ignored. In other words, isothermal assumption is applied in the model.
• The quality of the inlet gas is perfect, meaning the air only has oxygen and nitrogen and fuel only has hydrogen and steam.

In this section, models of major physical processes including electrochemical reaction, momentum transfer and mass transport are present. A summary of models used in this work is shown in Table 1.

3.1. Electrochemical reaction

Electrochemical reaction is the key part in modelling SOCs due to its direct relation to I-V curves and strongly coupled with other physics. Commonly, it is simulated by the Butler-Volmer equation in Equation (1) [19]

$$i=i_0\left[\exp \left(\frac{{\beta }_{\mathrm{a}}{n}_{\mathrm{e}}\mathrm{F}}{\mathrm{R}T}\eta \right)-\exp \left(\frac{-{\beta }_{\mathrm{c}}{n}_{\mathrm{e}}\mathrm{F}}{\mathrm{R}T}\eta \right)\right]$$

(1)

where i is the current density, $i_0$ is the exchange current density, ${\beta }_{\mathrm{a}}$ (${\beta }_{\mathrm{c}}$) is the anodic (cathodic) charge transfer coefficient, $n_e$ is the number of transferred electrons, $\mathrm{F}$ is the Faraday constant, $\mathrm{R}$ is the gas constant, T is the temperature, $\eta$ is the overpotential. In spite of the popularity of Equation (1), Mogensen et al. [20] has raised several arguments against using Equation (1) for SOCs, such as the reaction rate probably not being limited by the charge transfer. Similarly, Adler et al. [21] found that except for charge transfer, surface diffusion of chemical species and dissociative chemisorption were also important for reaction rates. As illustrated by Maria et al. [22], it could happen that high operation temperature of SOC made adsorption, diffusion and other processes be more rate-limiting than charge transfer. Additionally, in most cases linear I-V curves instead of exponentially-changed I-V curves are observed from measurement in FZJ.

In light of above reasons, in this work a linear expression of electrochemical kinetics is used shown in Equation (2) and Equation (3) [22,23]

$$i_{\mathrm{v}},\mathrm{fuel}=\frac{{\eta }_{\mathrm{fuel}}}{R_{\mathrm{fuel}}\exp \left(\frac{-E_{\mathrm{a}},\mathrm{fuel}}{\mathrm{R}T}\right)a_{\mathrm{H}}{2}^{0.1}{a}_{\mathrm{H}}2{\mathrm{O}}^{-0.33}}$$

(2)

$$i_{\mathrm{v}},\mathrm{air}=\frac{{\eta }_{\mathrm{air}}}{R_{\mathrm{air}}\exp \left(\frac{-E_{\mathrm{a}},\mathrm{air}}{\mathrm{R}T}\right)a_{\mathrm{O}}{2}^{-0.25}}$$

(3)

where $i_{\mathrm{v}}$ is the volumetric reaction current density, $\eta$ is the overpotential, R is a pre-factor, $E_{\mathrm{a}}$ is the energy barrier, a is the activity of the reactant. The overpotential can be calculated by [24]

$${\eta }_{\mathrm{air}}={\varphi }_{\mathrm{ele}},\mathrm{air}-{\varphi }_{\mathrm{io}},\mathrm{air}-{\varphi }_{\mathrm{eq}},\mathrm{air}$$

(4)

$${\eta }_{\mathrm{fuel}}={\varphi }_{\mathrm{ele}},\mathrm{fuel}-{\varphi }_{\mathrm{io}},\mathrm{fuel}-{\varphi }_{\mathrm{eq}},\mathrm{fuel}$$

(5)

where ${\varphi }_{\mathrm{io}}$ is the ionic potential, ${\varphi }_{\mathrm{ele}}$ is the electromotive potential and ${\varphi }_{\mathrm{eq}}$ is the equilibrium potential defined as [22]:

$${\varphi }_{\mathrm{eq}},\mathrm{air}=\frac{\mathrm{R}\mathrm{T}}{4\mathrm{F}}ln\left(Y_{{\mathrm{O}}_2}\right)$$

(6)

$${\varphi }_{\mathrm{eq}},\mathrm{fuel}=-\frac{\Delta G_{\mathrm{water}\mathrm{splitting}}}{2\mathrm{F}}-\frac{\mathrm{R}\mathrm{T}}{2\mathrm{F}}ln\left(\frac{Y_{{\mathrm{H}}_2}}{Y_{{\mathrm{H}}_2\mathrm{O}}}\right)$$

(7)

where $Y_{{\mathrm{O}}_2}$, $Y_{{\mathrm{H}}_2}$ and $Y_{{\mathrm{H}}_2\mathrm{O}}$ are molar fractions of oxygen, hydrogen and water respectively. $\Delta G_{\mathrm{water}\mathrm{splitting}}$ is the Gibbs free energy change of water splitting.

Two types of current exist in SOC: ionic current $i_{\mathrm{io}}$ and electronic current $i_{\mathrm{ele}}$. The current and potential obey Ohm’s law:

$$i_{\mathrm{io}}=-{\sigma }^{\mathrm{io}}\nabla {\varphi }_{\mathrm{io}}$$

(8)

$$i_{\mathrm{ele}}=-{\sigma }^{\mathrm{ele}}\nabla {\varphi }_{\mathrm{ele}}$$

(9)

where ${\sigma }^{\mathrm{io}}$ and ${\sigma }^{\mathrm{ele}}$ are ionic conductivity and electronic conductivity that can be found in Table 2. In a porous and composite medium, the conductivity needs to be corrected by considering the effect of solid volume fraction $\chi$ of and tortuosity $\tau$ of different materials. If the number of different material properties in the medium is n, the effective conductivity is [25]:

$${\sigma }^{\mathrm{ele}},\mathrm{eff}=\sum _{\mathrm{i}}=1^{\mathrm{n}}{\sigma }_i^{\mathrm{ele}}\frac{{\chi }_i}{{\tau }_i}$$

(10)

$${\sigma }^{\mathrm{io}},\mathrm{eff}=\sum _{\mathrm{i}}=1^{\mathrm{n}}{\sigma }_i^{\mathrm{io}}\frac{{\chi }_i}{{\tau }_i}$$

(11)

The conservation of current is guaranteed by

$$\nabla i=S_{\mathrm{current}}$$

(12)

where $S_{\mathrm{current}}$ is a current source defined as following:

$$S_{\mathrm{current}}=\left\{\begin{array}{c}{i}_{\mathrm{v}}\mathrm{in}\mathrm{electrochemical}\mathrm{active}\mathrm{regions}\hfill \\ 0\mathrm{in}\mathrm{electrochemical}\mathrm{inactive}\mathrm{regions}\hfill \end{array}\right.$$

(13)

and $i_{\mathrm{v}}$ is given in Equation (2) and Equation (3).

The electronic and ionic conductivity is present in Table 2. Other parameters, like the porosity and volume factions of the porous medium, are given in Table A1.

3.2. Momentum transfer

Momentum transfer of fluid happens in gas channels and porous medium. In gas channels, it is a common practice to apply Navier-Stokes (NS) equations to describe the momentum transfer as shown in Equation (14) [28]

$$\frac{\partial \left({\rho }_{\mathrm{f}}\overrightarrow{U}\right)}{\partial t}+{\rho }_{\mathrm{f}}(\overrightarrow{U}·\nabla )\overrightarrow{U}=-\nabla \left(P\overrightarrow{I}\right)+{\rho }_{\mathrm{f}}\overrightarrow{g}+\nabla \left[\mu \left(\nabla \overrightarrow{U}+{(\nabla \overrightarrow{U})}^{\mathrm{T}}\right)-\frac{2\mu }{3}(\nabla ·\overrightarrow{U})\overrightarrow{I}\right]$$

(14)

where ${\rho }_{\mathrm{f}}$ is the density of fluid, P is the pressure, $\overrightarrow{U}$ is the velocity, $\mu$ is the viscosity, $\overrightarrow{I}$ is the identity matrix. The continuity equation is:

$${\rho }_{\mathrm{f}}\nabla \overrightarrow{U}=S_{\mathrm{mass}}$$

(15)

where $S_{\mathrm{mass}}$ is the mass source.

In a porous medium, momentum transfer can be simulated by several models. The easiest one is the Darcy’s law considering the velocity of fluid should linearly respond to the pressure gradient:

$$\overrightarrow{U}=-\frac{\kappa }{\mu }\nabla P$$

(16)

where $\kappa$ is the permeability of the porous medium. In spite of its conciseness, it should be kept in mind that it is an empirical relation which was originated from experimental data of water passing through sands at low velocity [29]. Therefore there are some limitations of Equation (16). For example, Darcy’s law neglects viscous forces. Besides, assuming Darcy’s law is implemented in porous medium and NS equation is used in gas channels, two calculation domains need to be defined, because Equation (14) has second-order differential terms while Equation (16) misses it. This inherent conflict leads to a trouble in setting boundary conditions at the interface between channels and porous medium. [30].

Providing by the drawbacks in Darcy’s law, it is recommended to use Darcy-Forchheimer (DF) equation which is able to be implemented in both gas channels and porous medium, as given in Equation (17) [31,32]:

$$\frac{\partial ({\rho }_{\mathrm{f}}\overrightarrow{U}/\epsilon )}{\partial t}+{\rho }_{\mathrm{f}}(\frac{\overrightarrow{U}}{\epsilon }·\nabla )\frac{\overrightarrow{U}}{\epsilon }=-\nabla \left(P\overrightarrow{I}\right)+{\rho }_{\mathrm{f}}\overrightarrow{g}+\nabla \left[\frac{\mu }{\epsilon }\left(\nabla \overrightarrow{U}+{(\nabla \overrightarrow{U})}^{\mathrm{T}}\right)-\frac{2\mu }{3\epsilon }(\nabla ·\overrightarrow{U})\overrightarrow{I}\right]-\frac{\mu }{\kappa }\overrightarrow{U}$$

(17)

where $\epsilon$ is the porosity of the porous medium. In gas channels where permeability approaches to infinity and porosity becomes one, Equation (17) can automatically become Equation (14), which avoids to set another boundary condition at the interface between gas channels and porous medium.

The data of porosity and permeability is given in Table A1.

3.3. Mass transport

Mass is conserved by Equation (18):

$$\frac{\partial \left(c{Y}_i\right)}{\partial t}+\nabla \left(c\overrightarrow{U}{Y}_i\right)+\nabla N_i=S_{\mathrm{mole},i}$$

(18)

where c is the molar density, $Y_i$ is the molar fraction, $N_i$ is the molar diffusion flux of species i and $S_{\mathrm{mole},i}$ is the source term of moles of chemical specie i due to electrochemcial reactions and it is described by the following Equation (19)

$$S_{\mathrm{mole},\mathrm{i}}=\left\{\begin{array}{c}\frac{i_{\mathrm{v}}}{n_{\mathrm{e}}F}\mathrm{in}\mathrm{electrochemical}\mathrm{active}\mathrm{regions}\hfill \\ 0\mathrm{in}\mathrm{electrochemical}\mathrm{inactive}\mathrm{regions}\hfill \end{array}\right.$$

(19)

where $i_{\mathrm{v}}$ is the reaction current density, and $n_{\mathrm{e}}$ is the number of electrons transferred in electrochemical reactions. To solve Equation (18), $N_i$ needs to be calculated. Several diffusion models that can be chosen. For instance, Fick’s law can be used which is the most popular model due to its simplicity and it has been successfully implemented in SOC numerical modeling [33,34]. The mathematical description is shown in Equation (20)

$$N_i=-D_{ij}^{\mathrm{B}}\nabla \left(c{Y}_i\right)$$

(20)

where $D_{ij}^{\mathrm{B}}$ is the binary diffusion coefficient for species i and j. For a multicomponent system, it is more plausible to apply the Stefan-Maxwell equation to describe the transport phenomena which is the extension of Fick’s law. The Stefan-Maxwell equation is given in Equation (21)

$$\sum _{j=1,j\ne i}^{\mathrm{n}}\frac{Y_j{N}_i-Y_i{N}_j}{D_{ij}^{\mathrm{B},\mathrm{eff}}}=-\frac{P}{RT}\nabla Y_i-\frac{Y_i}{RT}\nabla P$$

(21)

where $D_{ij}^{\mathrm{B},\mathrm{eff}}$ is the effective binary diffusion coefficient. It should be noted that both Fick’s law and Stefan-Maxwell equations are factually applied for the open space in stead of the porous medium [35]. To simulate the behavior in the porous medium, effective diffusion coefficients are introduced which is related to porosity and tortuosity of the porous medium. In the model, Equation (22) is used to define the effective diffusion coefficient [25]:

$$D_{ij}^{\mathrm{B},\mathrm{eff}}=\frac{{\epsilon }_k}{{\tau }_k}{D}_{ij}^{\mathrm{B}}$$

(22)

where $\epsilon$ is the porosity and $\tau$ is the tortuosity. k is the component, such as the fuel electrode and the air electrode. The tortuosity is calculated through following relationship

$${\tau }_k={(1-{\epsilon }_k)}^{\frac{2-2D_{\mathrm{s}}}{2-D_{\mathrm{s}}}}$$

(23)

where $D_{\mathrm{s}}$ is usually chosen as 1.2 for SOC systems [36]. The binary diffusion coefficient $D_{ij}^{\mathrm{B}}$ is evaluated by the Chapman-Enskog theory [37]:

$$D_{ij}^{\mathrm{B}}=D_{ji}^{\mathrm{B}}=\frac{3.16\times {10}^{-8}{T}^{1.75}}{P{({\upsilon }_i^{1/3}+{\upsilon }_j^{1/3})}^2}{(\frac{1}{M_i}+\frac{1}{M_j})}^{1/2}$$

(24)

where $\upsilon$ is the diffusion volume and M is the molar mass.

Fick’s law and Stefan-Maxwell model function well mass transfer in porous medium but they will fail if interaction between species and solids can not be ignored. In this case, Knudsen diffusion should be taken into consideration in addition to molecular diffusion. One model including Knudsen diffusion is the Dusty Gas model as given in Equation (25)

$$\sum _{j=1,j\ne i}^{\mathrm{n}}\frac{Y_j{N}_i-Y_i{N}_j}{D_{ij}^{\mathrm{B},\mathrm{eff}}}+\frac{N_i}{D_i^{\mathrm{K},\mathrm{eff}}}=-\frac{P}{\mathrm{R}T}\nabla Y_i-\frac{Y_i}{\mathrm{R}T}\left(1+\frac{\kappa P}{\mu D_i^{\mathrm{K},\mathrm{eff}}}\right)\nabla P$$

(25)

where $\kappa$ is the permeability, $D_i^{\mathrm{K},\mathrm{eff}}$ is the effective Knudsen diffusion coefficient for the specie i and it can be calculated through Equation (26) [25]

$$D_i^{\mathrm{K},\mathrm{eff}}=\frac{{\epsilon }_k}{{\tau }_k}{D}_i^{\mathrm{K}}=\frac{d_{\mathrm{p}}{\epsilon }_k}{3{\tau }_k}\sqrt{\frac{8\mathrm{R}T}{\pi M_i}}$$

(26)

where $d_{\mathrm{p}}$ is the diameter of the pore size.

In brief, three models, Fick’s law, Stefan-Maxwell model and Dusty Gas model, can be chosen to simulate the mass transport. In this paper, Fick’s law is chosen after several considerations. First, it is easiest to achieve numerically as it has a simpler form than other. Secondly, Fick’s law actually can approximate the other two models well, particularly when the number of components in the system was less than four [38]. Thirdly, to improve the accuracy, Fick’s law can be modified to include the Knudsen diffusion [22,39,40] by employing the Bosanquet formula as shown in Equation (27)

$$\frac{1}{D_{ij}^{\mathrm{eff}}}=\frac{1}{D_{ij}^{\mathrm{B},\mathrm{eff}}}+\frac{1}{D_{ij}^{\mathrm{K},\mathrm{eff}}}$$

(27)

where $D_{ij}^{\mathrm{K},\mathrm{eff}}$ is a mean Knudsen diffusion coefficient that is obtained by replacing $M_i$ with $M_{ij}$ in Equation (26) and $M_{ij}$ is defined as

$$\frac{1}{M_{ij}}=\left(\frac{1}{M_i}+\frac{1}{M_j}\right)/2$$

(28)

Given the above, Fick’s law (Equation (20), (26) ∼ (28)) is applied in the model.

4. Governing equations of the degradation model of MIC oxidation

The typical material used for interconnects of SOC stacks are metals (e.g., Crofer 22 APU). It provides strong mechanical support and high electronic conductivity. However, it always suffers from oxidation [41] leading to the formation of the oxide scale. During the growth of the oxide scale, the resistance at the interface increases, which serves as one part of the total degradation. The model in this work only considers the MIC oxidation at the air side. On the fuel side, MIC oxidation is believed to have little influence on the performance of SOCs. The Ni mesh, as metal, results in good contact on the fuel support layer. Besides, spot welding is used to connect MIC and Ni mesh, which also provides a strong and reliable contact.

4.1. Thickness of the oxide scale on a clean surface

To simulate the growth of the oxide scale, it is a common practice to employ the parabolic law [42,43] given in Equation (29)

$$d^2=\Xi ·t$$

(29)

where d is the thickness of the oxide scale, t is time, and $\Xi$ is the parabolic constant. The meaning of "constant" is that its value does not depend on the thickness of the oxide scale. Before applying Equation (29), proof should be present that for SOCs the growth of the $C{r}_2{O}_3$ fulfils the parabolic format. It was pointed out that the growth of $C{r}_2{O}_3$ obeyed the parabolic law when the temperature was above 623 K [44], which is obviously lower than the operating temperature of SOCs. Besides, there are literature [42,45] where the parabolic law was used to make good curve fitting. In brief, it is reasonable to assume Equation (29) is satisfied during the whole operation of SOCs.

The next step is to obtain the parabolic constant $\Xi$. The typical method is Wagner’s theory which relates ions’ tracer diffusion coefficients to the parabolic constant. According to Wagner’s theory, the parabolic constant can be written as follows:

$$\Xi =\underset{p_{{\mathrm{O}}_2}^{\mathrm{metal}-\mathrm{oxide}}}{\overset{p_{{\mathrm{O}}_2}^{\mathrm{oxide}-\mathrm{gas}}}{\int }}\left[\left(Z_{C{r}^{3+}}/Z_{O^{2-}}\right)D_{C{r}^{3+}}^{\mathrm{eff}}+D_{O^{2-}}^{\mathrm{eff}}\right]dln{p}_{{\mathrm{O}}_2}$$

(30)

where Z is the absolute value of the valency, $D^{\mathrm{eff}}$ is the effective tracer diffusion coefficients which should include the bulk diffusion and grain-boundary diffusion [46,47], the superscript oxide-gas and metal-oxide refer to the interface of oxide-gas and the interface of metal-oxide respectively. Although Equation (30) is widely used for the simulation of alloy oxidation, it is not suitable for the model of SOCs due to the following reasons:

• In order to obtain tracer diffusion coefficients, the concentration of defects (e.g., $VC{r}^{\prime \prime \prime }$)served as the path for the ions needs to be known. However, there remains debates [47–49] on which defects are dominating inside Cr₂O₃.
• No literature about tracer diffusion coefficients inside the oxide scale on Crofer 22 APU can be found. If the data of other alloy is used (e.g., Ni-Cr alloy [49]), the parabolic constant obtained from Equation (30) will evidently deviate from the experimental findings.

In light of the above difficulty in applying Equation (30), an empirical relation, which was measured by FZJ [42] is used in the model.

4.2. Thickness of the oxide scale on the surface covered by a porous coating

It should be stressed that Equation (29) only works for a clean surface without coatings. However, in reality, the MIC is protected by WPS $MnOx$ or APS MCF. Considering the thickness is proportional to the mole of oxygen atoms adsorbed on the MIC, the following equation is obtained:

$$\begin{array}{cc}\hfill d_{\mathrm{poro}}\propto n_{\mathrm{O},\mathrm{poro}}& =\int \int {\dot{n}}_{\mathrm{O},\mathrm{poro}}d{A}_{\mathrm{poro}}dt\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & =\int \int {\dot{n}}_{\mathrm{O},\mathrm{poro}}d\left({\epsilon }_{\mathrm{coating}}A\right)dt\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & ={\epsilon }_{\mathrm{coating}}\int \int {\dot{n}}_{\mathrm{O},\mathrm{poro}}dAdt\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & ={\epsilon }_{\mathrm{coating}}\int \int {\dot{n}}_{\mathrm{O}}dAdt\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & ={\epsilon }_{\mathrm{coating}}{n}_{\mathrm{O}}\hfill \end{array}$$

(35)

which means

$$d_{\mathrm{poro}}={\epsilon }_{\mathrm{coating}}d$$

(36)

where $d_{\mathrm{poro}}$ is the thickness of the oxide scale under porous coatings (e.g., the protective coating), $n_{\mathrm{O},\mathrm{poro}}$ is the mole of oxygen atoms adsorbed on the MIC surface covered by coatings, ${\dot{n}}_{\mathrm{O},\mathrm{poro}}$ is the adsorption rate of oxygen atoms per area over the MIC surface covered by coatings, $A_{\mathrm{poro}}$ is the free surface area under a porous coating that can be reached by oxygen gas, A is the total surface area of MIC, ${\epsilon }_{\mathrm{coating}}$ is the porosity of porous coatings, ${\dot{n}}_{\mathrm{O}}$ is the adsorption rate of oxygen atoms of over the MIC surface without coatings and $n_{\mathrm{O}}$ is the the mole of oxygen atoms adsorbed on the MIC surface without coatings. Two underlying assumptions are used for derivation of Equation (36). First, homogenization assumption is applied in Equation (). This is a common assumption used in CFD models as it is hard for CFD to capture micro-structure values. Secondly, it is assumed in Equation () that the adsorption rate over the MIC surface is not affected by the coating. Since the most evident difference of physical phenomena between the case of applying the coating and the case of not applying the coating is gas transport of oxygen, this assumption means the oxygen partial pressure little affects the adsorption rate. If the porosity of the coating is higher than 0.3, this assumption is reasonable, as it was found unlimited access of oxygen could reach the surface [45]. For the situation where a dense coating is applied, currently no fact can directly support the second assumption. However, it is thought that usually the rate-limiting step during metal oxidation is the diffusion of ions instead of gas transport over the metal surface [43]. Therefore, the second assumption is thought to be generally valid for the growth of the oxide scale under a dense coating.

In brief, Equation (29) and (36) are used to simulate the growth of the oxide scale on MIC in SOCs.

4.3. Voltage drop due to MIC oxidation

To simulate the voltage drop due to MIC oxidation, an internal boundary condition is needed. In the model, this boundary is called the ultra-thin film resistance. The effect of the oxide scale is present by an internal surface boundary condition at the rib, as shown in Figure 2. The mesh of the rib surface is split into two sub-surfaces, and ohmic’s law is applied to each of them as follows:

$$-{\overrightarrow{n}}_{\mathrm{up}}·{\overrightarrow{i}}_{\mathrm{ele}}=-\frac{{\sigma }_{\mathrm{oxide}\mathrm{scale}}}{d_{\mathrm{poro}}}\left({\varphi }_{\mathrm{ele},\mathrm{up}}-{\varphi }_{\mathrm{ele},\mathrm{low}}\right)$$

(37)

$$-{\overrightarrow{n}}_{\mathrm{low}}·{\overrightarrow{i}}_{\mathrm{ele}}=-\frac{{\sigma }_{\mathrm{oxide}\mathrm{scale}}}{d_{\mathrm{poro}}}\left({\varphi }_{\mathrm{ele},\mathrm{low}}-{\varphi }_{\mathrm{ele},\mathrm{up}}\right)$$

(38)

where $\overrightarrow{n}$ is the unit normal vector, $\overrightarrow{i_{\mathrm{ele}}}$ is the electronic current density, ${\sigma }_{\mathrm{oxide}\mathrm{scale}}$ is the conductivity of the oxide scale and ${\varphi }_{\mathrm{ele}}$ is the electronic potential. The subscripts “up" and “low" refer to the upper surface (with higher electronic potential) and lower surface (with lower electronic potential). Directions of above vectors can be found in Figure 2. The difference between ${\varphi }_{\mathrm{ele},\mathrm{up}}$ and ${\varphi }_{\mathrm{ele},\mathrm{low}}$ arises from the resistance of the growing oxide scale, which can be obtained through:

$$\Delta {\varphi }_{\mathrm{ele}}={\varphi }_{\mathrm{ele},\mathrm{up}}-{\varphi }_{\mathrm{ele},\mathrm{low}}=\left|{\overrightarrow{i}}_{\mathrm{ele}}·\frac{d_{\mathrm{poro}}}{{\sigma }_{\mathrm{oxide}\mathrm{scale}}}\right|$$

(39)

where $\Delta {\varphi }_{\mathrm{ele}}$ is the voltage degradation due to the MIC oxidation.

4.4. Parameters

According to the experimental data [42], the parabolic constant of Crofer 22 APU (700 ∼ 900 ${}^{\circ }$C) is summarized in Equation (40)

$${\Xi }_{\mathrm{Crofer}}=5.5075\times {10}^{-9}\exp \left(\frac{-1.9992\times {10}^5[\mathrm{J}/\mathrm{mol}]}{\mathrm{R}T}\right)$$

(40)

It was found under 800 ${}^{\circ }$C, the growth rate of the oxide scale on ITM was half of that on Crofer 22 APU [50]. Assuming this finding is valid for the temperature range of 700 ∼ 900 ${}^{\circ }$C, the parabolic constant for ITM is:

$${\Xi }_{\mathrm{ITM}}=0.25\times {\Xi }_{\mathrm{Crofer}22\mathrm{APU}}=1.3769\times {10}^{-9}\exp \left(\frac{-1.9992\times {10}^5[\mathrm{J}/\mathrm{mol}]}{\mathrm{R}T}\right)$$

(41)

The conductivity of the oxide scale on Crofer 22 APU, ${\sigma }_{\mathrm{oxide}\mathrm{scale},\mathrm{Crofer}}$, is summarized as follows with the help of experimental data [43]:

$${\sigma }_{\mathrm{oxide}\mathrm{scale},\mathrm{Crofer}}=\frac{1}{T}·{10}^{-3228/T+6.7661}$$

(42)

The available conductivity data of the oxide scale on ITM is very limited. It was found that the increasing rate of ASR on ITM during oxidation was about 3.5 times as much as that on Crofer 22 APU [51], even if the thickness was half. The explanation was that if the coating was not a spinel phase, the oxide scale generated on ITM has some porosity while that on Crofer 22 APU was quite dense [51]. Since in history, ITM was usually combined with $MnOx$ coating (not a spinel phase) in FZJ SOC stacks design, it is assumed that the conductivity of the oxide scale on ITM, ${\sigma }_{\mathrm{oxide}\mathrm{scale},\mathrm{ITM}}$, is

$${\sigma }_{\mathrm{oxide}\mathrm{scale},\mathrm{ITM}}=\frac{1}{7}{\sigma }_{\mathrm{oxide}\mathrm{scale},\mathrm{Crofer}}=\frac{1}{7T}·{10}^{-3228/T+6.7661}$$

(43)

The porosity of WPS coating is 0.45 [52] while the porosity of APS coating is 0.03 [53].

5. Numerical procedure

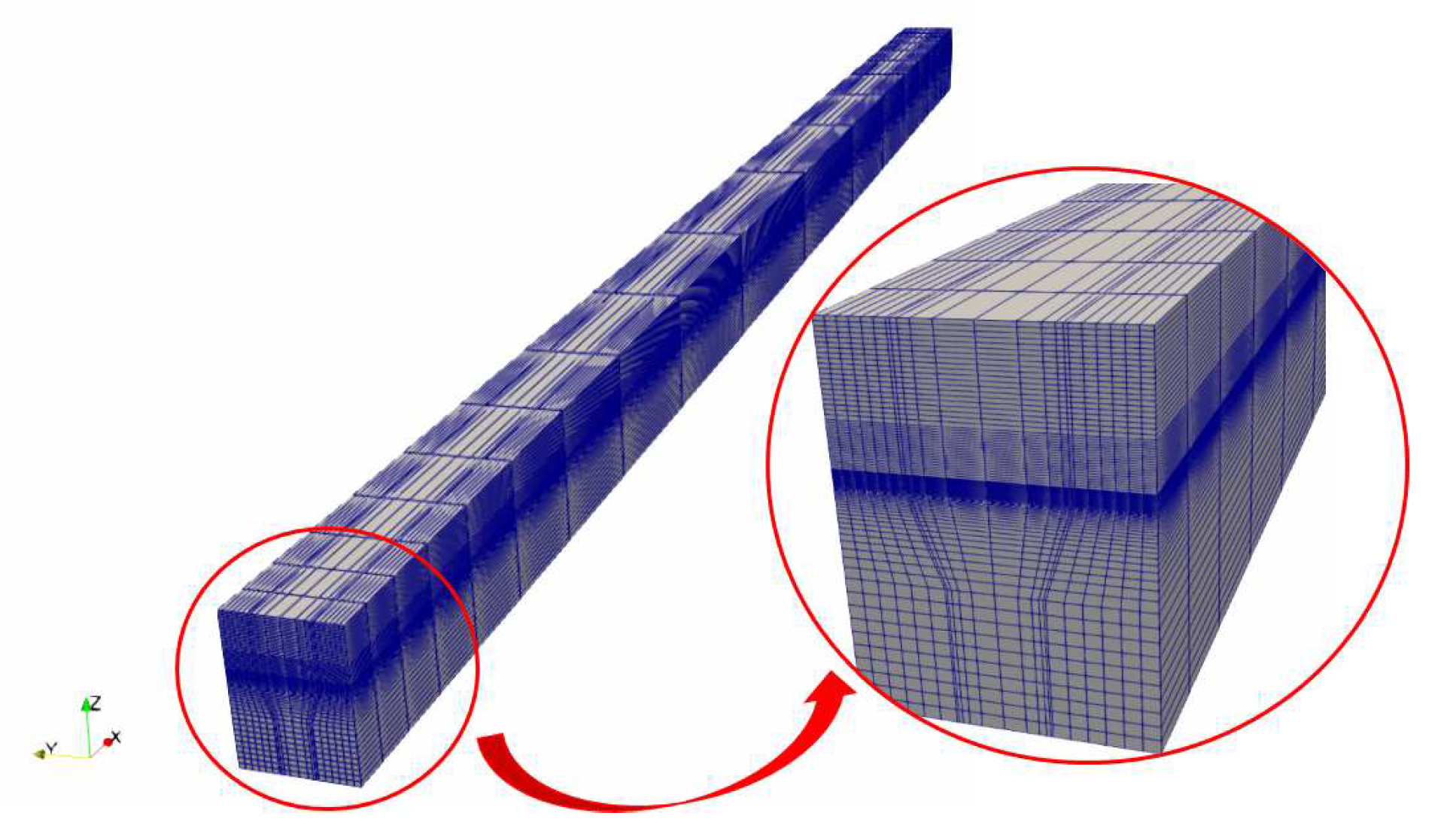
The mesh in the model is present in Figure 3, where totally 74800 elements are made. Mesh refinement is made at the interface to capture electrochemical reactions. In other areas a coarser mesh is used.

The basic model is steady-state while MIC oxidation is a time-dependent model. Discretization of the time derivative is achieved by Backward Euler method. To increase the convergence of the time-dependent simulation, the basic model is solved first. The time-dependent simulation of MIC oxidation is carried out with the initial values being results of the basic model. The time-step for the time-dependent simulation is 10 hours.

The solver and discretization used in COMSOL and OpenFOAM are different. The former employs a coupled solution manner, which solves all variables simultaneously. During time intervals, a direct solver, which solves the inverse of the matrix, is used. In contrast, the segregated solver is applied in OpenFOAM that subdivides the numerical calculation into several steps. For each iteration, the iterative solver is applied. Moreover, COMSOL implements the finite element method while OpenFOAM utilizes the finite volume method. Despite of above differences in numerical calculation, it is expected both software give similar results when it comes to the same model with same boundary conditions and parameters. All the simulations are conducted on a single core of a computer with CPU i7-9700K and 32 GB RAM.

6. Experiment

SOC stacks were operated in constant current mode with the gases supplied in a counter-flow scheme. The characterization and operation of SOC stacks were carried out in an oven test rig. Inside the oven, there were electric heating elements to maintain the temperature of stacks through heat radiation. Deionized water with a resistivity of 10 MΩ cm [54] was sent to the electrically-heated steam generator. Hydrogen with purity of minim 99.9 % was used for the inlet fuel. Dehumidified air with a dew point below -40 ${}^{\circ }$C was sent as the inlet air. The mass flow of inlet air and inlet fuel was controlled by the mass flow controllers (MFCs).Mica sealants between the test bench interface and the stack in combination with a compressive force of 1 kN were applied to prevent gas leakage. Table 3 shows details of MFCs, operation conditions and stack designs of several stacks, which are used for the validation of models. The temperature values in Table 3 are taken according to thermocouples that was roughly placed 10 mm-deep into the intermediate interconnector (details of the location can be found in reference [55]).

Table 3. Experimental details of SOC stacks

		F1002-97	F1002-95	F1004-67	F1004-115
Instrument	MFC	Bronkhorst, F-201CV	Bronkhorst, F-201CV	Bronkhorst, F-201CV	Brooks, 0254
Stack design	Contact layer	LCC12	LCC12	LSCF	LSCF
	MIC	ITM	Crofer 22 APU	Crofer 22 APU	Crofer 22 APU
	Protective coating	WPS MnOx	WPS MnOx	APS MCF	APS MCF
Operation conditions	Temperature	720 ${}^{\circ }$C	710 ${}^{\circ }$C	730 ${}^{\circ }$C
	Fuel mass flow	1.18$\times {10}^{-7}$ kg/s	1.15$\times {10}^{-7}$ kg/s	1.15$\times {10}^{-7}$ kg/s
	Molar ratio in fuel	H2/H2O = 79/21	H2/H2O = 80/20	H2/H2O = 80/20
	Air mass flow	1.9$\times {10}^{-6}$ kg/s	1.18$\times {10}^{-6}$ kg/s	1.18$\times {10}^{-6}$ kg/s
	Molar ratio in air	O2/N2 = 21/79	O2/N2 = 21/79	O2/N2 = 21/79
	Current density	0.5 A/cm${}^2$	0.5 A/cm${}^2$	0.5 A/cm${}^2$
	Time	100 kh	17 kh	25 kh
Conditions of I-V curves characterization	Temperature	700 ∼ 800 ${}^{\circ }$C		700 ∼ 800 ${}^{\circ }$C	700 ∼ 800 ${}^{\circ }$C
	Fuel mass flow	1.52$\times {10}^{-7}$ kg/s		1.85$\times {10}^{-7}$ kg/s	5.53$\times {10}^{-7}$ kg/s
	Molar ratio in fuel	H2/H2O = 88/12		H2/H2O = 80/20	H2/H2O = 50/50
	Air mass flow	2.38$\times {10}^{-6}$ kg/s		1.79$\times {10}^{-6}$ kg/s	2.83$\times {10}^{-6}$ kg/s
	Molar ratio in air	O2/N2 = 21/79		O2/N2 = 21/79	O2/N2 = 21/79
	Current density	0 ∼ 0.8 A/cm${}^2$		0 ∼ 0.8 A/cm${}^2$	-0.5 ∼ 0.5 A/cm${}^2$

Table 3. Experimental details of SOC stacks

		F1002-97	F1002-95	F1004-67	F1004-115
Instrument	MFC	Bronkhorst, F-201CV	Bronkhorst, F-201CV	Bronkhorst, F-201CV	Brooks, 0254
Stack design	Contact layer	LCC12	LCC12	LSCF	LSCF
	MIC	ITM	Crofer 22 APU	Crofer 22 APU	Crofer 22 APU
	Protective coating	WPS MnOx	WPS MnOx	APS MCF	APS MCF
Operation conditions	Temperature	720 ${}^{\circ }$C	710 ${}^{\circ }$C	730 ${}^{\circ }$C
	Fuel mass flow	1.18$\times {10}^{-7}$ kg/s	1.15$\times {10}^{-7}$ kg/s	1.15$\times {10}^{-7}$ kg/s
	Molar ratio in fuel	H2/H2O = 79/21	H2/H2O = 80/20	H2/H2O = 80/20
	Air mass flow	1.9$\times {10}^{-6}$ kg/s	1.18$\times {10}^{-6}$ kg/s	1.18$\times {10}^{-6}$ kg/s
	Molar ratio in air	O2/N2 = 21/79	O2/N2 = 21/79	O2/N2 = 21/79
	Current density	0.5 A/cm${}^2$	0.5 A/cm${}^2$	0.5 A/cm${}^2$
	Time	100 kh	17 kh	25 kh
Conditions of I-V curves characterization	Temperature	700 ∼ 800 ${}^{\circ }$C		700 ∼ 800 ${}^{\circ }$C	700 ∼ 800 ${}^{\circ }$C
	Fuel mass flow	1.52$\times {10}^{-7}$ kg/s		1.85$\times {10}^{-7}$ kg/s	5.53$\times {10}^{-7}$ kg/s
	Molar ratio in fuel	H2/H2O = 88/12		H2/H2O = 80/20	H2/H2O = 50/50
	Air mass flow	2.38$\times {10}^{-6}$ kg/s		1.79$\times {10}^{-6}$ kg/s	2.83$\times {10}^{-6}$ kg/s
	Molar ratio in air	O2/N2 = 21/79		O2/N2 = 21/79	O2/N2 = 21/79
	Current density	0 ∼ 0.8 A/cm${}^2$		0 ∼ 0.8 A/cm${}^2$	-0.5 ∼ 0.5 A/cm${}^2$

F1004-115 used a 400 µm thick support layer, 10 µm thick fuel electrode and a 6 µm thick electrolyte. Geometry of the rest parts of F1004-115 and other stacks can be found in Figure 1.

7. Validation

7.1. Validation of I-V curves of the basic model

The validation of the OpenFOAM simulation has two parts: 1) comparison between OpenFOAM simulation with COMSOL (a commercialized software) simulation. The same mesh, geometry, model, boundary conditions and parameters are used in both simulations. Although OpenFOAM and COMSOL use different discretization methods and solvers, their results are expected to be close; 2) comparison between OpenFOAM simulation and experimental results. The comparison is carried out under different operation modes (e.g., fuel cell and electrolysis modes) and various operation conditions (e.g., different operation temperature and humidity of inlet fuel).

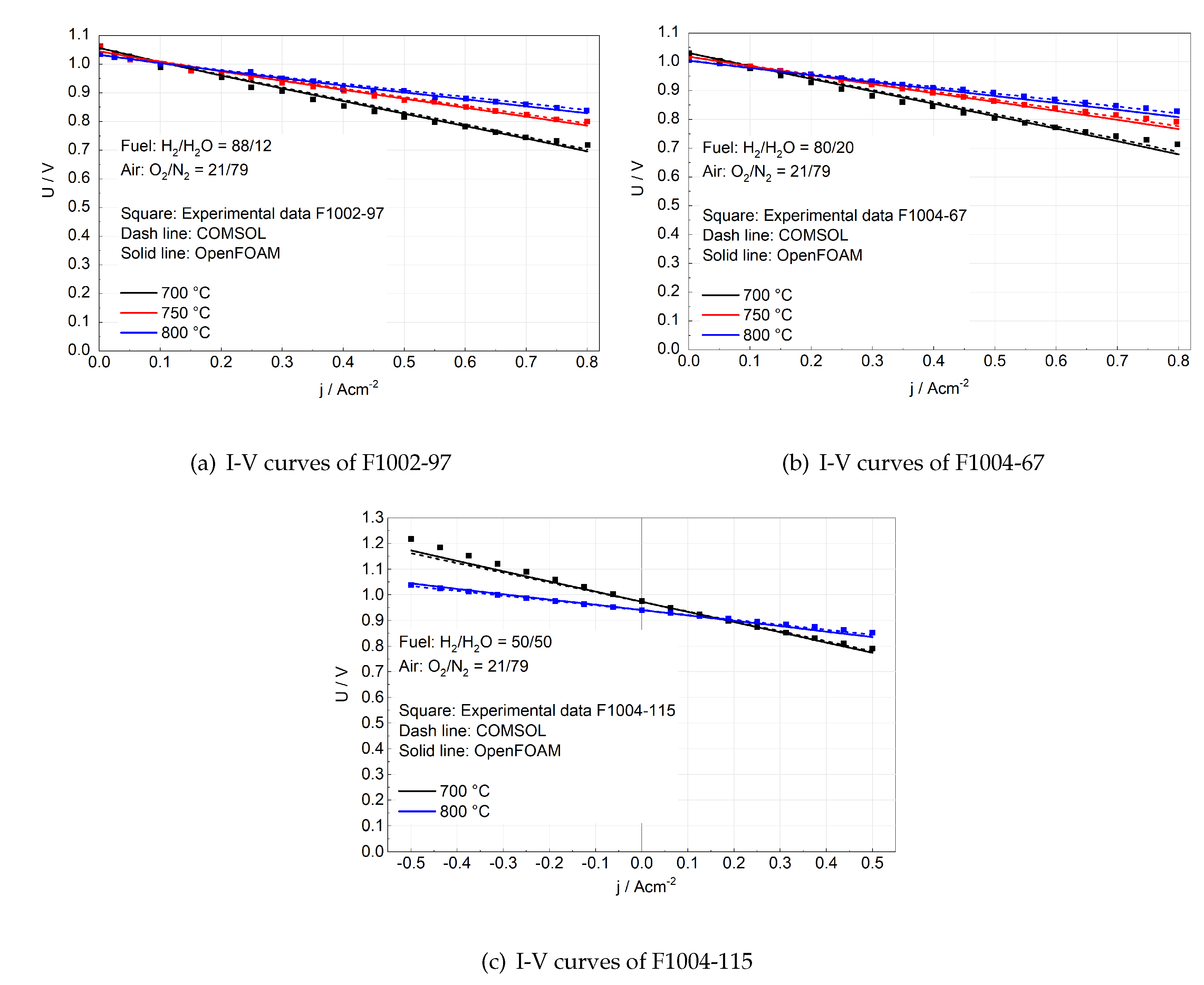
The validation by I-V curves is shown in Figure 4. Figure 4a and 4b presents the I-V curves only in the fuel cell mode. With various humidity and temperature, a very good match between OpenFOAM simulation and experimental data is found, where the maximum voltage deviation is only 4.5%. Figure 4c presents the I-V curves for reversible SOCs. The negative current density means electrolysis operation, while the positive current density indicates the fuel cell operation. Similarly, there is a good agreement between OpenFOAM and experimental measurement since the maximum voltage deviation is just 4.1%. Besides, the OpenFOAM simulation closely approximates the COMSOL simulation in all cases shown in Figure 4, which further proves the validity of the numerical model in OpenFOAM (assuming COMSOL simulation is reliable). The deviations between simulated and experimentally measured I-V curves could be due to the fluctuating temperature (5 ∼ 10 ${}^{\circ }$C) during I-V curves characterization.

7.2. Validation of MIC degradation model

The core equation of the MIC oxidation model is Equation (36), which describes the thickness of the oxide scale under a porous coating. In the following, examples are given to demonstrate the validity of Equation (36).

7.2.1. Result from Persson: Crofer 22 APU with and without $(La,Sr)Mn{O}_3$ (LSM) coating

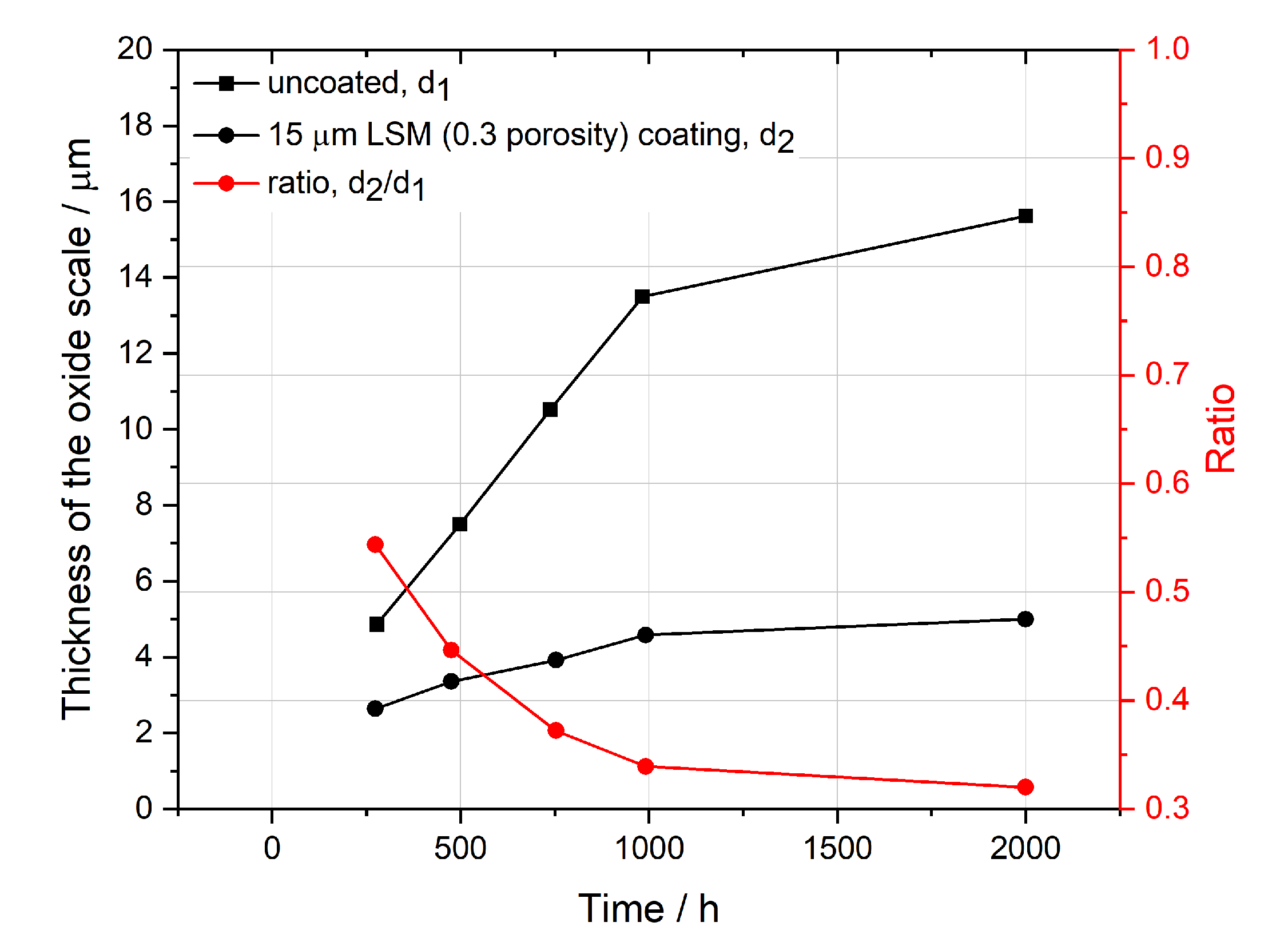
Persson et al. [45] did a series of oxidation tests on Crofer 22 APU. The experimental data were taken from thermogravimetric analysis (TGA), which made it possible to track the growth of the oxide scale during operation. If Equation (36) can approximate well to the experimental results, the ratio of the thickness of the oxide scale under the coating to the thickness of the oxide scale without coating should be close to the porosity of the coating, 0.3. From Figure 5, after 1000 h operation, the ratio was near 0.3, indicating the model’s validity. However, at the beginning of the operation, the ratio was clearly higher than 0.3. This could be due to the sintering process of the coating, as Persson used spray guns to add coatings on the MIC at room temperature and then started oxidation tests directly [45]. But in general, it can be claimed that the model is capable of predicting an accurate thickness of the oxide scale.

7.2.2. Result from FZJ: F1002-95 and F1002-97

Two stacks from FZJ are used for validation, F1002-97 and F1002-95. F1002-97 used ITM as the MIC and WPS MnO_x as the protective coating, while F1002-95 used Crofer 22 APU as the MIC and WPS MnO_x as the protective coating. Details of stacks can be found in Table 3.

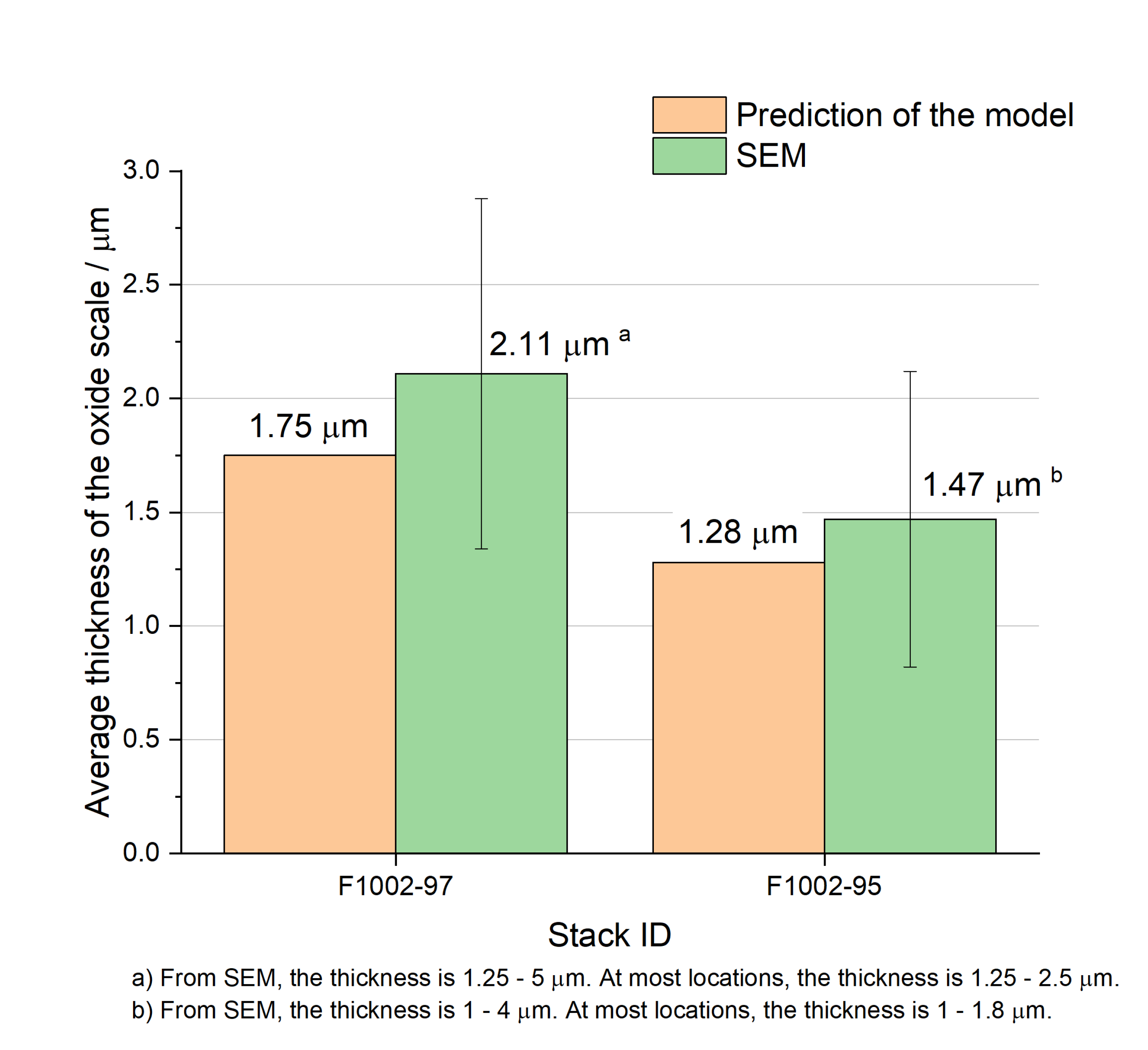
Unlike the TGA data in Figure 5, the validation data in this section are manually taken from SEM figures. This should be kept in mind during the following comparison since the model predicted the average thickness. As shown in Figure 6 where average thickness is compared, a good agreement is observed although there are some deviations between the simulation and the experimentally measured data. The deviations can be due to the limited choices of parameters (e.g., the porosity of the protective coating and properties of ITM) and manual errors when taking data from SEM images.

8. Results and discussions

8.1. Spatial distribution of mole fraction and overpotential

Distribution of mole fraction and overpotential affect the local degradation. Here only analysis of the SOEC is given.

Spatial distribution of mole fraction and overpotential are shown in Figure 7 and Figure 8 respectively. The simulation works for the electrolysis operation of F1004-115 under -0.5 A/cm${}^2$, fuel inlet composition H₂/H₂O = 50 : 50 and air inlet composition O₂/N₂ = 21 : 79. In the simulation, the flow field is the counter flow that fuel flows towards the x-coordinate while air flows against the x-coordinate.

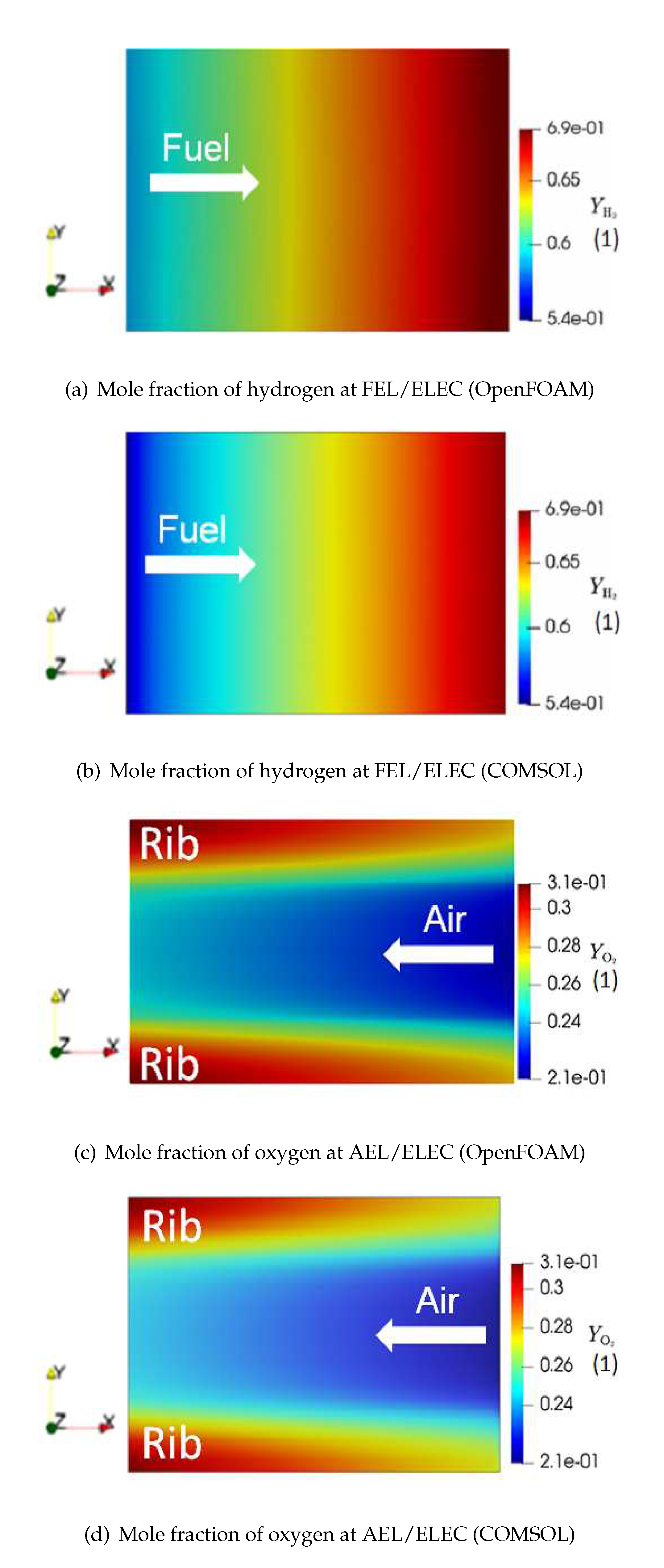
Figure 7 shows the mole fraction distribution in the electrolysis mode of F1004-115, at the interface between the fuel electrode and the electrolyte (FEL/ELEC) and the interface between the air electrode and the electrolyte (AEL/ELEC). From Figure 7a, it is found that along the x-coordinate, which is the fuel flow direction, $Y_{{\mathrm{H}}_2}$ gradually increases due to the electrochemical reaction. Similarly, as indicated by Figure 7c, $Y_{{\mathrm{O}}_2}$ increases along the flow direction (against the x-coordinate). In addition, it should be noted that $O_2$ tends to segregate at the rib. As a comparison, on the fuel side, $H_2$ is more uniformly distributed. The main reason behind this phenomenon is a gas channel is used for air distribution while the Ni mesh is used for sending the fuel. Unlike the Ni mesh, the air channel does not directly contact the rib. Hence $O_2$ transportation at the rib is mainly dependent on the diffusion process. However, the diffusion coefficient of $O_2$ is not high as it is one order of magnitude lower than that of hydrogen and water. Consequently, the lack of enough driving force of transportation leads to $O_2$ segregation at the rib. Besides, when it comes to the mole fraction, the OpenFOAM simulation is close to the COMSOL simulation. There is a slight difference between Figure 7a and Figure 7b, which can be caused by different solvers applied in OpenFOAM and COMSOL.

Figure 8 shows the overpotential distribution in the electrolysis mode of F1004-115, where ${\eta }_{\mathrm{fuel}}$ is negative and ${\eta }_{\mathrm{air}}$ is positive. According to Figure 8a and 8b, both overpotential, ${\eta }_{\mathrm{fuel}}$ and ${\eta }_{\mathrm{air}}$, reach the maximum absolute values close to the electrolyte as expected, because overpotential is the driving force for electrochemical reactions which majorly happen near the electrolyte interface. Compared to the COMSOL simulation (right column), the evolution tendency is the same while the values are slightly different.

8.2. Voltage degradation due to MIC oxidation in F1002-97

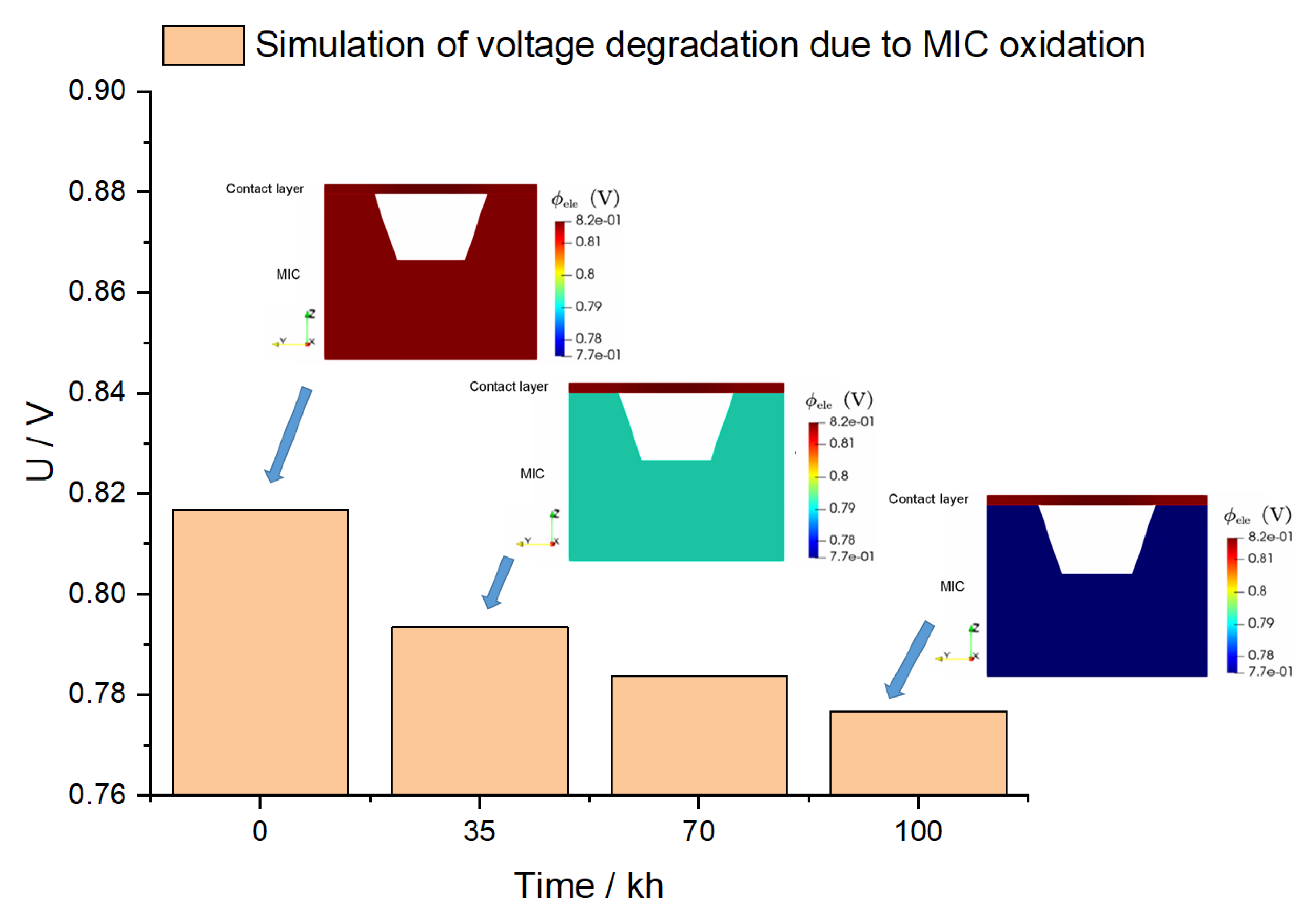
The details of the stack F1002-97 can be found in Table 3. Figure 9 shows stack voltage evolution predicted by simulation at four time points. The inserted figures present the distribution of the electronic potential in the contact layer and the MIC. At time = 0 h, when no oxide scale exists, the electronic potential is uniformly distributed, because the electronic conductivity of materials is high. With time going on, the oxide scale gradually grows, leading to degradation. It is clearly seen the ultra-thin film resistance model works as there is a sudden potential drop across the rib in the inserted figures. 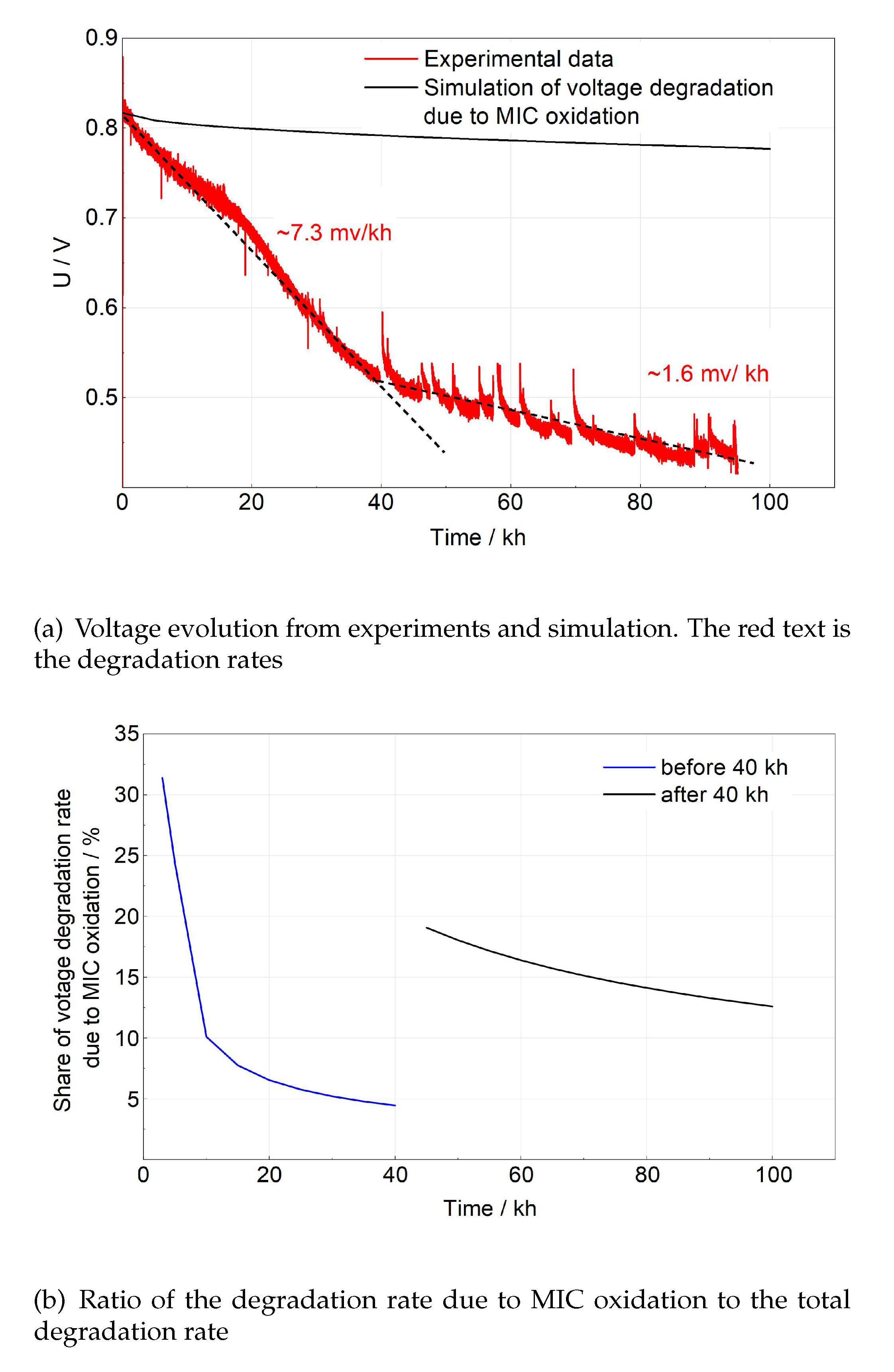Figure 10 gives the evolution of the voltage of the whole lifetime and the share of degradation rate only due to MIC oxidation. Due to unstable water supply, the voltage measured in experiments was fluctuating all the time. With the help of linear fitting, the degradation rate is determined as 7.3 mV/kh before 40 kh and 1.6 mV/kh after 40 kh. Figure 10a indicates the voltage drop as a consequence of MIC oxidation is not so important in the long term. However, as shown in Figure 10b, its influence on the total degradation rate could not be neglected, especially at the start of the operation (20% - 31% in the first 5 kh and 10% - 19% after 40 kh of the total degradation rate). The MIC oxidation contributes ∼ 11% of the total degradation rate.

8.3. Voltage degradation due to MIC oxidation in F1004-67

Crofer 22 APU was used as the MIC and APS MCF was applied as the protective coating for the stack F1004-67. It was operated at 730 ${}^{\circ }$C and 0.5 A/cm${}^2$ with a degradation rate of 3 mV/kh over 25 kh operation. Due to a dense coating, simulation predicts the voltage decreases at 0.016 mv/kh if MIC oxidation is the only degradation mechanism, which only contributes ∼ 0.53 % to the total degradation. The simulation result reveals that with APS MCF protective coating, degradation due to the MIC oxidation can be neglected. The degradation must mainly arise from other processes, such as Ni agglomeration and Cr poisoning.

A time-dependent model is built up via OpenFOAM, which can be used to simulate the MIC oxidation. It has been validated by several experiments that the accurate thickness of the oxide scale can be predicted by the model.

From the simulation, it is found if APS MCF Prot. Coat. is applied, the degradation due to the MIC oxidation is generally stopped. In contrast, if WPS $MnOx$ is used, the MIC oxidation can not be ignored, especially at the beginning of the operation. For the whole lifetime of F1002-97, the MIC oxidation contributes ∼11% of the total degradation rate.

The model gives a frame for future sophisticated modelling. For example, although currently an empirical equation is used to calculate the parabolic constant, a model with more physics can be added.