Surfaces Intersection and Flattening in 3D Models Through Computer Extended Descriptive Geometry (CeDG)

1. Introduction

Descriptive geometry (DG), a science that was systematized by Gaspard Monge in 1794, and its associated representation systems, such as the dihedral system, have determined the foundations of graphic representation in engineering since the second half of the 19th century. This discipline has a huge importance in the development of spatial vision and constitutes a fundamental pillar in university teaching, although its use in the professional field has been practically replaced by computer-aided design (CAD) software [1]. CAD technology emerged in the mid-1990s as a computer-based approach to create, modify, analyze and document 2D or 3D graphical representations of physical elements, providing an alternative to manual drafts and product prototypes. The main reason for the replacement of DG by CAD systems lies in the current wide availability of software packages capable of representing three-dimensional shapes. The geometry of the CAD model is essentially represented by curves and approximation surfaces, such as B-splines, which provide high control and accuracy [2].

The determination of the intersection between two surfaces of revolution as a problem in CAD has been around for 60 years and continues to be an active topic of research today. The main reason lies in the fact that the technique used has to balance three conflicting objectives such as accuracy, strength and efficiency [3]. The problem of intersection between surfaces involves the design of algorithms suitable for evaluating and performing geometric operations, as well as their representation. The exact requirements of the representation and algorithms depend on the particular application. Generally speaking, any representation should provide functionality to perform the operations of evaluating and rendering the intersection curve, deciding whether a point belongs to the intersection curve, organizing the points that lie on the intersection curve, and using it as the boundary edge of a trimmed surface.

The evaluation of the intersection between two rational parametric surfaces is a recurring operation in solid modelling and can be approached using algebraic sets in a higher dimensional space. Using results from elimination theory, it is possible to project the algebraic set to a lower dimensional space, using the matrix itself as the representation of the algebraic set in this space. Given this representation, properties of rectilinear programs and linear algebra results are used to perform geometric operations on the intersection curve. The accuracy of these operations can be improved by pivoting or other numerical techniques [4].

Nearly 30 years ago, the strength deficiencies shown in the methods of intersection between surfaces applied at the time [5] were being addressed. For this purpose, exact methods based on rational arithmetic (oriented to rational B-spline surfaces) began to be used, techniques that have been transferred to the usual CAD.

Subsequent studies presented a review of the problem of intersection between surfaces for CAD/CAM, also developing a new algorithm based on the geometric properties of the surfaces and their intersection curves, establishing an integration of the segmentation and tracing methods [6]. This algorithm translates the nonlinear problem of surface–surface intersection (SSI) curve finding into a series of steps for solving sets of linear equations. The starting points for the plotting are computed by a combination of numerical and subdivision techniques. In the plotting phase, the intersection curve is drawn in the direction of the combination of its tangent vector and the direction of the geodesic radius of curvature, and the size of the steps is adaptively adjusted according to the curvature of the intersection curve. Nevertheless, at the singular points, only the tangent direction was taken into account.

As an evolution of the previous methods, in [7] two hybrid models are generated for the calculation of the intersection of two Bezier surfaces, obtaining more accurate results, and therefore closer to the real solution, than using the plane/plane intersection. To calculate exactly intersection points, two marching methods were used, employing tangential or circular steps. An important difference between the two techniques lies in the step size. In the method using tangential steps, the step size must be fixed and predefined, while in the circular step method, the step size is dynamic and changes automatically. The choice of techniques to use will depend on the particular problem. If the result is twisted or sinuous, the circular pitch is recommended, otherwise, it is enough to use the tangential pitch.

A new improvement of the previous surface intersection methods is presented in [8] for surfaces based on NURBs. The results obtained in this study allow to eliminate some assumptions that were necessary to apply in the parameterization of surfaces, thus facilitating this process for two general surfaces. Finally, recent studies present new techniques targeting toroidal patches in which the intersection curve of two free-form surfaces is computed by employing a bounding volume hierarchy (BVH), where the leaf nodes contain oscillating toroidal patches [9]. The effectiveness of the technique applies, among other cases, to two nearly identical surfaces (such as Figure 7 of this article).

Computer Extended Descriptive Geometry (CeDG) constitutes a new way of undertaking computer modelling of 3D geometric systems [10], trying to offer a solution to the constraints of the current CAD systems previously pointed out [5]. As discussed, CAD tools favor the construction of virtual prototypes of 3D systems that can be manipulated in space and projected in a simple way according to the chosen representation system. Nevertheless, they do not allow the model to be generated when it depends on some implicit parameter (which can only be measured when the model is built). In addition, they still show important deficiencies in the calculation of flat patterns of sheet metal surfaces.

The CeDG approach combines the ability of DG to solve spatial geometric problems with the skill of dynamic geometry [11] in the evolution of geometric-algebraic model building. CeDG parametric models preserve the integrity of curves and surfaces, in contrast to CAD systems. A preliminary version of the CeDG approach implemented on the dynamic geometry software Geogebra [12] has proved its capability to overcome some of the above limitations [10].

The objective of this study is the development of theoretical methods for the computation of encounters between surfaces and for their flattening, based on CeDG. For this purpose, a methodology which is completely different from those presented so far will be used, not being oriented to NURBS-based surfaces.

The usual procedure used in DG to calculate the intersection between two surfaces consists of defining it by means of their projections, which are obtained through interpolation on a set of points belonging to them. The points are obtained by means of DG techniques, which are applied iteratively, so that the accuracy and complexity of the resulting curve is proportional to the number of points attained [13]. The CeDG approach uses an extension of the DG procedures, taking advantage of the existence of an exact algebraic function that defines the sought intersection curve, which represents the algebraic calculation of a general point of this curve. The algebraic function can be extracted by means of a locus function, which is automatically computed from the sequence of geometric-algebraic instructions associated with the calculation of a single generic point of the intersection [10].

This paper develops the theoretical technique that computes the intersections and flattening (first objective), which is used to solve the case study defined by a compound hopper, being its CeDG result (3D model and flat pattern) compared with the solution obtained using Solid Edge 2023 (second objective). The details of the comparison are presented in the Methods section.

2. Materials and Methods

The study follows two stages. The theoretical development of the $CeDG$ technique for surfaces intersection and flattening is presented in the first stage. We use the parametric 3D model of an oblique cone that intersects with an oblique cylinder (Figure 1) and it is subsequently flattened, to clarify the meaning and scope of the algebraic entities and procedures involved in the novel method.

The variables and other nomenclature used in the theoretical development are defined before their first use. Notwithstanding, those terms that refer to very relevant objects are listed also in the Abbreviations section. The 3D surfaces and entities are defined by their vertical and horizontal projections.

The technique is applied in the second stage to solve the hopper defined by the projections of Figure 2, computing the surface intersections and flat patterns (flattening) of the upper duct, ${\mathrm{D}}_{\mathrm{u}}$ (${\mathrm{d}\text{’}}_{\mathrm{u}}$ - ${\mathrm{d}}_{\mathrm{u}}$), and the lower duct, ${\mathrm{D}}_{\mathrm{l}}$ (${\mathrm{d}\text{’}}_{\mathrm{l}}$ - ${\mathrm{d}}_{\mathrm{l}}$), and comparing them against the flat patterns obtained through Solid Edge 2023. According with the methodology pointed in Prado-Velasco and Ortiz-Marín [13] the flat pattern refers to the neutral surface (fiber) of the hopper.

The hopper is completed by a fluid duct, ${\mathrm{D}}_{\mathrm{f}}$ (${\mathrm{d}\text{’}}_{\mathrm{f}}$ - ${\mathrm{d}}_{\mathrm{f}}$), which transports fluid towards the upper duct, and an oblique duct, ${\mathrm{D}}_{\mathrm{o}}$ (${\mathrm{d}\text{’}}_{\mathrm{o}}$ - ${\mathrm{d}}_{\mathrm{o}}$), where aggregates (small discrete mass of coarse - medium particles) from the aggregates border, ${\mathrm{B}}_{\mathrm{a}}$ (${\mathrm{b}\text{’}}_{\mathrm{a}}$ - ${\mathrm{b}}_{\mathrm{a}}$) go into the system. The fluid duct is a conical surface that discharges into ${\mathrm{D}}_{\mathrm{u}}$ through the discharge area, ${\mathrm{A}}_{\mathrm{d}}$, which assuming that the system operates in steady state, may be defined through the following equation:

$$G={\int }_{{\mathrm{S}}_{\mathrm{d}}}\rho \left(r\right)\overrightarrow{v}\left(r\right)\overrightarrow{dS}\left(r\right)={\rho }_d{v}_d{\mathrm{A}}_{\mathrm{d}},$$

(1)

in which G is the mass flow rate of fluid through ${\mathrm{D}}_{\mathrm{f}}$ and $\rho ,\overrightarrow{v}$ and $\overrightarrow{dS}$ are the density and velocity of fluid and a differential element of area perpendicular to $\overrightarrow{v}$ at the position r in the discharge surface, ${\mathrm{S}}_{\mathrm{d}}$. Thus, ${\rho }_d,v_d$ and ${\mathrm{A}}_{\mathrm{d}}$ are average values of density and fluid velocity, and the area of the discharge section.

The model wants to be optimized to achieve a very fast expansion of the fluid in the last portion of the conical duct (quasi - adiabatic expansion). With that aim, the 3D model must facilitate the research on the dimensional parameters that provide a fluid expansion given by the outlet / inlet area ratio ${\mathrm{A}}_{\mathrm{r}}$ = ${\mathrm{A}}_{\mathrm{d}}$/${\mathrm{A}}_{\mathrm{i}}$ > 3 (${\mathrm{A}}_{\mathrm{i}}$ is the fluid duct inlet area). The value of ${\mathrm{A}}_{\mathrm{r}}$ is controlled by the ${\mathrm{D}}_{\mathrm{u}}$ - ${\mathrm{D}}_{\mathrm{f}}$ connection curve, which depends on the conicity of ${\mathrm{D}}_{\mathrm{f}}$ (Con) and the horizontal distance between the ${\mathrm{D}}_{\mathrm{f}}$ axis and v (Eccentricity), Ecc, whereas the remaining dimensions of the hopper are constant. The conicity induces a smooth increment of area, whereas the eccentricity promotes a greater surface inside the ${\mathrm{D}}_{\mathrm{u}}$ - ${\mathrm{D}}_{\mathrm{f}}$ connection curve without a gradual increment along the fluid duct.

The other hopper dimensions taken as parameters are the diameter of the inlet fluid border (${\mathrm{b}\text{’}}_{\mathrm{f}}$ - ${\mathrm{b}}_{\mathrm{f}}$), ${\mathrm{D}}_{\mathrm{df}}$, diameter of the upper border (${\mathrm{b}\text{’}}_{\mathrm{u}}$ - ${\mathrm{b}}_{\mathrm{u}}$), ${\mathrm{D}}_{\mathrm{bu}}$, diameter of the lower border (${\mathrm{b}\text{’}}_{\mathrm{l}}$ - ${\mathrm{b}}_{\mathrm{l}}$), ${\mathrm{D}}_{\mathrm{bl}}$, height of the lower duct with respect to its vertex, ${\mathrm{H}}_{\mathrm{ld}}$, angle of fluid duct axis with respect to the vertical, ${\alpha }_{\mathrm{df}}$, and the angle of oblique duct with respect to the horizontal, ${\alpha }_{\mathrm{do}}$.

The discharge surface, ${\mathrm{S}}_{\mathrm{d}}$, may be defined by the cylindric surface inside the warped intersection curve between surfaces ${\mathrm{D}}_{\mathrm{f}}$ and ${\mathrm{D}}_{\mathrm{u}}$, which will be computed during the hopper modelling. According to the equation (1), the area ${\mathrm{A}}_{\mathrm{d}}$ may be considered perpendicular to the streamline. We are interested to perform an analysis focused on the 3D model and independent of the fluid system. Therefore, we will use the 3D hopper model to propose and compute a surrogate of ${\mathrm{A}}_{\mathrm{d}}$.

We define the following three specific targets in this second stage:

• Feasibility to reach the parametric 3D hopper’s model and the required flat patterns.
• Application of the 3D model to achieve ${\mathrm{A}}_{\mathrm{r}}$ > 3 with minimum conicity through the eccentricity dimension.
• Accuracy of the ${\mathrm{D}}_{\mathrm{u}}$ and ${\mathrm{D}}_{\mathrm{l}}$ flat patterns.

The values of model parameters were grouped in two main dimensional groups (Nom and Var) and several variations within these ones, as shown in Table 1. The parameters that are not set in this table were kept constant during the study. These are ${\mathrm{D}}_{\mathrm{bu}}$ = 6 m, ${\mathrm{D}}_{\mathrm{bl}}$ = 5 m, ${\mathrm{H}}_{\mathrm{ld}}$ = 7 m, ${\alpha }_{\mathrm{df}}=65°$ and ${\alpha }_{\mathrm{do}}=45°$. Nonetheless, they were modified to verify that the final model responds properly to their change.

The Nom dimensions’ group refers to the parameters used during the model building. ${\mathrm{Nom}}_0$ is the initial model, whereas ${\mathrm{Nom}}_1$ was the model achieved for minimal conicity and ${\mathrm{A}}_{\mathrm{r}}$ > 3 in the second target. The Var dimensions’ group is a variant group used to test the accuracy of the model. It changes the axis of ${\mathrm{D}}_{\mathrm{f}}$ and ${\mathrm{D}}_{\mathrm{o}}$, as well as the inlet fluid duct diameter, ${\mathrm{D}}_{\mathrm{df}}$. Conicity and eccentricity were swept across a wide set of values, including quasi non-conicity (Con = 0.09) and non - eccentricity (Ecc = 0).

The advantages and limitations of the ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ and Solid Edge 2023 approaches are evaluated through the first two targets. In order to simplify the metrics and extension of the third target, we use three key points of the intersection curves from flat patterns. Numeric precision will be limited to three decimals (mm).

3. Results

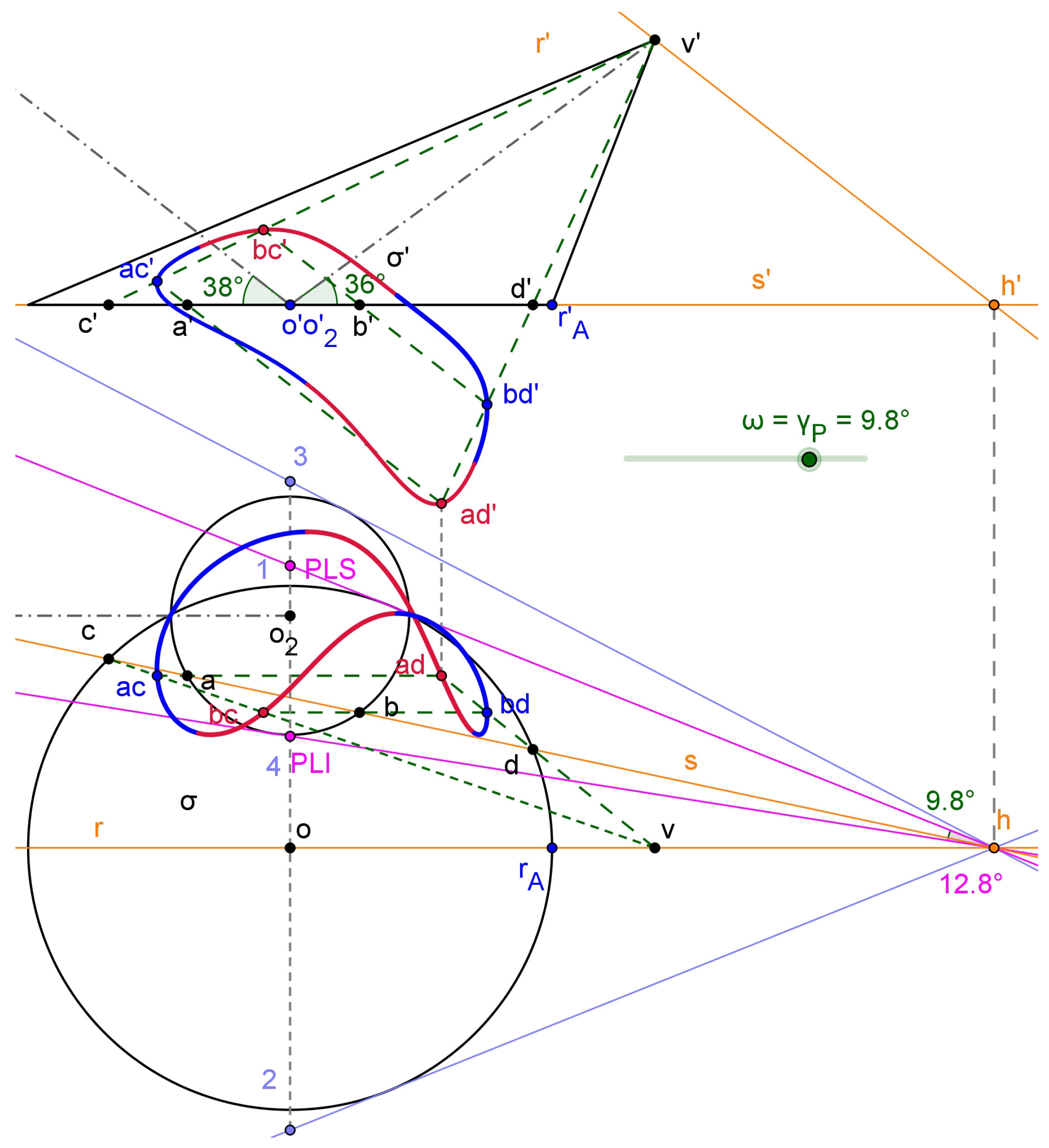
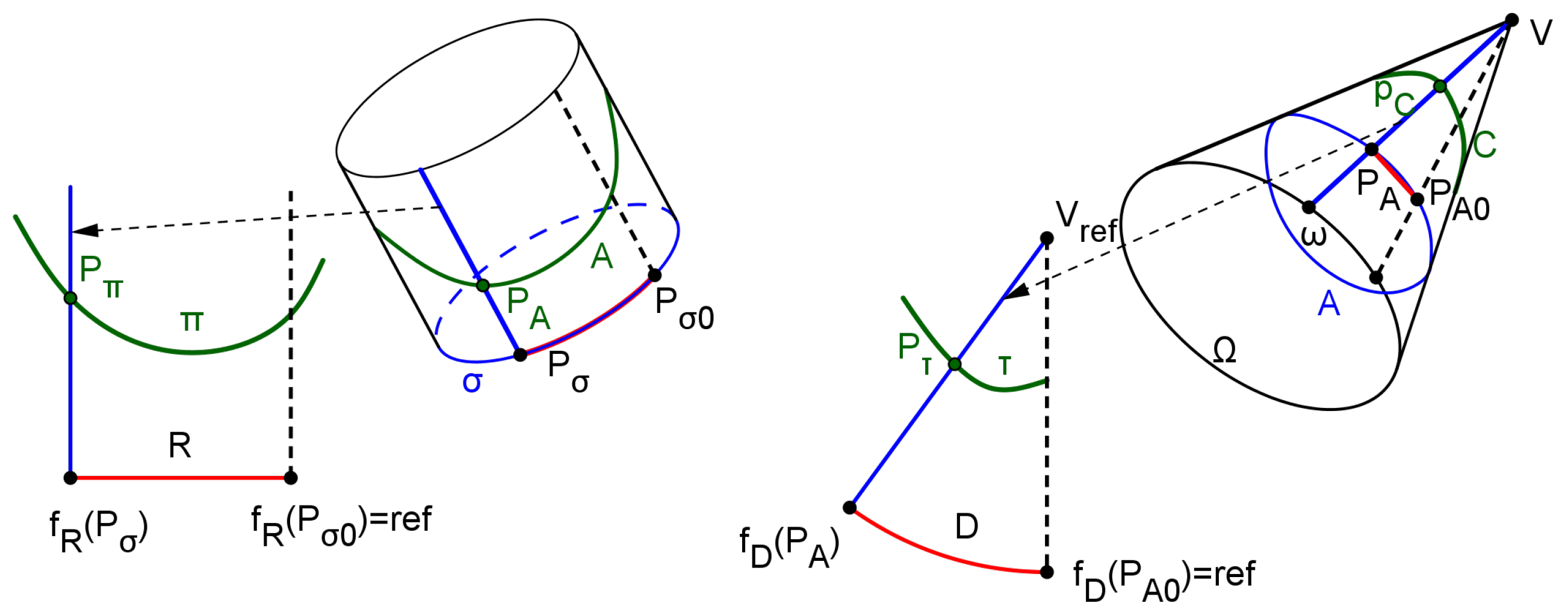
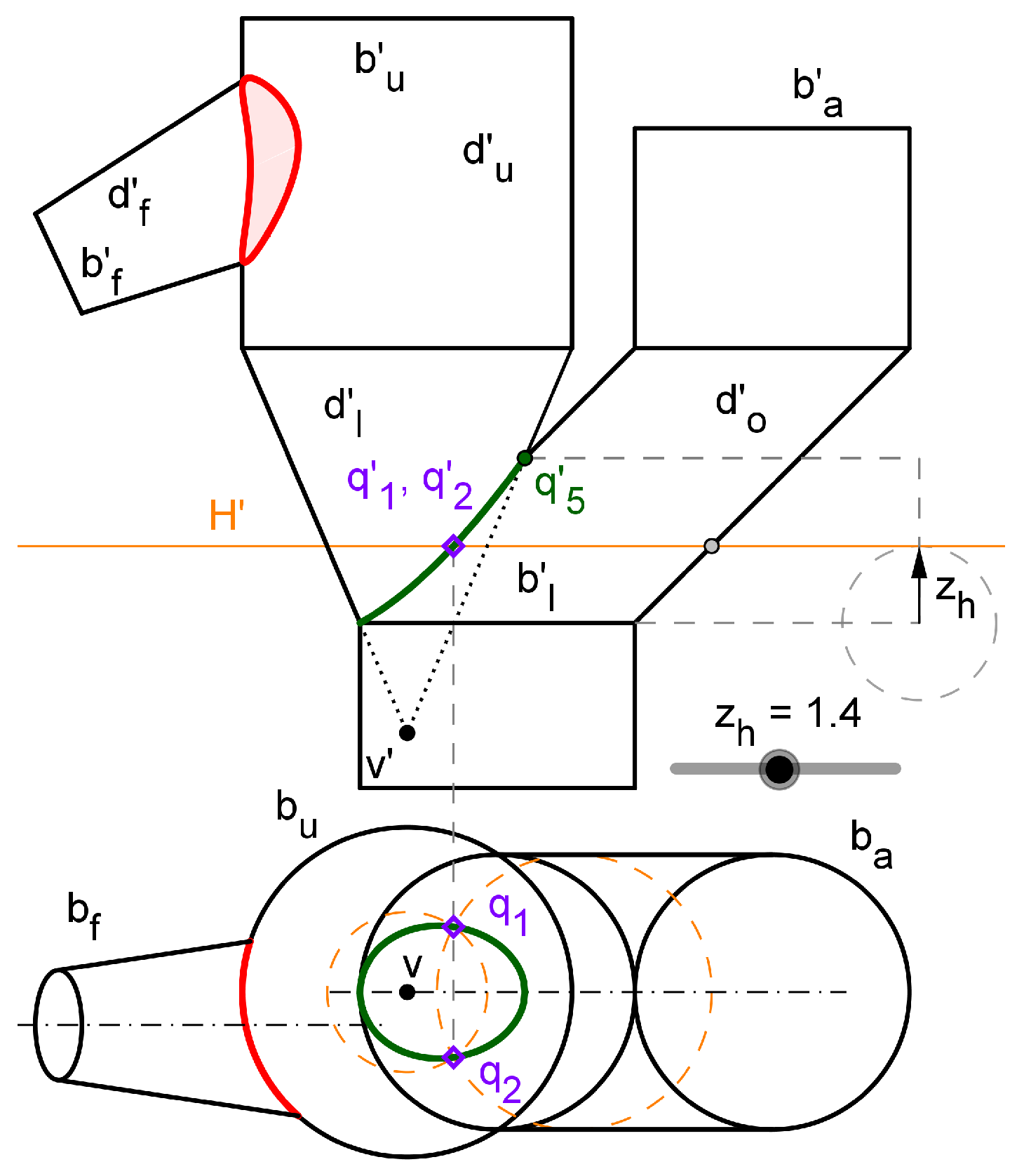
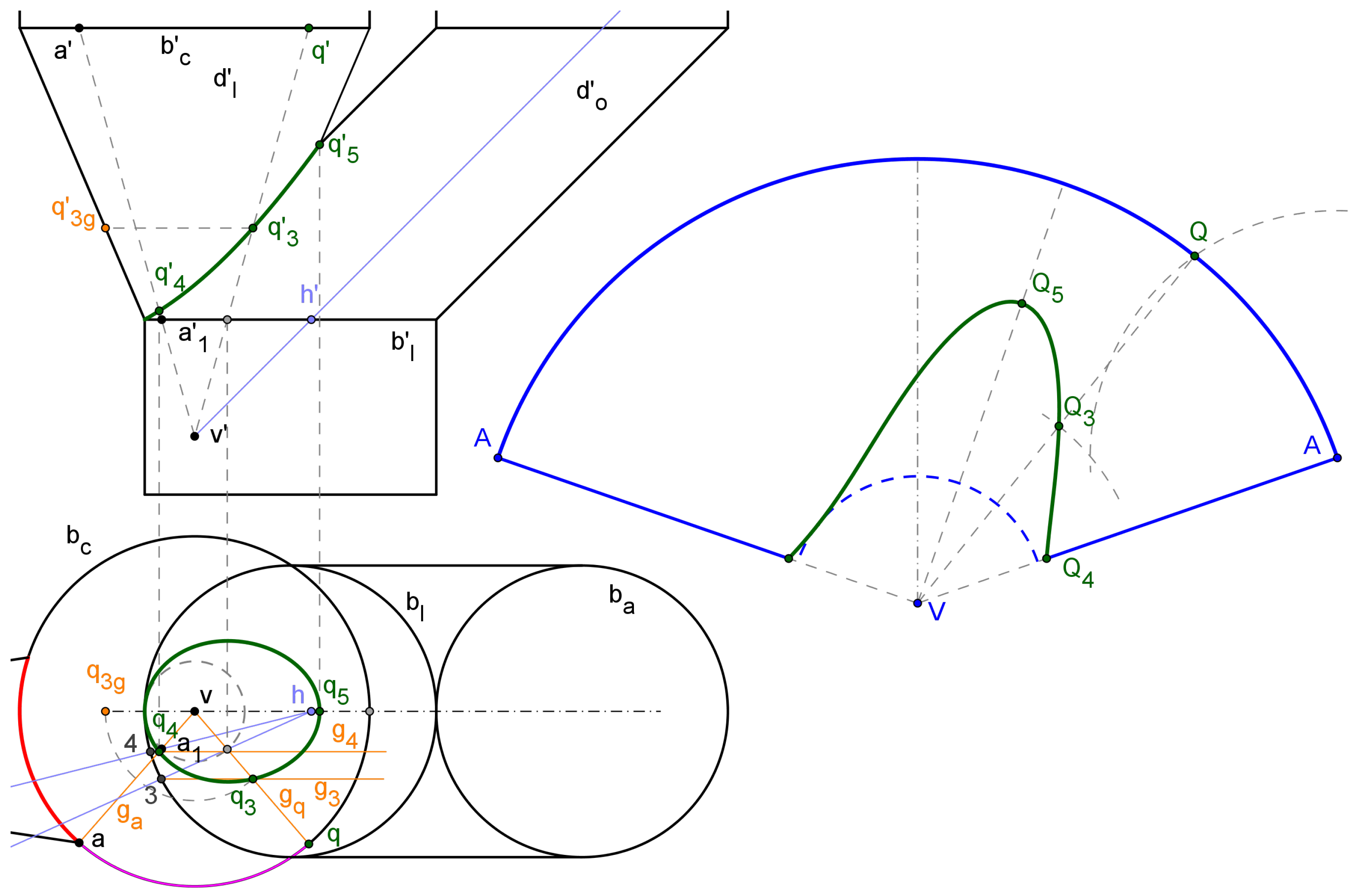
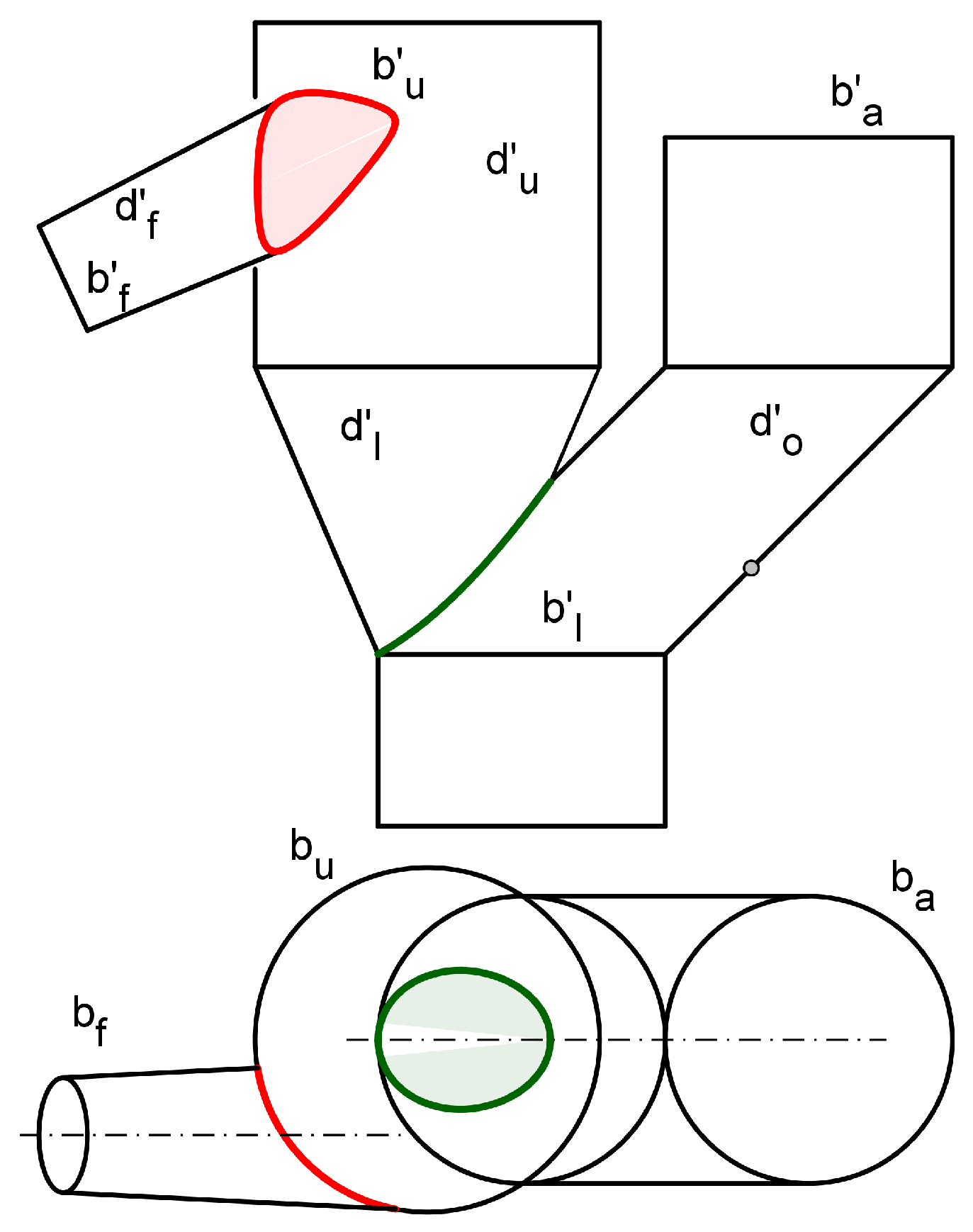
3.1. Surfaces’ intersection and flattening through locus - based parametric functions

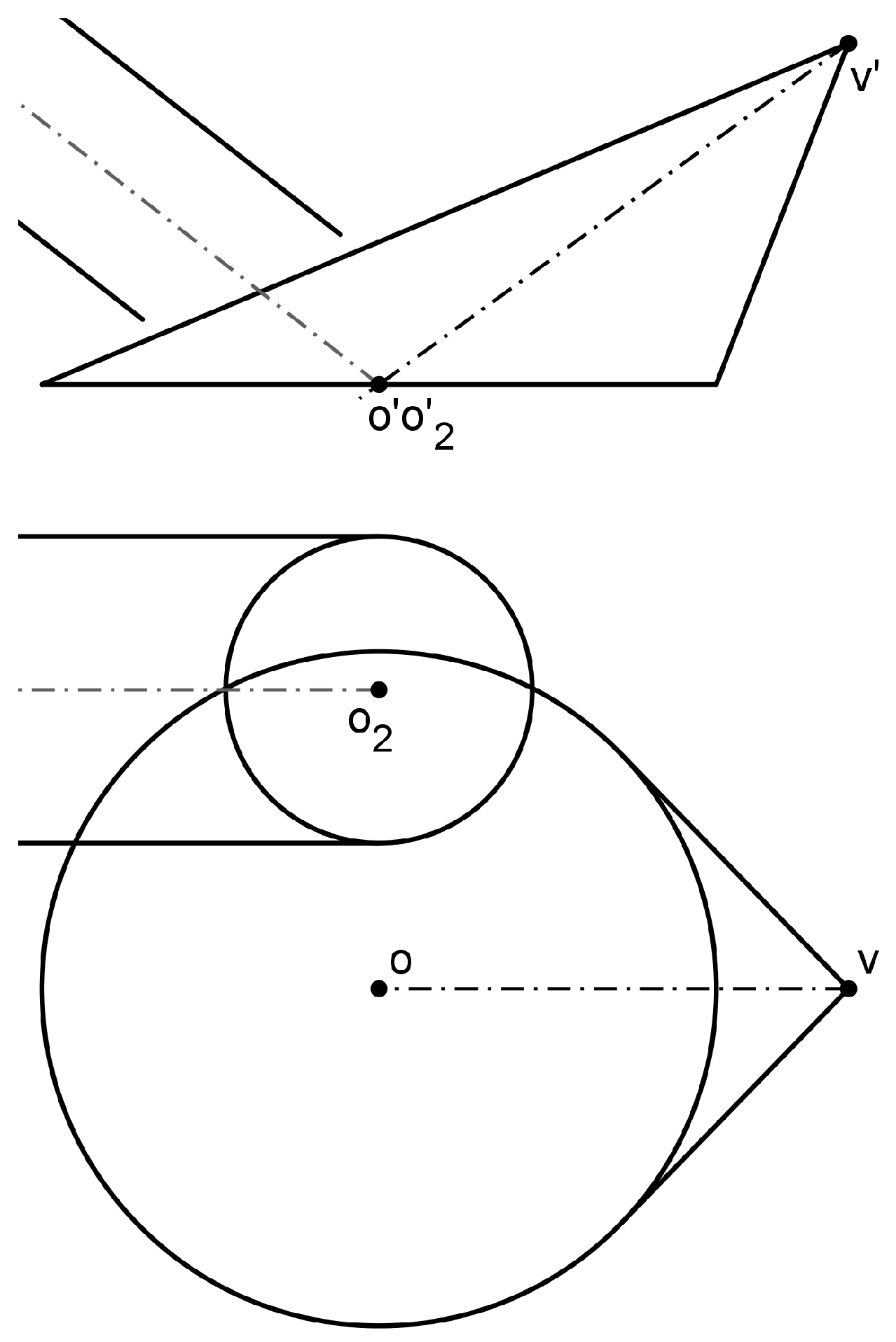
3.1.1. Surface to surface intersections

The encounter or intersection curve between two 3D surfaces, ${\mathbf{S}}_{\mathbf{1}}$ and ${\mathbf{S}}_{\mathbf{2}}$, $\mathbf{C}$, may be defined as the set of all 3D points, P, that pertain to both surfaces ($\mathrm{P}\in {\mathbf{S}}_{\mathbf{1}}\cap {\mathbf{S}}_{\mathbf{1}}$).

We define $\mathbf{S}\left(\omega \right)$ as collection of auxiliary surfaces that intersects both with ${\mathbf{S}}_{\mathbf{1}}$ and ${\mathbf{S}}_{\mathbf{2}}$ when the argument $\omega \in \Omega$, where $\Omega$ is a reference set on ${\Re }^n$ for n = 1 or $n=2$. Accordingly, the point $\mathrm{P}\left(\omega \right)={\mathbf{C}}_{\mathbf{1}}\left(\omega \right)\cap {\mathbf{C}}_{\mathbf{2}}\left(\omega \right)$ will pertain to $\mathbf{C}$, for ${\mathbf{C}}_{\mathbf{1}}\left(\omega \right)={\mathbf{S}}_{\mathbf{1}}\cap \mathbf{S}\left(\omega \right)$ and ${\mathbf{C}}_{\mathbf{2}}\left(\omega \right)={\mathbf{S}}_{\mathbf{2}}\cap \mathbf{S}\left(\omega \right)$.

If we choose a reference set $\Omega$, such that the collection $\mathbf{S}(\omega \in \Omega )$ sweeps all the points from ${\mathbf{S}}_{\mathbf{1}}$ and ${\mathbf{S}}_{\mathbf{2}}$, then we may set the intersection curve, $\mathbf{C}$, as the set of points $\mathrm{P}\left(\omega \right)={\mathbf{C}}_{\mathbf{1}}\left(\omega \right)\cap {\mathbf{C}}_{\mathbf{2}}\left(\omega \right)$ for $\omega \in \Omega$.

The projection of $\mathrm{P}\left(\omega \right)$ from $\mathbf{C}$ onto a plane is called ${\mathrm{p}}_{\sigma }$($\omega$), in such a way that $\sigma$ is the projection curve of $\mathbf{C}$ on that plane. As we may completely define a 3D curve from any two non-degenerated plane projections [14], we may compute the intersection curve $\mathbf{C}$ through their orthogonal projections on the dihedral planes, $\sigma$ (horizontal) and ${\sigma }^{\prime }$ (vertical).

Descriptive geometry gives algebraic procedures that solve ${\mathrm{p}}_{\sigma }$ projection for any value of $\omega$. The encapsulation of that sequence of algebraic procedures through dependent algebraic objects for the parameter $\omega$ may achieve a reliable locus entity, defining the following equation for the horizontal projection curve, $\sigma$:

$${\mathcal{L}}_{\sigma }\left(\omega \right)\equiv \sigma =locus({\mathrm{p}}_{\sigma }\left(\omega \right),\omega \in \Omega ),$$

(2)

where ${\mathcal{L}}_{\sigma }$ is a 2D parametric function in $\Omega$, and locus is the algebraic entity that gives the points ${\mathrm{p}}_{\sigma }$ associated with the value $\omega \in \Omega$. The vertical projection, ${\sigma }^{\prime }$, is achieved by the same equation when the horizontal projection of $\mathrm{P}\left(\omega \right)$ is substituted by the vertical projection, ${\mathrm{p}\text{’}}_{\sigma }$. This method was applied successfully to build ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ models using GeoGebra as dynamic geometry software [10].

Figure 3 presents the computation of the intersection between an oblique cone with an oblique cylinder using this method. They are defined by their circular sections with an horizontal plane (bases) and their axis. The vertical contour of the cone has been added to facilitate the interpretation.

We select the collection $\mathbf{S}\left(\omega \right)$ of planes that contain the cone vertex, v’ - v, and a line parallel to the cylinder axis, called r’ - r. As the incidence of this plane onto the horizontal plane is the h’ - h point, a plane from this collection may be defined through the s’ - s horizontal line, as shown in Figure 3. The line must intersect the two circular bases to assure that $\mathbf{S}\left(\omega \right)$ intersects the two surfaces. The lines h - PLI and h - PLS define the boundary planes of this collection for the relative position of the surfaces. These lines must be tangents to any of the circular bases. This manner, the PLS point is computed as PLS = If(y(1)<y(3) then point 1 else point 3), where 1 and 3 are presented in Figure 3 and y is the vertical coordinate. A similar condition with points 2 and 4 defines the PLI point. This conditional logic attends any relative position of these oblique surfaces.

We have defined $\omega$ as the angle ${\gamma }_{\mathrm{P}}$ between lines s and h - PLS (9.8° in the figure). Therefore the reference set, $\Omega$, is the interval [0, ${\gamma }_{\mathrm{Px}}$], where ${\gamma }_{\mathrm{Px}}$ is the angle between lines PLI - h - PLS (12.8° in the figure).

A general plane $\mathbf{S}\left(\omega \right)$ intersects in two generatrix lines (${\mathbf{C}}_{\mathbf{1}}\left(\omega \right)$) for the cylinder and other two for the cone (${\mathbf{C}}_{\mathbf{2}}\left(\omega \right)$), which intersects to gives four intersection points (${\mathrm{P}}_{\mathrm{i}}\left(\omega \right)={\mathbf{C}}_{\mathbf{1}}\left(\omega \right)\cap {\mathbf{C}}_{\mathbf{2}}\left(\omega \right),i=1,2,3,4$), from $\mathbf{C}$, as shown in Figure 3 (ac’ - ac, bc’ - bc, ad’ - ad, bd’ - bd) . The constructive procedure is shown. Therefore, the vertical projection of $\mathbf{C}$, ${\sigma }^{\prime }$, is given by the following four leaves parametric curve:

$${\sigma }^{\prime }\equiv {\mathcal{L}}_{{\sigma }^{\prime }}\left(\omega \right)=locus(\{a{c}^{\prime },b{c}^{\prime },a{d}^{\prime },b{d}^{\prime }\},\omega \in \Omega )$$

(3)

The leaves of ${\sigma }^{\prime }$ have been emphasized through alternating colours (see Figure 3). The horizontal projection of $\mathbf{C}$, $\sigma$, is also a four - leaves parametric curve given by

$$\sigma \equiv {\mathcal{L}}_{\sigma }\left(\omega \right)=locus(\{ac,bc,ad,bd\},\omega \in \Omega )$$

(4)

Figure 4. Projection curves of cone - cylinder intersection (penetration) in a ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ model.

Figure 4. Projection curves of cone - cylinder intersection (penetration) in a ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ model.

Reducing the distance between the centers of circular bases, o - ${\mathrm{o}}_2$, the bite between surfaces changes to a penetration of the cylinder into the cone, as shown in Figure 4. The boundary planes are now both tangent to the cylinder bases (PLS is 3 and PLI is 4). The intersection curve splits into two separates pieces, that are defined by the ${\mathcal{L}}_{{\sigma }^{\prime }}\left(\omega \right)$ parametric curve of equation (3) for the vertical projection and ${\mathcal{L}}_{\sigma }\left(\omega \right)$ of equation (4) for the horizontal projection.

An interesting property of this technique is that it keeps the geometric integrity of the intersection curve (i.e. these curves are not approximations but the true algebraic object). As Figure 3 and Figure 4 illustrate, it may be implemented in dynamic geometry tools through the graphical entities associated with the descriptive geometry’s algebraic objects. The input surfaces are not limited to ruled or quadric surfaces, but to smooth surfaces for which some computable auxiliary surface produces low complexity intersection curves. Most technical surfaces fulfil with these requirements.

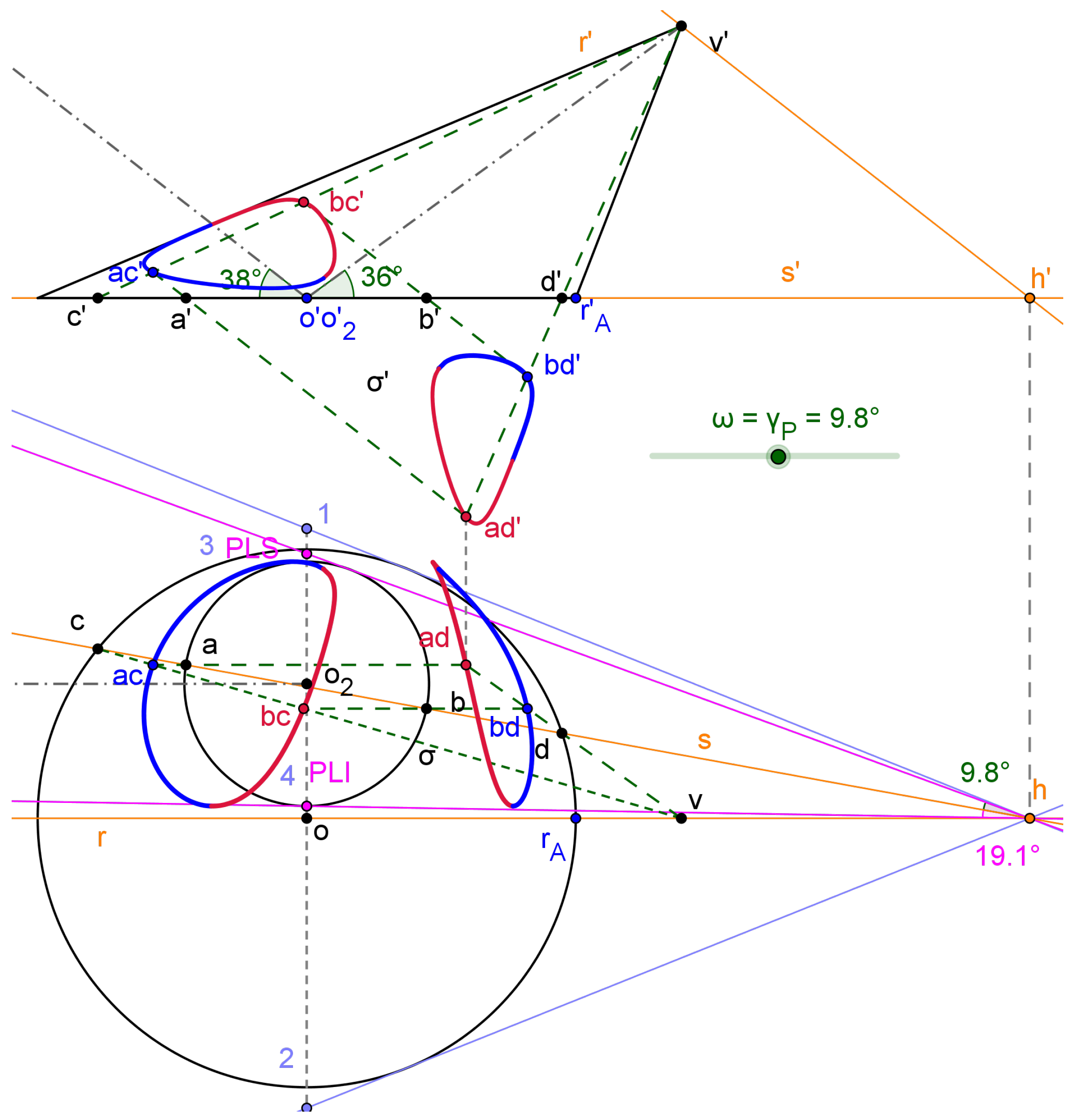
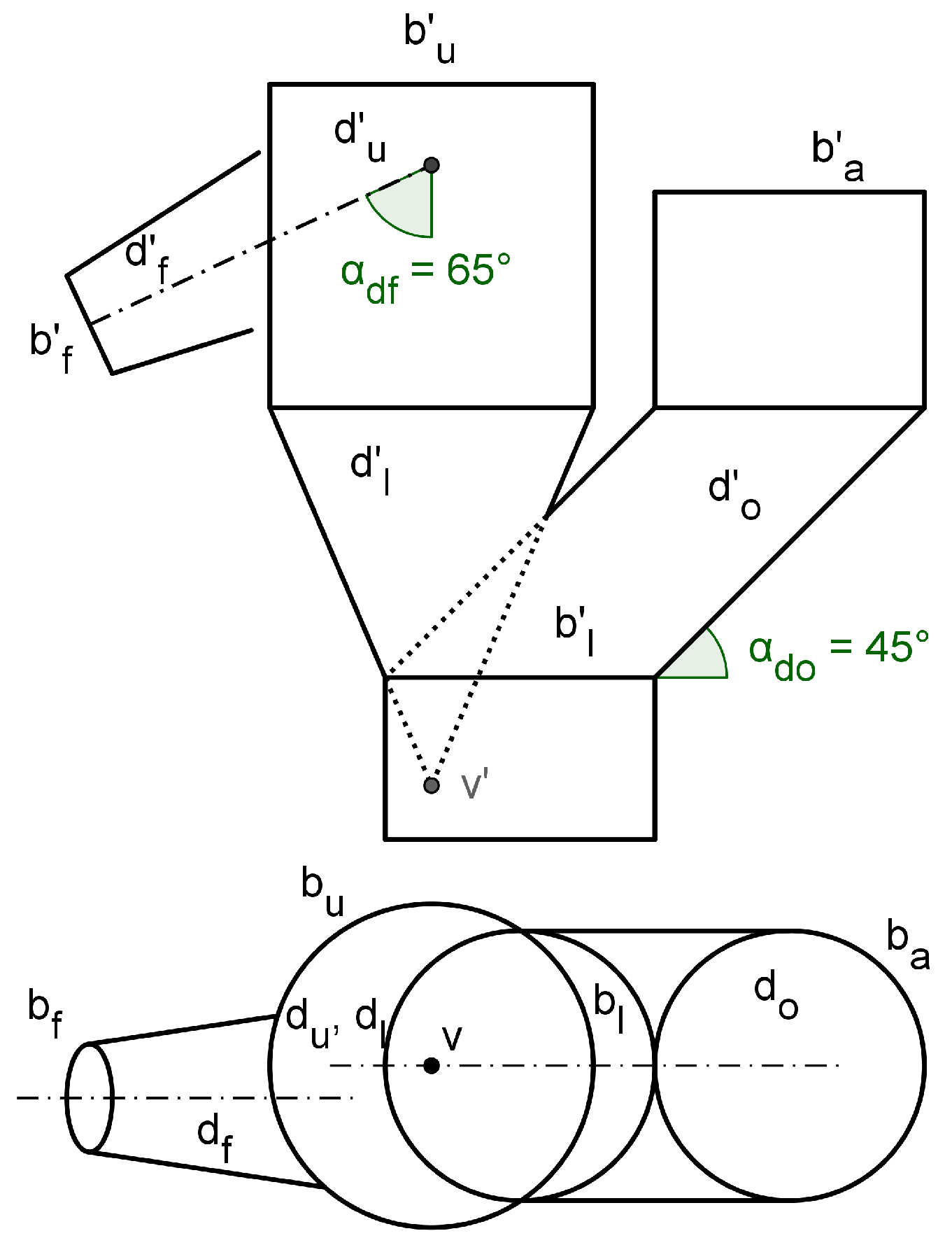
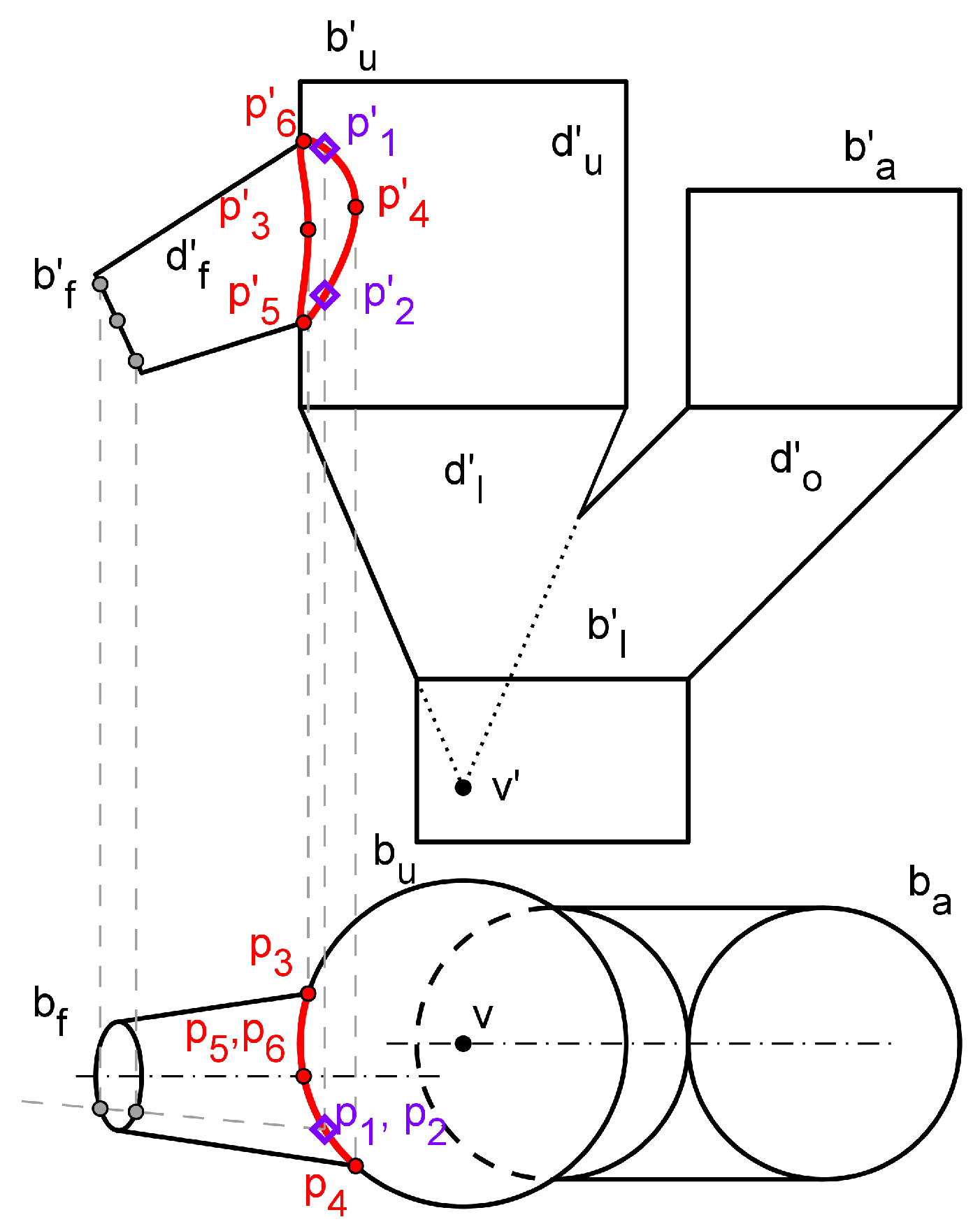
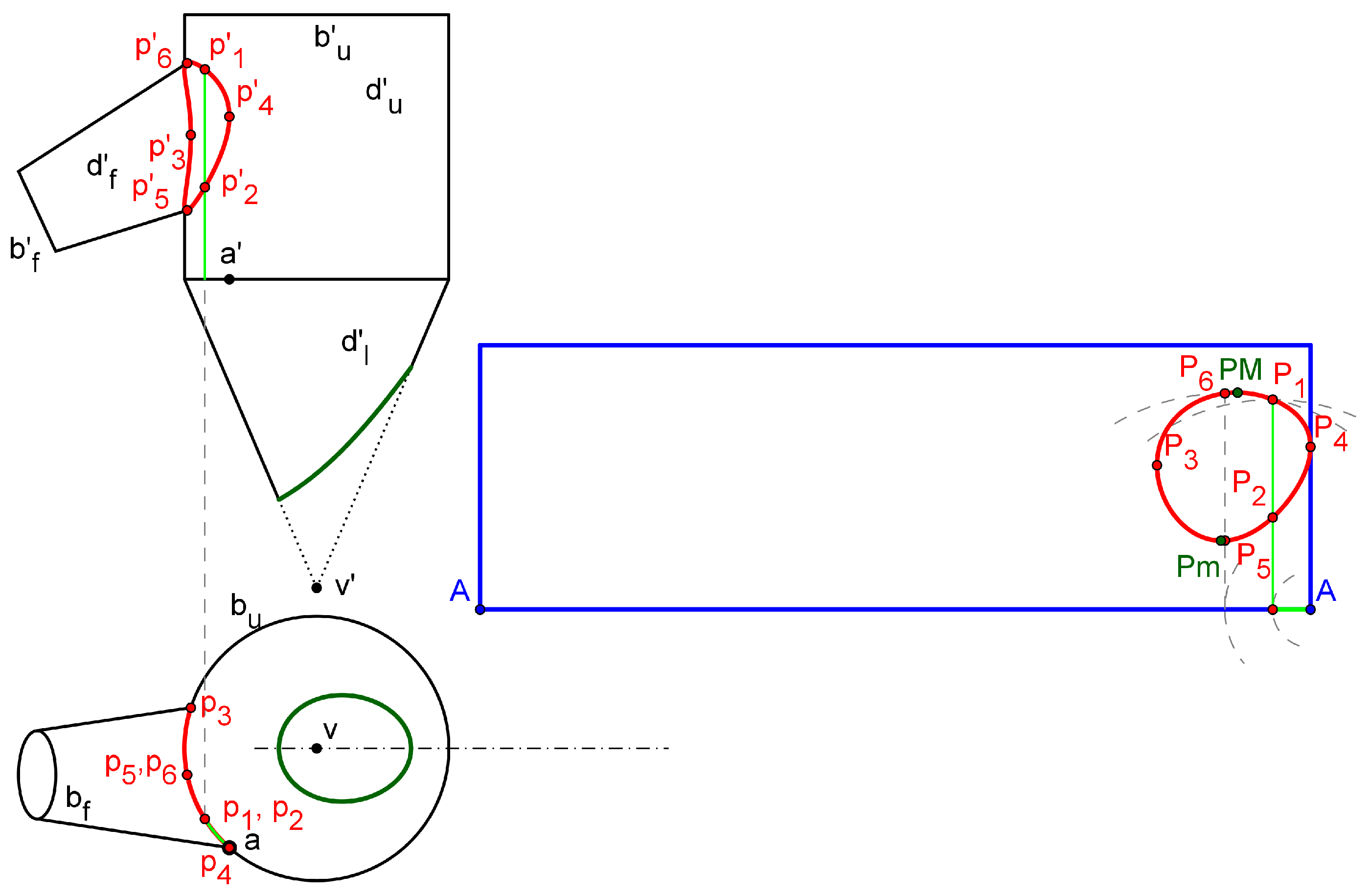
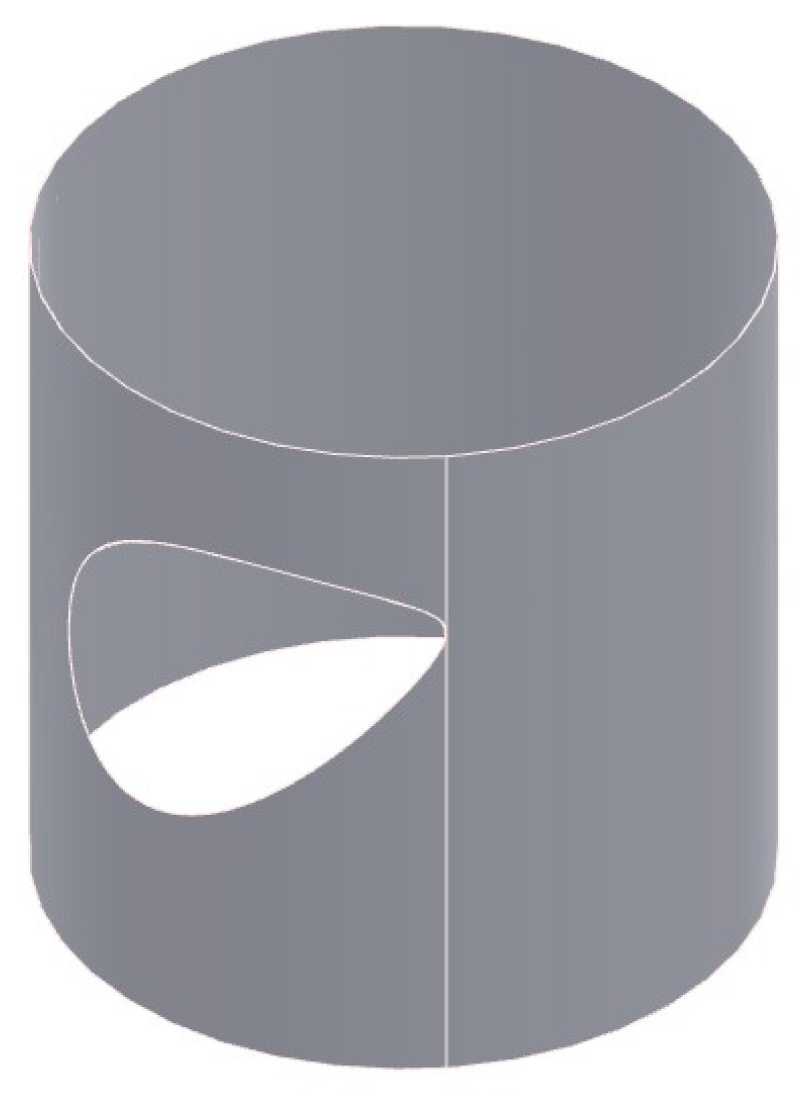
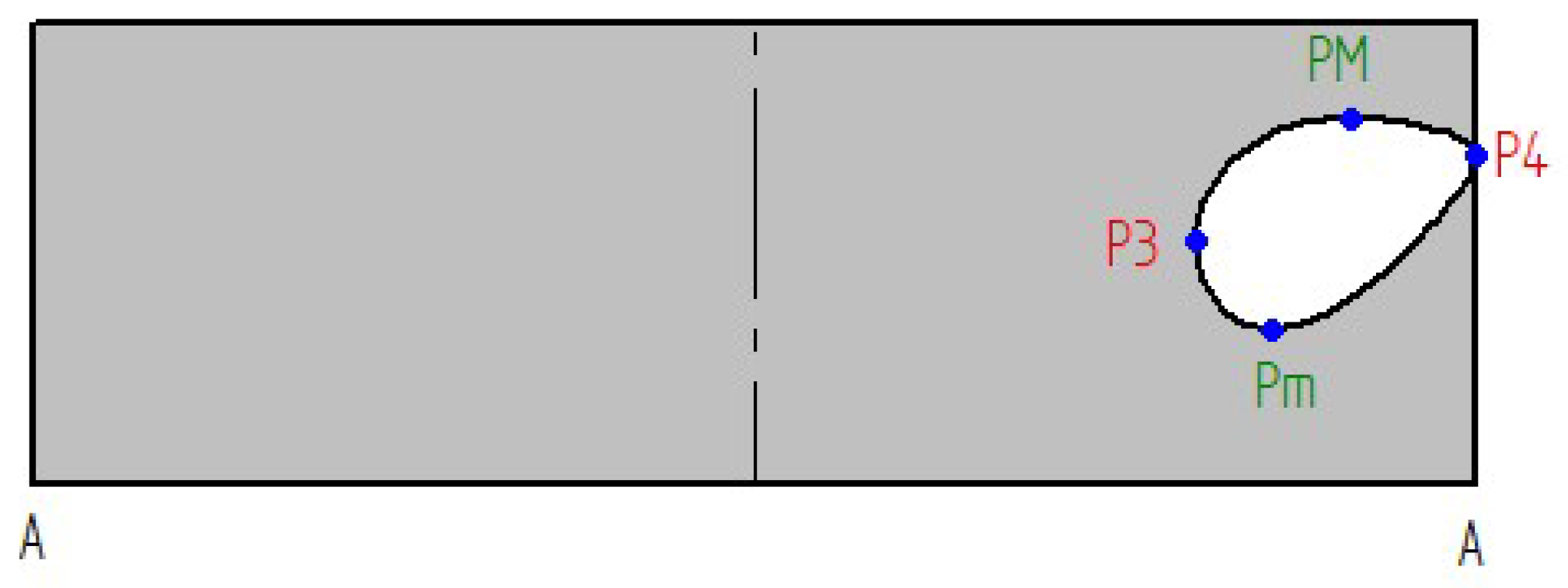
3.1.2. Surface flattening

Ruled single curvature surfaces can be flattened without deformation. Here we present a locus based technique that gives the exact flat transformed of any 3D curve in this type of surfaces. It has been implemented in GeoGebra as part of the built-in features of ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$.

The flat transformation of a curve $\mathbf{C}$ that pertains to a ruled single curvature surface, $\mathbf{S}$, may be formally computed by means of a two-stage procedure. First, a generic generatrix line of $\mathbf{S}$, g, that contains a point $\mathrm{P}\in \mathbf{C}$ is transformed to the flat domain. This transformation is equivalent to the placement of a line in the flat domain. Secondly, the point P is transformed to the flat domain, that is, it is placed onto the g transformed. This two-stage procedure defines a sequence of dependent algebraic objects, which builds the locus entity that defines the flat transformed of $\mathbf{C}$ through a parametric function. Figure 5 shows a scheme of this process for a cylinder and a cone, both oblique with generic directrix.

In the case of a cylinder (Figure 5 - left), we must intersect it with a plane perpendicular to the axis, to give the section $\sigma$. The flat transformed of $\sigma$ is the R straight line, perpendicular to transformed generatrix lines. We may use any generatrix line as reference in the flat domain, as shown in Figure 5 (dashed line). Then, defining ${\mathrm{p}}_{\sigma }$$\in \sigma$ as a parameter, it is transformed to ${\mathrm{f}}_{\mathrm{R}}$(${\mathrm{p}}_{\sigma }$) onto R, assuring the invariance of lengths of transformed paths. That is, the distance between ${\mathrm{f}}_{\mathrm{R}}$(${\mathrm{P}}_{\sigma }$) and ${\mathrm{f}}_{\mathrm{R}}$(${\mathrm{p}}_{\sigma 0}$) is equal to the length of $\sigma$ between ${\mathrm{P}}_{\sigma }$ and ${\mathrm{P}}_{\sigma 0}$. The flat transformed of the generatrix line through ${\mathrm{p}}_{\sigma }$ is parallel to the reference one. The function ${\mathrm{f}}_{\mathrm{R}}$ converts its argument from $\sigma$ into the transformed in R.

Finally, the flat transformed of ${\mathrm{P}}_{\mathrm{A}}\in \mathcal{A}$ in the cylinder is ${\mathrm{P}}_{\pi }$, which pertains to the flat transformed of its generatrix line, with a distance between ${\mathrm{P}}_{\pi }$ and ${\mathrm{f}}_{\mathrm{R}}$(${\mathrm{P}}_{\sigma }$) equal to the distance between ${\mathrm{P}}_{\mathrm{A}}$ and ${\mathrm{P}}_{\sigma }$.

Considering that descriptive geometry provides mathematical procedures to achieve the invariance conditions and manipulate the 3D space through algebraic objects, the flat transformed of $\mathcal{A}$, $\pi$, may be computed as:

$$\pi \equiv {\mathcal{L}}_{\pi }\left(\omega \right)=locus(P_{\pi }\left(f_R\left(\omega \right)\right),\omega \in \Omega ),$$

(5)

where ${\mathcal{L}}_{\pi }$ is a 2D parametric function of $\omega ={\mathrm{P}}_{\sigma }\in \sigma$, $\Omega$ is a subset of $\sigma$ that defines the cylinder piece to be flattened, and $P_{\pi }\left(f_R\left(\omega \right)\right)$ is a point of $\pi$ defined by the generatrix line through $f_R\left(\omega \right)$.

In the case of an oblique cone as surface $\mathbf{S}$ to be flattened (Figure 5 - right), we first intersect this surface with a sphere centered in cone’s vertex (V) to obtain a warped curve in $\mathbf{S}$, $\mathcal{A}$, which is called support curve. We know that the flat transformed of $\mathcal{A}$ is a circular arch (D) with the radius of the sphere. The flat transformed of ${\mathrm{P}}_{\mathrm{A}}\in \mathcal{A}$ is ${\mathrm{f}}_{\mathrm{D}}\left({\mathrm{P}}_{\mathrm{A}}\right)\in \mathrm{D}$, with a distance to the reference point ${\mathrm{f}}_{\mathrm{D}}\left({\mathrm{P}}_{\mathrm{A}0}\right)$ along D equal to the distance of ${\mathrm{P}}_{\mathrm{A}}$ to ${\mathrm{P}}_{\mathrm{A}0}$ along $\mathcal{A}$ (see Figure 5). The flat transformed of a generatrix line through ${\mathrm{P}}_{\mathrm{A}}\in \mathcal{A}$ contains the flat transformed of vertex (${\mathrm{V}}_{\mathrm{ref}}$ is placed together with the reference generatrix line) and ${\mathrm{f}}_{\mathrm{D}}\left({\mathrm{P}}_{\mathrm{A}}\right)$.

The flat transformed of ${\mathrm{P}}_{\mathrm{C}}\in \mathbf{C}$ in the cone is ${\mathrm{P}}_{\tau }$, which pertains to the flat transformed of its generatrix line, with a distance between ${\mathrm{P}}_{\tau }$ and ${\mathrm{f}}_{\mathrm{D}}$(${\mathrm{P}}_{\mathrm{A}}$) equal to the distance between ${\mathrm{P}}_{\mathrm{C}}$ and ${\mathrm{P}}_{\mathrm{A}}$. Under the same consideration of equation 5, the flat transformed of $\mathbf{C}$ ($\tau$) may be computed as:

$$\tau \equiv {\mathcal{L}}_{\tau }\left(\omega \right)=locus(P_{\tau }\left(f_D\left(\omega \right)\right),\omega \in \Omega ),$$

(6)

where ${\mathcal{L}}_{\tau }$ is a 2D parametric function of $\omega \in \Omega$, such that the generatrix line through $\omega$ contains ${\mathrm{P}}_{\mathrm{A}}$, and $\Omega$ is a plane section of the cone that facilitates the algebraic manipulation of this surface.

The variable $\omega \in \Omega$ may be substituted by other variable ${\mathrm{t}}_{\omega }$$\in \mathcal{T}$ , if there exists any mapping function between $\Omega$ and $\mathcal{T}$.

The computation of the distance from ${\mathrm{P}}_{\mathrm{A}}$ to ${\mathrm{P}}_{\mathrm{A}0}$ along $\mathcal{A}$ is not trivial since $\mathcal{A}$ is a warped curve with a geometry that depends on the conical surface. We use the flat transformed of $\mathcal{A}$ as pertaining to a cylinder, taking advantage of the invariance of lengths during the flat transformation.

This method for surface flattening is applied to the conical surface intersected with the cylinder (bite) from the previous ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ model, between two selected generatrix lines, as presented in Figure 6.

According to our nomenclature, projections are presented in lowercase, whereas flat transformations are in uppercase (excepting for Greek symbols). In Figure 6, ${\omega }_{\mathrm{R}}$ is a point in $\Omega$, which is the circular arch from ${\mathrm{r}}_{\mathrm{B}}$ to ${\mathrm{r}}_{\mathrm{A}}$ in the circular base of the conical surface (plane section). It is defined as ${\omega }_{\mathrm{R}}$ = Point(circular base, ${\mathrm{t}}_{\omega }\mathrm{R}$), where ${\mathrm{t}}_{\omega }\mathrm{R}$ is a real parameter in $\mathcal{T}=[0,1]$ and Point is the mapping function between $\Omega$ and $\mathcal{T}$.

The generatrix line through ${\omega }_{\mathrm{R}}$ intersects to the sphere (radius equal to segment v’ - ${\mathrm{r}\text{’}}_{\mathrm{A}}$) in ${\mathrm{p}\text{’}}_{\mathrm{AR}}$ - ${\mathrm{p}}_{\mathrm{AR}}$. Accordingly, ${\mathrm{p}}_{\mathrm{AR}}$ pertains to the horizontal projection of the support curve $\mathcal{A}$, which is calculated through equation (2) using ${\omega }_{\mathrm{c}}$ in the circular base, defined between ${\mathrm{r}}_{\mathrm{A}}$ and ${\omega }_{\mathrm{R}}$. Therefore, the horizontal projection of $\mathcal{A}$ between ${\mathrm{r}}_{\mathrm{A}}$ and ${\omega }_{\mathrm{R}}$ is locus(${\mathrm{p}}_{\mathrm{Ac}}$, ${\omega }_{\mathrm{c}}$) (orange horizontal projection).

We define a right cylinder from the horizontal projection of $\mathcal{A}$ (bottom base) to the support curve (warped) $\mathcal{A}$. The flat transformed of $\mathcal{A}$ as a curve of the cylinder is $\pi$, which is shown in Figure 6 (upper - right). According to the equation (5), $\pi$ is defined as locus(${\mathrm{P}}_{\mathrm{AR}}$, ${\mathrm{t}}_{\omega }\mathrm{R}$). The distance between ${\mathrm{r}}_{\mathrm{A}}$ and ${\mathrm{p}}_{\mathrm{ARL}}$ in the horizontal projection of $\mathcal{A}$ is computed through Perimeter(locus) command.

The distance between ${\mathrm{R}}_{\mathrm{A}}$ and ${\mathrm{P}}_{\mathrm{AR}}$ along D (circular arch in cone flat domain, Figure 6 bottom - right) must be equal to the distance between ${\mathrm{R}}_{\mathrm{A}}$ and ${\mathrm{P}}_{\mathrm{AR}}$ along $\pi$ curve, which is known. Therefore, ${\mathrm{P}}_{\mathrm{AR}}$ in D and its associated generatrix line through $\left({\omega }_{\mathrm{R}}\right)$ may be placed in the flat domain. The flat transformation of the cone base through ${\mathrm{R}}_{\mathrm{A}}$ to ${\mathrm{R}}_{\mathrm{B}}$ may be computed as locus((${\omega }_{\mathrm{R}}$), ${\mathrm{t}}_{\omega }\mathrm{R}$), according equation (6). Finally, the flat transformation of the cone - cylinder intersection inside the flat pattern is defined by two parametric functions: locus(${\omega }_{\mathrm{R}}$F, ${\mathrm{t}}_{\omega }\mathrm{R}$) and locus(${\omega }_{\mathrm{R}}$E, ${\mathrm{t}}_{\omega }\mathrm{R}$), since ${\omega }_{\mathrm{R}}$f’ - ${\omega }_{\mathrm{R}}$f and ${\omega }_{\mathrm{R}}$e’ - ${\omega }_{\mathrm{R}}$e are the intersections of the generatrix line through ${\omega }_{\mathrm{R}}$ with the cylinder.

The ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ model updates dynamically to changes of the parameters, what includes the modification of the intersection. This manner, if we reduce the distance between the centers of circular bases o - ${\mathrm{o}}_2$, as was performed in Figure 4, the bite will change to penetration, splitting in two pieces, and the flat pattern dynamically changes to give what shows Figure 7. It must be noted that we have also moved ${\mathrm{r}}_{\mathrm{B}}$ to increase the cone surface that is flattened.

Figure 7. Cone surface intersected with cylinder (penetrated, Figure 4) flattened between generatrix lines through ${\mathrm{r}}_{\mathrm{A}}$ and ${\mathrm{r}}_{\mathrm{B}}$.

Figure 7. Cone surface intersected with cylinder (penetrated, Figure 4) flattened between generatrix lines through ${\mathrm{r}}_{\mathrm{A}}$ and ${\mathrm{r}}_{\mathrm{B}}$.

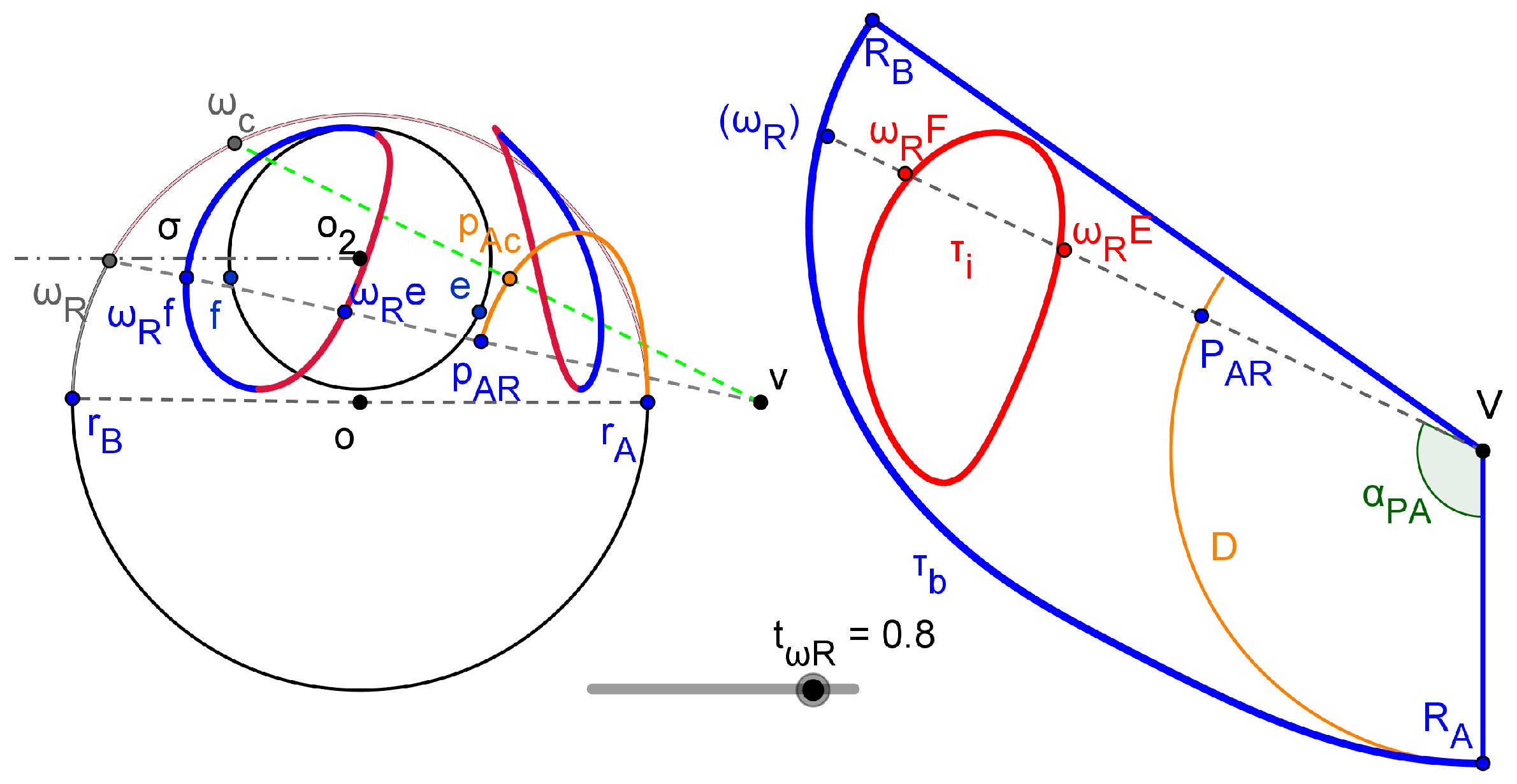
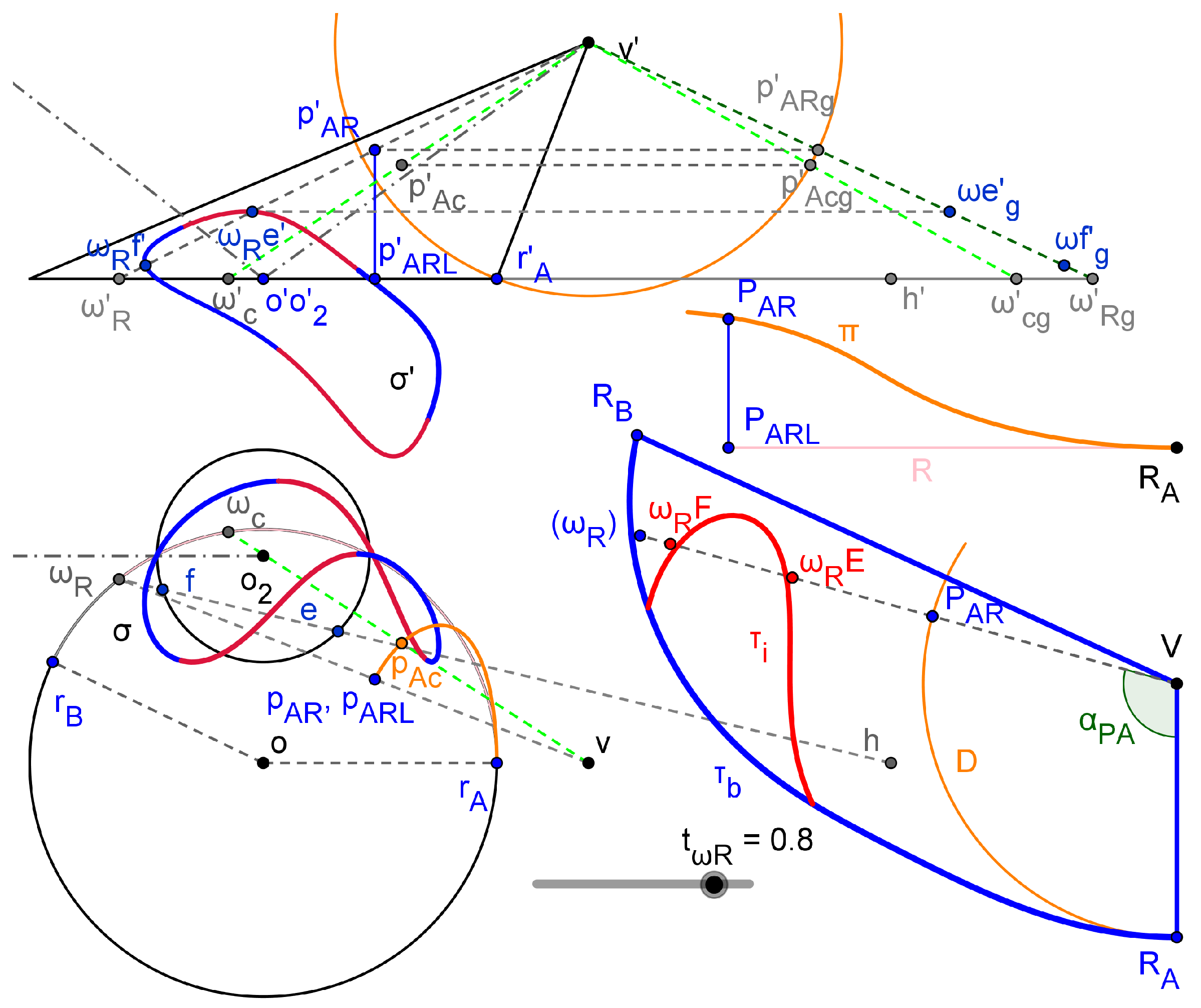
3.2. Hopper’s CeDG modelling

The Figure 8 shows the ${\mathrm{D}}_{\mathrm{u}}$ - ${\mathrm{D}}_{\mathrm{f}}$ connection, calculated according with the technique presented in Section 3.1.1.

We set a collection $\mathbf{S}\left(\omega \right)$ of auxiliary planes through the cone vertex (fluid duct) and parallel to the axis of the upper duct (vertical). The argument $\omega$ is a point in the circular base of the upper duct, between ${\mathrm{p}}_3$ and ${\mathrm{p}}_4$ ($\Omega$ is that circular arch). The auxiliar plane from $\mathbf{S}\left(\omega \right)$ with $\omega \in \Omega$ intersects to the fluid duct in two generatrix lines, ${\mathbf{C}}_{\mathbf{1}}\left(\omega \right)$, and to the upper duct in a generatrix line (at the inlet side), ${\mathbf{C}}_{\mathbf{2}}\left(\omega \right)$. These generatrix lines intersect themselves to give the points ${\mathrm{P}}_1$ and ${\mathrm{P}}_2$ through their projections. As seen, the horizontal projection is ${\mathrm{p}}_1$=${\mathrm{p}}_2$=$\omega$, whereas de vertical projection are ${\mathrm{p}\text{’}}_1$ and ${\mathrm{p}\text{’}}_2$.

Therefore, the ${\mathrm{D}}_{\mathrm{u}}$ - ${\mathrm{D}}_{\mathrm{f}}$ connection curve is given by the parametric functions locus(${\mathrm{p}\text{’}}_1$, $\omega$) and locus(${\mathrm{p}\text{’}}_2$, $\omega$) (vertical projection, two - leaves), and locus($\omega$, $\omega$) = $\Omega$ (horizontal projection, one leaf).

The intersection curve ${\mathrm{D}}_{\mathrm{l}}$ - ${\mathrm{D}}_{\mathrm{o}}$ is presented in Figure 9. It has been calculated using a collection of horizontal planes with heights from the low border, ${\mathrm{b}\text{’}}_{\mathrm{l}}$, to the height of ${\mathrm{Q}}_5$, as shown. This manner, we define $\omega ={\mathrm{z}}_{\mathrm{h}}$ (pointed out in figure) and $\Omega =[z\left({\mathrm{b}\text{’}}_{\mathrm{l}}\right),z\left({\mathrm{q}\text{’}}_5\right)]$. ${\mathbf{C}}_{\mathbf{1}}\left(\omega \right)$ and ${\mathbf{C}}_{\mathbf{2}}\left(\omega \right)$ are now circles that intersect in ${\mathrm{q}}_1$ and ${\mathrm{q}}_2$ (horizontal projection), and ${\mathrm{q}\text{’}}_1$=${\mathrm{q}\text{’}}_2$ (vertical projection), and thus the intersection curve is given by the parametric functions locus(${\mathrm{q}\text{’}}_1$, ${\mathrm{z}}_{\mathrm{h}}$) = locus(${\mathrm{q}\text{’}}_2$, ${\mathrm{z}}_{\mathrm{h}}$) (vertical projection, one leaf), and locus(${\mathrm{q}}_1$, ${\mathrm{z}}_{\mathrm{h}}$) - locus(${\mathrm{q}}_2$, ${\mathrm{z}}_{\mathrm{h}}$) (horizontal projection, two-leaves).

The ${\mathrm{D}}_{\mathrm{l}}$ - ${\mathrm{D}}_{\mathrm{o}}$ connection curve is warped despite its horizontal projection seems elliptic.

Once the connection curves are defined in our ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ model, the upper and lower ducts may be flattened. The flat pattern of the upper duct has been calculated as indicated in Figure 10. The section perpendicular to the axis of the cylinder is projected as the ${\mathrm{b}}_{\mathrm{u}}$ circle in the horizontal plane. We have taken the generatrix line through A (a’ - a) as reference in the flat domain. We define the $\Omega$ subset of the ${\mathrm{b}}_{\mathrm{u}}$ circular section as the circular arch from ${\mathrm{p}}_3$ to ${\mathrm{p}}_4$, which set the boundaries where the ${\mathrm{D}}_{\mathrm{f}}$ cone intersects with ${\mathrm{D}}_{\mathrm{u}}$ (Figure 10). The generatrix line through the point $\omega \in \Omega$ intersects the ${\mathrm{D}}_{\mathrm{u}}$-${\mathrm{D}}_{\mathrm{f}}$ connection in two points, ${\mathrm{p}\text{’}}_1$ and ${\mathrm{p}\text{’}}_2$, with horizontal projections ${\mathrm{p}}_1$=${\mathrm{p}}_2$=$\omega$. Then, they may be transformed to the flat domain thanks to the transformation length invariance to give ${\mathrm{P}}_1$ and ${\mathrm{P}}_2$.

We can apply now the equation (5) according to the surface flattening technique, which solves the flat transformation of the ${\mathrm{D}}_{\mathrm{u}}$-${\mathrm{D}}_{\mathrm{f}}$ connection curve as the parametric functions $locus({\mathrm{P}}_1,\omega$) and $locus({\mathrm{P}}_2,\omega$) with $\omega ={\mathrm{p}}_1={\mathrm{p}}_1$ (two leaves).

Figure 10 (right) also shows several relevant points within the intersection curve whose positions with respect A are used to verify the accuracy of the flat transformed. These area ${\mathrm{P}}_{\mathrm{M}}$ and ${\mathrm{P}}_{\mathrm{m}}$, with maximum and minimum height, ${\mathrm{P}}_3$ and ${\mathrm{P}}_4$, associated with the curve’s boundary limits, and ${\mathrm{P}}_6$ and ${\mathrm{P}}_5$ (which are defined below), will be used to compute ${\mathrm{A}}_{\mathrm{r}}$.

The lower duct, ${\mathrm{D}}_{\mathrm{l}}$, is a cone that is flattened according to equation (6). The process is presented in Figure 11, including the final flat pattern (right). As ${\mathrm{D}}_{\mathrm{l}}$ is a revolution circular cone, we have selected the sphere that generates the cone border, ${\mathrm{b}\text{’}}_{\mathrm{c}}$ - ${\mathrm{b}}_{\mathrm{c}}$, as support curve $\mathcal{A}$. We use again the point A (a’ - a) to set the reference generatrix line, which facilitates the patterns’ junction. As $\mathcal{A}$ is a flat curve, it may be also used as plane section and then $\Omega =\mathcal{A}$. Defining the point q (horizontal projection) from $\Omega$, it may be transported to the flat transformed of $\mathcal{A}$, D, keeping the length between its transformed, Q, and A (reference) along D, as shown. The intersection of the generatrix line through q with the ${\mathrm{D}}_{\mathrm{l}}$ - ${\mathrm{D}}_{\mathrm{o}}$ connection curve is ${\mathrm{q}\text{’}}_3$ - ${\mathrm{q}}_3$, which it is transported to the flat domain to deliver ${\mathrm{Q}}_3$ (keeping the distance V - ${\mathrm{Q}}_3$). Therefore, the ${\mathrm{D}}_{\mathrm{l}}$ - ${\mathrm{D}}_{\mathrm{o}}$ flat pattern is given by the parametric function $locus({\mathrm{Q}}_3,q)$.

The model solution also shows ${\mathrm{Q}}_4$, which is the intersection of the reference generatrix line with the ${\mathrm{D}}_{\mathrm{l}}$ - ${\mathrm{D}}_{\mathrm{o}}$ connection curve, and its highest point, ${\mathrm{Q}}_5$, which will be used subsequently in the comparative analysis against the CAD model. These points have been computed in the hopper projections, using the associated generatrix lines from ${\mathrm{D}}_{\mathrm{o}}$ and ${\mathrm{D}}_{\mathrm{l}}$, and transformed to the flat domain.

Table 2 presents the coordinates of the selected relevant points within the intersection curves flat patterns for each set of hopper dimensions’ values.

The ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ model of the hopper was visually inspected to propose a surrogate of the discharge area of the fluid duct (${\mathrm{A}}_{\mathrm{o}}$) that avoids a more complex computation in agreement with methods requirements (see Materials and Methods section). Figure 12a shows the connection curve ${\mathrm{D}}_{\mathrm{u}}$ - ${\mathrm{D}}_{\mathrm{f}}$ after two sequential rotations (${\varphi }_{\mathrm{ev}}$ and ${\varphi }_{\mathrm{eh}}$ with axis through ${\mathrm{D}}_{\mathrm{f}}$ vertex perpendicular to dihedral planes) in a position where the internal segment ${\mathrm{P}}_5$ - ${\mathrm{P}}_6$ (pertaining to a generatrix from ${\mathrm{D}}_{\mathrm{u}}$ that encounters with the ${\mathrm{D}}_{\mathrm{f}}$ contour generatrices in Figure 8) is parallel to the vertical projection plane. It is clear that the second internal segment ${\mathrm{P}}_3$ - ${\mathrm{P}}_4$ is approximately perpendicular to the first one. The product of the lengths of these segments is the area of a rectangular surface that keeps approximately perpendicular to the average streamline. Accordingly, we decided to define ${\mathrm{A}}_{\mathrm{o}}$ = $\overline{{\mathrm{P}}_5{\mathrm{P}}_6}·\overline{{\mathrm{P}}_3{\mathrm{P}}_4}$. The last column in Table 2 shows the outlet / inlet area ratio, ${\mathrm{A}}_{\mathrm{r}}$, in the fluid duct.

For the values of dimensions used during the model building (${\mathrm{Nom}}_0$, see Table 1), $\overline{{\mathrm{P}}_3{\mathrm{P}}_4}=3.320$ m, $\overline{{\mathrm{P}}_5{\mathrm{P}}_6}=3.339$ m, and thus ${\mathrm{A}}_{\mathrm{o}}$ = 11.085 m². The inlet area is ${\mathrm{A}}_{\mathrm{i}}=\pi {\mathrm{D}}_{\mathrm{df}}^2/4=\pi {\mathrm{m}}^2$, and then ${\mathrm{A}}_{\mathrm{r}}$ = 3.529. Although the area ratio is greater than 3 as wished, the conicity could be reduced.

The value ${\mathrm{A}}_{\mathrm{r}}$ as a function of the conicity, Con, and the eccentricity, Ecc, of the fluid duct is computed by the $C_{E}DG$ model and presented in Figure 12b. The values of conicity greater or equal than 0.25 are marked in red. The point marked in that plot achieves a ${\mathrm{A}}_{\mathrm{r}}$ value slightly greater than 3 (3.024) with 1.66 m of eccentricity and a minimum value of conicity (0.09). Although, it is possible to reduce even more the conicity, the sensitivity of ${\mathrm{A}}_{\mathrm{o}}$ to errors in the hopper’s dimensions increases excessively. Therefore, we select Con = 0.09 and Ecc = 1.66 m as design parameters (${\mathrm{Nom}}_1$ dimensions’ group).

The $C_{E}DG$ model of the hopper associated with the ${\mathrm{Nom}}_1$ design dimensions is presented in Figure 13.

3.3. Hopper’s CAD modelling

Figure 14 shows the ${\mathrm{D}}_{\mathrm{u}}$ - ${\mathrm{D}}_{\mathrm{f}}$ connection. Both bodies were modelled with the support of the 3D CAD solid modelling software, parametric features and synchronous technology Solid Edge 2023. We have made use of the protrusion command in the solids module to model both the cylinder and the truncated cone. In the case of the latter, a demolding operation has also been added to ensure the desired conicity in each case. Once the two solids were created, a thickness of 0.0001 mm was applied because Solid Edge 2023 does not allow to work with the neutral surface (fiber) of the hopper, as indicated in the methodology pointed out in Prado-Velasco and Ortiz-Marín [13] and the minimum thickness value allowed by this software is the one indicated above.

In Figure 15, ${\mathrm{D}}_{\mathrm{u}}$ cylinder is shown together with the intersection curve between it and the previous ${\mathrm{D}}_{\mathrm{f}}$ straight truncated cone. To obtain this part of the our whole 3D model in such a way that its flat pattern could be computed, we need to proceed as follows. First of all, the solid cylinder was created with the protrusion command and then a thickness of 0.0001 mm was applied. As it was said before, this is the minimum value allowed by the computer application. Next, a conical cut was applied with the characteristics of the ${\mathrm{D}}_{\mathrm{f}}$ duct, thus obtaining the cylinder together with the intersection curve produced by the truncated cone.

Subsequently, it was necessary to make a tiny cut in the lateral surface of the cylinder to generate a slot and be able to open the solid (see it at Figure 15). This is a fundamental condition if the solid cylinder is required to be converted into sheet metal module. Once the slot is created, it is possible to access the tools command and select the icon Convert into sheet metal part. Finally, by selecting the flat pattern button in the tools tab, the flat pattern of the cylinder together with the conical encounter of the ${\mathrm{D}}_{\mathrm{f}}$ duct is obtained, as shown in Figure 16 that was obtained by using Solid Edge’s draft module. The spatial points indicated are the same as those selected in the $C_{E}DG$ model. Models of Figure 14, Figure 15 and Figure 16 correspond to the ${\mathrm{Nom}}_1$ design dimensions.

The intersection curve ${\mathrm{D}}_{\mathrm{l}}$ - ${\mathrm{D}}_{\mathrm{o}}$ is presented in Figure 17. As in the case of the preceding cylinder, both bodies were modelled with the Solid Edge 2023 solids module. The truncated straight cone was generated with the protrusion by revolution command whereas the oblique cylinder was created by using the protrusion sweep command. Then, a thickness of 0.0001 mm was applied.

The ${\mathrm{D}}_{\mathrm{l}}$ truncated cone was processed in a similar manner than ${\mathrm{D}}_{\mathrm{u}}$ with the aim of solving its flat pattern. The protrusion by revolution command was used to generate the truncated cone, to which was subsequently made a swept hollowing with the same characteristics as ${\mathrm{D}}_{\mathrm{o}}$ oblique cylinder in order to generate on it the intersection curve produced by this cylinder, as shown in Figure 18. After applying a thickness command of 0.0001 mm, a tiny lateral slot was achieved to the truncated cone in order to open the lateral surface for subsequent application of the sheet metal module. Nevertheless, it was not possible to find a generatrix that would allow that flattening under the bite with the oblique cylinder.

We tried to use the Sheet Metal Body in Rough command to check if this option could work. After performing several tests, we concluded that the ${\mathrm{D}}_{\mathrm{l}}$ duct can only be flattened when the intersection with ${\mathrm{D}}_{\mathrm{o}}$ is a penetration (two holes) in opposition to a bite (one more complex hole). The Solid Edge surface module was also tested without success because it cannot compute the ${\mathrm{D}}_{\mathrm{l}}$ flat pattern.

Therefore, Table 3 has been created with the available information, in which the coordinates of the selected relevant points within the flat patterns of the intersection curves for each set of hopper values are presented together with the values of the outlet (discharge) / inlet area ratio, ${\mathrm{A}}_{\mathrm{r}}$, in the ${\mathrm{D}}_{\mathrm{f}}$ fluid conduit. We use the same surrogate of the discharge area than in ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ model, to facilitate the comparison.

The obtained values are very similar to those calculated using the ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ technique, as expected. Notwithstanding, we could not apply the 3D model from Solid Edge to extract the function ${\mathrm{A}}_{\mathrm{r}}$ as a function of the eccentricity and conicity, either others parameters.

Finally, the Solid Edge model of the hopper associated with the ${\mathrm{Nom}}_1$ design dimensions is presented in Figure 19.

4. Comparative analysis and discussion

According to the results obtained Solid Edge could not complete the hopper modelling. In addition, this CAD tool does not provide an easy method to compute and evaluate ${\mathrm{A}}_{\mathrm{r}}$, as a function of eccentricity and conicity of our 3D hopper. The comparison for each specific target of the second stage of our study (Methods) were as follows.

• Feasibility to reach the required models. The 3D model of the hopper, which include the ducts connections were properly obtained both in ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ and CAD, as shown in Figure 13 and Figure 19. Nonetheless, Solid Edge 2023 was not able to compute the flat pattern of the lower duct (truncated cone) because this duct encounters to the oblique cylindrical duct with an intersection of bite type. We used different strategies, as described in the Results section, without success.
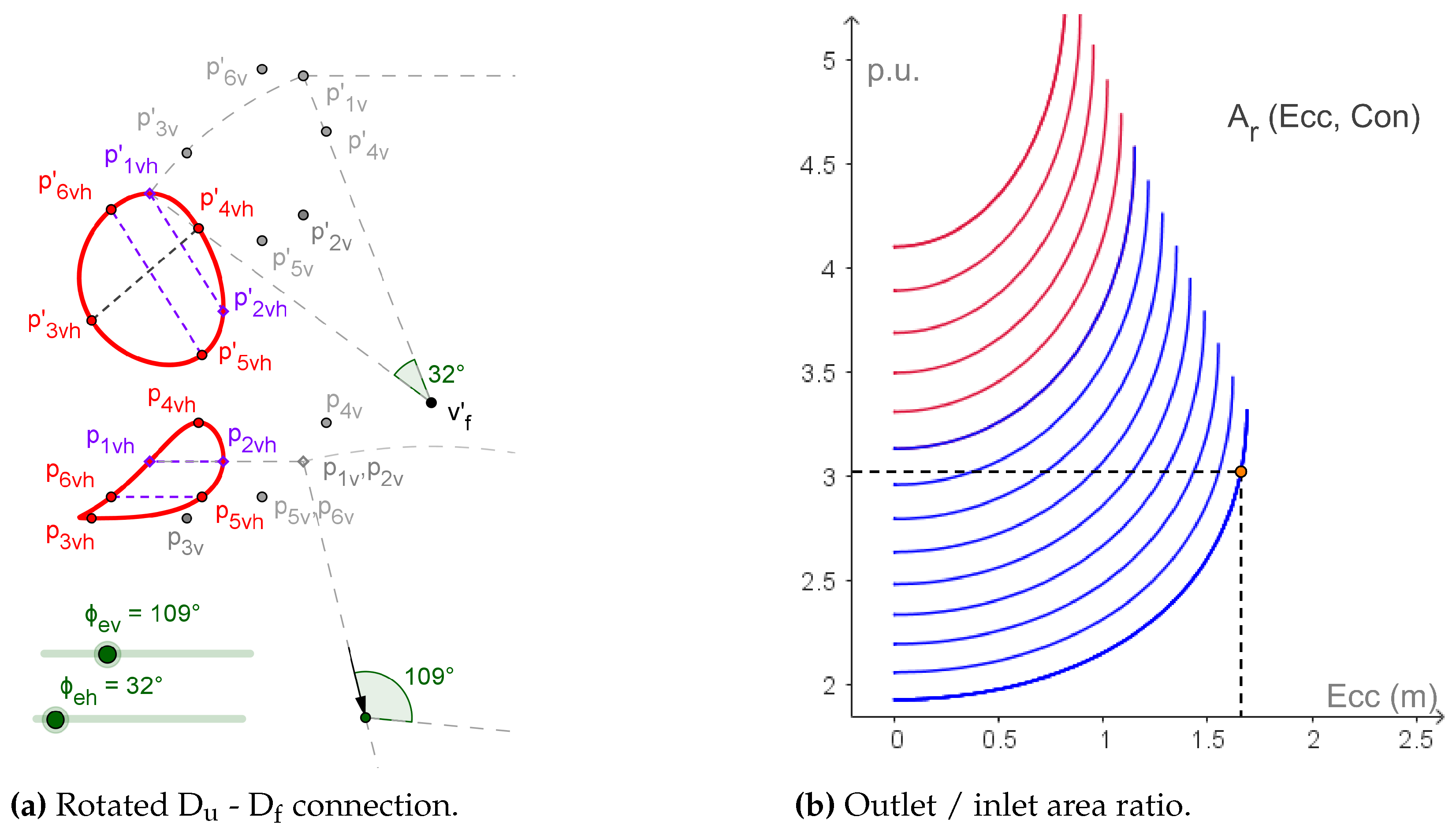
• Once the 3D models were computed, we tried to use them for the analysis of the influence of the geometrical parameters in the outlet / inlet area ratio of the fluid duct, ${\mathrm{A}}_{\mathrm{r}}$, and finally for the optimization of the hopper to achieve ${\mathrm{A}}_{\mathrm{r}}\ge 3$ in a fast expansion. The ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ model allowed a visual inspection of the fluid duct - upper duct connection through spatial rotation, as well as the plotting and quantitative computation of the relationship between ${\mathrm{A}}_{\mathrm{r}}$ and any geometrical parameter of the 3D system. We used this feature to plot ${\mathrm{A}}_{\mathrm{r}}$(Ecc, Con) and select the design values Ecc = 1.66 m and Con = 0.09 (Figure 12b). In opposition, the model computed with Solid Edge 2023 does not provide a direct manner to extract the ${\mathrm{A}}_{\mathrm{r}}$ function.
• With respect to the accuracy, the comparison between Table 2 and Table 3 shows that the position of ${\mathrm{P}}_3$ - ${\mathrm{P}}_4$ (boundary points) in the flat pattern had relative deviations lesser than 0.01 %. In the case of ${\mathrm{P}}_{\mathrm{m}}$ and ${\mathrm{P}}_{\mathrm{M}}$, z relative deviations were lesser than 0.02 %, whereas y relative deviations were lesser than 3.9 %. The relative deviations between ${\mathrm{A}}_{\mathrm{r}}$ values were lesser than 0.6 % with the exception of the value for ${\mathrm{Nom}}_0$ dimensions’ group which was 8.7 %. Values greater than 5 % occurred in those cases where a manual selection of some 3D object were needed. We conclude that the accuracy was high in both models.

The fail of Solid Edge 2023 to achieve the flat pattern of a particular surfaces’ configuration agrees with other comparative studies [13]. Although a more complete analysis of this lack exceeds the scope of this paper, the strategy of current CAD technology for surfaces’ flattening seems limited to a set of configurations previously defined in the software. This approach is clear in some CAD tools focused on sheet metal such as LogiTRACE v14.

As a consequence, our results validate the reliability and accuracy of the new theoretical method presented to compute surfaces intersections and their flattening. This method takes advantage of the mathematical procedures of descriptive geometry and extend them by means of a locus algebraic equation, within the novel ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ approach. The integrity of geometrical objects (i.e. handle without approximation) that characterizes ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ [10,13] is kept also in this method.

To the best of our knowledge, ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ is the first approach of computer parametric 3D modelling based on an extension of descriptive geometry supported by the locus algebraic concept. ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ is implemented in a software of dynamic geometry, which gives a technology different than the technology of current CAD systems. Others studies about 3D geometrical modelling have used the locus concept with a different goal. For instance, Gao et al. [15] uses the locus as a mathematical technique to solve some geometrical issues, like the geometric constraints problem that appear frequently in parametric CAD and other domains, and Oprea and Ruse [16] addressed the computation of some loci problems through descriptive geometry tools.

Other studies have tried to recover the interest in applying the locus concept to CAD software tools. This is the case of the study from Rojas-Sola et al. [17] that improved the set of available resources to build sketches by incorporating a locus tool to several geometrical cases, and implemented in Adobe Authorware v7 (e-learning authoring tool with a graphical programming language that was officially discontinued in 2007). A more recent study has advanced in that research line by implementing an algorithm to solve relevant loci cases, which was designed for educational use [18]. Certainly, the study of new mathematical algorithms that improve the locus equation computations is a ongoing research line on industrial and research [19].

Although ${\mathrm{C}}_{\mathrm{E}}\mathrm{D}\mathrm{G}$ is a computer parametric 3D approach designed for both educational and professional domains, it is still immature for the professional domain and it requires more research to improve the usability, computational efficiency, and capability to interact with other CAD tools. Concerning the GeoGebra implementation, although the Locus command gives the true parametric algebraic functional locus associated with a 2D point that has a complex dependency on the others mathematical objects, it cannot be used as a general 2D algebraic object and the measurement of lengths along it has limitations [12]. These issues define the ongoing research lines.