Submitted:
06 August 2024
Posted:
13 August 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. GMM Expansion
2.1. The Concept of GMM Expansion
- Observation X follows an unknown distribution with density ;
- is the density of GMM;
- ;
- is the i-th normal distribution with mean and standard deviation ;
- define as the interval for locating ;
- ;
- is a hyperparameter and the same for all Gaussian components, usually .
2.2. Approximate Arbitrary Density by GMM Expansion
2.3. Total Variation Distance Analysis For Small Region
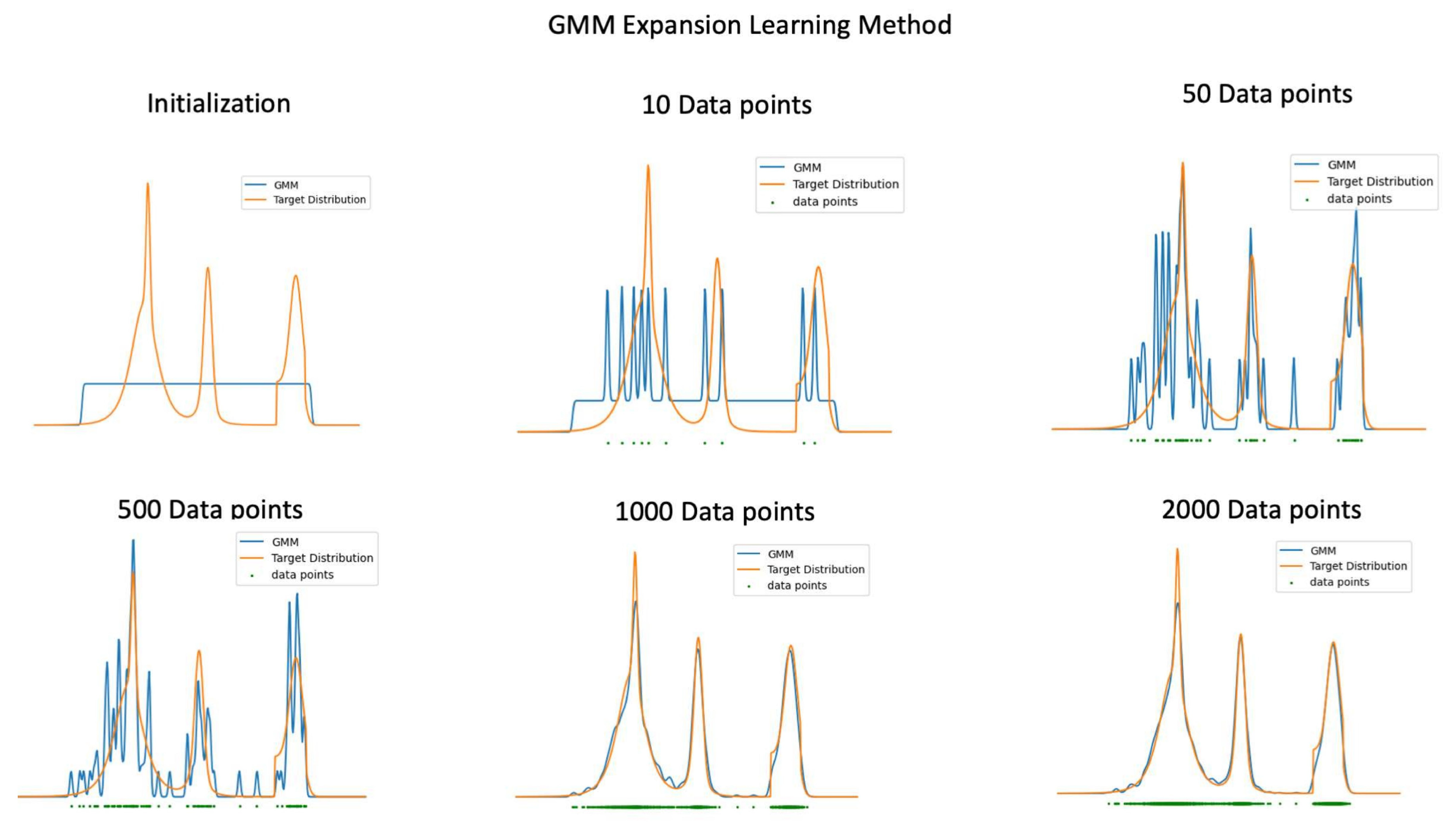
2.4. Learning Algorithm and Convergence
| Algorithm 1:GMM Expansion |
|
Initialization
Update Procedure
Finally, re-normalize s to ensure .
|
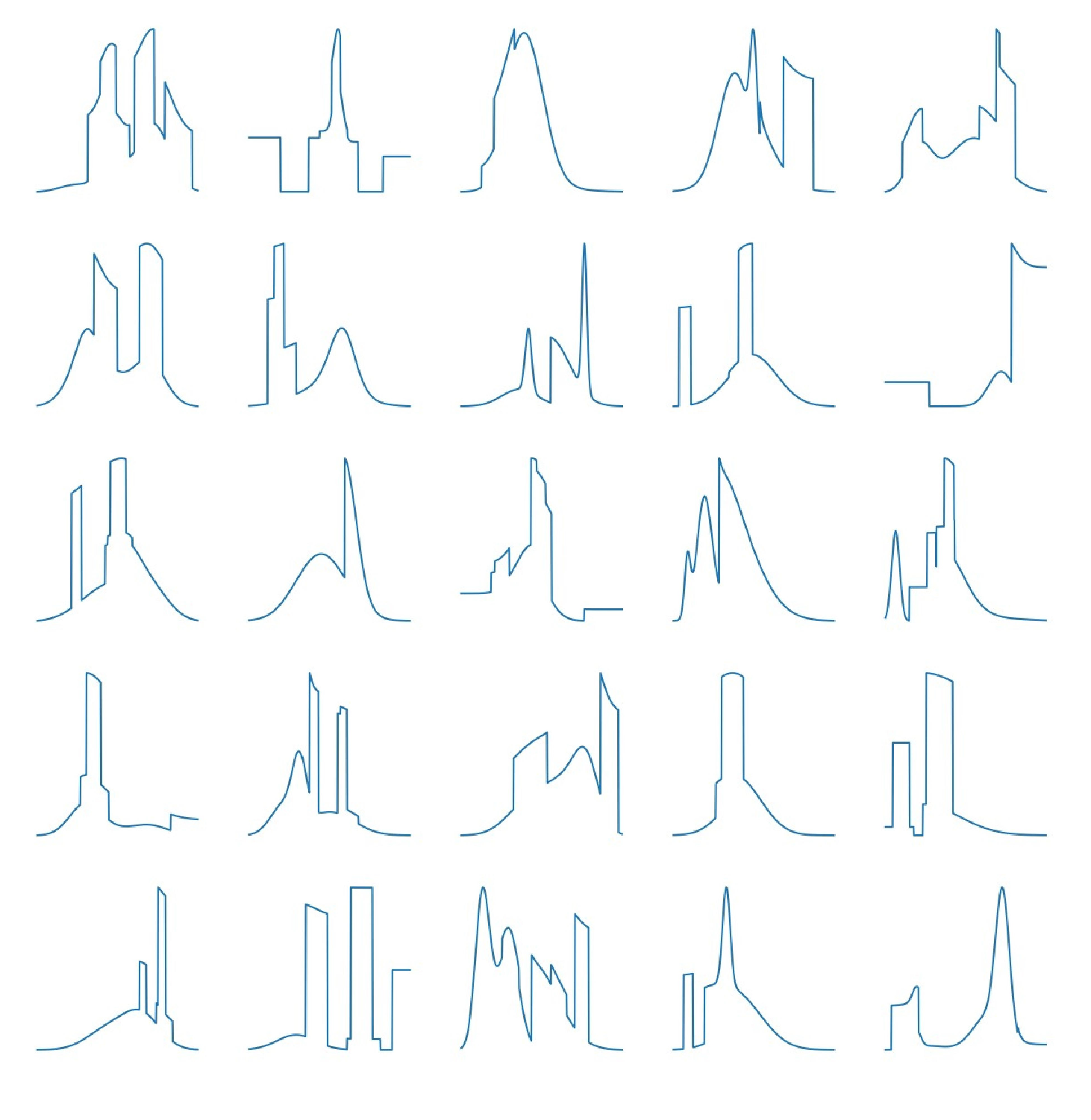
3. Numerical Experiments
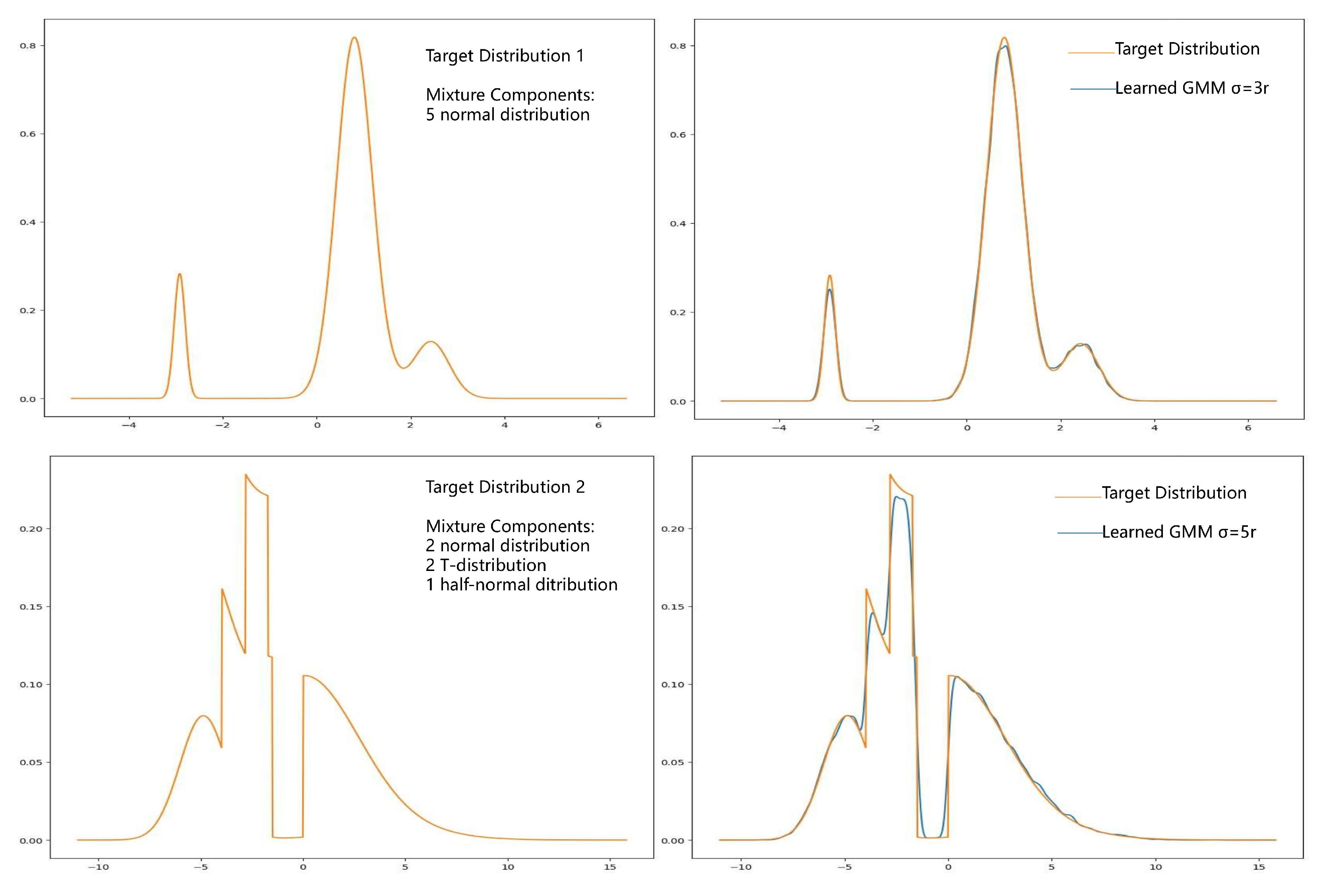
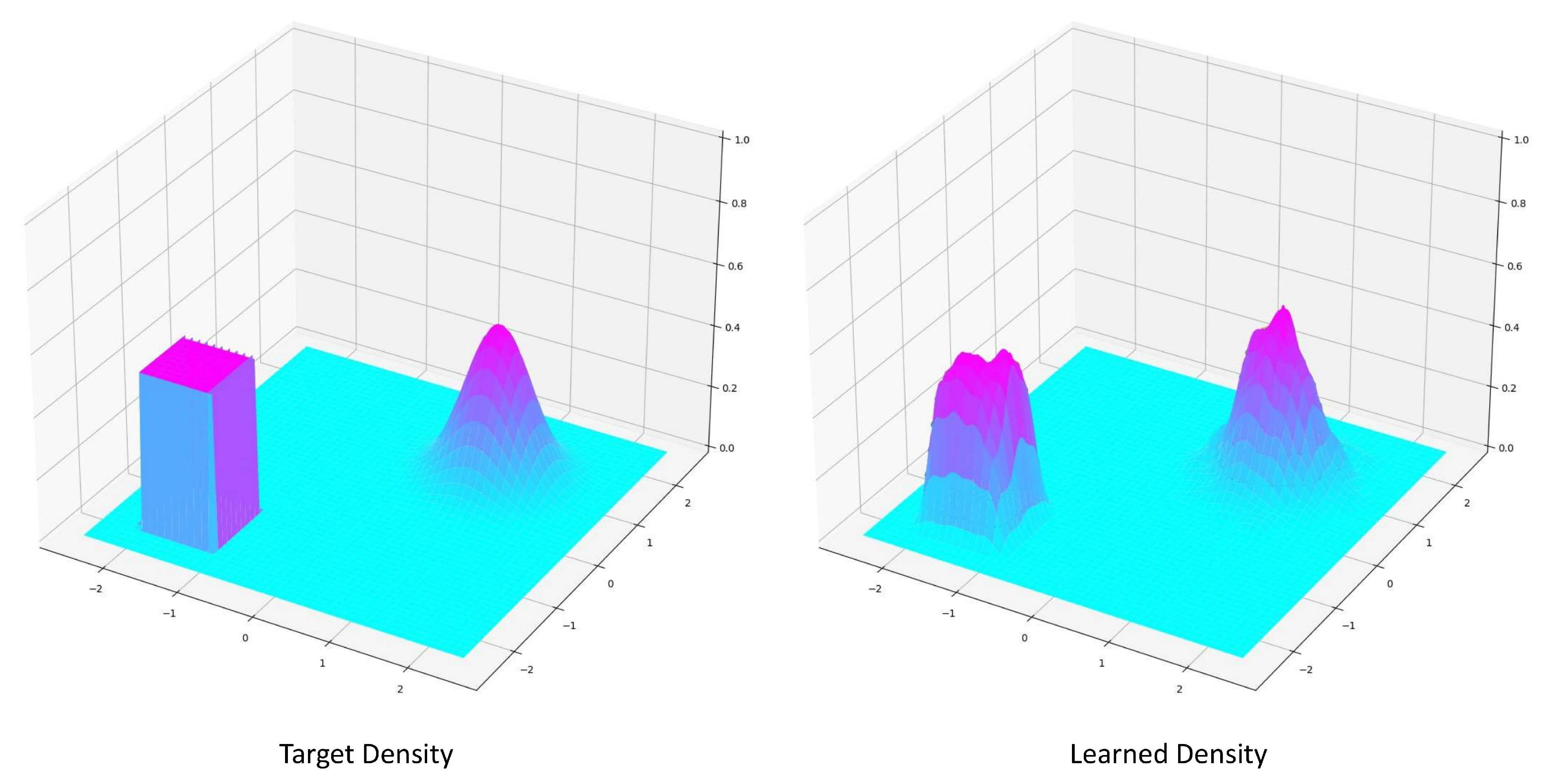
3.1. Density Approximation
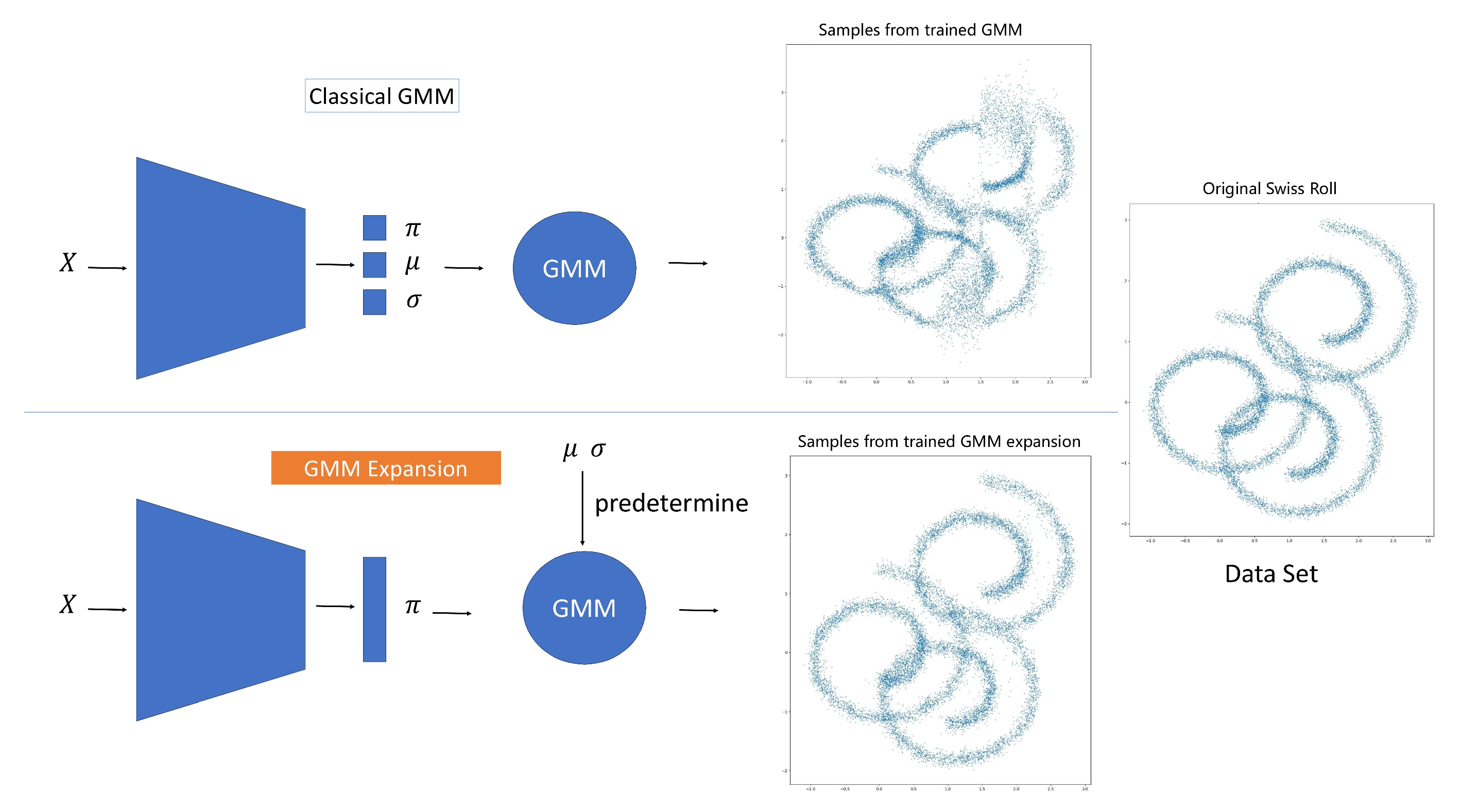
3.2. Comparison Study
4. Neural Network Application
4.1. Probabilistic Output
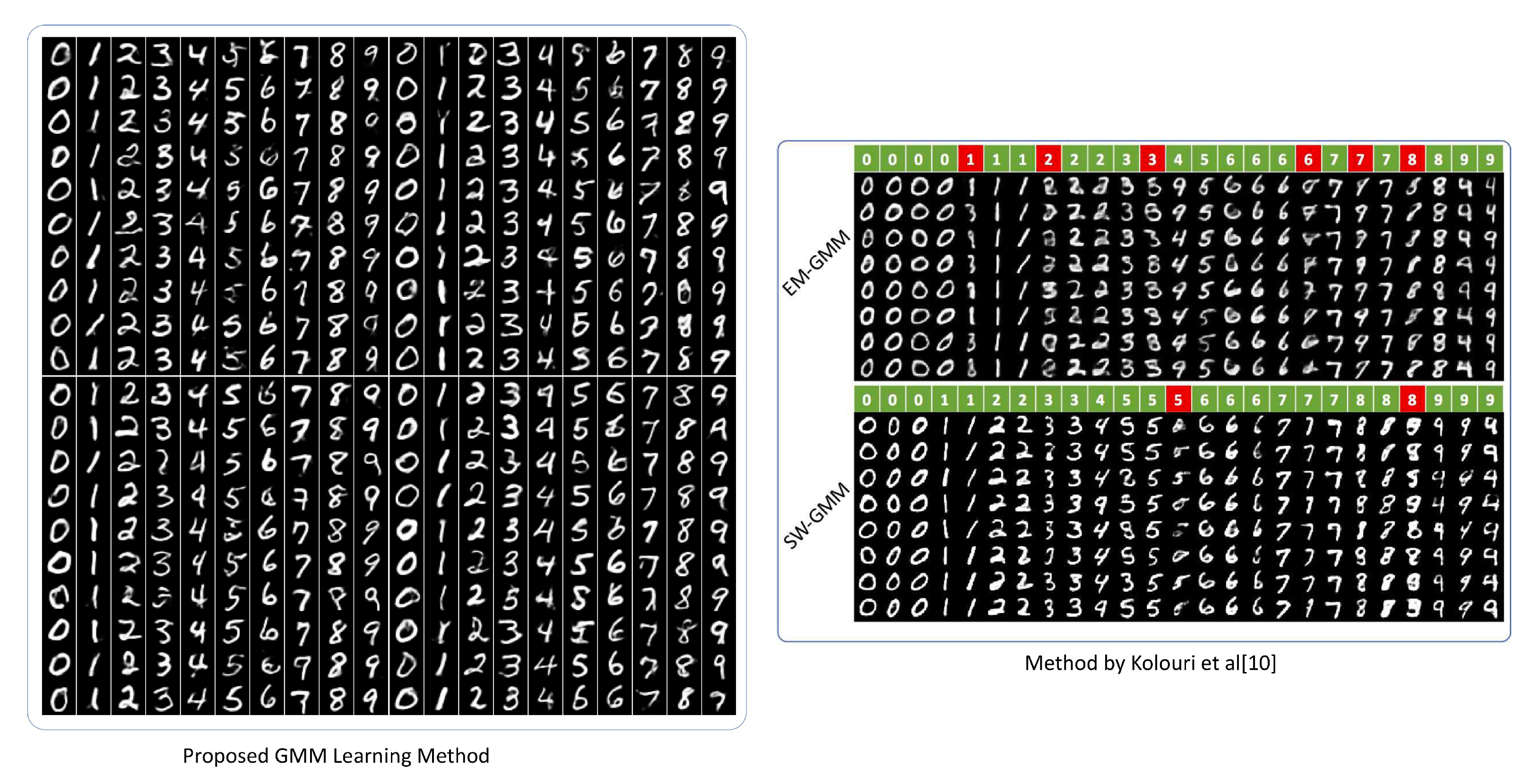
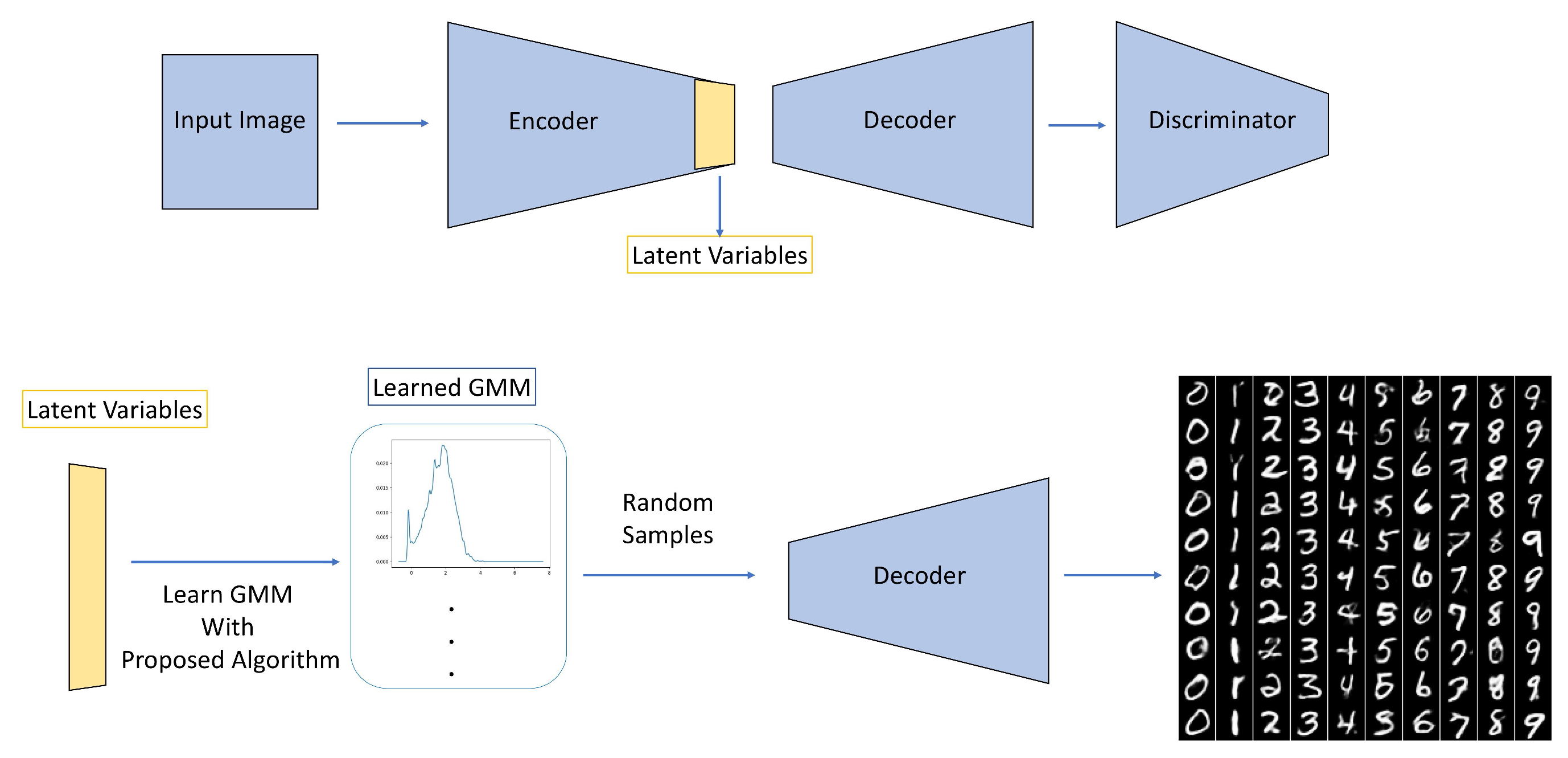
4.2. Mnist Data Set of Handwritten Digits Generation
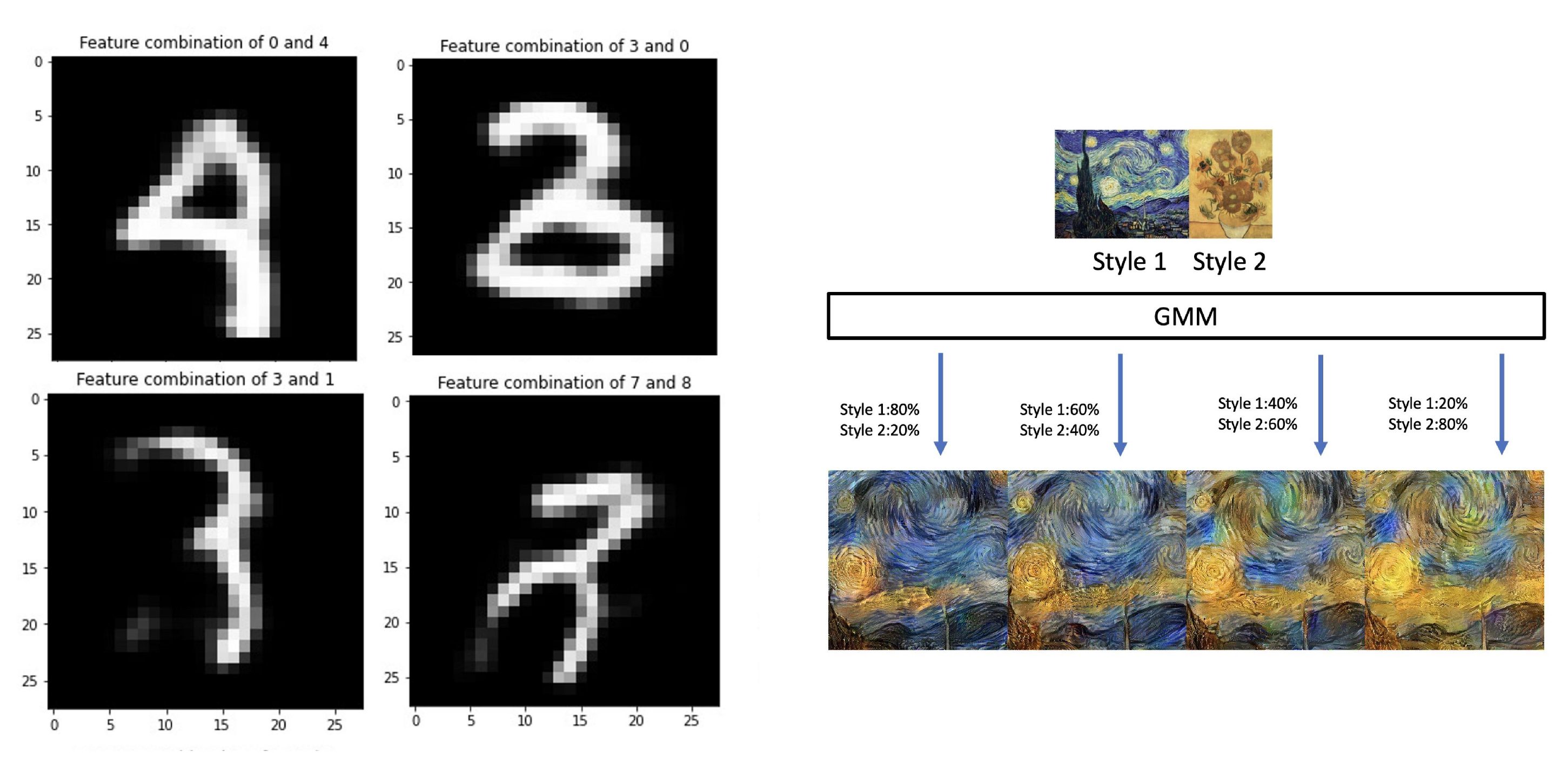
4.3. Style Transfer
5. Conclusions, Discussion and Future Work
Appendix A Uniform Distribution Approximation
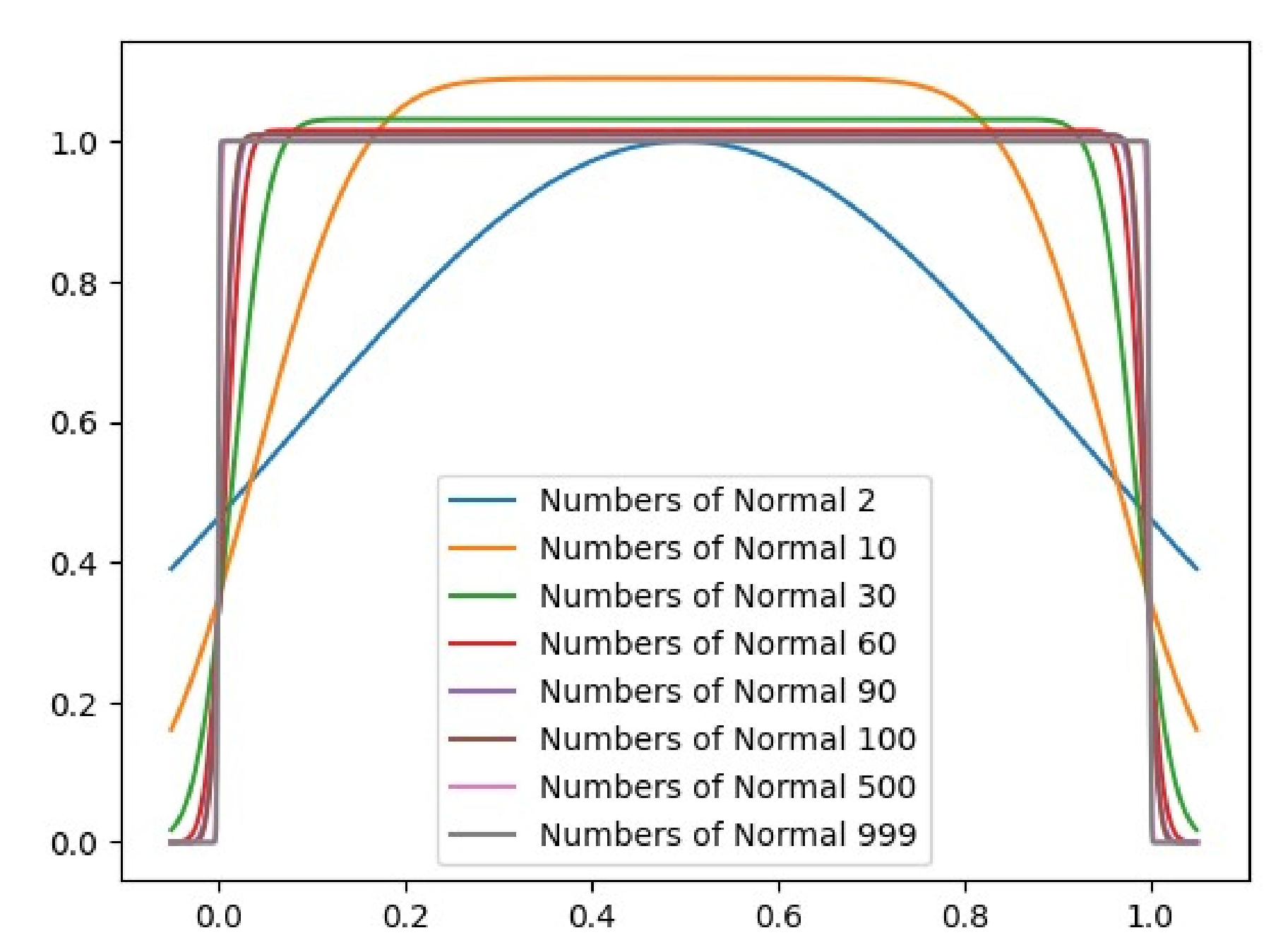

| 1-Wasserstein Distance of Mixture Gaussian and Uniform Distribution | ||||||||
| Numbers of Gaussian | 1 | 2 | 10 | 51 | 101 | 1001 | 1997 | 4997 |
| Wasserstein Distance | 0.1838 | 0.09098 | 0.01789 | 0.00463 | 0.00241 | 0.00024 | 0.00012 | |
Appendix B Further Analysis and Explanation
- 1.Does Eq.11 bounded?
- 2.Why in Algorithm 1 is this form?
- 3.Why can be treated as hyper-parameter?
- Condition 1: is small enough, the target density is approximately monotone and linear within
- Condition 2: GMM density within double crosses the target density.
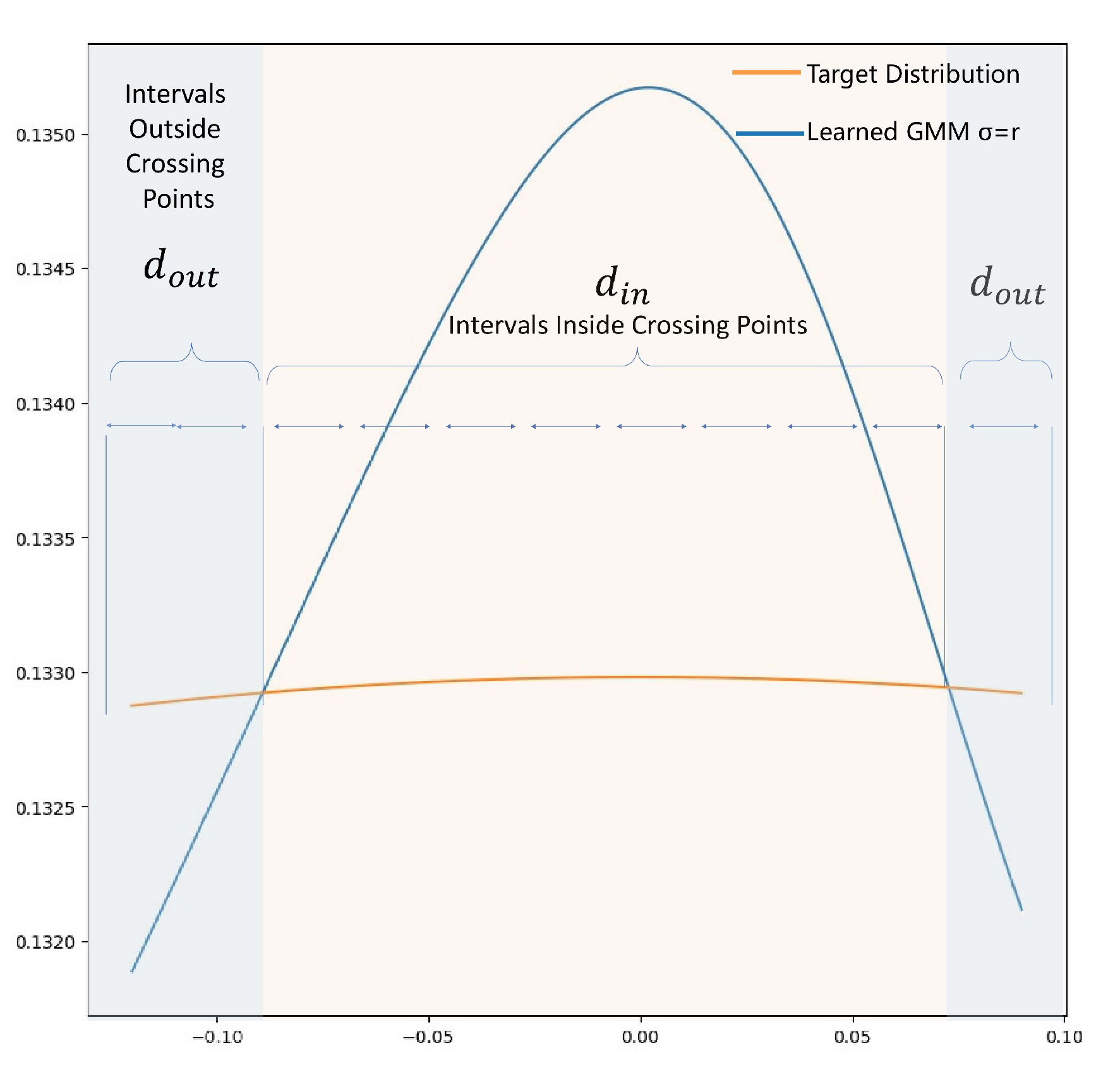
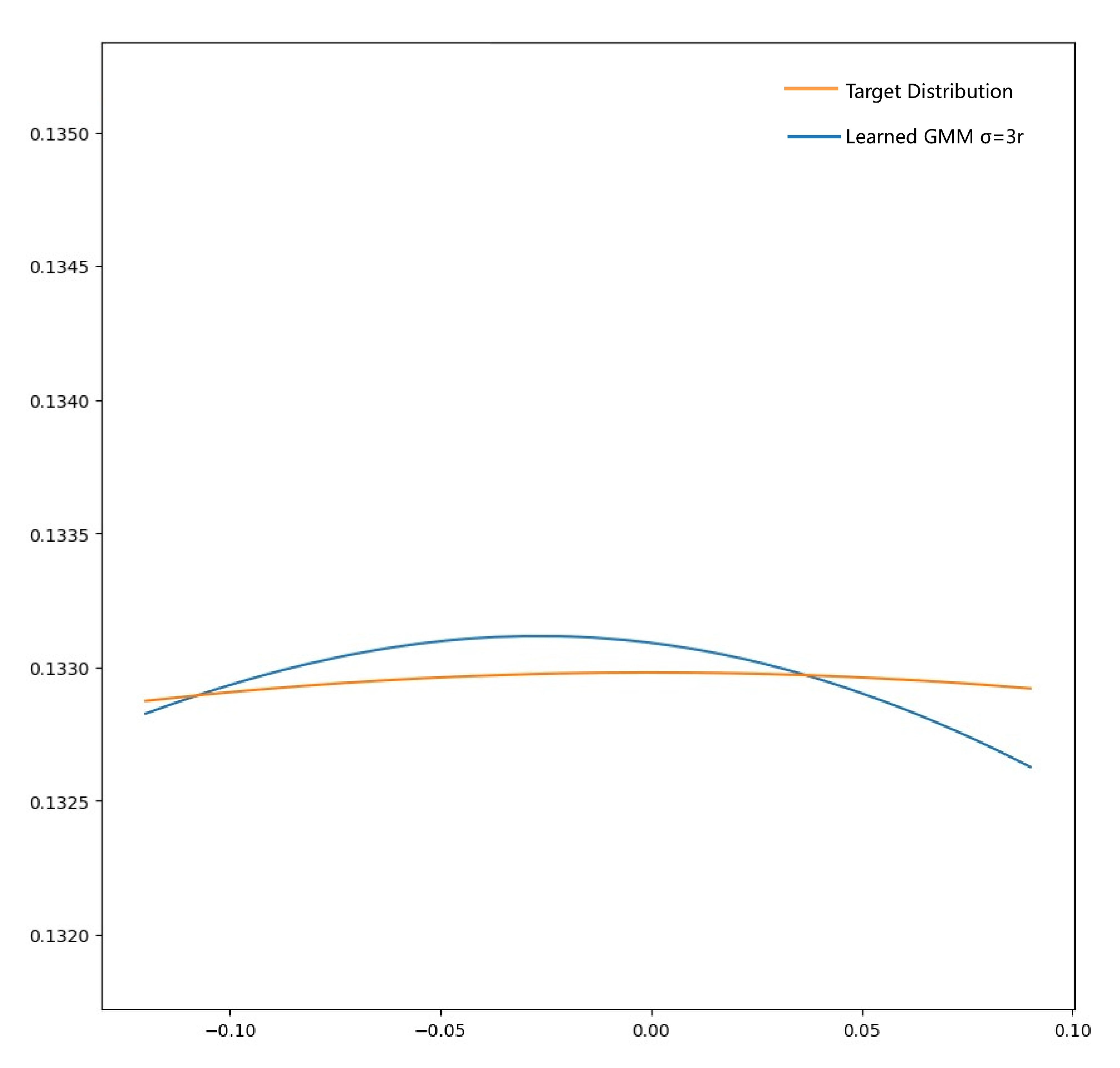
Appendix C Additional Experiment Results
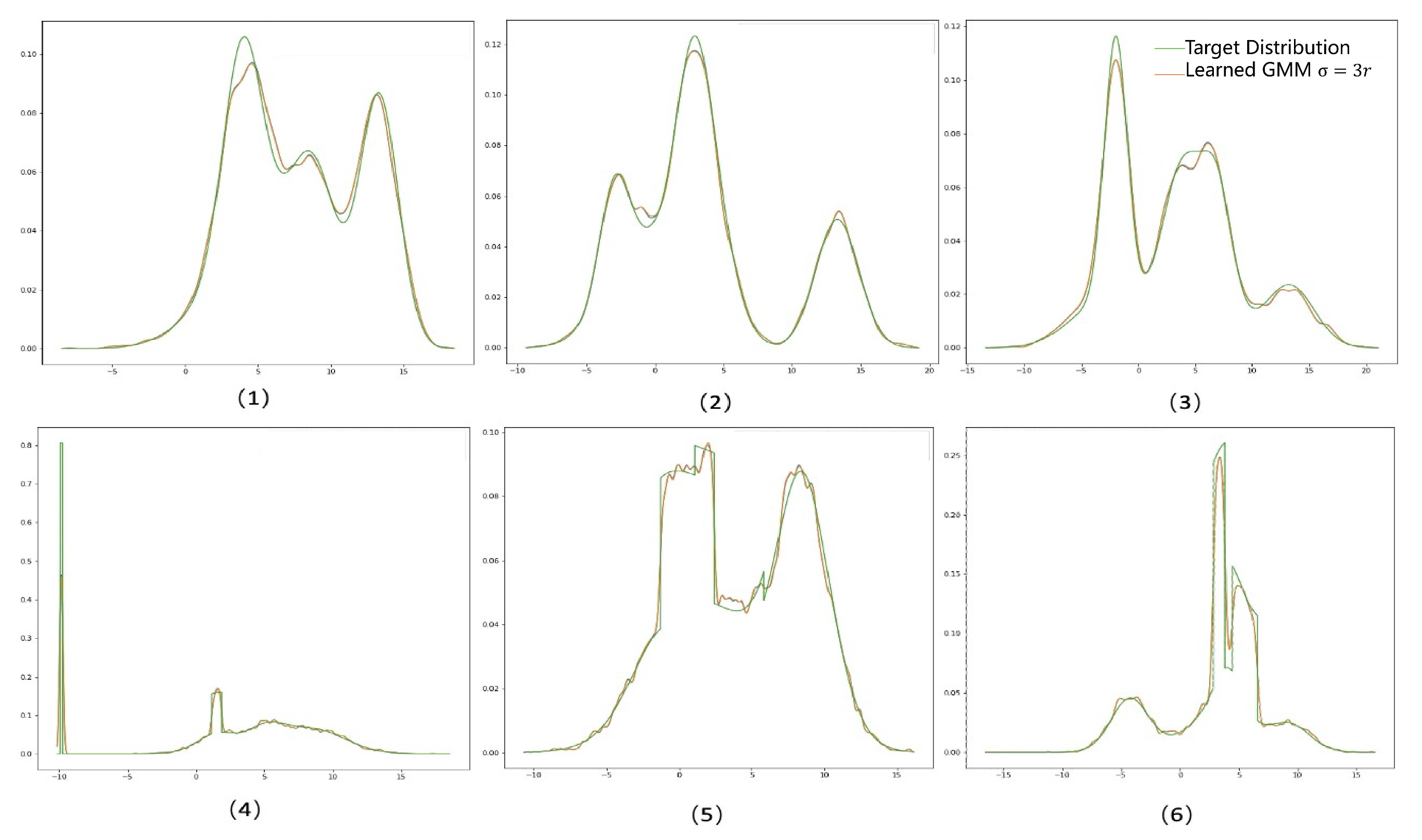
| 1 | |
| 2 | |
| 3 |
References
- G. J. McLachlan and S. Rathnayake, “On the number of components in a gaussian mixture model,” Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, vol. 4, no. 5, pp. 341–355, 2014.
- J. Li and A. Barron, “Mixture density estimation,” Advances in neural information processing systems, vol. 12, 1999.
- C. R. Genovese and L. Wasserman, “Rates of convergence for the gaussian mixture sieve,” The Annals of Statistics, vol. 28, no. 4, pp. 1105–1127, 2000.
- C. Blundell, J. Cornebise, K. Kavukcuoglu, and D. Wierstra, “Weight uncertainty in neural network,” in International Conference on Machine Learning. PMLR, 2015, pp. 1613–1622.
- Y. Gal, “What my deep model doesnât know,” Personal blog post, 2015.
- A. Kendall and Y. Gal, “What uncertainties do we need in bayesian deep learning for computer vision?” Advances in neural information processing systems, vol. 30, 2017.
- A. Der Kiureghian and O. Ditlevsen, “Aleatory or epistemic? does it matter?” Structural safety, vol. 31, no. 2, pp. 105–112, 2009.
- D. P. Kingma and M. Welling, “Auto-encoding variational bayes in 2nd international conference on learning representations,” in ICLR 2014-Conference Track Proceedings, 2014.
- L. A. Gatys, A. S. Ecker, and M. Bethge, “A neural algorithm of artistic style,” arXiv preprint arXiv:1508.06576, 2015.
- S. Kolouri, G. K. Rohde, and H. Hoffmann, “Sliced wasserstein distance for learning gaussian mixture models,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 3427–3436.
- A. P. Dempster, N. M. Laird, and D. B. Rubin, “Maximum likelihood from incomplete data via the em algorithm,” Journal of the Royal Statistical Society: Series B (Methodological), vol. 39, no. 1, pp. 1–22, 1977.
- J. Du, Y. Hu, and H. Jiang, “Boosted mixture learning of gaussian mixture hidden markov models based on maximum likelihood for speech recognition,” IEEE transactions on audio, speech, and language processing, vol. 19, no. 7, pp. 2091–2100, 2011.
- J. J. Verbeek, N. Vlassis, and B. Kröse, “Efficient greedy learning of gaussian mixture models,” Neural computation, vol. 15, no. 2, pp. 469–485, 2003.
- C. Jin, Y. Zhang, S. Balakrishnan, M. J. Wainwright, and M. I. Jordan, “Local maxima in the likelihood of gaussian mixture models: Structural results and algorithmic consequences,” Advances in neural information processing systems, vol. 29, 2016.
- C. Améndola, M. Drton, and B. Sturmfels, “Maximum likelihood estimates for gaussian mixtures are transcendental,” in International Conference on Mathematical Aspects of Computer and Information Sciences. Springer, 2015, pp. 579–590.
- N. Srebro, “Are there local maxima in the infinite-sample likelihood of gaussian mixture estimation?” in International Conference on Computational Learning Theory. Springer, 2007, pp. 628–629.
- Y. Chen, T. T. Georgiou, and A. Tannenbaum, “Optimal transport for gaussian mixture models,” IEEE Access, vol. 7, pp. 6269–6278, 2018.
- P. Li, Q. Wang, and L. Zhang, “A novel earth mover’s distance methodology for image matching with gaussian mixture models,” in Proceedings of the IEEE International Conference on Computer Vision, 2013, pp. 1689–1696.
- C. Beecks, A. M. Ivanescu, S. Kirchhoff, and T. Seidl, “Modeling image similarity by gaussian mixture models and the signature quadratic form distance,” in 2011 International Conference on Computer Vision. IEEE, 2011, pp. 1754–1761.
- B. Jian and B. C. Vemuri, “Robust point set registration using gaussian mixture models,” IEEE transactions on pattern analysis and machine intelligence, vol. 33, no. 8, pp. 1633–1645, 2010.
- G. Yu, G. Sapiro, and S. Mallat, “Solving inverse problems with piecewise linear estimators: From gaussian mixture models to structured sparsity,” IEEE Transactions on Image Processing, vol. 21, no. 5, pp. 2481–2499, 2011.
- W. M. Campbell, D. E. Sturim, and D. A. Reynolds, “Support vector machines using gmm supervectors for speaker verification,” IEEE signal processing letters, vol. 13, no. 5, pp. 308–311, 2006.
- K. P. Murphy, “Machine learning: A probabilistic perspective (adaptive computation and machine learning series),” pp. 344–345, 2018.
- H. Schwenk and Y. Bengio, “Training methods for adaptive boosting of neural networks,” Advances in neural information processing systems, vol. 10, 1997.
- G. E. Hinton and R. Zemel, “Autoencoders, minimum description length and helmholtz free energy,” Advances in neural information processing systems, vol. 6, 1993.
- Y. LeCun, “The mnist database of handwritten digits,” http://yann.lecun.com/exdb/mnist/, 1998.
- J. Li, W. Monroe, T. Shi, S. Jean, A. Ritter, and D. Jurafsky, “Adversarial learning for neural dialogue generation,” arXiv preprint arXiv:1701.06547, 2017.
- I. Goodfellow, “Nips 2016 tutorial: Generative adversarial networks,” arXiv preprint arXiv:1701.00160, 2016.
- K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” arXiv preprint arXiv:1409.1556, 2014.
- J. Ho, A. Jain, and P. Abbeel, “Denoising diffusion probabilistic models,” Advances in Neural Information Processing Systems, vol. 33, pp. 6840–6851, 2020.
- Y. Song and S. Ermon, “Generative modeling by estimating gradients of the data distribution,” Advances in Neural Information Processing Systems, vol. 32, 2019.
- J. Sohl-Dickstein, E. Weiss, N. Maheswaranathan, and S. Ganguli, “Deep unsupervised learning using nonequilibrium thermodynamics,” in International Conference on Machine Learning. PMLR, 2015, pp. 2256–2265.
- DM. Blei, A. Kucukelbir, and JD. McAuliffe, “Variational inference: A review for statisticians,” in Journal of the American statistical Association. 2017, 112(518), pp.859–877.
- C. Villani, “Optimal transport: old and new,” in Berlin: springer. 2009, 112(518), pp.93–113.
- CM. Bishop, NM. Nasrabadi, “Pattern recognition and machine learning,” in New York: springer. 2006, pp.423–517.
- S. Balakrishnan, MJ. Wainwright, B. Yu, “Statistical guarantees for the EM algorithm: From population to sample-based analysis.,” in Ann. Statist. 2017, 45 (1) 77 - 120. [CrossRef]
- H. Attias, “A variational baysian framework for graphical models,” in Advances in neural information processing systems, 12.. 1999.

| Average TVD For Smooth Densities | ||
| 0.035495 | 0.025455 | 0.022248 |
| Average TVD For Non-Smooth Densities | ||
| 0.04456 | 0.04369 | 0.04716 |
| Average TVD of 30 Experiments with Data size 20000 | ||||||
| Numbers of Components | ||||||
| 10 | 30 | 50 | 100 | 200 | 500 | 1000 |
| Average TVD of 30 Experiments with Data size 50000 | ||||||
| Numbers of Components | ||||||
| 10 | 30 | 50 | 100 | 200 | 500 | 1000 |
| Average TVD of 50 Experiments | |||||
| Numbers of Components | |||||
| 20 | 100 | 200 | 500 | 1000 | |
| Proposed Method | |||||
| EM K-mean | |||||
| EM Random | |||||
| BVI | |||||
| Average Training Time of 50 Experiments | |||||
| 20 | 100 | 200 | 500 | 1000 | |
| Proposed Method | |||||
| EM K-mean | |||||
| EM Random | |||||
| BVI | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





