An Efficient Gaussian Mixture Model and Its Application to Neural Network

Preprint

Article

An Efficient Gaussian Mixture Model and Its Application to Neural Network

Altmetrics

Downloads

453

Views

190

Comments

Weiguo Lu^*

Deng Ding,Fengyan Wu,

Gangnan Yuan^*

Weiguo Lu^*

Deng Ding,Fengyan Wu,

Gangnan Yuan^*

This version is not peer-reviewed

Submitted:

10 March 2023

Posted:

16 March 2023

Read the latest preprint version here

Alerts

Abstract

While modeling data in reality, uncertainties in both data (aleatoric) and model (epistemic) are not necessarily Gaussian. The uncertainties could appear with multimodality or any other particular forms which need to be captured. Gaussian mixture models (GMMs) are powerful tools that allow us to capture those features from a unknown density with a peculiar shape. Inspired by Fourier expansion, we propose a GMM model structure to decompose arbitrary unknown densities and prove the property of convergence. A simple learning method is introduced to learn GMMs through sampled datasets. We applied GMMs as well as our learning method to two classic neural network applications. The first one is learning encoder output of autoencoder as GMMs for handwritten digits images generation. The another one is learning gram matrices as GMMs for style-transfer algorithm. Comparing with the classic Expectation maximization (EM) algorithm, our method does not involve complex formulations and is capable of achieving applicable accuracy.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

Gaussian Mixture Models (GMMs) are powerful, parametric, and flexible models in the probabilistic realm. GMMs tackle two important problems. The first is known as the "inverse problem," in which

f^{- 1} (x)

and x are not unique one-to-one mappings [1]. The second issue is the uncertainty problem of both the data (aleatoric) and the model (epistemic)[2,3,4]. When we consider the two problems together, it is easy to see that if we deal with multimodal problems, classic model assumptions start falling apart. Traditionally, we attempt to discover the relationship between input x and output y, which is denoted as

y = f (x) + ϵ

with error

ϵ

. In a probabilistic sense, the above model assumption is equivalent to

y \sim Normal (f (x), σ)

. In terms of inverse and uncertainty problems, we purpose that the model assumption is

y \sim UnkownDistribution (θ (x))

. Under this condition, when y is no longer following any distribution in a known form, GMM becomes a viable option for model data. If

y \sim UnkownDistribution (θ (x)) \approx G M M (f (x))

could be satisfied, then we could use GMM as a general model regardless of whatever distribution y is following. The question remaining for us to answer is whether GMMs can approximate arbitrary densities. Some studies show that all normal mixture densities are dense in the set of all density functions under the

L 1

metric[5,6,7]. A model that can fit an arbitrary distribution density is relatively similar, as it requires the model to imitate all possible shapes of distribution density. In this work, taking ideas from Fourier expansion, we assume that any distribution density can be approximately seen as a combination with a set of finite Gaussian distributions. To put it another way, a set of Gaussian distribution bases with constant means and variances can be used to approximate any density by using data to determine the amplitudes (coefficients) of the Gaussian components. In summary, we have X as input data,

Y \sim {UnknownDistribution}_{y} = G_{y}

as output data, and

G M M (f (x)) + ϵ \approx G_{y},

here

f (x)

is the function that requires learning. To learn

f (x)

, which maps input x into GMM parameters, we can use any modeling technique.

We need to go through two stages of learning when utilizing GMM for modeling. Finding the right GMM parameters to approximate the target distribution

G_{y}

is the first step. Second, we may discover how model

f (x)

maps to

θ

. In this essay, we mostly talk about the first stage of learning. The best way to train a GMM to simulate the desired distribution. Fitting a GMM from the observed data related to two problems: 1) how many mixture components are needed; 2) how to estimate the parameters of the mixture components.

For the first problem, some techniques are introduced[5]. For the second problem, as early as 1977, the Expectation Maximization (EM) algorithm[8] was well developed and capable of fitting GMMs based on minimizing the negative log-likelihood (NLL). While the EM algorithm remains one of the most popular choices for learning GMMs, other methods have also been developed for learning GMMs[9,10,11]. The EM algorithm has a few drawbacks. Srebro [12] asked an open question that questioned the existence of local maxima between an arbitrary distribution and a GMM. That paper also addressed the possibility that the KL-divergence between an arbitrary distribution and mixture models may have non-global local minima. Especially in cases where the target distribution has more than k components but we fit it with a GMM with fewer than k components. Améndola at al.[13] has shown that the likelihood function for GMMs is transcendental. Jin et al.[14] resolved the problem that Srebro discovered and proved that with random initialization, the EM algorithm will converge to a bad critical point with high probability. The maximum likelihood function is transcendental and will cause arbitrarily many critical points. Intuitively speaking, when handling any distribution with multimodal analysis, if the size of the GMM components is less than the peaks that the target distribution contains, it will lead to an undesirable estimation.

Additionally, a single Gaussian component is limited in capturing these types of features and is unable to produce a good prediction if the target distribution’s peak appears as a flat top, similar to a roof, rather than a bell shape. The likelihood function could have poor local maxima and be arbitrarily worse than any global optimum. The Wasserstein distance is a topic of interest in several studies. Wasserstein distances are presented to replace the NLL function, which minimizes either the Kullback-Leibler divergence or the NLL function[11,15,16]. These methods avoid the downside of using NLL, but the calculation and formulation of the learning process are relatively complex.

Instead of following the EM algorithm, we take a different path. The main concept of our work is to take the idea of Fourier expansion and apply it to density decomposition. Similarly, like Fourier expansion, our model needs a set of base components, and their location is predetermined. Instead of using a couple of components, we use a relatively large number of components to construct this base. The benefit of this approach is that these bases represent how much detail our models can capture without going into a calculation process to decide how many GMM components are needed. Another benefit of this idea is that, on a predetermined basis, the learning parameters become relatively simple. To achieve the best approximation, we simply need to learn a suitable collection of

π

, which are the probability coefficients of normal components. A simple algorithm without heavy formulation is designed to achieve this task. More detailed explanations, formulations, and proofs are provided in the next section. It is important to note that, similar to cousin expansion, there will be information loss for the target sequence if base frequencies are insufficient. Similar information losses are experienced by this method due to insufficient Gaussian components. We provide a measurement of the information loss. In our experiments, our technique delivered a good estimation result.

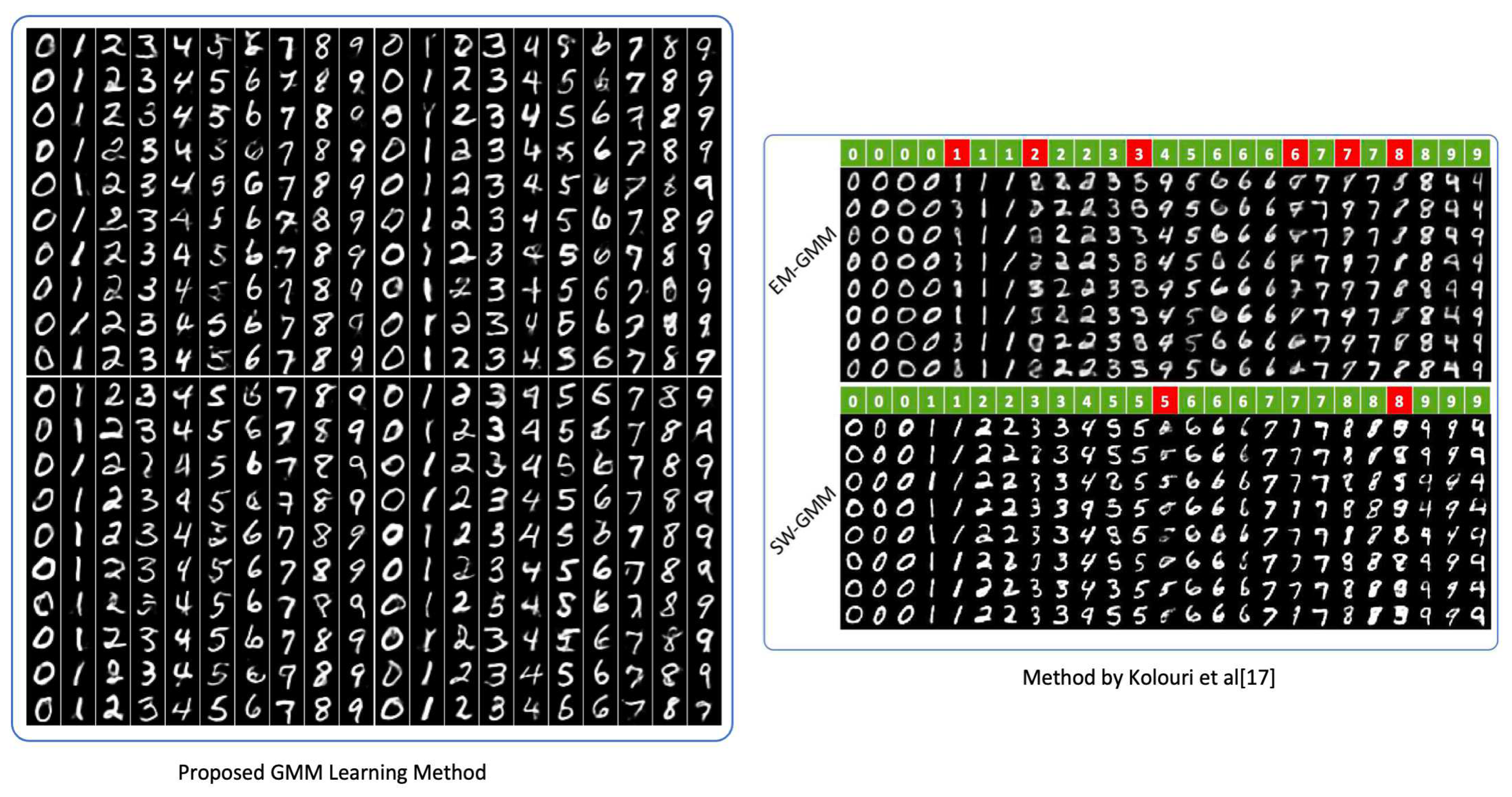
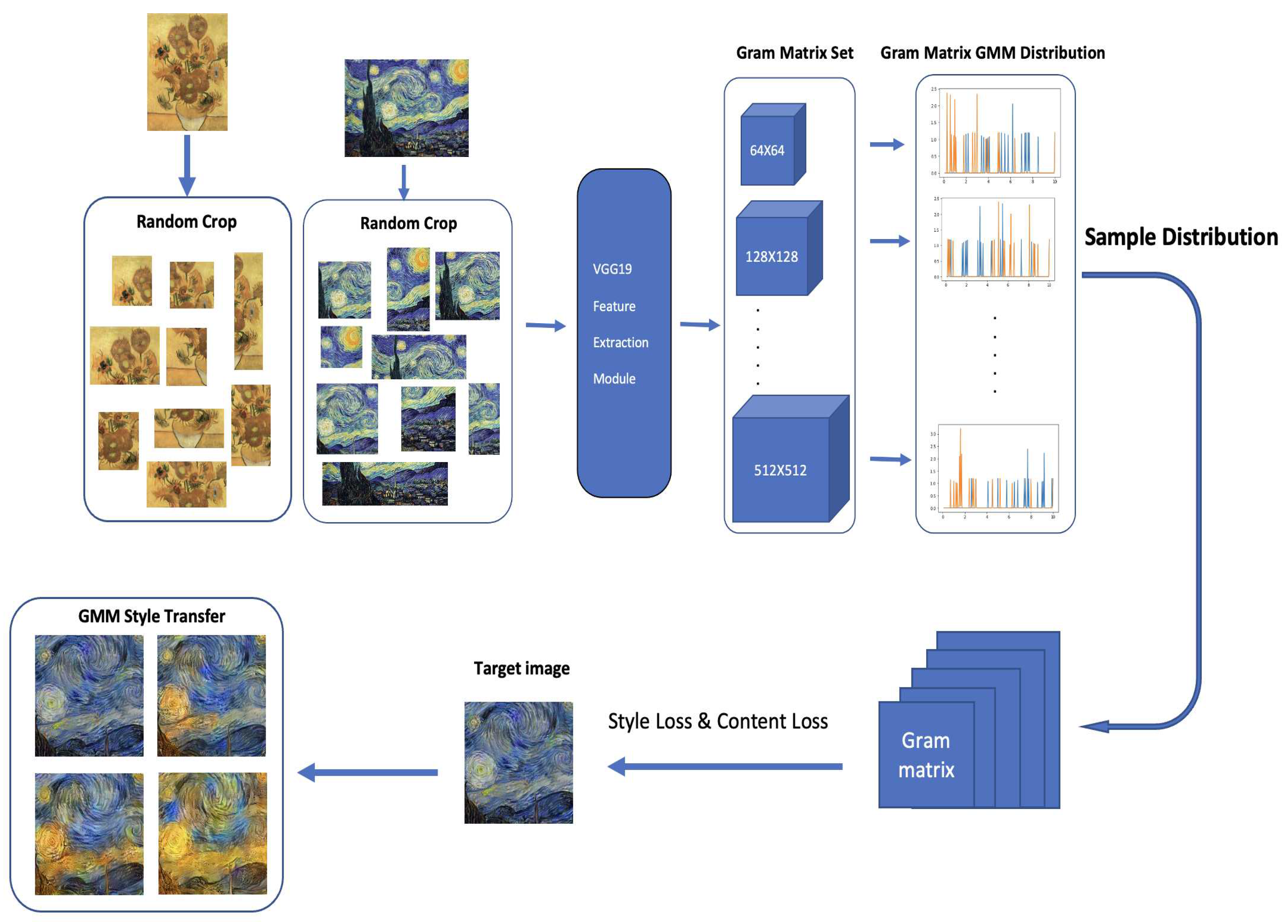
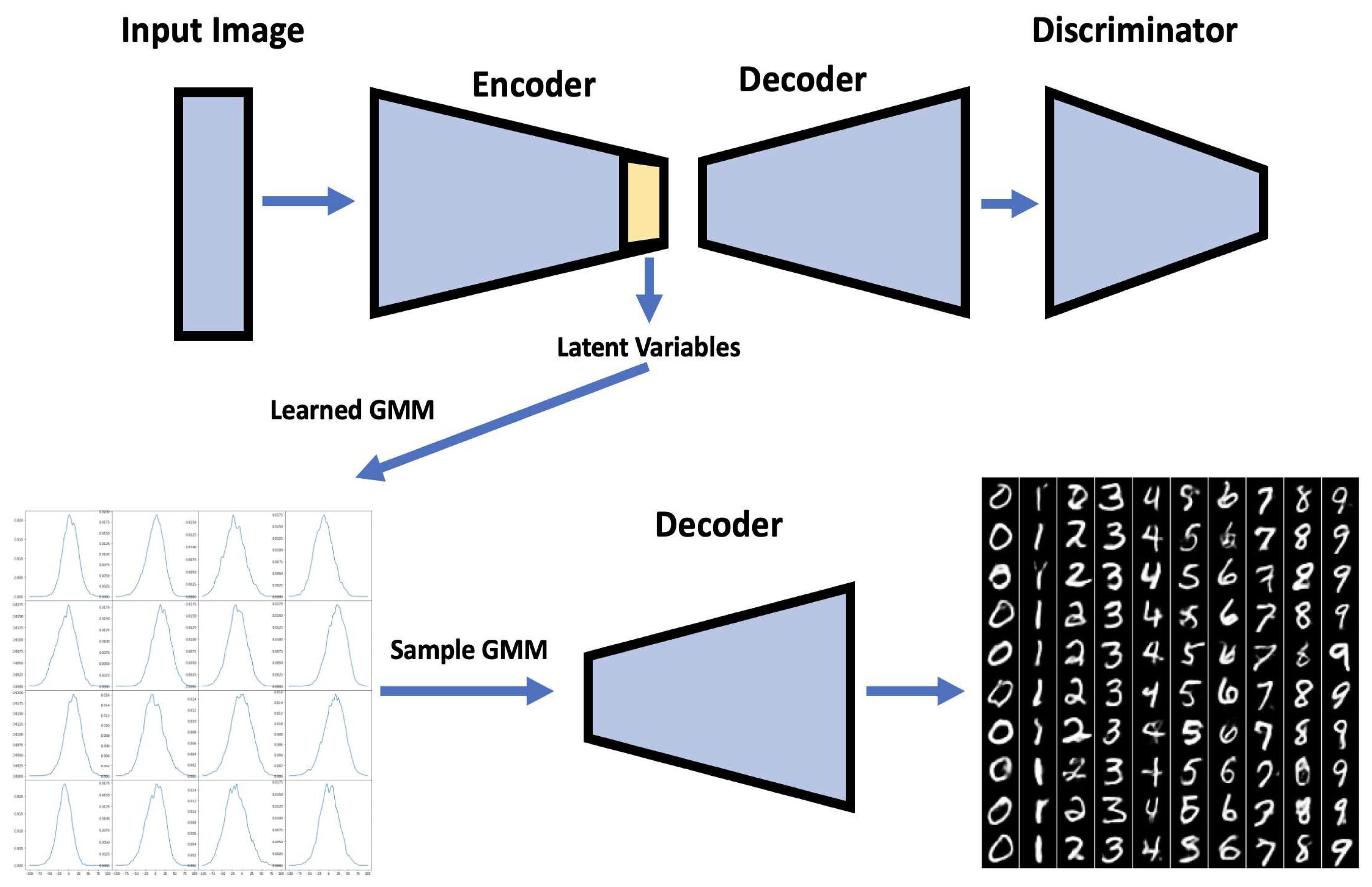
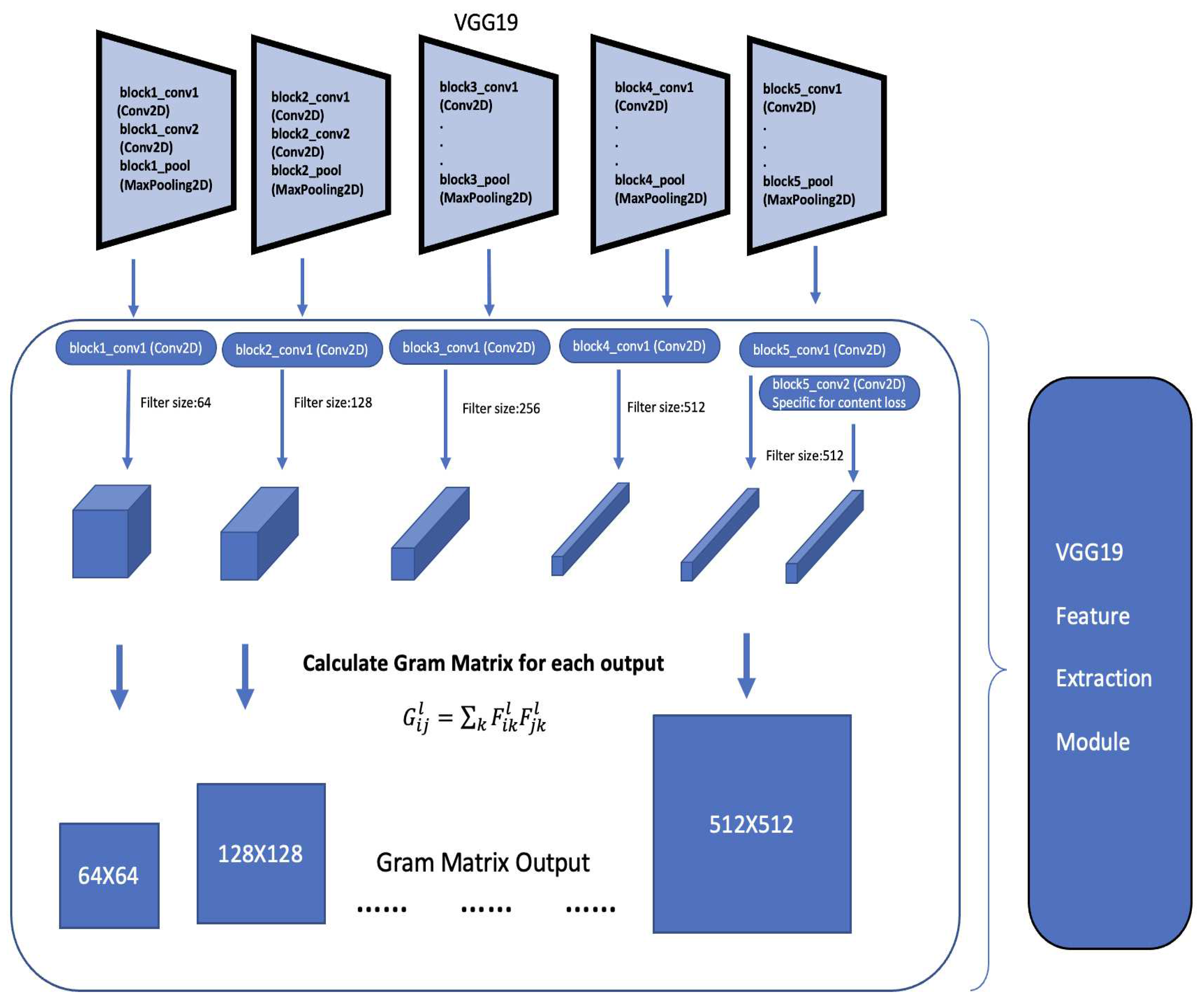
GMMs have been used across computer vision and pattern classification among many others [17,18,19,20]. Additionally, GMMs can also be used to learn embedded space in neural networks [11]. Similarly, as Kolouri et al., we apply our algorithm to learn embedded space in neural networks in two classic neural network applications of handwritten digits generation using autoencoders[21,22] and style transfer[23]. This helps us turn latent variables into a Gaussian Mixture distribution, which allows us to perform sampling to create variation. More detail is provided in Section 4.

Section 2 introduces Fourier expansion-inspired Gaussian mixture models, shows this method is capable of approximating arbitrary densities, discusses the convergency, defines a suitable metric, and details some of its properties. Section 3 provides our methodology for fitting a GMM through data, introduces two learning algorithms, and shows learning accuracy through experiments. Section 4 presents two neural network applications. The final section provides a summary and conclusions.

2. Decompose Arbitrary Density by GMM

The principle of density decomposition using GMM is demonstrated in this section, along with learning algorithms, and it is shown that it is possible to do so with bounded approximation error. In order to quantify the approximation error between the target density and the GMM, a metric called density information loss is proposed. Let’s start with the fundamental premise and notation:

Observed a dataset X, which is following a unknown distribution with density $f (x)$ ;
Assuming there is a GMM that matches the distribution of X : $f (x) \approx g (x) + ϵ$ ;
The density of GMM: $g (x) = \sum_{n} π_{i} ϕ_{i} (x)$ ;
As general definition of GMM, $\sum_{n} {\tilde{π}}_{i} = 1$ and $ϕ_{i} (x) \sim N (μ_{i}, σ_{i})$ .

We mostly examine one-dimensional examples in this study. Instead of multivariate Gaussian distributions, the GMM uses mixed Gaussian distributions.

2.1. General concept of GMM decomposition

The idea behind GMM decomposition is a Fourier series in probability that, assuming arbitrary density, can be approximately decomposed by infinite mixtures of Gaussian distributions. As mentioned earlier, a lot of studies prove that the likelihood of GMM has many critical points. There are far too many sets of

π, μ

and

σ

that could produce the same likelihood result on a given dataset. Learning three sets of parameters,

π, μ, σ

could increase the complexity of the learning process. Not to mention that these parameters interact with each other. Changing one of them could lead to new sets of optimal solutions for others. If we consider that GMM can decompose any density like the Fourier series into a periodic sequence, we can predetermine the base Gaussian distributions (component distributions).

In practice,

μ

can be set to be evenly spread out though the dataset space. The parameter

σ

can be treated as a hyper-parameter that adjusts overall GMM density smoothness. This means that

μ, σ

of the component distribution are non-parametric and do not need to be optimised. The parameter

π

is the only remaining problem for us to solve. Our goal shifted from finding the best set of

π, μ, σ

to finding the best set of

π

on a given dataset. With this idea, our GMM set-up becomes:

$g (x) = \sum_{n} π_{i} ϕ_{i} (x)$ is the density of GMM;
$\sum_{n} π_{i} = 1$ , $ϕ_{i} (x) \sim N (μ_{i}, σ)$ , n is the numbers of normal distributions;
$r = \frac{\max (X) - \min (X)}{n}$ is the interval for locating $μ_{i}$ ;
$μ_{i} = \min (X) + i \times r$ are means for Gaussian components;
$σ = t \times r$ is variance for all Gaussian components;
t is a real number hyper-parameter, usually $1 \leq t \leq 5$ .

2.2. Approximate arbitrary density by GMM

In this subsection, we show that, under certain conditions, if the component size of a mixture Gaussian model goes to infinity, the error of approximating an arbitrary density can go toward zero. Through the idea of Monte Carlo, we could assume that the accuracy of a fine frequency distribution estimation of the target probability mass through a dataset is good enough in general. A frequency distribution could also be seen as a mixture distribution with uniform distribution components. Elaborate from this: if we swap each uniform distribution into a Gaussian unit and push this toward infinite, we could have a correct probability mass approximation of any target distribution. Because we do not have access to the true density, the dataset is all we have, an accurate probability mass is generally good enough in practice. Let

ω_{i} = \{x \in (μ_{i} - r, μ_{i} + r]\}

, we have:

\begin{matrix} [\begin{matrix} \int_{ω_{0}} g (x) d x \\ . \\ . \\ . \\ \int_{ω_{n}} g (x) d x \end{matrix}] = [\begin{matrix} P_{g} \{ω_{0}\} \\ . \\ . \\ . \\ P_{g} \{ω_{n}\} \end{matrix}] \approx [\begin{matrix} P_{f} \{ω_{0}\} \\ . \\ . \\ . \\ P_{f} \{ω_{n}\} \end{matrix}] = [\begin{matrix} \int_{ω_{0}} f (x) d x \\ . \\ . \\ . \\ \int_{ω_{n}} f (x) d x \end{matrix}] . \end{matrix}

where

P_{g}

is the density function for GMM and

P_{f}

is the target density function. Expand the density of GMM

g (x)

results

[\begin{matrix} \int_{ω_{0}} ϕ_{0} (x) d x & . & \cdot & \cdot \int_{ω_{0}} ϕ_{n} (x) d x \\ ⋮ & ⋮ & ⋮ & ⋮ \\ \int_{ω_{n}} ϕ_{0} (x) d x & . & \cdot & \cdot \int_{ω_{n}} ϕ_{n} (x) d x \end{matrix}] [\begin{matrix} π_{0} \\ ⋮ \\ π_{n} \end{matrix}] = [\begin{matrix} P_{g} \{ω_{0}\} \\ ⋮ \\ P_{g} \{ω_{n}\} \end{matrix}] .

It is not hard to notice that, if

\int_{ω_{i}} ϕ_{i} (x) d x \approx 1

which means that each Gaussian component is very dense in their region, GMM become a discrete distribution that can be precisely 1:1 clone the estimation probability mass. It becomes:

[\begin{matrix} 1 & . & . & . 0 \\ ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & . & . & . 1 \end{matrix}] [\begin{matrix} π_{0} \\ ⋮ \\ π_{n} \end{matrix}] \approx [\begin{matrix} P_{g} \{ω_{0}\} \\ ⋮ \\ P_{g} \{ω_{n}\} \end{matrix}] \approx [\begin{matrix} P_{f} \{ω_{0}\} \\ ⋮ \\ P_{f} \{ω_{n}\} \end{matrix}]

These straightforward conclusions imply that, in this configuration, a GMM with a significant size component will perform as well as a frequency distribution. The same result might also be obtained by switching the mixing component from a regular Gaussian distribution to a truncated normal distribution or uniform distribution. One good thing about this configuration is that it might move discrete probability mass estimation to continuous density. Allow us to approach regression problems in a classification-based manner. We do suffer loss of information at some points in the density, but generally, in practice, a approximation of probability mass is what we are looking for. For example, let’s say we are trying to figure out the distribution of people’s height. Instead of looking for a precise density estimation of people’s height,

f \{height = 1.801 m\}

P \{1.80 m \leq height \leq 1.81 m\}

is what we targeting. Therefore, if we accept a discrete frequency distribution as one of our general approximation models, there is no reason that the GMM cannot be used to approximate an arbitrary density because it is capable of performing as good as frequency distribution estimation.

2.3. Density information loss

Even though GMM can approximate arbitrary densities similarly to frequency distribution, density information within

ω

remains a problem that needs to be discussed. In another word, even if we learn a model that probability mass is equal to target density

P_{g} \{ω\} = P_{f} \{ω\}

, the differentiation is not equal

\frac{d P_{g} \{ω\}}{d x} \neq \frac{d P_{f} \{ω\}}{d x}

. We could apply KL-divergence or Wasserstain distance to measure the difference between two densities. But in our setup, we introduce a simple metric to measure regional density information loss (DIL). If DIL is small enough under some conditions, then we may be able to conclude that GMM can be a generalized model to decompose arbitrary density.

First of all, assume we have already learned a GMM which achieves that probability mass is correctly mapped to the target distribution. We split the data space into n regions denoted as

ω_{i}

the same as Section 2.2. Assume we have

[\begin{matrix} P_{g} \{ω_{0}\} \\ ⋮ \\ P_{g} \{ω_{n}\} \end{matrix}] \approx [\begin{matrix} P_{f} \{ω_{0}\} \\ ⋮ \\ P_{f} \{ω_{n}\} \end{matrix}]

Then, the total density information loss is sum of absolute error is given by

\begin{matrix} D I L = \sum_{i = 1}^{n} \int_{ω_{i}} | f (x) - g (x) | d x . \end{matrix}

Since the integration is not easy to calculate, here we divide

ω_{i}

further into m smaller regions to estimate DIL:

\begin{matrix} \sum_{k = 1}^{m} d_{k} = ω_{i}, \\ D I L \approx \sum_{i = 1}^{n} \sum_{j = 1}^{m} \int_{d_{i j}} | f (x) - g (x) | d x \approx \sum_{i = 1}^{n} \sum_{j = 1}^{m} | P_{f} \{d_{i j}\} - P_{g} \{d_{i j}\} | . \end{matrix}

Denote that

L (ω_{i}) = \sum_{j = 1}^{m} | P_{f} \{d_{i j}\} - P_{g} \{d_{i j}\} | .

(1)

Here

L (ω_{i})

is the discrete approximation of density information loss within region

ω_{i}

. If

L (ω_{i})

is universally bounded in some conditions for all

ω

, the overall DIL is bounded. For any

x_{i j}

from

ω_{i}

, if

\begin{matrix} | P_{f} \{x_{i j} \pm d\} - P_{g} \{x_{i j} \pm d\} | \leq τ_{i} \leq τ, \end{matrix}

we have

\begin{matrix} D I L \leq n * m * τ . \end{matrix}

In fact,

L (ω_{i})

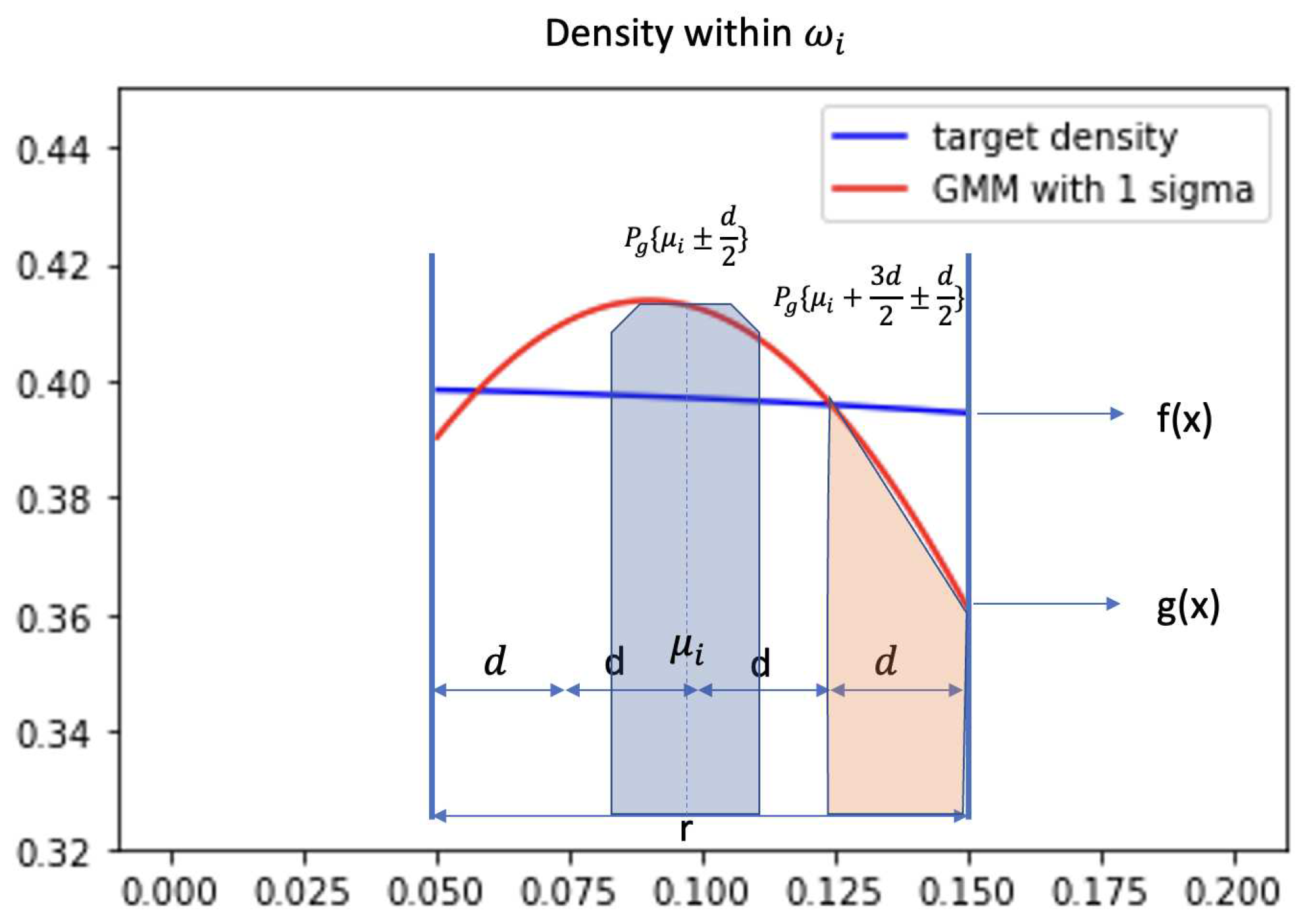
is bound within a comfortable condition. In Figure 1, the plot demonstrates the density of target distribution(blue) and GMM(red) in a small region

ω_{i}

. The probability

P_{f} \{ω_{i}\}

is equal to

P_{g} \{ω_{i}\}

. Evenly split

ω_{i}

into 4 smaller areas and each area has length d. When we look at this geometrical relationship between target distribution

f (x)

and GMM

g (x)

, we discover that for each small region d,

| P_{f} \{d_{j}\} - P_{g} \{d_{j}\} |

is bounded. Intuitively, the blue area which is shown in Figure 1 will always be larger than the orange area. Because we have learned a GMM that

P_{f} \{ω_{i}\} = P_{g} \{ω_{i}\}

and our GMM model is constructed by evenly spreading out Gaussian components, at each

ω_{i}

generally will share similar geometrical structure as Figure 1.

In brief, giving some conditions, the blue area subtracts the orange area in Figure 1 is guarantee larger than

| P_{f} \{d_{i j}\} - P_{g} \{d_{i j}\} |

. We will provide the proof below.

Given condition:

Condition 1: $P_{f} \{ω_{i}\} = P_{g} \{ω_{i}\}$
Condition 2: $ω_{i}$ is small enough, target density is approximately monotone and linear within change wi $ω_{i} \in (w_{i}, v_{i}]$
Condition 3: GMM density within $ω_{i}$ double cross the target density. Two cross points are named a, b and $b > a$ .

Set the spilt length

d \leq \min \{a - w_{i}, v_{i} - b\}

. Given condition that GMM density double cross the target density. Since

g (x) \geq f (x)

, for all

x \in [μ_{i} - \frac{d}{2}, μ_{i} + \frac{d}{2}]

, and

\begin{matrix} \int_{μ_{i} - \frac{d}{2}}^{μ_{i} + \frac{d}{2}} g (x) d x \geq \int_{μ_{i} - \frac{d}{2}}^{μ_{i} + \frac{d}{2}} f (x) d x, \end{matrix}

we have

\begin{matrix} P_{g} \{μ_{i} \pm \frac{d}{2}\} \geq P_{f} \{d_{i j}\} \geq P_{g} \{d_{i j}\}, \end{matrix}

and

| P_{f} \{d_{i j}\} - P_{g} \{d_{i j}\} | \leq P_{g} \{μ_{i} \pm \frac{d}{2}\} - P_{f} \{d_{i j}\},

(2)

By condition 2, if target density is monotonically decreasing, i.e.

g (x) \leq f (x)

, for all

x \in [μ_{i} + \frac{r}{2} - d, μ_{i} + \frac{r}{2}]

and

\begin{matrix} \int_{μ_{i} + \frac{r}{2} - d}^{μ_{i} + \frac{r}{2}} g (x) d x \leq \int_{μ_{i} + \frac{r}{2} - d}^{μ_{i} + \frac{r}{2}} f (x) d x . \end{matrix}

Therefore,

\begin{matrix} P_{g} \{μ_{i} + \frac{r}{2} - d < x \leq μ_{i} + \frac{r}{2}\} \leq P_{f} \{d_{i j}\} \leq P_{g} \{d_{i j}\} . \end{matrix}

With Eq.(2), we have:

\begin{matrix} | P_{f} \{d_{i j}\} - P_{g} \{d_{i j}\} | \leq P_{g} \{μ_{i} \pm \frac{d}{2}\} - P_{g} \{μ_{i} + \frac{r}{2} - d < x \leq μ_{i} + \frac{r}{2}\} \end{matrix}

(3)

Similarly, if target density is monotonically increasing:

\begin{matrix} | P_{f} \{d_{i j}\} - P_{g} \{d_{i j}\} | \leq P_{g} \{μ_{i} \pm \frac{d}{2}\} - P_{g} (μ_{i} - \frac{r}{2} \leq x \leq μ_{i} - \frac{r}{2} + d) \end{matrix}

(4)

The benefit of these two properties of Eq.(3) and Eq.(4) is that even though we do not know what the target density is, this system still guarantees the difference between GMM and target density, which is bounded by Eq.(3) or Eq.(4). As long as we are able to find a good approximation that satisfies condition 1, we will be able to reach an approximation that is not worse than a fully discrete frequency distribution, while keeping the density continuous. This will lead us to a simple algorithm to optimise GMM which shown in the next subsection.

Conditions 1-3 also provide another practical benefit. As long as these 3 conditions are satisfied,

σ

of each Gaussian component becomes a universal smoothness parameter which controls the kurtosis of each normal component. A larger

σ

produces an overall smoother density.

σ

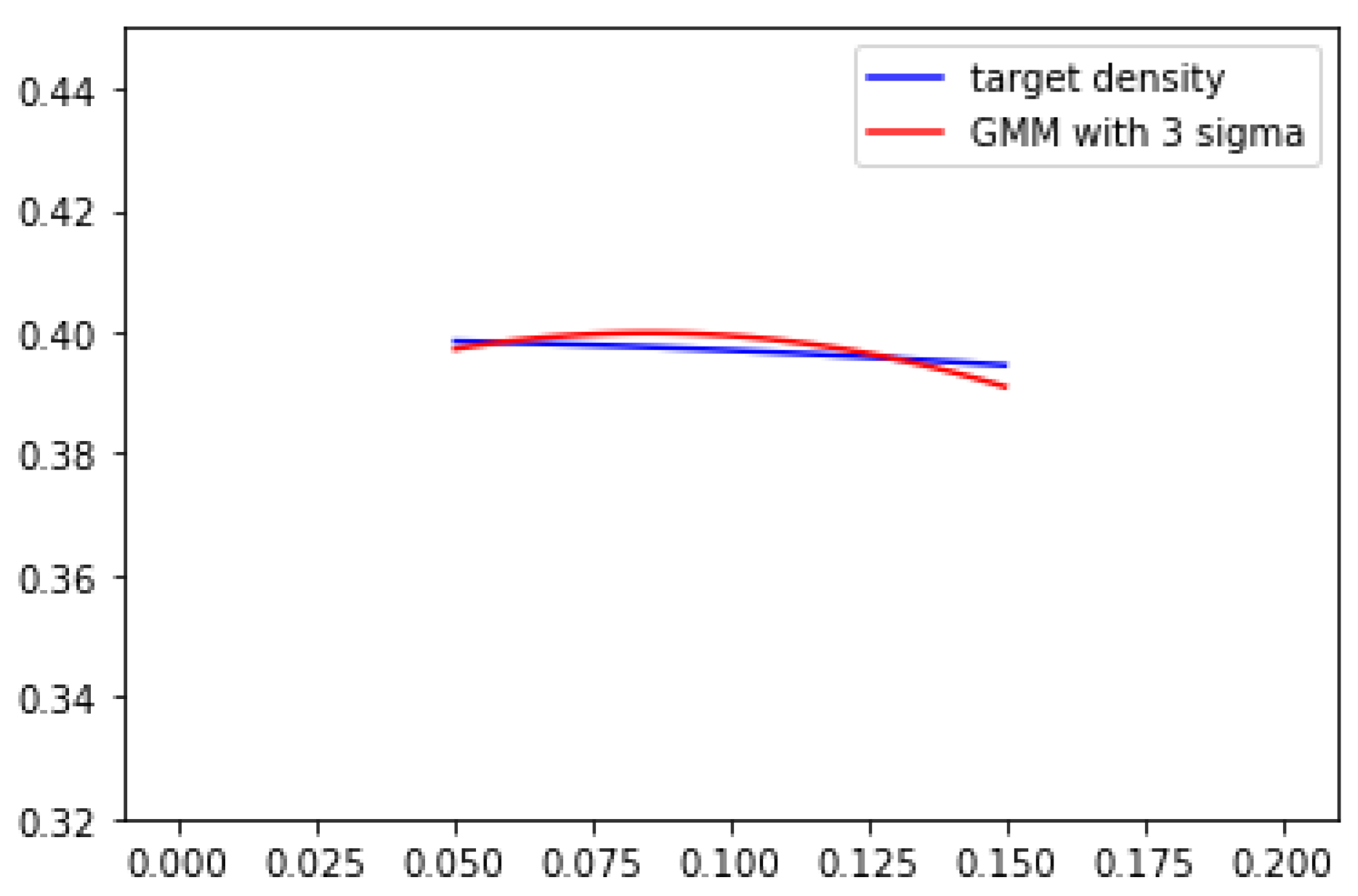
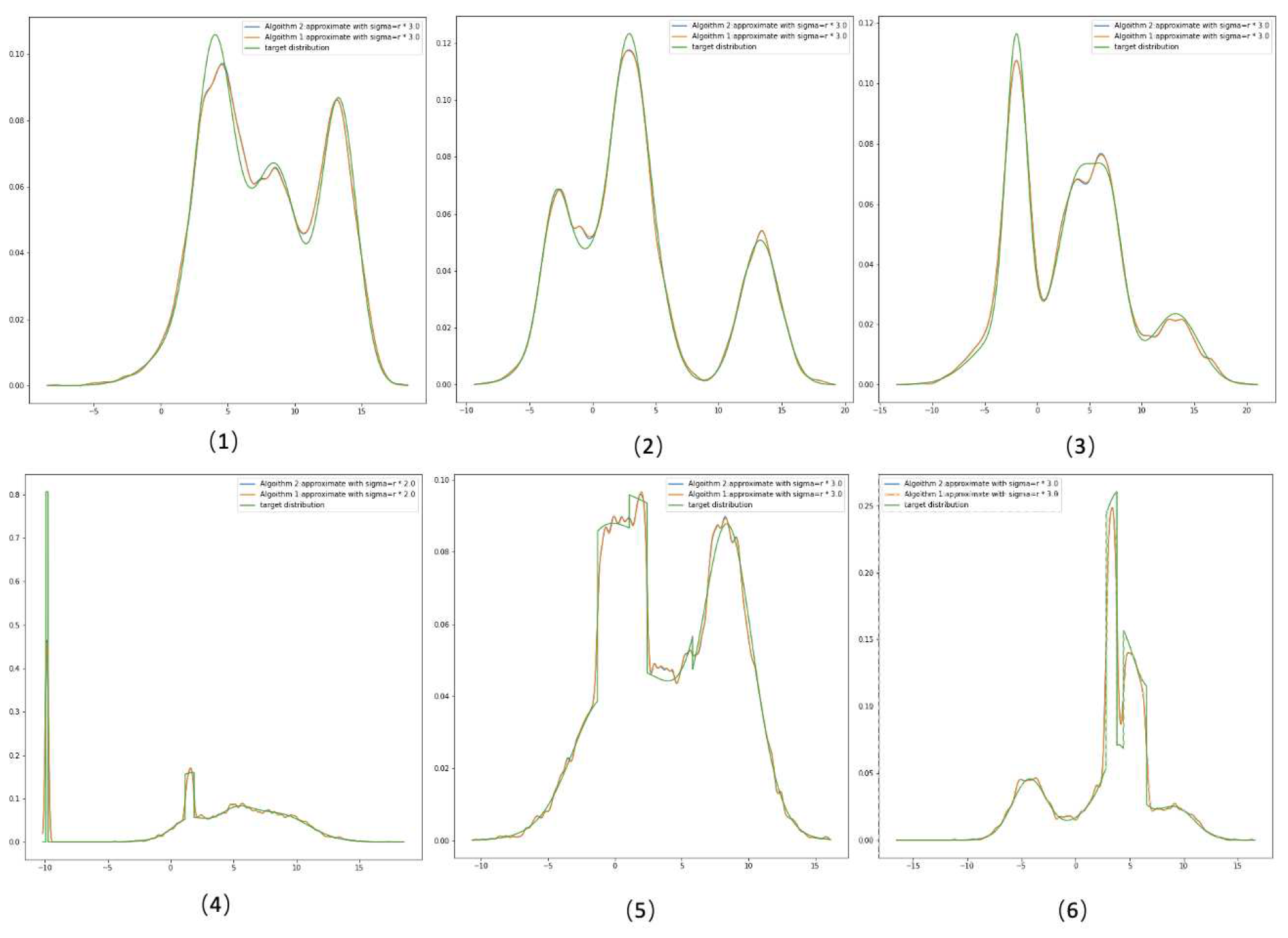
can be treated as a hyper-parameter which does not affect the learning process. GMM in Figure 1 uses

σ = 1 * r

. If we tune sigma larger, we will have the result shown in Figure 2, which is

σ = 3 * r

. The differences between target density and GMM are clearly smaller compared to 1 and 2. It also implies that if peaks of target density are not overly sharp(condituion 2), by stretching GMM components, resulting a better estimation of target density.

Here we can conclude that as long as the size of component distributions are large enough and satisfy given conditions 1-3, GMM can well approximate arbitrary distributions. The loss of density information between target density and GMM is controlled by Eq.(3) or Eq.(4).

2.4. Learning Algorithm

Most of the learning algorithms apply gradients iteratively to update target parameters until reaching an optimum position. There are no differences from ours. The key of the learning process is to find the right gradient for each parameter. In our model set up, this has become relatively simple. Begin with defining the loss function for the learning process.

L o s s (X) = \sum | P_{f} \{x_{j} \pm d\} - P_{g} \{x_{j} \pm d\} |

(5)

We want to find a set of parameters

π

which:

π = argmin \{L o s s (X)\} .

(6)

The Eq.(5) comes from Eq.(1). Because we do not have any access to the overall density information to calculate DIL, we change the region input

d_{j}

to the data points. From inequality in Eq.(3) and Eq.(4), instead of finding the precise gradient at each

x_{j}

, we apply Eq.(3) or Eq.(4) in Eq.(5):

\begin{matrix} L o s s (x_{j}) \leq \tilde{L o s s (x_{j})} = P_{g} (μ_{i} - \frac{d}{2} \leq x \leq μ_{i} + \frac{d}{2}) - P_{g} (μ_{i} - \frac{r}{2} \leq x \leq μ_{i} - \frac{r}{2} + d) \end{matrix}

\begin{matrix} L o s s (x_{j}) \leq \tilde{L o s s (x_{j})} = P_{g} (μ_{i} - \frac{d}{2} \leq x \leq μ_{i} + \frac{d}{2}) - P_{g} (μ_{i} + \frac{r}{2} - d \leq x \leq μ_{i} + \frac{r}{2}), \end{matrix}

where

μ_{i}

is the closest

μ

x_{j}

. Then,

\frac{\tilde{d L (k_{i}^{m i d}, k_{i}^{s i d e})}}{d π} = [\begin{matrix} \frac{d \tilde{L o s s (x_{j})}}{d π_{0}} \\ ⋮ \\ \frac{d \tilde{L o s s (x_{j})}}{d π_{n}} \end{matrix}] = [\begin{matrix} \tilde{P_{f_{0}}} (k_{i}^{m i d}) - \tilde{P_{f_{0}}} (k_{i}^{s i d e}) \\ ⋮ \\ \tilde{P_{f_{n}}} (k_{i}^{m i d}) - \tilde{P_{f_{n}}} (k_{i}^{s i d e}) \end{matrix}]

(7)

where

\tilde{P_{g_{i}}} (k_{i}) = \int_{k_{i}} ϕ_{i} (x) d x

ϕ_{i}

is the density of ith component distribution,

k_{i}^{m i d} \in (μ_{i} - d, μ_{i} + d]

, and

k_{i}^{s i d e} \in (μ_{i} + r, μ_{i} + r - d]

k_{i}^{s i d e} \in (μ_{i} - r, μ_{i} - r + d]

π^{+ 1} = π + \frac{\tilde{d L (k_{i}^{m i d}, k_{i}^{s i d e})}}{d π}

(8)

Eq.(7), the result is intuitively interpretative. For Gaussian distribution components where means are further away from data point

x_{j}

, gradient

\frac{d \tilde{L o s s (x_{j})}}{d π_{i}}

will be smaller and vice versa. For every data point, we perform Eq.(8) to update parameters.

Algorithm 1:

Algorithm 2:

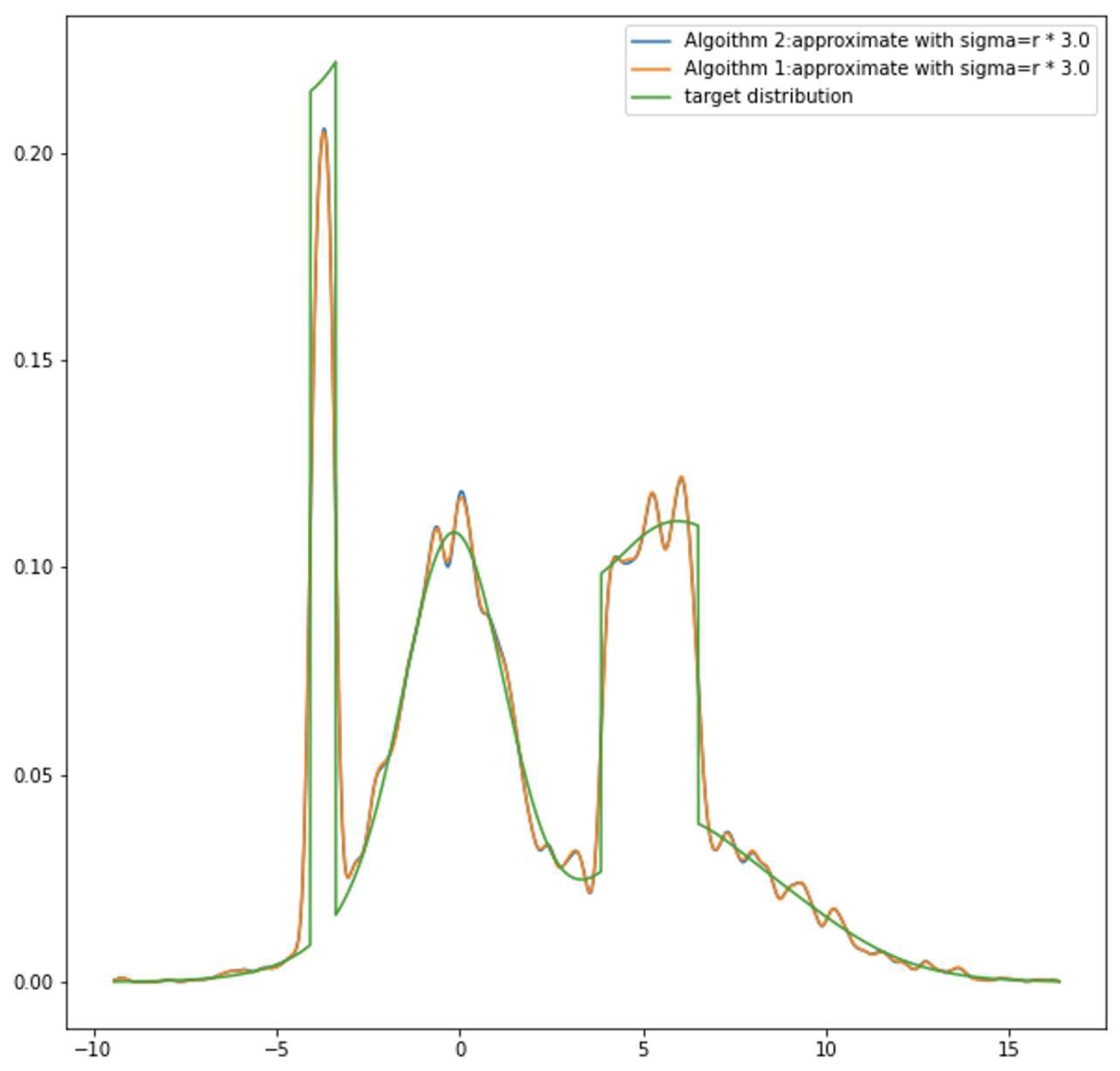
Based on Eq.(7), Here we developed two simple algorithms for learning GMM. Algorithm 1 computes the gradient following Eq.(7). Algorithm 2 is a simplified version where we only update the

π_{i}

which is the coefficient of

ϕ_{i}

that has

μ_{i}

closest to

x_{j}

. Algorithms’ performance comparison is shown in the next section. It is worth mentioning that

π

is initialized uniformly. After learning the whole dataset, the final step is re-normalization to ensure

\sum π_{i} = 1

3. Numerical Experiments

In this section, we demonstrate the correctness of our technique by approximating various probability densities. Two neural network applications are shown which incorporate GMM into neural network while applying our learning algorithm to learn feasible GMM. Eq.(9) provides a metric for measuring the accuracy of density estimation. It is an estimate for the DIL that is presented in Section 2.

\begin{matrix} L = & | P_{t r a g e t} \{x \leq μ_{1} - d\} - P_{g m m} \{x \leq μ_{1} - d\} | \\ + \sum_{i = 1}^{n} | P_{t r a g e t} \{μ_{i} \pm d\} - P_{g m m} \{μ_{i} \pm d\} | \\ + | P_{t r a g e t} \{x > μ_{n} + d\} - P_{g m m} \{x > μ_{n} + d\} | \end{matrix}

(9)

Measuring our estimation accuracy by Eq.(9) has a few advantages. It is firstly easy to calculate. Second, even without the target density in its current form, we can still calculate the loss using discrete statistical estimation. Its minimum and maximum values, which are

[0, 2]

, are also obvious. The evidence is provided below:

\begin{matrix} L & \leq | P_{t r a g e t} \{x \leq μ_{1} - d\} - 0 | + \sum_{i = 1}^{n} | P_{t r a g e t} \{μ_{i} \pm d\} - 0 | \\ + | P_{t r a g e t} \{x > μ_{n} + d\} - 0 | + | 0 - P_{g m m} \{x \leq μ_{1} - d\} | \\ + \sum_{i = 1}^{n} | 0 - P_{g m m} \{μ_{i} \pm d\} | + | 0 - P_{g m m} \{x > μ_{n} + d\} | \end{matrix}

That means

0 \leq L \leq 2

3.1. Random density approximation

In this subsection, we test the algorithm performance by learning randomly generated mixture distributions. Considering the conditions given by Section 2.4, mixture distributions with smooth forms are best for GMM to work with generally. In order to further investigate model efficacy, We also test our model with distributions that mix with non-smooth distributions; in our example, mixture with uniform, T and Gaussian distributions are employed to create these target mixed distributions.

The learning process is demonstrated using Figure 3, 4 and 5 for two randomly created examples. Target distribution 1, which is mixed with 8 normal distributions, is shown as the upper subplot in Figure 3. Target distribution 2 is mixed with normal distributions, T distributions, and uniform distributions in the lower subplot of Figure 3.

Figure 4 shows our initial GMM before learning. Target density and learned GMM are compared in 5 and Figure 6, respectively.

Using GMM with 200 components, the target distribution is learned. As a training dataset, we select 5000 data points from each target distribution. The target distribution 1 refers to those situations where GMM can perform best. Geometrically speaking, while target distributions are mixed with components which share a bell shape like structure, using GMM to approximate is an appropriate choice instinctively. But in situations like target distribution 2, while we add uniform distribution in the component distribution set, it becomes difficult for GMM to work with unless we have more components. Figure 4 provides a explanation. We can see that our initial GMM’s density is remarkably similar to a uniform distribution before training. Because there are more components, GMM may learn more structure. Deep cuts and straight lines, for example. This shows that if we want to simulate arbitrary densities that are not bound by multimodal, flat peaks, deep cuts, and all conceivable variations, higher order mixture components are required for GMM. When using the traditional EM algorithm and assuming that there are 200 Gaussian components, the parameters that we must learn for a GMM are

3 x 200

. By fixing

m u

and

s i g m a

as bases and smoothness, as we suggested in this study, the number of remaining parameters that must be learned is constrained to 200.

Figure 5 and Figure 6 demonstrate how well the suggested approach approximates target density. Comparing the two results, target density 1, which mixes with bell shape like distributions, works better than target distribution 2, which mixes with uniform distributions and others. Overall though, despite the fact that Figure 6’s output contains a lot of unwelcome sags and crests, GMM approximation still succeeds in capturing those crucial aspects of target density. In Figure 5 and Figure 6, demonstrate how two distinct algorithms discussed in Section 2.5 performed. On the graph, there are three curves. Green represents the target density, blue represents the taught GMM density from algorithm 2, and orange represents the learnt GMM density from method 1. The orange curve and the blue curve nearly cross each other. Algorithm differences are hardly discernible from one another.

Table 1 and Table 2 present average losses(L) in Eq.(9) over 20 experiments. In Table 1, the target distribution is randomly generated Gaussian mixture distributions. Some approximation examples are shown in Figure 7 subplots (1)-(3). Table 2 presents the average L by approximating the mixture distribution of which components contain Normal, T and Uniform distributions. Some examples are shown in Figure 7 subplots (4)-(6).

According to the tables, it is generally preferable to use GMM to approximate target distributions with normal components as opposed to mixing target distributions with distributions of different types. They also make the intriguing discovery that changing

σ

will alter accuracy across the board. Target distributions combined with normal distributions perform better when

σ

is increased from 1*r to 3*r. But when the target density gets more complex, a sigma with 2*r works the best. Distributions with extreme features need for a

σ

that is neither too large nor too small, as seen in comparison with subplots 1-3 and subplots 4-6 in Figure. 7. More expressiveness but less overall smoothness result as

σ

gets smaller. In cases where distribution density are not smooth, O ur experiments demonstrate that the proposed method is still able to capture all of the major characteristics of the target distributions and yield approximations that are generally good in practice. Table 1 and Table 2 imply that the error we make is less than 0.095.

0 \leq L \leq

is a definite upper and lower constraint for the metric function L. This indicates that the margin of error for our experiments is less than

5 %

. The performance of the overall model should be influenced by a link between the number of mixture components and the amount of the data. We have conducted tests to show the relationship between how data size impacts the accuracy under various amounts of mixed components, yet we have not yet found a suitable solution to this problem.

We conduct 30 experiments for each GMM with component sizes ranging from 10 to 1000, as shown in Table 3. We use method 2 and the learning process with

σ = 3 * r

. Target distributions are mixed distributions that were produced at random, identical to the experiments in Table 1 and Table 2. It demonstrates that with components under 200, an increase in data size does not improve performance when compared to the tests shown in Table 1. Information loss L for data sizes of 20000 and 50000 is 0.0778 and 0.065 for GMM with 100 components, which is worse than GMM with 200 components learning under 5000 data points. The performance of components with 200 components consistently improves from 0.04447 to 0.025 when data size is increased. After a certain point, increasing the size of components under the same data size may not always result in a better output. Component sizes 500 and 1000 perform no better than 200 with data size 20,000. Yet, a GMM with 500 components beats all other GMMs with a data size of 50,000. These discoveries reflect our understanding of GMM distribution decomposition intuitively. A specific number of components are required to obtain an appropriate level of detail representation of a density when we deconstruct a distribution. More data points and more components are required to discover finer details. In our investigation, the GMM with 200 components showed sufficient robustness for usage in practical applications. Model accuracy was able to rise even when the data amount was increased from 5000 to 50000.

3.2. Neural network application

We demonstrate a few neural network applications using GMMs and our GMMs learning techniques in this section. The first one involves creating handwritten numbers with an autoencoder while learning the output distribution of the encoder using GMM. In the second, known as style transfer, gram matrix distribution is learned using GMM.

3.2.1. Mnist Data set of handwritten digits generation

We replicate the numerical experiment from [11] in this experiment. In the Kolouri et al. experiment[11], they showed how to use Sliced Wasserstein Distance to learn an embedding layer (latent variables) through GMM. In our method, we train the GMM using suggested techniques. The proposed structure of the neural network model by [11] is exactly what is used. It was created by combining an autoencoder generator and a straightforward convolution neural network with classification output as the discriminator. [24,25,26,27,28] The whole process is illustrated in Figure 8.

We present our findings in Figure 9 and compare them with the learning strategy suggested at [11]. We have our results, which are randomly picked from our learnt GMM distributions, on the left side of Figure 9. Comparing with [11], our finding at the number 8 is more clear than SW-GMM and EM-GMM. Likewise, at number 9, our generation are less confused with number 4. Our results reveal more variety at number seven. Our learning method recognizes various varieties of the number 7. In addition, our learnt GMM captures some rounded shapes and writing habits that place dashes in the middle when writing a number 7. The majority of the random samples in our results don’t have a lot of unidentifiable generations, unlike the red-highlighted EM-GMM and SW-GMM results in Figure 9.

It is worth mentioning that, in our training process, in order to gain faster convergence, we slightly amended the loss function of GAN. The loss function for GAN is Eq.(10).

J^{(G)} = - α \frac{1}{2} E_{z} l o g (1 - D (G (z))) + {‖ x - G (z) ‖}^{2}

(10)

where

J^{(G)}

is the loss of a generator,

α

is a constant to adjust the level of discriminator loss,

\frac{1}{2} E_{z} l o g (1 - D (G (z)))

is the discriminator loss same as [29] and x is the target image and

G (z)

is output image generated by generator.

Following up the notation given on [29], for the generator loss, we multiply

α

to the cross-entropy loss to regulate how much we want to listen to the discriminator. Adding in Mean Square Loss guides the generator to generate images close to the dataset.

Another intriguing experiment is that we attempted random mixing of a few of GMM data through different classes. The examples in Figure 10 include 4 examples. Despite the fact that the number of those created images is getting intractable, our generated images continue to retain input category attributes. For instance, 0 and 4 produced an image that resembled 9. The image created by GMM samples randomly merged from classes 0 and 3 is shown in the example in the upper right.

The diffusion model employs stochastic processes to introduce noise and produce accurate data mapping. When similar images are diverted from an image by noise, a one-to-one path is created for the neural network to work with. [30,31,32]. In our work, using GMM as an intermediary for latent variables results in a comparable outcome. The fact that each class’s variables are well-segmented enables us to produce random combinations of features. As illustrated in Figure 10, it is simple to use and has more control over generated images. Language image models may find it advantageous to represent words as a GMM distribution. The values of latent variables are sampled at random, so the resulting images are less likely to become repetitive.

3.2.2. Style Transfer

Here we introduce a modified version of style transfer[23] algorithm where we turns gram matrix into GMM. The foundation of style transfer is the gram matrix. It shows the degree of correlation between each extracted feature as calculated by a neural network. In our trials, we applied trained VGG19 [33] for feature extraction in accordance with the original study. Variation is one of the causes for incorporating GMM into the algorithm. A specific gram matrix determines a specific algorithmic result. To provide diversity to the algorithm, we could change the learning rate or the weights assigned to style features and content features, although doing so aggressively could result in a chaotic result. Moreover, the traditional method struggles to manage the degree of feature mixing between two styles when we attempt to combine multiple styles at once. Turning a gram matrix into a distribution and doing random sampling is one method of solving these issues. The feature combination is randomized using a sample from a gram matrix. It is similar to what we show in the MNIST handwritten digits generation studies where blending characteristics stochastically can create new digits.

Figure 11 shows the process of how a gram matrix is produced. Passing an image into VGG19 produces output features from each layer. Take 5 output features from each block and perform Eq.(11) to calculate the gram matrix. For convenience, we call it VGG19 feature extraction module.

G_{i j}^{l} = \sum_{k} F_{i k}^{l} F_{j k}^{l},

(11)

We demonstrate how to put up a gram matrix data set as well as the entire algorithmic process in Figure 12. In order to get a data set of gram matrices for each layer, we first randomly crop two styles of photos and then send them to the VGG19 feature extraction module independently. Second, using Algorithm 2, we train GMM using a dataset of gram matrices for each layer. Third, sample the gram matrix and carry out the same optimization procedure as in the orginal work[23]. The probability of the features in the gram matrix is determined by the dataset. For instance, the gram matrix dataset comprises 1/4 of the data points from style 1 and 3/4 of the data points from style 2, if we arbitrarily crop 25 photos from style 1 and 75 images from style 2. The sampled gram matrix will probably comprise

25 %

values from style 1 and

75 %

values from style 2 as we sample the gram matrix distributions. Our method is illustrated graphically in Figure 13. We make use of two well-known Vincent Van Gogh works. Both "The Starry Night" and "Sunflowers" are used as the target and style images, respectively. The result image displays an increasing number of features from style image 2 as we steadily increase the size of style 2 photos in the data set. We discover that each output image shares the same style but has attributes that differ substantially from one to the next by learning several random sampling gram matrices. Nearly like altering position and angle of each stroke. When all output photographs are combined, the result will look like the painting’s features are flowing. Here is a youtube¹ video showcase the results. As shown in Figure 13, the feature blending levels between two styles are

0 %

10 %

20 %

, and

80 %

. Each mixing level generates 10 photos at once. Using this method, we can investigate the properties that neural networks can extract and how they impact the result.

4. Conclusions and Future Work

In this paper, we demonstrate that GMMs with large-sized components can approximate arbitrary distribution by using the Fourier decomposition concept. We offer two straightforward, easy-to-use GMM learning methods. Numerical tests are conducted to demonstrate the efficacy of our approach. Also, we showed how to use GMMs with natural networks. Our algorithm learns latent space for Autoencoder handwritten digits generation and gram matrix for style transfer. The neural network is able to produce meaningful images by merging characteristics from several categories by randomly mixing the sampled latent variables across multiple categories. We use GMM in the transfer gram matrix in the same way that we handle latent variables in the autoencoder.

In the future, we will work on a more explicit theoretical demonstration of the claim that the GMM can approximately decompose arbitrary distributions. We will continue to seek for ways to construct more sophisticated applications because our experiment demonstrates that GMM enables us to have greater control and variation over neural networks.

Notes

¹ https://youtu.be/yP22_ycAqMA

References

Murphy, K.P. Machine learning: A probabilistic perspective (adaptive computation and machine learning series), 2018.
Gal, Y. What my deep model doesn’t know. Personal blog post 2015. [Google Scholar]
Kendall, A.; Gal, Y. What uncertainties do we need in bayesian deep learning for computer vision? Advances in neural information processing systems 2017, 30. [Google Scholar]
Der Kiureghian, A.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Structural safety 2009, 31, 105–112. [Google Scholar] [CrossRef]
McLachlan, G.J.; Rathnayake, S. On the number of components in a Gaussian mixture model. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 2014, 4, 341–355. [Google Scholar] [CrossRef]
Li, J.; Barron, A. Mixture density estimation. Advances in neural information processing systems 1999, 12. [Google Scholar]
Genovese, C.R.; Wasserman, L. Rates of convergence for the Gaussian mixture sieve. The Annals of Statistics 2000, 28, 1105–1127. [Google Scholar] [CrossRef]
Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 1977, 39, 1–22. [Google Scholar] [CrossRef]
Verbeek, J.J.; Vlassis, N.; Kröse, B. Efficient greedy learning of Gaussian mixture models. Neural computation 2003, 15, 469–485. [Google Scholar] [CrossRef]
Du, J.; Hu, Y.; Jiang, H. Boosted mixture learning of Gaussian mixture hidden Markov models based on maximum likelihood for speech recognition. IEEE transactions on audio, speech, and language processing 2011, 19, 2091–2100. [Google Scholar] [CrossRef]
Kolouri, S.; Rohde, G.K.; Hoffmann, H. Sliced wasserstein distance for learning gaussian mixture models. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 3427–3436.
Srebro, N. Are there local maxima in the infinite-sample likelihood of Gaussian mixture estimation? International Conference on Computational Learning Theory. Springer, 2007, pp. 628–629.
Améndola, C.; Drton, M.; Sturmfels, B. Maximum likelihood estimates for gaussian mixtures are transcendental. International Conference on Mathematical Aspects of Computer and Information Sciences. Springer, 2015, pp. 579–590.
Jin, C.; Zhang, Y.; Balakrishnan, S.; Wainwright, M.J.; Jordan, M.I. Local maxima in the likelihood of gaussian mixture models: Structural results and algorithmic consequences. Advances in neural information processing systems 2016, 29. [Google Scholar]
Chen, Y.; Georgiou, T.T.; Tannenbaum, A. Optimal transport for Gaussian mixture models. IEEE Access 2018, 7, 6269–6278. [Google Scholar] [CrossRef]
Li, P.; Wang, Q.; Zhang, L. A novel earth mover’s distance methodology for image matching with gaussian mixture models. Proceedings of the IEEE International Conference on Computer Vision, 2013, pp. 1689–1696.
Beecks, C.; Ivanescu, A.M.; Kirchhoff, S.; Seidl, T. Modeling image similarity by gaussian mixture models and the signature quadratic form distance. 2011 International Conference on Computer Vision. IEEE, 2011, pp. 1754–1761.
Jian, B.; Vemuri, B.C. Robust point set registration using gaussian mixture models. IEEE transactions on pattern analysis and machine intelligence 2010, 33, 1633–1645. [Google Scholar] [CrossRef]
Yu, G.; Sapiro, G.; Mallat, S. Solving inverse problems with piecewise linear estimators: From Gaussian mixture models to structured sparsity. IEEE Transactions on Image Processing 2011, 21, 2481–2499. [Google Scholar]
Campbell, W.M.; Sturim, D.E.; Reynolds, D.A. Support vector machines using GMM supervectors for speaker verification. IEEE signal processing letters 2006, 13, 308–311. [Google Scholar] [CrossRef]
Ballard, D.H. Modular learning in neural networks. Aaai 1987, 647, 279–284. [Google Scholar]
LeCun, Y. PhD thesis: Modeles connexionnistes de l’apprentissage (connectionist learning models); Universite P. et M. Curie (Paris 6), 1987.
Gatys, L.A.; Ecker, A.S.; Bethge, M. A neural algorithm of artistic style. arXiv 2015, arXiv:1508.06576 2015. [Google Scholar] [CrossRef]
Hinton, G.E.; Zemel, R. Autoencoders, minimum description length and Helmholtz free energy. Advances in neural information processing systems 1993, 6. [Google Scholar]
Schwenk, H.; Bengio, Y. Training methods for adaptive boosting of neural networks. Advances in neural information processing systems 1997, 10. [Google Scholar]
LeCun, Y. The MNIST database of handwritten digits. http://yann. lecun. com/exdb/mnist/, 1998. [Google Scholar]
Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Communications of the ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
Li, J.; Monroe, W.; Shi, T.; Jean, S.; Ritter, A.; Jurafsky, D. Adversarial learning for neural dialogue generation. arXiv 2017, arXiv:1701.06547 2017. [Google Scholar]
Goodfellow, I. Nips 2016 tutorial: Generative adversarial networks. arXiv 2016, arXiv:1701.00160 2016. [Google Scholar]
Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. International Conference on Machine Learning. PMLR, 2015, pp. 2256–2265.
Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems 2020, 33, 6840–6851. [Google Scholar]
Song, Y.; Ermon, S. Generative modeling by estimating gradients of the data distribution. Advances in Neural Information Processing Systems 2019, 32. [Google Scholar]
Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556 2014. [Google Scholar]

Figure 1. Example of fitted GMM and target density in region

ω_{i}

Figure 1. Example of fitted GMM and target density in region

ω_{i}

Figure 2. Example of GMM and target density in region

ω_{i}

with larger

σ

Figure 2. Example of GMM and target density in region

ω_{i}

with larger

σ

Figure 3. Target Distributions.

Figure 4. Initialize GMM.

Figure 5. Trained GMM vs Target Distribution 1.

Figure 6. Trained GMM vs Target Distribution 2.

Figure 7. Other trained examples.

Figure 8. Model Structure.

Figure 9. Result comparison.

Figure 10. Random Mixing.

Figure 11. Result comparison.

Figure 12. Result comparison.

Figure 13. Random Mixing.

Table 1. Average Loss of 20 Experiments With 8 random Gaussian Components. Data size: 5000 data points.

Average Loss of 20 Experiments
Algorithm 1
$σ = 1 * r$	$σ = 2 * r$	$σ = 3 * r$
$L =$ 0.07099	$L =$ 0.05091	$L =$ 0.044296
Algorithm 2
$σ = 1 * r$	$σ = 2 * r$	$σ = 3 * r$
$L =$ 0.06866	$L =$ 0.05085	$L =$ 0.04447

Table 2. Average Loss of 20 Experiments With 8 Non-Gaussian random Components. Data size: 5000 data points.

Average Loss of 20 Experiments
Algorithm 1
$σ = 1 * r$	$σ = 2 * r$	$σ = 3 * r$
$L =$ 0.08912	$L =$ 0.08738	$L =$ 0.09432
Algorithm 2
$σ = 1 * r$	$σ = 2 * r$	$σ = 3 * r$
$L =$ 0.08678	$L =$ 0.08749	$L =$ 0.09446

Table 3. Average Loss of 25 Experiments With different numbers of components compare with data size 20000 data points and 50000 data points.

Average Loss of 30 Experiments with Data size 20000
Numbers of Components
10	30	50	100	200	500	1000
$L = 0.710$	$L = 0.336$	$L = 0.200$	$L = 0.0778$	$L = 0.0295$	$L = 0.0326$	$L = 0.0378$
Average Loss of 30 Experiments with Data size 50000
Numbers of Components
10	30	50	100	200	500	1000
$L = 0.715$	$L = 0.364$	$L = 0.210$	$L = 0.065$	$L = 0.025$	$L = 0.0203$	$L = 0.0289$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Efficient Gaussian Mixture Model and Its Application to Neural Network

Abstract

1. Introduction

2. Decompose Arbitrary Density by GMM

2.1. General concept of GMM decomposition

2.2. Approximate arbitrary density by GMM

2.3. Density information loss

2.4. Learning Algorithm

3. Numerical Experiments

3.1. Random density approximation

3.2. Neural network application

3.2.1. Mnist Data set of handwritten digits generation

3.2.2. Style Transfer

4. Conclusions and Future Work

Notes

References

MDPI Initiatives

Important Links

Subscribe