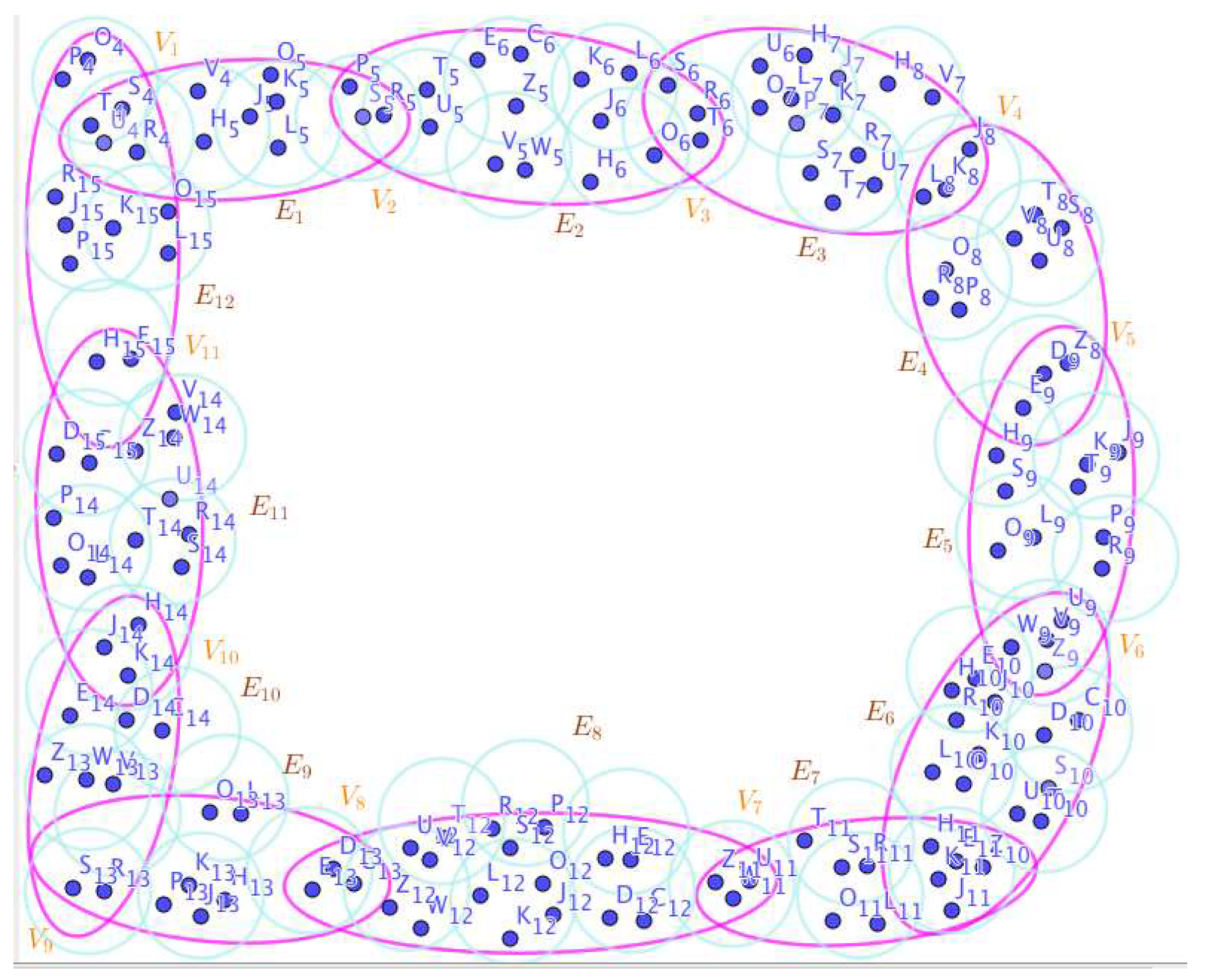
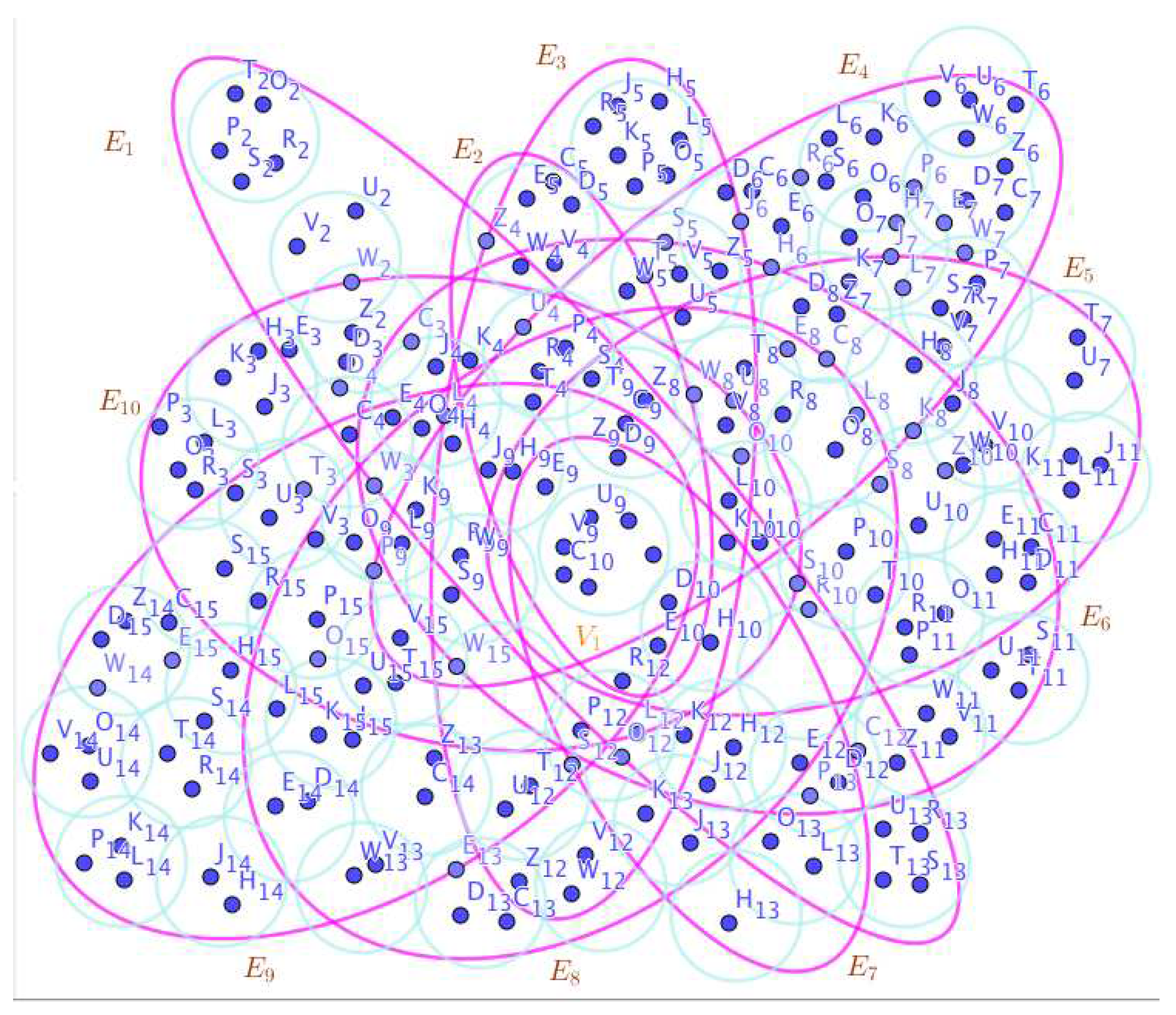
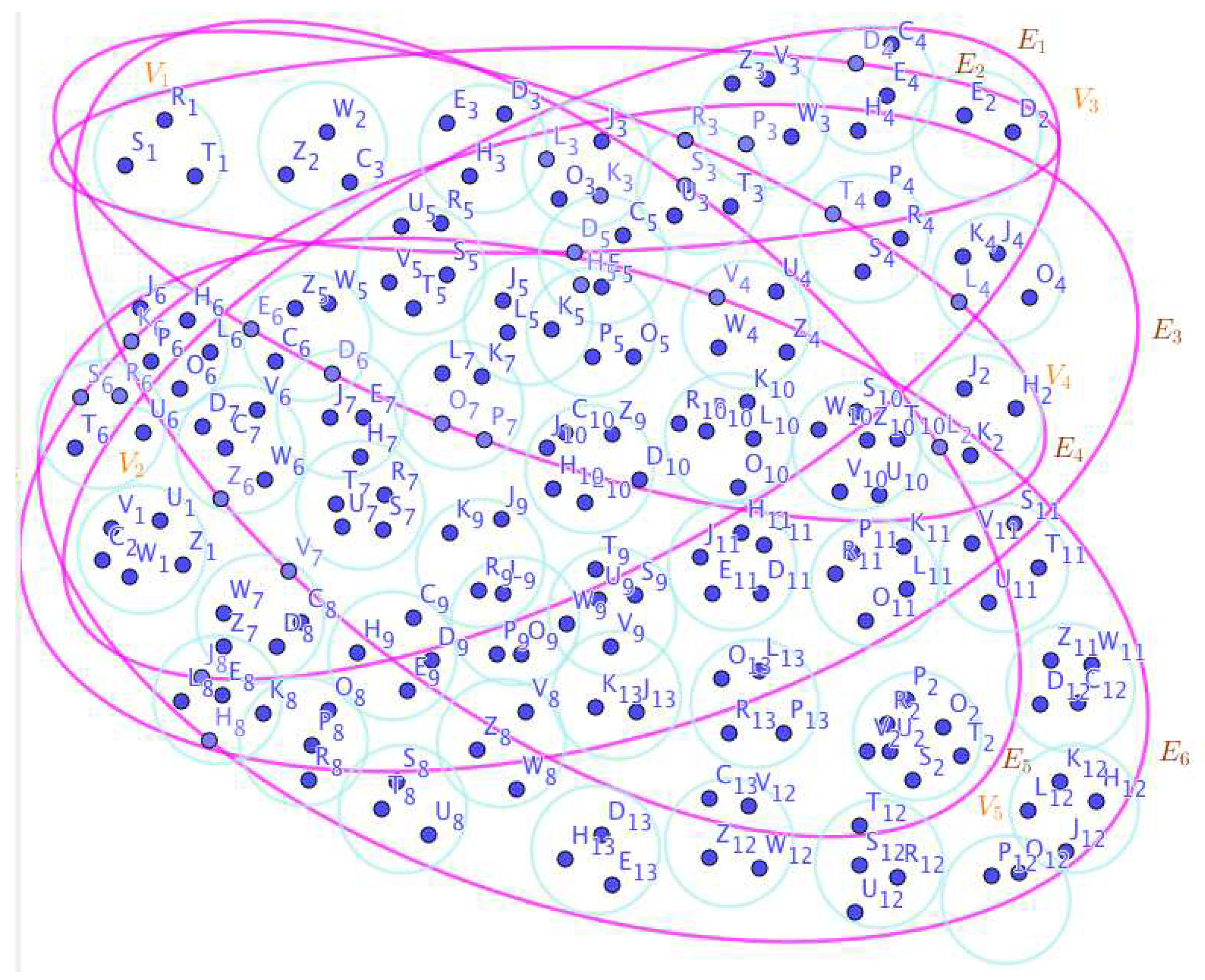
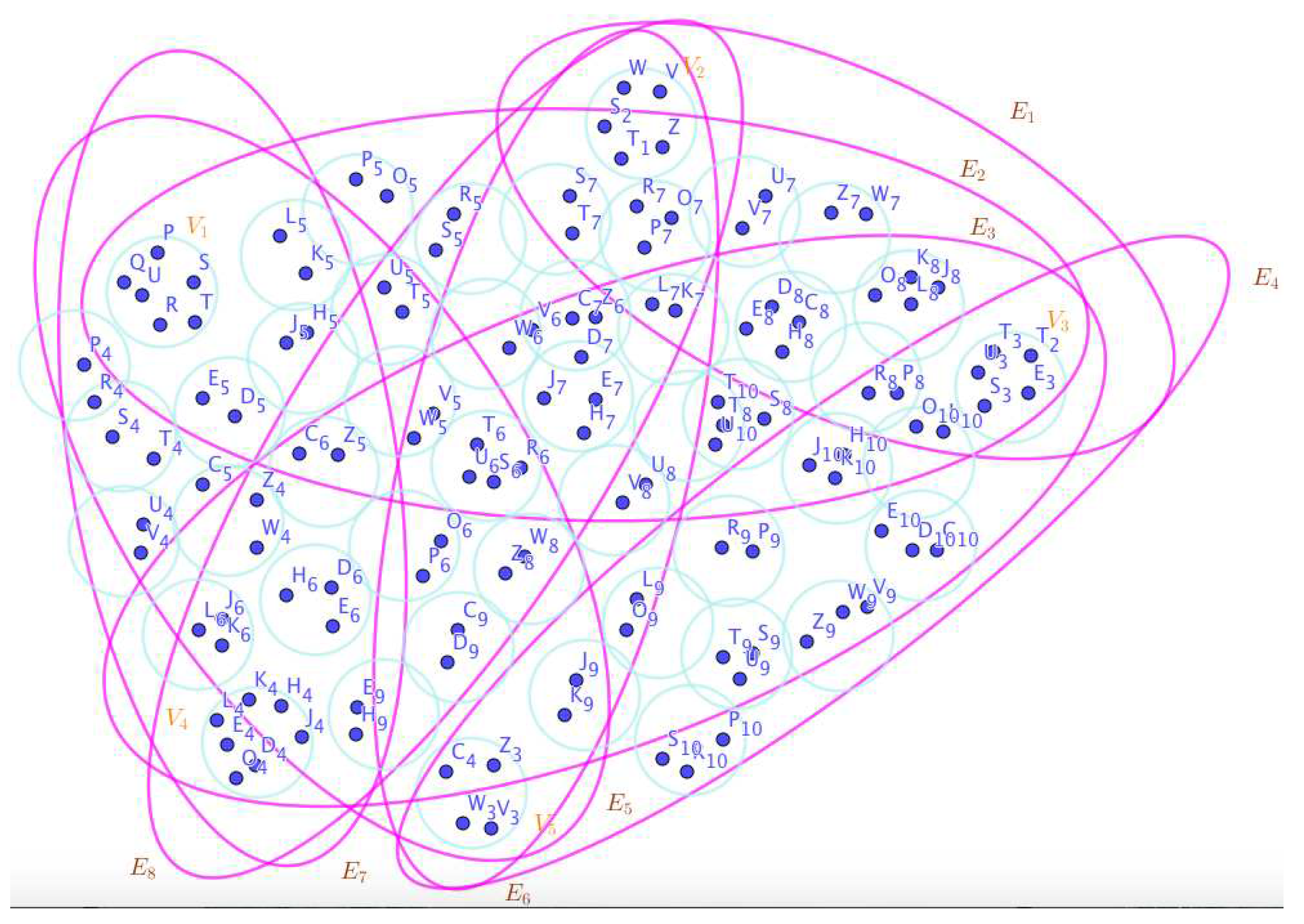
-
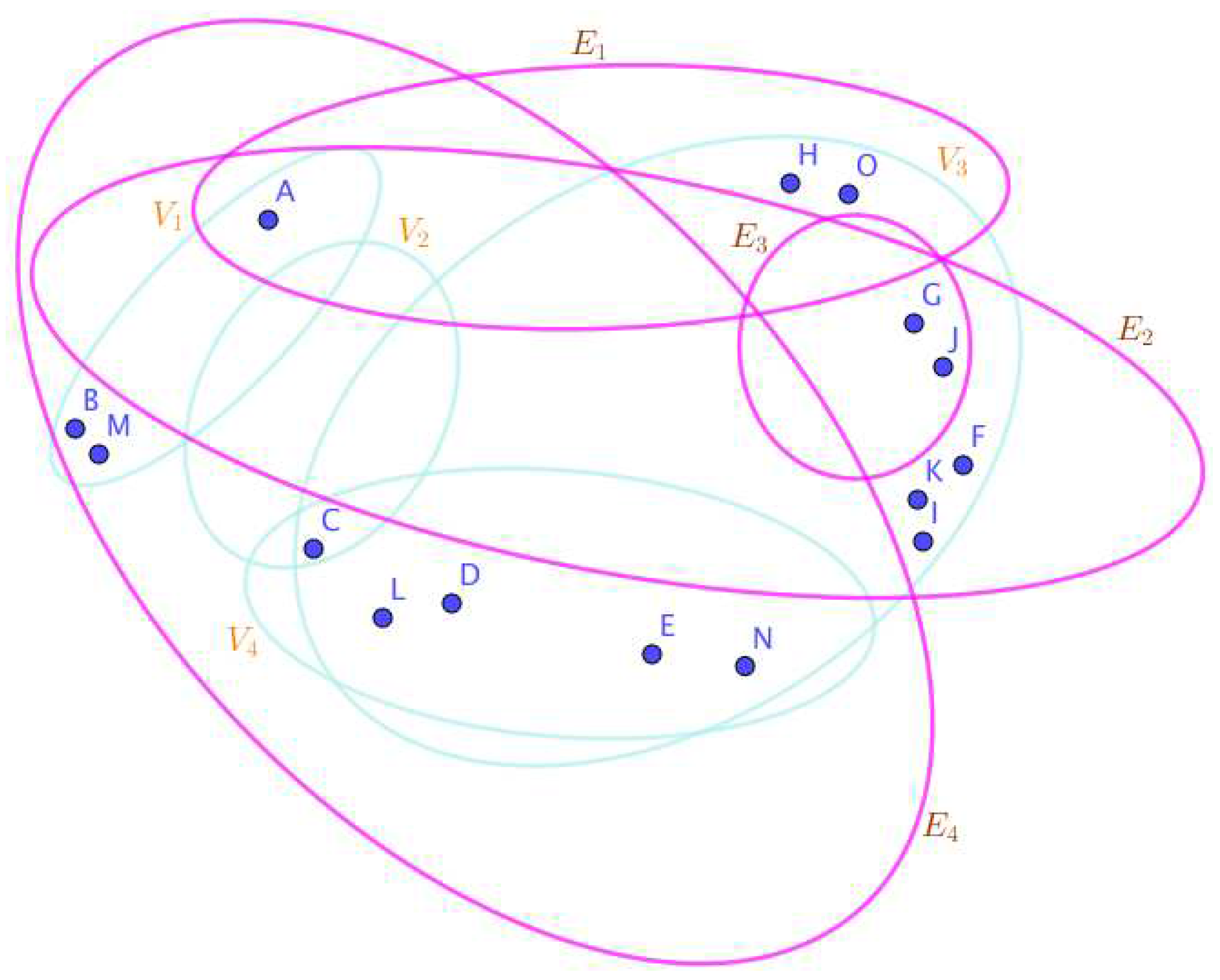
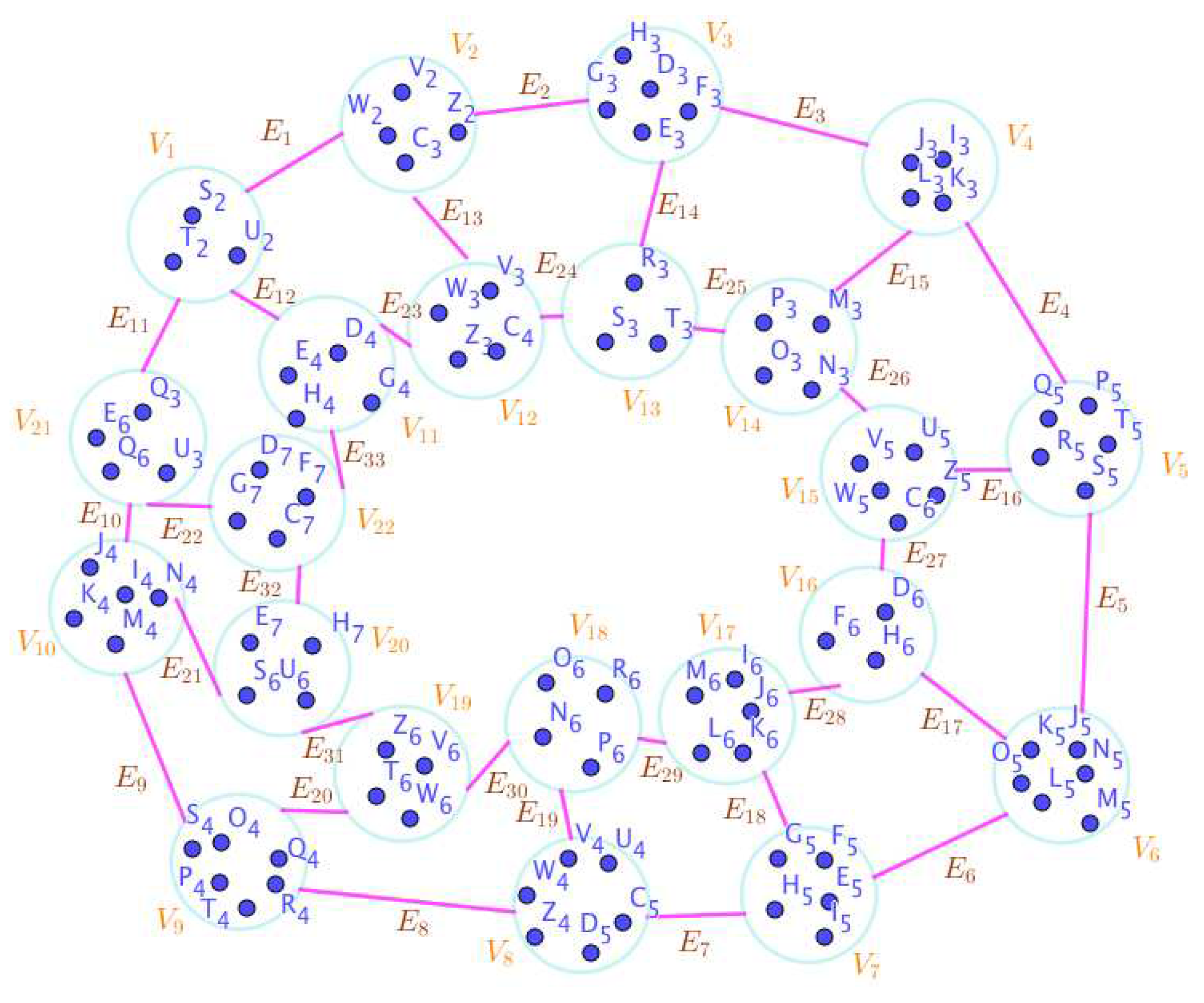
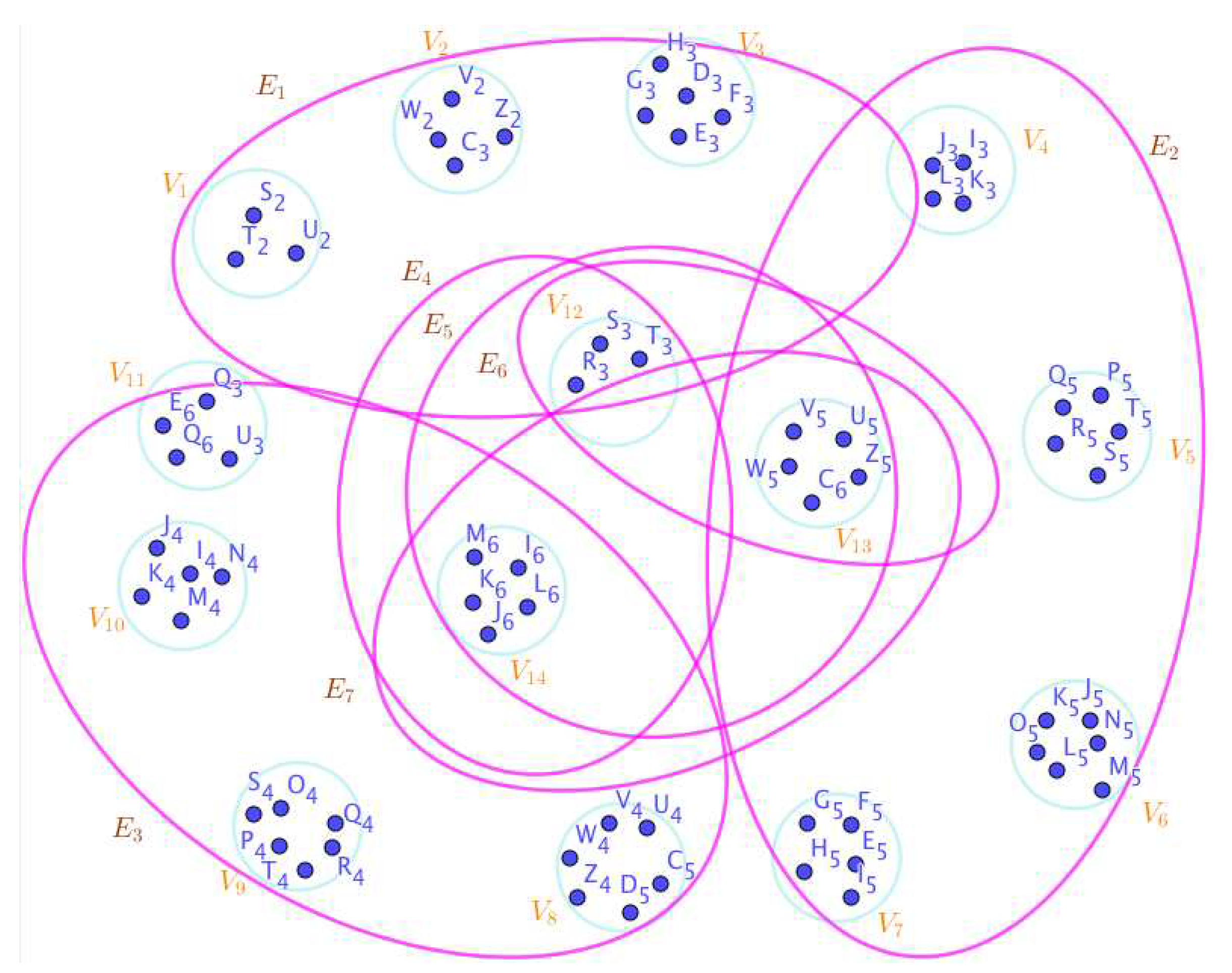
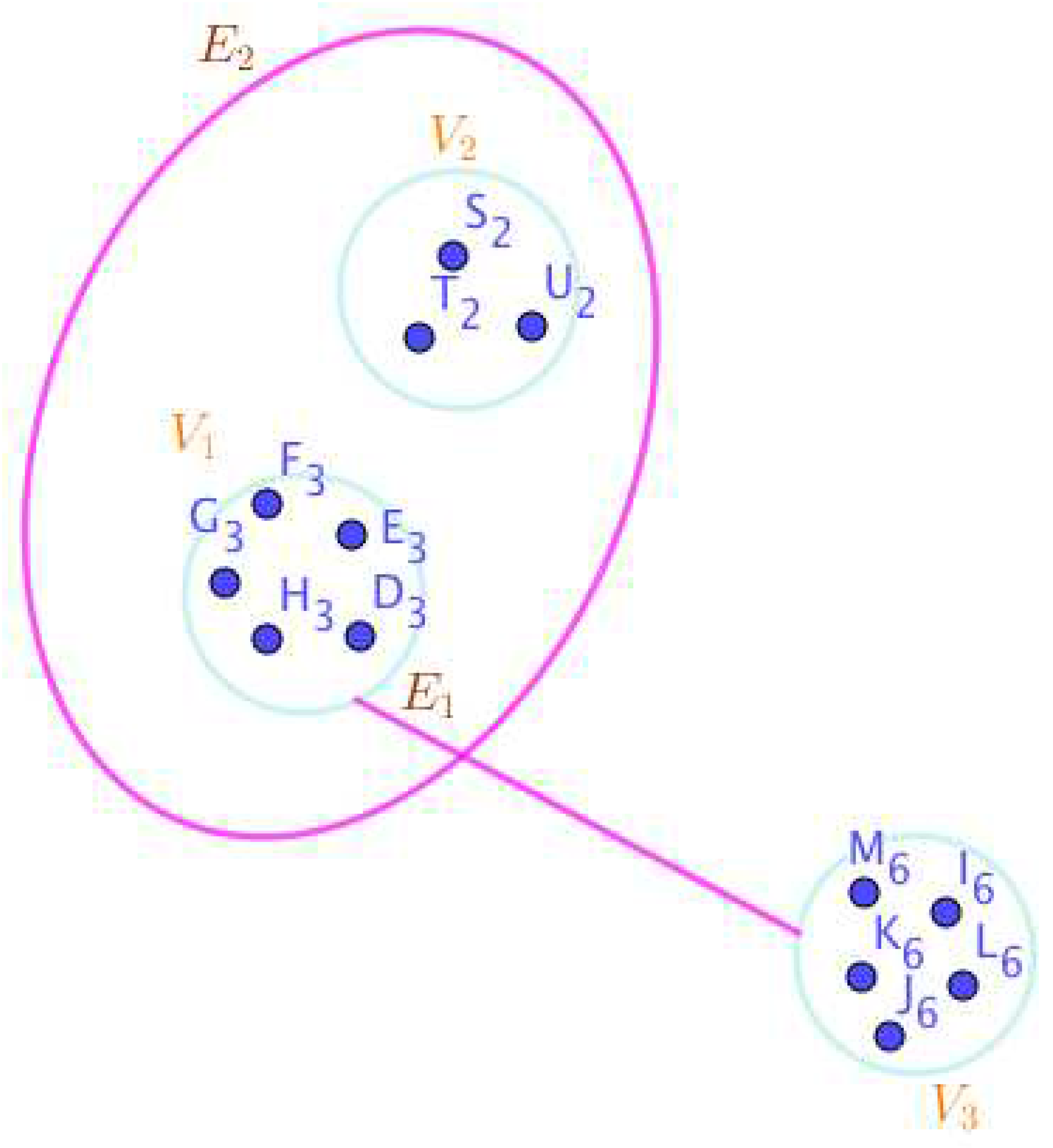
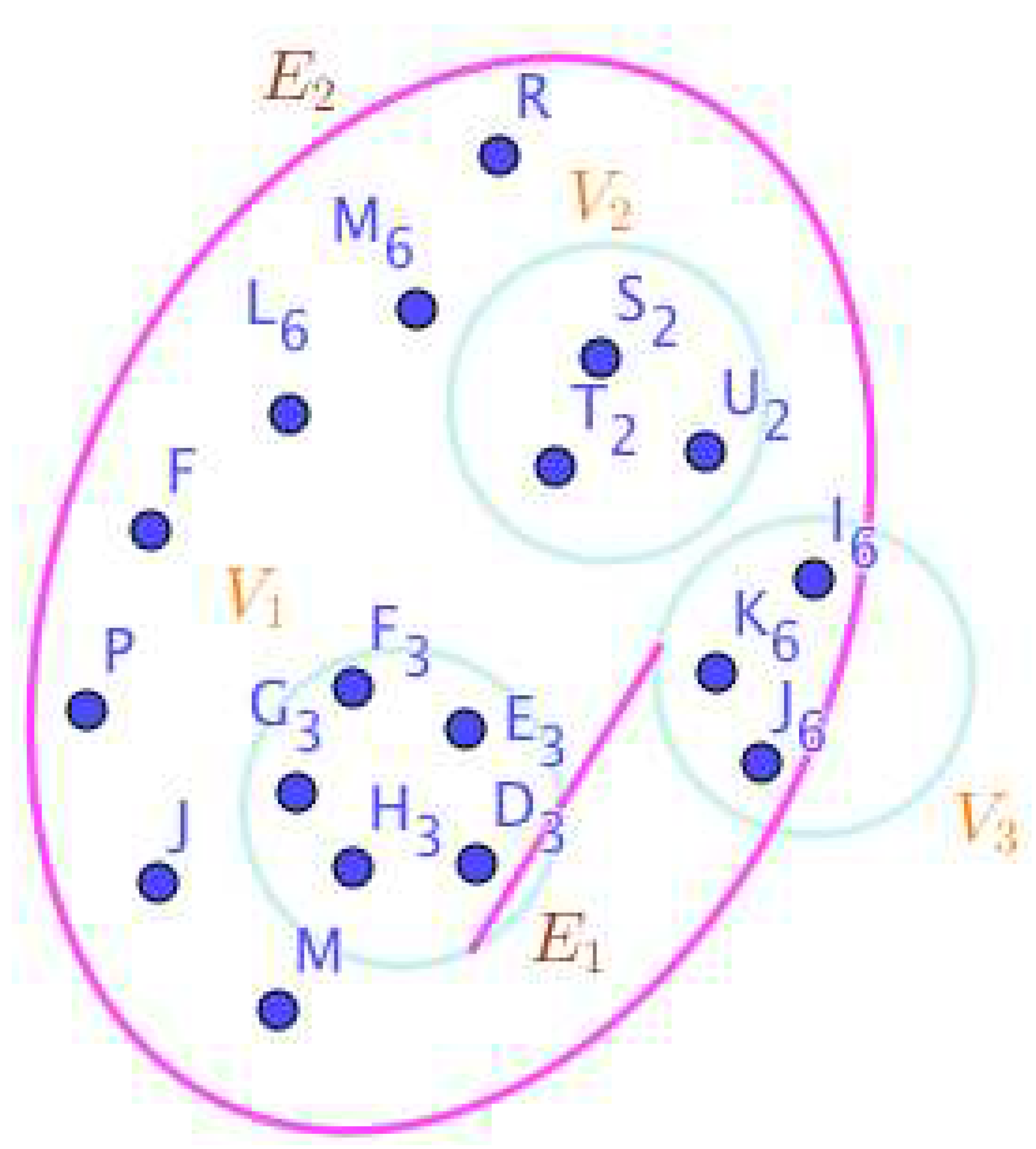
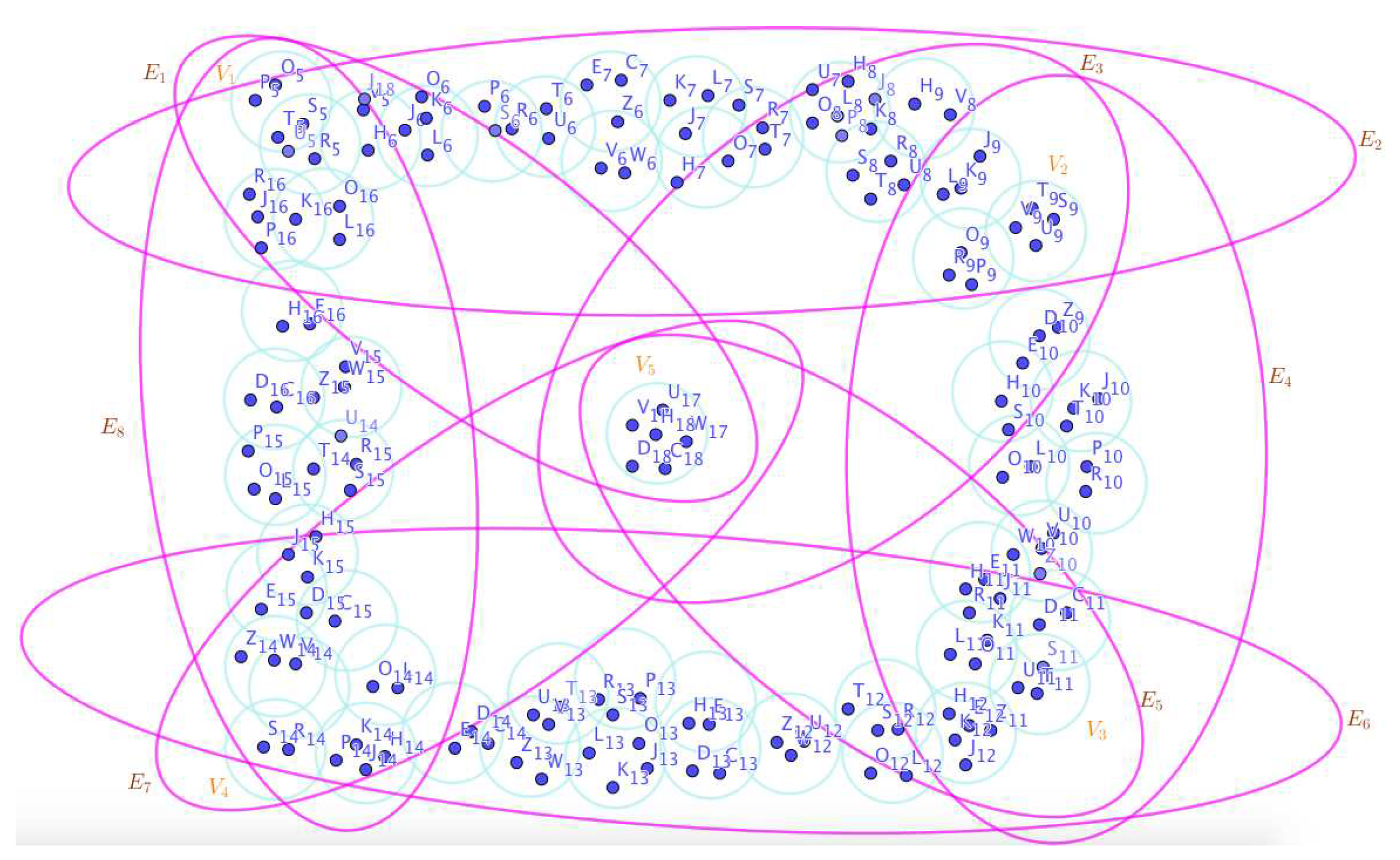
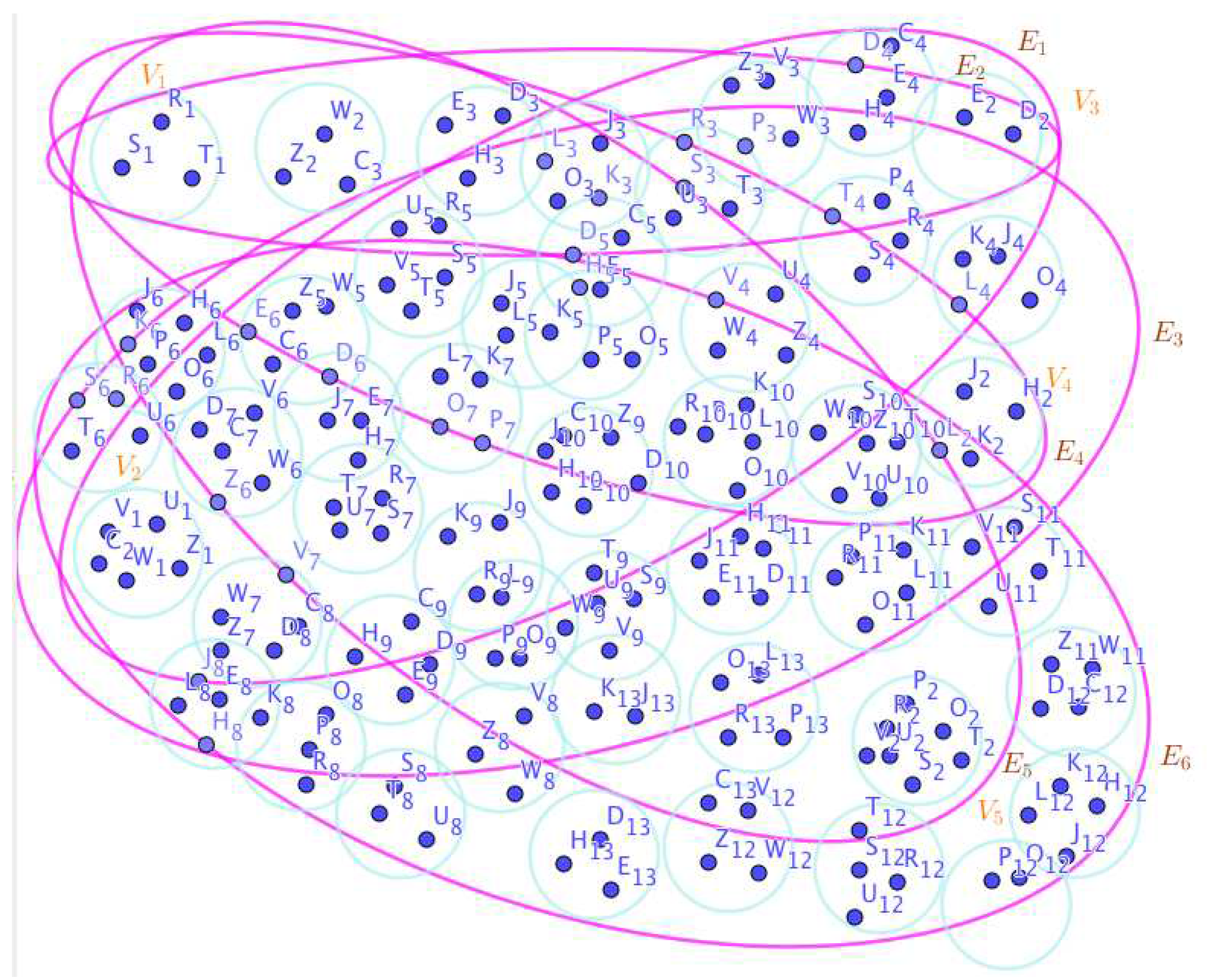
On the Figure 1, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. and are some empty SuperHyperEdges but is a loop SuperHyperEdge and is an SuperHyperEdge. Thus in the terms of SuperHyperNeighbor, there’s only one SuperHyperEdge, namely, The SuperHyperVertex, is isolated means that there’s no SuperHyperEdge has it as an endpoint. Thus SuperHyperVertex, is contained in every given neutrosophic SuperHyperForcing. All the following SuperHyperSets of SuperHyperVertices are the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing.
The SuperHyperSet of the SuperHyperVertices, is a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex but it isn’t a neutrosophic SuperHyperForcing. Since it doesn’t have the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only one SuperHyperVertex outside the intended SuperHyperSet. Thus the obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
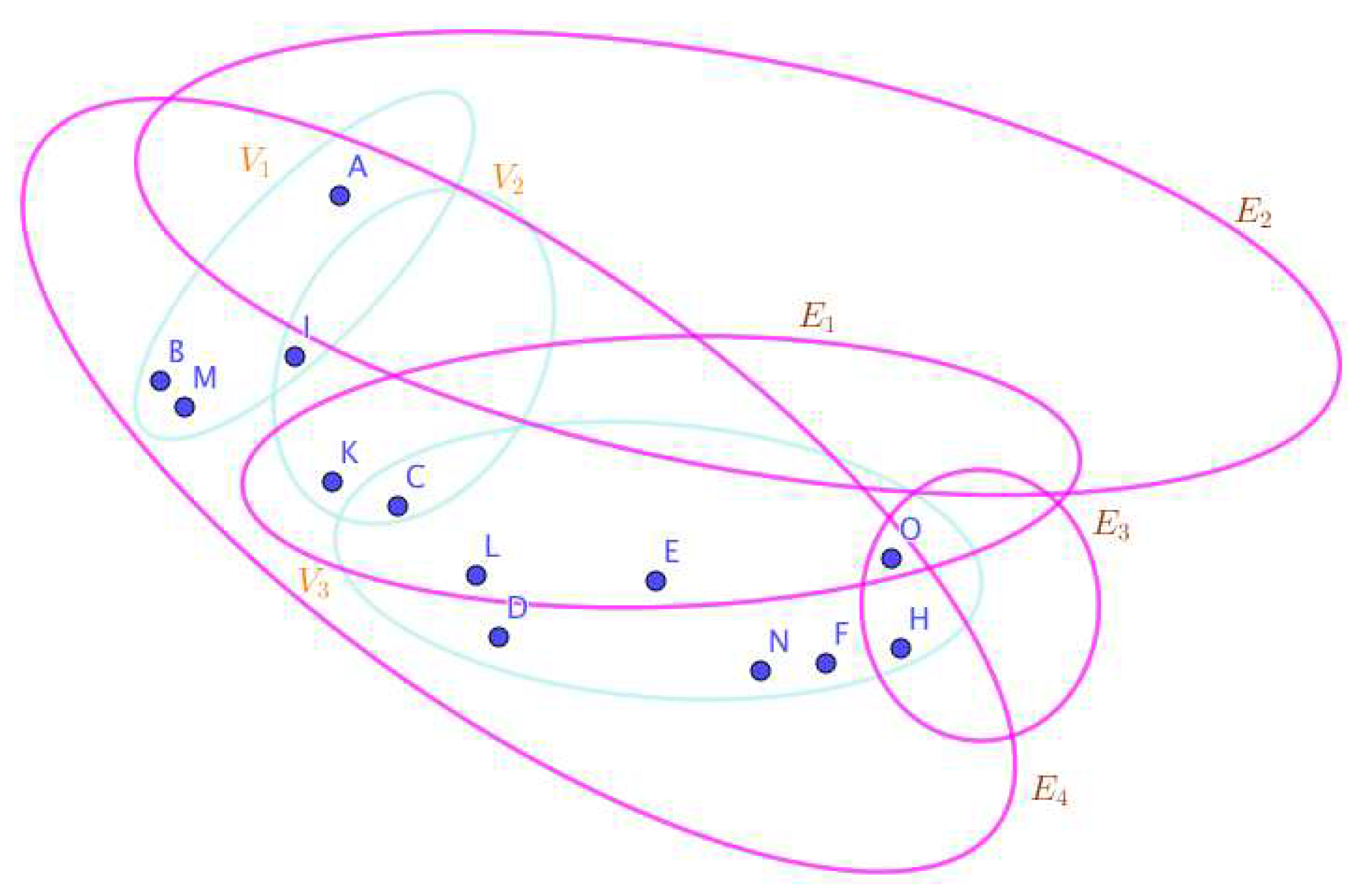
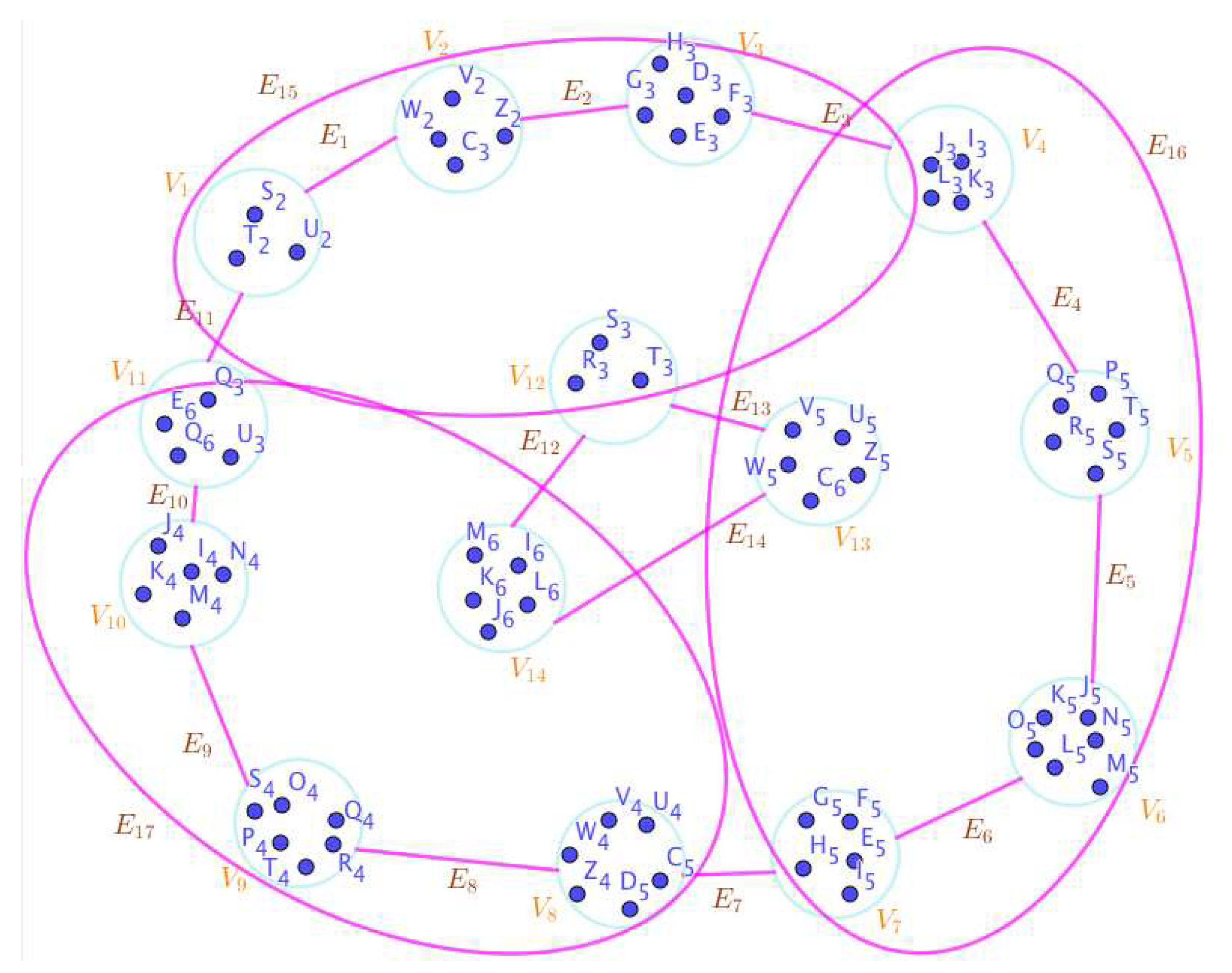
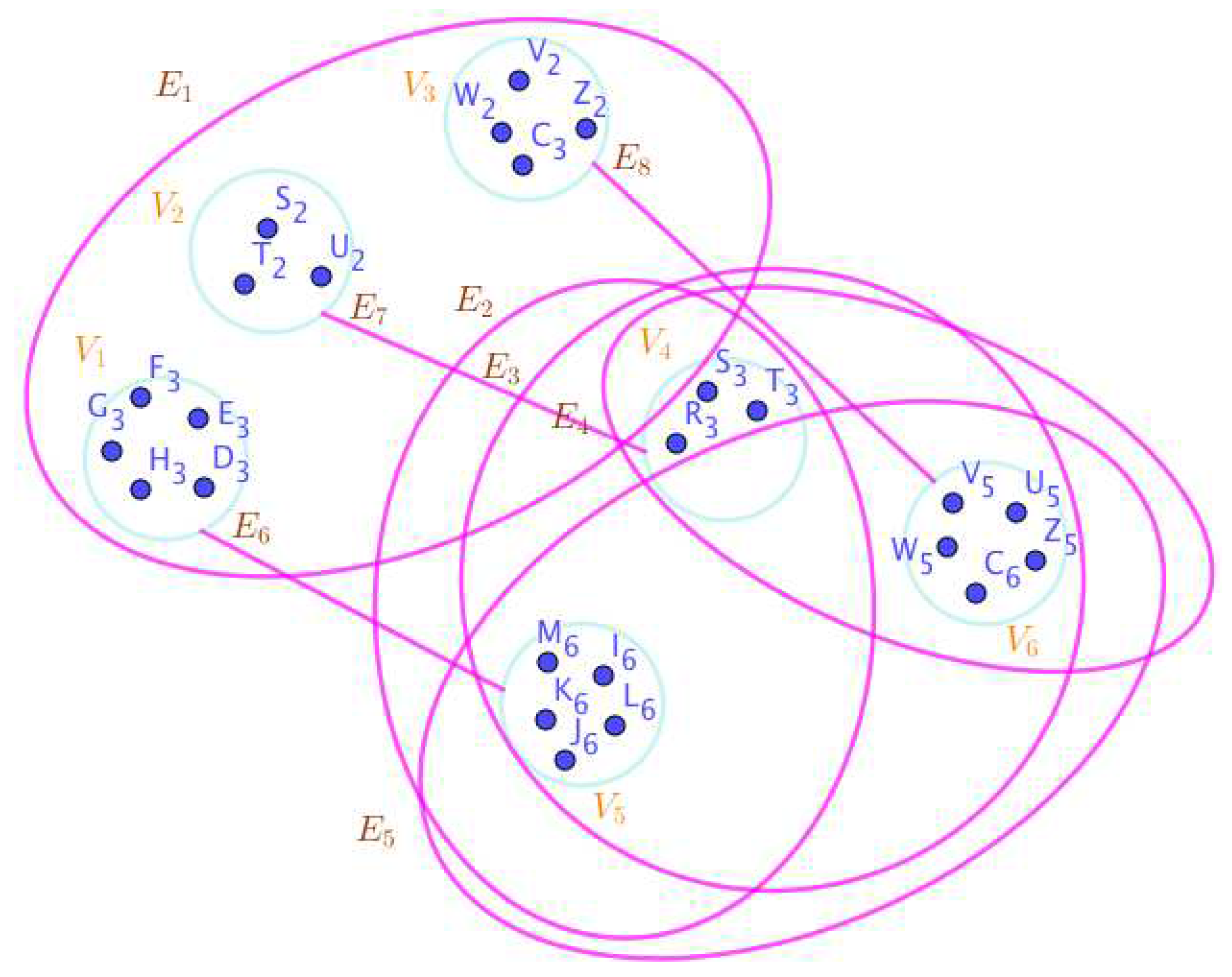
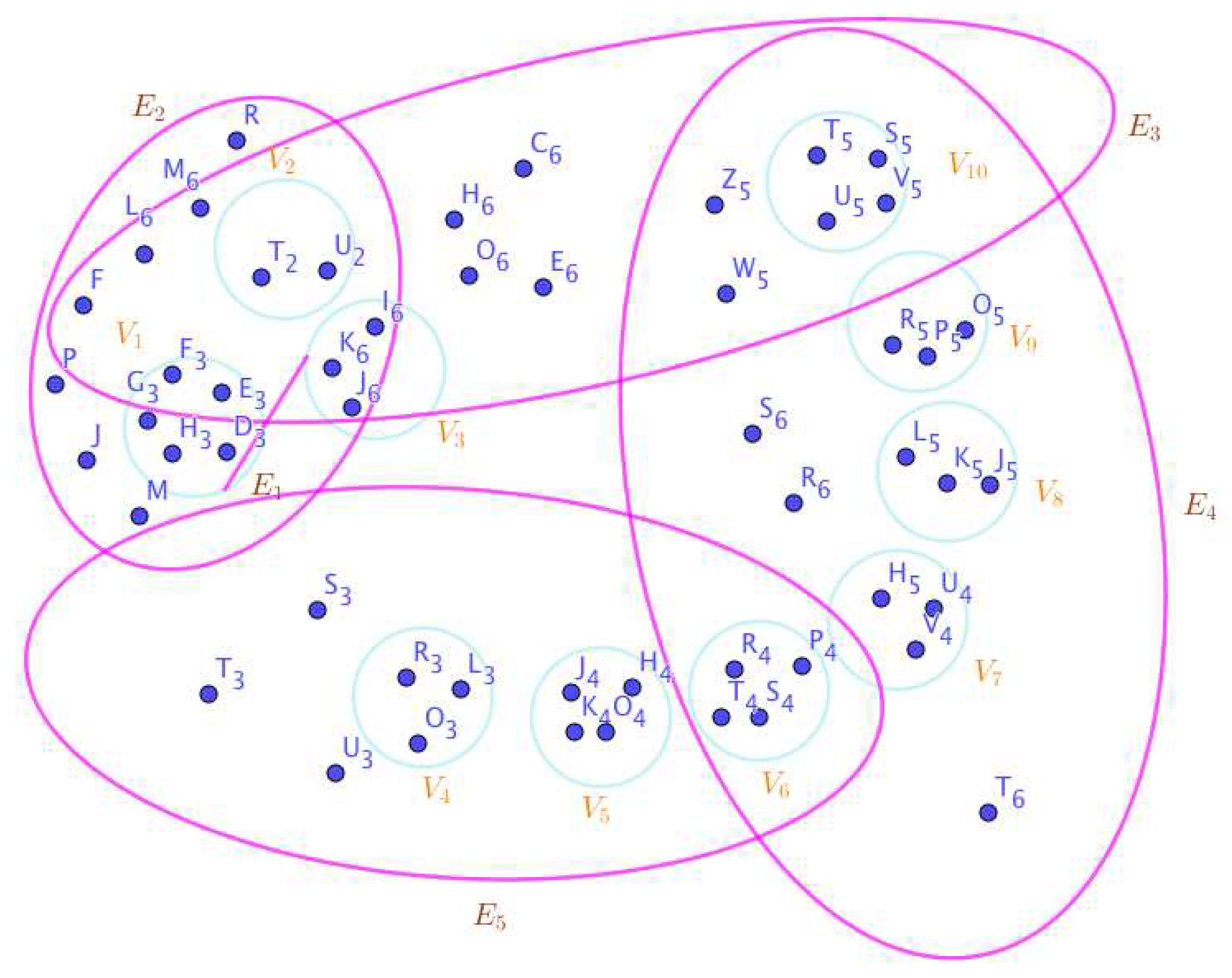
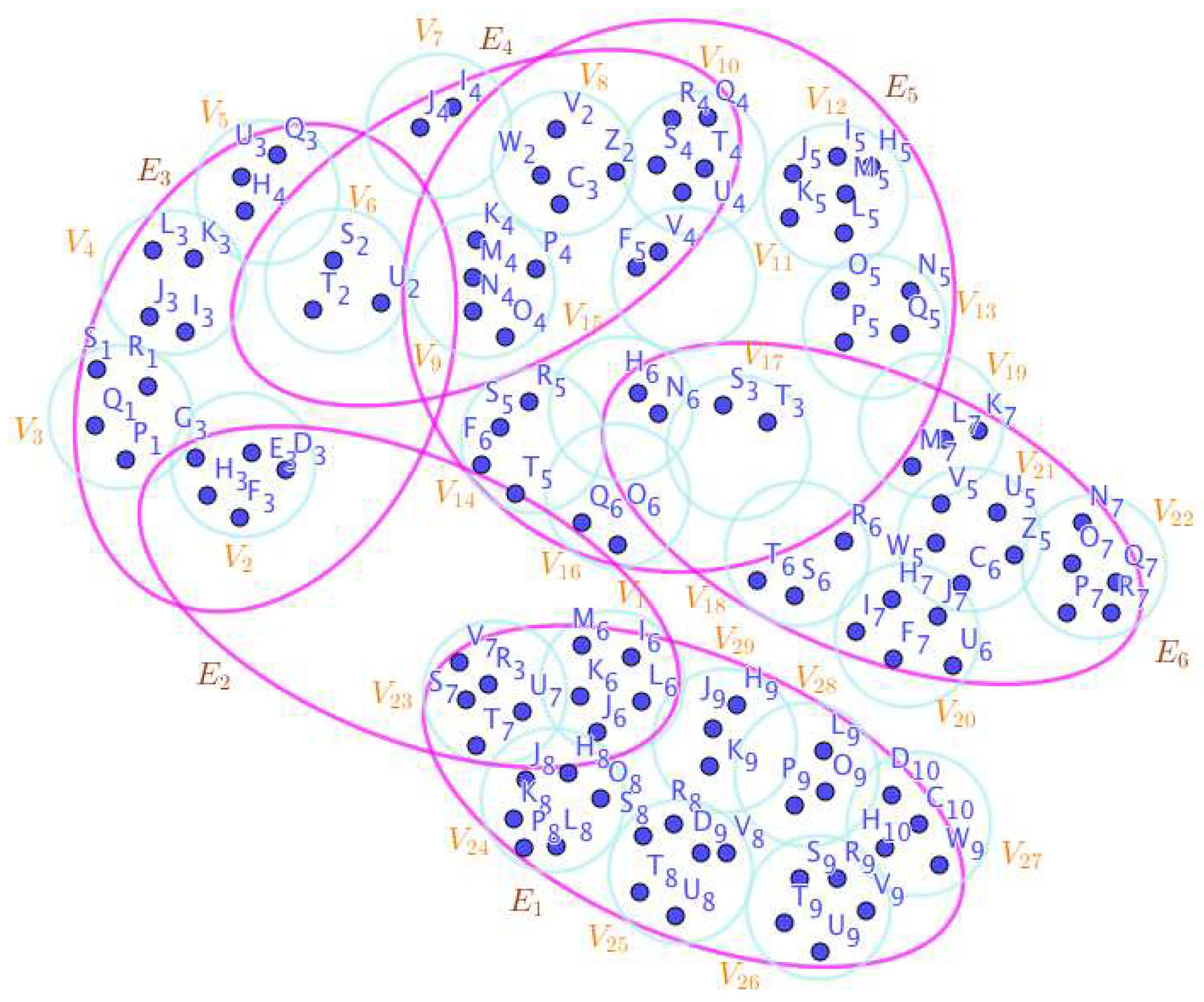
On the Figure 2, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. and are some empty SuperHyperEdges but is an SuperHyperEdge. Thus in the terms of SuperHyperNeighbor, there’s only one SuperHyperEdge, namely, The SuperHyperVertex, is isolated means that there’s no SuperHyperEdge has it as an endpoint. Thus SuperHyperVertex, is contained in every given neutrosophic SuperHyperForcing. All the following SuperHyperSets of SuperHyperVertices are the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing.
The SuperHyperSet of the SuperHyperVertices, is a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex but it isn’t a neutrosophic SuperHyperForcing. Since it doesn’t have the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only one SuperHyperVertex outside the intended SuperHyperSet. Thus the obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
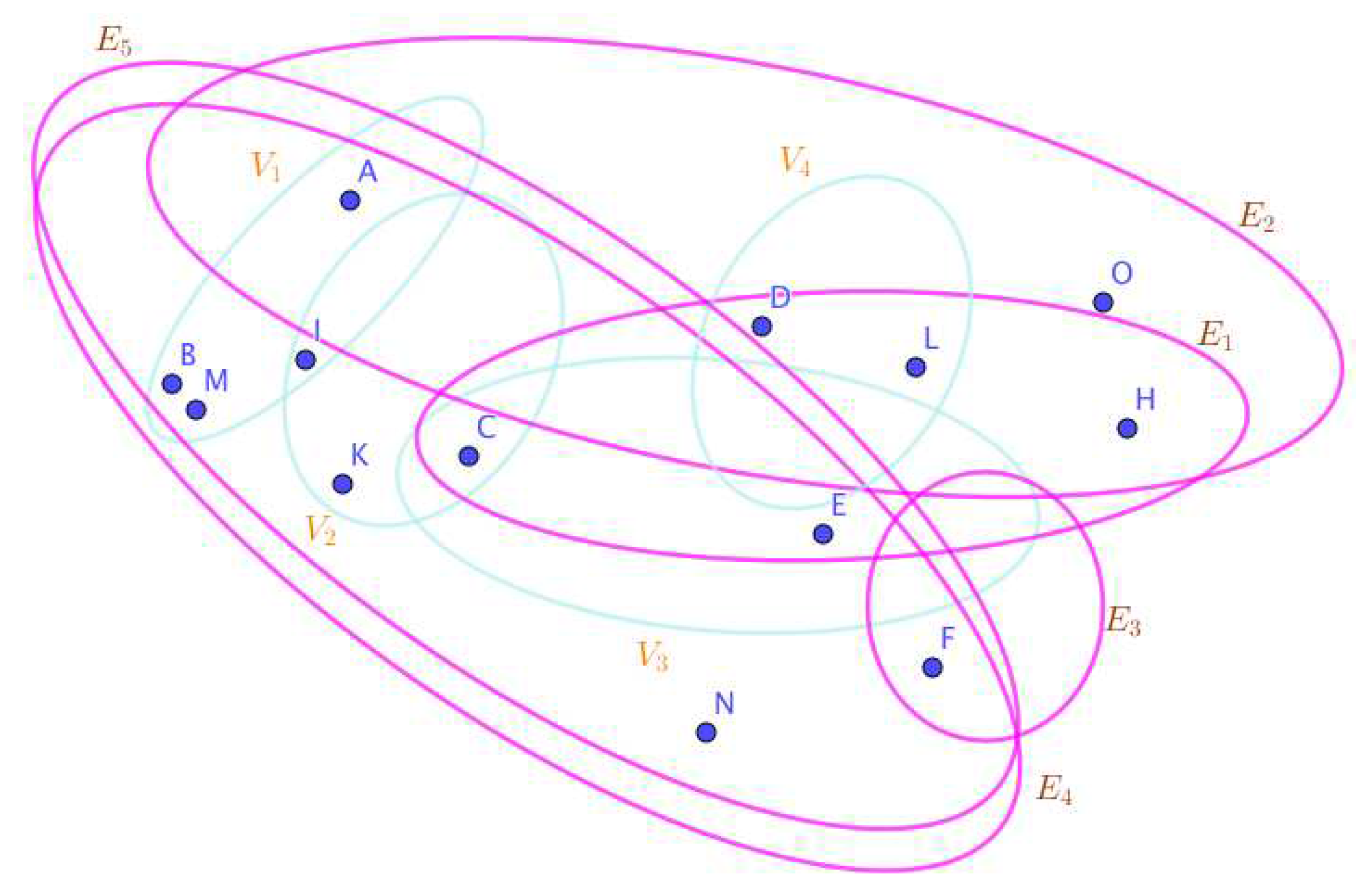
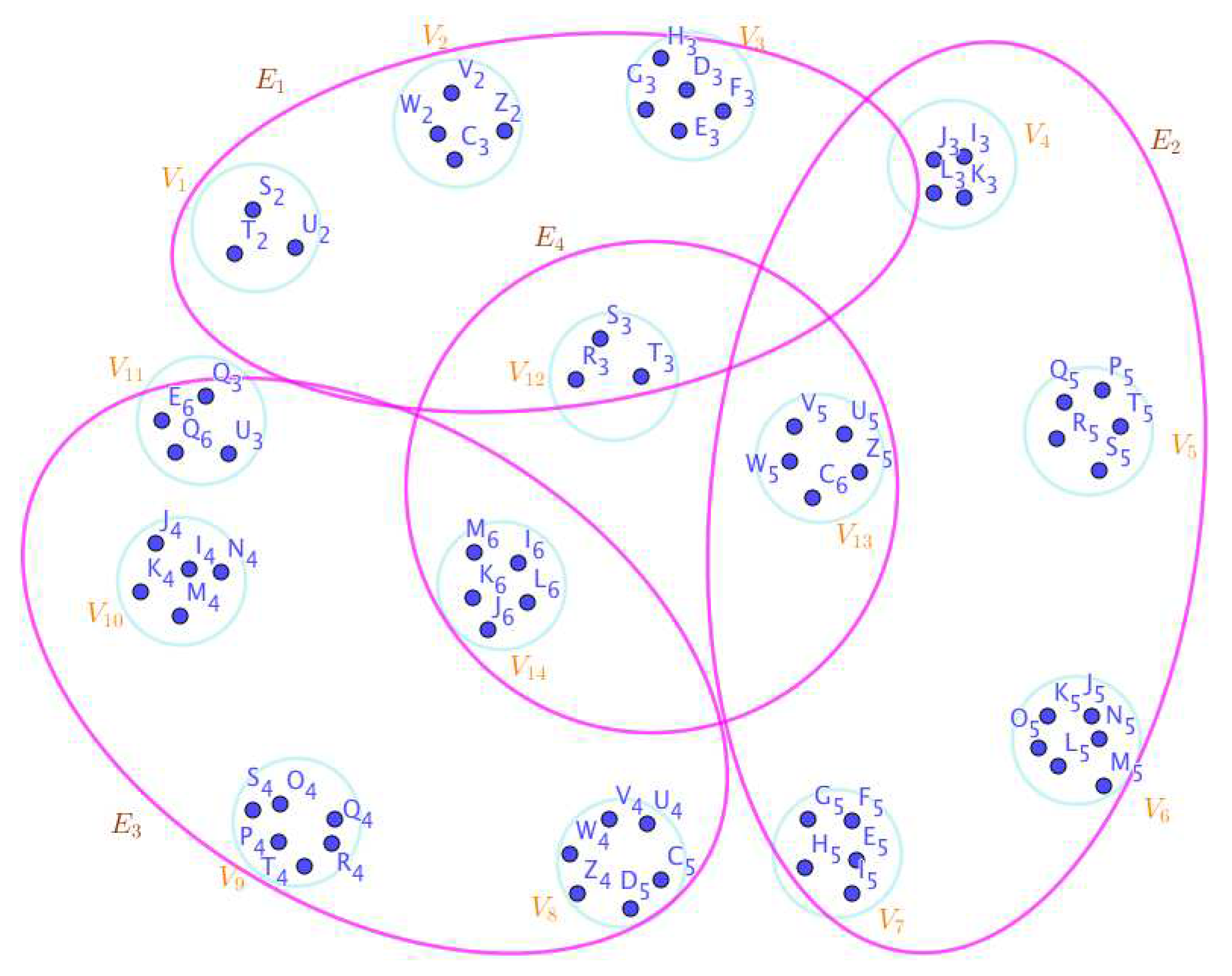
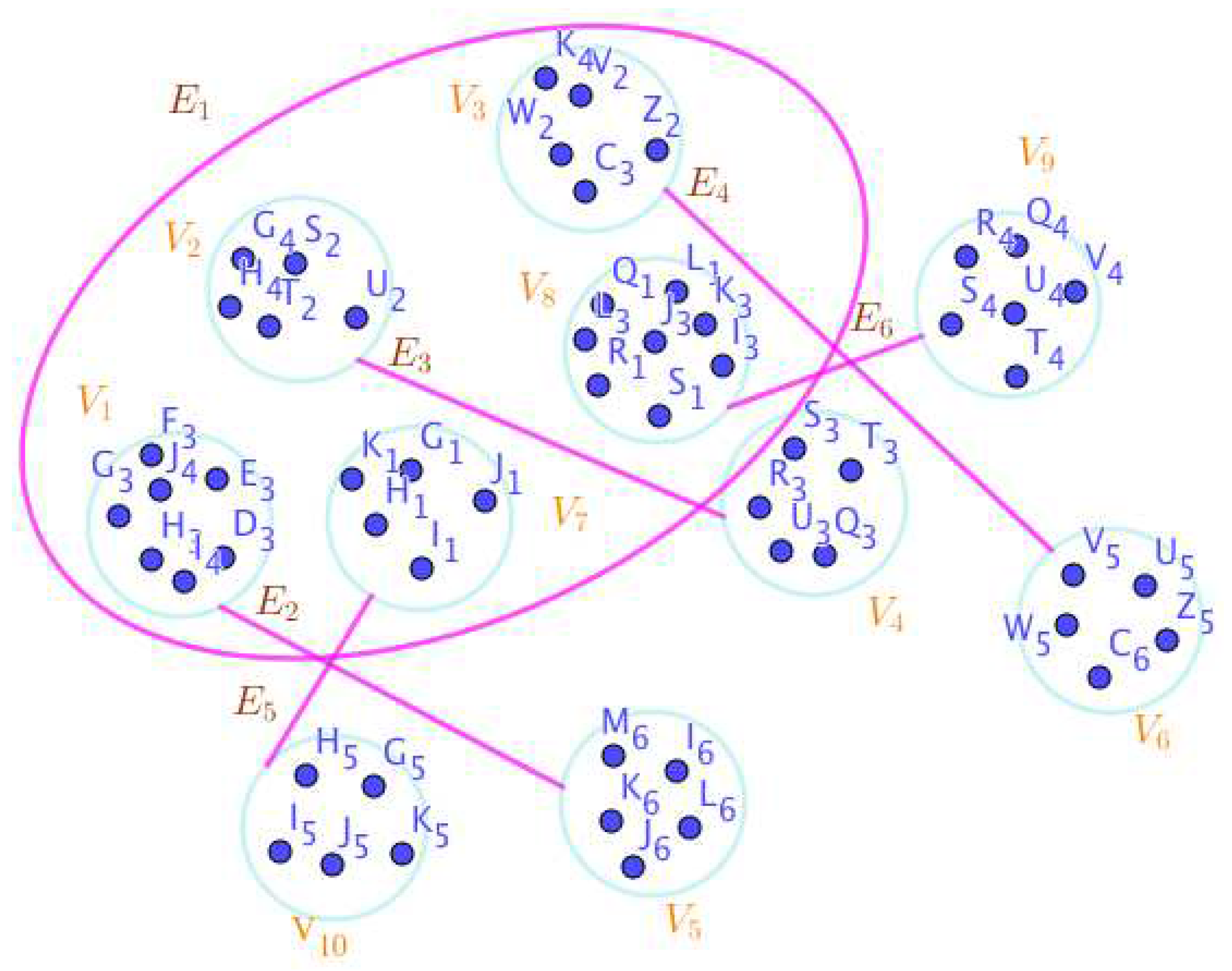
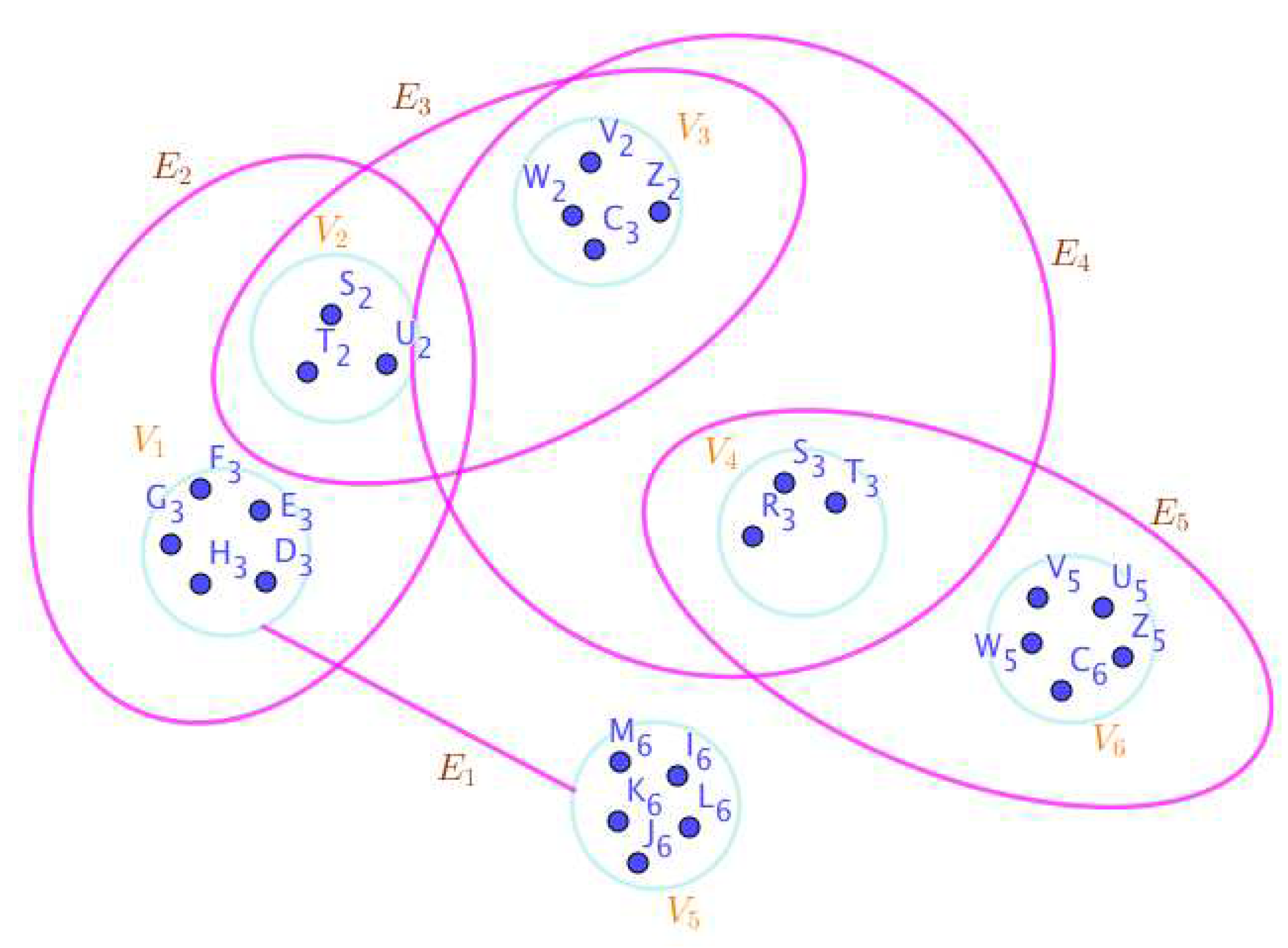
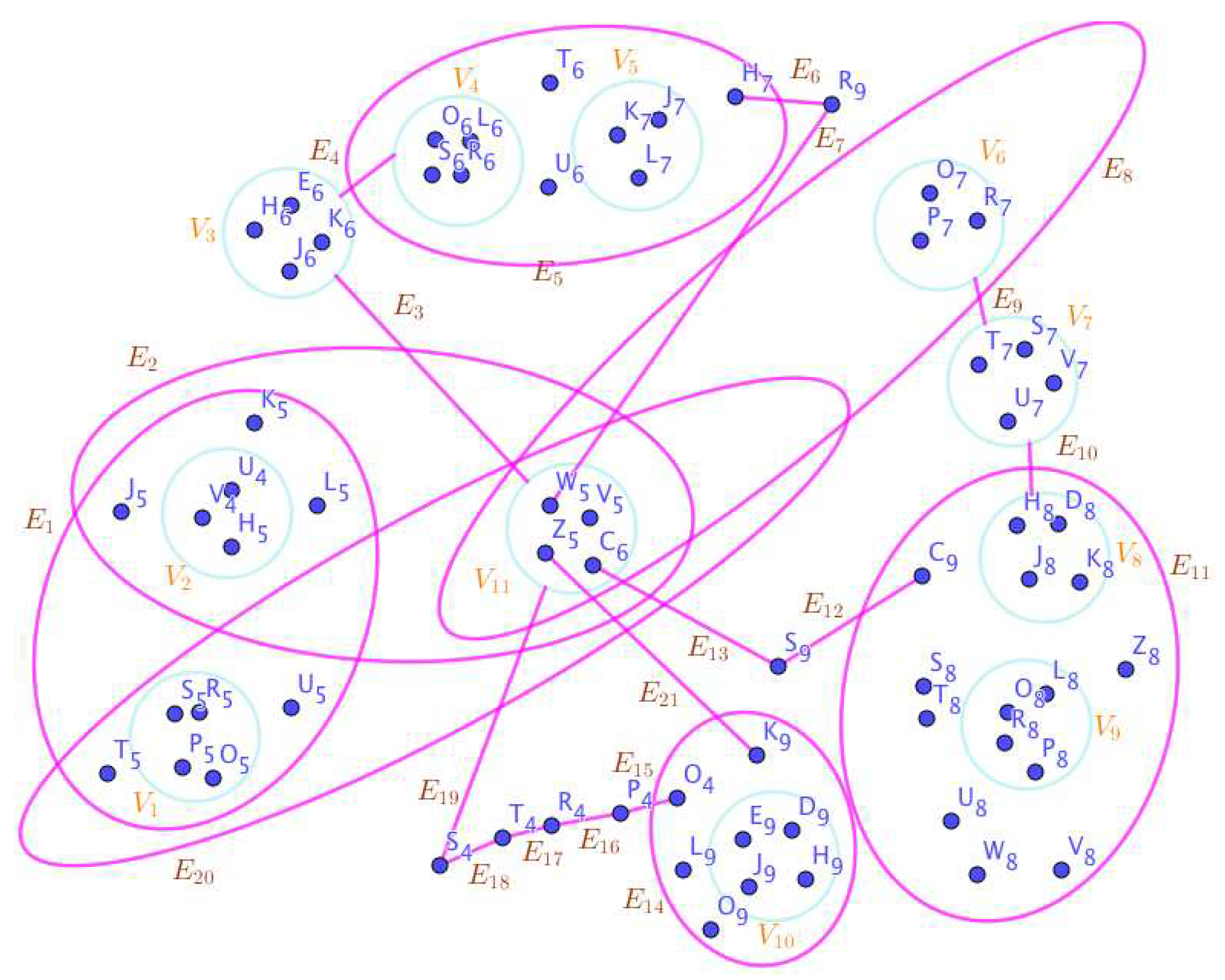
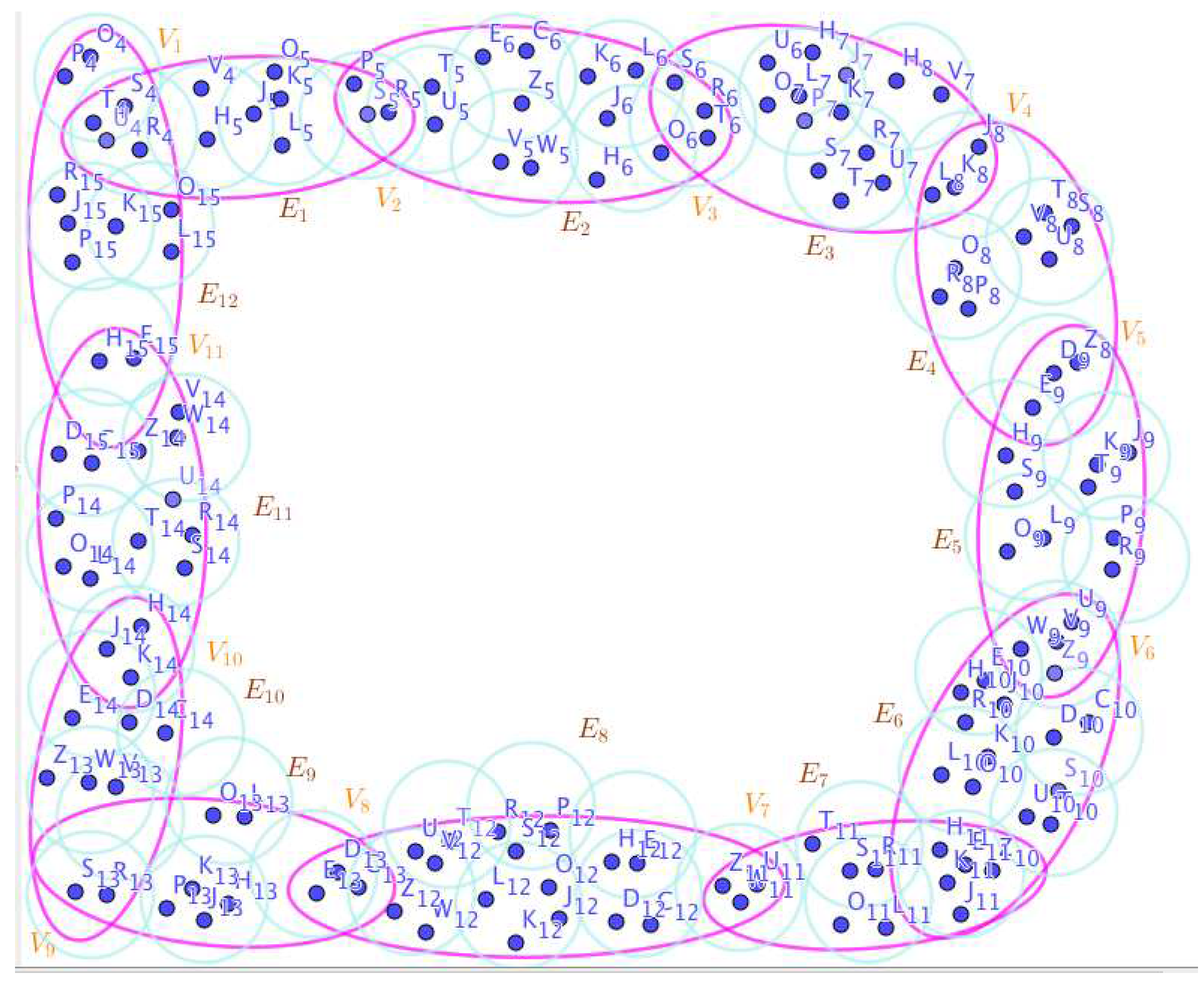
On the Figure 3, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. and are some empty SuperHyperEdges but is an SuperHyperEdge. Thus in the terms of SuperHyperNeighbor, there’s only one SuperHyperEdge, namely, All the following SuperHyperSets of SuperHyperVertices are the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing.
The SuperHyperSet of the SuperHyperVertices, is a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex but it isn’t a neutrosophic SuperHyperForcing. Since it doesn’t have the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only one SuperHyperVertex outside the intended SuperHyperSet. Thus the obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph Thus all the following SuperHyperSets of SuperHyperVertices are the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing.
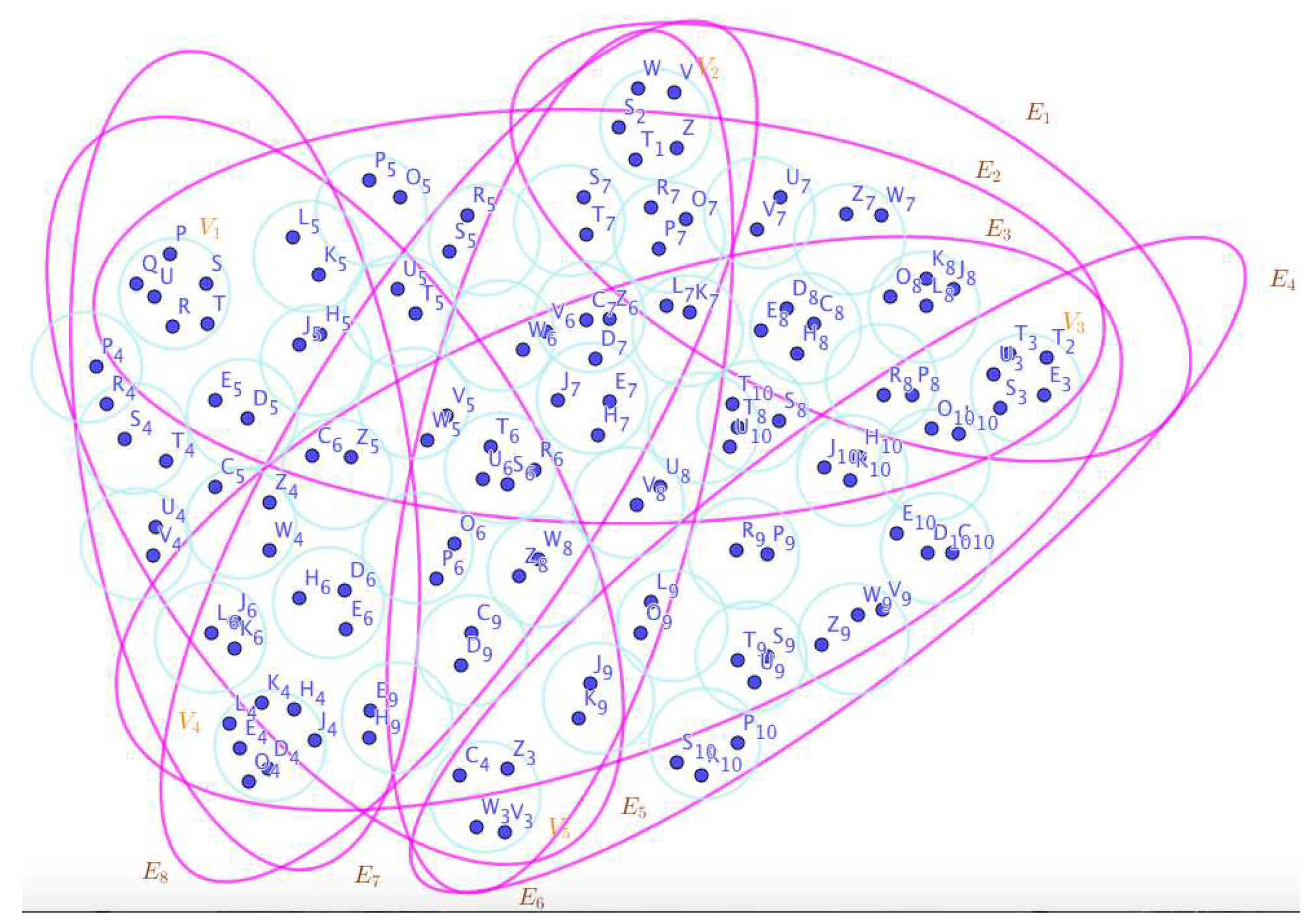
since the SuperHyperSets of the SuperHyperVertices, are the SuperHyperSets Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since they’vethe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only one SuperHyperVertex outside the intended SuperHyperSet, Thus the obvious neutrosophic SuperHyperForcing, is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
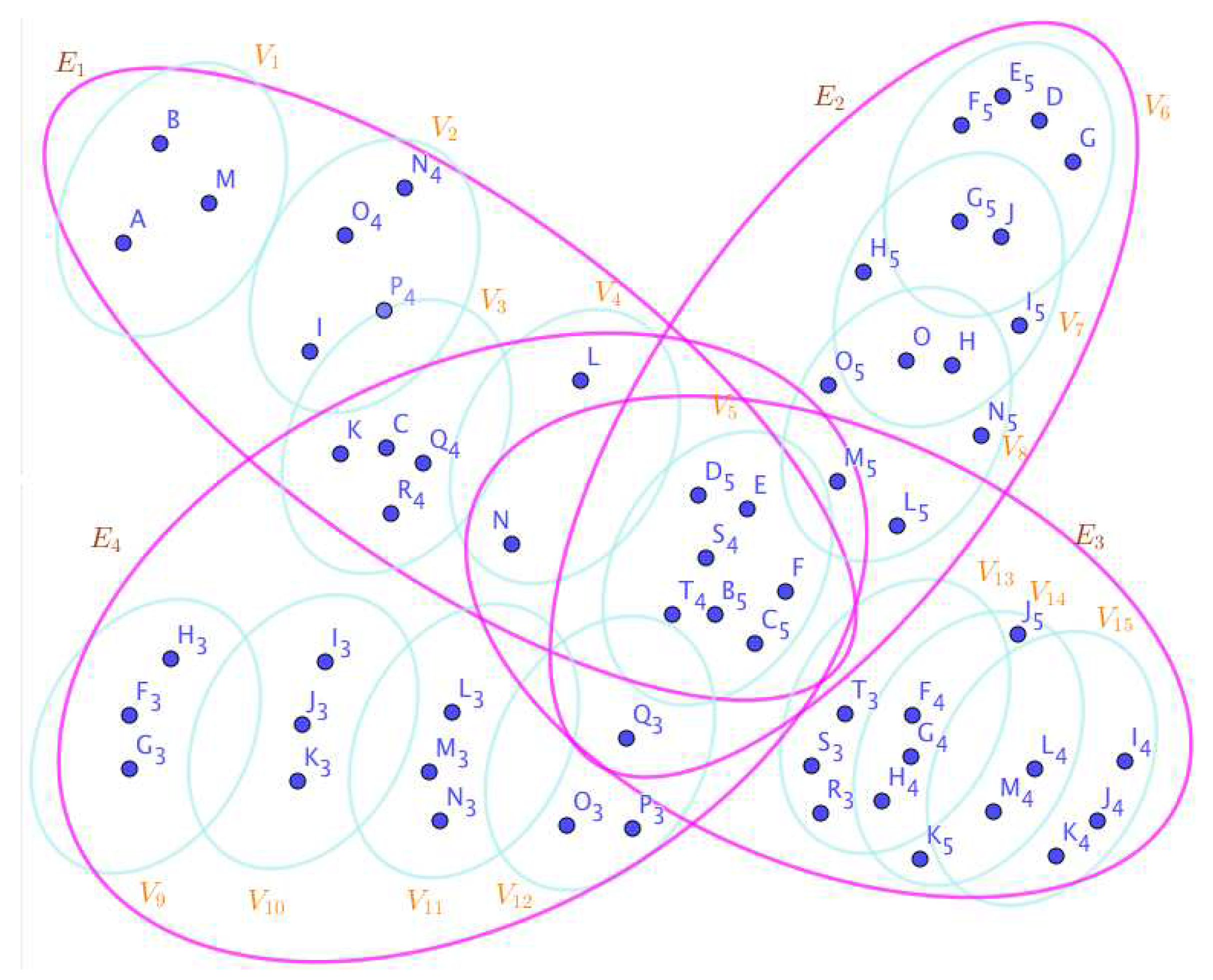
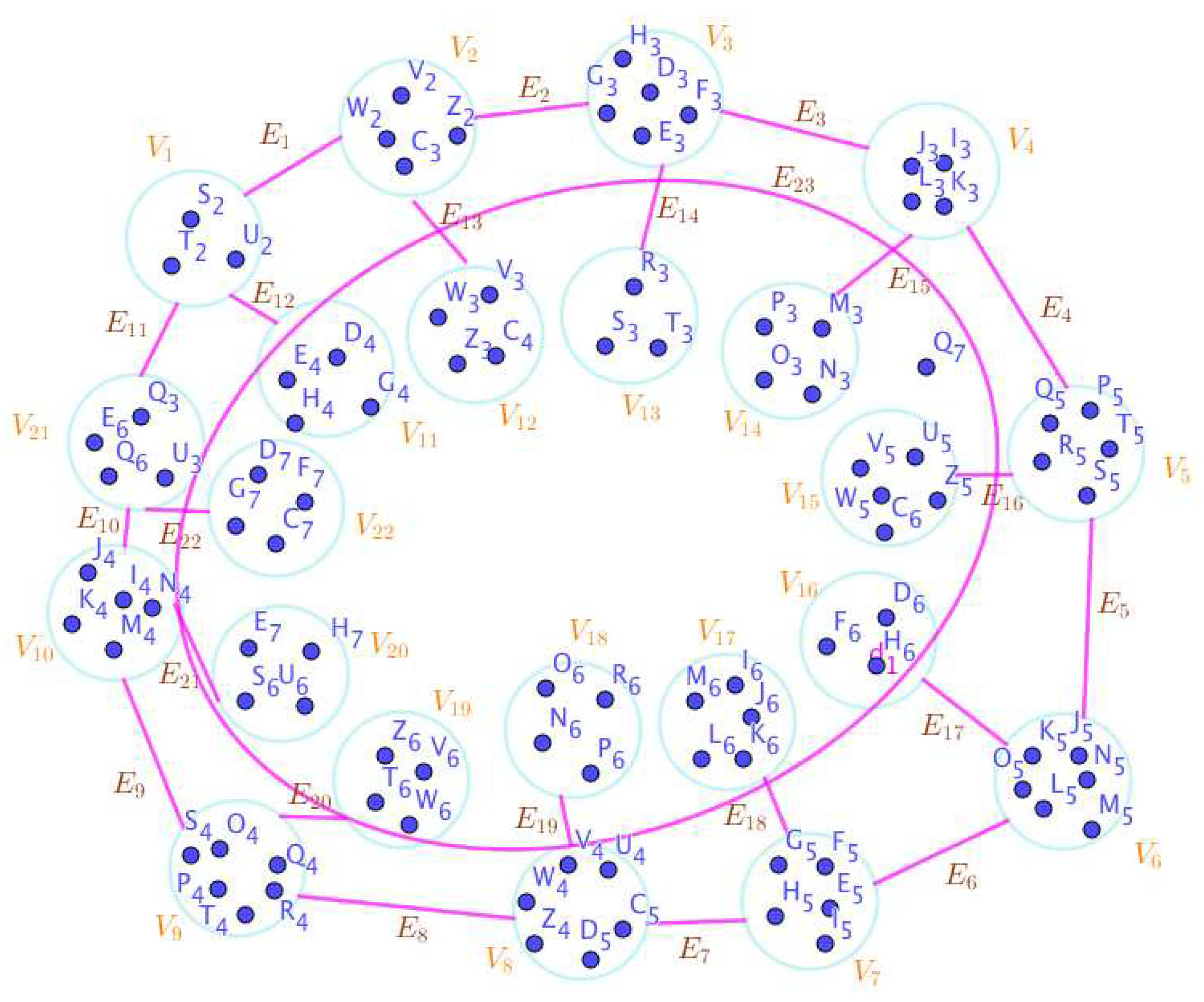
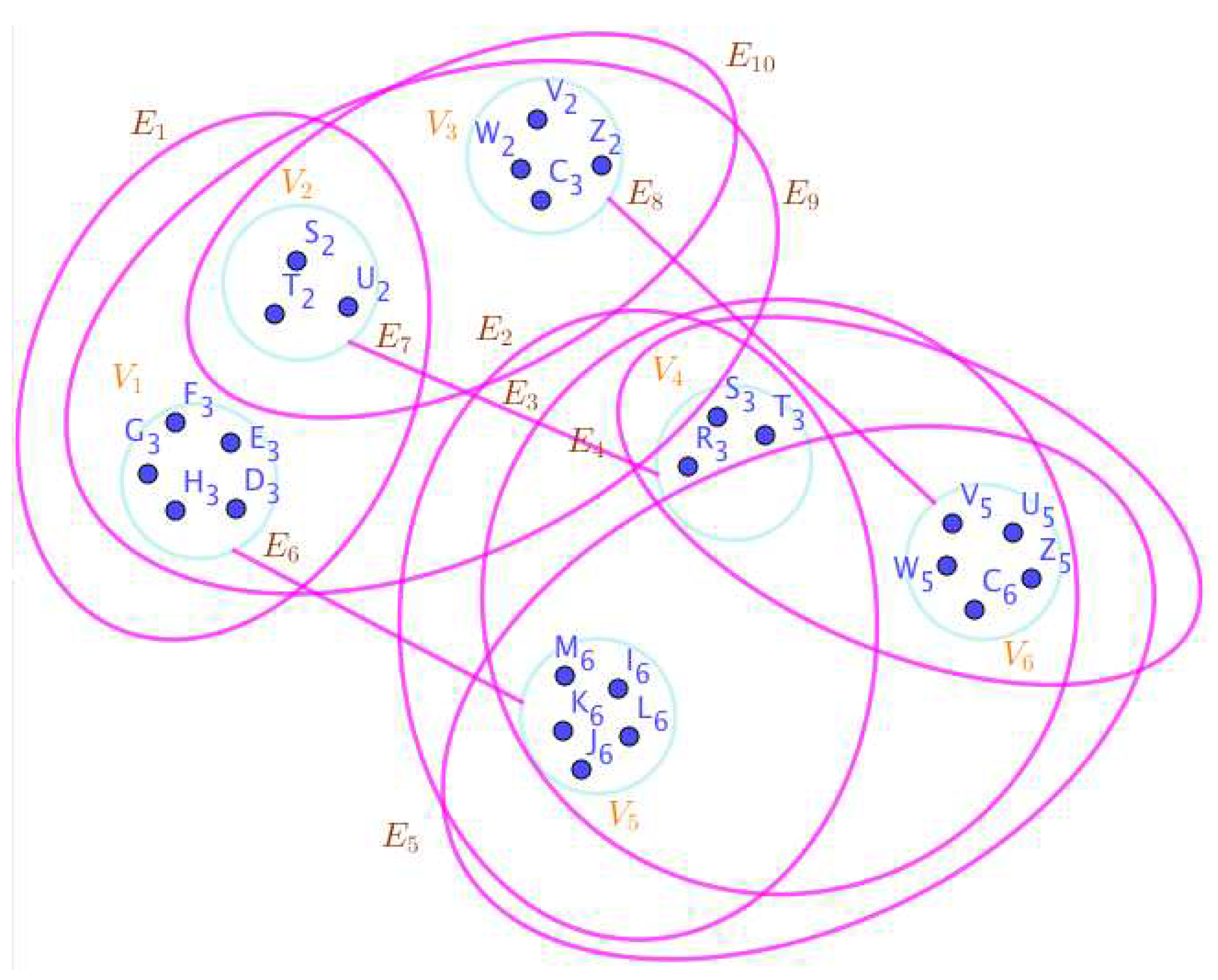
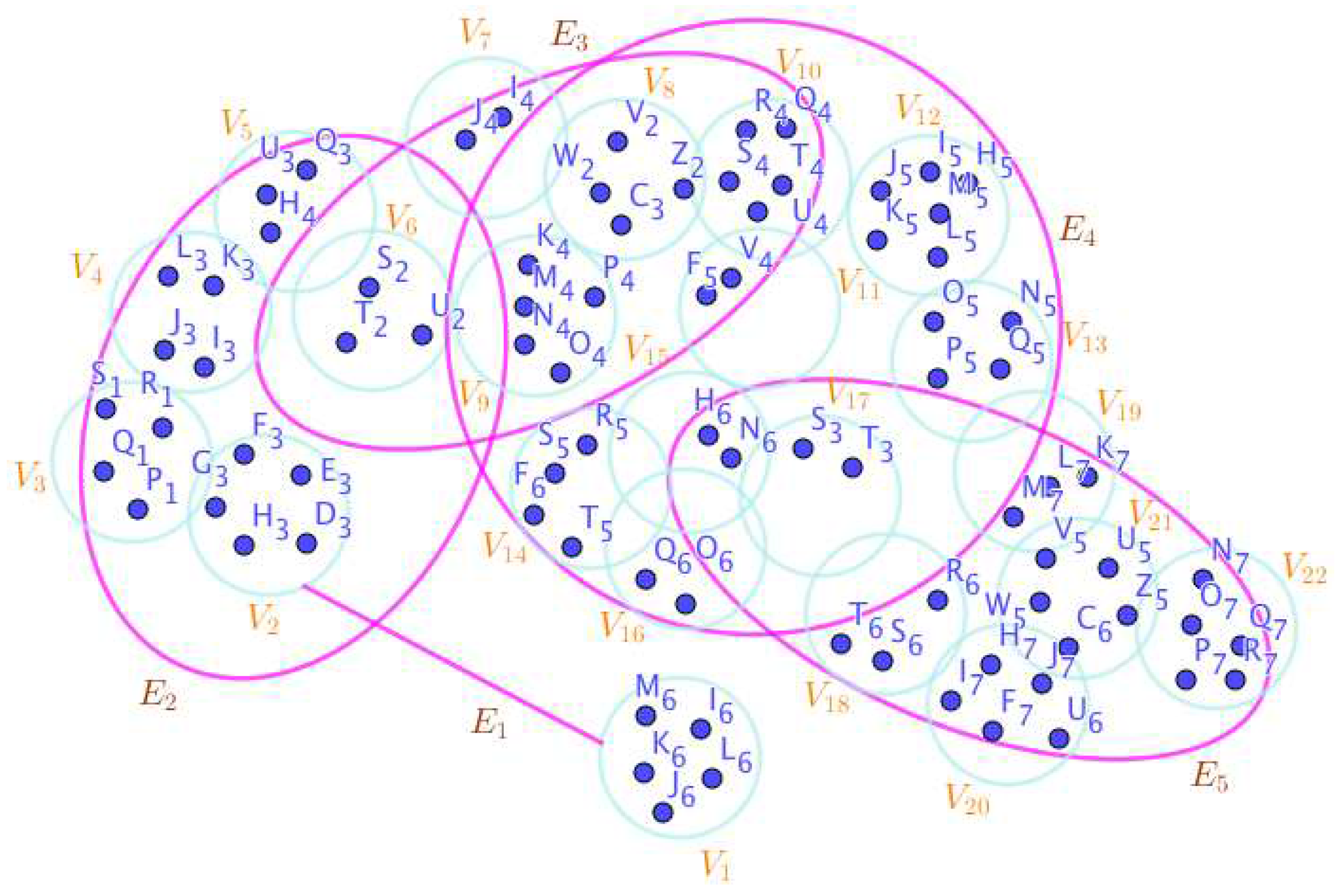
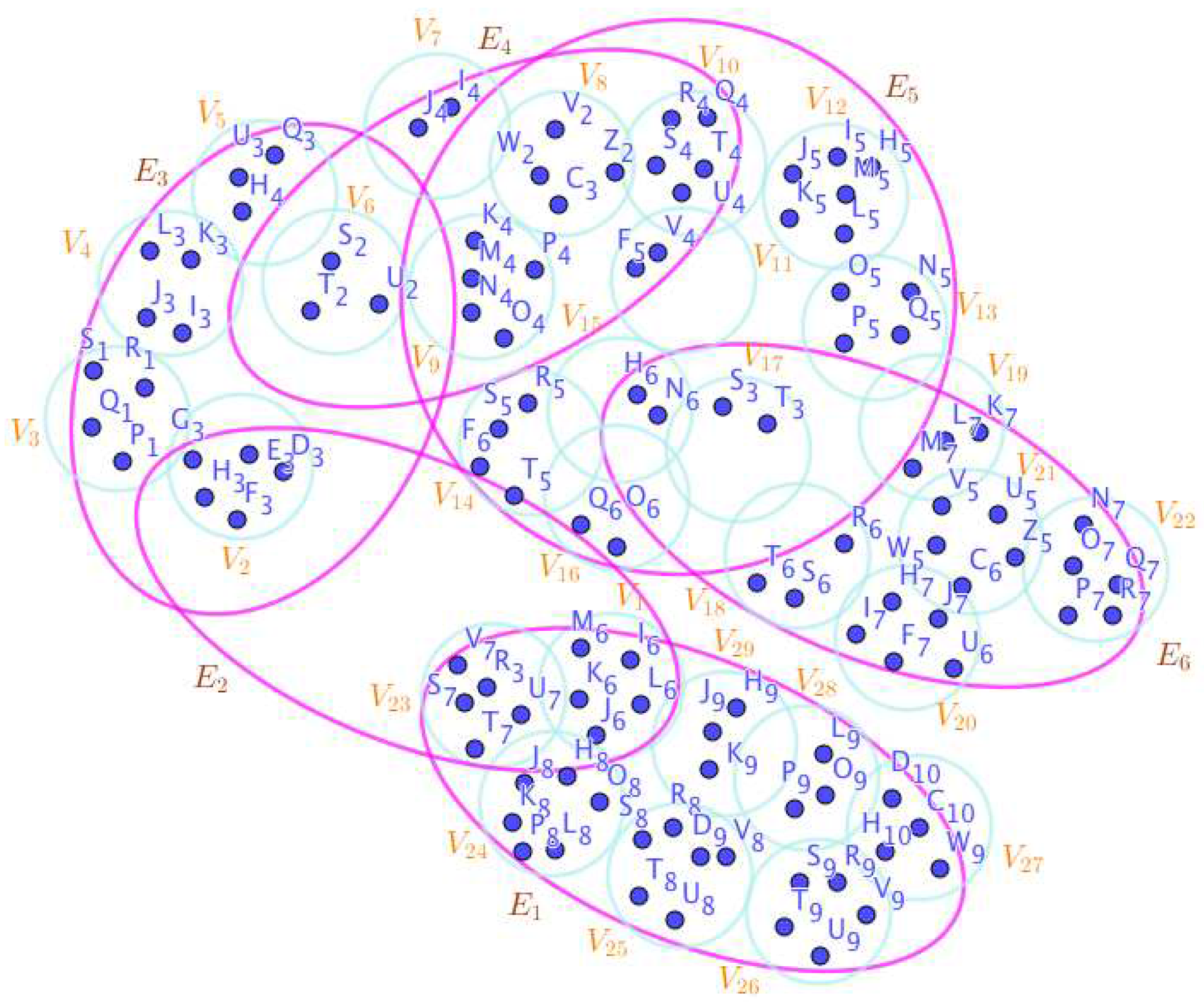
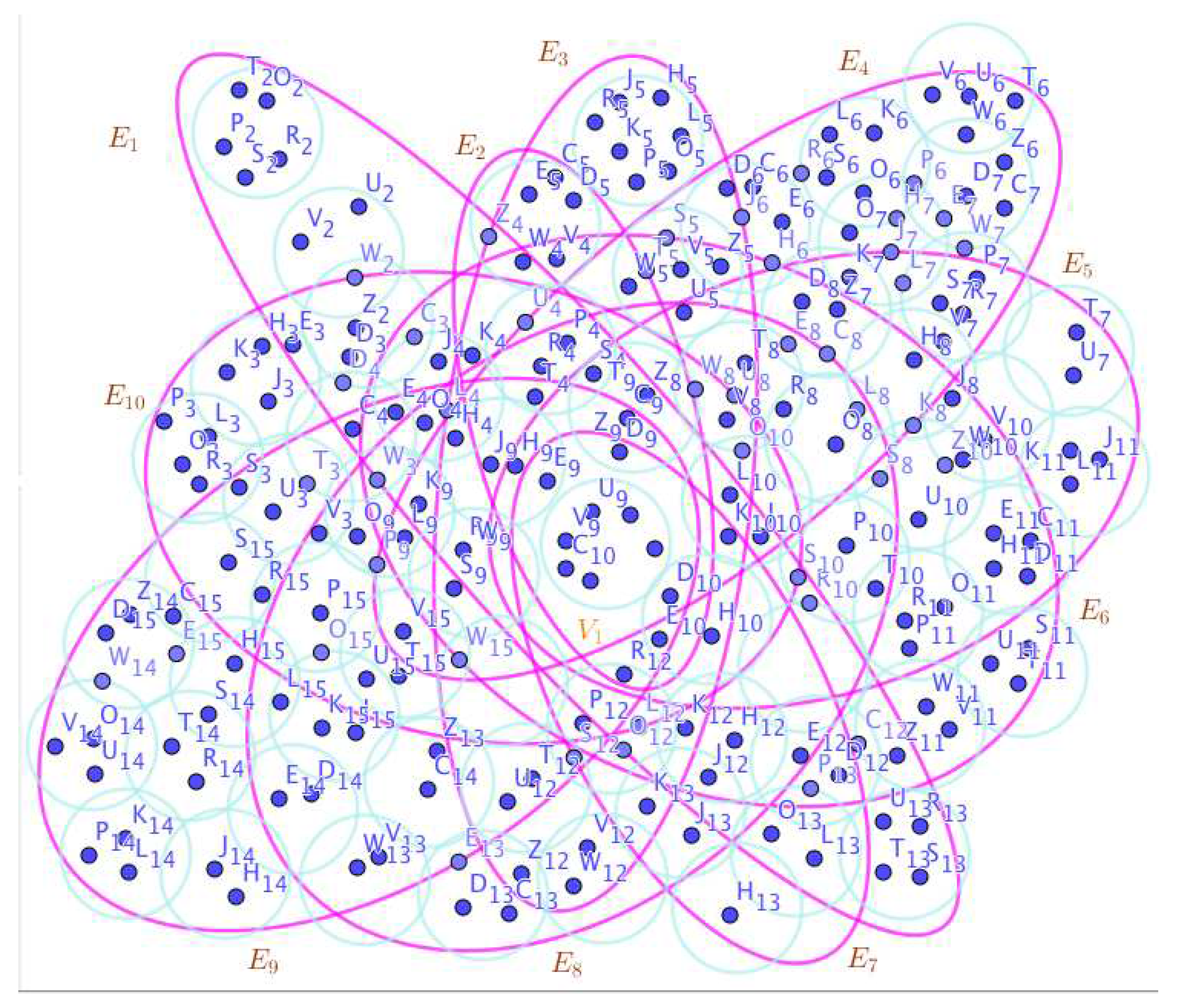
On the Figure 4, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s no empty SuperHyperEdge but are a loop SuperHyperEdge on and there are some SuperHyperEdges, namely, on alongside on and on The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph -
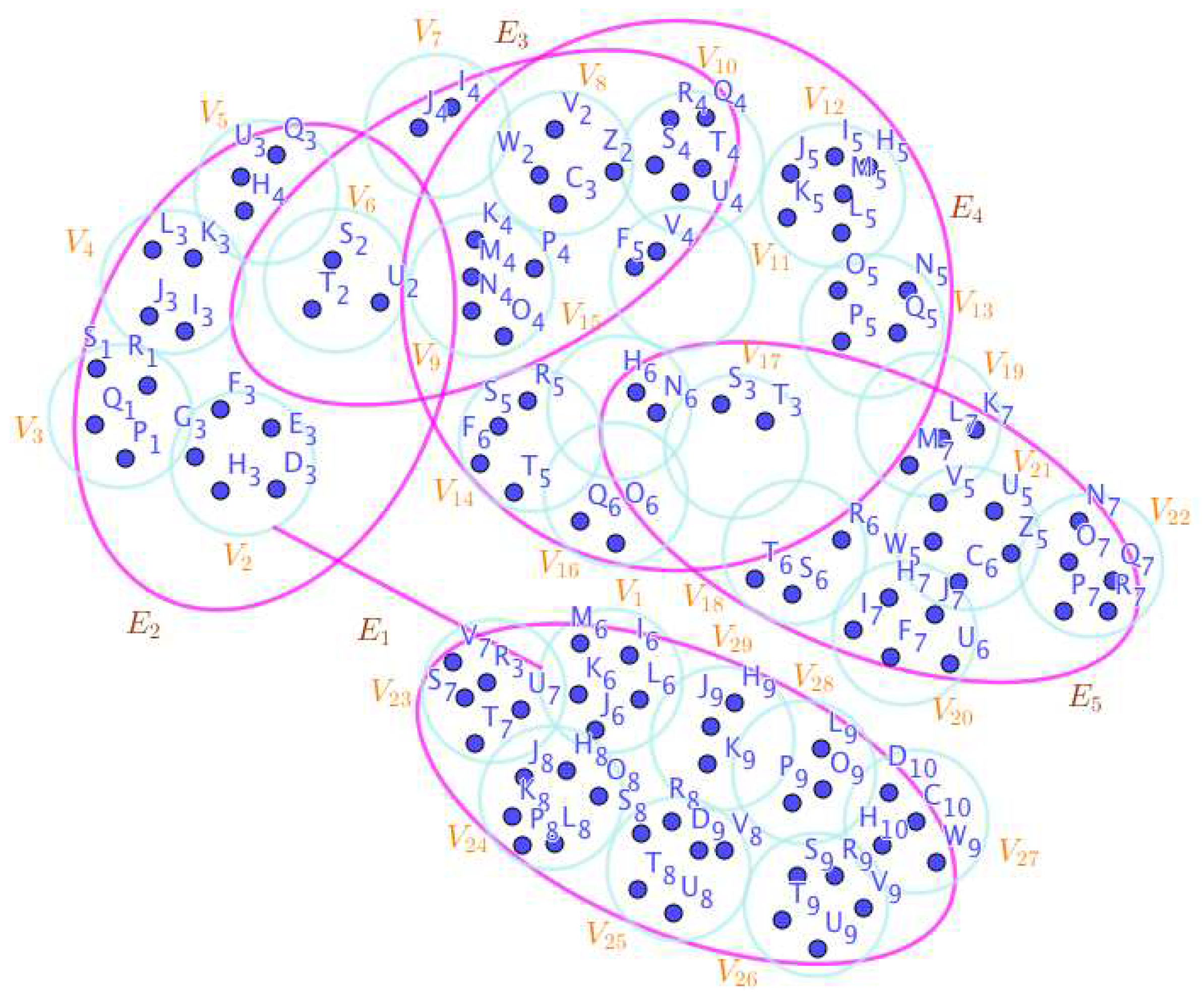
On the Figure 5, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
On the Figure 6, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
On the Figure 7, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
On the Figure 8, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
On the Figure 9, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
On the Figure 10, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph On the Figure 11, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph -
On the Figure 12, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
On the Figure 13, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph On the Figure 14, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph On the Figure 15, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up. is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph -
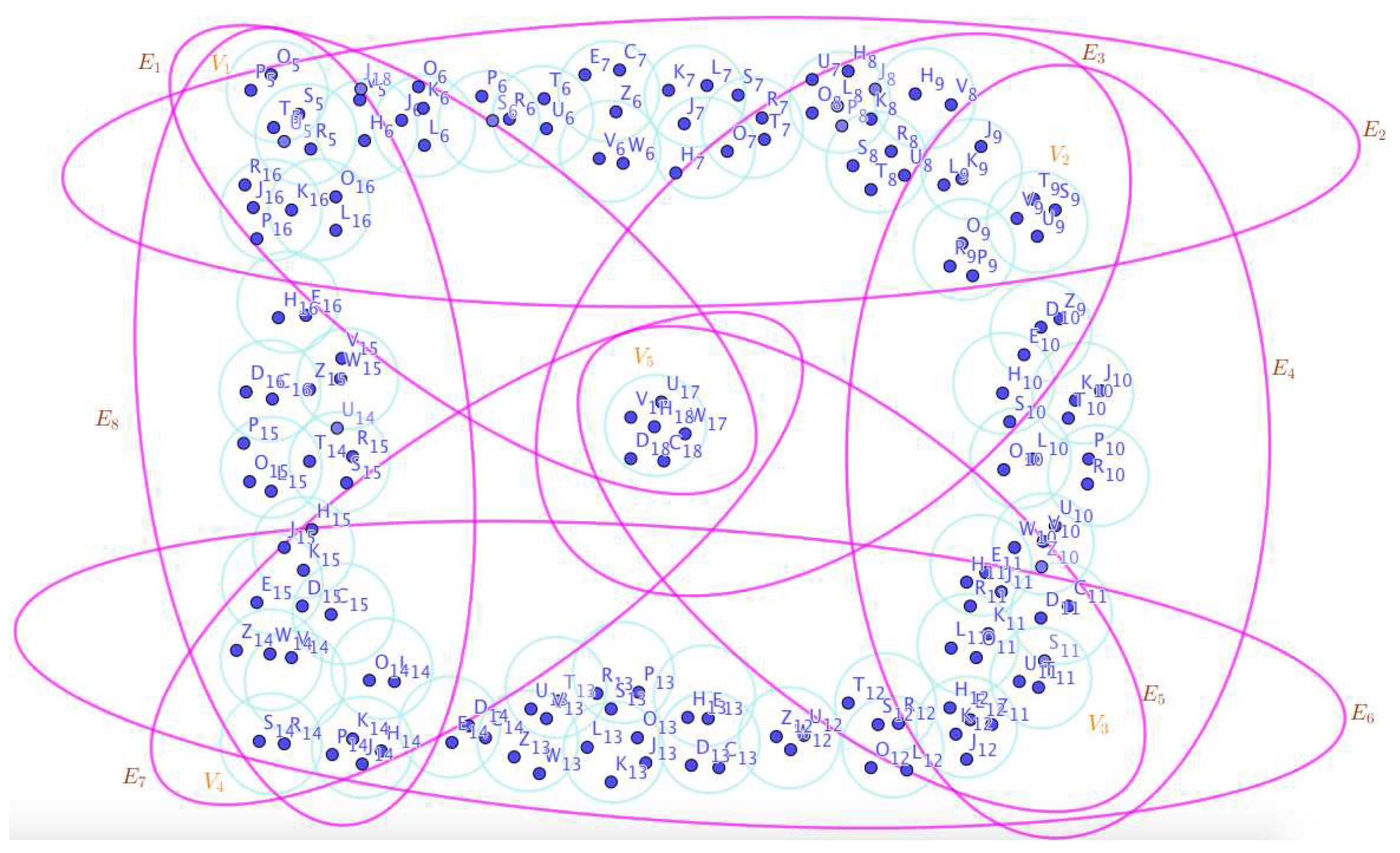
On the Figure 16, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices,
is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices,
is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices,
has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices,
is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices,
is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet,
Thus the non-obvious neutrosophic SuperHyperForcing,
is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing,
excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
On the Figure 17, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices,
is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices,
is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices,
has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices,
is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices,
is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet,
Thus the non-obvious neutrosophic SuperHyperForcing,
is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing,
excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
On the Figure 18, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices, is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices, is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices, has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices, is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices, is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet, Thus the non-obvious neutrosophic SuperHyperForcing, is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing, is a SuperHyperSet, excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
On the Figure 19, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements.There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices,
is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices,
is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices,
has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices,
is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices,
is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet,
Thus the non-obvious neutrosophic SuperHyperForcing,
is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing,
excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph
-
On the Figure 20, the neutrosophic SuperHyperNotion, namely, neutrosophic SuperHyperForcing, is up.
is the neutrosophic type-SuperHyperSet of the neutrosophic SuperHyperForcing. The details are followed by the upcoming statements. There’s neither empty SuperHyperEdge nor loop SuperHyperEdge. The SuperHyperSet of SuperHyperVertices,
is the simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. The SuperHyperSet of the SuperHyperVertices,
is the minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. In There’s not only one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious neutrosophic SuperHyperForcing is up. The obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is a SuperHyperSet excludes only one SuperHyperVertex in a connected neutrosophic SuperHyperGraph But the SuperHyperSet of SuperHyperVertices,
has more than one SuperHyperVertex outside the intended SuperHyperSet. Thus the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing is up. To sum them up, the SuperHyperSet of SuperHyperVertices,
is the non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing. Since the SuperHyperSet of the SuperHyperVertices,
is the SuperHyperSet Ss of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex and they are neutrosophic SuperHyperForcing. Since it’sthe minimum neutrosophic SuperHyperCardinality of a SuperHyperSet S of black SuperHyperVertices (whereas SuperHyperVertices in are colored white) such that is turned black after finitely many applications of “the color-change rule”: a white SuperHyperVertex is converted to a black SuperHyperVertex if it is the only white SuperHyperNeighbor of a black SuperHyperVertex. There’s only more than one SuperHyperVertex outside the intended SuperHyperSet,
Thus the non-obvious neutrosophic SuperHyperForcing,
is up. The non-obvious simple type-SuperHyperSet of the neutrosophic SuperHyperForcing,
excludes only more than one SuperHyperVertex in a connected neutrosophic SuperHyperGraph