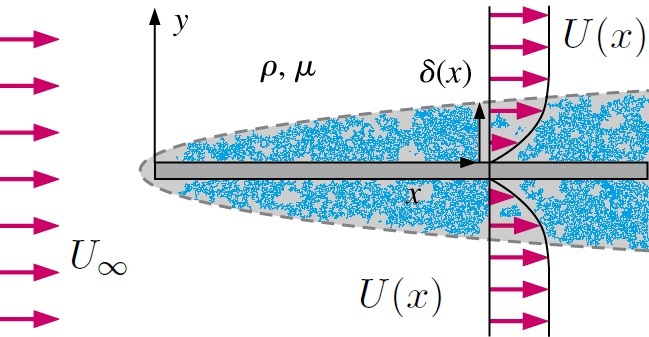
The exact similarity solutions (also called as special exact solutions) of two dimensional laminar boundary layer were obtained by Blasius in 1908, however, no similarity solutions for two dimensional turbulent boundary layers have been reported in the literature. With the help of dimensional analysis and invariance principle, Prandtl mixing length $\ell=\kappa y$ for one dimensional turbulent boundary layer is extended to $\ell(x,y)=\kappa y (1-\frac{y}{\delta})\sqrt{\frac{\nu}{U\delta}} $ for the two dimensional turbulent boundary layers, furthermore, with a similarity transformation, we successfully transform the two dimensional turbulent boundary layers partial differential equations into a single ordinary differential equation $f'''+ ff''+\beta(1-f'^2)+\kappa^2[\eta^2(1-\eta)^2f''|f''|]'=0$. As an application, similarity solutions of the two dimensional turbulent boundary layer on a flat plate at zero incidence have been studied in detail. To solve the ordinary differential equation numerically, a complete Maple code is provided.