A Proof Of The Riemann Hypothesis Based On A New Expression Of The Completed Zeta Function

1. Introduction

It has been almost 164 years since the Riemann Hypothesis (RH) was proposed in 1859 [1]. Many efforts and achievements have been made towards proving this celebrated hypothesis, but it is still an open problem [2,3]. The Riemann zeta function is the function of the complex variable s, defined in the half-plane $\Re \left(s\right)>1$ by the absolutely convergent series [2]

$$\zeta \left(s\right)=\sum _{n=1}^{\infty }\frac{1}{n^s},\Re \left(s\right)>1$$

(1)

The connection between the Riemann zeta function and prime numbers can be established through the well-known Euler product, i.e.

$$\zeta \left(s\right)=\sum _{n=1}^{\infty }\frac{1}{n^s}=\prod _p{(1-p^{-s})}^{-1},\Re \left(s\right)>1$$

(2)

where p runs over the prime numbers.

Riemann showed how to extend zeta function to the whole complex plane $\mathbb{C}$ by analytic continuation

$$\zeta \left(s\right)=\frac{{\pi }^{s/2}}{\mathsf{\Gamma }(s/2)}\{\frac{1}{s(s-1)}+{\int }_1^{\infty }(x^{\frac{s}{2}-1}+x^{-\frac{s}{2}-\frac{1}{2}})·\left(\frac{\theta \left(x\right)-1}{2}\right)dx\}$$

(3)

where $\theta \left(x\right)={\sum }_{-\infty }^{\infty }{e}^{-n^2\pi x}$ being the Jaccobi theta function, $\mathsf{\Gamma }$ being the Gamma function in the following Weierstrass expression (Meanwhile, there are also Gauss expression, Euler expression, and integral expression of the Gamma function.)

$$\frac{1}{\mathsf{\Gamma }\left(s\right)}=s·e^{\gamma s}\prod _{n=1}^{\infty }(1+\frac{s}{n})e^{-s/n}$$

(4)

where $\gamma$ is the Euler-Mascheroni constant.

As shown by Riemann, $\zeta \left(s\right)$ extends to $\mathbb{C}$ as a meromorphic function with only a simple pole at $s=1$, with residue 1, and satisfies the following functional equation

$${\pi }^{-\frac{s}{2}}\mathsf{\Gamma }\left(\frac{s}{2}\right)\zeta \left(s\right)={\pi }^{-\frac{1-s}{2}}\mathsf{\Gamma }\left(\frac{1-s}{2}\right)\zeta (1-s)$$

(5)

The Riemann zeta function $\zeta \left(s\right)$ has zeros at the negative even integers: $-2$, $-4$, $-6$, $-8$, ⋯ and one refers to them as the trivial zeros. The other zeros of $\zeta \left(s\right)$ are the complex numbers, i.e., non-trivial zeros [2].

In 1896, Hadamard [4] and Poussin [5] independently proved that no zeros could lie on the line $\Re \left(s\right)=1$. Together with the functional equation and the fact that there are no zeros with real part greater than 1, this showed that all non-trivial zeros must lie in the interior of the critical strip$0<\Re \left(s\right)<1$. This was a key step in their first proofs of the famous Prime Number Theorem.

Later on, Hardy (1914) [6], Hardy and Littlewood (1921) [7] showed that there are infinitely many zeros on the critical line $\Re \left(s\right)=\frac{1}{2}$, which was an astonishing result at that time.

As a summary, we have the following results on the properties of the non-trivial zeros of $\zeta \left(s\right)$ [4,5,6,7,8,9].

Lemma 1. 

Non-trivial zeroes of $\zeta \left(s\right)$, noted as $\rho =\alpha +j\beta$, have the following properties

1) The number of non-trivial zeroes is infinity;

2) $\beta \ne 0$;

3) $0<\alpha <1$;

4) $\rho ,\overline{\rho },1-\overline{\rho },1-\rho$ are all non-trivial zeroes.

As further study, a completed zeta function $\xi \left(s\right)$ is defined as

$$\xi \left(s\right)=\frac{1}{2}s(s-1){\pi }^{-\frac{s}{2}}\mathsf{\Gamma }\left(\frac{s}{2}\right)\zeta \left(s\right)$$

(6)

It is well-known that $\xi \left(s\right)$ is an entire function of order 1. This implies $\xi \left(s\right)$ is analytic, and can be expressed as infinite polynomial, in the whole complex plane $\mathbb{C}$.

In addition, replacing s with $1-s$ in Equation (6), and combining Equation (5), we have the following functional equation

$$\xi \left(s\right)=\xi (1-s)$$

(7)

Considering the definition of $\xi \left(s\right)$, and recalling Equation (4), the trivial zeros of $\zeta \left(s\right)$ are canceled by the poles of $\mathsf{\Gamma }\left(\frac{s}{2}\right)$. The zero of $s-1$ and the pole of $\zeta \left(s\right)$ cancel; the zero $s=0$ and the pole of $\mathsf{\Gamma }\left(\frac{s}{2}\right)$ cancel [9,10]. Thus, all the zeros of $\xi \left(s\right)$ are exactly the nontrivial zeros of $\zeta \left(s\right)$. Then we have the following Lemma 2.

Lemma 2. 

The zeros of $\xi \left(s\right)$ coincide with the non-trivial zeros of $\zeta \left(s\right)$.

According to Lemma 2, the following two statements for the RH are equivalent.

Statement 1 of the RH: All the non-trivial zeros of $\zeta \left(s\right)$ have real part equal to $\frac{1}{2}$.

Statement 2 of the RH: All the zeros of $\xi \left(s\right)$ have real part equal to $\frac{1}{2}$.

To prove the RH, a natural thinking is to estimate the numbers of non-trivial zeros of $\zeta \left(s\right)$ inside or outside some areas according to Argument Principle. Along this train of thought, there are many research works. Let $N\left(T\right)$ denote the number of zeros of $\zeta \left(s\right)$ inside the rectangle: $0<\alpha <1,0<\beta \le T$, and let $N_0\left(T\right)$ denote the number of zeros of $\zeta \left(s\right)$ on the line $\alpha =\frac{1}{2},0<\beta \le T$. Selberg proved that there exist positive constants c and $T_0$, such that $N_0\left(T\right)>cN\left(T\right),(T>T_0)$[11], later on, Levinson proved that $c\ge \frac{1}{3}$[12], Lou and Yao proved that $c\ge 0.3484$[13], Conrey proved that $c\ge \frac{2}{5}$[14], Bui, Conrey and Young proved that $c\ge 0.41$[15], Feng proved that $c\ge 0.4128$[16], Wu proved that $c\ge 0.4172$ [17].

On the other hand, many zeros have been calculated by hand or by computer programs. Among others, Riemann found the first three non-trivial zeros [18]. Gram found the first 15 zeros based on Euler-Maclaurin summation [19]. Titchmarsh calculated the 138^th to 195^th zeros using the Riemann-Siegel formula [20,21]. Here are the first three (pairs of) zeros: $\frac{1}{2}\pm j14.1347251;\frac{1}{2}\pm j21.0220396;\frac{1}{2}\pm j25.0108575$.

The idea of this paper is originated from Euler’s work on proving the following famous equality

$$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\cdots =\frac{{\pi }^2}{6}$$

(8)

This interesting result is deduced by comparing the like terms of two types of infinite expressions, i.e., infinite polynomial and infinite product, as shown in the following

$$\begin{array}{cc}\hfill \frac{sinx}{x}& =1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\cdots \hfill \\ \hfill & =(1-\frac{x^2}{{\pi }^2})(1-\frac{x^2}{4{\pi }^2})(1-\frac{x^2}{9{\pi }^2})\cdots \hfill \end{array}$$

(9)

Then it is conjectured that $\xi \left(s\right)$ should be factored into $(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2})$ or something like that, which was verified by paring ${\rho }_i$ and ${\overline{\rho }}_i$ in the Hadamard product of $\xi \left(s\right)$ to obtain

$$(1-\frac{s}{{\rho }_i})(1-\frac{s}{{\overline{\rho }}_i})=\frac{{\beta }_i^2}{{\alpha }_i^2+{\beta }_i^2}(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2})$$

The Hadamard product of $\xi \left(s\right)$ as shown in Equation (10) was first proposed by Riemann, however, it was Hadamard [22] who showed the validity of this infinite product expansion.

$$\xi \left(s\right)=\xi \left(0\right)\prod _{\rho }(1-\frac{s}{\rho })$$

(10)

where $\xi \left(0\right)=\frac{1}{2}$, $\rho$ runs over all the non-trivial zeros of the Riemann zeta function $\zeta \left(s\right)$, or in another word, $\rho$ runs over all the zeros of the completed zeta function $\xi \left(s\right)$.

To ensure the absolute convergence of the infinite product expansion, $\rho$ and $1-\rho$ are paired. Later in Section 4, we will show that $\rho$ and $\overline{\rho }$ can also be paired to ensure the absolute convergence of the infinite product expansion.

2. Lemmas

In this section, we first explain the concepts of multiple zeros of $\xi \left(s\right)$ with their real multiplicities. And then we give three lemmas to support the proof of the RH, in which Lemma 3 is the key lemma.

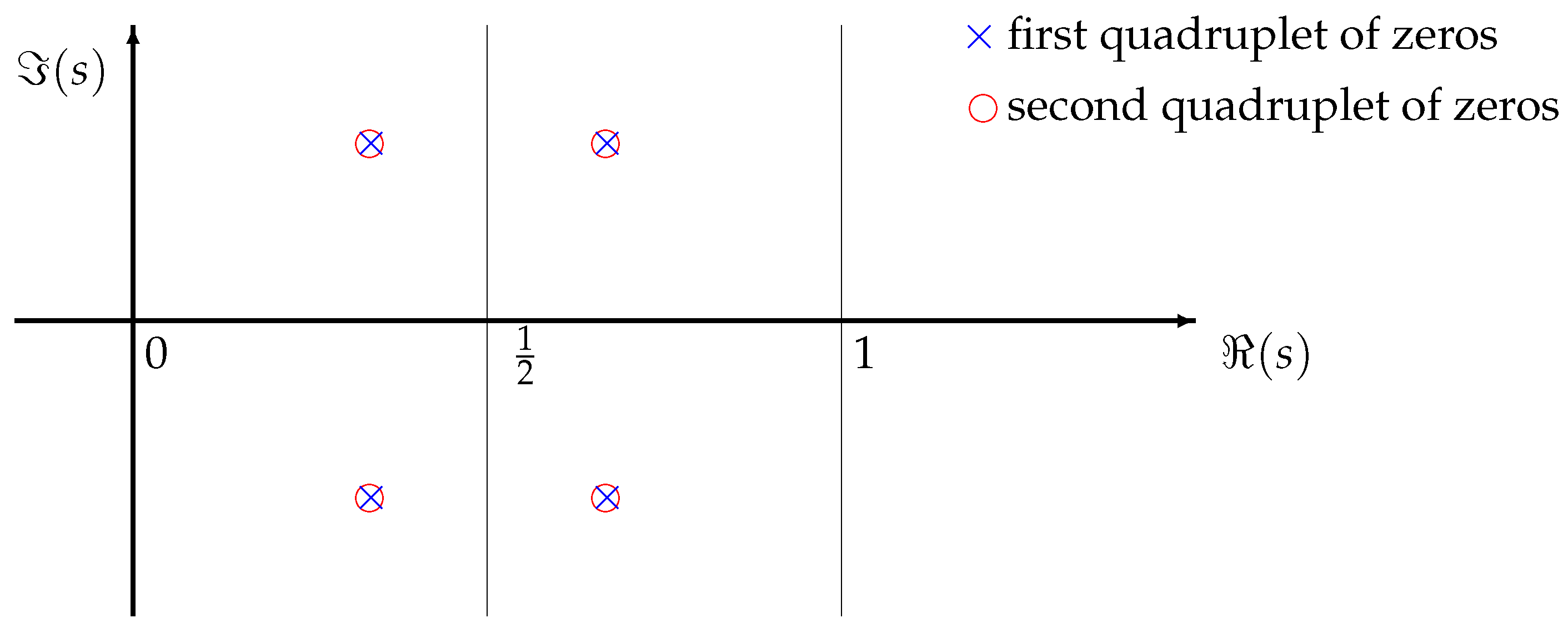
Multiple zeros of $\xi \left(s\right)$: As shown in Figure 1, the multiple zeros of $\xi \left(s\right)$ are defined in terms of the quadruplet, i.e., $\rho ,\overline{\rho },1-\rho ,1-\overline{\rho }$.

It should be noticed that the multiple zeros with their real multiplicities of $\xi \left(s\right)$ are objective existence, but the expression of the corresponding factors of $\xi \left(s\right)$ are optional to some extent. For example, the multiple zeros as shown in Figure 1 have two different expressions as factors of $\xi \left(s\right)$ and $\xi (1-s)$, respectively, i.e., $\left[\right(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^2,(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^2]$, or $\left[\right(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}\left)\right(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}),(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}\left)\right(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}),{\alpha }_1+{\alpha }_2=1,{\beta }_1^2={\beta }_2^2]$.

To exclude the latter expression, we stipulate that the multiple zeros ${\rho }_i$ related factors of $\xi \left(s\right)$ take the form of $(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}$, where $d_i\ge 1$ is the real multiplicity of ${\rho }_i$.

Lemma 3. 

Given two infinite products

$$f\left(s\right)=\prod _{i=1}^{\infty }(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}$$

(11)

and

$$f(1-s)=\prod _{i=1}^{\infty }(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}$$

(12)

where s is a complex variable, ${\rho }_i={\alpha }_i+j{\beta }_i$ and ${\overline{\rho }}_i={\alpha }_i-j{\beta }_i$ are the complex conjugate zeros of $\xi \left(s\right)$, $0<{\alpha }_i<1$ and ${\beta }_i\ne 0$ are real numbers, $d_i\ge 1$ are the real multiplicities of ${\rho }_i$, i are natural numbers from 1 to infinity, ${\beta }_i$ are in order of increasing $|{\beta }_i|$, i.e., $|{\beta }_1|\le |{\beta }_2|\le |{\beta }_3|\le \cdots$.

Then we have

$$f\left(s\right)=f(1-s)\iff \left\{\begin{array}{cc}& {\alpha }_i=\frac{1}{2},i=1,2,3,\cdots ,\infty \hfill \\ & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots \hfill \end{array}\right.$$

(13)

where $"\iff "$ is the equivalent sign.

Proof. 

First of all, we have the following fact:

$$\begin{array}{cc}\hfill & (1+\frac{{(s-\alpha )}^2}{{\beta }^2}{)}^d=(1+\frac{{(1-s-\alpha )}^2}{{\beta }^2}{)}^d\hfill \\ \hfill & \iff {(s-\alpha )}^2={(1-s-\alpha )}^2\iff \alpha =\frac{1}{2}\hfill \end{array}$$

(14)

where $d\ge 1$ is a natural number, $\alpha \ne 0$ and $\beta \ne 0$ are real numbers.

Next, the proof is based on Transfinite Induction. Let $P\left(n\right)$ be:

$$\begin{array}{cc}\hfill & \prod _{i=1}^n(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}=\prod _{i=1}^n(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\hfill \\ \hfill & \cdots \hfill \\ \hfill & (1+\frac{{(s-{\alpha }_n)}^2}{{\beta }_n^2}{)}^{d_n}=(1+\frac{{(1-s-{\alpha }_n)}^2}{{\beta }_n^2}{)}^{d_n}\hfill \\ \hfill & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots <|{\beta }_n|\hfill \end{array}\right.\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}& {\alpha }_i=\frac{1}{2},i=1\cdots n\hfill \\ & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots <|{\beta }_n|\hfill \end{array}\right.\hfill \end{array}$$

(15)

According to Equation (14), $P\left(1\right)$ is an obvious fact as the Base Case, i.e.,

$$\begin{array}{cc}\hfill & \prod _{i=1}^1(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}=\prod _{i=1}^1(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}\hfill \\ \hfill & \iff (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\hfill \\ \hfill & \iff {\alpha }_1=\frac{1}{2}\hfill \end{array}$$

(16)

To be more convincing, let’s further check $P\left(2\right)$, i.e.,

$$\begin{array}{cc}\hfill & \prod _{i=1}^2(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}=\prod _{i=1}^2(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\hfill \\ \hfill & (1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}\hfill \\ \hfill & |{\beta }_1|<|{\beta }_2|\hfill \end{array}\right.\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}& {\alpha }_1={\alpha }_2=\frac{1}{2}\hfill \\ & |{\beta }_1|<|{\beta }_2|\hfill \end{array}\right.\hfill \end{array}$$

(17)

which is also an obvious fact according to Lemma 5.

As the Successor Case, we need to prove $P\left(n\right)\Rightarrow P(n+1)$.

Actually, we have

$$\begin{array}{cc}\hfill & \prod _{i=1}^{n+1}(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}=\prod _{i=1}^{n+1}(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}\hfill \\ \hfill & \iff \hfill \\ \hfill & \prod _{i=1}^n(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}(1+\frac{{(s-{\alpha }_{n+1})}^2}{{\beta }_{n+1}^2}{)}^{d_{n+1}}=\prod _{i=1}^n(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}(1+\frac{{(1-s-{\alpha }_{n+1})}^2}{{\beta }_{n+1}^2}{)}^{d_{n+1}}\hfill \\ \hfill & \iff \left(\mathrm{by}\mathrm{Lemma}5\right)\hfill \\ \hfill & \left\{\begin{array}{cc}\hfill & \prod _{i=1}^n(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}=\prod _{i=1}^n(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}\hfill \\ \hfill & (1+\frac{{(s-{\alpha }_{n+1})}^2}{{\beta }_{n+1}^2}{)}^{d_{n+1}}=(1+\frac{{(1-s-{\alpha }_{n+1})}^2}{{\beta }_{n+1}^2}{)}^{d_{n+1}}\hfill \\ \hfill & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots <|{\beta }_n|<|{\beta }_{n+1}|\hfill \end{array}\right.\hfill \\ \hfill & \iff \left(\mathrm{by}\mathrm{Equation}\right(15\left)\right)\hfill \\ \hfill & \left\{\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\hfill \\ \hfill & \cdots \hfill \\ \hfill & (1+\frac{{(s-{\alpha }_{n+1})}^2}{{\beta }_{n+1}^2}{)}^{d_{n+1}}=(1+\frac{{(1-s-{\alpha }_{n+1})}^2}{{\beta }_{n+1}^2}{)}^{d_{n+1}}\hfill \\ \hfill & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots <|{\beta }_n|<|{\beta }_{n+1}|\hfill \end{array}\right.\hfill \\ \hfill & \iff \left(\mathrm{by}\mathrm{Equation}\right(14\left)\right)\hfill \\ \hfill & \left\{\begin{array}{cc}& {\alpha }_i=\frac{1}{2},i=1,2,3,\cdots ,n,n+1\hfill \\ & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots <|{\beta }_n|<|{\beta }_{n+1}|\hfill \end{array}\right.\hfill \end{array}$$

(18)

Thus the Successor Case is true, i.e., $P\left(n\right)\Rightarrow P(n+1)$.

Next, we prove that $P(\infty )$ holds by considering well-ordered ordinal set A indexing the family of statements $P(\gamma :\gamma \in A)$, $A=\mathbb{N}\bigcup \left\{\omega \right\}$ with the ordering that $n<\omega$ for all natural numbers n, $\omega$ is the first limit ordinal.

It is well-known that $\omega =\bigcup \{\gamma :\gamma <\omega \}$.

To prove that $P(\infty )$ holds, it suffices to prove the Limit Case, i.e., $P(\gamma <\omega )\Rightarrow P\left(\omega \right)$.

Actually, we have

$$\begin{array}{cc}\hfill & \prod _{i=1}^{\omega }(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}=\prod _{i=1}^{\omega }(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}\hfill \\ \hfill & \iff \hfill \\ \hfill & \prod _{i=1}^{\gamma <\omega }(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}(1+\frac{{(s-{\alpha }_{\omega })}^2}{{\beta }_{\omega }^2}{)}^{d_{\omega }}=\prod _{i=1}^{\gamma <\omega }(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}(1+\frac{{(1-s-{\alpha }_{\omega })}^2}{{\beta }_{\omega }^2}{)}^{d_{\omega }}\hfill \\ \hfill \\ \hfill & \iff \left(\mathrm{by}\mathrm{Lemma}5\right)\hfill \\ \hfill \\ \hfill & \left\{\begin{array}{cc}\hfill & \prod _{i=1}^{\gamma <\omega }(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}=\prod _{i=1}^{\gamma <\omega }(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}\hfill \\ \hfill & (1+\frac{{(s-{\alpha }_{\omega })}^2}{{\beta }_{\omega }^2}{)}^{d_{\omega }}=(1+\frac{{(1-s-{\alpha }_{\omega })}^2}{{\beta }_{\omega }^2}{)}^{d_{\omega }}\hfill \\ \hfill & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots <|{\beta }_{\omega }|\hfill \end{array}\right.\hfill \\ \hfill \\ \hfill & \iff \left(\mathrm{by}P\right(\alpha <\omega \left)\right)\hfill \\ \hfill \\ \hfill & \left\{\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\hfill \\ \hfill & \cdots \hfill \\ \hfill & (1+\frac{{(s-{\alpha }_{\omega })}^2}{{\beta }_{\omega }^2}{)}^{d_{\omega }}=(1+\frac{{(1-s-{\alpha }_{\omega })}^2}{{\beta }_{\omega }^2}{)}^{d_{\omega }}\hfill \\ \hfill & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots <|{\beta }_{\omega }|\hfill \end{array}\right.\hfill \\ \hfill \\ \hfill & \iff \left(\mathrm{by}\mathrm{Equation}\right(14\left)\right)\hfill \\ \hfill \\ \hfill & \left\{\begin{array}{cc}& {\alpha }_i=\frac{1}{2},i=1,2,3,\cdots ,\omega \hfill \\ & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots <|{\beta }_{\omega }|\hfill \end{array}\right.\hfill \end{array}$$

(19)

Thus the Limit Case is true, i.e., $P(\gamma <\omega )\Rightarrow P\left(\omega \right)$.

Hence we conclude by Transfinite Induction that $P(\infty )$ holds, i.e.,

$$\begin{array}{cc}\hfill & \prod _{i=1}^{\infty }(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}=\prod _{i=1}^{\infty }(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\hfill \\ \hfill & \cdots \hfill \\ \hfill & (1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}=(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}\hfill \\ \hfill & \cdots \hfill \\ \hfill & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots \hfill \end{array}\right.\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}& {\alpha }_i=\frac{1}{2},i=1\cdots \infty \hfill \\ & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots \hfill \end{array}\right.\hfill \end{array}$$

(20)

i.e.,

$$f\left(s\right)=f(1-s)\iff \left\{\begin{array}{cc}& {\alpha }_i=\frac{1}{2},i=1,2,3,\cdots ,\infty \hfill \\ & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots \hfill \end{array}\right.$$

(21)

That completes the proof of Lemma 3. □

Lemma 4. 

Given

$$(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2})$$

(22)

where s is a complex variable, $0<{\alpha }_i<1$ and ${\beta }_i\ne 0$ are real numbers, $|{\beta }_1|\le |{\beta }_2|$.

Then we have

$$\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2})\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}{\alpha }_1={\alpha }_2=\frac{1}{2},\hfill & |{\beta }_1|\le |{\beta }_2|\hfill \\ {\alpha }_1+{\alpha }_2=1,\hfill & |{\beta }_1|=|{\beta }_2|\hfill \end{array}\right.\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}),(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}),\hfill & |{\beta }_1|\le |{\beta }_2|\hfill \\ (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}),(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}),\hfill & |{\beta }_1|=|{\beta }_2|\hfill \end{array}\right.\hfill \end{array}$$

(23)

Proof. 

Expanding both sides of Equation (22), and comparing the coefficients of like terms, we obtain (details are omitted to save space)

$$\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2})\hfill \\ \hfill & \Rightarrow \hfill \\ \hfill & \left\{\begin{array}{cc}{\alpha }_1={\alpha }_2=\frac{1}{2},\hfill & |{\beta }_1|\le |{\beta }_2|\hfill \\ {\alpha }_1+{\alpha }_2=1,\hfill & |{\beta }_1|=|{\beta }_2|\hfill \end{array}\right.\hfill \end{array}$$

(24)

The inverse inference of Equation (24) is also an obvious fact. i.e.,

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}{\alpha }_1={\alpha }_2=\frac{1}{2},\hfill & |{\beta }_1|\le |{\beta }_2|\hfill \\ {\alpha }_1+{\alpha }_2=1,\hfill & |{\beta }_1|=|{\beta }_2|\hfill \end{array}\right.\hfill \\ \hfill & \Rightarrow \hfill \\ \hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2})\hfill \end{array}$$

Then we have

$$\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2})\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}{\alpha }_1={\alpha }_2=\frac{1}{2},\hfill & |{\beta }_1|\le |{\beta }_2|\hfill \\ {\alpha }_1+{\alpha }_2=1,\hfill & |{\beta }_1|=|{\beta }_2|\hfill \end{array}\right.\hfill \end{array}$$

(25)

Further, according to Equation (14), i.e.,

$$(1+\frac{{(s-\alpha )}^2}{{\beta }^2}{)}^d=(1+\frac{{(1-s-\alpha )}^2}{{\beta }^2}{)}^d\iff \alpha =\frac{1}{2}$$

and the following similar facts

$$(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2})\iff {\alpha }_1+{\alpha }_2=1,|{\beta }_1|=|{\beta }_2|$$

$$(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2})\iff {\alpha }_1+{\alpha }_2=1,|{\beta }_1|=|{\beta }_2|$$

we have

$$\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2})(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2})\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}{\alpha }_1={\alpha }_2=\frac{1}{2},\hfill & |{\beta }_1|\le |{\beta }_2|\hfill \\ {\alpha }_1+{\alpha }_2=1,\hfill & |{\beta }_1|=|{\beta }_2|\hfill \end{array}\right.\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}),(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}),\hfill & |{\beta }_1|\le |{\beta }_2|\hfill \\ (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}),(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}),\hfill & |{\beta }_1|=|{\beta }_2|\hfill \end{array}\right.\hfill \end{array}$$

(26)

That completes the proof of Lemma 4. □

Remark 1. 

From the viewpoint of the products of (polynomial) factors, Lemma 4 reveals a fact that there are only two possible cases to make Eq. (22) hold, i.e., Case 1: $(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2})$, $(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2})$; and Case 2: $(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2})=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2})$, $(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2})=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2})$, respectively. This result is quite different from the similar equation of products of factors $a·b=c·d$, which has infinite cases of solutions for real numbers $a,b,c,d$.

Remark 2. 

Given

$$(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}$$

(27)

where s is a complex variable, $0<{\alpha }_1<1,0<{\alpha }_2<1$ and ${\beta }_1\ne 0,{\beta }_2\ne 0$ are real numbers, $d_1\ge 1,d_2\ge 1$ are natural numbers, denoting the real multiplicities of ${\rho }_1={\alpha }_1+j{\beta }_1$ and ${\rho }_2={\alpha }_2+j{\beta }_2$, respectively, $|{\beta }_1|\le |{\beta }_2|$.

Then we have

$$\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}& {\alpha }_1={\alpha }_2=\frac{1}{2}\hfill \\ & |{\beta }_1|<|{\beta }_2|\hfill \end{array}\right.\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}& (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\hfill \\ & (1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}\hfill \\ & |{\beta }_1|<|{\beta }_2|\hfill \end{array}\right.\hfill \end{array}$$

(28)

Proof. 

Based on Lemma 4, and considering additional possibilities that $(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\mid (1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}$, $(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\mid (1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}$(where "∣" is the divisible sign), or vice versa, we have

$$\begin{array}{cc}\hfill & (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1},(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2},\hfill & |{\beta }_1|<|{\beta }_2|\hfill \\ \left\{\begin{array}{c}(1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\mid (1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2},(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\mid (1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}\hfill \\ (1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2-d_1}=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2-d_1}\hfill \end{array}\right.,\hfill & |{\beta }_1|=|{\beta }_2|,d_1<d_2\hfill \\ \left\{\begin{array}{c}(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}\mid (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1},(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}\mid (1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\hfill \\ (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1-d_2}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1-d_2}\hfill \end{array}\right.,\hfill & |{\beta }_1|=|{\beta }_2|,d_1>d_2\hfill \\ (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2},(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2},\hfill & |{\beta }_1|=|{\beta }_2|,d_1=d_2\hfill \end{array}\right.\hfill \\ \hfill & \iff \hfill \\ \hfill & \left\{\begin{array}{cc}{\alpha }_1={\alpha }_2=\frac{1}{2},\hfill & |{\beta }_1|<|{\beta }_2|\hfill \\ {\alpha }_1={\alpha }_2=\frac{1}{2},\hfill & |{\beta }_1|=|{\beta }_2|,d_1<d_2★\hfill \\ {\alpha }_1={\alpha }_2=\frac{1}{2},\hfill & |{\beta }_1|=|{\beta }_2|,d_1>d_2★\hfill \\ {\alpha }_1+{\alpha }_2=1,\hfill & |{\beta }_1|=|{\beta }_2|,d_1=d_2★\hfill \end{array}\right.\hfill \\ \hfill & \iff \hfill \\ \hfill & (\mathrm{To}\mathrm{exclude}\mathrm{the}\mathrm{duplication}\mathrm{situations}\mathrm{marked}\mathrm{by}★\mathrm{between}\mathrm{the}\mathrm{first}\mathrm{quadruplet}\mathrm{of}\mathrm{zeros}\mathrm{represented}\hfill \\ \hfill & \mathrm{by}{\rho }_1={\alpha }_1+j{\beta }_1\hfill \\ \hfill & \mathrm{and}\mathrm{the}\sec \mathrm{ond}\mathrm{quadruplet}\mathrm{of}\mathrm{zeros}\mathrm{represented}\mathrm{by}{\rho }_2={\alpha }_2+j{\beta }_2,\mathrm{which}\mathrm{contradict}\mathrm{the}\mathrm{given}\mathrm{condition}\hfill \\ \hfill & \mathrm{that}\mathrm{the}\mathrm{real}\mathrm{multiplicities}\mathrm{of}{\rho }_1\mathrm{and}{\rho }_2\mathrm{are}{d}_1\mathrm{and}{d}_2,\mathrm{respectively}.)\hfill \\ \hfill & \left\{\begin{array}{cc}& {\alpha }_1={\alpha }_2=\frac{1}{2}\hfill \\ & |{\beta }_1|<|{\beta }_2|\hfill \end{array}\right.\hfill \\ \hfill & \iff \left(\mathrm{by}\mathrm{Equation}\right(14\left)\right)\hfill \\ \hfill & \left\{\begin{array}{cc}& (1+\frac{{(s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}=(1+\frac{{(1-s-{\alpha }_1)}^2}{{\beta }_1^2}{)}^{d_1}\hfill \\ & (1+\frac{{(s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}=(1+\frac{{(1-s-{\alpha }_2)}^2}{{\beta }_2^2}{)}^{d_2}\hfill \\ & |{\beta }_1|<|{\beta }_2|\hfill \end{array}\right.\hfill \end{array}$$

(29)

That completes the proof of Lemma 5. □

3. A Proof of the RH

This section is planned to present a proof of the Riemann Hypothesis. We first prove that Statement 2 of the RH is true, and then by Lemma 2, Statement 1 of the RH is also true.

Proof of the RH. 

The details are delivered in three steps as follows.

Step 1: It is well-known that all the zeros of $\xi \left(s\right)$ always come in complex conjugate pairs. Then by pairing ${\rho }_i={\alpha }_i+j{\beta }_i$ and ${\overline{\rho }}_i={\alpha }_i-j{\beta }_i$ in the Hadamard product as shown in Equation (10), we have

$$\begin{array}{cc}\hfill \xi \left(s\right)& =\xi \left(0\right)\prod _{\rho }(1-\frac{s}{\rho })\hfill \\ \hfill & =\xi \left(0\right)\prod _{i=1}^{\infty }(1-\frac{s}{{\rho }_i})(1-\frac{s}{{\overline{\rho }}_i})\hfill \\ \hfill & =\xi \left(0\right)\prod _{i=1}^{\infty }(1-\frac{s}{{\alpha }_i+j{\beta }_i})(1-\frac{s}{{\alpha }_i-j{\beta }_i})\hfill \\ \hfill & =\xi \left(0\right)\prod _{i=1}^{\infty }(\frac{{\beta }_i^2}{{\alpha }_i^2+{\beta }_i^2}+\frac{{(s-{\alpha }_i)}^2}{{\alpha }_i^2+{\beta }_i^2})\hfill \end{array}$$

(30)

where $\xi \left(0\right)=\frac{1}{2},0<{\alpha }_i<1,{\beta }_i\ne 0$.

The absolute convergence of the infinite product in Equation (30) in the form

$$\xi \left(s\right)=\xi \left(0\right)\prod _{i=1}^{\infty }(1-\frac{s}{{\rho }_i})(1-\frac{s}{{\overline{\rho }}_i})=\xi \left(0\right)\prod _{i=1}^{\infty }(1-\frac{s(2{\alpha }_i-s)}{|{\rho }_i{|}^2})$$

(31)

depends on the convergence of infinite series ${\sum }_{i=1}^{\infty }\frac{1}{|{\rho }_i{|}^2}$, or equivalently, ${\sum }_{\rho }\frac{1}{{|\rho |}^2}$, which is an obvious fact according to Theorem 2 in Section 2, Chapter IV of Ref. [23], as shown in the following.

Theorem 1. 

([23]).The function $\xi \left(s\right)$ is an entire function of order one that has infinitely many zeros ${\rho }_n$ such that $0\le \mathbf{Re}{\rho }_n\le 1$. The series $\sum |{\rho }_n{|}^{-1}$ diverges, but the series $\sum |{\rho }_n{|}^{-1-\epsilon }$ converges for any $\epsilon >0$. The zeros of $\xi \left(s\right)$ are the nontrivial zeros of $\zeta \left(s\right)$.

Remark 3. 

In the Theorem 2 of Ref. [23], $\mathbf{Re}(·)$ is identical to $\Re (·)$ in this paper, both $\mathbf{Re}(·)$ and $\Re (·)$ mean the real part of any complex number.

Further, considering the absolute convergence of

$$\xi \left(s\right)=\xi \left(0\right)\prod _{i=1}^{\infty }(1-\frac{s(2{\alpha }_i-s)}{|{\rho }_i{|}^2})=\xi \left(0\right)\prod _{i=1}^{\infty }(\frac{{\beta }_i^2}{{\alpha }_i^2+{\beta }_i^2}+\frac{{(s-{\alpha }_i)}^2}{{\alpha }_i^2+{\beta }_i^2})$$

(32)

we have the following new expression of $\xi \left(s\right)$ by putting all the ${\rho }_i$ related multiple factors (zeros) together in the above Equation (32)

$$\xi \left(s\right)=\xi \left(0\right)\prod _{i=1}^{\infty }(\frac{{\beta }_i^2}{{\alpha }_i^2+{\beta }_i^2}+\frac{{(s-{\alpha }_i)}^2}{{\alpha }_i^2+{\beta }_i^2}{)}^{d_i}$$

(33)

where $d_i\ge 1$ are the real multiplicities of ${\rho }_i$, i are natural numbers from 1 to infinity.

Step 2: Replacing s with $1-s$ in Equation (33), we obtain the infinite product expression of $\xi (1-s)$, i.e.,

$$\xi (1-s)=\xi \left(0\right)\prod _{i=1}^{\infty }{(\frac{{\beta }_i^2}{{\alpha }_i^2+{\beta }_i^2}+\frac{{(1-s-{\alpha }_i)}^2}{{\alpha }_i^2+{\beta }_i^2})}^{d_i}$$

(34)

Remark 4. 

According to the new expressions of $\xi \left(s\right)$ and $\xi (1-s)$, i.e., Equation (33) and Equation (34), we may conclude that all ${\rho }_i$ and $1-{\rho }_i$ related multiple zeros, i.e., ${({\alpha }_i\pm j{\beta }_i)}^{d_i},{(1-{\alpha }_i\pm j{\beta }_i)}^{d_i}$ are included in the $i^{th}$ group of factors, $(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}$ and $(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2}{)}^{d_i}$, respectively, or in another word, before or after the $i^{th}$ group of factors of $\xi \left(s\right)$ and $\xi (1-s)$, there are no ${\rho }_i$ and $1-{\rho }_i$ related multiple zeros.

Actually, with such arrangement of ${\rho }_i$ and $1-{\rho }_i$ related multiple factors of $\xi \left(s\right)$ and $\xi (1-s)$, we "assigned" a reason for excluding, in the proof of Lemma 5 and Lemma 3, the "abnormal" situation, i.e., the successor factor and its predecessor factor represent the same quadruplet of zeros.

Step 3: According to the functional equation $\xi \left(s\right)=\xi (1-s)$, and considering Equation (33) and Equation (34), we have

$$\xi \left(0\right)\prod _{i=1}^{\infty }{(\frac{{\beta }_i^2}{{\alpha }_i^2+{\beta }_i^2}+\frac{{(s-{\alpha }_i)}^2}{{\alpha }_i^2+{\beta }_i^2})}^{d_i}=\xi \left(0\right)\prod _{i=1}^{\infty }{(\frac{{\beta }_i^2}{{\alpha }_i^2+{\beta }_i^2}+\frac{{(1-s-{\alpha }_i)}^2}{{\alpha }_i^2+{\beta }_i^2})}^{d_i}$$

(35)

which is equivalent to

$$\prod _{i=1}^{\infty }{(1+\frac{{(s-{\alpha }_i)}^2}{{\beta }_i^2})}^{d_i}=\prod _{i=1}^{\infty }{(1+\frac{{(1-s-{\alpha }_i)}^2}{{\beta }_i^2})}^{d_i}$$

(36)

And that ${\beta }_i$ can be certainly arranged in order of increasing $|{\beta }_i|$ , i.e., $|{\beta }_1|\le |{\beta }_2|\le |{\beta }_3|\le \cdots$.

Then, according to Lemma 3, Equation (36) is equivalent to

$$\left\{\begin{array}{cc}& {\alpha }_i=\frac{1}{2},i=1,2,3,\cdots ,\infty \hfill \\ & |{\beta }_1|<|{\beta }_2|<|{\beta }_3|<\cdots \hfill \end{array}\right.$$

Thus, we conclude that all the zeros of the completed zeta function $\xi \left(s\right)$ have real part equal to $\frac{1}{2}$, i.e., Statement 2 of the RH is true. According to Lemma 2, Statement 1 of the RH is also true, i.e., all the non-trivial zeros of the Riemann zeta function $\zeta \left(s\right)$ have real part equal to $\frac{1}{2}$.

That completes the proof of the RH. □

Remark 5. 

By Lemma 1, there are 2 pairs of complex zeros of $\zeta \left(s\right)$ simultaneously, i.e., $\rho =\alpha +j\beta ,\overline{\rho }=\alpha -j\beta ,1-\rho =1-\alpha -j\beta ,1-\overline{\rho }=1-\alpha +j\beta$ are all the non-trivial zeroes of $\zeta \left(s\right)$. With the proof of the RH, i.e., $\alpha =\frac{1}{2}$, these 2 pairs of zeros are actually only one pair, because $\rho =1-\overline{\rho }=\frac{1}{2}+j\beta ,\overline{\rho }=1-\rho =\frac{1}{2}-j\beta$. Thus Lemma 1 could be modified more precisely as follows.

Lemma 5. 

Non-trivial zeroes of $\zeta \left(s\right)$, noted as $\rho =\alpha +j\beta$, have the following properties

1) The number of non-trivial zeroes is infinity;

2) $\beta \ne 0$;

3) $0<\alpha <1$;

4) $\rho =1-\overline{\rho },\overline{\rho }=1-\rho$ are all non-trivial zeroes.

4. Conclusion

The celebrated Riemann Hypothesis is proved to be true based on a new expression of the completed zeta function $\xi \left(s\right)$, i.e.,

$$\xi \left(s\right)=\xi \left(0\right)\prod _{i=1}^{\infty }(\frac{{\beta }_i^2}{{\alpha }_i^2+{\beta }_i^2}+\frac{{(s-{\alpha }_i)}^2}{{\alpha }_i^2+{\beta }_i^2}{)}^{d_i}$$

where $\xi \left(0\right)=\frac{1}{2},{\rho }_i={\alpha }_i+j{\beta }_i$ and ${\overline{\rho }}_i={\alpha }_i-j{\beta }_i$ are the complex conjugate zeros of $\xi \left(s\right)$, $0<{\alpha }_i<1$ and ${\beta }_i\ne 0$ are real numbers, $d_i\ge 1$ are the real multiplicities of ${\rho }_i$, i are natural numbers from 1 to infinity, ${\beta }_i$ are in order of increasing $|{\beta }_i|$, i.e., $|{\beta }_1|\le |{\beta }_2|\le |{\beta }_3|\le \cdots$.