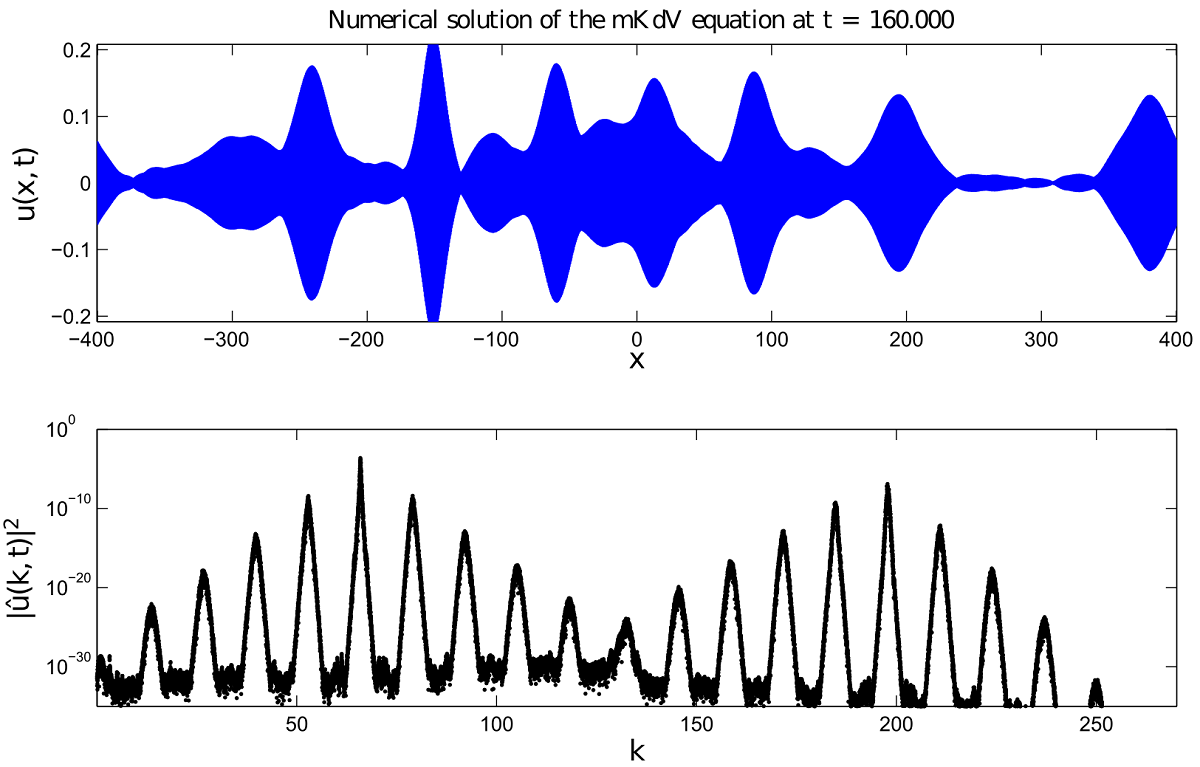
In this study we investigate the formation of dynamical energy cascades in higher order KdV-type equations. In the beginning we recall what is known about the dynamic cascades for the classical KdV (quadratic) and mKdV (cubic) equations. Then, we investigate further the mKdV case by considering a richer set of initial perturbations in order to check the validity and persistence of various facts previously established for the narrow-banded perturbations. Afterwards we focus on higher order nonlinearities (quartic and quintic) which are found to be quite different in many respects from the mKdV equation. Throughout this study we consider both the direct and double energy cascades. It was found that the dynamic cascade is always formed, but its formation is not necessarily accompanied by the nonlinear stage of the modulational instability. Direct cascade structure remains invariant regardless the size of the spectral domain. In contrast, the double cascade shape can depend on the size of the spectral domain, even if the total number of cascading modes remains invariant. Results obtained in this study can be potentially applied to plasmas, free surface and internal wave hydrodynamics.