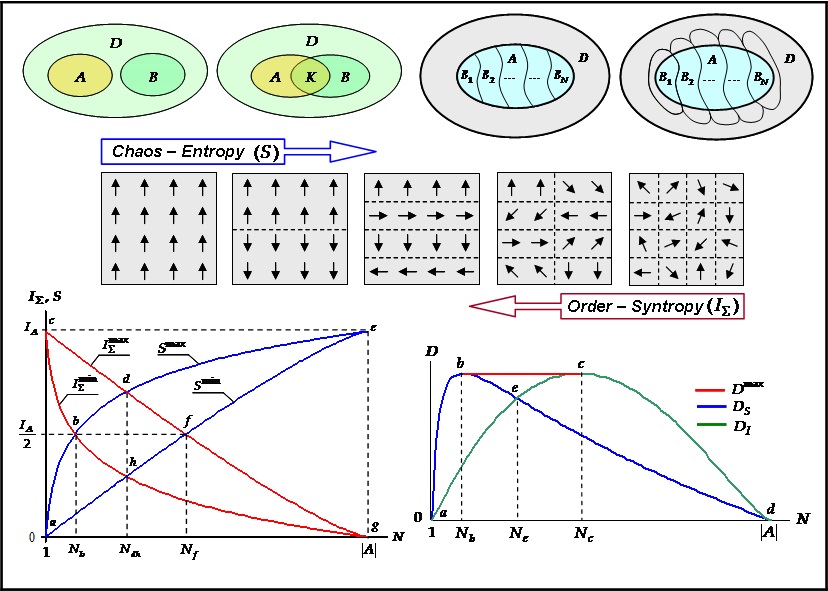
A new approach is presented to defining the amount of information, in which information is understood as the data about a finite set as a whole, whereas the average length of an integrative code of elements serves as a measure of information. We obtain a formula for the syntropy of reflection, that is, the information that two intersecting finite sets reflect about each other. The specificities of reflection of discrete systems through the combination of their parts are considered, and it is shown that the additive syntropy and entropy of reflection are measures of structural order and chaos. Three information laws have been established: the law of conservation of the sum of chaos and order; information law of reflection; the law of conservation and transformation of information. An assessment of the structural organization and the level of development of discrete systems is presented. It is shown that various measures of information are structural characteristics of integrative codes of elements of discrete systems. The conclusion is made that, from the informational-genetic positions, the synergetic theory of information is primary in relation to the Hartley-Shannon information theory. In the appendix we consider the asymmetry of the mutual reflection of finite sets and the proportionality of arbitrary quantities.