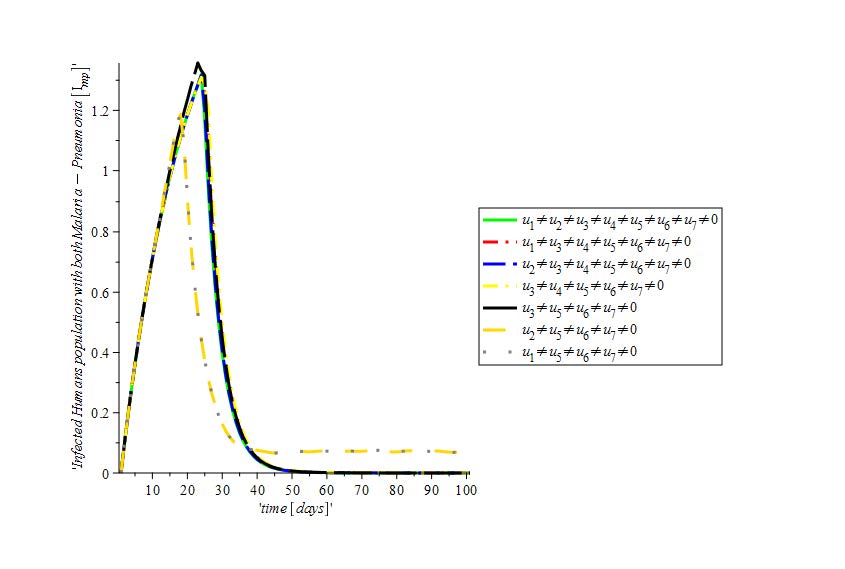
Malaria and Pneumonia are leading causes of serious illness in children and adults worldwide with their death rate and prevalence on the rise. Such alarming statistics may retard the milestones so far achieved in meeting the Millennium Development Goals 4 and 6 whose targets are to improve child survival and reverse the high prevalence of diseases such as pneumonia and malaria respectively. Two sub-models of malaria-pneumonia co-infection namely malaria model and pneumonia model were considered first and then followed by the full malaria-pneumonia co-infection model. The malaria model, pneumonia model and co-infection model basic reproduction numbers denoted by R_m, R_p and R_mp respectively was obtained using the Next Generation Matrix method. The model disease free equilibrium’s local and global stability was analysed using Descartes’ Rule of signs and Comparison method. The bifurcation analysis for the malaria, pneumonia and co-infection models was studied using the Centre Manifold Theory. The sensitivity indices of the model basic reproduction numbers R_m, R_p and R_mp to the parameters in the models were calculated. Optimal control theory was applied using the Pontryagins’ Maximum Principle to investigate optimal strategies for controlling the spread of malaria, pneumonia and co-infection models using insecticide treated bed nets (u₁(t)) spraying of mosquitoes insecticides (u₂(t)), sanitation (u₃(t)), vaccination (u₄(t)), anti-malaria drugs (u₅(t)), anti-pneumonia drugs (u₆(t)), both anti-malaria drugs and anti-pneumonia drugs (u₇(t)) as the system time control variables. Numerical simulations using a set of parameter values were provided to validate the analytical results.