Version 1
: Received: 15 February 2018 / Approved: 15 February 2018 / Online: 15 February 2018 (20:29:20 CET)
How to cite:
Pramanik, S.; Dey, P.P.; Smarandache, F. TOPSIS Based Algorithm for Solving Multi-objective Multi-level Programming Problem with Fuzzy Parameters. Preprints2018, 2018020105. https://doi.org/10.20944/preprints201802.0105.v1
Pramanik, S.; Dey, P.P.; Smarandache, F. TOPSIS Based Algorithm for Solving Multi-objective Multi-level Programming Problem with Fuzzy Parameters. Preprints 2018, 2018020105. https://doi.org/10.20944/preprints201802.0105.v1
Pramanik, S.; Dey, P.P.; Smarandache, F. TOPSIS Based Algorithm for Solving Multi-objective Multi-level Programming Problem with Fuzzy Parameters. Preprints2018, 2018020105. https://doi.org/10.20944/preprints201802.0105.v1
APA Style
Pramanik, S., Dey, P.P., & Smarandache, F. (2018). TOPSIS Based Algorithm for Solving Multi-objective Multi-level Programming Problem with Fuzzy Parameters. Preprints. https://doi.org/10.20944/preprints201802.0105.v1
Chicago/Turabian Style
Pramanik, S., Partha P. Dey and Florentin Smarandache. 2018 "TOPSIS Based Algorithm for Solving Multi-objective Multi-level Programming Problem with Fuzzy Parameters" Preprints. https://doi.org/10.20944/preprints201802.0105.v1
Abstract
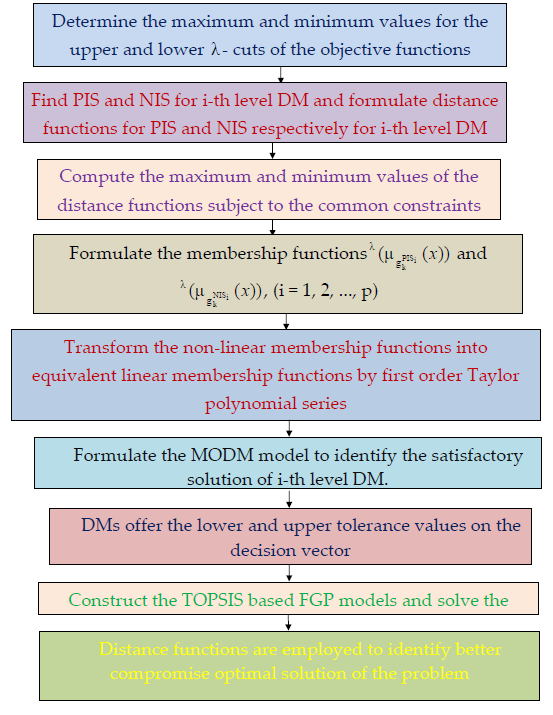
The paper proposes TOPSIS method for solving multi-objective multi-level programming problem (MO-MLPP) with fuzzy parameters via fuzzy goal programming (FGP). At first, - cut method is used to transform the fuzzily described MO-MLPP into deterministic MO-MLPP. Then, for specific , we construct the membership functions of distance functions from positive ideal solution (PIS) and negative ideal solution (NIS) of all level decision makers (DMs). Thereafter, FGP based multi-objective decision model is established for each level DM for obtaining individual optimal solution. A possible relaxation on decisions for all DMs is taken into account for satisfactory solution. Subsequently, two FGP models are developed and compromise optimal solutions are found by minimizing the sum of negative deviational variables. To recognize the better compromise optimal solution, the concept of distance functions is utilized. Finally, a novel algorithm for MO-MLPP involving fuzzy parameters is provided and an illustrative example is solved to verify the proposed procedure.
Computer Science and Mathematics, Applied Mathematics
Copyright:
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
